Cinemática del robot
|
|
|
- María Soledad Ríos Miranda
- hace 7 años
- Vistas:
Transcripción
1 Cinemática del robot
2 Cinemática del robot La cinemática del robot estudia el movimiento del mismo con respecto a un sistema de referencia. La cinemática se interesa por la descripción analítica del movimiento espacial del robot como una función del tiempo, y en particular por las relaciones entre la posición y la orientación del extremo final del robot con los valores ue toman sus coordenadas articulares. Existen dos problemas fundamentales a resolver en la cinemática del robot; el primero de ellos se conoce como el problema cinemático directo y el segundo como problema cinemático inverso.
3 Cinemática del robot El problema cinemático directo consiste en determinar cuál es la posición y orientación del extremo final del robot, con respecto a un sistema de coordenadas ue se toma como referencia, conocidos los valores de las articulaciones y los parámetros geométricos de los elementos del robot. El problema cinemático inverso, resuelve la configuración ue debe adoptar el robot para una posición y orientación del extremo conocidas.
4 Cinemática del robot Denavit y Hartenberg propusieron un método sistemático para describir y representar la geometría espacial de los elementos de una cadena cinemática, y en particular de un robot, con respecto a un sistema de referencia fijo. Este método utiliza una matriz de transformación homogénea para describir la relación espacial entre dos elementos rígidos adyacentes, reduciéndose así el problema cinemático a encontrar una matriz de transformación homogénea de 4x4 ue relacione la localización espacial del extremo del robot con respecto al sistema de coordenadas de su base.
5 Problema cinemático directo Dado ue un robot se puede considerar como una cadena cinemática formada por objetos rígidos o eslabones unidos entre sí mediante articulaciones, se puede establecer un sistema de referencia fijo situado en la base del robot y describir la localización de cada uno de los eslabones con respecto a dicho sistema de referencia. De esta forma, el problema cinemático directo se reduce a encontrar una matriz homogénea de transformación T ue relacione la posición y orientación del extremo del robot respecto del sistema fijo situado en la base del mismo. Esta matriz T será función de las coordenadas articulares.
6 Cadenas cinemáticas La resolución del problema cinemático directo consiste en encontrar las relaciones ue permiten conocer la localización espacial del extremo del robot a partir de los valores de sus coordenadas articulares. Así, si se han escogido coordenadas cartesianas y ángulos de Euler para representar la posición y orientación del extremo de un robot de seis grados de libertad, la solución al problema Cinemático directo vendrá dada por las relaciones:
7 Cadenas cinemáticas La obtención de estas relaciones no es en general complicada, siendo incluso en ciertos casos (robots de pocos GDL) fácil de encontrar mediante simples consideraciones geométricas. ( ) ( ) ( ) ( ) ( ) ( ) ,,,,,,,,,,,,,,,,,,,,,,,,,,,,,, f f f f z f y f x z y x γ β α γ β α = = = = = =
8 Cadenas cinemáticas Por ejemplo para un robot de 2 GDL ue se muestra en la figura, es fácil comprobar ue: x = l y = l cos + l2 cos sen + l 2 sen ( + 2 ) ( + ) 2 Para robots de más grados de libertad puede plantearse un método sistemático basado en la utilización de las matrices de transformación homogénea. Robot planar de 2 GDL
9 Cadenas cinemáticas En general, un robot de n grados de libertad está formado por n eslabones unidos por n articulaciones, de forma ue cada par articulación-eslabón constituye un grado de libertad. A cada eslabón se le puede asociar un sistema de r e f e r e n c i a s o l i d a r i o a é l y, u t i l i z a n d o l a s transformaciones homogéneas, es posible representar las rotaciones y traslaciones relativas entre los distintos eslabones ue componen el robot.
10 Cadenas cinemáticas Normalmente, la matriz de transformación homogénea ue representa la posición y orientación relativa entre los sistemas asociados a dos eslabones consecutivos del robot se suele denominar matriz i- A i. Así pues, A describe la posición y orientación del sistema de referencia solidario al primer eslabón con respecto al sistema de referencia solidario a la base, A 2 describe la posición y orientación del segundo eslabón respecto del primero, etc.
11 Cadenas cinemáticas Del mismo modo, denominando A k a las matrices resultantes del producto de las matrices i- A i con i desde hasta k, se puede representar de forma total o parcial la cadena cinemática ue forma el robot. Así, por ejemplo, la posición y orientación del sistema solidario con el segundo eslabón del robot con respecto al sistema de coordenadas de la base se puede expresar mediante la matriz A 2 : A 2 = A A 2
12 Cadenas cinemáticas De manera análoga, la matriz A 3 representa la localización del sistema del tercer eslabón: A 3 = A A 2 2 A 3 Cuando se consideran todos los grados de libertad a la matriz A n se le suele denominar T. Así, dado un robot de seis grados de libertad, se tiene ue la posición y orientación del eslabón final vendrá dada por la matriz T: T = A 6 = A A 2 2 A 3 3 A 4 4 A 5 5 A 6
13 Cadenas cinemáticas Aunue para describir la relación ue existe entre dos elementos contiguos se puede hacer uso de cualuier sistema de referencia ligado a cada elemento, la forma habitual ue se suele utilizar en robótica es la representación de Denavit-Hartenberg. Denvit-Hartenbarg en 955 propusieron un método matricial ue permite establecer de manera sistemática un sistema de coordenadas {S i } ligado a cada eslabón i de una cadena articulada, pudiéndose determinar a continuación las ecuaciones cinemáticas de la cadena completa.
14 Cadenas cinemáticas Según la representación de D-H, escogiendo adecuadamente los sistemas de coordenadas asociados a cada eslabón, será posible pasar de uno al siguiente mediante 4 transformaciones básicas ue dependen exclusivamente de las características geométricas del eslabón. Estas transformaciones básicas consisten en una sucesión de rotaciones y traslaciones ue permiten relacionar el sistema de referencia del elemento i con el sistema del elemento i-.
15 Cadenas cinemáticas Las transformaciones básicas son las siguientes:. Rotación alrededor del eje z i- un ángulo θ i. 2. Traslación a lo largo de z i- una distancia d i ; vector d i (,,d i ). 3. Traslación a lo largo de x i una distancia a i ; vector a i (a i,,). 4. Rotación alrededor del eje x i un ángulo α i.
16 Cadenas cinemáticas Dado ue el producto no es conmutativo las transformaciones se han de realizar en el orden indicado. De este modo se tiene ue: i- A i = Rot(z,θ i ) Tras(,,di) Tras(a i,,) Rot(x,α i ) y realizado el producto entre matrices: = = cos cos cos cos i i i i i i i i i i i i sen sen a d sen sen α α α α θ θ θ θ A
17 Cadenas cinemáticas i A i = cosθi senθi cosα senθ cosα cosθ i i senα i i i senα senθ i senα cosθ i cosα i i i ai cosθi a isenθi d i donde θ i, a i, d i, α i, son los parámetros D-H del eslabón i. De este modo, basta con identificar los parámetros θ i, a i, d i, α i para obtener las matrices A y relacionar así todos y cada uno de los eslabones del robot.
18 Algoritmo Denavit-Hartenberg para la obtención del modelo cinemático directo D-H. Numerar los eslabones comenzando con (primer eslabón móvil de la cadena) y acabando con n (último eslabón móvil). Se numerará como eslabón a la base fija del robot. D-H 2. Numerar cada articulación comenzando por (la correspondiente al primer grado de libertad) y acabando en n. D-H 3. Localizar el eje de cada articulación. Si ésta es rotativa, el eje será su propio eje de giro. Si es prismática, será el eje a lo largo del cual se produce el desplazamiento.
19 Algoritmo Denavit-Hartenberg para la obtención del modelo cinemático directo D.H 4. Situar el origen del sistema en la base {S } en cualuier punto del eje z. Los ejes x y y se situarán de modo ue formen un sistema de dextrógiro con z. D.H 5. Para i de a n-, situar el sistema {S i } (solidario al eslabón i) en la intersección del eje z i con la línea normal común a z i- y z i. Si ambos ejes se cortasen se situaría {S i } en el punto de corte. Si fuesen paralelos {S i } se situaría en la articulación i+. D-H 6. Situar x i en la línea normal común a z i- y z i o en la dirección normal a los planos z i- -z i si z i- y z i se intersectan.
20 Algoritmo Denavit-Hartenberg para la obtención del modelo cinemático directo D-H 7. Situar y i de modo ue forme un sistema dextrógiro con x i y z i. D-H 8. Situar el sistema {S n } en el extremo del robot de modo ue z n coincida con la dirección de z n- y x n sea normal a z n- y z n. D-H 9. Obtener θ i como el ángulo ue hay ue girar en torno a z i- para ue x i- y x i ueden paralelos.
21 Algoritmo Denavit-Hartenberg para la obtención del modelo cinemático directo D.H. Obtener d i como la distancia, medida a lo largo de z i-, ue habría ue desplazar {S i- } para ue x i y x i- ueden alineados. D.H. Obtener a i como la distancia medida a lo largo x i (ue ahora coincidiría con x i- ) ue habrá ue desplazar el nuevo {S i- } para ue su origen coincidiese con {S i }. D.H 2. Obtener α i como el ángulo ue habría ue girar en torno a x i (ue ahora coincidiría con x i- ), para ue el nuevo {S i- } coincidiese totalmente con {S i }.
22 Algoritmo Denavit-Hartenberg para la obtención del modelo cinemático directo D.H. 3. Obtener las matrices de transformación i- A i. D.H. 4. Obtener la matriz de transformación ue relaciona el sistema de la base con el del extremo del robot T = A, A 2,.. n- A n. D.H 5. La matriz T define la orientación y posición del extremo referido a la base en función de las n coordenadas articulares.
23 Algoritmo Denavit-Hartenberg para la obtención del modelo cinemático directo Los cuatro parámetros de D-H (θ i, a i, d i, α i ) dependen únicamente de las características geométricas de cada eslabón y de las articulaciones ue le unen con el anterior y el siguiente. Estos parámetros se muestran en la siguiente figura y representan: θ i es el ángulo ue forman los ejes x i- y x i medido en un plano perpendicular al eje z i-, utilizando la regla de la mano derecha. Se trata de un parámetro variable en articulaciones giratorias.
24 Algoritmo Denavit-Hartenberg para la obtención del modelo cinemático directo d i es la distancia a lo largo del eje z i- desde el origen del sistema de coordenadas (i-)-ésimo hasta la intersección del eje z i- con el eje x i. Se trata de un parámetro variable en articulaciones prismáticas. a i es la distancia a lo largo del eje x i ue va desde la intersección del eje z i- con el eje xi hasta el origen del sistema i-ésimo, en el caso de articulaciones giratorias. En el caso de articulaciones prismáticas, se calcula como la distancia más corta entre los ejes z i- y z i.
25 Algoritmo Denavit-Hartenberg para la obtención del modelo cinemático directo α i es el ángulo de separación del eje z i- y el eje z i, medido en un plano perpendicular al eje x i, utilizando la regla de la mano derecha. Una vez obtenidos los parámetros D-H, el cálculo de las relaciones entre los eslabones consecutivos del robot es inmediato. Obtenida la matriz T, ésta expresará la orientación y posición del extremo del robot en función de sus coordenadas articulares, con lo ue uedará resuelto el problema cinemático directo.
26 Algoritmo Denavit-Hartenberg para la obtención del modelo cinemático directo Representación D-H para un eslabón giratorio
27 Manipulador de dos eslabones Considere el robot de dos eslabones ue se muestra en la figura. Hallar la solución al problema cinemático directo. Manipulador de dos eslabones
28 Manipulador de dos eslabones Se obtiene la tabla de parámetros y se determinan las matrices A.
29 Manipulador de dos eslabones Obtenemos la matriz de transformación T La posición del efector final con respecto a la base está dada por:
30 Robot cilíndrico de tres eslabones Considere ahora el robot cilíndrico de 3 eslabones representado simbólicamente en la siguiente figura. Robot cilíndrico
31 Robot cilíndrico de tres eslabones Los parámetros se muestran en la siguiente tabla.
32 Robot cilíndrico de tres eslabones Se hallan las matrices A y T.
33 Muñeca esférica Una configuración de muñeca esférica se muestra en la siguiente figura, en la cual los ejes de las articulaciones z 3, z 4, z 5 se intersecan en o (origen).
34 Muñeca esférica Los parámetros Denavit-Hartenberg se muestran en la siguiente tabla. El manipulador Stanford es un ejemplo de un manipulador ue tiene una muñeca de este tipo.
35 Muñeca esférica Se calculan las matrices A.
36 Muñeca esférica Se resuelve la matriz de transformación T.
37 Manipulador cilíndrico con muñeca esférica Supongamos ue ahora fijamos una muñeca esférica al manipulador cilíndrico del ejemplo anterior. Note ue el eje de rotación del eslabón 4 es paralelo a z 2 y coincide con el eje z 3 del ejemplo anterior. Entonces podemos decir ue la cinemática directa está dada por:
38 Manipulador cilíndrico con muñeca esférica Manipulador cilíndrico con muñeca esférica.
39 Manipulador cilíndrico con muñeca esférica Desarrollamos la matriz T:
40 Robot SCARA Considere el robot SCARA ue se muestra en la figura.
41 Robot SCARA La tabla de parámetros D-H es:
42 Robot SCARA Las matrices A son las siguientes:
43 Robot SCARA La matriz de transformación T ueda como:
44 Resolución completa del problema cinemático directo para un robot cilíndrico Robot cilíndrico
45 Resolución completa del problema cinemático directo para un robot cilíndrico Se localizan los sistemas de referencia de cada una de las articulaciones del robot. Posteriormente se determinan los parámetros de Denavit-Hartenberg del robot con los ue se construye la siguiente tabla. Articulación θ d a α θ l 2 d d 3 4 θ 4 l 4
46 Resolución completa del problema cinemático directo para un robot cilíndrico Una vez calculados los parámetros de cada eslabón, se calculan las matrices A como sigue: = cos cos l sen sen θ θ θ θ A = cos cos l sen sen θ θ θ θ A = d A = 2 2 d A
47 Resolución completa del problema cinemático directo para un robot cilíndrico El resultado de la matriz T es el siguiente: ( ) ( ) = = l d C S l d S S C S C C l d C C S S S C A A A A T
48 Resolución completa del problema cinemático directo para un robot IRB64C En primer lugar y siguiendo el algoritmo Denavit- Hartenberg, se localizan los sistemas de referencia de cada una de las articulaciones del robot como se muestra en la figura. Posteriormente se determinan los parámetros de Denavit-Hartenberg del robot con los ue se construye la tabla de parámetros.
49 Resolución completa del problema cinemático directo para un robot IRB64C Asignación de ejes de referencia para el robot IRB64C.
50 Resolución completa del problema cinemático directo para un robot IRB64C Tabla de parámetros D-H. Articulación θ d a α θ -9 2 θ 2 l 9 3 l θ 4 l θ θ 6 l 4
51 Resolución completa del problema cinemático directo para un robot IRB64C Se calculan ahora las matrices A, sustituyendo en la expresión general de la siguiente manera:
52 Resolución completa del problema cinemático directo para un robot IRB64C Así pues, se puede calcular la matriz T ue indica la localización del sistema asociado al extremo del robot con respecto de referencia de la base del robot:
53 Resolución completa del problema cinemático directo para un robot IRB64C A continuación se desarrollan los términos de la matriz T.
54 Tarea Para el robot simple mostrado en la siguiente figura, asigne los sistemas coordenados necesarios basándose en el algoritmo D-H y llene la tabla con los parámetros. Por último halle la solución al problema cinemático directo.
55 Solución Se sitúan los ejes de acuerdo al algoritmo D-H
56 Solución Se hallan los parámetro de D-H y se llena la tabla
57 Solución Se escriben las transformaciones entre cada articulación sucesiva.
58 Solución
59 Solución La transformación total entre la base del robot y la mano es:
60 Ejercicio El brazo Stanford. Asigne los sistemas coordenados al brazo Stanford de la siguiente figura. El brazo Stanford es un brazo de coordenadas esféricas, lo ue significa ue sus dos primeras articulaciones son rotatorias y la tercera es prismática.
61 Solución del brazo Stanford La asignación de sistemas del brazo y la tabla de parámetros son los siguientes:
62 Solución del brazo Stanford
Cinemática del Robot
 Cinemática del Robot La cinemática del robot estudia el movimiento del mismo con respecto a un sistema de referencia. En primer término, la cinemática se interesa por la descripción analítica del movimiento
Cinemática del Robot La cinemática del robot estudia el movimiento del mismo con respecto a un sistema de referencia. En primer término, la cinemática se interesa por la descripción analítica del movimiento
CINEMÁTICA DEL ROBOT
 CINEMÁTICA DEL ROBOT Cinemática Directa Cinemática Inversa Matriz Jacobiana 1 Problema cinemático del robot Cinemática del robot: Estudio de su movimiento con respecto a un sistema de referencia: Descripción
CINEMÁTICA DEL ROBOT Cinemática Directa Cinemática Inversa Matriz Jacobiana 1 Problema cinemático del robot Cinemática del robot: Estudio de su movimiento con respecto a un sistema de referencia: Descripción
Dr. Roberto Carlos García Gómez
 Dr. Roberto Carlos García Gómez La cinemática del robot estudia el movimiento del mismo con respecto a un sistema de referencia. La cinemática se interesa por la descripción analítica del movimiento espacial
Dr. Roberto Carlos García Gómez La cinemática del robot estudia el movimiento del mismo con respecto a un sistema de referencia. La cinemática se interesa por la descripción analítica del movimiento espacial
Cinemática Directa del Robot. CI-2657 Robótica M.Sc. Kryscia Ramírez Benavides
 M.Sc. Kryscia Ramírez Benavides Introducción Consiste en determinar cual es la posición y orientación del extremo final del robot, con respecto a un sistema de coordenadas que se toma como referencia,
M.Sc. Kryscia Ramírez Benavides Introducción Consiste en determinar cual es la posición y orientación del extremo final del robot, con respecto a un sistema de coordenadas que se toma como referencia,
Cinemática Directa del Robot. UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides
 Cinemática Directa del Robot UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción Consiste en determinar cual es la posición y orientación del extremo final del robot, con
Cinemática Directa del Robot UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción Consiste en determinar cual es la posición y orientación del extremo final del robot, con
PARÁMETROS DE DENAVIT-HARTENBERG. Cristina Castejón
 PARÁMETROS DE DENAVIT-HARTENBERG Cristina Castejón Conceptos de robótica Cadena cinemática abierta formada por eslabones y articulaciones: Rotación Prismáticas Estudio cinemático Estudio dinámico Conceptos
PARÁMETROS DE DENAVIT-HARTENBERG Cristina Castejón Conceptos de robótica Cadena cinemática abierta formada por eslabones y articulaciones: Rotación Prismáticas Estudio cinemático Estudio dinámico Conceptos
Cinemática Directa. Facultad de Cs. de la Computación. Juan Carlos Conde Ramírez. Computer Animation
 Cinemática Directa Facultad de Cs. de la Computación Juan Carlos Conde Ramírez Computer Animation Contenido 1 Introducción 2 Transformaciones homogéneas 3 Cinemática directa 4 Método Denavit-Hartenberg
Cinemática Directa Facultad de Cs. de la Computación Juan Carlos Conde Ramírez Computer Animation Contenido 1 Introducción 2 Transformaciones homogéneas 3 Cinemática directa 4 Método Denavit-Hartenberg
Cinemática del Robot. UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides
 UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción La cinemática del robot estudia el movimiento del mismo con respecto a un sistema de referencia. Se interesa por la
UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción La cinemática del robot estudia el movimiento del mismo con respecto a un sistema de referencia. Se interesa por la
ROBÓTICA I. Cinemática Directa
 Cinemática Directa M. C. Jorge Luis Barahona Avalos 2 de mayo de 2012 Universidad Tecnológica de la Mixteca Instituto de Electrónica y Mecatrónica 1 / 42 Índice General 1 Cinemática Directa 2 Cadena Cinemática
Cinemática Directa M. C. Jorge Luis Barahona Avalos 2 de mayo de 2012 Universidad Tecnológica de la Mixteca Instituto de Electrónica y Mecatrónica 1 / 42 Índice General 1 Cinemática Directa 2 Cadena Cinemática
Robótica Industrial. Robótica Industrial
 TEMA 4: CINEMÁTICA DEL ROBOT Ingeniería de Sistemas y Automática Control de Robots y Sistemas Sensoriales Robótica Industrial Robótica Industrial ISA.- Ingeniería de Sistemas y Automática Cinemática del
TEMA 4: CINEMÁTICA DEL ROBOT Ingeniería de Sistemas y Automática Control de Robots y Sistemas Sensoriales Robótica Industrial Robótica Industrial ISA.- Ingeniería de Sistemas y Automática Cinemática del
Fundamentos de Robótica
 Fundamentos de Robótica Cinemática Directa Ricardo-Franco Mendoza-Garcia [email protected] Escuela Universitaria de Ingeniería Mecánica Universidad de Tarapacá Arica, Chile July 9, 2014 R. F. Mendoza-Garcia
Fundamentos de Robótica Cinemática Directa Ricardo-Franco Mendoza-Garcia [email protected] Escuela Universitaria de Ingeniería Mecánica Universidad de Tarapacá Arica, Chile July 9, 2014 R. F. Mendoza-Garcia
Cinemática de los manipuladores. Robótica
 Cinemática de los manipuladores Robótica Introducción Cinemática: Estudio del movimiento sin considerar las fuerzas que lo producen Propiedades geométricas y temporales Posición, velocidad, aceleración,
Cinemática de los manipuladores Robótica Introducción Cinemática: Estudio del movimiento sin considerar las fuerzas que lo producen Propiedades geométricas y temporales Posición, velocidad, aceleración,
ROBÓTICA I. Cinemática Directa
 Cinemática Directa M. C. Jorge Luis Barahona Avalos 11 de abril de 2011 Universidad Tecnológica de la Mixteca Instituto de Electrónica y Mecatrónica 1 / 34 Índice General 1 Cinemática Directa 2 Cadena
Cinemática Directa M. C. Jorge Luis Barahona Avalos 11 de abril de 2011 Universidad Tecnológica de la Mixteca Instituto de Electrónica y Mecatrónica 1 / 34 Índice General 1 Cinemática Directa 2 Cadena
Problema Cinemático Directo
 Problema Cinemático Directo Parámetros Denavit-Hartenberg Denavit-Hartenberg notación Craig Denavit-Hartenberg notación Craig Denavit-Hartenberg notación Craig Denavit-Hartenberg notación Craig Denavit-Hartenberg
Problema Cinemático Directo Parámetros Denavit-Hartenberg Denavit-Hartenberg notación Craig Denavit-Hartenberg notación Craig Denavit-Hartenberg notación Craig Denavit-Hartenberg notación Craig Denavit-Hartenberg
Control de un Robot Scara de 3 GDL
 Control de un Robot Scara de 3 GDL Jesús Soldevilla ureta Raúl Rivas Jimenez 13 de diciembre de 2010 Resumen El proyecto que se desarrolla en el siguiente informe plantea la aplicación de 4 técnicas de
Control de un Robot Scara de 3 GDL Jesús Soldevilla ureta Raúl Rivas Jimenez 13 de diciembre de 2010 Resumen El proyecto que se desarrolla en el siguiente informe plantea la aplicación de 4 técnicas de
CINEMÁTICA Y DINÁMICA DE ROBOTS MANIPULADORES: RESPUESTAS DE EJERCICIOS UNIDAD 03. Roger Miranda Colorado
 CINEMÁTICA Y DINÁMICA DE ROBOTS MANIPULADORES: RESPUESTAS DE EJERCICIOS UNIDAD 03 Roger Miranda Colorado 23 de mayo de 2016 Índice 1. RESPUESTAS DE EJERCICIOS UNIDAD 03 1 1. RESPUESTAS DE EJERCICIOS UNIDAD
CINEMÁTICA Y DINÁMICA DE ROBOTS MANIPULADORES: RESPUESTAS DE EJERCICIOS UNIDAD 03 Roger Miranda Colorado 23 de mayo de 2016 Índice 1. RESPUESTAS DE EJERCICIOS UNIDAD 03 1 1. RESPUESTAS DE EJERCICIOS UNIDAD
GUI y la Robótica. Figura 1. Robot manipulador KUKA KR-16
 RESUMEN GUI y la Robótica Miguel Durán 1, Jorge Gudiño 1, David Bolaños 1, Luís Avendaño 1 (1) Facultad de Ingeniería Electromecánica, Universidad de Colima, Colima (México) ([email protected]) El objetivo
RESUMEN GUI y la Robótica Miguel Durán 1, Jorge Gudiño 1, David Bolaños 1, Luís Avendaño 1 (1) Facultad de Ingeniería Electromecánica, Universidad de Colima, Colima (México) ([email protected]) El objetivo
Descripción de la posición y orientación.
 Indice TEMA 5. FUNDAMENTS MATEMÁTICS Descripción de la posición y orientación. Transformaciones básicas: traslación y rotación. Composición de transformaciones. Velocidades y aceleraciones. Momento de
Indice TEMA 5. FUNDAMENTS MATEMÁTICS Descripción de la posición y orientación. Transformaciones básicas: traslación y rotación. Composición de transformaciones. Velocidades y aceleraciones. Momento de
Cinemática Inversa. Facultad de Cs. de la Computación. Juan Carlos Conde R. Computer Animation
 Cinemática Inversa Facultad de Cs. de la Computación Juan Carlos Conde R. Computer Animation Contenido 1 Introducción 2 Métodos de resolución 3 Solución Geométrica 4 Solución Algebraica 1 / 23 Contenido
Cinemática Inversa Facultad de Cs. de la Computación Juan Carlos Conde R. Computer Animation Contenido 1 Introducción 2 Métodos de resolución 3 Solución Geométrica 4 Solución Algebraica 1 / 23 Contenido
Introducción. 2.2 Transformaciones de coordenadas: matriz de rotación y ángulos de Euler.
 Agosto 2011 Introducción El análisis cinemático directo nos permite determinar en donde se encuentra el elemento terminal del robot (mano) si se conoce la posición de todas las articulaciones. 15 50 Posición?
Agosto 2011 Introducción El análisis cinemático directo nos permite determinar en donde se encuentra el elemento terminal del robot (mano) si se conoce la posición de todas las articulaciones. 15 50 Posición?
Manipulación. Tarea de manipular con destreza, hacer operaciones con las manos. Es el manejo hábil de los objetos. V. Angélica García Vega
 Manipulación Tarea de manipular con destreza, hacer operaciones con las manos. Es el manejo hábil de los objetos Brazo robótico Manipulador Efector final o pinza Cinemática Estudia las relaciones entre
Manipulación Tarea de manipular con destreza, hacer operaciones con las manos. Es el manejo hábil de los objetos Brazo robótico Manipulador Efector final o pinza Cinemática Estudia las relaciones entre
Percepción visual aplicada a la robótica
 Percepción visual aplicada a la robótica Mario I. Chacón Murguía Rafael Sandoval Rodríguez Javier Vega Pineda Selecciona el libro para empezar Capítulo 2 Teoría de robótica Continuar Cinemática de robots
Percepción visual aplicada a la robótica Mario I. Chacón Murguía Rafael Sandoval Rodríguez Javier Vega Pineda Selecciona el libro para empezar Capítulo 2 Teoría de robótica Continuar Cinemática de robots
Fundamentos de Robótica
 Fundamentos de Robótica Introducción a la cinemática de manipuladores [email protected] http://scfi.uaemex.mx/hamontes 1 Recomendación No use estas diapositivas como referencia única de estudio durante
Fundamentos de Robótica Introducción a la cinemática de manipuladores [email protected] http://scfi.uaemex.mx/hamontes 1 Recomendación No use estas diapositivas como referencia única de estudio durante
INSTITUTO TECNOLÓGICO DE VERACRUZ. Materia: Robótica. Unidad 3: Cinemática. Tema: Cinemática Inversa. Catedrático: Dr. José Antonio Garrido Natarén
 INSTITUTO TECNOLÓGICO DE VERACRUZ Materia: Robótica Unidad 3: Cinemática Tema: Cinemática Inversa Catedrático: Dr. José Antonio Garrido Natarén H. Veracruz, Ver. Noviembre de 2014 La cinemática del robot
INSTITUTO TECNOLÓGICO DE VERACRUZ Materia: Robótica Unidad 3: Cinemática Tema: Cinemática Inversa Catedrático: Dr. José Antonio Garrido Natarén H. Veracruz, Ver. Noviembre de 2014 La cinemática del robot
Cinemática Inversa del Robot. UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides
 Cinemática Inversa del Robot UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción Resuelve la configuración que debe adoptar el robot para una posición y orientación del
Cinemática Inversa del Robot UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción Resuelve la configuración que debe adoptar el robot para una posición y orientación del
ANALISIS CINEMATICO DIRECTO E INVERSO
 ANALISIS CINEMATICO DIRECTO E INVERSO Cinematica directa x=f(q) [x,y,z] Articulaciones Posicion de la Herramienta Cinematica Inversa q=f -1 (x) El analisis cinematico inverso nos permite calcular la posicion
ANALISIS CINEMATICO DIRECTO E INVERSO Cinematica directa x=f(q) [x,y,z] Articulaciones Posicion de la Herramienta Cinematica Inversa q=f -1 (x) El analisis cinematico inverso nos permite calcular la posicion
PRÓLOGO PREFACIO... 21
 ÍNDICE PRÓLOGO... 17 PREFACIO... 21 CAPÍTULO 1. ENTORNO ACTUAL Y PERSPECTIVAS... 27 1.1 ORGANIZACIÓN DE UN SISTEMA ROBÓTICO... 29 1.2 ENTORNOS MATLAB Y SIMULINK... 31 1.3 TENDENCIAS EN ROBÓTICA Y MECATRÓNICA...
ÍNDICE PRÓLOGO... 17 PREFACIO... 21 CAPÍTULO 1. ENTORNO ACTUAL Y PERSPECTIVAS... 27 1.1 ORGANIZACIÓN DE UN SISTEMA ROBÓTICO... 29 1.2 ENTORNOS MATLAB Y SIMULINK... 31 1.3 TENDENCIAS EN ROBÓTICA Y MECATRÓNICA...
TSTC. Dpt. Teoría de la Señal, Telemática y Comunicaciones Tema 2 CINEMÁTICA DE MANIPULADORES
 Dpt. Teoría de la Señal, Telemática y Comunicaciones Tema 2 CINEMÁTICA DE MANIPULADORES Secciones 1. Introducción. 2. Coordenadas y Transformaciones Homogéneas. 3. Problema Cinemático Directo. Método de
Dpt. Teoría de la Señal, Telemática y Comunicaciones Tema 2 CINEMÁTICA DE MANIPULADORES Secciones 1. Introducción. 2. Coordenadas y Transformaciones Homogéneas. 3. Problema Cinemático Directo. Método de
Análisis Cinemático Directo del Robot RV-2AJ de Mitsubishi Utilizando Teoría de Screws
 1 Análisis Cinemático Directo del Robot RV-2AJ de Mitsubishi Utilizando Teoría de Screws Luis Villalobos, Karen Pimentel, Oscar Rivera, Manuel Cardona Facultad de Ingeniería, Universidad Don Bosco, El
1 Análisis Cinemático Directo del Robot RV-2AJ de Mitsubishi Utilizando Teoría de Screws Luis Villalobos, Karen Pimentel, Oscar Rivera, Manuel Cardona Facultad de Ingeniería, Universidad Don Bosco, El
Cinemática inversa del robot 4 gdl
 obótica y Visión por Computador - UMH Práctica 2 Cinemática inversa del robot gdl Ejemplo Solución del robot cilíndrico de grados de libertad En este caso particular, la solución geométrica es inmediata.
obótica y Visión por Computador - UMH Práctica 2 Cinemática inversa del robot gdl Ejemplo Solución del robot cilíndrico de grados de libertad En este caso particular, la solución geométrica es inmediata.
Capacitación Tecnológica Científica para Bolivia. Introducción al modelado de robots
 Catecbol Capacitación Tecnológica Científica para Bolivia www.catecbol.com facebook.com/catecbol @catecbol [email protected] Introducción al modelado de robots Ronald Terrazas Mallea Bélgica La unión
Catecbol Capacitación Tecnológica Científica para Bolivia www.catecbol.com facebook.com/catecbol @catecbol [email protected] Introducción al modelado de robots Ronald Terrazas Mallea Bélgica La unión
ESTUDIO DE UNA CADENA CINEMÁTICA UTILIZANDO LOS MÉTODOS DENAVIT-HARTENBERG Y CRAIG MODIFICADO
 ESTUDIO DE UNA CADENA CINEMÁTICA UTILIZANDO LOS MÉTODOS DENAVIT-HARTENBERG Y CRAIG MODIFICADO Dr. José Antonio Garrido Natarén 1, José Antonio Hernandez Reyes 2, MC. José Luis Fernando Palomeque Loyo 3,
ESTUDIO DE UNA CADENA CINEMÁTICA UTILIZANDO LOS MÉTODOS DENAVIT-HARTENBERG Y CRAIG MODIFICADO Dr. José Antonio Garrido Natarén 1, José Antonio Hernandez Reyes 2, MC. José Luis Fernando Palomeque Loyo 3,
Tema 5. Cinemática Inversa
 UNIVERSIDAD POLITÉCNICA DE MADRID E.U.I.T. Industrial TEMA: Cinemática Inversa FECHA: Enero de 01 Titulación: Grado en Ingeniería Electrónica y Automática Área: Ingeniería de Sistemas y Automática Departamento
UNIVERSIDAD POLITÉCNICA DE MADRID E.U.I.T. Industrial TEMA: Cinemática Inversa FECHA: Enero de 01 Titulación: Grado en Ingeniería Electrónica y Automática Área: Ingeniería de Sistemas y Automática Departamento
Clasificación de los robots según la AFRI (Asociación Francesa de Robótica Industrial) Manipulador con control manual o telemando.
 Tabla 1.1 Tipo A Clasificación de los robots según la AFRI (Asociación Francesa de Robótica Industrial) Manipulador con control manual o telemando. Tabla 1.1 Tipo A Tipo B Clasificación de los robots según
Tabla 1.1 Tipo A Clasificación de los robots según la AFRI (Asociación Francesa de Robótica Industrial) Manipulador con control manual o telemando. Tabla 1.1 Tipo A Tipo B Clasificación de los robots según
UNIVERSIDAD DON BOSCO VICERRECTORÍA DE ESTUDIOS DE POSTGRADO
 UNIVERSIDAD DON BOSCO VICERRECTORÍA DE ESTUDIOS DE POSTGRADO MAESTRÍA EN MANUFACTURA INTEGRADA POR COMPUTADORA ROBÓTICA INTEGRADA A LA MANUFACTURA Catedrático: Mg Manuel Napoleón Cardona Gutiérrez GUÍA
UNIVERSIDAD DON BOSCO VICERRECTORÍA DE ESTUDIOS DE POSTGRADO MAESTRÍA EN MANUFACTURA INTEGRADA POR COMPUTADORA ROBÓTICA INTEGRADA A LA MANUFACTURA Catedrático: Mg Manuel Napoleón Cardona Gutiérrez GUÍA
Cinemática del Robot. CI-2657 Robótica M.Sc. Kryscia Ramírez Benavides
 M.Sc. Kryscia Ramírez Benavides Sistema Robótico Cinemática Dinámica Planeamiento de Tareas Software Hardware Diseño Mecánico Actuadores Sistema de Control Sensores 2 Introducción Con el fin de controlar
M.Sc. Kryscia Ramírez Benavides Sistema Robótico Cinemática Dinámica Planeamiento de Tareas Software Hardware Diseño Mecánico Actuadores Sistema de Control Sensores 2 Introducción Con el fin de controlar
TECNOLOGICO NACIONAL DE MEXICO
 TECNOLOGICO NACIONAL DE MEXICO INSTITUTO TECNOLOGICO DE VERACRUZ ROBOTICA CLAVE 9F1A DR. JOSE ANTONIO GARRIDO NATAREN ING. MECATRONICA EQUIPO I UNIDAD I MORFOLOGIA DEL ROBOT 1.2 ESTRUCTURA MECANICA DE
TECNOLOGICO NACIONAL DE MEXICO INSTITUTO TECNOLOGICO DE VERACRUZ ROBOTICA CLAVE 9F1A DR. JOSE ANTONIO GARRIDO NATAREN ING. MECATRONICA EQUIPO I UNIDAD I MORFOLOGIA DEL ROBOT 1.2 ESTRUCTURA MECANICA DE
2015, Año del Generalísimo José María Morelos y Pavón
 Nombre de la Asignatura: ROBOTICA Línea de Investigación o Trabajo: PROCESAMIENTO DE SEÑALES ELECTRICAS Y ELECTRONICAS Tiempo de dedicación del estudiante a las actividades de: DOC-TIS-TPS-CRÉDITOS 48
Nombre de la Asignatura: ROBOTICA Línea de Investigación o Trabajo: PROCESAMIENTO DE SEÑALES ELECTRICAS Y ELECTRONICAS Tiempo de dedicación del estudiante a las actividades de: DOC-TIS-TPS-CRÉDITOS 48
SECRETARÍA DE EDUCACIÓN PÚBLICA TECNOLÓGICA NACIONAL DE MÉXICO INSTITUTIO TECNOLÓGICO DE VERACRUZ
 SECRETARÍA DE EDUCACIÓN PÚBLICA TECNOLÓGICA NACIONAL DE MÉXICO INSTITUTIO TECNOLÓGICO DE VERACRUZ Robótica Dr. José Antonio Garrido Natarén INGENIERÍA MECATRÓNICA Unidad 1 Morfología del robot 1.8 Grados
SECRETARÍA DE EDUCACIÓN PÚBLICA TECNOLÓGICA NACIONAL DE MÉXICO INSTITUTIO TECNOLÓGICO DE VERACRUZ Robótica Dr. José Antonio Garrido Natarén INGENIERÍA MECATRÓNICA Unidad 1 Morfología del robot 1.8 Grados
M.C. Cynthia Guerrero
 Algoritmo 2-6-1: Representación D-H 0. Numere las articulaciones de la 1 a la n comenzando con la base (cintura) y terminando con la herramienta, en el orden yaw, pitch y roll. 1. Asigne un sistema coordenado
Algoritmo 2-6-1: Representación D-H 0. Numere las articulaciones de la 1 a la n comenzando con la base (cintura) y terminando con la herramienta, en el orden yaw, pitch y roll. 1. Asigne un sistema coordenado
Control y programación de robots
 Control y programación de robots 11. Solución cinemática inversa y directa de robots seriales 11.1 El alumno, tras recibir y estudiar esta clase, debe ser capaz de: Comprender el modelado de la cinemática
Control y programación de robots 11. Solución cinemática inversa y directa de robots seriales 11.1 El alumno, tras recibir y estudiar esta clase, debe ser capaz de: Comprender el modelado de la cinemática
Cinemática inversa, Fanuc LR Mate 200ic
 Cinemática inversa, Fanuc LR Mate 200ic José Guadalupe Zavala Villalpando, Departamento de Ingeniería Mecatrónica Instituto Tecnológico de Celaya [email protected] Sebastián Alfonso Guzmán Blanco,
Cinemática inversa, Fanuc LR Mate 200ic José Guadalupe Zavala Villalpando, Departamento de Ingeniería Mecatrónica Instituto Tecnológico de Celaya [email protected] Sebastián Alfonso Guzmán Blanco,
UNIVERSIDAD NACIONAL DEL CALLAO FACULTAD DE INGENIERIA ELECTRICA Y ELECTRONICA. Informe Final de trabajo. De investigación
 UNIVERSIDAD NACIONAL DEL CALLAO FACULTAD DE INGENIERIA ELECTRICA Y ELECTRONICA Informe Final de trabajo De investigación CONTROL NO LINEAL DE UN ROBOT ESFÉRICO DE 3GL CON TÉCNICAS DE CONTROL DE LINEALIZACIÓN
UNIVERSIDAD NACIONAL DEL CALLAO FACULTAD DE INGENIERIA ELECTRICA Y ELECTRONICA Informe Final de trabajo De investigación CONTROL NO LINEAL DE UN ROBOT ESFÉRICO DE 3GL CON TÉCNICAS DE CONTROL DE LINEALIZACIÓN
CINEMÁTICA INVERSA DE ROBOTS INDUSTRIALES
 I EMETRE DE 00 CINEMÁTICA INVERA DE ROBOT INDUTRIALE GERMÁN ANDRÉ RAMO FUENTE * 1. Introducción El uso de robots en ambientes industriales, y más precisamente en procesos de manufactura, ha generado toda
I EMETRE DE 00 CINEMÁTICA INVERA DE ROBOT INDUTRIALE GERMÁN ANDRÉ RAMO FUENTE * 1. Introducción El uso de robots en ambientes industriales, y más precisamente en procesos de manufactura, ha generado toda
M.C. Cynthia Guerrero
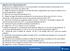 Algoritmo 2-6-1: Representación D-H 0. Numere las articulaciones de la 1 a la n comenzando con la base () y terminando con la herramienta, en el orden yaw, pitch y roll. 1. Asigne un sistema coordenado
Algoritmo 2-6-1: Representación D-H 0. Numere las articulaciones de la 1 a la n comenzando con la base () y terminando con la herramienta, en el orden yaw, pitch y roll. 1. Asigne un sistema coordenado
Se pide: (b) Ecuaciones que permiten obtener las coordenadas cartesianas en R en función de las de R.
 ÁLGEBRA Práctica 13 Espacios afines E 2 y E 3 (Curso 2004 2005) 1. En un espacio afín real de dimensión 3, se consideran dos sistemas de referencia R = {O, ē 1, ē 2, ē 3 } y R = {P, ū 1, ū 2, ū 3 }, donde
ÁLGEBRA Práctica 13 Espacios afines E 2 y E 3 (Curso 2004 2005) 1. En un espacio afín real de dimensión 3, se consideran dos sistemas de referencia R = {O, ē 1, ē 2, ē 3 } y R = {P, ū 1, ū 2, ū 3 }, donde
Modelado cinemático directo de un robot humanoide Universidad Politécnica de Sinaloa 1. Antecedentes 2. Marco teórico Espacio de articulaciones
 Modelado cinemático directo de un robot humanoide Dr. José Víctor Núñez Nalda M. C. Dora Rodríguez M. C. Víctor Rodríguez Velázquez Universidad Politécnica de Sinaloa jnunez, drodriguez, [email protected]
Modelado cinemático directo de un robot humanoide Dr. José Víctor Núñez Nalda M. C. Dora Rodríguez M. C. Víctor Rodríguez Velázquez Universidad Politécnica de Sinaloa jnunez, drodriguez, [email protected]
INTRODUCCIÓN A LA MECÁNICA DEL ROBOT. Curso de Extensión. Tema 2. Laboratorio de Robótica Aplicada (LABRA) 1
 Curso de Extensión INTRODUCCIÓN A LA ROBÓTICA MÓVILM (LABRA) 1 Curso de Introducción n a la Robótica MóvilM Tema 2 MECÁNICA DEL ROBOT (LABRA) 2 La Capa Física: F Diseño o Mecánico Configuración de las
Curso de Extensión INTRODUCCIÓN A LA ROBÓTICA MÓVILM (LABRA) 1 Curso de Introducción n a la Robótica MóvilM Tema 2 MECÁNICA DEL ROBOT (LABRA) 2 La Capa Física: F Diseño o Mecánico Configuración de las
TEMA 4. Geometría, cinemática y dinámica
 TEMA 4. Geometría, cinemática y dinámica 76 Índice: Geometría, cinemática y dinámica Geometría oordenadas propias y del mundo Representación de la posición. Tipos de coordenadas Matrices de rotación Representación
TEMA 4. Geometría, cinemática y dinámica 76 Índice: Geometría, cinemática y dinámica Geometría oordenadas propias y del mundo Representación de la posición. Tipos de coordenadas Matrices de rotación Representación
CONCEPTOS DE EQUILIBRIO DE CUERPOS VINCULADOS Y CINEMATICA PLANA
 CONCEPTOS DE EQUILIBRIO DE CUERPOS VINCULADOS Y CINEMATICA PLANA 1) LOS SISTEMAS PLANOS VINCULADOS Ing. Ramiro Piatti Ayudante Ad-Honorem 1.1) GENERALIDADES Se define como sistema de puntos materiales
CONCEPTOS DE EQUILIBRIO DE CUERPOS VINCULADOS Y CINEMATICA PLANA 1) LOS SISTEMAS PLANOS VINCULADOS Ing. Ramiro Piatti Ayudante Ad-Honorem 1.1) GENERALIDADES Se define como sistema de puntos materiales
UNIVERSIDAD DON BOSCO ROBÓTICA INTEGRADA A LA MANUFACTURA
 Mathematical tools: Denavit, Hartenberg and Screws, applied to direct cinematic analysis of the Mitsubishi Sergio Miguel García Perez, Master Student Computer Integrated Manufacturing, Don Bosco University,
Mathematical tools: Denavit, Hartenberg and Screws, applied to direct cinematic analysis of the Mitsubishi Sergio Miguel García Perez, Master Student Computer Integrated Manufacturing, Don Bosco University,
Geometría del plano y el espacio
 Geometría del plano y el espacio AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Geometría del plano y el espacio 1 / 21 Objetivos Al final de este tema tendréis que Conocer
Geometría del plano y el espacio AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Geometría del plano y el espacio 1 / 21 Objetivos Al final de este tema tendréis que Conocer
Primer Sumario de la Cinemática del Cuerpo Rígido.
 Primer Sumario de la Cinemática del Cuerpo Rígido. José María Rico Martínez. [email protected] Departamento de Ingeniería Mecánica División de Ingenierías, Campus Irapuato-Salamanca. Universidad de Guanajuato.
Primer Sumario de la Cinemática del Cuerpo Rígido. José María Rico Martínez. [email protected] Departamento de Ingeniería Mecánica División de Ingenierías, Campus Irapuato-Salamanca. Universidad de Guanajuato.
1. Obtener las coordenadas cartesianas del punto B simétrico del punto A(5,30 ), respecto al polo.
 SEMESTRE 018-1 SERIE CURVAS EN EL PLANO POLAR 1. Obtener las coordenadas cartesianas del punto B simétrico del punto A(5,30 ), respecto al polo.. Determinar las coordenadas polares del punto C simétrico
SEMESTRE 018-1 SERIE CURVAS EN EL PLANO POLAR 1. Obtener las coordenadas cartesianas del punto B simétrico del punto A(5,30 ), respecto al polo.. Determinar las coordenadas polares del punto C simétrico
Control cinemático y dinámico de robots omnidireccionales
 1 Diciembre 2013 Control cinemático y dinámico de robots omnidireccionales basado parcialmente en: Siegwart, Nourbakhsh y Scaramuzza, Introduction to Autonomous Mobile Robots Campion, et al., Structural
1 Diciembre 2013 Control cinemático y dinámico de robots omnidireccionales basado parcialmente en: Siegwart, Nourbakhsh y Scaramuzza, Introduction to Autonomous Mobile Robots Campion, et al., Structural
Introducción a la Robótica Mecanismos básicos: cinemática
 Introducción a la Robótica Mecanismos básicos: cinemática Dr José Martínez Carranza [email protected] Coordinación de Ciencias Computacionales, INAOE Cinemática (1) La cinemática es una rama de la Física
Introducción a la Robótica Mecanismos básicos: cinemática Dr José Martínez Carranza [email protected] Coordinación de Ciencias Computacionales, INAOE Cinemática (1) La cinemática es una rama de la Física
INGENIERÍA MECATRÓNICA EN COMPETENCIAS PROFESIONALES
 INGENIERÍA MECATRÓNICA EN COMPETENCIAS PROFESIONALES ASIGNATURA DE CINEMATICA DE ROBOTS PROPÓSITO DE APRENDIZAJE DE LA ASIGNATURA CUATRIMESTRE El alumno obtendrá el modelo cinemático de manipuladores,
INGENIERÍA MECATRÓNICA EN COMPETENCIAS PROFESIONALES ASIGNATURA DE CINEMATICA DE ROBOTS PROPÓSITO DE APRENDIZAJE DE LA ASIGNATURA CUATRIMESTRE El alumno obtendrá el modelo cinemático de manipuladores,
LA RECTA. Una recta r es el conjunto de los puntos del plano, alineados con un punto P y con una dirección dada.
 LA RECTA Una recta r es el conjunto de los puntos del plano, alineados con un punto P y con una dirección dada. En geometría euclidiana, la recta o la línea recta, se extiende en una misma dirección, existe
LA RECTA Una recta r es el conjunto de los puntos del plano, alineados con un punto P y con una dirección dada. En geometría euclidiana, la recta o la línea recta, se extiende en una misma dirección, existe
DENAVITHARTENBERG PA R A E L D E D O Í N D I C E D E L A M A N O
 D E T E R M I N A C I Ó N D E LO S PA R Á M E T R O S D E DENAVITHARTENBERG PA R A E L D E D O Í N D I C E D E L A M A N O M.C. José Salvador Antonio Méndez Aguirre1, Mario Arturo González Balderrama2
D E T E R M I N A C I Ó N D E LO S PA R Á M E T R O S D E DENAVITHARTENBERG PA R A E L D E D O Í N D I C E D E L A M A N O M.C. José Salvador Antonio Méndez Aguirre1, Mario Arturo González Balderrama2
Modelado de un brazo robótico Scorbot-ER III mediante cinemática directa
 XXIV CONVENCIÓN DE ESTUDIANTES DE CENTROAMÉRICA Y PANAMÁ, CONESCAPAN, EL SALVADOR, 25 Modelado de un brazo robótico Scorbot-ER III mediante cinemática directa Silvio Alejandro Urizar Salazar, Student Member
XXIV CONVENCIÓN DE ESTUDIANTES DE CENTROAMÉRICA Y PANAMÁ, CONESCAPAN, EL SALVADOR, 25 Modelado de un brazo robótico Scorbot-ER III mediante cinemática directa Silvio Alejandro Urizar Salazar, Student Member
Contenido. Prefacio... Acerca de los autores...
 Contenido Prefacio... Acerca de los autores... xi xvi Capítulo 1. Introducción... 1 1.1. Antecedentes históricos... 2 1.2. Origen y desarrollo de la robótica... 8 1.3. Definición del Robot... 16 1.3.1.
Contenido Prefacio... Acerca de los autores... xi xvi Capítulo 1. Introducción... 1 1.1. Antecedentes históricos... 2 1.2. Origen y desarrollo de la robótica... 8 1.3. Definición del Robot... 16 1.3.1.
TECNOLÓGICO DE ESTUDIOS SUPERIORES DE ECATEPEC
 TECNOLÓGICO DE ESTUDIOS SUPERIORES DE ECATEPEC DIVISIÓN DE INGENIERÍA ELECTRÓNICA Y TELEMÁTICA PRÁCTICAS DE LABORATORIO ASIGNATURA: ROBÓTICA I REALIZÓ: GERARDO PAZOS RODRÍGUEZ PRESENTACIÓN El presente
TECNOLÓGICO DE ESTUDIOS SUPERIORES DE ECATEPEC DIVISIÓN DE INGENIERÍA ELECTRÓNICA Y TELEMÁTICA PRÁCTICAS DE LABORATORIO ASIGNATURA: ROBÓTICA I REALIZÓ: GERARDO PAZOS RODRÍGUEZ PRESENTACIÓN El presente
Visión artificial y Robótica Geometría. Depto. de Ciencia de la Computación e Inteligencia Artificial
 Visión artificial y Robótica Geometría Depto. de Ciencia de la Computación e Inteligencia Artificial Contenidos Geometría 2D y 3D Transformación de coordenadas Calibración de la cámara Álgebra necesaria
Visión artificial y Robótica Geometría Depto. de Ciencia de la Computación e Inteligencia Artificial Contenidos Geometría 2D y 3D Transformación de coordenadas Calibración de la cámara Álgebra necesaria
Robots Autónomos Miguel Cazorla,, Otto Colomina Depto.. Ciencia de la Computación n e I.A. Universidad de Alicante
 Robots Autónomos Miguel Cazorla,, Otto Colomina Depto.. Ciencia de la Computación n e I.A. Universidad de Alicante Este ítem está licenciado bajo Licencia Creative Commons Tema 2: Modelos geométricos y
Robots Autónomos Miguel Cazorla,, Otto Colomina Depto.. Ciencia de la Computación n e I.A. Universidad de Alicante Este ítem está licenciado bajo Licencia Creative Commons Tema 2: Modelos geométricos y
Fundamentos de Robótica
 Fundamentos de Robótica Cinemática Inversa Ricardo-Franco Mendoza-Garcia [email protected] Escuela Universitaria de Ingeniería Mecánica Universidad de Tarapacá Arica, Chile June 16, 2015 R. F. Mendoza-Garcia
Fundamentos de Robótica Cinemática Inversa Ricardo-Franco Mendoza-Garcia [email protected] Escuela Universitaria de Ingeniería Mecánica Universidad de Tarapacá Arica, Chile June 16, 2015 R. F. Mendoza-Garcia
ap l i c a c i o n e s d e l a s
 Unidad 9 ap l i c a c i o n e s d e l a s transformaciones lineales Objetivos: Al inalizar la unidad, el alumno: Relacionará algunas transformaciones especiales con movimientos geométricos de vectores
Unidad 9 ap l i c a c i o n e s d e l a s transformaciones lineales Objetivos: Al inalizar la unidad, el alumno: Relacionará algunas transformaciones especiales con movimientos geométricos de vectores
VECTORES : Las Cantidades Vectoriales cantidades escalares
 VECTORES En física hay dos tipos de cantidades: Las Cantidades Vectoriales son aquellas que tiene tanto magnitud como dirección y sentido sobre la dirección), mientras que las cantidades escalares son
VECTORES En física hay dos tipos de cantidades: Las Cantidades Vectoriales son aquellas que tiene tanto magnitud como dirección y sentido sobre la dirección), mientras que las cantidades escalares son
CINEMÁTICA Y DINÁMICA DE ROBOTS MANIPULADORES: RESPUESTAS DE EJERCICIOS UNIDAD 01. Roger Miranda Colorado
 CINEMÁTICA Y DINÁMICA DE ROBOTS MANIPULADORES: RESPUESTAS DE EJERCICIOS UNIDAD 01 Roger Miranda Colorado 23 de mayo de 2016 Índice 1. RESPUESTAS DE EJERCICIOS UNIDAD 01 1 1. RESPUESTAS DE EJERCICIOS UNIDAD
CINEMÁTICA Y DINÁMICA DE ROBOTS MANIPULADORES: RESPUESTAS DE EJERCICIOS UNIDAD 01 Roger Miranda Colorado 23 de mayo de 2016 Índice 1. RESPUESTAS DE EJERCICIOS UNIDAD 01 1 1. RESPUESTAS DE EJERCICIOS UNIDAD
LOCOMOCION DE SISTEMAS ROBOTICOS
 CAPITULO II LOCOMOCION DE SISTEMAS ROBOTICOS P I N Z A B R A Z O A N T E B R A ZO B A S E 2.1. GRADOS DE LIBERTAD El componente principal en el robot está constituido por las articulaciones y sus eslabones.
CAPITULO II LOCOMOCION DE SISTEMAS ROBOTICOS P I N Z A B R A Z O A N T E B R A ZO B A S E 2.1. GRADOS DE LIBERTAD El componente principal en el robot está constituido por las articulaciones y sus eslabones.
Graficación CCOM-259. Benemérita Universidad Autónoma de Puebla. Facultad de Ciencias de la Computación. Daniel Alejandro Valdés Amaro, Ph.
 Graficación CCOM-9 Benemérita Universidad Autónoma de Puebla Facultad de Ciencias de la Computación Daniel Alejandro Valdés Amaro, Ph.D Objetivo: El alumno conocerá y aplicará los algoritmos y técnicas
Graficación CCOM-9 Benemérita Universidad Autónoma de Puebla Facultad de Ciencias de la Computación Daniel Alejandro Valdés Amaro, Ph.D Objetivo: El alumno conocerá y aplicará los algoritmos y técnicas
TRABAJO DE ELEMENTOS DE MÁQUINAS Y VIBRACIONES 3º INGENIERÍA INDUSTRIAL
 Trabajo 1: Dinámica de un sistema motor-volante de inercia-masa de un vehículo dinámico del sistema de la figura. Las variables que definen la posición del mecanismo serán las coordenadas indicadas en
Trabajo 1: Dinámica de un sistema motor-volante de inercia-masa de un vehículo dinámico del sistema de la figura. Las variables que definen la posición del mecanismo serán las coordenadas indicadas en
Universidad Politécnica de Madrid Escuela de Ingenieros Industriales. RoboTenis
 Universidad Politécnica de Madrid Escuela de Ingenieros Industriales RoboTenis Diseño, Simulación, Análisis Cinemático y Dinámico de un robot paralelo para Control Visual de altas prestaciones DISAM Luis
Universidad Politécnica de Madrid Escuela de Ingenieros Industriales RoboTenis Diseño, Simulación, Análisis Cinemático y Dinámico de un robot paralelo para Control Visual de altas prestaciones DISAM Luis
Escuela Politécnica Superior de Linares
 Escuela Politécnica Superior de Linares UNIVERSIDAD DE JAÉN Escuela Politécnica Superior de Linares Trabajo Fin de Grado PUESTA EN MARCHA DE BRAZO ROBÓTICO Y DESARROLLO DE APLICACIONES Alumno: Axel José
Escuela Politécnica Superior de Linares UNIVERSIDAD DE JAÉN Escuela Politécnica Superior de Linares Trabajo Fin de Grado PUESTA EN MARCHA DE BRAZO ROBÓTICO Y DESARROLLO DE APLICACIONES Alumno: Axel José
INSTITUTO POLITÉCNICO NACIONAL
 INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERIA MECÁNICA Y ELÉCTRICA UNIDAD ZACATENCO DEPARTAMENTO ACADÉMICO DE INGENIERIA EN CONTROL Y AITOMATIZACIÓN Diseño y construcción de un brazo mecánico,
INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERIA MECÁNICA Y ELÉCTRICA UNIDAD ZACATENCO DEPARTAMENTO ACADÉMICO DE INGENIERIA EN CONTROL Y AITOMATIZACIÓN Diseño y construcción de un brazo mecánico,
2 Transformaciones en 3D
 2 Transformaciones en 3D La manera más fácil de conseguir las transformaciones básicas (traslación, rotación, escalación, en general las transformaciones afines) es utilizando matrices de transformación.
2 Transformaciones en 3D La manera más fácil de conseguir las transformaciones básicas (traslación, rotación, escalación, en general las transformaciones afines) es utilizando matrices de transformación.
2.- (Puntuación máxima 2 puntos). Para cada valor del parámetro real a, se consideran los tres planos siguientes:
 1.- (Puntuación máxima 3 puntos). Se consideran las rectas: a) (1 punto) Calcular la distancia entre r y s. b) (1 punto) Hallar unas ecuaciones cartesianas de la recta perpendicular común a r y s y que
1.- (Puntuación máxima 3 puntos). Se consideran las rectas: a) (1 punto) Calcular la distancia entre r y s. b) (1 punto) Hallar unas ecuaciones cartesianas de la recta perpendicular común a r y s y que
Modelado Cinemático de la mano de Barrett
 Modelado Cinemático de la mano de Barrett Informe Técnico Proyecto: DPI2008-02647 Autores: Juan Antonio Corrales Ramón Fernando Torres Medina Grupo de Automática, Robótica y Visión Artificial Departamento
Modelado Cinemático de la mano de Barrett Informe Técnico Proyecto: DPI2008-02647 Autores: Juan Antonio Corrales Ramón Fernando Torres Medina Grupo de Automática, Robótica y Visión Artificial Departamento
INGENIERÍA PROFESIONAL EN INOCUIDAD ALIMENTARIA EN COMPETENCIAS PROFESIONALES ASIGNATURA DE ROBÓTICA
 INGENIERÍA PROFESIONAL EN INOCUIDAD ALIMENTARIA EN COMPETENCIAS PROFESIONALES ASIGNATURA DE ROBÓTICA UNIDADES DE APRENDIZAJE 1. Competencias Automatizar procesos de producción mediante la implementación
INGENIERÍA PROFESIONAL EN INOCUIDAD ALIMENTARIA EN COMPETENCIAS PROFESIONALES ASIGNATURA DE ROBÓTICA UNIDADES DE APRENDIZAJE 1. Competencias Automatizar procesos de producción mediante la implementación
EJERCICIOS PAU MATEMÁTICAS II ARAGÓN Autor: Fernando J. Nora Costa-Ribeiro Más ejercicios y soluciones en fisicaymat.wordpress.com
 GEOMETRÍA 1- Dados el punto P(1,-1,0) y la recta : 1 0 3 3 0 a) Determine la ecuación general del plano (Ax+By+Cz+D=0) que contiene al punto P y a la recta s. b) Determine el ángulo que forman el plano
GEOMETRÍA 1- Dados el punto P(1,-1,0) y la recta : 1 0 3 3 0 a) Determine la ecuación general del plano (Ax+By+Cz+D=0) que contiene al punto P y a la recta s. b) Determine el ángulo que forman el plano
Trabajo Práctico 3 - Cinemática del cuerpo rígido Edición 2014
 Facultad de Ingeniería - U.N.L.P. Mecánica Racional - urso 2016 / 1 semestre Trabajo Práctico 3 - inemática del cuerpo rígido Edición 2014 Problema 1. La barra de la figura, de longitud l, está unida mediante
Facultad de Ingeniería - U.N.L.P. Mecánica Racional - urso 2016 / 1 semestre Trabajo Práctico 3 - inemática del cuerpo rígido Edición 2014 Problema 1. La barra de la figura, de longitud l, está unida mediante
Tema 2 Campo de velocidades del sólido rígido
 Mecánica Clásica Tema Campo de velocidades del sólido rígido EIAE 5 de septiembre de 011 Velocidad de un punto del sólido. Deducción matricial.................................. Tensor velocidad angular......................................................
Mecánica Clásica Tema Campo de velocidades del sólido rígido EIAE 5 de septiembre de 011 Velocidad de un punto del sólido. Deducción matricial.................................. Tensor velocidad angular......................................................
Robótica Dr. José Antonio Garrido Natarén INGENIERÍA MECATRÓNICA. Unidad 1.- Morfología del robot. 1.2 Estructura mecánica de los robots.
 SECRETARÍA DE EDUCACIÓN PÚBLICA TECNOLÓGICA NACIONAL DE MÉXICO INSTITUTIO TECNOLÓGICO DE VERACRUZ Robótica Dr. José Antonio Garrido Natarén INGENIERÍA MECATRÓNICA Unidad 1.- Morfología del robot 1.2 Estructura
SECRETARÍA DE EDUCACIÓN PÚBLICA TECNOLÓGICA NACIONAL DE MÉXICO INSTITUTIO TECNOLÓGICO DE VERACRUZ Robótica Dr. José Antonio Garrido Natarén INGENIERÍA MECATRÓNICA Unidad 1.- Morfología del robot 1.2 Estructura
Ibarra Ecuador. B. Cinemática directa
 Diseño de un software que permite la simulación cinemática de un brazo robótico Kleber Andrés Calderón Martínez, Carlos Xavier Rosero [email protected], [email protected] Ingeniería en Mecatrónica Ibarra
Diseño de un software que permite la simulación cinemática de un brazo robótico Kleber Andrés Calderón Martínez, Carlos Xavier Rosero [email protected], [email protected] Ingeniería en Mecatrónica Ibarra
ESCUELA PREPARATORIA OFICIAL NO.16 MATERÍA: GEOMETRÍA ANALITICA GUÍA DE ESTUDIO PARA LA ÚLTIMA OPORTUNIDAD DE ACREDITAR LA MATERÍA
 Geometría analítica 1.- Ecuación de la recta 2.- Cónicas 3.-Ecuación de la parábola UNIDAD II: CONICAS (CIRCUNFERENCIA Y PARABOLAS) Una superficie cónica de revolución está engendrada por la rotación de
Geometría analítica 1.- Ecuación de la recta 2.- Cónicas 3.-Ecuación de la parábola UNIDAD II: CONICAS (CIRCUNFERENCIA Y PARABOLAS) Una superficie cónica de revolución está engendrada por la rotación de
TSTC. Dpt. Teoría de la Señal, Telemática y Comunicaciones Tema 1 INTRODUCCIÓN A LA ROBÓTICA
 Dpt. Teoría de la Señal, Telemática y Comunicaciones Tema 1 INTRODUCCIÓN A LA ROBÓTICA Secciones 1. Introducción y definiciones. 2. Visión General de la manipulación mecánica. 1. Posicionamiento y Cinemática
Dpt. Teoría de la Señal, Telemática y Comunicaciones Tema 1 INTRODUCCIÓN A LA ROBÓTICA Secciones 1. Introducción y definiciones. 2. Visión General de la manipulación mecánica. 1. Posicionamiento y Cinemática
GEOMETRÍA EN EL ESPACIO
 GEOMETRÍA EN EL ESPACIO 1. PUNTOS Y VECTORES OPERACIÓN TEORÍA Y FORMULACIÓN EJEMPLO Coordenadas de un punto Punto medio de un segmento Dividir un segmento en n partes iguales Coordenadas de un vector (
GEOMETRÍA EN EL ESPACIO 1. PUNTOS Y VECTORES OPERACIÓN TEORÍA Y FORMULACIÓN EJEMPLO Coordenadas de un punto Punto medio de un segmento Dividir un segmento en n partes iguales Coordenadas de un vector (
Visión artificial y Robótica Modelos de movimiento y mapas. Depto. de Ciencia de la Computación e Inteligencia Artificial
 Visión artificial y Robótica Modelos de movimiento y mapas Depto. de Ciencia de la Computación e Inteligencia Artificial Contenidos Sistemas de coordenadas Localización de objetos en el espacio Modelos
Visión artificial y Robótica Modelos de movimiento y mapas Depto. de Ciencia de la Computación e Inteligencia Artificial Contenidos Sistemas de coordenadas Localización de objetos en el espacio Modelos
Control y programación de robots
 Control y programación de robots 8. Cinemática directa robots seriales: Screws sucesivos 8. Objetivo Fórmula de Rodriguez espacial s ($), eje screw p2 sp t θ r p2 y2 pr 2 p r2 Bθ z2 p z t θ s x A x2 r
Control y programación de robots 8. Cinemática directa robots seriales: Screws sucesivos 8. Objetivo Fórmula de Rodriguez espacial s ($), eje screw p2 sp t θ r p2 y2 pr 2 p r2 Bθ z2 p z t θ s x A x2 r
