Tema 5. Cinemática Inversa
|
|
|
- Carlos Núñez Salas
- hace 8 años
- Vistas:
Transcripción
1 UNIVERSIDAD POLITÉCNICA DE MADRID E.U.I.T. Industrial TEMA: Cinemática Inversa FECHA: Enero de 01 Titulación: Grado en Ingeniería Electrónica y Automática Área: Ingeniería de Sistemas y Automática Departamento de Electrónica Automática e Informática Industrial Escuela Universitaria deingeniería Técnica Industrial Robótica Tema 5. Cinemática Inversa 1
2 Objetivos FECHA: Enero de Dada una localización en el espacio para el extremo operativo, encontrar una formulación matemática cerrada para cada una de las coordenadas generalizadas del robot a partir de la misma. Establecer la base que permite el control de trayectorias de la herramienta del robot, al formular el problema de localización referido a un sistema de referencia externo.
3 Contenido FECHA: Enero de Introducción al problema 5. Métodos Geométricos 5. Resolución por medio de las Matrices de Transformación Homogénea. 5.4Desacoplo o cinemático. átco 5.5 Consideraciones finales. 5.6 Ejemplos y problemas Bibliografía recomendada: Fundamentos de Robótica. (ª Edición) BarrientosA, Peñin L. F., BalaguerC., Aracil R.Ed. McGraw Hill ISBN:
4 5.1 Introducción al problema Justificación FECHA: Enero de 01
5 5.1 Introducción al problema Cinemática i Inversa FECHA: Enero de 01 Objetivo: encontrar losvaloresque deben adoptar las coordenadas articulares del robot para que su extremo se posicione y oriente según una determinada d localización li ió espacial il La resolución no es sistemática Depende de laconfig configuración racióndel robot (soluciones múltiples) No siempre existe solución en forma cerrada. o Condiciones suficientes para que exista: Tres ejes de articulación adyacentes interseccionan en un punto (robot PUMA y robot Stanford) Tres ejes de articulación adyacentes son paralelos entre sí (robot Elbow)
6 5.1 Introducción al problema Alternativas FECHA: Enero de 01 Procedimiento genérico a partir de los parámetros D H Método iterativo Problemas de velocidad y convergencia Búsqueda de solución cerrada: q k = f k (x,y,z,,,); k = 1,,n Posibilidad de resolución en tiempo real Posibilidad de selección de la solución más adecuada Posibilidad de simplificaciones No siempre es posible
7 5.1 Introducción al problema Métodos FECHA: Enero de 01 Métodos geométricos Se suele utilizar para las primeras variables articulares Uso de relaciones geométricas y trigonométricas (resolución de triángulos) Resolución a partir de las matrices de transformación homogénea Despejar las n variables ibl q i en función de las componentes de los vectores n, o, a y p. Desacoplamiento cinemático En robots de 6 GDL Separación de orientación y posicionamiento Otros: álgebrade tornillo, cuaterniones duales,métodos iterativos... 7 Robotica Industrial- Ci áti d l b t
8 5. Métodos geométricos r p z Método Geométrico Ejemplo(I) r FECHA: Enero de 01 q 1 p arctg p y x r pz l l llcosq Coseno del complementario px p y cosq px py pz l l l l sen q 1 cos q q arctg con cos q 1cos cos q q p p p l l ll x y z d l Teorema del coseno Dado un triángulo ABC, siendo α, β, γ, los ángulos, y a, b, c, los lados respectivamente opuestos a estos ángulos entonces:
9 FECHA: Enero de 01 Mé d G é i 5. Métodos geométricos Método Geométrico Ejemplo(II) q z z arct p g p arctg y x cos l l sen l arct r q q arctg p p g arctg cos l l q y x z c l l sen q l os q arctg p p p arctg q y
10 5. Basado en Matrices Homogéneas Concepto FECHA: Enero de 01 Resolución a partir de las matrices de transformación homogénea Se resuelve la cinemática directa y se obtienen las matrices A. Para evitar la aparición de ecuaciones trascendentes, se va premultiplicando por las matrices inversas. Se intenta obtener de esta forma una ecuación que aísle en uno de los lados una de las variables articulares La elección de los elementos ha de realizarse con sumo cuidado Por su complejidad a menudo este método se deshecha.
11 5. Basado en Matrices Homogéneas Ejemplo FECHA: Enero de 01 Artic. d a 1 q 1 l º q º 0 q C1 0 S1 0 C 0 S S1 0 C1 0 S 1 0 C A1 A A l q CC 1 S1 CS 1 0 CC 1 S1 CS 1 qcs 1 SC 1 C1 SS 1 0 SC A T 0 A 1 C1 SS 1 qss 1 S 0 C l1 S 0 C qc l
12 5. Basado en Matrices Homogéneas Ejemplo FECHA: Enero de 01 l é d d d á l d l d h d d El término izquierdo dependerá solo de q1 mientras que el derecho depende de q y q. Busco un elemento fácil, que relacione q1 con constantes:
13 5. Basado en Matrices Homogéneas Ejemplo FECHA: Enero de 01 Dado que q1 está obtenido, para q, buscare relaciones entre q1 y q con un elemento constante en el ladoderecho: derecho:
14 5.4 Desacoplo Cinemático Concepto FECHA: Enero de 01 Resolución mediante el desacoplo cinemático Habitualmente los tres último ejes del robot se cortan en un punto. La finalidad de estos es lograr la orientación de la herramienta, aunque como consecuencia de su movimiento tengan un efecto ligero sobre la posición Con la primera condición se puede simplificar enormemente el problema cinemático para 6 gdl, dado que la obtención de este punto de intersección es una operación sencilla. Este punto dependerá sólo de los primeros gdl, por lo que su obtención es asequible.
15 5.4 Desacoplo Cinemático Ejemplo FECHA: Enero de 01 Punto de desacoplo p m p r l a 4 6 Prof. Cecilia García
16 5.4 Desacoplo Cinemático Ejemplo FECHA: Enero de 01 Mediante alguno de los métodos anteriores se obtienen los valores de q1,q q y q. Qué hacemos con el resto? Nos centramos exclusivamente en la orientación por simplicidad, y aplicamos un método análogo al basado en las matrices homogéneas:
17 5.5 Consideraciones Finales Aspectos computacionales FECHA: Enero de 01 Para seguimiento de trayectorias es necesario resolver el problema cinemático a gran velocidad (0 veces/seg o más). Son S preferibles las soluciones cerradas explícitas (si (iexisten) a las iterativas. Para acelerar cálculos generalmente se emplean tablas previamente calculadas (look up tables) El coste de calcular n soluciones, no es necesariamente n veces el de calcular una única solución. Computacionalmente es más robusta la arcotangente por lo que es preferible buscar siempre este tipo de relación. 17
18 5.5 Consideraciones Finales Consideraciones i adicionales i FECHA: Enero de 01 Deben atenderse las múltiples soluciones: Elección que minimice los movimientos desde la posición actual Concepto de solución más cercana Mover los eslabones de menor peso Considerarobstáculos obstáculos (evitar colisiones). Teóricamente es resoluble todo sistema R y P con 6 grados de libertad. Métodos numéricos iterativos: lentitud. Se prefieren expresiones analíticas (soluciones cerradas): Métodos algebraicos Métodos geométricos. 18
19 5.5 Consideraciones Finales Robots Rd Redundantesd FECHA: Enero de 01 Se desea: Posicionar el elemento terminal en un punto del plano o Si Nº DoF del manipulador Nº DoF que requiere la tarea Dos soluciones o Si Nº DoF del manipulador > Nº de DoF que requiere la tarea Infinitas soluciones 19
Cinemática Inversa del Robot. UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides
 Cinemática Inversa del Robot UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción Resuelve la configuración que debe adoptar el robot para una posición y orientación del
Cinemática Inversa del Robot UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción Resuelve la configuración que debe adoptar el robot para una posición y orientación del
CINEMÁTICA DEL ROBOT
 CINEMÁTICA DEL ROBOT Cinemática Directa Cinemática Inversa Matriz Jacobiana 1 Problema cinemático del robot Cinemática del robot: Estudio de su movimiento con respecto a un sistema de referencia: Descripción
CINEMÁTICA DEL ROBOT Cinemática Directa Cinemática Inversa Matriz Jacobiana 1 Problema cinemático del robot Cinemática del robot: Estudio de su movimiento con respecto a un sistema de referencia: Descripción
Robótica Industrial. Robótica Industrial
 TEMA 4: CINEMÁTICA DEL ROBOT Ingeniería de Sistemas y Automática Control de Robots y Sistemas Sensoriales Robótica Industrial Robótica Industrial ISA.- Ingeniería de Sistemas y Automática Cinemática del
TEMA 4: CINEMÁTICA DEL ROBOT Ingeniería de Sistemas y Automática Control de Robots y Sistemas Sensoriales Robótica Industrial Robótica Industrial ISA.- Ingeniería de Sistemas y Automática Cinemática del
ANALISIS CINEMATICO DIRECTO E INVERSO
 ANALISIS CINEMATICO DIRECTO E INVERSO Cinematica directa x=f(q) [x,y,z] Articulaciones Posicion de la Herramienta Cinematica Inversa q=f -1 (x) El analisis cinematico inverso nos permite calcular la posicion
ANALISIS CINEMATICO DIRECTO E INVERSO Cinematica directa x=f(q) [x,y,z] Articulaciones Posicion de la Herramienta Cinematica Inversa q=f -1 (x) El analisis cinematico inverso nos permite calcular la posicion
Cinemática del Robot. UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides
 UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción La cinemática del robot estudia el movimiento del mismo con respecto a un sistema de referencia. Se interesa por la
UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción La cinemática del robot estudia el movimiento del mismo con respecto a un sistema de referencia. Se interesa por la
TSTC. Dpt. Teoría de la Señal, Telemática y Comunicaciones Tema 2 CINEMÁTICA DE MANIPULADORES
 Dpt. Teoría de la Señal, Telemática y Comunicaciones Tema 2 CINEMÁTICA DE MANIPULADORES Secciones 1. Introducción. 2. Coordenadas y Transformaciones Homogéneas. 3. Problema Cinemático Directo. Método de
Dpt. Teoría de la Señal, Telemática y Comunicaciones Tema 2 CINEMÁTICA DE MANIPULADORES Secciones 1. Introducción. 2. Coordenadas y Transformaciones Homogéneas. 3. Problema Cinemático Directo. Método de
Dr. Roberto Carlos García Gómez
 Dr. Roberto Carlos García Gómez La cinemática del robot estudia el movimiento del mismo con respecto a un sistema de referencia. La cinemática se interesa por la descripción analítica del movimiento espacial
Dr. Roberto Carlos García Gómez La cinemática del robot estudia el movimiento del mismo con respecto a un sistema de referencia. La cinemática se interesa por la descripción analítica del movimiento espacial
Cinemática del Robot
 Cinemática del Robot La cinemática del robot estudia el movimiento del mismo con respecto a un sistema de referencia. En primer término, la cinemática se interesa por la descripción analítica del movimiento
Cinemática del Robot La cinemática del robot estudia el movimiento del mismo con respecto a un sistema de referencia. En primer término, la cinemática se interesa por la descripción analítica del movimiento
Cinemática del Robot. CI-2657 Robótica M.Sc. Kryscia Ramírez Benavides
 M.Sc. Kryscia Ramírez Benavides Sistema Robótico Cinemática Dinámica Planeamiento de Tareas Software Hardware Diseño Mecánico Actuadores Sistema de Control Sensores 2 Introducción Con el fin de controlar
M.Sc. Kryscia Ramírez Benavides Sistema Robótico Cinemática Dinámica Planeamiento de Tareas Software Hardware Diseño Mecánico Actuadores Sistema de Control Sensores 2 Introducción Con el fin de controlar
ROBÓTICA I. Cinemática Directa
 Cinemática Directa M. C. Jorge Luis Barahona Avalos 11 de abril de 2011 Universidad Tecnológica de la Mixteca Instituto de Electrónica y Mecatrónica 1 / 34 Índice General 1 Cinemática Directa 2 Cadena
Cinemática Directa M. C. Jorge Luis Barahona Avalos 11 de abril de 2011 Universidad Tecnológica de la Mixteca Instituto de Electrónica y Mecatrónica 1 / 34 Índice General 1 Cinemática Directa 2 Cadena
Cinemática Inversa del Robot. CI-2657 Robótica M.Sc. Kryscia Ramírez Benavides
 Cinemática Inversa del Robot M.Sc. Kryscia Ramírez Benavides Introducción Resuelve la configuración que debe adoptar el robot para una posición y orientación del extremo conocidas. 2 Introducción (cont.)
Cinemática Inversa del Robot M.Sc. Kryscia Ramírez Benavides Introducción Resuelve la configuración que debe adoptar el robot para una posición y orientación del extremo conocidas. 2 Introducción (cont.)
ROBÓTICA I. Cinemática Directa
 Cinemática Directa M. C. Jorge Luis Barahona Avalos 2 de mayo de 2012 Universidad Tecnológica de la Mixteca Instituto de Electrónica y Mecatrónica 1 / 42 Índice General 1 Cinemática Directa 2 Cadena Cinemática
Cinemática Directa M. C. Jorge Luis Barahona Avalos 2 de mayo de 2012 Universidad Tecnológica de la Mixteca Instituto de Electrónica y Mecatrónica 1 / 42 Índice General 1 Cinemática Directa 2 Cadena Cinemática
Contenido. Prefacio... Acerca de los autores...
 Contenido Prefacio... Acerca de los autores... xi xvi Capítulo 1. Introducción... 1 1.1. Antecedentes históricos... 2 1.2. Origen y desarrollo de la robótica... 8 1.3. Definición del Robot... 16 1.3.1.
Contenido Prefacio... Acerca de los autores... xi xvi Capítulo 1. Introducción... 1 1.1. Antecedentes históricos... 2 1.2. Origen y desarrollo de la robótica... 8 1.3. Definición del Robot... 16 1.3.1.
INTRODUCCIÓN A LA MECÁNICA DEL ROBOT. Curso de Extensión. Tema 2. Laboratorio de Robótica Aplicada (LABRA) 1
 Curso de Extensión INTRODUCCIÓN A LA ROBÓTICA MÓVILM (LABRA) 1 Curso de Introducción n a la Robótica MóvilM Tema 2 MECÁNICA DEL ROBOT (LABRA) 2 La Capa Física: F Diseño o Mecánico Configuración de las
Curso de Extensión INTRODUCCIÓN A LA ROBÓTICA MÓVILM (LABRA) 1 Curso de Introducción n a la Robótica MóvilM Tema 2 MECÁNICA DEL ROBOT (LABRA) 2 La Capa Física: F Diseño o Mecánico Configuración de las
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE INGENIERÍA PROGRAMA DE ESTUDIO
 UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE INGENIERÍA PROGRAMA DE ESTUDIO ROBÓTICA 2135 9º 10 Asignatura Clave Semestre Créditos Ingeniería Mecánica e Industrial Ingeniería Mecatrónica Ingeniería
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE INGENIERÍA PROGRAMA DE ESTUDIO ROBÓTICA 2135 9º 10 Asignatura Clave Semestre Créditos Ingeniería Mecánica e Industrial Ingeniería Mecatrónica Ingeniería
TSTC. Dpt. Teoría de la Señal, Telemática y Comunicaciones Tema 1 INTRODUCCIÓN A LA ROBÓTICA
 Dpt. Teoría de la Señal, Telemática y Comunicaciones Tema 1 INTRODUCCIÓN A LA ROBÓTICA Secciones 1. Introducción y definiciones. 2. Visión General de la manipulación mecánica. 1. Posicionamiento y Cinemática
Dpt. Teoría de la Señal, Telemática y Comunicaciones Tema 1 INTRODUCCIÓN A LA ROBÓTICA Secciones 1. Introducción y definiciones. 2. Visión General de la manipulación mecánica. 1. Posicionamiento y Cinemática
ASIGNATURA: CONTROL Y PROGRAMACIÓN DE ROBOTS CÓDIGO: 2261
 ASIGNATURA: CONTROL Y PROGRAMACIÓN DE ROBOTS CÓDIGO: 221 DEPARTAMENTO: DEPARTAMENTO DE INGENIERÍA DE SISTEMAS Y AUTOMÁTICA ÁREAS DE CONOCIMIENTO: DEPARTAMENTO DE INGENIERÍA DE SISTEMAS Y AUTOMÁTICA DESCRIPTORES
ASIGNATURA: CONTROL Y PROGRAMACIÓN DE ROBOTS CÓDIGO: 221 DEPARTAMENTO: DEPARTAMENTO DE INGENIERÍA DE SISTEMAS Y AUTOMÁTICA ÁREAS DE CONOCIMIENTO: DEPARTAMENTO DE INGENIERÍA DE SISTEMAS Y AUTOMÁTICA DESCRIPTORES
Fundamentos de Robótica
 Fundamentos de Robótica Introducción a la cinemática de manipuladores [email protected] http://scfi.uaemex.mx/hamontes 1 Recomendación No use estas diapositivas como referencia única de estudio durante
Fundamentos de Robótica Introducción a la cinemática de manipuladores [email protected] http://scfi.uaemex.mx/hamontes 1 Recomendación No use estas diapositivas como referencia única de estudio durante
Modelado Cinemático de la mano de Barrett
 Modelado Cinemático de la mano de Barrett Informe Técnico Proyecto: DPI2008-02647 Autores: Juan Antonio Corrales Ramón Fernando Torres Medina Grupo de Automática, Robótica y Visión Artificial Departamento
Modelado Cinemático de la mano de Barrett Informe Técnico Proyecto: DPI2008-02647 Autores: Juan Antonio Corrales Ramón Fernando Torres Medina Grupo de Automática, Robótica y Visión Artificial Departamento
Cinemática Directa del Robot. CI-2657 Robótica M.Sc. Kryscia Ramírez Benavides
 M.Sc. Kryscia Ramírez Benavides Introducción Consiste en determinar cual es la posición y orientación del extremo final del robot, con respecto a un sistema de coordenadas que se toma como referencia,
M.Sc. Kryscia Ramírez Benavides Introducción Consiste en determinar cual es la posición y orientación del extremo final del robot, con respecto a un sistema de coordenadas que se toma como referencia,
Problema Cinemático Directo
 Problema Cinemático Directo Parámetros Denavit-Hartenberg Denavit-Hartenberg notación Craig Denavit-Hartenberg notación Craig Denavit-Hartenberg notación Craig Denavit-Hartenberg notación Craig Denavit-Hartenberg
Problema Cinemático Directo Parámetros Denavit-Hartenberg Denavit-Hartenberg notación Craig Denavit-Hartenberg notación Craig Denavit-Hartenberg notación Craig Denavit-Hartenberg notación Craig Denavit-Hartenberg
INSTITUTO TECNOLÓGICO DE TIJUANA SUBDIRECCIÓN ACADÉMICA DEPARTAMENTO DE SISTEMAS Y COMPUTACIÓN SEMESTRE AGOSTO-DICIEMBRE 2014
 INSTITUTO TECNOLÓGICO DE TIJUANA SUBDIRECCIÓN ACADÉMICA DEPARTAMENTO DE SISTEMAS Y COMPUTACIÓN SEMESTRE AGOSTO-DICIEMBRE 2014 Carrera: Ingeniería en sistemas computacionales. Materia: Métodos Numéricos.
INSTITUTO TECNOLÓGICO DE TIJUANA SUBDIRECCIÓN ACADÉMICA DEPARTAMENTO DE SISTEMAS Y COMPUTACIÓN SEMESTRE AGOSTO-DICIEMBRE 2014 Carrera: Ingeniería en sistemas computacionales. Materia: Métodos Numéricos.
Visión artificial y Robótica Modelos de movimiento y mapas. Depto. de Ciencia de la Computación e Inteligencia Artificial
 Visión artificial y Robótica Modelos de movimiento y mapas Depto. de Ciencia de la Computación e Inteligencia Artificial Contenidos Sistemas de coordenadas Localización de objetos en el espacio Modelos
Visión artificial y Robótica Modelos de movimiento y mapas Depto. de Ciencia de la Computación e Inteligencia Artificial Contenidos Sistemas de coordenadas Localización de objetos en el espacio Modelos
Control y programación de robots
 Control y programación de robots 11. Solución cinemática inversa y directa de robots seriales 11.1 El alumno, tras recibir y estudiar esta clase, debe ser capaz de: Comprender el modelado de la cinemática
Control y programación de robots 11. Solución cinemática inversa y directa de robots seriales 11.1 El alumno, tras recibir y estudiar esta clase, debe ser capaz de: Comprender el modelado de la cinemática
Cinemática Directa del Robot. UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides
 Cinemática Directa del Robot UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción Consiste en determinar cual es la posición y orientación del extremo final del robot, con
Cinemática Directa del Robot UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción Consiste en determinar cual es la posición y orientación del extremo final del robot, con
Dinámica del Robot. UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides
 UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción La dinámica se ocupa de la relación entre las fuerzas que actúan sobre un cuerpo y el movimiento en el que se origina.
UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción La dinámica se ocupa de la relación entre las fuerzas que actúan sobre un cuerpo y el movimiento en el que se origina.
PROGRAMA DE LA ASIGNATURA: Control y programación de robots. Código: Curso 2006/2007
 PROGRAMA DE LA ASIGNATURA: Control y programación de robots Código: 3042104010 Curso 2006/2007 CENTRO: ESCUELA TÉCNICA SUPERIOR DE INGENIEROS INDUSTRIALES TITULACIÓN: INGENIERÍA AUTOMÁTICA Y ELECTRÓNICA
PROGRAMA DE LA ASIGNATURA: Control y programación de robots Código: 3042104010 Curso 2006/2007 CENTRO: ESCUELA TÉCNICA SUPERIOR DE INGENIEROS INDUSTRIALES TITULACIÓN: INGENIERÍA AUTOMÁTICA Y ELECTRÓNICA
LOCOMOCION DE SISTEMAS ROBOTICOS
 CAPITULO II LOCOMOCION DE SISTEMAS ROBOTICOS P I N Z A B R A Z O A N T E B R A ZO B A S E 2.1. GRADOS DE LIBERTAD El componente principal en el robot está constituido por las articulaciones y sus eslabones.
CAPITULO II LOCOMOCION DE SISTEMAS ROBOTICOS P I N Z A B R A Z O A N T E B R A ZO B A S E 2.1. GRADOS DE LIBERTAD El componente principal en el robot está constituido por las articulaciones y sus eslabones.
FORMULARIO DE TRIGONOMETRIA PLANA Definicion de las seis razones trigonometricas 02.- Relaciones fundamentales entre las razones trigonometricas
 FORMULARIO DE TRIGONOMETRIA PLANA 01.- Definicion de las seis razones trigonometricas 02.- Relaciones fundamentales entre las razones trigonometricas 03.- Razones trigonometricas de la suma de dos angulos
FORMULARIO DE TRIGONOMETRIA PLANA 01.- Definicion de las seis razones trigonometricas 02.- Relaciones fundamentales entre las razones trigonometricas 03.- Razones trigonometricas de la suma de dos angulos
Introducción a la Robótica Mecanismos básicos: cinemática
 Introducción a la Robótica Mecanismos básicos: cinemática Dr José Martínez Carranza [email protected] Coordinación de Ciencias Computacionales, INAOE Cinemática (1) La cinemática es una rama de la Física
Introducción a la Robótica Mecanismos básicos: cinemática Dr José Martínez Carranza [email protected] Coordinación de Ciencias Computacionales, INAOE Cinemática (1) La cinemática es una rama de la Física
TEMAS 6 Y 7 RECTAS Y PLANOS EN EL ESPACIO
 Temas 6 y 7 Rectas y planos en el espacio Matemáticas II - 2º Bachillerato 1 TEMAS 6 Y 7 RECTAS Y PLANOS EN EL ESPACIO RECTAS Y PLANOS EJERCICIO 1 : Halla el volumen del tetraedro determinado por los ejes
Temas 6 y 7 Rectas y planos en el espacio Matemáticas II - 2º Bachillerato 1 TEMAS 6 Y 7 RECTAS Y PLANOS EN EL ESPACIO RECTAS Y PLANOS EJERCICIO 1 : Halla el volumen del tetraedro determinado por los ejes
INGENIERÍA PROFESIONAL EN INOCUIDAD ALIMENTARIA EN COMPETENCIAS PROFESIONALES ASIGNATURA DE ROBÓTICA
 INGENIERÍA PROFESIONAL EN INOCUIDAD ALIMENTARIA EN COMPETENCIAS PROFESIONALES ASIGNATURA DE ROBÓTICA UNIDADES DE APRENDIZAJE 1. Competencias Automatizar procesos de producción mediante la implementación
INGENIERÍA PROFESIONAL EN INOCUIDAD ALIMENTARIA EN COMPETENCIAS PROFESIONALES ASIGNATURA DE ROBÓTICA UNIDADES DE APRENDIZAJE 1. Competencias Automatizar procesos de producción mediante la implementación
2015, Año del Generalísimo José María Morelos y Pavón
 Nombre de la Asignatura: ROBOTICA Línea de Investigación o Trabajo: PROCESAMIENTO DE SEÑALES ELECTRICAS Y ELECTRONICAS Tiempo de dedicación del estudiante a las actividades de: DOC-TIS-TPS-CRÉDITOS 48
Nombre de la Asignatura: ROBOTICA Línea de Investigación o Trabajo: PROCESAMIENTO DE SEÑALES ELECTRICAS Y ELECTRONICAS Tiempo de dedicación del estudiante a las actividades de: DOC-TIS-TPS-CRÉDITOS 48
Parámetros Redundantes para Rotación y Traslación en Cinemática
 Parámetros Redundantes para Rotación y Traslación en Cinemática O. Altuzarra, A. Hernández, E. Amezua, V. Petuya Universidad del País Vasco - Euskal Herriko Unibertsitatea Departamento de Ingeniería Mecánica,
Parámetros Redundantes para Rotación y Traslación en Cinemática O. Altuzarra, A. Hernández, E. Amezua, V. Petuya Universidad del País Vasco - Euskal Herriko Unibertsitatea Departamento de Ingeniería Mecánica,
Capacitación Tecnológica Científica para Bolivia. Introducción al modelado de robots
 Catecbol Capacitación Tecnológica Científica para Bolivia www.catecbol.com facebook.com/catecbol @catecbol [email protected] Introducción al modelado de robots Ronald Terrazas Mallea Bélgica La unión
Catecbol Capacitación Tecnológica Científica para Bolivia www.catecbol.com facebook.com/catecbol @catecbol [email protected] Introducción al modelado de robots Ronald Terrazas Mallea Bélgica La unión
Visión artificial y Robótica Geometría. Depto. de Ciencia de la Computación e Inteligencia Artificial
 Visión artificial y Robótica Geometría Depto. de Ciencia de la Computación e Inteligencia Artificial Contenidos Geometría 2D y 3D Transformación de coordenadas Calibración de la cámara Álgebra necesaria
Visión artificial y Robótica Geometría Depto. de Ciencia de la Computación e Inteligencia Artificial Contenidos Geometría 2D y 3D Transformación de coordenadas Calibración de la cámara Álgebra necesaria
UNIVERSIDAD DE ORIENTE NUCLEO DE ANZOATEGUI PROGRAMA DE ASIGNATURA NOMBRE DE LA ASIGNATURA MATEMATICA I
 ESCUELA Ciencias Administrativas CODIGO PREREQUISITO(S) 008-1613 Ninguno HORAS SEMANALES TOTAL HORAS SEMESTRE 05 90 HORAS TEORICAS HORAS PRACTICAS 02 03 UNIVERSIDAD DE ORIENTE NUCLEO DE ANZOATEGUI PROGRAMA
ESCUELA Ciencias Administrativas CODIGO PREREQUISITO(S) 008-1613 Ninguno HORAS SEMANALES TOTAL HORAS SEMESTRE 05 90 HORAS TEORICAS HORAS PRACTICAS 02 03 UNIVERSIDAD DE ORIENTE NUCLEO DE ANZOATEGUI PROGRAMA
PLAN DE ESTUDIOS 2008-II SÍLABO
 UNIVERSIDAD RICARDO PALMA FACULTAD DE INGENIERÍA I. INFORMACIÓN GENERAL: DEPARTAMENTO ACADÉMICO DE INGENIERÍA PLAN DE ESTUDIOS 2008-II SÍLABO 1.1 Asignatura : ROBÓTICA 1.2. Ciclo : VIII 1.3 Carrera Profesional
UNIVERSIDAD RICARDO PALMA FACULTAD DE INGENIERÍA I. INFORMACIÓN GENERAL: DEPARTAMENTO ACADÉMICO DE INGENIERÍA PLAN DE ESTUDIOS 2008-II SÍLABO 1.1 Asignatura : ROBÓTICA 1.2. Ciclo : VIII 1.3 Carrera Profesional
ACTIVIDAD DE EVALUACIÓN % PESO PARA LA UNIDAD 40 PESO TOTAL DEL MÓDULO 100
 Guía Pedagógica y Evaluación 8. Tabla Ponración UNIDAD 1. Resolución problemas utilizando logaritmos y Moado angular, lineal, superficie y espacial. 3. Aplicación la trigonometría RA 1.1. Maneja sigualdas,
Guía Pedagógica y Evaluación 8. Tabla Ponración UNIDAD 1. Resolución problemas utilizando logaritmos y Moado angular, lineal, superficie y espacial. 3. Aplicación la trigonometría RA 1.1. Maneja sigualdas,
- Resolver problemas que involucren probabilidad clásica, unión e intersección de dos eventos
 ANGLO AMERICAN INTERNATIONAL SCHOOL ÁREA DE CIENCIAS, MATEMÁTICAS Y SALUD La formulación de un problema, es más importante que su solución Los Refugios del Arrayan 1653. Fonos 23215497-23215480 [email protected]
ANGLO AMERICAN INTERNATIONAL SCHOOL ÁREA DE CIENCIAS, MATEMÁTICAS Y SALUD La formulación de un problema, es más importante que su solución Los Refugios del Arrayan 1653. Fonos 23215497-23215480 [email protected]
RESOLUCIÓN DE SISTEMAS MEDIANTE DETERMINANTES
 UNIDD 4 RESOLUCIÓN DE SISTEMS MEDINTE DETERMINNTES Página 00 Resolución de sistemas mediante determinantes x y Resuelve, aplicando x = e y =, los siguientes sistemas de ecuaciones: x 5y = 7 5x + 4y = 6x
UNIDD 4 RESOLUCIÓN DE SISTEMS MEDINTE DETERMINNTES Página 00 Resolución de sistemas mediante determinantes x y Resuelve, aplicando x = e y =, los siguientes sistemas de ecuaciones: x 5y = 7 5x + 4y = 6x
Programa de Acceso Inclusivo, Equidad y Permanencia. PAIEP, Universidad de Santiago
 Guía de vectores. Vectores En matemática, un vector es una herramienta geométrica utilizada para representar una magnitud física definida en un sistema de referencia que se caracteriza por tener módulo
Guía de vectores. Vectores En matemática, un vector es una herramienta geométrica utilizada para representar una magnitud física definida en un sistema de referencia que se caracteriza por tener módulo
Facultad de Ingeniería Facultad de Tecnología Informática. Matemática Números reales Elementos de geometría analítica. Profesora: Silvia Mamone
 Facultad de Ingeniería Facultad de Tecnología Informática Matemática Números reales Elementos de geometría analítica 0 03936 Profesora: Silvia Mamone UB Facultad de Ingeniería Facultad de Tecnología Informática
Facultad de Ingeniería Facultad de Tecnología Informática Matemática Números reales Elementos de geometría analítica 0 03936 Profesora: Silvia Mamone UB Facultad de Ingeniería Facultad de Tecnología Informática
Geometría del plano y el espacio
 Geometría del plano y el espacio AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Geometría del plano y el espacio 1 / 21 Objetivos Al final de este tema tendréis que Conocer
Geometría del plano y el espacio AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Geometría del plano y el espacio 1 / 21 Objetivos Al final de este tema tendréis que Conocer
UNIDAD EDUCATIVA COLEGIO SAN GABRIEL PLAN DE MEJORA Y REFUERZO ACADÉMICO
 DATOS INFORMATIVOS UNIDAD EDUCATIVA COLEGIO SAN GABRIEL PLAN DE MEJORA Y REFUERZO ACADÉMICO Nombre del Estudiante: Curso: 1ro BGU Docente: Lic. Francisco Soria Fecha: 22 de febrero de 2016 DESTREZA A REFORZAR
DATOS INFORMATIVOS UNIDAD EDUCATIVA COLEGIO SAN GABRIEL PLAN DE MEJORA Y REFUERZO ACADÉMICO Nombre del Estudiante: Curso: 1ro BGU Docente: Lic. Francisco Soria Fecha: 22 de febrero de 2016 DESTREZA A REFORZAR
Control Cinemático. Funciones de control cinemático Tipos de trayectorias Interpolación de trayectorias. Robotica Industrial- Control cinemático 2
 Control Cinemático Funciones de control cinemático Tipos de trayectorias Interpolación de trayectorias Robotica Industrial- Control cinemático 2 Objetivos del control cinemático Establecer cuales son las
Control Cinemático Funciones de control cinemático Tipos de trayectorias Interpolación de trayectorias Robotica Industrial- Control cinemático 2 Objetivos del control cinemático Establecer cuales son las
EJEMPLO DE PREGU,TAS
 EJEMPLO DE PREGU,TAS MATEMÁTICAS PRIMERO, SEGU,DO Y TERCERO DE BACHILLERATO 1. Lógica proposicional Esta competencia se refiere al conocimiento que usted posee sobre el lenguaje de las proposiciones y
EJEMPLO DE PREGU,TAS MATEMÁTICAS PRIMERO, SEGU,DO Y TERCERO DE BACHILLERATO 1. Lógica proposicional Esta competencia se refiere al conocimiento que usted posee sobre el lenguaje de las proposiciones y
ROBOTICA II. UNIDAD 2
 ROBOTICA II. UNIDAD 2 MODELO DINÁMICO. En robótica, la cinemática y la dinámica se combinan para lograr el posicionamiento de una serie de eslabones articulados o brazo de robot. Las consideraciones cinemáticas
ROBOTICA II. UNIDAD 2 MODELO DINÁMICO. En robótica, la cinemática y la dinámica se combinan para lograr el posicionamiento de una serie de eslabones articulados o brazo de robot. Las consideraciones cinemáticas
TECNOLÓGICO DE ESTUDIOS SUPERIORES DE ECATEPEC
 TECNOLÓGICO DE ESTUDIOS SUPERIORES DE ECATEPEC DIVISIÓN DE INGENIERÍA ELECTRÓNICA Y TELEMÁTICA PRÁCTICAS DE LABORATORIO ASIGNATURA: ROBÓTICA I REALIZÓ: GERARDO PAZOS RODRÍGUEZ PRESENTACIÓN El presente
TECNOLÓGICO DE ESTUDIOS SUPERIORES DE ECATEPEC DIVISIÓN DE INGENIERÍA ELECTRÓNICA Y TELEMÁTICA PRÁCTICAS DE LABORATORIO ASIGNATURA: ROBÓTICA I REALIZÓ: GERARDO PAZOS RODRÍGUEZ PRESENTACIÓN El presente
SISTEMAS ROBOTIZADOS Asignatura optativa
 Área de Ingeniería de Sistemas y Automática Departamento de Lenguajes y Computación Universidad de Almería SISTEMAS ROBOTIZADOS Asignatura optativa PRACTICA 4 CONTROL DE ROBOTS MÓVILES UTILIZANDO EL MÉTODO
Área de Ingeniería de Sistemas y Automática Departamento de Lenguajes y Computación Universidad de Almería SISTEMAS ROBOTIZADOS Asignatura optativa PRACTICA 4 CONTROL DE ROBOTS MÓVILES UTILIZANDO EL MÉTODO
Álgebra II C PLANIFICACIONES Actualización: 2ºC/2017. Planificaciones Álgebra II C. Docente responsable: CAMMILLERI ADA LEONOR.
 Planificaciones 6122 - Álgebra II C Docente responsable: CAMMILLERI ADA LEONOR 1 de 9 OBJETIVOS Los objetivos centrales de la asignatura son que el alumno logre: - Conocimientos básicos sobre temas de
Planificaciones 6122 - Álgebra II C Docente responsable: CAMMILLERI ADA LEONOR 1 de 9 OBJETIVOS Los objetivos centrales de la asignatura son que el alumno logre: - Conocimientos básicos sobre temas de
Módulo. Representación Simbólica y Angular del entorno REAN-03 CONALEP IBQA
 Programa de estudios Unidad 2. Modelado angular, lineal, de superficie y espacial. Propósito de la unidad. Calculará dimensiones, angulares, lineales, superficiales y espaciales de figuras geométricas
Programa de estudios Unidad 2. Modelado angular, lineal, de superficie y espacial. Propósito de la unidad. Calculará dimensiones, angulares, lineales, superficiales y espaciales de figuras geométricas
FUNDAMENTOS DE ROBÓTICA
 ASIGNATURA DE GRADO: FUNDAMENTOS DE ROBÓTICA Curso 2015/2016 (Código:71013087) 1.PRESENTACIÓN DE LA ASIGNATURA Se trata de una asignatura cuatrimestral optativa, ubicada en el segundo cuatrimestre del
ASIGNATURA DE GRADO: FUNDAMENTOS DE ROBÓTICA Curso 2015/2016 (Código:71013087) 1.PRESENTACIÓN DE LA ASIGNATURA Se trata de una asignatura cuatrimestral optativa, ubicada en el segundo cuatrimestre del
Selección de un Robot Industrial. Prof. J. Milland
 Prof. J. Milland Si debemos robotizar un determinado proceso, debemos seleccionar el robot mas adecuado teniendo en consideración los servicios y el costo. Las características que debemos estar estudiando
Prof. J. Milland Si debemos robotizar un determinado proceso, debemos seleccionar el robot mas adecuado teniendo en consideración los servicios y el costo. Las características que debemos estar estudiando
MATHEMATICA. Geometría - Recta. Ricardo Villafaña Figueroa. Material realizado con Mathematica. Ricardo Villafaña Figueroa
 MATHEMATICA Geometría - Recta Material realizado con Mathematica 2 Contenido Sistema de Coordenadas... 3 Distancia entre dos puntos... 3 Punto Medio... 5 La Recta... 8 Definición de recta... 8 Pendiente
MATHEMATICA Geometría - Recta Material realizado con Mathematica 2 Contenido Sistema de Coordenadas... 3 Distancia entre dos puntos... 3 Punto Medio... 5 La Recta... 8 Definición de recta... 8 Pendiente
AL - Álgebra Lineal
 Unidad responsable: Unidad que imparte: Curso: Titulación: Créditos ECTS: 2016 230 - ETSETB - Escuela Técnica Superior de Ingeniería de Telecomunicación de Barcelona 749 - MAT - Departamento de Matemáticas
Unidad responsable: Unidad que imparte: Curso: Titulación: Créditos ECTS: 2016 230 - ETSETB - Escuela Técnica Superior de Ingeniería de Telecomunicación de Barcelona 749 - MAT - Departamento de Matemáticas
REPRESENTACIÓN DE FUERZAS. Hay dos tipos de magnitudes: ESCALARES y VECTORIALES
 VECTORES REPRESENTACIÓN DE UERZAS Hay dos tipos de magnitudes: ESCALARES y VECTORIALES Las magnitudes ESCALARES quedan determinadas mediante una cantidad y su unidad correspondiente: L (Longitud) 5 m m
VECTORES REPRESENTACIÓN DE UERZAS Hay dos tipos de magnitudes: ESCALARES y VECTORIALES Las magnitudes ESCALARES quedan determinadas mediante una cantidad y su unidad correspondiente: L (Longitud) 5 m m
Formato para prácticas de laboratorio
 CARRERA TRONCO COMÚN PLAN DE ESTUDIO CLAVE ASIGNATURA 2003-1 4347 ESTÁTICA NOMBRE DE LA ASIGNATURA PRÁCTICA No. LABORATORIO DE CIENCIAS BÁSICAS DURACIÓN(HORAS) NOMBRE DE LA DESCOMPOSICIÓN DE EST-02 2:00
CARRERA TRONCO COMÚN PLAN DE ESTUDIO CLAVE ASIGNATURA 2003-1 4347 ESTÁTICA NOMBRE DE LA ASIGNATURA PRÁCTICA No. LABORATORIO DE CIENCIAS BÁSICAS DURACIÓN(HORAS) NOMBRE DE LA DESCOMPOSICIÓN DE EST-02 2:00
Expresión decimal. Aproximación y estimación. Notación científica. Polinomios. Divisibilidad de polinomios. Regla de Ruffini.
 Otras páginas Matemáticas 5º Matemáticas I. Bloque I: ARITMÉTICA Y ÁLGEBRA Los números reales Los números reales, concepto y características. Estructura algebraica, orden, representación en la recta real
Otras páginas Matemáticas 5º Matemáticas I. Bloque I: ARITMÉTICA Y ÁLGEBRA Los números reales Los números reales, concepto y características. Estructura algebraica, orden, representación en la recta real
TEMAS 6 Y 7 GEOMETRÍA EN EL ESPACIO
 Ejercicios Selectividad Temas 6 y 7 Geometría en el espacio Mate II 2º Bach. 1 TEMAS 6 Y 7 GEOMETRÍA EN EL ESPACIO EJERCICIO 1 : Julio 11-12. Optativa (3 ptos) Para los puntos A(1,0,2) y B(-1,2,4) y la
Ejercicios Selectividad Temas 6 y 7 Geometría en el espacio Mate II 2º Bach. 1 TEMAS 6 Y 7 GEOMETRÍA EN EL ESPACIO EJERCICIO 1 : Julio 11-12. Optativa (3 ptos) Para los puntos A(1,0,2) y B(-1,2,4) y la
M.C. Cynthia Guerrero
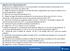 Algoritmo 2-6-1: Representación D-H 0. Numere las articulaciones de la 1 a la n comenzando con la base () y terminando con la herramienta, en el orden yaw, pitch y roll. 1. Asigne un sistema coordenado
Algoritmo 2-6-1: Representación D-H 0. Numere las articulaciones de la 1 a la n comenzando con la base () y terminando con la herramienta, en el orden yaw, pitch y roll. 1. Asigne un sistema coordenado
PROGRAMA DE RECUPERACIÓN PEDAGÓGICA
 DE RECUPERACIÓN PEDAGÓGICA 1er año de secundaria Estadística. Inecuaciones. Operaciones con números racionales. Ángulos. - Frecuencia absoluta y frecuencia relativa - Moda, mediana y media - Gráficas circulares
DE RECUPERACIÓN PEDAGÓGICA 1er año de secundaria Estadística. Inecuaciones. Operaciones con números racionales. Ángulos. - Frecuencia absoluta y frecuencia relativa - Moda, mediana y media - Gráficas circulares
GUÍA DE EJERCICIOS GEOMETRÍA ANALÍTICA (CURVAS CÓNICAS)
 U N E X P O INTRODUCCIÓN: UNIVERSIDAD NACIONAL EXPERIMENTAL POLITÉCNICA ANTONIO JOSÉ DE SUCRE VICE-RECTORADO PUERTO ORDAZ DEPARTAMENTO DE ESTUDIOS GENERALES SECCIÓN DE MATEMÁTICA GUÍA DE EJERCICIOS GEOMETRÍA
U N E X P O INTRODUCCIÓN: UNIVERSIDAD NACIONAL EXPERIMENTAL POLITÉCNICA ANTONIO JOSÉ DE SUCRE VICE-RECTORADO PUERTO ORDAZ DEPARTAMENTO DE ESTUDIOS GENERALES SECCIÓN DE MATEMÁTICA GUÍA DE EJERCICIOS GEOMETRÍA
VECTORES : Las Cantidades Vectoriales cantidades escalares
 VECTORES En física hay dos tipos de cantidades: Las Cantidades Vectoriales son aquellas que tiene tanto magnitud como dirección y sentido sobre la dirección), mientras que las cantidades escalares son
VECTORES En física hay dos tipos de cantidades: Las Cantidades Vectoriales son aquellas que tiene tanto magnitud como dirección y sentido sobre la dirección), mientras que las cantidades escalares son
CENTRO UNIVERSITARIO MONTEJO A. C. Temario de Matemáticas 3. Bloque I
 Bloque I Explica la diferencia entre eventos complementarios, mutuamente excluyentes e independientes. Resolución de problemas que impliquen el uso de ecuaciones cuadráticas sencillas, utilizando procedimientos
Bloque I Explica la diferencia entre eventos complementarios, mutuamente excluyentes e independientes. Resolución de problemas que impliquen el uso de ecuaciones cuadráticas sencillas, utilizando procedimientos
bloque i ejes aprendizajes esperados sentido numérico y PensaMiento algebraico forma, espacio y Medida Manejo de la información Patrones y ecuaciones
 TERCER GRADO bloque i Explica la diferencia entre eventos complementarios, mutuamente excluyentes e independientes. Resolución de problemas que impliquen el uso de ecuaciones cuadráticas sencillas, utilizando
TERCER GRADO bloque i Explica la diferencia entre eventos complementarios, mutuamente excluyentes e independientes. Resolución de problemas que impliquen el uso de ecuaciones cuadráticas sencillas, utilizando
Unidad 3: Razones trigonométricas.
 Unidad 3: Razones trigonométricas 1 Unidad 3: Razones trigonométricas. 1.- Medida de ángulos: grados y radianes. Las unidades de medida de ángulos más usuales son el grado sexagesimal y el radián. Se define
Unidad 3: Razones trigonométricas 1 Unidad 3: Razones trigonométricas. 1.- Medida de ángulos: grados y radianes. Las unidades de medida de ángulos más usuales son el grado sexagesimal y el radián. Se define
Producto Escalar. AMD Grado en Ingeniería Informática. AMD Grado en Ingeniería Informática (UM) Producto Escalar 1 / 31
 Producto Escalar AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Producto Escalar 1 / 31 Objetivos Al finalizar este tema tendrás que: Saber usar el producto escalar. Calcular
Producto Escalar AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Producto Escalar 1 / 31 Objetivos Al finalizar este tema tendrás que: Saber usar el producto escalar. Calcular
Longitud, áreas y volúmenes. Trigonometría. Circunferencia de radio R Círculo de radio R. 1 Triángulo de base B y altura H A = (BH ) 2
 Longitud, áreas y volúmenes Circunferencia de radio R Círculo de radio R A πr L πr Triángulo de base B y altura H A (BH ) Cuadrado de lado L A L Rectángulo de base B y altura H Superficie esférica A 4πR
Longitud, áreas y volúmenes Circunferencia de radio R Círculo de radio R A πr L πr Triángulo de base B y altura H A (BH ) Cuadrado de lado L A L Rectángulo de base B y altura H Superficie esférica A 4πR
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: MATEMÁTICAS II
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El alumno contestará a
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El alumno contestará a
Matemáticas II Bachillerato Ciencias y Tecnología 2º Curso. Espacio euclídeo Determinación de ángulos
 Espacio euclídeo 5.1. Determinación de ángulos.... - 2-5.1.1. Ángulo determinado por dos rectas secantes.... - 2-5.1.2. Ángulo determinado por planos secantes.... - 2-5.1.3. Ángulo determinado por una
Espacio euclídeo 5.1. Determinación de ángulos.... - 2-5.1.1. Ángulo determinado por dos rectas secantes.... - 2-5.1.2. Ángulo determinado por planos secantes.... - 2-5.1.3. Ángulo determinado por una
Diseño e implementación de un Manipulador Robótico con Tres Grados de Libertad para fines educativos
 Diseño e implementación de un Manipulador Robótico con Tres Grados de Libertad para fines educativos I. Aguirre G., L. J. Andueza C., C. Arismendi Universidad de Los Andes, Facultad de Ingeniería Escuela
Diseño e implementación de un Manipulador Robótico con Tres Grados de Libertad para fines educativos I. Aguirre G., L. J. Andueza C., C. Arismendi Universidad de Los Andes, Facultad de Ingeniería Escuela
TEMA 8. GEOMETRÍA ANALÍTICA.
 TEMA 8. GEOMETRÍA ANALÍTICA. 8..- El plano. Definimos el plano euclideo como el conjunto de puntos ( x, y) R. Así, cada punto del plano posee dos coordenadas. Para representar puntos del plano utilizaremos
TEMA 8. GEOMETRÍA ANALÍTICA. 8..- El plano. Definimos el plano euclideo como el conjunto de puntos ( x, y) R. Así, cada punto del plano posee dos coordenadas. Para representar puntos del plano utilizaremos
Programa de preparación para exámenes de ubicación
 GUÍA PARA EL EXAMEN DE UBICACIÓN DE MATEMÁTICAS TECNOLÓGICO DE MONTERREY INSTRUCCIONES Este examen debe ser presentado antes de las inscripciones, por los alumnos de primer ingreso que provengan de preparatorias
GUÍA PARA EL EXAMEN DE UBICACIÓN DE MATEMÁTICAS TECNOLÓGICO DE MONTERREY INSTRUCCIONES Este examen debe ser presentado antes de las inscripciones, por los alumnos de primer ingreso que provengan de preparatorias
ESTATICA. Debajo se encuentran las formulas para calcular las componentes y el ángulo α que determina la dirección de la fuerza.
 ESTATICA Es la parte de la física que estudia las fuerzas en equilibrio. Si sobre un cuerpo no actúan fuerzas o actúan varias fuerzas cuya resultante es cero, decimos que el cuerpo está en equilibrio.
ESTATICA Es la parte de la física que estudia las fuerzas en equilibrio. Si sobre un cuerpo no actúan fuerzas o actúan varias fuerzas cuya resultante es cero, decimos que el cuerpo está en equilibrio.
Universidad Politécnica de Madrid Escuela de Ingenieros Industriales. RoboTenis
 Universidad Politécnica de Madrid Escuela de Ingenieros Industriales RoboTenis Diseño, Simulación, Análisis Cinemático y Dinámico de un robot paralelo para Control Visual de altas prestaciones DISAM Luis
Universidad Politécnica de Madrid Escuela de Ingenieros Industriales RoboTenis Diseño, Simulación, Análisis Cinemático y Dinámico de un robot paralelo para Control Visual de altas prestaciones DISAM Luis
CÁLCULO INTEGRAL HORAS TEÓRICAS UNIDADES CRÉDITO HORAS PRÁCTICAS CODIGO (COMPUTACION) (SISTEMAS) CALCULO DIFERENCIAL III
 CÁLCULO INTEGRAL CODIGO HORAS TEÓRICAS HORAS PRÁCTICAS UNIDADES CRÉDITO SEMESTRE PRE REQUISITO 213154 (COMPUTACION) 223154 (SISTEMAS) 03 02 04 III CALCULO DIFERENCIAL ELABORADO POR REVISADO POR APROBADO
CÁLCULO INTEGRAL CODIGO HORAS TEÓRICAS HORAS PRÁCTICAS UNIDADES CRÉDITO SEMESTRE PRE REQUISITO 213154 (COMPUTACION) 223154 (SISTEMAS) 03 02 04 III CALCULO DIFERENCIAL ELABORADO POR REVISADO POR APROBADO
Razones trigonométricas en triangulo rectángulo EJEMPLO Nº 1 Solución: Se tienen los siguientes datos:
 Razones trigonométricas en triangulo rectángulo La trigonometría, enfocada en sus inicios solo al estudio de los triángulos, se utilizó durante siglos en topografía, navegación y astronomía. Esta rama
Razones trigonométricas en triangulo rectángulo La trigonometría, enfocada en sus inicios solo al estudio de los triángulos, se utilizó durante siglos en topografía, navegación y astronomía. Esta rama
DEPARTAMENTO DE MATEMÁTICAS Página 1
 DEPARTAMENTO DE MATEMÁTICAS Página 1 APROBADO EN EL CONSEJO DE LA FACULTAD DE CIENCIAS EXACTAS Y NATURALES ACTA 13 DEL 21 ABRIL 2010 PROGRAMAS DEL DEPARTAMENTO DE MATEMÁTICAS El presente formato tiene
DEPARTAMENTO DE MATEMÁTICAS Página 1 APROBADO EN EL CONSEJO DE LA FACULTAD DE CIENCIAS EXACTAS Y NATURALES ACTA 13 DEL 21 ABRIL 2010 PROGRAMAS DEL DEPARTAMENTO DE MATEMÁTICAS El presente formato tiene
Ecuación Vectorial de la Recta
 Ecuación Vectorial de la Recta Definimos una recta r como el conjunto de los puntos del plano, alineados con un punto P y con una dirección dada. Si P(x 1, y 1 ) es un punto de la recta r, el vector tiene
Ecuación Vectorial de la Recta Definimos una recta r como el conjunto de los puntos del plano, alineados con un punto P y con una dirección dada. Si P(x 1, y 1 ) es un punto de la recta r, el vector tiene
Modelamiento de un Robot de Cinco Grados de Libertad en un Módulo de Manufactura Flexible.
 Modelamiento de un Robot de Cinco Grados de Libertad en un Módulo de Manufactura Flexible. Yulieth Díaz*, Naidú Hernández** y Jairo Montoya*** *Universidad de La Salle, [email protected] ** Universidad
Modelamiento de un Robot de Cinco Grados de Libertad en un Módulo de Manufactura Flexible. Yulieth Díaz*, Naidú Hernández** y Jairo Montoya*** *Universidad de La Salle, [email protected] ** Universidad
27/01/2011 TRIGONOMETRÍA Página 1 de 7
 β 27/01/2011 TRIGONOMETRÍA Página 1 de 7 Notación en un triángulo: En un triángulo cualquiera llamaremos a, b y c a sus lados y A, B y C a sus vértices de forma que A sea el vértice formado por los lados
β 27/01/2011 TRIGONOMETRÍA Página 1 de 7 Notación en un triángulo: En un triángulo cualquiera llamaremos a, b y c a sus lados y A, B y C a sus vértices de forma que A sea el vértice formado por los lados
PROPUESTA A. f(x) = x 3 + ax 2 + bx + c,
 PROPUESTA A 1A. Dada la función f(x) = x 3 + ax 2 + bx + c, calcula los parámetros a, b, c R sabiendo que: La recta tangente a la gráfica de f(x) en el punto de abcisa x = 1 tiene pendiente 3. f(x) tiene
PROPUESTA A 1A. Dada la función f(x) = x 3 + ax 2 + bx + c, calcula los parámetros a, b, c R sabiendo que: La recta tangente a la gráfica de f(x) en el punto de abcisa x = 1 tiene pendiente 3. f(x) tiene
UNIVERSIDAD COMPLUTENSE DE MADRID
 Principales conceptos que se tendrán en cuenta en la elaboración de las pruebas de Acceso a la Universidad para los estudiantes provenientes del Bachillerato LOGSE de la materia "Matemáticas II" ÁLGEBRA
Principales conceptos que se tendrán en cuenta en la elaboración de las pruebas de Acceso a la Universidad para los estudiantes provenientes del Bachillerato LOGSE de la materia "Matemáticas II" ÁLGEBRA
INSTRUCCIONES GENERALES Y VALORACIÓN
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Examen-Modelo para el curso 2014-2015 MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Examen-Modelo para el curso 2014-2015 MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES
2.2 Rectas en el plano
 2.2 Al igual que ocurre con el punto, en geometría intrínseca, el concepto de recta no tiene definición, sino que constituye otro de sus conceptos iniciales, indefinibles. Desde luego se trata de un conjunto
2.2 Al igual que ocurre con el punto, en geometría intrínseca, el concepto de recta no tiene definición, sino que constituye otro de sus conceptos iniciales, indefinibles. Desde luego se trata de un conjunto
PROBLEMAS DE HOMOTECIAS Y SEMEJANZAS EN EL PLANO
 PROBLEMAS DE HOMOTECIAS Y SEMEJANZAS EN EL PLANO 1. Estudiar si la siguiente ecuación matricial corresponde a una homotecia del plano y, en su caso, calcular el centro y la razón: 1 1 1 ' = 3 y' 3 y. Estudiar
PROBLEMAS DE HOMOTECIAS Y SEMEJANZAS EN EL PLANO 1. Estudiar si la siguiente ecuación matricial corresponde a una homotecia del plano y, en su caso, calcular el centro y la razón: 1 1 1 ' = 3 y' 3 y. Estudiar
