Problema Cinemático Directo
|
|
|
- Felipe Coronel Núñez
- hace 9 años
- Vistas:
Transcripción
1 Problema Cinemático Directo Parámetros Denavit-Hartenberg
2 Denavit-Hartenberg notación Craig
3 Denavit-Hartenberg notación Craig
4 Denavit-Hartenberg notación Craig
5 Denavit-Hartenberg notación Craig
6 Denavit-Hartenberg notación Paul a i :(longitud eslabón) distancia entre ejes i, i+1 de las articulaciones a lo largo de la perp. común α i :(ángulo torsión) ángulo que existiría entre ejes i,i+1 si se cortasen en punto de corte de la perp común θ i :ángulo existiría entre las líneas normales de la articulación i si se cortasen en el mismo punto del eje i d i :distancia entre las intersecciones de las normales comunes al eje i, medida a lo largo de i
7 Parámetros Denavit-Hartenberg notación Paul 4 parámetros: a i, α i, θ i, d i 2 relativos a la forma y tamaño del eslabón a i, α i 2 describen posición relativa del eslabón respecto a su predecesor * θ i, d i Los parámetros de forma y tamaño quedan determinados en tempo de diseño Los parámetros de posición relativa varían Θ i variable si la rotación es articular (d i cte.) d i variable si la rotación es prismática (Θ i cte.) * En notación Craig es respecto al eslabón sucesivo a i-1, α i-1, θ i, d i
8 Asignación Sistemas de Referencia Objetivo: Resolver el PROBLEMA CINEMÁTICO DIRECTO: Encontrar una transformación homogénea (función de los parámetros vistos) que describa la posición y orientación del extremo del robot respecto a la base.
9 Asignación Sistemas de Referencia Método:Definir SR asociado a cada eslabón, realizar la transformación entre dos consecutivos con solo 2 giros y 2 traslaciones La asignación de SR no es única: e.g: Notación Paul, notación Craig [Paul]: SRi en el eje que le enlaza con el siguiente eslabón (al final del eslabón) [Craig]: SRi en el eje que le enlaza con el eslabón precedente (al inicio del eslabón) Las matrices de transformación intermedias varían, pero el resultado final es el mismo!
10 Asignación Sistemas de Referencia 1.- El eje z i del SR del eslabón i en eje de la articulación i El eje x i es normal común a ejes i, i+a, apuntando de i a i+1 * 3.- El eje y i trivialmente para que el sistema sea dextrogiro Y i-1 Z i-1 X i-1 Z i Y i * La normal común puede no ser única, necesitamos establecer convenciones X i
11 Asignación Sistemas de Referencia: Convenciones x i Si las articulaciones i, i+a son paralelas: Tenemos infinitas posibles perpendiculares comunes El origen del sistema de referencia queda indefinido ->Tomar origen en la articulación i+1
12 Asignación Sistemas de Referencia: Convenciones x i Si las articulaciones se cortan en un punto a i? 0 El origen en el punto de corte La dirección es perpendicular común al plano formado por z i-1, z i El sentido se toma arbitrariamente
13 Denavit-Hartenberg: Representación Y i-1 Z i-1 X i-1 Z i X i Y i
14 Denavit-Hartenberg: Representación Y i-1 Z i-1 X i-1 Z i X i Y i
15 Denavit-Hartenberg: Representación Y i Z i X i d i Z i X i Y i
16 Denavit-Hartenberg: Representación Z i Y i θ i d i X i Z i X i Y i
17 Denavit-Hartenberg: Representación θ i d i a i Y i Z i Z i Y i XX i i
18 Denavit-Hartenberg: Representación θ i α i Z i d i a i Z i Y i Y i XX i i
19 Denavit-Hartenberg: Representación Y i-1 Z i-1 X i-1 Z i Y i X i
20 Denavit-Hartenberg: Representación i# 1 A = T T T T i z, d z,! x, a x, " Y i-1 Z i-1 X i-1 Z i Y i X i
21 Denavit-Hartenberg: Representación i# 1 A $ cos! i # cos" i sen! i sen" i sen! i ai cos! i % & sen! i cos" i cos! i # sen" i cos! i ai sen! ' i = T T T T = & ' & 0 sen" i cos" i di ' & ' ( ) i z, d z,! x, a x, "
22 Denavit-Hartenberg: Representación i# 1 A $ cos! i # cos" i sen! i sen" i sen! i ai cos! i % & sen! i cos" i cos! i # sen" i cos! i ai sen! ' i = T T T T = & ' & 0 sen" i cos" i di ' & ' ( ) i z, d z,! x, a x, " Como es sabido, la inversa es la transpuesta i A i# 1 $ cos! i sen! i 0 # ai % & # cos" i sen! i cos" i cos! i sen" i # di sen" ' i = & ' & sen" i sen! i # sen" i cos! i cos" i # di cos" i ' & ' ( )
23 Denavit-Hartenberg: Representación NOTA: Las operaciones el resultado final es el mismo y se pueden conmutar
24 Denavit-Hartenberg: Algoritmo
25 Denavit-Hartenberg: Algoritmo
26 Denavit-Hartenberg: Algoritmo
Cinemática Directa del Robot. UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides
Cinemática Directa del Robot UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción Consiste en determinar cual es la posición y orientación del extremo final del robot, con
Cinemática Directa del Robot. CI-2657 Robótica M.Sc. Kryscia Ramírez Benavides
M.Sc. Kryscia Ramírez Benavides Introducción Consiste en determinar cual es la posición y orientación del extremo final del robot, con respecto a un sistema de coordenadas que se toma como referencia,
PARÁMETROS DE DENAVIT-HARTENBERG. Cristina Castejón
PARÁMETROS DE DENAVIT-HARTENBERG Cristina Castejón Conceptos de robótica Cadena cinemática abierta formada por eslabones y articulaciones: Rotación Prismáticas Estudio cinemático Estudio dinámico Conceptos
Dr. Roberto Carlos García Gómez
Dr. Roberto Carlos García Gómez La cinemática del robot estudia el movimiento del mismo con respecto a un sistema de referencia. La cinemática se interesa por la descripción analítica del movimiento espacial
CINEMÁTICA DEL ROBOT
CINEMÁTICA DEL ROBOT Cinemática Directa Cinemática Inversa Matriz Jacobiana 1 Problema cinemático del robot Cinemática del robot: Estudio de su movimiento con respecto a un sistema de referencia: Descripción
Cinemática del Robot
Cinemática del Robot La cinemática del robot estudia el movimiento del mismo con respecto a un sistema de referencia. En primer término, la cinemática se interesa por la descripción analítica del movimiento
Cinemática del robot
Cinemática del robot Cinemática del robot La cinemática del robot estudia el movimiento del mismo con respecto a un sistema de referencia. La cinemática se interesa por la descripción analítica del movimiento
Cinemática de los manipuladores. Robótica
Cinemática de los manipuladores Robótica Introducción Cinemática: Estudio del movimiento sin considerar las fuerzas que lo producen Propiedades geométricas y temporales Posición, velocidad, aceleración,
Cinemática Directa. Facultad de Cs. de la Computación. Juan Carlos Conde Ramírez. Computer Animation
Cinemática Directa Facultad de Cs. de la Computación Juan Carlos Conde Ramírez Computer Animation Contenido 1 Introducción 2 Transformaciones homogéneas 3 Cinemática directa 4 Método Denavit-Hartenberg
CINEMÁTICA Y DINÁMICA DE ROBOTS MANIPULADORES: RESPUESTAS DE EJERCICIOS UNIDAD 03. Roger Miranda Colorado
CINEMÁTICA Y DINÁMICA DE ROBOTS MANIPULADORES: RESPUESTAS DE EJERCICIOS UNIDAD 03 Roger Miranda Colorado 23 de mayo de 2016 Índice 1. RESPUESTAS DE EJERCICIOS UNIDAD 03 1 1. RESPUESTAS DE EJERCICIOS UNIDAD
Manipulación. Tarea de manipular con destreza, hacer operaciones con las manos. Es el manejo hábil de los objetos. V. Angélica García Vega
Manipulación Tarea de manipular con destreza, hacer operaciones con las manos. Es el manejo hábil de los objetos Brazo robótico Manipulador Efector final o pinza Cinemática Estudia las relaciones entre
ROBÓTICA I. Cinemática Directa
Cinemática Directa M. C. Jorge Luis Barahona Avalos 11 de abril de 2011 Universidad Tecnológica de la Mixteca Instituto de Electrónica y Mecatrónica 1 / 34 Índice General 1 Cinemática Directa 2 Cadena
UNIVERSIDAD DON BOSCO VICERRECTORÍA DE ESTUDIOS DE POSTGRADO
UNIVERSIDAD DON BOSCO VICERRECTORÍA DE ESTUDIOS DE POSTGRADO MAESTRÍA EN MANUFACTURA INTEGRADA POR COMPUTADORA ROBÓTICA INTEGRADA A LA MANUFACTURA Catedrático: Mg Manuel Napoleón Cardona Gutiérrez GUÍA
TSTC. Dpt. Teoría de la Señal, Telemática y Comunicaciones Tema 2 CINEMÁTICA DE MANIPULADORES
Dpt. Teoría de la Señal, Telemática y Comunicaciones Tema 2 CINEMÁTICA DE MANIPULADORES Secciones 1. Introducción. 2. Coordenadas y Transformaciones Homogéneas. 3. Problema Cinemático Directo. Método de
GUI y la Robótica. Figura 1. Robot manipulador KUKA KR-16
RESUMEN GUI y la Robótica Miguel Durán 1, Jorge Gudiño 1, David Bolaños 1, Luís Avendaño 1 (1) Facultad de Ingeniería Electromecánica, Universidad de Colima, Colima (México) ([email protected]) El objetivo
Fundamentos de Robótica
Fundamentos de Robótica Cinemática Directa Ricardo-Franco Mendoza-Garcia [email protected] Escuela Universitaria de Ingeniería Mecánica Universidad de Tarapacá Arica, Chile July 9, 2014 R. F. Mendoza-Garcia
Modelado Cinemático de la mano de Barrett
Modelado Cinemático de la mano de Barrett Informe Técnico Proyecto: DPI2008-02647 Autores: Juan Antonio Corrales Ramón Fernando Torres Medina Grupo de Automática, Robótica y Visión Artificial Departamento
Introducción. 2.2 Transformaciones de coordenadas: matriz de rotación y ángulos de Euler.
Agosto 2011 Introducción El análisis cinemático directo nos permite determinar en donde se encuentra el elemento terminal del robot (mano) si se conoce la posición de todas las articulaciones. 15 50 Posición?
ROBÓTICA I. Cinemática Directa
Cinemática Directa M. C. Jorge Luis Barahona Avalos 2 de mayo de 2012 Universidad Tecnológica de la Mixteca Instituto de Electrónica y Mecatrónica 1 / 42 Índice General 1 Cinemática Directa 2 Cadena Cinemática
ANALISIS CINEMATICO DIRECTO E INVERSO
ANALISIS CINEMATICO DIRECTO E INVERSO Cinematica directa x=f(q) [x,y,z] Articulaciones Posicion de la Herramienta Cinematica Inversa q=f -1 (x) El analisis cinematico inverso nos permite calcular la posicion
Fundamentos de Robótica
Fundamentos de Robótica Cinemática Inversa Ricardo-Franco Mendoza-Garcia [email protected] Escuela Universitaria de Ingeniería Mecánica Universidad de Tarapacá Arica, Chile June 16, 2015 R. F. Mendoza-Garcia
Capacitación Tecnológica Científica para Bolivia. Introducción al modelado de robots
Catecbol Capacitación Tecnológica Científica para Bolivia www.catecbol.com facebook.com/catecbol @catecbol [email protected] Introducción al modelado de robots Ronald Terrazas Mallea Bélgica La unión
PRÓLOGO PREFACIO... 21
ÍNDICE PRÓLOGO... 17 PREFACIO... 21 CAPÍTULO 1. ENTORNO ACTUAL Y PERSPECTIVAS... 27 1.1 ORGANIZACIÓN DE UN SISTEMA ROBÓTICO... 29 1.2 ENTORNOS MATLAB Y SIMULINK... 31 1.3 TENDENCIAS EN ROBÓTICA Y MECATRÓNICA...
Cinemática inversa, Fanuc LR Mate 200ic
Cinemática inversa, Fanuc LR Mate 200ic José Guadalupe Zavala Villalpando, Departamento de Ingeniería Mecatrónica Instituto Tecnológico de Celaya [email protected] Sebastián Alfonso Guzmán Blanco,
Cinemática Inversa del Robot. UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides
Cinemática Inversa del Robot UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción Resuelve la configuración que debe adoptar el robot para una posición y orientación del
M.C. Cynthia Guerrero
Algoritmo 2-6-1: Representación D-H 0. Numere las articulaciones de la 1 a la n comenzando con la base (cintura) y terminando con la herramienta, en el orden yaw, pitch y roll. 1. Asigne un sistema coordenado
Cinemática Inversa. Facultad de Cs. de la Computación. Juan Carlos Conde R. Computer Animation
Cinemática Inversa Facultad de Cs. de la Computación Juan Carlos Conde R. Computer Animation Contenido 1 Introducción 2 Métodos de resolución 3 Solución Geométrica 4 Solución Algebraica 1 / 23 Contenido
Descripción de la posición y orientación.
Indice TEMA 5. FUNDAMENTS MATEMÁTICS Descripción de la posición y orientación. Transformaciones básicas: traslación y rotación. Composición de transformaciones. Velocidades y aceleraciones. Momento de
INSTITUTO FRANCISCO POSSENTI A.C. Per crucem ad lucem PREPARATORIA (1085) GUÍA DE MATEMÁTICAS VI (1619) I. PROGRESIONES
INSTITUTO FRANCISCO POSSENTI A.C. Per crucem ad lucem PREPARATORIA (08) GUÍA DE MATEMÁTICAS VI (69) Sucesión: finita e infinita. Serie. Define progresión aritmética y geométrica. I. PROGRESIONES. Forma
Coordenadas polares. Facultad de Ciencias UNAM Geometría Analítica I. Prof. Esteban Rubén Hurtado Cruz 1
Coordenadas polares Si en un plano jamos un punto O que llamaremos polo u origen, y a partir de el trazamos un rayo o semirrecta L horizontal llamado eje polar, cualquier punto P del plano pertenece a
TSTC. Dpt. Teoría de la Señal, Telemática y Comunicaciones Tema 1 INTRODUCCIÓN A LA ROBÓTICA
Dpt. Teoría de la Señal, Telemática y Comunicaciones Tema 1 INTRODUCCIÓN A LA ROBÓTICA Secciones 1. Introducción y definiciones. 2. Visión General de la manipulación mecánica. 1. Posicionamiento y Cinemática
Control y programación de robots
Control y programación de robots 11. Solución cinemática inversa y directa de robots seriales 11.1 El alumno, tras recibir y estudiar esta clase, debe ser capaz de: Comprender el modelado de la cinemática
Cinemática del Robot. CI-2657 Robótica M.Sc. Kryscia Ramírez Benavides
M.Sc. Kryscia Ramírez Benavides Sistema Robótico Cinemática Dinámica Planeamiento de Tareas Software Hardware Diseño Mecánico Actuadores Sistema de Control Sensores 2 Introducción Con el fin de controlar
ESTUDIO DE UNA CADENA CINEMÁTICA UTILIZANDO LOS MÉTODOS DENAVIT-HARTENBERG Y CRAIG MODIFICADO
ESTUDIO DE UNA CADENA CINEMÁTICA UTILIZANDO LOS MÉTODOS DENAVIT-HARTENBERG Y CRAIG MODIFICADO Dr. José Antonio Garrido Natarén 1, José Antonio Hernandez Reyes 2, MC. José Luis Fernando Palomeque Loyo 3,
INSTITUTO TECNOLÓGICO DE VERACRUZ. Materia: Robótica. Unidad 3: Cinemática. Tema: Cinemática Inversa. Catedrático: Dr. José Antonio Garrido Natarén
INSTITUTO TECNOLÓGICO DE VERACRUZ Materia: Robótica Unidad 3: Cinemática Tema: Cinemática Inversa Catedrático: Dr. José Antonio Garrido Natarén H. Veracruz, Ver. Noviembre de 2014 La cinemática del robot
Robótica Industrial. Robótica Industrial
TEMA 4: CINEMÁTICA DEL ROBOT Ingeniería de Sistemas y Automática Control de Robots y Sistemas Sensoriales Robótica Industrial Robótica Industrial ISA.- Ingeniería de Sistemas y Automática Cinemática del
Se pide: (b) Ecuaciones que permiten obtener las coordenadas cartesianas en R en función de las de R.
ÁLGEBRA Práctica 13 Espacios afines E 2 y E 3 (Curso 2004 2005) 1. En un espacio afín real de dimensión 3, se consideran dos sistemas de referencia R = {O, ē 1, ē 2, ē 3 } y R = {P, ū 1, ū 2, ū 3 }, donde
Cinemática del Robot. UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides
UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción La cinemática del robot estudia el movimiento del mismo con respecto a un sistema de referencia. Se interesa por la
Fundamentos de Robótica
Fundamentos de Robótica Introducción a la cinemática de manipuladores [email protected] http://scfi.uaemex.mx/hamontes 1 Recomendación No use estas diapositivas como referencia única de estudio durante
Modelado de un brazo robótico Scorbot-ER III mediante cinemática directa
XXIV CONVENCIÓN DE ESTUDIANTES DE CENTROAMÉRICA Y PANAMÁ, CONESCAPAN, EL SALVADOR, 25 Modelado de un brazo robótico Scorbot-ER III mediante cinemática directa Silvio Alejandro Urizar Salazar, Student Member
M.C. Cynthia Guerrero
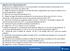Algoritmo 2-6-1: Representación D-H 0. Numere las articulaciones de la 1 a la n comenzando con la base () y terminando con la herramienta, en el orden yaw, pitch y roll. 1. Asigne un sistema coordenado
Tema 5. Cinemática Inversa
UNIVERSIDAD POLITÉCNICA DE MADRID E.U.I.T. Industrial TEMA: Cinemática Inversa FECHA: Enero de 01 Titulación: Grado en Ingeniería Electrónica y Automática Área: Ingeniería de Sistemas y Automática Departamento
El Método de Coordenadas de Pares en la Dinámica de Maquinaria.
El Método de Coordenadas de Pares en la Dinámica de Maquinaria. José María Rico Martínez Departamento de Ingeniería Mecánica División de Ingenierías, Campus Irapuato-Salamanca Universidad de Guanajuato
4, m = C) 2 D) 2. 3 m = B) 2. Sesión 9. Unidad IV Conceptos básicos. G. Pendiente de una recta.
Sesión 9.- La pendiente y ángulo de inclinación de la recta ilustrada es: Unidad IV Conceptos básicos. G. Pendiente de una recta..- La pendiente de recta R ilustrada m = m = m = m = E) m =.- Si la pendiente
CINEMÁTICA Y DINÁMICA DE ROBOTS MANIPULADORES: RESPUESTAS DE EJERCICIOS UNIDAD 02. Roger Miranda Colorado
CINEMÁTICA Y DINÁMICA DE ROBOTS MANIPULADORES: RESPUESTAS DE EJERCICIOS UNIDAD Roger Miranda Colorado de mayo de 6 Índice. RESPUESTAS DE EJERCICIOS UNIDAD . RESPUESTAS DE EJERCICIOS UNIDAD A continuación
Cinemática inversa del robot 4 gdl
obótica y Visión por Computador - UMH Práctica 2 Cinemática inversa del robot gdl Ejemplo Solución del robot cilíndrico de grados de libertad En este caso particular, la solución geométrica es inmediata.
ESTUDIO DE LA CINEMÁTICA DIRECTA DE UNA ARTICULACIÓN DE 3 GDL (RRR) UTILIZANDO LA METODOLOGÍA DENAVIT-HARTENBERG
ESTUDIO DE LA CINEMÁTICA DIRECTA DE UNA ARTICULACIÓN DE 3 GDL (RRR) UTILIZANDO LA METODOLOGÍA DENAVIT-HARTENBERG Dr. José Antonio Garrido Natarén 1, MC. Delia del Carmen Gamboa Olivares 2, MC. José Luis
Robots Autónomos Miguel Cazorla,, Otto Colomina Depto.. Ciencia de la Computación n e I.A. Universidad de Alicante
Robots Autónomos Miguel Cazorla,, Otto Colomina Depto.. Ciencia de la Computación n e I.A. Universidad de Alicante Este ítem está licenciado bajo Licencia Creative Commons Tema 2: Modelos geométricos y
Control de un Robot Scara de 3 GDL
Control de un Robot Scara de 3 GDL Jesús Soldevilla ureta Raúl Rivas Jimenez 13 de diciembre de 2010 Resumen El proyecto que se desarrolla en el siguiente informe plantea la aplicación de 4 técnicas de
Análisis Cinemático Directo del Robot RV-2AJ de Mitsubishi Utilizando Teoría de Screws
1 Análisis Cinemático Directo del Robot RV-2AJ de Mitsubishi Utilizando Teoría de Screws Luis Villalobos, Karen Pimentel, Oscar Rivera, Manuel Cardona Facultad de Ingeniería, Universidad Don Bosco, El
Visión artificial y Robótica Modelos de movimiento y mapas. Depto. de Ciencia de la Computación e Inteligencia Artificial
Visión artificial y Robótica Modelos de movimiento y mapas Depto. de Ciencia de la Computación e Inteligencia Artificial Contenidos Sistemas de coordenadas Localización de objetos en el espacio Modelos
Visión artificial y Robótica Geometría. Depto. de Ciencia de la Computación e Inteligencia Artificial
Visión artificial y Robótica Geometría Depto. de Ciencia de la Computación e Inteligencia Artificial Contenidos Geometría 2D y 3D Transformación de coordenadas Calibración de la cámara Álgebra necesaria
Mosaicos y frisos. Adela Salvador
Mosaicos y frisos Adela Salvador Isometrías en el plano Traslación Giro Simetría Simetría con deslizamiento Traslaciones La traslación queda definida al conocer el vector de traslación Busca dos vectores
20. TRANSFORMACIONES Y MOVIMIENTOS
20. TRANSFORMACIONES Y MOVIMIENTOS Los movimientos y las transformaciones son modificaciones aplicadas a los elementos del plano puntos, rectas, figuras_ con el fin de cambiar su posición o para convertirlos
2 Transformaciones en 3D
2 Transformaciones en 3D La manera más fácil de conseguir las transformaciones básicas (traslación, rotación, escalación, en general las transformaciones afines) es utilizando matrices de transformación.
Translaciones, giros, simetrías.
Translaciones, giros, simetrías. Transformaciones geométricas Transformación geométrica es una aplicación del plano en el plano tal que a cada punto de un plano le hace corresponder otro punto del mismo
Percepción visual aplicada a la robótica
Percepción visual aplicada a la robótica Mario I. Chacón Murguía Rafael Sandoval Rodríguez Javier Vega Pineda Selecciona el libro para empezar Capítulo 2 Teoría de robótica Continuar Cinemática de robots
DENAVITHARTENBERG PA R A E L D E D O Í N D I C E D E L A M A N O
D E T E R M I N A C I Ó N D E LO S PA R Á M E T R O S D E DENAVITHARTENBERG PA R A E L D E D O Í N D I C E D E L A M A N O M.C. José Salvador Antonio Méndez Aguirre1, Mario Arturo González Balderrama2
Control y programación de robots
Control y programación de robots 8. Cinemática directa robots seriales: Screws sucesivos 8. Objetivo Fórmula de Rodriguez espacial s ($), eje screw p2 sp t θ r p2 y2 pr 2 p r2 Bθ z2 p z t θ s x A x2 r
Graficación CCOM-259. Benemérita Universidad Autónoma de Puebla. Facultad de Ciencias de la Computación. Daniel Alejandro Valdés Amaro, Ph.
Graficación CCOM-9 Benemérita Universidad Autónoma de Puebla Facultad de Ciencias de la Computación Daniel Alejandro Valdés Amaro, Ph.D Objetivo: El alumno conocerá y aplicará los algoritmos y técnicas
Geometría del plano y el espacio
Geometría del plano y el espacio AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Geometría del plano y el espacio 1 / 21 Objetivos Al final de este tema tendréis que Conocer
MOVIMIENTOS Y TRANSFORMACIONES EN EL PLANO
MOVIMIENTOS Y TRANSFORMACIONES EN EL PLANO Traslación: Traslación (sin deslizadores) Traslación de un objeto: Traslación de una imagen: Actividad con geogebra: Construye un pentágono regular y trasládalo
Cinemática rotacional
Cinemática rotacional θ s r s = r θ ω = θ v = r ω rapidez t α = ω a t = r α acel. tangencial t a c = v2 r = r ω2 acel. radial o centrípeta θ = θ o + ω o t + 1 2 α t2 ω = ω o + α t ω 2 = ω 2 o + 2 α (θ
Elementos de geometría útiles para la localización espacial
Elementos de geometría útiles para la localización espacial Por qué los necesitamos un sistema de coordenadas? Ubicar espacialmente lo que se mide u observa Posicionar objetos Navegar Replantear Volver
TEMA 4. Geometría, cinemática y dinámica
TEMA 4. Geometría, cinemática y dinámica 76 Índice: Geometría, cinemática y dinámica Geometría oordenadas propias y del mundo Representación de la posición. Tipos de coordenadas Matrices de rotación Representación
1.18 Convertir de coordenadas cilíndricas a esféricas el campo vectorial H = (A/r), donde A es constante.
Problemas 1.5 Un campo vectorial está dado por G = 24xy + 12(x 2 + 2) + 18z 2. Dados dos puntos, P(1, 2, - 1) y Q(-2, 1, 3), encontrar: a) G en P; b) un vector unitario en la dirección de G en Q; c) un
2.- (Puntuación máxima 2 puntos). Para cada valor del parámetro real a, se consideran los tres planos siguientes:
1.- (Puntuación máxima 3 puntos). Se consideran las rectas: a) (1 punto) Calcular la distancia entre r y s. b) (1 punto) Hallar unas ecuaciones cartesianas de la recta perpendicular común a r y s y que
1. Obtener las coordenadas cartesianas del punto B simétrico del punto A(5,30 ), respecto al polo.
SEMESTRE 018-1 SERIE CURVAS EN EL PLANO POLAR 1. Obtener las coordenadas cartesianas del punto B simétrico del punto A(5,30 ), respecto al polo.. Determinar las coordenadas polares del punto C simétrico
Capítulo 2 Soluciones de ejercicios seleccionados
Capítulo Soluciones de ejercicios seleccionados Sección..4. (a) Sí. (b) No. (c) Sí.. (a) x = si α, pero si α = todo número real es solución de la ecuación. (b) (x, y) = (λ 7/, λ) para todo λ R.. Si k 6
VECTORES : Las Cantidades Vectoriales cantidades escalares
VECTORES En física hay dos tipos de cantidades: Las Cantidades Vectoriales son aquellas que tiene tanto magnitud como dirección y sentido sobre la dirección), mientras que las cantidades escalares son
CONCEPTOS DE EQUILIBRIO DE CUERPOS VINCULADOS Y CINEMATICA PLANA
CONCEPTOS DE EQUILIBRIO DE CUERPOS VINCULADOS Y CINEMATICA PLANA 1) LOS SISTEMAS PLANOS VINCULADOS Ing. Ramiro Piatti Ayudante Ad-Honorem 1.1) GENERALIDADES Se define como sistema de puntos materiales
Capítulo 10. Rotación de un Cuerpo Rígido
Capítulo 10 Rotación de un Cuerpo Rígido Contenido Velocidad angular y aceleración angular Cinemática rotacional Relaciones angulares y lineales Energía rotacional Cálculo de los momentos de inercia Teorema
Desplazamiento. Distancia en línea recta entre la posición inicial y final de un punto que se ha movido en un marco de referencia.
Tipos de Movimiento Conceptos Básicos Desplazamiento. Distancia en línea recta entre la posición inicial y final de un punto que se ha movido en un marco de referencia. Ciclo, periodo, fase y transmisión
SIMULADOR DE COMPORTAMIENTO CINEMÁTICO DE ROBOTS MANIPULADORES UTILIZANDO MATLAB
SIMULADOR DE COMPORTAMIENTO CINEMÁTICO DE ROBOTS MANIPULADORES UTILIZANDO MATLAB Enrique Cuan Duron a, Arnoldo Fernández Ramírez b, Elisa Urquizo Barraza a, Roxana García Andrade b,a División de Estudios
UNIVERSIDAD DEL NORTE Departamento de Matemáticas y Estadística. Álgebra Lineal. RESUMEN DE TEMAS DEL EXAMEN FINAL
1. Definiciones básicas. UNIVERSIDAD DEL NORTE Departamento de Matemáticas y Estadística. Álgebra Lineal. RESUMEN DE TEMAS DEL EXAMEN FINAL I. Sistemas homogéneos y subespacios de R n. (a) Para el sistema
INSTITUTO FRANCISCO POSSENTI A.C. Per crucem ad lucem PREPARATORIA (1085) GUÍA DE MATEMÁTICAS VI (1600 ) I. RELACIONES Y FUNCIONES
INSTITUTO FRANCISCO POSSENTI A.C. Per crucem ad lucem PREPARATORIA (085) GUÍA DE MATEMÁTICAS VI (600 ) I. RELACIONES Y FUNCIONES Funciones y relaciones. Dominio y rango. Determinar si es función o relación
Siete sistemas y catorce retículos
ESTRUCTURA CRISTALINA - PERFECCION Siete sistemas y catorce retículos Celda unitaria c a b Constantes reticulares o parámetros reticulares Longitud de los bordes Ángulos entre los ejes cristalográficos
CINEMÁTICA DE CUERPOS RÍGIDOS (Parte I)
UNIVERSIDAD JOSÉ ANTONIO PÁEZ FACULTAD DE INGENIERÍA ESCUELA DE INGENIERIA MECÁNICA MECÁNICA DINÁMICA SECCIÓN 204N1 CINEMÁTICA DE CUERPOS RÍGIDOS (Parte I) (Contenido correspondiente a parcial #3) CINEMÁTICA
INSTITUTO FRANCISCO POSSENTI A.C. Per crucem ad lucem PREPARATORIA (1085) GUÍA DE MATEMÁTICAS VI (1600) I. RELACIONES Y FUNCIONES
INSTITUTO FRANCISCO POSSENTI A.C. Per crucem ad lucem PREPARATORIA (085) GUÍA DE MATEMÁTICAS VI (600) I. RELACIONES Y FUNCIONES Funciones y relaciones. Dominio y rango. Determinar si es función o relación
Gráficos tridimensionales
9 de enero de 2013 1 / 25 Índice 1 2 Plano proyectivo Espacio proyectivo 3 4 2 / 25 Para los objetos en una escena usamos el sistema de referencia universal. Figura: Coordenadas universales y de vista.
TRANSF0RMACIONES GEOMÉTRICAS
DIBUJO TÉNCICO 2º BACH TRANSF0RMACIONES GEOMÉTRICAS Nos referimos a Transformaciones Geométricas cuando hablamos de la operación u operaciones necesarias para convertir una figura F en otra figura F portadora
Cambios del Sistema de Coordenadas. Transformación de
ASTRONOMÍA DE POSICIÓN Cambios del Sistema de. Transformación de Tema N Cambios del Sistema de. Transformación de.- Cambios del Sistema de Consideremos dos sistemas de coordenadas, uno denominado S=(,
Unidad 10. Rectas ángulos y movimientos.
Unidad 10. Rectas ángulos y movimientos. Recta, Semirecta y Segmento Una RECTA es una secuencia de puntos que se prolongan en sentidos opuestos y nunca tiene un fin. Una SEMIRRECTA es una secuencia de
Geometría 2. Halla a y b sabiendo que la recta que pasa por A y B corta perpendicularmente a la recta que pasa por C y D.
Geometría Ejercicio. Considera el plano π la recta r dados por π a 4 b r. 4 4 a) Halla los valores de a b para los que r está contenida en π. b) Eiste algún valor de a algún valor de b para los que la