Gráficos tridimensionales
|
|
|
- Patricia Eugenia Valenzuela Zúñiga
- hace 9 años
- Vistas:
Transcripción
1 9 de enero de / 25
2 Índice 1 2 Plano proyectivo Espacio proyectivo / 25
3 Para los objetos en una escena usamos el sistema de referencia universal. Figura: Coordenadas universales y de vista. La escena se proyecta en un plano, denominado cámara para lo cual se pasa al sistema de referencia de vista. Este proceso se denomina renderizado. 3 / 25
4 El comando pers en R es un modo de realizar dicha operación. Recibe xr, yr, zr, donde xr, yr son vectores ordenados y zr una matriz y dibuja la superficie. Devuelve una matriz de 4x4 que es la transformación aplicada. 4 / 25
5 Para transformar entre sistemas de coordenadas, utilizaremos matrices de la forma: x 2 y 2 z 2 1 a 11, a 12, a 13, a 14 = a 21, a 22, a 23, a 24 a 31, a 32, a 33, a 34 0, 0, 0, 1 x 1 y 1 z / 25
6 Traslación Para mover el punto (x 0, y 0, z 0 ) al origen: x 2 1, 0, 0, x 0 y 2 z 2 = 0, 1, 0, y 0 0, 0, 1, z 0 t 2 0, 0, 0, 1 x 1 y 1 z / 25
7 Rotación Una rotación de ángulo α respecto al eje z: x 2 cos(α), sin(α), 0, 0 x 1 y 2 z 2 = sin(α), cos(α), 0, 0 y 1 0, 0, 1, 0 z 1 t 2 0, 0, 0, / 25
8 Rotación Una rotación de ángulo α respecto al eje x: x 2 1, 0, 0, 0 x 1 y 2 z 2 = 0, cos(α), sin(α), 0 y 1 0, sin(α), cos(α), 0 z 1 t 2 0, 0, 0, / 25
9 Escalado Para multiplicar las coordenadas x por a, las y por b y las z por c, x 2 a, 0, 0, 0 x 1 y 2 z 2 = 0, b, 0, 0 y 1 0, 0, c, 0 z 1 t 2 0, 0, 0, / 25
10 Simetría respecto de un plano Simetría respecto al plano x = 0: x 2 1, 0, 0, 0 x 1 y 2 z 2 = 0, 1, 0, 0 y 1 0, 0, 1, 0 z 1 t 2 0, 0, 0, / 25
11 Transformaciones compuestas Toda transformación lineal puede descomponerse en producto de transformaciones simples. Por ejemplo, si queremos transformar el segmento (1, 1, 1)-(1, 0, 0) para que pase a ser el segmento (0, 0, 0)-(1, 0, 0), podemos: 1 Mover el punto (1, 0, 0) al origen (M 1 ). 2 Girar -45 o respecto al eje x (M 2 ). 3 Girar 90 o respecto al eje z (M 3 ). 4 Escalamos el eje x el factor 1/ 2 (M 4 ). La matriz que realiza el movimiento será: M = M 4 M 3 M 2 M 1 11 / 25
12 Proyecciones Las proyecciones paralelas se obtienen al proyectar en el plano de visión cada punto en una dirección dada. Normalmente esa dirección es la ortogonal al plano de visión. Podemos considerar que el plano de visión pasa por el origen. Para dar una proyección basta dar una transformación lineal (matriz) y tomar las coordenadas x, y. 12 / 25
13 a la normal al plano de visión Las proyecciones paralelas son planta, alzado y perfil. Las matrices de transformación son: , , / 25
14 Proyección isométrica Se elije el plano de visión de modo que la dirección ortogonal del plano de vista sea la de la recta x = y = z de las coordenadas universales. 1/ 6 2/ 6 1/ 6 0 1/ 2 0 1/ 2 0 1/ 3 1/ 3 1/ / 25
15 Proyección caballera Proyección caballera: Se realiza la transformación x v = y + xl 1 cos φ, y v = z + xl 1 sin φ. L 1 cos φ L 1 sin φ / 25
16 Plano proyectivo Plano proyectivo Espacio proyectivo El plano proyectivo se construye a partir del plano real R 2, añadiendo los siguientes puntos: Para cada familia de rectas paralelas, añadimos un punto. Dicho punto se denomina punto del infinito. Una manera alternativa es considerar R 3 y tomar como puntos las rectas {(λx, λy, λz), : λ R}. Los puntos de la forma (x, y, z) se denominan coordenadas homogéneas. Podemos pasar al plano afín mediante asignando a cada punto (x, y, z) del plano proyectivo el punto (x/z, y/z) del plano afín. 16 / 25
17 Plano proyectivo Plano proyectivo Espacio proyectivo Se denomina recta del infinito a la curva del plano proyectivo definida por z = 0 (es una circunferencia). Dos rectas del plano proyectivo siempre se cortan en un punto. Si tenemos una curva (x s, y s, z s ) en el plano proyectivo, entonces (x s /z s, y s /z s ) es su parte real. Si tenemos una curva (x s, y s, z s ) en el plano proyectivo, entonces z s = 0 nos da sus intersecciones con el infinito. 17 / 25
18 Plano proyectivo Plano proyectivo Espacio proyectivo Consideremos la hipérbola x 2 y 2 = 1. Podemos considerarla curva del plano proyectivo haciendo x x/z, y y/z. Entonces la hipérbola en el plano proyectivo es: x 2 y 2 = z 2 Corta a la recta del infinito (z = 0) en: x 2 y 2 = 0. x 2 = y 2, y = ±x. Luego y = ±x son paralelas a las asíntotas de las parábolas (de hecho son las asíntotas). 18 / 25
19 Espacio proyectivo Plano proyectivo Espacio proyectivo Denominamos espacio proyectivo a R 4 considerando como puntos las rectas {(λx, λy, λz, λt), : λ R}. Si existe λ tal que (x 1, y 1, z 1, t 1 ) = λ(x 2, y 2, z 2, t 2 ), entonces (x 1, y 1, z 1, t 1 ) y (x 2, y 2, z 2, t 2 ) son el mismo punto. 19 / 25
20 Espacio proyectivo Plano proyectivo Espacio proyectivo Dado un punto (x, y, z, t) tal que t 0, le asignamos el punto del espacio (afín) (x/t, y/t, z/t). Dado un punto (x, y, z) del espacio (afín), lo consideramos en el espacio proyectivo como (x/t, y/t, z/t, 1) (coordenadas homogéneas). 20 / 25
21 Plano proyectivo Espacio proyectivo Para definir una aplicación lineal en el espacio proyectivo, tenemos que dar una matriz de 4x4: x 2 a 11, a 12, a 13, a 14 x 1 y 2 z 2 = a 21, a 22, a 23, a 24 y 1 a 31, a 32, a 33, a 34 z 1 t 2 a 41, a 42, a 43, a 44 t 1 21 / 25
22 Proyección en perspectiva Plano proyectivo Espacio proyectivo Vamos a mover el plano del infinito para que esté en x = x y el plano x = x v se mantenga en proporción: x 2 y 2 z 2 = t 2 donde d = x x v. 1 + x v /d 0 0 x v x /d /d 0 0 x /d x 1 y 1 z / 25
23 se utiliza para renderizar una escena definida por caras planas. Consiste en dibujar las caras desde las más lejanas a las más cercanas. Falla cuando tres caras se solapan de modo cíclico. Para evitar esto existen algoritmos como el de bufer z. 23 / 25
24 Se ordenan las caras de más distante a menos distante al plano de vista. Para cada cara (S): Se compara con el resto de caras (S ), comprobando: No se superpone en z, No se superpone en y, No se superpone en x, Está detrás del plano que contiene a S, No hay superposición en el plano de vista. Si se cumple alguna condición se sigue con la cara siguiente. Si no se cumplen, se intercambian S y S y se vuelve a empezar. Se pintan las caras en el orden obtenido. 24 / 25
Geometría del plano y el espacio
 Geometría del plano y el espacio AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Geometría del plano y el espacio 1 / 21 Objetivos Al final de este tema tendréis que Conocer
Geometría del plano y el espacio AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Geometría del plano y el espacio 1 / 21 Objetivos Al final de este tema tendréis que Conocer
EJERCICIOS VOLUNTARIOS DE GEOMETRIA CON SOLUCIÓN. 2º BACHILLERATO
 EJERCICIOS VOLUNTARIOS DE GEOMETRIA CON SOLUCIÓN. 2º BACHILLERATO ESPACIO AFIN 1.Hallar la ecuación del plano que contenga al punto P(1, 1, 1) y sea paralelo a las rectas: r x 2y = 0 ; y 2z + 4 = 0; s
EJERCICIOS VOLUNTARIOS DE GEOMETRIA CON SOLUCIÓN. 2º BACHILLERATO ESPACIO AFIN 1.Hallar la ecuación del plano que contenga al punto P(1, 1, 1) y sea paralelo a las rectas: r x 2y = 0 ; y 2z + 4 = 0; s
Tema 5. Cónicas. Asi, para las identificaciones habituales, (punto proyectivo recta vectorial punto de un plano afín ampliado), RP 2 R3 {0}
 Tema 5. Cónicas. Introducción. Ejemplos.- El cono C = {(x, y, z) R 3 /x 2 + y 2 = z 2 } está formado por las rectas vectoriales 0 (x 1,x 2, 1) [x 1,x 2, 1] RP 2 con (x 1,x 2, 1) C Π 1 = C 1, circunferencia
Tema 5. Cónicas. Introducción. Ejemplos.- El cono C = {(x, y, z) R 3 /x 2 + y 2 = z 2 } está formado por las rectas vectoriales 0 (x 1,x 2, 1) [x 1,x 2, 1] RP 2 con (x 1,x 2, 1) C Π 1 = C 1, circunferencia
Parte II - Prácticas 8 a 9. Álgebra A 62 ÁLGEBRA A 62 (INGENIERÍA)
 Parte II - Prácticas 8 a 9 Álgebra A 62 Ingeniería 2015 CICLO BÁSICO COMÚN UBA ÁLGEBRA A 62 (INGENIERÍA) Práctica 8 Introducción a las transformaciones lineales Definiciones y propiedades Transformaciones
Parte II - Prácticas 8 a 9 Álgebra A 62 Ingeniería 2015 CICLO BÁSICO COMÚN UBA ÁLGEBRA A 62 (INGENIERÍA) Práctica 8 Introducción a las transformaciones lineales Definiciones y propiedades Transformaciones
Problemas de exámenes de Geometría
 1 Problemas de exámenes de Geometría 1. Consideramos los planos π 1 : X = P+λ 1 u 1 +λ 2 u 2 y π 2 : X = Q+µ 1 v 1 +µ 2 v 2. Cuál de las siguientes afirmaciones es incorrecta? a) Si π 1 π 2 Ø, entonces
1 Problemas de exámenes de Geometría 1. Consideramos los planos π 1 : X = P+λ 1 u 1 +λ 2 u 2 y π 2 : X = Q+µ 1 v 1 +µ 2 v 2. Cuál de las siguientes afirmaciones es incorrecta? a) Si π 1 π 2 Ø, entonces
1º BACH DIBUJO TÉCNICO I SISTEMA AXONOMÉTRICO PERSPECTIVA ISOMÉTRICA Y CABALLERA
 1º BACH SISTEMA AXONOMÉTRICO PERSPECTIVA ISOMÉTRICA Y CABALLERA 1- PERSPECTIVAS: SISTEMA AXONOMÉTRICO ORTOGONAL. INTRODUCCIÓN Sea un triedro trirrectángulo OXYZ, siendo el punto O el vértice del triedro
1º BACH SISTEMA AXONOMÉTRICO PERSPECTIVA ISOMÉTRICA Y CABALLERA 1- PERSPECTIVAS: SISTEMA AXONOMÉTRICO ORTOGONAL. INTRODUCCIÓN Sea un triedro trirrectángulo OXYZ, siendo el punto O el vértice del triedro
GEOMETRIA DESCRIPTIVA BASICA SISTEMAS DE REPRESENTACION EDUCACION PLASTICA Y VISUAL 3º ESO
 GEOMETRIA DESCRIPTIVA BASICA SISTEMAS DE REPRESENTACION EDUCACION PLASTICA Y VISUAL 3º ESO - 2-1. Qué es una proyección? 2. Tipos de proyección y relación con los sistemas de representación. 3. Diédrico.
GEOMETRIA DESCRIPTIVA BASICA SISTEMAS DE REPRESENTACION EDUCACION PLASTICA Y VISUAL 3º ESO - 2-1. Qué es una proyección? 2. Tipos de proyección y relación con los sistemas de representación. 3. Diédrico.
Unidad 1. Trazados fundamentales en el plano.
 MATERIA: CURSO: DIBUJO TÉCNICO 2º BACHILLERATO CONTENIDOS MÍNIMOS Unidad 1. Trazados fundamentales en el plano. Suma de segmentos. Diferencia de segmentos. Trazado de la mediatriz de un segmento. Trazado
MATERIA: CURSO: DIBUJO TÉCNICO 2º BACHILLERATO CONTENIDOS MÍNIMOS Unidad 1. Trazados fundamentales en el plano. Suma de segmentos. Diferencia de segmentos. Trazado de la mediatriz de un segmento. Trazado
CLASIFICACIÓN AFÍN DE CÓNICAS
 Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS CLASIFICACIÓN AFÍN DE CÓNICAS Sea E un R-espacio vectorial de dimensión. Sean E = e 1, e un plano vectorial de E y e 0 un
Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS CLASIFICACIÓN AFÍN DE CÓNICAS Sea E un R-espacio vectorial de dimensión. Sean E = e 1, e un plano vectorial de E y e 0 un
Planos y Rectas. 19 de Marzo de 2012
 el Geometría en el Planos y Rectas Universidad Autónoma Metropolitana Unidad Iztapalapa 19 de Marzo de 2012 el Anteriormente vimos que es posible encontrar un número infinito de vectores, no paralelos
el Geometría en el Planos y Rectas Universidad Autónoma Metropolitana Unidad Iztapalapa 19 de Marzo de 2012 el Anteriormente vimos que es posible encontrar un número infinito de vectores, no paralelos
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2006 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio 3, Opción A Reserva, Ejercicio
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio 3, Opción A Reserva, Ejercicio
ALGEBRA LINEAL. Capítulo III: Vectores en los espacios bidimensional y tridimensional. MsC. Andrés Baquero. jueves, 2 de julio de 15
 ALGEBRA LINEAL Capítulo III: Vectores en los espacios bidimensional y tridimensional MsC. Andrés Baquero jueves, 2 de julio de 15 Introducción a los vectores Vectores Geométricos Vectores Geométricos Vectores
ALGEBRA LINEAL Capítulo III: Vectores en los espacios bidimensional y tridimensional MsC. Andrés Baquero jueves, 2 de julio de 15 Introducción a los vectores Vectores Geométricos Vectores Geométricos Vectores
Tema 3. GEOMETRIA ANALITICA.
 Álgebra lineal. Curso 087-009. Tema. Hoja 1 Tema. GEOMETRIA ANALITICA. 1. Hallar la ecuación de la recta: a) que pase por ( 4, ) y tenga pendiente 1. b) que pase por (0, 5) y tenga pendiente. c) que pase
Álgebra lineal. Curso 087-009. Tema. Hoja 1 Tema. GEOMETRIA ANALITICA. 1. Hallar la ecuación de la recta: a) que pase por ( 4, ) y tenga pendiente 1. b) que pase por (0, 5) y tenga pendiente. c) que pase
Geometría Analítica Enero 2015
 Laboratorio #1 Distancia entre dos puntos I.- Hallar el perímetro del triángulo, cuyos vértices son los puntos dados. A( 2,, B( 8,, C( 5, 10) R( 6, 5) S( 2, - T(3,- U( -1, - V( 2, - W( 9, 4) II.- Demuestre
Laboratorio #1 Distancia entre dos puntos I.- Hallar el perímetro del triángulo, cuyos vértices son los puntos dados. A( 2,, B( 8,, C( 5, 10) R( 6, 5) S( 2, - T(3,- U( -1, - V( 2, - W( 9, 4) II.- Demuestre
20. TRANSFORMACIONES Y MOVIMIENTOS
 20. TRANSFORMACIONES Y MOVIMIENTOS Los movimientos y las transformaciones son modificaciones aplicadas a los elementos del plano puntos, rectas, figuras_ con el fin de cambiar su posición o para convertirlos
20. TRANSFORMACIONES Y MOVIMIENTOS Los movimientos y las transformaciones son modificaciones aplicadas a los elementos del plano puntos, rectas, figuras_ con el fin de cambiar su posición o para convertirlos
y v 0, 0, 1 y v 1, 0, 1 se tiene la ecuación
 SUPERFICIES Mostraremos varios métodos para generar superficies y encontrar sus ecuaciones. 1. Superficies cilíndricas Dada una curva en el plano de ecuación y un vector con Γ 0, es decir, no horizontal,
SUPERFICIES Mostraremos varios métodos para generar superficies y encontrar sus ecuaciones. 1. Superficies cilíndricas Dada una curva en el plano de ecuación y un vector con Γ 0, es decir, no horizontal,
2. Distancia entre dos puntos. Punto medio de un segmento
 Geometría 1 Geometría anaĺıtica Una ecuación de primer grado con dos incógnitas x e y tiene infinitas soluciones Por ejemplo x + y = 3 tiene como soluciones (0, 3), (1, ), ( 1, 4), etc Hasta ahora se han
Geometría 1 Geometría anaĺıtica Una ecuación de primer grado con dos incógnitas x e y tiene infinitas soluciones Por ejemplo x + y = 3 tiene como soluciones (0, 3), (1, ), ( 1, 4), etc Hasta ahora se han
ÁLGEBRA LINEAL II Práctica
 ÁLGEBRA LINEAL II Práctica 3.1-3.2 Geometría afín. (Curso 2012 2013) 1. En un espacio afín real de dimensión 3, se consideran dos sistemas de referencia R = O, ē 1, ē 2, ē 3 } y R = P, ū 1, ū 2, ū 3 },
ÁLGEBRA LINEAL II Práctica 3.1-3.2 Geometría afín. (Curso 2012 2013) 1. En un espacio afín real de dimensión 3, se consideran dos sistemas de referencia R = O, ē 1, ē 2, ē 3 } y R = P, ū 1, ū 2, ū 3 },
Fundamentos matemáticos básicos de la realidad virtual
 Fundamentos matemáticos básicos de la realidad virtual José Ignacio Ronda Prieto Grupo de Tratamiento de Imágenes, ETSIT, UPM [email protected] Fundamentos matemáticos básicos de la realidad virtual 1
Fundamentos matemáticos básicos de la realidad virtual José Ignacio Ronda Prieto Grupo de Tratamiento de Imágenes, ETSIT, UPM [email protected] Fundamentos matemáticos básicos de la realidad virtual 1
CÓNICAS. 1. Dada la cónica x 2 + 2xy y 2 2x 2y + 4 = 0, se pide su clasicación y los elementos característicos de la misma. = 1
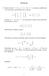 CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
ÁLGEBRA LINEAL II Práctica
 ÁLGEBRA LINEAL II Práctica 3.1-3.2 Geometría afín. (Curso 2013 2014) 1. En un espacio afín real de dimensión 3, se consideran dos sistemas de referencia R = O, ē 1, ē 2, ē 3 } y R = P, ū 1, ū 2, ū 3 },
ÁLGEBRA LINEAL II Práctica 3.1-3.2 Geometría afín. (Curso 2013 2014) 1. En un espacio afín real de dimensión 3, se consideran dos sistemas de referencia R = O, ē 1, ē 2, ē 3 } y R = P, ū 1, ū 2, ū 3 },
1 CÓNICAS Cónicas. Estudio particular. 1 x y. 1 x y. a 00 a 01 a 02 a 10 a 11 a 12 a 20 a 21 a 22
 CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular.
 ÁLGEBRA Práctica 15 Cónicas (Curso 2008 2009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
ÁLGEBRA Práctica 15 Cónicas (Curso 2008 2009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
CURVAS TÉCNICAS CURVAS CÓNICAS
 2º BACH CURVAS TÉCNICAS CURVAS CÓNICAS ANA BALLESTER JIMÉNEZ CURVAS TÉCNICAS 1. ÓVALOS. El óvalo es una curva cerrada, plana y convexa formada generalmente por cuatro arcos de circunferencia iguales dos
2º BACH CURVAS TÉCNICAS CURVAS CÓNICAS ANA BALLESTER JIMÉNEZ CURVAS TÉCNICAS 1. ÓVALOS. El óvalo es una curva cerrada, plana y convexa formada generalmente por cuatro arcos de circunferencia iguales dos
ESCUELA PREPARATORIA OFICIAL NO.16 MATERÍA: GEOMETRÍA ANALITICA GUÍA DE ESTUDIO PARA LA ÚLTIMA OPORTUNIDAD DE ACREDITAR LA MATERÍA
 Geometría analítica 1.- Ecuación de la recta 2.- Cónicas 3.-Ecuación de la parábola UNIDAD II: CONICAS (CIRCUNFERENCIA Y PARABOLAS) Una superficie cónica de revolución está engendrada por la rotación de
Geometría analítica 1.- Ecuación de la recta 2.- Cónicas 3.-Ecuación de la parábola UNIDAD II: CONICAS (CIRCUNFERENCIA Y PARABOLAS) Una superficie cónica de revolución está engendrada por la rotación de
Problemas de Geometría Proyectiva
 Problemas de Geometría Proyectiva José M. Sánchez Abril José M. Rodríguez-Sanjurjo, Jesús M. Ruiz 1995 * I. VARIEDADES PROYECTIVAS Número 1. Se consideran en el plano proyectivo P 2 los cuatro puntos a
Problemas de Geometría Proyectiva José M. Sánchez Abril José M. Rodríguez-Sanjurjo, Jesús M. Ruiz 1995 * I. VARIEDADES PROYECTIVAS Número 1. Se consideran en el plano proyectivo P 2 los cuatro puntos a
ESTUDIO GRÁFICO DE LA ELIPSE.
 Curvas Cónicas para Dibujo y Matemáticas. Aplicación web Dibujo Técnico para ESO y Bachillerato Matemáticas para Bachillerato Educación Plástica y Visual Autor: José Antonio Cuadrado Vicente. ESTUDIO GRÁFICO
Curvas Cónicas para Dibujo y Matemáticas. Aplicación web Dibujo Técnico para ESO y Bachillerato Matemáticas para Bachillerato Educación Plástica y Visual Autor: José Antonio Cuadrado Vicente. ESTUDIO GRÁFICO
Rectas y Cónicas. Sistema de Coordenadas Cartesianas. Guía de Ejercicios # Encuentre las coordenadas de los puntos mostrados en la figura.
 Universidad de Los Andes Facultad de Ciencias Forestales y Ambientales Escuela de ingeniería Forestal Departamento de Botánica y Ciencias Básicas Matemáticas I I 2014 Prof. K. Chang. Rectas y Cónicas Guía
Universidad de Los Andes Facultad de Ciencias Forestales y Ambientales Escuela de ingeniería Forestal Departamento de Botánica y Ciencias Básicas Matemáticas I I 2014 Prof. K. Chang. Rectas y Cónicas Guía
Geometría del Espacio. Física Geográfica. Licenciatura de Humanidades. Febrero-Mayo,
 Geometría del Espacio. Física Geográfica. Licenciatura de Humanidades. Febrero-Mayo, 2007. 42 Índice. 1. Superficies. 2. El espacio eucĺıdeo tridimensional. Coordenadas Cartesianas. 3. Distancia entre
Geometría del Espacio. Física Geográfica. Licenciatura de Humanidades. Febrero-Mayo, 2007. 42 Índice. 1. Superficies. 2. El espacio eucĺıdeo tridimensional. Coordenadas Cartesianas. 3. Distancia entre
1 Funciones de Varias Variables
 EJECICIOS DE FUNDAMENTOS MATEMÁTICOS (DISEO) Funciones de Varias Variables. Dada f(x, y) ln ( x + ln(y) ). a) Calcular la derivada direccional en el punto (x, y) (, e 2 ) en la dirección del vector v (3,
EJECICIOS DE FUNDAMENTOS MATEMÁTICOS (DISEO) Funciones de Varias Variables. Dada f(x, y) ln ( x + ln(y) ). a) Calcular la derivada direccional en el punto (x, y) (, e 2 ) en la dirección del vector v (3,
TEMA 5. CURVAS CÓNICAS.
 5.1. GENERALIDADES. TEMA 5. CURVAS CÓNICAS. Se denominan secciones cónicas a aquellas superficies que son producidas por la intersección de un plano con una superficie cónica de revolución (una superficie
5.1. GENERALIDADES. TEMA 5. CURVAS CÓNICAS. Se denominan secciones cónicas a aquellas superficies que son producidas por la intersección de un plano con una superficie cónica de revolución (una superficie
5 = z. 2. Hallar el valor de m para que los puntos A(3,m,1), B(1,1,-1) y C(-2,10,-4) pertenezcan a la misma recta.
 . Expresar en forma paramétrica y reducida la recta x+ 3 = y- 5 = z -. Hallar el valor de m para que los puntos A(3,m,), B(,,-) y C(-,0,-4) pertenezcan a la misma recta. 3. Probar que todos los planos
. Expresar en forma paramétrica y reducida la recta x+ 3 = y- 5 = z -. Hallar el valor de m para que los puntos A(3,m,), B(,,-) y C(-,0,-4) pertenezcan a la misma recta. 3. Probar que todos los planos
El pipeline de visualización es el conjunto de
 Sistemas de Visualización Pipeline de visualización 3D Definición del modelo geométrico Transformaciones geométricas Transformaciones de visualización Volumen de visualización Proyecciones Pipeline de
Sistemas de Visualización Pipeline de visualización 3D Definición del modelo geométrico Transformaciones geométricas Transformaciones de visualización Volumen de visualización Proyecciones Pipeline de
1. Escribir las ecuaciones paramétricas, reducida y continua de la recta que pasa por los puntos A(2,3,5) y B(-1,0,2).
 1. Escribir las ecuaciones paramétricas, reducida y continua de la recta que pasa por los puntos A(,3,5) y B(-1,0,).. Dados los puntos A(,3,-1) y B(-4,1,-), hallar las coordenadas de un punto C perteneciente
1. Escribir las ecuaciones paramétricas, reducida y continua de la recta que pasa por los puntos A(,3,5) y B(-1,0,).. Dados los puntos A(,3,-1) y B(-4,1,-), hallar las coordenadas de un punto C perteneciente
Transformaciones Isométricas
 Transformaciones Isométricas I o Medio Profesor: Alberto Alvaradejo Ojeda Índice 1. Transformación Isométrica 3 1.1. Traslación..................................... 3 1.2. Ejercicios.....................................
Transformaciones Isométricas I o Medio Profesor: Alberto Alvaradejo Ojeda Índice 1. Transformación Isométrica 3 1.1. Traslación..................................... 3 1.2. Ejercicios.....................................
V = v 1 +2v 2 +3v 3. v 2. v 1
 Coordenadas Hay muchas maneras de darle coordenadas a los puntos del espacio, las ecuaciones de las curvas o superficies dependen de las coordenadas que utilicemos y eligiendo las coordenadas adecuadas
Coordenadas Hay muchas maneras de darle coordenadas a los puntos del espacio, las ecuaciones de las curvas o superficies dependen de las coordenadas que utilicemos y eligiendo las coordenadas adecuadas
DIBUJO TÉCNICO. UNIDAD DIDÁCTICA VII: Geometría 2D (IV)
 UNIDAD DIDÁCTICA VII: Geometría 2D (IV) 1 ÍNDICE Página: 1 INTRODUCCIÓN. 2 2 ÁNGULOS VINCULADOS A LA CIRCUNFERENCIA... 2 3 TANGENCIAS ENTRE RECTAS Y CIRCUNFERENCIAS... 2 3.1 RECTAS TANGENTES A UNA CIRCUNFERENCIA
UNIDAD DIDÁCTICA VII: Geometría 2D (IV) 1 ÍNDICE Página: 1 INTRODUCCIÓN. 2 2 ÁNGULOS VINCULADOS A LA CIRCUNFERENCIA... 2 3 TANGENCIAS ENTRE RECTAS Y CIRCUNFERENCIAS... 2 3.1 RECTAS TANGENTES A UNA CIRCUNFERENCIA
Dibujo Técnico. Proyecciones Axonométricas. Prof. Juan Guerrero. Instituto Tecnológico de Costa Rica
 Proyecciones Axonométricas Dibujo Técnico Instituto Tecnológico de Costa Rica Prof. Juan Guerrero Proyecciones Axonométricas (Norma: ISO-5456-3) Definición El objeto a representar se sitúa con sus caras
Proyecciones Axonométricas Dibujo Técnico Instituto Tecnológico de Costa Rica Prof. Juan Guerrero Proyecciones Axonométricas (Norma: ISO-5456-3) Definición El objeto a representar se sitúa con sus caras
TRANSF0RMACIONES GEOMÉTRICAS
 DIBUJO TÉNCICO 2º BACH TRANSF0RMACIONES GEOMÉTRICAS Nos referimos a Transformaciones Geométricas cuando hablamos de la operación u operaciones necesarias para convertir una figura F en otra figura F portadora
DIBUJO TÉNCICO 2º BACH TRANSF0RMACIONES GEOMÉTRICAS Nos referimos a Transformaciones Geométricas cuando hablamos de la operación u operaciones necesarias para convertir una figura F en otra figura F portadora
Lugar Geométrico. Se llama lugar geométrico a un conjunto de puntos que cumplen una determinada propiedad. Mediatriz
 1 Lugar Geométrico Se llama lugar geométrico a un conjunto de puntos que cumplen una determinada propiedad. Mediatriz Mediatriz de un segmento es el lugar geométrico de los puntos del plano que equidistan
1 Lugar Geométrico Se llama lugar geométrico a un conjunto de puntos que cumplen una determinada propiedad. Mediatriz Mediatriz de un segmento es el lugar geométrico de los puntos del plano que equidistan
SERIE SUPERFICIES. 1.- Determinar la ecuación cartesiana del cilindro que contiene a la curva de ecuaciones:
 SERIE SUPERFICIES 1.- Determinar la ecuación cartesiana del cilindro que contiene a la curva de ecuaciones: 4x C z 0 y que se genera por rectas perpendiculares al plano: x + y + 3z + = 0.-Sea la superficie
SERIE SUPERFICIES 1.- Determinar la ecuación cartesiana del cilindro que contiene a la curva de ecuaciones: 4x C z 0 y que se genera por rectas perpendiculares al plano: x + y + 3z + = 0.-Sea la superficie
UNIVERSIDAD CENTROAMERICANA JOSÉ SIMEÓN CAÑAS ALGEBRA VECTORIAL Y MATRICES GUIA DE TRABAJO Secciones Cónicas Ciclo 02 de 2012
 UNIVERSIDAD CENTROAMERICANA JOSÉ SIMEÓN CAÑAS ALGEBRA VECTORIAL Y MATRICES GUIA DE TRABAJO Secciones Cónicas Ciclo 0 de 0 PARTE I: Ejercicios cortos de selección Múltiple. En cada uno de los siguientes
UNIVERSIDAD CENTROAMERICANA JOSÉ SIMEÓN CAÑAS ALGEBRA VECTORIAL Y MATRICES GUIA DE TRABAJO Secciones Cónicas Ciclo 0 de 0 PARTE I: Ejercicios cortos de selección Múltiple. En cada uno de los siguientes
ALGEBRA Y GEOMETRIA ANALITICA
 Diplomatura en Ciencia y Tecnología ALGEBRA Y GEOMETRIA ANALITICA SEGUNDO CUATRIMESTRE DE 009 Profesora Mariana Suarez PRACTICA N 8: RECTA EN EL ESPACIO PLANO ALGEBRA Y GEOMETRIA ANALITICA - Segundo cuatrimestre
Diplomatura en Ciencia y Tecnología ALGEBRA Y GEOMETRIA ANALITICA SEGUNDO CUATRIMESTRE DE 009 Profesora Mariana Suarez PRACTICA N 8: RECTA EN EL ESPACIO PLANO ALGEBRA Y GEOMETRIA ANALITICA - Segundo cuatrimestre
INDICE. 88 determinante 36. Familias de líneas rectas Resumen de resultados 96
 INDICE Geometría Analítica Plana Capitulo Primero Sistema de Coordenadas Articulo 1. Introducción 1 2. Segmento rectilíneo dirigido 1 3. Sistema coordenado lineal 3 4. Sistema coordenado en el plano 5
INDICE Geometría Analítica Plana Capitulo Primero Sistema de Coordenadas Articulo 1. Introducción 1 2. Segmento rectilíneo dirigido 1 3. Sistema coordenado lineal 3 4. Sistema coordenado en el plano 5
58 EJERCICIOS de RECTAS y PLANOS 2º BACH.
 58 EJERCICIOS de RECTAS y PLANOS 2º BACH. NOTA: En los ejercicios de Geometría se recomienda comenzar, antes de nada, por: Imaginarse la situación; podemos ayudarnos, para ello, de bolígrafos (para representar
58 EJERCICIOS de RECTAS y PLANOS 2º BACH. NOTA: En los ejercicios de Geometría se recomienda comenzar, antes de nada, por: Imaginarse la situación; podemos ayudarnos, para ello, de bolígrafos (para representar
22. CURVAS CÓNICAS-ELIPSE
 22. CURVAS CÓNICAS-ELIPSE 22.1. Características generales. Las curvas cónicas son las secciones planas de un cono de revolución. El cono de revolución es la superficie que genera una recta r al girar alrededor
22. CURVAS CÓNICAS-ELIPSE 22.1. Características generales. Las curvas cónicas son las secciones planas de un cono de revolución. El cono de revolución es la superficie que genera una recta r al girar alrededor
Ejercicios de Gráficos Proyecciones
 Ejercicios de Gráficos Proyecciones Pedro Pascual 17 de marzo de 2010 1. Indicar cuáles de las siguientes afirmaciones son verdaderas (V) y cúales son falsas (F): 1. La pseudodistancia 3D viene determinada
Ejercicios de Gráficos Proyecciones Pedro Pascual 17 de marzo de 2010 1. Indicar cuáles de las siguientes afirmaciones son verdaderas (V) y cúales son falsas (F): 1. La pseudodistancia 3D viene determinada
Cónicas. Dibujo I, Geometría Tema 7 ETSIN. Copyright All rights reserved.
 Cónicas Dibujo I, Geometría Tema 7 ETSIN http://debin.etsin.upm.es/~geometria/ Copyright 2008. All rights reserved. Objetivos Con este objeto de aprendizaje conseguirás: Recordar las propiedades de estas
Cónicas Dibujo I, Geometría Tema 7 ETSIN http://debin.etsin.upm.es/~geometria/ Copyright 2008. All rights reserved. Objetivos Con este objeto de aprendizaje conseguirás: Recordar las propiedades de estas
Resumen de Transformaciones Isométricas. Traslaciones
 Resumen de Transformaciones Isométricas Una transformación es un procedimiento geométrico o movimiento que produce cambios en una figura. La palabra isometría proviene del griego y significa igual medida
Resumen de Transformaciones Isométricas Una transformación es un procedimiento geométrico o movimiento que produce cambios en una figura. La palabra isometría proviene del griego y significa igual medida
Ejercicios Resueltos de Cálculo III.
 Ejercicios Resueltos de Cálculo III. 1.- Considere y. a) Demuestre que las rectas dadas se cortan. Encuentre el punto de intersección. b) Encuentre una ecuación del plano que contiene a esas rectas. Como
Ejercicios Resueltos de Cálculo III. 1.- Considere y. a) Demuestre que las rectas dadas se cortan. Encuentre el punto de intersección. b) Encuentre una ecuación del plano que contiene a esas rectas. Como
LA CIRCUNFERENCIA. La circunferencia es la sección producida por un plano perpendicular al eje.
 LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
DIBUJO MECÁNICO TEMA 3 PROYECCIONES. Prof. Andrés Meléndez
 DIBUJO MECÁNICO TEMA 3 PROYECCIONES Prof. Andrés Meléndez Contenido TEMA 3: PROYECCIONES Definiciones; Métodos de representación: Proyección Ortogonal; Axonométrica; En perspectiva (centro); Representación
DIBUJO MECÁNICO TEMA 3 PROYECCIONES Prof. Andrés Meléndez Contenido TEMA 3: PROYECCIONES Definiciones; Métodos de representación: Proyección Ortogonal; Axonométrica; En perspectiva (centro); Representación
Álgebra y Geometría Analítica I - LF 2016 Práctica 1: Algunos elementos de la Geometría Analítica
 Álgebra y Geometría Analítica I - LF 2016 Práctica 1: Algunos elementos de la Geometría Analítica 1. a) Marcar en un eje los puntos a(1);b( 2) y c(4). b) Hallar los puntos simétricos respecto al origen
Álgebra y Geometría Analítica I - LF 2016 Práctica 1: Algunos elementos de la Geometría Analítica 1. a) Marcar en un eje los puntos a(1);b( 2) y c(4). b) Hallar los puntos simétricos respecto al origen
PAU Madrid. Matemáticas II. Año Examen de septiembre. Opción A. Ejercicio 1. Valor: 2 puntos.
 Opción A. Ejercicio. Valor: 2 puntos. Se considera la función real de variable real definida por: f(x) = a) ( punto) Determinar sus máximos y mínimos relativos x x 2 + b) ( punto) Calcular el valor de
Opción A. Ejercicio. Valor: 2 puntos. Se considera la función real de variable real definida por: f(x) = a) ( punto) Determinar sus máximos y mínimos relativos x x 2 + b) ( punto) Calcular el valor de
Sistema axonométrico. Con el estudio de esta Unidad nos proponemos alcanzar los siguientes objetivos:
 UNIDAD 9 Sistema axonométrico E l sistema axonométrico se divide en ortogonal y oblicuo según sea la dirección de proyección. La axonometría ortogonal puede ser isométrica, dimétrica o trimétrica según
UNIDAD 9 Sistema axonométrico E l sistema axonométrico se divide en ortogonal y oblicuo según sea la dirección de proyección. La axonometría ortogonal puede ser isométrica, dimétrica o trimétrica según
Cambio de coordenadas
 Capítulo Cambio de coordenadas Problema Tenemos 3 puntos P, P y P 3, la idea es representar P en términos de esos puntos y de otros tres Q,Q y Q 3. El problema, es cómo ven P P P 3 a P y cómo Q Q Q 3 a
Capítulo Cambio de coordenadas Problema Tenemos 3 puntos P, P y P 3, la idea es representar P en términos de esos puntos y de otros tres Q,Q y Q 3. El problema, es cómo ven P P P 3 a P y cómo Q Q Q 3 a
Razonar si son ciertas o falsas las siguientes igualdades: Asociar cada función con su gráfica. (19) Si x 2 > 0, entonces x > 0.
 Razonar si son ciertas o falsas las siguientes igualdades: ) a + b) = a + b ) ) a + b = a + b e = e 4) a + ab b + a = a 5) 8 + = 6) a ) = a 5 7) 8) a = a 4 = 4 9) 9 = 0) ) e ) = e + = ) e ln = ) ln 0 =
Razonar si son ciertas o falsas las siguientes igualdades: ) a + b) = a + b ) ) a + b = a + b e = e 4) a + ab b + a = a 5) 8 + = 6) a ) = a 5 7) 8) a = a 4 = 4 9) 9 = 0) ) e ) = e + = ) e ln = ) ln 0 =
Cónicas. Clasificación.
 Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
B23 Curvas cónicas Curvas cónicas
 Geometría plana B23 Curvas cónicas Curvas cónicas Superficie cónica de revolución es la engendrada por una recta que gira alrededor de otra a la que corta. Curvas cónicas son las que resultan de la intersección
Geometría plana B23 Curvas cónicas Curvas cónicas Superficie cónica de revolución es la engendrada por una recta que gira alrededor de otra a la que corta. Curvas cónicas son las que resultan de la intersección
Fecha: 29/10/2013 MATEMÁTICAS
 Página: 1/5 MATEMÁTICAS Álgebra 1.- Conceptos y operaciones algebraicas fundamentales Terminología Operaciones fundamentales con monomios y polinomios o Reducción de términos semejantes o Suma, resta o
Página: 1/5 MATEMÁTICAS Álgebra 1.- Conceptos y operaciones algebraicas fundamentales Terminología Operaciones fundamentales con monomios y polinomios o Reducción de términos semejantes o Suma, resta o
Las curvas cónicas son las secciones producidas por un plano secante sobre una superficie cónica de revolución. (Fig. 31)
 Dibujo Trazado de Curvas cónicas Las curvas cónicas son las secciones producidas por un plano secante sobre una superficie cónica de revolución. (Fig. 31) Fig. 31 Una superficie cónica de revolución es
Dibujo Trazado de Curvas cónicas Las curvas cónicas son las secciones producidas por un plano secante sobre una superficie cónica de revolución. (Fig. 31) Fig. 31 Una superficie cónica de revolución es
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A Ejercicio 1.- Sea f : R R definida por f(x) = x 3 +ax 2 +bx+c. a) [1 75 puntos] Halla a,b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1 2 y que la recta tangente en
Opción A Ejercicio 1.- Sea f : R R definida por f(x) = x 3 +ax 2 +bx+c. a) [1 75 puntos] Halla a,b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1 2 y que la recta tangente en
EDUCACIÓN PLÁSTICA Y VISUAL UNIDAD 4: SISTEMA DIÉDRICO
 EDUCACIÓN PLÁSTICA Y VISUAL UNIDAD 4: SISTEMA DIÉDRICO INDICE 1. SISTEMAS DE REPRESENTACIÓN 1.1. Objetivo (de las 3D a las 2D y de las 2D a las 3D) 3 1.2. Operaciones básicas 3 1.3. Tipos de proyección
EDUCACIÓN PLÁSTICA Y VISUAL UNIDAD 4: SISTEMA DIÉDRICO INDICE 1. SISTEMAS DE REPRESENTACIÓN 1.1. Objetivo (de las 3D a las 2D y de las 2D a las 3D) 3 1.2. Operaciones básicas 3 1.3. Tipos de proyección
Análisis Matemático I (Ing. de Telecomunicación), Examen final, 26 de enero de 2010 RESPUESTAS A AMBOS MODELOS
 Análisis Matemático I (Ing. de Telecomunicación), 29-1 Examen final, 26 de enero de 21 RESPUESTAS A AMBOS MODELOS Primera Parte Las preguntas 1 14 son de tipo test. Se pide elegir una única respuesta en
Análisis Matemático I (Ing. de Telecomunicación), 29-1 Examen final, 26 de enero de 21 RESPUESTAS A AMBOS MODELOS Primera Parte Las preguntas 1 14 son de tipo test. Se pide elegir una única respuesta en
18. PERSPECTIVA CABALLERA.
 18. PERSPECTIVA CABALLERA. La perspectiva caballera es un sistema de representación que utiliza la proyección paralela oblicua, en el que las dimensiones del plano proyectante frontal, como las de los
18. PERSPECTIVA CABALLERA. La perspectiva caballera es un sistema de representación que utiliza la proyección paralela oblicua, en el que las dimensiones del plano proyectante frontal, como las de los
ECUACIONES DE RECTAS Y PLANOS
 ECUACIONES DE RECTAS Y PLANOS Una recta en el plano está determinada cuando se dan dos puntos cualesquiera de la recta, o un punto de la recta y su dirección (su pendiente o ángulo de inclinación). La
ECUACIONES DE RECTAS Y PLANOS Una recta en el plano está determinada cuando se dan dos puntos cualesquiera de la recta, o un punto de la recta y su dirección (su pendiente o ángulo de inclinación). La
Sistema Diédrico (II). Superficies poliédricas y radiadas. Secciones
 Sistema Diédrico (II). Superficies poliédricas y radiadas. Secciones En el tema anterior realizamos cambios en las superficies mediante intersecciones y tangencias con rectas o planos. Ahora vamos a ampliar
Sistema Diédrico (II). Superficies poliédricas y radiadas. Secciones En el tema anterior realizamos cambios en las superficies mediante intersecciones y tangencias con rectas o planos. Ahora vamos a ampliar
22 CURVAS CÓNICAS- HIPÉRBOLAS
 22 CURVAS CÓNICAS- HIPÉRBOLAS 22.1 Características generales. La hipérbola se obtiene al cortar la superficie cónica por un plano paralelo al eje que corta las dos hojas de la cónica. 22.2 Focos y directrices.
22 CURVAS CÓNICAS- HIPÉRBOLAS 22.1 Características generales. La hipérbola se obtiene al cortar la superficie cónica por un plano paralelo al eje que corta las dos hojas de la cónica. 22.2 Focos y directrices.
Clases de proyecciones
 REPRESENTACIÓN GRÁFICA VISTAS DE UNA PIEZA 1.Introducción Los sistemas de representación están basados en la proyección de objetos, situados en el espacio, sobre un plano de proyección en el papel. La
REPRESENTACIÓN GRÁFICA VISTAS DE UNA PIEZA 1.Introducción Los sistemas de representación están basados en la proyección de objetos, situados en el espacio, sobre un plano de proyección en el papel. La
EJERCICIOS DE REPASO DE MATEMÁTICAS I PENDIENTES
 EJERCICIOS DE REPASO DE MATEMÁTICAS I PENDIENTES 1 er PARCIAL 1. Obtén los valores reales que cumplen las siguientes condiciones: x+ x 3 5 x 1/ =1. Opera y expresa el resultado en notación científic (5,
EJERCICIOS DE REPASO DE MATEMÁTICAS I PENDIENTES 1 er PARCIAL 1. Obtén los valores reales que cumplen las siguientes condiciones: x+ x 3 5 x 1/ =1. Opera y expresa el resultado en notación científic (5,
Visualización y Realismo: Problemas Capítulo 2
 Visualización y Realismo: Problemas Capítulo 2 Carlos Ureña Almagro Curso 2011-12 1 Problema 2.1 Calcula los coeficientes de la ecuación implícita de la recta que pasa por los puntos p 0 y p 1 Y p 0 p
Visualización y Realismo: Problemas Capítulo 2 Carlos Ureña Almagro Curso 2011-12 1 Problema 2.1 Calcula los coeficientes de la ecuación implícita de la recta que pasa por los puntos p 0 y p 1 Y p 0 p
Una construcción del centro de curvatura en cónicas
 Una construcción del centro de curvatura en cónicas Previamente tratamos unos hechos relativos a transformaciones de curvas y proyectividades entre sus elementos, que nos sentarán las bases para las construcciones
Una construcción del centro de curvatura en cónicas Previamente tratamos unos hechos relativos a transformaciones de curvas y proyectividades entre sus elementos, que nos sentarán las bases para las construcciones
Es la elipse el conjunto de puntos fijos cuya suma de distancias a dos puntos fijos llamados focos es constante.
 ESQUEMA LAS CÓNICAS LA PARÁBOLA ECUACIONES DE LA PARÁBOLA ECUACIÓN DE LA TANGENTE A UNA PARÁBOLA ELIPSE ECUACIONES DE LA ELIPSE PROPIEDADES DE LA ELIPSE LA HIPÉRBOLA ECUACIONES DE LA HIPÉRBOLA 10 ASÍNTOTAS
ESQUEMA LAS CÓNICAS LA PARÁBOLA ECUACIONES DE LA PARÁBOLA ECUACIÓN DE LA TANGENTE A UNA PARÁBOLA ELIPSE ECUACIONES DE LA ELIPSE PROPIEDADES DE LA ELIPSE LA HIPÉRBOLA ECUACIONES DE LA HIPÉRBOLA 10 ASÍNTOTAS
Materia: Matemática de 5to Tema: Ecuación vectorial. Marco Teórico
 Materia: Matemática de 5to Tema: Ecuación vectorial Marco Teórico Como ya sabemos y = mx + b es la forma pendiente-intersección de una recta. Mientras que esta ecuación funciona bien en el espacio de dos
Materia: Matemática de 5to Tema: Ecuación vectorial Marco Teórico Como ya sabemos y = mx + b es la forma pendiente-intersección de una recta. Mientras que esta ecuación funciona bien en el espacio de dos
Dibujo Técnico Curvas cónicas-parábola
 22. CURVAS CÓNICAS-PARÁBOLAS 22.1. Características generales. Las curvas cónicas son las secciones planas de un cono de revolución. El cono de revolución es la superficie que genera una recta r al girar
22. CURVAS CÓNICAS-PARÁBOLAS 22.1. Características generales. Las curvas cónicas son las secciones planas de un cono de revolución. El cono de revolución es la superficie que genera una recta r al girar
Respuestas ejercicios edición 2007 Sección 3.3: Transformación de coordenadas Ejercicio 3-1
 Editorial Mc Graw Hill. Edición 007 Respuestas ejercicios edición 007 Sección 3.3: Transformación de coordenadas Ejercicio 3-1 a) Simetría respecto de ambos ejes y respecto del origen. b) Simetría respecto
Editorial Mc Graw Hill. Edición 007 Respuestas ejercicios edición 007 Sección 3.3: Transformación de coordenadas Ejercicio 3-1 a) Simetría respecto de ambos ejes y respecto del origen. b) Simetría respecto
Producto Escalar. AMD Grado en Ingeniería Informática. AMD Grado en Ingeniería Informática (UM) Producto Escalar 1 / 31
 Producto Escalar AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Producto Escalar 1 / 31 Objetivos Al finalizar este tema tendrás que: Saber usar el producto escalar. Calcular
Producto Escalar AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Producto Escalar 1 / 31 Objetivos Al finalizar este tema tendrás que: Saber usar el producto escalar. Calcular
- EJERCICIOS DE AMPLIACION DE GEOMETRIA - Curso 04-05
 - EJERCICIOS DE AMPLIACION DE GEOMETRIA - Curso 04-05 Nota previa: Los primeros 18 ejercicios constituyen un repaso de los conceptos de la asignatura GEOMETRIA, que se utilizarán profusamente a lo largo
- EJERCICIOS DE AMPLIACION DE GEOMETRIA - Curso 04-05 Nota previa: Los primeros 18 ejercicios constituyen un repaso de los conceptos de la asignatura GEOMETRIA, que se utilizarán profusamente a lo largo
Respuestas faltantes en ejercicios edición 2007 Sección 4.4: Superficie cuadráticas de revolución Ejercicio 4-1
 Editorial Mc Graw Hill. Edición 007 Respuestas faltantes en ejercicios edición 007 Sección 4.4: Superficie cuadráticas de revolución Ejercicio 4- R r + x + y Ejercicio 4-3 + R x + y + z Ecuaciones: x +
Editorial Mc Graw Hill. Edición 007 Respuestas faltantes en ejercicios edición 007 Sección 4.4: Superficie cuadráticas de revolución Ejercicio 4- R r + x + y Ejercicio 4-3 + R x + y + z Ecuaciones: x +
GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA
 ESCUELA PREPARATORIA OFICIAL No. 268 GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA Profra: Citlalli Artemisa García García 1) Qué es la pendiente? 2) Cómo es la pendiente de rectas
ESCUELA PREPARATORIA OFICIAL No. 268 GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA Profra: Citlalli Artemisa García García 1) Qué es la pendiente? 2) Cómo es la pendiente de rectas
D1 Generalidades: El punto
 El sistema diédrico D1 Generalidades: El punto Generalidades Proyección ortogonal de un punto sobre un plano Proyección ortogonal o, simplemente proyección de un punto sobre un plano, es el pie de la perpendicular
El sistema diédrico D1 Generalidades: El punto Generalidades Proyección ortogonal de un punto sobre un plano Proyección ortogonal o, simplemente proyección de un punto sobre un plano, es el pie de la perpendicular
SECCIONES CÓNICAS (1)Determinar y graficar el lugar geométrico de los puntos que equidistan de F(0, 2) y de la recta
 LOS EJERCICIOS DEBEN RESOLVERSE TAMBIÉN USANDO SOFTWARE MATEMÁTICO. LAS ECUACIONES PEDIDAS SON, EN TODOS LOS CASOS, LAS CANÓNICAS Y LAS PARAMÉTRICAS. I) GEOMETRÍA ANALÍTICA EN EL PLANO 1. Determinar y
LOS EJERCICIOS DEBEN RESOLVERSE TAMBIÉN USANDO SOFTWARE MATEMÁTICO. LAS ECUACIONES PEDIDAS SON, EN TODOS LOS CASOS, LAS CANÓNICAS Y LAS PARAMÉTRICAS. I) GEOMETRÍA ANALÍTICA EN EL PLANO 1. Determinar y
Tema 3: Transformaciones Geométricas
 J. Ribelles SIE020: Síntesis de Imagen y Animación Institute of New Imaging Technologies, Universitat Jaume I Contenido Introducción 1 Introducción 2 Traslación Escalado Rotación 3 4 5 6 Introducción Por
J. Ribelles SIE020: Síntesis de Imagen y Animación Institute of New Imaging Technologies, Universitat Jaume I Contenido Introducción 1 Introducción 2 Traslación Escalado Rotación 3 4 5 6 Introducción Por
A pesar de la importancia de las cónicas como secciones de una superficie cónica, para estudiar los elementos y propiedades de cada una de ellas en
 SECCIONES CÓNICAS Las secciones cónicas se pueden definir como lugares geométricos en el plano, sin embargo la definición clásica de las cónicas, que se debe a Apolonio de Perga, se hizo mediante un procedimiento
SECCIONES CÓNICAS Las secciones cónicas se pueden definir como lugares geométricos en el plano, sin embargo la definición clásica de las cónicas, que se debe a Apolonio de Perga, se hizo mediante un procedimiento
Interpretación geométrica de la derivada
 Interpretación geométrica de la derivada El matemático francés ierre de Fermat (60 665) al estudiar máimos mínimos de ciertas funciones observó que en aquellos puntos en los que la curva presenta un máimo
Interpretación geométrica de la derivada El matemático francés ierre de Fermat (60 665) al estudiar máimos mínimos de ciertas funciones observó que en aquellos puntos en los que la curva presenta un máimo
AXONOMETRÍA OBLICUA: PERSPECTIVA CABALLERA
 AXONOMETRÍA OBLICUA: PERSPECTIVA CABALLERA OBJETIVOS Conocer y analizar los fundamentos de los sistemas de proyección cilíndrica oblicua, diferenciando la perspectiva caballera frontal de la perspectiva
AXONOMETRÍA OBLICUA: PERSPECTIVA CABALLERA OBJETIVOS Conocer y analizar los fundamentos de los sistemas de proyección cilíndrica oblicua, diferenciando la perspectiva caballera frontal de la perspectiva
EJERCICIOS DE GEOMETRÍA
 EJERCICIOS DE GEOMETRÍA 1. Se consideran las rectas r x 2 = 0 x 2z = 1, s y + 3 = 0 y + z = 3 a) Estudiar la posición relativa de r y s. b) Hallar la mínima distancia entre ambas. Se pide: Sol: Se cruzan
EJERCICIOS DE GEOMETRÍA 1. Se consideran las rectas r x 2 = 0 x 2z = 1, s y + 3 = 0 y + z = 3 a) Estudiar la posición relativa de r y s. b) Hallar la mínima distancia entre ambas. Se pide: Sol: Se cruzan
x-z = 0 x+y+2 = [2012] [SEP-B] Halla el punto simétrico del P(2,1,-5) respecto de la recta r definida por
![x-z = 0 x+y+2 = [2012] [SEP-B] Halla el punto simétrico del P(2,1,-5) respecto de la recta r definida por x-z = 0 x+y+2 = [2012] [SEP-B] Halla el punto simétrico del P(2,1,-5) respecto de la recta r definida por](/thumbs/75/72263763.jpg) 1. [01] [SEP-B] Halla el punto simétrico del P(,1,-5) respecto de la recta r definida por x-z = 0 x+y+ = 0.. [01] [SEP-A] Sean los puntos A(0,0,1), B(1,0,-1), C(0,1,-) y D(1,,0). a) Halla la ecuación del
1. [01] [SEP-B] Halla el punto simétrico del P(,1,-5) respecto de la recta r definida por x-z = 0 x+y+ = 0.. [01] [SEP-A] Sean los puntos A(0,0,1), B(1,0,-1), C(0,1,-) y D(1,,0). a) Halla la ecuación del
1. Obtener las coordenadas cartesianas del punto B simétrico del punto A(5,30 ), respecto al polo.
 SEMESTRE 018-1 SERIE CURVAS EN EL PLANO POLAR 1. Obtener las coordenadas cartesianas del punto B simétrico del punto A(5,30 ), respecto al polo.. Determinar las coordenadas polares del punto C simétrico
SEMESTRE 018-1 SERIE CURVAS EN EL PLANO POLAR 1. Obtener las coordenadas cartesianas del punto B simétrico del punto A(5,30 ), respecto al polo.. Determinar las coordenadas polares del punto C simétrico
1.2. VECTOR DE POSICIÓN. VELOCIDAD Y ACELERACIÓN
 1.2. VECTOR DE POSICIÓN. VELOCIDAD Y ACELERACIÓN 1.2.1. Supuesto el vector de posición de un punto en el espacio: r = 2i-6j+4k, la mejor representación de dicho vector de todas las dadas es la: a) A b)
1.2. VECTOR DE POSICIÓN. VELOCIDAD Y ACELERACIÓN 1.2.1. Supuesto el vector de posición de un punto en el espacio: r = 2i-6j+4k, la mejor representación de dicho vector de todas las dadas es la: a) A b)
FUNCIONES ELEMENTALES
 FUNCIONES ELEMENTALES FUNCIONES POLINÓMICAS.- Son aquellas cuya expresión algebraica es un polinomio. El grado del polinomio es el grado de la función polinómica. Ejemplos.- f ( x) = 3 g ( x) = x + 1 h
FUNCIONES ELEMENTALES FUNCIONES POLINÓMICAS.- Son aquellas cuya expresión algebraica es un polinomio. El grado del polinomio es el grado de la función polinómica. Ejemplos.- f ( x) = 3 g ( x) = x + 1 h
TEMAS 6 Y 7 GEOMETRÍA EN EL ESPACIO
 Ejercicios Selectividad Temas 6 y 7 Geometría en el espacio Mate II 2º Bach. 1 TEMAS 6 Y 7 GEOMETRÍA EN EL ESPACIO EJERCICIO 1 : Julio 11-12. Optativa (3 ptos) Para los puntos A(1,0,2) y B(-1,2,4) y la
Ejercicios Selectividad Temas 6 y 7 Geometría en el espacio Mate II 2º Bach. 1 TEMAS 6 Y 7 GEOMETRÍA EN EL ESPACIO EJERCICIO 1 : Julio 11-12. Optativa (3 ptos) Para los puntos A(1,0,2) y B(-1,2,4) y la
Coordenadas polares. Si P es un punto cualquiera del plano, su posición queda determinada con el par ( r, ), donde: Ejemplo
 Coordenadas polares Sobre el plano elijamos un punto O, que denominamos Polo (u origen) y un rayo con origen O, que denominamos Eje Polar 1 2 Si P es un punto cualquiera del plano, su posición queda determinada
Coordenadas polares Sobre el plano elijamos un punto O, que denominamos Polo (u origen) y un rayo con origen O, que denominamos Eje Polar 1 2 Si P es un punto cualquiera del plano, su posición queda determinada
Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás
 Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás de mayo de 013 Capítulo 1 Año 011 1.1. Modelo 011 - Opción A Problema 1.1.1 (3 puntos) Dado el sistema: λx
Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás de mayo de 013 Capítulo 1 Año 011 1.1. Modelo 011 - Opción A Problema 1.1.1 (3 puntos) Dado el sistema: λx
INDICE. 88 determinante 36. Familias de líneas rectas Resumen de resultados 96 Capitulo IV
 INDICE Geometría Analítica Plana Capitulo Primero Artículo 1. Introducción 1 2. Segmento rectilíneo dirigido 1 3. Sistema coordenado lineal 3 4. Sistema coordenado en el plano 5 5. Carácter de la geografía
INDICE Geometría Analítica Plana Capitulo Primero Artículo 1. Introducción 1 2. Segmento rectilíneo dirigido 1 3. Sistema coordenado lineal 3 4. Sistema coordenado en el plano 5 5. Carácter de la geografía
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2011 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 0 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio 4, Opción A Reserva, Ejercicio 4,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 0 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio 4, Opción A Reserva, Ejercicio 4,
