Control y programación de robots
|
|
|
- María Ángeles Salas Villalba
- hace 7 años
- Vistas:
Transcripción
1 Control y programación de robots 8. Cinemática directa robots seriales: Screws sucesivos 8.
2 Objetivo
3 Fórmula de Rodriguez espacial s ($), eje screw p2 sp t θ r p2 y2 pr 2 p r2 Bθ z2 p z t θ s x A x2 r = p - s r2 = p 2 - s - ts A p = A R B Bp + A q A p = A A B B p y t Paso λ = θ
4 Método de desplazamientos screws sucesivos r = p - s Remplazando las anteriores expresiones en la formula de Rodrígues, obtenemos: r2 = p 2 - s - ts a = (s 2x - )( - cθ ) + A A p = RB p + q A B A p = A A B B p a 2 = s x s y ( - cθ ) s z sθ a 3 = s x s z ( - cθ ) + s ysθ a 2 = s ys x ( - cθ ) + s z sθ a 22 = (s 2y - )( - cθ ) + a + a 22 + a33 ) 2 a32 a 23 Sx = 2 sin(θ ) a3 a3 Sy = 2 sin(θ ) a 2 a2 Sz = 2 sin(θ ) θ = cos - ( SoT S = a 23 = s ys z ( - cθ ) s x sθ a 3 = s zs x ( - cθ ) s ysθ a 32 = s z s y ( - cθ ) + s x sθ a 33 = (s 2z - )( - cθ ) + a 4 = ts x - s x (a - ) - s y a 2 - s z a3 a 24 = ts y - s x a 2 - s y (a 22 - ) - s z a 23 a 34 = ts z - s x a 3 - s y a 32 - s z (a 33 - ) a 4 = a 42 = a 43 = ; a 44 =
5 Cinemática directa screws sucesivos P Creo la matriz de transf. Homogénea entre dos cuerpos a partir de: So= vector al eje de giro S= vector unitario del eje de giro Theta= angulo de giro alrededor de S t= translación a lo largo de S P P = T3 P 3
6 Cinemática directa screws sucesivos Para el movimiento del cuerpo 3 con relación al 2, identificar: So= vector al eje de giro S= vector unitario del eje de giro Theta= ángulo de giro alrededor de S t= translación a lo largo de S Generar la matriz 2 P = T3 P 2 3
7 Cinemática directa screws sucesivos Para el movimiento del cuerpo 2 con relación al, identificar: So= vector al eje de giro S= vector unitario del eje de giro Theta= ángulo de giro alrededor de S t= translación a lo largo de S Generar la matriz P = T2 P 2
8 Cinemática directa screws sucesivos Para el movimiento del cuerpo con relación al, identificar: So= vector al eje de giro S= vector unitario del eje de giro Theta= ángulo de giro alrededor de S t= translación a lo largo de S Generar la matriz P = T P
9 Ejemplo de un robot serial Halle las matrices de transformación homogénea para las articulaciones del siguiente robot Posición de referencia Primero identificamos una configuración de referencia del efector final, con respecto a la cual deben ser medidos las rotaciones y desplazamientos del robot
10 Ejemplo de un robot serial Construimos la tabla de los vectores si y soi Posición de referencia Joint si (,, ) 2 (, -, ) 3 (, -, ) 4 (, -, ) 5 (,, ) 6 (,, ) si (,, ) (,, ) (a2,, ) (a2 + a3,, ) (a2 + a3 + a4,, ) (,, )
11 Ejemplo del calculo de la submatriz de rotación de la primera transformada homogénea Para la configuración escogida asignamos los vectores unitarios s ($), s2 ($2), s2 ($2). y construimos la siguiente tabla. Posición de referencia Joint 2 3 si (,, ) (, -, ) (, -, )
12 Ejemplo de un robot serial Por ejemplo, para la primera matriz de rotación, reemplazando de la tabla anterior, tenemos: a = ( s x2 ) * ( cθ ) + a = ( ) * ( cθ ) + = cθ a2 = s x s y ( cθ ) s z sθ a2 = * * ( cθ ) * sθ = sθ a3 = s x s z ( cθ ) + s y sθ a3 = ** ( cθ ) + * sθ = a2 = s y s x ( cθ ) + s z sθ a2 = * * ( cθ ) + * sθ = sθ a22 = ( s y2 )( cθ ) + a22 = ( ) * ( cθ ) + = cθ a23 = s y s z ( cθ ) s x sθ a23 = ** (( cθ ) * sθ = a3 = s z s x ( cθ ) s y sθ a3 = * ( cθ ) * sθ a32 = s z s y ( cθ ) + s x sθ a32 = * * (( cθ ) * sθ = a33 = ( s z ) * ( cθ ) + a33 = (2 ) * ( cθ ) + = 2 cθ R = sθ. sθ. cθ...
13 Ejemplo de un robot serial: Matrices de transformación Nótese que tsi = [tsx tsy tsz]: ts = [ ], ts2 = [ ], ts3 = [a2 ] a = (s 2x - )( - cθ ) + a 2 = s x s y ( - cθ ) s zsθ a 3 = s x s z ( - cθ ) + s ysθ a 2 = s ys x ( - cθ ) + s z sθ a 22 = (s 2y - )( - cθ ) + a 23 = s ys z ( - cθ ) s x sθ a 3 = s z s x ( - cθ ) s ysθ a 32 = s z s y ( - cθ ) + s x sθ a 33 = (s 2z - )( - cθ ) + a 4 = ts x - s x (a - ) - s y a 2 - s z a3 a 24 = ts y - s x a 2 - s y (a 22 - ) - s z a 23 a 34 = ts z - s x a 3 - s y a 32 - s z (a 33 - ) a 4 = a 42 = a 43 = ; a 44 =
14 Ejemplo de un robot serial: Matrices de transformación Nótese que tsi = [tsx tsy tsz]: ts4 = [a2+ a3 ], ts5 = [a2+ a3+a4 ] ts6 = [ ] a = (s 2x - )( - cθ ) + a 2 = s x s y ( - cθ ) s zsθ a 3 = s x s z ( - cθ ) + s ysθ a 2 = s ys x ( - cθ ) + s z sθ a 22 = (s 2y - )( - cθ ) + a 23 = s ys z ( - cθ ) s x sθ a 3 = s z s x ( - cθ ) s ysθ a 32 = s z s y ( - cθ ) + s x sθ a 33 = (s 2z - )( - cθ ) + a 4 = ts x - s x (a - ) - s y a 2 - s z a3 a 24 = ts y - s x a 2 - s y (a 22 - ) - s z a 23 a 34 = ts z - s x a 3 - s y a 32 - s z (a 33 - ) a 4 = a 42 = a 43 = ; a 44 =
15 Tarea Hallar las matrices de transformación homogénea del siguiente robot SCARA
16 Tarea Hallar las matrices de transformación homogénea del siguiente robot SCARA $ S So theta P = T4 P 4 P =?? 4 Posición de ref. del efector final d
17 Tarea Hallar las matrices de transformación homogénea del siguiente robot SCARA $ S So theta d,,,, theta 2,,,a, theta2 3,,,a+a2, d3 4,,,a+a2, theta4 6 P =?? Posición de ref. del efector final
18 Ejemplo de un robot serial: Matrices de transformación Hallar las matrices de transformación: robot STANFORD
19 Ejemplo de un robot serial: Matrices de transformación Hallar las matrices de transformación: robot STANFORD P =T2 2 P P = T6 P 6 P =?? θ i ti = d i θ θ2 d3 θ4 θ5 θ6 6 Posición de ref. del efector final
20 Ejemplo de un robot serial: Matrices de transformación Hallar las matrices de transformación: robot STANFORD 6 P =??
21 Práctica Cinemática directa screws sucesivos Robot espacial 3-dof Para un dado robot entregar un archivo de word con: Tabla rellena matriz de transf. Hom. Simbólica: generada en un programa en Matlab que reciba: S_i, So_i, theta_i, d_i Grafico en 3d del robot (plot en Matlab) dados: los valores de theta_i=3deg, a_i=4,2, etc. $ S 2 3 So theta d Pos.Ref. Efector
22 Práctica Cinemática directa screws sucesivos Robot espacial Scorbot Para un dado robot entregar un $ archivo de word con: Tabla rellena matriz de transf. Hom. Simbólica: generada en un programa en Matlab que reciba: S_i, So_i, theta_i, d_i Grafico en 3d del robot (plot en Matlab) dados: los valores de theta_i=3deg, a_i=,4,4, d_5=. S So theta d Pos.Ref. Efector
23 Práctica Cinemática directa screws sucesivos Robot KUKA Para un dado robot entregar un archivo de word con: Tabla rellena matriz de transf. Hom. Simbólica: generada en un programa en Matlab que reciba: S_i, So_i, theta_i, d_i Grafico en 3d del robot (plot en Matlab) dados: los valores de theta_i=3deg, a_i=4,2etc. $ S So theta d Pos.Ref. Efector
24 Práctica Cinemática directa screws sucesivos Robot PUMA Staubli Para un dado robot entregar un archivo de word con: Tabla rellena matriz de transf. Hom. Simbólica: generada en un programa en Matlab que reciba: S_i, So_i, theta_i, d_i Grafico en 3d del robot (plot en Matlab) dados: los valores de theta_i=3deg, a_i= proporcional al dibujo. $ S So theta d Pos.Ref. Efector
UNIVERSIDAD DON BOSCO VICERRECTORÍA DE ESTUDIOS DE POSTGRADO
 UNIVERSIDAD DON BOSCO VICERRECTORÍA DE ESTUDIOS DE POSTGRADO MAESTRÍA EN MANUFACTURA INTEGRADA POR COMPUTADORA ROBÓTICA INTEGRADA A LA MANUFACTURA Catedrático: Mg Manuel Napoleón Cardona Gutiérrez GUÍA
UNIVERSIDAD DON BOSCO VICERRECTORÍA DE ESTUDIOS DE POSTGRADO MAESTRÍA EN MANUFACTURA INTEGRADA POR COMPUTADORA ROBÓTICA INTEGRADA A LA MANUFACTURA Catedrático: Mg Manuel Napoleón Cardona Gutiérrez GUÍA
Análisis Cinemático Directo del Robot RV-2AJ de Mitsubishi Utilizando Teoría de Screws
 1 Análisis Cinemático Directo del Robot RV-2AJ de Mitsubishi Utilizando Teoría de Screws Luis Villalobos, Karen Pimentel, Oscar Rivera, Manuel Cardona Facultad de Ingeniería, Universidad Don Bosco, El
1 Análisis Cinemático Directo del Robot RV-2AJ de Mitsubishi Utilizando Teoría de Screws Luis Villalobos, Karen Pimentel, Oscar Rivera, Manuel Cardona Facultad de Ingeniería, Universidad Don Bosco, El
Cinemática del robot
 Cinemática del robot Cinemática del robot La cinemática del robot estudia el movimiento del mismo con respecto a un sistema de referencia. La cinemática se interesa por la descripción analítica del movimiento
Cinemática del robot Cinemática del robot La cinemática del robot estudia el movimiento del mismo con respecto a un sistema de referencia. La cinemática se interesa por la descripción analítica del movimiento
Control y programación de robots
 Control y programación de robots 11. Solución cinemática inversa y directa de robots seriales 11.1 El alumno, tras recibir y estudiar esta clase, debe ser capaz de: Comprender el modelado de la cinemática
Control y programación de robots 11. Solución cinemática inversa y directa de robots seriales 11.1 El alumno, tras recibir y estudiar esta clase, debe ser capaz de: Comprender el modelado de la cinemática
CINEMÁTICA DEL ROBOT
 CINEMÁTICA DEL ROBOT Cinemática Directa Cinemática Inversa Matriz Jacobiana 1 Problema cinemático del robot Cinemática del robot: Estudio de su movimiento con respecto a un sistema de referencia: Descripción
CINEMÁTICA DEL ROBOT Cinemática Directa Cinemática Inversa Matriz Jacobiana 1 Problema cinemático del robot Cinemática del robot: Estudio de su movimiento con respecto a un sistema de referencia: Descripción
ANALISIS CINEMATICO DIRECTO E INVERSO
 ANALISIS CINEMATICO DIRECTO E INVERSO Cinematica directa x=f(q) [x,y,z] Articulaciones Posicion de la Herramienta Cinematica Inversa q=f -1 (x) El analisis cinematico inverso nos permite calcular la posicion
ANALISIS CINEMATICO DIRECTO E INVERSO Cinematica directa x=f(q) [x,y,z] Articulaciones Posicion de la Herramienta Cinematica Inversa q=f -1 (x) El analisis cinematico inverso nos permite calcular la posicion
Dr. Roberto Carlos García Gómez
 Dr. Roberto Carlos García Gómez La cinemática del robot estudia el movimiento del mismo con respecto a un sistema de referencia. La cinemática se interesa por la descripción analítica del movimiento espacial
Dr. Roberto Carlos García Gómez La cinemática del robot estudia el movimiento del mismo con respecto a un sistema de referencia. La cinemática se interesa por la descripción analítica del movimiento espacial
Robótica Industrial. Robótica Industrial
 TEMA 4: CINEMÁTICA DEL ROBOT Ingeniería de Sistemas y Automática Control de Robots y Sistemas Sensoriales Robótica Industrial Robótica Industrial ISA.- Ingeniería de Sistemas y Automática Cinemática del
TEMA 4: CINEMÁTICA DEL ROBOT Ingeniería de Sistemas y Automática Control de Robots y Sistemas Sensoriales Robótica Industrial Robótica Industrial ISA.- Ingeniería de Sistemas y Automática Cinemática del
PARÁMETROS DE DENAVIT-HARTENBERG. Cristina Castejón
 PARÁMETROS DE DENAVIT-HARTENBERG Cristina Castejón Conceptos de robótica Cadena cinemática abierta formada por eslabones y articulaciones: Rotación Prismáticas Estudio cinemático Estudio dinámico Conceptos
PARÁMETROS DE DENAVIT-HARTENBERG Cristina Castejón Conceptos de robótica Cadena cinemática abierta formada por eslabones y articulaciones: Rotación Prismáticas Estudio cinemático Estudio dinámico Conceptos
Capacitación Tecnológica Científica para Bolivia. Introducción al modelado de robots
 Catecbol Capacitación Tecnológica Científica para Bolivia www.catecbol.com facebook.com/catecbol @catecbol [email protected] Introducción al modelado de robots Ronald Terrazas Mallea Bélgica La unión
Catecbol Capacitación Tecnológica Científica para Bolivia www.catecbol.com facebook.com/catecbol @catecbol [email protected] Introducción al modelado de robots Ronald Terrazas Mallea Bélgica La unión
CINEMÁTICA Y DINÁMICA DE ROBOTS MANIPULADORES: RESPUESTAS DE EJERCICIOS UNIDAD 03. Roger Miranda Colorado
 CINEMÁTICA Y DINÁMICA DE ROBOTS MANIPULADORES: RESPUESTAS DE EJERCICIOS UNIDAD 03 Roger Miranda Colorado 23 de mayo de 2016 Índice 1. RESPUESTAS DE EJERCICIOS UNIDAD 03 1 1. RESPUESTAS DE EJERCICIOS UNIDAD
CINEMÁTICA Y DINÁMICA DE ROBOTS MANIPULADORES: RESPUESTAS DE EJERCICIOS UNIDAD 03 Roger Miranda Colorado 23 de mayo de 2016 Índice 1. RESPUESTAS DE EJERCICIOS UNIDAD 03 1 1. RESPUESTAS DE EJERCICIOS UNIDAD
UNIVERSIDAD DON BOSCO ROBÓTICA INTEGRADA A LA MANUFACTURA
 Mathematical tools: Denavit, Hartenberg and Screws, applied to direct cinematic analysis of the Mitsubishi Sergio Miguel García Perez, Master Student Computer Integrated Manufacturing, Don Bosco University,
Mathematical tools: Denavit, Hartenberg and Screws, applied to direct cinematic analysis of the Mitsubishi Sergio Miguel García Perez, Master Student Computer Integrated Manufacturing, Don Bosco University,
TSTC. Dpt. Teoría de la Señal, Telemática y Comunicaciones Tema 2 CINEMÁTICA DE MANIPULADORES
 Dpt. Teoría de la Señal, Telemática y Comunicaciones Tema 2 CINEMÁTICA DE MANIPULADORES Secciones 1. Introducción. 2. Coordenadas y Transformaciones Homogéneas. 3. Problema Cinemático Directo. Método de
Dpt. Teoría de la Señal, Telemática y Comunicaciones Tema 2 CINEMÁTICA DE MANIPULADORES Secciones 1. Introducción. 2. Coordenadas y Transformaciones Homogéneas. 3. Problema Cinemático Directo. Método de
Cinemática Directa. Facultad de Cs. de la Computación. Juan Carlos Conde Ramírez. Computer Animation
 Cinemática Directa Facultad de Cs. de la Computación Juan Carlos Conde Ramírez Computer Animation Contenido 1 Introducción 2 Transformaciones homogéneas 3 Cinemática directa 4 Método Denavit-Hartenberg
Cinemática Directa Facultad de Cs. de la Computación Juan Carlos Conde Ramírez Computer Animation Contenido 1 Introducción 2 Transformaciones homogéneas 3 Cinemática directa 4 Método Denavit-Hartenberg
Problema Cinemático Directo
 Problema Cinemático Directo Parámetros Denavit-Hartenberg Denavit-Hartenberg notación Craig Denavit-Hartenberg notación Craig Denavit-Hartenberg notación Craig Denavit-Hartenberg notación Craig Denavit-Hartenberg
Problema Cinemático Directo Parámetros Denavit-Hartenberg Denavit-Hartenberg notación Craig Denavit-Hartenberg notación Craig Denavit-Hartenberg notación Craig Denavit-Hartenberg notación Craig Denavit-Hartenberg
Fundamentos de Robótica
 Fundamentos de Robótica Introducción a la cinemática de manipuladores [email protected] http://scfi.uaemex.mx/hamontes 1 Recomendación No use estas diapositivas como referencia única de estudio durante
Fundamentos de Robótica Introducción a la cinemática de manipuladores [email protected] http://scfi.uaemex.mx/hamontes 1 Recomendación No use estas diapositivas como referencia única de estudio durante
PRÓLOGO PREFACIO... 21
 ÍNDICE PRÓLOGO... 17 PREFACIO... 21 CAPÍTULO 1. ENTORNO ACTUAL Y PERSPECTIVAS... 27 1.1 ORGANIZACIÓN DE UN SISTEMA ROBÓTICO... 29 1.2 ENTORNOS MATLAB Y SIMULINK... 31 1.3 TENDENCIAS EN ROBÓTICA Y MECATRÓNICA...
ÍNDICE PRÓLOGO... 17 PREFACIO... 21 CAPÍTULO 1. ENTORNO ACTUAL Y PERSPECTIVAS... 27 1.1 ORGANIZACIÓN DE UN SISTEMA ROBÓTICO... 29 1.2 ENTORNOS MATLAB Y SIMULINK... 31 1.3 TENDENCIAS EN ROBÓTICA Y MECATRÓNICA...
Fundamentos de Robótica
 Fundamentos de Robótica Cinemática Directa Ricardo-Franco Mendoza-Garcia [email protected] Escuela Universitaria de Ingeniería Mecánica Universidad de Tarapacá Arica, Chile July 9, 2014 R. F. Mendoza-Garcia
Fundamentos de Robótica Cinemática Directa Ricardo-Franco Mendoza-Garcia [email protected] Escuela Universitaria de Ingeniería Mecánica Universidad de Tarapacá Arica, Chile July 9, 2014 R. F. Mendoza-Garcia
Coordenadas Homogéneas y Transformaciones
 Computación Gráfica I Coordenadas Homogéneas y Transformaciones Daniel Fariña 06-39509 Laura Libretti 06-39796 Transformaciones Las transformaciones se usan para: o Posicionar objetos en escena o Cambiar
Computación Gráfica I Coordenadas Homogéneas y Transformaciones Daniel Fariña 06-39509 Laura Libretti 06-39796 Transformaciones Las transformaciones se usan para: o Posicionar objetos en escena o Cambiar
CINEMÁTICA Y DINÁMICA DE ROBOTS MANIPULADORES: RESPUESTAS DE EJERCICIOS UNIDAD 02. Roger Miranda Colorado
 CINEMÁTICA Y DINÁMICA DE ROBOTS MANIPULADORES: RESPUESTAS DE EJERCICIOS UNIDAD Roger Miranda Colorado de mayo de 6 Índice. RESPUESTAS DE EJERCICIOS UNIDAD . RESPUESTAS DE EJERCICIOS UNIDAD A continuación
CINEMÁTICA Y DINÁMICA DE ROBOTS MANIPULADORES: RESPUESTAS DE EJERCICIOS UNIDAD Roger Miranda Colorado de mayo de 6 Índice. RESPUESTAS DE EJERCICIOS UNIDAD . RESPUESTAS DE EJERCICIOS UNIDAD A continuación
Visión artificial y Robótica Geometría. Depto. de Ciencia de la Computación e Inteligencia Artificial
 Visión artificial y Robótica Geometría Depto. de Ciencia de la Computación e Inteligencia Artificial Contenidos Geometría 2D y 3D Transformación de coordenadas Calibración de la cámara Álgebra necesaria
Visión artificial y Robótica Geometría Depto. de Ciencia de la Computación e Inteligencia Artificial Contenidos Geometría 2D y 3D Transformación de coordenadas Calibración de la cámara Álgebra necesaria
Introducción. 2.2 Transformaciones de coordenadas: matriz de rotación y ángulos de Euler.
 Agosto 2011 Introducción El análisis cinemático directo nos permite determinar en donde se encuentra el elemento terminal del robot (mano) si se conoce la posición de todas las articulaciones. 15 50 Posición?
Agosto 2011 Introducción El análisis cinemático directo nos permite determinar en donde se encuentra el elemento terminal del robot (mano) si se conoce la posición de todas las articulaciones. 15 50 Posición?
Cinemática del Robot
 Cinemática del Robot La cinemática del robot estudia el movimiento del mismo con respecto a un sistema de referencia. En primer término, la cinemática se interesa por la descripción analítica del movimiento
Cinemática del Robot La cinemática del robot estudia el movimiento del mismo con respecto a un sistema de referencia. En primer término, la cinemática se interesa por la descripción analítica del movimiento
TECNOLÓGICO DE ESTUDIOS SUPERIORES DE ECATEPEC
 TECNOLÓGICO DE ESTUDIOS SUPERIORES DE ECATEPEC DIVISIÓN DE INGENIERÍA ELECTRÓNICA Y TELEMÁTICA PRÁCTICAS DE LABORATORIO ASIGNATURA: ROBÓTICA I REALIZÓ: GERARDO PAZOS RODRÍGUEZ PRESENTACIÓN El presente
TECNOLÓGICO DE ESTUDIOS SUPERIORES DE ECATEPEC DIVISIÓN DE INGENIERÍA ELECTRÓNICA Y TELEMÁTICA PRÁCTICAS DE LABORATORIO ASIGNATURA: ROBÓTICA I REALIZÓ: GERARDO PAZOS RODRÍGUEZ PRESENTACIÓN El presente
Cinemática Directa del Robot. CI-2657 Robótica M.Sc. Kryscia Ramírez Benavides
 M.Sc. Kryscia Ramírez Benavides Introducción Consiste en determinar cual es la posición y orientación del extremo final del robot, con respecto a un sistema de coordenadas que se toma como referencia,
M.Sc. Kryscia Ramírez Benavides Introducción Consiste en determinar cual es la posición y orientación del extremo final del robot, con respecto a un sistema de coordenadas que se toma como referencia,
Robots Autónomos Miguel Cazorla,, Otto Colomina Depto.. Ciencia de la Computación n e I.A. Universidad de Alicante
 Robots Autónomos Miguel Cazorla,, Otto Colomina Depto.. Ciencia de la Computación n e I.A. Universidad de Alicante Este ítem está licenciado bajo Licencia Creative Commons Tema 2: Modelos geométricos y
Robots Autónomos Miguel Cazorla,, Otto Colomina Depto.. Ciencia de la Computación n e I.A. Universidad de Alicante Este ítem está licenciado bajo Licencia Creative Commons Tema 2: Modelos geométricos y
Cinemática inversa, Fanuc LR Mate 200ic
 Cinemática inversa, Fanuc LR Mate 200ic José Guadalupe Zavala Villalpando, Departamento de Ingeniería Mecatrónica Instituto Tecnológico de Celaya [email protected] Sebastián Alfonso Guzmán Blanco,
Cinemática inversa, Fanuc LR Mate 200ic José Guadalupe Zavala Villalpando, Departamento de Ingeniería Mecatrónica Instituto Tecnológico de Celaya [email protected] Sebastián Alfonso Guzmán Blanco,
ROBÓTICA I. Cinemática Directa
 Cinemática Directa M. C. Jorge Luis Barahona Avalos 11 de abril de 2011 Universidad Tecnológica de la Mixteca Instituto de Electrónica y Mecatrónica 1 / 34 Índice General 1 Cinemática Directa 2 Cadena
Cinemática Directa M. C. Jorge Luis Barahona Avalos 11 de abril de 2011 Universidad Tecnológica de la Mixteca Instituto de Electrónica y Mecatrónica 1 / 34 Índice General 1 Cinemática Directa 2 Cadena
GUI y la Robótica. Figura 1. Robot manipulador KUKA KR-16
 RESUMEN GUI y la Robótica Miguel Durán 1, Jorge Gudiño 1, David Bolaños 1, Luís Avendaño 1 (1) Facultad de Ingeniería Electromecánica, Universidad de Colima, Colima (México) ([email protected]) El objetivo
RESUMEN GUI y la Robótica Miguel Durán 1, Jorge Gudiño 1, David Bolaños 1, Luís Avendaño 1 (1) Facultad de Ingeniería Electromecánica, Universidad de Colima, Colima (México) ([email protected]) El objetivo
Fundamentos de Robótica
 Fundamentos de Robótica Herramientas Matemáticas para la Localización Espacial Matrices de Transformación Homogéneas Ricardo-Franco Mendoza-Garcia [email protected] Escuela Universitaria de Ingeniería Mecánica
Fundamentos de Robótica Herramientas Matemáticas para la Localización Espacial Matrices de Transformación Homogéneas Ricardo-Franco Mendoza-Garcia [email protected] Escuela Universitaria de Ingeniería Mecánica
CINEMÁTICA INVERSA DE ROBOTS INDUSTRIALES
 I EMETRE DE 00 CINEMÁTICA INVERA DE ROBOT INDUTRIALE GERMÁN ANDRÉ RAMO FUENTE * 1. Introducción El uso de robots en ambientes industriales, y más precisamente en procesos de manufactura, ha generado toda
I EMETRE DE 00 CINEMÁTICA INVERA DE ROBOT INDUTRIALE GERMÁN ANDRÉ RAMO FUENTE * 1. Introducción El uso de robots en ambientes industriales, y más precisamente en procesos de manufactura, ha generado toda
Fundamentos de Robótica
 Fundamentos de Robótica Cinemática Inversa Ricardo-Franco Mendoza-Garcia [email protected] Escuela Universitaria de Ingeniería Mecánica Universidad de Tarapacá Arica, Chile June 16, 2015 R. F. Mendoza-Garcia
Fundamentos de Robótica Cinemática Inversa Ricardo-Franco Mendoza-Garcia [email protected] Escuela Universitaria de Ingeniería Mecánica Universidad de Tarapacá Arica, Chile June 16, 2015 R. F. Mendoza-Garcia
Solución de problemas III 1
 Solución de problemas III Álgebra II Curso 25-6. Espacio Afín.. Ejercicios Ejercicio.4.3 Encontrar la expresión analítica de las siguientes aplicaciones afines de R 2 : a Giro de centro (, ángulo π/2 b
Solución de problemas III Álgebra II Curso 25-6. Espacio Afín.. Ejercicios Ejercicio.4.3 Encontrar la expresión analítica de las siguientes aplicaciones afines de R 2 : a Giro de centro (, ángulo π/2 b
Control de un Robot Scara de 3 GDL
 Control de un Robot Scara de 3 GDL Jesús Soldevilla ureta Raúl Rivas Jimenez 13 de diciembre de 2010 Resumen El proyecto que se desarrolla en el siguiente informe plantea la aplicación de 4 técnicas de
Control de un Robot Scara de 3 GDL Jesús Soldevilla ureta Raúl Rivas Jimenez 13 de diciembre de 2010 Resumen El proyecto que se desarrolla en el siguiente informe plantea la aplicación de 4 técnicas de
MOVIMIENTOS EN EL PLANO
 Ejercicio nº 1.- MOVIMIENTOS EN EL PLANO a) Aplica una traslación de vector t 3, 2 a las figuras y F. F1 2 b Qué habríamos obtenido en cada caso si, en lugar de aplicar la traslación, hubiéramos aplicado
Ejercicio nº 1.- MOVIMIENTOS EN EL PLANO a) Aplica una traslación de vector t 3, 2 a las figuras y F. F1 2 b Qué habríamos obtenido en cada caso si, en lugar de aplicar la traslación, hubiéramos aplicado
Percepción visual aplicada a la robótica
 Percepción visual aplicada a la robótica Mario I. Chacón Murguía Rafael Sandoval Rodríguez Javier Vega Pineda Selecciona el libro para empezar Capítulo 2 Teoría de robótica Continuar Cinemática de robots
Percepción visual aplicada a la robótica Mario I. Chacón Murguía Rafael Sandoval Rodríguez Javier Vega Pineda Selecciona el libro para empezar Capítulo 2 Teoría de robótica Continuar Cinemática de robots
Cinemática del Robot. UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides
 UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción La cinemática del robot estudia el movimiento del mismo con respecto a un sistema de referencia. Se interesa por la
UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción La cinemática del robot estudia el movimiento del mismo con respecto a un sistema de referencia. Se interesa por la
ROBÓTICA I. Cinemática Directa
 Cinemática Directa M. C. Jorge Luis Barahona Avalos 2 de mayo de 2012 Universidad Tecnológica de la Mixteca Instituto de Electrónica y Mecatrónica 1 / 42 Índice General 1 Cinemática Directa 2 Cadena Cinemática
Cinemática Directa M. C. Jorge Luis Barahona Avalos 2 de mayo de 2012 Universidad Tecnológica de la Mixteca Instituto de Electrónica y Mecatrónica 1 / 42 Índice General 1 Cinemática Directa 2 Cadena Cinemática
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL. Facultad de Ingeniería en Mecánica y Ciencias de la. Producción
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL Facultad de Ingeniería en Mecánica y Ciencias de la Producción Modelo Cinemático Brazo Robótico de cinco grados de libertad para uso didáctico TRABAJO FINAL DE
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL Facultad de Ingeniería en Mecánica y Ciencias de la Producción Modelo Cinemático Brazo Robótico de cinco grados de libertad para uso didáctico TRABAJO FINAL DE
Visión artificial y Robótica Modelos de movimiento y mapas. Depto. de Ciencia de la Computación e Inteligencia Artificial
 Visión artificial y Robótica Modelos de movimiento y mapas Depto. de Ciencia de la Computación e Inteligencia Artificial Contenidos Sistemas de coordenadas Localización de objetos en el espacio Modelos
Visión artificial y Robótica Modelos de movimiento y mapas Depto. de Ciencia de la Computación e Inteligencia Artificial Contenidos Sistemas de coordenadas Localización de objetos en el espacio Modelos
Introducción a la Robótica Mecanismos básicos: cinemática
 Introducción a la Robótica Mecanismos básicos: cinemática Dr José Martínez Carranza [email protected] Coordinación de Ciencias Computacionales, INAOE Cinemática (1) La cinemática es una rama de la Física
Introducción a la Robótica Mecanismos básicos: cinemática Dr José Martínez Carranza [email protected] Coordinación de Ciencias Computacionales, INAOE Cinemática (1) La cinemática es una rama de la Física
Jeferson Corredor Salcedo. Director: Ing. Jorge Andrés García Barbosa Codirector: Ing. Ubaldo García Zaragoza
 IMPLEMENTACIÓN DE NUEVAS TECNOLOGIAS DE TOLERANCIAS GEOMÉTRICAS Y DIMENSIONALES PARA GARANTIZAR LOS REQUERIMIENTOS DE PRECISIÓN EN EL MOMENTO DE EMSAMBLE DE LOS COMPONENTES DEL ROBOT DELTA FIM-USTA. Jeferson
IMPLEMENTACIÓN DE NUEVAS TECNOLOGIAS DE TOLERANCIAS GEOMÉTRICAS Y DIMENSIONALES PARA GARANTIZAR LOS REQUERIMIENTOS DE PRECISIÓN EN EL MOMENTO DE EMSAMBLE DE LOS COMPONENTES DEL ROBOT DELTA FIM-USTA. Jeferson
Cinemática inversa del robot 4 gdl
 obótica y Visión por Computador - UMH Práctica 2 Cinemática inversa del robot gdl Ejemplo Solución del robot cilíndrico de grados de libertad En este caso particular, la solución geométrica es inmediata.
obótica y Visión por Computador - UMH Práctica 2 Cinemática inversa del robot gdl Ejemplo Solución del robot cilíndrico de grados de libertad En este caso particular, la solución geométrica es inmediata.
Cinemática Inversa. Facultad de Cs. de la Computación. Juan Carlos Conde R. Computer Animation
 Cinemática Inversa Facultad de Cs. de la Computación Juan Carlos Conde R. Computer Animation Contenido 1 Introducción 2 Métodos de resolución 3 Solución Geométrica 4 Solución Algebraica 1 / 23 Contenido
Cinemática Inversa Facultad de Cs. de la Computación Juan Carlos Conde R. Computer Animation Contenido 1 Introducción 2 Métodos de resolución 3 Solución Geométrica 4 Solución Algebraica 1 / 23 Contenido
CAPÍTULO 2 Modelado y Transformaciones Geométricas
 CAPÍTULO Modelado y Transformaciones Geométricas Antes que nada, en este trabajo veremos algunas animaciones, por lo cual se presenta en el presente capítulo algunos conceptos que explican el comportamiento
CAPÍTULO Modelado y Transformaciones Geométricas Antes que nada, en este trabajo veremos algunas animaciones, por lo cual se presenta en el presente capítulo algunos conceptos que explican el comportamiento
Clasificación de los robots según la AFRI (Asociación Francesa de Robótica Industrial) Manipulador con control manual o telemando.
 Tabla 1.1 Tipo A Clasificación de los robots según la AFRI (Asociación Francesa de Robótica Industrial) Manipulador con control manual o telemando. Tabla 1.1 Tipo A Tipo B Clasificación de los robots según
Tabla 1.1 Tipo A Clasificación de los robots según la AFRI (Asociación Francesa de Robótica Industrial) Manipulador con control manual o telemando. Tabla 1.1 Tipo A Tipo B Clasificación de los robots según
Cinemática de los manipuladores. Robótica
 Cinemática de los manipuladores Robótica Introducción Cinemática: Estudio del movimiento sin considerar las fuerzas que lo producen Propiedades geométricas y temporales Posición, velocidad, aceleración,
Cinemática de los manipuladores Robótica Introducción Cinemática: Estudio del movimiento sin considerar las fuerzas que lo producen Propiedades geométricas y temporales Posición, velocidad, aceleración,
SECRETARÍA DE EDUCACIÓN PÚBLICA TECNOLÓGICA NACIONAL DE MÉXICO INSTITUTIO TECNOLÓGICO DE VERACRUZ
 SECRETARÍA DE EDUCACIÓN PÚBLICA TECNOLÓGICA NACIONAL DE MÉXICO INSTITUTIO TECNOLÓGICO DE VERACRUZ Robótica Dr. José Antonio Garrido Natarén INGENIERÍA MECATRÓNICA Unidad 1 Morfología del robot 1.8 Grados
SECRETARÍA DE EDUCACIÓN PÚBLICA TECNOLÓGICA NACIONAL DE MÉXICO INSTITUTIO TECNOLÓGICO DE VERACRUZ Robótica Dr. José Antonio Garrido Natarén INGENIERÍA MECATRÓNICA Unidad 1 Morfología del robot 1.8 Grados
UNIVERSIDAD POLITÉCNICA. TEMA: Cinemática Diferencial. E.T.S.I. y Diseño Industrial. Titulación: Grado en Ingeniería Electrónica y Automática
 10/05/2017 UNIVERSIDAD POLITÉCNICA DE MADRID TEMA: Cinemática Diferencial Profesor: Miguel Hernando Gutiérrez & Cecilia García Cena E.T.S.I. y Diseño Industrial Titulación: Grado en Ingeniería Electrónica
10/05/2017 UNIVERSIDAD POLITÉCNICA DE MADRID TEMA: Cinemática Diferencial Profesor: Miguel Hernando Gutiérrez & Cecilia García Cena E.T.S.I. y Diseño Industrial Titulación: Grado en Ingeniería Electrónica
Ibarra Ecuador. B. Cinemática directa
 Diseño de un software que permite la simulación cinemática de un brazo robótico Kleber Andrés Calderón Martínez, Carlos Xavier Rosero [email protected], [email protected] Ingeniería en Mecatrónica Ibarra
Diseño de un software que permite la simulación cinemática de un brazo robótico Kleber Andrés Calderón Martínez, Carlos Xavier Rosero [email protected], [email protected] Ingeniería en Mecatrónica Ibarra
INSTITUTO TECNOLÓGICO DE VERACRUZ. Materia: Robótica. Unidad 3: Cinemática. Tema: Cinemática Inversa. Catedrático: Dr. José Antonio Garrido Natarén
 INSTITUTO TECNOLÓGICO DE VERACRUZ Materia: Robótica Unidad 3: Cinemática Tema: Cinemática Inversa Catedrático: Dr. José Antonio Garrido Natarén H. Veracruz, Ver. Noviembre de 2014 La cinemática del robot
INSTITUTO TECNOLÓGICO DE VERACRUZ Materia: Robótica Unidad 3: Cinemática Tema: Cinemática Inversa Catedrático: Dr. José Antonio Garrido Natarén H. Veracruz, Ver. Noviembre de 2014 La cinemática del robot
2015, Año del Generalísimo José María Morelos y Pavón
 Nombre de la Asignatura: ROBOTICA Línea de Investigación o Trabajo: PROCESAMIENTO DE SEÑALES ELECTRICAS Y ELECTRONICAS Tiempo de dedicación del estudiante a las actividades de: DOC-TIS-TPS-CRÉDITOS 48
Nombre de la Asignatura: ROBOTICA Línea de Investigación o Trabajo: PROCESAMIENTO DE SEÑALES ELECTRICAS Y ELECTRONICAS Tiempo de dedicación del estudiante a las actividades de: DOC-TIS-TPS-CRÉDITOS 48
M.C. Cynthia Guerrero
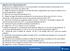 Algoritmo 2-6-1: Representación D-H 0. Numere las articulaciones de la 1 a la n comenzando con la base () y terminando con la herramienta, en el orden yaw, pitch y roll. 1. Asigne un sistema coordenado
Algoritmo 2-6-1: Representación D-H 0. Numere las articulaciones de la 1 a la n comenzando con la base () y terminando con la herramienta, en el orden yaw, pitch y roll. 1. Asigne un sistema coordenado
Control cinemático y dinámico de robots omnidireccionales
 1 Diciembre 2013 Control cinemático y dinámico de robots omnidireccionales basado parcialmente en: Siegwart, Nourbakhsh y Scaramuzza, Introduction to Autonomous Mobile Robots Campion, et al., Structural
1 Diciembre 2013 Control cinemático y dinámico de robots omnidireccionales basado parcialmente en: Siegwart, Nourbakhsh y Scaramuzza, Introduction to Autonomous Mobile Robots Campion, et al., Structural
Modelado de un brazo robótico Scorbot-ER III mediante cinemática directa
 XXIV CONVENCIÓN DE ESTUDIANTES DE CENTROAMÉRICA Y PANAMÁ, CONESCAPAN, EL SALVADOR, 25 Modelado de un brazo robótico Scorbot-ER III mediante cinemática directa Silvio Alejandro Urizar Salazar, Student Member
XXIV CONVENCIÓN DE ESTUDIANTES DE CENTROAMÉRICA Y PANAMÁ, CONESCAPAN, EL SALVADOR, 25 Modelado de un brazo robótico Scorbot-ER III mediante cinemática directa Silvio Alejandro Urizar Salazar, Student Member
Universidad Politécnica de Madrid Escuela de Ingenieros Industriales. RoboTenis
 Universidad Politécnica de Madrid Escuela de Ingenieros Industriales RoboTenis Diseño, Simulación, Análisis Cinemático y Dinámico de un robot paralelo para Control Visual de altas prestaciones DISAM Luis
Universidad Politécnica de Madrid Escuela de Ingenieros Industriales RoboTenis Diseño, Simulación, Análisis Cinemático y Dinámico de un robot paralelo para Control Visual de altas prestaciones DISAM Luis
Cinemática Inversa del Robot. UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides
 Cinemática Inversa del Robot UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción Resuelve la configuración que debe adoptar el robot para una posición y orientación del
Cinemática Inversa del Robot UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción Resuelve la configuración que debe adoptar el robot para una posición y orientación del
M.C. Cynthia Guerrero
 Algoritmo 2-6-1: Representación D-H 0. Numere las articulaciones de la 1 a la n comenzando con la base (cintura) y terminando con la herramienta, en el orden yaw, pitch y roll. 1. Asigne un sistema coordenado
Algoritmo 2-6-1: Representación D-H 0. Numere las articulaciones de la 1 a la n comenzando con la base (cintura) y terminando con la herramienta, en el orden yaw, pitch y roll. 1. Asigne un sistema coordenado
Fundamentos en Robótica. Unidad 4.1 Locomoción y cinemática
 Fundamentos en Robótica Unidad 4.1 Locomoción y cinemática Temas Manipulación Interacción con objetos físicos Locomoción Desplazamientos controlados en el medio Manipulación Brazos Sirven para ubicar al
Fundamentos en Robótica Unidad 4.1 Locomoción y cinemática Temas Manipulación Interacción con objetos físicos Locomoción Desplazamientos controlados en el medio Manipulación Brazos Sirven para ubicar al
Cinemática Directa del Robot. UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides
 Cinemática Directa del Robot UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción Consiste en determinar cual es la posición y orientación del extremo final del robot, con
Cinemática Directa del Robot UCR ECCI CI-2657 Robótica Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción Consiste en determinar cual es la posición y orientación del extremo final del robot, con
Vision por computadora, repaso 2
 Vision por computadora, repaso 2 Februar, 206 Geometria euclideana 2D.0. Transformaciones rigidas en el plano euclidiano Una transformación rígida (o isometría es una transformación que deja invariante
Vision por computadora, repaso 2 Februar, 206 Geometria euclideana 2D.0. Transformaciones rigidas en el plano euclidiano Una transformación rígida (o isometría es una transformación que deja invariante
TSTC. Dpt. Teoría de la Señal, Telemática y Comunicaciones Tema 1 INTRODUCCIÓN A LA ROBÓTICA
 Dpt. Teoría de la Señal, Telemática y Comunicaciones Tema 1 INTRODUCCIÓN A LA ROBÓTICA Secciones 1. Introducción y definiciones. 2. Visión General de la manipulación mecánica. 1. Posicionamiento y Cinemática
Dpt. Teoría de la Señal, Telemática y Comunicaciones Tema 1 INTRODUCCIÓN A LA ROBÓTICA Secciones 1. Introducción y definiciones. 2. Visión General de la manipulación mecánica. 1. Posicionamiento y Cinemática
Gráficos por Computadora. Mtro. J. Fco. Jafet Pérez L. Transformaciones Geométricas Bidimensionales
 Gráficos por Computadora Mtro. J. Fco. Jafet Pérez L. Transformaciones Geométricas Bidimensionales Objetivo Analizaremos los procedimientos estándares para realizar transformaciones geométricas bidimensionales
Gráficos por Computadora Mtro. J. Fco. Jafet Pérez L. Transformaciones Geométricas Bidimensionales Objetivo Analizaremos los procedimientos estándares para realizar transformaciones geométricas bidimensionales
Graficación CCOM-259. Benemérita Universidad Autónoma de Puebla. Facultad de Ciencias de la Computación. Daniel Alejandro Valdés Amaro, Ph.
 Graficación CCOM-9 Benemérita Universidad Autónoma de Puebla Facultad de Ciencias de la Computación Daniel Alejandro Valdés Amaro, Ph.D Objetivo: El alumno conocerá y aplicará los algoritmos y técnicas
Graficación CCOM-9 Benemérita Universidad Autónoma de Puebla Facultad de Ciencias de la Computación Daniel Alejandro Valdés Amaro, Ph.D Objetivo: El alumno conocerá y aplicará los algoritmos y técnicas
Representaciones Geométricas y Transformaciones en 2D
 Representaciones Geométricas y Transformaciones en 2D 7 de marzo de 20 Contenido Representación de lugares geométricos: polígonos Representaciones Geométricas Transformaciones geométricas en el espacio
Representaciones Geométricas y Transformaciones en 2D 7 de marzo de 20 Contenido Representación de lugares geométricos: polígonos Representaciones Geométricas Transformaciones geométricas en el espacio
TECNOLOGICO NACIONAL DE MEXICO
 TECNOLOGICO NACIONAL DE MEXICO INSTITUTO TECNOLOGICO DE VERACRUZ ROBOTICA CLAVE 9F1A DR. JOSE ANTONIO GARRIDO NATAREN ING. MECATRONICA EQUIPO I UNIDAD I MORFOLOGIA DEL ROBOT 1.2 ESTRUCTURA MECANICA DE
TECNOLOGICO NACIONAL DE MEXICO INSTITUTO TECNOLOGICO DE VERACRUZ ROBOTICA CLAVE 9F1A DR. JOSE ANTONIO GARRIDO NATAREN ING. MECATRONICA EQUIPO I UNIDAD I MORFOLOGIA DEL ROBOT 1.2 ESTRUCTURA MECANICA DE
Capítulo 6. Resultados Cinemáticos por Simulación
 Capítulo 6. Resultados Cinemáticos por Simulación Una vez que se tienen las ecuaciones de la descripción de la cinemática y la cinemática inversa del capítulo anterior, se tiene que corroborar que los
Capítulo 6. Resultados Cinemáticos por Simulación Una vez que se tienen las ecuaciones de la descripción de la cinemática y la cinemática inversa del capítulo anterior, se tiene que corroborar que los
Ejercicios de la acción de un campo Magnético sobre una Espira
 Ejercicios de la acción de un campo Magnético sobre una Espira Ejercicio resuelto nº 1 Una espira rectangular por las que circula una corriente de 5 A, de dimensiones 10 y 15 cm está en una región en la
Ejercicios de la acción de un campo Magnético sobre una Espira Ejercicio resuelto nº 1 Una espira rectangular por las que circula una corriente de 5 A, de dimensiones 10 y 15 cm está en una región en la
Translaciones, giros, simetrías.
 Translaciones, giros, simetrías. Transformaciones geométricas Transformación geométrica es una aplicación del plano en el plano tal que a cada punto de un plano le hace corresponder otro punto del mismo
Translaciones, giros, simetrías. Transformaciones geométricas Transformación geométrica es una aplicación del plano en el plano tal que a cada punto de un plano le hace corresponder otro punto del mismo
Monografía: Pares de fuerzas
 Monografía: Pares de fuerzas Par de fuerzas [1]: Son dos fuerzas paralelas que tienen la misma magnitud y dirección, sentidos contrarios y separados por una distancia perpendicular d (figura 1). Figura
Monografía: Pares de fuerzas Par de fuerzas [1]: Son dos fuerzas paralelas que tienen la misma magnitud y dirección, sentidos contrarios y separados por una distancia perpendicular d (figura 1). Figura
Parámetros Redundantes para Rotación y Traslación en Cinemática
 Parámetros Redundantes para Rotación y Traslación en Cinemática O. Altuzarra, A. Hernández, E. Amezua, V. Petuya Universidad del País Vasco - Euskal Herriko Unibertsitatea Departamento de Ingeniería Mecánica,
Parámetros Redundantes para Rotación y Traslación en Cinemática O. Altuzarra, A. Hernández, E. Amezua, V. Petuya Universidad del País Vasco - Euskal Herriko Unibertsitatea Departamento de Ingeniería Mecánica,
Estudio cinemático y dinámico de un robot dedicado a la reparación de. fallas menores en tuberías hidrosanitarias
 Estudio cinemático y dinámico de un robot dedicado a la reparación de fallas menores en tuberías hidrosanitarias Una Tesis Presentada Para Obtener El Título De Ingeniero en Mecatrónica Universidad Militar
Estudio cinemático y dinámico de un robot dedicado a la reparación de fallas menores en tuberías hidrosanitarias Una Tesis Presentada Para Obtener El Título De Ingeniero en Mecatrónica Universidad Militar
CINEMÁTICA DE CUERPOS RÍGIDOS (Parte I)
 UNIVERSIDAD JOSÉ ANTONIO PÁEZ FACULTAD DE INGENIERÍA ESCUELA DE INGENIERIA MECÁNICA MECÁNICA DINÁMICA SECCIÓN 204N1 CINEMÁTICA DE CUERPOS RÍGIDOS (Parte I) (Contenido correspondiente a parcial #3) CINEMÁTICA
UNIVERSIDAD JOSÉ ANTONIO PÁEZ FACULTAD DE INGENIERÍA ESCUELA DE INGENIERIA MECÁNICA MECÁNICA DINÁMICA SECCIÓN 204N1 CINEMÁTICA DE CUERPOS RÍGIDOS (Parte I) (Contenido correspondiente a parcial #3) CINEMÁTICA
Resumen de Transformaciones Isométricas. Traslaciones
 Resumen de Transformaciones Isométricas Una transformación es un procedimiento geométrico o movimiento que produce cambios en una figura. La palabra isometría proviene del griego y significa igual medida
Resumen de Transformaciones Isométricas Una transformación es un procedimiento geométrico o movimiento que produce cambios en una figura. La palabra isometría proviene del griego y significa igual medida
Alfaomega. Este documento pretende ser un breve manual de instalación y guía de ejecución. Guía de usuario
 Guía de usuario i Guía de usuario Este documento pretende ser un breve manual de instalación y guía de ejecución de los programas en código abierto de la obra MATLAB Aplicado a Robótica y Mecatrónica.
Guía de usuario i Guía de usuario Este documento pretende ser un breve manual de instalación y guía de ejecución de los programas en código abierto de la obra MATLAB Aplicado a Robótica y Mecatrónica.
6 DINAMICA DEL CUERPO RIGIDO
 6 DINAMICA DEL CUERPO RIGIDO 6. CINEMATICA 6.. Configuracion de un Cuerpo Rígido: Angulos de Euler Un cuerpo rígido se puede entender como una distribución continua de materia que se subdivide en pequeños
6 DINAMICA DEL CUERPO RIGIDO 6. CINEMATICA 6.. Configuracion de un Cuerpo Rígido: Angulos de Euler Un cuerpo rígido se puede entender como una distribución continua de materia que se subdivide en pequeños
TRANSFORMACIONES GEOMÉTRICAS Curso 03-04
 .-En el plano vectorial V, con la base ortonormal { i,j } vectores u (, ) y v (, ) éstos determinan. Hallar en la base { i,j } transformaciones ortogonales tales que f( D ) se consideran los y las semirrectas
.-En el plano vectorial V, con la base ortonormal { i,j } vectores u (, ) y v (, ) éstos determinan. Hallar en la base { i,j } transformaciones ortogonales tales que f( D ) se consideran los y las semirrectas
MODELADO Y CONTROL DINAMICO DE UN MANIPULADOR ROBOTICO CARTESIANO DE 3 GRADOS DE LIBERTAD
 MODELADO Y CONTROL DINAMICO DE UN MANIPULADOR ROBOTICO CARTESIANO DE 3 GRADOS DE LIBERTAD DYNAMIC MODELING AND CONTROL OF A CARTESIAN ROBOTIC MANIPULATOR OF 3 DOF Raúl Martínez Juárez Richar Suni Llanos
MODELADO Y CONTROL DINAMICO DE UN MANIPULADOR ROBOTICO CARTESIANO DE 3 GRADOS DE LIBERTAD DYNAMIC MODELING AND CONTROL OF A CARTESIAN ROBOTIC MANIPULATOR OF 3 DOF Raúl Martínez Juárez Richar Suni Llanos
ENSAMBLAJE Y CONTROL DE UN ROBOT DE TRES GRADOS DE LIBERTAD TIPO SCARA (SELECTIVE COMPLIANCE ASSEMBLY ROBOT ARM)
 ENSAMBLAJE Y CONTROL DE UN ROBOT DE TRES GRADOS DE LIBERTAD TIPO SCARA (SELECTIVE COMPLIANCE ASSEMBLY ROBOT ARM) Yadira Boada Acosta Luis Morales Escobar Nelson G. Sotomayor O, Msc. Profesor Principal
ENSAMBLAJE Y CONTROL DE UN ROBOT DE TRES GRADOS DE LIBERTAD TIPO SCARA (SELECTIVE COMPLIANCE ASSEMBLY ROBOT ARM) Yadira Boada Acosta Luis Morales Escobar Nelson G. Sotomayor O, Msc. Profesor Principal
Tema 5. Cinemática Inversa
 UNIVERSIDAD POLITÉCNICA DE MADRID E.U.I.T. Industrial TEMA: Cinemática Inversa FECHA: Enero de 01 Titulación: Grado en Ingeniería Electrónica y Automática Área: Ingeniería de Sistemas y Automática Departamento
UNIVERSIDAD POLITÉCNICA DE MADRID E.U.I.T. Industrial TEMA: Cinemática Inversa FECHA: Enero de 01 Titulación: Grado en Ingeniería Electrónica y Automática Área: Ingeniería de Sistemas y Automática Departamento
Universidad Surcolombiana NIT FACULTAD DE INGENIERÍA PROGRAMA DE INGENIERÍA ELECTRÓNICA
 Página de 8 FORMATO OFICIAL DE MICRODISEÑO CURRICULAR FACULTAD: INGENIERÍA PROGRAMA: INGENIERÍA ELECTRÓNICA. IDENTIFICACIÓN DEL CURSO Nombre del Curso Código ROBÓTICA Número de Créditos Académicos 3 Horas
Página de 8 FORMATO OFICIAL DE MICRODISEÑO CURRICULAR FACULTAD: INGENIERÍA PROGRAMA: INGENIERÍA ELECTRÓNICA. IDENTIFICACIÓN DEL CURSO Nombre del Curso Código ROBÓTICA Número de Créditos Académicos 3 Horas
ESTUDIO DE UNA CADENA CINEMÁTICA UTILIZANDO LOS MÉTODOS DENAVIT-HARTENBERG Y CRAIG MODIFICADO
 ESTUDIO DE UNA CADENA CINEMÁTICA UTILIZANDO LOS MÉTODOS DENAVIT-HARTENBERG Y CRAIG MODIFICADO Dr. José Antonio Garrido Natarén 1, José Antonio Hernandez Reyes 2, MC. José Luis Fernando Palomeque Loyo 3,
ESTUDIO DE UNA CADENA CINEMÁTICA UTILIZANDO LOS MÉTODOS DENAVIT-HARTENBERG Y CRAIG MODIFICADO Dr. José Antonio Garrido Natarén 1, José Antonio Hernandez Reyes 2, MC. José Luis Fernando Palomeque Loyo 3,
MODELADO DE UN ROBOT BÍPEDO DE MARCHA SEMI-ESTÁTICA CON SEIS GRADOS DE LIBERTAD USANDO EL MÉTODO DEL PRODUCTO DE EXPONENCIALES
 MODELADO DE UN ROBOT BÍPEDO DE MARCHA SEMI-ESTÁTICA CON SEIS GRADOS DE LIBERTAD USANDO EL MÉTODO DEL PRODUCTO DE EXPONENCIALES WILSON JAVIER ALMARIO RODRÍGUEZ JOSÉ LIBARDO LESMES MORA ESCUELA TECNOLÓGICA
MODELADO DE UN ROBOT BÍPEDO DE MARCHA SEMI-ESTÁTICA CON SEIS GRADOS DE LIBERTAD USANDO EL MÉTODO DEL PRODUCTO DE EXPONENCIALES WILSON JAVIER ALMARIO RODRÍGUEZ JOSÉ LIBARDO LESMES MORA ESCUELA TECNOLÓGICA
Escuela Politécnica Superior de Linares
 Escuela Politécnica Superior de Linares UNIVERSIDAD DE JAÉN Escuela Politécnica Superior de Linares Trabajo Fin de Grado PUESTA EN MARCHA DE BRAZO ROBÓTICO Y DESARROLLO DE APLICACIONES Alumno: Axel José
Escuela Politécnica Superior de Linares UNIVERSIDAD DE JAÉN Escuela Politécnica Superior de Linares Trabajo Fin de Grado PUESTA EN MARCHA DE BRAZO ROBÓTICO Y DESARROLLO DE APLICACIONES Alumno: Axel José
Análisis de Plataforma Sewart utilizando SimMechanics Aplicada al Desarrollo de Simuladores de Vuelo.
 Análisis de Plataforma Sewart utilizando SimMechanics Aplicada al Desarrollo de Simuladores de Vuelo. Griselda I. Cistac [1] -Aníbal Zanini [2] - Horacio Abbate [3] Facultad de Ingeniería-UNLPam [1] -
Análisis de Plataforma Sewart utilizando SimMechanics Aplicada al Desarrollo de Simuladores de Vuelo. Griselda I. Cistac [1] -Aníbal Zanini [2] - Horacio Abbate [3] Facultad de Ingeniería-UNLPam [1] -
