EXERCICIS - SOLUCIONS
|
|
|
- Estefania Ortíz García
- hace 7 años
- Vistas:
Transcripción
1 materials del curs de: MATEMÀTIQUES SISTEMES D EQUACIONS EXERCICIS - SOLUCIONS
2 AUTOR: Xavier Vilardell Bascompte CORRECCIÓ: Montse Ramos ÚLTIMA REVISIÓ: 1 d abril de 009 Aquests materials han estat realitzats per donar les classes al Centre de Formació Permanent d Osona Sud.
3 EXERCICI 1 Representa de forma gràfica les següents equacions lineals. Calcula prèviament la taula de valors. a) - -4 b) 3
4 c) 5 + d)
5 EXERCICI Representa gràficament el següent sistema d equacions. Quin és el punt d intersecció de les rectes? Quina és la solució del sistema?
6
7 EXERCICI 3 Resol els següents sistemes aplicant el mètode d igualació si aïllo les X: si aïllo les : solució del sistema: si aïllo les X: si aïllo les : solució del sistema: si aïllo les X: si aïllo les : solució del sistema:
8 EXERCICI 4 Resol els següents sistemes aplicant el mètode de substitució si aïllo les X: si aïllo les : solució del sistema: Primer arreglar si aïllo les X: si aïllo les : solució del sistema: si aïllo les X: si aïllo les : solució del sistema:
9 EXERCICI 5 Resol els següents sistemes aplicant el mètode de reducció si redueio les X: si redueio les : solució del sistema: si redueio les X: si redueio les : solució del sistema: Compte... primer hem d arreglar la segona equació: si redueio les X: si redueio les : solució del sistema:
10 PROBLEMES 1. La diferència entre dos nombres és 3. La meitat del més gran més el triple del més petit és 1. Quins són aquests nombres? X 3 X X número gran número petit X 6 3. Hem barrejat cafè de 6 /kg amb cafè de 9 /kg i hem obtingut una barreja de 300Kg que costa 7 /kg. Quants quilos de cafè hem posat de cada classe? X X kg café de 6 kg kg café de 9 kg X 00 kg 100 kg 3. El perímetre d un rectangle fa 16cm. Quines són les seves dimensions si la base és cm més gran que l altura. X + + X base altura 16 X 5 cm 3 cm 4. La Consol té 8 ans més que la Maria. D aquí a 6 ans el triple de l edat de la Consol serà igual a sis vegades la de la Maria. Quants ans té cada una? 3 X + 8 ( X + 6) 6 ( + 6) X 10 ans ans Ara D aquí 6 ans Consol X X+6 Maria +6
11 5. Dos nombres sumen 48. Si sumem 4 al quocient que s obté en dividir un per l altre el resultat dóna 9. De quins nombres estem parlant? X + X X PRIMER NOMBRE X 40 8 SEGON NOMBRE 6. A veure una pel lícula hi han anat 100 persones entre homes i dones. Abans d acabar la pel lícula han sortit 10 homes i, aleshores, ha quedat el doble nombre de dones que d homes. Quants homes i dones han anat al cine? X + ( X 10) 100 X HOMES DONES X 40 homes 60 dones 7. En Carles té 36 ans més que el seu fill. Quines edats tenen en Carles i el seu fill si d aquí a 4 ans l edat d en Carles serà 3 vegades la del seu fill? X ( + 4) X 50 ans 14 ans Ara D aquí 4 ans Carles X X+4 fill +4
12 8. La tercera part de la suma de dos nombres val 10, i el triple de la diferència més 1 és igual al més petit. Busca aquests dos nombres. 3 X ( X ) X X nombre petit nombre gran 9. Fa quatre ans, en Jordi tenia tres vegades l edat del seu germà David. Si en Jordi tingués 9 ans més i en David dos mens, l edat del més gran seria quatre vegades la del més petit. Quina edat té cada un? X ( 4) ( ) X 19 ans 9 ans Fa 4 ans Ara Jordi X - 4 X David La suma de les dues ifres d un nombre és 8. Si invertim l ordre de les dues ifres, la diferència és 36. De quin nombre es tracta? X + ( 10X + ) ( 10 + X ) 8 36 X primer nombre X segon nombre X 6 X Hem de pagar un cote de 4975 lliures, i només tenim bitllets de 100 i 5 lliures. El cobrador s emporta 64 bitllets. Quants bitllets de cada classe s emporta? X + 100X X bitllets de 100 lliures bitllets de 5 lliures X 45 bitllets de 100 lliures 19 bitllets de 5 lliures
13 1. Un pastor diu a un altre pastor: Dóna m una ovella, i aií en tindré el doble que tu. I l altre li contesta: Dóna-me n una tu, i aií en tindrem tots dos igual. Quantes ovelles té cada pastor? X + 1 X ( 1) X ovelles pastor1 ovelles pastor X 7 ovelles 5 ovelles 13. Avui al supermercat hem pagat amb 500 pessetes 3 kg de taronges i kg de pomes, i ens han tornat 105 pessetes. Si haguéssim comprat 4 kg de taronges i 1 kg de pomes, el canvi hauria estat de 90 pessetes. A quant hem comprat la fruita? 3X + 4X X pessetes kg taronges pessetes kg pomes X 85 pessetes kg 70 pessetes kg 14. Busca dos nombres tals que el doble del primer mens el triple del segon valgui 5, i que la vuitena part del primer per cinc sigui igual al segon. X 3 5 X X primer nombre 5 8 X 40 5 segon nombre 15. En una festa d aniversari hi ha el triple de nenes que de nens. Si havíem preparat dotze bosses de llaminadures i han vingut tots els convidats, quants nens i quantes nenes hi ha a la festa? X 3 X nenes nens X + 1 X 9 nenes 3 nens
EXERCICIS - SOLUCIONS
 materials del curs de: MATEMÀTIQUES SISTEMES D EQUACIONS EXERCICIS - SOLUCIONS AUTOR: Xavier Vilardell Bascompte [email protected] ÚLTIMA REVISIÓ: 21 d abril de 2009 Aquests materials han estat realitzats
materials del curs de: MATEMÀTIQUES SISTEMES D EQUACIONS EXERCICIS - SOLUCIONS AUTOR: Xavier Vilardell Bascompte [email protected] ÚLTIMA REVISIÓ: 21 d abril de 2009 Aquests materials han estat realitzats
1. Indica si les següents expressions són equacions o identitats: a. b. c. d.
 Dossier d equacions de primer grau 1. Indica si les següents expressions són equacions o identitats: Solucions: Equació / Identitat / Identitat / Identitat 2. Indica els elements d aquestes equacions (membres,
Dossier d equacions de primer grau 1. Indica si les següents expressions són equacions o identitats: Solucions: Equació / Identitat / Identitat / Identitat 2. Indica els elements d aquestes equacions (membres,
Pauta d estiu matemàtiques 2on E.S.O. curs
 Continguts: Pauta d estiu matemàtiques on E.S.O. curs 00-. Fraccions: suma, resta, producte, divisió, castells, operacions combinades i fracció generatriu.. Álgebra: suma, resta, producte i operacions
Continguts: Pauta d estiu matemàtiques on E.S.O. curs 00-. Fraccions: suma, resta, producte, divisió, castells, operacions combinades i fracció generatriu.. Álgebra: suma, resta, producte i operacions
Equacions i sistemes de segon grau
 Equacions i sistemes de segon grau 3 Equacions de segon grau. Resolució. a) L àrea del pati d una escola és quadrada i fa 0,5 m. Per calcular el perímetre del pati seguei els passos següents: Escriu l
Equacions i sistemes de segon grau 3 Equacions de segon grau. Resolució. a) L àrea del pati d una escola és quadrada i fa 0,5 m. Per calcular el perímetre del pati seguei els passos següents: Escriu l
Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera:
 Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera: ax + by = k a x + b y = k Coeficients de les incògnites: a, a, b, b. Termes independents:
Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera: ax + by = k a x + b y = k Coeficients de les incògnites: a, a, b, b. Termes independents:
I.E.S. Cirviànum Matemàtiques Segon Curs d E.S.O. EQUACIONS EQUACIONS DE PRIMER GRAU. Per resoldre equacions de primer grau cal seguir aquests passos:
 DE PRIMER GRAU Per resoldre equacions de primer grau cal seguir aquests passos: Treure parèntesis Traslladar totes les a un cantó de l igual Agrupar ambdós costats de l igual (les i els nombres) Aïllar
DE PRIMER GRAU Per resoldre equacions de primer grau cal seguir aquests passos: Treure parèntesis Traslladar totes les a un cantó de l igual Agrupar ambdós costats de l igual (les i els nombres) Aïllar
UNITAT 3: SISTEMES D EQUACIONS
 UNITAT 3: SISTEMES D EQUACIONS 1. EQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITES L equació x + y = 3 és una equació de primer grau amb dues incògnites : x i y. Per calcular les solucions escollim un valor
UNITAT 3: SISTEMES D EQUACIONS 1. EQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITES L equació x + y = 3 és una equació de primer grau amb dues incògnites : x i y. Per calcular les solucions escollim un valor
6Solucions a les activitats de cada epígraf
 PÀGINA 4 Pàg. Les equacions són igualtats algebraiques (amb nombres i lletres) que permeten establir relacions entre valors coneguts (dades) i valors desconeguts (incògnites). Aprenent a manejar-les, disposaràs
PÀGINA 4 Pàg. Les equacions són igualtats algebraiques (amb nombres i lletres) que permeten establir relacions entre valors coneguts (dades) i valors desconeguts (incògnites). Aprenent a manejar-les, disposaràs
SOLUCIONARI Unitat 5
 SOLUCIONARI Unitat 5 Comencem Escriu tres equacions que no tinguin solució en el conjunt. Resposta oberta. Per exemple: a) x b) 5x 0 c) x Estableix tres equacions que no tinguin solució en el conjunt.
SOLUCIONARI Unitat 5 Comencem Escriu tres equacions que no tinguin solució en el conjunt. Resposta oberta. Per exemple: a) x b) 5x 0 c) x Estableix tres equacions que no tinguin solució en el conjunt.
Unitat 2 EQUACIONS DE PRIMER GRAU. Matemàtiques, Ciència i Tecnologia 5. TRANSFORMACIONS D EXPRESSIONS ALGEBRAIQUES UNITAT 2 EQUACIONS DE PRIMER GRAU
 Unitat 2 EQUACIONS DE PRIMER GRAU 37 38 Matemàtiques, Ciència i Tecnologia 5. TRANSFORMACIONS D EXPRESSIONS ALGEBRAIQUES UNITAT 2 QUÈ TREBALLARÀS? què treballaràs? En acabar la unitat has de ser capaç
Unitat 2 EQUACIONS DE PRIMER GRAU 37 38 Matemàtiques, Ciència i Tecnologia 5. TRANSFORMACIONS D EXPRESSIONS ALGEBRAIQUES UNITAT 2 QUÈ TREBALLARÀS? què treballaràs? En acabar la unitat has de ser capaç
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 30 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE Activitat 1 Completa la taula següent: Graus Minuts Segons 30º 30 x 60 = 1.800 1.800 x 60 = 108.000 45º 2.700 162.000 120º 7.200 432.000 270º 16.200 972.000
30 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE Activitat 1 Completa la taula següent: Graus Minuts Segons 30º 30 x 60 = 1.800 1.800 x 60 = 108.000 45º 2.700 162.000 120º 7.200 432.000 270º 16.200 972.000
Institut d Educació Secundària. x b) A partir de la gràfica d aquesta funció, indica quin és el domini i el recorregut.
 Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques MS Àlgebra i uncions I Nom: Grup: ) Resol les següents equacions: a) 7+ 3+ c) 3 +
Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques MS Àlgebra i uncions I Nom: Grup: ) Resol les següents equacions: a) 7+ 3+ c) 3 +
Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera:
 Dossier de sistemes d'equacions lineals. / Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera: k b a k b a Coeficients de les incògnites:
Dossier de sistemes d'equacions lineals. / Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera: k b a k b a Coeficients de les incògnites:
( ) ( 6 5) (
 r d ESO EXERCICIS DE REPÀS 1. Determina el representant canònic de cadascun dels següents nombres racionals: 420 60 b) 12 14 c) 512 1024 d) 54 180 e) 117 247 2. Fes les següents operacions de nombres racionals
r d ESO EXERCICIS DE REPÀS 1. Determina el representant canònic de cadascun dels següents nombres racionals: 420 60 b) 12 14 c) 512 1024 d) 54 180 e) 117 247 2. Fes les següents operacions de nombres racionals
UIB 2 + f (x) + f(x) ց ց ր ր Per tant, el punt ( 3. Una altra forma de veure-ho és calcular la derivada segona i mirar el signe en x = 3: 2 f (x) =
 El cas positiu no té solució. Si analitzam el cas negatiu, ens surt x = x+, d on x =. A continuació fem la taula següent per veure si el valor obtingut és un màxim, mínim o un punt de sella. x + f (x)
El cas positiu no té solució. Si analitzam el cas negatiu, ens surt x = x+, d on x =. A continuació fem la taula següent per veure si el valor obtingut és un màxim, mínim o un punt de sella. x + f (x)
PROBLEMES D EQUACIONS DE PRIMER GRAU
 PROBLEMES D EQUACIONS DE PRIMER GRAU 1 Cerqueu un nombre tal que : el seu triple menys 5 és igual al seu doble més dos unitats. Sol: 7 2 El triple d un nombre és igual a cinc vegades ell mateix menys 20
PROBLEMES D EQUACIONS DE PRIMER GRAU 1 Cerqueu un nombre tal que : el seu triple menys 5 és igual al seu doble més dos unitats. Sol: 7 2 El triple d un nombre és igual a cinc vegades ell mateix menys 20
Unitat 4. El llenguatge algebraic.
 Unitat 4. El llenguatge algebraic. 1. Indica si aquestes expressions algebraiques son certes o faltes. a) El producte de dos nombres diferents és: x y. b) La sisena part d un nombre és: 6 x. c) Un nombre
Unitat 4. El llenguatge algebraic. 1. Indica si aquestes expressions algebraiques son certes o faltes. a) El producte de dos nombres diferents és: x y. b) La sisena part d un nombre és: 6 x. c) Un nombre
DOSSIER DE RECUPERACIÓ 3r ESO
 DOSSIER DE RECUPERACIÓ 3r ESO INS MARIANAO. Departament de matemàtiques La correcta realització d aquest dossier, i la posterior entrega el dia de l examen puntuarà un 20% de la nota total. Les activitats
DOSSIER DE RECUPERACIÓ 3r ESO INS MARIANAO. Departament de matemàtiques La correcta realització d aquest dossier, i la posterior entrega el dia de l examen puntuarà un 20% de la nota total. Les activitats
Equacions i sistemes de primer grau
 Equacions i sistemes de primer grau Equacions de primer grau amb una incògnita. Resolució 1. a) Llegeix atentament l endevinalla numèrica següent i resol-la començant amb tres nombres diferents: Pensa
Equacions i sistemes de primer grau Equacions de primer grau amb una incògnita. Resolució 1. a) Llegeix atentament l endevinalla numèrica següent i resol-la començant amb tres nombres diferents: Pensa
DOSSIER PREPARACIÓ RECUPERACIÓ MATEMÀTIQUES Setembre 3r ESO
 Generalitat de Catalunya Departament d Ensenyament Institut Pompeu Fabra DOSSIER PREPARACIÓ RECUPERACIÓ MATEMÀTIQUES Setembre 3r ESO Nom i Cognoms:... INSTRUCCIONS: - Aquest dossier serveix per a preparar
Generalitat de Catalunya Departament d Ensenyament Institut Pompeu Fabra DOSSIER PREPARACIÓ RECUPERACIÓ MATEMÀTIQUES Setembre 3r ESO Nom i Cognoms:... INSTRUCCIONS: - Aquest dossier serveix per a preparar
LA RECTA. Exercicis d autoaprenentatge 1. Siga la gràfica següent:
 LA RECTA Recordeu: Una recta és una funció de la forma y = mx + n, on m i n són nombres reals. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall
LA RECTA Recordeu: Una recta és una funció de la forma y = mx + n, on m i n són nombres reals. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall
1- Resol aquestes multiplicacions:
 EXERCICIS DE MATEMÁTIQUES 2n PRIMÀRIA 1- Resol aquestes multiplicacions: 2 X 4 =... 3 X 2 =... 4 X 5 =... 5 X 3 =... 6 X 2 =... 2 X 6 =... 3 X 9 =... 4 X 6 =... 5 X 8 =... 6 X 7 =... 2 X 7 =... 3 X 8 =...
EXERCICIS DE MATEMÁTIQUES 2n PRIMÀRIA 1- Resol aquestes multiplicacions: 2 X 4 =... 3 X 2 =... 4 X 5 =... 5 X 3 =... 6 X 2 =... 2 X 6 =... 3 X 9 =... 4 X 6 =... 5 X 8 =... 6 X 7 =... 2 X 7 =... 3 X 8 =...
avaluació educació primària curs competència matemàtica
 avaluació educació primària curs 2008-2009 competència matemàtica instruccions El material que necessites per fer la prova és un bolígraf. Llegeix atentament cada pregunta abans de contestar-la. En la
avaluació educació primària curs 2008-2009 competència matemàtica instruccions El material que necessites per fer la prova és un bolígraf. Llegeix atentament cada pregunta abans de contestar-la. En la
TEMES TREBALLATS A 3r d'eso
 TEMES TREBALLATS A r d'eso. Repàs de n d'eso. Nombres racionals. Equacions. Sistemes d'equacions de r grau. Funcions. Geometria en l'espai Recordeu que a part dels apunts teniu d'altres documents per preparar
TEMES TREBALLATS A r d'eso. Repàs de n d'eso. Nombres racionals. Equacions. Sistemes d'equacions de r grau. Funcions. Geometria en l'espai Recordeu que a part dels apunts teniu d'altres documents per preparar
Sistemes d Equacions. Objectius. Abans de començar. 1.Equacions lineals... pàg. 58 Definició. Solució
 4 Sistemes d Equacions Objectius En aquesta quinzena aprendràs a: Reconèixer i classificar els sistemes d'equacions segons el seu nombre de solucions. Obtenir la solució d'un sistema mitjançant una taula.
4 Sistemes d Equacions Objectius En aquesta quinzena aprendràs a: Reconèixer i classificar els sistemes d'equacions segons el seu nombre de solucions. Obtenir la solució d'un sistema mitjançant una taula.
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 3 Activitat Completa els productes següents. a) 0 = 5... e) 0 = 5... b)... = 5 3 f) 25 =... 5 c) 5 =... g) 55 = 5... d) 30 = 5... h) 40 =...... a) 0 = 5 0 e)
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 3 Activitat Completa els productes següents. a) 0 = 5... e) 0 = 5... b)... = 5 3 f) 25 =... 5 c) 5 =... g) 55 = 5... d) 30 = 5... h) 40 =...... a) 0 = 5 0 e)
Equacions. Solucions d una equació amb dues incògnites CLAUS PER COMENÇAR. Elements de l equació
 CLAUS PER COMENÇAR Equacions Elements de l equació Els membres d una equació són les expressions algebraiques que hi ha a cada costat de la igualtat, i cada sumand es diu terme. Les lletres que apareixen
CLAUS PER COMENÇAR Equacions Elements de l equació Els membres d una equació són les expressions algebraiques que hi ha a cada costat de la igualtat, i cada sumand es diu terme. Les lletres que apareixen
28 Sèries del Quinzet. Proves d avaluació
 Sèries del Quinzet. Proves d avaluació INSTRUCCIONS Les proves d avaluació de l aprenentatge del Quinzet estan dissenyades per fer l avaluació interna del centre. Aquestes proves, seguint les directrius
Sèries del Quinzet. Proves d avaluació INSTRUCCIONS Les proves d avaluació de l aprenentatge del Quinzet estan dissenyades per fer l avaluació interna del centre. Aquestes proves, seguint les directrius
x + 2 y = 3 2 x y = 1 4 x + 3 y = k a) Afegiu-hi una equació lineal de manera que el sistema resultant sigui incompatible.
 1998 - Sèrie 3 - Qüestió 4 Discutiu el sistema d'equacions a x y + 2 z = (2 a) 2 x + 3 y z = 3a x + 2 y z = 2a segons els valors del paràmetre a. 1999 - Sèrie 1 - Qüestió 1 Resoleu el sistema següent per
1998 - Sèrie 3 - Qüestió 4 Discutiu el sistema d'equacions a x y + 2 z = (2 a) 2 x + 3 y z = 3a x + 2 y z = 2a segons els valors del paràmetre a. 1999 - Sèrie 1 - Qüestió 1 Resoleu el sistema següent per
TEMA 1: EXPRESSIONS ALGEBRAIQUES. Activitats
 TEMA 1: EXPRESSIONS ALGEBRAIQUES Activitats 1.- Expressa en llenguatge algebraic: a) El doble d un nombre. b) El doble d un nombre menys tres unitats. c) El doble d un nombre menys tres unitats, més un
TEMA 1: EXPRESSIONS ALGEBRAIQUES Activitats 1.- Expressa en llenguatge algebraic: a) El doble d un nombre. b) El doble d un nombre menys tres unitats. c) El doble d un nombre menys tres unitats, més un
4.- Expressa en forma de potència única indicant el signe resultant.
 Pàgina 1 de 8 EXERCICIS PER LA RECUPARACIÓ 1A Avaluació 1.- Calcula de dues maneres (TP i RP): a) 25 + (-1+7) (18 9 + 15)= TP= RP= 9 (-12 + 5 8 = TP= RP= 2.- Treu factor comú i calcula: a) 5.(-3) + (-7).
Pàgina 1 de 8 EXERCICIS PER LA RECUPARACIÓ 1A Avaluació 1.- Calcula de dues maneres (TP i RP): a) 25 + (-1+7) (18 9 + 15)= TP= RP= 9 (-12 + 5 8 = TP= RP= 2.- Treu factor comú i calcula: a) 5.(-3) + (-7).
Resultat final, sense desenvolupar, dels exercicis i problemes proposats de cada unitat i de l apartat Resolució de problemes. En queden exclosos
 DE S L U S RE S I V I C LES Resultat final, sense desenvolupar, dels exercicis i problemes proposats de cada unitat i de l apartat Resolució de problemes. En queden exclosos aquells exercicis que requereixen
DE S L U S RE S I V I C LES Resultat final, sense desenvolupar, dels exercicis i problemes proposats de cada unitat i de l apartat Resolució de problemes. En queden exclosos aquells exercicis que requereixen
DERIVADES. TÈCNIQUES DE DERIVACIÓ
 UNITAT 7 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 56 Tangents a una corba y f (x) 5 5 9 4 Troba, mirant la gràfica i les rectes traçades, f'(), f'(9) i f'(4). f'() 0; f'(9) ; f'(4) 4 Digues uns altres
UNITAT 7 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 56 Tangents a una corba y f (x) 5 5 9 4 Troba, mirant la gràfica i les rectes traçades, f'(), f'(9) i f'(4). f'() 0; f'(9) ; f'(4) 4 Digues uns altres
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 PAU 2010
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 SÈRIE 1 Pregunta 1 3 1 lim = 3. Per tant, y = 3 és asímptota horitzontal de f. + 3 1 lim =. Per tant, = - és asímptota horitzontal
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 SÈRIE 1 Pregunta 1 3 1 lim = 3. Per tant, y = 3 és asímptota horitzontal de f. + 3 1 lim =. Per tant, = - és asímptota horitzontal
PAUTA D ESTIU MATEMÀ TIQUES 3R E.S.O. CURS
 PAUTA D ESTIU MATEMÀ TIQUES R E.S.O. CURS 00- Continguts: ) Fraccions: suma, resta, producte, divisió, castells, operacions combinades i fracció generatriu. ) Álgebra: suma, resta, producte i operacions
PAUTA D ESTIU MATEMÀ TIQUES R E.S.O. CURS 00- Continguts: ) Fraccions: suma, resta, producte, divisió, castells, operacions combinades i fracció generatriu. ) Álgebra: suma, resta, producte i operacions
Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS
 Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS 2.1. Divisió de polinomis. Podem fer la divisió entre dos monomis, sempre que m > n. Si hem de fer una divisió de dos polinomis, anirem calculant les divisions
Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS 2.1. Divisió de polinomis. Podem fer la divisió entre dos monomis, sempre que m > n. Si hem de fer una divisió de dos polinomis, anirem calculant les divisions
Districte Universitari de Catalunya
 Proves dʼaccés a la Universitat. Curs 2008-2009 Matemàtiques aplicades a les ciències socials Sèrie 4 Responeu a TRES de les quatre qüestions i resoleu UN dels dos problemes següents. En les respostes,
Proves dʼaccés a la Universitat. Curs 2008-2009 Matemàtiques aplicades a les ciències socials Sèrie 4 Responeu a TRES de les quatre qüestions i resoleu UN dels dos problemes següents. En les respostes,
Proves d accés a la Universitat per a més grans de 25 anys Convocatòria 2013
 Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
Àmbit de les matemàtiques, de la ciència i de la tecnologia M14 Operacions numèriques UNITAT 2 LES FRACCIONS
 M1 Operacions numèriques Unitat Les fraccions UNITAT LES FRACCIONS 1 M1 Operacions numèriques Unitat Les fraccions 1. Concepte de fracció La fracció es representa per dos nombres enters que s anomenen
M1 Operacions numèriques Unitat Les fraccions UNITAT LES FRACCIONS 1 M1 Operacions numèriques Unitat Les fraccions 1. Concepte de fracció La fracció es representa per dos nombres enters que s anomenen
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 55 Activitat 1 Dels nombres següents, indica quins són enters. a) 4 b) 0,25 c) 2 d) 3/5 e) 0 f) 1/2 g) 9 Els nombres enters són: 4, 2, 0 i 9. Activitat 2 Si la
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 55 Activitat 1 Dels nombres següents, indica quins són enters. a) 4 b) 0,25 c) 2 d) 3/5 e) 0 f) 1/2 g) 9 Els nombres enters són: 4, 2, 0 i 9. Activitat 2 Si la
DEURES D ESTIU PER ALS ALUMNES QUE HAN FET 3r D ESO EL CURS 16/17
 INSTITUT GORS Dept. de matemàtiques DEURES D ESTIU PER ALS ALUMNES QUE HAN FET r D ESO EL CURS 16/17 INSTITUT GORGS Dept. de Matemàtiques Juny 017 Benvolguts pares i alumnes de l institut Gorgs, Els professors
INSTITUT GORS Dept. de matemàtiques DEURES D ESTIU PER ALS ALUMNES QUE HAN FET r D ESO EL CURS 16/17 INSTITUT GORGS Dept. de Matemàtiques Juny 017 Benvolguts pares i alumnes de l institut Gorgs, Els professors
TEMA 4: Equacions de primer grau
 TEMA 4: Equacions de primer grau Full de preparació Aquest full s ha de lliurar el dia de la prova Nom:... Curs:... 1. Expressa algèbricament les operacions següents: a) Nombre de rodes necessàries per
TEMA 4: Equacions de primer grau Full de preparació Aquest full s ha de lliurar el dia de la prova Nom:... Curs:... 1. Expressa algèbricament les operacions següents: a) Nombre de rodes necessàries per
Bloc I. ARITMÈTICA I ÀLGEBRA. Tema 3: Els nombres enters TEORÍA
 1. NOMBRES ENTERS * El conjunt dels nombres enters està format pel conjunt dels nombres naturals N = {0, 1, 2, 3, 4, 5...} i els negatius { 1, 2, 3, 4, 5...}. Es representa amb el símbol Z. Per tant Z
1. NOMBRES ENTERS * El conjunt dels nombres enters està format pel conjunt dels nombres naturals N = {0, 1, 2, 3, 4, 5...} i els negatius { 1, 2, 3, 4, 5...}. Es representa amb el símbol Z. Per tant Z
PER ALS ALUMNES QUE HAN FET 2n D ESO EL CURS I PER ALS SEUS PARES
 PER ALS ALUMNES QUE HAN FET n D ESO EL CURS 0-07 I PER ALS SEUS PARES INSTITUT GORGS Dept. de Matemàtiques Juny 07 Benvolguts pares i alumnes de l institut Gorgs, Els professors del departament de matemàtiques
PER ALS ALUMNES QUE HAN FET n D ESO EL CURS 0-07 I PER ALS SEUS PARES INSTITUT GORGS Dept. de Matemàtiques Juny 07 Benvolguts pares i alumnes de l institut Gorgs, Els professors del departament de matemàtiques
Quadern de matemàtiques Decimals1
 Quadern de matemàtiques Decimals CENTENES DESENES UNITATS DECIMES CENTÈSIMES 3,5 Busca les vuit diferències que hi ha en aquests dos dibuixos Curs i grup: Data inici quadern Data acabament Seguiment Data
Quadern de matemàtiques Decimals CENTENES DESENES UNITATS DECIMES CENTÈSIMES 3,5 Busca les vuit diferències que hi ha en aquests dos dibuixos Curs i grup: Data inici quadern Data acabament Seguiment Data
MATEMÀTIQUES ÀREES I VOLUMS
 materials del curs de: MATEMÀTIQUES ÀREES I VOLUMS EXERCICIS RECULL D APUNTS I EXERCICIS D INTERNET FET PER: Xavier Vilardell Bascompte [email protected] ÚLTIMA REVISIÓ: 08 de febrer de 2010 Aquests materials
materials del curs de: MATEMÀTIQUES ÀREES I VOLUMS EXERCICIS RECULL D APUNTS I EXERCICIS D INTERNET FET PER: Xavier Vilardell Bascompte [email protected] ÚLTIMA REVISIÓ: 08 de febrer de 2010 Aquests materials
PROVA D APTITUD PERSONAL ACCÉS ALS GRAUS EDUCACIÓ INFANTIL I EDUCACIÓ PRIMÀRIA
 Nom i cognoms DNI / NIE PROVA D APTITUD PERSONAL ACCÉS ALS GRAUS EDUCACIÓ INFANTIL I EDUCACIÓ PRIMÀRIA COMPETÈNCIA LOGICOMATEMÀTICA 1. Està prohibit l ús de la calculadora o de qualsevol altre aparell
Nom i cognoms DNI / NIE PROVA D APTITUD PERSONAL ACCÉS ALS GRAUS EDUCACIÓ INFANTIL I EDUCACIÓ PRIMÀRIA COMPETÈNCIA LOGICOMATEMÀTICA 1. Està prohibit l ús de la calculadora o de qualsevol altre aparell
ACTIVITATS. a) b) c) d) INS JÚLIA MINGUELL 2n Batxillerat. dv, 18 de març Alumne:
 INS JÚLIA MINGUELL 2n Batxillerat Matemàtiques Tasca Continuada 4 «Matrius i Sistemes d equacions lineals» Alumne: dv, 18 de març 2016 LLIURAMENT: dm, 5 d abril 2016 NOTA: cal justificar matemàticament
INS JÚLIA MINGUELL 2n Batxillerat Matemàtiques Tasca Continuada 4 «Matrius i Sistemes d equacions lineals» Alumne: dv, 18 de març 2016 LLIURAMENT: dm, 5 d abril 2016 NOTA: cal justificar matemàticament
EQUACIONS DE PRIMER GRAU
 1.- Resol les equacions següents: a) x 6x + 10 b) 6x + 1 + 4x c) 5x + -10 d) 6(x 1) 4(x ) e) 1-4x + 6x f) 5(x ) + 4 (5x 1) + 1 g) 8( 10 x ) -6 h) 11 (x + 7) x (5x 6) i) 6( 7 x ) 8( 6 x ) j) ( 1) + 5x 1
1.- Resol les equacions següents: a) x 6x + 10 b) 6x + 1 + 4x c) 5x + -10 d) 6(x 1) 4(x ) e) 1-4x + 6x f) 5(x ) + 4 (5x 1) + 1 g) 8( 10 x ) -6 h) 11 (x + 7) x (5x 6) i) 6( 7 x ) 8( 6 x ) j) ( 1) + 5x 1
Igualdad. 2x + 3 = 5x 2. Una igualdad puede ser: Falsa: 2x + 1 = 2 (x + 1) 2x + 1 = 2x Cierta. 2x + 2 = 2 (x + 1) 2x + 2 = 2x = 2
 Cfgm Equacions 0 Ecuacions Igualdad Una igualdad se compone de dos expresiones unidas por el signo igual. 2x + 3 5x 2 Una igualdad puede ser: Falsa: 2x + 1 2 (x + 1) 2x + 1 2x + 2 1 2. Cierta 2x + 2 2
Cfgm Equacions 0 Ecuacions Igualdad Una igualdad se compone de dos expresiones unidas por el signo igual. 2x + 3 5x 2 Una igualdad puede ser: Falsa: 2x + 1 2 (x + 1) 2x + 1 2x + 2 1 2. Cierta 2x + 2 2
x = graduació del vi blanc y = graduació del vi negre
 Problemes ( pàgina 44 del llibre de classe, Editorial Casals ) (21) Barregem 60 L de vi blanc amb 20 L de vi negre i obtenim un vi de 10 graus (10% d alcohol). Si, contràriament, barregem 20 L de blanc
Problemes ( pàgina 44 del llibre de classe, Editorial Casals ) (21) Barregem 60 L de vi blanc amb 20 L de vi negre i obtenim un vi de 10 graus (10% d alcohol). Si, contràriament, barregem 20 L de blanc
INEQUACIONS I SISTEMES D'INEQUACIONS
 INEQUACIONS I SISTEMES D'INEQUACIONS 1- La mare de la Marta la fa anar a comprar quilos de taronges i ampolles de llet. Per això li dóna 40. Quan la Marta torna, ha perdut el canvi (o almenys, això és
INEQUACIONS I SISTEMES D'INEQUACIONS 1- La mare de la Marta la fa anar a comprar quilos de taronges i ampolles de llet. Per això li dóna 40. Quan la Marta torna, ha perdut el canvi (o almenys, això és
Quadern de matemàtiques Decimals2
 Quadern de matemàtiques Decimals2 1 2,7 0 3 Part entera: 12 Part decimal: 703 Curs i grup: Data inici quadern Data acabament Seguiment Data Observació Professorat Data Avaluació Professorat Índex Operacions
Quadern de matemàtiques Decimals2 1 2,7 0 3 Part entera: 12 Part decimal: 703 Curs i grup: Data inici quadern Data acabament Seguiment Data Observació Professorat Data Avaluació Professorat Índex Operacions
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 PAU 2008 QÜESTIONS
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 Aquestes pautes no preveuen tots els casos que en la pràctica es poden presentar. Tampoc no pretenen donar totes les possibles
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 Aquestes pautes no preveuen tots els casos que en la pràctica es poden presentar. Tampoc no pretenen donar totes les possibles
MATEMÀTIQUES. DOSSIER DE RECUPERACIÓ MATEMÀTIQUES 2n ESO. GRUP:2E. Nom i Cognoms (alumne):... Nom professor:...
 zz Curs: Departament d Educació Generalitat de Catalunya MATEMÀTIQUES DOSSIER DE RECUPERACIÓ MATEMÀTIQUES 2n ESO. GRUP:2E CURS 20-20 INS.PUIG CASTELLAR DATA: Nom i Cognoms (alumne):... Nom professor:...
zz Curs: Departament d Educació Generalitat de Catalunya MATEMÀTIQUES DOSSIER DE RECUPERACIÓ MATEMÀTIQUES 2n ESO. GRUP:2E CURS 20-20 INS.PUIG CASTELLAR DATA: Nom i Cognoms (alumne):... Nom professor:...
CUADERNO PREPARACIÓN MATEMÁTICAS 3 ESO
 CUADERNO PREPARACIÓN MATEMÁTICAS ESO NOMBRES, EQUACIONS i PROBLEMES: 1) Efectua les següents operacions, simplificant al màxim o expressant el resultat en forma de potència, segons convingui: 5 1 1 11
CUADERNO PREPARACIÓN MATEMÁTICAS ESO NOMBRES, EQUACIONS i PROBLEMES: 1) Efectua les següents operacions, simplificant al màxim o expressant el resultat en forma de potència, segons convingui: 5 1 1 11
Dossier d estiu 2n d ESO
 2011 Dossier d estiu 2n d ESO Aquest treball és obligatori per tots aquells alumnes que han passat a tercer amb les matemàtiques de segon suspeses. INSTITUT SABADELL DEPARTAMENT DE MATEMÀTIQUES Grup flexible:
2011 Dossier d estiu 2n d ESO Aquest treball és obligatori per tots aquells alumnes que han passat a tercer amb les matemàtiques de segon suspeses. INSTITUT SABADELL DEPARTAMENT DE MATEMÀTIQUES Grup flexible:
4. PROBLEMES AMB EQUACIONS
 4. PROBLEMES AMB EQUACIONS Molts problemes matemàtiques es poden resoldre amb ajuda d'equacions. Donar una mecànica per la resolució és difícil, doncs òbviament cada problema té la seva estratègia, però
4. PROBLEMES AMB EQUACIONS Molts problemes matemàtiques es poden resoldre amb ajuda d'equacions. Donar una mecànica per la resolució és difícil, doncs òbviament cada problema té la seva estratègia, però
TREBALL D ESTIU MATEMÀTIQUES 3r ESO. ALTRES ALUMNES: Es recomana que realitzeu aquells apartats on heu tingut més dificultats durant el curs. b.
 TREBALL D ESTIU MATEMÀTIQUES r ESO ESO 00 EAC mates Data: 18/05/018 Pàgina 1 de 6 OBSERVACIONS: ALUMNES SUSPESOS: Fer tot el treball obligatòriament ALTRES ALUMNES: Es recomana que realitzeu aquells apartats
TREBALL D ESTIU MATEMÀTIQUES r ESO ESO 00 EAC mates Data: 18/05/018 Pàgina 1 de 6 OBSERVACIONS: ALUMNES SUSPESOS: Fer tot el treball obligatòriament ALTRES ALUMNES: Es recomana que realitzeu aquells apartats
Prova de competència matemàtica
 PROVES DE QUALIFICACIO DE NIVELL 3 Prova de competència matemàtica Nombres naturals: jerarquia d operacions: La jerarquia es: 1. parèntesi 2. multiplicacions i divisions 3. sumes i restes a) 25 : 5 + 3.
PROVES DE QUALIFICACIO DE NIVELL 3 Prova de competència matemàtica Nombres naturals: jerarquia d operacions: La jerarquia es: 1. parèntesi 2. multiplicacions i divisions 3. sumes i restes a) 25 : 5 + 3.
Exercicis de matemàtiques de 1r ESO
 Exercicis de matemàtiques de 1r ESO NOMBRES NATURALS 1. Calcula el resultat d'aquestes operacions (treu primer els parèntesis): a) 63- (17-8) = b) 15+ (20-3) -12+ 2 = c) 8 + 42-6 -(12-4) + 1 = d) 4 + 3
Exercicis de matemàtiques de 1r ESO NOMBRES NATURALS 1. Calcula el resultat d'aquestes operacions (treu primer els parèntesis): a) 63- (17-8) = b) 15+ (20-3) -12+ 2 = c) 8 + 42-6 -(12-4) + 1 = d) 4 + 3
DEPARTAMENT DE MATEMÀTIQUES FEINA D ESTIU
 DEPARTAMENT DE MATEMÀTIQUES FEINA D ESTIU 4t BS 014-015 TEMA I : Intervals i radicals 1. Completa: Interval Desigualtat Representació (, 7 ] x 1 (,)U5,6) (-,-1]. Escriu en forma de desigualtat i representa:
DEPARTAMENT DE MATEMÀTIQUES FEINA D ESTIU 4t BS 014-015 TEMA I : Intervals i radicals 1. Completa: Interval Desigualtat Representació (, 7 ] x 1 (,)U5,6) (-,-1]. Escriu en forma de desigualtat i representa:
MATEMÀTIQUES 1r ESO DOSSIER D'ESTIU
 Col.legi DOMINIQUES DE L ENSENYAMENT Fundació Educativa Dominiques de l Ensenyament C/ Mallorca 349 08013 BARCELONA 932 073 165 MATEMÀTIQUES 1r ESO DOSSIER D'ESTIU - La realització d'aquest dossier d'estiu
Col.legi DOMINIQUES DE L ENSENYAMENT Fundació Educativa Dominiques de l Ensenyament C/ Mallorca 349 08013 BARCELONA 932 073 165 MATEMÀTIQUES 1r ESO DOSSIER D'ESTIU - La realització d'aquest dossier d'estiu
Curs Nombres decimals Fitxa unitats unitats
 1. Ordres d'unitats decimals. Completa: 1 dècima = 0'1 unitats = 1 centèsima = 0'01 unitats = 1 mil lèsima = 1 deumil lèsima = 1 centmil lèsima = 1 milionèsima = 2. Escriu amb xifres: Vint-i-quatre centèsimes:
1. Ordres d'unitats decimals. Completa: 1 dècima = 0'1 unitats = 1 centèsima = 0'01 unitats = 1 mil lèsima = 1 deumil lèsima = 1 centmil lèsima = 1 milionèsima = 2. Escriu amb xifres: Vint-i-quatre centèsimes:
Prova d accés a Cicles formatius de grau superior de formació professional, Ensenyaments d esports i Ensenyaments d arts plàstiques i disseny 2010
 Prova d accés a Cicles formatius de grau superior de formació professional, Ensenyaments d esports i Ensenyaments d arts plàstiques i disseny 2010 Matemàtiques Sèrie 1 Dades de la persona aspirant Qualificació
Prova d accés a Cicles formatius de grau superior de formació professional, Ensenyaments d esports i Ensenyaments d arts plàstiques i disseny 2010 Matemàtiques Sèrie 1 Dades de la persona aspirant Qualificació
( b) ( a) Matemàtiques - Activitats d estiu 4t ESO + = NOMBRES REALS. 1. Calcula, extraient factors fora dels radicals:
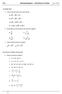 NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
DOSSIER D ACTIVITATS D ESTIU MATEMÀTIQUES 4t d ESO A I B
 DOSSIER D ACTIVITATS D ESTIU MATEMÀTIQUES 4t d ESO A I B A continuació tens una sèrie d'exercicis i activitats relacionats amb els continguts treballats durant el curs. El dossier s ha de presentar en
DOSSIER D ACTIVITATS D ESTIU MATEMÀTIQUES 4t d ESO A I B A continuació tens una sèrie d'exercicis i activitats relacionats amb els continguts treballats durant el curs. El dossier s ha de presentar en
DE FORMA ALGEBRAICA CERTES SITUACIONS
 EXPRESSAR OBJECTIU DE FORMA ALGEBRAICA CERTES SITUACIONS NOM: CURS: DATA: LLENGUATGE NUMÈRIC I LLENGUATGE ALGEBRAIC El llenguatge en què intervenen nombres i signes d operacions l anomenem llenguatge numèric.
EXPRESSAR OBJECTIU DE FORMA ALGEBRAICA CERTES SITUACIONS NOM: CURS: DATA: LLENGUATGE NUMÈRIC I LLENGUATGE ALGEBRAIC El llenguatge en què intervenen nombres i signes d operacions l anomenem llenguatge numèric.
Indiqueu en quins punts Y = f(x) no és contínua, el tipus de discontinuïtats de cada cas i les asímptotes que presenta. (0,1 9 +0,8=1,7 punts)
 Generalitat de Catalunya Departament d Ensenyament Institut Jaume Balmes Nom: 1.- Trobeu la funció inversa o recíproca de la funció recorregut de la funció yf(). f ( ) Departament de Matemàtiques 1MA:
Generalitat de Catalunya Departament d Ensenyament Institut Jaume Balmes Nom: 1.- Trobeu la funció inversa o recíproca de la funció recorregut de la funció yf(). f ( ) Departament de Matemàtiques 1MA:
Tema 3. La restricció pressupostària. Montse Vilalta Microeconomia II Universitat de Barcelona
 Tema 3. La restricció pressupostària Montse Vilalta Microeconomia II Universitat de Barcelona La restricció pressupostària Per desgràcia, no totes les cistelles de consum són assequibles al consumidor.
Tema 3. La restricció pressupostària Montse Vilalta Microeconomia II Universitat de Barcelona La restricció pressupostària Per desgràcia, no totes les cistelles de consum són assequibles al consumidor.
Prova d accés a la Universitat (2013) Matemàtiques II Model 1. (b) Suposant que a = 1, trobau totes les matrius X que satisfan AX + Id = A, on Id
 UIB Prova d accés a la Universitat () Matemàtiques II Model Contestau de manera clara i raonada una de les dues opcions proposades. Es disposa de 9 minuts. Cada qüestió es puntua sobre punts. La qualificació
UIB Prova d accés a la Universitat () Matemàtiques II Model Contestau de manera clara i raonada una de les dues opcions proposades. Es disposa de 9 minuts. Cada qüestió es puntua sobre punts. La qualificació
TEMA 5 : Resolució de sistemes d equacions
 TEMA 5 : Resolució de sistemes d equacions 5.1. EQUACIÓ LINEAL AMB n INCÒGNITES Una equació lineal de n incògnites es qualsevol expressió de la forma: a 1 x 1 + a 2 x 2 +... + a n x n = b, on a i b son
TEMA 5 : Resolució de sistemes d equacions 5.1. EQUACIÓ LINEAL AMB n INCÒGNITES Una equació lineal de n incògnites es qualsevol expressió de la forma: a 1 x 1 + a 2 x 2 +... + a n x n = b, on a i b son
Tema 2: Equacions i problemes de segon grau.
 Tema : Equacions i problemes de segon grau..1. Les equacions de n grau. Equacions del tipus x + 5x - 3 0, on la incògnita x es troba elevada al quadrat, diem que són equacions de segon grau. Exemples:
Tema : Equacions i problemes de segon grau..1. Les equacions de n grau. Equacions del tipus x + 5x - 3 0, on la incògnita x es troba elevada al quadrat, diem que són equacions de segon grau. Exemples:
avaluació diagnòstica educació secundària obligatòria competència matemàtica
 curs 2012-2013 avaluació diagnòstica educació secundària obligatòria competència matemàtica Nom i cognoms Grup Activitat 1: El telèfon mòbil Observa la figura següent, que representa la càrrega que queda
curs 2012-2013 avaluació diagnòstica educació secundària obligatòria competència matemàtica Nom i cognoms Grup Activitat 1: El telèfon mòbil Observa la figura següent, que representa la càrrega que queda
6 SISTEMES D EQUACIONS
 6 SISTEMES D EQUACIONS EXERCICIS PROPOSATS 6.1 Calcula les solucions de l equació 2x 6y 28 sabent el valor d una de les incògnites. a) x 5 c) y 1 e) y 3 b) x 10 d) y 0 f) x 1 2 a) x 5 2 5 6y 28 10 6y 28
6 SISTEMES D EQUACIONS EXERCICIS PROPOSATS 6.1 Calcula les solucions de l equació 2x 6y 28 sabent el valor d una de les incògnites. a) x 5 c) y 1 e) y 3 b) x 10 d) y 0 f) x 1 2 a) x 5 2 5 6y 28 10 6y 28
Matemà ate tiques 2n d ESO
 Matemàtiques 2n d ESO ELS NOMBRES NATURALS 1] Tradueix a numeració decimal aquests nombres egipcis: Pista: et pot ajudar aquest enllaç: http://static4.sobrehistoria.com/wp-content/uploads/2015/05/numeracion-egipcia-
Matemàtiques 2n d ESO ELS NOMBRES NATURALS 1] Tradueix a numeració decimal aquests nombres egipcis: Pista: et pot ajudar aquest enllaç: http://static4.sobrehistoria.com/wp-content/uploads/2015/05/numeracion-egipcia-
DOSSIER DE RECUPERACIÓ DE MATEMÀTIQUES DE 1R D ESO. 1R TRIMESTRE
 DOSSIER DE RECUPERACIÓ DE MATEMÀTIQUES DE 1R D ESO. 1R TRIMESTRE 2013-14 Cal fer totes les operacions en full a part i s han de veure tots els procediments. Les dates d entrega seran les que apareguin
DOSSIER DE RECUPERACIÓ DE MATEMÀTIQUES DE 1R D ESO. 1R TRIMESTRE 2013-14 Cal fer totes les operacions en full a part i s han de veure tots els procediments. Les dates d entrega seran les que apareguin
Tema 6 Proporcionalitat. 1r d ESO, Matemàtiques Editorial Teide, Weeras. Quants nombres, com a mínim, hem de tenir per parlar de proporció?
 Tema 6 Proporcionalitat 1r d ESO, Matemàtiques Editorial Teide, Weeras Què definim com raó de dos nombres? Quants nombres, com a mínim, hem de tenir per parlar de proporció? Com sabem si els nombres donats
Tema 6 Proporcionalitat 1r d ESO, Matemàtiques Editorial Teide, Weeras Què definim com raó de dos nombres? Quants nombres, com a mínim, hem de tenir per parlar de proporció? Com sabem si els nombres donats
Dossier recuperació 4t Curs:
 DEPARTAMENT de MATEMÀTIQUES Dossier recuperació 4t Curs: 2017-18 Data: Nom i Cognoms: Indicacions generals. Heu de presentar els exercicis i els problemes resolts de manera clara i neta en un quadern o
DEPARTAMENT de MATEMÀTIQUES Dossier recuperació 4t Curs: 2017-18 Data: Nom i Cognoms: Indicacions generals. Heu de presentar els exercicis i els problemes resolts de manera clara i neta en un quadern o
La recta. La paràbola
 LA RECTA, LA PARÀBOLA I LA HIPÈRBOLA La recta Una recta és una funció de la forma y = m + n. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall amb
LA RECTA, LA PARÀBOLA I LA HIPÈRBOLA La recta Una recta és una funció de la forma y = m + n. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall amb
FITXA 1: Angles consecutius i adjacents
 FITXA 1: Angles consecutius i adjacents A.1. OBSERVA AQUESTES FIGURES I FES EL QUE S INDICA: Consecutius Adjacents Oposats 1. Col loca aquests noms en la figura corresponent: angles adjacents, angles oposats
FITXA 1: Angles consecutius i adjacents A.1. OBSERVA AQUESTES FIGURES I FES EL QUE S INDICA: Consecutius Adjacents Oposats 1. Col loca aquests noms en la figura corresponent: angles adjacents, angles oposats
Districte Universitari de Catalunya
 Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val
Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val
Examen FINAL M2 FIB-UPC 12 de juny de 2015
 Examen FINAL M FIB-UPC 1 de juny de 015 1. ( punts Sigui a R, calculeu els límits següents segons els valors d a: n + n n + a+ a+n a n n n, n n + n!.. ( punts Considereu la integral següent: I = 1.8 1
Examen FINAL M FIB-UPC 1 de juny de 015 1. ( punts Sigui a R, calculeu els límits següents segons els valors d a: n + n n + a+ a+n a n n n, n n + n!.. ( punts Considereu la integral següent: I = 1.8 1
2n ESO A TREBALL D'ESTIU - MATEMÀTIQUES CURS
 INS PERE BORRELL C. Escoles Pies, 46 17520 PUIGCERDÂ Tel. 972880275 Fax 972141049 Departament de Matemàtiques 2n ESO A TREBALL D'ESTIU - MATEMÀTIQUES CURS 2015-2016 Exercicis que cal fer per preparar la
INS PERE BORRELL C. Escoles Pies, 46 17520 PUIGCERDÂ Tel. 972880275 Fax 972141049 Departament de Matemàtiques 2n ESO A TREBALL D'ESTIU - MATEMÀTIQUES CURS 2015-2016 Exercicis que cal fer per preparar la
5. Calcula: - 6 (- 8) = 9 9 = = -(-5) - 8 = 10 ( -8) = (-1) = 22 : (- 11) = - 45 : (- 9) = 10 : (- 5) = -9 : 3 = -14 : (-7) = 36.
 ELS NOMBRES ENTERS 1. Calcula les següents sumes de nombres enters. - 2 + ( - 10) = 13 + (- 14) = - 5 + 8 = 14 + (- 15) = -9 + 17 = - 6 + 0 = - 10 + (- 20) = 12 + 18 = 18 + (- 19) = 2. Calcula les restes
ELS NOMBRES ENTERS 1. Calcula les següents sumes de nombres enters. - 2 + ( - 10) = 13 + (- 14) = - 5 + 8 = 14 + (- 15) = -9 + 17 = - 6 + 0 = - 10 + (- 20) = 12 + 18 = 18 + (- 19) = 2. Calcula les restes
FITXA 1: Lectura i descomposició de nombres
 FITXA 1: Lectura i descomposició de nombres 1. ESCRIU AQUESTS NOMBRES: a) Tres mil dos-cents milions cent vuitanta mil. b) Sis-cents noranta mil noranta-set. c) Tres mil dos-cents milions cinc-cents cinquanta
FITXA 1: Lectura i descomposició de nombres 1. ESCRIU AQUESTS NOMBRES: a) Tres mil dos-cents milions cent vuitanta mil. b) Sis-cents noranta mil noranta-set. c) Tres mil dos-cents milions cinc-cents cinquanta
Prova de competència matemàtica
 PROVES DE QUALIFICACIO DE NIVELL 3 Prova de competència matemàtica Nombres naturals: jerarquia d operacions: La jerarquia es: 1. parèntesi 2. multiplicacions i divisions 3. sumes i restes a) 25 : 5 + 3.
PROVES DE QUALIFICACIO DE NIVELL 3 Prova de competència matemàtica Nombres naturals: jerarquia d operacions: La jerarquia es: 1. parèntesi 2. multiplicacions i divisions 3. sumes i restes a) 25 : 5 + 3.
PROVA DE MÍNIMS Cicle Superior CEIP TORRE LLAUDER PROVA D AVALUACIÓ DE MÍNIMS DE MATEMÀTIQUES C.S. ALUMNE/A:
 PROVA D AVALUACIÓ DE MÍNIMS DE MATEMÀTIQUES C.S. ALUMNE/A: DATA: CURS: 1.- Escriu amb xifres els nombres següents: Setanta-dos mil cinc-cents catorze Tres-cents vuit mil dues-cents vint-i-quatre Set milions
PROVA D AVALUACIÓ DE MÍNIMS DE MATEMÀTIQUES C.S. ALUMNE/A: DATA: CURS: 1.- Escriu amb xifres els nombres següents: Setanta-dos mil cinc-cents catorze Tres-cents vuit mil dues-cents vint-i-quatre Set milions
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 PAU 2009 QÜESTIONS
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 PAU 009 SÈRIE 4 QÜESTIONS 1. Considereu el sistema d inequacions següent: x 0, y 0 x+ 5y 10 3x+ 4y 1 a) Dibuixeu la regió de solucions
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 PAU 009 SÈRIE 4 QÜESTIONS 1. Considereu el sistema d inequacions següent: x 0, y 0 x+ 5y 10 3x+ 4y 1 a) Dibuixeu la regió de solucions
Dossier d estiu de Matemàtiques. 6è d Educació Primària.
 1. Completa les operacions següents: 6 5 4 1 2 x x 9 4 4 5 7 8 5 2 1 9 6 2 1 1 8 2. Quin nombre hem de multiplicar per 537 per obtenir 9.666? 3. Subratlla els nombres que siguin múltiples de 2 i encercla
1. Completa les operacions següents: 6 5 4 1 2 x x 9 4 4 5 7 8 5 2 1 9 6 2 1 1 8 2. Quin nombre hem de multiplicar per 537 per obtenir 9.666? 3. Subratlla els nombres que siguin múltiples de 2 i encercla
ÍNDEX 1 DEFINICIÓ 2 PER A QUÈ SERVEIX 3 COM ES REPRESENTA 4 PRIMER CONCEPTE 5 ESCALA DE REDUCCIÓ I ESCALA D AMPLIACIÓ 6 PROCEDIMENT DE CÀLCUL
 Francesc Sala, primera edició, abril de 1996 última revisió, desembre de 2007 ÍNDEX 1 DEFINICIÓ 2 PER A QUÈ SERVEIX COM ES REPRESENTA 4 PRIMER CONCEPTE 5 ESCALA DE REDUCCIÓ I ESCALA D AMPLIACIÓ 6 PROCEDIMENT
Francesc Sala, primera edició, abril de 1996 última revisió, desembre de 2007 ÍNDEX 1 DEFINICIÓ 2 PER A QUÈ SERVEIX COM ES REPRESENTA 4 PRIMER CONCEPTE 5 ESCALA DE REDUCCIÓ I ESCALA D AMPLIACIÓ 6 PROCEDIMENT
DERIVADES: exercicis bàsics ex D.1
 DERIVADES: eercicis bàsics e D.. Estudiar la derivabilitat de les funcions que s indiquen, calculant el seu camp de derivabilitat. Escriure l epressió de la funció derivada corresponent, en el cas de que
DERIVADES: eercicis bàsics e D.. Estudiar la derivabilitat de les funcions que s indiquen, calculant el seu camp de derivabilitat. Escriure l epressió de la funció derivada corresponent, en el cas de que
FUNCIONS EXPONENCIALS I LOGARÍTMIQUES. MATEMÀTIQUES-1
 FUNCIONS EXPONENCIALS I LOGARÍTMIQUES. 1. Funcions exponencials. 2. Equacions exponencials. 3. Definició de logaritme. Propietats. 4. Funcions logarítmiques. 5. Equacions logarítmiques. 1. Funcions exponencials.
FUNCIONS EXPONENCIALS I LOGARÍTMIQUES. 1. Funcions exponencials. 2. Equacions exponencials. 3. Definició de logaritme. Propietats. 4. Funcions logarítmiques. 5. Equacions logarítmiques. 1. Funcions exponencials.
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 59 Activitat 1 Llegeix atentament el teorema de Tales. Creus que també és certa la proporció següent? Per què? AB CD A B C D El teorema de Tales diu: AB (A B
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 59 Activitat 1 Llegeix atentament el teorema de Tales. Creus que també és certa la proporció següent? Per què? AB CD A B C D El teorema de Tales diu: AB (A B
CARACTERÍSTIQUES DE FUNCIONS ELEMENTALS
 CARACTERÍSTIQUES DE FUNCIONS ELEMENTALS 1. FUNCIÓ CONSTANT (document d'ajuda: 1_funcio_constant.html ) Expressió algèbrica: f(x) = n. Gràfica: 2. FUNCIÓ LINEAL (document d'ajuda: 2_funcio_lineal.html )
CARACTERÍSTIQUES DE FUNCIONS ELEMENTALS 1. FUNCIÓ CONSTANT (document d'ajuda: 1_funcio_constant.html ) Expressió algèbrica: f(x) = n. Gràfica: 2. FUNCIÓ LINEAL (document d'ajuda: 2_funcio_lineal.html )
TEMA 4: Equacions exponencials i logarítmiques
 TEMA 4: Equacions exponencials i logarítmiques 4.1. EXPONENCIALS Definim exponencial de base a i exponent n:. Propietats de les exponencials: (1). (2) (3) (4) 1 (5) 4.2. EQUACIONS EXPONENCIALS Anomenarem
TEMA 4: Equacions exponencials i logarítmiques 4.1. EXPONENCIALS Definim exponencial de base a i exponent n:. Propietats de les exponencials: (1). (2) (3) (4) 1 (5) 4.2. EQUACIONS EXPONENCIALS Anomenarem
2 desembre 2015 Límits i número exercicis. 2.1 Límits i número
 I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 2 desembre 205 Límits i número exercicis 2. Límits i número 4. Repàs de logaritmes i exponencials: troba totes les solucions de cadascuna de les següents equacions:
I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 2 desembre 205 Límits i número exercicis 2. Límits i número 4. Repàs de logaritmes i exponencials: troba totes les solucions de cadascuna de les següents equacions:
NO, la divisió no és exacta. SI, la divisió és exacta. SI, la divisió és exacta. NO, la divisió no és exacta. NO, la divisió no és exacta.
 1. Comprova si hi ha relació de divibilitat entre aquestos nombres. a) 224 i 40 1 NO, la divisió no és exacta. b) 450 i 50 c) 400 i 16 d) 654 i 32 NO, la divisió no és exacta. e) 568 i 46 NO, la divisió
1. Comprova si hi ha relació de divibilitat entre aquestos nombres. a) 224 i 40 1 NO, la divisió no és exacta. b) 450 i 50 c) 400 i 16 d) 654 i 32 NO, la divisió no és exacta. e) 568 i 46 NO, la divisió
