Circunferencia y sus elementos
|
|
|
- Eduardo Torres Naranjo
- hace 9 años
- Vistas:
Transcripción
1 Liceo Tecnológico Enrique Kirberg Departamento de Matemáticas Compendio Verano 2011 Séptimo y Octavo año Básico Circunferencia y sus elementos Una circunferencia es una figura geométrica formada por todos los puntos del plano que están a igual distancia de un punto llamado centro, al cual se le designa con la letra O. Cuerda: Es el segmento trazado entre dos puntos cualesquiera de la circunferencia. Radio: Es el segmento que une cualquier punto de la circunferencia con el centro de ésta. Diámetro: Es la cuerda que une dos puntos de la circunferencia pasando por el centro, es decir, el la cuerda de mayor longitud que podemos trazar. El diámetro mide el doble del radio. Arco: Es la parte de una circunferencia comprendida entre dos puntos de ella. Los arcos en una circunferencia se leen en sentido contrario de los punteros del reloj. Tangente a una circunferencia: Recta que tiene sólo un punto en común con la circunferencia, es decir, que la intersecta en un punto. Secante a una circunferencia: Recta que corta a la circunferencia en dos puntos. En la imagen el punto O es el centro de la circunferencia. El trazo es una cuerda. El segmento es el radio. El segmente es diámetro. La parte de la circunferencia que va desde el punto A hasta el punto B es el arco. La recta EF es secante a la circunferencia y la recta que la corta en H es tangente a ésta.
2 Ejercicios: 1. Cuántas rectas secantes puede tener una circunferencia? Por qué? 2. Cuántas rectas tangentes puede tener una circunferencia? Por qué? 3. Cuántas rectas tangentes pueden pasar por un solo punto de la circunferencia? Por qué? 4. Evalúa si cada afirmación es verdadera (V) o falsa (F) con respecto a la figura: a) El trazo AB es una cuerda de la circunferencia. b) La recta HL es secante a la circunferencia. c) La recta AB es secante a la circunferencia. d) El arco DE es el diámetro de la circunferencia. e) El segmento OH es radio de la circunferencia. f) Los trazos KA y DE son diámetros de la circunferencia. g) El segmento OK no es radio de la circunferencia. Círculo El círculo es el lugar geométrico formado por todos los puntos de una circunferencia y los puntos interiores que encierra dicha circunferencia. Regiones del círculo 1. Sector circular: 2. Segmento circular:
3 3. Corona Circular: 4. Trapecio circular: Ejercicios: 1. Qué relación hay entre el trapecio circular y la corona circular? Comenta. 2. Con qué concepto tratado anteriormente relacionarías cada uno de los siguientes objetos? a) Un trozo de pizza. b) Un anillo. c) Un plato. Polígonos regulares Un polígono es una figura geométrica plana cerrada, es la región del plano limitada por tres o más segmentos llamados lados, los cuales concurren en puntos denominados vértices. Un polígono regular es un polígono que tiene todos sus lados de igual medida y todos sus ángulos interiores son congruentes. Algunos de los polígonos regulares son: Triángulo equilátero (3 lados) Cuadrado (4 lados) Pentágono regular (5 lados) Hexágono regular (6 lados) Heptágono regular (7 lados) Octágono regular (8 lados) Eneágono regular (9 lados) Decágono regular (10 lados) Endecágono regular (11 lados) Ejercicios: 1. Investigue cuál es el valor de los ángulos interiores de los polígonos regulares nombrados anteriormente.
4 2. En los siguientes polígonos indique cuál o cuáles son regulares: 3. Investiga y completa la siguiente tabla: 4. Identifica la cantidad de segmentos circulares que determina cada uno de los polígonos regulares inscritos en la circunferencia. Note que un polígono regular inscrito en una circunferencia tiene todos sus vértices pertenecientes a ésta: 5. Cuántos segmentos circulares determina un polígono de n lados? Por qué? 6. Qué ocurre con las medidas de los ángulos interiores de un polígono regular a medida que la cantidad de lados crece? Perímetro y área El perímetro es la medida de la longitud del contorno de un figura geométrica, mientras que el área es una medida de la extensión de una superficie. La superficie es el conjunto de puntos del plano encerrados por una figura geométrica plana. Usted ya debería manejar algunas de la ecuaciones que facilitan el cálculo de áreas y perímetros de figuras planas, tales como:
5 Perímetro y área de polígonos regulares La siguiente señal de tránsito representa la forma de un polígono de ocho lados de igual medida y ángulos interiores congruentes. Si sus lados miden 25[cm] cada uno, cuál es la medida del perímetro y la del área del polígono representado? El polígono representado se denomina octágono regular (8 ángulos interiores iguales y 8 lados de igual medida). En este caso su perímetro P mide:
6 Su área se puede determinar descomponiéndolo en 8 triángulos isósceles de iguales dimensiones y área. Al medir la altura de cada triángulo, se tiene que ésta es de 30,2[cm] aproximadamente. Por lo que el área de cada triángulo es de: Finalmente, el área total mide: IMPORTANTE: Un polígono regular tiene todos sus ángulos interiores y lados de igual medida. El perímetro P de un polígono regular de n lados es: donde L es la medida del lado del polígono. El área A de un polígono regular está dada por: donde P es el perímetro del polígono y a la apotema. Apotema es la distancia desde el centro del polígono hasta uno de los lados de éste y que lo divide en dos segmentos iguales. Ejercicios: 1. Calcula la medida de la apotema a para cada polígono regular. Para ello, aplica el teorema de Pitágoras.
7 2. Calcule el perímetro P y el área A de cada uno de los polígonos regulares de la pregunta anterior. 3. La figura muestra un cuadrado inscrito en otro. Si el lado del cuadrado mide 4[cm], cuánto mide el perímetro del cuadrado? 4. Si el perímetro del polígono pintado es M, cuánto mide el perímetro del rectángulo? 5. Determine el perímetro del polígono regular que se muestra a continuación sabiendo que uno de sus lados mide 6. Calcula el área de la región pintada si el área del rectángulo ABCD es y M es un punto cualquiera del lado CD.
8 7. Se quiere construir un cuadrado que tenga igual perímetro que un rectángulo cuya área mide, en el que sus lados están en la razón 1 : 4. a) Cuál es el área del cuadrado? b) Qué conclusión relacionada con la variación de las áreas puedes obtener a partir de este problema? 8. Cuántos litros de pintura se ocupan en pintar un muro de de largo y de ancho, si con un litro se cubren? 9. Un cuadrado tiene igual perímetro que un rectángulo de de largo y de ancho. Calcula el lado del cuadrado. Longitud de una circunferencia Una rueda al dar un vuelta completa se desplaza una distancia que es igual a la longitud de su perímetro. Cuántas veces está contenido el diámetro en la longitud de este desplazamiento? Si se conoce el cociente entre el perímetro de la circunferencia que representa la rueda y su diámetro, se obtendrá un valor que es independiente del tamaño de ésta. Este número no se puede escribir como fracción, ya que es un número decimal infinito no periódico. Es representado con la letra griega y su valor aproximado a la centésima es. IMPORTANTE: Sea P la longitud o perímetro de una circunferencia y D el diámetro de la misma, entonces: El perímetro de una circunferencia está dado por: donde r es el radio de la circunferencia. El semiperímetro S de una circunferencia de perímetro P es:
9 Ejercicios: 1. Calcula el perímetro P de las siguientes circunferencias considerando. a) Una circunferencia de radio b) Una circunferencia de radio c) Una circunferencia de diámetro d) Una circunferencia de diámetro 2. Calcula la medida del radio y del diámetro de cada circunferencia. Para ello considera. a) El perímetro de la circunferencia es b) El semiperímetro de la circunferencia es 3. En un parque de diversiones, el carrusel da quince vueltas antes de detenerse a recoger nuevos pasajeros. Si el diámetro del carrusel mide, qué distancia recorre cada pasajero? 4. Aplica el teorema de Pitágoras y calcula la longitud de cada circunferencia. Considera que cada triángulo está inscrito en la circunferencia: 5. Si el radio de una circunferencia aumenta, qué variación porcentual experimenta su perímetro? 6. Al completar una vuelta, una rueda de bicicleta recorre. Cuál es aproximadamente la medida del radio de la rueda? Considere π. Área del círculo En una circunferencia se pueden inscribir polígonos regulares de n lados, con y
10 Se puede calcular el área de un círculo a partir del análisis de estos polígonos? Dado que el área de un polígono regular se calcula mediante la expresión se considera la circunferencia como un polígono de infinitos lados, la apotema se aproxima al radio de la circunferencia y se tiene que:, si IMPORTANTE: 1) El área de un círculo de radio r está dado por la ecuación: Ejercicios: 1. Calcule el área de los siguientes círculos: a) Un círculo de radio b) Un círculo de de diámetro. c) Un círculo inscrito en un cuadrado de lado d) Un círculo con semiperímetro igual a 2. Calcula la máxima distancia a la que se pueden encontrar dos vasos en una mesa redonda cuya cubierta tiene una superficie de 3. Cuál es el perímetro de la circunferencia que representa la cubierta de la mesa del problema anterior? 4. Si un cuadrado y un círculo tienen el mismo perímetro, se puede afirmar que estos tienen igual área? Justifica. 5. Cuánto mide el área del círculo que se forma con un cordel de de longitud? Considere. 6. Si la razón entre los radios de dos circunferencias es, en qué razón están sus áreas? 7. Si el radio de una circunferencia aumenta 20%, qué variación porcentual experimenta su área? 8. El área de un círculo es Determine su perímetro.
11 Perímetro de figuras compuestas El perímetro de una figura compuesta corresponde a la longitud de toda su frontera. Ejercicios: 1. Determine el perímetro de los siguientes polígonos compuestos: Área de figuras compuestas El área de figuras compuestas se puede calcular determinando el área de las figuras que la componen, sumándolas o restándolas según corresponda. Por ejemplo: ABCD rectángulo y AD diámetro del círculo de centro O. Entonces el área de la figura compuesta por el rectángulo y el semicírculo es:
12 En este segundo ejemplo ABCD rectángulo y el círculo de centro O tiene radio 2[cm]. El área pintada es: Ejercicios: 1. Determine el área pintada en cada caso:
13 2. Calcula el área sombreada, sabiendo que el lado de cuadrado es 3. Calcula el área de la parte sombreada, si el radio del círculo mayor mide y el radio de los círculos pequeños mide 4. La pared de una habitación mide 6[m] de ancho y de alto; además tiene 2 ventanas circulares de de radio cada una: a) Si no estuvieran las ventanas, qué superficie tendría la pared? b) Qué medida tiene la superficie de cada ventana? c) Si quieres pintar la pared, cuál es el área de la superficie a pintar? Explica tu procedimiento. d) Si un tarro de pintura alcanza para, cuántos tarros necesitas para pintar la pared? e) Si cada tarro cuesta $850, cuánto dinero se necesita para pintar la pared? Transformaciones isométricas Una transformación isométrica es un cambio que se realiza sobre figuras planas, que no modifican la forma ni el tamaño de éstas. La palabra isometría tiene origen griego: iso, que significa igual, y metría, que significa medir. Por lo tanto, esta palabra puede ser traducida como igual medida.
14 Ejercicios: 1. Identifica en cada caso si se realizó una transformación isométrica. Argumenta tu respuesta. a) b) c) d) 2. Se puede afirmar que las situaciones que muestran las fotografías representan transformaciones isométricas? Justifica. Mirarse al espejo Martillar un clavo Soltar una pelota Traslación La traslación de una figura plana es una transformación isométrica que mueve todos los puntos de la figura en una misma dirección, sentido y longitud. La translación de una figura geométrica plana se puede realizar utilizando un vector traslación, que tiene longitud, dirección y sentido.
15 Ejercicios: 1. Determine la traslación que se realizó a la siguientes figuras: 2. Traslada cada figura según el vector traslación dado: 3. Al trasladar el punto P = (-2, -2), 5 unidades hacia el norte, 3 unidades hacia el este y 1 unidad al sur. Cuáles son las nuevas coordenadas del punto P? Reflexión Una reflexión es una transformación isométrica en la que a cada punto de la figura original se le asocia otro punto llamado imagen. La reflexión puede ser de dos tipos: Simetría axial: Cada punto de la figura original y la imagen de cada uno de ellos bajo la reflexión, se encuentran a igual distancia de una recta llamada eje de simetría.
16 En la figura, la distancia que hay desde los puntos O, P y N al el eje de simetría es igual a la distancia que hay desde el eje de simetría hasta los puntos O', P' y N' respectivamente. Simetría central: Cada punto de la figura original y la imagen de cada uno de ellos bajo la reflexión, se encuentran a igual distancia de un punto llamado punto de simetría. En la figura, la distancia que hay desde los puntos A, B y C al el eje de simetría es igual a la distancia que hay desde el eje de simetría hasta los puntos A', B' y C' respectivamente. Ejercicios: 1. Refleja cada una de las siguientes figuras respecto al eje de simetría correspondiente:
17 2. Aplica el concepto de eje de simetría, con ayuda de una regla dibújalo en cada caso: 3. Plantea un procedimiento que te permita determinar el centro o punto de simetría entre las figuras: 4. Qué letras mayúsculas tienen simetría horizontal, pero no vertical? 5. Qué letras mayúsculas tienen simetría horizontal y vertical?
18 Rotación Una rotación es una transformación isométrica en la que todos los puntos de la figura de origen se mueven respecto de un punto fijo llamado centro de rotación en un determinado ángulo, llamado ángulo de rotación. El centro de rotación puede estar en el interior, en el contorno o en el exterior de la figura. El sentido positivo de la rotación es el sentido antihorario, es decir, contrario al movimiento de las manecillas del reloj. Mientras que el sentido negativo de la rotación es en el sentido horario. Para rotar una figura basta rotar sus vértices. Veamos cómo rotar un punto P respecto del centro de rotación O, para ello necesitaremos compás y transportador: Se traza el segmento OP. Se pone la marca de inicio del transportador en O y se marca 0º en el segmento OP. Con el lápiz se marca un punto sobre el transportador en grados. Se une dicho punto con el centro O. Con el compás se traza una circunferencia de centro O y radio OP hasta la intersectarse con el trazo recientemente dibujado.
19 Ejercicios: 1. Identifica cuál de las siguientes transformaciones corresponden a rotaciones. Justifica. 2. Rota en tu cuaderno las siguientes figuras en 90º respecto del punto indicado: 3. Realice una rotación con centro en D y un ángulo de 60º:
20 4. Realice una rotación con centro en E y un ángulo de 80º: Teselaciones La teselación es una técnica que permite recubrir el plano con figuras geométricas planas, de tal manera que todos los espacios resulten cubiertos, sin dejar vacíos, ni tampoco figuras superpuestas. Una teselación es regular cuando en el recubrimiento se utiliza un solo polígono regular. Este tipo de teselaciones sólo es posible utilizando triángulos equiláteros, cuadrados o hexágonos regulares. Por ejemplo: Una teselación es semirregular cuando en el recubrimiento se utilizan combinaciones de polígonos regulares. Para que esto sea posible, los polígonos que se juntan en un vértice deben tener ángulos interiores que sumen exactamente 360º. Por ejemplo:
21 Ejercicios: 1. Observa la siguiente teselación y responde: a) Qué tipo de teselación es? b) Cuál es el patrón de la teselación? (Figura[as] que se repiten y cubren completamente la superficie plana) c) Qué polígonos se utilizaron para construir esta teselación? d) Es posible construir una teselación semirregular utilizando solo un cuadrado y dos hexágonos regulares? Justifica. e) Es posible construir una teselación semirregular utilizando solo un cuadrado y dos octágonos regulares? Justifica. 2. Con qué polígonos regulares es posible construir una teselación? 3. Es posible teselar el plano con cualquier tipo de triángulo? Justifica. 4. Es posible teselar el plano con cualquier tipo de cuadrilátero? Justifica. 5. Construye dos teselaciones utilizando las dos combinaciones de polígonos que se muestran a continuación: 6. Describa en cada caso, la forma en que se puede aplicar transformaciones isométricas sobre la figura pintada que permitan teselar el plano como indica cada imagen:
22 Cuerpos geométricos Son objetos tridimensionales limitados por una o varias superficies. Se clasifican en cuerpos poliedros y cuerpos redondos: Cuerpos poliedros Es aquel cuerpo limitado por superficies planas y de contorno poligonal. Se llaman vértices y aristas del poliedro a los vértices y lados de sus caras, respectivamente. En cada vértice deben concurrir al menos tres aristas ya que es un objeto tridimensional. Los poliedros se designan según el número de sus caras: 4 caras Tetraedro 5 caras Pentaedro 6 caras Hexaedro 7 caras Heptaedro 8 caras Octaedro 10 caras Decaedro 12 caras Dodecaedro 20 caras Icosaedro, etc. Los poliedros se clasifican en regulares e irregulares: Poliedros regulares: Son aquellos cuyas caras son polígonos regulares congruentes entre sí y cuyos ángulos poliedros son iguales. En la figura se muestra qué es un ángulo poliedro, el cual está limitado por las caras del cuerpo. Los poliedros regulares son cinco: 1) Tetraedro regular: Formado por 4 caras que son triángulos equiláteros. 2) Hexaedro regular o cubo: Formado por 6 caras que son cuadrados. 3) Octaedro regular: Formado por 8 caras que son triángulos equiláteros.
23 4) Dodecaedro regular: Formado por 12 caras que son pentágonos regulares. 5) Icosaedro regular: Formado por 20 caras que son triángulos equiláteros. Poliedros irregulares: Son los que no cumplen con alguna de las condiciones de poliedro regular. Se pueden clasificar en prismas y pirámides. Prisma: Es el poliedro limitado por varios paralelógramos (caras laterales) y dos polígonos congruentes llamados bases cuyos planos son paralelos. Paralelepípedo: Prisma cuyas bases son paralelógramos. Si sus aristas laterales son perpendiculares a las bases, se llama paralelepípedo recto. Pirámide: Es el poliedro que tiene una cara que es un polígono al que se llama base y las caras laterales son triángulos que tienen un punto en común llamado vértice. Se designan de acuerdo con el polígono de la base. Si éste es un triángulo se llama pirámide triangular, si es un cuadrilátero, cuadrangular, etc.
24 Cuerpos redondos: Son aquellos que están limitados por superficies curvas o por superficies curvas y planas. Los principales son el cilindro, el cono y la esfera. Una superficie de revolución es una superficie generada por una línea que gira alrededor de una recta llamada eje de revolución. La línea que gira se llama generatriz. Sólido de revolución es el cuerpo generado por una superficie plana que gira alrededor de un eje situado en el miso plano. Cilindro circular recto: Es el cuerpo limitado por una superficie cilíndrica y dos secciones planas circulares paralelas (bases del cilindro). Su altura es la distancia entre las bases o, equivalentemente, la longitud de su generatriz. Es un cuerpo geométrico engendrado por la revolución completa de un rectángulo alrededor de un eje que puede ser cualquiera de sus lados.
25 Cono circular recto: Es el sólido de revolución engendrado al hacer girar un triángulo rectángulo en torno a un eje situado sobre uno de sus catetos. La altura es la distancia desde el vértice al plano de la base. Esfera: Es el conjunto de puntos de la superficie esférica más todos los puntos que están en su interior. Los puntos de la superficie esférica equidistan de un punto llamado centro. El segmento de recta que une el centro con cualquier punto de la superficie se llama radio. Podemos considerar la esfera como el cuerpo engendrado por la revolución de un semi círculo alrededor de un eje que contiene su diámetro. Ejercicios: 1. Qué es un cuerpo geométrico? 2. Defina los conceptos de cuerpo poliedro y cuerpo redondo. 3. Dibuje un hexaedro regular e indique cuáles son sus caras, aristas y vértices. 4. Qué es un poliedro regular? Indique cuántos y cuáles son. 5. Defina con sus palabras ángulo poliedro. 6. Qué es un polígono irregular? Indique al menos tres ejemplos. 7. Qué es un cuerpo redondo? 8. Dibuje tres prismas distintos. 9. Dibuje tres pirámides distintas. 10. Busca y dibuja en tu cuaderno las redes del tetraedro, el cubo, el paralelepípedo, el cilindro y el cono.
CORRECCIÓN DE ACTIVIDADES GEOMETRÍA LINEAL
 CORRECCIÓN DE ACTIVIDADES GEOMETRÍA LINEAL *. Responde a las siguientes preguntas en tu cuaderno. a) Qué es una recta? Dibújala. Recta: sucesión infinita de puntos (no tiene principio ni fin). Las rectas
CORRECCIÓN DE ACTIVIDADES GEOMETRÍA LINEAL *. Responde a las siguientes preguntas en tu cuaderno. a) Qué es una recta? Dibújala. Recta: sucesión infinita de puntos (no tiene principio ni fin). Las rectas
MATEMÁTICAS 1º DE ESO
 MATEMÁTICAS 1º DE ESO LOE TEMA XII: POLIEDROS Y CUERPOS DE REDONDOS Poliedros. o Elementos de un poliedro y desarrollo plano. Prismas. o Elementos y tipos de prismas. Pirámides. o Elementos y tipos de
MATEMÁTICAS 1º DE ESO LOE TEMA XII: POLIEDROS Y CUERPOS DE REDONDOS Poliedros. o Elementos de un poliedro y desarrollo plano. Prismas. o Elementos y tipos de prismas. Pirámides. o Elementos y tipos de
Sistemas de Representación y Dibujo Técnico Año 2015. Geometría Básica
 EL PUNTO Geometría Básica El punto es la entidad geométrica más pequeña y finita. Se puede definir por intersección de 2 rectas. En un plano, se puede definir por medio de 2 coordenadas. En el espacio,
EL PUNTO Geometría Básica El punto es la entidad geométrica más pequeña y finita. Se puede definir por intersección de 2 rectas. En un plano, se puede definir por medio de 2 coordenadas. En el espacio,
11 Cuerpos geométricos
 89485 _ 0369-0418.qxd 1/9/07 15:06 Página 369 Cuerpos geométricos INTRODUCCIÓN Los poliedros, sus elementos y tipos ya son conocidos por los alumnos del curso anterior. Descubrimos y reconocemos de nuevo
89485 _ 0369-0418.qxd 1/9/07 15:06 Página 369 Cuerpos geométricos INTRODUCCIÓN Los poliedros, sus elementos y tipos ya son conocidos por los alumnos del curso anterior. Descubrimos y reconocemos de nuevo
Colegio Universitario Boston. Geometría
 34 Conceptos ásicos Triángulo: Se define como la figura geométrica plana, cerrada de tres lados. Triángulo equilátero: Es el triángulo que tiene sus tres lados iguales y sus tres ángulos internos iguales,
34 Conceptos ásicos Triángulo: Se define como la figura geométrica plana, cerrada de tres lados. Triángulo equilátero: Es el triángulo que tiene sus tres lados iguales y sus tres ángulos internos iguales,
Los cuerpos geométricos
 Los cuerpos geométricos Se denominan cuerpos geométricos a aquellos elementos que, ya sean reales o ideales que existen en la realidad o pueden concebirse mentalmente ocupan un volumen en el espacio desarrollándose
Los cuerpos geométricos Se denominan cuerpos geométricos a aquellos elementos que, ya sean reales o ideales que existen en la realidad o pueden concebirse mentalmente ocupan un volumen en el espacio desarrollándose
Created with novapdf Printer (www.novapdf.com)
 GEOMETRÍA LONGITUDES Longitud de la circunferencia Es una línea curva cerrada que equidistan todos sus puntos del centro. Radio Centro: punto situado a igual distancia de todos los puntos de la circunferencia.
GEOMETRÍA LONGITUDES Longitud de la circunferencia Es una línea curva cerrada que equidistan todos sus puntos del centro. Radio Centro: punto situado a igual distancia de todos los puntos de la circunferencia.
9Soluciones a los ejercicios y problemas PÁGINA 200
 PÁGINA 200 Pág. 1 T ipos de cuerpos geométricos 1 Di, justificadamente, qué tipo de poliedro es cada uno de los siguientes: A B C D E F Hay entre ellos algún poliedro regular? A 8 Prisma pentagonal recto.
PÁGINA 200 Pág. 1 T ipos de cuerpos geométricos 1 Di, justificadamente, qué tipo de poliedro es cada uno de los siguientes: A B C D E F Hay entre ellos algún poliedro regular? A 8 Prisma pentagonal recto.
Polígonos y circunferencia
 826464 _ 055-070.qxd 12/2/07 09:22 Página 55 Polígonos y circunferencia INTRODUCCIÓN RESUMEN DE LA UNIDAD Nos introducimos en el estudio de los polígonos, recordando contenidos trabajados por los alumnos
826464 _ 055-070.qxd 12/2/07 09:22 Página 55 Polígonos y circunferencia INTRODUCCIÓN RESUMEN DE LA UNIDAD Nos introducimos en el estudio de los polígonos, recordando contenidos trabajados por los alumnos
Nº caras. Nº vértices
 Tipo De Caras (Ángulo Interior) Triángulo Equilátero (60º) Cuadrado (90º) Pentágono (108º) Hexágono (10º) Nº caras por vértice Suma de los ángulos de cada vértice Nº caras Nº vértices Nº aristas C + V
Tipo De Caras (Ángulo Interior) Triángulo Equilátero (60º) Cuadrado (90º) Pentágono (108º) Hexágono (10º) Nº caras por vértice Suma de los ángulos de cada vértice Nº caras Nº vértices Nº aristas C + V
UNIDAD 10. FIGURAS PLANAS: POLÍGONOS CIRCUNFERENCIA Y CÍRCULO
 UNIDAD 10. FIGURAS PLANAS: POLÍGONOS CIRCUNFERENCIA Y CÍRCULO 1. POLÍGONOS: DEFINÍCIÓN, ELEMENTOS Y CLASIFICACIÓN. 2. POLÍGONOS REGULARES E IRREGULARES. 3. TRIÁNGULOS Y CUADRILÁTEROS: CLASIFICACIÓN. 4.
UNIDAD 10. FIGURAS PLANAS: POLÍGONOS CIRCUNFERENCIA Y CÍRCULO 1. POLÍGONOS: DEFINÍCIÓN, ELEMENTOS Y CLASIFICACIÓN. 2. POLÍGONOS REGULARES E IRREGULARES. 3. TRIÁNGULOS Y CUADRILÁTEROS: CLASIFICACIÓN. 4.
ÁREAS DE CUERPOS GEOMÉTRICOS Poliedros. Para calcular el área de un poliedro calculamos el área de cada una de sus caras y las sumamos.
 TEMA 9: ÁREAS Y VOLÚMENES DE CUERPOS GEOMÉTRICOS POLIEDROS REGULARES Un poliedro se llama regular cunado cumple las dos condiciones siguientes: Sus caras son polígonos regulares idénticos. En cada vértice
TEMA 9: ÁREAS Y VOLÚMENES DE CUERPOS GEOMÉTRICOS POLIEDROS REGULARES Un poliedro se llama regular cunado cumple las dos condiciones siguientes: Sus caras son polígonos regulares idénticos. En cada vértice
EXAMEN GEOMETRÍA. 5. Halla el perímetro y el área de un triángulo isósceles cuyos lados miden 5, 5 y 8 cms., respectivamente.
 1. Supongamos una circunferencia de radio 90/ð cms. y un ángulo cuyo vértice coincida con el centro de la circunferencia. Halla: a) La longitud de arco de circunferencia que abarca un ángulo de 501. b)
1. Supongamos una circunferencia de radio 90/ð cms. y un ángulo cuyo vértice coincida con el centro de la circunferencia. Halla: a) La longitud de arco de circunferencia que abarca un ángulo de 501. b)
Manual de teoría: Geometría Matemática Bachillerato
 Manual de teoría: Geometría Matemática Bachillerato Realizado por José Pablo Flores Zúñiga Geometría: José Pablo Flores Zúñiga Página 1 Contenido: 3) Geometría 3.1 Círculo y Circunferencia 3. Polígonos
Manual de teoría: Geometría Matemática Bachillerato Realizado por José Pablo Flores Zúñiga Geometría: José Pablo Flores Zúñiga Página 1 Contenido: 3) Geometría 3.1 Círculo y Circunferencia 3. Polígonos
1.- Punto: Intersección de dos rectas. No tiene dimensiones (ni largo, ni ancho, ni alto).
 1.- Punto: Intersección de dos rectas. No tiene dimensiones (ni largo, ni ancho, ni alto). 6.- Espacio: Conjunto de puntos con tres dimensiones: largo, ancho y alto. Es infinito, sin límites. 2.- Recta:
1.- Punto: Intersección de dos rectas. No tiene dimensiones (ni largo, ni ancho, ni alto). 6.- Espacio: Conjunto de puntos con tres dimensiones: largo, ancho y alto. Es infinito, sin límites. 2.- Recta:
GEOMETRÍA. 1. Líneas y ángulos. Partimos de la existencia de infinitos puntos cuyo conjunto llamamos ESPACIO.
 1. Líneas y ángulos Partimos de la existencia de infinitos puntos cuyo conjunto llamamos ESPACIO. Los puntos del espacio se consideran agrupados en conjuntos parciales de infinitos puntos llamados PLANOS.
1. Líneas y ángulos Partimos de la existencia de infinitos puntos cuyo conjunto llamamos ESPACIO. Los puntos del espacio se consideran agrupados en conjuntos parciales de infinitos puntos llamados PLANOS.
Conceptos básicos de Geometría
 Conceptos básicos de geometría La geometría trata de la medición y de las propiedades de puntos, líneas, ángulos, planos y sólidos, así como de las relaciones que guardan entre sí. A continuación veremos
Conceptos básicos de geometría La geometría trata de la medición y de las propiedades de puntos, líneas, ángulos, planos y sólidos, así como de las relaciones que guardan entre sí. A continuación veremos
EJERCICIOS. ÁREAS Y VOLÚMENES.
 EJERCICIOS. ÁREAS Y VOLÚMENES. Teorema de Tales 1. Sean los triángulos ABC, AB'C'.Calcula el valor desconocido x. 2. Dos triángulos semejantes tienen una superficie de 20cm 2 y 30cm 2 respectivamente.
EJERCICIOS. ÁREAS Y VOLÚMENES. Teorema de Tales 1. Sean los triángulos ABC, AB'C'.Calcula el valor desconocido x. 2. Dos triángulos semejantes tienen una superficie de 20cm 2 y 30cm 2 respectivamente.
SUBRAYE LA RESPUESTA CORRECTA EN CADA PREGUNTA.
 CUADERNILLO DE GEOMETRIA I.- SUBRAYE LA RESPUESTA CORRECTA EN CADA PREGUNTA. 1.- SON LOS TRIÁNGULOS QUE TIENEN TODOS LOS ÁNGULOS IGUALES. A) EQUILÁTERO B) ACUTÁNGULO C) ISÓSCELES D) ESCALENO E) RECTÁNGULO
CUADERNILLO DE GEOMETRIA I.- SUBRAYE LA RESPUESTA CORRECTA EN CADA PREGUNTA. 1.- SON LOS TRIÁNGULOS QUE TIENEN TODOS LOS ÁNGULOS IGUALES. A) EQUILÁTERO B) ACUTÁNGULO C) ISÓSCELES D) ESCALENO E) RECTÁNGULO
13 POLIEDROS REPRESENTACIÓN DE POLIEDROS
 13-1 Curso de Dibujo Técnico. 2º de Bachillerato Patxi Aguirrezabal Martin 13 POLIEDROS TETRAEDRO. CUBO. OCTAEDRO. PRISMA. PIRÁMIDE. CONO. CILINDRO. ICOSAEDRO. DODECAEDRO. ESFERA. Contornos aparente y
13-1 Curso de Dibujo Técnico. 2º de Bachillerato Patxi Aguirrezabal Martin 13 POLIEDROS TETRAEDRO. CUBO. OCTAEDRO. PRISMA. PIRÁMIDE. CONO. CILINDRO. ICOSAEDRO. DODECAEDRO. ESFERA. Contornos aparente y
UNIDAD 10 CUERPOS GEOMÉTRICOS. Objetivo General.
 UNIDAD 10 CUERPOS GEOMÉTRICOS Objetivo General. Al terminar ésta unidad identificarás los diferentes tipos de Cuerpos Geométricos, resolverás ejercicios y problemas en los que apliques definiciones y fórmulas.
UNIDAD 10 CUERPOS GEOMÉTRICOS Objetivo General. Al terminar ésta unidad identificarás los diferentes tipos de Cuerpos Geométricos, resolverás ejercicios y problemas en los que apliques definiciones y fórmulas.
Desarrollo de Poliedros Regulares: Generalidades. Ejercicios Resueltos. Ejercicio 1 Ejercicio 2 Ejercicio 3 Ejercicio 4 Ejercicio 5
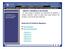 DESARROLLO DE POLIEDROS REGULARES UNIDAD IV: DESARROLLO DE SÓLIDOS En esta unidad se dibujarán las superficies de poliedros y cuerpos redondos modelos. Los temas de esta unidad son: sobre un plano para
DESARROLLO DE POLIEDROS REGULARES UNIDAD IV: DESARROLLO DE SÓLIDOS En esta unidad se dibujarán las superficies de poliedros y cuerpos redondos modelos. Los temas de esta unidad son: sobre un plano para
10 FIGURAS Y CUERPOS GEOMÉTRICOS
 10 FIGURAS Y CUERPOS GEOMÉTRICOS EJERCICIOS PROPUESTOS 10.1 Indica cuál de estos poliedros es cóncavo y cuál es convexo. a) Cóncavo b) Convexo 10. Completa la siguiente tabla. Caras (C ) Vértices (V )
10 FIGURAS Y CUERPOS GEOMÉTRICOS EJERCICIOS PROPUESTOS 10.1 Indica cuál de estos poliedros es cóncavo y cuál es convexo. a) Cóncavo b) Convexo 10. Completa la siguiente tabla. Caras (C ) Vértices (V )
FIGURAS PLANAS. Esto es un segmento: Esto es una línea poligonal abierta, formada por la unión de varios segmentos:
 FIGURAS PLANAS Esto es un segmento: Esto es una línea poligonal abierta, formada por la unión de varios segmentos: Y esto, una línea poligonal cerrada en la que se unen el extremo inicial del primer segmento
FIGURAS PLANAS Esto es un segmento: Esto es una línea poligonal abierta, formada por la unión de varios segmentos: Y esto, una línea poligonal cerrada en la que se unen el extremo inicial del primer segmento
VOLUMENES. Los cuerpos en el espacio (sólidos) poseen tres dimensiones: largo, ancho y profundidad
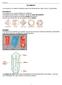 VOLUMENES Los cuerpos en el espacio (sólidos) poseen tres dimensiones: largo, ancho y profundidad POLIEDROS Un poliedro es un cuerpo limitado por polígonos Los polígonos que limiten el poliedro, se llaman
VOLUMENES Los cuerpos en el espacio (sólidos) poseen tres dimensiones: largo, ancho y profundidad POLIEDROS Un poliedro es un cuerpo limitado por polígonos Los polígonos que limiten el poliedro, se llaman
POSICIÓN DE DOS RECTAS
 POSICIÓN DE DOS RECTAS Un punto divide a una recta en dos semirrectas. Rectas paralelas son las que nunca se cortan por mucho que se prolonguen. Rectas secantes son las que se cortan. Rectas perpendiculares
POSICIÓN DE DOS RECTAS Un punto divide a una recta en dos semirrectas. Rectas paralelas son las que nunca se cortan por mucho que se prolonguen. Rectas secantes son las que se cortan. Rectas perpendiculares
La circunferencia y el círculo
 La circunferencia y el círculo Contenidos 1. La circunferencia. La circunferencia Elementos de la circunferencia. 2. Posiciones relativas. Punto y circunferencia. Recta y circunferencia. Dos circunferencias.
La circunferencia y el círculo Contenidos 1. La circunferencia. La circunferencia Elementos de la circunferencia. 2. Posiciones relativas. Punto y circunferencia. Recta y circunferencia. Dos circunferencias.
Guia PSU Matemática IV Medio PERÍMETROS, ÁREAS Y VOLÚMENES
 PERÍMETROS, ÁREAS Y VOLÚMENES Antes de entrar al análisis de fórmulas referente al perímetro, área y volumen de figuras geométricas, repasemos estos temas y efectuemos ejercicios pertinentes Llamamos área
PERÍMETROS, ÁREAS Y VOLÚMENES Antes de entrar al análisis de fórmulas referente al perímetro, área y volumen de figuras geométricas, repasemos estos temas y efectuemos ejercicios pertinentes Llamamos área
TETRAEDRO CUBO OCTAEDRO DODECAEDRO ICOSAEDRO
 6.- SÓLIDOS Al finalizar el sexto curso de Educación Primaria, los estudiantes deben describir cuerpos geométricos usando el vocabulario apropiado con términos como vértices, caras, aristas, planos, diedros,
6.- SÓLIDOS Al finalizar el sexto curso de Educación Primaria, los estudiantes deben describir cuerpos geométricos usando el vocabulario apropiado con términos como vértices, caras, aristas, planos, diedros,
AREA Y PERIMETRO DE LAS FIGURAS GEOMETRICAS
 AREA Y PERIMETRO DE LAS FIGURAS GEOMETRICAS Figura geométrica Consiste de una línea o de un conjunto de líneas que representarán un objeto dado. Polígono Es una poligonal cerrada (el origen del primer
AREA Y PERIMETRO DE LAS FIGURAS GEOMETRICAS Figura geométrica Consiste de una línea o de un conjunto de líneas que representarán un objeto dado. Polígono Es una poligonal cerrada (el origen del primer
-. B:... E:... ?A: Isósceles y acutángulo. .~~.-.. Triángulos y paralelogramos. Cómo se clasifican los triángulos PARA EMPEZAR
 111. TEOREMA DE PITAGORAS ).~~.-.. Triángulos y paralelogramos ~, PARA EMPEZAR Cómo se clasifican los triángulos Según sus lados: Equilátero Isósceles Escaleno Tiene los tres lados iguales. Tiene dos lados
111. TEOREMA DE PITAGORAS ).~~.-.. Triángulos y paralelogramos ~, PARA EMPEZAR Cómo se clasifican los triángulos Según sus lados: Equilátero Isósceles Escaleno Tiene los tres lados iguales. Tiene dos lados
CUERPOS GEOMÉTRICOS. Clases de cuerpos geométricos. Los poliedros. Los poliedros regulares.
 CUERPOS GEOMÉTRICOS. Se denominan cuerpos geométricos a aquellos elementos que, ya sean reales o ideales - que existen en la realidad o pueden concebirse mentalmente - ocupan un volumen en el espacio desarrollándose
CUERPOS GEOMÉTRICOS. Se denominan cuerpos geométricos a aquellos elementos que, ya sean reales o ideales - que existen en la realidad o pueden concebirse mentalmente - ocupan un volumen en el espacio desarrollándose
Los poliedros y sus elementos
 Los poliedros y sus elementos De las siguientes figuras, rodea las que sean poliedros o tengan forma de poliedro. Dibuja y escribe el nombre de tres objetos que tengan forma de poliedro. espuesta libre
Los poliedros y sus elementos De las siguientes figuras, rodea las que sean poliedros o tengan forma de poliedro. Dibuja y escribe el nombre de tres objetos que tengan forma de poliedro. espuesta libre
13 CUERPOS GEOMÉTRICOS
 13 CUERPOS GEOMÉTRICOS EJERCICIOS PROPUESTOS 13.1 Observa la figura y di qué elemento geométrico determinan la recta y el plano. r α La recta r y el plano determinan un punto. 13.2 Con los cuatro puntos
13 CUERPOS GEOMÉTRICOS EJERCICIOS PROPUESTOS 13.1 Observa la figura y di qué elemento geométrico determinan la recta y el plano. r α La recta r y el plano determinan un punto. 13.2 Con los cuatro puntos
Volúmenes de cuerpos geométricos
 Volúmenes de cuerpos geométricos TEORÍA Cuerpos geométricos En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
Volúmenes de cuerpos geométricos TEORÍA Cuerpos geométricos En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
9Soluciones a las actividades de cada epígrafe PÁGINA 186
 9Soluciones a las actividades de cada epígrafe PÁGINA 186 Pág. 1 En la Casa de la Cultura se ha montado una exposición fotográfica. En ella se recogen modernos edificios en los que los poliedros y los
9Soluciones a las actividades de cada epígrafe PÁGINA 186 Pág. 1 En la Casa de la Cultura se ha montado una exposición fotográfica. En ella se recogen modernos edificios en los que los poliedros y los
Unidad didáctica 3. Cálculo de superficies y volúmenes
 Unidad didáctica. Cálculo de superficies y volúmenes.1 Cálculo de superficies. En el presente apartado se estudiarán las superficies, perímetros y relaciones geométricas más importantes de las principales
Unidad didáctica. Cálculo de superficies y volúmenes.1 Cálculo de superficies. En el presente apartado se estudiarán las superficies, perímetros y relaciones geométricas más importantes de las principales
PÁGINA 196. 1 Di qué tipo de prisma es cada uno de los siguientes. Indica cuáles son regulares. Dibuja el desarrollo del primero de ellos.
 Soluciones a las actividades de cada epígrafe PÁGINA 196 1 Di qué tipo de prisma es cada uno de los siguientes. Indica cuáles son regulares. Dibuja el desarrollo del primero de ellos. a) b) c) d) a) Triangular,
Soluciones a las actividades de cada epígrafe PÁGINA 196 1 Di qué tipo de prisma es cada uno de los siguientes. Indica cuáles son regulares. Dibuja el desarrollo del primero de ellos. a) b) c) d) a) Triangular,
Las Figuras Planas. Vértice. Ángulo. Diagonal. Lado. Los polígonos. El Polígono. CEPA Carmen Conde Abellán Matemáticas II
 Las Figuras Planas Melilla Los polígonos Te has fijado alguna vez en el metro que usan los carpinteros? Está formado por segmentos de madera que se pliegan con facilidad. Este instrumento tiene forma de
Las Figuras Planas Melilla Los polígonos Te has fijado alguna vez en el metro que usan los carpinteros? Está formado por segmentos de madera que se pliegan con facilidad. Este instrumento tiene forma de
5. POLÍGONOS. 5.1 Definición y notación de polígonos
 5. POLÍGONOS 5.1 Definición y notación de polígonos Un polígono es una figura geométrica limitada por segmentos de recta denominados lados, donde el extremo de un segmento es el origen del otro. E D Etimológicamente,
5. POLÍGONOS 5.1 Definición y notación de polígonos Un polígono es una figura geométrica limitada por segmentos de recta denominados lados, donde el extremo de un segmento es el origen del otro. E D Etimológicamente,
Lección 17: Polígonos básicos
 Lección 17: Polígonos básicos Un polígono es una figura cerrada formada por segmentos de recta que no se cruzan entre sí. Los segmentos se llaman lados del polígono. Los polígonos pueden ser convexos,
Lección 17: Polígonos básicos Un polígono es una figura cerrada formada por segmentos de recta que no se cruzan entre sí. Los segmentos se llaman lados del polígono. Los polígonos pueden ser convexos,
Ángulos. Semejanza. ABE ˆ, ACE ˆ o ADE ˆ son ángulos inscritos en la. n 2 180º. En la circunferencia:
 GEOMETRÍA Ángulos En la circunferencia: ABE ˆ, ACE ˆ o ADE ˆ son ángulos inscritos en la circunferencia y son todos iguales. AOE ˆ es el ángulo central correspondiente y su medida es dos veces la medida
GEOMETRÍA Ángulos En la circunferencia: ABE ˆ, ACE ˆ o ADE ˆ son ángulos inscritos en la circunferencia y son todos iguales. AOE ˆ es el ángulo central correspondiente y su medida es dos veces la medida
1 Calcula en la siguiente figura el elemento que falta: 2 Calcula en la siguiente figura el elemento que falta:
 1 Calcula en la siguiente figura el elemento que falta: Calcula en la siguiente figura el elemento que falta: Calcula el valor de la diagonal de un ortoedro de aristas cm, 4 cm y 5 cm. 4 Comprueba la fórmula
1 Calcula en la siguiente figura el elemento que falta: Calcula en la siguiente figura el elemento que falta: Calcula el valor de la diagonal de un ortoedro de aristas cm, 4 cm y 5 cm. 4 Comprueba la fórmula
UNIDAD X - GEOMETRIA. Ejercitación
 UNIDAD X - GEOMETRIA Programa Analítico Segmentos. Operaciones con segmentos. Ángulos. Clasificación de los ángulos: Complementarios, suplementarios, adyacentes, alternos-internos, opuestos por el vértice.
UNIDAD X - GEOMETRIA Programa Analítico Segmentos. Operaciones con segmentos. Ángulos. Clasificación de los ángulos: Complementarios, suplementarios, adyacentes, alternos-internos, opuestos por el vértice.
ACTIVIDAD INTRODUCTORIA: El regalo para mi hermano.
 Grado 7 Matemáticas Conozcamos otros sistemas de medidas, el sistema internacional y el sistema inglés. TEMA: DESCRIPCIÓN DEL ÁREA EN CUERPOS GEOMÉTRICOS Nombre: Grado: ACTIVIDAD INTRODUCTORIA: El regalo
Grado 7 Matemáticas Conozcamos otros sistemas de medidas, el sistema internacional y el sistema inglés. TEMA: DESCRIPCIÓN DEL ÁREA EN CUERPOS GEOMÉTRICOS Nombre: Grado: ACTIVIDAD INTRODUCTORIA: El regalo
PERÍMETROS Y ÁREAS DE FIGURAS PLANAS UNIDADE 13 1º ESO 1 ) Halla la superficie y el perímetro del recinto marrón:
 PERÍMETROS Y ÁREAS DE FIGURAS PLANAS UNIDADE 13 1º ESO 1 ) Halla la superficie y el perímetro del recinto marrón: 2 ) Calcula el perímetro y el área de esta figura: 3 ) Calcula el perímetro y el área de
PERÍMETROS Y ÁREAS DE FIGURAS PLANAS UNIDADE 13 1º ESO 1 ) Halla la superficie y el perímetro del recinto marrón: 2 ) Calcula el perímetro y el área de esta figura: 3 ) Calcula el perímetro y el área de
SOLUCIONES A LAS ACTIVIDADES DE CADA EPÍGRAFE
 Pág. 1 PÁGINA 19 REFLEXIONA Las cajas, los contenedores y la caseta son poliedros. También es un poliedro la figura que forma la caja que pende de la grúa con las cuatro cuerdas que la sostienen. Cuántas
Pág. 1 PÁGINA 19 REFLEXIONA Las cajas, los contenedores y la caseta son poliedros. También es un poliedro la figura que forma la caja que pende de la grúa con las cuatro cuerdas que la sostienen. Cuántas
8. Si Â, Ê e Î son los ángulos de un triángulo, completa en tu cuaderno la siguiente tabla:
 5. Clasifica según sus lados los siguientes triángulos: a) Equilátero. b) Escaleno. c) Isósceles. 6. Clasifica según sus ángulos los siguientes triángulos: a) Acutángulo. b) Obtusángulo. c) Rectángulo.
5. Clasifica según sus lados los siguientes triángulos: a) Equilátero. b) Escaleno. c) Isósceles. 6. Clasifica según sus ángulos los siguientes triángulos: a) Acutángulo. b) Obtusángulo. c) Rectángulo.
Figuras Planas. 100 Ejercicios para practicar con soluciones. 1 Comprueba si los siguientes ángulos son complementarios: a) 72 + 35.
 Figuras Planas. 100 Ejercicios para practicar con soluciones 1 Comprueba si los siguientes ángulos son complementarios: a) 7º y 35 b) 6º y 64º a) 7 + 35 = 107 90 No son complementarios. b) 6 + 64 = 90
Figuras Planas. 100 Ejercicios para practicar con soluciones 1 Comprueba si los siguientes ángulos son complementarios: a) 7º y 35 b) 6º y 64º a) 7 + 35 = 107 90 No son complementarios. b) 6 + 64 = 90
TRANSFORMACIONES DEL PLANO
 PROBLEMAS DE GEOMETRÍA. TRANSFORMACIONES DEL PLANO 1. Un producto de dos simetrías axiales de ejes perpendiculares A qué transformación corresponde? En qué se transforma un segmento vertical? ( ) 2. Cuál
PROBLEMAS DE GEOMETRÍA. TRANSFORMACIONES DEL PLANO 1. Un producto de dos simetrías axiales de ejes perpendiculares A qué transformación corresponde? En qué se transforma un segmento vertical? ( ) 2. Cuál
Boletín de Actividades. Figuras Planas: Polígonos, Circunferencia y Círculo. Áreas y Perímetros de figuras complejas.
 Boletín de Actividades. Figuras Planas: Polígonos, Circunferencia y Círculo. Áreas y Perímetros de figuras complejas. 1.- Escribe el nombre de las siguientes líneas. 2.- Qué ángulos forman dos rectas perpendiculares?
Boletín de Actividades. Figuras Planas: Polígonos, Circunferencia y Círculo. Áreas y Perímetros de figuras complejas. 1.- Escribe el nombre de las siguientes líneas. 2.- Qué ángulos forman dos rectas perpendiculares?
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág. 1 PÁGINA 255 EJERCICIOS Construcciones y ejes de simetría 1 a) Halla el ángulo central de un octógono regular. b) Dibuja un octógono regular inscrito en una circunferencia de 5 cm de radio, construyendo
Pág. 1 PÁGINA 255 EJERCICIOS Construcciones y ejes de simetría 1 a) Halla el ángulo central de un octógono regular. b) Dibuja un octógono regular inscrito en una circunferencia de 5 cm de radio, construyendo
Práctica 06. Instituto Tecnológico de Costa Rica Escuela de Matemática Matemática General. I. Plantee y resuelva los siguientes problemas:
 Instituto Tecnológico de Costa Rica Escuela de Matemática Matemática General I. Plantee y resuelva los siguientes problemas: Práctica 06 Geometría 1) Un árbol proyecta una sombra de 5 m en el mismo instante
Instituto Tecnológico de Costa Rica Escuela de Matemática Matemática General I. Plantee y resuelva los siguientes problemas: Práctica 06 Geometría 1) Un árbol proyecta una sombra de 5 m en el mismo instante
POLIGONOS. Nº DE LADOS NOMBRE 3 Triángulos 4 Cuadriláteros 5 Pentágonos 6 Hexágonos 7 Heptágonos 8 Octógonos 9 Eneágonos 10 Decágonos
 1 POLIGONO POLIGONOS Polígono es la superficie plana limitada por una línea poligonal cerrada. Lados Vértices Polígono regular es el que tiene todos sus lados y ángulos iguales, mientras que polígono irregular
1 POLIGONO POLIGONOS Polígono es la superficie plana limitada por una línea poligonal cerrada. Lados Vértices Polígono regular es el que tiene todos sus lados y ángulos iguales, mientras que polígono irregular
10 FIGURAS Y CUERPOS GEOMÉTRICOS
 10 FIGURS Y UERPOS GEOMÉTRIOS EJERIIOS PR ENTRENRSE Poliedros y cuerpos redondos. Propiedades 10.2 Un poliedro regular tiene 8 vértices y 12 aristas. Utiliza la fórmula de Euler para saber de qué poliedro
10 FIGURS Y UERPOS GEOMÉTRIOS EJERIIOS PR ENTRENRSE Poliedros y cuerpos redondos. Propiedades 10.2 Un poliedro regular tiene 8 vértices y 12 aristas. Utiliza la fórmula de Euler para saber de qué poliedro
POLÍGONOS. α3 α 4 α 5. α 7 α 6. 1. Definición. Sean: A 1, A 2,...A n, n distintos puntos del plano. Trazamos los segmentos: A 1A 2,
 A 7 A 6 A 8 α 7 α 8 α A 5 α 6 A α α α α 5 A A A Un agricultor contrata a una compañía constructora para que realice el cálculo del área de un terreno que se encuentra en una explanada y que desea adquirir.
A 7 A 6 A 8 α 7 α 8 α A 5 α 6 A α α α α 5 A A A Un agricultor contrata a una compañía constructora para que realice el cálculo del área de un terreno que se encuentra en una explanada y que desea adquirir.
8. Elementos de geometría plana
 8. Elementos de geometría plana 1. Elementos básicos de la geometría 2. Ángulos 2.1. El sistema sexagesimal 2.1.1. Suma de ángulos 2.1.2. Resta de ángulos 2.1.3. Multiplicar por un número 2.1.4. Dividir
8. Elementos de geometría plana 1. Elementos básicos de la geometría 2. Ángulos 2.1. El sistema sexagesimal 2.1.1. Suma de ángulos 2.1.2. Resta de ángulos 2.1.3. Multiplicar por un número 2.1.4. Dividir
Los Cuerpos Geométricos
 06 Lección Apertura Matemáticas Los Cuerpos Geométricos APRENDO JUGANDO Competencia Describe qué son e identifica las características de los cuerpos geométricos. Diseño instruccional El maestro comenta
06 Lección Apertura Matemáticas Los Cuerpos Geométricos APRENDO JUGANDO Competencia Describe qué son e identifica las características de los cuerpos geométricos. Diseño instruccional El maestro comenta
1. ESQUEMA - RESUMEN Página 2. 2. EJERCICIOS DE INICIACIÓN Página 8. 3. EJERCICIOS DE DESARROLLO Página 20. 5. EJERCICIOS DE REFUERZO Página 36
 1. ESQUEMA - RESUMEN Página 2 2. EJERCICIOS DE INICIACIÓN Página 8 3. EJERCICIOS DE DESARROLLO Página 20 5. EJERCICIOS DE REFUERZO Página 36 1 1. ESQUEMA - RESUMEN Página 1.1. POLÍGONOS 2 1.2. TRIÁNGULOS
1. ESQUEMA - RESUMEN Página 2 2. EJERCICIOS DE INICIACIÓN Página 8 3. EJERCICIOS DE DESARROLLO Página 20 5. EJERCICIOS DE REFUERZO Página 36 1 1. ESQUEMA - RESUMEN Página 1.1. POLÍGONOS 2 1.2. TRIÁNGULOS
11-A-1/8. Nombre: Es un conjunto de segmentos unidos, formando diversos ángulos. Pueden ser:
 11-A-1/8 Geometría (polígonos) Líneas poligonales. Es un conjunto de segmentos unidos, formando diversos ángulos. Pueden ser: Abierta Cerrada El trozo de plano que hay dentro de una línea poligonal cerrada,
11-A-1/8 Geometría (polígonos) Líneas poligonales. Es un conjunto de segmentos unidos, formando diversos ángulos. Pueden ser: Abierta Cerrada El trozo de plano que hay dentro de una línea poligonal cerrada,
Poliedro cóncavo: es aquel que no cumple la propiedad anterior. Una recta puede cortarlo por más de dos puntos.
 El sistema diédrico D13 El prisma Poliedros Poliedro es un cuerpo geométrico limitado por polígonos. Caras del poliedro son los polígonos que lo limitan. Vértices son los vértices de las caras. Aristas
El sistema diédrico D13 El prisma Poliedros Poliedro es un cuerpo geométrico limitado por polígonos. Caras del poliedro son los polígonos que lo limitan. Vértices son los vértices de las caras. Aristas
ÁREAS Y VOLÚMENES DE CUERPOS GEOMÉTRICOS
 ÁRES Y VOLÚMENES DE CUERPOS GEOMÉTRICOS. CUERPOS GEOMÉTRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
ÁRES Y VOLÚMENES DE CUERPOS GEOMÉTRICOS. CUERPOS GEOMÉTRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
UNIDAD IV ÁREAS DE FIGURAS PLANAS
 UNIDAD IV ÁREAS DE FIGURAS PLANAS COMPETENCIAS E INDICADORES DE DESEMPEÑO Identifica las áreas de figuras planas, volumen y superficie. CONCEPTOS DE PERÍMETRO Y AREA DE UNA FIGURA PLANA Se llama perímetro
UNIDAD IV ÁREAS DE FIGURAS PLANAS COMPETENCIAS E INDICADORES DE DESEMPEÑO Identifica las áreas de figuras planas, volumen y superficie. CONCEPTOS DE PERÍMETRO Y AREA DE UNA FIGURA PLANA Se llama perímetro
1.- 3.- Las áreas de dos polígonos semejantes son 121 cm 2 y 324 cm 2. Si el perímetro del primero es 44 cm, cuál es el perímetro del segundo?
 olegio-laret 1.- 10m 7m 30m SMINRIO MTMÁTIS l dibujo presenta un método aproximado para medir la anchura de un río sin necesidad más que de tomar medidas en una orilla. Situándonos en el punto hemos realizado
olegio-laret 1.- 10m 7m 30m SMINRIO MTMÁTIS l dibujo presenta un método aproximado para medir la anchura de un río sin necesidad más que de tomar medidas en una orilla. Situándonos en el punto hemos realizado
Liceo N 1 Javiera Carrera 8 años 2011
 GUIA DE ESTUDIO : Cuerpos geométricos Prof. Juan Schuchhardt E. DEFINICIÓN: Los poliedros son aquellos cuerpos geométricos que están limitados por superficies planas y de contorno poligonal. Un poliedro
GUIA DE ESTUDIO : Cuerpos geométricos Prof. Juan Schuchhardt E. DEFINICIÓN: Los poliedros son aquellos cuerpos geométricos que están limitados por superficies planas y de contorno poligonal. Un poliedro
Tema 8 Cuerpos en el espacio
 Tema 8 Cuerpos en el espacio Poliedros La primera distinción que debemos hacer es entre los poliedros, que son cuerpos geométricos limitados por polígonos, y los cuerpos de revolución, donde una forma
Tema 8 Cuerpos en el espacio Poliedros La primera distinción que debemos hacer es entre los poliedros, que son cuerpos geométricos limitados por polígonos, y los cuerpos de revolución, donde una forma
RESUMEN DE FORMULAS EJERCICIOS de APLICACIÓN POLIEDROS
 RESUMEN DE FORMULAS EJERCICIOS de APLICACIÓN POLIEDROS. 1.-Calcule la superficie total de un tetraedro cuya arista mide 2 (12 3 ) 2.- Se tiene un tetraedro cuya arista mide 6 3 cm. Calcular.- 2.1.-La superficie
RESUMEN DE FORMULAS EJERCICIOS de APLICACIÓN POLIEDROS. 1.-Calcule la superficie total de un tetraedro cuya arista mide 2 (12 3 ) 2.- Se tiene un tetraedro cuya arista mide 6 3 cm. Calcular.- 2.1.-La superficie
Segmento : porción de recta comprendida entre dos de sus puntos, llamados extremos.
 ÍNDICE Elementos fundamentales Ángulos Triángulos y cuadriláteros Áreas y volúmenes Poliedros ELEMENTOS FUNDAMENTALES DE GEOMETRÍA Conceptos fundamentales Punto Recta Plano Semirecta : porción de recta
ÍNDICE Elementos fundamentales Ángulos Triángulos y cuadriláteros Áreas y volúmenes Poliedros ELEMENTOS FUNDAMENTALES DE GEOMETRÍA Conceptos fundamentales Punto Recta Plano Semirecta : porción de recta
1. Polígonos. 1.1 Definición
 1.1 Definición 1. Polígonos Es toda figura plana, cerrada, limitada por un número finito de lados rectos. De acuerdo al número de lados, los más utilizados se clasifican en: Triángulos 3 lados Cuadriláteros
1.1 Definición 1. Polígonos Es toda figura plana, cerrada, limitada por un número finito de lados rectos. De acuerdo al número de lados, los más utilizados se clasifican en: Triángulos 3 lados Cuadriláteros
Efa Moratalaz PCPI - Matemáticas GEOMETRÍA PLANA
 GEOMETRÍA PLANA Geometría Plana Ficha 1 (Ejercicios Cuadrado) Área de un cuadrado: Perímetro de un cuadrado: 1) Halla el perímetro y el área de un cuadrado de 3 m de lado. 2) Halla el perímetro y el área
GEOMETRÍA PLANA Geometría Plana Ficha 1 (Ejercicios Cuadrado) Área de un cuadrado: Perímetro de un cuadrado: 1) Halla el perímetro y el área de un cuadrado de 3 m de lado. 2) Halla el perímetro y el área
D18 Poliedros regulares
 El sistema diédrico D18 Poliedros regulares Clases de poliedros regulares convexos No pueden existir más de cinco clases de poliedros regulares convexos. Teniendo en cuenta que la suma de las caras de
El sistema diédrico D18 Poliedros regulares Clases de poliedros regulares convexos No pueden existir más de cinco clases de poliedros regulares convexos. Teniendo en cuenta que la suma de las caras de
13Soluciones a los ejercicios y problemas PÁGINA 250
 PÁGINA 50 Pág. 1 Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS Halla el área y el perímetro de las figuras coloreadas de los siguientes ejercicios: 1 a) b) 5 dm 4 cm cm 5 cm 8 cm a) 5 = 5 dm b) 8 = 8 cm P =
PÁGINA 50 Pág. 1 Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS Halla el área y el perímetro de las figuras coloreadas de los siguientes ejercicios: 1 a) b) 5 dm 4 cm cm 5 cm 8 cm a) 5 = 5 dm b) 8 = 8 cm P =
Hoja de problemas nº 7. Introducción a la Geometría
 Hoja de problemas nº 7 Introducción a la Geometría 1. Un rectángulo tiene de área 135 u 2 a. Si sus lados miden números enteros, averigua cuáles pueden ser sus dimensiones. b. Cortamos los vértices como
Hoja de problemas nº 7 Introducción a la Geometría 1. Un rectángulo tiene de área 135 u 2 a. Si sus lados miden números enteros, averigua cuáles pueden ser sus dimensiones. b. Cortamos los vértices como
Perímetro de un polígono regular: Si la longitud de un lado es y hay cantidad de lados en un polígono regular entonces el perímetro es.
 Materia: Matemática de Séptimo Tema: Área de Polígonos Qué pasa si te piden que encuentres la distancia del Pentágono en Arlington, VA? El Pentágono, que también alberga el Departamento de Defensa de EE.UU.,
Materia: Matemática de Séptimo Tema: Área de Polígonos Qué pasa si te piden que encuentres la distancia del Pentágono en Arlington, VA? El Pentágono, que también alberga el Departamento de Defensa de EE.UU.,
PENDIENTES 2º ESO. Tercer examen DEPARTAMENTO DE MATEMÁTICAS. Preparación del tercer examen de recuperación de MATEMÁTICAS DE 2º ESO Curso 2013-2014
 014 015 Preparación del tercer examen de recuperación de MATEMÁTICAS DE º ESO PENDIENTES º ESO Tercer examen DEPARTAMENTO DE MATEMÁTICAS 1.- En un triángulo rectángulo, los catetos miden 5 y 1cm, respectivamente.
014 015 Preparación del tercer examen de recuperación de MATEMÁTICAS DE º ESO PENDIENTES º ESO Tercer examen DEPARTAMENTO DE MATEMÁTICAS 1.- En un triángulo rectángulo, los catetos miden 5 y 1cm, respectivamente.
FIGURAS SEMEJANTES RAZÓN DE SEMEJANZA. Gráfica y numérica
 FIGURAS SEMEJANTES RAZÓN DE SEMEJANZA Ampliación / Reducción Escalas Teorema de Thales Gráfica y numérica Triángulos en posición de Thales Semejanza de triángulos Criterios de semezanza entre triángulos
FIGURAS SEMEJANTES RAZÓN DE SEMEJANZA Ampliación / Reducción Escalas Teorema de Thales Gráfica y numérica Triángulos en posición de Thales Semejanza de triángulos Criterios de semezanza entre triángulos
Trigonometría, figuras planas
 El polígono Un polígono es una figura plana limitada por tres o más segmentos. El perímetro de un polígono es igual a la suma de las longitudes de sus lados. El perímetro de una circunferencia se llama
El polígono Un polígono es una figura plana limitada por tres o más segmentos. El perímetro de un polígono es igual a la suma de las longitudes de sus lados. El perímetro de una circunferencia se llama
UNIDAD 12. GEOMETRÍA DEL ESPACIO (II). CUERPOS DE REVOLUCIÓN.
 UNIDAD 12. GEOMETRÍA DEL ESPACIO (II). CUERPOS DE REVOLUCIÓN. Unidad 12: Geometría del espacio (II). Cuerpos de revolución. Al final deberás haber aprendido... Describir cuerpos de revolución e identificar
UNIDAD 12. GEOMETRÍA DEL ESPACIO (II). CUERPOS DE REVOLUCIÓN. Unidad 12: Geometría del espacio (II). Cuerpos de revolución. Al final deberás haber aprendido... Describir cuerpos de revolución e identificar
PERÍMETROS Y ÁREAS DE FIGURAS PLANAS UNIDADE 13 1º ESO Halla la superficie y el perímetro del recinto marrón:
 PERÍMETROS Y ÁREAS DE FIGURAS PLANAS UNIDADE 13 1º ESO Halla la superficie y el perímetro del recinto marrón: Calcula el perímetro y el área de esta figura: Calcula el perímetro y el área de esta figura:
PERÍMETROS Y ÁREAS DE FIGURAS PLANAS UNIDADE 13 1º ESO Halla la superficie y el perímetro del recinto marrón: Calcula el perímetro y el área de esta figura: Calcula el perímetro y el área de esta figura:
Guía de Trabajo Volumen. Nombre: Curso: Fecha: Cuerpos geométricos
 Departamento de Matemática Profesora: Diosa Loyola Angel Âdâx àâ xáyâxüéé àx ÄÄxäx ÑÉÜ Ät áxçwt wxä vtâw ÄÄÉÊ Guía de Trabajo Volumen 1 Nombre: Curso: Fecha: Cuerpos geométricos Los cuerpos geométricos
Departamento de Matemática Profesora: Diosa Loyola Angel Âdâx àâ xáyâxüéé àx ÄÄxäx ÑÉÜ Ät áxçwt wxä vtâw ÄÄÉÊ Guía de Trabajo Volumen 1 Nombre: Curso: Fecha: Cuerpos geométricos Los cuerpos geométricos
CUERPOS GEOMÉTRICOS. ÁREAS Y VOLÚMENES
 º ESO CUEROS GEOMÉTRICOS. ÁREAS Y OLÚMENES DEARTAMENTO DE MATEMÁTICAS. COIRRAI_Julio César Abad Martínez-Losa CUEROS GEOMÉTRICOS. ÁREAS Y OLÚMENES 1.- CUEROS GEOMÉTRICOS Un cuerpo geométrico es una figura
º ESO CUEROS GEOMÉTRICOS. ÁREAS Y OLÚMENES DEARTAMENTO DE MATEMÁTICAS. COIRRAI_Julio César Abad Martínez-Losa CUEROS GEOMÉTRICOS. ÁREAS Y OLÚMENES 1.- CUEROS GEOMÉTRICOS Un cuerpo geométrico es una figura
Trigonometría y problemas métricos
 Trigonometría y problemas métricos 1) En un triángulo rectángulo, los catetos miden 6 y 8 centímetros. Calcula la medida de la altura sobre la hipotenusa y la distancia desde su pie hasta los extremos.
Trigonometría y problemas métricos 1) En un triángulo rectángulo, los catetos miden 6 y 8 centímetros. Calcula la medida de la altura sobre la hipotenusa y la distancia desde su pie hasta los extremos.
Tema 5: Polígonos. Mediatriz de un segmento : Es la recta perpendicular trazada en su punto medio.
 Tema 5: Polígonos 5.1 Elementos Fundamentales de Geometría Mediatriz de un segmento : Es la recta perpendicular trazada en su punto medio. A P * B Cualquier punto P de la mediatriz equidista de los extremos
Tema 5: Polígonos 5.1 Elementos Fundamentales de Geometría Mediatriz de un segmento : Es la recta perpendicular trazada en su punto medio. A P * B Cualquier punto P de la mediatriz equidista de los extremos
Área de paralelogramos, triángulos y trapecios (páginas 314 318)
 NOMRE FECHA PERÍODO Área de paralelogramos, triángulos y trapecios (páginas 34 38) Cualquier lado de un paralelogramo o triángulo puede usarse como base. La altitud de un paralelogramo es un segmento de
NOMRE FECHA PERÍODO Área de paralelogramos, triángulos y trapecios (páginas 34 38) Cualquier lado de un paralelogramo o triángulo puede usarse como base. La altitud de un paralelogramo es un segmento de
Ejercicios de geometría
 Ejercicios de geometría Ejercicio nº 1.- Los lados de un triángulo miden 16 cm, 11 cm y 8 cm. Comprueba si es un triángulo rectángulo. Ejercicio nº 2.- Calcula el área y el perímetro de estas figuras:
Ejercicios de geometría Ejercicio nº 1.- Los lados de un triángulo miden 16 cm, 11 cm y 8 cm. Comprueba si es un triángulo rectángulo. Ejercicio nº 2.- Calcula el área y el perímetro de estas figuras:
Colegio LOPE DE VEGA Luis de Medina, 12 28805 Alcalá de Henares DIBUJO TÉCNICO II EJERCICIOS DE APOYO
 Colegio LOPE DE VEGA Luis de Medina, 12 28805 Alcalá de Henares DIBUJO TÉCNICO II EJERCICIOS DE APOYO 1º.- Deducir razonadamente el valor del ángulo α marcado en la figura sabiendo que esta representa
Colegio LOPE DE VEGA Luis de Medina, 12 28805 Alcalá de Henares DIBUJO TÉCNICO II EJERCICIOS DE APOYO 1º.- Deducir razonadamente el valor del ángulo α marcado en la figura sabiendo que esta representa
Geometría y Trigonometría
 Geometría y Trigonometría Ejercicios para Politécnica Tema 1: En un cuadrado siempre se cumple que: I. Las diagonales son bisectrices de los ángulos interiores II. Las diagonales son perpendiculares entre
Geometría y Trigonometría Ejercicios para Politécnica Tema 1: En un cuadrado siempre se cumple que: I. Las diagonales son bisectrices de los ángulos interiores II. Las diagonales son perpendiculares entre
Poliedros y cuerpos de revolución
 12 Poliedros y cuerpos de revolución El cíclope matemático La tensión se apreciaba en el rostro de los presentes. La operación de cataratas parecía un éxito, pero la luz se fue apagando y Euler se quedó
12 Poliedros y cuerpos de revolución El cíclope matemático La tensión se apreciaba en el rostro de los presentes. La operación de cataratas parecía un éxito, pero la luz se fue apagando y Euler se quedó
ÁNGULOS EN POLÍGONOS. Ejercicio nº 1.- En los siguientes polígonos, halla la media del ángulo : a b c. Ejercicio nº 2.-
 ÁNGULOS EN POLÍGONOS Ejercicio nº 1.- En los siguientes polígonos, halla la media del ángulo : a b c Ejercicio nº.- Halla el valor del ángulo en cada uno de estos casos: a b c Ejercicio nº 3.- Halla el
ÁNGULOS EN POLÍGONOS Ejercicio nº 1.- En los siguientes polígonos, halla la media del ángulo : a b c Ejercicio nº.- Halla el valor del ángulo en cada uno de estos casos: a b c Ejercicio nº 3.- Halla el
8. LA CIRCUNFERENCIA Y EL CÍRCULO. 8.1. La Circunferencia. 8.2. El circulo. Dibujo Técnico La Circunferencia y el círculo
 8. LA CIRCUNFERENCIA Y EL CÍRCULO 8.1. La Circunferencia. Una circunferencia es una línea curva, cerrada y plana, cuyos puntos están a la misma distancia de otro interior al que llamamos centro, es decir:
8. LA CIRCUNFERENCIA Y EL CÍRCULO 8.1. La Circunferencia. Una circunferencia es una línea curva, cerrada y plana, cuyos puntos están a la misma distancia de otro interior al que llamamos centro, es decir:
1. ESQUEMA - RESUMEN Página. 2. EJERCICIOS DE INICIACIÓN Página. 3. EJERCICIOS DE DESARROLLO Página. 4. EJERCICIOS DE AMPLIACIÓN Página
 1. ESQUEMA - RESUMEN Página 2 2. EJERCICIOS DE INICIACIÓN Página 7 3. EJERCICIOS DE DESARROLLO Página 7 4. EJERCICIOS DE AMPLIACIÓN Página 9 5. EJERCICIOS DE REFUERZO Página 12 6. EJERCICIOS RESUELTOS
1. ESQUEMA - RESUMEN Página 2 2. EJERCICIOS DE INICIACIÓN Página 7 3. EJERCICIOS DE DESARROLLO Página 7 4. EJERCICIOS DE AMPLIACIÓN Página 9 5. EJERCICIOS DE REFUERZO Página 12 6. EJERCICIOS RESUELTOS
Cuerpos geométricos. Objetivos. Antes de empezar. 1. Poliedros...pág. 138 Definición Elementos de un poliedro
 8 Cuerpos geométricos. Objetivos En esta quincena aprenderás a: Identificar que es un poliedro. Determinar los elementos de un poliedro: Caras, aristas y vértices. Clasificar los poliedros. Especificar
8 Cuerpos geométricos. Objetivos En esta quincena aprenderás a: Identificar que es un poliedro. Determinar los elementos de un poliedro: Caras, aristas y vértices. Clasificar los poliedros. Especificar
ELEMENTS FONAMENTALS DE GEOMETRIA
 APUNTS DE GEOMETRIA. ELEMENTS FONAMENTALS DE GEOMETRIA Conceptes fonamentals Punt Recta Pla Semirrecta: porció de recta limitada en un extrem per un punt Semipla: es cadasquna de les parts en que queda
APUNTS DE GEOMETRIA. ELEMENTS FONAMENTALS DE GEOMETRIA Conceptes fonamentals Punt Recta Pla Semirrecta: porció de recta limitada en un extrem per un punt Semipla: es cadasquna de les parts en que queda
1 Indica cuál es el valor de los ángulo Â, Bˆ. en las siguientes figuras: a) b) 2 Calcula los ángulos dados por letras:
 1 Indica cuál es el valor de los ángulo Â, Bˆ y Ĉ en las siguientes figuras: a) b) Calcula los ángulos dados por letras: 3 Calcula el valor del ángulo A. 4 Dados los ángulos los mismos. a 45 0 30.y b 6
1 Indica cuál es el valor de los ángulo Â, Bˆ y Ĉ en las siguientes figuras: a) b) Calcula los ángulos dados por letras: 3 Calcula el valor del ángulo A. 4 Dados los ángulos los mismos. a 45 0 30.y b 6
Los Ángulos. 2. Cómo pueden ser los ángulos? Definir cada uno. Nulos: Si su medida es Cero. Ej.
 Los Ángulos 1. Qué es un ángulo y su notación? Son dos rayos cualesquiera que determinan dos regiones del plano. Su notación: Para nombrar los ángulos, utilizaremos los símbolos
Los Ángulos 1. Qué es un ángulo y su notación? Son dos rayos cualesquiera que determinan dos regiones del plano. Su notación: Para nombrar los ángulos, utilizaremos los símbolos
I.E.S VICENTE ALEIXANDRE BARBATE
 1. Calcula el área y el perímetro de estas figuras:. Un sector circular mide 80 y tiene 10 de radio. Cuál es su área y su perímetro? 3. El área de la zona sombreada es de 35. Cuál es la superficie del
1. Calcula el área y el perímetro de estas figuras:. Un sector circular mide 80 y tiene 10 de radio. Cuál es su área y su perímetro? 3. El área de la zona sombreada es de 35. Cuál es la superficie del
Proporcionalidad geométrica
 TEMA 9: Proporcionalidad geométrica INTRODUCCIÓN: THALES DE MILETO Thales, filósofo, astrónomo y matemático griego nació en Mileto en el año 624 a. de C. y murió a la edad de 78 años durante la quincuagésima
TEMA 9: Proporcionalidad geométrica INTRODUCCIÓN: THALES DE MILETO Thales, filósofo, astrónomo y matemático griego nació en Mileto en el año 624 a. de C. y murió a la edad de 78 años durante la quincuagésima
Conceptos Básicos. Las líneas rectas podemos encontrarlas en el doblez de una hoja de papel, en un hilo estirado, en la arista de una puerta, etc.
 3. Geometría Desde el jardinero que traza un jardín, el navegante que fija y traza la ruta del próximo viaje, el arquitecto que hace los planos para la construcción de un grandioso edificio, el ingeniero
3. Geometría Desde el jardinero que traza un jardín, el navegante que fija y traza la ruta del próximo viaje, el arquitecto que hace los planos para la construcción de un grandioso edificio, el ingeniero
Nombre: EJERCICIO 1 (1): Dado un rectángulo cuyos lados miden 4 cm y 3 cm, qué medidas tendrá una ampliación suya si la razón de semejanza es 2,5?
 Matemáticas 3ºESO D Examen: 1º 30. 04.14 EJERCICIO 1 (1): Dado un rectángulo cuyos lados miden 4 cm y 3 cm, qué medidas tendrá una ampliación suya si la razón de semejanza es 2,5? EJERCICIO 2: (2) Dado
Matemáticas 3ºESO D Examen: 1º 30. 04.14 EJERCICIO 1 (1): Dado un rectángulo cuyos lados miden 4 cm y 3 cm, qué medidas tendrá una ampliación suya si la razón de semejanza es 2,5? EJERCICIO 2: (2) Dado
TEOREMA DE PITÁGORAS. SEMEJANZA. (http://profeblog.es/blog/luismiglesias)
 Cuestiones 1. Qué polígonos son semejantes cuando tienen los lados proporcionales? a) Todos. c) Ninguno. b) Los cuadriláteros. d) Los triángulos. 2. La razón entre los perímetros de dos figuras semejantes
Cuestiones 1. Qué polígonos son semejantes cuando tienen los lados proporcionales? a) Todos. c) Ninguno. b) Los cuadriláteros. d) Los triángulos. 2. La razón entre los perímetros de dos figuras semejantes
