Minería de Datos. Redundancia en Reglas de Asociación. Fac. Ciencias Ing. Informática Otoño de Dept. Matesco, Universidad de Cantabria
|
|
|
- Raúl Ruiz Lozano
- hace 7 años
- Vistas:
Transcripción
1 Minería de Datos Redundancia en Reglas de Asociación Cristina Tîrnăucă Dept. Matesco, Universidad de Cantabria Fac. Ciencias Ing. Informática Otoño de 2012
2 Reglas de Asociación Estándar Fijamos unos umbrales mínimos de soporte y confianza. Calculamos conjuntos frecuentes : subconjuntos cuyo soporte supera el umbral. En cada conjunto frecuente, probamos todas las maneras de poner un item como consecuente de la regla y el resto como antecedente, y filtramos las que no alcancen el umbral de confianza. (Perdemos las reglas con varios consecuentes.) Alternativa: para todo conjunto frecuente X y cada Y X, calculamos c(x \Y Y ) y retornamos sólo las reglas que alcanzan el umbral de confianza.
3 Abundancia de Reglas de Asociación El gran problema de este enfoque Preprocesas los datos, lanzas tu asociador, afinas los parámetros... Y cuando, finalmente, aciertas con valores que te proporcionan reglas un poco interesantes...
4 Abundancia de Reglas de Asociación El gran problema de este enfoque Preprocesas los datos, lanzas tu asociador, afinas los parámetros... Y cuando, finalmente, aciertas con valores que te proporcionan reglas un poco interesantes......salen decenas de miles de reglas. Y muchas te sobran.
5 Abundancia de Reglas de Asociación El gran problema de este enfoque Preprocesas los datos, lanzas tu asociador, afinas los parámetros... Y cuando, finalmente, aciertas con valores que te proporcionan reglas un poco interesantes......salen decenas de miles de reglas. Y muchas te sobran. United-States, White Husband United-States, White Married-civ-spouse United-States, White (En general, todas las que los datos no desmienten.)
6 Abundancia de Reglas de Asociación El gran problema de este enfoque Preprocesas los datos, lanzas tu asociador, afinas los parámetros... Y cuando, finalmente, aciertas con valores que te proporcionan reglas un poco interesantes......salen decenas de miles de reglas. Y muchas te sobran. United-States, White Husband United-States, White Married-civ-spouse United-States, White (En general, todas las que los datos no desmienten.) Necesitamos: Nociones precisas de redundancia entre reglas de asociación, métodos para encontrar bases no redundantes mínimas, y maneras de descartar las reglas poco novedosas.
7 Hacía la eliminación de redundancia en las reglas Clausuras y conjuntos cerrados Conjuntos cerrados Son los que no puedes ampliar sin perder soporte. En el momento de extender un conjunto con un item, comprobamos si el soporte decrece; si no lo hace, el conjunto no es cerrado. Más formal, un conjunto X I es cerrado si X = X, donde X es la clausura de X y se calcula con una de las dos fórmulas: X = {a I s(x {a}) = s(x )} = {t D X t}
8 Cómo definimos una regla redundante? Definimos: F τ = {X I s(x ) τ} (conjuntos frecuentes) FC τ = {X F τ Z X, s(z) < s(x )} (cerrados frecuentes) FG τ = {X F τ Y X, s(y ) > s(x )} (generadores minimales frecuentes)
9 Cómo definimos una regla redundante? Definimos: F τ = {X I s(x ) τ} (conjuntos frecuentes) FC τ = {X F τ Z X, s(z) < s(x )} (cerrados frecuentes) FG τ = {X F τ Y X, s(y ) > s(x )} (generadores minimales frecuentes) Decimos que X 2 Y 2 es redundante con respecto a X 1 Y 1 C(X 1 Y 1 ) = {X 2 Y 2 X1 X 2 and X 2 Y 2 X 1 Y 1 }
10 Reglas Representativas, I Reglas de asociación AR τ,γ = {X Y s(x Y ) τ, c(x Y ) γ} Reglas Representativas RR τ,γ = {r AR τ,γ r AR τ,γ \{r} tal que r C(r )}.
11 Reglas Representativas, I Reglas de asociación AR τ,γ = {X Y s(x Y ) τ, c(x Y ) γ} Reglas Representativas RR τ,γ = {r AR τ,γ r AR τ,γ \{r} tal que r C(r )}. Condiciónes necesarias ( pero no suficientes!) Si X Y RR τ,γ entonces XY FC τ y X FG τ.
12 Reglas Representativas, II Denotemos RI τ,γ = {Z FC τ X Z tal que X Z\X RRτ,γ }
13 Reglas Representativas, II Denotemos RI τ,γ = {Z FC τ X Z tal que X Z\X RRτ,γ } Teorema RI τ,γ = {Z FC τ γ mxgsτ,γ (Z) > mxs τ (Z)}, donde mxs τ (X ) = max({s(z) Z FC τ, Z X } {0}), mns τ (X ) = min({s(y ) Y FG τ, Y X } { }, mxgs τ (X ) = max({s(y ) Y FG τ, Y X, γ s(y ) s(x )} {0}).
14 Reglas Representativas, II Denotemos RI τ,γ = {Z FC τ X Z tal que X Z\X RRτ,γ } Teorema RI τ,γ = {Z FC τ γ mxgsτ,γ (Z) > mxs τ (Z)}, donde mxs τ (X ) = max({s(z) Z FC τ, Z X } {0}), mns τ (X ) = min({s(y ) Y FG τ, Y X } { }, mxgs τ (X ) = max({s(y ) Y FG τ, Y X, γ s(y ) s(x )} {0}). Teorema RR τ,γ = {X Z\X Z RI τ,γ, X Z, mxs τ (Z) < γ s(x ) s(z) > γ mns τ (X )}
15 Ejemplo Consideremos el siguiente conjunto de datos D = {abcdef, abcde, ab, ac, bc, ad} y sunpongamos que el umbral de soporte es τ = 0. a b c d e f 1/0 1 a b c d e 2/1 2 f 6/1 1 a b c 3/2 2 e 6/2 2 a d 3/2 3 a b 4/2 3 a c 4/2 3 b c 4/2 3 b d 3/2 2 c d 3/2 2 d 6/3 3 a 6/3 5 b 6/3 4 c 6/3 4 /5 6
Topologías. Segundo cuatrimestre Práctica Encuentre todas las topologías sobre conjuntos de a lo sumo cuatro elementos.
 Topología Segundo cuatrimestre - 2011 Práctica 1 Topologías Ejemplos de topologías 1. Encuentre todas las topologías sobre conjuntos de a lo sumo cuatro elementos. 2. Sea X un conjunto. (a) Sea τ = {U
Topología Segundo cuatrimestre - 2011 Práctica 1 Topologías Ejemplos de topologías 1. Encuentre todas las topologías sobre conjuntos de a lo sumo cuatro elementos. 2. Sea X un conjunto. (a) Sea τ = {U
Procesadores de Lenguaje
 Procesadores de Lenguaje Repaso TALF Cristina Tîrnăucă Dept. Matesco, Universidad de Cantabria Fac. Ciencias Ing. Informática Primavera de 2013 La Jerarquía de Chomsky Cuatro niveles de lenguajes formales
Procesadores de Lenguaje Repaso TALF Cristina Tîrnăucă Dept. Matesco, Universidad de Cantabria Fac. Ciencias Ing. Informática Primavera de 2013 La Jerarquía de Chomsky Cuatro niveles de lenguajes formales
Procesadores de Lenguaje
 Procesadores de Lenguaje Analizadores sintácticos descendentes: LL(1) Cristina Tîrnăucă Dept. Matesco, Universidad de Cantabria Fac. Ciencias Ing. Informática Primavera de 2013 Analizadores sintácticos
Procesadores de Lenguaje Analizadores sintácticos descendentes: LL(1) Cristina Tîrnăucă Dept. Matesco, Universidad de Cantabria Fac. Ciencias Ing. Informática Primavera de 2013 Analizadores sintácticos
Números reales Conceptos básicos Algunas propiedades
 Números reales Conceptos básicos Algunas propiedades En álgebra es esencial manejar símbolos con objeto de transformar o reducir expresiones algebraicas y resolver ecuaciones algebraicas. Debido a que
Números reales Conceptos básicos Algunas propiedades En álgebra es esencial manejar símbolos con objeto de transformar o reducir expresiones algebraicas y resolver ecuaciones algebraicas. Debido a que
Núcleos por trayectorias monocromáticas. digráficas m-coloreada
 en digráficas m-coloreada Hortensia Galeana Sánchez Ma. Rocío Rojas Monroy Guadalupe Gaytán Gómez Marzo 20, 2013 Definiciones Básicas Definición Una digráfica D consiste de un conjunto finito no vacío
en digráficas m-coloreada Hortensia Galeana Sánchez Ma. Rocío Rojas Monroy Guadalupe Gaytán Gómez Marzo 20, 2013 Definiciones Básicas Definición Una digráfica D consiste de un conjunto finito no vacío
José F. Fernando y José Manuel Gamboa
 ECUACIONES ALGEBRAICAS, CURSO 2016-2017 José F. Fernando y José Manuel Gamboa Polinomios en varias variables 1. Calcular la suma de los cubos de las raíces en C del polinomio f(t) := t 3 2t 2 + 3t 4? 2.
ECUACIONES ALGEBRAICAS, CURSO 2016-2017 José F. Fernando y José Manuel Gamboa Polinomios en varias variables 1. Calcular la suma de los cubos de las raíces en C del polinomio f(t) := t 3 2t 2 + 3t 4? 2.
Procesadores de Lenguaje
 Procesadores de Lenguaje Bootstrapping de Compiladores y Diagramas en T Cristina Tîrnăucă Dept. Matesco, Universidad de Cantabria Fac. Ciencias Ing. Informática Primavera de 2012 Qué es un compilador?
Procesadores de Lenguaje Bootstrapping de Compiladores y Diagramas en T Cristina Tîrnăucă Dept. Matesco, Universidad de Cantabria Fac. Ciencias Ing. Informática Primavera de 2012 Qué es un compilador?
Bases de Grobner Natalia García 27 de febrero de 2009
 DEPARTAMENTO DE MATEMÁTICA FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CONCEPCIÓN Bases de Grobner Natalia García 27 de febrero de 2009 1. Introducción En este trabajo construiremos un algoritmo
DEPARTAMENTO DE MATEMÁTICA FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CONCEPCIÓN Bases de Grobner Natalia García 27 de febrero de 2009 1. Introducción En este trabajo construiremos un algoritmo
Ejercicios de Algebra III. Curso 00-01
 Ejercicios de Algebra III. Curso 00-01 Ejercicio 1. Sea x un elemento nilpotente de un anillo A. Probar que 1 + x es una unidad de A. Deducir que la suma de un elemento nilpotente y de una unidad es una
Ejercicios de Algebra III. Curso 00-01 Ejercicio 1. Sea x un elemento nilpotente de un anillo A. Probar que 1 + x es una unidad de A. Deducir que la suma de un elemento nilpotente y de una unidad es una
Ejemplo 66 Sea A = {los alumnos de este curso}, entonces podemos definir la siguiente relación el el conjunto A, dada por:
 Capítulo 3 Relaciones Definición 8 Sea A un conjunto no vacío. Se dice que R es una relación en A si y sólo si R A A. Ejemplo 65 Sea A = {a,b,c}, luego definimos los conjuntos: R 1 = {(a,a),(a,b),(b,c)},r
Capítulo 3 Relaciones Definición 8 Sea A un conjunto no vacío. Se dice que R es una relación en A si y sólo si R A A. Ejemplo 65 Sea A = {a,b,c}, luego definimos los conjuntos: R 1 = {(a,a),(a,b),(b,c)},r
Funciones Continuas Definiciones y Propiedades
 Capítulo 2 Funciones Continuas 2.1. Definiciones Propiedades Sean (X,T X ) e (Y,T Y ) dos espacios topológicos una función f : X Y. Se dice que f es continua, si sólo si, para todo V T Y, se tiene f 1
Capítulo 2 Funciones Continuas 2.1. Definiciones Propiedades Sean (X,T X ) e (Y,T Y ) dos espacios topológicos una función f : X Y. Se dice que f es continua, si sólo si, para todo V T Y, se tiene f 1
Clase 1: Funciones de Varias Variables
 Clase 1: Funciones de Varias Variables C. J. Vanegas 29 de abril de 2008 1. La geometría de funciones con valores reales Considere la siguiente función f: donde x = (x 1,..., x n ). f : A R n R m x A f(x)
Clase 1: Funciones de Varias Variables C. J. Vanegas 29 de abril de 2008 1. La geometría de funciones con valores reales Considere la siguiente función f: donde x = (x 1,..., x n ). f : A R n R m x A f(x)
5 DIVISIÓN DE POLINOMIOS. RAÍCES
 EJERCICIOS PARA ENTRENARSE División y regla de Ruffini 5.26 Realiza estas divisiones. a) (12x 2 yz 6xy 3 8xyz 2 ) (2xy) b) (15x 4 3x 3 9x 2 ) (3x 2 ) c) (5a 3 b 2 10ab 2 15a 3 b 4 ) (5ab 2 ) a) (12x 2
EJERCICIOS PARA ENTRENARSE División y regla de Ruffini 5.26 Realiza estas divisiones. a) (12x 2 yz 6xy 3 8xyz 2 ) (2xy) b) (15x 4 3x 3 9x 2 ) (3x 2 ) c) (5a 3 b 2 10ab 2 15a 3 b 4 ) (5ab 2 ) a) (12x 2
Tema 6: Funciones de varias variables
 Tema 6: Funciones de varias variables de febrero de 6 Preliminares: derivadas parciales. Sea F una función de dos variables, como por ejemplo la función definida por F(x; y) = x y 3 Podemos derivarla con
Tema 6: Funciones de varias variables de febrero de 6 Preliminares: derivadas parciales. Sea F una función de dos variables, como por ejemplo la función definida por F(x; y) = x y 3 Podemos derivarla con
Minería de Datos. Árboles de Decisión. Fac. Ciencias Ing. Informática Otoño de Dept. Matesco, Universidad de Cantabria
 Minería de Datos Árboles de Decisión Cristina Tîrnăucă Dept. Matesco, Universidad de Cantabria Fac. Ciencias Ing. Informática Otoño de 2012 Twenty questions Intuición sobre los árboles de decisión Juego
Minería de Datos Árboles de Decisión Cristina Tîrnăucă Dept. Matesco, Universidad de Cantabria Fac. Ciencias Ing. Informática Otoño de 2012 Twenty questions Intuición sobre los árboles de decisión Juego
GUÍA PRÁCTICA DE CONJUNTOS Y RELACIONES BINARIAS
 UNIVERSIDAD CATÓLICA ANDRÉS BELLO FACULTAD DE INGENIERÍA ESCUELA DE INGENIERÍA INFORMÁTICA CÁTEDRA DE LÓGICA COMPUTACIONAL GUÍA PRÁCTICA DE CONJUNTOS Y RELACIONES BINARIAS 1. Sean los conjuntos A = {x
UNIVERSIDAD CATÓLICA ANDRÉS BELLO FACULTAD DE INGENIERÍA ESCUELA DE INGENIERÍA INFORMÁTICA CÁTEDRA DE LÓGICA COMPUTACIONAL GUÍA PRÁCTICA DE CONJUNTOS Y RELACIONES BINARIAS 1. Sean los conjuntos A = {x
TEMA 3: CONTINUIDAD DE FUNCIONES
 TEMA 3: CONTINUIDAD DE FUNCIONES. Valor Absoluto Trabajaremos en el campo de los números reales, R. Para el estudio de las propiedades de las funciones necesitamos el concepto de valor absoluto de un número
TEMA 3: CONTINUIDAD DE FUNCIONES. Valor Absoluto Trabajaremos en el campo de los números reales, R. Para el estudio de las propiedades de las funciones necesitamos el concepto de valor absoluto de un número
Extensiones finitas.
 2. EXTENSIONES ALGEBRAICAS. Hemos dividido este tema en dos secciones: Extensiones finitas, y Clausura algebraica. En la primera relacionamos extensión finita y extensión algebraica: probamos que toda
2. EXTENSIONES ALGEBRAICAS. Hemos dividido este tema en dos secciones: Extensiones finitas, y Clausura algebraica. En la primera relacionamos extensión finita y extensión algebraica: probamos que toda
TEMA 3: CONTINUIDAD DE FUNCIONES
 TEMA 3: CONTINUIDAD DE FUNCIONES. Valor Absoluto Trabajaremos en el campo de los números reales, R. Para el estudio de las propiedades de las funciones necesitamos el concepto de valor absoluto de un número
TEMA 3: CONTINUIDAD DE FUNCIONES. Valor Absoluto Trabajaremos en el campo de los números reales, R. Para el estudio de las propiedades de las funciones necesitamos el concepto de valor absoluto de un número
Superficies Forma explícita
 Lección 7 Superficies En lo que sigue vamos a hacer un tratamiento básico de las superficies en R 3, que guarda cierto paralelismo con el estudio de las curvas en el plano hecho anteriormente. 7.1. Forma
Lección 7 Superficies En lo que sigue vamos a hacer un tratamiento básico de las superficies en R 3, que guarda cierto paralelismo con el estudio de las curvas en el plano hecho anteriormente. 7.1. Forma
Exámenes de Álgebra Local. Pedro Sancho
 Exámenes de Álgebra Local Pedro Sancho 2003 2 Índice General 1 Examen de Álgebra Local. Abril-2001 5 2 Examen de Álgebra Local. Abril-2001 7 3 Examen de Álgebra Local. Junio-2001 9 4 Examen de Álgebra
Exámenes de Álgebra Local Pedro Sancho 2003 2 Índice General 1 Examen de Álgebra Local. Abril-2001 5 2 Examen de Álgebra Local. Abril-2001 7 3 Examen de Álgebra Local. Junio-2001 9 4 Examen de Álgebra
Minería de Datos. Árboles de Decisión. Fac. Ciencias Ing. Informática Otoño de Dept. Matesco, Universidad de Cantabria
 Minería de Datos Árboles de Decisión Cristina Tîrnăucă Dept. Matesco, Universidad de Cantabria Fac. Ciencias Ing. Informática Otoño de 2012 Twenty questions Intuición sobre los árboles de decisión Juego
Minería de Datos Árboles de Decisión Cristina Tîrnăucă Dept. Matesco, Universidad de Cantabria Fac. Ciencias Ing. Informática Otoño de 2012 Twenty questions Intuición sobre los árboles de decisión Juego
Álgebra. Curso de junio de Grupo B
 Álgebra. Curso 2008-2009 9 de junio de 2009. Grupo B Primera parte Ejercicio. 1. Sea D un dominio noetheriano que no es un cuerpo. Demuestra que son equivalentes: (a) D es un dominio de Dedekind. (b) Todo
Álgebra. Curso 2008-2009 9 de junio de 2009. Grupo B Primera parte Ejercicio. 1. Sea D un dominio noetheriano que no es un cuerpo. Demuestra que son equivalentes: (a) D es un dominio de Dedekind. (b) Todo
Ecuaciones Diferenciales Ordinarias
 Ecuaciones Diferenciales Ordinarias (Teoremas de Existencia y Unicidad) Julio López jclopez@dim.uchile.cl Depto Ingeniería Matemática, Universidad de Chile Otoño 2011, Resumen clases Julio López EDO 1/15
Ecuaciones Diferenciales Ordinarias (Teoremas de Existencia y Unicidad) Julio López jclopez@dim.uchile.cl Depto Ingeniería Matemática, Universidad de Chile Otoño 2011, Resumen clases Julio López EDO 1/15
Notas sobre polinomios
 Notas sobre polinomios Glenier Bello 1. Definiciones y conceptos básicos 1.1. Un polinomio es una función f : C C del tipo f(x) = a n x n + a n 1 x n 1 + + a 1 x + a 0, donde n es un entero no negativo
Notas sobre polinomios Glenier Bello 1. Definiciones y conceptos básicos 1.1. Un polinomio es una función f : C C del tipo f(x) = a n x n + a n 1 x n 1 + + a 1 x + a 0, donde n es un entero no negativo
2. Cálculo diferencial de funciones de varias variables. Mayo, 2009
 Cálculo 2. Cálculo diferencial de funciones de varias variables Mayo, 2009 Definición IR 2 = {(x 1,x 2 )/x 1 IR,x 2 IR} Sean dos puntos a y b, de coordenadas respectivas (a 1,a 2 ) y (b 1,b 2 ). Definición
Cálculo 2. Cálculo diferencial de funciones de varias variables Mayo, 2009 Definición IR 2 = {(x 1,x 2 )/x 1 IR,x 2 IR} Sean dos puntos a y b, de coordenadas respectivas (a 1,a 2 ) y (b 1,b 2 ). Definición
1. Sumar monomios semejantes:
 HOJA 1: Monomios 1. Sumar monomios semejantes: a) 3x + 4x 5x b) 6x 3 x 3 + 3x 3 c) x 5 + 4x 5 7x 5 d) x 4 + 6x 4 + 3x 4 5x 4 e) 7x + 9x 8x + x f) y + 5y 3y g) 3x y 6x y + 5x y h) 4xy xy 7xy i) a 6 3a 6
HOJA 1: Monomios 1. Sumar monomios semejantes: a) 3x + 4x 5x b) 6x 3 x 3 + 3x 3 c) x 5 + 4x 5 7x 5 d) x 4 + 6x 4 + 3x 4 5x 4 e) 7x + 9x 8x + x f) y + 5y 3y g) 3x y 6x y + 5x y h) 4xy xy 7xy i) a 6 3a 6
Normalización Clase Práctica SPI y SPDF
 Normalización Clase Práctica Departamento de Computación - Facultad de Ciencias Exactas y Naturales Universidad de Buenos Aires Base de Datos 2do. Cuatrimestre 2015 Esquema General 1 Introducción 2 Sin
Normalización Clase Práctica Departamento de Computación - Facultad de Ciencias Exactas y Naturales Universidad de Buenos Aires Base de Datos 2do. Cuatrimestre 2015 Esquema General 1 Introducción 2 Sin
Problemas de Espacios Vectoriales
 Problemas de Espacios Vectoriales 1. Qué condiciones tiene que cumplir un súbconjunto no vacío de un espacio vectorial para que sea un subespacio vectorial de este? Pon un ejemplo. Sean E un espacio vectorial
Problemas de Espacios Vectoriales 1. Qué condiciones tiene que cumplir un súbconjunto no vacío de un espacio vectorial para que sea un subespacio vectorial de este? Pon un ejemplo. Sean E un espacio vectorial
Límite superior y límite inferior de una sucesión
 Límite superior y límite inferior de una sucesión Objetivos. Definir las nociones de los límites superior e inferior de una sucesión y estudiar sus propiedades básicas. Requisitos. Supremo e ínfimo de
Límite superior y límite inferior de una sucesión Objetivos. Definir las nociones de los límites superior e inferior de una sucesión y estudiar sus propiedades básicas. Requisitos. Supremo e ínfimo de
7. Seguiría siendo válida la proposición anterior si algunos de los conjuntos A, B, C y D son vacíos?
 UNIVERSIDAD SIMÓN BOLÍVAR DEPARTAMENTO DE COMPUTACIÓN Y TECNOLOGÍA DE LA INFROMACIÓN ESTRUCTURAS DISCRETAS I GUÍA PRÁCTICA Nº 2. Demuestre lo siguiente mediante inducción matemática: a) 3 + 2 4 + 3 5 +...
UNIVERSIDAD SIMÓN BOLÍVAR DEPARTAMENTO DE COMPUTACIÓN Y TECNOLOGÍA DE LA INFROMACIÓN ESTRUCTURAS DISCRETAS I GUÍA PRÁCTICA Nº 2. Demuestre lo siguiente mediante inducción matemática: a) 3 + 2 4 + 3 5 +...
CARACTERIZACIÓN DEL SOFTWARE DE COMPUTADORES Y PERIFÉRICOS
 CARACTRIZACIÓN L SOFTWAR COMPUTAORS Y PRIFÉRICOS CASO - FC - Revisión : Página de 8 Fecha de misión : 25/6/8 RSPONSABL: ING. ROGL MIGUZ Copia No Controlada, Impresa el día 25/6/8! CARACTRIZACIÓN L SOFTWAR
CARACTRIZACIÓN L SOFTWAR COMPUTAORS Y PRIFÉRICOS CASO - FC - Revisión : Página de 8 Fecha de misión : 25/6/8 RSPONSABL: ING. ROGL MIGUZ Copia No Controlada, Impresa el día 25/6/8! CARACTRIZACIÓN L SOFTWAR
El espacio n Consideremos el conjunto de todas las n adas ordenadas de números reales, denotado por n : 8. 1(x 1, x 2,, x n ) = (x 1, x 2,, x n )
 El espacio n Consideremos el conjunto de todas las n adas ordenadas de números reales, denotado por n : n = {(x 1,x,, x n ) / x 1,x,, x n } A cada uno de los números reales x 1,x,, x n que conforman la
El espacio n Consideremos el conjunto de todas las n adas ordenadas de números reales, denotado por n : n = {(x 1,x,, x n ) / x 1,x,, x n } A cada uno de los números reales x 1,x,, x n que conforman la
Conexión Motivación. Lección 10
 Lección 10 Conexión Estudiamos la propiedad topológica que nos va a permitir obtener una versión general para espacios métricos del teorema del valor intermedio que conocemos para funciones reales de variable
Lección 10 Conexión Estudiamos la propiedad topológica que nos va a permitir obtener una versión general para espacios métricos del teorema del valor intermedio que conocemos para funciones reales de variable
Espacios topológicos. 3.1 Espacio topológico
 Capítulo 3 Espacios topológicos 3.1 Espacio topológico Definición 3.1.1. Un espacio topológico es un par (X, τ), donde X es un conjunto, y τ es una familia de subconjuntos de X que verifica las siguientes
Capítulo 3 Espacios topológicos 3.1 Espacio topológico Definición 3.1.1. Un espacio topológico es un par (X, τ), donde X es un conjunto, y τ es una familia de subconjuntos de X que verifica las siguientes
Espacios conexos. Capítulo Conexidad
 Capítulo 5 Espacios conexos 1. Conexidad En este capítulo exploraremos el concepto de conexidad en un espacio métrico, y estudiaremos algunas de sus aplicaciones. Definición 5.1. Decimos que el espacio
Capítulo 5 Espacios conexos 1. Conexidad En este capítulo exploraremos el concepto de conexidad en un espacio métrico, y estudiaremos algunas de sus aplicaciones. Definición 5.1. Decimos que el espacio
Álgebra. Curso
 Álgebra. Curso 2012-2013 14 de junio de 2013 Resolución Ejercicio. 1. (2 puntos) Utiliza el teorema del descenso (o alternativamente la localización en primos) para probar el siguiente resultado: Sea K
Álgebra. Curso 2012-2013 14 de junio de 2013 Resolución Ejercicio. 1. (2 puntos) Utiliza el teorema del descenso (o alternativamente la localización en primos) para probar el siguiente resultado: Sea K
Paréntesis: Una aplicación en lenguajes formales
 Paréntesis: Una aplicación en lenguajes formales Vamos a ver una aplicación del Teorema de Immerman-Szelepcsényi en la área de lenguajes formales. IIC3242 Clases de Complejidad 35 / 69 Paréntesis: Una
Paréntesis: Una aplicación en lenguajes formales Vamos a ver una aplicación del Teorema de Immerman-Szelepcsényi en la área de lenguajes formales. IIC3242 Clases de Complejidad 35 / 69 Paréntesis: Una
LógicaS Modales. Ricardo Oscar Rodríguez Departamento de Computación, Fac. Ciencias Exactas y Naturales, Universidad de Buenos Aires, Argentina.
 Departamento de Computación, Fac. Ciencias Exactas y Naturales, Universidad de Buenos Aires, Argentina. Segunda Clase. 1er. Cuatrimestre, 2016 Outline 1 Repaso clase anterior Sintáxis Lógicas Modales Autocongruentes
Departamento de Computación, Fac. Ciencias Exactas y Naturales, Universidad de Buenos Aires, Argentina. Segunda Clase. 1er. Cuatrimestre, 2016 Outline 1 Repaso clase anterior Sintáxis Lógicas Modales Autocongruentes
Información importante
 Coordinación de Matemática I (MAT021) 1 er Semestre de 2010 Semana 8: Lunes 10 viernes 14 de Mayo Información importante El viernes 14 ser publicada la tarea preparatoria de Taller de Sala. Durante la
Coordinación de Matemática I (MAT021) 1 er Semestre de 2010 Semana 8: Lunes 10 viernes 14 de Mayo Información importante El viernes 14 ser publicada la tarea preparatoria de Taller de Sala. Durante la
Ejercicio 70 : En este ejercicio vamos a caracterizar completamente la expresión
 EJERCICIOS ESTRUCTURAS ALGEBRAICAS (2004-2005) 1 Ejercicio 70 : En este ejercicio vamos a caracterizar completamente la expresión f = a 1 f 1 +... + a s f s + r que se obtiene al aplicar el algoritmo de
EJERCICIOS ESTRUCTURAS ALGEBRAICAS (2004-2005) 1 Ejercicio 70 : En este ejercicio vamos a caracterizar completamente la expresión f = a 1 f 1 +... + a s f s + r que se obtiene al aplicar el algoritmo de
Clases Prácticas Base de Datos DF y FN 10 y 17/09/ C.2010
 Ej.1.- Sea la relación R = (A, B, C, D, E, F) y el conjunto de dependencias funcionales FD1: {A BD, B CD, AC E} FD2: {A BD, B CD, AC E, C A} FD3: {A BD, B ACD, AC E, C B} Cuál es la clausura de A, B y
Ej.1.- Sea la relación R = (A, B, C, D, E, F) y el conjunto de dependencias funcionales FD1: {A BD, B CD, AC E} FD2: {A BD, B CD, AC E, C A} FD3: {A BD, B ACD, AC E, C B} Cuál es la clausura de A, B y
EJERCICIOS DE ÁLGEBRA LINEAL TEMA 1 ESPACIOS VECTORIALES
 EJERCICIOS DE ÁLGEBRA LINEAL TEMA ESPACIOS VECTORIALES MATRICES. SISTEMAS DE ECUACIONES LINEALES Matrices ) Dada la matriz M=, prueba que n n M M, n. ) Demuestra la siguiente implicación: Si I A I AA A
EJERCICIOS DE ÁLGEBRA LINEAL TEMA ESPACIOS VECTORIALES MATRICES. SISTEMAS DE ECUACIONES LINEALES Matrices ) Dada la matriz M=, prueba que n n M M, n. ) Demuestra la siguiente implicación: Si I A I AA A
Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás
 Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás de mayo de 013 Capítulo 1 Año 011 1.1. Modelo 011 - Opción A Problema 1.1.1 (3 puntos) Dado el sistema: λx
Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás de mayo de 013 Capítulo 1 Año 011 1.1. Modelo 011 - Opción A Problema 1.1.1 (3 puntos) Dado el sistema: λx
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2001 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 001 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio 3, Opción B Junio, Ejercicio 4, Opción A Reserva 1, Ejercicio 4, Opción B Reserva, Ejercicio
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 001 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio 3, Opción B Junio, Ejercicio 4, Opción A Reserva 1, Ejercicio 4, Opción B Reserva, Ejercicio
Completitud en Lógica de Predicados
 Completitud en de Predicados Predicados - Completitud 1 Corrección. Significa que las derivaciones expresan una consecuencia lógica. Establece una correspondencia tal que partiendo de nociones sintácticas
Completitud en de Predicados Predicados - Completitud 1 Corrección. Significa que las derivaciones expresan una consecuencia lógica. Establece una correspondencia tal que partiendo de nociones sintácticas
Restricción de valor único. Indispensable para diseñar esquemas de bases de datos que eliminen al redundancia.
 CC42A Auxiliar #3 Dependencias funcionales, reglas, axiomas de Armstrong, cerradura de dependencias Martes, 03 de Septiembre de 2002 Profesor: Claudio Gutiérrez Auxiliar: Tania Gallardo Consultas a tgallard@dcc.uchile.cl
CC42A Auxiliar #3 Dependencias funcionales, reglas, axiomas de Armstrong, cerradura de dependencias Martes, 03 de Septiembre de 2002 Profesor: Claudio Gutiérrez Auxiliar: Tania Gallardo Consultas a tgallard@dcc.uchile.cl
EJERCICIOS DE ÁLGEBRA LINEAL TEMA 1 ESPACIOS VECTORIALES
 EJERCICIOS DE ÁLGEBRA LINEAL TEMA ESPACIOS VECTORIALES Formas reducidas y escalonada de una matriz SISTEMAS DE ECUACIONES LINEALES ) Encuentre una sucesión de matrices elementales E, E,..., E k tal que
EJERCICIOS DE ÁLGEBRA LINEAL TEMA ESPACIOS VECTORIALES Formas reducidas y escalonada de una matriz SISTEMAS DE ECUACIONES LINEALES ) Encuentre una sucesión de matrices elementales E, E,..., E k tal que
Teoría de la Computación Lenguajes Regulares (LR) - Propiedades
 Teoría de la Computación Lenguajes Regulares (LR) - Propiedades Prof. Hilda Y. Contreras Departamento de Computación hyelitza@ula.ve http://webdelprofesor.ula.ve/ingenieria/hyelitza Objetivo Lenguajes
Teoría de la Computación Lenguajes Regulares (LR) - Propiedades Prof. Hilda Y. Contreras Departamento de Computación hyelitza@ula.ve http://webdelprofesor.ula.ve/ingenieria/hyelitza Objetivo Lenguajes
Base y Dimensión de un Espacio Vectorial
 Base y Dimensión de un Espacio Vectorial 201 6Asturias: Red de Universidades Virtuales Iberoamericanas 1 Índice 1 Qué es un sistema generador?... 4 2 Base de un espacio vectorial... 4 3 Dimensión de un
Base y Dimensión de un Espacio Vectorial 201 6Asturias: Red de Universidades Virtuales Iberoamericanas 1 Índice 1 Qué es un sistema generador?... 4 2 Base de un espacio vectorial... 4 3 Dimensión de un
Relaciones IIC1253. IIC1253 Relaciones 1 / 32
 Relaciones IIC1253 IIC1253 Relaciones 1 / 32 Relaciones binarias Dado: conjunto A R es una relación binaria sobre A si R A A. Para indicar que a,b A están relacionados a través de R usamos las notaciones:
Relaciones IIC1253 IIC1253 Relaciones 1 / 32 Relaciones binarias Dado: conjunto A R es una relación binaria sobre A si R A A. Para indicar que a,b A están relacionados a través de R usamos las notaciones:
Álgebra básica Soluciones del examen de segunda convocatoria Curso 2016/ de septiembre de 2017
 Álgebra básica Soluciones del examen de segunda convocatoria Curso 2016/2017 12 de septiembre de 2017 Ejercicio 1. Se pide lo siguiente: 1. (2 puntos) Dados unos conjuntos X, Y, unos subconjuntos A X,
Álgebra básica Soluciones del examen de segunda convocatoria Curso 2016/2017 12 de septiembre de 2017 Ejercicio 1. Se pide lo siguiente: 1. (2 puntos) Dados unos conjuntos X, Y, unos subconjuntos A X,
Actividad: Figuras Semejantes
 Actividad: Figuras Semejantes Curso: Matemáticas Nivel: Septimo Grado Tiempo sugerido: 2 periodos de 50 minutos Estándar Expectativa Indicador Geometría: El estudiante es capaz de identificar formas geométricas,
Actividad: Figuras Semejantes Curso: Matemáticas Nivel: Septimo Grado Tiempo sugerido: 2 periodos de 50 minutos Estándar Expectativa Indicador Geometría: El estudiante es capaz de identificar formas geométricas,
ÁLGEBRA LINEAL Problemas, 2006/2007
 ÁLGEBRA LINEAL Problemas, 2006/2007 Nota: si no se especifíca lo contrario suponemos que las matrices y espacios vectoriales están definidos sobre un cuerpo K arbitrario 1 Una matriz A de orden n n se
ÁLGEBRA LINEAL Problemas, 2006/2007 Nota: si no se especifíca lo contrario suponemos que las matrices y espacios vectoriales están definidos sobre un cuerpo K arbitrario 1 Una matriz A de orden n n se
Álgebra y Trigonometría Clase 7 Sistemas de ecuaciones, Matrices y Determinantes
 Álgebra y Trigonometría Clase 7 Sistemas de ecuaciones, Matrices y Determinantes CNM-108 Departamento de Matemáticas Facultad de Ciencias Exactas y Naturales Universidad de Antioquia Copyleft c 2008. Reproducción
Álgebra y Trigonometría Clase 7 Sistemas de ecuaciones, Matrices y Determinantes CNM-108 Departamento de Matemáticas Facultad de Ciencias Exactas y Naturales Universidad de Antioquia Copyleft c 2008. Reproducción
Espacios conexos. 6.1 Conexos
 Capítulo 6 Espacios conexos 6.1 Conexos Definición 6.1.1 (Conjuntos separados). Dado un espacio topológico (X, τ) y dos subconjuntos A, B X, diremos que A y B están separados si A B = A B = Es evidente
Capítulo 6 Espacios conexos 6.1 Conexos Definición 6.1.1 (Conjuntos separados). Dado un espacio topológico (X, τ) y dos subconjuntos A, B X, diremos que A y B están separados si A B = A B = Es evidente
Capítulo 1: Fundamentos: Lógica y Demostraciones Clase 3: Relaciones, Funciones, y Notación Asintótica
 Capítulo 1: Fundamentos: Lógica y Demostraciones Clase 3: Relaciones, Funciones, y Notación Asintótica Matemática Discreta - CC3101 Profesor: Pablo Barceló P. Barceló Matemática Discreta - Cap. 1: Fundamentos:
Capítulo 1: Fundamentos: Lógica y Demostraciones Clase 3: Relaciones, Funciones, y Notación Asintótica Matemática Discreta - CC3101 Profesor: Pablo Barceló P. Barceló Matemática Discreta - Cap. 1: Fundamentos:
Conjuntos Abiertos y Conjuntos Cerrados
 El espacio R n 1 Conjuntos Abiertos y Conjuntos Cerrados Definición. Un conjunto V R n se dice que es abierto si para cada x V existe una bola abierta B( x, r) contenida en V. Es decir si para cada x V
El espacio R n 1 Conjuntos Abiertos y Conjuntos Cerrados Definición. Un conjunto V R n se dice que es abierto si para cada x V existe una bola abierta B( x, r) contenida en V. Es decir si para cada x V
Universidad Nacional del Sur Departamento de Ciencias e Ingeniería de la Computación Elementos de Bases de Datos 2do. Cuatrimestre de 2004
 2do. Cuatrimestre de 2004 Elementos de Bases de Datos Dpto.Ciencias e Ingeniería de la Computación Universidad Nacional del Sur Lic. María Mercedes Vitturini [mvitturi@cs.uns.edu.ar] Clase 9 1er. Cuatrimestre
2do. Cuatrimestre de 2004 Elementos de Bases de Datos Dpto.Ciencias e Ingeniería de la Computación Universidad Nacional del Sur Lic. María Mercedes Vitturini [mvitturi@cs.uns.edu.ar] Clase 9 1er. Cuatrimestre
Integral de Lebesgue
 Integral de Lebesgue Problemas para examen n todos los problemas se supone que (, F, µ) es un espacio de medida. Integración de funciones simples positivas. La representación canónica de una función simple
Integral de Lebesgue Problemas para examen n todos los problemas se supone que (, F, µ) es un espacio de medida. Integración de funciones simples positivas. La representación canónica de una función simple
MINISTERIO DE EDUCACIÓN Concurso Nacional de Matemática Educación Preuniversitaria Curso 2009 2010 Temario por Grados
 MINISTERIO DE EDUCACIÓN Concurso Nacional de Matemática Educación Preuniversitaria Curso 009 010 Temario por Grados Nombre: Grado: Escuela: Provincia: Municipio: Número C.I.: Calif: La distribución de
MINISTERIO DE EDUCACIÓN Concurso Nacional de Matemática Educación Preuniversitaria Curso 009 010 Temario por Grados Nombre: Grado: Escuela: Provincia: Municipio: Número C.I.: Calif: La distribución de
Lenguajes Incontextuales
 Tema 5: Gramáticas Formales Lenguajes Incontextuales Departamento de Sistemas Informáticos y Computación http://www.dsic.upv.es p.1/31 Tema 5: Gramáticas Formales Gramáticas. Tipos de Gramáticas. Jerarquía
Tema 5: Gramáticas Formales Lenguajes Incontextuales Departamento de Sistemas Informáticos y Computación http://www.dsic.upv.es p.1/31 Tema 5: Gramáticas Formales Gramáticas. Tipos de Gramáticas. Jerarquía
z-ultrafiltros y compactificación de Stone-Čech
 Universidad de Cantabria Departamento de Matemáticas, Estadística y Computación z-ultrafiltros y compactificación de Stone-Čech Víctor Diego Gutiérrez Trabajo dirigido en Matemática Fundamental por Jesús
Universidad de Cantabria Departamento de Matemáticas, Estadística y Computación z-ultrafiltros y compactificación de Stone-Čech Víctor Diego Gutiérrez Trabajo dirigido en Matemática Fundamental por Jesús
Continuidad. 5.1 Continuidad en un punto
 Capítulo 5 Continuidad 5.1 Continuidad en un punto Definición 5.1.1 (Aplicación continua en un punto). Sean (X, τ) e (Y, τ ) dos espacios topológicos, y sea f : X Y una aplicación entre ellos. Diremos
Capítulo 5 Continuidad 5.1 Continuidad en un punto Definición 5.1.1 (Aplicación continua en un punto). Sean (X, τ) e (Y, τ ) dos espacios topológicos, y sea f : X Y una aplicación entre ellos. Diremos
Álgebra Lineal V: Subespacios Vectoriales.
 Álgebra Lineal V: Subespacios Vectoriales. José María Rico Martínez Departamento de Ingeniería Mecánica Facultad de Ingeniería Mecánica Eléctrica y Electrónica Universidad de Guanajuato email: jrico@salamanca.ugto.mx
Álgebra Lineal V: Subespacios Vectoriales. José María Rico Martínez Departamento de Ingeniería Mecánica Facultad de Ingeniería Mecánica Eléctrica y Electrónica Universidad de Guanajuato email: jrico@salamanca.ugto.mx
Minería de Datos. Presentación de la asignatura. Fac. Ciencias Ing. Informática Otoño de 2012. Dept. Matesco, Universidad de Cantabria
 Minería de Datos Presentación de la asignatura Cristina Tîrnăucă Dept. Matesco, Universidad de Cantabria Fac. Ciencias Ing. Informática Otoño de 2012 Cuestiones Factuales De índole práctica Personal e
Minería de Datos Presentación de la asignatura Cristina Tîrnăucă Dept. Matesco, Universidad de Cantabria Fac. Ciencias Ing. Informática Otoño de 2012 Cuestiones Factuales De índole práctica Personal e
Series de potencias y modos de convergencia. Pedro Tamaroff
 Series de potencias y modos de convergencia Pedro Tamaroff 1. El álgebra de series de potencias I. Series formales Una serie de potencias formal con coeficientes complejos es una expresión f = ν 0 a ν
Series de potencias y modos de convergencia Pedro Tamaroff 1. El álgebra de series de potencias I. Series formales Una serie de potencias formal con coeficientes complejos es una expresión f = ν 0 a ν
Universidad Nacional del Sur Departamento de Ciencias e Ingeniería de la Computación Elementos de Bases de Datos 2do. Cuatrimestre de 2004
 do. Cuatrimestre de 004 Formas Normales Elementos de Bases de Datos Dpto.Ciencias e Ingeniería de la Computación Universidad Nacional del Sur Lic. María Mercedes Vitturini [mvitturi@cs.uns.edu.ar] Clase
do. Cuatrimestre de 004 Formas Normales Elementos de Bases de Datos Dpto.Ciencias e Ingeniería de la Computación Universidad Nacional del Sur Lic. María Mercedes Vitturini [mvitturi@cs.uns.edu.ar] Clase
Álgebras de Boole. Definición 1 Un álgebra de Boole es un conjunto parcialmente ordenado (B, ) que verifica las siguientes condiciones:
 Álgebras de Boole Sea (P, ) un conjunto parcialmente ordenado y sea S un subconjunto de P. Una cota superior de S es un elemento c P tal que s c para todo s S. Una cota inferior de S es un elemento d P
Álgebras de Boole Sea (P, ) un conjunto parcialmente ordenado y sea S un subconjunto de P. Una cota superior de S es un elemento c P tal que s c para todo s S. Una cota inferior de S es un elemento d P
Este documento ha sido generado para facilitar la impresión de los contenidos. Los enlaces a otras páginas no serán funcionales.
 Este documento ha sido generado para facilitar la impresión de los contenidos. Los enlaces a otras páginas no serán funcionales. Los segmentos se determinan por su longitud. Supongamos que tenemos dos
Este documento ha sido generado para facilitar la impresión de los contenidos. Los enlaces a otras páginas no serán funcionales. Los segmentos se determinan por su longitud. Supongamos que tenemos dos
1 Continuidad uniforme
 Centro de Matemática Facultad de Ciencias Universidad de la República Introducción a la Topología Curso 2016 NOTAS 6: ESPACIOS MÉTRICOS II: COMPLETITUD 1 Continuidad uniforme Denición. Sean (M, d 1 ) y
Centro de Matemática Facultad de Ciencias Universidad de la República Introducción a la Topología Curso 2016 NOTAS 6: ESPACIOS MÉTRICOS II: COMPLETITUD 1 Continuidad uniforme Denición. Sean (M, d 1 ) y
Diseño de Base de Datos Relacional. Diseño de Base de Datos Relacional
 Diseño de Base de Datos Relacional Temas: - Pautas informales para diseño de esquemas - Dependencias Funcionales - Formas Normales - Algoritmos de diseño - Dependencias multivaluadas y cuarta forma normal
Diseño de Base de Datos Relacional Temas: - Pautas informales para diseño de esquemas - Dependencias Funcionales - Formas Normales - Algoritmos de diseño - Dependencias multivaluadas y cuarta forma normal
Diseño de Base de Datos Relacional
 Diseño de Base de Datos Relacional Temas: - Pautas informales para diseño de esquemas - Dependencias Funcionales - Formas Normales - Algoritmos de diseño - Dependencias multivaluadas y cuarta forma normal
Diseño de Base de Datos Relacional Temas: - Pautas informales para diseño de esquemas - Dependencias Funcionales - Formas Normales - Algoritmos de diseño - Dependencias multivaluadas y cuarta forma normal
Sea P el conjunto de todos los poliedros convexos del espacio, esto es P X / X es
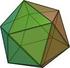 2. LA FUNCIÓN VOLUMEN Definición 9. Volumen de un poliedro convexo Sea P el conjunto de todos los poliedros convexos del espacio, esto es P X / X es un poliedro convexo, X E. Definimos una función que
2. LA FUNCIÓN VOLUMEN Definición 9. Volumen de un poliedro convexo Sea P el conjunto de todos los poliedros convexos del espacio, esto es P X / X es un poliedro convexo, X E. Definimos una función que
Tema 10: Teorema de Hahn-Banach. 14 y 17 de junio de 2010
 Tema 10: Teorema de Hahn-Banach 14 y 17 de junio de 2010 1 Versión anaĺıtica Enunciado del teorema Dual topológico Teoremas de extensión Duales de subespacios y cocientes Límites de Banach 2 Separación
Tema 10: Teorema de Hahn-Banach 14 y 17 de junio de 2010 1 Versión anaĺıtica Enunciado del teorema Dual topológico Teoremas de extensión Duales de subespacios y cocientes Límites de Banach 2 Separación
Las Gramáticas LL. Gramáticas con Parsing Eficiente. Universidad de Cantabria
 Las (k) Las Gramáticas con Parsing Eficiente Universidad de Cantabria Outline Las (k) 1 Las (k) 2 3 Las (k) Formalizalización del Concepto LL Definición Una gramática libre de contexto G = (V, Σ, Q 0,
Las (k) Las Gramáticas con Parsing Eficiente Universidad de Cantabria Outline Las (k) 1 Las (k) 2 3 Las (k) Formalizalización del Concepto LL Definición Una gramática libre de contexto G = (V, Σ, Q 0,
UNIVERSIDAD DE CONCEPCION FACULTAD DE CIENCIAS FISICAS Y MATEMATICAS DEPARTAMENTO DE INGENIERIA MATEMATICA
 AL GEBRA III UNIVERSIDAD DE CONCEPCION FACULTAD DE CIENCIAS FISICAS Y MATEMATICAS DEPARTAMENTO DE INGENIERIA MATEMATICA ALGEBRA III DEFINICION : Sea L : V V un operador lineal sobre el espacio vectorial
AL GEBRA III UNIVERSIDAD DE CONCEPCION FACULTAD DE CIENCIAS FISICAS Y MATEMATICAS DEPARTAMENTO DE INGENIERIA MATEMATICA ALGEBRA III DEFINICION : Sea L : V V un operador lineal sobre el espacio vectorial
Cambio de base. Objetivos. Estudiar la relación entre las coordenadas de un vector en dos bases.
 Cambio de base Objetivos Estudiar la relación entre las coordenadas de un vector en dos bases Requisitos Definición de una base, multiplicación de una matriz por un vector, delta de Kronecker Definición
Cambio de base Objetivos Estudiar la relación entre las coordenadas de un vector en dos bases Requisitos Definición de una base, multiplicación de una matriz por un vector, delta de Kronecker Definición
ax + by = 1 cx + dy = 0
 1.61. Considere el sistema ax + by = 1 cx + dy = 0 Muestre que si ad bc 0, el sistema tiene solución única x = d/(ad bc, y = c/(ad bc. Demostrar además que si ad bc = 0, c 0 o d 0, entonces el sistema
1.61. Considere el sistema ax + by = 1 cx + dy = 0 Muestre que si ad bc 0, el sistema tiene solución única x = d/(ad bc, y = c/(ad bc. Demostrar además que si ad bc = 0, c 0 o d 0, entonces el sistema
Ecuaciones Funcionales Involucrando Funciones Trigonométricas y Exponenciales
 Ecuaciones Funcionales Involucrando Funciones Trigonométricas y Exponenciales Alexandra K urepa Abstract Este artículo puede servir como una introducción al área de ecuaciones funcionales dando los ejemplos
Ecuaciones Funcionales Involucrando Funciones Trigonométricas y Exponenciales Alexandra K urepa Abstract Este artículo puede servir como una introducción al área de ecuaciones funcionales dando los ejemplos
Dependencias Funcionales. Bibliografía: Fundamentos de bases de datos Korth, Silberschatz
 Dependencias Funcionales Bibliografía: Fundamentos de bases de datos Korth, Silberschatz Conceptos básicos Las DF son un tipo particular de restricción. Permiten expresar hechos acerca de la realidad que
Dependencias Funcionales Bibliografía: Fundamentos de bases de datos Korth, Silberschatz Conceptos básicos Las DF son un tipo particular de restricción. Permiten expresar hechos acerca de la realidad que
1 NOCIONES BÁSICAS SOBRE CONJUNTOS. SÍMBOLOS.
 UNIDAD 1.- CONCEPTOS REQUERIDOS CONJUNTOS. AXIOMAS DE PERTENENCIA, PARALELISMO, ORDEN Y PARTICIÓN. 1 NOCIONES BÁSICAS SOBRE CONJUNTOS. SÍMBOLOS. 1.1 Determinaciones de un conjunto. Un conjunto queda determinado
UNIDAD 1.- CONCEPTOS REQUERIDOS CONJUNTOS. AXIOMAS DE PERTENENCIA, PARALELISMO, ORDEN Y PARTICIÓN. 1 NOCIONES BÁSICAS SOBRE CONJUNTOS. SÍMBOLOS. 1.1 Determinaciones de un conjunto. Un conjunto queda determinado
Dependencias funcionales
 CC42A/CC55A - BASES DE DATOS Profesor: Claudio Gutiérrez Auxiliar: Mauricio Monsalve Dependencias funcionales 1 El concepto de dependencia funcional 1.1 El concepto de dependencia funcional Hay veces en
CC42A/CC55A - BASES DE DATOS Profesor: Claudio Gutiérrez Auxiliar: Mauricio Monsalve Dependencias funcionales 1 El concepto de dependencia funcional 1.1 El concepto de dependencia funcional Hay veces en
11.1. Funciones uniformemente continuas
 Lección 11 Continuidad uniforme Completando el análisis de los principales teoremas que conocemos sobre continuidad de funciones reales de variable real, estudiamos ahora la versión general para espacios
Lección 11 Continuidad uniforme Completando el análisis de los principales teoremas que conocemos sobre continuidad de funciones reales de variable real, estudiamos ahora la versión general para espacios
Exámenes Selectivos para la Olimpiada Iberoamericana de Matemática
 Exámenes Selectivos para la Olimpiada Iberoamericana de Matemática Comisión de Olimpiadas de la Sociedad Matemática Peruana Edición: Jorge Tipe Versión: mayo 2016 Prólogo En la Olimpiada Iberoamericana
Exámenes Selectivos para la Olimpiada Iberoamericana de Matemática Comisión de Olimpiadas de la Sociedad Matemática Peruana Edición: Jorge Tipe Versión: mayo 2016 Prólogo En la Olimpiada Iberoamericana
Polinomios (II) Polinomios reales irreducibles. Pares de raíces conjugadas. Sesión teórica 4 (págs ) 27 de septiembre de 2010
 Polinomios (II) 1 Sesión teórica 4 (págs. 3-9) 7 de septiembre de 010 Pares de raíces conjugadas irreducibles Consideremos un polinomio f (x) =a0 + a1x + ax + + anx n R[x], es decir, con coeficientes reales
Polinomios (II) 1 Sesión teórica 4 (págs. 3-9) 7 de septiembre de 010 Pares de raíces conjugadas irreducibles Consideremos un polinomio f (x) =a0 + a1x + ax + + anx n R[x], es decir, con coeficientes reales
Algoritmos de Descomposición primaria
 Algoritmos de Descomposición primaria Santiago Laplagne Directora: Teresa Krick 10 de septiembre de 2004 1 Gracias! Voy a hacer como si fuera posible escribir todo el agradecimiento que siento hacia todos
Algoritmos de Descomposición primaria Santiago Laplagne Directora: Teresa Krick 10 de septiembre de 2004 1 Gracias! Voy a hacer como si fuera posible escribir todo el agradecimiento que siento hacia todos
V 2 : vectores libres en el plano
 V 2 : vectores libres en el plano Egor Maximenko ESFM del IPN 8 de agosto de 2009 Egor Maximenko (ESFM del IPN) V 2 : Vectores libres en el plano 8 de agosto de 2009 1 / 13 Contenido 1 Conjunto V 2 2 Operaciones
V 2 : vectores libres en el plano Egor Maximenko ESFM del IPN 8 de agosto de 2009 Egor Maximenko (ESFM del IPN) V 2 : Vectores libres en el plano 8 de agosto de 2009 1 / 13 Contenido 1 Conjunto V 2 2 Operaciones
Teorema de Lagrange. En esta sección demostramos algunos hechos básicos sobre grupos, que se pueden deducir de la definición
 Teorema de Lagrange Capítulo 3 3.1 Introducción En este capítulo estudiaremos uno de los teoremas más importantes de toda la teoría de grupos como lo es el Teorema de Lagrange. Daremos en primer lugar
Teorema de Lagrange Capítulo 3 3.1 Introducción En este capítulo estudiaremos uno de los teoremas más importantes de toda la teoría de grupos como lo es el Teorema de Lagrange. Daremos en primer lugar
Dilatación unitaria de semigrupos locales de contracciones con parámetro en los racionales diádicos. MSc. Angel Padilla. Cumaná, Marzo 2012
 Dilatación unitaria de semigrupos locales de contracciones con parámetro en los racionales diádicos Autor: MSc. Angel Padilla Cumaná, Marzo 2012 2 A continuación se fija algo de la notación que se utilizará
Dilatación unitaria de semigrupos locales de contracciones con parámetro en los racionales diádicos Autor: MSc. Angel Padilla Cumaná, Marzo 2012 2 A continuación se fija algo de la notación que se utilizará
Teoría de Galois de extensiones no normales
 Cuartas Jornadas de Teoría de Números Universidad Euskal Herriko del País Vasco Unibertsitatea 13 de julio de 2011 Teoría de Galois de extensiones no normales Teresa Crespo, Universitat de Barcelona Un
Cuartas Jornadas de Teoría de Números Universidad Euskal Herriko del País Vasco Unibertsitatea 13 de julio de 2011 Teoría de Galois de extensiones no normales Teresa Crespo, Universitat de Barcelona Un
TEMA Espacios métricos
 TEMA 55 Bolas abiertas y cerradas. Conjuntos abiertos y cerrados. Conjuntos compactos. Aplicaciones continuas de R n en R m. Propiedades de las aplicaciones continuas En la primera sección se introducen
TEMA 55 Bolas abiertas y cerradas. Conjuntos abiertos y cerrados. Conjuntos compactos. Aplicaciones continuas de R n en R m. Propiedades de las aplicaciones continuas En la primera sección se introducen
Tema 2: Determinantes
 Tema : Determinantes.- a) Encontrar los valores de λ para los que la matriz λ A = 0 λ λ 0 es invertible b) Para λ = hallar la inversa de A comprobar el resultado c) Resolver el sistema x 0 A = 0 z 0 para
Tema : Determinantes.- a) Encontrar los valores de λ para los que la matriz λ A = 0 λ λ 0 es invertible b) Para λ = hallar la inversa de A comprobar el resultado c) Resolver el sistema x 0 A = 0 z 0 para
Luego 72 = 2 3. Luego 48 = 2 3
 72 2 36 2 8 2 9 3 3 3 3 2 Luego 72 = 2 3 48 2 24 2 2 2 6 2 3 3 4 Luego 48 = 2 3 Así que el m.c.m. de 72 y 48 es 2 4 3 2 = 44. Como la rueda mayor tiene 72 dientes, para "recorrer" 44 dientes dee dar 44
72 2 36 2 8 2 9 3 3 3 3 2 Luego 72 = 2 3 48 2 24 2 2 2 6 2 3 3 4 Luego 48 = 2 3 Así que el m.c.m. de 72 y 48 es 2 4 3 2 = 44. Como la rueda mayor tiene 72 dientes, para "recorrer" 44 dientes dee dar 44
Grupos. Subgrupos. El Teorema de Lagrange. Grupo cociente. Teoremas de
 TEMA 8 Grupos. Subgrupos. El Teorema de Lagrange. Grupo cociente. Teoremas de Isomorfía En la primera sección introducimos los conceptos de grupo y subgrupo y, además de presentar varios ejemplos, prestamos
TEMA 8 Grupos. Subgrupos. El Teorema de Lagrange. Grupo cociente. Teoremas de Isomorfía En la primera sección introducimos los conceptos de grupo y subgrupo y, además de presentar varios ejemplos, prestamos
Reconocer y utilizar las propiedades sencillas de la topología métrica.
 3 Funciones continuas De entre todas las aplicaciones que pueden definirse entre dos espacios métrico, las aplicaciones continuas ocupan un papel preponderante. Su estudio es fundamental no sólo en topología,
3 Funciones continuas De entre todas las aplicaciones que pueden definirse entre dos espacios métrico, las aplicaciones continuas ocupan un papel preponderante. Su estudio es fundamental no sólo en topología,
CURVAS Y SUPERFICIES. RELACIÓN 2
 CURVAS Y SUPERFICIES. RELACIÓN 2 SUPERFICIES EN EL ESPACIO Curso 2015-16 1. Demostrar que las siguientes cuádricas reales son superficies. Obtener una parametrización de cada una de ellas. En cada caso,
CURVAS Y SUPERFICIES. RELACIÓN 2 SUPERFICIES EN EL ESPACIO Curso 2015-16 1. Demostrar que las siguientes cuádricas reales son superficies. Obtener una parametrización de cada una de ellas. En cada caso,
Sistemas Lineales y Matrices
 Profesores Hernán Giraldo y Omar Saldarriaga Instituto de Matemáticas Facultad de Ciencias Exactas y Naturales Universidad de Antioquia Ejemplo Solución de sistemas de ecuaciones lineales, usaremos este
Profesores Hernán Giraldo y Omar Saldarriaga Instituto de Matemáticas Facultad de Ciencias Exactas y Naturales Universidad de Antioquia Ejemplo Solución de sistemas de ecuaciones lineales, usaremos este
Los isomorfismos básicos de la teoría de cuerpos algebraicos.
 4. AUTOMORFISMOS DE CUERPOS. En este tema probaremos que dos elementos α y β, conjugados sobre un cuerpo F, determinan un isomorfismo entre los cuerpos F (α) y F (β). También cierto recíproco será válido.
4. AUTOMORFISMOS DE CUERPOS. En este tema probaremos que dos elementos α y β, conjugados sobre un cuerpo F, determinan un isomorfismo entre los cuerpos F (α) y F (β). También cierto recíproco será válido.
DISEÑO FACTORIAL MODELO JERÁRQUICO (0 ANIDADO)
 DISEÑO FACTORIAL Niveles de B Niveles de A 1 2 3 4 5 1 y 11 y 12 y 13 y 14 y 15 2 y 21 y 22 y 23 y y 3 y 31 y 32 y 33 y 34 y 35 4 y 41 y 42 y 43 y 44 y 45 Todos los niveles de cada factor están combinados
DISEÑO FACTORIAL Niveles de B Niveles de A 1 2 3 4 5 1 y 11 y 12 y 13 y 14 y 15 2 y 21 y 22 y 23 y y 3 y 31 y 32 y 33 y 34 y 35 4 y 41 y 42 y 43 y 44 y 45 Todos los niveles de cada factor están combinados
