NÚMEROS ENTEROS GBG 1
|
|
|
- Alfonso Santos Montes
- hace 8 años
- Vistas:
Transcripción
1 NÚMEROS ENTEROS Existen distintas situaciones en las que necesitamos otros números distintos a los números naturales y nos vemos obligados a realizar una ampliación de estos, considerando los números naturales distintos del cero como números positivos y añadiéndole los correspondientes números negativos. En un edificio usamos el número cero para indicar la planta baja y los números 1, 2, 3, para indicar las sucesivas plantas: primera, segunda, tercera, Todos ellos son números naturales. Para representar las plantas sótano necesitamos otros números, para ello consideramos los números naturales 1, 2, 3, como números positivos, es decir, +1, +2, +3, y para las plantas sótano usaremos números negativos: 1, 2, 3, para las distintas plantas sótano. Una situación análoga nos la encontramos al medir la temperatura. Habitualmente usamos la escala centígrada o escala celsius. En esta escala la temperatura de 0ºC la tenemos asignada al punto de congelación del agua y la de 100ºC a su punto de ebullición. Para las temperaturas inferiores al punto de congelación del agua usamos números negativos hablando por ejemplo de 4ºC. Anders Celsius ( ) fue un físico y astrónomo sueco, sus investigaciones en el campo de la astronomía fueron relevantes, sin embargo, es más conocido por ser el creador de la escala Celsius. En el año 1742 inventó un termómetro de mercurio que calibró empleando la escala celsius (llamada centígrada hasta 1948), establecida por él. El punto correspondiente a la temperatura 0 C coincidía con el punto de ebullición del agua, mientras que la temperatura de 100 ºC equivalía a la de congelación del agua al nivel del mar. La escala indicaba, por lo tanto, temperaturas positivas cuando descendían las temperaturas; este sentido se cambió después. Ese mismo año presentó ante la Academia de ciencias sueca su memoria sobre los puntos fijos de la escala termométrica, que contribuyó decisivamente a la aceptación del termómetro centígrado. En las cuentas corrientes se utilizan los números negativos llamados también números rojos para cuando el saldo de la cuenta es deudor. Si tenemos dinero en la cuenta, decimos que tenemos saldo positivo y estará representado por un número positivo (azul), pero si el banco ha tenido que abonar recibos por un importe superior a nuestro saldo, quedaremos con un saldo negativo (rojo) o deudor. GBG 1
2 El conjunto de los números naturales es = { 0,1, 2, 3,...} Desde un punto de vista aritmético, en la resta de números naturales teníamos la restricción de que el minuendo tenía que ser mayor o igual que el sustraendo. Minuendo Sustraendo = Diferencia Minuendo Sustraendo Así, en los números naturales podíamos restar 7 5, pero no 5 7. El resultado de 7 5 es un número natural, el 2, pero para 5 7 necesitamos otro tipo de números, los números enteros negativos. Diremos que el resultado de 5 7 es el número entero negativo = 2 y 5 7 = 2 A los números naturales distintos de cero vamos a considerarlos como números positivos y ampliamos el conjunto de los números naturales con los correspondientes números negativos, constituyendo juntos el conjunto de números enteros. El conjunto de los números naturales se representa por y el de los enteros por. 1. SI EL MINUENDO ES MAYOR QUE EL SUSTRAENDO NOS DARÁ UN NÚMERO POSITIVO = 3 2. SI EL MINUENDO ES MENOR QUE EL SUSTRAENDO NOS DARÁ UN NÚMERO NEGATIVO = 7 Se trata de hacer la diferencia en orden contrario al dado y ponerle signo menos: 12 5 = 7 y 5 12 = 7 Observa: 7 5= 2 y 5 7= 2 9 4= 5 y 4 9= 5 o bien: 5+ 7= 2 y 7+ 5= = 5 y 9+ 4= 5 GBG 2
3 El conjunto de los números enteros ENTEROS Enteros positivos Cero Enteros negativos NATURALES El conjunto de los números enteros es = {... 3, 2, 1,0, + 1, + 2, } El conjunto de los números enteros está formado por: Enteros positivos + = { + 1, + 2, } Cero 0 =... 3, 2, 1 Enteros negativos { } Teniendo que { 0} = + Los números enteros positivos los escribimos, habitualmente, prescindiendo del signo + que les precede, coincidiendo así su escritura con la de los números naturales. Por ejemplo, + 5= 5. Podemos escribir: = {... 3, 2, 1, 0, 1, 2, 3...} GBG 3
4 Ejemplos 1) Tengo cinco euros: 5. Debo cuatro euros: 4. 2) El récord de inmersión con botellas, pero sin asistencia exterior, está en 332 m de profundidad: 332 m. El viernes 24 de octubre de 2014 Eustace saltó desde un globo a metros de altura: m. Representación de los números enteros Los números enteros los representamos en una recta tomando un punto para el origen de la escala, el cero, y un segmento unidad. Los números positivos los representamos a la derecha del cero y los negativos a su izquierda. GBG 4
5 Opuesto de un número entero El opuesto de un número entero es el número que se obtiene al cambiarle el signo a dicho número. Op( a) = a Observa que Op( 3) = 3 ( ) Op 7 = 7 Valor absoluto de un número entero El valor absoluto de un número entero es el mismo número entero si este es positivo o cero y será su opuesto si el número es negativo El valor absoluto de un número entero siempre es positivo o cero. Nunca es negativo Ejemplos Si a es positivo, a = a Si a es cero, 0 = 0 Si a es negativo, a = a 4 = 4 0 = 0 6 = 6 El valor absoluto de un número entero es la distancia que hay de ese número a cero. Un número entero y su opuesto están a la misma distancia de cero y, por lo tanto, tienen el mismo valor absoluto. 3 = 3 y 3 = 3 GBG 5
6 Relación de orden en los números enteros Un número entero es menor que otro si está situado a la izquierda de este último en la recta numérica. Un número entero negativo es menor que cualquier número entero positivo. 5< 3 Cualquier número negativo es menor que cero. 4< 0 El cero es menor que cualquier número positivo. 0< 7 De dos números positivos es menor el que tiene menor valor absoluto. 6< 9 De dos números negativos es menor el que tiene mayor valor absoluto. 7< 2 GBG 6
7 OPERACIONES CON NÚMEROS ENTEROS Suma de números enteros Para sumar dos números enteros vamos a distinguir dos casos: Si los dos números tienen el mismo signo, se suman los valores absolutos de ambos números y se pone el signo común. Ejemplos ( + 4) + ( + 7) =+ 11 ( 9) + ( 6) = 15 Si tengo 4 y me dan 7, tengo 11. Si debo 9 a un amigo de ayer y de hoy le debo 6, entonces le debo 15. Si los dos números tienen distinto signo, se restan sus valores absolutos y se pone el signo del que tenga mayor valor absoluto (mayor peso). Ejemplos ( + 4) + ( 9) = 5 ( 7) + ( + 11) =+ 4 Si tengo 4 y debo 9, entonces debo 5. Si debo 7 y tengo 11, entonces, pagando la deuda, tendré 4. También podemos realizar las sumas de números enteros suprimiendo previamente los paréntesis teniendo en cuenta: Si el paréntesis va precedido del signo + se deja el signo del interior del paréntesis. + ( + a) =+ a y ( a) + = a Si el paréntesis va precedido del signo se cambia el signo del interior del paréntesis. Así, los ejemplos anteriores los haríamos de la siguiente forma: ( + 4) + ( + 7) = = 11 ( 9) + ( 6) = 9 6 = 15 + ( a) = a y ( a) =+ a ( + 4) + ( 9) =4 9= 5 ( 7) + ( + 11) = = 4 GBG 7
8 Resta de números enteros Para restar dos números enteros se le suma al minuendo el opuesto del sustraendo. Ejemplos ( + 2) ( 4) = ( + 2) + ( + 4) =+ 6 ( 2) ( 5) = ( 2) + ( + 5) =+ 3 ( 9) ( 4) = ( 9) + ( + 4) = 5 ( 3) ( 3) = ( 3) + ( + 3) = 0 ( 3) ( + 3) = ( 3) + ( 3) = 6 Ejemplos ( + 7) ( + 5) = ( + 7) + ( 5) =+ 2 ( + 4) ( + 7) = ( + 4) + ( 7) = 3 ( 2) ( + 6) = ( 2) + ( 6) = 8 ( + 3) ( + 3) = ( + 3) + ( 3) = 0 ( + 3) ( 3) = ( + 3) + ( + 3) =+ 6 También podemos realizar las restas de números enteros suprimiendo previamente los paréntesis: Si el paréntesis va precedido del signo + se mantiene el signo del número que haya dentro. + ( + a) =+ a y ( a) + = a Si el paréntesis va precedido del signo se cambia el signo del número que haya dentro. + ( a) = a y ( a) =+ a ( + 2) ( 4) = 2+ 4= 6 ( 2) ( 5) = 2+ 5= 3 ( 9) ( 4) = 9+ 4= 5 ( 3) ( 3) = 3+ 3= 0 ( 3) ( + 3) = 3 3= 6 ( + 7) ( + 5) = 7 5= 2 ( + 4) ( + 7) = 4 7= 3 ( 2) ( + 6) = 2 6= 8 ( + 3) ( + 3) = 3 3= 0 ( + 3) ( 3) = 3+ 3= 6 GBG 8
9 SUMAS Y RESTAS DE MÁS DE DOS NÚMEROS ENTEROS Para sumar y restar más de dos números enteros podemos proceder de dos formas diferentes: Ejemplo Método 1 Sumando y restando los números de izquierda a derecha sucesivamente = 4 Mentalmente vamos realizando las operaciones de izquierda a derecha: = = = = = 4 Método 2 Sumando en primer lugar todos los positivos, a continuación todos los negativos, y realizando, finalmente, la resta resultante = =23 27= 4 Ejercicio1 Efectúa las siguientes operaciones de izquierda a derecha: a) b) c) Ejercicio2 Efectúa las siguientes operaciones agrupando previamente los números de igual signo: a) b) c) GBG 9
10 Ejemplo ( 9) + ( + 5) ( 4) + ( 17) + ( 9) ( + 11) Primero quitamos los paréntesis y a continuación vamos sumando y restando de izquierda a derecha o agrupando positivos y negativos previamente = = 29 ( ) ( ) ( ) ( ) ( ) ( ) Ejercicio 3 a) ( 5) + ( 8) ( 3) + ( + 9) ( + 11) ( 7) b) ( 3) + ( + 14) ( 12) + ( 9) + ( 5) ( + 8) c) ( + 11) ( 3) + ( 1) ( 15) + ( + 12) ( + 4) d) ( + 7) ( + 6) ( 18) + ( 11) + ( + 9) ( 5) Ejemplo ( ) ( ) Método 1 Calculando en primer lugar el valor de las operaciones de los paréntesis: Realizamos las operaciones de los paréntesis, quitamos los paréntesis y calculamos de izquierda a derecha: = = = 7 ( ) ( ) ( ) ( ) Método 2 Quitando en primer lugar los paréntesis y operando de izquierda a derecha: = = 7 ( ) ( ) GBG 10
11 Ejercicio 4 Realiza las siguientes operaciones calculando en primer lugar el valor de las operaciones de los paréntesis: a) 14 + ( ) ( 11 18) b) ( 9 6 8) ( 13+ 4) + ( 19+ 3) c) ( ) ( ) ( 6 7) d) ( 7 13) + ( 9 17) ( 19 12) e) ( ) + 5 ( ) Ejercicio 5 Realiza las siguientes operaciones suprimiendo en primer lugar los paréntesis: a) ( 14 26) + ( 19 8) ( 9 14) b) ( ) 2 ( ) c) 3 + ( 1 8 5) ( 12 17) d) ( ) ( ) ( 9 7) e) ( ) ( ) + ( 9 + 6) GBG 11
12 EJERCICIOS 1. Efectúa: 1) ) 5 7 5) 7 3 7) 1 1 9) ) ) 9 6 4) ) ) ) ) Calcula: 1) ) ) ) ) ) ) ) ) ) ) ) ) ) ) Realiza eliminando previamente los paréntesis: 2 4 1) ( + 4) + ( + 3) 7) ( ) + ( + ) 13) ( 9) + ( 7) 19) ( + 28) + ( 23) 25) ( 15) + ( + 5) 2) ( + 9) + ( 7) 8) ( + 6) + ( 6) 14) ( 4) ) ( 6) + ( 8) 26) ( 7) + ( + 18) 3) ( 8) + ( + 6) 9) 0+ ( + 1) 15) ( + 8) + ( + 9) 21) ( 17) + ( + 9) 27) ( 14) + ( 21) 4) ( + 4) + ( 9) 10) ( + 1) + ( 5) 16) ( 15) + ( + 11) 22) ( 16) + ( 12) 28) ( + 16) + ( 17) 5) ( + 9) + ( 13) 11) ( + 3) + ( + 6) 17) ( 10) + ( 4) 23) ( + 3) + ( 11) 29) ( 13) + ( + 3) 6) ( 3) + ( 5) 12) ( + 2) + ( 9) 18) ( 15) + ( + 17) 24) 0 + ( 15) 30) ( + 13) + ( 3) 4. Realiza las siguientes restas eliminando previamente el paréntesis: ) ( + 8) ( + 5) 4) ( + ) ( + ) 7) ( ) ( ) 10) ( 4) ( + 4) 13) ( 9) ( 7) 2) ( + 3) ( + 9) 5) ( + 5) ( 3) 8) ( 2) ( 9) 11) 0 ( + 3) 14) ( + 7) ( 3) 3) ( + 6) ( + 2) 6) ( 9) ( + 7) 9) ( 3) ( + 11) 12) ( 8) ( + 7) 15) ( 8) ( 8) GBG 12
13 5. Calcula: 1) ( + 4) + ( + 9) + ( + 3) 4) ( + 3) + ( 11) + ( + 2) 7) ( 2) + ( 4) + ( + 6) 2) ( 6) + ( 3) + ( 8) 5) ( + 4) + ( 7) + ( 2) 8) ( 14) + ( + 8) + ( 11) 3) ( + 11) + ( 15) + ( + 6) 6) ( 6) + ( + 3) + ( + 7) 9) ( + 23) + ( 14) + ( + 6) 6. Realiza las siguientes operaciones: 1) ( + 4) ( + 3) ( 5) 6) ( + 4) ( 10) ( + 7) + ( 13) 11) ( 7) + ( 5) ( 12) + ( + 19) ( + 8) 2) ( + 7) ( + 8) + ( 14) 7) ( 3) ( + 5) + ( 16) ( + 5) 12) ( 11) ( 3) ( + 15) + ( 16) ( + 7) 3) ( 6) + ( + 4) ( 5) 8) ( 15) ( + 6) + ( + 4) + ( 2) 13) ( + 4) ( 19) + ( + 1) ( + 2) ( 6) 4) ( + 2) ( 4) ( 6) 9) ( + 7) ( 12) + ( + 1) ( + 9) 14) ( 15) + ( + 8) ( 6) + ( 17) ( + 3) 5) ( 7) ( + 3) ( + 8) 10) ( + 2) + ( 8) ( + 3) + ( 2) 15) ( + 14) ( + 21) ( + 5) + ( 4) ( 1) GBG 13
Por ejemplo, la necesidad de representar el dinero adeudado, temperatura bajo cero, profundidades con respecto al nivel del mar, etc.
 NÚMEROS ENTEROS 1. LOS NÚMEROS ENTEROS. Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el sustraendo, pero en la vida nos encontramos con operaciones de este
NÚMEROS ENTEROS 1. LOS NÚMEROS ENTEROS. Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el sustraendo, pero en la vida nos encontramos con operaciones de este
GAIA.- Números Enteros
 GAIA.- Números Enteros 1.- EL CONJUNTO DE LOS NÚMEROS ENTEROS.- El conjunto de los números enteros está formado por todos los números naturales (N) precedidos del signo más (+), los números naturales precedidos
GAIA.- Números Enteros 1.- EL CONJUNTO DE LOS NÚMEROS ENTEROS.- El conjunto de los números enteros está formado por todos los números naturales (N) precedidos del signo más (+), los números naturales precedidos
Los números enteros. Dado que los enteros contienen los enteros positivos, se considera a los números naturales son un subconjunto de los enteros.
 Los números enteros Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el que el sustraendo, pero en la vida nos encontramos con operaciones de este tipo donde
Los números enteros Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el que el sustraendo, pero en la vida nos encontramos con operaciones de este tipo donde
Apuntes de matemáticas 2º ESO Curso
 Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el que el sustraendo, pero en la vida nos encontramos con operaciones de este tipo donde a un número menor
Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el que el sustraendo, pero en la vida nos encontramos con operaciones de este tipo donde a un número menor
UNIDAD 7. LOS NÚMEROS ENTEROS
 UNIDAD 7. LOS NÚMEROS ENTEROS 1. LOS NÚMEROS ENTEROS 2. REPRESENTACIÓN Y ORDENACIÓN DE NÚMEROS ENTEROS 3. OPERACIONES CON NÚMEROS ENTEROS 1. LOS NÚMEROS ENTEROS En la vida se nos presentan muchas veces
UNIDAD 7. LOS NÚMEROS ENTEROS 1. LOS NÚMEROS ENTEROS 2. REPRESENTACIÓN Y ORDENACIÓN DE NÚMEROS ENTEROS 3. OPERACIONES CON NÚMEROS ENTEROS 1. LOS NÚMEROS ENTEROS En la vida se nos presentan muchas veces
NUMEROS ENTEROS ( Z)
 NUMEROS ENTEROS ( Z) En N la resta sólo está definida si el minuendo es mayor o igual al sustraendo. Para que dicha operación no sea tan restringida se creó el conjunto de enteros negativos ( notado por
NUMEROS ENTEROS ( Z) En N la resta sólo está definida si el minuendo es mayor o igual al sustraendo. Para que dicha operación no sea tan restringida se creó el conjunto de enteros negativos ( notado por
MATEMÁTICAS 1º DE ESO
 MATEMÁTICAS 1º DE ESO LOMCE TEMA III : LOS NÚMEROS ENTEROS Los números negativos. Su necesidad. El conjunto de los números enteros. Valor absoluto de un número entero. Opuesto de un número entero. Suma
MATEMÁTICAS 1º DE ESO LOMCE TEMA III : LOS NÚMEROS ENTEROS Los números negativos. Su necesidad. El conjunto de los números enteros. Valor absoluto de un número entero. Opuesto de un número entero. Suma
Opuesto de un número +3 + (-3) = (+5) = 0. N = 0,1, 2,3,4, Conjunto de los números naturales
 Números enteros Opuesto de un número Los números enteros son una extensión de los números naturales, de tal forma, que los números enteros tienen signo positivo (+) ó negativo (-). Los números positivos
Números enteros Opuesto de un número Los números enteros son una extensión de los números naturales, de tal forma, que los números enteros tienen signo positivo (+) ó negativo (-). Los números positivos
LibrosMareaVerde.tk Ilustraciones: Banco de Imágenes de INTEF
 30 CAPÍTULO 4: NÚMEROS ENTEROS 1. NÚMEROS ENTEROS 1.1. Números positivos, negativos y cero Existen ocasiones de la vida cotidiana en que es preciso usar números distintos de los naturales, números positivos
30 CAPÍTULO 4: NÚMEROS ENTEROS 1. NÚMEROS ENTEROS 1.1. Números positivos, negativos y cero Existen ocasiones de la vida cotidiana en que es preciso usar números distintos de los naturales, números positivos
1.-NÚMEROS ENTEROS POSITIVOS Y NEGATIVOS. EL CONJUNTO Z
 LECCIÓN 6: NÚMEROS ENTEROS 1.-NÚMEROS ENTEROS POSITIVOS Y NEGATIVOS. EL CONJUNTO Z 1.1.- EL CONJUNTO Z El conjunto de los números enteros se identifica con la letra Z, y está formado por - Los números
LECCIÓN 6: NÚMEROS ENTEROS 1.-NÚMEROS ENTEROS POSITIVOS Y NEGATIVOS. EL CONJUNTO Z 1.1.- EL CONJUNTO Z El conjunto de los números enteros se identifica con la letra Z, y está formado por - Los números
LOS NÚMEROS ENTEROS NÚMEROS POSITIVOS Y NÚMEROS NEGATIVOS
 LOS NÚMEROS ENTEROS NÚMEROS POSITIVOS Y NÚMEROS NEGATIVOS Para indicar las temperaturas por encima de cero ponemos delante del número el signo más y a las que son por debajo de cero, el signo menos. Para
LOS NÚMEROS ENTEROS NÚMEROS POSITIVOS Y NÚMEROS NEGATIVOS Para indicar las temperaturas por encima de cero ponemos delante del número el signo más y a las que son por debajo de cero, el signo menos. Para
MATEMÁTICAS I CICLO COMÚN UNIDAD DIDÁCTICA #6
 UNIDAD DIDÁCTICA #6 INDICE PÁGINA Ampliación del conjunto de los números naturales ------------------------------------------------------2 Uso de los números enteros y su representación en la recta numérica
UNIDAD DIDÁCTICA #6 INDICE PÁGINA Ampliación del conjunto de los números naturales ------------------------------------------------------2 Uso de los números enteros y su representación en la recta numérica
TEMA 2: NÚMEROS ENTEROS
 TEMA : NÚMEROS ENTEROS 1. NÚMEROS ENTEROS Los números naturales se utilizan para expresar matemáticamente multitud de situaciones cotidianas. Sin embargo, a veces no sirven para cuantificar las situaciones
TEMA : NÚMEROS ENTEROS 1. NÚMEROS ENTEROS Los números naturales se utilizan para expresar matemáticamente multitud de situaciones cotidianas. Sin embargo, a veces no sirven para cuantificar las situaciones
LIMPIEZA Y ORGANIZACIÓN
 SATISFACTORIO ACEPTABLE MEJORABLE Cuaderno: LIMPIEZA Y ORGANIZACIÓN Realización de TAREAS TEMA 4 NÚMEROS ENTEROS ALUMNO/A: Nº Ejercicios TEMA 4 NÚMEROS ENTEROS (1º ESO) Página 1 N Ú M E R O S P O S I T
SATISFACTORIO ACEPTABLE MEJORABLE Cuaderno: LIMPIEZA Y ORGANIZACIÓN Realización de TAREAS TEMA 4 NÚMEROS ENTEROS ALUMNO/A: Nº Ejercicios TEMA 4 NÚMEROS ENTEROS (1º ESO) Página 1 N Ú M E R O S P O S I T
El conjunto de números enteros está formado por los números naturales, sus opuestos (negativos) y el cero.
 1 1. NÚMEROS ENTEROS El conjunto de números enteros está formado por los números naturales, sus opuestos (negativos) y el cero. La necesidad de representar el dinero adeudado, la temperatura bajo cero,
1 1. NÚMEROS ENTEROS El conjunto de números enteros está formado por los números naturales, sus opuestos (negativos) y el cero. La necesidad de representar el dinero adeudado, la temperatura bajo cero,
Suma de números enteros
 NÚMEROS ENTEROS. RESUMEN Los números enteros son del tipo: = {... 5, 4, 3, 2, 1, 0, 1, 2, 3, 4, 5...} Es decir, los naturales, sus opuestos (negativos) y el cero. Valor absoluto El valor absoluto de un
NÚMEROS ENTEROS. RESUMEN Los números enteros son del tipo: = {... 5, 4, 3, 2, 1, 0, 1, 2, 3, 4, 5...} Es decir, los naturales, sus opuestos (negativos) y el cero. Valor absoluto El valor absoluto de un
TEMA 1. Los números enteros. Matemáticas
 1 Introducción En esta unidad veremos propiedades de los números enteros, como se opera con ellos (con y sin calculadora), los números primos, máximo común divisor y mínimo común múltiplo y por últimos
1 Introducción En esta unidad veremos propiedades de los números enteros, como se opera con ellos (con y sin calculadora), los números primos, máximo común divisor y mínimo común múltiplo y por últimos
Fíjate en algo muy importante: los números enteros tienen signo. Puede ser positivo o negativo. El único número que no tiene signo es el 0.
 4. NÚMEROS ENTEROS En Jujulandia están en invierno. Está previsto la entrada de un frente de aire frío que va a bajar las temperaturas una media de 10º C. Hoy, la temperatura máxima ha sido de 6º C. Qué
4. NÚMEROS ENTEROS En Jujulandia están en invierno. Está previsto la entrada de un frente de aire frío que va a bajar las temperaturas una media de 10º C. Hoy, la temperatura máxima ha sido de 6º C. Qué
Guía 1: Operaciones numéricas en los Números enteros (Z)
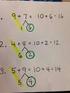 Guía 1: Operaciones numéricas en los Números enteros (Z) NÚMEROS ENTEROS (Z): Existen números con signo, que son los números enteros (Z+ son los positivos y Z- son los negativos). Según se sabe, nos los
Guía 1: Operaciones numéricas en los Números enteros (Z) NÚMEROS ENTEROS (Z): Existen números con signo, que son los números enteros (Z+ son los positivos y Z- son los negativos). Según se sabe, nos los
Suma de números enteros
 NÚMEROS ENTEROS. RESUMEN Los números enteros son del tipo: = {... 5, 4, 3, 2, 1, 0, 1, 2, 3, 4, 5...} Es decir, los naturales, sus opuestos (negativos) y el cero. Valor absoluto El valor absoluto de un
NÚMEROS ENTEROS. RESUMEN Los números enteros son del tipo: = {... 5, 4, 3, 2, 1, 0, 1, 2, 3, 4, 5...} Es decir, los naturales, sus opuestos (negativos) y el cero. Valor absoluto El valor absoluto de un
Semana 1: Números Reales y sus Operaciones
 Semana 1: Números Reales y sus Operaciones Taller de Preparación para Prueba PLANEA Ing. Jonathan Quiroga Tinoco Conalep Tehuacán P.T.B. en ADMO, SOMA y EMEC UNIDAD 04 Los números enteros y sus operaciones
Semana 1: Números Reales y sus Operaciones Taller de Preparación para Prueba PLANEA Ing. Jonathan Quiroga Tinoco Conalep Tehuacán P.T.B. en ADMO, SOMA y EMEC UNIDAD 04 Los números enteros y sus operaciones
CAPÍTULO 4: NÚMEROS ENTEROS. TEORÍA. Matemáticas 1º y 2º de ESO
 24 CAPÍTULO 4: NÚMEROS ENTEROS.. Matemáticas 1º y 2º de ESO 1. NÚMEROS ENTEROS 1.1. Números positivos, negativos y cero Existen ocasiones de la vida cotidiana en que es preciso usar números distintos de
24 CAPÍTULO 4: NÚMEROS ENTEROS.. Matemáticas 1º y 2º de ESO 1. NÚMEROS ENTEROS 1.1. Números positivos, negativos y cero Existen ocasiones de la vida cotidiana en que es preciso usar números distintos de
Divisibilidad I. Nombre Curso Fecha
 Matemáticas 2.º ESO Unidad 1 Ficha 1 Divisibilidad I Un número b es divisor de otro número a si al dividir a entre b la división es exacta. Se dice también que a es múltiplo de b. 1. Completa con la palabra
Matemáticas 2.º ESO Unidad 1 Ficha 1 Divisibilidad I Un número b es divisor de otro número a si al dividir a entre b la división es exacta. Se dice también que a es múltiplo de b. 1. Completa con la palabra
Unidad didáctica 1. Operaciones básicas con números enteros
 Unidad didáctica 1 Operaciones básicas con números enteros 1.- Representación y ordenación de números enteros Para representar números enteros en una recta hay que seguir estos pasos: a) Se dibuja una
Unidad didáctica 1 Operaciones básicas con números enteros 1.- Representación y ordenación de números enteros Para representar números enteros en una recta hay que seguir estos pasos: a) Se dibuja una
TEMA 10. EL CONJUNTO DE LOS NÚMEROS ENTEROS
 TEMA 10. EL CONJUNTO DE LOS NÚMEROS ENTEROS 1. LOS NÚMEROS ENTEROS Hasta ahora sólo has conocido el conjunto de los números naturales (N), que está formado por todos los números positivos desde el cero
TEMA 10. EL CONJUNTO DE LOS NÚMEROS ENTEROS 1. LOS NÚMEROS ENTEROS Hasta ahora sólo has conocido el conjunto de los números naturales (N), que está formado por todos los números positivos desde el cero
ESCUELA PREPARATORIA OFICIAL NO.16 MATERÍA: PENSAMIENTO NUMÉRICO Y ALGEBRAICO I
 ARITMÉTICA 1. Números naturales 2. Divisibilidad 3. Números enteros 4. Números decimales 5. Fracciones y números racionales 6. Proporcionalidad 7. Sistema métrico decimal 8. Sistema sexagesimal 9. Números
ARITMÉTICA 1. Números naturales 2. Divisibilidad 3. Números enteros 4. Números decimales 5. Fracciones y números racionales 6. Proporcionalidad 7. Sistema métrico decimal 8. Sistema sexagesimal 9. Números
Bloque 1. Aritmética y Álgebra
 Bloque 1. Aritmética y Álgebra 2. Los números enteros 1. Los números enteros Es el conjunto de los números negativos, el cero y los positivos, y se representan como: Z...,-5,-4,-3,-2,-1,0, 1, 2, 3, 4,
Bloque 1. Aritmética y Álgebra 2. Los números enteros 1. Los números enteros Es el conjunto de los números negativos, el cero y los positivos, y se representan como: Z...,-5,-4,-3,-2,-1,0, 1, 2, 3, 4,
Números Enteros. 1º de ESO 1º ESO CAPÍTULO 4: NÚMEROS ENTEROS
 65 1º ESO CAPÍTULO 4: NÚMEROS ENTEROS Autora: Ana Lorente Revisora: Adela Salvador Ilustraciones: Banco de imágenes del INTEF 66 Índice 1. NÚMEROS ENTEROS 1.1. NÚMEROS POSITIVOS, NEGATIVOS Y CERO 1.2.
65 1º ESO CAPÍTULO 4: NÚMEROS ENTEROS Autora: Ana Lorente Revisora: Adela Salvador Ilustraciones: Banco de imágenes del INTEF 66 Índice 1. NÚMEROS ENTEROS 1.1. NÚMEROS POSITIVOS, NEGATIVOS Y CERO 1.2.
Vamos a repasar cómo se hacen las operaciones básicas con los distintos números que seguro has estudiado en secundaria:
 TEMA 0: REPASO DE NÚMEROS. Vamos a repasar cómo se hacen las operaciones básicas con los distintos números que seguro has estudiado en secundaria: Suma de números enteros 1. Si los sumandos son del mismo
TEMA 0: REPASO DE NÚMEROS. Vamos a repasar cómo se hacen las operaciones básicas con los distintos números que seguro has estudiado en secundaria: Suma de números enteros 1. Si los sumandos son del mismo
TEMA 1: NÚMEROS ENTEROS
 Números enteros 1 OBJETIVO 1: Significado de los números enteros TEMA 1: NÚMEROS ENTEROS 1. Expresa las siguientes situaciones con números enteros a) El año 2500 a.c... b) Pasear por la orilla del mar...
Números enteros 1 OBJETIVO 1: Significado de los números enteros TEMA 1: NÚMEROS ENTEROS 1. Expresa las siguientes situaciones con números enteros a) El año 2500 a.c... b) Pasear por la orilla del mar...
Tema 1: NUMEROS ENTEROS
 COLEGIO EL LIMONAR. MÁLAGA DEPARTAMENTO DE MÁTEMÁTICAS RELACIONES DE EJERCICIOS 1º ESO. NÚMEROS ENTEROS Tema 1: NUMEROS ENTEROS Los números enteros (representados por la letra Z), son un conjunto de número
COLEGIO EL LIMONAR. MÁLAGA DEPARTAMENTO DE MÁTEMÁTICAS RELACIONES DE EJERCICIOS 1º ESO. NÚMEROS ENTEROS Tema 1: NUMEROS ENTEROS Los números enteros (representados por la letra Z), son un conjunto de número
Lección 8: Suma y resta de en teros
 LECCIÓN 8 bajo el nivel del mar, y el buzo B baja a 81 metros bajo el nivel del mar. Cuál de los dos está más cerca de la superficie? d) El saldo de la empresa Caluro, S.A. es de $12 807 en números rojos,
LECCIÓN 8 bajo el nivel del mar, y el buzo B baja a 81 metros bajo el nivel del mar. Cuál de los dos está más cerca de la superficie? d) El saldo de la empresa Caluro, S.A. es de $12 807 en números rojos,
Lección 7: Números enteros y orden
 El Sr. Martínez va a enmarcar con canaleta de bronce un espejo cuadrado que tiene de área 1369 cm 2. De qué largo es cada orilla del espejo? LECCIÓN 7 Lección 7: Números enteros y orden Recordemos un ejemplo
El Sr. Martínez va a enmarcar con canaleta de bronce un espejo cuadrado que tiene de área 1369 cm 2. De qué largo es cada orilla del espejo? LECCIÓN 7 Lección 7: Números enteros y orden Recordemos un ejemplo
Teoría (resumen) Por ejemplo, los múltiplos de 3 son: 3, 6, 9, 12, 15, 18, ; los múltiplos de 2 son: 2, 4, 6, 8, 10, 12, ; o sea los números pares.
 1.- Divisibilidad Teoría (resumen) Múltiplos de un número. Son aquellos que se obtienen al multiplicar dicho número por los números naturales 1, 2, 3,. Por ejemplo, los múltiplos de 3 son: 3, 6, 9, 12,
1.- Divisibilidad Teoría (resumen) Múltiplos de un número. Son aquellos que se obtienen al multiplicar dicho número por los números naturales 1, 2, 3,. Por ejemplo, los múltiplos de 3 son: 3, 6, 9, 12,
NÚMEROS ENTEROS. Números naturales: sirven para contar, ordenar y comunicar información.
 NÚMEROS ENTEROS 15 Números naturales: sirven para contar, ordenar y comunicar información. representa al conjunto de todos los número naturales. = {0, 1, 2, 3, 4, 5, 6, } Hay infinitos números naturales.
NÚMEROS ENTEROS 15 Números naturales: sirven para contar, ordenar y comunicar información. representa al conjunto de todos los número naturales. = {0, 1, 2, 3, 4, 5, 6, } Hay infinitos números naturales.
Números enteros. 1. En una recta horizontal, se toma un punto cualquiera que se señala como cero.
 Números enteros Son el conjunto de números naturales, sus opuestos (negativos) y el cero. Se dividen en tres partes: enteros positivos o números naturales (+1, +2, +3,...), enteros negativos (-1, -2, -3,.)
Números enteros Son el conjunto de números naturales, sus opuestos (negativos) y el cero. Se dividen en tres partes: enteros positivos o números naturales (+1, +2, +3,...), enteros negativos (-1, -2, -3,.)
LOS NUMEROS ENTEROS. I. Introducción a los Números Enteros
 LOS NUMEROS ENTEROS I. Introducción a los Números Enteros Hasta ahora hemos visto los números naturales, que comienzan en 0 e incluyen los números mayores que 0, sumando siempre 1 al número anterior. Cuando
LOS NUMEROS ENTEROS I. Introducción a los Números Enteros Hasta ahora hemos visto los números naturales, que comienzan en 0 e incluyen los números mayores que 0, sumando siempre 1 al número anterior. Cuando
Lección 1: Números en teros. Orden, suma y resta
 LECCIÓN 1 Lección 1: Números en teros. Orden, suma y resta En esta lección se hará un repaso de los temas abordados en las lecciones 7 y 8 del curso anterior. Los números enteros Como usted recordará,
LECCIÓN 1 Lección 1: Números en teros. Orden, suma y resta En esta lección se hará un repaso de los temas abordados en las lecciones 7 y 8 del curso anterior. Los números enteros Como usted recordará,
7.1 Números Racionales: números enteros, propiedades de los números y orden de operaciones. Prof. Kyria A. Pérez
 7.1 Números Racionales: números enteros, propiedades de los números y orden de operaciones Prof. Kyria A. Pérez Estándares de contenido y expectativas N.SO.7.2.1- Modela la suma, Resta, multiplicación
7.1 Números Racionales: números enteros, propiedades de los números y orden de operaciones Prof. Kyria A. Pérez Estándares de contenido y expectativas N.SO.7.2.1- Modela la suma, Resta, multiplicación
LOS NÚMEROS ENTEROS QUÉ ES UN NÚMERO ENTERO? VALOR ABSOLUTO EL OPUESTO DE UN NÚMERO ENTERO OPERACIONES CON ENTEROS ORDENACIÓN DE NÚMEROS ENTEROS
 LOS NÚMEROS ENTEROS QUÉ ES UN NÚMERO ENTERO? VALOR ABSOLUTO EL OPUESTO DE UN NÚMERO ENTERO ORDENACIÓN DE NÚMEROS ENTEROS OPERACIONES CON ENTEROS Suma Resta Multiplicación División Potencia JERARQUÍA RESOLUCIÓN
LOS NÚMEROS ENTEROS QUÉ ES UN NÚMERO ENTERO? VALOR ABSOLUTO EL OPUESTO DE UN NÚMERO ENTERO ORDENACIÓN DE NÚMEROS ENTEROS OPERACIONES CON ENTEROS Suma Resta Multiplicación División Potencia JERARQUÍA RESOLUCIÓN
Los números enteros Z = {,-3, -2, -1, 0, 1, 2, 3, }
 Los números enteros La unión de los números naturales y los enteros negativos forma el conjunto de los números enteros, que se designa con la palabra Z. Está constituido por infinitos elementos y se representan
Los números enteros La unión de los números naturales y los enteros negativos forma el conjunto de los números enteros, que se designa con la palabra Z. Está constituido por infinitos elementos y se representan
FICHAS REPASO 3º ESO. Para restar números enteros, se suma al minuendo el opuesto del sustraendo y después se aplican las reglas de la suma.
 FICHAS REPASO º ESO OPERACIONES CON NÚMEROS ENTEROS El valor absoluto de un número entero es el número natural que resulta al prescindir del signo. Por ejemplo, el valor absoluto de es y el valor absoluto
FICHAS REPASO º ESO OPERACIONES CON NÚMEROS ENTEROS El valor absoluto de un número entero es el número natural que resulta al prescindir del signo. Por ejemplo, el valor absoluto de es y el valor absoluto
INSTITUCIÓN EDUCATIVA JORGE ROBLEDO PLAN DE APOYO
 FECHA:07-0-204 Página de 4 ÁREA/ASIGNATURA: ARITMÉTICA PARA LA PROMOCIÓN ANTICIPADA GRADO: SEXTO AÑO: 207 INSTRUCCIONES: La entrega de la solución, por escrito y bien presentada, es requisito indispensable
FECHA:07-0-204 Página de 4 ÁREA/ASIGNATURA: ARITMÉTICA PARA LA PROMOCIÓN ANTICIPADA GRADO: SEXTO AÑO: 207 INSTRUCCIONES: La entrega de la solución, por escrito y bien presentada, es requisito indispensable
OPERACIÓN CON NÚMEROS ENTEROS(Z)
 OPERACIÓN CON NÚMEROS ENTEROS(Z) Imagina que un día estas de visita en un apartamento de unos amigos, al despedirte bajas al sótano 2 a buscar tu carro y te das cuenta que dejaste las llaves en casa de
OPERACIÓN CON NÚMEROS ENTEROS(Z) Imagina que un día estas de visita en un apartamento de unos amigos, al despedirte bajas al sótano 2 a buscar tu carro y te das cuenta que dejaste las llaves en casa de
TEMA 1: LOS NÚMEROS ENTEROS. Segundo Curso de Educación Secundaria Obligatoria. I.E.S de Fuentesaúco. Manuel González de León.
 TEMA 1: LOS NÚMEROS ENTEROS Segundo Curso de Educación Secundaria Obligatoria. I.E.S de Fuentesaúco. Manuel González de León. CURSO 2011-2012 1. Los Números Enteros. 2. Suma y resta de números enteros.
TEMA 1: LOS NÚMEROS ENTEROS Segundo Curso de Educación Secundaria Obligatoria. I.E.S de Fuentesaúco. Manuel González de León. CURSO 2011-2012 1. Los Números Enteros. 2. Suma y resta de números enteros.
SIGNIFICADO DE LOS NÚMEROS ENTEROS: POSITIVOS Y NEGATIVOS
 OBJETIVO 1 SIGNIICADO DE LOS NÚMEROS ENTEROS: POSITIVOS Y NEGATIVOS NOMBRE: CURSO: ECHA: NÚMEROS NEGATIVOS En nuestra vida diaria observamos, leemos y decimos expresiones del tipo: a) Hemos dejado el coche
OBJETIVO 1 SIGNIICADO DE LOS NÚMEROS ENTEROS: POSITIVOS Y NEGATIVOS NOMBRE: CURSO: ECHA: NÚMEROS NEGATIVOS En nuestra vida diaria observamos, leemos y decimos expresiones del tipo: a) Hemos dejado el coche
Números enteros. Los números enteros son los formados por los números naturales (1), sus opuestos (2) y el número 0
 Los números enteros son los formados por los números naturales, sus opuestos (2) y el número 0 Números enteros Los números naturales son aquellos que nos permiten contar las cosas. Ej. 2 sillas, 4 patas,
Los números enteros son los formados por los números naturales, sus opuestos (2) y el número 0 Números enteros Los números naturales son aquellos que nos permiten contar las cosas. Ej. 2 sillas, 4 patas,
*Número natural, el que sirve para designar la cantidad de. *El cero, a veces, se excluye del conjunto de los números
 *Número natural, el que sirve para designar la cantidad de elementos que tiene un cierto conjunto, y se llama cardinal de dicho conjunto. *Los números naturales son infinitos. El conjunto de todos ellos
*Número natural, el que sirve para designar la cantidad de elementos que tiene un cierto conjunto, y se llama cardinal de dicho conjunto. *Los números naturales son infinitos. El conjunto de todos ellos
Unidad n.º 6. Números enteros
 Unidad n.º 6 Números enteros Actividades NIVEL I 1. Haz una clasificación de los números enteros. 2. Utiliza los números enteros para expresar: a) Me han ingresado 42.000 pesetas en la cuenta de ahorros.
Unidad n.º 6 Números enteros Actividades NIVEL I 1. Haz una clasificación de los números enteros. 2. Utiliza los números enteros para expresar: a) Me han ingresado 42.000 pesetas en la cuenta de ahorros.
5 Números enteros OBJETIVOS CONTENIDOS PROCEDIMIENTOS. Números negativos y positivos. Números enteros.
 826464 _ 0289-0300.qxd 12/2/07 09:47 Página 289 Números enteros INTRODUCCIÓN El concepto de número entero negativo implica la inclusión en el sistema numérico de unos números que superan el concepto de
826464 _ 0289-0300.qxd 12/2/07 09:47 Página 289 Números enteros INTRODUCCIÓN El concepto de número entero negativo implica la inclusión en el sistema numérico de unos números que superan el concepto de
Números enteros CLAVES PARA EMPEZAR VIDA COTIDIANA RESUELVE EL RETO. a) 8 o C b) c) Planta 2
 CLAVES PARA EMPEZAR a) 8 o C b) 200 000 c) Planta 2 a) 8 : 4 7 2 7 9 b) 15 6 : 6 15 1 14 c) 9 2 2 18 2 16 VIDA COTIDIANA En el congelador está a 18 o, si se sube a la zona de verduras, en la que estará
CLAVES PARA EMPEZAR a) 8 o C b) 200 000 c) Planta 2 a) 8 : 4 7 2 7 9 b) 15 6 : 6 15 1 14 c) 9 2 2 18 2 16 VIDA COTIDIANA En el congelador está a 18 o, si se sube a la zona de verduras, en la que estará
4Soluciones a las actividades de cada epígrafe PÁGINA 74
 PÁGINA 74 Pág. 1 Con qué tipo de números podrías expresar la posición de cada objeto con relación al nivel del mar? Y sus posibles movimientos? Comprobarás que los números naturales (0, 1, 2, 3, ) no bastan.
PÁGINA 74 Pág. 1 Con qué tipo de números podrías expresar la posición de cada objeto con relación al nivel del mar? Y sus posibles movimientos? Comprobarás que los números naturales (0, 1, 2, 3, ) no bastan.
TEMA 4 NÚMEROS ENTEROS
 TEMA 4 NÚMEROS ENTEROS 1 2 3 Recta numérica. -9-8 -7-6 -5-4 -3-2 -1 0 +1 +2 +3 +4 +5 +6 +7 +8 +9 Enteros negativos A la izquierda del 0 están los números enteros negativos Enteros positivos A la derecha
TEMA 4 NÚMEROS ENTEROS 1 2 3 Recta numérica. -9-8 -7-6 -5-4 -3-2 -1 0 +1 +2 +3 +4 +5 +6 +7 +8 +9 Enteros negativos A la izquierda del 0 están los números enteros negativos Enteros positivos A la derecha
Matemáticas: Operaciones con números enteros
 Matemáticas: Operaciones con números enteros Profesor: Jorge Granados Romero Descripción y objetivos del curso Este curso está dirigido a quienes deseen refrescar sus conocimientos de matemáticas, y para
Matemáticas: Operaciones con números enteros Profesor: Jorge Granados Romero Descripción y objetivos del curso Este curso está dirigido a quienes deseen refrescar sus conocimientos de matemáticas, y para
ESCUELA PREPARATORIA OFICIAL NO.16 MATERÍA: PENSAMIENTO NUMÉRICO Y ALGEBRAICO I
 Fracción Una fracción es el cociente de dos números enteros a y b, que representamos de la siguiente forma: b a denominador, indica el número de partes en que se ha dividido la unidad. numerador, indica
Fracción Una fracción es el cociente de dos números enteros a y b, que representamos de la siguiente forma: b a denominador, indica el número de partes en que se ha dividido la unidad. numerador, indica
GUIA DE TRABAJO # 13. Materia: Matemáticas. Tema: Adición en Z. Fecha: Profesor: Fernando Viso. Nombre del alumno: Sección del alumno:
 GUIA DE TRABAJO # 13. Materia: Matemáticas. Tema: Adición en Z. Fecha: Profesor: Fernando Viso Nombre del alumno: Sección del alumno: CONDICIONES: Trabajo individual. Sin libros, ni cuadernos, ni notas.
GUIA DE TRABAJO # 13. Materia: Matemáticas. Tema: Adición en Z. Fecha: Profesor: Fernando Viso Nombre del alumno: Sección del alumno: CONDICIONES: Trabajo individual. Sin libros, ni cuadernos, ni notas.
Tema 4: Los números enteros Z
 4.1 Números positivos y negativos Tema 4: Los números enteros Z Describe las siguientes situaciones mediante números positivos y negativos: 1. Estamos en la planta treinta y siete de un rascacielos 37
4.1 Números positivos y negativos Tema 4: Los números enteros Z Describe las siguientes situaciones mediante números positivos y negativos: 1. Estamos en la planta treinta y siete de un rascacielos 37
Los números enteros. > significa "mayor que". Ejemplo: 58 > 12 < significa "menor que". Ejemplo: 3 < 12 Cualquier número positivo siempre es mayor
 Los números enteros Los números enteros Los números enteros son aquellos que permiten contar tanto los objetos que se tienen, como los objetos que se deben. Enteros positivos: precedidos por el signo +
Los números enteros Los números enteros Los números enteros son aquellos que permiten contar tanto los objetos que se tienen, como los objetos que se deben. Enteros positivos: precedidos por el signo +
Escuela Pública Experimental Desconcentrada Nº3 Dr. Carlos Juan Rodríguez Matemática 1º Año Ciclo Básico de Secundaria Teoría Nº 2 Segundo Trimestre
 CONJUNTO DE LOS NÚMEROS ENTEROS Los números enteros están formados por: los números naturales (o enteros positivos y el cero) y los números negativos. El cero no tiene signo, no es ni positivo ni negativo.
CONJUNTO DE LOS NÚMEROS ENTEROS Los números enteros están formados por: los números naturales (o enteros positivos y el cero) y los números negativos. El cero no tiene signo, no es ni positivo ni negativo.
Operaciones con números enteros
 Operaciones con números enteros Suma de números enteros Cuando tienen el mismo signo: Se suman los valores y se deja el signo que tengan, si son positivos signo positivo y si son negativos signo negativo.
Operaciones con números enteros Suma de números enteros Cuando tienen el mismo signo: Se suman los valores y se deja el signo que tengan, si son positivos signo positivo y si son negativos signo negativo.
Los números enteros. 1. Los números negativos
 3 Los números enteros 1. Los números negativos a) Alejandro ha dejado el coche en el segundo sótano de un aparcamiento subterráneo. Al volver por el coche, ve los botones 0, 1 y 2 en el ascensor. En qué
3 Los números enteros 1. Los números negativos a) Alejandro ha dejado el coche en el segundo sótano de un aparcamiento subterráneo. Al volver por el coche, ve los botones 0, 1 y 2 en el ascensor. En qué
ESCUELA SECUNDARIA OFICIAL No MIGUEL LEON PORTILLA. GUIA DE EXAMEN DE RECUPERACION 3er. BIMESTRE MATEMATICAS I
 ESCUELA SECUNDARIA OFICIAL No. 00 MIGUEL LEON PORTILLA GUIA DE EXAMEN DE RECUPERACION er. BIMESTRE MATEMATICAS I NOMBRE DEL ALUMNO: GRADO: _º_GRUPO: _B_ REPRESENTACIÓN DE NÚMEROS FRACCIONARIOS Y DECIMALES
ESCUELA SECUNDARIA OFICIAL No. 00 MIGUEL LEON PORTILLA GUIA DE EXAMEN DE RECUPERACION er. BIMESTRE MATEMATICAS I NOMBRE DEL ALUMNO: GRADO: _º_GRUPO: _B_ REPRESENTACIÓN DE NÚMEROS FRACCIONARIOS Y DECIMALES
NÚMEROS ENTEROS. En la recta numérica se pueden representar los números naturales, el cero y los números negativos.
 NÚMEROS ENTEROS El conjunto de los números enteros está formado por: Los números positivos (1, 2, 3, 4, 5, ) Los números negativos ( El cero (no tiene signo) Recta numérica En la recta numérica se pueden
NÚMEROS ENTEROS El conjunto de los números enteros está formado por: Los números positivos (1, 2, 3, 4, 5, ) Los números negativos ( El cero (no tiene signo) Recta numérica En la recta numérica se pueden
MATEMÁTICAS UNIDAD 4 GRADO 6º. Números naturales
 1 Franklin Eduardo Pérez Quintero MATEMÁTICAS UNIDAD 4 GRADO 6º Números naturales 1 2 Franklin Eduardo Pérez Quintero LOGRO: Estudiar, analizar y profundizar las operaciones y propiedades de los números
1 Franklin Eduardo Pérez Quintero MATEMÁTICAS UNIDAD 4 GRADO 6º Números naturales 1 2 Franklin Eduardo Pérez Quintero LOGRO: Estudiar, analizar y profundizar las operaciones y propiedades de los números
CURSO UNICO DE INGRESO 2010
 INSTITUTO SUPERIOR ZARELA MOYANO DE TOLEDO PROF. ING. ELSA MEDINA CURSO UNICO DE INGRESO 2010 MATEMATICAS INTRODUCCION El presente material supone un REPASO sobre los temas fundamentales y necesarios para
INSTITUTO SUPERIOR ZARELA MOYANO DE TOLEDO PROF. ING. ELSA MEDINA CURSO UNICO DE INGRESO 2010 MATEMATICAS INTRODUCCION El presente material supone un REPASO sobre los temas fundamentales y necesarios para
POTENCIAS. MÚLTIPLOS Y DIVISORES. MÁXIMO COMÚN DIVISOR Y MÍNIMO COMÚN MÚLTIPLO.
 1. LOS NÚMEROS NATURALES POTENCIAS. MÚLTIPLOS Y DIVISORES. MÁXIMO COMÚN DIVISOR Y MÍNIMO COMÚN MÚLTIPLO. 2. LOS NÚMEROS ENTEROS. VALOR ABSOLUTO DE UN NÚMERO ENTERO. REPRESENTACIÓN GRÁFICA. OPERACIONES.
1. LOS NÚMEROS NATURALES POTENCIAS. MÚLTIPLOS Y DIVISORES. MÁXIMO COMÚN DIVISOR Y MÍNIMO COMÚN MÚLTIPLO. 2. LOS NÚMEROS ENTEROS. VALOR ABSOLUTO DE UN NÚMERO ENTERO. REPRESENTACIÓN GRÁFICA. OPERACIONES.
Los Números Enteros (Z)
 Los Números Enteros (Z) Los números enteros: representación gráfica, orden, modulo o valor absoluto. Operaciones en Z, procedimientos y propiedades de estas. Prioridades de operaciones y paréntesis. Problemas
Los Números Enteros (Z) Los números enteros: representación gráfica, orden, modulo o valor absoluto. Operaciones en Z, procedimientos y propiedades de estas. Prioridades de operaciones y paréntesis. Problemas
TEMA 2: NÚMEROS ENTEROS 1º ESO. MATEMÁTICAS
 TEMA 2: NÚMEROS ENTEROS 1º ESO. MATEMÁTICAS Por qué aparecen los números enteros? Por qué aparecen los números enteros? La cueva de Voronia, es la cueva conocida más profunda de la Tierra, localizada
TEMA 2: NÚMEROS ENTEROS 1º ESO. MATEMÁTICAS Por qué aparecen los números enteros? Por qué aparecen los números enteros? La cueva de Voronia, es la cueva conocida más profunda de la Tierra, localizada
TEMA 1. Las cuentas de andar por casa
 TEMA 1. Las cuentas de andar por casa 1.-Los distintos tipos de números Módulo 3 1.1. Los números naturales El conjunto de los números naturales está formado por: N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9,...}
TEMA 1. Las cuentas de andar por casa 1.-Los distintos tipos de números Módulo 3 1.1. Los números naturales El conjunto de los números naturales está formado por: N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9,...}
SOLUCIONES A LAS ACTIVIDADES DE CADA EPÍGRAFE
 Pág. 1 PÁGINA 76 REFLEXIONA Vamos a pensar en los números que se necesita para expresar las distintas paradas del montacargas del barco, así como sus posibles movimientos. Comprobarás que los números naturales
Pág. 1 PÁGINA 76 REFLEXIONA Vamos a pensar en los números que se necesita para expresar las distintas paradas del montacargas del barco, así como sus posibles movimientos. Comprobarás que los números naturales
LOS NÙMEROS ENTEROS. Crucigrama de enteros: Vertical
 Crucigrama de enteros: Vertical 1. ( - 65 ) : ( - 13 ) 2. Vertical 2. 8 x ( - 2 ) x ( - 2 ) 3. 15 + ( - 14 ) + ( - 2 ) + 3 4. Opuesto de - 23. 7. 2 + ( - 3 ) x ( - 5 ) 10. ( - ) x ( + ) Horizontal 2. Subir
Crucigrama de enteros: Vertical 1. ( - 65 ) : ( - 13 ) 2. Vertical 2. 8 x ( - 2 ) x ( - 2 ) 3. 15 + ( - 14 ) + ( - 2 ) + 3 4. Opuesto de - 23. 7. 2 + ( - 3 ) x ( - 5 ) 10. ( - ) x ( + ) Horizontal 2. Subir
UNIDAD 1 NÚMEROS ENTEROS. 7 Básico. Autor. Thomas Bustos Ortiz
 UNIDAD 1 NÚMEROS ENTEROS 7 Básico Autor Thomas Bustos Ortiz I ESQUEMA SINÓPTICO DE LAS CLASES Clase 1 Clase 2 Clase 3 Clase 4 Clase 5 Clase 6 Clase 7 Problemas aditivos Adición Sustracción Composición,
UNIDAD 1 NÚMEROS ENTEROS 7 Básico Autor Thomas Bustos Ortiz I ESQUEMA SINÓPTICO DE LAS CLASES Clase 1 Clase 2 Clase 3 Clase 4 Clase 5 Clase 6 Clase 7 Problemas aditivos Adición Sustracción Composición,
Tema 2 : NÚMEROS ENTEROS. Primero de Educación Secundaria Obligatoria. I.e.s Fuentesaúco.
 2010 Tema 2 : NÚMEROS ENTEROS. Primero de Educación Secundaria Obligatoria. I.e.s Fuentesaúco. Manuel González de León mgdl 01/01/2010 INDICE: 01. DE LOS NÚMEROS NATURALES A LOS NÚMEROS ENTEROS. 02. VALOR
2010 Tema 2 : NÚMEROS ENTEROS. Primero de Educación Secundaria Obligatoria. I.e.s Fuentesaúco. Manuel González de León mgdl 01/01/2010 INDICE: 01. DE LOS NÚMEROS NATURALES A LOS NÚMEROS ENTEROS. 02. VALOR
NÚMEROS ENTEROS. Números enteros positivos y números enteros negativos. Su representación gráfica en la recta. Número entero positivo.
 NÚMEROS ENTEROS Números enteros positivos y números enteros negativos. Su representación gráfica en la recta. Número entero positivo. - Es todo aquel número mayor que 0. - Se utiliza para representar valores
NÚMEROS ENTEROS Números enteros positivos y números enteros negativos. Su representación gráfica en la recta. Número entero positivo. - Es todo aquel número mayor que 0. - Se utiliza para representar valores
6º lección TEMA 10.- LOS NÚMEROS ENTEROS
 Los números negativos sirven para expresar cantidades menores que cero. Recuerda que los números pueden ser positivos o negativos. -.Expresar con números enteros las siguientes situaciones: Recuerda Ejemplo:
Los números negativos sirven para expresar cantidades menores que cero. Recuerda que los números pueden ser positivos o negativos. -.Expresar con números enteros las siguientes situaciones: Recuerda Ejemplo:
CONTENIDO INFORMATIVO ARITMÉTICA
 NÚMEROS CON SIGNO. CONTENIDO INFORMATIVO ARITMÉTICA Los signos de más (+) positivo o de menos (-) negativo, cuando acompañan a un número o cantidad es para indicar el sentido: positivo o negativo. Positivo
NÚMEROS CON SIGNO. CONTENIDO INFORMATIVO ARITMÉTICA Los signos de más (+) positivo o de menos (-) negativo, cuando acompañan a un número o cantidad es para indicar el sentido: positivo o negativo. Positivo
Recuerda: la décima parte de la unidad
 Recuerda: la décima parte de la unidad -. Relaciona las expresiones con las cifras correspondientes: Dos Seis Cuatro Ocho Tres Nueve Cinco 0,3 0,2 0,8 0,6 0,5 0,4 0,9 -. Escribe en forma de fracción y
Recuerda: la décima parte de la unidad -. Relaciona las expresiones con las cifras correspondientes: Dos Seis Cuatro Ocho Tres Nueve Cinco 0,3 0,2 0,8 0,6 0,5 0,4 0,9 -. Escribe en forma de fracción y
Expresiones algebraicas (1º ESO)
 Epresiones algebraicas (º ESO) Lenguaje numérico y lenguaje algebraico. El lenguaje en el que intervienen números y signos de operaciones se denomina lenguaje numérico. Lenguaje usual Lenguaje numérico
Epresiones algebraicas (º ESO) Lenguaje numérico y lenguaje algebraico. El lenguaje en el que intervienen números y signos de operaciones se denomina lenguaje numérico. Lenguaje usual Lenguaje numérico
TEMA 2 NÚMEROS ENTEROS
 TEMA 2 NÚMEROS ENTEROS 1. Dibuja una recta numérica y ubica en ella, los siguientes números enteros: a) 4 b) 7 c) +2 d) 0 e) 5 (Encierra con un círculo de color azul los enteros positivos y uno de color
TEMA 2 NÚMEROS ENTEROS 1. Dibuja una recta numérica y ubica en ella, los siguientes números enteros: a) 4 b) 7 c) +2 d) 0 e) 5 (Encierra con un círculo de color azul los enteros positivos y uno de color
FIN EDUCATIVO FIN INSTRUCTIVO
 FIN EDUCATIVO Todos somos números en las Matemáticas de la vida, con valores: absolutos, relativos, positivos y negativos. Los primeros representan a nuestras cualidades y virtudes ; los segundos a los
FIN EDUCATIVO Todos somos números en las Matemáticas de la vida, con valores: absolutos, relativos, positivos y negativos. Los primeros representan a nuestras cualidades y virtudes ; los segundos a los
CONJUTOS NÚMERICOS NÚMEROS NATURALES
 CONJUTOS NÚMERICOS NÚMEROS NATURALES El conjunto de números naturales tiene gran importancia en la vida práctica ya que con sus elementos se pueden encontrar elementos u objetos de otros conjuntos. El
CONJUTOS NÚMERICOS NÚMEROS NATURALES El conjunto de números naturales tiene gran importancia en la vida práctica ya que con sus elementos se pueden encontrar elementos u objetos de otros conjuntos. El
Expresa con lenguaje numérico los enunciados siguientes:
 Pág. 1 de 16 UNIDAD 4 NÚMEROS ENTEROS 1. ORDENACIÓN DE NÚMEROS ENTEROS Actividades de clase 1.1. NÚMEROS POSITIVOS O NEGATIVOS Expresa con lenguaje numérico los enunciados siguientes: El avión vuela a
Pág. 1 de 16 UNIDAD 4 NÚMEROS ENTEROS 1. ORDENACIÓN DE NÚMEROS ENTEROS Actividades de clase 1.1. NÚMEROS POSITIVOS O NEGATIVOS Expresa con lenguaje numérico los enunciados siguientes: El avión vuela a
Y LOS ELEMENTOS QUE FORMAN UN POLINOMIO. Nombre: Curso: Fecha: F Cómo es el polinomio, completo o incompleto?
 REPASO Y APOYO OBJETIVO 1 3 RECONOCER EL GRADO Y LOS ELEMENTOS QUE ORMAN UN POLINOMIO Nombre: Curso: echa: Un polinomio es una expresión algebraica formada por la suma algebraica de monomios, que son los
REPASO Y APOYO OBJETIVO 1 3 RECONOCER EL GRADO Y LOS ELEMENTOS QUE ORMAN UN POLINOMIO Nombre: Curso: echa: Un polinomio es una expresión algebraica formada por la suma algebraica de monomios, que son los
TEMA 2 NÚMEROS ENTEROS
 TEMA 2 NÚMEROS ENTEROS Criterios De Evaluación de la Unidad 1. Utilizar de forma adecuada los números enteros. 2. Representar sobre la recta los números enteros. 3. Hallar el valor absoluto de cualquier
TEMA 2 NÚMEROS ENTEROS Criterios De Evaluación de la Unidad 1. Utilizar de forma adecuada los números enteros. 2. Representar sobre la recta los números enteros. 3. Hallar el valor absoluto de cualquier
NÚMEROS DECIMALES. Teoría 3 er Ciclo Primaria Colegio Romareda 2011/2012 Página 28
 Teoría 3 er Ciclo Primaria Colegio Romareda 20/202 Página 28 NÚMEROS DECIMALES Los números decimales nacen como una forma especial de escritura de las fracciones decimales, de manera que la coma separa
Teoría 3 er Ciclo Primaria Colegio Romareda 20/202 Página 28 NÚMEROS DECIMALES Los números decimales nacen como una forma especial de escritura de las fracciones decimales, de manera que la coma separa
Operaciones con números enteros
 1. Identificación Nivel: Primario Área: Matemática Grado: Sexto SC 10: Resumen: En esta Unidad Didáctica se identifican los números enteros positivos y negativos. Se resuelven operaciones de adición y
1. Identificación Nivel: Primario Área: Matemática Grado: Sexto SC 10: Resumen: En esta Unidad Didáctica se identifican los números enteros positivos y negativos. Se resuelven operaciones de adición y
CONJUNTO DE LOS NUMEROS ENTEROS
 República Bolivariana de Venezuela Ministerio de la Defensa Universidad Nacional Experimental Politécnica de la Fuerza Armada Núcleo Caracas CIU Cátedra: Razonamiento Matemático CONJUNTO DE LOS NUMEROS
República Bolivariana de Venezuela Ministerio de la Defensa Universidad Nacional Experimental Politécnica de la Fuerza Armada Núcleo Caracas CIU Cátedra: Razonamiento Matemático CONJUNTO DE LOS NUMEROS
SESIÓN 1 PRE-ALGEBRA, CONCEPTOS Y OPERACIONES ARITMÉTICAS BÁSICAS
 SESIÓN 1 PRE-ALGEBRA, CONCEPTOS Y OPERACIONES ARITMÉTICAS BÁSICAS I. CONTENIDOS: 1. Introducción: de la aritmética al álgebra. 2. Números reales y recta numérica. 3. Operaciones aritméticas básicas con
SESIÓN 1 PRE-ALGEBRA, CONCEPTOS Y OPERACIONES ARITMÉTICAS BÁSICAS I. CONTENIDOS: 1. Introducción: de la aritmética al álgebra. 2. Números reales y recta numérica. 3. Operaciones aritméticas básicas con
1 Números enteros OBJETIVOS CONTENIDOS PROCEDIMIENTOS
 898 _ 0-008.qxd /9/07 :0 Página Números enteros INTRODUCCIÓN La representación numérica en la recta de los números enteros nos introduce en el estudio de su ordenación y comparación, el concepto de valor
898 _ 0-008.qxd /9/07 :0 Página Números enteros INTRODUCCIÓN La representación numérica en la recta de los números enteros nos introduce en el estudio de su ordenación y comparación, el concepto de valor
Operaciones de enteros. Prof. Yaritza González Adaptado por: Yuitza T. Humarán Departamento de Matemáticas UPRA
 Operaciones de enteros Prof. Yaritza González Adaptado por: Yuitza T. Humarán Departamento de Matemáticas UPRA Suma de enteros: Reglas Suma de dos enteros negativos o dos enteros positivos El total es
Operaciones de enteros Prof. Yaritza González Adaptado por: Yuitza T. Humarán Departamento de Matemáticas UPRA Suma de enteros: Reglas Suma de dos enteros negativos o dos enteros positivos El total es
Expresa con lenguaje numérico los enunciados siguientes:
 Pág. 1 de 13 UNIDAD 4 NÚMEROS ENTEROS 1. ORDENACIÓN DE NÚMEROS ENTEROS Actividades de clase 1.1. NÚMEROS POSITIVOS O NEGATIVOS Expresa con lenguaje numérico los enunciados siguientes: El avión vuela a
Pág. 1 de 13 UNIDAD 4 NÚMEROS ENTEROS 1. ORDENACIÓN DE NÚMEROS ENTEROS Actividades de clase 1.1. NÚMEROS POSITIVOS O NEGATIVOS Expresa con lenguaje numérico los enunciados siguientes: El avión vuela a
MANEJO DE ESPACIOS Y CANTIDADES
 INTRODUCCIÓN AL ÁLGEBRA (TÉRMINOS, ADICIÓN Y SUSTRACCIÓN) Material: cartulina roja cartulina azul cartulina amarilla cartulina verde tijeras regla goma de pegar Construcción del material : a) Dividir cada
INTRODUCCIÓN AL ÁLGEBRA (TÉRMINOS, ADICIÓN Y SUSTRACCIÓN) Material: cartulina roja cartulina azul cartulina amarilla cartulina verde tijeras regla goma de pegar Construcción del material : a) Dividir cada
2) Si debo a un amigo $80 y a otro amigo $30, en total debo la suma de $110. Esto es: $80 $30= $110
 1.2.1. SUMA DE NÚMEROS ENTEROS. En los siguientes ejemplos se muestra como realizar la suma de números enteros. 1) Si tengo en mi bolsillo $50 y en la cartera tengo $350 en total tengo la cantidad de $400
1.2.1. SUMA DE NÚMEROS ENTEROS. En los siguientes ejemplos se muestra como realizar la suma de números enteros. 1) Si tengo en mi bolsillo $50 y en la cartera tengo $350 en total tengo la cantidad de $400
Representación de números enteros: el convenio exceso Z
 Representación de números enteros: el convenio exceso Z Apellidos, nombre Martí Campoy, Antonio ([email protected]) Departamento Centro Informàtica de Sistemes i Computadors Escola Tècnica Superior d
Representación de números enteros: el convenio exceso Z Apellidos, nombre Martí Campoy, Antonio ([email protected]) Departamento Centro Informàtica de Sistemes i Computadors Escola Tècnica Superior d
OBJETIVO 1 EL SIGNIFICADO DE LOS NÚMEROS POSITIVOS Y NEGATIVOS
 COMPRENDER OBJETIVO EL SIGNIICADO DE LOS NÚMEROS POSITIVOS Y NEGATIVOS NOMBRE: CURSO: ECHA: NÚMEROS NEGATIVOS En nuestra vida diaria observamos, leemos y decimos expresiones del siguiente tipo. EXPRESIONES
COMPRENDER OBJETIVO EL SIGNIICADO DE LOS NÚMEROS POSITIVOS Y NEGATIVOS NOMBRE: CURSO: ECHA: NÚMEROS NEGATIVOS En nuestra vida diaria observamos, leemos y decimos expresiones del siguiente tipo. EXPRESIONES
Ejes cartesianos. Coordenadas de un punto
 Ejes cartesianos. Coordenadas de un punto Los elementos de una función son: la variable independiente la variable dependiente, que se representa sobre el eje horizontal o eje de abscisas,, que se representa
Ejes cartesianos. Coordenadas de un punto Los elementos de una función son: la variable independiente la variable dependiente, que se representa sobre el eje horizontal o eje de abscisas,, que se representa
LOGRO: Reconoce distintas representaciones de los números reales y usa sus propiedades para resolver Problemas.
 ESTANDARES Utilizo números reales en sus diferentes representaciones y en diversos contextos. Resuelvo problemas y simplifico cálculos usando propiedades y relaciones de los números reales y de las relaciones
ESTANDARES Utilizo números reales en sus diferentes representaciones y en diversos contextos. Resuelvo problemas y simplifico cálculos usando propiedades y relaciones de los números reales y de las relaciones
OPERACIONES CON NÚMEROS BINARIOS
 OPERACIONES CON NÚMEROS BINARIOS Centro CFP/ES SUMA BINARIA La información tenemos que transformarla, compararla y procesarla. Para ello empleamos la aritmética binaria, es decir, procesos matemáticos
OPERACIONES CON NÚMEROS BINARIOS Centro CFP/ES SUMA BINARIA La información tenemos que transformarla, compararla y procesarla. Para ello empleamos la aritmética binaria, es decir, procesos matemáticos
LOS NÚMEROS ENTEROS. Para restar un número entero, se quita el paréntesis y se pone al número el signo contrario al que tenía.
 Melilla Los números Enteros y operaciones elementales LOS NÚMEROS ENTEROS 1º LOS NÚMEROS ENTEROS. El conjunto de los números enteros Z está formado por los números naturales (enteros positivos) el cero
Melilla Los números Enteros y operaciones elementales LOS NÚMEROS ENTEROS 1º LOS NÚMEROS ENTEROS. El conjunto de los números enteros Z está formado por los números naturales (enteros positivos) el cero
