CONJUNTO DE LOS NUMEROS ENTEROS
|
|
|
- María José Cano Gallego
- hace 9 años
- Vistas:
Transcripción
1 República Bolivariana de Venezuela Ministerio de la Defensa Universidad Nacional Experimental Politécnica de la Fuerza Armada Núcleo Caracas CIU Cátedra: Razonamiento Matemático CONJUNTO DE LOS NUMEROS ENTEROS GUIA CIU NRO: 2 COMISIÓN DE APOYO A RAZONAMIENTO MATEMATICO INTEGRANTES: Ing. Beliana Gómez Ing. Elvia Moreno Ing. Mixef Rojas Lic. Teresa Gómez Prof. Neida González VERSION OCTUBRE 2006
2 2 CONJUNTO DE LOS NÚMEROS ENTEROS 1.- DEFINICIÓN DEL CONJUNTO DE LOS NÚMEROS ENTEROS En ciertas ocasiones necesitamos expresar valores que están antes o por debajo del valor que consideramos punto de partida o valor cero. Ha sido necesario ampliar el conjunto de los números incluyendo también los negativos, para ello añadimos al número natural un signo + o -. De esta manera han surgido los números enteros, que expresan valores que van de uno en uno, pero permiten expresar valores positivos y también valores negativos. Los números enteros son del tipo: -59, -3, 0, 1, 5, 78, 34567, etc., es decir, los naturales, sus opuestos (negativos) y el cero. Se dividen en tres partes: enteros positivos o números naturales, enteros negativos y cero. Dado que los enteros contienen los enteros positivos, se considera a los números naturales un subconjunto de los enteros. Los números negativos pueden aplicarse en distintos contextos, como la representación de deudas, profundidades bajo el nivel del mar, temperaturas bajo cero, entre otros. Históricamente, durante mucho tiempo fueron rechazados por creer que "no existían" y no fue sino hasta el siglo XVII que tuvieron aceptación en trabajos científicos, aunque matemáticos italianos del renacimiento como Tartaglia y Cardano los hubiesen ya advertido en sus trabajos acerca de solución de ecuaciones de tercer grado. El hecho de que un número sea entero, significa que no tiene parte decimal. Imaginemos que disponemos de dos barras de chocolate, cada una con tres divisiones, las cuales van a repartirse entre tres personas. Es claro que esta operación puede realizarse convenientemente si a cada persona le tocan dos partes de las tres que tiene cada barra. Ahora bien, imaginemos que tenemos 7 esferas de metal que queremos repartir entre las mismas tres personas. Es claro que no puede partirse una esfera para que a cada persona le toque la misma cantidad de esferas, así que a cada uno le deben tocar dos esferas y regalar una para que la repartición sea justa, o bien conseguir otras dos esferas para que a cada uno le toquen tres.
3 3 Representación gráfica del Conjunto : El conjunto de los números enteros se representa de la siguiente forma: = { , -6, -5, -4, -3, -2, -1, 0, +1, +2, +3, +4, +5, +6, } En forma gráfica: VALOR ABSOLUTO DE UN NÚMERO El valor absoluto será la distancia que haya entre determinado número al origen de la recta numérica o también llamado el cero (0). El valor absoluto de un número se representa entre dos líneas paralelas. La representación es la siguiente: a a Valor absoluto de: a = a a = a -a 0 a En la práctica el valor absoluto es simplemente la magnitud del número que tenemos, sin importar el signo ( positivo o negativo). Ejemplos: a) Para hallar el valor absoluto de -33: -33 = 33 b) Para hallar el valor absoluto de +15: +15 = 15 c) El resultado de la siguiente operación es: = = RELACIÓN DE ORDEN EN :
4 4 Para que se cumpla la relación de orden en Si a Ζ y b Ζ, se cumple sólo y sólo una vez que: a es mayor que b, o a es igual a b o b es menor que a es decir, a > b a Z, b Z a = b a < b, se deben establecer ciertas condiciones: (Mayor) (Menor) Según lo expresado anteriormente, se pueden afirmar las siguientes aseveraciones: a. Todos los números enteros positivos son mayores que cero (0): x Z +, x > 0 6 > 0 b. Todos los números enteros negativos son menores que cero (0): y Z, y < 0-6 < 0 c. Todos los números enteros positivos son mayores que todos los números enteros negativos: x Z +, y Z x > y 6 > - 6 d. Entre números positivos será mayor el que represente la mayor cantidad. Por ejemplo: +5 es mayor que +3, ya que 5 representa mayor cantidad que 3. e. Entre números negativos será mayor aquel cuyo valor absoluto represente la menor cantidad. Por ejemplo: -2 es mayor que -5, ya que 2 representa menor cantidad que 5. Ejemplos: Para los siguientes números, vamos a identificar cuál es el mayor: i) 58 y 65 Según la afirmación (c), 58 es un número positivo y 65 es un número negativo, por lo que el número mayor será el 58.
5 5 ii) 9 y 156 Según la afirmación (e), 9 es un número negativo y 156 es negativo, y entre estas dos cantidades, aquella cuyo valor absoluto representa la menor cantidad es el 9, por lo que -9 debe ser el número mayor. iii) + 37 y + 39 En este caso, los dos números representan cantidades positivas, por lo que se aplica la afirmación (d), en la que el número + 39 representa una mayor cantidad que el + 37, por lo que el + 39 debe ser el número mayor. 3.- ADICIÓN EN : Se tienen dos posibilidades, según sea el caso. Las posibilidades son las siguientes: Caso I: Si se suman números de igual signo Cuando tengamos dos o más números de igual signo, lo que se tiene que hacer es sumar las cantidades y al resultado anteponerle el mismo signo. Observe el siguiente caso: En esta operación se tienen tres números positivos: +35, +46 y Entonces lo que se debe hacer es sumar los tres números, el resultado será: = 92 Por último, se define el signo del resultado, que para este caso será positivo. Otro ejemplo podrá ser: En esta operación se tienen tres números negativos: -12, -28 y Entonces lo que se debe hacer es sumar los tres números, el resultado será: El signo del resultado será negativo también, ya que el signo se mantiene.
6 6 Caso II: Si se suman números de signos diferentes Si se tienen números de diferentes signos, se resta el número de mayor cantidad con el número de menor cantidad, y el resultado llevará el signo del número de mayor cantidad. Se tiene el siguiente ejemplo: En esta operación se tienen dos números, uno positivo y otro negativo El de mayor cantidad es 46 y el de menor es 35, entonces: = Como el número de mayor cantidad es 46, y este es negativo, el resultado será también negativo. Otro ejemplo: En esta operación se tiene un número negativo y otro positivo El de mayor cantidad es 28 y el de menor 12, entonces: = = 16 Como el número de mayor cantidad es 28, y este es positivo, el resultado será también positivo (3.1) Propiedades de la Adición en Z (3.1.1) Ley conmutativa La adición de números enteros es conmutativa, ya que no depende del orden de los sumandos: Es decir, al cambiar el orden de los sumandos la suma no varía. a + b = b + a ( 2) = ( 2) + 4
7 7 Otro ejemplo de la aplicación de la ley conmutativa será: ( 25) + (56) = (56) + ( 25) 21 = 21 (3.1.2) Ley asociativa La adición de números enteros es asociativa, ya que no depende de la forma que se asocien los sumandos. Es decir, al agrupar los sumandos no cambia la suma total: ( a + b) + c = a + ( b + c) (6 + 5) + 12 = 6 + (5 + 12) = = 23 (3.1.3) Elemento Neutro El número cero es el elemento neutro de la adición y sustracción de números enteros. (3.1.4) Elemento Simétrico Todo número entero tiene su simétrico llamado opuesto, de modo que la suma de ese número y su simétrico es igual al elemento neutro, cero. El simétrico de un número no es más que el mismo número pero con signo contrario. a + ( a) = 0
8 8 4.- SUSTRACCIÓN EN : Para restar dos números enteros, se suma al minuendo el opuesto al sustraendo, por lo tanto, toda sustracción se transforma en una adición. Por ejemplo: a) (-58) (65) = = b) (+45) (63) = = -18 Observe: La sustracción de números enteros no es conmutativa: La sustracción de números enteros no es asociativa. ( 15 6) 5 15 ( 6 5) MULTIPLICACIÓN O PRODUCTO EN : Al realizar el producto de números enteros se pueden distinguir dos casos: Caso I: Producto de números de igual signo
9 9 Al multiplicar dos números de igual signo, el resultado es la multiplicación de esos números con signo positivo. Es decir, multiplicación de números de igual signo, el resultado será positivo. Ejemplos: a) (-5).(-6) = + (5. 6) = + 30 b) (+5).(+3) = + (5. 3) = + 15 Caso II: Producto de números de distinto signo Al multiplicar dos números de signos diferentes, el resultado es la multiplicación de esos números con signo negativo. Es decir, multiplicación de números de signos diferentes, el resultado será negativo. Ejemplos: a) (-15).(+2) = - (15. 2) = - 30 b) (+5).(-11) = - (5. 11) = - 55 (5.1) Propiedades de la Multiplicación en Z (5.1.1) Ley conmutativa El producto de números enteros es conmutativo, ya que no depende del orden de los factores. Es decir, el orden de los factores no afecta el producto. a b = b a ( 3) (2) = (2) (3)
10 10 (5.1.2) Ley asociativa El producto de números enteros es asociativo, ya que no depende de la forma que se asocien los factores. Es decir, si se reemplazan dos factores por su producto efectuado, el resultado no varía. 2 [( 4) ( 5) ] = [ 2 ( 4) ] ( 5) 2 ( + 20) = ( 8) ( 5) + 40 = + 40 (5.1.3) Elemento Neutro El número 1 es el elemento neutro del producto de números enteros, en donde todo número multiplicado por uno, da como resultado al mismo número. Ejemplos: a) 4. 1 = 4 b) 1. (-5) = -5 (5.1.4) Elemento Absorbente El número 0 es el elemento absorbente del producto de números enteros. El producto de cero por cualquier número entero es igual a cero. Ejemplos: a) 8. 0 = 0 b) 0. (-9) = 0 (5.1.5) Propiedad Distributiva con Respecto a la Adición y a la Sustracción El producto de una suma por un número entero es igual a la suma de los productos de cada sumando por ese número entero.
11 11 4 [( 3) + ( 8) ] = 4 ( 3) + 4 ( 8) = ( 12) + ( 32) = 44 El producto de una resta por un número entero es igual a la diferencia entre el producto del minuendo por ese número entero y el producto del sustraendo por ese mismo número. ( 5) [ 4 ( 3) ] = ( 5) 4 ( 5) ( 3) = ( 20) ( + 15) = ( 20) + ( 15) = DIVISIÓN EN : La división de dos números enteros, es igual a la división de los valores absolutos del dividendo y el divisor, y cuyo signo es positivo cuando ambos tienen el mismo signo y es negativo cuando los números tienen distinto signo. En esta división, se debe cumplir que el valor de b tiene que ser diferente de cero para que la división pueda realizarse. Sino, la división se convierte en indefinida. Ejemplos: a) 4 2 = 2 b) ( 6) 2 = 3 c) ( 16) 4 = 4 d) 15 ( 5) = 3 Nota: En la división entre números no es posible que el divisor sea cero. (6.1) Propiedades de la Multiplicación en Z
12 12 (6.1.1) Elemento Neutro El número 1 es el elemento neutro de la división de números enteros, por lo que todo número divido entre uno, da como resultado el mismo número. Ejemplos: a) 4 1 = 4 b) (-5) 1 = -5 (6.1.2) Elemento Absorbente El número 0 es el elemento absorbente de la división de números enteros. La división de cero entre cualquier número entero es igual a cero. Ejemplos: a) 0 8 = 0 b) 0 (-9) = 0 Nota: Observe que en este caso el dividendo si puede ser cero. (6.1.3) Propiedad Distributiva con Respecto a la Adición y a la Sustracción La división de una suma entre un número entero es igual a la suma de las divisiones de cada sumando entre ese número entero. ( ) ( 4) = 12 ( 4) + 8 ( 4) + 20 ( 4) = ( 3) + ( 2) + ( 5) = 10 La división de una resta entre un número entero es igual a la diferencia entre la división del minuendo entre ese número entero y la división del sustraendo entre ese mismo número entero.
13 13 ( 21 9) ( 3) = 21 ( 3) + ( 9) ( 3) = ( 7) + ( 3) = 4 (6.1.4) Notas sobre las propiedades de la división en Z 1.- La división de números enteros no cumple la propiedad conmutativa La división de números enteros no cumple la propiedad asociativa. ( 24 4) 2 24 ( 4 2) POTENCIACIÓN EN : Sean a, b y c números pertenecientes al conjunto de los números enteros, se tiene que: ( a) b = a a a... a = c Ejemplos: a) ( 2) 3 = ( 2) ( 2) ( 2) = 8 b) ( 3) 4 = = 81 b veces, donde b representa al exponente
14 14 Se puede determinar el signo que resulta de elevar una potencia a un cierto exponente, con solo analizar los siguientes casos: Caso I: (+) impar = (+) Caso II: (+) par = (+) Caso III: (-) impar = (-) Caso IV: (-) par = (+) Cualquier número positivo elevado a exponente impar tiene resultado positivo Cualquier número positivo elevado a exponente par tiene resultado positivo Cualquier número negativo elevado a exponente impar tiene resultado negativo Cualquier número negativo elevado a exponente par tiene resultado positivo Ejemplos: a) ( 2) = 4 = Base positiva, siempre será positivo el resultado. b) ( 2) = 8 = Base positiva, siempre será positivo el resultado. c) ( 2) 2 = ( 2 )(. 2) = 4 Base negativa y exponente par, el resultado será d) ( 2) 3 = ( 2)(. 2 )(. 2) = 8 positivo. Base negativa y exponente par, el resultado será negativo. Nota: Para revisar las propiedades de la potenciación de los números enteros, basta revisar la guía de Números Naturales, sección 4.5.1, ya que las propiedades se cumplen exactamente igual a las descritas en esa sección. 7.- USO DE LOS SIGNOS DE AGRUPACIÓN En las operaciones con cualquier tipo de números, sean Naturales, Enteros o perteneciente a otro conjunto, se pueden agrupar a los mismos usando los llamados Signos de Agrupación. Estos sirven para determinar como se realizarán las operaciones, sean de adición,
15 15 sustracción, multiplicación, división y potenciación entre otras, y agrupar en mucho de los casos los términos que sean semejantes. Estos signos de agrupación son: a) (...) Paréntesis b) [...] Corchetes c) {... } Llaves El uso de los mismos lo determina la operación, utilizando los paréntesis para las operaciones más internas, los corchetes para las operaciones en las que contienen algún paréntesis, y las llaves cuando las operaciones contienen algún corchete. Es importante revisar los siguientes casos antes de resolver un ejercicio en las que estén involucrados los signos de agrupación: 7.1) Si delante de un paréntesis, corchete o llave no hay nada entonces hay un signo positivo que no se escribe: {[( 3 2) ] + 5} = {[ 3 2] + 5} = { } = 6 Hay un signo positivo 7.2) Cuando delante de un paréntesis, corchete o llave hay: 7.2.1) Un Signo Negativo, se elimina el paréntesis, corchete o llave y se CAMBIAN todos los signos de los números que están adentro del mismo. - ( 4-3 ) = Se cambian los signos 7.2.2) Un Signo Positivo, se elimina el paréntesis, corchete o llave y se NO SE CAMBIAN los signos de los números que están adentro.
16 16 ( 4-3 ) = 4-3 No se cambian los signos Recomendaciones Si se tienen varios números para sumar algunos positivos, con otros negativos: =??? 1 er PASO: Sumar los positivos: ( ) = 13 2 do PASO: Sumar los negativos anteponiendo el signo menos al paréntesis: - ( ) = er PASO: Al final resulta: ( ) - ( ) Buscando la diferencia entre los dos y colocando el signo del mayor: = - 4 La diferencia entre 17 y 13 es de 4 y como el mayor, que es el 17, tiene signo negativo, el resultado da negativo. Ejemplo tipo, usando los signos de agrupación. Se desea obtener el resultado de la siguiente operación: { 7 + [ 5 ( 7 2) ]} + 5 { [ 9 ( 14 5) + 3] 5} 8 =??? Caso 1: Eliminando los signos de agrupación primero: Paso 1: Eliminar Paréntesis: Recordando que si hay un signo negativo delante, se elimina el paréntesis y se cambian los signos de todos los números adentro, y si es positivo el signo de adelante entonces todos los números se dejan con su mismo signo:
17 { 7 + [ ] } + 5 { [ ] 5} = 8 Paso 2: Eliminar los corchetes utilizando el mismo procedimiento que en el paso 1: { } + 5 { } = 8 Paso 3: Eliminar las llaves utilizando el mismo procedimiento que en el paso 1: = Paso 4: Sumar los positivos por un lado y los negativos por otro, anteponiendo a estos últimos el signo negativo: ( ) ( ) = = Paso 5: Hallar la diferencia entre ambos valores y colocar el signo del mayor: = agrupación: Caso 2: Resolviendo primero las operaciones internas y luego eliminando los signos de Paso 1: Se resuelve primero lo que está dentro de los paréntesis: { 7 + [ 5 ( 9) ]} + 5 { [ 9 ( 9) + 3] 5} = 8 Paso 2: Eliminar Paréntesis: Recordando que si hay un signo negativo delante, se elimina el paréntesis y se cambian los signos de todos los números adentro, y si es positivo el signo de adelante entonces todos los números se dejan con su mismo signo: { 7 + [ 5 + 9] } + 5 { [ ] 5} = 8 Paso 3: Se resuelve lo que está dentro de los corchetes: { 7 + [ 14] } + 5 { [ 3] 5} = 8 Paso 4: Eliminar los corchetes utilizando el mismo procedimiento que en el paso 2: { } + 5 { 3 5} = 8 Paso 5: Se resuelve lo que está dentro de las llaves: { 21 } + 5 { 8} = 8 Paso 6: Eliminar las llaves utilizando el mismo procedimiento que en el paso 2: =
18 18 Paso 7: Sumar los positivos por un lado y los negativos por otro, anteponiendo a estos últimos el signo negativo: ( 5 + 8) ( 21+ 8) = Paso 8: Hallar la diferencia entre ambos valores y colocar el signo del mayor: = = 16 Nota: Es de notar que no importa el procedimiento que se tome para resolver el ejercicio, el resultado en los dos casos anteriores es el mismo. Es de entender entonces que siempre que se realicen operaciones matemáticas, en las cuales se siga un procedimiento valido, el resultado debe ser el correcto. 7.3) Si detrás de un número hay un número negativo entre paréntesis, quiere decir que entre los dos hay un signo de multiplicación que puede no escribirse: 2 ( 3) = 6 Hay un Signo de Multiplicación 7.4) Cuando dos paréntesis, corchetes o llaves están juntos uno cerrado y el otro abierto y no hay ningún signo entre ellos, hay un signo de multiplicación que puede no escribirse: ( )(2 1+ 3) = ( ) (2 1+ 3) = ( 2) (4) = 8 Hay un Signo de Multiplicación 7.5) Cuando hay un número al lado de un paréntesis, corchete entre el cual no hay ningún signo, entonces hay un signo de multiplicación que puede no escribirse.
19 19 4 (2 1+ 3) = 4 4 = 16 Hay un Signo de Multiplicación 7.6) Separación De Términos: Para resolver ejercicios combinados con suma o resta y multiplicación o división, se debe primero separar en términos. Los signos que separan términos son los de suma o resta y se resuelve primero lo que está en cada término. Por ejemplo: Si el ejercicio combinado tiene paréntesis, corchetes y/o llaves, se procede así: Resolver: { 4 ( 7) 4[ 4 : ( 2) 5( : 3) ]} =??? Paso 1: Separar en términos lo que está dentro del paréntesis y resolver: 4 ( 7) 4 4 : ( 2) 5 { {: 3 = 1er Término 2do Término ( 7) 4[ 4 : ( 2) 5( 12 + )] { 4 3 }= ( 7) 4[ 4 : ( 2) 5( )] { 4 9 }= Paso 2: Separar en términos lo que está dentro de los corchetes y resolver: er Término 123 ( 7) 4 4 : ( 2) 5( 9) = 2do Término { 4 45 }= ( 7) 4[ 2 + ] { 4 43 }= ( 7) 4[ ]
20 20 Paso 3: Separar en términos lo que está dentro de las llaves y resolver: er Término { = ( 7) 4[ 43] 2do Término { } = 144
Apuntes de matemáticas 2º ESO Curso
 Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el que el sustraendo, pero en la vida nos encontramos con operaciones de este tipo donde a un número menor
Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el que el sustraendo, pero en la vida nos encontramos con operaciones de este tipo donde a un número menor
Opuesto de un número +3 + (-3) = (+5) = 0. N = 0,1, 2,3,4, Conjunto de los números naturales
 Números enteros Opuesto de un número Los números enteros son una extensión de los números naturales, de tal forma, que los números enteros tienen signo positivo (+) ó negativo (-). Los números positivos
Números enteros Opuesto de un número Los números enteros son una extensión de los números naturales, de tal forma, que los números enteros tienen signo positivo (+) ó negativo (-). Los números positivos
Semana 1: Números Reales y sus Operaciones
 Semana 1: Números Reales y sus Operaciones Taller de Preparación para Prueba PLANEA Ing. Jonathan Quiroga Tinoco Conalep Tehuacán P.T.B. en ADMO, SOMA y EMEC UNIDAD 04 Los números enteros y sus operaciones
Semana 1: Números Reales y sus Operaciones Taller de Preparación para Prueba PLANEA Ing. Jonathan Quiroga Tinoco Conalep Tehuacán P.T.B. en ADMO, SOMA y EMEC UNIDAD 04 Los números enteros y sus operaciones
Los números enteros. Dado que los enteros contienen los enteros positivos, se considera a los números naturales son un subconjunto de los enteros.
 Los números enteros Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el que el sustraendo, pero en la vida nos encontramos con operaciones de este tipo donde
Los números enteros Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el que el sustraendo, pero en la vida nos encontramos con operaciones de este tipo donde
NUMEROS ENTEROS ( Z)
 NUMEROS ENTEROS ( Z) En N la resta sólo está definida si el minuendo es mayor o igual al sustraendo. Para que dicha operación no sea tan restringida se creó el conjunto de enteros negativos ( notado por
NUMEROS ENTEROS ( Z) En N la resta sólo está definida si el minuendo es mayor o igual al sustraendo. Para que dicha operación no sea tan restringida se creó el conjunto de enteros negativos ( notado por
Capítulo 5. Los números reales y sus representaciones Pearson Education, Inc. Diapositiva 5-2-1
 Capítulo 5 Los números reales y sus representaciones 2012 Pearson Education, Inc. Diapositiva 5-2-1 Capítulo 5: Los números reales y sus representaciones 5.1 Números reales, orden y valor absoluto 5.2
Capítulo 5 Los números reales y sus representaciones 2012 Pearson Education, Inc. Diapositiva 5-2-1 Capítulo 5: Los números reales y sus representaciones 5.1 Números reales, orden y valor absoluto 5.2
ESCUELA PREPARATORIA OFICIAL NO.16 MATERÍA: PENSAMIENTO NUMÉRICO Y ALGEBRAICO I
 ARITMÉTICA 1. Números naturales 2. Divisibilidad 3. Números enteros 4. Números decimales 5. Fracciones y números racionales 6. Proporcionalidad 7. Sistema métrico decimal 8. Sistema sexagesimal 9. Números
ARITMÉTICA 1. Números naturales 2. Divisibilidad 3. Números enteros 4. Números decimales 5. Fracciones y números racionales 6. Proporcionalidad 7. Sistema métrico decimal 8. Sistema sexagesimal 9. Números
Suma. Propiedades de la suma.
 Suma. La suma es la operación matemática que resulta al reunir en una sola a varias cantidades. También se conoce a la suma como adición. Las cantidades que se suman se llaman sumandos y el resultado suma
Suma. La suma es la operación matemática que resulta al reunir en una sola a varias cantidades. También se conoce a la suma como adición. Las cantidades que se suman se llaman sumandos y el resultado suma
UNIDAD DIDÁCTICA #1 CONTENIDO
 UNIDAD DIDÁCTICA #1 CONTENIDO OPERACIONES CON DECIMALES MULTIPLICACION DE DECIMALES DIVISIÓN DE DECIMALES OPERACIONES COMBINADAS CON DECIMALES POTENCIACIÓN DE DECIMALES HOJA DE EVALUACIÓN BIBLIOGRAFÍA
UNIDAD DIDÁCTICA #1 CONTENIDO OPERACIONES CON DECIMALES MULTIPLICACION DE DECIMALES DIVISIÓN DE DECIMALES OPERACIONES COMBINADAS CON DECIMALES POTENCIACIÓN DE DECIMALES HOJA DE EVALUACIÓN BIBLIOGRAFÍA
Definiciones de: Matematica y Aritmetica
 1 GUIA 1 MATEMATICA Definiciones de: Matematica y Aritmetica 1. DESARROLLO DE LOS SISTEMAS DE NUMERACION: a. Por los instrumentos que ha utilizado el hombre para contar: Marcas en arboles Maquinas Piedras
1 GUIA 1 MATEMATICA Definiciones de: Matematica y Aritmetica 1. DESARROLLO DE LOS SISTEMAS DE NUMERACION: a. Por los instrumentos que ha utilizado el hombre para contar: Marcas en arboles Maquinas Piedras
Escuela Pública Experimental Desconcentrada Nº3 Dr. Carlos Juan Rodríguez Matemática 1º Año Ciclo Básico de Secundaria Teoría Nº 1 Primer Trimestre
 CONJUNTO DE LOS NÚMEROS NATURALES Los números naturales son aquellos números exactos; es decir, que no tienen parte decimal ni fraccionaria; además son todos positivos. Sistema de numeración decimal El
CONJUNTO DE LOS NÚMEROS NATURALES Los números naturales son aquellos números exactos; es decir, que no tienen parte decimal ni fraccionaria; además son todos positivos. Sistema de numeración decimal El
MATEMÁTICAS 1º DE ESO
 MATEMÁTICAS 1º DE ESO LOMCE TEMA I : NÚMEROS NATURALES Sistema de numeración romano. Los números naturales. Números naturales como cardinales y ordinales. o Recta numérica. El sistema de numeración decimal.
MATEMÁTICAS 1º DE ESO LOMCE TEMA I : NÚMEROS NATURALES Sistema de numeración romano. Los números naturales. Números naturales como cardinales y ordinales. o Recta numérica. El sistema de numeración decimal.
Tema 22 Resumen Operaciones de cálculo y procedimientos del mismo
 Tema 22 Resumen Operaciones de cálculo y procedimientos del mismo Operaciones con número naturales Cardinal obtenido al unir dos conjuntos distintos Los términos se denominan. Operación interna N. (Tª
Tema 22 Resumen Operaciones de cálculo y procedimientos del mismo Operaciones con número naturales Cardinal obtenido al unir dos conjuntos distintos Los términos se denominan. Operación interna N. (Tª
TERMINOS HOMOGENEOS: Son los que tienen el mismo grado absoluto, son homogéneos porque ambos son de quinto grado absoluto.
 TERMINOS HOMOGENEOS: Son los que tienen el mismo grado absoluto, son homogéneos porque ambos son de quinto grado absoluto. 4xy y 6xy. Hallando la suma de los exponentes: 4 + 1 = 5 2 + 3 = 5 TERMINOS HETEROGENEOS:
TERMINOS HOMOGENEOS: Son los que tienen el mismo grado absoluto, son homogéneos porque ambos son de quinto grado absoluto. 4xy y 6xy. Hallando la suma de los exponentes: 4 + 1 = 5 2 + 3 = 5 TERMINOS HETEROGENEOS:
TEMA 1. Los números enteros. Matemáticas
 1 Introducción En esta unidad veremos propiedades de los números enteros, como se opera con ellos (con y sin calculadora), los números primos, máximo común divisor y mínimo común múltiplo y por últimos
1 Introducción En esta unidad veremos propiedades de los números enteros, como se opera con ellos (con y sin calculadora), los números primos, máximo común divisor y mínimo común múltiplo y por últimos
ADICIÓN DE NÚMEROS ENTEROS
 ADICIÓN DE NÚMEROS ENTEROS Suma de enteros con signos iguales: Para sumar dos números enteros del mismo signo. Se suma el valor absoluto de las cantidades dadas. Ejemplos: 1) 5 + 7 + 18 = 30 2) ( 8) +
ADICIÓN DE NÚMEROS ENTEROS Suma de enteros con signos iguales: Para sumar dos números enteros del mismo signo. Se suma el valor absoluto de las cantidades dadas. Ejemplos: 1) 5 + 7 + 18 = 30 2) ( 8) +
Los números enteros Z = {,-3, -2, -1, 0, 1, 2, 3, }
 Los números enteros La unión de los números naturales y los enteros negativos forma el conjunto de los números enteros, que se designa con la palabra Z. Está constituido por infinitos elementos y se representan
Los números enteros La unión de los números naturales y los enteros negativos forma el conjunto de los números enteros, que se designa con la palabra Z. Está constituido por infinitos elementos y se representan
TEMA 1: LOS NÚMEROS ENTEROS. Segundo Curso de Educación Secundaria Obligatoria. I.E.S de Fuentesaúco. Manuel González de León.
 TEMA 1: LOS NÚMEROS ENTEROS Segundo Curso de Educación Secundaria Obligatoria. I.E.S de Fuentesaúco. Manuel González de León. CURSO 2011-2012 1. Los Números Enteros. 2. Suma y resta de números enteros.
TEMA 1: LOS NÚMEROS ENTEROS Segundo Curso de Educación Secundaria Obligatoria. I.E.S de Fuentesaúco. Manuel González de León. CURSO 2011-2012 1. Los Números Enteros. 2. Suma y resta de números enteros.
MATEMÁTICAS 1º DE ESO
 MATEMÁTICAS 1º DE ESO LOMCE TEMA III : LOS NÚMEROS ENTEROS Los números negativos. Su necesidad. El conjunto de los números enteros. Valor absoluto de un número entero. Opuesto de un número entero. Suma
MATEMÁTICAS 1º DE ESO LOMCE TEMA III : LOS NÚMEROS ENTEROS Los números negativos. Su necesidad. El conjunto de los números enteros. Valor absoluto de un número entero. Opuesto de un número entero. Suma
INSTITUTO TECNICO MARIA INMACULADA Formando líderes estudiantiles para un futuro mejor
 INSTITUTO TECNICO MARIA INMACULADA Formando líderes estudiantiles para un futuro mejor Coordinación Vo. Bo. Eje temático: OPERACIONES Y PROPIEDADES EN LOS NÚMEROS REALES Área: MATEMÁTICAS Asignatura: Matemáticas
INSTITUTO TECNICO MARIA INMACULADA Formando líderes estudiantiles para un futuro mejor Coordinación Vo. Bo. Eje temático: OPERACIONES Y PROPIEDADES EN LOS NÚMEROS REALES Área: MATEMÁTICAS Asignatura: Matemáticas
CONJUNTO DE LOS NÚMEROS NATURALES
 República Bolivariana de Venezuela Ministerio de la Defensa Universidad Nacional Experimental de las Fuerzas Armadas Curso de Inducción Universitaria CIU Cátedra: Razonamiento Matemático CONJUNTO DE LOS
República Bolivariana de Venezuela Ministerio de la Defensa Universidad Nacional Experimental de las Fuerzas Armadas Curso de Inducción Universitaria CIU Cátedra: Razonamiento Matemático CONJUNTO DE LOS
Números Naturales. Cero elemento neutro: = 12 Sucesión fundamental : se obtiene el siguiente número = 9
 Números Naturales Cuando comenzamos a contar los objetos, los años, etc, nos hemos encontrado con los números de forma natural; por eso a este conjunto de números así aprendidos se les denomina números
Números Naturales Cuando comenzamos a contar los objetos, los años, etc, nos hemos encontrado con los números de forma natural; por eso a este conjunto de números así aprendidos se les denomina números
FIN EDUCATIVO FIN INSTRUCTIVO
 FIN EDUCATIVO Todos somos números en las Matemáticas de la vida, con valores: absolutos, relativos, positivos y negativos. Los primeros representan a nuestras cualidades y virtudes ; los segundos a los
FIN EDUCATIVO Todos somos números en las Matemáticas de la vida, con valores: absolutos, relativos, positivos y negativos. Los primeros representan a nuestras cualidades y virtudes ; los segundos a los
Bloque 1. Aritmética y Álgebra
 Bloque 1. Aritmética y Álgebra 2. Los números enteros 1. Los números enteros Es el conjunto de los números negativos, el cero y los positivos, y se representan como: Z...,-5,-4,-3,-2,-1,0, 1, 2, 3, 4,
Bloque 1. Aritmética y Álgebra 2. Los números enteros 1. Los números enteros Es el conjunto de los números negativos, el cero y los positivos, y se representan como: Z...,-5,-4,-3,-2,-1,0, 1, 2, 3, 4,
FISICA I Repaso. Si el alumno no supera al maestro, ni es bueno el alumno; ni es bueno el maestro (Proverbio Chino)
 Si el alumno no supera al maestro, ni es bueno el alumno; ni es bueno el maestro (Proverbio Chino) Profesor: Cazzaniga, Alejandro J. Física I E.T.N : 28 - República Francesa Pág. 1 de 9 Conjuntos numéricos
Si el alumno no supera al maestro, ni es bueno el alumno; ni es bueno el maestro (Proverbio Chino) Profesor: Cazzaniga, Alejandro J. Física I E.T.N : 28 - República Francesa Pág. 1 de 9 Conjuntos numéricos
5.1 Números Reales Mate 3041 Milena Salcedo V. Copyright Cengage Learning. All rights reserved.
 5.1 Números Reales Mate 3041 Milena Salcedo V R Copyright Cengage Learning. All rights reserved. Números Reales Números Naturales: N = 1,2,3, Números Enteros no negativos (Cardinales): 0,1,2,3, Números
5.1 Números Reales Mate 3041 Milena Salcedo V R Copyright Cengage Learning. All rights reserved. Números Reales Números Naturales: N = 1,2,3, Números Enteros no negativos (Cardinales): 0,1,2,3, Números
Escuela Pública Experimental Desconcentrada Nº3 Dr. Carlos Juan Rodríguez Matemática 1º Año Ciclo Básico de Secundaria Teoría Nº 2 Segundo Trimestre
 CONJUNTO DE LOS NÚMEROS ENTEROS Los números enteros están formados por: los números naturales (o enteros positivos y el cero) y los números negativos. El cero no tiene signo, no es ni positivo ni negativo.
CONJUNTO DE LOS NÚMEROS ENTEROS Los números enteros están formados por: los números naturales (o enteros positivos y el cero) y los números negativos. El cero no tiene signo, no es ni positivo ni negativo.
OPERACIÓN CON NÚMEROS ENTEROS(Z)
 OPERACIÓN CON NÚMEROS ENTEROS(Z) Imagina que un día estas de visita en un apartamento de unos amigos, al despedirte bajas al sótano 2 a buscar tu carro y te das cuenta que dejaste las llaves en casa de
OPERACIÓN CON NÚMEROS ENTEROS(Z) Imagina que un día estas de visita en un apartamento de unos amigos, al despedirte bajas al sótano 2 a buscar tu carro y te das cuenta que dejaste las llaves en casa de
Pre-Universitario Manuel Guerrero Ceballos
 Pre-Universitario Manuel Guerrero Ceballos Clase N 02 Operatoria Resumen de la clase anterior NÚMEROS Conjuntos numéricos Definiciones Orden Q Q* IN IN 0 R II C 9 número impar múltiplos {9, 18, 27, } divisores
Pre-Universitario Manuel Guerrero Ceballos Clase N 02 Operatoria Resumen de la clase anterior NÚMEROS Conjuntos numéricos Definiciones Orden Q Q* IN IN 0 R II C 9 número impar múltiplos {9, 18, 27, } divisores
Los Números Enteros (Z)
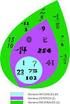 Los Números Enteros (Z) Los números enteros: representación gráfica, orden, modulo o valor absoluto. Operaciones en Z, procedimientos y propiedades de estas. Prioridades de operaciones y paréntesis. Problemas
Los Números Enteros (Z) Los números enteros: representación gráfica, orden, modulo o valor absoluto. Operaciones en Z, procedimientos y propiedades de estas. Prioridades de operaciones y paréntesis. Problemas
Departamento de Matemática TEORÍA DEL CONJUNTO DE LOS NÚNEROS ENTEROS Primer Año
 Departamento de Matemática TEORÍA DEL CONJUNTO DE LOS NÚNEROS ENTEROS Primer Año - 015 Introducción: Tanto en tablas que informan temperaturas como en resúmenes bancarios, en líneas de tiempo de historia,
Departamento de Matemática TEORÍA DEL CONJUNTO DE LOS NÚNEROS ENTEROS Primer Año - 015 Introducción: Tanto en tablas que informan temperaturas como en resúmenes bancarios, en líneas de tiempo de historia,
Operaciones de enteros. Prof. Yaritza González Adaptado por: Yuitza T. Humarán Departamento de Matemáticas UPRA
 Operaciones de enteros Prof. Yaritza González Adaptado por: Yuitza T. Humarán Departamento de Matemáticas UPRA Suma de enteros: Reglas Suma de dos enteros negativos o dos enteros positivos El total es
Operaciones de enteros Prof. Yaritza González Adaptado por: Yuitza T. Humarán Departamento de Matemáticas UPRA Suma de enteros: Reglas Suma de dos enteros negativos o dos enteros positivos El total es
Lic. Manuel de Jesús Campos Boc
 UNIVERSIDAD MARIANO GÁLVEZ DE GUATEMALA FACULTAD DE CIENCIAS DE LA ADMINISTRACIÓN DIRECCIÓN GENERAL DE CENTRO UNIVERSITARIOS CENTRO UNIVERSITARIO DE VILLA NUEVA CURSO MATEMÁTICAS APLICADA I 015 Lic. Manuel
UNIVERSIDAD MARIANO GÁLVEZ DE GUATEMALA FACULTAD DE CIENCIAS DE LA ADMINISTRACIÓN DIRECCIÓN GENERAL DE CENTRO UNIVERSITARIOS CENTRO UNIVERSITARIO DE VILLA NUEVA CURSO MATEMÁTICAS APLICADA I 015 Lic. Manuel
Números enteros. Los números enteros son los formados por los números naturales (1), sus opuestos (2) y el número 0
 Los números enteros son los formados por los números naturales, sus opuestos (2) y el número 0 Números enteros Los números naturales son aquellos que nos permiten contar las cosas. Ej. 2 sillas, 4 patas,
Los números enteros son los formados por los números naturales, sus opuestos (2) y el número 0 Números enteros Los números naturales son aquellos que nos permiten contar las cosas. Ej. 2 sillas, 4 patas,
Tema 1.- Los números reales
 Tema 1.- Los números reales Los números irracionales Un número es irracional si posee infinitas cifras decimales no periódicas, por tanto no se puede expresar en forma de fracción. El número irracional
Tema 1.- Los números reales Los números irracionales Un número es irracional si posee infinitas cifras decimales no periódicas, por tanto no se puede expresar en forma de fracción. El número irracional
CONJUTOS NÚMERICOS NÚMEROS NATURALES
 CONJUTOS NÚMERICOS NÚMEROS NATURALES El conjunto de números naturales tiene gran importancia en la vida práctica ya que con sus elementos se pueden encontrar elementos u objetos de otros conjuntos. El
CONJUTOS NÚMERICOS NÚMEROS NATURALES El conjunto de números naturales tiene gran importancia en la vida práctica ya que con sus elementos se pueden encontrar elementos u objetos de otros conjuntos. El
Suma de números enteros
 NÚMEROS ENTEROS. RESUMEN Los números enteros son del tipo: = {... 5, 4, 3, 2, 1, 0, 1, 2, 3, 4, 5...} Es decir, los naturales, sus opuestos (negativos) y el cero. Valor absoluto El valor absoluto de un
NÚMEROS ENTEROS. RESUMEN Los números enteros son del tipo: = {... 5, 4, 3, 2, 1, 0, 1, 2, 3, 4, 5...} Es decir, los naturales, sus opuestos (negativos) y el cero. Valor absoluto El valor absoluto de un
Operaciones con números enteros
 1. Identificación Nivel: Primario Área: Matemática Grado: Sexto SC 10: Resumen: En esta Unidad Didáctica se identifican los números enteros positivos y negativos. Se resuelven operaciones de adición y
1. Identificación Nivel: Primario Área: Matemática Grado: Sexto SC 10: Resumen: En esta Unidad Didáctica se identifican los números enteros positivos y negativos. Se resuelven operaciones de adición y
Def.- Los números naturales son aquellos que utilizamos para contar o designar los elementos que existen en un conjunto.
 3 LANDLFORMACION Los Conjuntos Numéricos. Los Números Naturales. Introducción Def.- Los números naturales son aquellos que utilizamos para contar o designar los elementos que existen en un conjunto. Pueden
3 LANDLFORMACION Los Conjuntos Numéricos. Los Números Naturales. Introducción Def.- Los números naturales son aquellos que utilizamos para contar o designar los elementos que existen en un conjunto. Pueden
Catedrático: I.S.C. Iván de J. Moscoso Navarro Contenido:
 Materia: Matemáticas I Catedrático: I.S.C. Iván de J. Moscoso Navarro Contenido: UNIDAD TEMATICA II.- SISTEMAS NUMÉRICOS 2.1 Números Naturales ( N )... Introducción Propiedades de la adición de los números
Materia: Matemáticas I Catedrático: I.S.C. Iván de J. Moscoso Navarro Contenido: UNIDAD TEMATICA II.- SISTEMAS NUMÉRICOS 2.1 Números Naturales ( N )... Introducción Propiedades de la adición de los números
Comparación y Orden: El termómetro marca -3ºC a la tarde y 7ºC a la noche, la temperatura, bajó o subió? Ubiquemos esos valores en la recta numérica:
 Números Enteros: En nuestro país tenemos un relieve montañoso al oeste y llano al este. Esto da por resultado una pendiente general del terreno hacia el Océano Atlántico. Pero la tierra se extiende bajo
Números Enteros: En nuestro país tenemos un relieve montañoso al oeste y llano al este. Esto da por resultado una pendiente general del terreno hacia el Océano Atlántico. Pero la tierra se extiende bajo
PROPEDEUTICO DE MATEMATICAS I UNIDAD ARITMETICA
 PROPEDEUTICO DE MATEMATICAS I UNIDAD ARITMETICA 1.1 CLASIFICACION DE LOS NUMEROS Los números REALES (denotados por R ) son el conjunto de números creados por el hombre para poder transmitir mediante un
PROPEDEUTICO DE MATEMATICAS I UNIDAD ARITMETICA 1.1 CLASIFICACION DE LOS NUMEROS Los números REALES (denotados por R ) son el conjunto de números creados por el hombre para poder transmitir mediante un
Tema 3. Números Enteros
 Tema 3. Números Enteros Javier Rodríguez Ruiz Curso 2012-2013 Índice 1. Introducción a los números enteros (Z) 2 2. Sumas y restas de números enteros 5 3. Productos y divisiones de números enteros 8 4.
Tema 3. Números Enteros Javier Rodríguez Ruiz Curso 2012-2013 Índice 1. Introducción a los números enteros (Z) 2 2. Sumas y restas de números enteros 5 3. Productos y divisiones de números enteros 8 4.
7.1 Números Racionales: números enteros, propiedades de los números y orden de operaciones. Prof. Kyria A. Pérez
 7.1 Números Racionales: números enteros, propiedades de los números y orden de operaciones Prof. Kyria A. Pérez Estándares de contenido y expectativas N.SO.7.2.1- Modela la suma, Resta, multiplicación
7.1 Números Racionales: números enteros, propiedades de los números y orden de operaciones Prof. Kyria A. Pérez Estándares de contenido y expectativas N.SO.7.2.1- Modela la suma, Resta, multiplicación
ASIGNATURA: MATEMATICAS NOTA TIPO DE GUIA: CONCEPTUAL - EJERCITACION PERIODO GRADO FECHA N DURACION 2 6 ABRIL 06 / UNIDADES
 INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMATICAS ASIGNATURA: MATEMATICAS NOTA DOCENTE: HUGO HERNAN BEDOYA TIPO DE GUIA: CONCEPTUAL - EJERCITACION PERIODO GRADO FECHA N DURACION 2
INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMATICAS ASIGNATURA: MATEMATICAS NOTA DOCENTE: HUGO HERNAN BEDOYA TIPO DE GUIA: CONCEPTUAL - EJERCITACION PERIODO GRADO FECHA N DURACION 2
5. División exacta de números enteros. 6. Operaciones combinadas. Regla de prioridades. 7. Potencia de números enteros con exponente natural.
 1 MATEMÁTICAS Nivel 2º E.S.O. Tema 2º NÚMEROS ENTEROS Conocimientos que puedes adquirir: 1. El conjunto de números enteros: a) Positivos, negativos y el cero. b) Representación gráfica. c) Valor absoluto.
1 MATEMÁTICAS Nivel 2º E.S.O. Tema 2º NÚMEROS ENTEROS Conocimientos que puedes adquirir: 1. El conjunto de números enteros: a) Positivos, negativos y el cero. b) Representación gráfica. c) Valor absoluto.
El conjunto de números enteros está formado por los números naturales, sus opuestos (negativos) y el cero.
 1 1. NÚMEROS ENTEROS El conjunto de números enteros está formado por los números naturales, sus opuestos (negativos) y el cero. La necesidad de representar el dinero adeudado, la temperatura bajo cero,
1 1. NÚMEROS ENTEROS El conjunto de números enteros está formado por los números naturales, sus opuestos (negativos) y el cero. La necesidad de representar el dinero adeudado, la temperatura bajo cero,
UNIDAD DE APRENDIZAJE II
 UNIDAD DE APRENDIZAJE II NÚMEROS RACIONALES Jerarquía de Operaciones En matemáticas una operación es una acción realizada sobre un número (en el caso de la raíz y potencia) o donde se involucran dos números
UNIDAD DE APRENDIZAJE II NÚMEROS RACIONALES Jerarquía de Operaciones En matemáticas una operación es una acción realizada sobre un número (en el caso de la raíz y potencia) o donde se involucran dos números
Materia: Matemática de Octavo Tema: Operaciones en Q Propiedades de la Multiplicación en Q
 Materia: Matemática de Octavo Tema: Operaciones en Q Propiedades de la Multiplicación en Q Las propiedades de la multiplicación en el conjunto, ya las hemos estudiado para el conjunto de los números naturales
Materia: Matemática de Octavo Tema: Operaciones en Q Propiedades de la Multiplicación en Q Las propiedades de la multiplicación en el conjunto, ya las hemos estudiado para el conjunto de los números naturales
El número áureo,, utilizado por artistas de todas las épocas (Fidias, Leonardo da Vinci, Alberto Durero, Dalí,..) en las proporciones de sus obras.
 1.- LOS NÚMEROS REALES Los números irracionales Un número es irracional si posee infinitas cifras decimales no periódicas, por tanto no se pueden expresar en forma de fracción. El número irracional más
1.- LOS NÚMEROS REALES Los números irracionales Un número es irracional si posee infinitas cifras decimales no periódicas, por tanto no se pueden expresar en forma de fracción. El número irracional más
Números Reales. Números Irracionales
 INSTITUTO FRAY MAMERTO ESQUIU Números Reales La unión del conjunto de los números racionales con el conjunto de los números irracionales recibe el nombre de conjunto de los números reales, y se denota
INSTITUTO FRAY MAMERTO ESQUIU Números Reales La unión del conjunto de los números racionales con el conjunto de los números irracionales recibe el nombre de conjunto de los números reales, y se denota
TEMA 1 NÚMEROS NATURALES
 TEMA 1 NÚMEROS NATURALES Criterios De Evaluación de la Unidad 1 Efectuar correctamente operaciones combinadas de números naturales, aplicando correctamente las reglas de prioridad y haciendo un uso adecuado
TEMA 1 NÚMEROS NATURALES Criterios De Evaluación de la Unidad 1 Efectuar correctamente operaciones combinadas de números naturales, aplicando correctamente las reglas de prioridad y haciendo un uso adecuado
1.1.- LA SUMA O ADICIÓN: Sumar es añadir una cantidad a otra; juntar o reunir varias cantidades en una sola.
 LECCIÓN 2: OPERACIONES CON NÚMEROS ENTEROS 1.- SUMA DE NÚMEROS ENTEROS 1.1.- LA SUMA O ADICIÓN: Sumar es añadir una cantidad a otra; juntar o reunir varias cantidades en una sola. SIGNO DE LA SUMA: Es
LECCIÓN 2: OPERACIONES CON NÚMEROS ENTEROS 1.- SUMA DE NÚMEROS ENTEROS 1.1.- LA SUMA O ADICIÓN: Sumar es añadir una cantidad a otra; juntar o reunir varias cantidades en una sola. SIGNO DE LA SUMA: Es
LEY DE LOS SIGNOS, TEORÍA DE AGRUPAMIENTO Y ORDEN DE OPERACIONES
 LEY DE LOS SIGNOS, TEORÍA DE AGRUPAMIENTO Y ORDEN DE OPERACIONES LEY DE LOS SIGNOS SUMA Si los números tienen el mismo signo se suman se deja el mismo signo. 3 + 5 = 8 ( 3) + ( 5) = 8 Si números tienen
LEY DE LOS SIGNOS, TEORÍA DE AGRUPAMIENTO Y ORDEN DE OPERACIONES LEY DE LOS SIGNOS SUMA Si los números tienen el mismo signo se suman se deja el mismo signo. 3 + 5 = 8 ( 3) + ( 5) = 8 Si números tienen
1 ESO MATEMÁTICAS TEMA 3: NÚMEROS ENTEROS
 IES Alcarria Baja MONDÉJAR 1 ESO MATEMÁTICAS TEMA 3: NÚMEROS ENTEROS EJERCICIOS NÚMEROS ENTEROS 1. Completa los huecos para que las afirmaciones siguientes sean ciertas: a) El cero es..................
IES Alcarria Baja MONDÉJAR 1 ESO MATEMÁTICAS TEMA 3: NÚMEROS ENTEROS EJERCICIOS NÚMEROS ENTEROS 1. Completa los huecos para que las afirmaciones siguientes sean ciertas: a) El cero es..................
OPERACIONES CON NÚMEROS REALES
 NÚMEROS REALES Por número real llamaremos a un número que puede ser racional o irracional, por consiguiente, el conjunto de los números reales es la unión del conjunto de números racionales y el conjunto
NÚMEROS REALES Por número real llamaremos a un número que puede ser racional o irracional, por consiguiente, el conjunto de los números reales es la unión del conjunto de números racionales y el conjunto
Representación de los números naturales
 Números naturales El conjunto de los números naturales se representa por la letra, y está formado por: N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9,...} Los números naturales sirven para contar los elementos de un
Números naturales El conjunto de los números naturales se representa por la letra, y está formado por: N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9,...} Los números naturales sirven para contar los elementos de un
CONJUNTO DE LOS NÚMEROS NATURALES
 CONJUNTO DE LOS NÚMEROS NATURALES 1.- DEFINICIÓN DEL CONJUNTO DE LOS NÚMEROS NATURALES (Conjunto N): Un número natural es cualquier número que se puede usar para contar los elementos de un conjunto finito.
CONJUNTO DE LOS NÚMEROS NATURALES 1.- DEFINICIÓN DEL CONJUNTO DE LOS NÚMEROS NATURALES (Conjunto N): Un número natural es cualquier número que se puede usar para contar los elementos de un conjunto finito.
 Titulo: MULTIPLICACION Y DIVISIÓN DE POLINOMIOS Año escolar: 3ER: año de bachillerato Autor: José Luis Albornoz Salazar Ocupación: Ing Civil. Docente Universitario País de residencia: Venezuela Correo
Titulo: MULTIPLICACION Y DIVISIÓN DE POLINOMIOS Año escolar: 3ER: año de bachillerato Autor: José Luis Albornoz Salazar Ocupación: Ing Civil. Docente Universitario País de residencia: Venezuela Correo
Unidad didáctica 1. Operaciones básicas con números enteros
 Unidad didáctica 1 Operaciones básicas con números enteros 1.- Representación y ordenación de números enteros. Para representar números enteros en una recta hay que seguir estos pasos: a) Se dibuja una
Unidad didáctica 1 Operaciones básicas con números enteros 1.- Representación y ordenación de números enteros. Para representar números enteros en una recta hay que seguir estos pasos: a) Se dibuja una
UNIDAD II: CONJUNTOS NUMÉRICOS
 Presentación En esta unidad se aborda el estudio de los conjuntos numéricos, la operatoria y propiedades en ellos, dando énfasis al trabajo de operatoria básica en IR, potencias, raíces y logaritmos. En
Presentación En esta unidad se aborda el estudio de los conjuntos numéricos, la operatoria y propiedades en ellos, dando énfasis al trabajo de operatoria básica en IR, potencias, raíces y logaritmos. En
= RESP = + 7 se suman los del mismo signo 3 3 = 6 se suman los del mismo signo
 SUMA Y RESTA DE NUMEROS ENTEROS y ALGEBRAICOS A) SUMA Y RESTA 3 + 2 + 5 3 = RESP + 1 2 + 5 = + 7 se suman los del mismo signo 3 3 = 6 se suman los del mismo signo + 7 6 = + 1 se restan signos contrarios
SUMA Y RESTA DE NUMEROS ENTEROS y ALGEBRAICOS A) SUMA Y RESTA 3 + 2 + 5 3 = RESP + 1 2 + 5 = + 7 se suman los del mismo signo 3 3 = 6 se suman los del mismo signo + 7 6 = + 1 se restan signos contrarios
ALGEBRA. a b. abc. Álgebra. Rama de las matemáticas que generaliza los métodos y procedimientos para efectuar Cálculos y resolver problemas.
 ALGEBRA Álgebra. Rama de las matemáticas que generaliza los métodos procedimientos para efectuar Cálculos resolver problemas. Área del círculo.= r Volumen del cilindro = r h LENGUAJE ALGEBRAICO El lenguaje
ALGEBRA Álgebra. Rama de las matemáticas que generaliza los métodos procedimientos para efectuar Cálculos resolver problemas. Área del círculo.= r Volumen del cilindro = r h LENGUAJE ALGEBRAICO El lenguaje
Operaciones con números enteros
 Operaciones con números enteros Suma de números enteros Cuando tienen el mismo signo: Se suman los valores y se deja el signo que tengan, si son positivos signo positivo y si son negativos signo negativo.
Operaciones con números enteros Suma de números enteros Cuando tienen el mismo signo: Se suman los valores y se deja el signo que tengan, si son positivos signo positivo y si son negativos signo negativo.
Suma de números enteros
 NÚMEROS ENTEROS. RESUMEN Los números enteros son del tipo: = {... 5, 4, 3, 2, 1, 0, 1, 2, 3, 4, 5...} Es decir, los naturales, sus opuestos (negativos) y el cero. Valor absoluto El valor absoluto de un
NÚMEROS ENTEROS. RESUMEN Los números enteros son del tipo: = {... 5, 4, 3, 2, 1, 0, 1, 2, 3, 4, 5...} Es decir, los naturales, sus opuestos (negativos) y el cero. Valor absoluto El valor absoluto de un
INSTITUTO DE ESTUDIOS BANCARIOS GUILLERMO SUBERCASEAUX Fundado en Matemáticas I. Técnico Financiero Semestre CONJUNTOS NUMERICOS
 Matemáticas I Técnico Financiero Semestre 1-2008 CONJUNTOS NUMERICOS I. Números naturales El conjunto de los números naturales se representa por IN y corresponde al siguiente conjunto numérico: IN = {1,
Matemáticas I Técnico Financiero Semestre 1-2008 CONJUNTOS NUMERICOS I. Números naturales El conjunto de los números naturales se representa por IN y corresponde al siguiente conjunto numérico: IN = {1,
PRIMER CURSO AÑO LECTIVO El módulo de la multiplicación es el 0 V F. 4. La división de Z si cumple la propiedad conmutativa V F
 BANCO DE PREGUNTAS PRIMER SEMESTRE PRIMER CURSO AÑO LECTIVO 007-008 I. Establezca si las siguientes proposiciones son verdaderas o falsas 1. En el ejercicio 1 + 4 48 el factor común es 1 V F. Los términos
BANCO DE PREGUNTAS PRIMER SEMESTRE PRIMER CURSO AÑO LECTIVO 007-008 I. Establezca si las siguientes proposiciones son verdaderas o falsas 1. En el ejercicio 1 + 4 48 el factor común es 1 V F. Los términos
NÚMEROS NATURALES. DIVISIBILIDAD. NÚMEROS ENTEROS
 UNIDAD 0: NÚMEROS NATURALES. DIVISIBILIDAD. NÚMEROS ENTEROS ESTRUCTURA DEL SISTEMA DE NUMERACIÓN DECIMAL Nuestro sistema de numeración es decimal y posicional. Para escribir cualquier número se utilizan
UNIDAD 0: NÚMEROS NATURALES. DIVISIBILIDAD. NÚMEROS ENTEROS ESTRUCTURA DEL SISTEMA DE NUMERACIÓN DECIMAL Nuestro sistema de numeración es decimal y posicional. Para escribir cualquier número se utilizan
FICHAS REPASO 3º ESO. Para restar números enteros, se suma al minuendo el opuesto del sustraendo y después se aplican las reglas de la suma.
 FICHAS REPASO º ESO OPERACIONES CON NÚMEROS ENTEROS El valor absoluto de un número entero es el número natural que resulta al prescindir del signo. Por ejemplo, el valor absoluto de es y el valor absoluto
FICHAS REPASO º ESO OPERACIONES CON NÚMEROS ENTEROS El valor absoluto de un número entero es el número natural que resulta al prescindir del signo. Por ejemplo, el valor absoluto de es y el valor absoluto
ESCUELA PREPARATORIA OFICIAL NO.16 MATERÍA: PENSAMIENTO NUMÉRICO Y ALGEBRAICO I
 Fracción Una fracción es el cociente de dos números enteros a y b, que representamos de la siguiente forma: b a denominador, indica el número de partes en que se ha dividido la unidad. numerador, indica
Fracción Una fracción es el cociente de dos números enteros a y b, que representamos de la siguiente forma: b a denominador, indica el número de partes en que se ha dividido la unidad. numerador, indica
CONJUNTO DE LOS NÚMEROS NATURALES
 CONJUNTO DE LOS NÚMEROS NATURALES NÚMEROS: Hace referencia a los signos o conjunto de signos que permiten expresar una cantidad con relación a su unidad. Existen distintos grupos de números, como los números
CONJUNTO DE LOS NÚMEROS NATURALES NÚMEROS: Hace referencia a los signos o conjunto de signos que permiten expresar una cantidad con relación a su unidad. Existen distintos grupos de números, como los números
MÓDULO 3: HERRAMIENTAS
 MÓDULO 3: HERRAMIENTAS MATEMÁTICAS PARA FÍSICA (PARTE I). Física Lenguaje algebraico. UTN Facultad Regional Trenque Lauquen 27/01/2015 MÓDULO 3: HERRAMIENTAS MATEMÁTICAS PARA FÍSICA (PARTE I). Física El
MÓDULO 3: HERRAMIENTAS MATEMÁTICAS PARA FÍSICA (PARTE I). Física Lenguaje algebraico. UTN Facultad Regional Trenque Lauquen 27/01/2015 MÓDULO 3: HERRAMIENTAS MATEMÁTICAS PARA FÍSICA (PARTE I). Física El
MATEMÁTICAS I CICLO COMÚN UNIDAD DIDÁCTICA #6
 UNIDAD DIDÁCTICA #6 INDICE PÁGINA Ampliación del conjunto de los números naturales ------------------------------------------------------2 Uso de los números enteros y su representación en la recta numérica
UNIDAD DIDÁCTICA #6 INDICE PÁGINA Ampliación del conjunto de los números naturales ------------------------------------------------------2 Uso de los números enteros y su representación en la recta numérica
NÚMEROS ENTEROS. En la recta numérica se pueden representar los números naturales, el cero y los números negativos.
 NÚMEROS ENTEROS El conjunto de los números enteros está formado por: Los números positivos (1, 2, 3, 4, 5, ) Los números negativos ( El cero (no tiene signo) Recta numérica En la recta numérica se pueden
NÚMEROS ENTEROS El conjunto de los números enteros está formado por: Los números positivos (1, 2, 3, 4, 5, ) Los números negativos ( El cero (no tiene signo) Recta numérica En la recta numérica se pueden
Y LOS ELEMENTOS QUE FORMAN UN POLINOMIO. Nombre: Curso: Fecha: F Cómo es el polinomio, completo o incompleto?
 REPASO Y APOYO OBJETIVO 1 3 RECONOCER EL GRADO Y LOS ELEMENTOS QUE ORMAN UN POLINOMIO Nombre: Curso: echa: Un polinomio es una expresión algebraica formada por la suma algebraica de monomios, que son los
REPASO Y APOYO OBJETIVO 1 3 RECONOCER EL GRADO Y LOS ELEMENTOS QUE ORMAN UN POLINOMIO Nombre: Curso: echa: Un polinomio es una expresión algebraica formada por la suma algebraica de monomios, que son los
Ley distributiva Asocia las operaciones de suma y producto de la siguiente manera a x (b + c) = a x b + a x c
 Unidad 1- Trabajo Práctico 1 Operaciones Básicas con Números Reales Las operaciones básicas que pueden realizarse con los Números Reales son las de Suma Resta Producto Cociente Potencia Radicación Leyes
Unidad 1- Trabajo Práctico 1 Operaciones Básicas con Números Reales Las operaciones básicas que pueden realizarse con los Números Reales son las de Suma Resta Producto Cociente Potencia Radicación Leyes
Por ejemplo, la necesidad de representar el dinero adeudado, temperatura bajo cero, profundidades con respecto al nivel del mar, etc.
 NÚMEROS ENTEROS 1. LOS NÚMEROS ENTEROS. Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el sustraendo, pero en la vida nos encontramos con operaciones de este
NÚMEROS ENTEROS 1. LOS NÚMEROS ENTEROS. Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el sustraendo, pero en la vida nos encontramos con operaciones de este
Unidad didáctica 1. Operaciones básicas con números enteros
 Unidad didáctica 1 Operaciones básicas con números enteros 1.- Representación y ordenación de números enteros Para representar números enteros en una recta hay que seguir estos pasos: a) Se dibuja una
Unidad didáctica 1 Operaciones básicas con números enteros 1.- Representación y ordenación de números enteros Para representar números enteros en una recta hay que seguir estos pasos: a) Se dibuja una
INSTITUCIÓN EDUCATIVA JORGE ROBLEDO PLAN DE APOYO
 FECHA:07-0-204 Página de 4 ÁREA/ASIGNATURA: ARITMÉTICA PARA LA PROMOCIÓN ANTICIPADA GRADO: SEXTO AÑO: 207 INSTRUCCIONES: La entrega de la solución, por escrito y bien presentada, es requisito indispensable
FECHA:07-0-204 Página de 4 ÁREA/ASIGNATURA: ARITMÉTICA PARA LA PROMOCIÓN ANTICIPADA GRADO: SEXTO AÑO: 207 INSTRUCCIONES: La entrega de la solución, por escrito y bien presentada, es requisito indispensable
RESUMEN DE ALGEBRA. CONCEPTO: El pensador principal del algebra es Al-Hwarizmi; es de origen árabe.
 RESUMEN DE ALGEBRA CONCEPTO: El pensador principal del algebra es Al-Hwarizmi; es de origen árabe. El álgebra es la rama del conocimiento de la matemática; es decir se desprende de ella. Estudia realidades
RESUMEN DE ALGEBRA CONCEPTO: El pensador principal del algebra es Al-Hwarizmi; es de origen árabe. El álgebra es la rama del conocimiento de la matemática; es decir se desprende de ella. Estudia realidades
M.E.M. RAMSES ANTONIO BARBERI ROSAS
 MATEMÁTICAS I Chic@s les mando el cuadernillo el cual esta explicado de una manera muy sencilla y práctica, la solución de ejercicios y problemas los vamos a revisar continuamente en fechas que por whatsapp
MATEMÁTICAS I Chic@s les mando el cuadernillo el cual esta explicado de una manera muy sencilla y práctica, la solución de ejercicios y problemas los vamos a revisar continuamente en fechas que por whatsapp
Teoría (resumen) Por ejemplo, los múltiplos de 3 son: 3, 6, 9, 12, 15, 18, ; los múltiplos de 2 son: 2, 4, 6, 8, 10, 12, ; o sea los números pares.
 1.- Divisibilidad Teoría (resumen) Múltiplos de un número. Son aquellos que se obtienen al multiplicar dicho número por los números naturales 1, 2, 3,. Por ejemplo, los múltiplos de 3 son: 3, 6, 9, 12,
1.- Divisibilidad Teoría (resumen) Múltiplos de un número. Son aquellos que se obtienen al multiplicar dicho número por los números naturales 1, 2, 3,. Por ejemplo, los múltiplos de 3 son: 3, 6, 9, 12,
*Número natural, el que sirve para designar la cantidad de. *El cero, a veces, se excluye del conjunto de los números
 *Número natural, el que sirve para designar la cantidad de elementos que tiene un cierto conjunto, y se llama cardinal de dicho conjunto. *Los números naturales son infinitos. El conjunto de todos ellos
*Número natural, el que sirve para designar la cantidad de elementos que tiene un cierto conjunto, y se llama cardinal de dicho conjunto. *Los números naturales son infinitos. El conjunto de todos ellos
TEMA Nº 1. Conjuntos numéricos
 TEMA Nº 1 Conjuntos numéricos Aprendizajes esperados: Utilizar y clasificar los distintos conjuntos numéricos en sus diversas formas de expresión, tanto en las ciencias exactas como en las ciencias sociales
TEMA Nº 1 Conjuntos numéricos Aprendizajes esperados: Utilizar y clasificar los distintos conjuntos numéricos en sus diversas formas de expresión, tanto en las ciencias exactas como en las ciencias sociales
OPERACIONES CON POLINOMIOS
 4. 1 UNIDAD 4 OPERACIONES CON POLINOMIOS Objetivo general. Al terminar esta Unidad resolverás ejercicios y problemas en los que apliques las operaciones de suma, resta, multiplicación y división de polinomios.
4. 1 UNIDAD 4 OPERACIONES CON POLINOMIOS Objetivo general. Al terminar esta Unidad resolverás ejercicios y problemas en los que apliques las operaciones de suma, resta, multiplicación y división de polinomios.
TEMA 2: NÚMEROS ENTEROS 1º ESO. MATEMÁTICAS
 TEMA 2: NÚMEROS ENTEROS 1º ESO. MATEMÁTICAS Por qué aparecen los números enteros? Por qué aparecen los números enteros? La cueva de Voronia, es la cueva conocida más profunda de la Tierra, localizada
TEMA 2: NÚMEROS ENTEROS 1º ESO. MATEMÁTICAS Por qué aparecen los números enteros? Por qué aparecen los números enteros? La cueva de Voronia, es la cueva conocida más profunda de la Tierra, localizada
REPASO ALGEBRA ELEMENTAL
 REPASO ALGEBRA ELEMENTAL OPERACIONES MATEMÁTICAS POR: DRA. KARILUZ DÁVILA DÍAZ Operaciones matemáticas comunes Operaciones matemáticas comunes que se utilizan en el curso de Química General son: Operación
REPASO ALGEBRA ELEMENTAL OPERACIONES MATEMÁTICAS POR: DRA. KARILUZ DÁVILA DÍAZ Operaciones matemáticas comunes Operaciones matemáticas comunes que se utilizan en el curso de Química General son: Operación
CURSO CEPA LOS LLANOS
 Módulo 2 CURSO 2017-18 CEPA LOS LLANOS ÁMBITO CIENTÍFICO Y TECNOLÓGICO Bloque 4. Números enteros y potencias. Expresiones algebraicas, ecuaciones de primer grado y representaciones gráficas. La célula
Módulo 2 CURSO 2017-18 CEPA LOS LLANOS ÁMBITO CIENTÍFICO Y TECNOLÓGICO Bloque 4. Números enteros y potencias. Expresiones algebraicas, ecuaciones de primer grado y representaciones gráficas. La célula
MANEJO DE ESPACIOS Y CANTIDADES ALGEBRA
 MANEJO DE ESPACIOS Y CANTIDADES ALGEBRA ALGEBRA: es el nombre que identifica a una rama de la Matemática que emplea números, letras y signos para poder hacer referencia a múltiples operaciones aritméticas.
MANEJO DE ESPACIOS Y CANTIDADES ALGEBRA ALGEBRA: es el nombre que identifica a una rama de la Matemática que emplea números, letras y signos para poder hacer referencia a múltiples operaciones aritméticas.
1. Escribir los Z del 7 al 23: 2. Completar con el signo < o >, según corresponda (véase el primer ejemplo):
 EJERCICIOS de ENTEROS º ESO FICHA 1: Concepto de nº entero. Representación en la recta R 1. Escribir los Z del 7 al :. Completar con el signo < o >, según corresponda (véase el primer ejemplo): a) < 7
EJERCICIOS de ENTEROS º ESO FICHA 1: Concepto de nº entero. Representación en la recta R 1. Escribir los Z del 7 al :. Completar con el signo < o >, según corresponda (véase el primer ejemplo): a) < 7
LOS NÚMEROS ENTEROS. Para restar un número entero, se quita el paréntesis y se pone al número el signo contrario al que tenía.
 Melilla Los números Enteros y operaciones elementales LOS NÚMEROS ENTEROS 1º LOS NÚMEROS ENTEROS. El conjunto de los números enteros Z está formado por los números naturales (enteros positivos) el cero
Melilla Los números Enteros y operaciones elementales LOS NÚMEROS ENTEROS 1º LOS NÚMEROS ENTEROS. El conjunto de los números enteros Z está formado por los números naturales (enteros positivos) el cero
Los números naturales están ordenados, lo que nos permite comparar dos números naturales:
 LOS NUMEROS NATURALES. El conjunto de los números naturales está formado por: N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9,...} Con los números naturales contamos los elementos de un conjunto (número cardinal). O
LOS NUMEROS NATURALES. El conjunto de los números naturales está formado por: N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9,...} Con los números naturales contamos los elementos de un conjunto (número cardinal). O
1.- DE LOS NÚMEROS NATURALES A LOS NÚMEROS ENTEROS
 1.- DE LOS NÚMEROS NATURALES A LOS NÚMEROS ENTEROS Conjunto de los números naturales: N 1, 2, 3,. Conjunto de los números enteros: Z Positivos: +1, +2, + 3, El 0 Negativos: -1, -2, -3, Los enteros positivos
1.- DE LOS NÚMEROS NATURALES A LOS NÚMEROS ENTEROS Conjunto de los números naturales: N 1, 2, 3,. Conjunto de los números enteros: Z Positivos: +1, +2, + 3, El 0 Negativos: -1, -2, -3, Los enteros positivos
T. P. Números Racionales: Q. a es igual a 1?, cuándo es menor?, cuándo es mayor?
 T P Números Racionales Q Si a b pertenecen a los enteros, a b SIEMPRE pertenece a los enteros? Exploren las distintas posibilidades (positivos negativos Den ejemplos de acuerdo con cada caso posible Qué
T P Números Racionales Q Si a b pertenecen a los enteros, a b SIEMPRE pertenece a los enteros? Exploren las distintas posibilidades (positivos negativos Den ejemplos de acuerdo con cada caso posible Qué
sumando sumando sumando sumandos sumandos = 38.6 Cualquier número que se suma.
 sumando sumando 33 + 4.7 + 0.9 = 38.6 sumandos sumando 33 + 4.7 + 0.9 = 38.6 sumandos Cualquier número que se suma. algoritmo Ejemplo de producto parcial algoritmo 555 x 7 35 Paso 1: Multiplicar las unidades
sumando sumando 33 + 4.7 + 0.9 = 38.6 sumandos sumando 33 + 4.7 + 0.9 = 38.6 sumandos Cualquier número que se suma. algoritmo Ejemplo de producto parcial algoritmo 555 x 7 35 Paso 1: Multiplicar las unidades
LOGRO: Reconoce distintas representaciones de los números reales y usa sus propiedades para resolver Problemas.
 ESTANDARES Utilizo números reales en sus diferentes representaciones y en diversos contextos. Resuelvo problemas y simplifico cálculos usando propiedades y relaciones de los números reales y de las relaciones
ESTANDARES Utilizo números reales en sus diferentes representaciones y en diversos contextos. Resuelvo problemas y simplifico cálculos usando propiedades y relaciones de los números reales y de las relaciones
NUMEROS NATURALES. En esta unidad se da un repaso de los diferentes conjuntos de números que existen en matemáticas.
 LOS NUMEROS En esta unidad se da un repaso de los diferentes conjuntos de números que existen en matemáticas. Un conjunto es una "colección de objetos"; Así, se puede hablar de un conjunto de personas,
LOS NUMEROS En esta unidad se da un repaso de los diferentes conjuntos de números que existen en matemáticas. Un conjunto es una "colección de objetos"; Así, se puede hablar de un conjunto de personas,
Suma. Propiedades de la suma. Asociativa
 Suma La suma es la operación matemática que resulta de reunir en una sola varias cantidades. También se conoce a la suma como adición. Las cantidades que se suman se llaman sumandos y el resultado suma
Suma La suma es la operación matemática que resulta de reunir en una sola varias cantidades. También se conoce a la suma como adición. Las cantidades que se suman se llaman sumandos y el resultado suma
