9. MEDIDA DE LA DENSIDAD DE LÍQUIDOS
|
|
|
- Juan Manuel Domínguez Sosa
- hace 7 años
- Vistas:
Transcripción
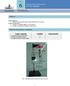
1 9. MEDIDA DE LA DENSIDAD DE LÍQUIDOS OBJETIVO El objetivo de la practica es determinar la densidad de líquidos utilizando la balanza de Möhr y su aplicación a la determinación de la densidad de disoluciones con distinta concentración. MATERIAL Balanza de Möhr (1) Inmersor sólido () Jinetillos de tres pesos (3) Probetas (4) Agua destilada y disolución problema. FUNDAMENTO TEÓRICO Según el principio de Arquímedes: todo cuerpo sumergido en un fluido, experimenta un empuje vertical, E, de igual magnitud pero de sentido opuesto al peso del fluido que desplaza dicho cuerpo. E1 ρ1 = V g [9-1] en donde ρ 1 es la densidad del líquido y g la aceleración de la gravedad. Si el mismo cuerpo se introduce en un líquido de densidad distinta, ρ, el nuevo empuje será: = V g [9-] E ρ 1
2 Por lo tanto, la densidad de un líquido ρ, puede obtenerse a partir de una densidad conocida ρ 1 y de la determinación del empuje relativo E / E 1, utilizando la relación: E ρ = ρ1 [9-3] E1 Descripción de la balanza de Möhr Definimos el momento de una fuerza o torque,, como el producto vectorial entre la fuerza y la distancia ( = r xf ) donde r es el brazo medido desde el punto de aplicación de la fuerza F al punto fijo del sistema. La balanza de Möhr es una palanca de primer género con brazos desiguales, cuyo equilibrio se alcanza cuando los momentos debidos a los pesos suspendidos de ambos brazos se igualan. El brazo más corto está formado por un contrapeso montado sobre un tornillo de forma que se puede ajustar su distancia al eje de giro de la balanza, y con ello, el momento que genera. El brazo más largo está dividido en 10 partes iguales. Para conseguir el equilibrio, se utilizan unos jinetillos, cuyos pesos están en la proporción p, 0.1p y 0.01p siendo p el peso del jinetillo mayor. Los jinetillos colocados en distintas posiciones sobre el brazo largo de la balanza originan diferentes momentos Determinación del empuje relativo MÉTODO Para determinar el empuje relativo que el inmersor experimenta al ser sumergido en el líquido problema, respecto del, procederemos del modo siguiente: a) Se equilibra la balanza con el inmersor seco, fuera de la probeta, suspendido del extremo del brazo largo de la balanza, utilizando el tornillo del contrapeso, sin poner ningún jinetillo. Se tiene entonces que los momentos generados por el contrapeso, contrapeso y el inmersor, inmersor son iguales: contrapeso= inmersor [9-4] b) Se ponen unos 150 cm 3 de en la probeta más ancha, y se introduce el inmersor, y sin tocar el contrapeso, se colocan jinetillos sobre el brazo largo de la balanza hasta equilibrarla. Debe ponerse especial cuidado en que el inmersor esté totalmente sumergido y que no toque paredes ni fondo. En esta situación, el momento generado por el contrapeso se equilibra con el momento resultante del inmersor, empuje y jinetillos: contrapeso = + 1 [9-5] inmersor jinetillos E
3 De las ecuaciones [9-4] y [9-5] se deduce que: jinetillos 1 = E [9-6] c) Se repite una operación idéntica a la anterior, pero con el inmersor sumergido en el líquido problema. Por un razonamiento análogo se llega a que: jinetillos = Elíquido [9-7] Dividiendo las ecuaciones [9-6], [9-7] y teniendo en cuenta la ecuación [9-3] se llega a: jinetillos 1 jinetillos = E E lxe = lxe E = E = ρ ρ [9-8] Donde l es la longitud del brazo largo de la balanza. Utilizando la ec. [9-3] tenemos que la densidad del podemos ponerla en función de la densidad del y de los momentos relativos o de los empujes relativos: ρ = ρ [9-9] El valor de la densidad del, para una temperatura igual a la temperatura ambiente del laboratorio, puede encontrarse en la tabla siguiente: (Consideraremos ρ =0). Tabla (9.1): T(º C) ρ (g/cm 3 ) T (º C) ρ (g/cm 3 ) 0 0, , , , , , , , , , , , , , , , ,99 Para realizar el cálculo de los momentos se busca el equilibrio primero con el jinetillo mayor, de peso p, colocándolo en la ranura del brazo largo de la balanza más cercana al fulcro (o punto de giro), y desplazándolo hacia el extremo. Si así no se consigue el equilibrio utilizaremos el jinetillo mediano, de peso 0.1p, e iremos colocándolo en las distintas ranuras hasta equilibrar la balanza. Si tampoco se alcanza el equilibrio con éste, utilizaremos el jinetillo menor, de peso 0.01p, y procederemos de la misma manera. Según la ecuación [9-9], necesitamos conocer la proporción que guardan los momentos del y del problema, no sus valores reales; por ello normalizamos a la unidad 3
4 los momentos, considerando 1 el momento generado por el jinetillo mayor situado en la posición más alejado del fulcro, expresado en unidades arbitrarias (u.a.), ver tabla (9.): Tabla (9.): Momento (u.a.) División Grande Mediano Pequeño Un ejemplo del cálculo del momento creado por el peso de los jinetillos se muestra a continuación : jinetillos = = 0.54 u.a. El error cometido en, también relativo, será el mínimo momento que somos capaces de medir..- Determinación de la densidad en función de la concentración. Vacíese un volumen V' 0 cm 3 de la disolución inicial problema, y sustitúyase por un volumen igual de destilada. Operando como se indica en el apartado, determínese la densidad de esta nueva disolución. Repítase esta operación (vaciado y sustitución por destilada) hasta 5 veces. Calcúlense las concentraciones de cada disolución mediante la relación: C V V Cm m ( ') = 1 V [9-10] siendo m un índice de orden que nos va indicando el número de veces que hemos realizado la operación de dilución. Calcúlense todas las concentraciones suponiendo que la concentración de la disolución original C o es del 10%. 4
5 Nombre Curso Fecha Apellidos Grupo Letra de prácticas DATOS EXPERIMENTALES Medida Posición de los jinetillos (1-10) jinetillos Grande Mediano Pequeño (u.a.) H O Líquido problema Dilución 1 Dilución Dilución 3 Dilución 4 Dilución 5 Escribir en la tabla los valores de la incertidumbre de medida directa al usar los jinetillos y al medir el volumen. Variable Valor Unidades jinetillos V Indicar la densidad del para la temperatura a la que trabajas, a partir de los datos de la tabla (9.1) de densidades, interpolando si es necesario. AGUA T (ºC) DENSIDAD (g/cm 3 ) 5
6 Nombre Curso Fecha Apellidos Grupo Letra de prácticas RESUMEN DE RESULTADOS Calcular las incertidumbres de medida indirecta de las densidades y de las concentraciones, teniendo en cuenta que vienen determinadas por las incertidumbres de medida directa de los momentos y del volumen del y de la concentración, respectivamente. FÓRMULAS CALCULADAS ρ LIQUIDO Cm 6
7 Medida ρ LIQ (g/cm 3 ) ρ LIQ (g/cm 3 ) ρ LIQ ± ρ LIQ (g/cm 3 ) Cm (%) Cm (%) Cm ± Cm H O Líquido problema 10 0 Dilución 1 Dilución Dilución 3 Dilución 4 Dilución 5 Representar gráficamente, reflejando la escala y las unidades correspondientes, los datos experimentales obtenidos para la concentración en función de la densidad. 7
8 Ajusta a una recta por el método de regresión lineal (Cm = a ρ LIQUIDO + b) los valores experimentales obtenidos para la concentración en función de la densidad del. Rellena en los paréntesis de la tabla las unidades que asignas a las variables Y i y X i, respectivamente. i Y i ( ) X i ( ) X i Y i X i Σ Calcula los valores de la pendiente de ajuste, a, y del término independiente, b, con sus respectivas unidades: Variable Valor Unidades Pendiente Tno. Indep. 8
9 Cuestiones : 1.- Por qué es importante que el inmersor esté totalmente sumergido en el líquido?.- Por qué hay que tener en cuenta la división n en que se coloca cada uno de los jinetillos? 3.- Es correcto afirmar que el peso de los jinetillos usados para equilibrar la balanza con el inmersor sumergido en es exactamente igual al empuje que experimenta? Por qué? 4.- Se coloca un cubo de en un platillo de una balanza y un peso igual en el otro platillo. Atendiendo a la definición de empuje y a la 3ª ley de Newton (principio de acción y reacción), Se desequilibrará el sistema por introducir un dedo en el sin tocar el cubo? 9
8. DETERMINACIÓN DE LA DENSIDAD DE UN SÓLIDO
 8. DETERMINACIÓN DE LA DENSIDAD DE UN SÓLIDO OBJETIVO El objetivo de la práctica es determinar la densidad de un sólido. Para ello vamos a utilizar dos métodos: Método 1 : Cálculo de la densidad de un
8. DETERMINACIÓN DE LA DENSIDAD DE UN SÓLIDO OBJETIVO El objetivo de la práctica es determinar la densidad de un sólido. Para ello vamos a utilizar dos métodos: Método 1 : Cálculo de la densidad de un
8. DETERMINACIÓN DE LA DENSIDAD DE UN SÓLIDO
 8. DETERMINACIÓN DE LA DENSIDAD DE UN SÓLIDO OBJETIVO El objetivo de la practica es determinar la densidad de un sólido. Para ello vamos a utilizar dos métodos: Método 1 : Cálculo de la densidad de un
8. DETERMINACIÓN DE LA DENSIDAD DE UN SÓLIDO OBJETIVO El objetivo de la practica es determinar la densidad de un sólido. Para ello vamos a utilizar dos métodos: Método 1 : Cálculo de la densidad de un
FUNDAMENTOS FÍSICOS DE LA INGENIERÍA CUARTA SESIÓN DE PRÁCTICAS
 DEPARTAMENTO DE FÍSICA APLICADA ESCUELA TÉCNICA SUPERIOR DE INGENIEROS AGRÓNOMOS Y DE MONTES UNIVERSIDAD DE CÓRDOBA FUNDAMENTOS FÍSICOS DE LA INGENIERÍA CUARTA SESIÓN DE PRÁCTICAS 6.- Principio de Arquímedes.
DEPARTAMENTO DE FÍSICA APLICADA ESCUELA TÉCNICA SUPERIOR DE INGENIEROS AGRÓNOMOS Y DE MONTES UNIVERSIDAD DE CÓRDOBA FUNDAMENTOS FÍSICOS DE LA INGENIERÍA CUARTA SESIÓN DE PRÁCTICAS 6.- Principio de Arquímedes.
PRÁCTICA: MOMENTOS DE INERCIA Y PÉNDULO FÍSICO
 PRÁCTICA: MOMENTOS DE INERCIA Y PÉNDULO FÍSICO Parte I: MOMENTOS DE INERCIA Objetivo: Determinar experimentalmente el momento de inercia de un disco respecto a su centro de gravedad y respecto a distintos
PRÁCTICA: MOMENTOS DE INERCIA Y PÉNDULO FÍSICO Parte I: MOMENTOS DE INERCIA Objetivo: Determinar experimentalmente el momento de inercia de un disco respecto a su centro de gravedad y respecto a distintos
23. MICROSCOPIO COMPUESTO: DETERMINACIÓN DE SU AUMENTO y MEDIDA DE ÁREAS MICROSCÓPICAS
 23. MICROSCOPIO COMPUESTO: DETERMINACIÓN DE SU AUMENTO y MEDIDA DE ÁREAS MICROSCÓPICAS OBJETIVO El objetivo de la práctica es familiarizarse con el uso del microscopio, determinar el aumento lineal de
23. MICROSCOPIO COMPUESTO: DETERMINACIÓN DE SU AUMENTO y MEDIDA DE ÁREAS MICROSCÓPICAS OBJETIVO El objetivo de la práctica es familiarizarse con el uso del microscopio, determinar el aumento lineal de
BALANZA DE MOHR - WESTPHAL : DENSIDAD ABSOLUTA DE SÓLIDOS
 BALANZA DE OHR - WESTPHAL : DENSIDAD ABSOLUTA DE SÓLIDOS OBJETIVO DE LA PRÁCTICA: Determinación de la densidad de un sólido. PRINCIPIO: Aplicación del Principio de Arquímedes. APLICACIONES: - En el equilibrio
BALANZA DE OHR - WESTPHAL : DENSIDAD ABSOLUTA DE SÓLIDOS OBJETIVO DE LA PRÁCTICA: Determinación de la densidad de un sólido. PRINCIPIO: Aplicación del Principio de Arquímedes. APLICACIONES: - En el equilibrio
PRÁCTICA 3: MEDIDAS DE LONGITUDES, PESOS Y TIEMPOS.
 PRÁCTICA : MEDIDAS DE LONGITUDES, PESOS Y TIEMPOS. MEDIDA DE DIMENSIONES GEOMÉTRICAS CON EL PALMER Y EL CALIRADOR. Con esta práctica se pretende que el alumno se familiarice con el manejo de distintos
PRÁCTICA : MEDIDAS DE LONGITUDES, PESOS Y TIEMPOS. MEDIDA DE DIMENSIONES GEOMÉTRICAS CON EL PALMER Y EL CALIRADOR. Con esta práctica se pretende que el alumno se familiarice con el manejo de distintos
Medidas y errores. Introducción teórica: Recordemos que medir es comparar una magnitud con otra de la misma especie que
 Medidas y errores. Introducción teórica: Recordemos que medir es comparar una magnitud con otra de la misma especie que se toma como unidad. El proceso de medida se puede realizar comparando directamente
Medidas y errores. Introducción teórica: Recordemos que medir es comparar una magnitud con otra de la misma especie que se toma como unidad. El proceso de medida se puede realizar comparando directamente
El resultado se expresa mediante una cantidad seguida de la unidad elegida. La cantidad representa el número de veces que se repite la unidad.
 LA MEDIDA Magnitudes físicas Todas las propiedades que podemos medir se denominan magnitudes. Para medir una magnitud hay que determinar previamente una cantidad de esta, llamada unidad. Al medir, se comparan
LA MEDIDA Magnitudes físicas Todas las propiedades que podemos medir se denominan magnitudes. Para medir una magnitud hay que determinar previamente una cantidad de esta, llamada unidad. Al medir, se comparan
Descripción del funcionamiento de la balanza de Mohr-Westphal Redactado por : Matías Zapata.-Grupo IEC- FRLP-UTN.
 Descripción del funcionamiento de la balanza de Mohr-Westphal Redactado por : Matías Zapata.-Grupo IEC- FRLP-UTN. Balanza de Mohr-Westphal La balanza de Mohr-Westphal es un dispositivo utilizado para medir
Descripción del funcionamiento de la balanza de Mohr-Westphal Redactado por : Matías Zapata.-Grupo IEC- FRLP-UTN. Balanza de Mohr-Westphal La balanza de Mohr-Westphal es un dispositivo utilizado para medir
Con la ayuda de el dinamómetro implementamos el segundo método de aplicación y medición de fuerzas.
 EXPERIMENTO # 1: LEY DE HOOKE MEDICIÓN DE FUERZAS Objetivo: Estudios de las propiedades de un dinamómetro mediante la aplicación de fuerza conocidas. Fundamento Teórico: El concepto de fuerza es definido
EXPERIMENTO # 1: LEY DE HOOKE MEDICIÓN DE FUERZAS Objetivo: Estudios de las propiedades de un dinamómetro mediante la aplicación de fuerza conocidas. Fundamento Teórico: El concepto de fuerza es definido
La densidad es la masa específica, es decir, la masa por unidad de volumen. ρ ' m V
 Página 1 I INTRODUCCIÓN. FUNDAMENTO TEORICO La densidad es la masa específica, es decir, la masa por unidad de volumen ρ ' m V Existen muchos procedimientos para determinar la densidad. Unos se basan en
Página 1 I INTRODUCCIÓN. FUNDAMENTO TEORICO La densidad es la masa específica, es decir, la masa por unidad de volumen ρ ' m V Existen muchos procedimientos para determinar la densidad. Unos se basan en
ρ 20º/20º = ρ a /ρ ref (I)
 Práctica N 1 Determinación de Densidad en los Alimentos Objetivos Determinar la densidad de diferentes muestras de alimentos utilizando el picnómetro. Determinar la densidad de diferentes muestras de alimentos
Práctica N 1 Determinación de Densidad en los Alimentos Objetivos Determinar la densidad de diferentes muestras de alimentos utilizando el picnómetro. Determinar la densidad de diferentes muestras de alimentos
LABORATORIO DE FÍSICA GENERAL 10ª Edición EXPERIENCIA N 06
 ABORATORIO DE FÍSIA GENERA 10ª Edición DAFI FF UNMSM DENSIDAD DE SÓIDOS Y ÍQUIDOS EXPERIENIA N 06 Arquímedes (Siracusa, actual Italia, h. 287 a..-id., 212 a..) Matemático e ingeniero griego, considerado
ABORATORIO DE FÍSIA GENERA 10ª Edición DAFI FF UNMSM DENSIDAD DE SÓIDOS Y ÍQUIDOS EXPERIENIA N 06 Arquímedes (Siracusa, actual Italia, h. 287 a..-id., 212 a..) Matemático e ingeniero griego, considerado
Definición de vectores
 Definición de vectores Un vector es todo segmento de recta dirigido en el espacio. Cada vector posee unas características que son: Origen O también denominado Punto de aplicación. Es el punto exacto sobre
Definición de vectores Un vector es todo segmento de recta dirigido en el espacio. Cada vector posee unas características que son: Origen O también denominado Punto de aplicación. Es el punto exacto sobre
Práctica 2 DENSIDAD RELATIVA Y DENSIDAD APARENTE DE UN MATERIAL EN POLVO
 Práctica 2 DENSIDAD RELATIVA Y DENSIDAD APARENTE DE UN MATERIAL EN POLVO 1. Objetivos docentes Conocer un método para determinar la densidad de un material en polvo. Conocer los distintos tipos de densidades
Práctica 2 DENSIDAD RELATIVA Y DENSIDAD APARENTE DE UN MATERIAL EN POLVO 1. Objetivos docentes Conocer un método para determinar la densidad de un material en polvo. Conocer los distintos tipos de densidades
Fecha de realización:... Fecha de entrega:... Comisión:... Apellidos Nombres:...
 ASIGNATURA: FÍSICA I TRABAJO PRÁCTICO Nº 1: GRÁFICOS Y ESCALAS Fecha de realización:... Fecha de entrega:... Comisión:... Apellidos Nombres:... y......... 1. Objetivo del trabajo: Construcción de gráficos,
ASIGNATURA: FÍSICA I TRABAJO PRÁCTICO Nº 1: GRÁFICOS Y ESCALAS Fecha de realización:... Fecha de entrega:... Comisión:... Apellidos Nombres:... y......... 1. Objetivo del trabajo: Construcción de gráficos,
Tema 13: La materia Ciencias Naturales 1º ESO página 1. Materia es todo aquello que posee masa y ocupa un volumen. Está formada de partículas muy
 Tema 13: La materia Ciencias Naturales 1º ESO página 1 TEMA 13: LA MATERIA, BASE DEL UNIVERSO 1. Qué es materia? Materia es todo aquello que posee masa y ocupa un volumen. Está formada de partículas muy
Tema 13: La materia Ciencias Naturales 1º ESO página 1 TEMA 13: LA MATERIA, BASE DEL UNIVERSO 1. Qué es materia? Materia es todo aquello que posee masa y ocupa un volumen. Está formada de partículas muy
4. Mecánica Rotacional
 4. Mecánica Rotacional Cinemática Rotacional: (Conceptos básicos) Radián Velocidad angular Aceleración angular Frecuencia y período Velocidad tangencial Aceleración tangencial Aceleración centrípeta Torca
4. Mecánica Rotacional Cinemática Rotacional: (Conceptos básicos) Radián Velocidad angular Aceleración angular Frecuencia y período Velocidad tangencial Aceleración tangencial Aceleración centrípeta Torca
MEDIDA DE PEQUEÑAS LONGITUDES.
 EDIDA DE PEQUEÑAS LOGITUDES. PROPÓSITO: Conocimiento de los instrumentos del laboratorio y su uso en la determinación de la longitud, masa y densidad. Instrumento especial: Calibrador o pié de Rey. Instrumento
EDIDA DE PEQUEÑAS LOGITUDES. PROPÓSITO: Conocimiento de los instrumentos del laboratorio y su uso en la determinación de la longitud, masa y densidad. Instrumento especial: Calibrador o pié de Rey. Instrumento
MOVIMIENTO ARMÓNICO AMORTIGUADO
 MOVIMIENTO ARMÓNICO AMORTIGUADO OBJETIVO Medida experimental de la variación exponencial decreciente de la oscilación en un sistema oscilatorio de bajo amortiguamiento. FUNDAMENTO TEÓRICO A) SISTEMA SIN
MOVIMIENTO ARMÓNICO AMORTIGUADO OBJETIVO Medida experimental de la variación exponencial decreciente de la oscilación en un sistema oscilatorio de bajo amortiguamiento. FUNDAMENTO TEÓRICO A) SISTEMA SIN
Aplicaciones de la integral
 CAPÍTULO 1 Aplicaciones de la integral 3.6 uerza y presión de un fluido Cuando en un fluido contenido por un recipiente se encuentra un cuerpo sumergido, este experimenta una fuerza, perpendicular a cualquiera
CAPÍTULO 1 Aplicaciones de la integral 3.6 uerza y presión de un fluido Cuando en un fluido contenido por un recipiente se encuentra un cuerpo sumergido, este experimenta una fuerza, perpendicular a cualquiera
PRÁCTICA 1: DETERMINACIÓN EXPERIMENTAL DE LA VELOCIDAD DE SEDIMENTACIÓN
 PRÁCTICA 1: DETERMINACIÓN EXPERIMENTAL DE LA VELOCIDAD DE SEDIMENTACIÓN 1. Introducción Se llama sedimentación a la operación que consiste en separar de una suspensión, un líquido claro que sobrenada en
PRÁCTICA 1: DETERMINACIÓN EXPERIMENTAL DE LA VELOCIDAD DE SEDIMENTACIÓN 1. Introducción Se llama sedimentación a la operación que consiste en separar de una suspensión, un líquido claro que sobrenada en
PROPIEDADES DE LOS FLUIDOS
 PROPIEDADES DE LOS FLUIDOS CRUDO Objetivo: Determinar las propiedades importantes del Crudo, tales como la Densidad, Gravedad API, Viscosidad Cinemática y Viscosidad Dinámica; utilizando diferentes métodos.
PROPIEDADES DE LOS FLUIDOS CRUDO Objetivo: Determinar las propiedades importantes del Crudo, tales como la Densidad, Gravedad API, Viscosidad Cinemática y Viscosidad Dinámica; utilizando diferentes métodos.
Campo Eléctrico. Fig. 1. Problema número 1.
 Campo Eléctrico 1. Cuatro cargas del mismo valor están dispuestas en los vértices de un cuadrado de lado L, tal como se indica en la figura 1. a) Hallar el módulo, dirección y sentido de la fuerza eléctrica
Campo Eléctrico 1. Cuatro cargas del mismo valor están dispuestas en los vértices de un cuadrado de lado L, tal como se indica en la figura 1. a) Hallar el módulo, dirección y sentido de la fuerza eléctrica
PRÁCTICA 1. Mediciones
 PRÁCTICA 1 Mediciones Objetivo General El alumno determinará la incertidumbre de las mediciones. Objetivos particulares 1. El alumno determinará las incertidumbres a partir de los instrumentos de medición..
PRÁCTICA 1 Mediciones Objetivo General El alumno determinará la incertidumbre de las mediciones. Objetivos particulares 1. El alumno determinará las incertidumbres a partir de los instrumentos de medición..
Respecto a la fuerza neta que actúa sobre un cuerpo, es correcto afirmar que
 Guía práctica Dinámica I: fuerza y leyes de Newton Física Estándar Anual Nº Ejercicios PSU Para esta guía considere que la magnitud de la aceleración de gravedad (g) es 10 1. 2. GUICES016CB32-A16V1 m.
Guía práctica Dinámica I: fuerza y leyes de Newton Física Estándar Anual Nº Ejercicios PSU Para esta guía considere que la magnitud de la aceleración de gravedad (g) es 10 1. 2. GUICES016CB32-A16V1 m.
F2 Bach. Movimiento armónico simple
 F Bach Movimiento armónico simple 1. Movimientos periódicos. Movimientos vibratorios 3. Movimiento armónico simple (MAS) 4. Cinemática del MAS 5. Dinámica del MAS 6. Energía de un oscilador armónico 7.
F Bach Movimiento armónico simple 1. Movimientos periódicos. Movimientos vibratorios 3. Movimiento armónico simple (MAS) 4. Cinemática del MAS 5. Dinámica del MAS 6. Energía de un oscilador armónico 7.
Ejercicios resueltos sobre el estado de agregación de la materia. Estudio de las disoluciones
 Ejercicios resueltos sobre el estado de agregación de la materia. Estudio de las disoluciones Recordemos algunos conceptos teóricos en nuestro nivel. Toda disolución tiene dos componentes: a) Soluto b)
Ejercicios resueltos sobre el estado de agregación de la materia. Estudio de las disoluciones Recordemos algunos conceptos teóricos en nuestro nivel. Toda disolución tiene dos componentes: a) Soluto b)
PLANO INCLINADO. Para la realización de esta práctica el alumno deberá venir al laboratorio provisto con hojas de papel milimetrado.
 PLANO INCLINADO Para la realización de esta práctica el alumno deberá venir al laboratorio provisto con hojas de papel milimetrado. Objetivo: Verificar experimentalmente la descomposición de fuerzas en
PLANO INCLINADO Para la realización de esta práctica el alumno deberá venir al laboratorio provisto con hojas de papel milimetrado. Objetivo: Verificar experimentalmente la descomposición de fuerzas en
LABORATORIO DE MECANICA LEY DE HOOKE
 No 6 LABORATORIO DE MECANICA LEY DE HOOKE DEPARTAMENTO DE FISICA Y GEOLOGIA UNIVERSIDAD DE PAMPLONA FACULTAD DE CIENCIAS BÁSICAS Objetivos Objetivo general: Estudiar experimentalmente el comportamiento
No 6 LABORATORIO DE MECANICA LEY DE HOOKE DEPARTAMENTO DE FISICA Y GEOLOGIA UNIVERSIDAD DE PAMPLONA FACULTAD DE CIENCIAS BÁSICAS Objetivos Objetivo general: Estudiar experimentalmente el comportamiento
Física Mecánica. Sesión de Problemas Experimento. TEMA: TEOREMA DEL TRABAJO Y LA ENERGÍA. PRINCIPIO DE CONSERVACIÓN DE LA ENERGÍA.
 TEM: TEOREM DEL TRJO Y L ENERGÍ. PRINCIPIO DE CONSERVCIÓN DE L ENERGÍ. Problema experimento #10: Trabajo y Conservación de la energía con plano inclinado. Medir el espesor de un pequeño bloque de madera
TEM: TEOREM DEL TRJO Y L ENERGÍ. PRINCIPIO DE CONSERVCIÓN DE L ENERGÍ. Problema experimento #10: Trabajo y Conservación de la energía con plano inclinado. Medir el espesor de un pequeño bloque de madera
CINÉTICA DE HIDRÓLISIS DEL ACETATO DE METILO Eva Mª Talavera Rodríguez y Francisco A. Ocaña Lara
 CINÉTICA DE HIDRÓLISIS DEL ACETATO DE METILO Eva Mª Talavera Rodríguez y Francisco A. Ocaña Lara OBJETIVOS 1.- Estudiar la cinética de la reacción de hidrólisis ácida del acetato de metilo en disolución
CINÉTICA DE HIDRÓLISIS DEL ACETATO DE METILO Eva Mª Talavera Rodríguez y Francisco A. Ocaña Lara OBJETIVOS 1.- Estudiar la cinética de la reacción de hidrólisis ácida del acetato de metilo en disolución
TEMA N 2 RECTAS EN EL PLANO
 2.1 Distancia entre dos puntos1 TEMA N 2 RECTAS EN EL PLANO Sean P 1 (x 1, y 1 ) y P 2 (x 2, y 2 ) dos puntos en el plano. La distancia entre los puntos P 1 y P 2 denotada por d = esta dada por: (1) Demostración
2.1 Distancia entre dos puntos1 TEMA N 2 RECTAS EN EL PLANO Sean P 1 (x 1, y 1 ) y P 2 (x 2, y 2 ) dos puntos en el plano. La distancia entre los puntos P 1 y P 2 denotada por d = esta dada por: (1) Demostración
Ejercicios resueltos de funciones
 Ejercicios resueltos de funciones 1) Representa en un eje de coordenadas los siguientes puntos: A(1,5), B(-3,3), C(0, -4), D (2,0). 2) Representa en dos ejes de coordenadas las funciones siguientes: a)
Ejercicios resueltos de funciones 1) Representa en un eje de coordenadas los siguientes puntos: A(1,5), B(-3,3), C(0, -4), D (2,0). 2) Representa en dos ejes de coordenadas las funciones siguientes: a)
UNIDAD II FUNCIONES. Ing. Ronny Altuve Esp.
 República Bolivariana de Venezuela Universidad Alonso de Ojeda Administración Mención Gerencia y Mercadeo UNIDAD II FUNCIONES Ing. Ronny Altuve Esp. Ciudad Ojeda, Septiembre de 2015 Función Universidad
República Bolivariana de Venezuela Universidad Alonso de Ojeda Administración Mención Gerencia y Mercadeo UNIDAD II FUNCIONES Ing. Ronny Altuve Esp. Ciudad Ojeda, Septiembre de 2015 Función Universidad
Fluidos. Presión. Principio de Pascal.
 Fluidos. Presión. Principio de Pascal. CHOQUES ELASTICOS E INELASTICOS Se debe tener en cuenta que tanto la cantidad de movimiento como la energía cinética deben conservarse en los choques. Durante una
Fluidos. Presión. Principio de Pascal. CHOQUES ELASTICOS E INELASTICOS Se debe tener en cuenta que tanto la cantidad de movimiento como la energía cinética deben conservarse en los choques. Durante una
APUNTES DE MATEMÁTICAS 1º BACHILLERATO TEMA 5: GEOMETRÍA AFÍN PROBLEMAS MÉTRICOS
 APUNTES DE MATEMÁTICAS TEMA 5: GEOMETRÍA AFÍN PROBLEMAS MÉTRICOS º BACHILLERATO ÍNDICE. ECUACIONES DE LA RECTA EN EL PLANO.... 4.. SISTEMAS DE REFERENCIA... 4.. COORDENADAS DE UN PUNTO... 4.3. COORDENADAS
APUNTES DE MATEMÁTICAS TEMA 5: GEOMETRÍA AFÍN PROBLEMAS MÉTRICOS º BACHILLERATO ÍNDICE. ECUACIONES DE LA RECTA EN EL PLANO.... 4.. SISTEMAS DE REFERENCIA... 4.. COORDENADAS DE UN PUNTO... 4.3. COORDENADAS
5. PÉNDULO SIMPLE. MEDIDA DE g
 5. PÉNDULO SIMPLE. MEDIDA DE g OBJETIVO El objetivo de la práctica es medir la aceleración de la gravedad en el laboratorio, g, a partir del estudio del movimiento armónico de un péndulo simple. MATERIAL
5. PÉNDULO SIMPLE. MEDIDA DE g OBJETIVO El objetivo de la práctica es medir la aceleración de la gravedad en el laboratorio, g, a partir del estudio del movimiento armónico de un péndulo simple. MATERIAL
Tema: TRATAMIENTO DE DATOS
 1 Facultad Escuela Lugar de Ejecución : Ingeniería. : Biomédica : Laboratorio de Biomédica Tema: TRATAMIENTO DE DATOS Objetivos 1. Que el estudiante se familiarice con el concepto de error en una medición.
1 Facultad Escuela Lugar de Ejecución : Ingeniería. : Biomédica : Laboratorio de Biomédica Tema: TRATAMIENTO DE DATOS Objetivos 1. Que el estudiante se familiarice con el concepto de error en una medición.
FICHA DE EVALUACION - PRACTICA Nro. 3: Mediciones directas e indirectas. Propagación de errores.
 FICHA DE EVALUACION - PRACTICA Nro. 3: Mediciones directas e indirectas. Propagación de errores. LABORATORIO DE FISICA I (Licenciatura en Bioquímica) GRUPO Día: Hora: Docente: 1 3 4 5 6 Subgrupo Nro. Nombres
FICHA DE EVALUACION - PRACTICA Nro. 3: Mediciones directas e indirectas. Propagación de errores. LABORATORIO DE FISICA I (Licenciatura en Bioquímica) GRUPO Día: Hora: Docente: 1 3 4 5 6 Subgrupo Nro. Nombres
La Densidad, es la masa de un cuerpo por unidad de volumen.
 Práctica INTRODUCCIÓN.- La Densidad, es la masa de un cuerpo por unidad de volumen. En ocasiones se habla de densidad relativa es significa la relación entre la densidad de un cuerpo y la densidad del
Práctica INTRODUCCIÓN.- La Densidad, es la masa de un cuerpo por unidad de volumen. En ocasiones se habla de densidad relativa es significa la relación entre la densidad de un cuerpo y la densidad del
EXPERIMENTO 8 MÁQUINAS SIMPLES
 EXPERIMENTO 8 MÁQUINAS SIMPLES 1. Objetivos 1.1 Estudiar sistemas en equilibrio estático traslacional y rotacional. 1.2 Calcular la ventaja mecánica para diferentes sistemas de poleas y palancas. 1.3 Adquirir
EXPERIMENTO 8 MÁQUINAS SIMPLES 1. Objetivos 1.1 Estudiar sistemas en equilibrio estático traslacional y rotacional. 1.2 Calcular la ventaja mecánica para diferentes sistemas de poleas y palancas. 1.3 Adquirir
Medición de los trabajos de Poliuretano Proyectado
 Medición de los trabajos de Poliuretano Proyectado A continuación se recoge un resumen de la Norma UNE 92310:2003, Criterios de medición y cuantificación para trabajos de aislamiento térmico en instalaciones
Medición de los trabajos de Poliuretano Proyectado A continuación se recoge un resumen de la Norma UNE 92310:2003, Criterios de medición y cuantificación para trabajos de aislamiento térmico en instalaciones
Laboratorio de Física 1 (ByG) Guía 4: Viscosidad, empuje y oscilaciones amortiguadas
 Laboratorio de Física 1 (ByG) Guía 4: Viscosidad, empuje y oscilaciones amortiguadas Verano 2008 Objetivos Experiencia 1: Viscosidad y Empuje En esta experiencia de laboratorio vamos a estudiar el movimiento
Laboratorio de Física 1 (ByG) Guía 4: Viscosidad, empuje y oscilaciones amortiguadas Verano 2008 Objetivos Experiencia 1: Viscosidad y Empuje En esta experiencia de laboratorio vamos a estudiar el movimiento
SISTEMAS DE ECUACIONES LINEALES
 1 SISTEMAS DE ECUACIONES LINEALES Una ecuación es un enunciado o proposición que plantea la igualdad de dos expresiones, donde al menos una de ellas contiene cantidades desconocidas llamadas variables
1 SISTEMAS DE ECUACIONES LINEALES Una ecuación es un enunciado o proposición que plantea la igualdad de dos expresiones, donde al menos una de ellas contiene cantidades desconocidas llamadas variables
TORQUE. Estudiar los torques producidos por fuerzas perpendiculares al brazo de palanca.
 TORQUE Experimento 1. Objetivo: Estudiar los torques producidos por fuerzas perpendiculares al brazo de palanca. Fundamento teórico: En experiencias anteriores se calcularon fuerzas resultantes y equilibrantes
TORQUE Experimento 1. Objetivo: Estudiar los torques producidos por fuerzas perpendiculares al brazo de palanca. Fundamento teórico: En experiencias anteriores se calcularon fuerzas resultantes y equilibrantes
SEGMENTOS RECTILÍNEOS: DIRIGIDOS Y NO DIRIGIDOS
 SEGMENTOS RECTILÍNEOS: DIRIGIDOS Y NO DIRIGIDOS A la porción de una línea recta comprendida entre dos de sus puntos se llama segmento rectilíneo o simplemente segmento. Los dos puntos se llaman extremos
SEGMENTOS RECTILÍNEOS: DIRIGIDOS Y NO DIRIGIDOS A la porción de una línea recta comprendida entre dos de sus puntos se llama segmento rectilíneo o simplemente segmento. Los dos puntos se llaman extremos
N = {1, 2, 3, 4, 5,...}
 Números y Funciones.. Números Los principales tipos de números son:. Los números naturales son aquellos que sirven para contar. N = {,,, 4, 5,...}. Los números enteros incluyen a los naturales y a sus
Números y Funciones.. Números Los principales tipos de números son:. Los números naturales son aquellos que sirven para contar. N = {,,, 4, 5,...}. Los números enteros incluyen a los naturales y a sus
CAPÍTULO III MOMENTO DE INERCIA EN ÁREAS PLANAS. Este capítulo comprende diversas propiedades geométricas de secciones (para casos
 CAPÍTULO III MOMENTO DE INERCIA EN ÁREAS PLANAS Este capítulo comprende diversas propiedades geométricas de secciones (para casos prácticos, secciones de vigas) siendo la más importante el momento de inercia.
CAPÍTULO III MOMENTO DE INERCIA EN ÁREAS PLANAS Este capítulo comprende diversas propiedades geométricas de secciones (para casos prácticos, secciones de vigas) siendo la más importante el momento de inercia.
Figura 3.-(a) Movimiento curvilíneo. (b) Concepto de radio de curvatura
 Componentes intrínsecas de la aceleración: Componentes tangencial y normal Alfonso Calera Departamento de Física Aplicada. ETSIA. Albacete. UCLM En muchas ocasiones el análisis del movimiento es más sencillo
Componentes intrínsecas de la aceleración: Componentes tangencial y normal Alfonso Calera Departamento de Física Aplicada. ETSIA. Albacete. UCLM En muchas ocasiones el análisis del movimiento es más sencillo
Práctica No 2. Determinación experimental del factor de compresibilidad
 Práctica No 2 Determinación experimental del factor de compresibilidad 1. Objetivo general: Determinación del comportamiento de un gas a diferentes presiones, mediante el cálculo experimental del factor
Práctica No 2 Determinación experimental del factor de compresibilidad 1. Objetivo general: Determinación del comportamiento de un gas a diferentes presiones, mediante el cálculo experimental del factor
11. Desgaste de herramientas. Contenido: 1. Desgaste de herramientas 2. Medida del desgaste 3. Ensayos de duración de herramientas
 11. Desgaste de herramientas Contenido: 1. Desgaste de herramientas 2. Medida del desgaste 3. Ensayos de duración de herramientas Desgaste de herramientas La herramienta durante su trabajo está sometida
11. Desgaste de herramientas Contenido: 1. Desgaste de herramientas 2. Medida del desgaste 3. Ensayos de duración de herramientas Desgaste de herramientas La herramienta durante su trabajo está sometida
POTENCIAS. MÚLTIPLOS Y DIVISORES. MÁXIMO COMÚN DIVISOR Y MÍNIMO COMÚN MÚLTIPLO.
 1. LOS NÚMEROS NATURALES POTENCIAS. MÚLTIPLOS Y DIVISORES. MÁXIMO COMÚN DIVISOR Y MÍNIMO COMÚN MÚLTIPLO. 2. LOS NÚMEROS ENTEROS. VALOR ABSOLUTO DE UN NÚMERO ENTERO. REPRESENTACIÓN GRÁFICA. OPERACIONES.
1. LOS NÚMEROS NATURALES POTENCIAS. MÚLTIPLOS Y DIVISORES. MÁXIMO COMÚN DIVISOR Y MÍNIMO COMÚN MÚLTIPLO. 2. LOS NÚMEROS ENTEROS. VALOR ABSOLUTO DE UN NÚMERO ENTERO. REPRESENTACIÓN GRÁFICA. OPERACIONES.
PRÁCTICA 1: MANEJO DEL ERROR EXPERIMENTAL Y PROPIEDADES DE LOS FLUIDOS
 Universidad Nacional Experimental Francisco de Miranda Área de Tecnología Programa de Ingeniería Industrial Departamento de Energética Laboratorio de Fenómenos de Transporte PRÁCTIC 1: MNEJO DEL ERROR
Universidad Nacional Experimental Francisco de Miranda Área de Tecnología Programa de Ingeniería Industrial Departamento de Energética Laboratorio de Fenómenos de Transporte PRÁCTIC 1: MNEJO DEL ERROR
4 LAS FUERZAS Y EL EQUILIBRIO DE LOS SÓLIDOS
 4 LAS FUERZAS Y EL EQUILIBRI DE LS SÓLIDS EJERCICIS PRPUESTS 4.1 Nombra cinco sólidos rígidos que se encuentren en tu aula. Mesa, silla, pizarra, libro, bolígrafo, etc. 4.2 Justifica si una moneda se comporta
4 LAS FUERZAS Y EL EQUILIBRI DE LS SÓLIDS EJERCICIS PRPUESTS 4.1 Nombra cinco sólidos rígidos que se encuentren en tu aula. Mesa, silla, pizarra, libro, bolígrafo, etc. 4.2 Justifica si una moneda se comporta
EJERCICIOS DE PALANCAS. 2. Aplicamos 100 N de fuerza en cada mango de estos alicates. Qué fuerza resultará en cada punta?
 EJERCICIOS DE PALANCAS 1. Indica la fuerza que debe realizar el cilindro hidráulico de esta grúa para levantar un peso de 1000 Kg. El brazo de la fuerza mide 1,5 m y el brazo de la resistencia 5 m. Qué
EJERCICIOS DE PALANCAS 1. Indica la fuerza que debe realizar el cilindro hidráulico de esta grúa para levantar un peso de 1000 Kg. El brazo de la fuerza mide 1,5 m y el brazo de la resistencia 5 m. Qué
Tema 11: Intervalos de confianza.
 Tema 11: Intervalos de confianza. Presentación y Objetivos. En este tema se trata la estimación de parámetros por intervalos de confianza. Consiste en aproximar el valor de un parámetro desconocido por
Tema 11: Intervalos de confianza. Presentación y Objetivos. En este tema se trata la estimación de parámetros por intervalos de confianza. Consiste en aproximar el valor de un parámetro desconocido por
INSTRUMENTOS DE MEDIDAS Y TEORÍA DEL ERROR
 INSTRUMENTOS DE MEDIDAS Y TEORÍA DEL ERROR Adaptación del Experimento Nº1 de la Guía de Ensayos y Teoría del Error del profesor Ricardo Nitsche, página 36-42. Autorizado por el Autor. Materiales: Cilindros
INSTRUMENTOS DE MEDIDAS Y TEORÍA DEL ERROR Adaptación del Experimento Nº1 de la Guía de Ensayos y Teoría del Error del profesor Ricardo Nitsche, página 36-42. Autorizado por el Autor. Materiales: Cilindros
GEOMETRÍA ANALÍTICA DEL PLANO
 GEOMETRÍA ANALÍTICA DEL PLANO 1 UNIDAD DIDÁCTICA 5: Geometría analítica del plano 1. ÍNDICE 1. Sistemas de referencia y coordenadas puntuales 2. Distancia entre dos puntos del plano 3. Coordenadas del
GEOMETRÍA ANALÍTICA DEL PLANO 1 UNIDAD DIDÁCTICA 5: Geometría analítica del plano 1. ÍNDICE 1. Sistemas de referencia y coordenadas puntuales 2. Distancia entre dos puntos del plano 3. Coordenadas del
UNIDAD DIDÁCTICA 5: Geometría analítica del plano
 UNIDAD DIDÁCTICA 5: Geometría analítica del plano 1. ÍNDICE 1. Sistemas de referencia y coordenadas puntuales 2. Distancia entre dos puntos del plano 3. Coordenadas del punto medio de un segmento 4. La
UNIDAD DIDÁCTICA 5: Geometría analítica del plano 1. ÍNDICE 1. Sistemas de referencia y coordenadas puntuales 2. Distancia entre dos puntos del plano 3. Coordenadas del punto medio de un segmento 4. La
Calor específico de un metal
 Calor específico de un metal Objetivos Determinar el calor específico del Cobre (Cu). Comprobar experimentalmente la ley cero de la Termodinámica. Introducción Diferentes sustancias requieren diferentes
Calor específico de un metal Objetivos Determinar el calor específico del Cobre (Cu). Comprobar experimentalmente la ley cero de la Termodinámica. Introducción Diferentes sustancias requieren diferentes
Ix ʹ = 8 mb 2, I. c) El momento de inercia respecto de un eje perpendicular al plano de la figura y que pase por una de las masas (eje z ʹ ) será:
 CALCULO DE MOMENTOS DE INECIA Se unen cuatro partículas de masa m mediante varillas sin masa, formando un rectángulo de lados a b. El sistema gira alrededor de un eje en el plano de la figura que pasa
CALCULO DE MOMENTOS DE INECIA Se unen cuatro partículas de masa m mediante varillas sin masa, formando un rectángulo de lados a b. El sistema gira alrededor de un eje en el plano de la figura que pasa
Una matriz es una tabla ordenada (por filas y columnas) de escalares a i j de la forma: ... ... a... ...
 MATRICES Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de las derivadas parciales. Tienen también muchas aplicaciones
MATRICES Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de las derivadas parciales. Tienen también muchas aplicaciones
Figura 1.3.1. Sobre la definición de flujo ΔΦ.
 1.3. Teorema de Gauss Clases de Electromagnetismo. Ariel Becerra La ley de Coulomb y el principio de superposición permiten de una manera completa describir el campo electrostático de un sistema dado de
1.3. Teorema de Gauss Clases de Electromagnetismo. Ariel Becerra La ley de Coulomb y el principio de superposición permiten de una manera completa describir el campo electrostático de un sistema dado de
operaciones inversas Para unificar ambas operaciones, se define la potencia de exponente fraccionario:
 Potencias y raíces Potencias y raíces Potencia operaciones inversas Raíz exponente índice 7 = 7 7 7 = 4 4 = 7 base base Para unificar ambas operaciones, se define la potencia de exponente fraccionario:
Potencias y raíces Potencias y raíces Potencia operaciones inversas Raíz exponente índice 7 = 7 7 7 = 4 4 = 7 base base Para unificar ambas operaciones, se define la potencia de exponente fraccionario:
ESTÁTICA. Objetivos: Material: Introducción: 1. Suma y descomposición de fuerzas.
 ESTÁTICA Objetivos: 1. Sumar y descomponer fuerzas (analizando su carácter vectorial) 2. Medir fuerzas resultantes y momentos resultantes de fuerzas paralelas y no paralelas. Analizar el equilibrio mecánico
ESTÁTICA Objetivos: 1. Sumar y descomponer fuerzas (analizando su carácter vectorial) 2. Medir fuerzas resultantes y momentos resultantes de fuerzas paralelas y no paralelas. Analizar el equilibrio mecánico
FÍSICA Y QUÍMICA 4º ESO. OBJETIVOS, CONTENIDOS Y CRITERIOS DE EVALUACIÓN. 1ª Evaluación
 FÍSICA Y QUÍMICA 4º ESO. OBJETIVOS, CONTENIDOS Y CRITERIOS DE EVALUACIÓN. 1ª Evaluación Unidad 1: El movimiento de los cuerpos i. Objetivos Observar las distintas magnitudes físicas que se ponen de manifiesto
FÍSICA Y QUÍMICA 4º ESO. OBJETIVOS, CONTENIDOS Y CRITERIOS DE EVALUACIÓN. 1ª Evaluación Unidad 1: El movimiento de los cuerpos i. Objetivos Observar las distintas magnitudes físicas que se ponen de manifiesto
PRÁCTICA 3 DETERMINACIÓN ESPECTROFOTOMÉTRICA DEL pk DE UN INDICADOR
 PRÁCTICA 3 DETERMINACIÓN ESPECTROFOTOMÉTRICA DEL pk DE UN INDICADOR Material Productos 2 matraces aforados de 250 ml Hidróxido de sodio en lentejas 2 matraces aforados de 25 ml Disolución de hidróxido
PRÁCTICA 3 DETERMINACIÓN ESPECTROFOTOMÉTRICA DEL pk DE UN INDICADOR Material Productos 2 matraces aforados de 250 ml Hidróxido de sodio en lentejas 2 matraces aforados de 25 ml Disolución de hidróxido
2º ESO. matemáticas IES Montevil tema 2: NÚMEROS ENTEROS curso 2010/2011 2 34 0-7 -1 5 4-12 10 2 0-7 00 0 15
 nombre: apellidos: números enteros El conjunto de los números enteros es el que está formado por los números positivos y negativos que no tienen decimales, es decir que son enteros. Los números enteros
nombre: apellidos: números enteros El conjunto de los números enteros es el que está formado por los números positivos y negativos que no tienen decimales, es decir que son enteros. Los números enteros
Academia, Librería, Informática Diego FUERZAS Y PRESIONES I (4º E.S.O.) Fuerzas
 FUERZAS Y PRESIONES I (4º E.S.O.) Fuerzas 1. Con un dinamómetro, cuya constante elástica es k = 500 N/m, se han medido los pesos de dos cuerpos, obteniéndose un alargamiento de 4 y 8 cm, respectivamente.
FUERZAS Y PRESIONES I (4º E.S.O.) Fuerzas 1. Con un dinamómetro, cuya constante elástica es k = 500 N/m, se han medido los pesos de dos cuerpos, obteniéndose un alargamiento de 4 y 8 cm, respectivamente.
TRABAJO DE ENTRADA= TRABAJO ÚTIL DE SALIDA + TRABAJO NECESARIO PARA VENCER LA FRICCIÓN
 UNA MÁQUINA: es cualquier dispositivo con el cual se puede cambiar la magnitud, la dirección o el método de aplicación de una fuerza para obtener algún provecho. Como ejemplos de máquinas simples tenemos
UNA MÁQUINA: es cualquier dispositivo con el cual se puede cambiar la magnitud, la dirección o el método de aplicación de una fuerza para obtener algún provecho. Como ejemplos de máquinas simples tenemos
Producto cartesiano. X Y = {(x, y) : x X, y Y }. Ejemplo En el tablero de ajedrez, X = números del 1-8, Y = letras de A-H.
 Producto cartesiano Motivación: Has oido hablar sobre gente que juega ajedrez sin tener que mirar nunca el tablero?. Esto es posible, y se debe a una herramienta llamada coordenadas de un punto. En un
Producto cartesiano Motivación: Has oido hablar sobre gente que juega ajedrez sin tener que mirar nunca el tablero?. Esto es posible, y se debe a una herramienta llamada coordenadas de un punto. En un
"OBSERVACIÓN DE LA CAÍDA DE UNA ESFERA A TRAVÉS DE UN MEDIO VISCOSO"
 EXPERIMENTO FA6 LABORATORIO DE FÍSICA AMBIENTAL "OBSERVACIÓN DE LA CAÍDA DE UNA ESFERA A TRAVÉS DE UN MEDIO VISCOSO" MATERIAL: () VISCOSÍMETRO ESFERAS DE ACERO 3 () MICROMETRO. ESCALA (O.00mm) (D x=0.0mm).
EXPERIMENTO FA6 LABORATORIO DE FÍSICA AMBIENTAL "OBSERVACIÓN DE LA CAÍDA DE UNA ESFERA A TRAVÉS DE UN MEDIO VISCOSO" MATERIAL: () VISCOSÍMETRO ESFERAS DE ACERO 3 () MICROMETRO. ESCALA (O.00mm) (D x=0.0mm).
RESUMEN DE HIDROSTÁTICA E HIDRODINÁMICA
 Fluidos: RESUMEN DE HIDROSTÁTICA E HIDRODINÁMICA Materiales que fluyen, que no tienen forma propia, materiales que se comportan de manera diferente de los sólidos ya que estos tienen forma y volumen definido.
Fluidos: RESUMEN DE HIDROSTÁTICA E HIDRODINÁMICA Materiales que fluyen, que no tienen forma propia, materiales que se comportan de manera diferente de los sólidos ya que estos tienen forma y volumen definido.
FUNCIONES CUADRÁTICAS. PARÁBOLAS
 FUNCIONES CUADRÁTICAS. PARÁBOLAS 1. FUNCIONES CUADRÁTICAS Representemos, en función de la longitud de la base (x), el área (y) de todos los rectángulos de perímetro 1 metros. De ellos, cuáles son las medidas
FUNCIONES CUADRÁTICAS. PARÁBOLAS 1. FUNCIONES CUADRÁTICAS Representemos, en función de la longitud de la base (x), el área (y) de todos los rectángulos de perímetro 1 metros. De ellos, cuáles son las medidas
ECUACIÓN DE ESTADO DE LOS GASES IDEALES
 ECUACIÓN DE ESTADO DE LOS GASES IDEALES Laboratorio de Física 1. OBJETIVO Se estudiará, tomando como ejemplo el aire, el comportamiento de un gas ideal cuando varían sus variables de estado, y se comprobarán
ECUACIÓN DE ESTADO DE LOS GASES IDEALES Laboratorio de Física 1. OBJETIVO Se estudiará, tomando como ejemplo el aire, el comportamiento de un gas ideal cuando varían sus variables de estado, y se comprobarán
de una reacción n en la cual, tanto reactivos como productos están n en condiciones estándar (p = 1 atm; ; T = 298 K = 25 ºC;
 Entalpía a estándar de la reacción Es el incremento entálpico de una reacción n en la cual, tanto reactivos como productos están n en condiciones estándar (p = 1 atm; ; T = 298 K = 25 ºC; conc.. = 1 M).
Entalpía a estándar de la reacción Es el incremento entálpico de una reacción n en la cual, tanto reactivos como productos están n en condiciones estándar (p = 1 atm; ; T = 298 K = 25 ºC; conc.. = 1 M).
TEMA 4: BALANCES DE ENERGÍA. IngQui-4 [1]
![TEMA 4: BALANCES DE ENERGÍA. IngQui-4 [1] TEMA 4: BALANCES DE ENERGÍA. IngQui-4 [1]](/thumbs/40/22050892.jpg) TEMA 4: BALANCES DE ENERGÍA IngQui-4 [1] OBJETIVOS! Aplicar la ecuación de conservación al análisis de la energía involucrada en un sistema.! Recordar las componentes de la energía (cinética, potencial
TEMA 4: BALANCES DE ENERGÍA IngQui-4 [1] OBJETIVOS! Aplicar la ecuación de conservación al análisis de la energía involucrada en un sistema.! Recordar las componentes de la energía (cinética, potencial
A = A < θ R = A + B + C = C+ B + A. b) RESTA O DIFERENCIA DE VECTORES ANÁLISIS VECTORIAL. Es una operación que tiene por finalidad hallar un
 ANÁLISIS VECTORIAL MAGNITUD FÍSICA Es todo aquello que se puede medir. CLASIFICACIÓN DE MAGNITUDES POR NATURALEZA MAGNITUD ESCALAR: Magnitud definida por completo mediante un número y la unidad de medida
ANÁLISIS VECTORIAL MAGNITUD FÍSICA Es todo aquello que se puede medir. CLASIFICACIÓN DE MAGNITUDES POR NATURALEZA MAGNITUD ESCALAR: Magnitud definida por completo mediante un número y la unidad de medida
y por lo tanto se tiene (5)
 FISICA GENERAL II 2011 Guía de Trabajo Practico N o 1 MEDICIÓN DE VISCOSIDAD EN LÍQUIDOS Método 1: El viscosímetro de Ostwald Introducción: El fundamento de la mayor parte de los viscosímetros que se utilizan
FISICA GENERAL II 2011 Guía de Trabajo Practico N o 1 MEDICIÓN DE VISCOSIDAD EN LÍQUIDOS Método 1: El viscosímetro de Ostwald Introducción: El fundamento de la mayor parte de los viscosímetros que se utilizan
SAN JUAN DE AZNALFARACHE (SEVILLA) PROBLEMAS DE MECANISMOS
 IES MTEO LEMÁN SN JUN DE ZNLFRCHE (SEVILL) PROBLEMS DE MECNISMOS º ESO MOTOR D 4 5 6 7 B C P PEDRO J. CSTEL GIL-TORESNO DEPRTMENTO DE TECNOLOGÍ PROBLEMS DE MECNISMOS Calcula la fuerza F y el desplazamiento
IES MTEO LEMÁN SN JUN DE ZNLFRCHE (SEVILL) PROBLEMS DE MECNISMOS º ESO MOTOR D 4 5 6 7 B C P PEDRO J. CSTEL GIL-TORESNO DEPRTMENTO DE TECNOLOGÍ PROBLEMS DE MECNISMOS Calcula la fuerza F y el desplazamiento
APÉNDICE E. Cálculo de la capacidad volumétrica del sitio. E.1 Cálculo de áreas
 Apéndices 79 APÉNDICE E Cálculo de la capacidad volumétrica del sitio E.1 Cálculo de áreas El área de cualquier figura que se haya levantado puede calcularse a partir de:? Las anotaciones de campo? El
Apéndices 79 APÉNDICE E Cálculo de la capacidad volumétrica del sitio E.1 Cálculo de áreas El área de cualquier figura que se haya levantado puede calcularse a partir de:? Las anotaciones de campo? El
Tema: Movimiento rectilíneo uniformemente variado.
 LABORATORIO DE FÍSICA Tema: Movimiento rectilíneo uniformemente variado. 1. Objetivo: Establecer las leyes y ecuaciones para una partícula que tiene una trayectoria rectilínea con M.R.U.V. 2. Introducción
LABORATORIO DE FÍSICA Tema: Movimiento rectilíneo uniformemente variado. 1. Objetivo: Establecer las leyes y ecuaciones para una partícula que tiene una trayectoria rectilínea con M.R.U.V. 2. Introducción
www.matesxronda.net José A. Jiménez Nieto
 NÚMEROS REALES 1. NÚMEROS IRRACIONALES: CARACTERIZACIÓN. En el tema correspondiente a números racionales hemos visto que estos números tienen una característica esencial: su expresión decimal es exacta
NÚMEROS REALES 1. NÚMEROS IRRACIONALES: CARACTERIZACIÓN. En el tema correspondiente a números racionales hemos visto que estos números tienen una característica esencial: su expresión decimal es exacta
UNIVERSIDAD DON BOSCO DEPARTAMENTO DE CIENCIAS BÁSICAS Asignatura: FÍSICA II
 UNIVERSIDAD DON BOSCO DEPARTAMENTO DE CIENCIAS BÁSICAS Asignatura: FÍSICA II LABORATORIO DE FÍSICA CICLO: AÑO: Laboratorio: 08 Laboratorio 08: CALOR ESPECÍFICO DE UN METAL I. OBJETIVOS General Aplicar
UNIVERSIDAD DON BOSCO DEPARTAMENTO DE CIENCIAS BÁSICAS Asignatura: FÍSICA II LABORATORIO DE FÍSICA CICLO: AÑO: Laboratorio: 08 Laboratorio 08: CALOR ESPECÍFICO DE UN METAL I. OBJETIVOS General Aplicar
Prácticas Integrales I Año Lectivo 2007-2008 Modulo I Procedimientos e instrumentación Básica en el Laboratorio
 Práctica N 2 Mediciones y Tipos de Errores 1.- Objetivos: Seleccionar el instrumento más apropiado para realizar una medición considerando su precisión y exactitud. Realizar transformaciones de unidades
Práctica N 2 Mediciones y Tipos de Errores 1.- Objetivos: Seleccionar el instrumento más apropiado para realizar una medición considerando su precisión y exactitud. Realizar transformaciones de unidades
Las condiciones ambientales, especialmente la temperatura y la presión afectan a la viscosidad.
 4. PRUEBAS 4.1. VISCOSIDAD 4.1.1. Definición La viscosidad, es la propiedad de un fluido al oponerse a su flujo cuando se aplica una fuerza. Los fluidos de alta viscosidad presentan una cierta resistencia
4. PRUEBAS 4.1. VISCOSIDAD 4.1.1. Definición La viscosidad, es la propiedad de un fluido al oponerse a su flujo cuando se aplica una fuerza. Los fluidos de alta viscosidad presentan una cierta resistencia
Universidad Alonso de Ojeda. Facultad de Ingeniería GUIA DE ESTUDIO ALGEBRA LINEAL.
 UNIDAD IV: VECTORES EN R2 Y R3 VECTOR Se puede considerar un vector como un segmento de recta con una flecha en uno de sus extremos. De esta forma lo podemos distinguir por cuatro partes fundamentales:
UNIDAD IV: VECTORES EN R2 Y R3 VECTOR Se puede considerar un vector como un segmento de recta con una flecha en uno de sus extremos. De esta forma lo podemos distinguir por cuatro partes fundamentales:
Manual de laboratorio de termodinámica I. Ley de Gay-Lussac
 Ley de Gay-Lussac Conceptos relacionados Presión, temperatura, volumen, coeficiente de expansión térmica, ecuación de estado de los gases ideales, constante universal de los gases. Principio El estado
Ley de Gay-Lussac Conceptos relacionados Presión, temperatura, volumen, coeficiente de expansión térmica, ecuación de estado de los gases ideales, constante universal de los gases. Principio El estado
Interacción aire - agua. Termómetro húmedo
 Interacción aire - agua. Termómetro húmedo Objetivos de la práctica! Obtener experimentalmente la denominada temperatura húmeda.! Estudiar las magnitudes psicrométricas de dos corrientes de aire húmedo,
Interacción aire - agua. Termómetro húmedo Objetivos de la práctica! Obtener experimentalmente la denominada temperatura húmeda.! Estudiar las magnitudes psicrométricas de dos corrientes de aire húmedo,
DIFERENCIA ENTRE FLUIDOS Y SÓLIDOS
 DIFERENCIA ENTRE FLUIDOS Y SÓLIDOS Se le llama fluido a toda aquella sustancia continua que puede fluir. Los fluidos pueden ser gaseosos y líquidos. Esta es la diferencia fundamental entre un sólido, cuya
DIFERENCIA ENTRE FLUIDOS Y SÓLIDOS Se le llama fluido a toda aquella sustancia continua que puede fluir. Los fluidos pueden ser gaseosos y líquidos. Esta es la diferencia fundamental entre un sólido, cuya
La función cuadrática
 La función cuadrática En primer semestre estudiamos las ecuaciones cuadráticas. También resolvimos estas ecuaciones por el método gráfico. Para esto, tuvimos que convertir la ecuación en una función igualándola
La función cuadrática En primer semestre estudiamos las ecuaciones cuadráticas. También resolvimos estas ecuaciones por el método gráfico. Para esto, tuvimos que convertir la ecuación en una función igualándola
Teoría de errores. Departamento de Análisis Matemático Universidad de La Laguna
 Teoría de errores BENITO J. GONZÁLEZ RODRÍGUEZ (bjglez@ull.es) DOMINGO HERNÁNDEZ ABREU (dhabreu@ull.es) MATEO M. JIMÉNEZ PAIZ (mjimenez@ull.es) M. ISABEL MARRERO RODRÍGUEZ (imarrero@ull.es) ALEJANDRO SANABRIA
Teoría de errores BENITO J. GONZÁLEZ RODRÍGUEZ (bjglez@ull.es) DOMINGO HERNÁNDEZ ABREU (dhabreu@ull.es) MATEO M. JIMÉNEZ PAIZ (mjimenez@ull.es) M. ISABEL MARRERO RODRÍGUEZ (imarrero@ull.es) ALEJANDRO SANABRIA
Determinación de la constante elástica, k, de un resorte. Estudio estático y dinámico.
 Determinación de la constante elástica, k, de un resorte. Estudio estático y dinámico. Nombre: Manuel Apellidos: Fernandez Nuñez Curso: 2º A Fecha: 29/02/2008 Índice Introducción pag. 3 a 6 Objetivos.
Determinación de la constante elástica, k, de un resorte. Estudio estático y dinámico. Nombre: Manuel Apellidos: Fernandez Nuñez Curso: 2º A Fecha: 29/02/2008 Índice Introducción pag. 3 a 6 Objetivos.
Determinación de la densidad de distintos cuerpos - Estudio experimental del principio de Arquímedes.
 Determinación de la densidad de distintos cuerpos - Estudio experimental del principio de Arquímedes. P. D Angelo Campos, N. C. Cagliotti y A. Sterverlynck Universidad de San Andrés - Mayo 2001 RESUMEN
Determinación de la densidad de distintos cuerpos - Estudio experimental del principio de Arquímedes. P. D Angelo Campos, N. C. Cagliotti y A. Sterverlynck Universidad de San Andrés - Mayo 2001 RESUMEN
TRABAJO PRÁCTICO N 2 DETERMINACIÓN DE DENSIDADES
 0 TRABAJO PRÁCTICO N 2 DETERMINACIÓN DE DENSIDADES a) Determinación de la densidad de hidrógeno Objetivos Determinar la densidad de un gas Conceptos Gases ideales, presión de vapor, rendimiento, pureza,
0 TRABAJO PRÁCTICO N 2 DETERMINACIÓN DE DENSIDADES a) Determinación de la densidad de hidrógeno Objetivos Determinar la densidad de un gas Conceptos Gases ideales, presión de vapor, rendimiento, pureza,
TEMA 6: CINÉTICA HETEROGÉNEA FLUIDO - FLUIDO CQA-6/1
 TEMA 6: CINÉTICA HETEROGÉNEA FLUIDO - FLUIDO CQA-6/1 PLANTEAMIENTO DEL MODELO CINÉTICO Objetivos de las reacciones heterogéneas fluido-fluido:! Obtener productos valiosos mediante reacciones gas-líquido!
TEMA 6: CINÉTICA HETEROGÉNEA FLUIDO - FLUIDO CQA-6/1 PLANTEAMIENTO DEL MODELO CINÉTICO Objetivos de las reacciones heterogéneas fluido-fluido:! Obtener productos valiosos mediante reacciones gas-líquido!
Introducción a la Física Experimental Guía de la experiencia Balanza de Mohr-Westpal Un método para determinar la densidad de un
 Introducción a la Física Experimental Guía de la experiencia Balanza de Mohr-Westpal Un método para determinar la densidad de un líquido Departamento de Física Aplicada. Universidad de Cantabria. Febrero
Introducción a la Física Experimental Guía de la experiencia Balanza de Mohr-Westpal Un método para determinar la densidad de un líquido Departamento de Física Aplicada. Universidad de Cantabria. Febrero
UNIDAD 2: DINÁMICA. LAS FUERZAS Y SUS EFECTOS.
 UNIDAD 2: DINÁMICA. LAS FUERZAS Y SUS EFECTOS. 1. FUERZAS Y SUS EFECTOS. La Dinámica es una parte de la Física que estudia el movimiento de los cuerpos, atendiendo a las causas que lo producen. Son las
UNIDAD 2: DINÁMICA. LAS FUERZAS Y SUS EFECTOS. 1. FUERZAS Y SUS EFECTOS. La Dinámica es una parte de la Física que estudia el movimiento de los cuerpos, atendiendo a las causas que lo producen. Son las
