Diseño de Filtros Digitales (Parte
|
|
|
- José Carlos Núñez Parra
- hace 7 años
- Vistas:
Transcripción
1 Diseño de Filtros Digitales (Parte 2) Filtros FIR Secuencias Simétricas Método de las Series de Fourier Método de Muestreo en Frecuencia Métodos Iterativos basados en condiciones óptimas Diseño de Filtros FIR con MATLAB
2 Secuencias Simétricas 5º Curso-Tratamiento Digital de Señal El diseño de filtros FIR requieren la selección de la secuencia que mejor representa la respuesta a impulso de un filtro ideal. Los filtros FIR son siempre estables y son capaces de tener una respuesta de fase que es lineal, lo que equivale a decir que su respuesta tiene un retraso constante. El mayor problema de los filtros FIR es que para unas especificaciones dadas requieren un filtro de orden mucho mayor que los filtros IIR. Un filtro FIR de longitud M con entrada x[n] y salida y[n] se describe mediante la ecuación diferencia: [ ] = [ ] + [ ] + + [ + ] = [ ] yn bxn bxn b xn M bxn k M donde b k son los coeficientes del filtro. M k= k 2
3 Secuencias Simétricas 5º Curso-Tratamiento Digital de Señal Por otra parte podemos expresar la salida del filtro y[n] como una convolución de la entrada x[n] con la respuesta a impulso del filtro h[n]: M [ ] [ ] [ ] yn = hk xn k k= Ya que estas dos ecuaciones son idénticas, y por tanto, los coeficientes b k =h[k]. Se puede demostrar que la respuesta de un filtro FIR es de fase lineal si los coeficientes h[n] cumplen : hn [ ] =± h[ M n] n=,,, M Es decir los coeficientes tienen algún tipo de simetría. La función de Transferencia Z del filtro FIR, aplicando esta condición es : M k 2 ( M 2) ( M ) () = hk [] z = h[] + h[] z + h[] 2 z + + h[ M 2] z + h[ M ] z H z k= z = /2 [ z ± z ] ( M 3) /2 ( M )/2 M [] ( M 2k ) /2 ( M 2k ) h z 2 + /2 [ z ± z ] ( M )/2 ( M )/2 [] ( M 2k ) /2 ( M 2k ) k= hk k= hk Mimpar M par = 3
4 Secuencias Simétricas De esta última expresión se deduce que 5º Curso-Tratamiento Digital de Señal ( M ) ( ) ( ) z H z =± H z lo que significa que la raíces de H(z) son las mismas que las de H(z - ). Es decir las raíces (en este caso, los ceros) ocurren en pares recíprocos. Si z es un cero de H(z), /z es también un cero. Además, si z es un cero complejo, su conjugado z * es también un cero, 2 así como /z *
5 4 Secuencias Simétricas 5º Curso-Tratamiento Digital de Señal La longitud N de una secuencia simétrica puede ser par o impar. Esto significa que el punto medio cae en un punto de la secuencia si N es impar y entre dos puntos si N es par. Como tengo dos tipos de simetría (par o impar), tendré cuatro posibles tipos de secuencias simétricas, las cuales se muestran en la Tabla junto con la DTFT de cada secuencia. Secuencias Simétricas L=½(N-), M=½N, F es la frecuecia digital=f/f s, donde f s es la frecuencia de muestreo Tipo Simetría N H(F) H() H(½) L L L Par Impar h[] + 2 h[] k cos( 2kπ F) h[] + 2 h[] k k= h[] + 2 ( ) k h[] k k= k = M L 2 Par Par 2 = h[] k cos [ 2π F( k )] k 2 2 hk [] k= L 3 Impar Impar j2 h[] k sin( 2kπF) k = k = 2 M M k 4 Impar Par j2 h[] k sin [ 2πF( k )] 2 ( ) hk [] k = Tabla : Secuencias Simétricas 5
6 Secuencias Simétricas 5º Curso-Tratamiento Digital de Señal De esta tabla se pueden sacar las siguientes conclusiones acerca de la aplicabilidad de cada una de los tipos de secuencia. Para las secuencias del tipo 2 H(½) =, por lo que sólo pueden ser utilizadas para filtros pasabaja y pasabanda. Las secuencias del tipo 3 ( H() == H(½) ) sólo pueden ser utilizadas para filtros pasabanda. Las secuencias tipo 4 ( H() =) son apropiadas para filtros pasaalta y pasabanda. La secuencia tipo puede implementar cualquier tipo de filtro. Es el único tipo capaz de realizar filtros parabanda. Aplicaciones de las Secuencias Simétricas Tipo H(F) Aplicación Todo tipo de filtros 2 H(½)= Sólo LP y BP 3 H() == H(½) Sólo BP 4 H()= Sólo HP y BP 6
7 5º Curso-Tratamiento Digital de Señal Hay tres métodos de diseño de filtros FIR: Método de las Series de Fourier. Método del Muestreo en Frecuencia. Métodos Iterativos basados en condiciones óptimas de diseño. Método de las Series de Fourier El método se basa en seleccionar la respuesta a impulso h N [n] como una versión truncada de la respuesta a impulso h[n] de un filtro ideal con repuesta frecuencial H(F). Proceso de Diseño de Filtros FIR por este método: Normalización de frecuencias por la frecuencia de muestreo. Conversión de especificaciones a la de un Prototipo de Filtro Pasobajo. Truncamiento de la respuesta a impulso de un filtro ideal h[n]=2f C sinc(2nf C ) a h N [n] de longitud N. El orden del filtro es N-. Selecionar una ventana w[n] de N puntos para obtener h w [n]=h N [n] w[n]. Convertir del Protipo de Filtro Pasobajo al Filtro deseado h F [n]. Retrasar h F [n] para asegurarse que el filtro es causal. 7
8 Nos planteamos realizar un filtro pasobajo ideal (digital) con una frecuencia de corte F c, tal y como indica la figura..5 -F c H(F) F c.5 F Si expresamos matemáticamente la respuesta frecuencial deseada: j F N H d ( ) F 2π ( )/ 2 e F Fc = F > Fc Haciendo la Transformada inversa de Fourier discreta en el tiempo de esta función H d (F), nos queda: [ ] ( ) hn j F N c n j Fn = 2π Hd F e df = e df = F 2π 2 2 Fc N s j2π n 2 F j F N 2 2π n 2 2j = N j2π n 2 = F F N 2 csinc 2 c n 2 F N sin 2π c n F 2 = 2 c e F N sin 2π c n 2 = F N 2π c n 2 F c = F c 8
9 La función sinc(x) está definida para todo valor de x, y además decae muy lentamente. Utilizar los valores de h[n] definidos por la ecuación anterior como coeficientes del filtro FIR, dará lugar a sobreimpulsos en la respuesta frecuencial del filtro. Debido a la lentitud de la función sinc(x), necesitaré un filtro de elevado orden (gran número de puntos) para diseñar filtros con transiciones rápidas entre bandas
10 Necesidad de utilizar ventanas espectrales : El truncamiento de h[n] equivale a multiplicar h[n] por una ventana rectangular w[n] de longitud N. El espectro de h N [n]=h[n] w[n] es la convolución de H(F) y W(F). La función W(F) va a producir rizados y sobreimpulsos en la señal de salida, de la misma forma que se producía el efecto Gibbs al reconstruir una señal discontinua con un número finito de coeficientes espectrales. Aquí el efecto Gibbs se da en el dominio frecuencial al usar un truncamineto de la respuesta a impulso. Para reducir los efectos de un truncamiento abrupto se utilizan ventanas espectrales que tienden a suavizar esos efectos. Por ejemplo, en el caso de una ventana rectangular, en la que w[n]=, para n=,...,n-, la DTFT es, W N N N j 2πFk j 2πFk j2πf ( F ) = w[] k e = e = ( e ) k = e = e j 2πF N 2 j 2π F 2 j e e 2πF N 2 j2π F 2 k = e e j 2πF N 2 j 2π F 2 k = = e j2πf k e = e j2πfn j2πf ( N ) 2 sin( πfn ) sin( πf) =
11 El módulo de esta función (llamada función de Dirichlet) se muestra en la figura de la página siguiente. Las ventanas más comunmente utilizadas en el diseño de filtros FIR están listadas en la Tabla 2. Sus características espectrales principales se especifican en la Tabla 3. De los espectros de las ventanas se hacen notar dos cosas: El ancho del lóbulo principal y el de transición decrece al aumentar N. La amplitud de los lóbulos de los lados permanece constante con N. Idealmente el espectro de una ventana debe estar confinado en el lóbulo principal, sin casi energía en los lóbulos de los lados.
12 A continuación se muestran algunas ventanas espectrales y sus espectros Boxcar Indice n Frecuencia Digital f/fs Hamming Indice n Frecuencia Digital f/fs 2
13 vonhann Indice n Frecuencia Digital f/fs Blackman Indice n Frecuencia Digital f/fs 3
14 Bartlett Indice n Frecuencia Digital f/fs Papoulis Indice n Frecuencia Digital f/fs 4
15 Kaiser β= Indice n Frecuencia Digital f/fs Parzen Indice n Frecuencia Digital f/fs 5
16 Las ventanas más utilizadas son vonhann, Hamming y Kaiser. A la hora de escoger la ventana adecuada tendremos un cuenta dos criterios principales de diseño : Asegurarse que el parámetro P S de la ventana esté por encima de la atenuación A s especificada para la parabanda del filtro. Como mucho puede estar unos 8 db por encima. Es decir P s A s Una transición más ancha permite utilizar un filtro de menor orden, pero a costa de una menor atenuación en los lóbulos. Ejemplo: Diseñar un filtro FIR pasobajo con una frecuencia de corte de 5KHz y una frecuencia de muestreo de 2KHz. h N [n]=2f C sinc(2nf C )=2 (5/2) sinc(2n5/2)=.5 sinc(.5n). (a) Con N=9, -4 n 4, y una ventana tipo Bartlett : 2n w[] n = { w[] n } = {,,2,3,4,3,2,, } N 4 { hn [] n } = {,.6,,.383,.5,.383,,.6, } h [] n = h n w n =, { } { [][]} {.265,,.2387,.5,.2387,,.265,} W N 6
17 Para que el filtro sea causal tendremos que retrasar 4 muestreos, por lo que el filtro a aplicar es: Hz ( ) =. 265z z +. 5z z z + = =. 265z z +. 5z z. 265z Como el primer muestreo de h W [n]=, podemos hacer Hz ( ) = z +. 5z z. 265z (b) Con N=6, -2.5 n 2.5 y una ventana vonhann wn [] = cos[ 2nπ ( N ) ] { wn []} = {,. 3455,. 945,. 945,. 3455, } { hn[] n} = {. 9,. 5,. 452,. 452,. 5,. 9} { hw[] n} = hn[][] n w n =,. 58,. 472,. 472,. 58, { } { } Hz () = z z +. 58z 2 3 7
18 magnitude vs digital frequency F 2 phase in degrees vs digital frequency F Bartlett N= unwrapped phase in degrees vs digital frequency F magnitude vs digital frequency F 2 phase in degrees vs digital frequency F vonhann N= unwrapped phase in degrees vs digital frequency F
19 Características de algunas ventanas espectrales Window Atenuación en lóbulo de los lados (db) Ancho de Banda de la Transición Rectangular -3 2π.9/N -2 Hanning -3 2π 3./N -44 Hamming -4 2π 3.3/N -53 Blackman -57 2π 5.5/N -74 Máximo Rizado en Parabanda (db) Características de la ventana Kaiser para distintos parámetros Parámetro β Atenuación en lóbulo de los lados (db) Ancho de Banda de la Transición Máximo Rizado en Parabanda (db π.5/N π 2./N π 2.6/N π 3.2/N π 3.8/N π 4.5/N π 5./N π 5.7/N π 6.4/N -99 9
20 Podemos estimar la longitud del filtro (N) a partir del ancho de banda en la transición ( ω). Por ejemplo, si se pide un filtro con una transición entre ω p y ω s, llamamos banda de transición a la diferencia normalizada por la frecuencia de muestreo F m, entre las frecuencias de parabanda y pasabanda (en rad/s), ( ωs ω p ) 2πk 2πk k ω = = N = N ω F F m Para el caso de un filtro de Kaiser hay que calcular la longitud del filtro y el valor del parámetro β. Esto se realiza mediantes las siguientes ecuaciones, As 7.95 N 4.36 F.2 ( As 8.7), As 5 β = ( As 2) ( As 2 ), 2 < As < 5 2
21 Otro criterio es tomar N de acuerdo a la siguiente fórmula, donde W S es la mitad de la anchura del lóbulo principal (Tabla 2), y F p y F s la frecuencias digitales de pasabanda y parabanda. W ( Fs Fp) Transformaciones Espectrales : Se trata de convertir diseños de filtros pasobajo a otras formas y viceversa. Las tablas y 2 del apéndice muestran todas las posibles transformaciones. N S Ejemplo : Diseñar un filtro pasobajo con las siguientes especificaciones f p =KHz, f s =2KHz, S f =KHz, A p =2 db y A s =4dB. Las frecuencias digitales son F p =f p /S f =., F s =f s /S f =.2. Aplicando este último criterio y acudiendo a las tablas vemos que de acuerdo a los valores de P S, los filtros más adecuados son vonhann, Hamming y Blackman. Aplicando la fórmula de N para cada uno de estos filtros obtenemos, 2
22 vonhann : N = Hamming : N =.9. 2 Blackman : N = A partir de aquí procedemos por el científico método de intentar y errar. De la Tabla, obtenemos h N [n] para una frecuencia de corte que no se nos especifica claramente. Sólo se nos da las frecuencias en los bordes de la pasabanda y la parabanda. Por ello escogemos una frecuencia de corte un 2% superior a f p, es decir f C =.2 KHz. h n F nf n [] = 2 sinc ( 2 ) = 24sinc. ( 24. ) N C C Ahora se intenta con cada uno de los filtros partiendo de la longitud calculada y se observa si se cumplen las especificaciones. En caso de no cumplirse, debe aumentarse el orden del filtro o modificar la frecuencia de corte elegida y volver comprobar las especificaciones. Este proceso ha sido utilizado en este problema y hemos llegado a los siguientes resultados: vonhann: N=23 F C =.37 Ap=.9 db As=4dB Hamming: N=23 F C =.32 Ap=.58 db As=4.dB Blackman: N=29 F C =.28 Ap=.98 db As=4.dB El filtro Blackman tiene la mayor longitud y un mayor ancho de transición pero el nivel de los lóbulos de los lados es el menor. 22
23 2 vonhann - hamming - blackman -2 Magnitud (db) Frecuencia Digital 23
24 Ejemplo : Diseñar un filtro pasabanda con las siguientes especificaciones: Pasabanda [4,8]KHz, Parabanda [2,2]KHz A p =3dB A s =45dB S F =25KHz Calculamos primero la frecuencia central f =6KHz. Para hacer que la Parabanda tenga una frecuencia central igual a la Pasabanda por lo que cambiamos la frecuencia de 2KHz por una frecuancia de KHz. Normalizamos las frecuencias y aplicamos las fórmulas de la Tabla 2, para pasarlo al protipo pasobajo : PasaBanda[.6,.32] ParaBanda[.8,.4] F =.24 F p =(F p2 -F p )/2=.8 F s =(F s2 -F s )/2=.6 Utilizamos el filtro de Hamming, para el que N W S /(F s -F p ) 24 y comenzamos el proceso de intentar y errar hasta que llegamos a una solución aceptable. Una vez determinada la secuencia h w [n] que especifica el filtro, lo convertimos a un filtro pasabanda a través de la relación de la Tabla : h BP [n]=2cos(2πnf ) h w [n]=2cos(.48πn) h w [n]. El resultado final obtenido es un filtro con N=27, F C =.956, A p =3.dB a 4 KHz y 8 KHz, A s =45.dB a 2KHz y db a 2 KHz. 24
25 Filtro Pasabanda usando una ventana de Hamming Frecuencia Digital 25
26 Filtros FIR de Media Banda : Veamos qué sucede si diseñamos un filtro pasabaja en el que la frecuencia de corte es F C =.25. La respuesta a impulso es h[n]=2f C sinc(2nf C )=.5sinc(.5n), de forma que si el orden N es impar, h[n]= para n par (ver ejemplo T). En este caso la frecuencia de muestreo debe ser S F =4f (o 4f c ). La función de Transferencia H(F) tiene antisimetría respecto a F=.25 : H(F)=-H(.25-F) Filtros de Media Banda usando la ventana Kaiser : Para esta ventana con N=9 y β=.5, w[n]={.588,.7497,.8838,.972,,.972,.8838,.7497,.588}, y h N [n] w[n]={,-.795,,.388,.5,.388,,-.795,}=h w [n]. H(z)= z z z z -6. Este tipo de filtros con la ventana Kaiser muestra un rizado tanto en la pasabanda (δ p ) como en la parabanda (δ s ). Estos dependerán de las atenuaciones especificadas en las dos bandas. Con estos datos se diseña la ventana Kaiser con el parámetro β más adecuado. 26
27 .2 +δ p -δ p δ s δ s Frecuencia Digital Dos importantes características de los filtros de media banda son : Su implementación requiere sólo de aprox. N/2 multiplicadores debido a los ceros de los coeficientes del filtro. Se puede obtener un filtro pasoalto a partir del espectro complementario : H HP (z)=z -(N-)/2 H co (z). 27
28 5º Curso-Tratamiento Digital de Señal Ejemplo : Diseñar un filtro parabanda de media banda con las siguientes especificaciones : Parabanda [2 KHz-3 KHz], Pasabanda [ KHz-4 KHz], A p =db y A s =5dB. Calculamos la frecuencia de muestreo necesaria para realizar el filtro. S F =4f =4(3+2)/2= KHz. Ahora se determinar las frecuencias digitales Fp y Fs de acuerdo con la Tabla 2, diseñandose un prototipo de filtro pasabaja. Una vez obtenido se transforma a un filtro parabanda con las expresiones de la Tabla. El resultado final para un filtro de este tipo con una ventana Kaiser es : N=3, A p =.46 db a 2 KHz y 3 KHz y A s =53.2 db a y 4 KHz. Los pasos a realizar no se muestran explicitamente puesto que este tipo de diseño se realiza de forma automática por métodos de CAD. En concreto, haremos estos diseños utilizando MATLAB. Especificaremos el tipo de filtro a realizar (pasobajo, pasoalto, etc), la frecuencia de muestreo, las frecuancias de pasabanda y parabanda y sus respectivas atenuaciones, así como el tipo de ventana que deseamos utilizar. Con estos datos el programa realiza el diseño del filtro proporcionando el orden, los coeficientes y las especificaciones reales del filtro. 28
29 kaiser window: n = 3 Fc =. ap = as = Digital Freq F 29
30 5º Curso-Tratamiento Digital de Señal Método del Muestreo Frecuencial Se trata de reconstruir el espectro continuo X(F) de una señal discreta a partir de los muestreos de la función X(F). El espectro reconstruido X N (F) será igual a X(F) sólo en las frecuencias de muestreo. Se puede considerar el DFT de la señal h N [n] de longitud N como N muestreos de su DTFT (H(F)) en F=k/N, k=,,...,n-. N H ( F) = h [] n exp( j2πnf) df H [] k = h [] n exp( j2πnk N) N N N N k= La respuesta a impulso h N [n] se calcula con el IDFT, h N N N [] n = H [] k exp( j2πnk N) k= N Proceso de diseño Los muestreos deben hacerse en un periodo (,) de la extensión periódica de H(F). La fase de H(F) es lineal y por tanto cada uno de los muestreos tiene una fase dada por φ(k)=-πk(n-)/n, k=,...,n. 3
31 Para minimizar el efecto Gibbs en las discontinuidades, permitimos que los valores de muestreo varíen lentamente en las discontinuidades. Ejemplo : Diseñar un filtro pasobajo dado por la respuesta frecuencial de la figura. Tomamos muestras. La fase de cada una de las muestras es -πk(n-)/n H[]= H[]=exp(-j.9π) H[2]=exp(-j.8π) H[3]= H[4]= H[5]=. H[]=-.95-j.39 H[2]=.89+j Los valores H[5]... H[9] se calculan teniendo en cuenta que la respuesta frecuencial debe ser simétrica en módulo y asimétrica en fase: H[6]= H[7]= H[8]=.89-j.5878 H[9]=-.95+j.39. Haciendo la IDFT de estos H[k] obtenemos la secuencia h[n], h[n]={.76,-.794,-.,.558,.452,.452,.558,-.,-.794,.76} En la respuesta frecuencial de este filtro se observa que efectivamente pasa por los puntos de muestreo pero a costa de un sobreimpulso. Para suavizarlo, se puede sustituir los muestreos H[3] por.5exp(-j2.7π). Haciendo el IDFT de la nueva secuencia de muestreos H[k] obtenemos el filtro, h[n]={.28,.57,-.,.66,.58,.58,.66, -.,.57,.28} 3
32 .2 Filtro Pasobajo usando Muestreo Frecuencial Frecuencia Digital 32
33 Podemos combinar las ventajas del diseño con ventanas estudiado anteriormente y el método de muestreo frecuencial para tener un método de diseño de filtros de respuesta frecuencial arbitraria. Se muestrea la respuesta frecuencial deseada con un número alto de puntos (M=52). Hacemos el IDFT y obtenemos la respuesta h[n]. h[n] es demasiado largo, así que debemos truncarlo a una secuencia más pequeña con una ventana. Si el diseño no cumple las especificaciones podemos cambiar N, el ancho de pasabanda o ajustar los muestreos en la zona de transición. Métodos Basados en criterios de optimización Se trata de utilizar criterios para minimizar el máximo error en la aproximación. Hay tres importantes conceptos en diseño óptimo, El error entre la aprox. H(F) y la respuesta deseada D(F) debe tener igual rizado. 33
34 La respuesta frecuencial H(F) de un filtro cuya respuesta a impulso h[n] es una secuencia simétrica puede ponerse como M HF ( ) = α n( F) cos( 2πnF) k= donde M está relacionado con la longitud del filtro N. Esta forma es un polinomio de Chebyshev. Debemos escogerα n para que el diseño se óptimo. El teorema de la alternancia ofrece una pista para seleccionarα n. El Teorema de la Alternancia : Aproximamos D(F) por una forma polinomial de Chebyshev obteniendo H(F). Se define el error ponderado en la aproximación ε(f) como ε(f)=w(f)[d(f)-h(f)] El teorema dice que se pueden encontrar al menos M+2 frecuencias F k, k=,2,...,m+2 llamadas frecuencias extremas donde El error varía entre dos máximos y mínimos iguales ε(f k ) = -ε(f k+ ) k=,2,...,m+ El error en la frecuencia F k es igual al máximo error absoluto. ε(f k ) = ε(f) max k=,2,...,m+2 34
35 Existe un algoritmo llamado Parks-McClellan (PM) para determinar esas frecuencias. Este algoritmo necesita los siguientes datos: las frecuencias F p y F s, la relación δ /δ 2 de los errores en la pasabanda y en la parabanda y la longitud N del filtro. Devuelve los coeficientes α n y los valores reales de δ y δ 2. El filtro parabanda diseñado anteriormente ha sido rediseñado utilizando este algoritmo. El resultado es un filtro de N=2, δ =.2225dB y δ 2 =56.79 db. La respuesta frecuencial se muestra en la figura. 35
36 Length N = 2 PB/SB Attn from db = [ ] db Digital Frequency F 36
37 Filtros FIR de horizontalidad máxima Se trata de diseñar un filtro cuyas 2L- derivadas en F= y sus 2K- derivadas en F=.5 sean cero. La longitud del filtro viene dada por N=2(K+L)- y es por tanto impar. Los enteros K y L se determinan a partir de las frecuencias de pasabanda y parabanda que corresponden a atenuaciones de.5 db y 26 db. Por ejemplo, se pide un filtro pasobajo cuyas frecuencias digitales F p =.2 y F s =.4. Obtenemos un filtro de N=27..2 Filtro Pasobajo de Horizontalidad Máxima Frecuencia Digital 37
38 Diseño de Filtros FIR con MATLAB Funciones de MATLAB para realizar filtros FIR: Función FIR >> B = fir(n,wn,type,window); Diseña un filtro FIR pasobajo de orden N (longitud N+) y frecuencia de corte Wn (normalizada con respecto a la frecuencia de Nyquists, Wn ). Se pueden especificar otro tipo de filtros de la misma forma que con los filtros IIR mediante el parámetro type. Por ejemplo, para un filtro parabanda: >> B = fir(n,[w W2],'stop'); Por defecto la función FIR usa la ventana de Hamming. Otro tipo de ventanas pueden también especificarse: >> B = fir(n,wn,bartlett(n+)); >> B = fir(n,wn,'high',chebwin(n+,r)); Función FIR2 >> B = fir2(n,f,m,window); Diseña un filtro FIR utilizando el método del muestreo frecuencial. Los parámetros de entrada es el orden del filtro N (longitud N+) y dos vectores F y M que especifican la frecuencia y la magnitud, de forma que plot(f,m) es una gráfica de la respuesta deseada del filtro. 38
39 Diseño de Filtros FIR con MATLAB Se pueden indicar saltos bruscos en la respuesta frecuencial duplicando el valor de la frecuencia de corte. F debe estar entre y, en orden creciente, siendo el primer elemento igual a y el último. El parámetro window indica el tipo de ventana a utilizar. Por defecto, usa la ventana de Hamming. >> B = fir2(n,f,m, bartlett(n+) ); Se pueden especificar más parámetros en esta función, >> B = fir2(n,f,m,npt,lap,window); La función fir2 interpola la respuesta frecuencial deseada (F,M) con npt puntos (por defecto, npt=52). Si dos valores sucesivos de F son iguales, se crea una región de lap puntos alrededor de este punto (por defecto, lap=25). Función FIRLS >> B = firls(n,f,m); Diseño de filtros FIR usando la minimización del error por mínimos cuadrados. Los argumentos de entrada son el orden del filtro N, y dos vectores F y M, cuyo formato difiere de los análogos en la función fir2. El filtro obtenido es la mejor aproximación a (F,M) por mínimos cuadrados. 39
40 Diseño de Filtros FIR con MATLAB F es un vector que indica los límites de las bandas de frecuencia en parejas (por tanto el tamaño de F debe ser par), y en orden ascendente entre y. M es un vector del mismo tamaño que F que indica la magnitud deseada para cada banda de frecuencias. La respuesta deseada es la línea que conecta los puntos (F(k),M(k)) y (F(k+),M(k+)) para k impar. Las bandas de frecuencia entre F(k+) y F(k+2) para k impar son tratadas por firls como bandas de transición. También existe un argumento opcional que consiste en un vector W cuyo tamaño es la mitad de F. W es un factor de ponderación del error para cada banda de frecuencias. >> B = firls(n,f,m,w); H(F) Bandas de Transición M() M(2) M(5) M(3) M(4) M(6) F()= F(2) F(3) F(4) F(5) F(6)= F 4
41 5º Curso-Tratamiento Digital de Señal Diseño de Filtros FIR con MATLAB Algoritmo de Parks-McClellan Hay dos funciones en MATLAB para realizar este algoritmo: remezord y remez. >> [N,Fo,Mo,W] = remezord(f,m,dev,fs) Calcula el orden N, las bandas de frecuencia normalizadas Fo, las magnitudes en esas bandas Mo y los factores de ponderación W que luego serán utilizados como argumentos de entrada de la función remez. Estos valores cumplen las especificaciones dadas por F, M, DEV. F es un vector de frecuencias de corte en Hz, en orden ascendente entre y Fs/2. Si no se especifica Fs, Fs=2 por defecto. El primer elemento de F es siempre y el último es siempre Fs/2, pero no deben ser especificados en el vector F. El vector M indica la respuesta deseada en cada banda. Por tanto, el vector M tiene un tamaño igual a (length(f)+2)/2. DEV es un vector que indica el máximo rizado permitido en cada banda. Ver la gráfica de la página siguiente. >> b = remez(n,fo,mo,w); Con los valores obtenidos en la función remezord, podemos implemantar el algoritmo de Parks-McClellan. Fo y Mo son dos vectores de igual magnitud. Fo(k) y Fo(k+) k impar especifica bandas de frecuencia y Mo(k) y Mo(k+) la correspondiente magnitud para cada frecuencia. El filtro obtenido es la mejor aproximación por minimax. 4
42 Diseño de Filtros FIR con MATLAB H(F) Bandas de Transición M() M(3) M(2) F= F() F(2) F(3) F(4) F=F s /2 F Ejemplo : Diseñar un filtro FIR pasabanda a frecuencias de 3 Hz y 35 Hz por cada uno de los diferentes métodos. Utilizar un mismo orden de filtro (por ejemplo N=44) y comparar las respuestas frecuenciales. >> N=44;Fs=2;Fny=Fs/2; >> Bfir = fir(n,[3 35]/Fny); >> Bfir2 = fir2(n,[ Fny]/Fny,[ ]); >> Bfirls = firls(n,[ Fny]/Fny,[ ]); >> Bremez = remez(n,[ Fny]/Fny,[ ]); 42
43 Diseño de Filtros FIR con MATLAB >> F=::5; >> Hfir=abs(freqz(Bfir,,F,Fs); >> Hfir2=abs(freqz(Bfir2,,F,Fs); >> Hfirls=abs(freqz(Bfirls,,F,Fs); >> Hremez=abs(freqz(Bremez,,F,Fs); >> semilogy(f,hfir,'r',f,hfir2,'g',f,hfirls,'y',f,hremez,'m'); Respuesta frecuencial: -- fir, -- fir2, -- firls, -- remez
44 Apéndice Tablas de Transformaciones Espectrales 44
45 Tabla Transformaciones de Filtros pasobajo Tipo H(F) ideal Respuesta a Impulso h[n] H F F F h n = 2F sinc 2nF Pasobajo ( ) = rect LP ( 2 C ) [] ( ) LP C C Pasoalto H ( F) H ( F) Pasoalto ( ) = ( ) = rect ( - ) HP = - LP hhp[] n = δ[] n hlp[] n [ 2 2 ] H F H F F F HP LP 2 C rect Pasabanda HBP( F) = rect [( F F ) 2FC ] ( F F ) 2FC + + [ ] 2 cos π ( ) n h [] n LP ( 2 nf ) h [] n Parabanda H ( F) = H ( F) δn [] h [] n BS BP BP LP 45
46 Tabla 2 Transformaciones a Prototipos de Pasobajo F p, F p2, F s y F s2 = límites de pasabanda y parabanda, F = Frecuencia Central Para BS y BP se asume que tienen simetría respecto a F Transformación Límite de Pasabanda Límite de Parabanda Frecuencia Central HP2LP Fp = FsHP Fs = FpHP Si h HP [n]=δ[n]-h LP [n] HP2LP Fp = F F php s = F shp Si h HP [n]=( ) n h[n] 2 2 F ( F F ) BP2LP p = 2 F p 2 p s = ( Fs F 2 2 s ) F = 2( Fp2 + Fp ) F ( F F ) BS2LP p = 2 s 2 s Fs = 2( Fp2 Fp ) F = 2( Fp2 + Fp ) 46
En general, el diseño de cualquier filtro digital es llevado a cabo en 3 pasos:
 En general, el diseño de cualquier filtro digital es llevado a cabo en 3 pasos: 1. Especificaciones: Antes de poder diseñar un filtro debemos tener algunas especificaciones, las cuales son determinadas
En general, el diseño de cualquier filtro digital es llevado a cabo en 3 pasos: 1. Especificaciones: Antes de poder diseñar un filtro debemos tener algunas especificaciones, las cuales son determinadas
Filtros senoc-enventanado Filtros personalizados. clase 11
 Filtros senoc-enventanado Filtros personalizados clase 11 Temas Introducción a los filtros digitales Clasificación, Caracterización, Parámetros Filtros FIR (Respuesta al impulso finita) Filtros de media
Filtros senoc-enventanado Filtros personalizados clase 11 Temas Introducción a los filtros digitales Clasificación, Caracterización, Parámetros Filtros FIR (Respuesta al impulso finita) Filtros de media
Procesamiento Digital de Señal
 Procesamiento Digital de Señal Tema 6 : Diseño de iltros digitales Transformada Z Análisis de sistemas digitales unción de Transferencia Respuesta en recuencia Síntesis de Sistemas digitales Diseño de
Procesamiento Digital de Señal Tema 6 : Diseño de iltros digitales Transformada Z Análisis de sistemas digitales unción de Transferencia Respuesta en recuencia Síntesis de Sistemas digitales Diseño de
FILTRADO DIGITAL. División de Ingenierías Campus Irapuato-Salamanca
 FILTRADO DIGITAL Divisió de Igeierías Campus Irapuato-Salamaca Filtros ideales Pasabajas: Pasaaltas Pasabada Rechazabada 2 2 2 1 1 1 1 1 1 2 2 2 ) si( 2 ) si( 2 ) ( ) si( 2 ) si( 2 ) ( 1) )/( ( ) ( ) si(
FILTRADO DIGITAL Divisió de Igeierías Campus Irapuato-Salamaca Filtros ideales Pasabajas: Pasaaltas Pasabada Rechazabada 2 2 2 1 1 1 1 1 1 2 2 2 ) si( 2 ) si( 2 ) ( ) si( 2 ) si( 2 ) ( 1) )/( ( ) ( ) si(
ICTP Latin-American Advanced Course on FPGADesign for Scientific Instrumentation. 19 November - 7 December, 2012.
 2384-25 ICTP Latin-American Advanced Course on FPGADesign for Scientific Instrumentation 19 November - 7 December, 2012 Filtros digitales COSTA Diego Esteban Laboratorio de Electronica, Investigacion y
2384-25 ICTP Latin-American Advanced Course on FPGADesign for Scientific Instrumentation 19 November - 7 December, 2012 Filtros digitales COSTA Diego Esteban Laboratorio de Electronica, Investigacion y
10. Vigesimotercera clase. Diseño de filtros FIR de fase lineal mediante ventanas
 Universidad Distrital Francisco José de Caldas - Análisis de Señales y Sistemas - Marco A. Alzate. Vigesimotercera clase. Diseño de filtros FIR de fase lineal mediante ventanas De acuerdo con las propiedades
Universidad Distrital Francisco José de Caldas - Análisis de Señales y Sistemas - Marco A. Alzate. Vigesimotercera clase. Diseño de filtros FIR de fase lineal mediante ventanas De acuerdo con las propiedades
Procesamiento Digital de. Ing. Biomédica, Ing. Electrónica e Ing. en Telecomunicaciones Capitulo VII Diseño de Filtros Digitales
 Procesamiento Digital de Señales Ing. Biomédica, Ing. Electrónica e Ing. en Telecomunicaciones Capitulo VII Diseño de Filtros Digitales D.U. Campos-Delgado Facultad de Ciencias UASLP Enero-Junio/014 1
Procesamiento Digital de Señales Ing. Biomédica, Ing. Electrónica e Ing. en Telecomunicaciones Capitulo VII Diseño de Filtros Digitales D.U. Campos-Delgado Facultad de Ciencias UASLP Enero-Junio/014 1
Introducción al Diseño de Filtros Digitales
 Introducción al Diseño de Filtros Digitales Diego Milone Procesamiento Digital de Señales Ingeniería Informática FICH-UNL 3 de mayo de 2012 Organización de la clase Introducción Concepto y clasificación
Introducción al Diseño de Filtros Digitales Diego Milone Procesamiento Digital de Señales Ingeniería Informática FICH-UNL 3 de mayo de 2012 Organización de la clase Introducción Concepto y clasificación
Taller de Filtros Digitales 2016 Práctica 2
 Taller de Filtros Digitales 2016 Práctica 2 1. Objetivo Familiarizarse con distintas técnicas de diseño de filtros digitales. 2. FIR - Diseño por ventanas Se desea diseñar un filtro pasabanda de fase lineal
Taller de Filtros Digitales 2016 Práctica 2 1. Objetivo Familiarizarse con distintas técnicas de diseño de filtros digitales. 2. FIR - Diseño por ventanas Se desea diseñar un filtro pasabanda de fase lineal
Desarrollo de una interfase para el diseño de filtros FIR a través del Método de Remez integrado a MFilters CAPITULO II FILTROS.
 CAPITULO II FILTROS 6 2.1 Introducción. La palabra filtro significa: material encargado de separar una cosa de otra. En otras palabras, un filtro tiene la capacidad de rechazar partes indeseables de la
CAPITULO II FILTROS 6 2.1 Introducción. La palabra filtro significa: material encargado de separar una cosa de otra. En otras palabras, un filtro tiene la capacidad de rechazar partes indeseables de la
Primera parte (3 puntos, 25 minutos):
 TRATAMIENTO DIGITAL DE SEÑALES EXAMEN FINAL 18/01/2013 APELLIDOS NOMBRE DNI NO DE LA VUELTA A ESTA HOJA HASTA QUE SE LO INDIQUE EL PROFESOR MIENTRAS TANTO, LEA ATENTAMENTE LAS INSTRUCCIONES PARA LA REALIZACIÓN
TRATAMIENTO DIGITAL DE SEÑALES EXAMEN FINAL 18/01/2013 APELLIDOS NOMBRE DNI NO DE LA VUELTA A ESTA HOJA HASTA QUE SE LO INDIQUE EL PROFESOR MIENTRAS TANTO, LEA ATENTAMENTE LAS INSTRUCCIONES PARA LA REALIZACIÓN
Problemas de Filtros Digitales FIR. VENTANAS
 Problemas de Filtros Digitales FIR. VENTANAS Síntesis de Filtros Digitales FIR. Ventanas 1.- Se pretende diseñar un filtro FIR de fase lineal tipo II (número de coeficientes par y simetría par en la respuesta
Problemas de Filtros Digitales FIR. VENTANAS Síntesis de Filtros Digitales FIR. Ventanas 1.- Se pretende diseñar un filtro FIR de fase lineal tipo II (número de coeficientes par y simetría par en la respuesta
ELO 385 Laboratorio de Procesamiento Digital de Señales Laboratorio 5: Transformada Discreta de Fourier Parte I
 1 ELO 385 Laboratorio de Procesamiento Digital de Señales Laboratorio 5: Transformada Discreta de Fourier Parte I Este laboratorio está compuesto por dos sesiones en la cuales se estudiará la transformada
1 ELO 385 Laboratorio de Procesamiento Digital de Señales Laboratorio 5: Transformada Discreta de Fourier Parte I Este laboratorio está compuesto por dos sesiones en la cuales se estudiará la transformada
Capítulo 5: Ejemplos Prácticos
 Capítulo 5: Ejemplos Prácticos Ya se han detallado los aspectos constitutivos de los resultados logrados en este trabajo. Estamos en disposición, entonces, de presentar algunos ejemplos interesantes derivados
Capítulo 5: Ejemplos Prácticos Ya se han detallado los aspectos constitutivos de los resultados logrados en este trabajo. Estamos en disposición, entonces, de presentar algunos ejemplos interesantes derivados
INDICE 1. Panorama 2. Señales Analógicas 3. Señales Discretas 4. Sistemas Analógicos 5. Sistemas en Tiempo Discreto
 INDICE Prefacio XI Del Prefacio a la Primera Edición XIII 1. Panorama 1.0. Introducción 1 1.1. Señales 1 1.2. Sistemas 3 1.3. El dominio de la frecuencia 4 1.4. Del concepto a la aplicación 7 2. Señales
INDICE Prefacio XI Del Prefacio a la Primera Edición XIII 1. Panorama 1.0. Introducción 1 1.1. Señales 1 1.2. Sistemas 3 1.3. El dominio de la frecuencia 4 1.4. Del concepto a la aplicación 7 2. Señales
Técnicas Digitales III
 Universidad Tecnológica Nacional Facultad Regional San Nicolás Técnicas Digitales III Trabajo Práctico nro. 6 FILTROS con MATLAB Rev.2015 Trabajo Práctico 6 OBJETIVO: Conocer las herramientas que este
Universidad Tecnológica Nacional Facultad Regional San Nicolás Técnicas Digitales III Trabajo Práctico nro. 6 FILTROS con MATLAB Rev.2015 Trabajo Práctico 6 OBJETIVO: Conocer las herramientas que este
LABORATORIO No 6: FILTROS FIR Y ESTRUCTURAS
 CURSO: PROCESAMIENTO DIGITAL DE SEÑALES PROFESOR: M. I. JORGE ANTONIO POLANÍA P. PROCEDIMIENTO LABORATORIO No 6: FILTROS FIR Y ESTRUCTURAS 1. VENTANAS PARA FILTROS FIR Utilizando wvtool grafique las respuesta
CURSO: PROCESAMIENTO DIGITAL DE SEÑALES PROFESOR: M. I. JORGE ANTONIO POLANÍA P. PROCEDIMIENTO LABORATORIO No 6: FILTROS FIR Y ESTRUCTURAS 1. VENTANAS PARA FILTROS FIR Utilizando wvtool grafique las respuesta
Primera parte (2.5 puntos, 20 minutos):
 TRATAMIENTO DIGITAL DE SEÑALES EXAMEN FINAL 24/06/2013 APELLIDOS NOMBRE DNI NO DE LA VUELTA A ESTA HOJA HASTA QUE SE LO INDIQUE EL PROFESOR MIENTRAS TANTO, LEA ATENTAMENTE LAS INSTRUCCIONES PARA LA REALIZACIÓN
TRATAMIENTO DIGITAL DE SEÑALES EXAMEN FINAL 24/06/2013 APELLIDOS NOMBRE DNI NO DE LA VUELTA A ESTA HOJA HASTA QUE SE LO INDIQUE EL PROFESOR MIENTRAS TANTO, LEA ATENTAMENTE LAS INSTRUCCIONES PARA LA REALIZACIÓN
Primera parte (2.5 puntos, 20 minutos):
 TRATAMIENTO DIGITAL DE SEÑALES EXAMEN FINAL 24/06/2013 APELLIDOS NOMBRE DNI NO DE LA VUELTA A ESTA HOJA HASTA QUE SE LO INDIQUE EL PROFESOR MIENTRAS TANTO, LEA ATENTAMENTE LAS INSTRUCCIONES PARA LA REALIZACIÓN
TRATAMIENTO DIGITAL DE SEÑALES EXAMEN FINAL 24/06/2013 APELLIDOS NOMBRE DNI NO DE LA VUELTA A ESTA HOJA HASTA QUE SE LO INDIQUE EL PROFESOR MIENTRAS TANTO, LEA ATENTAMENTE LAS INSTRUCCIONES PARA LA REALIZACIÓN
ELO 385 Laboratorio de Procesamiento Digital de Señales Laboratorio 4: Filtros digitales Parte I
 1 ELO 385 Laboratorio de Procesamiento Digital de Señales Laboratorio 4: Filtros digitales Parte I 0. Introducción Este laboratorio está compuesto por dos sesiones en la cuales se estudiarán filtros digitales.
1 ELO 385 Laboratorio de Procesamiento Digital de Señales Laboratorio 4: Filtros digitales Parte I 0. Introducción Este laboratorio está compuesto por dos sesiones en la cuales se estudiarán filtros digitales.
Análisis de Señales en Geofísica
 Análisis de Señales en Geofísica 8 Clase Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata, Argentina Todos los sistemas lineales e invariantes pueden ser pensados como filtros.
Análisis de Señales en Geofísica 8 Clase Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata, Argentina Todos los sistemas lineales e invariantes pueden ser pensados como filtros.
FILTROS DIGITALES VENTAJAS INCONVENIENTES
 FILTROS DIGITALES VENTAJAS - Características imposibles con filtros analógicos (fase lineal) - No cambian cualquiera que sea el entorno - Procesamiento de varias señales con un único filtro - Posibilidad
FILTROS DIGITALES VENTAJAS - Características imposibles con filtros analógicos (fase lineal) - No cambian cualquiera que sea el entorno - Procesamiento de varias señales con un único filtro - Posibilidad
TEMA4: Implementación de Filtros Discretos
 TEMA4: Implementación de Filtros Discretos Contenidos del tema: El muestreo y sus consecuencias Relaciones entre señales y sus transformadas: Especificaciones de filtros continuos y discretos Aproximaciones
TEMA4: Implementación de Filtros Discretos Contenidos del tema: El muestreo y sus consecuencias Relaciones entre señales y sus transformadas: Especificaciones de filtros continuos y discretos Aproximaciones
Introducción al Diseño de Filtros Digitales
 Introducción al Diseño de Filtros Digitales Diego Milone Muestreo y Procesamiento Digital Ingeniería Informática FICH-UNL 7 de mayo de 2009 Organización de la clase Introducción Concepto y clasicación
Introducción al Diseño de Filtros Digitales Diego Milone Muestreo y Procesamiento Digital Ingeniería Informática FICH-UNL 7 de mayo de 2009 Organización de la clase Introducción Concepto y clasicación
Análisis de un filtro IIR Butterworth mediante Sptool de Matlab. TEORÍA DE SISTEMAS. ANÁLISIS DE FILTRO IIR BUTTERWORTH (PASABAJOS) 1.
 Análisis de un filtro IIR Butterworth mediante Sptool de Matlab. TEORÍA DE SISTEMAS. ANÁLISIS DE FILTRO IIR BUTTERWORTH (PASABAJOS) 1. Filtro ideal: La definición del filtro ideal pasabajos, es un concepto
Análisis de un filtro IIR Butterworth mediante Sptool de Matlab. TEORÍA DE SISTEMAS. ANÁLISIS DE FILTRO IIR BUTTERWORTH (PASABAJOS) 1. Filtro ideal: La definición del filtro ideal pasabajos, es un concepto
Circuitos de RF y las Comunicaciones Analógicas. Capítulo 3 Filtros en RF
 Capítulo 3 Filtros en RF 37 38 FILTROS EN RF Filtrado en RF: circuito que modifica la magnitud y la fase de las componentes de las frecuencias de la señal de RF que pasa a través de ellos. Un filtro de
Capítulo 3 Filtros en RF 37 38 FILTROS EN RF Filtrado en RF: circuito que modifica la magnitud y la fase de las componentes de las frecuencias de la señal de RF que pasa a través de ellos. Un filtro de
Estructura de Sistemas Digitales Introducción a las Técnicas de diseño de filtros Digitales
 Estructura de Sistemas Digitales Introducción a las Técnicas de diseño de filtros Digitales Asignatura: Procesamiento Digital de Señales Carrera: Bioinformática-FIUNER Bibliografía: Tratamiento de Señales
Estructura de Sistemas Digitales Introducción a las Técnicas de diseño de filtros Digitales Asignatura: Procesamiento Digital de Señales Carrera: Bioinformática-FIUNER Bibliografía: Tratamiento de Señales
Tratamiento Digital de Señales
 Departamento de Teoría de la Señal y Communicaciones Tratamiento Digital de Señales Transformada Discreta de Fourier (DFT) Prof.: Manuel Blanco Velasco Sumario Definición e interpretación La DFT como transformación
Departamento de Teoría de la Señal y Communicaciones Tratamiento Digital de Señales Transformada Discreta de Fourier (DFT) Prof.: Manuel Blanco Velasco Sumario Definición e interpretación La DFT como transformación
Seminario de Procesamiento Digital de Señales
 Seminario de Procesamiento Digital de Señales Unidad 5: Diseño de Filtros Digitales - Parte I Marcelo A. Pérez Departamento Electrónica Universidad Técnica Federico Santa María Contenidos 1 Conceptos Básicos
Seminario de Procesamiento Digital de Señales Unidad 5: Diseño de Filtros Digitales - Parte I Marcelo A. Pérez Departamento Electrónica Universidad Técnica Federico Santa María Contenidos 1 Conceptos Básicos
Sistemas Lineales e Invariantes PRÁCTICA 2
 Sistemas Lineales e Invariantes PRÁCTICA 2 (1 sesión) Laboratorio de Señales y Comunicaciones PRÁCTICA 2 Sistemas Lineales e Invariantes 1. Objetivo Los objetivos de esta práctica son: Revisar los sistemas
Sistemas Lineales e Invariantes PRÁCTICA 2 (1 sesión) Laboratorio de Señales y Comunicaciones PRÁCTICA 2 Sistemas Lineales e Invariantes 1. Objetivo Los objetivos de esta práctica son: Revisar los sistemas
ELO Procesamiento Digital de Señales Lab. 3 - Parte I: Filtros Digitales en MatLab
 ELO 314 - Procesamiento Digital de Señales Lab. 3 - Parte I: Filtros Digitales en MatLab Preparado por Dr. Matías Zañartu, e-mail: Matias.Zanartu@usm.cl Dr. Christian Rojas, e-mail: Christian.Rojas@usm.cl
ELO 314 - Procesamiento Digital de Señales Lab. 3 - Parte I: Filtros Digitales en MatLab Preparado por Dr. Matías Zañartu, e-mail: Matias.Zanartu@usm.cl Dr. Christian Rojas, e-mail: Christian.Rojas@usm.cl
2 Diseño de filtros de interpolación
 Diseño de filtros de interpolación Una parte fundamental de un interpolador es el filtro de interpolación paso baja. Dicho filtro se encarga de filtrar las imágenes que se forman al realizar el proceso
Diseño de filtros de interpolación Una parte fundamental de un interpolador es el filtro de interpolación paso baja. Dicho filtro se encarga de filtrar las imágenes que se forman al realizar el proceso
Escuela Politécnica Superior 3º Ingeniería Informática. Laboratorio TAAO1. Curso 2004/2005. Autor de la práctica: Prof. Doroteo Torre Toledano
 Escuela Politécnica Superior 3º Ingeniería Informática Laboratorio TAAO1 Curso 2004/2005 Autor de la práctica: Prof. Doroteo Torre Toledano Práctica 6 Técnicas de diseño de filtros digitales. Primer Apellido
Escuela Politécnica Superior 3º Ingeniería Informática Laboratorio TAAO1 Curso 2004/2005 Autor de la práctica: Prof. Doroteo Torre Toledano Práctica 6 Técnicas de diseño de filtros digitales. Primer Apellido
Formulario Procesamiento Digital de Señales
 Formulario Procesamiento Digital de Señales M n=0 n=0 α n = αm+ α ( α n =, a < ( α sen(a ± B = sen(a cos(b ± cos(a sen(b (3 cos(a ± B = cos(a cos(b sen(a sen(b (4 cos (A = ( + cos(a (5 sen (A = ( cos(a
Formulario Procesamiento Digital de Señales M n=0 n=0 α n = αm+ α ( α n =, a < ( α sen(a ± B = sen(a cos(b ± cos(a sen(b (3 cos(a ± B = cos(a cos(b sen(a sen(b (4 cos (A = ( + cos(a (5 sen (A = ( cos(a
Integral de Fourier y espectros continuos
 9 2 2 2 Esta expresión se denomina forma de Angulo fase (o forma armónica) de la serie de Fourier. Integral de Fourier y espectros continuos Las series de Fourier son una herramienta útil para representar
9 2 2 2 Esta expresión se denomina forma de Angulo fase (o forma armónica) de la serie de Fourier. Integral de Fourier y espectros continuos Las series de Fourier son una herramienta útil para representar
Transformada Z Filtros recursivos. clase 12
 Transformada Z Filtros recursivos clase 12 Temas Introducción a los filtros digitales Clasificación, Caracterización, Parámetros Filtros FIR (Respuesta al impulso finita) Filtros de media móvil, filtros
Transformada Z Filtros recursivos clase 12 Temas Introducción a los filtros digitales Clasificación, Caracterización, Parámetros Filtros FIR (Respuesta al impulso finita) Filtros de media móvil, filtros
PRÁCTICA 6: DISEÑO DE FILTROS FIR
 PRÁCTICA 6: DISEÑO DE FILTROS FIR Objetivo Específico: El alumno utilizará herramientas computacionales para el diseño de filtros de respuesta finita al impulso (FIR). Comparará las características que
PRÁCTICA 6: DISEÑO DE FILTROS FIR Objetivo Específico: El alumno utilizará herramientas computacionales para el diseño de filtros de respuesta finita al impulso (FIR). Comparará las características que
GUÍA DE LABORATORIO 2 FILTROS DIGITALES FILTROS FIR E IIR
 UNIVERSIDAD TÉCNICA FEDERICO SANTA MARÍA Departamento de Electrónica GUÍA DE LABORATORIO 2 FILTROS DIGITALES FILTROS FIR E IIR CURSO LABORATORIO DE PROCESAMIENTO DIGITAL DE SEÑALES SIGLA ELO 385 PROFESOR
UNIVERSIDAD TÉCNICA FEDERICO SANTA MARÍA Departamento de Electrónica GUÍA DE LABORATORIO 2 FILTROS DIGITALES FILTROS FIR E IIR CURSO LABORATORIO DE PROCESAMIENTO DIGITAL DE SEÑALES SIGLA ELO 385 PROFESOR
DISEÑO DE FILTROS IIR
 Los filtros digitales se pueden clasificar en dos grandes grupos: aquellos que presentan una respuesta al impulso de duración infinita (IIR) y, por el contrario, los sistemas FIR o de respuesta al impulso
Los filtros digitales se pueden clasificar en dos grandes grupos: aquellos que presentan una respuesta al impulso de duración infinita (IIR) y, por el contrario, los sistemas FIR o de respuesta al impulso
Sistemas Lineales. Examen de Junio SOluciones
 . Considere la señal xt) sinπt) Sistemas Lineales Examen de Junio 22. SOluciones a) Obtenga su transformada de Fourier, X), y represéntela para 7π. b) Calcule la potencia y la energía de xt). c) Considere
. Considere la señal xt) sinπt) Sistemas Lineales Examen de Junio 22. SOluciones a) Obtenga su transformada de Fourier, X), y represéntela para 7π. b) Calcule la potencia y la energía de xt). c) Considere
PROBLEMAS TEMA 1 INTRODUCCIÓN. DEFINICIONES BÁSICAS
 INTRODUCCIÓN. DEFINICIONES BÁSICAS PROBLEMA 1 Se desea obtener un filtro paso banda que cumpla las especificaciones indicadas en la plantilla de atenuación de la figura a partir de un filtro paso bajo
INTRODUCCIÓN. DEFINICIONES BÁSICAS PROBLEMA 1 Se desea obtener un filtro paso banda que cumpla las especificaciones indicadas en la plantilla de atenuación de la figura a partir de un filtro paso bajo
ESTUDIO COMPARATIVO SOBRE DISTINTOS TIPOS DE FILTROS FIR IMPLEMENTADOS EN UN DSPIC
 ESTUDIO COMPARATIVO SOBRE DISTINTOS TIPOS DE FILTROS FIR IMPLEMENTADOS EN UN DSPIC Autores: Matías L. Martini, Gastón Oviedo Tutor: Ing. Franco M. Salvático (fmsalvatico@hotmail.com) Departamento de Ingeniería
ESTUDIO COMPARATIVO SOBRE DISTINTOS TIPOS DE FILTROS FIR IMPLEMENTADOS EN UN DSPIC Autores: Matías L. Martini, Gastón Oviedo Tutor: Ing. Franco M. Salvático (fmsalvatico@hotmail.com) Departamento de Ingeniería
Transformada Discreta de Fourier (DFT)
 Transformada Discreta de Fourier (DFT) Transformada Discreta de Fourier FFT (Fast Fourier Transform) Transformada Discreta de Fourier Antes de definir la DFT, analizaremos primero la Transformada de Fourier
Transformada Discreta de Fourier (DFT) Transformada Discreta de Fourier FFT (Fast Fourier Transform) Transformada Discreta de Fourier Antes de definir la DFT, analizaremos primero la Transformada de Fourier
Filtrado Digital. Lectura 2: Estructuras Básicas de Filtros Digitales
 Lectura 2: Estructuras Básicas de Filtros Digitales Filtros FIR sencillos Filtro de promedio móvil de 2 puntos (M=1 1er orden): Es el filtro FIR más simple. Note que H(z) tiene un cero en z=-1, y un polo
Lectura 2: Estructuras Básicas de Filtros Digitales Filtros FIR sencillos Filtro de promedio móvil de 2 puntos (M=1 1er orden): Es el filtro FIR más simple. Note que H(z) tiene un cero en z=-1, y un polo
Sistemas Lineales. Examen de Septiembre Soluciones
 Sistemas Lineales Examen de Septiembre 25. Soluciones. (2.5 pt.) La señal y(t) [sinc( t)] 4 puede escribirse como y(t) [sinc( t)] 4 [ ] sin(o πt) 4 o πt [ sin(o πt) ] 4 4 πt 4 [y (t)] 4 4 y (t) y (t) y
Sistemas Lineales Examen de Septiembre 25. Soluciones. (2.5 pt.) La señal y(t) [sinc( t)] 4 puede escribirse como y(t) [sinc( t)] 4 [ ] sin(o πt) 4 o πt [ sin(o πt) ] 4 4 πt 4 [y (t)] 4 4 y (t) y (t) y
Filtros Activos. Teoría. Autor: José Cabrera Peña
 Filtros Activos Teoría Autor: José Cabrera Peña Definición y clasificaciones Un filtro es un sistema que permite el paso de señales eléctricas a un rango de frecuencias determinadas e impide el paso del
Filtros Activos Teoría Autor: José Cabrera Peña Definición y clasificaciones Un filtro es un sistema que permite el paso de señales eléctricas a un rango de frecuencias determinadas e impide el paso del
Tratamiento Digital de Señales TEMA 2 : DFT (I)
 Tratamiento Digital de Señales TEMA 2 : DFT (I) Universidade de Vigo ETSE Telecomunicación CONTENIDOS 1. Repaso de conceptos asociados con la TF 2. Formulación de la DFT 3. Propiedades de la DFT 4. Métodos
Tratamiento Digital de Señales TEMA 2 : DFT (I) Universidade de Vigo ETSE Telecomunicación CONTENIDOS 1. Repaso de conceptos asociados con la TF 2. Formulación de la DFT 3. Propiedades de la DFT 4. Métodos
Aplicaciones del Tratamiento de Señales. Parte 1: Grabación y Reproducción de Señales de Voz
 Aplicaciones del Tratamiento de Señales Curso 2004-2005 Herramientas Básicas de Análisis de Voz y Audio Parte 1: Grabación y Reproducción de Señales de Voz INTRODUCCIÓN Se pretende en esta parte que el
Aplicaciones del Tratamiento de Señales Curso 2004-2005 Herramientas Básicas de Análisis de Voz y Audio Parte 1: Grabación y Reproducción de Señales de Voz INTRODUCCIÓN Se pretende en esta parte que el
UNIVERSIDAD TECNOLÓGICA DE PEREIRA FACULTAD DE INGENIERÍAS MAESTRÍA EN INGENIERÍA DE SISTEMAS Y COMPUTACIÓN
 UNIVERSIDAD TECNOLÓGICA DE PEREIRA FACULTAD DE INGENIERÍAS MAESTRÍA EN INGENIERÍA DE SISTEMAS Y COMPUTACIÓN TEORÍA DE SEÑALES OBJETIVO GENERAL Estudiar los conceptos fundamentales de representación de
UNIVERSIDAD TECNOLÓGICA DE PEREIRA FACULTAD DE INGENIERÍAS MAESTRÍA EN INGENIERÍA DE SISTEMAS Y COMPUTACIÓN TEORÍA DE SEÑALES OBJETIVO GENERAL Estudiar los conceptos fundamentales de representación de
Dar una breve semblanza sobre los Filtros Digitales, sus fundamentos y su principales características.
 Filtros Digitales Objetivo Dar una breve semblanza sobre los Filtros Digitales, sus fundamentos y su principales características. Revisar la convolución como fundamentos de los filtros digitales junto
Filtros Digitales Objetivo Dar una breve semblanza sobre los Filtros Digitales, sus fundamentos y su principales características. Revisar la convolución como fundamentos de los filtros digitales junto
Análisis Espectral mediante DFT PRÁCTICA 4
 Análisis Espectral mediante DFT PRÁCTICA 4 (2 sesiones) Laboratorio de Señales y Comunicaciones 1 PRÁCTICA 4 Análisis Espectral mediante DFT 1. Objetivo Habitualmente, el análisis de señales y sistemas
Análisis Espectral mediante DFT PRÁCTICA 4 (2 sesiones) Laboratorio de Señales y Comunicaciones 1 PRÁCTICA 4 Análisis Espectral mediante DFT 1. Objetivo Habitualmente, el análisis de señales y sistemas
Un filtro con h(t) real es ideal si: H(f) =1 en la banda de paso H(f) =0 en la banda atenuada ΦΗ(f)= 2παf en la banda de paso
 PROCESAMIENTO DIGITAL DE SEÑALES PROFESOR: ING. JORGE A. POLANÍA P. 4.1 FILTROS ANÁLOGOS 1. INTRODUCCIÓN En ocasiones, las señales de interés están mezcladas con otras señales y no es posible distinguirlas
PROCESAMIENTO DIGITAL DE SEÑALES PROFESOR: ING. JORGE A. POLANÍA P. 4.1 FILTROS ANÁLOGOS 1. INTRODUCCIÓN En ocasiones, las señales de interés están mezcladas con otras señales y no es posible distinguirlas
IDENTIFICACION DE SISTEMAS IDENTIFICACION NO PARAMETRICA
 IDENTIFICACION DE SISTEMAS IDENTIFICACION NO PARAMETRICA Ing. Fredy Ruiz Ph.D. ruizf@javeriana.edu.co Maestría en Ingeniería Electrónica Pontificia Universidad Javeriana 2013 SISTEMAS LTI En general un
IDENTIFICACION DE SISTEMAS IDENTIFICACION NO PARAMETRICA Ing. Fredy Ruiz Ph.D. ruizf@javeriana.edu.co Maestría en Ingeniería Electrónica Pontificia Universidad Javeriana 2013 SISTEMAS LTI En general un
3. Señales. Introducción y outline
 3. Señales Introducción y outline Outline Señales y Sistemas Discretos: SLIT, Muestreo, análisis tiempo-frecuencia, autocorrelación, espectro, transformada Z, DTFT, DFT, FFT Filtros y Estimación: Filtros
3. Señales Introducción y outline Outline Señales y Sistemas Discretos: SLIT, Muestreo, análisis tiempo-frecuencia, autocorrelación, espectro, transformada Z, DTFT, DFT, FFT Filtros y Estimación: Filtros
CAPITULO IV DESARROLLO DE UNA INTERFASE PARA EL DISEÑO DE FILTROS FIR MEDIANTE EL METODO DE REMEZ INTEGRADO A MFILTERS.
 CAPITULO IV DESARROLLO DE UNA INTERFASE PARA EL DISEÑO DE FILTROS FIR MEDIANTE EL METODO DE REMEZ INTEGRADO A MFILTERS. 29 4.1 Propiedades y Funcionamiento de MFilters MFilters fue creado mediante archivos.m
CAPITULO IV DESARROLLO DE UNA INTERFASE PARA EL DISEÑO DE FILTROS FIR MEDIANTE EL METODO DE REMEZ INTEGRADO A MFILTERS. 29 4.1 Propiedades y Funcionamiento de MFilters MFilters fue creado mediante archivos.m
Sistemas Lineales. Tema 7. Problemas
 Sistemas Lineales ema 7. Problemas. Se sabe que una señal de valor real x(t) ha sido determinada sólo por sus muestras cuando la frecuencia de muestreo es s = 0 4 π. Para qué valores de se garantiza que
Sistemas Lineales ema 7. Problemas. Se sabe que una señal de valor real x(t) ha sido determinada sólo por sus muestras cuando la frecuencia de muestreo es s = 0 4 π. Para qué valores de se garantiza que
Figura 1. Espectro de la señal x(t) FPBanda π/3 -- 2π/3 (ideal) T Figura 2. Diagrama de bloques del sistema discreto
 EXAMEN DE PROCESADO DIGITAL DE LA SEÑAL EXAMEN DE PROCESADO DE LA SEÑAL AUDIOVISUAL Universidad Politécnica de Madrid. E.U.I.T. Telecomunicación Departamento de Ingeniería Audiovisual y Comunicaciones
EXAMEN DE PROCESADO DIGITAL DE LA SEÑAL EXAMEN DE PROCESADO DE LA SEÑAL AUDIOVISUAL Universidad Politécnica de Madrid. E.U.I.T. Telecomunicación Departamento de Ingeniería Audiovisual y Comunicaciones
Segunda parte (2h 30 ):
 TRATAMIENTO DIGITAL DE SEÑALES EXAMEN FINAL SEPTIEMBRE 2008 05/09/2008 APELLIDOS NOMBRE DNI NO DE LA VUELTA A ESTA HOJA HASTA QUE SE LO INDIQUE EL PROFESOR MIENTRAS TANTO, LEA ATENTAMENTE LAS INSTRUCCIONES
TRATAMIENTO DIGITAL DE SEÑALES EXAMEN FINAL SEPTIEMBRE 2008 05/09/2008 APELLIDOS NOMBRE DNI NO DE LA VUELTA A ESTA HOJA HASTA QUE SE LO INDIQUE EL PROFESOR MIENTRAS TANTO, LEA ATENTAMENTE LAS INSTRUCCIONES
Práctica 1 INTRODUCCIÓN A MATLAB
 UNIVERSIDAD AUTÓNOMA DE BAJA CALIFORNIA FACULTAD DE INGENIERÍA, ARQUITECTURA Y DISEÑO Laboratorio de Procesamiento Digital de Señales Práctica 1 INTRODUCCIÓN A MATLAB OBJETIVO: Que el alumno realice gráficos
UNIVERSIDAD AUTÓNOMA DE BAJA CALIFORNIA FACULTAD DE INGENIERÍA, ARQUITECTURA Y DISEÑO Laboratorio de Procesamiento Digital de Señales Práctica 1 INTRODUCCIÓN A MATLAB OBJETIVO: Que el alumno realice gráficos
Procesamiento digital de señales Semana 9. Filtros Digitales
 Procesamiento digital de señales Semana 9. Filtros Digitales Dra. María del Pilar Gómez Gil Otoño 2017 Coordinación de computación INAOE Versión: 24 de Octubre 2017 (c) P.Gómez Gil, INAOE 2017 1 Tema Filtros
Procesamiento digital de señales Semana 9. Filtros Digitales Dra. María del Pilar Gómez Gil Otoño 2017 Coordinación de computación INAOE Versión: 24 de Octubre 2017 (c) P.Gómez Gil, INAOE 2017 1 Tema Filtros
REPRESENTACION DE SEÑALES Y SISTEMAS
 REPRESENTACION DE SEÑALES Y SISTEMAS TRANSFORMADA DE FOURIER La serie de Fourier nos permite obtener una representación en el dominio de la frecuencia de funciones periódicas f(t). La transformada de Fourier
REPRESENTACION DE SEÑALES Y SISTEMAS TRANSFORMADA DE FOURIER La serie de Fourier nos permite obtener una representación en el dominio de la frecuencia de funciones periódicas f(t). La transformada de Fourier
INGENIERIA DE TELECOMUNICACIÓN TRATAMIENTO DIGITAL DE LA SEÑAL I CURSO 2005/2006 TEMA 5: ANALISIS ESPECTRAL DE SEÑALES MEDIANTE LA DFT
 Departamento de Ingeniería Electrónica, de Telecomunicación y Automática UNIVERSIDAD DE JAÉN INGENIERIA DE TELECOMUNICACIÓN TRATAMIENTO DIGITAL DE LA SEÑAL I CURSO 2005/2006 TEMA 5: ANALISIS ESPECTRAL
Departamento de Ingeniería Electrónica, de Telecomunicación y Automática UNIVERSIDAD DE JAÉN INGENIERIA DE TELECOMUNICACIÓN TRATAMIENTO DIGITAL DE LA SEÑAL I CURSO 2005/2006 TEMA 5: ANALISIS ESPECTRAL
A502 - Teoría de Sistemas y Señales
 A50 - Teoría de Sistemas y Señales Transparencias Densidad Espectral de Energía de Señales Aperiódicas Autor: Dr. Juan Carlos Gómez Señales de Potencia Verifican TD: TC: Algunas Definiciones N 1 < P lim
A50 - Teoría de Sistemas y Señales Transparencias Densidad Espectral de Energía de Señales Aperiódicas Autor: Dr. Juan Carlos Gómez Señales de Potencia Verifican TD: TC: Algunas Definiciones N 1 < P lim
Problemas de diseño de filtros y sus soluciones
 Problemas de diseño de filtros y sus soluciones 1. Diseñe un filtro paso-bajo de Butterworth con una frecuencia de corte fc=10khz y una atenuación mínima de A t =36 db a f r =100Khz. a. Cuánto vale el
Problemas de diseño de filtros y sus soluciones 1. Diseñe un filtro paso-bajo de Butterworth con una frecuencia de corte fc=10khz y una atenuación mínima de A t =36 db a f r =100Khz. a. Cuánto vale el
Procesamiento de Señales 1D. 2.1 El mundo análogo de sistemas LIT. Se tiene un sistema H. se puede descomponer
 2. Procesamiento de Señales 1D Generalizando, para sistemas lineales e Inv. a la traslación 2.1 El mundo análogo de sistemas LIT Se tiene un sistema H usando.:. En general la salida Si tenemos x 0(t),
2. Procesamiento de Señales 1D Generalizando, para sistemas lineales e Inv. a la traslación 2.1 El mundo análogo de sistemas LIT Se tiene un sistema H usando.:. En general la salida Si tenemos x 0(t),
Filtrado Digital. Lectura 3: Diseño de Filtros FIR
 Lectura 3: Diseño de Filtros FIR Diseño de Filtros Objetivo: Obtener una función de transferencia H(z) realizable aproximándola a una respuesta en frecuencia deseable. El diseño de filtros digitales es
Lectura 3: Diseño de Filtros FIR Diseño de Filtros Objetivo: Obtener una función de transferencia H(z) realizable aproximándola a una respuesta en frecuencia deseable. El diseño de filtros digitales es
Procesamiento Digital Tren de pulsos
 2. Procesamiento Digital Una formulación general para las series de Fourier es = donde se utiliza otro tipo de función φ k diferente a las funciones sinusoidales. 2.1 Interpolación Se puede expresar una
2. Procesamiento Digital Una formulación general para las series de Fourier es = donde se utiliza otro tipo de función φ k diferente a las funciones sinusoidales. 2.1 Interpolación Se puede expresar una
Filtrado Digital. Lectura 1: Conceptos de Filtrado
 Filtrado Digital Lectura 1: Conceptos de Filtrado Respuesta en Frecuencia La salida de un sistema LTI en el dominio de la frecuencia es: Donde H(ω) es llamada la respuesta en frecuencia del sistema, la
Filtrado Digital Lectura 1: Conceptos de Filtrado Respuesta en Frecuencia La salida de un sistema LTI en el dominio de la frecuencia es: Donde H(ω) es llamada la respuesta en frecuencia del sistema, la
Transformada Discreta de Fourier (II)
 Transformada Discreta de Fourier (II) 1 Más problemas...ahora computacionales La DFT de orden de una señal x(n) viene definida por la siguiente expresión #1 % X(k) = x(n) "e n= 0 # j"2"$ "k"n Para cada
Transformada Discreta de Fourier (II) 1 Más problemas...ahora computacionales La DFT de orden de una señal x(n) viene definida por la siguiente expresión #1 % X(k) = x(n) "e n= 0 # j"2"$ "k"n Para cada
Si conocemos x(n) y obtenemos la salida del sistema podemos determinar la respuesta al impulso del sistema obteniendo en primer lugar H(z) con: = n(
 58 Funciones de transferencia de sistemas LTI Como ya conocemos la salida de un sistema LTI en el tiempo (en reposo) para una secuencia de entrada x(n) se podía obtener como la convolución de esa secuencia
58 Funciones de transferencia de sistemas LTI Como ya conocemos la salida de un sistema LTI en el tiempo (en reposo) para una secuencia de entrada x(n) se podía obtener como la convolución de esa secuencia
Procesamiento digital de señales de audio
 Procesamiento digital de señales de audio Filtros digitales Instituto de Ingeniería Eléctrica, Facultad de Ingeniería Universidad de la República, Uruguay Grupo de Procesamiento de Audio Filtros digitales
Procesamiento digital de señales de audio Filtros digitales Instituto de Ingeniería Eléctrica, Facultad de Ingeniería Universidad de la República, Uruguay Grupo de Procesamiento de Audio Filtros digitales
Ampliación de Señales y Sistemas
 Grados Ing. de Telecomunicación. Universidad Rey Juan Carlos Página 1/6 Ampliación de Señales y Sistemas PRÁCTICA 2: La DFT en Matlab Profesora responsable de esta práctica: Alicia Guerrero Bibliografía:
Grados Ing. de Telecomunicación. Universidad Rey Juan Carlos Página 1/6 Ampliación de Señales y Sistemas PRÁCTICA 2: La DFT en Matlab Profesora responsable de esta práctica: Alicia Guerrero Bibliografía:
PROBLEMAS TEMA 2 TEORÍA DE LA APROXIMACIÓN
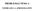 PROBLEMAS TEMA TEORÍA DE LA APROXIMACIÓN PROBLEMA : Determinar la función de transferencia de un filtro paso bajo máximamente plano que cumplan las especificaciones de la figura: a) Determinar el orden
PROBLEMAS TEMA TEORÍA DE LA APROXIMACIÓN PROBLEMA : Determinar la función de transferencia de un filtro paso bajo máximamente plano que cumplan las especificaciones de la figura: a) Determinar el orden
IMPLEMENTACIÓN DE FILTROS DIGITALES EN LÓGICA RECONFIGURABLE
 IMPLEMENTACIÓN DE FILTROS DIGITALES EN LÓGICA RECONFIGURABLE TESIS QUE PRESENTA Rodrigo Cruz González PARA OBTENER EL GRADO DE MAESTRO EN CIENCIAS Asesor: Dr. Gonzalo I. Duchén Sánchez ESCUELA SUPERIOR
IMPLEMENTACIÓN DE FILTROS DIGITALES EN LÓGICA RECONFIGURABLE TESIS QUE PRESENTA Rodrigo Cruz González PARA OBTENER EL GRADO DE MAESTRO EN CIENCIAS Asesor: Dr. Gonzalo I. Duchén Sánchez ESCUELA SUPERIOR
INDICE Capitulo 1. Introducción Capitulo 2. Descripción matemática de señales 2.1. Introducción y objetivos
 INDICE Prefacio XIII Capitulo 1. Introducción 1 1.1. Definición de señales y sistemas 1 1.2. Tipos de señales 1 1.3. Ejemplo de una señal y un sistema 8 1.4. Uso de MATLAB 13 Capitulo 2. Descripción matemática
INDICE Prefacio XIII Capitulo 1. Introducción 1 1.1. Definición de señales y sistemas 1 1.2. Tipos de señales 1 1.3. Ejemplo de una señal y un sistema 8 1.4. Uso de MATLAB 13 Capitulo 2. Descripción matemática
DEPARTAMENTO DE TEORÍA DE LA SEÑAL Y COMUNICACIONES ANÁLISIS Y SÍNTESIS DE CIRCUITOS PRÁCTICA 2: Diseño de Filtros. Aproximación
 DEPARTAMENTO DE TEORÍA DE LA SEÑAL Y COMUNICACIONES ANÁLISIS Y SÍNTESIS DE CIRCUITOS PRÁCTICA 2: Diseño de Filtros. Aproximación Curso 2010-2011 ÍNDICE 1. Objetivos.... 2 2. Herramientas.... 2 3. Introducción
DEPARTAMENTO DE TEORÍA DE LA SEÑAL Y COMUNICACIONES ANÁLISIS Y SÍNTESIS DE CIRCUITOS PRÁCTICA 2: Diseño de Filtros. Aproximación Curso 2010-2011 ÍNDICE 1. Objetivos.... 2 2. Herramientas.... 2 3. Introducción
SOLUCIONES. 2 Xm 2 n ,953mv W, determinar la relación señal a ruido de
 PROCESADO DIGITAL DE SEÑAL (Sonido e Imagen) Universidad Politécnica de Madrid. E.U.I.T. Telecomunicación Departamento de Ingeniería Audiovisual y Comunicaciones Examen de teoría, Plan 000 15 de Junio
PROCESADO DIGITAL DE SEÑAL (Sonido e Imagen) Universidad Politécnica de Madrid. E.U.I.T. Telecomunicación Departamento de Ingeniería Audiovisual y Comunicaciones Examen de teoría, Plan 000 15 de Junio
TEMA 1. Principios de Teoría de la Señal
 Tecnología de Comunicaciones Inalámbrica (TCI) 2012-2013 TEMA 1. Principios de Teoría de la Señal Juan Carlos Crespo crespozj@dtf.fi.upm.es 1 INTRODUCCIÓN En este capítulo estudiaremos la naturaleza de
Tecnología de Comunicaciones Inalámbrica (TCI) 2012-2013 TEMA 1. Principios de Teoría de la Señal Juan Carlos Crespo crespozj@dtf.fi.upm.es 1 INTRODUCCIÓN En este capítulo estudiaremos la naturaleza de
Victrola de La Transformada de Fourier
 Victrola de La Transformada de Fourier p. 1/2 Victrola de La Transformada de Fourier Introducción para Músicos Juan I Reyes juanig@maginvent.org artelab Laboratorios de Artes Electrónicas Victrola de La
Victrola de La Transformada de Fourier p. 1/2 Victrola de La Transformada de Fourier Introducción para Músicos Juan I Reyes juanig@maginvent.org artelab Laboratorios de Artes Electrónicas Victrola de La
SÍNTESIS DE FILTROS DIGITALES
 Prácticas de la Asignatura Tratamiento Digital de Señales SÍNTESIS DE FILTROS DIGITALES Fernando Cruz Roldán Índice Práctica de Diseño de Filtros Digitales. Práctica de Efectos de la Cuantificación de
Prácticas de la Asignatura Tratamiento Digital de Señales SÍNTESIS DE FILTROS DIGITALES Fernando Cruz Roldán Índice Práctica de Diseño de Filtros Digitales. Práctica de Efectos de la Cuantificación de
Temas Avanzados en Procesado de Señales Tratamiento Digital de Señales Visuales
 Temas Avanzados en Procesado de Señales Tratamiento Digital de Señales Visuales Tema 5: Operadores Globales transformadas lineales, transformadas morfológicas gicas José María Martínez Sánchez Escuela
Temas Avanzados en Procesado de Señales Tratamiento Digital de Señales Visuales Tema 5: Operadores Globales transformadas lineales, transformadas morfológicas gicas José María Martínez Sánchez Escuela
DISEÑO E IMPLEMENTACION DE UN FILTRO PASA BANDA. Realizado por Luis Salcedo, Andrés Basto, Rubén martín, Andrés Urrea
 DISEÑO E IMPLEMENTACION DE UN FILTRO PASA BANDA Realizado por Luis Salcedo, Andrés Basto, Rubén martín, Andrés Urrea PLANTEAMIENTO DEL PROBLEMA Se nos pide modificar una señal de audio, la mejor manera
DISEÑO E IMPLEMENTACION DE UN FILTRO PASA BANDA Realizado por Luis Salcedo, Andrés Basto, Rubén martín, Andrés Urrea PLANTEAMIENTO DEL PROBLEMA Se nos pide modificar una señal de audio, la mejor manera
Respuesta en fase Filtros Chebyshev. clase 13
 Respuesta en fase Filtros Chebyshev clase 13 Temas Introducción a los filtros digitales Clasificación, Caracterización, Parámetros Filtros FIR (Respuesta al impulso finita) Filtros de media móvil, filtros
Respuesta en fase Filtros Chebyshev clase 13 Temas Introducción a los filtros digitales Clasificación, Caracterización, Parámetros Filtros FIR (Respuesta al impulso finita) Filtros de media móvil, filtros
Tema 3. Análisis de Fourier de señales y sistemas de tiempo continuo.
 Tema 3. Análisis de Fourier de señales y sistemas de tiempo continuo. 205-206 Tema 3. Análisis de Fourier de tiempo continuo 205-206 / 23 Índice Introducción 2 Respuesta de sistemas LTI a exponenciales
Tema 3. Análisis de Fourier de señales y sistemas de tiempo continuo. 205-206 Tema 3. Análisis de Fourier de tiempo continuo 205-206 / 23 Índice Introducción 2 Respuesta de sistemas LTI a exponenciales
Preguntas IE TEC. Total de Puntos: 47 Puntos obtenidos: Porcentaje: Nota:
 IE TEC Nombre: Instituto Tecnológico de Costa Rica Escuela de Ingeniería en Electrónica EL-5805 Procesamiento Digital de Señales Profesor: Dr. Pablo Alvarado Moya II Semestre, 2010 Examen Final Total de
IE TEC Nombre: Instituto Tecnológico de Costa Rica Escuela de Ingeniería en Electrónica EL-5805 Procesamiento Digital de Señales Profesor: Dr. Pablo Alvarado Moya II Semestre, 2010 Examen Final Total de
Filtros Digitales 2. Contenidos. Juan-Pablo Cáceres CCRMA Stanford University. Agosto, Un Filtro Lowpass Simple
 Filtros Digitales 2 Juan-Pablo Cáceres CCRMA Stanford University Agosto, 2007 Contenidos Un Filtro Lowpass Simple Obtención de la Respuesta en Frecuencia Función de Transferencia Propiedad de Linealidad
Filtros Digitales 2 Juan-Pablo Cáceres CCRMA Stanford University Agosto, 2007 Contenidos Un Filtro Lowpass Simple Obtención de la Respuesta en Frecuencia Función de Transferencia Propiedad de Linealidad
Adquisición de datos y acondicionamiento de la señal Tema 5. Esta lección describe los pasos para el procesado de señales
 PROCESADO DE SEÑALES Esta lección describe los pasos para el procesado de señales Tenemos los siguientes apartados: A. Trasformada discreta de Fourier (DFT) y Transformada rápida de Fourier (FFT) B. Magnitud
PROCESADO DE SEÑALES Esta lección describe los pasos para el procesado de señales Tenemos los siguientes apartados: A. Trasformada discreta de Fourier (DFT) y Transformada rápida de Fourier (FFT) B. Magnitud
CAPÍTULO V: IMPLEMENTACIÓN FILTROS DIGITALES EN FPGA's IMPLEMENTACIÓN DE FILTROS DIGITALES EN FPGA'S IEC FRANCISCO JAVIER TORRES VALLE
 V IMPLEMENTACIÓN DE FILTROS DIGITALES EN FPGA'S 83 5.1 INTRODUCCIÓN Un FPGA es un dispositivo cuyas características pueden ser modificadas, manipuladas o almacenadas mediante programación. La arquitectura
V IMPLEMENTACIÓN DE FILTROS DIGITALES EN FPGA'S 83 5.1 INTRODUCCIÓN Un FPGA es un dispositivo cuyas características pueden ser modificadas, manipuladas o almacenadas mediante programación. La arquitectura
Sistemas Lineales. Problemas de Muestreo (V2.0)
 Sistemas Lineales Problemas de Muestreo (V2.0). Una señal continua x(t) se obtiene a la salida de un filtro pasobajo ideal con frecuencia de corte c = 000π. Si el muestreo con tren de impulsos se realiza
Sistemas Lineales Problemas de Muestreo (V2.0). Una señal continua x(t) se obtiene a la salida de un filtro pasobajo ideal con frecuencia de corte c = 000π. Si el muestreo con tren de impulsos se realiza
Programa. Introducción 1. Generación y percepción de la señal de voz 2. Técnicas avanzadas
 Programa Introducción 1. Generación y percepción de la señal de voz 2. Técnicas avanzadas Análisis localizado en tiempo y en frecuencia Predicción lineal Cepstrum Realce 3. Reconocimiento automático del
Programa Introducción 1. Generación y percepción de la señal de voz 2. Técnicas avanzadas Análisis localizado en tiempo y en frecuencia Predicción lineal Cepstrum Realce 3. Reconocimiento automático del
1. Implementación de filtros IIR: Formas Directas I y II
 1 ELO 385 Laboratorio de Procesamiento Digital de Señales Laboratorio 4: Filtros digitales Parte II 1. Implementación de filtros IIR: Formas Directas I y II Existen varios tipos de estructuras para la
1 ELO 385 Laboratorio de Procesamiento Digital de Señales Laboratorio 4: Filtros digitales Parte II 1. Implementación de filtros IIR: Formas Directas I y II Existen varios tipos de estructuras para la
ELECTRONICA II BIOINGENIERIA 1ra. Parte FILTROS ANALOGICOS
 ELECTRONICA II BIOINGENIERIA 1ra. Parte FILTROS ANALOGICOS Los filtros analógicos son indispensables en muchas situaciones, por ejemplo los filtros anti-aliasing que se utilizan antes del procesamiento
ELECTRONICA II BIOINGENIERIA 1ra. Parte FILTROS ANALOGICOS Los filtros analógicos son indispensables en muchas situaciones, por ejemplo los filtros anti-aliasing que se utilizan antes del procesamiento
Análisis de Señales en Geofísica
 Análisis de Señales en Geofísica 14 Clase Transformada Bidimensional de Fourier Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata, Argentina Introducción: La extensión de
Análisis de Señales en Geofísica 14 Clase Transformada Bidimensional de Fourier Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata, Argentina Introducción: La extensión de
Procesamiento Digital de Imágenes
 3. Procesamiento Digital de Imágenes 3.1 Transformada discreta de Fourier en 2D Una señal periódica con períodos N 1 y N 2 en sus coordenadas x 1 y x 2, respectivamente, tiene una trasformada de Fourier
3. Procesamiento Digital de Imágenes 3.1 Transformada discreta de Fourier en 2D Una señal periódica con períodos N 1 y N 2 en sus coordenadas x 1 y x 2, respectivamente, tiene una trasformada de Fourier
Capítulo 2: Introducción Teórica
 Capítulo 2: Introducción Teórica En este capítulo se muestran los fundamentos teóricos del trabajo desarrollado. En concreto, todo lo relativo a los conceptos básicos de la citada asignatura de tratamiento
Capítulo 2: Introducción Teórica En este capítulo se muestran los fundamentos teóricos del trabajo desarrollado. En concreto, todo lo relativo a los conceptos básicos de la citada asignatura de tratamiento
Conceptos de Señales
 Conceptos de Señales ELO 313 Procesamiento Digital de Señales con Aplicaciones Primer semestre - 2012 Matías Zañartu, Ph.D. Departamento de Electrónica Universidad Técnica Federico Santa María Conceptos
Conceptos de Señales ELO 313 Procesamiento Digital de Señales con Aplicaciones Primer semestre - 2012 Matías Zañartu, Ph.D. Departamento de Electrónica Universidad Técnica Federico Santa María Conceptos
PROGRAMA ANALÍTICO DEPARTAMENTO: TELECOMUNICACIONES CARRERA: INGENIERÍA EN TELECOMUNICACIONES ASIGNATURA: SISTEMAS Y SEÑALES II CÓDIGO: 0021
 PROGRAMA ANALÍTICO DEPARTAMENTO: TELECOMUNICACIONES CARRERA: INGENIERÍA EN TELECOMUNICACIONES ASIGNATURA: SISTEMAS Y SEÑALES II CÓDIGO: 0021 AÑO ACADÉMICO: 2015 PLAN DE ESTUDIO: 2010 UBICACIÓN EN EL PLAN
PROGRAMA ANALÍTICO DEPARTAMENTO: TELECOMUNICACIONES CARRERA: INGENIERÍA EN TELECOMUNICACIONES ASIGNATURA: SISTEMAS Y SEÑALES II CÓDIGO: 0021 AÑO ACADÉMICO: 2015 PLAN DE ESTUDIO: 2010 UBICACIÓN EN EL PLAN
INGENIERÍA ELÉCTRICA CIRCUITOS III EJERCICIOS
 INGENIEÍA EÉTIA IUITOS III EJEIIOS Transformada de aplace y función de transferencia. Para el siguiente circuito calcular v c (t) t 0. = 2 Ω, = 0,5 H, = 0,25 F, = e t cos 2t V, v c (0 ) = V, i (0 ) = A
INGENIEÍA EÉTIA IUITOS III EJEIIOS Transformada de aplace y función de transferencia. Para el siguiente circuito calcular v c (t) t 0. = 2 Ω, = 0,5 H, = 0,25 F, = e t cos 2t V, v c (0 ) = V, i (0 ) = A
TEMA III. Análisis de sistemas LIT mediante transformadas.
 TEA III Análisis de sistemas LIT mediante transformadas. Representación de ecuaciones en diferencias lineales con coeficientes constantes mediante diagramas de bloque y diagramas de flujo de señal 20/0/2002
TEA III Análisis de sistemas LIT mediante transformadas. Representación de ecuaciones en diferencias lineales con coeficientes constantes mediante diagramas de bloque y diagramas de flujo de señal 20/0/2002
