Resolución de Problemas Geométricos
|
|
|
- Eva María Valdéz Contreras
- hace 10 años
- Vistas:
Transcripción
1 Resolución de Problemas Geométricos renes, ITR Resumen El presente trabajo brinda una aplicación de la Teoría de ampos onceptuales, de Gérard Vergnaud, a la resolución de problemas geométricos. La resolución de cierto tipo de problemas geométricos no puede ser algoritmizadas y requiere un proceso de reflexión y exploración que recurre a varios esquemas adquiridos. Se introduce el concepto de esquema principal que permite alimentar la intuición necesaria para la resolución de estos problemas. Palabras claves: Geometría, Didáctica, ampos onceptuales. 1 Introducción Las habilidades que una persona requiera para resolver con éxito un problema matemático son variadas y dependen del tipo de problema a resolver, estás involucras procesos de reflexión, de ensayo y error, de conjetura, de búsqueda de patrones, de razonamiento inducción y deducción, entre otras. Particularmente, estos procesos se evidencian en una gran variedad de problemas geométricos. Estos problemas son calificados usualmente como los más difíciles, quizás por que no hay un camino trazado para resolverlos. En su resolución se distinguen dos componentes principales: la escritura y los procesos a seguir para resolverlo. El primer componente se debe caracterizar por su rigurosidad y formalidad. El otro componente requiere educar la intuición y el ordenamiento de ideas, para deducir intuitivamente la manera de resolver el problema. l considerar las matemáticas como un lenguaje, los componentes anteriormente señalados son llamados: sintáctico y semántico. El componente sintáctico nos permite comunicarnos con los demás, se caracteriza por una serie de reglas que regulan la forma de conectar las "palabras", para formar "oraciones" que permitan expresarnos. La semántica, por un lado le da significado a las oraciones que recibimos, y por otro, nos permite comunicarnos con 1
2 nosotros mismos y organizar, con la intuición, nuestras ideas para luego expresarlas por medio de "oraciones" a los demás. Quién domina en matemática: la sintaxis o la semántica? Gödel responde a esta interrogante: la sintáctica y la semántica son equivalentes, es decir hay una relación bidirreccional entre ambos componentes. sí, se concluyen dos aspectos importantes: 1. La rigurosidad (sintaxis) regula y enrumba la intuición (semántica). No basta con tener la idea de como demostrar un teorema, la escritura nos permite ordenar las ideas y desechar aquellas que se alejan del razonamiento y de dudosa validez. 2. La intuición es el motor de la rigurosidad. No es suficiente con saberse de memoria los teoremas, las definiciones y manejar el uso de los símbolos, la intuición nos traza el camino poco a poco a la solución del problema. ómo educar la intuición en la resolución de problemas geométricos? El presente trabajo desarrollará algunas técnicas elementales que permiten alimentar la intuición para hacer frente a los problemas geométricos. 2 Los problemas Geométricos ntes de enfocarse en los problemas Geométricos, se debe responder, al menos parcialmente, a la pregunta: ómo resolver problemas? Para responderla se toma como marco de referencia para la resolución de problemas la Teoría de ampos onceptuales de Gérard Vergnaud, pues como señala Vergnaud su teoría cognitivista pretende proporcionar un marco coherente y algunos principios de base para el estudio del desarrollo y del aprendizaje de competencias complejas. Un concepto importante en esta teoría es el concepto de esquema: organización invariante de la conducta para una clase de situaciones (problemas) dada. En un esquema hay cierta automatización sin impedir el control de la situación. Son como algoritmos pero tienen mucho implícito. Ejemplo 1 Un ejemplo de esquema es la Resolución de Ecuaciones ax+b=c. Desde este punto de vista, los problemas geométricos se pueden clasificar en dos tipos: los ejercicios (situaciones problema tipo1) y los verdaderos problemas (situaciones problema tipo2). Seguidamente se explican ambos tipos de situaciones. 2
3 2.1 Situaciones tipo 1 lase de situaciones para las cuales el sujeto dispone, en su repertorio, de las competencias necesarias para su tratamiento. En este tipo de situaciones las conductas son muy automatizadas y organizadas por un esquema único. Estas situaciones más que problemas son ejercicios. Ejemplo 2 lgunas situaciones tipo 1 en geometría son: 1. alcular un área 2. Deducir que dos triángulos son semejantes. 3. plicar la desigualdad triangular 2.2 Situaciones tipo 2 lase de situaciones para las cuales el sujeto no dispone de todas las competencias necesarias para su tratamiento. Esto obliga al sujeto a entrar en un proceso de reflexión, exploración, ensayo y error,... En este tipo de situaciones las conductas no son automatizadas y se evocan varios esquemas adquiridos que pueden competir entre sí y que por lo tanto deben ser acomodados, separados y recombinados. Estas situaciones son los verdaderos problemas. Es este tipo de situaciones entran los problemas olímpicos de geometría, algunos problemas de secundaria y los problemas de demostración. Para iniciar la resolución de uno de estos problemas hay dos caminos que no sin totalmente disjuntos: 1. Exploración. Realizar un dibujo, hacer deducciones (aplicación de esquemas adquiridos) a partir de las hipótesis con la esperanza de que sean útiles o que arroguen la luz necesaria para ver la solución. En este caso, el sujeto camina inicialmente sin rumbo obteniendo deducciones desconectadas, en busca del camino que lo lleve a la solución. 2. Definición de un esquema principal. Para los problemas de conclusión conocida, el sujeto puede recurrir a un esquema adquirido (un problema resuelto o un teorema) que brinde una conclusión similar a la buscada. Si bien, no es la simple aplicación del esquema, algunos elementos de este esquema principal (ruptura del esquema) combinado con elementos de otros esquemas (filiaciones) permitirán obtener la solución al problema. El esquema principal traza un camino que tiene una buena posibilidad de que lleve al sujeto a la solución. La conclusión conocida en un información que se le debe sacar provecho. 3
4 uál de los dos caminos es mejor? mbos puede conducir al éxito o a errores: con la exploración puede que no se halle el camino a la solución (se obtuvieron deducciones aisladas) y esquema principal nos puede señalar un camino incorrecto. En realidad no hay un camino mejor que el otro, quizás lo optimo es combinar ambos. uál camino utilizan más los estudiantes a nivel nacional? En su mayoría utilizan la exploración, la utilización del esquema principal es poco desarrollada. Por esta razón centraremos la atención en el segundo camino. sí, seguidamente se presentan algunos ejemplos utilizando este enfoque Problemas de desigualdades Ejemplo 3 En el triángulo sea M el punto medio de ysea MQ la mediatriz de con Q. Pruebe que >. Solución: Dado que la conclusión es una desigualdad Que resultados sobre desigualdades geométricas conoce? Posibles esquemas principales: Desigualdad triangular, En un triángulo, a ángulo mayor se opone lado mayor y viceversa. En este caso ambos sirve como esquema principal: 1. Utilizando la Desigualdad triangular. Se debe formar un triángulo de manera que al aplicarle la desigualdad triangular se obtenga que >. Porlotanto,eneltriángulo a formar la suma de la medida de dos de sus lados debe ser igual a. Tracemos Q Q M Por el criterio LL se tiene que MQ = MQ por lo tanto Q = Q = = Q + Q = Q + Q (1) plicando desigualdad triangular al Q se obtiene que Q + Q > (2) De (1) y (2) se obtiene el resultado 4
5 2. Utilizando que en un triángulo, a ángulo mayor se opone lado mayor y viceversa. En este caso se debe probar que en el triángulo el ángulo opuesto a es mayor que el ángulo opuesto a. Para ello, tracemos Q : Q M Por el criterio LL se tiene que MQ = MQ por lo tanto Por hipótesis Q entonces m]mq = m]mq = m]q (1) m] > m]q (2) De (1) y (2) se obtiene que m] > m]mq = m], comoaángulomayorse opone lado mayor entonces se concluye el resultado. Otros problemas similares: 1. Pruebe que la mediana de un lado de un triángulo es menor que la semisuma de los otros dos lados. 2. Pruebe que la mediana de un lado de un triángulo es mayor que la diferencia entre la semisuma de los otros dos lados y la mitad del tercer lado Problemas de Igualdades Ejemplo 4 (Olimpiada nacional 2007, final ) Sean y D puntos sobre un semicírculo con diámetro ycentros de manera que el punto este sobre el arco D yel]sd sea recto. onsidere los puntos E y F tales que E es la intersección entre las rectas y D, y F es la intersección entre las rectas D y. Pruebe que EF =. Solución: Dado que la conclusión es una igualdad de dos medidas de segmentos, algunos posibles esquemas principales son: 1) la congruencia de triángulos 2) medida de lados de triángulos isósceles 5
6 Realizando un dibujo se puede ver que la mejor opción es la #2 sí, como se quiere que EF =, se deben buscar dos triángulos congruentes, uno con lado EF yotrolado. Recurriendoaldibujocomoguíasepuedesuponerquelostriángulosrectángulos FE y son candidatos a ser congruentes. Para ello se debería cumplir que = F, cayendo en el mismo tipo de problema pero esta vez se elige la opción #2, así se debe probar que el F es rectángulo isósceles, lo cual se deduce de las hipótesis. Finalmente, para lograr la congruencia, se debe probar que m]ef = m] o que E =. Eligiendo el primer camino, se extiende el segmento EF para obtener triángulos semejantes que permiten deducir la congruencia de ángulos. Veamos la demostración con detalle: D D y omo y D están sobre el semicírculo entonces E F D S Note que F es el ortocentro del E, entoncesef. omo el ángulo central ]SD es recto entonces la medida del ángulo inscrito ]D es 45, por lo tanto el F es rectángulo isósceles, así = F (1) Por otro lado, sea 0 la intersección de las rectas EF y, como m]ef = m] =90 (2) note que FE 0 E por.. entonces m]ef = m] (3) 6
7 De 1, 2 y 3, por el criterio L se tiene que FE = yporlotanto Otros problemas similares: EF = 1. En el sea M el punto medio de tal que m M = m M. Pruebe que =. 2. onsidere el triángulo isósceles ( = ), sean D y E dos puntos tales que D, E y DEk. Pruebe que D = E Problemas de proporciones Ejemplo 5 En la figura, P es un punto exterior al círculo, con PT tangente al círculo en T.Muestreque P PT = PT (Sug. Trace las cuerdas T y T ). P T P Solución: Dado que la conclusión es una proporción de segmentos Qué resultados sobre proporción de segmentos conoce? algunos posibles esquemas principales son: 1) Semejanza de triángulos 2) áreas. Por ejemplo, recuerde que la razón del áreas de dos triángulos con igual altura es igual a la razón de sus bases La opción 1 es la que mejor se adapta al problema. Dado que se quiere demostrar que P PT = PT, entonces se deben buscar o formar dos triángulos semejantes, el primero con P dos lados de medida P y PT; y el segundo con lados de medida PT y P. Recurriendo al 7
8 dibujo se intuye que estos triángulos son: PT y PT. Observe la demostración: Note que por idempotencia ]P = ]P (1) Dado que el ] es inscrito, el ]PT es semi-inscrito y estos ángulos subtienden el mismo arco, entonces m] = m T a = m]pt (2) 2 De 1 y 2, por el criterio se tiene que PT PT yporlotanto P PT = PT P Otros problemas similares: 1. (Teorema de eva) Dado un. Sean X, Y, Z puntos de los lados, y respectivamente. Si los tres segmentos X, Y y Z son concurrentes, entonces X X Y Y Z Z =1 Y X Z 2. En la figura adjunta, E es el punto medio de, EF, ED D y D. F E D Pruebe FE = ED. 8
9 2.2.4 Problemas de rectas paralelas o perpendiculares Ejemplo 6 Sea.D, con la hipotenusa del y D =. SeaM la bisectriz del, con M D, N y N M. Pruebe que D es paralelo a M Solución: Dado que la conclusión es que dos rectas son paralelas, un posible esquema principal: congruencia de ángulos, esto incluye congruencias de triángulos, semejanza de triángulos, triángulos isósceles. N M D sí, se debe probar que ]D = ]NM. Dado que el triángulo D es isósceles basta demostrar que el triángulo MN es isósceles, es decir se debe probar que ]MN = ]NM, lo cual se deduce de la semejanza entre N y M. Veamos la prueba: Note que es la bisectriz del ] entonces ]N = ]M. Por el criterio.. seobtienequelostriángulosrectángulosn y M son semejantes por lo tanto ]N = ]MN, como ]N = ]MN, porseropuestosporelvértice,entonces ]MN = ]MN. Por lo tanto, MN es isósceles al igual que el, y como comparten el ángulo desigual (]), entonces ]D = ]NM De lo anterior, se concluye que D es paralelo a M. 9
10 Otros problemas similares: 1. Sea.D, con la hipotenusa del y D =. SeaM la bisectriz del, N, M y D N ). Pruebe que D es perpendicular a M. 2. En el, la bisectriz del interseca a en D, la mediatriz de D interseca a en G. Demuestre que GDk. 3 onsideraciones finales lgunas observaciones que debe tener en cuenta el lector sobre el trabajo presentado son: 1. Lo expuesto no establece una manera de resolver problemas geométricos sino tomar en cuenta la conclusión para inicial la resolución del problema. 2. No siempre es posible hallar un esquema principal para resolver el problema, sobre todo en problemas muy nuevos, donde es necesario la exploración. 3. En cada resolución de un problema hay un proceso de asimilación y acomodación de esquemas y se mejora o incrementa el repertorio de competencias del sujeto. 4 ibiografía 1. ntibí,. Didáctica de las Matemáticas: Métodos de Resolución de problemas. Serie abecar, osta Rica (2000). 2. rousseau, Guy.Fundamentos y Métodos de la Didáctica de las Matemáticas, traducción de Fondements et méthodes de la didactiques des mathématiques. Revista Recherches en Didactique des Mathématiques, Vol 7, n 2, pp (1986). 3. hevallard, Yves. La Transposición Didáctica. Del saber sabio al saber enseñado. ique grupo Editor S.., rgentina (1991). 4. Moise, Edwin. Elementos de Geometría Superior. ompañia Editorial ontinental, S.. México, (1968). 5. Verguard G. : La Théore des hamps onceptuels. Revista Recherches en Didactique des Mathemátiques, vol 10, N o 23, pp (1991) 10
El rincón de los problemas. Oportunidades para estimular el pensamiento matemático. Triángulos de área máxima o de área mínima Problema
 www.fisem.org/web/union El rincón de los problemas ISSN: 1815-0640 Número 37. Marzo 2014 páginas 139-145 Pontificia Universidad Católica del Perú [email protected] Oportunidades para estimular el pensamiento
www.fisem.org/web/union El rincón de los problemas ISSN: 1815-0640 Número 37. Marzo 2014 páginas 139-145 Pontificia Universidad Católica del Perú [email protected] Oportunidades para estimular el pensamiento
Soluciones a los problemas Olimpiada de Matemáticas Fase local Extremadura Enero de 2015
 Olimpiada atemática Española RSE Soluciones a los problemas Olimpiada de atemáticas Fase local Extremadura Enero de 2015 1. lrededor de una mesa circular están sentadas seis personas. ada una lleva un
Olimpiada atemática Española RSE Soluciones a los problemas Olimpiada de atemáticas Fase local Extremadura Enero de 2015 1. lrededor de una mesa circular están sentadas seis personas. ada una lleva un
Análisis de propuestas de evaluación en las aulas de América Latina
 Este trabajo de evaluación tiene como objetivo la caracterización de figuras del espacio. Para ello el alumno debe establecer la correspondencia entre la representación de la figura y algunas de sus propiedades.
Este trabajo de evaluación tiene como objetivo la caracterización de figuras del espacio. Para ello el alumno debe establecer la correspondencia entre la representación de la figura y algunas de sus propiedades.
SOLUCIONES ELEMENTALES A PROBLEMAS ELEMENTALES. Darío Durán Cepeda
 1 SOLUIONES ELEMENTLES ROLEMS ELEMENTLES arío urán epeda He sido profesor de matemática desde el año de 1960 hasta la fecha y he aprendido que la matemática no se enseña aunque sí se aprende. Mucha gente
1 SOLUIONES ELEMENTLES ROLEMS ELEMENTLES arío urán epeda He sido profesor de matemática desde el año de 1960 hasta la fecha y he aprendido que la matemática no se enseña aunque sí se aprende. Mucha gente
Revista digital Matemática, Educación e Internet (www.cidse.itcr.ac.cr/revistamate/). Vol. 8, N o 2. 2007
 Sección Tecnologías de Internet Revista digital Matemática, Educación e Internet (www.cidse.itcr.ac.cr/revistamate/). Vol. 8, N o 2. 2007 Hacia una propuesta didáctica para la enseñanza de Métodos Numéricos
Sección Tecnologías de Internet Revista digital Matemática, Educación e Internet (www.cidse.itcr.ac.cr/revistamate/). Vol. 8, N o 2. 2007 Hacia una propuesta didáctica para la enseñanza de Métodos Numéricos
TEMA 8: TRAZADOS GEOMÉTRICOS
 EDUCACIÓN PLÁSTICA Y VISUAL 3º DE LA E.S.O. TEMA 8: TRAZADOS GEOMÉTRICOS En dibujo técnico, es fundamental conocer los trazados geométricos básicos para construir posteriormente formas o figuras de mayor
EDUCACIÓN PLÁSTICA Y VISUAL 3º DE LA E.S.O. TEMA 8: TRAZADOS GEOMÉTRICOS En dibujo técnico, es fundamental conocer los trazados geométricos básicos para construir posteriormente formas o figuras de mayor
El rincón de los problemas
 Marzo de 2010, Número 21, páginas 165-172 ISSN: 1815-0640 El rincón de los problemas Pontificia Universidad Católica del Perú [email protected] De lo particular a lo general, usando grafos Problema En
Marzo de 2010, Número 21, páginas 165-172 ISSN: 1815-0640 El rincón de los problemas Pontificia Universidad Católica del Perú [email protected] De lo particular a lo general, usando grafos Problema En
TEMA 6: LA GEOMETRÍA DEL TRIÁNGULO
 TEMA 6: LA GEOMETRÍA DEL TRIÁNGULO Matías Arce, Sonsoles Blázquez, Tomás Ortega, Cristina Pecharromán 1. INTRODUCCIÓN... 1 2. CLASIFICACIÓN DE TRIÁNGULOS... 2 3. PUNTOS Y RECTAS NOTABLES... 3 4. SEMEJANZA
TEMA 6: LA GEOMETRÍA DEL TRIÁNGULO Matías Arce, Sonsoles Blázquez, Tomás Ortega, Cristina Pecharromán 1. INTRODUCCIÓN... 1 2. CLASIFICACIÓN DE TRIÁNGULOS... 2 3. PUNTOS Y RECTAS NOTABLES... 3 4. SEMEJANZA
Geometría Tridimensional
 Capítulo 4 Geometría Tridimensional En dos dimensiones trabajamos en el plano mientras que en tres dimensiones trabajaremos en el espacio, también provisto de un sistema de coordenadas. En el espacio,
Capítulo 4 Geometría Tridimensional En dos dimensiones trabajamos en el plano mientras que en tres dimensiones trabajaremos en el espacio, también provisto de un sistema de coordenadas. En el espacio,
Tarea 4 Soluciones. la parte literal es x3 y 4
 Tarea 4 Soluciones Extracto del libro Baldor. Definición. Término.-es una expresión algebraica que consta de un solo símbolo o de varios símbolos no separados entre sí por el signo + o -. Así, a, 3b, 2xy,
Tarea 4 Soluciones Extracto del libro Baldor. Definición. Término.-es una expresión algebraica que consta de un solo símbolo o de varios símbolos no separados entre sí por el signo + o -. Así, a, 3b, 2xy,
Análisis de propuestas de evaluación en las aulas de América Latina
 Esta propuesta tiene como objetivo la operatoria con fracciones. Se espera del alumno la aplicación de un algoritmo para resolver las operaciones. Estas actividades comúnmente presentan numerosos ejercicios
Esta propuesta tiene como objetivo la operatoria con fracciones. Se espera del alumno la aplicación de un algoritmo para resolver las operaciones. Estas actividades comúnmente presentan numerosos ejercicios
Ecuación ordinaria de la circunferencia
 Ecuación ordinaria de la circunferencia En esta sección estudiatemos la ecuación de la circunferencia en la forma ordinaria. Cuando hablemos de la forma ordinaria de una cónica, generalmente nos referiremos
Ecuación ordinaria de la circunferencia En esta sección estudiatemos la ecuación de la circunferencia en la forma ordinaria. Cuando hablemos de la forma ordinaria de una cónica, generalmente nos referiremos
VECTORES. Módulo, dirección y sentido de un vector fijo En un vector fijo se llama módulo del mismo a la longitud del segmento que lo define.
 VECTORES El estudio de los vectores es uno de tantos conocimientos de las matemáticas que provienen de la física. En esta ciencia se distingue entre magnitudes escalares y magnitudes vectoriales. Se llaman
VECTORES El estudio de los vectores es uno de tantos conocimientos de las matemáticas que provienen de la física. En esta ciencia se distingue entre magnitudes escalares y magnitudes vectoriales. Se llaman
Vectores: Producto escalar y vectorial
 Nivelación de Matemática MTHA UNLP 1 Vectores: Producto escalar y vectorial Versores fundamentales Dado un sistema de coordenadas ortogonales, se considera sobre cada uno de los ejes y coincidiendo con
Nivelación de Matemática MTHA UNLP 1 Vectores: Producto escalar y vectorial Versores fundamentales Dado un sistema de coordenadas ortogonales, se considera sobre cada uno de los ejes y coincidiendo con
KIG: LA GEOMETRÍA A GOLPE DE RATÓN. Asesor de Tecnologías de la Información y de las Comunicaciones
 KIG: LA GEOMETRÍA A GOLPE DE RATÓN Asesor de Tecnologías de la Información y de las Comunicaciones GNU/LINEX Mariano Real Pérez KIG KDE Interactive geometry (Geometría interactiva de KDE) es una aplicación
KIG: LA GEOMETRÍA A GOLPE DE RATÓN Asesor de Tecnologías de la Información y de las Comunicaciones GNU/LINEX Mariano Real Pérez KIG KDE Interactive geometry (Geometría interactiva de KDE) es una aplicación
MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas
 Universidad de Cádiz Departamento de Matemáticas MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas Tema 4 La recta en el plano Elaborado por la Profesora Doctora María Teresa
Universidad de Cádiz Departamento de Matemáticas MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas Tema 4 La recta en el plano Elaborado por la Profesora Doctora María Teresa
CENAFE MATEMÁTICAS POLÍGONOS
 POLÍGONOS Es la porción del plano comprendida dentro de una línea poligonal cerrada. Es la superficie del plano limitada por una línea poligonal. La medida de un polígono es su área. Criterios de clasificación:
POLÍGONOS Es la porción del plano comprendida dentro de una línea poligonal cerrada. Es la superficie del plano limitada por una línea poligonal. La medida de un polígono es su área. Criterios de clasificación:
_ Antología de Física I. Unidad II Vectores. Elaboró: Ing. Víctor H. Alcalá-Octaviano
 24 Unidad II Vectores 2.1 Magnitudes escalares y vectoriales Unidad II. VECTORES Para muchas magnitudes físicas basta con indicar su valor para que estén perfectamente definidas y estas son las denominadas
24 Unidad II Vectores 2.1 Magnitudes escalares y vectoriales Unidad II. VECTORES Para muchas magnitudes físicas basta con indicar su valor para que estén perfectamente definidas y estas son las denominadas
Dirección de Evaluación de la Calidad Educativa
 Operaciones: Resolver problemas con dos operaciones Dentro del núcleo estructurante Operaciones, uno de los Saberes Básicos Fundamentales, donde se observa tienen más dificultades los alumnos es respecto
Operaciones: Resolver problemas con dos operaciones Dentro del núcleo estructurante Operaciones, uno de los Saberes Básicos Fundamentales, donde se observa tienen más dificultades los alumnos es respecto
EL TRIÁNGULO. Recordemos algunas propiedades elementales de los triángulos
 EL TRIÁNGULO 1. EL TRIÁNGULO. PRIMERAS PROPIEDADES El triángulo es un polígono que tiene tres lados y tres ángulos. Es, por tanto, el polígono más simple y el conocimiento de sus características y propiedades
EL TRIÁNGULO 1. EL TRIÁNGULO. PRIMERAS PROPIEDADES El triángulo es un polígono que tiene tres lados y tres ángulos. Es, por tanto, el polígono más simple y el conocimiento de sus características y propiedades
GEOMETRÍA 1.- INTRODUCCIÓN:
 GEOMETRÍA 1.- INTRODUCCIÓN: Etimológicamente hablando, la palabra Geometría procede del griego y significa Medida de la Tierra. La Geometría es la parte de las Matemáticas que estudia las idealizaciones
GEOMETRÍA 1.- INTRODUCCIÓN: Etimológicamente hablando, la palabra Geometría procede del griego y significa Medida de la Tierra. La Geometría es la parte de las Matemáticas que estudia las idealizaciones
Programa para el Mejoramiento de la Enseñanza de la Matemática en ANEP Proyecto: Análisis, Reflexión y Producción. Fracciones
 Fracciones. Las fracciones y los números Racionales Las fracciones se utilizan cotidianamente en contextos relacionados con la medida, el reparto o como forma de relacionar dos cantidades. Tenemos entonces
Fracciones. Las fracciones y los números Racionales Las fracciones se utilizan cotidianamente en contextos relacionados con la medida, el reparto o como forma de relacionar dos cantidades. Tenemos entonces
Preparación para la XLVII Olimpiada Matemática Española (II) Soluciones
 Preparación para la XLVII Olimpiada Matemática Española (II) Soluciones Eva Elduque Laburta y Adrián Rodrigo Escudero 5 de noviembre de 010 Problema 1. Construir un triángulo conocidos 1. un lado, su ángulo
Preparación para la XLVII Olimpiada Matemática Española (II) Soluciones Eva Elduque Laburta y Adrián Rodrigo Escudero 5 de noviembre de 010 Problema 1. Construir un triángulo conocidos 1. un lado, su ángulo
Matrices Invertibles y Elementos de Álgebra Matricial
 Matrices Invertibles y Elementos de Álgebra Matricial Departamento de Matemáticas, CCIR/ITESM 12 de enero de 2011 Índice 91 Introducción 1 92 Transpuesta 1 93 Propiedades de la transpuesta 2 94 Matrices
Matrices Invertibles y Elementos de Álgebra Matricial Departamento de Matemáticas, CCIR/ITESM 12 de enero de 2011 Índice 91 Introducción 1 92 Transpuesta 1 93 Propiedades de la transpuesta 2 94 Matrices
MICROECONOMÍA II PRÁCTICA TEMA III: MONOPOLIO
 MICROECONOMÍA II PRÁCTICA TEMA III: MONOPOLIO EJERCICIO 1 Primero analizamos el equilibrio bajo el monopolio. El monopolista escoge la cantidad que maximiza sus beneficios; en particular, escoge la cantidad
MICROECONOMÍA II PRÁCTICA TEMA III: MONOPOLIO EJERCICIO 1 Primero analizamos el equilibrio bajo el monopolio. El monopolista escoge la cantidad que maximiza sus beneficios; en particular, escoge la cantidad
Espacios generados, dependencia lineal y bases
 Espacios generados dependencia lineal y bases Departamento de Matemáticas CCIR/ITESM 14 de enero de 2011 Índice 14.1. Introducción............................................... 1 14.2. Espacio Generado............................................
Espacios generados dependencia lineal y bases Departamento de Matemáticas CCIR/ITESM 14 de enero de 2011 Índice 14.1. Introducción............................................... 1 14.2. Espacio Generado............................................
Tema 2 Límites de Funciones
 Tema 2 Límites de Funciones 2.1.- Definición de Límite Idea de límite de una función en un punto: Sea la función. Si x tiende a 2, a qué valor se aproxima? Construyendo - + una tabla de valores próximos
Tema 2 Límites de Funciones 2.1.- Definición de Límite Idea de límite de una función en un punto: Sea la función. Si x tiende a 2, a qué valor se aproxima? Construyendo - + una tabla de valores próximos
1. SOLUCIONES A LOS EJERCICIOS PROPUESTOS
 1 1. SOLUCIONES A LOS EJERCICIOS PROPUESTOS 1.1. ESPACIOS VECTORIALES 1. Analizar cuáles de los siguientes subconjuntos de R 3 son subespacios vectoriales. a) A = {(2x, x, 7x)/x R} El conjunto A es una
1 1. SOLUCIONES A LOS EJERCICIOS PROPUESTOS 1.1. ESPACIOS VECTORIALES 1. Analizar cuáles de los siguientes subconjuntos de R 3 son subespacios vectoriales. a) A = {(2x, x, 7x)/x R} El conjunto A es una
DEMOSTRACIONES GEOMÉTRICAS
 DEMOSTRACIONES GEOMÉTRICAS Ana M. Martín Caraballo, Universidad Pablo de Olavide de Sevilla. José Muñoz Santonja, IES Macarena de Sevilla. ESTALMAT ANDALUCÍA SEDE SEVILLA ÍNDICE INTRODUCCIÓN PRIMERA PARTE:
DEMOSTRACIONES GEOMÉTRICAS Ana M. Martín Caraballo, Universidad Pablo de Olavide de Sevilla. José Muñoz Santonja, IES Macarena de Sevilla. ESTALMAT ANDALUCÍA SEDE SEVILLA ÍNDICE INTRODUCCIÓN PRIMERA PARTE:
ESTÁTICA 2. VECTORES. Figura tomada de http://www.juntadeandalucia.es/averroes/~04001205/fisiqui/imagenes/vectores/473396841_e1de1dd225_o.
 ESTÁTICA Sesión 2 2 VECTORES 2.1. Escalares y vectores 2.2. Cómo operar con vectores 2.2.1. Suma vectorial 2.2.2. Producto de un escalar y un vector 2.2.3. Resta vectorial 2.2.4. Vectores unitarios 2.2.5.
ESTÁTICA Sesión 2 2 VECTORES 2.1. Escalares y vectores 2.2. Cómo operar con vectores 2.2.1. Suma vectorial 2.2.2. Producto de un escalar y un vector 2.2.3. Resta vectorial 2.2.4. Vectores unitarios 2.2.5.
TORNEO DE LAS CUENCAS. 2013 Primera Ronda Soluciones PRIMER NIVEL
 TORNEO DE LAS CUENCAS 2013 Primera Ronda Soluciones PRIMER NIVEL Problema 1- La figura adjunta está formada por un rectángulo y un cuadrado. Trazar una recta que la divida en dos figuras de igual área.
TORNEO DE LAS CUENCAS 2013 Primera Ronda Soluciones PRIMER NIVEL Problema 1- La figura adjunta está formada por un rectángulo y un cuadrado. Trazar una recta que la divida en dos figuras de igual área.
MINISTERIO DE EDUCACIÓN Concurso Nacional de Matemática Educación Preuniversitaria Curso 2009 2010 Temario por Grados
 MINISTERIO DE EDUCACIÓN Concurso Nacional de Matemática Educación Preuniversitaria Curso 009 010 Temario por Grados Nombre: Grado: Escuela: Provincia: Municipio: Número C.I.: Calif: La distribución de
MINISTERIO DE EDUCACIÓN Concurso Nacional de Matemática Educación Preuniversitaria Curso 009 010 Temario por Grados Nombre: Grado: Escuela: Provincia: Municipio: Número C.I.: Calif: La distribución de
UNIVERSIDAD DE COSTA RICA FACULTAD DE CIENCIAS BÁSICAS ESCUELA DE MATEMÁTICA DEPARTAMENTO DE ENSEÑANZA DE LA MATEMÁTICA CARTA AL ESTUDIANTE
 UNIVERSIDAD DE COSTA RICA FACULTAD DE CIENCIAS BÁSICAS ESCUELA DE MATEMÁTICA DEPARTAMENTO DE ENSEÑANZA DE LA MATEMÁTICA MA-0270 Geometría I I Ciclo del 2014 Curso del I año de carrera, I ciclo 5 horas
UNIVERSIDAD DE COSTA RICA FACULTAD DE CIENCIAS BÁSICAS ESCUELA DE MATEMÁTICA DEPARTAMENTO DE ENSEÑANZA DE LA MATEMÁTICA MA-0270 Geometría I I Ciclo del 2014 Curso del I año de carrera, I ciclo 5 horas
SISTEMA DIÉDRICO PARA INGENIEROS. David Peribáñez Martínez DEMO
 SISTEMA DIÉDRICO PARA INGENIEROS David Peribáñez Martínez SISTEMA DIÉDRICO PARA INGENIEROS David Peribáñez Martínez Valderrebollo 20, 1 A 28031 MADRID 1ª Edición Ninguna parte de esta publicación, incluido
SISTEMA DIÉDRICO PARA INGENIEROS David Peribáñez Martínez SISTEMA DIÉDRICO PARA INGENIEROS David Peribáñez Martínez Valderrebollo 20, 1 A 28031 MADRID 1ª Edición Ninguna parte de esta publicación, incluido
no descompone no descompone no descompone
 Problema 1. Sea I n el conjunto de los n primeros números naturales impares. Por ejemplo: I 3 = {1, 3, 5, I 6 = {1, 3, 5, 7, 9, 11, etc. Para qué números n el conjunto I n se puede descomponer en dos partes
Problema 1. Sea I n el conjunto de los n primeros números naturales impares. Por ejemplo: I 3 = {1, 3, 5, I 6 = {1, 3, 5, 7, 9, 11, etc. Para qué números n el conjunto I n se puede descomponer en dos partes
GEOMETRÍA CON LA CLASSPAD 300
 8. GEOMETRÍA CON LA CLASSPAD 300 LA APLICACIÓN GEOMETRÍA Para acceder a la aplicación para trabajar con distintas construcciones geométricas bastará con pulsar el icono correspondiente a Geometry en el
8. GEOMETRÍA CON LA CLASSPAD 300 LA APLICACIÓN GEOMETRÍA Para acceder a la aplicación para trabajar con distintas construcciones geométricas bastará con pulsar el icono correspondiente a Geometry en el
Los Aprendizajes en 6º grado de Primaria
 Los Aprendizajes en 6º grado de Primaria Matemática El análisis de las puntuaciones medias en Matemática de los estudiantes de 6º de Primaria evidencia disparidades en los resultados. La diferencia del
Los Aprendizajes en 6º grado de Primaria Matemática El análisis de las puntuaciones medias en Matemática de los estudiantes de 6º de Primaria evidencia disparidades en los resultados. La diferencia del
Profr. Efraín Soto Apolinar. Factorización
 Factorización La factorización es la otra parte de la historia de los productos notables. Esto es, ambas cosas se refieren a las mismas fórmulas, pero en los productos notables se nos daba una operación
Factorización La factorización es la otra parte de la historia de los productos notables. Esto es, ambas cosas se refieren a las mismas fórmulas, pero en los productos notables se nos daba una operación
Caracterización geométrica
 Caracterización geométrica Ahora vamos a centrar nuestra atención en la elipe. Esta figura geométrica tiene la misma esencia que la circunferencia, pero ésta está dilatada en uno de sus ejes. Recuerda
Caracterización geométrica Ahora vamos a centrar nuestra atención en la elipe. Esta figura geométrica tiene la misma esencia que la circunferencia, pero ésta está dilatada en uno de sus ejes. Recuerda
Este documento ha sido generado para facilitar la impresión de los contenidos. Los enlaces a otras páginas no serán funcionales.
 Este documento ha sido generado para facilitar la impresión de los contenidos. Los enlaces a otras páginas no serán funcionales. Introducción Por qué La Geometría? La Geometría tiene como objetivo fundamental
Este documento ha sido generado para facilitar la impresión de los contenidos. Los enlaces a otras páginas no serán funcionales. Introducción Por qué La Geometría? La Geometría tiene como objetivo fundamental
El proyecto Eratóstenes. Guía para el estudiante.
 El proyecto Eratóstenes. Guía para el estudiante. En esta actividad vas a trabajar en colaboración con estudiantes de otra escuela para medir el radio de la Tierra. Vas a usar los mismos métodos y principios
El proyecto Eratóstenes. Guía para el estudiante. En esta actividad vas a trabajar en colaboración con estudiantes de otra escuela para medir el radio de la Tierra. Vas a usar los mismos métodos y principios
VENTAJAS Y DESVENTAJAS DE LAS TECNOLOGIAS
 VENTAJAS Y DESVENTAJAS DE LAS TECNOLOGIAS EN NUESTRAS VIDAS JOCABED VALENZUELA GARCIA ESLI GUADALUPE LAZCANO RODRIGUEZ INTRODUCCION: Le tecnología es un sinónimo de innovación y de cosas nuevas para facilitar
VENTAJAS Y DESVENTAJAS DE LAS TECNOLOGIAS EN NUESTRAS VIDAS JOCABED VALENZUELA GARCIA ESLI GUADALUPE LAZCANO RODRIGUEZ INTRODUCCION: Le tecnología es un sinónimo de innovación y de cosas nuevas para facilitar
El cuadrante del éxito en la Empresa
 Cursos para EMPRESARIOS y EMPRESARIAS El cuadrante del éxito en la Empresa Cómo hacerse inmune a las crisis? Capítulo 3. - El Negocio Síntesis del vídeo 1.- En esta lección abordaremos qué hacer en el
Cursos para EMPRESARIOS y EMPRESARIAS El cuadrante del éxito en la Empresa Cómo hacerse inmune a las crisis? Capítulo 3. - El Negocio Síntesis del vídeo 1.- En esta lección abordaremos qué hacer en el
Guía del Usuario ANEXOS
 DataSoft 6.0 Guía del Usuario ANEXOS Tarija, julio del 2012 TABLA DE CONTENIDO 1. METODOS DE CONTROL DE INVENTARIO...1 1.1 Selección del Método De Control... 1 1.2 Método PEPS: Primeros en Entrar, Primeros
DataSoft 6.0 Guía del Usuario ANEXOS Tarija, julio del 2012 TABLA DE CONTENIDO 1. METODOS DE CONTROL DE INVENTARIO...1 1.1 Selección del Método De Control... 1 1.2 Método PEPS: Primeros en Entrar, Primeros
Tema 1: Fundamentos de lógica, teoría de conjuntos y estructuras algebraicas: Apéndice
 Tema 1: Fundamentos de lógica, teoría de conjuntos y estructuras algebraicas: Apéndice 1 Polinomios Dedicaremos este apartado al repaso de los polinomios. Se define R[x] ={a 0 + a 1 x + a 2 x 2 +... +
Tema 1: Fundamentos de lógica, teoría de conjuntos y estructuras algebraicas: Apéndice 1 Polinomios Dedicaremos este apartado al repaso de los polinomios. Se define R[x] ={a 0 + a 1 x + a 2 x 2 +... +
1 IES Salvador Allende/Extracto de la programación/recuperación Matemáticas 1º ESO
 1. CONTENIDOS BÁSICOS. Escritura y lectura de cantidades sencillas en el sistema de numeración decimal. Operar con rigor y precisión en N, respetando la jerarquía de operaciones. Resolver problemas sencillos
1. CONTENIDOS BÁSICOS. Escritura y lectura de cantidades sencillas en el sistema de numeración decimal. Operar con rigor y precisión en N, respetando la jerarquía de operaciones. Resolver problemas sencillos
1.3 Números racionales
 1.3 1.3.1 El concepto de número racional Figura 1.2: Un reparto no equitativo: 12 5 =?. Figura 1.3: Un quinto de la unidad. Con los números naturales y enteros es imposible resolver cuestiones tan simples
1.3 1.3.1 El concepto de número racional Figura 1.2: Un reparto no equitativo: 12 5 =?. Figura 1.3: Un quinto de la unidad. Con los números naturales y enteros es imposible resolver cuestiones tan simples
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID. PRUEBAS DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) Curso 2001-2002 OPCIÓN A
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBAS DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) Curso 2001-2002 MATERIA: DIBUJO TÉCNICO Junio Septiembre R1 R2 INSTRUCCIONES GENERALES La prueba consiste
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBAS DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) Curso 2001-2002 MATERIA: DIBUJO TÉCNICO Junio Septiembre R1 R2 INSTRUCCIONES GENERALES La prueba consiste
La lección de hoy es sobre Resolver Ecuaciones. El cuál es la expectativa para el aprendizaje del estudiante SEI.2.A1.1
 SEI.2.A1.1-Solving Equations-Student Learning Expectation. La lección de hoy es sobre Resolver Ecuaciones. El cuál es la expectativa para el aprendizaje del estudiante SEI.2.A1.1 En esta lección aprenderemos
SEI.2.A1.1-Solving Equations-Student Learning Expectation. La lección de hoy es sobre Resolver Ecuaciones. El cuál es la expectativa para el aprendizaje del estudiante SEI.2.A1.1 En esta lección aprenderemos
Lección 1-Introducción a los Polinomios y Suma y Resta de Polinomios. Dra. Noemí L. Ruiz Limardo 2009
 Lección 1-Introducción a los Polinomios y Suma y Resta de Polinomios Dra. Noemí L. Ruiz Limardo 2009 Objetivos de la Lección Al finalizar esta lección los estudiantes: Identificarán, de una lista de expresiones
Lección 1-Introducción a los Polinomios y Suma y Resta de Polinomios Dra. Noemí L. Ruiz Limardo 2009 Objetivos de la Lección Al finalizar esta lección los estudiantes: Identificarán, de una lista de expresiones
A RG. Giro de un punto A respecto del eje vertical, e. Giro de un punto A respecto del eje de punta, e.
 Giro de un punto A respecto del eje vertical, e. A''' A''' 2 e A'' 60 El giro es otro de los procedimietos utilizados en diédrico para resolver construcciones. Aquí vamos a ver solo uno de sus aspectos:
Giro de un punto A respecto del eje vertical, e. A''' A''' 2 e A'' 60 El giro es otro de los procedimietos utilizados en diédrico para resolver construcciones. Aquí vamos a ver solo uno de sus aspectos:
1.4.- D E S I G U A L D A D E S
 1.4.- D E S I G U A L D A D E S OBJETIVO: Que el alumno conozca y maneje las reglas empleadas en la resolución de desigualdades y las use para determinar el conjunto solución de una desigualdad dada y
1.4.- D E S I G U A L D A D E S OBJETIVO: Que el alumno conozca y maneje las reglas empleadas en la resolución de desigualdades y las use para determinar el conjunto solución de una desigualdad dada y
Seminario de problemas-eso. Curso 2012-13. Hoja 7
 Seminario de problemas-eso. Curso 2012-13. Hoja 7 43. La suma de las edades de mamá, papá, mi hermano y yo es 83. Seis veces la edad de papá es igual a siete veces la edad de mamá, y la edad de mamá es
Seminario de problemas-eso. Curso 2012-13. Hoja 7 43. La suma de las edades de mamá, papá, mi hermano y yo es 83. Seis veces la edad de papá es igual a siete veces la edad de mamá, y la edad de mamá es
VALOR SOCIAL LA GESTIÓN DEL VALOR SOCIAL EN LA ADMINISTRACIÓN PÚBLICA
 VALOR SOCIAL LA DEL EN LA ADMINISTRACIÓN PÚBLICA LA DEL EN LAS ADMINISTRACIONES PÚBLICAS La medición del valor social y medioambiental es una oportunidad para ampliar la capacidad de gestión de cualquier
VALOR SOCIAL LA DEL EN LA ADMINISTRACIÓN PÚBLICA LA DEL EN LAS ADMINISTRACIONES PÚBLICAS La medición del valor social y medioambiental es una oportunidad para ampliar la capacidad de gestión de cualquier
Colegio Alexander von Humboldt - Lima. Tema: La enseñanza de la matemática está en un proceso de cambio
 Refo 07 2004 15 al 19 de noviembre 2004 Colegio Alexander von Humboldt - Lima Tema: La enseñanza de la matemática está en un proceso de cambio La enseñanza de la matemática debe tener dos objetivos principales:
Refo 07 2004 15 al 19 de noviembre 2004 Colegio Alexander von Humboldt - Lima Tema: La enseñanza de la matemática está en un proceso de cambio La enseñanza de la matemática debe tener dos objetivos principales:
Ejercicios de Trigonometría
 Ejercicios de Trigonometría 1) Indica la medida de estos ángulos en radianes: a) 0º b) 45º c) 60º d) 120º Recuerda que 360º son 2π radianes, con lo que para hacer la conversión realizaremos una simple
Ejercicios de Trigonometría 1) Indica la medida de estos ángulos en radianes: a) 0º b) 45º c) 60º d) 120º Recuerda que 360º son 2π radianes, con lo que para hacer la conversión realizaremos una simple
Una desigualdad se obtiene al escribir dos expresiones numéricas o algebraicas relacionadas con alguno de los símbolos
 MATEMÁTICAS BÁSICAS DESIGUALDADES DESIGUALDADES DE PRIMER GRADO EN UNA VARIABLE La epresión a b significa que "a" no es igual a "b ". Según los valores particulares de a de b, puede tenerse a > b, que
MATEMÁTICAS BÁSICAS DESIGUALDADES DESIGUALDADES DE PRIMER GRADO EN UNA VARIABLE La epresión a b significa que "a" no es igual a "b ". Según los valores particulares de a de b, puede tenerse a > b, que
1. Producto escalar, métrica y norma asociada
 1. asociada Consideramos el espacio vectorial R n sobre el cuerpo R; escribimos los vectores o puntos de R n, indistintamente, como x = (x 1,..., x n ) = n x i e i i=1 donde e i son los vectores de la
1. asociada Consideramos el espacio vectorial R n sobre el cuerpo R; escribimos los vectores o puntos de R n, indistintamente, como x = (x 1,..., x n ) = n x i e i i=1 donde e i son los vectores de la
NÚMEROS NATURALES Y NÚMEROS ENTEROS
 NÚMEROS NATURALES Y NÚMEROS ENTEROS Los números naturales surgen como respuesta a la necesidad de nuestros antepasados de contar los elementos de un conjunto (por ejemplo los animales de un rebaño) y de
NÚMEROS NATURALES Y NÚMEROS ENTEROS Los números naturales surgen como respuesta a la necesidad de nuestros antepasados de contar los elementos de un conjunto (por ejemplo los animales de un rebaño) y de
TEMA 5: CIRCUNFERENCIA Y CÍRCULO
 TEMA 5: CIRCUNFERENCIA Y CÍRCULO Matías Arce, Sonsoles Blázquez, Tomás Ortega, Cristina Pecharromán 1. INTRODUCCIÓN... 1 2. LA CIRCUNFERENCIA Y EL CÍRCULO... 1 3. MEDICIÓN DE ÁNGULOS... 3 4. ÁNGULOS EN
TEMA 5: CIRCUNFERENCIA Y CÍRCULO Matías Arce, Sonsoles Blázquez, Tomás Ortega, Cristina Pecharromán 1. INTRODUCCIÓN... 1 2. LA CIRCUNFERENCIA Y EL CÍRCULO... 1 3. MEDICIÓN DE ÁNGULOS... 3 4. ÁNGULOS EN
Lección 24: Lenguaje algebraico y sustituciones
 LECCIÓN Lección : Lenguaje algebraico y sustituciones En lecciones anteriores usted ya trabajó con ecuaciones. Las ecuaciones expresan una igualdad entre ciertas relaciones numéricas en las que se desconoce
LECCIÓN Lección : Lenguaje algebraico y sustituciones En lecciones anteriores usted ya trabajó con ecuaciones. Las ecuaciones expresan una igualdad entre ciertas relaciones numéricas en las que se desconoce
EJEMPLO DE REPORTE DE LIBERTAD FINANCIERA
 EJEMPLO DE REPORTE DE LIBERTAD FINANCIERA 1. Introduccio n El propósito de este reporte es describir de manera detallada un diagnóstico de su habilidad para generar ingresos pasivos, es decir, ingresos
EJEMPLO DE REPORTE DE LIBERTAD FINANCIERA 1. Introduccio n El propósito de este reporte es describir de manera detallada un diagnóstico de su habilidad para generar ingresos pasivos, es decir, ingresos
RAZONAMIENTOS LÓGICOS EN LOS PROBLEMAS DE MATEMÁTICAS
 RAZONAMIENTOS LÓGICOS EN LOS PROBLEMAS DE MATEMÁTICAS AUTORÍA SERGIO BALLESTER SAMPEDRO TEMÁTICA MATEMÁTICAS ETAPA ESO, BACHILLERATO Resumen En este artículo comienzo definiendo proposición y los distintos
RAZONAMIENTOS LÓGICOS EN LOS PROBLEMAS DE MATEMÁTICAS AUTORÍA SERGIO BALLESTER SAMPEDRO TEMÁTICA MATEMÁTICAS ETAPA ESO, BACHILLERATO Resumen En este artículo comienzo definiendo proposición y los distintos
PROBLEMAS DE ECUACIONES SIMULTÁNEAS
 PROBLEMAS DE ECUACIONES SIMULTÁNEAS Por: ELÍAS LOYOLA CAMPOS 1. En un recinto del zoológico se tienen dos tipos de animales: avestruces y jirafas. Hay 30 ojos y 44 patas, cuántos animales hay de cada tipo?
PROBLEMAS DE ECUACIONES SIMULTÁNEAS Por: ELÍAS LOYOLA CAMPOS 1. En un recinto del zoológico se tienen dos tipos de animales: avestruces y jirafas. Hay 30 ojos y 44 patas, cuántos animales hay de cada tipo?
Recursos para el Estudio en Carreras de Ingeniería 2006 UNIDAD TEMÁTICA Nº 4 LA TOMA DE APUNTES
 UNIDAD TEMÁTICA Nº 4 LA TOMA DE APUNTES En esta unidad te invitamos a que: Adviertas la importancia de los apuntes como un recurso para iniciar el estudio de un tema. Te apropies de algunas estrategias
UNIDAD TEMÁTICA Nº 4 LA TOMA DE APUNTES En esta unidad te invitamos a que: Adviertas la importancia de los apuntes como un recurso para iniciar el estudio de un tema. Te apropies de algunas estrategias
Definición 1.1.1. Dados dos números naturales m y n, una matriz de orden o dimensión m n es una tabla numérica rectangular con m filas y n columnas.
 Tema 1 Matrices Estructura del tema. Conceptos básicos y ejemplos Operaciones básicas con matrices Método de Gauss Rango de una matriz Concepto de matriz regular y propiedades Determinante asociado a una
Tema 1 Matrices Estructura del tema. Conceptos básicos y ejemplos Operaciones básicas con matrices Método de Gauss Rango de una matriz Concepto de matriz regular y propiedades Determinante asociado a una
Apuntes de Matemática Discreta 1. Conjuntos y Subconjuntos
 Apuntes de Matemática Discreta 1. Conjuntos y Subconjuntos Francisco José González Gutiérrez Cádiz, Octubre de 2004 Universidad de Cádiz Departamento de Matemáticas ii Lección 1 Conjuntos y Subconjuntos
Apuntes de Matemática Discreta 1. Conjuntos y Subconjuntos Francisco José González Gutiérrez Cádiz, Octubre de 2004 Universidad de Cádiz Departamento de Matemáticas ii Lección 1 Conjuntos y Subconjuntos
XLIV Olimpiada Matemática Española Fase nacional 2008 (Valencia) PRIMERA SESIÓN (28 de marzo)
 Fase nacional 008 (Valencia) PRIMERA SESIÓN (8 de marzo).- Halla dos enteros positivos a y b conociendo su suma y su mínimo común múltiplo. Aplícalo en el caso de ue la suma sea 97 y el mínimo común múltiplo
Fase nacional 008 (Valencia) PRIMERA SESIÓN (8 de marzo).- Halla dos enteros positivos a y b conociendo su suma y su mínimo común múltiplo. Aplícalo en el caso de ue la suma sea 97 y el mínimo común múltiplo
Ecuaciones de primer grado con dos incógnitas
 Ecuaciones de primer grado con dos incógnitas Si decimos: "las edades de mis padres suman 120 años", podemos expresar esta frase algebraicamente de la siguiente forma: Entonces, Denominamos x a la edad
Ecuaciones de primer grado con dos incógnitas Si decimos: "las edades de mis padres suman 120 años", podemos expresar esta frase algebraicamente de la siguiente forma: Entonces, Denominamos x a la edad
Problemas a la carta
 Problemas a la carta Enseñanza Alfinio Flores Peñafiel y Nora G. Ramírez Arizona State University Maricopa Community Colleges resumen Se presentan cinco problemas que pueden ser resueltos mediante la utilización
Problemas a la carta Enseñanza Alfinio Flores Peñafiel y Nora G. Ramírez Arizona State University Maricopa Community Colleges resumen Se presentan cinco problemas que pueden ser resueltos mediante la utilización
TRANSFORMADORES EN PARALELO
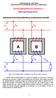 UNIVERIDD DE CNTRI TRNFORMDORE EN PRLELO Miguel ngel Rodríguez Pozueta Condiciones para que varios transformadores se puedan conectar en paralelo Fig. 0: Dos transformadores monofásicos ( y ) conectados
UNIVERIDD DE CNTRI TRNFORMDORE EN PRLELO Miguel ngel Rodríguez Pozueta Condiciones para que varios transformadores se puedan conectar en paralelo Fig. 0: Dos transformadores monofásicos ( y ) conectados
MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas
 Universidad de ádiz Departamento de Matemáticas MATEMÁTIAS para estudiantes de primer curso de facultades y escuelas técnicas Tema 5 La circunferencia Elaborado por la Profesora Doctora María Teresa González
Universidad de ádiz Departamento de Matemáticas MATEMÁTIAS para estudiantes de primer curso de facultades y escuelas técnicas Tema 5 La circunferencia Elaborado por la Profesora Doctora María Teresa González
GUÍA TÉCNICA PARA LA DEFINICIÓN DE COMPROMISOS DE CALIDAD Y SUS INDICADORES
 GUÍA TÉCNICA PARA LA DEFINICIÓN DE COMPROMISOS DE CALIDAD Y SUS INDICADORES Tema: Cartas de Servicios Primera versión: 2008 Datos de contacto: Evaluación y Calidad. Gobierno de Navarra. [email protected]
GUÍA TÉCNICA PARA LA DEFINICIÓN DE COMPROMISOS DE CALIDAD Y SUS INDICADORES Tema: Cartas de Servicios Primera versión: 2008 Datos de contacto: Evaluación y Calidad. Gobierno de Navarra. [email protected]
Áreas de rectángulos y paralelogramos
 LECCIÓN CONDENSADA 8.1 Áreas de rectángulos y paralelogramos En esta lección Revisarás la fórmula del área de un rectángulo Usarás la fórmula del área de un rectángulo para encontrar las áreas de otras
LECCIÓN CONDENSADA 8.1 Áreas de rectángulos y paralelogramos En esta lección Revisarás la fórmula del área de un rectángulo Usarás la fórmula del área de un rectángulo para encontrar las áreas de otras
VECTORES. Se representa gráficamente por medio de una flecha, por ejemplo: Todos los vectores poseen las siguientes características:
 Un vector v es un segmento orientado. VECTORES Se representa gráficamente por medio de una flecha, por ejemplo: Todos los vectores poseen las siguientes características: Punto de aplicación: es el lugar
Un vector v es un segmento orientado. VECTORES Se representa gráficamente por medio de una flecha, por ejemplo: Todos los vectores poseen las siguientes características: Punto de aplicación: es el lugar
Biblioteca Virtual Ejercicios Resueltos
 EJERCICIO 13 13 V a l o r n u m é r i c o Valor numérico de expresiones compuestas P r o c e d i m i e n t o 1. Se reemplaza cada letra por su valor numérico 2. Se efectúan las operaciones indicadas Hallar
EJERCICIO 13 13 V a l o r n u m é r i c o Valor numérico de expresiones compuestas P r o c e d i m i e n t o 1. Se reemplaza cada letra por su valor numérico 2. Se efectúan las operaciones indicadas Hallar
Universidad de Costa Rica Escuela de Matemática Departamento de Enseñanza de la Matemática. Carta al Estudiante MA0270 Geometría I II Ciclo - 2011
 Universidad de Costa Rica Escuela de Matemática Departamento de Enseñanza de la Matemática Carta al Estudiante MA0270 Geometría I II Ciclo - 2011 Número de créditos: 4. Horas lectivas por semana: 5. Requisitos
Universidad de Costa Rica Escuela de Matemática Departamento de Enseñanza de la Matemática Carta al Estudiante MA0270 Geometría I II Ciclo - 2011 Número de créditos: 4. Horas lectivas por semana: 5. Requisitos
Vectores en el plano con punto inicial fijo
 Vectores en el plano con punto inicial fijo bjetivos. Considerar el conjunto V 2 () de los vectores en el plano euclidiano (también llamados segmentos dirigidos o flechas) con un punto inicial fijo. Definir
Vectores en el plano con punto inicial fijo bjetivos. Considerar el conjunto V 2 () de los vectores en el plano euclidiano (también llamados segmentos dirigidos o flechas) con un punto inicial fijo. Definir
DESIGUALDADES página 1
 DESIGUALDADES página 1 1.1 CONCEPTOS Y DEFINICIONES Una igualdad en Álgebra es aquella relación que establece equivalencia entre dos entes matemáticos. Es una afirmación, a través del signo =, de que dos
DESIGUALDADES página 1 1.1 CONCEPTOS Y DEFINICIONES Una igualdad en Álgebra es aquella relación que establece equivalencia entre dos entes matemáticos. Es una afirmación, a través del signo =, de que dos
1. Vectores 1.1. Definición de un vector en R2, R3 (Interpretación geométrica), y su generalización en Rn.
 1. VECTORES INDICE 1.1. Definición de un vector en R 2, R 3 (Interpretación geométrica), y su generalización en R n...2 1.2. Operaciones con vectores y sus propiedades...6 1.3. Producto escalar y vectorial
1. VECTORES INDICE 1.1. Definición de un vector en R 2, R 3 (Interpretación geométrica), y su generalización en R n...2 1.2. Operaciones con vectores y sus propiedades...6 1.3. Producto escalar y vectorial
Subespacios vectoriales en R n
 Subespacios vectoriales en R n Víctor Domínguez Octubre 2011 1. Introducción Con estas notas resumimos los conceptos fundamentales del tema 3 que, en pocas palabras, se puede resumir en técnicas de manejo
Subespacios vectoriales en R n Víctor Domínguez Octubre 2011 1. Introducción Con estas notas resumimos los conceptos fundamentales del tema 3 que, en pocas palabras, se puede resumir en técnicas de manejo
Integrales paramétricas e integrales dobles y triples.
 Integrales paramétricas e integrales dobles y triples. Eleonora Catsigeras * 19 de julio de 2006 PRÓLOGO: Notas para el curso de Cálculo II de la Facultad de Ingeniería. Este texto es complementario al
Integrales paramétricas e integrales dobles y triples. Eleonora Catsigeras * 19 de julio de 2006 PRÓLOGO: Notas para el curso de Cálculo II de la Facultad de Ingeniería. Este texto es complementario al
Unidad 3 Direccionamiento IP (Subnetting)
 Unidad 3 Direccionamiento IP (Subnetting) Las direcciones denominadas IPv4 se expresan por combinaciones de números de hasta 32 bits que permiten hasta 2 32 posibilidades (4.294.967.296 en total). Los
Unidad 3 Direccionamiento IP (Subnetting) Las direcciones denominadas IPv4 se expresan por combinaciones de números de hasta 32 bits que permiten hasta 2 32 posibilidades (4.294.967.296 en total). Los
3.1 DEFINICIÓN. Figura Nº 1. Vector
 3.1 DEFINICIÓN Un vector (A) una magnitud física caracterizable mediante un módulo y una dirección (u orientación) en el espacio. Todo vector debe tener un origen marcado (M) con un punto y un final marcado
3.1 DEFINICIÓN Un vector (A) una magnitud física caracterizable mediante un módulo y una dirección (u orientación) en el espacio. Todo vector debe tener un origen marcado (M) con un punto y un final marcado
Vectores no colineales.
 Vectores no colineales. Por definición son aquellos vectores que no tienen igual dirección. La resultante de los mismos no surge de la suma algebraica de los módulos de dichos vectores, sino que deben
Vectores no colineales. Por definición son aquellos vectores que no tienen igual dirección. La resultante de los mismos no surge de la suma algebraica de los módulos de dichos vectores, sino que deben
Inter American Accreditation Cooperation. Grupo de prácticas de auditoría de acreditación Directriz sobre:
 Grupo de prácticas de auditoría de acreditación Directriz sobre: Auditando la competencia de los auditores y equipos de auditores de organismos de certificación / registro de Sistemas de Gestión de Calidad
Grupo de prácticas de auditoría de acreditación Directriz sobre: Auditando la competencia de los auditores y equipos de auditores de organismos de certificación / registro de Sistemas de Gestión de Calidad
Estrategias para la enseñanza de ecuaciones para niños con discapacidad visual
 Estrategias para la enseñanza de ecuaciones para niños con discapacidad visual Por: Yenifer Paola Correa Hernández Erika Julieth Pulido Mahecha Compartir Resumen Los procedimientos, gráficos, operaciones
Estrategias para la enseñanza de ecuaciones para niños con discapacidad visual Por: Yenifer Paola Correa Hernández Erika Julieth Pulido Mahecha Compartir Resumen Los procedimientos, gráficos, operaciones
PRISMA OBLICUO > REPRESENTACIÓN Y DESARROLLO POR EL MÉTODO DE LA SECCIÓN NORMAL
 1. CARACTERÍSTICAS GENERALES DEL PRISMA OBLICUO Desde el punto de vista de la representación en SISTEMA DIÉDRICO, el prisma oblicuo presenta dos características importantes que lo diferencian del prisma
1. CARACTERÍSTICAS GENERALES DEL PRISMA OBLICUO Desde el punto de vista de la representación en SISTEMA DIÉDRICO, el prisma oblicuo presenta dos características importantes que lo diferencian del prisma
FUNDACION PUERTORRIQUEÑA DE LAS HUMANIDADES ENCICLOPEDIA DE PUERTO RICO EN LINEA. Política Editorial y Guía para Autores
 FUNDACION PUERTORRIQUEÑA DE LAS HUMANIDADES ENCICLOPEDIA DE PUERTO RICO EN LINEA Política Editorial y Guía para Autores I. Misión y descripción de la Enciclopedia de Puerto Rico en Línea La Enciclopedia
FUNDACION PUERTORRIQUEÑA DE LAS HUMANIDADES ENCICLOPEDIA DE PUERTO RICO EN LINEA Política Editorial y Guía para Autores I. Misión y descripción de la Enciclopedia de Puerto Rico en Línea La Enciclopedia
Soluciones de los ejercicios de Selectividad sobre Probabilidad de Matemáticas Aplicadas a las Ciencias Sociales II
 Soluciones de los ejercicios de Selectividad sobre Probabilidad de ntonio Francisco Roldán López de Hierro * Convocatoria de 2007 Las siguientes páginas contienen las soluciones de los ejercicios propuestos
Soluciones de los ejercicios de Selectividad sobre Probabilidad de ntonio Francisco Roldán López de Hierro * Convocatoria de 2007 Las siguientes páginas contienen las soluciones de los ejercicios propuestos
Los números racionales
 Los números racionales Los números racionales Los números fraccionarios o fracciones permiten representar aquellas situaciones en las que se obtiene o se debe una parte de un objeto. Todas las fracciones
Los números racionales Los números racionales Los números fraccionarios o fracciones permiten representar aquellas situaciones en las que se obtiene o se debe una parte de un objeto. Todas las fracciones
Matemática I Extremos de una Función. Definiciones-Teoremas
 Universidad Centroccidental Lisandro Alvarado Decanato de Agronomía Programa Ingeniería Agroindustrial Departamento de Gerencia Estudios Generales Matemática I Etremos de una Función. Definiciones-Teoremas
Universidad Centroccidental Lisandro Alvarado Decanato de Agronomía Programa Ingeniería Agroindustrial Departamento de Gerencia Estudios Generales Matemática I Etremos de una Función. Definiciones-Teoremas
Universidad de la Frontera. Geometría Anaĺıtica: Departamento de Matemática y Estadística. Cĺınica de Matemática. J. Labrin - G.
 Universidad de la Frontera Departamento de Matemática y Estadística Cĺınica de Matemática 1 Geometría Anaĺıtica: J. Labrin - G.Riquelme 1. Los puntos extremos de un segmento son P 1 (2,4) y P 2 (8, 4).
Universidad de la Frontera Departamento de Matemática y Estadística Cĺınica de Matemática 1 Geometría Anaĺıtica: J. Labrin - G.Riquelme 1. Los puntos extremos de un segmento son P 1 (2,4) y P 2 (8, 4).
Tema 6: Ecuaciones e inecuaciones.
 Tema 6: Ecuaciones e inecuaciones. Ejercicio 1. Encontrar, tanteando, alguna solución de cada una de las siguientes ecuaciones: 3 a) + 5 = 69 Probamos para =,3,4,... = = 3 3 = 4 4 3 3 3 + 5 = 13. + 5 =
Tema 6: Ecuaciones e inecuaciones. Ejercicio 1. Encontrar, tanteando, alguna solución de cada una de las siguientes ecuaciones: 3 a) + 5 = 69 Probamos para =,3,4,... = = 3 3 = 4 4 3 3 3 + 5 = 13. + 5 =
Tema 1: Cuerpos geométricos. Aplicaciones
 Tema 1: Cuerpos geométricos. Aplicaciones 1.- los polígonos. Un polígono es un trozo de plano limitado por una línea poligonal (sin curvas) cerrada. Es un polígono No son polígonos Hay dos clases de polígonos:
Tema 1: Cuerpos geométricos. Aplicaciones 1.- los polígonos. Un polígono es un trozo de plano limitado por una línea poligonal (sin curvas) cerrada. Es un polígono No son polígonos Hay dos clases de polígonos:
CAPÍTULO 1 PROYECTO JURÍDICO PRÁCTICAS MONOPÓLICAS EN LOS CONTRATOS DE FRANQUICIAS EN MÉXICO
 CAPÍTULO 1 PROYECTO JURÍDICO PRÁCTICAS MONOPÓLICAS EN LOS CONTRATOS DE FRANQUICIAS EN MÉXICO SUMARIO. 1.1 Introducción. 1.2 Breve Descripción del Tema. 1.3 Objetivo General 1.4 Objetivo Específico 1.5
CAPÍTULO 1 PROYECTO JURÍDICO PRÁCTICAS MONOPÓLICAS EN LOS CONTRATOS DE FRANQUICIAS EN MÉXICO SUMARIO. 1.1 Introducción. 1.2 Breve Descripción del Tema. 1.3 Objetivo General 1.4 Objetivo Específico 1.5
MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN CLASES # 13 y #14
 MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN CLASES # 3 y #4 Desigualdades Al inicio del Capítulo 3, estudiamos las relaciones de orden en los número reales y el signi cado de expresiones
MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN CLASES # 3 y #4 Desigualdades Al inicio del Capítulo 3, estudiamos las relaciones de orden en los número reales y el signi cado de expresiones
Qué son los monomios?
 Qué son los monomios? Recordemos qué es una expresión algebraica. Definición Una expresión algebraica es aquella en la que se utilizan letras, números y signos de operaciones. Si se observan las siguientes
Qué son los monomios? Recordemos qué es una expresión algebraica. Definición Una expresión algebraica es aquella en la que se utilizan letras, números y signos de operaciones. Si se observan las siguientes

 TALES DE MILETO -625 / -547 Qalh
TALES DE MILETO -625 / -547 Qalh