Ejemplo de Presentación Beamer
|
|
|
- Samuel Guzmán Fidalgo
- hace 9 años
- Vistas:
Transcripción
1 Noviembre 2010 Departamento de Informática Universidad de Valladolid
2 Índice Introducción 1 Introducción Modelos Basados en Adaptación Social
3 Índice Introducción 1 Introducción Modelos Basados en Adaptación Social 2 Un algoritmo
4 Índice Introducción 1 Introducción Modelos Basados en Adaptación Social 2 Un algoritmo 3
5 Modelos Basados en Adaptación Social Qué es un modelo basado en adaptación social? Definición Algoritmos o mecanismos distribuidos de resolución de problemas inspirados en el comportamiento colectivo de colonias de insectos sociales u otras sociedades de animales.
6 Modelos Basados en Adaptación Social Qué es un modelo basado en adaptación social? Definición Algoritmos o mecanismos distribuidos de resolución de problemas inspirados en el comportamiento colectivo de colonias de insectos sociales u otras sociedades de animales. Ejemplo Insectos
7 Modelos Basados en Adaptación Social Qué es un modelo basado en adaptación social? Definición Algoritmos o mecanismos distribuidos de resolución de problemas inspirados en el comportamiento colectivo de colonias de insectos sociales u otras sociedades de animales. Ejemplo Insectos Aves
8 Modelos Basados en Adaptación Social Qué es un modelo basado en adaptación social? Definición Algoritmos o mecanismos distribuidos de resolución de problemas inspirados en el comportamiento colectivo de colonias de insectos sociales u otras sociedades de animales. Ejemplo Insectos Aves Peces
9 Modelos Basados en Adaptación Social Qué es un modelo basado en adaptación social? Definición Algoritmos o mecanismos distribuidos de resolución de problemas inspirados en el comportamiento colectivo de colonias de insectos sociales u otras sociedades de animales. Ejemplo Insectos Aves Peces Mamíferos
10 Un algoritmo Un bloque Texto
11 Un algoritmo Un bloque Texto 1 Texto Texto Texto Texto Texto Texto Texto Texto Texto Texto Texto Texto Texto Texto
12 Un algoritmo Un bloque Texto 2 Texto Texto Texto Texto Texto Texto Texto Texto Texto Texto Texto Texto Texto Texto
13 Un algoritmo Un bloque Texto 3 Texto Texto Texto Texto Texto Texto Texto Texto Texto Texto Texto Texto Texto Texto
14 Un algoritmo Un bloque Texto 3 Texto Texto Texto Texto Texto Texto Texto Texto Texto Texto Texto Texto Texto Texto Otro bloque Texto Texto Texto Texto
15 Ecuaciones Introducción Una ecuación du
16 Ecuaciones Introducción Una ecuación du = 1 2 sec2 (x/2)dx
17 Ecuaciones Introducción Una ecuación du = 1 2 sec2 (x/2)dx = 2 cos 2 (x/2)du
18 Ecuaciones Introducción Una ecuación du = 1 2 sec2 (x/2)dx = 2 cos 2 (x/2)du = 2du 1 + u 2
19 Ecuaciones Introducción Una ecuación du = 1 2 sec2 (x/2)dx = 2 cos 2 (x/2)du = 2du 1 + u 2 Otra ecuación du u 2 + 4
20 Ecuaciones Introducción Una ecuación du = 1 2 sec2 (x/2)dx = 2 cos 2 (x/2)du = 2du 1 + u 2 Otra ecuación du u = 1 2 arctan(u/2) + c
21 Ecuaciones Introducción Una ecuación du = 1 2 sec2 (x/2)dx = 2 cos 2 (x/2)du = 2du 1 + u 2 Otra ecuación du u = 1 2 arctan(u/2) + c = 1 2 arctan(1 2 tan(x/2)) + c
C.P. Montgo Ana Vallés Aula P.T. TEMA 2 LOS ANIMALES
 TEMA 2 LOS ANIMALES Autor pictogramas: Sergio Palao Procedencia: ARASAAC http://catedu.es/arasaac/ Licencia: CC (BY-NC) Autora: Amaya Padilla Collado http://www.garachicoenclave.blogspot.com Fotos e imágenes:
TEMA 2 LOS ANIMALES Autor pictogramas: Sergio Palao Procedencia: ARASAAC http://catedu.es/arasaac/ Licencia: CC (BY-NC) Autora: Amaya Padilla Collado http://www.garachicoenclave.blogspot.com Fotos e imágenes:
CECyT No. 1 Gonzalo Vázquez Vela PROBLEMARIO. Materia: Cálculo Integral. Prof.: Escoto Villaseñor Martha Guadalupe.
 Instituto Politécnico Nacional CECyT No. 1 Gonzalo Vázquez Vela PROBLEMARIO Materia: Prof.: Escoto Villaseñor Martha Guadalupe. Prof. Martha Guadalupe Escoto Villaseñor Página 1 Trabajo: Temas visto en
Instituto Politécnico Nacional CECyT No. 1 Gonzalo Vázquez Vela PROBLEMARIO Materia: Prof.: Escoto Villaseñor Martha Guadalupe. Prof. Martha Guadalupe Escoto Villaseñor Página 1 Trabajo: Temas visto en
7 Sistemas de ecuaciones
 89485 _ 0309-0368.qxd 1/9/0 15:3 Página 31 Sistemas de ecuaciones INTRODUCCIÓN Aunque no es el objetivo de este curso, los alumnos deben ser capaces de reconocer ecuaciones con dos incógnitas y obtener
89485 _ 0309-0368.qxd 1/9/0 15:3 Página 31 Sistemas de ecuaciones INTRODUCCIÓN Aunque no es el objetivo de este curso, los alumnos deben ser capaces de reconocer ecuaciones con dos incógnitas y obtener
Nombre: Kinder: Autoras: Mª Victoria López Cecilia Rodríguez. Fundación Astoreca Versión preliminar Programa matemática Nivel Kinder
 Nombre: Kinder: Autoras: Mª Victoria López Cecilia Rodríguez 1 uno Dibuje 1(un) elemento: 2 Repase con el dedo índice 3 veces el número 1: Ahora escríbalo. 3 Encierre en un círculo azul los números 1:
Nombre: Kinder: Autoras: Mª Victoria López Cecilia Rodríguez 1 uno Dibuje 1(un) elemento: 2 Repase con el dedo índice 3 veces el número 1: Ahora escríbalo. 3 Encierre en un círculo azul los números 1:
ALGORITMO DE OPTIMIZACIÓN BASADO EN EL APAREAMIENTO DE LAS ABEJAS(HBMO). UN NUEVO ENFOQUE HEURÍSTICO DE OPTIMIZACIÓN.
 DE OPTIMIZACIÓN BASADO EN EL APAREAMIENTO DE LAS (HBMO). UN NUEVO ENFOQUE HEURÍSTICO DE OPTIMIZACIÓN. OMID BOZORG HADDAD, ABBAS AFSHAR, MIGUEL A. MARIÑO Víctor Fernández Mora Manuel Sifón Miralles Raquel
DE OPTIMIZACIÓN BASADO EN EL APAREAMIENTO DE LAS (HBMO). UN NUEVO ENFOQUE HEURÍSTICO DE OPTIMIZACIÓN. OMID BOZORG HADDAD, ABBAS AFSHAR, MIGUEL A. MARIÑO Víctor Fernández Mora Manuel Sifón Miralles Raquel
Matrices escalonadas y escalonadas reducidas
 Matrices escalonadas y escalonadas reducidas Objetivos. Estudiar las definiciones formales de matrices escalonadas y escalonadas reducidas. Comprender qué importancia tienen estas matrices para resolver
Matrices escalonadas y escalonadas reducidas Objetivos. Estudiar las definiciones formales de matrices escalonadas y escalonadas reducidas. Comprender qué importancia tienen estas matrices para resolver
2 Métodos de solución de ED de primer orden
 CAPÍTULO Métodos de solución de E de primer orden.5 Ecuaciones diferenciales homogéneas Al tratar con polinomios de más de una variable, se define el grado de cada término como la suma de los grados de
CAPÍTULO Métodos de solución de E de primer orden.5 Ecuaciones diferenciales homogéneas Al tratar con polinomios de más de una variable, se define el grado de cada término como la suma de los grados de
INTRODUCCIÓN. Página 1
 INTRODUCCIÓN Página 1 INTRODUCCIÓN Página 2 INTRODUCCIÓN Página 3 INTRODUCCIÓN Página 4 INTRODUCCIÓN Página 5 INTRODUCCIÓN Página 6 INTRODUCCIÓN Página 7 CAPÍTULO 1 Página 8 CAPÍTULO 1 Página 9 CAPÍTULO
INTRODUCCIÓN Página 1 INTRODUCCIÓN Página 2 INTRODUCCIÓN Página 3 INTRODUCCIÓN Página 4 INTRODUCCIÓN Página 5 INTRODUCCIÓN Página 6 INTRODUCCIÓN Página 7 CAPÍTULO 1 Página 8 CAPÍTULO 1 Página 9 CAPÍTULO
Curso de Matemática. Unidad 2. Operaciones Elementales II: Potenciación. Profesora: Sofía Fuhrman. Definición
 Curso de Matemática Unidad 2 Profesora: Sofía Fuhrman Operaciones Elementales II: Potenciación Definición a n = a. a.a a multiplicado por sí mismo n veces. a) Regla de los signos Exponente Par Exponente
Curso de Matemática Unidad 2 Profesora: Sofía Fuhrman Operaciones Elementales II: Potenciación Definición a n = a. a.a a multiplicado por sí mismo n veces. a) Regla de los signos Exponente Par Exponente
Es cierta para x = 0. d) Sí, son soluciones. Se trata de una identidad pues es cierta para cualquier valor de x.
 EJERCICIOS RESUELTOS MÍNIMOS 3º ESO TEMA 4 ECUACIONES Ejercicio nº 1.- Dada la siguiente igualdad: x 1 3 9 x 5 3x = x responde razonadamente: a) Es cierta si sustituimos la incógnita por el valor cero?
EJERCICIOS RESUELTOS MÍNIMOS 3º ESO TEMA 4 ECUACIONES Ejercicio nº 1.- Dada la siguiente igualdad: x 1 3 9 x 5 3x = x responde razonadamente: a) Es cierta si sustituimos la incógnita por el valor cero?
INTEGRACIÓN POR CAMBIO DE VARIABLE
 INTEGRACIÓN POR CAMBIO DE VARIABLE Propósitos Identificar las operaciones algebraicas que convierten una integral a una forma inmediata (cambio de variable). Utilizar las tablas de integrales inmediatas
INTEGRACIÓN POR CAMBIO DE VARIABLE Propósitos Identificar las operaciones algebraicas que convierten una integral a una forma inmediata (cambio de variable). Utilizar las tablas de integrales inmediatas
5 Sistemas de ecuaciones
 863 _ 099-031.qxd 7/4/07 13:3 Página 99 Sistemas de ecuaciones INTRODUCCIÓN La resolución de problemas es uno de los fundamentos de las Matemáticas. A la hora de resolver muchos problemas reales se hace
863 _ 099-031.qxd 7/4/07 13:3 Página 99 Sistemas de ecuaciones INTRODUCCIÓN La resolución de problemas es uno de los fundamentos de las Matemáticas. A la hora de resolver muchos problemas reales se hace
EJERCICIOS RESUELTOS DE ECUACIONES LOGARÍTMICAS Y EXPONENCIALES
 MATEMÁTICAS EJERCICIOS RESUELTOS DE ECUACIONES LOGARÍTMICAS Y EXPONENCIALES Juan Jesús Pascual ECUACIONES LOGARÍTMICAS Y EXPONENCIALES A. Introducción teórica B. Ejercicios resueltos A. INTRODUCCIÓN TEÓRICA
MATEMÁTICAS EJERCICIOS RESUELTOS DE ECUACIONES LOGARÍTMICAS Y EXPONENCIALES Juan Jesús Pascual ECUACIONES LOGARÍTMICAS Y EXPONENCIALES A. Introducción teórica B. Ejercicios resueltos A. INTRODUCCIÓN TEÓRICA
Métodos Numéricos Grado en Informática Tema 5: Diferenciación e Integración Numérica
 Métodos Numéricos Grado en Informática Tema 5: Diferenciación e Integración Numérica Luis Alvarez León Univ. de Las Palmas de G.C. Luis Alvarez León () Métodos Numéricos Univ. de Las Palmas de G.C. 1 /
Métodos Numéricos Grado en Informática Tema 5: Diferenciación e Integración Numérica Luis Alvarez León Univ. de Las Palmas de G.C. Luis Alvarez León () Métodos Numéricos Univ. de Las Palmas de G.C. 1 /
Ecuaciones. 3º de ESO
 Ecuaciones 3º de ESO El signo igual El signo igual se utiliza en: Igualdades numéricas: 2 + 3 = 5 Identidades algebraicas: (x + 4) x = x 2 + 4 4x Fórmulas: El área, A,, de un círculo de radio r es: A =
Ecuaciones 3º de ESO El signo igual El signo igual se utiliza en: Igualdades numéricas: 2 + 3 = 5 Identidades algebraicas: (x + 4) x = x 2 + 4 4x Fórmulas: El área, A,, de un círculo de radio r es: A =
La herramienta ArtEM: Aritmética Entera y Modular
 La herramienta ArtEM: Aritmética Entera y Modular 1. Introducción La herramienta ArtEM (Aritmética Entera y Modular) es una aplicación informática programada en Visual Basic y desarrollada con el fin de
La herramienta ArtEM: Aritmética Entera y Modular 1. Introducción La herramienta ArtEM (Aritmética Entera y Modular) es una aplicación informática programada en Visual Basic y desarrollada con el fin de
Juan Ruiz Álvarez. Matemáticas (Grado en Biología)
 Método de las isóclinas. 1 1 Departamento de Matemáticas. Universidad de Alcalá de Henares. Contenidos Introducción 1 Introducción 2 3 4 Índice Introducción 1 Introducción 2 3 4 Introducción Desafortunadamente,
Método de las isóclinas. 1 1 Departamento de Matemáticas. Universidad de Alcalá de Henares. Contenidos Introducción 1 Introducción 2 3 4 Índice Introducción 1 Introducción 2 3 4 Introducción Desafortunadamente,
AUTORES... 11 PRÓLOGO...13 INTRODUCCIÓN... 15 CAPÍTULO 1. INICIACIÓN A LA PROGRAMACIÓN EN MAPLE...19
 ÍNDICE AUTORES... 11 PRÓLOGO...13 INTRODUCCIÓN... 15 CAPÍTULO 1. INICIACIÓN A LA PROGRAMACIÓN EN MAPLE...19 1.1. ESTRUCTURA BÁSICA... 19 1.2. BREVE RECORRIDO POR MAPLE...23 1.2.1. Números, Polinomios y
ÍNDICE AUTORES... 11 PRÓLOGO...13 INTRODUCCIÓN... 15 CAPÍTULO 1. INICIACIÓN A LA PROGRAMACIÓN EN MAPLE...19 1.1. ESTRUCTURA BÁSICA... 19 1.2. BREVE RECORRIDO POR MAPLE...23 1.2.1. Números, Polinomios y
Problemas de 4 o ESO. Isaac Musat Hervás
 Problemas de 4 o ESO Isaac Musat Hervás 5 de febrero de 01 Índice general 1. Problemas de Álgebra 7 1.1. Números Reales.......................... 7 1.1.1. Los números....................... 7 1.1.. Intervalos.........................
Problemas de 4 o ESO Isaac Musat Hervás 5 de febrero de 01 Índice general 1. Problemas de Álgebra 7 1.1. Números Reales.......................... 7 1.1.1. Los números....................... 7 1.1.. Intervalos.........................
Ecuaciones de primer grado con denominadores
 Ecuaciones de primer grado con denominadores x 1 3 =x 1 3 ) x 1 3 =x 3 1 ) 4x 1 3 =x 3 1 3 ) x 5 =3x 8 5 5 ) 3x 3 5 = x 7 5 4 5 ) x 3 = x 1 3 ) x 3 1 5 = x 6 3 6 15 ) 4x 6 =5 x 4 3 17 ) 6x 5 =3 x 1 ) 5x
Ecuaciones de primer grado con denominadores x 1 3 =x 1 3 ) x 1 3 =x 3 1 ) 4x 1 3 =x 3 1 3 ) x 5 =3x 8 5 5 ) 3x 3 5 = x 7 5 4 5 ) x 3 = x 1 3 ) x 3 1 5 = x 6 3 6 15 ) 4x 6 =5 x 4 3 17 ) 6x 5 =3 x 1 ) 5x
Habilidades Directivas y Técnicas de Liderazgo
 HABILIDADES DIRECTIVAS Y TÉCNICAS DE LIDERAZGO Su Aplicación en la Gestión de Equipos de Trabajo EDITORIAL Habilidades Directivas y Técnicas de Liderazgo Habilidades Directivas y Técnicas de Liderazgo
HABILIDADES DIRECTIVAS Y TÉCNICAS DE LIDERAZGO Su Aplicación en la Gestión de Equipos de Trabajo EDITORIAL Habilidades Directivas y Técnicas de Liderazgo Habilidades Directivas y Técnicas de Liderazgo
ACIS. ADAPTACIÓN CURRICULAR INDIVIDUAL SIGNIFICATIVA
 ACIS. ADAPTACIÓN CURRICULAR INDIVIDUAL SIGNIFICATIVA Alumno /a: Unidad didáctica: La Tierra en el cosmos a) Que el alumno /a comprenda cómo 1.- El Universo. Libro de adaptación curricular CCNN. es el Universo.
ACIS. ADAPTACIÓN CURRICULAR INDIVIDUAL SIGNIFICATIVA Alumno /a: Unidad didáctica: La Tierra en el cosmos a) Que el alumno /a comprenda cómo 1.- El Universo. Libro de adaptación curricular CCNN. es el Universo.
CURSO CERO DE MATEMATICAS. Apuntes elaborados por Domingo Pestana Galván. y José Manuel Rodríguez García
 INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES CURSO CERO DE MATEMATICAS Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica
INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES CURSO CERO DE MATEMATICAS Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica
Complementos de Matemáticas, ITT Telemática
 Introducción Métodos de punto fijo Complementos de Matemáticas, ITT Telemática Tema 1. Solución numérica de ecuaciones no lineales Departamento de Matemáticas, Universidad de Alcalá Introducción Métodos
Introducción Métodos de punto fijo Complementos de Matemáticas, ITT Telemática Tema 1. Solución numérica de ecuaciones no lineales Departamento de Matemáticas, Universidad de Alcalá Introducción Métodos
E.T.S. Minas: Métodos Matemáticos Ejercicios resueltos Tema 7 Ecuaciones diferenciales de primer orden
 E.T.S. Minas: Métodos Matemáticos Ejercicios resueltos Tema 7 Ecuaciones diferenciales de primer orden Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de
E.T.S. Minas: Métodos Matemáticos Ejercicios resueltos Tema 7 Ecuaciones diferenciales de primer orden Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de
INDICE Parte Uno: El Control Interno Capitulo. Qué es el sistema de Control Intenso (SCI)
 INDICE Introducción Parte Uno: El Control Interno Capitulo. Qué es el sistema de Control Intenso (SCI) 3 Objetivos de capitulo 3 Definición de control 3 Evolución del control interno 5 Por qué y para qué
INDICE Introducción Parte Uno: El Control Interno Capitulo. Qué es el sistema de Control Intenso (SCI) 3 Objetivos de capitulo 3 Definición de control 3 Evolución del control interno 5 Por qué y para qué
INSTITUTO TECNOLÓGICO DE TIJUANA ECUACIONES DIFERENCIALES. Portafolio Parte 2
 INSTITUTO TECNOLÓGICO DE TIJUANA DEPARTAMENTO DE SISTEMAS Y COMPUTACIÓN SEMESTRE ENERO JUNIO 2014 INGENIERÍA EN SISTEMAS COMPUTACIONALES ECUACIONES DIFERENCIALES Portafolio Parte 2 Indicadores 19-23, 25,
INSTITUTO TECNOLÓGICO DE TIJUANA DEPARTAMENTO DE SISTEMAS Y COMPUTACIÓN SEMESTRE ENERO JUNIO 2014 INGENIERÍA EN SISTEMAS COMPUTACIONALES ECUACIONES DIFERENCIALES Portafolio Parte 2 Indicadores 19-23, 25,
Curso y ejercicios de matemáticas para la Selectividad y su fase específica Eric Dubon
 Curso y ejercicios de matemáticas para la Selectividad y su fase específica Eric Dubon Profesor de matemáticas del Liceo Francés de Alicante Pierre Deschamps. Doctorando del departamento de Análisis Matemático
Curso y ejercicios de matemáticas para la Selectividad y su fase específica Eric Dubon Profesor de matemáticas del Liceo Francés de Alicante Pierre Deschamps. Doctorando del departamento de Análisis Matemático
Llamamos a F una antiderivada de f en el intervalo I si D x F(x) = f (x) en I; esto es, si F (x) = f (x) para toda x en I.
 Sección 3.8 Antiderivadas 197 C Después de derivar y hacer el resultado igual a cero, muchos problemas prácticos de máximos y mínimos conducen a una ecuación que no puede resolverse de manera exacta. Para
Sección 3.8 Antiderivadas 197 C Después de derivar y hacer el resultado igual a cero, muchos problemas prácticos de máximos y mínimos conducen a una ecuación que no puede resolverse de manera exacta. Para
CARACTERÍSTICAS DE LA REPRODUCCIÓN SEXUAL Y ASEXUAL
 CARACTERÍSTICAS DE LA REPRODUCCIÓN SEXUAL Y ASEXUAL Los seres vivos (incluido el ser humano) tiene que cumplir a diario con unas funciones que les permiten mantenerse con vida y perpetuar su especie, asegurando
CARACTERÍSTICAS DE LA REPRODUCCIÓN SEXUAL Y ASEXUAL Los seres vivos (incluido el ser humano) tiene que cumplir a diario con unas funciones que les permiten mantenerse con vida y perpetuar su especie, asegurando
Noviembre 2006, Versión 1.1. Ejercicio 1 Resuelve las siguientes ecuaciones diferenciales ordinarias. 1. 4y 00 + y 0 =0. 2. y 00 y 0 6y =0.
 E.T.S. Minas: Métodos Matemáticos Ejercicios resueltos Tema 8 EDOs de orden superior Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Curso 006/07
E.T.S. Minas: Métodos Matemáticos Ejercicios resueltos Tema 8 EDOs de orden superior Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Curso 006/07
b 11 cm y la hipotenusa
 . RESOLUCIÓN DE TRIÁNGULOS RECTÁNGULOS UNIDAD : Trigonometría II Resolver un triángulo es conocer la longitud de cada uno de sus lados y la medida de cada uno de sus ángulos. En el caso de triángulos rectángulos,
. RESOLUCIÓN DE TRIÁNGULOS RECTÁNGULOS UNIDAD : Trigonometría II Resolver un triángulo es conocer la longitud de cada uno de sus lados y la medida de cada uno de sus ángulos. En el caso de triángulos rectángulos,
Ecuaciones Diferenciales, Fracciones Parciales y Fórmulas de Heaviside
 Ecuaciones Diferenciales, Fracciones Parciales y Fórmulas de Heaviside Dr. Julián Gpe. Tapia Aguilar E S F M Instituto Politécnico Nacional [email protected] Agosto de 2008 Índice 1. Introducción 1
Ecuaciones Diferenciales, Fracciones Parciales y Fórmulas de Heaviside Dr. Julián Gpe. Tapia Aguilar E S F M Instituto Politécnico Nacional [email protected] Agosto de 2008 Índice 1. Introducción 1
UNIVERSIDAD NACIONAL EXPERIMENTAL DE GUAYANA GERENCIA ACADEMICA COORDINACION DE PREGRADO PROYECTO INGENIERIA 1272-416/ALGEBRA DE ESTRUCTURAS SEMESTRE:
 GERENCIA ACADEMICA COORDINACION DE PREGRADO PROYECTO INGENIERIA PROGRAMA: ALGEBRA LINEAL CÓDIGO ASIGNATURA: 1272-521 PRE-REQUISITO: 1272-416/ALGEBRA DE ESTRUCTURAS SEMESTRE: 90-II UNIDADES DE CRÉDITO:
GERENCIA ACADEMICA COORDINACION DE PREGRADO PROYECTO INGENIERIA PROGRAMA: ALGEBRA LINEAL CÓDIGO ASIGNATURA: 1272-521 PRE-REQUISITO: 1272-416/ALGEBRA DE ESTRUCTURAS SEMESTRE: 90-II UNIDADES DE CRÉDITO:
SISTEMAS DE ECUACIONES LINEALES
 1 SISTEMAS DE ECUACIONES LINEALES Una ecuación es un enunciado o proposición que plantea la igualdad de dos expresiones, donde al menos una de ellas contiene cantidades desconocidas llamadas variables
1 SISTEMAS DE ECUACIONES LINEALES Una ecuación es un enunciado o proposición que plantea la igualdad de dos expresiones, donde al menos una de ellas contiene cantidades desconocidas llamadas variables
5 Sistemas de ecuaciones
 8966 _ 09-008.qd 7/6/08 09: Página 97 Sistemas de ecuaciones INTRODUCCIÓN Los sistemas de ecuaciones son necesarios para plantear solucionar numerosos problemas reales, por lo que los alumnos deben ser
8966 _ 09-008.qd 7/6/08 09: Página 97 Sistemas de ecuaciones INTRODUCCIÓN Los sistemas de ecuaciones son necesarios para plantear solucionar numerosos problemas reales, por lo que los alumnos deben ser
SOLUCIONES DE LOS EJERCICIOS DEL TEMA 4
 SOLUCIONES E LOS EJERCICIOS EL TEMA 4 EJERCICIO 1 Verdadero. La demanda será superior a la oferta, con lo cual habrá un exceso de demanda o escasez. b) Falso. No tendrá efecto alguno, ya que en el mercado
SOLUCIONES E LOS EJERCICIOS EL TEMA 4 EJERCICIO 1 Verdadero. La demanda será superior a la oferta, con lo cual habrá un exceso de demanda o escasez. b) Falso. No tendrá efecto alguno, ya que en el mercado
DEPARTAMENTO DE CÁLCULO Y GEOMETRIA ANALITICA SEMESTRE 2017-1 SERIE CURVAS EN EL ESPACIO
 SEMESTRE 017-1 1. Obtener una ecuación vectorial de la curva que se obtiene por el desplazamiento de un punto tal que su abscisa es -5 mientras que su cota es el triple de la tangente de su ordenada..
SEMESTRE 017-1 1. Obtener una ecuación vectorial de la curva que se obtiene por el desplazamiento de un punto tal que su abscisa es -5 mientras que su cota es el triple de la tangente de su ordenada..
Los animales vertebrados
 Área Conocimiento del Medio. Adaptación de Textos. Libro de la Editorial Santillana, Proyecto La Casa del Saber. Los animales vertebrados 1 Los animales vertebrados tienen huesos en el interior de su cuerpo.
Área Conocimiento del Medio. Adaptación de Textos. Libro de la Editorial Santillana, Proyecto La Casa del Saber. Los animales vertebrados 1 Los animales vertebrados tienen huesos en el interior de su cuerpo.
Funciones exponenciales y logarítmicas
 Funciones exponenciales y logarítmicas - Funciones exponenciales y sus gráficas Un terremoto de 85 grados en la escala de Richter es 00 veces más potente que uno de 65, por qué?, cómo es la escala de Richter?
Funciones exponenciales y logarítmicas - Funciones exponenciales y sus gráficas Un terremoto de 85 grados en la escala de Richter es 00 veces más potente que uno de 65, por qué?, cómo es la escala de Richter?
UNIDAD 3 LOGARITMOS EJERCICIOS RESUELTOS. Objetivo general.
 . UNIDAD LOGARITMOS EJERCICIOS RESUELTOS Objetivo general. Al terminar esta Unidad comprenderás la importancia histórica de los logaritmos y resolverás ejercicios y problemas en los que apliques los logaritmos
. UNIDAD LOGARITMOS EJERCICIOS RESUELTOS Objetivo general. Al terminar esta Unidad comprenderás la importancia histórica de los logaritmos y resolverás ejercicios y problemas en los que apliques los logaritmos
Cinemática de la partícula
 Cinemática de la partícula Física I Grado en Ingeniería de Organización Industrial Primer Curso Ana Mª Marco Ramírez Curso 2013/2014 Dpto.Física Aplicada III Universidad de Sevilla Índice Introducción
Cinemática de la partícula Física I Grado en Ingeniería de Organización Industrial Primer Curso Ana Mª Marco Ramírez Curso 2013/2014 Dpto.Física Aplicada III Universidad de Sevilla Índice Introducción
Conservación n y Mantenimiento de Colecciones de Historia Natural y Materiales didácticos en IES con fondos históricos 9-11 de diciembre de 2010
 Técnicas básicas b de Conservación n y Mantenimiento de Colecciones de Historia Natural y Materiales didácticos en IES con fondos históricos 9-11 de diciembre de 2010 Introducción Celia Santos. Colección
Técnicas básicas b de Conservación n y Mantenimiento de Colecciones de Historia Natural y Materiales didácticos en IES con fondos históricos 9-11 de diciembre de 2010 Introducción Celia Santos. Colección
GRADO EN INGENIERÍA DE TECNOLOGÍAS Y SERVICIOS DE TELECOMUNICACIÓN
 GRADO EN INGENIERÍA DE TECNOLOGÍAS Y SERVICIOS DE TELECOMUNICACIÓN CURSO ACADÉMICO 202/ Estudios Grado en Ingeniería de Tecnologías y Servicios de Telecomunicación (Publicado en BOE) (.2.200) (En el presente
GRADO EN INGENIERÍA DE TECNOLOGÍAS Y SERVICIOS DE TELECOMUNICACIÓN CURSO ACADÉMICO 202/ Estudios Grado en Ingeniería de Tecnologías y Servicios de Telecomunicación (Publicado en BOE) (.2.200) (En el presente
Introducción a las ecuaciones diferenciales
 Matemáticas. 1 de Biología http://orion.ciencias.uniovi.es/asignaturas/biomat Facultad de Biología Curso 25-26 Introducción a las ecuaciones diferenciales 1. Probar que cada función dada es solución de
Matemáticas. 1 de Biología http://orion.ciencias.uniovi.es/asignaturas/biomat Facultad de Biología Curso 25-26 Introducción a las ecuaciones diferenciales 1. Probar que cada función dada es solución de
TEMARIO EXAMEN MATEMÁTICA SÉPTIMO AÑO BÁSICO 2012 3 DE DICIEMBRE
 SÉPTIMO AÑO BÁSICO 2012 NÚMEROS Ejercicios combinados con enteros, con y sin paréntesis. Solución de problemas con enteros Solución de problemas, aplicando proporción directa e inversa. Propiedades de
SÉPTIMO AÑO BÁSICO 2012 NÚMEROS Ejercicios combinados con enteros, con y sin paréntesis. Solución de problemas con enteros Solución de problemas, aplicando proporción directa e inversa. Propiedades de
LOS ANIMALES NATIVOS DE QUITO. Stella de la Torre COCIBA USFQ
 LOS ANIMALES NATIVOS DE QUITO Stella de la Torre COCIBA USFQ Qué es un animal? Organismo eucariota, pluricelular, heterótrofo de ingestión Reservas en glucógeno Reproducción sexual (asexual) Sistema nervioso
LOS ANIMALES NATIVOS DE QUITO Stella de la Torre COCIBA USFQ Qué es un animal? Organismo eucariota, pluricelular, heterótrofo de ingestión Reservas en glucógeno Reproducción sexual (asexual) Sistema nervioso
2 ln x dx. Solución: Resolvemos la integral por partes. Si hacemos u = ln x y dv = dx, entonces u =ln x du = 1 x dx dv = dx v = x y por tanto
 Tema 6 Integración Definida Ejercicios resueltos Ejercicio Calcular la integral definida ln x dx Solución: Resolvemos la integral por partes. Si hacemos u = ln x y dv = dx, entonces u =ln x du = x dx dv
Tema 6 Integración Definida Ejercicios resueltos Ejercicio Calcular la integral definida ln x dx Solución: Resolvemos la integral por partes. Si hacemos u = ln x y dv = dx, entonces u =ln x du = x dx dv
EXAMEN DE SISTEMAS DE ECUACIONES LINEALES Y NO LINEALES
 EXAMEN DE SISTEMAS DE ECUACIONES LINEALES Y NO LINEALES Se recomienda: a) Antes de hacer algo, lee todo el examen. b) Resuelve antes las preguntas que se te den mejor. c) Responde a cada parte del examen
EXAMEN DE SISTEMAS DE ECUACIONES LINEALES Y NO LINEALES Se recomienda: a) Antes de hacer algo, lee todo el examen. b) Resuelve antes las preguntas que se te den mejor. c) Responde a cada parte del examen
Problemas resueltos de subespacios vectoriales, base y dimensión. Matemáticas I curso 2012 13
 29. Calcular la dimensión, una base, unas ecuaciones implícitas y unas ecuaciones explícitas (paramétricas) de los siguientes subespacios. En qué espacio vectorial están contenidos?,,, Dato: Tenemos las
29. Calcular la dimensión, una base, unas ecuaciones implícitas y unas ecuaciones explícitas (paramétricas) de los siguientes subespacios. En qué espacio vectorial están contenidos?,,, Dato: Tenemos las
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE INGENIERÍA DIVISIÓN DE CIENCIAS BÁSICAS COORDINACIÓN DE MATEMÁTICAS LOGARITMOS
 LOGARITMOS Introducción El empleo de los logaritmos es de gran utilidad para entender muchos de los desarrollos que se analizan en la Matemática, y para explicar una variedad muy extensa de problemas que
LOGARITMOS Introducción El empleo de los logaritmos es de gran utilidad para entender muchos de los desarrollos que se analizan en la Matemática, y para explicar una variedad muy extensa de problemas que
x ln x dx Solución: Resolvemos la integral por partes. Si hacemos u = ln x y dv = xdx, entonces u =ln x du = 1 x dx x 2 dx = 1 2 x2 ln x x2
 Tema 5 Integración Indefinida Ejercicios resueltos Ejercicio Calcular la integral x ln x dx Solución: Resolvemos la integral por partes. Si hacemos u = ln x y dv = xdx, entonces u =ln x du = x dx dv =
Tema 5 Integración Indefinida Ejercicios resueltos Ejercicio Calcular la integral x ln x dx Solución: Resolvemos la integral por partes. Si hacemos u = ln x y dv = xdx, entonces u =ln x du = x dx dv =
TEMA 3: La Matriz Inversa y Las Ecuaciones Matriciales
 MATEMÁTICAS 2º Bach. BLOQUE : ALGEBRA José Ramón Padrón TEMA 3: La Matriz Inversa y Las Ecuaciones Matriciales Dándole vueltas a las matrices: La matriz inversa INTRODUCCIÓN Observa los precios de tres
MATEMÁTICAS 2º Bach. BLOQUE : ALGEBRA José Ramón Padrón TEMA 3: La Matriz Inversa y Las Ecuaciones Matriciales Dándole vueltas a las matrices: La matriz inversa INTRODUCCIÓN Observa los precios de tres
Clase 9 Sistemas de ecuaciones no lineales
 Clase 9 Instituto de Ciencias Básicas Facultad de Ingeniería Universidad Diego Portales Marzo, 2013 Problemas resueltos Problema 4: Considere el sistema de ecuaciones x y = 3 (x 2) 2 +y = 1 Problemas resueltos
Clase 9 Instituto de Ciencias Básicas Facultad de Ingeniería Universidad Diego Portales Marzo, 2013 Problemas resueltos Problema 4: Considere el sistema de ecuaciones x y = 3 (x 2) 2 +y = 1 Problemas resueltos
INTRODUCCIÓN. FUNCIONES EXPONENCIALES Y LOGARÍTMICAS
 INTRODUCCIÓN. FUNCIONES EXPONENCIALES Y LOGARÍTMICAS Tradicionalmente, el estudio de los logaritmos ha ido inevitablemente acompañado de las tablas logarítmicas y del estudio de conceptos tales como el
INTRODUCCIÓN. FUNCIONES EXPONENCIALES Y LOGARÍTMICAS Tradicionalmente, el estudio de los logaritmos ha ido inevitablemente acompañado de las tablas logarítmicas y del estudio de conceptos tales como el
1. Determinar el volumen del solido que se genera al rotar la región acotada por las parabolas x = y 2 3 y x = y y 2,alrededor de la recta x = 4.
 Practica. Determinar el volumen del solido que se genera al rotar la región acotada or las arabolas x = y y x = y y,alrededor de la recta x = 4. Encontremos los untos de interceccion de ambas curvas: y
Practica. Determinar el volumen del solido que se genera al rotar la región acotada or las arabolas x = y y x = y y,alrededor de la recta x = 4. Encontremos los untos de interceccion de ambas curvas: y
λ autovalor / valor propio v autovector / vector propio
 1. INTRODUCCIÓN Problema estándar Problema generalizado CÁLCULO DE AUTOVALORES λ autovalor / valor propio v autovector / vector propio Laboratori de Càlcul Numèric (LaCàN) Departament de Matemàtica Aplicada
1. INTRODUCCIÓN Problema estándar Problema generalizado CÁLCULO DE AUTOVALORES λ autovalor / valor propio v autovector / vector propio Laboratori de Càlcul Numèric (LaCàN) Departament de Matemàtica Aplicada
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE INGENIERÍA DIVISIÓN DE CIENCIAS BÁSICAS COORDINACIÓN DE MATEMÁTICAS LA RECTA
 LA RECTA Definición Se llama línea recta al lugar geométrico de todos los puntos contenidos en el, Q x, y de la plano tales que, tomados dos puntos cualesquiera P( x y ) y ( ) recta, el valor de la pendiente
LA RECTA Definición Se llama línea recta al lugar geométrico de todos los puntos contenidos en el, Q x, y de la plano tales que, tomados dos puntos cualesquiera P( x y ) y ( ) recta, el valor de la pendiente
Estudio del tiempo de ejecución de algoritmos recursivos a través de relaciones de recurrencia lineal
 Estudio del tiempo de ejecución de algoritmos recursivos a través de relaciones de recurrencia lineal Apellidos, nombre Centro Sanabria Codesal, Esther 1 ([email protected]) Casanova Faus, Assumpció
Estudio del tiempo de ejecución de algoritmos recursivos a través de relaciones de recurrencia lineal Apellidos, nombre Centro Sanabria Codesal, Esther 1 ([email protected]) Casanova Faus, Assumpció
CADENA ALIMENTARIA. Una de las relaciones más importantes entre los seres vivos surge de la necesidad de alimentarse
 INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE LUMNA: AREA : CIENCIAS NATURALES Y EDUCACION AMBIENTAL ASIGNATURA: CIENCIAS NATURALES DOCENTE: MARA CELINA MAZO TAPIAS TIPO DE GUIA: CONCEPTUAL y DE EJECUCION
INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE LUMNA: AREA : CIENCIAS NATURALES Y EDUCACION AMBIENTAL ASIGNATURA: CIENCIAS NATURALES DOCENTE: MARA CELINA MAZO TAPIAS TIPO DE GUIA: CONCEPTUAL y DE EJECUCION
La respiración en los animales
 La respiración en los animales En el interior de las células, en las mitocondrias, mediante la respiración celular, los nutrientes son degradados con oxígeno y se obtienen energía y sustancias de desecho,
La respiración en los animales En el interior de las células, en las mitocondrias, mediante la respiración celular, los nutrientes son degradados con oxígeno y se obtienen energía y sustancias de desecho,
CÁLCULO DE PRIMITIVAS
 CÁLCULO DE PRIMITIVAS David Ariza-Ruiz Departamento de Análisis Matemático Seminario I 7 de noviembre de 202 (Universidad de Sevilla) David Ariza Ruiz 7 de noviembre de 202 / 42 Definición y propiedades
CÁLCULO DE PRIMITIVAS David Ariza-Ruiz Departamento de Análisis Matemático Seminario I 7 de noviembre de 202 (Universidad de Sevilla) David Ariza Ruiz 7 de noviembre de 202 / 42 Definición y propiedades
Ingeniería Informática
 Grado en Ingeniería Informática PLAN DE ESTUDIOS Explicación general del plan de estudios El plan de estudios contendrá toda la formación teórica y práctica que el alumnado deba adquirir: aspectos básicos
Grado en Ingeniería Informática PLAN DE ESTUDIOS Explicación general del plan de estudios El plan de estudios contendrá toda la formación teórica y práctica que el alumnado deba adquirir: aspectos básicos
Ejemplo 1. Ejemplo introductorio
 . -Jordan. Ejemplo 1. Ejemplo introductorio. -Jordan Dos especies de insectos se crían juntas en un recipiente de laboratorio. Todos los días se les proporcionan dos tipos de alimento A y B. 1 individuo
. -Jordan. Ejemplo 1. Ejemplo introductorio. -Jordan Dos especies de insectos se crían juntas en un recipiente de laboratorio. Todos los días se les proporcionan dos tipos de alimento A y B. 1 individuo
Diseño y desarrollo Web con HTML 5, CSS y Dreamweaver CS4 - URJC
 Diseño y desarrollo Web con HTML 5, CSS y Dreamweaver CS4 - URJC Código: 13119 Modalidad Distancia 150 Duración Qué aprenderás? Con este curso aprenderás conocimientos teóricos y prácticos para poder desarrollar
Diseño y desarrollo Web con HTML 5, CSS y Dreamweaver CS4 - URJC Código: 13119 Modalidad Distancia 150 Duración Qué aprenderás? Con este curso aprenderás conocimientos teóricos y prácticos para poder desarrollar
RESOLUCIÓN DE ECUACIONES E INECUACIONES
 Matemáticas con la calculadora Classpad. RESOLUCIÓN DE ECUACIONES E INECUACIONES INTRODUCCIÓN La calculadora posee en el menú Principal un submenú de Acción en él, un menú secundario llamado [Ecuación/Desigualdad]
Matemáticas con la calculadora Classpad. RESOLUCIÓN DE ECUACIONES E INECUACIONES INTRODUCCIÓN La calculadora posee en el menú Principal un submenú de Acción en él, un menú secundario llamado [Ecuación/Desigualdad]
Solución de ecuaciones algebraicas y trascendentes: Método de Newton Raphson
 Solución de ecuaciones algebraicas y trascendentes: Método de Newton Raphson Ing. Jesús Javier Cortés Rosas M. en A. Miguel Eduardo González Cárdenas M. en A. Víctor D. Pinilla Morán Facultad de Ingeniería,
Solución de ecuaciones algebraicas y trascendentes: Método de Newton Raphson Ing. Jesús Javier Cortés Rosas M. en A. Miguel Eduardo González Cárdenas M. en A. Víctor D. Pinilla Morán Facultad de Ingeniería,
Introducción a las Bases de Datos Evaluación de Archivos - 13/05/2011 tema 2 1. El proceso de baja en un archivo con registros de longitud variable 2.
 Introducción a las Bases de Datos Evaluación de Archivos - 13/05/2011 tema 1 1. Cual de las siguientes definiciones corresponde a Archivo?: 2. Un archivo que maneja registros de longitud fija necesita:
Introducción a las Bases de Datos Evaluación de Archivos - 13/05/2011 tema 1 1. Cual de las siguientes definiciones corresponde a Archivo?: 2. Un archivo que maneja registros de longitud fija necesita:
Pauta Segundo Certamen de Matemática II (MAT022) 2 do Semestre de Febrero 2012
 1. Alternativas Pauta Segundo Certamen de Matemática II (MAT0 do Semestre 011 7 de Febrero 01 Nombre: Rut: Paralelo: En las siguientes preguntas de alternativas, justifique claramente su respuesta. (10
1. Alternativas Pauta Segundo Certamen de Matemática II (MAT0 do Semestre 011 7 de Febrero 01 Nombre: Rut: Paralelo: En las siguientes preguntas de alternativas, justifique claramente su respuesta. (10
Microcurrículo del ÁREA DE: MATEMÁTICAS. Unidad y temas. Logro e Indicadores Indicadores De Logro
 Microcurrículo del ÁREA DE: MATEMÁTICAS fecha Grado noveno Sesión 1-10 (semanas) Unidad Unidad y temas Temas Unidad #1.Conjunto de los números imaginarios. Números Imaginarios: Concepto, operaciones básicas
Microcurrículo del ÁREA DE: MATEMÁTICAS fecha Grado noveno Sesión 1-10 (semanas) Unidad Unidad y temas Temas Unidad #1.Conjunto de los números imaginarios. Números Imaginarios: Concepto, operaciones básicas
Clasificación de los seres vivos Técnico en masoterapia
 Clasificación de los seres vivos Técnico en masoterapia Objetivo :Identificar y definir las principales características de los 5 reinos de los seres vivos. Introducción A nuestro alrededor vemos multitud
Clasificación de los seres vivos Técnico en masoterapia Objetivo :Identificar y definir las principales características de los 5 reinos de los seres vivos. Introducción A nuestro alrededor vemos multitud
RESOLUCIÓN DE PROBLEMAS MEDIANTE ECUACIONES. 2.- La suma de dos números es 15 y su producto es 26. Cuáles son dichos números?
 RESOLUCIÓN DE PROBLEMAS MEDIANTE ECUACIONES 1.- El perímetro de un rectángulo es 4 cm y su área es 0 cm. Cuáles son sus dimensiones? Sea = altura ; y = base Como perímetro es 4: + y = 1 y = 1 Como el área
RESOLUCIÓN DE PROBLEMAS MEDIANTE ECUACIONES 1.- El perímetro de un rectángulo es 4 cm y su área es 0 cm. Cuáles son sus dimensiones? Sea = altura ; y = base Como perímetro es 4: + y = 1 y = 1 Como el área
UNIVERSIDAD COMPLUTENSE DE MADRID
 INSTRUCCIONES GENERALES Y VALORACIÓN TIEMPO: Una hora y treinta minutos. INSTRUCCIONES: El examen presenta dos opciones A y B; el alumno deberá elegir una de ellas y contestar razonadamente a los cuatro
INSTRUCCIONES GENERALES Y VALORACIÓN TIEMPO: Una hora y treinta minutos. INSTRUCCIONES: El examen presenta dos opciones A y B; el alumno deberá elegir una de ellas y contestar razonadamente a los cuatro
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE V
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-107-1-V-1-00-2018 CURSO: CÓDIGO DEL CURSO: 107 SEMESTRE: Primer Semestre JORNADA: Vespertina TIPO DE EXAMEN:
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-107-1-V-1-00-2018 CURSO: CÓDIGO DEL CURSO: 107 SEMESTRE: Primer Semestre JORNADA: Vespertina TIPO DE EXAMEN:
Ecuaciones matriciales AX = B y XA = B. Cálculo de la matriz inversa
 Ecuaciones matriciales AX = B y XA = B Cálculo de la matriz inversa Objetivos Aprender a resolver ecuaciones matriciales de la forma AX = B y XA = B Aprender a calcular la matriz inversa con la eliminación
Ecuaciones matriciales AX = B y XA = B Cálculo de la matriz inversa Objetivos Aprender a resolver ecuaciones matriciales de la forma AX = B y XA = B Aprender a calcular la matriz inversa con la eliminación
CENTRO UNIVERSITARIO DE LA DEFENSA. ZARAGOZA CURSO 2011-12. Curso cero de Matemáticas
 CENTRO UNIVERSITARIO DE LA DEFENSA. ZARAGOZA CURSO 2011-12 Curso cero de Matemáticas Página 1 de 10 Página 2 de 10 1. OBJETO: El acceso al Centro Universitario de la Defensa supone para el alumno un cambio
CENTRO UNIVERSITARIO DE LA DEFENSA. ZARAGOZA CURSO 2011-12 Curso cero de Matemáticas Página 1 de 10 Página 2 de 10 1. OBJETO: El acceso al Centro Universitario de la Defensa supone para el alumno un cambio
Titulación Universitaria. Curso Universitario en Análisis y Gestión de Conflictos en la Empresa + 4 Créditos ECTS
 Titulación Universitaria Curso Universitario en Análisis y Gestión de Conflictos en la Empresa + 4 Créditos ECTS Índice Curso Universitario en Análisis y Gestión de Conflictos en la Empresa + 4 Créditos
Titulación Universitaria Curso Universitario en Análisis y Gestión de Conflictos en la Empresa + 4 Créditos ECTS Índice Curso Universitario en Análisis y Gestión de Conflictos en la Empresa + 4 Créditos
- Conoce los modelos planetarios clásicos y explica la organización del sistema solar.
 MATERIA: CIENCIAS NATURALES NIVEL: 1º ESO DURACIÓN: 1h 15 min. CRITERIOS DE EVALUACIÓN. UNIDAD 1: EL UNIVERSO Y EL SISTEMA SOLAR. - Conoce los modelos planetarios clásicos y explica la organización del
MATERIA: CIENCIAS NATURALES NIVEL: 1º ESO DURACIÓN: 1h 15 min. CRITERIOS DE EVALUACIÓN. UNIDAD 1: EL UNIVERSO Y EL SISTEMA SOLAR. - Conoce los modelos planetarios clásicos y explica la organización del
Reproducción: una introducción
 Universidad de Sonora Licenciatura en Biología Curso: Ecología Reproducción: una introducción Francisco Molina Freaner [email protected] Biósfera Región Objetivo Paisaje Ecosistema Comunidad Interacción
Universidad de Sonora Licenciatura en Biología Curso: Ecología Reproducción: una introducción Francisco Molina Freaner [email protected] Biósfera Región Objetivo Paisaje Ecosistema Comunidad Interacción
Capas y recursos de la Tierra
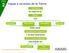 La Tierra Se organiza en Capas Son Geosfera Hidrosfera Atmósfera Estas capas Se relacionan entre sí Y de ellas obtenemos Los recursos naturales Que pueden ser Renovables No renovables Biosfera Layers y
La Tierra Se organiza en Capas Son Geosfera Hidrosfera Atmósfera Estas capas Se relacionan entre sí Y de ellas obtenemos Los recursos naturales Que pueden ser Renovables No renovables Biosfera Layers y
Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos:
 1 CONOCIMIENTOS PREVIOS. 1 Logaritmos. 1. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Operaciones básicas con números reales. Propiedades de
1 CONOCIMIENTOS PREVIOS. 1 Logaritmos. 1. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Operaciones básicas con números reales. Propiedades de
RAZONES TRIGONOMÉTRICAS
 RAZONES TRIGONOMÉTRICAS.- PRIMERAS DEFINICIONES Se denomina ángulo en el plano a la porción de plano comprendida entre dos semirrectas con un origen común denominado vértice. Ángulo central es el ángulo
RAZONES TRIGONOMÉTRICAS.- PRIMERAS DEFINICIONES Se denomina ángulo en el plano a la porción de plano comprendida entre dos semirrectas con un origen común denominado vértice. Ángulo central es el ángulo
Lección 4.1. Sistemas de Ecuaciones. 03/06/2013 Prof. José G. Rodríguez Ahumada 1 de 21
 Lección 4.1 Sistemas de Ecuaciones 03/06/013 Prof. José G. Rodríguez Ahumada 1 de 1 Actividades 4.1 Referencia Texto: Seccíón 9.1 Sistema de Ecuaciones; Problemas impares 1-9 páginas 64 (593 y 594); Sección
Lección 4.1 Sistemas de Ecuaciones 03/06/013 Prof. José G. Rodríguez Ahumada 1 de 1 Actividades 4.1 Referencia Texto: Seccíón 9.1 Sistema de Ecuaciones; Problemas impares 1-9 páginas 64 (593 y 594); Sección
UNIDAD DIDÁCTICA 2: SISTEMAS DE ECUACIONES LINEALES
 CURSO PAU 5 UNIDAD DIDÁCTICA : SISTEMAS DE ECUACIONES LINEALES. ÍNDICE. Introducción: descripción. Resolución de sistemas sistemas equivalentes. Clasificación de sistemas. Métodos de resolución de sistemas
CURSO PAU 5 UNIDAD DIDÁCTICA : SISTEMAS DE ECUACIONES LINEALES. ÍNDICE. Introducción: descripción. Resolución de sistemas sistemas equivalentes. Clasificación de sistemas. Métodos de resolución de sistemas
Profesorado para el 3º Ciclo de la EGB y Educación Polimodal en Tecnología Espacio de Definición Institucional LA TRANSFORMACIÓN DE DATOS EN
 LA TRANSFORMACIÓN DE DATOS EN INFORMACIÓN CONTABLE -1- -2- -3- -4- -5- LA ECUACIÓN CONTABLE BÁSICA -6- -7- -8- -9- - 10 - - 11 - REGISTRACIÓN EN EL LIBRO DIARIO - 12 - - 13 - - 14 - - 15 - - 16 - - 17
LA TRANSFORMACIÓN DE DATOS EN INFORMACIÓN CONTABLE -1- -2- -3- -4- -5- LA ECUACIÓN CONTABLE BÁSICA -6- -7- -8- -9- - 10 - - 11 - REGISTRACIÓN EN EL LIBRO DIARIO - 12 - - 13 - - 14 - - 15 - - 16 - - 17
UNIDAD DIDÁCTICA: RADIACTIVIDAD
 UNIDAD DIDÁCTICA: RADIACTIVIDAD INTRODUCCIÓN: El alto grado de desarrollo alcanzado en los últimos años en las técnicas computacionales ha permitido que ciertos modelos informáticos fueran elaborados para
UNIDAD DIDÁCTICA: RADIACTIVIDAD INTRODUCCIÓN: El alto grado de desarrollo alcanzado en los últimos años en las técnicas computacionales ha permitido que ciertos modelos informáticos fueran elaborados para
DEPARTAMENTO DE GEOMETRÍA ANALÍTICA
 DEPARTAMENTO DE GEOMETRÍA ANALÍTICA SERIE No. 4 010 - CURVAS 1. Obtener una ecuación vectorial de la curva que se obtiene por el desplazamiento de un punto tal que su abscisa es -5 mientras que su cota
DEPARTAMENTO DE GEOMETRÍA ANALÍTICA SERIE No. 4 010 - CURVAS 1. Obtener una ecuación vectorial de la curva que se obtiene por el desplazamiento de un punto tal que su abscisa es -5 mientras que su cota
Notación de Conjuntos
 1 A. Introducción UNIVERSIDAD INTERAMERICANA DE PUERTO RICO DEPARTAMENTO DE ADMINISTRACIÓN DE EMPRESAS MAEC 2140: Métodos Cuantitativos Prof. J.L.Cotto Conferencia: Conceptos Matemáticos Básicos Notación
1 A. Introducción UNIVERSIDAD INTERAMERICANA DE PUERTO RICO DEPARTAMENTO DE ADMINISTRACIÓN DE EMPRESAS MAEC 2140: Métodos Cuantitativos Prof. J.L.Cotto Conferencia: Conceptos Matemáticos Básicos Notación
TEMA 2: Algoritmos y Programas. Fundamentos de Informática (Grados en Ingenierías Industriales)
 TEMA 2: Algoritmos y Programas Fundamentos de Informática (Grados en Ingenierías Industriales) Índice de contenidos 1. Introducción. Conceptos básicos 2. Representación de algoritmos. 3. Metodología de
TEMA 2: Algoritmos y Programas Fundamentos de Informática (Grados en Ingenierías Industriales) Índice de contenidos 1. Introducción. Conceptos básicos 2. Representación de algoritmos. 3. Metodología de
Tema Contenido Contenidos Mínimos
 1 Números racionales - Fracciones equivalentes. - Simplificación de fracciones. - Representación y comparación de los números fraccionarios. - Operaciones con números fraccionarios. - Ordenación de los
1 Números racionales - Fracciones equivalentes. - Simplificación de fracciones. - Representación y comparación de los números fraccionarios. - Operaciones con números fraccionarios. - Ordenación de los
Contenidos mínimos 4B ESO. 1. Contenidos. Bloque I: Aritmética y álgebra.
 Contenidos mínimos 4B ESO. 1. Contenidos. Bloque I: Aritmética y álgebra. 1. Clasificar distintos tipos de números: naturales, enteros, racionales y reales. 2. Operar con números reales y aplicar las propiedades
Contenidos mínimos 4B ESO. 1. Contenidos. Bloque I: Aritmética y álgebra. 1. Clasificar distintos tipos de números: naturales, enteros, racionales y reales. 2. Operar con números reales y aplicar las propiedades

