TEMA IV.- PRINCIPIOS ÓPTICOS
|
|
|
- Rodrigo Serrano Toledo
- hace 9 años
- Vistas:
Transcripción
1 Master en Optometría y Ciencias de la Visión ª Edición (99-0) TEMA IV.- PRINCIPIOS ÓPTICOS En este tema, vamos a describir las principales características de los instrumentos ópticos más utilizados, como ayudas para pacientes con baja visión. Para este fin, no es necesario referirnos aquí a problemas o necesidades de estos pacientes, que se han tratado o se tratarán en otros temas, porque estos instrumentos son también utilizados por personas con visión normal para realizar tareas específicas. Todos los instrumentos que vamos a ver son, en realidad, ayudas para la visión. Los ojos emétropes y sanos también tienen sus limitaciones, la Agudeza Visual (AV) y el punto próximo (P), por ejemplo, son un límite en la visión de detalles espaciales. Generalmente, tendemos a acercarnos los objetos y y P u u u u p Figura.- Los objetos subtienden un ángulo mayor al acercarlos al ojo. Podrán ser vistos si el valor de su tamaño angular, u, supera el valor límite dado por la AV, siendo la distancia p entre el ojo y el punto próximo el máximo acercamiento posible. pequeños para aumentar así el valor del ángulo bajo el que son vistos desde la pupila de entrada, PE, del ojo. La imagen que se forma sobre la retina es mayor cuando el objeto se acerca, como puede verse en la Figura. Sin embargo, no es posible enfocar el objeto si está más cerca del ojo que el punto P, siendo éste nuestro límite de acercamiento.
2 y y Master en Optometría y Ciencias de la Visión ª Edición (99-0) Qué podemos hacer entonces para ver objetos cuyo tamaño está por debajo de nuestra AV? La lupa y el microscopio compuesto solucionan este problema, permitiéndonos aumentar en visión de cerca el ángulo u subtendido por el objeto. Un caso distinto, es el que se nos presenta al mirar a lo lejos e intentar ver un objeto que subtiende un ángulo demasiado pequeño para nuestra AV. Ahora no se trata de acercarnos al objeto, que quizá está en el horizonte, pero necesitamos algo que aumente su tamaño angular u. Los instrumentos llamados telescopios o anteojos (también prismáticos o binoculares) son los que sirven de ayuda al ojo para ver objetos lejanos que subtienden un ángulo pequeño. IV. - LA LUPA Cualquier lente converge trabajando con el objeto situado entre la lente y el foco F, es decir, con distancia objeto, x, menor (en valor absoluto) que la distancia focal objeto f, actúa como lupa. En este instrumento la imagen es siempre virtual, directa y mayor que el objeto. y y F X f / F x f Figura.- Una lente delgada convergente actuando como lupa. La imagen es virtual, directa y mayor que el objeto. β y /y (III.)
3 Master en Optometría y Ciencias de la Visión ª Edición (99-0) IV.. AUMENTO LINEAL El aumento lineal (o aumento lateral) es, por definición, la razón entre el tamaño de la imagen, y, y el tamaño del objeto, y. Esto es: En la lupa: β y / y >+; donde el signo positivo indica que la imagen es directa y virtual. En algunos textos a este aumento se le denomina aumento relativo a la distancia. La razón por la que se usa este nombre es evidente, si consideramos que en el caso de una lente en aire (como la lupa), este aumento puede calcularse como el cociente entre las distancias imagen y objeto (medidas desde la lente) respectivamente, es decir: β y / y x / x (IV.). Es importante resaltar que el valor de este aumento crece muy rápidamente cuando el objeto se sitúa cada vez más cerca del foco F. En la Figura pueden verse, como ejemplo, la imagen de dos objetos y e y situados a diferente distancia de la lupa. Al objeto y a distancia x f/ de la lente, le corresponde la imagen y sobre el foco, de modo que x f. En efecto, de la ecuación de Gauss se obtiene: x' x + x' f f f x' f y el aumento : β' y' y x' x + Al objeto y, que está situado más cerca del foco que el anterior, le corresponde una imagen y de mayor tamaño y más alejada de la lente. En resumen, recordemos que el aumento lineal de la lupa es tal que: a) Si el objeto está situado entre la posición de la lente, x0, y la posición xf/, el aumento β sólo varía entre + y +. b) Pero al cambiar la posición del objeto entre xf/ y xf el aumento toma valores desde + hasta infinito. En consecuencia, la lupa deberá utilizarse con el objeto situado en el foco F o muy cerca de éste para que el aumento lineal sea máximo. 3
4 Master en Optometría y Ciencias de la Visión ª Edición (99-0) Cualquier lente converge trabajando con el objeto a una distancia entre f y f de la lente, ya no actúa como lupa sino como un sistema de proyección, proporcionando una imagen real, invertida y mayor que el objeto, como se deduce del valor que toma el aumento lateral β y / y - y tal como vemos en la Figura 3. Aunque este caso no tiene relación directa con este tema, viene bien compararlo con la lupa para establecer las diferencias entre las imágenes reales y virtuales cuando son vistas por el ojo. En efecto, las imágenes reales de la Figura 3 no se ven sino utilizando una pantalla en el plano imagen, cuya posición está perfectamente establecida, ya que situando la pantalla en otro plano ligeramente anterior o posterior la imagen se vería desenfocada. Pensemos, por ejemplo en un proyector de diapositivas qué se ve sin pantalla? Un haz de luz, pero no una imagen. y y F F y y f Figura 3.- Una lente delgada convergente actuando como sistema de proyección. La imagen es real invertida y mayor que el objeto. Además, en este caso, el valor del aumento está perfectamente establecido para cada pareja de planos conjugados. Así entre y e y el aumento lateral es y entre y e y el aumento es, en donde el signo menos sólo indica la posición invertida de la imagen respecto del objeto. El ojo percibe las imágenes de acuerdo con estos valores del aumento, por lo que verá y del mismo tamaño que y e y de tamaño doble del de y. 4
5 Master en Optometría y Ciencias de la Visión ª Edición (99-0) Por el contrario, en el caso de la lupa al ser las imágenes virtuales no pueden ser recogidas sobre una pantalla, el ojo las ve con sólo situarse detrás de la lente y recibir la luz procedente de la imagen. Para el ojo que ve la imagen virtual, es como si el objeto que está viendo estuviese allí ya que desde allí él ve llegar los rayos. Para recordar cómo en ojo ve las imágenes virtuales basta pensar un momento en las imágenes formadas por un espejo plano y que estamos tan acostumbrados a ver. En cualquiera de los instrumentos de ayuda que vamos a describir, el ojo va a ver imágenes virtuales. Casi siempre se suele formar la imagen en el infinito, para que el ojo la pueda ver con mayor comodidad y utilice el instrumento sin fatigarse a causa de la acomodación. La principal diferencia entre el caso de la imagen real (Figura 3) y la imagen virtual (Figura ) cuando son vistas por el ojo es que el aumento, cuando vemos imágenes virtuales, ya no está tan claramente establecido. Con el tamaño de las imágenes percibidas por el ojo se producen algunas paradojas. Por ejemplo: Cuando cambia el ángulo u con el cual es visto el objeto desde el ojo, cambia el tamaño aparente o tamaño percibido aunque no cambie el tamaño real. Esta paradoja de percibir un aumento que realmente no existe, se pone de manifiesto con frecuencia en nuestra vida cotidiana, aunque muchas veces, por costumbre, nos pasa desapercibida.. n.33 n y y u u Figura 4.- En un dioptrio plano (agua-aire en este caso) el aumento lineal es +. Sin embargo el ojo percibe un aumento angular al que llamaremos aumento visual. Basta recordar la visión a través de unas gafas submarinas o la percepción de una moneda en el fondo de un estanque, por ejemplo, para darnos cuenta de 5
6 Master en Optometría y Ciencias de la Visión ª Edición (99-0) que el tamaño aparente de los objetos vistos a través de un dioptrio plano (Figura 4) es diferente de su tamaño real aunque, como sabemos, en estos dioptrios la imagen es siempre del mismo tamaño que el objeto: el aumento es siempre, para cualquier posición del objeto, β + Sin embargo, sí que apreciamos un aumento distinto de la unidad. En cualquier caso, estamos viendo un cambio de tamaño que teóricamente no existe. La explicación se encuentra en el hecho que se ha representado en la Figura : dos objetos del mismo tamaño el ojo los ve con tamaño diferente si subtienden distinto ángulo. Otras veces, se produce la paradoja contraria: El ojo forma una imagen de igual tamaño sobre la retina de todos los objetos o imágenes que ve bajo el mismo ángulo u como se observa en la Figura-5. Aunque tengan tamaños lineales muy diferentes. podrían parecer iguales para el ojo. u N N u Figura 5.- Objetos de diferentes tamaños lineales, pero con el mismo tamaño angular, u, tienen el mismo tamaño sobre la retina del ojo. El ojo podría interpretar que son iguales. IV.. AUMENTO ANGULAR De las paradojas descritas en el párrafo anterior se deduce que para el ojo, y todos los instrumentos que trabajan asociados con él, existe, además del aumento lineal o lateral, otro aumento al que llamaremos aumento angular o aumento visual, Γ, (para distinguirlo de otro aumento angular, γ, que se utiliza para la definición de puntos nodales) que se define como:. En algunos aspectos, este hecho es similar al cambio de tamaño aparente de la luna o el sol que se observa en determinadas circunstancias. 6
7 Master en Optometría y Ciencias de la Visión ª Edición (99-0) tg u' Γ tg u (IV.) Siendo u y u los ángulos bajo los cuales se perciben los objetos desde el ojo con y sin instrumento respectivamente. En el ejemplo de la Figura 4, la gafa submarina tendría un aumento lineal β + pero un aumento angular que podría valer Γ + si consideramos tg u tg u. Sea una lupa de potencia P L que se utiliza a distancia h de la pupila de entrada, PE, del ojo, calculemos el valor del aumento Γ apoyándonos en la Figura 6. y LUPA P L y u PE u O O x h x Figura 6.- Una lupa de potencia P L forma de un objeto de tamaño y una imagen y. El aumento visual Γ compara el tamaño angular del objeto desde la PE del ojo, visto con y sin instrumento. De la Figura deducimos los valores de las distancias desde O y O a la PE que son: O PE O H +H PE -x + h OPE OH + H PE -x + h con estos valores el aumento se escribe como: Γ tg u' tg u y' h x' y h x y' h x y h x' x' h x x h x' 7
8 Master en Optometría y Ciencias de la Visión ª Edición (99-0) además podemos expresar la distancia imagen x en función de la distancia objeto x, a través de la ecuación de Gauss, siendo entonces: x' x x + Sustituyendo este valor en la ecuación anterior y considerando que la potencia de la lupa P L /f, con las simplificaciones oportunas el aumento angular resulta: Γ x h x h( + xp L ) (IV.3) En esta expresión se ve claramente que el valor que toma este aumento depende, además de la potencia de la lupa P L, de dos factores: ) posición del ojo respecto de la lente, h ) posición del objeto, x. A estos dos hay que añadir un tercero: 3) elección de una distancia de referencia, d. Este último factor, que no se refleja en la ecuación anterior, resulta lógico si tratamos de comparar los tamaños angulares del objeto y su imagen en las mismas condiciones. ) Posición del ojo: Cómo depende el aumento Γ de la posición h del ojo respecto de la lupa? Para verlo, a) hagamos en (IV.3) h f, lo que implica suponer que el ojo está situado en el foco imagen de la lente. Se obtiene: Γ xp L (IV.4) b) hagamos h 0 en la ecuación (IV.), esto significa considerar el ojo pegado a la lente. En este caso el valor de Γ resulta constante e igual a la unidad, independientemente de la posición del objeto. Así se tiene: Γ (IV.5) 8
9 Master en Optometría y Ciencias de la Visión ª Edición (99-0) con lo que este aumento no cuenta y sólo es considerable el aumento lineal que, como ya vimos, es máximo si el objeto se sitúa en el foco F o muy próximo a esa posición. ) Posición del objeto: Cuando el objeto se sitúa en el foco de la lente F, además de conseguirse el máximo aumento lineal, se tiene la ventaja de que la imagen virtual se forma en el infinito. En este caso no importa la acomodación del sujeto y, en principio tampoco debería de influir la situación del ojo del sujeto respecto de la lente ya que los rayos le llegarían paralelos en cualquier situación. Pero, en la práctica, sí que tiene importancia la distancia, h, del ojo a la lente en este caso porque, aunque la imagen en la retina es siempre la misma, cuanto más se aleja el ojo menor es el ángulo con el que se ve el objeto y también la lente de modo que, por comparación, se aprecia un incremento del aumento angular. y u d y y y u x d x Figura 7.- El aumento convencional de una lupa compara el tamaño aparente u del objeto visto a una distancia d (cuyo valor es convenido) con el tamaño aparente u de la imagen que forma la lupa a la misma distancia d. En ambos casos la acomodación del ojo es de +4 dioptrías si la distancia convencional es de 5 cm. Haciendo x f -f en la ecuación (IV.3) se tiene para este caso: 9
10 Master en Optometría y Ciencias de la Visión ª Edición (99-0) Γ + hp L (IV.6) 3) Distancia, d, de referencia: Para poder comparar el aumento de diferentes lupas conviene establecer una distancia estandar o de referencia de modo que, en el aumento visual, comparemos el ángulo u que da el tamaño del objeto sin lupa a una determinada distancia, d, del ojo con el ángulo u que da el tamaño de la imagen formada por la lupa, cuando situamos el objeto a una distancia x tal que x d. De este modo los tamaños angulares con y sin lupa se están comparando a la misma distancia, como se ve en la Figura 7. Calculemos ahora el valor del aumento visual: Γ tg u' tg u y x y x' x' x Γ d x' + PL 4 Γ d Γ dp (IV.7) L Este aumento convencional, llamado así porque asignamos a la distancia d un valor convencional (negativo) de 5 cm, compara el tamaño aparente (u ) de la imagen y formada por la lupa a 5 cm del ojo, con el tamaño aparente (u) del objeto, y, si estuviera a 5 cm del ojo. Esta fórmula supone que el error refractivo ha sido corregido por una lente diferente a la que se considera y que, con o sin lente, se está utilizando una acomodación de +4 dioptrias. Objeto en el foco: Cuando el objeto se sitúa en el foco la imagen se forma en el infinito, como vemos en la Figura 8. El aumento toma el valor: Γ y f y d d d dpl f y haciendo d - 5 cm resulta : Γ C PL (IV.8) 4 0
11 Master en Optometría y Ciencias de la Visión ª Edición (99-0) Este es el llamado aumento efectivo o comercial de la lupa. Si la distancia de comparación se considera d -40 cm, como recomiendan algunos autores, el aumento comercial sería: Γ C PL.5 La ecuación (IV.8) compara el tamaño aparente de la imagen y formada por la lupa en el infinito con el tamaño aparente del objeto, y, si estuviera a 5 cm (o a 40 cm). Se está comparando una imagen que no requiere acomodación para ser enfocada con un objeto que requiere +4 dioptrias de acomodación para ser enfocado por el ojo. Esta ecuación supone que el error refractivo ha sido corregido por otra lente y que no se utiliza la acomodación cuando se mira a través de la lupa. y u F f Figura 8.- Cuando el objeto se coloca en el Foco de la lupa la imagen se forma en el infinito. El aumento comercial compara el tamaño aparente u del objeto visto a una distancia d (normalmente de 5 cm) con el tamaño aparente u de la imagen que se forma en el infinito. El objeto requiere una acomodación del ojo de +4 dioptrías mientras que la imagen se ve sin acomodación. Si el error refractivo no ha sido corregido con otra lente, el aumento comercial de la lupa se calculará mediante la ecuación:
12 Master en Optometría y Ciencias de la Visión ª Edición (99-0) PL R Γ 4 (IV.9) siendo R el valor de la refracción que se toma con signo positivo para los hipermétropes y negativo para los miopes. Las ecuaciones (IV.7) y (IV.8) no son contradictorias sino que representan la misma idea bajo condiciones diferentes. En (IV.7) objeto e imagen se contemplan a igual distancia del ojo por lo que se está utilizando la misma acomodación para ver a ambos. En cambio, en (IV.8) el objeto se considera visto a distancia d y el ojo realiza la acomodación correspondiente para enfocarlo en la retina, mientras que la imagen puede verse sin acomodación por estar situada en el infinito. En resumen, el aumento angular de la lupa:.- Si se utiliza la lupa pegada al ojo (h0) este aumento angular es constante e igual a la unidad. Por lo tanto sólo el aumento lineal será importante para el ojo. Por esta razón suele utilizarse la lupa separada del ojo porque así el aumento angular es subjetivamente mayor. Este crecimiento del valor del aumento angular a medida que separamos la lupa del ojo no es objetivamente cierto (si no cambiamos el tamaño de la imagen) pero se explica porque disminuye el campo angular que ocupa la lupa por lo que, por comparación, aumenta subjetivamente el tamaño angular de la imagen (Figura 0)..- Si se trabaja con el objeto en el foco de la lente (xf) (que es el caso más común por dos razones:ª el aumento lineal es máximo y ª no se necesita acomodación porque la imagen se forma en el infinito), y considerando la distancia de referencia de 5 cm para el objeto, se tiene el llamado aumento efectivo o comercial: Γ C PL 4
13 Master en Optometría y Ciencias de la Visión ª Edición (99-0) IV..3 CAMPO DE LA LUPA El campo de la lupa depende de la potencia de la lente, P L, de la distancia al ojo, h, y del valor de los radios de la lente, r, y de la pupila del ojo r p. En la Figura 9 se representa el campo de plena iluminación que es una zona de radio OP sobre el plano del objeto. El valor de OP puede calcularse de la expresión: (r rp ) OP h P L (IV.0) Esta ecuación nos dice que el campo disminuye al aumentar la potencia de la lente y la distancia h de la lente al ojo. El campo aumenta con el radio r de la lente, mientras que el radio r P de la pupila del ojo prácticamente no influye nada en el valor del campo. P PE P r OF OF r P h c P Figura 9.- El campo objeto de plena iluminación en la lupa es una zona de radio OP sobre el plano del objeto. El objeto está en el foco F de la lupa, la cual es de radio r y dista h de la PE del ojo que tiene un radio r P. El rayo de luz que pasa por el extremo superior de la lupa y de la PE corta al eje óptico a la distancia c, cuyo valor se deduce de la semejanza de los triángulos que forma dicho rayo con el eje. Se han representado dos posiciones distintas del plano objeto(que es además el plano focal) para poner de manifiesto que el campo se reduce al aumentar la potencia de la lente (el objeto está más cerca). 3
14 Master en Optometría y Ciencias de la Visión ª Edición (99-0) La expresión (IV.0) se ha deducido desde la Figura 9 como sigue: OP r r f OP en donde el valor de c es : f h + c h + c r rp rp h r c rp h + rp c c h + c c r rp sustituyendo este valor en la expresión de OP queda : r f r f r f r rp OP rp h r r h r h P p + r p L h + h r r r r p r r p p y Figura 0. El campo angular que abarca la lente disminuye cuando la lente se separa del ojo. El tamaño ángular u de la imagen y, aunque no varía, resulta subjetivamente mayor por comparación con el de la la lente al alejarse. El campo de la lupa dado por la ecuación (IV.0) es un valor teórico que, en la práctica, puede verse bastante reducido por la presencia de aberraciones, como puede verse en la Figura. Principalmente son la distorsión, el coma, el astigmatismo por incidencia oblícua y la curvatura de campo las que más afectan. La aberración esférica y la cromática de posición son más fáciles de evitar combinando adecuadamente las curvaturas de las caras de las lentes (dobletes de lentes) o utilizando superficies asféricas. Las lentes de Fresnel se han considerado una buena solución porque ) permiten diámetros grandes ) se reduce mucho el grosor y peso 3) se reducen las aberracuiones y 4) ofrecen la posibilidad de grandes efectos prismáticos por descentramiento. Sin embargo, el gran inconveniente que presentan es la bajada de contraste que hace que las rechacen muchos pacientes. 4
15 Master en Optometría y Ciencias de la Visión ª Edición (99-0) Figura.- Las aberraciones reducen el campo óptico de la lupa y demás instrumentos. ADVERTENCIA: Las lentes de alta potencia que se utilizan como microscopios (para ver de cerca) tienen una variación apreciable en el valor de la potencia, según se considere ésta desde el vértice posterior o se estime desde el vértice frontal. La forma y el grosor de estas lentes es un factor muy importante y puede cometerse un error considerable al pedir al fabricante la lente prescrita para cataratas (que se calcula en función del vértice posterior) por la potencia del microscopio probado (ya que la potencia de los microscopios se calcula en función de la potencia al vértice frontal) sin utilizar la correspondiente compensación. IV. EL MICROSCOPIO COMPUESTO 5
16 Master en Optometría y Ciencias de la Visión ª Edición (99-0) El microscopio compuesto consta de dos sistemas ópticos, acoplados a una distancia tal, que desde el foco imagen del primero al foco objeto del segundo hay una distancia t positiva llamada longitud óptica. Por simplicidad, representaremos como lentes delgadas convergentes a estos dos sistemas: ) el objetivo proporciona una imagen real e invertida del objeto (imagen intermedia) con un aumento lineal β ) el ocular es una lupa trabajando con objeto en su foco F oc, su aumento será Γ 50/f oc P L /4. En conjunto, el microscopio compuesto trabaja como una lupa, ya que se enfoca de tal manera que el objeto se sitúe en el foco F del sistema total. En la Figura vemos un esquema de su funcionamiento. IV.. AUMENTO El aumento del microscopio compuesto es el producto de los aumentos de objetivo y ocular: Γ β' ob Γ oc (IV.) P (oc) 5 y' P (tot) en donde Γ L ; β ' y Γ L oc 4 ob y 4 oc 5 Objetivo Ocular ω F oc ω F PE f + t f PS Figura.- El microscopio compuesto funciona como una lupa. El aumento es el producto del aumento lateral del objetivo por el aumento comercial del ocular. 6
17 Master en Optometría y Ciencias de la Visión ª Edición (99-0) conocidas las focales f y f del objetivo y ocular respectivamente y la longitud óptica del microscopio t (distancia de F a F ) el aumento puede calcularse como: Γ tgω tgω + t IV.. CAMPO DEL MICROSCOPIO Todo lo que se ha tratado con detalle para la lupa o microscopìo simple es aplicable también al microscopio compuesto. Sin embargo la expresión para calcular el campo objeto de plena iluminación es más compleja y, aunque de sencilla demostración, no la vamos a deducir aquí por no extender más estos apuntes. El tamaño del citado campo es: OP t ( + t) R ( + t) R R ( + t) + t + t Γ R + t + (IV.) donde R y R son los radios de abertura útil de objetivo y ocular respectivamente. IV..3 APERTURA NUMÉRICA Este dato viene reseñado en todos los microscopios y es fundamental para conocer la iluminación en la imagen. Como es sabido, esta magnitud está directamente relacionada con el tamaño de las pupilas de entrada y salida, el cual indica la cantidad de luz que llega a la imagen a través del instrumento. Su valor es: AN n sen σ siendo n el índice de refracción del espacio objeto y σ el ángulo que forma con el eje óptico el rayo que parte del pie del objeto y alcanza el extremo de la PE (que está en el objetivo). La relación entre el diámetro de la PS y la AN es: Φ AN 500 Γ PS AN P L (IV.3) 7
18 Master en Optometría y Ciencias de la Visión ª Edición (99-0) siendo Γ y P L el aumento y la potencia del microscopio completo. Esta relación pone de manifiesto la poca luminosidad que se tiene con microscopios de alta potencia. IV.3 EL TELESCOPIO Al igual que el microscopio compuesto, el telescopio está formado por dos sistemas ópticos: objetivo y ocular. Sin embargo, éstos están acoplados entre sí de tal forma que el foco imagen del objetivo coincide con el foco objeto del ocular, F ob F oc, resultando así que t0. A los sistemas que cumplen esta condición se les llama afocales (por carecer de puntos focales F y F ) o telescópicos (por ser la característica propia de estos instrumentos). Los telescopios suelen utilizarse para mirar al infinito, pero también pueden usarse para ver objetos más cercanos y entonces se les suele llamar anteojos (también los llamados binoculares o prismáticos son sistemas basados en el mismo principio). Objetivo Ocular ω F ob F oc ω Figura 3. El telescopio forma, de un objeto lejano que subtiende un pequeño ángulo ω, una imagen en el infinito que subtiende un ángulo mayor ω, de modo que el aumento es tg ω /tg ω. IV.3. AUMENTO En la figura 3 se observa que la imagen intermedia y es real e invertida, está relaciona con las focales de objetivo y ocular, f y f respectivamente, así como, con los ángulos objeto ω e imagen ω, de modo que podemos escribir: 8
19 Master en Optometría y Ciencias de la Visión ª Edición (99-0) Γ tg ω' y'/ tg ω y'/ (IV.4) el signo negativo del aumento sólo indica la inversión de la imagen. IV.3. APERTURA RELATIVA La abertura relativa se utiliza en estos instrumentos que trabajan con objetos lejanos, indicando lo mismo que la A.N. en el microscopio. Su valor se obtiene por el cociente entre el diámetro de la PE, que es el objetivo, y la focal de éste. Φ AR ob ob (IV.5) IV.3.3.EMERGENCIA PUPILAR Para una buena calidad de visión, el ojo debería situarse en la PS del instrumento, de lo contrario se tienen recortes en la imagen. Por ello interesa conocer la distancia desde el ocular hasta la pupila de salida llamada emergencia popular + e x' PS donde e es la distancia entre objetivo y ocular y Γ' es negativo Γ por otra parte sabemos que el diámetro de la pupila de salida es: Φ PS Φ Γ' ob IV.3.4 CAMPO DEL TELESCOPIO En el telescopio, el valor del campo objeto de plena iluminación es angular ya que el objeto está en el infinito. El ángulo ω P que da el semi-campo de plena iluminación se calcula de la ecuación: tgω P R R x' Γ' PS PS R e R + Γ' (IV.6) 9
20 Master en Optometría y Ciencias de la Visión ª Edición (99-0) donde R y R son los radios de abertura útil de objetivo y ocular respectivamente y e la distancia de acoplamiento entre objetivo y ocular. La especificación comercial que normalmente se encuentra en estos instrumentos es a x d: aumento x diámetro del objetivo. La imagen que da un telescopio como el de la Figura 3 es, como se ha dicho, invertida lo cual no es inconveniente en los telescopios que se utilizan para observaciones astronómicas; sin embargo, los telescopios utilizados para visión terrestre lejana llevan, entre objetivo y ocular, un dispositivo inversor de imagen para enderezar la imagen intermedia y. A un telescopio así se le conoce como anteojo terrestre. IV.4 EL ANTEOJO DE GALILEO Su funcionamiento es igual al del telescopio anterior, con la diferencia de ser el ocular divergente lo cual evita la inversión de la imagen. El esquema de funcionamiento se ve en la Figura 4. El objetivo dirige los rayos que vienen del objeto lejano hacia la imagen intermedia y, pero antes de llegar a ese punto (Foco imagen del objetivo Foco objeto del ocular) el ocular divergente hace que salgan los rayos paralelos entre sí y hacia el infinito. PS F ob F oc y ω ω Figura 4. El anteojo de Galileo utiliza un ocular divergente con lo que se evita la inversión de la imagen. La pupila de salida es virtual lo que impide situar el ojo correctamente. 0
21 IV.4. AUMENTO Master en Optometría y Ciencias de la Visión ª Edición (99-0) La única diferencia con el aumento del telescopio es el signo del aumento que en este instrumento es positivo, dado que la imagen es directa y no invertida. Γ tg ω' y'/ tg ω y'/ (IV.7) destaquemos el hecho de que en esta relación las focales de objetivo y ocular son de signo contrario por lo que el aumento resulta positivo. IV.4. APERTURA RELATIVA En este apartado no existe ninguna diferencia con el caso del telescopio. IV.4.3.PUPILA DE SALIDA Un inconveniente del anteojo de Galileo es que la pupila de salida es virtual y está situada en el interior del instrumento (Figura 4). Esto hace que el sujeto no pueda situar el ojo correctamente y puede tener recortes en el campo visual en forma de ojo de herradura. La posición y diámetro de la PS se expresan en las siguientes relaciones: que son las mismas que las del telescopio con la salvedad ya indicada del signo del aumento. Φ PS Φ e ob ; x' PS donde e es la distancia entre objetivo y ocular y Γ' es positivo Γ' Γ IV.4.4 CAMPO ANGULAR En este instrumento no puede situarse el diafragma de campo sobre la imagen intermedia, como se hace en los telescopios en que esta imagen es real, lo que da lugar a que la limitación del campo no sea la más adecuada. En lugar de tener todo el campo con plena iluminación se tiene el efecto de viñeteado de los haces de luz, que hace que la iluminación vaya decreciendo
22 Master en Optometría y Ciencias de la Visión ª Edición (99-0) hasta el valor límite del campo. Por esta razón daremos el valor del campo de iluminación media: tgω m Φ ob ' eγ (IV.8) en donde se ha considerado el ojo pegado al ocular.
Bolilla 12: Óptica Geométrica
 Bolilla 12: Óptica Geométrica 1 Bolilla 12: Óptica Geométrica Los contenidos de esta bolilla están relacionados con los principios primarios que rigen el comportamiento de los instrumentos ópticos. La
Bolilla 12: Óptica Geométrica 1 Bolilla 12: Óptica Geométrica Los contenidos de esta bolilla están relacionados con los principios primarios que rigen el comportamiento de los instrumentos ópticos. La
Lentes delgadas Clasificación de las lentes Según su forma Lentes convergentes Lentes divergentes Según su grosor
 Lentes delgadas Una lente delgada es un sistema óptico centrado formado por dos dioptrios, uno de los cuales, al menos, es esférico, y en el que los dos medios refringentes extremos poseen el mismo índice
Lentes delgadas Una lente delgada es un sistema óptico centrado formado por dos dioptrios, uno de los cuales, al menos, es esférico, y en el que los dos medios refringentes extremos poseen el mismo índice
Práctica 5: El telemicroscopio
 LABORATORIO DE ÓPTICA (ÓPTICA INSTRUMENTAL) CURSO 009/10 Práctica 5: El telemicroscopio 5.1 Objetivo de la práctica El objetivo de esta práctica es el estudio y comprensión de los fundamentos ópticos del
LABORATORIO DE ÓPTICA (ÓPTICA INSTRUMENTAL) CURSO 009/10 Práctica 5: El telemicroscopio 5.1 Objetivo de la práctica El objetivo de esta práctica es el estudio y comprensión de los fundamentos ópticos del
Práctica 3: Sistemas telescópicos. Objeto lejano.
 LABORATORIO DE ÓPTICA (ÓPTICA INSTRUMENTAL) CURSO 2009/10 Práctica 3: Sistemas telescópicos. Objeto lejano. 3.1 Objetivo de la práctica El objetivo de esta práctica es el conocimiento y manejo de los distintos
LABORATORIO DE ÓPTICA (ÓPTICA INSTRUMENTAL) CURSO 2009/10 Práctica 3: Sistemas telescópicos. Objeto lejano. 3.1 Objetivo de la práctica El objetivo de esta práctica es el conocimiento y manejo de los distintos
TEMA IV EL OJO EMÉTROPE. VI - Tamaño de la imagen sobre la retina de un objeto extenso
 TEMA IV EL OJO EMÉTRO I - Concepto de ojo emétropre II - Punto remoto III - La ecuación de Gauss en el ojo emétrope IV - Imagen de un punto enfocado V - El círculo de desenfoque VI - Tamaño de la imagen
TEMA IV EL OJO EMÉTRO I - Concepto de ojo emétropre II - Punto remoto III - La ecuación de Gauss en el ojo emétrope IV - Imagen de un punto enfocado V - El círculo de desenfoque VI - Tamaño de la imagen
Capítulo 23. Microscopios
 Capítulo 23 Microscopios 1 Aumento angular El aumento angular m (a) de una lente convergente viene dado por: m (a) = tan θ rmim tan θ ob = q 0.25 (d + q )p en donde d es la separación entre la lente y
Capítulo 23 Microscopios 1 Aumento angular El aumento angular m (a) de una lente convergente viene dado por: m (a) = tan θ rmim tan θ ob = q 0.25 (d + q )p en donde d es la separación entre la lente y
LAS LENTES Y SUS CARACTERÍSTICAS
 LAS LENTES Y SUS CARACTERÍSTICAS Las lentes son cuerpos transparentes limitados por dos superficies esféricas o por una esférica y una plana, las lentes se emplean a fin de desviar las rayos luminosos
LAS LENTES Y SUS CARACTERÍSTICAS Las lentes son cuerpos transparentes limitados por dos superficies esféricas o por una esférica y una plana, las lentes se emplean a fin de desviar las rayos luminosos
ÓPTICA GEOMÉTRICA. Es el fenómeno que se observa cuando un rayo de luz incide sobre una superficie y se refleja. Su estudio se basa en dos leyes:
 ONDAS LUMINOSAS La luz que nos llega del sol (luz blanca), está compuesta por rayos de luz de diferentes colores. Este conjunto de rayos constituye lo que se llama espectro visible, el cual, es una zona
ONDAS LUMINOSAS La luz que nos llega del sol (luz blanca), está compuesta por rayos de luz de diferentes colores. Este conjunto de rayos constituye lo que se llama espectro visible, el cual, es una zona
Ejercicios Repaso Tema 5: Óptica geométrica
 Cuestiones y Problemas Ejercicios Repaso Tema 5: Óptica geométrica Dpto. de Física 1. Una esfera de vidrio de paredes delgadas y radio R está llena de agua. A una distancia 3R de su superficie se coloca
Cuestiones y Problemas Ejercicios Repaso Tema 5: Óptica geométrica Dpto. de Física 1. Una esfera de vidrio de paredes delgadas y radio R está llena de agua. A una distancia 3R de su superficie se coloca
3.3.6 Introducción a los Instrumentos Ópticos
 GUÍA DE ESTUDIO Complemento a la Unidad 3.3 LUZ 3.3.6 Introducción a los Instrumentos Ópticos. Instrumentos de Lente.. Imágenes Reales... El Proyector Opera con el objeto (diapositiva) muy cerca de la
GUÍA DE ESTUDIO Complemento a la Unidad 3.3 LUZ 3.3.6 Introducción a los Instrumentos Ópticos. Instrumentos de Lente.. Imágenes Reales... El Proyector Opera con el objeto (diapositiva) muy cerca de la
13. Por qué no se observa dispersión cuando la luz blanca atraviesa una lámina de vidrio de caras planas y paralelas? 14. Sobre una lámina de vidrio,
 PROBLEMAS ÓPTICA 1. Una de las frecuencias utilizadas en telefonía móvil (sistema GSM) es de 900 MHz. Cuántos fotones GSM necesitamos para obtener la misma energía que con un solo fotón de luz violeta,
PROBLEMAS ÓPTICA 1. Una de las frecuencias utilizadas en telefonía móvil (sistema GSM) es de 900 MHz. Cuántos fotones GSM necesitamos para obtener la misma energía que con un solo fotón de luz violeta,
Porqué es útil estudiar los espejos y las lentes como elementos ópticos? A qué se le conoce como distancia focal de una lente o espejo?
 Porqué es útil estudiar los espejos y las lentes como elementos ópticos? A qué se le conoce como distancia focal de una lente o espejo? Cómo depende la distancia focal del material que forma un espejo?
Porqué es útil estudiar los espejos y las lentes como elementos ópticos? A qué se le conoce como distancia focal de una lente o espejo? Cómo depende la distancia focal del material que forma un espejo?
4. Dioptrios. Vamos a estudiar dioptrios esféricos con rayos paraxiales. La ecuación de un dioptrio esférico para rayos paraxiales
 4. Dioptrios. Un dioptrio es la superficie de separación entre dos medios con distinto índice de refracción, pero isótropos, homogéneos y transparente. Un rayo paraxial es aquel que forma un ángulo muy
4. Dioptrios. Un dioptrio es la superficie de separación entre dos medios con distinto índice de refracción, pero isótropos, homogéneos y transparente. Un rayo paraxial es aquel que forma un ángulo muy
Física 2 Biólogos y Geólogos - Curso de Verano 2006 Turno: Tarde
 Física 2 Biólogos y Geólogos - Curso de Verano 2006 Turno: Tarde Serie 2: Objetos. Formación de imágenes. Imágenes. Dioptras esféricas y planas. Espejos esféricos y planos. Lentes delgadas, sistemas de
Física 2 Biólogos y Geólogos - Curso de Verano 2006 Turno: Tarde Serie 2: Objetos. Formación de imágenes. Imágenes. Dioptras esféricas y planas. Espejos esféricos y planos. Lentes delgadas, sistemas de
Distancia focal de una lente convergente (método del desplazamiento) Fundamento
 Distancia focal de una lente convergente (método del desplazamiento) Fundamento En una lente convergente delgada se considera el eje principal como la recta perpendicular a la lente y que pasa por su centro.
Distancia focal de una lente convergente (método del desplazamiento) Fundamento En una lente convergente delgada se considera el eje principal como la recta perpendicular a la lente y que pasa por su centro.
TEMA 10: INSTRUMENTOS ÓPTICOS.
 TEMA 10: INSTRUMENTOS ÓPTICOS. 10.1. El ojo humano. De forma muy simplificada, podemos considerar que el ojo humano está constituido por una lente (formada por la córnea y el cristalino) y una superficie
TEMA 10: INSTRUMENTOS ÓPTICOS. 10.1. El ojo humano. De forma muy simplificada, podemos considerar que el ojo humano está constituido por una lente (formada por la córnea y el cristalino) y una superficie
TEMA 4: ACOMODACIÓN Y PRESBICIA
 TEMA 4: ACOMODACIÓN Y PRESBICIA ACOMODACIÓN Y PRESBICIA 1.- Acomodación: concepto y definición. Amplitud y recorrido de acomodación 2.- Modificaciones del ojo durante la acomodación 3.- El ojo teórico
TEMA 4: ACOMODACIÓN Y PRESBICIA ACOMODACIÓN Y PRESBICIA 1.- Acomodación: concepto y definición. Amplitud y recorrido de acomodación 2.- Modificaciones del ojo durante la acomodación 3.- El ojo teórico
Problemas de Óptica II. Óptica geométrica 2º de bachillerato. Física
 1 Problemas de Óptica II. Óptica geométrica 2º de bachillerato. Física 1. Los índices de refracción de un dioptrio esférico cóncavo, de 20,0 cm de radio, son 1,33 y 1,54 para el primero y el segundo medios.
1 Problemas de Óptica II. Óptica geométrica 2º de bachillerato. Física 1. Los índices de refracción de un dioptrio esférico cóncavo, de 20,0 cm de radio, son 1,33 y 1,54 para el primero y el segundo medios.
1. El (los) espejo(s) que puede(n) formar una imagen virtual, derecha y de igual tamaño que el objeto observado, es (son)
 Programa Estándar Anual Nº Guía práctica Ondas V: imágenes en espejos y lentes Ejercicios PSU 1. El (los) espejo(s) que puede(n) formar una imagen virtual, derecha y de igual tamaño que el objeto observado,
Programa Estándar Anual Nº Guía práctica Ondas V: imágenes en espejos y lentes Ejercicios PSU 1. El (los) espejo(s) que puede(n) formar una imagen virtual, derecha y de igual tamaño que el objeto observado,
Lentes Clasificación Se clasifican en dos grupos convergentes (positivas) y divergentes (negativas), las cuales a su vez pueden adoptar formas
 Lentes Clasificación Se clasifican en dos grupos convergentes (positivas) y divergentes (negativas), las cuales a su vez pueden adoptar formas distintas. Estas geometrías de lentes tienen las siguientes
Lentes Clasificación Se clasifican en dos grupos convergentes (positivas) y divergentes (negativas), las cuales a su vez pueden adoptar formas distintas. Estas geometrías de lentes tienen las siguientes
ÓPTICA GEOMÉTRICA 1. Conceptos básicos. 2. Espejos planos. 3. Espejos esféricos. 4. Dioptrios. 5. Lentes delgadas. 6. La visión.
 ÓPTICA GEOMÉTRICA 1. Conceptos básicos. 2. Espejos planos. 3. Espejos esféricos. 4. Dioptrios. 5. Lentes delgadas. 6. La visión. Física 2º bachillerato Óptica geométrica 1 ÓPTICA GEOMÉTRICA La óptica geométrica
ÓPTICA GEOMÉTRICA 1. Conceptos básicos. 2. Espejos planos. 3. Espejos esféricos. 4. Dioptrios. 5. Lentes delgadas. 6. La visión. Física 2º bachillerato Óptica geométrica 1 ÓPTICA GEOMÉTRICA La óptica geométrica
TEMA 4: OPTICA. s, y s, y Espejos y lentes FINALIDAD: dado un objeto imagen
 4.2.- Espejos y lentes FINALIDAD: dado un objeto imagen s, y s, y Objeto o imagen real: aquél para el cual los rayos de luz se cruzan de forma real. El punto de corte se puede recoger en una pantalla Figura
4.2.- Espejos y lentes FINALIDAD: dado un objeto imagen s, y s, y Objeto o imagen real: aquél para el cual los rayos de luz se cruzan de forma real. El punto de corte se puede recoger en una pantalla Figura
TEMA 4: OPTICA. Ojo normal! 4.4 El ojo como sistema óptico Características del ojo normal (emétrope): Córnea: parte protuberante del ojo
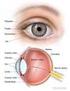 Ojo normal! Características del ojo normal (emétrope): Córnea: parte protuberante del ojo Figura 32.45 Tipler 5ª Ed. Características del ojo normal (emétrope): Córnea: parte protuberante del ojo Iris:
Ojo normal! Características del ojo normal (emétrope): Córnea: parte protuberante del ojo Figura 32.45 Tipler 5ª Ed. Características del ojo normal (emétrope): Córnea: parte protuberante del ojo Iris:
ÁREA DE FÍSICA GUÍA DE APLICACIÓN TEMA: ACÚSTICA Y ÓPTICA GUÍA: 1203 ESTUDIANTE: FECHA:
 ÁREA DE FÍSICA GUÍA DE APLICACIÓN TEMA: ACÚSTICA Y ÓPTICA GUÍA: 1203 ESTUDIANTE: E-MAIL: FECHA: ACÚSTICA Resuelva cada uno de los siguientes problemas haciendo el proceso completo. 1. Un estudiante golpea
ÁREA DE FÍSICA GUÍA DE APLICACIÓN TEMA: ACÚSTICA Y ÓPTICA GUÍA: 1203 ESTUDIANTE: E-MAIL: FECHA: ACÚSTICA Resuelva cada uno de los siguientes problemas haciendo el proceso completo. 1. Un estudiante golpea
INVESTIGACIÓN 3: MODELO DEL OJO HUMANO
 INVESTIGACIÓN 3: MODELO DEL OJO HUMANO MATERIALES Y EQUIPO Fuente de luz muy distante o fuente de luz colimada (para simular un objeto distante) Fuente de luz/diapositiva objeto (transparencia con flecha
INVESTIGACIÓN 3: MODELO DEL OJO HUMANO MATERIALES Y EQUIPO Fuente de luz muy distante o fuente de luz colimada (para simular un objeto distante) Fuente de luz/diapositiva objeto (transparencia con flecha
Tema 1. Consideraciones. CONTACTOLOGIA II María Isabel Soro Martínez Diego García Ayuso
 Tema 1. Consideraciones ópticas de las LC Introducción Objetivo adaptación LC Compensación óptica de ametropías y anisometropías. Debemos conocer: Potencia de la LC (plano de SCA). Cambios visuales respecto
Tema 1. Consideraciones ópticas de las LC Introducción Objetivo adaptación LC Compensación óptica de ametropías y anisometropías. Debemos conocer: Potencia de la LC (plano de SCA). Cambios visuales respecto
LUZ Y ÓPTICA. Propagación de la luz
 LUZ Y ÓPTICA Propagación de la luz La luz se propaga en línea recta en un medio homogéneo. La hipótesis de la propagación de la luz explica varios fenómenos entre los que se puede resaltar: Cuando un rayo
LUZ Y ÓPTICA Propagación de la luz La luz se propaga en línea recta en un medio homogéneo. La hipótesis de la propagación de la luz explica varios fenómenos entre los que se puede resaltar: Cuando un rayo
LENTES Y ÓPTICA DEL OJO
 LENTES Y ÓPTICA DEL OJO OBJETIVOS En las investigaciones 2 y 3 vimos que si la luz atraviesa superficies de separación entre dos medios diferentes se desvía. Este hecho ha sido empleado para la construcción
LENTES Y ÓPTICA DEL OJO OBJETIVOS En las investigaciones 2 y 3 vimos que si la luz atraviesa superficies de separación entre dos medios diferentes se desvía. Este hecho ha sido empleado para la construcción
Física P.A.U. ÓPTICA 1 ÓPTICA
 Física P.A.U. ÓPTICA 1 ÓPTICA PROBLEMAS DIOPTRIO PLANO 1. Un rayo de luz de frecuencia 5 10¹⁴ Hz incide con un ángulo de incidencia de 30 sobre una lámina de vidrio de caras plano-paralelas de espesor
Física P.A.U. ÓPTICA 1 ÓPTICA PROBLEMAS DIOPTRIO PLANO 1. Un rayo de luz de frecuencia 5 10¹⁴ Hz incide con un ángulo de incidencia de 30 sobre una lámina de vidrio de caras plano-paralelas de espesor
Introducción. Flujo Eléctrico.
 Introducción La descripción cualitativa del campo eléctrico mediante las líneas de fuerza, está relacionada con una ecuación matemática llamada Ley de Gauss, que relaciona el campo eléctrico sobre una
Introducción La descripción cualitativa del campo eléctrico mediante las líneas de fuerza, está relacionada con una ecuación matemática llamada Ley de Gauss, que relaciona el campo eléctrico sobre una
LAS LENTES PROGRESIVAS
 IMAGEN PERIODISMO CON VISIÓN COMPENDIO DE OFTÁLMICA / LAS LENTES PROGRESIVAS LAS LENTES PROGRESIVAS CAPÍTULO 1 DE 4 Fig. 1: Los présbitas una población en aumento. Introducción Desde su introducción por
IMAGEN PERIODISMO CON VISIÓN COMPENDIO DE OFTÁLMICA / LAS LENTES PROGRESIVAS LAS LENTES PROGRESIVAS CAPÍTULO 1 DE 4 Fig. 1: Los présbitas una población en aumento. Introducción Desde su introducción por
UNIVERSIDAD NACIONAL DE MISIONES
 OPTICA GEOMÉTRICA PROBLEMAS PROPUESTOS 1: Un rayo que se propaga por el aire incide en la superficie de un bloque de hielo transparente (n h =1,309) formando un ángulo de 40º con la normal a dicha superficie.
OPTICA GEOMÉTRICA PROBLEMAS PROPUESTOS 1: Un rayo que se propaga por el aire incide en la superficie de un bloque de hielo transparente (n h =1,309) formando un ángulo de 40º con la normal a dicha superficie.
TEMA 2 EL OJO TEÓRICO
 TEMA 2 EL OJO TEÓRICO MODELIZACIÓN DEL OJO HUMANO 2.1.-Constantes ópticas del ojo 2.2.-Aproximaciones en el modelo del ojo teórico: sistema centrado, aproximación paraxial 2.3.-La córnea: potencia, planos
TEMA 2 EL OJO TEÓRICO MODELIZACIÓN DEL OJO HUMANO 2.1.-Constantes ópticas del ojo 2.2.-Aproximaciones en el modelo del ojo teórico: sistema centrado, aproximación paraxial 2.3.-La córnea: potencia, planos
UN SISTEMA PARA RESOLVER PROBLEMAS DE ÓPTICA. Guillermo Becerra Córdova. Universidad Autónoma Chapingo. Dpto. de Preparatoria Agrícola.
 UN SISTEMA PARA RESOLVER PROBLEMAS DE ÓPTICA Guillermo Becerra Córdova Universidad Autónoma Chapingo Dpto. de Preparatoria Agrícola Área de Física E-mail: [email protected] Resumen Dentro de los cursos
UN SISTEMA PARA RESOLVER PROBLEMAS DE ÓPTICA Guillermo Becerra Córdova Universidad Autónoma Chapingo Dpto. de Preparatoria Agrícola Área de Física E-mail: [email protected] Resumen Dentro de los cursos
SESIÓN 3: MICROSCOPIO TRABAJO PREVIO CONCEPTOS FUNDAMENTALES
 SESIÓN 3: MICROSCOPIO TRABAJO PREVIO CONCEPTOS FUNDAMENTALES En esta sección se describen algunas de las características del microscopio compuesto. También la propiedad de las láminas planoparalelas de
SESIÓN 3: MICROSCOPIO TRABAJO PREVIO CONCEPTOS FUNDAMENTALES En esta sección se describen algunas de las características del microscopio compuesto. También la propiedad de las láminas planoparalelas de
COMPROBACIÓN DE RELACIONES PARAXIALES
 SESIÓN 4: COMPROBACIÓN DE RELACIONES PARAXIALES TRABAJO PREVIO CONCEPTOS FUNDAMENTALES Aproximación paraxial Aproximación de ángulos con el eje óptico pequeños (sen σ σ, tg σ σ). En aproximación paraxial
SESIÓN 4: COMPROBACIÓN DE RELACIONES PARAXIALES TRABAJO PREVIO CONCEPTOS FUNDAMENTALES Aproximación paraxial Aproximación de ángulos con el eje óptico pequeños (sen σ σ, tg σ σ). En aproximación paraxial
Práctica de Óptica Geométrica
 Práctica de Determinación de la distancia focal de lentes delgadas convergentes y divergentes 2 Pre - requisitos para realizar la práctica.. 2 Bibliografía recomendada en referencia al modelo teórico 2
Práctica de Determinación de la distancia focal de lentes delgadas convergentes y divergentes 2 Pre - requisitos para realizar la práctica.. 2 Bibliografía recomendada en referencia al modelo teórico 2
ÓPTICA. Agradecimientos al profesor Camilo Reyes
 ÓPTICA Agradecimientos al profesor Camilo Reyes ÓPTICA Aplicación de lentes, espejos y prismas a instrumentos que controlan y manipulan la luz. CONVERGENTES (positivas) DIVERGENTES (negativas) TIPOS BÁSICOS
ÓPTICA Agradecimientos al profesor Camilo Reyes ÓPTICA Aplicación de lentes, espejos y prismas a instrumentos que controlan y manipulan la luz. CONVERGENTES (positivas) DIVERGENTES (negativas) TIPOS BÁSICOS
ÓPTICA GEOMÉTRICA: REFLEXIÓN Y REFRACCIÓN DE LA LUZ
 1 ÓPTICA GEOMÉTRICA: REFLEXIÓN Y REFRACCIÓN DE LA LUZ INTRODUCCIÓN TEÓRICA: La característica fundamental de una onda propagándose por un medio es su velocidad (v), y naturalmente, cuando la onda cambia
1 ÓPTICA GEOMÉTRICA: REFLEXIÓN Y REFRACCIÓN DE LA LUZ INTRODUCCIÓN TEÓRICA: La característica fundamental de una onda propagándose por un medio es su velocidad (v), y naturalmente, cuando la onda cambia
a) la imagen de un plano perpendicular al eje óptico es otro plano perpendicular
 .- CONCEPTOS BÁSICOS: RAYO, DIOPTRIO, OBJETO, IMAGEN... La Óptica geométrica se ocupa de la propagación de la luz y de la formación de las imágenes que ésta produce sin tener para nada en cuenta su naturaleza.
.- CONCEPTOS BÁSICOS: RAYO, DIOPTRIO, OBJETO, IMAGEN... La Óptica geométrica se ocupa de la propagación de la luz y de la formación de las imágenes que ésta produce sin tener para nada en cuenta su naturaleza.
TEMA 2 EL OJO TEÓRICO
 TEMA 2 EL OJO TEÓRICO 2.1.-Constantes ópticas del ojo 2.2.-Aproximaciones en el modelo del ojo teórico: sistema centrado, aproximación paraxial 2.3.-La córnea: potencia, planos principales y focales 2.4.-El
TEMA 2 EL OJO TEÓRICO 2.1.-Constantes ópticas del ojo 2.2.-Aproximaciones en el modelo del ojo teórico: sistema centrado, aproximación paraxial 2.3.-La córnea: potencia, planos principales y focales 2.4.-El
PROBLEMAS RESUELTOS MOVIMIENTO ONDULATORIO
 PROBLEMAS RESUELTOS MOVIMIENTO ONDULATORIO 1. Una onda transversal se propaga en una cuerda según la ecuación (unidades en el S.I.) Calcular la velocidad de propagación de la onda y el estado de vibración
PROBLEMAS RESUELTOS MOVIMIENTO ONDULATORIO 1. Una onda transversal se propaga en una cuerda según la ecuación (unidades en el S.I.) Calcular la velocidad de propagación de la onda y el estado de vibración
TEMA 7.- SISTEMAS TELESCÓPICOS
 1/ 6 TEMA 7.- SISTEMAS TELESCÓPICOS Introducción. La condición aocal. Anteojo Astronómico. Aumento visual. Campo angular. Diaragma de campo y retículos. Proundidad de enoque. Oculares dles. Sistema inversor.
1/ 6 TEMA 7.- SISTEMAS TELESCÓPICOS Introducción. La condición aocal. Anteojo Astronómico. Aumento visual. Campo angular. Diaragma de campo y retículos. Proundidad de enoque. Oculares dles. Sistema inversor.
3.1 Ametropías Miopía
 3 A m e t r o p í a s y A l t e r a c i o n e s d e l a V isi ó n B i n o c u l a r En este capítulo se abordarán tanto los problemas de refracción, que necesitan una compensación óptica, como los más
3 A m e t r o p í a s y A l t e r a c i o n e s d e l a V isi ó n B i n o c u l a r En este capítulo se abordarán tanto los problemas de refracción, que necesitan una compensación óptica, como los más
MEDIDA DE FOCALES Y RADIOS DE CURVATURA DE ESPEJOS
 SESIÓN 1 MEDIDA DE FOCALES Y RADIOS DE CURVATURA DE ESPEJOS TRABAJO PREVIO: MEDIDA DE FOCALES CONCEPTOS FUNDAMENTALES Aproximación paraxial Los ángulos con el eje óptico se aproximan por ángulos pequeños
SESIÓN 1 MEDIDA DE FOCALES Y RADIOS DE CURVATURA DE ESPEJOS TRABAJO PREVIO: MEDIDA DE FOCALES CONCEPTOS FUNDAMENTALES Aproximación paraxial Los ángulos con el eje óptico se aproximan por ángulos pequeños
Física 2º Bach. Óptica 01/04/09
 Física 2º Bach. Óptica 0/04/09 DEPARTAMENTO DE FÍSICA E QUÍMICA Problemas Nombre: [3 PUNTO /UNO]. Un objeto O está situado a 30 cm del vértice de un espejo cóncavo, tal y como indica la figura. Se observa
Física 2º Bach. Óptica 0/04/09 DEPARTAMENTO DE FÍSICA E QUÍMICA Problemas Nombre: [3 PUNTO /UNO]. Un objeto O está situado a 30 cm del vértice de un espejo cóncavo, tal y como indica la figura. Se observa
Óptica Física y Geométrica
 Óptica Física y Geométrica INDICE Diversas teorías acerca de la luz 1 Propagación de las ondas electromagnéticas 3 Ondas electromagnéticas. La luz. 3 Índice de refracción de la luz 4 Reflexión de la luz
Óptica Física y Geométrica INDICE Diversas teorías acerca de la luz 1 Propagación de las ondas electromagnéticas 3 Ondas electromagnéticas. La luz. 3 Índice de refracción de la luz 4 Reflexión de la luz
Cámara réflex digital. DSRL (Digital Single Lens Réflex)
 Cámara réflex digital DSRL (Digital Single Lens Réflex) Cuerpo Lente, Objetivo, óptica objetivo pentaprisma Sensor o película obturador 1. Visor Réflex: Lo cual significa, que cuando miramos a través del
Cámara réflex digital DSRL (Digital Single Lens Réflex) Cuerpo Lente, Objetivo, óptica objetivo pentaprisma Sensor o película obturador 1. Visor Réflex: Lo cual significa, que cuando miramos a través del
BLOQUE 4.2 ÓPTICA GEOMÉTRICA
 BLOQUE 4.2 ÓPTICA GEOMÉTRICA 1- DE QUÉ TRATA LA ÓPTICA GEOMÉTRICA? El desarrollo de la Óptica y de sus usos o aplicaciones discurrió prácticamente al margen de la discusión relativa a la naturaleza de
BLOQUE 4.2 ÓPTICA GEOMÉTRICA 1- DE QUÉ TRATA LA ÓPTICA GEOMÉTRICA? El desarrollo de la Óptica y de sus usos o aplicaciones discurrió prácticamente al margen de la discusión relativa a la naturaleza de
REFRACCIÓN DE LA LUZ
 1 Nombre OBJETIVOS: Ud. Deberá ser capaz de : 1. definir la refracción de la luz 2. comprender el comportamiento que tiene la luz frente a distintos medios 3. describir la ley de refracción 4. describir
1 Nombre OBJETIVOS: Ud. Deberá ser capaz de : 1. definir la refracción de la luz 2. comprender el comportamiento que tiene la luz frente a distintos medios 3. describir la ley de refracción 4. describir
TEMA: LA LUZ. - Concepto - Tipos - Leyes. - Concepto. - Espejos. - Concepto. - Índice de refracción. - Lentes. - Prisma óptico
 TEMA: LA LUZ LA LUZ - Concepto - Características - Propagación - La materia y la luz - Instrumentos ópticos -Reflexión - Refracción - Concepto - Tipos - Leyes - Espejos - Concepto - Índice de refracción
TEMA: LA LUZ LA LUZ - Concepto - Características - Propagación - La materia y la luz - Instrumentos ópticos -Reflexión - Refracción - Concepto - Tipos - Leyes - Espejos - Concepto - Índice de refracción
Formación de imágenes
 ormación de imágenes Espejos esféricos: Cóncavos Convexos Lentes Convergentes Divergentes Salir Espejos esféricos cóncavos ormación de imágenes en el espejo esférico. a mayor distancia que el centro de
ormación de imágenes Espejos esféricos: Cóncavos Convexos Lentes Convergentes Divergentes Salir Espejos esféricos cóncavos ormación de imágenes en el espejo esférico. a mayor distancia que el centro de
ESPEJOS ESFERICOS. Figura 29. Definición de términos para los espejos esféricos.
 ESPEJOS ESFERICOS Los mismos métodos geométricos aplicados a la reflexión de la luz desde un espejo plano se pueden utilizar para un espejo curvo. El ángulo de incidencia sigue siendo igual que el ángulo
ESPEJOS ESFERICOS Los mismos métodos geométricos aplicados a la reflexión de la luz desde un espejo plano se pueden utilizar para un espejo curvo. El ángulo de incidencia sigue siendo igual que el ángulo
23. MICROSCOPIO COMPUESTO: DETERMINACIÓN DE SU AUMENTO y MEDIDA DE ÁREAS MICROSCÓPICAS
 23. MICROSCOPIO COMPUESTO: DETERMINACIÓN DE SU AUMENTO y MEDIDA DE ÁREAS MICROSCÓPICAS OBJETIVO El objetivo de la práctica es familiarizarse con el uso del microscopio, determinar el aumento lineal de
23. MICROSCOPIO COMPUESTO: DETERMINACIÓN DE SU AUMENTO y MEDIDA DE ÁREAS MICROSCÓPICAS OBJETIVO El objetivo de la práctica es familiarizarse con el uso del microscopio, determinar el aumento lineal de
Reflexión de la luz MATERIALES MONTAJE
 Reflexión de la luz Espejos planos Estamos acostumbrados a usar los espejos sin plantearnos que ocurre con los rayos de luz que inciden sobre ellos. Vamos a estudiar el comportamiento de la luz primero
Reflexión de la luz Espejos planos Estamos acostumbrados a usar los espejos sin plantearnos que ocurre con los rayos de luz que inciden sobre ellos. Vamos a estudiar el comportamiento de la luz primero
Ver objetos minúsculos que los tenemos cerca lo hacemos gracias al microscopio.
 1 Ver objetos minúsculos que los tenemos cerca lo hacemos gracias al microscopio. Ver objetos grandes que están muy lejos de la Tierra lo conseguimos gracias al telescopio. Las invenciones del microscopio
1 Ver objetos minúsculos que los tenemos cerca lo hacemos gracias al microscopio. Ver objetos grandes que están muy lejos de la Tierra lo conseguimos gracias al telescopio. Las invenciones del microscopio
PRÁCTICA Nº.- LENTES.
 PRÁCTICA Nº.- LENTES. Objetivo: Estudiar la ormación de imágenes de lentes delgadas y determinar la distancia ocal y la potencia de una lente convergente y de una lente divergente. undamento teórico: La
PRÁCTICA Nº.- LENTES. Objetivo: Estudiar la ormación de imágenes de lentes delgadas y determinar la distancia ocal y la potencia de una lente convergente y de una lente divergente. undamento teórico: La
TEMA 8.- NORMAS DE MATRICES Y
 Álgebra II: Tema 8. TEMA 8.- NORMAS DE MATRICES Y NúMERO DE CONDICIóN Índice. Introducción 2. Norma vectorial y norma matricial. 2 2.. Norma matricial inducida por normas vectoriales......... 4 2.2. Algunos
Álgebra II: Tema 8. TEMA 8.- NORMAS DE MATRICES Y NúMERO DE CONDICIóN Índice. Introducción 2. Norma vectorial y norma matricial. 2 2.. Norma matricial inducida por normas vectoriales......... 4 2.2. Algunos
OPTICA GEOMÉTRICA. Física de 2º de Bachillerato
 OPTICA GEOMÉTRICA Física de 2º de Bachillerato La luz se propaga en el vacío a la velocidad de la luz, que es constante, nunca se detiene. Da igual a qué velocidad persigamos un rayo de luz; siempre se
OPTICA GEOMÉTRICA Física de 2º de Bachillerato La luz se propaga en el vacío a la velocidad de la luz, que es constante, nunca se detiene. Da igual a qué velocidad persigamos un rayo de luz; siempre se
7. Difracción n de la luz
 7. Difracción n de la luz 7.1. La difracción 1 7. Difracción de la luz. 2 Experiencia de Grimaldi (1665) Al iluminar una pantalla opaca con una abertura pequeña, se esperaba que en la pantalla de observación
7. Difracción n de la luz 7.1. La difracción 1 7. Difracción de la luz. 2 Experiencia de Grimaldi (1665) Al iluminar una pantalla opaca con una abertura pequeña, se esperaba que en la pantalla de observación
Representación de números enteros: el convenio exceso Z
 Representación de números enteros: el convenio exceso Z Apellidos, nombre Martí Campoy, Antonio ([email protected]) Departamento Centro Informàtica de Sistemes i Computadors Escola Tècnica Superior d
Representación de números enteros: el convenio exceso Z Apellidos, nombre Martí Campoy, Antonio ([email protected]) Departamento Centro Informàtica de Sistemes i Computadors Escola Tècnica Superior d
ÓPTICA GEOMÉTRICA IDEAS PRINCIPALES
 3 ÓPTICA GEOMÉTRICA IDEAS PRINCIPALES Modelo de rayos Sombras y penumbras Velocidad de la luz Imágenes reales y virtuales Mecanismo de visión Reflexión especular y difusa Espejos planos y esféricos Lentes
3 ÓPTICA GEOMÉTRICA IDEAS PRINCIPALES Modelo de rayos Sombras y penumbras Velocidad de la luz Imágenes reales y virtuales Mecanismo de visión Reflexión especular y difusa Espejos planos y esféricos Lentes
FICHAS COMPLEMENTARIAS. REFLEXIÓN
 FICHAS COMPLEMENTARIAS. REFLEXIÓN I.- DESCRIPCIÓN DE LOS COMPONENTES Para realizar las prácticas de óptica vas a usar: 1.- Banco óptico: es una base metálica sobre la que colocar los diferentes montajes.
FICHAS COMPLEMENTARIAS. REFLEXIÓN I.- DESCRIPCIÓN DE LOS COMPONENTES Para realizar las prácticas de óptica vas a usar: 1.- Banco óptico: es una base metálica sobre la que colocar los diferentes montajes.
Laboratorio de Optica
 Laboratorio de Optica 5. Lentes Delgadas Neil Bruce Laboratorio de Optica Aplicada, Centro de Instrumentos, U.N.A.M., A.P. 70-186, México, 04510, D.F. Objetivos Veriicar las ecuaciones que relacionan la
Laboratorio de Optica 5. Lentes Delgadas Neil Bruce Laboratorio de Optica Aplicada, Centro de Instrumentos, U.N.A.M., A.P. 70-186, México, 04510, D.F. Objetivos Veriicar las ecuaciones que relacionan la
Sistemas de dos ecuaciones lineales de primer grado con dos incógnitas
 Un sistema de dos ecuaciones lineales de primer grado con dos incógnitas tiene la siguiente forma Ax + By + C = 0 A x + B y + C (1) = 0 Ya sabemos que una ecuación lineal de primer grado con dos incógnitas
Un sistema de dos ecuaciones lineales de primer grado con dos incógnitas tiene la siguiente forma Ax + By + C = 0 A x + B y + C (1) = 0 Ya sabemos que una ecuación lineal de primer grado con dos incógnitas
Tema 1. Elementos de un sistema de Visión por Computador. Esquema general de un sistema de visión por computador
 Tema 1 Elementos de un sistema de Visión por Computador Índice Esquema general de un sistema de visión por computador Esquema de un proceso de visión por computador Estructura típica de un sistema Fundamentos
Tema 1 Elementos de un sistema de Visión por Computador Índice Esquema general de un sistema de visión por computador Esquema de un proceso de visión por computador Estructura típica de un sistema Fundamentos
Observando el cielo con prismáticos y telescopios
 Observando el cielo con prismáticos y telescopios Ángel Serrano y Jacobo Aguirre Universidad de Mayores de URJC http://www.tallerdeastronomia.es/ Introducción Luz: onda electromagnética que viaja en el
Observando el cielo con prismáticos y telescopios Ángel Serrano y Jacobo Aguirre Universidad de Mayores de URJC http://www.tallerdeastronomia.es/ Introducción Luz: onda electromagnética que viaja en el
Capítulo 21 Óptica 1
 Capítulo 21 Óptica 1 Reflexión y refracción Las leyes de la reflexión y de la refracción nos dicen lo siguiente: Los rayos incidente, reflejado y transmitido están todos en un mismo plano, perpendicular
Capítulo 21 Óptica 1 Reflexión y refracción Las leyes de la reflexión y de la refracción nos dicen lo siguiente: Los rayos incidente, reflejado y transmitido están todos en un mismo plano, perpendicular
1. Análisis Teórico. 1.1. Microscopio Óptico. 1.2. Teoría de Formación de Imágenes de Abbe. Resolución. Laboratorio de Ondas y Óptica.
 Laboratorio de Ondas y Óptica Práctica N 7 Microscopía Óptica Digital Departamento de Física, FaCyT. Universidad de Carabobo, Venezuela. Objetivos Estudiar el funcionamiento de un Microscopio Óptico Preparación
Laboratorio de Ondas y Óptica Práctica N 7 Microscopía Óptica Digital Departamento de Física, FaCyT. Universidad de Carabobo, Venezuela. Objetivos Estudiar el funcionamiento de un Microscopio Óptico Preparación
Cartografía Temática Recopilación Apuntes Juan E. Gutiérrez Palacios
 IV. MAPAS DE PUNTOS 4.1. INTRODUCCIÓN En los mapas de puntos la información cuantitativa se representa por medio de la repetición de puntos que, a diferencia de los mapas de símbolos proporcionales, no
IV. MAPAS DE PUNTOS 4.1. INTRODUCCIÓN En los mapas de puntos la información cuantitativa se representa por medio de la repetición de puntos que, a diferencia de los mapas de símbolos proporcionales, no
FÍSICA de 2º de BACHILLERATO ÓPTICA -GEOMÉTRICA-
 FÍSICA de 2º de BACHILLERATO ÓPTICA -GEOMÉTRICA- EJERCICIOS RESUELTOS QUE HAN SIDO PROPUESTOS EN LOS EXÁMENES DE LAS PRUEBAS DE ACCESO A ESTUDIOS UNIVERSITARIOS EN LA COMUNIDAD DE MADRID (1996 2013) DOMINGO
FÍSICA de 2º de BACHILLERATO ÓPTICA -GEOMÉTRICA- EJERCICIOS RESUELTOS QUE HAN SIDO PROPUESTOS EN LOS EXÁMENES DE LAS PRUEBAS DE ACCESO A ESTUDIOS UNIVERSITARIOS EN LA COMUNIDAD DE MADRID (1996 2013) DOMINGO
MATEMÁTICAS 2º ESO SEMEJANZA Y TEOREMA DE THALES
 MATEMÁTICAS º ESO SEMEJANZA Y TEOREMA DE THALES S1 SEMEJANZA DE FIGURAS. RAZÓN DE SEMEJANZA O ESCALA. Dos figuras son semejantes si tienen la misma forma, aunque quizá distinto tamaño. La razón de semejanza
MATEMÁTICAS º ESO SEMEJANZA Y TEOREMA DE THALES S1 SEMEJANZA DE FIGURAS. RAZÓN DE SEMEJANZA O ESCALA. Dos figuras son semejantes si tienen la misma forma, aunque quizá distinto tamaño. La razón de semejanza
Espejos CAPÍTULO 4. Editorial Contexto - - Canelones Espejos planos, imágenes
 APÍTULO 4 interacciones campos y ondas / física 1º b.d. ESPEJOS apítulo 4 43 Espejos Espejos planos, imágenes En la figura 1 representamos un fuente puntual de luz ubicada en A y un espejo plano. En ella
APÍTULO 4 interacciones campos y ondas / física 1º b.d. ESPEJOS apítulo 4 43 Espejos Espejos planos, imágenes En la figura 1 representamos un fuente puntual de luz ubicada en A y un espejo plano. En ella
NIVEL 1 ADIESTRAMIENTO PARA ASESOR JUNIOR MODULO 2 AMETROPIAS
 NIVEL 1 ADIESTRAMIENTO PARA ASESOR JUNIOR MODULO 2 AMETROPIAS EL OJO NORMAL (EMETROPE) AMETROPIAS LA HIPERMETROPÍA LA MIOPÍA EL ASTIGMATISMO LA PRESBICIA RX DIOPTRIA INTERPRETACION DEL Rx EL OJO NORMAL
NIVEL 1 ADIESTRAMIENTO PARA ASESOR JUNIOR MODULO 2 AMETROPIAS EL OJO NORMAL (EMETROPE) AMETROPIAS LA HIPERMETROPÍA LA MIOPÍA EL ASTIGMATISMO LA PRESBICIA RX DIOPTRIA INTERPRETACION DEL Rx EL OJO NORMAL
TEMA: Formación de imágenes en lentes convergentes
 TEMA: Formación de imágenes en lentes convergentes Objetivos 1. Estudiar un sistema óptico simple. 2. Determinar experimentalmente la longitud focal de una lente convergente. 3. Verificar experimentalmente
TEMA: Formación de imágenes en lentes convergentes Objetivos 1. Estudiar un sistema óptico simple. 2. Determinar experimentalmente la longitud focal de una lente convergente. 3. Verificar experimentalmente
UNIDAD DIDÁCTICA 5: Geometría analítica del plano
 UNIDAD DIDÁCTICA 5: Geometría analítica del plano 1. ÍNDICE 1. Sistemas de referencia y coordenadas puntuales 2. Distancia entre dos puntos del plano 3. Coordenadas del punto medio de un segmento 4. La
UNIDAD DIDÁCTICA 5: Geometría analítica del plano 1. ÍNDICE 1. Sistemas de referencia y coordenadas puntuales 2. Distancia entre dos puntos del plano 3. Coordenadas del punto medio de un segmento 4. La
Óptica. Radio Microondas Infrarrojo Visible Ultravioleta Rayos X Rayos. plano. 2ª ley: el ángulo de incidencia es igual que el ángulo de reflexión.
 Óptica Espectro electromagnético (m) 10-1 10-3 7 10-7 4,5 10-7 10-9 10-11 Radio Microondas Inrarrojo Visible Ultravioleta Rayos X Rayos (Hz) 10 9 10 11 4 10 14 8 10 14 10 17 10 19 Hipótesis de Planck Energía
Óptica Espectro electromagnético (m) 10-1 10-3 7 10-7 4,5 10-7 10-9 10-11 Radio Microondas Inrarrojo Visible Ultravioleta Rayos X Rayos (Hz) 10 9 10 11 4 10 14 8 10 14 10 17 10 19 Hipótesis de Planck Energía
CORRIENTE CONTINUA I : RESISTENCIA INTERNA DE UNA FUENTE
 eman ta zabal zazu Departamento de Física de la Materia Condensada universidad del país vasco euskal herriko unibertsitatea FACULTAD DE CIENCIA Y TECNOLOGÍA UNIVERSIDAD DEL PAÍS VASCO DEPARTAMENTO de FÍSICA
eman ta zabal zazu Departamento de Física de la Materia Condensada universidad del país vasco euskal herriko unibertsitatea FACULTAD DE CIENCIA Y TECNOLOGÍA UNIVERSIDAD DEL PAÍS VASCO DEPARTAMENTO de FÍSICA
FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS
 FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS Página 8. Aunque el método para resolver las siguientes preguntas se sistematiza en la página siguiente, puedes resolverlas ahora: a) Cuántos radianes corresponden
FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS Página 8. Aunque el método para resolver las siguientes preguntas se sistematiza en la página siguiente, puedes resolverlas ahora: a) Cuántos radianes corresponden
UD Trigonometría Ejercicios Resueltos y Propuestos Col La Presentación
 En este documento se da una relación de los tipos de ejercicios que nos podemos encontrar en el tema de Trigonometría de º de Bachillerato. En todo el documento se sigue el mismo esquema: Enunciado tipo
En este documento se da una relación de los tipos de ejercicios que nos podemos encontrar en el tema de Trigonometría de º de Bachillerato. En todo el documento se sigue el mismo esquema: Enunciado tipo
TEMA 18. Sistemas de Baja Visión para cerca: Microscopios y Lupas.
 TEMA 18. Sistemas de Baja Visión para cerca: Microscopios y Lupas. Microscopios Se denomina microscopio en rehabilitación visual a una lente muy positiva o combinación de lentes montadas en gafa, para
TEMA 18. Sistemas de Baja Visión para cerca: Microscopios y Lupas. Microscopios Se denomina microscopio en rehabilitación visual a una lente muy positiva o combinación de lentes montadas en gafa, para
Física. Choque de un meteorito sobre la tierra
 Física Choque de un meteorito sobre la tierra Hace 65 millones de años la Tierra cambió de forma repentina, muchas especies desaparecieron, plantas, animales terrestres y marinos y sobre todo, los grandes
Física Choque de un meteorito sobre la tierra Hace 65 millones de años la Tierra cambió de forma repentina, muchas especies desaparecieron, plantas, animales terrestres y marinos y sobre todo, los grandes
Proyecto. Tema 6 sesión 2: Generación de Rectas, Circunferencias y Curvas. Geometría Analítica. Isidro Huesca Zavaleta
 Geometría Analítica Tema 6 sesión 2: Generación de Rectas, Circunferencias y Curvas Isidro Huesca Zavaleta La Integración de dos Ciencias La Geometría Analítica nació de la integración de dos ciencias
Geometría Analítica Tema 6 sesión 2: Generación de Rectas, Circunferencias y Curvas Isidro Huesca Zavaleta La Integración de dos Ciencias La Geometría Analítica nació de la integración de dos ciencias
TEMA 1. MATRICES, DETERMINANTES Y APLICACIÓN DE LOS DETERMINANTES. CONCEPTO DE MATRIZ. LA MATRIZ COMO EXPRESIÓN DE TABLAS Y GRAFOS.
 TEMA 1. MATRICES, DETERMINANTES Y APLICACIÓN DE LOS DETERMINANTES. 1. MATRICES. CONCEPTO DE MATRIZ. LA MATRIZ COMO EXPRESIÓN DE TABLAS Y GRAFOS. DEFINICIÓN: Las matrices son tablas numéricas rectangulares
TEMA 1. MATRICES, DETERMINANTES Y APLICACIÓN DE LOS DETERMINANTES. 1. MATRICES. CONCEPTO DE MATRIZ. LA MATRIZ COMO EXPRESIÓN DE TABLAS Y GRAFOS. DEFINICIÓN: Las matrices son tablas numéricas rectangulares
ÁLGEBRA LINEAL II Algunas soluciones a la práctica 2.3
 ÁLGEBRA LINEAL II Algunas soluciones a la práctica 2. Transformaciones ortogonales (Curso 2010 2011) 1. Se considera el espacio vectorial euclídeo IR referido a una base ortonormal. Obtener la expresión
ÁLGEBRA LINEAL II Algunas soluciones a la práctica 2. Transformaciones ortogonales (Curso 2010 2011) 1. Se considera el espacio vectorial euclídeo IR referido a una base ortonormal. Obtener la expresión
Magnetismo y Óptica Departamento de Física Universidad de Sonora. Óptica Geométrica
 Magnetismo y Óptica 2006 Departamento de Física Universidad de Sonora 1 Óptica Geométrica 2 1 Temas 1. Formación de imágenes por reflexión: En espejos planos En espejos esféricos 2. Formación de imágenes
Magnetismo y Óptica 2006 Departamento de Física Universidad de Sonora 1 Óptica Geométrica 2 1 Temas 1. Formación de imágenes por reflexión: En espejos planos En espejos esféricos 2. Formación de imágenes
Unidad 3: Razones trigonométricas.
 Unidad 3: Razones trigonométricas 1 Unidad 3: Razones trigonométricas. 1.- Medida de ángulos: grados y radianes. Las unidades de medida de ángulos más usuales son el grado sexagesimal y el radián. Se define
Unidad 3: Razones trigonométricas 1 Unidad 3: Razones trigonométricas. 1.- Medida de ángulos: grados y radianes. Las unidades de medida de ángulos más usuales son el grado sexagesimal y el radián. Se define
SEDNAOFFICE OCUPACIONAL DE ALTA DEFINICIÓN
 SEDNAOFFICE OCUPACIONAL DE ALTA DEFINICIÓN 2 SEDNAOFICCE sedna HD office ha sido diseñada priorizando las zonas de visión intermedia y cerca para poder realizar cómodamente actividades con ordenador, lectura,
SEDNAOFFICE OCUPACIONAL DE ALTA DEFINICIÓN 2 SEDNAOFICCE sedna HD office ha sido diseñada priorizando las zonas de visión intermedia y cerca para poder realizar cómodamente actividades con ordenador, lectura,
3. ASOCIACIÓN ENTRE DOS VARIABLES CUALITATIVAS
 1. INTRODUCCIÓN Este tema se centra en el estudio conjunto de dos variables. Dos variables cualitativas - Tabla de datos - Tabla de contingencia - Diagrama de barras - Tabla de diferencias entre frecuencias
1. INTRODUCCIÓN Este tema se centra en el estudio conjunto de dos variables. Dos variables cualitativas - Tabla de datos - Tabla de contingencia - Diagrama de barras - Tabla de diferencias entre frecuencias
SISTEMAS DE ECUACIONES LINEALES. Método de reducción o de Gauss. 1º DE BACHILLERATO DPTO DE MATEMÁTICAS COLEGIO MARAVILLAS AUTORA: Teresa González.
 SISTEMAS DE ECUACIONES LINEALES Método de reducción o de Gauss 1º DE BACHILLERATO DPTO DE MATEMÁTICAS COLEGIO MARAVILLAS AUTORA: Teresa González. SISTEMAS DE DOS ECUACIONES LINEALES CON DOS INCÓGNITAS.
SISTEMAS DE ECUACIONES LINEALES Método de reducción o de Gauss 1º DE BACHILLERATO DPTO DE MATEMÁTICAS COLEGIO MARAVILLAS AUTORA: Teresa González. SISTEMAS DE DOS ECUACIONES LINEALES CON DOS INCÓGNITAS.
GEOMETRÍA ANALÍTICA DEL PLANO
 GEOMETRÍA ANALÍTICA DEL PLANO 1 UNIDAD DIDÁCTICA 5: Geometría analítica del plano 1. ÍNDICE 1. Sistemas de referencia y coordenadas puntuales 2. Distancia entre dos puntos del plano 3. Coordenadas del
GEOMETRÍA ANALÍTICA DEL PLANO 1 UNIDAD DIDÁCTICA 5: Geometría analítica del plano 1. ÍNDICE 1. Sistemas de referencia y coordenadas puntuales 2. Distancia entre dos puntos del plano 3. Coordenadas del
UNIVERSIDAD COMPLUTENSE. GRADO EN FARMACIA VESILE SAMI RAMADAN Mª DAIRIS SUÁREZ SUÁREZ
 ÓPTICA UNIVERSIDAD COMPLUTENSE. GRADO EN FARMACIA VESILE SAMI RAMADAN Mª DAIRIS SUÁREZ SUÁREZ El ojo humano -Es el órgano que detecta la luz y es la base del sentido de la vista. -Función principal: transformar
ÓPTICA UNIVERSIDAD COMPLUTENSE. GRADO EN FARMACIA VESILE SAMI RAMADAN Mª DAIRIS SUÁREZ SUÁREZ El ojo humano -Es el órgano que detecta la luz y es la base del sentido de la vista. -Función principal: transformar
FISICA 2º BACHILLERATO CAMPO MAGNÉTICO E INDUCCIÓN ELECTROMAGNÉTICA
 A) CAMPO MAGNÉTICO El Campo Magnético es la perturbación que un imán o una corriente eléctrica producen en el espacio que los rodea. Esta perturbación del espacio se manifiesta en la fuerza magnética que
A) CAMPO MAGNÉTICO El Campo Magnético es la perturbación que un imán o una corriente eléctrica producen en el espacio que los rodea. Esta perturbación del espacio se manifiesta en la fuerza magnética que
PRIMER CÁLCULO DE LA UNIDAD ASTRONÓMICA MEDIANTE EL TRÁNSITO DE VENUS
 PRIMER CÁLCULO DE LA UNIDAD ASTRONÓMICA MEDIANTE EL TRÁNSITO DE VENUS (adaptado y traducido de textos de Internet por Luis E.) Hacia 1700 gracias a Kepler- las distancias relativas entre los seis planetas
PRIMER CÁLCULO DE LA UNIDAD ASTRONÓMICA MEDIANTE EL TRÁNSITO DE VENUS (adaptado y traducido de textos de Internet por Luis E.) Hacia 1700 gracias a Kepler- las distancias relativas entre los seis planetas
10. ÓPTICA GEOMÉTRICA.
 Optica 19 10. ÓPTICA GEOMÉTRICA. Desarrollamos la unidad de acuerdo con el siguiente hilo conductor: 1. De qué trata la Óptica geométrica? Conceptos básicos en Óptica geométrica. 2. Cómo se forman las
Optica 19 10. ÓPTICA GEOMÉTRICA. Desarrollamos la unidad de acuerdo con el siguiente hilo conductor: 1. De qué trata la Óptica geométrica? Conceptos básicos en Óptica geométrica. 2. Cómo se forman las
II Unidad Diagramas en bloque de transmisores /receptores
 1 Diagramas en bloque de transmisores /receptores 10-04-2015 2 Amplitud modulada AM Frecuencia modulada FM Diagramas en bloque de transmisores /receptores Amplitud modulada AM En la modulación de amplitud
1 Diagramas en bloque de transmisores /receptores 10-04-2015 2 Amplitud modulada AM Frecuencia modulada FM Diagramas en bloque de transmisores /receptores Amplitud modulada AM En la modulación de amplitud
Algunos conceptos básicos de Trigonometría DEFINICIÓN FIGURA OBSERVACIONES. Nombre y definición Figura Característica
 Ángulos. DEFINICIÓN FIGURA OBSERVACIONES Ángulo. Es la abertura formada por dos semirrectas unidas en un solo punto llamado vértice. Donde: α = Ángulo O = Vértice OA = Lado inicial OB = Lado terminal Un
Ángulos. DEFINICIÓN FIGURA OBSERVACIONES Ángulo. Es la abertura formada por dos semirrectas unidas en un solo punto llamado vértice. Donde: α = Ángulo O = Vértice OA = Lado inicial OB = Lado terminal Un
Problema a) En un triángulo rectángulo OAB una recta r paralela a la hipotenusa corta a los catetos OA y OB en los puntos A y B respectivamente.
 Problema 717.- a) En un triángulo rectángulo OAB una recta r paralela a la hipotenusa corta a los catetos OA y OB en los puntos A y B respectivamente. Hallar el lugar geométrico de los puntos comunes a
Problema 717.- a) En un triángulo rectángulo OAB una recta r paralela a la hipotenusa corta a los catetos OA y OB en los puntos A y B respectivamente. Hallar el lugar geométrico de los puntos comunes a
Solución: I.T.I. 96, 98, 02, 05, I.T.T. 96, 99, 01, curso cero de física
 VECTORES: TRIÁNGULOS Demostrar que en una semicircunferencia cualquier triángulo inscrito con el diámetro como uno de sus lados es un triángulo rectángulo. Solución: I.T.I. 96, 98, 02, 05, I.T.T. 96, 99,
VECTORES: TRIÁNGULOS Demostrar que en una semicircunferencia cualquier triángulo inscrito con el diámetro como uno de sus lados es un triángulo rectángulo. Solución: I.T.I. 96, 98, 02, 05, I.T.T. 96, 99,
Sumario. Efectos ópticos de un prisma. Objeto binocular efectivo. Neutralización óptica con prismas en visión binocular
 Sumario Efectos ópticos de un prisma Objeto binocular efectivo Neutralización óptica con prismas en visión binocular 7-1 1. Efectos ópticos de un prisma 1 Prisma oftálmico o delgado Ángulo apical < 10
Sumario Efectos ópticos de un prisma Objeto binocular efectivo Neutralización óptica con prismas en visión binocular 7-1 1. Efectos ópticos de un prisma 1 Prisma oftálmico o delgado Ángulo apical < 10
