TEMA 7.- SISTEMAS TELESCÓPICOS
|
|
|
- José Luis Toledo Bustamante
- hace 9 años
- Vistas:
Transcripción
1 1/ 6 TEMA 7.- SISTEMAS TELESCÓPICOS Introducción. La condición aocal. Anteojo Astronómico. Aumento visual. Campo angular. Diaragma de campo y retículos. Proundidad de enoque. Oculares dles. Sistema inversor. Luminosidad. Poder separador. Anteojo de Galileo. Campo angular. Proundidad de enoque. Luminosidad. Poder separador. Ventajas e inconvenientes del Anteojo de Galileo. Telescopios relectores. Propiedades de los Telescopios relectores. Telescopio de Newton. Telescopio de Cassegrain. Denominación comercial y ejemplos.
2 / Introducción SISTEMAS TELESCÓPICOS Telescopios: Instrumentos ópticos subjetivos para la servación de jetos lejanos. Están compuestos, básicamente, por dos elementos: Objetivo: Elemento convergente. Ocular: Convergente o divergente. Características generales: Son sistemas aocales : Dado un jeto situado en el ininito, proporcionan una imagen situada también en el ininito. Presentan al ojo una imagen aumentada de jetos extensos. Para la servación de jetos puntuales son instrumentos muy luminosos.
3 7.1.- Introducción TIPOS DE TELESCOPIOS: 3/ 6 TELESCOPIOS REFRACTORES (o Anteojos): El Objetivo está ormado por una lente o acoplamiento de lentes. Anteojo Astronómico o de Kepler Anteojo de Galileo TELESCOPIOS REFLECTORES: El Objetivo es un espejo o acoplamiento de espejos. Telescopio de Newton Telescopio de Cassegrain
4 4/ La condición aocal Todos los Telescopios son Sistemas aocales : Transorman un haz colimado incidente en un haz emergente también colimado pero con una inclinación mayor. Sistema aocal más simple: está ormado por el acoplamiento de dos lentes convergentes, de orma que el oco imagen de la primera coincide con el oco jeto de la segunda:
5 5/ La condición aocal Los Sistemas aocales carecen de puntos cardinales y, por tanto, para su estudio no puede utilizarse las ecuaciones de conjugación Gauss o de Newton. Pueden analizarse de modo muy simple adaptando las ecuaciones de conjugación de Gauss generalizadas. Ecuaciones de conjugación de Gauss generalizadas + = βp x x n n β P n o o β 0 nx = nx o o 1 β P n= n = Ecuaciones de conjugación de Gauss generalizadas para Sistemas aocales β x 0 = x0 βp x = = βp x0 βp
6 Ecuaciones de correspondencia para los Sistemas aocales 6/ 6 β x 0 = x0 βp x = = βp x0 βp En los Sistemas telescópicos, el ojo del servador se debe situar, al igual que en el Microscopio, de modo que su Pupila de Entrada coincida con la Pupila de Salida del instrumento y, por ello, es conveniente tomar como orígenes para las distancias axiales: L 1 : Objetivo (PE) en el espacio jeto. L 1 : Conjugado del Objetivo (PS) en el espacio imagen.
7 Ecuaciones de correspondencia para los Sistemas aocales 7/ 6 β x 0 = x0 βp x = = βp x0 βp zz p p = z β p = = p z p β P P = = β 0 1 z P P
8 7.3.- Anteojo Astronómico (o de Kepler) Objetivo (convergente) Ocular (convergente) 8/ 6 Johannes Kepler
9 7.3.- Anteojo Astronómico 9/ Aumento visual Se deine el Aumento visual del Anteojo Astronómico como el cociente entre el tamaño angular aparente, w, de la imagen y el tamaño angular, w, del jeto cuando es servado directamente. w tan w Γ K = w tan w 1 Γ K = = β oc P
10 Aumento visual 10 / 6 1 Γ K = = β oc P El Aumento visual es negativo: No es importante en la servación astronómica. El Anteojo Astronómico no sirve para la servación terrestre. Para tener valores altos del aumento visual es necesario que Características de los Objetivos: oc varía entre unos decímetros y varios metros Apertura Relativa: AR φ = Características de los Oculares: varía entre 100mm y 10mm 1 1 varía entre y 10 0 Γ oc (.5 5) oc
11 Campo angular 11 / 6 El Campo visual del Anteojo Astronómico es angular ya que el plano jeto está situado en el ininito. Cálculo del Campo de iluminación media en el espacio óptico imagen: El ocular y la pupila del ojo están en el espacio imagen. Hay que calcular la posición del conjugado del jetivo en el espacio imagen. La imagen inal proporcionada por el Anteojo está en el ininito. En los Sistemas telescópicos la montura del jetivo actúa como Diaragma de Apertura (y Pupila de Entrada) y, por tanto, su conjugado en el espacio imagen es la Pupila de Salida. Objetivo Pupila de entrada Ocular
12 a Campo angular Posición y tamaño de la Pupila de Salida del Anteojo Astronómico Ocular Objetivo p p = a a p p ( ) oc oc a = + = e ap oc ( + oc ) oc + oc e = = = = a + ( + ) + / Γ PS p p oc oc oc oc K Pupila de entrada φ φ = β φ = Diámetro de la Pupila de Salida Γ Para una servación óptima la Pupila del ojo ha de situarse sre la Pupila de Salida del Anteojo K Emergencia pupilar 1 / 6
13 Objetivo Pupila de entrada Ocular 13 / 6 w m Cálculo del Campo de iluminación media en el espacio óptico imagen El semicampo imagen de iluminación media es el ángulo subtendido por la montura del Ocular desde el centro de la Pupila del ojo Campo de iluminación media en el espacio óptico jeto (Campo visual) tan w tan m w m φ = oc ap φoc = e
14 Diaragma de campo y retículos 14 / 6 El Anteojo Astronómico tiene la ventaja de proporcionar una imagen intermedia real. Sre el plano de la imagen intermedia pueden situarse, para mejorar la calidad de la servación, los siguientes elementos : Diaragma de campo: Elemento opaco con una abertura circular que permite limitar el campo de servación eliminando el viñeteado. Retículo: Elemento transparente, con dibujo de líneas o escala. Se serva nítidamente a la vez que el jeto. Sirve para ijar la dirección del punto de mira o medir: El tamaño angular del jeto. La separación angular de dos jetos puntuales.
15 Proundidad de enoque 15 / 6 { } ANTEOJO Δ e = O% RO % P { IV.. N. = OROP} Límites de enoque Aplicando las ecuaciones de conjugación para Sistemas aocales x = Γ xr = AOR = r xr R = = x RΓK β p xr r K x = Γ xp = AOP = p xp P = = x PΓK β p xp p K e xp xr ( p r) K Δ = = Γ
16 16 / 6 Δ = % % = = Γ e OO R P xp xr ( p r) K r = Δ OBSERVADOR EMÉTROPE e independientemente de la posición de OBSERVADOR HIPERMÉTROPE OR es virtual O% R es virtual Campo axial: O es real es real ( OR ) y, virtualmente, ( OP) P O% P % % Δ e = ( p r) Γ toma un valor inito y negativo No describe ielmente las dimensiones del campo axial O% P
17 17 / 6 Δ = % % = = Γ e OO R P xp xr ( p r) K En los Sistemas telescópicos la Proundidad de enoque es un parámetro poco adecuado para representar la magnitud del campo axial. Lo realmente relevante son los valores de x P y x R, que indican las posiciones de los Límites de enoque Límites de enoque
18 Oculares dles. Lente de Campo Para aumentar el Campo visual de los Sistemas telescópicos y minimizar la inluencia del viñeteado, se utilizan Oculares dles. Al igual que en el Microscopio, la coniguración más simple consiste en insertar una Lente de campo en el plano de la imagen intermedia que produce los siguientes eectos: El Aumento visual del Anteojo no varía El diámetro de la Pupila de Salida no cambia La Emergencia pupilar disminuye El Campo visual aumenta Lente de campo tan w m = φ Lente de ojo oc ap 18 / 6
19 H oc H oc oc = E 19 / 6 tan w tan w m m φe = a p φe φe = = a p e E + ΓK F tan w HFF oc = 0 H F = m E oc E El Campo aumenta al utilizar oculares compuestos L F E F L E wm φe K E e F tan = = Γ
20 Sistema Inversor El Anteojo Astronómico proporciona una imagen invertida de los jetos servados. Sin embargo, para la servación de jetos situados en la supericie terrestre se necesita que la imagen inal esté derecha. Una de las soluciones para lograr que la imagen inal esté derecha consiste en añadir un Sistema Inversor: Sistema convergente, situado entre el Objetivo y el ocular, que produce una inversión de la imagen intermedia. El Sistema Inversor más sencillo es una lente convergente en coniguración 4. Al Sistema Inversor se le llama también Vehículo ya que, adicionalmente, transporta la imagen intermedia a otro plano. 0 / 6
21 Sistema Inversor A los Anteojos que incorporan un Sistema Inversor se les denomina Anteojos Terrestres. La utilización de un Sistema Inversor aecta a: Aumento visual. Pupila de Salida. Campo visual. El estudio del Anteojo Terrestre se simpliica al considerar el instrumento como el acoplamiento del Objetivo y un Ocular triple constituido por el Sistema Inversor y el Ocular dle 1 / 6
22 Lente Inversora H H I I Ocular triple Ocular dle H oc H oc Distancia ocal imagen del Ocular triple T = 1 = I 1 = = I E E T = = E 1 + e I + E ( I + E) e = I + E oc = E HFF oc = 0 H F = E oc E / 6 E F
23 Posición de los Focos del Ocular triple 3 / 6 FT F T H I H I F I "OCULAR" LI LF + L O T oc "OCULAR" O F T Lente Inversora Posición del Foco imagen respecto de la Lente de ojo Z Ocular dle H oc E F F O H oc L I LF L O F + E F I T Z Plano de la imagen intermedia F F y T z = E I E F H EFT = HEFoc + FocFT = E + F T 1 E I
24 4 / 6 T = E El Anteojo terrestre es un Sistema aocal. El Aumento visual es positivo y, por tanto, la imagen inal está derecha. Pupila de salida E E E p p p I I F E T E H F E E I F = + E E Γ t = = Γ φ φ a = a + = a + φ PS = = No cambia Γ Γ Campo angular tan w m φe = = a p t tan w = m t tan w Γ t m K
25 Práctica de laboratorio 5 / 6 Construcción del Anteojo Astronómico (Anteojo de Kepler) Determinación de la posición y tamaño de la Pupila de Salida
26 6 / 6 Determinación del campo angular jeto (campo visual) Determinación del tamaño angular de un jeto utilizando un Retículo ρ tan wm = m c
27 7 / 6 Medida del Aumento visual del Anteojo y r tan w = tan w A Γ= tan wa ya tan wa = A
28 8 / 6 Construcción de un Anteojo con Ocular dle. Estudio de la inluencia de la Lente de campo: Posición y tamaño de la Pupila de salida: La emergencia pupilar disminuye. El diámetro de la P.S. no cambia. Campo visual: Aumenta. Aumento visual: No varía.
29 9 / 6 Construcción de un Anteojo Terrestre con Ocular dle. Estudio de la inluencia de la Lente Inversora: Posición y tamaño de la Pupila de salida: La emergencia pupilar aumenta. El diámetro de la P.S. no cambia. Campo visual: Disminuye. Aumento visual: Es positivo.
30 EJERCICIOS 30 / 6 Para un Sistema aocal ormado por el acoplamiento de dos sistemas de ocales 1 y, demuestre que el valor del aumento lateral entre dos planos conjugados: a) Es una constante, es decir, no depende de la posición del jeto. b) Viene dado por la expresión: Demuestre que en un Anteojo terrestre el campo visual viene dado por la expresión: tan w m β = φe = E E e + I F 1
31 Luminosidad Para el caso de jetos extensos, se deine la Luminosidad como el cociente entre la iluminación retiniana en visión a través del instrumento óptico, y la tenida en visión directa. C e e E r φ PS = = τ E A φa donde φ = min, φa Γ es el diámetro de la Pupila de Salida Eectiva del acoplamiento entre el Anteojo y la Pupila de Entrada del ojo del servador. φ φ C τ φ = φ C = τ e PS = PS e = Γ φ A e PS A e C e φ φ = min τ, τ φ Γ A Variación de la Luminosidad en unción del Aumento visual C φ e PS τ φ e = Γ φ A C e =τ 31 / 6
32 Variación de la Luminosidad en unción del Aumento visual 3 / 6 para φ Γ C = φ A τ φ e = Γ φ A φ Γ = φ A C e =τ Γ eq C e E r φ PS Ce = = τ E A φa e φ φps = min, φa Γ e φ = min τ, τ φ Γ A Aumento equipupilar Mayor valor del aumento visual que permite tener una luminosidad máxima. Para tener un valor alto del Aumento equipupilar es necesario que el diámetro del jetivo ( φ ) sea grande. φ PS = φ A
33 33 / 6 Cuando el jeto servado está muy alejado y es puntual, o sus dimensiones tan reducidas que su imagen impresiona un único otorreceptor, la luminosidad vale En general: φ C e PE P φ A C e C p e φps e φ r φ PE = = τ = τ Γ = C Γ φ A φa φa Ganancia en contraste : G c e La Luminosidad del Anteojo, para el caso de jetos puntuales, es mucho mayor que la unidad = C C p e = Γ Las estrellas (jetos puntuales) se servan con un contraste muy elevado sre el ondo celeste
34 34 / 6 Ejemplo = 500mm 0 Γ= oc = 5mm e= 55mm 60 φ = 60mm φ φ = = 3mm φ 0 φa = 4mm τ = 0,75 C e PE PS PS p C e e φ PE 60 = τ = (0.75) = φa 4 e φ PS 3 = τ = (0.75) = φa 4 Imagen de un cúmulo de estrellas tenida con el Telescopio espacial Hubble p == e(0) = 400 e C C C
35 Poder Separador 35 / 6 Si nos centramos en la servación astronómica, el poder separador mide la capacidad del Anteojo para discernir las imágenes de dos estrellas cuya separación angular es pequeña. Objetivo Imagen de dos puntos igual de intensos, localizados en el ininito y separados un ángulo ψ
36 Poder Separador 36 / 6 Supuesto que las aberraciones han sido convenientemente corregidas, el poder separador está limitado por el enómeno de la diracción y por la estructura discreta de la retina. A los eectos de la diracción, y asumiendo que la Pupila de Entrada eectiva del Anteojo es el Objetivo, el límite de resolución angular del acoplamiento entre el Anteojo y la pupila de Entrada del ojo vale : ψ di 140" 140" = = e φ ( mm) φ ( mm) PE Con respecto a la inluencia de la estructura discreta de la retina, recordemos que dos jetos puntuales son discernibles por el ojo, si sus imágenes a través del Instrumento están separadas un ángulo αa 80 Por tanto, el límite de resolución vale: α 80" ψ A ret = = Γ Γ
37 Poder Separador Si consideramos conjuntamente ambos actores: ψ Zona de Aumento vacío Anteojo 37 / 6 140" 80" = máx, φ Γ La intersección de las dos curvas deine el Aumento útil o superresolvente: Γ = 4 7 φ ( ) u mm ψ di ψ ret 140" = φ ( mm ) 80" = Γ
38 38 / Anteojo de Galileo El Anteojo de Galileo es el Anteojo terrestre de diseño más antiguo y presenta una solución dierente a la del Sistema Inversor para conseguir una imagen inal derecha. Está ormado por un Objetivo convergente y un Ocular divergente acoplados de modo aocal. Objetivo (convergente) Ocular (divergente) Galileo Galilei
39 Aumento visual 39 / 6 Γ = w tan w Γ G = G w Γ tan w es positivo G Posición y tamaño de la Pupila de Salida e a p = a p < 0 Γ φ PS G = Γ φ G oc Objetivo Pupila de Salida PE Ocular PS φ φ φ La Pupila de Salida del Anteojo es virtual No es posible situar la Pupila del ojo sre ella La imagen intermedia es virtual y, por tanto, no es posible utilizar elementos como una Lente de campo, un diaragma o un retículo
40 Campo visual Objetivo No es posible situar la Pupila de entrada del ojo sre la Pupila de Salida del Anteojo. Generalmente La Pupila de entrada del ojo actúa como Pupila de Salida eectiva del acoplamiento entre el Anteojo de Galileo y el ojo. La imagen del Objetivo actúa como Lucarna de Salida ya que el Ocular divergente se diseña para que no intervenga en la limitación de rayos. Ocular φ A < φ PS Pupila de Salida eectiva 40 / 6
41 Objetivo φ Ocular Cálculo del Campo de iluminación media en el espacio óptico imagen El semicampo imagen de iluminación media es el ángulo subtendido por la Lucarna de Salida desde el centro de la pupila del ojo Campo de iluminación media en el espacio óptico jeto (Campo visual) tan w tan w m m Pupila de Salida eectiva φ = ( s a ) p φ = Γ G s + e Γ G 41 / 6
42 Campo visual φ tan wm = e Γ G s + Γ G El Campo visual es proporcional al diámetro del Objetivo y aumenta al acercar el ojo al Ocular. En el caso límite, ideal, de que la Pupila de Entrada del ojo se sitúe sre el Ocular: tan w m φ = eγ El campo visual es inversamente proporcional al aumento visual El Aumento del Anteojo de Galileo no puede tomar valores altos ya que se reduciría mucho el campo. Por ello: El Aumento no suele exceder del valor 6 y los valores más usuales son de.5 a 4. La singular coniguración de los diaragmas en el Anteojo de Galileo produce una servación del tipo Ojo de cerradura G 4 / 6
43 Proundidad de enoque Límites de enoque { } ANTEOJO Δ e = O% RO % P { IV.. N. = OROP} Al aplicar las ecuaciones de conjugación para Sistemas aocales tomando como orígenes de distancias el Objetivo y su homólogo en el espacio imagen R G p P G p x =Γ ( s a + r) x =Γ ( s a + p) Objetivo Ocular e xp xr ( p r) G Δ = = Γ Las dimensiones del campo axial son las mismas que en el Anteojo Astronómico. Sin embargo: En el Anteojo de Galileo los Límites de enoque dependen explícitamente de la posición del ojo del servador. 43 / 6
44 Luminosidad En la actualidad el anteojo de Galileo se utiliza únicamente para la servación terrestre, por lo cual analizaremos sólo el caso de jetos extensos C e e E r φ PS = = τ E A φa e φ = φ C = τ 0.8 PS A e Considerando τ L 0.9 El Anteojo de Galileo es un Instrumento óptico muy luminoso Poder Separador La Pupila del ojo constituye la Pupila de Salida del sistema El Aumento visual toma siempre valores pequeños El Anteojo de Galileo trabaja siempre por debajo del Aumento útil La estructura discreta de la retina determina el Límite de resolución α Γ A ψ = = G 80" Γ G El Anteojo de Galileo tiene un Poder Separador muy débil 44 / 6
45 45 / 6 Ventajas e inconvenientes del Anteojo de Galileo Campo visual muy limitado. Visión tipo ojo de cerradura. Valores bajos del Aumento. Poder Separador muy débil. Imagen intermedia virtual. Instrumento muy luminoso. Muy sencillo y de dimensiones reducidas en comparación con otros Anteojos que incorporan un Sistema Inversor. Muy útil cuando se requieren Aumentos bajos o como complemento de otros Instrumentos (convertidores para Objetivos otográicos, por ejemplo).
46 Práctica de laboratorio 46 / 6 Construcción de un Anteojo de Galileo. Estudio de la inluencia del Ocular divergente: La Pupila de salida es virtual: Campo visual: Visión tipo ojo de cerradura. Aumento visual: Es positivo.
47 7.5.- Telescopios relectores 47 / 6 Los Telescopios relectores se utilizan undamentalmente para la servación astronómica. El Objetivo es un espejo o acoplamiento de espejos, con lo cual no presenta aberración cromática. Pueden utilizarse espejos de gran diámetro aumentando así la Luminosidad y el Poder separador (con las limitaciones debidas a las variaciones del índice de reracción de la Atmósera). Un prlema de diseño es la ubicación del Ocular para que no intercepte el haz incidente. Existen undamentalmente dos tipos de Telescopios relectores: Telescopio de Newton. Telescopio de Cassegrain. Todas las órmulas establecidas para el estudio del Anteojo Astronómico son aplicables a los Telescopios relectores ya que la naturaleza del Objetivo (reractor o relector) no inluye.
48 Telescopio de Newton La Pupila de Entrada es una corona circular En la práctica el Espejo primario es paraboloidal para minimizar las aberraciones Objetivo Espejo secundario Isaac Newton Ocular Espejo primario r Convergente Divergente Lente de campo Sistema inversor r = Plano de imagen intermedia Retículo Diaragma 48 / 6
49 49 / 6 Telescopio de Cassegrain La Pupila de Entrada es una corona circular Espejo secundario Objetivo (E 1 + E ) Espejo primario E 1 y E son espejos eséricos concéntricos Ocular Convergente Divergente Lente de campo Sistema inversor Plano de imagen intermedia Retículo Diaragma
50 Práctica de laboratorio 50 / 6 Campo visual y Aumento. Lente de campo Retículo y diaragma Ocular divergente Objetivo Construcción de un Telescopio relector.
51 51 / 6 Ejercicio El Objetivo de un Telescopio es de distancia ocal y diámetro φ = 114mm Se dispone de tres Oculares dles de las siguientes características: Ocular (1) = 5 mm w = 45º oc Ocular () = 16 mm w = 45º oc Ocular (3) = 9.5 mm w = 45º oc m m m = 910 mm Analice la Luminosidad (para jetos extensos), el Poder separador y el Campo visual del Telescopio con cada uno de los Oculares. Nota: Considere que la Pupila del servador es de diámetro 3 φ = 4mm y que τ = (0.95) A
52 C e φ Objetivo = 910mm e φ PS = τ φa = 114mm φ e PS φ = min, φa Γ Ocular (1) = 5 mm w = 45º oc Ocular () = 16 mm w = 45º oc Ocular (3) = 9.5 mm w = 45º oc C e m m m φ = min τ, τ φ Γ A 5 / 6
53 φ Objetivo = 910mm ψ = 114mm 140" 80" = máx { ψ, ψ t} = máx, φ Γ Anteojo di re Ocular (1) = 5 mm w = 45º oc Ocular () = 16 mm w = 45º oc Ocular (3) = 9.5 mm w = 45º oc m m m Campo visual w / 6 m (1) wm = = 1.3º w 56.9 m () wm = = 0.79º w w = = 95.8 m (3) m 0.47º
54 7.6.- Denominación comercial y ejemplos Desde un punto de vista comercial los Anteojos se especiican de dierentes ormas: Telescopios (reractores y relectores): m n m n m= n= φ Prismáticos: o / donde y m n donde m= Γ y n= φ Para los Oculares se emplea la misma notación que en los microscopios Γ oc = 50 / oc ( mm). Sin embargo, se indica el valor de la distancia ocal imagen, oc, que resulta más útil para calcular el Aumento total. A veces se indica también el valor del campo angular. Conocer el diámetro del jetivo,, es muy importante ya que inluye en: Luminosidad Poder separador φ 54 / 6
55 55 / 6 Anteojo de Galileo, S XVI Telescopio reractor de Lick, S XIX San Fransisco φ = 910mm
56 56 / 6 Telescopio relector 1400/150 = 1400mm φ = 150mm Anteojo terrestre 100 x 90 Sistema inversor de prismas φ = 100mm = 90mm
57 PRISMÁTICOS Anteojo terrestre en el que el Sistema Inversor está constituido por prismas 57 / 6 Esquema de un Prismático Γ x φ Prismático monocular 45 x 90 Cámara digital incorporada Prismático binocular 10 x 50
58 58 / 6 Prismático monocular 8 x 1 Γ = 8 φ = 1mm Retículo especial calibrado para medir distancias Límites de enoque: 1m a 1000m Aplicación: Gol
59 59 / 6 Observatorio de Keck, Mauna Kea. Hawai
60 60 / 6 φ Telescopio ROBótico de Aras φ = 030mm = 03mm Telescopio relector. Campus de Burjassot = 4800mm = 600mm
61 61 / 6 Telescopio espacial Hubble
62 6 / 6 Interacción de dos Galaxias Saturno Imágenes tenidas con el Telescopio espacial Hubble
TEMA 6.- EL MICROSCOPIO
 TEMA 6.- EL MICROSCOPIO 1/ 48 Introducción. Estructura del microscopio. Aumento visual. Distancia de enfoque. Campo visual. Profundidad de enfoque. Diafragma de campo y retículos. Los oculares. Apertura
TEMA 6.- EL MICROSCOPIO 1/ 48 Introducción. Estructura del microscopio. Aumento visual. Distancia de enfoque. Campo visual. Profundidad de enfoque. Diafragma de campo y retículos. Los oculares. Apertura
TEMA 5.- LA LUPA (MICROSCOPIO SIMPLE)
 1/ 27 TEM 5.- L LUP (MICROSCOPIO SIMPLE) Introducción. umento visual. Distancia de visión equivalente. Potencia equivalente. Valores normalizados del aumento visual. Campo visual. Profundidad de enfoque.
1/ 27 TEM 5.- L LUP (MICROSCOPIO SIMPLE) Introducción. umento visual. Distancia de visión equivalente. Potencia equivalente. Valores normalizados del aumento visual. Campo visual. Profundidad de enfoque.
Práctica 3: Sistemas telescópicos. Objeto lejano.
 LABORATORIO DE ÓPTICA (ÓPTICA INSTRUMENTAL) CURSO 2009/10 Práctica 3: Sistemas telescópicos. Objeto lejano. 3.1 Objetivo de la práctica El objetivo de esta práctica es el conocimiento y manejo de los distintos
LABORATORIO DE ÓPTICA (ÓPTICA INSTRUMENTAL) CURSO 2009/10 Práctica 3: Sistemas telescópicos. Objeto lejano. 3.1 Objetivo de la práctica El objetivo de esta práctica es el conocimiento y manejo de los distintos
Práctica 5: El telemicroscopio
 LABORATORIO DE ÓPTICA (ÓPTICA INSTRUMENTAL) CURSO 009/10 Práctica 5: El telemicroscopio 5.1 Objetivo de la práctica El objetivo de esta práctica es el estudio y comprensión de los fundamentos ópticos del
LABORATORIO DE ÓPTICA (ÓPTICA INSTRUMENTAL) CURSO 009/10 Práctica 5: El telemicroscopio 5.1 Objetivo de la práctica El objetivo de esta práctica es el estudio y comprensión de los fundamentos ópticos del
TEMA IV.- PRINCIPIOS ÓPTICOS
 Master en Optometría y Ciencias de la Visión ª Edición (99-0) TEMA IV.- PRINCIPIOS ÓPTICOS En este tema, vamos a describir las principales características de los instrumentos ópticos más utilizados, como
Master en Optometría y Ciencias de la Visión ª Edición (99-0) TEMA IV.- PRINCIPIOS ÓPTICOS En este tema, vamos a describir las principales características de los instrumentos ópticos más utilizados, como
ÓPTICA ÓPTICA GEOMÉTRICA
 ÓPTICA ÓPTICA GEOMÉTRICA IES La Magdalena. Avilés. Asturias En la óptica geométrica se estudian los cambios de dirección experimentados por los rayos de luz cuando son relejados o reractados mediante representaciones
ÓPTICA ÓPTICA GEOMÉTRICA IES La Magdalena. Avilés. Asturias En la óptica geométrica se estudian los cambios de dirección experimentados por los rayos de luz cuando son relejados o reractados mediante representaciones
Seminario 3: Lentes, espejos y formación de imágenes
 Seminario 3: Lentes, espejos y ormación de imágenes Fabián Andrés Torres Ruiz Departamento de Física,, Chile 4 de Abril de 2007. Problemas. (Problema 8, capitulo 35,Física, Raymond A. Serway, las supericies
Seminario 3: Lentes, espejos y ormación de imágenes Fabián Andrés Torres Ruiz Departamento de Física,, Chile 4 de Abril de 2007. Problemas. (Problema 8, capitulo 35,Física, Raymond A. Serway, las supericies
Laboratorio de Optica
 Laboratorio de Optica 5. Lentes Delgadas Neil Bruce Laboratorio de Optica Aplicada, Centro de Instrumentos, U.N.A.M., A.P. 70-186, México, 04510, D.F. Objetivos Veriicar las ecuaciones que relacionan la
Laboratorio de Optica 5. Lentes Delgadas Neil Bruce Laboratorio de Optica Aplicada, Centro de Instrumentos, U.N.A.M., A.P. 70-186, México, 04510, D.F. Objetivos Veriicar las ecuaciones que relacionan la
TEMA 8.- INSTRUMENTACIÓN ÓPTICA PARA BAJA VISIÓN
 1/ 27 EMA 8.- INSRUMENACIÓN ÓPICA PARA BAJA VISIÓN Concepto de baja visión. Ayudas convencionales para visión cercana. Ayudas convencionales para visión intermedia. Ayudas ópticas no convencionales. 8.1.-
1/ 27 EMA 8.- INSRUMENACIÓN ÓPICA PARA BAJA VISIÓN Concepto de baja visión. Ayudas convencionales para visión cercana. Ayudas convencionales para visión intermedia. Ayudas ópticas no convencionales. 8.1.-
TEMA 4.- PODER SEPARADOR DE LOS INSTRUMENTOS ÓPTICOS
 1/ 17 Definición. TEMA 4.- PODER SEPARADOR DE LOS INSTRUMENTOS ÓPTICOS Factores que influyen en el Poder separador. Poder separador de los Instrumentos Ópticos. Capacidad de los Instrumentos Ópticos para
1/ 17 Definición. TEMA 4.- PODER SEPARADOR DE LOS INSTRUMENTOS ÓPTICOS Factores que influyen en el Poder separador. Poder separador de los Instrumentos Ópticos. Capacidad de los Instrumentos Ópticos para
Instrumentos ópticos
 Instrumentos ópticos Ojo Humano: sistema óptico ormado por un dióptrico esérico (córnea) y una lente (cristalino) orman la imagen del objeto en la retina. Punto remoto: la distancia máxima a la que puede
Instrumentos ópticos Ojo Humano: sistema óptico ormado por un dióptrico esérico (córnea) y una lente (cristalino) orman la imagen del objeto en la retina. Punto remoto: la distancia máxima a la que puede
ÓPTICA GEOMÉTRICA. Es el fenómeno que se observa cuando un rayo de luz incide sobre una superficie y se refleja. Su estudio se basa en dos leyes:
 ONDAS LUMINOSAS La luz que nos llega del sol (luz blanca), está compuesta por rayos de luz de diferentes colores. Este conjunto de rayos constituye lo que se llama espectro visible, el cual, es una zona
ONDAS LUMINOSAS La luz que nos llega del sol (luz blanca), está compuesta por rayos de luz de diferentes colores. Este conjunto de rayos constituye lo que se llama espectro visible, el cual, es una zona
Bolilla 12: Óptica Geométrica
 Bolilla 12: Óptica Geométrica 1 Bolilla 12: Óptica Geométrica Los contenidos de esta bolilla están relacionados con los principios primarios que rigen el comportamiento de los instrumentos ópticos. La
Bolilla 12: Óptica Geométrica 1 Bolilla 12: Óptica Geométrica Los contenidos de esta bolilla están relacionados con los principios primarios que rigen el comportamiento de los instrumentos ópticos. La
Observando el cielo con prismáticos y telescopios
 Observando el cielo con prismáticos y telescopios Ángel Serrano y Jacobo Aguirre Universidad de Mayores de URJC http://www.tallerdeastronomia.es/ Introducción Luz: onda electromagnética que viaja en el
Observando el cielo con prismáticos y telescopios Ángel Serrano y Jacobo Aguirre Universidad de Mayores de URJC http://www.tallerdeastronomia.es/ Introducción Luz: onda electromagnética que viaja en el
1. Dada una dioptra esférica, establecidas las siguientes convenciones de signos:
 Física 2 Biólogos y Geólogos -Curso de Verano 2012 Serie 2: Objetos. Formación de imágenes. Imágenes. Dioptras esféricas y planas. Espejos esféricos y planos. Lentes delgadas, sistemas de lentes o instrumentos.
Física 2 Biólogos y Geólogos -Curso de Verano 2012 Serie 2: Objetos. Formación de imágenes. Imágenes. Dioptras esféricas y planas. Espejos esféricos y planos. Lentes delgadas, sistemas de lentes o instrumentos.
TEMA 1.- INTRODUCCIÓN A LA ÓPTICA INSTRUMENTAL
 1/ 16 TEMA 1.- INTRODUCCIÓN A LA ÓPTICA INSTRUMENTAL Introducción. Clasificación de los Instrumentos Ópticos. Características generales de los Instrumentos Ópticos. El ojo como receptor de la información
1/ 16 TEMA 1.- INTRODUCCIÓN A LA ÓPTICA INSTRUMENTAL Introducción. Clasificación de los Instrumentos Ópticos. Características generales de los Instrumentos Ópticos. El ojo como receptor de la información
ÓPTICA GEOMÉTRICA Tipos de imágenes Imagen real Imagen virtual Imágenes en los espejos planos
 ÓPTICA GEOMÉTRICA Tipos de imágenes Imagen real, es cuando está formada sobre los propios rayos. Estas imágenes se pueden recoger sobre una pantalla. Imagen virtual, es cuando está formada por la prolongación
ÓPTICA GEOMÉTRICA Tipos de imágenes Imagen real, es cuando está formada sobre los propios rayos. Estas imágenes se pueden recoger sobre una pantalla. Imagen virtual, es cuando está formada por la prolongación
Óptica. Radio Microondas Infrarrojo Visible Ultravioleta Rayos X Rayos. plano. 2ª ley: el ángulo de incidencia es igual que el ángulo de reflexión.
 Óptica Espectro electromagnético (m) 10-1 10-3 7 10-7 4,5 10-7 10-9 10-11 Radio Microondas Inrarrojo Visible Ultravioleta Rayos X Rayos (Hz) 10 9 10 11 4 10 14 8 10 14 10 17 10 19 Hipótesis de Planck Energía
Óptica Espectro electromagnético (m) 10-1 10-3 7 10-7 4,5 10-7 10-9 10-11 Radio Microondas Inrarrojo Visible Ultravioleta Rayos X Rayos (Hz) 10 9 10 11 4 10 14 8 10 14 10 17 10 19 Hipótesis de Planck Energía
Guía Óptica. Área de Físico-Química. 4to año 2016
 Guía Óptica Área de Físico-Química 4to año 2016 Pág. 1 de 10 Espejos Reflexión de la luz: Es el fenómeno que se observa cuando un rayo de luz incide sobre una superficie y se refleja. En este fenómeno
Guía Óptica Área de Físico-Química 4to año 2016 Pág. 1 de 10 Espejos Reflexión de la luz: Es el fenómeno que se observa cuando un rayo de luz incide sobre una superficie y se refleja. En este fenómeno
SESIÓN Nº 1: MEDIDA DE FOCALES.
 Sesión nº 1: Medida de Focales. SESIÓN Nº 1: MEDIDA DE FOCALES. TRABAJO PREVIO 1. Conceptos fundamentales 2. Cuestiones 1. Conceptos fundamentales Aproximación paraxial: aproximación de ángulos con el
Sesión nº 1: Medida de Focales. SESIÓN Nº 1: MEDIDA DE FOCALES. TRABAJO PREVIO 1. Conceptos fundamentales 2. Cuestiones 1. Conceptos fundamentales Aproximación paraxial: aproximación de ángulos con el
CASO 1 - Tipo de Instrumento: LENTE PARA CÁMARA FOTOGRÁFICA RÉFLEX (Marca: SIGMA)
 Casos Prácticos - Tema 1: INSTRUMENTOS ÓPTICOS CASO 1 - Tipo de Instrumento: LENTE PARA CÁMARA FOTOGRÁFICA RÉFLEX (Marca: SIGMA) 1 CASO 1 - Tipo de Instrumento: LENTE PARA CÁMARA FOTOGRÁFICA RÉFLEX (Marca:
Casos Prácticos - Tema 1: INSTRUMENTOS ÓPTICOS CASO 1 - Tipo de Instrumento: LENTE PARA CÁMARA FOTOGRÁFICA RÉFLEX (Marca: SIGMA) 1 CASO 1 - Tipo de Instrumento: LENTE PARA CÁMARA FOTOGRÁFICA RÉFLEX (Marca:
TEMA 3: IMÁGENES FORMADAS POR EL OJO
 TEMA 3: IMÁGENES FORMADAS POR EL OJO IMÁGENES FORMADAS POR EL OJO 3.1.- Imagen dióptrica e imagen retiniana 3.2.- Tamaño de la imagen retiniana 3.3.- Grado de borrosidad de la imagen retiniana 3.4.- Profundidad
TEMA 3: IMÁGENES FORMADAS POR EL OJO IMÁGENES FORMADAS POR EL OJO 3.1.- Imagen dióptrica e imagen retiniana 3.2.- Tamaño de la imagen retiniana 3.3.- Grado de borrosidad de la imagen retiniana 3.4.- Profundidad
ÓPTICA ÓPTICA GEOMÉTRICA
 ÓPTICA La óptica es la parte de la física que estudia los fenómenos de la luz. Se divide en tres ramas: Óptica Geométrica: estudia la naturaleza particular de la luz desde el punto de vista corpuscular,
ÓPTICA La óptica es la parte de la física que estudia los fenómenos de la luz. Se divide en tres ramas: Óptica Geométrica: estudia la naturaleza particular de la luz desde el punto de vista corpuscular,
TEMA 4: OPTICA. Límite: el punto próximo. Figura Tipler 5ª Ed.
 (a) La lupa (microscopio simple) Tamaño aparente de un objeto: tamaño de la imagen formada en la retina. Objeto lejano imagen pequeña Mismo objeto más cerca imagen más grande Límite: el punto próximo Figura
(a) La lupa (microscopio simple) Tamaño aparente de un objeto: tamaño de la imagen formada en la retina. Objeto lejano imagen pequeña Mismo objeto más cerca imagen más grande Límite: el punto próximo Figura
INSTRUMENTOS ÓPTICOS: Casos Prácticos
 Objetivos: INSTRUMENTOS ÓPTICOS: Casos Prácticos 1. Identificar las características ópticas de diversos instrumentos y dispositivos a partir de la información técnica y/o comercial proporcionada por el
Objetivos: INSTRUMENTOS ÓPTICOS: Casos Prácticos 1. Identificar las características ópticas de diversos instrumentos y dispositivos a partir de la información técnica y/o comercial proporcionada por el
CAPÍTULO aletos Física para Ciencias e Ingeniería Contacto: Conceptos fundamentales
 aletos.6.04- Conceptos undamentales CAPÍTULO.6.04 Un conjunto de supericies que separan medios de distinto índice de reracción constituyen un sistema óptico. Si, como caso particular, estas supericies
aletos.6.04- Conceptos undamentales CAPÍTULO.6.04 Un conjunto de supericies que separan medios de distinto índice de reracción constituyen un sistema óptico. Si, como caso particular, estas supericies
FÍSICA. BLOQUE 3: Ondas y Óptica ÓPTICA GEOMÉTRICA 2º CURSO
 BLOQUE 3: Ondas y Óptica ÓPTICA GEOMÉTRICA El estudio de la Óptica Geométrica, se restringe al marco de la aproximación paraxial. Las ecuaciones de los sistemas ópticos se presentan desde un punto de vista
BLOQUE 3: Ondas y Óptica ÓPTICA GEOMÉTRICA El estudio de la Óptica Geométrica, se restringe al marco de la aproximación paraxial. Las ecuaciones de los sistemas ópticos se presentan desde un punto de vista
Lentes delgadas (aprox. paraxial + delgadas)
 Lentes delgadas (aprox. paraxial + delgadas) Formación de imágenes con lentes CONVERGENTES O POSITIVAS Objeto más allá del foco: Imagen REAL, INVERTIDA Objeto más cerca del foco: Imagen VIRTUAL, DERECHA,
Lentes delgadas (aprox. paraxial + delgadas) Formación de imágenes con lentes CONVERGENTES O POSITIVAS Objeto más allá del foco: Imagen REAL, INVERTIDA Objeto más cerca del foco: Imagen VIRTUAL, DERECHA,
FÍSICA 2 (FÍCOS) - CÉDRA PROF. SKIGIN SEGUNDO CUATRIMESTRE DE 2016 GUÍA 3: DESCRIPCIÓN GEOMÉTRICA DE MOVIMIENTOS ONDULATORIOS
 FÍSICA 2 (FÍCOS) - CÉDRA PROF. SKIGIN SEGUNDO CUATRIMESTRE DE 2016 GUÍA 3: DESCRIPCIÓN GEOMÉTRICA DE MOVIMIENTOS ONDULATORIOS 1. a) Si un rayo parte del punto A = (0,1,0), se refleja en el espejo plano
FÍSICA 2 (FÍCOS) - CÉDRA PROF. SKIGIN SEGUNDO CUATRIMESTRE DE 2016 GUÍA 3: DESCRIPCIÓN GEOMÉTRICA DE MOVIMIENTOS ONDULATORIOS 1. a) Si un rayo parte del punto A = (0,1,0), se refleja en el espejo plano
ÓPTICA GEOMÉTRICA. ESPEJOS Y LENTES
 80 0 ÓPTICA GEOMÉTRICA. ESPEJOS Y LENTES j Actividades. Define los siguientes conceptos: dioptrio, eje óptico, radio de curvatura, imagen real y centro óptico. Dioptrio: conjunto formado por dos medios
80 0 ÓPTICA GEOMÉTRICA. ESPEJOS Y LENTES j Actividades. Define los siguientes conceptos: dioptrio, eje óptico, radio de curvatura, imagen real y centro óptico. Dioptrio: conjunto formado por dos medios
Lentes, Espejos, Aberraciones.
 Lentes, Espejos, Aberraciones. La imagen formada en un telescopio de una estrella es un disco de difracción, y entre mas resolución tenga el telescopio, mas pequeño será ese disco. Cuando se colocan oculares
Lentes, Espejos, Aberraciones. La imagen formada en un telescopio de una estrella es un disco de difracción, y entre mas resolución tenga el telescopio, mas pequeño será ese disco. Cuando se colocan oculares
Un dioptrio es una superficie de separación entre dos medios de diferente índice de refracción. Vamos a estudiar dos: el esférico y el plano.
 Un dioptrio es una supericie de separación entre dos medios de dierente índice de reracción. Vamos a estudiar dos: el esérico el plano. Dioptrio esérico Vamos a trabajar con raos paraxiales: raos próximos
Un dioptrio es una supericie de separación entre dos medios de dierente índice de reracción. Vamos a estudiar dos: el esérico el plano. Dioptrio esérico Vamos a trabajar con raos paraxiales: raos próximos
Imagen retiniana: posición y tamaño.
 Tema IV. Imagen retiniana: posición y tamaño. La imagen retiniana es invertida y menor que el objeto (como son las imágenes formadas por una lente convexa) y es reinvertida psicológicamente en la corteza
Tema IV. Imagen retiniana: posición y tamaño. La imagen retiniana es invertida y menor que el objeto (como son las imágenes formadas por una lente convexa) y es reinvertida psicológicamente en la corteza
Física II- Curso de Verano. Clase 7
 Física II- Curso de Verano Clase 7 Formación de imágenes: ESPEJOS PLANOS Leyes de reflexión Imagen virtual, formada por la prolongación de los rayos Distancia imagen = distancia objeto d o =d i No invierte
Física II- Curso de Verano Clase 7 Formación de imágenes: ESPEJOS PLANOS Leyes de reflexión Imagen virtual, formada por la prolongación de los rayos Distancia imagen = distancia objeto d o =d i No invierte
ÓPTICA GEOMÉTRICA. Teniendo en cuenta que se trata de ángulos paraxiales, la expresión se puede simplificar a: En el triángulo APC:
 ÓPTICA GEOMÉTRICA Conceptos generales: Imágenes reales. No se ven a simple vista, pero pueden recogerse sobre una pantalla. Se forman por la intersección de rayos convergentes. Imágenes virtuales. No existen
ÓPTICA GEOMÉTRICA Conceptos generales: Imágenes reales. No se ven a simple vista, pero pueden recogerse sobre una pantalla. Se forman por la intersección de rayos convergentes. Imágenes virtuales. No existen
LUZ Y ÓPTICA. Propagación de la luz
 LUZ Y ÓPTICA Propagación de la luz La luz se propaga en línea recta en un medio homogéneo. La hipótesis de la propagación de la luz explica varios fenómenos entre los que se puede resaltar: Cuando un rayo
LUZ Y ÓPTICA Propagación de la luz La luz se propaga en línea recta en un medio homogéneo. La hipótesis de la propagación de la luz explica varios fenómenos entre los que se puede resaltar: Cuando un rayo
GUIÓN DE LA SESIÓN DE PRÁCTICAS Nº 1 Medida de focales.
 GUIÓN DE LA SESIÓN DE PRÁCTICAS Nº 1 Medida de focales. Objetivos de la práctica: Medida de la distancia focal de una lente convergente por tres métodos distintos (uno de los cuales permite la localización
GUIÓN DE LA SESIÓN DE PRÁCTICAS Nº 1 Medida de focales. Objetivos de la práctica: Medida de la distancia focal de una lente convergente por tres métodos distintos (uno de los cuales permite la localización
CUESTIONARIO DE ÓPTICA.
 CUESTIONARIO DE ÓPTICA. 1.- Qué es la luz, onda o partícula? 2.- Menciona la aportación que realizaron los personajes siguientes, acerca de la naturaleza de la luz: Arquimedes: Huygens: Young: Newton:
CUESTIONARIO DE ÓPTICA. 1.- Qué es la luz, onda o partícula? 2.- Menciona la aportación que realizaron los personajes siguientes, acerca de la naturaleza de la luz: Arquimedes: Huygens: Young: Newton:
LENTES DELGADAS 2.1. INTRODUCCIÓN
 LENTE DELGADA.. INTRODUCCIÓN En la práctica anterior se realizó un estudio de las leyes de relexión y reracción de la luz, utilizando espejos y sólidos transparentes con dierentes geometrías. Uno de los
LENTE DELGADA.. INTRODUCCIÓN En la práctica anterior se realizó un estudio de las leyes de relexión y reracción de la luz, utilizando espejos y sólidos transparentes con dierentes geometrías. Uno de los
TEMA 11 : ÓPTICA GEOMÉTRICA
 . INTRODUCCIÓN A LA ÓPTICA GEOMÉTRICA Las leyes sobre las que se estructura la óptica geométrica son: Ley de propagación rectilínea de la luz Ley de independencia de los rayos luminosos. Cada rayo es independiente
. INTRODUCCIÓN A LA ÓPTICA GEOMÉTRICA Las leyes sobre las que se estructura la óptica geométrica son: Ley de propagación rectilínea de la luz Ley de independencia de los rayos luminosos. Cada rayo es independiente
FÍSICA 2 (FÍSICOS) - CÁTEDRA DRA. ARBÓ SEGUNDO CUATRIMESTRE 2012 GUÍA 3: DESCRIPCIÓN GEOMÉTRICA DE MOVIMIENTOS ONDULATORIOS
 FÍSICA 2 (FÍSICOS) - CÁTEDRA DRA. ARBÓ SEGUNDO CUATRIMESTRE 2012 GUÍA 3: DESCRIPCIÓN GEOMÉTRICA DE MOVIMIENTOS ONDULATORIOS 1. a) Si un rayo parte del punto A = (0,1,0), se refleja en el espejo plano (x,0,z)
FÍSICA 2 (FÍSICOS) - CÁTEDRA DRA. ARBÓ SEGUNDO CUATRIMESTRE 2012 GUÍA 3: DESCRIPCIÓN GEOMÉTRICA DE MOVIMIENTOS ONDULATORIOS 1. a) Si un rayo parte del punto A = (0,1,0), se refleja en el espejo plano (x,0,z)
FÍSICA 2 (FÍSICOS) - CÁTEDRA PROF. MANDRINI VERANO DE 2016 GUÍA 3: DESCRIPCIÓN GEOMÉTRICA DE MOVIMIENTOS ONDULATORIOS
 FÍSICA 2 (FÍSICOS) - CÁTEDRA PROF. MANDRINI VERANO DE 2016 GUÍA 3: DESCRIPCIÓN GEOMÉTRICA DE MOVIMIENTOS ONDULATORIOS 1. a) Si un rayo parte del punto A = (0,1,0), se refleja en el espejo plano (x,0,z)
FÍSICA 2 (FÍSICOS) - CÁTEDRA PROF. MANDRINI VERANO DE 2016 GUÍA 3: DESCRIPCIÓN GEOMÉTRICA DE MOVIMIENTOS ONDULATORIOS 1. a) Si un rayo parte del punto A = (0,1,0), se refleja en el espejo plano (x,0,z)
1. Un faro sumergido en un lago dirige un haz de luz hacia la superficie del lago con î = 40º
 1. Un faro sumergido en un lago dirige un haz de luz hacia la superficie del lago con î = 40º. Encuentra el ángulo refractado ( n agua = 1, 33 ).. Encuentra el ángulo límite para la reflexión total interna
1. Un faro sumergido en un lago dirige un haz de luz hacia la superficie del lago con î = 40º. Encuentra el ángulo refractado ( n agua = 1, 33 ).. Encuentra el ángulo límite para la reflexión total interna
Física 2 ByG / curso de verano 2017 Guía 2: Óptica geométrica. Dioptras, espejos, lentes delgadas e instrumentos.
 Guía 2: Óptica geométrica. Dioptras, espejos, lentes delgadas e instrumentos. A. Dioptras Espacio objeto : Espacio imagen : semi-espacio de donde viene la luz el otro semi-espacio, hacia donde avanza la
Guía 2: Óptica geométrica. Dioptras, espejos, lentes delgadas e instrumentos. A. Dioptras Espacio objeto : Espacio imagen : semi-espacio de donde viene la luz el otro semi-espacio, hacia donde avanza la
TEMA IV EL OJO EMÉTROPE. VI - Tamaño de la imagen sobre la retina de un objeto extenso
 TEMA IV EL OJO EMÉTRO I - Concepto de ojo emétropre II - Punto remoto III - La ecuación de Gauss en el ojo emétrope IV - Imagen de un punto enfocado V - El círculo de desenfoque VI - Tamaño de la imagen
TEMA IV EL OJO EMÉTRO I - Concepto de ojo emétropre II - Punto remoto III - La ecuación de Gauss en el ojo emétrope IV - Imagen de un punto enfocado V - El círculo de desenfoque VI - Tamaño de la imagen
Tema II. Modelos teóricos del ojo humano: esquemático, simplicado y reducido. Pupilas.
 Tema II. Modelos teóricos del ojo humano: esquemático, simplicado y reducido. Pupilas. En este tema, una vez fijados los parámetros ópticos del ojo, vamos a calcular la posición de sus planos principales
Tema II. Modelos teóricos del ojo humano: esquemático, simplicado y reducido. Pupilas. En este tema, una vez fijados los parámetros ópticos del ojo, vamos a calcular la posición de sus planos principales
GALICIA/ JUNIO 01. LOGSE / FÍSICA / EXAMEN COMPLETO
 Desarrollar una de las dos opciones propuestas. Cada problema puntúa 3 (1,5 cada apartado) y cada cuestión teórica o práctica 1. OPCIÓN 1 Un cilindro macizo y homogéneo de 3 kg de masa y 0,1 m de radio
Desarrollar una de las dos opciones propuestas. Cada problema puntúa 3 (1,5 cada apartado) y cada cuestión teórica o práctica 1. OPCIÓN 1 Un cilindro macizo y homogéneo de 3 kg de masa y 0,1 m de radio
En este artículo pretendo de una forma breve, explicar los tipos de telescopio que un aficionado a la astronomía puede encontrar en el mercado.
 Telescopio En este artículo pretendo de una forma breve, explicar los tipos de telescopio que un aficionado a la astronomía puede encontrar en el mercado. Antes de entrar en materia, la definición de telescopio:
Telescopio En este artículo pretendo de una forma breve, explicar los tipos de telescopio que un aficionado a la astronomía puede encontrar en el mercado. Antes de entrar en materia, la definición de telescopio:
BACHILLERATO FÍSICA 9. ÓPTICA GEOMÉTRICA. Dpto. de Física y Química. R. Artacho
 BACHILLERATO FÍSICA 9. ÓPTICA GEOMÉTRICA R. Artacho Dpto. de Física y Química Índice CONTENIDOS 1. Introducción a la óptica geométrica 2. Óptica de la reflexión. Espejos planos y esféricos 3. Óptica de
BACHILLERATO FÍSICA 9. ÓPTICA GEOMÉTRICA R. Artacho Dpto. de Física y Química Índice CONTENIDOS 1. Introducción a la óptica geométrica 2. Óptica de la reflexión. Espejos planos y esféricos 3. Óptica de
Óptica Eddie L. Segura C. ÓPTICA GEOMÉTRICA
 ÓPTICA GEOMÉTRICA 1. INTRODUCCIÓN A LA ÓPTICA GEOMÉTRICA Las leyes sobre las que se estructuró la óptica geométrica son: Ley de propagación rectilínea de la luz Ley de independencia de los rayos luminosos.
ÓPTICA GEOMÉTRICA 1. INTRODUCCIÓN A LA ÓPTICA GEOMÉTRICA Las leyes sobre las que se estructuró la óptica geométrica son: Ley de propagación rectilínea de la luz Ley de independencia de los rayos luminosos.
Ver objetos minúsculos que los tenemos cerca lo hacemos gracias al microscopio.
 1 Ver objetos minúsculos que los tenemos cerca lo hacemos gracias al microscopio. Ver objetos grandes que están muy lejos de la Tierra lo conseguimos gracias al telescopio. Las invenciones del microscopio
1 Ver objetos minúsculos que los tenemos cerca lo hacemos gracias al microscopio. Ver objetos grandes que están muy lejos de la Tierra lo conseguimos gracias al telescopio. Las invenciones del microscopio
La luz. Óptica geométrica. J.M.L.C. - Chena Física 2 o Bachillerato
 Óptica geométrica J.M.L.C. - Chena [email protected] www.iesaguilarycano.com Física 2 o Bachillerato Conceptos Los fenómenos relacionados con la reflexión y refracción de la luz pueden justificarse prescindiendo
Óptica geométrica J.M.L.C. - Chena [email protected] www.iesaguilarycano.com Física 2 o Bachillerato Conceptos Los fenómenos relacionados con la reflexión y refracción de la luz pueden justificarse prescindiendo
Reflexión y refracción en superficies planas y curvas
 Física II (Biólogos y Geólogos) SERIE 1 Reflexión y refracción en superficies planas y curvas 1. Considere un conjunto de 10 superficies planas paralelas separadas entre sí por la misma distancia d. Cada
Física II (Biólogos y Geólogos) SERIE 1 Reflexión y refracción en superficies planas y curvas 1. Considere un conjunto de 10 superficies planas paralelas separadas entre sí por la misma distancia d. Cada
ÓPTICA ÓPTICA GEOMÉTRICA
 ÓPTICA ÓPTICA GEOMÉTRICA IES La Magdalena. Avilés. Asturias En la óptica geométrica se estudian los cambios de dirección experimentados por los rayos de luz cuando son reflejados o refractados mediante
ÓPTICA ÓPTICA GEOMÉTRICA IES La Magdalena. Avilés. Asturias En la óptica geométrica se estudian los cambios de dirección experimentados por los rayos de luz cuando son reflejados o refractados mediante
Hipermetropía: concepto, clasificación, punto remoto, grado de ametropía.
 Tema VI. Hipermetropía: concepto, clasificación, punto remoto, grado de ametropía. La hipermetropía es una ametropía esférica en la que los rayos procedentes de un punto objeto distante (rayos paralelos
Tema VI. Hipermetropía: concepto, clasificación, punto remoto, grado de ametropía. La hipermetropía es una ametropía esférica en la que los rayos procedentes de un punto objeto distante (rayos paralelos
Física 2 Biólogos y Geólogos - Curso de Verano 2006 Turno: Tarde
 Física 2 Biólogos y Geólogos - Curso de Verano 2006 Turno: Tarde Serie 2: Objetos. Formación de imágenes. Imágenes. Dioptras esféricas y planas. Espejos esféricos y planos. Lentes delgadas, sistemas de
Física 2 Biólogos y Geólogos - Curso de Verano 2006 Turno: Tarde Serie 2: Objetos. Formación de imágenes. Imágenes. Dioptras esféricas y planas. Espejos esféricos y planos. Lentes delgadas, sistemas de
Óptica Geométrica. Física III - Primer Semestre de Fernando Cuturrufo - Karina Ávalos
 Óptica Geométrica - Primer Semestre de 2018 Fernando Cuturrufo - Karina Ávalos 1. Un espejo cóncavo tiene un radio de curvatura con un valor absoluto de 20 cm. Halle por medios gráficos la imagen de un
Óptica Geométrica - Primer Semestre de 2018 Fernando Cuturrufo - Karina Ávalos 1. Un espejo cóncavo tiene un radio de curvatura con un valor absoluto de 20 cm. Halle por medios gráficos la imagen de un
Examen de Selectividad de Física. Modelo 2.008/09
 Examen de electividad de Física. Modelo 2.008/09 Primera parte Cuestión 1.- a) Enuncie la tercera ley de Kepler y demuéstrela para el caso de órbitas circulares. Aplique dicha ley para calcular la masa
Examen de electividad de Física. Modelo 2.008/09 Primera parte Cuestión 1.- a) Enuncie la tercera ley de Kepler y demuéstrela para el caso de órbitas circulares. Aplique dicha ley para calcular la masa
PROBLEMA EXPERIMENTAL 1
 Física Aplicada a Farmacia. //00 PROBLEMA EXPERIMENTAL 3 puntos El constantán es una aleación de cobre y níquel cuya resistividad es constante en un amplio rango de temperaturas. Esta resistividad debe
Física Aplicada a Farmacia. //00 PROBLEMA EXPERIMENTAL 3 puntos El constantán es una aleación de cobre y níquel cuya resistividad es constante en un amplio rango de temperaturas. Esta resistividad debe
Óptica Geométrica. Física III - Segundo Semestre de Fernando Cuturrufo - Karina Ávalos
 Óptica Geométrica - Segundo Semestre de 2017 Fernando Cuturrufo - Karina Ávalos 1. Un espejo cóncavo tiene un radio de curvatura con un valor absoluto de 20 cm. Halle por medios gráficos la imagen de un
Óptica Geométrica - Segundo Semestre de 2017 Fernando Cuturrufo - Karina Ávalos 1. Un espejo cóncavo tiene un radio de curvatura con un valor absoluto de 20 cm. Halle por medios gráficos la imagen de un
Resumen de Optica. Miguel Silvera Alonso. Octubre de 2000
 Resumen de Optica Miguel Silvera Alonso Octubre de 2000 Índice 1. Sistemas Opticos ideales 2 1.1. Espejo Plano................. 2 1.2. Espejo Esférico................ 2 1.3. lámina delgada................
Resumen de Optica Miguel Silvera Alonso Octubre de 2000 Índice 1. Sistemas Opticos ideales 2 1.1. Espejo Plano................. 2 1.2. Espejo Esférico................ 2 1.3. lámina delgada................
Tema 12. Lentes. Lic. María Silvia Aguirre 1
 Tema 2 Lentes Lic. María Silvia Aguirre Objetivos específicos Que el alumno logre: Diferenciar los distintos tipos de lentes. Obtener gráfica, analítica y experimentalmente la posición de la imagen de
Tema 2 Lentes Lic. María Silvia Aguirre Objetivos específicos Que el alumno logre: Diferenciar los distintos tipos de lentes. Obtener gráfica, analítica y experimentalmente la posición de la imagen de
6. ÓPTICA GEOMÉTRICA. 6.1 Espejos
 6. Óptica Geométrica 6. ÓPTICA GEOMÉTRICA La longitud de onda de la luz suele ser muy pequeña en comparación con el tamaño de obstáculos ó aberturas que se encuentra a su paso. Esto permite en general
6. Óptica Geométrica 6. ÓPTICA GEOMÉTRICA La longitud de onda de la luz suele ser muy pequeña en comparación con el tamaño de obstáculos ó aberturas que se encuentra a su paso. Esto permite en general
La luz. Refracción. Experimenta. Reflexión. Produce imágenes en. Produce imágenes en. Espejos. Lentes. Divergentes. Convergentes.
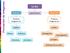 Formación de imágenes Planos Reflexión Produce imágenes en Espejos Esféricos La luz Experimenta Divergentes Refracción Produce imágenes en Lentes Convergentes Cóncavos Convexos Corrigen Defectos de la
Formación de imágenes Planos Reflexión Produce imágenes en Espejos Esféricos La luz Experimenta Divergentes Refracción Produce imágenes en Lentes Convergentes Cóncavos Convexos Corrigen Defectos de la
LAS LENTES Y SUS CARACTERÍSTICAS
 LAS LENTES Y SUS CARACTERÍSTICAS Las lentes son cuerpos transparentes limitados por dos superficies esféricas o por una esférica y una plana, las lentes se emplean a fin de desviar las rayos luminosos
LAS LENTES Y SUS CARACTERÍSTICAS Las lentes son cuerpos transparentes limitados por dos superficies esféricas o por una esférica y una plana, las lentes se emplean a fin de desviar las rayos luminosos
Optica del Microscopio Compuesto
 Optica del Microscopio Compuesto Prof. Iván Rebolledo El microscopio compuesto convencional está formado por dos sistemas de lentes de aumento ubicados en los extremos de un tubo: el ocular, en el extremo
Optica del Microscopio Compuesto Prof. Iván Rebolledo El microscopio compuesto convencional está formado por dos sistemas de lentes de aumento ubicados en los extremos de un tubo: el ocular, en el extremo
LENTES ESFÉRICAS convergentes o divergentes.
 LENTES Objetivos Conocer los tipos de lentes y los elementos de las lentes. Conocer los rayos principales y la formación de imágenes en lentes convergentes y divergentes. Conocer las partes del ojo, las
LENTES Objetivos Conocer los tipos de lentes y los elementos de las lentes. Conocer los rayos principales y la formación de imágenes en lentes convergentes y divergentes. Conocer las partes del ojo, las
Como elegir un telescopio?
 Como elegir un telescopio? Fuente: Claudio Martinez [email protected] Para elegir un telescopio hay que tener en cuenta varios aspectos, para poder tener un instrumento que no sea un juguete, y que
Como elegir un telescopio? Fuente: Claudio Martinez [email protected] Para elegir un telescopio hay que tener en cuenta varios aspectos, para poder tener un instrumento que no sea un juguete, y que
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL INSTITUTO DE CIENCIAS FÍSICAS I TÉRMINO PRIMERA EVALUACIÓN DE FÍSICA D SOLUCIÓN
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL INSTITUTO DE CIENCIAS FÍSICAS I TÉRMINO 2011-2012 PRIMERA EVALUACIÓN DE FÍSICA D SOLUCIÓN PRIMERA PARTE: Ejercicios de opción múltiple (2 puntos c/u) 1) Un rayo
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL INSTITUTO DE CIENCIAS FÍSICAS I TÉRMINO 2011-2012 PRIMERA EVALUACIÓN DE FÍSICA D SOLUCIÓN PRIMERA PARTE: Ejercicios de opción múltiple (2 puntos c/u) 1) Un rayo
Capítulo 2 Instrumentos ópticos. Características generales
 Instrumentos ópticos. Características generales 49 Capítulo 2 Instrumentos ópticos. Características generales 2.1 Clasificación Si no se cuentan entre los instrumentos ópticos los aparatos que tienen por
Instrumentos ópticos. Características generales 49 Capítulo 2 Instrumentos ópticos. Características generales 2.1 Clasificación Si no se cuentan entre los instrumentos ópticos los aparatos que tienen por
Bolilla 09. Óptica Geométrica (parte 2)
 Bolilla 09 Óptica Geométrica (parte 2) La óptica geométrica es la parte de la Física que estudia, mediante leyes geométricas sencillas, los cambios de dirección que experimentan los rayos de luz en la
Bolilla 09 Óptica Geométrica (parte 2) La óptica geométrica es la parte de la Física que estudia, mediante leyes geométricas sencillas, los cambios de dirección que experimentan los rayos de luz en la
TEMA II EL OJO TEÓRICO
 TEMA II EL OJO TEÓRICO I - El ojo como sistema óptico: ojos teóricos. II - La córnea II. - La córnea en el ojo teórico II. - La córnea simplificada III - El cristalino IV - El ojo teórico de Legrand IV.
TEMA II EL OJO TEÓRICO I - El ojo como sistema óptico: ojos teóricos. II - La córnea II. - La córnea en el ojo teórico II. - La córnea simplificada III - El cristalino IV - El ojo teórico de Legrand IV.
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL INSTITUTO DE CIENCIAS FÍSICAS II TÉRMINO PRIMERA EVALUACIÓN DE FÍSICA GENERAL II SOLUCIÓN
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL INSTITUTO DE CIENCIAS FÍSICAS II TÉRMINO 2011-2012 PRIMERA EVALUACIÓN DE FÍSICA GENERAL II SOLUCIÓN PRIMERA PARTE: Ejercicios de opción múltiple (2 puntos c/u)
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL INSTITUTO DE CIENCIAS FÍSICAS II TÉRMINO 2011-2012 PRIMERA EVALUACIÓN DE FÍSICA GENERAL II SOLUCIÓN PRIMERA PARTE: Ejercicios de opción múltiple (2 puntos c/u)
A-PDF Manual Split Demo. Purchase from to remove the watermark
 0 A-PD Manual Split Demo. Purchase from www.a-pd.com to remove the watermark 86 ÓPTIA GEOMÉTRIA j Sigue practicando. a) onstruya gráficamente la imagen obtenida en un espejo cóncavo de un objeto situado
0 A-PD Manual Split Demo. Purchase from www.a-pd.com to remove the watermark 86 ÓPTIA GEOMÉTRIA j Sigue practicando. a) onstruya gráficamente la imagen obtenida en un espejo cóncavo de un objeto situado
PROBLEMAS DE ÓPTICA GEOMÉTRICA E INSTRUMENTAL
 PROBLEMAS DE ÓPTICA GEOMÉTRICA E INSTRUMENTAL Unidad 6: 6.1. Dioptrio esférico Jaume Escofet Unidad 6: 6.1 Dioptrio esférico Uso de este material Copyright 2011 by Jaume Escofet El autor autoriza la distribución
PROBLEMAS DE ÓPTICA GEOMÉTRICA E INSTRUMENTAL Unidad 6: 6.1. Dioptrio esférico Jaume Escofet Unidad 6: 6.1 Dioptrio esférico Uso de este material Copyright 2011 by Jaume Escofet El autor autoriza la distribución
Los objetivos fotográficos
 Los objetivos fotográficos Objetivo fotográfico Un objetivo es un tubo que dirige el haz de la luz hacia la cámara fotográfica. Contiene lentes, que pueden ser de cristal o de plástico, convergentes y
Los objetivos fotográficos Objetivo fotográfico Un objetivo es un tubo que dirige el haz de la luz hacia la cámara fotográfica. Contiene lentes, que pueden ser de cristal o de plástico, convergentes y
n = 7, s 1 λ = c ν = , = 4, m
 . (Andalucía, Jun. 206) Un rayo de luz con una longitud de onda de 300 nm se propaga en el interior de una fibra de vidrio, de forma que sufre reflexión total en sus caras. a) Determine para qué valores
. (Andalucía, Jun. 206) Un rayo de luz con una longitud de onda de 300 nm se propaga en el interior de una fibra de vidrio, de forma que sufre reflexión total en sus caras. a) Determine para qué valores
IV - ÓPTICA PAU.98 PAU.98
 1.- Dónde debe colocarse un objeto para que un espejo cóncavo forme imágenes virtuales?. Qué tamaño tienen estas imágenes?. Realiza las construcciones geométricas necesarias para su explicación PAU.94
1.- Dónde debe colocarse un objeto para que un espejo cóncavo forme imágenes virtuales?. Qué tamaño tienen estas imágenes?. Realiza las construcciones geométricas necesarias para su explicación PAU.94
Como funciona el telescopio?
 Como funciona el telescopio? Espejos curvos y lentes convexos han sido usados desde tiempos muy remotos para concentrar la luz que nos llega del sol y así crear fuego; como es el caso de un lente de rocas
Como funciona el telescopio? Espejos curvos y lentes convexos han sido usados desde tiempos muy remotos para concentrar la luz que nos llega del sol y así crear fuego; como es el caso de un lente de rocas
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL INSTITUTO DE CIENCIAS FÍSICAS II TÉRMINO PRIMERA EVALUACIÓN DE FÍSICA D.
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL INSTITUTO DE CIENCIAS FÍSICAS II TÉRMINO 2011-2012 PRIMERA EVALUACIÓN DE FÍSICA D Nombre: Paralelo: PRIMERA PARTE: Ejercicios de opción múltiple (2 puntos c/u)
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL INSTITUTO DE CIENCIAS FÍSICAS II TÉRMINO 2011-2012 PRIMERA EVALUACIÓN DE FÍSICA D Nombre: Paralelo: PRIMERA PARTE: Ejercicios de opción múltiple (2 puntos c/u)
CARACTERISTICAS DE LOS TELESCOPIOS
 TELESCOPIOS CARACTERISTICAS DE LOS TELESCOPIOS Un telescopio es básicamente un instrumento óptico que recoge cierta cantidad de luz y la concentra en un punto. La cantidad de luz captada por el instrumento
TELESCOPIOS CARACTERISTICAS DE LOS TELESCOPIOS Un telescopio es básicamente un instrumento óptico que recoge cierta cantidad de luz y la concentra en un punto. La cantidad de luz captada por el instrumento
9 ÓPTICA GEOMÉTRICA: REFLEXIÓN Y REFRACCIÓN
 9 ÓPTICA GEOMÉTRICA: REFLEXIÓN Y REFRACCIÓN OBJETIVOS Uso de instrumentos ópticos. Comprobación de las leyes de la reflexión y la refracción. Estudio de la desviación de la luz en un prisma. Determinación
9 ÓPTICA GEOMÉTRICA: REFLEXIÓN Y REFRACCIÓN OBJETIVOS Uso de instrumentos ópticos. Comprobación de las leyes de la reflexión y la refracción. Estudio de la desviación de la luz en un prisma. Determinación
transparent ÓPTICA GEOMÉTRICA Prof. Jorge Rojo Carrascosa 27 de febrero de 2017
 transparent www.profesorjrc.es 27 de febrero de 2017 Conceptos Básicos 1 En medios isótropos y homogeneos, el rayo luminoso se propaga en ĺınea recta. 2 El cruce de dos o más rayos no afectan a la trayectoria.
transparent www.profesorjrc.es 27 de febrero de 2017 Conceptos Básicos 1 En medios isótropos y homogeneos, el rayo luminoso se propaga en ĺınea recta. 2 El cruce de dos o más rayos no afectan a la trayectoria.
SESIÓN Nº 3: MICROSCOPIO.
 Sesión nº 3:Microscopio. SESIÓN Nº 3: MICROSCOPIO. TRABAJO PREVIO 1. Conceptos fundamentales 2. Cuestiones 1. Conceptos fundamentales Microscopio compuesto Elementos constituyentes El microscopio compuesto
Sesión nº 3:Microscopio. SESIÓN Nº 3: MICROSCOPIO. TRABAJO PREVIO 1. Conceptos fundamentales 2. Cuestiones 1. Conceptos fundamentales Microscopio compuesto Elementos constituyentes El microscopio compuesto
10. Óptica geométrica (I)
 10. Óptica geométrica (I) Elementos de óptica geométrica Centro de curvatura: centro de la superficie esférica a la que pertenece el dioptrio esférico Radio de curvatura: radio de la superficie esférica
10. Óptica geométrica (I) Elementos de óptica geométrica Centro de curvatura: centro de la superficie esférica a la que pertenece el dioptrio esférico Radio de curvatura: radio de la superficie esférica
