Capítulo 2: Formulación matemática del problema
|
|
|
- Ángeles Blázquez Rey
- hace 9 años
- Vistas:
Transcripción
1 Capítulo : Formulación matemática del problema. Introducción El análisis del comportamiento en régimen permanente o transitorio de una red de puesta a tierra se fundamenta en la teoría electromagnética clásica. Cuando se aplica una corriente eléctrica o una tensión a un conjunto de electrodos localizados en un medio físico se origina un campo electromagnético dependiente de la fuente de excitación, de la geometría de los electrodos y del medio circundante. En el siglo XIX Maxwell [7,7] unificó las ecuaciones del electromagnetismo. La solución de estas ecuaciones permite calcular el campo eléctrico y magnético para una situación dada. Una vez que se determinan los campos asociados con un problema, es posible calcular diferencias de potencial y distribuciones de la densidad de corriente en el espacio y en el tiempo, debidas a una excitación.. Ecuaciones de Maxwell Las ecuaciones de Maxwell para cualquier sistema de coordenadas se pueden enunciar en su forma diferencial como [5]: x E = - B t x H = J + D t. D = ρ (Ley de Faraday). (Ley de Ampère). (Ley de Gauss).3. B =0 (Ley de Gauss).4 De las ecuaciones. y.3 se obtiene la ecuación de conservación de la carga: ρ. J = - t.5 Se unen a las ecuaciones de Maxwell. a.4 las relaciones constitutivas que ligan el comportamiento de los diferentes campos en los medios materiales. Estas ecuaciones relacionan la densidad de corriente J con el campo eléctrico E, la densidad de campo eléctrico D con el campo eléctrico E, y la densidad de campo magnético B con la intensidad de campo magnético H: J = σ E (Ley de Ohm).6 - -
2 E T = E T.9 donde: D = ε E.7 B = µ H.8 σ es la conductividad eléctrica del medio ε es la permitividad dieléctrica del medio y µ es la permeabilidad magnética del medio. En el caso de dos medios materiales con una superficie común de separación, se pueden deducir a partir de las ecuaciones de Maxwell las siguientes condiciones de continuidad entre los dos medios [5]: D N = D N + σ q.0 B N = B N. H = H + J x T T s n. En las condiciones de continuidad.9,.0,. y. el subíndice T se refiere a la componente tangencial a la superficie de separación, y el subíndice N a la componente normal. En la ecuación.0, σ q se refiere a la densidad de carga superficial entre las dos capas. En la ecuación., J s representa la densidad de corriente superficial entre las dos capas y n es el vector unitario normal a la superficie de separación entre las dos capas..3 Análisis con excitación constante en el tiempo Para resolver las ecuaciones de Maxwell es conveniente considerar inicialmente que las corrientes o densidades de corriente son conocidas, es decir, la densidad de corriente J se define como variable independiente. Si la densidad de corriente J es constante en el tiempo, los campos eléctricos y magnéticos también son constantes en el tiempo. Definiendo el potencial escalar φ, mediante la relación: E = - φ.3 y considerando que en un punto del espacio de solución, las cargas eléctricas libres ρ son cero, las ecuaciones. a.4 se pueden reducir a la conocida ecuación de - -
3 Laplace para el potencial eléctrico escalar [84,96]: φ = 0.4 Si el medio material es uniforme, isotrópico e infinito, la solución del potencial para un punto del espacio libre de carga eléctrica y separado una distancia r de la carga puntual q, es: q φ (r) = 4π ε r.5 Como la carga eléctrica q, aplicada en un medio de conductividad σ y permitividad dieléctrica ε pueden ser reemplazada por una inyección de corriente I utilizando la relación [5]: ε q = σ I.6 se obtiene de esta forma, la distribución espacial del potencial eléctrico producido por una inyección puntual de corriente I en un medio de conductividad uniforme σ: I φ (r) = 4π σ r.7 Cuando la inyección de corriente no se encuentra en el origen de coordenadas, sino en el punto (x o, y o, z o ), la ecuación.7 se puede expresar en el sistema de coordenadas cartesianas, de la siguiente forma: I φ (x, y, z) = 4πσ [ ] (x-x o ) + (y-y o ) + (z-z o ).8 Una vez determinado el potencial eléctrico φ producido por la inyección de una corriente puntual I en un medio conductivo uniforme, se puede calcular el vector J de densidades de corriente, aplicando.6: I J (r) = σ. E (r) = r 4π r.9 Si el medio conductivo no es uniforme, la función φ no depende exclusivamente de la distancia r entre la inyección de corriente I y el punto de interés. En cualquier caso la ecuación.4 sigue siendo válida y puede ser representada en los principales sistemas de coordenadas ortogonales [84]. La solución de la ecuación de Laplace en coordenadas cartesianas, es de la forma [84]: φ (x, y, z) = X (x). Y (y). Z (z).0 con: - 3 -
4 X (x) = A x e j m + m x+ Bx e - j m + m x - Y (y) = A y e - Z (z) = A z e m y m z m y + B y e m z + B z e...3 En coordenadas cilíndricas la solución es de la forma: φ (r, z, ψ) = R (r). Z (z). Ψ (ψ).4 con: R (r) = A r J m (m r ) + B r J - m (m r ).5 - m z m z Z (z) = A z e + B z e.6 - m ψ m ψ Ψ (ψ) = A ψ e + B ψ e.7 donde m y m son variables auxiliares que pueden tener cualquier valor en el conjunto de los números complejos. El dominio de estas variables puede quedar reducido, debido a las simetrías implícitas en el problema. El empleo de uno u otro sistema de coordenadas, depende de las condiciones de contorno o frontera de cada problema. En el caso particular del análisis del comportamiento de las redes de tierra, es habitual modelar el subsuelo en estratos horizontales que se extienden hasta el infinito. El potencial eléctrico producido por una inyección puntual de corriente en un medio semejante es independiente de la coordenada azimutal ψ en un sistema de coordenadas cilíndricas cuyo eje z es normal a las capas horizontales. Por esta razón resulta ventajoso utilizar este sistema de coordenadas para representar el comportamiento del potencial y del campo eléctrico en un sistema estratificado horizontalmente. La solución general para este tipo de problemas se puede obtener a partir de las ecuaciones.5 y.6: - φ (r, z) = R (r). Z (z) = [ A r J o (mr) + B r Y o (mr) ].[ A z e mz mz + B z e ].8 La función de Bessel de segunda especie de grado cero Y o (mr) tiende a menos infinito cuando el argumento tiende a cero. Por esta razón en la solución de problemas físicos es frecuente asignar a B r el valor cero, para permitir que el - 4 -
5 potencial en el punto de inyección de la corriente (r=0) obtenga un valor finito. En estas condiciones el potencial se expresa de la siguiente forma: - φ (r, z) = J o (mr) [ A e mz mz + B e ].9 La ecuación.9 representa una familia de funciones ortogonales, solución de la ecuación de Laplace.4 para un medio conductivo estratificado horizontalmente. La solución del problema se obtiene superponiendo todas las soluciones posibles y determinando el valor de los coeficientes indeterminados A(m) y B(m) que satisfacen las condiciones de contorno del problema: φ (r, z) = [ A(m) e - mz + B(m) e mz ] J o (mr) dm Análisis con excitación senoidal en el tiempo Si el sistema analizado es lineal se puede aplicar el principio de superposición. De esta forma un sistema excitado mediante una fuente variable en el tiempo puede ser estudiado mediante la superposición de las respuestas a un conjunto de inyecciones senoidales cuya suma coinciden con la fuente. Por esta razón resulta de gran interés determinar el comportamiento de un sistema electromagnético excitado mediante inyecciones de corriente senoidales de frecuencia ω. Cuando la fuente de excitación es variable con el tiempo, el campo eléctrico E y el magnético H también lo son. Si la excitación es senoidal, los campos electromagnéticos tienen este mismo comportamiento y las ecuaciones de Maxwell se pueden expresar fasorialmente para la frecuencia ω de la siguiente forma: x E = - j ω B x H = J + j ω D. D = ρ B = J = - j ω ρ.35 en donde, los vectores B, D, E, H y J representan fasores que giran sincrónicamente con la velocidad angular ω. Las relaciones.6 a. siguen siendo válidas, considerando como fasores los vectores correspondientes
6 Si las densidades de corriente son constantes en el tiempo, el rotacional del campo eléctrico E es nulo y se puede utilizar el concepto de potencial eléctrico escalar φ para definir todos los campos del sistema. En el caso que se está analizando, el rotacional del campo eléctrico no es nulo y por esta razón no se puede definir el campo eléctrico E mediante una función potencial escalar φ tal como se hizo en la sección anterior. Sin embargo es posible utilizar el concepto de potencial magnético vectorial A para obtener una formulación semejante. El campo eléctrico E, y la densidad de campo magnético B, se calculan en estas condiciones como [57]: E = - φ - j ω A.36 B = x A.37 En este caso, el campo eléctrico E depende por un lado del gradiente de un potencial escalar φ y por otro del potencial vectorial A. El potencial vectorial contiene la información del comportamiento inductivo del sistema. El potencial escalar φ determina el comportamiento capacitivo-conductivo del sistema. En función de estos dos potenciales se puede obtener una descripción del sistema electromagnético con excitación senoidal similar al caso analizado en la sección.3 para excitación constante en el tiempo. La ecuación.37 no define completamente el potencial vectorial, es necesario imponer una condición arbitraria adicional que relacione el potencial vectorial A y el potencial escalar φ. Para este fin, se usará la condición de Lorentz para medios conductivos [5,93]:. A = - µ ( σ + j ωε ) φ.38 que permite desacoplar el sistema formado por las ecuaciones.36 y.37 en dos ecuaciones independientes: donde: A - γ A = - µ J iny.39 φ - γ φ = - ε ρ.40 γ = - ω µε + j ωµσ.4 La ecuación.39 se puede resolver directamente debido a que la densidad de corriente J iny se refiere a la densidad de corriente inyectada externamente a través de la fuente de excitación del sistema. Si en un punto del espacio no existe corriente inyectada, la ecuación.39 se convierte en la ecuación de Helmholtz [84]: - 6 -
7 A - γ A = 0.4 Las ecuaciones.39 y.4 son relaciones fasoriales tridimensionales. En el sistema de coordenadas cartesianas la ecuación.39 se puede representar mediante el sistema de ecuaciones: A x - γ A x = - µj inyx.43 A y - γ A y = - µj inyy.44 A z - γ A z = - µj inyz.45 Para un medio uniforme, isotrópico e infinito cada una de las coordenadas del potencial magnético vectorial A depende unicamente de la distancia r al punto de interés. Las tres ecuaciones escalares.43,.44 y.45 se pueden expresar en el sistema de coordenadas esféricas de la siguiente forma: A x + R R A y + R R A x - γ A x = - µ J R iny A y - γ A y = - µ J R iny x y A z + A z - γ A z = - µ J iny R R R z.48 En un punto cualquiera del espacio sin inyección de corriente, la solución de las ecuaciones.46,.47 y.48 es [84]: µ - γ A = e R µ - γ [ I x + Iinyyy + Iinyzz ] = e R (R) I 4π R inyx 4π R iny.49 donde I iny es la corriente total inyectada en un diferencial de volumen ubicado a una distancia R del punto de interés. Una vez determinado el potencial vectorial A, se puede obtener el potencial escalar φ a partir de la ecuación.38: φ = -. A µ ( σ + j ωε ) j ω = -. A γ.50 El campo eléctrico fasorial E se puede calcular sustituyendo las ecuaciones - 7 -
8 .49 y.50 en la ecuación.36: (. A) E ( R )= - φ - j ω A = j ω [ - A ] γ.5 El campo eléctrico E de la ecuación.5 está compuesto por la superposición de dos campos, un campo conservativo representado por el gradiente de la divergencia del vector potencial magnético A, que es independiente de la trayectoria de integración cuando se determina la diferencia de potencial entre dos puntos del espacio, y un campo no conservativo jωa, que hace depender la fuerza electromotriz resultante, de la trayectoria utilizada para ir de un punto al otro. El término jωa de la ecuación.5 representa los fenómenos de caracter inductivo y el término φ representa los fenómenos capacitivos y conductivos presentes en el sistema. Para evaluar la diferencia de potencial V ab entre dos puntos del espacio en un medio infinito y homogéneo es necesario calcular la integral de línea del campo eléctrico E definido mediante la ecuación.5 entre los puntos a y b para una trayectoria dada L: b V = E(r). dl = j ω ab [ a γ b a ω b [. A (b) -. A (a) - γ a b (. A) dl - A. dl ] = a = j γ A (r). dl ].5 Si el medio conductivo posee una estratificación horizontal, el vector potencial magnético A depende de tres coordenadas ortogonales. En el sistema de coordenadas cilíndricas cada una de las ecuaciones.43,.44 y.45, para un punto del medio sin inyección de corriente, se puede expresar de la siguiente forma: A + r r A + r r Cuya solución se puede representar mediante: A + A - γ ψ z A = 0.53 donde: A (r, z, ψ) = R (r). Z (z). Ψ (ψ) R (r) = A r J m (m r ) + B r J - m (m r ) Z (z) = A z e - λz + B z e λz
9 siendo: Ψ (ψ) = A ψ sen (m ψ) + B ψ cos (m ψ).57 λ = m + γ cuando m es un número natural, la ecuación.55 queda:.58 R (r) = A r J m (m r) + B r Y m (m r) si m IN.59 Si el eje z del sistema de coordenadas cilíndricas está orientado perpendicularmente a los estratos horizontales del medio, la coordenada azimutal ψ, tiene una periodicidad de π radianes y simetría par. Con estas condiciones el valor del parámetro m puede tener solamente los valores cero o uno. El valor cero para el caso en que la componente del potencial vectorial A sea independiente del ángulo azimutal ψ, y uno si existe dependencia con esta coordenada. Debido a la simetría par con respecto a la variación de la coordenada ψ, la expansión en función coseno representa completamente la solución. Adicionalmente, para garantizar que el potencial vectorial sea finito cuando la distancia al punto de inyección de la corriente tiende a cero, se debe anular el valor del coeficiente indeterminado que acompaña a la funciones de Bessel de segunda especie Y m. La solución general cuando existe dependencia en las tres coordenadas cilíndricas de las componentes del vector potencial magnético es: A (r, z, ψ) = (C e - λz + D e λz ) J (mr) cosψ.60 y si no existe dependencia en la componente del vector potencial magnético con el ángulo azimutal ψ, se tiene: A (r, z) = (C e - λz + D e λz ) J o (mr).6 Las ecuaciones.60 y.6 representan familias de funciones ortogonales solución de la ecuación de Helmholtz.53 para un medio conductivo estratificado horizontalmente. Para cualquier valor complejo de la variable λ, las ecuaciones.60 y.6 son soluciones válidas. El problema queda resuelto superponiendo todas las posibles soluciones y calculando el valor de los coeficientes indeterminados que hacen que la solución general satisfaga las condiciones de contorno del problema. De esta forma la solución general se puede expresar como: A (r, z, ψ) = cos ψ [ C(m) e - λz + D(m) e λz ] J (mr) dm 0.6 ó: - 9 -
10 donde: A (r, z) = [ C(m) e - λz + D(m) e λz ] J o (mr) dm 0.63 λ = m + γ.64 En las ecuaciones.6 y.63 es necesario obtener las funciones indeterminadas C(m) y D(m) que satisfagan a todas de las condiciones de contorno del problema. La ecuación.49 se puede reescribir en su forma integral [07], para facilitar la obtención de las funciones indeterminadas en la variable m, mediante la siguiente expresión: µ A (r, z) = e - γ r + z µ I = Iiny m 4π r + z iny 4π e - λz Jo (mr) dm λ 0.65 En la ecuación.65 el valor de λ queda determinado mediante la ecuación.64. Expresar de esta forma la solución particular, semejante a la utilizada en.6 y.63 para la homogénea resulta conveniente para simplificar el cálculo de las funciones indeterminadas C(m) y D(m). Con el desarrollo anterior, el problema queda matemáticamente resuelto para una frecuencia ω determinada. Si se resuelven las ecuaciones para todas las frecuencias de excitación, se obtiene la respuesta en frecuencia del sistema a la perturbación transitoria. Mediante la transformación inversa de Fourier [5] se puede obtener la respuesta temporal del sistema a la excitación transitoria
un sistema de conductores cargados. Energía electrostática en función de los vectores de campo. Fuerza electrostática. Presión electrostática.
 11 ÍNDICE GENERAL INTRODUCCIÓN 13 CÁLCULO VECTORIAL 17 Escalares y vectores. Operaciones con vectores. Campos escalares y vectoriales. Sistemas de coordenadas. Transformación de coordenadas. Vector de
11 ÍNDICE GENERAL INTRODUCCIÓN 13 CÁLCULO VECTORIAL 17 Escalares y vectores. Operaciones con vectores. Campos escalares y vectoriales. Sistemas de coordenadas. Transformación de coordenadas. Vector de
Ingeniería Electrónica ELECTROMAGNETISMO Cátedra Ramos-Lavia Versión
 Versión 2013 1 TRABAJO PRÁCTICO N 0: Modelo Electromagnético 0.1 - Cuáles son las cuatro unidades SI fundamentales del electromagnetismo? 0.2 - Cuáles son las cuatro unidades de campo fundamentales del
Versión 2013 1 TRABAJO PRÁCTICO N 0: Modelo Electromagnético 0.1 - Cuáles son las cuatro unidades SI fundamentales del electromagnetismo? 0.2 - Cuáles son las cuatro unidades de campo fundamentales del
CAMPOS ELÉCTRICOS DEBIDOS A DISTRIBUCIONES CONTINUAS DE CARGA
 CAMPOS ELÉCTRICOS DEBIDOS A DISTRIBUCIONES CONTINUAS DE CARGA Este documento enuncia de forma más detallada la formulación matemática que permite el estudio de campos eléctricos debido a distribuciones
CAMPOS ELÉCTRICOS DEBIDOS A DISTRIBUCIONES CONTINUAS DE CARGA Este documento enuncia de forma más detallada la formulación matemática que permite el estudio de campos eléctricos debido a distribuciones
Lección 7. Ecuaciones de Maxwell. Ondas electromagnéticas.
 Lección 7. Ecuaciones de Maxwell. Ondas electromagnéticas. 201. Escribir las ecuaciones de Maxwell válidas en medios materiales. Definir los diferentes términos y su significado físico. Deducir las condiciones
Lección 7. Ecuaciones de Maxwell. Ondas electromagnéticas. 201. Escribir las ecuaciones de Maxwell válidas en medios materiales. Definir los diferentes términos y su significado físico. Deducir las condiciones
AUXILIAR 1 PROBLEMA 1
 AUXILIAR 1 PROBLEMA 1 Calcular el campo eléctrico en cualquier punto del espacio, producido por una recta de carga infinita (con densidad lineal de carga λ0). Luego, aplicar el teorema de Gauss para obtener
AUXILIAR 1 PROBLEMA 1 Calcular el campo eléctrico en cualquier punto del espacio, producido por una recta de carga infinita (con densidad lineal de carga λ0). Luego, aplicar el teorema de Gauss para obtener
Electrotecnia General (Prof. Dr. José Andrés Sancho Llerandi) Tema 14 CORRIENTES ALTERNAS
 TEMA 14 CORRIENTES ALTERNAS 14.1. VALORES ASOCIADOS A LAS ONDAS SENOIDALES. Sea un cuadro rectangular de lados h y l, formado por N espiras devanadas en serie, que gira a velocidad angular constante ω
TEMA 14 CORRIENTES ALTERNAS 14.1. VALORES ASOCIADOS A LAS ONDAS SENOIDALES. Sea un cuadro rectangular de lados h y l, formado por N espiras devanadas en serie, que gira a velocidad angular constante ω
LEY DE COULOMB E INTENSIDAD DE CAMPO ELECTRICO
 INDICE Prefacio XIV Visita Guiada 1 Análisis Vectorial 1 2 Ley Coulomb e Intensidad de Campo Eléctrico 26 3 Densidad de Flujo Eléctrico, Ley de Gauss y Divergencia 51 4 Energía y Potencial 80 5 Corriente
INDICE Prefacio XIV Visita Guiada 1 Análisis Vectorial 1 2 Ley Coulomb e Intensidad de Campo Eléctrico 26 3 Densidad de Flujo Eléctrico, Ley de Gauss y Divergencia 51 4 Energía y Potencial 80 5 Corriente
1. V F El producto escalar de dos vectores es siempre un número real y positivo.
 TEORIA TEST (30 %) Indique si las siguientes propuestas son VERDADERAS o FALSAS encerrando con un círculo la opción que crea correcta. Acierto=1 punto; blanco=0; error= 1. 1. V F El producto escalar de
TEORIA TEST (30 %) Indique si las siguientes propuestas son VERDADERAS o FALSAS encerrando con un círculo la opción que crea correcta. Acierto=1 punto; blanco=0; error= 1. 1. V F El producto escalar de
Medios materiales y desarrollo multipolar.
 Física Teórica 1 Guia 3 - Medios materiales y multipolos 1 cuat. 2014 Medios materiales y desarrollo multipolar. Medios materiales. 1. Una esfera de radio a está uniformemente magnetizada con densidad
Física Teórica 1 Guia 3 - Medios materiales y multipolos 1 cuat. 2014 Medios materiales y desarrollo multipolar. Medios materiales. 1. Una esfera de radio a está uniformemente magnetizada con densidad
Período Vigente: 2005
 Tópicos de Física General (0333), Redes Eléctricas I (2107), Cálculo Vectorial (025) PAG.: 1 PROPÓSITO La finalidad de esta asignatura es presentar en una forma clara y directa las leyes generales que
Tópicos de Física General (0333), Redes Eléctricas I (2107), Cálculo Vectorial (025) PAG.: 1 PROPÓSITO La finalidad de esta asignatura es presentar en una forma clara y directa las leyes generales que
Anejo 1. Teoría de Airy. Solución lineal de la ecuación de ondas.
 Anejo 1. Teoría de Airy. Solución lineal de la ecuación de ondas. Introducción y ecuaciones que rigen la propagación del oleaje. La propagación de oleaje en un fluido es un proceso no lineal. Podemos tratar
Anejo 1. Teoría de Airy. Solución lineal de la ecuación de ondas. Introducción y ecuaciones que rigen la propagación del oleaje. La propagación de oleaje en un fluido es un proceso no lineal. Podemos tratar
Ecuaciones de Maxwell y Ondas Electromagnéticas
 Capítulo 7: Ecuaciones de Maxwell y Ondas Electromagnéticas Hasta ahora: Ley de Gauss Ley de Faraday-Henry Ley de Gauss para el magnetismo Ley de Ampere Veremos que la Ley de Ampere presenta problemas
Capítulo 7: Ecuaciones de Maxwell y Ondas Electromagnéticas Hasta ahora: Ley de Gauss Ley de Faraday-Henry Ley de Gauss para el magnetismo Ley de Ampere Veremos que la Ley de Ampere presenta problemas
ECUACIONES DE POISSON Y LAPLACE
 ECUACIONES DE POISSON Y LAPLACE Partiendo de: D ρ (forma punto de Ley de Gauss ( D E ( E (3 por sustitución de (3 en ( y luego en ( se tiene: D ( E ( ρ Ésta es la ecuación de Poisson para un medio NO homogéneo
ECUACIONES DE POISSON Y LAPLACE Partiendo de: D ρ (forma punto de Ley de Gauss ( D E ( E (3 por sustitución de (3 en ( y luego en ( se tiene: D ( E ( ρ Ésta es la ecuación de Poisson para un medio NO homogéneo
Tema 7: Polarización. Índice
 Tema 7: Polarización 1 Índice Introducción Vector polarización Vector desplazamiento Leyes constitutivas Energía en presencia de dieléctricos Fuerzas sobre dieléctricos 2 Introducción Conductores: poseen
Tema 7: Polarización 1 Índice Introducción Vector polarización Vector desplazamiento Leyes constitutivas Energía en presencia de dieléctricos Fuerzas sobre dieléctricos 2 Introducción Conductores: poseen
Figura Trabajo de las fuerzas eléctricas al desplazar en Δ la carga q.
 1.4. Trabajo en un campo eléctrico. Potencial Clases de Electromagnetismo. Ariel Becerra Al desplazar una carga de prueba q en un campo eléctrico, las fuerzas eléctricas realizan un trabajo. Este trabajo
1.4. Trabajo en un campo eléctrico. Potencial Clases de Electromagnetismo. Ariel Becerra Al desplazar una carga de prueba q en un campo eléctrico, las fuerzas eléctricas realizan un trabajo. Este trabajo
CAPÍTULO III Electrostática
 CAPÍTULO III Electrostática Fundamento teórico I.- Ley de Coulomb Ia.- Ley de Coulomb La fuerza electrostática F que una carga puntual q con vector posición r ejerce sobre una carga puntual q con vector
CAPÍTULO III Electrostática Fundamento teórico I.- Ley de Coulomb Ia.- Ley de Coulomb La fuerza electrostática F que una carga puntual q con vector posición r ejerce sobre una carga puntual q con vector
Electromagnetismo I. Semestre: TAREA 2 Y SU SOLUCIÓN Dr. A. Reyes-Coronado
 Electromagnetismo I Semestre: 214-2 TAREA 2 Y SU SOLUCIÓN Dr. A. Reyes-Coronado Solución por Carlos Andrés Escobar Ruíz 1.- Problema: (2pts) a) Una carga puntual q está localizada en el centro de un cubo
Electromagnetismo I Semestre: 214-2 TAREA 2 Y SU SOLUCIÓN Dr. A. Reyes-Coronado Solución por Carlos Andrés Escobar Ruíz 1.- Problema: (2pts) a) Una carga puntual q está localizada en el centro de un cubo
Departamento de Física Aplicada III
 Departamento de Física Aplicada III Escuela Superior de Ingenieros Camino de los Descubrimientos s/n 4109 Sevilla Examen de Campos electromagnéticos. o Curso de Ingeniería Industrial. Septiembre de 011
Departamento de Física Aplicada III Escuela Superior de Ingenieros Camino de los Descubrimientos s/n 4109 Sevilla Examen de Campos electromagnéticos. o Curso de Ingeniería Industrial. Septiembre de 011
UNIVERSIDAD DE ANTIOQUIA FACULTAD DE CIENCIAS EXACTAS Y NATURALES PREGRADO EN MATEMÁTICAS
 UNIVERSIDAD DE ANTIOQUIA FACULTAD DE CIENCIAS EXACTAS Y NATURALES PREGRADO EN MATEMÁTICAS Código: CNM- 517 Nombre: Análisis vectorial Prerrequisitos: CNM-295 Duración del semestre: 16 semanas Intensidad
UNIVERSIDAD DE ANTIOQUIA FACULTAD DE CIENCIAS EXACTAS Y NATURALES PREGRADO EN MATEMÁTICAS Código: CNM- 517 Nombre: Análisis vectorial Prerrequisitos: CNM-295 Duración del semestre: 16 semanas Intensidad
El campo magnético de las corrientes estacionarias
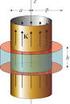 El campo magnético de las corrientes estacionarias Introducción Propiedades diferenciales del campo magnético Propiedades integrales del campo magnético Teorema de Ampère El potencial vector Ecuaciones
El campo magnético de las corrientes estacionarias Introducción Propiedades diferenciales del campo magnético Propiedades integrales del campo magnético Teorema de Ampère El potencial vector Ecuaciones
Lección 3. El campo de las corrientes estacionarias. El campo magnetostático.
 Lección 3. El campo de las corrientes estacionarias. El campo magnetostático. 81. Un campo vectorial está definido por B = B 0 u x (r < a) B r = A cos ϕ ; B r 2 ϕ = C sin ϕ (r > a) r 2 donde r y ϕ son
Lección 3. El campo de las corrientes estacionarias. El campo magnetostático. 81. Un campo vectorial está definido por B = B 0 u x (r < a) B r = A cos ϕ ; B r 2 ϕ = C sin ϕ (r > a) r 2 donde r y ϕ son
Electromagnetismo. Introducción. Líneas de campo magnético. Experimento de Oersted. El campo magnético de las corrientes estacionarias
 El campo magnético de las corrientes estacionarias Electromagnetismo Andrés Cantarero Sáez Curso 25-26 Grupo C ntroducción Propiedades diferenciales del campo magnético Propiedades integrales del campo
El campo magnético de las corrientes estacionarias Electromagnetismo Andrés Cantarero Sáez Curso 25-26 Grupo C ntroducción Propiedades diferenciales del campo magnético Propiedades integrales del campo
REPÚBLICA BOLIVARIANA DE VENEZUELA UNIVERSIDAD BICENTENARIA DE ARAGUA SECRETARIA DIRECCIÓN DE ADMISIÓN Y CONTROL DE ESTUDIOS
 FACULTAD: CARRERA: INGENIERIA INGENIERIA ELECTRICA AÑO: 94 UNIDAD CURRICULAR: CODIGO: REQUISITOS: TEORIA ELECTROMAGNETICA ELC-714 MAT-505/ELC-505 UNIDAD DE CREDITOS: 04 DENSIDAD DE HORARIO: 05 HORAS TEORICA:
FACULTAD: CARRERA: INGENIERIA INGENIERIA ELECTRICA AÑO: 94 UNIDAD CURRICULAR: CODIGO: REQUISITOS: TEORIA ELECTROMAGNETICA ELC-714 MAT-505/ELC-505 UNIDAD DE CREDITOS: 04 DENSIDAD DE HORARIO: 05 HORAS TEORICA:
EXAMEN PARCIAL DE FÍSICA DE PRIMER CURSO. 7 DE FEBRERO DE GRUPOS C Y D.
 Página 1 de 14 Al índice de exámenes EXAMEN PARCIAL DE FÍSICA DE PRIMER CURSO. 7 DE FEBRERO DE 1994. GRUPOS C Y D. E1. Deducir la ecuación de dimensiones de las siguientes magnitudes: 1- velocidad; 2-
Página 1 de 14 Al índice de exámenes EXAMEN PARCIAL DE FÍSICA DE PRIMER CURSO. 7 DE FEBRERO DE 1994. GRUPOS C Y D. E1. Deducir la ecuación de dimensiones de las siguientes magnitudes: 1- velocidad; 2-
Sílabo de Teoría Electromagnética
 Sílabo de Teoría Electromagnética I. Datos Generales Código Carácter A0559 Obligatorio Créditos 3 Periodo Académico 2017 Prerrequisito Física II Horas Teóricas: 2 Prácticas: 2 II. Sumilla de la Asignatura
Sílabo de Teoría Electromagnética I. Datos Generales Código Carácter A0559 Obligatorio Créditos 3 Periodo Académico 2017 Prerrequisito Física II Horas Teóricas: 2 Prácticas: 2 II. Sumilla de la Asignatura
Temario 4.Campo Eléctrico
 Campo Eléctrico 1 1 Temario 4.Campo Eléctrico 4.1 Concepto y definición de campo eléctrico 4.2 Campo eléctrico producido por una y varias cargas puntuales. 4.3 Lineas de Campo 4.4 Un conductor eléctrico
Campo Eléctrico 1 1 Temario 4.Campo Eléctrico 4.1 Concepto y definición de campo eléctrico 4.2 Campo eléctrico producido por una y varias cargas puntuales. 4.3 Lineas de Campo 4.4 Un conductor eléctrico
Módulo 1: Electrostática Potencial eléctrico
 Módulo 1: Electrostática Potencial eléctrico 1 Energía potencial electrostática Se tiene una analogía entre la energía potencial gravitatoria (debida a la fuerza de la gravedad) y la energía potencial
Módulo 1: Electrostática Potencial eléctrico 1 Energía potencial electrostática Se tiene una analogía entre la energía potencial gravitatoria (debida a la fuerza de la gravedad) y la energía potencial
Definición. Tema 12: Teoremas de Integración del Cálculo Vectorial. Gradiente de un campo escalar. Rotacional de un campo vectorial.
 Tema 12: Teoremas de Integración del Cálculo Vectorial El operador nabla e conoce como operador nabla al pseudo-vector = ( x, y, ) Juan Ignacio Del Valle Gamboa ede de Guanacaste Universidad de Costa Rica
Tema 12: Teoremas de Integración del Cálculo Vectorial El operador nabla e conoce como operador nabla al pseudo-vector = ( x, y, ) Juan Ignacio Del Valle Gamboa ede de Guanacaste Universidad de Costa Rica
Capítulo 7: Ecuaciones de Maxwell y Ondas Electromagnéticas
 Capítulo 7: Ecuaciones de Maxwell y Ondas Electromagnéticas Hasta ahora: Ley de Gauss Ley de Faraday-Henry Ley de Gauss para el magnetismo Ley de Ampere Veremos que la Ley de Ampere presenta problemas
Capítulo 7: Ecuaciones de Maxwell y Ondas Electromagnéticas Hasta ahora: Ley de Gauss Ley de Faraday-Henry Ley de Gauss para el magnetismo Ley de Ampere Veremos que la Ley de Ampere presenta problemas
Potencial escalar magnético y cargas de magnetización. Cálculo de la intensidad magnética en ausencia de corrientes libres.
 c Rafael R. Boix y Francisco Medina 1 Potencial escalar magnético y cargas de magnetización. Cálculo de la intensidad magnética en ausencia de corrientes libres. Consideremos un cuerpo magnetizado en ausencia
c Rafael R. Boix y Francisco Medina 1 Potencial escalar magnético y cargas de magnetización. Cálculo de la intensidad magnética en ausencia de corrientes libres. Consideremos un cuerpo magnetizado en ausencia
INDICE 1. Sistemas de Coordenadas e Integrales 2. Gradiente, Divergente y Rotacional 3. Campos Electrostáticos
 INDICE Prefacio XVII 1. Sistemas de Coordenadas e Integrales 1 1.1. Conceptos generales 1 1.2. Coordenadas de un punto 2 1.3. Los campos escalares y cómo se transforman 4 1.4. Campos vectoriales y cómo
INDICE Prefacio XVII 1. Sistemas de Coordenadas e Integrales 1 1.1. Conceptos generales 1 1.2. Coordenadas de un punto 2 1.3. Los campos escalares y cómo se transforman 4 1.4. Campos vectoriales y cómo
Operadores diferenciales
 Apéndice A Operadores diferenciales A.1. Los conceptos de gradiente, divergencia y rotor Sobre el concepto de gradiente. Si f r) es una función escalar, entonces su gradiente, en coordenadas cartesianas
Apéndice A Operadores diferenciales A.1. Los conceptos de gradiente, divergencia y rotor Sobre el concepto de gradiente. Si f r) es una función escalar, entonces su gradiente, en coordenadas cartesianas
PROBLEMA 1 *( ) + SOLUCIÓN: Sea la superficie de la parte esférica superior, parametrizada con coordenadas cilíndricas de la siguiente manera:
 PROBLEMA 1 A una esfera maciza de radio unidad se le hace una perforación cilíndrica siguiendo un eje diametral de la esfera. Suponiendo que el cilindro es circular de radio, con y que el eje que se usa
PROBLEMA 1 A una esfera maciza de radio unidad se le hace una perforación cilíndrica siguiendo un eje diametral de la esfera. Suponiendo que el cilindro es circular de radio, con y que el eje que se usa
Rotacional del campo magnético creado por corrientes estacionarias. Ley de Ampère
 c Rafael R. Boix y Francisco Medina 1 Rotacional del campo magnético creado por corrientes estacionarias. Ley de Ampère Consideremos un conductor que ocupa un volumen τ. Sea r el vector de posición de
c Rafael R. Boix y Francisco Medina 1 Rotacional del campo magnético creado por corrientes estacionarias. Ley de Ampère Consideremos un conductor que ocupa un volumen τ. Sea r el vector de posición de
TEORIA DE LOS RADIADORES LECTROMAGNETICOS ELEMENTALES
 TEORIA DE LOS RADIADORES LECTROMAGNETICOS ELEMENTALES Teoría de antenas Antena es un dispositivo que permite acoplar la energía radio eléctrica de una línea de transmisión al espacio libre o viceversa
TEORIA DE LOS RADIADORES LECTROMAGNETICOS ELEMENTALES Teoría de antenas Antena es un dispositivo que permite acoplar la energía radio eléctrica de una línea de transmisión al espacio libre o viceversa
Campo de un hilo infinito. Fuerzas magnéticas. Teorema de Ampère. Campo magnético de una espira circular
 El campo magnético de las corrientes estacionarias ntroducción Propiedades diferenciales del campo magnético Propiedades integrales del campo magnético Teorema de Ampère El potencial vector Ecuaciones
El campo magnético de las corrientes estacionarias ntroducción Propiedades diferenciales del campo magnético Propiedades integrales del campo magnético Teorema de Ampère El potencial vector Ecuaciones
UNIDAD CURRICULAR: TEORÍA DE ONDAS VII Prof. Juan Hernández Octubre Eje de Formación Prelación HAD HTIE
 PROGRAMA ANALÌTICO FACULTAD: INGENIERÌA ESCUELA: INGENIERÍA ELECTRÓNICA UNIDAD CURRICULAR: TEORÍA DE ONDAS Código de la Escuela Código Período Elaborado por Fecha Elaboración Plan de Estudios 25 25-0927
PROGRAMA ANALÌTICO FACULTAD: INGENIERÌA ESCUELA: INGENIERÍA ELECTRÓNICA UNIDAD CURRICULAR: TEORÍA DE ONDAS Código de la Escuela Código Período Elaborado por Fecha Elaboración Plan de Estudios 25 25-0927
PROGRAMA DE: ELECTROMAGNETISMO II IDENTIFICACION DE LA ASIGNATURA CODIGO OPTICO:
 UNIVERSIDAD DEL ZULIA FACULTAD EXPERIMENTAL DE CIENCIAS D.E.B.S. COORDINACION ACADEMICA DE LA FEC DEPARTAMENTO DE FISICA UNIDAD ACADÉMICA ELECTROMAGNETISMO PROGRAMA DE: ELECTROMAGNETISMO II IDENTIFICACION
UNIVERSIDAD DEL ZULIA FACULTAD EXPERIMENTAL DE CIENCIAS D.E.B.S. COORDINACION ACADEMICA DE LA FEC DEPARTAMENTO DE FISICA UNIDAD ACADÉMICA ELECTROMAGNETISMO PROGRAMA DE: ELECTROMAGNETISMO II IDENTIFICACION
Relaciones esfuerzo deformación
 Capítulo Relaciones esfuerzo deformación En esta sección se emplea la primera ley de la termodinámica para derivar la relación esfuerzo deformación..1. Relaciones constitutivas Se llama modelo constitutivo
Capítulo Relaciones esfuerzo deformación En esta sección se emplea la primera ley de la termodinámica para derivar la relación esfuerzo deformación..1. Relaciones constitutivas Se llama modelo constitutivo
Los potenciales electromagnéticos. Tema 8 Electromagnetismo
 Los potenciales electromagnéticos Tema 8 Electromagnetismo Los potenciales electromagnéticos Los potenciales electromagnéticos. Transformaciones de contraste. Ecuación de ondas para los potenciales. Soluciones
Los potenciales electromagnéticos Tema 8 Electromagnetismo Los potenciales electromagnéticos Los potenciales electromagnéticos. Transformaciones de contraste. Ecuación de ondas para los potenciales. Soluciones
01/07/2009. Ecuaciones dinámicas del motor. Fig. 1 circuito equivalente del motor de CD con excitación independiente.
 Control de Máquinas Eléctricas Primavera 2009 1. Análisis vectorial de sistema trifásicos 1. Campo magnético 2. Devanado trifásico 3. Vector espacial de un sistema de corrientes 4. Representación gráfica
Control de Máquinas Eléctricas Primavera 2009 1. Análisis vectorial de sistema trifásicos 1. Campo magnético 2. Devanado trifásico 3. Vector espacial de un sistema de corrientes 4. Representación gráfica
, Ind ice general. 1-1 Descripción general El modelo electromagnético Unidades en el SI y constantes universales 8 Resumen 10
 , Ind ice general CAPíTULO1 EL MODELO ELECTROMAGNÉTICO 2 1-1 Descripción general 2 1-2 El modelo electromagnético 4 1-3 Unidades en el SI y constantes universales 8 Resumen 10 CAPíTULO2 ANÁLISIS VECTORIAL
, Ind ice general CAPíTULO1 EL MODELO ELECTROMAGNÉTICO 2 1-1 Descripción general 2 1-2 El modelo electromagnético 4 1-3 Unidades en el SI y constantes universales 8 Resumen 10 CAPíTULO2 ANÁLISIS VECTORIAL
Física 3: Septiembre-Diciembre 2011 Clase 13,Lunes 24 de octubre de 2011
 Clase 13 Potencial Eléctrico Cálculo del potencial eléctrico Ejemplo 35: Efecto punta En un conductor el campo eléctrico es mas intenso cerca de las puntas y protuberancias pues el exceso de carga tiende
Clase 13 Potencial Eléctrico Cálculo del potencial eléctrico Ejemplo 35: Efecto punta En un conductor el campo eléctrico es mas intenso cerca de las puntas y protuberancias pues el exceso de carga tiende
EXAMEN DE FÍSICA. 5 DE FEBRERO DE GRUPOS C Y D. TEORÍA
 Página 1 de 8 Índice de exámenes EXAMEN DE FÍSICA. 5 DE FEBRERO DE 1997. GRUPOS C Y D. TEORÍA T3. Si tenemos 2 cargas puntuales separadas un adistancia l, Hay puntos fuera de la recta que las une en que
Página 1 de 8 Índice de exámenes EXAMEN DE FÍSICA. 5 DE FEBRERO DE 1997. GRUPOS C Y D. TEORÍA T3. Si tenemos 2 cargas puntuales separadas un adistancia l, Hay puntos fuera de la recta que las une en que
Electromagnetismo I. Semestre: TAREA 1 Y SU SOLUCIÓN Dr. A. Reyes-Coronado
 Electromagnetismo I Semestre: 01- TAREA 1 Y SU SOLUCIÓN Dr. A. Reyes-Coronado Solución por Carlos Andrés Escobar Ruí 1.- Problema: (5pts) (a) Doce cargas iguales q se encuentran localiadas en los vérices
Electromagnetismo I Semestre: 01- TAREA 1 Y SU SOLUCIÓN Dr. A. Reyes-Coronado Solución por Carlos Andrés Escobar Ruí 1.- Problema: (5pts) (a) Doce cargas iguales q se encuentran localiadas en los vérices
Repaso de electrostática y magnetostática. 1. En cada una de las siguientes distribuciones de carga:
 Física Teórica 1 Guia 1 - Repaso 1 cuat. 2015 Repaso de electrostática y magnetostática. Transformaciones de simetría. Ley de Gauss. Ley de Ampere. 1. En cada una de las siguientes distribuciones de carga:
Física Teórica 1 Guia 1 - Repaso 1 cuat. 2015 Repaso de electrostática y magnetostática. Transformaciones de simetría. Ley de Gauss. Ley de Ampere. 1. En cada una de las siguientes distribuciones de carga:
ACTA DE CONSEJO DE FACULTAD/DEPTO./CENTRO: ÁREA/MÓDULO: CIENCIAS BÁSICAS PRERREQUISITOS/CORREQUISITOS: FÍSICA BÁSICA Y LABORATORIO VERSIÓN: UNO
 Página 1 de 6 PROGRAMA: INGENIERÍA DE TELECOMUNICACIONES PLAN DE ESTUDIOS: 4 ACTA DE CONSEJO DE FACULTAD/DEPTO./CENTRO: 68 1. DATOS GENERALES ASIGNATURA/MÓDULO/SEMINARIO: ELECTRICIDAD, MAGNETISMO Y LABORATORIO
Página 1 de 6 PROGRAMA: INGENIERÍA DE TELECOMUNICACIONES PLAN DE ESTUDIOS: 4 ACTA DE CONSEJO DE FACULTAD/DEPTO./CENTRO: 68 1. DATOS GENERALES ASIGNATURA/MÓDULO/SEMINARIO: ELECTRICIDAD, MAGNETISMO Y LABORATORIO
TEORIA ELECTROMAGNETICA CLASE 10 SOLUCIONES DE LA ECUACION DE ONDA
 TEORIA ELECTROMAGNETICA CLASE 10 SOLUCIONES DE LA ECUACION DE ONDA Onda Electromagnética ESTA FORMADA POR UN PAR DE CAMPOS (UNO ELECTRICO Y OTRO MAGNETICO) QUE VARIAN CON LA POSICION Y EL TIEMPO ESA ONDA
TEORIA ELECTROMAGNETICA CLASE 10 SOLUCIONES DE LA ECUACION DE ONDA Onda Electromagnética ESTA FORMADA POR UN PAR DE CAMPOS (UNO ELECTRICO Y OTRO MAGNETICO) QUE VARIAN CON LA POSICION Y EL TIEMPO ESA ONDA
FISICA 2º BACHILLERATO CAMPO MAGNÉTICO E INDUCCIÓN ELECTROMAGNÉTICA
 A) CAMPO MAGNÉTICO El Campo Magnético es la perturbación que un imán o una corriente eléctrica producen en el espacio que los rodea. Esta perturbación del espacio se manifiesta en la fuerza magnética que
A) CAMPO MAGNÉTICO El Campo Magnético es la perturbación que un imán o una corriente eléctrica producen en el espacio que los rodea. Esta perturbación del espacio se manifiesta en la fuerza magnética que
CORRIENTE ALTERNA. Onda senoidal:
 CORRIENTE ALTERNA Onda senoidal: En corriente alterna, la tensión varía continuamente en el tiempo, tomando valores positivos y negativos. La forma más común de corriente alterna es la senoidal. Se debe
CORRIENTE ALTERNA Onda senoidal: En corriente alterna, la tensión varía continuamente en el tiempo, tomando valores positivos y negativos. La forma más común de corriente alterna es la senoidal. Se debe
El flujo de un campo vectorial
 Ley de Gauss Ley de Gauss Hasta ahora todo lo que hemos hecho en electrostática se basa en la ley de Coulomb. A partir de esa ley hemos definido el campo eléctrico de una carga puntual. Al generalizar
Ley de Gauss Ley de Gauss Hasta ahora todo lo que hemos hecho en electrostática se basa en la ley de Coulomb. A partir de esa ley hemos definido el campo eléctrico de una carga puntual. Al generalizar
1. Las funciones periódicas. Ondas sinusoidales. 3. La representación vectorial de una onda.
 DESARROLLO DEL AMA: 1. Las funciones periódicas. Ondas sinusoidales.. Características de una onda. 3. La representación vectorial de una onda. 4. Ondas sinusoidales simultáneas con la misma frecuencia:
DESARROLLO DEL AMA: 1. Las funciones periódicas. Ondas sinusoidales.. Características de una onda. 3. La representación vectorial de una onda. 4. Ondas sinusoidales simultáneas con la misma frecuencia:
CAMPO ELÉCTRICO MODELO 2016
 CAMPO ELÉCTRICO MODELO 2016 1- Una carga puntual, q = 3 μc, se encuentra situada en el origen de coordenadas, tal y como se muestra en la figura. Una segunda carga q 1 = 1 μc se encuentra inicialmente
CAMPO ELÉCTRICO MODELO 2016 1- Una carga puntual, q = 3 μc, se encuentra situada en el origen de coordenadas, tal y como se muestra en la figura. Una segunda carga q 1 = 1 μc se encuentra inicialmente
Capítulo 1: Introducción
 Capítulo 1: Introducción Los sistemas de puesta a tierra, contribuyen de forma importante a la protección y el buen funcionamiento de los sistemas de energía eléctrica. La red de puesta a tierra tiene
Capítulo 1: Introducción Los sistemas de puesta a tierra, contribuyen de forma importante a la protección y el buen funcionamiento de los sistemas de energía eléctrica. La red de puesta a tierra tiene
ELECTROMAGNETISMO I El Rotor de H. ELECTROMAGNETISMO I El Rotor de H
 El Rotor de H Escribamos la expresión para Iy.. =? + + + + + + = = esto es igual a la corriente dentro del área analizada 139 El Rotor de H Dividiendo ambos miembros por el área dxdz y tomando el límite
El Rotor de H Escribamos la expresión para Iy.. =? + + + + + + = = esto es igual a la corriente dentro del área analizada 139 El Rotor de H Dividiendo ambos miembros por el área dxdz y tomando el límite
Consiste en provocar una corriente eléctrica mediante un campo magnético variable.
 www.clasesalacarta.com 1 Inducción electromagnética Inducción Electromagnética Consiste en provocar una corriente eléctrica mediante un campo magnético variable. Flujo magnético ( m ) El flujo magnético
www.clasesalacarta.com 1 Inducción electromagnética Inducción Electromagnética Consiste en provocar una corriente eléctrica mediante un campo magnético variable. Flujo magnético ( m ) El flujo magnético
Fuerzas superficiales
 1.2 Fuerzas 1.2. Fuerzas Las fuerzas que pueden actuar sobre un medio continuo pueden ser de dos tipos: Fuerzas superficiales y de cuerpo. 1.2.1. Fuerzas superficiales Se define como fuerzas superficiales
1.2 Fuerzas 1.2. Fuerzas Las fuerzas que pueden actuar sobre un medio continuo pueden ser de dos tipos: Fuerzas superficiales y de cuerpo. 1.2.1. Fuerzas superficiales Se define como fuerzas superficiales
INDICE Capitulo 1. Números Capitulo 2. Secuencias Capitulo 3. Funciones, Límites y Continuidad
 INDICE Capitulo 1. Números 1 Conjuntos 1 Números reales 1 Representación decimal de los números reales 2 Representación geométrica de los números reales 2 Operación con los números reales 2 Desigualdades
INDICE Capitulo 1. Números 1 Conjuntos 1 Números reales 1 Representación decimal de los números reales 2 Representación geométrica de los números reales 2 Operación con los números reales 2 Desigualdades
Tema 3: Campos estáticos
 Tema 3: Campos estáticos 1 Índice Ecuaciones en el caso estacionario Electrostática Solución del problema electrostático Cálculo de campos mediante Ley de Gauss Energía electrostática Desarrollo multipolar
Tema 3: Campos estáticos 1 Índice Ecuaciones en el caso estacionario Electrostática Solución del problema electrostático Cálculo de campos mediante Ley de Gauss Energía electrostática Desarrollo multipolar
Campo Magnético en un alambre recto.
 Campo Magnético en un alambre recto. A.M. Velasco (133384) J.P. Soler (133380) O.A. Botina (133268) Departamento de física, facultad de ciencias, Universidad Nacional de Colombia Resumen. Se hizo pasar
Campo Magnético en un alambre recto. A.M. Velasco (133384) J.P. Soler (133380) O.A. Botina (133268) Departamento de física, facultad de ciencias, Universidad Nacional de Colombia Resumen. Se hizo pasar
2- El flujo de un campo vectorial se define para una superficie abierta o cerrada?
 ASIGNATURA FISICA II AÑO 2012 GUIA NRO. 2 LEY DE GAUSS Bibliografía Obligatoria (mínima) Capítulo 24 Física de Serway Tomo II Apunte de la cátedra: Capìtulo III PREGUNTAS SOBRE LA TEORIA Las preguntas
ASIGNATURA FISICA II AÑO 2012 GUIA NRO. 2 LEY DE GAUSS Bibliografía Obligatoria (mínima) Capítulo 24 Física de Serway Tomo II Apunte de la cátedra: Capìtulo III PREGUNTAS SOBRE LA TEORIA Las preguntas
Teoría electromagnética: fotones y luz. Leyes bá sicas de la Teoría Electromagnética.
 Teoría electromagnética: fotones y luz. Leyes bá sicas de la Teoría Electromagnética. Teoría electromagnética. El electromagnetismo es una teoría de campos que estudia y unifica los fenómenos eléctricos
Teoría electromagnética: fotones y luz. Leyes bá sicas de la Teoría Electromagnética. Teoría electromagnética. El electromagnetismo es una teoría de campos que estudia y unifica los fenómenos eléctricos
Campo de velocidades se puede representar mediante una función potencial φ, escalar
 Flujo Potencial Campo de velocidades se puede representar mediante una función potencial φ, escalar Condición necesaria flujo irrotacional, V=0. Hipótesis: Flujo irrotacional, incompresible y permanente
Flujo Potencial Campo de velocidades se puede representar mediante una función potencial φ, escalar Condición necesaria flujo irrotacional, V=0. Hipótesis: Flujo irrotacional, incompresible y permanente
2 =0 (3.146) Expresando, las componentes del tensor de esfuerzos en coordenadas cartesianas como: 2 ; = 2 2 ; =
 3.7. Función de Airy Cuando las fuerzas de cuerpo b son constantes en un sólido con estado de deformación o esfuerzo plano, el problema elástico se simplifica considerablemente mediante el uso de una función
3.7. Función de Airy Cuando las fuerzas de cuerpo b son constantes en un sólido con estado de deformación o esfuerzo plano, el problema elástico se simplifica considerablemente mediante el uso de una función
Tema 3: Campos estáticos
 Tema 3: Campos estáticos 1 Índice (I) Ecuaciones en el caso estacionario Electrostática Solución del problema electrostático Cálculo de campos mediante Ley de Gauss Energía electrostática Desarrollo multipolar
Tema 3: Campos estáticos 1 Índice (I) Ecuaciones en el caso estacionario Electrostática Solución del problema electrostático Cálculo de campos mediante Ley de Gauss Energía electrostática Desarrollo multipolar
a) Analice la continuidad en (1,0). E1) Dada F : IR 2 π g : D IR 2 I R 2 2 2
 Ejemplos de parcial de Análisis Matemático II Los ítems E1, E, E3 E4 corresponden a la parte práctica Los ítems T1 T son teóricos (sólo para promoción) T1) Sea F : IR IR diferenciable tal que F(,) 00 =
Ejemplos de parcial de Análisis Matemático II Los ítems E1, E, E3 E4 corresponden a la parte práctica Los ítems T1 T son teóricos (sólo para promoción) T1) Sea F : IR IR diferenciable tal que F(,) 00 =
Sistemas de Coordenadas
 C.U. UAEM Valle de Teotihuacán Licenciatura en Ingeniería en Computación Sistemas de Coordenadas Unidad de Aprendizaje: Fundamentos de Robótica Unidad de competencia V Elaborado por: M. en I. José Francisco
C.U. UAEM Valle de Teotihuacán Licenciatura en Ingeniería en Computación Sistemas de Coordenadas Unidad de Aprendizaje: Fundamentos de Robótica Unidad de competencia V Elaborado por: M. en I. José Francisco
Soluciones de la ecuación de onda ( ) ( ) ( ) ONDAS PLANAS. Ecuación de onda en coordenadas cartesianas. Separación de variables.
 ONDAS PLANAS Soluciones de la ecuación de onda cuación de onda en coordenadas cartesianas Ω+ Ω Ω Ω Ω + + + Ω Separación de variables Ω X Y Z d X dy dz + + + X d Y d Z d X d Y d d X dy Z d dz + + cuaciones
ONDAS PLANAS Soluciones de la ecuación de onda cuación de onda en coordenadas cartesianas Ω+ Ω Ω Ω Ω + + + Ω Separación de variables Ω X Y Z d X dy dz + + + X d Y d Z d X d Y d d X dy Z d dz + + cuaciones
Postulados de Cauchy
 1.4. Tracción 1.4.1. Postulados de Cauchy Consideremos un medio continuo sobre el que actúan las correspondientes fuerzas de cuerpo ysuperficiales (ver Fig. 1.14). Consideremos también una partícula P
1.4. Tracción 1.4.1. Postulados de Cauchy Consideremos un medio continuo sobre el que actúan las correspondientes fuerzas de cuerpo ysuperficiales (ver Fig. 1.14). Consideremos también una partícula P
Teoremas que se derivan de las ecuaciones de Poisson y Laplace.
 c Rafael R. Boix y Francisco Medina Teoremas que se derivan de las ecuaciones de Poisson y Laplace. Identidades de Green Consideremos dos campos escalares u = u(r) y v = v(r).teniendo en cuenta que se
c Rafael R. Boix y Francisco Medina Teoremas que se derivan de las ecuaciones de Poisson y Laplace. Identidades de Green Consideremos dos campos escalares u = u(r) y v = v(r).teniendo en cuenta que se
Instituto de Física Universidad de Guanajuato Agosto 2007
 Instituto de Física Universidad de Guanajuato Agosto 2007 Física III Capítulo I José Luis Lucio Martínez El material que se presenta en estas notas se encuentra, en su mayor parte, en las referencias que
Instituto de Física Universidad de Guanajuato Agosto 2007 Física III Capítulo I José Luis Lucio Martínez El material que se presenta en estas notas se encuentra, en su mayor parte, en las referencias que
ds = ds = 4πr2 Kq r 2 φ = q ε
 1 El teorema de Gauss. Supongamos una superficie que es atravesada por las líneas de fuerza de un campo eléctrico. Definimos flujo de dicho campo eléctrico a través de la superficie como φ = E S = E S
1 El teorema de Gauss. Supongamos una superficie que es atravesada por las líneas de fuerza de un campo eléctrico. Definimos flujo de dicho campo eléctrico a través de la superficie como φ = E S = E S
Cargas puntuales en movimiento
 Cargas puntuales en movimiento manuel fernández guasti 8 de agosto de 009 1. potenciales ardados Se debe evaluar el campo o los potenciales tomando en cuenta el tiempo de ardo de la distancia que deben
Cargas puntuales en movimiento manuel fernández guasti 8 de agosto de 009 1. potenciales ardados Se debe evaluar el campo o los potenciales tomando en cuenta el tiempo de ardo de la distancia que deben
INDICE 1. Desigualdades 2. Relaciones, Funciones, Graficas 3. La Línea Recta 4. Introducción al Cálculo. Límites
 INDICE 1. Desigualdades 1 1. Desigualdades 1 2. Valor absoluto 8 3. Valor absoluto y desigualdades 11 2. Relaciones, Funciones, Graficas 16 1. Conjunto. Notación de conjuntos 16 2. El plano coordenado.
INDICE 1. Desigualdades 1 1. Desigualdades 1 2. Valor absoluto 8 3. Valor absoluto y desigualdades 11 2. Relaciones, Funciones, Graficas 16 1. Conjunto. Notación de conjuntos 16 2. El plano coordenado.
Planos y Rectas. 19 de Marzo de 2012
 el Geometría en el Planos y Rectas Universidad Autónoma Metropolitana Unidad Iztapalapa 19 de Marzo de 2012 el Anteriormente vimos que es posible encontrar un número infinito de vectores, no paralelos
el Geometría en el Planos y Rectas Universidad Autónoma Metropolitana Unidad Iztapalapa 19 de Marzo de 2012 el Anteriormente vimos que es posible encontrar un número infinito de vectores, no paralelos
Física 2º Bach. Campo eléctrico 19/02/ Calcula: a) La intensidad del campo eléctrico en el centro M de la base de un triángulo
 Física 2º Bach. Campo eléctrico 19/02/10 DEPARTAMENTO DE FÍSICA E QUÍMICA Problemas Nombre: [3 PUNTOS /UNO] 1. Dos conductores esféricos concéntricos huecos, de radios 6,00 y 10,0 cm, están cargados con
Física 2º Bach. Campo eléctrico 19/02/10 DEPARTAMENTO DE FÍSICA E QUÍMICA Problemas Nombre: [3 PUNTOS /UNO] 1. Dos conductores esféricos concéntricos huecos, de radios 6,00 y 10,0 cm, están cargados con
Guía n 9: Materiales Magnéticos Ecuaciones de Maxwell Ondas Electromagnéticas
 Guía n 9: Materiales Magnéticos Ecuaciones de Maxwell Ondas Electromagnéticas Problema 1 Dos imanes permanentes iguales A y B, cuyo momento magnético es P m están situados como indica la figura. La distancia
Guía n 9: Materiales Magnéticos Ecuaciones de Maxwell Ondas Electromagnéticas Problema 1 Dos imanes permanentes iguales A y B, cuyo momento magnético es P m están situados como indica la figura. La distancia
Potencia y energía electromagnética.
 Potencia y energía electromagnética. Importancia. Existen muchos dispositivos de interés práctico para los ingenieros electrónicos y eléctricos que se basan en la transmisión o conversión de energía electromagnética.
Potencia y energía electromagnética. Importancia. Existen muchos dispositivos de interés práctico para los ingenieros electrónicos y eléctricos que se basan en la transmisión o conversión de energía electromagnética.
FISICA 2º BACHILLERATO CAMPO ELECTRICO
 ) CMPO ELÉCTRICO Cuando en el espacio vacío se introduce una partícula cargada, ésta lo perturba, modifica, haciendo cambiar su geometría, de modo que otra partícula cargada que se sitúa en él, estará
) CMPO ELÉCTRICO Cuando en el espacio vacío se introduce una partícula cargada, ésta lo perturba, modifica, haciendo cambiar su geometría, de modo que otra partícula cargada que se sitúa en él, estará
MAGNITUDES VECTORIALES
 MGNITUDES VECTORILES ÍNDICE 1. Magnitudes escalares y magnitudes vectoriales 2. Componentes de un vector 3. Coordenadas polares 4. Clasificación de los vectores 5. Suma y resta de vectores 6. Producto
MGNITUDES VECTORILES ÍNDICE 1. Magnitudes escalares y magnitudes vectoriales 2. Componentes de un vector 3. Coordenadas polares 4. Clasificación de los vectores 5. Suma y resta de vectores 6. Producto
Ecuaciones generales Modelo de Maxwell
 Ecuaciones generales Modelo de Maxwell Introducción Fuentes de campo: arga eléctrica. orriente eléctrica. Ecuación de continuidad. Definición del campo electromagnético. Ecuaciones de Maxwell. Forma Integral.
Ecuaciones generales Modelo de Maxwell Introducción Fuentes de campo: arga eléctrica. orriente eléctrica. Ecuación de continuidad. Definición del campo electromagnético. Ecuaciones de Maxwell. Forma Integral.
Procesos transitorios y frecuencia compleja
 Procesos transitorios y frecuencia compleja Objetivos 1. Comprender y familiarizarse con los procesos transitorios en circuitos de primer orden estimulados con corriente alterna, aplicando el método clásico
Procesos transitorios y frecuencia compleja Objetivos 1. Comprender y familiarizarse con los procesos transitorios en circuitos de primer orden estimulados con corriente alterna, aplicando el método clásico
Inducción Electromagnética
 Inducción Electromagnética Área Física Resultados de aprendizaje Calcular diferentes magnitudes físicas en circuitos sujetos a inducción magnética. Contenidos 1. Introducción teórica. 2. Ejercicios. Debo
Inducción Electromagnética Área Física Resultados de aprendizaje Calcular diferentes magnitudes físicas en circuitos sujetos a inducción magnética. Contenidos 1. Introducción teórica. 2. Ejercicios. Debo
ESCUELA: UNIVERSIDAD DEL ISTMO
 1.-IDENTIFICACIÓN ESCUELA: UNIVERSIDAD DEL ISTMO CLAVE: 3034 GRADO: ING. EN COMPUTACIÓN, TERCER SEMESTRE TIPO DE TEÓRICA / PRÁCTICA ANTECEDENTE CURRICULAR: 304.- OBJETIVO GENERAL Proporcionar al alumno
1.-IDENTIFICACIÓN ESCUELA: UNIVERSIDAD DEL ISTMO CLAVE: 3034 GRADO: ING. EN COMPUTACIÓN, TERCER SEMESTRE TIPO DE TEÓRICA / PRÁCTICA ANTECEDENTE CURRICULAR: 304.- OBJETIVO GENERAL Proporcionar al alumno
A. No existe. B. Es una elipse. C. Es una circunferencia. D. Es una hipérbola equilátera.
 CUESTIONES SOBRE CAMPO ELECTROSTÁTICO 1.- En un campo electrostático, el corte de dos superficies equiescalares con forma de elipsoide, con sus centros separados y un mismo eje mayor: No existe. B. Es
CUESTIONES SOBRE CAMPO ELECTROSTÁTICO 1.- En un campo electrostático, el corte de dos superficies equiescalares con forma de elipsoide, con sus centros separados y un mismo eje mayor: No existe. B. Es
Unidad Nº 10. Magnetismo
 Unidad Nº 10 Magnetismo 10.1. Definición y propiedades del campo magnético. Fuerza magnética en una corriente. Movimiento de cargas en un campo magnético. 10.2. Campos magnéticos creados por corrientes.
Unidad Nº 10 Magnetismo 10.1. Definición y propiedades del campo magnético. Fuerza magnética en una corriente. Movimiento de cargas en un campo magnético. 10.2. Campos magnéticos creados por corrientes.
