Álgebra Lineal Ma1010
|
|
|
- Arturo Vázquez Villalobos
- hace 6 años
- Vistas:
Transcripción
1 Álgebra Lineal Ma1010 Aplicaciones de Sistemas de Ecuaciones Lineales Departamento de Matemáticas ITESM Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 1/47
2 En esta lectura veremos algunas aplicaciones de los sistemas de ecuaciones lineales. Las aplicaciones de la resoluciones de sistemas son innumerables, y por consiguiente es imposible pretender cubrir las aplicaciones. Queda como reto personal encontrar situaciones donde surgan este tipo de problemas. Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 2/47
3 La lectura pretende que usted conozca algunas de las situaciones que conducen a la resolución de un sistema de ecuaciones lineales. blemente, la técnica de las fracciones parciales, el ajuste de curvas y algunos más. Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 3/47
4 parciales Una técnica muy conveniente utilizada en algunas tareas matemáticas es aquella conocida como fracciones parciales. Ésta se aplica para simplificar integrales o transformadas de Laplace, por citar algunos ejemplos. La idea principal consiste en cambiar la forma que puede ser expresado un cociente entre polinomios a otra forma más conveniente para cierto tipo de cálculo. Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 4/47
5 Ejemplo Determine los valores de las constantes a y b para que satisfagan: 1 (x 2)(x+3) = a x 2 + b x+3 Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 5/47
6 Solución Se debe cumplir: 1 (x 2)(x+3) = a x 2 + b x+3 = a(x+3)+b(x 2) (x 2)(x+3) = ax+3a+bx 2b (x 2)(x+3) = (3a 2b)+(a+b)x (x 2)(x+3) Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 6/47
7 Esto se cumple si: Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 7/47
8 Esto se cumple si: Es decir, si: 1+0 x = 1 = (3a 2b)+(a+b)x 3a 2b = 1 a + b = 0 El cual tiene como solución: a = 1 5 y b = 1 5 Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 7/47
9 Ejemplo (Forma dudosa) Determine los valores de las constantes a y b para que satisfagan: 2+2x+2x 2 (x+1)(x 2 +1) = a x+1 + b x 2 +1 Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 8/47
10 Solución Se debe cumplir: 2+2x+2x 2 (x+1)(x 2 +1) = a x+1 + b x 2 +1 = a(x2 +1)+b(x+1) (x+1)(x 2 +1) = ax2 +a+bx+b (x+1)(x 2 +1) = (a+b)+(b)x+ax2 (x+1)(x 2 +1) Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 9/47
11 Esto se cumple si: Es decir, si: 2+2x+2x 2 = (a+b) + (b)x+ax 2 a + b = 2 + b = 2 a = 2 Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 10/47
12 Esto se cumple si: Es decir, si: 2+2x+2x 2 = (a+b) + (b)x+ax 2 El cual no tiene solución. a + b = 2 + b = 2 a = 2 Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 10/47
13 Esto se cumple si: Es decir, si: 2+2x+2x 2 = (a+b) + (b)x+ax 2 a + b = 2 + b = 2 a = 2 El cual no tiene solución. Qué puede andar mal? Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 10/47
14 Esto se cumple si: Es decir, si: 2+2x+2x 2 = (a+b) + (b)x+ax 2 a + b = 2 + b = 2 a = 2 El cual no tiene solución. Qué puede andar mal? La forma propuesta para la expresión en fracciones parciales. Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 10/47
15 Ejemplo Determine los valores de las constantes a, b y c para que satisfagan: 2+2x+2x 2 (x+1)(x 2 +1) = a x+1 + bx+c x 2 +1 Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 11/47
16 Solución Se debe cumplir: 2x 2 +2x+2 (x+1)(x 2 +1) = a x+1 + bx+c x 2 +1 = a(x2 +1)+(bx+c)(x+1) (x+1)(x 2 +1) = ax2 +a+bx 2 +bx+cx+c (x+1)(x 2 +1) = (a+b)x2 +(b+c)x+(a+c) (x+1)(x 2 +1) Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 12/47
17 Esto se cumple si: 2x 2 +2x+2 = (a+b)x 2 +(b+c)x+(a+c) Es decir, si: a + b = 2 b + c = 2 a + c = 2 Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 13/47
18 Esto se cumple si: 2x 2 +2x+2 = (a+b)x 2 +(b+c)x+(a+c) Es decir, si: a + b = 2 b + c = 2 a + c = 2 El cual tiene como solución: a = 1, b = 1 y c = 1 Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 13/47
19 Determinación de curvas Un problema comun en diferentes áreas es la determinación de curvas. es decir el problema de encontrar la función que pasa por un conjunto de puntos. Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 14/47
20 Determinación de curvas Un problema comun en diferentes áreas es la determinación de curvas. es decir el problema de encontrar la función que pasa por un conjunto de puntos. Usualmente se conoce la naturaleza de la función, es decir, se conoce la forma que debe tener la función. Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 14/47
21 Determinación de curvas Un problema comun en diferentes áreas es la determinación de curvas. es decir el problema de encontrar la función que pasa por un conjunto de puntos. Usualmente se conoce la naturaleza de la función, es decir, se conoce la forma que debe tener la función. Por ejemplo, línea recta, parábola o exponencial etc. Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 14/47
22 Determinación de curvas Un problema comun en diferentes áreas es la determinación de curvas. es decir el problema de encontrar la función que pasa por un conjunto de puntos. Usualmente se conoce la naturaleza de la función, es decir, se conoce la forma que debe tener la función. Por ejemplo, línea recta, parábola o exponencial etc. Lo que se hace para resolver este tipo de problemas es describir la forma más general de la función mediante parámetros constantes. Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 14/47
23 Determinación de curvas Un problema comun en diferentes áreas es la determinación de curvas. es decir el problema de encontrar la función que pasa por un conjunto de puntos. Usualmente se conoce la naturaleza de la función, es decir, se conoce la forma que debe tener la función. Por ejemplo, línea recta, parábola o exponencial etc. Lo que se hace para resolver este tipo de problemas es describir la forma más general de la función mediante parámetros constantes. Y posteriormente se determinan estos parámetros haciendo pasar la función por los puntos conocidos. Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 14/47
24 Ejemplo Determine la función cudrática que pasa por los puntos P(1,4), Q( 1,2), y R(2,3). Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 15/47
25 Ejemplo Determine la función cudrática que pasa por los puntos P(1,4), Q( 1,2), y R(2,3). Solución La forma más general de una cuadrática es: f(x) = ax 2 +bx+c donde los coeficientes a, b, y c son constantes numéricas. El problema consiste en determinar estos coeficientes. Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 15/47
26 Ejemplo Determine la función cudrática que pasa por los puntos P(1,4), Q( 1,2), y R(2,3). Solución La forma más general de una cuadrática es: f(x) = ax 2 +bx+c donde los coeficientes a, b, y c son constantes numéricas. El problema consiste en determinar estos coeficientes. Así pues los parámetros a, b, y c se vuelven ahora las incógnitas. Y para poderlas determinar requerimos de ecuaciones o igualdades que deben satisfacer. Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 15/47
27 Para determinar estas ecuaciones debemos usar los puntos. Para que la función pase por el punto P(1,4) se debe cumplir que f(x = 1) = 4 Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 16/47
28 Para determinar estas ecuaciones debemos usar los puntos. Para que la función pase por el punto P(1,4) se debe cumplir que f(x = 1) = 4 es decir, se debe cumplir: a(1) 2 +b(1)+c = 4 Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 16/47
29 Para determinar estas ecuaciones debemos usar los puntos. Para que la función pase por el punto P(1,4) se debe cumplir que f(x = 1) = 4 es decir, se debe cumplir: a(1) 2 +b(1)+c = 4 es decir, se debe cumplir: a+b+c = 4 Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 16/47
30 Procediendo de igual manera con el punto Q( 1, 2): formulamos la ecuación: y para R(2,3): a b+c = 2 4a+2b+c = 3 Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 17/47
31 Resumiendo para que la función f(x) = ax 2 +bx+c pase por los puntos P, Q, y R deben cumplirse las ecuaciones: a + b + c = 4 a b + c = 2 4a + 2b + c = 3 Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 18/47
32 Resumiendo para que la función f(x) = ax 2 +bx+c pase por los puntos P, Q, y R deben cumplirse las ecuaciones: a + b + c = 4 a b + c = 2 4a + 2b + c = 3 La solución a este sistema es: a = 2 3,b = 1, y c = 11 3 Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 18/47
33 La misma situación presentada en el problema de las fracciones parciales que originaba un sistema inconsistente, se puede presentar en la determinación de funciones. Y la conclusión es similar: si el sistema originado es inconsistente lo que se concluye es que no existe una función con esa forma general que pase exactamente por los puntos dados. Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 19/47
34 Ejemplo Conociendo la solución general a una ED: y(t) = C 1 e t +C 2 e t +C 3 e 3t Determine en orden los valores de las constantes C 1, C 2, y C 3 para que se cumpla: y(0) = 0, y (0) = 1, y (0) = 2 Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 20/47
35 Ejemplo Conociendo la solución general a una ED: y(t) = C 1 e t +C 2 e t +C 3 e 3t Determine en orden los valores de las constantes C 1, C 2, y C 3 para que se cumpla: Solución y(0) = 0, y (0) = 1, y (0) = 2 y(t) = C 1 e t +C 2 e t +C 3 e 3t y (t) = C 1 e t C 2 e t +3C 3 e 3t y (t) = C 1 e t +C 2 e t +9C 3 e 3t Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 20/47
36 Usando las condiciones iniciales y las derivadas calculadas tenemos: 0 = C 1 +C 2 +C 3 1 = C 1 C 2 +3C 3 2 = C 1 +C 2 +9C 3 Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 21/47
37 Usando las condiciones iniciales y las derivadas calculadas tenemos: 0 = C 1 +C 2 +C 3 1 = C 1 C 2 +3C 3 2 = C 1 +C 2 +9C 3 La solución es: C 1 = 0, C 2 = 1/4 y C 3 = 1/4. Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 21/47
38 Balanceo de Una aplicación sencilla de los sistemas de ecuaciones se da en el balanceo de reacciones químicas. Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 22/47
39 Balanceo de Una aplicación sencilla de los sistemas de ecuaciones se da en el balanceo de reacciones químicas. La problemática consiste en determinar el número entero de moléculas que intervienen en una reacción química cuidando siempre que el número de átomos de cada sustancia se preserve. Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 22/47
40 Ejemplo Balancee la reacción química ach 4 +bo 2 cco 2 +dh 2 O Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 23/47
41 Ejemplo Balancee la reacción química ach 4 +bo 2 cco 2 +dh 2 O Solución Para determinar los coeficientes a, b, c, y d que representan el número de moléculas de las sustancias en la reacción debemos igualar el número de átomos en cada miembro: Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 23/47
42 Por los átomos de carbono Por los átomos de oxígeno a = c 2b = 2c+d Por los átomos de hidrógeno 4a = 2d Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 24/47
43 Este sistema es consistente y origina infinitas soluciones. La fórmula general para las soluciones queda: a = 1 2 d b = d c = 1 2 d Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 25/47
44 Este sistema es consistente y origina infinitas soluciones. La fórmula general para las soluciones queda: a = 1 2 d b = d c = 1 2 d El valor más pequeño de d que hace que los números de moléculas sean enteros positivos es d = 2: a = 1,b = 2,c = 1, y d = 2 Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 25/47
45 Aplicaciones a Manufactura Ejemplo Patito computers fabrica tres modelos de computadoras personales: cañon, clon, y lenta-pero-segura. Para armar una computadora modelo cañon necesita 12 horas de ensamblado, 2.5 para probarla, y 2 más para instalar sus programas. Para una clon requiere 10 horas de ensamblado, 2 para probarla, y 2 para instalar programas. Y por último, para una lenta-pero-segura requiere 6 para ensamblado, 1.5 para probarla, y 1.5 para instalar programas. Si la fábrica dispone en horas por mes de 556 para ensamble, 120 para pruebas, y 103 horas para instalación de programas, cuántas computadoras se pueden producir por mes? Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 26/47
46 Solución En nuestro caso las incógnitas el número de cada tipo de computadora a producir: x = número de computadoras cañon y = número de computadoras clon z = número de computadoras lenta-pero-segura Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 27/47
47 Solución En nuestro caso las incógnitas el número de cada tipo de computadora a producir: x = número de computadoras cañon y = número de computadoras clon z = número de computadoras lenta-pero-segura Para determinar las ecuaciones debemos utilizar los tiempos de ensamblado, pruebas, e instalación de programas. Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 27/47
48 Ensamblado 556(total) = 12x(cañon)+10y(clon)+6z(lenta) Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 28/47
49 Ensamblado Pruebas 556(total) = 12x(cañon)+10y(clon)+6z(lenta) 120(total) = 2.5x(cañon)+2y(clon)+1.5z(lenta) Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 28/47
50 Ensamblado Pruebas 556(total) = 12x(cañon)+10y(clon)+6z(lenta) 120(total) = 2.5x(cañon)+2y(clon)+1.5z(lenta) Instalación de programas 103(total) = 2x(cañon)+2y(clon)+1.5z(lenta) Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 28/47
51 Al resolver este sistema obtenemos: x = 34,y = 4,z = 18 Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 29/47
52 Dado lo común de las aplicaciones hacia el área de manufactura, existe una forma simple de construir la matriz del sistema de ecuaciones que en general se trabaja como una tabla: En la última columna aparecen los recursos: un renglón para cada tipo de recursos y en cuya posición final se pone el total de recursos disponibles. En las primera columnas se colocan los objetos o modelos a ser ensamblados o construidos: en cada posición se coloca el total de recursos que consume en forma unitaria cada tipo de objeto. Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 30/47
53 Recursos requeridos por unidad Recurso Cañon Clon Lenta Total Ensamble Pruebas Instalación Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 31/47
54 Aplicaciones Diversas Ejemplo Un negociante internacional necesita, en promedio, cantidades fijas de yenes japoneses, francos franceses, y marcos alemanes para cada uno de sus viajes de negocios. Este año viajó tres veces. La primera vez cambió un total de $434 a la siguiente paridad: 100 yenes, 1.5 francos y 1.2 marcos por dolar. La segunda vez, cambió un total de $406 con las siguientes tasas: 100 yenes, 1.2 francos, y 1.5 marcos por dolar. La tercera vez cambió $434 en total, a $125 yenes, 1.2 francos, y 1.2 marcos por dolar. Qué cantidades de yenes, francos y marcos compró cada vez? Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 32/47
55 Solución En nuestro caso las incógnitas son las cantidades de moneda extranjera requerida que se mantuvo fija en los tres viajes: Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 33/47
56 Solución En nuestro caso las incógnitas son las cantidades de moneda extranjera requerida que se mantuvo fija en los tres viajes: x = cantidad de yenes y = cantidad de francos z = cantidad de marcos Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 33/47
57 Primera vez: 434(total) = x y z Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 34/47
58 Primera vez: Segunda vez: 434(total) = x y z 406(total) = x y z Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 34/47
59 Primera vez: Segunda vez: Tercera vez: 434(total) = x y z 406(total) = x y z 434(total) = x y z Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 34/47
60 Resolviendo el sistema anterior obtenemos: x = 10500,y = 126,z = 294 Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 35/47
61 Transferencia de Calor Ejemplo Suponga que la placa de la siguiente figura representa una sección transversal perpendicular a la placa. T CO T CN T 1 T 4 T CS T CE Sean T 1, T 2, T 3, T 4, T 5, y T 6 las tempreaturas interiores de los nodos de la red. La temperatura en un nodo es aproximadamente igual al promedio de las temperaturas de los cuatro nodos más cercanos arriba, abajo, a la derecha, y a la izquierda. T 2 T 5 T 3 T 6 Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 36/47
62 Así por ejemplo T 1 = (T CN +T 2 +T 4 +T CO )/4. Determine las temperaturas T 1 a T 6 sabiendo que T CN = 25 o, T CE = 37 o, T CS = 10 o, T CO = 31 o Reporte sólo el valor de T 2. Solución Las ecuaciones para las temperaturas de los puntos interiores a la placa T 1 a T 6 quedan: T 1 = (T CN +T 2 +T 4 +T CO )/4 T 2 = (T CN +T 3 +T 5 +T 1 )/4 T 3 = (T CN +T CE +T 6 +T 2 )/4 T 4 = (T 1 +T 5 +T CS +T CO )/4 T 5 = (T 2 +T 6 +T CS +T 4 )/4 T 6 = (T 3 +T CE +T CS +T 5 )/4 Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 37/47
63 Usando los datos de las temperaturas a los costados de la placa y convirtiendo cada ecuación a la forma canónica queda (conviene multiplicar por 4 cada ecuación): 4T 1 T 2 T 4 = 56 T 1 + 4T 2 T 3 T 5 = 25 T 2 + 4T 3 T 6 = 62 T 1 + 4T 4 T 5 = 41 T 2 T 4 + 4T 5 T 6 = 10 T 3 T 5 + 4T 6 = 47 Quedando T 1 T 2 T 3 T 4 T 5 T Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 38/47
64 Al reducir la matriz obtenemos la solución: T 1 = T 2 = T 3 = T 4 = T 5 = T 6 = Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 39/47
65 Splines cúbicos Ejemplo Determine los coeficientes que deben tener los polinomios S 1 (x) = A 1 +B 1 (x 0.4)+C 1 (x 0.4) 2 +D 1 (x 0.4) 3 S 2 (x) = A 2 +B 2 (x 0.5)+C 2 (x 0.5) 2 +D 2 (x 0.5) 3 para que se cumpla: 1. S 1 (0.4) = S 1 (0.5) = S 2 (0.5) = S 2 (0.6) = S 1(0.5) = S 2(0.5) 6. S 1(0.5) = S 2(0.5) 7. S 1(0.4) = 0 8. S 2(0.6) = 0 Lo que debe hacer es tomar como incógnitas dichos coeficientes, usar las condiciones anteriores para construir ecuaciones, y resolver el sistema que se forma. Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 40/47
66 La condición 1. lleva a la ecuación A 1 = La condición 2. lleva a la ecuación A 1 +.1B C D 1 = La condición 3. lleva a la ecuación A 2 = La condición 4. lleva a la ecuación A 2 +.1B C D 2 = La condición 5. lleva a la ecuación B 1 +.2C D 1 = B 2 La condición 6. lleva a la ecuación 2C 1 +.6D 1 = 2C 2 La condición 7. lleva a la ecuación 2C 1 = 0 La condición 8. lleva a la ecuación 2C 2 +.6D 2 = 0. Al resolver este sistema de 8 ecuaciones con 8 incógintas daa la solución: A 1 = B 1 = C 1 = 0.0 D 1 = A 2 = B 2 = C 2 = D 2 = Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 41/47
67 Suma de los primeros cuadrados Ejemplo Existe una fórmula para calcular la suma n 2. Sabiendo que la fórmula es un polinomio de grado tres en la variable n, encuentre dicha fórmula. Sugerencia: Proponga como fórmula F(n) = An 3 +Bn 2 +Cn+D donde A,B,C y D son incógnitas. Dando los valores n = 1, n = 2, n = 3 y n = 4 y conociendo los resultados que dan esas sumas, plantea y resuelve el sistema. Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 42/47
68 Solución Para n = 1 la suma da: 1 i 2 = 1 2 = 1 Por tanto, la fórmula para n = 1 debe dar 1. La ecuación queda: A1 3 +B1 2 +C1+D = A+B +C +D = 1 Para n = 2 la suma da: 2 i 2 = = 1+4 = 5 i=1 Por tanto, la fórmula para n = 2 debe dar 5. La ecuación queda: A2 3 +B2 2 +C2+D = 8A+4B +2C +D = 5 i=1 Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 43/47
69 Para n = 3 la suma da: 3 i 2 = = = 14 i=1 Por tanto, la fórmula para n = 3 debe dar 14. La ecuación queda: A3 3 +B3 2 +C3+D = 27A+9B +3C +D = 27 Para n = 4 la suma da: 4 i 2 = = = 30 i=1 Por tanto, la fórmula para n = 3 debe dar 14. La ecuación queda: A4 3 +B4 2 +C4+D = 64A+16B +4C +D = 30 Al resolver este sistema de 4 ecuaciones para A, B, C y D obtenemos: A = 1 3, B = 1 2, C = 1 6 Por tanto la fórmula de la sumatoria queda: n n N, i 2 = 1 3 n n n i=1 Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 44/47
70 Integración numérica Ejemplo La integral de una función en un intervalo se puede aproximar dividiendo el intervalo en un número de puntos adecuado (2n+1) y en cada 3 puntos consecutivos cambiar la función a integrar por la parábola (polinomio cuadrático) que pasa ellos. Utilice esta técnica para calcular la integral f(x)dx Utilizando los datos: i x i f(x i ) Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 45/47
71 Solución Primero calculemos la parábola que pasa por los 3 primeros puntos. La parábola será f 1 (x) = a 1 x 2 +b 1 x+c 1. Al aplicar las condiciones de que pase por esos puntos quedan las ecuaciones Para(1.0, ) 1.00a b 1 +c 1 = Para(1.2, ) 1.44a b 1 +c 1 = Para(1.4, ) 1.96a b 1 +c 1 = Resolviendo el sistema se obtiene a 1 = ,b 1 = ,c 1 = Por tanto, f(x)dx f 1 (x)dx = Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 46/47
72 Por otro lado, para últimos 3 puntos la parábola será f 2 (x) = a 2 x 2 +b 2 x+c 2. Al aplicar las condiciones de que pase por esos puntos quedan las ecuaciones Para(1.4, ) 1.96a b 2 +c 2 = Para(1.6, ) 2.56a b 2 +c 2 = Para(1.8, ) 3.24a b 2 +c 2 = Resolviendo el sistema se obtiene a 2 = ,b 2 = ,c 2 = Por tanto, Así f(x)dx = f(x)dx f(x)dx+ f 2 (x)dx = f(x)dx Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 47/47
Álgebra Lineal Ma1010
 Álgebra Lineal Ma1010 Aplicaciones de Sistemas de Ecuaciones Lineales Departamento de Matemáticas ITESM Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 1/38 En esta lectura veremos
Álgebra Lineal Ma1010 Aplicaciones de Sistemas de Ecuaciones Lineales Departamento de Matemáticas ITESM Aplicaciones de Sistemas de Ecuaciones Lineales Álgebra Lineal - p. 1/38 En esta lectura veremos
Aplicaciones de Sistemas de Ecuaciones Lineales
 Aplicaciones de Sistemas de Ecuaciones Lineales Departamento de Matemáticas, CCIR/ITESM 10 de enero de 2011 Índice 3.1. Introducción............................................... 1 3.2. Objetivo.................................................
Aplicaciones de Sistemas de Ecuaciones Lineales Departamento de Matemáticas, CCIR/ITESM 10 de enero de 2011 Índice 3.1. Introducción............................................... 1 3.2. Objetivo.................................................
Mínimos Cuadrados. Departamento de Matemáticas, CCIR/ITESM. 30 de junio de 2011
 Mínimos Cuadrados Departamento de Matemáticas, CCIR/ITESM 30 de junio de 011 Índice 4.1.Introducción............................................... 1 4..Error Cuadrático............................................
Mínimos Cuadrados Departamento de Matemáticas, CCIR/ITESM 30 de junio de 011 Índice 4.1.Introducción............................................... 1 4..Error Cuadrático............................................
Clase 4 Ecuaciones lineales y cuadráticas
 Clase 4 Instituto de Ciencias Básicas Facultad de Ingeniería Universidad Diego Portales Marzo de 2013 Introducción Muchos de los errores que los estudiantes cometen en Matemática no se deben al tema que
Clase 4 Instituto de Ciencias Básicas Facultad de Ingeniería Universidad Diego Portales Marzo de 2013 Introducción Muchos de los errores que los estudiantes cometen en Matemática no se deben al tema que
MANUAL DE FRACCIONES PARCIALES
 Universidad Politécnica Salesiana MANUAL DE FRACCIONES PARCIALES Xavier Espinoza Xavier Espinoza MANUAL DE FRACCIONES PARCIALES 2012 MANUAL DE FRACCIONES PARCIALES Xavier Espinoza 1era. edición: c Editorial
Universidad Politécnica Salesiana MANUAL DE FRACCIONES PARCIALES Xavier Espinoza Xavier Espinoza MANUAL DE FRACCIONES PARCIALES 2012 MANUAL DE FRACCIONES PARCIALES Xavier Espinoza 1era. edición: c Editorial
INTERVALOS Y SEMIRRECTAS.
 el blog de mate de aida CSI: Inecuaciones pág 1 INTERVALOS Y SEMIRRECTAS La ordenación de números permite definir algunos conjuntos de números que tienen una representación geométrica en la recta real
el blog de mate de aida CSI: Inecuaciones pág 1 INTERVALOS Y SEMIRRECTAS La ordenación de números permite definir algunos conjuntos de números que tienen una representación geométrica en la recta real
Unidad 2: Ecuaciones, inecuaciones y sistemas.
 Unidad 2: Ecuaciones, inecuaciones y sistemas 1 Unidad 2: Ecuaciones, inecuaciones y sistemas. 1.- Factorización de polinomios. M. C. D y m.c.m de polinomios. Un número a es raíz de un polinomio es 0.
Unidad 2: Ecuaciones, inecuaciones y sistemas 1 Unidad 2: Ecuaciones, inecuaciones y sistemas. 1.- Factorización de polinomios. M. C. D y m.c.m de polinomios. Un número a es raíz de un polinomio es 0.
TRABAJO DE MATEMÁTICAS. PENDIENTES DE 1º ESO. (2ª parte)
 TRABAJO DE MATEMÁTICAS PENDIENTES DE 1º ESO. (2ª parte) NÚMEROS RACIONALES REDUCCIÓN DE FRACCIONES AL MISMO DENOMINADOR Para reducir varias fracciones al mismo denominador se siguen los siguientes pasos:
TRABAJO DE MATEMÁTICAS PENDIENTES DE 1º ESO. (2ª parte) NÚMEROS RACIONALES REDUCCIÓN DE FRACCIONES AL MISMO DENOMINADOR Para reducir varias fracciones al mismo denominador se siguen los siguientes pasos:
Una ecuación puede tener ninguna, una o varias soluciones. Por ejemplo: 5x 9 = 1 es una ecuación con una incógnita con una solución, x = 2
 Podemos definir a las ecuaciones como una igualdad entre expresiones algebraicas (encadenamiento de números y letras ligados por operaciones matemáticas diversas),en la que intervienen una o más letras,
Podemos definir a las ecuaciones como una igualdad entre expresiones algebraicas (encadenamiento de números y letras ligados por operaciones matemáticas diversas),en la que intervienen una o más letras,
Ecuaciones cuadráticas Resolver ecuaciones cuadráticas casos especiales
 Ecuaciones cuadráticas Resolver ecuaciones cuadráticas casos especiales Departamento de Matemáticas Universidad de Puerto Rico - Arecibo Ecuación cuadrática en forma general Una ecuación cuadrática tiene
Ecuaciones cuadráticas Resolver ecuaciones cuadráticas casos especiales Departamento de Matemáticas Universidad de Puerto Rico - Arecibo Ecuación cuadrática en forma general Una ecuación cuadrática tiene
ECUACIONES POLINÓMICAS CON UNA INCÓGNITA
 Unidad didáctica. Ecuaciones, inecuaciones y sistemas de ecuaciones e inecuaciones ECUACIONES POLINÓMICAS CON UNA INCÓGNITA Las ecuaciones polinómicas son aquellas equivalentes a una ecuación cuyo primer
Unidad didáctica. Ecuaciones, inecuaciones y sistemas de ecuaciones e inecuaciones ECUACIONES POLINÓMICAS CON UNA INCÓGNITA Las ecuaciones polinómicas son aquellas equivalentes a una ecuación cuyo primer
Álgebra Lineal Ma1010
 Álgebra Lineal Ma1010 Líneas y s en el Espacio Departamento de Matemáticas ITESM Líneas y s en el Espacio Álgebra Lineal - p. 1/34 Los conjuntos solución a un sistema de ecuaciones lineales cuando tienen
Álgebra Lineal Ma1010 Líneas y s en el Espacio Departamento de Matemáticas ITESM Líneas y s en el Espacio Álgebra Lineal - p. 1/34 Los conjuntos solución a un sistema de ecuaciones lineales cuando tienen
MODELOS LINEALES. Alejandro Vera Trejo
 MODELOS LINEALES Alejandro Vera Trejo Objetivo Se representará una situación determinada a través de la construcción de una o varias ecuaciones lineales. Se resolverán situaciones reales por medio de ecuaciones
MODELOS LINEALES Alejandro Vera Trejo Objetivo Se representará una situación determinada a través de la construcción de una o varias ecuaciones lineales. Se resolverán situaciones reales por medio de ecuaciones
Álgebra Lineal Ma1010
 Álgebra Lineal Ma1010 Métodos Iterativos para Resolver Sistemas Lineales Departamento de Matemáticas ITESM Métodos Iterativos para Resolver Sistemas Lineales Álgebra Lineal - p. 1/30 En esta lectura veremos
Álgebra Lineal Ma1010 Métodos Iterativos para Resolver Sistemas Lineales Departamento de Matemáticas ITESM Métodos Iterativos para Resolver Sistemas Lineales Álgebra Lineal - p. 1/30 En esta lectura veremos
REPASO DE FUNCIONES FUNCIONES REALES DE VARIABLE REAL
 REPASO DE FUNCIONES FUNCIONES REALES DE VARIABLE REAL CORRESPONDENCIA. Se llama CORRESPONDENCIA entre dos conjuntos A y B a toda ley que asocia elementos del conjunto A con elementos del conjunto B. Se
REPASO DE FUNCIONES FUNCIONES REALES DE VARIABLE REAL CORRESPONDENCIA. Se llama CORRESPONDENCIA entre dos conjuntos A y B a toda ley que asocia elementos del conjunto A con elementos del conjunto B. Se
Matrices Invertibles y Elementos de Álgebra Matricial
 Matrices Invertibles y Elementos de Álgebra Matricial Departamento de Matemáticas, CSI/ITESM 20 de agosto de 2008 Índice 121 Introducción 1 122 Transpuesta 1 123 Propiedades de la transpuesta 2 124 Matrices
Matrices Invertibles y Elementos de Álgebra Matricial Departamento de Matemáticas, CSI/ITESM 20 de agosto de 2008 Índice 121 Introducción 1 122 Transpuesta 1 123 Propiedades de la transpuesta 2 124 Matrices
T0. TRANSFORMADAS DE LAPLACE
 ESCUELA TÉCNICA SUPERIOR DE NÁUTICA Y MÁQUINAS NAVALES / NAUTIKAKO ETA ITSASONTZI MAKINETAKO GOI ESKOLA TEKNIKOA MATEMATICAS T0. TRANSFORMADAS DE LAPLACE Mediante transformadas de Laplace (por Pierre-Simon
ESCUELA TÉCNICA SUPERIOR DE NÁUTICA Y MÁQUINAS NAVALES / NAUTIKAKO ETA ITSASONTZI MAKINETAKO GOI ESKOLA TEKNIKOA MATEMATICAS T0. TRANSFORMADAS DE LAPLACE Mediante transformadas de Laplace (por Pierre-Simon
Preliminares Métodos de Ajuste de Curvas AJUSTE DE CURVAS AJUSTE DE CURVAS
 Contenido 1 Preliminares Definiciones 2 Definiciones Contenido 1 Preliminares Definiciones 2 Definiciones Definiciones En ciencias e ingeniería es frecuente que un experimento produzca un conjunto de datos
Contenido 1 Preliminares Definiciones 2 Definiciones Contenido 1 Preliminares Definiciones 2 Definiciones Definiciones En ciencias e ingeniería es frecuente que un experimento produzca un conjunto de datos
Reemplazos Algebraicos. Gabriel Darío Uribe Guerra Universidad de Antioquia. XIII COLOQUIO REGIONAL DE MATEMÁTICAS y III SIMPOSIO DE ESTADÍSTICA.
 Reemplazos Algebraicos Gabriel Darío Uribe Guerra Universidad de Antioquia XIII COLOQUIO REGIONAL DE MATEMÁTICAS y III SIMPOSIO DE ESTADÍSTICA. Universidad de Nariño San Juan de Pasto Mayo 2016 1/23 Introducción
Reemplazos Algebraicos Gabriel Darío Uribe Guerra Universidad de Antioquia XIII COLOQUIO REGIONAL DE MATEMÁTICAS y III SIMPOSIO DE ESTADÍSTICA. Universidad de Nariño San Juan de Pasto Mayo 2016 1/23 Introducción
Clase 3 Funciones lineal y cuadrática
 Clase 3 Instituto de Ciencias Básicas Facultad de Ingeniería Universidad Diego Portales Marzo de 2014 Función lineal Definición Una relación de la forma f(x) = mx+n, donde m, n R, se llama función lineal
Clase 3 Instituto de Ciencias Básicas Facultad de Ingeniería Universidad Diego Portales Marzo de 2014 Función lineal Definición Una relación de la forma f(x) = mx+n, donde m, n R, se llama función lineal
Tema 3 Álgebra Matemáticas I 1º Bachillerato. 1
 Tema 3 Álgebra Matemáticas I 1º Bachillerato. 1 TEMA 3 ÁLGEBRA 3.1 FACTORIZACIÓN DE POLINOMIOS LA DIVISIBILIDAD EN LOS POLINOMIOS Un polinomio P(x) es divisible por otro polinomio Q(x) cuando el cociente
Tema 3 Álgebra Matemáticas I 1º Bachillerato. 1 TEMA 3 ÁLGEBRA 3.1 FACTORIZACIÓN DE POLINOMIOS LA DIVISIBILIDAD EN LOS POLINOMIOS Un polinomio P(x) es divisible por otro polinomio Q(x) cuando el cociente
5.1 DISTINTOS TIPOS DE FUNCIONES LINEALES
 Tema 5 : Funciones elementales - Matemáticas B 4º E.S.O. 1 TEMA 5 FUNCIONES ELEMENTALES 5.1 DISTINTOS TIPOS DE FUNCIONES LINEALES 3º 5.1.1 - FUNCIONES DE PROPORCIONALIDAD: y = mx Las funciones de proporcionalidad
Tema 5 : Funciones elementales - Matemáticas B 4º E.S.O. 1 TEMA 5 FUNCIONES ELEMENTALES 5.1 DISTINTOS TIPOS DE FUNCIONES LINEALES 3º 5.1.1 - FUNCIONES DE PROPORCIONALIDAD: y = mx Las funciones de proporcionalidad
4.3 Aproximación por mínimos cuadrados.
 4.3 Aproximación por mínimos cuadrados. Como ya hemos dicho anteriormente la búsqueda de un modelo matemático que represente lo mejor posible a unos datos experimentales puede abordarse, entre otras, de
4.3 Aproximación por mínimos cuadrados. Como ya hemos dicho anteriormente la búsqueda de un modelo matemático que represente lo mejor posible a unos datos experimentales puede abordarse, entre otras, de
METODOS DE INTEGRACION IV FRACCIONES PARCIALES
 METODOS DE INTEGRACION IV FRACCIONES PARCIALES Una función racional es una función de la forma En la que f(x) y g(x) son polinomios. Si el frado de f(x) es menor que el de g(x), F(x) se denomina fracción
METODOS DE INTEGRACION IV FRACCIONES PARCIALES Una función racional es una función de la forma En la que f(x) y g(x) son polinomios. Si el frado de f(x) es menor que el de g(x), F(x) se denomina fracción
Contenidos Mínimos MATEMÁTICAS 3º ESO ENSEÑANZAS ACADÉMICAS. U 1 Fracciones y decimales. CRITERIOS DE EVALUACIÓN. ESTÁNDARES DE APRENDIZAJE EVALUABLES
 Septiembre 2.016 Contenidos Mínimos MATEMÁTICAS 3º ESO ENSEÑANZAS ACADÉMICAS U 1 Fracciones y decimales. Números racionales. Expresión fraccionaria - Números enteros. - Fracciones. - Fracciones propias
Septiembre 2.016 Contenidos Mínimos MATEMÁTICAS 3º ESO ENSEÑANZAS ACADÉMICAS U 1 Fracciones y decimales. Números racionales. Expresión fraccionaria - Números enteros. - Fracciones. - Fracciones propias
FUNCIONES DE PROPORCIONALIDAD: y = mx. Su pendiente es 0. La recta y = 0 coincide con el eje
 Funciones elementales - Matemáticas B 4º E.S.O. FUNCIONES ELEMENTALES DISTINTOS TIPOS DE FUNCIONES LINEALES FUNCIONES DE PROPORCIONALIDAD: y = mx FUNCIÓN CONSTANTE: y = n Las funciones de proporcionalidad
Funciones elementales - Matemáticas B 4º E.S.O. FUNCIONES ELEMENTALES DISTINTOS TIPOS DE FUNCIONES LINEALES FUNCIONES DE PROPORCIONALIDAD: y = mx FUNCIÓN CONSTANTE: y = n Las funciones de proporcionalidad
Unidad II. Si una función f(x) tiene primitiva, tiene infinitas primitivas, diferenciándose todas ellas en unaconstante.
 Unidad II Integral indefinida y métodos de integración. 2.1 Definición de integral indefinida. Integrar es el proceso recíproco del de derivar, es decir, dada una función f(x), busca aquellas funciones
Unidad II Integral indefinida y métodos de integración. 2.1 Definición de integral indefinida. Integrar es el proceso recíproco del de derivar, es decir, dada una función f(x), busca aquellas funciones
Definiciones I. Una solución de una ecuación son aquellos valores que al sustituirlos en la ecuación hacen que la igualdad sea cierta.
 Ecuaciones Definiciones I Una ecuación es una igualdad algebraica que se verifica únicamente para un conjunto determinado de valores de las variables o indeterminadas que forman la ecuación. a + b 2 =
Ecuaciones Definiciones I Una ecuación es una igualdad algebraica que se verifica únicamente para un conjunto determinado de valores de las variables o indeterminadas que forman la ecuación. a + b 2 =
Álgebra Lineal Ma1010
 Álgebra Ma1010 Departamento de Matemáticas ITESM Álgebra - p. 1/31 En este apartado se introduce uno de los conceptos más importantes del curso: el de combinación lineal entre vectores. Se establece la
Álgebra Ma1010 Departamento de Matemáticas ITESM Álgebra - p. 1/31 En este apartado se introduce uno de los conceptos más importantes del curso: el de combinación lineal entre vectores. Se establece la
Ecuaciones, inecuaciones y sistemas
 Ecuaciones, inecuaciones y sistemas. Matemáticas Aplicadas a las Ciencias Sociales I 1 Ecuaciones, inecuaciones y sistemas Ecuaciones con una incógnita. Ecuación.- Una ecuación es una igualdad de expresiones
Ecuaciones, inecuaciones y sistemas. Matemáticas Aplicadas a las Ciencias Sociales I 1 Ecuaciones, inecuaciones y sistemas Ecuaciones con una incógnita. Ecuación.- Una ecuación es una igualdad de expresiones
Splines (funciones polinomiales por trozos)
 Splines (funciones polinomiales por trozos) Problemas para examen Interpolación lineal y cúbica 1. Fórmulas para la interpolación lineal. Dados t 1,..., t n, x 1,..., x n R tales que t 1
Splines (funciones polinomiales por trozos) Problemas para examen Interpolación lineal y cúbica 1. Fórmulas para la interpolación lineal. Dados t 1,..., t n, x 1,..., x n R tales que t 1
UNIVERSIDAD SIMON BOLIVAR MA1116 abril-julio de 2009 Departamento de Matemáticas Puras y Aplicadas. Ejercicios sugeridos para :
 II / 7 UNIVERSIDAD SIMON BOLIVAR MA6 abril-julio de 29 Ejercicios sugeridos para : los temas de las clases del 28 y de abril de 29. Temas : Métodos de Gauss y Gauss-Jordan. Sistemas homogéneos y no homogéneos.
II / 7 UNIVERSIDAD SIMON BOLIVAR MA6 abril-julio de 29 Ejercicios sugeridos para : los temas de las clases del 28 y de abril de 29. Temas : Métodos de Gauss y Gauss-Jordan. Sistemas homogéneos y no homogéneos.
FUNCIÓN CUADRÁTICA. Tres formas para identificar una parábola según los datos:
 FUNCIÓN CUADRÁTICA Una función cuadrática es una función polinómica de segundo grado de la forma y=ax +bx+c, cuya gráfica es una parábola de eje vertical, donde a representa la abertura de la parábola.
FUNCIÓN CUADRÁTICA Una función cuadrática es una función polinómica de segundo grado de la forma y=ax +bx+c, cuya gráfica es una parábola de eje vertical, donde a representa la abertura de la parábola.
11.SISTEMAS DE ECUACIONES LINEALES DEFINICIÓN DE ECUACIÓN LINEAL DEFINICIÓN DE SISTEMA LINEAL Y CONJUNTO SOLUCIÓN
 ÍNDICE 11SISTEMAS DE ECUACIONES LINEALES 219 111 DEFINICIÓN DE ECUACIÓN LINEAL 219 112 DEFINICIÓN DE SISTEMA LINEAL Y CONJUNTO SOLUCIÓN 220 113 EQUIVALENCIA Y COMPATIBILIDAD 220 11 REPRESENTACIÓN MATRICIAL
ÍNDICE 11SISTEMAS DE ECUACIONES LINEALES 219 111 DEFINICIÓN DE ECUACIÓN LINEAL 219 112 DEFINICIÓN DE SISTEMA LINEAL Y CONJUNTO SOLUCIÓN 220 113 EQUIVALENCIA Y COMPATIBILIDAD 220 11 REPRESENTACIÓN MATRICIAL
Para verificar que el sistema converge se deberán cumplir con las siguientes condiciones en las formulas con derivadas parciales: + 1
 MAT 5 B Sistemas de ecuaciones no lineales EJERCICIOS RESUELTOS. Resuelva el siguiente sistema de ecuaciones no lineales, utilizando el método de punto fijo multivariable: x cos x x SOLUCIÓN x 8 x +. +
MAT 5 B Sistemas de ecuaciones no lineales EJERCICIOS RESUELTOS. Resuelva el siguiente sistema de ecuaciones no lineales, utilizando el método de punto fijo multivariable: x cos x x SOLUCIÓN x 8 x +. +
INECUACIONES LINEALES
 INECUACIONES POLINÓMICAS EN UNA VARIABLE Las inecuaciones en general, son desigualdades entre epresiones algebraicas en las que intervienen una o más variables. Cuando las epresiones algebraicas de cada
INECUACIONES POLINÓMICAS EN UNA VARIABLE Las inecuaciones en general, son desigualdades entre epresiones algebraicas en las que intervienen una o más variables. Cuando las epresiones algebraicas de cada
EJERCICIOS RESUELTOS DE INTERPOLACION NUMERICA. 1) *Probar que si g interpola a la función f en,,, y h interpola a f en,,,,
 Universidad de Santiago de Chile Facultad de Ciencia Departamento de Matemática y Ciencias de la Computación EJERCICIOS RESUELTOS DE INTERPOLACION NUMERICA Profesor: Jaime Álvarez Maldonado Ayudante: Rodrigo
Universidad de Santiago de Chile Facultad de Ciencia Departamento de Matemática y Ciencias de la Computación EJERCICIOS RESUELTOS DE INTERPOLACION NUMERICA Profesor: Jaime Álvarez Maldonado Ayudante: Rodrigo
A)2011 B)2012 B)2013 D)2014 E)2015. C) a5 +b 5
 ENCUENTRO # 6 TEMA: Fracciones algebraicas CONTENIDOS:. Máximo común divisor 2. Mínimo común múltiplo 3. Simplificación de fracciones algebraicas 4. Suma de fracciones algebraicas 5. Resta de fracciones
ENCUENTRO # 6 TEMA: Fracciones algebraicas CONTENIDOS:. Máximo común divisor 2. Mínimo común múltiplo 3. Simplificación de fracciones algebraicas 4. Suma de fracciones algebraicas 5. Resta de fracciones
Algunas Aplicaciones de Sistemas de Ecuaciones Lineales
 Universidad Central de Venezuela Facultad de Ingeniería Departamento de Matemática Aplicada Álgebra Lineal Prof. Norma Guzmán Algunas Aplicaciones de Sistemas de Ecuaciones Lineales 1. Modelo Insumo-Producto
Universidad Central de Venezuela Facultad de Ingeniería Departamento de Matemática Aplicada Álgebra Lineal Prof. Norma Guzmán Algunas Aplicaciones de Sistemas de Ecuaciones Lineales 1. Modelo Insumo-Producto
Revisora: María Molero
 57 Capítulo 5: INECUACIONES. Matemáticas 4ºB ESO 1. INTERVALOS 1.1. Tipos de intervalos Intervalo abierto: I = (a, b) = {x a < x < b}. Intervalo cerrado: I = [a, b] = {x a x b}. Intervalo semiabierto por
57 Capítulo 5: INECUACIONES. Matemáticas 4ºB ESO 1. INTERVALOS 1.1. Tipos de intervalos Intervalo abierto: I = (a, b) = {x a < x < b}. Intervalo cerrado: I = [a, b] = {x a x b}. Intervalo semiabierto por
Las desigualdades absolutas son aquellas que se cumplen sea cual sea el valor real que se sustituye. Por ejemplo:
 MATEMÁTICAS BÁSICAS INECUACIONES INTERVALOS DE NÚMEROS REALES Una desigualdad es la epresión de dos cantidades tales que una es mayor que otra. Las desigualdades en general se clasifican en absolutas y
MATEMÁTICAS BÁSICAS INECUACIONES INTERVALOS DE NÚMEROS REALES Una desigualdad es la epresión de dos cantidades tales que una es mayor que otra. Las desigualdades en general se clasifican en absolutas y
TEMA 2.- ECUACIONES E INECUACIONES
 TEMA.- ECUACIONES E INECUACIONES 1.- INECUACIONES 1.1.- Repaso De Ecuaciones De Primer Y Segundo Grado Ecuaciones de primer grado x 3 4x 4x 3 x 6 4x 4x 1 x 4 x 5x 7 x 7 3x 14 35x 7 x 7 6 3x 14 3 15x 1
TEMA.- ECUACIONES E INECUACIONES 1.- INECUACIONES 1.1.- Repaso De Ecuaciones De Primer Y Segundo Grado Ecuaciones de primer grado x 3 4x 4x 3 x 6 4x 4x 1 x 4 x 5x 7 x 7 3x 14 35x 7 x 7 6 3x 14 3 15x 1
ECUACIONES DE PRIMER GRADO CON UNA INCÓGNITA
 UNIDAD OBJETIVO: Resolverá situaciones y problemas en los que se apliquen ecuaciones de primer grado con una incógnita, sistemas de ecuaciones lineales con dos y tres incógnitas, mediante métodos algebraicos
UNIDAD OBJETIVO: Resolverá situaciones y problemas en los que se apliquen ecuaciones de primer grado con una incógnita, sistemas de ecuaciones lineales con dos y tres incógnitas, mediante métodos algebraicos
Preparación para Álgebra universitaria con trigonometría
 Preparación para Álgebra universitaria con trigonometría Este curso cubre los siguientes temas. Usted puede personalizar la gama y la secuencia de este curso para satisfacer sus necesidades curriculares.
Preparación para Álgebra universitaria con trigonometría Este curso cubre los siguientes temas. Usted puede personalizar la gama y la secuencia de este curso para satisfacer sus necesidades curriculares.
FICHAS REPASO 3º ESO. Para restar números enteros, se suma al minuendo el opuesto del sustraendo y después se aplican las reglas de la suma.
 FICHAS REPASO º ESO OPERACIONES CON NÚMEROS ENTEROS El valor absoluto de un número entero es el número natural que resulta al prescindir del signo. Por ejemplo, el valor absoluto de es y el valor absoluto
FICHAS REPASO º ESO OPERACIONES CON NÚMEROS ENTEROS El valor absoluto de un número entero es el número natural que resulta al prescindir del signo. Por ejemplo, el valor absoluto de es y el valor absoluto
Fundamentos matemáticos. Tema 8 Ecuaciones diferenciales
 Grado en Ingeniería agrícola y del medio rural Tema 8 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2016 Licencia Creative Commons 4.0 Internacional J.
Grado en Ingeniería agrícola y del medio rural Tema 8 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2016 Licencia Creative Commons 4.0 Internacional J.
LA ECUACIÓN CUADRÁTICA
 INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : ASIGNATURA: DOCENTE: TIPO DE GUIA: MATEMÁTICAS MATEMÁTICAS EDISON MEJIA MONSALVE CONCEPTUAL - EJERCITACION PERIODO GRADO 9 N 0 4 FECHA 7 DE ABRIL
INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : ASIGNATURA: DOCENTE: TIPO DE GUIA: MATEMÁTICAS MATEMÁTICAS EDISON MEJIA MONSALVE CONCEPTUAL - EJERCITACION PERIODO GRADO 9 N 0 4 FECHA 7 DE ABRIL
ECUACIONES. Ecuaciones. Indicadores. Contenido ECUACIÓN
 Indicadores ECUACIONES Determina el conjunto solución de una ecuación. Resuelve ecuaciones de primer y segundo grado, así como sistemas de ecuaciones Contenido Ecuaciones De primer grado Sistemas de ecuaciones
Indicadores ECUACIONES Determina el conjunto solución de una ecuación. Resuelve ecuaciones de primer y segundo grado, así como sistemas de ecuaciones Contenido Ecuaciones De primer grado Sistemas de ecuaciones
TALLER DE MATEMÁTICAS 1 ECUACIONES POLINÓMICAS
 TALLER DE MATEMÁTICAS 1 ECUACIONES POLINÓMICAS NOTAS Toda expresión algebraica del tipo a n x n + a n 1 x n 1 + + a 1 x + a 0 es un polinomio de grado n, si a n 0. Es bien conocida la fórmula que da las
TALLER DE MATEMÁTICAS 1 ECUACIONES POLINÓMICAS NOTAS Toda expresión algebraica del tipo a n x n + a n 1 x n 1 + + a 1 x + a 0 es un polinomio de grado n, si a n 0. Es bien conocida la fórmula que da las
1. Introducción. Fundación Uno. Ejercicio Reto. ENCUENTRO # 33 TEMA: Exponenciales y Logaritmos CONTENIDOS: 1. Ecuaciones Exponenciales.
 ENCUENTRO # 33 TEMA: Exponenciales y Logaritmos CONTENIDOS: 1. Ecuaciones Exponenciales. (a) Leyes de los Exponentes (b) Como resolver ecuaciones exponenciales Ejercicio Reto 1. Si a y b las soluciones
ENCUENTRO # 33 TEMA: Exponenciales y Logaritmos CONTENIDOS: 1. Ecuaciones Exponenciales. (a) Leyes de los Exponentes (b) Como resolver ecuaciones exponenciales Ejercicio Reto 1. Si a y b las soluciones
Matemáticas III. Geometría analítica
 Matemáticas III. Geometría analítica Este curso cubre los conceptos mostrados a continuación. El estudiante navega por trayectos de aprendizaje basados en su nivel de preparación. Usuarios institucionales
Matemáticas III. Geometría analítica Este curso cubre los conceptos mostrados a continuación. El estudiante navega por trayectos de aprendizaje basados en su nivel de preparación. Usuarios institucionales
Cuadratura de Newton-Cotes
 Profesor: Jaime Álvarez Maldonado Universidad de Santiago de Chile Facultad de Ciencia Departamento de Matemática y Ciencias de la Computación INTEGRACION NUMERICA Ayudante: Rodrigo Torres Aguirre INTEGRACION
Profesor: Jaime Álvarez Maldonado Universidad de Santiago de Chile Facultad de Ciencia Departamento de Matemática y Ciencias de la Computación INTEGRACION NUMERICA Ayudante: Rodrigo Torres Aguirre INTEGRACION
Álgebra 2. Plan de estudios (305 temas)
 Álgebra 2 Este curso cubre los conceptos mostrados a continuación. El estudiante navega por trayectos de aprendizaje basados en su nivel de preparación. Usuarios institucionales pueden personalizar el
Álgebra 2 Este curso cubre los conceptos mostrados a continuación. El estudiante navega por trayectos de aprendizaje basados en su nivel de preparación. Usuarios institucionales pueden personalizar el
CURSO CERO DE MATEMATICAS. Apuntes elaborados por Domingo Pestana Galván. y José Manuel Rodríguez García
 INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES CURSO CERO DE MATEMATICAS Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica
INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES CURSO CERO DE MATEMATICAS Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: MATEMÁTICAS II
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El alumno contestará a
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El alumno contestará a
Tema 3 Algebra. Ecuaciones. Sistemas de ecuaciones: Inecuaciones Índice
 Tema 3 Algebra. Ecuaciones. Sistemas de ecuaciones: Inecuaciones Índice 1. ECUACIONES... 2 1.1. Ecuaciones de primer grado... 2 1.2. Ecuaciones de segundo grado... 3 1.2.1. Ecuación de segundo grado completa...
Tema 3 Algebra. Ecuaciones. Sistemas de ecuaciones: Inecuaciones Índice 1. ECUACIONES... 2 1.1. Ecuaciones de primer grado... 2 1.2. Ecuaciones de segundo grado... 3 1.2.1. Ecuación de segundo grado completa...
( 3) esto no es igual a 3 ya que sería
 MATEMÁTICA MÓDULO 3 Eje temático: Álgebra y Funciones 1. RAÍCES CUADRADAS Y CÚBICAS Comencemos el estudio de las raíces haciéndonos la siguiente pregunta: si el área de un cuadrado es 15 cm, cuál es su
MATEMÁTICA MÓDULO 3 Eje temático: Álgebra y Funciones 1. RAÍCES CUADRADAS Y CÚBICAS Comencemos el estudio de las raíces haciéndonos la siguiente pregunta: si el área de un cuadrado es 15 cm, cuál es su
1 - Ecuaciones. Sistemas de Ecuaciones Mixtos
 Nivelación de Matemática MTHA UNLP 1 1 - Ecuaciones. Sistemas de Ecuaciones Mixtos 1. Conjuntos numéricos Los números mas comunes son los llamados NATURALES O ENTEROS POSI- TIVOS: 1,, 3,... Para designar
Nivelación de Matemática MTHA UNLP 1 1 - Ecuaciones. Sistemas de Ecuaciones Mixtos 1. Conjuntos numéricos Los números mas comunes son los llamados NATURALES O ENTEROS POSI- TIVOS: 1,, 3,... Para designar
Determinación de la trasformada inversa mediante el uso de las fracciones parciales
 3.6. Determinación de la trasformada inversa mediante el uso de las fracciones parciales 95 3.6. Determinación de la trasformada inversa mediante el uso de las fracciones parciales Transformadas de Ecuaciones
3.6. Determinación de la trasformada inversa mediante el uso de las fracciones parciales 95 3.6. Determinación de la trasformada inversa mediante el uso de las fracciones parciales Transformadas de Ecuaciones
Una forma fácil de recordar esta suma (regla de Sarrus): Primero vamos a estudiar algunas propiedades de los determinantes.
 Una forma fácil de recordar esta suma (regla de Sarrus): Ejemplos: Tarea: realizar al menos tres ejercicios de cálculo de determinantes de matrices de 2x2 y otros tres de 3x3. PARA DETERMINANTES DE MATRICES
Una forma fácil de recordar esta suma (regla de Sarrus): Ejemplos: Tarea: realizar al menos tres ejercicios de cálculo de determinantes de matrices de 2x2 y otros tres de 3x3. PARA DETERMINANTES DE MATRICES
Fundación Uno A)2011 B)2012 B)2013 D)2014 E)2015. es equivalente a 12 b 7 + a 7 b 12 a 19 a 19 a 13 a 6 b 7 + a 7 b 6 b13 a: D) a8 +a 3 b 5 +b 8
 ENCUENTRO # 6 TEMA:Fracciones Algebraicas CONTENIDOS:. Máximo Común Divisor 2. Mínimo Común Múltiplo 3. Simplificación de Fraciones Algebraicas 4. Suma de Fracciones Algebraicas 5. Resta de Fracciones
ENCUENTRO # 6 TEMA:Fracciones Algebraicas CONTENIDOS:. Máximo Común Divisor 2. Mínimo Común Múltiplo 3. Simplificación de Fraciones Algebraicas 4. Suma de Fracciones Algebraicas 5. Resta de Fracciones
Cuánto vale x si la balanza está equilibrada? Hay que resolver le ecuación x + 3 = 7 x = 7 3 x = 4. La solución es x = 4 porque = 7
 TEMA 3. ECUACIONES DE PRIMER Y SEGUNDO GRADO 1. ECUACIÓN DE PRIMER GRADO 1.1 Planteamiento general Identidad: Es una expresión con una igualdad que se cumple siempre. Identidad numérica: Sólo aparecen
TEMA 3. ECUACIONES DE PRIMER Y SEGUNDO GRADO 1. ECUACIÓN DE PRIMER GRADO 1.1 Planteamiento general Identidad: Es una expresión con una igualdad que se cumple siempre. Identidad numérica: Sólo aparecen
TEMA 4: ECUACIONES Y SISTEMAS DE ECUACIONES
 TEMA 4: ECUACIONES Y SISTEMAS DE ECUACIONES 1. ECUACIONES. Una ecuación es una igualdad entre dos expresiones algebraicas. Las variables en este caso se denominan incógnitas. Las soluciones de una ecuación
TEMA 4: ECUACIONES Y SISTEMAS DE ECUACIONES 1. ECUACIONES. Una ecuación es una igualdad entre dos expresiones algebraicas. Las variables en este caso se denominan incógnitas. Las soluciones de una ecuación
OLIMPIADAS COSTARRICENSES DE MATEMÁTICAS
 OLIMPIADAS COSTARRICENSES DE MATEMÁTICAS UNA - UCR - TEC - UNED - MEP - MICITT Álgebra e iπ + φ φ 0 III Nivel I Eliminatoria Marzo 06 Índice. Presentación. Contenidos 3. Algunos consejos útiles 4. Problemas
OLIMPIADAS COSTARRICENSES DE MATEMÁTICAS UNA - UCR - TEC - UNED - MEP - MICITT Álgebra e iπ + φ φ 0 III Nivel I Eliminatoria Marzo 06 Índice. Presentación. Contenidos 3. Algunos consejos útiles 4. Problemas
TEMA 1.- POLINOMIOS Y FRACCIONES ALGEBRAICAS
 TEMA 1.- POLINOMIOS Y FRACCIONES ALGEBRAICAS 1.- POLINOMIOS Recordemos que un monomio es una expresión algebraica (combinación de letras y números) en la que las únicas operaciones que aparecen entre las
TEMA 1.- POLINOMIOS Y FRACCIONES ALGEBRAICAS 1.- POLINOMIOS Recordemos que un monomio es una expresión algebraica (combinación de letras y números) en la que las únicas operaciones que aparecen entre las
Matemáticas II PRUEBA DE ACCESO A LA UNIVERSIDAD 2012 BACHILLERATO FORMACIÓN PROFESIONAL CICLOS FORMATIVOS DE GRADO SUPERIOR.
 PRUEBA DE ACCESO A LA UNIVERSIDAD 2012 Matemáticas II BACHILLERATO FORMACIÓN PROFESIONAL CICLOS FORMATIVOS DE GRADO SUPERIOR Examen Criterios de Corrección y Calificación UNIBERTSITATERA SARTZEKO PROBAK
PRUEBA DE ACCESO A LA UNIVERSIDAD 2012 Matemáticas II BACHILLERATO FORMACIÓN PROFESIONAL CICLOS FORMATIVOS DE GRADO SUPERIOR Examen Criterios de Corrección y Calificación UNIBERTSITATERA SARTZEKO PROBAK
Ecuaciones de primer ysegundo grado
 86 _ 087-098.qxd 7//07 : Página 87 Ecuaciones de primer ysegundo grado INTRODUCCIÓN La unidad comienza diferenciando entre ecuaciones e identidades, para pasar luego a la exposición de los conceptos asociados
86 _ 087-098.qxd 7//07 : Página 87 Ecuaciones de primer ysegundo grado INTRODUCCIÓN La unidad comienza diferenciando entre ecuaciones e identidades, para pasar luego a la exposición de los conceptos asociados
Ejercicio 1 Completa: Monomio Coeficiente Parte literal Grado
 Soluciones a los ejercicios de Álgebra, primera parte: Ejercicio 1 Completa: Monomio Coeficiente Parte literal Grado 3xz 3 xz 3 1x zy 1 4 abc 1 5 x 5 3 x zy 6 4 abc 6 x 1 Ejercicio Halla el valor numérico
Soluciones a los ejercicios de Álgebra, primera parte: Ejercicio 1 Completa: Monomio Coeficiente Parte literal Grado 3xz 3 xz 3 1x zy 1 4 abc 1 5 x 5 3 x zy 6 4 abc 6 x 1 Ejercicio Halla el valor numérico
Matemáticas. Matías Puello Chamorro. Algebra Operativa. 9 de agosto de 2016
 Matemáticas Algebra Operativa Matías Puello Chamorro http://www.unilibrebaq.edu.co 9 de agosto de 2016 Índice 1. Introducción 3 2. Definiciones básicas del Algebra 4 2.1. Definición de igualdad............................
Matemáticas Algebra Operativa Matías Puello Chamorro http://www.unilibrebaq.edu.co 9 de agosto de 2016 Índice 1. Introducción 3 2. Definiciones básicas del Algebra 4 2.1. Definición de igualdad............................
SISTEMAS DE ECUACIONES LINEALES. Método de reducción o de Gauss. 1º DE BACHILLERATO DPTO DE MATEMÁTICAS COLEGIO MARAVILLAS AUTORA: Teresa González.
 SISTEMAS DE ECUACIONES LINEALES Método de reducción o de Gauss 1º DE BACHILLERATO DPTO DE MATEMÁTICAS COLEGIO MARAVILLAS AUTORA: Teresa González. SISTEMAS DE DOS ECUACIONES LINEALES CON DOS INCÓGNITAS.
SISTEMAS DE ECUACIONES LINEALES Método de reducción o de Gauss 1º DE BACHILLERATO DPTO DE MATEMÁTICAS COLEGIO MARAVILLAS AUTORA: Teresa González. SISTEMAS DE DOS ECUACIONES LINEALES CON DOS INCÓGNITAS.
DEPARTAMENTO DE MATEMÁTICAS. IES GALLICUM
 UNIDAD I: NÚMEROS (6 Horas) 1.- Repasar el cálculo con números racionales y potencias de exponente entero. 2.- Resolver problemas de la vida cotidiana en los que intervengan los números racionales. 1.-
UNIDAD I: NÚMEROS (6 Horas) 1.- Repasar el cálculo con números racionales y potencias de exponente entero. 2.- Resolver problemas de la vida cotidiana en los que intervengan los números racionales. 1.-
LA ECUACIÓN CUADRÁTICA
 INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMÁTICAS ASIGNATURA: MATEMÁTICAS DOCENTE: EDISON MEJIA MONSALVE TIPO DE GUIA: CONCEPTUAL - EJERCITACION PERIODO GRADO N 0 FECHA DURACION 3
INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMÁTICAS ASIGNATURA: MATEMÁTICAS DOCENTE: EDISON MEJIA MONSALVE TIPO DE GUIA: CONCEPTUAL - EJERCITACION PERIODO GRADO N 0 FECHA DURACION 3
Capitulo IV - Inecuaciones
 Capitulo IV - Inecuaciones Definición: Una inecuación es una desigualdad en las que hay una o más cantidades desconocidas (incógnita) y que sólo se verifica para determinados valores de la incógnita o
Capitulo IV - Inecuaciones Definición: Una inecuación es una desigualdad en las que hay una o más cantidades desconocidas (incógnita) y que sólo se verifica para determinados valores de la incógnita o
GUÍA DE APLICACIÓN POR FRACCIONES PARCIALES
 GUÍA DE APLICACIÓN POR FRACCIONES PARCIALES El método de fracciones parciales se utiliza cuando quiere integrarse una expresión de la forma, donde el numerador y el denominador son polinomios y el grado
GUÍA DE APLICACIÓN POR FRACCIONES PARCIALES El método de fracciones parciales se utiliza cuando quiere integrarse una expresión de la forma, donde el numerador y el denominador son polinomios y el grado
OBJETIVOS CONTENIDOS PROCEDIMIENTOS
 Polinomios INTRODUCCIÓN Son múltiples los contextos en los que aparecen los polinomios: fórmulas económicas, químicas, físicas, de ahí la importancia de comprender el concepto de polinomio y otros asociados
Polinomios INTRODUCCIÓN Son múltiples los contextos en los que aparecen los polinomios: fórmulas económicas, químicas, físicas, de ahí la importancia de comprender el concepto de polinomio y otros asociados
FUNDAMENTOS NUMÉRICOS SEMANA 4
 FUNDAMENTOS NUMÉRICOS SEMANA 4 ÍNDICE INECUACIONES Y DESIGUALDADES... 3 APRENDIZAJES ESPERADOS... 3 INTRODUCCIÓN... 3 INECUACIONES... 4 REGLAS DE LAS DESIGUALDADES... 4 INECUACIONES LINEALES... 5 INECUACIONES
FUNDAMENTOS NUMÉRICOS SEMANA 4 ÍNDICE INECUACIONES Y DESIGUALDADES... 3 APRENDIZAJES ESPERADOS... 3 INTRODUCCIÓN... 3 INECUACIONES... 4 REGLAS DE LAS DESIGUALDADES... 4 INECUACIONES LINEALES... 5 INECUACIONES
CONCRECIÓN DE LOS CRITERIOS DE EVALUACIÓN Curso: PRIMERO de BACHILLERATO CIENCIAS Asignatura: MATEMÁTICAS I Profesor: ALFONSO BdV
 CONCRECIÓN DE LOS CRITERIOS DE EVALUACIÓN Curso: PRIMERO de BACHILLERATO CIENCIAS Asignatura: MATEMÁTICAS I Profesor: ALFONSO BdV 1. Números reales. Aritmética y álgebra 1.1. Operar con fracciones de números
CONCRECIÓN DE LOS CRITERIOS DE EVALUACIÓN Curso: PRIMERO de BACHILLERATO CIENCIAS Asignatura: MATEMÁTICAS I Profesor: ALFONSO BdV 1. Números reales. Aritmética y álgebra 1.1. Operar con fracciones de números
numerador 15 como el denominador 18 tienen como divisor común este número:
 MATEMÁTICA MÓDULO Eje temático: álgebra y funciones 1. LENGUAJE ALGEBRAICO 1.1. Simplificación de fracciones algebraicas Si tenemos la fracción 15, la puedes simplificar por 3, ya que tanto el 18 numerador
MATEMÁTICA MÓDULO Eje temático: álgebra y funciones 1. LENGUAJE ALGEBRAICO 1.1. Simplificación de fracciones algebraicas Si tenemos la fracción 15, la puedes simplificar por 3, ya que tanto el 18 numerador
Bloque 1. Aritmética y Álgebra
 Bloque 1. Aritmética y Álgebra 12. Sistemas de ecuaciones 1. Sistemas de ecuaciones Un sistema de ecuaciones es un conjunto de dos o más ecuaciones con varias incógnitas que conforman un problema matemático
Bloque 1. Aritmética y Álgebra 12. Sistemas de ecuaciones 1. Sistemas de ecuaciones Un sistema de ecuaciones es un conjunto de dos o más ecuaciones con varias incógnitas que conforman un problema matemático
Ecuaciones de primer grado
 Matemáticas Unidad 16 Ecuaciones de primer grado Objetivos Resolver problemas que impliquen el planteamiento y la resolución de ecuaciones de primer grado de la forma x + a = b; ax = b; ax + b = c, utilizando
Matemáticas Unidad 16 Ecuaciones de primer grado Objetivos Resolver problemas que impliquen el planteamiento y la resolución de ecuaciones de primer grado de la forma x + a = b; ax = b; ax + b = c, utilizando
1. x = 2. Solución : x = 2 o x = x = 2. Solución x = 2 o x= x = 0. Solución: x = 0
 Problemas que involucran igualdades con valor absoluto. x =. Solución : x = o x = -. x =. Solución x = o x= -.. x = 0. Solución: x = 0. x =. No hay solución posible. No existen valores absolutos negativos.
Problemas que involucran igualdades con valor absoluto. x =. Solución : x = o x = -. x =. Solución x = o x= -.. x = 0. Solución: x = 0. x =. No hay solución posible. No existen valores absolutos negativos.
IES Francisco Ayala Modelo 2 (Septiembre) de 2008 Soluciones Germán Jesús Rubio Luna. Opción A. x - bx - 4 si x > 2
 IES Francisco Ayala Modelo (Septiembre) de 008 Soluciones Germán Jesús Rubio Luna Opción A Ejercicio n 1 de la opción A de septiembre de 008 ax + x si x Sea f: R R la función definida por: f(x). x - bx
IES Francisco Ayala Modelo (Septiembre) de 008 Soluciones Germán Jesús Rubio Luna Opción A Ejercicio n 1 de la opción A de septiembre de 008 ax + x si x Sea f: R R la función definida por: f(x). x - bx
LÍMITES. Ing. Ronny Altuve
 UNIVERSIDAD ALONSO DE OJEDA FACULTAD DE CIENCIAS ADMINISTRATIVAS Unidad Curricular: Matemática II LÍMITES Elaborado por: Ing. Ronny Altuve Ciudad Ojeda, septiembre 2016 INDICADOR DE LOGRO Aplicar la definición
UNIVERSIDAD ALONSO DE OJEDA FACULTAD DE CIENCIAS ADMINISTRATIVAS Unidad Curricular: Matemática II LÍMITES Elaborado por: Ing. Ronny Altuve Ciudad Ojeda, septiembre 2016 INDICADOR DE LOGRO Aplicar la definición
Algebra Lineal Tarea No 9: Líneas y planos en R 3 Solución a algunos problemas de la tarea (al 29 de junio de 2014)
 lgebra Lineal Tarea No 9: Líneas planos en R 3 a algunos problemas de la tarea (al 9 de junio de 0). Indique las opciones que no contienen ecuaciones de líneas rectas en R 3 :. x = + t, =, z = 3. = = 3
lgebra Lineal Tarea No 9: Líneas planos en R 3 a algunos problemas de la tarea (al 9 de junio de 0). Indique las opciones que no contienen ecuaciones de líneas rectas en R 3 :. x = + t, =, z = 3. = = 3
1. GENERALIDADES SOBRE LOS POLINOMIOS.
 GENERALIDADES SOBRE LOS POLINOMIOS Funciones polinómicas LAS DEFINICIONES Sea p la función definida por: p ( ) = 2( 2 ) + 2 ( 2 ) + 2 2, p es una función de R en R Y para todo real, se tiene p ( ) = 2
GENERALIDADES SOBRE LOS POLINOMIOS Funciones polinómicas LAS DEFINICIONES Sea p la función definida por: p ( ) = 2( 2 ) + 2 ( 2 ) + 2 2, p es una función de R en R Y para todo real, se tiene p ( ) = 2
Ecuaciones e inecuaciones. Sistemas de ecuaciones e inecuaciones
 Ecuaciones e inecuaciones. Sistemas de ecuaciones e inecuaciones Álvarez S., Caballero M.V. y Sánchez M. a M. salvarez@um.es, m.victori@um.es, marvega@um.es Índice 1. Herramientas 6 1.1. Factorización
Ecuaciones e inecuaciones. Sistemas de ecuaciones e inecuaciones Álvarez S., Caballero M.V. y Sánchez M. a M. salvarez@um.es, m.victori@um.es, marvega@um.es Índice 1. Herramientas 6 1.1. Factorización
De grados tres y cuatro
 De grados tres y cuatro Comportamiento general de las funciones polinomiales de grados tres y cuatro Funciones de grado tres. La forma general de las funciones de grado tres (cúbicas) esf x = ax 3 + bx
De grados tres y cuatro Comportamiento general de las funciones polinomiales de grados tres y cuatro Funciones de grado tres. La forma general de las funciones de grado tres (cúbicas) esf x = ax 3 + bx
CÓNICAS. 1. Dada la cónica x 2 + 2xy y 2 2x 2y + 4 = 0, se pide su clasicación y los elementos característicos de la misma. = 1
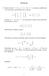 CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
III) INTERPOLACIÓN INTRODUCCIÓN
 III) INTERPOLACIÓN INTRODUCCIÓN En numerosos fenómenos de la naturaleza observamos una cierta regularidad en la forma de producirse, esto nos permite sacar conclusiones de la marcha de un fenómeno en situaciones
III) INTERPOLACIÓN INTRODUCCIÓN En numerosos fenómenos de la naturaleza observamos una cierta regularidad en la forma de producirse, esto nos permite sacar conclusiones de la marcha de un fenómeno en situaciones
Título: mar 6-1:39 PM (Página 1 de 20)
 TEMA 5. ÁLGEBRA El lenguaje algebraico es un lenguaje matemático que combina números y letras unidos mediante operaciones aritméticas (+, -,, :) para expresar la realidad de forma concisa, inequívoca y
TEMA 5. ÁLGEBRA El lenguaje algebraico es un lenguaje matemático que combina números y letras unidos mediante operaciones aritméticas (+, -,, :) para expresar la realidad de forma concisa, inequívoca y
Colegio Beato Carlos Manuel Rodríguez Departamento de Matemáticas. Mapa curricular Algebra I 9 no grado
 Colegio Beato Carlos Manuel Rodríguez Departamento de Matemáticas Mapa curricular Algebra I 9 no grado Colegio Beato Carlos Manuel Rodríguez Mapa curricular Algebra I 9 no grado periodo contenido Dos semanas
Colegio Beato Carlos Manuel Rodríguez Departamento de Matemáticas Mapa curricular Algebra I 9 no grado Colegio Beato Carlos Manuel Rodríguez Mapa curricular Algebra I 9 no grado periodo contenido Dos semanas
Expresiones algebraicas
 Expresiones algebraicas Trabajar en álgebra consiste en manejar relaciones numéricas en las que una o más cantidades son desconocidas. Estas cantidades se llaman variables, incógnitas o indeterminadas
Expresiones algebraicas Trabajar en álgebra consiste en manejar relaciones numéricas en las que una o más cantidades son desconocidas. Estas cantidades se llaman variables, incógnitas o indeterminadas
Límites y continuidad. Cálculo 1
 Límites y continuidad Cálculo 1 Razones de cambio y límites La rapidez promedio de un móvil es la distancia recorrida durante un intervalo de tiempo dividida entre la longitud del intervalo. Ejemplo 1
Límites y continuidad Cálculo 1 Razones de cambio y límites La rapidez promedio de un móvil es la distancia recorrida durante un intervalo de tiempo dividida entre la longitud del intervalo. Ejemplo 1
EJEMPLO DE PREGU,TAS
 EJEMPLO DE PREGU,TAS MATEMÁTICAS PRIMERO, SEGU,DO Y TERCERO DE BACHILLERATO 1. Lógica proposicional Esta competencia se refiere al conocimiento que usted posee sobre el lenguaje de las proposiciones y
EJEMPLO DE PREGU,TAS MATEMÁTICAS PRIMERO, SEGU,DO Y TERCERO DE BACHILLERATO 1. Lógica proposicional Esta competencia se refiere al conocimiento que usted posee sobre el lenguaje de las proposiciones y
Colegio Nacional Rafael Hernández
 Programa de Matemática de 3º año Ciclo lectivo 2014 HILOS CONDUCTORES Colegio Nacional Rafael Hernández Ángulos entre rectas, nuevos ángulos? El álgebra y la geometría: dos caras de una misma moneda. Más
Programa de Matemática de 3º año Ciclo lectivo 2014 HILOS CONDUCTORES Colegio Nacional Rafael Hernández Ángulos entre rectas, nuevos ángulos? El álgebra y la geometría: dos caras de una misma moneda. Más
TEMA 3. POLINOMIOS Y FRACCIONES ALGEBRAICAS. Ficha 0
 Ficha 0 Un monomio es una expresión algebraica formada por el producto de un número, llamado coeficiente, por una o más variables con exponente natural o cero, llamadas parte literal. El grado es la suma
Ficha 0 Un monomio es una expresión algebraica formada por el producto de un número, llamado coeficiente, por una o más variables con exponente natural o cero, llamadas parte literal. El grado es la suma
Área Académica: Matemáticas (Cálculo Diferencial) Tema: Números reales y clasificación de funciones. Profesor(a):Mtra. Judith Ramírez Hernández.
 Área Académica: Matemáticas (Cálculo Diferencial) Tema: Números reales y clasificación de funciones Profesor(a):Mtra. Judith Ramírez Hernández. Periodo: Enero Junio 2012 Topic: Real Numbers and classification
Área Académica: Matemáticas (Cálculo Diferencial) Tema: Números reales y clasificación de funciones Profesor(a):Mtra. Judith Ramírez Hernández. Periodo: Enero Junio 2012 Topic: Real Numbers and classification
Trabajo de Matemáticas AMPLIACIÓN 3º ESO
 Trabajo de Matemáticas AMPLIACIÓN º ESO ACTIVIDADES DE AMPLIACIÓN TEMA : NÚMEROS FRACCIONARIOS O RACIONALES Problema nº Un grifo tarda en llenar un depósito horas y otro tarda en llenar el mismo depósito
Trabajo de Matemáticas AMPLIACIÓN º ESO ACTIVIDADES DE AMPLIACIÓN TEMA : NÚMEROS FRACCIONARIOS O RACIONALES Problema nº Un grifo tarda en llenar un depósito horas y otro tarda en llenar el mismo depósito
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A Ejercicio 1.- Sea f : R R definida por f(x) = x 3 +ax 2 +bx+c. a) [1 75 puntos] Halla a,b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1 2 y que la recta tangente en
Opción A Ejercicio 1.- Sea f : R R definida por f(x) = x 3 +ax 2 +bx+c. a) [1 75 puntos] Halla a,b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1 2 y que la recta tangente en
UNIDAD 8 INECUACIONES. Objetivo general.
 8. 1 UNIDAD 8 INECUACIONES Objetivo general. Al terminar esta Unidad resolverás inecuaciones lineales y cuadráticas e inecuaciones que incluyan valores absolutos, identificarás sus conjuntos solución en
8. 1 UNIDAD 8 INECUACIONES Objetivo general. Al terminar esta Unidad resolverás inecuaciones lineales y cuadráticas e inecuaciones que incluyan valores absolutos, identificarás sus conjuntos solución en
