Electromagnetismo II

Transcripción

1 Electromagnetismo II Semestre: TAREA 9: Solución Dr. A. Reyes-Coronado Por: Jesús Castrejón Figueroa Problema 1 (10pts) Demuestra que para cualquier vector constante c se cumple que: ( c r)d l = a c. Sea T ( r ) una función escalar. Definimos a la función vectorial v como: v = c T, (1) donde c es un vector arbitrario constante distinto de cero. Aplicando el teorema de Stokes a la función v, tenemos que: v d a = v d l, (2) mientras que el rotacional de v es: y la Ec. (2) queda como: v = T c, (3) T c d a = T c d l. (4) Debido a que c es un vector constante puede salir de la integral, por lo que la Ec. anterior queda como: c T d a = c T d l, (5) dicha igualdad es válida para todo vector c, por lo que: T d a = T d l (6) Ahora definimos a T = c r en la ecuación anterior: ( c r) d a = ( c r)d l, (7) pero tenemos que: ( c r) = c, (8) 1

2 ya que c es un vector constante, y entonces: el vector c puede salir de la integral, y finalmente: c d a = ( c r)d l, (9) c a = ( c r)d l (10) Problema 2 (15pts) (a) Recordarás que en clase discutimos que el triángulo magnetoestático estaba incompleto porque faltaba una expresión para calcular el potencial vectorial A dado B. Ahora bien, una forma de llenar el enlace faltante en el triángulo magnetoestático es emplear la analogía entre las definiciones del potencial vectorial ( A = 0; A = B) y las ecuaciones de Maxwell para B ( B = 0; B = µ 0 J). Evidentemente A depende de B de la misma manera que B depende de µ 0 J (por medio de la ley de Biot-Savart). Usando esta observación escribe una ecuación para A en términos de B. (b) El análogo eléctrico para tu resultado en (a) es: Φ( r ) = 1 E( r ) ( r r ) 4π r r 3 d 3 r. Deriva éste resultado haciendo uso de la analogía apropiada. (a) La ley de Biot-Savart, la cual relaciona a B con µ 0 J, viene dada por: Notemos que: y B( r) = µ 0 J( r ) ( r r ) 4π r r 3 d 3 r. (11) A = B, (12) B = µ 0 J, A = 0, (13) B = 0, por lo que A se relaciona con B de la misma manera que B se relaciona con µ 0 J, y entonces: A( r) = 1 B( r ) ( r r ) 4π r r 3 d 3 r (14) 2

3 (b) En este caso E se relaciona con ρ de la siguiente manera: mientras que se cumple que: E( r) = 1 4πε 0 ρ( r )( r r ) r r 3 d 3 r, (15) E = ρ ε 0, (16) Φ = E, por lo que Φ se relaciona con E de la misma manera que E se relaciona con ρ/ε 0 (agregando un producto punto debido a la divergencia): Φ( r) = 1 E( r ) ( r r ) 4π r r 3 d 3 r (17) Problema 3 (20pts) En el polo norte magnético, el campo magnético de la tierra es vertical y tiene una magnitud de 0.62 gauss. El campo magnético terrestre en su superficie (y mas allá), es aproximadamente igual al de un dipolo localizado en el centro de la Tierra. (a) Calcula la magnitud del momento dipolar en joules/tesla. (b) Imagina que la fuente del campo magnético terrestre es un anillo de corriente situada en el ecuador"del centro esférico metálico de la tierra, que tiene un radio de 1, 200 Km (según mediciones sismológicas reportadas en el 2010 en la prestigiada revista Science: doi: /science ), que es casi el radio de la luna (1, 738 Km aprox.). Calcula qué tan grande tiene que ser esta corriente. El campo magnético de un dipolo magnético puntual viene dado por: B = µ 0 3( m ê r )ê r m 4π r 3, (18) por lo que el campo magnético sobre el polo norte viene dado por: B = µ 0 2 m 4π R 3, (19) con R el radio terrestre. Entonces la magnitud del momento dipolar terrestre es: m = iπw 2 = 4πR3 2µ 0 B, (20) con w el radio del ecuador del centro esférico metálico de la tierra e i es la corriente que produce el campo. Sustituyendo valores numéricos, tenemos que: m = J/T (21) i = A (22) Notese que, ya que el joule y el tesla son unidades del SI, al igual que el ampere y el metro, entonces joule/tesla representa la misma unidad que el ampere metro 2. 3

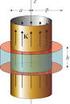
4 Problema 4 (25pts) Una esfera sólida de radio R posee una magnetización uniforme M. Demuestra que la densidad de corriente superficial es la misma que la generada por una esfera hueca del mismo radio con densidad superficial de carga σ, girando con una velocidad angular ω específica. Cómo se debe relacionar los parámetros en el problema? Calculamos las corrientes inducidas, dadas por: Por otro lado, para la esfera que gira, tenemos que: J b = M = 0, (23) K b = M ˆn = M(ê z ê r ) = M sin θê φ. (24) J = ρ v = 0 (25) K = σ v = σωr sin θê φ, (26) por lo que tenemos que la solución es análoga a la de la esfera uniformemente magnetizada si hacemos el cambio: Problema 5 (30pts) M σr ω (27) Hace algunas clases, en la parte de electrostática, determinamos el campo eléctrico dentro de una esfera sólida uniformemente polarizada, encontrando el potencial sobre la superficie de la esfera y luego usando el teorema de unicidad de la solución para calcular el potencial dentro de la esfera. Ahora, puedes seguir la misma estrategia para calcular el campo magnético dentro de una esfera sólida uniformemente magnetizada. Los pasos a seguir son los siguientes: (a) El campo debido a un dipolo magnético está dado por: B r = µ 0m cos θ, 2πr3 B θ = µ 0m 4πr 3 sin θ, B φ = 0. (28) que tiene la misma forma que el campo producido por un dipolo eléctrico: p E r = 2πε 0 r 3 cos θ, E p θ = 4πε 0 r 3 sin θ, E φ = 0. (29) Explica por qué este hecho implica que el campo magnético externo debido a una esfera sólida uniformemente magnetizada de radio R, es el mismo que el campo producido por un dipolo magnético (puntual) m 0 localizado en el centro de la esfera, con magnitud m 0 = (4πR 3 /3)M. (b) Si m 0 apunta en la dirección ê z, entonces las componentes del potencial vectorial A en coordenadas cartesianas sobre la superficie de la esfera, están dadas por: A x = µ 0my 4πr 3, A y = µ 0mx 4πr 3, A z = 0. (30) Explica por qué se puede aplicar en este caso el teorema de unicidad de la solución y calcula A dentro de la esfera. Calcula también el rotacional de A para obtener B. Qué similitudes y/o diferencias encuentras del campo magnético B calculado con los resultados obtenidos para E dentro de una esfera uniformemente polarizada? 4

5 a) Debido a que no hay corrientes libres ( J free = 0), tenemos que: H = 0, (31) y el campo auxiliar H puede ser escrito como el gradiente de una función escalar: donde el campo W cumple la ecuación de Poisson, H = W, (32) 2 W = M (33) Como M es uniforme, M = 0, y W cumple la ecuación de laplace, cuya solución en coordenadas esfericas son los polinomios de Legendre, al igual que en caso electroestático. Entonces la solución fuera de la esfera es proporcional a P 1 (cos θ), lo que equivale a un dipolo puntual. b) El valor máximo (mínimo) del potencial vectorial A es en la frontera, por lo que dentro de la esfera, A debe ser constante y debe tener el valor que tiene en la frontera, esto es: cuyo rotacional es: A x = µ 0my 4πR 3, Tomando en cuenta que m = 4 3 πr3 M, tenemos que: A y = µ 0mx 4πR 3, A z = 0, (34) ( A Ay = x A ) x ê z (35) y = 2µ 0m 4πR 3 êz. B = 2 3 Mê z (36) Problema TORITO (20pts) Una esfera sólida de radio R tiene una densidad volumétrica de carga ρ y gira con una velocidad angular ω. Usando los resultados de los problemas 4 y 5 de esta tarea, muestra que el campo magnético en el polo norte de la esfera es igual a 2µ 0 ρωr 2 /15. Hasta ahora podemos resolver el caso de una esfera hueca, para encontrar el resultado correspondiente a una esfera sólida, consideraremos a esta última como formada por una sucesión de cascarones con radios comprendidos entre (0, R) y con grosor dr infinitesimal, la densidad superficial de carga asociada a uno de estos cascarones es: σ = ρdr. (37) 5

6 La magnetización asociada a las corrientes que produce esta carga en movimiento (visto en el problema 4) viene dada por: dm = ρωrdr, (38) para el caso de un cascarón de radio r. El dipolo puntual asociado es: dm = 4π 3 r3 dm, (39) = 4π 3 ρωr4 dr, y el campo magnético que produce (visto en el problema 5) es: por lo que la magnitud el campo magnético de la esfera sólida es: B = db = 2µ 0dm 4πR 3, (40) R Tomando en cuenta la dirección de la rotación de la esfera, tenemos que: 0 2µ 0 ρω 3R 3 r4 dr. (41) B = 2 15 µ 0ρR 2 ω (42) 6