1. Control de Mínima Varianza
|
|
|
- Vicenta Bustamante Agüero
- hace 6 años
- Vistas:
Transcripción
1 . Control de Mínima Varianza. CONTROL DE MÍNIMA VARIANZA..... PLANTEO DEL PROBLEMA..... CRITERIO DE OPTIMIZACIÓN PREDICCIÓN ÓPTIMA Forma intuitiva Caso General Cálculo del Predictor Óptimo Raíces de C Sobre el Círculo Unidad CONTROL DE MÍNIMA VARIANZA Interpretación como Ubicación de Polos Sistemas con Inversa Inestable REGULADOR LINEAL ÓPTIMO ESTOCÁSTICO (LQG) Factorización Espectral Discusión Heurística Demostración Formal REFERENCIAS...48 Clase 3b Control de Mínima Varianza.doc
2 x.. Planteo del Problema Proceso B ( q) = u [.] A q y = x + v [.] C ( q) v = e A q [.3] con e ruido blanco, A q puede ser inestable, por lo tanto v puede no ser estacionario. Haciendo A = AA B = BA [.4] C = C A se despeja v A q y = B q u + C q e [.5] Se supone que C tiene todos sus raíces dentro del círculo unidad. Clase 3b Control de Mínima Varianza.doc
3 Ejemplo.. Modificación de C Sea z C z n φ = + [.6] sea la señal = C q e [.7] si e es ruido blanco, el espectro de n es π jwt jwt jwt ( e ) C( e ) C( e ) = [.8] se cumple = ( + )( + ) = ( + )( + ) = ( z+ )( z + ) = 4( z+ 0,5)( z + 0,5) C z C z z z z z o sea que n se puede representar ( ) n = C q e = z+ e [.0] * [.9] Clase 3b Control de Mínima Varianza.doc 3
4 si algunas raíces de C están fuera del círculo se las reemplaza de esta manera C = C C C + = C C * + * [.] Clase 3b Control de Mínima Varianza.doc 4
5 J.. Criterio de Optimización mv { } = E y [.] control de mínima varianza J E y N = lim N N [.3] = control lineal cuadrático (lqr) { ρ } J = E y + u [.4] lqr Clase 3b Control de Mínima Varianza.doc 5
6 Ejemplo.. Control de Mínima Varianza y + ay = bu + e + ce [.5] + + con c < e tiene media nula y varianza unitaria. Se trata de mantener la salida lo más próxima a cero que se pueda. Como e + es independiente de y se cumplirá ( y ) ( e ) var var = [.6] + + Si se toma la ley de control u = ( ay ce) [.7] b y u en el siguiente instante resultará + = e+ [.8] esto se cumple para todo instante o sea que el control se reduce a c b a = y [.9] es un control proporcional Clase 3b Control de Mínima Varianza.doc 6
7 El denominador de lazo cerrado es C( z) = z+ c [.0] de aquí la importancia de que este polinomio sea estable La salida, con este control será 0 y = e + c y e [.] 0 0 como c<, el segundo término tiende a cero. Este control da la mínima varianza de la salida. La cantidad ay + bu + ce [.] se puede interpretar como la mejor predicción de la salida en + la cantidad e + es el error de predicción El control se puede redefinir como el que hace que el error de predicción sea mínimo En este caso el error de control es igual al error de predicción Predicción y control están ligados Clase 3b Control de Mínima Varianza.doc 7
8 .3. Predicción Óptima Se asume: que el sistema está perturbado por ruido blanco gaussiano y que el mejor predictor es el que minimiza el error de predicción en sentido medio cuadrático..3.. Forma intuitiva ( q ) * C q C y = e = e * [.3] Aq A q donde * n A q = q A q [.4] (se hace esto por una cuestión de causalidad) Se asume que A y C son de orden n. En el instante se conocen y, y, y se desea predecir y + m Clase 3b Control de Mínima Varianza.doc 8
9 Si se desarrolla en serie, se obtiene ( q ) ( q ) * C y = e = e + f e + + f e + f e + f e + [.5] e + m * + m + m + m m + m m+ A desconocidos conocidos Si C es estable se puede calcular e en base a las medidas de y. A ( q ) ( q ) * = y * [.6] C La mejor predicción será y = f e + f e + [.7] ˆ + m / m m + y el error de predicción es y = e + f e + + f e [.8] + m/ + m + m m + Resta calcular los f i Clase 3b Control de Mínima Varianza.doc 9
10 ... Caso General El predictor de mínima varianza a m pasos está dado por ( q ) * G q G yˆ + m / = q y = y * [.9] C q C q donde F y G son el cociente y el resto de la división m q C q A q F q G q = + [.30] m+ q El error de predicción es un promedio móvil con media nula y = y yˆ = e + f e + + f e + m/ + m + m/ + m + m m + = F q e + su varianza es { } + m/ = ( m) E y f f σ [.3] [.3] C, es decir: A Clase 3b Control de Mínima Varianza.doc 0
11 - Demostración El polinomio F es de grado m- y mónico. El grado de G es menor a n F q = q + f q + + f m m m G q = g q + g q + + g o n n 0 n F q = + f q + + f q * m+ m G q = g + g q + + g q * n+ 0 n se debe cumplir [.33] [.34] m * * * * C q = A q F q + q G q [.35] las ecuaciones [.3] y [.5] se pueden reescribir desconocido * * C q G q * y+ m= e * + m= F ( q ) e+ m+ e * [.36] A q A q conocido Clase 3b Control de Mínima Varianza.doc
12 sabiendo la relación entre e e y ( q ) ( q ) * G * y+ m= F ( q ) e+ m+ y * [.37] C Suponiendo que la predicción es una combinación lineal arbitraria de medidas de la salida, la varianza del error de predicción será ( q ) ( q ) * { } {( ) } G * E y yˆ = E F q e + E y yˆ C * G * ( q ) + E ( F ( q ) e+ m) y ˆ * y + m/ C ( q ) + m + m/ + m * + m/ el último término tiende a cero ya que e es incorrelado con la salida. El predictor que minimiza esta varianza es el que hace cero el segundo término o sea G ( q ) ( q ) * yˆ + m / = y * [.39] C Clase 3b Control de Mínima Varianza.doc [.38]
13 El mejor predictor es lineal. Esto surge al poder eliminar el tercer término en el cálculo de la varianza. El error de predicción es y = y yˆ = e [.40] + / Por esto se dice que la variable e es la innovación del proceso y. Con este predictor el funcional resulta { } + m/ ( m) J m = E y = + f + + f σ [.4] Clase 3b Control de Mínima Varianza.doc 3
14 .3.. Cálculo del Predictor Óptimo Igualando términos en la ecuación [.30] c = a + f c = a + a f + f c = a + a f + + a f + f m m m m m c = a + a f + + a f + g m m m m 0 c = a + a f + + a f + g m+ m+ m m c = a + a f + + a f + g n n n n m+ m nm 0 = a f + a f + + a f + g n n n m+ m n m+ [.4] 0 = a f + g n m n es la solución de una ecuación diofantina Clase 3b Control de Mínima Varianza.doc 4
15 Ejemplo.3. Predictor Aq q q =,5 + 0, 7 C q q q = 0, + 0,5 [.43] El predictor a 3 pasos se calcula ( 0, 0,5) (,5 0,7) q q q q q q fq f g0q g + = [.44] ( ) ( ) ( 0,7 f,5 f g ) q 0, q + 0,5q =,5 + f q + 0, 7 +,5 f + f q f f g g =, 3 =, 75 =,75 =,5 [.46] ,7 f + g El predictor resulta 0 qg q q q yˆ y y C q q 0,q+ 0,5,75,5 + 3/ = [.47] [.45] Clase 3b Control de Mínima Varianza.doc 5
16 y su varianza es { } [.48] E y = +,3 +,75 = 5,755 Clase 3b Control de Mínima Varianza.doc 6
17 Ejemplo.4. Influencia del horizonte de predicción La varianza depende de los términos de F. Estos aumenta con el horizonte m. Como F se obtiene dividiendo C con A, sus elementos corresponden a la respuesta impulsional del sistema C q q 0,q+ 0,5 = y e e Aq q,5q+ 0, (,3,75,75 ) = + q + q + q + e = j= 0 fe j j y el costo de la predicción { } E y m = σ f j [.50] j= figuras [.49] Clase 3b Control de Mínima Varianza.doc 7
18 .3.3. Raíces de C Sobre el Círculo Unidad Ejemplo.5. Una Raíz en Uno y e e y = [.5] e ˆ + / = [.5] calculando e en base a y = + i = + [.53] e e y e z 0 0 i= 0 no va a cero ya que e0 no se anula usar filtro Kalman Clase 3b Control de Mínima Varianza.doc 8
19 Ejemplo.6. Modelo de Señal Continua A q y = C q e + b [.54] se puede eliminar b haciendo ( ) ( ) q A q y = q C q e + b [.55] y considerar una nueva variable ( ) A q y = q C q e = C q e [.56] pero en C ( q) aparece una raíz en uno. Hay que evitar estos modelos. Clase 3b Control de Mínima Varianza.doc 9
20 .4. Control de Mínima Varianza * * B q C q B q C q d y = u e q u * e * Aq + Aq = A q + A q [.57] B estable d = gradoa gradob gradoc = gradoa = n haciendo m=d, se obtiene * * * * C q B q G q B q * y+ d= e * + d+ u * = F ( q ) e+ d+ e * + u * [.58] A q A q A q A q se sabe además, que para las muestras conocidas se puede calcular e * * A q B q d e = y * q u * C q C q [.59] reemplazando, Clase 3b Control de Mínima Varianza.doc 0
21 * * * * G q G q B q B q y = F ( q ) e + y q u + u C q A q C q A q * d + d + d * * * * G q B q F q = + + C q C q * * * * F ( q ) e+ d y * u * Se debe calcular la acción de control tal que minimice la varianza de la salida * * * { } { ( ) } G q B q F q * E y = E F q e + E y + u C q C q + d + d * * el único término manejable es el segundo, que debe ser cero, *( ) ( ) ( ) G q G q u = y * * y B q F q = B q F q [.6] se interpreta como una predicción a d-pasos La salida entonces resulta ( ) * = = d d+ [.63] y F q e e f e f e es un promedio móvil de longitud d-. Clase 3b Control de Mínima Varianza.doc [.60] [.6]
22 La covarianza se extinguirá para separaciones mayores a d-. Esto se utiliza como diagnóstico Hay cancelación de los ceros del proceso Clase 3b Control de Mínima Varianza.doc
23 Ejemplo.7. Control de mínima Varianza 3 A q q, 7q 0, 7q B q = + = q+ 0,5 C q = q 0,9q d = [.65] F q = q+ 3 0,8 G q = 0,66q 0,56q u = q( 0,66q 0,56) ( q+ 0,5)( q+ 0,8) [.66] y [.64] [.67] u =,3u 0,4u 0,66 y + 0,56 y [.68] { } 0,8,64 E y = + = [.69] Clase 3b Control de Mínima Varianza.doc 3
24 Clase 3b Control de Mínima Varianza.doc 4
25 Ejemplo.8. Influencia del Retardo =,5 + 0,7 d = ( + 0,5 ) = 0, + 0,5 A q q q * B q q q * C q q q * d = 3 5 [.7] [.70] Clase 3b Control de Mínima Varianza.doc 5
26 .4.. Seguimiento de Referencias La planta se escribe * * * G q B q F q * y+ d= F ( q ) e+ d+ y * + u * [.7] C q C q Se debe calcular la acción de control tal que minimice la varianza de la salida ( ) { } {( ) } * * * G q B q F q * E y r = E F q e + E y + u r C q C q + d + d + d * * + d el único término manejable es el segundo, que debe ser cero, * u = C * * ( q ) r+ d G ( q ) y B q F q [.74] [.73] Clase 3b Control de Mínima Varianza.doc 6
27 Diagrama en Bloques ω C A r + d C + - FB u z -d B A + + y G Relación entrada salida y = r + F q e [.75] * Clase 3b Control de Mínima Varianza.doc 7
28 .4.. Mínima Varianza Ponderado Funcional a minimizar { } + d + λ d J = E y r + u [.76] ( ) { } { ( ) } E y r λu E F q e E y u r u C q C q [.77] * * * * G q B q F q + d + d + = + d + * + * + d + λ Su mínimo está cuando * u = C( q ) r + G ( q ) y B q F q C q + λ * * d [.78] Clase 3b Control de Mínima Varianza.doc 8
29 Diagrama en Bloques ω C A r + d C + - FB + λc u z -d B A + + y G Relación entrada salida λ + λ λ * * * B q F q B q C q y = r + e B q + A q B q + A q * * * * [.79] Clase 3b Control de Mínima Varianza.doc 9
30 .4.3. Expresión Vectorial del Controlador y Planta Controlador: * u = C( q ) r + G ( q ) y B q F q C q + λ * * d con lo que u resulta, [.80] b λ u = Cr G y - F B - b + (C - ) u b b 0 + d 0 0+ λ 0 Por lo tanto la ley de control en forma vectorial será: donde: = p T u x [9-] T b0 b0c b0 g0 b0gn- b0 λ p =,, fb + c b0+ λ b0+ λ b0+ λ b0+ λ b0+ λ b0 x [ + + y y u ] = r,r - -, - T d d -n+ - [9-] [9-3] Clase 3b Control de Mínima Varianza.doc 30
31 Planta: * * * G q B q F q * y+ d= F ( q ) e+ d+ y * + u * [.8] C q C q Predictor * * * G ( q ) B ( q ) F ( q ) + = + [.8] * * C ( q ) C ( q ) ˆ = + d [.83] λ ˆ + *( * ) ( * ) + λ ( ) [ ˆ = d λ ] ( + + ) y y u ˆ d * * * * B q F q u C q y G q y B q F q u + C q u = C q y G q y + C q λu [.84] * * * d B q F q C q u C q y u G q y [.85] b0 + λ λ λ u = C y ˆ+ d+ u - G y - F B - b + ( C - ) u b0 b0 b0 0 b0 λ λ u = C y ˆ + d+ u - G y - F B - b + (C - ) u b0+ λ b0 b0 0 [9-4] Clase 3b Control de Mínima Varianza.doc 3
32 es: por lo tanto, la expresión de la actuación de acuerdo a la ecuación de la planta donde x = p T u x [9-5] λ λ = y ˆ +, y ˆ b b T + d u + d u- y y-n+ u- u-m-d+ 0 0 T b0 b0c b0 g0 b0gn- b0 λ p =,, ( fb + c ) b0+ λ b0+ λ b0+ λ b0+ λ b0+ λ b0 [9-6] Clase 3b Control de Mínima Varianza.doc 3
33 .4.4. Interpretación como Ubicación de Polos Aq Bq y C q e G q F q B q = u 0 [.86] despejando la acción de control, resulta el siguiente polinomio característico d A q F q B q + G q B q = q C q B q [.87] esto se puede interpretar como una ubicación de polos. Es decir, se elige el regulador, G( q) S q u = y y F q B q = R q [.88] con, S q = G q R q = F q B q [.89] reemplazando, d q C q B q A q F q B q G q B q A q R q B q S q = + == + [.90] Clase 3b Control de Mínima Varianza.doc 33
34 .4.5. Sistemas con Inversa Inestable Si B tiene raíces inestables, aparecerán modos inestables que no son observados desde la salida. y u F q e = d q [.9] B( q) G q e = d [.9] q Ejemplo.9. Cancelación de Ceros Inestables = 0,9q+ Aq = q q = q q+ B q 0,7,7 0,7 C q = q q 0,7 = q 0,7q d = [.94] F q = G q = q0,7 [.95] [.93] verificar simulación Clase 3b Control de Mínima Varianza.doc 34
35 Teorema. Control de Mínima Varianza Generalizado Sea el sistema A q y = B q u + C q e [.96] con + B q B q B q u = [.97] + todos los ceros de B ( q) todos los ceros de B ( q) todos los ceros de C( q ) están fuera del círculo unidad A( q ) y B ( q) no tienen raíces comunes. están dentro del círculo unidad están fuera del círculo unidad Entonces, el control de mínima varianza sigue la ley G( q) ( q) F( q) = + [.98] B siendo, y d q C q A q F q B q G q = + [.99] Clase 3b Control de Mínima Varianza.doc 35
36 con grado F = d + grado B grado G < grado A = n [.00] - Demostración Sea el operador a > q+ a [.0] Clase 3b Control de Mínima Varianza.doc 36
37 .5. Regulador Lineal Óptimo Estocástico (LQG) Proceso x =Φ x +Γ u + Ke + y = Cx + e [.0] el grado de C es igual al grado de A a 0 0 b ca a 0 0 b c a Φ= Γ= = C = a 0 0 b c a n n n n an bn cn an el filtro de Kalman resulta xˆ =Φ xˆ +Γ u + K y Cxˆ [.04] + / / / el polinomio característico es ( ) det zi Φ KC = C z [.05] Si el retardo es uno, la ley de control es [ 0 0] [.03] Clase 3b Control de Mínima Varianza.doc 37
38 u Lxˆ = / [.06] y la función de transferencia del regulador es S z Hr ( z) =L( zi Φ+ KC+Γ L) = [.07] R z donde det R z = zi Φ+ KC+Γ L [.08] el grado de R es n y el grado de S<n los polos en lazo cerrado son los de C det P z = zi Φ+Γ L = C z [.09] P se obtiene de la ecuación de Ricatti. Se tratará de dejar la ley de control en función de la salida en lugar del estado La ecuación a minimizar es { ρ } J = E y + u [.0] lqr es el mismo caso de variables de estado en donde Q = C C Q = 0 Q = ρ [.] T Clase 3b Control de Mínima Varianza.doc 38
39 haciendo igual cálculo se llega a que L = L v Φ [.] la ley de control en variables de estados es u =Lxˆ L vˆ =Lxˆ L K y Cxˆ / v / / v / =L ΦKC xˆ L Ky v / v reemplazando el observador v v ( Φ+ ) [.3] u =L ΦKC qi Φ+ KC Γ u + Ky L Ky v v =L ΦKC qi Φ+ KC Γu L Φ KC+ qi +Φ+ KC qi Φ+ KC Ky v =L ΦKC qi Φ+ KC Γu L qi KC Ky v haciendo R = det ( qi Φ+ KC) [.5] se obtiene [.4] Clase 3b Control de Mínima Varianza.doc 39
40 R q S q u = u y [.6] R q R q donde grado R 0 = 0 ( ) < n grado R = grado S = n S con lo que queda S( q) + [.7] S q u = y = y R q R q R q [.8] Clase 3b Control de Mínima Varianza.doc 40
41 es.5.. Factorización Espectral de lo visto en variables de estado, el polinomio característico P en lazo cerrado, ( ) ( ρ ) ( ) rp z P z = A z A z + B z B z [.9] Otra forma de verlo, es encontrar un polinomio P que cumpla con esta ecuación. Esto se llama factorización espectral. Sea n n n+ n n F z = f z + f z + + f z + f z + f z + + f z+ f [.0] 0 n n n 0 este polinomio coincide con su recíproco n F z = z F z = F z [.] si a es raíz de F ( z ), también es raíz. a Además, si los coeficientes de F son reales, los conjugadosa y también son a raíces. Clase 3b Control de Mínima Varianza.doc 4
42 Teorema. Se cumple que, si A y B son primos, grado de A mayor al grado de B, grado de P = grado A = n Existe un único P con sus raíces dentro o sobre el círculo unidad, y si ρ > 0, P no tiene raíces sobre el círculo unidad. - Demostración: n Multiplicando la ecuación [.9] por z n n n n+ n n zpzpz = pz + pz + + p z + pz + p z + + pz+ p [.] queda de la forma de F. 0 n n n 0 Por lo tanto el lado derecho de la ecuación [.9] tiene raíces espejadas. Tampoco puede tenerlas sobre el círculo unidad ya que, para j ( ω j ) ( ω j ) ( ω j j j ) ( ω ) ρ ( ω ) ( ω ) ρae Ae + Be Be = Ae + Be = 0 [.3] como ρ > 0, implica que z j e ω j = e ω es raíz de A y de B, pero estos son primos. La condición de que el grado de P sea n, asegura la unicidad de P. Clase 3b Control de Mínima Varianza.doc 4 z =
43 Nota : si se introduce el recíproco P * ( z) z n P( z ) * ρ * * rp z P z = A z A z + B z B z [.4] = resulta l Nota : si P satisface la ecuación [.9] entonces zp( z ) Clase 3b Control de Mínima Varianza.doc 43
44 .5.. Discusión Heurística En el problema de ubicación de polos se debe definir el polinomio característico A z. en lazo cerrado Ac( z) Ao( z ) donde o En el problema LQG A ( z) = C( z) y el polinomio A ( z) P( z) factorización espectral. o c = que se obtiene por Se puede pensar en la ubicación de polos con estas condiciones de diseño, resultando el control óptimo: u S q = y [.5] con R q A( z) R( z) + B( z) S( z) = P( z) C( z) [.6] Hay muchos polinomios que satisfacen esta ecuación. Si hay retardo es mejor calcular la siguiente ecuación: d ( ) ( ) * * * * * * A z R z z B z S z P z C z + = [.7] d = grado A z grado B z [.8] Clase 3b Control de Mínima Varianza.doc 44
45 .5.3. Demostración Formal Teorema 3. Control LQG Sea P( z) el polinomio calculado por factorización espectral, A( z) mónico A( z) y B( z) no tienen raíces comunes fuera del o sobre el círculo unidad. Entonces existe una única solución a las ecuaciones * * * A z X z + rp z S z = B z C z =ρ d * * * z B z X z rp z R z A z C z con ( ) * * grado X z < n < = ( ) grado R z n grado S z n grado A z [.30] [.9] Clase 3b Control de Mínima Varianza.doc 45
46 - Demostración Primero se supone que raíces serán z i < P z tiene raíces distintas z i, como es estable todas las Por hipótesis, los polinomios A y B no se pueden hacer cero simultaneamente. Evaluando [.9] en z = z ( i) ( i) = ( i) ( i) =ρ * * A z X z B z C z d * * i i i i i z B z X z A z C z i [.3] si A y B son distintos de cero se puede hacer ( i) ( i) B z ρ A z A z z B z = [.3] * d * i i i * * si A ( z i ) = 0 y B ( zi ) 0, de[.4] resulta ( i ) 0 cumple A * ( 0) =. Esto implica z 0. Se puede despejar X de la ecuación A z X z B z C z * * i i = i i [.33] i B z =. Como A es mónico se Clase 3b Control de Mínima Varianza.doc 46
47 X z i * ( i) ( i) d * ( z ) ρ A z C z = [.34] z B i i Clase 3b Control de Mínima Varianza.doc 47
48 .6. Referencias Goodwin, G. Sin: Adaptive Filtering, Prediction and Control, Prentice Hall 984. Clase 3b Control de Mínima Varianza.doc 48
1. Diseño Óptimo en Función de Transferencia. 1. Diseño Óptimo en Función de Transferencia 1
 . Diseño Óptimo en Función de Transferencia. Diseño Óptimo en Función de Transferencia.. Planteo del Problema.. Criterio de Optimización 3.. Predicción Óptima 4... Forma intuitiva 5... Caso General 5..3.
. Diseño Óptimo en Función de Transferencia. Diseño Óptimo en Función de Transferencia.. Planteo del Problema.. Criterio de Optimización 3.. Predicción Óptima 4... Forma intuitiva 5... Caso General 5..3.
Procesos autorregresivos
 Capítulo 3 Procesos autorregresivos Los procesos autorregresivos deben su nombre a la regresión y son los primeros procesos estacionarios que se estudiaron. Proceso autorregresivo: Un proceso autorregresivo
Capítulo 3 Procesos autorregresivos Los procesos autorregresivos deben su nombre a la regresión y son los primeros procesos estacionarios que se estudiaron. Proceso autorregresivo: Un proceso autorregresivo
PROBLEMAS PROPUESTOS. TEMAS 5 Y 6 SOLUCIONES
 Grado en Ingeniería Mecánica Teoría de Sistemas PROBLEMAS PROPUESTOS. TEMAS 5 Y 6 SOLUCIONES Transformada Z. Función de transferencia discreta. Modelado de sistemas discretos. PROBLEMA 1. Sistema discreto
Grado en Ingeniería Mecánica Teoría de Sistemas PROBLEMAS PROPUESTOS. TEMAS 5 Y 6 SOLUCIONES Transformada Z. Función de transferencia discreta. Modelado de sistemas discretos. PROBLEMA 1. Sistema discreto
Modelado en el dominio de la frecuencia Utilizar la transformada Laplace para representar ecuaciones diferenciales lineales
 2.3 OBJETIVOS Transformada Laplace (Repaso) Modelado en el dominio de la frecuencia Utilizar la transformada Laplace para representar ecuaciones diferenciales lineales CONTENIDOS Transformada de Laplace
2.3 OBJETIVOS Transformada Laplace (Repaso) Modelado en el dominio de la frecuencia Utilizar la transformada Laplace para representar ecuaciones diferenciales lineales CONTENIDOS Transformada de Laplace
Identificación Paramétrica
 Identificación Paramétrica Métodos para la Obtención de un Modelo Discreto Un modelo, incluyendo el ruido o perturbación, a tiempo discreto puede ser representado por la siguiente i ecuación Donde: ( )
Identificación Paramétrica Métodos para la Obtención de un Modelo Discreto Un modelo, incluyendo el ruido o perturbación, a tiempo discreto puede ser representado por la siguiente i ecuación Donde: ( )
1. Modelo de Perturbaciones. 1. Modelo de Perturbaciones 1
 . Modelo de Perturbaciones. Modelo de Perturbaciones.. Introducción 3.. Reducción del efecto de las Perturbaciones 4.3. Modelo de Perturbaciones 8.4. Perturbaciones Determísticas a Tramos.4.. Modelo en
. Modelo de Perturbaciones. Modelo de Perturbaciones.. Introducción 3.. Reducción del efecto de las Perturbaciones 4.3. Modelo de Perturbaciones 8.4. Perturbaciones Determísticas a Tramos.4.. Modelo en
EJERCICIOS RESUELTOS Y PROPUESTOS
 UNIVERSIDAD NACIONAL DE INGENIERÍA Facultad de Ingeniería Mecánica MT 227 Control Moderno y Óptimo EJERCICIOS RESUELTOS Y PROPUESTOS Estabilidad según Lyapunov (1) Un buen modelo de un niño impulsandose
UNIVERSIDAD NACIONAL DE INGENIERÍA Facultad de Ingeniería Mecánica MT 227 Control Moderno y Óptimo EJERCICIOS RESUELTOS Y PROPUESTOS Estabilidad según Lyapunov (1) Un buen modelo de un niño impulsandose
AUTOMATIZACION Y CONTROL DE PROCESOS FACEyT UNT ESTABILIDAD DE LOS SISTEMAS EN LAZO CERRADO
 Análisis Cualitativo de la Respuesta Temporal de un Sistema Si se conocen la función de transferencia G(s) de un dado sistema y la entrada x(t), se puede evaluar la salida y(t) a partir de: y(s) G (s )
Análisis Cualitativo de la Respuesta Temporal de un Sistema Si se conocen la función de transferencia G(s) de un dado sistema y la entrada x(t), se puede evaluar la salida y(t) a partir de: y(s) G (s )
Parte 3. Vectores y valores propios
 Parte 3. Vectores y valores propios Gustavo Montero Escuela Universitaria Politécnica Universidad de Las Palmas de Gran Canaria Curso 2006-2007 Valores y vectores propios Valor propio Se dice que el número
Parte 3. Vectores y valores propios Gustavo Montero Escuela Universitaria Politécnica Universidad de Las Palmas de Gran Canaria Curso 2006-2007 Valores y vectores propios Valor propio Se dice que el número
Sistemas de control con realimentación de la salida
 Capítulo 7 Sistemas de control con realimentación de la salida 7.1. Introducción En el capítulo 5 se supuso que estaba disponible el vector de estado completamente. Relajando esta suposición y estudiando
Capítulo 7 Sistemas de control con realimentación de la salida 7.1. Introducción En el capítulo 5 se supuso que estaba disponible el vector de estado completamente. Relajando esta suposición y estudiando
MODELOS DE SERIES DE TIEMPO 1. Modelos capaces de predecir, interpretar y evaluar hipótesis con datos económicos y financieros.
 MODELOS DE SERIES DE TIEMPO 1 Introducción Modelos capaces de predecir, interpretar y evaluar hipótesis con datos económicos y financieros. Originalmente tuvieron como objetivo hacer predicciones. Descomposición
MODELOS DE SERIES DE TIEMPO 1 Introducción Modelos capaces de predecir, interpretar y evaluar hipótesis con datos económicos y financieros. Originalmente tuvieron como objetivo hacer predicciones. Descomposición
Parte 3. Vectores y valores propios
 Parte 3. Vectores y valores propios Gustavo Montero Escuela Universitaria Politécnica Universidad de Las Palmas de Gran Canaria Curso 2004-2005 1 Introducción a los valores y vectores propios 2 3 4 5 Valores
Parte 3. Vectores y valores propios Gustavo Montero Escuela Universitaria Politécnica Universidad de Las Palmas de Gran Canaria Curso 2004-2005 1 Introducción a los valores y vectores propios 2 3 4 5 Valores
ECONOMETRÍA II: ECONOMETRÍA DE SERIES TEMPORALES. Modelos ARMA
 ECONOMETRÍA II: ECONOMETRÍA DE SERIES TEMPORALES Modelos ARMA Definición: Ruido blanco. Se dice que el proceso {ɛ t } es ruido blanco ( white noise ) si: E(ɛ t ) = 0 Var(ɛ t ) = E(ɛ 2 t ) = σ 2 Para todo
ECONOMETRÍA II: ECONOMETRÍA DE SERIES TEMPORALES Modelos ARMA Definición: Ruido blanco. Se dice que el proceso {ɛ t } es ruido blanco ( white noise ) si: E(ɛ t ) = 0 Var(ɛ t ) = E(ɛ 2 t ) = σ 2 Para todo
Estabilidad de Sistemas en Tiempo Discreto.
 CAPIULO 3 Estabilidad de Sistemas en iempo Discreto. El hombre de talento es naturalmente inclinado a la crítica, porque ve más cosas que los otros hombres y las ve mejor. Montesquieu Contenido: ema 3.:
CAPIULO 3 Estabilidad de Sistemas en iempo Discreto. El hombre de talento es naturalmente inclinado a la crítica, porque ve más cosas que los otros hombres y las ve mejor. Montesquieu Contenido: ema 3.:
Las desigualdades absolutas son aquellas que se cumplen sea cual sea el valor real que se sustituye. Por ejemplo:
 MATEMÁTICAS BÁSICAS INECUACIONES INTERVALOS DE NÚMEROS REALES Una desigualdad es la epresión de dos cantidades tales que una es mayor que otra. Las desigualdades en general se clasifican en absolutas y
MATEMÁTICAS BÁSICAS INECUACIONES INTERVALOS DE NÚMEROS REALES Una desigualdad es la epresión de dos cantidades tales que una es mayor que otra. Las desigualdades en general se clasifican en absolutas y
Control Moderno. Ene.-Jun Diseño de controlador por retroalimentación de estado. Dr. Rodolfo Salinas. mayo 2007
 UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN Facultad de Ingeniería Mecánica y Eléctrica Control Moderno Ene.-Jun. 2007 Diseño de controlador por retroalimentación de estado Dr. Rodolfo Salinas mayo 2007 Control
UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN Facultad de Ingeniería Mecánica y Eléctrica Control Moderno Ene.-Jun. 2007 Diseño de controlador por retroalimentación de estado Dr. Rodolfo Salinas mayo 2007 Control
Elementos de control en lazo cerrado 14 de diciembre de 2011
 . Introducción Elementos de control en lazo cerrado 4 de diciembre de 2 d i d o r C u G o y d m Figura : Lazo de control estándar. La Figura muestra un lazo de control elemental. En dicha figura, G o corresponde
. Introducción Elementos de control en lazo cerrado 4 de diciembre de 2 d i d o r C u G o y d m Figura : Lazo de control estándar. La Figura muestra un lazo de control elemental. En dicha figura, G o corresponde
Introducción. Por favor. No olvide bajar el tono a su. Franco E., Rosero E., Ramírez J.M. () SISTEMAS DE CONTROL II GICI / 42
 Introducción Por favor No olvide bajar el tono a su teléfono móvil!. Franco E., Rosero E., Ramírez J.M. () SISTEMAS DE CONTROL II GICI 2008 1 / 42 Introducción UNIDAD I ESTABILIDAD DE SISTEMAS DINÁMICOS
Introducción Por favor No olvide bajar el tono a su teléfono móvil!. Franco E., Rosero E., Ramírez J.M. () SISTEMAS DE CONTROL II GICI 2008 1 / 42 Introducción UNIDAD I ESTABILIDAD DE SISTEMAS DINÁMICOS
PROBLEMA 1 *( ) + SOLUCIÓN: Sea la superficie de la parte esférica superior, parametrizada con coordenadas cilíndricas de la siguiente manera:
 PROBLEMA 1 A una esfera maciza de radio unidad se le hace una perforación cilíndrica siguiendo un eje diametral de la esfera. Suponiendo que el cilindro es circular de radio, con y que el eje que se usa
PROBLEMA 1 A una esfera maciza de radio unidad se le hace una perforación cilíndrica siguiendo un eje diametral de la esfera. Suponiendo que el cilindro es circular de radio, con y que el eje que se usa
Práctico 2 Análisis de proceso autorregresivo de orden 2 Proceso WSS filtrado
 Práctico Análisis de proceso autorregresivo de orden Proceso WSS filtrado Tratamiento Estadístico de Señales Pablo Musé, Ernesto López & Luís Di Martino {pmuse, elopez, dimartino}@fing.edu.uy Departamento
Práctico Análisis de proceso autorregresivo de orden Proceso WSS filtrado Tratamiento Estadístico de Señales Pablo Musé, Ernesto López & Luís Di Martino {pmuse, elopez, dimartino}@fing.edu.uy Departamento
Control Moderno. Ene.-Jun Diseño de controlador con referencia a la entrada, servosistemas. Dr. Rodolfo Salinas. mayo 2007
 UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN Facultad de Ingeniería Mecánica y Eléctrica Control Moderno Ene.-Jun. 2007 Diseño de controlador con referencia a la entrada, servosistemas Dr. Rodolfo Salinas mayo 2007
UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN Facultad de Ingeniería Mecánica y Eléctrica Control Moderno Ene.-Jun. 2007 Diseño de controlador con referencia a la entrada, servosistemas Dr. Rodolfo Salinas mayo 2007
Ingeniería de Control I Tema 11. Reguladores PID
 Ingeniería de Control I Tema 11 Reguladores PID 1 Tema 11. Reguladores PID Introducción Especificaciones de funcionamiento Acciones básicas de control Ajuste empírico de reguladores. Métodos de Ziegler-
Ingeniería de Control I Tema 11 Reguladores PID 1 Tema 11. Reguladores PID Introducción Especificaciones de funcionamiento Acciones básicas de control Ajuste empírico de reguladores. Métodos de Ziegler-
Procesos Integrados. Si (Y t ) no es estacionario pero la serie (Z t ) de las primeras diferencias. Z t = Y t = Y t Y t 1,
 Capítulo 5 Procesos Integrados Un proceso no estacionario puede no ser estable en la media, en la varianza o en las autocorrelaciones. Por ejemplo, las series 3, 5-13, 19, 29-31, 35-37, y 39 del Capítulo
Capítulo 5 Procesos Integrados Un proceso no estacionario puede no ser estable en la media, en la varianza o en las autocorrelaciones. Por ejemplo, las series 3, 5-13, 19, 29-31, 35-37, y 39 del Capítulo
Técnicas de Predicción Solución Examen Final
 Técnicas de Predicción Solución Examen Final Administración y Dirección de Empresas 23 de Junio, 2008 Prof. Antoni Espasa Secciones 3h Nota: Todas las respuestas deben ser adecuadamente razonadas. Respuestas
Técnicas de Predicción Solución Examen Final Administración y Dirección de Empresas 23 de Junio, 2008 Prof. Antoni Espasa Secciones 3h Nota: Todas las respuestas deben ser adecuadamente razonadas. Respuestas
ECONOMETRÍA II: ECONOMETRÍA DE SERIES TEMPORALES. Modelos econométricos dinámicos uniecuacionales
 ECONOMETRÍA II: ECONOMETRÍA DE SERIES TEMPORALES Modelos econométricos dinámicos uniecuacionales Introducción: Hemos estudiado modelos de tipo: y t = φ 0 + p i=1 φ iy t i + q j=0 θ jɛ t j y t = β x t +
ECONOMETRÍA II: ECONOMETRÍA DE SERIES TEMPORALES Modelos econométricos dinámicos uniecuacionales Introducción: Hemos estudiado modelos de tipo: y t = φ 0 + p i=1 φ iy t i + q j=0 θ jɛ t j y t = β x t +
Tema 2: Modelos probabilísticos de series
 Tema 2: Modelos probabilísticos de Tema 2: Modelos probabilísticos de 1 2 3 4 5 6 Definición Un proceso estocástico con conjunto de índices T es una colección de variables aleatorias {X t } t T sobre (Ω,
Tema 2: Modelos probabilísticos de Tema 2: Modelos probabilísticos de 1 2 3 4 5 6 Definición Un proceso estocástico con conjunto de índices T es una colección de variables aleatorias {X t } t T sobre (Ω,
Antecedentes de Control
 Apéndice A Antecedentes de Control Para cualquier tipo de análisis de sistemas de control, es importante establecer ciertos conceptos básicos. Sistemas de control retroalimentados Un sistema que mantiene
Apéndice A Antecedentes de Control Para cualquier tipo de análisis de sistemas de control, es importante establecer ciertos conceptos básicos. Sistemas de control retroalimentados Un sistema que mantiene
COLECCIÓN DE PROBLEMAS DE EXÁMENES DE INGENIERÍA DE CONTROL
 COLECCIÓN DE PROBLEMAS DE EXÁMENES DE INGENIERÍA DE CONTROL A continuación se incluyen preguntas de examen de los últimos años, tanto de teoría como de problemas. Lo indicado entre paréntesis es la puntuación
COLECCIÓN DE PROBLEMAS DE EXÁMENES DE INGENIERÍA DE CONTROL A continuación se incluyen preguntas de examen de los últimos años, tanto de teoría como de problemas. Lo indicado entre paréntesis es la puntuación
Sistemas lineales de ecuaciones diferenciales. Juan-Miguel Gracia
 Sistemas lineales de ecuaciones diferenciales Juan-Miguel Gracia Índice Sistemas lineales 2 Búsqueda de una solución especial 3 Aplicación a sistemas 4 Problema de condiciones iniciales 2 / 2 Sistemas
Sistemas lineales de ecuaciones diferenciales Juan-Miguel Gracia Índice Sistemas lineales 2 Búsqueda de una solución especial 3 Aplicación a sistemas 4 Problema de condiciones iniciales 2 / 2 Sistemas
SEGUNDO TURNO TEMA 1
 TEMA 1 Ejercicio 1 ( puntos) Dada la función polinómica f(x) = x + 2x 2 x 2, hallar los intervalos de positividad y negatividad de f sabiendo que el gráfico de dicha función corta al eje x en el punto
TEMA 1 Ejercicio 1 ( puntos) Dada la función polinómica f(x) = x + 2x 2 x 2, hallar los intervalos de positividad y negatividad de f sabiendo que el gráfico de dicha función corta al eje x en el punto
Aplicaciones Industriales del Control Automático ESC
 Aplicaciones Industriales del Control Automático Controladores Predictivos Aníbal Zanini azanini@fi.uba.ar Departamento de Electrónica Facultad de Ingeniería de la Universidad de Buenos Aires CIITI 2005
Aplicaciones Industriales del Control Automático Controladores Predictivos Aníbal Zanini azanini@fi.uba.ar Departamento de Electrónica Facultad de Ingeniería de la Universidad de Buenos Aires CIITI 2005
1: EL CONCEPTO DE CONTROL INVERSO ADAPTATIVO
 Capítulo 1: EL CONCEPTO DE CONTROL INVERSO ADAPTATIVO INTRODUCCIÓN 1.1. INTRODUCCIÓN Las técnicas de filtrado adaptativo han sido aplicadas con éxito a los sistemas de antenas adaptativas, a problemas
Capítulo 1: EL CONCEPTO DE CONTROL INVERSO ADAPTATIVO INTRODUCCIÓN 1.1. INTRODUCCIÓN Las técnicas de filtrado adaptativo han sido aplicadas con éxito a los sistemas de antenas adaptativas, a problemas
SISTEMAS DE CONTROL ANÁLISIS Y DISEÑO DE SISTEMAS DE CONTROL EN EL DOMINIO DE LA FRECUENCIA. Profesor: Adrián Peidró
 SISTEMAS DE CONTROL PRÁCTICAS DE SISTEMAS DE CONTROL ANÁLISIS Y DISEÑO DE SISTEMAS DE CONTROL EN EL DOMINIO DE LA FRECUENCIA Profesor: Adrián Peidró (apeidro@umh.es) OBJETIVOS Afianzar los conocimientos
SISTEMAS DE CONTROL PRÁCTICAS DE SISTEMAS DE CONTROL ANÁLISIS Y DISEÑO DE SISTEMAS DE CONTROL EN EL DOMINIO DE LA FRECUENCIA Profesor: Adrián Peidró (apeidro@umh.es) OBJETIVOS Afianzar los conocimientos
1. Ajuste de los Modelos 1
 03 b Ajuste de Modelos Identificacion.doc. Ajuste de los Modelos. Ajuste de los Modelos.. Introducción 2.2. Obtención Experimental del Modelo 2.2.. Modelado en Lazo Abierto 3.3. Otros Métodos 2.4. Obtención
03 b Ajuste de Modelos Identificacion.doc. Ajuste de los Modelos. Ajuste de los Modelos.. Introducción 2.2. Obtención Experimental del Modelo 2.2.. Modelado en Lazo Abierto 3.3. Otros Métodos 2.4. Obtención
Clase 7 Herramientas de Álgebra Lineal
 Clase 7 Herramientas de Álgebra Lineal 1 Formas cuadráticas La descomposición en valores singulares 3 Normas de matrices 4 Ejercicios Dada una matriz M R n n, la función escalar x T Mx, donde x R n, es
Clase 7 Herramientas de Álgebra Lineal 1 Formas cuadráticas La descomposición en valores singulares 3 Normas de matrices 4 Ejercicios Dada una matriz M R n n, la función escalar x T Mx, donde x R n, es
4.- ANALISIS DE SISTEMAS EN TIEMPO CONTINUO
 ANALISIS DE SISTEMAS EN TIEMPO CONTINUO Dinámica de Sistemas 4. 4.- ANALISIS DE SISTEMAS EN TIEMPO CONTINUO 4..- Efecto de los polos en el comportamiento del sistema. 4..- Estabilidad. 4.3.- Análisis de
ANALISIS DE SISTEMAS EN TIEMPO CONTINUO Dinámica de Sistemas 4. 4.- ANALISIS DE SISTEMAS EN TIEMPO CONTINUO 4..- Efecto de los polos en el comportamiento del sistema. 4..- Estabilidad. 4.3.- Análisis de
1. Método del Lugar de las Raíces
 . Método del Lugar de las Raíces. MÉTODO DEL LUGAR DE LAS RAÍCES..... IDEA BÁSICA... 3.. LUGAR DE LAS RAÍCES DE SISTEMAS SIMPLES... 0.3. LUGAR DE GANANCIA CONSTANTE....4. REGLAS PARA LA CONSTRUCCIÓN DEL
. Método del Lugar de las Raíces. MÉTODO DEL LUGAR DE LAS RAÍCES..... IDEA BÁSICA... 3.. LUGAR DE LAS RAÍCES DE SISTEMAS SIMPLES... 0.3. LUGAR DE GANANCIA CONSTANTE....4. REGLAS PARA LA CONSTRUCCIÓN DEL
6. Diseño Básico de controladores SISO
 6. Diseño Básico de controladores SISO Parte 1 Panorama: Enfoque polinomial Ajuste de PI y PID mediante asignación de polos El predictor de Smith CAUT1 Clase 9 1 Introducción En el capítulo anterior examinamos
6. Diseño Básico de controladores SISO Parte 1 Panorama: Enfoque polinomial Ajuste de PI y PID mediante asignación de polos El predictor de Smith CAUT1 Clase 9 1 Introducción En el capítulo anterior examinamos
1.1. Introducción Método de Identificación por Mínimos Cuadrados Forma Recursiva: Inclusión del Factor de Olvido.
 . Mínimos Cuadrados. Mínimos Cuadrados.. Introducción 2.2. Método de Identificación por Mínimos Cuadrados 3.2.. Forma Recursiva: 6.2.2. Inclusión del Factor de Olvido. 0.3. Características Estadísticas
. Mínimos Cuadrados. Mínimos Cuadrados.. Introducción 2.2. Método de Identificación por Mínimos Cuadrados 3.2.. Forma Recursiva: 6.2.2. Inclusión del Factor de Olvido. 0.3. Características Estadísticas
SOLUCIONES EJERCICIOS PROPUESTOS TEMA SOLUCIÓN DE ECUACIONES POLINÓMICAS POR FACTORIZACIÓN
 CURSO MATE 0066 Verano 009 SOLUCIONES EJERCICIOS PROPUESTOS TEMA SOLUCIÓN DE ECUACIONES POLINÓMICAS POR FACTORIZACIÓN 1. Igualando a cero la epresión tenemos una ecuación polinómica de la forma + b + c.
CURSO MATE 0066 Verano 009 SOLUCIONES EJERCICIOS PROPUESTOS TEMA SOLUCIÓN DE ECUACIONES POLINÓMICAS POR FACTORIZACIÓN 1. Igualando a cero la epresión tenemos una ecuación polinómica de la forma + b + c.
ii. f 1 (x) = 1 + x v.ninguna de las anteriores
 UPR Departamento de Ciencias Matemáticas RUM MATE 7 Práctica # //09 Profesor Nombre Instrucciones. Resuelva cada uno de los ejercicios por usted mismo y si tienen dudas preguntele a su instructor o busque
UPR Departamento de Ciencias Matemáticas RUM MATE 7 Práctica # //09 Profesor Nombre Instrucciones. Resuelva cada uno de los ejercicios por usted mismo y si tienen dudas preguntele a su instructor o busque
Concepto de VA bidimensional. Tema 3: VARIABLE ALEATORIA BIDIMENSIONAL. Concepto de VA bidimensional. Concepto de VA bidimensional
 Concepto de VA bidimensional Tema 3: VARIABLE ALEATORIA BIDIMENSIONAL Carlos Alberola López Lab. rocesado de Imagen, ETSI Telecomunicación Despacho D04 caralb@tel.uva.es, jcasasec@tel.uva.es, http://www.lpi.tel.uva.es/sar
Concepto de VA bidimensional Tema 3: VARIABLE ALEATORIA BIDIMENSIONAL Carlos Alberola López Lab. rocesado de Imagen, ETSI Telecomunicación Despacho D04 caralb@tel.uva.es, jcasasec@tel.uva.es, http://www.lpi.tel.uva.es/sar
OLIMPIADAS COSTARRICENSES DE MATEMÁTICAS
 OLIMPIADAS COSTARRICENSES DE MATEMÁTICAS UNA - UCR - TEC - UNED - MEP - MICITT Álgebra e iπ + φ φ 0 III Nivel I Eliminatoria Marzo 06 Índice. Presentación. Contenidos 3. Algunos consejos útiles 4. Problemas
OLIMPIADAS COSTARRICENSES DE MATEMÁTICAS UNA - UCR - TEC - UNED - MEP - MICITT Álgebra e iπ + φ φ 0 III Nivel I Eliminatoria Marzo 06 Índice. Presentación. Contenidos 3. Algunos consejos útiles 4. Problemas
Álgebra I Práctica 7 - Polinomios
 FCEyN - UBA - 2do cuatrimestre 2016 Generalidades Álgebra I Práctica 7 - Polinomios 1. Calcular el grado y el coeficiente principal de f Q[X] en los casos i) f = (4X 6 2X 5 + 3X 2 2X + 7) 77. ii) f = (
FCEyN - UBA - 2do cuatrimestre 2016 Generalidades Álgebra I Práctica 7 - Polinomios 1. Calcular el grado y el coeficiente principal de f Q[X] en los casos i) f = (4X 6 2X 5 + 3X 2 2X + 7) 77. ii) f = (
solucionario matemáticas II
 solucionario matemáticas II UNIDADES 8-4 bachillerato 8 Determinantes 4 9 Sistemas de ecuaciones lineales 46 Fin bloque II 0 Vectores 8 Rectas planos en el espacio 68 Propiedades métricas 08 Fin bloque
solucionario matemáticas II UNIDADES 8-4 bachillerato 8 Determinantes 4 9 Sistemas de ecuaciones lineales 46 Fin bloque II 0 Vectores 8 Rectas planos en el espacio 68 Propiedades métricas 08 Fin bloque
INECUACIONES LINEALES
 INECUACIONES POLINÓMICAS EN UNA VARIABLE Las inecuaciones en general, son desigualdades entre epresiones algebraicas en las que intervienen una o más variables. Cuando las epresiones algebraicas de cada
INECUACIONES POLINÓMICAS EN UNA VARIABLE Las inecuaciones en general, son desigualdades entre epresiones algebraicas en las que intervienen una o más variables. Cuando las epresiones algebraicas de cada
Universidad Simón Bolívar Departamento de Procesos y Sistemas
 Universidad Simón Bolívar Departamento de Procesos y Sistemas Guía de Ejercicios de Sistemas de Control I PS-3 Prof. Alexander Hoyo Junio 00 http://prof.usb.ve/ahoyo ahoyo@usb.ve ÍNDICE Pág. Modelaje Matemático
Universidad Simón Bolívar Departamento de Procesos y Sistemas Guía de Ejercicios de Sistemas de Control I PS-3 Prof. Alexander Hoyo Junio 00 http://prof.usb.ve/ahoyo ahoyo@usb.ve ÍNDICE Pág. Modelaje Matemático
Econometría II Grado en finanzas y contabilidad
 Econometría II Grado en finanzas y contabilidad Variables aleatorias y procesos estocásticos. La FAC y el correlograma Profesora: Dolores García Martos E-mail:mdgmarto@est-econ.uc3m.es Este documento es
Econometría II Grado en finanzas y contabilidad Variables aleatorias y procesos estocásticos. La FAC y el correlograma Profesora: Dolores García Martos E-mail:mdgmarto@est-econ.uc3m.es Este documento es
Un sistema con realimentación unitaria tiene una función de transferencia en lazo abierto
 Un sistema con realimentación unitaria tiene una función de transferencia en lazo abierto G p ( s) k s( s + )( s + 5) a)para el sistema en lazo abierto, y suponiendo el valor k : Obtener la expresión analítica
Un sistema con realimentación unitaria tiene una función de transferencia en lazo abierto G p ( s) k s( s + )( s + 5) a)para el sistema en lazo abierto, y suponiendo el valor k : Obtener la expresión analítica
Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS
 Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS Grado en Matemáticas Curso 203-204 . Ecuaciones lineales con coeficientes constantes Ecuaciones de primer orden. Encontrar la solución de los siguientes
Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS Grado en Matemáticas Curso 203-204 . Ecuaciones lineales con coeficientes constantes Ecuaciones de primer orden. Encontrar la solución de los siguientes
Ejercicio 3 Un sistema de control de velocidad de un motor de corriente continua se modela mediante la ecuación
 Trabajo práctico Nº 4 Fundamentos de control realimentado - Segundo cuatrimestre 2017 Ejercicio 1 Aplicando el criterio de estabilidad de Routh: i) Determine la cantidad de raíces en el semiplano derecho
Trabajo práctico Nº 4 Fundamentos de control realimentado - Segundo cuatrimestre 2017 Ejercicio 1 Aplicando el criterio de estabilidad de Routh: i) Determine la cantidad de raíces en el semiplano derecho
1. Sensibilidad en caso de restricciones de igualdad
 FACULTAD CS. FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE MA57B Optimización No Lineal. Semestre 2007-1 Profesor: Héctor Ramírez C. Auxiliar: Oscar Peredo. Clase Auxiliar #4 Análisis de Sensibilidad en Optimización
FACULTAD CS. FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE MA57B Optimización No Lineal. Semestre 2007-1 Profesor: Héctor Ramírez C. Auxiliar: Oscar Peredo. Clase Auxiliar #4 Análisis de Sensibilidad en Optimización
x^new = x^old + K(b new A new x^old )
 El Filtro de Kalman: La idea fundamental del filtro de Kalman es la actualización La llegada de una nueva observación supone un cambio en la mejor estimación mínimo cuatrática del parámetro x Se desea
El Filtro de Kalman: La idea fundamental del filtro de Kalman es la actualización La llegada de una nueva observación supone un cambio en la mejor estimación mínimo cuatrática del parámetro x Se desea
Departamento de Ingenierías Eléctrica y Electrónica Universidad del Norte
 christianq@uninorte.edu.co Departamento de Ingenierías Eléctrica y Electrónica Universidad del Norte Ejemplo: Considere el sistema de la figura: G(s) tiene un par de polos complejos conjugados en s = 1
christianq@uninorte.edu.co Departamento de Ingenierías Eléctrica y Electrónica Universidad del Norte Ejemplo: Considere el sistema de la figura: G(s) tiene un par de polos complejos conjugados en s = 1
MATEMÁTICAS. Posgrado en Nanotecnología. Dr. Roberto Pedro Duarte Zamorano 2016 Departamento de Física
 MATEMÁTICAS Posgrado en Nanotecnología Dr. Roberto Pedro Duarte Zamorano 016 Departamento de Física TEMARIO 3. Transformada de Fourier 1. Transformadas integrales.. La Transformada de Fourier. 3. Teorema
MATEMÁTICAS Posgrado en Nanotecnología Dr. Roberto Pedro Duarte Zamorano 016 Departamento de Física TEMARIO 3. Transformada de Fourier 1. Transformadas integrales.. La Transformada de Fourier. 3. Teorema
Conceptos Básicos de Errores y Lugar de la Raíz
 Departamento de Ingeniería Eléctrica Universidad de Magallanes Conceptos Básicos de Errores y Lugar de la Raíz Apuntes del curso de Control Automático Roberto Cárdenas Dobson Ingeniero Electricista Msc.
Departamento de Ingeniería Eléctrica Universidad de Magallanes Conceptos Básicos de Errores y Lugar de la Raíz Apuntes del curso de Control Automático Roberto Cárdenas Dobson Ingeniero Electricista Msc.
Polinomios: Definición: Se llama polinomio en "x" de grado "n" a una expresión del tipo
 Polinomios: Definición: Se llama polinomio en "x" de grado "n" a una expresión del tipo P (x) = a 0 x n + a 1 x n 1 +... + a n Donde n N (número natural) ; a 0, a 1, a 2,..., a n son coeficientes reales
Polinomios: Definición: Se llama polinomio en "x" de grado "n" a una expresión del tipo P (x) = a 0 x n + a 1 x n 1 +... + a n Donde n N (número natural) ; a 0, a 1, a 2,..., a n son coeficientes reales
TECNICAS DE DISEÑO Y COMPENSACION
 TECNICAS DE DISEÑO Y COMPENSACION Técnicas para sistemas SISO invariantes en el tiempo Basadas en el lugar de las raices y respuesta en frecuencia Especificaciones de funcionamiento Exactitud o precisión
TECNICAS DE DISEÑO Y COMPENSACION Técnicas para sistemas SISO invariantes en el tiempo Basadas en el lugar de las raices y respuesta en frecuencia Especificaciones de funcionamiento Exactitud o precisión
FUNCIONES MEROMORFAS. EL TEOREMA DE LOS RESIDUOS Y ALGUNAS DE SUS CONSECUENCIAS
 FUNCIONES MEROMORFAS. EL TEOREMA DE LOS RESIDUOS Y ALGUNAS DE SUS CONSECUENCIAS. FUNCIONES MEROMORFAS Definición.. Se dice que una función es meromorfa en un abierto Ω de C si f es holomorfa en Ω excepto
FUNCIONES MEROMORFAS. EL TEOREMA DE LOS RESIDUOS Y ALGUNAS DE SUS CONSECUENCIAS. FUNCIONES MEROMORFAS Definición.. Se dice que una función es meromorfa en un abierto Ω de C si f es holomorfa en Ω excepto
Apéndice sobre ecuaciones diferenciales lineales
 Apéndice sobre ecuaciones diferenciales lineales Juan-Miguel Gracia 10 de febrero de 2008 Índice 2 Determinante wronskiano. Wronskiano de f 1 (t), f 2 (t),..., f n (t). Derivada de un determinante de funciones.
Apéndice sobre ecuaciones diferenciales lineales Juan-Miguel Gracia 10 de febrero de 2008 Índice 2 Determinante wronskiano. Wronskiano de f 1 (t), f 2 (t),..., f n (t). Derivada de un determinante de funciones.
Es decir, det A = producto de diagonal principal producto de diagonal secundaria. Determinante de una matriz cuadrada de orden 3
 1.- DETERMINANTE DE UNA MATRIZ CUADRADA Determinante de una matriz cuadrada de orden 1 Dada una matriz cuadrada de orden 1, A = (a), se define det A = det (a) = a Determinante de una matriz cuadrada de
1.- DETERMINANTE DE UNA MATRIZ CUADRADA Determinante de una matriz cuadrada de orden 1 Dada una matriz cuadrada de orden 1, A = (a), se define det A = det (a) = a Determinante de una matriz cuadrada de
Lugar Geométrico de las Raíces Herramienta para diseño de sistemas de control
 Lugar Geométrico de las Raíces Herramienta para diseño de sistemas de control Elizabeth Villota Curso: Ingeniería de Control (MT221) Facultad de Ingeniería Mecánica UNI-FIM 1 Modelado Modelo: representación
Lugar Geométrico de las Raíces Herramienta para diseño de sistemas de control Elizabeth Villota Curso: Ingeniería de Control (MT221) Facultad de Ingeniería Mecánica UNI-FIM 1 Modelado Modelo: representación
6.1. Condición de magnitud y ángulo
 Capítulo 6 Lugar de las raíces La respuesta transitoria de un sistema en lazo cerrado, está ligada con la ubicación de los polos de lazo cerrado en el plano complejo S. Si el sistema tiene una ganancia
Capítulo 6 Lugar de las raíces La respuesta transitoria de un sistema en lazo cerrado, está ligada con la ubicación de los polos de lazo cerrado en el plano complejo S. Si el sistema tiene una ganancia
es el lugar geométrico de los puntos p tales que ; R (1)
 LA RECTA DEL PLANO ECUACIÓN VECTORIAL Y ECUACIONES PARAMÉTRICAS La recta en el plano como lugar geométrico Dados un punto p un vector no nulo u, la recta T paralela a u que pasa por p es el lugar geométrico
LA RECTA DEL PLANO ECUACIÓN VECTORIAL Y ECUACIONES PARAMÉTRICAS La recta en el plano como lugar geométrico Dados un punto p un vector no nulo u, la recta T paralela a u que pasa por p es el lugar geométrico
Sistemas lineales con parámetros
 4 Sistemas lineales con parámetros. Teorema de Rouché Piensa y calcula Dado el siguiente sistema en forma matricial, escribe sus ecuaciones: 3 0 y = 0 z + y 3z = 0 y = Aplica la teoría. Escribe los siguientes
4 Sistemas lineales con parámetros. Teorema de Rouché Piensa y calcula Dado el siguiente sistema en forma matricial, escribe sus ecuaciones: 3 0 y = 0 z + y 3z = 0 y = Aplica la teoría. Escribe los siguientes
Problemas Ampliación de Matemáticas. Sistemas lineales 1.- Encontrar la factorización L U de las siguientes matrices:
 Problemas Ampliación de Matemáticas. Sistemas lineales 1.- Encontrar la factorización L U de las siguientes matrices: 5 2 1 1 0 3 1 0 3 3 1 6. 3 1 6 5 2 1 2.- Dada la matriz A = 10 7 8 7 5 6, 8 6 10 hallar
Problemas Ampliación de Matemáticas. Sistemas lineales 1.- Encontrar la factorización L U de las siguientes matrices: 5 2 1 1 0 3 1 0 3 3 1 6. 3 1 6 5 2 1 2.- Dada la matriz A = 10 7 8 7 5 6, 8 6 10 hallar
Ejercicio 1 de la Opción A del modelo 1 de Solución
 Ejercicio 1 de la Opción A del modelo 1 de 2008 Sean f : R R y g : R R las funciones definidas por f(x) = x 2 -(x + 1) + ax + b y g(x) = ce Se sabe que las gráficas de f y g se cortan en el punto ( 1,
Ejercicio 1 de la Opción A del modelo 1 de 2008 Sean f : R R y g : R R las funciones definidas por f(x) = x 2 -(x + 1) + ax + b y g(x) = ce Se sabe que las gráficas de f y g se cortan en el punto ( 1,
Cambio de base. Objetivos. Estudiar la relación entre las coordenadas de un vector en dos bases.
 Cambio de base Objetivos Estudiar la relación entre las coordenadas de un vector en dos bases Requisitos Definición de una base, multiplicación de una matriz por un vector, delta de Kronecker Definición
Cambio de base Objetivos Estudiar la relación entre las coordenadas de un vector en dos bases Requisitos Definición de una base, multiplicación de una matriz por un vector, delta de Kronecker Definición
15. Teoría de los residuos.
 162 Funciones de variable compleja. Eleonora Catsigeras. 12 Julio 2006. 15. Teoría de los residuos. 15.1. Residuos. Definición 15.1.1. Residuo de una función en una singularidad aislada. Dada una función
162 Funciones de variable compleja. Eleonora Catsigeras. 12 Julio 2006. 15. Teoría de los residuos. 15.1. Residuos. Definición 15.1.1. Residuo de una función en una singularidad aislada. Dada una función
0.1. Error en Estado Estacionario
 0. Error en Estado Estacionario 0.. Error en Estado Estacionario La respuesta permanente es aquella que se alcanza cuando el sistema se establece y es muy importante su estudio pues informa lo que sucede
0. Error en Estado Estacionario 0.. Error en Estado Estacionario La respuesta permanente es aquella que se alcanza cuando el sistema se establece y es muy importante su estudio pues informa lo que sucede
Matrices y Sistemas Lineales
 Matrices y Sistemas Lineales Álvarez S, Caballero MV y Sánchez M a M salvarez@umes, mvictori@umes, marvega@umes 1 ÍNDICE Matemáticas Cero Índice 1 Definiciones 3 11 Matrices 3 12 Sistemas lineales 5 2
Matrices y Sistemas Lineales Álvarez S, Caballero MV y Sánchez M a M salvarez@umes, mvictori@umes, marvega@umes 1 ÍNDICE Matemáticas Cero Índice 1 Definiciones 3 11 Matrices 3 12 Sistemas lineales 5 2
Universidad Técnica de Babahoyo CORRELACIÓN DE VARIABLES Y REGRESIÓN LINEAL
 Universidad Técnica de Babahoyo CORRELACIÓN DE VARIABLES Y REGRESIÓN LINEAL OBJETIVO Analizar las Diferentes formas de Describir la Relación entre dos variables numéricas Trazar un diagrama de dispersión
Universidad Técnica de Babahoyo CORRELACIÓN DE VARIABLES Y REGRESIÓN LINEAL OBJETIVO Analizar las Diferentes formas de Describir la Relación entre dos variables numéricas Trazar un diagrama de dispersión
Pontificia Universidad Católica del Perú ICA624: Control Robusto. 11. Factorización Prima Sobre RH. Parametrización de Controles Estabilizantes
 Pontificia Universidad Católica del Perú ICA624: Control Robusto 11. Factorización Prima Sobre Hanz Richter, PhD Profesor Visitante Cleveland State University Mechanical Engineering Department 1 / 14 Polinomios
Pontificia Universidad Católica del Perú ICA624: Control Robusto 11. Factorización Prima Sobre Hanz Richter, PhD Profesor Visitante Cleveland State University Mechanical Engineering Department 1 / 14 Polinomios
Control Óptimo. Diseño y Propiedades del LQR. Dr. Fernando Ornelas Tellez
 Control Óptimo Diseño y Propiedades del LQR Dr. Fernando Ornelas Tellez Universidad Michoacana de San Nicolás de Hidalgo División de Estudios de Posgrado Facultad de Ingeniería Eléctrica Morelia, Michoacan
Control Óptimo Diseño y Propiedades del LQR Dr. Fernando Ornelas Tellez Universidad Michoacana de San Nicolás de Hidalgo División de Estudios de Posgrado Facultad de Ingeniería Eléctrica Morelia, Michoacan
Preliminares Métodos de Ajuste de Curvas AJUSTE DE CURVAS AJUSTE DE CURVAS
 Contenido 1 Preliminares Definiciones 2 Definiciones Contenido 1 Preliminares Definiciones 2 Definiciones Definiciones En ciencias e ingeniería es frecuente que un experimento produzca un conjunto de datos
Contenido 1 Preliminares Definiciones 2 Definiciones Contenido 1 Preliminares Definiciones 2 Definiciones Definiciones En ciencias e ingeniería es frecuente que un experimento produzca un conjunto de datos
Información sobre Gastos de Consumo Personal y Producto Interno Bruto ( ) en miles de millones de dólares de 1992.
 Universidad Nacional Autónoma de Nicaragua UNAN-Managua Curso de Análisis y Diseño de Modelos Econométricos Profesor: MSc. Julio Rito Vargas Avilés. Participantes: Docentes /FAREM-Carazo Encuentro No.4
Universidad Nacional Autónoma de Nicaragua UNAN-Managua Curso de Análisis y Diseño de Modelos Econométricos Profesor: MSc. Julio Rito Vargas Avilés. Participantes: Docentes /FAREM-Carazo Encuentro No.4
Vectores y rectas. 4º curso de E.S.O., opción B. Modelo de examen (ficticio)
 demattematicaswordpresscom Vectores y rectas º curso de ESO, opción B Modelo de examen (ficticio) Sean los vectores u = (,5) y v = (, ) a) Analiza si tienen la misma dirección No tienen la misma dirección
demattematicaswordpresscom Vectores y rectas º curso de ESO, opción B Modelo de examen (ficticio) Sean los vectores u = (,5) y v = (, ) a) Analiza si tienen la misma dirección No tienen la misma dirección
c-inversa o inversa generalizada de Rao
 c-inversa o inversa generalizada de Rao Definición.- Sea A m n. Se dice que una matriz A c de orden n m es una c-inversa o inversa generalizada en el sentido de Rao si y sólo si se verifica AA c A = A.
c-inversa o inversa generalizada de Rao Definición.- Sea A m n. Se dice que una matriz A c de orden n m es una c-inversa o inversa generalizada en el sentido de Rao si y sólo si se verifica AA c A = A.
El Teorema Fundamental del Álgebra
 El Teorema Fundamental del Álgebra 1. Repaso de polinomios Definiciones básicas Un monomio en una indeterminada x es una expresión de la forma ax n que representa el producto de un número, a, por una potencia
El Teorema Fundamental del Álgebra 1. Repaso de polinomios Definiciones básicas Un monomio en una indeterminada x es una expresión de la forma ax n que representa el producto de un número, a, por una potencia
El Movimiento Browniano en la modelización del par EUR/USD
 MÁSTER UNIVERSITARIO EN DIRECCIÓN FINANCIERA Y FISCAL TESINA FIN DE MÁSTER El Movimiento Browniano en la modelización del par EUR/USD Autor: José Vicente González Cervera Directores: Dr. Juan Carlos Cortés
MÁSTER UNIVERSITARIO EN DIRECCIÓN FINANCIERA Y FISCAL TESINA FIN DE MÁSTER El Movimiento Browniano en la modelización del par EUR/USD Autor: José Vicente González Cervera Directores: Dr. Juan Carlos Cortés
Introducción a la Identificación de sistemas
 Ingeniería de Control Introducción a la Identificación de sistemas Daniel Rodríguez Ramírez Teodoro Alamo Cantarero Contextualización del tema Conocimientos que se adquieren en este tema: Modelos deterministas
Ingeniería de Control Introducción a la Identificación de sistemas Daniel Rodríguez Ramírez Teodoro Alamo Cantarero Contextualización del tema Conocimientos que se adquieren en este tema: Modelos deterministas
Función de transferencia
 3 Función de transferencia En el capítulo anterior se presentó la transformada de Laplace y se explicó cómo utilizar sus propiedades para la resolución de una ecuación diferencial lineal de coeficientes
3 Función de transferencia En el capítulo anterior se presentó la transformada de Laplace y se explicó cómo utilizar sus propiedades para la resolución de una ecuación diferencial lineal de coeficientes
Matrices y Sistemas Lineales
 Matrices y Sistemas Lineales Álvarez S, Caballero MV y Sánchez M a M salvarez@umes, mvictori@umes, marvega@umes Índice 1 Definiciones 3 11 Matrices 3 12 Sistemas lineales 6 2 Herramientas 8 21 Operaciones
Matrices y Sistemas Lineales Álvarez S, Caballero MV y Sánchez M a M salvarez@umes, mvictori@umes, marvega@umes Índice 1 Definiciones 3 11 Matrices 3 12 Sistemas lineales 6 2 Herramientas 8 21 Operaciones
Nombre y Apellidos:... EXAMEN ECONOMETRÍA II (Enero 2010)
 Nombre y Apellidos:... NIU:... Grupo:... EXAMEN ECONOMETRÍA II (Enero 2010) Lea cuidadosamente cada pregunta. Marque muy claramente la respuesta de cada pregunta en la hoja de respuestas. Observe que los
Nombre y Apellidos:... NIU:... Grupo:... EXAMEN ECONOMETRÍA II (Enero 2010) Lea cuidadosamente cada pregunta. Marque muy claramente la respuesta de cada pregunta en la hoja de respuestas. Observe que los
Serie 10 ESTABILIDAD
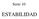 Serie 0 ESTABILIDAD Condición de estabilidad U u Gu U R r + + - Gc Gv Gp C G V G P + c C H G( G (. G (. G (. H ( C V P + G( 0 G( G φ 80 Localización de las raíces Plano s E S T A B L E I N E S T A B L
Serie 0 ESTABILIDAD Condición de estabilidad U u Gu U R r + + - Gc Gv Gp C G V G P + c C H G( G (. G (. G (. H ( C V P + G( 0 G( G φ 80 Localización de las raíces Plano s E S T A B L E I N E S T A B L
1. El Teorema de Rolle Generalizado.
 Proyecto III: Los Teoremas de Rolle y del valor Medio Objetivos: Profundizar el estudio de algunos teoremas del cálculo diferencial 1 El Teorema de Rolle Generalizado La formulación más común del Teorema
Proyecto III: Los Teoremas de Rolle y del valor Medio Objetivos: Profundizar el estudio de algunos teoremas del cálculo diferencial 1 El Teorema de Rolle Generalizado La formulación más común del Teorema
4. Análisis de Sistemas Realimentados
 4. Análisis de Sistemas Realimentados Panorama: Dados un controlador y una planta conectados en realimentación, vamos a plantear y contestar las siguientes preguntas: Es el lazo cerrado estable? Cuáles
4. Análisis de Sistemas Realimentados Panorama: Dados un controlador y una planta conectados en realimentación, vamos a plantear y contestar las siguientes preguntas: Es el lazo cerrado estable? Cuáles
Seguimiento de los parámetros del modelo del tracto vocal
 Algoritmos para el seguimiento de los parámetros del modelo de tracto vocal Monografía de Tratamiento Estadístico de Señales parias@fing.edu.uy Instituto de Ingeniería Eléctrica Facultad de Ingeniería
Algoritmos para el seguimiento de los parámetros del modelo de tracto vocal Monografía de Tratamiento Estadístico de Señales parias@fing.edu.uy Instituto de Ingeniería Eléctrica Facultad de Ingeniería
Filtro. k k. determinan la respuesta en frecuencia del filtro. Una señal x(n) que pase a través del sistema tendrá una salida Y ( ω)
 7.- Introducción a los filtros digitales 7..- Introducción. El término FILTRO hace referencia a cualquier sistema que discrimina lo que pasa a su través de acuerdo con alguno de los atributos de la entrada.
7.- Introducción a los filtros digitales 7..- Introducción. El término FILTRO hace referencia a cualquier sistema que discrimina lo que pasa a su través de acuerdo con alguno de los atributos de la entrada.
PFC: Localización de robots mediante filtro de Kalman
 6.- FILTRO DE KALMAN 6.1.- MOTIVACIÓN Los sistemas de navegación se han convertido en un estándar, ya que se venden más y más, sobre todo con los coches nuevos. La mayoría de estos sistemas de navegación
6.- FILTRO DE KALMAN 6.1.- MOTIVACIÓN Los sistemas de navegación se han convertido en un estándar, ya que se venden más y más, sobre todo con los coches nuevos. La mayoría de estos sistemas de navegación
Ejercicio 1. Ejercicio 2
 Guía de Ejercicios Ejercicio. Calcular los momentos de primer y segundo orden (media y varianza) de una variable aleatoria continua con distribución uniforme entre los límites a y b.. Sabiendo que la función
Guía de Ejercicios Ejercicio. Calcular los momentos de primer y segundo orden (media y varianza) de una variable aleatoria continua con distribución uniforme entre los límites a y b.. Sabiendo que la función
Correlación. El coeficiente de correlación mide la fuerza o el grado de asociación entre dos variables (r)
 Correlación El coeficiente de correlación mide la fuerza o el grado de asociación entre dos variables (r) El coeficiente de correlación lineal de Pearson (r) permite medir el grado de asociación entre
Correlación El coeficiente de correlación mide la fuerza o el grado de asociación entre dos variables (r) El coeficiente de correlación lineal de Pearson (r) permite medir el grado de asociación entre
4.1. Polinomios y teoría de ecuaciones
 CAPÍTULO 4 Polinomios y teoría de ecuaciones 4.1. Polinomios y teoría de ecuaciones Un polinomio real en x, o simplemente polinomio en x es una expresión algebraica de la forma a n x n + a n 1 x n 1 +
CAPÍTULO 4 Polinomios y teoría de ecuaciones 4.1. Polinomios y teoría de ecuaciones Un polinomio real en x, o simplemente polinomio en x es una expresión algebraica de la forma a n x n + a n 1 x n 1 +
SISTEMAS LINEALES DE ECUACIONES DIFERENCIALES
 SISTEMAS LINEALES DE ECUACIONES DIFERENCIALES En esta sección se estudiaran los sistemas de ecuaciones diferenciales lineales de primer orden, así como los de orden superior, con dos o más funciones desconocidas,
SISTEMAS LINEALES DE ECUACIONES DIFERENCIALES En esta sección se estudiaran los sistemas de ecuaciones diferenciales lineales de primer orden, así como los de orden superior, con dos o más funciones desconocidas,
Tema 1. 1 Álgebra lineal. Aurea Grané Departamento de Estadística Universidad Carlos III de Madrid. 1.1 Vectores de R n. 1. Vectores. 2.
 Aurea Grané. Máster en Estadística. Universidade Pedagógica. 1 Aurea Grané. Máster en Estadística. Universidade Pedagógica. 2 Tema 1 Álgebra lineal 1. Vectores 2. Matrices 1 Álgebra lineal Aurea Grané
Aurea Grané. Máster en Estadística. Universidade Pedagógica. 1 Aurea Grané. Máster en Estadística. Universidade Pedagógica. 2 Tema 1 Álgebra lineal 1. Vectores 2. Matrices 1 Álgebra lineal Aurea Grané
Geometría Diferencial Preguntas de la teoría para el examen
 Geometría Diferencial - 2015 Preguntas de la teoría para el examen Observaciones: Una pregunta del examen puede ser sólo una parte de una de las preguntas siguientes. Si en esta lista una pregunta tiene
Geometría Diferencial - 2015 Preguntas de la teoría para el examen Observaciones: Una pregunta del examen puede ser sólo una parte de una de las preguntas siguientes. Si en esta lista una pregunta tiene
Luego 72 = 2 3. Luego 48 = 2 3
 72 2 36 2 8 2 9 3 3 3 3 2 Luego 72 = 2 3 48 2 24 2 2 2 6 2 3 3 4 Luego 48 = 2 3 Así que el m.c.m. de 72 y 48 es 2 4 3 2 = 44. Como la rueda mayor tiene 72 dientes, para "recorrer" 44 dientes dee dar 44
72 2 36 2 8 2 9 3 3 3 3 2 Luego 72 = 2 3 48 2 24 2 2 2 6 2 3 3 4 Luego 48 = 2 3 Así que el m.c.m. de 72 y 48 es 2 4 3 2 = 44. Como la rueda mayor tiene 72 dientes, para "recorrer" 44 dientes dee dar 44
MATE Dr. Pedro Vásquez UPRM. P. Vásquez (UPRM) Conferencia 1 / 10
 Dr. Pedro Vásquez UPRM P. Vásquez (UPRM) Conferencia / 0 Ceros complejos y el teorema fundamental del álgebra En las secciones anteriores se ha discutido que un polinomio de grado n puede tener a lo más
Dr. Pedro Vásquez UPRM P. Vásquez (UPRM) Conferencia / 0 Ceros complejos y el teorema fundamental del álgebra En las secciones anteriores se ha discutido que un polinomio de grado n puede tener a lo más
Lugar Geométrico de las Raíces
 ELC-33103 Teoría de Control Lugar Geométrico de las Raíces Prof. Francisco M. Gonzalez-Longatt fglongatt@ieee.org http://www.giaelec.org/fglongatt/sp.htm 1. Introducción La característica básica de la
ELC-33103 Teoría de Control Lugar Geométrico de las Raíces Prof. Francisco M. Gonzalez-Longatt fglongatt@ieee.org http://www.giaelec.org/fglongatt/sp.htm 1. Introducción La característica básica de la
Como ejemplo, consideremos la función compleja P(s)= s 2 +1.
 Criterio de Estabilidad de Nyquist El criterio de Estabilidad de Nyquist está basado en un teorema de la variable compleja. Para entender este criterio primero se utilizarán los conceptos de transferencia
Criterio de Estabilidad de Nyquist El criterio de Estabilidad de Nyquist está basado en un teorema de la variable compleja. Para entender este criterio primero se utilizarán los conceptos de transferencia
