CONTRASTE DE HIPÓTESIS
|
|
|
- Esteban Calderón Juárez
- hace 8 años
- Vistas:
Transcripción
1 CONTRASTE DE HIPÓTESIS
2 Índice: 1. Contraste de hipótesis Errores de tipo I y tipo II Contraste para el parámetro p de una distribución Contraste para la media de una distribución normal Analogías entre el contraste de hipótesis e intervalos de confianza Página 1
3 1. Contraste de hipótesis. Antes de comenzar con un ejemplo que podamos ilustrar en que consiste un contraste de hipótesis, veamos algunas definiciones que vamos a utilizar a lo largo de este tema Contraste de hipótesis.- Es un procedimiento estadístico mediante el cual se investiga la verdad o falsedad de una hipótesis acerca de una población o poblaciones. Hipótesis nula H 0.- Es la hipótesis que se fórmula y que se quiere contrastar; es, por tanto, la hipótesis que se acepta o se rechaza como consecuencia del contraste. Hipótesis alternativa H a.- Es cualquier otra hipótesis que difiere o es contraria a la hipótesis nula, de forma que si se rechaza H 0 se acepta H a y si se acepta H a se rechaza H 0. Estadístico del contraste.- Es función de valores muestrales. Es una variable aleatoria que sigue una distribución en el muestreo. Toma un valor para cada muestra. Región de aceptación.- Es la formada por el conjunto de puntos tales que los valores del estadístico del contraste nos lleva a aceptar la hipótesis nula. Región de crítica.- Es la formada por el conjunto de puntos tales que los valores del estadístico del contraste nos lleva a rechazar la hipótesis nula. Contraste bilateral.- Cuando la región crítica está formada por dos conjuntos de puntos disjuntos. Contraste unilateral.- Cuando la región crítica está formada por un solo conjunto de puntos disjuntos. # Ejemplo.- Si en una investigación anterior se ha estimado que la temperatura media del cuerpo humano para los adultos sanos se distribuye según una N (μ, σ=n (37º C ;0,9º C. Si denominamos, Hipótesis nula: H 0 : μ=37º C. Hipótesis alternativa: H a : μ 37º C. Para contrastar la hipótesis nula, elegimos una muestra aleatoria de 10 personas adultas sanas, obteniendo las siguientes temperaturas en grados centígrados: 37,7; 36,7; 37,5; 37; 37,9; 37,6; 37,1; 37; 36,8; 37,1 Si calculemos la media muestral y obtenemos x=37,4 º C, que es un valor particular del estadístico X, que sigue una distribución N( n μ, σ ( =N 0,9 37, =N (37,0, Página
4 Por tanto, la diferencia μ x = 37º C 37,4º C =0,4º C, puede ser debida al azar, en cuyo caso diremos que no es significativa, o puede ser debida o otras causas, en cuyo caso diremos que es significativa. Como podemos saber cuando es significativa o no?. Fijamos previamente el nivel de confianza que queremos, por ejemplo 1 α=0,95, y tipificando la variable X, para el valor particular x, obtenemos Y existirá un valor z α tal que P ( z α 37,4 37 z 0,85 α P ( 0,93 z α =0,975, que mirando en la tabla normal N (0,1 se obtiene Luego, aceptaremos la hipótesis nula si el estadístico del contraste dentro del intervalo ( z, z α α, es decir, del intervalo ( 1,96,1,96. Como 0,93 cae dentro de dicho intervalo, aceptaremos la hipótesis nula. Es decir, la muestra es realmente compatible con la población en el 95% de los casos. O también decimos, que a partir de los datos muestrales se acepta la hipótesis de que la temperatura media del cuerpo humano para adultos sanos es 37º C, con un nivel de confianza del 95% Los valores críticos α mas usuales para contrastar hipótesis son 37,4 37 =0,93. 0,85 =0,95, que equivale a z α =1,96. 37,4 37 =0,93 cae 0,85 Nivel de significación α Valores críticos: contrastes unilaterales z α Valores críticos: contrastes bilaterales z α 0,100 ±1,8 ±1,645 0,050 ±1,64 ±1,96 0,010 ±,33 ±,58 0,005 ±,58 ±,81 0 ±,88 ±3,08 Página 3
5 . Errores de tipo I y tipo II Todo contraste de hipótesis lleva a aceptar o rechazar la hipótesis nula planteada. Ahora bien, pueden ocurrir los siguientes casos: 1º Aceptar la hipótesis nula siendo verdadera. Ésta es una decisión correcta. º Rechazar la hipótesis nula siendo falsa. Esta es otra decisión correcta. 3º Rechazar la hipótesis nula siendo verdadera. Cometemos un error de tipo I. 4º Aceptar la hipótesis nula siendo falsa. Cometemos un error de tipo II. La probabilidad P, de cometer el error de tipo I se llama nivel de significación y lo representamos por α. Este determinado valor es conocido de antemano, ya que se debe de fijar antes de efectuar el contraste. La probabilidad P, de cometer el error de tipo II la denominamos por β. Y la probabilidad 1 β se llama nivel potencia del contraste, que es la probabilidad de rechazar la hipótesis nula cuando es falsa. Podemos resumir este tipo de errores en la siguiente tabla Aceptar H 0 Decisión correcta P=1 α Rechazar H 0 Cometer error de tipo I P=α H 0 : verdadera H 0 : falsa Y que podemos representar mediante las áreas correspondientes Cometer error de tipo II P=β Decisión correcta P=1 β Potencia del contraste Página 4
6 3. Contraste para el parámetro p de una distribución binomial Supongamos que partimos de una distribución binomial de parámetros B(n, p y que queremos contrastar el valor p= p 0, fijado un nivel de significación α, si elegimos una muestra para la cual un valor determinado de p es p. Entonces, se tiene H 0 H a Tipo de contraste Estadístico Región de aceptación p= p 0 p p p p 0 bilateral Z= 0 ( z α, z α p 0.(1 p 0 p p 0 p> p 0 unilateral n (, z α que sigue una distribución p p 0 p< p 0 unilateral N (0,1 ( z α,+ # Ejemplo.- El ayuntamiento de una ciudad afirma que el 65% de los accidentes juveniles de los fines de semana son debidos al alcohol. Un investigador decide contrastar dicha hipótesis, para lo cual toma una muestra formada por 35 accidentes y observa que 4 de ellos han sido debidos al alcohol. Qué podemos decir sobre la afirmación del ayuntamiento? Efectuamos los siguientes pasos 1º PASO.- formulamos las hipótesis H 0 : p=0,65= p 0 H a : p 0,65 º PASO.- elegimos un nivel de significación α, por ejemplo α=0,01. p p Z= 0 3º PASO.- elegimos el estadístico de contraste p 0.(1 p 0 n 4º PASO.- elegimos la región de aceptación. Que como es un contraste bilateral, para α=0,01, se tiene el intervalo ( z, z α α =(,58 ;,58 5º PASO.- Calculamos p= 4 35 =0,686 ; n=35 z= 0,686 0,65 0,65.(1 0,65 35 =0,444 6º PASO.- Como 0,444 (,58 ;,58, se acepta la hipótesis nula y decimos que el nivel 1 se acepta la proporción de accidentes debidos al alcohol es del 65 Página 5
7 # Ejemplo.- Un entrenador asegura que sus jugadores en los entrenamientos encestan más del 9% de los tiros libres. Con el fin de contrastar esta afirmación de ha elegido aleatoriamente una muestra de 60 lanzamientos, de los que 4 han entrado en la canasta. Estos resultados, ponen en duda al entrenador o no? Efectuamos los siguientes pasos 1º PASO.- formulamos las hipótesis H 0 : p 0,9= p 0 H a : p<0,9 º PASO.- elegimos un nivel de significación α, por ejemplo α=0,1. p p Z= 0 3º PASO.- elegimos el estadístico de contraste p 0.(1 p 0 n 4º PASO.- elegimos la región de aceptación. Que como es un contraste unilateral, para α=0,1, se tiene el intervalo ( z α,+ =( 1,88 ;+ 5º PASO.- Calculamos p= 4 60 =0,7 ; n=60 z= 0,7 0,9 0,9.(1 0,9 60 = 6,8 6º PASO.- Como 6,38 ( 1,8 ;+, se rechaza la hipótesis nula; por tanto, al nivel de 10% se pone en duda la afirmación del entrenador. 4. Contraste para la media de una población normal Si σ es conocida Supongamos que partimos de una distribución N (μ, σ, donde σ es conocida, y queremos contrastar el valor μ=μ 0. Para ello, fijado un determinado nivel de significación α, elegimos una muestra de tamaño n para la cual la media muestral x se tiene H 0 H a Tipo de contraste Estadístico Región de aceptación μ=μ 0 μ μ 0 bilateral Z= x μ 0 ( z α, z α σ μ μ 0 μ>μ 0 unilateral (, z n α que sigue una distribución μ μ 0 μ<μ 0 unilateral N (0,1 ( z α,+ Página 6
8 Si σ es desconocida y el tamaño de la muestra n es grande ( n 30 Sustituiremos la varianza σ por la cuasivarianza muestral ŝ. Por tanto el estadístico del contraste z= x μ 0 ŝ n sigue N (0,1. # Ejemplo.- Se cree que el tiempo medio de ocio que dedican al día los estudiantes de Bachillerato sigue una distribución normal de media 350 minutos y desviación típica poblacional de 60 minutos. Para contrastar esta hipótesis, se toma una muestra aleatoria formada por 100 alumnos, y se observa que el tiempo medio es 30 minutos. Qué se puede decir de esta afirmación al nivel 10%? 1º PASO.- formulamos las hipótesis H 0 :μ=350=μ 0 H a :μ 350 º PASO.- elegimos un nivel de significación α, por ejemplo α=0,1. 3º PASO.- elegimos el estadístico de contraste Z= x μ 0 σ n 4º PASO.- elegimos la región de aceptación. Que como es un contraste bilateral, para α=0,1, se tiene el intervalo ( z, z α α =( 1,645;1,645 5º PASO.- Calculamos x=30 ; n=100 ; σ=60 z= = º PASO.- Como 5 ( 1,645 ;1,645, se rechaza la hipótesis nula; por tanto, al nivel del 10% se pone en duda que el tiempo medio diario dedicado al ocio por los alumnos de Bachillerato sea 350 minutos. # Ejemplo.- Se quiere contrastar el contenido de azúcar de distintos cargamentos de remolacha. Se sabe que el contenido medio de azúcar para remolacha de regadío es de 18% y con media superior para el de secano, siendo la desviación típica 6% para ambos casos. Se toma una muestra de 0 cargamentos. Qué valor de la media permitirá tomar la decisión si es de secano o Página 7
9 de regadío al nivel del 5%? Contraste de hipótesis º curso de Bachillerato Ciencias Sociales 1º PASO.- formulamos las hipótesis H 0 :μ 18=μ 0 H a :μ>18 º PASO.- elegimos un nivel de significación α, por ejemplo α=0,05. 3º PASO.- elegimos el estadístico de contraste Z= x μ 0 σ n 4º PASO.- elegimos la región de aceptación. Que como es un contraste unilateral, para α=0,05, se tiene el intervalo (, z α =( ;1,645 5º PASO.- Calculamos x=? ; n=0 ; σ=6 z= x º PASO.- Como z= x 18 <1,645 x<0, % 6 0 Luego el 0, % es el punto crítico. Por tanto, Si Si x<0,% remolacha de regadío x 0,% remolacha de secano 5. Analogías entre el contraste de hipótesis e intervalos de confianza Para ver la analogía entre el contraste de hipótesis y los intervalos de confianza, veamos el siguiente ejemplo. # Ejemplo.- Supongamos que el gremio de restaurantes de Madrid afirma que el precio medio del menú del día es 11 y queremos contrastar esta hipótesis. Para lo cual efectuamos un contraste de hipótesis, mediante los siguiente pasos 1º PASO.- formulamos las hipótesis H 0 :μ=11 =μ 0 H a :μ 11 º PASO.- elegimos un nivel de significación α, por ejemplo α=0,05, de donde 1 α=0,95. Página 8
10 3º PASO.- elegimos el estadístico de contraste N (0,1 Z= x μ 0 s n que sigue una distribución 4º PASO.- elegimos la región de aceptación. Que como es un contraste bilateral, para α=0,05, se tiene el intervalo ( z, z α α =( 1,96 ;1,96 5º PASO.- Elegimos una muestra, por ejemplo de 40 restaurantes y hallamos el precio medio de la muestra y la desviación típica muestral; sean por ejemplo: x=11,50 ; n=40 ; s=1, Y efectuamos los cálculo para el caso particular de X ; x=11,50 z= 11,50 11 =,635 1, 40 6º PASO.- Como,635 ( 1,96 ; 1,96, se rechaza la hipótesis nula; y decimos que al nivel de significación del 5% existe evidencia suficiente de que el precio del menú del día es distinto de 11. Sin hallamos un intervalo de confianza para la media poblacional al nivel del 5 % para el enunciado anterior, será IC= ( x± z α s n ( = 1, 11,5±1, =(11,13;11,87 Y dado que μ 0 =11 (11,13 ;11,87 al nivel de significación del 5%, vemos que existe una relación entre el contraste de hipótesis y le intervalo de confianza. El error de tipo I del contraste de hipótesis se corresponde con la probabilidad de que el intervalo de confianza no cubra el valor parámetro. El error de tipo I del contraste de hipótesis se corresponde con la probabilidad de que el intervalo de confianza no cubra valores erróneos. Página 9
Contraste de hipótesis Tema Pasos del contraste de hipótesis. 1.1 Hipótesis estadísticas: nula y alternativa. 1.3 Estadístico de contraste
 1 Contraste de hipótesis Tema 3 1. Pasos del contraste de hipótesis 1.1 Hipótesis estadísticas: nula y alternativa 1.2 Supuestos 1.3 Estadístico de contraste 1.4 Regla de decisión: zona de aceptación y
1 Contraste de hipótesis Tema 3 1. Pasos del contraste de hipótesis 1.1 Hipótesis estadísticas: nula y alternativa 1.2 Supuestos 1.3 Estadístico de contraste 1.4 Regla de decisión: zona de aceptación y
Tema 8: Contraste de hipótesis
 Tema 8: Contraste de hipótesis 1 En este tema: Conceptos fundamentales: hipótesis nula y alternativa, nivel de significación, error de tipo I y tipo II, p-valor. Contraste de hipótesis e IC. Contraste
Tema 8: Contraste de hipótesis 1 En este tema: Conceptos fundamentales: hipótesis nula y alternativa, nivel de significación, error de tipo I y tipo II, p-valor. Contraste de hipótesis e IC. Contraste
Estadística y sus aplicaciones en Ciencias Sociales 6. Prueba de hipótesis. Facultad de Ciencias Sociales, UdelaR
 Estadística y sus aplicaciones en Ciencias Sociales 6. Prueba de hipótesis Facultad de Ciencias Sociales, UdelaR Índice 1. Introducción: hipótesis estadística, tipos de hipótesis, prueba de hipótesis 2.
Estadística y sus aplicaciones en Ciencias Sociales 6. Prueba de hipótesis Facultad de Ciencias Sociales, UdelaR Índice 1. Introducción: hipótesis estadística, tipos de hipótesis, prueba de hipótesis 2.
ESTIMACIÓN Y PRUEBA DE HIPÓTESIS INTERVALOS DE CONFIANZA
 www.jmontenegro.wordpress.com UNI ESTIMACIÓN Y PRUEBA DE HIPÓTESIS INTERVALOS DE CONFIANZA PROF. JOHNNY MONTENEGRO MOLINA Objetivos Desarrollar el concepto de estimación de parámetros Explicar qué es una
www.jmontenegro.wordpress.com UNI ESTIMACIÓN Y PRUEBA DE HIPÓTESIS INTERVALOS DE CONFIANZA PROF. JOHNNY MONTENEGRO MOLINA Objetivos Desarrollar el concepto de estimación de parámetros Explicar qué es una
Ejemplos Resueltos Tema 4
 Ejemplos Resueltos Tema 4 2012 1. Contraste de Hipótesis para la Media µ (con σ conocida) Dada una muestra de tamaño n y conocida la desviación típica de la población σ, se desea contrastar la hipótesis
Ejemplos Resueltos Tema 4 2012 1. Contraste de Hipótesis para la Media µ (con σ conocida) Dada una muestra de tamaño n y conocida la desviación típica de la población σ, se desea contrastar la hipótesis
Contrastes de hipótesis. 1: Ideas generales
 Contrastes de hipótesis 1: Ideas generales 1 Inferencia Estadística paramétrica población Muestra de individuos Técnicas de muestreo X 1 X 2 X 3.. X n Inferencia Estadística: métodos y procedimientos que
Contrastes de hipótesis 1: Ideas generales 1 Inferencia Estadística paramétrica población Muestra de individuos Técnicas de muestreo X 1 X 2 X 3.. X n Inferencia Estadística: métodos y procedimientos que
Tema 7. Contrastes de Hipótesis
 7.1. Conceptos básicos Tema 7. Contrastes de Hipótesis Uno de los problemas comunes en inferencia consiste en contrastar una hipótesis estadística. Ejemplo: El fabricante de un determinado tipo de piezas
7.1. Conceptos básicos Tema 7. Contrastes de Hipótesis Uno de los problemas comunes en inferencia consiste en contrastar una hipótesis estadística. Ejemplo: El fabricante de un determinado tipo de piezas
Universidad Rafael Belloso Chacín (URBE) Cátedra: Fundamentos de Estadística y Simulación Básica Semestre Profesor: Jaime Soto
 Universidad Rafael Belloso Chacín (URBE) Cátedra: Fundamentos de Estadística y Simulación Básica Semestre 2011-1 Profesor: Jaime Soto PRUEBA DE HIPÓTESIS Ejemplo El jefe de la Biblioteca de la URBE manifiesta
Universidad Rafael Belloso Chacín (URBE) Cátedra: Fundamentos de Estadística y Simulación Básica Semestre 2011-1 Profesor: Jaime Soto PRUEBA DE HIPÓTESIS Ejemplo El jefe de la Biblioteca de la URBE manifiesta
Caso particular: Contraste de homocedasticidad
 36 Bioestadística: Métodos y Aplicaciones 9.5.5. Caso particular: Contraste de homocedasticidad En la práctica un contraste de gran interés es el de la homocedasticidad o igualdad de varianzas. Decimos
36 Bioestadística: Métodos y Aplicaciones 9.5.5. Caso particular: Contraste de homocedasticidad En la práctica un contraste de gran interés es el de la homocedasticidad o igualdad de varianzas. Decimos
Tema 9: Contraste de hipótesis.
 Estadística 84 Tema 9: Contraste de hipótesis. 9.1 Introducción. El objetivo de este tema es proporcionar métodos que permiten decidir si una hipótesis estadística debe o no ser rechazada, en base a los
Estadística 84 Tema 9: Contraste de hipótesis. 9.1 Introducción. El objetivo de este tema es proporcionar métodos que permiten decidir si una hipótesis estadística debe o no ser rechazada, en base a los
Estructura de este tema. Tema 3 Contrastes de hipótesis. Ejemplo
 Estructura de este tema Tema 3 Contrastes de hipótesis José R. Berrendero Departamento de Matemáticas Universidad Autónoma de Madrid Qué es un contraste de hipótesis? Elementos de un contraste: hipótesis,
Estructura de este tema Tema 3 Contrastes de hipótesis José R. Berrendero Departamento de Matemáticas Universidad Autónoma de Madrid Qué es un contraste de hipótesis? Elementos de un contraste: hipótesis,
Contrastes de hipótesis paramétricos
 Estadística II Universidad de Salamanca Curso 2011/2012 Outline Introducción 1 Introducción 2 Contraste de Neyman-Pearson Sea X f X (x, θ). Desonocemos θ y queremos saber que valor toma este parámetro,
Estadística II Universidad de Salamanca Curso 2011/2012 Outline Introducción 1 Introducción 2 Contraste de Neyman-Pearson Sea X f X (x, θ). Desonocemos θ y queremos saber que valor toma este parámetro,
Introducción a la Inferencia Estadística
 Introducción a la Inferencia Estadística Prof. Jose Jacobo Zubcoff Universidad de Alicante 2008 1 Introducción En este tema explicaremos los contrastes para la media de una población normal. e estudiarán
Introducción a la Inferencia Estadística Prof. Jose Jacobo Zubcoff Universidad de Alicante 2008 1 Introducción En este tema explicaremos los contrastes para la media de una población normal. e estudiarán
Tema 5. Contraste de hipótesis (I)
 Tema 5. Contraste de hipótesis (I) CA UNED de Huelva, "Profesor Dr. José Carlos Vílchez Martín" Introducción Bienvenida Objetivos pedagógicos: Conocer el concepto de hipótesis estadística Conocer y estimar
Tema 5. Contraste de hipótesis (I) CA UNED de Huelva, "Profesor Dr. José Carlos Vílchez Martín" Introducción Bienvenida Objetivos pedagógicos: Conocer el concepto de hipótesis estadística Conocer y estimar
Métodos Estadísticos de la Ingeniería Tema 11: Contrastes de Hipótesis Grupo B
 Métodos Estadísticos de la Ingeniería Tema 11: Contrastes de Hipótesis Grupo B Área de Estadística e Investigación Operativa Licesio J. Rodríguez-Aragón Abril 2010 Contenidos...............................................................
Métodos Estadísticos de la Ingeniería Tema 11: Contrastes de Hipótesis Grupo B Área de Estadística e Investigación Operativa Licesio J. Rodríguez-Aragón Abril 2010 Contenidos...............................................................
El primer paso en la realización de una investigación es planear las hipótesis de investigación. Definamos el concepto de hipótesis:
 El primer paso en la realización de una investigación es planear las hipótesis de investigación. Definamos el concepto de hipótesis Definición 1.- Una hipótesis es una afirmación que está sujeta a verificación
El primer paso en la realización de una investigación es planear las hipótesis de investigación. Definamos el concepto de hipótesis Definición 1.- Una hipótesis es una afirmación que está sujeta a verificación
INFERENCIA ESTADISTICA
 1 INFERENCIA ESTADISTICA Es una rama de la Estadística que se ocupa de los procedimientos que nos permiten analizar y extraer conclusiones de una población a partir de los datos de una muestra aleatoria,
1 INFERENCIA ESTADISTICA Es una rama de la Estadística que se ocupa de los procedimientos que nos permiten analizar y extraer conclusiones de una población a partir de los datos de una muestra aleatoria,
Contrastes de hipótesis estadísticas. Contrastes paramétricos
 Índice 7 Contrastes de hipótesis estadísticas. Contrastes paramétricos 7.1 7.1 Introducción.......................................... 7.1 7.2 Conceptos básicos...................................... 7.2
Índice 7 Contrastes de hipótesis estadísticas. Contrastes paramétricos 7.1 7.1 Introducción.......................................... 7.1 7.2 Conceptos básicos...................................... 7.2
Esta proposición recibe el nombre de hipótesis
 Pruebas de hipótesis tesis. Refs: Apuntes de Estadística, Mtra Leticia de la Torre Instituto Tecnológico de Chiuhuahua, Apuntes de Estadística, Dr. Pedro Juan Rodríguez Esquerdo, Departamento de Matemáticas,
Pruebas de hipótesis tesis. Refs: Apuntes de Estadística, Mtra Leticia de la Torre Instituto Tecnológico de Chiuhuahua, Apuntes de Estadística, Dr. Pedro Juan Rodríguez Esquerdo, Departamento de Matemáticas,
para una muestra Ref: Apuntes de Estadística, Mtra Leticia de la Torre Instituto Tecnológico de Chiuhuahua
 Pruebas de hipótesis para una muestra Ref: Apuntes de Estadística, Mtra Leticia de la Torre Instituto Tecnológico de Chiuhuahua En muchas situaciones cuando queremos sacar conclusiones sobre una muestra,
Pruebas de hipótesis para una muestra Ref: Apuntes de Estadística, Mtra Leticia de la Torre Instituto Tecnológico de Chiuhuahua En muchas situaciones cuando queremos sacar conclusiones sobre una muestra,
Introducción al Tema 6. Tema 5. Intervalos de confianza Definición. Ejemplos de intervalos de confianza. Determinación del tamaño muestral.
 Introducción al Tema 6 1 Tema 5. Intervalos de confianza Definición. Ejemplos de intervalos de confianza. Determinación del tamaño muestral. Esta θ en el intervalo de confianza? Tema 6. Contraste de hipótesis
Introducción al Tema 6 1 Tema 5. Intervalos de confianza Definición. Ejemplos de intervalos de confianza. Determinación del tamaño muestral. Esta θ en el intervalo de confianza? Tema 6. Contraste de hipótesis
INFERENCIA ESTADÍSTICA: CONTRASTES DE HIPÓTESIS
 INFERENCIA ESTADÍSTICA: CONTRASTES DE HIPÓTESIS Autor: Clara Laguna 6.1 INTRODUCCIÓN En el tema anterior estudiamos cómo a partir de una muestra podemos obtener una estimación puntual o bien establecer
INFERENCIA ESTADÍSTICA: CONTRASTES DE HIPÓTESIS Autor: Clara Laguna 6.1 INTRODUCCIÓN En el tema anterior estudiamos cómo a partir de una muestra podemos obtener una estimación puntual o bien establecer
CONTROL ESTADISTICO DE LA CALIDAD
 CICLO 2012-I Módulo:2 Unidad:2 Semana: 2 CONTROL ESTADISTICO DE LA CALIDAD ING. ENRIQUE MONTENEGRO MARCELO PRUEBAS DE HIPOTESIS CONTENIDOS TEMÁTICOS 1. DEFINICIÓN DE HIPOTESIS 2. PROCEDIMIENTO DE UNA PRUEBA
CICLO 2012-I Módulo:2 Unidad:2 Semana: 2 CONTROL ESTADISTICO DE LA CALIDAD ING. ENRIQUE MONTENEGRO MARCELO PRUEBAS DE HIPOTESIS CONTENIDOS TEMÁTICOS 1. DEFINICIÓN DE HIPOTESIS 2. PROCEDIMIENTO DE UNA PRUEBA
EJERCICIOS DE SELECTIVIDAD
 EJERCICIOS DE SELECTIVIDAD INFERENCIA 1998 JUNIO OPCIÓN A Un fabricante de electrodomésticos sabe que la vida media de éstos sigue una distribución normal con media μ = 100 meses y desviación típica σ
EJERCICIOS DE SELECTIVIDAD INFERENCIA 1998 JUNIO OPCIÓN A Un fabricante de electrodomésticos sabe que la vida media de éstos sigue una distribución normal con media μ = 100 meses y desviación típica σ
4. Prueba de Hipótesis
 4. Prueba de Hipótesis Como se ha indicado anteriormente, nuestro objetivo al tomar una muestra es extraer alguna conclusión o inferencia sobre una población. En nuestro interés es conocer acerca de los
4. Prueba de Hipótesis Como se ha indicado anteriormente, nuestro objetivo al tomar una muestra es extraer alguna conclusión o inferencia sobre una población. En nuestro interés es conocer acerca de los
EJERCICIOS DE PRUEBA DE HIPOTESIS
 EJERCICIOS DE PRUEBA DE HIPOTESIS Protocolo 1. Identifique la aseveración original que se probará y exprésela en forma simbólica 1. 2. Dar la forma simbólica que debe ser verdad si la aseveración original
EJERCICIOS DE PRUEBA DE HIPOTESIS Protocolo 1. Identifique la aseveración original que se probará y exprésela en forma simbólica 1. 2. Dar la forma simbólica que debe ser verdad si la aseveración original
para una muestra Ref: Apuntes de Estadística, Mtra Leticia de la Torre Instituto Tecnológico de Chiuhuahua
 Pruebas de hipótesis para una muestra Ref: Apuntes de Estadística, Mtra Leticia de la Torre Instituto Tecnológico de Chiuhuahua Las secciones anteriores han mostrado cómo puede estimarse un parámetro de
Pruebas de hipótesis para una muestra Ref: Apuntes de Estadística, Mtra Leticia de la Torre Instituto Tecnológico de Chiuhuahua Las secciones anteriores han mostrado cómo puede estimarse un parámetro de
Contrastes de Hipótesis paramétricos y no-paramétricos.
 Capítulo 1 Contrastes de Hiptesis paramétricos y no-paramétricos. Estadística Inductiva o Inferencia Estadística: Conjunto de métodos que se fundamentan en la Teoría de la Probabilidad y que tienen por
Capítulo 1 Contrastes de Hiptesis paramétricos y no-paramétricos. Estadística Inductiva o Inferencia Estadística: Conjunto de métodos que se fundamentan en la Teoría de la Probabilidad y que tienen por
Podemos definir un contraste de hipótesis como un procedimiento que se basa en lo observado en las muestras y en la teoría de la probabilidad para
 VII. Pruebas de Hipótesis VII. Concepto de contraste de hipótesis Podemos definir un contraste de hipótesis como un procedimiento que se basa en lo observado en las muestras y en la teoría de la probabilidad
VII. Pruebas de Hipótesis VII. Concepto de contraste de hipótesis Podemos definir un contraste de hipótesis como un procedimiento que se basa en lo observado en las muestras y en la teoría de la probabilidad
Tests de Hipótesis basados en una muestra. ESTADÍSTICA (Q) 5. TESTS DE HIPÓTESIS PARA LA MEDIA DE UNA POBLACIÓN NORMAL CON VARIANZA CONOCIDA
 2 5. TESTS DE HIPÓTESIS PARA LA MEDIA DE UNA POBLACIÓN NORMAL CON VARIANZA CONOCIDA 5. Desarrollo de un ejemplo Interesa saber si el método de absorción atómica de vapor frío para determinar mercurio introduce
2 5. TESTS DE HIPÓTESIS PARA LA MEDIA DE UNA POBLACIÓN NORMAL CON VARIANZA CONOCIDA 5. Desarrollo de un ejemplo Interesa saber si el método de absorción atómica de vapor frío para determinar mercurio introduce
SOLUCIÓN EXAMEN IV Nombres: Apellidos: C.I.: Firma: Fecha: 19/11/2004
 Nombres: Apellidos: C.I.: Firma: Fecha: 19/11/004 MÉTODOS ESTADÍSTICOS I EXAMEN IV PARTE I: Encierre con un círculo la respuesta correcta (0,5 puntos c/u): 1. (V F) Los contrastes de hipótesis de dos muestras
Nombres: Apellidos: C.I.: Firma: Fecha: 19/11/004 MÉTODOS ESTADÍSTICOS I EXAMEN IV PARTE I: Encierre con un círculo la respuesta correcta (0,5 puntos c/u): 1. (V F) Los contrastes de hipótesis de dos muestras
Pruebas de hipótesis
 Pruebas de hipótesis Álvaro José Flórez 1 Escuela de Ingeniería Industrial y Estadística Facultad de Ingenierías Febrero - Junio 2012 Prueba de hipótesis Uno de los objetivos de la estadística es hacer
Pruebas de hipótesis Álvaro José Flórez 1 Escuela de Ingeniería Industrial y Estadística Facultad de Ingenierías Febrero - Junio 2012 Prueba de hipótesis Uno de los objetivos de la estadística es hacer
Pruebas de Hipótesis. Diseño Estadístico y Herramientas para la Calidad. Pruebas de Hipótesis. Hipótesis
 Diseño Estadístico y Herramientas para la Calidad Pruebas de Hipótesis Expositor: Dr. Juan José Flores Romero [email protected] http://lsc.fie.umich.mx/~juan M. en Calidad Total y Competitividad Pruebas de
Diseño Estadístico y Herramientas para la Calidad Pruebas de Hipótesis Expositor: Dr. Juan José Flores Romero [email protected] http://lsc.fie.umich.mx/~juan M. en Calidad Total y Competitividad Pruebas de
CONTRASTE DE HIPÓTESIS
 CONTRASTE DE HIPÓTESIS Antonio Morillas A. Morillas: Contraste de hipótesis 1 CONTRASTE DE HIPÓTESIS 1. Introducción 2. Conceptos básicos 3. Región crítica óptima i. Teorema de Neyman-Pearson ii. Región
CONTRASTE DE HIPÓTESIS Antonio Morillas A. Morillas: Contraste de hipótesis 1 CONTRASTE DE HIPÓTESIS 1. Introducción 2. Conceptos básicos 3. Región crítica óptima i. Teorema de Neyman-Pearson ii. Región
PLAN DE TRABAJO 9 Período 3/09/07 al 28/09/07
 PLAN DE TRABAJO 9 Período 3/09/07 al 28/09/07 TEMAS A ESTUDIAR En esta guía nos dedicaremos a estudiar el tema de Estimación por intervalo y comenzaremos a estudiar las pruebas de hipótesis paramétricas.
PLAN DE TRABAJO 9 Período 3/09/07 al 28/09/07 TEMAS A ESTUDIAR En esta guía nos dedicaremos a estudiar el tema de Estimación por intervalo y comenzaremos a estudiar las pruebas de hipótesis paramétricas.
Contraste de hipótesis paramétricas
 Contraste de hipótesis paramétricas Prof, Dr. Jose Jacobo Zubcoff Departamento de Ciencias del Mar y Biología Aplicada Proceso de la investigación estadística Etapas PROBLEMA HIPÓTESIS DISEÑO RECOLECCIÓN
Contraste de hipótesis paramétricas Prof, Dr. Jose Jacobo Zubcoff Departamento de Ciencias del Mar y Biología Aplicada Proceso de la investigación estadística Etapas PROBLEMA HIPÓTESIS DISEÑO RECOLECCIÓN
Teoría de muestras. Distribución de variables aleatorias en el muestreo. 1. Distribución de medias muestrales
 Teoría de muestras Distribución de variables aleatorias en el muestreo 1. Distribución de medias muestrales Dada una variable estadística observada en una población, se puede calcular se media y su desviación
Teoría de muestras Distribución de variables aleatorias en el muestreo 1. Distribución de medias muestrales Dada una variable estadística observada en una población, se puede calcular se media y su desviación
Curso de Estadística Aplicada a las Ciencias Sociales. Tema 12. Contraste de hipótesis. Introducción. Introducción
 Curso de Estadística Aplicada a las Ciencias Sociales Tema 12. Contraste de (Cap. 22 del libro) Tema 12. Contraste de 1. Tipos de 2. La nula y la Ejercicios Tema 12, Contraste de 2 En muchas investigaciones
Curso de Estadística Aplicada a las Ciencias Sociales Tema 12. Contraste de (Cap. 22 del libro) Tema 12. Contraste de 1. Tipos de 2. La nula y la Ejercicios Tema 12, Contraste de 2 En muchas investigaciones
Conceptos del contraste de hipótesis
 Análisis de datos y gestión veterinaria Contraste de hipótesis Departamento de Producción Animal Facultad de Veterinaria Universidad de Córdoba Córdoba, 14 de Diciembre de 211 Conceptos del contraste de
Análisis de datos y gestión veterinaria Contraste de hipótesis Departamento de Producción Animal Facultad de Veterinaria Universidad de Córdoba Córdoba, 14 de Diciembre de 211 Conceptos del contraste de
Práctica 4. Contraste de hipótesis
 Práctica 4. Contraste de hipótesis Estadística Facultad de Física Objetivos Ajuste a una distribución discreta uniforme Test χ 2 Comparación de muestras Ajuste a una distribución normal 1 Introducción
Práctica 4. Contraste de hipótesis Estadística Facultad de Física Objetivos Ajuste a una distribución discreta uniforme Test χ 2 Comparación de muestras Ajuste a una distribución normal 1 Introducción
Objetivos del tema. Qué es una hipótesis? Test de Hipótesis Introducción a la Probabilidad y Estadística. Contrastando una hipótesis
 Objetivos del tema Conocer el proceso para contrastar hipótesis y su relación con el método científico. Diferenciar entre hipótesis nula y alternativa Nivel de significación Test de Hipótesis Introducción
Objetivos del tema Conocer el proceso para contrastar hipótesis y su relación con el método científico. Diferenciar entre hipótesis nula y alternativa Nivel de significación Test de Hipótesis Introducción
Tema 8: Introducción a la Teoría sobre Contraste de hipótesis
 Tema 8: Introducción a la Teoría sobre Contraste de hipótesis Estadística. 4 o Curso. Licenciatura en Ciencias Ambientales Licenciatura en Ciencias Ambientales (4 o Curso) Tema 8: Introducción a la Teoría
Tema 8: Introducción a la Teoría sobre Contraste de hipótesis Estadística. 4 o Curso. Licenciatura en Ciencias Ambientales Licenciatura en Ciencias Ambientales (4 o Curso) Tema 8: Introducción a la Teoría
Solución Examen Parcial IV Nombres: Apellidos: C.I.: Firma: Fecha: 22/06/2005
 Nombres: Apellidos: C.I.: Firma: Fecha: 22/06/2005 MÉTODOS ESTADÍSTICOS I EXAMEN IV PARTE I: Encierre con un círculo la respuesta correcta o llene los espacios en blanco (0,5 puntos c/u): 1. (V F) La prueba
Nombres: Apellidos: C.I.: Firma: Fecha: 22/06/2005 MÉTODOS ESTADÍSTICOS I EXAMEN IV PARTE I: Encierre con un círculo la respuesta correcta o llene los espacios en blanco (0,5 puntos c/u): 1. (V F) La prueba
Práctica 5 ANÁLISIS DE UNA MUESTRA INTERVALOS DE CONFIANZA CONTRASTE DE HIPÓTESIS
 Práctica. Intervalos de confianza 1 Práctica ANÁLISIS DE UNA MUESTRA INTERVALOS DE CONFIANZA CONTRASTE DE HIPÓTESIS Objetivos: Ilustrar el grado de fiabilidad de un intervalo de confianza cuando se utiliza
Práctica. Intervalos de confianza 1 Práctica ANÁLISIS DE UNA MUESTRA INTERVALOS DE CONFIANZA CONTRASTE DE HIPÓTESIS Objetivos: Ilustrar el grado de fiabilidad de un intervalo de confianza cuando se utiliza
Estadísticas Pueden ser
 Principios Básicos Para iniciar en el curso de Diseño de experimentos, es necesario tener algunos conceptos claros en la parte de probabilidad y estadística. A continuación se presentan los conceptos más
Principios Básicos Para iniciar en el curso de Diseño de experimentos, es necesario tener algunos conceptos claros en la parte de probabilidad y estadística. A continuación se presentan los conceptos más
Teorema Central del Límite (1)
 Teorema Central del Límite (1) Definición. Cualquier cantidad calculada a partir de las observaciones de una muestra se llama estadístico. La distribución de los valores que puede tomar un estadístico
Teorema Central del Límite (1) Definición. Cualquier cantidad calculada a partir de las observaciones de una muestra se llama estadístico. La distribución de los valores que puede tomar un estadístico
Teoría de muestras 2º curso de Bachillerato Ciencias Sociales
 TEORÍA DE MUESTRAS Índice: 1. Introducción----------------------------------------------------------------------------------------- 2 2. Muestras y población-------------------------------------------------------------------------------
TEORÍA DE MUESTRAS Índice: 1. Introducción----------------------------------------------------------------------------------------- 2 2. Muestras y población-------------------------------------------------------------------------------
Es una proposición o supuesto sobre los parámetros de una o más poblaciones
 HIPOTESIS ESTADISTICA Es una proposición o supuesto sobre los parámetros de una o más poblaciones http://www.itch.edu.mx/academic/industrial/estadistica1/cap02.html POR LUIS M. BAQUERO ROSAS, MBA JUNIO
HIPOTESIS ESTADISTICA Es una proposición o supuesto sobre los parámetros de una o más poblaciones http://www.itch.edu.mx/academic/industrial/estadistica1/cap02.html POR LUIS M. BAQUERO ROSAS, MBA JUNIO
Tema 6. Inferencia estadística
 Cuestiones de Verdadero/Falso Tema 6. Inferencia estadística 508 Estadística. ETDI. Curs 2002/03 1. La Estimación puntual supone obtener un único valor como estimación del parámetro desconocido. 2. La
Cuestiones de Verdadero/Falso Tema 6. Inferencia estadística 508 Estadística. ETDI. Curs 2002/03 1. La Estimación puntual supone obtener un único valor como estimación del parámetro desconocido. 2. La
= P (Z ) - P (Z ) = P (Z 1 25) P (Z -1 25)= P (Z 1 25) [P (Z 1 25)] = P (Z 1 25) [1- P (Z 1 25)] =
![= P (Z ) - P (Z ) = P (Z 1 25) P (Z -1 25)= P (Z 1 25) [P (Z 1 25)] = P (Z 1 25) [1- P (Z 1 25)] = = P (Z ) - P (Z ) = P (Z 1 25) P (Z -1 25)= P (Z 1 25) [P (Z 1 25)] = P (Z 1 25) [1- P (Z 1 25)] =](/thumbs/52/30362634.jpg) El peso en kg de los estudiantes universitarios de una gran ciudad se supone aproximado por una distribución normal con media 60kg y desviación típica 8kg. Se toman 100 muestras aleatorias simples de 64
El peso en kg de los estudiantes universitarios de una gran ciudad se supone aproximado por una distribución normal con media 60kg y desviación típica 8kg. Se toman 100 muestras aleatorias simples de 64
Germán Jesús Rubio Luna Catedrático de Matemáticas del IES Francisco Ayala
 Decisión estadística. Contraste de hipótesis Nota.- Cuando tratábamos la estimación de parámetros, intentábamos obtener un valor o un intervalo de valores que constituyesen la mejor estimación del parámetro
Decisión estadística. Contraste de hipótesis Nota.- Cuando tratábamos la estimación de parámetros, intentábamos obtener un valor o un intervalo de valores que constituyesen la mejor estimación del parámetro
INTERVALO DE CONFIANZA PARA LA PROPORCIÓN
 INTERVALO DE CONFIANZA PARA LA PROPORCIÓN Si deseamos estimar la proporción p con que una determinada característica se da en una población, a partir de la proporción p' observada en una muestra de tamaño
INTERVALO DE CONFIANZA PARA LA PROPORCIÓN Si deseamos estimar la proporción p con que una determinada característica se da en una población, a partir de la proporción p' observada en una muestra de tamaño
Proyecto Tema 8: Tests de hipótesis. Resumen teórico
 Temas de Estadística Práctica Antonio Roldán Martínez Proyecto http://www.hojamat.es/ Tema 8: Tests de hipótesis Resumen teórico Tests de hipótesis Concepto de test de hipótesis Un test de hipótesis (o
Temas de Estadística Práctica Antonio Roldán Martínez Proyecto http://www.hojamat.es/ Tema 8: Tests de hipótesis Resumen teórico Tests de hipótesis Concepto de test de hipótesis Un test de hipótesis (o
INFERENCIA ESTADISTICA
 INFERENCIA ESTADISTICA ESTIMACION 2 maneras de estimar: Estimaciones puntuales x s 2 Estimaciones por intervalo 2 ESTIMACION Estimaciones por intervalo Limites de Confianza LCI
INFERENCIA ESTADISTICA ESTIMACION 2 maneras de estimar: Estimaciones puntuales x s 2 Estimaciones por intervalo 2 ESTIMACION Estimaciones por intervalo Limites de Confianza LCI
Hipótesis Alternativa H 1 : ϑ Θ 1
 INFERENCIA ESTADÍSTICA Tema 3.3: Contrastes de signicación Objetivos Dominar el esquema conceptual y el lenguaje propios de los contrastes de hipótesis. Construir contrastes de hipótesis para los parámetros
INFERENCIA ESTADÍSTICA Tema 3.3: Contrastes de signicación Objetivos Dominar el esquema conceptual y el lenguaje propios de los contrastes de hipótesis. Construir contrastes de hipótesis para los parámetros
Departamento de Estadística y Econometría. Curso EJERCICIOS DE ESTADÍSTICA APLICADA A LA EMPRESA II. L.A.D.E. TEMA 2
 Departamento de Estadística y Econometría. Curso 2002-2003 EJERCICIOS DE ESTADÍSTICA APLICADA A LA EMPRESA II. L.A.D.E. TEMA 2 1.- Una empresa de elaboración de materiales pone en práctica un nuevo método
Departamento de Estadística y Econometría. Curso 2002-2003 EJERCICIOS DE ESTADÍSTICA APLICADA A LA EMPRESA II. L.A.D.E. TEMA 2 1.- Una empresa de elaboración de materiales pone en práctica un nuevo método
Caso 105. Tamaño de muestra y potencia de una prueba. Diseño de experimentos. Jesús López Fidalgo
 Caso 105. Tamaño de muestra y potencia de una prueba. Diseño de experimentos. Jesús López Fidalgo Caso Práctico El objetivo de este ejercicio es analizar diferentes tipos de pruebas estadísticas en las
Caso 105. Tamaño de muestra y potencia de una prueba. Diseño de experimentos. Jesús López Fidalgo Caso Práctico El objetivo de este ejercicio es analizar diferentes tipos de pruebas estadísticas en las
Bloque 3 Tema 14 ANÁLISIS DE LA VARIANZA. PRUEBA F
 Bloque 3 Tema 4 AÁLISIS DE LA VARIAZA. PRUEBA F El objetivo fundamental de la experimentación es estudiar la posible relación de causalidad existente entre dos o más variables. Este estudio representa
Bloque 3 Tema 4 AÁLISIS DE LA VARIAZA. PRUEBA F El objetivo fundamental de la experimentación es estudiar la posible relación de causalidad existente entre dos o más variables. Este estudio representa
Tema 13 : Intervalos de probabilidad y confianza. Hipótesis y decisiones estadísticas.
 Tema 13 : Intervalos de probabilidad y confianza. Hipótesis y decisiones estadísticas. ---Intervalo de probabilidad (IP) Permite predecir el comportamiento de las muestras. Si de una población se sacan
Tema 13 : Intervalos de probabilidad y confianza. Hipótesis y decisiones estadísticas. ---Intervalo de probabilidad (IP) Permite predecir el comportamiento de las muestras. Si de una población se sacan
Ejercicios T.5 CONTRASTES PARAMÉTRICOS
 Ejercicios T.5 CONTRASTES PARAMÉTRICOS 1. Un fabricante de perfume asegura que los frascos que produce contienen por término medio 100 ml. distribuyéndose el contenido de dichos frascos según una distribución
Ejercicios T.5 CONTRASTES PARAMÉTRICOS 1. Un fabricante de perfume asegura que los frascos que produce contienen por término medio 100 ml. distribuyéndose el contenido de dichos frascos según una distribución
Prueba de Hipótesis. Bondad de Ajuste. Tuesday, August 5, 14
 Prueba de Hipótesis Bondad de Ajuste Conceptos Generales Hipótesis: Enunciado que se quiere demostrar. Prueba de Hipótesis: Procedimiento para determinar si se debe rechazar o no una afirmación acerca
Prueba de Hipótesis Bondad de Ajuste Conceptos Generales Hipótesis: Enunciado que se quiere demostrar. Prueba de Hipótesis: Procedimiento para determinar si se debe rechazar o no una afirmación acerca
JUNIO Encuentra, si existen, matrices cuadradas A, de orden 2, distintas de la matriz identidad, tales que: A
 Bloque A JUNIO 2003 1.- Encuentra, si existen, matrices cuadradas A, de orden 2, distintas de la matriz identidad, tales que: 1 0 A = 1 0 A Cuántas matrices A existen con esa condición? Razona tu respuesta.
Bloque A JUNIO 2003 1.- Encuentra, si existen, matrices cuadradas A, de orden 2, distintas de la matriz identidad, tales que: 1 0 A = 1 0 A Cuántas matrices A existen con esa condición? Razona tu respuesta.
Estadística Inferencial
 Estadística Inferencial 1 Sesión No. 5 Nombre: Prueba de hipótesis Contextualización En la práctica, es frecuente tener que tomar decisiones acerca de poblaciones con base en información de muestreo. Tales
Estadística Inferencial 1 Sesión No. 5 Nombre: Prueba de hipótesis Contextualización En la práctica, es frecuente tener que tomar decisiones acerca de poblaciones con base en información de muestreo. Tales
R E S O L U C I Ó N. a) El intervalo de confianza de la media poblacional viene dado por: I. C. z
 Un estudio realizado sobre 100 usuarios revela que un automóvil recorre anualmente un promedio de 15.00 Km con una desviación típica de.50 Km. a) Determine un intervalo de confianza, al 99%, para la cantidad
Un estudio realizado sobre 100 usuarios revela que un automóvil recorre anualmente un promedio de 15.00 Km con una desviación típica de.50 Km. a) Determine un intervalo de confianza, al 99%, para la cantidad
ETSI de Topografía, Geodesia y Cartografía
 Disttool Es una herramienta de MATLAB que permite visualizar de forma gráfica las características de cada distribución con la posibilidad de variar sus parámetros. Las funciones que muestra son: Función
Disttool Es una herramienta de MATLAB que permite visualizar de forma gráfica las características de cada distribución con la posibilidad de variar sus parámetros. Las funciones que muestra son: Función
Inferencia estadística Selectividad CCSS Murcia. MasMates.com Colecciones de ejercicios
 1. [2014] [EXT-A] Según un informe de una universidad, la edad media de finalización de un determinado grado no supera los 23 años. Sabiendo que la edad de finalización sigue una normal con desviación
1. [2014] [EXT-A] Según un informe de una universidad, la edad media de finalización de un determinado grado no supera los 23 años. Sabiendo que la edad de finalización sigue una normal con desviación
Tabla de Test de Hipótesis ( Caso: Una muestra ) A. Test para µ con σ 2 conocida: Suponga que X 1, X 2,, X n, es una m.a.(n) desde N( µ, σ 2 )
 Test de Hipótesis II Tabla de Test de Hipótesis ( Caso: Una muestra ) A. Test para µ con σ conocida: Suponga que X, X,, X n, es una m.a.(n) desde N( µ, σ ) Estadística de Prueba X - μ Z 0 = σ / n ~ N(0,)
Test de Hipótesis II Tabla de Test de Hipótesis ( Caso: Una muestra ) A. Test para µ con σ conocida: Suponga que X, X,, X n, es una m.a.(n) desde N( µ, σ ) Estadística de Prueba X - μ Z 0 = σ / n ~ N(0,)
1) Características del diseño en un estudio de cohortes.
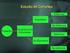 Departamento de Estadística Universidad Carlos III de Madrid BIOESTADISTICA (55-10536) Estudios de cohortes CONCEPTOS CLAVE 1) Características del diseño en un estudio de cohortes. ) Elección del tamaño
Departamento de Estadística Universidad Carlos III de Madrid BIOESTADISTICA (55-10536) Estudios de cohortes CONCEPTOS CLAVE 1) Características del diseño en un estudio de cohortes. ) Elección del tamaño
Cómo introducir Prueba de Hipótesis para una media, utilizando experimentos en el salón de clase.
 Cómo introducir Prueba de Hipótesis para una media, utilizando experimentos en el salón de clase. M. C. Blanca Evelia Flores Soto. Dpto. de Matemáticas Universidad de Sonora Introducción. Actividad desarrollada
Cómo introducir Prueba de Hipótesis para una media, utilizando experimentos en el salón de clase. M. C. Blanca Evelia Flores Soto. Dpto. de Matemáticas Universidad de Sonora Introducción. Actividad desarrollada
Matemáticas 2.º Bachillerato. Intervalos de confianza. Contraste de hipótesis
 Matemáticas 2.º Bachillerato Intervalos de confianza. Contraste de hipótesis Depto. Matemáticas IES Elaios Tema: Estadística Inferencial 1. MUESTREO ALEATORIO Presentación elaborada por el profesor José
Matemáticas 2.º Bachillerato Intervalos de confianza. Contraste de hipótesis Depto. Matemáticas IES Elaios Tema: Estadística Inferencial 1. MUESTREO ALEATORIO Presentación elaborada por el profesor José
Teoría de la decisión Estadística
 Pruebas de hìpótesis Unidad 8. Pruebas de hipótesis. Formulación general. Distribución de varianza conocida. Prueba para la bondad del ajuste. Validación de modelos 1 Formulación Una Hipótesis es una proposición
Pruebas de hìpótesis Unidad 8. Pruebas de hipótesis. Formulación general. Distribución de varianza conocida. Prueba para la bondad del ajuste. Validación de modelos 1 Formulación Una Hipótesis es una proposición
Inferencia con una variable Tema 2
 Inferencia con una variable Tema 2 1. Contraste sobre una proporción 2. Bondad de ajuste 3. Contraste de hipótesis sobre una media 3.1. Con σ 2 conocida, prueba Z 3.2. Con σ 2 desconocida, prueba T 4.
Inferencia con una variable Tema 2 1. Contraste sobre una proporción 2. Bondad de ajuste 3. Contraste de hipótesis sobre una media 3.1. Con σ 2 conocida, prueba Z 3.2. Con σ 2 desconocida, prueba T 4.
PRUEBAS DE ACCESO A LA UNIVERSIDAD L.O.G.S.E
 PRUEBAS DE ACCESO A LA UNIVERSIDAD L.O.G.S.E CURSO 00-.003 - CONVOCATORIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES - Cada alumno debe elegir sólo una de las pruebas (A o B) y, dentro de ella, sólo
PRUEBAS DE ACCESO A LA UNIVERSIDAD L.O.G.S.E CURSO 00-.003 - CONVOCATORIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES - Cada alumno debe elegir sólo una de las pruebas (A o B) y, dentro de ella, sólo
Estadística II / PRUEBAS DE HIPOTESIS. Una hipótesis estadística es una afirmación o conjetura acerca de una o mas poblaciones.
 PRUEBAS DE HIPOTESIS La prueba de hipótesis es un procedimiento estadístico que comienza con una suposición que se hace con respecto a un parámetro de población, luego se recolectan datos de muestra, se
PRUEBAS DE HIPOTESIS La prueba de hipótesis es un procedimiento estadístico que comienza con una suposición que se hace con respecto a un parámetro de población, luego se recolectan datos de muestra, se
TAMAÑO DE MUESTRA EN LA ESTIMACIÓN DE LA MEDIA DE UNA POBLACIÓN
 TAMAÑO DE MUESTRA EN LA ESTIMACIÓN DE LA MEDIA DE UNA POBLACIÓN En este artículo, se trata de explicar una metodología estadística sencilla y sobre todo práctica, para la estimación del tamaño de muestra
TAMAÑO DE MUESTRA EN LA ESTIMACIÓN DE LA MEDIA DE UNA POBLACIÓN En este artículo, se trata de explicar una metodología estadística sencilla y sobre todo práctica, para la estimación del tamaño de muestra
Inferencia estadística Selectividad CCSS Andalucía. MasMates.com Colecciones de ejercicios
 1. [2014] [EXT-A] La concejalía de Educación de una determinada localidad afirma que el tiempo medio dedicado a la lectura por los jóvenes de entre 15 y 20 años de edad es, a lo sumo, de 8 horas semanales.
1. [2014] [EXT-A] La concejalía de Educación de una determinada localidad afirma que el tiempo medio dedicado a la lectura por los jóvenes de entre 15 y 20 años de edad es, a lo sumo, de 8 horas semanales.
ENUNCIADO y SOLUCIONES. Problema 1
 Ingeniería Industrial Métodos estadísticos de la Ingeniería Examen Junio 007. ENUNCIADO y SOLUCIONES Problema La memoria RAM para un ordenador se puede recibir de dos fabricantes A y B con igual probabilidad.
Ingeniería Industrial Métodos estadísticos de la Ingeniería Examen Junio 007. ENUNCIADO y SOLUCIONES Problema La memoria RAM para un ordenador se puede recibir de dos fabricantes A y B con igual probabilidad.
Sesión 13. Introducción a la Prueba de Hipótesis. Estadística II Equipo Docente: Iris Gallardo - Andrés Antivilo Francisco Marro
 Sesión 13 Introducción a la Prueba de Hipótesis Introducción ( Porqué debemos realizar pruebas de hipótesis?) El objetivo último del análisis de datos es el de extraer conclusiones de tipo general a partir
Sesión 13 Introducción a la Prueba de Hipótesis Introducción ( Porqué debemos realizar pruebas de hipótesis?) El objetivo último del análisis de datos es el de extraer conclusiones de tipo general a partir
DISEÑO Y ANÁLISIS DE DATOS EN PSICOLOGÍA II
 DISEÑO Y ANÁLISIS DE DATOS EN PSICOLOGÍA II PRÁCTICA 5 En una determinada investigación se estudió el rendimiento en matemáticas en función del estilo de aprendizaje de una serie de estudiantes de educación
DISEÑO Y ANÁLISIS DE DATOS EN PSICOLOGÍA II PRÁCTICA 5 En una determinada investigación se estudió el rendimiento en matemáticas en función del estilo de aprendizaje de una serie de estudiantes de educación
ANOVA. Análisis de la Varianza. Univariante Efectos fijos Muestras independientes
 ANOVA Análisis de la Varianza Univariante Efectos fijos Muestras independientes De la t a la F En el test de la t de Student para muestras independientes, aprendimos como usar la distribución t para contrastar
ANOVA Análisis de la Varianza Univariante Efectos fijos Muestras independientes De la t a la F En el test de la t de Student para muestras independientes, aprendimos como usar la distribución t para contrastar
INFERENCIA DE LA PROPORCIÓN
 ESTADISTICA INFERENCIA DE LA PROPORCIÓN DISTRIBUCIÓN MUESTRAL DE PROPORCIONES En una población la proporción de elementos (personas, animales, cosas o entes) que posee una cierta característica es p. En
ESTADISTICA INFERENCIA DE LA PROPORCIÓN DISTRIBUCIÓN MUESTRAL DE PROPORCIONES En una población la proporción de elementos (personas, animales, cosas o entes) que posee una cierta característica es p. En
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2011 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 6: TEORÍA DE MUESTRAS
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 011 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 6: TEORÍA DE MUESTRAS Junio, Ejercicio 4, Opción B Reserva 1, Ejercicio 4, Opción B Reserva, Ejercicio
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 011 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 6: TEORÍA DE MUESTRAS Junio, Ejercicio 4, Opción B Reserva 1, Ejercicio 4, Opción B Reserva, Ejercicio
TEMA 3: Contrastes de Hipótesis en el MRL
 TEMA 3: Contrastes de Hipótesis en el MRL Econometría I M. Angeles Carnero Departamento de Fundamentos del Análisis Económico Curso 2011-12 Econometría I (UA) Tema 3: Contrastes de Hipótesis Curso 2011-12
TEMA 3: Contrastes de Hipótesis en el MRL Econometría I M. Angeles Carnero Departamento de Fundamentos del Análisis Económico Curso 2011-12 Econometría I (UA) Tema 3: Contrastes de Hipótesis Curso 2011-12
a. N(19 5, 1 2) P(19 X 21) = P( Z ) = = P = P P = = P P = P = = = El 55 72% no son adecuados.
 El diámetro de los tubos de cartón para un envase ha de estar entre 19 y 21mm. La maquina prepara tubos cuyos diámetros están distribuidos como una manual de media 19 5mm y desviación típica 1 2mm. Qué
El diámetro de los tubos de cartón para un envase ha de estar entre 19 y 21mm. La maquina prepara tubos cuyos diámetros están distribuidos como una manual de media 19 5mm y desviación típica 1 2mm. Qué
ESTADÍSTICA. Población Individuo Muestra Muestreo Valor Dato Variable Cualitativa ordinal nominal. continua
 ESTADÍSTICA Población Individuo Muestra Muestreo Valor Dato Variable Cualitativa ordinal nominal Cuantitativa discreta continua DISTRIBUCIÓN DE FRECUENCIAS Frecuencia absoluta: fi Frecuencia relativa:
ESTADÍSTICA Población Individuo Muestra Muestreo Valor Dato Variable Cualitativa ordinal nominal Cuantitativa discreta continua DISTRIBUCIÓN DE FRECUENCIAS Frecuencia absoluta: fi Frecuencia relativa:
INTERVALOS DE CONFIANZA. La estadística en cómic (L. Gonick y W. Smith)
 INTERVALOS DE CONFIANZA La estadística en cómic (L. Gonick y W. Smith) EJEMPLO: Será elegido el senador Astuto? 2 tamaño muestral Estimador de p variable aleatoria poblacional? proporción de personas que
INTERVALOS DE CONFIANZA La estadística en cómic (L. Gonick y W. Smith) EJEMPLO: Será elegido el senador Astuto? 2 tamaño muestral Estimador de p variable aleatoria poblacional? proporción de personas que
Tema 8. Muestreo. Indice
 Tema 8. Muestreo Indice 1. Población y muestra.... 2 2. Tipos de muestreos.... 3 3. Distribución muestral de las medias.... 4 4. Distribución muestral de las proporciones.... 6 Apuntes realizados por José
Tema 8. Muestreo Indice 1. Población y muestra.... 2 2. Tipos de muestreos.... 3 3. Distribución muestral de las medias.... 4 4. Distribución muestral de las proporciones.... 6 Apuntes realizados por José
478 Índice alfabético
 Índice alfabético Símbolos A, suceso contrario de A, 187 A B, diferencia de los sucesos A y B, 188 A/B, suceso A condicionado por el suceso B, 194 A B, intersección de los sucesos A y B, 188 A B, unión
Índice alfabético Símbolos A, suceso contrario de A, 187 A B, diferencia de los sucesos A y B, 188 A/B, suceso A condicionado por el suceso B, 194 A B, intersección de los sucesos A y B, 188 A B, unión
1. Ejercicios. 2 a parte
 1. Ejercicios. 2 a parte Ejercicio 1 Calcule 1. P (χ 2 9 3 33) 2. P (χ 2 15 7 26). 3. P (15 51 χ 2 8 22). 4. P (χ 2 70 82). Ejercicio 2 Si X χ 2 26, obtenga un intervalo [a, b] que contenga un 95 % de
1. Ejercicios. 2 a parte Ejercicio 1 Calcule 1. P (χ 2 9 3 33) 2. P (χ 2 15 7 26). 3. P (15 51 χ 2 8 22). 4. P (χ 2 70 82). Ejercicio 2 Si X χ 2 26, obtenga un intervalo [a, b] que contenga un 95 % de
Pruebas de Hipótesis
 Pruebas de Hipótesis Tipos de errores Se pueden cometer dos tipos de errores: Decisión Población Ho es erdadera Ho es falsa No rechazar Ho Decisión correcta. Error tipo II Rechazar Ho Error tipo I Decisión
Pruebas de Hipótesis Tipos de errores Se pueden cometer dos tipos de errores: Decisión Población Ho es erdadera Ho es falsa No rechazar Ho Decisión correcta. Error tipo II Rechazar Ho Error tipo I Decisión
Estadística II / PRUEBAS DE HIPOTESIS. Una hipótesis estadística es una afirmación o conjetura acerca de una o mas poblaciones.
 La prueba de hipótesis es un procedimiento estadístico que comienza con una suposición que se hace con respecto a un parámetro de población, luego se recolectan datos de muestra, se producen estadísticas
La prueba de hipótesis es un procedimiento estadístico que comienza con una suposición que se hace con respecto a un parámetro de población, luego se recolectan datos de muestra, se producen estadísticas
PRÁCTICA 8: CONTRASTES DE HIPÓTESIS PARAMÉTRICOS
 PRÁCTICA 8: CONTRASTES DE HIPÓTESIS PARAMÉTRICOS Objetivos Plantear y resolver problemas mediante la técnica de contraste de hipótesis. Asimilar los conceptos relativos a contrastes de hipótesis, tales
PRÁCTICA 8: CONTRASTES DE HIPÓTESIS PARAMÉTRICOS Objetivos Plantear y resolver problemas mediante la técnica de contraste de hipótesis. Asimilar los conceptos relativos a contrastes de hipótesis, tales
Análisis Estadístico de Datos Climáticos. Pruebas de Hipótesis (Wilks, cap. 5)
 Análisis Estadístico de Datos Climáticos Pruebas de Hipótesis (Wilks, cap. 5) 2015 PRUEBAS DE HIPÓTESIS (o pruebas de significación) Objetivo: A partir del análisis de una muestra de datos, decidir si
Análisis Estadístico de Datos Climáticos Pruebas de Hipótesis (Wilks, cap. 5) 2015 PRUEBAS DE HIPÓTESIS (o pruebas de significación) Objetivo: A partir del análisis de una muestra de datos, decidir si
Estadística y sus aplicaciones en Ciencias Sociales 5. Estimación. Facultad de Ciencias Sociales, UdelaR
 Estadística y sus aplicaciones en Ciencias Sociales 5. Estimación Facultad de Ciencias Sociales, UdelaR Índice 1. Repaso: estimadores y estimaciones. Propiedades de los estimadores. 2. Estimación puntual.
Estadística y sus aplicaciones en Ciencias Sociales 5. Estimación Facultad de Ciencias Sociales, UdelaR Índice 1. Repaso: estimadores y estimaciones. Propiedades de los estimadores. 2. Estimación puntual.
Determinación del tamaño de muestra (para una sola muestra)
 STATGRAPHICS Rev. 4/5/007 Determinación del tamaño de muestra (para una sola muestra) Este procedimiento determina un tamaño de muestra adecuado para la estimación o la prueba de hipótesis con respecto
STATGRAPHICS Rev. 4/5/007 Determinación del tamaño de muestra (para una sola muestra) Este procedimiento determina un tamaño de muestra adecuado para la estimación o la prueba de hipótesis con respecto
EJERCICIOS RESUELTOS DE ESTADÍSTICA II
 EJERCICIOS RESUELTOS DE ESTADÍSTICA II RESUMEN DE EJERCICIOS DADOS EN CLASES POR: EILEEN JOHANA ARAGONES GENEY DISTRIBUCIONES DOCENTE: JUAN CARLOS VERGARA SCHMALBACH ESTIMACIÓN PRUEBAS DE HIPÓTESIS Grupo
EJERCICIOS RESUELTOS DE ESTADÍSTICA II RESUMEN DE EJERCICIOS DADOS EN CLASES POR: EILEEN JOHANA ARAGONES GENEY DISTRIBUCIONES DOCENTE: JUAN CARLOS VERGARA SCHMALBACH ESTIMACIÓN PRUEBAS DE HIPÓTESIS Grupo
INFERENCIA ESTADÍSTICA
 INFERENCIA ESTADÍSTICA 1. DEFINICIÓN DE INFERENCIA ESTADÍSTICA Llamamos Inferencia Estadística al proceso de sacar conclusiones generales para toda una población a partir del estudio de una muestra, así
INFERENCIA ESTADÍSTICA 1. DEFINICIÓN DE INFERENCIA ESTADÍSTICA Llamamos Inferencia Estadística al proceso de sacar conclusiones generales para toda una población a partir del estudio de una muestra, así
Estadística II Tema 2. Conceptos básicos en el contraste de. Curso 2010/11
 Estadística II Tema 2. Conceptos básicos en el contraste de hipótesis Curso 2010/11 Tema 2. Conceptos básicos en el contraste de hipótesis Contenidos Definición de contraste e hipótesis estadística. Hipótesis
Estadística II Tema 2. Conceptos básicos en el contraste de hipótesis Curso 2010/11 Tema 2. Conceptos básicos en el contraste de hipótesis Contenidos Definición de contraste e hipótesis estadística. Hipótesis
