TRABAJO PRÁCTICO 3 PROBLEMA TÉRMICO
|
|
|
- Rodrigo Córdoba Rojo
- hace 7 años
- Vistas:
Transcripción
1 INTRODUCCIÓN AL MÉTODO DE LOS ELEMENTOS FINITOS TRABAJO PRÁCTICO 3 PROBLEMA TÉRMICO Estudiante FREDY ANDRÉS MERCADO NAVARRO Pasaporte: Maestría en Simulación Numérica y Control Cuatrimestre: II de Diciembre de 2011 Universidad de Buenos Aires Ciudad Autónoma de Buenos Aires Argentina
2 PROBLEMA 1 El principio de las temperaturas virtuales corresponde a la condición estacionaria del siguiente funcional, propuesto por Bathe et al en la ecuación 7.10 de la referencia [1]: Π= Naturalmente, nuestro problema es bidimensional, por lo cual asumimos que la dimensión en Z es unitaria. Al mismo tiempo, asumimos que la conductividad es igual tanto en X como en Y, y preparamos la ecuación para la introducción de la variación que nos permitirá deducir las ecuaciones que gobiernan nuestro problema: Π= 1 2 Luego, invocando Π=0, se obtiene: + Π= + =0 Ecuación 1 Aplicando las reglas operativas de los operadores diferenciales para el operador variacional, obtenemos: = Realizamos la transformación anterior y reemplazamos en los dos términos de la primera integral en la Ecuación 1. Posteriormente, aplicamos la teoría contenida en el apéndice G de la referencia [2], donde integramos por partes y aplicamos el teorema de Green para transformar una integral sobre un área en una integral de línea sobre el contorno: Primer término, en x: Segundo término, en y: = Ecuación 2 = Ecuación 3 Γ Γ Donde y son las componentes del vector normal a la superficie o línea de contorno en el caso 2D. La suma de la Ecuación 2 y Ecuación 3 resulta: Page 2 of 19
3 + = + Γ + Reemplazamos la expresión anterior en la Ecuación 1: Γ Γ =0 Luego agrupamos los términos con factores y operadores comunes. En este paso también se asume que las conductividades térmicas en x e y, y, son constantes e iguales: + + Γ =0 La variación puede ser arbitraria pero debe ser cero en el contorno esencial (en la superficie, o en este caso, en los bordes). Para cumplir con la ecuación se requiere entonces, que: Equilibrio de calor al interior del cuerpo: Condición de equilibrio en la superficie: Sio: + =0 =0 =, = La expresión siguiente resume la ecuación que gobierna el equilibrio del flujo de calor en el área de nuestro problema. A esta ecuación solo resta aplicarle la discretización para elementos finitos, transformándola a matrices y vectores para ser utilizada en la resolución de nuestro problema isotrópo lineal de conducción bidimensional. = Page 3 of 19
4 PROBLEMA 2 En este problema se calculará la temperatura en los nodos 3 y 4 de la siguiente figura, integrando numéricamente mediante el método de Gauss-Legre utilizando 2 x 2 puntos de integración. Definimos primero las siguientes expresiones: = Para los cálculos numéricos se utilizará la conductividad térmica indicada para el problema 3 (k=440 K.W/m). = =., = 0 0, =det =. Dado que ambos elementos son cuadriláteros con 1 nodo en cada vértice, las funciones de forma para ambos elementos son las mismas. La numeración de los nodos se desarrolló en base a la Ilustración 1:
5 Ilustración 1. Convención para numeración de nodos locales. Para Para = = = = Para = =1 4 1 Para = = = = =1 4 1 = A continuación se desarrolla la ilustración del programa desarrollado para el cálculo numérico de las temperaturas. El programa utilizado para los cálculos es el Matlab. Código Desarrollado Se ilustrará directamente con el código el algoritmo desarrollado para los cálculos: %PARA TODOS LOS ELEMENTOS 1. Definimos una matriz con las conductividades en las direcciones x e y. kx=440; ky=440; k=[kx 0;0 ky]; 2. Definimos un vector con los puntos de Gauss a ser evaluados más adelante. puntogauss=[-1/sqrt(3), 1/sqrt(3)]; %PARA ELEMENTOS 1 Y 2 3. Definimos las coordenadas de los nodos de cada elemento. coord1=[1 1;0 1;0 0;1.5 0] coord2=[2.5 1;1 1;1.5 0;2.5 0] 4. Se define el tamaño de las matrices elementales. Inicialmente, llenas con valores de cero. K1=zeros(4,4); K2=zeros(4,4); Page 5 of 19
6 %CÁLCULO DE MATRICES DE RIGIDEZ ELEMENTALES 5. En los dos ciclos siguientes se llenan las matrices de rigidez elementales, calculando el aporte a la matriz de rigidez elemental a partir de la aplicación de la siguiente ecuación en las coordenadas de cada punto de Gauss: for j=1:2 for i=1:2 r=puntogauss(i); s=puntogauss(j); dh1dr=(1/4)*(1+s); dh1ds=(1/4)*(1+r); dh2dr=-(1/4)*(1+s); dh2ds=(1/4)*(1-r); dh3dr=-(1/4)*(1-s); dh3ds=-(1/4)*(1-r); dh4dr=(1/4)*(1-s); dh4ds=-(1/4)*(1+r); = matrizdhdr=[dh1dr dh2dr dh3dr dh4dr;... dh1ds dh2ds dh3ds dh4ds]; J1=matrizdhdr*coord1; %Op. Jacobiano Elemento 1 J2=matrizdhdr*coord2; %Op. Jacobiano Elemento 2 B1=inv(J1)*matrizdhdr; %Gradiente de H Elemento 1 B2=inv(J2)*matrizdhdr; %Gradiente de H Elemento 2 F1=B1'*k*B1*det(J1); %Aporte por cada evaluación de ri,si a Elem. 1 F2=B2'*k*B2*det(J2); %Aporte por cada evaluación de ri,si a Elem. 2 K1=F1+K1; %Llenado de matriz elemental Elemento 1 K2=F2+K2; %Llenado de matriz elemental Elemento 2 K1 K2 %ENSAMBLE DE MATRIZ DE RIGIDEZ GLOBAL 6. Se define el tamaño de la matriz de rigidez global y se llena de ceros. También se define la matriz de conectividad de acuerdo a la siguiente tabla: Numeración Global Elemento Nodo local Page 6 of 19
7 K=zeros(6,6); cgl=[3 5;1 3;2 4;4 6] %Matriz de conectividad Nodo # Local <-> # Global 7. Con los siguientes ciclos se recorren las matrices de rigidez elementales y sus valores se suman a la matriz de rigidez global. for j=1:4 e=1; for i=1:4 K(cgl(i,e),cgl(j,e))=K(cgl(i,e),cgl(j,e))+K1(i,j); e=2; for i=1:4 K(cgl(i,e),cgl(j,e))=K(cgl(i,e),cgl(j,e))+K2(i,j); K %CONDICIONES DE BORDE 8. Se definen las temperturas a izquierda y derecha del objeto discretizado. Se crea el vector b en el cual se sumarán las evaluaciones de las temperturas conocidas para la ecuación de cada nodo. El vector b1 posee los valores nodales de temperatura conocidos. Tizq=273; Tder=278; b=zeros(6,1); b1=zeros(6,1); %Temperaturas Conocidas en los bordes del objeto b1(1)=273; b1(2)=273; b1(5)=278; b1(6)=278; %Vector Auxiliar para la programación de las CB 9. Se define un vector auxiliar para facilitar la identificación de aquellas filas que pertenecen a valores nodales conocidos. aux=zeros(6,1); aux(1)=1; aux(2)=1; aux(5)=1; aux(6)=1; %Preparación de matriz K y vector b % #1 % Se iguala a 1 el coeficiente de las T conocidas. % Se calculan los K*T conocidos y se pasan al vector b. Page 7 of 19
8 % Se iguala a cero el coeficiente (i,j) tras el cálculo. for j=1:6 if aux(j,1)==1 for i=1:6 if i==j K(i,j)=1; else b(i,1)=-k(i,j)*b1(j,1)+b(i,1); K(i,j)=0; % #2 % Se le imponen las temperturas conocidas al vector b. for i=1:6 if aux(i)==1 b(i)=b1(i); % #3 % Se igualan a cero las filas de temperturas conocidas % a excepción de la diagonal. for i=1:6 if aux(i)==1 for j=1:6 if i~=j K(i,j)=0; aux b K %Cálculo de incógnitas T3 y T4 T=K\b Resultados Los valores de temperatura, en Kelvin, de los nodos globales 3 y 4 corresponden a las filas 3 y 4 del vector T. T = Page 8 of 19
9 PROBLEMA 3 En este problema se calcularán los flujos de calor q de los cuatro puntos de Gauss. El flujo de calor es un vector y se transforma de la misma forma que un desplazamiento. A continuación se desarrolla la formulación matricial para el cálculo de los flujos de calor en cada punto de Gauss. Tenemos que el flujo de calor obedece la ley de Fourier, donde el flujo se produce en la dirección en la cual existe un gradiente de temperaturas: =. T = 0. 0 El gradiente se puede expresar en términos de coordenadas naturales para cada elemento. Así: =. Reemplazando en la ecuación para el flujo de calor tenemos: = La temperatura en cualquier punto dentro del elemento se puede expresar en términos de las funciones de forma y las temperaturas nodales:,= A continuación observamos que podemos calcular una de las matrices como el operador jacobiano inverso. Esto se desarrollará en forma numérica. Hacio uso de la expresión anterior, también expresamos las derivadas respecto a las coordenadas naturales en términos de las derivadas de las funciones de forma y los valores nodales de temperatura. =, =. Reemplazamos en la ecuación para los flujos de calor: Page 9 of 19
10 = A continuación definimos la matriz B: = =. Finalmente, derivamos una expresión matricial para el cálculo de los flujos de calor en los puntos de Gauss, la cual se implementa directamente en el código computacional. Código Desarrollado =.. =.. Las líneas de código siguientes son consecutivas con las líneas de código suministradas en el desarrollo del Problema Se definen dos vectores de temperatura local. %CÁLCULO DE FLUJOS DE CALOR EN PUNTOS DE GAUSS T1=zeros(4,1); T2=zeros(4,1); %Asignación de temperaturas correspondientes a Elementos 1 y 2 2. Se llenan los dos vectores de acuerdo a la numeración otorgada por la matriz de conectividad. for i=1:4 T1(i,1)=T(cgl(i,1)); T2(i,1)=T(cgl(i,2)); T1 T2 % Cálculo de vectores de flujo de calor en X e Y % Se requieren los vectores T1 Y T2. 'FLUJO EN LOS PUNTOS DE GAUSS' 3. En los siguientes ciclos se evalúan las expresiones en los puntos de Gauss. En cada ciclo se calcula el flujo de calor para uno de los puntos. Se utilizan los vectores de temperatura T1 y T2 hallados en el problema 2. for j=1:2 for i=1:2 r=puntogauss(i); s=puntogauss(j); Page 10 of 19
11 dh1dr=(1/4)*(1+s); dh1ds=(1/4)*(1+r); dh2dr=-(1/4)*(1+s); dh2ds=(1/4)*(1-r); dh3dr=-(1/4)*(1-s); dh3ds=-(1/4)*(1-r); dh4dr=(1/4)*(1-s); dh4ds=-(1/4)*(1+r); matrizdhdr=[dh1dr dh2dr dh3dr dh4dr;... dh1ds dh2ds dh3ds dh4ds]; J1=matrizdhdr*coord1; J2=matrizdhdr*coord2; B1=inv(J1)*matrizdhdr; B2=inv(J2)*matrizdhdr; ' ' r s q1=-k*b1*t1 q2=-k*b2*t2 Resultados Los valores del flujo de calor, en Watts, a través de cada nodo es igual para todos los puntos y solo posee componente en la dirección X. Así: = Page 11 of 19
12 %TRABAJO PRÁCTICO 3 - IMEF format compact clear all clc %PARA TODOS LOS ELEMENTOS kx=440; ky=440; k=[kx 0;0 ky]; puntogauss=[-1/sqrt(3), 1/sqrt(3)]; %PARA ELEMENTOS 1 Y 2 coord1=[1 1;0 1;0 0;1.5 0] coord2=[2.5 1;1 1;1.5 0;2.5 0] K1=zeros(4,4); K2=zeros(4,4); ANEXO CÓDIGO COMPLETO PERTENECIENTE A PROBLEMAS 2 Y 3 %CÁLCULO DE MATRICES DE RIGIDEZ ELEMENTALES for j=1:2 for i=1:2 r=puntogauss(i); s=puntogauss(j); dh1dr=(1/4)*(1+s); dh1ds=(1/4)*(1+r); dh2dr=-(1/4)*(1+s); dh2ds=(1/4)*(1-r); dh3dr=-(1/4)*(1-s); dh3ds=-(1/4)*(1-r); dh4dr=(1/4)*(1-s); dh4ds=-(1/4)*(1+r); matrizdhdr=[dh1dr dh2dr dh3dr dh4dr;... dh1ds dh2ds dh3ds dh4ds]; J1=matrizdhdr*coord1; %Op. Jacobiano Elemento 1 J2=matrizdhdr*coord2; %Op. Jacobiano Elemento 2 B1=inv(J1)*matrizdhdr; %Gradiente de H Elemento 1 B2=inv(J2)*matrizdhdr; %Gradiente de H Elemento 2 F1=B1'*k*B1*det(J1); %Aporte por cada evaluación de ri,si a Elem. 1 F2=B2'*k*B2*det(J2); %Aporte por cada evaluación de ri,si a Elem. 2 Page 12 of 19
13 K1=F1+K1; %Llenado de matriz elemental Elemento 1 K2=F2+K2; %Llenado de matriz elemental Elemento 2 K1 K2 %ENSAMBLE DE MATRIZ DE RIGIDEZ GLOBAL K=zeros(6,6); cgl=[3 5;1 3;2 4;4 6] %Matriz de conectividad Nodo # Local <-> # Global for j=1:4 e=1; for i=1:4 K(cgl(i,e),cgl(j,e))=K(cgl(i,e),cgl(j,e))+K1(i,j); e=2; for i=1:4 K(cgl(i,e),cgl(j,e))=K(cgl(i,e),cgl(j,e))+K2(i,j); K %CONDICIONES DE BORDE Tizq=273; Tder=278; b=zeros(6,1); b1=zeros(6,1); %Temperaturas Conocidas en los bordes del objeto b1(1)=273; b1(2)=273; b1(5)=278; b1(6)=278; %Vector Auxiliar para la programación de las CB aux=zeros(6,1); aux(1)=1; aux(2)=1; aux(5)=1; aux(6)=1; %Preparación de matriz K y vector b % #1 % Se iguala a 1 el coeficiente de las T conocidas. % Se calculan los K*T conocidos y se pasan al vector b. % Se iguala a cero el coeficiente (i,j) tras el cálculo. for j=1:6 if aux(j,1)==1 for i=1:6 Page 13 of 19
14 if i==j K(i,j)=1; else b(i,1)=-k(i,j)*b1(j,1)+b(i,1); K(i,j)=0; % #2 % Se le imponen las temperturas conocidas al vector b. for i=1:6 if aux(i)==1 b(i)=b1(i); % #3 % Se igualan a cero las filas de temperturas conocidas % a excepción de la diagonal. for i=1:6 if aux(i)==1 for j=1:6 if i~=j K(i,j)=0; aux b K %Cálculo de incógnitas T3 y T4 T=K\b %CÁLCULO DE FLUJOS DE CALOR EN PUNTOS DE GAUSS T1=zeros(4,1); T2=zeros(4,1); %Asignación de temperaturas correspondientes a Elementos 1 y 2 for i=1:4 T1(i,1)=T(cgl(i,1)); T2(i,1)=T(cgl(i,2)); T1 T2 % Cálculo de vectores de flujo de calor en X e Y % Se requieren los vectores T1 Y T2. Page 14 of 19
15 'FLUJO EN LOS PUNTOS DE GAUSS' for j=1:2 for i=1:2 r=puntogauss(i); s=puntogauss(j); dh1dr=(1/4)*(1+s); dh1ds=(1/4)*(1+r); dh2dr=-(1/4)*(1+s); dh2ds=(1/4)*(1-r); dh3dr=-(1/4)*(1-s); dh3ds=-(1/4)*(1-r); dh4dr=(1/4)*(1-s); dh4ds=-(1/4)*(1+r); matrizdhdr=[dh1dr dh2dr dh3dr dh4dr;... dh1ds dh2ds dh3ds dh4ds]; J1=matrizdhdr*coord1; J2=matrizdhdr*coord2; B1=inv(J1)*matrizdhdr; B2=inv(J2)*matrizdhdr; ' ' r s q1=-k*b1*t1 q2=-k*b2*t2 SALIDA DEL CÓDIGO PARA PROBLEMAS 2 Y 3 coord1 = coord2 = K1 = Page 15 of 19
16 K2 = cgl = K = aux = b = 1.0e+005 * K = T = Page 16 of 19
17 T1 = T2 = ans = FLUJO EN LOS PUNTOS DE GAUSS ans = r = s = q1 = q2 = ans = r = s = q1 = q2 = ans = r = s = q1 = Page 17 of 19
18 q2 = ans = r = s = q1 = q2 = >> Page 18 of 19
19 REFERENCIAS BIBLIOGRÁFICAS 1. BATHE, Klaus-Jurgen. Finite Element Procedures. Prentice-Hall PP ZIENKIEWICS, O.C. TAYLOR, R.L. The Finite Element Method. Volume I: The Basis. Fifth Edition Page 19 of 19
TRABAJO PRÁCTICO 4 PROBLEMA DE ELASTICIDAD LINEAL
 INTRODUCCIÓN AL MÉTODO DE LOS ELEMENTOS FINITOS TRABAJO PRÁCTICO 4 PROBLEMA DE ELASTICIDAD LINEAL Estudiante FREDY ANDRÉS MERCADO NAVARRO Pasaporte: 98 773.532 Maestría en Simulación Numérica y Control
INTRODUCCIÓN AL MÉTODO DE LOS ELEMENTOS FINITOS TRABAJO PRÁCTICO 4 PROBLEMA DE ELASTICIDAD LINEAL Estudiante FREDY ANDRÉS MERCADO NAVARRO Pasaporte: 98 773.532 Maestría en Simulación Numérica y Control
TRABAJO PRÁCTICO 6 PROBLEMA DE CONVECCIÓN-DIFUSIÓN
 INTRODUCCIÓN AL MÉTODO DE LOS ELEMENTOS FINITOS TRABAJO PRÁCTICO 6 PROBLEMA DE CONVECCIÓN-DIFUSIÓN Estudiante FREDY ANDRÉS MERCADO NAVARRO Pasaporte: 98 773.53 Maestría en Simulación Numérica y Control
INTRODUCCIÓN AL MÉTODO DE LOS ELEMENTOS FINITOS TRABAJO PRÁCTICO 6 PROBLEMA DE CONVECCIÓN-DIFUSIÓN Estudiante FREDY ANDRÉS MERCADO NAVARRO Pasaporte: 98 773.53 Maestría en Simulación Numérica y Control
67.58 INTRODUCCIÓN AL MÉTODO DE LOS ELEMENTOS FINITOS
 67.58 INTRODUCCIÓN AL MÉTODO DE LOS ELEMENTOS FINITOS TRABAJO PRÁCTICO 7 (ESPECIAL) SIMULACIÓN NUMÉRICA DE LA DISTRIBUCIÓN DE TEMPERATURAS EN UN INTERCAMBIADOR DE CALOR Estudiante FREDY ANDRÉS MERCADO
67.58 INTRODUCCIÓN AL MÉTODO DE LOS ELEMENTOS FINITOS TRABAJO PRÁCTICO 7 (ESPECIAL) SIMULACIÓN NUMÉRICA DE LA DISTRIBUCIÓN DE TEMPERATURAS EN UN INTERCAMBIADOR DE CALOR Estudiante FREDY ANDRÉS MERCADO
TRABAJO PRÁCTICO 5 (CORREGIDO) PROBLEMA TÉRMICO TRANSITORIO UNIDIMENSIONAL
 INTRODUCCIÓN AL MÉTODO DE LOS ELEMENTOS FINITOS TRABAJO PRÁCTICO 5 (CORREGIDO) PROBLEMA TÉRMICO TRANSITORIO UNIDIMENSIONAL Estudiante FREDY ANDRÉS MERCADO NAVARRO Pasaporte: 98 773.532 Maestría en Simulación
INTRODUCCIÓN AL MÉTODO DE LOS ELEMENTOS FINITOS TRABAJO PRÁCTICO 5 (CORREGIDO) PROBLEMA TÉRMICO TRANSITORIO UNIDIMENSIONAL Estudiante FREDY ANDRÉS MERCADO NAVARRO Pasaporte: 98 773.532 Maestría en Simulación
FEM para Mecánica 3D. Miguel Ángel Otaduy. Animación Avanzada 7 de Marzo de 2014
 FEM para Mecánica 3D Miguel Ángel Otaduy Animación Avanzada 7 de Marzo de 2014 Índice Repaso Hoy Funciones de forma Formulación fuerte formulación débil Matriz de rigidez Ec. de elasticidad en 3D Deformación
FEM para Mecánica 3D Miguel Ángel Otaduy Animación Avanzada 7 de Marzo de 2014 Índice Repaso Hoy Funciones de forma Formulación fuerte formulación débil Matriz de rigidez Ec. de elasticidad en 3D Deformación
Interp r o p la l c a ió i n seccio i nal a l (S ( pl p i l n i e) Val a o l re r s pr p e r scri r t i os N (x)
 Introducción al método de los elementos finitos Métodos Numéricos 2 Laboratori de Càlcul Numèric (LaCàN) Dep. de Matemàtica Aplicada III Universitat Politècnica de Catalunya www-lacan.upc.es Ventajas del
Introducción al método de los elementos finitos Métodos Numéricos 2 Laboratori de Càlcul Numèric (LaCàN) Dep. de Matemàtica Aplicada III Universitat Politècnica de Catalunya www-lacan.upc.es Ventajas del
4. Método del elemento finito (formulación de desplazamientos)
 4 Método del elemento finito (formulación de desplazamientos) 41 Introducción El método del elemento finito es un método numérico que permite encontrar soluciones aproximadas a problemas físicos gobernados
4 Método del elemento finito (formulación de desplazamientos) 41 Introducción El método del elemento finito es un método numérico que permite encontrar soluciones aproximadas a problemas físicos gobernados
MN - Métodos Numéricos
 Unidad responsable: 295 - EEBE - Escuela de Ingeniería de Barcelona Este Unidad que imparte: 737 - RMEE - Departamento de Resistencia de Materiales y Estructuras en la Ingeniería Curso: Titulación: 2018
Unidad responsable: 295 - EEBE - Escuela de Ingeniería de Barcelona Este Unidad que imparte: 737 - RMEE - Departamento de Resistencia de Materiales y Estructuras en la Ingeniería Curso: Titulación: 2018
MÉTODO DE LOS ELEMENTOS FINITOS.
 de MÉTODO DE LOS ELEMENTOS FINITOS. Castillo Madrid, 23 de Noviembre de 26 Índice de 2 3 4 de de El de los Elementos Finitos (M.E.F.) es un procedimiento numérico para resolver ecuaciones diferenciales
de MÉTODO DE LOS ELEMENTOS FINITOS. Castillo Madrid, 23 de Noviembre de 26 Índice de 2 3 4 de de El de los Elementos Finitos (M.E.F.) es un procedimiento numérico para resolver ecuaciones diferenciales
dx = x El tensor x/ X se denomina tensor gradiente de la deformación F = x
 Capítulo 2 Cinemática El desarrollo de las expresiones contenidas en este capítulo se lleva a cabo en un sistema de referencia general cartesiano {I 1 I 2 I 3 }. La notación es, con algunas diferencias,
Capítulo 2 Cinemática El desarrollo de las expresiones contenidas en este capítulo se lleva a cabo en un sistema de referencia general cartesiano {I 1 I 2 I 3 }. La notación es, con algunas diferencias,
Métodos de elemento finito Formulación n de elemento finito en 2 dimensiones
 Métodos de elemento finito 7.4.. Método de Galerkin 7.4.. Formulación n de elemento finito en dimensiones Los métodos m de elemento finito (MEF) son una estrategia numérica alternativa muy popular para
Métodos de elemento finito 7.4.. Método de Galerkin 7.4.. Formulación n de elemento finito en dimensiones Los métodos m de elemento finito (MEF) son una estrategia numérica alternativa muy popular para
1. ANALISIS DE UN RESERVORIO CIRCULAR MEDIANTE FEM
 . ANALISIS DE UN RESERVORIO CIRCULAR MEDIANTE FEM Analizar la pared de un reservorio circular de radio interior m, espesor de la pared.m, altura de la pared desde la losa de fondo m. Considerar solamente
. ANALISIS DE UN RESERVORIO CIRCULAR MEDIANTE FEM Analizar la pared de un reservorio circular de radio interior m, espesor de la pared.m, altura de la pared desde la losa de fondo m. Considerar solamente
ASIGNATURA: EL MÉTODO DE LOS ELEMENTOS FINITOS EN INGENIERÍA. Código: Titulación: INGENIERO INDUSTRIAL Curso: 4
 ASIGNATURA: EL MÉTODO DE LOS ELEMENTOS FINITOS EN INGENIERÍA Código: 141214001 Titulación: INGENIERO INDUSTRIAL Curso: 4 Profesor(es) responsable(s): PEDRO JESÚS MARTÍNEZ CASTEJÓN Departamento: ESTRUCTURAS
ASIGNATURA: EL MÉTODO DE LOS ELEMENTOS FINITOS EN INGENIERÍA Código: 141214001 Titulación: INGENIERO INDUSTRIAL Curso: 4 Profesor(es) responsable(s): PEDRO JESÚS MARTÍNEZ CASTEJÓN Departamento: ESTRUCTURAS
Matemáticas 2ºBachillerato Aplicadas a las Ciencias Sociales. Un sistema de ecuaciones lineales es un conjunto de ecuaciones lineales de la forma:
 Matemáticas 2ºBachillerato Aplicadas a las Ciencias Sociales 1era evaluación. Sistemas de Ecuaciones Lineales 1) SISTEMAS DE ECUACIONES LINEALES Un sistema de ecuaciones lineales es un conjunto de ecuaciones
Matemáticas 2ºBachillerato Aplicadas a las Ciencias Sociales 1era evaluación. Sistemas de Ecuaciones Lineales 1) SISTEMAS DE ECUACIONES LINEALES Un sistema de ecuaciones lineales es un conjunto de ecuaciones
ME Capítulo 2 Introducción al Análisis por Elementos Finitos. Alejandro Ortiz Bernardin. Universidad de Chile
 Diseño de Elementos Mecánicos ME-5600 Capítulo 2 Introducción al Análisis por Elementos Finitos Alejandro Ortiz Bernardin www.cec.uchile.cl/~aortizb Departamento de Ingeniería Mecánica Universidad de Chile
Diseño de Elementos Mecánicos ME-5600 Capítulo 2 Introducción al Análisis por Elementos Finitos Alejandro Ortiz Bernardin www.cec.uchile.cl/~aortizb Departamento de Ingeniería Mecánica Universidad de Chile
Capítulo V. Introducción al análisis por el método de elemento finito
 Capítulo V Introducción al análisis por el método de elemento finito El método de elemento finito es una técnica para resolver ecuaciones diferenciales parciales, primero, discretando las ecuaciones al
Capítulo V Introducción al análisis por el método de elemento finito El método de elemento finito es una técnica para resolver ecuaciones diferenciales parciales, primero, discretando las ecuaciones al
Solución de ecuaciones diferenciales por el método de elementos finitos
 Solución de ecuaciones diferenciales por el método de elementos finitos Departamento de Matemáticas Método de elemento finito Un problema del método de diferencias finitas es que al aplicarlo obtenemos
Solución de ecuaciones diferenciales por el método de elementos finitos Departamento de Matemáticas Método de elemento finito Un problema del método de diferencias finitas es que al aplicarlo obtenemos
CMAM - Aplicaciones de Mecánica Computacional
 Unidad responsable: Unidad que imparte: Curso: Titulación: Créditos ECTS: 2016 295 - EEBE - Escuela de Ingeniería de Barcelona Este 737 - RMEE - Departamento de Resistencia de Materiales y Estructuras
Unidad responsable: Unidad que imparte: Curso: Titulación: Créditos ECTS: 2016 295 - EEBE - Escuela de Ingeniería de Barcelona Este 737 - RMEE - Departamento de Resistencia de Materiales y Estructuras
Formulación del problema de la ruta más corta en programación lineal
 Formulación del problema de la ruta más corta en programación lineal En esta sección se describen dos formulaciones de programación lineal para el problema de la ruta más corta. Las formulaciones son generales,
Formulación del problema de la ruta más corta en programación lineal En esta sección se describen dos formulaciones de programación lineal para el problema de la ruta más corta. Las formulaciones son generales,
08 Losas delgadas Teoría de Kirchhoff. Diego Andrés Alvarez Marín Profesor Asistente Universidad Nacional de Colombia Sede Manizales
 08 Losas delgadas Teoría de Kirchhoff Diego Andrés Alvarez Marín Profesor Asistente Universidad Nacional de Colombia Sede Manizales 1 Introducción Elementos laminares delgados Losas o placas (son elementos
08 Losas delgadas Teoría de Kirchhoff Diego Andrés Alvarez Marín Profesor Asistente Universidad Nacional de Colombia Sede Manizales 1 Introducción Elementos laminares delgados Losas o placas (son elementos
MNEM - Métodos Numéricos en la Ingeniería Mecánica
 Unidad responsable: Unidad que imparte: Curso: Titulación: Créditos ECTS: 2016 295 - EEBE - Escuela de Ingeniería de Barcelona Este 737 - RMEE - Departamento de Resistencia de Materiales y Estructuras
Unidad responsable: Unidad que imparte: Curso: Titulación: Créditos ECTS: 2016 295 - EEBE - Escuela de Ingeniería de Barcelona Este 737 - RMEE - Departamento de Resistencia de Materiales y Estructuras
Una forma fácil de recordar esta suma (regla de Sarrus): Primero vamos a estudiar algunas propiedades de los determinantes.
 Una forma fácil de recordar esta suma (regla de Sarrus): Ejemplos: Tarea: realizar al menos tres ejercicios de cálculo de determinantes de matrices de 2x2 y otros tres de 3x3. PARA DETERMINANTES DE MATRICES
Una forma fácil de recordar esta suma (regla de Sarrus): Ejemplos: Tarea: realizar al menos tres ejercicios de cálculo de determinantes de matrices de 2x2 y otros tres de 3x3. PARA DETERMINANTES DE MATRICES
08 Losas delgadas Teoría de Kirchhoff. Diego Andrés Alvarez Marín Profesor Asistente Universidad Nacional de Colombia Sede Manizales
 08 Losas delgadas Teoría de Kirchhoff Diego Andrés Alvarez Marín Profesor Asistente Universidad Nacional de Colombia Sede Manizales 1 Introducción Elementos laminares delgados Losas o placas (son elementos
08 Losas delgadas Teoría de Kirchhoff Diego Andrés Alvarez Marín Profesor Asistente Universidad Nacional de Colombia Sede Manizales 1 Introducción Elementos laminares delgados Losas o placas (son elementos
Tema 12: Ecuaciones diferenciales de primer orden Métodos elementales de integración. Teoremas de existencia y unicidad. Aplicaciones.
 Álgebra Tema 1: Fundamentos Lógica matemática. Teoría de conjuntos. Tema 2: Combinatoria Combinatoria. Conjuntos parcialmente ordenados. Tema 3: Sistemas de ecuaciones lineales Eliminación gaussiana. Sistemas
Álgebra Tema 1: Fundamentos Lógica matemática. Teoría de conjuntos. Tema 2: Combinatoria Combinatoria. Conjuntos parcialmente ordenados. Tema 3: Sistemas de ecuaciones lineales Eliminación gaussiana. Sistemas
Elementos de Cálculo Numérico
 Universidad de Buenos Aires - Facultad de Ciencias Exactas y Naturales - Depto. de Matemática Elementos de Cálculo Numérico Primer cuatrimestre 2006 Práctica N 2: Condicionamiento de una matriz. Descomposición
Universidad de Buenos Aires - Facultad de Ciencias Exactas y Naturales - Depto. de Matemática Elementos de Cálculo Numérico Primer cuatrimestre 2006 Práctica N 2: Condicionamiento de una matriz. Descomposición
TEORIA MATEMATICAS 5 PRIMER PARCIAL
 Def: Grafica de una función TEORIA MATEMATICAS 5 PRIMER PARCIAL Sea:. Definimos la grafica de f como el subconjunto de formado por los puntos, de en los que es un punto de U. Simbólicamente grafica es:
Def: Grafica de una función TEORIA MATEMATICAS 5 PRIMER PARCIAL Sea:. Definimos la grafica de f como el subconjunto de formado por los puntos, de en los que es un punto de U. Simbólicamente grafica es:
APLICACIONES COMPUTACIONALES
 APLICACIONES COMPUTACIONALES INGENIERÍA EJECUCIÓN MECÁNICA ECUACIONES DIFERENCIALES PARCIALES (EDP) MOTIVACIÓN Una ecuación que tiene derivadas parciales de una función desconocida, de dos o más variables
APLICACIONES COMPUTACIONALES INGENIERÍA EJECUCIÓN MECÁNICA ECUACIONES DIFERENCIALES PARCIALES (EDP) MOTIVACIÓN Una ecuación que tiene derivadas parciales de una función desconocida, de dos o más variables
UNIVERSIDAD NACIONAL DE INGENIERÍA FACULTAD DE INGENIERÍA MECÁNICA DEPARTAMENTO ACADÉMICO DE CIENCIAS DE INGENIERÍA SILABO
 UNIVERSIDAD NACIONAL DE INGENIERÍA FACULTAD DE INGENIERÍA MECÁNICA DEPARTAMENTO ACADÉMICO DE CIENCIAS DE INGENIERÍA SILABO CÁLCULO POR ELEMENTOS FINITOS (MC-516) 2010-II UNIVERSIDAD NACIONAL DE INGENIERÍA
UNIVERSIDAD NACIONAL DE INGENIERÍA FACULTAD DE INGENIERÍA MECÁNICA DEPARTAMENTO ACADÉMICO DE CIENCIAS DE INGENIERÍA SILABO CÁLCULO POR ELEMENTOS FINITOS (MC-516) 2010-II UNIVERSIDAD NACIONAL DE INGENIERÍA
Clase 8 Matrices Álgebra Lineal
 Clase 8 Matrices Álgebra Lineal Código Escuela de Matemáticas - Facultad de Ciencias Universidad Nacional de Colombia Matrices Definición Una matriz es un arreglo rectangular de números denominados entradas
Clase 8 Matrices Álgebra Lineal Código Escuela de Matemáticas - Facultad de Ciencias Universidad Nacional de Colombia Matrices Definición Una matriz es un arreglo rectangular de números denominados entradas
Matemáticas de la Especialidad de Ingeniería Mecánica
 Matemáticas de la Especialidad de Ingeniería Mecánica Módulo 1: Introducción Plan 2010: Programa curso 2013 14 Clase 01 Introducción a la asignatura. Introducción a Matlab. Clases 02, 03 Primer ejemplo
Matemáticas de la Especialidad de Ingeniería Mecánica Módulo 1: Introducción Plan 2010: Programa curso 2013 14 Clase 01 Introducción a la asignatura. Introducción a Matlab. Clases 02, 03 Primer ejemplo
ETAPAS BÁSICAS DEL ANÁLISIS MATRICIAL DE UN SISTEMA DISCRETO. Mercedes López Salinas
 ETAPAS BÁSICAS DEL ANÁLISIS MATRICIAL DE UN SISTEMA DISCRETO Mercedes López Salinas PhD. Ing. Civil [email protected] ELEMENTOS FINITOS Facultad de Ciencia y Tecnología Escuela de Ingeniería Civil y
ETAPAS BÁSICAS DEL ANÁLISIS MATRICIAL DE UN SISTEMA DISCRETO Mercedes López Salinas PhD. Ing. Civil [email protected] ELEMENTOS FINITOS Facultad de Ciencia y Tecnología Escuela de Ingeniería Civil y
MÉTODO MATRICIAL PARA EL ANÁLISIS DE ARMADURAS PLANAS Y ESPACIALES. Gabriel Santiago Silva Vega
 MÉTODO MATRICIAL PARA EL ANÁLISIS DE ARMADURAS PLANAS Y ESPACIALES Gabriel Santiago Silva Vega Objetivo Propuesta de un procedimiento alternativo para el análisis y diseño de armaduras Implementación computacional
MÉTODO MATRICIAL PARA EL ANÁLISIS DE ARMADURAS PLANAS Y ESPACIALES Gabriel Santiago Silva Vega Objetivo Propuesta de un procedimiento alternativo para el análisis y diseño de armaduras Implementación computacional
05 Problemas de elasticidad bidimensional. Diego Andrés Alvarez Marín Profesor Asistente Universidad Nacional de Colombia Sede Manizales
 05 Problemas de elasticidad bidimensional Diego Andrés Alvarez Marín Profesor Asistente Universidad Nacional de Colombia Sede Manizales 1 Convención para los esfuerzos positivos 2 Deformaciones 3 Ley de
05 Problemas de elasticidad bidimensional Diego Andrés Alvarez Marín Profesor Asistente Universidad Nacional de Colombia Sede Manizales 1 Convención para los esfuerzos positivos 2 Deformaciones 3 Ley de
MÉTODO DE LAS FUERZAS.
 UNIVERSIDAD DE CARABOBO FACULTAD DE INGENIERÍA ESCUELA DE INGENIERÍA CIVIL DEPARTAMENTO DE INGENIERIA ESTRUCTURAL INTRODUCCIÓN AL ANÁLISIS ESTRUCTURAL MÉTODO DE LAS FUERZAS. APUNTES DE CLASE Y EJERCICIOS
UNIVERSIDAD DE CARABOBO FACULTAD DE INGENIERÍA ESCUELA DE INGENIERÍA CIVIL DEPARTAMENTO DE INGENIERIA ESTRUCTURAL INTRODUCCIÓN AL ANÁLISIS ESTRUCTURAL MÉTODO DE LAS FUERZAS. APUNTES DE CLASE Y EJERCICIOS
CONCEPTOS BÁSICOS DEL ANÁLISIS MATRICIAL DE ESTRUCTURAS DE BARRA. Mercedes López Salinas
 CONCEPTOS BÁSICOS DEL ANÁLISIS MATRICIAL DE ESTRUCTURAS DE BARRA Mercedes López Salinas PhD. Ing. Civil [email protected] ELEMENTOS FINITOS Facultad de Ciencia y Tecnología Escuela de Ingeniería Civil
CONCEPTOS BÁSICOS DEL ANÁLISIS MATRICIAL DE ESTRUCTURAS DE BARRA Mercedes López Salinas PhD. Ing. Civil [email protected] ELEMENTOS FINITOS Facultad de Ciencia y Tecnología Escuela de Ingeniería Civil
CONTENIDOS MATEMÁTICAS II SEGUNDA EVALUACIÓN CURSO 2017/2018 MATRICES
 CONTENIDOS MATEMÁTICAS II SEGUNDA EVALUACIÓN CURSO 2017/2018 Unidades: - Matrices (Bloque Álgebra) - Determinantes (Bloque Álgebra) - Sistemas de ecuaciones lineales (Bloque Álgebra) - Vectores (Bloque
CONTENIDOS MATEMÁTICAS II SEGUNDA EVALUACIÓN CURSO 2017/2018 Unidades: - Matrices (Bloque Álgebra) - Determinantes (Bloque Álgebra) - Sistemas de ecuaciones lineales (Bloque Álgebra) - Vectores (Bloque
RESOLUCIÓN DE SISTEMAS LINEALES
 Contenido 1 Métodos de Solución Contenido Métodos de Solución 1 Métodos de Solución Desarrollamos el algoritmo de sustitución regresiva, con el que podremos resolver un sistema de ecuaciones lineales cuya
Contenido 1 Métodos de Solución Contenido Métodos de Solución 1 Métodos de Solución Desarrollamos el algoritmo de sustitución regresiva, con el que podremos resolver un sistema de ecuaciones lineales cuya
Método del elemento finito Código ( )
 Código (8084283) Por : Euro CASANOVA Departamento de Mecánica, USB Ofc.: MEU-317B Tel: 906-4091 / 906-4056 email: [email protected] web: http://prof.usb.ve/ecasanov 1 Datos del curso Horario: Miércoles 17H
Código (8084283) Por : Euro CASANOVA Departamento de Mecánica, USB Ofc.: MEU-317B Tel: 906-4091 / 906-4056 email: [email protected] web: http://prof.usb.ve/ecasanov 1 Datos del curso Horario: Miércoles 17H
08 Losas delgadas Teoría de Kirchhoff. Diego Andrés Alvarez Marín Profesor Asociado Universidad Nacional de Colombia Sede Manizales
 08 Losas delgadas Teoría de Kirchhoff Diego Andrés Alvarez Marín Profesor Asociado Universidad Nacional de Colombia Sede Manizales 1 Introducción Elementos laminares delgados Losas o placas (son elementos
08 Losas delgadas Teoría de Kirchhoff Diego Andrés Alvarez Marín Profesor Asociado Universidad Nacional de Colombia Sede Manizales 1 Introducción Elementos laminares delgados Losas o placas (son elementos
Capítulo 3 El Método de los Elementos de Contorno y la Formulación Hipersingular.
 Capítulo 3 El Método de los Elementos de Contorno y la Formulación Hipersingular. 3.1. Introducción El Método de los Elementos de Contorno (MEC) se ha implantado firmemente en numerosos campos de la ingeniería
Capítulo 3 El Método de los Elementos de Contorno y la Formulación Hipersingular. 3.1. Introducción El Método de los Elementos de Contorno (MEC) se ha implantado firmemente en numerosos campos de la ingeniería
05 Problemas de elasticidad bidimensional. Diego Andrés Alvarez Marín Profesor Asistente Universidad Nacional de Colombia Sede Manizales
 05 Problemas de elasticidad bidimensional Diego Andrés Alvarez Marín Profesor Asistente Universidad Nacional de Colombia Sede Manizales 1 Convención para los esfuerzos positivos 2 Deformaciones 3 Ley de
05 Problemas de elasticidad bidimensional Diego Andrés Alvarez Marín Profesor Asistente Universidad Nacional de Colombia Sede Manizales 1 Convención para los esfuerzos positivos 2 Deformaciones 3 Ley de
I.PROGRAMA DE ESTUDIOS. Unidad 1. Conceptos básicos de la teoría de las estructuras
 I.PROGRAMA DE ESTUDIOS Unidad 1 Conceptos básicos de la teoría de las estructuras 1.1.Equilibrio 1.2.Relación fuerza desplazamiento 1.3.Compatibilidad 1.4.Principio de superposición 1.5.Enfoque de solución
I.PROGRAMA DE ESTUDIOS Unidad 1 Conceptos básicos de la teoría de las estructuras 1.1.Equilibrio 1.2.Relación fuerza desplazamiento 1.3.Compatibilidad 1.4.Principio de superposición 1.5.Enfoque de solución
Tema 1. Espacios Vectoriales. Sistemas de ecuaciones.
 Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada Fortes)
Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada Fortes)
Determinantes. Determinante de orden uno. a 11 = a 11 5 = 5
 DETERMINANTES Determinantes Concepto de determinante A cada matriz cuadrada A se le asigna un escalar particular denominado determinante de A, denotado por A o por det (A). A = Determinante de orden uno
DETERMINANTES Determinantes Concepto de determinante A cada matriz cuadrada A se le asigna un escalar particular denominado determinante de A, denotado por A o por det (A). A = Determinante de orden uno
1 ÁLGEBRA DE MATRICES
 1 ÁLGEBRA DE MATRICES 1.1 DEFINICIONES Las matrices son tablas numéricas rectangulares. Se dice que una matriz es de dimensión m n si tiene m filas y n columnas. Cada elemento de una matriz se designa
1 ÁLGEBRA DE MATRICES 1.1 DEFINICIONES Las matrices son tablas numéricas rectangulares. Se dice que una matriz es de dimensión m n si tiene m filas y n columnas. Cada elemento de una matriz se designa
Capítulo 7. Subterráneo
 Capítulo 7 Solución n Numérica de la Ecuación n de Flujo Subterráneo Teoría a de Flujo Subterráneo Semestre 2008-1 Alberto Rosas Medina 1 Índice Polinomios de Lagrange Diferencias Finitas en una Dimensión
Capítulo 7 Solución n Numérica de la Ecuación n de Flujo Subterráneo Teoría a de Flujo Subterráneo Semestre 2008-1 Alberto Rosas Medina 1 Índice Polinomios de Lagrange Diferencias Finitas en una Dimensión
2. ANÁLISIS DEL TECHO DE UN AUDITORIO MEDIANTE FEM
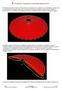 . ANÁLISIS DEL TECHO DE UN AUDITORIO MEDIANTE FEM El Objetivo es analizar el techo en forma de cono con abertura de un auditorio circular de diámetro igual a m, la altura total del cono sería.m, pero a
. ANÁLISIS DEL TECHO DE UN AUDITORIO MEDIANTE FEM El Objetivo es analizar el techo en forma de cono con abertura de un auditorio circular de diámetro igual a m, la altura total del cono sería.m, pero a
Solución de la ecuación de Stokes
 REVISTA Solución de la ecuación de Stokes Doctora en Ciencias Matemáticas, Resumen Palabras clave Método de los elementos Elementos cuadriláteros Solution of the Stokes equation using the quadrilateral
REVISTA Solución de la ecuación de Stokes Doctora en Ciencias Matemáticas, Resumen Palabras clave Método de los elementos Elementos cuadriláteros Solution of the Stokes equation using the quadrilateral
Relaciones esfuerzo deformación
 Capítulo Relaciones esfuerzo deformación En esta sección se emplea la primera ley de la termodinámica para derivar la relación esfuerzo deformación..1. Relaciones constitutivas Se llama modelo constitutivo
Capítulo Relaciones esfuerzo deformación En esta sección se emplea la primera ley de la termodinámica para derivar la relación esfuerzo deformación..1. Relaciones constitutivas Se llama modelo constitutivo
Capítulo V. Valores y vectores propios. Diagonalización de operadores lineales.
 Capítulo V Valores y vectores propios. Diagonalización de operadores lineales. Hemos visto que la aplicaciones lineales de en están definidas a través de una expresión de la forma ; pero esta fórmula puede
Capítulo V Valores y vectores propios. Diagonalización de operadores lineales. Hemos visto que la aplicaciones lineales de en están definidas a través de una expresión de la forma ; pero esta fórmula puede
Simulación Numérica de Yacimientos
 Simulación Numérica de Yacimientos Dr. Fernando Rodríguez de la Garza e-mail: [email protected] Tel: 5550872, 5622 307 al 9 Capítulo 4. Simulación Numérica de Flujo Multifásico Unidimensional 4.
Simulación Numérica de Yacimientos Dr. Fernando Rodríguez de la Garza e-mail: [email protected] Tel: 5550872, 5622 307 al 9 Capítulo 4. Simulación Numérica de Flujo Multifásico Unidimensional 4.
Índice. Programación de las unidades. Unidad 1 Matrices 6. Unidad 2 Determinantes 8. Unidad 3 Sistemas de ecuaciones lineales 10
 Índice Programación de las unidades Unidad 1 Matrices 6 Unidad 2 Determinantes 8 Unidad 3 Sistemas de ecuaciones lineales 10 Unidad 4 Geometría en el espacio 12 Unidad 5 Producto escalar 14 Unidad 6 Productos
Índice Programación de las unidades Unidad 1 Matrices 6 Unidad 2 Determinantes 8 Unidad 3 Sistemas de ecuaciones lineales 10 Unidad 4 Geometría en el espacio 12 Unidad 5 Producto escalar 14 Unidad 6 Productos
Curso de Elemento Finito con el software ALGOR
 Curso de Elemento Finito con el software ALGOR Facultad de Ingeniería, UNAM www.algor.com M. en I. Alejandro Farah Instituto de Astronomía, UNAM www.astroscu.unam.mx/~farah Contenido general: - La teoría
Curso de Elemento Finito con el software ALGOR Facultad de Ingeniería, UNAM www.algor.com M. en I. Alejandro Farah Instituto de Astronomía, UNAM www.astroscu.unam.mx/~farah Contenido general: - La teoría
MC-5122 Método del elemento finito
 MC-5122 Método del elemento finito Por : Euro CASANOVA Departamento de Mecánica, USB Ofc.: MEU-317B Tel: 96-491 / 96-456 email: [email protected] web: http://prof.usb.ve/ecasanov 1 Datos del curso Horario:
MC-5122 Método del elemento finito Por : Euro CASANOVA Departamento de Mecánica, USB Ofc.: MEU-317B Tel: 96-491 / 96-456 email: [email protected] web: http://prof.usb.ve/ecasanov 1 Datos del curso Horario:
1. Para la función f(x) = x sen x, halle su polinomio de Taylor de orden 2 en a = 0. x x3 3!, x x3
 Cálculo I (Grado en Ingeniería Informática) Problemas resueltos, - y -4 (tercera parte) Preparado por los profesores de la asignatura: Pablo Fernández, Dragan Vukotić (coordinadores), Luis Guijarro, Kazaros
Cálculo I (Grado en Ingeniería Informática) Problemas resueltos, - y -4 (tercera parte) Preparado por los profesores de la asignatura: Pablo Fernández, Dragan Vukotić (coordinadores), Luis Guijarro, Kazaros
Integración numérica MAT 1105 F EJERCICIOS RESUELTOS. 1. Obtenga: a) Integrando por el método del trapecio. Se utilizan las siguientes formulas:
 MAT 1105 F Integración numérica EJERCICIOS RESUELTOS 1 1. Obtenga: a) Integrando por el método del trapecio. Se utilizan las siguientes formulas: Donde: 4 2 Ecuación lineal Luego, Área del trapecio -1-1
MAT 1105 F Integración numérica EJERCICIOS RESUELTOS 1 1. Obtenga: a) Integrando por el método del trapecio. Se utilizan las siguientes formulas: Donde: 4 2 Ecuación lineal Luego, Área del trapecio -1-1
Aquí veremos la armadura de cuatro barras del ejemplo 4.1 pero con carga diferente. Considere E=29.5E6psi y α=1/ por ºF.
 Ejemplo 4. (Página ) Introducción al estudio del Elemento Finito en Ingeniería Segunda Edición TITUPATHI R. CHANDRUPATLA ASHOK D. BELEGUNDU PRENTICE HALL Aquí veremos la armadura de cuatro barras del ejemplo
Ejemplo 4. (Página ) Introducción al estudio del Elemento Finito en Ingeniería Segunda Edición TITUPATHI R. CHANDRUPATLA ASHOK D. BELEGUNDU PRENTICE HALL Aquí veremos la armadura de cuatro barras del ejemplo
Tema 1: Matrices. El concepto de matriz alcanza múltiples aplicaciones tanto en la representación y manipulación de datos como en el cálculo numérico.
 Tema 1: Matrices El concepto de matriz alcanza múltiples aplicaciones tanto en la representación y manipulación de datos como en el cálculo numérico. 1. Terminología Comenzamos con la definición de matriz
Tema 1: Matrices El concepto de matriz alcanza múltiples aplicaciones tanto en la representación y manipulación de datos como en el cálculo numérico. 1. Terminología Comenzamos con la definición de matriz
O.C. Zienkiewicz, R.L. Taylor. El Método de los Elementos Finitos. Vols 1 y 2. CIMNE-Mc Graw Hill, 1994.
 Índice de la teoría 1. Presentación. Estas lecciones sólo pretenden ser una introducción que sirva para orientar sobre los conceptos, para un estudio más amplio se recomienda leer alguna publicación especializada,
Índice de la teoría 1. Presentación. Estas lecciones sólo pretenden ser una introducción que sirva para orientar sobre los conceptos, para un estudio más amplio se recomienda leer alguna publicación especializada,
Tema 1. Espacios Vectoriales. Sistemas de ecuaciones.
 Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada Fortes)
Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada Fortes)
SISTEMAS DE ECUACIONES
 1 SISTEMAS DE ECUACIONES OBJETIVO: RESOLVER SISTEMAS DE ECUACIONES LINEALES UTILIZANDO DIVERSOS MÉTODOS DE SOLUCIÓN CONTENIDO: Representación matricial de un sistema de ecuaciones. Transformaciones elementales.
1 SISTEMAS DE ECUACIONES OBJETIVO: RESOLVER SISTEMAS DE ECUACIONES LINEALES UTILIZANDO DIVERSOS MÉTODOS DE SOLUCIÓN CONTENIDO: Representación matricial de un sistema de ecuaciones. Transformaciones elementales.
Álgebra y Geometría Analítica 4-Sistemas de ecuaciones lineales. Resumen
 Álgebra y Geometría Analítica 4-Sistemas de ecuaciones lineales Docente: Ernesto Aljinovic Resumen Sistema de n ecuaciones lineales con m incógnitas (Sistema de n m) Forma matricial del sistema Matriz
Álgebra y Geometría Analítica 4-Sistemas de ecuaciones lineales Docente: Ernesto Aljinovic Resumen Sistema de n ecuaciones lineales con m incógnitas (Sistema de n m) Forma matricial del sistema Matriz
Método de diferencias finitas para ecuaciones diferenciales parciales elípticas. (Parte I)
 Método de diferencias finitas para ecuaciones diferenciales parciales elípticas (Parte I) Contenido Ecuaciones en derivadas parciales Ecuaciones en derivadas parciales elípticas Ecuación de Laplace Aproximación
Método de diferencias finitas para ecuaciones diferenciales parciales elípticas (Parte I) Contenido Ecuaciones en derivadas parciales Ecuaciones en derivadas parciales elípticas Ecuación de Laplace Aproximación
02 Elementos finitos para tensión/ compresión axial. Diego Andrés Alvarez Marín Profesor Asistente Universidad Nacional de Colombia Sede Manizales
 02 Elementos finitos para tensión/ compresión axial Diego Andrés Alvarez Marín Profesor Asistente Universidad Nacional de Colombia Sede Manizales 1 El método de los elementos finitos El método de los elementos
02 Elementos finitos para tensión/ compresión axial Diego Andrés Alvarez Marín Profesor Asistente Universidad Nacional de Colombia Sede Manizales 1 El método de los elementos finitos El método de los elementos
Algebra lineal y conjuntos convexos
 Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Módulo 6 Simulación Formulación Implementación MEF v Prof. Dr. José L Oliver
 7. Elementos Cuadrilátero de CUATRO NODOS para el Problema de la Tensión Plana. 7.1. Cuadriláteros de Cuatro Nodos para Tensión Plana Carlos A. Felippa. En esta sección seguiremos observando cómo funciona
7. Elementos Cuadrilátero de CUATRO NODOS para el Problema de la Tensión Plana. 7.1. Cuadriláteros de Cuatro Nodos para Tensión Plana Carlos A. Felippa. En esta sección seguiremos observando cómo funciona
Sistema de ecuaciones lineales
 1 El sistema de ecuaciones lineales Sistema de ecuaciones lineales puede ser escrito en forma matricial como, donde: es llamada matriz de los coeficientes (reales) del sistema es el vector de las incógnitas
1 El sistema de ecuaciones lineales Sistema de ecuaciones lineales puede ser escrito en forma matricial como, donde: es llamada matriz de los coeficientes (reales) del sistema es el vector de las incógnitas
de la forma ), i =1,..., m, j =1,..., n, o simplemente por (a i j ).
 INTRODUCCIÓN. MATRICES Y DETERMINANTES Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de las derivadas parciales.
INTRODUCCIÓN. MATRICES Y DETERMINANTES Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de las derivadas parciales.
Matrices y Sistemas Lineales
 Matrices y Sistemas Lineales Álvarez S, Caballero MV y Sánchez M a M salvarez@umes, mvictori@umes, marvega@umes 1 ÍNDICE Matemáticas Cero Índice 1 Definiciones 3 11 Matrices 3 12 Sistemas lineales 5 2
Matrices y Sistemas Lineales Álvarez S, Caballero MV y Sánchez M a M salvarez@umes, mvictori@umes, marvega@umes 1 ÍNDICE Matemáticas Cero Índice 1 Definiciones 3 11 Matrices 3 12 Sistemas lineales 5 2
PROPUESTA A. 3A. a) Despeja X en la ecuación matricial X A B = 2X donde A, B y X son matrices cuadradas
 PROPUESTA A 1A a) Calcula el valor de a R, a > 0, para que la función sea continua en x = 0. b) Calcula el límite 2A. Calcula las siguientes integrales (1 25 puntos por cada integral) Observación: El cambio
PROPUESTA A 1A a) Calcula el valor de a R, a > 0, para que la función sea continua en x = 0. b) Calcula el límite 2A. Calcula las siguientes integrales (1 25 puntos por cada integral) Observación: El cambio
Tema 2. Sistemas de ecuaciones lineales
 Tema 2 Sistemas de ecuaciones lineales Ecuaciones lineales ( x,, x n ) Una ecuación lineal tiene variables 1 término independiente (b) y coeficientes (reales o complejos) a a x a x a x b 1 1 2 2 n n,,
Tema 2 Sistemas de ecuaciones lineales Ecuaciones lineales ( x,, x n ) Una ecuación lineal tiene variables 1 término independiente (b) y coeficientes (reales o complejos) a a x a x a x b 1 1 2 2 n n,,
Una matriz es un arreglo rectangular de números. Los números en el arreglo se llaman elementos de la matriz. ) ( + ( ) ( )
 MATRICES Una matriz es un arreglo rectangular de números. Los números en el arreglo se llaman elementos de la matriz. Ejemplo 1. Algunos ejemplos de matrices ( + ( ) ( + ( ) El tamaño o el orden de una
MATRICES Una matriz es un arreglo rectangular de números. Los números en el arreglo se llaman elementos de la matriz. Ejemplo 1. Algunos ejemplos de matrices ( + ( ) ( + ( ) El tamaño o el orden de una
Mecánica de las Estructuras II
 Mecánica de las Estructuras II Página 1 de 5 Programa de: UNIVERSIDAD NACIONAL DE CÓRDOBA Facultad de Ciencias Exactas, Físicas y Naturales República Argentina Carrera: Ingeniería Civil Escuela: Ingeniería
Mecánica de las Estructuras II Página 1 de 5 Programa de: UNIVERSIDAD NACIONAL DE CÓRDOBA Facultad de Ciencias Exactas, Físicas y Naturales República Argentina Carrera: Ingeniería Civil Escuela: Ingeniería
Elementos de Cálculo Numérico (M) - Cálculo Numérico
 Universidad de Buenos Aires - Facultad de Ciencias Exactas y Naturales - Depto. de Matemática Elementos de Cálculo Numérico (M) - Cálculo Numérico Primer Cuatrimestre 204 Práctica N 2: Normas y Condicionamiento.
Universidad de Buenos Aires - Facultad de Ciencias Exactas y Naturales - Depto. de Matemática Elementos de Cálculo Numérico (M) - Cálculo Numérico Primer Cuatrimestre 204 Práctica N 2: Normas y Condicionamiento.
4 MÉTODOS DIRECTOS PARA RESOLVER SISTEMAS DE ECUACIONES LINEALES
 57 4 MÉTODOS DIRECTOS PARA RESOLVER SISTEMAS DE ECUACIONES LINEALES En este capítulo se estudia el componente algorítmico y computacional de los métodos directos para resolver sistemas de ecuaciones lineales.
57 4 MÉTODOS DIRECTOS PARA RESOLVER SISTEMAS DE ECUACIONES LINEALES En este capítulo se estudia el componente algorítmico y computacional de los métodos directos para resolver sistemas de ecuaciones lineales.
Matrices y Sistemas de Ecuaciones lineales
 Matrices y Sistemas de Ecuaciones lineales Llamaremos M m n (K) al conjunto de las matrices A = (a ij ) (i = 1, 2,..., m; j = 1, 2,..., n) donde los elementos a ij pertenecen a un cuerpo K. Las matrices,
Matrices y Sistemas de Ecuaciones lineales Llamaremos M m n (K) al conjunto de las matrices A = (a ij ) (i = 1, 2,..., m; j = 1, 2,..., n) donde los elementos a ij pertenecen a un cuerpo K. Las matrices,
Matrices: repaso. Denotaremos con M m n el conjunto de matrices de tamaño m n, o sea, de m filas y n columnas. Una matriz A M m n es de la forma A =
 Matrices: repaso Denotaremos con M m n el conjunto de matrices de tamaño m n, o sea, de m filas y n columnas Una matriz A M m n es de la forma a 11 a 1n A = a m1 a mn Denotaremos A ij = a ij el coeficiente
Matrices: repaso Denotaremos con M m n el conjunto de matrices de tamaño m n, o sea, de m filas y n columnas Una matriz A M m n es de la forma a 11 a 1n A = a m1 a mn Denotaremos A ij = a ij el coeficiente
Resumen 3: Matrices, determinantes y sistemas de ecuaciones
 Resumen 3: Matrices, determinantes y sistemas de ecuaciones lineales 1 Matrices Una matriz con coeficientes sobre un cuerpo K (normalmente K R) consiste en una colección de números (o escalares) del cuerpo
Resumen 3: Matrices, determinantes y sistemas de ecuaciones lineales 1 Matrices Una matriz con coeficientes sobre un cuerpo K (normalmente K R) consiste en una colección de números (o escalares) del cuerpo
UNIVERSIDAD CENTRAL DE VENEZUELA FACULTAD DE INGENIERÍA ESCUELA DE INGENIERÍA CIVIL DEPARTAMENTO DE INGENIERÍA ESTRUCTURAL
 TIPO DE 122 11, 117 FUNDAMENTACIÓN El programa de la asignatura pretende vincular al estudiante con las técnicas básicas utilizadas en el desarrollo de sistemas computacionales en el área de Ingeniería
TIPO DE 122 11, 117 FUNDAMENTACIÓN El programa de la asignatura pretende vincular al estudiante con las técnicas básicas utilizadas en el desarrollo de sistemas computacionales en el área de Ingeniería
Matrices y Sistemas Lineales
 Matrices y Sistemas Lineales Álvarez S, Caballero MV y Sánchez M a M salvarez@umes, mvictori@umes, marvega@umes Índice 1 Definiciones 3 11 Matrices 3 12 Sistemas lineales 6 2 Herramientas 8 21 Operaciones
Matrices y Sistemas Lineales Álvarez S, Caballero MV y Sánchez M a M salvarez@umes, mvictori@umes, marvega@umes Índice 1 Definiciones 3 11 Matrices 3 12 Sistemas lineales 6 2 Herramientas 8 21 Operaciones
