El espacio n. Consideremos el conjunto de todas las n adas ordenadas de números reales, denotado por n :
|
|
|
- Agustín Henríquez Benítez
- hace 5 años
- Vistas:
Transcripción
1 El espacio n Consideremos el conjunto de todas las n adas ordenadas de números reales, denotado por n : n = {(x 1,x 2,, x n ) / x 1,x 2,, x n } A cada uno de los números reales x 1,x 2,, x n que conforman la n ada (x 1,x 2,, x n ) n, se le llama componente o cooordenada de la n-ada correspondiente. Al elemento x i, de la n ada (x 1,x 2,, x n ), lo denominaremos la i - ésima coordenada de (x 1,x 2,, x n ), donde i = 1, 2,..., n. Ejemplos: = no es más que el conjunto de los números reales 2 = {(x,y) / x, y } 3 = {(x,y,z) / x, y, z } 1 1 Igualdad en n Dos n-adas de n, se dicen ser iguales, cuando todos y cada una de sus coordenadas son iguales, es decir: (x 1,x 2,, x n ) = (y 1,y 2,, y n ) x 1 = y 1, x 2 = y 2,..., x n = y n 2
2 OPERACIONES EN n Las operaciones que definiremos en n son: a. Suma de n-adas ordenadas Si (x 1, x 2,, x n ), (y 1, y 2,, y n ), son dos elementos de n, definimos la suma, denotada por (x 1, x 2,, x n ) + (y 1, y 2,, y n ), como: (x 1, x 2,, x n ) + (y 1, y 2,, y n ) = (x 1 + y 1, x 2 + y 2,, x n + y n ) b. Producto de una n-ada ordenada por un escalar El producto de una n-ada (x 1, x 2,, x n ) n por el escalar c, denotado por c(x 1, x 2,, x n ), se define por: c(x 1, x 2,, x n ) = ( c x 1, c x 2,, c x n ) 3 PROPIEDADES 1. La suma es conmutativa, es decir (x 1, x 2,, x n ) + (y 1, y 2,, y n ) =(y 1, y 2,, y n ) + (x 1, x 2,, x n ) 2. La suma es asociativa, es decir (x 1, x 2,, x n ) + [ (y 1, y 2,, y n ) +(z 1, z 2,, z n )] =[(x 1, x 2,, x n ) + (y 1, y 2,, y n )] +(z 1, z 2,, z n ) 3. Existe un elemento en n, llamado cero 0 =(0,0,...,0), que actua de manera neutro para la suma: (x 1, x 2,, x n ) + (0,0,, 0) = (x 1, x 2,, x n ) 4. Cada n-ada de n tiene un inverso aditivo, el cual es un elemento de n que tiene la propiedad de que, sumado con la n-ada original, produce el cero de n. El inverso aditivo de (x 1, x 2,, x n ), es (- x 1, -x 2,,- x n ), pues: (x 1, x 2,, x n ) + (- x 1, -x 2,,- x n ) = (0,0,, 0) 4
3 5. Si es un escalar, se tiene que: [ (x 1, x 2,, x n ) + (y 1, y 2,, y n ) ] = (x 1, x 2,, x n ) + (y 1, y 2,, y n ) 6. Si, son escalares, se tiene que: ( + ) (x 1, x 2,, x n ) = (x 1, x 2,, x n ) + (x 1, x 2,, x n ) 7. Si, son escalares, se tiene que: ( ) (x 1, x 2,, x n ) = [ (x 1, x 2,, x n )] = [ (x 1, x 2,, x n ) ] 8. 1(x 1, x 2,, x n ) = (x 1, x 2,, x n ) 5 SISTEMA CARTESIANO EN EL ESPACIO (0,0,c) (0,b,c) (a,0,c) (0,b,0) (a,0,0) (a,b,0) 6
4 NORMA Y DISTANCIA La norma euclideana de un vector x n denotada por x, se define como: x = 2 x+x+...+x 1 2 n La distancia entre los vectores x, y n, denotada por d(x,y), se define como: d(x,y) = x- y Ejemplos: Calcular la distancia entre los puntos: i) P(-3) y Q(5.5) ii) P(-3, 2) y Q(1,1.5) iii) P(1.5,-1,1) y Q(0,0,3) 7 BOLAS ABIERTAS Sea x 0 n y r > 0. La bola abierta de centro en x 0 y radio r, denotada por B(x 0,r), es el conjunto de puntos de n que distan de x 0 en menos de r, es decir: B(x 0,r) = { x n / x- x 0 < r } : B(X o,r) 2 : B(X o,r) 3 : B(X o,r) y 0 z 0 x 0 y 0 x 0 8
5 CONJUNTO ABIERTOS Se dice que el conjunto U n es un conjunto abierto en n, si para cada x 0 U existe un r > 0 tal que B(x 0,r) U. CONJUNTOS CERRADOS Se dice que el conjunto U n es cerrado, si el complemento de U es un conjunto abierto en n. Ejemplos Indicar si el conjunto es abierto ó cerrado en: i) A = < 7, > ii) A = [-3, 6 ] iii) A = [-5, 6 > iv) A = {(x,y) 2 / x>1, y>0 } v) A ={(x,y) 2 / x 0, y 0 } 9 FUNCIONES DE VARIAS VARIABLES La explicación ó descripción del mundo real y social han planteado, la necesidad de considerar funciones de más de una sola variable. Por ejemplo, considere la temperatura T en un punto de la superficie de la tierra depende en todo momento de la longitud x y la latitud y del punto. Podemos pensar en T como una función de dos variables x e y ó como una función del par (x,y). Esta dependencia funcional lo representaremos por T= f(x,y). Una función f de n variables f: D n, es una regla que asigna a cada elemento (x 1, x 2,, x n ) de D un único número real f(x 1, x 2,, x n ). Al conjunto D se conoce como dominio de f. A menudo escribimos z = f(x 1, x 2,, x n ) para hacer explícito el valor que toma f en el punto general (x 1, x 2,, x n ). Las variables x 1, x 2,, x n son las variables independientes y z es la variable dependiente. 10
6 El rango de f, denotado por Rg(f), es el conjunto de valores que toma f, es decir: Rg(f) ={ f(x 1, x 2,, x n )/ (x 1, x 2,, x n ) D} Ejemplo: Determinar el dominio, rango de la función f(x,y) = 4 x y Sea f: D n, una función con dominio D. La gráfica de f, es el conjunto: G(f) = { (x 1, x 2,, x n, z)/ z = f(x 1, x 2,, x n ), (x 1, x 2,, x n ) D)} (x,y,z) (x,y) 11 Observación: i) Si f: D, su gráfica se encuentra en 2 ii) Si f: D 2, su gráfica se encuentra en 3 Ejemplo: Obtener la gráfica de la función f, definida por: f(x,y) = 4 12
7 CONJUNTO DE NIVEL Sea f: D n, una función y k. Entonces el conjunto de nivel de valor k, se define como: { x D/ f(x, y) = k } n Si: n = 2, el conjunto de nivel será una curva de nivel (de valor k) Si: n = 3, el conjunto de nivel será una superficie de nivel (de valor k) NOTA. Las curvas de nivel se usan frecuentemente en la elaboración de mapas hidrográficos, meteorológicos, etc. 13 Ejemplo: Determine las curvas de nivel de: z = x 2 + y
8 OPERACIONES CON FUNCIONES DE VARIAS VARIABLES Sean f, g: D n, funciones de n variables con dominios Df y Dg f, respectivamente, entonces f + g, f - g, f. g, f / g, se definen como: i) (f + g )(x) = f(x) + g(x), D f+g = D f D g ii) iii) (f - g )(x) = f(x) - g(x), D f-g = D f D g (f. g )(x) = f(x) g(x), D f.g = D f D g Ejercicio. Determinar el dominio de la función: f(x,y) = 15 LÍMITE DE UNA FUNCIÓN DE VARIAS VARIABLES y Lámina de metal Temperatura (a, b) (x, y) L f(x, y) x 0 Si la temperatura f(x,y) se acerca a un valor fijo L, cuando (x,y) se aproxima cada vez más a un punto fijo (a,b), entonces esto se denotará como: lim (x,y) (a,b) f(x,y) = L y puede leerse: el límite de f(x,y) cuando (x,y) tiende a (a,b) es L 16
9 17 Ejercicio 1. Analizar si xy lim =0 x y (x,y) (0,0) Ejercicio 2. Analizar si 3 4 xy lim =0 4 4 x y (x,y) (0,0) 7x y Ejercicio 3. Analizar si lim =0 (x,y) (0,0) 2x y 18
10 CALCULO DE LIMITES MEDIANTE OPERACIONES ALGEBRAICAS Ejemplo: Calcular los siguientes límites: 1. lim x y (x,y) (1,5) x 2 2. lim x y (x,y) (0,0) x y 3 4 ( x 1)( y 16) 4. lim x y 3. lim (x,y) (1,2) ( 2 1)( 4) (x,y) (0,0) x x y y TEOREMA DEL ENCAJE Dadas las funciones f, h, g tal que f(x) h(x) g(x), x D n., Si lim f(x)= lim g(x),entonces, x x x x 0 0 lim h(x)= lim f(x)= lim g(x) x x0 x x0 x x0 TEOREMA DE LA ACOTACIÓN Si f es una función tal que lim f(x)=0 x x 0 ; g(x) una función acotada (es decir existe una constante k>0 de modo que: -k g(x) k ), entonces, lim f(x)g(x)=0 x x 0 Este teorema nos indica que si una función tiene límite cero en un punto, y otra función está acotada en los alrededores del punto, entonces, su producto también tiene límite cero en dicho punto. 20
11 Ejemplo: Calcular: i) lim (x + y )cos ii) (x,y) (0,0) xy (x,y) (0,0) 1 3 x lim x +y 21 PUNTO DE ACUMULACIÓN Se dice que p 0 es un punto de acumulación de un conjunto D n, si toda bola abierta reducida B (p0,r):= B(p 0,r) { p 0 } contiene infinitos puntos de D, es decir: B (p 0,r) D. Ejemplo Analizar si el punto (0,0) es un punto de acumulación de S= {(x,y) 2 / x > 0, y > 0} REGLA DE LA TRAYECTORIA Sea S 1 y S 2 limf(x) limf(x) x p x p x S x S2 conjuntos de n que tienen al punto p 0 como un punto de acumulación. Si entonces, lim f(x) x p 0, no existe. 22
12 Ejemplo. Calcular: i), x y si existe. ii) x y lim lim (, xy) (0,0) 2 x y ( xy, ) (2,2) x 3xy iii) lim (, xyz,) (0,0,0) x yx z x 4 x y z 4 3 si existe 23 CONTINUIDAD DE FUNCIONES DE VARIAS VARIABLES Sea f es una función de n variables y sea p un punto en n Se dice que f es continua en el punto p si se cumplen la tres condiciones: i) f (p) esta definida ii) lim f(x) x p existe iii) lim f(x) = f(p) x p Sea f una función de n variables, definida en el conjunto abierto D de n. Se dice que f es continua en el conjunto D (o simplemente que f es continua) si f es continua en cada uno de los puntos x o D. 24
13 Propiedad Sean f, g: D n funciones definidas en el conjunto abierto D de n. Si f y g son funciones continua en el punto x o, entonces 1. la función f+ g: D n, (f + g)(x)= f(x)+g(x), es continua en x o 2. la función fg: D n, (f g)(x)= f(x) g(x), es continua en x o 3. la función f/ g: D n, (f /g)(x)= f(x) /g(x), es continua en x o, siempre que g(x o ) 0 Nota. Cualquier función polinómica f: n es continua en n. Ejemplo: Analizar si la función f(x,y,z)= su dominio x xy y x y, es continua en todo 25 Ejercicios En cada caso, analizar si f es continua en (0,0), si i) x y x y si x y f( x, y) 0, si( x, y) (0,0) 2 ( )/( ), (, ) (0,0) ii) xy x y si x y f( x, y) 0, si( x, y) (0,0) /( ), (, ) (0,0) iii) x y x y si x y f( x, y) 0, si( x, y) (0,0) ( )/( ), (, ) (0,0) 26
14 Propiedad Si f: D n es un función continua xo y g es una función continua en f(xo), entonces, la función compuesta definida por (gof)(x)=g(f(x)) es continua en xo, es decir: lim g( f( x)) g(lim( f( x)) x x x x 0 0 Ejemplo. Analizar si f(x,y)=sen(x 2 -y 2 ) es continua en todo su dominio. 27
El espacio n Consideremos el conjunto de todas las n adas ordenadas de números reales, denotado por n : 8. 1(x 1, x 2,, x n ) = (x 1, x 2,, x n )
 El espacio n Consideremos el conjunto de todas las n adas ordenadas de números reales, denotado por n : n = {(x 1,x,, x n ) / x 1,x,, x n } A cada uno de los números reales x 1,x,, x n que conforman la
El espacio n Consideremos el conjunto de todas las n adas ordenadas de números reales, denotado por n : n = {(x 1,x,, x n ) / x 1,x,, x n } A cada uno de los números reales x 1,x,, x n que conforman la
Sea f: D n, una función con dominio D. La gráfica de f, es el conjunto: G(f) = { (x 1, x 2,, x n, z)/ z = f(x 1, x 2,, x n ), (x 1, x 2,, x n ) D)}
 FUNCIONES DE VARIAS VARIABLES La eplicación ó descripción del mundo real y social han planteado, la necesidad de considerar funciones de más de una sola variable. Por ejemplo, considere la temperatura
FUNCIONES DE VARIAS VARIABLES La eplicación ó descripción del mundo real y social han planteado, la necesidad de considerar funciones de más de una sola variable. Por ejemplo, considere la temperatura
FUNCIONES DE VARIAS VARIABLES
 CAPITULO III CALCULO II FUNCIONES DE VARIAS VARIABLES 3.1 DEFINICIÓN Se denomina función de varias variables a la función que tiene n variables independientes y m variables dependientes. Una función de
CAPITULO III CALCULO II FUNCIONES DE VARIAS VARIABLES 3.1 DEFINICIÓN Se denomina función de varias variables a la función que tiene n variables independientes y m variables dependientes. Una función de
Funciones Reales de Varias Variables
 Funciones Reales de Varias Variables Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica II Hermes Pantoja Carhuavilca 1 de 54 CONTENIDO Funciones
Funciones Reales de Varias Variables Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica II Hermes Pantoja Carhuavilca 1 de 54 CONTENIDO Funciones
Continuidad de funciones reales y vectoriales de variable vectorial
 Capítulo 6 Continuidad de funciones reales y vectoriales de variable vectorial 6.1. Introducción Hasta el momento hemos estudiado funciones reales de variable real, es decir, funciones de la forma f :
Capítulo 6 Continuidad de funciones reales y vectoriales de variable vectorial 6.1. Introducción Hasta el momento hemos estudiado funciones reales de variable real, es decir, funciones de la forma f :
Funciones de varias variables. Continuidad
 Capítulo 1 Funciones de varias variables. Continuidad 1. Topología en R n Definición (Norma, espacio vectorial normado). Una norma sobre R n es una aplicación: : R n [0,+ [ x x, que satisface las siguientes
Capítulo 1 Funciones de varias variables. Continuidad 1. Topología en R n Definición (Norma, espacio vectorial normado). Una norma sobre R n es una aplicación: : R n [0,+ [ x x, que satisface las siguientes
TEORÍA DE CÁLCULO II PARA GRADOS DE INGENIERÍA Elaborada por Domingo Pestana y José Manuel Rodríguez 1. CÁLCULO DIFERENCIAL EN VARIAS VARIABLES
 TEORÍA DE CÁLCULO II PARA GRADOS DE INGENIERÍA Elaborada por Domingo Pestana y José Manuel Rodríguez 1 CÁLCULO DIFERENCIAL EN VARIAS VARIABLES 11 CONCEPTOS BÁSICOS Definición La norma de un vector x =
TEORÍA DE CÁLCULO II PARA GRADOS DE INGENIERÍA Elaborada por Domingo Pestana y José Manuel Rodríguez 1 CÁLCULO DIFERENCIAL EN VARIAS VARIABLES 11 CONCEPTOS BÁSICOS Definición La norma de un vector x =
Funciones Reales de Varias Variables
 Funciones Reales de Varias Variables Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica II Hermes Pantoja Carhuavilca 1 de 162 CONTENIDO Funciones
Funciones Reales de Varias Variables Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica II Hermes Pantoja Carhuavilca 1 de 162 CONTENIDO Funciones
2. Cálculo diferencial de funciones de varias variables. Mayo, 2009
 Cálculo 2. Cálculo diferencial de funciones de varias variables Mayo, 2009 Definición IR 2 = {(x 1,x 2 )/x 1 IR,x 2 IR} Sean dos puntos a y b, de coordenadas respectivas (a 1,a 2 ) y (b 1,b 2 ). Definición
Cálculo 2. Cálculo diferencial de funciones de varias variables Mayo, 2009 Definición IR 2 = {(x 1,x 2 )/x 1 IR,x 2 IR} Sean dos puntos a y b, de coordenadas respectivas (a 1,a 2 ) y (b 1,b 2 ). Definición
TEMA 3: CONTINUIDAD DE FUNCIONES
 TEMA 3: CONTINUIDAD DE FUNCIONES. Valor Absoluto Trabajaremos en el campo de los números reales, R. Para el estudio de las propiedades de las funciones necesitamos el concepto de valor absoluto de un número
TEMA 3: CONTINUIDAD DE FUNCIONES. Valor Absoluto Trabajaremos en el campo de los números reales, R. Para el estudio de las propiedades de las funciones necesitamos el concepto de valor absoluto de un número
TEORÍA DE CÁLCULO I. Para Grados en Ingeniería. Capítulo 1: Funciones de una variable real. Domingo Pestana Galván José Manuel Rodríguez García
 TEORÍA DE CÁLCULO I Para Grados en Ingeniería Capítulo 1: Funciones de una variable real Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez 1 CAPÍTULO 1.
TEORÍA DE CÁLCULO I Para Grados en Ingeniería Capítulo 1: Funciones de una variable real Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez 1 CAPÍTULO 1.
INSTITUTO SUPERIOR TECNOLÓGICO NORBERT WIENER
 INSTITUTO SUPERIOR TECNOLÓGICO NORBERT WIENER ASIGNATURA: Matemática Aplicada II PROGRAMA: S3C LIMA-PERU 2 MANUAL DE MATEMATICA APLICADA II INDICE.- SECCION 1 : MATRICES Ejercicios 1 SECCION 2 : OPERACIONES
INSTITUTO SUPERIOR TECNOLÓGICO NORBERT WIENER ASIGNATURA: Matemática Aplicada II PROGRAMA: S3C LIMA-PERU 2 MANUAL DE MATEMATICA APLICADA II INDICE.- SECCION 1 : MATRICES Ejercicios 1 SECCION 2 : OPERACIONES
En lo que resta de esta unidad se considera una región o dominio (ver Apéndice )
 1 Derivadas Parciales (Parte 1) FUNCIONES DE VARIAS VARIABLES Hasta ahora nos hemos preocupado del Cálculo Diferencial e Integral de funciones de una variable, sin embargo, en el mundo real las cantidades
1 Derivadas Parciales (Parte 1) FUNCIONES DE VARIAS VARIABLES Hasta ahora nos hemos preocupado del Cálculo Diferencial e Integral de funciones de una variable, sin embargo, en el mundo real las cantidades
Números reales Conceptos básicos Algunas propiedades
 Números reales Conceptos básicos Algunas propiedades En álgebra es esencial manejar símbolos con objeto de transformar o reducir expresiones algebraicas y resolver ecuaciones algebraicas. Debido a que
Números reales Conceptos básicos Algunas propiedades En álgebra es esencial manejar símbolos con objeto de transformar o reducir expresiones algebraicas y resolver ecuaciones algebraicas. Debido a que
son dos elementos de Rⁿ, definimos su suma, denotada por
 1.1 Definición de un vector en R², R³ y su Interpretación geométrica. 1.2 Introducción a los campos escalares y vectoriales. 1.3 La geometría de las operaciones vectoriales. 1.4 Operaciones con vectores
1.1 Definición de un vector en R², R³ y su Interpretación geométrica. 1.2 Introducción a los campos escalares y vectoriales. 1.3 La geometría de las operaciones vectoriales. 1.4 Operaciones con vectores
Parte I. FUNCIONES. LÍMITES Y CONTINUIDAD. ACOTACIÓN
 Parte I. FUNCIONES. LÍMITES Y CONTINUIDAD. ACOTACIÓN I.1. DEFINICIONES. Una función real de variable real (f: Domf R Recf R) es una relación que a cada elemento x de un subconjunto de R (Domf) le asigna
Parte I. FUNCIONES. LÍMITES Y CONTINUIDAD. ACOTACIÓN I.1. DEFINICIONES. Una función real de variable real (f: Domf R Recf R) es una relación que a cada elemento x de un subconjunto de R (Domf) le asigna
Una operación interna: Suma Una operación externa: Multiplicación por un escalar
 El conjunto R n Es el conjunto de las n-adas formadas por el producto cartesiano RRR.R, donde R es el conjunto de los números reales. Así pues, dos elementos X y Y de R n serán iguales si y solo si tienen
El conjunto R n Es el conjunto de las n-adas formadas por el producto cartesiano RRR.R, donde R es el conjunto de los números reales. Así pues, dos elementos X y Y de R n serán iguales si y solo si tienen
Objetivos. Conjuntos numéricos. Funciones reales de una variable real. Límites de funciones. Continuidad de funciones. Derivabilidad.
 TEMA 1 Objetivos. Conjuntos numéricos. Funciones reales de una variable real. Límites de funciones. Continuidad de funciones. Derivabilidad. Propiedades de las funciones derivables. Polinomio de Taylor.
TEMA 1 Objetivos. Conjuntos numéricos. Funciones reales de una variable real. Límites de funciones. Continuidad de funciones. Derivabilidad. Propiedades de las funciones derivables. Polinomio de Taylor.
Capítulo 3. Limites y continuidad
 Capítulo 3. Limites y continuidad Objetivo: El alumno calculará el límite de una función real de variable real y analizará la continuidad de la misma. Contenido: 3.1 Concepto de límite de una función en
Capítulo 3. Limites y continuidad Objetivo: El alumno calculará el límite de una función real de variable real y analizará la continuidad de la misma. Contenido: 3.1 Concepto de límite de una función en
CÁLCULO III. Pablo Torres. Funciones definidas en R n. Facultad de Ciencias Exactas, Ingeniería y Agrimensura - Universidad Nacional de Rosario
 CÁLCULO III Pablo Torres Facultad de Ciencias Exactas, Ingeniería y Agrimensura - Universidad Nacional de Rosario Funciones definidas en R n. INTRODUCCIÓN Sean n,m N y A R n. Una función f : A R m se denomina
CÁLCULO III Pablo Torres Facultad de Ciencias Exactas, Ingeniería y Agrimensura - Universidad Nacional de Rosario Funciones definidas en R n. INTRODUCCIÓN Sean n,m N y A R n. Una función f : A R m se denomina
NOCIONES PRELIMINARES (*) 1
 CONJUNTOS NOCIONES PRELIMINARES (*) 1 Conjunto no es un término definible, pero da idea de una reunión de cosas ( elementos ) que tienen algo en común. En matemática los conjuntos se designan con letras
CONJUNTOS NOCIONES PRELIMINARES (*) 1 Conjunto no es un término definible, pero da idea de una reunión de cosas ( elementos ) que tienen algo en común. En matemática los conjuntos se designan con letras
520142: ALGEBRA y ALGEBRA LINEAL
 520142: ALGEBRA y ALGEBRA LINEAL Segundo Semestre 2008, Universidad de Concepción CAPITULO 10: Espacios Vectoriales DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas 1 Definición
520142: ALGEBRA y ALGEBRA LINEAL Segundo Semestre 2008, Universidad de Concepción CAPITULO 10: Espacios Vectoriales DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas 1 Definición
Funciones elementales
 Tema Funciones elementales.1. Función real de variable real Una función real de variable real es cualquier aplicación f : D R! R. Se dice que el conjunto D es el dominio de f. El rango de f es el conjunto
Tema Funciones elementales.1. Función real de variable real Una función real de variable real es cualquier aplicación f : D R! R. Se dice que el conjunto D es el dominio de f. El rango de f es el conjunto
Tema X: LÍMITES Y CONTINUIDAD DE FUNCIONES X.2. Límites. Tema X: LÍMITES Y CONTINUIDAD DE FUNCIONES X.2. Límites
 Tema X: LÍMITES Y CONTINUIDAD DE FUNCIONES X.2. Límites 1. Definición de límite DEF. Sea f : A R R y a A Se dice que l R es el límite de f cuando x tiende a a, si para todo entorno de l, existe un entorno
Tema X: LÍMITES Y CONTINUIDAD DE FUNCIONES X.2. Límites 1. Definición de límite DEF. Sea f : A R R y a A Se dice que l R es el límite de f cuando x tiende a a, si para todo entorno de l, existe un entorno
Función de dos variables
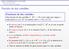 Funciones escalares de dos variables Función de dos variables Funciones de dos variables Una función de dos variables F : R 2 R es una regla que asigna a cada punto (x, y) R 2 un número real z = F (x,
Funciones escalares de dos variables Función de dos variables Funciones de dos variables Una función de dos variables F : R 2 R es una regla que asigna a cada punto (x, y) R 2 un número real z = F (x,
Álgebra y Trigonometría
 Álgebra y Trigonometría Conceptos fundamentales del Álgebra Universidad de Antioquia Departamento de Matemáticas 1. Números Reales El conjunto de los números reales está constituido por diferentes clases
Álgebra y Trigonometría Conceptos fundamentales del Álgebra Universidad de Antioquia Departamento de Matemáticas 1. Números Reales El conjunto de los números reales está constituido por diferentes clases
ESTRUCTURAS ALGEBRAICAS. Parte 1
 ESTRUCTURAS ALGEBRAICAS Parte 1 ESTRUCTURAS ALGEBRAICAS Una estructura algebraica es una n-tupla (a 1,a 2,...,a n ), donde a 1 es un conjunto dado no vacío, y {a 2,...,a n } un conjunto de operaciones
ESTRUCTURAS ALGEBRAICAS Parte 1 ESTRUCTURAS ALGEBRAICAS Una estructura algebraica es una n-tupla (a 1,a 2,...,a n ), donde a 1 es un conjunto dado no vacío, y {a 2,...,a n } un conjunto de operaciones
8. FUNCIONES DE VARIAS VARIABLES.
 8. FUNCIONES DE VARIAS VARIABLES. En este tema comenzamos el análisis de funciones de varias variables reales. Comenzaremos estudiando el espacio euclídeo n-dimensional para continuar el estudio (sencillo)
8. FUNCIONES DE VARIAS VARIABLES. En este tema comenzamos el análisis de funciones de varias variables reales. Comenzaremos estudiando el espacio euclídeo n-dimensional para continuar el estudio (sencillo)
Funciones de Variable Real
 Tema 1 Funciones de Variable Real 1.1. La Recta Real Los números reales se pueden ordenar como los puntos de una recta. Los enteros positivos {1, 2, 3, 4,...} que surgen al contar, se llaman números naturales
Tema 1 Funciones de Variable Real 1.1. La Recta Real Los números reales se pueden ordenar como los puntos de una recta. Los enteros positivos {1, 2, 3, 4,...} que surgen al contar, se llaman números naturales
PRIMER PARCIAL
 PRIMER PARCIAL 25-26 decimales. Cuando termines un ejercicio cambia de página () Pregunta de teoría: (a) (.5 puntos) Enuncia y demuestra el Teorema del valor medio para funciones vectoriales. (b) (.5 puntos)
PRIMER PARCIAL 25-26 decimales. Cuando termines un ejercicio cambia de página () Pregunta de teoría: (a) (.5 puntos) Enuncia y demuestra el Teorema del valor medio para funciones vectoriales. (b) (.5 puntos)
5 Continuidad y derivabilidad de funciones reales de varias variables reales.
 5 Continuidad y derivabilidad de funciones reales de varias variables reales. 5.1 Funciones reales de varias variables reales. Curvas de nivel. Continuidad. 5.1.1 Introducción al Análisis Matemático. El
5 Continuidad y derivabilidad de funciones reales de varias variables reales. 5.1 Funciones reales de varias variables reales. Curvas de nivel. Continuidad. 5.1.1 Introducción al Análisis Matemático. El
FUNCIONES Y SUPERFICIES
 FUNCIONES Y SUPERFICIES Sergio Stive Solano Sabié 1 Abril de 2013 1 Visita http://sergiosolanosabie.wikispaces.com FUNCIONES Y SUPERFICIES Sergio Stive Solano Sabié 1 Abril de 2013 1 Visita http://sergiosolanosabie.wikispaces.com
FUNCIONES Y SUPERFICIES Sergio Stive Solano Sabié 1 Abril de 2013 1 Visita http://sergiosolanosabie.wikispaces.com FUNCIONES Y SUPERFICIES Sergio Stive Solano Sabié 1 Abril de 2013 1 Visita http://sergiosolanosabie.wikispaces.com
Nociones topológicas elementales de R n
 Nociones topológicas elementales de R n 1 Espacio vectorial R n Consideremos el conunto R n de las n-uplas de números reales, donde n es un número natural arbitrario fio. Los elementos de R n, que llamamos
Nociones topológicas elementales de R n 1 Espacio vectorial R n Consideremos el conunto R n de las n-uplas de números reales, donde n es un número natural arbitrario fio. Los elementos de R n, que llamamos
Tema 1. Números Complejos
 Tema 1. Números Complejos Prof. William La Cruz Bastidas 27 de septiembre de 2002 Capítulo 1 Números Complejos Definición 1.1 Un número complejo, z, es un número que se expresa como z = x + iy o, de manera
Tema 1. Números Complejos Prof. William La Cruz Bastidas 27 de septiembre de 2002 Capítulo 1 Números Complejos Definición 1.1 Un número complejo, z, es un número que se expresa como z = x + iy o, de manera
Preliminares. 1. Notación simbólica. Conjuntos. También se da en el curso de Conjuntos y Numeros.
 CAPíTULO 1 Preliminares 1. Notación simbólica. Conjuntos. También se da en el curso de Conjuntos y Numeros. El método matemático es axiomático y deductivo: a partir de unos principios aceptados inicialmente
CAPíTULO 1 Preliminares 1. Notación simbólica. Conjuntos. También se da en el curso de Conjuntos y Numeros. El método matemático es axiomático y deductivo: a partir de unos principios aceptados inicialmente
(Forman pares, pares cartesianos)
 FUNCIONES ALGEBRAICAS. 29.1 Relación entre conjuntos todos con todos. Es la correspondencia, que existe entre los elementos de los conjuntos A y B, sean los conjuntos que se representan: CONJUNTO SIEMPRE
FUNCIONES ALGEBRAICAS. 29.1 Relación entre conjuntos todos con todos. Es la correspondencia, que existe entre los elementos de los conjuntos A y B, sean los conjuntos que se representan: CONJUNTO SIEMPRE
Tema 7: Funciones de una variable. Límites y continuidad.
 Tema 7: Funciones de una variable. Límites y continuidad. José M. Salazar Noviembre de 2016 Tema 7: Funciones de una variable. Límites y continuidad. Lección 8. Funciones de una variable. Límites y continuidad.
Tema 7: Funciones de una variable. Límites y continuidad. José M. Salazar Noviembre de 2016 Tema 7: Funciones de una variable. Límites y continuidad. Lección 8. Funciones de una variable. Límites y continuidad.
CÁLCULO II Grados en Ingeniería
 CÁLCULO II Grados en Ingeniería Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez Capítulo 1. Cálculo diferencial 1.1 Funciones. Límites y continuidad
CÁLCULO II Grados en Ingeniería Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez Capítulo 1. Cálculo diferencial 1.1 Funciones. Límites y continuidad
Inducción Matemática Conjuntos Funciones. Matemática Discreta. Agustín G. Bonifacio UNSL. Repaso de Inducción, Conjuntos y Funciones
 UNSL Repaso de Inducción, y Inducción Matemática (Sección 1.7 del libro) Supongamos que queremos demostrar enunciados del siguiente tipo: P(n) : La suma de los primeros n números naturales es n(n+1)
UNSL Repaso de Inducción, y Inducción Matemática (Sección 1.7 del libro) Supongamos que queremos demostrar enunciados del siguiente tipo: P(n) : La suma de los primeros n números naturales es n(n+1)
Tema 1: Fundamentos.
 Tema 1: Fundamentos. 1. Nociones básicas de la Teoría de Conjuntos. Definición. Un conjunto es una colección de objetos. A los objetos de un conjunto se les llama elementos del conjunto. Se denominará
Tema 1: Fundamentos. 1. Nociones básicas de la Teoría de Conjuntos. Definición. Un conjunto es una colección de objetos. A los objetos de un conjunto se les llama elementos del conjunto. Se denominará
Tema 10: Continuidad en varias variables.
 Tema 10: Continuidad en varias variables. José M. Salazar Noviembre de 2016 Tema 10: Continuidad en varias variables. Lección 13. Continuidad en varias variables. Índice 1 Nociones básicas en R n. Funciones
Tema 10: Continuidad en varias variables. José M. Salazar Noviembre de 2016 Tema 10: Continuidad en varias variables. Lección 13. Continuidad en varias variables. Índice 1 Nociones básicas en R n. Funciones
Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) x u + f
 1 228 Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) z u = f x x u + f y y u z v = f x x v + f y y v z w = f x
1 228 Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) z u = f x x u + f y y u z v = f x x v + f y y v z w = f x
Geometría Analítica Espacios Vectoriales VECTORES EN EL PLANO
 VECTORES EN EL PLANO 1 ESPACIO VECTORIAL Un vector fijo es una pareja ordenada de puntos en el plano (origen y extremo) Si A y B son dichos puntos, representaremos el vector por AB Gráficamente, lo representamos
VECTORES EN EL PLANO 1 ESPACIO VECTORIAL Un vector fijo es una pareja ordenada de puntos en el plano (origen y extremo) Si A y B son dichos puntos, representaremos el vector por AB Gráficamente, lo representamos
Límite y Continuidad de funciones de una variable
 Introducción Límite y de funciones de una variable Departamento de Matemática Aplicada Universitat Politècnica de València, España Fundamentos Matemáticos para la Ingenieria Civil Límite y de funciones
Introducción Límite y de funciones de una variable Departamento de Matemática Aplicada Universitat Politècnica de València, España Fundamentos Matemáticos para la Ingenieria Civil Límite y de funciones
Matemáticas III Tema 1 Funciones de varias variables. Diferenciabilidad
 Matemáticas III Tema 1 Funciones de varias variables. Diferenciabilidad Rodríguez Sánchez, F.J. Muñoz Ruiz, M.L. Merino Córdoba, S. 2014. OCW-Universidad de Málaga, http://ocw.uma.es. Bajo licencia Creative
Matemáticas III Tema 1 Funciones de varias variables. Diferenciabilidad Rodríguez Sánchez, F.J. Muñoz Ruiz, M.L. Merino Córdoba, S. 2014. OCW-Universidad de Málaga, http://ocw.uma.es. Bajo licencia Creative
Funciones de R m R n
 Funciones de R n R m Funciones de R m R n Una funcion f : R n R m es una función cuyo dominio es un subconjunto Ω R n. Denotada por f : Ω R m donde a cada x R n f le asigna un vector f(x) R m. Ejemplo.-
Funciones de R n R m Funciones de R m R n Una funcion f : R n R m es una función cuyo dominio es un subconjunto Ω R n. Denotada por f : Ω R m donde a cada x R n f le asigna un vector f(x) R m. Ejemplo.-
Funciones de varias variables
 Funciones de varias variables 1. Conceptos elementales Funciones IR n IR m. Definición Una función f (también f o f): A IR n IR m es una aplicación que a cada x (también x o x) A IR n le hace corresponder
Funciones de varias variables 1. Conceptos elementales Funciones IR n IR m. Definición Una función f (también f o f): A IR n IR m es una aplicación que a cada x (también x o x) A IR n le hace corresponder
Números Complejos. Contenido. Definición
 U Contenido Facultad de Ingeniería Escuela de Ingeniería Eléctrica Departamento de Electrónica, Computación y Control Variable Compleja y Cálculo Operacional Números Complejos William La Cruz Números Complejos...3
U Contenido Facultad de Ingeniería Escuela de Ingeniería Eléctrica Departamento de Electrónica, Computación y Control Variable Compleja y Cálculo Operacional Números Complejos William La Cruz Números Complejos...3
UNIDAD DE APRENDIZAJE I
 UNIDAD DE APRENDIZAJE I Saberes procedimentales 1. Define en forma correcta el concepto de desigualdad y el de valor absoluto. 2. Explica la diferencia entre constante, parámetro y variable. 3. Define
UNIDAD DE APRENDIZAJE I Saberes procedimentales 1. Define en forma correcta el concepto de desigualdad y el de valor absoluto. 2. Explica la diferencia entre constante, parámetro y variable. 3. Define
Módulo 1 - Diapositiva 7 Números Complejos. Universidad de Antioquia. Facultad de Ciencias Exactas y Naturales
 Módulo 1 - Diapositiva 7 Números Complejos Facultad de Ciencias Exactas y Naturales Temas Números complejos C Axiomas de campo para C Plano complejo y módulo Solución de ecuaciones lineales y cuadráticas
Módulo 1 - Diapositiva 7 Números Complejos Facultad de Ciencias Exactas y Naturales Temas Números complejos C Axiomas de campo para C Plano complejo y módulo Solución de ecuaciones lineales y cuadráticas
Curso 2010/ de julio de (2.75 p.) 1) Se considera la función f : (0, ) (0, ) definida por
 Cálculo I Curso 2010/2011 Universidade de Vigo Departamento de Matemática Aplicada II ETSI Minas 5 de julio de 2011 (275 p) 1) Se considera la función f : (0, ) (0, ) definida por f(x) = 1 + ex x e x a)
Cálculo I Curso 2010/2011 Universidade de Vigo Departamento de Matemática Aplicada II ETSI Minas 5 de julio de 2011 (275 p) 1) Se considera la función f : (0, ) (0, ) definida por f(x) = 1 + ex x e x a)
Análisis Matemático I: Numeros Reales y Complejos
 Contents : Numeros Reales y Complejos Universidad de Murcia Curso 2008-2009 Contents 1 Definición axiomática de R Objetivos Definición axiomática de R Objetivos 1 Definir (y entender) R introducido axiomáticamente.
Contents : Numeros Reales y Complejos Universidad de Murcia Curso 2008-2009 Contents 1 Definición axiomática de R Objetivos Definición axiomática de R Objetivos 1 Definir (y entender) R introducido axiomáticamente.
DERIVADAS PARCIALES Y APLICACIONES
 CAPITULO IV CALCULO II 4.1 DEFINICIÓN DERIVADAS PARCIALES Y APLICACIONES En cálculo una derivada parcial de una función de diversas variables es su derivada respecto a una de esas variables con las otras
CAPITULO IV CALCULO II 4.1 DEFINICIÓN DERIVADAS PARCIALES Y APLICACIONES En cálculo una derivada parcial de una función de diversas variables es su derivada respecto a una de esas variables con las otras
REPASO DE FUNCIONES FUNCIONES REALES DE VARIABLE REAL
 REPASO DE FUNCIONES FUNCIONES REALES DE VARIABLE REAL CORRESPONDENCIA. Se llama CORRESPONDENCIA entre dos conjuntos A y B a toda ley que asocia elementos del conjunto A con elementos del conjunto B. Se
REPASO DE FUNCIONES FUNCIONES REALES DE VARIABLE REAL CORRESPONDENCIA. Se llama CORRESPONDENCIA entre dos conjuntos A y B a toda ley que asocia elementos del conjunto A con elementos del conjunto B. Se
Algebra Lineal XI: Funciones y Transformaciones Lineales
 Algebra Lineal XI: Funciones y Transformaciones Lineales José María Rico Martínez Departamento de Ingeniería Mecánica Facultad de Ingeniería Mecánica Eléctrica y Electrónica Universidad de Guanajuato email:
Algebra Lineal XI: Funciones y Transformaciones Lineales José María Rico Martínez Departamento de Ingeniería Mecánica Facultad de Ingeniería Mecánica Eléctrica y Electrónica Universidad de Guanajuato email:
Espacios vectoriales reales.
 Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
FUNCIONES DE VARIAS VARIABLES PRIMEROS CONCEPTOS
 Índice Presentación... 3 Funciones de varias variables... 4 Ejemplos... 5 Otros ejemplos económicos... 7 Dominio e imagen... 9 Gráficas... 10 Curvas de nivel... 11 Ejemplos de curva de nivel... 12 Curvas
Índice Presentación... 3 Funciones de varias variables... 4 Ejemplos... 5 Otros ejemplos económicos... 7 Dominio e imagen... 9 Gráficas... 10 Curvas de nivel... 11 Ejemplos de curva de nivel... 12 Curvas
9. Diferenciación de funciones reales de varias variables reales Diferenciación DERIVADAS PARCIALES
 9.1. Diferenciación 9.1.1. DERIVADAS PARCIALES Derivadas parciales de una función de dos variables Se llaman primeras derivadas parciales de una función f(x, y) respecto de x e y a las funciones: f x (x,
9.1. Diferenciación 9.1.1. DERIVADAS PARCIALES Derivadas parciales de una función de dos variables Se llaman primeras derivadas parciales de una función f(x, y) respecto de x e y a las funciones: f x (x,
Clase 4: Diferenciación
 Clase 4: Diferenciación C.J Vanegas 27 de abril de 2008 1. Derivadas Parciales Recordemos que la definición de derivada parcial: sea fa R R, definida sobre un f(x) f(x 0 ) intervalo abierto A. f es derivable
Clase 4: Diferenciación C.J Vanegas 27 de abril de 2008 1. Derivadas Parciales Recordemos que la definición de derivada parcial: sea fa R R, definida sobre un f(x) f(x 0 ) intervalo abierto A. f es derivable
CÁLCULO DIFERENCIAL Muestras de examen
 CÁLCULO DIFERENCIAL Muestras de examen Febrero 2012 T1. [2] Demostrar que la imagen continua de un conjunto compacto es compacto. T2. [2.5] Definir la diferencial de una función en un punto y demostrar
CÁLCULO DIFERENCIAL Muestras de examen Febrero 2012 T1. [2] Demostrar que la imagen continua de un conjunto compacto es compacto. T2. [2.5] Definir la diferencial de una función en un punto y demostrar
PROBLEMAS RESUELTOS ÁLGEBRA LINEAL Tema 2. Espacios Vectoriales
 SUBTEMA: ESPACIOS VECTORIALES Problema 1: Sea V = {a} el conjunto con el único elemento a. Determinar si V es un Espacio Vectorial sobre los reales con las operaciones de adición y multiplicación por un
SUBTEMA: ESPACIOS VECTORIALES Problema 1: Sea V = {a} el conjunto con el único elemento a. Determinar si V es un Espacio Vectorial sobre los reales con las operaciones de adición y multiplicación por un
Capítulo 2. Funciones
 Capítulo 2. Funciones Objetivo: El alumno analizará las características principales de las funciones reales de variable real y formulará modelos matemáticos. Contenido: 2.1 Definición de función real de
Capítulo 2. Funciones Objetivo: El alumno analizará las características principales de las funciones reales de variable real y formulará modelos matemáticos. Contenido: 2.1 Definición de función real de
9. DIFERENCIACIÓN DE FUNCIONES DE VARIAS VARIABLES.
 9 DIFERENCIACIÓN DE FUNCIONES DE VARIAS VARIABLES 91 Derivadas parciales y direccionales de un campo escalar La noción de derivada intenta describir cómo resulta afectada una función y = f(x) por un cambio
9 DIFERENCIACIÓN DE FUNCIONES DE VARIAS VARIABLES 91 Derivadas parciales y direccionales de un campo escalar La noción de derivada intenta describir cómo resulta afectada una función y = f(x) por un cambio
Modelo 3. Ejercicio 1 de la Opción A de Sobrantes de 2010
 Modelo 3. Ejercicio 1 de la Opción A de Sobrantes de 2010 [2 5 puntos] Sea la función f : R R dada por f(x) = Calcula las constantes a, b y c sabiendo que f es derivable y que la recta tangente a la gráfica
Modelo 3. Ejercicio 1 de la Opción A de Sobrantes de 2010 [2 5 puntos] Sea la función f : R R dada por f(x) = Calcula las constantes a, b y c sabiendo que f es derivable y que la recta tangente a la gráfica
TEORIA MATEMATICAS 5 PRIMER PARCIAL
 Def: Grafica de una función TEORIA MATEMATICAS 5 PRIMER PARCIAL Sea:. Definimos la grafica de f como el subconjunto de formado por los puntos, de en los que es un punto de U. Simbólicamente grafica es:
Def: Grafica de una función TEORIA MATEMATICAS 5 PRIMER PARCIAL Sea:. Definimos la grafica de f como el subconjunto de formado por los puntos, de en los que es un punto de U. Simbólicamente grafica es:
UNIDAD 1 : ELEMENTOS ALGEBRAICOS
 UNIDAD 1 : ELEMENTOS ALGEBRAICOS 1.D FUNCIONES 1.D.1 Características de una función para graficarla Si necesitamos graficar una función f se pueden prescindir de las tablas de valores y reconocer ciertas
UNIDAD 1 : ELEMENTOS ALGEBRAICOS 1.D FUNCIONES 1.D.1 Características de una función para graficarla Si necesitamos graficar una función f se pueden prescindir de las tablas de valores y reconocer ciertas
Matemáticas. para administración y economía Ernest F. Haeussler, Jr.* Richard S. Paul
 Matemáticas para administración y economía Ernest F. Haeussler, Jr.* Richard S. Paul Unidad I (Capítulos 3 y 5 del texto) Funciones y Gráficas 1.1 Definición y notación de función. 1.2 Dominio y rango
Matemáticas para administración y economía Ernest F. Haeussler, Jr.* Richard S. Paul Unidad I (Capítulos 3 y 5 del texto) Funciones y Gráficas 1.1 Definición y notación de función. 1.2 Dominio y rango
Parte II. Cálculo Diferencial para Funciones de Varias Variables Reales
 Parte II Cálculo Diferencial para Funciones de Varias Variables Reales Capítulo 5 Derivadas Direccionales y Derivadas Parciales Iniciamos, con este capítulo, el cálculo diferencial para funciones de varias
Parte II Cálculo Diferencial para Funciones de Varias Variables Reales Capítulo 5 Derivadas Direccionales y Derivadas Parciales Iniciamos, con este capítulo, el cálculo diferencial para funciones de varias
SECCIÓN 7.3 INTRODUCCION A VECTORES. Capítulo 7
 SECCIÓN 7.3 INTRODUCCION A VECTORES Capítulo 7 Introducción Cantidades tales como área, volumen, longitud, temperatura y tiempo se componen únicamente de una magnitud y se pueden describir completamente
SECCIÓN 7.3 INTRODUCCION A VECTORES Capítulo 7 Introducción Cantidades tales como área, volumen, longitud, temperatura y tiempo se componen únicamente de una magnitud y se pueden describir completamente
Teorema de la Función Implícita
 Teorema de la Función Implícita El círculo de radio 1 con centro en el origen, puede representarse implícitamente mediante la ecuación x 2 + y 2 1 ó explícitamente por las ecuaciones y 1 x 2 y y 1 x 2
Teorema de la Función Implícita El círculo de radio 1 con centro en el origen, puede representarse implícitamente mediante la ecuación x 2 + y 2 1 ó explícitamente por las ecuaciones y 1 x 2 y y 1 x 2
Funciones de dos variables: Límites. Continuidad. Derivadas parciales. Derivadas de orden superior.
 de orden superior Funciones de dos variables:. Continuidad.. Derivadas de orden superior. 1 1 Departamento de Matemáticas. Universidad de Alcalá de Henares. de orden superior Contenidos 1 Introducción
de orden superior Funciones de dos variables:. Continuidad.. Derivadas de orden superior. 1 1 Departamento de Matemáticas. Universidad de Alcalá de Henares. de orden superior Contenidos 1 Introducción
Problemas de exámenes de Formas Bilineales y Determinantes
 1 Problemas de exámenes de Formas Bilineales y Determinantes 1. Sea R 3 con el producto escalar ordinario. Sea f un endomorfismo de R 3 definido por las condiciones: a) La matriz de f respecto de la base
1 Problemas de exámenes de Formas Bilineales y Determinantes 1. Sea R 3 con el producto escalar ordinario. Sea f un endomorfismo de R 3 definido por las condiciones: a) La matriz de f respecto de la base
Clase 10: Extremos condicionados y multiplicadores de Lagrange
 Clase 10: Extremos condicionados y multiplicadores de Lagrange C.J. Vanegas 7 de abril de 008 1. Extremos condicionados y multiplicadores de Lagrange Estamos interesados en maximizar o minimizar una función
Clase 10: Extremos condicionados y multiplicadores de Lagrange C.J. Vanegas 7 de abril de 008 1. Extremos condicionados y multiplicadores de Lagrange Estamos interesados en maximizar o minimizar una función
LÍMITE DE FUNCIONES. Análisis Matemático A
 LÍMITE DE FUNCIONES Nos aproximamos intuitivamente al límite ε ε δ = Mín(δ 1, δ 2 ) δ 1 δ 2 lim x 2 f x = 7 f 2 Otro ejemplo Algunas observaciones: ε es cualquier número real positivo, tan pequeño como
LÍMITE DE FUNCIONES Nos aproximamos intuitivamente al límite ε ε δ = Mín(δ 1, δ 2 ) δ 1 δ 2 lim x 2 f x = 7 f 2 Otro ejemplo Algunas observaciones: ε es cualquier número real positivo, tan pequeño como
Cálculo en varias variables
 Cálculo en varias variables Dpto. Matemática Aplicada Universidad de Málaga Resumen Límites y continuidad Funciones de varias variables Límites y continuidad en varias variables 1 Límites y continuidad
Cálculo en varias variables Dpto. Matemática Aplicada Universidad de Málaga Resumen Límites y continuidad Funciones de varias variables Límites y continuidad en varias variables 1 Límites y continuidad
Espacios Conexos Espacio Conexo
 Capítulo 4 Espacios Conexos Una forma natural de construir nuevos espacios topológicos es pegando en forma disjunta, es decir. Sean (X,T X ),(Y,T Y ) dos espacios topológicos, luego definimos Z = X {0}
Capítulo 4 Espacios Conexos Una forma natural de construir nuevos espacios topológicos es pegando en forma disjunta, es decir. Sean (X,T X ),(Y,T Y ) dos espacios topológicos, luego definimos Z = X {0}
Tema 1: ESPACIOS VECTORIALES
 Tema 1: ESPACIOS VECTORIALES Prof. Rafael López Camino Departamento de Geometría y Topología Universidad de Granada Material docente para el alumno Asignatura: Geometría I. Curso 1998/99 Licenciatura:
Tema 1: ESPACIOS VECTORIALES Prof. Rafael López Camino Departamento de Geometría y Topología Universidad de Granada Material docente para el alumno Asignatura: Geometría I. Curso 1998/99 Licenciatura:
Introducción al Cál lculo Infinitesimal
 Tema 3 1. Conceptos básicos: dominio, recorrido.. Funciones reales de dos variables reales. 3. Gráficas. 4. Curvas de nivel. 5. Trazas. 6. Concepto de límite. 7. Límites reiterados, según trayectorias
Tema 3 1. Conceptos básicos: dominio, recorrido.. Funciones reales de dos variables reales. 3. Gráficas. 4. Curvas de nivel. 5. Trazas. 6. Concepto de límite. 7. Límites reiterados, según trayectorias
Práctica 3: Espacios Métricos. Métricas en R n
 Cálculo Avanzado Segundo Cuatrimestre de 2009 Práctica 3: Espacios Métricos Thought is only a flash between two long nights, but this flash is everything. Henri Poincare (1854-1912). I would never die
Cálculo Avanzado Segundo Cuatrimestre de 2009 Práctica 3: Espacios Métricos Thought is only a flash between two long nights, but this flash is everything. Henri Poincare (1854-1912). I would never die
DIPLOMA EN ECONOMÍA PARA NO ECONOMISTAS
 UNIVERSIDAD DE LA REPÚBLICA FACULTAD DE CIENCIAS SOCIALES - DEPARTAMENTO DE ECONOMÍA DIPLOMA EN ECONOMÍA PARA NO ECONOMISTAS CURSO: MATEMÁTICA APLICADA A LA ECONOMÍA NOTAS DEL CURSO Y APLICACIONES PRÁCTICAS
UNIVERSIDAD DE LA REPÚBLICA FACULTAD DE CIENCIAS SOCIALES - DEPARTAMENTO DE ECONOMÍA DIPLOMA EN ECONOMÍA PARA NO ECONOMISTAS CURSO: MATEMÁTICA APLICADA A LA ECONOMÍA NOTAS DEL CURSO Y APLICACIONES PRÁCTICAS
Álgebra Lineal Ma1010
 Álgebra Lineal Ma1010 Espacios Vectoriales Departamento de Matemáticas ITESM Espacios Vectoriales Álgebra Lineal - p. 1/80 En esta lectura se introduce el concepto de espacio vectorial. Este concepto generaliza
Álgebra Lineal Ma1010 Espacios Vectoriales Departamento de Matemáticas ITESM Espacios Vectoriales Álgebra Lineal - p. 1/80 En esta lectura se introduce el concepto de espacio vectorial. Este concepto generaliza
Clase 1: Funciones de Varias Variables
 Clase 1: Funciones de Varias Variables C. J. Vanegas 29 de abril de 2008 1. La geometría de funciones con valores reales Considere la siguiente función f: donde x = (x 1,..., x n ). f : A R n R m x A f(x)
Clase 1: Funciones de Varias Variables C. J. Vanegas 29 de abril de 2008 1. La geometría de funciones con valores reales Considere la siguiente función f: donde x = (x 1,..., x n ). f : A R n R m x A f(x)
1. El sistema: F(x,y,z) = =
 > 1. El sistema: F(x,y,z) = = Define implícitamente a la función (y, z) =f(x) en un entorno del punto x0=1. Encuentre la ecuación EXPLICITA de la recta tangente a la curva definida por f en el punto x0.
> 1. El sistema: F(x,y,z) = = Define implícitamente a la función (y, z) =f(x) en un entorno del punto x0=1. Encuentre la ecuación EXPLICITA de la recta tangente a la curva definida por f en el punto x0.
Álgebra y Trigonometría Clase 2 Ecuaciones, desigualdades y Funciones
 Álgebra y Trigonometría Clase 2 Ecuaciones, desigualdades y Funciones CNM-108 Departamento de Matemáticas Facultad de Ciencias Exactas y Naturales Universidad de Antioquia Copyleft c 2008. Reproducción
Álgebra y Trigonometría Clase 2 Ecuaciones, desigualdades y Funciones CNM-108 Departamento de Matemáticas Facultad de Ciencias Exactas y Naturales Universidad de Antioquia Copyleft c 2008. Reproducción
TEMA 3: CONTINUIDAD DE FUNCIONES
 TEMA 3: CONTINUIDAD DE FUNCIONES. Valor Absoluto Trabajaremos en el campo de los números reales, R. Para el estudio de las propiedades de las funciones necesitamos el concepto de valor absoluto de un número
TEMA 3: CONTINUIDAD DE FUNCIONES. Valor Absoluto Trabajaremos en el campo de los números reales, R. Para el estudio de las propiedades de las funciones necesitamos el concepto de valor absoluto de un número
Forma binomial de números complejos (ejercicios)
 Forma binomial de números complejos (ejercicios) Objetivos. Mostrar que los números reales x se pueden identificar con números complejos de la forma (x, 0), y cada número complejo (x, y) se puede escribir
Forma binomial de números complejos (ejercicios) Objetivos. Mostrar que los números reales x se pueden identificar con números complejos de la forma (x, 0), y cada número complejo (x, y) se puede escribir
FUNCIONES VECTORIALES DE VARIABLE ESCALAR
 CAPITULO II CALCULO II 2.1 CONCEPTOS BÁSICOS FUNCIONES VECTORIALES DE VARIABLE ESCALAR Una función vectorial (o a valores vectoriales) de una variable real (escalar), es una función del en la cual, a cada
CAPITULO II CALCULO II 2.1 CONCEPTOS BÁSICOS FUNCIONES VECTORIALES DE VARIABLE ESCALAR Una función vectorial (o a valores vectoriales) de una variable real (escalar), es una función del en la cual, a cada
Geometría afín y proyectiva, 2016 SEMANA 3
 Geometría afín y proyectiva, 2016 SEMANA 3 Sonia L. Rueda ETS Arquitectura. UPM September 20, 2016 Geometría afín y proyectiva 1. Álgebra Lineal 2. Geometría afín y eucĺıdea 3. Cónicas y cuádricas Álgebra
Geometría afín y proyectiva, 2016 SEMANA 3 Sonia L. Rueda ETS Arquitectura. UPM September 20, 2016 Geometría afín y proyectiva 1. Álgebra Lineal 2. Geometría afín y eucĺıdea 3. Cónicas y cuádricas Álgebra
Conceptos Preliminares
 Conceptos Preliminares Igualdad de matrices Definición: Dos matrices son iguales cuando tienen la misma dimensión y los elementos que ocupan la misma posición en ambas son iguales. Estas matrices cumplen
Conceptos Preliminares Igualdad de matrices Definición: Dos matrices son iguales cuando tienen la misma dimensión y los elementos que ocupan la misma posición en ambas son iguales. Estas matrices cumplen
Topología en R n. Continuidad de funciones de varias variables
 . Continuidad de funciones de varias variables María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I (1 o Grado en Ingeniería Electrónica Industrial y Automática) M. Muñoz (U.P.C.T.) Continuidad
. Continuidad de funciones de varias variables María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I (1 o Grado en Ingeniería Electrónica Industrial y Automática) M. Muñoz (U.P.C.T.) Continuidad
Algebra lineal y conjuntos convexos
 Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Funciones de varias variables
 Funciones de varias variables 7 de febrero de 008 1. Definiciones básicas Sean a, b puntos de R n (donde n N) con coordenadas: a = (a 1, a,, a n ); b = (b 1, b,, b n ) Se define la distancia euclídea entre
Funciones de varias variables 7 de febrero de 008 1. Definiciones básicas Sean a, b puntos de R n (donde n N) con coordenadas: a = (a 1, a,, a n ); b = (b 1, b,, b n ) Se define la distancia euclídea entre
Funciones reales de varias variables.
 Tema 4 Funciones reales de varias variables. 4.1. El espacio euclídeo R n. Definición 4.1.1. Se define el producto escalar entre vectores de R n como la aplicación: ( ) : R n R n R : x y = (x 1, x 2,...,
Tema 4 Funciones reales de varias variables. 4.1. El espacio euclídeo R n. Definición 4.1.1. Se define el producto escalar entre vectores de R n como la aplicación: ( ) : R n R n R : x y = (x 1, x 2,...,
TEMA 8. FUNCIONES, LÍMITES Y CONTINIDAD.
 TEMA 8. FUNCIONES, LÍMITES Y CONTINIDAD. 1. Concepto de función.. Dominio e imagen de una función. 3. Tipos de funciones. 4. Operaciones con funciones. 5. Concepto de límite. 6. Cálculo de límites. 7.
TEMA 8. FUNCIONES, LÍMITES Y CONTINIDAD. 1. Concepto de función.. Dominio e imagen de una función. 3. Tipos de funciones. 4. Operaciones con funciones. 5. Concepto de límite. 6. Cálculo de límites. 7.
1. Funciones diferenciables
 1. diferenciables Volvamos sobre el significado de la derivada de una función real de una variable real, Como vimos en el capítulo anterior, f : (a, b) R derivable en x 0, equivale a que f(x) f(x 0 ) =
1. diferenciables Volvamos sobre el significado de la derivada de una función real de una variable real, Como vimos en el capítulo anterior, f : (a, b) R derivable en x 0, equivale a que f(x) f(x 0 ) =
TEMA 7. FUNCIONES. a) Mediante una grafica. Es la forma en la que mejor se puede apreciar el comportamiento global de una función.
 . INTRODUCCIÓN. TEMA 7. FUNCIONES Las funciones estudian la relación existente entre dos variables. Para expresar esta relación, las funciones se pueden presentar de diferentes formas: a) Mediante una
. INTRODUCCIÓN. TEMA 7. FUNCIONES Las funciones estudian la relación existente entre dos variables. Para expresar esta relación, las funciones se pueden presentar de diferentes formas: a) Mediante una
1. La curva C es definida implícitamente por la expresión:
 1. La curva C es definida implícitamente por la expresión: 3 y - x - 2x + y + 7 0 Sea la función compuesta, donde es una función real. Suponga que. Cuál es la variación en la cota de F si a partir del
1. La curva C es definida implícitamente por la expresión: 3 y - x - 2x + y + 7 0 Sea la función compuesta, donde es una función real. Suponga que. Cuál es la variación en la cota de F si a partir del
DERIVADAS. TÉCNICAS DE DERIVACIÓN
 9 DERIVADAS. TÉCNICAS DE DERIVACIÓN REFLEXIONA Y RESUELVE Tangentes a una curva y = f (x) 5 3 5 3 9 14 Halla, mirando la gráfica y las rectas trazadas, f'(3), f'(9) y f'(14). Di otros tres puntos en los
9 DERIVADAS. TÉCNICAS DE DERIVACIÓN REFLEXIONA Y RESUELVE Tangentes a una curva y = f (x) 5 3 5 3 9 14 Halla, mirando la gráfica y las rectas trazadas, f'(3), f'(9) y f'(14). Di otros tres puntos en los
VECTORES. A cada clase de vectores equipolentes se denomina vector libre.!
 VECTORES Vectores libres del plano Definiciones Sean A y B dos puntos del plano de la geometría elemental. Se llama vector AB al par ordenado A, B. El punto A se denomina origen y al punto B extremo. (
VECTORES Vectores libres del plano Definiciones Sean A y B dos puntos del plano de la geometría elemental. Se llama vector AB al par ordenado A, B. El punto A se denomina origen y al punto B extremo. (
