FUNCIONES Y SUPERFICIES
|
|
|
- José Miguel Núñez Carmona
- hace 9 años
- Vistas:
Transcripción
1 FUNCIONES Y SUPERFICIES Sergio Stive Solano Sabié 1 Abril de Visita
2 FUNCIONES Y SUPERFICIES Sergio Stive Solano Sabié 1 Abril de Visita
3 Funciones de dos variables 1 La temperatura T en un punto de la superficie de la Tierra en cualquier instante determinado depende en todo momento de la longitud x y latitud y del punto. Podemos pensar en T como una función de dos variables x y y. Indicamos esta dependencia funcional escribienfo T (x, y). 2 El volumen V de un cilindro circular depende de su radio r y de su altura h. Sabemos que V = πr 2 h. Decimos que V es una función de r y h, y escribimos esto como V (r, h) = πr 2 h. Definición 1.1 Una función de dos variables es una regla que le asigna a cada par de números reales (x, y) en el conjunto D un número real único denotado con f(x, y). El conjunto D es el dominio de f y su rango es el conjunto de valores que f toma; es decir, {f(x, y) (x, y) D}.
4 Funciones de dos variables 1 La temperatura T en un punto de la superficie de la Tierra en cualquier instante determinado depende en todo momento de la longitud x y latitud y del punto. Podemos pensar en T como una función de dos variables x y y. Indicamos esta dependencia funcional escribienfo T (x, y). 2 El volumen V de un cilindro circular depende de su radio r y de su altura h. Sabemos que V = πr 2 h. Decimos que V es una función de r y h, y escribimos esto como V (r, h) = πr 2 h. Definición 1.1 Una función de dos variables es una regla que le asigna a cada par de números reales (x, y) en el conjunto D un número real único denotado con f(x, y). El conjunto D es el dominio de f y su rango es el conjunto de valores que f toma; es decir, {f(x, y) (x, y) D}.
5 Funciones de dos variables 1 La temperatura T en un punto de la superficie de la Tierra en cualquier instante determinado depende en todo momento de la longitud x y latitud y del punto. Podemos pensar en T como una función de dos variables x y y. Indicamos esta dependencia funcional escribienfo T (x, y). 2 El volumen V de un cilindro circular depende de su radio r y de su altura h. Sabemos que V = πr 2 h. Decimos que V es una función de r y h, y escribimos esto como V (r, h) = πr 2 h. Definición 1.1 Una función de dos variables es una regla que le asigna a cada par de números reales (x, y) en el conjunto D un número real único denotado con f(x, y). El conjunto D es el dominio de f y su rango es el conjunto de valores que f toma; es decir, {f(x, y) (x, y) D}.
6 Funciones de dos variables 1 La temperatura T en un punto de la superficie de la Tierra en cualquier instante determinado depende en todo momento de la longitud x y latitud y del punto. Podemos pensar en T como una función de dos variables x y y. Indicamos esta dependencia funcional escribienfo T (x, y). 2 El volumen V de un cilindro circular depende de su radio r y de su altura h. Sabemos que V = πr 2 h. Decimos que V es una función de r y h, y escribimos esto como V (r, h) = πr 2 h. Definición 1.1 Una función de dos variables es una regla que le asigna a cada par de números reales (x, y) en el conjunto D un número real único denotado con f(x, y). El conjunto D es el dominio de f y su rango es el conjunto de valores que f toma; es decir, {f(x, y) (x, y) D}.
7 Funciones de dos variables Ejemplo 1.1 Encuentre el dominio de cada una de las siguientes funciones y evalúe f(3, 2). 1 f(x, y) = x+y+1 x 1 2 f(x, y) = x ln(y 2 x) Solución. 1 La expresión para f tiene sentido si el denominador es distinto de 0 y la cantidad que está bajo el radical no es negativa. Así que el dominio de f es D = {(x, y) x + y + 1 0, x 1}. 2 Puesto que ln(y 2 x) está definida sólo cuando y 2 x > 0, es decir, x < y 2, el dominio de f es D = {(x, y) x < y 2 }.
8 Gráficas Definición 1.2 Funciones de dos variables Si f es una función f de dos variables con dominio D, entonces la gráfica de f es el conjunto de todos los puntos (x, y, z) en R 3, tal que z = f(x, y) y (x, y) D. La gráfica de una función f de dos variables es una superficie S con ecuación z = f(x, y). Podemos visualizar la gráfica de S como si estuviera abajo o arriba de su dominio en el plano xy. Ejemplo 1.2 Trace la gráfica de la función. 1 f(x, y, z) = 6 3x 2y (plano) 2 f(x, y) = x 2 (cilindro parabólico) 3 f(x, y) = 4x 2 + y 2 (paraboloide elíptico) 4 f(x, y) = y 2 x 2 (paraboloide hiperbólico)
9 Gráficas Funciones de dos variables Para representar una función de dos variables, a menudo resulya útil determinar la forma de las secciones transversales (rebanadas) de la gráfica. Por ejemplo, si mantenemos a x fija al hacer x = k (una constante) y dejar que y varíe, el resultado es una función de una variable z = f(k, y), cuya grafica es la curva que resulta de intersectar la superficie z = f(x, y) con el plano vertical x = k. De una forma similar, podemos cortar la superficie con el plano vertical y = k y observar las curvas z = f(x, k). También podemos cortarlas con los planos horizontales z = k. Estos tres tipos de curvas se llaman trazas (o secciones transversales) de la superficie z = f(x, y).
10 Gráficas Funciones de dos variables Ejemplo 1.3 Dibuja la superficie cuadrática cuya ecuación es x 2 + y2 9 + z2 4 = 1 Solución. La traza en el plano xy(z = 0) es x 2 + y2 9 = 1, la cual reconocemos como una ecuación de una elipse. En general, la traza horizontal en el plano z = k es x 2 + y2 9 = 1 k2 4 (z = k) que es una elipse, dado que k 2 < 4, es decir, 2 < k < 2. De manera análoga, las trazas verticales también son elipses: y z2 4 = 1 k2 x = k (si 1 < k < 1) x 2 + z2 4 = 1 k2 9 y = k (si 3 < k < 3)
11 Gráficas Funciones de dos variables Ejemplo 1.3 Dibuja la superficie cuadrática cuya ecuación es x 2 + y2 9 + z2 4 = 1 Solución. La traza en el plano xy(z = 0) es x 2 + y2 9 = 1, la cual reconocemos como una ecuación de una elipse. En general, la traza horizontal en el plano z = k es x 2 + y2 9 = 1 k2 4 (z = k) que es una elipse, dado que k 2 < 4, es decir, 2 < k < 2. De manera análoga, las trazas verticales también son elipses: y z2 4 = 1 k2 x = k (si 1 < k < 1) x 2 + z2 4 = 1 k2 9 y = k (si 3 < k < 3)
12 Gráficas Funciones de dos variables En la siguiente figura se muestra cómo al dibujar algunas de esas trazas se esboza la forma de la superficie. Se llama elipsoide debido a que todas sus trazas son elipses.
13 Definición 2.1 La gráfica de una ecuación de segundo grado de tres variables x, y y z se llama superficie cuadrática. A continuación se muestran gráficas de los seis tipos básicos de superficies cuadráticas en su forma convencional.
14
15
16 Ejemplo 2.1 Clasifica la superficie cuadrática x 2 + 2z 2 6x y + 10 = 0. Solución. Al completar el cuadrado, la ecuación se escribe como y 1 = (x 3) 2 + 2z 2 Al comparar esta ecuación con la tabla anterior, la ecuación representa un paraboloide elíptico. El eje de la parábola es paralelo ala eje y y se le desplazo de tal manera que su vértice es el punto (3, 1, 0). Las trazas en el plano y = k (k > 1) son las elipses (x 3) 2 + 2z 2 = k 1, y = k > 1 Las trazas en el plano xy es la parábola con ecuación y = 1 + (x 3) 2, z = 0.
17 En la siguiente figura se muestra el paraboloide
18 Definición 3.1 La curvas de nivel de una función f de dos variables son la curvas con ecuación f(x, y) = k, donde k es una constante (en el recorrido de f). Ejemplo 3.1 Dibuje las curvas de nivel de la función g(x, y) = 9 x 2 y 2. Solución. Las curvas de nivel son 9 x 2 y 2 = k o bien x 2 y 2 = 9 k 2 Ésta es una familia de círculos concéntricos con centro (0, 0) y radio 9 k 2.
19 Un ejemplo usual de las curvas de nivel ocurren en los mapas topográficos de las regiones montañosas:
20 GRACIAS POR SU ATENCIÓN
FUNCIONES Y SUPERFICIES
 FUNCIONES Y SUPERFICIES Sergio Stive Solano Sabié 1 Octubre de 2012 1 Visita http://sergiosolanosabie.wikispaces.com FUNCIONES Y SUPERFICIES Sergio Stive Solano Sabié 1 Octubre de 2012 1 Visita http://sergiosolanosabie.wikispaces.com
FUNCIONES Y SUPERFICIES Sergio Stive Solano Sabié 1 Octubre de 2012 1 Visita http://sergiosolanosabie.wikispaces.com FUNCIONES Y SUPERFICIES Sergio Stive Solano Sabié 1 Octubre de 2012 1 Visita http://sergiosolanosabie.wikispaces.com
Función de dos variables
 Funciones de dos y más variables, dominio y rango, y curva de nivel Marlon Fajardo Molinares - [email protected] 1. Función de dos variables 2. Funciones de varias variables 3. Método para hallar el
Funciones de dos y más variables, dominio y rango, y curva de nivel Marlon Fajardo Molinares - [email protected] 1. Función de dos variables 2. Funciones de varias variables 3. Método para hallar el
CLASE 1: Funciones y Gráficas
 CLASE 1: Funciones y Gráficas Sergio Stive Solano Sabié Agosto de 2011 CLASE 1: Funciones y Gráficas Sergio Stive Solano Sabié Agosto de 2011 Cuatro maneras de representar una función Definición 1.1 Una
CLASE 1: Funciones y Gráficas Sergio Stive Solano Sabié Agosto de 2011 CLASE 1: Funciones y Gráficas Sergio Stive Solano Sabié Agosto de 2011 Cuatro maneras de representar una función Definición 1.1 Una
VALORES MÁXIMOS Y MÍNIMOS DE FUNCIONES DE DOS VARIABLES
 VALORES MÁXIMOS Y MÍNIMOS DE FUNCIONES DE DOS VARIABLES Sergio Stive Solano Sabié 1 Mayo de 2013 1 Visita http://sergiosolanosabie.wikispaces.com VALORES MÁXIMOS Y MÍNIMOS DE FUNCIONES DE DOS VARIABLES
VALORES MÁXIMOS Y MÍNIMOS DE FUNCIONES DE DOS VARIABLES Sergio Stive Solano Sabié 1 Mayo de 2013 1 Visita http://sergiosolanosabie.wikispaces.com VALORES MÁXIMOS Y MÍNIMOS DE FUNCIONES DE DOS VARIABLES
SECCIONES CÓNICAS (1)Determinar y graficar el lugar geométrico de los puntos que equidistan de F(0, 2) y de la recta
 LOS EJERCICIOS DEBEN RESOLVERSE TAMBIÉN USANDO SOFTWARE MATEMÁTICO. LAS ECUACIONES PEDIDAS SON, EN TODOS LOS CASOS, LAS CANÓNICAS Y LAS PARAMÉTRICAS. I) GEOMETRÍA ANALÍTICA EN EL PLANO 1. Determinar y
LOS EJERCICIOS DEBEN RESOLVERSE TAMBIÉN USANDO SOFTWARE MATEMÁTICO. LAS ECUACIONES PEDIDAS SON, EN TODOS LOS CASOS, LAS CANÓNICAS Y LAS PARAMÉTRICAS. I) GEOMETRÍA ANALÍTICA EN EL PLANO 1. Determinar y
SUPERFICIES CUÁDRICAS
 SUPERFICIES CUÁDRICAS Un cuarto tipo de superficie en el espacio tridimensional son las cuádricas. Una superficie cuádrica en el espacio es una ecuación de segundo grado de la forma Ax + By + Cz + Dx +
SUPERFICIES CUÁDRICAS Un cuarto tipo de superficie en el espacio tridimensional son las cuádricas. Una superficie cuádrica en el espacio es una ecuación de segundo grado de la forma Ax + By + Cz + Dx +
Una curva del plano correspondiente a la gráfica de una función si y sólo si ninguna recta vertical intercepta a la curva más de una vez
 Función Una función f de un conjunto D a un conjunto E, es una regla de correspondencia que asigna a cada elemento x de D un elemento único y de E. Características de las funciones Dominio de una función:
Función Una función f de un conjunto D a un conjunto E, es una regla de correspondencia que asigna a cada elemento x de D un elemento único y de E. Características de las funciones Dominio de una función:
TALLER DE CONICAS. Ejemplo 1: En las siguientes ecuaciones diga que posible curva es:
 TALLER DE CONICAS Ejemplo 1: En las siguientes ecuaciones diga que posible curva es: 1. y -4x =4. x=y. x-y+6=0 4. 9x +4y -18x+16y-11=0 5. 9x -4y -18x-16y-4=0 6. 4x +y =4 7. 4x 9y =6 8. 4x+=0 9. 5y-=0 10.
TALLER DE CONICAS Ejemplo 1: En las siguientes ecuaciones diga que posible curva es: 1. y -4x =4. x=y. x-y+6=0 4. 9x +4y -18x+16y-11=0 5. 9x -4y -18x-16y-4=0 6. 4x +y =4 7. 4x 9y =6 8. 4x+=0 9. 5y-=0 10.
CM2 ENRICH CREUS CARNICERO Nivel 2
 CM ENRICH CREUS CARNICERO Nivel Unidad Anexo Superficies en 3D 01 Anexo de la Unidad : Superficies en 3D Anexo 1: valor absoluto o módulo El valor absoluto o módulo de un número a, que se anota a, es la
CM ENRICH CREUS CARNICERO Nivel Unidad Anexo Superficies en 3D 01 Anexo de la Unidad : Superficies en 3D Anexo 1: valor absoluto o módulo El valor absoluto o módulo de un número a, que se anota a, es la
Prof. Enrique Mateus Nieves. Doctorando en Educación Matemática. Cálculo multivariado REPASO DE SECCIONES CONICAS
 REPASO DE SECCIONES CONICAS SUPERFICIES CUADRICAS Y SUS TRAZAS Elipsoide x z Ecuación canónica: 1 a b c Secciones paralelas al plano x: Elipses; Secciones paralelas al plano xz: Elipses; Secciones paralelas
REPASO DE SECCIONES CONICAS SUPERFICIES CUADRICAS Y SUS TRAZAS Elipsoide x z Ecuación canónica: 1 a b c Secciones paralelas al plano x: Elipses; Secciones paralelas al plano xz: Elipses; Secciones paralelas
1.2 CONJUNTOS DEFINIDOS MEDIANTE FUNCIONES
 1.. Conjuntos definidos mediante funciones 1. CONJUNTOS DEFINIDOS MEDIANTE FUNCIONES A lo largo de este texto se verá la necesidad de diferenciar dos eventos: dada una función, encontrar los diferentes
1.. Conjuntos definidos mediante funciones 1. CONJUNTOS DEFINIDOS MEDIANTE FUNCIONES A lo largo de este texto se verá la necesidad de diferenciar dos eventos: dada una función, encontrar los diferentes
FUNCIONES 1. DEFINICION DOMINIO Y RANGO
 1. DEFINICION DOMINIO Y RANGO FUNCIONES Antes de definir función, uno de los conceptos fundamentales y de mayor importancia de todas las matemáticas, plantearemos algunos ejercicios que nos eran de utilidad
1. DEFINICION DOMINIO Y RANGO FUNCIONES Antes de definir función, uno de los conceptos fundamentales y de mayor importancia de todas las matemáticas, plantearemos algunos ejercicios que nos eran de utilidad
TEMA 5: DERIVADAS PARCIALES
 Matemáticas. Curso 2011/2012 Graos en ADE e Consultoría. Universidade de Vigo. En muchos problemas comunes aparecen funciones de dos o más variables, por ejemplo: w = F D (Trabajo realizado por una fuerza)
Matemáticas. Curso 2011/2012 Graos en ADE e Consultoría. Universidade de Vigo. En muchos problemas comunes aparecen funciones de dos o más variables, por ejemplo: w = F D (Trabajo realizado por una fuerza)
y v 0, 0, 1 y v 1, 0, 1 se tiene la ecuación
 SUPERFICIES Mostraremos varios métodos para generar superficies y encontrar sus ecuaciones. 1. Superficies cilíndricas Dada una curva en el plano de ecuación y un vector con Γ 0, es decir, no horizontal,
SUPERFICIES Mostraremos varios métodos para generar superficies y encontrar sus ecuaciones. 1. Superficies cilíndricas Dada una curva en el plano de ecuación y un vector con Γ 0, es decir, no horizontal,
1. Halla los máximos, mínimos y puntos de inflexión de las siguientes funciones:
 APLICACIONES DE DERIVADAS 1. Halla los máximos, mínimos y puntos de inflexión de las siguientes funciones: a. 6 9 b. c. 2 d. 2 e. f. 1 2. Estudia los intervalos de crecimiento y decrecimiento de las siguientes
APLICACIONES DE DERIVADAS 1. Halla los máximos, mínimos y puntos de inflexión de las siguientes funciones: a. 6 9 b. c. 2 d. 2 e. f. 1 2. Estudia los intervalos de crecimiento y decrecimiento de las siguientes
Álgebra y trigonometría: Gráficas de ecuaciones y funciones
 Álgebra y trigonometría: Gráficas de ecuaciones y funciones CNM-108 Instituto de Matemáticas Facultad de Ciencias Exactas y Naturales Universidad de Antioquia Este documento es distribuido bajo una licencia
Álgebra y trigonometría: Gráficas de ecuaciones y funciones CNM-108 Instituto de Matemáticas Facultad de Ciencias Exactas y Naturales Universidad de Antioquia Este documento es distribuido bajo una licencia
FUNCIÓN. La Respuesta correcta es D
 FUNCIONES FUNCIÓN La Respuesta correcta es D FUNCIÓN Función Continua: Es aquella en la que su gráfica se puede recorrer en forma ininterrumpida en toda su extensión. FUNCIÓN Función Discontinua: Es aquella
FUNCIONES FUNCIÓN La Respuesta correcta es D FUNCIÓN Función Continua: Es aquella en la que su gráfica se puede recorrer en forma ininterrumpida en toda su extensión. FUNCIÓN Función Discontinua: Es aquella
Álgebra y Trigonometría Clase 2 Ecuaciones, desigualdades y Funciones
 Álgebra y Trigonometría Clase 2 Ecuaciones, desigualdades y Funciones CNM-108 Departamento de Matemáticas Facultad de Ciencias Exactas y Naturales Universidad de Antioquia Copyleft c 2008. Reproducción
Álgebra y Trigonometría Clase 2 Ecuaciones, desigualdades y Funciones CNM-108 Departamento de Matemáticas Facultad de Ciencias Exactas y Naturales Universidad de Antioquia Copyleft c 2008. Reproducción
SERIE # 2 CÁLCULO VECTORIAL
 SERIE # CÁLCULO VECTORIAL SERIE 1) Calcular las coordenadas del punto P de la curva: en el que el vector P 1, 1, r t es paralelo a r t Página 1 t1 r t 1 t i ( t ) j e k ) Una partícula se mueve a lo largo
SERIE # CÁLCULO VECTORIAL SERIE 1) Calcular las coordenadas del punto P de la curva: en el que el vector P 1, 1, r t es paralelo a r t Página 1 t1 r t 1 t i ( t ) j e k ) Una partícula se mueve a lo largo
Universidad Icesi Departamento de Matemáticas y Estadística
 Universidad Icesi Departamento de Matemáticas y Estadística Solución del primer examen parcial del curso Cálculo de una variable Grupo: Once Período: Inicial del año 000 Prof: Rubén D. Nieto C. PUNTO 1.
Universidad Icesi Departamento de Matemáticas y Estadística Solución del primer examen parcial del curso Cálculo de una variable Grupo: Once Período: Inicial del año 000 Prof: Rubén D. Nieto C. PUNTO 1.
LOGO TEMA: FUNCIONES
 LOGO TEMA: FUNCIONES 1 Función Cuadrática 2 Función Exponencial 3 Función Logarìtmica 4 Comprender los diferentes tipos de comportamientos de las funciones cuadráticas, exponencial y logarítmica Identificar
LOGO TEMA: FUNCIONES 1 Función Cuadrática 2 Función Exponencial 3 Función Logarìtmica 4 Comprender los diferentes tipos de comportamientos de las funciones cuadráticas, exponencial y logarítmica Identificar
FUNCIONES y = f(x) ESO3
 Las correspondencias entre conjunto de valores o magnitudes se pueden expresar de varias formas: con un enunciado, con una tabla, con una gráfica, o con una fórmula o expresión algebraica o analítica.
Las correspondencias entre conjunto de valores o magnitudes se pueden expresar de varias formas: con un enunciado, con una tabla, con una gráfica, o con una fórmula o expresión algebraica o analítica.
GIMNASIO VIRTUAL SAN FRANCISCO JAVIER Valores y Tecnología para la Formación Integral del Ser Humano UNIDAD I FUNCIONES
 UNIDAD I FUNCIONES Una función es una correspondencia entre dos conjuntos, que asocia a cada elemento del primer conjunto exactamente un elemento del otro conjunto. Una función f definida entre dos conjuntos
UNIDAD I FUNCIONES Una función es una correspondencia entre dos conjuntos, que asocia a cada elemento del primer conjunto exactamente un elemento del otro conjunto. Una función f definida entre dos conjuntos
5 Continuidad y derivabilidad de funciones reales de varias variables reales.
 5 Continuidad y derivabilidad de funciones reales de varias variables reales. 5.1 Funciones reales de varias variables reales. Curvas de nivel. Continuidad. 5.1.1 Introducción al Análisis Matemático. El
5 Continuidad y derivabilidad de funciones reales de varias variables reales. 5.1 Funciones reales de varias variables reales. Curvas de nivel. Continuidad. 5.1.1 Introducción al Análisis Matemático. El
Formulario de Geometría Analítica
 1. El Punto 1.1. Distancia entre dos puntos Sean A(x 1, y 1 ) y B(x, y ) dos puntos en el plano. La distancia d entre ambos está dada por la ecuación: d(a, B) = (x x 1 ) + (y y 1 ) 1.. Punto medio: Sean
1. El Punto 1.1. Distancia entre dos puntos Sean A(x 1, y 1 ) y B(x, y ) dos puntos en el plano. La distancia d entre ambos está dada por la ecuación: d(a, B) = (x x 1 ) + (y y 1 ) 1.. Punto medio: Sean
y = 2x + 8x 7, y = x 4. y = 4 x, y = x + 2, x = 2, x = 3. x = 16 y, x = 6 y. y = a x, y = x, x y = a. (1 x)dx. y = 9 x, y = 0.
 . Encuentre el área de la región limitada por las curvas indicadas:.. y = x, y = x +... x = y, x = y +... y = x +, y = x +, y = x....5..6..7..8..9..0....... y = x + 8x 7, y = x. y = x, y = x +, x =, x
. Encuentre el área de la región limitada por las curvas indicadas:.. y = x, y = x +... x = y, x = y +... y = x +, y = x +, y = x....5..6..7..8..9..0....... y = x + 8x 7, y = x. y = x, y = x +, x =, x
REPASO DE FUNCIONES FUNCIONES REALES DE VARIABLE REAL
 REPASO DE FUNCIONES FUNCIONES REALES DE VARIABLE REAL CORRESPONDENCIA. Se llama CORRESPONDENCIA entre dos conjuntos A y B a toda ley que asocia elementos del conjunto A con elementos del conjunto B. Se
REPASO DE FUNCIONES FUNCIONES REALES DE VARIABLE REAL CORRESPONDENCIA. Se llama CORRESPONDENCIA entre dos conjuntos A y B a toda ley que asocia elementos del conjunto A con elementos del conjunto B. Se
SESIÓN 10 FUNCIONES Y GRÁFICAS
 SESIÓN 10 FUNCIONES Y GRÁFICAS I. CONTENIDOS: 1. Funciones. 2. Variables dependientes e independientes. 3. Gráfica de funciones y su aplicación. II. OBJETIVOS: Al término de la Sesión, el alumno: Comprenderá
SESIÓN 10 FUNCIONES Y GRÁFICAS I. CONTENIDOS: 1. Funciones. 2. Variables dependientes e independientes. 3. Gráfica de funciones y su aplicación. II. OBJETIVOS: Al término de la Sesión, el alumno: Comprenderá
Funciones cuadráticas MATE 3171
 Funciones cuadráticas MATE 3171 Funciones cuadráticas Una función, f, es una función cuadrática si f(x) = ax 2 + bx + c, a, b, y c se llaman coeficientes. o a es el coeficiente principal o b es el coeficiente
Funciones cuadráticas MATE 3171 Funciones cuadráticas Una función, f, es una función cuadrática si f(x) = ax 2 + bx + c, a, b, y c se llaman coeficientes. o a es el coeficiente principal o b es el coeficiente
3 Polinomios y funciones racionales
 Programa Inmersión, Verano 06 Notas escritas por Dr. M Notas del cursos. Basadas en los prontuarios de MATE 300 y MATE 303 Clase #8: jueves, 3 de junio de 06. 3 Polinomios y funciones racionales 3. Funciones
Programa Inmersión, Verano 06 Notas escritas por Dr. M Notas del cursos. Basadas en los prontuarios de MATE 300 y MATE 303 Clase #8: jueves, 3 de junio de 06. 3 Polinomios y funciones racionales 3. Funciones
Funciones de varias variables: continuidad derivadas parciales y optimización
 Titulación: Ingeniero en Telecomunicación. Asignatura: Cálculo. Relación de problemas número 4. Funciones de varias variables: continuidad derivadas parciales y optimización Problema 1. Determinar el dominio
Titulación: Ingeniero en Telecomunicación. Asignatura: Cálculo. Relación de problemas número 4. Funciones de varias variables: continuidad derivadas parciales y optimización Problema 1. Determinar el dominio
Contenido 1. Integrales Dobles 2. Integrales Triples
 Integración Contenido 1. Integrales Dobles 2 1.1. Integrales iteradas............................. 2 1.2. Regiones en R 2.............................. 3 1.3. Volumen..................................
Integración Contenido 1. Integrales Dobles 2 1.1. Integrales iteradas............................. 2 1.2. Regiones en R 2.............................. 3 1.3. Volumen..................................
1. INTEGRALES MÚLTIPLES
 1. INTEGALES MÚLTIPLES 1. Calcular las siguientes integrales iteradas: 1. x x 7 y dy dx dx 1. x x y y dx dy 1 1 7. (1 + xy) dx dy 1 1 π/. x sen y dy dx 5. (x + y) dx dy 6/ 1 6. (x + y) 8 dx dy 616 5 1
1. INTEGALES MÚLTIPLES 1. Calcular las siguientes integrales iteradas: 1. x x 7 y dy dx dx 1. x x y y dx dy 1 1 7. (1 + xy) dx dy 1 1 π/. x sen y dy dx 5. (x + y) dx dy 6/ 1 6. (x + y) 8 dx dy 616 5 1
CÁLCULO DIFERENCIAL E INTEGRAL I TERCERA EVALUACIÓN PARCIAL E0600 TRIMESTRE 00-P. 8 x 2 + y 2 + xy3 x 4 =1
 CÁLCULO DIFERENCIAL E INTEGRAL I TERCERA EVALUACIÓN PARCIAL E0600 TRIMESTRE 00-P (1) Obtener la ecuación de la tangente a la curva en el punto (2, 2). x 2 + y 2 + xy3 x 4 =1 (2) Se requiere construir un
CÁLCULO DIFERENCIAL E INTEGRAL I TERCERA EVALUACIÓN PARCIAL E0600 TRIMESTRE 00-P (1) Obtener la ecuación de la tangente a la curva en el punto (2, 2). x 2 + y 2 + xy3 x 4 =1 (2) Se requiere construir un
La variable independiente x es aquella cuyo valor se fija previamente. La variable dependiente y es aquella cuyo valor se deduce a partir de x.
 Bloque 8. FUNCIONES. (En el libro Temas 10, 11 y 12, páginas 179, 197 y 211) 1. Definiciones: función, variables, ecuación, tabla y gráfica. 2. Características o propiedades de una función: 2.1. Dominio
Bloque 8. FUNCIONES. (En el libro Temas 10, 11 y 12, páginas 179, 197 y 211) 1. Definiciones: función, variables, ecuación, tabla y gráfica. 2. Características o propiedades de una función: 2.1. Dominio
TEMA 4 FUNCIONES ELEMENTALES
 Tema 4 Funciones elementales Matemáticas CCSSI º Bachillerato TEMA 4 FUNCIONES ELEMENTALES FUNCIÓN EJERCICIO : Indica cuáles de las siguientes representaciones corresponden a la gráfica de una función.
Tema 4 Funciones elementales Matemáticas CCSSI º Bachillerato TEMA 4 FUNCIONES ELEMENTALES FUNCIÓN EJERCICIO : Indica cuáles de las siguientes representaciones corresponden a la gráfica de una función.
Fundamentos matemáticos. Tema 3 Geometría del plano y del espacio
 Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna [email protected]
Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna [email protected]
Funciones cuadráticas: valor mínimo, valor máximo y el vértice
 Funciones cuadráticas: valor mínimo, valor máximo y el vértice Definiciones Si la gráfica de una función sube en el plano de izquierda a derecha, se dice que es creciente en ese intervalo. Definiciones
Funciones cuadráticas: valor mínimo, valor máximo y el vértice Definiciones Si la gráfica de una función sube en el plano de izquierda a derecha, se dice que es creciente en ese intervalo. Definiciones
No es otra cosa, que la representación de los resultados de una función sobre el plano carteciano.
 FUNCIONES GRAFICAS No es otra cosa, que la representación de los resultados de una función sobre el plano carteciano. INTÉRVALOS Un intervalo es el conjunto de todos los números reales entre dos números
FUNCIONES GRAFICAS No es otra cosa, que la representación de los resultados de una función sobre el plano carteciano. INTÉRVALOS Un intervalo es el conjunto de todos los números reales entre dos números
Aplicaciones físicas
 Problemas propuestos con solución Aplicaciones físicas ISABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna imarrero@ulles Índice 1 Integral doble: valor medio 1 2 Integral doble:
Problemas propuestos con solución Aplicaciones físicas ISABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna imarrero@ulles Índice 1 Integral doble: valor medio 1 2 Integral doble:
1. Parábola. P(F,d) = {P : d(p,f) = d(p,d)}.
 Facultad de Ciencias Exactas, Ingeniería y Agrimensura Departamento de Matemática - Escuela de Ciencias Exactas y Naturales Álgebra y Geometría Analítica I Lic. en Fisica - Año 2014 Docentes: Viviana del
Facultad de Ciencias Exactas, Ingeniería y Agrimensura Departamento de Matemática - Escuela de Ciencias Exactas y Naturales Álgebra y Geometría Analítica I Lic. en Fisica - Año 2014 Docentes: Viviana del
FUNCIONES LINEALES Y CUADRÁTICAS
 . FUNCIONES LINEALES FUNCIONES LINEALES CUADRÁTICAS Aquéllas cua fórmula es un polinomio de grado. = + 9ºESO Se corresponden con los fenómenos de proporcionalidad; es decir, que la variación de la '' sea
. FUNCIONES LINEALES FUNCIONES LINEALES CUADRÁTICAS Aquéllas cua fórmula es un polinomio de grado. = + 9ºESO Se corresponden con los fenómenos de proporcionalidad; es decir, que la variación de la '' sea
(B) Segundo parcial (1) Dibuje una gráfica de una función f que satisfaga todas las condiciones siguientes:
 CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN GLOBAL E1600 (A) Primer parcial (1) Si se lanza una pelota verticalmente hacia arriba con una velocidad de 5 m/seg, entonces su altura después de t segundos
CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN GLOBAL E1600 (A) Primer parcial (1) Si se lanza una pelota verticalmente hacia arriba con una velocidad de 5 m/seg, entonces su altura después de t segundos
El espacio n Consideremos el conjunto de todas las n adas ordenadas de números reales, denotado por n : 8. 1(x 1, x 2,, x n ) = (x 1, x 2,, x n )
 El espacio n Consideremos el conjunto de todas las n adas ordenadas de números reales, denotado por n : n = {(x 1,x,, x n ) / x 1,x,, x n } A cada uno de los números reales x 1,x,, x n que conforman la
El espacio n Consideremos el conjunto de todas las n adas ordenadas de números reales, denotado por n : n = {(x 1,x,, x n ) / x 1,x,, x n } A cada uno de los números reales x 1,x,, x n que conforman la
Secciones Cónicas. 0.1 Parábolas
 Secciones Cónicas 0.1 Parábolas Las secciones cónicas, también llamadas cónicas, se obtienen cortando un cono circular recto doble con un plano. Al cambiar la posición del plano se tiene un círculo, una
Secciones Cónicas 0.1 Parábolas Las secciones cónicas, también llamadas cónicas, se obtienen cortando un cono circular recto doble con un plano. Al cambiar la posición del plano se tiene un círculo, una
Volumen de Sólidos de Revolución
 60 CAPÍTULO 4 Volumen de Sólidos de Revolución 6 Volumen de sólidos de revolución Cuando una región del plano de coordenadas gira alrededor de una recta l, se genera un cuerpo geométrico denominado sólido
60 CAPÍTULO 4 Volumen de Sólidos de Revolución 6 Volumen de sólidos de revolución Cuando una región del plano de coordenadas gira alrededor de una recta l, se genera un cuerpo geométrico denominado sólido
Si se pueden obtener las imágenes de x por simple sustitución.
 TEMA 0: REPASO DE FUNCIONES FUNCIONES: TIPOS DE FUNCIONES Funciones algebraicas En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción,
TEMA 0: REPASO DE FUNCIONES FUNCIONES: TIPOS DE FUNCIONES Funciones algebraicas En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción,
Funciones de dos variables. Gráficas y superficies.
 Univ. de Alcalá de Henares Ingeniería de Telecomunicación Cálculo. Segundo parcial. Curso 2004-2005 Funciones de dos variables. Gráficas y superficies. Puede ser conveniente la visualización en pantalla
Univ. de Alcalá de Henares Ingeniería de Telecomunicación Cálculo. Segundo parcial. Curso 2004-2005 Funciones de dos variables. Gráficas y superficies. Puede ser conveniente la visualización en pantalla
Listo para seguir? Intervención de destrezas
 9A Listo para seguir? Intervención de destrezas 9-1 Cómo identificar funciones cuadráticas Busca estas palabras de vocabulario en la Lección 9-1 el Glosario multilingüe. Vocabulario función cuadrática
9A Listo para seguir? Intervención de destrezas 9-1 Cómo identificar funciones cuadráticas Busca estas palabras de vocabulario en la Lección 9-1 el Glosario multilingüe. Vocabulario función cuadrática
GUIA DIDACTICA MATEMATICA 5to PARABOLA
 UNIDAD EDUCATIVA COLEGIO LOS PIRINEOS DON BOSCO INSCRITO EN EL M.P.P.L N S2991D2023 RIF: J-09009977-8 GUIA DIDACTICA MATEMATICA 5to PARABOLA Asignatura: Matemática Año Escolar: 2013-2014 Lapso: 2do Año:
UNIDAD EDUCATIVA COLEGIO LOS PIRINEOS DON BOSCO INSCRITO EN EL M.P.P.L N S2991D2023 RIF: J-09009977-8 GUIA DIDACTICA MATEMATICA 5to PARABOLA Asignatura: Matemática Año Escolar: 2013-2014 Lapso: 2do Año:
Funciones de dos o más variables. Gráficas. Curvas de nivel
 Funciones de dos o más variables. Gráficas. Curvas de nivel 1 1 Departamento de Matemáticas. Universidad de Alcalá de Henares. Contenidos 1 Introducción 2 3 4 5 6 Índice Introducción 1 Introducción 2 3
Funciones de dos o más variables. Gráficas. Curvas de nivel 1 1 Departamento de Matemáticas. Universidad de Alcalá de Henares. Contenidos 1 Introducción 2 3 4 5 6 Índice Introducción 1 Introducción 2 3
ÁLGEBRA VECTORIAL Y MATRICES. Ciclo 02 de Circunferencia.
 ÁLGEBRA VECTORIAL Y MATRICES. Ciclo 02 de 2012. Circunferencia. Elementos de la circunferencia. El segmento de recta es una cuerda. El segmento de recta es una cuerda que pasa por el centro, por lo tanto
ÁLGEBRA VECTORIAL Y MATRICES. Ciclo 02 de 2012. Circunferencia. Elementos de la circunferencia. El segmento de recta es una cuerda. El segmento de recta es una cuerda que pasa por el centro, por lo tanto
Funciones. Guía de Ejercicios
 . Módulo 4 Funciones Guía de Ejercicios Índice Unidad I. Concepto de función, dominio y recorrido Ejercicios Resueltos... pág. 02 Ejercicios Propuestos... pág. 06 Unidad II. Gráfico de funciones Ejercicios
. Módulo 4 Funciones Guía de Ejercicios Índice Unidad I. Concepto de función, dominio y recorrido Ejercicios Resueltos... pág. 02 Ejercicios Propuestos... pág. 06 Unidad II. Gráfico de funciones Ejercicios
Funciones. Rectas y parábolas
 0 Funciones. Rectas y parábolas. Funciones Dado el rectángulo de la figura, calcula: el perímetro. el área. P I E N S A C A L C U L A Perímetro = ( + ) = 6 Área = = Indica cuál de las siguientes gráficas
0 Funciones. Rectas y parábolas. Funciones Dado el rectángulo de la figura, calcula: el perímetro. el área. P I E N S A C A L C U L A Perímetro = ( + ) = 6 Área = = Indica cuál de las siguientes gráficas
Lección 2.4. Funciones Polinómicas. 08/10/2013 Prof. José G. Rodríguez Ahumada 1 de 24
 Lección.4 Funciones Polinómicas 08/10/013 Prof. José G. Rodríguez Ahumada 1 de 4 Actividades.4 Referencia Texto: Seccíón 3.6 Funciones Cuadráticas; Ejercicios de Práctica: Problemas impares 13-1, 37-41
Lección.4 Funciones Polinómicas 08/10/013 Prof. José G. Rodríguez Ahumada 1 de 4 Actividades.4 Referencia Texto: Seccíón 3.6 Funciones Cuadráticas; Ejercicios de Práctica: Problemas impares 13-1, 37-41
Para ver una explicación detallada de cada gráfica, haga Click sobre el nombre.
 Para ver una explicación detallada de cada gráfica, haga Click sobre el nombre. La Parábola La Circunferencia La Elipse La Hipérbola La Parábola La parábola se define como: el lugar geométrico de los puntos
Para ver una explicación detallada de cada gráfica, haga Click sobre el nombre. La Parábola La Circunferencia La Elipse La Hipérbola La Parábola La parábola se define como: el lugar geométrico de los puntos
Conjuntos de nivel, diagramas de contorno, gráficas. Funciones vectoriales de una y dos variables.
 Empezaremos el curso introduciendo algunos conceptos básicos para el estudio de funciones de varias variables, que son el objetivo de la asignatura: Funciones escalares de dos y tres variables. Conjuntos
Empezaremos el curso introduciendo algunos conceptos básicos para el estudio de funciones de varias variables, que son el objetivo de la asignatura: Funciones escalares de dos y tres variables. Conjuntos
2.4 Analizando gráficas de funciones cuadráticas
 2.4 Analizando gráficas de funciones cuadráticas Definiciones Si la gráfica de una función sube de izquierda a derecha, se dice que es creciente en ese intervalo. Una función f se dice que es creciente
2.4 Analizando gráficas de funciones cuadráticas Definiciones Si la gráfica de una función sube de izquierda a derecha, se dice que es creciente en ese intervalo. Una función f se dice que es creciente
Capítulo 3 Soluciones de ejercicios seleccionados
 Capítulo 3 Soluciones de ejercicios seleccionados Sección 3.1.4 1. Dom a = [ 1, 1]. Dom b = R. Dom c = (, 4). Dom d = ( 1, ). Dom e = R ( 1, 3] y Dom f = R {, }. 5x 4 x < 1, (x 1)(3x ) x < 1,. (f + g)(x)
Capítulo 3 Soluciones de ejercicios seleccionados Sección 3.1.4 1. Dom a = [ 1, 1]. Dom b = R. Dom c = (, 4). Dom d = ( 1, ). Dom e = R ( 1, 3] y Dom f = R {, }. 5x 4 x < 1, (x 1)(3x ) x < 1,. (f + g)(x)
Respuestas ejercicios edición 2007 Sección 3.3: Transformación de coordenadas Ejercicio 3-1
 Editorial Mc Graw Hill. Edición 007 Respuestas ejercicios edición 007 Sección 3.3: Transformación de coordenadas Ejercicio 3-1 a) Simetría respecto de ambos ejes y respecto del origen. b) Simetría respecto
Editorial Mc Graw Hill. Edición 007 Respuestas ejercicios edición 007 Sección 3.3: Transformación de coordenadas Ejercicio 3-1 a) Simetría respecto de ambos ejes y respecto del origen. b) Simetría respecto
PARÁBOLA IX.
 IX. PARÁBOLA Lugar geométrico de todos los puntos tales que la distancia de éstos a un punto fijo (foco) es siempre la misma a una recta fija (directriz). p = distancia del vértice al foco o del vértice
IX. PARÁBOLA Lugar geométrico de todos los puntos tales que la distancia de éstos a un punto fijo (foco) es siempre la misma a una recta fija (directriz). p = distancia del vértice al foco o del vértice
Matemáticas 2 Agosto 2015
 Laboratorio # 1 Línea recta I.-Determina la ecuación de la recta que satisface las siguientes condiciones y exprésala en la forma general. Pasa por el punto (1,5) y tiene pendiente 2 Pasa por y Pendiente
Laboratorio # 1 Línea recta I.-Determina la ecuación de la recta que satisface las siguientes condiciones y exprésala en la forma general. Pasa por el punto (1,5) y tiene pendiente 2 Pasa por y Pendiente
PROBLEMAS DE REPASO. Solución: Si llamamos x e y a las longitudes de cada uno de los catetos, sabemos que: x 2 y 2 1 y 2 1 x 2 El volumen del cono es:
 PROBLEMAS DE REPASO 1. La hipotenusa de un triángulo rectángulo mide 1 dm. Hacemos girar el triángulo alrededor de uno de sus catetos. Determina la longitud de los catetos de forma que el cono engendrado
PROBLEMAS DE REPASO 1. La hipotenusa de un triángulo rectángulo mide 1 dm. Hacemos girar el triángulo alrededor de uno de sus catetos. Determina la longitud de los catetos de forma que el cono engendrado
(B) Segundo parcial (1) Una función f se dice que es acotada si existe M 0 tal que f(x) M para toda x en dominio de f.
 CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN GLOBAL E00 A) Primer parcial 1) Completando el trinomio cuadrado perfecto, dibujar la gráfica de + 6 = y ) + 6 ) 1 6 4) Sea + si < 1 f) = 4 si < 1 si 1 4 a)
CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN GLOBAL E00 A) Primer parcial 1) Completando el trinomio cuadrado perfecto, dibujar la gráfica de + 6 = y ) + 6 ) 1 6 4) Sea + si < 1 f) = 4 si < 1 si 1 4 a)
EJERCICIOS RESUELTOS TEMA 11 Y 12. FUNCIONES. FUNCIÓN LINEAL Y CUADRÁTICA. Apellidos y Nombre:.Curso: 3º E.S.O. Grupo:.
 EJERCICIS RESUELTS TEMA 11 1. FUNCINES. FUNCIÓN LINEAL CUADRÁTICA Apellidos y Nombre:.Curso: º E.S.. Grupo:. 1 El coste del recibo del teléfono depende de los minutos hablados y una cuota fija de 1 euros.
EJERCICIS RESUELTS TEMA 11 1. FUNCINES. FUNCIÓN LINEAL CUADRÁTICA Apellidos y Nombre:.Curso: º E.S.. Grupo:. 1 El coste del recibo del teléfono depende de los minutos hablados y una cuota fija de 1 euros.
Las únicas funciones cuyas gráficas son rectas son las siguientes:
 Funciones, 3º ESO () RECTAS Las únicas funciones cuyas gráficas son rectas son las siguientes: - Lineales, de fórmula y mx. Las gráficas de estas funciones pasan por el origen de coordenadas. m es la pendiente
Funciones, 3º ESO () RECTAS Las únicas funciones cuyas gráficas son rectas son las siguientes: - Lineales, de fórmula y mx. Las gráficas de estas funciones pasan por el origen de coordenadas. m es la pendiente
Este trabajo debe realizarce después de haber trabajado el taller virtual
 Este trabajo debe realizarce después de haber trabajado el taller virtual qué se encuentra en la http://ceciba.escuelaing.edu.co/mre página bajo la pestaña de Talleres Virtuales.. Para las guientes funciones:
Este trabajo debe realizarce después de haber trabajado el taller virtual qué se encuentra en la http://ceciba.escuelaing.edu.co/mre página bajo la pestaña de Talleres Virtuales.. Para las guientes funciones:
Módulo 2 - Diapositiva 6 Funciones y sus gráficas. Universidad de Antioquia
 Módulo 2 - Diapositiva 6 Funciones y sus gráficas Facultad de Ciencias Exactas y Naturales Temas Funciones Funciones Funciones Lineales Función Funciones Dominio y rango de una función Gráfica de funciones
Módulo 2 - Diapositiva 6 Funciones y sus gráficas Facultad de Ciencias Exactas y Naturales Temas Funciones Funciones Funciones Lineales Función Funciones Dominio y rango de una función Gráfica de funciones
Funciones polinomiales de grados cero, uno y dos
 Funciones polinomiales de grados cero, uno y dos A una función p se le llama polinomio si: p x = a n x n + a n 1 x n 1 + + a 2 x 2 + a 1x + a 0 Donde un entero no negativo y los números a 0, a 1, a 2,
Funciones polinomiales de grados cero, uno y dos A una función p se le llama polinomio si: p x = a n x n + a n 1 x n 1 + + a 2 x 2 + a 1x + a 0 Donde un entero no negativo y los números a 0, a 1, a 2,
TEMA 0: REPASO DE FUNCIONES
 TEMA 0: REPASO DE FUNCIONES Recordamos que una función real de variable real es una aplicación de un subconjunto de los números reales A en el conjunto de los números reales de forma que a cada elemento
TEMA 0: REPASO DE FUNCIONES Recordamos que una función real de variable real es una aplicación de un subconjunto de los números reales A en el conjunto de los números reales de forma que a cada elemento
V. DISCUSIÓN DE ECUACIONES ALGEBRAICAS
 V. DISCUSIÓN DE ECUACIONES ALGEBRAICAS A. ANÁLISIS DE UNA ECUACIÓN En la geometría analítica hay dos problemas por resolver: 1. Dada la ecuación de una curva construir una gráfica.. Dadas algunas condiciones
V. DISCUSIÓN DE ECUACIONES ALGEBRAICAS A. ANÁLISIS DE UNA ECUACIÓN En la geometría analítica hay dos problemas por resolver: 1. Dada la ecuación de una curva construir una gráfica.. Dadas algunas condiciones
ANALISIS MATEMATICO II Grupo Ciencias 2015
 ANALISIS MATEMATICO II Grupo Ciencias 05 Práctica : Geometría Analítica: Vectores, Rectas y Planos A. Vectores Hasta el 9 de marzo. Sean v = (0,, ) y w = (,, 4) dos vectores de IR 3. (a) Obtener el coseno
ANALISIS MATEMATICO II Grupo Ciencias 05 Práctica : Geometría Analítica: Vectores, Rectas y Planos A. Vectores Hasta el 9 de marzo. Sean v = (0,, ) y w = (,, 4) dos vectores de IR 3. (a) Obtener el coseno
GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA
 ESCUELA PREPARATORIA OFICIAL No. 268 GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA Profra: Citlalli Artemisa García García 1) Qué es la pendiente? 2) Cómo es la pendiente de rectas
ESCUELA PREPARATORIA OFICIAL No. 268 GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA Profra: Citlalli Artemisa García García 1) Qué es la pendiente? 2) Cómo es la pendiente de rectas
A RG. Diédrico 22. Sección 3. Cilindro recto por un proyectante Hoja 1/2
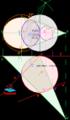 Dibujar la sección producida por el plano α al cilindro recto de base circular y altura 50 mm, obteniendo su verdadera magnitud. en la parte inferior de la lámina obtener el desarrollo del prisma y de
Dibujar la sección producida por el plano α al cilindro recto de base circular y altura 50 mm, obteniendo su verdadera magnitud. en la parte inferior de la lámina obtener el desarrollo del prisma y de
FUNCIONES REALES DE VARIABLE REAL
 MatemáticasNM Curso 0- FUNCIONES REALES DE VARIABLE REAL. Determina gráficamente el dominio y recorrido de cada una de las siguientes funciones: a) f() = b) f() = c) f() = d) f() = + d) f() = + e) f()
MatemáticasNM Curso 0- FUNCIONES REALES DE VARIABLE REAL. Determina gráficamente el dominio y recorrido de cada una de las siguientes funciones: a) f() = b) f() = c) f() = d) f() = + d) f() = + e) f()
7. Cónicas. Propiedades métricas y ópticas
 Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 49 7. Cónicas. Propiedades métricas y ópticas Cónicas Círcunferencias, elipses, parábolas, e hipérbolas son llamadas secciones cónicas
Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 49 7. Cónicas. Propiedades métricas y ópticas Cónicas Círcunferencias, elipses, parábolas, e hipérbolas son llamadas secciones cónicas
Guía de Estudio Algebra y Trigonometría Para Ciencias Agropecuarias
 Guía de Estudio Para Ciencias Agropecuarias Unidad: Geometría Analítica Los siguientes ejercicios están relacionados con los principales temas de Geometría Analítica e involucra todos los conocimientos
Guía de Estudio Para Ciencias Agropecuarias Unidad: Geometría Analítica Los siguientes ejercicios están relacionados con los principales temas de Geometría Analítica e involucra todos los conocimientos
UNIDADES TECNOLÓGICAS DE SANTANDER DEPARTAMENTO DE CIENCIAS BÁSICAS CÁLCULO MULTIVARIABLE Primer Parcial
 Primer Parcial Identifica los criterios de convergencia para determinar si una serie es convergente o no. 1,2 Representa una función mediante una serie de potencias estableciendo el intervalo de convergencia.
Primer Parcial Identifica los criterios de convergencia para determinar si una serie es convergente o no. 1,2 Representa una función mediante una serie de potencias estableciendo el intervalo de convergencia.
LA PARÁBOLA ECUACIÓN CANÓNICA DE LA PARÁBOLA DEFINICIÓN ELEMENTOS DE LA PARÁBOLA. x 2px p y x 2px p. Geometría Analítica
 ECUACIÓN CANÓNICA DE LA PARÁBOLA DEFINICIÓN LA PARÁBOLA Parábola es el lugar geométrico de todos los puntos P del plano que equidistan de una recta fija llamada directriz (L) y de un punto fijo exterior
ECUACIÓN CANÓNICA DE LA PARÁBOLA DEFINICIÓN LA PARÁBOLA Parábola es el lugar geométrico de todos los puntos P del plano que equidistan de una recta fija llamada directriz (L) y de un punto fijo exterior
4 E.M. Curso: Colegio SSCC Concepción - Depto. de Matemáticas. Nombre: Unidad de Aprendizaje: Función Cuadrática y Función Raíz Cuadrada.
 Curso: Colegio SSCC Concepción - Depto. de Matemáticas Unidad de Aprendizaje: Función Cuadrática y Función Raíz Cuadrada Habilidad: 4 E.M. 8 Racionamiento Matemático/ Comprensión, Aplicación/ A.S.E. Valores/
Curso: Colegio SSCC Concepción - Depto. de Matemáticas Unidad de Aprendizaje: Función Cuadrática y Función Raíz Cuadrada Habilidad: 4 E.M. 8 Racionamiento Matemático/ Comprensión, Aplicación/ A.S.E. Valores/
Integral definida. dx es diferencial de x, e indica cuál es la variable de la función que se integra.
 Integral definida Integral definida Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x =
Integral definida Integral definida Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x =
1 Indica cuáles de las siguientes parábolas están abiertas hacia arriba y cuáles hacia abajo:
 Indica cuáles de las siguientes parábolas están abiertas hacia arriba y cuáles hacia abajo: 3 + x y = 3 x x + x 3 + x y = 3 x x + x Abierta hacia arriba Abierta hacia abajo Abierta hacia abajo Calcula
Indica cuáles de las siguientes parábolas están abiertas hacia arriba y cuáles hacia abajo: 3 + x y = 3 x x + x 3 + x y = 3 x x + x Abierta hacia arriba Abierta hacia abajo Abierta hacia abajo Calcula
DE LA GRÁFICA A LA EXPRESIÓN ALGEBRAICA
 De la gráfica a la expresión algebraica DE LA GRÁFICA A LA EXPRESIÓN ALGEBRAICA Rectas, Parábolas, Hipérbolas, Exponenciales Logarítmicas LA RECTA Comencemos localizando el punto donde la recta corta al
De la gráfica a la expresión algebraica DE LA GRÁFICA A LA EXPRESIÓN ALGEBRAICA Rectas, Parábolas, Hipérbolas, Exponenciales Logarítmicas LA RECTA Comencemos localizando el punto donde la recta corta al
Cónicas y Cuádricas con Surfer
 Cónicas y Cuádricas con Surfer Daniel Alejandro Grimaldi 29/08/2016-2do Cuatrimestre de 2016 Denición: Se conoce como cuádrica a la supercie en R n que representa los ceros de un polinomio de grado 2 con
Cónicas y Cuádricas con Surfer Daniel Alejandro Grimaldi 29/08/2016-2do Cuatrimestre de 2016 Denición: Se conoce como cuádrica a la supercie en R n que representa los ceros de un polinomio de grado 2 con
Funciones y gráficas (1)
 Funciones y gráficas (1) Introducción Uno de los conceptos más importantes en matemática es el de función. El término función fue usado por primera vez en 1637 por el matemático francés René Descartes
Funciones y gráficas (1) Introducción Uno de los conceptos más importantes en matemática es el de función. El término función fue usado por primera vez en 1637 por el matemático francés René Descartes
LECCIÓN Nº 04 LA PARABOLA
 LECCIÓN Nº 04 LA PARABOLA Parábola El conjunto de puntos del plano tales que están a la misma distancia de una recta dada y de un punto dado F que no este sobre recibe el nombre de parábola. El punto F
LECCIÓN Nº 04 LA PARABOLA Parábola El conjunto de puntos del plano tales que están a la misma distancia de una recta dada y de un punto dado F que no este sobre recibe el nombre de parábola. El punto F
Rectas y Cónicas. Sistema de Coordenadas Cartesianas. Guía de Ejercicios # Encuentre las coordenadas de los puntos mostrados en la figura.
 Universidad de Los Andes Facultad de Ciencias Forestales y Ambientales Escuela de ingeniería Forestal Departamento de Botánica y Ciencias Básicas Matemáticas I I 2014 Prof. K. Chang. Rectas y Cónicas Guía
Universidad de Los Andes Facultad de Ciencias Forestales y Ambientales Escuela de ingeniería Forestal Departamento de Botánica y Ciencias Básicas Matemáticas I I 2014 Prof. K. Chang. Rectas y Cónicas Guía
CAPITULO 3. Aplicaciones de la Derivada. Licda. Elsie Hernández Saborío. Instituto Tecnológico de Costa Rica. Escuela de Matemática
 CAPITULO Aplicaciones de la Derivada Licda. Elsie Hernández Saborío Instituto Tecnológico de Costa Rica Escuela de Matemática Créditos Primera edición impresa: Rosario Álvarez, 1988. Edición Latex: Marieth
CAPITULO Aplicaciones de la Derivada Licda. Elsie Hernández Saborío Instituto Tecnológico de Costa Rica Escuela de Matemática Créditos Primera edición impresa: Rosario Álvarez, 1988. Edición Latex: Marieth
INTEGRAL DEFINIDA. APLICACIONES
 COLEGIO SAN ALBERTO MAGNO MATEMÁTICAS II INTEGRAL DEFINIDA. APLICACIONES. 008 MODELO OPCIÓN A. Ejercicio. [ 5 puntos] Dadas las funciones f : [0,+ ) R y g : [0, + ) R definidas por y calcula el área del
COLEGIO SAN ALBERTO MAGNO MATEMÁTICAS II INTEGRAL DEFINIDA. APLICACIONES. 008 MODELO OPCIÓN A. Ejercicio. [ 5 puntos] Dadas las funciones f : [0,+ ) R y g : [0, + ) R definidas por y calcula el área del
Funciones de varias variables.
 Funciones de varias variables. Definición. Hasta ahora se han estudiado funciones de la forma y = f (x), f :D Estas funciones recibían el nombre de funciones reales de variable real ya que su valor y dependía
Funciones de varias variables. Definición. Hasta ahora se han estudiado funciones de la forma y = f (x), f :D Estas funciones recibían el nombre de funciones reales de variable real ya que su valor y dependía
Sección 2.5. Gráficas de Funciones Transformaciones en el plano
 Sección 2.5 Gráficas de Funciones Transformaciones en el plano Funciones Pares e Impares Las funciones se clasifican como pares o impares dependiendo del tipo de simetría que reflejan sus gráficas. Terminología
Sección 2.5 Gráficas de Funciones Transformaciones en el plano Funciones Pares e Impares Las funciones se clasifican como pares o impares dependiendo del tipo de simetría que reflejan sus gráficas. Terminología
Matemáticas. para administración y economía Ernest F. Haeussler, Jr.* Richard S. Paul
 Matemáticas para administración y economía Ernest F. Haeussler, Jr.* Richard S. Paul Unidad I (Capítulos 3 y 5 del texto) Funciones y Gráficas 1.1 Definición y notación de función. 1.2 Dominio y rango
Matemáticas para administración y economía Ernest F. Haeussler, Jr.* Richard S. Paul Unidad I (Capítulos 3 y 5 del texto) Funciones y Gráficas 1.1 Definición y notación de función. 1.2 Dominio y rango
C U R S O : MATEMÁTICA
 C U R S O : MATEMÁTICA UNIDAD: ÁLGEBRA Y FUNCIONES FUNCIÓN CUADRÁTICA GUÍA TEÓRICO PRÁCTICA Nº8 A la función de segundo grado f() = a + b + c, siendo a, b, c lr a 0 se le denomina función cuadrática. La
C U R S O : MATEMÁTICA UNIDAD: ÁLGEBRA Y FUNCIONES FUNCIÓN CUADRÁTICA GUÍA TEÓRICO PRÁCTICA Nº8 A la función de segundo grado f() = a + b + c, siendo a, b, c lr a 0 se le denomina función cuadrática. La
CALCULO DE CENTROS DE MASA
 CALCULO DE CENTOS DE MASA Determinar la posición del C.M. de un semicono. Solución: I.T.I., I.T.T., 4 Sea el semicono de la figura orientado a lo largo del eje X, de altura radio. Dado que el plano XY
CALCULO DE CENTOS DE MASA Determinar la posición del C.M. de un semicono. Solución: I.T.I., I.T.T., 4 Sea el semicono de la figura orientado a lo largo del eje X, de altura radio. Dado que el plano XY
Otras Funciones Relevantes
 PreUnAB Clase # 14 Septiembre 2014 Función Cuadrática o de Segundo Grado Definición de la función cuadrática La función cuadrática tiene la forma general: f(x) = ax 2 + bx + c Dominio y recorrido de la
PreUnAB Clase # 14 Septiembre 2014 Función Cuadrática o de Segundo Grado Definición de la función cuadrática La función cuadrática tiene la forma general: f(x) = ax 2 + bx + c Dominio y recorrido de la
4 Integrales de línea y de superficie
 a t e a PROBLEMA DE ÁLULO II t i c a s 1 o Ings. Industrial y de Telecomunicación URO 2009 2010 4 Integrales de línea y de superficie 4.1 Integrales sobre curvas y campos conservativos. Problema 4.1 Integra
a t e a PROBLEMA DE ÁLULO II t i c a s 1 o Ings. Industrial y de Telecomunicación URO 2009 2010 4 Integrales de línea y de superficie 4.1 Integrales sobre curvas y campos conservativos. Problema 4.1 Integra
3 Polinomios y funciones racionales
 Programa Inmersión, Verano 2016 Notas escritas por Dr. M Notas del cursos. Basadas en los prontuarios de MATE 3001 y MATE 3023 Clase #19: viernes, 24 de junio de 2016. 3 Polinomios y funciones racionales
Programa Inmersión, Verano 2016 Notas escritas por Dr. M Notas del cursos. Basadas en los prontuarios de MATE 3001 y MATE 3023 Clase #19: viernes, 24 de junio de 2016. 3 Polinomios y funciones racionales
P(x,y) F Foco PF PA. e =
 MATEMÁTICAS BÁSICAS CÓNICAS DEFINICIÓN DE CÓNICA Dada una recta fija L un fijo F no contenido en esa recta, se llama cónica al lugar geométrico de un que se mueve en el plano, de tal manera que la razón
MATEMÁTICAS BÁSICAS CÓNICAS DEFINICIÓN DE CÓNICA Dada una recta fija L un fijo F no contenido en esa recta, se llama cónica al lugar geométrico de un que se mueve en el plano, de tal manera que la razón
Guía de aprendizaje Nº 2
 Liceo Polivalente Juan Antonio Ríos Quinta Normal NIVEL : TERCERO MEDIO Guía de aprendizaje Nº 2 Unidad Temática: FUNCION CUADRATICA Objetivo General: Graficar y analizar las raices de la funcion cuadratica.
Liceo Polivalente Juan Antonio Ríos Quinta Normal NIVEL : TERCERO MEDIO Guía de aprendizaje Nº 2 Unidad Temática: FUNCION CUADRATICA Objetivo General: Graficar y analizar las raices de la funcion cuadratica.
