MEF1-dim. (Mètode dels Elements Finits 1-dim) Mètodes Numèrics-Dept. MA1-ETSEIB. Toni Susin
|
|
|
- Celia Carmona Naranjo
- hace 5 años
- Vistas:
Transcripción
1 MEF1-dim (Mètode dels Elements Finits 1-dim) Mètodes Numèrics-Dept. MA1-ETSEIB Toni Susin
2 Visió General: Modelització
3 Visió General: Descomposició
4 Element 1-dim: LINK Barra (Link): Element 1 2 Nodes(locals) Conjunt d elements: E1 E2 E3 E Nodes(globals)
5 Geometria:Especificar coordenades dels nodes (globals) Dim 1: = Dim 2: = Dim3:... Element 1-dim: LINK
6 Element 1-dim: LINK Elements(especificar la connectivitat) E1 E2 E3 E Matriu de Connectivitat: Nodes Elements B=
7 Element 1-dim: LINK Exemple 1: 3 Elements Nodes 1 2 B= Exemple 2: B=
8 Element 1-dim: LINK Contribució Estructuralper cada element (dim1). = : desplaçaments : forces : Matriu de Rigidesa 2x2 (justificat a teoria): = E: Mòdul de Young(coef. d elasticitat) A: Areade seccióde la barra L: Longituddel la barra
9 Sistema Global (1-dim) Sistema Global(contribucions de TOTS els elements): : vector de desplaçaments. : vector de forces. :matriu de rigidesa global formada per l acoblament de tots els elements.
10 Matriu de Rigidesa: Acoblament(1-dim) Exemple E1 E2 E3 E Matriu Global: =
11 Matriu de Rigidesa: Acoblament(1-dim) B= Exemple = =! E1 E2 E3 E4 Ke
12 Matriu de Rigidesa: Acoblament(1-dim) B= Exemple = = +! E1 E2 E3 E4 Ke
13 Matriu de Rigidesa: Acoblament(1-dim) B= Exemple = E1 E2 E3 E4 Ke
14 Matriu de Rigidesa: Acoblament(1-dim) B= Exemple = E1 E2 E3 E4 Ke
15 Matriu de Rigidesa: Acoblament(1-dim) B= Exemple = E1 E2 E3 E EA/L
16 Forces i Restriccions (1-dim) Imposem Forces i Condicions de Contorn (Loads): = Restriccions del Moviment:(CC essencials) =, = Forces:(CC naturals) E1 E2 E3 E4 =
17 Sistema Global: Imposem les condicions de contorn(cc): EA/L = 6
18 Sistema Global: Imposem les condicions de contorn(cc): EA/L = 6 Solució amb E=1, A=.1, L=1 =, =1.5, =3, =4.5, =
19 FEM 1-Dim (Codi MATLAB) Estructura del programa: Preprocés: Carregar la geometria Propietats del Material Constants Reals Solució: Imposar Condicions de Contorn (CC/LOADS) Resoldre el sistema Postprocés: Forces de reacció, Tensions axials, etc.
20 FEM 1-Dim (Codi MATLAB) Preprocés: Carregar fitxers de dades: Coordenades dels Nodes Elements Definir Propietats del material i Àrees de Secció Coeficient d Elasticitat Areade secció nod=load('nodes.txt','-ascii'); [num_nod,ndim]=size(nod); elem=load('conectivitat.txt','-ascii'); [num_elem,ndim_elem]=size(elem); Y=1; %modul de Young E=Y*ones(1,num_elem); %tots iguals Area=.1; A=Area*ones(1,num_elem); %tots iguals
21 FEM 1-Dim (Codi MATLAB) Acoblament: Solució: K=zeros(num_nod*ndim); %iniciem a zeros for e=1:num_elem Ke=LinkBar_Mrigidesa(nod, elem,e,e,a); files=[elem(e,1); elem(e,2)]; colums=files; K(files,colums)=K(files,colums)+Ke; %acoblament end f=zeros(num_nod,1); %forces f(4)=6; fixed=[1,num_nod]; %fixem punts primer i últim val=[,]; [Km,fm]=ImposemCC1dim(K,f,fixed,val); u=km\fm %solució
22 FEM 1-Dim (Codi MATLAB) Funció LinkBar_Mrigidesa: function Ke=LinkBar_Mrigidesa(nod,elem,e,E,A) x1=nod(elem(e,1),1); x2=nod(elem(e,2),1); x21=x2-x1; Le=abs(x21); %Longitud de l element coef=((e(e)*a(e))/le); % %Matriu de cada element % Ke=[1, -1; -1, 1]; Ke=coef*Ke;
23 FEM 1-Dim (Codi MATLAB) Funció ImposemCC1dim: function[km,fm]=imposemcc1dim(k,f,fixed,val) Km=K; fm=f; nfix=size(fixed,2); %modifiquem el vector de forces(loads) %passem cap els termes independents les columnes %associadesa valorsfixats. for i=1:nfix fm=fm-val(1,i)*km(:,fixed(i)); end %fixem els valors donats f(fixed)=val; %fem que les equacions corresponents als valors fixats %siguin la identitat. Km(fixed,:)=; Km(:,fixed)=; for i=1:nfix ni=fixed(i); Km(ni,ni)=1; %diagonal igual a 1 end
24 2-Dim: Element 2-dim: PlaneLINK
25 Element 2-dim: PlaneLINK Matriu de rigidesa 2-Dim: On
26 Element 2-dim: PlaneLINK(Codi MATLAB) Funció PlaneLinkBar_Mrigidesa: function Ke=PlaneLinkBar_Mrigidesa(nod,elem,e,E,A) x1=nod(elem(e,1),1); y1=nod(elem(e,1),2); x2=nod(elem(e,2),1); y2=nod(elem(e,2),2); x21=x2-x1; y21=y2-y1; Le=sqrt(x21*x21+y21*y21); %Longitud coef=((e(e)*a(e))/le^3); Ke=[x21*x21, x21*y21, -x21*x21, -x21*y21; x21*y21, y21*y21, -x21*y21, -y21*y21; -x21*x21, -x21*y21, x21*x21, x21*y21; -x21*y21, -y21*y21, x21*y21, y21*y21]; Ke=coef*Ke;
27 Exemple 2D: Element 2-dim: LINK
28 % % Exemple de FEM per elements lineals: LINK % (2-Dim: desplaçaments en x i y) % nod=load('nodes2.txt','-ascii'); [num_nod,ndim]=size(nod); elem=load('conectivitat2.txt','-ascii'); [num_elem,ndim_elem]=size(elem); % %Pintem els nodes i els elements % figure(1) pintemnodelem(nod,elem); % %Propietats del material % % mòdul de Young Y=5; E=Y*ones(1, num_elem); %tots els elements del mateix material E(3)=1; % %Constants reals: Area de secció de la barra % Area=2; A=Area*ones(1,num_elem); A(2)=1; A(3)=2*sqrt(2); % %Pintem la matriu de rigidesa % figure(2) K=zeros(num_nod*ndim); for e=1:num_elem Ke=PlaneLinkBar_Mrigidesa(nod,elem,e,E,A) files=[elem(e,1)*2-1; elem(e,1)*2; elem(e,2)*2-1; elem(e,2)*2]; colums=files; K(files,colums)=K(files,colums)+Ke; spy(k) pause(.1); end %matriu de rigidesa K % % SOLVE: Apliquem condicions de contorn % %Inicialitzem forces f=zeros(num_nod*ndim,1); fixed=zeros(1,num_nod*ndim); val=zeros(1,num_nod*ndim); fapp=zeros(num_nod*ndim,1); %Fixem els punts: 1 all DOF, 3 % codifiquem amb un 1 els punts en els que fixem desplaçaments % exemp: fixed=[1,1,,1,,]; fixed(1*ndim-1)=1; %(u1_x=) fixed(1*ndim)=1; %(u1_y=) fixed(2*ndim)=1; %(u2_y=) % codifiquem les forces i els valors dels desplaçaments % exemp: val=[,,,,2,1]; % forces al node3 : (fx=2, fy=1) nodf=3; %node en el que apliquem la força val(nodf*ndim-1)=2; val(nodf*ndim)=1; fapp(nodf*ndim-1)=2;%copiem les forces aplicades fapp(nodf*ndim)=1; %per aplicar-ho a les forces de reacció [Km,fm]=ImposemBC(K,f,fixed,val); Km fm % % SOLVE: Resolem el sistema i calculem els desplaçaments % u=km\fm % % POSTPROCES: Pintem desplaçaments i calculem forces i tensions % % Representem la solució desplaçada figure(3) esc=2; %escala per representar els desplaçaments pintemnodelemdespl(nod,elem,u,esc); %Forces de Reacció fr=k*u-fapp %Tensions Axials [T, F]=calculTensionsAxials (nod,elem,u,e,a) Exemple 2D: (Codi Matlab)
29 function[tensions Forces]=calculTensionsAxials(nod,elem,u,E,A) [num_nod,ndim]=size(nod); [num_elem,ndim_elem]=size(elem); Forces=zeros(1,num_elem); Tensions=zeros(1,num_elem); for e=1:num_elem x1=nod(elem(e,1),1); x2=nod(elem(e,2),1); if(ndim==1) y1=; y2=; ux1=u(elem(e,1)); ux2=u(elem(e,2)); uy1=; uy2=; else y1=nod(elem(e,1),2); y2=nod(elem(e,2),2); ux1=u(elem(e,1)*ndim-1); uy1=u(elem(e,1)*ndim); ux2=u(elem(e,2)*ndim-1); uy2=u(elem(e,2)*ndim); end x21=x2-x1; y21=y2-y1; Le=sqrt(x21*x21+y21*y21); ux21=ux2-ux1; uy21=uy2-uy1; d=(x21*ux21+y21*uy21)/le; Forces(e)=E(e)*A(e)*d/Le; Tensions(e)=Forces(e)/A(e); end Exemple 2D: (Codi Matlab)
30 Element 2-dim: LINK Exemple 2D: Un problema típic en enginyeria és dissenyar un pont. Considereu el següent model format per barres d'acer que tenen un mòdul de Young de E = 2GPa i un àrea de secció A = 325mm^2. Les fletxes indiquen les càrregues del pont. Són forces puntuals de 28, 21, 28 i 36 kn. L'objectiu és l'estudi de les deformacions, les forces de reacció i les tensions axials.
31 Exemple 2D: Nodes: Element 2-dim: LINK Elements:
32 Exemple 2D: Nodes: Element 2-dim: LINK Elements:
33 3-Dim: Element 3-dim: LINK
34 Element 3-dim: LINK Matriu de rigidesa 3-Dim: On i
1. SISTEMA D EQUACIONS LINEALS
 1. SISTEMA D EQUACIONS LINEALS 1.1 Equacions lineals Una equació lineal està composta de coeficients (nombres reals) acompanyats d incògnites (x, y, z,t..o ) s igualen a un terme independent, i les solucions
1. SISTEMA D EQUACIONS LINEALS 1.1 Equacions lineals Una equació lineal està composta de coeficients (nombres reals) acompanyats d incògnites (x, y, z,t..o ) s igualen a un terme independent, i les solucions
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 PAU 2012
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 1 1 k 1.- Determineu el rang de la matriu A = 1 k 1 en funció del valor del paràmetre k. k 1 1 [2 punts] En ser la matriu
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 1 1 k 1.- Determineu el rang de la matriu A = 1 k 1 en funció del valor del paràmetre k. k 1 1 [2 punts] En ser la matriu
TEMA 5 : Resolució de sistemes d equacions
 TEMA 5 : Resolució de sistemes d equacions 5.1. EQUACIÓ LINEAL AMB n INCÒGNITES Una equació lineal de n incògnites es qualsevol expressió de la forma: a 1 x 1 + a 2 x 2 +... + a n x n = b, on a i b son
TEMA 5 : Resolució de sistemes d equacions 5.1. EQUACIÓ LINEAL AMB n INCÒGNITES Una equació lineal de n incògnites es qualsevol expressió de la forma: a 1 x 1 + a 2 x 2 +... + a n x n = b, on a i b son
1.- Sabem que el vector (2, 1, 1) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c. . cx by +2z = b
 Oficina d Organització de Proves d Accés a la Universitat Pàgina de 5 PAU 0 - Sabem que el vector (,, ) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c cx by +z = b Calculeu el valor
Oficina d Organització de Proves d Accés a la Universitat Pàgina de 5 PAU 0 - Sabem que el vector (,, ) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c cx by +z = b Calculeu el valor
Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera:
 Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera: ax + by = k a x + b y = k Coeficients de les incògnites: a, a, b, b. Termes independents:
Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera: ax + by = k a x + b y = k Coeficients de les incògnites: a, a, b, b. Termes independents:
( 2 3, utilitzeu la matriu inversa B 1 ( 1 4 ( 2 1. Matrius i determinants Sèrie 3 - Qüestió 4. Donada la matriu B =
 1998 - Sèrie 3 - Qüestió 4 Donada la matriu B = ( 2 3, utilitzeu la matriu inversa B 1 1 1) B X B = ( 1 4 3 2). per trobar una matriu X tal que 2004 - Sèrie 1 - Qüestió 3 Considereu les matrius Trobeu
1998 - Sèrie 3 - Qüestió 4 Donada la matriu B = ( 2 3, utilitzeu la matriu inversa B 1 1 1) B X B = ( 1 4 3 2). per trobar una matriu X tal que 2004 - Sèrie 1 - Qüestió 3 Considereu les matrius Trobeu
TEMA 4 : Matrius i Determinants
 TEMA 4 : Matrius i Determinants MATRIUS 4.1. NOMENCLATURA. DEFINICIÓ Una matriu és un conjunt de mxn elements distribuïts en m files i n columnes, A= Aquesta és una matriu de m files per n columnes. És
TEMA 4 : Matrius i Determinants MATRIUS 4.1. NOMENCLATURA. DEFINICIÓ Una matriu és un conjunt de mxn elements distribuïts en m files i n columnes, A= Aquesta és una matriu de m files per n columnes. És
Districte Universitari de Catalunya
 Proves d Accés a la Universitat. Curs 2012-2013 Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts.
Proves d Accés a la Universitat. Curs 2012-2013 Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts.
UIB 2 + f (x) + f(x) ց ց ր ր Per tant, el punt ( 3. Una altra forma de veure-ho és calcular la derivada segona i mirar el signe en x = 3: 2 f (x) =
 El cas positiu no té solució. Si analitzam el cas negatiu, ens surt x = x+, d on x =. A continuació fem la taula següent per veure si el valor obtingut és un màxim, mínim o un punt de sella. x + f (x)
El cas positiu no té solució. Si analitzam el cas negatiu, ens surt x = x+, d on x =. A continuació fem la taula següent per veure si el valor obtingut és un màxim, mínim o un punt de sella. x + f (x)
TEMA 4: Equacions exponencials i logarítmiques
 TEMA 4: Equacions exponencials i logarítmiques 4.1. EXPONENCIALS Definim exponencial de base a i exponent n:. Propietats de les exponencials: (1). (2) (3) (4) 1 (5) 4.2. EQUACIONS EXPONENCIALS Anomenarem
TEMA 4: Equacions exponencials i logarítmiques 4.1. EXPONENCIALS Definim exponencial de base a i exponent n:. Propietats de les exponencials: (1). (2) (3) (4) 1 (5) 4.2. EQUACIONS EXPONENCIALS Anomenarem
Sèrie 5. Resolució: 1. Siguin i les rectes de d equacions. a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i.
 Oficina d Accés a la Universitat Pàgina 1 de 11 Sèrie 5 1. Siguin i les rectes de d equacions : 55 3 2 : 3 2 1 2 3 1 a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i. b) Trobeu l
Oficina d Accés a la Universitat Pàgina 1 de 11 Sèrie 5 1. Siguin i les rectes de d equacions : 55 3 2 : 3 2 1 2 3 1 a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i. b) Trobeu l
Propietats de les desigualtats.
 Inequacions Desigualtats Direm que a < b a és menor que b si b a és un nombre positiu. Gràficament, a queda a l esquerra de b. Direm que a > b a major que b si a b és un nombre positiu. Gràficament, a
Inequacions Desigualtats Direm que a < b a és menor que b si b a és un nombre positiu. Gràficament, a queda a l esquerra de b. Direm que a > b a major que b si a b és un nombre positiu. Gràficament, a
SOLUCIONARI Unitat 5
 SOLUCIONARI Unitat 5 Comencem Escriu tres equacions que no tinguin solució en el conjunt. Resposta oberta. Per exemple: a) x b) 5x 0 c) x Estableix tres equacions que no tinguin solució en el conjunt.
SOLUCIONARI Unitat 5 Comencem Escriu tres equacions que no tinguin solució en el conjunt. Resposta oberta. Per exemple: a) x b) 5x 0 c) x Estableix tres equacions que no tinguin solució en el conjunt.
Resolucions de l autoavaluació del llibre de text
 Pàg. 1 de 1 Tenim els vectors u(3,, 1), v ( 4, 0, 3) i w (3,, 0): a) Formen una base de Á 3? b) Troba m per tal que el vector (, 6, m) sigui perpendicular a u. c) Calcula u, ì v i ( u, v). a) Per tal que
Pàg. 1 de 1 Tenim els vectors u(3,, 1), v ( 4, 0, 3) i w (3,, 0): a) Formen una base de Á 3? b) Troba m per tal que el vector (, 6, m) sigui perpendicular a u. c) Calcula u, ì v i ( u, v). a) Per tal que
Inferència de Tipus a Haskell
 Inferència de Tipus a Haskell Mateu Villaret 21 d abril de 2008 1 Exemple d inferència de tipus Considerem la definició en Haskell de la funció map Haskell Code 1 map f [] = [] 2 map f (x: xs) = (f x)
Inferència de Tipus a Haskell Mateu Villaret 21 d abril de 2008 1 Exemple d inferència de tipus Considerem la definició en Haskell de la funció map Haskell Code 1 map f [] = [] 2 map f (x: xs) = (f x)
1.- Elements d una recta Vector director d una recta Vector normal d una recta Pendent d una recta
 .- Elements d una recta..- Vector director d una recta..- Vector normal d una recta.3.- Pendent d una recta.- Equacions d una recta..- Equació ectorial, paramètrica i contínua..- Equació explícita.3.-
.- Elements d una recta..- Vector director d una recta..- Vector normal d una recta.3.- Pendent d una recta.- Equacions d una recta..- Equació ectorial, paramètrica i contínua..- Equació explícita.3.-
RESOLUCIÓ DE PROBLEMES
 RESOLUCIÓ DE PROBLEMES MOVIMENT UNIFORMEMENT ACCELERAT 1.- Llegir el problema. 2.- Fer-se una idea de la situació, dibuixar-la i col locar el sistema de referència. 3.- Buscar les constants del moviment:
RESOLUCIÓ DE PROBLEMES MOVIMENT UNIFORMEMENT ACCELERAT 1.- Llegir el problema. 2.- Fer-se una idea de la situació, dibuixar-la i col locar el sistema de referència. 3.- Buscar les constants del moviment:
E1. Exercicis comentats
 ETSAV-UPC Matemàtiques I [títol_ ] Exercicis de matemàtiques I. Lliçó. [versió_ ] Setembre 200 [matèria_ ] Sistemes d equacions lineals. [assignatura_ ] Matemàtiques I [centre_ ] E. T. S. d'arquitectura
ETSAV-UPC Matemàtiques I [títol_ ] Exercicis de matemàtiques I. Lliçó. [versió_ ] Setembre 200 [matèria_ ] Sistemes d equacions lineals. [assignatura_ ] Matemàtiques I [centre_ ] E. T. S. d'arquitectura
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 PAU 2008 QÜESTIONS
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 Aquestes pautes no preveuen tots els casos que en la pràctica es poden presentar. Tampoc no pretenen donar totes les possibles
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 Aquestes pautes no preveuen tots els casos que en la pràctica es poden presentar. Tampoc no pretenen donar totes les possibles
Districte Universitari de Catalunya
 Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val
Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val
Geometria / GE 2. Perpendicularitat S. Xambó
 Geometria / GE 2. Perpendicularitat S. Xambó Vectors perpendiculars Ortogonal d un subespai Varietats lineals ortogonals Projecció ortogonal Càlcul efectiu de la projecció ortogonal Aplicació: ortonormalització
Geometria / GE 2. Perpendicularitat S. Xambó Vectors perpendiculars Ortogonal d un subespai Varietats lineals ortogonals Projecció ortogonal Càlcul efectiu de la projecció ortogonal Aplicació: ortonormalització
Equacions Diferencials 10 de Gener de 2014
 Equacions Diferencials de Gener de 24 243 - Problemes Temps: 2 hores 5 minuts 2,5 punts Contesteu les següents preguntes independents entre sí a Considereu el sistema X α t = AXt amb A =, α R. α a. Classifiqueu-lo.
Equacions Diferencials de Gener de 24 243 - Problemes Temps: 2 hores 5 minuts 2,5 punts Contesteu les següents preguntes independents entre sí a Considereu el sistema X α t = AXt amb A =, α R. α a. Classifiqueu-lo.
Matemàtiques 1 - FIB
 Matemàtiques - FI 7--7 Examen Final F Àlgebra lineal JUSTIFIQUEU TOTES LES RESPOSTES. [ punts] Siguin E i F dos espais vectorials, f : E F una aplicació lineal. (a) Digueu què ha de satisfer f per tal
Matemàtiques - FI 7--7 Examen Final F Àlgebra lineal JUSTIFIQUEU TOTES LES RESPOSTES. [ punts] Siguin E i F dos espais vectorials, f : E F una aplicació lineal. (a) Digueu què ha de satisfer f per tal
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 PAU 2009
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 1 QÜESTIONS 1.- Considereu la matriu A = ( ) A 2 1 0 =. 2 1 [2 punts] ( ) a 0. Calculeu el valor dels paràmetres a i b perquè
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 1 QÜESTIONS 1.- Considereu la matriu A = ( ) A 2 1 0 =. 2 1 [2 punts] ( ) a 0. Calculeu el valor dels paràmetres a i b perquè
UNITAT 3: SISTEMES D EQUACIONS
 UNITAT 3: SISTEMES D EQUACIONS 1. EQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITES L equació x + y = 3 és una equació de primer grau amb dues incògnites : x i y. Per calcular les solucions escollim un valor
UNITAT 3: SISTEMES D EQUACIONS 1. EQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITES L equació x + y = 3 és una equació de primer grau amb dues incògnites : x i y. Per calcular les solucions escollim un valor
j Introducció al càlcul vectorial
 FÍSICA 00 9 j Introducció al càlcul vectorial j Activitats finals h Qüestions 1. La suma dels vectors unitaris i, j és un altre vector unitari? Justifiqueu la resposta fent un gràfic. Els vectors unitaris
FÍSICA 00 9 j Introducció al càlcul vectorial j Activitats finals h Qüestions 1. La suma dels vectors unitaris i, j és un altre vector unitari? Justifiqueu la resposta fent un gràfic. Els vectors unitaris
P =
 RECULL DE PROBLEMES SOBRE MTRIUS I DETERMINNTS QUE HN SORTIT LES PROVES DE SELECTIVITT ) PU LOGSE 004 Sèrie Qüestió 3: Considereu les matrius compleixi X + = B. = i B =. Trobeu una matriu X que ) PU LOGSE
RECULL DE PROBLEMES SOBRE MTRIUS I DETERMINNTS QUE HN SORTIT LES PROVES DE SELECTIVITT ) PU LOGSE 004 Sèrie Qüestió 3: Considereu les matrius compleixi X + = B. = i B =. Trobeu una matriu X que ) PU LOGSE
Nom i Cognoms: Grup: Data:
 n BATX MA ) Raoneu la certesa o falsedat de les afirmacions següents: a) Si A és la matriu dels coeficients d'un sistema d'equacions lineals i Ampl és la matriu ampliada del mateix sistema. Rang(A) Rang
n BATX MA ) Raoneu la certesa o falsedat de les afirmacions següents: a) Si A és la matriu dels coeficients d'un sistema d'equacions lineals i Ampl és la matriu ampliada del mateix sistema. Rang(A) Rang
Apèndix Àlgebra lineal amb wxmaxima
 Apèndix Àlgebra lineal amb wxmaxima Objectius 1. Definir matrius amb wxmaxima. 2. Aplicar amb wxmaxima operacions amb matrius. 3. Aplicar transformacions elementals de matrius. 4. Calcular el determinant
Apèndix Àlgebra lineal amb wxmaxima Objectius 1. Definir matrius amb wxmaxima. 2. Aplicar amb wxmaxima operacions amb matrius. 3. Aplicar transformacions elementals de matrius. 4. Calcular el determinant
1. Què tenen en comú aquestes dues rectes? Com són entre elles? 2. En què es diferencien aquestes dues rectes?
 En la nostra vida diària trobem moltes situacions de relació entre dues variable que es poden interpretar mitjançant una funció de primer grau. La seva expressió algebraica és del tipus f(x)=mx+n. També
En la nostra vida diària trobem moltes situacions de relació entre dues variable que es poden interpretar mitjançant una funció de primer grau. La seva expressió algebraica és del tipus f(x)=mx+n. També
Vector unitari Els vectors unitaris tenen de mòdul la unitat. Calculem el vector unitari del vector següent manera: ( ) ( )
 GEOMETRIA EN L ESPAI VECTORS EN L ESPAI OPERACIONS AMB VECTORS Un vector és un segment orientat en l espai que té un mòdul, una direcció i un sentit coneguts: té un extrem i un origen (Exemple: vector
GEOMETRIA EN L ESPAI VECTORS EN L ESPAI OPERACIONS AMB VECTORS Un vector és un segment orientat en l espai que té un mòdul, una direcció i un sentit coneguts: té un extrem i un origen (Exemple: vector
Prova d accés a la Universitat (2013) Matemàtiques II Model 1. (b) Suposant que a = 1, trobau totes les matrius X que satisfan AX + Id = A, on Id
 UIB Prova d accés a la Universitat () Matemàtiques II Model Contestau de manera clara i raonada una de les dues opcions proposades. Es disposa de 9 minuts. Cada qüestió es puntua sobre punts. La qualificació
UIB Prova d accés a la Universitat () Matemàtiques II Model Contestau de manera clara i raonada una de les dues opcions proposades. Es disposa de 9 minuts. Cada qüestió es puntua sobre punts. La qualificació
Unitat 2 EQUACIONS DE PRIMER GRAU. Matemàtiques, Ciència i Tecnologia 5. TRANSFORMACIONS D EXPRESSIONS ALGEBRAIQUES UNITAT 2 EQUACIONS DE PRIMER GRAU
 Unitat 2 EQUACIONS DE PRIMER GRAU 37 38 Matemàtiques, Ciència i Tecnologia 5. TRANSFORMACIONS D EXPRESSIONS ALGEBRAIQUES UNITAT 2 QUÈ TREBALLARÀS? què treballaràs? En acabar la unitat has de ser capaç
Unitat 2 EQUACIONS DE PRIMER GRAU 37 38 Matemàtiques, Ciència i Tecnologia 5. TRANSFORMACIONS D EXPRESSIONS ALGEBRAIQUES UNITAT 2 QUÈ TREBALLARÀS? què treballaràs? En acabar la unitat has de ser capaç
MNEM - Mètodes Numèrics a l'enginyeria Mecànica
 Unitat responsable: Unitat que imparteix: Curs: Titulació: Crèdits ECTS: 2018 295 - EEBE - Escola d'enginyeria de Barcelona Est 737 - RMEE - Departament de Resistència de Materials i Estructures a l'enginyeria
Unitat responsable: Unitat que imparteix: Curs: Titulació: Crèdits ECTS: 2018 295 - EEBE - Escola d'enginyeria de Barcelona Est 737 - RMEE - Departament de Resistència de Materials i Estructures a l'enginyeria
Convocatòria Matemàtiques. Proves d accés a la universitat per a més grans de 25 anys. Sèrie 1. Fase específica
 Proves d accés a la universitat per a més grans de 25 anys Matemàtiques Sèrie 1 Fase específica Exercicis Qualificació 1 2 3 Convocatòria 2017 4 5 Problema Suma de notes parcials Qualificació final Qualificació
Proves d accés a la universitat per a més grans de 25 anys Matemàtiques Sèrie 1 Fase específica Exercicis Qualificació 1 2 3 Convocatòria 2017 4 5 Problema Suma de notes parcials Qualificació final Qualificació
t2 Donat el PVI següent, que depèn d un paràmetre µ R,
 Nom i cognoms: A 1 Equacions Diferencials (40131 Examen Final Juny 018 Temps: 3h... [Test ] [ Nota important: respostes correctes +1 punt incorrectes 0.5 punts ] { t1 x Donat el sistema d EDOs 3x y y y
Nom i cognoms: A 1 Equacions Diferencials (40131 Examen Final Juny 018 Temps: 3h... [Test ] [ Nota important: respostes correctes +1 punt incorrectes 0.5 punts ] { t1 x Donat el sistema d EDOs 3x y y y
x + 2 y = 3 2 x y = 1 4 x + 3 y = k a) Afegiu-hi una equació lineal de manera que el sistema resultant sigui incompatible.
 1998 - Sèrie 3 - Qüestió 4 Discutiu el sistema d'equacions a x y + 2 z = (2 a) 2 x + 3 y z = 3a x + 2 y z = 2a segons els valors del paràmetre a. 1999 - Sèrie 1 - Qüestió 1 Resoleu el sistema següent per
1998 - Sèrie 3 - Qüestió 4 Discutiu el sistema d'equacions a x y + 2 z = (2 a) 2 x + 3 y z = 3a x + 2 y z = 2a segons els valors del paràmetre a. 1999 - Sèrie 1 - Qüestió 1 Resoleu el sistema següent per
GEOMETRÍA ANALÍTICA PLANA
 GEOMETRÍA ANALÍTICA PLANA Un vector fijo es un segmento orientado que va del punto A (origen) al punto B (extremo). Módulo del vector : Es la longitud del segmento AB, se representa por. Dirección del
GEOMETRÍA ANALÍTICA PLANA Un vector fijo es un segmento orientado que va del punto A (origen) al punto B (extremo). Módulo del vector : Es la longitud del segmento AB, se representa por. Dirección del
2 desembre 2015 Límits i número exercicis. 2.1 Límits i número
 I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 2 desembre 205 Límits i número exercicis 2. Límits i número 4. Repàs de logaritmes i exponencials: troba totes les solucions de cadascuna de les següents equacions:
I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 2 desembre 205 Límits i número exercicis 2. Límits i número 4. Repàs de logaritmes i exponencials: troba totes les solucions de cadascuna de les següents equacions:
Generalitat de Catalunya Departament d Ensenyament Institut Obert de Catalunya. Avaluació contínua. Cognoms. Centre: Trimestre: Tardor 11
 Generalitat de Catalunya Departament d Ensenyament Institut Obert de Catalunya valuació contínua Qualificació prova TOTL Cognoms una lletra majúscula a cada casella: Nom: Centre: Trimestre: Tardor 11 M4
Generalitat de Catalunya Departament d Ensenyament Institut Obert de Catalunya valuació contínua Qualificació prova TOTL Cognoms una lletra majúscula a cada casella: Nom: Centre: Trimestre: Tardor 11 M4
Àlgebra lineal i equacions diferencials. Curs 2001/02 Exemple de diagonalització.
 Considerem la matriu Àlgebra lineal i equacions diferencials Química Curs 2001/02 Exemple de diagonalització. A = M 3 (R). Calculeu els valors propis de la matriu A. Calculeu els vectors propis pels valors
Considerem la matriu Àlgebra lineal i equacions diferencials Química Curs 2001/02 Exemple de diagonalització. A = M 3 (R). Calculeu els valors propis de la matriu A. Calculeu els vectors propis pels valors
Oficina d'organització de Proves d'accés a la Universitat Pàgina 1 de 8 PAU 2004
 Oficina d'organització de Proves d'accés a la Universitat Pàgina de 8 PAU 004 SÈRIE 3 Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals (ara bé, dins de cada pregunta podeu utilitzar
Oficina d'organització de Proves d'accés a la Universitat Pàgina de 8 PAU 004 SÈRIE 3 Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals (ara bé, dins de cada pregunta podeu utilitzar
Examen FINAL M2 FIB-UPC 11 de gener de 2017
 Examen FINAL M FIB-UPC 11 de gener de 017 1. (3 punts) Sigui {a n } la successió tal que: a 1 = 56 i a n+1 = a n per a tot n > 1. a) Proveu que 1 a n 56, per a tot n 1. b) Proveu que {a n } és decreixent.
Examen FINAL M FIB-UPC 11 de gener de 017 1. (3 punts) Sigui {a n } la successió tal que: a 1 = 56 i a n+1 = a n per a tot n > 1. a) Proveu que 1 a n 56, per a tot n 1. b) Proveu que {a n } és decreixent.
ACTIVITATS. a) b) c) d) INS JÚLIA MINGUELL 2n Batxillerat. dv, 18 de març Alumne:
 INS JÚLIA MINGUELL 2n Batxillerat Matemàtiques Tasca Continuada 4 «Matrius i Sistemes d equacions lineals» Alumne: dv, 18 de març 2016 LLIURAMENT: dm, 5 d abril 2016 NOTA: cal justificar matemàticament
INS JÚLIA MINGUELL 2n Batxillerat Matemàtiques Tasca Continuada 4 «Matrius i Sistemes d equacions lineals» Alumne: dv, 18 de març 2016 LLIURAMENT: dm, 5 d abril 2016 NOTA: cal justificar matemàticament
Examen Final 17 de gener de 2013
 MATEMÀTIQUES FIB-UPC Examen Final 7 de gener de 03 a) Representeu gràficament la corba definida per l equació y = x 5x. b) Determineu si el conjunt C = { x R x 5x 6 } és fitat superiorment inferiorment)
MATEMÀTIQUES FIB-UPC Examen Final 7 de gener de 03 a) Representeu gràficament la corba definida per l equació y = x 5x. b) Determineu si el conjunt C = { x R x 5x 6 } és fitat superiorment inferiorment)
VECTORS I RECTES AL PLA. Exercici 1 Tenint en compte quin és l'origen i quin és l'extrem, anomena els següents vectors: D
 VECTORS I RECTES AL PLA Un vector és un segment orientat que és determinat per dos punts, A i B, i l'ordre d'aquests. El primer dels punts s'anomena origen i el segons es denomina extrem, i s'escriu AB.
VECTORS I RECTES AL PLA Un vector és un segment orientat que és determinat per dos punts, A i B, i l'ordre d'aquests. El primer dels punts s'anomena origen i el segons es denomina extrem, i s'escriu AB.
Examen FINAL M2 FIB-UPC 12 de juny de 2015
 Examen FINAL M FIB-UPC 1 de juny de 015 1. ( punts Sigui a R, calculeu els límits següents segons els valors d a: n + n n + a+ a+n a n n n, n n + n!.. ( punts Considereu la integral següent: I = 1.8 1
Examen FINAL M FIB-UPC 1 de juny de 015 1. ( punts Sigui a R, calculeu els límits següents segons els valors d a: n + n n + a+ a+n a n n n, n n + n!.. ( punts Considereu la integral següent: I = 1.8 1
Oficina d Accés a la Universitat Pàgina 1 de 12 PAU 2015
 Oficina d Accés a la Universitat Pàgina 1 de 12 Sèrie 5 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar
Oficina d Accés a la Universitat Pàgina 1 de 12 Sèrie 5 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar
Universitat Pompeu Fabra Anàlisi Multivariant, curs Prof. Albert Satorra Prof. Ajudant. Ferran Carrascosa. Deure 4
 Universitat Pompeu Fabra Anàlisi Multivariant, curs 2011-2012 Prof. Albert Satorra Prof. Ajudant. Ferran Carrascosa Deure 4 Exercici 1. Considereu la matriu X següent: X = 0 1 2 1 0 3 2 3 0 3 4 1 6 3 2
Universitat Pompeu Fabra Anàlisi Multivariant, curs 2011-2012 Prof. Albert Satorra Prof. Ajudant. Ferran Carrascosa Deure 4 Exercici 1. Considereu la matriu X següent: X = 0 1 2 1 0 3 2 3 0 3 4 1 6 3 2
Tema 2: GEOMETRIA ANALÍTICA AL PLA
 Tema : GEOMETRIA ANALÍTICA AL PLA Vector El vector AB és el segment orientat amb origen al punt A i extrem al punt B b a A B Les projeccions del vector sobre els eixos són les components del vector: a
Tema : GEOMETRIA ANALÍTICA AL PLA Vector El vector AB és el segment orientat amb origen al punt A i extrem al punt B b a A B Les projeccions del vector sobre els eixos són les components del vector: a
4. EQUACIONS DE PRIMER GRAU AMB UNA INCÒGNITA
 Definició d'equació. Equacions de primer grau amb una incògnita 1. EQUACIONS: DEFINICIONS Equació: igualtat entre dues expressions algebraiques. L'expressió de l'esquerra de la igualtat rep el nom de PRIMER
Definició d'equació. Equacions de primer grau amb una incògnita 1. EQUACIONS: DEFINICIONS Equació: igualtat entre dues expressions algebraiques. L'expressió de l'esquerra de la igualtat rep el nom de PRIMER
z 2 4z + 5 = 0, z = x + iy, i 1,
 Àlgebra i Geometria I Tema I NOMBRES COMPLEXOS 1- Necessitat dels nombres complexos i definició (a) Les solucions de les equacions polinòmiques El nombre imaginari i 1 Els enters Z, els racionals Q i els
Àlgebra i Geometria I Tema I NOMBRES COMPLEXOS 1- Necessitat dels nombres complexos i definició (a) Les solucions de les equacions polinòmiques El nombre imaginari i 1 Els enters Z, els racionals Q i els
TEMA 6 : Geometria en l espai. Activitats
 TEMA 6 : Geometria en l espai Activitats 1. Siguin els punts A(1,2,3), B(0,1,3) i C(2,3,1) a) Trobeu el vector b) Calculeu el mòdul del vector c) Trobeu el vector unitari d igual direcció que el vector
TEMA 6 : Geometria en l espai Activitats 1. Siguin els punts A(1,2,3), B(0,1,3) i C(2,3,1) a) Trobeu el vector b) Calculeu el mòdul del vector c) Trobeu el vector unitari d igual direcció que el vector
PRIMERA MODEL B Codi B2. A1. C
 TOT n 15-16 -1/1 PRIMERA MODEL B Codi B A1 C1 15-16 1- (1) a) Raoneu que els polinomis són funcions contínues a tots el reals (1) b) Digueu que entenem per discontinuïtat de salt i poseu-ne un exemple
TOT n 15-16 -1/1 PRIMERA MODEL B Codi B A1 C1 15-16 1- (1) a) Raoneu que els polinomis són funcions contínues a tots el reals (1) b) Digueu que entenem per discontinuïtat de salt i poseu-ne un exemple
TEMA 4 : Programació lineal
 TEMA 4 : Programació lineal 4.1. SISTEMES D INEQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITA La solució d aquest sistema és l intersecció de les regions que correspon a la solució de cadascuna de les inequacions
TEMA 4 : Programació lineal 4.1. SISTEMES D INEQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITA La solució d aquest sistema és l intersecció de les regions que correspon a la solució de cadascuna de les inequacions
Fitxa per recollir informació sobre activitats d aula realitzades amb TAC d interès especial. Es treballa sobre els següents continguts:
 Fitxa per recollir informació sobre activitats d aula realitzades amb TAC d interès especial Títol de l activitat REPRESENTACIÓ DE FUNCIONS Mestre/a - Professor/a Nom i Cognoms Adreça electrònica Cristina
Fitxa per recollir informació sobre activitats d aula realitzades amb TAC d interès especial Títol de l activitat REPRESENTACIÓ DE FUNCIONS Mestre/a - Professor/a Nom i Cognoms Adreça electrònica Cristina
c) C = (c ij ) de tres files i tres columnes per a) u r = (1, 2, 3, 4), c) u r = (1, 1, 1), v r = (2, 4, 8) i w r = (3, 9, 27)
 SOLUCONAR Unitat 8 Comencem Cada 100 g de producte d un determinat aliment conté 0,06 g de vitamina A, 0,3 g de vitamina B i 0, g de calci. Anàlogament, un altre aliment conté 0,1 g de vitamina A, 0, g
SOLUCONAR Unitat 8 Comencem Cada 100 g de producte d un determinat aliment conté 0,06 g de vitamina A, 0,3 g de vitamina B i 0, g de calci. Anàlogament, un altre aliment conté 0,1 g de vitamina A, 0, g
XXXV OLIMPÍADA MATEMÀTICA
 XXXV OLIMPÍADA MATEMÀTICA Primera fase (Catalunya) 10 de desembre de 1999, de 16 a 0h. 1. Amb quadrats i triangles equilàters de costat unitat es poden construir polígons convexos. Per exemple, es poden
XXXV OLIMPÍADA MATEMÀTICA Primera fase (Catalunya) 10 de desembre de 1999, de 16 a 0h. 1. Amb quadrats i triangles equilàters de costat unitat es poden construir polígons convexos. Per exemple, es poden
Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS
 Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS 2.1. Divisió de polinomis. Podem fer la divisió entre dos monomis, sempre que m > n. Si hem de fer una divisió de dos polinomis, anirem calculant les divisions
Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS 2.1. Divisió de polinomis. Podem fer la divisió entre dos monomis, sempre que m > n. Si hem de fer una divisió de dos polinomis, anirem calculant les divisions
Estudiem la funció (,, ) en un domini obert on existeixen, i són contínues, totes les seves derivades parcials fins l ordre que sigui necessari.
 Estudiem la funció (,, ) en un domini obert on existeixen, i són contínues, totes les seves derivades parcials fins l ordre que sigui necessari. PUNT CRÍTIC (o ESTACIONARI): (,, ) és punt estacionari d
Estudiem la funció (,, ) en un domini obert on existeixen, i són contínues, totes les seves derivades parcials fins l ordre que sigui necessari. PUNT CRÍTIC (o ESTACIONARI): (,, ) és punt estacionari d
Proves d accés a la Universitat per a més grans de 25 anys Convocatòria 2013
 Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes. Nom i Cognoms: Grup: Data:
 Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques n BATX MA Eamen FINAL Nom i Cognoms: Grup: Data: -5-007 r BLOC: ) Trobeu els límits:
Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques n BATX MA Eamen FINAL Nom i Cognoms: Grup: Data: -5-007 r BLOC: ) Trobeu els límits:
Aquí veremos la armadura de cuatro barras del ejemplo 4.1 pero con carga diferente. Considere E=29.5E6psi. y Ae=1in2
 Ejemplo 4.b (Página ) Introducción al estudio del Elemento Finito en Ingeniería Segunda Edición TITUPATHI R. CHANDRUPATLA ASHOK D. BELEGUNDU PRENTICE HALL Aquí veremos la armadura de cuatro barras del
Ejemplo 4.b (Página ) Introducción al estudio del Elemento Finito en Ingeniería Segunda Edición TITUPATHI R. CHANDRUPATLA ASHOK D. BELEGUNDU PRENTICE HALL Aquí veremos la armadura de cuatro barras del
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 16 PAU cx by + 2z = b. 2a+b c = a+c 2b 1 b = a b c
 Oficina d Organització de Proves d Accés a la Universitat Pàgina de 6 PAU 0 SÈRIE 4.- Sabem que el vector (,, ) és solució del sistema ax + by + cz = a+c bx y + bz = a b c. cx by + z = b Calculeu el valor
Oficina d Organització de Proves d Accés a la Universitat Pàgina de 6 PAU 0 SÈRIE 4.- Sabem que el vector (,, ) és solució del sistema ax + by + cz = a+c bx y + bz = a b c. cx by + z = b Calculeu el valor
Llei de Kirchhoff. Mètode de les malles. Càlcul resistència equivalent. on I>0, si la intensitat és entrant I<0, si la intensitat és isquent
 lei de Kirchhoff. ètode de les malles. Càlcul resistència equivalent l hora d estudiar el règim d intensitats que circula per una xarxa elèctrica, necessitem tantes equacions com branques té la xarxa,
lei de Kirchhoff. ètode de les malles. Càlcul resistència equivalent l hora d estudiar el règim d intensitats que circula per una xarxa elèctrica, necessitem tantes equacions com branques té la xarxa,
= 1+ β, essent α i β paràmetres reals. a la recta r 2. i el pla Π d equació
 Problema A Setembre 0 + y z = En l espai es té la recta r i el pla Π d equacions r x + mz = 0, on x y z = 0 m és un paràmetre real a) Un vector director de la recta r b) El valor de m per al qual la recta
Problema A Setembre 0 + y z = En l espai es té la recta r i el pla Π d equacions r x + mz = 0, on x y z = 0 m és un paràmetre real a) Un vector director de la recta r b) El valor de m per al qual la recta
U.N.S.C.H. Escuela Profesional de Ingeniería Civil
 Análisis de Armadura por el Método de Rigidez Curso : Análisis Estructural II / IC 4 Profesor : Estudiante : CANCHARI GUIÉRREZ, Edmundo. Cod. Est. : 65 U.N.S.C.H Escuela Profesional de Ingeniería Civil
Análisis de Armadura por el Método de Rigidez Curso : Análisis Estructural II / IC 4 Profesor : Estudiante : CANCHARI GUIÉRREZ, Edmundo. Cod. Est. : 65 U.N.S.C.H Escuela Profesional de Ingeniería Civil
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 PAU 2009
 Oficina d Organització de Proves d Accés a la Universitat Pàgina de 0 SÈRIE 4 QÜESTIONS.- Donats el punt P =(,, ) ilarectar : x = y + = z 5 : a) Trobeu l equació cartesiana (és a dir, de la forma Ax +
Oficina d Organització de Proves d Accés a la Universitat Pàgina de 0 SÈRIE 4 QÜESTIONS.- Donats el punt P =(,, ) ilarectar : x = y + = z 5 : a) Trobeu l equació cartesiana (és a dir, de la forma Ax +
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 11 PAU 2005
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 11 PAU 005 SÈRIE. Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals. Ara bé, dins de cada pregunta podeu utilitzar
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 11 PAU 005 SÈRIE. Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals. Ara bé, dins de cada pregunta podeu utilitzar
Equacions i sistemes de segon grau
 Equacions i sistemes de segon grau 3 Equacions de segon grau. Resolució. a) L àrea del pati d una escola és quadrada i fa 0,5 m. Per calcular el perímetre del pati seguei els passos següents: Escriu l
Equacions i sistemes de segon grau 3 Equacions de segon grau. Resolució. a) L àrea del pati d una escola és quadrada i fa 0,5 m. Per calcular el perímetre del pati seguei els passos següents: Escriu l
TEMA 3: Polinomis 3.1 DEFINICIONS:
 TEMA 3: Polinomis 3.1 DEFINICIONS: Anomenarem monomi qualsevol expressió algèbrica formada per la multiplicació d un nombre real i d una variable elevada a un exponent natural. El nombre es diu coeficient
TEMA 3: Polinomis 3.1 DEFINICIONS: Anomenarem monomi qualsevol expressió algèbrica formada per la multiplicació d un nombre real i d una variable elevada a un exponent natural. El nombre es diu coeficient
POLINOMIS. p(x) = a 0 + a 1 x + a 2 x a n x n,
 POLINOMIS Un monomi és una expressió de la forma ax m, on el coeficient a és un nombre real o complex, x és una indeterminada i m és un nombre natural o zero. Un polinomi és una suma finita de monomis,
POLINOMIS Un monomi és una expressió de la forma ax m, on el coeficient a és un nombre real o complex, x és una indeterminada i m és un nombre natural o zero. Un polinomi és una suma finita de monomis,
1- Preguntes breus (resposta correcta del apartat són 0.5 punts. Total de punts, 5 sobre 10).
 UPF, Anàlisi Multivariant, Examen Final, de desembre de, De. a 7.,Aula 4. Professor: Albert Satorra Instruccions: Aquest examen consta de tres apartats. El primer són preguntes breus sobre temes diversos.
UPF, Anàlisi Multivariant, Examen Final, de desembre de, De. a 7.,Aula 4. Professor: Albert Satorra Instruccions: Aquest examen consta de tres apartats. El primer són preguntes breus sobre temes diversos.
TEMA 4 : Geometria analítica al pla. Vectors i la Recta. Activitats
 TEMA 4 : Geometria analítica al pla. Vectors i la Recta Activitats 1. Donats els punts A(2,1), B(6,5),i C(-1,4): a) Representa els vectors AB i CA i estudia totes les seves característiques b) Calcula
TEMA 4 : Geometria analítica al pla. Vectors i la Recta Activitats 1. Donats els punts A(2,1), B(6,5),i C(-1,4): a) Representa els vectors AB i CA i estudia totes les seves característiques b) Calcula
CARACTERÍSTIQUES DE FUNCIONS ELEMENTALS
 CARACTERÍSTIQUES DE FUNCIONS ELEMENTALS 1. FUNCIÓ CONSTANT (document d'ajuda: 1_funcio_constant.html ) Expressió algèbrica: f(x) = n. Gràfica: 2. FUNCIÓ LINEAL (document d'ajuda: 2_funcio_lineal.html )
CARACTERÍSTIQUES DE FUNCIONS ELEMENTALS 1. FUNCIÓ CONSTANT (document d'ajuda: 1_funcio_constant.html ) Expressió algèbrica: f(x) = n. Gràfica: 2. FUNCIÓ LINEAL (document d'ajuda: 2_funcio_lineal.html )
DOSSIER DE RECUPERACIÓ 3r ESO
 DOSSIER DE RECUPERACIÓ 3r ESO INS MARIANAO. Departament de matemàtiques La correcta realització d aquest dossier, i la posterior entrega el dia de l examen puntuarà un 20% de la nota total. Les activitats
DOSSIER DE RECUPERACIÓ 3r ESO INS MARIANAO. Departament de matemàtiques La correcta realització d aquest dossier, i la posterior entrega el dia de l examen puntuarà un 20% de la nota total. Les activitats
LA FUNCIÓ EXPONENCIAL I LA FUNCIÓ LOGARÍTMICA. FUNCIONS DEFINIDES A TROSSOS. Funció exponencial
 LA FUNCIÓ EXPONENCIAL I LA FUNCIÓ LOGARÍTMICA. FUNCIONS DEFINIDES A TROSSOS. Funció eponencial La funció eponencial és de la forma f () = a, on a > 0, a 1 El valor a s anomena base de la funció eponencial.
LA FUNCIÓ EXPONENCIAL I LA FUNCIÓ LOGARÍTMICA. FUNCIONS DEFINIDES A TROSSOS. Funció eponencial La funció eponencial és de la forma f () = a, on a > 0, a 1 El valor a s anomena base de la funció eponencial.
8 Geometria analítica
 Geometria analítica INTRODUCCIÓ Els vectors s utilitzen en diverses branques de la física que fan servir magnituds vectorials, per això és important que els alumnes en coneguin els elements i les operacions.
Geometria analítica INTRODUCCIÓ Els vectors s utilitzen en diverses branques de la física que fan servir magnituds vectorials, per això és important que els alumnes en coneguin els elements i les operacions.
ETSAV-UPC Matemàtiques I 5
 ETSAV-UPC Matemàtiques I 5 [títol_ ] Lliçó 3. Exercicis [versió_ ] Octubre 8 [matèria_ ] Sistemes de referència. [assignatura_ ] Matemàtiques I [centre_ ] E. T. S. d'arquitectura del Vallès - Universitat
ETSAV-UPC Matemàtiques I 5 [títol_ ] Lliçó 3. Exercicis [versió_ ] Octubre 8 [matèria_ ] Sistemes de referència. [assignatura_ ] Matemàtiques I [centre_ ] E. T. S. d'arquitectura del Vallès - Universitat
GEOMETRIA ANALÍTICA PLANA
 GEOMETRIA ANALÍTICA PLANA Un vector fix és un segment orientat que va del punt A (origen) al punto B (extrem). M òdul del vector AB, es representa pe r. : É s la long itud del segment Direc ció del vector
GEOMETRIA ANALÍTICA PLANA Un vector fix és un segment orientat que va del punt A (origen) al punto B (extrem). M òdul del vector AB, es representa pe r. : É s la long itud del segment Direc ció del vector
EXAMEN D ENLLAÇ QUÍMIC I ESTRUCTURA. 25 DE GENER DE 2010
 EXAMEN D ENLLAÇ QUÍMIC I ESTRUCTURA. 1ª CONVOCATÒRIA Nom:... 25 DE GENER DE 2010 1. (15 punts) a) Una làmina d un determinat metall només emet electrons quan és irradiada amb radiació de longituds d ona
EXAMEN D ENLLAÇ QUÍMIC I ESTRUCTURA. 1ª CONVOCATÒRIA Nom:... 25 DE GENER DE 2010 1. (15 punts) a) Una làmina d un determinat metall només emet electrons quan és irradiada amb radiació de longituds d ona
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 PAU 2009 QÜESTIONS
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 PAU 009 SÈRIE 4 QÜESTIONS 1. Considereu el sistema d inequacions següent: x 0, y 0 x+ 5y 10 3x+ 4y 1 a) Dibuixeu la regió de solucions
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 PAU 009 SÈRIE 4 QÜESTIONS 1. Considereu el sistema d inequacions següent: x 0, y 0 x+ 5y 10 3x+ 4y 1 a) Dibuixeu la regió de solucions
Matemàtiques Sèrie 1
 Proves d accés a cicles formatius de grau superior de formació professional inicial, d ensenyaments d arts plàstiques i disseny, i d ensenyaments esportius 013 Matemàtiques Sèrie 1 SOLUCIONS, CRITERIS
Proves d accés a cicles formatius de grau superior de formació professional inicial, d ensenyaments d arts plàstiques i disseny, i d ensenyaments esportius 013 Matemàtiques Sèrie 1 SOLUCIONS, CRITERIS
( b) ( a) Matemàtiques - Activitats d estiu 4t ESO + = NOMBRES REALS. 1. Calcula, extraient factors fora dels radicals:
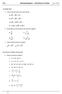 NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
Tema 1. La teoria cineticomolecular de la matèria PRIMERES LLEIS CIENTÍFIQUES DE LA QUÍMICA
 Tema 1. La teoria cineticomolecular de la matèria PRIMERES LLEIS CIENTÍFIQUES DE LA QUÍMICA Les primeres lleis relatives a les reaccions químiques han estat desenvolupades al segle XVIII. Hi ha lleis referents
Tema 1. La teoria cineticomolecular de la matèria PRIMERES LLEIS CIENTÍFIQUES DE LA QUÍMICA Les primeres lleis relatives a les reaccions químiques han estat desenvolupades al segle XVIII. Hi ha lleis referents
TEMA 5 : Derivades. Tècniques de derivació. Activitats
 TEMA 5 : Derivades. Tècniques de derivació Activitats. Calculeu, mitjançant la definició de derivada, la derivada de les funcions següents en els punts indicats: a) f() en f() + 4 5 en - c) f() 6 + 5 en
TEMA 5 : Derivades. Tècniques de derivació Activitats. Calculeu, mitjançant la definició de derivada, la derivada de les funcions següents en els punts indicats: a) f() en f() + 4 5 en - c) f() 6 + 5 en
GEOMETRIA ANALÍTICA DEL PLA. MATEMÀTIQUES-1
 GEOMETRIA ANALÍTICA DEL PLA. 1. Vectors en el pla.. Equacions de la recta. 3. Posició relativa de dues rectes. 4. Paral lelisme de rectes. 5. Producte escalar de dos vectors. 6. Perpendicularitat de rectes.
GEOMETRIA ANALÍTICA DEL PLA. 1. Vectors en el pla.. Equacions de la recta. 3. Posició relativa de dues rectes. 4. Paral lelisme de rectes. 5. Producte escalar de dos vectors. 6. Perpendicularitat de rectes.
ESTUDI COMPUTACIONAL DEL COMPORTAMENT EN GRANS DEFORMACIONS D'ESTRUCTURES INFLABLES
 Titulació: ENGINYERIA AERONÀUTICA Alumna: ANNA MIR MAÑÉ Títol PFC: ESTUDI COMPUTACIONAL DEL COMPORTAMENT EN GRANS DEFORMACIONS D'ESTRUCTURES INFLABLES Director del PFC: JORDI MARCÉ NOGUÉ Convocatòria de
Titulació: ENGINYERIA AERONÀUTICA Alumna: ANNA MIR MAÑÉ Títol PFC: ESTUDI COMPUTACIONAL DEL COMPORTAMENT EN GRANS DEFORMACIONS D'ESTRUCTURES INFLABLES Director del PFC: JORDI MARCÉ NOGUÉ Convocatòria de
Semblança. Teorema de Tales
 Semblança. Teorema de Tales Dos polígons són semblants si el angles corresponents són iguals i els costats corresponents són proporcionals. ABCDE A'B'C'D'E' si: Â = Â',Bˆ = Bˆ', Ĉ = Ĉ', Dˆ = Dˆ', Ê = Ê'
Semblança. Teorema de Tales Dos polígons són semblants si el angles corresponents són iguals i els costats corresponents són proporcionals. ABCDE A'B'C'D'E' si: Â = Â',Bˆ = Bˆ', Ĉ = Ĉ', Dˆ = Dˆ', Ê = Ê'
EXERCICIS - SOLUCIONS
 materials del curs de: MATEMÀTIQUES SISTEMES D EQUACIONS EXERCICIS - SOLUCIONS AUTOR: Xavier Vilardell Bascompte xevi.vb@gmail.com ÚLTIMA REVISIÓ: 21 d abril de 2009 Aquests materials han estat realitzats
materials del curs de: MATEMÀTIQUES SISTEMES D EQUACIONS EXERCICIS - SOLUCIONS AUTOR: Xavier Vilardell Bascompte xevi.vb@gmail.com ÚLTIMA REVISIÓ: 21 d abril de 2009 Aquests materials han estat realitzats
Tema 3: EQUACIONS I INEQUACIONS
 Tema 3: EQUACIONS I INEQUACIONS Igualtats algebraiques Es poden diferenciar: identitats i equacions a) Identitats Són igualtats que sempre es compleixen, per qualsevol valor numèric que donem a les lletres.
Tema 3: EQUACIONS I INEQUACIONS Igualtats algebraiques Es poden diferenciar: identitats i equacions a) Identitats Són igualtats que sempre es compleixen, per qualsevol valor numèric que donem a les lletres.
VALASAIG - Validació i Assaig de Màquines
 Unitat responsable: 840 - EUPMT - Escola Universitària Politècnica de Mataró Unitat que imparteix: 840 - EUPMT - Escola Universitària Politècnica de Mataró Curs: Titulació: 2016 GRAU EN ENGINYERIA MECÀNICA
Unitat responsable: 840 - EUPMT - Escola Universitària Politècnica de Mataró Unitat que imparteix: 840 - EUPMT - Escola Universitària Politècnica de Mataró Curs: Titulació: 2016 GRAU EN ENGINYERIA MECÀNICA
ÀLGEBRA LINEAL I GEOMETRIA. PROBLEMES
 TEXTOS DOCENTS 199 ÀLGEBRA LINEAL I GEOMETRIA. PROBLEMES Robert Estalella Guillem Anglada Rosendo Vílchez Rosario López Ferran Sala Departament d Astronomia i Meteorologia U UNIVERSITAT DE BARCELONA B
TEXTOS DOCENTS 199 ÀLGEBRA LINEAL I GEOMETRIA. PROBLEMES Robert Estalella Guillem Anglada Rosendo Vílchez Rosario López Ferran Sala Departament d Astronomia i Meteorologia U UNIVERSITAT DE BARCELONA B
Un breu resum de teoria
 SISTEMES MULTICOMPONENTS. Regla de les fases Un breu resum de teoria Els sistemes químics són en general mescles de més d un component. Les funcions termodinàmiques depenen de la temperatura i de la pressió
SISTEMES MULTICOMPONENTS. Regla de les fases Un breu resum de teoria Els sistemes químics són en general mescles de més d un component. Les funcions termodinàmiques depenen de la temperatura i de la pressió
program el_meu_primer_programa write(*,*) 'Hello, cruel world!' end --------------------------------------------------------------------
 program el_meu_primer_programa write(,) 'Hello, cruel world!' end -------------------------------------------------------------------- program segon_programa read(,) a write(,) 'Has entrat el numero ',a
program el_meu_primer_programa write(,) 'Hello, cruel world!' end -------------------------------------------------------------------- program segon_programa read(,) a write(,) 'Has entrat el numero ',a
POLÍGONS, CIRCUMFERÈNCIA I CERCLE
 POLÍGONS, CIRCUMFERÈNCIA I CERCLE POLÍGONS Polígon és la figura plana tancada formada per n segments P 1P,PP3,P3P4,...,Pn P1 ( n 3 ) anomenats costats, essent els punts P,P,... els vèrtexs. 1 Pn L angle
POLÍGONS, CIRCUMFERÈNCIA I CERCLE POLÍGONS Polígon és la figura plana tancada formada per n segments P 1P,PP3,P3P4,...,Pn P1 ( n 3 ) anomenats costats, essent els punts P,P,... els vèrtexs. 1 Pn L angle
DERIVADES. TÈCNIQUES DE DERIVACIÓ
 UNITAT 7 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 56 Tangents a una corba y f (x) 5 5 9 4 Troba, mirant la gràfica i les rectes traçades, f'(), f'(9) i f'(4). f'() 0; f'(9) ; f'(4) 4 Digues uns altres
UNITAT 7 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 56 Tangents a una corba y f (x) 5 5 9 4 Troba, mirant la gràfica i les rectes traçades, f'(), f'(9) i f'(4). f'() 0; f'(9) ; f'(4) 4 Digues uns altres
Oficina d Accés a la Universitat Pàgina 1 de 10 PAU 2014 Criteris específics de correcció i qualificació per ser fets públics un cop finalitzades
 Oficina d Accés a la Universitat Pàgina 1 de 10 SÈRIE 3 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val punts. Podeu utilitzar
Oficina d Accés a la Universitat Pàgina 1 de 10 SÈRIE 3 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val punts. Podeu utilitzar
FUNCIONS REALS. MATEMÀTIQUES-1
 FUNCIONS REALS. 1. El concepte de funció. 2. Domini i recorregut d una funció. 3. Característiques generals d una funció. 4. Funcions definides a intervals. 5. Operacions amb funcions. 6. Les successions
FUNCIONS REALS. 1. El concepte de funció. 2. Domini i recorregut d una funció. 3. Característiques generals d una funció. 4. Funcions definides a intervals. 5. Operacions amb funcions. 6. Les successions
