Clasificación Afín de las Cuádricas
|
|
|
- Gloria Lozano Sevilla
- hace 5 años
- Vistas:
Transcripción
1 Capítulo VIII Clasificación Afín de las Cuádricas Como no puede ser de otro modo, en este capítulo seguiremos suponiendo que k es un cuerpo conmutativo de característica distinta de 2, que todos los espacios vectoriales que aparezcan lo son sobre k y de dimensión finita, y que E es un k-espacio vectorial de dimensión n. 1 Preliminares Empezaremos dando unas propiedades sencillas de las métricas simétricas que nos serán muy útiles en el resto del capítulo. Lema 1.1 Sea T 2 una métrica no singular sobre E, y sea E un hiperplano vectorial de E. Se cumple dim(rad E ) 1. Demostración. Basta tener en cuenta las igualdades dim(e ) = dim E dim E = 1 y rad E = E (E ). Lema 1.2 Sean E y E 0 subespacios vectoriales de E. Si E es un hiperplano de E entonces: E 0 E ó dim(e 0 E ) = dim E 0 1. Demostración. Si E 0 E entonces E 0 + E = E (porque E es un hiperplano de E ), y para terminar basta aplicar la fórmula de la dimensión para los subespacios vectoriales. 1.3 Sea T 2 una métrica no singular sobre E. Si {e i } es una base de E y A es la matriz de T 2 en esa base, entonces podemos considerar el escalar A k. Dicho escalar no es un invariante de la métrica T 2, ya que depende de la base elegida. Veamos cómo varía al cambiar la base: si {e i } es otra base de E, y si B es la matriz de cambio de la base {e i } a la base {e i}, entonces la matriz de T 2 en la base {e i } es A = B t AB ; por lo tanto A = B 2 A. Si consideramos el grupo multiplicativo k, y si k 2 denota el conjunto de los elementos de k que son iguales al cuadrado de algún elemento de k, entonces k 2 es un subgrupo de k y podemos considerar el grupo cociente k /k 2. En el párrafo anterior hemos probado que la clase del escalar no nulo A en el grupo cociente k /k 2 no depende de la base elegida en E, y por lo tanto dicha clase sí es un invariante de la métrica no singular T
2 130 Capítulo VIII. Clasificación Afín de las Cuádricas Definición 1.4 Sea T 2 una métrica no singular sobre E. Llamaremos discriminante de T 2 a la clase de A en el grupo k /k 2, siendo A el determinante de la matriz de T 2 en una base cualquiera de E (véase 1.3). El discriminante de T 2 lo denotaremos dis T 2, ó dis E si la referencia a la métrica considerada sobre E es clara. Lema 1.5 Sea T 2 una métrica no singular sobre E ( dim E = n). Si λ k entonces la métrica λt 2 es no singular y se cumple dis(λt 2 ) = λ n dis T 2 (donde λ n dis T 2 debe entenderse como la clase de λ n en k /k 2 multiplicada por dis T 2 ). Además, si E = E 1 E 2 con E 1 y E 2 no singulares entonces dis E = dis E 1 dis E 2. Demostración. Es un sencillo ejercicio. Lema 1.6 Sean E 1 y E 2 espacios vectoriales de dimensión uno dotados de sendas métricas simétricas no singulares. Tenemos: E 1 y E 2 son isométricos dis E 1 = dis E 2. Demostración. Es un sencillo ejercicio. 2 Posiciones Relativas de un Hiperplano Respecto de una Cuádrica Para todo lo que resta de capítulo fijaremos en P(E) una cuádrica T 2, cuyo lugar denotaremos por C, y un hiperplano H = π(e ). Por simplificar la notación identificaremos la cuádrica T 2 con su lugar y hablaremos de la cuádrica C ; del mismo modo, hablaremos de la cuádrica C H refiriéndonos a la cuádrica T 2 restringida al hiperplano H (aunque puede ocurrir que dicha cuádrica restringida no exista porque H C ). 2.1 En esta sección supondremos que no se satisface el caso trivial H = C, es decir, C no es el hiperplano H doble (o sea, descartamos el caso rad E = E, el cual se corresponde con las igualdades rg E = 1 y rg E = 0). Recordemos que el hiperplano H se dice que es tangente a la cuádrica C, si H C (en cuyo caso no existe la cuádrica C restringida a H ), ó si el vértice de la cuádrica restringida C H contiene estrictamente al corte de H con el vértice de C. Recordemos también que el vértice de C es la subvariedad lineal definida por el subespacio rad E, y que el vértice de C H es la subvariedad lineal definida por el subespacio rad E. (Véase VI.2.12.) Lema 2.2 Las posibles posiciones relativas del hiperplano H respecto de la cuádrica C son: Caso (a): H no contiene al vértice de C ( lo que equivale a la condición rad E rad E ). Caso (b): H contiene al vértice de C y no es tangente a C ( lo que equivale a la condición rad E = rad E ). Caso (c): H contiene al vértice de C y es tangente a C (lo que equivale a la condición rad E rad E ). Demostración. De la definición de radical se sigue trivialmente: rad E E rad E rad E. Por lo tanto: H contiene al vértice de C rad E E rad E rad E.
3 Posiciones Relativas de un Hiperplano Respecto de una Cuádrica 131 Probemos: H es tangente a C rad E rad E. La implicación es fácil y se deja como ejercicio. Veamos la implicación. Si H C entonces E es totalmente isótropo, y como E es un hiperplano debe se maximal, de modo que rad E E = rad E ; además, según 2.1 la inclusión debe ser estricta: rad E rad E. Si H C, por definición de tangencia tenemos (rad E) E rad E. Si rad E E, entonces existe e rad E tal que E = e E y por lo tanto rad E = e rad E ; de la anterior igualdad se sigue (rad E) E = rad E, lo cual está en contra de la condición de tangencia. Por lo tanto debe ser rad E E y obtenemos rad E = (rad E) E rad E. De todo lo dicho se sigue que el que H contenga al vértice de C y no sea tangente a C es equivalente a la condición rad E = rad E. Lema 2.3 Con la notación e hipótesis introducidas hasta ahora tenemos: En el caso (a): existe un subespacio no singular Ē en E tal que E = rad E Ē y E = [ (rad E) E ] Ē. En el caso (b): existe un subespacio no singular Ē en E tal que E = rad E Ē y E = rad E Ē, Ē hiperplano no singular de Ē. En el caso (c): existe un subespacio no singular Ē en E tal que E = rad E Ē y E = rad E Ē, Ē hiperplano singular de Ē. Demostración. Supongamos en primer lugar que rad E rad E (ó equivalentemente, que rad E E ). Existe e rad E tal que E = e E, y existe un subespacio no singular Ē tal que E = rad E Ē. Por lo tanto E = e rad E Ē y obtenemos las igualdades rad E = e rad E, rad E = (rad E) E. Supongamos ahora que H contiene al vértice de C : rad E rad E. Si Ē es un subespacio no singular de E tal que E = rad E Ē, entonces Ē E (pues si Ē E tendríamos E = rad E Ē rad E + E = E ). Por lo tanto Ē = E Ē es un hiperplano de Ē en virtud del lema 1.2, y aplicando la fórmula de la dimensión obtenemos E = rad E Ē. Si rad E = rad E (caso (b)) entonces rad Ē = 0 (Ē es un hiperplano no singular de Ē ), y si rad E rad E (caso (c)) entonces rad Ē 0 (Ē es un hiperplano singular de Ē ). 2.4 En lo que sigue, r e i denotarán el rango y el índice de la cuádrica C, y r e i denotarán el rango y el índice de la cuádrica restringida C H. Teorema 2.5 Con la notación e hipótesis introducidas hasta ahora en esta sección tenemos: En el caso (a): (r, i ) = (r, i). En el caso (b): (r, i ) = (r 1, i) ó (r, i ) = (r 1, i 1). En el caso (c): (r, i ) = (r 2, i 1).
4 132 Capítulo VIII. Clasificación Afín de las Cuádricas Demostración. Se sigue del lema 2.3. En el caso (a), E y E tienen la misma parte no singular, por lo tanto E y E tienen el mismo rango y el mismo índice. En el caso (b), sean Ē y Ē la parte no singular de E y E, respectivamente, donde Ē es un hiperplano de Ē. Tenemos r = dim Ē = dim Ē 1 = r 1. Ahora, por una parte, todo subespacio totalmente isótropo de Ē es un subespacio totalmente isótropo de Ē y por lo tanto i i ; por otra parte, si F es un subespacio totalmente isótropo maximal de Ē, entonces Ē F es un subespacio totalmente isótropo de Ē y por lo tanto (véase el lema 1.2) i 1 = dim F 1 dim(ē F ) i. En el caso (c), si Ē es la parte no singular de E, existe un hiperplano singular Ē de Ē tal que E = rad E Ē y por tanto rad E = rad E rad Ē. Como, según el lema 1.1, es dim(rad Ē ) = 1, obtenemos r = dim E dim(rad E ) = dim E dim(rad E) dim(rad Ē ) = (n 1) (n r) 1 = r 2. Ahora, como la parte no singular de E es igual a la parte no singular de Ē tenemos que el índice de E es igual al índice de Ē, así que calculemos éste último. La dimensión de los subespacios totalmente isótropos maximales de Ē es i, y la dimensión de los subespacios totalmente isótropos maximales de Ē es 1 + i porque dim(rad Ē ) = 1 (véase el problema V.4.1 (c)). Por lo tanto, si vemos que existe un subespacio totalmente isotropo maximal de Ē que también es maximal en Ē tendremos i = 1 + i, que es lo que nos falta probar. Sea e 1 Ē tal que rad Ē = e 1, de modo que e 1 = Ē (ortogonal tomado dentro de Ē ); como e 1 es un subespacio totalmente isótropo de Ē, e 1 está contenido en un subespacio totalmente isótropo maximal F de Ē; en particular, F e 1, por lo que F es un subespacio totalmente isótropo de Ē que debe ser maximal (si F no fuera maximal en Ē, entonces tampoco sería maximal en Ē ). Observación 2.6 Conocidos los rangos de C y C H, el teorema 2.5 nos permite deducir la posición relativa del hiperplano H respecto de la cuádrica C. Esta observación es válida incluso en el caso trivial que no hemos considerado en los anteriores resultados (véase 2.1): C es el hiperplano H doble r = 1 y r = 0. 3 Teoremas de Clasificación Consideremos en lo que sigue el espacio afín A = (P(E), H) que el hiperplano H = π(e ) define en P(E), y fijemos otra cuádrica T 2 de P(E) cuyo lugar denotaremos C. 3.1 Recordemos que las cuádricas C y C son (proyectivamente) equivalentes si existe una proyectividad τ : P(E) P(E) que transforma la cuádrica C en la cuádrica C, lo que expresaremos abreviadamente escribiendo τ(c) = C. Recordemos también que una proyectividad τ : P(E) P(E) transforma la cuádrica C en la cuádrica C si existen un escalar λ k y un representante lineal T : E E de τ tales que T : (E, λt 2 ) (E, T 2 ) es una isometría. Por último, recordemos que una autoafinidad de A es una autoproyectividad de P(E) que deja invariante al hiperplano H (véase III.6.3).
5 3. Teoremas de Clasificación 133 Definiciones 3.2 Llamaremos cuádrica sobre el espacio afín A a toda cuádrica sobre el espacio proyectivo P(E). Diremos que las cuádricas C y C de A son afínmente equivalentes si existe una afinidad τ : A A tal que τ(c) = C. Es decir, C y C de son afínmente equivalentes si existen un escalar λ k y un isomorfismo lineal T : E E tales que T : (E, λt 2 ) (E, T 2 ) es una isometría que manda el hiperplano vectorial E a él mismo. Teorema 3.3 Si H 1 y H 2 son hiperplanos de P(E) tales que las cuádricas C H 1 y C H 2 son proyectivamente equivalentes, entonces existe una proyectividad τ : P(E) P(E) tal que τ(c) = C y τ(h 1 ) = H 2. Demostración. Nótese que C H 1 y C H 2 tienen el mismo rango (porque son equivalentes), y por consiguiente las posiciones relativas de H 1 y H 2 respecto de C son la misma (véase la observación 2.6). Analicemos los tres casos posibles, para lo cual consideremos los hiperplanos vectoriales E 1 y E 2 de E tales que H 1 = π(e 1 ) y H 2 = π(e 2 ). (El teorema es trivialmente cierto cuando C es el hiperplano H 1 doble, pues en ese caso debe ser H 1 = H 2.) (a) H 1 y H 2 no contienen al vértice de C. En este caso, según el lema 2.3 tenemos E = rad E Ē1 = rad E Ē2, E 1 = rad E 1 Ē1, E 2 = rad E 2 Ē2, donde Ēi = parte no singular de E i y rad E i = rad E E i, i = 1, 2. Si F i es un subespacio suplementario de rad E i en rad E, entonces E = rad E Ēi = F i rad E i Ēi = F i E i. La hipótesis C H 1 y C H 2 son equivalentes significa que existe λ k y una isometría f : (E 1, λt 2 ) (E 2, T 2 ). Si g : F 1 F 2 es un isomorfismo cualquiera (existe porque dim F 1 = dim F 2 ), entonces g : (F 1, λt 2 ) (F 2, T 2 ) es una isometría (porque F 1 y F 2 son totalmente isótropos), y por lo tanto T = g f : (F 1 E 1, λt 2 ) (F 2 E 2, T 2 ) es una isometría que satisface T (E 1 ) = E 2, por lo que τ = T es la proyectividad buscada. (b) H 1 y H 2 contienen al vértice de C y no son tangentes a C. En este caso tenemos las descomposiciones E = rad E Ē, E 1 = rad E Ē1, E 2 = rad E Ē2, donde Ē1 = E 1 Ē y Ē2 = E 2 Ē son hiperplanos no singulares de Ē (véase el lema 2.3 y su demostración). Sean e 1, e 2 Ē vectores no nulos tales que e 1 = Ē 1 y e 2 = Ē 2 (ortogonales tomados dentro de Ē ), y sean a 1 = T 2 (e 1, e 1 ), a 2 = T 2 (e 2, e 2 ). Por una parte, tomando discriminantes en las igualdades Ē = Ē1 e 1 = Ē2 e 2 resulta (véase el lema 1.5) (dis Ē1) a 1 = (dis Ē2) a 2. Por otra parte, la equivalencia de C H 1 y C H 2 implica que existe λ k tal que los espacios (Ē1, λt 2 ) y (Ē2, T 2 ) son isométricos, y por lo tanto (véase el lema 1.5) dis Ē2 = λ m dis Ē1 (m = dim Ē1). De todo lo anterior resulta a 1 = λ m a 2 (en k /k 2 ).
6 134 Capítulo VIII. Clasificación Afín de las Cuádricas Distiguimos ahora dos casos. Si λ m es un cuadrado, entonces a 1 = a 2 (en k /k 2 ) y por lo tanto existe una isometría e 1 e 2 (véase el lema 1.6). Por el teorema de Witt, esta isometría extiende a una isometría g : Ē Ē que transforma e 1 = Ē1 en e 2 = Ē2. La proyectividad buscada es la proyectivización de la isometría T = Id g : E = rad E Ē rad E Ē = E. Si λ m no es un cuadrado, entonces m es impar y por lo tanto a 1 = λ 1 a 2 (en k /k 2 ). Esto implica que ( e 1, λt 2 ) y ( e 2, T 2 ) son isométricos, y como (Ē1, λt 2 ) y (Ē2, T 2 ) también son isométricos tenemos en conjunto una isometría (E, λt 2 ) = (rad E Ē1 e 1, λt 2 ) (rad E Ē2 e 2, T 2 ) = (E, T 2 ) que induce la proyectividad buscada. (c) H 1 y H 2 contienen al vértice de C y son tangentes a C. En este caso tenemos las descomposiciones E = rad E Ē, E 1 = rad E Ē1, E 2 = rad E Ē2, donde Ē1 = E 1 Ē y Ē2 = E 2 Ē son hiperplanos singulares de Ē cuyos radicales tienen dimensión 1 (véanse los lemas 2.3 y 1.1). Sean e 1, e 2 Ē vectores no nulos tales que e 1 = rad Ē1 y e 2 = rad Ē2. Como e 1 y e 2 son totalmente isótropos existe una isometría e 1 e 2, la cual extiende por el teorema de Witt a una isometría h : Ē Ē que transforma e 1 = Ē1 en e 2 = Ē2 (ortogonales tomados dentro de Ē ); entonces la isometría induce la proyectividad buscada. T = Id h : E = rad E Ē rad E Ē = E Teorema 3.4 Las cuádricas C y C de A son afínmente equivalentes, si y sólo si, son proyectivamente equivalentes y sus restricciones al hiperplano del infinito, C H y C H, también son proyectivamente equivalentes. Demostración. Si C y C son afínmente equivalentes, entonces existe una proyectividad τ : P(E) P(E) tal que τ(c) = C y τ(h) = H ; en particular C y C son proyectivamente equivalentes. Además, la restricción de τ a H define una autoproyectividad de H que transforma C H en C H, por lo que las cuádricas C H y C H también son proyectivamente equivalentes. Supongamos ahora que C y C son proyectivamente equivalentes, y que C H y C H son proyectivamente equivalentes. Sea τ : P(E) P(E) una proyectividad que trasforma C en C, y denotemos H = τ (H). Es claro que las cuádricas C H y C H son equivalentes, y como por hipótesis las cuádricas C H y C H son equivalentes, obtenemos que C H y C H son cuádricas equivalentes. Por el teorema 3.3 aplicado a la cuádrica C y a los hiperplanos H y H, existe una proyectividad τ : P(E) P(E) tal que τ (C ) = C y τ (H ) = H. Entonces τ = τ τ es una autoafinidad de A (porque τ(h) = H ) que transforma C en C, con lo que concluimos que C y C son afínmente equivalentes.
7 4. Ecuaciones Reducidas 135 Combinando el resultado anterior con los teoremas VII.5.3 y VII.5.5 obtenemos los teoremas de clasificación afín de las cuádricas en los dos casos que venimos considerando habitualmente: el algebraicamente cerrado y el real: 3.5 Teorema de clasificación: Si el cuerpo k es algebraicamente cerrado, entonces C y C son afínmente equivalentes, si y sólo si, C y C tienen igual rango y C H y C H también tienen igual rango. 3.6 Teorema de clasificación: Si k = R, entonces C y C son afínmente equivalentes, si y sólo si, C y C tienen igual rango e índice y C H y C H también tienen igual rango e índice. 4 Ecuaciones Reducidas Veamos a continuación la expresión en coordenadas de las cuádricas afines respecto de un sistema de referencia apropiado. 4.1 Como hasta ahora, C = T 2 es una cuádrica en P(E) de rango r e índice i, H = π(e ) es un hiperplano de P(E), y r e i denotan el rango y el índice de la cuádrica restringida C H. Recordemos que dar una referencia afín en el espacio afín A = (P(E), H) significa dar una referencia proyectiva (P 0, P 1,..., P n, U) en el espacio proyectivo P(E) tal que P 1 + +P n = H. Es decir, una referencia afín de A es una referencia proyectiva de P(E) respecto de la cual la ecuación del hiperplano del infinito H es x 0 = 0. Recordemos también que, fijada una referencia afín, si (x 0, x 1,..., x n ) son las coordenadas homogéneas de un punto P A, entonces las coordenadas afines de P son (y 1,..., y n ), donde y 1 = x 1 x 0,..., y n = x n x Cuerpo algebraicamente cerrado: Caso (a): El hiperplano H no contiene al vértice de C, es decir, r = r. En este caso E = rad E Ē y E = [(rad E) E ] Ē, por lo que existe un vector no nulo e 0 rad E tal que E = e 0 E. Si {e r+1,..., e n } es una base de (rad E) E y {e 1,..., e r } una base ortonormal de Ē, entonces {e 1,..., e r, e r+1,..., e n } es una base de E, por lo que {e 0, e 1,..., e r, e r+1,..., e n } es una base de E en la cual la ecuación de E es x 0 = 0. Proyectivizando dicha base de E obtenemos una referencia afín de A en la cual la ecuación de (el lugar de) la cuádrica C en coordenadas homogéneas es y la ecuación de C en coordenadas afines es x x 2 r = 0, 1 r n, y y 2 r = 0, 1 r n. Caso (b): El hiperplano H contiene al vértice de C y no es tangente a C, es decir, r = r 1; como además la posibilidad (r, r ) = (1, 0) la consideramos aparte debe ser r 2. En este caso E = rad E Ē y E = rad E Ē, siendo Ē un hiperplano no singular de Ē. Sea {e 0, e 1,..., e r 1 } una base ortonormal de Ē tal que Ē = e 0 Ē. Si {e r,..., e n } es una base
8 136 Capítulo VIII. Clasificación Afín de las Cuádricas de rad E, entonces {e 0, e 1,..., e r 1, e r,..., e n } es una base de E que define una referencia afín de A, en la cual la ecuación de C en coordenadas homogéneas es y la ecuación de C en coordenadas afines es x x 2 r 1 = 0, 2 r n + 1, 1 + y y 2 r 1 = 0, 2 r n + 1. Caso (c): El hiperplano H contiene al vértice de C y es tangente a C, es decir, r = r 2 ( r 2). En este caso E = rad E Ē y E = rad E Ē, siendo Ē un hiperplano singular de Ē. Del lema 1.1 se sigue que existe un vector isótropo e 1 Ē y un subespacio no singular F tal que Ē = e 1 F. En particular, existe un vector v Ē tal que F = v, e 1 (ortogonal tomado dentro de Ē ), de modo que F es un espacio vectorial de dimensión 2 que es no singular (Ē y F son no singulares) y que es no elíptico (el vector e 1 es isótropo), es decir, F es un plano hiperbólico. Por lo tanto existe un par hiperbólico (u, e 1 ) tal que F = u, e 1 (véase el lema V.3.2). Si definimos e 0 = 1 2 u, entonces {e 0, e 1 } es una base de F formada por vectores isótropos tales que T 2 (e 0, e 1 ) = 1 2. Si {e 2,..., e r 1 } es una base ortonormal de F y {e r,..., e n } es una base de rad E, entonces {e 0, e 1,..., e r 1, e r,..., e n } es una base de E en la cual la matriz de T 2 es r 2) , por lo que la ecuación de C en coordenadas homogéneas respecto de la referencia afín que dicha base de E define es x 0 x 1 + x x 2 r 1 = 0, 2 r n + 1, y la ecuación de C en coordenadas afines es y 1 + y y 2 r 1 = 0, 2 r n + 1. Caso (r, r ) = (1, 0): C es el hiperplano H doble. En este caso es claro que en cualquier referencia afín de A la ecuación en coordenadas homogéneas de C es x 2 0 = 0, de modo que su ecuación en coordenadas afines es 1 = 0, que es la ecuación del vacío. Es decir, C no tiene puntos afines en su lugar. A continuación aparecen, para dimensiones bajas, las tablas de clasificación de las cuádricas afines sobre el cuerpo C de los números complejos:
9 4. Ecuaciones Reducidas 137 Cónicas en A 2 (C) r r 0 1 = 0 y 1 = 0 vacío 1 y 2 1 = 0 recta doble una recta 1 + y 2 1 = 0 dos rectas paralelas y 1 + y 2 2 = 0 parábola 2 y y 2 2 = 0 dos rectas no paralelas 1 + y y 2 2 = 0 hipérbola Cuádricas en A 3 (C) r r = 0 y 1 = 0 vacío 1 y 2 1 = 0 plano doble un plano 1 + y 2 1 = 0 dos planos paralelos y 1 + y 2 2 = 0 cilindro parabólico 2 y y 2 2 = 0 dos planos no paralelos 1 + y y 2 2 = 0 cilindro hiperbólico y 1 + y y 2 3 = 0 paraboloide 3 y y y 2 3 = 0 cono de vértice un punto 1 + y y y 2 3 = 0 hiperboloide
10 138 Capítulo VIII. Clasificación Afín de las Cuádricas Cuádricas en A 1 (C) r r = 0 y 1 = 0 vacío 1 y 2 1 = 0 punto doble un punto 1 + y 2 1 = 0 dos puntos distintos 4.3 Cuerpo real: Procediendo como en 4.2 para el caso algebraicamente cerrado, se llega a que existe una base B de E tal que, respecto del sistema de referencia proyectivo que define B, la ecuación en coordenadas homogéneas del lugar de la cuádrica C es: si (r, i ) = (r, i), x x 2 r i x 2 r i+1 x 2 r = 0, ( 1 r n i r 2 ) ; si (r, i ) = (r 1, i), x x 2 r i 1 x 2 r i x 2 r 1 = 0, ( 2 r n + 1 i < r 2 ) ; si (r, i ) = (r 1, i 1), x x x 2 r i x 2 r i+1 x 2 r 1 = 0, ( 2 r n + 1 i r 2 ) ; si (r, i ) = (r 2, i 1), x 0 x 1 x 2 2 x 2 i + x 2 i x 2 r 1 = 0, ( 2 r n + 1 i r 2 ). La referencia proyectiva respecto de la cual se obtienen las anteriores ecuaciones se construye de modo que la ecuación homogénea del hiperplano H es x 0 = 0 (es decir, en la base B la ecuación del subespacio E es x 0 = 0), por lo tanto es una referencia afín de A en la cual la ecuación de C en coordenadas afines es: si (r, i ) = (r, i), y y 2 r i y 2 r i+1 y 2 r = 0, ( 1 r n i r 2 ) ;
11 4. Ecuaciones Reducidas 139 si (r, i ) = (r 1, i), y yr i 1 2 yr i 2 yr 1 2 = 1, si (r, i ) = (r 1, i 1), y yr i 2 yr i+1 2 yr 1 2 = 1, ( 2 r n + 1 i < r 2 ( 2 r n + 1 i r 2 ) ; ) ; si (r, i ) = (r 2, i 1), y 1 = y y 2 i y 2 i+1 y 2 r 1, ( 2 r n + 1 i r 2 ). Cuádricas en A 3 (R) (..\..) (r, i) (r, i ) (0,0) 1 = 0 (1,0) (2,0) (2,1) (3,0) y 1 = 0 vacío (1,0) y 2 1 = 0 plano doble y 2 1 = 1 planos imaginarios paralelos un plano y 2 1 = 1 par de planos paralelos (2,0) y y 2 2 = 0 planos imaginarios no paralelos y y 2 2 = 1 cilindro imaginario (2,1) y 2 1 y 2 2 = 0 par de planos no paralelos (3,0) y y y 2 3 = 0 (3,1) cono imaginario
12 140 Capítulo VIII. Clasificación Afín de las Cuádricas Cuádricas en A 3 (R) (continuación) (r, i) (r, i ) (0,0) (3,1) (4,0) (4,1) (4,2) (1,0) y 1 = y 2 2 cilindro parabólico (2,0) y y 2 2 = 1 cilindro elíptico y 1 = y y 2 3 paraboloide no reglado (2,1) y 2 1 y 2 2 = 1 cilindro hiperbólico y 1 = y 2 2 y 2 3 paraboloide reglado (3,0) y y y 2 3 = 1 (3,1) y y 2 2 y 2 3 = 0 cono elipsoide imaginario y y y 2 3 = 1 elipsoide real y 2 1 y 2 2 y 2 3 = 1 hiperboloide no reglado y y 2 2 y 2 3 = 1 hiperboloide reglado
13 4. Ecuaciones Reducidas 141 Cónicas en A 2 (R) (r, i) (r, i ) (0,0) 1 = 0 (1,0) (2,0) (2,1) (3,0) (3,1) y 1 = 0 vacío una recta (1,0) y 2 1 = 0 y 2 1 = 1 y 2 1 = 1 y 1 = y 2 2 recta doble rectas imaginarias paralelas par de rectas paralelas parábola (2,0) y y 2 2 = 0 rectas imaginarias no paralelas (2,1) y 2 1 y 2 2 = 0 par de rectas no paralelas y y 2 2 = 1 elipse imaginaria y1 2 + y2 2 = 1 elipse real y1 2 y2 2 = 1 hipérbola Cuádricas en A 1 (R) (r, i) (r, i ) (0,0) 1 = 0 (1,0) (2,0) (2,1) y 1 = 0 vacío (1,0) y 2 1 = 0 punto doble y 2 1 = 1 dos puntos imaginarios un punto y 2 1 = 1 dos puntos distintos
14 142 Capítulo VIII. Clasificación Afín de las Cuádricas 5 Elementos Afines de las Cuádricas Continuamos con la notación introducida en las secciones anteriores. Definiciones 5.1 Llamaremos centro de la cuádrica C a todo punto afín que sea conjugado (respecto de C ) de todo punto del infinito. Es decir, los centros son los puntos afines de la subariedad lineal H, la cual se denomina subvariedad de centros de la cuádrica C. El significado geométrico de la proposición VI.2.3 es el siguiente: si P 0 es un centro de C y r es una recta afín que pasa por P 0 y corta a la cuádrica en dos puntos afines Q 1 y Q 2, entonces P 0 es el punto medio de Q 1 y Q 2. Si la cuádrica C es no singular entonces H es un punto, y cuando dicho punto es afín es el único centro de la cuádrica. Una cuádrica no singular con un único centro de denomina cuádrica central, y una cuádrica no singular sin centro se llama paraboloide. Es decir, las cuádricas centrales son las cuádricas no singulares que no son tangentes al hiperplano del infinito, y los paraboloides son las cuádricas no singulares que son tangentes al hiperplano del infinito. Definiciones 5.2 Supongamos que la subvariedad de centros de la cuádrica C es no vacía y sea r una recta de A que pasa por uno de los centros de C. Diremos que r es un diámetro de C si no es tangente a la cuádrica, y diremos que r es una asíntota de C si es tangente a la cuádrica. Dos diámetros de C se dice que son conjugados si sus direcciones son puntos de H conjugados respecto de C. Supongamos ahora que C es un paraboloide y sea P = H (es decir, C es no singular y el hiperplano del infinito H es tangente a C en el punto del infinito P ); entonces se definen los diámetros de C como las rectas afines que pasan por P (es decir, las rectas afines cuya dirección es P ). Ejemplos 5.3 Veamos los elementos afines de las cónicas reales. Como es usual, denotaremos las coordenadas afín del plano por (x, y) (en lugar de (y 1, y 2 )). (a) Cónicas sin centros. Parábola: y = x 2. En este caso la cónica es tangente en un punto a la recta del infinito, y los diámetros son las rectas afines cuya dirección es dicho punto (todo los diámetros son paralelos). El origen de la referencia afín es un punto de la cónica, el eje y = 0 es la tangente a la cónica en el origen, y el eje x = 0 es el diámetro que pasa por el origen. Una recta: x = 0. El origen de la referencia es un punto de la cónica, y el eje y = 0 es una recta que pasa por el origen y no está contenida en la cónica. (b) Cónicas con un único centro. Elipse real: x 2 + y 2 = 1. Los diámetros son las rectas que pasan por el centro (no hay asíntotas). El origen de la referencia es el centro de la cónica y los ejes son dos diámetros conjugados. Elipse imaginaria: x 2 + y 2 = 1. Los diámetros son las rectas que pasan por el centro (no hay asíntotas). El origen de la referencia es el centro de la cónica y los ejes son dos diámetros conjugados.
15 5. Elementos Afines de las Cuádricas 143 (c) Hipérbola: x 2 y 2 = 1. De las rectas que pasan por el centro, dos son asíntotas y el resto son diámetros. El origen de la referencia es el centro de la cónica y los ejes son dos diámetros conjugados. Par de rectas no paralelas: x 2 y 2 = 0. El centro es la intersección de las dos rectas, las asíntotas son las dos rectas, y los diámetros son las rectas que pasan por el centro distintas de las del lugar de la cónica. El origen de la referencia es el centro de la cónica y los ejes son dos diámetros conjugados. Par de rectas imaginarias no paralelas: x 2 + y 2 = 0. El centro es la intersección de las dos rectas, y todas las rectas que pasan por el centro son diámetros (no hay asíntotas). El origen de la referencia es el centro de la cónica y los ejes son dos diámetros conjugados. Cónicas con una recta de centros. Par de rectas paralelas: x 2 = 1. La recta de centros es x = 0. Toda recta afín no paralela a x = 0 es diámetro. El origen de la referencia es un punto afín de x = 0, y el eje y = 0 es una recta afín que pasa por el origen y es distinta de la recta de centros. Par de rectas imaginarias paralelas: x 2 = 1. La recta de centros es x = 0. Los diámetros son todas las rectas afines no paralelas a x = 0. El origen de la referencia es un punto afín de x = 0, y el eje y = 0 es una recta (distinta de x = 0) que pasa por el origen. Recta doble: x 2 = 0. La recta de centros es x = 0. Toda recta afín no paralela a x = 0 es diámetro. El origen de la referencia es un punto afín de x = 0, y el eje y = 0 es una recta afín (distinta de x = 0) que pasa por el origen. (d) Para la cónica que en coordenadas homogéneas tiene por ecuación x 2 0 = 0 (en cuyo lugar no hay puntos afines), todo punto afín es centro, toda recta afín es diámetro, y en cualquier referencia afín su ecuación en coordenadas homogéneas es x 2 0 = 0. Ejercicio 5.4 A continuación damos la lista de todas las cuádricas del espacio proyectivo real de dimensión 3, agrupadas según la dimensión de su variedad de centros. Dígase en cada caso si hay ó no hay asíntotas, y cómo es un sistema de referencia afín respecto del cual se obtiene la ecuación reducida. (a) Cuádricas sin centro: Paraboloide reglado: z = x 2 y 2. Paraboloide no reglado: z = x 2 + y 2. Cilindro parabólico: y = x 2. Un plano: x = 0. (b) Cuádricas con un único centro: Elipse real: x 2 + y 2 + z 2 = 1. Elipse imaginaria: x 2 + y 2 + z 2 = 1. Hiperboloide reglado: x 2 + y 2 z 2 = 1. Hiperboloide no reglado: x 2 + y 2 z 2 = 1. Cono real: x 2 + y 2 z 2 = 0. Cono imaginario: x 2 + y 2 + z 2 = 0. (c) Cuádricas con una recta de centros: Cilindro hiperbólico: x 2 y 2 = 1. Cilindro elíptico: x 2 + y 2 = 1. Cilindro imaginario: x 2 + y 2 = 1. Par de planos no paralelos: x 2 y 2 = 0. Par de planos imaginarios no paralelos: x 2 + y 2 = 0. (d) Cuádricas con un plano de centros: Par de planos paralelos: x 2 = 1. Par de planos imaginarios paralelos: x 2 = 1. Plano doble: x 2 = 0.
16 144 Capítulo VIII. Clasificación Afín de las Cuádricas 6 Problemas En todos los problemas enunciados a continuación, el cuerpo base será R. 6.1 Hágase la clasificación afín de las cónicas (a), (b) y de las cuádricas (c), (d): (a) 3x 2 5xy + y 2 x + 2y 1 = 0 ; (b) x y 2 10xy + 6x 30y = 0 ; (c) 2x 2 + 2y 2 + 2z 2 2xy + 2xz 2yz + 1 = 0 ; (d) x 2 3y 2 2z 2 + xy xz + 5x 3y 1 = Hágase la clasificación afín (según el valor del parámetro m ) de la cuádrica x 2 + (2m 2 + 1)(y 2 + z 2 ) 2(xy + yz + zx) = 2m 2 3m Hállese la ecuación de la cuádrica cuyo corte con el plano x = 0 es la cónica yz 2y+z = 0, que contiene la recta y = 0 = z y la recta del infinito del plano y = 0, y que pasa por el punto (1, 1, 0). 6.4 Dada la parábola cuya ecuación en un sistema de referencia afín (O; v 1, v 2 ) es x 2 + y 2 + 2xy 2y 1 = 0, hállese otro sistema de referencia afín en el cual la ecuación de dicha parábola sea ȳ = x Dada la hipérbola cuya ecuación en un sistema de referencia afín (O; v 1, v 2 ) es x 2 + y 2 + 4xy 2y = 0, hállese otro sistema de referencia afín en el cual la ecuación de dicha hipérbola sea x 2 ȳ 2 = 1. Encuéntrese también un tercer sistema de referencia en el que la ecuación de la hipérbola sea x ȳ = Dada la elipse cuya ecuación en un sistema de referencia afín (O; v 1, v 2 ) es x 2 + y 2 + 2x 3 = 0, hállese otro sistema de referencia afín en el cual la ecuación de dicha elipse sea x 2 + ȳ 2 = Clasifíquese la cuádrica de ecuación 3x 2 +2y 2 +3z 2 2xz 2x 4y 2z = 5, y obténgase un sistema de referencia afín en la que se obtenga su ecuación reducida. Hágase lo mismo con las cuádricas x 2 + y 2 + z 2 4xz 4y = 2 y 4xz + y = El lugar geométrico de las centros de las cónicas del haz x 2 + 4axy + 4y 2 2ax + 4y = 3, (a R) forman una hipérbola. Calcúlense las asíntotas de las cónicas del haz. 6.9 Hállese el cilindro circunscrito a la cuádrica 2x 2 + 3y 2 2z = 0 y cuyas generatrices son paralelas a la recta x = y = 2z Calcúlese la cuádrica que corta al plano z = 0 en la cónica x 2 + y 2 xy + 2x = 1, pasa por los puntos (0, 1, 2) y (2, 0, 3), y es tangente al eje z en el punto (0, 0, 1).
17 6. Problemas Determínese los planos tangentes a la cuádrica 2x 2 + 3y 2 = 2z que pasan por la recta 2y 1 = 0 2x + 6y z 4 = Hállese una cuádrica que pase por las tres siguientes rectas: } x + y = y + 1 = ( z 1)/2, x 1 = (y 1)/2 = (1 z)/3, (x 2)/2 = y 2 = (2 1)/ Al cortar la cuádrica 6xz 3x + 2yz + y + 3z 2 4z + 3 = 0 con los dos planos paralelos x + y + 2z = 0, x + y + 2z = 1 se obtienen dos cónicas homotéticas. Hállense los centros de las homotecias que transforman una de dichas cónicas en la otra. Qué ocurre si cortamos los mismos planos con la cuádrica 4x 2 + 3y 2 12z 2 = 1? 6.14 Redúzcase el cálculo de las raíces del polinomio x 4 + ax 3 + bx 2 + cx + d al cálculo de las raíces de un polinomio de grado Dado un punto P de una elipse C, demuéstrese que el lugar geométrico de los puntos medios de los segmentos P X, donde X recorre C, es una elipse tangente a C en P. Calcúlese dicho lugar cuando C es x 2 + 2y 2 2x 4y + 2 = 0 y P = (2, 1) Las rectas paralelas a las de un hiperboloide reglado trazadas desde un punto cualquiera del espacio forman un cono Sea C el lugar de una cuádrica no singular reglada de P 3 (R). Tenemos: (a) Por cada punto P de C pasan exactamente dos rectas contenidas en C. Dichas rectas son el corte con C del plano tangente a C en P. (b) En el conjunto de las rectas contenidas en C se define la relación: r 1, r 2 C, r 1 r 2. r 1 = r 2, ó r 1 r 2 =. La relación es de equivalencia y para ella hay exactamente 2 clases de equivalencia Determínense las dos rectas que pasan por el punto (1, 1, 1) y que están contenidas en el hiperboloide reglado x 2 y 2 + z 2 1 = 0. Determínense también las dos rectas que pasan por el punto (1, 1, 0) y que están contenidas en el paraboloide reglado x 2 y 2 + z = Si r 1, r 2, r 3 son tres rectas de P 3 (R) que se cruzan, entonces hay una única cuádrica en P 3 (R) que pasa por esas rectas. El lugar de dicha cuádrica, que es no singular y reglada, es la unión de las rectas que se apoyan a la vez en r 1, r 2 y r 3. Así se describe toda cuádrica no singular reglada de P 3 (R).
18 146 Capítulo VIII. Clasificación Afín de las Cuádricas 6.20 En el espacio afín A 3 (R), dadas tres rectas que se cruzan y son paralelas a un plano, la superficie engendrada por una recta que se mueve apoyándose sobre las tres rectas dadas es un paraboloide reglado. Puede generarse de este modo todo paraboloide reglado? 6.21 Demuéstrese que las cuerdas 1 de una elipse cuyo punto medio yace sobre una recta fija (que no es diámetro) envuelven una parábola Las diagonales de un paralelogramo circunscrito a una elipse (o una hipérbola) son diámetros conjugados de la misma Dado un cuadrivértice completo en un plano afín, los puntos medios de sus seis lados yacen sobre una cónica que pasa por los tres puntos diagonales Sea P un punto de una cónica central C, y sea d un diámetro de C que no pasa por P y que corta a C en puntos distintos Q 1 y Q 2. Las rectas P + Q 1 y P + Q 2 son paralelas a diámetros conjugados Sea d un diámetro de una cónica central y sea d el diámetro conjugado de d. Toda cuerda de la cónica paralela a d es cortada por d en su punto medio Fijada una recta r y una parábola, existe un diámetro de la parábola tal que los puntos medios de las cuerdas de la parábola que son paralelas a r yacen sobre dicho diámetro Dada una cónica afín no singular cuya ecuación en una referencia afín (P 0 ; v 1, v 2 ) es ax 2 + 2bxy + cy 2 a b + 2(dx + fy) + e = 0, denotemos = b c. (a) Cuando = 0 la cónica es una parábola y su punto del infinito es la dirección que define el vector bv 1 av 2. (b) Cuando 0 la cónica es central y su centro es el punto cuyas coodenadas afines son la solución del sistema de ecuaciones lineales } ax + by = d. bx + cy = f 1 La noción de cuerda debe entenderse en sentido general, esto es, una cuerda puede cortar a la cónica en dos puntos imaginarios conjugados.
G. SERRANO SOTELO. H = e 0 + E
 CLASIFICACIÓN AFÍN DE CÓNICAS Y CUÁDRICAS G. SERRANO SOTELO 1. Cuádricas en un hiperplano afín Sea E un R-espacio vectorial de dimensión n +1. Sean E = e 1,...,e n un hiperplano vectorial de E y e un vector
CLASIFICACIÓN AFÍN DE CÓNICAS Y CUÁDRICAS G. SERRANO SOTELO 1. Cuádricas en un hiperplano afín Sea E un R-espacio vectorial de dimensión n +1. Sean E = e 1,...,e n un hiperplano vectorial de E y e un vector
Hipercuádricas afines. Clasificación. Interpretación proyectiva de propiedades afines.
 Tema 8- Hipercuádricas afines Clasificación Interpretación proyectiva de propiedades afines 81 Hipercuádricas afines Sea k un cuerpo de característica distinta de dos Definición 811 Una hipercuádrica afín
Tema 8- Hipercuádricas afines Clasificación Interpretación proyectiva de propiedades afines 81 Hipercuádricas afines Sea k un cuerpo de característica distinta de dos Definición 811 Una hipercuádrica afín
Clasificación de Métricas y
 Capítulo VII Clasificación de Métricas y Cuádricas Dada una métrica T 2 sobre un k-espacio vectorial E, para simplificar la notación, y siempre que no haya motivo de confusión, cualesquiera que sean e,
Capítulo VII Clasificación de Métricas y Cuádricas Dada una métrica T 2 sobre un k-espacio vectorial E, para simplificar la notación, y siempre que no haya motivo de confusión, cualesquiera que sean e,
Clasificación Euclídea de las
 Capítulo X Clasificación Euclídea de las Cuádricas Fijemos en todo este capítulo un espacio afín euclídeo (A, V, Ω 2 ) de dimensión n y una métrica euclídea Ω 2 representante del absoluto. Las bases asociadas
Capítulo X Clasificación Euclídea de las Cuádricas Fijemos en todo este capítulo un espacio afín euclídeo (A, V, Ω 2 ) de dimensión n y una métrica euclídea Ω 2 representante del absoluto. Las bases asociadas
Capítulo V. T 2 (e, e
 Capítulo V Métricas En este capítulo y en los siguientes, el cuerpo base de los espacios vectoriales que se consideren será de característica distinta de 2. Empecemos recordando las nociones básicas que
Capítulo V Métricas En este capítulo y en los siguientes, el cuerpo base de los espacios vectoriales que se consideren será de característica distinta de 2. Empecemos recordando las nociones básicas que
Hipercuádricas afines. Clasificación. Elementos afines y euclídeos.
 Capítulo 6 Hipercuádricas afines. Clasificación. Elementos afines y euclídeos. Sea k un cuerpo de característica distinta de dos. Definición 6.0.1. Una hipercuádrica afín en k n es una ecuación de segundo
Capítulo 6 Hipercuádricas afines. Clasificación. Elementos afines y euclídeos. Sea k un cuerpo de característica distinta de dos. Definición 6.0.1. Una hipercuádrica afín en k n es una ecuación de segundo
CLASIFICACIÓN AFÍN DE CÓNICAS
 Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS CLASIFICACIÓN AFÍN DE CÓNICAS Sea E un R-espacio vectorial de dimensión. Sean E = e 1, e un plano vectorial de E y e 0 un
Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS CLASIFICACIÓN AFÍN DE CÓNICAS Sea E un R-espacio vectorial de dimensión. Sean E = e 1, e un plano vectorial de E y e 0 un
Teoría de la Dimensión
 Capítulo II Teoría de la Dimensión En este capítulo introduciremos una de las propiedades más importantes que tienen los espacios vectoriales: la dimensión. Dos son los modos posibles de llegar a la noción
Capítulo II Teoría de la Dimensión En este capítulo introduciremos una de las propiedades más importantes que tienen los espacios vectoriales: la dimensión. Dos son los modos posibles de llegar a la noción
Autor: Francisco Martín Cabrera, Departamento Matemática Fundamental, Universidad de La Laguna, Islas Canarias, España TEMA IV
 52 Variedades Cuadráticas Autor: Francisco Martín Cabrera, Departamento Matemática Fundamental, Universidad de La Laguna, Islas Canarias, España http://creativecommons.org/licenses/by-nc-sa/2.5/es/ TEMA
52 Variedades Cuadráticas Autor: Francisco Martín Cabrera, Departamento Matemática Fundamental, Universidad de La Laguna, Islas Canarias, España http://creativecommons.org/licenses/by-nc-sa/2.5/es/ TEMA
Tema 5. Cónicas. Asi, para las identificaciones habituales, (punto proyectivo recta vectorial punto de un plano afín ampliado), RP 2 R3 {0}
 Tema 5. Cónicas. Introducción. Ejemplos.- El cono C = {(x, y, z) R 3 /x 2 + y 2 = z 2 } está formado por las rectas vectoriales 0 (x 1,x 2, 1) [x 1,x 2, 1] RP 2 con (x 1,x 2, 1) C Π 1 = C 1, circunferencia
Tema 5. Cónicas. Introducción. Ejemplos.- El cono C = {(x, y, z) R 3 /x 2 + y 2 = z 2 } está formado por las rectas vectoriales 0 (x 1,x 2, 1) [x 1,x 2, 1] RP 2 con (x 1,x 2, 1) C Π 1 = C 1, circunferencia
Interpretación proyectiva de propiedades euclídeas. Elementos
 Tema 9.- Interpretación proyectiva de propiedades euclídeas. Elementos de las cónicas y cuádricas euclídeas 9.1 El espacio euclídeo como subespacio del proyectivo. Consideramos el espacio euclídeo R n
Tema 9.- Interpretación proyectiva de propiedades euclídeas. Elementos de las cónicas y cuádricas euclídeas 9.1 El espacio euclídeo como subespacio del proyectivo. Consideramos el espacio euclídeo R n
Hipercuádricas. Polaridad. Estudio geométrico de las cónicas y cuádricas
 Capítulo 4 Hipercuádricas. Polaridad. Estudio geométrico de las cónicas y cuádricas Comenzamos con el objeto básico de este curso. Hemos estudiado hasta ahora variedades lineales proyectivas, que están
Capítulo 4 Hipercuádricas. Polaridad. Estudio geométrico de las cónicas y cuádricas Comenzamos con el objeto básico de este curso. Hemos estudiado hasta ahora variedades lineales proyectivas, que están
Coordenadas Homogéneas
 Capítulo II Coordenadas Homogéneas En lo que sigue E será un espacio vectorial de dimensión n + 1, de modo que el espacio proyectivo P(E) tendrá dimensión n. 1 Sistemas de Referencia Proyectivos Definición
Capítulo II Coordenadas Homogéneas En lo que sigue E será un espacio vectorial de dimensión n + 1, de modo que el espacio proyectivo P(E) tendrá dimensión n. 1 Sistemas de Referencia Proyectivos Definición
Álgebra lineal y Geometría II. Métricas y formas cuadráticas. 1. La matriz de la métrica T 2 ((x, y, z), (x, y, z )) = xx + yy + 3zz 2xz 2zx es:
 Álgebra lineal y Geometría II Gloria Serrano Sotelo Departamento de MATEMÁTICAS ÁLGEBRA LINEAL Y GEOMETRÍA. 0 FÍSICAS Métricas y formas cuadráticas.. La matriz de la métrica T ((x, y, z), (x, y, z )) =
Álgebra lineal y Geometría II Gloria Serrano Sotelo Departamento de MATEMÁTICAS ÁLGEBRA LINEAL Y GEOMETRÍA. 0 FÍSICAS Métricas y formas cuadráticas.. La matriz de la métrica T ((x, y, z), (x, y, z )) =
El grupo lineal proyectivo. Homologías. Afinidades.
 Tema 3- El grupo lineal proyectivo Homologías Afinidades 31 El grupo lineal proyectivo Recordamos que en el tema anterior hemos definido, para una variedad lineal proyectiva L P n no vacía, el grupo lineal
Tema 3- El grupo lineal proyectivo Homologías Afinidades 31 El grupo lineal proyectivo Recordamos que en el tema anterior hemos definido, para una variedad lineal proyectiva L P n no vacía, el grupo lineal
- EJERCICIOS DE AMPLIACION DE GEOMETRIA - Curso 04-05
 - EJERCICIOS DE AMPLIACION DE GEOMETRIA - Curso 04-05 Nota previa: Los primeros 18 ejercicios constituyen un repaso de los conceptos de la asignatura GEOMETRIA, que se utilizarán profusamente a lo largo
- EJERCICIOS DE AMPLIACION DE GEOMETRIA - Curso 04-05 Nota previa: Los primeros 18 ejercicios constituyen un repaso de los conceptos de la asignatura GEOMETRIA, que se utilizarán profusamente a lo largo
El Espacio Proyectivo
 Capítulo I El Espacio Proyectivo En este cap tulo todos los espacios vectoriales considerados se supondrán de dimensión finita sobre un cuerpo conmutativo k, y E será uno de tales espacios. 1 Espacio Proyectivo
Capítulo I El Espacio Proyectivo En este cap tulo todos los espacios vectoriales considerados se supondrán de dimensión finita sobre un cuerpo conmutativo k, y E será uno de tales espacios. 1 Espacio Proyectivo
Problemas de Geometría Proyectiva
 Problemas de Geometría Proyectiva José M. Sánchez Abril José M. Rodríguez-Sanjurjo, Jesús M. Ruiz 1995 * I. VARIEDADES PROYECTIVAS Número 1. Se consideran en el plano proyectivo P 2 los cuatro puntos a
Problemas de Geometría Proyectiva José M. Sánchez Abril José M. Rodríguez-Sanjurjo, Jesús M. Ruiz 1995 * I. VARIEDADES PROYECTIVAS Número 1. Se consideran en el plano proyectivo P 2 los cuatro puntos a
SOLUCIONES. ÁLGEBRA LINEAL Y GEOMETRÍA (Examen Ordinario : ) Grado en Matemáticas Curso
 ÁLGEBRA LINEAL Y GEOMETRÍA Eamen Ordinario : 6--7 Grado en Matemáticas Curso 6-7 SOLUCIONES Dados tres puntos distintos alineados A, A, A A R, al número real r tal que A A = r A A lo llamaremos raón simple
ÁLGEBRA LINEAL Y GEOMETRÍA Eamen Ordinario : 6--7 Grado en Matemáticas Curso 6-7 SOLUCIONES Dados tres puntos distintos alineados A, A, A A R, al número real r tal que A A = r A A lo llamaremos raón simple
- EJERCICIOS - - Álgebra Lineal y Geometría II - Curso 10-11
 - EJERCICIOS - - Álgebra Lineal y Geometría II - Curso 10-11 Nota: Los primeros 18 ejercicios constituyen un repaso de los conceptos de la asignatura Álgebra Lineal y Geometría I. EJERCICIO 1. Sean P 1,...,
- EJERCICIOS - - Álgebra Lineal y Geometría II - Curso 10-11 Nota: Los primeros 18 ejercicios constituyen un repaso de los conceptos de la asignatura Álgebra Lineal y Geometría I. EJERCICIO 1. Sean P 1,...,
Index. Ángulo, 80 entre dos planos, 80 entre dos rectas, 80 entre dos vectores, 59 entre recta y plano, 80
 Index Ángulo, 80 entre dos planos, 80 entre dos rectas, 80 entre dos vectores, 59 entre recta y plano, 80 Adjunto, 14 Aplicación, 2 bilineal, 47 biyectiva, 3 compuesta, 3 identidad, 3 inversa, 3 inyectiva,
Index Ángulo, 80 entre dos planos, 80 entre dos rectas, 80 entre dos vectores, 59 entre recta y plano, 80 Adjunto, 14 Aplicación, 2 bilineal, 47 biyectiva, 3 compuesta, 3 identidad, 3 inversa, 3 inyectiva,
El Espacio Afín Euclídeo
 Capítulo IX El Espacio Afín Euclídeo Todos los espacios vectoriales que aparezcan lo serán de dimensión finita y sobre el cuerpo R de los números reales 1 Espacio Vectorial Euclídeo Definición 11 Un espacio
Capítulo IX El Espacio Afín Euclídeo Todos los espacios vectoriales que aparezcan lo serán de dimensión finita y sobre el cuerpo R de los números reales 1 Espacio Vectorial Euclídeo Definición 11 Un espacio
1 CUÁDRICAS Cuádricas. Estudio particular. 1 x y z. 1 x y z. a 00 a 01 a 02 a 03 a 10 a 11 a 12 a 13 a 20 a 21 a 22 a 23 a 30 a 31 a 32 a 33
 CUÁDRICAS. CUÁDRICAS.. Cuádricas. Estudio particular. Una cuádrica se dene como el lugar geométrico de los puntos del espacio euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen
CUÁDRICAS. CUÁDRICAS.. Cuádricas. Estudio particular. Una cuádrica se dene como el lugar geométrico de los puntos del espacio euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen
Haces de hipercuádricas. Clasificación de los haces de cónicas. Determinación de cónicas.
 Tema 7- Haces de hipercuádricas Clasificación de los haces de cónicas Determinación de cónicas 71 Puntos base y fundamentales de un haz Definición 711 Sea el espacio proyectivo Pn(k) de dimensión n sobre
Tema 7- Haces de hipercuádricas Clasificación de los haces de cónicas Determinación de cónicas 71 Puntos base y fundamentales de un haz Definición 711 Sea el espacio proyectivo Pn(k) de dimensión n sobre
Polaridad. Tangentes. Estudio geométrico de cónicas y cuádricas
 Tema 6- Polaridad Tangentes Estudio geométrico de cónicas y cuádricas En este tema pretendemos estudiar propiedades de V(Q), especialmente en los casos real y complejo, con n =2,3 Para ello, necesitamos
Tema 6- Polaridad Tangentes Estudio geométrico de cónicas y cuádricas En este tema pretendemos estudiar propiedades de V(Q), especialmente en los casos real y complejo, con n =2,3 Para ello, necesitamos
Las variedades lineales en un K-espacio vectorial V pueden definirse como sigue a partir de los subespacios de V.
 Capítulo 9 Variedades lineales Al considerar los subespacios de R 2, vimos que éstos son el conjunto {(0, 0)}, el espacio R 2 y las rectas que pasan por el origen. Ahora, en algunos contextos, por ejemplo
Capítulo 9 Variedades lineales Al considerar los subespacios de R 2, vimos que éstos son el conjunto {(0, 0)}, el espacio R 2 y las rectas que pasan por el origen. Ahora, en algunos contextos, por ejemplo
Fundamentos matemáticos. Tema 3 Geometría del plano y del espacio
 Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es
Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es
1 CÓNICAS Cónicas. Estudio particular. 1 x y. 1 x y. a 00 a 01 a 02 a 10 a 11 a 12 a 20 a 21 a 22
 CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
2 Intersección de una recta y una cuádrica. 1 Definición y ecuaciones. ( x y z
 2. Cuádricas. En todo este capítulo trabajaremos en el espacio afín euclídeo E 3 con respecto a una referencia rectangular {O; ē 1, ē 2, ē 3}. Denotaremos por (x, y, las coordenadas cartesianas respecto
2. Cuádricas. En todo este capítulo trabajaremos en el espacio afín euclídeo E 3 con respecto a una referencia rectangular {O; ē 1, ē 2, ē 3}. Denotaremos por (x, y, las coordenadas cartesianas respecto
Ejercicios de Ampliación de Geometría. Hoja 2
 Ejercicios de Ampliación de Geometría Licenciatura en Ciencias Matemáticas, 2 Curso 27 de Octubre de 2008 Hoja 2 Dualidad y radiaciones. 1. Formular y resolver en el espacio proyectivo dual los siguientes
Ejercicios de Ampliación de Geometría Licenciatura en Ciencias Matemáticas, 2 Curso 27 de Octubre de 2008 Hoja 2 Dualidad y radiaciones. 1. Formular y resolver en el espacio proyectivo dual los siguientes
Fundamentos matemáticos. Tema 3 Geometría del plano y del espacio
 Grado en Ingeniería agrícola y del medio rural Tema 3 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2017 Licencia Creative Commons 4.0 Internacional J.
Grado en Ingeniería agrícola y del medio rural Tema 3 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2017 Licencia Creative Commons 4.0 Internacional J.
- RELACION COMPLEMENTARIA DE AMPLIACION DE GEOMETRIA - Curso 04-05
 - RELACION COMPLEMENTARIA DE AMPLIACION DE GEOMETRIA - Curso 04-05 Ejercicio 1. Junio 98 En el espacio proyectivo ordinario de dimensión 4, se consideran dos rectas, r y s, que se cruzan. Probar la verdad
- RELACION COMPLEMENTARIA DE AMPLIACION DE GEOMETRIA - Curso 04-05 Ejercicio 1. Junio 98 En el espacio proyectivo ordinario de dimensión 4, se consideran dos rectas, r y s, que se cruzan. Probar la verdad
Espacios vectoriales
 CAPíTULO 2 Espacios vectoriales 1. Definición de espacio vectorial Es frecuente representar ciertas magnitudes físicas (velocidad, fuerza,...) mediante segmentos orientados o vectores. Dados dos de tales
CAPíTULO 2 Espacios vectoriales 1. Definición de espacio vectorial Es frecuente representar ciertas magnitudes físicas (velocidad, fuerza,...) mediante segmentos orientados o vectores. Dados dos de tales
B23 Curvas cónicas Curvas cónicas
 Geometría plana B23 Curvas cónicas Curvas cónicas Superficie cónica de revolución es la engendrada por una recta que gira alrededor de otra a la que corta. Curvas cónicas son las que resultan de la intersección
Geometría plana B23 Curvas cónicas Curvas cónicas Superficie cónica de revolución es la engendrada por una recta que gira alrededor de otra a la que corta. Curvas cónicas son las que resultan de la intersección
V = v 1 +2v 2 +3v 3. v 2. v 1
 Coordenadas Hay muchas maneras de darle coordenadas a los puntos del espacio, las ecuaciones de las curvas o superficies dependen de las coordenadas que utilicemos y eligiendo las coordenadas adecuadas
Coordenadas Hay muchas maneras de darle coordenadas a los puntos del espacio, las ecuaciones de las curvas o superficies dependen de las coordenadas que utilicemos y eligiendo las coordenadas adecuadas
El espacio proyectivo. Sistemas de referencia. Dualidad.
 Capítulo 1 El espacio proyectivo Sistemas de referencia Dualidad En todo lo que sigue k designará un cuerpo arbitrario 11 Espacio afín como subespacio del proyectivo Definición 111 Sea un entero n 0 El
Capítulo 1 El espacio proyectivo Sistemas de referencia Dualidad En todo lo que sigue k designará un cuerpo arbitrario 11 Espacio afín como subespacio del proyectivo Definición 111 Sea un entero n 0 El
SERIE SUPERFICIES. 1.- Determinar la ecuación cartesiana del cilindro que contiene a la curva de ecuaciones:
 SERIE SUPERFICIES 1.- Determinar la ecuación cartesiana del cilindro que contiene a la curva de ecuaciones: 4x C z 0 y que se genera por rectas perpendiculares al plano: x + y + 3z + = 0.-Sea la superficie
SERIE SUPERFICIES 1.- Determinar la ecuación cartesiana del cilindro que contiene a la curva de ecuaciones: 4x C z 0 y que se genera por rectas perpendiculares al plano: x + y + 3z + = 0.-Sea la superficie
E E V (P, Q) v = P Q AA + AB = AB AA = 0.
 Espacios afines. 1 Definición y propiedades. Definición 1.1 Sea E un conjunto no vacío. Se dice que E está dotado de estructura de espacio afín asociado a un espacio vectorial V, si existe una aplicación:
Espacios afines. 1 Definición y propiedades. Definición 1.1 Sea E un conjunto no vacío. Se dice que E está dotado de estructura de espacio afín asociado a un espacio vectorial V, si existe una aplicación:
Reflexiones sobre el Punto de Frégier José Araujo - Luis C. Maiarú - Norma Pietrocola
 Reflexiones sobre el Punto de Frégier José Araujo - Luis C. Maiarú - Norma Pietrocola Resumen En estas notas vamos a referirnos al punto de Frégier de una cónica y a la generalización de este resultado
Reflexiones sobre el Punto de Frégier José Araujo - Luis C. Maiarú - Norma Pietrocola Resumen En estas notas vamos a referirnos al punto de Frégier de una cónica y a la generalización de este resultado
Cada recta vectorial se llama punto proyectivo. Se llama dimensión del espacio proyectivo a dim P(V ) = dim V 1.
 "Con eso francamente que nunca he sentido gusto por el estudio o la investigación en física o en geometría, a no ser que pudiera servir como medio de llegar a algún tipo de conocimiento de las causas próximas...para
"Con eso francamente que nunca he sentido gusto por el estudio o la investigación en física o en geometría, a no ser que pudiera servir como medio de llegar a algún tipo de conocimiento de las causas próximas...para
Tema 3.3. Aplicaciones afines. Cónicas y cuádricas
 Tema 3.3. Aplicaciones afines. Cónicas y cuádricas Definición 1. Sean A = (P, V, f) y A = (P, V, f ) dos espacios afines tales que V y V son espacios vectoriales sobre un mismo cuerpo. Una función θ :
Tema 3.3. Aplicaciones afines. Cónicas y cuádricas Definición 1. Sean A = (P, V, f) y A = (P, V, f ) dos espacios afines tales que V y V son espacios vectoriales sobre un mismo cuerpo. Una función θ :
+ : X V X. (+) P : V X u P + u. (P + u) + v = P + (u + v). Nota La propiedad 1) de la definición anterior implica, en primer lugar, que
 Capítulo 1 El espacio afín 11 Introducción Dependencia lineal afín La Geometría afín sobre un cuerpo k tiene como objetos básicos los siguientes: un conjunto no vacío X, cuyos elementos serán llamados
Capítulo 1 El espacio afín 11 Introducción Dependencia lineal afín La Geometría afín sobre un cuerpo k tiene como objetos básicos los siguientes: un conjunto no vacío X, cuyos elementos serán llamados
Cónicas. Clasificación.
 Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Examen extraordinario Ejercicio 4 (55 minutos) 4 de septiembre de 2006
 ÁLGEBRA Examen extraordinario Ejercicio 4 (55 minutos) 4 de septiembre de 006 1. Calcular la ecuación de una hipérbola que tiene por asíntota a la recta x = y, por eje la recta x+y = 1 y que pasa por el
ÁLGEBRA Examen extraordinario Ejercicio 4 (55 minutos) 4 de septiembre de 006 1. Calcular la ecuación de una hipérbola que tiene por asíntota a la recta x = y, por eje la recta x+y = 1 y que pasa por el
Definición: Se llama pendiente de una recta a la tangente de un ángulo de inclinación formado por el eje X y la
 Geometría Analítica Preliminares Identidades Trigonométricas Definición: Se llama pendiente de una recta a la tangente de un ángulo de inclinación formado por el eje X y la recta, tal que, esto es Recta
Geometría Analítica Preliminares Identidades Trigonométricas Definición: Se llama pendiente de una recta a la tangente de un ángulo de inclinación formado por el eje X y la recta, tal que, esto es Recta
Cónicas y cuádricas. Circunferencia Elipse Parábola Hipérbola
 Grado en Óptica y Optometría Curso 2009-2010 Cónicas y cuádricas. Curvas cónicas Entre las curvas, quizás más importante y con más renombre, figuran las conocidas como curvas cónicas, cuyo nombre proviene
Grado en Óptica y Optometría Curso 2009-2010 Cónicas y cuádricas. Curvas cónicas Entre las curvas, quizás más importante y con más renombre, figuran las conocidas como curvas cónicas, cuyo nombre proviene
Algebra Lineal y Geometría
 Algebra Lineal y Geometría Unidad n 11:Ecuación General de Segundo Grado en Tres Variables. Algebra Lineal y Geometría Esp.Liliana Eva Mata 1 Contenidos Superficies. Relaciones elementales entre propiedades
Algebra Lineal y Geometría Unidad n 11:Ecuación General de Segundo Grado en Tres Variables. Algebra Lineal y Geometría Esp.Liliana Eva Mata 1 Contenidos Superficies. Relaciones elementales entre propiedades
Concepto de superficie
 Capítulo IV Concepto de superficie 1. Parametrizaciones regulares Intuitivamente, una superficie de R 3 es un subconjunto S R 3 con la siguiente propiedad: cada punto P S tiene un entorno abierto en S
Capítulo IV Concepto de superficie 1. Parametrizaciones regulares Intuitivamente, una superficie de R 3 es un subconjunto S R 3 con la siguiente propiedad: cada punto P S tiene un entorno abierto en S
Ejercicios N 3 (MAT 021)
 Ejercicios N 3 (MAT 021) Universidad Técnica Federico Santa María Departamento de Matemática Septiembre 2009 1 Rectas 1. En cada caso determine la ecuación de la recta L (a) L pasa por el punto P ( 1,
Ejercicios N 3 (MAT 021) Universidad Técnica Federico Santa María Departamento de Matemática Septiembre 2009 1 Rectas 1. En cada caso determine la ecuación de la recta L (a) L pasa por el punto P ( 1,
SUPERFICIES CUÁDRICAS
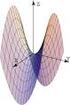 SUPERFICIES CUÁDRICAS Un cuarto tipo de superficie en el espacio tridimensional son las cuádricas. Una superficie cuádrica en el espacio es una ecuación de segundo grado de la forma Ax + By + Cz + Dx +
SUPERFICIES CUÁDRICAS Un cuarto tipo de superficie en el espacio tridimensional son las cuádricas. Una superficie cuádrica en el espacio es una ecuación de segundo grado de la forma Ax + By + Cz + Dx +
Problemas de geometría afín
 Problemas de geometría afín Teóricos Problema A Para un subconjunto no vacío X de R n se cumple: X es subvariedad afín cada recta que pasa por dos puntos distintos de X está totalmente contenida en X Problema
Problemas de geometría afín Teóricos Problema A Para un subconjunto no vacío X de R n se cumple: X es subvariedad afín cada recta que pasa por dos puntos distintos de X está totalmente contenida en X Problema
El Espacio Afín. Capítulo III. 1 Espacio Afín y Subvariedades Afines
 Capítulo III El Espacio Afín Como en los capítulos anteriores todos los cuerpos serán conmutativos Lo mismo ocurrirá (y ya no insistiremos más en ello) en todos los capítulos siguientes Si en algún momento
Capítulo III El Espacio Afín Como en los capítulos anteriores todos los cuerpos serán conmutativos Lo mismo ocurrirá (y ya no insistiremos más en ello) en todos los capítulos siguientes Si en algún momento
Es la elipse el conjunto de puntos fijos cuya suma de distancias a dos puntos fijos llamados focos es constante.
 ESQUEMA LAS CÓNICAS LA PARÁBOLA ECUACIONES DE LA PARÁBOLA ECUACIÓN DE LA TANGENTE A UNA PARÁBOLA ELIPSE ECUACIONES DE LA ELIPSE PROPIEDADES DE LA ELIPSE LA HIPÉRBOLA ECUACIONES DE LA HIPÉRBOLA 10 ASÍNTOTAS
ESQUEMA LAS CÓNICAS LA PARÁBOLA ECUACIONES DE LA PARÁBOLA ECUACIÓN DE LA TANGENTE A UNA PARÁBOLA ELIPSE ECUACIONES DE LA ELIPSE PROPIEDADES DE LA ELIPSE LA HIPÉRBOLA ECUACIONES DE LA HIPÉRBOLA 10 ASÍNTOTAS
Respuestas faltantes en ejercicios edición 2007 Sección 4.4: Superficie cuadráticas de revolución Ejercicio 4-1
 Editorial Mc Graw Hill. Edición 007 Respuestas faltantes en ejercicios edición 007 Sección 4.4: Superficie cuadráticas de revolución Ejercicio 4- R r + x + y Ejercicio 4-3 + R x + y + z Ecuaciones: x +
Editorial Mc Graw Hill. Edición 007 Respuestas faltantes en ejercicios edición 007 Sección 4.4: Superficie cuadráticas de revolución Ejercicio 4- R r + x + y Ejercicio 4-3 + R x + y + z Ecuaciones: x +
CÓNICAS. 1. Dada la cónica x 2 + 2xy y 2 2x 2y + 4 = 0, se pide su clasicación y los elementos característicos de la misma. = 1
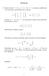 CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
TEMA 5. CURVAS CÓNICAS.
 5.1. GENERALIDADES. TEMA 5. CURVAS CÓNICAS. Se denominan secciones cónicas a aquellas superficies que son producidas por la intersección de un plano con una superficie cónica de revolución (una superficie
5.1. GENERALIDADES. TEMA 5. CURVAS CÓNICAS. Se denominan secciones cónicas a aquellas superficies que son producidas por la intersección de un plano con una superficie cónica de revolución (una superficie
GEOMETRÍA I 23 de septiembre del 2011
 GEOMETRÍA I 3 de septiembre del 011 1. En el espacio ordinario se consideran las rectas l 1 : { x y + z = 1 x + y z = l : x 3 = y + 1 = z a. Hallar a IR para que exista un plano π que contenga a l 1 y
GEOMETRÍA I 3 de septiembre del 011 1. En el espacio ordinario se consideran las rectas l 1 : { x y + z = 1 x + y z = l : x 3 = y + 1 = z a. Hallar a IR para que exista un plano π que contenga a l 1 y
EJERCICIOS DE ÁLGEBRA LINEAL TEMA 1 ESPACIOS VECTORIALES
 EJERCICIOS DE ÁLGEBRA LINEAL TEMA ESPACIOS VECTORIALES Formas reducidas y escalonada de una matriz SISTEMAS DE ECUACIONES LINEALES ) Encuentre una sucesión de matrices elementales E, E,..., E k tal que
EJERCICIOS DE ÁLGEBRA LINEAL TEMA ESPACIOS VECTORIALES Formas reducidas y escalonada de una matriz SISTEMAS DE ECUACIONES LINEALES ) Encuentre una sucesión de matrices elementales E, E,..., E k tal que
El espacio proyectivo P n (k). Sistemas de referencia. Dualidad. Departamento de Algebra Septiembre El espacio proyectivo P n (k).
 Notas de la asignatura AMPLIACIÓN DE GEOMETRÍA de la Licenciatura de Matemáticas, Facultad de Matemáticas, Universidad de Sevilla, para el curso 2000-01 Departamento de Algebra Septiembre 2000 Tema 1-
Notas de la asignatura AMPLIACIÓN DE GEOMETRÍA de la Licenciatura de Matemáticas, Facultad de Matemáticas, Universidad de Sevilla, para el curso 2000-01 Departamento de Algebra Septiembre 2000 Tema 1-
Ejercicios de cónicas.
 Ejercicios de cónicas. 1. Demuéstrese que un rayo lanzado en cualquier dirección desde un foco de una elipse y que se refleje en la cónica pasa por el otro foco. 2. Demuéstrese que un rayo lanzado paralelamente
Ejercicios de cónicas. 1. Demuéstrese que un rayo lanzado en cualquier dirección desde un foco de una elipse y que se refleje en la cónica pasa por el otro foco. 2. Demuéstrese que un rayo lanzado paralelamente
3. Calcular una base normalizada asociada a esa referencia y las coordenadas en ella del punto [1, 2, 5, 3]
![3. Calcular una base normalizada asociada a esa referencia y las coordenadas en ella del punto [1, 2, 5, 3] 3. Calcular una base normalizada asociada a esa referencia y las coordenadas en ella del punto [1, 2, 5, 3]](/thumbs/68/59191793.jpg) Ejercicio 0.1 Sea K un cuerpo con q elementos y sea V un espacio vectorial de dimensión n + 1 sobre K. Calcular cuantas bases distintas (como subconjuntos) tiene V, cuantas referencias distintas hay en
Ejercicio 0.1 Sea K un cuerpo con q elementos y sea V un espacio vectorial de dimensión n + 1 sobre K. Calcular cuantas bases distintas (como subconjuntos) tiene V, cuantas referencias distintas hay en
Se puede considerar una superficie, como una lámina infinitamente delgada, que recubre un cuerpo, separa dos medios o dos regiones del espacio.
 SUPERFICIES SUPERFICIES Se puede considerar una superficie, como una lámina infinitamente delgada, que recubre un cuerpo, separa dos medios o dos regiones del espacio. Una Superficie puede estar engendrada
SUPERFICIES SUPERFICIES Se puede considerar una superficie, como una lámina infinitamente delgada, que recubre un cuerpo, separa dos medios o dos regiones del espacio. Una Superficie puede estar engendrada
Movimientos. Teorema de Cartan-Dieudonné. Semejanzas.
 Capítulo 5 Movimientos. Teorema de Cartan-Dieudonné. Semejanzas. 5.1 Isometrías y movimientos Partimos de un espacio euclídeo (X, V, +) y recordemos que una isometría de V es un elemento ϕ Gl(V ) que conserva
Capítulo 5 Movimientos. Teorema de Cartan-Dieudonné. Semejanzas. 5.1 Isometrías y movimientos Partimos de un espacio euclídeo (X, V, +) y recordemos que una isometría de V es un elemento ϕ Gl(V ) que conserva
CURVAS Y SUPERFICIES. RELACIÓN 2
 CURVAS Y SUPERFICIES. RELACIÓN 2 SUPERFICIES EN EL ESPACIO Curso 2015-16 1. Demostrar que las siguientes cuádricas reales son superficies. Obtener una parametrización de cada una de ellas. En cada caso,
CURVAS Y SUPERFICIES. RELACIÓN 2 SUPERFICIES EN EL ESPACIO Curso 2015-16 1. Demostrar que las siguientes cuádricas reales son superficies. Obtener una parametrización de cada una de ellas. En cada caso,
Haces de hipercuádricas. Clasificación de los haces de cónicas. Determinación de
 Capítulo 5 Haces de hipercuádricas. Clasificación de los haces de cónicas. Determinación de cónicas. 5.1. Definición y ecuaciones Definición 5.1.1. Sea (X, T, π) un espacio proyectivo de dimensión n sobre
Capítulo 5 Haces de hipercuádricas. Clasificación de los haces de cónicas. Determinación de cónicas. 5.1. Definición y ecuaciones Definición 5.1.1. Sea (X, T, π) un espacio proyectivo de dimensión n sobre
Capítulo VI. Diferenciabilidad de funciones de varias variables
 Capítulo VI Diferenciabilidad de funciones de varias variables La definición de diferenciabilidad para funciones el cociente no tiene sentido, puesto que no está definido, porque el cociente entre el vector
Capítulo VI Diferenciabilidad de funciones de varias variables La definición de diferenciabilidad para funciones el cociente no tiene sentido, puesto que no está definido, porque el cociente entre el vector
Este documento es de distribución gratuita y llega gracias a El mayor portal de recursos educativos a tu servicio!
 Este documento es de distribución gratuita y llega gracias a Ciencia Matemática El mayor portal de recursos educativos a tu servicio! Capítulo 5 Cónicas 5.1 Definiciones y ecuaciones reducidas Nota En
Este documento es de distribución gratuita y llega gracias a Ciencia Matemática El mayor portal de recursos educativos a tu servicio! Capítulo 5 Cónicas 5.1 Definiciones y ecuaciones reducidas Nota En
Tema 1. Espacios Vectoriales Definición de Espacio Vectorial
 Tema 1 Espacios Vectoriales. 1.1. Definición de Espacio Vectorial Notas 1.1.1. Denotaremos por N, Z, Q, R, C, a los conjuntos de los números Naturales, Enteros, Racionales, Reales y Complejos, respectivamente.
Tema 1 Espacios Vectoriales. 1.1. Definición de Espacio Vectorial Notas 1.1.1. Denotaremos por N, Z, Q, R, C, a los conjuntos de los números Naturales, Enteros, Racionales, Reales y Complejos, respectivamente.
Grupos y Subgrupos El concepto de grupo Sea G un conjunto no vacío y sea G G G
 Capítulo 1 Grupos y Subgrupos 001. El concepto de grupo Sea G un conjunto no vacío y sea G G G una operación interna en G para la cual denotaremos a la imagen de un par (x, y) mediante xy. Supongamos que
Capítulo 1 Grupos y Subgrupos 001. El concepto de grupo Sea G un conjunto no vacío y sea G G G una operación interna en G para la cual denotaremos a la imagen de un par (x, y) mediante xy. Supongamos que
II.3 CUÁDRICAS EN EL AFÍN
 II.3 CUÁDRICAS EN EL AFÍN Índice del capítulo. 1 Posición relativa de una cuádrica y un hiperplano 2 Extensiones proyectivas de una cuádrica afín 3 Clasificación afín de las cuádricas 4 Ejercicios CUÁDRICAS
II.3 CUÁDRICAS EN EL AFÍN Índice del capítulo. 1 Posición relativa de una cuádrica y un hiperplano 2 Extensiones proyectivas de una cuádrica afín 3 Clasificación afín de las cuádricas 4 Ejercicios CUÁDRICAS
IDENTIFICACIÓN DE SUPERFICES CUÁDRICAS
 IDENTIFICACIÓN DE SUPERFICES CUÁDRICAS LUIS HUMBERTO SORIANO SÁNCHE Captura: Hanna Leslye García Guerra Evelyn Salazar Guerrero IDENTIFICACIÓN DE SUPERFICIES CUÁDRICAS Definición. Se llama superficie al
IDENTIFICACIÓN DE SUPERFICES CUÁDRICAS LUIS HUMBERTO SORIANO SÁNCHE Captura: Hanna Leslye García Guerra Evelyn Salazar Guerrero IDENTIFICACIÓN DE SUPERFICIES CUÁDRICAS Definición. Se llama superficie al
Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados
 Capítulo 5 Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados En este tema iniciamos el estudio de los conceptos geométricos de distancia y perpendicularidad en K n. Empezaremos con las definiciones
Capítulo 5 Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados En este tema iniciamos el estudio de los conceptos geométricos de distancia y perpendicularidad en K n. Empezaremos con las definiciones
Unidad 8 Lugares geométricos. Cónicas
 Unidad 8 Lugares geométricos. Cónicas PÁGINA 75 SOLUCIONES. La elipse es una cónica obtenida al cortar una superficie cónica por un plano oblicuo al eje y que corte a todas las generatrices. La hipérbola
Unidad 8 Lugares geométricos. Cónicas PÁGINA 75 SOLUCIONES. La elipse es una cónica obtenida al cortar una superficie cónica por un plano oblicuo al eje y que corte a todas las generatrices. La hipérbola
ESTUDIO GRÁFICO DE LA ELIPSE.
 Curvas Cónicas para Dibujo y Matemáticas. Aplicación web Dibujo Técnico para ESO y Bachillerato Matemáticas para Bachillerato Educación Plástica y Visual Autor: José Antonio Cuadrado Vicente. ESTUDIO GRÁFICO
Curvas Cónicas para Dibujo y Matemáticas. Aplicación web Dibujo Técnico para ESO y Bachillerato Matemáticas para Bachillerato Educación Plástica y Visual Autor: José Antonio Cuadrado Vicente. ESTUDIO GRÁFICO
ÁLGEBRA LINEAL II Práctica 4.1
 ÁLGEBRA LINEAL II Práctica 4.1 Cónicas (Curso 2012 2013) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo
ÁLGEBRA LINEAL II Práctica 4.1 Cónicas (Curso 2012 2013) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo
Ejercicios resueltos de Álgebra, hoja 2. Beatriz Graña Otero
 Ejercicios resueltos de Álgebra, hoja 2. Beatriz Graña Otero 11 de Diciembre de 2008 2 B.G.O. 104.- Determina si los siguientes subconjuntos del espacio vectorial correspondiente son subvariedades afines:
Ejercicios resueltos de Álgebra, hoja 2. Beatriz Graña Otero 11 de Diciembre de 2008 2 B.G.O. 104.- Determina si los siguientes subconjuntos del espacio vectorial correspondiente son subvariedades afines:
UNIVERSIDAD DEL NORTE Departamento de Matemáticas y Estadística. Álgebra Lineal. RESUMEN DE TEMAS DEL EXAMEN FINAL
 1. Definiciones básicas. UNIVERSIDAD DEL NORTE Departamento de Matemáticas y Estadística. Álgebra Lineal. RESUMEN DE TEMAS DEL EXAMEN FINAL I. Sistemas homogéneos y subespacios de R n. (a) Para el sistema
1. Definiciones básicas. UNIVERSIDAD DEL NORTE Departamento de Matemáticas y Estadística. Álgebra Lineal. RESUMEN DE TEMAS DEL EXAMEN FINAL I. Sistemas homogéneos y subespacios de R n. (a) Para el sistema
Facultad de Ingeniería Facultad de Tecnología Informática. Matemática Números reales Elementos de geometría analítica. Profesora: Silvia Mamone
 Facultad de Ingeniería Facultad de Tecnología Informática Matemática Números reales Elementos de geometría analítica 0 03936 Profesora: Silvia Mamone UB Facultad de Ingeniería Facultad de Tecnología Informática
Facultad de Ingeniería Facultad de Tecnología Informática Matemática Números reales Elementos de geometría analítica 0 03936 Profesora: Silvia Mamone UB Facultad de Ingeniería Facultad de Tecnología Informática
11. Cónicas proyectivas
 24 FRANCISCO JAVIER GALLEGO RODRIGO. Cónicas proyectivas Recordemos que una de las razones para construir el espacio proyectivo fue estudiar qué les pasa a los objetos afines cuando nos vamos al infinito.
24 FRANCISCO JAVIER GALLEGO RODRIGO. Cónicas proyectivas Recordemos que una de las razones para construir el espacio proyectivo fue estudiar qué les pasa a los objetos afines cuando nos vamos al infinito.
6 Vectores. Dependencia e independencia lineal.
 6 Vectores. Dependencia e independencia lineal. Introducción Hay fenómenos reales que se pueden representar adecuadamente mediante un número con su adecuada unidad de medida. Sin embargo para representar
6 Vectores. Dependencia e independencia lineal. Introducción Hay fenómenos reales que se pueden representar adecuadamente mediante un número con su adecuada unidad de medida. Sin embargo para representar
22. CURVAS CÓNICAS-ELIPSE
 22. CURVAS CÓNICAS-ELIPSE 22.1. Características generales. Las curvas cónicas son las secciones planas de un cono de revolución. El cono de revolución es la superficie que genera una recta r al girar alrededor
22. CURVAS CÓNICAS-ELIPSE 22.1. Características generales. Las curvas cónicas son las secciones planas de un cono de revolución. El cono de revolución es la superficie que genera una recta r al girar alrededor
Tema 3. GEOMETRIA ANALITICA.
 Álgebra lineal. Curso 087-009. Tema. Hoja 1 Tema. GEOMETRIA ANALITICA. 1. Hallar la ecuación de la recta: a) que pase por ( 4, ) y tenga pendiente 1. b) que pase por (0, 5) y tenga pendiente. c) que pase
Álgebra lineal. Curso 087-009. Tema. Hoja 1 Tema. GEOMETRIA ANALITICA. 1. Hallar la ecuación de la recta: a) que pase por ( 4, ) y tenga pendiente 1. b) que pase por (0, 5) y tenga pendiente. c) que pase
INDICE. 88 determinante 36. Familias de líneas rectas Resumen de resultados 96 Capitulo IV
 INDICE Geometría Analítica Plana Capitulo Primero Artículo 1. Introducción 1 2. Segmento rectilíneo dirigido 1 3. Sistema coordenado lineal 3 4. Sistema coordenado en el plano 5 5. Carácter de la geografía
INDICE Geometría Analítica Plana Capitulo Primero Artículo 1. Introducción 1 2. Segmento rectilíneo dirigido 1 3. Sistema coordenado lineal 3 4. Sistema coordenado en el plano 5 5. Carácter de la geografía
Ba s e, d i M e n s i ó n y Mat r i z
 Unidad 4 Ba s e, d i M e n s i ó n y Mat r i z de transición Objetivos: Al inalizar la unidad, el alumno: Conocerá la deinición de base de un espacio vectorial Identiicará bases canónicas para algunos
Unidad 4 Ba s e, d i M e n s i ó n y Mat r i z de transición Objetivos: Al inalizar la unidad, el alumno: Conocerá la deinición de base de un espacio vectorial Identiicará bases canónicas para algunos
Álgebra Lineal y Geometría I. Prueba 3. Grupo A. 12 de marzo de (
 Álgebra Lineal y Geometría I. Prueba 3. Grupo A. 2 de marzo de 208. Apellidos: Nombre: DNI: Ejercicio.-(4 puntos) Se considera la matriz siguiente: A = 2 0 3 0 2. Calcule W = null(a 2I), W 2 = null(a 4I)
Álgebra Lineal y Geometría I. Prueba 3. Grupo A. 2 de marzo de 208. Apellidos: Nombre: DNI: Ejercicio.-(4 puntos) Se considera la matriz siguiente: A = 2 0 3 0 2. Calcule W = null(a 2I), W 2 = null(a 4I)
Sea V un conjunto no vacío (cuyos elementos se llamarán vectores) y sea K un cuerpo (cuyos elementos se llamarán escalares).
 Capítulo 6 Espacios Vectoriales 6.1 Definiciones Sea V un conjunto no vacío (cuyos elementos se llamarán vectores) y sea K un cuerpo (cuyos elementos se llamarán escalares). Definición 6.1.1 Se dice que
Capítulo 6 Espacios Vectoriales 6.1 Definiciones Sea V un conjunto no vacío (cuyos elementos se llamarán vectores) y sea K un cuerpo (cuyos elementos se llamarán escalares). Definición 6.1.1 Se dice que
El Espacio Dual. Capítulo IV. 1 El Espacio Dual. Fijemos en todo este capítulo un cuerpo k.
 Capítulo IV El Espacio Dual Fijemos en todo este capítulo un cuerpo k. 1 El Espacio Dual Definición 1.1 Dado un espacio vectorial E, llamaremos espacio dual de E al k-espacio vectorial E = Hom k (E, k).
Capítulo IV El Espacio Dual Fijemos en todo este capítulo un cuerpo k. 1 El Espacio Dual Definición 1.1 Dado un espacio vectorial E, llamaremos espacio dual de E al k-espacio vectorial E = Hom k (E, k).
Semana 13: Determinación de cónicas. Haces de cónicas proyectivas.
 Semana 13: Determinación de cónicas. Haces de cónicas proyectivas. Sonia L. Rueda ETS Arquitectura. UPM Geometría afín y proyectiva, 2015 Geometría afín y proyectiva 1. Álgebra lineal 2. Geometría afín
Semana 13: Determinación de cónicas. Haces de cónicas proyectivas. Sonia L. Rueda ETS Arquitectura. UPM Geometría afín y proyectiva, 2015 Geometría afín y proyectiva 1. Álgebra lineal 2. Geometría afín
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID. PRUEBAS DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) MODELO DE EXAMEN (Curso )
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBAS DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) MODELO DE EXAMEN (Curso 00-003) MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN INSTRUCCIONES:
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBAS DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) MODELO DE EXAMEN (Curso 00-003) MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN INSTRUCCIONES:
ÁLGEBRA LINEAL II Práctica 4.1
 ÁLGEBRA LINEAL II Práctica 4.1 Cónicas (Curso 2010 2011) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo
ÁLGEBRA LINEAL II Práctica 4.1 Cónicas (Curso 2010 2011) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo
Geometría afín y proyectiva, 2016 SEMANA 2
 Geometría afín y proyectiva, 2016 SEMANA 2 Sonia L. Rueda ETS Arquitectura. UPM September 20, 2016 Geometría afín y proyectiva 1. Álgebra Lineal 2. Geometría afín y eucĺıdea 3. Cónicas y cuádricas Álgebra
Geometría afín y proyectiva, 2016 SEMANA 2 Sonia L. Rueda ETS Arquitectura. UPM September 20, 2016 Geometría afín y proyectiva 1. Álgebra Lineal 2. Geometría afín y eucĺıdea 3. Cónicas y cuádricas Álgebra
Una construcción del centro de curvatura en cónicas
 Una construcción del centro de curvatura en cónicas Previamente tratamos unos hechos relativos a transformaciones de curvas y proyectividades entre sus elementos, que nos sentarán las bases para las construcciones
Una construcción del centro de curvatura en cónicas Previamente tratamos unos hechos relativos a transformaciones de curvas y proyectividades entre sus elementos, que nos sentarán las bases para las construcciones
Capitulo I. Variedades algebraicas afines.
 Capitulo I. Variedades algebraicas afines. Al conjunto solución de un sistema de ecuaciones algebraicas lo llamamos variedad algebraica afín. Uno lo considera como objetos de la geometría en espacios afines.
Capitulo I. Variedades algebraicas afines. Al conjunto solución de un sistema de ecuaciones algebraicas lo llamamos variedad algebraica afín. Uno lo considera como objetos de la geometría en espacios afines.
CAPÍTULO II. Índice del capítulo. Definición general de las cónicas Cónicas sin centro. Coordenadas polares Problemas propuestos Bibliografía
 CAPÍTULO II CÓNICAS Índice del capítulo Definición general de las cónicas Cónicas con centro Cónicas sin centro Coordenadas polares Problemas propuestos Bibliografía 1 8. Cónicas. Las cónicas son curvas
CAPÍTULO II CÓNICAS Índice del capítulo Definición general de las cónicas Cónicas con centro Cónicas sin centro Coordenadas polares Problemas propuestos Bibliografía 1 8. Cónicas. Las cónicas son curvas
3.1 El espacio afín R n
 3. Geometría analítica 3.1 El espacio afín R n Consideremos el conjunto R n, formado por las listas ordenadas (x 1,...,x n ) de números reales. Convengamos en llamar puntos a los elementos de R n. Pero
3. Geometría analítica 3.1 El espacio afín R n Consideremos el conjunto R n, formado por las listas ordenadas (x 1,...,x n ) de números reales. Convengamos en llamar puntos a los elementos de R n. Pero
