- EJERCICIOS - - Álgebra Lineal y Geometría II - Curso 10-11
|
|
|
- Manuel Domínguez Jiménez
- hace 6 años
- Vistas:
Transcripción
1 - EJERCICIOS - - Álgebra Lineal y Geometría II - Curso Nota: Los primeros 18 ejercicios constituyen un repaso de los conceptos de la asignatura Álgebra Lineal y Geometría I. EJERCICIO 1. Sean P 1,..., P m puntos de P n (k). Probar que son linealmente dependientes si y sólo existe un i {1,..., m} tal que P i depende linealmente de P 1,..., P i 1, P i+1,..., P m. EJERCICIO 2. Estudiar la posición relativa de dos variedades lineales de un espacio proyectivo de dimensión 3. EJERCICIO 3. Hallar las ecuaciones paramétricas e implícitas de la recta r que pasa por los puntos (1 : 1 : 2) y (2 : 1 : 1) de P 2 (k). Hallar también el punto de intersección de r con la recta s de ecuación x 0 + x 1 + x 2 = 0. Hallar las ecuaciones del haz de rectas que pasan por r s. EJERCICIO 4. Estudiar las posiciones relativas de tres rectas en un plano proyectivo. EJERCICIO 5. Determinar las posiciones relativas de las siguientes ternas de rectas en P 2 (R): a) x 0 x 1 + x 2 = 0 3x 0 + x 2 = 0 x 0 x 1 x 2 = 0 b) x 0 + x 1 + x 2 = 0 x 0 + 3x 1 3x 2 = 0 x 0 + 3x 2 = 0 c) x 0 + x 1 = 0 x 0 + x 2 = 0 x 1 + x 2 = 0. Nota.- En los ejercicios siguientes se considerará el espacio proyectivo P 3 (k). EJERCICIO 6. Determinar las ecuaciones paramétricas e implícitas del plano que pasa por los puntos (1 : 0 : 1 : 3), (2 : 1 : 1 : 1) y (1 : 1 : 0 : 1). EJERCICIO 7. Hallar las ecuaciones paramétricas e implícitas de la recta que pasa por los puntos (2 : 1 : 3 : 0) y (0 : 1 : 0 : 1). EJERCICIO 8. Sean r y s dos rectas distintas. Probar que son equivalentes: a) r y s se cruzan. b) Si P 0, P 1, P 2, P 3 son puntos distintos con P 0, P 1 r, P 2, P 3 s, entonces {P 0, P 1, P 2, P 3 } es un conjunto linealmente independiente. EJERCICIO 9. Determinar las posiciones relativas de los siguientes pares de rectas: a) x 0 = 5λ + µ x 0 = 4λ 5µ x 1 = 2λ 3µ x 1 = λ 3µ x 2 = 4λ + 2µ x 2 = 2λ + µ x 3 = 7λ + µ x 3 = λ b) x 0 5x 1 + 5x 2 = 0 4x 0 3x 1 + 7x 2 + 2x 3 = 0 P + Q, con P = (7 : 5 : 2 : 0) Q = (1 : 3 : 0 : 2) c) x 0 2x 1 + 3x 2 + 3x 3 = 0 4x 0 x 1 + 5x 2 + 2x 3 = 0 10x 0 x 1 9x 2 = 0 3x 0 x 1 2x 2 x 3 = 0 d) r = P + Q, s = R + S P = (1 : 0 : 1 : 0), Q = (1 : 1 : 0 : 0) R = (0 : 1 : 0 : 1), S = (0 : 0 : 1 : 1) EJERCICIO 10. Determinar las posiciones relativas de la recta r y del plano H en cada uno de los casos siguientes: { { 2x0 6x a) r x 2 = 0 plano determinado por los puntos: H 4x 0 26x x x 3 = 0 (1 : 1 : 2 : 3), (4 : 5 : 1 : 2), (3 : 1 : 0 : 1) { x0 = λ + 2µ, x b) r 1 = λ + µ x 2 = λ µ, x 3 = λ + µ H { 3x 0 + 2x 1 + 5x 2 + 7x 3 = 0. EJERCICIO 11. Sea r la recta que pasa por los puntos (5 : 4 : 1 : 6) y (1 : 1 : 2 : 3), y s la recta que pasa por los puntos (4 : 5 : 1 : 2) y (3 : 1 : 0 : 1).
2 a) Probar que r y s se cruzan. b) Probar que el punto P = (1 : 1 : 1 : 1) no está ni en r ni en s. c) Determinar las ecuaciones de la recta t que pasa por P y que sea coplanaria con r y s (separadamente). d) Tendría solución el apartado c) si P r ó P s ó r s? Nota: Aunque este ejercicio está enunciado con unos datos particulares, debe ser entendido en general, es decir, pruébese que, dados un punto P y dos rectas r y s que se cruzan en P 3, hay una recta (única, si P / r s) que se apoya en las tres variedades dadas. EJERCICIO 12. Estudiar las posiciones relativas de dos planos de P 4 (k), probando que dos planos se cortan en un punto si y sólo si no están contenidos en un mismo hiperplano. EJERCICIO 13. Estudiar las posiciones relativas de una recta y plano en P 4 (k). EJERCICIO 14. Determinar las posiciones relativas de las siguientes variedades de P 4 (k): { x 0 = µ x0 x L 1 x 2 x 3 = 0 x 1 = λ + µ x 1 x 3 x 4 = 0 M x 2 = λ N = (1 : 1 : 0 : 1 : 1) x 3 = µ x 4 = λ + µ EJERCICIO 15. Consideremos las rectas de P 3 (k) siguientes: t { x0 x 1 = 0 x 2 x 3 = 0 a { x0 + x 2 x 3 = 0 x 1 x 3 = 0 b { x0 + x 1 x 3 = 0 x 2 = 0 c { x1 = 0 x 0 x 2 = 0 d { 2x0 x 3 = 0 x 1 x 2 = 0. a) Probar que por cada punto de t pasa una única recta r que se apoya en a y en c y una única recta s que se apoya en b y d. b) Con la notación anterior, sea P = (1 : 1 : 0 : 0), A = r a, C = r c, B = s b, D = s d. Calcular Q = AB CD. c) Dado cualquier otro punto de t, se siguen cortando AB y CD? Razónese la respuesta. EJERCICIO 16. Para las variedades afines que se dan se pide: a) Hallar unas ecuaciones implícitas independientes de las mínimas variedades proyectivas que contienen a su imagen por ϕ. b) Hallar, para cada una, un sistema de puntos l.i. que las generen, y que el mayor número de ellos esté en el infinito. L 1 x 1 + x 2 x 3 2x 4 = 1 x 1 + 3x 2 + x 3 2x 4 = 1 x 1 3x 2 5x 3 2x 4 = 5 L 3 x 1 x 2 + x 3 + 2x 4 = 1 x 1 + 2x 3 + x 4 = 2 5x 1 3x 2 x 3 + 4x 4 = 6. L 2 { x1 x 2 + x 3 3x 4 = 1 x 1 + x 2 x 3 + 2x 4 = 1 EJERCICIO 17. En cada uno de los casos siguientes se da una variedad lineal proyectiva M i generada por los puntos que se indican. Hallar un sistema de puntos en k 4, independientes, que generen ϕ 1 (M i ) y unas ecuaciones implícitas independientes de esta variedad lineal afín: M 1 : (0 : 3 : 1 : 2 : 4), (0 : 2 : 1 : 1 : 1), (1 : 1 : 1 : 2 : 1) M 2 : (0 : 2 : 1 : 1 : 1), (1 : 1 : 2 : 0 : 1), (3 : 1 : 4 : 2 : 1), (0 : 1 : 1 : 2 : 1) M 3 : (0 : 1 : 2 : 1 : 1), (0 : 1 : 1 : 1 : 1).
3 EJERCICIO 18. Con el mismo enunciado que el ejercicio anterior y las M i dadas por sus ecuaciones implícitas: M 1 Fin de los ejercicios de repaso x 0 + 2x 1 5x 2 + x 3 + 2x 4 = 0 3x 0 + x 1 4x 2 + 2x 4 = 0 x 0 x 1 + x 2 + x 3 + x 4 = 0 M 3 M 2 x 0 x 1 = 0 x 0 + x 1 = 0 x 0 + x 1 + x 2 + x 3 + x 4 = 0. x 0 + x 1 x 2 + 2x 3 = 0 x 1 2x 2 + x 3 + x 4 = 0 x 0 + x 1 2x 2 + x 3 + x 4 = 0 2x 0 + x 1 + x 2 + 4x 3 2x 4 = 0 EJERCICIO 19. En el espacio proyectivo P 7 (k) se consideran tres planos H 1, H 2 y H 3 tales que se cruzan dos a dos y no existe ningún hiperplano que contenga a los tres. a) Calcular dim((h 1 + H 2 ) H 3 ). b) Determinar el número de rectas que son secantes a los tres planos. EJERCICIO 20. Sea L una variedad lineal proyectiva de P n (k) dada por las ecuaciones implícitas a 10 x a 1n x n = a r0 x a rn x n = 0 Probar que un hiperplano contiene a L si y sólo si tiene una ecuación de la forma: con µ 1,..., µ r k no todos nulos. µ 1 (a 10 x a 1n x n ) µ r (a r0 x a rn x n ) = 0 EJERCICIO 21. Dado un sistema de referencia R de P 2 (k) probar que {(1 : 2 : 0), (1 : 1 : 2), (1 : 2 : 1), (1 : 0 : 1)} es otro sistema de referencia. Calcular una base normalizada asociada a este otro sistema. EJERCICIO 22. Dados los siguientes sistemas de referencia en P 2 (R), R = {(1 : 0 : 0), (0 : 1 : 0), (0 : 0 : 1), (1 : 1 : 1)}, R = {(2 : 1 : 0), (1 : 0 : 1), (0 : 2 : 1), (1 : 1 : 1)}, se pide: a) Encontrar dos bases normalizadas asociadas a R y R. b) Encontrar las ecuaciones del cambio de sistemas de referencia. EJERCICIO 23. Se da el espacio proyectivo P 4 (R) y un sistema de referencia R = {A 0, A 1, A 2, A 3, A 4, U} en él, respecto del cual se tomarán coordenadas. a) Se da una recta r, un punto P r y un plano L tal que P L. Se trata de hallar todas las rectas que pasen por P y sean secantes a r y a L. Discutir la existencia y el número de soluciones del problema según la posición de P, r y L. b) Sea r la recta de ecuaciones implícitas: x 1 + x 3 = 0 x 2 = 0 x 4 = 0 P : (0 : 0 : 1 : 0 : 0) y L el plano que pasa por los puntos P 0 : (1 : 1 : 2 : 0 : 0), P 1 : (1 : 1 : 0 : 2 : 0) y P 2 : (1 : 0 : 0 : 0 : 1). Hallar todas las rectas que pasan por P y son secantes a L y a r. c) Sea U : (0 : 5 : 4 : 6 : 1). Probar que R = {P 0, P 1, P 2, U } es un sistema de referencia en L. d) Sea r la recta determinada por los puntos de coordenadas (3 : 1 : 2 : 5 : 4) y (2 : 1 : 3 : 4 : 4). Probar que r es secante a L y calcular las coordenadas de r L respecto de R. e) Sea L el plano determinado por r y el punto de coordenadas ( 2 : 5 : 4 : 6 : 1). Probar que L L es una recta y hallar su ecuación respecto de R.
4 EJERCICIO 24. Sea R un sistema de referencia en el espacio proyectivo tridimensional real. Sea L un plano de ecuación x 0 + x 1 = 0. Encontrar un sistema de referencia R L de L. Expresar las coordenadas del punto P = (1 : 1 : 0 : 2) R L respecto de R L. Dado el punto Q L de coordenadas respecto de R L (1 : 1 : 2), hallar sus coordenadas respecto de R. EJERCICIO 25. En la situación del ejercicio anterior, sea L de ecuación x 0 = 0. Encontrar un sistema de referencia R L de L de modo que un punto P L coordenadas (0 : a : b : c) respecto de R tenga coordenadas (a : b : c) respecto de R L. EJERCICIO 26. En el plano proyectivo real se considera la homografía F que respecto de un sistema de referencia tiene por matriz: a) Probar que para todo P, la recta P + F (P ) pasa por el punto (1 : 1 : 1). b) Probar que para todo par de puntos P, Q las rectas P + Q y F (P ) + F (Q) se cortan sobre la recta de ecuación 2x 0 x 1 + 2x 2 = 0. c) Sabiendo que F (1 : 1 : 1) = (0 : 1 : 1), obtener F (1 : 1 : 0) sin usar la matriz de F. EJERCICIO 27. Sea R un sistema de referencia en P n (R), P, Q puntos distintos de una recta r, de coordenadas (a 0 :... : a n ), (b 0 :... : b n ) respectivamente. Sea R r un punto distinto de los anteriores: R : (a 0 + αb 0 :... : a n + αb n ) con α 0. Demostrar que el cuarto armónico de P, Q, R es el punto S : (a 0 αb 0 :... : a n αb n ). EJERCICIO 28. Dado un cuadrivértice plano, probar que dos puntos diagonales cualesquiera separan armónicamente al par de puntos de intersección con la recta que determinan y los lados que pasan por el otro punto diagonal. Como consecuencia deducir que, dados tres puntos alineados distintos A, B, C, se puede construir, usando sólo una regla, un cuarto punto D tal que ABCD = 1. EJERCICIO 29. Se considera la inmersión natural ϕ : R n P n (R) del espacio afín real en el espacio proyectivo real. 1. Sean A, B, C R n tres puntos distintos dos a dos y alineados. Se recuerda que la razón simple (CBA) es el único escalar tal que CA= (CBA) CB. Probar que (CBA) = ϕ(a)ϕ(b)ϕ(c)d donde D es el punto del infinito de la recta afín A + B. 2. Consideremos el dibujo adjunto como una parte del plano afín real R 2. Dar un procedimiento geométrico para calcular (usando sólo una regla no graduada) el punto medio del segmento AB. (Utilizar la recta t, paralela a A + B) t EJERCICIO 30. A B 1. Dados los puntos A, B y C alineados, justificar un procedimiento geométrico, usando únicamente una regla no graduada, para calcular un punto D con ABCD = 2. La respuesta no es únicamente un dibujo. 2. Dados cuatro planos H 1, H 2, H 3 y H 4 de P 3 (R) conteniendo una recta fija s, y dada otra recta r que se cruce con s, se llama razón doble de H 1, H 2, H 3, H 4 a (H1 r)(h 2 r)(h 3 r)(h 4 r). Sean H 1 = {x 3 = 0}, H 2 = {x 1 x 3 = 0}, H 3 = {x 1 = 0}, y r la recta de ecuaciones {x 0 = 0, x 1 + x 2 = 0}. Calcular el cuarto armónico de H 1, H 2, H 3.
5 EJERCICIO 31. En P 2 (R) se considera un sistema de referencia R y respecto de él las cónicas cuyas ecuaciones son: a) x 2 1 x x 1 x 2 x 2 2 = 0. b) 3x 2 0 x 0 x 1 + x 1 x 2 4x 0 x 2 + x 2 2 = 0. c) 5x x x 2 2 8x 0 x 1 + 4x 1 x 2 2x 0 x 2 = 0. d) 2x 2 1 2x x x 0 x 1 2x 1 x 2 2x 0 x 2 = 0. Clasificarlas. EJERCICIO 32. Sea Q la cuádrica en P 3 (R) que respecto de un sistema de referencia tiene por ecuación xax t = 0, siendo A = a) Clasificarla y dar una ecuación reducida. b) Calcular los planos polares de (1:0:0:0) y (0:1:0:0), y los polos de x 0 + x 3 = 0, y x 0 + x 1 + x 2 + x 3 = 0. c) Calcular la variedad polar de L = {x 0 = x 1 = 0}. d) Idem con L = {x 0 + x 1 = x 2 = 0}, L + L, L L. EJERCICIO 33. Sea C una cónica-lugar no degenerada del plano proyectivo real no vacía. Se dice que un punto que no pertenece a C es interior (resp. exterior) si y sólo si su polar no corta a C (resp. su polar corta a C en dos puntos distintos). Se pide: a) Probar que por un punto exterior a C pasan dos tangentes a la cónica. b) Probar que por un punto interior a C no pasa ninguna tangente a la cónica y que toda recta que pasa por él corta a la cónica en dos puntos distintos. EJERCICIO 34. Sea Q una cuádrica de puntos elípticos, P / V(Q), y r una recta que pasa por P y corta a V(Q) en dos puntos distintos. Probar que el conjugado armónico de P respecto de los puntos r V(Q) está en el plano polar de P. EJERCICIO 35. Sea Q una cuádrica real no degenerada de P 3, P / V(Q), L su plano polar. Supongamos que L V(Q) y P L V(Q). a) Probar que la recta P P es tangente a Q en P. b) Probar que el conjunto de rectas que pasa por P y cortan a V(Q) en un punto de L es una cuádrica degenerada que tiene a P como punto singular, llamada cono tangente a Q en P. EJERCICIO 36. Se considera en P 3 (R) la cuádrica Q de ecuación xax t = 0 respecto de un sistema de referencia, con A = a) Clasificar Q y hallar sus puntos singulares. b) Demostrar que todos sus puntos no singulares son parabólicos, i.e. el plano tangente corta a V(Q) en una cónica de rango y signatura 1. c) Sea r la recta de ecuaciones x 1 + x 3 = 0, x 0 x 1 + x 2 = 0. Demostrar que los planos polares de todos sus puntos (salvo uno) coinciden. Calcúlese este plano común d) Demostrar que toda recta que pase por el punto singular verifica lo anterior
6 e) Sea s la recta de ecuaciones x 1 + x 3 = 0, x 0 x 1 + x 3 = 0. Demostrar que los planos polares de sus puntos son todos distintos, y pasan por una recta que contiene a un punto singular. Calcúlese esta recta. f) Demostrar que toda recta que no pase por un punto singular verifica lo anterior. g) Compruébese que el plano polar obtenido en el apartado c) es el determinado por las rectas de contacto de los planos tangentes a Q que pasan por r. EJERCICIO 37. Sea Q una cónica real no degenerada y A, B, C, D Q un cuadrivértice plano inscrito en Q. Probar que los puntos diagonales forma un trivértice autoconjugado (i.e. la polar de cada vértice es la recta que pasa por los otros dos). Indicación: usar el haz de cónicas de base A, B, C, D. EJERCICIO 38. Determinar las cónicas del plano real que pasan por los puntos A = (1 : 0 : 0), B = (1 : 0 : 2), C = (1 : 2 : 0), D = (1 : 2 : 10) y son tangentes a r : x 0 = 0. EJERCICIO 39. Determinar las cónicas tangentes a las cinco rectas siguientes: r 1 : x 1 + 3x 2 = 0, r 2 : 2x 0 + 3x 1 + x 2 = 0, r 3 : 2x 0 + 5x 1 + 3x 2 = 0, r 4 : x 1 x 2 = 0, r 5 : x 0 + 2x 1 x 2 = 0. EJERCICIO 40. Determinar las cónicas que pasan por el punto (3:1:2) y son tangentes a las rectas x 0 x 1 x 2 = 0, x 0 x 1 + x 2 = 0, x 0 + x 1 + x 2 = 0, x 0 + x 1 x 2 = 0. EJERCICIO 41. Determinar las cónicas que pasan por los puntos (3:2:1), (4:2:1), (5:3:2), (6:5:2) y son tangentes a la recta x 0 + 2x 1 7x 2 = 0. EJERCICIO 42. Determinar las cónicas que pasan por los puntos (1:0:1), (3:-2:0) y son tangentes a las rectas x 0 + 2x 1 = 0, x 1 = 0, x 0 + x 1 2x 2 = 0. EJERCICIO 43. Determinar las cónicas que pasan por los puntos (1:0:2), (3:1:2) y son tangentes a las rectas x 1 = 0, x 0 + 3x 1 3x 2 = 0, x 0 x 1 = 0. EJERCICIO 44. Determinar las cónicas que tienen un contacto de orden 2 (osculatrices) con la cónica de ecuación x 0 x 1 + x 0 x 2 + x 1 x 2 = 0 en el punto (0:1:0) y que pasa por los puntos (3 : 6 : 2),(1 : 0 : 1). EJERCICIO 45. Determinar las cónicas que tienen un contacto de 2 o orden en el punto (1:1:0) con la cónica de ecuación x x 0 x 1 + 4x 0 x 2 x x 1 x 2 + 2x 2 2 = 0 y pasan por (1:1:-1) y (2:1:2). EJERCICIO 46. Determinar las cónicas que tienen un contacto de orden 3 (super-osculatrices) con la cónica de ecuación x 2 0 x x 2 2 2x 0 x 1 = 0 en el punto (1:1:1) y que pasan por (1:2:1). Nota.- Los siguientes ejercicios se refieren al espacio afín como subespacio del proyectivo. EJERCICIO 47. En el plano proyectivo real y respecto de un sistema de referencia dado se consideran las cónicas de matrices siguientes: a) b) c) Sea H la recta x 0 = 0. Clasificar las cónicas afines en el plano afín resultante de quitar H. Calcular centros, diámetros, asíntotas, ejes y focos, cuando los haya. EJERCICIO 48. Se considera un sistema de referencia en el espacio proyectivo real de dimensión tres y, respecto de él, el plano H de ecuación x 0 = 0 y la cuádrica de ecuación: a) b) c) Clasificar las cuádricas afines que resultan al quitar el plano H dando los centros, planos asintóticos. EJERCICIO 49. Clasificar las familias de cuádricas afines: a) m mx 2 + y 2 + z 2 + 2z = 0 b) 3x 2 + 4myz + 2x 2y + m = 0
7 c) x 2 + (m + 1)y 2 + mz 2 + 2xy 2yz + 2x + 2z + 4 = 0 d) x 2 + y 2 + z 2 + 2mxy 2mx + 2y + 2z + 3 = 0. EJERCICIO 50. En el espacio proyectivo tridimensional real, y con respecto a un sistema de referencia fijo, se consideran las cuádricas Q : x x 0 x 1 x x 2 x 3 = 0, Q : x 2 0 x 0 x 1 x 2 2 x 2 x 3 = 0 y el haz H determinado por ambas. a) Hallar las cuádricas degeneradas de H. Si alguna de ellas fuese la unión de dos planos, escribir las ecuaciones (por separado) de cada uno de esos planos. b) Clasificar las cuádricas de H. c) Hallar los puntos base de del haz H. d) Hallar los planos tangentes comunes a Q y Q. EJERCICIO 51. Hallar la ecuación de una hipérbola una de cuyas asíntotas es la recta x+2y 2 = 0, la otra asíntota es paralela al eje OY y sabiendo que la polar del punto (1, 0) es la recta x + y 3 = 0. EJERCICIO 52. Hallar la ecuación de una cónica, cuyo centro es el punto (1,0), tiene por asíntota el eje OX y es tangente al eje OY en el punto (0,1). EJERCICIO 53. Determinar la cónica que teniendo las mismas direcciones asintóticas que la pase por el origen y tenga su centro en el punto (1,1). x 2 + 2xy 2y 2 x + y + 1 = 0 EJERCICIO 54. Hallar la ecuación de la cónica que pase por el origen, tenga un foco en el punto F = (1, 3) y su directriz correspondiente sea x + 2y 1 = 0. EJERCICIO 55. x 2y + 1 = 0. Determinar la hipérbola equilátera uno de cuyos focos es el punto (1,2) y la directriz correspondiente es EJERCICIO 56. Hallar la ecuación de una cónica tangente a la recta 2x 1 = 0, y cuyos focos son (1,3), ( 2, 1). EJERCICIO 57. Hallar la ecuación de una hipérbola tangente a la cónica C siguiente, en los puntos de intersección de C con la recta x 2y = 0 y teniendo una asíntota paralela al eje OY : C : 3x 2 2xy + 5y 2 x + y = 0 EJERCICIO 58. Consideremos la cuádrica real afín Q de ecuación: x 2 + y 2 + 2z 2 2xz 2yz 1 = 0, el plano π de ecuación z = 0 y el par de rectas r, s de ecuaciones: r = {x 1 = y z = 0}, s = {y 1 = x z = 0}. a) Clasificar la cuádrica afín real Q. Hallar sus planos principales y ejes. b) Hallar la posición relativa de la cónica C = Q π y del par de rectas r s. c) Existe alguna cuádrica degenerada que contenga a C r s? Razonar la respuesta. En caso afirmativo, hallar la ecuación de una tal cuádrica. d) Idem que el apartado c) para el caso de una cuádrica no degenerada. EJERCICIO 59. En el plano euclídeo R 2, sumergido de la forma habitual en P 2 (R), se pide:
8 1) Calcular la ecuación general de las hipérbolas cuyas asíntotas son las rectas x + 2y = 0, 2x y = 0. 2) Calcular los focos reales de cada una de las hipérbolas del apartado anterior. Qué lugar geométrico determinan? EJERCICIO 60. a) Probar que dos parábolas superosculatrices en su punto del infinito tienen el mismo eje. Es cierto el recíproco? b) Comprobar que las parábolas de ecuaciones y x 2 = 0, y x 2 + x = 0 son osculatrices en su punto del infinito. EJERCICIO 61. Calcular la ecuación general de las parábolas de R 2 cuyo eje es la recta x = 0 y cuyo foco es el punto (0, 1). EJERCICIO Calcule la ecuación de todas las parábolas de eje x + y = 0 y tangentes a las rectas x = 0 e y = De ellas, cúantas y cuáles pasan por ( 1, 1)? 3. Halle el foco y directriz (polar del foco) de las parábolas del apartado anterior. EJERCICIO 63. Calcular las secciones circulares del elipsoide 2x 2 + 3y 2 + z 2 = 1. EJERCICIO 64. Consideremos, en P 2 (C), la familia F de cónicas no degeneradas con focos reales F 1 = (1, 1) y F 2 = (3, 3), considerando el espacio afín C 2 inmerso en P 2 (C) de la forma habitual. a) Dar una ecuación general de la familia. Hallar los otros dos focos de cada una de las cónicas de F. b) Probar que toda cónica de la familia es tangente a cuatro rectas fijas y dar una ecuación de cada una de estas rectas. c) Sea F R la familia de cónicas afines reales inducida por F en R 2. Clasificar las cónicas de F R (considerando R 2 inmerso en P 2 (R) de la forma habitual, es decir, con x 0 = 0 como recta del infinito). d) Cuántas cónicas de F R pasan por cada punto de R 2? De qué tipo son? Deducir de aquí si F puede estar incluida en un haz de cónicas en P 2 (C). e) Determinar la(s) hipérbola(s) de R 2 con focos reales F 1 = (1, 1) y F 2 = (3, 3) y tales que la recta 2y x 2 = 0 sea una de sus asíntotas. Calcular, para cada una de estas hipérbolas, la otra asíntota. EJERCICIO 65. Consideremos la cuádrica afín de ecuación: 1 + 2x + x 2 + 2xz + 2y 2 + z 2 = 0 Clasificarla. Hallar su(s) direccion(es) principal(es) y diámetro(s) principal(es). Calcular su(s) eje(s) y el cono tangente a ella desde el punto (0, 0, 0). EJERCICIO 66. En el plano proyectivo real P 2 (R) se considera la familia F de cónicas definidas por la matriz A m = m2 m m m m 1 1 m 1 m 1 donde m R. 1. Probar que la familia F no es un haz de cónicas proyectivo y clasificar las cónicas de F. 2. Se considera, a partir de ahora, el plano R 2 inmerso en P 2 (R) tomando x 0 = 0 como recta del infinito. Sea F a la familia de cónicas afines en R 2 definida por F. Clasificar las cónicas de F a.
9 3. Hallar los ejes de las cónicas no degeneradas de la familia F a. 4. Hallar los puntos de R 2 por los que pasan dos cónicas de F a. 5. Hallar las asíntotas (si existen) y los focos (si existen) de la cónica que se obtiene para m = 1. EJERCICIO 67. Se da la familia F de cuádricas de P 3 (R) de ecuaciones siguientes: λ 2 x 0 x 2 + λx 1 x 2 + x 0 x 3 = 0 con λ un parámetro real. 1. Clasificar las cuádricas degeneradas de F. 2. Deducir si x 0 = 0 es un plano tangente a todas las cuádricas de F, y hallar los puntos de tangencia en su caso. 3. Usando lo anterior, dar la clasificación de todas las cuádricas de F, en función del parámetro λ. 4. Deducir si la recta r : x 0 = x 1, x 2 = x 3 es tangente a alguna cuádrica de F. EJERCICIO 68. Hallar la ecuación general de la familia de parábolas cuya tangente en el vértice es la recta s de ecuación x + 2y = 4. La familia es un haz de cónicas afines? b) Hallar la ecuación de la(s) parábola(s) de vértice V = (0, 2) y de tangente en V la recta s. Cuáles de estas parábolas pasan por el punto (4, 0)? EJERCICIO 69. Consideremos la cuádrica afín Q de ecuación 2 + 2x 2xy y 2 z 2 = 0 1. Clasificarla y hallar su centro. 2. Calcular las rectas contenidas en Q que pasan por el punto ( 1, 0, 0). 3. Calcular la ecuación del cono tangente a Q desde el punto (0, 0, 1). 4. Consideremos la familia de cuádricas afines de ecuación 2 + 2x 2xy y 2 z 2 + λ(1 + x + y) = 0 λ R utilizando exclusivamente los apartados anteriores junto con razonamientos geométricos (tanto en el afín como en el proyectivo) se pide clasificar todas las cuádricas de la familia. EJERCICIO 70. Sea la cónica afín Q de ecuación x 2 + 2x + 2y = 0. Clasificarla. Sea Q la cónica proyectiva asociada y consideremos el cuadrivértice P 1, P 2, P 3, P 4, con P 1 = (1 : 0 : 0), P 2 = (1 : 2 : 0), P 3 = (1 : 2 : 4), P 4 = (0 : 0 : 1). Calcular los puntos diagonales de este cuadrivértice y comprobar que la polar del punto diagonal alineado con P 1 y P 2 es la recta que pasa por los otros dos puntos diagonales (digamos P, P ). EJERCICIO 71. Consideremos la cuádrica afín Q de ecuación 2x 2 + y 2 + z 2 + 6yz + 2 = Clasificarla, hallar sus planos principales, ejes y sus vértices. 2. Qué tipos de cónicas afines se pueden obtener al cortar la cuádrica Q por un plano? Dar la ecuación de algún plano afín L que corte a Q en un par de rectas imaginarias (secantes en un punto real). EJERCICIO 72. En el espacio afín euclídeo R 3 consideramos la cuádrica Q de ecuación x 2 + 4y 2 10yz + 4z 2 1 = Clasificarla. 2. Calcular su centro, sus direcciones principales, sus planos principales y sus ejes. 3. Calcular su cono asintótico (es decir, el cono tangente con vértice en el centro).
10 EJERCICIO 73. Se dan los puntos A = (0, 0), B = (2, 2) y C = (3, 3) del plano afín R 2, que se considera sumergido en el plano proyectivo P 2 (R) del modo usual. Sea r la recta afín AB. 1. En la clausura proyectiva r P 2 (R) se considera el sistema de referencia R = {A, B; C}; hallar las coordenadas respecto de R de r, punto del infinito de r. 2. Sea P = (x, x) un punto genérico de r y P = (y, y) el cuarto armónico de A, B, P (cuando esté definido). Demostrar que se verifica que xy x y = Clasificar la ecuación anterior en R 2. Hallar sus asíntotas, si las tiene. EJERCICIO 74. A.- Teniendo en cuenta que la tangente en el vértice a una cónica es perpendicular al eje al que pertenece, determinar la(s) parábola(s) de eje 2x + y = 0 y vértice (0, 0) que pasan por el punto ( 1, 3). B.- Se considera la familia de cónicas afines de ecuación 1. Clasificarlas. Q α : 2αx x 2 + 2αxy y 2 = 0 2. Hallar las direcciones principales y los ejes de Q α en cada caso. 3. Para el caso α = 1, calcular los focos de la cónica obtenida. EJERCICIO 75. Se considera fijo el espacio proyectivo tridimensional real P 3 (R) y, dentro de él, el espacio euclídeo de dimensión 3, sumergido de la forma usual respecto de un sistema de coordenadas. Responder a las cuestiones siguientes: 1. Sea Q una cuádrica proyectiva no degenerada (es decir, de rango 4) y real (es decir, de signatura proyectiva 2 ó 0). Se puede averiguar si Q es de puntos elípticos o hiperbólicos (es decir, signatura 2, ó 0 respectivamente) cortando por planos transversales (es decir, no tangentes) a Q? En caso de respuesta afirmativa, decir cómo. 2. En un paraboloide elíptico de revolución Q, de qué tipo es la cónica del infinito Q de Q? Cuál de los puntos fundamentales del haz H determinado por el absoluto Ω y Q es el de tangencia del plano del infinito? 3. Dada la cuádrica Q de ecuación x 2 0 2x 0 x 1 2x 0 x 3 x x x 2 1 2x 3 x 1 = 0, de la que se sabe que es no degenerada, demostrar que la recta r que pasa por los puntos P 1 = (1 : 0 : 1 : 0), P 2 = (1 : 0 : 0 : 1) está contenida en ella. Cuál es la signatura proyectiva de esa cuádrica?. 4. Hallar el plano tangente L a la cuádrica Q en P 1. La intersección L V(Q) son dos rectas; hallar ecuaciones implícitas de cada una de ellas. 5. Razonar por qué los planos tangentes a Q en los puntos de r forman el haz de planos P de base r. EJERCICIO Describir la configuración de los puntos base y fundamentales de todos los haces de cónicas complejas. 2. Calcular la(s) parábola(s) superosculatrices (tipo 5) con 2x + 2xy x 2 1 = 0 en el punto (1, 0). Para cada solución hallada, calcular el eje y el foco. EJERCICIO 77. Se considera el espacio proyectivo tridimensional real P 3 (R). Se da la familia de cuádricas proyectivas λ(x 2 0 4x 2 1) + µ(x x 2 x 3 2x 2 3) = 0. 1). Clasificarla según los valores de λ y µ.
11 2). Para λ = µ = 1 obtenemos una cuádrica de puntos hiperbólicos. Se sabe que el punto P = (2 : 1 : 1 : 1) pertenece a la cuádrica lugar. Hallar dos puntos Q 1, Q 2 de la cuádrica lugar, distintos de P, tales que las rectas P Q 1 y P Q 2 sean las generatrices que pasan por P. 3). Se considera el espacio euclídeo sumergido en el proyectivo a la manera usual, es decir, tomando como hiperplano del infinito x 0 = 0. Las coordenadas afines serán designadas por x, y, z. Se pide clasificar la familia afín correspondiente según los valores de λ y µ. 4). Para λ = µ = 1 obtenemos una cuádrica afín. Hallar su centro y su cono asintótico. EJERCICIO 78. Dados cuatro planos H 1, H 2, H 3 y H 4 de P 3 (R) conteniendo una recta fija s, y dada otra recta r que se cruce con s, se llama razón doble de H 1, H 2, H 3, H 4 a (H1 r)(h 2 r)(h 3 r)(h 4 r). Sean H 1 = {x 3 = 0}, H 2 = {x 1 x 3 = 0}, H 3 = {x 1 = 0}, y r la recta de ecuaciones {x 0 = 0, x 1 + x 2 = 0}. Calcular el cuarto armónico de H 1, H 2, H 3. EJERCICIO 79. a) Defina centro de una hipercuádrica afín y enuncie sus propiedades de simetría. b) Pruebe que las cónicas afines de centro (0,0) y cuya tangente en ( 1, 1) es la recta x y + 2 = 0 forman parte de un haz de bitangentes. c) Determine las cónicas de centro (0,0), cuya tangente en ( 1, 1) es la recta x y + 2 = 0 y que pasen por el punto ( 2, 3). EJERCICIO 80. Dada la cuádrica Q en R 3 de ecuación x + y z x 2 + z 2 = 0, se pide: a) Clasificarla. b) Calcular su centro, planos principales y ejes, si los hay. c) Calcular las ecuaciones de cada una de las rectas contenidas en el lugar de Q que pasan por el origen de coordenadas, si las hay. d) Calcular el cilindro tangente a Q de dirección (1, 0, 0). Para ello calcular el cono tangente a Q desde (0 : 1 : 0 : 0). EJERCICIO 81. Consideremos la familia de cuádricas en R 3, de ecuación Q λ : x 2 z 2 + x + y + z + λ(x + y + z) = 0, λ R. 1.- Cuántas cuádricas degeneradas hay en la familia? Clasificarlas. 2.- Es el plano π : x + y + z = 0 tangente a todas las cuádricas no degeneradas de la familia? 3.- Clasificar (Q λ ) para cada valor de λ. 4.-Sin hacer cálculos, clasificar las cuádricas Q λ. 5.- Calcular los centros y ejes de cada una de las cuádricas no degeneradas de la familia. EJERCICIO Sea Q una cónica afín no degenerada en R 2. Defina el concepto de asíntota de Q. Deduzca, según sea V(Q ), el número de asíntotas de Q. 2. Calcule las ecuaciones de las cónicas que tienen la asíntota x = 1 y el foco (0, 0). 3. Verifique que la ecuación 1 2x 2y + 2xy = 0 es de una cónica del apartado anterior, hallando sus asíntotas y sus focos. EJERCICIO 83. Consideremos en el espacio proyectivo real tridimensional P 3 (R) el haz de cuádricas {Q λ,µ / (λ : µ) P 1 (R)}, con Q λ,µ = λ(x 0 x 1 + x 0 x 2 ) + µ( x x x x 2 3) = 0. a) Q 1,0 es un par de planos. Calcular sus polos respecto de Q 0,1 y deducir de la posición de éstos respecto de Q 0,1 los puntos base del haz, especificando si son reales o imaginarios. b) Sin hacer cálculos, determinar cuántas cuádricas proyectivas degeneradas hay en el haz, y clasificarlas. c) Sin hacer cálculos, clasificar las cuádricas afines no degeneradas (Q λ,µ ) a del espacio afín.
12 d) Calcular unas ecuaciones implícitas del lugar geométrico de los centros de las cuádricas afines anteriores. EJERCICIO 84. Contestar brevemente a las siguientes cuestiones: a) Enumerar los tipos de cuádricas proyectivas reales cuyos lugares contienen al menos una recta. b) Enumerar los tipos de cuádricas proyectivas reales cuyos lugares contienen al menos dos rectas que se cruzan. c) Enumerar los tipos de cuádricas afines reales cuyo lugar es vacío. d) Existen paraboloides elípticos de revolución? Y paraboloides hiperbólicos de revolución? Contestar razonadamente. e) Enumerar los tipos afines de cuádricas del espacio euclídeo tridimensional que pueden ser de revolución. f) Cuántos ejes tiene un cono afín real en el espacio euclídeo tridimensional que no sea de revolución? Contestar razonadamente. EJERCICIO 85. En el espacio proyectivo P n (R) se dan tres rectas L 1, L 2, L 3 tales que (L i + L j ) L k = para {i, j, k} = {1, 2, 3}. 1. Pruebe que n > 4, hallando la dimensión de la suma de las tres rectas. 2. En ese caso, pruebe que no existe ningún plano que contenga a una de las rectas y corte a las otras dos. EJERCICIO 86. Sean A y B dos puntos distintos del plano afín, y C el punto del infinito de la recta AB. 1. Indique razonadamente un procedimiento geométrico para construir, con escuadra y cartabón, el punto D tal que ACBD = Si D es el punto anterior, demuestre que un punto E verifica que ACBE = 1 4 si y sólo si ACDE = 1 2. Usando lo anterior, indique un procedimiento geométrico para construir un punto E tal que ACBE = Si A = (0, 0) y B = (1, 2), calcule las coordenadas de los puntos D y E anteriores. EJERCICIO 87. Sea Q la cuádrica afín de R 3 de ecuación 2x + y 2 + 2yz + z 2 = Clasifíquela. Calcule sus centros, planos principales y ejes, si los hay. 2.- Consideremos la cónica afín Q π, restricción de Q al plano π : x + y = 0. Clasificar esta cónica y calcular las coordenadas de su centro, focos y la ecuación de sus ejes (si los hubiera) respecto del sistema de referencia canónico de R 3. EJERCICIO 88. Sean la cónica no degenerada Q de ecuación 2x 0 x 1 + x 2 2 = 0 y la recta r 2x 0 + x 1 = 0. Probar que si A y B son los puntos de corte de la cónica con la recta y P el punto de coordenadas (0 : 0 : 1), se tiene que el punto P que hace que P P AB = 1 pertenece a la polar de la recta respecto de la cónica. Utilizando el apartado anterior, dar un procedimiento geométrico para calcular la polar del punto. EJERCICIO 89. Se tienen las dos cónicas Q 1 y Q 2 cuyas ecuaciones son respectivamente x 2 1 x x 0 x 2 = 0 y 3x 0 x 2 + 2x 1 x 2 + 4x x 2 2 = 0. Calcular el haz H(Q 1, Q 2 ). Calcular las cónicas degeneradas y los puntos fundamentales del haz, Fund(H). Calcular los puntos base del haz. Determinar de qué tipo es el haz. Encontrar las posibles cónicas del haz que sean tangentes a la recta x 1 = 0. Enumerar los tipos de haces que tengan una infinidad de puntos fundamentales describiendo sus cónicas degeneradas y sus puntos base. EJERCICIO 90. Se tiene la cuádrica afín x 2 + 2y 2 + z 2 + yz + 3xz + xy. 1. Clasificarla.
13 2. Calcular el centro, direcciones principales y ejes. Razonar si se trata de una cuádrica de revolución. 3. Calcular las tangentes desde el punto (1, 1, 1). EJERCICIO 91. De un haz de cónicas se sabe que: La cónica no degenerada Q de ecuación 2x 0 x 1 + x 2 2 = 0 pertenece al haz. Todas las cónicas del haz son tangentes en el mismo punto a la recta r de ecuación x 0 + 2x 1 + 2x 2 = 0. Todas las cónicas, salvo las degeneradas, son parábolas que intersecan con la recta del infinito en un punto común. Determinar el haz. EJERCICIO 92. Dada la cuádrica afín Q en R 3 de ecuación 2x 2 2y 2 z 2 4xz + 2y + 2 = 0, se pide: 1. Clasificarla. 2. Calcular sus direcciones principales. Es de revolución? En caso afirmativo calcular su eje de revolución. 3. Calcular los focos reales de la cónica restricción de Q al plano y = 0. EJERCICIO 93. Enumerar, razonadamente, las cuádricas proyectivas reales cuya sección por un plano pueda ser vacía. EJERCICIO 94. Sea la familia de cónicas x 2 + 4λxy + 4y 2 2λx + 4y 3 = 0. Discutir razonamente si se trata de un haz. Calcular el lugar geométrico que describen los centros de las cónicas de la familia. EJERCICIO 95. Sean r y s dos rectas distintas del plano proyectivo real y A su punto de intersección. Sean {B, C, D} y {B, C, D } ternas de puntos de r y s respectivamente, distintos entre sí y distintos de A. Demostrar que si ABCD = A B C D, las tres rectas AA, BB y CC son concurrentes. EJERCICIO 96. Consideremos la cuádrica Q de P 3 (R) de ecuación 2x x 0 x 2 + 2x x 1 x 3 + x 2 3 = 0 y la recta r de ecuaciones x 1 x 3 = x 1 + x 3 = 0. Sea f : r r la homografía definida como f(p ) := polar Q (P ) r. Se pide: 1. Calcular la imagen de un punto genérico de r y expresar la homografía matricialmente respecto de un sistema de referencia que se deba elegir. 2. Calcular (si existen) los puntos dobles para f, y expresar sus coordenadas respecto del sistema de referencia canónico de P 3 (R) EJERCICIO 97. Consideremos la cuádrica Q de P 3 (R) de ecuación 1. Clasificarla. 2x 0 x 1 + x 2 2 x 2 3 = 0 2. Dado el plano H : x 0 + x 2 x 3 = 0 calcular la restricción Q H. Clasificar dicha restricción. 3. Probar que el plano H es tangente en un punto P y encontrar dicho punto de contacto. 4. Dado el punto P del apartado anterior, Es posible encontrar dos rectas r, s (Q) que le contengan?. Calcularlas en caso afirmativo.
- EJERCICIOS DE AMPLIACION DE GEOMETRIA - Curso 04-05
 - EJERCICIOS DE AMPLIACION DE GEOMETRIA - Curso 04-05 Nota previa: Los primeros 18 ejercicios constituyen un repaso de los conceptos de la asignatura GEOMETRIA, que se utilizarán profusamente a lo largo
- EJERCICIOS DE AMPLIACION DE GEOMETRIA - Curso 04-05 Nota previa: Los primeros 18 ejercicios constituyen un repaso de los conceptos de la asignatura GEOMETRIA, que se utilizarán profusamente a lo largo
NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular.
 ÁLGEBRA Práctica 15 Cónicas (Curso 2008 2009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
ÁLGEBRA Práctica 15 Cónicas (Curso 2008 2009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
Problemas de Geometría Proyectiva
 Problemas de Geometría Proyectiva José M. Sánchez Abril José M. Rodríguez-Sanjurjo, Jesús M. Ruiz 1995 * I. VARIEDADES PROYECTIVAS Número 1. Se consideran en el plano proyectivo P 2 los cuatro puntos a
Problemas de Geometría Proyectiva José M. Sánchez Abril José M. Rodríguez-Sanjurjo, Jesús M. Ruiz 1995 * I. VARIEDADES PROYECTIVAS Número 1. Se consideran en el plano proyectivo P 2 los cuatro puntos a
ÁLGEBRA LINEAL II Práctica 4.1
 ÁLGEBRA LINEAL II Práctica 4.1 Cónicas (Curso 2010 2011) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo
ÁLGEBRA LINEAL II Práctica 4.1 Cónicas (Curso 2010 2011) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo
Tema 3. GEOMETRIA ANALITICA.
 Álgebra lineal. Curso 087-009. Tema. Hoja 1 Tema. GEOMETRIA ANALITICA. 1. Hallar la ecuación de la recta: a) que pase por ( 4, ) y tenga pendiente 1. b) que pase por (0, 5) y tenga pendiente. c) que pase
Álgebra lineal. Curso 087-009. Tema. Hoja 1 Tema. GEOMETRIA ANALITICA. 1. Hallar la ecuación de la recta: a) que pase por ( 4, ) y tenga pendiente 1. b) que pase por (0, 5) y tenga pendiente. c) que pase
GEOMETRÍA. (x 1) 2 +(y 2) 2 =1. Razónalo. x y + z = 2. :3x 3z +1= 0 es doble de la distancia al plano π 2. : x + y 1= 0. Razónalo.
 GEOMETRÍA 1. (Junio, 1994) Sin resolver el sistema, determina si la recta x +3y +1= 0 es exterior, secante o tangente a la circunferencia (x 1) +(y ) =1. Razónalo.. (Junio, 1994) Dadas las ecuaciones de
GEOMETRÍA 1. (Junio, 1994) Sin resolver el sistema, determina si la recta x +3y +1= 0 es exterior, secante o tangente a la circunferencia (x 1) +(y ) =1. Razónalo.. (Junio, 1994) Dadas las ecuaciones de
Autor: Francisco Martín Cabrera, Departamento Matemática Fundamental, Universidad de La Laguna, Islas Canarias, España TEMA IV
 52 Variedades Cuadráticas Autor: Francisco Martín Cabrera, Departamento Matemática Fundamental, Universidad de La Laguna, Islas Canarias, España http://creativecommons.org/licenses/by-nc-sa/2.5/es/ TEMA
52 Variedades Cuadráticas Autor: Francisco Martín Cabrera, Departamento Matemática Fundamental, Universidad de La Laguna, Islas Canarias, España http://creativecommons.org/licenses/by-nc-sa/2.5/es/ TEMA
EJERCICIOS DE GEOMETRÍA
 1) Sean las rectas EJERCICIOS DE GEOMETRÍA x 2y 6z 1 r : x y 0 x y 1 s: z 2 a a) Determinar la posición relativa de r y s según los valores de a. b) Calcular la distancia entre las rectas r y s cuando
1) Sean las rectas EJERCICIOS DE GEOMETRÍA x 2y 6z 1 r : x y 0 x y 1 s: z 2 a a) Determinar la posición relativa de r y s según los valores de a. b) Calcular la distancia entre las rectas r y s cuando
Polaridad. Tangentes. Estudio geométrico de cónicas y cuádricas
 Tema 6- Polaridad Tangentes Estudio geométrico de cónicas y cuádricas En este tema pretendemos estudiar propiedades de V(Q), especialmente en los casos real y complejo, con n =2,3 Para ello, necesitamos
Tema 6- Polaridad Tangentes Estudio geométrico de cónicas y cuádricas En este tema pretendemos estudiar propiedades de V(Q), especialmente en los casos real y complejo, con n =2,3 Para ello, necesitamos
Ejercicios de Ampliación de Geometría. Hoja 2
 Ejercicios de Ampliación de Geometría Licenciatura en Ciencias Matemáticas, 2 Curso 27 de Octubre de 2008 Hoja 2 Dualidad y radiaciones. 1. Formular y resolver en el espacio proyectivo dual los siguientes
Ejercicios de Ampliación de Geometría Licenciatura en Ciencias Matemáticas, 2 Curso 27 de Octubre de 2008 Hoja 2 Dualidad y radiaciones. 1. Formular y resolver en el espacio proyectivo dual los siguientes
EJERCICIOS VOLUNTARIOS DE GEOMETRIA CON SOLUCIÓN. 2º BACHILLERATO
 EJERCICIOS VOLUNTARIOS DE GEOMETRIA CON SOLUCIÓN. 2º BACHILLERATO ESPACIO AFIN 1.Hallar la ecuación del plano que contenga al punto P(1, 1, 1) y sea paralelo a las rectas: r x 2y = 0 ; y 2z + 4 = 0; s
EJERCICIOS VOLUNTARIOS DE GEOMETRIA CON SOLUCIÓN. 2º BACHILLERATO ESPACIO AFIN 1.Hallar la ecuación del plano que contenga al punto P(1, 1, 1) y sea paralelo a las rectas: r x 2y = 0 ; y 2z + 4 = 0; s
Geometría. 2 (el " " representa el producto vectorial)? En caso afirmativo, justifíquese. En caso contrario, póngase un ejemplo que lo confirme.
 Geometría 1 (Junio-96 Dados los vectores a,b y c tales que a, b 1 y c 4 y a b c, calcular la siguiente suma de productos escalares: a b b c a c (Sol: -1 (Junio-96 Señalar si las siguientes afirmaciones
Geometría 1 (Junio-96 Dados los vectores a,b y c tales que a, b 1 y c 4 y a b c, calcular la siguiente suma de productos escalares: a b b c a c (Sol: -1 (Junio-96 Señalar si las siguientes afirmaciones
EJERCICIOS DE SELECTIVIDAD DE GEOMETRIA
 EJERCICIOS DE SELECTIVIDAD DE GEOMETRIA 2003 (4) Ejercicio 1. Considera los vectores u = (1,1,1), v = (2,2,a) y w = (2,0,0), (a) [1'25 puntos] Halla los valores de a para que los vectores u, v y w sean
EJERCICIOS DE SELECTIVIDAD DE GEOMETRIA 2003 (4) Ejercicio 1. Considera los vectores u = (1,1,1), v = (2,2,a) y w = (2,0,0), (a) [1'25 puntos] Halla los valores de a para que los vectores u, v y w sean
Problemas de geometría afín
 Problemas de geometría afín Teóricos Problema A Para un subconjunto no vacío X de R n se cumple: X es subvariedad afín cada recta que pasa por dos puntos distintos de X está totalmente contenida en X Problema
Problemas de geometría afín Teóricos Problema A Para un subconjunto no vacío X de R n se cumple: X es subvariedad afín cada recta que pasa por dos puntos distintos de X está totalmente contenida en X Problema
B23 Curvas cónicas Curvas cónicas
 Geometría plana B23 Curvas cónicas Curvas cónicas Superficie cónica de revolución es la engendrada por una recta que gira alrededor de otra a la que corta. Curvas cónicas son las que resultan de la intersección
Geometría plana B23 Curvas cónicas Curvas cónicas Superficie cónica de revolución es la engendrada por una recta que gira alrededor de otra a la que corta. Curvas cónicas son las que resultan de la intersección
Respuestas faltantes en ejercicios edición 2007 Sección 4.4: Superficie cuadráticas de revolución Ejercicio 4-1
 Editorial Mc Graw Hill. Edición 007 Respuestas faltantes en ejercicios edición 007 Sección 4.4: Superficie cuadráticas de revolución Ejercicio 4- R r + x + y Ejercicio 4-3 + R x + y + z Ecuaciones: x +
Editorial Mc Graw Hill. Edición 007 Respuestas faltantes en ejercicios edición 007 Sección 4.4: Superficie cuadráticas de revolución Ejercicio 4- R r + x + y Ejercicio 4-3 + R x + y + z Ecuaciones: x +
x-z = 0 x+y+2 = [2012] [EXT-B] Halla el punto simétrico del P(2,1,-5) respecto de la recta r definida por
![x-z = 0 x+y+2 = [2012] [EXT-B] Halla el punto simétrico del P(2,1,-5) respecto de la recta r definida por x-z = 0 x+y+2 = [2012] [EXT-B] Halla el punto simétrico del P(2,1,-5) respecto de la recta r definida por](/thumbs/55/35462313.jpg) x = 1+t 1. [014] [EXT-A] Considera los puntos A(1,1,) y B(1,-1,-) y la recta dada por y = t. z = 1 a) Halla la ecuación general del plano que que contiene a r y es paralelo a la recta que pasa por A y
x = 1+t 1. [014] [EXT-A] Considera los puntos A(1,1,) y B(1,-1,-) y la recta dada por y = t. z = 1 a) Halla la ecuación general del plano que que contiene a r y es paralelo a la recta que pasa por A y
Tema 5. Cónicas. Asi, para las identificaciones habituales, (punto proyectivo recta vectorial punto de un plano afín ampliado), RP 2 R3 {0}
 Tema 5. Cónicas. Introducción. Ejemplos.- El cono C = {(x, y, z) R 3 /x 2 + y 2 = z 2 } está formado por las rectas vectoriales 0 (x 1,x 2, 1) [x 1,x 2, 1] RP 2 con (x 1,x 2, 1) C Π 1 = C 1, circunferencia
Tema 5. Cónicas. Introducción. Ejemplos.- El cono C = {(x, y, z) R 3 /x 2 + y 2 = z 2 } está formado por las rectas vectoriales 0 (x 1,x 2, 1) [x 1,x 2, 1] RP 2 con (x 1,x 2, 1) C Π 1 = C 1, circunferencia
x-z = 0 x+y+2 = [2012] [SEP-B] Halla el punto simétrico del P(2,1,-5) respecto de la recta r definida por
![x-z = 0 x+y+2 = [2012] [SEP-B] Halla el punto simétrico del P(2,1,-5) respecto de la recta r definida por x-z = 0 x+y+2 = [2012] [SEP-B] Halla el punto simétrico del P(2,1,-5) respecto de la recta r definida por](/thumbs/75/72263763.jpg) 1. [01] [SEP-B] Halla el punto simétrico del P(,1,-5) respecto de la recta r definida por x-z = 0 x+y+ = 0.. [01] [SEP-A] Sean los puntos A(0,0,1), B(1,0,-1), C(0,1,-) y D(1,,0). a) Halla la ecuación del
1. [01] [SEP-B] Halla el punto simétrico del P(,1,-5) respecto de la recta r definida por x-z = 0 x+y+ = 0.. [01] [SEP-A] Sean los puntos A(0,0,1), B(1,0,-1), C(0,1,-) y D(1,,0). a) Halla la ecuación del
COLEGIO NUESTRA SEÑORA DEL BUEN CONSEJO. Melilla LUGARES GEOMÉTRICOS Y CÓNICAS
 LUGARES GEOMÉTRICOS Y CÓNICAS 01. Halla la ecuación de la circunferencia de centro ( 5, 12) y radio 13. Comprueba que pasa por el punto (0, 0). 02. Halla las ecuaciones de los siguientes lugares geométricos:
LUGARES GEOMÉTRICOS Y CÓNICAS 01. Halla la ecuación de la circunferencia de centro ( 5, 12) y radio 13. Comprueba que pasa por el punto (0, 0). 02. Halla las ecuaciones de los siguientes lugares geométricos:
1. Determine el valor de la constante k para que la recta kx + (3 k)y + 7 = 0 sea perpendicular a la recta x + 7y + 1 = 0
 Universidad Técnica Federico Santa María Departamento de Matemática Campus Santiago Geometría Analítica 1. Determine el valor de la constante k para que la recta kx + (3 k)y + 7 = 0 sea perpendicular a
Universidad Técnica Federico Santa María Departamento de Matemática Campus Santiago Geometría Analítica 1. Determine el valor de la constante k para que la recta kx + (3 k)y + 7 = 0 sea perpendicular a
Matemáticas II. d) Perpendicular al plano π: 2x y + 3z 1 = 0, paralelo a la recta r : x 1 2 = y 3 = z 8
 I.E.S. Juan Carlos I Ciempozuelos (Madrid) Matemáticas II * Geometría analítica en R 3 * 1. Determina cuáles de las siguientes ternas de puntos son puntos alineados. Encuentra la ecuación de la recta que
I.E.S. Juan Carlos I Ciempozuelos (Madrid) Matemáticas II * Geometría analítica en R 3 * 1. Determina cuáles de las siguientes ternas de puntos son puntos alineados. Encuentra la ecuación de la recta que
Semana 13: Determinación de cónicas. Haces de cónicas proyectivas.
 Semana 13: Determinación de cónicas. Haces de cónicas proyectivas. Sonia L. Rueda ETS Arquitectura. UPM Geometría afín y proyectiva, 2015 Geometría afín y proyectiva 1. Álgebra lineal 2. Geometría afín
Semana 13: Determinación de cónicas. Haces de cónicas proyectivas. Sonia L. Rueda ETS Arquitectura. UPM Geometría afín y proyectiva, 2015 Geometría afín y proyectiva 1. Álgebra lineal 2. Geometría afín
Colegio Internacional Torrequebrada. Departamento de Matemáticas
 Geometría. Problema 1: Calcula la distancia del punto P(1, 1, 1) a la recta Problema 2: Dadas las rectas, se pide: a) Analiza su posición relativa. b) Halla la ecuación general del plano π que contiene
Geometría. Problema 1: Calcula la distancia del punto P(1, 1, 1) a la recta Problema 2: Dadas las rectas, se pide: a) Analiza su posición relativa. b) Halla la ecuación general del plano π que contiene
Problemas de exámenes de Geometría
 1 Problemas de exámenes de Geometría 1. Consideramos los planos π 1 : X = P+λ 1 u 1 +λ 2 u 2 y π 2 : X = Q+µ 1 v 1 +µ 2 v 2. Cuál de las siguientes afirmaciones es incorrecta? a) Si π 1 π 2 Ø, entonces
1 Problemas de exámenes de Geometría 1. Consideramos los planos π 1 : X = P+λ 1 u 1 +λ 2 u 2 y π 2 : X = Q+µ 1 v 1 +µ 2 v 2. Cuál de las siguientes afirmaciones es incorrecta? a) Si π 1 π 2 Ø, entonces
Espacios vectoriales. Vectores del espacio.
 Espacios vectoriales. Vectores del espacio. Consideremos un paralelepípedo de bases ABCD y EFGH, siendo A(1,1,1), B(2,1,1), C(2,4,1) y E(1,2,7). Halla: a) el área de una de las bases; b) el volumen del
Espacios vectoriales. Vectores del espacio. Consideremos un paralelepípedo de bases ABCD y EFGH, siendo A(1,1,1), B(2,1,1), C(2,4,1) y E(1,2,7). Halla: a) el área de una de las bases; b) el volumen del
, 2 x+y+z = 2, = z 5 y s: 4x-2y+z = 0. ( ) ( ) y dado el punto P(0,3,-1) exterior a, obtener las ecuaciones en
 x+y-z = 0 1. [2014] [EXT-A] Sea P el punto de coordenadas P(1,0,1) y r la recta de ecuación r x-2z = 1. a) Hallar la ecuación en forma continua de una recta que pase por el punto P y sea paralela a la
x+y-z = 0 1. [2014] [EXT-A] Sea P el punto de coordenadas P(1,0,1) y r la recta de ecuación r x-2z = 1. a) Hallar la ecuación en forma continua de una recta que pase por el punto P y sea paralela a la
3. Calcular una base normalizada asociada a esa referencia y las coordenadas en ella del punto [1, 2, 5, 3]
![3. Calcular una base normalizada asociada a esa referencia y las coordenadas en ella del punto [1, 2, 5, 3] 3. Calcular una base normalizada asociada a esa referencia y las coordenadas en ella del punto [1, 2, 5, 3]](/thumbs/68/59191793.jpg) Ejercicio 0.1 Sea K un cuerpo con q elementos y sea V un espacio vectorial de dimensión n + 1 sobre K. Calcular cuantas bases distintas (como subconjuntos) tiene V, cuantas referencias distintas hay en
Ejercicio 0.1 Sea K un cuerpo con q elementos y sea V un espacio vectorial de dimensión n + 1 sobre K. Calcular cuantas bases distintas (como subconjuntos) tiene V, cuantas referencias distintas hay en
Cónicas. Clasificación.
 Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Bloque 2. Geometría. 4. Iniciación a las Cónicas
 Bloque 2. Geometría 4. Iniciación a las Cónicas 1. La circunferencia Se llama circunferencia al lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. Elevando al cuadrado
Bloque 2. Geometría 4. Iniciación a las Cónicas 1. La circunferencia Se llama circunferencia al lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. Elevando al cuadrado
1. Escribir las ecuaciones paramétricas, reducida y continua de la recta que pasa por los puntos A(2,3,5) y B(-1,0,2).
 1. Escribir las ecuaciones paramétricas, reducida y continua de la recta que pasa por los puntos A(,3,5) y B(-1,0,).. Dados los puntos A(,3,-1) y B(-4,1,-), hallar las coordenadas de un punto C perteneciente
1. Escribir las ecuaciones paramétricas, reducida y continua de la recta que pasa por los puntos A(,3,5) y B(-1,0,).. Dados los puntos A(,3,-1) y B(-4,1,-), hallar las coordenadas de un punto C perteneciente
7. [2013] [JUN-A] a) Pueden existir vectores u y v tales que u = 2, v = 3 y u v = 8? Justifique la respuesta.
![7. [2013] [JUN-A] a) Pueden existir vectores u y v tales que u = 2, v = 3 y u v = 8? Justifique la respuesta. 7. [2013] [JUN-A] a) Pueden existir vectores u y v tales que u = 2, v = 3 y u v = 8? Justifique la respuesta.](/thumbs/71/65551146.jpg) 1. [014] [EXT-A] a) Determine el valor o valores de m, si existen, para que la recta r: mx+y = x+ mz = : x-y-z+6 = 0. b) Determine la distancia del punto P= (,1,1) a la recta r cuando m =. sea paralela
1. [014] [EXT-A] a) Determine el valor o valores de m, si existen, para que la recta r: mx+y = x+ mz = : x-y-z+6 = 0. b) Determine la distancia del punto P= (,1,1) a la recta r cuando m =. sea paralela
ALUMNO: GRUPO: Sean dos formas homológicas F y F' de planos superpuestos, una circunferencia c perteneciente a F y su cónica homóloga c' en F'.
 ESCUELA TÉCNICA SUPERIOR DE INGENIEROS DE CAMINOS, CANALES Y PUERTOS DE GRANADA GEOMETRÍA APLICADA. EXAMEN FINAL. 28 DE JUNIO DE 2012. EJERCICIO TEÓRICO ALUMNO: GRUPO: NOTAS - El test consta de un total
ESCUELA TÉCNICA SUPERIOR DE INGENIEROS DE CAMINOS, CANALES Y PUERTOS DE GRANADA GEOMETRÍA APLICADA. EXAMEN FINAL. 28 DE JUNIO DE 2012. EJERCICIO TEÓRICO ALUMNO: GRUPO: NOTAS - El test consta de un total
SOLUCIONES. ÁLGEBRA LINEAL Y GEOMETRÍA (Examen Ordinario : ) Grado en Matemáticas Curso
 ÁLGEBRA LINEAL Y GEOMETRÍA Eamen Ordinario : 6--7 Grado en Matemáticas Curso 6-7 SOLUCIONES Dados tres puntos distintos alineados A, A, A A R, al número real r tal que A A = r A A lo llamaremos raón simple
ÁLGEBRA LINEAL Y GEOMETRÍA Eamen Ordinario : 6--7 Grado en Matemáticas Curso 6-7 SOLUCIONES Dados tres puntos distintos alineados A, A, A A R, al número real r tal que A A = r A A lo llamaremos raón simple
EJERCICIOS DE GEOMETRÍA
 EJERCICIOS DE GEOMETRÍA 1. Se consideran las rectas r x 2 = 0 x 2z = 1, s y + 3 = 0 y + z = 3 a) Estudiar la posición relativa de r y s. b) Hallar la mínima distancia entre ambas. Se pide: Sol: Se cruzan
EJERCICIOS DE GEOMETRÍA 1. Se consideran las rectas r x 2 = 0 x 2z = 1, s y + 3 = 0 y + z = 3 a) Estudiar la posición relativa de r y s. b) Hallar la mínima distancia entre ambas. Se pide: Sol: Se cruzan
GEOMETRÍA I 23 de septiembre del 2011
 GEOMETRÍA I 3 de septiembre del 011 1. En el espacio ordinario se consideran las rectas l 1 : { x y + z = 1 x + y z = l : x 3 = y + 1 = z a. Hallar a IR para que exista un plano π que contenga a l 1 y
GEOMETRÍA I 3 de septiembre del 011 1. En el espacio ordinario se consideran las rectas l 1 : { x y + z = 1 x + y z = l : x 3 = y + 1 = z a. Hallar a IR para que exista un plano π que contenga a l 1 y
Fundamentos matemáticos. Tema 3 Geometría del plano y del espacio
 Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es
Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es
. Halla los valores de α en cada uno de los siguientes casos: a) (1 punto) u r, v
 EJERCICIOS BLOQUE III: GEOMETRÍA (04-M;Jun-A-4) Considera la recta r que pasa por los puntos A (,0, ) y (,,0 ) a) ( punto) Halla la ecuación de la recta s paralela a r que pasa por C (,,) b) (5 puntos)
EJERCICIOS BLOQUE III: GEOMETRÍA (04-M;Jun-A-4) Considera la recta r que pasa por los puntos A (,0, ) y (,,0 ) a) ( punto) Halla la ecuación de la recta s paralela a r que pasa por C (,,) b) (5 puntos)
EJERCICIOS BLOQUE III: GEOMETRÍA
 EJERCICIOS BLOQUE III: GEOMETRÍA (05-M4;Jun-B-4) Sea el plano π x + y z + 8 a) (5 puntos) Calcula el punto, P simétrico del punto (,,5 ) b) ( punto) Calcula la recta r, simétrica de la recta plano π P
EJERCICIOS BLOQUE III: GEOMETRÍA (05-M4;Jun-B-4) Sea el plano π x + y z + 8 a) (5 puntos) Calcula el punto, P simétrico del punto (,,5 ) b) ( punto) Calcula la recta r, simétrica de la recta plano π P
TEMAS 6 Y 7 RECTAS Y PLANOS EN EL ESPACIO
 Temas 6 y 7 Rectas y planos en el espacio Matemáticas II - 2º Bachillerato 1 TEMAS 6 Y 7 RECTAS Y PLANOS EN EL ESPACIO RECTAS Y PLANOS EJERCICIO 1 : Halla el volumen del tetraedro determinado por los ejes
Temas 6 y 7 Rectas y planos en el espacio Matemáticas II - 2º Bachillerato 1 TEMAS 6 Y 7 RECTAS Y PLANOS EN EL ESPACIO RECTAS Y PLANOS EJERCICIO 1 : Halla el volumen del tetraedro determinado por los ejes
ESTUDIO GRÁFICO DE LA ELIPSE.
 Curvas Cónicas para Dibujo y Matemáticas. Aplicación web Dibujo Técnico para ESO y Bachillerato Matemáticas para Bachillerato Educación Plástica y Visual Autor: José Antonio Cuadrado Vicente. ESTUDIO GRÁFICO
Curvas Cónicas para Dibujo y Matemáticas. Aplicación web Dibujo Técnico para ESO y Bachillerato Matemáticas para Bachillerato Educación Plástica y Visual Autor: José Antonio Cuadrado Vicente. ESTUDIO GRÁFICO
TEMAS 6 Y 7 GEOMETRÍA EN EL ESPACIO
 Ejercicios Selectividad Temas 6 y 7 Geometría en el espacio Mate II 2º Bach. 1 TEMAS 6 Y 7 GEOMETRÍA EN EL ESPACIO EJERCICIO 1 : Julio 11-12. Optativa (3 ptos) Para los puntos A(1,0,2) y B(-1,2,4) y la
Ejercicios Selectividad Temas 6 y 7 Geometría en el espacio Mate II 2º Bach. 1 TEMAS 6 Y 7 GEOMETRÍA EN EL ESPACIO EJERCICIO 1 : Julio 11-12. Optativa (3 ptos) Para los puntos A(1,0,2) y B(-1,2,4) y la
ALGEBRA Y GEOMETRIA ANALITICA
 Diplomatura en Ciencia y Tecnología ALGEBRA Y GEOMETRIA ANALITICA SEGUNDO CUATRIMESTRE DE 009 Profesora Mariana Suarez PRACTICA N 8: RECTA EN EL ESPACIO PLANO ALGEBRA Y GEOMETRIA ANALITICA - Segundo cuatrimestre
Diplomatura en Ciencia y Tecnología ALGEBRA Y GEOMETRIA ANALITICA SEGUNDO CUATRIMESTRE DE 009 Profesora Mariana Suarez PRACTICA N 8: RECTA EN EL ESPACIO PLANO ALGEBRA Y GEOMETRIA ANALITICA - Segundo cuatrimestre
Hipercuádricas. Polaridad. Estudio geométrico de las cónicas y cuádricas
 Capítulo 4 Hipercuádricas. Polaridad. Estudio geométrico de las cónicas y cuádricas Comenzamos con el objeto básico de este curso. Hemos estudiado hasta ahora variedades lineales proyectivas, que están
Capítulo 4 Hipercuádricas. Polaridad. Estudio geométrico de las cónicas y cuádricas Comenzamos con el objeto básico de este curso. Hemos estudiado hasta ahora variedades lineales proyectivas, que están
TEMA 5. CURVAS CÓNICAS.
 5.1. GENERALIDADES. TEMA 5. CURVAS CÓNICAS. Se denominan secciones cónicas a aquellas superficies que son producidas por la intersección de un plano con una superficie cónica de revolución (una superficie
5.1. GENERALIDADES. TEMA 5. CURVAS CÓNICAS. Se denominan secciones cónicas a aquellas superficies que son producidas por la intersección de un plano con una superficie cónica de revolución (una superficie
12. Espacios afines euclídeos
 12. Espacios afines euclídeos Distancia y sistema de referencia métrico Ejercicio 12.1. Teorema de Sylvester-Gallai. Sean P 1,...,P n,n 3 puntos del espacio euclídeo afín A 2 (R) que no están sobre una
12. Espacios afines euclídeos Distancia y sistema de referencia métrico Ejercicio 12.1. Teorema de Sylvester-Gallai. Sean P 1,...,P n,n 3 puntos del espacio euclídeo afín A 2 (R) que no están sobre una
Lugar Geométrico. Se llama lugar geométrico a un conjunto de puntos que cumplen una determinada propiedad. Mediatriz
 1 Lugar Geométrico Se llama lugar geométrico a un conjunto de puntos que cumplen una determinada propiedad. Mediatriz Mediatriz de un segmento es el lugar geométrico de los puntos del plano que equidistan
1 Lugar Geométrico Se llama lugar geométrico a un conjunto de puntos que cumplen una determinada propiedad. Mediatriz Mediatriz de un segmento es el lugar geométrico de los puntos del plano que equidistan
LA CIRCUNFERENCIA. La circunferencia es la sección producida por un plano perpendicular al eje.
 LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
x-y+2 = 0 z = [2014] [JUN-A] Sea el plano que pasa por los puntos A(1,-1,1), B(2,3,2), C(3,1,0) y r la recta dada por r x-7 2 = y+6
![x-y+2 = 0 z = [2014] [JUN-A] Sea el plano que pasa por los puntos A(1,-1,1), B(2,3,2), C(3,1,0) y r la recta dada por r x-7 2 = y+6 x-y+2 = 0 z = [2014] [JUN-A] Sea el plano que pasa por los puntos A(1,-1,1), B(2,3,2), C(3,1,0) y r la recta dada por r x-7 2 = y+6](/thumbs/56/38320881.jpg) 1. [014] [EXT-A] Sea el punto A(1,1,) y la recta de ecuación r a) Calcular el plano perpendicular a la recta r que pase por A. b) Calcular la distancia del punto A a la recta r. x-y+ = 0 z =.. [014] [EXT-B]
1. [014] [EXT-A] Sea el punto A(1,1,) y la recta de ecuación r a) Calcular el plano perpendicular a la recta r que pase por A. b) Calcular la distancia del punto A a la recta r. x-y+ = 0 z =.. [014] [EXT-B]
BLOQUE II. GEOMETRÍA.
 BLOQUE II. GEOMETRÍA. PROBLEMAS SELECTIVIDAD (PAU) CANTABRIA 2000-204 I.E.S. LA MARINA. CURSO 204/205. MATEMÁTICAS II. Condidera el plano y la recta r dados por : ax + 2y 4z 23 = 0, r: 3 a) ( PUNTO) Halla
BLOQUE II. GEOMETRÍA. PROBLEMAS SELECTIVIDAD (PAU) CANTABRIA 2000-204 I.E.S. LA MARINA. CURSO 204/205. MATEMÁTICAS II. Condidera el plano y la recta r dados por : ax + 2y 4z 23 = 0, r: 3 a) ( PUNTO) Halla
EJERCICIOS DE ÁLGEBRA LINEAL TEMA 1 ESPACIOS VECTORIALES
 EJERCICIOS DE ÁLGEBRA LINEAL TEMA ESPACIOS VECTORIALES Formas reducidas y escalonada de una matriz SISTEMAS DE ECUACIONES LINEALES ) Encuentre una sucesión de matrices elementales E, E,..., E k tal que
EJERCICIOS DE ÁLGEBRA LINEAL TEMA ESPACIOS VECTORIALES Formas reducidas y escalonada de una matriz SISTEMAS DE ECUACIONES LINEALES ) Encuentre una sucesión de matrices elementales E, E,..., E k tal que
CAPÍTULO 4 ESPACIOS VECTORIALES
 CAPÍTULO 4 ESPACIOS VECTORIALES 4.1.- Concepto y definición de espacio vectorial. 4.2.- Propiedades de los espacios vectoriales. 4.3.- Subespacios vectoriales. 4.4.- Combinación lineal de vectores. 4.5.-
CAPÍTULO 4 ESPACIOS VECTORIALES 4.1.- Concepto y definición de espacio vectorial. 4.2.- Propiedades de los espacios vectoriales. 4.3.- Subespacios vectoriales. 4.4.- Combinación lineal de vectores. 4.5.-
SERIE SUPERFICIES. 1.- Determinar la ecuación cartesiana del cilindro que contiene a la curva de ecuaciones:
 SERIE SUPERFICIES 1.- Determinar la ecuación cartesiana del cilindro que contiene a la curva de ecuaciones: 4x C z 0 y que se genera por rectas perpendiculares al plano: x + y + 3z + = 0.-Sea la superficie
SERIE SUPERFICIES 1.- Determinar la ecuación cartesiana del cilindro que contiene a la curva de ecuaciones: 4x C z 0 y que se genera por rectas perpendiculares al plano: x + y + 3z + = 0.-Sea la superficie
x = 1-2t 3. [2014] [EXT-B] Dados el plano y la recta r siguentes: 2x-y+2z+3 = 0, r z = 1+t
![x = 1-2t 3. [2014] [EXT-B] Dados el plano y la recta r siguentes: 2x-y+2z+3 = 0, r z = 1+t x = 1-2t 3. [2014] [EXT-B] Dados el plano y la recta r siguentes: 2x-y+2z+3 = 0, r z = 1+t](/thumbs/54/34881211.jpg) . [04] [EXT-A] Dados los puntos A(,0,-), B(,-4,-), C(5,4,-) y D(0,,4) a) Calcular el área del triángulo de vértices A, B y C. b) Calcular el volumen del tetraedro ABCD.. [04] [EXT-A] Dados los planos x-z-
. [04] [EXT-A] Dados los puntos A(,0,-), B(,-4,-), C(5,4,-) y D(0,,4) a) Calcular el área del triángulo de vértices A, B y C. b) Calcular el volumen del tetraedro ABCD.. [04] [EXT-A] Dados los planos x-z-
58 EJERCICIOS de RECTAS y PLANOS 2º BACH.
 58 EJERCICIOS de RECTAS y PLANOS 2º BACH. NOTA: En los ejercicios de Geometría se recomienda comenzar, antes de nada, por: Imaginarse la situación; podemos ayudarnos, para ello, de bolígrafos (para representar
58 EJERCICIOS de RECTAS y PLANOS 2º BACH. NOTA: En los ejercicios de Geometría se recomienda comenzar, antes de nada, por: Imaginarse la situación; podemos ayudarnos, para ello, de bolígrafos (para representar
CLASIFICACIÓN AFÍN DE CÓNICAS
 Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS CLASIFICACIÓN AFÍN DE CÓNICAS Sea E un R-espacio vectorial de dimensión. Sean E = e 1, e un plano vectorial de E y e 0 un
Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS CLASIFICACIÓN AFÍN DE CÓNICAS Sea E un R-espacio vectorial de dimensión. Sean E = e 1, e un plano vectorial de E y e 0 un
Fundamentos matemáticos. Tema 3 Geometría del plano y del espacio
 Grado en Ingeniería agrícola y del medio rural Tema 3 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2017 Licencia Creative Commons 4.0 Internacional J.
Grado en Ingeniería agrícola y del medio rural Tema 3 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2017 Licencia Creative Commons 4.0 Internacional J.
5 = z. 2. Hallar el valor de m para que los puntos A(3,m,1), B(1,1,-1) y C(-2,10,-4) pertenezcan a la misma recta.
 . Expresar en forma paramétrica y reducida la recta x+ 3 = y- 5 = z -. Hallar el valor de m para que los puntos A(3,m,), B(,,-) y C(-,0,-4) pertenezcan a la misma recta. 3. Probar que todos los planos
. Expresar en forma paramétrica y reducida la recta x+ 3 = y- 5 = z -. Hallar el valor de m para que los puntos A(3,m,), B(,,-) y C(-,0,-4) pertenezcan a la misma recta. 3. Probar que todos los planos
RECTAS Y PLANOS EN EL ESPACIO
 RECTAS Y PLANOS EN EL ESPACIO 4 6 7 8 9 0 Calcula las ecuaciones paramétricas de la recta que pasa por el punto P(7,, ) y tiene la dirección del vector k. ACTIVIDADES x 7 y z Halla la ecuación continua
RECTAS Y PLANOS EN EL ESPACIO 4 6 7 8 9 0 Calcula las ecuaciones paramétricas de la recta que pasa por el punto P(7,, ) y tiene la dirección del vector k. ACTIVIDADES x 7 y z Halla la ecuación continua
Profesor: Fernando Ureña Portero
 Curso 13-14 1.-Los puntos A(1,3,1) y B(2,1,3) son vértices consecutivos de un cuadrado. Los otros dos vértices pertenecen a una recta r que pasa por el punto P(2,7,0). a) (3p) Hallar la ecuación de la
Curso 13-14 1.-Los puntos A(1,3,1) y B(2,1,3) son vértices consecutivos de un cuadrado. Los otros dos vértices pertenecen a una recta r que pasa por el punto P(2,7,0). a) (3p) Hallar la ecuación de la
TEMA V. Espacios vectoriales
 TEMA V. Espacios vectoriales 1 1. Demostrar que cada uno de los siguientes conjuntos tiene estructura de espacio vectorial sobre el cuerpo de los reales: a El conjunto (R 2, +,, R. b El conjunto (R 3,
TEMA V. Espacios vectoriales 1 1. Demostrar que cada uno de los siguientes conjuntos tiene estructura de espacio vectorial sobre el cuerpo de los reales: a El conjunto (R 2, +,, R. b El conjunto (R 3,
Rectas y Cónicas. Sistema de Coordenadas Cartesianas. Guía de Ejercicios # Encuentre las coordenadas de los puntos mostrados en la figura.
 Universidad de Los Andes Facultad de Ciencias Forestales y Ambientales Escuela de ingeniería Forestal Departamento de Botánica y Ciencias Básicas Matemáticas I I 2014 Prof. K. Chang. Rectas y Cónicas Guía
Universidad de Los Andes Facultad de Ciencias Forestales y Ambientales Escuela de ingeniería Forestal Departamento de Botánica y Ciencias Básicas Matemáticas I I 2014 Prof. K. Chang. Rectas y Cónicas Guía
2 Intersección de una recta y una cuádrica. 1 Definición y ecuaciones. ( x y z
 2. Cuádricas. En todo este capítulo trabajaremos en el espacio afín euclídeo E 3 con respecto a una referencia rectangular {O; ē 1, ē 2, ē 3}. Denotaremos por (x, y, las coordenadas cartesianas respecto
2. Cuádricas. En todo este capítulo trabajaremos en el espacio afín euclídeo E 3 con respecto a una referencia rectangular {O; ē 1, ē 2, ē 3}. Denotaremos por (x, y, las coordenadas cartesianas respecto
El grupo lineal proyectivo. Homologías. Afinidades.
 Tema 3- El grupo lineal proyectivo Homologías Afinidades 31 El grupo lineal proyectivo Recordamos que en el tema anterior hemos definido, para una variedad lineal proyectiva L P n no vacía, el grupo lineal
Tema 3- El grupo lineal proyectivo Homologías Afinidades 31 El grupo lineal proyectivo Recordamos que en el tema anterior hemos definido, para una variedad lineal proyectiva L P n no vacía, el grupo lineal
Seis problemas resueltos de geometría
 Problema 1 a) Dados los puntos P(4, 2, 3) y Q(2, 0, 5), da la ecuación implícita del plano π de modo que el punto simétrico de P respecto a π es Q. b) Calcula el valor del parámetro λ R para que el plano
Problema 1 a) Dados los puntos P(4, 2, 3) y Q(2, 0, 5), da la ecuación implícita del plano π de modo que el punto simétrico de P respecto a π es Q. b) Calcula el valor del parámetro λ R para que el plano
Bloque 2. Geometría. 3. La recta. 1. Definición de recta
 Bloque 2. Geometría 3. La recta 1. Definición de recta Para representar puntos en un plano (superficie de dos dimensiones) utilizamos dos rectas graduadas y perpendiculares, cuyo corte es el punto 0 de
Bloque 2. Geometría 3. La recta 1. Definición de recta Para representar puntos en un plano (superficie de dos dimensiones) utilizamos dos rectas graduadas y perpendiculares, cuyo corte es el punto 0 de
Cónicas y cuádricas. Circunferencia Elipse Parábola Hipérbola
 Grado en Óptica y Optometría Curso 2009-2010 Cónicas y cuádricas. Curvas cónicas Entre las curvas, quizás más importante y con más renombre, figuran las conocidas como curvas cónicas, cuyo nombre proviene
Grado en Óptica y Optometría Curso 2009-2010 Cónicas y cuádricas. Curvas cónicas Entre las curvas, quizás más importante y con más renombre, figuran las conocidas como curvas cónicas, cuyo nombre proviene
a) La ecuación del plano que pasa por el punto ( 1, 1, 0 ). (3 puntos) b) La ecuación del plano que es paralelo a la recta r.
 PROBLEMAS DE SELECTIVIDAD. BLOQUE GEOMETRÍA 1. En el espacio se dan las rectas Obtener a) El valor de para el que las rectas r y s están contenidas en un plano. (4 puntos) b) La ecuación del plano que
PROBLEMAS DE SELECTIVIDAD. BLOQUE GEOMETRÍA 1. En el espacio se dan las rectas Obtener a) El valor de para el que las rectas r y s están contenidas en un plano. (4 puntos) b) La ecuación del plano que
Taller de Construcciones clásicas de Geometría con Cabri-Géomètre
 Taller de Construcciones clásicas de Geometría con Cabri-Géomètre Días 11, 12 y 13 de noviembre de 2008 Juan Francisco Padial y Eugenia Rosado jf.padial@upm.es eugenia.rosado@upm.es El taller consiste
Taller de Construcciones clásicas de Geometría con Cabri-Géomètre Días 11, 12 y 13 de noviembre de 2008 Juan Francisco Padial y Eugenia Rosado jf.padial@upm.es eugenia.rosado@upm.es El taller consiste
Geometría (Selectividad) 1. Dados los puntos A(1,3,5) y B(-2,4,1), hallar las coordenadas del punto C, perteneciente
 Geometría (Selectividad) 1. Dados los puntos A(1,3,5) y B(-2,4,1), hallar las coordenadas del punto C, perteneciente al plano OXY de forma que A, B y C estén alineados. Sol: 2. Considera la recta de ecuaciones.
Geometría (Selectividad) 1. Dados los puntos A(1,3,5) y B(-2,4,1), hallar las coordenadas del punto C, perteneciente al plano OXY de forma que A, B y C estén alineados. Sol: 2. Considera la recta de ecuaciones.
MATEMÁTICASII Curso académico BLOQUE GEOMETRÍA TEMA 2: Puntos, rectas y planos del espacio.
 MATEMÁTICASII Curso académico 2015-2016 BLOQUE GEOMETRÍA TEMA 2: Puntos, rectas y planos del espacio. 2.1 SISTEMA DE REFERENCIA. COORDENADAS DE UN PUNTO Elegimos un punto del espacio que llamamos origen
MATEMÁTICASII Curso académico 2015-2016 BLOQUE GEOMETRÍA TEMA 2: Puntos, rectas y planos del espacio. 2.1 SISTEMA DE REFERENCIA. COORDENADAS DE UN PUNTO Elegimos un punto del espacio que llamamos origen
GEOMETRÍA ANALÍTICA - Ejercicios de Selectividad
 GEOMETRÍA ANALÍTICA - Ejercicios de Selectividad 1 Se sabe que los puntos A (1,0,-1), B (3,, 1) y C (-7, 1, 5) son los vértices consecutivos de un paralelogramo ABCD. (a) Calcula las coordenadas del punto
GEOMETRÍA ANALÍTICA - Ejercicios de Selectividad 1 Se sabe que los puntos A (1,0,-1), B (3,, 1) y C (-7, 1, 5) son los vértices consecutivos de un paralelogramo ABCD. (a) Calcula las coordenadas del punto
101 EJERCICIOS de RECTAS
 101 EJERCICIOS de RECTAS Forma paramétrica: 1. Dado el punto A(5,3) y el vector director ur = (1, ), se pide: a) Hallar las ecuaciones paramétricas de la recta r que determinan. b) Obtener otros tres puntos
101 EJERCICIOS de RECTAS Forma paramétrica: 1. Dado el punto A(5,3) y el vector director ur = (1, ), se pide: a) Hallar las ecuaciones paramétricas de la recta r que determinan. b) Obtener otros tres puntos
1) Clasifica las siguientes cónicas y expresa sus focos y su excentricidad: a)
 Ejercicios de cónicas 1º bachillerato C 1) Clasifica las siguientes cónicas y expresa sus focos y su excentricidad: a) b) c) d) e) f) g) h) i) Soluciones: a) Circunferencia de centro ( y radio 3. Excentricidad
Ejercicios de cónicas 1º bachillerato C 1) Clasifica las siguientes cónicas y expresa sus focos y su excentricidad: a) b) c) d) e) f) g) h) i) Soluciones: a) Circunferencia de centro ( y radio 3. Excentricidad
= λ + 1 y el punto A(0, 7, 5)
 94 GEOMETRÍA ANALÍTICA DEL ESPACIO en las PAU de Asturias Dados los puntos A(1, 0, 1), B(l, 1, 1) y C(l, 6, a), se pide: a) hallar para qué valores del parámetro a están alineados b) hallar si existen
94 GEOMETRÍA ANALÍTICA DEL ESPACIO en las PAU de Asturias Dados los puntos A(1, 0, 1), B(l, 1, 1) y C(l, 6, a), se pide: a) hallar para qué valores del parámetro a están alineados b) hallar si existen
CÓNICAS. 1. Dada la cónica x 2 + 2xy y 2 2x 2y + 4 = 0, se pide su clasicación y los elementos característicos de la misma. = 1
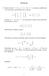 CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
Geometría 2. Halla a y b sabiendo que la recta que pasa por A y B corta perpendicularmente a la recta que pasa por C y D.
 Geometría Ejercicio. Considera el plano π la recta r dados por π a 4 b r. 4 4 a) Halla los valores de a b para los que r está contenida en π. b) Eiste algún valor de a algún valor de b para los que la
Geometría Ejercicio. Considera el plano π la recta r dados por π a 4 b r. 4 4 a) Halla los valores de a b para los que r está contenida en π. b) Eiste algún valor de a algún valor de b para los que la
CURVAS TÉCNICAS CURVAS CÓNICAS
 2º BACH CURVAS TÉCNICAS CURVAS CÓNICAS ANA BALLESTER JIMÉNEZ CURVAS TÉCNICAS 1. ÓVALOS. El óvalo es una curva cerrada, plana y convexa formada generalmente por cuatro arcos de circunferencia iguales dos
2º BACH CURVAS TÉCNICAS CURVAS CÓNICAS ANA BALLESTER JIMÉNEZ CURVAS TÉCNICAS 1. ÓVALOS. El óvalo es una curva cerrada, plana y convexa formada generalmente por cuatro arcos de circunferencia iguales dos
Tema 7 Rectas y planos en el espacio Matemáticas II - 2º Bachillerato 1
 Tema 7 Rectas y planos en el espacio Matemáticas II - º Bachillerato 1 ÁNGULOS EJERCICIO 33 : Halla el ángulo que forma la recta y el plano π: x y + 4z 0. 3x y z + 1 0 r : x + y 3z 0 EJERCICIO 34 : En
Tema 7 Rectas y planos en el espacio Matemáticas II - º Bachillerato 1 ÁNGULOS EJERCICIO 33 : Halla el ángulo que forma la recta y el plano π: x y + 4z 0. 3x y z + 1 0 r : x + y 3z 0 EJERCICIO 34 : En
hallar; a) Ecuación del plano que pasa por r y por (1, 3, 8) b) Distancia desde el origen al plano anterior
 x 1 y 1. Distancia entre la recta = = z y el plano (x, y, z) = (0, 1, 0) + τ(, 5, 1) + λ(1, 0, ) 3 5. Distancia del punto (, 3, 5) a la recta x 1 z = y = x + z y 3. Distancia entre las rectas r = y = y
x 1 y 1. Distancia entre la recta = = z y el plano (x, y, z) = (0, 1, 0) + τ(, 5, 1) + λ(1, 0, ) 3 5. Distancia del punto (, 3, 5) a la recta x 1 z = y = x + z y 3. Distancia entre las rectas r = y = y
TEMA 5. RECTAS Y PLANOS. INCIDENCIA.
 TEMA 5. RECTAS Y PLANOS. INCIDENCIA. SISTEMA DE REFERENCIA EN EL ESPACIO. Un sistema de referencia en el espacio está formado por un punto y tres vectores linealmente independientes. A partir de ahora
TEMA 5. RECTAS Y PLANOS. INCIDENCIA. SISTEMA DE REFERENCIA EN EL ESPACIO. Un sistema de referencia en el espacio está formado por un punto y tres vectores linealmente independientes. A partir de ahora
ALUMNO: GRUPO: Sean las series de bases r y r' y el haz de vértice V de la figura, todos ellos coplanarios.
 CANALES Y PUERTOS DE GRANADA INGENIERÍA GRÁFICA II. EXAMEN FINAL. 31 DE ENERO DE 2012 EJERCICIO TEÓRICO ALUMNO: GRUPO: NOTAS - El test consta de un total de 40 preguntas que se valorarán con las puntuaciones
CANALES Y PUERTOS DE GRANADA INGENIERÍA GRÁFICA II. EXAMEN FINAL. 31 DE ENERO DE 2012 EJERCICIO TEÓRICO ALUMNO: GRUPO: NOTAS - El test consta de un total de 40 preguntas que se valorarán con las puntuaciones
Haces de hipercuádricas. Clasificación de los haces de cónicas. Determinación de
 Capítulo 5 Haces de hipercuádricas. Clasificación de los haces de cónicas. Determinación de cónicas. 5.1. Definición y ecuaciones Definición 5.1.1. Sea (X, T, π) un espacio proyectivo de dimensión n sobre
Capítulo 5 Haces de hipercuádricas. Clasificación de los haces de cónicas. Determinación de cónicas. 5.1. Definición y ecuaciones Definición 5.1.1. Sea (X, T, π) un espacio proyectivo de dimensión n sobre
MODELOS DE EXÁMENES. Pruebas de acceso a la universidad Matemáticas II. Universidad Complutense (Madrid)
 COLEGIO INTERNACIONAL SEK EL CASTILLO Departamento de Ciencias MODELOS DE EXÁMENES Pruebas de acceso a la universidad Matemáticas II Universidad Complutense (Madrid) UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD
COLEGIO INTERNACIONAL SEK EL CASTILLO Departamento de Ciencias MODELOS DE EXÁMENES Pruebas de acceso a la universidad Matemáticas II Universidad Complutense (Madrid) UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD
4. [ANDA] [JUN-B] Dados los puntos A(2,1,1) y B(0,0,1), halla los puntos C en el eje OX tales que el área del triángulo de vértices A, B y C es 2.
![4. [ANDA] [JUN-B] Dados los puntos A(2,1,1) y B(0,0,1), halla los puntos C en el eje OX tales que el área del triángulo de vértices A, B y C es 2. 4. [ANDA] [JUN-B] Dados los puntos A(2,1,1) y B(0,0,1), halla los puntos C en el eje OX tales que el área del triángulo de vértices A, B y C es 2.](/thumbs/57/40567115.jpg) Selectividad CCNN 008 x-z = -. [ANDA] [SEP-A] Sea la recta dada por y+z = a) Halla la ecuación del plano que es paralelo a la recta s y contiene a la recta r, dada por x- = -y+ = z-. b) Estudia la posición
Selectividad CCNN 008 x-z = -. [ANDA] [SEP-A] Sea la recta dada por y+z = a) Halla la ecuación del plano que es paralelo a la recta s y contiene a la recta r, dada por x- = -y+ = z-. b) Estudia la posición
SECCIONES CÓNICAS (1)Determinar y graficar el lugar geométrico de los puntos que equidistan de F(0, 2) y de la recta
 LOS EJERCICIOS DEBEN RESOLVERSE TAMBIÉN USANDO SOFTWARE MATEMÁTICO. LAS ECUACIONES PEDIDAS SON, EN TODOS LOS CASOS, LAS CANÓNICAS Y LAS PARAMÉTRICAS. I) GEOMETRÍA ANALÍTICA EN EL PLANO 1. Determinar y
LOS EJERCICIOS DEBEN RESOLVERSE TAMBIÉN USANDO SOFTWARE MATEMÁTICO. LAS ECUACIONES PEDIDAS SON, EN TODOS LOS CASOS, LAS CANÓNICAS Y LAS PARAMÉTRICAS. I) GEOMETRÍA ANALÍTICA EN EL PLANO 1. Determinar y
Parte II - Prácticas 8 a 9. Álgebra A 62 ÁLGEBRA A 62 (INGENIERÍA)
 Parte II - Prácticas 8 a 9 Álgebra A 62 Ingeniería 2015 CICLO BÁSICO COMÚN UBA ÁLGEBRA A 62 (INGENIERÍA) Práctica 8 Introducción a las transformaciones lineales Definiciones y propiedades Transformaciones
Parte II - Prácticas 8 a 9 Álgebra A 62 Ingeniería 2015 CICLO BÁSICO COMÚN UBA ÁLGEBRA A 62 (INGENIERÍA) Práctica 8 Introducción a las transformaciones lineales Definiciones y propiedades Transformaciones
Facultad de Ingeniería Facultad de Tecnología Informática. Matemática Números reales Elementos de geometría analítica. Profesora: Silvia Mamone
 Facultad de Ingeniería Facultad de Tecnología Informática Matemática Números reales Elementos de geometría analítica 0 03936 Profesora: Silvia Mamone UB Facultad de Ingeniería Facultad de Tecnología Informática
Facultad de Ingeniería Facultad de Tecnología Informática Matemática Números reales Elementos de geometría analítica 0 03936 Profesora: Silvia Mamone UB Facultad de Ingeniería Facultad de Tecnología Informática
Observa que : OA + AB = OB a + AB = b AB = b a
 .- PUNTOS EN EL ESPACIO Sistema de referencia Un sistema de referencia en el espacio es un conjunto formado por un punto de referencia O y la base ortonormal canónica B = i, j, k. Se representa así:. En
.- PUNTOS EN EL ESPACIO Sistema de referencia Un sistema de referencia en el espacio es un conjunto formado por un punto de referencia O y la base ortonormal canónica B = i, j, k. Se representa así:. En
GUIA ADICIONAL CÁLCULO 1 GEOMETRÍA ANALÍTICA. 1.- Grafique los siguientes puntos y encuentre la distancia entre ellos:
 GUIA ADICIONAL CÁLCULO GEOMETRÍA ANALÍTICA ELEMENTOS DE GEOMETRÍA ANALÍTICA.- Grafique los siguientes puntos y encuentre la distancia entre ellos: a ) A(, 3) B( 5,3) b ) A( 4, 5) B(5, 3) c ) A(4, ) B(6,
GUIA ADICIONAL CÁLCULO GEOMETRÍA ANALÍTICA ELEMENTOS DE GEOMETRÍA ANALÍTICA.- Grafique los siguientes puntos y encuentre la distancia entre ellos: a ) A(, 3) B( 5,3) b ) A( 4, 5) B(5, 3) c ) A(4, ) B(6,
Matemáticas II Bachillerato Ciencias y Tecnología 2º Curso ESPACIO AFÍN Introducción Ecuaciones de la recta...
 Unidad 5 ESPACIO AFÍN 5.. Introducción.... - - 5.. Ecuaciones de la recta.... - - 5.3. Ecuaciones del plano.... - 4-5.4. Posiciones relativas (Incidencia y paralelismo).... - 6 - Anexo I.- EJERCICIOS...
Unidad 5 ESPACIO AFÍN 5.. Introducción.... - - 5.. Ecuaciones de la recta.... - - 5.3. Ecuaciones del plano.... - 4-5.4. Posiciones relativas (Incidencia y paralelismo).... - 6 - Anexo I.- EJERCICIOS...
ESCUELA PREPARATORIA OFICIAL NO.16 MATERÍA: GEOMETRÍA ANALITICA GUÍA DE ESTUDIO PARA LA ÚLTIMA OPORTUNIDAD DE ACREDITAR LA MATERÍA
 Geometría analítica 1.- Ecuación de la recta 2.- Cónicas 3.-Ecuación de la parábola UNIDAD II: CONICAS (CIRCUNFERENCIA Y PARABOLAS) Una superficie cónica de revolución está engendrada por la rotación de
Geometría analítica 1.- Ecuación de la recta 2.- Cónicas 3.-Ecuación de la parábola UNIDAD II: CONICAS (CIRCUNFERENCIA Y PARABOLAS) Una superficie cónica de revolución está engendrada por la rotación de
ejerciciosyexamenes.com GEOMETRIA
 GEOMETRIA 1.- Dado el vector AB= (2,-1,3) y el punto B(3,1,2) halla las coordenadas del punto A. Sol: A =(1,2,-1) 2.- Comprobar si los vectores AB y CD son equipolentes, siendo A(1,2,-1), B(0,3,1), C(1,1,1)
GEOMETRIA 1.- Dado el vector AB= (2,-1,3) y el punto B(3,1,2) halla las coordenadas del punto A. Sol: A =(1,2,-1) 2.- Comprobar si los vectores AB y CD son equipolentes, siendo A(1,2,-1), B(0,3,1), C(1,1,1)
UNIVERSIDAD CENTROAMERICANA JOSÉ SIMEÓN CAÑAS ALGEBRA VECTORIAL Y MATRICES GUIA DE TRABAJO Secciones Cónicas Ciclo 02 de 2012
 UNIVERSIDAD CENTROAMERICANA JOSÉ SIMEÓN CAÑAS ALGEBRA VECTORIAL Y MATRICES GUIA DE TRABAJO Secciones Cónicas Ciclo 0 de 0 PARTE I: Ejercicios cortos de selección Múltiple. En cada uno de los siguientes
UNIVERSIDAD CENTROAMERICANA JOSÉ SIMEÓN CAÑAS ALGEBRA VECTORIAL Y MATRICES GUIA DE TRABAJO Secciones Cónicas Ciclo 0 de 0 PARTE I: Ejercicios cortos de selección Múltiple. En cada uno de los siguientes
ÁLGEBRA LINEAL II Práctica
 ÁLGEBRA LINEAL II Práctica 3.1-3.2 Geometría afín. (Curso 2013 2014) 1. En un espacio afín real de dimensión 3, se consideran dos sistemas de referencia R = O, ē 1, ē 2, ē 3 } y R = P, ū 1, ū 2, ū 3 },
ÁLGEBRA LINEAL II Práctica 3.1-3.2 Geometría afín. (Curso 2013 2014) 1. En un espacio afín real de dimensión 3, se consideran dos sistemas de referencia R = O, ē 1, ē 2, ē 3 } y R = P, ū 1, ū 2, ū 3 },
Algebra Lineal y Geometría
 Algebra Lineal y Geometría Unidad n 11:Ecuación General de Segundo Grado en Tres Variables. Algebra Lineal y Geometría Esp.Liliana Eva Mata 1 Contenidos Superficies. Relaciones elementales entre propiedades
Algebra Lineal y Geometría Unidad n 11:Ecuación General de Segundo Grado en Tres Variables. Algebra Lineal y Geometría Esp.Liliana Eva Mata 1 Contenidos Superficies. Relaciones elementales entre propiedades
4. Escribe la ecuación de la circunferencia de centro C(-2,3) y radio 4. Sol: (x+2) 2 +(y-3) 2 =16.
 Problemas de circunferencias 4. Escribe la ecuación de la circunferencia de centro C(-2,3) y radio 4. Sol: (x+2) 2 +(y-3) 2 =16. 10. 5. Calcula la potencia del punto P(-1,2) a la circunferencia: x 2 +y
Problemas de circunferencias 4. Escribe la ecuación de la circunferencia de centro C(-2,3) y radio 4. Sol: (x+2) 2 +(y-3) 2 =16. 10. 5. Calcula la potencia del punto P(-1,2) a la circunferencia: x 2 +y
