Hipercuádricas. Polaridad. Estudio geométrico de las cónicas y cuádricas
|
|
|
- Trinidad Domínguez Tebar
- hace 6 años
- Vistas:
Transcripción
1 Capítulo 4 Hipercuádricas. Polaridad. Estudio geométrico de las cónicas y cuádricas Comenzamos con el objeto básico de este curso. Hemos estudiado hasta ahora variedades lineales proyectivas, que están definidas por ecuaciones homogéneas de primer grado. Dando un paso adelante, vamos a estudiar hipercuádricas que van a venir dadas por ecuaciones homogéneas de segundo grado. Veamos algunos preliminares. Supondremos siempre que k es un cuerpo de característica distinta de 2, aun cuando la mayoría de los resultados se referirán a C y R. Definición Un polinomio f de k[x 0, x 1,..., x n ] se dice homogéneo de grado d si es de la forma f = c c0c 1...c n x c0 0 xc xcn n, c 0+c c n=d con c c0c 1...c n k. La propiedad fundamental que verifican los polinomios homogéneos es la siguiente, debida a Euler: Lema Si f(x 0,..., x n ) es un polinomio homogéneo de grado d y λ k, entonces f(λx 0,..., λx n ) = λ d f(x 0,..., x n ) Definición Una hipercuádrica Q del espacio proyectivo P n (k) es una ecuación f = 0 definida por un polinomio homogéneo de segundo grado, salvo escalar. Es decir, la ecuación λf = 0 define la misma hipercuádrica Q, para cualquier λ k no nulo. En los casos n = 2, 3, utilizaremos para las hipercuádricas los nombres clásicos de cónicas y cuádricas, respectivamente. Con la siguiente definición distinguiremos la ecuación de sus soluciones.
2 Definición La hipercuádrica-lugar asociada a Q, será el conjunto de sus soluciones en P n (k), es decir V(Q) = {(a 0 : : a n ) P n f(a 0,..., a n ) = 0}. Nótese que la definición anterior es consistente, gracias al lema de Euler, porque un punto proyectivo está definido salvo escalar. Teorema Sean k un cuerpo algebraicamente cerrado y Q, Q dos hipercuádricas en P n (k). Entonces Q = Q si y sólo si V(Q) = V(Q ). Nota La clave del estudio de las hipercuádricas está en la posibilidad de traducir el carácter cuadrático de sus ecuaciones a las formas bilineales simétricas. Sea Q una hipercuádrica de P n (k) definida por una ecuación f = 0 donde f es un polinomio homogéneo de grado dos en las variables (x 0,..., x n ) y con coeficientes en k. Separamos los monomios puros (cuadrado de una variable) de los mixtos (producto de dos variables distintas): f = f(x 0,..., x n ) = n c ii x 2 i + i=0 si notamos por A a la matriz simétrica se tiene fácilmente que A = c 00 c 01 c 01 0 i<j n 2 c ij x i x j k[x 0,..., x n ], c 0n 2 c 1n 2 2 c c 0n c 1n 2 2 c nn, f(x 0,..., x n ) = (x 0,..., x n )A(x 0,..., x n ) t. De este modo se asocia a cada polinomio homogéneo de segundo grado f una única matriz simétrica A de orden n + 1, cuya diagonal está formada por los coeficientes de los monomios puros de f, y los elementos extradiagonales de A, por los coeficientes de los monomios mixtos correspondientes de f, divididos por 2 ( aquí es fundamental la hipótesis sobre la característica de k!), y que verifica la anterior ecuación. En la anterior descripción de A, y en lo sucesivo, es útil numerar las filas y columnas de A de 0 a n, así como denotar por X al vector (x 0,..., x n ) de modo que la ecuación de Q se escribe XAX t = 0. Por tanto la hipercuádrica Q tiene asociada la clase-matriz [A], con A matriz simétrica de orden n + 1. Definición Dos hipercuádricas Q y Q, de ecuaciones XAX t = 0 y XBX t = 0, se dicen (proyectivamente) equivalentes, y se notará Q Q, si se diferencian en un cambio de sistema de referencia, es decir, si existe una matriz M, con M 0, tal que [B] = [MAM t ], o bien, A y B son congruentes salvo escalar. Se trata de resolver dos problemas, íntimamente relacionados: Problema 1. Dada una hipercuádrica Q encontrar un sistema de referencia en el que Q tenga una ecuación lo más simple posible. 2
3 Problema 2. Dadas dos hipercuádricas Q y Q deducir si son o no equivalentes. Para la respuesta a ambas cuestiones será fundamental el cuerpo base k. Como nos apoyaremos en resultados de Álgebra Lineal relativos a congruencias de matrices reales y complejas, la solución a los problemas citados se limita a k = R o k = C. Resultados previos de Álgebra Lineal 1. Sea A una matriz simétrica con elementos en k. Existe una matriz inversible M tal que la matriz MAM t es diagonal. 2. Sea A una matriz simétrica compleja. Existe una matriz M compleja, inversible, tal que 1... MAM t = Más aún, si M y M son dos matrices complejas inversibles tales que D = MAM t y D = M A(M ) t son diagonales, entonces el número de elementos no nulos en las diagonales de D y D coincide y por tanto este número no depende más que de A (de hecho este número es el rango de A). Se deduce fácilmente de lo anterior que dos matrices simétricas complejas son congruentes si y sólo si tienen el mismo rango. 3. Sea A una matriz simétrica real. Existe una matriz M real inversible tal que MAM t = Más aún, si M y M son dos matrices reales inversibles tales que D = MAM t y D = M A(M ) t son diagonales, entonces el número de elementos positivos en las diagonales de D y D coincide y por tanto este número no depende más que de A, se llama signatura lineal de A, y lo notaremos por sl(a). Se deduce fácilmente de lo anterior que dos matrices simétricas reales son congruentes si y sólo si tienen el mismo rango y la misma signatura lineal. A partir de estos resultados se pueden resolver fácilmente los problemas enunciados. Teorema (Clasificación de hipercuádricas complejas) 3
4 1. Sea Q una hipercuádrica compleja. El rango de cualquier matriz de cualquier ecuación de Q no varía, y se denominará rango de Q. 2. Si Q tiene rango r + 1, existe un sistema de referencia en P n (C) en el que x x 2 r = 0 es una ecuación (reducida) de Q. 3. Sean Q y Q dos hipercuádricas complejas. Q Q si y sólo si Q y Q tienen el mismo rango. Teorema (Clasificación de hipercuádricas reales) 1. Sea Q una hipercuádrica real. El rango de cualquier matriz A de cualquier ecuación XAX t = 0 de Q no varía, y se denominará rango de Q. El número sl(a) sl( A) sólo depende de Q y se denominará signatura proyectiva de Q, y la notaremos sp(q). 2. Existe un sistema de referencia en P n (R) tal que una ecuación (reducida) de Q es x x 2 p x 2 p+1... x 2 r = 0, donde r + 1 es el rango de Q y la diferencia entre coeficientes positivos y negativos, en valor absoluto ( 2p r + 1 ), es la signatura proyectiva de Q. 3. Sean Q y Q dos hipercuádricas reales. Q Q si y sólo si Q y Q tienen el mismo rango y la misma signatura proyectiva. Definición Llamaremos hipercuádricas no degeneradas de P n (k) a aquellas que tienen rango máximo n + 1, y las llamaremos degeneradas en caso contrario. Ejemplo HIPERCUÁDRICAS DE LA RECTA PROYECTIVA COMPLEJA. Como hemos visto, hay tres tipos de hipercuádricas: 1. rango(q)=2 (no degeneradas). Su ecuación reducida es x x 2 1 = 0. Así V(Q) son dos puntos distintos de P 1 (C). 2. rango(q)=1. Su ecuación reducida es x 2 0 = 0. Así V(Q) es un punto de P 1 (C). 3. rango(q)=0. Su ecuación es 0=0 y V(Q) = P 1 (C). Ejemplo HIPERCUÁDRICAS DE LA RECTA PROYECTIVA REAL. Por el teorema de clasificación hay 4 tipos de hipercuádricas. 1. rango(q)=2, sp(q)=2. Su ecuación reducida es x x 2 1 = 0. Así V(Q) =. Se llama hipercuádrica no degenerada imaginaria. 2. rango(q)=2, sp(q)=0. Su ecuación reducida es x 2 0 x 2 1 = 0. Así V(Q) son dos puntos. Se llama hipercuádrica no degenerada real. 3. rango(q)=sp(q)=1. Su ecuación reducida es x 2 0 = 0. Así V(Q) es un punto. 4. rango(q)=0. Su ecuación es 0=0 y V(Q) = P 1 (R). 4
5 El estudio de cónicas y cuádricas lo dejaremos para más adelante siguiente, puesto que necesitaremos el concepto de polaridad. Para terminar presentamos un método rápido de cálculo de la signatura proyectiva de una hipercuádrica real. Para ello necesitamos recordar algunos resultados. Teorema Sea Q una hipercuádrica real de ecuación XAX t = 0. Se verifica que sp(q) coincide con la diferencia, en valor absoluto, entre el número de cambios de signo y de permanencias de la sucesión de coeficientes del polinomio q(λ), obtenido dividiendo el polinomio característico de A, p(λ) = λi A, por la máxima potencia de λ por la que sea divisible Puntos conjugados respecto de una hipercuádrica Recordemos que una hipercuádrica Q en X = P n (k) se dice degenerada si el rango de Q es estrictamente menor que dim(x) y se dice no degenerada en otro caso. Definición Sea Q una hipercuádrica en X. Un punto P 1 X se dice conjugado con P 2 X respecto de Q, si x 1 Ax t 2 = 0 donde Q = [A], [x 1 ] = P 1 y [x 2 ] = P 2. Un punto P se dice autoconjugado respecto de Q si P es conjugado consigo mismo (respecto de Q). Lema Sean Q una hipercuádrica y P X. El conjunto de puntos de X conjugados con P, respecto de Q, es una variedad lineal proyectiva, llamada la variedad polar (o simplemente la polar) de P respecto de Q y notada polar Q (P ). Si P L(Q), la polar de P se llamará la variedad tangente a Q en P. Si Q es no degenerada, entonces para todo P X, polar Q (P ) es un hiperplano (llamado el hiperplano polar de P respecto de Q). Definición Sean Q una hipercuádrica y L una variedad lineal proyectiva de X. Diremos que L es tangente a Q en P si P L y L polar Q (P ). Definición Sea Q una hipercuádrica en X. Un punto P L(Q) se dice singular si P es conjugado (respecto de Q) con todo punto de X. El conjunto de los puntos singulares de Q se notará Sing(Q). Lema Sea Q una hipercuádrica de rango r. El conjunto Sing(Q) es una variedad lineal proyectiva de dimensión n r. En particular, si Q es no degenerada entonces Sing(Q) =. Nótese que todo punto singular pertenece a la hipercuádrica por ser autoconjugado. Además, si P Sing(Q) y P L(Q) entonces P + P L(Q) Polaridad Teorema Sean Q una hipercuádrica y L una variedad lineal proyectiva de X. El conjunto de los puntos de X conjugados con todos los puntos de L es una variedad lineal 5
6 proyectiva que será denotada polar Q (L) y que será llamada la polar de L respecto de Q. Además se tiene que si L variedad lineal proyectiva: 1. L 1 L 2 polar Q (L 1 ) polar Q (L 2 ). 2. polar Q (L) Sing(Q) = polar Q (P n ). 3. polar Q ( i L i) = i polar Q (L i ). 4. polar Q (L) = P L polar Q (P ). 5. polar Q ( L i ) polar Q (L i ). 6. polar Q (polar Q (L)) L. 7. dim polar Q (L) n dim(l) + 1. Teorema Sean Q una hipercuádrica no degenerada y H un hiperplano de X. Entonces, el polo de H (respecto de Q) es la intersección de los hiperplanos polares de los puntos de H. Esto es polo Q (H) = polar Q (P ). P H El teorema anterior se llama Teorema de la Polaridad Hipercuádricas sobre variedades lineales proyectivas Sea L una subvariedad lineal proyectiva de dimensión s (0 s n) de P n (k). Sea R = {R 0,..., R s, V } un sistema de referencia en L. Se llama hipercuádrica restricción de Q sobre L, respecto de R, la clase de equivalencia (respecto de la equivalencia escalar) de una matriz no nula de MS(s + 1, k). Si R = {R 0,..., R s, V } es otro sistema de referencia en L y si C es una matriz del cambio (i.e. (x 0,..., x s ) R = (x 0,..., x s) R C) entonces una matriz de Q respecto de R es CAC t. La ecuación de Q respecto de R es (x 0,..., x s )A(x 0,..., x s ) t = 0. El conjunto de soluciones (en L) de la ecuación anterior se denota L(Q) y se llama la hipercuádrica lugar de Q (respecto de R) Intersección de una hipercuádrica con una variedad lineal proyectiva. Sea Q = [A] una hipercuádrica el X 1. Sea L una variedad lineal proyectiva de dimensión s, 0 s n. Si R = {R 0,..., R s, V } es un sistema de referencia en L, 1 Si no se precisa lo contrario, se entenderá que A es una matriz de Q respecto del sistema de referencia canónico 6
7 notaremos R = {R 0,..., R s, R s+1,..., R n, U} una extensión de R a un sistema de referencia en X = P n (k) de manera que, si P L entonces las coordenadas de P respecto de R son (a 0 :... : a s ) si y sólo si, respecto de R, las coordenadas de P son (a 0 :... : a s : 0 :... : 0). Sea à = CACt una matriz de Q respecto de R, donde C es una matriz del cambio de sistema de R al sistema de referencia canónico. Notaremos à L la matriz que se obtiene suprimiendo en à las últimas (n s) filas y columnas. Definición Si à L no es la matriz nula, llamaremos restricción de Q a L, respecto de R, (y notaremos Q L ) a la hipercuádrica de L, respecto de R, definida por Ã. Proposición Con las notaciones anteriores 1. Sean P, P L, P Q L P P Q P. 2. Si P L, polar Q L (P ) = polar Q (P ) L. 3. Si L L, polar Q L (L ) = polar Q (L ) L. 4. (Q L ) = (Q) L. 5. (Q) L polar Q (L) L. 6. rg(q L ) = dim(l) dim(l polar Q (L)). Teorema Sean Q una hipercuádrica no degenerada y H un hiperplano de X. Entonces se tiene: 1. Si H no es tangente a Q entonces rango(q H ) = n. 2. Si H es tangente a Q entonces rango(q H ) = n Si k = R y H es tangente a Q entonces, además, sp(q) = sp(q H ) 4.5. Cónicas en P 2 (C) De acuerdo con el teorema sólo existen tres clases de equivalencia proyectiva de cónicas complejas. rango(q) = 3 Una ecuación reducida de una cónica de esta clase es x 2 0+x 2 1+x 2 2 = 0. Una cónica de esta clase no tiene ningún punto singular. Recibe el nombre de Cónica no degenerada compleja. rango(q) = 2 Una ecuación reducida es x x 2 1 = 0. La cónica lugar consiste por tanto en dos rectas complejas y distintas que se cortan en el único punto singular de la cónica. Recibe el nombre de Par de rectas complejas distintas. 7
8 rango(q) = 1 Una ecuación reducida es x 2 0 = 0. La cónica lugar consiste por tanto en una recta compleja. Todos los puntos de la cónica son singulares. Recibe el nombre de Recta doble compleja Cónicas en P 2 (R) De acuerdo con el teorema existen cinco clases de equivalencia proyectiva de cónicas reales rango(q) = 3, sp(q) = 3 Una ecuación reducida de una cónica de esta clase es x 2 0+ x x 2 2 = 0. Por tanto la cónica lugar es. Recibe el nombre de Cónica imaginaria no degenerada. rango(q) = 3, sp(q) = 1 Una ecuación reducida es x 2 0+x 2 1 x 2 2 = 0. No hay puntos singulares. La cónica lugar es no vacía. Recibe el nombre de Cónica real no degenerada. rango(q) = 2, sp(q) = 2 Una ecuación reducida es x x 2 1 = 0. La cónica lugar consta sólo de un punto que es singular. Recibe el nombre de Par de rectas imaginarias secantes en un punto real. rango(q) = 2, sp(q) = 0 Una ecuación reducida es x 2 0 x 2 1 = 0. La cónica lugar consta de dos rectas distintas que se cortan en el único punto singular de la cónica. Recibe el nombre de Par de rectas reales y distintas. rango(q) = 1, sp(q) = 1 Una ecuación reducida es x 2 0 = 0. La cónica lugar consta de una recta. Todos los puntos de la cónica son singulares. Recibe el nombre de Recta doble real Cuádricas en P 3 (C) De acuerdo con el teorema existen cuatro clases de equivalencia proyectiva de cuádricas complejas. rango(q) = 4 Una ecuación reducida de una cuádrica de esta clase es x x x 2 2 +x 2 3 = 0. Una cuádrica de esta clase no tiene ningún punto singular. Recibe el nombre de Cuádrica compleja no degenerada. rango(q) = 3 Una ecuación reducida es x x x 2 2 = 0. La cuádrica tiene un único punto singular P. Este punto tiene la siguiente propiedad: Para todo P L(Q), P P, la recta P + P está contenida en L(Q). Debido a esta propiedad, la cuádrica recibe el nombre de Cono proyectivo complejo de vértice P. 8
9 rango(q) = 2 Una ecuación reducida es x 2 0+x 2 1 = 0. La cuádrica lugar es la reunión de dos planos distintos. La recta intersección de estos planos es el conjunto de puntos singulares de la cuádrica. Recibe el nombre de Par de planos complejos y distintos. rango(q) = 1 Una ecuación reducida es x 2 0 = 0. La cuádrica lugar es un plano. Todos los puntos de ese plano son singulares. Recibe el nombre de Plano doble complejo Cuádricas en P 3 (R) De acuerdo con el teorema existen ocho clases de equivalencia proyectiva de cuádricas reales. rango(q) = 4, sp(q) = 4 Una ecuación reducida de una cuádrica de esta clase es x x x x 2 3 = 0. La cuádrica lugar es el vacío. Recibe el nombre de Cuádrica imaginaria no degenerada. rango(q) = 4, sp(q) = 2 Una ecuación reducida es x x x 2 2 x 2 3 = 0. La cuádrica no tiene puntos singulares. De acuerdo con el teorema se verifica la siguiente propiedad: Para todo P L(Q) el hiperplano polar de P corta a L(Q) sólo en el punto P. Debido a esta propiedad, la cuádrica recibe el nombre de Cuádrica (no degenerada) real de puntos elípticos. rango(q) = 4, sp(q) = 0 Una ecuación reducida es x x 2 1 x 2 2 x 2 3 = 0. La cuádrica no tiene puntos singulares. De acuerdo con el teorema se verifica la siguiente propiedad: Para todo P L(Q) el hiperplano polar de P corta a L(Q) en dos rectas distintas que se cortan en P. Debido a esta propiedad, la cuádrica recibe el nombre de Cuádrica (no degenerada) real de puntos hiperbólicos. Además esta cuádrica es reglada (ver 4.8.1). rango(q) = 3, sp(q) = 3 Una ecuación reducida es x x x 2 2 = 0. La cuádrica lugar consta de un sólo punto que es singular. Puesto que su complexificado es un cono esta cuádrica recibe el nombre de Cono imaginario de vértice su punto singular. rango(q) = 3, sp(q) = 1 Una ecuación reducida es x x 2 1 x 2 2 = 0. La cuádrica tiene un sólo punto singular P. Este punto tiene la siguiente propiedad: Para todo P L(Q), P P, la recta P + P está contenida en L(Q). Debido a esta propiedad, la cuádrica recibe el nombre de Cono proyectivo real de vértice P. rango(q) = 2, sp(q) = 2 Una ecuación reducida es x x 2 1 = 0. La cuádrica lugar es una recta que coincide con Sing(Q). Como su complexificado es un par de planos, la cuádrica recibe el nombre de par de planos imaginarios y distintos que se cortan en una recta real. 9
10 rango(q) = 2, sp(q) = 0 Una ecuación reducida es x 2 0 x 2 1 = 0. La cuádrica lugar es la reunión de dos planos distintos. La recta intersección de estos planos es el conjunto de puntos singulares de la cuádrica. Recibe el nombre de Par de planos reales y distintos. rango(q) = 1, sp(q) = 1 Una ecuación reducida es x 2 0 = 0. La cuádrica lugar es un plano. Todos los puntos de ese plano son singulares. Recibe el nombre de Plano doble real. Proposición Toda cuádrica real de puntos hiperbólicos, Q, es reglada. Más aún, existen dos familias de rectas F 1 y F 2 verificando: 1. Toda recta de F 1 (resp. de F 2 ) está contenida en Q. 2. Si r, r F 1 y r r entonces r r =. 3. Si s, s F 2 y s s entonces s s =. 4. Si r F 1 y s F 2 entonces r y s se cortan en un punto. Si este punto es P, entonces polar Q (P ) L(Q) = r s. 5. L(Q) = ( r F 1 r) = ( s F 2 s). 10
Polaridad. Tangentes. Estudio geométrico de cónicas y cuádricas
 Tema 6- Polaridad Tangentes Estudio geométrico de cónicas y cuádricas En este tema pretendemos estudiar propiedades de V(Q), especialmente en los casos real y complejo, con n =2,3 Para ello, necesitamos
Tema 6- Polaridad Tangentes Estudio geométrico de cónicas y cuádricas En este tema pretendemos estudiar propiedades de V(Q), especialmente en los casos real y complejo, con n =2,3 Para ello, necesitamos
Haces de hipercuádricas. Clasificación de los haces de cónicas. Determinación de
 Capítulo 5 Haces de hipercuádricas. Clasificación de los haces de cónicas. Determinación de cónicas. 5.1. Definición y ecuaciones Definición 5.1.1. Sea (X, T, π) un espacio proyectivo de dimensión n sobre
Capítulo 5 Haces de hipercuádricas. Clasificación de los haces de cónicas. Determinación de cónicas. 5.1. Definición y ecuaciones Definición 5.1.1. Sea (X, T, π) un espacio proyectivo de dimensión n sobre
Tema 11.- Autovalores y Autovectores.
 Álgebra 004-005 Ingenieros Industriales Departamento de Matemática Aplicada II Universidad de Sevilla Tema - Autovalores y Autovectores Definición, propiedades e interpretación geométrica La ecuación característica
Álgebra 004-005 Ingenieros Industriales Departamento de Matemática Aplicada II Universidad de Sevilla Tema - Autovalores y Autovectores Definición, propiedades e interpretación geométrica La ecuación característica
a ij x i x j = [x] t B A+At ) t = At +(A t ) t = At +A x i x j + a ij + a ji x j x i = s ij x i x j + s ji x j x i 2
![a ij x i x j = [x] t B A+At ) t = At +(A t ) t = At +A x i x j + a ij + a ji x j x i = s ij x i x j + s ji x j x i 2 a ij x i x j = [x] t B A+At ) t = At +(A t ) t = At +A x i x j + a ij + a ji x j x i = s ij x i x j + s ji x j x i 2](/thumbs/65/53464617.jpg) 68 Matemáticas I : Álgebra Lineal Tema 7 Formas cuadráticas Aunque, pueda parecernos que vamos a estudiar un nuevo concepto, un caso particular de las formas cudráticas ya ha sido estudiado, pues el cuadrado
68 Matemáticas I : Álgebra Lineal Tema 7 Formas cuadráticas Aunque, pueda parecernos que vamos a estudiar un nuevo concepto, un caso particular de las formas cudráticas ya ha sido estudiado, pues el cuadrado
El grupo lineal proyectivo. Homologías. Afinidades.
 Tema 3- El grupo lineal proyectivo Homologías Afinidades 31 El grupo lineal proyectivo Recordamos que en el tema anterior hemos definido, para una variedad lineal proyectiva L P n no vacía, el grupo lineal
Tema 3- El grupo lineal proyectivo Homologías Afinidades 31 El grupo lineal proyectivo Recordamos que en el tema anterior hemos definido, para una variedad lineal proyectiva L P n no vacía, el grupo lineal
Tema 2. Aplicaciones lineales. Diagonalización de endomorfismos.
 Tema 2. Aplicaciones lineales. Diagonalización de endomorfismos. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada
Tema 2. Aplicaciones lineales. Diagonalización de endomorfismos. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada
2 Espacios vectoriales
 Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 2 Espacios vectoriales 2.1 Espacio vectorial Un espacio vectorial sobre un cuerpo K (en general R o C) es un conjunto V sobre el que hay
Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 2 Espacios vectoriales 2.1 Espacio vectorial Un espacio vectorial sobre un cuerpo K (en general R o C) es un conjunto V sobre el que hay
Esta expresión polinómica puede expresarse como una expresión matricial de la forma; a 11 a 12 a 1n x 1 x 2 q(x 1, x 2,, x n ) = (x 1, x 2,, x n )
 Tema 3 Formas cuadráticas. 3.1. Definición y expresión matricial Definición 3.1.1. Una forma cuadrática sobre R es una aplicación q : R n R que a cada vector x = (x 1, x 2,, x n ) R n le hace corresponder
Tema 3 Formas cuadráticas. 3.1. Definición y expresión matricial Definición 3.1.1. Una forma cuadrática sobre R es una aplicación q : R n R que a cada vector x = (x 1, x 2,, x n ) R n le hace corresponder
Autovalores y autovectores Diagonalización y formas canónicas
 Autovalores y autovectores Diagonalización y formas canónicas Autovalores y autovectores.propiedades Sea V un espacio vectorial sobre K y f End(V ). Fijada una base de V, existirá una matriz cuadrada A,
Autovalores y autovectores Diagonalización y formas canónicas Autovalores y autovectores.propiedades Sea V un espacio vectorial sobre K y f End(V ). Fijada una base de V, existirá una matriz cuadrada A,
Geometría afín y proyectiva, 2016 SEMANA 4
 Geometría afín y proyectiva, 2016 SEMANA 4 Sonia L. Rueda ETS Arquitectura. UPM September 30, 2016 Geometría afín y proyectiva 1. Álgebra Lineal 2. Geometría afín y eucĺıdea 3. Cónicas y cuádricas Álgebra
Geometría afín y proyectiva, 2016 SEMANA 4 Sonia L. Rueda ETS Arquitectura. UPM September 30, 2016 Geometría afín y proyectiva 1. Álgebra Lineal 2. Geometría afín y eucĺıdea 3. Cónicas y cuádricas Álgebra
2 Intersección de una recta y una cuádrica. 1 Definición y ecuaciones. ( x y z
 2. Cuádricas. En todo este capítulo trabajaremos en el espacio afín euclídeo E 3 con respecto a una referencia rectangular {O; ē 1, ē 2, ē 3}. Denotaremos por (x, y, las coordenadas cartesianas respecto
2. Cuádricas. En todo este capítulo trabajaremos en el espacio afín euclídeo E 3 con respecto a una referencia rectangular {O; ē 1, ē 2, ē 3}. Denotaremos por (x, y, las coordenadas cartesianas respecto
Semana 13: Determinación de cónicas. Haces de cónicas proyectivas.
 Semana 13: Determinación de cónicas. Haces de cónicas proyectivas. Sonia L. Rueda ETS Arquitectura. UPM Geometría afín y proyectiva, 2015 Geometría afín y proyectiva 1. Álgebra lineal 2. Geometría afín
Semana 13: Determinación de cónicas. Haces de cónicas proyectivas. Sonia L. Rueda ETS Arquitectura. UPM Geometría afín y proyectiva, 2015 Geometría afín y proyectiva 1. Álgebra lineal 2. Geometría afín
Tema 3: Espacios vectoriales
 Tema 3: Espacios vectoriales K denotará un cuerpo. Definición. Se dice que un conjunto no vacio V es un espacio vectorial sobre K o que es un K-espacio vectorial si: 1. En V está definida una operación
Tema 3: Espacios vectoriales K denotará un cuerpo. Definición. Se dice que un conjunto no vacio V es un espacio vectorial sobre K o que es un K-espacio vectorial si: 1. En V está definida una operación
Departamento de Ingeniería Matemática - Universidad de Chile
 Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 8-7 Formas cuadráticas SEMANA 4: FORMAS CUADRÁTICAS 7 Formas cuadráticas y matrices definidas positivas
Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 8-7 Formas cuadráticas SEMANA 4: FORMAS CUADRÁTICAS 7 Formas cuadráticas y matrices definidas positivas
Cónicas. Clasificación.
 Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
1 CÓNICAS Cónicas. Estudio particular. 1 x y. 1 x y. a 00 a 01 a 02 a 10 a 11 a 12 a 20 a 21 a 22
 CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
Diagonalización. Tema Valores y vectores propios Planteamiento del problema Valores y vectores propios
 61 Matemáticas I : Álgebra Lineal Tema 6 Diagonalización 61 Valores y vectores propios 611 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial
61 Matemáticas I : Álgebra Lineal Tema 6 Diagonalización 61 Valores y vectores propios 611 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial
si existe un entorno V de a contenido en A, tal que la diferencia f(x) f(a) no cambia de signo cuando x V :
 Capítulo 7 Extremos Relativos Una aplicación clásica del Teorema Local de Taylor es el estudio de los extremos relativos de una función escalar. Aunque la analogía con el caso de una variable es total,
Capítulo 7 Extremos Relativos Una aplicación clásica del Teorema Local de Taylor es el estudio de los extremos relativos de una función escalar. Aunque la analogía con el caso de una variable es total,
Espacios vectoriales reales.
 Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
Podemos pues formular los dos problemas anteriores en términos de matrices.
 Tema 5 Diagonalización 51 Introducción Valores y vectores propios 511 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial V de dimensión
Tema 5 Diagonalización 51 Introducción Valores y vectores propios 511 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial V de dimensión
Aquella que tiene nulos los elementos nos situados en la diagonal principal. Los elementos situados por encima de la diagonal principal son nulos.
 Álgebra lineal Matrices Rango de una matriz Orden del mayor menor complementario no nulo. Matriz regular det A Diagonal principal Elementos a ii de la matriz. Si la matriz es cuadrado son los elementos
Álgebra lineal Matrices Rango de una matriz Orden del mayor menor complementario no nulo. Matriz regular det A Diagonal principal Elementos a ii de la matriz. Si la matriz es cuadrado son los elementos
Formas cuadráticas. Natalia Boal María Luisa Sein-Echaluce Universidad de Zaragoza
 Formas cuadráticas Natalia Boal María Luisa Sein-Echaluce Universidad de Zaragoza A lo largo de todo el capítulo consideraremos que V un espacio vectorial real de dimensión finita n. 1 Formas bilineales
Formas cuadráticas Natalia Boal María Luisa Sein-Echaluce Universidad de Zaragoza A lo largo de todo el capítulo consideraremos que V un espacio vectorial real de dimensión finita n. 1 Formas bilineales
1 CUÁDRICAS Cuádricas. Estudio particular. 1 x y z. 1 x y z. a 00 a 01 a 02 a 03 a 10 a 11 a 12 a 13 a 20 a 21 a 22 a 23 a 30 a 31 a 32 a 33
 CUÁDRICAS. CUÁDRICAS.. Cuádricas. Estudio particular. Una cuádrica se dene como el lugar geométrico de los puntos del espacio euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen
CUÁDRICAS. CUÁDRICAS.. Cuádricas. Estudio particular. Una cuádrica se dene como el lugar geométrico de los puntos del espacio euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen
6 Vectores. Dependencia e independencia lineal.
 6 Vectores. Dependencia e independencia lineal. Introducción Hay fenómenos reales que se pueden representar adecuadamente mediante un número con su adecuada unidad de medida. Sin embargo para representar
6 Vectores. Dependencia e independencia lineal. Introducción Hay fenómenos reales que se pueden representar adecuadamente mediante un número con su adecuada unidad de medida. Sin embargo para representar
Tema 2.- Formas Cuadráticas.
 Álgebra. 004 005. Ingenieros Industriales. Departamento de Matemática Aplicada II. Universidad de Sevilla. Tema.- Formas Cuadráticas. Definición y representación matricial. Clasificación de las formas
Álgebra. 004 005. Ingenieros Industriales. Departamento de Matemática Aplicada II. Universidad de Sevilla. Tema.- Formas Cuadráticas. Definición y representación matricial. Clasificación de las formas
Matrices, determinantes y sistemas de ecuaciones lineales
 Matrices, determinantes y sistemas de ecuaciones lineales David Ariza-Ruiz 10 de octubre de 2012 1 Matrices Una matriz es una tabla numérica rectangular de m filas y n columnas dispuesta de la siguiente
Matrices, determinantes y sistemas de ecuaciones lineales David Ariza-Ruiz 10 de octubre de 2012 1 Matrices Una matriz es una tabla numérica rectangular de m filas y n columnas dispuesta de la siguiente
Problemas de Geometría Proyectiva
 Problemas de Geometría Proyectiva José M. Sánchez Abril José M. Rodríguez-Sanjurjo, Jesús M. Ruiz 1995 * I. VARIEDADES PROYECTIVAS Número 1. Se consideran en el plano proyectivo P 2 los cuatro puntos a
Problemas de Geometría Proyectiva José M. Sánchez Abril José M. Rodríguez-Sanjurjo, Jesús M. Ruiz 1995 * I. VARIEDADES PROYECTIVAS Número 1. Se consideran en el plano proyectivo P 2 los cuatro puntos a
x, y = x 0 y 0 + x 1 y 1 + x 2 y 2 + x 3 y 3. Es fácil ver que verifica 1. Es simétrica. x, y = y, x para todo x, y R 4.
 1 Tema 2. Sección 1. Espacio vectorial de Minkowski. Manuel Gutiérrez. Departamento de Álgebra, Geometría y Topología. Universidad de Málaga. 29071-Málaga. Spain. Abril de 2010. En este capítulo se recordará
1 Tema 2. Sección 1. Espacio vectorial de Minkowski. Manuel Gutiérrez. Departamento de Álgebra, Geometría y Topología. Universidad de Málaga. 29071-Málaga. Spain. Abril de 2010. En este capítulo se recordará
Tema 2: Diagonalización
 TEORÍA DE ÁLGEBRA II: Tema 2. DIPLOMATURA DE ESTADÍSTICA 1 Tema 2: Diagonalización 1 Introducción Sea f : R n R n lineal. Dada una base B de R n podemos asociar a f la matriz A 1 = [f, B] M n. Si C es
TEORÍA DE ÁLGEBRA II: Tema 2. DIPLOMATURA DE ESTADÍSTICA 1 Tema 2: Diagonalización 1 Introducción Sea f : R n R n lineal. Dada una base B de R n podemos asociar a f la matriz A 1 = [f, B] M n. Si C es
Matrices. Álgebra de matrices.
 Matrices. Álgebra de matrices. 1. Definiciones generales Definición 1.1 Si m y n son dos números naturales, se llama matriz de números reales de orden m n a una aplicación A : {1, 2, 3,..., m} {1, 2, 3,...,
Matrices. Álgebra de matrices. 1. Definiciones generales Definición 1.1 Si m y n son dos números naturales, se llama matriz de números reales de orden m n a una aplicación A : {1, 2, 3,..., m} {1, 2, 3,...,
Diagonalización de matrices
 7 Diagonalización de matrices 7.1. Matrices diagonalizables Existen diversos procesos en los que el estado en cada uno de sus pasos se puede representar por un determinado vector y en los que, además,
7 Diagonalización de matrices 7.1. Matrices diagonalizables Existen diversos procesos en los que el estado en cada uno de sus pasos se puede representar por un determinado vector y en los que, además,
Las variedades lineales en un K-espacio vectorial V pueden definirse como sigue a partir de los subespacios de V.
 Capítulo 9 Variedades lineales Al considerar los subespacios de R 2, vimos que éstos son el conjunto {(0, 0)}, el espacio R 2 y las rectas que pasan por el origen. Ahora, en algunos contextos, por ejemplo
Capítulo 9 Variedades lineales Al considerar los subespacios de R 2, vimos que éstos son el conjunto {(0, 0)}, el espacio R 2 y las rectas que pasan por el origen. Ahora, en algunos contextos, por ejemplo
6.7. Clasificación de formas cuadráticas
 6.7 Clasificación de s s 1.1. Definición de s s en R n El concepto básico que sirve para definir una es el de polinomio homogéneo de segundo grado en varias variables. En toda esta sección sobreentenderemos
6.7 Clasificación de s s 1.1. Definición de s s en R n El concepto básico que sirve para definir una es el de polinomio homogéneo de segundo grado en varias variables. En toda esta sección sobreentenderemos
CLASIFICACIÓN AFÍN DE CÓNICAS
 Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS CLASIFICACIÓN AFÍN DE CÓNICAS Sea E un R-espacio vectorial de dimensión. Sean E = e 1, e un plano vectorial de E y e 0 un
Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS CLASIFICACIÓN AFÍN DE CÓNICAS Sea E un R-espacio vectorial de dimensión. Sean E = e 1, e un plano vectorial de E y e 0 un
520142: ALGEBRA y ALGEBRA LINEAL
 520142: ALGEBRA y ALGEBRA LINEAL Segundo Semestre 2008, Universidad de Concepción CAPITULO 10: Espacios Vectoriales DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas 1 Definición
520142: ALGEBRA y ALGEBRA LINEAL Segundo Semestre 2008, Universidad de Concepción CAPITULO 10: Espacios Vectoriales DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas 1 Definición
11. Cónicas proyectivas
 24 FRANCISCO JAVIER GALLEGO RODRIGO. Cónicas proyectivas Recordemos que una de las razones para construir el espacio proyectivo fue estudiar qué les pasa a los objetos afines cuando nos vamos al infinito.
24 FRANCISCO JAVIER GALLEGO RODRIGO. Cónicas proyectivas Recordemos que una de las razones para construir el espacio proyectivo fue estudiar qué les pasa a los objetos afines cuando nos vamos al infinito.
ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- Espacios vectoriales
 Resumen teoría Prof. Alcón ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- Espacios vectoriales Sea (K, +,.) un cuerpo con característica 0. Podemos pensar K = Q, R o C. Si V es un conjunto cualquiera en el que
Resumen teoría Prof. Alcón ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- Espacios vectoriales Sea (K, +,.) un cuerpo con característica 0. Podemos pensar K = Q, R o C. Si V es un conjunto cualquiera en el que
Tema II. Capítulo 5. Aplicaciones bilineales y formas cuadráticas.
 Tema II Capítulo 5 Aplicaciones bilineales y formas cuadráticas Álgebra Departamento de Métodos Matemáticos y de Representación UDC 5 Aplicaciones bilineales y formas cuadráticas o simplemente f( x, ȳ)
Tema II Capítulo 5 Aplicaciones bilineales y formas cuadráticas Álgebra Departamento de Métodos Matemáticos y de Representación UDC 5 Aplicaciones bilineales y formas cuadráticas o simplemente f( x, ȳ)
Tema 5. Cónicas. Asi, para las identificaciones habituales, (punto proyectivo recta vectorial punto de un plano afín ampliado), RP 2 R3 {0}
 Tema 5. Cónicas. Introducción. Ejemplos.- El cono C = {(x, y, z) R 3 /x 2 + y 2 = z 2 } está formado por las rectas vectoriales 0 (x 1,x 2, 1) [x 1,x 2, 1] RP 2 con (x 1,x 2, 1) C Π 1 = C 1, circunferencia
Tema 5. Cónicas. Introducción. Ejemplos.- El cono C = {(x, y, z) R 3 /x 2 + y 2 = z 2 } está formado por las rectas vectoriales 0 (x 1,x 2, 1) [x 1,x 2, 1] RP 2 con (x 1,x 2, 1) C Π 1 = C 1, circunferencia
Clase 8 Matrices Álgebra Lineal
 Clase 8 Matrices Álgebra Lineal Código Escuela de Matemáticas - Facultad de Ciencias Universidad Nacional de Colombia Matrices Definición Una matriz es un arreglo rectangular de números denominados entradas
Clase 8 Matrices Álgebra Lineal Código Escuela de Matemáticas - Facultad de Ciencias Universidad Nacional de Colombia Matrices Definición Una matriz es un arreglo rectangular de números denominados entradas
Clase 7 Herramientas de Álgebra Lineal
 Clase 7 Herramientas de Álgebra Lineal 1 Formas cuadráticas La descomposición en valores singulares 3 Normas de matrices 4 Ejercicios Dada una matriz M R n n, la función escalar x T Mx, donde x R n, es
Clase 7 Herramientas de Álgebra Lineal 1 Formas cuadráticas La descomposición en valores singulares 3 Normas de matrices 4 Ejercicios Dada una matriz M R n n, la función escalar x T Mx, donde x R n, es
2. Formas cuadráticas. Expresiones diagonales. Clasificación respecto a su signo.
 2. Formas cuadráticas. Expresiones diagonales. Clasificación respecto a su signo. 2.1 Formas cuadráticas. Expresión matricial y analítica. Expresiones diagonales. Definición 2.1 (Expresión matricial) Una
2. Formas cuadráticas. Expresiones diagonales. Clasificación respecto a su signo. 2.1 Formas cuadráticas. Expresión matricial y analítica. Expresiones diagonales. Definición 2.1 (Expresión matricial) Una
Tema 2: Espacios Vectoriales
 Tema 2: Espacios Vectoriales José M. Salazar Octubre de 2016 Tema 2: Espacios Vectoriales Lección 2. Espacios vectoriales. Subespacios vectoriales. Bases. Lección 3. Coordenadas respecto de una base. Ecuaciones.
Tema 2: Espacios Vectoriales José M. Salazar Octubre de 2016 Tema 2: Espacios Vectoriales Lección 2. Espacios vectoriales. Subespacios vectoriales. Bases. Lección 3. Coordenadas respecto de una base. Ecuaciones.
Aplicaciones Lineales. Diagonalización de matrices.
 Tema 2 Aplicaciones Lineales. Diagonalización de matrices. 2.1. Definiciones y propiedades Nota 2.1.1. En este tema trabajaremos con los Espacios Vectoriales R n y R m definidos sobre el cuerpo R. Definición
Tema 2 Aplicaciones Lineales. Diagonalización de matrices. 2.1. Definiciones y propiedades Nota 2.1.1. En este tema trabajaremos con los Espacios Vectoriales R n y R m definidos sobre el cuerpo R. Definición
Tema 1: Matrices. Sistemas de ecuaciones. Determinantes
 Tema 1: Matrices. Sistemas de ecuaciones. Determinantes José M. Salazar Octubre de 2016 Tema 1: Matrices. Sistemas de ecuaciones. Determinantes Lección 1. Matrices. Sistemas de ecuaciones. Determinantes
Tema 1: Matrices. Sistemas de ecuaciones. Determinantes José M. Salazar Octubre de 2016 Tema 1: Matrices. Sistemas de ecuaciones. Determinantes Lección 1. Matrices. Sistemas de ecuaciones. Determinantes
Este documento es de distribución gratuita y llega gracias a El mayor portal de recursos educativos a tu servicio!
 Este documento es de distribución gratuita y llega gracias a Ciencia Matemática El mayor portal de recursos educativos a tu servicio! Capítulo 5 Cónicas 5.1 Definiciones y ecuaciones reducidas Nota En
Este documento es de distribución gratuita y llega gracias a Ciencia Matemática El mayor portal de recursos educativos a tu servicio! Capítulo 5 Cónicas 5.1 Definiciones y ecuaciones reducidas Nota En
Tema 1. Espacios Vectoriales Definición de Espacio Vectorial
 Tema 1 Espacios Vectoriales. 1.1. Definición de Espacio Vectorial Notas 1.1.1. Denotaremos por N, Z, Q, R, C, a los conjuntos de los números Naturales, Enteros, Racionales, Reales y Complejos, respectivamente.
Tema 1 Espacios Vectoriales. 1.1. Definición de Espacio Vectorial Notas 1.1.1. Denotaremos por N, Z, Q, R, C, a los conjuntos de los números Naturales, Enteros, Racionales, Reales y Complejos, respectivamente.
Espacios Vectoriales
 Espacios Vectoriales Espacios Vectoriales Verónica Briceño V. noviembre 2013 Verónica Briceño V. () Espacios Vectoriales noviembre 2013 1 / 47 En esta Presentación... En esta Presentación veremos: Espacios
Espacios Vectoriales Espacios Vectoriales Verónica Briceño V. noviembre 2013 Verónica Briceño V. () Espacios Vectoriales noviembre 2013 1 / 47 En esta Presentación... En esta Presentación veremos: Espacios
un conjunto cuyos elementos denominaremos vectores y denotaremos por es un espacio vectorial si verifica las siguientes propiedades:
 CAPÍTULO 2: ESPACIOS VECTORIALES 2.1- Definición y propiedades. 2.1.1-Definición: espacio vectorial. Sea un cuerpo conmutativo a cuyos elementos denominaremos escalares o números. No es necesario preocuparse
CAPÍTULO 2: ESPACIOS VECTORIALES 2.1- Definición y propiedades. 2.1.1-Definición: espacio vectorial. Sea un cuerpo conmutativo a cuyos elementos denominaremos escalares o números. No es necesario preocuparse
Sistemas lineales de ecuaciones diferenciales. Juan-Miguel Gracia
 Sistemas lineales de ecuaciones diferenciales Juan-Miguel Gracia Índice Sistemas lineales 2 Búsqueda de una solución especial 3 Aplicación a sistemas 4 Problema de condiciones iniciales 2 / 2 Sistemas
Sistemas lineales de ecuaciones diferenciales Juan-Miguel Gracia Índice Sistemas lineales 2 Búsqueda de una solución especial 3 Aplicación a sistemas 4 Problema de condiciones iniciales 2 / 2 Sistemas
Álgebra Lineal EDITORIAL UNIVERSITAT POLITÈCNICA DE VALÈNCIA
 Josefa Marín Molina Ángel Balaguer Beser María José Felipe Román María Teresa Capilla Romá Álgebra Lineal EDITORIAL UNIVERSITAT POLITÈCNICA DE VALÈNCIA Colección Académica Para referenciar esta publicación
Josefa Marín Molina Ángel Balaguer Beser María José Felipe Román María Teresa Capilla Romá Álgebra Lineal EDITORIAL UNIVERSITAT POLITÈCNICA DE VALÈNCIA Colección Académica Para referenciar esta publicación
Tema 5: Sistemas de ecuaciones lineales.
 TEORÍA DE ÁLGEBRA: Tema 5 DIPLOMATURA DE ESTADÍSTICA 1 Tema 5: Sistemas de ecuaciones lineales 1 Definiciones generales Definición 11 Una ecuación lineal con n incognitas es una expresión del tipo a 1
TEORÍA DE ÁLGEBRA: Tema 5 DIPLOMATURA DE ESTADÍSTICA 1 Tema 5: Sistemas de ecuaciones lineales 1 Definiciones generales Definición 11 Una ecuación lineal con n incognitas es una expresión del tipo a 1
Capítulo 7. Espacios vectoriales. 7.1 Definición y ejemplos
 Capítulo Espacios vectoriales.1 Definición y ejemplos Un espacio vectorial sobre un cuerpo K (que supondremos conmutativo es un conjunto no vacío junto con 1. una operación interna, +, a la que llamaremos
Capítulo Espacios vectoriales.1 Definición y ejemplos Un espacio vectorial sobre un cuerpo K (que supondremos conmutativo es un conjunto no vacío junto con 1. una operación interna, +, a la que llamaremos
ÁLGEBRA LINEAL. EXAMEN FINAL 18 de Enero de b) (0, 5 puntos) Estudia si la siguiente afirmación es verdadera o falsa, justificando
 ÁLGEBRA LINEAL EXAMEN FINAL 8 de Enero de Apellidos y Nombre: Duración del examen: 3 horas Publicación de notas: enero Revisión de Examen: feb Ejercicio. ( puntos a (, puntos Estudia si la siguiente afirmación
ÁLGEBRA LINEAL EXAMEN FINAL 8 de Enero de Apellidos y Nombre: Duración del examen: 3 horas Publicación de notas: enero Revisión de Examen: feb Ejercicio. ( puntos a (, puntos Estudia si la siguiente afirmación
Una matriz es un arreglo rectangular de números. Los números en el arreglo se llaman elementos de la matriz. ) ( + ( ) ( )
 MATRICES Una matriz es un arreglo rectangular de números. Los números en el arreglo se llaman elementos de la matriz. Ejemplo 1. Algunos ejemplos de matrices ( + ( ) ( + ( ) El tamaño o el orden de una
MATRICES Una matriz es un arreglo rectangular de números. Los números en el arreglo se llaman elementos de la matriz. Ejemplo 1. Algunos ejemplos de matrices ( + ( ) ( + ( ) El tamaño o el orden de una
CAPÍTULO 4. Sistemas de ecuaciones lineales de primer orden
 CAPÍTULO 4 Sistemas de ecuaciones lineales de primer orden Hasta ahora hemos considerado únicamente ecuaciones diferenciales aisladas Sin embargo, en muchas aplicaciones aparecen situaciones en las que
CAPÍTULO 4 Sistemas de ecuaciones lineales de primer orden Hasta ahora hemos considerado únicamente ecuaciones diferenciales aisladas Sin embargo, en muchas aplicaciones aparecen situaciones en las que
Matrices y Sistemas de Ecuaciones lineales
 Matrices y Sistemas de Ecuaciones lineales Llamaremos M m n (K) al conjunto de las matrices A = (a ij ) (i = 1, 2,..., m; j = 1, 2,..., n) donde los elementos a ij pertenecen a un cuerpo K. Las matrices,
Matrices y Sistemas de Ecuaciones lineales Llamaremos M m n (K) al conjunto de las matrices A = (a ij ) (i = 1, 2,..., m; j = 1, 2,..., n) donde los elementos a ij pertenecen a un cuerpo K. Las matrices,
Ejercicios resueltos de Álgebra, hoja 2. Beatriz Graña Otero
 Ejercicios resueltos de Álgebra, hoja 2. Beatriz Graña Otero 11 de Diciembre de 2008 2 B.G.O. 104.- Determina si los siguientes subconjuntos del espacio vectorial correspondiente son subvariedades afines:
Ejercicios resueltos de Álgebra, hoja 2. Beatriz Graña Otero 11 de Diciembre de 2008 2 B.G.O. 104.- Determina si los siguientes subconjuntos del espacio vectorial correspondiente son subvariedades afines:
Algebra Lineal: Valores y Vectores Propios. Departamento de Matemáticas. Intro. Eigenvalues. Multiplicidades
 Algebra ducción Los valores y vectores propios son muy importantes en el análisis sistemas lineales. En esta presentación veremos su finición y cómo se calculan. vectores propios Sea A una matriz cuadrada,
Algebra ducción Los valores y vectores propios son muy importantes en el análisis sistemas lineales. En esta presentación veremos su finición y cómo se calculan. vectores propios Sea A una matriz cuadrada,
Algunos Tipos de matrices. Matrices. Algunos Tipos de matrices. Algunos Tipos de matrices
 Matrices Una matriz de orden m n es un conjunto ordenado de m n números reales dispuestos en m filas y n columnas de la forma: A = a 11 a 12 a 1j a 1n a 21 a 22 a 2j a 2n a i1 a i2 a ij a in a m1 a m2
Matrices Una matriz de orden m n es un conjunto ordenado de m n números reales dispuestos en m filas y n columnas de la forma: A = a 11 a 12 a 1j a 1n a 21 a 22 a 2j a 2n a i1 a i2 a ij a in a m1 a m2
Apéndice sobre ecuaciones diferenciales lineales
 Apéndice sobre ecuaciones diferenciales lineales Juan-Miguel Gracia 10 de febrero de 2008 Índice 2 Determinante wronskiano. Wronskiano de f 1 (t), f 2 (t),..., f n (t). Derivada de un determinante de funciones.
Apéndice sobre ecuaciones diferenciales lineales Juan-Miguel Gracia 10 de febrero de 2008 Índice 2 Determinante wronskiano. Wronskiano de f 1 (t), f 2 (t),..., f n (t). Derivada de un determinante de funciones.
Sistemas de Ecuaciones Lineales y Matrices
 Capítulo 4 Sistemas de Ecuaciones Lineales y Matrices El problema central del Álgebra Lineal es la resolución de ecuaciones lineales simultáneas Una ecuación lineal con n-incógnitas x 1, x 2,, x n es una
Capítulo 4 Sistemas de Ecuaciones Lineales y Matrices El problema central del Álgebra Lineal es la resolución de ecuaciones lineales simultáneas Una ecuación lineal con n-incógnitas x 1, x 2,, x n es una
INGENÍERIA INFORMÁTICA. PROBLEMAS DE ALGEBRA
 INGENÍERIA INFORMÁTICA. PROBLEMAS DE ALGEBRA C. Galindo 1. Resolver el siguiente sistema de ecuaciones x 1 + 3x 2 2x 3 + 2x 5 = 0 2x 1 + 6x 2 5x 3 2x 4 + 4x 5 3x 6 = 1 5x 3 + 10x 4 + 15x 6 = 5 2x 1 + 6x
INGENÍERIA INFORMÁTICA. PROBLEMAS DE ALGEBRA C. Galindo 1. Resolver el siguiente sistema de ecuaciones x 1 + 3x 2 2x 3 + 2x 5 = 0 2x 1 + 6x 2 5x 3 2x 4 + 4x 5 3x 6 = 1 5x 3 + 10x 4 + 15x 6 = 5 2x 1 + 6x
APÉNDICE A. Algebra matricial
 APÉNDICE A Algebra matricial El estudio de la econometría requiere cierta familiaridad con el álgebra matricial. La teoría de matrices simplifica la descripción, desarrollo y aplicación de los métodos
APÉNDICE A Algebra matricial El estudio de la econometría requiere cierta familiaridad con el álgebra matricial. La teoría de matrices simplifica la descripción, desarrollo y aplicación de los métodos
Álgebra Lineal V: Subespacios Vectoriales.
 Álgebra Lineal V: Subespacios Vectoriales. José María Rico Martínez Departamento de Ingeniería Mecánica Facultad de Ingeniería Mecánica Eléctrica y Electrónica Universidad de Guanajuato email: jrico@salamanca.ugto.mx
Álgebra Lineal V: Subespacios Vectoriales. José María Rico Martínez Departamento de Ingeniería Mecánica Facultad de Ingeniería Mecánica Eléctrica y Electrónica Universidad de Guanajuato email: jrico@salamanca.ugto.mx
1. Matrices. Operaciones con matrices
 REPASO MUY BÁSICO DE MATRICES. Matrices. Operaciones con matrices.. Introducción Las matrices aparecieron por primera vez hacia el año 850, introducidas por el inglés J. J. Sylvester. Su desarrollo se
REPASO MUY BÁSICO DE MATRICES. Matrices. Operaciones con matrices.. Introducción Las matrices aparecieron por primera vez hacia el año 850, introducidas por el inglés J. J. Sylvester. Su desarrollo se
a de un conjunto S de R n si
 1 235 Máximos, mínimos y puntos de ensilladura Definición.- Se dice que una función real f( x) tiene un máximo absoluto en un punto a de un conjunto S de R n si f( x) f( a) (2) para todo x S. El número
1 235 Máximos, mínimos y puntos de ensilladura Definición.- Se dice que una función real f( x) tiene un máximo absoluto en un punto a de un conjunto S de R n si f( x) f( a) (2) para todo x S. El número
Tema 4: FORMAS BILINEALES Y CUADRÁTICAS
 Tema 4: FORMAS BILINEALES Y CUADRÁTICAS Prof. Rafael López Camino Departamento de Geometría y Topología Universidad de Granada Material docente para el alumno Asignatura: Geometría I. Curso 2003/04 Licenciatura:
Tema 4: FORMAS BILINEALES Y CUADRÁTICAS Prof. Rafael López Camino Departamento de Geometría y Topología Universidad de Granada Material docente para el alumno Asignatura: Geometría I. Curso 2003/04 Licenciatura:
Matrices: repaso. Denotaremos con M m n el conjunto de matrices de tamaño m n, o sea, de m filas y n columnas. Una matriz A M m n es de la forma A =
 Matrices: repaso Denotaremos con M m n el conjunto de matrices de tamaño m n, o sea, de m filas y n columnas Una matriz A M m n es de la forma a 11 a 1n A = a m1 a mn Denotaremos A ij = a ij el coeficiente
Matrices: repaso Denotaremos con M m n el conjunto de matrices de tamaño m n, o sea, de m filas y n columnas Una matriz A M m n es de la forma a 11 a 1n A = a m1 a mn Denotaremos A ij = a ij el coeficiente
MATRICES. Se simboliza tal matriz por y se le llamará una matriz x o matriz de orden x (que se lee por ).
 1 MATRICES 1 Una matriz es una disposición rectangular de números (Reales); la forma general de una matriz con filas y columnas es Se simboliza tal matriz por y se le llamará una matriz x o matriz de orden
1 MATRICES 1 Una matriz es una disposición rectangular de números (Reales); la forma general de una matriz con filas y columnas es Se simboliza tal matriz por y se le llamará una matriz x o matriz de orden
EJERCICIOS DE ÁLGEBRA LINEAL TEMA 1 ESPACIOS VECTORIALES
 EJERCICIOS DE ÁLGEBRA LINEAL TEMA ESPACIOS VECTORIALES Formas reducidas y escalonada de una matriz SISTEMAS DE ECUACIONES LINEALES ) Encuentre una sucesión de matrices elementales E, E,..., E k tal que
EJERCICIOS DE ÁLGEBRA LINEAL TEMA ESPACIOS VECTORIALES Formas reducidas y escalonada de una matriz SISTEMAS DE ECUACIONES LINEALES ) Encuentre una sucesión de matrices elementales E, E,..., E k tal que
TEMA 7: MATRICES. OPERACIONES.
 TEMA 7: MATRICES. OPERACIONES. 1. MATRICES. TIPOS DE MATRICES. Se llama matriz de orden m x n (m filas y n columnas) a un conjunto de m n elementos, distribuidos en m filas y n columnas y encerrados entre
TEMA 7: MATRICES. OPERACIONES. 1. MATRICES. TIPOS DE MATRICES. Se llama matriz de orden m x n (m filas y n columnas) a un conjunto de m n elementos, distribuidos en m filas y n columnas y encerrados entre
Capítulo 4: Conjuntos
 Capítulo 4: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2014 Olalla (Universidad de Sevilla) Capítulo 4: Conjuntos Septiembre de
Capítulo 4: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2014 Olalla (Universidad de Sevilla) Capítulo 4: Conjuntos Septiembre de
CÓNICAS. 1. Dada la cónica x 2 + 2xy y 2 2x 2y + 4 = 0, se pide su clasicación y los elementos característicos de la misma. = 1
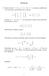 CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
Aplicaciones lineales.
 Tema 4 Aplicaciones lineales. Definición 4. Sea f: V W una aplicación entre los espacios vectoriales reales V y W. Se dice que f es una aplicación lineal si: a f(u + v = f(u + f(v; u, v V, b f(ku = kf(u;
Tema 4 Aplicaciones lineales. Definición 4. Sea f: V W una aplicación entre los espacios vectoriales reales V y W. Se dice que f es una aplicación lineal si: a f(u + v = f(u + f(v; u, v V, b f(ku = kf(u;
Introducción a los espacios vectoriales
 1 / 64 Introducción a los espacios vectoriales Pablo Olaso Redondo Informática Universidad Francisco de Vitoria November 19, 2015 2 / 64 Espacios vectoriales 1 Las 10 propiedades de un espacio vectorial
1 / 64 Introducción a los espacios vectoriales Pablo Olaso Redondo Informática Universidad Francisco de Vitoria November 19, 2015 2 / 64 Espacios vectoriales 1 Las 10 propiedades de un espacio vectorial
RESUMEN DEL TEMA 7 VALORES Y VECTORES PROPIOS
 RESUMEN DEL TEMA 7 VALORES Y VECTORES PROPIOS 1. Determinantes El determinante de una matriz cuadrada n n A = a 21 a 22 a 2n a n1 a n2 a nn es un número real, y se representa por: A = a 21 a 22 a 2n a
RESUMEN DEL TEMA 7 VALORES Y VECTORES PROPIOS 1. Determinantes El determinante de una matriz cuadrada n n A = a 21 a 22 a 2n a n1 a n2 a nn es un número real, y se representa por: A = a 21 a 22 a 2n a
Tema 1. 1 Álgebra lineal. Aurea Grané Departamento de Estadística Universidad Carlos III de Madrid. 1.1 Vectores de R n. 1. Vectores. 2.
 Aurea Grané. Máster en Estadística. Universidade Pedagógica. 1 Aurea Grané. Máster en Estadística. Universidade Pedagógica. 2 Tema 1 Álgebra lineal 1. Vectores 2. Matrices 1 Álgebra lineal Aurea Grané
Aurea Grané. Máster en Estadística. Universidade Pedagógica. 1 Aurea Grané. Máster en Estadística. Universidade Pedagógica. 2 Tema 1 Álgebra lineal 1. Vectores 2. Matrices 1 Álgebra lineal Aurea Grané
Funciones de varias variables
 Funciones de varias variables 1. Conceptos elementales Funciones IR n IR m. Definición Una función f (también f o f): A IR n IR m es una aplicación que a cada x (también x o x) A IR n le hace corresponder
Funciones de varias variables 1. Conceptos elementales Funciones IR n IR m. Definición Una función f (también f o f): A IR n IR m es una aplicación que a cada x (también x o x) A IR n le hace corresponder
TEMA 1: MATRICES Y DETERMINANTES
 TEMA 1: MATRICES Y DETERMINANTES 1 Matrices Definición 11 Una matriz es un arreglo rectangular de números reales de la forma a 11 a 12 a 1m a 21 a 22 a 2m A = a n1 a n2 a nm Las líneas horizontales (verticales)
TEMA 1: MATRICES Y DETERMINANTES 1 Matrices Definición 11 Una matriz es un arreglo rectangular de números reales de la forma a 11 a 12 a 1m a 21 a 22 a 2m A = a n1 a n2 a nm Las líneas horizontales (verticales)
Definición Dados dos números naturales m y n, una matriz de orden o dimensión m n es una tabla numérica rectangular con m filas y n columnas.
 Tema 1 Matrices 1.1. Conceptos básicos y ejemplos Definición 1.1.1. Dados dos números naturales m y n, una matriz de orden o dimensión m n es una tabla numérica rectangular con m filas y n columnas. NOTA:
Tema 1 Matrices 1.1. Conceptos básicos y ejemplos Definición 1.1.1. Dados dos números naturales m y n, una matriz de orden o dimensión m n es una tabla numérica rectangular con m filas y n columnas. NOTA:
Estructuras Algebraicas
 Tema 1 Estructuras Algebraicas Definición 1 Sea A un conjunto no vacío Una operación binaria (u operación interna) en A es una aplicación : A A A Es decir, tenemos una regla que a cada par de elementos
Tema 1 Estructuras Algebraicas Definición 1 Sea A un conjunto no vacío Una operación binaria (u operación interna) en A es una aplicación : A A A Es decir, tenemos una regla que a cada par de elementos
Algebra lineal y conjuntos convexos
 Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
UNIDAD I: SISTEMAS DE DOS ECUACIONES CON DOS INCÓGNITAS
 UNIDAD I: SISTEMAS DE DOS ECUACIONES CON DOS INCÓGNITAS Sistemas de dos ecuaciones con dos incógnitas. Método de igualación. Método de reducción. Método de sustitución Método de eliminación Gaussiana.
UNIDAD I: SISTEMAS DE DOS ECUACIONES CON DOS INCÓGNITAS Sistemas de dos ecuaciones con dos incógnitas. Método de igualación. Método de reducción. Método de sustitución Método de eliminación Gaussiana.
EJERCICIOS DE ÁLGEBRA LINEAL TEMA 1 ESPACIOS VECTORIALES
 EJERCICIOS DE ÁLGEBRA LINEAL TEMA ESPACIOS VECTORIALES MATRICES. SISTEMAS DE ECUACIONES LINEALES Matrices ) Dada la matriz M=, prueba que n n M M, n. ) Demuestra la siguiente implicación: Si I A I AA A
EJERCICIOS DE ÁLGEBRA LINEAL TEMA ESPACIOS VECTORIALES MATRICES. SISTEMAS DE ECUACIONES LINEALES Matrices ) Dada la matriz M=, prueba que n n M M, n. ) Demuestra la siguiente implicación: Si I A I AA A
Aplicaciones Lineales
 Aplicaciones Lineales AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Aplicaciones Lineales 1 / 47 Objetivos Al finalizar este tema tendrás que: Saber si una aplicación es
Aplicaciones Lineales AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Aplicaciones Lineales 1 / 47 Objetivos Al finalizar este tema tendrás que: Saber si una aplicación es
Funciones de Clase C 1
 Capítulo 7 Funciones de Clase C 1 Vamos a considerar ahora la extensión a varias variables del concepto de función de clase C 1. Cada vez que establezcamos una propiedad de las funciones diferenciables,
Capítulo 7 Funciones de Clase C 1 Vamos a considerar ahora la extensión a varias variables del concepto de función de clase C 1. Cada vez que establezcamos una propiedad de las funciones diferenciables,
Diagonalización de matrices
 Capítulo 6 Diagonalización de matrices 6.. Introducción 6... Un ejemplo preliminar Antes de plantearlo de manera general, estudiaremos un ejemplo que servirá para situar el problema. Supongamos que, en
Capítulo 6 Diagonalización de matrices 6.. Introducción 6... Un ejemplo preliminar Antes de plantearlo de manera general, estudiaremos un ejemplo que servirá para situar el problema. Supongamos que, en
1 Autovalores y autovectores asociados a un endomor smo f. Diagonalización.
 utovalores y autovectores asociados a un endomor smo f Diagonalización Dado un endomor smo f de un espacio vectorial real V y jada una base B de V obtenemos una única matriz asociada a f respecto de la
utovalores y autovectores asociados a un endomor smo f Diagonalización Dado un endomor smo f de un espacio vectorial real V y jada una base B de V obtenemos una única matriz asociada a f respecto de la
6. Forma canónica de matrices
 6. Forma canónica de matrices Manuel Palacios Departamento de Matemática Aplicada Centro Politécnico Superior Universidad de Zaragoza Otoño 2010 Contents 6 6. Forma canónica de matrices 7 6.1 Introducción....................................
6. Forma canónica de matrices Manuel Palacios Departamento de Matemática Aplicada Centro Politécnico Superior Universidad de Zaragoza Otoño 2010 Contents 6 6. Forma canónica de matrices 7 6.1 Introducción....................................
Resumen de Teoría de Matrices
 Resumen de Teoría de Matrices Rubén Alexis Sáez Morcillo Ana Isabel Martínez Domínguez 1 de Octubre de 2004 1. Matrices. Generalidades. Definición 1.1. Se llama matriz de orden m n sobre un cuerpo K a
Resumen de Teoría de Matrices Rubén Alexis Sáez Morcillo Ana Isabel Martínez Domínguez 1 de Octubre de 2004 1. Matrices. Generalidades. Definición 1.1. Se llama matriz de orden m n sobre un cuerpo K a
Espacios vectoriales. Capítulo Espacios vectoriales y subespacios Preliminares
 Capítulo 1 Espacios vectoriales En diversos conjuntos conocidos, por ejemplo los de vectores en el plano o en el espacio (R 2 y R 3 ), o también el de los polinomios (R[X]), sabemos sumar sus elementos
Capítulo 1 Espacios vectoriales En diversos conjuntos conocidos, por ejemplo los de vectores en el plano o en el espacio (R 2 y R 3 ), o también el de los polinomios (R[X]), sabemos sumar sus elementos
como el número real que resulta del producto matricial y se nota por:
 Espacio euclídeo 2 2. ESPACIO EUCLÍDEO 2.. PRODUCTO ESCALAR En el espacio vectorial se define el producto escalar de dos vectores y como el número real que resulta del producto matricial y se nota por:,
Espacio euclídeo 2 2. ESPACIO EUCLÍDEO 2.. PRODUCTO ESCALAR En el espacio vectorial se define el producto escalar de dos vectores y como el número real que resulta del producto matricial y se nota por:,
Es trivial generalizar la definición al caso de varios conjuntos: A B C, etc.
 Tema 1 Espacios Vectoriales 1.1 Repaso de Estructuras Algebraicas 1. Producto cartesiano de conjuntos. Dados los conjuntos A y B, se llama producto cartesiano de A y B, y se denota por A B al conjunto
Tema 1 Espacios Vectoriales 1.1 Repaso de Estructuras Algebraicas 1. Producto cartesiano de conjuntos. Dados los conjuntos A y B, se llama producto cartesiano de A y B, y se denota por A B al conjunto
GUIA DE EJERCICIOS TIPO PSU ECUACIONES Y FUNCIONES DE SEGUNDO GRADO MATEMÁTICA COMÚN
 GUIA DE EJERCICIOS TIPO PSU ECUACIONES Y FUNCIONES DE SEGUNDO GRADO MATEMÁTICA COMÚN 1) El vértice de la parábola f ( x) x² 8x 5 corresponde al par ordenado: a) (4,11) b) (4, 11) c) ( 8,5) d) ( 4,11) e)
GUIA DE EJERCICIOS TIPO PSU ECUACIONES Y FUNCIONES DE SEGUNDO GRADO MATEMÁTICA COMÚN 1) El vértice de la parábola f ( x) x² 8x 5 corresponde al par ordenado: a) (4,11) b) (4, 11) c) ( 8,5) d) ( 4,11) e)
Problemas y Ejercicios Resueltos. Tema 6: Diagonalizacion.
 Problemas y Ejercicios Resueltos. Tema 6: Diagonalizacion. Ejercicios 1.- Sea f End V. Demostrar que la suma de subespacios f-invariantes es f-invariante. Solución. Sean U, W dos subespacios f-invariantes
Problemas y Ejercicios Resueltos. Tema 6: Diagonalizacion. Ejercicios 1.- Sea f End V. Demostrar que la suma de subespacios f-invariantes es f-invariante. Solución. Sean U, W dos subespacios f-invariantes
Departamento de Ingeniería Matemática - Universidad de Chile
 Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 08-2 SEMANA 7: ESPACIOS VECTORIALES 3.5. Generadores de un espacio vectorial Sea V un espacio vectorial
Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 08-2 SEMANA 7: ESPACIOS VECTORIALES 3.5. Generadores de un espacio vectorial Sea V un espacio vectorial
Tema 3: MATRICES. Prof. Rafael López Camino Departamento de Geometría y Topología Universidad de Granada
 Tema 3: MATRICES Prof. Rafael López Camino Departamento de Geometría y Topología Universidad de Granada Material docente para el alumno Asignatura: Geometría I. Curso 2003/04 Licenciatura: Matemáticas
Tema 3: MATRICES Prof. Rafael López Camino Departamento de Geometría y Topología Universidad de Granada Material docente para el alumno Asignatura: Geometría I. Curso 2003/04 Licenciatura: Matemáticas
Grado en Edificación MATERIAL DOCENTE: PRESENTACIÓN DEL TEMA III. Ana Isabel Garralda Guillem y Manuel Ruiz Galán
 MATEMÁTICAS TICAS I Grado en Edificación MATERIAL DOCENTE: PRESENTACIÓN DEL TEMA III Ana Isabel Garralda Guillem y Manuel Ruiz Galán Tema. Diagonalización de matrices.1. Diagonalización de matrices por
MATEMÁTICAS TICAS I Grado en Edificación MATERIAL DOCENTE: PRESENTACIÓN DEL TEMA III Ana Isabel Garralda Guillem y Manuel Ruiz Galán Tema. Diagonalización de matrices.1. Diagonalización de matrices por
SISTEMAS DE ECUACIONES LINEALES Y MATRICES
 y SISTEMAS DE ECUACIONES ES Y MATRICES Sergio Stive Solano 1 Febrero de 2015 1 Visita http://sergiosolanosabie.wikispaces.com y SISTEMAS DE ECUACIONES ES Y MATRICES Sergio Stive Solano 1 Febrero de 2015
y SISTEMAS DE ECUACIONES ES Y MATRICES Sergio Stive Solano 1 Febrero de 2015 1 Visita http://sergiosolanosabie.wikispaces.com y SISTEMAS DE ECUACIONES ES Y MATRICES Sergio Stive Solano 1 Febrero de 2015
