Introducción a los espacios vectoriales
|
|
|
- Adrián Franco Guzmán
- hace 9 años
- Vistas:
Transcripción
1 1 / 64 Introducción a los espacios vectoriales Pablo Olaso Redondo Informática Universidad Francisco de Vitoria November 19, 2015
2 2 / 64 Espacios vectoriales 1 Las 10 propiedades de un espacio vectorial 2 Subespacios Vectoriales 3 Conjuntos Generadores y Bases 4 Coordenadas y Cambio de Base
3 3 / 64 Espacios vectoriales 1 Las 10 propiedades de un espacio vectorial 2 Subespacios Vectoriales 3 Conjuntos Generadores y Bases 4 Coordenadas y Cambio de Base
4 4 / 64 Espacios vectoriales 1 Las 10 propiedades de un espacio vectorial 2 Subespacios Vectoriales 3 Conjuntos Generadores y Bases 4 Coordenadas y Cambio de Base
5 5 / 64 Espacios vectoriales 1 Las 10 propiedades de un espacio vectorial 2 Subespacios Vectoriales 3 Conjuntos Generadores y Bases 4 Coordenadas y Cambio de Base
6 6 / 64 Espacios Vectoriales 1 Las 10 propiedades de un espacio vectorial 2 Subespacios Vectoriales 3 Conjuntos Generadores y Bases 4 Coordenadas y Cambio de Base
7 Definición Un espacio vectorial está compuesto por un conjunto de vectores, V, un conjunto de escalares (generalmente, un cuerpo, pero nosotros vamos a considerar únicamente el cuerpo de los números reales, R, que todos conocéis) y dos operaciones, (a las que llamaremos suma vectorial y multiplicación escalar), que cumplen las siguientes propiedades: 7 / 64
8 Suma. Para todos los vectores u, v y w en V: 1. u + v está en V(propiedad de cierre bajo la suma) 2. u + v = v + u (propiedad conmutativa de la suma) 3. u + (v + w) = (u + v) + w (propiedad asociativa de la suma) 4. Existe en V un vector, 0, tal que para todo u en V, u + 0 = u (elemento neutro de la suma) 5. Para todo u en V, existe un vector u en V tal que u + ( u) = 0 (elemento inverso de la suma) Multiplicación escalar. Para todos los vectores u, v y w en V y para todos los escalares c y d: 6. cu está en V (propiedad de cierre bajo la multiplicación escalar) 7. c(u + v) = cu + cv (propiedad distributiva) 8. (c + d)u = cu + du (propiedad distributiva) 9. c(du) = (cd)u (propiedad asociativa) 10. 1u = u (elemento neutro) 8 / 64
9 Suma. Para todos los vectores u, v y w en V: 1. u + v está en V(propiedad de cierre bajo la suma) 2. u + v = v + u (propiedad conmutativa de la suma) 3. u + (v + w) = (u + v) + w (propiedad asociativa de la suma) 4. Existe en V un vector, 0, tal que para todo u en V, u + 0 = u (elemento neutro de la suma) 5. Para todo u en V, existe un vector u en V tal que u + ( u) = 0 (elemento inverso de la suma) Multiplicación escalar. Para todos los vectores u, v y w en V y para todos los escalares c y d: 6. cu está en V (propiedad de cierre bajo la multiplicación escalar) 7. c(u + v) = cu + cv (propiedad distributiva) 8. (c + d)u = cu + du (propiedad distributiva) 9. c(du) = (cd)u (propiedad asociativa) 10. 1u = u (elemento neutro) 9 / 64
10 10 / 64 Aplicando estas 10 propiedades de los espacios vectoriales, se pueden realizar manipulaciones algebraicas con vectores, como en R n, casi del mismo modo en que se haría con los números reales. Ejemplo Sean u = (2, 1, 5, 0), v = (4, 3, 2, 2) y w = ( 5, 3, 8, 1) vectores de R 4. Calcula: x = 2u (v + 3w); x = 5(x + 2u w). Despeja: el vector x: 4x 2(u + v + x) 3w = 2.
11 11 / 64 Aplicando estas 10 propiedades de los espacios vectoriales, se pueden realizar manipulaciones algebraicas con vectores, como en R n, casi del mismo modo en que se haría con los números reales. Ejemplo Sean u = (2, 1, 5, 0), v = (4, 3, 2, 2) y w = ( 5, 3, 8, 1) vectores de R 4. Calcula: x = 2u (v + 3w); x = 5(x + 2u w). Despeja: el vector x: 4x 2(u + v + x) 3w = 2.
12 12 / 64 Estas 10 propiedades de la suma vectorial y de la multiplicación escalar son compartidas por muchas estructuras matemáticas, como el espacio euclideo R 3 y en general en los espacios R n, las matrices, los polinomios y las funciones. Por otra parte, de dichas propiedades se pueden concluir otras muchas propiedades, y además permiten, como hemos visto, una serie de operaciones algebraicas. Por todo esto, es útil abstraer dichas propiedades (que de este modo pasan a denominarse axiomas) y extraer conclusiones generales aplicables a todos los espacios vectoriales.
13 13 / 64 Estas 10 propiedades de la suma vectorial y de la multiplicación escalar son compartidas por muchas estructuras matemáticas, como el espacio euclideo R 3 y en general en los espacios R n, las matrices, los polinomios y las funciones. Por otra parte, de dichas propiedades se pueden concluir otras muchas propiedades, y además permiten, como hemos visto, una serie de operaciones algebraicas. Por todo esto, es útil abstraer dichas propiedades (que de este modo pasan a denominarse axiomas) y extraer conclusiones generales aplicables a todos los espacios vectoriales.
14 Ejemplos de espacios vectoriales: R 2 R R n Las matrices de 3x5 (M 3,5 ) con la suma de matrices y la multiplicación por un escalar. En general, las matrices M m,n P 2, el conjunto de polinomios de grado (menor o igual que) 2 (p(x) = a 2 x 2 + a 1 x + a 0 con la suma y producto escalar) El espacio vectorial de las funciones continuas C(, ) 14 / 64
15 15 / 64 Hemos visto que un vector puede ser un número real, una n-upla, una matriz, un polinomio, una función continua, etc. Para qué sirve esta abstracción? Eficiencia: A partir de ahora, todo lo que demostremos para un espacio vectorial abstracto, se aplica a todos los espacios vectoriales que hemos visto y a cualquier otro con el que nos encontremos.
16 Si v es un vector en R n y c un escalar, entonces se cumplen las siguientes propiedades: 1 El idéntico (nulo) aditivo es único: si u + v = v, entonces u = 0 2 El inverso aditivo de v es único: si v + u = 0 entonces u = v. 3 0v = 0 4 c0 = 0 5 si cv = 0, entonces c = 0 o v = 0 6 ( 1)v = v 7 ( v) = v (Estas propiedades se deducen de las 10 anteriores que definen un espacio vectorial. Demuéstralas tú mismo) 16 / 64
17 Si v es un vector en R n y c un escalar, entonces se cumplen las siguientes propiedades: 1 El idéntico (nulo) aditivo es único: si u + v = v, entonces u = 0 2 El inverso aditivo de v es único: si v + u = 0 entonces u = v. 3 0v = 0 4 c0 = 0 5 si cv = 0, entonces c = 0 o v = 0 6 ( 1)v = v 7 ( v) = v (Estas propiedades se deducen de las 10 anteriores que definen un espacio vectorial. Demuéstralas tú mismo) 17 / 64
18 Si v es un vector en R n y c un escalar, entonces se cumplen las siguientes propiedades: 1 El idéntico (nulo) aditivo es único: si u + v = v, entonces u = 0 2 El inverso aditivo de v es único: si v + u = 0 entonces u = v. 3 0v = 0 4 c0 = 0 5 si cv = 0, entonces c = 0 o v = 0 6 ( 1)v = v 7 ( v) = v (Estas propiedades se deducen de las 10 anteriores que definen un espacio vectorial. Demuéstralas tú mismo) 18 / 64
19 19 / 64 Escribir un vector v como combinacion lineal de otros vectores v 1,..., v n es encontrar unos escalares a 1,..., a n tales que v = a 1 v a n v n Observa: se puede expresar el vector (4, 5) como combinación lineal de ( 2, 1) y (4, 2)?
20 20 / 64 Escribir un vector v como combinacion lineal de otros vectores v 1,..., v n es encontrar unos escalares a 1,..., a n tales que v = a 1 v a n v n Observa: se puede expresar el vector (4, 5) como combinación lineal de ( 2, 1) y (4, 2)?
21 21 / 64 Son los enteros, Z, un espacio vectorial?
22 22 / 64 Espacios Vectoriales 1 Las 10 propiedades de un espacio vectorial 2 Subespacios Vectoriales 3 Conjuntos Generadores y Bases 4 Coordenadas y Cambio de Base
23 En muchas ocasiones los Espacios Vectoriales (EV) resultan ser subespacios de otros más grandes. Definición Decimos que W es un Subespacio Vectorial (SEV) de V si es un subconjunto de V y es un EV bajo las operaciones de suma y multiplicación escalar definidas sobre V. En particular, observa que para que la suma y multiplicación escalar estén bien definidas sobre W, ambas operaciones deben ser cerradas en W. Es más, para demostrar que un subconjunto W de V es un subespacio vectorial, no será necesario demostrar que se cumplen las 10 propiedades que caracterizan a los EV, basta con comprobar que las dos operaciones son cerradas. 23 / 64
24 En muchas ocasiones los Espacios Vectoriales (EV) resultan ser subespacios de otros más grandes. Definición Decimos que W es un Subespacio Vectorial (SEV) de V si es un subconjunto de V y es un EV bajo las operaciones de suma y multiplicación escalar definidas sobre V. En particular, observa que para que la suma y multiplicación escalar estén bien definidas sobre W, ambas operaciones deben ser cerradas en W. Es más, para demostrar que un subconjunto W de V es un subespacio vectorial, no será necesario demostrar que se cumplen las 10 propiedades que caracterizan a los EV, basta con comprobar que las dos operaciones son cerradas. 24 / 64
25 En muchas ocasiones los Espacios Vectoriales (EV) resultan ser subespacios de otros más grandes. Definición Decimos que W es un Subespacio Vectorial (SEV) de V si es un subconjunto de V y es un EV bajo las operaciones de suma y multiplicación escalar definidas sobre V. En particular, observa que para que la suma y multiplicación escalar estén bien definidas sobre W, ambas operaciones deben ser cerradas en W. Es más, para demostrar que un subconjunto W de V es un subespacio vectorial, no será necesario demostrar que se cumplen las 10 propiedades que caracterizan a los EV, basta con comprobar que las dos operaciones son cerradas. 25 / 64
26 26 / 64 Es fácil comprobar que entonces el elemento neutro de la suma, 0, está en W (recordar que 0u = 0) y que para todo u en W su inverso, u, tambien está en W (( 1)u = u). Las demás propiedades ya sabemos que se verifican al tratarse V de un EV. Ojo, además de la cerradura de las operaciones, hay que comprobar que W es no vacío, ya que el conjunto vacío no se puede considerar un EV. Un modo de comprobarlo es ver que, por ejemplo, el neutro de la suma, 0, está efectivamente en W.
27 27 / 64 Es fácil comprobar que entonces el elemento neutro de la suma, 0, está en W (recordar que 0u = 0) y que para todo u en W su inverso, u, tambien está en W (( 1)u = u). Las demás propiedades ya sabemos que se verifican al tratarse V de un EV. Ojo, además de la cerradura de las operaciones, hay que comprobar que W es no vacío, ya que el conjunto vacío no se puede considerar un EV. Un modo de comprobarlo es ver que, por ejemplo, el neutro de la suma, 0, está efectivamente en W.
28 28 / 64 Ejemplo Sea W el conjunto de puntos de la recta x + 3y = 1. W no es un SEV de R 2. Para verificarlo basta comprobar que el neutro, 0 = (0, 0) no está en W. Sin embargo, el conjunto de puntos de la recta dada por 2x + 3y = 0 sí es un SEV de R 2. Compruébalo tú mismo. En general, el conjunto de soluciones de un sistema de ecuaciones lineales homogéneo (y el anterior lo es, con una única ecuación) con n incógnitas, es un SEV de R n. Esto también es fácil de demostrar.
29 29 / 64 Ejemplo Sea W el conjunto de puntos de la recta x + 3y = 1. W no es un SEV de R 2. Para verificarlo basta comprobar que el neutro, 0 = (0, 0) no está en W. Sin embargo, el conjunto de puntos de la recta dada por 2x + 3y = 0 sí es un SEV de R 2. Compruébalo tú mismo. En general, el conjunto de soluciones de un sistema de ecuaciones lineales homogéneo (y el anterior lo es, con una única ecuación) con n incógnitas, es un SEV de R n. Esto también es fácil de demostrar.
30 30 / 64 Ejemplo Sea W el conjunto de puntos de la recta x + 3y = 1. W no es un SEV de R 2. Para verificarlo basta comprobar que el neutro, 0 = (0, 0) no está en W. Sin embargo, el conjunto de puntos de la recta dada por 2x + 3y = 0 sí es un SEV de R 2. Compruébalo tú mismo. En general, el conjunto de soluciones de un sistema de ecuaciones lineales homogéneo (y el anterior lo es, con una única ecuación) con n incógnitas, es un SEV de R n. Esto también es fácil de demostrar.
31 31 / 64 Ejemplo W = {(x 1, 0) x 1 R} es un subespacio vectorial (SEV) de R 2 con las operaciones estándar. Es W = {(x 1, x 2, 3x 1 x 2 ) : x 1, x 2, x 3 R} un SEV? Observa que W = {0} y el propio V son subespacios de V. Estos son los subespacios más sencillos de todo EV, y se llaman subespacios triviales. Los demás subespacios se llamarán subespacios propios.
32 32 / 64 Ejemplo W = {(x 1, 0) x 1 R} es un subespacio vectorial (SEV) de R 2 con las operaciones estándar. Es W = {(x 1, x 2, 3x 1 x 2 ) : x 1, x 2, x 3 R} un SEV? Observa que W = {0} y el propio V son subespacios de V. Estos son los subespacios más sencillos de todo EV, y se llaman subespacios triviales. Los demás subespacios se llamarán subespacios propios.
33 33 / 64 Ejemplo W = {(x 1, 0) x 1 R} es un subespacio vectorial (SEV) de R 2 con las operaciones estándar. Es W = {(x 1, x 2, 3x 1 x 2 ) : x 1, x 2, x 3 R} un SEV? Observa que W = {0} y el propio V son subespacios de V. Estos son los subespacios más sencillos de todo EV, y se llaman subespacios triviales. Los demás subespacios se llamarán subespacios propios.
34 Ejemplo El conjunto W M n,n de las matrices simétricas es un SEV. Las matrices singulares (no invertibles) no son un SEV. Las matrices invertibles tampoco son un SEV (basta ver que la matriz nula no está en dicho conjunto) Podrías demostrar estas 3 afirmaciones previas? Demuestra que la interseccion de 2 subespacios de V, tambien es un subespacio de V. Ojo, no olvides comprobar que la intersección no es vacía. En general, los subespacios propios de R 3 son las rectas y planos que pasan por el origen de coordenadas, (0, 0, 0). 34 / 64
35 Ejemplo El conjunto W M n,n de las matrices simétricas es un SEV. Las matrices singulares (no invertibles) no son un SEV. Las matrices invertibles tampoco son un SEV (basta ver que la matriz nula no está en dicho conjunto) Podrías demostrar estas 3 afirmaciones previas? Demuestra que la interseccion de 2 subespacios de V, tambien es un subespacio de V. Ojo, no olvides comprobar que la intersección no es vacía. En general, los subespacios propios de R 3 son las rectas y planos que pasan por el origen de coordenadas, (0, 0, 0). 35 / 64
36 Ejemplo El conjunto W M n,n de las matrices simétricas es un SEV. Las matrices singulares (no invertibles) no son un SEV. Las matrices invertibles tampoco son un SEV (basta ver que la matriz nula no está en dicho conjunto) Podrías demostrar estas 3 afirmaciones previas? Demuestra que la interseccion de 2 subespacios de V, tambien es un subespacio de V. Ojo, no olvides comprobar que la intersección no es vacía. En general, los subespacios propios de R 3 son las rectas y planos que pasan por el origen de coordenadas, (0, 0, 0). 36 / 64
37 Ejemplo El conjunto W M n,n de las matrices simétricas es un SEV. Las matrices singulares (no invertibles) no son un SEV. Las matrices invertibles tampoco son un SEV (basta ver que la matriz nula no está en dicho conjunto) Podrías demostrar estas 3 afirmaciones previas? Demuestra que la interseccion de 2 subespacios de V, tambien es un subespacio de V. Ojo, no olvides comprobar que la intersección no es vacía. En general, los subespacios propios de R 3 son las rectas y planos que pasan por el origen de coordenadas, (0, 0, 0). 37 / 64
38 38 / 64 Espacios Vectoriales 1 Las 10 propiedades de un espacio vectorial 2 Subespacios Vectoriales 3 Conjuntos Generadores y Bases 4 Coordenadas y Cambio de Base
39 Definición Sea v un vector en V, un EV dado. Decimos que v es combinación lineal del conjunto de vectores {v i : i = 1,..., n}, contenido en V, si v se puede expresar de la forma v = a 1 v a n v n, donde a i son escalares para i = 1,..., n. Definición Sea S = {v 1, v 2,..., v k } un subconjunto de V. Definimos el generador de S como el conjunto de todas las posibles combinaciones lineales de los vectores en S: < S >= {a 1 v a k v k : a i R, i} 39 / 64
40 Definición Sea v un vector en V, un EV dado. Decimos que v es combinación lineal del conjunto de vectores {v i : i = 1,..., n}, contenido en V, si v se puede expresar de la forma v = a 1 v a n v n, donde a i son escalares para i = 1,..., n. Definición Sea S = {v 1, v 2,..., v k } un subconjunto de V. Definimos el generador de S como el conjunto de todas las posibles combinaciones lineales de los vectores en S: < S >= {a 1 v a k v k : a i R, i} 40 / 64
41 Definición S es un conjunto generador de V si todo vector de V se puede expresar como combinación lineal de los vectores de S, o lo que es lo mismo si < S >= V. Decimos que V es generado por S o que S genera a V. Si S no genera a V, genera un SEV de V: < S > es siempre un subespacio de V. Además, es el menor subespacio que contiene a S, es decir, si W es un subespacio que contiene a S, entonces < S > está contenido en W. Demuéstralo. 41 / 64
42 Definición S es un conjunto generador de V si todo vector de V se puede expresar como combinación lineal de los vectores de S, o lo que es lo mismo si < S >= V. Decimos que V es generado por S o que S genera a V. Si S no genera a V, genera un SEV de V: < S > es siempre un subespacio de V. Además, es el menor subespacio que contiene a S, es decir, si W es un subespacio que contiene a S, entonces < S > está contenido en W. Demuéstralo. 42 / 64
43 Definición S es un conjunto generador de V si todo vector de V se puede expresar como combinación lineal de los vectores de S, o lo que es lo mismo si < S >= V. Decimos que V es generado por S o que S genera a V. Si S no genera a V, genera un SEV de V: < S > es siempre un subespacio de V. Además, es el menor subespacio que contiene a S, es decir, si W es un subespacio que contiene a S, entonces < S > está contenido en W. Demuéstralo. 43 / 64
44 Dado un conjunto de vectores S = {v 1, v 2,..., v k } en V, un EV, la ecuación: a 1 v a k v k = 0 tiene al menos la solución trivial a 1 = a 2 =... = a k = 0 Definición Es posible que haya otras soluciones donde al menos algún a i 0 En este caso se dice que S es linealmente dependiente (l.d.), mientras que cuando la única solución posible es la trivial (a 1 =... = a k = 0), S es linealmente independiente (l.i.) 44 / 64
45 Dado un conjunto de vectores S = {v 1, v 2,..., v k } en V, un EV, la ecuación: a 1 v a k v k = 0 tiene al menos la solución trivial a 1 = a 2 =... = a k = 0 Definición Es posible que haya otras soluciones donde al menos algún a i 0 En este caso se dice que S es linealmente dependiente (l.d.), mientras que cuando la única solución posible es la trivial (a 1 =... = a k = 0), S es linealmente independiente (l.i.) 45 / 64
46 46 / 64 Veamos que esta definición de dependencia lineal tiene sentido: Si hay algún a i 0, entonces podemos despejar el vector correspondiente y expresarlo como combinación lineal de los demás, es decir, v i será linealmente dependiente de los demás vectores: v i = (a 1v 1 + +a i 1 v i 1 +a i+1 v i+1 + +a k v k ) a i De hecho, si uno de los vectores se puede expresar como combinación lineal de los demás, podemos demostrar que S será l.d. Demuéstralo tú mismo.
47 47 / 64 Veamos que esta definición de dependencia lineal tiene sentido: Si hay algún a i 0, entonces podemos despejar el vector correspondiente y expresarlo como combinación lineal de los demás, es decir, v i será linealmente dependiente de los demás vectores: v i = (a 1v 1 + +a i 1 v i 1 +a i+1 v i+1 + +a k v k ) a i De hecho, si uno de los vectores se puede expresar como combinación lineal de los demás, podemos demostrar que S será l.d. Demuéstralo tú mismo.
48 48 / 64 Veamos que esta definición de dependencia lineal tiene sentido: Si hay algún a i 0, entonces podemos despejar el vector correspondiente y expresarlo como combinación lineal de los demás, es decir, v i será linealmente dependiente de los demás vectores: v i = (a 1v 1 + +a i 1 v i 1 +a i+1 v i+1 + +a k v k ) a i De hecho, si uno de los vectores se puede expresar como combinación lineal de los demás, podemos demostrar que S será l.d. Demuéstralo tú mismo.
49 49 / 64 Veamos que esta definición de dependencia lineal tiene sentido: Si hay algún a i 0, entonces podemos despejar el vector correspondiente y expresarlo como combinación lineal de los demás, es decir, v i será linealmente dependiente de los demás vectores: v i = (a 1v 1 + +a i 1 v i 1 +a i+1 v i+1 + +a k v k ) a i De hecho, si uno de los vectores se puede expresar como combinación lineal de los demás, podemos demostrar que S será l.d. Demuéstralo tú mismo.
50 Definición Un conjunto de vectores S = {v 1, v 2,..., v n } en un espacio vectorial V, es una base de V, si: < S >= V S es l.i. Es decir, S genera a V y además es maximal, es decir, no sobra ningún vector. Definición Si S es una base de V, diremos que V tiene dimensión n. Observa que para que el concepto esté bien definido, todas las posibles bases de V deben tener el mismo número, n, de vectores, es esto cierto? 50 / 64
51 Definición Un conjunto de vectores S = {v 1, v 2,..., v n } en un espacio vectorial V, es una base de V, si: < S >= V S es l.i. Es decir, S genera a V y además es maximal, es decir, no sobra ningún vector. Definición Si S es una base de V, diremos que V tiene dimensión n. Observa que para que el concepto esté bien definido, todas las posibles bases de V deben tener el mismo número, n, de vectores, es esto cierto? 51 / 64
52 52 / 64 Existen EV de dimensión infinita, cuyas bases tienen infinitos vectores, pero no vamos a estudiarlas en este curso (por ejemplo, el EV formado por todos los polinomios) Cual es la dimensión de un EV que consta de un único punto, es decir V = {0}?
53 53 / 64 Existen EV de dimensión infinita, cuyas bases tienen infinitos vectores, pero no vamos a estudiarlas en este curso (por ejemplo, el EV formado por todos los polinomios) Cual es la dimensión de un EV que consta de un único punto, es decir V = {0}?
54 Ejemplo Algunos ejemplos de bases: {(1, 0, 0), (0, 1, 0), (0, 0, 1)} se llama base estándar o canónica de R 3 {1, x, x 2,..., x n } se llama base canónica del EV P n, formado por los polinomios de grado (menor o igual que) n. Dada una base, todo vector v en V puede expresarse de una única forma como combinación lineal de los vectores de S. Demuéstralo. Así a simple vista y sin realizar ningún cálculo, responde a esta pregunta: En R 3, S = {(1, 1, 0), (0, 1, 0), (1, 0, 1), (0, 1, 1)}, puede ser l.i.? 54 / 64
55 Ejemplo Algunos ejemplos de bases: {(1, 0, 0), (0, 1, 0), (0, 0, 1)} se llama base estándar o canónica de R 3 {1, x, x 2,..., x n } se llama base canónica del EV P n, formado por los polinomios de grado (menor o igual que) n. Dada una base, todo vector v en V puede expresarse de una única forma como combinación lineal de los vectores de S. Demuéstralo. Así a simple vista y sin realizar ningún cálculo, responde a esta pregunta: En R 3, S = {(1, 1, 0), (0, 1, 0), (1, 0, 1), (0, 1, 1)}, puede ser l.i.? 55 / 64
56 Ejemplo Algunos ejemplos de bases: {(1, 0, 0), (0, 1, 0), (0, 0, 1)} se llama base estándar o canónica de R 3 {1, x, x 2,..., x n } se llama base canónica del EV P n, formado por los polinomios de grado (menor o igual que) n. Dada una base, todo vector v en V puede expresarse de una única forma como combinación lineal de los vectores de S. Demuéstralo. Así a simple vista y sin realizar ningún cálculo, responde a esta pregunta: En R 3, S = {(1, 1, 0), (0, 1, 0), (1, 0, 1), (0, 1, 1)}, puede ser l.i.? 56 / 64
57 Ejemplo Algunos ejemplos de bases: {(1, 0, 0), (0, 1, 0), (0, 0, 1)} se llama base estándar o canónica de R 3 {1, x, x 2,..., x n } se llama base canónica del EV P n, formado por los polinomios de grado (menor o igual que) n. Dada una base, todo vector v en V puede expresarse de una única forma como combinación lineal de los vectores de S. Demuéstralo. Así a simple vista y sin realizar ningún cálculo, responde a esta pregunta: En R 3, S = {(1, 1, 0), (0, 1, 0), (1, 0, 1), (0, 1, 1)}, puede ser l.i.? 57 / 64
58 58 / 64 Espacios Vectoriales 1 Las 10 propiedades de un espacio vectorial 2 Subespacios Vectoriales 3 Conjuntos Generadores y Bases 4 Coordenadas y Cambio de Base
59 Dada una base B = {v 1,..., v n } del EV V, todo vector v en V se puede expresar como combinación lineal de los vectores de B: v = a 1 v a n v n Pues bien, esta combinación lineal es única, es decir, para cualesquiera c i tales que v = c i v c n v n, necesariamente c i = a i para todo i. Definición Estos a i se llaman coordenadas de v con respecto a la base B, y representamos el vector de coordenadas así: (v) B = (a 1,..., a n ) Ejemplo Si (v) B = (4, 5) son las coordenadas de v respecto a la base {(1, 1), (1, 1)}, sus coordenadas en la base canónica serán: v = 4(1, 1) + 5(1, 1) = (9, 1) 0 59 / 64
60 Dada una base B = {v 1,..., v n } del EV V, todo vector v en V se puede expresar como combinación lineal de los vectores de B: v = a 1 v a n v n Pues bien, esta combinación lineal es única, es decir, para cualesquiera c i tales que v = c i v c n v n, necesariamente c i = a i para todo i. Definición Estos a i se llaman coordenadas de v con respecto a la base B, y representamos el vector de coordenadas así: (v) B = (a 1,..., a n ) Ejemplo Si (v) B = (4, 5) son las coordenadas de v respecto a la base {(1, 1), (1, 1)}, sus coordenadas en la base canónica serán: v = 4(1, 1) + 5(1, 1) = (9, 1) 0 60 / 64
61 Dada una base B = {v 1,..., v n } del EV V, todo vector v en V se puede expresar como combinación lineal de los vectores de B: v = a 1 v a n v n Pues bien, esta combinación lineal es única, es decir, para cualesquiera c i tales que v = c i v c n v n, necesariamente c i = a i para todo i. Definición Estos a i se llaman coordenadas de v con respecto a la base B, y representamos el vector de coordenadas así: (v) B = (a 1,..., a n ) Ejemplo Si (v) B = (4, 5) son las coordenadas de v respecto a la base {(1, 1), (1, 1)}, sus coordenadas en la base canónica serán: v = 4(1, 1) + 5(1, 1) = (9, 1) 0 61 / 64
62 Cómo obtener las coordenadas de un vector en una base dada si tenemos sus coordenadas en la base canónica? Sea v = (1, 2, 3) en R 3, cuáles son sus cordenadas en la base B = {(1, 0, 5), (0, 1, 2), (3, 2, 2)}? En general este problema lo vamos a resolver mediante la llamada matriz de transición P de la base B a la base B, que cumple: [v] B = P[v] B. Esta matriz es invertible y su inversa, P 1, es la matriz de transición de la base B a B. Un modo sencillo de encontrar esta matriz es el siguiente: Primero construimos dos matrices, B y B, cuyas columnas se corresponden con los vectores de las bases B y B, respectivamente, y luego aplicamos la eliminación de Gauss-Jordan a la matriz [B B] hasta obtener la matriz [I P 1 ]. 62 / 64
63 Cómo obtener las coordenadas de un vector en una base dada si tenemos sus coordenadas en la base canónica? Sea v = (1, 2, 3) en R 3, cuáles son sus cordenadas en la base B = {(1, 0, 5), (0, 1, 2), (3, 2, 2)}? En general este problema lo vamos a resolver mediante la llamada matriz de transición P de la base B a la base B, que cumple: [v] B = P[v] B. Esta matriz es invertible y su inversa, P 1, es la matriz de transición de la base B a B. Un modo sencillo de encontrar esta matriz es el siguiente: Primero construimos dos matrices, B y B, cuyas columnas se corresponden con los vectores de las bases B y B, respectivamente, y luego aplicamos la eliminación de Gauss-Jordan a la matriz [B B] hasta obtener la matriz [I P 1 ]. 63 / 64
64 Cómo obtener las coordenadas de un vector en una base dada si tenemos sus coordenadas en la base canónica? Sea v = (1, 2, 3) en R 3, cuáles son sus cordenadas en la base B = {(1, 0, 5), (0, 1, 2), (3, 2, 2)}? En general este problema lo vamos a resolver mediante la llamada matriz de transición P de la base B a la base B, que cumple: [v] B = P[v] B. Esta matriz es invertible y su inversa, P 1, es la matriz de transición de la base B a B. Un modo sencillo de encontrar esta matriz es el siguiente: Primero construimos dos matrices, B y B, cuyas columnas se corresponden con los vectores de las bases B y B, respectivamente, y luego aplicamos la eliminación de Gauss-Jordan a la matriz [B B] hasta obtener la matriz [I P 1 ]. 64 / 64
Tema 2: Espacios Vectoriales
 Tema 2: Espacios Vectoriales José M. Salazar Octubre de 2016 Tema 2: Espacios Vectoriales Lección 2. Espacios vectoriales. Subespacios vectoriales. Bases. Lección 3. Coordenadas respecto de una base. Ecuaciones.
Tema 2: Espacios Vectoriales José M. Salazar Octubre de 2016 Tema 2: Espacios Vectoriales Lección 2. Espacios vectoriales. Subespacios vectoriales. Bases. Lección 3. Coordenadas respecto de una base. Ecuaciones.
520142: ALGEBRA y ALGEBRA LINEAL
 520142: ALGEBRA y ALGEBRA LINEAL Segundo Semestre 2008, Universidad de Concepción CAPITULO 10: Espacios Vectoriales DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas 1 Definición
520142: ALGEBRA y ALGEBRA LINEAL Segundo Semestre 2008, Universidad de Concepción CAPITULO 10: Espacios Vectoriales DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas 1 Definición
CONCEPTOS BÁSICOS DE ESPACIOS VECTORIALES Alumno. Cristina Mª Méndez Suero
 Fundamento Científico del Currículum de Matemáticas en Enseñanza Secundaria CONCEPTOS BÁSICOS DE ESPACIOS VECTORIALES Alumno. Cristina Mª Méndez Suero ESPACIOS VECTORIALES DEFINICIÓN... 1 PROPIEDADES DE
Fundamento Científico del Currículum de Matemáticas en Enseñanza Secundaria CONCEPTOS BÁSICOS DE ESPACIOS VECTORIALES Alumno. Cristina Mª Méndez Suero ESPACIOS VECTORIALES DEFINICIÓN... 1 PROPIEDADES DE
Tema 1. Espacios Vectoriales Definición de Espacio Vectorial
 Tema 1 Espacios Vectoriales. 1.1. Definición de Espacio Vectorial Notas 1.1.1. Denotaremos por N, Z, Q, R, C, a los conjuntos de los números Naturales, Enteros, Racionales, Reales y Complejos, respectivamente.
Tema 1 Espacios Vectoriales. 1.1. Definición de Espacio Vectorial Notas 1.1.1. Denotaremos por N, Z, Q, R, C, a los conjuntos de los números Naturales, Enteros, Racionales, Reales y Complejos, respectivamente.
Algebra lineal y conjuntos convexos
 Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Un subconjunto no vacío H de un espacio vectorial V es un subespacio de V si se cumplen las dos reglas de cerradura:
 4 Subespacios 29 b) x 5 [25;5], 5 [;24], z 5 [4;4] Use a 5 2, a 5 / a 5 2 / 2 c) Su propia elección de x,, z /o a 2 a) Elija algunos valores para n m genere tres matrices aleatorias de n m, llamadas X,
4 Subespacios 29 b) x 5 [25;5], 5 [;24], z 5 [4;4] Use a 5 2, a 5 / a 5 2 / 2 c) Su propia elección de x,, z /o a 2 a) Elija algunos valores para n m genere tres matrices aleatorias de n m, llamadas X,
Espacios Vectoriales
 Espacios Vectoriales Espacios Vectoriales Verónica Briceño V. noviembre 2013 Verónica Briceño V. () Espacios Vectoriales noviembre 2013 1 / 47 En esta Presentación... En esta Presentación veremos: Espacios
Espacios Vectoriales Espacios Vectoriales Verónica Briceño V. noviembre 2013 Verónica Briceño V. () Espacios Vectoriales noviembre 2013 1 / 47 En esta Presentación... En esta Presentación veremos: Espacios
Espacios vectoriales
 Espacios vectoriales [Versión preliminar] Prof. Isabel Arratia Z. Algebra Lineal 1 En el estudio de las matrices y, en particular, de los sistemas de ecuaciones lineales realizamos sumas y multiplicación
Espacios vectoriales [Versión preliminar] Prof. Isabel Arratia Z. Algebra Lineal 1 En el estudio de las matrices y, en particular, de los sistemas de ecuaciones lineales realizamos sumas y multiplicación
un conjunto cuyos elementos denominaremos vectores y denotaremos por es un espacio vectorial si verifica las siguientes propiedades:
 CAPÍTULO 2: ESPACIOS VECTORIALES 2.1- Definición y propiedades. 2.1.1-Definición: espacio vectorial. Sea un cuerpo conmutativo a cuyos elementos denominaremos escalares o números. No es necesario preocuparse
CAPÍTULO 2: ESPACIOS VECTORIALES 2.1- Definición y propiedades. 2.1.1-Definición: espacio vectorial. Sea un cuerpo conmutativo a cuyos elementos denominaremos escalares o números. No es necesario preocuparse
ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- Espacios vectoriales
 Resumen teoría Prof. Alcón ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- Espacios vectoriales Sea (K, +,.) un cuerpo con característica 0. Podemos pensar K = Q, R o C. Si V es un conjunto cualquiera en el que
Resumen teoría Prof. Alcón ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- Espacios vectoriales Sea (K, +,.) un cuerpo con característica 0. Podemos pensar K = Q, R o C. Si V es un conjunto cualquiera en el que
Tema 3: Espacios vectoriales
 Tema 3: Espacios vectoriales K denotará un cuerpo. Definición. Se dice que un conjunto no vacio V es un espacio vectorial sobre K o que es un K-espacio vectorial si: 1. En V está definida una operación
Tema 3: Espacios vectoriales K denotará un cuerpo. Definición. Se dice que un conjunto no vacio V es un espacio vectorial sobre K o que es un K-espacio vectorial si: 1. En V está definida una operación
ESPACIOS VECTORIALES
 MATEMÁTICA I - - Capítulo 8 ------------------------------------------------------------------------------------ ESPACIOS VECTORIALES.. Espacios Vectoriales y Subespacios... Definición. Un espacio vectorial
MATEMÁTICA I - - Capítulo 8 ------------------------------------------------------------------------------------ ESPACIOS VECTORIALES.. Espacios Vectoriales y Subespacios... Definición. Un espacio vectorial
Trabajo Práctico N 5: ESPACIOS VECTORIALES. Ejercicio 1:
 6 Trabajo Práctico N 5: ESPACIOS VECTORIALES Ejercicio : Determine si los siguientes conjuntos con las operaciones definidas en cada caso son o no espacios vectoriales. Para aquellos que no lo sean, indique
6 Trabajo Práctico N 5: ESPACIOS VECTORIALES Ejercicio : Determine si los siguientes conjuntos con las operaciones definidas en cada caso son o no espacios vectoriales. Para aquellos que no lo sean, indique
Espacios Vectoriales. AMD Grado en Ingeniería Informática. AMD Grado en Ingeniería Informática (UM) Espacios Vectoriales 1 / 21
 Espacios Vectoriales AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Espacios Vectoriales 1 / 21 Objetivos Al finalizar este tema tendrás que: Saber si unos vectores son independientes.
Espacios Vectoriales AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Espacios Vectoriales 1 / 21 Objetivos Al finalizar este tema tendrás que: Saber si unos vectores son independientes.
Trabajo Práctico N 5: ESPACIOS VECTORIALES
 Trabajo Práctico N 5: ESPACIOS VECTORIALES Ejercicio 1: Determine si los siguientes conjuntos con las operaciones definidas en cada caso son o no espacios vectoriales. Para aquellos que no lo sean, indique
Trabajo Práctico N 5: ESPACIOS VECTORIALES Ejercicio 1: Determine si los siguientes conjuntos con las operaciones definidas en cada caso son o no espacios vectoriales. Para aquellos que no lo sean, indique
Espacios Vectoriales, Valores y Vectores Propios
 , Valores y Vectores Propios José Juan Rincón Pasaye, División de Estudios de Postgrado FIE-UMSNH Curso Propedéutico de Matemáticas para la Maestría en Ciencias opciones: Sistemas de Control y Sistemas
, Valores y Vectores Propios José Juan Rincón Pasaye, División de Estudios de Postgrado FIE-UMSNH Curso Propedéutico de Matemáticas para la Maestría en Ciencias opciones: Sistemas de Control y Sistemas
Matrices, Determinantes y Sistemas Lineales.
 12 de octubre de 2014 Matrices Una matriz A m n es una colección de números ordenados en filas y columnas a 11 a 12 a 1n f 1 a 21 a 22 a 2n f 2....... a m1 a m2 a mn f m c 1 c 2 c n Decimos que la dimensión
12 de octubre de 2014 Matrices Una matriz A m n es una colección de números ordenados en filas y columnas a 11 a 12 a 1n f 1 a 21 a 22 a 2n f 2....... a m1 a m2 a mn f m c 1 c 2 c n Decimos que la dimensión
Espacios vectoriales reales.
 Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
Algebra Lineal Tarea No 9: Espacios vectoriales Maestra Dora Elia Cienfuegos, Enero-Mayo 2017
 Algebra Lineal Tarea No 9: Espacios vectoriales Maestra Dora Elia Cienfuegos, Enero-Mayo 2017 Grupo: Matrícula: Nombre: Tipo:-1 1. Suponga que V = R 2 y que se definen las operaciones: y Si Calcule: 1.
Algebra Lineal Tarea No 9: Espacios vectoriales Maestra Dora Elia Cienfuegos, Enero-Mayo 2017 Grupo: Matrícula: Nombre: Tipo:-1 1. Suponga que V = R 2 y que se definen las operaciones: y Si Calcule: 1.
Tema 1: Matrices. El concepto de matriz alcanza múltiples aplicaciones tanto en la representación y manipulación de datos como en el cálculo numérico.
 Tema 1: Matrices El concepto de matriz alcanza múltiples aplicaciones tanto en la representación y manipulación de datos como en el cálculo numérico. 1. Terminología Comenzamos con la definición de matriz
Tema 1: Matrices El concepto de matriz alcanza múltiples aplicaciones tanto en la representación y manipulación de datos como en el cálculo numérico. 1. Terminología Comenzamos con la definición de matriz
Espacios Vectoriales Asturias: Red de Universidades Virtuales Iberoamericanas 1
 Espacios Vectoriales 201 6Asturias: Red de Universidades Virtuales Iberoamericanas 1 Índice 1 Espacios Vectoriales... 4 1.1 Definición de espacio vectorial... 4 1.2 Definición de subespacio vectorial...
Espacios Vectoriales 201 6Asturias: Red de Universidades Virtuales Iberoamericanas 1 Índice 1 Espacios Vectoriales... 4 1.1 Definición de espacio vectorial... 4 1.2 Definición de subespacio vectorial...
Espacios Vectoriales www.math.com.mx
 Espacios Vectoriales Definiciones básicas de Espacios Vectoriales www.math.com.mx José de Jesús Angel Angel [email protected] MathCon c 007-009 Contenido. Espacios Vectoriales.. Idea Básica de Espacio Vectorial.................................
Espacios Vectoriales Definiciones básicas de Espacios Vectoriales www.math.com.mx José de Jesús Angel Angel [email protected] MathCon c 007-009 Contenido. Espacios Vectoriales.. Idea Básica de Espacio Vectorial.................................
Capítulo 7. Espacios vectoriales. 7.1 Definición y ejemplos
 Capítulo Espacios vectoriales.1 Definición y ejemplos Un espacio vectorial sobre un cuerpo K (que supondremos conmutativo es un conjunto no vacío junto con 1. una operación interna, +, a la que llamaremos
Capítulo Espacios vectoriales.1 Definición y ejemplos Un espacio vectorial sobre un cuerpo K (que supondremos conmutativo es un conjunto no vacío junto con 1. una operación interna, +, a la que llamaremos
PAIEP. Complemento Ortogonal
 Programa de Acceso Inclusivo, Equidad y Permanencia PAIEP Universidad de Santiago de Chile Complemento Ortogonal Veamos ahora una aplicación de los vectores ortogonales a la caracterización de subespacios
Programa de Acceso Inclusivo, Equidad y Permanencia PAIEP Universidad de Santiago de Chile Complemento Ortogonal Veamos ahora una aplicación de los vectores ortogonales a la caracterización de subespacios
Una operación interna: Suma Una operación externa: Multiplicación por un escalar
 El conjunto R n Es el conjunto de las n-adas formadas por el producto cartesiano RRR.R, donde R es el conjunto de los números reales. Así pues, dos elementos X y Y de R n serán iguales si y solo si tienen
El conjunto R n Es el conjunto de las n-adas formadas por el producto cartesiano RRR.R, donde R es el conjunto de los números reales. Así pues, dos elementos X y Y de R n serán iguales si y solo si tienen
Álgebra Lineal V: Subespacios Vectoriales.
 Álgebra Lineal V: Subespacios Vectoriales. José María Rico Martínez Departamento de Ingeniería Mecánica Facultad de Ingeniería Mecánica Eléctrica y Electrónica Universidad de Guanajuato email: [email protected]
Álgebra Lineal V: Subespacios Vectoriales. José María Rico Martínez Departamento de Ingeniería Mecánica Facultad de Ingeniería Mecánica Eléctrica y Electrónica Universidad de Guanajuato email: [email protected]
MMAF: Espacios normados y espacios de Banach
 MMAF: Espacios normados y espacios de Banach Licenciatura en Estadística R. Álvarez-Nodarse Universidad de Sevilla Curso 2011/2012 Espacios vectoriales Definición Sea V un conjunto de elementos sobre el
MMAF: Espacios normados y espacios de Banach Licenciatura en Estadística R. Álvarez-Nodarse Universidad de Sevilla Curso 2011/2012 Espacios vectoriales Definición Sea V un conjunto de elementos sobre el
DEFINICIONES TIPOS DE MATRICES DETERMINANTES Y PROPIEDADES OPERACIONES MATRICIALES INVERSA DE UNA MATRIZ SISTEMAS DE ECUACIONES
 ALGEBRA DE MATRICES DEFINICIONES TIPOS DE MATRICES DETERMINANTES Y PROPIEDADES OPERACIONES MATRICIALES INVERSA DE UNA MATRIZ SISTEMAS DE ECUACIONES DEFINICIONES 2 Las matrices y los determinantes son herramientas
ALGEBRA DE MATRICES DEFINICIONES TIPOS DE MATRICES DETERMINANTES Y PROPIEDADES OPERACIONES MATRICIALES INVERSA DE UNA MATRIZ SISTEMAS DE ECUACIONES DEFINICIONES 2 Las matrices y los determinantes son herramientas
Base y Dimensión de un Espacio Vectorial
 Base y Dimensión de un Espacio Vectorial 201 6Asturias: Red de Universidades Virtuales Iberoamericanas 1 Índice 1 Qué es un sistema generador?... 4 2 Base de un espacio vectorial... 4 3 Dimensión de un
Base y Dimensión de un Espacio Vectorial 201 6Asturias: Red de Universidades Virtuales Iberoamericanas 1 Índice 1 Qué es un sistema generador?... 4 2 Base de un espacio vectorial... 4 3 Dimensión de un
LEYES DE COMPOSICIÓN INTERNA Y ELEMENTOS DISTINGUIDOS
 LEYES DE COMPOSICIÓN INTERNA Y ELEMENTOS DISTINGUIDOS Sea una estructura formada por un conjunto A, sobre cuyos elementos se ha definido una operación o ley interna, comúnmente denotada por " * ", que
LEYES DE COMPOSICIÓN INTERNA Y ELEMENTOS DISTINGUIDOS Sea una estructura formada por un conjunto A, sobre cuyos elementos se ha definido una operación o ley interna, comúnmente denotada por " * ", que
SESIÓN 4: ESPACIOS VECTORIALES
 SESIÓN 4: ESPACIOS VECTORIALES Un espacio vectorial sobre un campo (como el cuerpo de los números reales o los números complejos) es un conjunto no vacío, dotado de dos operaciones para las cuales será
SESIÓN 4: ESPACIOS VECTORIALES Un espacio vectorial sobre un campo (como el cuerpo de los números reales o los números complejos) es un conjunto no vacío, dotado de dos operaciones para las cuales será
ESPACIOS VECTORIALES
 01 de Junio de 2011 ESPACIOS VECTORIALES (Clase 02) Departamento de Matemática Aplicada Facultad de Ingeniería Universidad Central de Venezuela 1 Puntos a tratar 1. Combinación lineal 2. Subespacio vectorial
01 de Junio de 2011 ESPACIOS VECTORIALES (Clase 02) Departamento de Matemática Aplicada Facultad de Ingeniería Universidad Central de Venezuela 1 Puntos a tratar 1. Combinación lineal 2. Subespacio vectorial
Espacios topológicos. 3.1 Espacio topológico
 Capítulo 3 Espacios topológicos 3.1 Espacio topológico Definición 3.1.1. Un espacio topológico es un par (X, τ), donde X es un conjunto, y τ es una familia de subconjuntos de X que verifica las siguientes
Capítulo 3 Espacios topológicos 3.1 Espacio topológico Definición 3.1.1. Un espacio topológico es un par (X, τ), donde X es un conjunto, y τ es una familia de subconjuntos de X que verifica las siguientes
Algebra Lineal. Gustavo Rodríguez Gómez. Verano 2011 INAOE. Gustavo Rodríguez Gómez (INAOE) Algebra Lineal Verano / 21
 Algebra Lineal Gustavo Rodríguez Gómez INAOE Verano 2011 Gustavo Rodríguez Gómez (INAOE) Algebra Lineal Verano 2011 1 / 21 Espacios Vectoriales Espacios Vectoriales INAOE Gustavo Rodríguez Gómez (INAOE)
Algebra Lineal Gustavo Rodríguez Gómez INAOE Verano 2011 Gustavo Rodríguez Gómez (INAOE) Algebra Lineal Verano 2011 1 / 21 Espacios Vectoriales Espacios Vectoriales INAOE Gustavo Rodríguez Gómez (INAOE)
Definición 1 Un semigrupo es un conjunto E provisto de una operación binaria asociativa sobre E, se denota por (E, ).
 ALGEBRA La primera parte del presente libro está dedicada a las estructuras algebraicas. En esta parte vamos a iniciar agregándole a los conjuntos operaciones. Cuando las operaciones tienen determinadas
ALGEBRA La primera parte del presente libro está dedicada a las estructuras algebraicas. En esta parte vamos a iniciar agregándole a los conjuntos operaciones. Cuando las operaciones tienen determinadas
1. Lección 1 - Espacio Vectorial
 1. Lección 1 - Espacio Vectorial Definiremos espacio vectorial como la estructura algebraica consistente en: 1. Grupo abeliano {V, +, } cuyos elementos se denominan vectores. Para que los elementos de
1. Lección 1 - Espacio Vectorial Definiremos espacio vectorial como la estructura algebraica consistente en: 1. Grupo abeliano {V, +, } cuyos elementos se denominan vectores. Para que los elementos de
Problemas de Espacios Vectoriales
 Problemas de Espacios Vectoriales 1. Qué condiciones tiene que cumplir un súbconjunto no vacío de un espacio vectorial para que sea un subespacio vectorial de este? Pon un ejemplo. Sean E un espacio vectorial
Problemas de Espacios Vectoriales 1. Qué condiciones tiene que cumplir un súbconjunto no vacío de un espacio vectorial para que sea un subespacio vectorial de este? Pon un ejemplo. Sean E un espacio vectorial
EJERCICIOS DE ÁLGEBRA LINEAL TEMA 1 ESPACIOS VECTORIALES
 EJERCICIOS DE ÁLGEBRA LINEAL TEMA ESPACIOS VECTORIALES Formas reducidas y escalonada de una matriz SISTEMAS DE ECUACIONES LINEALES ) Encuentre una sucesión de matrices elementales E, E,..., E k tal que
EJERCICIOS DE ÁLGEBRA LINEAL TEMA ESPACIOS VECTORIALES Formas reducidas y escalonada de una matriz SISTEMAS DE ECUACIONES LINEALES ) Encuentre una sucesión de matrices elementales E, E,..., E k tal que
Autovalores y autovectores Diagonalización y formas canónicas
 Autovalores y autovectores Diagonalización y formas canónicas Autovalores y autovectores.propiedades Sea V un espacio vectorial sobre K y f End(V ). Fijada una base de V, existirá una matriz cuadrada A,
Autovalores y autovectores Diagonalización y formas canónicas Autovalores y autovectores.propiedades Sea V un espacio vectorial sobre K y f End(V ). Fijada una base de V, existirá una matriz cuadrada A,
1 SISTEMAS DE ECUACIONES LINEALES. MÉTODO DE GAUSS
 1 SISTEMAS DE ECUACIONES LINEALES. MÉTODO DE GAUSS 1.1 SISTEMAS DE ECUACIONES LINEALES Una ecuación lineal es una ecuación polinómica de grado 1, con una o varias incógnitas. Dos ecuaciones son equivalentes
1 SISTEMAS DE ECUACIONES LINEALES. MÉTODO DE GAUSS 1.1 SISTEMAS DE ECUACIONES LINEALES Una ecuación lineal es una ecuación polinómica de grado 1, con una o varias incógnitas. Dos ecuaciones son equivalentes
Espacios Vectoriales
 Espacios Vectoriales Departamento de Matemáticas, CSI/ITESM 7 de junio de 28 Índice 5.. Objetivos................................................ 5.2. Motivación...............................................
Espacios Vectoriales Departamento de Matemáticas, CSI/ITESM 7 de junio de 28 Índice 5.. Objetivos................................................ 5.2. Motivación...............................................
TEMA 1. MATRICES, DETERMINANTES Y APLICACIÓN DE LOS DETERMINANTES. CONCEPTO DE MATRIZ. LA MATRIZ COMO EXPRESIÓN DE TABLAS Y GRAFOS.
 TEMA 1. MATRICES, DETERMINANTES Y APLICACIÓN DE LOS DETERMINANTES. 1. MATRICES. CONCEPTO DE MATRIZ. LA MATRIZ COMO EXPRESIÓN DE TABLAS Y GRAFOS. DEFINICIÓN: Las matrices son tablas numéricas rectangulares
TEMA 1. MATRICES, DETERMINANTES Y APLICACIÓN DE LOS DETERMINANTES. 1. MATRICES. CONCEPTO DE MATRIZ. LA MATRIZ COMO EXPRESIÓN DE TABLAS Y GRAFOS. DEFINICIÓN: Las matrices son tablas numéricas rectangulares
Subespacios Vectoriales
 Subespacios Vectoriales Prof. Apuntes del Postgrado en Ingeniería 31 Mayo 2008 Subespacio Definición de Subespacio y Ejemplos. Definición Sea H un subconjunto no vacio de un espacio vectorial V(K). Si
Subespacios Vectoriales Prof. Apuntes del Postgrado en Ingeniería 31 Mayo 2008 Subespacio Definición de Subespacio y Ejemplos. Definición Sea H un subconjunto no vacio de un espacio vectorial V(K). Si
Espacios vectoriales. Capítulo Espacios vectoriales y subespacios Preliminares
 Capítulo 1 Espacios vectoriales En diversos conjuntos conocidos, por ejemplo los de vectores en el plano o en el espacio (R 2 y R 3 ), o también el de los polinomios (R[X]), sabemos sumar sus elementos
Capítulo 1 Espacios vectoriales En diversos conjuntos conocidos, por ejemplo los de vectores en el plano o en el espacio (R 2 y R 3 ), o también el de los polinomios (R[X]), sabemos sumar sus elementos
BLOQUE 1. LOS NÚMEROS
 BLOQUE 1. LOS NÚMEROS Números naturales, enteros y racionales. El número real. Intervalos. Valor absoluto. Tanto el Cálculo como el Álgebra que estudiaremos en esta asignatura, descansan en los números
BLOQUE 1. LOS NÚMEROS Números naturales, enteros y racionales. El número real. Intervalos. Valor absoluto. Tanto el Cálculo como el Álgebra que estudiaremos en esta asignatura, descansan en los números
Espacios Vectoriales
 Leandro Marín Octubre 2010 Índice Definición y Ejemplos Paramétricas vs. Impĺıcitas Bases y Coordenadas Para definir un espacio vectorial tenemos que empezar determinando un cuerpo sobre el que esté definido
Leandro Marín Octubre 2010 Índice Definición y Ejemplos Paramétricas vs. Impĺıcitas Bases y Coordenadas Para definir un espacio vectorial tenemos que empezar determinando un cuerpo sobre el que esté definido
1 ÁLGEBRA DE MATRICES
 1 ÁLGEBRA DE MATRICES 1.1 DEFINICIONES Las matrices son tablas numéricas rectangulares. Se dice que una matriz es de dimensión m n si tiene m filas y n columnas. Cada elemento de una matriz se designa
1 ÁLGEBRA DE MATRICES 1.1 DEFINICIONES Las matrices son tablas numéricas rectangulares. Se dice que una matriz es de dimensión m n si tiene m filas y n columnas. Cada elemento de una matriz se designa
Algebra Lineal y Geometría.
 Algebra Lineal y Geometría. Unidad n 6: Subespacios Vectoriales. Algebra Lineal y Geometría Esp. Liliana Eva Mata 1 Contenidos. Subespacios Vectoriales. Operaciones con Subespacios: Intersección, unión,
Algebra Lineal y Geometría. Unidad n 6: Subespacios Vectoriales. Algebra Lineal y Geometría Esp. Liliana Eva Mata 1 Contenidos. Subespacios Vectoriales. Operaciones con Subespacios: Intersección, unión,
Estructuras Algebraicas
 Tema 1 Estructuras Algebraicas Definición 1 Sea A un conjunto no vacío Una operación binaria (u operación interna) en A es una aplicación : A A A Es decir, tenemos una regla que a cada par de elementos
Tema 1 Estructuras Algebraicas Definición 1 Sea A un conjunto no vacío Una operación binaria (u operación interna) en A es una aplicación : A A A Es decir, tenemos una regla que a cada par de elementos
MATRICES. Se simboliza tal matriz por y se le llamará una matriz x o matriz de orden x (que se lee por ).
 1 MATRICES 1 Una matriz es una disposición rectangular de números (Reales); la forma general de una matriz con filas y columnas es Se simboliza tal matriz por y se le llamará una matriz x o matriz de orden
1 MATRICES 1 Una matriz es una disposición rectangular de números (Reales); la forma general de una matriz con filas y columnas es Se simboliza tal matriz por y se le llamará una matriz x o matriz de orden
Dos matrices son iguales cuando tienen la misma dimensión y los elementos que ocupan el mismo lugar en ambas son iguales
 Introducción Las matrices aparecen por primera vez hacia el año 1850, introducidas por J.J. Sylvester. El desarrollo inicial de la teoría se debe al matemático W.R. Hamilton en 1853. En 1858, A. Cayley
Introducción Las matrices aparecen por primera vez hacia el año 1850, introducidas por J.J. Sylvester. El desarrollo inicial de la teoría se debe al matemático W.R. Hamilton en 1853. En 1858, A. Cayley
TEMA 2. ESPACIOS VECTORIALES
 TEMA 2. ESPACIOS VECTORIALES CÉSAR ROSALES GEOMETRÍA I En este tema comenzaremos el estudio de los objetos que nos interesarán en esta asignatura: los espacios vectoriales. Estos son estructuras básicas
TEMA 2. ESPACIOS VECTORIALES CÉSAR ROSALES GEOMETRÍA I En este tema comenzaremos el estudio de los objetos que nos interesarán en esta asignatura: los espacios vectoriales. Estos son estructuras básicas
TEMA 11. VECTORES EN EL ESPACIO
 TEMA 11. VECTORES EN EL ESPACIO Dados dos puntos y, se define el vector como el segmento orientado caracterizado por su módulo, su dirección y su sentido. Dos vectores son equipolentes si tienen el mismo
TEMA 11. VECTORES EN EL ESPACIO Dados dos puntos y, se define el vector como el segmento orientado caracterizado por su módulo, su dirección y su sentido. Dos vectores son equipolentes si tienen el mismo
Álgebra Lineal VII: Independencia Lineal.
 Álgebra Lineal VII: Independencia Lineal José María Rico Martínez Departamento de Ingeniería Mecánica División de Ingenierías, Campus Irapuato-Salamanca Universidad de Guanajuato email: jrico@salamancaugtomx
Álgebra Lineal VII: Independencia Lineal José María Rico Martínez Departamento de Ingeniería Mecánica División de Ingenierías, Campus Irapuato-Salamanca Universidad de Guanajuato email: jrico@salamancaugtomx
DOCENTE: JESÚS E. BARRIOS P.
 DOCENTE: JESÚS E. BARRIOS P. DEFINICIONES Es larga la historia del uso de las matrices para resolver ecuaciones lineales. Un texto matemático chino que proviene del año 300 A. C. a 200 A. C., Nueve capítulos
DOCENTE: JESÚS E. BARRIOS P. DEFINICIONES Es larga la historia del uso de las matrices para resolver ecuaciones lineales. Un texto matemático chino que proviene del año 300 A. C. a 200 A. C., Nueve capítulos
Resumen 3: Matrices, determinantes y sistemas de ecuaciones
 Resumen 3: Matrices, determinantes y sistemas de ecuaciones lineales 1 Matrices Una matriz con coeficientes sobre un cuerpo K (normalmente K R) consiste en una colección de números (o escalares) del cuerpo
Resumen 3: Matrices, determinantes y sistemas de ecuaciones lineales 1 Matrices Una matriz con coeficientes sobre un cuerpo K (normalmente K R) consiste en una colección de números (o escalares) del cuerpo
Tema 2: Teorema de estructura de los grupos abelianos finitamente generados.
 ESTRUCTURAS ALGEBRAICAS GRADO EN MATEMÁTICAS. CURSO 215/216 Tema 2: Teorema de estructura de los grupos abelianos finitamente generados. 1.1. Grupo abeliano libre. Bases. Definición 1.1. El grupo Z n con
ESTRUCTURAS ALGEBRAICAS GRADO EN MATEMÁTICAS. CURSO 215/216 Tema 2: Teorema de estructura de los grupos abelianos finitamente generados. 1.1. Grupo abeliano libre. Bases. Definición 1.1. El grupo Z n con
Vectores y Matrices. Tema 3: Repaso de Álgebra Lineal Parte I. Contenidos
 Tema 3: Repaso de Álgebra Lineal Parte I Virginia Mazzone Contenidos Vectores y Matrices Bases y Ortonormailizaciòn Norma de Vectores Ecuaciones Lineales Algenraicas Ejercicios Vectores y Matrices Los
Tema 3: Repaso de Álgebra Lineal Parte I Virginia Mazzone Contenidos Vectores y Matrices Bases y Ortonormailizaciòn Norma de Vectores Ecuaciones Lineales Algenraicas Ejercicios Vectores y Matrices Los
2.1. Estructura algebraica de espacio vectorial
 Tema 2 Espacios vectoriales de dimensión finita 21 Estructura algebraica de espacio vectorial Los vectores libres en el plano son el sustento geométrico del concepto de espacio vectorial Se trata de segmentos
Tema 2 Espacios vectoriales de dimensión finita 21 Estructura algebraica de espacio vectorial Los vectores libres en el plano son el sustento geométrico del concepto de espacio vectorial Se trata de segmentos
Es trivial generalizar la definición al caso de varios conjuntos: A B C, etc.
 Tema 1 Espacios Vectoriales 1.1 Introducción Estas notas están elaboradas pensando simplemente en facilitar al estudiante una guía para el estudio de la asignatura, y en consecuencia se caracterizan por
Tema 1 Espacios Vectoriales 1.1 Introducción Estas notas están elaboradas pensando simplemente en facilitar al estudiante una guía para el estudio de la asignatura, y en consecuencia se caracterizan por
Sistemas de Ecuaciones Lineales y Matrices
 Capítulo 4 Sistemas de Ecuaciones Lineales y Matrices El problema central del Álgebra Lineal es la resolución de ecuaciones lineales simultáneas Una ecuación lineal con n-incógnitas x 1, x 2,, x n es una
Capítulo 4 Sistemas de Ecuaciones Lineales y Matrices El problema central del Álgebra Lineal es la resolución de ecuaciones lineales simultáneas Una ecuación lineal con n-incógnitas x 1, x 2,, x n es una
Tema 2: El grupo de las permutaciones
 Tema 2: El grupo de las permutaciones Miguel Ángel Olalla Acosta [email protected] Departamento de Álgebra Universidad de Sevilla Octubre de 2014 Olalla (Universidad de Sevilla) Tema 2: El grupo de las
Tema 2: El grupo de las permutaciones Miguel Ángel Olalla Acosta [email protected] Departamento de Álgebra Universidad de Sevilla Octubre de 2014 Olalla (Universidad de Sevilla) Tema 2: El grupo de las
Definición Dados dos números naturales m y n, una matriz de orden o dimensión m n es una tabla numérica rectangular con m filas y n columnas.
 Tema 1 Matrices 1.1. Conceptos básicos y ejemplos Definición 1.1.1. Dados dos números naturales m y n, una matriz de orden o dimensión m n es una tabla numérica rectangular con m filas y n columnas. NOTA:
Tema 1 Matrices 1.1. Conceptos básicos y ejemplos Definición 1.1.1. Dados dos números naturales m y n, una matriz de orden o dimensión m n es una tabla numérica rectangular con m filas y n columnas. NOTA:
Herramientas digitales de auto-aprendizaje para Matemáticas
 real de con Herramientas digitales de auto-aprendizaje para Matemáticas, Grupo de Innovación Didáctica Departamento de Matemáticas Universidad de Extremadura real de con Índice real de con real de con.
real de con Herramientas digitales de auto-aprendizaje para Matemáticas, Grupo de Innovación Didáctica Departamento de Matemáticas Universidad de Extremadura real de con Índice real de con real de con.
TEMA 8. GEOMETRÍA ANALÍTICA.
 TEMA 8. GEOMETRÍA ANALÍTICA. 8..- El plano. Definimos el plano euclideo como el conjunto de puntos ( x, y) R. Así, cada punto del plano posee dos coordenadas. Para representar puntos del plano utilizaremos
TEMA 8. GEOMETRÍA ANALÍTICA. 8..- El plano. Definimos el plano euclideo como el conjunto de puntos ( x, y) R. Así, cada punto del plano posee dos coordenadas. Para representar puntos del plano utilizaremos
BLOQUE DE ÁLGEBRA: TEMA 1: MATRICES.
 BLOQUE DE ÁLGEBRA: TEMA 1: MATRICES. Matrices: Se llama matriz de dimensión m n a un conjunto de números reales dispuestos en m filas y n columnas de la siguiente forma: 11 a 12 a 13... a 1n A= a a 21
BLOQUE DE ÁLGEBRA: TEMA 1: MATRICES. Matrices: Se llama matriz de dimensión m n a un conjunto de números reales dispuestos en m filas y n columnas de la siguiente forma: 11 a 12 a 13... a 1n A= a a 21
Matrices y determinantes
 Matrices y determinantes 1 Ejemplo Cuál es el tamaño de las siguientes matrices? Cuál es el elemento a 21, b 23, c 42? 2 Tipos de matrices Matriz renglón o vector renglón Matriz columna o vector columna
Matrices y determinantes 1 Ejemplo Cuál es el tamaño de las siguientes matrices? Cuál es el elemento a 21, b 23, c 42? 2 Tipos de matrices Matriz renglón o vector renglón Matriz columna o vector columna
1. Si están situados en rectas paralelas: la recta que une los orígenes, deja sus extremos en un mismo semiplano.
 CAPÍTULO El plano vectorial Consideremos P como el plano intuitivo de puntos: A,,C..... El espacio vectorial de los vectores Definición. Vectores fijos Dado dos puntos cualesquiera A e del espacio nos
CAPÍTULO El plano vectorial Consideremos P como el plano intuitivo de puntos: A,,C..... El espacio vectorial de los vectores Definición. Vectores fijos Dado dos puntos cualesquiera A e del espacio nos
Conjunto R 3 y operaciones lineales en R 3
 Conjunto R 3 y operaciones lineales en R 3 Objetivos. Definir el conjunto R 3 y operaciones lineales en R 3. Requisitos. Conjunto de los números reales R, propiedades de las operaciones aritméticas en
Conjunto R 3 y operaciones lineales en R 3 Objetivos. Definir el conjunto R 3 y operaciones lineales en R 3. Requisitos. Conjunto de los números reales R, propiedades de las operaciones aritméticas en
Tema I 1. EL CUERPO DE LOS REALES, EL CUERPO DE LOS COMPLEJOS
 1 Tema I 1. EL CUERPO DE LOS REALES, EL CUERPO DE LOS COMPLEJOS 1.1 Los Números Naturales. Los números naturales aparecen por la necesidad que tiene el hombre (primitivo) tanto de contar como de ordenar
1 Tema I 1. EL CUERPO DE LOS REALES, EL CUERPO DE LOS COMPLEJOS 1.1 Los Números Naturales. Los números naturales aparecen por la necesidad que tiene el hombre (primitivo) tanto de contar como de ordenar
Clase 8 Matrices Álgebra Lineal
 Clase 8 Matrices Álgebra Lineal Código Escuela de Matemáticas - Facultad de Ciencias Universidad Nacional de Colombia Matrices Definición Una matriz es un arreglo rectangular de números denominados entradas
Clase 8 Matrices Álgebra Lineal Código Escuela de Matemáticas - Facultad de Ciencias Universidad Nacional de Colombia Matrices Definición Una matriz es un arreglo rectangular de números denominados entradas
Tema 11.- Autovalores y Autovectores.
 Álgebra 004-005 Ingenieros Industriales Departamento de Matemática Aplicada II Universidad de Sevilla Tema - Autovalores y Autovectores Definición, propiedades e interpretación geométrica La ecuación característica
Álgebra 004-005 Ingenieros Industriales Departamento de Matemática Aplicada II Universidad de Sevilla Tema - Autovalores y Autovectores Definición, propiedades e interpretación geométrica La ecuación característica
Definición: Dos matrices A y B son iguales si tienen el mismo orden y coinciden los elementos que ocupan el mismo lugar.
 UNIDAD 03: MATRICES Y DETERMINANTES. 3.1 Conceptos de Matrices. 3.1.1 Definición de matriz. Definición: Se lama matriz de orden m x n a un arreglo rectangular de números dispuestos en m renglones y n columnas.
UNIDAD 03: MATRICES Y DETERMINANTES. 3.1 Conceptos de Matrices. 3.1.1 Definición de matriz. Definición: Se lama matriz de orden m x n a un arreglo rectangular de números dispuestos en m renglones y n columnas.
Espacios Vectoriales. Tema Introducción. 1.2 Repaso de Estructuras Algebraicas
 Tema 1 Espacios Vectoriales 1.1 Introducción Estas notas se han escrito con el ánimo de facilitar al estudiante una guía para el estudio de la asignatura, y no como un libro de texto o manual de Álgebra
Tema 1 Espacios Vectoriales 1.1 Introducción Estas notas se han escrito con el ánimo de facilitar al estudiante una guía para el estudio de la asignatura, y no como un libro de texto o manual de Álgebra
Funciones y Cardinalidad
 Funciones y Cardinalidad Definición 1 Llamaremos función f entre dos conjuntos A y B a una relación que verifica las siguientes propiedades: i) Dom(f) = A ii) Si (a, b), (a, c) f entonces b = c Dicho de
Funciones y Cardinalidad Definición 1 Llamaremos función f entre dos conjuntos A y B a una relación que verifica las siguientes propiedades: i) Dom(f) = A ii) Si (a, b), (a, c) f entonces b = c Dicho de
Una matriz es un arreglo rectangular de elementos. Por ejemplo:
 1 MATRICES CONCEPTOS BÁSICOS Definición: Matriz Una matriz es un arreglo rectangular de elementos. Por ejemplo: es una matriz de 3 x 2 (que se lee 3 por 2 ) pues es un arreglo rectangular de números con
1 MATRICES CONCEPTOS BÁSICOS Definición: Matriz Una matriz es un arreglo rectangular de elementos. Por ejemplo: es una matriz de 3 x 2 (que se lee 3 por 2 ) pues es un arreglo rectangular de números con
ELEMENTOS DE GEOMETRÍA. Eduardo P. Serrano
 ELEMENTOS DE GEOMETRÍA Eduardo P. Serrano Este Apunte de Clase está dirigido a los alumnos de la materia Elementos de Cálculo Numérico para Biólogos. Tiene por objeto exponer algunos conceptos básicos
ELEMENTOS DE GEOMETRÍA Eduardo P. Serrano Este Apunte de Clase está dirigido a los alumnos de la materia Elementos de Cálculo Numérico para Biólogos. Tiene por objeto exponer algunos conceptos básicos
MATEMÁTICAS 2º BACH TECNOL. MATRICES. Profesor: Fernando Ureña Portero MATRICES
 CONCEPTO DE MATRIZ Definición: Se denomina matriz A o (a ij ) a todo conjunto de números o expresiones dispuestos en forma rectangular, formando filas y columnas : Columnas Filas Elemento a ij : Cada uno
CONCEPTO DE MATRIZ Definición: Se denomina matriz A o (a ij ) a todo conjunto de números o expresiones dispuestos en forma rectangular, formando filas y columnas : Columnas Filas Elemento a ij : Cada uno
ESPACIOS VECTORIALES
 1. Introducción: 1.1 Grupo Abeliano 1. Cuerpo. Estructura de espacio vectorial 3. Propiedades 4. Subespacio vectorial 5. Combinación lineal de vectores 5.1 Propiedades 6. Dependencia e independencia lineal
1. Introducción: 1.1 Grupo Abeliano 1. Cuerpo. Estructura de espacio vectorial 3. Propiedades 4. Subespacio vectorial 5. Combinación lineal de vectores 5.1 Propiedades 6. Dependencia e independencia lineal
Conjuntos, relaciones y funciones Susana Puddu
 Susana Puddu 1. Repaso sobre la teoría de conjuntos. Denotaremos por IN al conjunto de los números naturales y por ZZ al de los enteros. Dados dos conjuntos A y B decimos que A está contenido en B o también
Susana Puddu 1. Repaso sobre la teoría de conjuntos. Denotaremos por IN al conjunto de los números naturales y por ZZ al de los enteros. Dados dos conjuntos A y B decimos que A está contenido en B o también
Tema 1: MATRICES. OPERACIONES CON MATRICES
 Tema 1: MATRICES. OPERACIONES CON MATRICES 1. DEFINICIÓN Y TIPO DE MATRICES DEFINICIÓN. Una matriz es un conjunto de números reales dispuestos en filas y columnas. Si en ese conjunto hay m n números escritos
Tema 1: MATRICES. OPERACIONES CON MATRICES 1. DEFINICIÓN Y TIPO DE MATRICES DEFINICIÓN. Una matriz es un conjunto de números reales dispuestos en filas y columnas. Si en ese conjunto hay m n números escritos
Matrices: repaso. Denotaremos con M m n el conjunto de matrices de tamaño m n, o sea, de m filas y n columnas. Una matriz A M m n es de la forma A =
 Matrices: repaso Denotaremos con M m n el conjunto de matrices de tamaño m n, o sea, de m filas y n columnas Una matriz A M m n es de la forma a 11 a 1n A = a m1 a mn Denotaremos A ij = a ij el coeficiente
Matrices: repaso Denotaremos con M m n el conjunto de matrices de tamaño m n, o sea, de m filas y n columnas Una matriz A M m n es de la forma a 11 a 1n A = a m1 a mn Denotaremos A ij = a ij el coeficiente
UNIDAD I: SISTEMAS DE DOS ECUACIONES CON DOS INCÓGNITAS
 UNIDAD I: SISTEMAS DE DOS ECUACIONES CON DOS INCÓGNITAS Sistemas de dos ecuaciones con dos incógnitas. Método de igualación. Método de reducción. Método de sustitución Método de eliminación Gaussiana.
UNIDAD I: SISTEMAS DE DOS ECUACIONES CON DOS INCÓGNITAS Sistemas de dos ecuaciones con dos incógnitas. Método de igualación. Método de reducción. Método de sustitución Método de eliminación Gaussiana.
Si A es una matriz cuadrada n x n, tal que A 2 = A, e I es la matriz unidad ( n x n ), qué matriz es B 2, si B = 2ª - I?
 MATRICES Si A es una matriz cuadrada n x n, tal que A 2 = A, e I es la matriz unidad ( n x n ), qué matriz es B 2, si B = 2ª - I? La multiplicación de matrices cuadradas, tiene la propiedad conmutativa?
MATRICES Si A es una matriz cuadrada n x n, tal que A 2 = A, e I es la matriz unidad ( n x n ), qué matriz es B 2, si B = 2ª - I? La multiplicación de matrices cuadradas, tiene la propiedad conmutativa?
IN Guía de Problemas Resueltos de Geometría de Programación Lineal v1.0
 IN3701 - Guía de Problemas Resueltos de Geometría de Programación Lineal v1.0 Acá va una pequeña guía con problemas resueltos de Geometría en Programación Lineal con problemas básicamente extraídos del
IN3701 - Guía de Problemas Resueltos de Geometría de Programación Lineal v1.0 Acá va una pequeña guía con problemas resueltos de Geometría en Programación Lineal con problemas básicamente extraídos del
MATRICES. Rango de una matriz. Matriz Inversa. Determinante de una matriz cuadrada. Sistemas de Ecuaciones Lineales. Nociones de espacios vectoriales
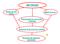 MATRICES Rango de una matriz Matriz Inversa Determinante de una matriz cuadrada Sistemas de Ecuaciones Lineales Nociones de espacios vectoriales MATRICES -DEFINICIÓN DE MATRIZ. -ALGUNOS TIPOS DE MATRICES.
MATRICES Rango de una matriz Matriz Inversa Determinante de una matriz cuadrada Sistemas de Ecuaciones Lineales Nociones de espacios vectoriales MATRICES -DEFINICIÓN DE MATRIZ. -ALGUNOS TIPOS DE MATRICES.
Ecuaciones de la recta en el espacio
 Ecuaciones de la recta en el espacio Ecuación vectorial de la recta Sea P(x 1, y 1 ) es un punto de la recta r y uu su vector director, el vector PPXX tiene igual dirección que uu, luego es igual a uu
Ecuaciones de la recta en el espacio Ecuación vectorial de la recta Sea P(x 1, y 1 ) es un punto de la recta r y uu su vector director, el vector PPXX tiene igual dirección que uu, luego es igual a uu
Ejercicios del Tema 2: Estructuras algebraicas básicas
 Ejercicios del Tema 2: Estructuras algebraicas básicas En los ejercicios 1, 2, 8 y 9 se utilizará que si G = {g 1,...,g n } es un conjunto finito y * una operación interna definida en G, podemos utilizar
Ejercicios del Tema 2: Estructuras algebraicas básicas En los ejercicios 1, 2, 8 y 9 se utilizará que si G = {g 1,...,g n } es un conjunto finito y * una operación interna definida en G, podemos utilizar
como el número real que resulta del producto matricial y se nota por:
 Espacio euclídeo 2 2. ESPACIO EUCLÍDEO 2.. PRODUCTO ESCALAR En el espacio vectorial se define el producto escalar de dos vectores y como el número real que resulta del producto matricial y se nota por:,
Espacio euclídeo 2 2. ESPACIO EUCLÍDEO 2.. PRODUCTO ESCALAR En el espacio vectorial se define el producto escalar de dos vectores y como el número real que resulta del producto matricial y se nota por:,
Matrices. José Vicente Romero Bauset. ETSIT-curso 2009/2010. José Vicente Romero Bauset Tema 1.- Matrices. 1
 Matrices José Vicente Romero Bauset ETSIT-curso 2009/2010 José Vicente Romero Bauset Tema 1- Matrices 1 Introducción Por qué estudiar las matrices? Son muchas las situaciones de la vida real en las que
Matrices José Vicente Romero Bauset ETSIT-curso 2009/2010 José Vicente Romero Bauset Tema 1- Matrices 1 Introducción Por qué estudiar las matrices? Son muchas las situaciones de la vida real en las que
MATEMÁTICASII Curso académico BLOQUE GEOMETRÍA. TEMA 1: VECTORES
 MATEMÁTICASII Curso académico 2015-2016 BLOQUE GEOMETRÍA. TEMA 1: VECTORES 1.1 VECTORES DEL ESPACIO. VECTORES LIBRES DEL ESPACIO Sean y dos puntos del espacio. Llamaremos vector (fijo) a un segmento orientado
MATEMÁTICASII Curso académico 2015-2016 BLOQUE GEOMETRÍA. TEMA 1: VECTORES 1.1 VECTORES DEL ESPACIO. VECTORES LIBRES DEL ESPACIO Sean y dos puntos del espacio. Llamaremos vector (fijo) a un segmento orientado
Forma binomial de números complejos (ejercicios)
 Forma binomial de números complejos (ejercicios) Objetivos. Mostrar que los números reales x se pueden identificar con números complejos de la forma (x, 0), y cada número complejo (x, y) se puede escribir
Forma binomial de números complejos (ejercicios) Objetivos. Mostrar que los números reales x se pueden identificar con números complejos de la forma (x, 0), y cada número complejo (x, y) se puede escribir
Matriz sobre K = R o C de dimensión m n
 2 Matrices y Determinantes 21 Matrices Matriz sobre K = R o C de dimensión m n A = a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a mn Tipos de matrices: Cuadrada: n n = (a ij) i=1,,m j=1,,n Nula: (0) i,j 1 0
2 Matrices y Determinantes 21 Matrices Matriz sobre K = R o C de dimensión m n A = a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a mn Tipos de matrices: Cuadrada: n n = (a ij) i=1,,m j=1,,n Nula: (0) i,j 1 0
TRA NSFORMACIO N ES LIN EA LES
 TRA NSFORMACIO N ES LIN EA LES C o m p uta c i ó n G r á fica Tipos de Datos Geométricos T Un punto se puede representar con tres números reales [x,y,z] que llamaremos vector coordenado. Los números especifican
TRA NSFORMACIO N ES LIN EA LES C o m p uta c i ó n G r á fica Tipos de Datos Geométricos T Un punto se puede representar con tres números reales [x,y,z] que llamaremos vector coordenado. Los números especifican
I.E.S. Miguel de Cervantes (Granada) Departamento de Matemáticas GBG 1
 PRODUCTO ESCALAR INTRODUCCIÓN El espacio vectorial de los vectores libres del plano se caracteriza por tener definidas dos operaciones: una interna, suma de vectores, y otra externa, producto de un número
PRODUCTO ESCALAR INTRODUCCIÓN El espacio vectorial de los vectores libres del plano se caracteriza por tener definidas dos operaciones: una interna, suma de vectores, y otra externa, producto de un número
