Hipercuádricas afines. Clasificación. Elementos afines y euclídeos.
|
|
|
- María Pilar Rey Carrasco
- hace 5 años
- Vistas:
Transcripción
1 Capítulo 6 Hipercuádricas afines. Clasificación. Elementos afines y euclídeos. Sea k un cuerpo de característica distinta de dos. Definición Una hipercuádrica afín en k n es una ecuación de segundo grado en n variables, salvo escalar A cada polinomio f = f(y 1,..., y n ) = α ij y i y j i+j 2 se le asocia una matriz simétrica A f con coeficientes en k tal que f(y 1,..., y n ) = (1, y 1,..., y n )A f (1, y 1,..., y n ) t (se ha utilizado aquí que el cuerpo es de característica distinta de dos). Por tanto una hipercuádrica afín de k n es, salvo escalar, una ecuación Y AY t = 0, con Y = (1, y 1,..., y n ) y A una matriz simétrica de orden n + 1. Definición Si Q es una hipercuádrica afín en k n se llama hipercuádrica lugar asociada a Q al conjunto V a (Q) = {(a 1,..., a n ) k n f(a 1,..., a n ) = 0}, donde f = 0 es una ecuación de Q. Nota Obviamente la definición anterior es consistente, es decir, el conjunto V a (Q) no depende del representante f elegido. Nota Recordamos que un sistema de referencia afín en k n está dado por R = {O; B}, donde O es un punto de k n y B es una base del espacio vectorial k n. El ejemplo más elemental es el del sistema de referencia canónico, dado por 1
2 O = (0,..., 0) y por la base canónica de k n, en donde el punto (a 1,..., a n ) de k n tiene coordenadas (a 1,..., a n ) respecto del sistema de referencia canónico. Por otra parte, si R = {O ; B } es otro sistema de referencia afín en k n, las ecuaciones del cambio de sistema de referencia afín son de la forma: 1 m m 0n (1, y 1,..., y n ) = (1, y 1,..., y n) 0 m m 1n..., 0 m n0... m nn o bien, Y = Y M, con la notación obvia. Por tanto, dada una hipercuádrica afín Q de ecuación Y AY t = 0, respecto de un sistema de referencia afín R, en otro sistema de referencia afín R, una ecuación de Q es: 0 = (Y M)A(Y M) t = Y BY t con B = MAM t también simétrica, siendo M una matriz de cambio de sistema de referencia afín. Nótese que esta matriz M es una matriz de orden n + 1 inversible especial por su primera columna. Definición Sean Q y Q dos hipercuádricas afines en k n. Se dice que Q es afínmente equivalente a Q (y se representa Q a Q ) si existe un cambio de sistema de referencia afín de k n que transforma una ecuación de Q en una ecuación de Q. Es decir, si Y AY t = 0, Y BY t = 0, son ecuaciones de Q y Q respectivamente, entonces A y B son congruentes con una matriz de paso especial. Se trata de encontrar invariantes de las hipercuádricas afines que las clasifiquen, por analogía a lo hecho en el caso proyectivo. Se considera el espacio afín k n sumergido en el espacio proyectivo P n (k) de la manera habitual : k n P n (k) donde se identifica el punto (a 1,..., a n ) k n con (1 : a 1 :... : a n ) P n (k). Denotaremos por H al hiperplano del infinito x 0 = 0. Definición Sea Q una hipercuádrica afín en k n definida por una ecuación Y AY t = 0. Se llama clausura proyectiva de Q (y se denota por Q) a la hipercuádrica proyectiva definida en P n (k) por la ecuación XAX t = 0, con X = (x 0, x 1,..., x n ). Nótese que la ecuación de Q se obtiene homogeneizando la ecuación de Q, igual que sucedía con las ecuaciones de las variedades lineales afines, al hallar sus clausuras proyectivas. Definición Se llama hipercuádrica del infinito asociada a Q (y se denota por Q ) a la hipercuádrica proyectiva Q H definida en el hiperplano del infinito por Q. Por tanto, la ecuación de Q es (0, x 1,..., x n )A 0 x 1. x n = (x 1,..., x n )A 0 x 1. x n = 0, 2
3 donde A 0 es la submatriz de A obtenida eliminando la primera fila y columna. Lema Con las notaciones anteriores se tiene: V a (Q) V(Q ) = V(Q) Teorema Sea k = R ó C. Sean Q y Q dos hipercuádricas afines en k n. Son equivalentes: 1. Q es afínmente equivalente a Q. 2. Q es proyectivamente equivalente a Q y Q es proyectivamente equivalente a Q. Como en el caso k = C las hipercuádricas proyectivas se clasifican según su rango, las hipercuádricas afines complejas se clasifican por los rangos de su clausura proyectiva y de su restricción al infinito. En términos matriciales, si A es una matriz de una ecuación de una hipercuádrica afín, los rangos de A y A 0, la clasifican. En el caso real, la situación es análoga, salvo que hay dos invariantes que clasifican hipercuádricas: rango y signatura proyectiva. Vamos a describir los distintos tipos de cónicas y cuádricas afines reales, dando sus nombres y sus ecuaciones canónicas o reducidas, en función de estos cuatro invariantes. Cónicas afines reales Q rang(q) : 3 rang(q) : 2 rang(q) : 1 sp(q) : 3 sp(q) : 1 sp(q) : 2 sp(q) : 0 sp(q) = 1 2 Elipse Elipse Par rectas afines imaginaria real imaginarias secantes Q 2 0 Hipérbola Par rectas afines reales secantes 1 1 Parábola Par rectas afines Par rectas afines recta afín imaginarias paralelas reales paralelas doble 0 0 recta afín Para construir la tabla se utilizan varios argumentos: el lema y la posición relativa de una cónica real no degenerada y una recta, que dimos al describir a aquella. Las ecuaciones reducidas son: elipse imaginaria: 1 + y y 2 2 = 0 elipse real: 1 + y y 2 2 = 0 hipérbola: 1 + y 2 1 y 2 2 = 0 parábola: 2y 1 + y 2 2 = 0 3
4 par de rectas afines imaginarias secantes: y1 2 + y2 2 = 0 par de rectas afines reales secantes: y1 2 y2 2 = 0 par de rectas afines imaginarias paralelas: 1 + y1 2 = 0 par de rectas afines reales paralelas: 1 y1 2 = 0 recta afín doble: y1 2 = 0 recta afín: y 1 = 0 Cuádricas afines reales Q rang(q) : 4 rang(q) : 3 rang(q) : 2 rang(q) : 1 sp(q) : 4 sp(q) : 2 sp(q) : 0 sp(q) : 3 sp(q) : 1 sp(q) : 2 sp(q) : 0 sp(q) : 1 3 Elipsoide Elipsoide cono af. imag. real imag. 3 1 hiperboloide hiperboloide cono af. elíptico hiperbólico real Q 2 Paraboloide cilindro cilindro par planos elíptico imag. elíptico af. imag. secantes 2 0 Paraboloide cilindro par planos hiperbólico hiperb. af. reales secantes 1 1 cilindro Par planos Par planos plano af. parab. af. imag. af. reales doble paralelos paralelos 0 0 plano afín Para construir la tabla se utilizan varios argumentos: el lema y la posición relativa de las cuádricas reales no degeneradas y un plano, que dimos al describir a aquellas. Las ecuaciones reducidas son: elipsoide imaginario: 1 + y y y 2 3 = 0 elipsoide real: 1 + y y y 2 3 = 0 hiperboloide elíptico: 1 + y y 2 2 y 2 3 = 0 hiperboloide hiperbólico: 1 + y 2 1 y 2 2 y 2 3 = 0 paraboloide elíptico: 2y 1 + y y 2 3 = 0 paraboloide hiperbólico: 2y 1 + y 2 2 y 2 3 = 0 cono afín imaginario: y y y 2 3 = 0 4
5 cono afín real: y y 2 2 y 2 3 = 0 cilindro imaginario: 1 + y y 2 2 = 0 cilindro elíptico: 1 + y y 2 2 = 0 cilindro hiperbólico: 1 + y 2 1 y 2 2 = 0 cilindro parabólico: 2y 1 + y 2 2 = 0 par de planos afines imaginarios secantes: y y 2 2 = 0 par de planos afines reales secantes: y 2 1 y 2 2 = 0 par de planos afines imaginarios paralelos: 1 + y 2 1 = 0 par de planos afines reales paralelos: 1 y 2 1 = 0 plano afín doble: y 2 1 = 0 plano afín: y 1 = 0 Definición Sea Q una hipercuádrica afín. Se llama variedad de centros de Q al conjunto ϕ 1 (pol Q (H)). Lema Sea Q una hipercuádrica proyectiva de P n (k) y L una recta proyectiva, no tangente a Q. La aplicación f : L L que lleva cada punto P P n (k) en L pol Q (P ) está bien definida, y es una homografía involutiva (o involución), es decir f 2 = id. Corolario Si O es un centro de una hipercuádrica afín (real o compleja) Q y L es una recta afín que pasa por O y corta a V a (Q) en dos puntos distintos P 1 y P 2, entonces O es el punto medio del segmento P 1 P 2. Definición Se llama hiperplano diametral (diámetro, en dimensión 2) de una hipercuádrica afín Q al hiperplano afín correspondiente a la polar (respecto de Q) de un punto del infinito, es decir ϕ 1 (pol Q (P )), para cada P H. Definición Sea Q una hipercuádrica afín. Se llama hiperplano asintótico (asíntota, en dimensión 2) de Q a todo hiperplano afín de la forma ϕ 1 (pol Q (P )) donde P V(Q) H = V(Q ) (estos puntos se llaman direcciones asintóticas). Lema Sea Q una hipercuádrica real no degenerada de P 3 (k), P / V(Q), L su hiperplano polar. Supongamos que L V(Q) y P L V(Q). Se tiene: 1. La recta P P es tangente a Q en P. 2. El conjunto de rectas que pasan por P y cortan a V(Q) en un punto de L es una cuádrica degenerada que tiene a P como punto singular, llamada cono tangente a Q en P. Definición Se llama cono asintótico de una cuádrica afín con centro único, al cono tangente desde este centro. 5
6 6.1. Interpretación proyectiva de la perpendicularidad. A partir de ahora, consideraremos el espacio afín R n sumergido en P n (R) de la manera habitual (i.e. considerando H (x 0 = 0) como el hiperplano del infinito). En el espacio afín R n consideraremos el producto escalar habitual x.y = n i=1 x iy i (este producto escalar dota a R n de estructura de espacio euclídeo). En H P n 1 (R) consideraremos la hipercuádrica (que llamaremos hipercuádrica del absoluto y notaremos Ω) de ecuación n i=1 x2 i = 0. Nótese que la hipercuádrica lugar de Ω es el conjunto vacío. Teorema Se verifica: 1. Si r, s son dos rectas de R n, entonces r es perpendicular a s si y sólo si los puntos r H y s H son conjugados respecto de Ω. 2. Si r y H son respectivamente una recta y un hiperplano de R n, entonces r es perpendicular a H si y sólo si el punto r H es el polo (respecto de Ω) de H H. 3. Dos hiperplanos de R n (notados H 1, H 2 ) son perpendiculares si y sólo si polar Ω (H 1 H ) pertenece a H 2 H Sea ahora Q una hipercuádrica afín de R n. Recuérdese que define a Q = Q H en H. Por tanto en H hay dos hipercuádricas: Q y Ω. En lo sucesivo, suponemos que Ω está definido por el producto escalar clásico, dado por la matriz identidad, es decir, x y = n i=1 x iy i. Definición Se dice que Q es una esfera de R n si Q = Ω. En dimensión dos se dirá circunferencia. En casos distintos a las esferas, Q y Ω definen un haz H de hipercuádricas en H P n (C). En el caso n = 3, podemos decir algo sobre el haz de cónicas H. Proposición Si Q es una cuádrica de R 3 distinta de una esfera, el haz de cónicas H es del tipo 1 o 3. Definición Se dice que Q es una cuádrica de revolución de R 3 si, Q es una esfera, o bien Q y Ω definen un haz de bitangentes. Más adelante justificaremos esta definición. Volvemos ahora al caso general de R n Hiperplanos principales de las hipercuádricas. Definición Sea Q una hipercuádrica de R n distinta de una esfera, se llaman direcciones principales de Q a los puntos del conjunto F (H(Q, Ω)) \ Sing(Q ) H. En el caso de la esfera, todas las direcciones son principales. Se 6
7 llaman hiperplanos principales de Q (ejes en dimensión 2) a los hiperplanos afines k n pol Q (P ), para cada P dirección principal. Proposición Sea Q una hipercuádrica de R n, L un hiperplano principal y r L una recta que corta a V a (Q) en dos puntos distintos P 1 y P 2. Entonces r L es el punto medio de P 1 P 2. Definición Se llaman ejes de una cuádrica la intersección de dos planos principales. (Atención: no confundir con ejes de una cónica!) Proposición Una cuádrica Q de R 3, de ecuación Y AY t = 0 es de revolución si y sólo si la submatriz A 0 tiene un autovalor doble Focos de las cónicas Sea Q una cónica afín no degenerada el C 2. Sea F un punto del plano afín C 2 que no esté en Q. La polaridad (respecto de Q) induce una homografía (que es una involución) sobre el haz de rectas P 2 (C)/F. En efecto, esta involución es: η Q : P 2(C) F P 2(C) F definida por η Q (r) = polar Q (r)+f. Por otra parte la ortogonalidad define también una homografía sobre el haz de rectas P 2 (C)/F (es decir la imagen de una recta pasando por F es la recta que pasa por F y es ortogonal a la recta de partida). Concretamente, y respecto del sistema de referencia canónico, suponiendo que el punto F tenga coordenadas (1 : a 1 : a 2 ), esta involución asocia a una recta genérica α(x 1 a 1 x 0 ) + β(x 2 a 2 x 0 ) = 0 (pasando por F ) la recta β(x 1 a 1 x 0 ) α(x 2 a 2 x 0 ) = 0. Definición Sea Q una cónica afín no degenerada en C 2 y sea F un punto de C 2 que no esté en Q. Se dice que F es un foco de Q si la homografía inducida por la polaridad coincide con la inducida por la ortogonalidad. Lema El la situación anterior, F es un foco de Q si y sólo si por F pasan dos tangentes a Q y autoperpendiculares. Sea Q una cónica afín no degenerada en R 2, es decir una elipse, hipérbola o parábola. Por tanto Q es una cónica real no degenerada de P 2 (R). Se puede hablar así de Q en P 2 (R), que es también una cónica real no degenerada. En este caso Ω es la hipercuádrica de la recta del infinito H de ecuación x x 2 2 = 0, luego V(Ω) = {P 0, P 0 }, con P 0 = (0 : 1 : i), que se llaman puntos cíclicos del plano, al ser los puntos por donde pasan todas las circunferencias (Q = Ω). Definimos en P 2 (R) la cónica degenerada de ecuación u u 2 2 = 0, que notamos por Ω, ya que V(Ω ) está formado por la unión de las rectas duales de los puntos cíclicos: (P 0 ) y (P 0 ). Así en P 2 (R) hay un haz H definido por Q y por Ω. Definición Se llaman focos de la cónica Q a los puntos de R 2 cuyos duales son rectas de P 2 (R) del lugar de una cónica degenerada del haz H. 7
8 Caso circunferencia. En este caso los puntos cíclicos P 0, P 0 están en V(Q), por tanto (P 0 ) y (P 0 ) son tangentes a Q, por lo que H es un haz de cónicas bitangentes. Hay dos puntos base P 1 y P 1. La recta P 1 P 1 (real) de P 2 (R) es la dual del único foco F de la circunferencia. Caso parábola. Suponemos que Q es tangente a H en el punto A. Al revés que antes, (P 0 ) y (P 0 ) no son tangentes a Q, pero (H) = (P 0 ) (P 0 ) está en V(Q ), porque H es tangente a Q. Además (A) es tangente a Q. Por tanto H es un haz de cónicas del tipo 2, con tres puntos base: {P 1, P 1, (H)}. La recta P 1 P 1 (real) de P 2 (R) es la dual del único foco F de la parábola. Caso elipse (no circunferencia) e hipérbola. En este caso (P 0 ) y (P 0 ) no son tangentes a Q, y (H) = (P 0 ) (P 0 ) no está en V(Q ). Por tanto H es un haz de cónicas del tipo 1, con cuatro puntos base: {P 1, P 1, P 2, P 2 }. Las rectas reales P 1 P 1 y P 2 P 2 de P 2 (R) son las duales de sendos puntos F 1 y F 2 de R 2, que son focos de la elipse o hipérbola Q. En algunos textos también se llaman, en este caso, focos imaginarios a los puntos (imaginarios) duales de las rectas P 1 P 2 y P 2 P 1. Proposición Los focos de una cónica real no degenerada Q de R 2 son los puntos de corte de rectas tangentes a Q y autoperpendiculares. 8
Hipercuádricas afines. Clasificación. Interpretación proyectiva de propiedades afines.
 Tema 8- Hipercuádricas afines Clasificación Interpretación proyectiva de propiedades afines 81 Hipercuádricas afines Sea k un cuerpo de característica distinta de dos Definición 811 Una hipercuádrica afín
Tema 8- Hipercuádricas afines Clasificación Interpretación proyectiva de propiedades afines 81 Hipercuádricas afines Sea k un cuerpo de característica distinta de dos Definición 811 Una hipercuádrica afín
Interpretación proyectiva de propiedades euclídeas. Elementos
 Tema 9.- Interpretación proyectiva de propiedades euclídeas. Elementos de las cónicas y cuádricas euclídeas 9.1 El espacio euclídeo como subespacio del proyectivo. Consideramos el espacio euclídeo R n
Tema 9.- Interpretación proyectiva de propiedades euclídeas. Elementos de las cónicas y cuádricas euclídeas 9.1 El espacio euclídeo como subespacio del proyectivo. Consideramos el espacio euclídeo R n
Hipercuádricas. Polaridad. Estudio geométrico de las cónicas y cuádricas
 Capítulo 4 Hipercuádricas. Polaridad. Estudio geométrico de las cónicas y cuádricas Comenzamos con el objeto básico de este curso. Hemos estudiado hasta ahora variedades lineales proyectivas, que están
Capítulo 4 Hipercuádricas. Polaridad. Estudio geométrico de las cónicas y cuádricas Comenzamos con el objeto básico de este curso. Hemos estudiado hasta ahora variedades lineales proyectivas, que están
Polaridad. Tangentes. Estudio geométrico de cónicas y cuádricas
 Tema 6- Polaridad Tangentes Estudio geométrico de cónicas y cuádricas En este tema pretendemos estudiar propiedades de V(Q), especialmente en los casos real y complejo, con n =2,3 Para ello, necesitamos
Tema 6- Polaridad Tangentes Estudio geométrico de cónicas y cuádricas En este tema pretendemos estudiar propiedades de V(Q), especialmente en los casos real y complejo, con n =2,3 Para ello, necesitamos
- EJERCICIOS DE AMPLIACION DE GEOMETRIA - Curso 04-05
 - EJERCICIOS DE AMPLIACION DE GEOMETRIA - Curso 04-05 Nota previa: Los primeros 18 ejercicios constituyen un repaso de los conceptos de la asignatura GEOMETRIA, que se utilizarán profusamente a lo largo
- EJERCICIOS DE AMPLIACION DE GEOMETRIA - Curso 04-05 Nota previa: Los primeros 18 ejercicios constituyen un repaso de los conceptos de la asignatura GEOMETRIA, que se utilizarán profusamente a lo largo
- EJERCICIOS - - Álgebra Lineal y Geometría II - Curso 10-11
 - EJERCICIOS - - Álgebra Lineal y Geometría II - Curso 10-11 Nota: Los primeros 18 ejercicios constituyen un repaso de los conceptos de la asignatura Álgebra Lineal y Geometría I. EJERCICIO 1. Sean P 1,...,
- EJERCICIOS - - Álgebra Lineal y Geometría II - Curso 10-11 Nota: Los primeros 18 ejercicios constituyen un repaso de los conceptos de la asignatura Álgebra Lineal y Geometría I. EJERCICIO 1. Sean P 1,...,
Index. Ángulo, 80 entre dos planos, 80 entre dos rectas, 80 entre dos vectores, 59 entre recta y plano, 80
 Index Ángulo, 80 entre dos planos, 80 entre dos rectas, 80 entre dos vectores, 59 entre recta y plano, 80 Adjunto, 14 Aplicación, 2 bilineal, 47 biyectiva, 3 compuesta, 3 identidad, 3 inversa, 3 inyectiva,
Index Ángulo, 80 entre dos planos, 80 entre dos rectas, 80 entre dos vectores, 59 entre recta y plano, 80 Adjunto, 14 Aplicación, 2 bilineal, 47 biyectiva, 3 compuesta, 3 identidad, 3 inversa, 3 inyectiva,
G. SERRANO SOTELO. H = e 0 + E
 CLASIFICACIÓN AFÍN DE CÓNICAS Y CUÁDRICAS G. SERRANO SOTELO 1. Cuádricas en un hiperplano afín Sea E un R-espacio vectorial de dimensión n +1. Sean E = e 1,...,e n un hiperplano vectorial de E y e un vector
CLASIFICACIÓN AFÍN DE CÓNICAS Y CUÁDRICAS G. SERRANO SOTELO 1. Cuádricas en un hiperplano afín Sea E un R-espacio vectorial de dimensión n +1. Sean E = e 1,...,e n un hiperplano vectorial de E y e un vector
Autor: Francisco Martín Cabrera, Departamento Matemática Fundamental, Universidad de La Laguna, Islas Canarias, España TEMA IV
 52 Variedades Cuadráticas Autor: Francisco Martín Cabrera, Departamento Matemática Fundamental, Universidad de La Laguna, Islas Canarias, España http://creativecommons.org/licenses/by-nc-sa/2.5/es/ TEMA
52 Variedades Cuadráticas Autor: Francisco Martín Cabrera, Departamento Matemática Fundamental, Universidad de La Laguna, Islas Canarias, España http://creativecommons.org/licenses/by-nc-sa/2.5/es/ TEMA
- RELACION COMPLEMENTARIA DE AMPLIACION DE GEOMETRIA - Curso 04-05
 - RELACION COMPLEMENTARIA DE AMPLIACION DE GEOMETRIA - Curso 04-05 Ejercicio 1. Junio 98 En el espacio proyectivo ordinario de dimensión 4, se consideran dos rectas, r y s, que se cruzan. Probar la verdad
- RELACION COMPLEMENTARIA DE AMPLIACION DE GEOMETRIA - Curso 04-05 Ejercicio 1. Junio 98 En el espacio proyectivo ordinario de dimensión 4, se consideran dos rectas, r y s, que se cruzan. Probar la verdad
ÁLGEBRA LINEAL II Práctica 4.1
 ÁLGEBRA LINEAL II Práctica 4.1 Cónicas (Curso 2010 2011) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo
ÁLGEBRA LINEAL II Práctica 4.1 Cónicas (Curso 2010 2011) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo
Tema 5. Cónicas. Asi, para las identificaciones habituales, (punto proyectivo recta vectorial punto de un plano afín ampliado), RP 2 R3 {0}
 Tema 5. Cónicas. Introducción. Ejemplos.- El cono C = {(x, y, z) R 3 /x 2 + y 2 = z 2 } está formado por las rectas vectoriales 0 (x 1,x 2, 1) [x 1,x 2, 1] RP 2 con (x 1,x 2, 1) C Π 1 = C 1, circunferencia
Tema 5. Cónicas. Introducción. Ejemplos.- El cono C = {(x, y, z) R 3 /x 2 + y 2 = z 2 } está formado por las rectas vectoriales 0 (x 1,x 2, 1) [x 1,x 2, 1] RP 2 con (x 1,x 2, 1) C Π 1 = C 1, circunferencia
Semana 13: Determinación de cónicas. Haces de cónicas proyectivas.
 Semana 13: Determinación de cónicas. Haces de cónicas proyectivas. Sonia L. Rueda ETS Arquitectura. UPM Geometría afín y proyectiva, 2015 Geometría afín y proyectiva 1. Álgebra lineal 2. Geometría afín
Semana 13: Determinación de cónicas. Haces de cónicas proyectivas. Sonia L. Rueda ETS Arquitectura. UPM Geometría afín y proyectiva, 2015 Geometría afín y proyectiva 1. Álgebra lineal 2. Geometría afín
ÁLGEBRA LINEAL II Práctica 4.1
 ÁLGEBRA LINEAL II Práctica 4.1 Cónicas (Curso 2012 2013) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo
ÁLGEBRA LINEAL II Práctica 4.1 Cónicas (Curso 2012 2013) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo
ÁLGEBRA Práctica Clasificar según los valores de λ IR las cónicas de los siguientes haces: 2. Para las siguientes cónicas
 ÁLGEBRA Práctica 14 Cónicas (Curso 2006 2007) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Clasificar según los valores de λ
ÁLGEBRA Práctica 14 Cónicas (Curso 2006 2007) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Clasificar según los valores de λ
2 Intersección de una recta y una cuádrica. 1 Definición y ecuaciones. ( x y z
 2. Cuádricas. En todo este capítulo trabajaremos en el espacio afín euclídeo E 3 con respecto a una referencia rectangular {O; ē 1, ē 2, ē 3}. Denotaremos por (x, y, las coordenadas cartesianas respecto
2. Cuádricas. En todo este capítulo trabajaremos en el espacio afín euclídeo E 3 con respecto a una referencia rectangular {O; ē 1, ē 2, ē 3}. Denotaremos por (x, y, las coordenadas cartesianas respecto
Clasificación Euclídea de las
 Capítulo X Clasificación Euclídea de las Cuádricas Fijemos en todo este capítulo un espacio afín euclídeo (A, V, Ω 2 ) de dimensión n y una métrica euclídea Ω 2 representante del absoluto. Las bases asociadas
Capítulo X Clasificación Euclídea de las Cuádricas Fijemos en todo este capítulo un espacio afín euclídeo (A, V, Ω 2 ) de dimensión n y una métrica euclídea Ω 2 representante del absoluto. Las bases asociadas
NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular.
 ÁLGEBRA Práctica 14 Cónicas (Curso 2007 2008) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
ÁLGEBRA Práctica 14 Cónicas (Curso 2007 2008) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
Haces de hipercuádricas. Clasificación de los haces de cónicas. Determinación de cónicas.
 Tema 7- Haces de hipercuádricas Clasificación de los haces de cónicas Determinación de cónicas 71 Puntos base y fundamentales de un haz Definición 711 Sea el espacio proyectivo Pn(k) de dimensión n sobre
Tema 7- Haces de hipercuádricas Clasificación de los haces de cónicas Determinación de cónicas 71 Puntos base y fundamentales de un haz Definición 711 Sea el espacio proyectivo Pn(k) de dimensión n sobre
Clasificación Afín de las Cuádricas
 Capítulo VIII Clasificación Afín de las Cuádricas Como no puede ser de otro modo, en este capítulo seguiremos suponiendo que k es un cuerpo conmutativo de característica distinta de 2, que todos los espacios
Capítulo VIII Clasificación Afín de las Cuádricas Como no puede ser de otro modo, en este capítulo seguiremos suponiendo que k es un cuerpo conmutativo de característica distinta de 2, que todos los espacios
NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular.
 ÁLGEBRA Práctica 15 Cónicas (Curso 2008 2009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo y con respecto
ÁLGEBRA Práctica 15 Cónicas (Curso 2008 2009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo y con respecto
NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular.
 ÁLGEBRA Práctica 15 Cónicas (Curso 2008 2009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
ÁLGEBRA Práctica 15 Cónicas (Curso 2008 2009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
Formulario: Geometría Analítica
 Universidad Autónoma del Estado de México UAEM Facultad de Ingeniería Formulario: Geometría Analítica Elaborado por: Estudiante en Ingeniería en Electrónica Formulario Geometría Analítica 1. VECTORES EN
Universidad Autónoma del Estado de México UAEM Facultad de Ingeniería Formulario: Geometría Analítica Elaborado por: Estudiante en Ingeniería en Electrónica Formulario Geometría Analítica 1. VECTORES EN
CLASIFICACIÓN AFÍN DE CÓNICAS
 Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS CLASIFICACIÓN AFÍN DE CÓNICAS Sea E un R-espacio vectorial de dimensión. Sean E = e 1, e un plano vectorial de E y e 0 un
Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS CLASIFICACIÓN AFÍN DE CÓNICAS Sea E un R-espacio vectorial de dimensión. Sean E = e 1, e un plano vectorial de E y e 0 un
Definición: Se llama pendiente de una recta a la tangente de un ángulo de inclinación formado por el eje X y la
 Geometría Analítica Preliminares Identidades Trigonométricas Definición: Se llama pendiente de una recta a la tangente de un ángulo de inclinación formado por el eje X y la recta, tal que, esto es Recta
Geometría Analítica Preliminares Identidades Trigonométricas Definición: Se llama pendiente de una recta a la tangente de un ángulo de inclinación formado por el eje X y la recta, tal que, esto es Recta
Examen extraordinario Ejercicio 4 (55 minutos) 4 de septiembre de 2006
 ÁLGEBRA Examen extraordinario Ejercicio 4 (55 minutos) 4 de septiembre de 006 1. Calcular la ecuación de una hipérbola que tiene por asíntota a la recta x = y, por eje la recta x+y = 1 y que pasa por el
ÁLGEBRA Examen extraordinario Ejercicio 4 (55 minutos) 4 de septiembre de 006 1. Calcular la ecuación de una hipérbola que tiene por asíntota a la recta x = y, por eje la recta x+y = 1 y que pasa por el
Cónicas. Clasificación.
 Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Problemas de Geometría Proyectiva
 Problemas de Geometría Proyectiva José M. Sánchez Abril José M. Rodríguez-Sanjurjo, Jesús M. Ruiz 1995 * I. VARIEDADES PROYECTIVAS Número 1. Se consideran en el plano proyectivo P 2 los cuatro puntos a
Problemas de Geometría Proyectiva José M. Sánchez Abril José M. Rodríguez-Sanjurjo, Jesús M. Ruiz 1995 * I. VARIEDADES PROYECTIVAS Número 1. Se consideran en el plano proyectivo P 2 los cuatro puntos a
El espacio proyectivo. Sistemas de referencia. Dualidad.
 Capítulo 1 El espacio proyectivo Sistemas de referencia Dualidad En todo lo que sigue k designará un cuerpo arbitrario 11 Espacio afín como subespacio del proyectivo Definición 111 Sea un entero n 0 El
Capítulo 1 El espacio proyectivo Sistemas de referencia Dualidad En todo lo que sigue k designará un cuerpo arbitrario 11 Espacio afín como subespacio del proyectivo Definición 111 Sea un entero n 0 El
El grupo lineal proyectivo. Homologías. Afinidades.
 Tema 3- El grupo lineal proyectivo Homologías Afinidades 31 El grupo lineal proyectivo Recordamos que en el tema anterior hemos definido, para una variedad lineal proyectiva L P n no vacía, el grupo lineal
Tema 3- El grupo lineal proyectivo Homologías Afinidades 31 El grupo lineal proyectivo Recordamos que en el tema anterior hemos definido, para una variedad lineal proyectiva L P n no vacía, el grupo lineal
1 CUÁDRICAS Cuádricas. Estudio particular. 1 x y z. 1 x y z. a 00 a 01 a 02 a 03 a 10 a 11 a 12 a 13 a 20 a 21 a 22 a 23 a 30 a 31 a 32 a 33
 CUÁDRICAS. CUÁDRICAS.. Cuádricas. Estudio particular. Una cuádrica se dene como el lugar geométrico de los puntos del espacio euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen
CUÁDRICAS. CUÁDRICAS.. Cuádricas. Estudio particular. Una cuádrica se dene como el lugar geométrico de los puntos del espacio euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen
SERIE SUPERFICIES. 1.- Determinar la ecuación cartesiana del cilindro que contiene a la curva de ecuaciones:
 SERIE SUPERFICIES 1.- Determinar la ecuación cartesiana del cilindro que contiene a la curva de ecuaciones: 4x C z 0 y que se genera por rectas perpendiculares al plano: x + y + 3z + = 0.-Sea la superficie
SERIE SUPERFICIES 1.- Determinar la ecuación cartesiana del cilindro que contiene a la curva de ecuaciones: 4x C z 0 y que se genera por rectas perpendiculares al plano: x + y + 3z + = 0.-Sea la superficie
SOLUCIONES. ÁLGEBRA LINEAL Y GEOMETRÍA (Examen Ordinario : ) Grado en Matemáticas Curso
 ÁLGEBRA LINEAL Y GEOMETRÍA Eamen Ordinario : 6--7 Grado en Matemáticas Curso 6-7 SOLUCIONES Dados tres puntos distintos alineados A, A, A A R, al número real r tal que A A = r A A lo llamaremos raón simple
ÁLGEBRA LINEAL Y GEOMETRÍA Eamen Ordinario : 6--7 Grado en Matemáticas Curso 6-7 SOLUCIONES Dados tres puntos distintos alineados A, A, A A R, al número real r tal que A A = r A A lo llamaremos raón simple
Estudio proyectivo 23. Autor: Francisco Martín Cabrera, Departamento Matemática Fundamental, Universidad de La Laguna, Islas Canarias, España TEMA II
 Estudio proyectivo 23 Autor: Francisco Martín Cabrera, Departamento Matemática Fundamental, Universidad de La Laguna, Islas Canarias, España http://creativecommons.org/licenses/by-nc-sa/2.5/es/ TEMA II
Estudio proyectivo 23 Autor: Francisco Martín Cabrera, Departamento Matemática Fundamental, Universidad de La Laguna, Islas Canarias, España http://creativecommons.org/licenses/by-nc-sa/2.5/es/ TEMA II
Tema 1 (Resultados).- Cónicas y Cuádricas.
 Ingenierías: Aeroespacial, Civil y Química Matemáticas I 010-011 Departamento de Matemática Aplicada II Escuela Superior de Ingenieros Universidad de Sevilla Tema 1 (Resultados)- Cónicas y Cuádricas Ejercicio
Ingenierías: Aeroespacial, Civil y Química Matemáticas I 010-011 Departamento de Matemática Aplicada II Escuela Superior de Ingenieros Universidad de Sevilla Tema 1 (Resultados)- Cónicas y Cuádricas Ejercicio
11. Cónicas proyectivas
 24 FRANCISCO JAVIER GALLEGO RODRIGO. Cónicas proyectivas Recordemos que una de las razones para construir el espacio proyectivo fue estudiar qué les pasa a los objetos afines cuando nos vamos al infinito.
24 FRANCISCO JAVIER GALLEGO RODRIGO. Cónicas proyectivas Recordemos que una de las razones para construir el espacio proyectivo fue estudiar qué les pasa a los objetos afines cuando nos vamos al infinito.
Respuestas faltantes en ejercicios edición 2007 Sección 4.4: Superficie cuadráticas de revolución Ejercicio 4-1
 Editorial Mc Graw Hill. Edición 007 Respuestas faltantes en ejercicios edición 007 Sección 4.4: Superficie cuadráticas de revolución Ejercicio 4- R r + x + y Ejercicio 4-3 + R x + y + z Ecuaciones: x +
Editorial Mc Graw Hill. Edición 007 Respuestas faltantes en ejercicios edición 007 Sección 4.4: Superficie cuadráticas de revolución Ejercicio 4- R r + x + y Ejercicio 4-3 + R x + y + z Ecuaciones: x +
Reflexiones sobre el Punto de Frégier José Araujo - Luis C. Maiarú - Norma Pietrocola
 Reflexiones sobre el Punto de Frégier José Araujo - Luis C. Maiarú - Norma Pietrocola Resumen En estas notas vamos a referirnos al punto de Frégier de una cónica y a la generalización de este resultado
Reflexiones sobre el Punto de Frégier José Araujo - Luis C. Maiarú - Norma Pietrocola Resumen En estas notas vamos a referirnos al punto de Frégier de una cónica y a la generalización de este resultado
Aquella que tiene nulos los elementos nos situados en la diagonal principal. Los elementos situados por encima de la diagonal principal son nulos.
 Álgebra lineal Matrices Rango de una matriz Orden del mayor menor complementario no nulo. Matriz regular det A Diagonal principal Elementos a ii de la matriz. Si la matriz es cuadrado son los elementos
Álgebra lineal Matrices Rango de una matriz Orden del mayor menor complementario no nulo. Matriz regular det A Diagonal principal Elementos a ii de la matriz. Si la matriz es cuadrado son los elementos
B23 Curvas cónicas Curvas cónicas
 Geometría plana B23 Curvas cónicas Curvas cónicas Superficie cónica de revolución es la engendrada por una recta que gira alrededor de otra a la que corta. Curvas cónicas son las que resultan de la intersección
Geometría plana B23 Curvas cónicas Curvas cónicas Superficie cónica de revolución es la engendrada por una recta que gira alrededor de otra a la que corta. Curvas cónicas son las que resultan de la intersección
GEOMETRÍA I 23 de septiembre del 2011
 GEOMETRÍA I 3 de septiembre del 011 1. En el espacio ordinario se consideran las rectas l 1 : { x y + z = 1 x + y z = l : x 3 = y + 1 = z a. Hallar a IR para que exista un plano π que contenga a l 1 y
GEOMETRÍA I 3 de septiembre del 011 1. En el espacio ordinario se consideran las rectas l 1 : { x y + z = 1 x + y z = l : x 3 = y + 1 = z a. Hallar a IR para que exista un plano π que contenga a l 1 y
+ : X V X. (+) P : V X u P + u. (P + u) + v = P + (u + v). Nota La propiedad 1) de la definición anterior implica, en primer lugar, que
 Capítulo 1 El espacio afín 11 Introducción Dependencia lineal afín La Geometría afín sobre un cuerpo k tiene como objetos básicos los siguientes: un conjunto no vacío X, cuyos elementos serán llamados
Capítulo 1 El espacio afín 11 Introducción Dependencia lineal afín La Geometría afín sobre un cuerpo k tiene como objetos básicos los siguientes: un conjunto no vacío X, cuyos elementos serán llamados
Haces de hipercuádricas. Clasificación de los haces de cónicas. Determinación de
 Capítulo 5 Haces de hipercuádricas. Clasificación de los haces de cónicas. Determinación de cónicas. 5.1. Definición y ecuaciones Definición 5.1.1. Sea (X, T, π) un espacio proyectivo de dimensión n sobre
Capítulo 5 Haces de hipercuádricas. Clasificación de los haces de cónicas. Determinación de cónicas. 5.1. Definición y ecuaciones Definición 5.1.1. Sea (X, T, π) un espacio proyectivo de dimensión n sobre
Ejercicios de Ampliación de Geometría. Hoja 2
 Ejercicios de Ampliación de Geometría Licenciatura en Ciencias Matemáticas, 2 Curso 27 de Octubre de 2008 Hoja 2 Dualidad y radiaciones. 1. Formular y resolver en el espacio proyectivo dual los siguientes
Ejercicios de Ampliación de Geometría Licenciatura en Ciencias Matemáticas, 2 Curso 27 de Octubre de 2008 Hoja 2 Dualidad y radiaciones. 1. Formular y resolver en el espacio proyectivo dual los siguientes
Cada recta vectorial se llama punto proyectivo. Se llama dimensión del espacio proyectivo a dim P(V ) = dim V 1.
 "Con eso francamente que nunca he sentido gusto por el estudio o la investigación en física o en geometría, a no ser que pudiera servir como medio de llegar a algún tipo de conocimiento de las causas próximas...para
"Con eso francamente que nunca he sentido gusto por el estudio o la investigación en física o en geometría, a no ser que pudiera servir como medio de llegar a algún tipo de conocimiento de las causas próximas...para
1 CÓNICAS Cónicas. Estudio particular. 1 x y. 1 x y. a 00 a 01 a 02 a 10 a 11 a 12 a 20 a 21 a 22
 CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
2º BACH CURVAS TÉCNICAS CURVAS CÓNICAS
 2º BACH CURVAS TÉCNICAS CURVAS CÓNICAS CURVAS TÉCNICAS 1. ÓVALOS. El óvalo es una curva cerrada, plana y convexa formada generalmente por cuatro arcos de circunferencia iguales dos a dos; tiene dos ejes
2º BACH CURVAS TÉCNICAS CURVAS CÓNICAS CURVAS TÉCNICAS 1. ÓVALOS. El óvalo es una curva cerrada, plana y convexa formada generalmente por cuatro arcos de circunferencia iguales dos a dos; tiene dos ejes
Movimientos. Teorema de Cartan-Dieudonné. Semejanzas.
 Capítulo 5 Movimientos. Teorema de Cartan-Dieudonné. Semejanzas. 5.1 Isometrías y movimientos Partimos de un espacio euclídeo (X, V, +) y recordemos que una isometría de V es un elemento ϕ Gl(V ) que conserva
Capítulo 5 Movimientos. Teorema de Cartan-Dieudonné. Semejanzas. 5.1 Isometrías y movimientos Partimos de un espacio euclídeo (X, V, +) y recordemos que una isometría de V es un elemento ϕ Gl(V ) que conserva
CÓNICAS. 1. Dada la cónica x 2 + 2xy y 2 2x 2y + 4 = 0, se pide su clasicación y los elementos característicos de la misma. = 1
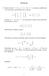 CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
El espacio proyectivo P n (k). Sistemas de referencia. Dualidad. Departamento de Algebra Septiembre El espacio proyectivo P n (k).
 Notas de la asignatura AMPLIACIÓN DE GEOMETRÍA de la Licenciatura de Matemáticas, Facultad de Matemáticas, Universidad de Sevilla, para el curso 2000-01 Departamento de Algebra Septiembre 2000 Tema 1-
Notas de la asignatura AMPLIACIÓN DE GEOMETRÍA de la Licenciatura de Matemáticas, Facultad de Matemáticas, Universidad de Sevilla, para el curso 2000-01 Departamento de Algebra Septiembre 2000 Tema 1-
ESTUDIO GRÁFICO DE LA ELIPSE.
 Curvas Cónicas para Dibujo y Matemáticas. Aplicación web Dibujo Técnico para ESO y Bachillerato Matemáticas para Bachillerato Educación Plástica y Visual Autor: José Antonio Cuadrado Vicente. ESTUDIO GRÁFICO
Curvas Cónicas para Dibujo y Matemáticas. Aplicación web Dibujo Técnico para ESO y Bachillerato Matemáticas para Bachillerato Educación Plástica y Visual Autor: José Antonio Cuadrado Vicente. ESTUDIO GRÁFICO
Cónicas. Marcos Marvá Departamento de Física y Matemáticas, Universidad de Alcalá. November 27,
 Cónicas Marcos Marvá Departamento de Física y Matemáticas, Universidad de Alcalá November 27, 2013 marcos.marva@uah.es Cómo definir una cónica Como intersección de un plano y un cono recto de doble hoja
Cónicas Marcos Marvá Departamento de Física y Matemáticas, Universidad de Alcalá November 27, 2013 marcos.marva@uah.es Cómo definir una cónica Como intersección de un plano y un cono recto de doble hoja
Se puede considerar una superficie, como una lámina infinitamente delgada, que recubre un cuerpo, separa dos medios o dos regiones del espacio.
 SUPERFICIES SUPERFICIES Se puede considerar una superficie, como una lámina infinitamente delgada, que recubre un cuerpo, separa dos medios o dos regiones del espacio. Una Superficie puede estar engendrada
SUPERFICIES SUPERFICIES Se puede considerar una superficie, como una lámina infinitamente delgada, que recubre un cuerpo, separa dos medios o dos regiones del espacio. Una Superficie puede estar engendrada
2. Distancia entre dos puntos. Punto medio de un segmento
 Geometría 1 Geometría anaĺıtica Una ecuación de primer grado con dos incógnitas x e y tiene infinitas soluciones Por ejemplo x + y = 3 tiene como soluciones (0, 3), (1, ), ( 1, 4), etc Hasta ahora se han
Geometría 1 Geometría anaĺıtica Una ecuación de primer grado con dos incógnitas x e y tiene infinitas soluciones Por ejemplo x + y = 3 tiene como soluciones (0, 3), (1, ), ( 1, 4), etc Hasta ahora se han
CURVAS TÉCNICAS CURVAS CÓNICAS
 2º BACH CURVAS TÉCNICAS CURVAS CÓNICAS ANA BALLESTER JIMÉNEZ CURVAS TÉCNICAS 1. ÓVALOS. El óvalo es una curva cerrada, plana y convexa formada generalmente por cuatro arcos de circunferencia iguales dos
2º BACH CURVAS TÉCNICAS CURVAS CÓNICAS ANA BALLESTER JIMÉNEZ CURVAS TÉCNICAS 1. ÓVALOS. El óvalo es una curva cerrada, plana y convexa formada generalmente por cuatro arcos de circunferencia iguales dos
Superficies cuádricas
 Superficies cuádricas Jana Rodriguez Hertz GAL2 IMERL 9 de noviembre de 2010 definición superficie cuádrica definición (forma cuadrática) una superficie cuádrica está dada por la ecuación: definición superficie
Superficies cuádricas Jana Rodriguez Hertz GAL2 IMERL 9 de noviembre de 2010 definición superficie cuádrica definición (forma cuadrática) una superficie cuádrica está dada por la ecuación: definición superficie
ALUMNO: GRUPO: Sean dos formas homológicas F y F' de planos superpuestos, una circunferencia c perteneciente a F y su cónica homóloga c' en F'.
 ESCUELA TÉCNICA SUPERIOR DE INGENIEROS DE CAMINOS, CANALES Y PUERTOS DE GRANADA GEOMETRÍA APLICADA. EXAMEN FINAL. 28 DE JUNIO DE 2012. EJERCICIO TEÓRICO ALUMNO: GRUPO: NOTAS - El test consta de un total
ESCUELA TÉCNICA SUPERIOR DE INGENIEROS DE CAMINOS, CANALES Y PUERTOS DE GRANADA GEOMETRÍA APLICADA. EXAMEN FINAL. 28 DE JUNIO DE 2012. EJERCICIO TEÓRICO ALUMNO: GRUPO: NOTAS - El test consta de un total
7 Superficies cuadráticas
 La esfera Planteamiento de problemas Otras superficies cuadráticas El elipsoide Cilindros Hiperboloides Paraboloides Conos Planteamiento de problemas Problemas y ejercicios del capítulo 7 Superficies cuadráticas
La esfera Planteamiento de problemas Otras superficies cuadráticas El elipsoide Cilindros Hiperboloides Paraboloides Conos Planteamiento de problemas Problemas y ejercicios del capítulo 7 Superficies cuadráticas
Algebra Lineal y Geometría
 Algebra Lineal y Geometría Unidad n 11:Ecuación General de Segundo Grado en Tres Variables. Algebra Lineal y Geometría Esp.Liliana Eva Mata 1 Contenidos Superficies. Relaciones elementales entre propiedades
Algebra Lineal y Geometría Unidad n 11:Ecuación General de Segundo Grado en Tres Variables. Algebra Lineal y Geometría Esp.Liliana Eva Mata 1 Contenidos Superficies. Relaciones elementales entre propiedades
CURVAS Y SUPERFICIES. RELACIÓN 2
 CURVAS Y SUPERFICIES. RELACIÓN 2 SUPERFICIES EN EL ESPACIO Curso 2015-16 1. Demostrar que las siguientes cuádricas reales son superficies. Obtener una parametrización de cada una de ellas. En cada caso,
CURVAS Y SUPERFICIES. RELACIÓN 2 SUPERFICIES EN EL ESPACIO Curso 2015-16 1. Demostrar que las siguientes cuádricas reales son superficies. Obtener una parametrización de cada una de ellas. En cada caso,
Ejercicios de Álgebra y Geometría Analítica
 Ejercicios de Álgebra y Geometría Analítica Profr. Fausto Cervantes Ortiz Recta Dibujar las rectas indicadas 1. y = x + 1 2. y = 2x + 5 2 3. y = x + 2 4. y = x + 2 5. y = 2x 3 2 6. y = 3 2 x + 1 2 7. y
Ejercicios de Álgebra y Geometría Analítica Profr. Fausto Cervantes Ortiz Recta Dibujar las rectas indicadas 1. y = x + 1 2. y = 2x + 5 2 3. y = x + 2 4. y = x + 2 5. y = 2x 3 2 6. y = 3 2 x + 1 2 7. y
Tema 1.- Cónicas y Cuádricas.
 Ingeniería Química. Matemáticas I. 013-014. Departamento de Matemática Aplicada II. Escuela Superior de Ingenieros. Universidad de Sevilla. Tema 1.- Cónicas y Cuádricas. 1.1.- Las cónicas. Ecuaciones reducidas.
Ingeniería Química. Matemáticas I. 013-014. Departamento de Matemática Aplicada II. Escuela Superior de Ingenieros. Universidad de Sevilla. Tema 1.- Cónicas y Cuádricas. 1.1.- Las cónicas. Ecuaciones reducidas.
10.1 Rectas en el plano
 10 CAPÍTULO DIEZ Ejercicios propuestos 10.1 Rectas en el plano 1. Determine la distancia y el punto medio entre los siguientes pares de puntos: a. (1, 2) ; ( 2, 3) b. (0, 3) ; (1, 5) c. ( 2, 1) ; ( 3,
10 CAPÍTULO DIEZ Ejercicios propuestos 10.1 Rectas en el plano 1. Determine la distancia y el punto medio entre los siguientes pares de puntos: a. (1, 2) ; ( 2, 3) b. (0, 3) ; (1, 5) c. ( 2, 1) ; ( 3,
22. CURVAS CÓNICAS-ELIPSE
 22. CURVAS CÓNICAS-ELIPSE 22.1. Características generales. Las curvas cónicas son las secciones planas de un cono de revolución. El cono de revolución es la superficie que genera una recta r al girar alrededor
22. CURVAS CÓNICAS-ELIPSE 22.1. Características generales. Las curvas cónicas son las secciones planas de un cono de revolución. El cono de revolución es la superficie que genera una recta r al girar alrededor
3. Calcular una base normalizada asociada a esa referencia y las coordenadas en ella del punto [1, 2, 5, 3]
![3. Calcular una base normalizada asociada a esa referencia y las coordenadas en ella del punto [1, 2, 5, 3] 3. Calcular una base normalizada asociada a esa referencia y las coordenadas en ella del punto [1, 2, 5, 3]](/thumbs/68/59191793.jpg) Ejercicio 0.1 Sea K un cuerpo con q elementos y sea V un espacio vectorial de dimensión n + 1 sobre K. Calcular cuantas bases distintas (como subconjuntos) tiene V, cuantas referencias distintas hay en
Ejercicio 0.1 Sea K un cuerpo con q elementos y sea V un espacio vectorial de dimensión n + 1 sobre K. Calcular cuantas bases distintas (como subconjuntos) tiene V, cuantas referencias distintas hay en
COLEGIO NUESTRA SEÑORA DEL BUEN CONSEJO. Melilla LUGARES GEOMÉTRICOS Y CÓNICAS
 LUGARES GEOMÉTRICOS Y CÓNICAS 01. Halla la ecuación de la circunferencia de centro ( 5, 12) y radio 13. Comprueba que pasa por el punto (0, 0). 02. Halla las ecuaciones de los siguientes lugares geométricos:
LUGARES GEOMÉTRICOS Y CÓNICAS 01. Halla la ecuación de la circunferencia de centro ( 5, 12) y radio 13. Comprueba que pasa por el punto (0, 0). 02. Halla las ecuaciones de los siguientes lugares geométricos:
y v 0, 0, 1 y v 1, 0, 1 se tiene la ecuación
 SUPERFICIES Mostraremos varios métodos para generar superficies y encontrar sus ecuaciones. 1. Superficies cilíndricas Dada una curva en el plano de ecuación y un vector con Γ 0, es decir, no horizontal,
SUPERFICIES Mostraremos varios métodos para generar superficies y encontrar sus ecuaciones. 1. Superficies cilíndricas Dada una curva en el plano de ecuación y un vector con Γ 0, es decir, no horizontal,
Se llaman curvas cónicas a las curvas que se obtienen de la intersección de una superficie cónica por un plano.
 CURVAS CÓNICAS Se llaman curvas cónicas a las curvas que se obtienen de la intersección de una superficie cónica por un plano. Secciones de un cono Supongamos un cono de revolución de dos ramas; según
CURVAS CÓNICAS Se llaman curvas cónicas a las curvas que se obtienen de la intersección de una superficie cónica por un plano. Secciones de un cono Supongamos un cono de revolución de dos ramas; según
Ejercicios de cónicas.
 Ejercicios de cónicas. 1. Demuéstrese que un rayo lanzado en cualquier dirección desde un foco de una elipse y que se refleje en la cónica pasa por el otro foco. 2. Demuéstrese que un rayo lanzado paralelamente
Ejercicios de cónicas. 1. Demuéstrese que un rayo lanzado en cualquier dirección desde un foco de una elipse y que se refleje en la cónica pasa por el otro foco. 2. Demuéstrese que un rayo lanzado paralelamente
Cónicas y cuádricas. Circunferencia Elipse Parábola Hipérbola
 Grado en Óptica y Optometría Curso 2009-2010 Cónicas y cuádricas. Curvas cónicas Entre las curvas, quizás más importante y con más renombre, figuran las conocidas como curvas cónicas, cuyo nombre proviene
Grado en Óptica y Optometría Curso 2009-2010 Cónicas y cuádricas. Curvas cónicas Entre las curvas, quizás más importante y con más renombre, figuran las conocidas como curvas cónicas, cuyo nombre proviene
Este documento es de distribución gratuita y llega gracias a El mayor portal de recursos educativos a tu servicio!
 Este documento es de distribución gratuita y llega gracias a Ciencia Matemática El mayor portal de recursos educativos a tu servicio! Capítulo 5 Cónicas 5.1 Definiciones y ecuaciones reducidas Nota En
Este documento es de distribución gratuita y llega gracias a Ciencia Matemática El mayor portal de recursos educativos a tu servicio! Capítulo 5 Cónicas 5.1 Definiciones y ecuaciones reducidas Nota En
UNIVERSIDAD CENTROAMERICANA JOSÉ SIMEÓN CAÑAS ALGEBRA VECTORIAL Y MATRICES GUIA DE TRABAJO Secciones Cónicas Ciclo 02 de 2012
 UNIVERSIDAD CENTROAMERICANA JOSÉ SIMEÓN CAÑAS ALGEBRA VECTORIAL Y MATRICES GUIA DE TRABAJO Secciones Cónicas Ciclo 0 de 0 PARTE I: Ejercicios cortos de selección Múltiple. En cada uno de los siguientes
UNIVERSIDAD CENTROAMERICANA JOSÉ SIMEÓN CAÑAS ALGEBRA VECTORIAL Y MATRICES GUIA DE TRABAJO Secciones Cónicas Ciclo 0 de 0 PARTE I: Ejercicios cortos de selección Múltiple. En cada uno de los siguientes
Tema 3. GEOMETRIA ANALITICA.
 Álgebra lineal. Curso 087-009. Tema. Hoja 1 Tema. GEOMETRIA ANALITICA. 1. Hallar la ecuación de la recta: a) que pase por ( 4, ) y tenga pendiente 1. b) que pase por (0, 5) y tenga pendiente. c) que pase
Álgebra lineal. Curso 087-009. Tema. Hoja 1 Tema. GEOMETRIA ANALITICA. 1. Hallar la ecuación de la recta: a) que pase por ( 4, ) y tenga pendiente 1. b) que pase por (0, 5) y tenga pendiente. c) que pase
IDENTIFICACIÓN DE SUPERFICES CUÁDRICAS
 IDENTIFICACIÓN DE SUPERFICES CUÁDRICAS LUIS HUMBERTO SORIANO SÁNCHE Captura: Hanna Leslye García Guerra Evelyn Salazar Guerrero IDENTIFICACIÓN DE SUPERFICIES CUÁDRICAS Definición. Se llama superficie al
IDENTIFICACIÓN DE SUPERFICES CUÁDRICAS LUIS HUMBERTO SORIANO SÁNCHE Captura: Hanna Leslye García Guerra Evelyn Salazar Guerrero IDENTIFICACIÓN DE SUPERFICIES CUÁDRICAS Definición. Se llama superficie al
ESCUELA PREPARATORIA OFICIAL NO.16 MATERÍA: GEOMETRÍA ANALITICA GUÍA DE ESTUDIO PARA LA ÚLTIMA OPORTUNIDAD DE ACREDITAR LA MATERÍA
 Geometría analítica 1.- Ecuación de la recta 2.- Cónicas 3.-Ecuación de la parábola UNIDAD II: CONICAS (CIRCUNFERENCIA Y PARABOLAS) Una superficie cónica de revolución está engendrada por la rotación de
Geometría analítica 1.- Ecuación de la recta 2.- Cónicas 3.-Ecuación de la parábola UNIDAD II: CONICAS (CIRCUNFERENCIA Y PARABOLAS) Una superficie cónica de revolución está engendrada por la rotación de
Introducción La Circunferencia Parábola Elipse Hiperbola. Conicas. Hermes Pantoja Carhuavilca
 Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica I Contenido 1 Introducción 2 La Circunferencia 3 Parábola 4 Elipse 5 Hiperbola Objetivos Se persigue que el estudiante:
Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica I Contenido 1 Introducción 2 La Circunferencia 3 Parábola 4 Elipse 5 Hiperbola Objetivos Se persigue que el estudiante:
ALUMNO: GRUPO: Sean las series de bases r y r' y el haz de vértice V de la figura, todos ellos coplanarios.
 CANALES Y PUERTOS DE GRANADA INGENIERÍA GRÁFICA II. EXAMEN FINAL. 31 DE ENERO DE 2012 EJERCICIO TEÓRICO ALUMNO: GRUPO: NOTAS - El test consta de un total de 40 preguntas que se valorarán con las puntuaciones
CANALES Y PUERTOS DE GRANADA INGENIERÍA GRÁFICA II. EXAMEN FINAL. 31 DE ENERO DE 2012 EJERCICIO TEÓRICO ALUMNO: GRUPO: NOTAS - El test consta de un total de 40 preguntas que se valorarán con las puntuaciones
Fundamentos matemáticos. Tema 3 Geometría del plano y del espacio
 Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es
Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es
Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados
 Capítulo 5 Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados En este tema iniciamos el estudio de los conceptos geométricos de distancia y perpendicularidad en K n. Empezaremos con las definiciones
Capítulo 5 Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados En este tema iniciamos el estudio de los conceptos geométricos de distancia y perpendicularidad en K n. Empezaremos con las definiciones
1) Clasifica las siguientes cónicas y expresa sus focos y su excentricidad: a)
 Ejercicios de cónicas 1º bachillerato C 1) Clasifica las siguientes cónicas y expresa sus focos y su excentricidad: a) b) c) d) e) f) g) h) i) Soluciones: a) Circunferencia de centro ( y radio 3. Excentricidad
Ejercicios de cónicas 1º bachillerato C 1) Clasifica las siguientes cónicas y expresa sus focos y su excentricidad: a) b) c) d) e) f) g) h) i) Soluciones: a) Circunferencia de centro ( y radio 3. Excentricidad
V = v 1 +2v 2 +3v 3. v 2. v 1
 Coordenadas Hay muchas maneras de darle coordenadas a los puntos del espacio, las ecuaciones de las curvas o superficies dependen de las coordenadas que utilicemos y eligiendo las coordenadas adecuadas
Coordenadas Hay muchas maneras de darle coordenadas a los puntos del espacio, las ecuaciones de las curvas o superficies dependen de las coordenadas que utilicemos y eligiendo las coordenadas adecuadas
UNIDAD TEMÁTICA Nº: 1
 Objetivos de la materia: Que el alumno: Aprecie el valor instrumental del álgebra y la geometría, relacionándolas con los demás espacios curriculares. Articule el registro algebraico con el del lenguaje
Objetivos de la materia: Que el alumno: Aprecie el valor instrumental del álgebra y la geometría, relacionándolas con los demás espacios curriculares. Articule el registro algebraico con el del lenguaje
( ) 2 +( 1) 2. BLOQUE III Geometría analítica plana. Resoluciones de la autoevaluación del libro de texto
 Pág. de Dados los vectores u, y v0,, calcula: a u b u + v c u v u, v0, 5 a u = = = + b u + v =, + 0, =, + 0, 6 =, c u v = u v = 0 + = Determina el valor de k para que los vectores a, y b6, k sean ortogonales.
Pág. de Dados los vectores u, y v0,, calcula: a u b u + v c u v u, v0, 5 a u = = = + b u + v =, + 0, =, + 0, 6 =, c u v = u v = 0 + = Determina el valor de k para que los vectores a, y b6, k sean ortogonales.
INDICE. 88 determinante 36. Familias de líneas rectas Resumen de resultados 96
 INDICE Geometría Analítica Plana Capitulo Primero Sistema de Coordenadas Articulo 1. Introducción 1 2. Segmento rectilíneo dirigido 1 3. Sistema coordenado lineal 3 4. Sistema coordenado en el plano 5
INDICE Geometría Analítica Plana Capitulo Primero Sistema de Coordenadas Articulo 1. Introducción 1 2. Segmento rectilíneo dirigido 1 3. Sistema coordenado lineal 3 4. Sistema coordenado en el plano 5
GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA
 ESCUELA PREPARATORIA OFICIAL No. 268 GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA Profra: Citlalli Artemisa García García 1) Qué es la pendiente? 2) Cómo es la pendiente de rectas
ESCUELA PREPARATORIA OFICIAL No. 268 GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA Profra: Citlalli Artemisa García García 1) Qué es la pendiente? 2) Cómo es la pendiente de rectas
SUPERFICIES CUÁDRICAS
 SUPERFICIES CUÁDRICAS Un cuarto tipo de superficie en el espacio tridimensional son las cuádricas. Una superficie cuádrica en el espacio es una ecuación de segundo grado de la forma Ax + By + Cz + Dx +
SUPERFICIES CUÁDRICAS Un cuarto tipo de superficie en el espacio tridimensional son las cuádricas. Una superficie cuádrica en el espacio es una ecuación de segundo grado de la forma Ax + By + Cz + Dx +
SECCIONES CÓNICAS (1)Determinar y graficar el lugar geométrico de los puntos que equidistan de F(0, 2) y de la recta
 LOS EJERCICIOS DEBEN RESOLVERSE TAMBIÉN USANDO SOFTWARE MATEMÁTICO. LAS ECUACIONES PEDIDAS SON, EN TODOS LOS CASOS, LAS CANÓNICAS Y LAS PARAMÉTRICAS. I) GEOMETRÍA ANALÍTICA EN EL PLANO 1. Determinar y
LOS EJERCICIOS DEBEN RESOLVERSE TAMBIÉN USANDO SOFTWARE MATEMÁTICO. LAS ECUACIONES PEDIDAS SON, EN TODOS LOS CASOS, LAS CANÓNICAS Y LAS PARAMÉTRICAS. I) GEOMETRÍA ANALÍTICA EN EL PLANO 1. Determinar y
+ : X V X. (+) P : V X u P + u. (P + u) + v = P + (u + v). Nota La propiedad 1) de la definición anterior implica, en primer lugar, que
 Capítulo 1 El espacio afín 11 Introducción Dependencia lineal afín La Geometría afín sobre un cuerpo k tiene como objetos básicos los siguientes: un conjunto no vacío X, cuyos elementos serán llamados
Capítulo 1 El espacio afín 11 Introducción Dependencia lineal afín La Geometría afín sobre un cuerpo k tiene como objetos básicos los siguientes: un conjunto no vacío X, cuyos elementos serán llamados
TEMA 5. CURVAS CÓNICAS.
 5.1. GENERALIDADES. TEMA 5. CURVAS CÓNICAS. Se denominan secciones cónicas a aquellas superficies que son producidas por la intersección de un plano con una superficie cónica de revolución (una superficie
5.1. GENERALIDADES. TEMA 5. CURVAS CÓNICAS. Se denominan secciones cónicas a aquellas superficies que son producidas por la intersección de un plano con una superficie cónica de revolución (una superficie
Ejercicios y Talleres. puedes enviarlos a
 Ejercicios y Talleres puedes enviarlos a klasesdematematicasymas@gmail.com TALLER-LABORATORIO SUPERFICIES CUADRICAS - CILINDROS APLICACIONES OBJETIVOS Analizar características y propiedades en la representacion
Ejercicios y Talleres puedes enviarlos a klasesdematematicasymas@gmail.com TALLER-LABORATORIO SUPERFICIES CUADRICAS - CILINDROS APLICACIONES OBJETIVOS Analizar características y propiedades en la representacion
Tema 3: Espacios vectoriales
 Tema 3: Espacios vectoriales K denotará un cuerpo. Definición. Se dice que un conjunto no vacio V es un espacio vectorial sobre K o que es un K-espacio vectorial si: 1. En V está definida una operación
Tema 3: Espacios vectoriales K denotará un cuerpo. Definición. Se dice que un conjunto no vacio V es un espacio vectorial sobre K o que es un K-espacio vectorial si: 1. En V está definida una operación
INDICE. 88 determinante 36. Familias de líneas rectas Resumen de resultados 96 Capitulo IV
 INDICE Geometría Analítica Plana Capitulo Primero Artículo 1. Introducción 1 2. Segmento rectilíneo dirigido 1 3. Sistema coordenado lineal 3 4. Sistema coordenado en el plano 5 5. Carácter de la geografía
INDICE Geometría Analítica Plana Capitulo Primero Artículo 1. Introducción 1 2. Segmento rectilíneo dirigido 1 3. Sistema coordenado lineal 3 4. Sistema coordenado en el plano 5 5. Carácter de la geografía
EJERCICIOS DE ÁLGEBRA LINEAL TEMA 1 ESPACIOS VECTORIALES
 EJERCICIOS DE ÁLGEBRA LINEAL TEMA ESPACIOS VECTORIALES Formas reducidas y escalonada de una matriz SISTEMAS DE ECUACIONES LINEALES ) Encuentre una sucesión de matrices elementales E, E,..., E k tal que
EJERCICIOS DE ÁLGEBRA LINEAL TEMA ESPACIOS VECTORIALES Formas reducidas y escalonada de una matriz SISTEMAS DE ECUACIONES LINEALES ) Encuentre una sucesión de matrices elementales E, E,..., E k tal que
4. Escribe la ecuación de la circunferencia de centro C(-2,3) y radio 4. Sol: (x+2) 2 +(y-3) 2 =16.
 Problemas de circunferencias 4. Escribe la ecuación de la circunferencia de centro C(-2,3) y radio 4. Sol: (x+2) 2 +(y-3) 2 =16. 10. 5. Calcula la potencia del punto P(-1,2) a la circunferencia: x 2 +y
Problemas de circunferencias 4. Escribe la ecuación de la circunferencia de centro C(-2,3) y radio 4. Sol: (x+2) 2 +(y-3) 2 =16. 10. 5. Calcula la potencia del punto P(-1,2) a la circunferencia: x 2 +y
Dibujo Técnico Curvas cónicas
 23. CURVAS CÓNICAS 23.1. Características generales. Las curvas cónicas son las secciones planas de un cono de revolución. El cono de revolución es la superficie que genera una recta r al girar alrededor
23. CURVAS CÓNICAS 23.1. Características generales. Las curvas cónicas son las secciones planas de un cono de revolución. El cono de revolución es la superficie que genera una recta r al girar alrededor
Geometría del plano y del espacio
 Tema 6 Geometría del plano y del espacio 6.. Sistemas de coordenadas 6... Sistema de coordenadas en el plano Vamos a describir dos sistemas de coordenadas en el plano: sistema de coordenadas cartesiano
Tema 6 Geometría del plano y del espacio 6.. Sistemas de coordenadas 6... Sistema de coordenadas en el plano Vamos a describir dos sistemas de coordenadas en el plano: sistema de coordenadas cartesiano
Sumario Prólogo Unidad didáctica 1. Funciones reales de una variable real. Límites y continuidad Objetivos de la Unidad...
 ÍNDICE SISTEMÁTICO PÁGINA Sumario... 5 Prólogo... 7 Unidad didáctica 1. Funciones reales de una variable real. Límites y continuidad... 9 Objetivos de la Unidad... 11 1. Topología de la recta real... 12
ÍNDICE SISTEMÁTICO PÁGINA Sumario... 5 Prólogo... 7 Unidad didáctica 1. Funciones reales de una variable real. Límites y continuidad... 9 Objetivos de la Unidad... 11 1. Topología de la recta real... 12
