El teorema de isomorfismo
|
|
|
- Belén Méndez Castro
- hace 5 años
- Vistas:
Transcripción
1 El teorema de isomorfismo Si dos estructuras A y B son isomorfas, entonces son idénticas excepto por sus dominios. A y B son indistinguibles IIC2213 Lógica de Primer Orden 40 / 65
2 El teorema de isomorfismo Si dos estructuras A y B son isomorfas, entonces son idénticas excepto por sus dominios. A y B son indistinguibles En particular: La lógica de primer orden no debería poder distinguir entre estructuras isomorfas IIC2213 Lógica de Primer Orden 40 / 65
3 El teorema de isomorfismo Si dos estructuras A y B son isomorfas, entonces son idénticas excepto por sus dominios. A y B son indistinguibles En particular: La lógica de primer orden no debería poder distinguir entre estructuras isomorfas Vamos a demostrar esto IIC2213 Lógica de Primer Orden 40 / 65
4 El teorema de isomorfismo Si dos estructuras A y B son isomorfas, entonces son idénticas excepto por sus dominios. A y B son indistinguibles En particular: La lógica de primer orden no debería poder distinguir entre estructuras isomorfas Vamos a demostrar esto Por qué este resultado es fundamental? IIC2213 Lógica de Primer Orden 40 / 65
5 El teorema de isomorfismo: Una primera versión Teorema Si A y B son L-estructuras isomorfas, entonces para cada L-oración ϕ se tiene que: A = ϕ si y sólo si B = ϕ IIC2213 Lógica de Primer Orden 41 / 65
6 El teorema de isomorfismo: Una primera versión Teorema Si A y B son L-estructuras isomorfas, entonces para cada L-oración ϕ se tiene que: A = ϕ si y sólo si B = ϕ Cómo podemos demostrar este Teorema? IIC2213 Lógica de Primer Orden 41 / 65
7 El teorema de isomorfismo: Una primera versión Teorema Si A y B son L-estructuras isomorfas, entonces para cada L-oración ϕ se tiene que: A = ϕ si y sólo si B = ϕ Cómo podemos demostrar este Teorema? Podemos usar inducción? IIC2213 Lógica de Primer Orden 41 / 65
8 El teorema de isomorfismo: Una primera versión Teorema Si A y B son L-estructuras isomorfas, entonces para cada L-oración ϕ se tiene que: A = ϕ si y sólo si B = ϕ Cómo podemos demostrar este Teorema? Podemos usar inducción? Tenemos que demostrar una versión mas fuerte del teorema IIC2213 Lógica de Primer Orden 41 / 65
9 El teorema de isomorfismo: Una segunda versión Notación Si h : A B es una biyección que muestra que A y B son estructuras isomorfas, entonces h es un isomorfismo de A en B. IIC2213 Lógica de Primer Orden 42 / 65
10 El teorema de isomorfismo: Una segunda versión Notación Si h : A B es una biyección que muestra que A y B son estructuras isomorfas, entonces h es un isomorfismo de A en B. Nota: Si σ es una asignación para A, entoncesh σ es una asignación para B. IIC2213 Lógica de Primer Orden 42 / 65
11 El teorema de isomorfismo: Una segunda versión Teorema (Isomorfismo) Sea σ una asignación para A y h un isomorfismo de A en B. Entonces para toda L-fórmula ϕ: (A,σ) = ϕ si y sólo si (B, h σ) = ϕ IIC2213 Lógica de Primer Orden 43 / 65
12 El teorema de isomorfismo: Una segunda versión Teorema (Isomorfismo) Sea σ una asignación para A y h un isomorfismo de A en B. Entonces para toda L-fórmula ϕ: (A,σ) = ϕ si y sólo si (B, h σ) = ϕ La primera versión del teorema es un corolario de esta versión más fuerte. IIC2213 Lógica de Primer Orden 43 / 65
13 El teorema de isomorfismo: Aplicaciones Antes de demostrar el teorema de isomorfismo, vamos a ver una de sus aplicaciones. Notación Si (A,σ) = ϕ(x 1,...,x k ) y σ(x i )=a i (i [1, k]), entoncesdecimosque A = ϕ(a 1,...,a k ) IIC2213 Lógica de Primer Orden 44 / 65
14 El teorema de isomorfismo: Aplicaciones Antes de demostrar el teorema de isomorfismo, vamos a ver una de sus aplicaciones. Notación Si (A,σ) = ϕ(x 1,...,x k ) y σ(x i )=a i (i [1, k]), entoncesdecimosque A = ϕ(a 1,...,a k ) Problema de Definibilidad Dada una estructura A con dominio A y S A k (k 1), decimos que S es definible en A si existe una fórmula ϕ(x 1,...,x k )talque S = {(a 1,...,a k ) A k A = ϕ(a 1,...,a k )} IIC2213 Lógica de Primer Orden 44 / 65
15 El problema de definibilidad: Ejemplos Ejemplo Qué conjuntos definen en N, +, las siguientes fórmulas? ϕ 1 (x) = y(x + y = y) ϕ 2 (x) = y(x y = y) ϕ 3 (x, y) = z( ϕ 1 (z) x + z = y) IIC2213 Lógica de Primer Orden 45 / 65
16 El problema de definibilidad: Ejemplos Ejemplo Qué conjuntos definen en N, +, las siguientes fórmulas? ϕ 1 (x) = y(x + y = y) ϕ 2 (x) = y(x y = y) ϕ 3 (x, y) = z( ϕ 1 (z) x + z = y) Para demostrar que un conjunto es definible tenemos que construir una fórmula. IIC2213 Lógica de Primer Orden 45 / 65
17 El problema de definibilidad: Ejemplos Ejemplo Qué conjuntos definen en N, +, las siguientes fórmulas? ϕ 1 (x) = y(x + y = y) ϕ 2 (x) = y(x y = y) ϕ 3 (x, y) = z( ϕ 1 (z) x + z = y) Para demostrar que un conjunto es definible tenemos que construir una fórmula. Cómo podemos demostrar que un conjunto no es definible? IIC2213 Lógica de Primer Orden 45 / 65
18 El problema de definibilidad: Ejemplos Ejemplo Qué conjuntos definen en N, +, las siguientes fórmulas? ϕ 1 (x) = y(x + y = y) ϕ 2 (x) = y(x y = y) ϕ 3 (x, y) = z( ϕ 1 (z) x + z = y) Para demostrar que un conjunto es definible tenemos que construir una fórmula. Cómo podemos demostrar que un conjunto no es definible? Podemos usar el teorema de isomorfismo! IIC2213 Lógica de Primer Orden 45 / 65
19 El problema de definibilidad y el teorema de isomorfismo Es la multiplicación definible en R, +? IIC2213 Lógica de Primer Orden 46 / 65
20 El problema de definibilidad y el teorema de isomorfismo Es la multiplicación definible en R, +? Si esto es cierto, entonces existe ϕ(x, y, z) talqueparatodoa, b, c R: R, + = ϕ(a, b, c) si y sólo si a b = c IIC2213 Lógica de Primer Orden 46 / 65
21 El problema de definibilidad y el teorema de isomorfismo Es la multiplicación definible en R, +? Si esto es cierto, entonces existe ϕ(x, y, z) talqueparatodoa, b, c R: R, + = ϕ(a, b, c) si y sólo si a b = c Entonces para todo isomorfismo h de R, + en R, +, setieneque: R, + = ϕ(a, b, c) si y sólo si R, + = ϕ(h(a), h(b), h(c)) IIC2213 Lógica de Primer Orden 46 / 65
22 El problema de definibilidad y el teorema de isomorfismo Es la multiplicación definible en R, +? Si esto es cierto, entonces existe ϕ(x, y, z) talqueparatodoa, b, c R: R, + = ϕ(a, b, c) si y sólo si a b = c Entonces para todo isomorfismo h de R, + en R, +, setieneque: R, + = ϕ(a, b, c) si y sólo si R, + = ϕ(h(a), h(b), h(c)) Sea h : R R definida por h(x) = x 2 IIC2213 Lógica de Primer Orden 46 / 65
23 El problema de definibilidad y el teorema de isomorfismo Es la multiplicación definible en R, +? Si esto es cierto, entonces existe ϕ(x, y, z) talqueparatodoa, b, c R: R, + = ϕ(a, b, c) si y sólo si a b = c Entonces para todo isomorfismo h de R, + en R, +, setieneque: R, + = ϕ(a, b, c) si y sólo si R, + = ϕ(h(a), h(b), h(c)) Sea h : R R definida por h(x) = x 2 h es un isomorfismo de R, + en R, + IIC2213 Lógica de Primer Orden 46 / 65
24 El problema de definibilidad y el teorema de isomorfismo Es la multiplicación definible en R, +? Si esto es cierto, entonces existe ϕ(x, y, z) talqueparatodoa, b, c R: R, + = ϕ(a, b, c) si y sólo si a b = c Entonces para todo isomorfismo h de R, + en R, +, setieneque: R, + = ϕ(a, b, c) si y sólo si R, + = ϕ(h(a), h(b), h(c)) Sea h : R R definida por h(x) = x 2 h es un isomorfismo de R, + en R, + R, + = ϕ(2, 2, 4) y R, + = ϕ(h(2), h(2), h(4)). Tenemos una contradicción! IIC2213 Lógica de Primer Orden 46 / 65
25 El problema de definibilidad y el teorema de isomorfismo Ejercicios 1. Demuestre que la suma no es definible en R, 2. Demuestre que la suma no es definible en N, 3. Puede usarse el teorema de isomorfismo para mostrar que la multiplicación no es definible en N, +? IIC2213 Lógica de Primer Orden 47 / 65
26 El teorema de isomorfismo: Demostración Ahora vamos a demostrar por inducción la versión fuerte del teorema de isomorfismo. Dado: un vocabulario L y L-estructuras A y B IIC2213 Lógica de Primer Orden 48 / 65
27 El teorema de isomorfismo: Demostración Ahora vamos a demostrar por inducción la versión fuerte del teorema de isomorfismo. Dado: un vocabulario L y L-estructuras A y B Necesitamos el siguiente lema: Lemma Si σ es una asignación para A yhesunisomorfismodea en B, entonces ĥ σ = h ˆσ. IIC2213 Lógica de Primer Orden 48 / 65
28 El teorema de isomorfismo: Demostración Ahora vamos a demostrar por inducción la versión fuerte del teorema de isomorfismo. Dado: un vocabulario L y L-estructuras A y B Necesitamos el siguiente lema: Lemma Si σ es una asignación para A yhesunisomorfismodea en B, entonces ĥ σ = h ˆσ. Demostración: Por inducción en los L-términos. Para cada constante c L: ĥ σ(c) =c B = h(c A )=h(ˆσ(c)) = (h ˆσ)(c) IIC2213 Lógica de Primer Orden 48 / 65
29 El teorema de isomorfismo: Demostración Para cada variable x: ĥ σ(x) =(h σ)(x) = h(σ(x)) = h(ˆσ(x)) = (h ˆσ)(x) IIC2213 Lógica de Primer Orden 49 / 65
30 El teorema de isomorfismo: Demostración Para cada variable x: ĥ σ(x) =(h σ)(x) = h(σ(x)) = h(ˆσ(x)) = (h ˆσ)(x) Para cada función n-aria f L: Si ĥ σ(t i )=(h ˆσ)(t i ) para todo i [1, n], entonces ĥ σ(f (t 1,...,t n )) = f B (ĥ σ(t 1 ),...,ĥ σ(t n )) = f B ((h ˆσ)(t 1 ),...,(h ˆσ)(t n )) = f B (h(ˆσ(t 1 )),...,h(ˆσ(t n ))) = h(f A (ˆσ(t 1 ),...,ˆσ(t n ))) = h(ˆσ(f (t 1,...,t n ))) = (h ˆσ)(f (t 1,...,t n )) IIC2213 Lógica de Primer Orden 49 / 65
31 El teorema de isomorfismo: Demostración Vamos a demostrar el teorema por inducción en la estructura de ϕ: Si ϕ = t 1 = t 2,entonces: (A,σ) = t 1 = t 2 si y sólo si ˆσ(t 1 )=ˆσ(t 2 ) si y sólo si h(ˆσ(t 1 )) = h(ˆσ(t 2 )) si y sólo si (h ˆσ)(t 1 )=(h ˆσ)(t 2 ) si y sólo si ĥ σ(t 1 )=ĥ σ(t 2 ) si y sólo si (B, h σ) = t 1 = t 2 IIC2213 Lógica de Primer Orden 50 / 65
32 El teorema de isomorfismo: Demostración Si ϕ = R(t 1,...,t n ), entonces: (A,σ) = R(t 1,...,t n ) si y sólo si (ˆσ(t 1 ),...,ˆσ(t n )) R A si y sólo si (h(ˆσ(t 1 )),...,h(ˆσ(t n ))) R B si y sólo si ((h ˆσ)(t 1 ),...,(h ˆσ)(t n )) R B si y sólo si (ĥ σ(t 1 ),...,ĥ σ(t n )) R B si y sólo si (B, h σ) = R(t 1,...,t n ) IIC2213 Lógica de Primer Orden 51 / 65
33 El teorema de isomorfismo: Demostración Finalmente suponemos que la propiedad se cumple para ψ y θ IIC2213 Lógica de Primer Orden 52 / 65
34 El teorema de isomorfismo: Demostración Finalmente suponemos que la propiedad se cumple para ψ y θ Si ϕ = ψ, entonces: IIC2213 Lógica de Primer Orden 52 / 65
35 El teorema de isomorfismo: Demostración Finalmente suponemos que la propiedad se cumple para ψ y θ Si ϕ = ψ, entonces: (A,σ) = ϕ si y sólo si (A,σ) = ψ si y sólo si (B, h σ) = ψ si y sólo si (B, h σ) = ϕ IIC2213 Lógica de Primer Orden 52 / 65
36 El teorema de isomorfismo: Demostración Si ϕ = ψ θ, entonces: (A,σ) = ϕ si y sólo si (A,σ) = ψ y(a,σ) = θ si y sólo si (B, h σ) = ψ y(b, h σ) = θ si y sólo si (B, h σ) = ϕ IIC2213 Lógica de Primer Orden 53 / 65
37 El teorema de isomorfismo: Demostración Suponga que ϕ = x ψ. IIC2213 Lógica de Primer Orden 54 / 65
38 El teorema de isomorfismo: Demostración Suponga que ϕ = x ψ. Sólo vamos a demostrar una dirección. La otra dirección se demuestra de la misma forma pero considerando h 1 en lugar de h. IIC2213 Lógica de Primer Orden 54 / 65
39 El teorema de isomorfismo: Demostración Suponga que ϕ = x ψ. Sólo vamos a demostrar una dirección. La otra dirección se demuestra de la misma forma pero considerando h 1 en lugar de h. Si (A,σ) = ϕ: Existe a A tal que (A,σ[x/a]) = ψ. Por hipótesis de inducción: Existe a A tal que (B, h σ[x/a]) = ψ. Pero: h σ[x/a] =(h σ)[x/h(a)]. Tenemos que: Existe b B tal que (B, (h σ)[x/b]) = ψ. Por lo tanto: (B, h σ) = ϕ. IIC2213 Lógica de Primer Orden 54 / 65
Lógica de Primer Orden
Lógica de Primer Orden IIC2213 IIC2213 Lógica de Primer Orden 1 / 60 Lógica de primer orden Dos de los objetivos de la lógica proposicional: Poder modelar el proceso de razonamiento. Poder formalizar la
Repaso de Lógica de Primer Orden
Repaso de Lógica de Primer Orden IIC3260 IIC3260 Repaso de Lógica de Primer Orden 1 / 29 Lógica de primer orden: Vocabulario Una fórmula en lógica de primer orden está definida sobre algunas constantes
Lógica de primer orden: Repaso y notación
Lógica de primer orden: Repaso y notación IIC3263 IIC3263 Lógica de primer orden: Repaso y notación 1 / 29 Lógica de primer orden: Vocabulario Una fórmula en lógica de primer orden está definida sobre
Nociones de Localidad
Nociones de Localidad IIC3260 IIC3260 Nociones de Localidad 1 / 48 Notación: Grafo de Gaifman Dado: Vocabulario L y L-estructura A Primero suponemos que L sólo contiene símbolos de relación IIC3260 Nociones
Teorema de incompletitud de Gödel
Teorema de incompletitud de Gödel Theorem (Gödel) Th(N) es una teoría indecidible. IIC2213 Teorías 79 / 109 Teorema de incompletitud de Gödel Theorem (Gödel) Th(N) es una teoría indecidible. Corolario
Leyes 0-1 IIC3263. IIC3263 Leyes 0-1 1/77
Leyes 0-1 IIC3263 IIC3263 Leyes 0-1 1/77 Leyes 0-1: Notación Dado: Vocabulario L Recuerde que una propiedad P sobre L (L-propiedad) es un subconjunto de Struct[L] IIC3263 Leyes 0-1 2/77 Leyes 0-1: Notación
Leyes 0-1 IIC3260. IIC3260 Leyes / 77
Leyes 0-1 IIC3260 IIC3260 Leyes 0-1 1 / 77 Leyes 0-1: Notación Dado: Vocabulario L Recuerde que una propiedad P sobre L (L-propiedad) es un subconjunto de Struct[L] Notación sl n : Número de L-estructuras
IIC2213. IIC2213 Teorías 1 / 42
Teorías IIC2213 IIC2213 Teorías 1 / 42 Qué es una teoría? Una teoría es un cúmulo de información. Debe estar libre de contradicciones. Debe ser cerrada con respecto a lo que se puede deducir de ella. Inicialmente
El sistema deductivo de Hilbert
El sistema deductivo de Hilbert IIC2213 IIC2213 El sistema deductivo de Hilbert 1 / 17 Completidad de resolución proposicional Qué tenemos que agregar a nuestro sistema de deducción para que sea completo?
El problema de satisfacción
El problema de satisfacción Definición Un conjunto de fórmulas Σ es satisfacible si existe una valuación σ tal que σ(σ) = 1. En caso contrario, Σ es inconsistente. IIC2213 Lógica Proposicional 33 / 42
Juegos de Ehrenfeucht-Fraïssé
Juegos de Ehrenfeucht-Fraïssé IIC3263 IIC3263 Juegos de Ehrenfeucht-Fraïssé 1/65 Terminología Restricción Recuerde que en este curso consideramos vocabularios sin funciones. De hecho, inicialmente nos
La lógica de segundo orden: Sintaxis
La lógica de segundo orden: Sintaxis Dado: Vocabulario L Definición La lógica de segundo orden (LSO) sobre L es definida como la extensión de LPO que incluye las siguientes reglas: Si t 1,..., t k son
La clase de hoy. 22 de abril de 2017
La clase de hoy 22 de abril de 2017 1. Satisfacibilidad 1.1. Vamos a extender ahora nuestra noción de verdad bajo una interpretación de enunciados a fórmulas. Por supuesto, el tema es cómo interpretar
Lógica Proposicional IIC2213. IIC2213 Lógica Proposicional 1/42
Lógica Proposicional IIC2213 IIC2213 Lógica Proposicional 1/42 Por qué necesitamos la lógica? Necesitamos un lenguaje con una sintaxis precisa y una semántica bien definida. Queremos usar este lenguaje
Nuestro objetivo es demostrar que autómata = lógica. IIC3260 Una Aplicación de Teoría de Modelos Finitos: Lógica = Autómata 35 / 60
Autómata = Lógica Nuestro objetivo es demostrar que autómata = lógica IIC3260 Una Aplicación de Teoría de Modelos Finitos: Lógica = Autómata 35 / 60 Autómata = Lógica Nuestro objetivo es demostrar que
Nuestro objetivo es demostrar que autómata = lógica Qué significa esto? Queremos encontrar una lógica que defina a los lenguajes regulares
Autómata = Lógica Nuestro objetivo es demostrar que autómata = lógica Qué significa esto? Queremos encontrar una lógica que defina a los lenguajes regulares Pero antes: Vamos a hacer un breve repaso sobre
Lógica Proposicional IIC2213. IIC2213 Lógica Proposicional 1/42
Lógica Proposicional IIC2213 IIC2213 Lógica Proposicional 1/42 Por qué necesitamos la lógica? Necesitamos un lenguaje con una sintaxis precisa y una semántica bien definida. Queremos usar este lenguaje
Lógica proposicional: Lectura única
Lógica proposicional: Lectura única Una fórmula ϕ es atómica si ϕ = p, donde p P. Una fórmula ϕ es compuesta si no es atómica. - Si ϕ = ( α), entonces es un conectivo primario de ϕ y α es una subfórmula
Resolución Proposicional
Resolución Proposicional IIC2213 IIC2213 Resolución Proposicional 1 / 19 Resolución proposicional Sabemos que Σ = ϕ si y sólo si Σ { ϕ} es inconsistente. Cómo verificamos si Σ { ϕ} es inconsistente? El
Repaso de Lógica de Primer Orden
Repaso de Lógica de Primer Orden IIC3260 IIC3260 Repaso de Lógica de Primer Orden 1 / 29 Lógica de primer orden: Vocabulario Una fórmula en lógica de primer orden está definida sobre algunas constantes
Eliminación de cuantificadores
Eliminación de cuantificadores Teorema Si una teoría admite eliminación de cuantificadores, y existe un algoritmo que construye ϕ sc a partir de ϕ, entonces es decidible. Cómo se demuestra este teorema?
Teoría de Anillos y Campos
Teoría de Anillos y Campos Presentación 2: anillos, homomorfismos e ideales Luis Felipe González Rivas UANL 21 de agosto de 2018 Contenido 1 Anillos 2 Homomorfismos 3 Ideales Luis Felipe González Rivas
PONTIFICIA UNIVERSIDAD CATOLICA DE CHILE ESCUELA DE INGENIERIA DEPARTAMENTO DE CIENCIA DE LA COMPUTACION
PONTIFICIA UNIVERSIDAD CATOLICA DE CHILE ESCUELA DE INGENIERIA DEPARTAMENTO DE CIENCIA DE LA COMPUTACION Lógica para Ciencia de la Computación - IIC2213 Guía 1 - Lógica proposicional 1. Dados dos strings
IIC1253. IIC1253 Una introducción a la teoría de números (y a la criptografía) 1/45
Una introducción a la teoría de números (y a la criptografía) IIC1253 IIC1253 Una introducción a la teoría de números (y a la criptografía) 1/45 Motivación: Criptografía de clave pública Se tiene dos funciones
R no es enumerable. Por contradicción, supongamos que existe una biyección f : N! R. diagonalización de Cantor. Para cada i 2 N:
R no es enumerable Por contradicción, supongamos que existe una biyección f : N! R. I Vamos a obtener una contradicción usando el método de diagonalización de Cantor. Para cada i 2 N: f (i) = n i.d i,0
Teoría de Modelos Finitos: Motivación
Teoría de Modelos Finitos: Motivación IIC3260 IIC3260 Teoría de Modelos Finitos: Motivación 1 / 29 Poder expresivo de una lógica: Caso finito Desde ahora en adelante nos vamos a concentrar en las estructuras
Homomorfismos de cuerpos. Extensiones normales. Teorema fundamental de la teoría de Galois.
1 Tema 9.-. Homomorfismos de cuerpos. Extensiones normales. Teorema fundamental de la teoría de Galois. 9.1. Caracteres de un grupo. A la hora de resolver una ecuación f(x) = 0 con f(x) k[x], tomamos un
Teorías decidibles. Definición. Ejercicio
Teorías decidibles Definición Una teoría Σ sobre un vocabulario L es decidible si existe un algoritmo que, dada una L-oración ϕ, verificasiϕ Σ. Ejercicio Sea Ord k el siguiente conjunto de axiomas sobre
Un tercer ejemplo: verificación de primalidad
Un tercer ejemplo: verificación de primalidad Vamos a ver un algoritmo aleatorizado para verificar si un número es primo. I Este algoritmo es más eficiente que los algoritmos sin componentes aleatorias
Algoritmos en teoría de números
Algoritmos en teoría de números IIC2283 IIC2283 Algoritmos en teoría de números 1 / 92 Para recordar: aritmética modular Dados dos números a, b Z, si b > 0 entonces existen α, β Z tales que 0 β < b y a
Lógica Proposicional IIC1253. IIC1253 Lógica Proposicional 1/64
Lógica Proposicional IIC1253 IIC1253 Lógica Proposicional 1/64 Inicio de la Lógica Originalmente, la Lógica trataba con argumentos en el lenguaje natural. Ejemplo Es el siguiente argumento válido? Todos
Lógica Proposicional. Del conjunto de hipótesis Γ se deduce α?
Proposicional Metateoría: Corrección y Completitud Proposicional - 1 Del conjunto de hipótesis Γ se deduce α? Γ = α? -Tablas de verdad - Equivalencia lógicas Existen métodos que siempre responden SI o
Teorema de Lagrange. En esta sección demostramos algunos hechos básicos sobre grupos, que se pueden deducir de la definición
Teorema de Lagrange Capítulo 3 3.1 Introducción En este capítulo estudiaremos uno de los teoremas más importantes de toda la teoría de grupos como lo es el Teorema de Lagrange. Daremos en primer lugar
MATE 4032: Álgebra Abstracta. 1. Suponga que I, J son ideales de un anillo R. Demuestre que I J es un ideal
Solución Asignación 9. Universidad de Puerto Rico Río Piedras Facultad de Ciencias Naturales Departamento de Matemáticas San Juan Puerto Rico MATE 4032: Álgebra Abstracta 1. Suponga que I J son ideales
El sistema de Hilbert: Lógica de Primer Orden
El sistema de Hilbert: Lógica de Primer Orden El sistema de deducción de Hilbert para la lógica de primer orden consta de los siguientes elementos: IIC2213 Lógica de Primer Orden 55 / 65 El sistema de
Teorema de Carathéodory
Teorema de Carathéodory Objetivos. Dada una medida exterior ϕ, definir conjuntos Carathéodory-medibles respecto a ϕ, mostrar que esos conjuntos forman una σ-álgebra y la medida exterior ϕ restringida a
Clase 2: Distribuciones y Derivadas Generalizadas.
Clase 2: Distribuciones y Derivadas Generalizadas. Peter Hummelgens 9 de enero de 2007 1. Distribuciones. Nuestro espacio vectorial básico será D(R) = C0 (R), el espacio de las funciones de prueba. Una
Completitud en Lógica de Predicados
Completitud en de Predicados Predicados - Completitud 1 Corrección. Significa que las derivaciones expresan una consecuencia lógica. Establece una correspondencia tal que partiendo de nociones sintácticas
8.1. Extensiones algebraicas. Grado.
1 Tema 8.-. Extensiones algebraicas. Cuerpos de descomposición. Elemento primitivo. 8.1. Extensiones algebraicas. Grado. Si k es un subcuerpo de K, diremos que K es una extensión de k, que notaremos K
Terminaremos el capítulo con una breve referencia a la teoría de cardinales.
TEMA 5. CARDINALES 241 Tema 5. Cardinales Terminaremos el capítulo con una breve referencia a la teoría de cardinales. Definición A.5.1. Diremos que el conjunto X tiene el mismo cardinal que el conjunto
COMPACIDAD Y COMPLETITUD: DOS TEOREMAS CLÁSICOS DE LA TEORÍA DE MODELOS
COMPACIDAD Y COMPLETITUD: DOS TEOREMAS CLÁSICOS DE LA TEORÍA DE MODELOS JOEL TORRES DEL VALLE 1 1 Universidad Cartagena Resumen. Se presentan dos teoremas clásicos de la Teoría de Modelos: Teorema de La
Ejercicio. Usando la formulación del principio de inducción mostrada en la transparencia anterior, demuestre que: 2 2 n 1esdivisiblepor3. =2 n.
Ejercicio Usando la formulación del principio de inducción mostrada en la transparencia anterior, demuestre que: n 1esdivisiblepor3 n i=0 ( ) n i = n IIC153 Inducción 18 / 30 Inducción estructural La forma
Resumen ANÁLISIS LÓGICO INDUCCIÓN Y RECURSIÓN. Conjuntos inductivos. Definiciones circulares
Resumen ANÁLISIS LÓGICO INDUCCIÓN Y RECURSIÓN Francisco Hernández Quiroz Departamento de Matemáticas Facultad de Ciencias, UNAM E-mail: fhq@ciencias.unam.mx Página Web: www.matematicas.unam.mx/fhq En este
Anuladores. Objetivos. Definir el concepto de anuladores y estudiar sus propiedades principales.
Anuladores Objetivos. Definir el concepto de anuladores y estudiar sus propiedades principales. Requisitos. Espacio dual, espacio bidual, base dual.. Definición (anulador de un subconjunto de un espacio
Introdución a la Lógica Proposicional
Introdución a la Lógica Proposicional Pablo Barceló P. Barceló Lógica Proposicional - CC52A 1 / 24 Lógica proposicional: Sintaxis Tenemos los siguientes elementos: - Variables proposicionales (P): p, q,
Introducción a la Lógica y la Computación
Clase del 9 de septiembre de 2014 Cuestión a resolver Todas las Álgebras de Boole vistas (aunque estén camufladas como D 6 o D 30 ) son en definitiva (vía isomorfismo) de la forma P(X). O sea, son álgebras
Paréntesis: Una aplicación en lenguajes formales
Paréntesis: Una aplicación en lenguajes formales Vamos a ver una aplicación del Teorema de Immerman-Szelepcsényi en la área de lenguajes formales. IIC3242 Clases de Complejidad 35 / 69 Paréntesis: Una
Teoremas de Tonelli y Fubini
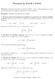Teoremas de Tonelli y Fubini Objetivos. Demostrar teoremas de Tonelli y Fubini, conocer contraejemplos que muestran la importancia de algunas condiciones de estos teoremas. Requisitos. Definición del producto
Un tercer problema NP-completo: Programación entera
Un tercer problema NP-completo: Programación entera Un problema muy estudiado por su utilidad práctica: PROG-ENT = {(A, b) A x b es un sistema de ecuaciones lineales enteras que tiene solución}. Teorema
Multiplicación de matrices simétricas
Multiplicación de matrices simétricas La traspuesta de una matriz A n n es definida como una matriz A T n n tal que A T [i, j] =A[j, i] paracadai, j 2{1,...,n} Además, una matriz A es simétrica si A =
Los isomorfismos básicos de la teoría de cuerpos algebraicos.
4. AUTOMORFISMOS DE CUERPOS. En este tema probaremos que dos elementos α y β, conjugados sobre un cuerpo F, determinan un isomorfismo entre los cuerpos F (α) y F (β). También cierto recíproco será válido.
Relaciones IIC1253. IIC1253 Relaciones 1 / 32
Relaciones IIC1253 IIC1253 Relaciones 1 / 32 Relaciones binarias Dado: conjunto A R es una relación binaria sobre A si R A A. Para indicar que a,b A están relacionados a través de R usamos las notaciones:
Teorema de Hahn-Banach
Capítulo 3 Teorema de Hahn-Banach 3.1. Introducción Una vez introducidos los espacios vectoriales más importantes donde se tiene una estructura métrica a saber, los espacios de Hilbert y los espacios de
Extensiones algebraicas. Cuerpos de descomposición.
Temas 10-11.- 10-11.1 Extensiones algebraicas. Cuerpos de descomposición. Si k es un subcuerpo de K, diremos que K es una extensión de k, que notaremos K k. Si K k es una extensión y E K es un subconjunto,
Una pregunta pendiente
Una pregunta pendiente Cómo podemos construir un generador (casi) uniforme para una relación? Recuerde el problema KS definido en la sección anterior y la relación: R KS = {((~a, b), ~x) ~a 2 N n y ~x
Cardinalidad IIC1253. IIC1253 Cardinalidad 1 / 23
Cardinalidad IIC1253 IIC1253 Cardinalidad 1 / 23 Conjuntos con la misma cardinalidad Definición Decimos que dos conjuntos A y B son equinumerosos, denotado como A B, si existe una biyección f : A B. Ejemplo
1. CONTINUIDAD EN VARIAS VARIABLES
1 1. CONTINUIDAD EN VARIAS VARIABLES 1.1. PRIMERAS DEFINICIONES. LÍMITES Definición 1.1. Sea A R n. Una función real de varias variables es una aplicación f : A R n R m con f(x 1,..., x n ) = (y 1,...,
Teorema de Compacidad
Teorema de Compacidad Seminario de Teoría de Modelos - FCEyN - UBA 1 de septiembre de 2011 Teorema 1 (Compacidad). Una L-teoría T es satisfacible si y solo si todo subconjunto finito de T es satisfacible.
Cardinalidad IIC1253. IIC1253 Cardinalidad 1 / 23
Cardinalidad IIC1253 IIC1253 Cardinalidad 1 / 23 Conjuntos con la misma cardinalidad Definición Decimos que dos conjuntos A y B son equinumerosos, denotado como A B, si existe una biyección f : A B. IIC1253
Teorema de la Función Implícita
Teorema de la Función Implícita Sea F : U R p+1 R U abierto F (x 1, x 2,..., x q, y) y un punto a (a 1, a 2,..., a q, b) en U tal que i)f (a 1, a 2,..., a q, b) 0 ii) 0 y continua, existe entonces una
RSA: Autentificación y firma digitales
RSA: Autentificación y firma digitales Escenario usual para RSA: E B A M = E B (M) E A B E A, D A E B, D B C E A, E B Dos preguntas a responder: Autentificación: Cómo puede saber A si E B es efectivamente
Guía. Álgebra II. Examen parcial III. Transformaciones lineales. Teoremas los más importantes cuyas demostraciones se pueden incluir en el examen
Guía. Álgebra II. Examen parcial III. Transformaciones lineales. Teoremas los más importantes cuyas demostraciones se pueden incluir en el examen 1. Teorema de la representación matricial de una transformación
RSA: Autentificación y firma digitales
RSA: Autentificación y firma digitales Escenario usual para RSA: E B A M = E B (M) E A B E A, D A E B, D B C E A, E B Dos preguntas a responder: Autentificación: Cómo puede saber A si E B es efectivamente
Estructuras algebraicas. Departamento de Álgebra. Apuntes de teoría
ESTRUCTURAS ALGEBRAICAS GRADO EN MATEMÁTICAS. CURSO 2015/2016 Apuntes de teoría Tema 1: Grupos y subgrupos. 1.1. Introducción Definición 1.1. Un grupo es un par (G, ), donde G es un conjunto no vacío,
El algoritmo de Resolución
El algoritmo de Resolución El algoritmo de resolución es casi idéntico al de lógica proposicional: Suponga que quiere demostrar que ϕ es consecuencia lógica de Σ. El método es el siguiente: Transforme
Modelos. Capítulo La clase V
Capítulo 6 Modelos En este capítulo veremos ejemplos de como demostrar la independencia de un axioma o su consistencia relativa a los otros. Si A es un sistema de axiomas: 1. A + es el sistema de axiomas
Definición 1 Sean E, F y G tres espacios vectoriales. Una transformación ϕ : E F G se llama bilineal si satisface las siguientes condiciones:
Producto tensorial 0.1 Transformaciones multilineales Definición 1 Sean E, F y G tres espacios vectoriales. Una transformación ϕ : E F G se llama bilineal si satisface las siguientes condiciones: ϕ(λx
Anillos. a + (b + c) = (a + b) + c. 3) Existe un elemento 0 en R, el cual llamaremos cero, tal que. a + 0 = 0 + a = a para todo a en R.
Capítulo 7 Anillos 7.1 Definiciones Básicas El concepto de Anillo se obtiene como una generalización de los números enteros, en donde están definidas un par de operaciones, la suma y el producto, relacionadas
AMPLIACIÓN DE MATEMÁTICAS
AMPLIACIÓN DE MATEMÁTICAS CLASIFICACIÓN DE GRUPOS FINITOS. Vamos a ver una clasificación de los grupos finitos. Va a ser un poco superficial, pero nos dará una idea de como puede ser usada en algunas aplicaciones.
Diferenciación de funciones f : R n R m. f(x, y) = ( e xy, x 2 + y, 2x 3 y 2) r(h) (h 1, h 2 ) e. 2(1 + h 1 ) 3 (3 + h 2 ) h 1 12h 2
Funciones de R n en R m Diferenciación de funciones f : R n R m Definición. Considere la función f : A R n R m definida en un conjunto abierto A de R n y sea x 0 A. Se dice que esta función es diferenciable
Ejemplos de expresiones que no son proposiciones. Teorema 1. Existe una innidad de números primos.
Proposición Es una oración o una expresión matemática que arma o niega algo. s de proposiciones verdaderas 5 es un número impar 2 es un número par s de proposiciones falsas 14 es un número impar 2=5 s
Teorema de la Función Implícita (f : R R)
Funciones de R n en R 1 Teorema de la Función Implícita f : R R) Teorema 1. Considere la función y = fx). Sea x 0, y 0 ) R 2 un punto tal que F x 0, y 0 ) = 0. Suponga que la función F tiene derivadas
Elementos de lógica de predicados *
Elementos de lógica de predicados * 1. Lenguaje Definimos un lenguaje L para la lógica de predicados de primer orden como el par A, F, donde A representa el alfabeto o conjunto de signos de L y F el conjunto
Resumen LÓGICA COMPUTACIONAL INDUCCIÓN Y RECURSIÓN. Conjuntos inductivos. Definiciones circulares
Resumen LÓGICA COMPUTACIONAL INDUCCIÓN Y RECURSIÓN Francisco Hernández Quiroz Departamento de Matemáticas Facultad de Ciencias, UNAM E-mail: fhq@ciencias.unam.mx Página Web: www.matematicas.unam.mx/fhq
NÚMEROS COMPLEJOS 1.1. INTRODUCCIÓN 1.2. OPERACIONES CON COMPLEJOS
NÚMEROS COMPLEJOS 1.1. INTRODUCCIÓN La ecuación x + 1 0 no tiene solución en el cuerpo de los números reales R ya que no existe un número real x tal que x 1. Necesitamos un conjunto que contenga a R, que
Introducción a la Lógica y la Computación
Clase del 21 de agosto de 2015 Estructura Algebraica Esta formada por un conjunto con operaciones Por ejemplo, los números enteros dotados de las operaciones suma, producto y las constantes 0 y 1 tienen
Grupos libres. Presentaciones.
S _ Tema 12.- Grupos libres. Presentaciones. 12.1 Grupos libres. En el grupo Z de los enteros vimos una propiedad (cf. ejemplos.5), que lo caracteriza como grupo libre. Lo enunciamos al modo de una Propiedad
La Diferencial de Fréchet
Capítulo 6 La Diferencial de Fréchet Es bien conocido que una función de una variable f es derivable en un punto a si y sólo si su gráfica admite una recta tangente (no vertical) en el punto (a, f(a)).
Resumen de aritmética de Peano
Resumen de aritmética de Peano UDELAR/FING/IMERL 16 de febrero de 2017 1. Fundamentos de la Aritmética de Peano. Axioma 1.1. Existe un conjunto al que denotamos N, un elemento 0 N y una función s : N N
a los anillos no conmutativos
Tema 7.- Representaciones de grupos finitos. Introducción a los anillos no conmutativos 7.1 Nociones básicas En lo que sigue, k denotará un cuerpo arbitrario y los espacios vectoriales lo serán sobre k.
Problemas recursivamente enumerables
Problemas recursivamente enumerables Definición Un problema L es recursivamente enumerable si existe una máquina de Turing M tal que L = L(M). Nótese que M en la definición no necesariamente se detiene
Teorías. Una teoría acerca de una base de conocimiento Σ contendrá no sólo a Σ sino que a todo lo que se puede deducir de Σ.
Teorías Qué es una teoría? Ya hemos usado antes la noción de base de conocimiento Este concepto se refiere a un conocimiento, representado a través de axiomas. Una teoría acerca de una base de conocimiento
Es claro que es una relación de equivalencia. Para ver que tener la misma cardinalidad y la cardinalidad están bien definidas queremos ver que
Capítulo II Cardinalidad Finita II.1. Cardinalidad Definimos I n para n N como I n = {k N : 1 k n}. En particular I 0 =, puesto que 0 < 1. Esto es equivalente a la definición recursiva { si n = 0 I n =
Lógica proposicional. Semántica Lógica 2018
Lógica proposicional. Semántica Lógica 2018 Instituto de Computación 20 de marzo Instituto de Computación (InCo) Lógica proposicional. Semántica Curso 2018 1 / 1 Significado de una fórmula proposicional
sup si A no es acotado.
Capítulo 5 Teoría de Baire 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y la
Límites Laterales. El límite por la derecha se denota. x 2 + x 2 = 1. x 2. x + x 2. x = x + x 2. El límite por la izquierda se denota
Límites Laterales Denición. Si f : D R R y x 0 es un punto de D, decimos que l d es ite de f en x 0 por la derecha si ɛ > 0 δ ɛ > 0 f(x) l d < ɛ si 0 < x x 0 < δ ɛ ɛ > 0 δ ɛ > 0 f(x) l d < ɛ si x 0 < x
Espacios vectoriales con producto interno
Espacios vectoriales con producto interno Problemas teóricos En todos los problemas relacionados con el caso complejo se supone que el producto interno es lineal con respecto al segundo argumento. Definición
Cuadrados mágicos y matrices de permutación
Cuadrados mágicos y matrices de permutación Alexey Beshenov (cadadr@gmail.com) 13 de agosto de 016 Estos son mis apuntes para una pequeña presentación para los alumnos del Programa Jóvenes Talento de la
CIENCIAS FORMALES CIENCIAS FÁCTICAS
UNA CLASIFICACIÓN DE LAS CIENCIAS CIENCIAS FORMALES CIENCIAS FÁCTICAS CIENCIAS FORMALES MATEMÁTICA LÓGICA CIENCIAS FÁCTICAS FÍSICA BIOLOGÍA QUÍMICA CIENCIAS SOCIALES OTRAS CIENCIAS FORMALES VOCABULARIO
En primer lugar, vamos a precisar un concepto al que ya nos hemos referido anteriormente, el de σ-álgebra.
Capítulo 20 Conjuntos de Borel Hemos demostrado ya que la familia M de los conjuntos medibles contiene a todos los abiertos de R n y, por tanto, a todos los conjuntos que podamos formar a partir de los
Problemas recursivamente enumerables
Problemas recursivamente enumerables Definición Un problema L es recursivamente enumerable si existe una máquina de Turing M tal que L = L(M). Nótese que M en la definición no necesariamente se detiene
(MAT021) 1 er Semestre de z + e = (x + iy) + (e 1 + ie 2 ) = (x + e 1 ) + i(y + e 2 ) = x + iy
(MAT01) 1 er Semestre de 010 1 Números Complejos Se define el conjunto de los números complejos como: C = {a + bi / a, b R, i = 1} Definición 1.1. Sea z, w C tal que z = x + iy en donde x, y R. Se define:
Funciones continuas e inyectivas
Nuestro último teorema afirmaba que toda función continua en un intervalo cerrado y acotado tiene máximo y mínimo absolutos, pero nada nos informa sobre los puntos en los que se alcanzan. Bajo la hipótesis
1. MEDIDA E INTEGRACIÓN.
1. MEDID E INTEGRCIÓN. En este capítulo repasamos algunos conceptos que se vieron en la asignatura mpliación de la Teoría de Funciones de Varias Variables. 1. MEDIDS POSITIVS. (1,1,1) Definición. Una σ-álgebra
Con los dos conectivos y en las formulas que tienen una sola variable proposicional distinta, no hay forma de construir una contradicción.
1) No se puede formar una contradicción usando solamente los dos conectivos, {*,->}, en las formulas que tienen una sola variable proposicional distinta. Con los dos conectivos y en las formulas que tienen
Estructura de los Grupos
Capítulo 6 Estructura de los Grupos 6.1 Introducción En nuestro viaje dentro de la teoría de grupos, hemos estudiado muchos ejemplos de grupos interesantes, como los grupos de simetría, los enteros módulo
Muchas de las ecuaciones de recurrencia que vamos a usar en este curso tienen la siguiente forma: ( c n =0 T (n) = a T (b n b.
El Teorema Maestro Muchas de las ecuaciones de recurrencia que vamos a usar en este curso tienen la siguiente forma: ( c n =0 T (n) = a T (b n b c)+f (n) n 1 donde a, b y c son constantes, y f (n) es una