Capítulo 2 SECCIÓN DE FIGURAS PLANAS
|
|
|
- Rafael Río Domínguez
- hace 7 años
- Vistas:
Transcripción
1 Capítulo SECCIÓN DE FIGURAS PLANAS 1
2 .1. INTRODUCCIÓN Una figura plana, tiene todos sus puntos sobre un mismo plano. En la Figura 1, las rectas m y n se intersectan en un punto. En la Figura, r intersecta a la figura f en dos puntos y para la Figura 3, la intersección de s y la figura L, es de tres puntos. En todos los casos anteriores diremos que las figuras son secantes, se cortan en 1, ó 3 puntos respectivamente... LÍNEAS CONVEXAS Son aquellas que se intersectan con alguna recta, en un mximo de dos puntos. Ejemplos:.3. LÍNEAS NO CONVEXAS Si alguna recta secante determina sobre ellas, más de dos puntos de corte. La Geometría clásica, menciona estas figuras cóncavas. Ejemplos:
3 .4. OBSERVACIONES 1. Dos rectas contenidas en un mismo plano y que no se intersectan, reciben el nombre de paralelas. Ejemplo: m y q. En este caso, escribiremos: m q ( m es paralela a q ). A veces, suele decirse que las rectas se intersectan, para este caso, en el infinito.. Una recta y una circunferencia, pueden ser: Recta y circunferencia, tangentes entre sí. Recta y circunferencia, secantes entre sí. ( puntos de intersección). Nose Intersectan. (Cero puntos de intersección). 3. Veamos algunos gráficos de intersección entre un triángulo y una circunferencia: Por supuesto que, podrían hacerse otros gráficos para encontrar un número determinado de puntos: 1; ; 3; 4; 5 ó 6.
4 Notamos que, el mínimo número de puntos de intersección (diferente de cero), entre estas figuras, es uno y el máximo: Las fórmulas que damos a continuación, permiten encontrar el máximo número de puntos de intersección entre figuras del mismo tipo, así como entre dos grupos diferentes..5. MÁXIMO NÚMERO DE PUNTOS DE CORTE 1. Para n rectas secantes n(n 1) puntos. Así por ejemplo, 4 rectas se cortan como máximo, en: 4(3). Para n circunferencias secantes: n(n 1) puntos. = 6 puntos. 3 circunferencias secantes se cortan, como máximo, en 3() = 6 puntos. 3. Para n triángulos: 3n(n 1) puntos.
5 Si se tienen 10 triángulos, encontraremos como máximo: 3 10(9) = 70 punto de corte. 4. Para n cuadriláteros convexos: 4n(n 1) puntos. 5. n pentágonos convexos se cortan, como máximo, en: 5n(n 1) puntos. 6. En general, n polígonos convexos de L lados cada uno, se cortan como máximo, en Ln(n 1) puntos. Por ejemplo n polígonos de 11 lados cada uno (convexos) tienen como fórmula para el máximo número de puntos de corte: 11n(n 1). De modo que, 5 de estas figuras se cortarán en un máximo de: 11 5(4) = 0 puntos. Problema 1 En cuántos puntos se intersectan, como máximo, 10 icoságonos convexos? Resolución Un icoságono es el polígono de 0 lados. Luego, en la fórmula del (6), debemos reemplazar: L = 0 número de lados. n = 10 número de polígonos. Ln(n 1) = 0 10(9) = 1800 puntos Problema En cuántos puntos se intersectan, como máximo, 5 octógonos convexos? Resolución El octógono es un polígono de 8 lados. Entonces: L = 8 y n = 5. En la fórmula de (6): Ln(n 1) = 8 5(4) = 160 puntos 7. Dos polígonos convexos, de diferente número de lados, se intersectan, como máximo, en un número de puntos equivalente al doble del número de lados del menor. Por ejemplo:
6 1 triángulo y 1 cuadriátero: 1 cuadrilátero y 1 pentágono: 1 decágono (10 lados) y 1 octógono (8 lados), convexos, se cortan como máximo en: 8 = 16 puntos. 1 cuadrilátero y 1 circunferencia: Observación La circunferencia se considera como un polígono de infinitos lados. Por ejemplo. Calcular el máximo número de puntos de corte entre: a) Un triángulo y un pentágono convexo, es:. b) Un dodecágono convexo (1 lados) y un icoságono convexo (0 lados), es:. c) Un polígono convexo de 50 lados y una circunferencia, es:. 8. Para n figuras cualesquiera (convexas o no convexas), del mismo tipo, el máximo número de puntos de corte, es: kn(n 1)
7 Siendo k, el número máximo de puntos en que se cortan de dichas figuras. Por ejemplo: Encontremos la fórmula para calcular el máximo número de puntos de corte entre n elipses. Una elipse, es de la forma: Hallamos el valor de k graficando dos elipses, de modo que se tenga el número máximo de puntos de intersección entre ellas. Entonces para n elipses, la fórmula se obtiene al reemplazar este valor de k en la expresión anterior: 4n(n 1) n(n 1) puntos Ejemplo: Hallar una fórmula para calcular al máximo número de puntos de corte entre n figuras de la forma: Graficamos dos de dichas figuras a fin de obtener el valor de k:
8 Para n de estas figuras 9n(n 1) puntos, luego de reemplazar el valor de k en la fórmula de (8).
9 PROBLEMAS RESUELTOS Nota: Vamos a reemplazar el enunciado Máximo número de puntos de corte, por: MNPC. 1. Hallar el MNPC entre 10 rectas y 5 circunferencias, al cortarse todas estas figuras entre sí. El método de resolución consiste en contar por separados los puntos de corte: rectas solas, circunferencias solas y al final la combinación. El resultado se obtiene sumandos los parciales, Así: a) Las 10 rectas solas, se cortan como máximo, en: 10(9) = 45 b) Las 5 circunferencias: 5(4) = 0 puntos. c) Para el número de puntos entre rectas y circunferencias: Como cada recta corta a una circunferencia en puntos y son 5 circunferencias, entonces una recta corta a las 5 circunferencias en 5 = 10 puntos. Pero, son 10 rectas, entonces tendremos aquí: esto mismo, es: = 100 puntos
10 10 5 = 100 puntos Número de puntos entre una recta y una circunferencia Número de circunferencias Número de rectas Finalmente, sumando los resultados parciales de (a), (b) y (c): = 165 puntos. Hallar el MNPC entre 11 rectas secantes y 5 triángulos, al cortarse todas estas figuras entre sí. Veamos: a) Las 11 rectas, por sí solas: 11(10) = 55 puntos. b) Los 5 triángulos entre sí: 3 5(4) = 60 puntos. c) Las 11 rectas a los 5 triángulos:
11 11 5 = 100 puntos Número de puntos entre una recta y un triángulos Número de rectas Número de triángulos Luego, sumando los resultados (a), (b) y (c) : = 5 puntos. 3. Hallar el MNPC entre 1 rectas secantes, 15 circunferencias y 1 triángulos, al intersectarse todas estas figuras entre sí. El método es similar; evaluamos el máximo número de puntos de corte entre las rectas solas, las circunferencias entre sí, los triángulos por si solos y luego hacemos las combinaciones en grupos de dos. Así: a) Las 1 : 1(0) = 10 puntos b) Las 15 : 15(14) = 10 puntos c) Los 1 : 3 1(11) = 396 puntos d) 1 a 15 : 1 15 = 630 puntos Dos puntos
12 e) Las 1 a los 1 : 1 1 = 504 puntos Dos puntos f ) Las 15 a los = 1080 puntos Seis puntos El MNPC total lo obtenemos sumando los resultados parciales de (a) a (f): = 3030 puntos 4. Hallar el MNPC entre 1 triángulos y 10 cuadriláteros convexos, todos secantes entre sí.
13 Procedemos como antes: a) Los 1 triángulos se cortan como máximo, en 3 1(0) = 160 puntos. b) Los 10 cuadriláteros convexos: 4 10(9) = 360 puntos. c) Los 1 a los = 160 puntos 3 = 6 pts. Sumando lo obtenido en (a), (b) y (c): MNPC = = 880 puntos. 5. Hallar el MNPC entre 10 rectas paralelas, 5 rectas secantes y 6 triángulos, al intersectarse todas estas figuras entre sí. Tenemos: a) Las 10 rectas paralelas entre sí: cero puntos de corte. b) Las 5 rectas secantes por sí solas: 5(4) = 10 puntos
14 c) Los 6 : 3 6(5) = 90 puntos Ahora, en grupos de : d) 10 rectas paralelas y 5 secantes = 50 puntos Nros. de pts. entre una paralela y una secante Nros. de paralelas Nros. de secantes e) Las 10 rectas paralelas a los 6 triángulos: 10 6 = 10 puntos puntos paralelas triángulos f ) 5 rectas secantes y 6 triángulos:
15 5 6 = 60 puntos puntos secantes triángulos Sumando ahora, todos los resultados parciales: MNPC = MNPC = 330 puntos. 6. Si a un grupo de rectas de un plano, se le agrega una, el máximo número de puntos de corte se duplicaría. Hallar el número de rectas original. Si, inicialmente, hubieran n rectas, el número máximo de puntos de corte sería Al agregar una al grupo anterior (n + 1) rectas, éstas se cortan, en n(n + 1) puntos. n(n 1) puntos. (n + 1)(n + 1 1) Según enunciado, el segundo resultado debe ser el doble del primero. Luego, resolviendo esta sencilla ecuación: n = 3 rectas. 7. Si a un grupo de n rectas secantes se agrega una recta, el máximo número de puntos de corte aumentaría en 1. Hallar el valor de n. Como, al agregar una recta al grupo existente de n rectas, la nueva debe contar a cada una de las anteriores en un punto, entonces el MNPC se incrementará en n. Por lo tanto, n = Si a un grupo de n triángulos se le quita uno, el máximo número de puntos de corte disminuye en 18. Hallar n. Un triángulo corta a otro en 6 puntos, como máximo. Al extraer un triángulo al grupo de n, éste cortará a cada uno de los (n 1) restantes, en 6 puntos. Luego, 6(n 1) = 18 n = 4 9. Al duplicarse el número de rectas secantes, el máximo número de puntos de corte se quintuplica. Hallar el número inicial de rectas. n(n 1) Sean n el número inicial de rectas. Ellas determinan puntos.
16 Si se duplica el número de rectas, ahora tendremos n rectas que se cortan en Según el enunciado, este último resultado debe ser cinco veces el anterior. n(n 1) puntos. n(n 1) = 5 n(n 1), despejando n tenemos: n(n 1) 1 n(n 1) 1 n(n 1 1) n 1 = 5 = 5 = 5 4n = 5n 5 n(n 1) n(n 1) (n 1) 5n + 4n = 5 + n = 3 n = 3 / 1 / n 10. Si a un grupo de n polígonos convexos, de L lados cada uno, se agrega otro de la misma naturaleza y cantidad de lados, el máximo número de puntos que corta se duplica. Hallar n. Es fácil deducir que dos polígonos convexo de L lados cada uno se cortan como máximo en L puntos. Luego, el nuevo polígono corta al grupo de n, en Ln puntos. Como los n polígonos de L lados se cortan en Ln(n 1) puntos, según la fórmula, y al colocar el nuevo polígono, esta cantidad se duplica, entonces: Ln = Ln(n 1) = (n 1), donde n = Encontrar la cantidad de decágonos que se intersectan, sabiendo que al hacerlo determinan como máximo 650 puntos, en los cuales están también considerados los vértices. Sea n el número de decágonos. Luego: Número total de vértices: 10n Número máximo de puntos de intersección : 10n(n 1), donde 10n + 10n(n 1) = 650. n = 65 n = 5 1. Si a un conjunto de rectas secantes, se le agregase una cantidad igual de rectas, su número máximo de puntos de corte aumentaría en 330. Calcular cuántas rectas tiene el conjunto.
17 Si, inicialmente, hubieran n rectas, éstas se cortarían, en n(n 1) puntos. Al agregar otras n rectas al grupo anterior, habrán n rectas que se cortarían en puntos. n(n 1) Usando el dato numérico n(n 1) = n(n 1) En efecto, 3n n 660 = 0 (3n + 44)(n 15) = 0, de donde n = Se tiene n circunferencias secantes. Si se quitan dos circunferencias, al número máximo de puntos de corte disminuye en 30. Hallar n. Las n circunferencias secantes: n(n 1) puntos. Al quitar, las (n ) circunferencias restantes, se cortan en: (n ) [(n ) 1] puntos. Con el dato: n(n 1) 30 = (n ) [(n ) 1] Resolviendo, hallamos n = Encontrar el número máximo de puntos de corte que hay entre F decágonos convexos y F cuadriláteros convexos. { F decágonos convexos F Cuadriláteros convexos a) Los F decágonos (10 lados cada uno): 10F (F 1) b) Los F cuadriláteros: 4F (F 1) c) Los F decágonos con los F cuadriláteros.
18 Número de puntos de corte entre (Número de decágonos ) 1 decágono y 1 cuadrilátero Así ( 4) (F )(F ) = 8F ( ) Número de cuadriláteros Finalmente, sumanod los resultados parciales: 10F (F 1)+4F (F 1)+8F F (11F 7) puntos. 15. Hallar el máximo número de puntos de intersección de 10 cuadriláteros no convexos. Debemos usar la fórmula vista en el número (8) de la teoría, para encontrar el MNPC entre n cuadriláteros no convexos y aquí reemplazar el valor de n: MNP C = Kn(n 1) puntos K es el número máximo de puntos en que se cortan cuadriáteros no convexos. Para ello, tenemos el siguiente gráfico: K = 16 puntos Entonces, para n de estas figuras, la fórmula es: MNP C = puntos. Y si n = 10: MNP C = 8 10(9) = 70 puntos. 16n(n 1) MNP C = 8n(n 1) 16. Deducir una fórmula para encontrar el número total de puntos en que se cortan n circunferencias dispuestas como se indica:
19 El análisis lo hacemos incrementando cada vez, en uno, el número de circunferencias. Debemos relacionar el número de puntos con el número de circunferencias. Así: Número de circunferencias Número de puntos puntos ( 1) 4 puntos (3 1) 6 puntos (4 1) 8 puntos (5 1) 10 puntos (6 1). n circunferencias. (n 1) puntos (fórmula) 17. En la figura, las rectas L 1 y L son paralelas entre sí; sobre L 1 se toman m puntos y sobre L, n puntos. Hallar el máximo número de puntos de corte en que las rectas determinadas por los m puntos de L 1 y n puntos de L, cortan a la circunferencia.
20 Cada recta intersecta a la circunferencia, como máximo, en puntos. El número de rectas determinadas, lo obtenemos así: Un punto de L 1 con los N puntos de L determinan n rectas. Luego, los m puntos de L 1 con los n puntos de L, determinan m n rectas. Entonces, el número de puntos en que esta cantidad (m n) de rectas corta a la circunferencia, es: m n, como máximo. 18. Hallar MNPC entre n circunferencias, n rectas secantes y n triángulos, al cortarse todas estas figuras entre sí. n MNP C = n n circunferencias rectas triángulos a) Las n circunferencias: n(n 1) puntos. b) Las n rectas secantes: n(n 1) = n(n 1) c) Los n triángulos: 3n(n 1) puntos. d) n circunferencias a n rectas: n n = 4n punto. e) n circunferencias a n triángulos: 6 n n = 6n puntos. f ) n rectas a n triángulos: n n = 4n puntos. Sumamos los resultados parciales: efectuando, MNP C = 5n(4n 1) puntos.
21 19. Se muestran n circunferencias concéntricas y otras n circunferencias menores formando una argolla. El máximo número de puntos de corte, es: a) El número de puntos entre las circunferencias que forman la argolla se determina así: La argolla se obtiene al intersectar las circunferencias extremas ( puntos más): n circunferencias en esta posición: (n 1) puntos. Entonces, el número de puntos en la argolla será: (n 1) + = n puntos... (1). b) Cada circunferencia de la argolla corta a una de las concéntricas, en puntos. Así que, las n circunferencias de la argolla cortan a las n concéntricas, en: n n = n... () el número total de puntos de corte se obtiene sumando los resultados (1) y (): MNP C = n + n = n(n + 1) 0. Al número máximo de puntos de corte entre n polígonos convexos, de L lados cad auno, se le suma el máximo número de puntos de corte entre n polígonos de L lados cada uno, obteniéndose en total 630 puntos. Hallar L + n MNPC entre n polígonos de L lados es Ln(n 1). MNPC entre n polígonos de L lados es Ln(n 1). Según enunciado: Ln(n 1) + Ln(n 1) = 630 3Ln(n 1) = 630 Ln(n 1) = 10 En factores primos, 10 es Escrito este producto en forma que contenga dos factores consecutivos, para luego comparar con el primer miembro, tenemos: Ln(n 1) = De donde: L = 7 y n = 6 L + n = 13
22 PROBLEMAS PROPUESTOS 1. Hallar el MNPC entre 11 circunferencias y 8 triángulos al intersectarse todas estas figuras entre sí. a) 76 b) 706 c) 806 d) 906 e) 78. Hallar el MNPC entre 6 cuadriláteros convexos, 11 pentágonos convexos y 1 ocógonos convexos, al intersectarse todas estas figuras entre sí. 7. n polígonos convexos de l lados cada uno se intersectan en 640 puntos, como máximo. Si quitamos un polígono, el número de puntos de intersección disminuye en 31. Hallar (l + n). a) 33 b) 40 c) 4 d) 46 e) Hallar el MNPC entre 5 elipses y 11 cuadriláteros no convexos. a) 7414 b) 7604 c) 6704 d) 4706 e) 7456 a) 1360 b) 160 c) 1460 d) 1560 e) Si a un grupo de n rectas secantes se agregan dos rectas, el máximo número de puntos de corte aumentaría en 15. Hallar n. a) 5 b) 6 c) 7 d) 8 e) N.A. 4. Hallar el número máximo de puntos que corte, entre 5 octógonos y 10 icoságonos, todos convexos. a) 670 b) 770 c) 760 d) 870 e) Encontrar el número máximo de puntos de corte que hay entre 3 polígonos convexos de k lados y 6 polígonos convexos de 3k lados cada uno. a) 10K b) 11K c) 1K d) 164K e) 174K 10. Luego de disponer 50 circunferencias y 0 rectas paralelas, como indica la figura siguiente, hallar el máximo número de puntos de corte. 5. Hallar el máximo número de puntos de corte entre 10 rectas secantes, 6 triángulos y 11 cuadriláteros convexos. a) 1311 b) 131 c) 113 d) 131 e) N.A. a) 098 b) 089 c) 090 d) 080 e) Calcular el máximo número de puntos de intersección de 10 rectas paralelas, 1 rectas ecantes y 16 circunferencias secantes rectas secantes, 8 circunferencias y 9 triángulos, se cortan como máximo, en: a) 1130 c) 316 e) 1098 a) 963 pts. c) 693 pts. e) N.A. b) 306 d) 746 b) 396 pts. d) 973 pts.
23 1. 5 ángulos y 8 circunferencias, se cortan como máximo, en: a) 60 b) 61 c) 6 d) 63 e) 64 a) 136 pts. b) 96 pts. c) 160 pts. d) 46 pts. e) 16 pts rectas paralelas, 6 secantes y 1 pentágonos se cortan como máximo en: a) 109 pts. b) 99 pts. c) 119 pts. d) 1309 pts. e) N.A. 14. Se tiene n triángulos secantes. si se quitan 3 triángulos, el número máximo de puntos de corte disminuye en 54. Hallar n. a) 10 b) 6 c) 7 d) 5 e) Hallar el máximo número de puntos de corte entre n elipses y n rectas, todas secantes. a) 4n(3n 1) b) n(n+) c) 4n(n 1) d) 3n(4n 1) e) 3n(4n + 1) 16. Hallar el máximo número de puntos de interseccion entre 5 octógonos y 6 decágonos convexos. a) 460 b) 480 c) 940 d) 840 e) N.A. 17. n rectas secantes, n cicunferencias y n triángulos, se cortan como máximo, en: a) n(9n 9) c) n(n 1) b) n (9n 9) d) n (9n 9) 18. Hallar el máximo número de puntos de corte de 5 rectas que tienen un punto común y 5 circunferencias que tienen un punto común. 19. Hallar el número máximo de puntos de corte, entre 10 rectas paralelas y 50 curcunferencias dispuestas así: a) 1980 b) 1890 c) 1098 d) 1690 e) N.A. 0. Hallar el número de puntos de corte entre 10 curcunferencias concéntricas y 0 rectas que pasan por el centro común. a) 400 b) 401 c) 00 d) 01 e) De un conjunto de 30 rectas, 18 son secantes, 8 son paralelas que tienen una determinada dirección y las 4 restantes son también paralelas pero tienen una dirección distintas a las anteriores. Hallar el máximo número de puntos de corte. a) 400 b) 401 c) 40 d) 403 e) 404. Se tiene un grupo de recta secantes, cuyo número se desea calcular sabiendo que si se tuviera rectas más, se obtendrían 18 puntos de corte más que si se tuviera una recta menos. a) b) 4 c) 6 d) 8 e) 9 3. Existen varias rectas coplanares que determinan 9 puntos de corte como máximo. Si de
24 ellas son paralelas entre sí, hallar el número de rectas. a) 10 b) 9 c) 8 d) 5 e) 7 4. Si se tienen 5 grupos de 3 rectas paralelas entre sí cada una, hallar el máximo número de puntos de corte de las rectas. a) 60 b) 70 c) 80 d) 90 e) Cuatro rectas secantes y tres circunferencias originan el mimo número de puntos de corte de n triángulos. Hallar n. a) 6 b) 8 c) 4 d) 7 e) 9 6. Hallar el máximo número de puntos de corte de cuatro grupos de triángulos de a 3, si los triángulos de cada grupo no se cortan entre sí, pero sons ecantes con los triángulos de los otros grupos. a) 360 b) 308 c) 70 d) 34 e) Hallar el máximo número de puntos de corte de 10 cuadriláteros convexos secantes y 0 circunferencias, que no se cortan entre sí. a) 1960 b) 1980 c) 1700 d) 140 e) Hallar el máximo número de puntos de corte de los siguientes grupos: cuatro cuadriláteros convexos, cinco pentágonos convexos. Los polígonos de cada grupo no se cortan entre ellos pero sí cortan a los polígonos del otro grupo. a) 160 b) 10 c) 150 d) 170 e) Hallar el máximo número de puntos de corte para 10 cuadriláteros convexos, 10 octógonos convexos y 10 icoságonos convexos. a) 700 b) 6080 c) 600 d) 700 e) Hallar el máximo número de puntos de corte para 30 triángulos que tienen un punto en común. a) 100 b) 176 c) 716 d) 160 e) Se tiene n triángulos y n cuadriláteros convexos. Si al máximo número de puntos de corte de los triángulos se aumenta el número total de lados de los triángulos, más el máximo número de puntos de corte de los cuadriláteros, más el número total de los ángulos de los cuadriláteros se obtiene Hallar n. a) 16 b) 18 c) 14 d) 1 e) 0 3. Cuál es el máximo número de puntos de corte de N cuadriláteros secantes y N triángulos secantes (polígonos convexos)? a) 1N b) N(13N 7) c) N(7n 6) d) N(N ) e) N(1N 5) 33. Cuál es el máximo número de puntos de corte para N circufnerencias secnates y N pentágonos convexos secantes? a) N(8N ) b) N(8n 1) c) N(8N 3) d) N(8N 5) e) N
25 34. Cuál es el máximo número de puntos de corte de N cuadriláteros convexos y N pentágonos convexos? a) N(17N 9) b) N(9N 4) c) N(7N 3) d) N(17N 8) e) 3N 35. En cuánto disminuye el máximo número de puntos de corte de 8 cuadriláteros secantes y 6 hexágonos secantes, si se quitan 3 cuadriláteros y 3 hexágonos (polígonos convexos). a) 40 b) 360 c) 45 d) 51 e) Si se anulan 3 rectas de un grupo que se están cortando, el máximo número de puntos de corte disminuirá en 57.? Cuántas rectas forman dicho grupo inicial? a) 31 b) 1 c) 19 d) 7 e) Hallar el máximo número de rectas que pasan por el máximo número de puntos de intersección de 15 rectas secantes. a) 5460 b) 5640 c) 4560 d) 560 e) Hallar el máximo número de puntos de corte de los siguientes grupos: cuatro hexágonos convexos, cinco decágonos convexos y seis octógonos convexos. Los polígonos de cada grupo no se cortan entre ellas pero sí con los polígonos de los otros grupos. a) 1000 b) 100 c) 1004 d) 1006 e) Hallar el máximo número de puntos de corte de n pentágonos, n octógonos y n decágonos (todos convexos). 40. Hallar el máximo número de puntos de corte para 30 triángulos que tienen puntos comunes. a) 70 b) 600 c) 76 d) 67 e) Hallar el máximo número de puntos de corte de 5 cuadriláteros cóncavos y 10 triángulos. a) 80 b) 830 c) 840 d) 850 e) Cuál es el máximo número de puntos de corte de 4 octógonos convexos secantes, 5 decágonos convexos secantes y 6 dodecágonos convexos secantes? a) 1960 b) 1690 c) 1980 d) 1890 e) Hallar el máximo número de puntos de corte para n polígonos convexos de n lados, que tienen puntos comunes. a) n(n 1) b) n(n 1) + c) n(n 1) + d) n + e) (n 1) Hallar el máximo número de puntos de corte de n grupos de n polígonos convexos de n lados, conociendo que los polígonos de cada grupo entre ellos no se cortan pero sí con los polígonos de los otros grupos. a) n (n 1) b) n 3 (n 1) c) n(n 1) d) n 4 (n 1) e) n (n + 1) 45. Hallar el máximo número de puntos de corte de n rectas secantes, n rectas paralelas y n circunferencias secantes. a) n (13n 3) d) n (7n 3) a) 1000 b) 100 c) 1004 d) 1006 e) 1008 b) n (11n ) c) n (9n 5) e) n (13n 1)
MATEMÁTICA I GEOMETRÍA PLANA. POLÍGONOS DE MÁS DE CUATRO LADOS ING. SANTIAGO FIGUEROA LORENZO
 MATEMÁTICA I GEOMETRÍA PLANA. POLÍGONOS DE MÁS DE CUATRO LADOS ING. SANTIAGO FIGUEROA LORENZO LÍNEA POLIGONAL POLÍGONOS Es la figura que esta formado por segmento de recta unido por sus extremos dos a
MATEMÁTICA I GEOMETRÍA PLANA. POLÍGONOS DE MÁS DE CUATRO LADOS ING. SANTIAGO FIGUEROA LORENZO LÍNEA POLIGONAL POLÍGONOS Es la figura que esta formado por segmento de recta unido por sus extremos dos a
polígono 3 Triángulo 4 Cuadrilátero 5 Pentágono 6 Hexágono 7 Heptágono 8 Octógono 9 Eneágono 10 Decágono 11 Undecágono 12 Dodecágono 20 Icoságono
 TEMA: POLÍGONOS Y ÁNGULOS. POLÍGONOS REGULARES. POLÍGONOS Un polígono es una figura cerrada cuyos lados son segmentos. La palabra polígonos se puede interpretar como: figura de muchos ángulos. Los triángulos,
TEMA: POLÍGONOS Y ÁNGULOS. POLÍGONOS REGULARES. POLÍGONOS Un polígono es una figura cerrada cuyos lados son segmentos. La palabra polígonos se puede interpretar como: figura de muchos ángulos. Los triángulos,
Polígonos IES BELLAVISTA
 Polígonos IES BELLAVISTA Polígonos: definiciones Un polígono es la porción de plano limitada por rectas que se cortan. Polígono regular: el que tiene todos los lados y ángulos iguales. Polígono irregular:
Polígonos IES BELLAVISTA Polígonos: definiciones Un polígono es la porción de plano limitada por rectas que se cortan. Polígono regular: el que tiene todos los lados y ángulos iguales. Polígono irregular:
Objet ivo. Reconocer los elementos del polígono y relacionarlos. en cualquier polígono conociendo su número de lados.
 POLÍGONOS I Objet ivo Reconocer los elementos del polígono y relacionarlos en cualquier polígono conociendo su número de lados. DEFINICIÓN Son figuras formadas por segmentos no alineados y de extremos
POLÍGONOS I Objet ivo Reconocer los elementos del polígono y relacionarlos en cualquier polígono conociendo su número de lados. DEFINICIÓN Son figuras formadas por segmentos no alineados y de extremos
Clasificación de polígonos según sus lados
 POLÍGONOS Polígonos Un polígono es la región del plano limitada por tres o más segmentos. Elementos de un polígono Lados Son los segmentos que lo limitan. Vértices Son los puntos donde concurren dos lados.
POLÍGONOS Polígonos Un polígono es la región del plano limitada por tres o más segmentos. Elementos de un polígono Lados Son los segmentos que lo limitan. Vértices Son los puntos donde concurren dos lados.
Cuadriláteros y circunferencia
 CLAVES PARA EMPEZAR Un triángulo isósceles tiene dos lados iguales: b c. Como es rectángulo, se cumple el teorema de Pitágoras: 10 2 b 2 b 2 100 2b 2 b 7,07. Los dos lados miden 7,07 cm cada uno. r A C
CLAVES PARA EMPEZAR Un triángulo isósceles tiene dos lados iguales: b c. Como es rectángulo, se cumple el teorema de Pitágoras: 10 2 b 2 b 2 100 2b 2 b 7,07. Los dos lados miden 7,07 cm cada uno. r A C
POLÍGONOS P 6 P 1 P 3. Interior del polígono P 8. P n 1 P 7
 POLÍGONOS DEFINICIÓN Sean P 1, P 2,..., P n un conjunto de n puntos distintos de un plano con n 3 y sean los n segmentos P1P 2, P 2 P 3,..., P n 1P n, P n P 1 tales que: (1) Ningún par de segmentos se
POLÍGONOS DEFINICIÓN Sean P 1, P 2,..., P n un conjunto de n puntos distintos de un plano con n 3 y sean los n segmentos P1P 2, P 2 P 3,..., P n 1P n, P n P 1 tales que: (1) Ningún par de segmentos se
INSTITUTO RAÚL SCALABRINI ORTIZ GEOMETRIA POLÍGONOS
 GEOMETRIA POLÍGONOS (1) Si un polígono tiene un ángulo central de 45º Cuántos lados tiene? (2) Inscribir en distintas circunferencias los siguientes polígonos: a) Triángulo equilátero b) Pentágono regular
GEOMETRIA POLÍGONOS (1) Si un polígono tiene un ángulo central de 45º Cuántos lados tiene? (2) Inscribir en distintas circunferencias los siguientes polígonos: a) Triángulo equilátero b) Pentágono regular
Geometría Básica 43 UNIVERSIDAD DE LOS ANDES - TÁCHIRA DEPARTAMENTO DE CIENCIAS CARRERA EDUCACIÓN BÁSICA INTEGRAL
 Geometría Básica 43 POLIGONOS UNIVERSIDAD DE LOS ANDES - TÁCHIRA DEPARTAMENTO DE CIENCIAS CARRERA EDUCACIÓN BÁSICA INTEGRAL SEGMENTOS CONCATENADOS Y CONSECUTIVOS Consideremos los segmentos ab y bc, donde
Geometría Básica 43 POLIGONOS UNIVERSIDAD DE LOS ANDES - TÁCHIRA DEPARTAMENTO DE CIENCIAS CARRERA EDUCACIÓN BÁSICA INTEGRAL SEGMENTOS CONCATENADOS Y CONSECUTIVOS Consideremos los segmentos ab y bc, donde
- 1 - RECTAS Y ÁNGULOS. Tipos de ángulos Los ángulos se clasifican según su apertura: -Agudos: menores de 90º. Rectas
 Alonso Fernández Galián Geometría plana elemental Rectas RECTAS Y ÁNGULOS Una recta es una línea que no está curvada, y que no tiene principio ni final. Tipos de ángulos Los ángulos se clasifican según
Alonso Fernández Galián Geometría plana elemental Rectas RECTAS Y ÁNGULOS Una recta es una línea que no está curvada, y que no tiene principio ni final. Tipos de ángulos Los ángulos se clasifican según
TEMA 9. RECTAS Y ÁNGULOS. Bisectriz de un ángulo
 TEMA 9. RECTAS Y ÁNGULOS RECTAS EN EL PLANO ÁNGULOS Rectas Segmento Semirrectas Mediatriz de un segmento Ángulos según su abertura: Recto, agudo, obtuso, llano, completo, cóncavo, Ángulos según su posición:
TEMA 9. RECTAS Y ÁNGULOS RECTAS EN EL PLANO ÁNGULOS Rectas Segmento Semirrectas Mediatriz de un segmento Ángulos según su abertura: Recto, agudo, obtuso, llano, completo, cóncavo, Ángulos según su posición:
Polígono. Superficie plana limitada por una línea poligonal cerrada.
 POLÍGONO B C r A d O a l E D Polígono. Superficie plana limitada por una línea poligonal cerrada. r O r =a Elementos, puntos y líneas en los polígonos. (Regulares) LADO Cada uno de los segmentos de la
POLÍGONO B C r A d O a l E D Polígono. Superficie plana limitada por una línea poligonal cerrada. r O r =a Elementos, puntos y líneas en los polígonos. (Regulares) LADO Cada uno de los segmentos de la
Polígonos Regulares: Definición de polígono:
 1 Polígonos Regulares: Definición de polígono: Un polígono es una figura plana cerrada, limitada por segmentos de recta llamados lados del polígono. Los puntos donde se unen dos lados consecutivos se llaman
1 Polígonos Regulares: Definición de polígono: Un polígono es una figura plana cerrada, limitada por segmentos de recta llamados lados del polígono. Los puntos donde se unen dos lados consecutivos se llaman
8. UNIDAD DIDACTICA 8: TANGENCIAS Y ENLACES
 8. UNIDAD DIDACTICA 8: TANGENCIAS Y ENLACES 8.1. TANGENCIAS Se dice que dos figuras planas son tangentes cuando tienen un solo punto en común, al que se conoce como punto de tangencia. Las tangencias pueden
8. UNIDAD DIDACTICA 8: TANGENCIAS Y ENLACES 8.1. TANGENCIAS Se dice que dos figuras planas son tangentes cuando tienen un solo punto en común, al que se conoce como punto de tangencia. Las tangencias pueden
- Propiedades de las figuras planas
 MATEMÁTICAS 1ºESO TEMA 10 PROPIEDADES DE LAS FIGURAS PLANAS 1 Tema 10 - Propiedades de las figuras planas 1 Escribe de línea poligonal y dibuja una: 2 Escribe el concepto de polígono. Dibuja un polígono
MATEMÁTICAS 1ºESO TEMA 10 PROPIEDADES DE LAS FIGURAS PLANAS 1 Tema 10 - Propiedades de las figuras planas 1 Escribe de línea poligonal y dibuja una: 2 Escribe el concepto de polígono. Dibuja un polígono
Colegio Internacional Torrequebrada. Departamento de Matemáticas
 Geometría. Problema 1: Calcula la distancia del punto P(1, 1, 1) a la recta Problema 2: Dadas las rectas, se pide: a) Analiza su posición relativa. b) Halla la ecuación general del plano π que contiene
Geometría. Problema 1: Calcula la distancia del punto P(1, 1, 1) a la recta Problema 2: Dadas las rectas, se pide: a) Analiza su posición relativa. b) Halla la ecuación general del plano π que contiene
FIGURAS PLANAS. Es una figura plana delimitada por una línea poligonal cerrada.
 1.- Qué es un polígono? FIGURAS PLANAS Es una figura plana delimitada por una línea poligonal cerrada. Los elementos de un polígono son: - Lado: Se llama lado a cada segmento que limita un polígono - Vértice:
1.- Qué es un polígono? FIGURAS PLANAS Es una figura plana delimitada por una línea poligonal cerrada. Los elementos de un polígono son: - Lado: Se llama lado a cada segmento que limita un polígono - Vértice:
Figuras planas. Definiciones
 Figuras planas Definiciones Polígono: definición Un polígono es una figura plana (yace en un plano) cerrada por tres o más segmentos. Los lados de un polígono son cada uno de los segmentos que delimitan
Figuras planas Definiciones Polígono: definición Un polígono es una figura plana (yace en un plano) cerrada por tres o más segmentos. Los lados de un polígono son cada uno de los segmentos que delimitan
Trazado de rectas paralelas y perpendiculares
 Trazado de rectas paralelas y perpendiculares Recuerda Dos rectas paralelas son aquellas que no llegan nunca a cortarse, y son perpendiculares cuando se cortan formando ángulos rectos. Dibuja una recta
Trazado de rectas paralelas y perpendiculares Recuerda Dos rectas paralelas son aquellas que no llegan nunca a cortarse, y son perpendiculares cuando se cortan formando ángulos rectos. Dibuja una recta
TEMA 12: PROBLEMAS MÉTRICOS EN EL ESPACIO.
 TEMA 12: PROBLEMAS MÉTRICOS EN EL ESPACIO. 1. Distancia entre dos puntos: Si A= (a 1, a 2, a 3 ) y B= (b 1, b 2, b 3 ), entonces: 2.Ángulo entre elementos del espacio: Ángulo entre dos rectas: d (A, B)
TEMA 12: PROBLEMAS MÉTRICOS EN EL ESPACIO. 1. Distancia entre dos puntos: Si A= (a 1, a 2, a 3 ) y B= (b 1, b 2, b 3 ), entonces: 2.Ángulo entre elementos del espacio: Ángulo entre dos rectas: d (A, B)
ESCUELA PREPARATORIA OFICIAL NO.16 MATERÍA: GEOMETRÍA ANALITICA GUÍA DE ESTUDIO PARA LA ÚLTIMA OPORTUNIDAD DE ACREDITAR LA MATERÍA
 Geometría analítica 1.- Ecuación de la recta 2.- Cónicas 3.-Ecuación de la parábola UNIDAD II: CONICAS (CIRCUNFERENCIA Y PARABOLAS) Una superficie cónica de revolución está engendrada por la rotación de
Geometría analítica 1.- Ecuación de la recta 2.- Cónicas 3.-Ecuación de la parábola UNIDAD II: CONICAS (CIRCUNFERENCIA Y PARABOLAS) Una superficie cónica de revolución está engendrada por la rotación de
Departamento de matemáticas
 Geometría con solución Problema 1: Sea r y s las rectas dadas por: a) Hállese el valor de m para que ambas rectas se corten. b) Para m = 1, hállese la ecuación del plano que contiene a r y s Problema 2:
Geometría con solución Problema 1: Sea r y s las rectas dadas por: a) Hállese el valor de m para que ambas rectas se corten. b) Para m = 1, hállese la ecuación del plano que contiene a r y s Problema 2:
Una recta es una línea (de puntos) que no tiene ni principio ni final. Un segmento es la parte de una recta que se encuentra entre 2 puntos.
 RECTAS Y ÁNGULOS RECTAS Una recta es una línea (de puntos) que no tiene ni principio ni final. Un punto divide a una recta en 2 semirrectas. Un segmento es la parte de una recta que se encuentra entre
RECTAS Y ÁNGULOS RECTAS Una recta es una línea (de puntos) que no tiene ni principio ni final. Un punto divide a una recta en 2 semirrectas. Un segmento es la parte de una recta que se encuentra entre
TEMA 10: FORMAS Y FIGURAS PLANAS. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco.
 2009 TEMA 10: FORMAS Y FIGURAS PLANAS. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/2009 TEMA 10: FORMAS Y FIGURAS PLANAS. 1. Polígonos. 2.
2009 TEMA 10: FORMAS Y FIGURAS PLANAS. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/2009 TEMA 10: FORMAS Y FIGURAS PLANAS. 1. Polígonos. 2.
Polígonos y Triángulos
 7 o Básico 2015 Profesor Alberto Alvaradejo Ojeda 1. Polígono Un polígono es una figura plana cerrada formada por trazos o segmentos. Los polígonos se pueden clasificar en: Cóncavos: son los aquellos polígonos
7 o Básico 2015 Profesor Alberto Alvaradejo Ojeda 1. Polígono Un polígono es una figura plana cerrada formada por trazos o segmentos. Los polígonos se pueden clasificar en: Cóncavos: son los aquellos polígonos
Proyecto Guao POLÍGONOS
 POLÍGONOS Qué pasaría si te preguntaran cuántos lados tiene un polígono? Cómo describirías el polígono? Después de leer este concepto, vas a poder clasificar un polígono en función de su número de lados.
POLÍGONOS Qué pasaría si te preguntaran cuántos lados tiene un polígono? Cómo describirías el polígono? Después de leer este concepto, vas a poder clasificar un polígono en función de su número de lados.
UNIDAD 3 : ELEMENTOS GEOMÉTRICOS
 UNIDAD 3 : ELEMENTOS GEOMÉTRICOS 3.A.1 Características de un lugar geométrico 3.A ELEMENTOS DE GEOMETRÍA PLANA Se denomina lugar geométrico a todo conjunto de puntos que cumplen una misma propiedad o que
UNIDAD 3 : ELEMENTOS GEOMÉTRICOS 3.A.1 Características de un lugar geométrico 3.A ELEMENTOS DE GEOMETRÍA PLANA Se denomina lugar geométrico a todo conjunto de puntos que cumplen una misma propiedad o que
Carrera: Diseño Industrial
 POLÍGONOS 1) Dados los siguientes polígonos se pide determinar cuales de ellos son cóncavos y cuales convexos. Justifique sus respuestas. a) b) c) 2) En los polígonos graficados a continuación indique
POLÍGONOS 1) Dados los siguientes polígonos se pide determinar cuales de ellos son cóncavos y cuales convexos. Justifique sus respuestas. a) b) c) 2) En los polígonos graficados a continuación indique
POLÍGONOS POLÍGONOS. APM Página 1
 POLÍGONOS 1. Polígonos. 1.1. Elementos de un polígono. 1.2. Suma de los ángulos interiores de un polígono. 1.3. Diagonales de un polígono. 1.4. Clasificación de los polígonos. 2. Polígonos regulares. Elementos.
POLÍGONOS 1. Polígonos. 1.1. Elementos de un polígono. 1.2. Suma de los ángulos interiores de un polígono. 1.3. Diagonales de un polígono. 1.4. Clasificación de los polígonos. 2. Polígonos regulares. Elementos.
n Por ejemplo, en un pentágono tenemos que saber que sus ángulos suman 540º y cada ángulo del pentágono son 108º.
 MATEMÁTICAS 3º ESO TEMA 10 PROBLEMAS MÉTRICOS EM EL PLANO- 1. ÁNGULOS EN LOS POLÍGONOS La suma de los ángulos de un polígono de n lados es: 180º (n-2) 180º(n - 2) La medida de cada ángulo de un polígono
MATEMÁTICAS 3º ESO TEMA 10 PROBLEMAS MÉTRICOS EM EL PLANO- 1. ÁNGULOS EN LOS POLÍGONOS La suma de los ángulos de un polígono de n lados es: 180º (n-2) 180º(n - 2) La medida de cada ángulo de un polígono
Líneas paralelas. Se llaman líneas paralelas las que se hallan en un mismo plano y no se intersectan por mas que se prolonguen.
 1.1 ngulos entre paralelas. apítulo 1. onceptos ásicos de Geometría Líneas paralelas. Se llaman líneas paralelas las que se hallan en un mismo plano y no se intersectan por mas que se prolonguen. Si una
1.1 ngulos entre paralelas. apítulo 1. onceptos ásicos de Geometría Líneas paralelas. Se llaman líneas paralelas las que se hallan en un mismo plano y no se intersectan por mas que se prolonguen. Si una
XXIX TORNEO INTERNACIONAL DE LAS CIUDADES PRIMAVERA DEL HEMISFERIO NORTE NIVEL JUVENIL
 XXIX TORNEO INTERNACIONAL DE LAS CIUDADES PRIMAVERA DEL HEMISFERIO NORTE NIVEL JUVENIL 1. Juan multiplicó dos números enteros positivos consecutivos. a) Demostrar que Pedro puede agregar dos dígitos a
XXIX TORNEO INTERNACIONAL DE LAS CIUDADES PRIMAVERA DEL HEMISFERIO NORTE NIVEL JUVENIL 1. Juan multiplicó dos números enteros positivos consecutivos. a) Demostrar que Pedro puede agregar dos dígitos a
POLÍGONOS REGULARES. Ejemplo: Hexágono 360º / 6 = 60º. TRIÁNGULO 3 120º 60º 180º (3-2)= 180º CUADRADO 4 90º 90º 180º (4-2)= 360º
 A B G C F LADO D E A B G C F D E APOTEMA DIAGONALES RADIO 360º / n (180º- ) ELEMENTOS Y PROPIEDADES DE LOS POLÍGONOS REGULARES. (Ilustración nº 1). Diagonal: Es el segmento que une dos vértices no consecutivos.
A B G C F LADO D E A B G C F D E APOTEMA DIAGONALES RADIO 360º / n (180º- ) ELEMENTOS Y PROPIEDADES DE LOS POLÍGONOS REGULARES. (Ilustración nº 1). Diagonal: Es el segmento que une dos vértices no consecutivos.
CICLO ESCOLAR: FEBRERO JULIO 2016
 SECRETARIA DE EDUCACIÓN PÚBLICA SUBSECRETARIA DE EDUCACIÓN MEDIA SUPERIOR DIRECCION GENERAL DE EDUCACIÓN TECNOLOGICA INDUSTRIAL CENTRO DE ESTUDIOS TECNOLOGICO INDUSTRIAL Y DE SERVICIOS, No. 5 GERTRUDIS
SECRETARIA DE EDUCACIÓN PÚBLICA SUBSECRETARIA DE EDUCACIÓN MEDIA SUPERIOR DIRECCION GENERAL DE EDUCACIÓN TECNOLOGICA INDUSTRIAL CENTRO DE ESTUDIOS TECNOLOGICO INDUSTRIAL Y DE SERVICIOS, No. 5 GERTRUDIS
El polígono es una porción del plano limitado por una línea poligonal cerrada.
 UNIDAD 12: GEOMETRÍA PLANA 12.1. Los polígonos: Elementos El polígono es una porción del plano limitado por una línea poligonal cerrada. Un polígono se nombra con las letras mayúsculas situadas en los
UNIDAD 12: GEOMETRÍA PLANA 12.1. Los polígonos: Elementos El polígono es una porción del plano limitado por una línea poligonal cerrada. Un polígono se nombra con las letras mayúsculas situadas en los
SOLUCIONES A LAS ACTIVIDADES DE CADA EPÍGRAFE
 Pág. 1 PÁGINA 246 REFLEXIONA En la inauguración de la Casa de la Cultura observamos, entre otras, las siguientes figuras: Todas ellas son polígonos. Cuáles crees que son regulares? Explica por qué crees
Pág. 1 PÁGINA 246 REFLEXIONA En la inauguración de la Casa de la Cultura observamos, entre otras, las siguientes figuras: Todas ellas son polígonos. Cuáles crees que son regulares? Explica por qué crees
Tema 7: Geometría Analítica. Rectas.
 Tema 7: Geometría Analítica. Rectas. En este tema nos centraremos en estudiar la geometría en el plano, así como los elementos que en este aparecen como son los puntos, segmentos, vectores y rectas. Estudiaremos
Tema 7: Geometría Analítica. Rectas. En este tema nos centraremos en estudiar la geometría en el plano, así como los elementos que en este aparecen como son los puntos, segmentos, vectores y rectas. Estudiaremos
Los elementos básicos de la Geometría Plana son el punto, la línea, y el plano.
 GEOMETRÍA PLANA Dibujo Geométrico La geometría es la parte de las matemáticas que estudia las propiedades y las medidas de las figuras planas y tridimensionales en el espacio. La palabra procede de dos
GEOMETRÍA PLANA Dibujo Geométrico La geometría es la parte de las matemáticas que estudia las propiedades y las medidas de las figuras planas y tridimensionales en el espacio. La palabra procede de dos
Ángulos consecutivos, suplementarios, adyacentes, opuestos por el vértice y complementarios.
 ÁNGULOS Dadas dos semirrectas de origen común (Ox, Oy), no opuestas ni coincidentes, llamaremos ángulo convexo de vértice O, a la intersección del semiplano de borde la recta sostén de Ox, que contiene
ÁNGULOS Dadas dos semirrectas de origen común (Ox, Oy), no opuestas ni coincidentes, llamaremos ángulo convexo de vértice O, a la intersección del semiplano de borde la recta sostén de Ox, que contiene
open green road Guía Matemática CUADRILÁTEROS tutora: Jacky Moreno .co
 Guía Matemática CUADRILÁTEROS tutora: Jacky Moreno.co 1. Polígonos Epistemológicamente, la palabra polígono significa muchos ángulos. Los polígonos son figuras cerradas planas que están formadas por la
Guía Matemática CUADRILÁTEROS tutora: Jacky Moreno.co 1. Polígonos Epistemológicamente, la palabra polígono significa muchos ángulos. Los polígonos son figuras cerradas planas que están formadas por la
El punto de unión de cada par de segmentos se denomina ángulo. El numero de lados, ( y por tanto de ángulos) ha de ser mayor o igual a tres.
 POLÍGONOS: POLÍGONOS REGULARES y POLÍGONOS REGULARES ESTRELLADOS. Polígono es la superficie plana encerrada dentro de un contorno formado por segmentos rectos unidos en sus extremos. Cada uno de los segmentos
POLÍGONOS: POLÍGONOS REGULARES y POLÍGONOS REGULARES ESTRELLADOS. Polígono es la superficie plana encerrada dentro de un contorno formado por segmentos rectos unidos en sus extremos. Cada uno de los segmentos
TEMA 1. TRAZADOS GEOMÉTRICOS ELEMENTALES
 TEMA 1. TRAZADOS GEOMÉTRICOS ELEMENTALES GEOMETRÍA: Rama de las matemáticas que se ocupa del estudio de las figuras geométricas, incluyendo puntos, rectas, planos Proviene del Griego GEO (tierra) METRÍA
TEMA 1. TRAZADOS GEOMÉTRICOS ELEMENTALES GEOMETRÍA: Rama de las matemáticas que se ocupa del estudio de las figuras geométricas, incluyendo puntos, rectas, planos Proviene del Griego GEO (tierra) METRÍA
ENCUENTRO NÚMERO CINCO La circunferencia y el círculo
 MODULO III - GEOMETRIA ENCUENTRO NÚMERO CINCO La circunferencia y el círculo 24 DEAGOSTO DE 2014 MANAGUA FINANCIADO POR: FUNDACIÓN UNO 1 Circunferencia: Una circunferencia es una línea curva cerrada cuyos
MODULO III - GEOMETRIA ENCUENTRO NÚMERO CINCO La circunferencia y el círculo 24 DEAGOSTO DE 2014 MANAGUA FINANCIADO POR: FUNDACIÓN UNO 1 Circunferencia: Una circunferencia es una línea curva cerrada cuyos
TRAZADOS GEOMÉTRICOS
 ELEMENTOS GEOMÉTRICOS Punto Línea recta/curva direcciones posiciones Ángulo tipos posiciones TRAZADOS GEOMÉTRICOS Lugares Geométricos mediatriz bisectriz circunferencia División de la Circunferencia 2-4-8
ELEMENTOS GEOMÉTRICOS Punto Línea recta/curva direcciones posiciones Ángulo tipos posiciones TRAZADOS GEOMÉTRICOS Lugares Geométricos mediatriz bisectriz circunferencia División de la Circunferencia 2-4-8
LA GEOMETRÍA PLANA. Llanos: Si su medida es de 180º. Agudos: Si su medida esta comprendida entre 0 y 90. Rectos: si su medida es 90
 LA GEOMETRÍA PLANA La geometría plana trata de aquellos elementos que solo tienen dos dimensiones y, que por lo tanto, se encuentran y operan en un plano. Los elementos básicos con los que se suele trabajar
LA GEOMETRÍA PLANA La geometría plana trata de aquellos elementos que solo tienen dos dimensiones y, que por lo tanto, se encuentran y operan en un plano. Los elementos básicos con los que se suele trabajar
Unidad Didáctica 8. Dibujo Geométrico
 Unidad Didáctica 8 Dibujo Geométrico 1.- Tazados Geométricos Básicos Trazados Rectas Paralelas Rectas paralelas. Las que no llegan nunca a cortarse, o se cortan en el infinito. Con Escuadra y Cartabón:
Unidad Didáctica 8 Dibujo Geométrico 1.- Tazados Geométricos Básicos Trazados Rectas Paralelas Rectas paralelas. Las que no llegan nunca a cortarse, o se cortan en el infinito. Con Escuadra y Cartabón:
Departamento de Educación Plástica y Visual. Unidad 3: Polígonos. 3º ESO EDUCACIÓN PLÁSTICA Y VISUAL UNIDAD 3: POLÍGONOS.
 EDUCACIÓN PLÁSTICA Y VISUAL UNIDAD 3: POLÍGONOS Página 1 de 15 1. POLÍGONOS 1.1. Conocimiento de los polígonos regulares Polígono: Proviene de la palabra compuesta de Poli (muchos) Gonos (ángulos). Se
EDUCACIÓN PLÁSTICA Y VISUAL UNIDAD 3: POLÍGONOS Página 1 de 15 1. POLÍGONOS 1.1. Conocimiento de los polígonos regulares Polígono: Proviene de la palabra compuesta de Poli (muchos) Gonos (ángulos). Se
A 2 TEMA 10. POLÍGONOS ÁREAS Y PERÍMETROS TRIÁNGULOS CUADRILÁTEROS POLÍGONOS REGULARES CIRCUNFERENCIA CÍRCULO TEOREMA DE PITÁGORAS:
 TEMA 10. POLÍGONOS ÁREAS Y PERÍMETROS ELEMENTOS CLASIFICACIÓN TRIÁNGULOS CUADRILÁTEROS POLÍGONOS REGULARES CIRCUNFERENCIA CÍRCULO A b h A b a A perímetro apotema A r TEOREMA DE PITÁGORAS: a b c 1 POLÍGONOS
TEMA 10. POLÍGONOS ÁREAS Y PERÍMETROS ELEMENTOS CLASIFICACIÓN TRIÁNGULOS CUADRILÁTEROS POLÍGONOS REGULARES CIRCUNFERENCIA CÍRCULO A b h A b a A perímetro apotema A r TEOREMA DE PITÁGORAS: a b c 1 POLÍGONOS
Nuestro punto de partida será el teorema que Blaise Pascal descubrió a la edad de dieciseís años y que se conoce Hexagrama Misticum:
 1. roblema 505 de triánguloscabri ado un triángulo y un punto X sobre la recta, (a) Inscribir una parábola en los lados del triángulo de manera que X sea el punto de tangencia con la recta. (b) emostrar
1. roblema 505 de triánguloscabri ado un triángulo y un punto X sobre la recta, (a) Inscribir una parábola en los lados del triángulo de manera que X sea el punto de tangencia con la recta. (b) emostrar
Preguntas Propuestas
 reguntas ropuestas 2 ... olígonos 1. alcule la suma de lados de dos polígonos si se sabe que las sumas de las medidas de sus ángulos interiores difieren en 540º y el número de diagonales del polígono de
reguntas ropuestas 2 ... olígonos 1. alcule la suma de lados de dos polígonos si se sabe que las sumas de las medidas de sus ángulos interiores difieren en 540º y el número de diagonales del polígono de
POLIGONOS. Nº DE LADOS NOMBRE 3 Triángulos 4 Cuadriláteros 5 Pentágonos 6 Hexágonos 7 Heptágonos 8 Octógonos 9 Eneágonos 10 Decágonos
 1 POLIGONO POLIGONOS Polígono es la superficie plana limitada por una línea poligonal cerrada. Lados Vértices Polígono regular es el que tiene todos sus lados y ángulos iguales, mientras que polígono irregular
1 POLIGONO POLIGONOS Polígono es la superficie plana limitada por una línea poligonal cerrada. Lados Vértices Polígono regular es el que tiene todos sus lados y ángulos iguales, mientras que polígono irregular
MATEMÁTICAS (GEOMÉTRÍA)
 COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS (GEOMÉTRÍA) GRADO:6 O DOCENTE: Nubia E. Niño C. FECHA: 9 / 06 / 15 Guía Didáctica 3 1 Desempeños: * Identifica, clasifica
COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS (GEOMÉTRÍA) GRADO:6 O DOCENTE: Nubia E. Niño C. FECHA: 9 / 06 / 15 Guía Didáctica 3 1 Desempeños: * Identifica, clasifica
CONCEPTO DE POLÍGONO. RECONOCER Y CLASIFICAR POLÍGONOS
 OBJETIVO 1 CONCEPTO DE POLÍGONO. RECONOCER Y CLASIICAR POLÍGONOS NOMBRE: CURSO: ECHA: POLÍGONOS Varios segmentos unidos entre sí forman una línea poligonal. Una línea poligonal cerrada es un polígono.
OBJETIVO 1 CONCEPTO DE POLÍGONO. RECONOCER Y CLASIICAR POLÍGONOS NOMBRE: CURSO: ECHA: POLÍGONOS Varios segmentos unidos entre sí forman una línea poligonal. Una línea poligonal cerrada es un polígono.
ACTIVIDADES DE GEOMETRÍA PARA 4º ESO DE EPV Nombre y apellidos:
 ACTIVIDADES DE GEOMETRÍA PARA 4º ESO DE EPV Nombre y apellidos: Curso: TEMA 1: TRAZADOS BÁSICOS. 1. RECTAS PARALELAS Las rectas paralelas son aquellas que por mucho que las prolongues nunca se van a cortar.
ACTIVIDADES DE GEOMETRÍA PARA 4º ESO DE EPV Nombre y apellidos: Curso: TEMA 1: TRAZADOS BÁSICOS. 1. RECTAS PARALELAS Las rectas paralelas son aquellas que por mucho que las prolongues nunca se van a cortar.
Facultad de Ingeniería Facultad de Tecnología Informática. Matemática Números reales Elementos de geometría analítica. Profesora: Silvia Mamone
 Facultad de Ingeniería Facultad de Tecnología Informática Matemática Números reales Elementos de geometría analítica 0 03936 Profesora: Silvia Mamone UB Facultad de Ingeniería Facultad de Tecnología Informática
Facultad de Ingeniería Facultad de Tecnología Informática Matemática Números reales Elementos de geometría analítica 0 03936 Profesora: Silvia Mamone UB Facultad de Ingeniería Facultad de Tecnología Informática
Punto. Recta. Semirrecta. Segmento. Rectas Secantes. Rectas Paralelas. Rectas Perpendiculares
 Punto El punto es un objeto geométrico que no tiene dimensión y que sirve para indicar una posición. A Recta Es una sucesión continua e indefinida de puntos en una sola dimensión. Semirrecta Es una línea
Punto El punto es un objeto geométrico que no tiene dimensión y que sirve para indicar una posición. A Recta Es una sucesión continua e indefinida de puntos en una sola dimensión. Semirrecta Es una línea
Se llama lugar geométrico a todos los puntos del plano que cumplen una propiedad geométrica. Ejemplo:
 3º ESO E UNIDAD 11.- GEOMETRÍA DEL PLANO PROFESOR: RAFAEL NÚÑEZ ------------------------------------------------------------------------------------------------------------------------------------- 1.-
3º ESO E UNIDAD 11.- GEOMETRÍA DEL PLANO PROFESOR: RAFAEL NÚÑEZ ------------------------------------------------------------------------------------------------------------------------------------- 1.-
Trazados geométricos con escuadra, cartabón y compás. 1. Traza la mediatriz del segmento dado AB.
 1. Traza la mediatriz del segmento dado AB. 2. A la semirrecta s trázale una perpendicular en su extremo.. ª.2. Construye un triángulo sabiendo A= 30º, B= 45º Y se A B x s 3. Dada la recta r, trázale desde
1. Traza la mediatriz del segmento dado AB. 2. A la semirrecta s trázale una perpendicular en su extremo.. ª.2. Construye un triángulo sabiendo A= 30º, B= 45º Y se A B x s 3. Dada la recta r, trázale desde
GEOMETRÍA LLANA: CONCEPTOS BÁSICOS (1ESO)
 GEOMETRÍA LLANA: CONCEPTOS BÁSICOS (1ESO) PUNTOS, RECTOS Y PLANES 1.- Punto: Intersección de dos rectos. No tiene dimensiones (ni largo, ni ancho, ni alto). 2.- Recta: Conjunto de puntos con una sola dimensión.
GEOMETRÍA LLANA: CONCEPTOS BÁSICOS (1ESO) PUNTOS, RECTOS Y PLANES 1.- Punto: Intersección de dos rectos. No tiene dimensiones (ni largo, ni ancho, ni alto). 2.- Recta: Conjunto de puntos con una sola dimensión.
TEMA 5: GEOMETRÍA PLANA. Contenidos:
 Contenidos: - Elementos básicos del plano: punto, recta y segmento. Rectas paralelas y perpendiculares. Ángulos: definición, clasificación y medida. - Instrumentos de dibujo. Construcción de segmentos,
Contenidos: - Elementos básicos del plano: punto, recta y segmento. Rectas paralelas y perpendiculares. Ángulos: definición, clasificación y medida. - Instrumentos de dibujo. Construcción de segmentos,
Mª Rosa Villegas Pérez
 Mª Rosa Villegas Pérez FIGURAS PLANAS G.T. Elaboración de Materiales y Recursos Didácticos en un Centro TIC. Polígonos.- / 14 POLÍGONOS Un polígono es una figura plana y cerrada formada al unir tres o
Mª Rosa Villegas Pérez FIGURAS PLANAS G.T. Elaboración de Materiales y Recursos Didácticos en un Centro TIC. Polígonos.- / 14 POLÍGONOS Un polígono es una figura plana y cerrada formada al unir tres o
TIPOS DE LÍNEAS Las rectas no tienen principio ni fin. La recta es una línea formada por una serie de puntos en una misma dirección...
 TEMA 8 RECTAS Y ÁNGULOS TIPOS DE LÍNEAS Las rectas no tienen principio ni fin. La recta es una línea formada por una serie de puntos en una misma dirección....... Línea recta Cada una de las partes en
TEMA 8 RECTAS Y ÁNGULOS TIPOS DE LÍNEAS Las rectas no tienen principio ni fin. La recta es una línea formada por una serie de puntos en una misma dirección....... Línea recta Cada una de las partes en
TEMA 3 TRAZADO GEOMETRICO. CONICAS
 TEM 3 TRZDO GEOMETRICO. CONICS 1. CIRCUNFERENCIS...2 1.1 TNGENCIS...2 2. DIVISION DE CIRCUNFERENCIS...9 2.1 EN TRES Y SEIS PRTES IGULES...9 2.2 EN CUTRO Y OCHO PRTES IGULES...10 2.3 EN CINCO Y DIEZ PRTES
TEM 3 TRZDO GEOMETRICO. CONICS 1. CIRCUNFERENCIS...2 1.1 TNGENCIS...2 2. DIVISION DE CIRCUNFERENCIS...9 2.1 EN TRES Y SEIS PRTES IGULES...9 2.2 EN CUTRO Y OCHO PRTES IGULES...10 2.3 EN CINCO Y DIEZ PRTES
1) Clasifica las siguientes cónicas y expresa sus focos y su excentricidad: a)
 Ejercicios de cónicas 1º bachillerato C 1) Clasifica las siguientes cónicas y expresa sus focos y su excentricidad: a) b) c) d) e) f) g) h) i) Soluciones: a) Circunferencia de centro ( y radio 3. Excentricidad
Ejercicios de cónicas 1º bachillerato C 1) Clasifica las siguientes cónicas y expresa sus focos y su excentricidad: a) b) c) d) e) f) g) h) i) Soluciones: a) Circunferencia de centro ( y radio 3. Excentricidad
ARITMÉTICA. 1. Resolver las siguientes ecuaciones en Q. 2 x + 5. d) ( ) 2. g) 0,86 x 0,73 = 1. x = 1 4 3x. = x + + l) ( ) ( )( ) m) ( )( ) ( ) 2
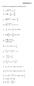 1. Resolver las siguientes ecuaciones en Q. ARITMÉTICA a) b) 3. x + 1 = 3 83 3,90x x = 3 31 c) 0,x + x 4,16 = 6 x + 3 1 + 4 = x + 1 d) ( ) e) f) x x + = 0,3 0, 6x 3 0, 6 1x + 6x = 0,3 8 g) 0,86 x 0,73
1. Resolver las siguientes ecuaciones en Q. ARITMÉTICA a) b) 3. x + 1 = 3 83 3,90x x = 3 31 c) 0,x + x 4,16 = 6 x + 3 1 + 4 = x + 1 d) ( ) e) f) x x + = 0,3 0, 6x 3 0, 6 1x + 6x = 0,3 8 g) 0,86 x 0,73
Lados. Posee 4 lados que son representados por los segmentos: AB, Vértice. Posee 4 vértices, a saber: A, Lados opuestos. Son los lados no adyacentes:
 Identificación de las propiedades de los cuadriláteros Cuadrilátero. Es un polígono de cuatro lados. Se le representa con sus cuatro vértices. Características Dado este cuadrilátero ABCD, se tiene: Clasificación.
Identificación de las propiedades de los cuadriláteros Cuadrilátero. Es un polígono de cuatro lados. Se le representa con sus cuatro vértices. Características Dado este cuadrilátero ABCD, se tiene: Clasificación.
PROBLEMAS RESUELTOS DE LA ECUACIÓN DE LA RECTA
 PROLEMS RESUELTOS DE L ECUCIÓN DE L RECT 1) Hallar la pendiente el ángulo de inclinación de la recta que pasa por los puntos (-, ) (7, -) 1 m 1 m 7 1 comom tan entonces 1 1 tan 1,4 ) Los segmentos que
PROLEMS RESUELTOS DE L ECUCIÓN DE L RECT 1) Hallar la pendiente el ángulo de inclinación de la recta que pasa por los puntos (-, ) (7, -) 1 m 1 m 7 1 comom tan entonces 1 1 tan 1,4 ) Los segmentos que
Lámina 1: Rectas paralelas horizontales, verticales, inclinadas y cruzadas.
 Lámina 1: Rectas paralelas horizontales, verticales, inclinadas y cruzadas. Lámina 2: Realiza los siguientes patrones Traza un segmento de 50 mm por el punto R paralelo a la recta r. Divide el segmento
Lámina 1: Rectas paralelas horizontales, verticales, inclinadas y cruzadas. Lámina 2: Realiza los siguientes patrones Traza un segmento de 50 mm por el punto R paralelo a la recta r. Divide el segmento
MATEMATICAS. BC2 TEMA 6: Rectas y Planos en R 3
 MATEMATICAS. BC2 TEMA 6: Rectas y Planos en R 3 1. Las coordenadas de los vértices consecutivos de un paralelogramo son A (1, 0, 0) y B(0, 1, 0). Las coordenadas del centro M son M(0, 0, 1). Hallar las
MATEMATICAS. BC2 TEMA 6: Rectas y Planos en R 3 1. Las coordenadas de los vértices consecutivos de un paralelogramo son A (1, 0, 0) y B(0, 1, 0). Las coordenadas del centro M son M(0, 0, 1). Hallar las
Elementos de geometría analítica
 UNIDAD 7: APLIQUEMOS ELEMENTOS DE GEOMETRIA ANALITICA. Introducción Elementos de geometría analítica En esta unidad última nos ocuparemos del estudio de los conceptos más fundamentales de la geometría
UNIDAD 7: APLIQUEMOS ELEMENTOS DE GEOMETRIA ANALITICA. Introducción Elementos de geometría analítica En esta unidad última nos ocuparemos del estudio de los conceptos más fundamentales de la geometría
Estrella es la figura obtenida cuando todos los vértices del polígono inicial están conectados.
 CONSTRUCCIÓN 1ª A partir de un polígono regular de n lados. Se elige uno de sus vértices y, a partir de él, se trazan segmentos que unen dos vértices no consecutivos. Este trazado se realiza de manera
CONSTRUCCIÓN 1ª A partir de un polígono regular de n lados. Se elige uno de sus vértices y, a partir de él, se trazan segmentos que unen dos vértices no consecutivos. Este trazado se realiza de manera
MATEMÁTICAS 1º DE ESO
 MATEMÁTICAS 1º DE ESO LOMCE TEMA IX: RECTAS Y ÁNGULOS Puntos, rectas, semirrectas y segmentos en el plano. Posiciones relativas de rectas en el plano. Mediatriz de un segmento. Ángulos. Elementos. Clasificación
MATEMÁTICAS 1º DE ESO LOMCE TEMA IX: RECTAS Y ÁNGULOS Puntos, rectas, semirrectas y segmentos en el plano. Posiciones relativas de rectas en el plano. Mediatriz de un segmento. Ángulos. Elementos. Clasificación
Las diagonales de un polígono convexo son segmentos de línea que conectan los vértices (no son lados)
 Materia: Matemática de Séptimo Tema: Polígonos Qué pasaría si te preguntaran cuántos lados tiene un polígono? Cómo describirías el polígono? Después de leer este concepto, vas a poder clasificar un polígono
Materia: Matemática de Séptimo Tema: Polígonos Qué pasaría si te preguntaran cuántos lados tiene un polígono? Cómo describirías el polígono? Después de leer este concepto, vas a poder clasificar un polígono
MATHEMATICA. Geometría - Recta. Ricardo Villafaña Figueroa. Material realizado con Mathematica. Ricardo Villafaña Figueroa
 MATHEMATICA Geometría - Recta Material realizado con Mathematica 2 Contenido Sistema de Coordenadas... 3 Distancia entre dos puntos... 3 Punto Medio... 5 La Recta... 8 Definición de recta... 8 Pendiente
MATHEMATICA Geometría - Recta Material realizado con Mathematica 2 Contenido Sistema de Coordenadas... 3 Distancia entre dos puntos... 3 Punto Medio... 5 La Recta... 8 Definición de recta... 8 Pendiente
ACTIVIDADES DE 2ºESO DE EPV DEL PRIMER TRIMESTRE Nombre y apellidos: TEMA 1: TRAZADOS BÁSICOS
 ACTIVIDADES DE 2ºESO DE EPV DEL PRIMER TRIMESTRE Nombre y apellidos: Curso: TEMA 1: TRAZADOS BÁSICOS 1. LA ESCUADRA Y EL CARTABÓN. Observando tu escuadra y tu cartabón describe su forma y sus ángulos.
ACTIVIDADES DE 2ºESO DE EPV DEL PRIMER TRIMESTRE Nombre y apellidos: Curso: TEMA 1: TRAZADOS BÁSICOS 1. LA ESCUADRA Y EL CARTABÓN. Observando tu escuadra y tu cartabón describe su forma y sus ángulos.
Indice....1 Recta Punto Semirrecta Segmento Posición relativa de dos rectas en el plano Ángulo.-...
 Geometría plana1 2017.odt Departamento de Matemáticas IES Isaac Díaz Pardo. Sada Geometría del plano Curso 1º Nombre: Nº : - 1- Indice....1 Recta.-...2 Punto.-...2 Semirrecta.-...2 Segmento.-...2 Posición
Geometría plana1 2017.odt Departamento de Matemáticas IES Isaac Díaz Pardo. Sada Geometría del plano Curso 1º Nombre: Nº : - 1- Indice....1 Recta.-...2 Punto.-...2 Semirrecta.-...2 Segmento.-...2 Posición
EJERCICIOS DE GEOMETRÍA
 1) Sean las rectas EJERCICIOS DE GEOMETRÍA x 2y 6z 1 r : x y 0 x y 1 s: z 2 a a) Determinar la posición relativa de r y s según los valores de a. b) Calcular la distancia entre las rectas r y s cuando
1) Sean las rectas EJERCICIOS DE GEOMETRÍA x 2y 6z 1 r : x y 0 x y 1 s: z 2 a a) Determinar la posición relativa de r y s según los valores de a. b) Calcular la distancia entre las rectas r y s cuando
Perpendiculares, mediatrices, simetrías y proyecciones
 Perpendiculares, mediatrices, simetrías y proyecciones 1. Calcular en cada caso la ecuación de la recta perpendicular a la dada, y que pasa por el punto P que se indica: a) 5x 2y 3 0 P( 1, 3) b) x 4 y
Perpendiculares, mediatrices, simetrías y proyecciones 1. Calcular en cada caso la ecuación de la recta perpendicular a la dada, y que pasa por el punto P que se indica: a) 5x 2y 3 0 P( 1, 3) b) x 4 y
1. Recta exterior a la circunferencia: cuando la distancia de la recta al centro de la circunferencia es mayor que el radio de esta.
 TEMA 4. TANGENCIAS 4.1 CONCEPTO DE TANGENCIA 4.1.1. Concepto El término viene del latín TANGERE = Tocar. Se emplea en geometría para designar líneas, curvas y superficies que se tocan, sin llegar a cortarse.
TEMA 4. TANGENCIAS 4.1 CONCEPTO DE TANGENCIA 4.1.1. Concepto El término viene del latín TANGERE = Tocar. Se emplea en geometría para designar líneas, curvas y superficies que se tocan, sin llegar a cortarse.
MATEMÁTICAS 1º BACH. C. N. Y S. 25 de enero de 2010 Geometría y Logaritmos
 MATEMÁTICAS 1º BACH. C. N. Y S. 5 de enero de 010 Geometría y Logaritmos x yz 1) Tomar logaritmos, y desarrollar, en la siguiente expresión: A 4 ab log x log b 4log a log y ) Quitar logaritmos: log A )
MATEMÁTICAS 1º BACH. C. N. Y S. 5 de enero de 010 Geometría y Logaritmos x yz 1) Tomar logaritmos, y desarrollar, en la siguiente expresión: A 4 ab log x log b 4log a log y ) Quitar logaritmos: log A )
MYP (MIDDLE YEARS PROGRAMME)
 MYP (MIDDLE YEARS PROGRAMME) 2014-2015 Fecha 19/05/2015 APUNTES DE GEOMETRÍA 2º ESO 1. EL TEOREMA DE PITÁGORAS El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa
MYP (MIDDLE YEARS PROGRAMME) 2014-2015 Fecha 19/05/2015 APUNTES DE GEOMETRÍA 2º ESO 1. EL TEOREMA DE PITÁGORAS El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa
Propiedades TEMA 3: POLÍGONOS DEFINICIÓN, PROPIEDADES Y CLASIFICACIÓN D TRIÁNGULOS. Clasificación. Definición
 TRIÁNGULOS/CUADRILÁTEROAS/POLÍGONOS TEMA 3:2º- BACH/Página 1 de 30 TEMA 3: POLÍGONOS DEFINICIÓN, PROPIEDADES Y CLASIFICACIÓN D TRIÁNGULOS. Definición Triángulo es una superficie plana limitada por tres
TRIÁNGULOS/CUADRILÁTEROAS/POLÍGONOS TEMA 3:2º- BACH/Página 1 de 30 TEMA 3: POLÍGONOS DEFINICIÓN, PROPIEDADES Y CLASIFICACIÓN D TRIÁNGULOS. Definición Triángulo es una superficie plana limitada por tres
4. UNIDAD DIDÁCTICA 4: FORMAS GEOMÉTRICAS II
 4. UNIDAD DIDÁCTICA 4: FORMAS GEOMÉTRICAS II En el tema anterior empezamos a conocer lo más básico de las formas geométricas. En este tema vamos a aprender a trazar otras formas un poco más complejas,
4. UNIDAD DIDÁCTICA 4: FORMAS GEOMÉTRICAS II En el tema anterior empezamos a conocer lo más básico de las formas geométricas. En este tema vamos a aprender a trazar otras formas un poco más complejas,
III: Geometría para maestros. Capitulo 1: Figuras geométricas
 III: Geometría para maestros. Capitulo : Figuras geométricas SELECCIÓN DE EJERCICIOS RESUELTOS SITUACIONES INTRODUCTORIAS En un libro de primaria encontramos este enunciado: Dibuja un polígono convexo
III: Geometría para maestros. Capitulo : Figuras geométricas SELECCIÓN DE EJERCICIOS RESUELTOS SITUACIONES INTRODUCTORIAS En un libro de primaria encontramos este enunciado: Dibuja un polígono convexo
. a) Comprueba que forman una base de los vectores libres del plano. b) Encuentra las componentes del vector w ( 1,5)
 Curso: º Bachillerato Recuperación Fecha: 5 de Junio de 05 º Trimestre.- Dados los vectores u (, ) implica una penalización del 5% de la nota. y v (,). a) Comprueba que forman una base de los vectores
Curso: º Bachillerato Recuperación Fecha: 5 de Junio de 05 º Trimestre.- Dados los vectores u (, ) implica una penalización del 5% de la nota. y v (,). a) Comprueba que forman una base de los vectores
ECUACIONES, SISTEMAS DE ECUACIONES E INECUACIONES
 ECUACIONES, SISTEMAS DE ECUACIONES E INECUACIONES Ejercicio. a) Halle los valores de m para los que la ecuación de segundo grado 8 m 7 m no tiene solución real. b) Resuelva la siguiente inecuación indicando
ECUACIONES, SISTEMAS DE ECUACIONES E INECUACIONES Ejercicio. a) Halle los valores de m para los que la ecuación de segundo grado 8 m 7 m no tiene solución real. b) Resuelva la siguiente inecuación indicando
ARITMÉTICA. 1. Resolver las siguientes ecuaciones en Q. 2 x + 5. d) ( x ) ( x ) x = x + = x. l) ( ) ( )( ) + = + + o) ( x ) 2.
 1. Resolver las siguientes ecuaciones en Q. ARITMÉTICA a) b) 3. x + 1 = 3 83 3,90x x = 3 31 c) 0,x + x 4,16 = 6 d) ( x ) ( x ) + 3 1 = + 1 4 e) f) g) x x + = 0,3 0, 6x 3 0, 6 1x + 6x = 0,3 8 0,86x 0,73
1. Resolver las siguientes ecuaciones en Q. ARITMÉTICA a) b) 3. x + 1 = 3 83 3,90x x = 3 31 c) 0,x + x 4,16 = 6 d) ( x ) ( x ) + 3 1 = + 1 4 e) f) g) x x + = 0,3 0, 6x 3 0, 6 1x + 6x = 0,3 8 0,86x 0,73
INSTITUCIÓN EDUCATIVA ESCUELA NORMAL SUPERIOR DEL BAJO CAUCA
 Las matemáticas, históricamente, comenzaron con la geometría. La geometría es la ciencia que estudia la forma y posición de la figuras y nos enseña a medir su extensión. Geometría (del griego geo, tierra,
Las matemáticas, históricamente, comenzaron con la geometría. La geometría es la ciencia que estudia la forma y posición de la figuras y nos enseña a medir su extensión. Geometría (del griego geo, tierra,
Tema 2: Figuras geométricas
 Tema 2: Figuras geométricas En este tema empezaremos a estudiar: 1. la circunferencia. 2. los triángulos. 3. los cuadriláteros. 4. los poĺıgonos. 1 2 La circunferencia (p. 31) El cerebro humano es muy
Tema 2: Figuras geométricas En este tema empezaremos a estudiar: 1. la circunferencia. 2. los triángulos. 3. los cuadriláteros. 4. los poĺıgonos. 1 2 La circunferencia (p. 31) El cerebro humano es muy
FIGURAS GEOMETRICAS PLANAS
 UNIDAD 9 FIGURAS GEOMETRICAS PLANAS Objetivo General Al terminar esta Unidad entenderás y aplicaras los conceptos generales de las figuras geométricas planas, y resolverás ejercicios y problemas con figuras
UNIDAD 9 FIGURAS GEOMETRICAS PLANAS Objetivo General Al terminar esta Unidad entenderás y aplicaras los conceptos generales de las figuras geométricas planas, y resolverás ejercicios y problemas con figuras
POLÍGONO ÁNGULOS DE UN POLÍGONO CLASIFICACIÓN: La denominación de polígono palabra compuesta de poli, del griego: muchos; y gonos del griego: ángulos
 POLÍGONO La denominación de polígono palabra compuesta de poli, del griego: muchos; y gonos del griego: ángulos Un polígono es una porción del plano limitada por una línea poligonal cerrada. Los segmentos
POLÍGONO La denominación de polígono palabra compuesta de poli, del griego: muchos; y gonos del griego: ángulos Un polígono es una porción del plano limitada por una línea poligonal cerrada. Los segmentos
GEOMETRÍA POLÍGONOS - 1
 GEOMETRÍA POLÍGONOS - 1 TRIÁNGULOS Los triángulos son figuras planas formadas por tres puntos no alineados y por tres segmentos que los unen dos a dos (los tres puntos son los vértices y los tres segmentos
GEOMETRÍA POLÍGONOS - 1 TRIÁNGULOS Los triángulos son figuras planas formadas por tres puntos no alineados y por tres segmentos que los unen dos a dos (los tres puntos son los vértices y los tres segmentos
CONICAS Y LUGARES GEOMÉTRICOS ( problemas resueltos)
 CONICAS Y LUGARES GEOMÉTRICOS ( problemas resueltos) Ejercicio nº 1.- Escribe la ecuación de la circunferencia con centro en el punto (, 3) que es tangente a la recta 3 4 + 5 = 0. El radio, R, de la circunferencia
CONICAS Y LUGARES GEOMÉTRICOS ( problemas resueltos) Ejercicio nº 1.- Escribe la ecuación de la circunferencia con centro en el punto (, 3) que es tangente a la recta 3 4 + 5 = 0. El radio, R, de la circunferencia
Lección 1.1: Perímetro y área. Parte A - Figuras regulares e irregulares
 Unidad 7.5: Geometría Tema 1: Figuras bidimensionales Lección 1.1: Perímetro y área Parte A - Figuras regulares e irregulares Los polígonos Los ángulos son las regiones que forman los lados al cortarse.
Unidad 7.5: Geometría Tema 1: Figuras bidimensionales Lección 1.1: Perímetro y área Parte A - Figuras regulares e irregulares Los polígonos Los ángulos son las regiones que forman los lados al cortarse.
1. Halla la ecuación de la recta r, sabiendo que pasa por A(1,-2) y B(-1,2)
 1. Halla la ecuación de la recta r, sabiendo que pasa por A(1,-2) y B(-1,2) 2. Halla la ecuación de la recta r, sabiendo que es paralela a y=2x-3 y pasa por el punto (1,3). 3. Halla la ecuación de la recta
1. Halla la ecuación de la recta r, sabiendo que pasa por A(1,-2) y B(-1,2) 2. Halla la ecuación de la recta r, sabiendo que es paralela a y=2x-3 y pasa por el punto (1,3). 3. Halla la ecuación de la recta
Definición y Clasificación de Polígonos. Definición
 Definición y Clasificación de Polígonos Además del triángulo hay una gran cantidad de otras figuras geométricas delimitadas por segmentos de recta que son importantes en geometría. Definición Polígono
Definición y Clasificación de Polígonos Además del triángulo hay una gran cantidad de otras figuras geométricas delimitadas por segmentos de recta que son importantes en geometría. Definición Polígono
