Valores propios de matrices de Toeplitz hermitianas: aproximación uniforme por medio de la función cuantil
|
|
|
- Tomás Quintana Roldán
- hace 5 años
- Vistas:
Transcripción
1 Valores propios de matrices de Toeplitz hermitianas: aproximación uniforme por medio de la función cuantil Egor Maximenko usando trabajos conjuntos con Johan Manuel Bogoya, Albrecht Böttcher y Sergei Grudsky Instituto Politécnico Nacional, ESFM, México Escuela de verano 206 CINVESTAV, México / 37
2 Convergencia uniforme Matrices de Toeplitz Aplicación a matrices Función cuantil 2 / 37
3 Operador de convolución en l 2 (Z) (repaso) Sea a l (Z). Definimos C(a): l 2 (Z) l 2 (Z), C(a)x := a x = a j k x k. k Z j Z El operador C(a) se puede identificar con la matriz infinita [ a j k ]j,k Z : a0 a a 2 a 3 a a a 0 a a 2 a.. 3 C(a) =.... a2 a a 0 a a a3 a 2 a a 0 a a4 a 3 a 2 a a / 37
4 Diagonalización del operador de convolución (repaso) F := la transformada de Fourier Plancherel sobre el grupo Z: F : l 2 (Z) L 2 (0, 2π), (x n ) n Z x(θ) = n Z x n e n i θ. 4 / 37
5 Diagonalización del operador de convolución (repaso) F := la transformada de Fourier Plancherel sobre el grupo Z: F : l 2 (Z) L 2 (0, 2π), (x n ) n Z x(θ) = n Z x n e n i θ. M(a) := el operador de multiplicación por la función a: M(a): L 2 (0, 2π) L 2 (0, 2π), (M(a)f )(θ) = a(θ)f (θ). 4 / 37
6 Diagonalización del operador de convolución (repaso) F := la transformada de Fourier Plancherel sobre el grupo Z: F : l 2 (Z) L 2 (0, 2π), (x n ) n Z x(θ) = n Z x n e n i θ. M(a) := el operador de multiplicación por la función a: M(a): L 2 (0, 2π) L 2 (0, 2π), (M(a)f )(θ) = a(θ)f (θ). Teorema de convolución: F(a x) = (Fa)(Fx). 4 / 37
7 Diagonalización del operador de convolución (repaso) F := la transformada de Fourier Plancherel sobre el grupo Z: F : l 2 (Z) L 2 (0, 2π), (x n ) n Z x(θ) = n Z x n e n i θ. M(a) := el operador de multiplicación por la función a: M(a): L 2 (0, 2π) L 2 (0, 2π), (M(a)f )(θ) = a(θ)f (θ). Teorema de convolución: Por el teorema de convolución, F(a x) = (Fa)(Fx). FC(a)F = M(a), esto es, C(a) = F M(a)F. 4 / 37
8 Corolarios de la diagonalización de C(a) De la igualdad C(a) = F M(a)F se deduce fácilmente que C(a)C(b) = C(ab), C(a) = M(a) = max a(θ), 0 θ 2π sp(c(a)) = sp(m(a)) = a([0, 2π]) = {a(θ): 0 θ 2π}. 5 / 37
9 Matrices de Toeplitz T 5 (a) = a 0 a a 2 a 3 a 4 a a 0 a a 2 a 3 a 2 a a 0 a a 2 a 3 a 2 a a 0 a a 4 a 3 a 2 a a 0. 6 / 37
10 Matrices de Toeplitz T 5 (a) = a 0 a a 2 a 3 a 4 a a 0 a a 2 a 3 a 2 a a 0 a a 2 a 3 a 2 a a 0 a a 4 a 3 a 2 a a 0. Suponemos que a = (a k ) k Z es una sucesión sumable: a k < +. k Z Consideramos la serie de Fourier con estos coeficientes: a(θ) = a k e k i θ (0 θ 2π). k Z La función a se llama el símbolo generador de las matrices T n (a) = [ a j k ] n j,k=. 6 / 37
11 La matriz T n (a) es un corte finito del operador de convolución a0 a a 2 a 3 a a a 0 a a 2 a.. 3 C(a) =.... a2 a a 0 a a a3 a 2 a a 0 a a4 a 3 a 2 a a T 3 (a) = a 0 a a 2 a a 0 a a 2 a a 0. 7 / 37
12 Matrices de Toeplitz autoadjuntas Suponemos que el símbolo generador es continuo y real: a C([0, 2π], R). En este caso las matrices T n (a) son hermíticas: a k = a k, a 0 R. T 5 (a) = a 0 a a 2 a 3 a 4 a a 0 a a 2 a 3 a 2 a a 0 a a 2 a 3 a 2 a a 0 a a 4 a 3 a 2 a a 0. 8 / 37
13 stealed from loveiscomix.com 9 / 37
14 [ a0 ] a a 2 a 3 a a 0 a a 2 a 2 a a 0 a a 3 a 2 a a 0 Entender a una matriz autoadjunta es... 9 / 37
15 [ a0 ] a a 2 a 3 a a 0 a a 2 a 2 a a 0 a a 3 a 2 a a 0 [ λ ] λ λ λ 4 Entender a una matriz autoadjunta es entender el comportamiento de sus valores y vectores propios. 9 / 37
16 Problema: valores propios de matrices de Toeplitz El objetivo es describir propiedades asintóticas de T n (a), en particular, el comportamiento asintótico de sus valores propios. Los ordenamos de manera ascendente: λ (n)... λ (n) n. 0 / 37
17 Valores propios de matrices de Toeplitz Gráfica de a Valores propios de T 8 (a) 0 π 2π 0 / 37
18 Valores propios de matrices de Toeplitz Gráfica de a Valores propios de T 6 (a) 0 π 2π 0 / 37
19 Valores propios de matrices de Toeplitz Gráfica de a Valores propios de T 32 (a) 0 π 2π 0 / 37
20 Valores propios de matrices de Toeplitz Gráfica de a Valores propios de T 32 (a) β cuántos? 0 π 2π α 0 Primera pregunta: #{ j : λ (n) j [α, β] }? (Szegő, 920) / 37
21 Valores propios de matrices de Toeplitz Gráfica de a Valores propios de T 32 (a) λ (32) 20? 0 π 2π 0 Primera pregunta: Segunda pregunta: #{ j : λ (n) j [α, β] }? (Szegő, 920) λ (n) j? / 37
22 La traza generalizada de una matriz de Toeplitz Es fácil calcular la traza de una matriz de Toeplitz: tr(t n (a)) = na 0 = n 2π a(θ) dθ. 2π 0 2 / 37
23 La traza generalizada de una matriz de Toeplitz Es fácil calcular la traza de una matriz de Toeplitz: tr(t n (a)) = na 0 = n 2π a(θ) dθ. 2π 0 Dada una función ϕ C(R), la ϕ-traza de T n (a) se define como tr(ϕ(t n (a))) = n j= ϕ(λ (n) j ). 2 / 37
24 La traza generalizada de una matriz de Toeplitz Es fácil calcular la traza de una matriz de Toeplitz: tr(t n (a)) = na 0 = n 2π a(θ) dθ. 2π 0 Dada una función ϕ C(R), la ϕ-traza de T n (a) se define como tr(ϕ(t n (a))) = n j= ϕ(λ (n) j ). Consideremos el comportamiento asintótico de esta expresión, cuando n. 2 / 37
25 T n (a)t n (b) T n (ab) en cierto sentido Lema Sean a, b : [0, 2π] R funciones suaves. Entonces ( ) lim n n T n(a)t n (b) T n (ab) tr = 0, donde tr es la norma nuclear ( norma traza ) de la matriz. 3 / 37
26 T n (a)t n (b) T n (ab) en cierto sentido Lema Sean a, b : [0, 2π] R funciones suaves. Entonces ( ) lim n n T n(a)t n (b) T n (ab) tr = 0, donde tr es la norma nuclear ( norma traza ) de la matriz. Este lema permite demostrar que n tr(t n p (a)) n tr(t n(a p )) = 2π 2π 0 a p (θ) dθ, 3 / 37
27 T n (a)t n (b) T n (ab) en cierto sentido Lema Sean a, b : [0, 2π] R funciones suaves. Entonces ( ) lim n n T n(a)t n (b) T n (ab) tr = 0, donde tr es la norma nuclear ( norma traza ) de la matriz. Este lema permite demostrar que luego n tr(t n p (a)) n tr(t n(a p )) = 2π 2π 0 a p (θ) dθ, n tr(ϕ(t n(a))) n tr(t n(ϕ a)) = 2π ϕ(a(θ)) dθ, 2π 0 para cualquier polinomio ϕ. 3 / 37
28 Teorema de Szegő a C([0, 2π], R) ϕ C(R) n n j= ϕ(λ (n) j ) 2π ϕ(a(θ)) dθ 2π 0 4 / 37
29 Corolario del teorema ĺımite de Szegő distribución de los valores propios de matrices de Toeplitz a C([0, 2π], R) α < β a α, β c.t.p. #{j : α λ (n) j β} n µ R {θ [0, 2π]: α a(θ) β} 2π 5 / 37
30 Ejemplo para ilustrar el corolario Gráfica de a Valores propios de T 32 (a) π 0 6 / 37
31 Ejemplo para ilustrar el corolario Gráfica de a Valores propios de T 32 (a) valores propios 0 2π / 37
32 Ejemplo para ilustrar el corolario Gráfica de a Valores propios de T 32 (a) valores propios 0 2π / 37
33 Ejemplo para ilustrar el corolario Gráfica de a Valores propios de T 32 (a) valores propios 0 2π / 37
34 Ejemplo para ilustrar el corolario Gráfica de a Valores propios de T 32 (a) valores propios 0 2π 0 µ R {θ : 0 a(θ) 0.4} 2π = / 37
35 Szegő describió la distribución asintótica de los valores propios de T n (a) cuando n. Otra pregunta se quedó sin respuesta: λ (n) j? 7 / 37
36 Idea clave Sean ξ,..., ξ 000 algunos números reales tales que ξ... ξ 000, todas las diferencias ξ j+ ξ j son pequeñas, y # { j {..., 000}: ξ j 2 } Entonces podemos afirmar que ξ??????. 8 / 37
37 Idea clave En general, si # { j {..., 000}: ξ j v } 000 F (v), entonces podemos afirmar que ξ??????. Para aproximar ξ j con j dado, hay que invertir F. 9 / 37
38 Convergencia uniforme Matrices de Toeplitz Aplicación a matrices Función cuantil 20 / 37
39 La función cuantil asociada a una variable aleatoria Sea (Ω, F, P) un espacio de probabilidad, y sea X : Ω R una función F-medible. Le asociamos la función de distribución y la función cuantil: F X (v) := P(X (, v]), Q X (p) := inf{v R: F X (v) p}. Se puede decir que Q X es la inversa derecha superior de la función F X. 2 / 37
40 Una lista de números como una variable aleatoria Sea ξ = (ξ,..., ξ n ) una lista de números reales. Dotamos {,..., n} con la medida de conteo normalizada: µ n (J) = #J n y consideramos ξ como una variable aleatoria. (J {,..., n}), Si la lista (ξ,..., ξ n ) es ordenada de manera ascendente, entonces y F ξ (v) = max{j {,..., d}: ξ j v} d Q ξ (j/d) = ξ j. 22 / 37
41 Ejemplo Consideremos una lista de tres números reales: ξ = (, 0.6,.). Los dibujos muestran la función de distribución y la función cuantil:. 2/3 0.6 / / 37
42 Otro ejemplo Los mismos números en el orden ascendente: Q(/3) = 8 porque 8 es el número más pequeño entre los números v tales que al menos /3 de los elementos son menores o iguales a v. 24 / 37
43 Construcción de la función cuantil asociada a un símbolo generador lineal a trozos Gráfica de a Gráfica de Q a π 2 π 3π 2 2π / 37
44 Construcción de la función cuantil asociada a un símbolo generador lineal a trozos Gráfica de a Gráfica de Q a 3 4 v v 4 0 π 2 π 3π 2 2π a y Q a son identicamente distribuidas: 2π µ R{θ [0, 2π]: a(θ) v} = µ R {p [0, ]: Q a (p) v} 25 / 37
45 Construcción de la función cuantil asociada a un símbolo generador lineal a trozos Gráfica de a Gráfica de Q a π 2 π 3π 2 2π a reordenamiento en el estilo de Lebesgue Q a 25 / 37
46 Convergencia uniforme Matrices de Toeplitz Aplicación a matrices Función cuantil 26 / 37
47 Puntos de continuidad de una función Sean X, Y algunos espacios topológicos y sea f : X Y una función. C(f ) := { x X : f es continua en x }. Por ejemplo, si f : R R, entonces f (x) = + x + x 2, C(f ) = 27 / 37
48 Puntos de continuidad de una función Sean X, Y algunos espacios topológicos y sea f : X Y una función. C(f ) := { x X : f es continua en x }. Por ejemplo, si f : R R, entonces f (x) = + x + x 2, C(f ) = R \ Z. 27 / 37
49 Criterio de convergencia en distribución (X n Y ) Sea Y una variable aleatoria, y sea (X n ) n= una sucesión de v.a. Entonces las siguientes condiciones son equivalentes. ϕ C b (R) lim ϕ X n dµ n = ϕ Y dµ n Ω n Ω v C(F Y ) lim n F X n (v) = F Y (v) p C(Q Y ) lim Q X n n (p) = Q Y (p) 28 / 37
50 Lema sobre la convergencia uniforme f n (p) g(p) p [0, ] f n : [0, ] R f n son crecientes g : [0, ] R g es continua f n [0,] ==== g 29 / 37
51 Teorema (resultado principal): de la convergencia más débil a la convergencia más fuerte X n Y n N X n (Ω n ) [α, β] Y C([0, 2π], R) Y ([0, 2π]) = [α, β] Q Xn [0,] = Q Y 30 / 37
52 Corolario: de la distribución asintótica de tuplas a la convergencia uniforme Supongamos que (ξ (n) ) n= = ( ξ (n),..., d(n)) ξ(n) es una sucesión de tuplas en R. n= a C([0, 2π]) y a([0, 2π]) = [α, β]. α ξ (n) α (n) 2 α (n) n β para cada n N. ξ es asintóticamente distribuida como a, esto es, ξ (n) a. Entonces lim max n j n ξ(n) j Q a (j/n) = 0. 3 / 37
53 Convergencia uniforme Matrices de Toeplitz Aplicación a matrices Función cuantil 32 / 37
54 Convergencia uniforme de los valores propios de matrices de Toeplitz a C([0, 2π]) a([0, 2π]) R max j n λ (n) j Q a ( j/n) 0 33 / 37
55 Ejemplo Gráfica de a Gráfica de Q a Val. prop. de T 64 (a) 3/4 3/4 /4 /4 0 π/2 π 3π/2 2π 0 9/48 /6 64 Cada valor propio λ (n) j se muestra como el punto ( ) j n, λ(n) j. Se ve que el tercer dibujo parece mucho al segundo. 34 / 37
56 Ejemplo Gráfica de a Gráfica de Q a 3/4 3/4 /4 /4 0 π/2 π 3π/2 2π 0 9/48 /6 35 / 37
57 Ejemplo Gráfica de a Gráfica de Q a 3/4 3/4 /4 /4 0 π/2 π 3π/2 2π 0 9/48 /6 y los puntos ( j/n, λ (n) j ) 35 / 37
58 Ejemplo Gráfica de a 3/4 3/4 /4 /4 0 π/2 π 3π/2 2π 0 9/48 /6 ( ) 3 64, λ(64) 3 35 / 37
59 Ejemplo Gráfica de a ( 3 64, Q a ( )) /4 3/4 /4 /4 0 π/2 π 3π/2 2π 0 9/48 /6 ( ) 3 64, λ(64) 3 35 / 37
60 36 / 37
61 El teorema ĺımite de Szegő combinado con el concepto de función cuantil nos proporciona el término principal de la asintótica de los valores propios: λ (n) j Q a ( j n ) suponiendo que a C([0, 2π], R). 36 / 37
62 Antecedentes Fabio Di Benedetto, Giuseppe Fiorentino, Stefano Serra (993): C. G. Preconditioning for Toeplitz matrices. doi:0.06/ (93) Demostraron la convergencia puntual, suponiendo que a C([0, 2π], R) y que F a es continua. 37 / 37
63 Antecedentes Fabio Di Benedetto, Giuseppe Fiorentino, Stefano Serra (993): C. G. Preconditioning for Toeplitz matrices. doi:0.06/ (93) Demostraron la convergencia puntual, suponiendo que a C([0, 2π], R) y que F a es continua. William Trench (202): An elementary view of Weyl s theory of equal distribution. doi:0.469/amer.math.monthly Demostró la convergencia en promedio. 37 / 37
De la convergencia en distribución a la aproximación uniforme
 De la convergencia en distribución a la aproximación uniforme Egor Maximenko utilizando trabajos juntos con Johan Manuel Bogoya, Albrecht Böttcher y Sergei Grudsky Instituto Politécnico Nacional, ESFM,
De la convergencia en distribución a la aproximación uniforme Egor Maximenko utilizando trabajos juntos con Johan Manuel Bogoya, Albrecht Böttcher y Sergei Grudsky Instituto Politécnico Nacional, ESFM,
Matrices de Toeplitz autoadjuntas y el teorema ĺımite de Szegő
 Matrices de Toeplitz autoadjuntas y el teorema ĺımite de Szegő Egor Maximenko para un proyecto conjunto con Víctor Hugo Ibarra Mercado, Eliseo Sarmiento Rosales y José Eliud Silva Urrutia Instituto Politécnico
Matrices de Toeplitz autoadjuntas y el teorema ĺımite de Szegő Egor Maximenko para un proyecto conjunto con Víctor Hugo Ibarra Mercado, Eliseo Sarmiento Rosales y José Eliud Silva Urrutia Instituto Politécnico
Análisis III. Introducción
 Análisis III. Introducción Egor Maximenko ESFM del IPN 3 de agosto de 2009 Egor Maximenko (ESFM del IPN) Análisis III. Introducción 3 de agosto de 2009 1 / 30 Contenido 1 Programa del curso Lista de unidades
Análisis III. Introducción Egor Maximenko ESFM del IPN 3 de agosto de 2009 Egor Maximenko (ESFM del IPN) Análisis III. Introducción 3 de agosto de 2009 1 / 30 Contenido 1 Programa del curso Lista de unidades
1. MEDIDA E INTEGRACIÓN.
 1. MEDID E INTEGRCIÓN. En este capítulo repasamos algunos conceptos que se vieron en la asignatura mpliación de la Teoría de Funciones de Varias Variables. 1. MEDIDS POSITIVS. (1,1,1) Definición. Una σ-álgebra
1. MEDID E INTEGRCIÓN. En este capítulo repasamos algunos conceptos que se vieron en la asignatura mpliación de la Teoría de Funciones de Varias Variables. 1. MEDIDS POSITIVS. (1,1,1) Definición. Una σ-álgebra
Ejercicios Variable Real
 UNIVERSIDAD AUTÓNOMA DE MADRID FACULTAD DE MATEMÁTICAS Ejercicios Variable Real Antonio Córdoba (Manuel Mellado Cuerno) 1º Cuatrimestre del curso 2016-2017 manuel.mellado@estudiante.uam.es 2 Capítulo 1
UNIVERSIDAD AUTÓNOMA DE MADRID FACULTAD DE MATEMÁTICAS Ejercicios Variable Real Antonio Córdoba (Manuel Mellado Cuerno) 1º Cuatrimestre del curso 2016-2017 manuel.mellado@estudiante.uam.es 2 Capítulo 1
Integral de Lebesgue
 Integral de Lebesgue Problemas para examen n todos los problemas se supone que (, F, µ) es un espacio de medida. Integración de funciones simples positivas. La representación canónica de una función simple
Integral de Lebesgue Problemas para examen n todos los problemas se supone que (, F, µ) es un espacio de medida. Integración de funciones simples positivas. La representación canónica de una función simple
Medidas. Problemas para examen. Estos problemas están redactados por Egor Maximenko y Breitner Arley Ocampo Gómez.
 Medidas Problemas para examen Estos problemas están redactados por Egor Maximenko y Breitner Arley Ocampo Gómez. Sigma-álgebras 1. Propiedades elementales de σ-álgebras. Demuestre que una σ-álgebra es
Medidas Problemas para examen Estos problemas están redactados por Egor Maximenko y Breitner Arley Ocampo Gómez. Sigma-álgebras 1. Propiedades elementales de σ-álgebras. Demuestre que una σ-álgebra es
Teoremas de Tonelli y Fubini
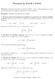 Teoremas de Tonelli y Fubini Objetivos. Demostrar teoremas de Tonelli y Fubini, conocer contraejemplos que muestran la importancia de algunas condiciones de estos teoremas. Requisitos. Definición del producto
Teoremas de Tonelli y Fubini Objetivos. Demostrar teoremas de Tonelli y Fubini, conocer contraejemplos que muestran la importancia de algunas condiciones de estos teoremas. Requisitos. Definición del producto
Lista de problemas de álgebra, 2016
 Instituto Politécnico Nacional Escuela Superior de Física y Matemáticas Posgrado en Ciencias Físicomatemáticas Línea de Matemáticas Lista de problemas de álgebra 2016 Egor Maximenko: En mi opinión cualquier
Instituto Politécnico Nacional Escuela Superior de Física y Matemáticas Posgrado en Ciencias Físicomatemáticas Línea de Matemáticas Lista de problemas de álgebra 2016 Egor Maximenko: En mi opinión cualquier
Ejercicios de teoría de la medida
 Ejercicios de teoría de la medida Pedro Alegría Capítulo. Dada una aplicación F : Ω Ω, demostrar que: a) Si A es una σ-álgebra de Ω, A = {B Ω : F B) A} lo es de Ω. b) Si A es una σ-álgebra de Ω, A = F
Ejercicios de teoría de la medida Pedro Alegría Capítulo. Dada una aplicación F : Ω Ω, demostrar que: a) Si A es una σ-álgebra de Ω, A = {B Ω : F B) A} lo es de Ω. b) Si A es una σ-álgebra de Ω, A = F
Valores y vectores propios
 Valores y vectores propios Tareas adicionales Algunos de estos problemas compuso Gustavo Antonio Sandoval Angeles (como parte de su servicio social). Estos problemas son más difíciles o más laboriosos
Valores y vectores propios Tareas adicionales Algunos de estos problemas compuso Gustavo Antonio Sandoval Angeles (como parte de su servicio social). Estos problemas son más difíciles o más laboriosos
Transformación adjunta a una transformación lineal
 Transformación adjunta a una transformación lineal Objetivos. Estudiar la construcción y las propiedades básicas de la transformación lineal adjunta. Requisitos. Transformación lineal, producto interno,
Transformación adjunta a una transformación lineal Objetivos. Estudiar la construcción y las propiedades básicas de la transformación lineal adjunta. Requisitos. Transformación lineal, producto interno,
ESTADÍSTICA I Tema 2: Algunas ideas básicas sobre inferencia estadística. Muestreo aleatorio
 ESTADÍSTICA I Tema 2: Algunas ideas básicas sobre inferencia estadística. Muestreo aleatorio Muestra aleatoria Conceptos probabiĺısticos básicos El problema de inferencia Estadísticos. Media y varianza
ESTADÍSTICA I Tema 2: Algunas ideas básicas sobre inferencia estadística. Muestreo aleatorio Muestra aleatoria Conceptos probabiĺısticos básicos El problema de inferencia Estadísticos. Media y varianza
Análisis de Fourier. Resumen de los apuntes de D. Antonio Cañada Villar. Sergio Cruz Blázquez. Curso 2015/2016
 Análisis de Fourier Resumen de los apuntes de D. Antonio Cañada Villar Curso 2015/2016 Sergio Cruz Blázquez Índice 1 El espacio L 2 (a, b) Definición y primeras notas El espacio L 1 (a, b) L 2 (a, b) como
Análisis de Fourier Resumen de los apuntes de D. Antonio Cañada Villar Curso 2015/2016 Sergio Cruz Blázquez Índice 1 El espacio L 2 (a, b) Definición y primeras notas El espacio L 1 (a, b) L 2 (a, b) como
Transformaciones lineales autoadjuntas (hermíticas)
 Transformaciones lineales autoadjuntas (hermíticas) Objetivos. Estudiar propiedades elementales de transformaciones lineales autoadjuntas. Demostrar que para toda transformación lineal autoadjunta en un
Transformaciones lineales autoadjuntas (hermíticas) Objetivos. Estudiar propiedades elementales de transformaciones lineales autoadjuntas. Demostrar que para toda transformación lineal autoadjunta en un
Tema 6: Modelos de probabilidad.
 Estadística 60 Tema 6: Modelos de probabilidad. 6.1 Modelos discretos. (a) Distribución uniforme discreta: La variable aleatoria X tiene una distribución uniforme discreta de parámetro n,que denoteramos
Estadística 60 Tema 6: Modelos de probabilidad. 6.1 Modelos discretos. (a) Distribución uniforme discreta: La variable aleatoria X tiene una distribución uniforme discreta de parámetro n,que denoteramos
Estadística. Tema 2. Variables Aleatorias Funciones de distribución y probabilidad Ejemplos distribuciones discretas y continuas
 Estadística Tema 2 Variables Aleatorias 21 Funciones de distribución y probabilidad 22 Ejemplos distribuciones discretas y continuas 23 Distribuciones conjuntas y marginales 24 Ejemplos distribuciones
Estadística Tema 2 Variables Aleatorias 21 Funciones de distribución y probabilidad 22 Ejemplos distribuciones discretas y continuas 23 Distribuciones conjuntas y marginales 24 Ejemplos distribuciones
Algunos algoritmos para matrices de Toeplitz
 Algunos algoritmos para matrices de Toeplitz Estos apuntes están escritos por varios estudiantes de la ESFM del IPN, bajo la dirección del profesor Egor Maximenko. Participaron Jocelyn Hernández, Jareth
Algunos algoritmos para matrices de Toeplitz Estos apuntes están escritos por varios estudiantes de la ESFM del IPN, bajo la dirección del profesor Egor Maximenko. Participaron Jocelyn Hernández, Jareth
El Teorema del Modulo Máximo
 Capítulo 5 El Teorema del Modulo Máximo. El Principio del Máximo. Pruebe el siguiente Principio del Mínimo. Si f es una función analítica no constante sobre un conjunto abierto G acotado y es continua
Capítulo 5 El Teorema del Modulo Máximo. El Principio del Máximo. Pruebe el siguiente Principio del Mínimo. Si f es una función analítica no constante sobre un conjunto abierto G acotado y es continua
Métodos matemáticos: Análisis funcional
 Métodos matemáticos: Análisis funcional Conceptos y resultados fundamentales Curso 2011/2012 Aquí encontrarás los Teoremas hay que saber para el primer parcial ( 1) así como las definiciones, problemas
Métodos matemáticos: Análisis funcional Conceptos y resultados fundamentales Curso 2011/2012 Aquí encontrarás los Teoremas hay que saber para el primer parcial ( 1) así como las definiciones, problemas
Órdenes de la convergencia de sucesiones. Condiciones de la convergencia lineal y cuadrática del método de iteración simple
 Órdenes de la convergencia de sucesiones. Condiciones de la convergencia lineal y cuadrática del método de iteración simple Estos apuntes están redactados por Maria de los Angeles Isidro Pérez y Egor Maximenko.
Órdenes de la convergencia de sucesiones. Condiciones de la convergencia lineal y cuadrática del método de iteración simple Estos apuntes están redactados por Maria de los Angeles Isidro Pérez y Egor Maximenko.
Polinomios de Schur y soluciones básicas de las recurrencias lineales
 Polinomios de Schur y soluciones básicas de las recurrencias lineales Egor Maximenko, Mario Alberto Moctezuma Salazar Instituto Politécnico Nacional, ESFM, México 50 o Congreso Nacional de la Sociedad
Polinomios de Schur y soluciones básicas de las recurrencias lineales Egor Maximenko, Mario Alberto Moctezuma Salazar Instituto Politécnico Nacional, ESFM, México 50 o Congreso Nacional de la Sociedad
Teoremas de Convergencia
 Capítulo 24 Teoremas de Convergencia El teorema de la convergencia monótona (Lema 21.3) establece ciertas condiciones sobre una sucesión de funciones medibles para que se puedan permutar los símbolos y
Capítulo 24 Teoremas de Convergencia El teorema de la convergencia monótona (Lema 21.3) establece ciertas condiciones sobre una sucesión de funciones medibles para que se puedan permutar los símbolos y
Introducción a la Probabilidad No-Conmutativa
 Introducción a la Probabilidad No-Conmutativa Tulio Gaxiola CIMAT 18 de abril de 2016 Sesión de Probabilidad No-Conmutativa, Matrices Aleatorias y Gráficas Tulio Gaxiola (CIMAT) EPNC y Gráficas 18 de abril
Introducción a la Probabilidad No-Conmutativa Tulio Gaxiola CIMAT 18 de abril de 2016 Sesión de Probabilidad No-Conmutativa, Matrices Aleatorias y Gráficas Tulio Gaxiola (CIMAT) EPNC y Gráficas 18 de abril
Espacios vectoriales con producto interno
 Espacios vectoriales con producto interno Problemas teóricos En todos los problemas relacionados con el caso complejo se supone que el producto interno es lineal con respecto al segundo argumento. Definición
Espacios vectoriales con producto interno Problemas teóricos En todos los problemas relacionados con el caso complejo se supone que el producto interno es lineal con respecto al segundo argumento. Definición
Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS
 Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS Grado en Matemáticas Curso 203-204 . Ecuaciones lineales con coeficientes constantes Ecuaciones de primer orden. Encontrar la solución de los siguientes
Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS Grado en Matemáticas Curso 203-204 . Ecuaciones lineales con coeficientes constantes Ecuaciones de primer orden. Encontrar la solución de los siguientes
Ortogonalización de Gram Schmidt
 Ortogonalización de Gram Schmidt Objetivos. Estudiar el proceso de ortogonalización de Gram Schmidt que permite construir de una lista arbitraria de vectores a,..., a m una lista ortogonal b,..., b m que
Ortogonalización de Gram Schmidt Objetivos. Estudiar el proceso de ortogonalización de Gram Schmidt que permite construir de una lista arbitraria de vectores a,..., a m una lista ortogonal b,..., b m que
Métodos Matemáticos: Análisis Funcional
 Licenciatura en Ciencias y Técnicas Estadísticas Universidad de Sevilla http://euler.us.es/ renato/clases.html Espacios eucĺıdeos Definición Se dice que un espacio vectorial E es un espacio eucĺıdeo si
Licenciatura en Ciencias y Técnicas Estadísticas Universidad de Sevilla http://euler.us.es/ renato/clases.html Espacios eucĺıdeos Definición Se dice que un espacio vectorial E es un espacio eucĺıdeo si
4. Complementos sobre Problemas de Contorno para S.D.O. Lineales. 4. Complementos sobre Problemas de Contorno
 para S.D.O. Lineales 4.1. Problemas de contorno para s.d.o. lineales. Teorema de alternativa 4.1. Problemas de contorno. Teorema de alternativa Fijemos A C 0 ([α, β]; L(R N )) y b C 0 ([α, β]; R N ), dos
para S.D.O. Lineales 4.1. Problemas de contorno para s.d.o. lineales. Teorema de alternativa 4.1. Problemas de contorno. Teorema de alternativa Fijemos A C 0 ([α, β]; L(R N )) y b C 0 ([α, β]; R N ), dos
Teoremas del Límite Central No-Conmutativos y Productos de Gráficas
 Teoremas del Límite Central No-Conmutativos y Productos de Gráficas Marco Tulio Gaxiola Leyva CIMAT 16 de Octubre de 2014 Seminario Interinstitucional Centro Norte de México, de Combinatoria y Probabilidad
Teoremas del Límite Central No-Conmutativos y Productos de Gráficas Marco Tulio Gaxiola Leyva CIMAT 16 de Octubre de 2014 Seminario Interinstitucional Centro Norte de México, de Combinatoria y Probabilidad
Métodos Matemáticos: Análisis Funcional
 Licenciatura en Ciencias y Técnicas Estadísticas Universidad de Sevilla http://euler.us.es/ renato/clases.html Qué son esos espacios de Hilbert? Qué son esos espacios de Hilbert? David Hilbert Para relajarnos
Licenciatura en Ciencias y Técnicas Estadísticas Universidad de Sevilla http://euler.us.es/ renato/clases.html Qué son esos espacios de Hilbert? Qué son esos espacios de Hilbert? David Hilbert Para relajarnos
Introducción. Capítulo Introducción. Sea {X n, n 1} una sucesión de v.a.i.i.d. con f.d. común F y definamos
 Capítulo 1 Introducción 1.1. Introducción Sea {X n, n 1} una sucesión de v.a.i.i.d. con f.d. común F y definamos La distribución de esta variable aleatoria es Definimos M n = máx i n X i. P (M n x) = P
Capítulo 1 Introducción 1.1. Introducción Sea {X n, n 1} una sucesión de v.a.i.i.d. con f.d. común F y definamos La distribución de esta variable aleatoria es Definimos M n = máx i n X i. P (M n x) = P
Correspondencia entre vectores y columnas de sus coordenadas respecto a una base fija
 Correspondencia entre vectores y columnas de sus coordenadas respecto a una base fija Objetivos. Mostrar que la correspondencia entre vectores y columnas de sus coordenadas (respecto a una base fija) preserva
Correspondencia entre vectores y columnas de sus coordenadas respecto a una base fija Objetivos. Mostrar que la correspondencia entre vectores y columnas de sus coordenadas (respecto a una base fija) preserva
Práctica 2 -Cardinalidad- A. Propiedades básicas de los Conjuntos
 Cálculo Avanzado Segundo Cuatrimestre de 2012 Práctica 2 -Cardinalidad- A. Propiedades básicas de los Conjuntos Ejercicio 1. Demostrar las siguientes igualdades de conjuntos: i) B i I A i = i I(B A i ).
Cálculo Avanzado Segundo Cuatrimestre de 2012 Práctica 2 -Cardinalidad- A. Propiedades básicas de los Conjuntos Ejercicio 1. Demostrar las siguientes igualdades de conjuntos: i) B i I A i = i I(B A i ).
Notas de clase sobre la Transformada de Fourier
 Notas de clase sobre la Transformada de Fourier Pablo L. De Nápoli 3 de noviembre de 205. La definición de la transformada de Fourier Definición. Si f L ( ) definimos su transformada de fourier por f(ξ)
Notas de clase sobre la Transformada de Fourier Pablo L. De Nápoli 3 de noviembre de 205. La definición de la transformada de Fourier Definición. Si f L ( ) definimos su transformada de fourier por f(ξ)
Principio minimax para los valores propios de matrices hermitianas
 Principio minimax para los valores propios de matrices hermitianas El propósito de estos apuntes (escritos por Egor Maximenko, Rogelio Rocha Hernández, Eliseo Sarmiento Rosales y Zacarías Sánchez Francisco
Principio minimax para los valores propios de matrices hermitianas El propósito de estos apuntes (escritos por Egor Maximenko, Rogelio Rocha Hernández, Eliseo Sarmiento Rosales y Zacarías Sánchez Francisco
Momentos de Funciones de Vectores Aleatorios
 Capítulo 1 Momentos de Funciones de Vectores Aleatorios 1.1 Esperanza de Funciones de Vectores Aleatorios Definición 1.1 Sea X = (X 1,..., X n ) un vector aleatorio (absolutamente continuo o discreto)
Capítulo 1 Momentos de Funciones de Vectores Aleatorios 1.1 Esperanza de Funciones de Vectores Aleatorios Definición 1.1 Sea X = (X 1,..., X n ) un vector aleatorio (absolutamente continuo o discreto)
Intersección y suma de subespacios
 Intersección y suma de subespacios Objetivos Demostrar que la intersección y la suma de dos subespacios de un espacio vectorial también son sus subespaicios Requisitos Espacio vectorial, subespacio vectorial
Intersección y suma de subespacios Objetivos Demostrar que la intersección y la suma de dos subespacios de un espacio vectorial también son sus subespaicios Requisitos Espacio vectorial, subespacio vectorial
Cálculo Numérico III Curso 2010/11
 Cálculo Numérico III Curso 2010/11 Problemas del Tema 1 1. Sean {x 0, x 1,..., x n } IR con x i x j si i j. Hoja de problemas - Parte I a) Hallar el polinomio de grado n que interpola a la función en los
Cálculo Numérico III Curso 2010/11 Problemas del Tema 1 1. Sean {x 0, x 1,..., x n } IR con x i x j si i j. Hoja de problemas - Parte I a) Hallar el polinomio de grado n que interpola a la función en los
Lección 3: Aproximación de funciones. por polinomios. Fórmula de Taylor para
 Lección 3: Aproximación de funciones por polinomios. Fórmula de Taylor para funciones escalares 3.1 Introducción Cuando es difícil trabajar con una función complicada, tratamos a veces de hallar una función
Lección 3: Aproximación de funciones por polinomios. Fórmula de Taylor para funciones escalares 3.1 Introducción Cuando es difícil trabajar con una función complicada, tratamos a veces de hallar una función
Práctica 5 Martingalas a tiempo discreto
 Práctica 5 Martingalas a tiempo discreto 1. Tiempos de Parada A lo largo de esta sección vamos a fijar un espacio de probabilidad (Ω, F, P ) junto con una filtración (F n ) n N definida en este espacio.
Práctica 5 Martingalas a tiempo discreto 1. Tiempos de Parada A lo largo de esta sección vamos a fijar un espacio de probabilidad (Ω, F, P ) junto con una filtración (F n ) n N definida en este espacio.
Determinantes de matrices de Toeplitz autoadjuntas generadas por polinomios de Laurent
 INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE FÍSICA Y MATEMÁTICAS Determinantes de matrices de Toeplitz autoadjuntas generadas por polinomios de Laurent Tesis para obtener el grado de maestro en
INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE FÍSICA Y MATEMÁTICAS Determinantes de matrices de Toeplitz autoadjuntas generadas por polinomios de Laurent Tesis para obtener el grado de maestro en
Cuerpos Finitos. XXVII Escuela Venezolana de Matemáticas EMALCA. Edgar Martínez-Moro Sept. 2014
 Cuerpos Finitos XXVII Escuela Venezolana de Matemáticas EMALCA Edgar Martínez-Moro Sept. 2014 Cuerpos y extensiones de cuerpos Un cuerpo (F, +, ) es un conjunto no vacío en el que se han definido dos operaciones
Cuerpos Finitos XXVII Escuela Venezolana de Matemáticas EMALCA Edgar Martínez-Moro Sept. 2014 Cuerpos y extensiones de cuerpos Un cuerpo (F, +, ) es un conjunto no vacío en el que se han definido dos operaciones
Diferenciciación en R n
 Diferenciciación en R n R. Álvarez-Nodarse Universidad de Sevilla Cómo definir la derivada? Definición Sea A un abierto de R n, a A y f : A R n R m. La derivada parcial i-ésima (1 i n) de f en a se define
Diferenciciación en R n R. Álvarez-Nodarse Universidad de Sevilla Cómo definir la derivada? Definición Sea A un abierto de R n, a A y f : A R n R m. La derivada parcial i-ésima (1 i n) de f en a se define
520142: ALGEBRA y ALGEBRA LINEAL
 520142: ALGEBRA y ALGEBRA LINEAL Segundo Semestre 2008, Universidad de Concepción CAPITULO 10: Espacios Vectoriales DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas 1 Definición
520142: ALGEBRA y ALGEBRA LINEAL Segundo Semestre 2008, Universidad de Concepción CAPITULO 10: Espacios Vectoriales DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas 1 Definición
Formulación de Galerkin El método de los elementos finitos
 Clase No. 28: MAT 251 Formulación de Galerkin El método de los elementos finitos Dr. Alonso Ramírez Manzanares Depto. de Matemáticas Univ. de Guanajuato e-mail: alram@ cimat.mx web: http://www.cimat.mx/
Clase No. 28: MAT 251 Formulación de Galerkin El método de los elementos finitos Dr. Alonso Ramírez Manzanares Depto. de Matemáticas Univ. de Guanajuato e-mail: alram@ cimat.mx web: http://www.cimat.mx/
UNIVERSIDAD DE EXTREMADURA Departamento de Matemáticas. Matemáticas. Manuel Fernández García-Hierro Badajoz, Febrero 2008
 UNIVERSIDAD DE EXTREMADURA Departamento de Matemáticas Matemáticas Manuel Fernández García-Hierro Badajoz, Febrero 2008 Capítulo X Integración numérica Introducción La integral definida I(f) = b a f(x)
UNIVERSIDAD DE EXTREMADURA Departamento de Matemáticas Matemáticas Manuel Fernández García-Hierro Badajoz, Febrero 2008 Capítulo X Integración numérica Introducción La integral definida I(f) = b a f(x)
MAT2715 VARIABLE COMPLEJA II Ayudantia 1 Rodrigo Vargas. f n (z)dz = 0.
 PONTIFICIA UNIVERSIDAD CATÓLICA DE CHILE FACULTAD DE MATEMÁTICAS MAT2715 VARIABLE COMPLEJA II Ayudantia 1 Rodrigo Vargas 1. Si f n : Ω C analítica y {f n } converge uniformemente en compactos de Ω, entonces
PONTIFICIA UNIVERSIDAD CATÓLICA DE CHILE FACULTAD DE MATEMÁTICAS MAT2715 VARIABLE COMPLEJA II Ayudantia 1 Rodrigo Vargas 1. Si f n : Ω C analítica y {f n } converge uniformemente en compactos de Ω, entonces
Lección: Ortogonalidad y Series de Fourier
 Lección: Ortogonalidad y Series de Fourier Dr. Miguel Angel Uh Zapata, Centro de Investigación en Matemáticas, Unidad Mérida Facultad de Matemáticas, UADY Octubre 2015 Miguel Uh Lección: Ortogonalidad
Lección: Ortogonalidad y Series de Fourier Dr. Miguel Angel Uh Zapata, Centro de Investigación en Matemáticas, Unidad Mérida Facultad de Matemáticas, UADY Octubre 2015 Miguel Uh Lección: Ortogonalidad
TEMA VI: ESPACIOS DE HILBERT
 TEMA VI: ESPACIOS DE HILBERT. Espacios con producto escalar Definición: Sea L un espacio vectorial sobre el cuerpo K (R ó C). Por un producto escalar (o interno) sobre L entedemos una aplicación :
TEMA VI: ESPACIOS DE HILBERT. Espacios con producto escalar Definición: Sea L un espacio vectorial sobre el cuerpo K (R ó C). Por un producto escalar (o interno) sobre L entedemos una aplicación :
Hoja 4 Variables aleatorias multidimensionales
 Hoja 4 Variables aleatorias multidimensionales 1.- Estudiar si F (x, y) = 1, si x + 2y 1, 0, si x + 2y < 1, es una función de distribución en IR 2. 2.- Dada la variable aleatoria 2-dimensional (X, Y )
Hoja 4 Variables aleatorias multidimensionales 1.- Estudiar si F (x, y) = 1, si x + 2y 1, 0, si x + 2y < 1, es una función de distribución en IR 2. 2.- Dada la variable aleatoria 2-dimensional (X, Y )
Práctica 3 Esperanza Condicional
 1. Generalidades Práctica 3 Esperanza Condicional 1. Sea (X i ) i I una familia de variables aleatorias definidas sobre un mismo espacio medible (Ω, F) y sea Y otra variable aleatoria en este espacio.
1. Generalidades Práctica 3 Esperanza Condicional 1. Sea (X i ) i I una familia de variables aleatorias definidas sobre un mismo espacio medible (Ω, F) y sea Y otra variable aleatoria en este espacio.
UNIVERSIDAD DE CONCEPCION FACULTAD DE CIENCIAS FISICAS Y MATEMATICAS DEPARTAMENTO DE INGENIERIA MATEMATICA
 AL GEBRA III UNIVERSIDAD DE CONCEPCION FACULTAD DE CIENCIAS FISICAS Y MATEMATICAS DEPARTAMENTO DE INGENIERIA MATEMATICA ALGEBRA III DEFINICION : Sea L : V V un operador lineal sobre el espacio vectorial
AL GEBRA III UNIVERSIDAD DE CONCEPCION FACULTAD DE CIENCIAS FISICAS Y MATEMATICAS DEPARTAMENTO DE INGENIERIA MATEMATICA ALGEBRA III DEFINICION : Sea L : V V un operador lineal sobre el espacio vectorial
Integración de Funciones Reales
 Capítulo 20 Integración de Funciones Reales Nos proponemos estudiar en este capítulo las propiedades fundamentales del operador integral. n particular, extenderemos aquí al caso de funciones medibles con
Capítulo 20 Integración de Funciones Reales Nos proponemos estudiar en este capítulo las propiedades fundamentales del operador integral. n particular, extenderemos aquí al caso de funciones medibles con
Parte 4: Teoremas de convergencia.
 Parte 4: Teoremas de convergencia. Como siempre, si no se dice lo contrario, se supone que (, M, µ) es un espacio de medida y trabajamos con funciones de dominio y recorrido contenido en C o R o R. Empezamos
Parte 4: Teoremas de convergencia. Como siempre, si no se dice lo contrario, se supone que (, M, µ) es un espacio de medida y trabajamos con funciones de dominio y recorrido contenido en C o R o R. Empezamos
Cálculo de Probabilidades II Preguntas Tema 2
 Cálculo de Probabilidades II Preguntas Tema 2 1. Demuestre que la suma de n v.a. Bernuolli(p) independientes tiene una distribución Binomial con parametros (n, p). 2. Se dice que una v.a tiene una distribución
Cálculo de Probabilidades II Preguntas Tema 2 1. Demuestre que la suma de n v.a. Bernuolli(p) independientes tiene una distribución Binomial con parametros (n, p). 2. Se dice que una v.a tiene una distribución
Kolmogorov y la teoría de la la probabilidad. David Nualart. Academia de Ciencias y Universidad de Barcelona
 Kolmogorov y la teoría de la la probabilidad David Nualart Academia de Ciencias y Universidad de Barcelona 1 La axiomatización del cálculo de probabilidades A. N. Kolmogorov: Grundbegriffe des Wahrscheinlichkeitsrechnung
Kolmogorov y la teoría de la la probabilidad David Nualart Academia de Ciencias y Universidad de Barcelona 1 La axiomatización del cálculo de probabilidades A. N. Kolmogorov: Grundbegriffe des Wahrscheinlichkeitsrechnung
Espacios de Hilbert y Notación de Dirac
 Espacios de Hilbert y Notación de Dirac Alonso Contreras-Astorga CINVESTAV, México Diciembre 2012 Índice Espacios de Hilbert Operadores lineales en espacios de Hilbert Notación de Dirac 2 / 46 Espacios
Espacios de Hilbert y Notación de Dirac Alonso Contreras-Astorga CINVESTAV, México Diciembre 2012 Índice Espacios de Hilbert Operadores lineales en espacios de Hilbert Notación de Dirac 2 / 46 Espacios
Valores y vectores propios
 Valores y vectores propios Problemas teóricos El los siguientes problemas se denota por L(V ) conjunto de los operadores lineales en un espacio vectorial V (en otras palabras, de las transformaciones lineales
Valores y vectores propios Problemas teóricos El los siguientes problemas se denota por L(V ) conjunto de los operadores lineales en un espacio vectorial V (en otras palabras, de las transformaciones lineales
Problemas de VC para EDVC elaborados por C. Mora, Tema 4
 Problemas de VC para EDVC elaborados por C. Mora, Tema 4 Ejercicio Determinar las funciones enteras f para las que Solución f( + w) = f()f(w), w C. En primer lugar, f(0) = f(0 + 0) = f(0)f(0) = f(0) 2,
Problemas de VC para EDVC elaborados por C. Mora, Tema 4 Ejercicio Determinar las funciones enteras f para las que Solución f( + w) = f()f(w), w C. En primer lugar, f(0) = f(0 + 0) = f(0)f(0) = f(0) 2,
Una invitación al estudio de las cadenas de Markov
 Una invitación al estudio de las cadenas de Markov Víctor RIVERO Centro de Investigación en Matemáticas A. C. Taller de solución de problemas de probabilidad, 21-25 de Enero de 2008. 1/ 1 Potencias de
Una invitación al estudio de las cadenas de Markov Víctor RIVERO Centro de Investigación en Matemáticas A. C. Taller de solución de problemas de probabilidad, 21-25 de Enero de 2008. 1/ 1 Potencias de
El Teorema de la Convergencia Dominada
 Capítulo 22 l Teorema de la Convergencia Dominada Los dos teoremas de convergencia básicos en la integración Lebesgue son el teorema de la convergencia monótona (Lema 19.10), que vimos el capítulo y el
Capítulo 22 l Teorema de la Convergencia Dominada Los dos teoremas de convergencia básicos en la integración Lebesgue son el teorema de la convergencia monótona (Lema 19.10), que vimos el capítulo y el
Tema 2. Aplicaciones lineales. Diagonalización de endomorfismos.
 Tema 2. Aplicaciones lineales. Diagonalización de endomorfismos. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada
Tema 2. Aplicaciones lineales. Diagonalización de endomorfismos. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada
Ejemplo 1 Sea V un espacio con producto interno sobre un cuerpo K. A las transformaciones lineales T : V K las llamamos funcionales lineales.
 Facultad de Ingeniería - IMERL - Geometría y Álgebra Lineal 2 - Curso 2008. 1 Transformaciones lineales en espacios con producto interno Notas para el curso de Geometría y Algebra Lineal 2 de la Facultad
Facultad de Ingeniería - IMERL - Geometría y Álgebra Lineal 2 - Curso 2008. 1 Transformaciones lineales en espacios con producto interno Notas para el curso de Geometría y Algebra Lineal 2 de la Facultad
Problemas con soluciones
 Departamento de Matemática, Universidad Técnica Federico Santa María, MAT-223. Problemas con soluciones 1) Muestre que si A es una base de una toplogía en X, entonces la topología generada por A es iqual
Departamento de Matemática, Universidad Técnica Federico Santa María, MAT-223. Problemas con soluciones 1) Muestre que si A es una base de una toplogía en X, entonces la topología generada por A es iqual
1. Conjuntos y funciones
 Centro de Matemática Facultad de Ciencias Universidad de la República Introducción a la Topología Curso 2016 PRACTICO 1: CONJUNTOS. 1 1. Conjuntos y funciones Ejercicio 1. Si I es un conjunto y A α es
Centro de Matemática Facultad de Ciencias Universidad de la República Introducción a la Topología Curso 2016 PRACTICO 1: CONJUNTOS. 1 1. Conjuntos y funciones Ejercicio 1. Si I es un conjunto y A α es
Una norma en un espacio lineal (o vectorial) X es una función. : X R con las siguientes propiedades: (a) x 0, para todo x X (no negatividad);
 MATEMÁTICA APLICADA II Segundo cuatrimestre 20 Licenciatura en Física, Universidad Nacional de Rosario Espacios de Banach. Introducción Frecuentemente estamos interesados en qué tan grande. es una función.
MATEMÁTICA APLICADA II Segundo cuatrimestre 20 Licenciatura en Física, Universidad Nacional de Rosario Espacios de Banach. Introducción Frecuentemente estamos interesados en qué tan grande. es una función.
Examen de Admisión a la Maestría / Doctorado 24 de Junio de 2016
 Examen de Admisión a la Maestría / Doctorado 4 de Junio de 6 Nombre: Instrucciones: En cada reactivo seleccione la respuesta correcta encerrando en un círculo la letra correspondiente. Puede hacer cálculos
Examen de Admisión a la Maestría / Doctorado 4 de Junio de 6 Nombre: Instrucciones: En cada reactivo seleccione la respuesta correcta encerrando en un círculo la letra correspondiente. Puede hacer cálculos
Técnicas de Inferencia Estadística II. Tema 5. Estadísticos de orden
 Técnicas de Inferencia Estadística II Tema 5. Estadísticos de orden M. Concepción Ausín Universidad Carlos III de Madrid Grado en Estadística y Empresa Curso 2010/11 Tema 5. Estadísticos de orden Contenidos
Técnicas de Inferencia Estadística II Tema 5. Estadísticos de orden M. Concepción Ausín Universidad Carlos III de Madrid Grado en Estadística y Empresa Curso 2010/11 Tema 5. Estadísticos de orden Contenidos
Construcción de Paul Lévy del Movimiento Browniano Estándar, según P. Morters y Y. Peres. August 31, 2016
 del Movimiento Browniano Estándar, según P. Morters y Y. Peres August 31, 016 Algunos preliminares Definición Una función de distribución (de probabilidades) es una función F : R R tal que 1. F es no decreciente.
del Movimiento Browniano Estándar, según P. Morters y Y. Peres August 31, 016 Algunos preliminares Definición Una función de distribución (de probabilidades) es una función F : R R tal que 1. F es no decreciente.
Olimpiada Iberoamericana de Matemática Universitaria 2012 Problemas, soluciones y criterios
 Olimpiada Iberoamericana de Matemática Universitaria 202 Problemas, soluciones y criterios. Problemas. (3 puntos) Sea Z el anillo de los enteros. Los conjuntos Z, 2Z y 3Z son semigrupos con respecto a
Olimpiada Iberoamericana de Matemática Universitaria 202 Problemas, soluciones y criterios. Problemas. (3 puntos) Sea Z el anillo de los enteros. Los conjuntos Z, 2Z y 3Z son semigrupos con respecto a
Espacios vectoriales
 CAPíTULO 2 Espacios vectoriales 1. Definición de espacio vectorial Es frecuente representar ciertas magnitudes físicas (velocidad, fuerza,...) mediante segmentos orientados o vectores. Dados dos de tales
CAPíTULO 2 Espacios vectoriales 1. Definición de espacio vectorial Es frecuente representar ciertas magnitudes físicas (velocidad, fuerza,...) mediante segmentos orientados o vectores. Dados dos de tales
Variables aleatorias continuas y Teorema Central del Limite
 Variables aleatorias continuas y Teorema Central del Limite FaMAF 17 de marzo, 2015 Variables aleatorias continuas Definición Una variable aleatoria X se dice (absolutamente continua) si existe f : R R
Variables aleatorias continuas y Teorema Central del Limite FaMAF 17 de marzo, 2015 Variables aleatorias continuas Definición Una variable aleatoria X se dice (absolutamente continua) si existe f : R R
Ejercicios Análisis II
 Ejercicios Análisis II Ejercicios resueltos del libro Real and Complex Analysis de Walter Rudin Mauricio Bravo Vera mauro.bravo@gmail.com Segundo semestre 2010 Índice general 1. Integración Abstracta
Ejercicios Análisis II Ejercicios resueltos del libro Real and Complex Analysis de Walter Rudin Mauricio Bravo Vera mauro.bravo@gmail.com Segundo semestre 2010 Índice general 1. Integración Abstracta
EXÁMEN INFERENCIA ESTADÍSTICA I Diplomado en Estadística Convocatoria de Febrero 2006
 EXÁMEN INFERENCIA ESTADÍSTICA I Diplomado en Estadística Convocatoria de Febrero 6 Problema ( ptos) Considera un experimento aleatorio con espacio muestral Ω. a) Definir una σ-álgebra A sobre Ω. b) Dar
EXÁMEN INFERENCIA ESTADÍSTICA I Diplomado en Estadística Convocatoria de Febrero 6 Problema ( ptos) Considera un experimento aleatorio con espacio muestral Ω. a) Definir una σ-álgebra A sobre Ω. b) Dar
Tema 10: Teorema de Hahn-Banach. 14 y 17 de junio de 2010
 Tema 10: Teorema de Hahn-Banach 14 y 17 de junio de 2010 1 Versión anaĺıtica Enunciado del teorema Dual topológico Teoremas de extensión Duales de subespacios y cocientes Límites de Banach 2 Separación
Tema 10: Teorema de Hahn-Banach 14 y 17 de junio de 2010 1 Versión anaĺıtica Enunciado del teorema Dual topológico Teoremas de extensión Duales de subespacios y cocientes Límites de Banach 2 Separación
Apéndice 2: Series de Fourier.
 Apéndice 2: Series de Fourier. 19 de noviembre de 2014 1. Conjuntos ortonormales y proyecciones. Sea V un espacio vectorial con un producto interno . Sea {e 1,..., e n } un conjunto ortonormal, V
Apéndice 2: Series de Fourier. 19 de noviembre de 2014 1. Conjuntos ortonormales y proyecciones. Sea V un espacio vectorial con un producto interno . Sea {e 1,..., e n } un conjunto ortonormal, V
Coordinación de Matemática II (MAT022)
 Coordinación de Matemática II (MAT022) Guía de ejercicios N 6 parte Complementos Espacios Vectoriales En los ejercicios que siguen utilizamos la siguientes notaciones: R n [x es el espacio vectorial sobre
Coordinación de Matemática II (MAT022) Guía de ejercicios N 6 parte Complementos Espacios Vectoriales En los ejercicios que siguen utilizamos la siguientes notaciones: R n [x es el espacio vectorial sobre
Ejercicios de Análisis Funcional
 Ejercicios de Análisis Funcional Rafael Payá Albert Departamento de Análisis Matemático Universidad de Granada ANÁLISIS FUNCIONAL Relación de Ejercicios N o 1 1. Dar un ejemplo de una distancia en un espacio
Ejercicios de Análisis Funcional Rafael Payá Albert Departamento de Análisis Matemático Universidad de Granada ANÁLISIS FUNCIONAL Relación de Ejercicios N o 1 1. Dar un ejemplo de una distancia en un espacio
Funciones Continuas Definiciones y Propiedades
 Capítulo 2 Funciones Continuas 2.1. Definiciones Propiedades Sean (X,T X ) e (Y,T Y ) dos espacios topológicos una función f : X Y. Se dice que f es continua, si sólo si, para todo V T Y, se tiene f 1
Capítulo 2 Funciones Continuas 2.1. Definiciones Propiedades Sean (X,T X ) e (Y,T Y ) dos espacios topológicos una función f : X Y. Se dice que f es continua, si sólo si, para todo V T Y, se tiene f 1
0 a b X = b c 0. f X (A) = AX XA.
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Industriales Álgebra Lineal Convocatoria de Junio 8 de Junio de 2007 (3 ptos.). Sea V = {A M 3 3 (R) / A t = A}. (a) Demostrar que toda
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Industriales Álgebra Lineal Convocatoria de Junio 8 de Junio de 2007 (3 ptos.). Sea V = {A M 3 3 (R) / A t = A}. (a) Demostrar que toda
x (0) si f (x) = 2s 1, s > 1 d) f 3. Analizar la existencia de derivadas laterales y de derivada en a = 0, para las siguientes funciones:
 FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
Procesamiento Digital Tren de pulsos
 2. Procesamiento Digital Una formulación general para las series de Fourier es = donde se utiliza otro tipo de función φ k diferente a las funciones sinusoidales. 2.1 Interpolación Se puede expresar una
2. Procesamiento Digital Una formulación general para las series de Fourier es = donde se utiliza otro tipo de función φ k diferente a las funciones sinusoidales. 2.1 Interpolación Se puede expresar una
Fórmulas de cuadratura positivas en la circunferencia unidad con nodos prefijados
 Fórmulas de cuadratura positivas en la circunferencia unidad con nodos prefijados Francisco José Perdomo Pío Departamento de Análisis Matemático, Universidad de La Laguna Preprint: Positive quadrature
Fórmulas de cuadratura positivas en la circunferencia unidad con nodos prefijados Francisco José Perdomo Pío Departamento de Análisis Matemático, Universidad de La Laguna Preprint: Positive quadrature
El Teorema de Stone-Weierstrass
 Capítulo 3 El Teorema de Stone-Weierstrass Vamos a ver en esta lección el teorema clásico de Weierstrass y la importante generalización del mismo dada por Stone. El teorema de Weierstrass El teorema de
Capítulo 3 El Teorema de Stone-Weierstrass Vamos a ver en esta lección el teorema clásico de Weierstrass y la importante generalización del mismo dada por Stone. El teorema de Weierstrass El teorema de
Comisión de Pedagogía - Diego Chamorro Un (corto) panorama de Análisis Armónico (Nivel 3).
 AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Un (corto) panorama de Análisis Armónico (Nivel 3). Lección n : La ecuación de ondas como punto de partida UCE, otoño 04 Introducción El objetivo
AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Un (corto) panorama de Análisis Armónico (Nivel 3). Lección n : La ecuación de ondas como punto de partida UCE, otoño 04 Introducción El objetivo
Elementos Básicos de Análisis Funcional en. Dr. Oldemar Rodríguez Rojas
 Elementos Básicos de Análisis Funcional en Análisis Numérico Dr. Oldemar Rodríguez Rojas Agosto 2008 Contents 1 Elementos Básicos de Análisis Funcional 2 1.1 Espacios normados...........................
Elementos Básicos de Análisis Funcional en Análisis Numérico Dr. Oldemar Rodríguez Rojas Agosto 2008 Contents 1 Elementos Básicos de Análisis Funcional 2 1.1 Espacios normados...........................
5. Aplicaciones Lineales
 Contents 5 Aplicaciones Lineales 2 5.1 Aplicaciones lineales. Definición y propiedades........................ 2 5.2 Núcleo e Imagen.................................................... 3 5.3 Descomposición
Contents 5 Aplicaciones Lineales 2 5.1 Aplicaciones lineales. Definición y propiedades........................ 2 5.2 Núcleo e Imagen.................................................... 3 5.3 Descomposición
Polinomios ortogonalmente aditivos y aplicaciones.
 Polinomios ortogonalmente aditivos y aplicaciones. Pablo Linares conjuntamente con A. Ibort y J. G. Llavona. Universidad Complutense Salobreña, 3-5 Abril 2008 1 Polinomios ortogonalmente aditivos. Introducción.
Polinomios ortogonalmente aditivos y aplicaciones. Pablo Linares conjuntamente con A. Ibort y J. G. Llavona. Universidad Complutense Salobreña, 3-5 Abril 2008 1 Polinomios ortogonalmente aditivos. Introducción.
1. Teoría de Littlewood-Paley
 AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Análisis armónico y espacios funcionales (Nivel 3). Lección n 2: Teoría y Descomposiciones de Littlewood-Paley. EPN, verano 2010 1. Teoría de
AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Análisis armónico y espacios funcionales (Nivel 3). Lección n 2: Teoría y Descomposiciones de Littlewood-Paley. EPN, verano 2010 1. Teoría de
7. CONVOLUCION Y DENSIDAD
 Hemos definido una relación de inclusión (7.1) 7. CONVOLUCION Y DENSIDAD Esta relación nos permite "pensar en" S n ) como un sub-espacio de S' n ); lo que indica que normalmente identificaremos uϕ con
Hemos definido una relación de inclusión (7.1) 7. CONVOLUCION Y DENSIDAD Esta relación nos permite "pensar en" S n ) como un sub-espacio de S' n ); lo que indica que normalmente identificaremos uϕ con
Estimación por intervalos
 Capítulo 9 Estimación por intervalos 9.1. Introducción En este capítulo se desarrolla la estimación por intervalos donde el proceso de inferencia se realiza de la forma θ C, donde C = Cx) es un conjunto
Capítulo 9 Estimación por intervalos 9.1. Introducción En este capítulo se desarrolla la estimación por intervalos donde el proceso de inferencia se realiza de la forma θ C, donde C = Cx) es un conjunto
Algoritmos en teoría de números
 Algoritmos en teoría de números IIC2283 IIC2283 Algoritmos en teoría de números 1 / 92 Para recordar: aritmética modular Dados dos números a, b Z, si b > 0 entonces existen α, β Z tales que 0 β < b y a
Algoritmos en teoría de números IIC2283 IIC2283 Algoritmos en teoría de números 1 / 92 Para recordar: aritmética modular Dados dos números a, b Z, si b > 0 entonces existen α, β Z tales que 0 β < b y a
Función característica. Sean X e Y v.a. en (Ω,A,P), Z = X + iy es una variable aleatoria compleja, es decir, Z : Ω C
 Dada una variable aleatoria X, introduciremos la función caracteística de X, que se denotará φ X (t). El objetivo de los Teoremas que se enuncian a continuación es probar que X n D X φ Xn (t) φ X (t) t
Dada una variable aleatoria X, introduciremos la función caracteística de X, que se denotará φ X (t). El objetivo de los Teoremas que se enuncian a continuación es probar que X n D X φ Xn (t) φ X (t) t
Clase 1: Simulación de variables aleatorias *
 Clase 1: Simulación de variables aleatorias * Índice 1. Simulación de variables aleatorias 1 1.1. Espacio de Probabilidad. Axiomas de Kolmogorov...... 1 2. Variables aleatorias y distribución de probabilidad
Clase 1: Simulación de variables aleatorias * Índice 1. Simulación de variables aleatorias 1 1.1. Espacio de Probabilidad. Axiomas de Kolmogorov...... 1 2. Variables aleatorias y distribución de probabilidad
Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados
 Capítulo 5 Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados En este tema iniciamos el estudio de los conceptos geométricos de distancia y perpendicularidad en K n. Empezaremos con las definiciones
Capítulo 5 Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados En este tema iniciamos el estudio de los conceptos geométricos de distancia y perpendicularidad en K n. Empezaremos con las definiciones
Topologías. Segundo cuatrimestre Práctica Encuentre todas las topologías sobre conjuntos de a lo sumo cuatro elementos.
 Topología Segundo cuatrimestre - 2011 Práctica 1 Topologías Ejemplos de topologías 1. Encuentre todas las topologías sobre conjuntos de a lo sumo cuatro elementos. 2. Sea X un conjunto. (a) Sea τ = {U
Topología Segundo cuatrimestre - 2011 Práctica 1 Topologías Ejemplos de topologías 1. Encuentre todas las topologías sobre conjuntos de a lo sumo cuatro elementos. 2. Sea X un conjunto. (a) Sea τ = {U
Análisis Matemático para Estadística. Hoja 1
 Análisis Matemático para Estadística. Hoja Funciones de variable compleja. Teoremas básicos.. Describe el conjunto de puntos del plano complejo que cumplen la ecuación: (a) Im(z + 5i) = ; (b) Re(z + 3
Análisis Matemático para Estadística. Hoja Funciones de variable compleja. Teoremas básicos.. Describe el conjunto de puntos del plano complejo que cumplen la ecuación: (a) Im(z + 5i) = ; (b) Re(z + 3
Parte 3. Vectores y valores propios
 Parte 3. Vectores y valores propios Gustavo Montero Escuela Universitaria Politécnica Universidad de Las Palmas de Gran Canaria Curso 2004-2005 1 Introducción a los valores y vectores propios 2 3 4 5 Valores
Parte 3. Vectores y valores propios Gustavo Montero Escuela Universitaria Politécnica Universidad de Las Palmas de Gran Canaria Curso 2004-2005 1 Introducción a los valores y vectores propios 2 3 4 5 Valores
Espacios Vectoriales
 Espacios Vectoriales Espacios Vectoriales Verónica Briceño V. noviembre 2013 Verónica Briceño V. () Espacios Vectoriales noviembre 2013 1 / 47 En esta Presentación... En esta Presentación veremos: Espacios
Espacios Vectoriales Espacios Vectoriales Verónica Briceño V. noviembre 2013 Verónica Briceño V. () Espacios Vectoriales noviembre 2013 1 / 47 En esta Presentación... En esta Presentación veremos: Espacios
