Números complejos y Polinomios
|
|
|
- Monica Castro Arroyo
- hace 9 años
- Vistas:
Transcripción
1 Semana 13 [1/14] 23 de mayo de 2007
2 Forma polar de los complejos Semana 13 [2/14] Raíces de la unidad Raíz n-ésima de la unidad Sean z C y n 2. Diremos que z es una raíz n-ésima de la unidad si z n = 1 Si escribimos en forma polar z = re iθ, entonces (gracias a la fórmula de Moivre) z n = r n e inθ Entonces, para que z sea raíz n-ésima de la unidad, debe cumplirse r n = 1 ( k ) nθ = 2kπ Como r 0 es un número real, debe tenerse que r = 1. La condición sobre θ es: ( k ) θ = 2kπ n Obtenemos que todos los complejos de la forma z = e i 2kπ n son raíces n-ésimas de la unidad. Cuántos números complejos cumplen esto? Elijamos r {0,...,n 1} tal que k n r, es decir que k = r + nl con l. Entonces e i 2kπ n = e 2rπ i( n +2lπ) = e i 2rπ n e i 2lπ = e i 2rπ n 1 = e i 2rπ n Así, todos los posibles valores de θ dados anteriormente definen sólo n números complejos distintos: éstos son e i 2rπ n (r = 0,...,n 1) Estos valores son las exactamente n raíces n-ésimas de la unidad.
3 Forma polar de los complejos Semana 13 [3/14] Raíces de un complejo cualquiera Raíces de un complejo cualquiera Sean w C \ {0} y n 2. Diremos que z es una raíz n-ésima de w si z n = w Escribiendo las formas polares z = re iθ y w = Re iφ, entonces debe cumplirse r n e inθ = Re iφ Como r 0 es real, esta vez obtenemos que r = n R, y la condición se reduce a e inθ = e iφ lo que equivale a ( e i(θ φ n ) ) n = 1 es decir, v = e i(θ φ n ) debe ser una raíz n-ésima de la unidad. Así, existe r {0,...,n 1} tal que θ φ n = 2rπ n Nuestra condición para θ es, finalmente, ( r {0,...,n 1}) θ = φ + 2rπ n
4 Forma polar de los complejos Semana 13 [4/14] Raíces de un complejo cualquiera Concluimos que w tiene también exactamente n raíces n-ésimas, las cuales son n R e i φ+2rπ n (r = 0,...,n 1) Gracias a este análisis, sabemos ahora que la ecuación z 2 = 1 posee exactamente dos soluciones en C: las dos raíces cuadradas de -1. La forma polar de -1 es e iπ, por lo que las mencionadas raíces son y e i π 2 = cos π 2 + i sin π 2 = i e i π+2π 2 = cos 3π 2 + i sin 3π 2 = i
5 Forma polar de los complejos Semana 13 [5/14] Ejercicio: suma de las raíces de la unidad Propiedad Sea n 2. La suma de las n raíces n-ésimas de la unidad vale cero. Demostración. Las raíces n-ésimas de la unidad son e i 2rπ n (r = 0,...,n 1) Su suma es, entonces, ( ) r, Observamos que e i 2rπ n = e i 2π n por lo que n 1 S = r=0 e i 2rπ n Como n 2, tenemos que e i 2π n 1, y así S = n 1 S = r=0 ( ) 0 ( ) n e i 2π n e i 2π n 1 e i 2π n ( ) r e i 2π n = e i 2π n = 0
6 Polinomios Semana 13 [6/14] Definición Polinomio Sea (Ã, +, ) un cuerpo, Ê ó C. Un polinomio es un tipo particular de función de à en Ã, dado por p : à à x p(x)= a 0 + a 1 x + a 2 x a n x n = n a kx k donde a 0, a 1, a 2,...,a n son constantes en Ã. Se llaman coeficientes del polinomio p. Al conjunto de todos los polinomios con coeficientes en à se le denota Ã[x]. Proposición Sean p, q dos polinomios en Ã[x]. Se tiene que Demostración. Por doble implicancia. ) Ésta es directa, y queda de ejercicio para el lector. ) Supongamos que p y q son iguales Sus coeficientes son iguales p(x) = a 0 + a 1 x + a 2 x a n x n q(x) = b 0 + b 1 x + b 2 x b m x m Notemos que podemos suponer que m = n. En efecto, si m < n, entonces podemos escribir q(x) = b 0 + b 1 x + b 2 x b n x n tomando b m+1 = 0, b m+2 = 0,..., b n = 0. Se procede de modo similar si m > n. Continúa...
7 Polinomios Semana 13 [7/14] Igualdad de polinomios Continuación demostración. Debemos demostrar, entonces, que ( k = 0,...,n) a k = b k. Lo haremos siguiendo un argumento de tipo inductivo (similar a la segunda forma del principio de inducción): Caso base k = 0: Sabemos que los polinomios p y q son iguales (como funciones), por lo que p(0) = q(0). Pero p(0) = a 0 y q(0) = b 0, con lo que concluimos que a 0 = b 0. Paso inductivo: Sea k {1,...,n}, y supongamos que a 0 = b 0, a 1 = b 1,...,a k 1 = b k 1. Debemos demostrar que a k = b k. Como p y q son iguales, entonces para cualquier x Ã: a 0 + a 1 x + a 2 x a n x n = b 0 + b 1 x + b 2 x b n x n Usando la hipótesis inductiva, podemos cancelar los primeros k términos a cada lado, y obtener Podemos a ambos lados factorizar x k : Así, para todo x à \ {0} tenemos a k x k a n x n = b k x k b n x n x k (a k a n x n k ) = x k (b k b n x n k ) a k a n x n k = b k b n x n k pues podemos dividir por x k. Recordando que à es Ê ó C, podemos tomar el límite x 0 a ambos lados de la última igualdad, y así a k = b k. Por lo tanto, los coeficientes de ambos polinomios son iguales.
8 Polinomios Semana 13 [8/14] Grado de un polinomio Grado de un polinomio Sea p(x) = a 0 + a 1 x a n x n un polinomio. Diremos que es de grado n si a n 0, en cuyo caso notaremos gr(p) = n. Si p(x) = 0 (el llamado polinomio nulo), diremos que es de grado, y lo notaremos por gr(p) =. Es decir, gr(p) es el k más grande posible tal que a k es no nulo. Respecto de, se usa las siguientes convenciones: para cualquier n Æ y además n + ( ) = n > ( ) + ( ) = Ejemplos gr(1 + 5x + 18x 4 ) = 4 gr(x + 3) = 1 gr(37) = 0 gr(0) =
9 Polinomios Semana 13 [9/14] Grado de un polinomio Importante Los polinomios de grado 0 son exactamente los polinomios constantes (que no dependen de x) p(x) = a 0 con a 0 0. Sea p Ã[x] un polinomio. Diremos que p es mónico si a n = 1 donde n = gr(p) es decir, si el coeficiente asociado a la potencia de x más grande vale 1. Ejemplos Son polinomios mónicos: x + x x 2 x 5 + 5x 2 25
10 Polinomios Semana 13 [10/14] Operaciones entre polinomios Sean p, q Ã[x] dos polinomios: p(x) = n a k x k, q(x) = n b k x k (recordar que eventualmente hay que rellenar con ceros para que ambos polinomios tengan la misma cantidad de coeficientes) Definimos la suma y multiplicación de polinomios del modo siguiente: Suma y multiplicación de polinomios El polinomio suma se define como el polinomio formado por la suma de los coeficientes de p y q. (p + q)(x) = n (a k + b k )x k El polinomio producto tiene una definición en apariencia más complicada. ( 2n k ) (p q)(x) = a i b k i x k i=0 Sin embargo, ésta corresponde a la forma intuitiva de multiplicar distribuyendo: (1 x + 3x 2 ) (x 2 x 4 ) = 1(x 2 x 4 ) x(x 2 x 4 ) + 3x 2 (x 2 x 4 ) = x 2 x 4 x 3 + x 5 + 3x 4 3x 6 = x 2 x 3 + 2x 4 + x 5 3x 6
11 Polinomios Semana 13 [11/14] Operaciones entre polinomios: Consideraciones de grado Estas operaciones cumplen: gr(p + q) m«ax{gr(p), gr(q)} gr(p q) = gr(p) + gr(q) Es importante recalcar que en el caso de la suma sólo tenemos una desigualdad, y no una igualdad. Un posible ejemplo es considerar p(x) = 1 + 5x + 7x 2 y q(x) = 2 + 8x 7x 2. Se tiene que gr(p) = gr(q) = 2, pero gr(p + q) = gr(3 + 13x) = 1. Observemos que la fórmula para calcular el grado de un producto también es válida cuando alguno de los polinomios es el polinomio nulo: en efecto, si p(x) = 0, entonces (p q)(x) = 0, por lo que y ambos lados valen. gr(0) = gr(p q) = gr(p) + gr(q) = ( ) + gr(q)
12 Polinomios Semana 13 [12/14] Estructura de Ã[x] Propiedad (Ã[x], +, ) es un anillo conmutativo con unidad, que no posee divisores de cero. Demostración. Esta demostración queda como ejercicio para el lector, aquí revisaremos sólo algunas partes. La unidad de (Ã[x], +, ) es el polinomio constante p(x) = 1. Observemos que los coeficientes de este polinomio son { 1 k = 0 a k = 0 k 0 Así, si q = b 0 + b 1 x b n x n Ã[x] es de grado n Continúa... (p q)(x) = = = = 2n 2n 2n 2n ( k ) a i b k i ( ( i=0 a 0 b k + 1 b k + b k x k x k ) k a i b k i i=1 x k ) k 0 b k i i=1 x k
13 Polinomios Semana 13 [13/14] Estructura de Ã[x] Continuación demostración. Como q es de grado n, entonces b k = 0 para k = n + 1,...,2n. Entonces (p q)(x) = n b k x k = q(x) (Ã[x], +, ) no posee divisores de cero. En efecto, si p, q Ã[x] son tales que p q = 0, entonces obtenemos que gr(p) + gr(q) = Dadas las reglas de suma que definimos, al menos uno de los dos grados debe valer, es decir al menos uno de los dos polinomios debe ser igual a cero.
14 Polinomios Semana 13 [14/14] Es (Ã[x], +, ) cuerpo? Veremos que (Ã[x], +, ) es un ejemplo de un anillo conmutativo con unidad sin divisores de cero, que sin embargo no es cuerpo. ( Qué anillos conmutativos con unidad sin divisores de cero sí son cuerpos?) Proposición En (Ã[x], +, ), los únicos polinomios que poseen inverso son las constantes no nulas, es decir los polinomios de grado 0. Demostración. Sea p Ã[x] de grado 0. Entonces p(x) = a 0 con a 0 0. Es fácil ver que p posee inverso, el cual es q(x) = 1 a 0. Sea ahora p Ã[x] tal que posee un inverso q Ã[x]. Entonces p q = 1, con lo que gr(p) + gr(q) = 0 Como el grado de un polinomio es siempre positivo (con la excepción de que valga ), debe tenerse en particular que gr(p) = 0.
Semana 14 [1/19] Polinomios. 8 de junio de Polinomios
![Semana 14 [1/19] Polinomios. 8 de junio de Polinomios Semana 14 [1/19] Polinomios. 8 de junio de Polinomios](/thumbs/57/40923686.jpg) Semana 14 [1/19] 8 de junio de 2007 División Semana 14 [2/19] Teorema de la División Al ser (K[x], +, ) un anillo, ocurre un fenómeno similar al de : Las divisiones deben considerar un posible resto. Teorema
Semana 14 [1/19] 8 de junio de 2007 División Semana 14 [2/19] Teorema de la División Al ser (K[x], +, ) un anillo, ocurre un fenómeno similar al de : Las divisiones deben considerar un posible resto. Teorema
Definición 1.2. Sea (K, +, ) un dominio de integridad. Un polinomio de grado n sobre K es una expresión de la forma
 Polinomios Definición 1.1. Un conjunto K junto con dos operaciones definidas en él que denotaremos por + : K K K : K K K para las cuales se cumplen las siguientes propiedades: Asociatividad Conmutatividad
Polinomios Definición 1.1. Un conjunto K junto con dos operaciones definidas en él que denotaremos por + : K K K : K K K para las cuales se cumplen las siguientes propiedades: Asociatividad Conmutatividad
Estructuras algebraicas
 Semana 11[1/22] 4 de mayo de 2007 Anillos y cuerpos Semana 11[2/22] Anillos Comenzamos ahora el estudio de estructuras algebraicas que tengan definidas dos operaciones, y las clasificaremos en anillos
Semana 11[1/22] 4 de mayo de 2007 Anillos y cuerpos Semana 11[2/22] Anillos Comenzamos ahora el estudio de estructuras algebraicas que tengan definidas dos operaciones, y las clasificaremos en anillos
Problemas de VC para EDVC elaborados por C. Mora, Tema 1. Escribir en forma binómica los siguientes números complejos:, n N; 3 i ; (1+i 3) 20 ; e 1/z
 Problemas de VC para EDVC elaborados por C. Mora, Tema 1 Ejercicio 1 Escribir en forma binómica los siguientes números complejos: i n, n Z; ( 1 + i ) n, n N; ( ) ( ) 4 5 1 + i 3 i ; (1+i 3) 0 ; e 1/z 1
Problemas de VC para EDVC elaborados por C. Mora, Tema 1 Ejercicio 1 Escribir en forma binómica los siguientes números complejos: i n, n Z; ( 1 + i ) n, n N; ( ) ( ) 4 5 1 + i 3 i ; (1+i 3) 0 ; e 1/z 1
MATEMÁTICA D y D 1 Módulo I: Análisis de Variable Compleja
 Matemática D y D MATEMÁTICA D y D Módulo I: Análisis de Variable Compleja Unidad 0 Números Complejos Mag. María Inés Baragatti Números complejos. Generalidades Un número complejo es un par ordenado de
Matemática D y D MATEMÁTICA D y D Módulo I: Análisis de Variable Compleja Unidad 0 Números Complejos Mag. María Inés Baragatti Números complejos. Generalidades Un número complejo es un par ordenado de
ALGEBRA I, ALGEBRA Y TRIGONOMETRIA , Segundo Semestre CAPITULO 6: POLINOMIOS.
 ALGEBRA I, ALGEBRA Y TRIGONOMETRIA 520135, 522115 Segundo Semestre CAPITULO 6: POLINOMIOS. DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas 1 Definición: Polinomio Sea K
ALGEBRA I, ALGEBRA Y TRIGONOMETRIA 520135, 522115 Segundo Semestre CAPITULO 6: POLINOMIOS. DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas 1 Definición: Polinomio Sea K
Principio de inducción y Sumatorias
 Semana06[1/14] 3 de abril de 007 Principio de inducción: Primera forma Semana06[/14] Una categoría importante de proposiciones y teoremas es la de las propiedades de los números naturales. Aquí tenemos,
Semana06[1/14] 3 de abril de 007 Principio de inducción: Primera forma Semana06[/14] Una categoría importante de proposiciones y teoremas es la de las propiedades de los números naturales. Aquí tenemos,
1. Conjuntos de números
 1.2. Números complejos 1.2.1. FORMA BINÓMICA Números complejos en forma binómica Se llama número complejo a cualquier expresión de la forma z = x + yi donde x e y son números reales cualesquiera e i =
1.2. Números complejos 1.2.1. FORMA BINÓMICA Números complejos en forma binómica Se llama número complejo a cualquier expresión de la forma z = x + yi donde x e y son números reales cualesquiera e i =
NÚMEROS COMPLEJOS: C
 NÚMEROS COMPLEJOS: C Alejandro Lugon 21 de mayo de 2010 Resumen Este es un pequeño estudio de los números complejos con el objetivo de poder usar las técnicas de solución de ecuaciones y sistemas diferenciales
NÚMEROS COMPLEJOS: C Alejandro Lugon 21 de mayo de 2010 Resumen Este es un pequeño estudio de los números complejos con el objetivo de poder usar las técnicas de solución de ecuaciones y sistemas diferenciales
Semana 12 [1/8] Números complejos. 15 de mayo de Números complejos
![Semana 12 [1/8] Números complejos. 15 de mayo de Números complejos Semana 12 [1/8] Números complejos. 15 de mayo de Números complejos](/thumbs/58/41243274.jpg) Semana 12 [1/8] 15 de mayo de 2007 Aviso Semana 12 [2/8] Importante Los contenidos asociados a números complejos en la tutoría de la semana 11, se consideran como parte de esta semana. Esto se reflejará
Semana 12 [1/8] 15 de mayo de 2007 Aviso Semana 12 [2/8] Importante Los contenidos asociados a números complejos en la tutoría de la semana 11, se consideran como parte de esta semana. Esto se reflejará
Anillo de polinomios con coeficientes en un cuerpo
 Capítulo 2 Anillo de polinomios con coeficientes en un cuerpo En el conjunto Z se ha visto cómo la relación ser congruente módulo m para un entero m > 1, es compatible con las operaciones suma y producto.
Capítulo 2 Anillo de polinomios con coeficientes en un cuerpo En el conjunto Z se ha visto cómo la relación ser congruente módulo m para un entero m > 1, es compatible con las operaciones suma y producto.
Departamento de Ingeniería Matemática - Universidad de Chile
 5. Principio de inducción Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Introducción al Álgebra 08-1 5.1. Principio de inducción: Primera forma Importante: Visita
5. Principio de inducción Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Introducción al Álgebra 08-1 5.1. Principio de inducción: Primera forma Importante: Visita
FUNCIONES REALES DE UNA VARIABLE CONCEPTOS FUNDAMENTALES
 FUNCIONES REALES DE UNA VARIABLE Índice Presentación... 3 Conjunto de los números reales... 4 Los intervalos... 6 Las potencias... 7 Los polinomios... 8 La factorización de polinomios (I)... 9 La factorización
FUNCIONES REALES DE UNA VARIABLE Índice Presentación... 3 Conjunto de los números reales... 4 Los intervalos... 6 Las potencias... 7 Los polinomios... 8 La factorización de polinomios (I)... 9 La factorización
ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- Polinomios
 Resumen teoría Prof. Alcón ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- Polinomios Sea (A, +,.) un anillo conmutativo. Indicamos con A[x] al conjunto de polinomios en una indeterminada x con coeficientes en
Resumen teoría Prof. Alcón ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- Polinomios Sea (A, +,.) un anillo conmutativo. Indicamos con A[x] al conjunto de polinomios en una indeterminada x con coeficientes en
ALGEBRA y ALGEBRA LINEAL. Primer Semestre CAPITULO 6. POLINOMIOS DE UNA VARIABLE.
 ALGEBRA y ALGEBRA LINEAL 520142 Primer Semestre CAPITULO 6. POLINOMIOS DE UNA VARIABLE. DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas 1 Definición: Polinomio Sea K (Q,
ALGEBRA y ALGEBRA LINEAL 520142 Primer Semestre CAPITULO 6. POLINOMIOS DE UNA VARIABLE. DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas 1 Definición: Polinomio Sea K (Q,
Semana03[1/17] Funciones. 16 de marzo de Funciones
![Semana03[1/17] Funciones. 16 de marzo de Funciones Semana03[1/17] Funciones. 16 de marzo de Funciones](/thumbs/48/24900626.jpg) Semana03[1/17] 16 de marzo de 2007 Introducción Semana03[2/17] Ya que conocemos el producto cartesiano A B entre dos conjuntos A y B, podemos definir entre ellos algún tipo de correspondencia. Es decir,
Semana03[1/17] 16 de marzo de 2007 Introducción Semana03[2/17] Ya que conocemos el producto cartesiano A B entre dos conjuntos A y B, podemos definir entre ellos algún tipo de correspondencia. Es decir,
1. DEFINICIÓN. ax = b, x 2 = b, 2 + 5i, 0 + ( 2)i, 2 + 3i, 5 + 0i, 1 + 1i. 0 + ( 2)i = 2i, 5 + 0i = 5, 1 + 1i = 1 + i.
 NÚMEROS COMPLEJOS PATRICIA KISBYE 1. DEFINICIÓN En los números reales es posible resolver cualquier ecuación lineal en una variable: ax = b, siempre que a sea distinto de 0. Pero las ecuaciones cuadráticas,
NÚMEROS COMPLEJOS PATRICIA KISBYE 1. DEFINICIÓN En los números reales es posible resolver cualquier ecuación lineal en una variable: ax = b, siempre que a sea distinto de 0. Pero las ecuaciones cuadráticas,
Una matriz es un arreglo rectangular de números. Los números en el arreglo se llaman elementos de la matriz. ) ( + ( ) ( )
 MATRICES Una matriz es un arreglo rectangular de números. Los números en el arreglo se llaman elementos de la matriz. Ejemplo 1. Algunos ejemplos de matrices ( + ( ) ( + ( ) El tamaño o el orden de una
MATRICES Una matriz es un arreglo rectangular de números. Los números en el arreglo se llaman elementos de la matriz. Ejemplo 1. Algunos ejemplos de matrices ( + ( ) ( + ( ) El tamaño o el orden de una
Números complejos. por. Ramón Espinosa Armenta
 Números complejos por Ramón Espinosa Armenta En el siglo XVI, el matemático italiano Gerolamo Cardano se preguntó si tenía sentido considerar raíces cuadradas de números negativos. Tal raíz cuadrada debería
Números complejos por Ramón Espinosa Armenta En el siglo XVI, el matemático italiano Gerolamo Cardano se preguntó si tenía sentido considerar raíces cuadradas de números negativos. Tal raíz cuadrada debería
Semana 07[1/21] Sumatorias. 12 de abril de Sumatorias
![Semana 07[1/21] Sumatorias. 12 de abril de Sumatorias Semana 07[1/21] Sumatorias. 12 de abril de Sumatorias](/thumbs/70/63260960.jpg) Semana 07[/] de abril de 007 Semana 07[/] Progresiones aritméticas Progresión aritmética Es una sumatoria del tipo (A + d) es decir, donde a A + d, para valores A, d Ê. Utilizando las propiedades de sumatoria,
Semana 07[/] de abril de 007 Semana 07[/] Progresiones aritméticas Progresión aritmética Es una sumatoria del tipo (A + d) es decir, donde a A + d, para valores A, d Ê. Utilizando las propiedades de sumatoria,
Departamento de Ingeniería Matemática - Universidad de Chile
 Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 08-2 SEMANA 7: ESPACIOS VECTORIALES 3.5. Generadores de un espacio vectorial Sea V un espacio vectorial
Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 08-2 SEMANA 7: ESPACIOS VECTORIALES 3.5. Generadores de un espacio vectorial Sea V un espacio vectorial
El cuerpo de los números complejos
 Capítulo 1 El cuerpo de los números complejos En este primer capítulo se revisan los conceptos elementales relativos a los números complejos. El capítulo comienza con una breve nota histórica y después
Capítulo 1 El cuerpo de los números complejos En este primer capítulo se revisan los conceptos elementales relativos a los números complejos. El capítulo comienza con una breve nota histórica y después
NÚMEROS COMPLEJOS 1.1. INTRODUCCIÓN 1.2. OPERACIONES CON COMPLEJOS
 NÚMEROS COMPLEJOS 1.1. INTRODUCCIÓN La ecuación x + 1 0 no tiene solución en el cuerpo de los números reales R ya que no existe un número real x tal que x 1. Necesitamos un conjunto que contenga a R, que
NÚMEROS COMPLEJOS 1.1. INTRODUCCIÓN La ecuación x + 1 0 no tiene solución en el cuerpo de los números reales R ya que no existe un número real x tal que x 1. Necesitamos un conjunto que contenga a R, que
Estructuras algebraicas
 Semana 10[1/14] 26 de abril de 2007 Semana 10[2/14] Grupos Un grupo es un caso particular de una estructura algebraica. Veremos que esta noción rescata ampliamente las propiedades de estructuras tales
Semana 10[1/14] 26 de abril de 2007 Semana 10[2/14] Grupos Un grupo es un caso particular de una estructura algebraica. Veremos que esta noción rescata ampliamente las propiedades de estructuras tales
GUÍA DE EJERCICIOS. Área Matemática - Polinomios
 GUÍA DE EJERCICIOS Área Matemática - Polinomios Resultados de aprendizaje. Realizar operaciones entre polinomios. Aplicar Regla de Ruffini, para determinar raíces de un polinomio. Aplicar los procedimientos
GUÍA DE EJERCICIOS Área Matemática - Polinomios Resultados de aprendizaje. Realizar operaciones entre polinomios. Aplicar Regla de Ruffini, para determinar raíces de un polinomio. Aplicar los procedimientos
CURSO CERO DE MATEMATICAS. Apuntes elaborados por Domingo Pestana Galván. y José Manuel Rodríguez García
 INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES CURSO CERO DE MATEMATICAS Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica
INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES CURSO CERO DE MATEMATICAS Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica
Capítulo 4: Polinomios
 Capítulo 4: Polinomios Miguel Ángel Olalla Acosta [email protected] Departamento de Álgebra Universidad de Sevilla Diciembre de 2017 Olalla (Universidad de Sevilla) Capítulo 4: Polinomios Diciembre de
Capítulo 4: Polinomios Miguel Ángel Olalla Acosta [email protected] Departamento de Álgebra Universidad de Sevilla Diciembre de 2017 Olalla (Universidad de Sevilla) Capítulo 4: Polinomios Diciembre de
Raíces de polinomios
 Raíces de polinomios En ésta página podrás conocer las herramientas necesarias para poder encontrar las raíces de polinomios de una variable con coeficientes enteros. Para ello hemos dividido esta página
Raíces de polinomios En ésta página podrás conocer las herramientas necesarias para poder encontrar las raíces de polinomios de una variable con coeficientes enteros. Para ello hemos dividido esta página
Polinomios. Capítulo El cuerpo de los números complejos C.
 Capítulo 5 Polinomios. Este capítulo trata sobre los polinomios con coeficientes en un cuerpo K. Hasta ahora mencionamos en la materia varios ejemplos de cuerpos: el cuerpo de los números racionales Q,
Capítulo 5 Polinomios. Este capítulo trata sobre los polinomios con coeficientes en un cuerpo K. Hasta ahora mencionamos en la materia varios ejemplos de cuerpos: el cuerpo de los números racionales Q,
Capítulo 4: Polinomios
 Capítulo 4: Polinomios Miguel Ángel Olalla Acosta [email protected] Departamento de Álgebra Universidad de Sevilla Diciembre de 2015 Olalla (Universidad de Sevilla) Capítulo 4: Polinomios Diciembre de
Capítulo 4: Polinomios Miguel Ángel Olalla Acosta [email protected] Departamento de Álgebra Universidad de Sevilla Diciembre de 2015 Olalla (Universidad de Sevilla) Capítulo 4: Polinomios Diciembre de
UNIDAD 1 NUMEROS COMPLEJOS
 UNIDAD 1 NUMEROS COMPLEJOS El conjunto de los números complejos fue creado para poder resolver algunos problemas matemáticos que no tienen solución dentro del conjunto de los números reales. Por ejemplo
UNIDAD 1 NUMEROS COMPLEJOS El conjunto de los números complejos fue creado para poder resolver algunos problemas matemáticos que no tienen solución dentro del conjunto de los números reales. Por ejemplo
Números Complejos. Contenido. Definición
 U Contenido Facultad de Ingeniería Escuela de Ingeniería Eléctrica Departamento de Electrónica, Computación y Control Variable Compleja y Cálculo Operacional Números Complejos William La Cruz Números Complejos...3
U Contenido Facultad de Ingeniería Escuela de Ingeniería Eléctrica Departamento de Electrónica, Computación y Control Variable Compleja y Cálculo Operacional Números Complejos William La Cruz Números Complejos...3
Notas del cursos. Basadas en los prontuarios de MATE 3001 y MATE 3023
 Programa Inmersión, Verano 2016 Notas escritas por Dr. M Notas del cursos. Basadas en los prontuarios de MATE 3001 y MATE 3023 Clase #8: jueves, 9 de junio de 2016. 8 Factorización Conceptos básicos Hasta
Programa Inmersión, Verano 2016 Notas escritas por Dr. M Notas del cursos. Basadas en los prontuarios de MATE 3001 y MATE 3023 Clase #8: jueves, 9 de junio de 2016. 8 Factorización Conceptos básicos Hasta
Variable Compleja I. Maite Fernández Unzieta Universidad de Guanajuato Enero Junio Eugenio Daniel Flores Alatorre
 Variable Compleja I Maite Fernández Unzieta Universidad de Guanajuato Enero Junio 2012 Eugenio Daniel Flores Alatorre Bibliografía Complex Analysis 3rd ed. Ahlfors Basic Complex Analysis Functions of one
Variable Compleja I Maite Fernández Unzieta Universidad de Guanajuato Enero Junio 2012 Eugenio Daniel Flores Alatorre Bibliografía Complex Analysis 3rd ed. Ahlfors Basic Complex Analysis Functions of one
TRABAJO PRÁCTICO Nº 4: POLINOMIOS
 TRABAJO PRÁCTICO Nº : POLINOMIOS EJERCICIOS A DESARROLLAR Clase ) Dados los polinomios reales P(x) =.x ; Q(x) = 3x3 x + y los polinomios complejos R(x) = i.x ; S(x) = x + ( + i).x i, calcular: a) 3x. P(x)
TRABAJO PRÁCTICO Nº : POLINOMIOS EJERCICIOS A DESARROLLAR Clase ) Dados los polinomios reales P(x) =.x ; Q(x) = 3x3 x + y los polinomios complejos R(x) = i.x ; S(x) = x + ( + i).x i, calcular: a) 3x. P(x)
Tema 4. Polinomios Operaciones
 Tema 4. Polinomios Operaciones 1. Expresiones algebraicas. Identidades y ecuaciones.. Monomios.1. Definiciones.. Operaciones con monomios. Polinomios.1. Definiciones.. Operaciones con polinomios Tema.
Tema 4. Polinomios Operaciones 1. Expresiones algebraicas. Identidades y ecuaciones.. Monomios.1. Definiciones.. Operaciones con monomios. Polinomios.1. Definiciones.. Operaciones con polinomios Tema.
Números complejos ( 1)(25) =
 Números complejos 1. Introducción Podemos pensar en las progresivas ampliaciones de los conjuntos numéricos como el método necesario para resolver ecuaciones algebraicas progresivamente complicadas. Así,
Números complejos 1. Introducción Podemos pensar en las progresivas ampliaciones de los conjuntos numéricos como el método necesario para resolver ecuaciones algebraicas progresivamente complicadas. Así,
Si el producto de dos números es cero
 Matemáticas I, 2012-I Si el producto de dos números es cero Empezamos con un acertijo: Silvia tiene dos números. Si los multiplica sale 0 y si los suma sale 256. Cuáles son estos dos números que tiene
Matemáticas I, 2012-I Si el producto de dos números es cero Empezamos con un acertijo: Silvia tiene dos números. Si los multiplica sale 0 y si los suma sale 256. Cuáles son estos dos números que tiene
Los números complejos
 Universidad Autónoma de Madrid Actualización en Análisis Matemático, abril de 2012 Cardano (1501 1576) Dividir un segmento de longitud 10 en dos trozos tales que el rectángulo cuyos lados tienen la longitud
Universidad Autónoma de Madrid Actualización en Análisis Matemático, abril de 2012 Cardano (1501 1576) Dividir un segmento de longitud 10 en dos trozos tales que el rectángulo cuyos lados tienen la longitud
AMPLIACIÓN DE MATEMÁTICAS
 AMPLIACIÓN DE MATEMÁTICAS RAÍCES MÚLTIPLES. Dado un polinomio con coeficientes en un cuerpo existirá siempre un elemento del cuerpo que anula el polinomio? Siempre existe un cuerpo donde podamos encontrar
AMPLIACIÓN DE MATEMÁTICAS RAÍCES MÚLTIPLES. Dado un polinomio con coeficientes en un cuerpo existirá siempre un elemento del cuerpo que anula el polinomio? Siempre existe un cuerpo donde podamos encontrar
6 Vectores. Dependencia e independencia lineal.
 6 Vectores. Dependencia e independencia lineal. Introducción Hay fenómenos reales que se pueden representar adecuadamente mediante un número con su adecuada unidad de medida. Sin embargo para representar
6 Vectores. Dependencia e independencia lineal. Introducción Hay fenómenos reales que se pueden representar adecuadamente mediante un número con su adecuada unidad de medida. Sin embargo para representar
ALGEBRA y ALGEBRA LINEAL. Primer Semestre CAPITULO 5
 ALGEBRA y ALGEBRA LINEAL 520142 Primer Semestre CAPITULO 5 DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas 1 Definición: Números Complejos Se define el conjunto de los
ALGEBRA y ALGEBRA LINEAL 520142 Primer Semestre CAPITULO 5 DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas 1 Definición: Números Complejos Se define el conjunto de los
Números complejos (lista de problemas para examen)
 Números complejos (lista de problemas para examen) En esta lista de problemas trabajamos con la construcción de números complejos (como pares ordenados de los reales) y con su representación en la forma
Números complejos (lista de problemas para examen) En esta lista de problemas trabajamos con la construcción de números complejos (como pares ordenados de los reales) y con su representación en la forma
Semana02[1/23] Conjuntos. 9 de marzo de Conjuntos
![Semana02[1/23] Conjuntos. 9 de marzo de Conjuntos Semana02[1/23] Conjuntos. 9 de marzo de Conjuntos](/thumbs/53/31721818.jpg) Semana02[1/23] 9 de marzo de 2007 Introducción Semana02[2/23] La teoría de conjuntos gira en torno a la función proposicional x A. Los valores que hacen verdadera la función proposicional x A son aquellos
Semana02[1/23] 9 de marzo de 2007 Introducción Semana02[2/23] La teoría de conjuntos gira en torno a la función proposicional x A. Los valores que hacen verdadera la función proposicional x A son aquellos
Anillo de Polinomios.
 Capítulo 6 Anillo de Polinomios. Una forma de definir los polinomios en forma intuitiva es la siguiente: Sea (K,+, ) un cuerpo, entonces un polinomio con coeficiente en K es de la siguiente forma p(x)
Capítulo 6 Anillo de Polinomios. Una forma de definir los polinomios en forma intuitiva es la siguiente: Sea (K,+, ) un cuerpo, entonces un polinomio con coeficiente en K es de la siguiente forma p(x)
Capítulo 4 Desarrollos en Serie de Taylor y de Laurent.
 Capítulo 4 Desarrollos en Serie de Taylor y de Laurent. El desarrollo en serie de potencias, que comúnmente se restringe a potencias positivas en el campo real toma forma definitiva en el campo complejo
Capítulo 4 Desarrollos en Serie de Taylor y de Laurent. El desarrollo en serie de potencias, que comúnmente se restringe a potencias positivas en el campo real toma forma definitiva en el campo complejo
Polinomios II. I. Regla de Ruffini
 Polinomios II En las matemáticas se define el polinomio como una expresión que está formada por un número finito de variables (no conocidas) y constantes (coeficientes) siendo muy utilizados en las matemáticas
Polinomios II En las matemáticas se define el polinomio como una expresión que está formada por un número finito de variables (no conocidas) y constantes (coeficientes) siendo muy utilizados en las matemáticas
14/02/2017. TEMA 3: EL CUERPO DE LOS NUMEROS REALES Esp. Prof. Liliana N. Caputo
 TEMA 3: EL CUERPO DE LOS NUMEROS REALES Esp. Prof. Liliana N. Caputo Así como al estudiar conjuntos hablamos de la existencia de términos primitivos (que no se definen), para definir algunos conjuntos,
TEMA 3: EL CUERPO DE LOS NUMEROS REALES Esp. Prof. Liliana N. Caputo Así como al estudiar conjuntos hablamos de la existencia de términos primitivos (que no se definen), para definir algunos conjuntos,
Anexo: El anillo de polinomios K[x].
![Anexo: El anillo de polinomios K[x]. Anexo: El anillo de polinomios K[x].](/thumbs/67/56852452.jpg) El anillo de polinomios K[x] 1 Anexo: El anillo de polinomios K[x]. 1. Construcción del anillo de polinomios K[x]. Dado un cuerpo K, se define m K[x] = { a i x i a i K, i = 0,..., m, m N {0}}, i=0 donde
El anillo de polinomios K[x] 1 Anexo: El anillo de polinomios K[x]. 1. Construcción del anillo de polinomios K[x]. Dado un cuerpo K, se define m K[x] = { a i x i a i K, i = 0,..., m, m N {0}}, i=0 donde
Polinomios (lista de problemas para examen)
 Polinomios (lista de problemas para examen) En esta lista de problemas el conjunto de los polinomios de una variable con coeficientes complejos se denota por P(C). También se usa la notación C[x], si la
Polinomios (lista de problemas para examen) En esta lista de problemas el conjunto de los polinomios de una variable con coeficientes complejos se denota por P(C). También se usa la notación C[x], si la
6.1. Anillos de polinomios.
 1 Tema 6.-. Anillo de polinomios. División y factorización. Lema de Gauss. 6.1. Anillos de polinomios. Definición 6.1.1. Sea A un anillo. El anillo de polinomios en la indeterminada X con coeficientes
1 Tema 6.-. Anillo de polinomios. División y factorización. Lema de Gauss. 6.1. Anillos de polinomios. Definición 6.1.1. Sea A un anillo. El anillo de polinomios en la indeterminada X con coeficientes
OPERACIONES CON MONOMIOS Y POLINOMIOS. Suma de monomios
 OPERACIONES CON MONOMIOS Y POLINOMIOS Suma de monomios Sólo podemos sumar monomios semejantes. La suma de los monomios es otro monomio que tiene la misma parte literal y cuyo coeficiente es la suma de
OPERACIONES CON MONOMIOS Y POLINOMIOS Suma de monomios Sólo podemos sumar monomios semejantes. La suma de los monomios es otro monomio que tiene la misma parte literal y cuyo coeficiente es la suma de
La trascendencia de e y π
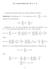 La trascendencia de e y π Comenzamos introduciendo unos convenios útiles de notación: Definición 1 Escribiremos h r = r!, de modo que si fz) = m c r z r C[z], entonces fh) representará fh) = m c r h r
La trascendencia de e y π Comenzamos introduciendo unos convenios útiles de notación: Definición 1 Escribiremos h r = r!, de modo que si fz) = m c r z r C[z], entonces fh) representará fh) = m c r h r
Semana02[1/33] Números Reales. March 9, Números Reales
![Semana02[1/33] Números Reales. March 9, Números Reales Semana02[1/33] Números Reales. March 9, Números Reales](/thumbs/57/41059919.jpg) Semana02[1/33] March 9, 2007 Axiomas de R en torno a la desigualdad Números reales positivos Semana02[2/33] Para introducir la idea de orden en los reales y poder trabajar con desigualdades, existen diversas
Semana02[1/33] March 9, 2007 Axiomas de R en torno a la desigualdad Números reales positivos Semana02[2/33] Para introducir la idea de orden en los reales y poder trabajar con desigualdades, existen diversas
TEMA 1.- POLINOMIOS Y FRACCIONES ALGEBRAICAS
 TEMA 1.- POLINOMIOS Y FRACCIONES ALGEBRAICAS 1.- POLINOMIOS Recordemos que un monomio es una expresión algebraica (combinación de letras y números) en la que las únicas operaciones que aparecen entre las
TEMA 1.- POLINOMIOS Y FRACCIONES ALGEBRAICAS 1.- POLINOMIOS Recordemos que un monomio es una expresión algebraica (combinación de letras y números) en la que las únicas operaciones que aparecen entre las
TEMA 2. ESPACIOS VECTORIALES
 TEMA 2. ESPACIOS VECTORIALES CÉSAR ROSALES GEOMETRÍA I En este tema comenzaremos el estudio de los objetos que nos interesarán en esta asignatura: los espacios vectoriales. Estos son estructuras básicas
TEMA 2. ESPACIOS VECTORIALES CÉSAR ROSALES GEOMETRÍA I En este tema comenzaremos el estudio de los objetos que nos interesarán en esta asignatura: los espacios vectoriales. Estos son estructuras básicas
Fracciones Algebraicas
 Fracciones Algebraicas 1 Conceptos básicos Definición 1 Una fracción algebraica en la indeterminada x (o cualquier otra letra) es una expresión de la forma, donde tanto P como Q son polinomios con coeficientes
Fracciones Algebraicas 1 Conceptos básicos Definición 1 Una fracción algebraica en la indeterminada x (o cualquier otra letra) es una expresión de la forma, donde tanto P como Q son polinomios con coeficientes
TEMA 6: DIVISIÓN DE POLINOMIOS RAÍCES MATEMÁTICAS 3º ESO
 TEMA 6: DIVISIÓN DE POLINOMIOS RAÍCES MATEMÁTICAS 3º ESO 1. División de polinomios Dados dos polinomios P (el dividendo) y D (el divisor), dividir P entre D es encontrar dos polinomios Q (el cociente)
TEMA 6: DIVISIÓN DE POLINOMIOS RAÍCES MATEMÁTICAS 3º ESO 1. División de polinomios Dados dos polinomios P (el dividendo) y D (el divisor), dividir P entre D es encontrar dos polinomios Q (el cociente)
Álgebra II Primer Cuatrimestre 2016
 Álgebra II Primer Cuatrimestre 2016 Práctica 3: Anillos Ejemplos construcciones 1. Probar que los siguientes conjuntos son anillos con las operaciones indicadas. Decidir en cada caso si son conmutativos,
Álgebra II Primer Cuatrimestre 2016 Práctica 3: Anillos Ejemplos construcciones 1. Probar que los siguientes conjuntos son anillos con las operaciones indicadas. Decidir en cada caso si son conmutativos,
Polinomios: Definición: Se llama polinomio en "x" de grado "n" a una expresión del tipo
 Polinomios: Definición: Se llama polinomio en "x" de grado "n" a una expresión del tipo P (x) = a 0 x n + a 1 x n 1 +... + a n Donde n N (número natural) ; a 0, a 1, a 2,..., a n son coeficientes reales
Polinomios: Definición: Se llama polinomio en "x" de grado "n" a una expresión del tipo P (x) = a 0 x n + a 1 x n 1 +... + a n Donde n N (número natural) ; a 0, a 1, a 2,..., a n son coeficientes reales
Semana05[1/14] Relaciones. 28 de marzo de Relaciones
![Semana05[1/14] Relaciones. 28 de marzo de Relaciones Semana05[1/14] Relaciones. 28 de marzo de Relaciones](/thumbs/50/26257926.jpg) Semana05[1/14] 28 de marzo de 2007 Introducción Semana05[2/14] Ya en los capítulos anteriores nos acercamos al concepto de relación. Relación Dados un par de conjuntos no vacíos A y B, llamaremos relación
Semana05[1/14] 28 de marzo de 2007 Introducción Semana05[2/14] Ya en los capítulos anteriores nos acercamos al concepto de relación. Relación Dados un par de conjuntos no vacíos A y B, llamaremos relación
Cuerpo de Fracciones de un Anillo Íntegro
 Cuerpo de Fracciones de un Anillo Íntegro René A Hernández Toledo 1997 * Cuando se desarrollan los sistemas numéricos a partir los conjuntos, primeramente se construyen los números naturales. A partir
Cuerpo de Fracciones de un Anillo Íntegro René A Hernández Toledo 1997 * Cuando se desarrollan los sistemas numéricos a partir los conjuntos, primeramente se construyen los números naturales. A partir
MATRICES. Se simboliza tal matriz por y se le llamará una matriz x o matriz de orden x (que se lee por ).
 1 MATRICES 1 Una matriz es una disposición rectangular de números (Reales); la forma general de una matriz con filas y columnas es Se simboliza tal matriz por y se le llamará una matriz x o matriz de orden
1 MATRICES 1 Una matriz es una disposición rectangular de números (Reales); la forma general de una matriz con filas y columnas es Se simboliza tal matriz por y se le llamará una matriz x o matriz de orden
4.1. Polinomios y teoría de ecuaciones
 CAPÍTULO 4 Polinomios y teoría de ecuaciones 4.1. Polinomios y teoría de ecuaciones Un polinomio real en x, o simplemente polinomio en x es una expresión algebraica de la forma a n x n + a n 1 x n 1 +
CAPÍTULO 4 Polinomios y teoría de ecuaciones 4.1. Polinomios y teoría de ecuaciones Un polinomio real en x, o simplemente polinomio en x es una expresión algebraica de la forma a n x n + a n 1 x n 1 +
Clase 4 Funciones polinomiales y racionales
 Clase 4 Instituto de Ciencias Básicas Facultad de Ingeniería Universidad Diego Portales Marzo de 2014 Polinomios Definición Se llama polinomio en x a toda expresión de la forma p(x) = a 0 + a 1x+ +a n
Clase 4 Instituto de Ciencias Básicas Facultad de Ingeniería Universidad Diego Portales Marzo de 2014 Polinomios Definición Se llama polinomio en x a toda expresión de la forma p(x) = a 0 + a 1x+ +a n
El Teorema Fundamental del Álgebra
 El Teorema Fundamental del Álgebra 1. Repaso de polinomios Definiciones básicas Un monomio en una indeterminada x es una expresión de la forma ax n que representa el producto de un número, a, por una potencia
El Teorema Fundamental del Álgebra 1. Repaso de polinomios Definiciones básicas Un monomio en una indeterminada x es una expresión de la forma ax n que representa el producto de un número, a, por una potencia
POLINOMIOS En esta unidad aprenderás a:
 POLINOMIOS En esta unidad aprenderás a: Reconocer polinomios y calcular su valor numérico Realizar operaciones con polinomios. Manejar la regla de Ruffini y el teorema del resto para encontrar las raíces
POLINOMIOS En esta unidad aprenderás a: Reconocer polinomios y calcular su valor numérico Realizar operaciones con polinomios. Manejar la regla de Ruffini y el teorema del resto para encontrar las raíces
Números complejos ( 1)(25) =
 Números complejos Introducción Podemos pensar en las progresivas ampliaciones de los conjuntos numéricos como el método necesario para resolver ecuaciones algebraicas progresivamente complicadas. Así,
Números complejos Introducción Podemos pensar en las progresivas ampliaciones de los conjuntos numéricos como el método necesario para resolver ecuaciones algebraicas progresivamente complicadas. Así,
POLINOMIOS Y DIVISIÓN DE POLINOMIOS MATEMÁTICAS 3º ESO
 POLINOMIOS Y DIVISIÓN DE POLINOMIOS MATEMÁTICAS 3º ESO Dado que los polinomios se utilizan para describir curvas de diferentes tipos, la gente los utiliza en el mundo real para dibujar curvas. Por ejemplo,
POLINOMIOS Y DIVISIÓN DE POLINOMIOS MATEMÁTICAS 3º ESO Dado que los polinomios se utilizan para describir curvas de diferentes tipos, la gente los utiliza en el mundo real para dibujar curvas. Por ejemplo,
Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones
![Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones](/thumbs/49/25360651.jpg) Semana 09 [1/28] 29 de abril de 2007 Semana 09 [2/28] Definición Sucesión Una sucesión real es una función: f : N R n f (n) Observaciones Para distinguir a una sucesión de las demás funciones, se ocupará
Semana 09 [1/28] 29 de abril de 2007 Semana 09 [2/28] Definición Sucesión Una sucesión real es una función: f : N R n f (n) Observaciones Para distinguir a una sucesión de las demás funciones, se ocupará
Tema 4: Funciones. Límites de funciones
 Tema 4: Funciones. Límites de funciones 1. Concepto de función Una aplicación entre dos conjuntos A y B es una transformación que asocia a cada elemento del conjunto A un único elemento del conjunto B.
Tema 4: Funciones. Límites de funciones 1. Concepto de función Una aplicación entre dos conjuntos A y B es una transformación que asocia a cada elemento del conjunto A un único elemento del conjunto B.
Clase 2: Algoritmo de Euclídes
 Clase 2: Algoritmo de Euclídes Dr. Daniel A. Jaume, * 8 de agosto de 2011 1. Máximo común divisor Para entender que es el máximo común divisor de un par de enteros (no simultáneamente nulos). Lidearemos
Clase 2: Algoritmo de Euclídes Dr. Daniel A. Jaume, * 8 de agosto de 2011 1. Máximo común divisor Para entender que es el máximo común divisor de un par de enteros (no simultáneamente nulos). Lidearemos
Fracciones Parciales. Ramón Espinoza Armenta AVC APOYO VIRTUAL PARA EL CONOCIMIENTO
 Ramón Espinoza Armenta AVC APOYO VIRTUAL PARA EL CONOCIMIENTO Una expresión racional con coeficientes en un campo K, es una expresión de la forma ax ( ) bx ( ) donde ax ( ), bx ( ) K[ x] ax ( ) cx ( )
Ramón Espinoza Armenta AVC APOYO VIRTUAL PARA EL CONOCIMIENTO Una expresión racional con coeficientes en un campo K, es una expresión de la forma ax ( ) bx ( ) donde ax ( ), bx ( ) K[ x] ax ( ) cx ( )
Estructuras Algebraicas
 Tema 1 Estructuras Algebraicas Definición 1 Sea A un conjunto no vacío Una operación binaria (u operación interna) en A es una aplicación : A A A Es decir, tenemos una regla que a cada par de elementos
Tema 1 Estructuras Algebraicas Definición 1 Sea A un conjunto no vacío Una operación binaria (u operación interna) en A es una aplicación : A A A Es decir, tenemos una regla que a cada par de elementos
TERCER EXAMEN PARCIAL ALGEBRA LINEAL I 23 DE MAYO DE 2014 (CON SOLUCIONES)
 TERCER EXAMEN PARCIAL ALGEBRA LINEAL I 23 DE MAYO DE 2014 (CON SOLUCIONES) Instrucciones: Resolver los 5 problemas justificando todas sus afirmaciones y presentando todos sus cálculos. 1. Sea F un campo.
TERCER EXAMEN PARCIAL ALGEBRA LINEAL I 23 DE MAYO DE 2014 (CON SOLUCIONES) Instrucciones: Resolver los 5 problemas justificando todas sus afirmaciones y presentando todos sus cálculos. 1. Sea F un campo.
3.1. Operaciones con matrices. (Suma, resta, producto y traspuesta)
 Operaciones con matrices Suma, resta, producto y traspuesta Suma, resta y multiplicación por escalares Las matrices de un tamaño fijo m n se pueden sumar entre sí y esta operación de sumar se puede definir
Operaciones con matrices Suma, resta, producto y traspuesta Suma, resta y multiplicación por escalares Las matrices de un tamaño fijo m n se pueden sumar entre sí y esta operación de sumar se puede definir
Q(x,t) = -2x 2 t 3 - xt x 5-3x 3 + 4x 2 +2x- 7 22/03/2016. División de polinomios. P(x) = -x 4 + 3x 2-5 R(x) = 5x 4-2x 3 + 3x
 S Escribe un polinomio que cumpla las siguientes condiciones: A)Se llama P(x, y) B)Tiene 5 términos C)Es de grado seis D)No tiene término independiente S Escribe un polinomio que cumpla las siguientes
S Escribe un polinomio que cumpla las siguientes condiciones: A)Se llama P(x, y) B)Tiene 5 términos C)Es de grado seis D)No tiene término independiente S Escribe un polinomio que cumpla las siguientes
Tema 3. Polinomios y fracciones algebraicas
 Tema. Polinomios y fracciones algebraicas. Monomios.. Definiciones.. Operaciones con monomios. Polinomios.. Definiciones.. Operaciones con polinomios. Factorización de un polinomio.. Teorema del resto.
Tema. Polinomios y fracciones algebraicas. Monomios.. Definiciones.. Operaciones con monomios. Polinomios.. Definiciones.. Operaciones con polinomios. Factorización de un polinomio.. Teorema del resto.
La estructura de un cuerpo finito.
 9. CUERPOS FINITOS El objetivo de este capítulo es determinar la estructura de todos los cuerpos finitos. Probaremos en primer lugar que todo cuerpo finito tiene p n elementos, donde p es la característica
9. CUERPOS FINITOS El objetivo de este capítulo es determinar la estructura de todos los cuerpos finitos. Probaremos en primer lugar que todo cuerpo finito tiene p n elementos, donde p es la característica
Álgebra I Práctica 5 - Polinomios
 Álgebra I Práctica 5 - Polinomios 1. Para los siguientes z C, hallar Rez), Imz), z, Rez 1 ), Imz 1 ), Re i z) e Imi z). i) z = 2 + i)1 + 3 i). ii) z = 5 i1 + i) 4. iii) z = 2 + 3 i) 2 1 3 i). iv) z = i
Álgebra I Práctica 5 - Polinomios 1. Para los siguientes z C, hallar Rez), Imz), z, Rez 1 ), Imz 1 ), Re i z) e Imi z). i) z = 2 + i)1 + 3 i). ii) z = 5 i1 + i) 4. iii) z = 2 + 3 i) 2 1 3 i). iv) z = i
CURSO CERO DE MATEMATICAS. Apuntes elaborados por Domingo Pestana Galván. y José Manuel Rodríguez García
 INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES CURSO CERO DE MATEMATICAS Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica
INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES CURSO CERO DE MATEMATICAS Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica
Familiarizar al alumno con las distintas maneras de expresar números complejos.
 Capítulo 2 Aritmética compleja Objetivos Familiarizar al alumno con las distintas maneras de expresar números complejos. Manejar con soltura las operaciones aritméticas con números complejos. 2.1. Representaciones
Capítulo 2 Aritmética compleja Objetivos Familiarizar al alumno con las distintas maneras de expresar números complejos. Manejar con soltura las operaciones aritméticas con números complejos. 2.1. Representaciones
Ceros en extensiones.
 1. EXTENSIONES DE CUERPOS. Varios son los objetivos de este tema. El primero de ellos, resultado debido a Kronecker, es probar que todo polinomio con coeficientes en un cuerpo tiene una raíz en un cuerpo
1. EXTENSIONES DE CUERPOS. Varios son los objetivos de este tema. El primero de ellos, resultado debido a Kronecker, es probar que todo polinomio con coeficientes en un cuerpo tiene una raíz en un cuerpo
Números reales. por. Ramón Espinosa
 Números reales por Ramón Espinosa Existe un conjunto R, cuyos elementos son llamados números reales. Los números reales satisfacen ciertas propiedades algebraicas y de orden que describimos a continuación.
Números reales por Ramón Espinosa Existe un conjunto R, cuyos elementos son llamados números reales. Los números reales satisfacen ciertas propiedades algebraicas y de orden que describimos a continuación.
TEMA 7. DIAGONALIZACION Y Y FORMAS CANONICAS 1. ENDOMORFISMOS NILPOTENTES
 TEMA 7. DIAGONALIZACION Y Y FORMAS CANONICAS 1. ENDOMORFISMOS NILPOTENTES Definición 1.1. Endomorfismo Nilpotente. Un endomorfismo T End(V ) es nilpotente si existe n N tal que f n 0. Definición 1.. Matriz
TEMA 7. DIAGONALIZACION Y Y FORMAS CANONICAS 1. ENDOMORFISMOS NILPOTENTES Definición 1.1. Endomorfismo Nilpotente. Un endomorfismo T End(V ) es nilpotente si existe n N tal que f n 0. Definición 1.. Matriz
Números complejos en la forma polar (lista de problemas para examen)
 Números complejos en la forma polar lista de problemas para examen) En esta lista de problemas trabajamos con números complejos en la forma polar llamada también la forma trigonométrica) El sentido geométrico
Números complejos en la forma polar lista de problemas para examen) En esta lista de problemas trabajamos con números complejos en la forma polar llamada también la forma trigonométrica) El sentido geométrico
2. El conjunto de los números complejos
 Números complejos 1 Introducción El nacimiento de los números complejos se debió a la necesidad de dar solución a un problema: no todas las ecuaciones polinómicas poseen una solución real El ejemplo más
Números complejos 1 Introducción El nacimiento de los números complejos se debió a la necesidad de dar solución a un problema: no todas las ecuaciones polinómicas poseen una solución real El ejemplo más
TEMA: 5 ÁLGEBRA 3º ESO
 TEMA: 5 ÁLGEBRA 3º ESO 1. MONOMIO Un monomio es una expresión algebraica en la que las únicas operaciones que aparecen entre las variables son el producto y la potencia de exponente natural. Ejemplo: x
TEMA: 5 ÁLGEBRA 3º ESO 1. MONOMIO Un monomio es una expresión algebraica en la que las únicas operaciones que aparecen entre las variables son el producto y la potencia de exponente natural. Ejemplo: x
Llamaremos número real a cualquier fracción decimal. Las fracciones decimales periódicas se llaman números racionales, así:
 Capítulo 1 Números Reales 1.1. Introducción Llamaremos número real a cualquier fracción decimal. Ejemplos:, 0;, 3333...;, 5; 0,785; 3, 14159...;,718818...; 1,414136... Las fracciones decimales periódicas
Capítulo 1 Números Reales 1.1. Introducción Llamaremos número real a cualquier fracción decimal. Ejemplos:, 0;, 3333...;, 5; 0,785; 3, 14159...;,718818...; 1,414136... Las fracciones decimales periódicas
Método de integración por fracciones parciales
 Método de integración por fracciones parciales Temas Fracciones parciales. Método de integración por fracciones parciales. Capacidades Descomponer una fracción en suma de fracciones parciales. Conocer
Método de integración por fracciones parciales Temas Fracciones parciales. Método de integración por fracciones parciales. Capacidades Descomponer una fracción en suma de fracciones parciales. Conocer
Polinomios. 1.- Funciones cuadráticas
 Polinomios 1.- Funciones cuadráticas Definición 1 (Función polinomial) Sea n un entero no negativo y sean a n, a n 1,..., a, a 1, a 0 número s reales con a n 0. La función se denomina función polinomial
Polinomios 1.- Funciones cuadráticas Definición 1 (Función polinomial) Sea n un entero no negativo y sean a n, a n 1,..., a, a 1, a 0 número s reales con a n 0. La función se denomina función polinomial
Unidad 6. Raíces de polinomios. Objetivos. Al finalizar la unidad, el alumno:
 Unidad 6 Raíces de polinomios Objetivos Al finalizar la unidad, el alumno: Comprenderá el Teorema Fundamental del Álgebra. Aplicará los teoremas del residuo y del factor en la obtención de las raíces de
Unidad 6 Raíces de polinomios Objetivos Al finalizar la unidad, el alumno: Comprenderá el Teorema Fundamental del Álgebra. Aplicará los teoremas del residuo y del factor en la obtención de las raíces de
