Semana 14 [1/19] Polinomios. 8 de junio de Polinomios
|
|
|
- Yolanda Río Saavedra
- hace 7 años
- Vistas:
Transcripción
1 Semana 14 [1/19] 8 de junio de 2007
2 División Semana 14 [2/19] Teorema de la División Al ser (K[x], +, ) un anillo, ocurre un fenómeno similar al de : Las divisiones deben considerar un posible resto. Teorema de la División Sean p, d K[x] con d 0. Entonces existe un único par q, r K[x] tal que 1 p = q d + r 2 gr(r) < gr(d) Notación La ecuación (1), se llama división con resto de p por d. El polinomio q se llama cuociente. El polinomio r se llama resto. Cuando r(x) = 0, diremos que d divide a p, lo cual notaremos d p, al igual que en Æ \ {0}. Es decir, d p ( q K[x]) p = q d Para probar este teorema, usaremos un método de división similar al que conocemos en. Lo ejemplificaremos a partir de un ejemplo.
3 División Semana 14 [3/19] Teorema de la División: Ejemplo Calculemos la división entre p(x) = 3x 3 + 2x 2 y q(x) = x 4. 3x 3 +2x 2 : x 4 = Para obtener el cuociente, debemos preguntarnos por qué multiplicar el término de mayor exponente de x 4 para obtener el de 3x 3 + 2x 2: es decir, por qué multiplicar x para obtener 3x 3. La respuesta es 3x 2. Entonces 3x 3 +2x 2 : x 4 = 3x 2 (3x 3 12x 2 ) 12x 2 +2x 2 El término 3x 3 12x 2 corresponde a la multiplicación de 3x 2 por el divisor x 4, y aparece restándose para calcular el resto parcial correspondiente. El polinomio 12x 2 + 2x 2 es el resultado de calcular la resta entre el polinomio original y el término recién obtenido. El proceso continúa iterativamente: x debe ser multiplicado por 12x para obtener 12x 2, así que sumamos 12x al cuociente parcial 3x 2 que llevábamos. 3x 3 +2x 2 : x 4 = 3x 2 +12x (3x 3 12x 2 ) 12x 2 +2x 2 (12x 2 48x) 50x 2
4 División Semana 14 [4/19] Teorema de la División: Ejemplo En cada etapa vamos calculando un nuevo resto parcial, y detenemos el proceso cuando este resto tiene grado menor que el de x 4: 3x 3 +2x 2 : x 4 = 3x 2 +12x+50 (3x 3 12x 2 ) 12x 2 +2x 2 (12x 2 48x) 50x 2 (50x 200) 198 Obtenemos así que el cuociente de esta división es q(x) = 3x x + 50, y el resto es r(x) = 198. En términos del teorema de la división, podemos entonces escribir 3x 3 + 2x 2 = (x 4)(3x x + 50)
5 División Semana 14 [5/19] Teorema de la División Demostración (Teorema de la División). Primero probaremos la existencia de q y r. Veamos dos casos posibles: Si gr(d) > gr(p). Basta notar que p = 0 d + p. De donde q = 0 y r = p, satisfacen las condiciones del Teorema. Si gr(d) gr(p). Ocupamos el procedimiento de división ejemplificado anteriormente, obteniendo: p = q 1 d + r 1 r 1 = q 2 d + r 2 r 2 = q 3 d + r 3. r n = q n+1 d + r n+1, con gr(r n+1 ) < gr(d). Por qué gr(r n+1 ) < gr(d)? Porque el grado de los restos r i disminuye en al menos 1 en cada etapa y gr(d) 0 (pues d 0). Continúa...
6 División Semana 14 [6/19] Teorema de la División Continuación demostración. Reemplazamos ahora en la primera ecuación, las posteriores: p = q 1 d + r 1. = (q 1 + q 2 ) d + r 2 = (q 1 + q 2 + q 3 ) d + r 3 = (q 1 + q q n+1 ) d + r n+1, con gr(r n+1 ) < gr(d). Basta entonces definir q = q 1 + q q n+1, y r = r n+1. Estos polinomios satisfacen el Teorema de la División. Como ejercicio para el lector, queda formalizar esta demostración como una inducción en el grado de p. Resta ahora probar la unicidad de dichos polinomios. Supongamos que tenemos dos descomposiciones (y probemos que son la misma): p = q 1 d + r 1 = q 2 d + r 2. En donde gr(r 1 ) < gr(d) y gr(r 2 ) < gr(d). Reagrupando, obtenemos (q 1 q 2 ) d = r 2 r 1. Pero como gr(r 2 r 1 ) m«ax(gr(r 2 ), gr(r 1 )) < gr(d), entonces gr(d) > gr((q 1 q 2 ) d) = gr(q 1 q 2 ) + gr(d), lo cual sólo puede ocurrir si gr(q 1 q 2 ) =, o sea, si Como consecuencia, r 2 r 1 = 0 d = 0 y luego r 1 = r 2. q 1 q 2 = 0 q 1 = q 2.
7 Raíces y factorización Semana 14 [7/19] Raíces de un polinomio Teorema del Resto Sean p K[x] y c K. El resto de dividir p por el polinomio (x c) es exactamente p(c). Demostración. Por el teorema anterior, existen únicos q, r K[x] con gr(r) < 1 tales que p(x) = q(x)(x c) + r(x) Como gr(r) < 1, existe r 0 K tal que r(x) = r 0. Evaluando la relación de división antes obtenida en x = c, obtenemos p(c) = q(c) 0 + r 0 por lo que el resto vale r 0 = p(c). Raíz Diremos que c K es una raíz del polinomio p K[x] si p(c) = 0.
8 Raíces y factorización Semana 14 [8/19] Raíces de un polinomio Propiedad c à es raíz de p (x c) p(x) Demostración. ) Sabemos que p(c) es el resto de dividir p por (x c), es decir existe q K[x] tal que p(x) = q(x)(x c) + p(c) Como c es raíz de p, p(c) = 0, y así p(x) = q(x)(x c) con lo que (x c) p(x). ) Si (x c) p(x), entonces existe q K[x] tal que p(x) = q(x)(x c) Entonces p(c) = q(c) 0 = 0.
9 Raíces y factorización Semana 14 [9/19] Raíces de un polinomio: Propiedades Se tienen las siguientes propiedades: Propiedades 1 Si c 1, c 2,...,c k son raíces distintas de p, entonces (x c 1 )(x c 2 )...(x c k ) p(x) 2 Sea n 1. Si p K[x] es tal que gr(p) = n, entonces p posee a lo más n raíces distintas. 3 Sean n 1, y p, q K[x] tales que gr(p) n y gr(q) n. Si p y q coinciden en n + 1 puntos distintos, entonces son iguales (como polinomios). Demostración. Demostraremos (1) y (2). (3) se obtiene como consecuencia de (2), aplicándola al polinomio (p q). Para (1): Por inducción en k. El caso k = 1 está demostrado en el teorema anterior. Sean c 1, c 2,...,c k raíces distintas de p. Usando hipótesis inductiva, sabemos que o, equivalentemente, existe q K[x] tal que Como c k también es raíz de p, Continúa... (x c 1 )(x c 2 )...(x c k 1 ) p(x) p(x) = q(x)(x c 1 )(x c 2 )...(x c k 1 ) 0 = p(c k ) = q(c k )(c k c 1 )(c k c 2 )...(c k c k 1 )
10 Raíces y factorización Semana 14 [10/19] Raíces de un polinomio: Propiedades Continuación demostración. Gracias a que los valores c i son todos distintos, tenemos necesariamente que q(c k ) = 0, con lo que concluimos que c k es raíz del polinomio q. Así, (x c k ) q(x), y existe q K[x] tal que q(x) = q (x)(x c k ) Reemplazando esto en la descomposición de p, nos queda p(x) = q (x)(x c 1 )(x c 2 )...(x c k ) Es decir, (x c 1 )(x c 2 )...(x c k ) p(x) Para (2): Sea k el número de raíces distintas que posee p, y sean c 1,...,c k estas raíces. Aplicando (??), tenemos que existe q K[x] tal que p(x) = q(x)(x c 1 )...(x c k ) Luego de donde obtenemos que n = gr(p) = gr(q) + gr(x c 1 ) gr(x c k ) n = gr(q) + k pues gr(x c i ) = 1 para i = 1,..., k. Como gr(p) = n 1, entonces p no puede ser el polinomio nulo. Así, q tampoco puede ser el polinomio nulo (razonar por contradicción), y por lo tanto gr(q) 0. Entonces k = n gr(q) n 0 = n es decir, p posee a lo más n raíces distintas.
11 Teorema Fundamental del Álgebra Semana 14 [11/19] Teorema Fundamental del Álgebra En la sección anterior demostramos un resultado que dice que un polinomio de grado n posee a lo más n raíces distintas, pero deja la posibilidad abierta de que pudiera no tener raíces. Cuando consideramos raíces en Ê, el caso puede darse. Tan sólo consideremos p(x) = 1 + x 2 Las raíces de este polinomio son i y i, sin embargo éstas no son reales, sino complejas. El polinomio p no posee raíces en Ê. El Teorema Fundamental del Álgebra da una versión general de este caso, generalizando además el resultado de la sección anterior. Teorema Fundamental del Álgebra Sea p un polinomio con coeficientes en C[x], tal que gr(p) = n 1. Entonces p posee al menos una raíz en C. No demostraremos este teorema, ya que para eso requerimos herramientas más avanzadas. Sin embargo, estudiaremos la siguiente aplicación.
12 Teorema Fundamental del Álgebra Semana 14 [12/19] Factorización de un polinomio en C[x] Proposición Sea p un polinomio con coeficientes en C[x], tal que gr(p) = n 1. Entonces existen valores α, c 1,..., c m C y naturales l 1,..., l m 1 tales que p(x) = α(x c 1 ) l 1...(x c m ) lm Demostración. Como gr(p) 1, utilizamos el Teorema Fundamental del Álgebra para encontrar r 1 C que es raíz de p. Entonces podemos escribir p(x) = q 1 (x)(x r 1 ) para algún q 1 C[x]. El grado de q 1 es gr(q 1 ) = gr(p) gr(x r 1 ) = n 1. Si n 1 1, entonces podemos seguir aplicando el Teorema Fundamental, esta vez a q 1. Así, existe una raíz r 2 C de q 1, y podemos escribir p(x) = q 2 (x)(x r 1 )(x r 2 ) para algún q 2 C[x]. Si continuamos iterando este proceso mientras gr(q i ) 1, llegamos a una descomposición p(x) = q n (x)(x r 1 )(x r 2 )...(x r n ) donde r 1,...,r n C y q n C[x] es de grado 0. Por lo tanto, q n (x) = α donde α es un valor fijo en C. Continúa...
13 Teorema Fundamental del Álgebra Semana 14 [13/19] Factorización de un polinomio en C[x] Continuación demostración. Para terminar de escribir la descomposición deseada, notamos que los valores r i no necesariamente son distintos, así que los agrupamos de modo que El valor c 1 C aparece l 1 veces. El valor c 2 C aparece l 2 veces.... El valor c m C aparece l m veces. Así p(x) = α(x c 1 ) l 1...(x c m ) lm Notar que si existe una demostración del tipo mencionado, entonces gr(p) = l l m Queda como ejercicio para el lector demostrar que el complejo α que aparece en la descomposición de p es exactamente su coeficiente a n.
14 Acerca de las raíces complejas Semana 14 [14/19] Raíces complejas Proposición Sea p Ê[x], y sea z C una raíz de p. Entonces, el conjugado z también es raíz de p. Demostración. Escribamos donde a k Ê para k = 0,...,n. Se tiene que n p(x) = a k x k k=0 n p( z) = a k ( z) k k=0 Observemos que, como a k Ê, entonces a k = a k, y así a k ( z) k = a k z k (k = 0,...,n) Reemplazando esta expresión, obtenemos p( z) = n a k z k = k=0 n a k z k = p(z) k=0 Como z es raíz de p, entonces p(z) = 0, y así p( z) = 0 = 0, con lo que z también es raíz de p.
15 Acerca de las raíces complejas Semana 14 [15/19] Factorización de un polinomio en Ê[x] Proposición Sea p un polinomio con coeficientes en Ê[x], tal que gr(p) = n 1. Entonces existen valores α, c 1,..., c m, a 1, b 1, a 2, b 2... a s, b s Ê tales que p(x) = α(x c 1 )(x c 2 )...(x c m )(x 2 + a 1 x + b 1 )(x 2 + a 2 x + b 2 )...(x 2 + a s x + b s ). En donde c 1,...,c m son las raíces reales de p y x 2 + a 1 x + b 1,..., x 2 + a s x + b s son polinomios sin raíces reales (con posible repetición). α es el coeficiente a n de p. Demostración. La demostración se basa en la descomposición anterior, salvo que consideramos primero todas las raíces reales de p (posiblemente repetidas), obteniendo: p(x) = (x c 1 )(x c 2 )...(x c m )q(x). Luego por cada raíz compleja z C \ Ê de p, por la proposición anterior (ya que p Ê[x]) sabemos que z es también raíz de p. Así, (x z)(x z) divide a p. Pero esto no nos sirve para factorizar a p en Ê[x]. Sin embargo: (x z)(x z) = x 2 (z + z)x + zz = x 2 2Re(z) x + z 2 Ê[x]. Definimos entonces a i = 2Re(z) y b i = z 2, en cada paso (con posible repetición). Obtenemos así la descomposición. Queda como ejercicio para el lector el formalizar esta demostración.
16 Algunos resultados útiles Semana 14 [16/19] a coeficientes enteros Proposición Sea p Ê[x], con coeficientes a 0,...,a n. Si r É (se asume que r y s son primos relativos) es una raíz s de p, entonces: r a 0 s a n. Demostración. Como r es raíz de p, luego s ( r ( r ) n ( r ) n 1 ( r p = a n + an a1 + a 0 = 0 s) s s s) r ( ) a n r n 1 + a n 1 sr n s n a 1 = a0 s n. De aquí, r divide a a 0 s n. Sin embargo, como r y s son primos relativos, r y s n también lo son. Luego necesariamente r a 0. Queda propuesto como ejercicio probar que s a n.
17 Algunos resultados útiles Semana 14 [17/19] Aplicación El siguiente corolario es útil para explorar cuáles son las raíces enteras de un polinomio mónico con coeficientes enteros. Corolario Sea p Ê[x] mónico, con coeficientes a 0,...,a n 1. Entonces toda raíz racional de p es entera y divide a a 0. Ejemplo Consideremos el polinomo (mónico y con coeficientes enteros) p(x) = x 3 + 6x 2 3x 4. Gracias al resultado anterior, sabemos que toda raíz x É de p, debe ser un entero y ser divisor de a 0 = 4. Luego, si x É es raíz de p, entonces x {±1, ±2, ±4}. Podríamos evaluar p en x = 1534 para ver si es raíz. Pero para qué? Lo anterior nos dice que eso sería tiempo perdido.
18 Algunos resultados útiles Semana 14 [18/19] Regla de Ruffini A continuación veremos un método para dividir un polinomio p por (x c), de manera rápida. Regla de Ruffini Sea p(x) = n k=0 a kx k Ê[x] y c Ê. Para dividir p por (x c), construimos la siguiente tabla para calcular los números b i, con i {0,... n 1}: c a n a n 1 a 1 a 0 b n 1 = a n En el paso i 1, multiplicamos b i+1 por c y sumamos el resultado a a i+1. O sea b i = a i+1 + b i+1 c. a n a n 1 a 1 a 0 c b n 1 c b 1 c b 0 c b n 1 = a n b n 2 = a n 1 + b n 1 c b 0 = a 1 + b 1 c r = a 0 + b 0 c Luego, el cuociente de dividir p por (x c) es: q(x) = b n 1 x n 1 + b n 2 x n b 1 x + b 0. Además, el último término calculado en la tabla es el resto de dividir p por (x c): O sea, r(x) = r = a 0 + b 0 c. p(x) = q(x)(x c) + r(x). Queda propuesto para el lector probar que el método recién presentado funciona.
19 Algunos resultados útiles Semana 14 [19/19] Algoritmo de Horner Notemos que gracias al Teorema del Resto, el resto r entregado por la Regla de Ruffini, es la evaluación de p en c. Así, la Regla de Ruffini puede ser usada para estudiar las raíces reales de un polinomio en Ê[x]. Este uso es denominado Algoritmo de Horner. Ejemplo Consideremos el polinomio anterior: p(x) = x 3 + 6x 2 3x 4 (aunque la Regla de Ruffini no requiere que sea mónico). Dividamos p por (x 1): Es decir p(x) = (x 2 + 7x + 4)(x 1) + 0 y luego x = 1 es raíz de p. Sin embargo, al dividir por (x 2): Luego p(x) = (x 2 + 8x + 13)(x 2) + 22 y por lo tanto p(2) = 22 (x = 2 no es raíz de p).
ALGEBRA y ALGEBRA LINEAL. Primer Semestre CAPITULO 6. POLINOMIOS DE UNA VARIABLE.
 ALGEBRA y ALGEBRA LINEAL 520142 Primer Semestre CAPITULO 6. POLINOMIOS DE UNA VARIABLE. DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas 1 Definición: Polinomio Sea K (Q,
ALGEBRA y ALGEBRA LINEAL 520142 Primer Semestre CAPITULO 6. POLINOMIOS DE UNA VARIABLE. DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas 1 Definición: Polinomio Sea K (Q,
Números complejos y Polinomios
 Semana 13 [1/14] 23 de mayo de 2007 Forma polar de los complejos Semana 13 [2/14] Raíces de la unidad Raíz n-ésima de la unidad Sean z C y n 2. Diremos que z es una raíz n-ésima de la unidad si z n = 1
Semana 13 [1/14] 23 de mayo de 2007 Forma polar de los complejos Semana 13 [2/14] Raíces de la unidad Raíz n-ésima de la unidad Sean z C y n 2. Diremos que z es una raíz n-ésima de la unidad si z n = 1
ALGEBRA I, ALGEBRA Y TRIGONOMETRIA , Segundo Semestre CAPITULO 6: POLINOMIOS.
 ALGEBRA I, ALGEBRA Y TRIGONOMETRIA 520135, 522115 Segundo Semestre CAPITULO 6: POLINOMIOS. DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas 1 Definición: Polinomio Sea K
ALGEBRA I, ALGEBRA Y TRIGONOMETRIA 520135, 522115 Segundo Semestre CAPITULO 6: POLINOMIOS. DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas 1 Definición: Polinomio Sea K
Definición 1.2. Sea (K, +, ) un dominio de integridad. Un polinomio de grado n sobre K es una expresión de la forma
 Polinomios Definición 1.1. Un conjunto K junto con dos operaciones definidas en él que denotaremos por + : K K K : K K K para las cuales se cumplen las siguientes propiedades: Asociatividad Conmutatividad
Polinomios Definición 1.1. Un conjunto K junto con dos operaciones definidas en él que denotaremos por + : K K K : K K K para las cuales se cumplen las siguientes propiedades: Asociatividad Conmutatividad
ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- Polinomios
 Resumen teoría Prof. Alcón ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- Polinomios Sea (A, +,.) un anillo conmutativo. Indicamos con A[x] al conjunto de polinomios en una indeterminada x con coeficientes en
Resumen teoría Prof. Alcón ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- Polinomios Sea (A, +,.) un anillo conmutativo. Indicamos con A[x] al conjunto de polinomios en una indeterminada x con coeficientes en
Apéndice 1: Fundamentos de lógica, teoría de conjuntos y estructuras algebraicas. . Analizando el
 Apéndice 1: Fundamentos de lógica, teoría de conjuntos y estructuras algebraicas Polinomios Dedicaremos este apartado al repaso de los polinomios. Se define Rx a 0 a 1 x a 2 x 2...a n x n a 0,a 1,a 2,...,a
Apéndice 1: Fundamentos de lógica, teoría de conjuntos y estructuras algebraicas Polinomios Dedicaremos este apartado al repaso de los polinomios. Se define Rx a 0 a 1 x a 2 x 2...a n x n a 0,a 1,a 2,...,a
4.1 Anillo de polinomios con coeficientes en un cuerpo
 Tema 4 Polinomios 4.1 Anillo de polinomios con coeficientes en un cuerpo Aunque se puede definir el conjunto de los polinomios con coeficientes en un anillo, nuestro estudio se va a centrar en el conjunto
Tema 4 Polinomios 4.1 Anillo de polinomios con coeficientes en un cuerpo Aunque se puede definir el conjunto de los polinomios con coeficientes en un anillo, nuestro estudio se va a centrar en el conjunto
Ejercicios de Álgebra Básica. Curso 2016/17
 Tema 4: Polinomios Ejercicios de Álgebra Básica. Curso 2016/17 El anillo k[x]. Divisibilidad Ejercicio 1. Sea A un anillo. Prueba que, si A es dominio de integridad, A[x] = A y demuestra con un contraejemplo
Tema 4: Polinomios Ejercicios de Álgebra Básica. Curso 2016/17 El anillo k[x]. Divisibilidad Ejercicio 1. Sea A un anillo. Prueba que, si A es dominio de integridad, A[x] = A y demuestra con un contraejemplo
Anexo: El anillo de polinomios K[x].
![Anexo: El anillo de polinomios K[x]. Anexo: El anillo de polinomios K[x].](/thumbs/67/56852452.jpg) El anillo de polinomios K[x] 1 Anexo: El anillo de polinomios K[x]. 1. Construcción del anillo de polinomios K[x]. Dado un cuerpo K, se define m K[x] = { a i x i a i K, i = 0,..., m, m N {0}}, i=0 donde
El anillo de polinomios K[x] 1 Anexo: El anillo de polinomios K[x]. 1. Construcción del anillo de polinomios K[x]. Dado un cuerpo K, se define m K[x] = { a i x i a i K, i = 0,..., m, m N {0}}, i=0 donde
Capítulo 4: Polinomios
 Capítulo 4: Polinomios Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Diciembre de 2015 Olalla (Universidad de Sevilla) Capítulo 4: Polinomios Diciembre de
Capítulo 4: Polinomios Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Diciembre de 2015 Olalla (Universidad de Sevilla) Capítulo 4: Polinomios Diciembre de
Capítulo 4: Polinomios
 Capítulo 4: Polinomios Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Diciembre de 2017 Olalla (Universidad de Sevilla) Capítulo 4: Polinomios Diciembre de
Capítulo 4: Polinomios Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Diciembre de 2017 Olalla (Universidad de Sevilla) Capítulo 4: Polinomios Diciembre de
Principio de inducción y Sumatorias
 Semana06[1/14] 3 de abril de 007 Principio de inducción: Primera forma Semana06[/14] Una categoría importante de proposiciones y teoremas es la de las propiedades de los números naturales. Aquí tenemos,
Semana06[1/14] 3 de abril de 007 Principio de inducción: Primera forma Semana06[/14] Una categoría importante de proposiciones y teoremas es la de las propiedades de los números naturales. Aquí tenemos,
AMPLIACIÓN DE MATEMÁTICAS DIVISIBILIDAD DE POLINOMIOS.
 AMPLIACIÓN DE MATEMÁTICAS DIVISIBILIDAD DE POLINOMIOS. Ejemplo 1. Dados dos polinomios p, q Z[x] con q mónico se puede dividir p entre q. x 2 + 2x + 1 x + 1 0 x + 1 ; x 2 + 2x + 2 x + 1 1 x + 1 ; 3x2 +
AMPLIACIÓN DE MATEMÁTICAS DIVISIBILIDAD DE POLINOMIOS. Ejemplo 1. Dados dos polinomios p, q Z[x] con q mónico se puede dividir p entre q. x 2 + 2x + 1 x + 1 0 x + 1 ; x 2 + 2x + 2 x + 1 1 x + 1 ; 3x2 +
Anillo de polinomios con coeficientes en un cuerpo
 Capítulo 2 Anillo de polinomios con coeficientes en un cuerpo En el conjunto Z se ha visto cómo la relación ser congruente módulo m para un entero m > 1, es compatible con las operaciones suma y producto.
Capítulo 2 Anillo de polinomios con coeficientes en un cuerpo En el conjunto Z se ha visto cómo la relación ser congruente módulo m para un entero m > 1, es compatible con las operaciones suma y producto.
AMPLIACIÓN DE MATEMÁTICAS
 AMPLIACIÓN DE MATEMÁTICAS RAÍCES MÚLTIPLES. Dado un polinomio con coeficientes en un cuerpo existirá siempre un elemento del cuerpo que anula el polinomio? Siempre existe un cuerpo donde podamos encontrar
AMPLIACIÓN DE MATEMÁTICAS RAÍCES MÚLTIPLES. Dado un polinomio con coeficientes en un cuerpo existirá siempre un elemento del cuerpo que anula el polinomio? Siempre existe un cuerpo donde podamos encontrar
Anillo de Polinomios.
 Capítulo 6 Anillo de Polinomios. Una forma de definir los polinomios en forma intuitiva es la siguiente: Sea (K,+, ) un cuerpo, entonces un polinomio con coeficiente en K es de la siguiente forma p(x)
Capítulo 6 Anillo de Polinomios. Una forma de definir los polinomios en forma intuitiva es la siguiente: Sea (K,+, ) un cuerpo, entonces un polinomio con coeficiente en K es de la siguiente forma p(x)
Departamento de Ingeniería Matemática - Universidad de Chile
 5. Principio de inducción Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Introducción al Álgebra 08-1 5.1. Principio de inducción: Primera forma Importante: Visita
5. Principio de inducción Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Introducción al Álgebra 08-1 5.1. Principio de inducción: Primera forma Importante: Visita
Tema 1. Anillos e ideales. Operaciones. Divisibilidad
 Tema 1. Anillos e ideales. Operaciones. Divisibilidad y factorización. La parte correspondiente a Anillos e ideales. Operaciones se corresponde con el capítulo 1 del libro Atiyah, M.F., Macdonald, I.G.,
Tema 1. Anillos e ideales. Operaciones. Divisibilidad y factorización. La parte correspondiente a Anillos e ideales. Operaciones se corresponde con el capítulo 1 del libro Atiyah, M.F., Macdonald, I.G.,
COMPLEMENTO DEL TEÓRICO
 ÁLGEBRA I PRIMER CUATRIMESTRE - AÑO 2016 COMPLEMENTO DEL TEÓRICO El material de estas notas fue dictado en las clases teóricas pero no se encuentra en el texto que seguimos en las mismas ( Álgebra I -
ÁLGEBRA I PRIMER CUATRIMESTRE - AÑO 2016 COMPLEMENTO DEL TEÓRICO El material de estas notas fue dictado en las clases teóricas pero no se encuentra en el texto que seguimos en las mismas ( Álgebra I -
Ejercicios de Polinomios y Fracciones Algebráicas
 Matemáticas 1º Bach CCSS. Ejercicios Tema 2. Polinomios y Fracciones Algebráicas. Pág 1/12 1. Dados los polinomios: Ejercicios de Polinomios y Fracciones Algebráicas 1. P(x) = 4x 2 1 2. Q(x) = x 3 3x 2
Matemáticas 1º Bach CCSS. Ejercicios Tema 2. Polinomios y Fracciones Algebráicas. Pág 1/12 1. Dados los polinomios: Ejercicios de Polinomios y Fracciones Algebráicas 1. P(x) = 4x 2 1 2. Q(x) = x 3 3x 2
Estructuras algebraicas
 Semana 11[1/22] 4 de mayo de 2007 Anillos y cuerpos Semana 11[2/22] Anillos Comenzamos ahora el estudio de estructuras algebraicas que tengan definidas dos operaciones, y las clasificaremos en anillos
Semana 11[1/22] 4 de mayo de 2007 Anillos y cuerpos Semana 11[2/22] Anillos Comenzamos ahora el estudio de estructuras algebraicas que tengan definidas dos operaciones, y las clasificaremos en anillos
Semana 14. Carlos Hernandez. Helena de Oteyza. Alfredo.
 Semana 4 Carlos Hernandez Los apuntes los encuentran en: http://wwwcimatmx/especialidadseg/documentos/algoritmospdf Helena de Oteyza http://wwwcimatmx/especialidadseg/documentos/desigualdadespdf Alfredo
Semana 4 Carlos Hernandez Los apuntes los encuentran en: http://wwwcimatmx/especialidadseg/documentos/algoritmospdf Helena de Oteyza http://wwwcimatmx/especialidadseg/documentos/desigualdadespdf Alfredo
GUÍA DE EJERCICIOS. Área Matemática - Polinomios
 GUÍA DE EJERCICIOS Área Matemática - Polinomios Resultados de aprendizaje. Realizar operaciones entre polinomios. Aplicar Regla de Ruffini, para determinar raíces de un polinomio. Aplicar los procedimientos
GUÍA DE EJERCICIOS Área Matemática - Polinomios Resultados de aprendizaje. Realizar operaciones entre polinomios. Aplicar Regla de Ruffini, para determinar raíces de un polinomio. Aplicar los procedimientos
6.1. Anillos de polinomios.
 1 Tema 6.-. Anillo de polinomios. División y factorización. Lema de Gauss. 6.1. Anillos de polinomios. Definición 6.1.1. Sea A un anillo. El anillo de polinomios en la indeterminada X con coeficientes
1 Tema 6.-. Anillo de polinomios. División y factorización. Lema de Gauss. 6.1. Anillos de polinomios. Definición 6.1.1. Sea A un anillo. El anillo de polinomios en la indeterminada X con coeficientes
Semana 07[1/21] Sumatorias. 12 de abril de Sumatorias
![Semana 07[1/21] Sumatorias. 12 de abril de Sumatorias Semana 07[1/21] Sumatorias. 12 de abril de Sumatorias](/thumbs/70/63260960.jpg) Semana 07[/] de abril de 007 Semana 07[/] Progresiones aritméticas Progresión aritmética Es una sumatoria del tipo (A + d) es decir, donde a A + d, para valores A, d Ê. Utilizando las propiedades de sumatoria,
Semana 07[/] de abril de 007 Semana 07[/] Progresiones aritméticas Progresión aritmética Es una sumatoria del tipo (A + d) es decir, donde a A + d, para valores A, d Ê. Utilizando las propiedades de sumatoria,
Álgebra Básica 11/01/2017 Grado en Matemáticas. Grupo C. Curso 2016/2017
 Álgebra Básica 11/01/2017 Grado en Matemáticas. Grupo C. Curso 2016/2017 SOLUCIONES Ejercicio 1 (5 puntos). Sea A un anillo conmutativo y K un cuerpo. a) Definir: i) Unidad en A. ii) Elemento irreducible
Álgebra Básica 11/01/2017 Grado en Matemáticas. Grupo C. Curso 2016/2017 SOLUCIONES Ejercicio 1 (5 puntos). Sea A un anillo conmutativo y K un cuerpo. a) Definir: i) Unidad en A. ii) Elemento irreducible
EJERCICIOS. 7.3 Valor de un polinomio para x = a. Por lo tanto: para determinar expresiones
 or lo tanto: para determinar epresiones a que sean divisores de un polinomio con coeficientes enteros, se deben asignar valores al número a que dividan al término independiente. Apliquemos este resultado
or lo tanto: para determinar epresiones a que sean divisores de un polinomio con coeficientes enteros, se deben asignar valores al número a que dividan al término independiente. Apliquemos este resultado
x a que sean divisores de un polinomio con coeficientes enteros, se deben asignar valores al número a que dividan al término independiente.
 or lo tanto: para determinar epresiones a que sean divisores de un polinomio con coeficientes enteros, se deben asignar valores al número a que dividan al término independiente. Apliquemos este resultado
or lo tanto: para determinar epresiones a que sean divisores de un polinomio con coeficientes enteros, se deben asignar valores al número a que dividan al término independiente. Apliquemos este resultado
6. Ortogonalidad. Universidad de Chile Conjuntos ortogonales y ortonormales. Ingeniería Matemática SEMANA 12: ORTOGONALIDAD
 FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 7- SEMANA : ORTOGONALIDAD 6 Ortogonalidad 6 Conjuntos ortogonales y ortonormales Recordemos que la proyección de u sobre v
FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 7- SEMANA : ORTOGONALIDAD 6 Ortogonalidad 6 Conjuntos ortogonales y ortonormales Recordemos que la proyección de u sobre v
Tema 2: Teorema de estructura de los grupos abelianos finitamente generados.
 ESTRUCTURAS ALGEBRAICAS GRADO EN MATEMÁTICAS. CURSO 215/216 Tema 2: Teorema de estructura de los grupos abelianos finitamente generados. 1.1. Grupo abeliano libre. Bases. Definición 1.1. El grupo Z n con
ESTRUCTURAS ALGEBRAICAS GRADO EN MATEMÁTICAS. CURSO 215/216 Tema 2: Teorema de estructura de los grupos abelianos finitamente generados. 1.1. Grupo abeliano libre. Bases. Definición 1.1. El grupo Z n con
TRABAJO PRÁCTICO Nº 4: POLINOMIOS
 TRABAJO PRÁCTICO Nº : POLINOMIOS EJERCICIOS A DESARROLLAR Clase ) Dados los polinomios reales P(x) =.x ; Q(x) = 3x3 x + y los polinomios complejos R(x) = i.x ; S(x) = x + ( + i).x i, calcular: a) 3x. P(x)
TRABAJO PRÁCTICO Nº : POLINOMIOS EJERCICIOS A DESARROLLAR Clase ) Dados los polinomios reales P(x) =.x ; Q(x) = 3x3 x + y los polinomios complejos R(x) = i.x ; S(x) = x + ( + i).x i, calcular: a) 3x. P(x)
IV Taller de Olimpiadas Matemáticas para Profesores 2014
 IV Taller de Olimpiadas Matemáticas para Profesores 204 Polinomios Jorge Tipe Villanueva. Polinomios Un polinomio es una expresión de la forma a n x n +a n x n + +a x+a 0, donde los números a i son complejos.
IV Taller de Olimpiadas Matemáticas para Profesores 204 Polinomios Jorge Tipe Villanueva. Polinomios Un polinomio es una expresión de la forma a n x n +a n x n + +a x+a 0, donde los números a i son complejos.
Unidad 6. Raíces de polinomios. Objetivos. Al finalizar la unidad, el alumno:
 Unidad 6 Raíces de polinomios Objetivos Al finalizar la unidad, el alumno: Comprenderá el Teorema Fundamental del Álgebra. Aplicará los teoremas del residuo y del factor en la obtención de las raíces de
Unidad 6 Raíces de polinomios Objetivos Al finalizar la unidad, el alumno: Comprenderá el Teorema Fundamental del Álgebra. Aplicará los teoremas del residuo y del factor en la obtención de las raíces de
Álgebra básica Soluciones del examen de segunda convocatoria Curso 2016/ de septiembre de 2017
 Álgebra básica Soluciones del examen de segunda convocatoria Curso 2016/2017 12 de septiembre de 2017 Ejercicio 1. Se pide lo siguiente: 1. (2 puntos) Dados unos conjuntos X, Y, unos subconjuntos A X,
Álgebra básica Soluciones del examen de segunda convocatoria Curso 2016/2017 12 de septiembre de 2017 Ejercicio 1. Se pide lo siguiente: 1. (2 puntos) Dados unos conjuntos X, Y, unos subconjuntos A X,
Semana02[1/23] Conjuntos. 9 de marzo de Conjuntos
![Semana02[1/23] Conjuntos. 9 de marzo de Conjuntos Semana02[1/23] Conjuntos. 9 de marzo de Conjuntos](/thumbs/53/31721818.jpg) Semana02[1/23] 9 de marzo de 2007 Introducción Semana02[2/23] La teoría de conjuntos gira en torno a la función proposicional x A. Los valores que hacen verdadera la función proposicional x A son aquellos
Semana02[1/23] 9 de marzo de 2007 Introducción Semana02[2/23] La teoría de conjuntos gira en torno a la función proposicional x A. Los valores que hacen verdadera la función proposicional x A son aquellos
El Teorema Fundamental del Álgebra
 El Teorema Fundamental del Álgebra 1. Repaso de polinomios Definiciones básicas Un monomio en una indeterminada x es una expresión de la forma ax n que representa el producto de un número, a, por una potencia
El Teorema Fundamental del Álgebra 1. Repaso de polinomios Definiciones básicas Un monomio en una indeterminada x es una expresión de la forma ax n que representa el producto de un número, a, por una potencia
Q(x,t) = -2x 2 t 3 - xt x 5-3x 3 + 4x 2 +2x- 7 22/03/2016. División de polinomios. P(x) = -x 4 + 3x 2-5 R(x) = 5x 4-2x 3 + 3x
 S Escribe un polinomio que cumpla las siguientes condiciones: A)Se llama P(x, y) B)Tiene 5 términos C)Es de grado seis D)No tiene término independiente S Escribe un polinomio que cumpla las siguientes
S Escribe un polinomio que cumpla las siguientes condiciones: A)Se llama P(x, y) B)Tiene 5 términos C)Es de grado seis D)No tiene término independiente S Escribe un polinomio que cumpla las siguientes
POLINOMIOS. (Versión Preliminar) Un polinomio en la variable x es una expresión de la forma. p(x) = a n x n + a n 1 x n
 POLINOMIOS (Versión Preliminar) Estas notas deben ser complementadas con ejercicios de la guía o de algun texto. En esta sección denotaremos por N al conjunto de los números naturales incluido el cero.
POLINOMIOS (Versión Preliminar) Estas notas deben ser complementadas con ejercicios de la guía o de algun texto. En esta sección denotaremos por N al conjunto de los números naturales incluido el cero.
Semana 09[1/14] Cardinalidad. 25 de abril de Cardinalidad
![Semana 09[1/14] Cardinalidad. 25 de abril de Cardinalidad Semana 09[1/14] Cardinalidad. 25 de abril de Cardinalidad](/thumbs/84/90149636.jpg) Semana 09[1/14] 25 de abril de 2007 Semana 09[2/14] Conjunto no numerables Vimos cuáles son los conjuntos numerables, una serie de propiedades acerca de ellos, y conocimos varios conjuntos numerables,
Semana 09[1/14] 25 de abril de 2007 Semana 09[2/14] Conjunto no numerables Vimos cuáles son los conjuntos numerables, una serie de propiedades acerca de ellos, y conocimos varios conjuntos numerables,
Semana05[1/14] Relaciones. 28 de marzo de Relaciones
![Semana05[1/14] Relaciones. 28 de marzo de Relaciones Semana05[1/14] Relaciones. 28 de marzo de Relaciones](/thumbs/50/26257926.jpg) Semana05[1/14] 28 de marzo de 2007 Introducción Semana05[2/14] Ya en los capítulos anteriores nos acercamos al concepto de relación. Relación Dados un par de conjuntos no vacíos A y B, llamaremos relación
Semana05[1/14] 28 de marzo de 2007 Introducción Semana05[2/14] Ya en los capítulos anteriores nos acercamos al concepto de relación. Relación Dados un par de conjuntos no vacíos A y B, llamaremos relación
Álgebra I Práctica 7 - Polinomios
 FCEyN - UBA - 1er cuatrimestre 2016 Generalidades Álgebra I Práctica 7 - Polinomios 1. Calcular el grado y el coeficiente principal de f Q[X] en los casos i) f = (4X 6 2X 5 + 3X 2 2X + 7) 77. ii) f = (
FCEyN - UBA - 1er cuatrimestre 2016 Generalidades Álgebra I Práctica 7 - Polinomios 1. Calcular el grado y el coeficiente principal de f Q[X] en los casos i) f = (4X 6 2X 5 + 3X 2 2X + 7) 77. ii) f = (
Factorización de Polinomios
 Factorización de Polinomios Curso de Nivelación Ingreso FaMAF 2016 Marcelo E. Rubio Abstract En este apunte se introduce el concepto de factorización de polinomios, y se muestran algunas herramientas útiles
Factorización de Polinomios Curso de Nivelación Ingreso FaMAF 2016 Marcelo E. Rubio Abstract En este apunte se introduce el concepto de factorización de polinomios, y se muestran algunas herramientas útiles
Clase 4 Funciones polinomiales y racionales
 Clase 4 Instituto de Ciencias Básicas Facultad de Ingeniería Universidad Diego Portales Marzo de 2014 Polinomios Definición Se llama polinomio en x a toda expresión de la forma p(x) = a 0 + a 1x+ +a n
Clase 4 Instituto de Ciencias Básicas Facultad de Ingeniería Universidad Diego Portales Marzo de 2014 Polinomios Definición Se llama polinomio en x a toda expresión de la forma p(x) = a 0 + a 1x+ +a n
5 DIVISIÓN DE POLINOMIOS. RAÍCES
 AMPLIACIÓN 5.74 Halla los valores que han de tomar m y n, para que el polinomio P(x) 2x 5 x 4 x 3 mx 2 nx 2 sea divisible por x 2 1. 2x 5 x 4 3x 3 (m 1mx 2 (3 )nx 2(m x 2 1 2x 5 x 3 2x 3 6x 1 2x 3 x 2
AMPLIACIÓN 5.74 Halla los valores que han de tomar m y n, para que el polinomio P(x) 2x 5 x 4 x 3 mx 2 nx 2 sea divisible por x 2 1. 2x 5 x 4 3x 3 (m 1mx 2 (3 )nx 2(m x 2 1 2x 5 x 3 2x 3 6x 1 2x 3 x 2
Algoritmos en teoría de números
 Algoritmos en teoría de números IIC2283 IIC2283 Algoritmos en teoría de números 1 / 92 Para recordar: aritmética modular Dados dos números a, b Z, si b > 0 entonces existen α, β Z tales que 0 β < b y a
Algoritmos en teoría de números IIC2283 IIC2283 Algoritmos en teoría de números 1 / 92 Para recordar: aritmética modular Dados dos números a, b Z, si b > 0 entonces existen α, β Z tales que 0 β < b y a
Semana03[1/17] Funciones. 16 de marzo de Funciones
![Semana03[1/17] Funciones. 16 de marzo de Funciones Semana03[1/17] Funciones. 16 de marzo de Funciones](/thumbs/48/24900626.jpg) Semana03[1/17] 16 de marzo de 2007 Introducción Semana03[2/17] Ya que conocemos el producto cartesiano A B entre dos conjuntos A y B, podemos definir entre ellos algún tipo de correspondencia. Es decir,
Semana03[1/17] 16 de marzo de 2007 Introducción Semana03[2/17] Ya que conocemos el producto cartesiano A B entre dos conjuntos A y B, podemos definir entre ellos algún tipo de correspondencia. Es decir,
Polinomios (II) Polinomios reales irreducibles. Pares de raíces conjugadas. Sesión teórica 4 (págs ) 27 de septiembre de 2010
 Polinomios (II) 1 Sesión teórica 4 (págs. 3-9) 7 de septiembre de 010 Pares de raíces conjugadas irreducibles Consideremos un polinomio f (x) =a0 + a1x + ax + + anx n R[x], es decir, con coeficientes reales
Polinomios (II) 1 Sesión teórica 4 (págs. 3-9) 7 de septiembre de 010 Pares de raíces conjugadas irreducibles Consideremos un polinomio f (x) =a0 + a1x + ax + + anx n R[x], es decir, con coeficientes reales
MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN CLASE # 8
 MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN CLASE # 8 Teorema del Residuo Si un polinomio P (x) se divide entre x c, entonces, el residuo de la división es P (c). Sin realizar
MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN CLASE # 8 Teorema del Residuo Si un polinomio P (x) se divide entre x c, entonces, el residuo de la división es P (c). Sin realizar
POLINOMIOS. FACTORIZACIÓN
 POLINOMIOS FACTORIZACIÓN JUSTIFICACIÓN Es muy fácil realizar multiplicaciones de números naturales Más dificultad entraña el problema inverso: la factorización Así, realizar la multiplicación 7 es trivial,
POLINOMIOS FACTORIZACIÓN JUSTIFICACIÓN Es muy fácil realizar multiplicaciones de números naturales Más dificultad entraña el problema inverso: la factorización Así, realizar la multiplicación 7 es trivial,
5 REPASO Y APOYO OBJETIVO 1
 5 REPASO Y APOYO OBJETIVO 1 RECONOCER EL GRADO, LOS TÉRMINOS Y EL TÉRMINO INDEPENDIENTE DE UN POLINOMIO Nombre: Curso: echa: Un monomio es una expresión algebraica formada por el producto de un número,
5 REPASO Y APOYO OBJETIVO 1 RECONOCER EL GRADO, LOS TÉRMINOS Y EL TÉRMINO INDEPENDIENTE DE UN POLINOMIO Nombre: Curso: echa: Un monomio es una expresión algebraica formada por el producto de un número,
Factorización de polinomios FACTORIZACIÓN DE POLINOMIOS
 FACTORIZACIÓN DE POLINOMIOS 1. Polinomios Un monomio es el producto de un número real por una o más letras que pueden estar elevadas a exponentes que sean números naturales. La suma de los exponentes de
FACTORIZACIÓN DE POLINOMIOS 1. Polinomios Un monomio es el producto de un número real por una o más letras que pueden estar elevadas a exponentes que sean números naturales. La suma de los exponentes de
TEMA 6: DIVISIÓN DE POLINOMIOS RAÍCES MATEMÁTICAS 3º ESO
 TEMA 6: DIVISIÓN DE POLINOMIOS RAÍCES MATEMÁTICAS 3º ESO 1. División de polinomios Dados dos polinomios P (el dividendo) y D (el divisor), dividir P entre D es encontrar dos polinomios Q (el cociente)
TEMA 6: DIVISIÓN DE POLINOMIOS RAÍCES MATEMÁTICAS 3º ESO 1. División de polinomios Dados dos polinomios P (el dividendo) y D (el divisor), dividir P entre D es encontrar dos polinomios Q (el cociente)
Capítulo 4: Polinomios
 Capítulo 4: Polinomios Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Diciembre de 2016 Olalla (Universidad de Sevilla) Capítulo 4: Polinomios Diciembre de
Capítulo 4: Polinomios Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Diciembre de 2016 Olalla (Universidad de Sevilla) Capítulo 4: Polinomios Diciembre de
Homomorfismos de cuerpos. Extensiones normales. Teorema fundamental de la teoría de Galois.
 1 Tema 9.-. Homomorfismos de cuerpos. Extensiones normales. Teorema fundamental de la teoría de Galois. 9.1. Caracteres de un grupo. A la hora de resolver una ecuación f(x) = 0 con f(x) k[x], tomamos un
1 Tema 9.-. Homomorfismos de cuerpos. Extensiones normales. Teorema fundamental de la teoría de Galois. 9.1. Caracteres de un grupo. A la hora de resolver una ecuación f(x) = 0 con f(x) k[x], tomamos un
Álgebra Básica Primera parte
 Álgebra Básica Primera parte 21-1-2016 apellidos nombre Observaciones: -) Todos los ejercicios tienen el mismo valor. Cada ejercicio será puntuado sobre 10 para después calcular la nota global, según se
Álgebra Básica Primera parte 21-1-2016 apellidos nombre Observaciones: -) Todos los ejercicios tienen el mismo valor. Cada ejercicio será puntuado sobre 10 para después calcular la nota global, según se
Capítulo 4: Polinomios
 Capítulo 4: Polinomios Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Diciembre de 2016 Olalla (Universidad de Sevilla) Capítulo 4: Polinomios Diciembre de
Capítulo 4: Polinomios Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Diciembre de 2016 Olalla (Universidad de Sevilla) Capítulo 4: Polinomios Diciembre de
Fracciones Algebraicas
 Fracciones Algebraicas 1 Conceptos básicos Definición 1 Una fracción algebraica en la indeterminada x (o cualquier otra letra) es una expresión de la forma, donde tanto P como Q son polinomios con coeficientes
Fracciones Algebraicas 1 Conceptos básicos Definición 1 Una fracción algebraica en la indeterminada x (o cualquier otra letra) es una expresión de la forma, donde tanto P como Q son polinomios con coeficientes
4.1. Polinomios y teoría de ecuaciones
 CAPÍTULO 4 Polinomios y teoría de ecuaciones 4.1. Polinomios y teoría de ecuaciones Un polinomio real en x, o simplemente polinomio en x es una expresión algebraica de la forma a n x n + a n 1 x n 1 +
CAPÍTULO 4 Polinomios y teoría de ecuaciones 4.1. Polinomios y teoría de ecuaciones Un polinomio real en x, o simplemente polinomio en x es una expresión algebraica de la forma a n x n + a n 1 x n 1 +
TEMA 5. FACTORIZACIÓN DE POLINOMIOS.
 TEMA 5. FACTORIZACIÓN DE POLINOMIOS. 1. SACAR FACTOR COMÚN Cuando todos los términos de un polinomio, P(x), son múltiplos de un mismo monomio, M(x), podemos extraer M(x) como factor común. Por ejemplo:
TEMA 5. FACTORIZACIÓN DE POLINOMIOS. 1. SACAR FACTOR COMÚN Cuando todos los términos de un polinomio, P(x), son múltiplos de un mismo monomio, M(x), podemos extraer M(x) como factor común. Por ejemplo:
FUNCIONES REALES DE UNA VARIABLE CONCEPTOS FUNDAMENTALES
 FUNCIONES REALES DE UNA VARIABLE Índice Presentación... 3 Conjunto de los números reales... 4 Los intervalos... 6 Las potencias... 7 Los polinomios... 8 La factorización de polinomios (I)... 9 La factorización
FUNCIONES REALES DE UNA VARIABLE Índice Presentación... 3 Conjunto de los números reales... 4 Los intervalos... 6 Las potencias... 7 Los polinomios... 8 La factorización de polinomios (I)... 9 La factorización
Cociente. Resto Cómo procedimos? 3 x por 2
 COLEGIO SECUNDARIO LA PLATA Colegio Secundario La Plata Educar para un mundo mejor DIVISIÓN DE POLINOMIOS Definición: Dados dos polinomios, P() y Q(), siempre eisten polinomios C() y R(), únicos, llamados
COLEGIO SECUNDARIO LA PLATA Colegio Secundario La Plata Educar para un mundo mejor DIVISIÓN DE POLINOMIOS Definición: Dados dos polinomios, P() y Q(), siempre eisten polinomios C() y R(), únicos, llamados
TEMA 1.- POLINOMIOS Y FRACCIONES ALGEBRAICAS
 TEMA 1.- POLINOMIOS Y FRACCIONES ALGEBRAICAS 1.- POLINOMIOS Recordemos que un monomio es una expresión algebraica (combinación de letras y números) en la que las únicas operaciones que aparecen entre las
TEMA 1.- POLINOMIOS Y FRACCIONES ALGEBRAICAS 1.- POLINOMIOS Recordemos que un monomio es una expresión algebraica (combinación de letras y números) en la que las únicas operaciones que aparecen entre las
gr(p(x)) = n = deg(p(x)), cuando a n 0. El conjunto de todos los polinomios con coeficiente en K lo denotamos por K[x]
![gr(p(x)) = n = deg(p(x)), cuando a n 0. El conjunto de todos los polinomios con coeficiente en K lo denotamos por K[x] gr(p(x)) = n = deg(p(x)), cuando a n 0. El conjunto de todos los polinomios con coeficiente en K lo denotamos por K[x]](/thumbs/54/35320321.jpg) Capítulo 5 Polinomios Definición 22 Sea K igual a Z,Q,R,C, un polinomio en la variable x con coeficientes en K es una expresión de la forma p(x) = a n x n +a n 1 x n 1 + +a 1 x+a 0, donde a i con i desde
Capítulo 5 Polinomios Definición 22 Sea K igual a Z,Q,R,C, un polinomio en la variable x con coeficientes en K es una expresión de la forma p(x) = a n x n +a n 1 x n 1 + +a 1 x+a 0, donde a i con i desde
La trascendencia de e y π
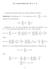 La trascendencia de e y π Comenzamos introduciendo unos convenios útiles de notación: Definición 1 Escribiremos h r = r!, de modo que si fz) = m c r z r C[z], entonces fh) representará fh) = m c r h r
La trascendencia de e y π Comenzamos introduciendo unos convenios útiles de notación: Definición 1 Escribiremos h r = r!, de modo que si fz) = m c r z r C[z], entonces fh) representará fh) = m c r h r
OPERACIONES CON MONOMIOS Y POLINOMIOS. Suma de monomios
 OPERACIONES CON MONOMIOS Y POLINOMIOS Suma de monomios Sólo podemos sumar monomios semejantes. La suma de los monomios es otro monomio que tiene la misma parte literal y cuyo coeficiente es la suma de
OPERACIONES CON MONOMIOS Y POLINOMIOS Suma de monomios Sólo podemos sumar monomios semejantes. La suma de los monomios es otro monomio que tiene la misma parte literal y cuyo coeficiente es la suma de
Anillos. 3.1 Anillos. a b c d e a a a a a a b a b c d e c a c e b d d a d b e c e a e d c b
 Capítulo 3 Anillos Hemos utilizado estructuras en las que hay dos operaciones, como la suma y el producto en Z. El objeto más básico de este tipo es un anillo, cuyos axiomas son bastante parecidos a los
Capítulo 3 Anillos Hemos utilizado estructuras en las que hay dos operaciones, como la suma y el producto en Z. El objeto más básico de este tipo es un anillo, cuyos axiomas son bastante parecidos a los
Dominios de factorización única
 CAPíTULO 3 Dominios de factorización única 1. Dominios euclídeos En la sección dedicada a los números enteros hemos descrito todos los ideales de Z. En este apartado introducimos una familia de anillos
CAPíTULO 3 Dominios de factorización única 1. Dominios euclídeos En la sección dedicada a los números enteros hemos descrito todos los ideales de Z. En este apartado introducimos una familia de anillos
Álgebra I Práctica 5 - Polinomios
 Álgebra I Práctica 5 - Polinomios Números complejos 1. Para los siguientes z C, hallar Re(z), Im(z), z, Re(z 1 ), Im(z 1 ), Re( i z) e Im(i z). i) z = (2 + i)(1 + 3 i). ii) z = 5 i(1 + i) 4. iii) z = (
Álgebra I Práctica 5 - Polinomios Números complejos 1. Para los siguientes z C, hallar Re(z), Im(z), z, Re(z 1 ), Im(z 1 ), Re( i z) e Im(i z). i) z = (2 + i)(1 + 3 i). ii) z = 5 i(1 + i) 4. iii) z = (
Álgebra I Práctica 5 - Polinomios
 Álgebra I Práctica 5 - Polinomios 1. Para los siguientes z C, hallar Rez), Imz), z, Rez 1 ), Imz 1 ), Re i z) e Imi z). i) z = 2 + i)1 + 3 i). ii) z = 5 i1 + i) 4. iii) z = 2 + 3 i) 2 1 3 i). iv) z = i
Álgebra I Práctica 5 - Polinomios 1. Para los siguientes z C, hallar Rez), Imz), z, Rez 1 ), Imz 1 ), Re i z) e Imi z). i) z = 2 + i)1 + 3 i). ii) z = 5 i1 + i) 4. iii) z = 2 + 3 i) 2 1 3 i). iv) z = i
Departamento de Ingeniería Matemática - Universidad de Chile
 Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 08-2 SEMANA 7: ESPACIOS VECTORIALES 3.5. Generadores de un espacio vectorial Sea V un espacio vectorial
Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 08-2 SEMANA 7: ESPACIOS VECTORIALES 3.5. Generadores de un espacio vectorial Sea V un espacio vectorial
S2: Polinomios complejos
 S: Polinomios complejos Un polinomio complejo de grado n es un polinomio de la forma: p x = a 0 + a 1 x + a x + + a n x n Donde los a i C se llaman coeficientes y a n 0. Observa que como R C los coeficientes
S: Polinomios complejos Un polinomio complejo de grado n es un polinomio de la forma: p x = a 0 + a 1 x + a x + + a n x n Donde los a i C se llaman coeficientes y a n 0. Observa que como R C los coeficientes
Apéndice 5: Diagonalización de matrices
 Apéndice 5: Diagonalización de matrices Más aplicaciones de la diagonalización. Resolución de ecuaciones en diferencias Hay cierto tipo de problemas cuya resolución depende de la potencia de una matriz.
Apéndice 5: Diagonalización de matrices Más aplicaciones de la diagonalización. Resolución de ecuaciones en diferencias Hay cierto tipo de problemas cuya resolución depende de la potencia de una matriz.
Álgebra Lineal y Estructuras Matemáticas. J. C. Rosales y P. A. García Sánchez. Departamento de Álgebra, Universidad de Granada
 Álgebra Lineal y Estructuras Matemáticas J. C. Rosales y P. A. García Sánchez Departamento de Álgebra, Universidad de Granada Capítulo 3 El anillo de los polinomios sobre un cuerpo 1. Divisibilidad Un
Álgebra Lineal y Estructuras Matemáticas J. C. Rosales y P. A. García Sánchez Departamento de Álgebra, Universidad de Granada Capítulo 3 El anillo de los polinomios sobre un cuerpo 1. Divisibilidad Un
Polinomios (lista de problemas para examen)
 Polinomios (lista de problemas para examen) En esta lista de problemas el conjunto de los polinomios de una variable con coeficientes complejos se denota por P(C). También se usa la notación C[x], si la
Polinomios (lista de problemas para examen) En esta lista de problemas el conjunto de los polinomios de una variable con coeficientes complejos se denota por P(C). También se usa la notación C[x], si la
ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- Enteros
 Resumen teoría Prof. Alcón ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- Z = N {0} N Enteros Las operaciones + y. son cerradas en Z, es decir la suma de dos números enteros es un número entero y el producto
Resumen teoría Prof. Alcón ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- Z = N {0} N Enteros Las operaciones + y. son cerradas en Z, es decir la suma de dos números enteros es un número entero y el producto
a + b 2 ab + a2 + b 2 Si aplicamos la desigualdad entre las medias aritmética y geométrica al miembro de la izquierda obtenemos 2 2ab + a2 + b =
 Sesión 3 1. Sean a, b números positivos. Probar que a + b a + b ab +. Solución 1. La desigualdad equivale a ab + a +b a + b. Si aplicamos la desigualdad entre las medias aritmética y geométrica al miembro
Sesión 3 1. Sean a, b números positivos. Probar que a + b a + b ab +. Solución 1. La desigualdad equivale a ab + a +b a + b. Si aplicamos la desigualdad entre las medias aritmética y geométrica al miembro
Álgebra I Práctica 7 - Polinomios
 FCEyN - UBA - 2do cuatrimestre 2016 Generalidades Álgebra I Práctica 7 - Polinomios 1. Calcular el grado y el coeficiente principal de f Q[X] en los casos i) f = (4X 6 2X 5 + 3X 2 2X + 7) 77. ii) f = (
FCEyN - UBA - 2do cuatrimestre 2016 Generalidades Álgebra I Práctica 7 - Polinomios 1. Calcular el grado y el coeficiente principal de f Q[X] en los casos i) f = (4X 6 2X 5 + 3X 2 2X + 7) 77. ii) f = (
Unidad 2 Polinomios PÁGINA 28 SOLUCIONES. Sacar factor común. a) b) Evaluar un polinomio en un punto.
 Unidad Polinomios PÁGINA 8 SOLUCIONES Sacar factor común. a) b) 3x 6 3 ( x ) 3 5x 10x 5x 5 x( x x1) Evaluar un polinomio en un punto. Dado el polinomio P(x) = x 4 x 3 x + 1, podemos asegurar que: a) P(1)
Unidad Polinomios PÁGINA 8 SOLUCIONES Sacar factor común. a) b) 3x 6 3 ( x ) 3 5x 10x 5x 5 x( x x1) Evaluar un polinomio en un punto. Dado el polinomio P(x) = x 4 x 3 x + 1, podemos asegurar que: a) P(1)
TEÓRICO PRÁCTICO Nº 4: FUNCIÓN POLINÓMICA
 Departamento de Matemática TEÓRICO PRÁCTICO Nº 4: FUNCIÓN POLINÓMICA Primera parte La función polinómica es del tipo: O como y, se escribe directamente: es decir, tiene la expresión de un polinomio. Los
Departamento de Matemática TEÓRICO PRÁCTICO Nº 4: FUNCIÓN POLINÓMICA Primera parte La función polinómica es del tipo: O como y, se escribe directamente: es decir, tiene la expresión de un polinomio. Los
Notas sobre polinomios
 Notas sobre polinomios Glenier Bello 1. Definiciones y conceptos básicos 1.1. Un polinomio es una función f : C C del tipo f(x) = a n x n + a n 1 x n 1 + + a 1 x + a 0, donde n es un entero no negativo
Notas sobre polinomios Glenier Bello 1. Definiciones y conceptos básicos 1.1. Un polinomio es una función f : C C del tipo f(x) = a n x n + a n 1 x n 1 + + a 1 x + a 0, donde n es un entero no negativo
Conjuntos, relaciones y funciones Susana Puddu
 Susana Puddu 1. Repaso sobre la teoría de conjuntos. Denotaremos por IN al conjunto de los números naturales y por ZZ al de los enteros. Dados dos conjuntos A y B decimos que A está contenido en B o también
Susana Puddu 1. Repaso sobre la teoría de conjuntos. Denotaremos por IN al conjunto de los números naturales y por ZZ al de los enteros. Dados dos conjuntos A y B decimos que A está contenido en B o también
Estructuras algebraicas
 Semana 10[1/14] 26 de abril de 2007 Semana 10[2/14] Grupos Un grupo es un caso particular de una estructura algebraica. Veremos que esta noción rescata ampliamente las propiedades de estructuras tales
Semana 10[1/14] 26 de abril de 2007 Semana 10[2/14] Grupos Un grupo es un caso particular de una estructura algebraica. Veremos que esta noción rescata ampliamente las propiedades de estructuras tales
Reporte de Actividades 13
 Reporte de Actividades 13 Profesores: Alejandro Díaz Barriga, Ricardo Vila. Tutores: Paulina Salcedo, Yury García. 1. Sesión del 25 de mayo de 2011 1.1 Apuntes de la clase con Alejandro Díaz Barriga. 1.1.1.
Reporte de Actividades 13 Profesores: Alejandro Díaz Barriga, Ricardo Vila. Tutores: Paulina Salcedo, Yury García. 1. Sesión del 25 de mayo de 2011 1.1 Apuntes de la clase con Alejandro Díaz Barriga. 1.1.1.
Semana04[1/17] Funciones. 21 de marzo de Funciones
![Semana04[1/17] Funciones. 21 de marzo de Funciones Semana04[1/17] Funciones. 21 de marzo de Funciones](/thumbs/73/69418199.jpg) Semana04[1/17] 21 de marzo de 2007 Composición de funciones Semana04[2/17] Pensemos que tenemos tres conjuntos no vacíos A, B, C, y dos funciones, f : A B y g : B C, como en el siguiente diagrama: Figura:
Semana04[1/17] 21 de marzo de 2007 Composición de funciones Semana04[2/17] Pensemos que tenemos tres conjuntos no vacíos A, B, C, y dos funciones, f : A B y g : B C, como en el siguiente diagrama: Figura:
Exámenes de álgebra básica de enero de Grupos 1 y 3.
 Exámenes de álgebra básica de enero de 2019. Grupos 1 y 3. GRUPOS 1. Calcular razonadamente todos los subgrupos normales de S 4. Un subgrupo H de un grupo G es normal si y solamente si para cada g G se
Exámenes de álgebra básica de enero de 2019. Grupos 1 y 3. GRUPOS 1. Calcular razonadamente todos los subgrupos normales de S 4. Un subgrupo H de un grupo G es normal si y solamente si para cada g G se
FACTORIZACIÓN BÁSICA Y RAÍCES
 FACTORIZACIÓN BÁSICA Y RAÍCES Genaro Luna Carreto 1 1 Profesor de la Benemérita Universidad Autónoma de Puebla, México. 0.1. Algoritmo de la división El símbolo K[X] representa al conjunto de polinomios
FACTORIZACIÓN BÁSICA Y RAÍCES Genaro Luna Carreto 1 1 Profesor de la Benemérita Universidad Autónoma de Puebla, México. 0.1. Algoritmo de la división El símbolo K[X] representa al conjunto de polinomios
Fundamentos matemáticos. Tema 1 Números reales. Polinomios
 Grado en Ingeniería agrícola y del medio rural Tema 1 Números reales. Polinomios José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2017 Licencia Creative
Grado en Ingeniería agrícola y del medio rural Tema 1 Números reales. Polinomios José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2017 Licencia Creative
Álgebra I Práctica 5 - Polinomios
 Números complejos Álgebra I Práctica 5 - Polinomios 1. Para los siguientes z C, hallar Re(z), Im(z), z, Re(z 1 ), Im(z 1 ), Re( i z) e Im(i z). i) z = (2 + i)(1 + 3 i). ii) z = 5 i(1 + i) 4. iii) z = (
Números complejos Álgebra I Práctica 5 - Polinomios 1. Para los siguientes z C, hallar Re(z), Im(z), z, Re(z 1 ), Im(z 1 ), Re( i z) e Im(i z). i) z = (2 + i)(1 + 3 i). ii) z = 5 i(1 + i) 4. iii) z = (
TEMA: 5 ÁLGEBRA 3º ESO
 TEMA: 5 ÁLGEBRA 3º ESO 1. MONOMIO Un monomio es una expresión algebraica en la que las únicas operaciones que aparecen entre las variables son el producto y la potencia de exponente natural. Ejemplo: x
TEMA: 5 ÁLGEBRA 3º ESO 1. MONOMIO Un monomio es una expresión algebraica en la que las únicas operaciones que aparecen entre las variables son el producto y la potencia de exponente natural. Ejemplo: x
AMPLIACIÓN DE MATEMÁTICAS. DIVISIBILIDAD DE NÚMEROS ENTEROS. En el conjunto de los números enteros
 AMPLIACIÓN DE MATEMÁTICAS DIVISIBILIDAD DE NÚMEROS ENTEROS. En el conjunto de los números enteros Z = {..., n,..., 2, 1, 0, 1, 2, 3,..., n, n + 1,...} tenemos definidos una suma y un producto para los
AMPLIACIÓN DE MATEMÁTICAS DIVISIBILIDAD DE NÚMEROS ENTEROS. En el conjunto de los números enteros Z = {..., n,..., 2, 1, 0, 1, 2, 3,..., n, n + 1,...} tenemos definidos una suma y un producto para los
La estructura de un cuerpo finito.
 9. CUERPOS FINITOS El objetivo de este capítulo es determinar la estructura de todos los cuerpos finitos. Probaremos en primer lugar que todo cuerpo finito tiene p n elementos, donde p es la característica
9. CUERPOS FINITOS El objetivo de este capítulo es determinar la estructura de todos los cuerpos finitos. Probaremos en primer lugar que todo cuerpo finito tiene p n elementos, donde p es la característica
ÁLGEBRA MODERNA. Índice 1. El grupo de permutaciones y el grupo alternante 1
 ÁLGEBRA MODERNA DANIEL LABARDINI FRAGOSO TOMÓ ESTAS NOTAS: ALEJANDRO DE LAS PEÑAS CASTAÑO FECHA: 9/MARZO/2016 Índice 1. El grupo de permutaciones y el grupo alternante 1 1. El grupo de permutaciones y
ÁLGEBRA MODERNA DANIEL LABARDINI FRAGOSO TOMÓ ESTAS NOTAS: ALEJANDRO DE LAS PEÑAS CASTAÑO FECHA: 9/MARZO/2016 Índice 1. El grupo de permutaciones y el grupo alternante 1 1. El grupo de permutaciones y
10. Series de potencias
 FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 7-2 Basado en el apunte del curso Cálculo (2do semestre), de Roberto Cominetti, Martín Matamala y Jorge San
FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 7-2 Basado en el apunte del curso Cálculo (2do semestre), de Roberto Cominetti, Martín Matamala y Jorge San
Raíces de polinomios
 Raíces de polinomios En ésta página podrás conocer las herramientas necesarias para poder encontrar las raíces de polinomios de una variable con coeficientes enteros. Para ello hemos dividido esta página
Raíces de polinomios En ésta página podrás conocer las herramientas necesarias para poder encontrar las raíces de polinomios de una variable con coeficientes enteros. Para ello hemos dividido esta página
CURSO CERO DE MATEMATICAS. Apuntes elaborados por Domingo Pestana Galván. y José Manuel Rodríguez García
 INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES CURSO CERO DE MATEMATICAS Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica
INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES CURSO CERO DE MATEMATICAS Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica
Ejercicios Resueltos 1 / Algebra / 2008
 Ejercicios Resueltos 1 / Algebra / 008 Profesora: María Leonor Varas (Sección 4) Auxiliares: Sebastián Astroza & Diego Morán A continuación veremos un ejemplo de un tipo de problemas de inducción, los
Ejercicios Resueltos 1 / Algebra / 008 Profesora: María Leonor Varas (Sección 4) Auxiliares: Sebastián Astroza & Diego Morán A continuación veremos un ejemplo de un tipo de problemas de inducción, los
