MATEMATICA. Primer Año Módulo 3
|
|
|
- Esteban Muñoz Blázquez
- hace 9 años
- Vistas:
Transcripción
1 Centro Educativo de Nivel Secundario Nº 451 Anexo Universidad Tecnológica Nacional Dirección de Capacitación No Docente Dirección General de Cultura y Educación Provincia de Buenos Aires MATEMATICA Primer Año Módulo 3 LIBROS BACHILLER 2011 Formato digital PDF Publicación de edutecne Editorial de la U. T. N. Sarmiento 440 (C1041AAJ) Ciudad Autónoma de Buenos Aires Argentina [email protected] Universidad Tecnológica Nacional U.T.N. Argentina. La Editorial de la U.T.N. recuerda que las obras publicadas en su sitio web son de libre acceso para fines académicos y como un medio de difundir el conocimiento generado por autores universitarios, pero que los mismos y edutecne se reservan el derecho de autoría a todos los fines que correspondan.
2 Números enteros: Representación y orden de números enteros : números opuestos, valor absoluto. Operaciones con números enteros: suma, resta, producto, cociente, Potenciación, radicación. Cálculos combinados en Z. Propiedades de la radicación y potenciación, ejercicios combinados Cuadrado de un binomio. NÚMEROS ENTEROS Cómo surge la necesidad de definir otro conjunto numérico, además del conjunto de los naturales (N) con el que ya hemos trabajado? Cuando hablamos de arriba o abajo, antes o después etc. estamos estableciendo puntos de referencia. Muchas veces en situaciones de la vida cotidiana establecemos esos puntos aunque no lo hagamos concientemente. Por ejemplo... El cerro Gris tiene 235 m de altura,... en Puerto Madryn la sensación térmica es de 5 grados bajo 0,...si subimos a un ascensor y deseamos ir al segundo subsuelo apretamos el botón -2 0 m Nivel del mar 200 m 150 m 100 m 50 m -50 m -100 m -150 m 35 C 22 C -5 C PB Subsuelos En el primer caso el punto de referencia es el nivel del mar al que llamamos 0 metros, a partir de dicho punto, los que se encuentren por encima del mismo serán positivos y los que se encuentren debajo negativos. Entonces si se dice 100 m se estará hablando de una altura de 100m y si se dice m todos comprenderán que se trata de una profundidad de 100 metros. En el caso de las temperaturas será 0, en el ejemplo del ascensor será la PB. Surge entonces la necesidad de un nuevo conjunto de números llamado conjunto de los números enteros, que se nota con la letra Z. 53
3 Al conjunto formado por los números naturales o enteros positivos, los enteros negativos y el 0 lo llamamos conjunto de los números enteros y lo indicamos con: Z = {...-5, -4, -3, -2, -1, 0, 1, 2, 3, 4,...} Vamos a ver varios ejemplos. Ejemplo N 1 (volvamos a José y el supermercado). José compró 3 tortas de frutilla, 2 kilos de frutillas, 6 botellas de vino blanco y 3 de vino tinto y 2 kilos de carne y gastó $ 78, que hubiera pasado sin en lugar de pagar con $ 100, pagaba con $ 50? En realidad no hubiera podido hacer la compra pues el gasto superaría al dinero que tiene, la deuda sería de $ 28 y para indicar que es una deuda diriamos - $ 28. No es lo mismo decir tengo $ 28 que debo $ 28, por eso la deuda se escribirá como - $ 28. $50 $78 $28 Ejemplo N 2 Pablo está preocupado pues acaba de recibir el resumen de su cuenta bancaria con una deuda de $ A los diez días, va al banco y paga $ en efectivo. Cuando al mes siguiente le llega el resumen bancario observa lo siguiente: Banco Irlandés Cuenta Nº /8 Fecha Señor: Pablo González Ahorro y Servicios Deuda Anterior Pago en Efectivo Interés por deuda SALDO AL
4 Pablo miró el resumen y observó que todavía debía $ Cómo llegó el banco a esa suma? Pablo leyó una y otra vez el resumen, buscó lápiz, papel y comenzó a anotar. debía $ pagué - $ debo $ debo intereses + $ $ Sin embargo, el banco había hecho la cuenta de otro modo: deuda anterior (- 4500) + intereses por deuda (- 150), el cliente debe (- 4650); pagó $1200, debe entonces (- 3450). El cliente sigue debiendo por que lo que pagó es menor que su deuda. Debe = Pagó = Representación y orden de números enteros En general los números enteros se representan en una recta en la que se marca el 0 (cero) y un segmento unidad con el objeto de fijar el punto de referencia. En dicha recta a partir del cero hacia la derecha, estarán representados los números positivos y del cero hacia la izquierda los números negativos. El 0 no es ni positivo ni negativo. Teniendo en cuenta lo expuesto cualquier número de la recta numérica es mayor que otro que se encuentre a su izquierda. negativos positivos El orden de los naturales se establece de la siguiente forma 1 < 2 < 3 < 4 < 5 < 6... El orden de los enteros se establece de la siguiente forma -8< -7 < -6 < -5 < -4 < -3 < -2< -1 < 0 < 1 <2 <3 <4 <
5 Si consideramos en la recta numérica, 2 y 2 están a la misma distancia del cero. A estos números se los denomina números opuestos Números opuestos: Se denomina así a los números cuya distancia al cero es la misma. Módulo o valor absoluto de un número: La distancia entre cualquier número entero y el cero se denomina valor absoluto o módulo. En cualquier número se pueden distinguir dos propiedades 1) su signo. ( positivo o negativo). 2) su valor absoluto o módulo (cantidad de unidades que ocupa en la recta numérica). ejemplo: El módulo de - 2 = 2 (ocupa dos unidades) y el módulo de 2 = 2 aunque ambos tienen distinto signo tiene igual modulo Módulo se representa por medio de dos barras donde queda encerrado el número. 2 2 El número que esta dentro del modulo puede ser positivo o negativo, pero el modulo de cualquier número (sea positivo o negativo) es positivo, pues se asocia al concepto de distancia, y las distancias son siempre positivas. Ordenar de menor a mayor los siguientes números: -15; 4; -7; 2; 9; -20; 5; 0; 1; -12; -1; 3; ; -15; -12; -7; -1; 0; 1; 2; 3; 4; 5; 9; Ordenamos de menor a mayor: -2; 7; 0; 45; -1;-32; 20; 17;
6 7 Problema 1) Dibujen una recta numérica y ubiquen los siguientes números. a) Marquen con un color los números naturales y con otro los números enteros. b) Marquen si existen pares de números opuestos. c) Indiquen el módulo o valor absoluto de cada número. -5, -9, 3, 8, -5, 7, 2, 2,-7, Problema 2) Completen el siguiente cuadro número opuesto módulo consecutivo doble Problema 3) Si tenemos en cuenta los años mas importantes en la vida de Juan: Nació 1951 Terminó la primaria 1963 Terminó la secundaria 1968 Se recibió de abogado en 1975 Se casó en 1978 Tuvo su primer hijo en 1980 Tuvo su segundo hijo en 1983 Se divorció en
7 Tomen como punto de referencia el año en el que terminó la secundaria e indiquen mediante un número entero cuantos años antes o después ocurrieron los otros acontecimientos. Nació Terminó la primaria Terminó la secundaria Se recibió de abogado Se casó Tuvo su primer hijo Tuvo su segundo hijo Se divorció Problema 4) En un edificio de Belgrano, en el ascensor la PB esta indicada con el 0, y los subsuelos con números negativos. Completen el siguiente cuadro. Sube en el piso Viaja en el ascensor Baja en el piso -3 5 pisos hacia arriba 4 5 pisos hacia abajo 6 pisos hacia arriba 4 7 pisos hacia abajo
8 OPERACIONES FUNDAMENTALES CON NÚMEROS ENTEROS Suma y resta Para sumar y restar dos números enteros se tiene 8 posibilidades Suma de dos enteros positivos. ( + 3 ) + ( + 4 ) = 7 Resta de dos enteros positivos. ( + 3 ) - ( + 4 ) 3 4 = - 1 Suma de dos enteros de distinto signo. ( + 3 ) + ( - 4 ) 3 4 = -1 ( - 3 ) + ( + 4 ) = 1 Resta de dos enteros de distinto signo. ( - 3 ) - ( + 4 ) = - 7 ( + 3 ) - ( -4 ) = 7 Suma de dos enteros negativos. ( - 3 ) + ( - 4 ) = -7 Resta de dos enteros negativos. ( - 3 ) - ( - 4 ) = 1 Si recordamos lo visto en el capitulo anterior, para sumar o restar enteros operamos igual que con naturales, eliminamos los paréntesis y luego se opera A esta sucesión de sumas y restas en Z, se la conoce con el nombre de suma algebraica. Cómo se resuelve? Agrupamos los números positivos por un lado y los negativos por otro de la siguiente manera: ( ) - ( ) = positivos negativos Como existe un delante de un paréntesis significa que son negativos a pesar de que dentro del paréntesis figuren como positivos. ( 15 ) - ( 22 ) = = -7 Si la suma de los positivos es mayor que la de los negativos, entonces el resultado final, será positivo. Si la suma de los positivos es igual a la de los negativos, entonces el resultado final será 0. 59
9 Si la suma de los negativos es mayor que la de los positivos, entonces el resultado final era negativo. Al resolver las sumas algebraicas, se puede pensar que los números positivos es el dinero con que se cuenta para pagar una deuda, los números negativos son la deuda. Retomando: Si lo que se tiene es mayor que la deuda, abono y me quedo con efectivo. Si lo que se tiene es igual a la deuda, abono y no me queda nada. Si lo que se tiene es menor a la deuda, abono y quedo con deuda. Multiplicación en Z: Definición: Si a y n son números enteros, el producto a. n (se lee a por n ) es también un número entero. El producto a. n se define mediante: a. 0 = 0 a. 1 = a a (-1) = - a Es decir, multiplicar un número entero a por otro n mayor que 1, significa sumar n veces a; en cambio multiplicarlo por n; significa sumar n veces el opuesto de a. Es decir: el producto de dos números es positivo si ambos son del mismo signo; negativo si uno de ellos es negativo, cero si alguno de los dos es cero, o ambos son ceros. Esto se conoce con el nombre de regla de los signos 1) (+). (+) = (+) 2) (+). (- ) = (- ) 3) (- ). (+) = (- ) 4) (- ). (- ) = (+) En 1) y 4) observamos que siendo los 2 del mismo signo (es decir ambos + o ambos negativos) da positivo (+) En 2) y 3) cuando uno de ellos es negativo da negativo (- ) La regla de los signos se utiliza para la multiplicación y la división. ejemplos: 1) 2. 3 = 6 4) ( - 5 ). 7 = ) ( - 2 ). (- 3 ) = 6 5) 7. (- 8) = ) ( - 4 ). 8 = ) ( - 4 ). (- 8) = 32 Si se tienen más de dos enteros se multiplican de a 2 : (- 3). (- 4). (- 8) =
10 8 ( +). ( - ) = ( - ) Para dividir también se aplica la regla de los signos: a) (- 4) : 2 = - 2 b) (- 6) : (- 3) = 2 c) (- 8) : (- 2) = 4 d) 16 : ( - 2) = - 8 e) (- 18) : (- 9) = 2 f) (- 15) : 3 = - 5 Ejercicio1) Resuelvan las siguientes sumas y restas eliminando previamente los paréntesis. a) ( + 3) + (-4) =... b) ( - 7 ) + (+5) + (-2) =... d) ( - 5) ( -3) =... d) ( +9) + (+7) =. e)( - 5) + ( - 4) =... f) ( +9) (-8) - (6) =... Ejercicio 2) Resuelvan las siguientes sumas algebraicas: a) =... b) =... c) = d) = Ejercicio 3) Completen el siguiente cuadro a b c a. b. c a. b : c
11 Ejercicio 4) Según corresponda en cada caso indique si es V (verdadero) o F (falso). a) (-3): (-3) = (3): (3) d) (-5).(1) = (-1). (5) b) (-5). (-1) = (5).(-1) e) (-2).0 = 0. (-5) c) (-3): (-1) = (-1): (-3) f) (-5) (2) = (-2). (5) Ejercicio 5) Coloquen los paréntesis necesarios donde correspondan para que las operaciones combinadas den el resultado indicado =5-2: =-21 Ejercicio 6) Completen el siguiente cuadro: a b c a+b-c a+b-(c+a) a.b.c a-(b+c)
12 POTENCIACIÓN EN Z Dado un número a que a Z y otro n que a N definimos una nueva operación a la que llamamos potenciación que cumple: a n = b Donde a se llama base, n exponente y b potencia. Ejemplo numérico: 2 3 = 8 2 es la base, 3 el exponente y 8 la potencia cómo se calcula una potencia? En realidad la potenciación es una multiplicación abreviada, el número n nos indica la cantidad de veces que se multiplica la base: 2 3 = = 8 23 = = 8 3 veces ( n = 3) 22 = 2. 2 = 4 2 veces ( n = 2) Para tener en cuenta a 0 = 1 cualquier número distinto de 0 elevado a la 0 es igual a 1 (por ahora lo tomamos sin discusión ya veremos cual es el motivo cuando estudiemos propiedades de las potencias). a 1 = a cualquier número elevado a la 1(primera) es el mismo número. Si el exponente es 2 se denomina al cuadrado. Si el exponente es 3 se denomina al cubo 63
13 En esta primera instancia hemos definido al exponente como un número natural, por lo que no puede ser negativo, pero hemos definido a la base como un numero entero por lo que puede ser positivo o negativo. Por lo tanto estudiaremos todas las posibilidades teniendo en cuenta los signos de la base. Sigan la secuencia del grafico analizando el ejemplo numérico para comprender mejor las distintas situaciones que se plantean. POTENCIACIÓN a n = b Base positiva a > 0 Ej. a = 5 Base negativa a < 0 Ej. a = -2 Exponente par n = 2 Exponente impar n = 3 Exponente par n = 2 Exponente impar n = 3 Resultado siempre positivo 5 2 = 5.5 = = 5.5.5= 125 Resultado Positivo (-2) 2 = (-2). (-2) = = + Resultado Negativo (-2) 3 = (-2). (-2).(.2)= = - Conclusión: Cuando la base es positiva ya sea el exponente par o impar siempre arroja por resultado un número positivo. Conclusión: Cuando la base es negativa y el exponente es par da por resultado un número positivo. Conclusión: Cuando la base es negativa y el exponente es impar es en el único caso en el que el resultado es un número negativo. Ojo queda pendiente el caso en el que el exponente es negativo. Importante -2 2 (-2) (-2). (-2) -4 4 En una caso la base es 2 y en el otro (-2) 64
14 Propiedades de la potenciación La potenciación no es distributiva con respecto a la adición o a la sustracción. Es decir; en símbolos: (a + b)2 a2 + b2 (2 + 3) Primero se efectúa la suma y después se eleva a la potencia correspondiente. La potenciación es distributiva con respecto a la multiplicación y a la división: En símbolos: (a. b)n = an. bn (a : b)n = an : bn ( 2. 3 ) 2 = = = 36 En el producto y en el cociente el resultado es el mismo aplicando o no la propiedad distributiva. Producto de potencias de igual base = 25 = = 5 Conclusión: en el producto de potencias de igual base se suman los exponentes. 65
15 Ejemplo 1: = 39 Cociente de potencias de igual base 45 : 43 = Si observamos los exponentes: 5-3 = = 4 2 Propiedad: En el cociente de potencias de igual base se restan los exponentes. ejemplo 2: 84 : 82 = 84-2 = 82 Potencia de potencia (22) 3 =(2. 2 ) 3 = = 23+3 = 26 aplico propiedad distributiva aplico propiedad de producto de potencias de igual base Si observamos los exponentes 2. 3 = 6 Propiedad En la potencia de potencia se multiplican los exponentes ( 25 )2 = = 210 Potenciación 1) Calcular las siguientes potencias: a) ( - 3 )2 =... e) (- 2 )4 =... b) ( - 3 )3 =... f) (- 2 )5 =... c) ( - 7 )2 =.. g) ( - 1 )2 =... d) ( - 7 )3 =.. h) ( - 1 )3 =... 66
16 Propiedades de la potenciación Producto de potencias de igual base Cociente de potencias de igual base Potencia de potencia Se suman los exponentes Se restan los exponentes Se multiplican los exponentes RADICACIÓN La radicación es la operación inversa de la potenciación n a = b entonces a = bn siendo n: índice de la raíz a: radicando b: raíz enésima signo radical La raíz de índice 2 se llama raíz cuadrada y generalmente el 2 no se escribe en el signo radical, o sea a se lee raíz cuadrada de a. La raíz de índice 3, se llama cúbica. ejemplos: 4 = 2 porque 22 = = 2 porque 23 = 8 Las raíces de índice par tienen algunas particularidades : Si x 2 = 4, nos encontramos con una ecuación y para resolverla deberemos encontrar el o los valores de x que verifiquen la igualdad, entonces surge la pregunta cuáles son los valores de x que elevados al cuadrado darán como resultado 4? En realidad los números que satisfacen esa condición son x = 2 ó x = -2 67
17 2 x x = 2 = x x = 2 o x = Resumiendo si n es par: x = x Este tema resulta un poco difícil de comprender, pero pensemos que: 22 = 4 y (-2)2 = 4 Propiedades de la radicación La radicación goza de las mismas propiedades que la potenciación. Es decir: No es distributiva respecto a la adición y/o a la sustracción: a + b a + b ejemplo numérico: Verificar realizando los cálculos con la calculadora. Es distributiva respecto a la multiplicación y a la división. a. b = a. b ejemplo numérico: = = 8 sin aplicar propiedad distributiva distributiva = 2. 4 = 8 aplicando propiedad Al igual que en la potenciación, las raíces de índice impar y radicando negativo son las únicas que me dan por resultado un número negativo. 68
18 Radicación Usando la Calculadora Radicando positivo a > 0 Radicando negativo a < 0 Índice par n = 2 4 = 2 Índice impar n = Índice par n = Índice impar n = Resultado siempre positivo La calculadora marca error No tiene resultado pues no existe ningún número que multiplicado por sí mismo sea negativo. Recordemos que +.+=+ -.- =+ Resultado Negativo entonces 4 qué significa?, qué era? Como no se puede encontrar el resultado se dice que la solución es vacía. 69
19 Se ha visto que la potenciación no es distributiva con respecto a la suma o a la resta y entonces como se opera en una situación como la que sigue? (x-2) 2 1) Se sabe que si un número o una expresión está elevada al cuadrado, la base debe multiplicarse por sí misma dos veces. Entonces: (x 2 ) 2 = (x - 2) (x - 2) 2)Se aplica propiedad distributiva 1 (x + 2) (x + 2) = x. x + 2. x x Otro ejemplo Cuadrado de Binomio 2 1 (x + 5) 2 = (x + 5) (x + 5) = x 2 + 2x x = x 2 + 2x + 2x + 4 = x 2 + 4x + 4 Agrupamos las x (x + 5) (x + 5) = x. x + 5. x + 5. x = x 2 + 5x + 5x +25 = x x + 25 En general (a b) 2 = a 2 2 a b + b 2 (a + b) 2 = a a b + b 2 (a - b) 2 = a 2-2 a b + b 2 2 Si se tiene una suma al cuadrado el resultado es: el cuadrado del primer número, más el doble producto del primer número por el segundo, más el cuadrado del segundo. En caso de una resta, el resultado es el mismo, pero el doble producto será negativo. 70
20 Ejercicio Marque con una x la ecuación que corresponde a cada uno de los siguientes enunciados 1) La suma de los cuadrados de dos números distintos es igual a 25. a. (x+y) 2 =25 b. x 2 +y 2 =25 c. x + y 2 =25 2)El triple de un número aumentado en 6 es igual a 36. a. 3x+6=36 b. 3x=36+6 c. 3(x+6)=36 3) La suma de tres números consecutivos es 63. a. 3w=63 b. w+w+1+w+2=63 c. 3(w+1)=63 4)El triple de un número es igual al doble de su consecutivo. a. 3t=2t+1 b. t+3=2t+1 c. 3t=2(t+1) 5) Si un número se lo eleva al cuadrado se obtiene por resultado el cuádruple de dicho número. a. g=4g 2 b. 4g=g 2 c. g 2 =g+4 9 Ejercicio Planten la ecuación y resuelvan los siguientes problemas. 1. La suma entre un número y el doble de su consecutivo es igual a 35 Cuál es el número?
21 2.El doble del anterior de un número sumado a su triplo es igual a 13. Cuál es el número? El triple de la suma entre dos números consecutivos es igual a 45. Cuál es el número? El cuádruple de la edad que tenía Yolanda hace 2 años es igual al doble de la que tendra dentro de 10. Qué edad tiene Yolanda? Ejercicio Observen como se resuelve cada ecuación y resuelvan las de la última página 1. ( x 2 3) : x x 2 +3=28 4x 2 =36 x 2 =28+3 x 2 =9 x 2 =25 x =5 ó x = -5 x = 3 ó x = x x = -6 2x = (-6) 2 2x = 36 x = ( x 3 1) 27 x 3-1= -27 : 3 x 3-1= -9 x 3 = -8 x = x x 2 = -2 x + 2 = (-2) 3 x +2 = -8 x = x 1 2 5x+1 = 2 4 5x+1 = 16 5x = 15 x = x 5 8 = 2x 2 4 = x 2 x = 2 ó x = x x = (-2) x = = 11x 3 = x 72
22 EJERCICIOS PARA HACER EN CASA: NÚMEROS ENTEROS 1 ) ESCRIBIR LOS PLANETAS ORDENADOS SEGÚN SU TEMPERATURA MEDIA EN SUPERFICIE, ORDENADOS DE MAYOR A MENOR. 480 C 220 C 350 C 210 C 150 C 180 C 22 C 23 C 230 C 2 ) SABIENDO QUE UN PAÍS OBTIENE DINERO AL EXPORTAR ( ) Y AL IMPORTAR LO PIERDE ( ). CALCULAR EL SALDO OBTENIDO PARA CADA MES E INDICAR FINALMENTE CUÁL FUE EL MES DE MAYOR INGRESO Y EL DE MAYOR EGRESO. (en millones de dólares) Mes Export. Import. Saldo Abril Mayo Junio Julio
23 3 ) EN UN PUEBLO DE LA SIERRA DE CÓRDOBA SE HIZO UN ESTUDIODEL MOVIMIENTO DE POBLACIÓN OCURRIDO EL AÑO PASADO. TOMANDO LOS DATOS DEL GRÁFICO Y USANDO NÚMEROS ENTEROS, DETERMINAR SI FINALMENTE HUBO UN AUMENTO O UNA REDUCCIÓN EN LA POBLACIÓN INICIAL PUEBLO ) CALCULAR LA TEMPERATURA PROMEDIO ANUAL A PARTIR DE LA MÁXIMA Y LA MÍNIMA, PARA CADA CIUDAD CHILENA. TEMP. MAX. TEMP. MIN. TEMP. PROM. TEMP. MAX. TEMP. MIN. TEMP. PROM. SANTIAGO 34 C 6 C... VALDIVIA 33 C 3 C... PUNTA ARENAS 26 C 10 C... BAHÍA ORANGE 23 C 7 C... 5 ) CALCULAR CUÁNTOS GRADOS DE LATITUD HAY QUE RECORRER AL REALIZAR LOS SIGUIENTES VIAJES: (USANDO LA FÓRMULA DE VARIACIÓN) BRASILIA TEGUCIGALPA; TEGUCIGALPA BRASILIA; QUITO PANAMÁ; BRASILIA QUITO; PANAMÁ TEGUCIGALPA POLO NORTE: 90 TEGUCIGALPA: 14 PANAMÁ: 8 ECUADOR: 0 QUITO: 1 BRASILIA: 22 POLO SUR: 90 74
24 6 ) DETERMINAR EL TIEMPO DE DURACIÓN QUE TUVO CADA IMPERIO DE LA ANTIGÛEDAD: (USANDO LA FÓRMULA DE VARIACIÓN) BABILONIA : desde hasta 600 EGIPTO: desde hasta 332 GRECIA: desde hasta 100 ROMA: desde 750 hasta ) EL MERCURIO ES UNA SUSTANCIA QUE CONGELA A 39 C Y VAPORIZA A 357 C. SÍ INICIALMENTE SE ENCUENTRA EN ESTADO LÍQUIDO, A LA TEMPERATURA AMBIENTE DE 12 C. CALCULAR (USANDO LA FÓMULA DE VARIACIÓN): 1 ) LA VARIACIÓN DE TEMPERATURA QUE EXPERIMENTARÁ PARA LLEGAR A SOLIDIFICAR. 2 ) LA VARIACIÓN DE TEMPERATURA QUE EXPERIMENTARÁ PARA LLEGAR A VAPORIZAR. SÓLIDO LQUIDO GAS 357 C 0 C 39 C 75
25 8 ) INDICAR CON FLECHAS PARA C/ CUENTA EL SIGNO DEL RESULTADO. pos. pos. pos. pos. pos. neg. NEGATIVO neg. neg. NEGATIVO neg. pos. POSITIVO neg. par POSITIVO neg. neg. neg. impar LA REGLA DE LOS SIGNOS SEGÚN LOS CALCULADORES HINDÚES: "EL PRODUCTO DE DOS BIENES O DE DOS DEUDAS ES UN BIEN". 9 ) RESOLVER LAS SIGUIENTES OPERACIONES COMBINADAS: 1. ( 16) ( 22) ( 13) ( 20) = 2. ( 49):( 7) ( 18):( 1) ( 30):( 3) 3. ( 6) 3 :( 3) 2 = 4. ( 1).( 14) ( 5).( 4) ( 8).( 4) = 5. ( ( 4):( 1) ) 3 = 6. ( ( 39) ( 13) ( 45) ( 5) ) 3 = 10 ) CONSTRUIR LAS RELACIONES UTILIZANDO FLECHAS: NEGATIVO POSITIVO NEGATIVO POSITIVO RADICACIÓN 2 soluciones 1 solución sin solución BHASKARA, MATEMÁTICO HINDÚ DEL SIGLO XII, INDICA QUE LA RAÍZ CUADRADA DE UN NÚMERO POSITIVO TIENE DOS VALORES, PERO AFIRMA QUE NO HAY NINGUNA RAÍZ CUADRADA DE UN N NEGATIVO PORQUE ESTOS NÚMEROS NO SON CUADRADOS. 76
26 11 ) RESOLVER LAS SIGUIENTES OPERACIONES COMBINADAS: 1) ( 38) ( 17) ( 27) 2 ( 42) ( 26) ( 13) 2 = 2) ( 1) 2 ( 2) 3 ( 3) 4 ( 10)= 3) 12 2 : ) 10 3 : : 5 : 10 = ALGUNAS RESPUESTAS: 2 ) Saldo de mayo: 65 millones 3 ) 89 hab. 4 ) Santiago: 20 C; Punta Arenas: 8 C 5 ) Brasilia Tegucigalpa: 36 ; Quito a Panamá 9 C 6 ) Duración del imperio babilónio: años, del imperio egípcio: 4332 años. 7 ): 1 ): 345 C 2 ): 51 C 9 ) ) ) ( x 2 6) : ) 2x ) 3x ) 3x
27 78
Colegio Nacional Bartolomé Mitre. Profesora: Hasure Ana Valeria Curso: 2º año Turno: Noche
 1 Colegio Nacional Bartolomé Mitre Profesora: Hasure Ana Valeria Curso: 2º año Turno: Noche 2 PROGRAMA COLEGIO NACIONAL BARTOLOME MITRE CURSO: 2º año TURNO: Noche AÑO: 2016 PROFESORA: Hasure Ana Valeria
1 Colegio Nacional Bartolomé Mitre Profesora: Hasure Ana Valeria Curso: 2º año Turno: Noche 2 PROGRAMA COLEGIO NACIONAL BARTOLOME MITRE CURSO: 2º año TURNO: Noche AÑO: 2016 PROFESORA: Hasure Ana Valeria
ESCUELA TÉCNICA N 26 D.E. 6. Confederación Suiza. Carpeta de Trabajos Prácticos de MATEMÁTICA. Parte I para 1 Año APELLIDO Y NOMBRE DEL ALUMNO:...
 ESCUELA TÉCNICA N 26 D.E. 6 Confederación Suiza Carpeta de Trabajos Prácticos de MATEMÁTICA Parte I para 1 Año APELLIDO Y NOMBRE DEL ALUMNO:... PROFESOR:... DIVISIÓN:... Página 1 UNIDAD 1 NÚMEROS ENTEROS
ESCUELA TÉCNICA N 26 D.E. 6 Confederación Suiza Carpeta de Trabajos Prácticos de MATEMÁTICA Parte I para 1 Año APELLIDO Y NOMBRE DEL ALUMNO:... PROFESOR:... DIVISIÓN:... Página 1 UNIDAD 1 NÚMEROS ENTEROS
Números enteros. Capítulo 1
 Capítulo 1 Números enteros El conjunto de los números enteros (Z). Representación en la recta numérica. El orden en Z. Módulo o valor absoluto. Números opuestos y consecutivos. Adición y sustracción. Multiplicación
Capítulo 1 Números enteros El conjunto de los números enteros (Z). Representación en la recta numérica. El orden en Z. Módulo o valor absoluto. Números opuestos y consecutivos. Adición y sustracción. Multiplicación
El conjunto de los números enteros está formado por los números naturales, el cero y los naturales negativos. Este conjunto se simboliza con la letra
 INSTITUTO FRAY MAMERTO ESQUIÚ MATEMÁTICA 2 C E.S.B. Prof. Virginia Penedo Unidad 1 NÚMEROS ENTEROS Para asignar números enteros a ciertas situaciones de la vida cotidiana es necesario establecer un punto
INSTITUTO FRAY MAMERTO ESQUIÚ MATEMÁTICA 2 C E.S.B. Prof. Virginia Penedo Unidad 1 NÚMEROS ENTEROS Para asignar números enteros a ciertas situaciones de la vida cotidiana es necesario establecer un punto
La potenciación es una forma abreviada de escribir una multiplicación de factores iguales. a n = a. a. a. a. a. a a a 0 = 1 (con a 0) a 1 = a.
 Potenciación y sus propiedades infoactiva La potenciación es una forma abreviada de escribir una multiplicación de factores iguales. exponente base a n a. a. a. a. a. a a a 0 1 (con a 0) a 1 a n veces
Potenciación y sus propiedades infoactiva La potenciación es una forma abreviada de escribir una multiplicación de factores iguales. exponente base a n a. a. a. a. a. a a a 0 1 (con a 0) a 1 a n veces
INSTITUCION EDUCATIVA LA PRESENTACION
 INSTITUCION EDUCATIVA LA PRESENTACION Nombre de la alumna: Área: MATEMATICAS Asignatura: Matemáticas Docente: Luis López Zuleta Tipo de Guía: Conceptual PERIODO GRADO FECHA DURACION DOS 6º 04 de mayo de
INSTITUCION EDUCATIVA LA PRESENTACION Nombre de la alumna: Área: MATEMATICAS Asignatura: Matemáticas Docente: Luis López Zuleta Tipo de Guía: Conceptual PERIODO GRADO FECHA DURACION DOS 6º 04 de mayo de
Tema 3. Números Enteros
 Tema 3. Números Enteros Javier Rodríguez Ruiz Curso 2012-2013 Índice 1. Introducción a los números enteros (Z) 2 2. Sumas y restas de números enteros 5 3. Productos y divisiones de números enteros 8 4.
Tema 3. Números Enteros Javier Rodríguez Ruiz Curso 2012-2013 Índice 1. Introducción a los números enteros (Z) 2 2. Sumas y restas de números enteros 5 3. Productos y divisiones de números enteros 8 4.
LOS NÚMEROS ENTEROS. Para restar un número entero, se quita el paréntesis y se pone al número el signo contrario al que tenía.
 Melilla Los números Enteros y operaciones elementales LOS NÚMEROS ENTEROS 1º LOS NÚMEROS ENTEROS. El conjunto de los números enteros Z está formado por los números naturales (enteros positivos) el cero
Melilla Los números Enteros y operaciones elementales LOS NÚMEROS ENTEROS 1º LOS NÚMEROS ENTEROS. El conjunto de los números enteros Z está formado por los números naturales (enteros positivos) el cero
Espacio curricular: Matemática. Curso: 1 año D Turno tarde. Alumno: ... Profesora :María Elisa Palmas
 Colegio Secundario Nº Gregorio Álvarez. Maestro Patagónico Lucio Mansilla Nº 55. Tel 85-77 Caleta Olivia. Santa Cruz Espacio curricular: Matemática Curso: 1 año D Turno tarde Alumno: EJE TEMÁTICO I: Números
Colegio Secundario Nº Gregorio Álvarez. Maestro Patagónico Lucio Mansilla Nº 55. Tel 85-77 Caleta Olivia. Santa Cruz Espacio curricular: Matemática Curso: 1 año D Turno tarde Alumno: EJE TEMÁTICO I: Números
NÚMEROS ENTEROS. Lengua:.. Música: Historia: Contabilidad:.. Geografía:.. Matemática: Biología:.. Inglés:..
 NÚMEROS ENTEROS 1 Ejercicio 1: Expresar cada una de estas situaciones con el número entero correspondiente: a) Alejandro Magno murió años a.c.. b) El Aconcagua está a 6959 m sobre el nivel del mar.. c)
NÚMEROS ENTEROS 1 Ejercicio 1: Expresar cada una de estas situaciones con el número entero correspondiente: a) Alejandro Magno murió años a.c.. b) El Aconcagua está a 6959 m sobre el nivel del mar.. c)
PRIMER CURSO AÑO LECTIVO El módulo de la multiplicación es el 0 V F. 4. La división de Z si cumple la propiedad conmutativa V F
 BANCO DE PREGUNTAS PRIMER SEMESTRE PRIMER CURSO AÑO LECTIVO 007-008 I. Establezca si las siguientes proposiciones son verdaderas o falsas 1. En el ejercicio 1 + 4 48 el factor común es 1 V F. Los términos
BANCO DE PREGUNTAS PRIMER SEMESTRE PRIMER CURSO AÑO LECTIVO 007-008 I. Establezca si las siguientes proposiciones son verdaderas o falsas 1. En el ejercicio 1 + 4 48 el factor común es 1 V F. Los términos
Bloque 1. Aritmética y Álgebra
 Bloque 1. Aritmética y Álgebra 2. Los números enteros 1. Los números enteros Es el conjunto de los números negativos, el cero y los positivos, y se representan como: Z...,-5,-4,-3,-2,-1,0, 1, 2, 3, 4,
Bloque 1. Aritmética y Álgebra 2. Los números enteros 1. Los números enteros Es el conjunto de los números negativos, el cero y los positivos, y se representan como: Z...,-5,-4,-3,-2,-1,0, 1, 2, 3, 4,
Primer Año EL CONJUNTO DE LOS NÚMEROS ENTEROS
 EL CONJUNTO DE LOS NÚMEROS ENTEROS Contenidos a desarrollar: Producción de fórmulas en N. Elaboración de fórmulas para calcular el paso n de un proceso que cumple cierta regularidad (suma de los n primeros
EL CONJUNTO DE LOS NÚMEROS ENTEROS Contenidos a desarrollar: Producción de fórmulas en N. Elaboración de fórmulas para calcular el paso n de un proceso que cumple cierta regularidad (suma de los n primeros
5. División exacta de números enteros. 6. Operaciones combinadas. Regla de prioridades. 7. Potencia de números enteros con exponente natural.
 1 MATEMÁTICAS Nivel 2º E.S.O. Tema 2º NÚMEROS ENTEROS Conocimientos que puedes adquirir: 1. El conjunto de números enteros: a) Positivos, negativos y el cero. b) Representación gráfica. c) Valor absoluto.
1 MATEMÁTICAS Nivel 2º E.S.O. Tema 2º NÚMEROS ENTEROS Conocimientos que puedes adquirir: 1. El conjunto de números enteros: a) Positivos, negativos y el cero. b) Representación gráfica. c) Valor absoluto.
Semana 1: Números Reales y sus Operaciones
 Semana 1: Números Reales y sus Operaciones Taller de Preparación para Prueba PLANEA Ing. Jonathan Quiroga Tinoco Conalep Tehuacán P.T.B. en ADMO, SOMA y EMEC UNIDAD 04 Los números enteros y sus operaciones
Semana 1: Números Reales y sus Operaciones Taller de Preparación para Prueba PLANEA Ing. Jonathan Quiroga Tinoco Conalep Tehuacán P.T.B. en ADMO, SOMA y EMEC UNIDAD 04 Los números enteros y sus operaciones
CURSO CEPA LOS LLANOS
 Módulo 2 CURSO 2017-18 CEPA LOS LLANOS ÁMBITO CIENTÍFICO Y TECNOLÓGICO Bloque 4. Números enteros y potencias. Expresiones algebraicas, ecuaciones de primer grado y representaciones gráficas. La célula
Módulo 2 CURSO 2017-18 CEPA LOS LLANOS ÁMBITO CIENTÍFICO Y TECNOLÓGICO Bloque 4. Números enteros y potencias. Expresiones algebraicas, ecuaciones de primer grado y representaciones gráficas. La célula
NÚMEROS ENTEROS. (1) Laura anotó en fichas las temperaturas a partir de las 8 de la mañana, pero las fichas de le
 NÚMEROS ENTEROS Matemática Año (1) Laura anotó en fichas las temperaturas a partir de las 8 de la mañana, pero las fichas de le desordenaron. Ayudá a Laura a escribir la temperatura correspondiente a cada
NÚMEROS ENTEROS Matemática Año (1) Laura anotó en fichas las temperaturas a partir de las 8 de la mañana, pero las fichas de le desordenaron. Ayudá a Laura a escribir la temperatura correspondiente a cada
TEMA 2: NÚMEROS ENTEROS
 TEMA : NÚMEROS ENTEROS 1. NÚMEROS ENTEROS Los números naturales se utilizan para expresar matemáticamente multitud de situaciones cotidianas. Sin embargo, a veces no sirven para cuantificar las situaciones
TEMA : NÚMEROS ENTEROS 1. NÚMEROS ENTEROS Los números naturales se utilizan para expresar matemáticamente multitud de situaciones cotidianas. Sin embargo, a veces no sirven para cuantificar las situaciones
Primer Año EL CONJUNTO DE LOS NÚMEROS ENTEROS
 EL CONJUNTO DE LOS NÚMEROS ENTEROS Contenidos a desarrollar: Producción de fórmulas en N. Elaboración de fórmulas para calcular el paso n de un proceso que cumple cierta regularidad (suma de los n primeros
EL CONJUNTO DE LOS NÚMEROS ENTEROS Contenidos a desarrollar: Producción de fórmulas en N. Elaboración de fórmulas para calcular el paso n de un proceso que cumple cierta regularidad (suma de los n primeros
LOGRO: Reconoce distintas representaciones de los números reales y usa sus propiedades para resolver Problemas.
 ESTANDARES Utilizo números reales en sus diferentes representaciones y en diversos contextos. Resuelvo problemas y simplifico cálculos usando propiedades y relaciones de los números reales y de las relaciones
ESTANDARES Utilizo números reales en sus diferentes representaciones y en diversos contextos. Resuelvo problemas y simplifico cálculos usando propiedades y relaciones de los números reales y de las relaciones
ESCUELA PREPARATORIA OFICIAL NO.16 MATERÍA: PENSAMIENTO NUMÉRICO Y ALGEBRAICO I
 ARITMÉTICA 1. Números naturales 2. Divisibilidad 3. Números enteros 4. Números decimales 5. Fracciones y números racionales 6. Proporcionalidad 7. Sistema métrico decimal 8. Sistema sexagesimal 9. Números
ARITMÉTICA 1. Números naturales 2. Divisibilidad 3. Números enteros 4. Números decimales 5. Fracciones y números racionales 6. Proporcionalidad 7. Sistema métrico decimal 8. Sistema sexagesimal 9. Números
NUMEROS ENTEROS ( Z)
 NUMEROS ENTEROS ( Z) En N la resta sólo está definida si el minuendo es mayor o igual al sustraendo. Para que dicha operación no sea tan restringida se creó el conjunto de enteros negativos ( notado por
NUMEROS ENTEROS ( Z) En N la resta sólo está definida si el minuendo es mayor o igual al sustraendo. Para que dicha operación no sea tan restringida se creó el conjunto de enteros negativos ( notado por
TEMA 2: LOS NÚMEROS ENTEROS
 1 TEMA : LOS NÚMEROS ENTEROS VALOR ABSOLUTO DE UN NÚMERO ENTERO El valor absoluto de un número entero es la distancia, en unidades, que le separa del cero en la recta numérica. Se escribe entre dos barras,,
1 TEMA : LOS NÚMEROS ENTEROS VALOR ABSOLUTO DE UN NÚMERO ENTERO El valor absoluto de un número entero es la distancia, en unidades, que le separa del cero en la recta numérica. Se escribe entre dos barras,,
Comparación y Orden: El termómetro marca -3ºC a la tarde y 7ºC a la noche, la temperatura, bajó o subió? Ubiquemos esos valores en la recta numérica:
 Números Enteros: En nuestro país tenemos un relieve montañoso al oeste y llano al este. Esto da por resultado una pendiente general del terreno hacia el Océano Atlántico. Pero la tierra se extiende bajo
Números Enteros: En nuestro país tenemos un relieve montañoso al oeste y llano al este. Esto da por resultado una pendiente general del terreno hacia el Océano Atlántico. Pero la tierra se extiende bajo
Tema 2 Algebra. Expresiones algebraicas Índice
 Tema 2 Algebra. Expresiones algebraicas Índice 1. Expresiones algebraicas comunes... 2 2. Valor numérico de una expresión algebraica... 2 3. Tipos de expresiones algebraicas... 2 4. Monomios... 2 4.1.
Tema 2 Algebra. Expresiones algebraicas Índice 1. Expresiones algebraicas comunes... 2 2. Valor numérico de una expresión algebraica... 2 3. Tipos de expresiones algebraicas... 2 4. Monomios... 2 4.1.
Potencias y raíces Matemáticas 1º ESO
 Potencias y raíces Matemáticas 1º ESO ÍNDICE 1. Potencias 2. Propiedades de potencias 3. Cuadrados perfectos 4. Raíces cuadradas 1 1. POTENCIAS Una potencia es una multiplicación en la que todos los factores
Potencias y raíces Matemáticas 1º ESO ÍNDICE 1. Potencias 2. Propiedades de potencias 3. Cuadrados perfectos 4. Raíces cuadradas 1 1. POTENCIAS Una potencia es una multiplicación en la que todos los factores
j) El beneficio que se obtiene en la venta de un artículo que cuesta a euros y se vende por b euros.
 TEMA 5: ALGEBRA EXPRESIONES ALGEBRAICAS El álgebra es la parte de las matemáticas en la que se utilizan letras para epresar números de valor desconocido. Es un lenguaje que facilita mucho los procesos
TEMA 5: ALGEBRA EXPRESIONES ALGEBRAICAS El álgebra es la parte de las matemáticas en la que se utilizan letras para epresar números de valor desconocido. Es un lenguaje que facilita mucho los procesos
Suma. Propiedades de la suma.
 Suma. La suma es la operación matemática que resulta al reunir en una sola a varias cantidades. También se conoce a la suma como adición. Las cantidades que se suman se llaman sumandos y el resultado suma
Suma. La suma es la operación matemática que resulta al reunir en una sola a varias cantidades. También se conoce a la suma como adición. Las cantidades que se suman se llaman sumandos y el resultado suma
CONJUTOS NÚMERICOS NÚMEROS NATURALES
 CONJUTOS NÚMERICOS NÚMEROS NATURALES El conjunto de números naturales tiene gran importancia en la vida práctica ya que con sus elementos se pueden encontrar elementos u objetos de otros conjuntos. El
CONJUTOS NÚMERICOS NÚMEROS NATURALES El conjunto de números naturales tiene gran importancia en la vida práctica ya que con sus elementos se pueden encontrar elementos u objetos de otros conjuntos. El
N Ú M E R O S P O S I T I V O S Y N E G A T I V O S
 N Ú M E R O S P O S I T I V O S Y N E G A T I V O S Llamamos números negativos a los que están por debajo del cero. Los números negativos se escriben precedidos del signo menos: - 1, -2, -3, -4, -5,. Cuando
N Ú M E R O S P O S I T I V O S Y N E G A T I V O S Llamamos números negativos a los que están por debajo del cero. Los números negativos se escriben precedidos del signo menos: - 1, -2, -3, -4, -5,. Cuando
MONOMIOS Y POLINOMIOS
 Trabajar en álgebra consiste en manejar relaciones numéricas en las que una o más cantidades son desconocidas. Estas cantidades se llaman variables, incógnitas o indeterminadas y se representan por letras.
Trabajar en álgebra consiste en manejar relaciones numéricas en las que una o más cantidades son desconocidas. Estas cantidades se llaman variables, incógnitas o indeterminadas y se representan por letras.
TEMA 5: ÁLGEBRA EXPRESIONES ALGEBRAICAS
 1 TEMA 5: ÁLGEBRA EXPRESIONES ALGEBRAICAS Una expresión algebraica es un conjunto de números y letras unidos entre sí por las operaciones de sumar, restar, multiplicar, dividir y/o por paréntesis. Las
1 TEMA 5: ÁLGEBRA EXPRESIONES ALGEBRAICAS Una expresión algebraica es un conjunto de números y letras unidos entre sí por las operaciones de sumar, restar, multiplicar, dividir y/o por paréntesis. Las
Números Naturales. Cero elemento neutro: = 12 Sucesión fundamental : se obtiene el siguiente número = 9
 Números Naturales Cuando comenzamos a contar los objetos, los años, etc, nos hemos encontrado con los números de forma natural; por eso a este conjunto de números así aprendidos se les denomina números
Números Naturales Cuando comenzamos a contar los objetos, los años, etc, nos hemos encontrado con los números de forma natural; por eso a este conjunto de números así aprendidos se les denomina números
LEY DE LOS SIGNOS, TEORÍA DE AGRUPAMIENTO Y ORDEN DE OPERACIONES
 LEY DE LOS SIGNOS, TEORÍA DE AGRUPAMIENTO Y ORDEN DE OPERACIONES LEY DE LOS SIGNOS SUMA Si los números tienen el mismo signo se suman se deja el mismo signo. 3 + 5 = 8 ( 3) + ( 5) = 8 Si números tienen
LEY DE LOS SIGNOS, TEORÍA DE AGRUPAMIENTO Y ORDEN DE OPERACIONES LEY DE LOS SIGNOS SUMA Si los números tienen el mismo signo se suman se deja el mismo signo. 3 + 5 = 8 ( 3) + ( 5) = 8 Si números tienen
RESUMEN DE ALGEBRA. CONCEPTO: El pensador principal del algebra es Al-Hwarizmi; es de origen árabe.
 RESUMEN DE ALGEBRA CONCEPTO: El pensador principal del algebra es Al-Hwarizmi; es de origen árabe. El álgebra es la rama del conocimiento de la matemática; es decir se desprende de ella. Estudia realidades
RESUMEN DE ALGEBRA CONCEPTO: El pensador principal del algebra es Al-Hwarizmi; es de origen árabe. El álgebra es la rama del conocimiento de la matemática; es decir se desprende de ella. Estudia realidades
Apuntes de matemáticas 2º ESO Curso
 Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el que el sustraendo, pero en la vida nos encontramos con operaciones de este tipo donde a un número menor
Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el que el sustraendo, pero en la vida nos encontramos con operaciones de este tipo donde a un número menor
Los números enteros. Dado que los enteros contienen los enteros positivos, se considera a los números naturales son un subconjunto de los enteros.
 Los números enteros Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el que el sustraendo, pero en la vida nos encontramos con operaciones de este tipo donde
Los números enteros Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el que el sustraendo, pero en la vida nos encontramos con operaciones de este tipo donde
Escuela Pública Experimental Desconcentrada Nº3 Dr. Carlos Juan Rodríguez Matemática 1º Año Ciclo Básico de Secundaria Teoría Nº 1 Primer Trimestre
 CONJUNTO DE LOS NÚMEROS NATURALES Los números naturales son aquellos números exactos; es decir, que no tienen parte decimal ni fraccionaria; además son todos positivos. Sistema de numeración decimal El
CONJUNTO DE LOS NÚMEROS NATURALES Los números naturales son aquellos números exactos; es decir, que no tienen parte decimal ni fraccionaria; además son todos positivos. Sistema de numeración decimal El
UNA ECUACIÓN es una igualdad de dos expresiones algebraicas.
 UNA EXPRESIÓN ALGEBRAICA es una combinación de números, variables (o símbolos) y operaciones como la suma, resta, multiplicación, división, potenciación y radicación. Ejemplos. UNA ECUACIÓN es una igualdad
UNA EXPRESIÓN ALGEBRAICA es una combinación de números, variables (o símbolos) y operaciones como la suma, resta, multiplicación, división, potenciación y radicación. Ejemplos. UNA ECUACIÓN es una igualdad
Expresiones algebraicas
 Expresiones algebraicas Trabajar en álgebra consiste en manejar relaciones numéricas en las que una o más cantidades son desconocidas. Estas cantidades se llaman variables, incógnitas o indeterminadas
Expresiones algebraicas Trabajar en álgebra consiste en manejar relaciones numéricas en las que una o más cantidades son desconocidas. Estas cantidades se llaman variables, incógnitas o indeterminadas
INSTITUCIÓN EDUCATIVA JORGE ROBLEDO PLAN DE APOYO
 FECHA:07-0-204 Página de 4 ÁREA/ASIGNATURA: ARITMÉTICA PARA LA PROMOCIÓN ANTICIPADA GRADO: SEXTO AÑO: 207 INSTRUCCIONES: La entrega de la solución, por escrito y bien presentada, es requisito indispensable
FECHA:07-0-204 Página de 4 ÁREA/ASIGNATURA: ARITMÉTICA PARA LA PROMOCIÓN ANTICIPADA GRADO: SEXTO AÑO: 207 INSTRUCCIONES: La entrega de la solución, por escrito y bien presentada, es requisito indispensable
LIMPIEZA Y ORGANIZACIÓN
 SATISFACTORIO ACEPTABLE MEJORABLE Cuaderno: LIMPIEZA Y ORGANIZACIÓN Realización de TAREAS TEMA 4 NÚMEROS ENTEROS ALUMNO/A: Nº Ejercicios TEMA 4 NÚMEROS ENTEROS (1º ESO) Página 1 N Ú M E R O S P O S I T
SATISFACTORIO ACEPTABLE MEJORABLE Cuaderno: LIMPIEZA Y ORGANIZACIÓN Realización de TAREAS TEMA 4 NÚMEROS ENTEROS ALUMNO/A: Nº Ejercicios TEMA 4 NÚMEROS ENTEROS (1º ESO) Página 1 N Ú M E R O S P O S I T
UNIDAD DIDÁCTICA #1 CONTENIDO
 UNIDAD DIDÁCTICA #1 CONTENIDO OPERACIONES CON DECIMALES MULTIPLICACION DE DECIMALES DIVISIÓN DE DECIMALES OPERACIONES COMBINADAS CON DECIMALES POTENCIACIÓN DE DECIMALES HOJA DE EVALUACIÓN BIBLIOGRAFÍA
UNIDAD DIDÁCTICA #1 CONTENIDO OPERACIONES CON DECIMALES MULTIPLICACION DE DECIMALES DIVISIÓN DE DECIMALES OPERACIONES COMBINADAS CON DECIMALES POTENCIACIÓN DE DECIMALES HOJA DE EVALUACIÓN BIBLIOGRAFÍA
UNIDAD DE APRENDIZAJE II
 UNIDAD DE APRENDIZAJE II NÚMEROS RACIONALES Jerarquía de Operaciones En matemáticas una operación es una acción realizada sobre un número (en el caso de la raíz y potencia) o donde se involucran dos números
UNIDAD DE APRENDIZAJE II NÚMEROS RACIONALES Jerarquía de Operaciones En matemáticas una operación es una acción realizada sobre un número (en el caso de la raíz y potencia) o donde se involucran dos números
Y LOS ELEMENTOS QUE FORMAN UN POLINOMIO. Nombre: Curso: Fecha: F Cómo es el polinomio, completo o incompleto?
 REPASO Y APOYO OBJETIVO 1 3 RECONOCER EL GRADO Y LOS ELEMENTOS QUE ORMAN UN POLINOMIO Nombre: Curso: echa: Un polinomio es una expresión algebraica formada por la suma algebraica de monomios, que son los
REPASO Y APOYO OBJETIVO 1 3 RECONOCER EL GRADO Y LOS ELEMENTOS QUE ORMAN UN POLINOMIO Nombre: Curso: echa: Un polinomio es una expresión algebraica formada por la suma algebraica de monomios, que son los
Matemáticas de 1ºPCPI - Tema
 . TEMA 1 1.- LA SUMA Y LA RESTA DE LOS NÚMEROS NATURALES. 1. Efectúa las siguientes sumas y restas: 2.345 45.890 48.719 754 4.589 28.807 33.957 187 7.082 9.870 45.890 16.907 94 6.529 13.885 61.959 347
. TEMA 1 1.- LA SUMA Y LA RESTA DE LOS NÚMEROS NATURALES. 1. Efectúa las siguientes sumas y restas: 2.345 45.890 48.719 754 4.589 28.807 33.957 187 7.082 9.870 45.890 16.907 94 6.529 13.885 61.959 347
Departamento de Matemática TEORÍA DEL CONJUNTO DE LOS NÚNEROS ENTEROS Primer Año
 Departamento de Matemática TEORÍA DEL CONJUNTO DE LOS NÚNEROS ENTEROS Primer Año - 015 Introducción: Tanto en tablas que informan temperaturas como en resúmenes bancarios, en líneas de tiempo de historia,
Departamento de Matemática TEORÍA DEL CONJUNTO DE LOS NÚNEROS ENTEROS Primer Año - 015 Introducción: Tanto en tablas que informan temperaturas como en resúmenes bancarios, en líneas de tiempo de historia,
TEMA 1 CONJUNTOS NUMÉRICOS
 TEMA 1 CONJUNTOS NUMÉRICOS. Objetivos / Criterios de evaluación O.1.1 Realizar correctamente operaciones con fracciones: Suma, resta, producto, cociente, potencia y radicación. O.1.2 Resolver operaciones
TEMA 1 CONJUNTOS NUMÉRICOS. Objetivos / Criterios de evaluación O.1.1 Realizar correctamente operaciones con fracciones: Suma, resta, producto, cociente, potencia y radicación. O.1.2 Resolver operaciones
Signos del álgebra. Notación algebraica. a) Signos de operación. b) Signos de relación. c) Signos de agrupación. a) Los signos de operación son:
 Notación algebraica Al estudiar el lenguaje algebraico observamos la relación entre signos, letras y números a lo que llamamos notación algebraica. A continuación estudiaremos los elementos que son básicos
Notación algebraica Al estudiar el lenguaje algebraico observamos la relación entre signos, letras y números a lo que llamamos notación algebraica. A continuación estudiaremos los elementos que son básicos
Escuela Pública Experimental Desconcentrada Nº3 Dr. Carlos Juan Rodríguez Matemática 1º Año Ciclo Básico de Secundaria Teoría Nº 2 Segundo Trimestre
 CONJUNTO DE LOS NÚMEROS ENTEROS Los números enteros están formados por: los números naturales (o enteros positivos y el cero) y los números negativos. El cero no tiene signo, no es ni positivo ni negativo.
CONJUNTO DE LOS NÚMEROS ENTEROS Los números enteros están formados por: los números naturales (o enteros positivos y el cero) y los números negativos. El cero no tiene signo, no es ni positivo ni negativo.
TEORIA DE EXPONENTES ING. CRISTHIAN VELANDIA
 TEORIA DE EXPONENTES ING. CRISTHIAN VELANDIA Conceptos preliminares. Epresión algebraica.- es el conjunto de letras y números interrelacionados entre si, mediante las operaciones de adición y sustracción,
TEORIA DE EXPONENTES ING. CRISTHIAN VELANDIA Conceptos preliminares. Epresión algebraica.- es el conjunto de letras y números interrelacionados entre si, mediante las operaciones de adición y sustracción,
1.- DE LOS NÚMEROS NATURALES A LOS NÚMEROS ENTEROS
 1.- DE LOS NÚMEROS NATURALES A LOS NÚMEROS ENTEROS Conjunto de los números naturales: N 1, 2, 3,. Conjunto de los números enteros: Z Positivos: +1, +2, + 3, El 0 Negativos: -1, -2, -3, Los enteros positivos
1.- DE LOS NÚMEROS NATURALES A LOS NÚMEROS ENTEROS Conjunto de los números naturales: N 1, 2, 3,. Conjunto de los números enteros: Z Positivos: +1, +2, + 3, El 0 Negativos: -1, -2, -3, Los enteros positivos
FICHAS REPASO 3º ESO. Para restar números enteros, se suma al minuendo el opuesto del sustraendo y después se aplican las reglas de la suma.
 FICHAS REPASO º ESO OPERACIONES CON NÚMEROS ENTEROS El valor absoluto de un número entero es el número natural que resulta al prescindir del signo. Por ejemplo, el valor absoluto de es y el valor absoluto
FICHAS REPASO º ESO OPERACIONES CON NÚMEROS ENTEROS El valor absoluto de un número entero es el número natural que resulta al prescindir del signo. Por ejemplo, el valor absoluto de es y el valor absoluto
Nombre estudiante: Fecha: D / M / A Asignatura: MATEMÁT. Educador: Luz Dari Lindarte Clavijo. Socialización con estudiante y padre familia, firma:
 EVALUACIÓN ACADÉMICA Gestión Académica Versión 3 / 12-2-2016 Nombre estudiante: Fecha: D / M / A Asignatura: MATEMÁT DBA: Utiliza las propiedades de los números enteros y racionales y las propiedades de
EVALUACIÓN ACADÉMICA Gestión Académica Versión 3 / 12-2-2016 Nombre estudiante: Fecha: D / M / A Asignatura: MATEMÁT DBA: Utiliza las propiedades de los números enteros y racionales y las propiedades de
NÚMEROS ENTEROS. En la recta numérica se pueden representar los números naturales, el cero y los números negativos.
 NÚMEROS ENTEROS El conjunto de los números enteros está formado por: Los números positivos (1, 2, 3, 4, 5, ) Los números negativos ( El cero (no tiene signo) Recta numérica En la recta numérica se pueden
NÚMEROS ENTEROS El conjunto de los números enteros está formado por: Los números positivos (1, 2, 3, 4, 5, ) Los números negativos ( El cero (no tiene signo) Recta numérica En la recta numérica se pueden
1. ADICIÓN O SUMA Caso (a): Adición de un número Racional con uno Irracional: La suma de un número racional con uno Irracional es otro irracional.
 ADICIÓN, SUSTRACCIÓN, MULTIPLICACIÓN, DIVISIÓN, POTENCIACIÓN Y RADICACIÓN EN LOS NÚMEROS REALES. Hoy en día si hablamos de números seguramente nos damos cuenta de que es un tema muy extenso. Pero, hace
ADICIÓN, SUSTRACCIÓN, MULTIPLICACIÓN, DIVISIÓN, POTENCIACIÓN Y RADICACIÓN EN LOS NÚMEROS REALES. Hoy en día si hablamos de números seguramente nos damos cuenta de que es un tema muy extenso. Pero, hace
LibrosMareaVerde.tk Ilustraciones: Banco de Imágenes de INTEF
 30 CAPÍTULO 4: NÚMEROS ENTEROS 1. NÚMEROS ENTEROS 1.1. Números positivos, negativos y cero Existen ocasiones de la vida cotidiana en que es preciso usar números distintos de los naturales, números positivos
30 CAPÍTULO 4: NÚMEROS ENTEROS 1. NÚMEROS ENTEROS 1.1. Números positivos, negativos y cero Existen ocasiones de la vida cotidiana en que es preciso usar números distintos de los naturales, números positivos
Unidad didáctica 1. Operaciones básicas con números enteros
 Unidad didáctica 1 Operaciones básicas con números enteros 1.- Representación y ordenación de números enteros Para representar números enteros en una recta hay que seguir estos pasos: a) Se dibuja una
Unidad didáctica 1 Operaciones básicas con números enteros 1.- Representación y ordenación de números enteros Para representar números enteros en una recta hay que seguir estos pasos: a) Se dibuja una
MATEMÁTICAS ÁLGEBRA (TIC)
 COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS ÁLGEBRA (TIC) GRADO:8 O A, B DOCENTE: Nubia E. Niño C. FECHA: 23 / 02 / 15 GUÍA UNIFICADA: # 1 5; # 1-6 y 1-7 DESEMPEÑOS:
COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS ÁLGEBRA (TIC) GRADO:8 O A, B DOCENTE: Nubia E. Niño C. FECHA: 23 / 02 / 15 GUÍA UNIFICADA: # 1 5; # 1-6 y 1-7 DESEMPEÑOS:
MATEMÁTICAS 1º DE ESO
 MATEMÁTICAS 1º DE ESO LOMCE TEMA III : LOS NÚMEROS ENTEROS Los números negativos. Su necesidad. El conjunto de los números enteros. Valor absoluto de un número entero. Opuesto de un número entero. Suma
MATEMÁTICAS 1º DE ESO LOMCE TEMA III : LOS NÚMEROS ENTEROS Los números negativos. Su necesidad. El conjunto de los números enteros. Valor absoluto de un número entero. Opuesto de un número entero. Suma
Capítulo 3: POTENCIAS Y RAÍCES. TEORÍA. Matemáticas 1º y 2º de ESO
 19 1. POTENCIAS Capítulo 3: POTENCIAS Y RAÍCES.. Matemáticas 1º y 2º de ESO 1.1. Concepto de potencia. Base y exponente Ejemplo 1: María guarda 5 collares en una bolsa, cada 5 bolsas en una caja y cada
19 1. POTENCIAS Capítulo 3: POTENCIAS Y RAÍCES.. Matemáticas 1º y 2º de ESO 1.1. Concepto de potencia. Base y exponente Ejemplo 1: María guarda 5 collares en una bolsa, cada 5 bolsas en una caja y cada
Números enteros. Los números enteros son los formados por los números naturales (1), sus opuestos (2) y el número 0
 Los números enteros son los formados por los números naturales, sus opuestos (2) y el número 0 Números enteros Los números naturales son aquellos que nos permiten contar las cosas. Ej. 2 sillas, 4 patas,
Los números enteros son los formados por los números naturales, sus opuestos (2) y el número 0 Números enteros Los números naturales son aquellos que nos permiten contar las cosas. Ej. 2 sillas, 4 patas,
Este documento es de distribución gratuita y llega gracias a El mayor portal de recursos educativos a tu servicio!
 Este documento es de distribución gratuita y llega gracias a Ciencia Matemática www.cienciamatematica.com El mayor portal de recursos educativos a tu servicio! Recuerdas qué es? Expresión algebraica Es
Este documento es de distribución gratuita y llega gracias a Ciencia Matemática www.cienciamatematica.com El mayor portal de recursos educativos a tu servicio! Recuerdas qué es? Expresión algebraica Es
UNIDAD 1. NÚMEROS. (Página 223 del libro) Nivel II. Distancia. Ámbito Científico Tecnológico.
 UNIDAD 1. NÚMEROS. (Página 22 del libro) Nivel II. Distancia. Ámbito Científico Tecnológico. Clasificación de los números Números naturales son aquellos que utilizamos para contar. N = 0,1,2,,,5,6, Números
UNIDAD 1. NÚMEROS. (Página 22 del libro) Nivel II. Distancia. Ámbito Científico Tecnológico. Clasificación de los números Números naturales son aquellos que utilizamos para contar. N = 0,1,2,,,5,6, Números
Lenguaje coloquial y simbólico:
 TRABAJO PRÁCTICO N 2. Expresiones algebraicas. Ecuaciones e inecuaciones con números enteros Lenguaje coloquial y simbólico: El lenguaje coloquial es el que se utiliza normalmente y está compuesto por
TRABAJO PRÁCTICO N 2. Expresiones algebraicas. Ecuaciones e inecuaciones con números enteros Lenguaje coloquial y simbólico: El lenguaje coloquial es el que se utiliza normalmente y está compuesto por
I CICLO COMÚN MATEMÁTICAS INBAC UNIDAD DIDÁCTICA #8
 UNIDAD DIDÁCTICA #8 INDICE PÁGINA Operaciones Combinadas --------------------------------------------------------------------------------------2 Potenciación de enteros -----------------------------------------------------------------------------------------3
UNIDAD DIDÁCTICA #8 INDICE PÁGINA Operaciones Combinadas --------------------------------------------------------------------------------------2 Potenciación de enteros -----------------------------------------------------------------------------------------3
I.E.S. ANTONIO DOMÍNGUEZ ORTIZ
 I.E.S. ANTONIO DOMÍNGUEZ ORTIZ 3º DE E.S.O TEMA 5 LENGUAJE ALGEBRAICO 1 ÍNDICE 1 DEFINICIONES 1.1 Expresiones algebraicas 1.2 Incógnitas o variables. 1.3 Términos 1.4 Valor numérico de una expresión algebraica.
I.E.S. ANTONIO DOMÍNGUEZ ORTIZ 3º DE E.S.O TEMA 5 LENGUAJE ALGEBRAICO 1 ÍNDICE 1 DEFINICIONES 1.1 Expresiones algebraicas 1.2 Incógnitas o variables. 1.3 Términos 1.4 Valor numérico de una expresión algebraica.
GUÍA DE APRENDIZAJE 7 BÁSICO Educación Matemática (CARLA ORELLANA M.)
 GUÍA DE APRENDIZAJE 7 BÁSICO Educación Matemática (CARLA ORELLANA M.) Nombre alumno(a) I. Resuelve 1) Con la ayuda de la recta numérica, escribe el antecesor y sucesor de los siguientes números enteros:
GUÍA DE APRENDIZAJE 7 BÁSICO Educación Matemática (CARLA ORELLANA M.) Nombre alumno(a) I. Resuelve 1) Con la ayuda de la recta numérica, escribe el antecesor y sucesor de los siguientes números enteros:
PLAN DE RECUPERACIÓN DE MATEMÁTICAS 2º ESO (Primer Trimestre) (Para alumnos de 3º de ESO)
 PLAN DE RECUPERACIÓN DE MATEMÁTICAS 2º ESO (Primer Trimestre) (Para alumnos de 3º de ESO) NOMBRE: Para aprobar las matemáticas pendientes de cursos anteriores es obligatorio realizar el plan de recuperación
PLAN DE RECUPERACIÓN DE MATEMÁTICAS 2º ESO (Primer Trimestre) (Para alumnos de 3º de ESO) NOMBRE: Para aprobar las matemáticas pendientes de cursos anteriores es obligatorio realizar el plan de recuperación
INSTITUTO FRAY MAMERTO ESQUIÚ MATEMÁTICA 2 C E.S.B. Prof. Virginia Penedo
 INSTITUTO FRAY MAMERTO ESQUIÚ MATEMÁTICA 2 C E.S.B. Prof. Virginia Penedo Unidad 2 EXPRESIONES ALGEBRAICAS Expresiones algebraicas. Ecuaciones e inecuaciones con números enteros Lenguaje coloquial y simbólico:
INSTITUTO FRAY MAMERTO ESQUIÚ MATEMÁTICA 2 C E.S.B. Prof. Virginia Penedo Unidad 2 EXPRESIONES ALGEBRAICAS Expresiones algebraicas. Ecuaciones e inecuaciones con números enteros Lenguaje coloquial y simbólico:
MANEJO DE ESPACIOS Y CANTIDADES ALGEBRA
 MANEJO DE ESPACIOS Y CANTIDADES ALGEBRA ALGEBRA: es el nombre que identifica a una rama de la Matemática que emplea números, letras y signos para poder hacer referencia a múltiples operaciones aritméticas.
MANEJO DE ESPACIOS Y CANTIDADES ALGEBRA ALGEBRA: es el nombre que identifica a una rama de la Matemática que emplea números, letras y signos para poder hacer referencia a múltiples operaciones aritméticas.
Números naturales. Marquen con una X la o las descomposiciones correctas en cada caso. a c
 Nombre y apellido: Curso: 2 c Números naturales Sistema de numeración decimal para iniciar Dónde hay más habitantes? Jujuy: 6707 Río Negro: 68645 Unan con flechas según corresponda. a. El 5 vale 500 000.
Nombre y apellido: Curso: 2 c Números naturales Sistema de numeración decimal para iniciar Dónde hay más habitantes? Jujuy: 6707 Río Negro: 68645 Unan con flechas según corresponda. a. El 5 vale 500 000.
POTENCIACIÓN - PROPIEDADES
 POTENCIACIÓN - PROPIEDADES Haga Click sobre la opción que desee ver: 1. Concepto general 2. Propiedades de la potenciación Potencia de exponente cero Potencia de exponente uno Producto (multiplicación)
POTENCIACIÓN - PROPIEDADES Haga Click sobre la opción que desee ver: 1. Concepto general 2. Propiedades de la potenciación Potencia de exponente cero Potencia de exponente uno Producto (multiplicación)
Guía 1: Operaciones numéricas en los Números enteros (Z)
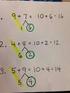 Guía 1: Operaciones numéricas en los Números enteros (Z) NÚMEROS ENTEROS (Z): Existen números con signo, que son los números enteros (Z+ son los positivos y Z- son los negativos). Según se sabe, nos los
Guía 1: Operaciones numéricas en los Números enteros (Z) NÚMEROS ENTEROS (Z): Existen números con signo, que son los números enteros (Z+ son los positivos y Z- son los negativos). Según se sabe, nos los
INSTITUTO FRAY MAMERTO ESQUIÚ MATEMÁTICA 2 A E.S.B. Prof. Oliveros Lorena
 INSTITUTO FRAY MAMERTO ESQUIÚ MATEMÁTICA 2 A E.S.B. Prof. Oliveros Lorena Unidad 2 EXPRESIONES ALGEBRAICAS Expresiones algebraicas. Ecuaciones e inecuaciones con números enteros Lenguaje coloquial y simbólico:
INSTITUTO FRAY MAMERTO ESQUIÚ MATEMÁTICA 2 A E.S.B. Prof. Oliveros Lorena Unidad 2 EXPRESIONES ALGEBRAICAS Expresiones algebraicas. Ecuaciones e inecuaciones con números enteros Lenguaje coloquial y simbólico:
Ley distributiva Asocia las operaciones de suma y producto de la siguiente manera a x (b + c) = a x b + a x c
 Unidad 1- Trabajo Práctico 1 Operaciones Básicas con Números Reales Las operaciones básicas que pueden realizarse con los Números Reales son las de Suma Resta Producto Cociente Potencia Radicación Leyes
Unidad 1- Trabajo Práctico 1 Operaciones Básicas con Números Reales Las operaciones básicas que pueden realizarse con los Números Reales son las de Suma Resta Producto Cociente Potencia Radicación Leyes
Unidad didáctica 1. Operaciones básicas con números enteros
 Unidad didáctica 1 Operaciones básicas con números enteros 1.- Representación y ordenación de números enteros. Para representar números enteros en una recta hay que seguir estos pasos: a) Se dibuja una
Unidad didáctica 1 Operaciones básicas con números enteros 1.- Representación y ordenación de números enteros. Para representar números enteros en una recta hay que seguir estos pasos: a) Se dibuja una
LOS NÚMEROS ENTEROS QUÉ ES UN NÚMERO ENTERO? VALOR ABSOLUTO EL OPUESTO DE UN NÚMERO ENTERO OPERACIONES CON ENTEROS ORDENACIÓN DE NÚMEROS ENTEROS
 LOS NÚMEROS ENTEROS QUÉ ES UN NÚMERO ENTERO? VALOR ABSOLUTO EL OPUESTO DE UN NÚMERO ENTERO ORDENACIÓN DE NÚMEROS ENTEROS OPERACIONES CON ENTEROS Suma Resta Multiplicación División Potencia JERARQUÍA RESOLUCIÓN
LOS NÚMEROS ENTEROS QUÉ ES UN NÚMERO ENTERO? VALOR ABSOLUTO EL OPUESTO DE UN NÚMERO ENTERO ORDENACIÓN DE NÚMEROS ENTEROS OPERACIONES CON ENTEROS Suma Resta Multiplicación División Potencia JERARQUÍA RESOLUCIÓN
OPERACIÓN CON NÚMEROS ENTEROS(Z)
 OPERACIÓN CON NÚMEROS ENTEROS(Z) Imagina que un día estas de visita en un apartamento de unos amigos, al despedirte bajas al sótano 2 a buscar tu carro y te das cuenta que dejaste las llaves en casa de
OPERACIÓN CON NÚMEROS ENTEROS(Z) Imagina que un día estas de visita en un apartamento de unos amigos, al despedirte bajas al sótano 2 a buscar tu carro y te das cuenta que dejaste las llaves en casa de
Catedrático: I.S.C. Iván de J. Moscoso Navarro Contenido:
 Materia: Matemáticas I Catedrático: I.S.C. Iván de J. Moscoso Navarro Contenido: UNIDAD TEMATICA II.- SISTEMAS NUMÉRICOS 2.1 Números Naturales ( N )... Introducción Propiedades de la adición de los números
Materia: Matemáticas I Catedrático: I.S.C. Iván de J. Moscoso Navarro Contenido: UNIDAD TEMATICA II.- SISTEMAS NUMÉRICOS 2.1 Números Naturales ( N )... Introducción Propiedades de la adición de los números
APÉNDICE MATEMÁTICO DEL MÓDULO DE: GESTIÓN FINANCIERA
 APÉNDICE MATEMÁTICO DEL MÓDULO DE: GESTIÓN FINANCIERA 1º CURSO DEL CICLO DE GRADO SUPERIOR DE ADMINISTRACIÓN Y FINANZAS. CONTENIDO: Números enteros Fracciones Potencias Igualdades algebraicas notables
APÉNDICE MATEMÁTICO DEL MÓDULO DE: GESTIÓN FINANCIERA 1º CURSO DEL CICLO DE GRADO SUPERIOR DE ADMINISTRACIÓN Y FINANZAS. CONTENIDO: Números enteros Fracciones Potencias Igualdades algebraicas notables
Teoría (resumen) Por ejemplo, los múltiplos de 3 son: 3, 6, 9, 12, 15, 18, ; los múltiplos de 2 son: 2, 4, 6, 8, 10, 12, ; o sea los números pares.
 1.- Divisibilidad Teoría (resumen) Múltiplos de un número. Son aquellos que se obtienen al multiplicar dicho número por los números naturales 1, 2, 3,. Por ejemplo, los múltiplos de 3 son: 3, 6, 9, 12,
1.- Divisibilidad Teoría (resumen) Múltiplos de un número. Son aquellos que se obtienen al multiplicar dicho número por los números naturales 1, 2, 3,. Por ejemplo, los múltiplos de 3 son: 3, 6, 9, 12,
cómo expresarías?. ÁLGEBRA Álgebra Unidad 4. El lenguaje algebraico. TEMA 4: POLINOMIOS Grupo: 3º A Expresiones algebraicas Álgebra vs Aritmética
 16/01/01 ÁLGEBRA Álgebra Unidad 4. El lenguaje algebraico. TEMA 4: POLINOMIOS Grupo: º A cómo expresarías?. La altura de mi hermano si te digo que mide 10 cm más que mi hermana: El perímetro de un triángulo
16/01/01 ÁLGEBRA Álgebra Unidad 4. El lenguaje algebraico. TEMA 4: POLINOMIOS Grupo: º A cómo expresarías?. La altura de mi hermano si te digo que mide 10 cm más que mi hermana: El perímetro de un triángulo
UNIDAD III. EXPONENTES Y RADICALES. RAZONES, PROPORCIONES Y VARIACIONES.
 UNIDAD III. EXPONENTES Y RADICALES. RAZONES, PROPORCIONES Y VARIACIONES. Ley asociativa El producto de tres o más números, es el mismo sin importar la manera en que se agrupan al multiplicarlos. abc=(ac)b=c(ab)
UNIDAD III. EXPONENTES Y RADICALES. RAZONES, PROPORCIONES Y VARIACIONES. Ley asociativa El producto de tres o más números, es el mismo sin importar la manera en que se agrupan al multiplicarlos. abc=(ac)b=c(ab)
Instituto Superior de Formación Técnica Nº 177
 Instituto Superior de Formación Técnica Nº 177 Ciudad de Libertad (Merlo) Curso de Ingreso Matemática Página 1 Los números naturales también sirven para ordenar. Así, decimos que la Tierra es el tercer
Instituto Superior de Formación Técnica Nº 177 Ciudad de Libertad (Merlo) Curso de Ingreso Matemática Página 1 Los números naturales también sirven para ordenar. Así, decimos que la Tierra es el tercer
Operaciones con números enteros
 1. Identificación Nivel: Primario Área: Matemática Grado: Sexto SC 10: Resumen: En esta Unidad Didáctica se identifican los números enteros positivos y negativos. Se resuelven operaciones de adición y
1. Identificación Nivel: Primario Área: Matemática Grado: Sexto SC 10: Resumen: En esta Unidad Didáctica se identifican los números enteros positivos y negativos. Se resuelven operaciones de adición y
5 REPASO Y APOYO OBJETIVO 1
 5 REPASO Y APOYO OBJETIVO 1 RECONOCER EL GRADO, LOS TÉRMINOS Y EL TÉRMINO INDEPENDIENTE DE UN POLINOMIO Nombre: Curso: echa: Un monomio es una expresión algebraica formada por el producto de un número,
5 REPASO Y APOYO OBJETIVO 1 RECONOCER EL GRADO, LOS TÉRMINOS Y EL TÉRMINO INDEPENDIENTE DE UN POLINOMIO Nombre: Curso: echa: Un monomio es una expresión algebraica formada por el producto de un número,
Potencias y raíces Matemáticas 1º ESO
 ÍNDICE Potencias y raíces Matemáticas 1º ESO 1. Potencias 2. Propiedades de potencias 3. Cuadrados perfectos 4. Raíces cuadradas 1. POTENCIAS Una potencia es una multiplicación en la que todos los factores
ÍNDICE Potencias y raíces Matemáticas 1º ESO 1. Potencias 2. Propiedades de potencias 3. Cuadrados perfectos 4. Raíces cuadradas 1. POTENCIAS Una potencia es una multiplicación en la que todos los factores
TEMA 1: NÚMEROS ENTEROS
 Números enteros 1 OBJETIVO 1: Significado de los números enteros TEMA 1: NÚMEROS ENTEROS 1. Expresa las siguientes situaciones con números enteros a) El año 2500 a.c... b) Pasear por la orilla del mar...
Números enteros 1 OBJETIVO 1: Significado de los números enteros TEMA 1: NÚMEROS ENTEROS 1. Expresa las siguientes situaciones con números enteros a) El año 2500 a.c... b) Pasear por la orilla del mar...
Colegio La Salle Envigado FORMANDO EN VALORES PARA LA VIDA GUIA FACTORIZACION
 GUIA FACTORIZACION Esta guía tiene como objetivo afianzar los conocimientos teórico-prácticos en los diferentes casos de factorización, para ello se darán en esta guía algunos ejercicios de factorización
GUIA FACTORIZACION Esta guía tiene como objetivo afianzar los conocimientos teórico-prácticos en los diferentes casos de factorización, para ello se darán en esta guía algunos ejercicios de factorización
EXPRESIONES ALGEBRAICAS. POLINOMIOS
 Unidad didáctica 5 EXPRESIONES ALGEBRAICAS. POLINOMIOS. EXPRESIONES ALGEBRAICAS. Estas expresiones del área son expresiones algebraicas, ya que además de números aparecen letras. Son también expresiones
Unidad didáctica 5 EXPRESIONES ALGEBRAICAS. POLINOMIOS. EXPRESIONES ALGEBRAICAS. Estas expresiones del área son expresiones algebraicas, ya que además de números aparecen letras. Son también expresiones
MATEMÁTICA CPU MÓDULO 1. Números reales Ecuaciones e inecuaciones. Representaciones en la recta y en el plano.
 MATEMÁTICA CPU MÓDULO Números reales. Ecuaciones e inecuaciones. Representaciones en la recta y en el plano.. Marcar con una cruz los conjuntos a los cuales pertenecen los siguientes números: N Z Q R 8
MATEMÁTICA CPU MÓDULO Números reales. Ecuaciones e inecuaciones. Representaciones en la recta y en el plano.. Marcar con una cruz los conjuntos a los cuales pertenecen los siguientes números: N Z Q R 8
Los Números Enteros (Z)
 Los Números Enteros (Z) Los números enteros: representación gráfica, orden, modulo o valor absoluto. Operaciones en Z, procedimientos y propiedades de estas. Prioridades de operaciones y paréntesis. Problemas
Los Números Enteros (Z) Los números enteros: representación gráfica, orden, modulo o valor absoluto. Operaciones en Z, procedimientos y propiedades de estas. Prioridades de operaciones y paréntesis. Problemas
UNIDAD: NÚMEROS Y PROPORCIONALIDAD. Los elementos del conjunto IN = {1, 2, 3, 4, 5, 6, 7,...} se denominan números
 GUÍA Nº 2 UNIDAD: NÚMEROS Y PROPORCIONALIDAD NÚMEROS ENTEROS NÚMEROS NATURALES (ln) Los elementos del conjunto IN = {1, 2, 3, 4, 5, 6, 7,...} se denominan números naturales NÚMEROS ENTEROS (Z) Los elementos
GUÍA Nº 2 UNIDAD: NÚMEROS Y PROPORCIONALIDAD NÚMEROS ENTEROS NÚMEROS NATURALES (ln) Los elementos del conjunto IN = {1, 2, 3, 4, 5, 6, 7,...} se denominan números naturales NÚMEROS ENTEROS (Z) Los elementos
UNIDAD DOS FACTORIZACIÓN
 UNIDAD DOS FACTORIZACIÓN Factorizar quiere decir descomponer en factores, los factores son divisores de una expresión que, multiplicados entre sí, dan como resultado la primera expresión. FACTOR COMÚN
UNIDAD DOS FACTORIZACIÓN Factorizar quiere decir descomponer en factores, los factores son divisores de una expresión que, multiplicados entre sí, dan como resultado la primera expresión. FACTOR COMÚN
Llamamos potencia a todo producto de factores iguales. Por ejemplo: 3 4 =
 1. NÚMEROS NATURALES POTENCIAS DE UN NÚMERO NATURAL Llamamos potencia a todo producto de factores iguales. Por ejemplo: 3 4 = 3 3 3 3 El factor que se repite es la base, y el número de veces que se repite
1. NÚMEROS NATURALES POTENCIAS DE UN NÚMERO NATURAL Llamamos potencia a todo producto de factores iguales. Por ejemplo: 3 4 = 3 3 3 3 El factor que se repite es la base, y el número de veces que se repite
FIN EDUCATIVO FIN INSTRUCTIVO
 FIN EDUCATIVO Todos somos números en las Matemáticas de la vida, con valores: absolutos, relativos, positivos y negativos. Los primeros representan a nuestras cualidades y virtudes ; los segundos a los
FIN EDUCATIVO Todos somos números en las Matemáticas de la vida, con valores: absolutos, relativos, positivos y negativos. Los primeros representan a nuestras cualidades y virtudes ; los segundos a los
