Estimadores de regresión logística para tratamiento de no respuesta en el caso de cocientes de variables dicotómicas
|
|
|
- Andrea Morales Luna
- hace 7 años
- Vistas:
Transcripción
1 Comunicaciones en Estadística Junio 2009, Vol. 2, No. 1 Estimadores de regresión logística para tratamiento de no respuesta en el caso de cocientes de variables dicotómicas Logistic Regression Estimators for the Treatment of Nonresponse for the Ratio of Dichotomic Variables Pedro César Del Campo Neira a pcampo@icfes.gov.co Resumen Para la estimación de un cociente de variables dicotómicas en un diseño MAS 2 se utiliza información auxiliar para los elementos de la segunda etapa. La información auxiliar se usa en el numerador y el denominador a través de regresión logística. Para distintas funciones de enlace en el modelo de regresión y tratamiento de la no respuesta, se compara la eficiencia del uso de distintos tipos de información auxiliar binaria en el numerador y el denominador. Usando el proceso de simulación de Monte Carlo se realiza la comparación de estos distintos escenarios. Palabras clave: muestreo, estimación de cocientes, modelos lineales generalizados, regresión logística, tratamiento de la no respuesta. Abstract To make the estimate of ratio with dichotomic variables in a SISI design is used auxiliary information for the second stage elements. Auxiliary information is used in the numerator and denominator with the use of logistic regression. To different link functions in the logistic regression model and the treatment of the nonresponse, it is compared the efficiency of the use of different types of binary auxiliary information for numerator and denominator. Through of a Monte Carlo Simulation process is made the comparison of the different approaches. Key words: survey sampling, estimate of ratio, generalized linear model, logistic regression, treatment of nonresponse. a Asesor estadístico. Subdirección académica. Instituto Colombiano para el Fomento de la Educación Superior (ICFES). 11
2 12 Pedro César Del Campo Neira 1. Introducción Para muchos estudios de muestreo se tiene interés en estimar razones de totales de variables dicotómicas. Un ejemplo son las encuestas de tipo electoral, donde se desea estimar la razón entre el total de personas que votan por un determinado candidato sobre el total de personas que votan. También son un ejemplo las encuestas de tipo médico, donde se desea estimar la razón entre el total de personas que sufren de una determinada enfermedad y que viven en una región sobre el total de personas que viven en esa región. En particular se desea formular estimadores de cocientes de variables dicotómicas que se obtienen con el uso de información auxiliar y modelos de regresión logística para un diseño MAS 2 con distintas funciones de enlace y teniendo en cuenta la no respuesta para elementos de la segunda etapa. Se trabaja con estimadores de cocientes sin información auxiliar, con información auxiliar para el denominador, información auxiliar para el numerador e información auxiliar para el denominador y el numerador. La información auxiliar se trabaja a través de regresión logística para las funciones de enlace Logit y Probit. Posteriormente, se compararásu eficiencia en términos de sesgo y varianza a través de procesos de simulación. 2. Estimación de cocientes de totales asistidos por modelos Sea U un conjunto considerado como una población con N elementos {e 1,e 2,...,e N }. Se tienen dos variables dicotómicas y k y z k para cada elemento de U. Sea U y := {e k y k =1} y U z := {e k z k =1}. En particular se tiene que U y U z U. El objetivo es estimar el cociente C representado en la ecuación (1). C = U y k U z k = N y N z (1) Debido a que U y U z se puede ver claramente que C representa la proporción de elementos de U y en U z. Para el caso de diseño muestral MAS 2 la estimación del cociente C depende de la información disponible para la variables Y y Z. La varianza y el estimador de la varianza del estimador del cociente C se obtienen mediante el método de linealización de Taylor (Särndal et al. 1993) 2.1. Estimación de cocientes en un modelo MAS 2 Para un diseño muestral MAS 2 se tiene en particular que el estimador de un cociente de variables dicotómicas sin el uso de información auxiliar está dado por la ecuación (2).
3 Estimadores de regresión logística para tratamiento de no respuesta 13 Ĉ π = mi mi y k mi mi y k = N y N z (2) Para la estimación de totales bajo un diseño muestral en dos etapas se debe tener en cuenta qué tipo de información auxiliar se tiene. En particular cuando se dispone de información auxiliar sólo para los elementos de la segunda etapa, y en particular de sus totales poblacionales, se plantea la estimación del total de una variable mediante la ecuación (3), según Särndal et al. (1993) muestra en el capítulo 8. Es decir se dispone de t x = U x k. donde, t ybr = m g ksb y k (3) g ksb =1+ [ U I t xi m I t xiπ π Ii ] t T 1 x k σ 2 k (4) Luego con el uso de información auxiliar se determina que el estimador de un cociente es como indica la ecuación (5), donde se dispone de información auxiliar para el numerador y el denominador. Ĉ xw = m m [ 1+ t xi ] t t xiπ 1 T x U I m I π Ii [ 1+ t wi ] t t wiπ 1 T w U I m I π Ii x k σk 2 w k σ 2 k y k y k (5) Se asume que el vector x k es información auxiliar para los elementos y k y el vector w k es información auxiliar para los elementos z k. La información auxiliar también puede ser utilizada en solo uno de los términos del cociente, en el numerador o en el denominador, dando como resultados estimadores de los cocientes, como se representa en las ecuaciones (6) y (7). Ĉ x = [ 1+ t xi ] t t xiπ 1 T x U I m I π Ii m x k σk 2 y k (6) N z
4 14 Pedro César Del Campo Neira Ĉ w = m N y [ 1+ t wi ] t t wiπ 1 T w U I m I π Ii w k σ 2 k y k (7) En particular x t k =(1,x k)yw t k =(1,w k) son los vectores de información auxiliar. Las variables x k y w k son variables dicotómicas que poseen un grado de correlación con las variables y k y z k respectivamente Modelo Lineal Generalizado (MLG) Los modelos lineales generalizados extienden el caso de los modelos lineales, incorporando de esta manera la posibilidad de modelar variables respuesta con distribuciones no necesariamente normales según estudios de Nelder y Wedderburn(1972, citado por Dobson, 1990). Para este trabajo en particular las variables provienen de una distribución bernoulli. Sea y 1,y 2,...y n valores muestrales de variables aleatorias que provienen de una distribución binomial. Para un modelo lineal generalizado se considera un conjunto de parámetros β =(β 1,β 2,...,β p ) t donde p<ntal que una combinación lineal de estos parámetros sea igual a una función que dependa del valor esperado μ i de y i. g(μ i )=η i = x t iβ = p x t ijβ j (8) Los parámetros del modelo lineal generalizado, representados en la ecuación (8), se estiman a través de un proceso iterativo descrito en la ecuación (9). El proceso iterativo se da porque la matriz W de tamaño nxn y el vector z y el vector n dependen directamente de los parámetros del modelo. j=1 X t W (m) Xb (m+1) = X t W (m) z (m) (9) La matriz W es una matriz diagonal con los elementos dados por la ecuación (10). w ii = 1 V (y i ) ( ) 2 μi (10) El vector z tiene los elementos representados en la ecuación 11. z i = p k=1 x ik b (m) k η i +(y i μ i ) η i μ i (11)
5 Estimadores de regresión logística para tratamiento de no respuesta 15 Para efectos de este trabajo se van a considerar grupos de un solo individuo que provienen de una distribución binomial Z i bin(1, p i ) o distribución Bernoulli. A continuación se va a presentar la forma de estimación de los parámetros del modelo de regresión lineal generalizado teniendo en cuenta los dos tipos distintos de función de enlace Logit y Probit Estimación de parámetros función de enlace Logit Teniendo en cuenta que los datos y 1,y 2,...,y G se distribuyen Y g bin(n g, p g )se tiene que E[y g ]=μ g = n g p g y V [y g ]=n g p g (1 p g ). Luego se desea determinar los parámetros de la matriz diagonal W y del vector z según las ecuaciones (10) y (11) respectivamente. Como primera medida se determina la derivada η g / μ g donde η g está representado con la función de enlace Logit. η g = η [ g p g 1 = + 1 ] 1 = μ g p g μ g p g 1 p g n g [ ] 1 pg + p g 1 = p g (1 p g ) n g 1 n g p g (1 p g ) = 1 V (y g ) Luego, utilizando este resultado se obtiene el resultado de los elementos de la matriz diagonal W para la iteración m-ésima. ( w gg (m) 1 μg = V (y g ) (m) η g ) 2 (m) = (V (y g)) 2 V (y g ) = n g p g (1 p g ) exp {x t gb (m)} exp {x t gb (m)} = n g 1 + exp {x t gb (m)} exp {x t gb (m)} exp {x t gb (m)} = n g ( 1 + exp {x t gb (m)}) 2 (12) Luego, utilizando en parte el resultado de la ecuación (12) se obtiene la forma de los elementos del vector z reflejados en la ecuación (13).
6 16 Pedro César Del Campo Neira ( ) ( ) z g (m) = x t gb (m) + y g μ (m) η g g μ g (m) exp {x t gb (m)} ( 1 + exp {x t gb (m)}) 2 = x t gb (m) + y g n g 1 + exp {x t gb (m)} (13) n g exp {x t (m)} gb Finalmente, se estima β utilizando las ecuaciones (12) y (13), y el método iterativo dado en la ecuación (9) partiendo de un valor b (0) Estimación de parámetros función de enlace Probit Teniendo en cuenta que los datos y 1,y 2,...,y G se distribuyen Y g bin(n g, p g )se tiene que E[y g ]=μ g = n g p g y V [y g ]=n g p g (1 p g ). Luego se desea determinar los parámetros de la matriz diagonal W y del vector z según las ecuaciones (10) y (11) respectivamente. Como primera medida se determina la derivada μ g / η g usando el teorema de diferencias de Lebesgue. η g está representado con la función de enlace Probit. μ g η g = μ g p g p g η g = n g f N (η g )=n g f N ( x t g b ) Donde f N representa la función de distribución normal estándar. Luego, utilizando este resultado se obtienen los elementos de la matriz diagonal W para la iteración m-ésima. ( w gg (m) 1 μg = V (y g ) (m) η g = ) 2 (m) n 2 g f N ( x t gb (m)) 2 ( Φ x t gb (m))( 1 Φ (14) (x t (m))) gb Luego se obtienen los elementos del vector z reflejados en la ecuación (15). ( ) ( ) z g (m) = x t gb (m) + y g μ g (m) η g μ g (m) y g n g Φ (x t gb (m)) = x t gb (m) + ( (15) n g f N x t (m)) gb
7 Estimadores de regresión logística para tratamiento de no respuesta 17 Finalmente se estima β utilizando las ecuaciones (14) y (15), y el método iterativo dado en la ecuación (9) partiendo de un valor b (0) Estimación de cocientes bajo modelo logístico Teniendo en cuenta los desarrollos de la estimación de un total asistido por regresión dado en la ecuación (3) se puede obtener otra manera de escribir esta estimación según la ecuación (16). t ybr = g ksb y k m = [ 1+ t xi ] t t xiπ 1 x k T y k m U I m I π Ii = y k + [ t xi ] t t xiπ 1 x k T m m U I m I π Ii = m = m = m y k + [ U I t xi m I t xiπ π Ii σ 2 k ] t T 1 [ y k + x k U I U ] t x k B i m m y k σk 2 x k y k σk 2 y k + x m I U t B k x t B k (16) i m Teniendo en cuenta que en un modelo lineal generalizado se relaciona el predictor lineal x t k β con el valor esperado de la variable respuesta E[y k]=p k mediante la función g(p k )=x t kβ. Se obtiene que el estimador del total de la variable Y asistido por un modelo lineal generalizado está dado por la ecuación (17), el cual es una generalización de la ecuación (16). t yglm = m y k + m I ( g 1 x t B ) k U i m g (x 1 t B ) k (17) En particular g (x 1 t B ) k es la probabilidad estimada p k de que un individuo tome el valor y k = 1, dado que posee un vector de información auxiliar x k bajo el uso de las funciones de enlace Logit y Probit. La estimación de β dada por B se obtiene mediante la ecuación (18). X t Ŵ (m) Π 1 X B (m+1) = X t W (m) Π 1 ẑ (m) (18)
8 18 Pedro César Del Campo Neira En un modelo lineal generalizado la estimación de los parámetros del modelo se obtiene mediante un proceso iterativo como se refleja en la ecuación (9). La ecuación (18) es un caso general de la ecuación (9), donde Π es una matriz cuadrada diagonal con las probabilidades de inclusión para los elementos de la muestra. Los elementos de la matriz diagonal Ŵ (m) para la iteración m se calculan sobre los elementos de la muestra como indica la ecuación (10), y los elementos del vector ẑ (m) para la iteración m se calculan sobre los elementos de la muestra como indica la ecuación (11). Luego para estimar el cociente de dos variables dicotómicas en un diseño muestral de dos etapas se propone el estimador dado por la ecuación (19), el cual utiliza toda la información auxiliar del universo.. Ĉ GLM = N yglm N zglm = m m y k + m I z k + m I U i g 1 ( U i g 1 ( x t B ) k w t B ) k g (x 1 t B ) k m g (w 1 t B ) k m (19) 3. Medidas de asociación de variables binarias En estimación de totales, el nivel de asociación de las variable de interés y las variables auxiliares es importante para determinar la precisión del modelo. Por lo tanto, es de interés conocer cuál es el nivel de asociación de las variables y k y z k con las variables x k y w k respectivamente. Teniendo en cuenta que el conjunto de variables es de carácter dicotómico, se establece su nivel de asociación a través de un distinto conjunto de medidas. La siguiente tabla ayuda a determinar los coeficientes que se explican a continuación. x k 0 1 y k 0 n 00 n 01 n 0 1 n 10 n 11 n 1 n 0 n 1 n Tabla 1: Tabla de contingencia de dos variables binarias y k y x k 3.1. Coeficiente de contingencia En el caso de variables dicotómicas se obtiene el coeficiente de contingencia a partir de la Tabla 1. En primer lugar, se calcula el estadístico de Ji-cuadrado como se
9 Estimadores de regresión logística para tratamiento de no respuesta 19 muestra en la ecuación (20), y finalmente se obtiene el coeficiente de contingencia como indica la ecuación (21). χ 2 = 1 i=0 j=0 ( 1 n ij n i n j n n i n j n χ 2 C C = χ 2 + n ) 2 (20) (21) En el caso de variables dicotómicas, el coeficiente de contingencia tiene un rango entre 0 CC 1/2. El coeficiente de contingencia es un parámetro importante en el que se busca un estimador óptimo en este trabajo Coeficiente φ El coeficiente de asociación φ es una medida de asociación derivada del estadístico de Pearson Ji-cuadrado. El coeficiente φ tiene un rango en [ 1, 1] para tablas 2x2. El coeficiente φ es calculado como: φ = n 00n 11 n 01 n 10 n 0 n 1 n 0 n 1 (22) 3.3. Coeficiente de Yule El coeficiente de Yule se basa en el número de concordantes y discordances en los pares de observaciones. El coeficiente de Yule es apropiado solo cuando las variables son de escala ordinal. El rango del coeficiente de Yule está entre 1 y1. Si las dos variables son independientes, el coeficiente de Yule se acerca a cero. El coeficiente de Yule se calcula como: C Y = n 00n 11 n 01 n 10 n 11 n 00 + n 01 n 10 (23) En este trabajo se utiliza en particular la medida de asociación dada por el coeficiente de contingencia, ya que esta medida tiene en cuenta la asociación indiferentemente si la tendencia es creciente o decreciente. 4. No respuesta La no respuesta es una característica frecuente pero indeseable de un estudio y puede afectar severamente la calidad de los estimativos que se calculan y se publi-
10 20 Pedro César Del Campo Neira can. La idea es utilizar técnicas estadísticas que se desempeñen bien en presencia de no respuesta, ya que las inferencias estadísticas que se hacen basadas en datos afectados por tal fenómeno, corren un alto riesgo de ser inválidas. Hay dos caminos: evitar la no respuesta antes de que ocurra, o utilizar las técnicas de estimación adecuadas para manejar la no respuesta que ocurre. Esto último se conoce como ajuste por no respuesta (Särndal & Lundström 2005). En particular para las variables y k y z k se tiene no respuesta por item, bajo distintos modelos de distribución de la respuesta. El tratamiento de la no respuesta se realiza mediante el proceso de imputación. Dada una muestra m se define r como el conjunto de los datos respondientes. Para todo e k U se define θ k como la probabilidad de respuesta del individuo e k, Donde θ k [0, 1]. Generalmente la probabilidad de respuesta θ k es desconocida. La distribución de la respuesta generalmente depende de variables de factores desconocidos. En particular Särndal & Lundström (2005) muestran dos formas de modelar la respuesta: θ k = cte para todo e k U o distribución constante de la respuesta, e incremento exponencial de la distribución de la respuesta evaluado como θ k = 1 exp( cb k ), donde b k es una variable desconocida. La tasa de respuesta se evalúa como el promedio de los valores θ k en el universo. La imputación es el procedimiento mediante el cual los valores faltantes de una o más variables de estudio son sustituidas. Esta sustitución puede ser construida en gran variedad de formas. En particular, entre la imputación por reglas estadísticas se utiliza la imputación por regresión. Si e k m r su imputación es de la forma que indica la ecuación (24). ŷ k = h(x t k β m ) (24) El coeficiente de regresión β m es el resultado de regresión usando (y k, x k ) disponible para e k m. 5. Comportamiento empírico del sesgo y la varianza de estimadores asistidos por modelos Con el fin de evaluar la precisión y la exactitud de los estimadores de cocientes, se genera una población con un diseño de dos etapas. La primera etapa con N I = 240 conglomerados de muestreo. Cada conglomerado posee aproximadamente N i = 1900 elementos para generar una población de N = elementos aproximadamente. En cada población se generan variables binarias y k y z k tal que si zk = 0 entonces y k = 0. Se fija un tamaño muestral de n I =15yn i =0.2N i para todo U i U I, buscando obtener valores comparables de la precisión de los estimadores de cocientes. Se realizan dos simulaciones de Monte Carlo con las siguientes características: la primera para obtener un escenario deseable según las asociación de las variables
11 Estimadores de regresión logística para tratamiento de no respuesta 21 auxiliares utilizadas, la segunda incluye la no respuesta para dos escenarios de distribución de la no respuesta para numerador y denominador Escenarios de variables auxiliares según coeficiente de contingencia Se generan variables auxiliares binarias x k y w k que guardan un cierto grado de asociación con las variables y k y z k respectivamente. La asociación entre las variables se define como alto, medio y bajo según el coeficiente de contingencia dado en la sección 3. Siendo C CA 0.7,C CM 0.3 yc CB Lo anterior se realiza para establecer la asociación entre y k, x k y z k, w k, originando nueve escenarios posibles para comparar. El parámetro de interés para el universo generado es C = N y /N z = Para este universo se extrajeron 1500 muestras mediante diseño muestral MAS 2. En particular para cada uno de los nueve escenarios de información auxiliar se trabajó con 6 estimadores de cocientes que se presentan a continuación. 1. Estimador convencional del cociente Ĉπ = N yπ /N zπ 2. Estimador con uso de información auxiliar en el numerador dado por el modelo y k = β 0 + β 1 x k. Cociente Ĉx = N yreg / N zπ. 3. Estimador con uso de información auxiliar en el denominador dado por el modelo z k = β 0 + β 1 w k. Cociente Ĉw = N yπ / N zreg. 4. Estimador con uso de información auxiliar en el numerador y el denominador dado por los modelos y k = β 0 + β 1 x k y z k = β 0 + β 1 w k respectivamente. Cociente Ĉxw = N yreg / N zreg. 5. Estimador con uso de información auxiliar tanto en el numerador como en el denominador dado por los modelos lineales generalizados con función de enlace Logit, Logit(p yk )=β 0 + β 1 x k y Logit(p zk )=β 0 + β 1 w k respectivamente. Cociente ĈLogit = N yglml / N zglml. 6. Estimador con uso de información auxiliar en el numerador y el denominador dado por los modelos lineales generalizados con función de enlace Probit, Φ(p yk )=β 0 +β 1 x k yφ(p zk )=β 0 +β 1 w k respectivamente. Cociente Ĉ P robit = N yglmp / N zglmp. Para las 1500 simulaciones dadas por el método de Monte Carlo en los seis estimadores, se toma el promedio de las estimaciones como estimador de la esperanza del estimador del cociente dado en la Tabla 2, la varianza muestral como estimador de la varianza del estimador del cociente. Se obtiene el cálculo del sesgo relativo estimado en la Tabla 3 y el coeficiente de variación estimado en la Tabla 4.
12 22 Pedro César Del Campo Neira Asociación Asociación numerador denominador Ĉ π Ĉ x Ĉ w Ĉ xw Ĉ Logit Ĉ P robit Alta Alta Media Baja Alta Media Media Baja Alta Baja Media Baja Tabla 2: Estimaciones de la esperanza de Cocientes de método Monte Carlo por tipo de información auxiliar, según estimador de Cociente ( C =0.321) En la Tabla 2, los promedios de las estimaciones son prácticamente iguales al valor poblacional del cociente C = No hay cambios significativos según el tipo de información auxiliar en el denominador y el numerador. El promedio de las estimaciones no tiene cambio por el tipo de estimador utilizado. Asociación Asociación numerador denominador Ĉ π Ĉ x Ĉ w Ĉ xw Ĉ Logit Ĉ P robit Alta Alta Media Baja Alta Media Media Baja Alta Baja Media Baja Tabla 3: Estimaciones del sesgo relativo porcentual de método Monte Carlo por tipo de información auxiliar, según estimador de Cociente En la Tabla 3 de sesgo relativo se puede observar que hay una ligera sobreestimación por parte de los estimadores que no utilizan regresión logística y para los que utilizan información de mala calidad en el numerador, observado en los sesgos relativos negativos. Los estimadores asistidos por regresión logística con uso de información auxiliar alta y media para el numerador muestran una ligera sub-estimación observada en los signos positivos del sesgo relativo. Sin embargo, ningún sesgo relativo porcentual sobrepasa el 10 %, por lo que se considera que el sesgo es insignificante. En la Tabla 4 se puede ver que los estimadores asistidos por regresión logística son más adecuados que el convencional C π y los asistidos por regresión lineal. En particular, los mejores escenarios en cuanto a precisión se observan cuando existe la información auxiliar para asistir el total del numerador, ya que ésta es alta.
13 Estimadores de regresión logística para tratamiento de no respuesta 23 Asociación Asociación numerador denominador Ĉ π Ĉ x Ĉ w Ĉ xw Ĉ Logit Ĉ P robit Alta Alta Media Baja Alta Media Media Baja Alta Baja Media Baja Tabla 4: Estimaciones del coeficiente de variación porcentual de método Monte Carlo por tipo de información auxiliar, según estimador de Cociente Figura 1: Comparación de estimadores de cocientes según tipo de información auxiliar. La Figura 1 ilustra claramente que el sesgo no es relevante para ninguno de los estimadores en ninguno de los escenarios de uso de información auxiliar. Sin embargo, se observa una clara diferencia de variación en los estimadores asistidos por regresión logística cuando la información auxiliar para el denominador es alta. Bajo estas condiciones se selecciona de los mejores escenarios el más simple: información auxiliar de alta calidad para el numerador e información auxiliar de baja calidad para el denominador.
14 24 Pedro César Del Campo Neira 5.2. Imputación por regresión logística El objetivo de esta simulación es dar un ilustración del comportamiento de los estimadores asistidos por regresión logística bajo condiciones de no respuesta. El tratamiento de no respuesta elegido es la imputación mediante uso de regresión logística como lo indica la ecuación (24). A partir del universo generado en la sección 5.1, en la vida real la distribución de la respuesta es desconocida. Por lo tanto, la simulación cubre dos tipos de distribución de la respuesta posibles. Distribución de respuesta constante: esta se basa en que la probabilidad que un individuo conteste es constante para todos los individuos del universo θ k = cte. Incremento exponencial de la respuesta: esta probabilidad es calculada por θ k =1 exp( cb k ). Bajo esta estructura con c y b k mayores que cero, se ve claramente que la probabilidad de ser respondiente es mayor a medida que la variable b k aumente. La variable b k es un valor desconocido en las encuestas reales. Para la no respuesta de z k se tomaron las dos distribuciones de la respuesta tal que la taza de respuesta sea del 82 %. En particular para la distribución de respuesta constante θ kz =0.82 para todo e k U, para el Incremento exponencial de la respuesta θ kz =1 exp( c z b kz ) se genera una variable ordinal v zk de seis categorías tal que si z k = 1 la variable categórica toma con mayor probabilidad los valores 4, 5 y 6 que 1, 2 y 3; cuando z k = 0 la variable categórica v zk toma con mayor probabilidad los valores 1, 2 y 3 que 4, 5y6.Luego b k es una variable continua de valores positivos que toma valores grandes a medida que la categoría toma valores numéricos más altos. La Tabla 5 da una idea de la relación de las seis categorías y la variable z k Total z k % % % % 6.64 % 6.57 % 100 % % 6.70 % % % % % 100 % Total Categorías 9.63 % 8.74 % % % % % 100 % Tabla 5: Tabla de contingencia variable v zk contra z k Luego con el uso de método de Newton-Raphson para solución de ecuaciones se obtienen que c z = Análogamente se establecen dos modelos de distribución de la respuesta para la variable y k esperando una taza de respuesta del 70 % bajo el modelo de distribución constante e incremento exponencial de la respuesta. Obteniendo un valor c y =
15 Estimadores de regresión logística para tratamiento de no respuesta 25 En particular se manejan cuatro escenarios que dependen de la distribución de la respuesta para el numerador y el denominador. Se toman 1500 muestras con n I =15yn i =0.2N i para cada conglomerado U i m I. Para cada muestra se crea la no respuesta para el numerador y el denominador. Para cada elemento e k de la muestra m se origino un experimento Bernoulli con parámetro θ k. Esto es, el elemento pertenece a la muestra con probabilidad θ k y a los no respondientes con probabilidad 1 θ k, donde θ k es conocido para todo e k U en ambas distribuciones. Así, se realizó un experimento Bernoulli para cada individuo de la muestra m, obteniendo un conjunto de 1500 muestras de respondientes; para cada conjunto escenario de distribución de respondientes en el numerador y el denominador, se calculan cinco diferentes estimadores. Ĉ π0 estimador convencional de un cociente con no respuesta imputada de la forma simple ŷ k =0yẑ k =0. Ĉ π1 estimador convencional de un cociente con no respuesta imputada mediante regresión logística, función de enlace Logit. Ĉ π2 estimador convencional de un cociente con no respuesta imputada mediante regresión logística, función de enlace Probit. Ĉ Logit estimador con uso de información auxiliar en el numerador y el denominador dado por los modelos lineales generalizados con función de enlace Logit, Logit(p yk )=β 0 + β 1 x k y Logit(p zk )=β 0 + β 1 w k respectivamente. Estimador con no respuesta imputada mediante regresión logística, función de enlace Logit. Ĉ P robit estimador con uso de información auxiliar en el numerador y el denominador dado por los modelos lineales generalizados con función de enlace Probit, Φ(p yk )=β 0 + β 1 x k y Φ(p zk )=β 0 + β 1 w k respectivamente. Estimador con no respuesta imputada mediante regresión logística, función de enlace Probit. Análogamente a la simulación de Monte Carlo bajo distintos escenarios de información auxiliar, se obtienen resultados de esperanza del cociente estimada (Tabla 6), sesgo relativo estimado (Tabla 7) y coeficiente de variación estimado (Tabla 8). Distribución respuesta numerador Distribución respuesta denominador Ĉ π0 Ĉ π1 Ĉ π2 Ĉ Logit Ĉ P robit Constante Constante Exponencial Constante Exponencial Exponencial Tabla 6: Estimaciones de la esperanza de Cocientes de método Monte Carlo por tipo de distribución de respuesta, según estimador de Cociente ( C =0.321)
16 26 Pedro César Del Campo Neira En los cuatro estimadores y los cuatro escenarios de distribución de la respuesta, el estimador con imputación simple subestima el cociente de las variables dicotómicas. Distribución respuesta numerador Distribución respuesta denominador Ĉ π0 Ĉ π1 Ĉ π2 Ĉ Logit Ĉ P robit Constante Constante Exponencial Constante Exponencial Exponencial Tabla 7: Estimaciones del sesgo relativo porcentual de método Monte Carlo por distribución de la respuesta, según estimador de Cociente El sesgo relativo es mayor de diez en todos los escenarios y estimadores. Aunque es menor en los estimadores que utilizan imputación por modelo logístico y estimadores convencionales. Distribución respuesta numerador Distribución respuesta denominador Ĉ π0 Ĉ π1 Ĉ π2 Ĉ Logit Ĉ P robit Constante Constante Exponencial Constante Exponencial Exponencial Tabla 8: Estimaciones del coeficiente de variación porcentual de método Monte Carlo por distribución de la respuesta, según estimador de Cociente En la Tabla 8 se puede ver que la precisión es mejor para estimadores asistidos por regresión logística que sin el uso de información auxiliar. Bajo imputación logística la precisión no cambia en comparación con el estimador con imputación simple. En la Figura 2 el estimador que utiliza imputación simple subestima el cociente. La alta variabilidad de los estimadores que no usan información auxiliar amortigua el efecto causado por el sesgo; sin embargo, los estimadores asistidos por regresión logística tiene un sesgo visible debido a su baja variabilidad. 6. Resultados Este trabajo compara inicialmente distintos estimadores de un cociente de variables dicotómicas, asistidos por regresión lineal simple y modelos lineales generalizados. Estos estimadores se utilizan bajo distintos escenarios de información auxiliar para el numerador y el denominador. Luego, para el mejor escenario se generan distintos escenarios de no respuesta para el numerador y el denominador con el uso de estimadores de cocientes asistidos por modelos lineales generalizados. El proceso
17 Estimadores de regresión logística para tratamiento de no respuesta 27 Figura 2: Comparación de estimadores de cocientes según tipo de distribución de la respuesta de programación de generación y obtención de estimadores mediante simulación de Monte Carlo se realizó en SAS (2004), el proceso de análisis de resultados se realizó en lenguaje de programación R Development Core Team (2006) versión Como resultado de los ejercicios realizados en este trabajo, se propone, para la estimación de un cociente de variables dicotómicas con un diseño muestral MAS 2, el uso de un estimador que utilice información auxiliar de tipo binario en el numerador tal que discrimine prácticamente la variable y k. Se recomienda el uso de información auxiliar para el denominador sin importar su nivel de asociación con la variable z k. Esto reducirá drásticamente el coeficiente de variación del estimador como se puede ver en la Tabla 4, donde los coeficientes de variación más bajos se encuentran con el uso de buena información auxiliar en el numerador. También la Figura 1 muestra que los cambios de variabilidad de los estimadores se ven reflejados en estimadores con buen uso de información auxiliar en el denominador. Según la Tabla 3, el sesgo relativo porcentual no es mayor de 10 %, en valor absoluto, para ninguno de los estimadores. Además la Figura 1 muestra que la media de todos los estimadores está muy cercana al cociente verdadero a estimar, reflejado en la linea horizontal que atraviesa cada gráfico. Por lo tanto, el sesgo relativo es insignificante para cualquiera de los escenarios propuestos de información auxiliar en el numerador y el denominador.
18 28 Pedro César Del Campo Neira Bajo no respuesta el estimador con imputación simple muestra una subestimación significativa que se puede ver en la Tabla 6 y la Figura 2. La imputación soluciona problemas en la exactitud del estimador. La asistencia de un modelo logístico soluciona problemas de precisión. El estimador que utiliza función de enlace Logit es ligeramente mejor que el estimador que utiliza función de enlace Probit en términos de precisión. El estimador asistido por regresión logística con función de enlace Logit es ligeramente mejor que el de función de enlace Probit bajo condiciones de respuesta completa como de no respuesta. El sesgo relativo es relativamente el mismo bajo las condiciones de respuesta completa y bajo la no respuesta. Agradecimientos Gracias al profesor Leonardo Bautista por introducirme en el mundo del muestreo, por colaborarme y sobrellevarme en el desarrollo de este trabajo. Agradezco a la Universidad Nacional de Colombia por darme las herramientas para mi desarrollo como profesional y a la Universidad Santo Tomás por invitarme a ser parte en este volumen. 1 Recibido: 5 de febrero de 2009 Aceptado: 18 de mayo de 2009 Referencias Dobson, A. (1990), An introduction to Generalized Linear Models, Chapman & Hall, Australia. Lehtonen, R. & Pahkinen, E. (2004), Practical Methods for design and Analisys of Complex Surveys, Jhon wiley & Sons, Ltd, Finland. R Development Core Team (2006), R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria. * Särndal, C.-E. & Lundström, S. (2005), Estimation in Surveys with nonresponse, Jhon wiley & Sons, Ltd, Sweden. 1 Este artículo es resultado del trabajo de grado para optar por el titulo de estadístico titulado Estimadores de regresión logística para tratamiento de no respuesta en el caso de cocientes de variables dicotómicas, dirigido por el maestro Leonardo Bautista y presentado en la Universidad Nacional de Colombia en 2007.
19 Estimadores de regresión logística para tratamiento de no respuesta 29 Särndal, C.-E., Swensson, B. & Wretman, J. (1993), Model Assisted Survey Sampling, Springer, New York. SAS (2004), Sas onlinedoc , SAS Institute Inc, Cary, NC. *
Análisis de datos Categóricos
 Introducción a los Modelos Lineales Generalizados Universidad Nacional Agraria La Molina 2016-1 Introducción Modelos Lineales Generalizados Introducción Componentes Estimación En los capítulos anteriores
Introducción a los Modelos Lineales Generalizados Universidad Nacional Agraria La Molina 2016-1 Introducción Modelos Lineales Generalizados Introducción Componentes Estimación En los capítulos anteriores
Muestreo en Poblaciones Finitas
 Información Adicional. Estimadores de Razón y Regresión 1/25 Muestreo en Poblaciones Finitas Información Adicional. Estimadores de Razón y Regresión José A. Mayor Gallego Departamento de Estadística e
Información Adicional. Estimadores de Razón y Regresión 1/25 Muestreo en Poblaciones Finitas Información Adicional. Estimadores de Razón y Regresión José A. Mayor Gallego Departamento de Estadística e
Cálculo y estimación de la varianza en la aplicación del estimador de rastrillo (Raking)
 Comunicaciones en Estadística Junio 009, Vol., No. Cálculo y estimación de la varianza en la aplicación del estimador de rastrillo (Raking) Variance Computation and Estimation for the Application of the
Comunicaciones en Estadística Junio 009, Vol., No. Cálculo y estimación de la varianza en la aplicación del estimador de rastrillo (Raking) Variance Computation and Estimation for the Application of the
MODELOS LINEALES GENERALIZADOS
 MODELOS LINEALES GENERALIZADOS Conceptos básicos Ignacio Méndez Gómez-Humarán imendez@cimat.mx Los Modelos Lineales Generalizados (GLM por sus siglas en inglés) son una familia de modelos estadísticos
MODELOS LINEALES GENERALIZADOS Conceptos básicos Ignacio Méndez Gómez-Humarán imendez@cimat.mx Los Modelos Lineales Generalizados (GLM por sus siglas en inglés) son una familia de modelos estadísticos
COMPARACIÓN DE TRES MÉTODOS DE REGRESIÓN LINEAL USANDO PROCEDIMIENTOS DE SIMULACIÓN
 Revista Colombiana de Estadística Volumen 24 (2001) N o 1, páginas 33 a 43 COMPARACIÓN DE TRES MÉTODOS DE REGRESIÓN LINEAL USANDO PROCEDIMIENTOS DE SIMULACIÓN JUAN C. TORRES C. * Resumen Cuando desea ajustarse
Revista Colombiana de Estadística Volumen 24 (2001) N o 1, páginas 33 a 43 COMPARACIÓN DE TRES MÉTODOS DE REGRESIÓN LINEAL USANDO PROCEDIMIENTOS DE SIMULACIÓN JUAN C. TORRES C. * Resumen Cuando desea ajustarse
ANÁLISIS DE REGRESIÓN
 ANÁLISIS DE REGRESIÓN INTRODUCCIÓN Francis Galtón DEFINICIÓN Análisis de Regresión Es una técnica estadística que se usa para investigar y modelar la relación entre variables. Respuesta Independiente Y
ANÁLISIS DE REGRESIÓN INTRODUCCIÓN Francis Galtón DEFINICIÓN Análisis de Regresión Es una técnica estadística que se usa para investigar y modelar la relación entre variables. Respuesta Independiente Y
1. Modelos para conteos
 1. Modelos para conteos En esta sección se modelarán conteos, que resultan de diversas situaciones, por ejemplo: el número de accidentes en una carretera, el número de caries que tiene una persona, el
1. Modelos para conteos En esta sección se modelarán conteos, que resultan de diversas situaciones, por ejemplo: el número de accidentes en una carretera, el número de caries que tiene una persona, el
El diseño P.P.T. con variables categóricas para la estimación de dico razones
 Revista Colombiana de Estadística Volumen 28 N o. Págs. 99 a 4. Junio 25 El diseño P.P.T. con variables categóricas para la estimación de dico razones Jairo Alberto Fúquene P. * Jaime Leonardo Bautista
Revista Colombiana de Estadística Volumen 28 N o. Págs. 99 a 4. Junio 25 El diseño P.P.T. con variables categóricas para la estimación de dico razones Jairo Alberto Fúquene P. * Jaime Leonardo Bautista
Estimación del Índice de Gini en Poblaciones Finitas. José Antonio Mayor Gallego
 Estimación del Índice de Gini en Poblaciones Finitas José Antonio Mayor Gallego Departamento de Estadística e Investigación Operativa Universidad de Sevilla. Facultad de Matemáticas Abril, 2009 José A.
Estimación del Índice de Gini en Poblaciones Finitas José Antonio Mayor Gallego Departamento de Estadística e Investigación Operativa Universidad de Sevilla. Facultad de Matemáticas Abril, 2009 José A.
Un estimador jackknife de varianza en muestreo en dos fases con probabilidades desiguales
 Revista Colombiana de Estadística Volumen 30 No. 2. pp. 203 a 212. Diciembre 2007 Un estimador jackknife de varianza en muestreo en dos fases con probabilidades desiguales A Jackknife Variance Estimator
Revista Colombiana de Estadística Volumen 30 No. 2. pp. 203 a 212. Diciembre 2007 Un estimador jackknife de varianza en muestreo en dos fases con probabilidades desiguales A Jackknife Variance Estimator
Modelos Lineales Generalizados
 Modelos Lineales Generalizados 1 DefinicióndeunMLG Y1,Y2,...,Yn,conmediasµ1,µ2,...,µn,Yi, i=1,...,n,tienefdpmiembrodela familia exponencial a un parámetro, con las siguientes propiedades: 1.LadistribucióndecadaunodelosYi,paratodoi,estáenlaformacanónica,i.e.:
Modelos Lineales Generalizados 1 DefinicióndeunMLG Y1,Y2,...,Yn,conmediasµ1,µ2,...,µn,Yi, i=1,...,n,tienefdpmiembrodela familia exponencial a un parámetro, con las siguientes propiedades: 1.LadistribucióndecadaunodelosYi,paratodoi,estáenlaformacanónica,i.e.:
Agro 6998 Conferencia 2. Introducción a los modelos estadísticos mixtos
 Agro 6998 Conferencia Introducción a los modelos estadísticos mixtos Los modelos estadísticos permiten modelar la respuesta de un estudio experimental u observacional en función de factores (tratamientos,
Agro 6998 Conferencia Introducción a los modelos estadísticos mixtos Los modelos estadísticos permiten modelar la respuesta de un estudio experimental u observacional en función de factores (tratamientos,
Estimación de Parámetros. Jhon Jairo Padilla A., PhD.
 Estimación de Parámetros Jhon Jairo Padilla A., PhD. Inferencia Estadística La inferencia estadística puede dividirse en dos áreas principales: Estimación de Parámetros Prueba de Hipótesis Estimación de
Estimación de Parámetros Jhon Jairo Padilla A., PhD. Inferencia Estadística La inferencia estadística puede dividirse en dos áreas principales: Estimación de Parámetros Prueba de Hipótesis Estimación de
Estimación de Parámetros. Jhon Jairo Padilla A., PhD.
 Estimación de Parámetros Jhon Jairo Padilla A., PhD. Inferencia Estadística La inferencia estadística puede dividirse en dos áreas principales: Estimación de Parámetros Prueba de Hipótesis Estimación de
Estimación de Parámetros Jhon Jairo Padilla A., PhD. Inferencia Estadística La inferencia estadística puede dividirse en dos áreas principales: Estimación de Parámetros Prueba de Hipótesis Estimación de
Estadística y sus aplicaciones en Ciencias Sociales 5. Estimación. Facultad de Ciencias Sociales, UdelaR
 Estadística y sus aplicaciones en Ciencias Sociales 5. Estimación Facultad de Ciencias Sociales, UdelaR Índice 1. Repaso: estimadores y estimaciones. Propiedades de los estimadores. 2. Estimación puntual.
Estadística y sus aplicaciones en Ciencias Sociales 5. Estimación Facultad de Ciencias Sociales, UdelaR Índice 1. Repaso: estimadores y estimaciones. Propiedades de los estimadores. 2. Estimación puntual.
UNIVERSIDAD AUTÓNOMA CHAPINGO DIVISIÓN DE CIENCIAS FORESTALES CARRERA DE: Licenciatura en Estadística PROGRAMA DE LA ASIGNATURA DE MUESTREO I
 UNIVERSIDAD AUTÓNOMA CHAPINGO DIVISIÓN DE CIENCIAS FORESTALES CARRERA DE: Licenciatura en Estadística PROGRAMA DE LA ASIGNATURA DE MUESTREO I DATOS GENERALES Departamento (División): Nombre del Programa
UNIVERSIDAD AUTÓNOMA CHAPINGO DIVISIÓN DE CIENCIAS FORESTALES CARRERA DE: Licenciatura en Estadística PROGRAMA DE LA ASIGNATURA DE MUESTREO I DATOS GENERALES Departamento (División): Nombre del Programa
Estadistica II Tema 0. Repaso de conceptos básicos. Curso 2009/10
 Estadistica II Tema 0. Repaso de conceptos básicos Curso 2009/10 Tema 0. Repaso de conceptos básicos Contenidos Variables aleatorias y distribuciones de probabilidad La distribución normal Muestras aleatorias,
Estadistica II Tema 0. Repaso de conceptos básicos Curso 2009/10 Tema 0. Repaso de conceptos básicos Contenidos Variables aleatorias y distribuciones de probabilidad La distribución normal Muestras aleatorias,
viii CAPÍTULO 2 Métodos de muestreo CAPÍTULO 3 Análisis exploratorio de datos
 Contenido Acerca de los autores.............................. Prefacio.... xvii CAPÍTULO 1 Introducción... 1 Introducción.............................................. 1 1.1 Ideas de la estadística.........................................
Contenido Acerca de los autores.............................. Prefacio.... xvii CAPÍTULO 1 Introducción... 1 Introducción.............................................. 1 1.1 Ideas de la estadística.........................................
Modelos lineales generalizados
 GoBack Modelos lineales Guillermo Ayala Gallego Universidad de Valencia 20 de enero de 2009 1 / 57 Verosimilitud de Ajuste de un GLM mediante Fisher Scoring Method s de un modelo lineal generalizado Identifica
GoBack Modelos lineales Guillermo Ayala Gallego Universidad de Valencia 20 de enero de 2009 1 / 57 Verosimilitud de Ajuste de un GLM mediante Fisher Scoring Method s de un modelo lineal generalizado Identifica
Una revisión de los estimadores óptimos de calibración usando métodos de cuasi-verosimilitud en muestreo bifásico
 Comunicaciones en Estadística Junio 2009, Vol. 2, No. 1 Una revisión de los estimadores óptimos de calibración usando métodos de cuasi-verosimilitud en muestreo bifásico A Revision about Optimal Calibration
Comunicaciones en Estadística Junio 2009, Vol. 2, No. 1 Una revisión de los estimadores óptimos de calibración usando métodos de cuasi-verosimilitud en muestreo bifásico A Revision about Optimal Calibration
Distribuciones Fundamentales de Muestreo. UCR ECCI CI-0115 Probabilidad y Estadística Prof. Kryscia Daviana Ramírez Benavides
 Distribuciones Fundamentales de Muestreo UCR ECCI CI-0115 Probabilidad y Estadística Prof. Kryscia Daviana Ramírez Benavides Distribuciones Muestrales La distribución de probabilidad de un estadístico
Distribuciones Fundamentales de Muestreo UCR ECCI CI-0115 Probabilidad y Estadística Prof. Kryscia Daviana Ramírez Benavides Distribuciones Muestrales La distribución de probabilidad de un estadístico
Sampling Strategy using Generalized Regression Estimators for Presidential Elections Favoritism Rate in Colombia
 Comunicaciones en Estadística Junio 2009, Vol. 2, No. 1 Estrategia de muestreo usando estimadores de regresión generalizada para la estimación de tasas de favoritismo en elecciones presidenciales en Colombia
Comunicaciones en Estadística Junio 2009, Vol. 2, No. 1 Estrategia de muestreo usando estimadores de regresión generalizada para la estimación de tasas de favoritismo en elecciones presidenciales en Colombia
UN TAMAÑO DE MUESTRA PRELIMINAR EN LA ESTIMACION DE LA MEDIA, EN POBLACIONES CON DISTRIBUCIONES UNIFORMES Y TRIANGULARES
 Revista Colombiana de Estadística Volumen 24 (2001) N o 1, páginas 27 a 32 UN TAMAÑO DE MUESTRA PRELIMINAR EN LA ESTIMACION DE LA MEDIA, EN POBLACIONES CON DISTRIBUCIONES UNIFORMES Y TRIANGULARES CARLOS
Revista Colombiana de Estadística Volumen 24 (2001) N o 1, páginas 27 a 32 UN TAMAÑO DE MUESTRA PRELIMINAR EN LA ESTIMACION DE LA MEDIA, EN POBLACIONES CON DISTRIBUCIONES UNIFORMES Y TRIANGULARES CARLOS
INFORMACIÓN FALTANTE Y/O CONFUSA EN VARIABLES DISCRETAS DE LA ENCUESTA PERMANENTE DE HOGARES (EPH)
 Badler, Clara E. Alsina, Sara M. 1 Puigsubirá, Cristina B. 1 Vitelleschi, María S. 1 Instituto de Investigaciones Teóricas y Aplicadas de la Escuela de Estadística (IITAE) INFORMACIÓN FALTANTE Y/O CONFUSA
Badler, Clara E. Alsina, Sara M. 1 Puigsubirá, Cristina B. 1 Vitelleschi, María S. 1 Instituto de Investigaciones Teóricas y Aplicadas de la Escuela de Estadística (IITAE) INFORMACIÓN FALTANTE Y/O CONFUSA
Análisis de Datos Categóricos. Leticia Gracia Medrano
 Análisis de Datos Categóricos Leticia Gracia Medrano ii Contents 1 Modelo Logístico 1 1.1 Estimación de parámetros.................... 1 1.2 Interpretación de los parámetros................. 2 1.3 Ejemplo..............................
Análisis de Datos Categóricos Leticia Gracia Medrano ii Contents 1 Modelo Logístico 1 1.1 Estimación de parámetros.................... 1 1.2 Interpretación de los parámetros................. 2 1.3 Ejemplo..............................
INTRODUCCIÓN A LA INFERENCIA ESTADÍSTICA
 UNIVERSIDAD AUTÓNOMA CHAPINGO DIVISIÓN DE CIENCIAS FORESTALES CARRERA DE: Licenciado en Estadística PROGRAMA DE LA ASIGNATURA DE INTRODUCCIÓN A LA INFERENCIA ESTADÍSTICA DATOS GENERALES Departamento (División):
UNIVERSIDAD AUTÓNOMA CHAPINGO DIVISIÓN DE CIENCIAS FORESTALES CARRERA DE: Licenciado en Estadística PROGRAMA DE LA ASIGNATURA DE INTRODUCCIÓN A LA INFERENCIA ESTADÍSTICA DATOS GENERALES Departamento (División):
INDICE. Prólogo a la Segunda Edición
 INDICE Prólogo a la Segunda Edición XV Prefacio XVI Capitulo 1. Análisis de datos de Negocios 1 1.1. Definición de estadística de negocios 1 1.2. Estadística descriptiva r inferencia estadística 1 1.3.
INDICE Prólogo a la Segunda Edición XV Prefacio XVI Capitulo 1. Análisis de datos de Negocios 1 1.1. Definición de estadística de negocios 1 1.2. Estadística descriptiva r inferencia estadística 1 1.3.
Regresión polinomial y factores
 Capítulo Regresión polinomial y factores.. Regresión polinomial Si una función media tiene un predictor X pueden usarse sus potencias enteras para aproximar E (Y X). El caso más simple es la regresión
Capítulo Regresión polinomial y factores.. Regresión polinomial Si una función media tiene un predictor X pueden usarse sus potencias enteras para aproximar E (Y X). El caso más simple es la regresión
5.5 Modelo de regresión. se especificó en los términos siguientes: (6.3.1) 1,2,3,..N. Donde:
 5.5 Modelo de regresión El modelo de regresión lineal que se aplicó para explicar la relación entre producción antigüedad, edad, capital humano, apiarios y camioneta de los apicultores nayaritas se especificó
5.5 Modelo de regresión El modelo de regresión lineal que se aplicó para explicar la relación entre producción antigüedad, edad, capital humano, apiarios y camioneta de los apicultores nayaritas se especificó
ESTIMACIÓN DE CAUDALES MÁXIMOS EN EL DISEÑO DE ALCANTARILLAS MEDIANTE EL MODELO GAMMA
 ESTIMACIÓN DE CAUDALES MÁXIMOS EN EL DISEÑO DE ALCANTARILLAS MEDIANTE EL MODELO GAMMA OZÁN NÉLIDA SUSANA1 1, GOMEZ MARIANA2 2 y FERNANDEZ MARIO3 3 1 Dpto. Matemática. Facultad de Ingeniería. Universidad
ESTIMACIÓN DE CAUDALES MÁXIMOS EN EL DISEÑO DE ALCANTARILLAS MEDIANTE EL MODELO GAMMA OZÁN NÉLIDA SUSANA1 1, GOMEZ MARIANA2 2 y FERNANDEZ MARIO3 3 1 Dpto. Matemática. Facultad de Ingeniería. Universidad
Estadística I Tema 5: Introducción a la inferencia estadística
 Estadística I Tema 5: Introducción a la inferencia estadística Tema 5. Introducción a la inferencia estadística Contenidos Objetivos. Estimación puntual. Bondad de ajuste a una distribución. Distribución
Estadística I Tema 5: Introducción a la inferencia estadística Tema 5. Introducción a la inferencia estadística Contenidos Objetivos. Estimación puntual. Bondad de ajuste a una distribución. Distribución
EL PRINCIPIO DE MÁXIMA VEROSIMILITUD (LIKELIHOOD)
 EL PRINCIPIO DE MÁXIMA VEROSIMILITUD (LIKELIHOOD) Fortino Vela Peón fvela@correo.xoc.uam.mx FVela-0 Objetivo Introducir las ideas básicas del principio de máxima verosimilitud. Problema Considere el experimento
EL PRINCIPIO DE MÁXIMA VEROSIMILITUD (LIKELIHOOD) Fortino Vela Peón fvela@correo.xoc.uam.mx FVela-0 Objetivo Introducir las ideas básicas del principio de máxima verosimilitud. Problema Considere el experimento
Estadística Computacional. M. González
 Estadística Computacional M. González Facultad de Medicina. Universidad de Extremadura M. González (UEx) Estadística Computacional 1 / 23 Índice Modelos Lineales Generalizados Bioensayos: Modelos Dosis-Respuesta
Estadística Computacional M. González Facultad de Medicina. Universidad de Extremadura M. González (UEx) Estadística Computacional 1 / 23 Índice Modelos Lineales Generalizados Bioensayos: Modelos Dosis-Respuesta
Tema 2: Introducción a la Inferencia Estadística
 Tema 2: Introducción a la Inferencia Estadística 1.- En m.a.s. el estadístico varianza muestral es: a) Un estimador insesgado de la varianza poblacional. b) Un estimador insesgado de la media poblacional.
Tema 2: Introducción a la Inferencia Estadística 1.- En m.a.s. el estadístico varianza muestral es: a) Un estimador insesgado de la varianza poblacional. b) Un estimador insesgado de la media poblacional.
Econometría III Examen. 29 de Marzo de 2012
 Econometría III Examen. 29 de Marzo de 2012 El examen consta de 20 preguntas de respuesta múltiple. El tiempo máximo es 1:10 minutos. nota: no se pueden hacer preguntas durante el examen a no ser que sean
Econometría III Examen. 29 de Marzo de 2012 El examen consta de 20 preguntas de respuesta múltiple. El tiempo máximo es 1:10 minutos. nota: no se pueden hacer preguntas durante el examen a no ser que sean
ESTIMACIÓN DE FUNCIONES DE DENSIDAD DE DATOS CORRELACIONADOS Y/O CON VALORES ATÍPICOS
 Servy, Elsa Cuesta, Cristina Marí, Gonzalo Instituto de Investigaciones Teóricas y Aplicadas, Escuela de Estadística ESTIMACIÓN DE FUNCIONES DE DENSIDAD DE DATOS CORRELACIONADOS Y/O CON VALORES ATÍPICOS
Servy, Elsa Cuesta, Cristina Marí, Gonzalo Instituto de Investigaciones Teóricas y Aplicadas, Escuela de Estadística ESTIMACIÓN DE FUNCIONES DE DENSIDAD DE DATOS CORRELACIONADOS Y/O CON VALORES ATÍPICOS
PROGRAMA OFICIAL DE POSTGRADO EN ESTADÍSTICA E INVESTIGACIÓN OPERATIVA
 PROGRAMA OFICIAL DE POSTGRADO EN ESTADÍSTICA E INVESTIGACIÓN OPERATIVA DATOS IDENTIFICATIVOS DE LA MATERIA Código de la materia: P1061101 Nombre de la materia: Modelos de Regresión Número de créditos ECTS:
PROGRAMA OFICIAL DE POSTGRADO EN ESTADÍSTICA E INVESTIGACIÓN OPERATIVA DATOS IDENTIFICATIVOS DE LA MATERIA Código de la materia: P1061101 Nombre de la materia: Modelos de Regresión Número de créditos ECTS:
Programa Educativo: Licenciatura en PROGRAMA DE ESTUDIO
 Programa Educativo: Licenciatura en PROGRAMA DE ESTUDIO Matemáticas Área de Formación : Integral Profesional Horas teóricas: 3 Horas prácticas: 2 Total de Horas: 5 Confiabilidad Total de créditos: 8 Clave:
Programa Educativo: Licenciatura en PROGRAMA DE ESTUDIO Matemáticas Área de Formación : Integral Profesional Horas teóricas: 3 Horas prácticas: 2 Total de Horas: 5 Confiabilidad Total de créditos: 8 Clave:
ºBONDAD DE LOS ESTIMADORES JACKNIFE PARA DISTINTOS TIPOS DE POBLACIÓN
 ºBONDAD DE LOS ESTIMADORES JACKNIFE PARA DISTINTOS TIPOS DE POBLACIÓN Raquel Plúa Morán 1, Gaudencio Zurita 2 1 Ingeniera en Estadística Informática 2003 2 Director de Tesis, Master en Ciencias Matemáticas,
ºBONDAD DE LOS ESTIMADORES JACKNIFE PARA DISTINTOS TIPOS DE POBLACIÓN Raquel Plúa Morán 1, Gaudencio Zurita 2 1 Ingeniera en Estadística Informática 2003 2 Director de Tesis, Master en Ciencias Matemáticas,
Propiedades Una distribución pertenece a la familia exponencial si su función de densidad puede expresarse como:
 Familia Exponencial Propiedades Una distribución pertenece a la familia exponencial si su función de densidad puede expresarse como: f (y; θ) = s(y)t(θ)exp[a(y)b(θ)] = exp[a(y)b(θ)+c(θ)+d(y)] (1) con s(y)
Familia Exponencial Propiedades Una distribución pertenece a la familia exponencial si su función de densidad puede expresarse como: f (y; θ) = s(y)t(θ)exp[a(y)b(θ)] = exp[a(y)b(θ)+c(θ)+d(y)] (1) con s(y)
REGRESIÓN Y ESTIMACIÓN TEMA 1: REGRESIÓN LINEAL SIMPLE
 UNIDAD 3 REGRESIÓN Y ESTIMACIÓN TEMA 1: REGRESIÓN LINEAL SIMPLE Relación entre variables de interés 1 Relación entre variables de interés Muchas decisiones gerenciales se basan en la relación entre 2 o
UNIDAD 3 REGRESIÓN Y ESTIMACIÓN TEMA 1: REGRESIÓN LINEAL SIMPLE Relación entre variables de interés 1 Relación entre variables de interés Muchas decisiones gerenciales se basan en la relación entre 2 o
Regresión Lineal Múltiple
 Unidad 4 Regresión Lineal Múltiple Javier Santibáñez (IIMAS, UNAM) Regresión Semestre 2017-2 1 / 35 Introducción La idea de la regresión lineal múltiple es modelar el valor esperado de la variable respuesta
Unidad 4 Regresión Lineal Múltiple Javier Santibáñez (IIMAS, UNAM) Regresión Semestre 2017-2 1 / 35 Introducción La idea de la regresión lineal múltiple es modelar el valor esperado de la variable respuesta
Universidad Autónoma de Sinaloa
 Séptima Edición del Diplomado en Estadística Mc. José V. Jiménez Ramírez Director de la Escuela de Ciencias Fisico-Matemáticas Tel. : 7 16 11 54 vidaljr@uas.uasnet.mx Dr. René Castro Montoya Coordinador
Séptima Edición del Diplomado en Estadística Mc. José V. Jiménez Ramírez Director de la Escuela de Ciencias Fisico-Matemáticas Tel. : 7 16 11 54 vidaljr@uas.uasnet.mx Dr. René Castro Montoya Coordinador
Modelo de Regresión Lineal
 Modelo de Regresión Lineal Álvaro José Flórez 1 Escuela de Ingeniería Industrial y Estadística Facultad de Ingenierías Febrero - Junio 2012 Introducción Un ingeniero, empleado por un embotellador de gaseosas,
Modelo de Regresión Lineal Álvaro José Flórez 1 Escuela de Ingeniería Industrial y Estadística Facultad de Ingenierías Febrero - Junio 2012 Introducción Un ingeniero, empleado por un embotellador de gaseosas,
Inferencia Estadística
 Inferencia Estadística 2do C. 2018 Mg. Stella Figueroa Clase Nº10 Población y Muestra- Parámetro y Estimación puntual Población: Es el conjunto de todos los elementos o unidades elementales con características
Inferencia Estadística 2do C. 2018 Mg. Stella Figueroa Clase Nº10 Población y Muestra- Parámetro y Estimación puntual Población: Es el conjunto de todos los elementos o unidades elementales con características
Regresión lineal simple
 Regresión lineal simple Unidad 1 Javier Santibáñez IIMAS, UNAM jsantibanez@sigma.iimas.unam.mx Semestre 2018-2 Javier Santibáñez (IIMAS, UNAM) Regresión simple Semestre 2018-2 1 / 62 Contenido 1 Planteamiento
Regresión lineal simple Unidad 1 Javier Santibáñez IIMAS, UNAM jsantibanez@sigma.iimas.unam.mx Semestre 2018-2 Javier Santibáñez (IIMAS, UNAM) Regresión simple Semestre 2018-2 1 / 62 Contenido 1 Planteamiento
Está formado por nueve cursos:
 Revisión de los programas de estudio de la Fase de Especialización del área de Estadística de la Licenciatura en Matemáticas del plan de estudios enviado por Lucio 110203 Está formado por nueve cursos:
Revisión de los programas de estudio de la Fase de Especialización del área de Estadística de la Licenciatura en Matemáticas del plan de estudios enviado por Lucio 110203 Está formado por nueve cursos:
Estimación de Parámetros
 Estimación de Parámetros Jhon Jairo Padilla A., PhD. Inferencia Estadística La inferencia estadística puede dividirse en dos áreas principales: p Estimación de Parámetros Prueba de Hipótesis Estimación
Estimación de Parámetros Jhon Jairo Padilla A., PhD. Inferencia Estadística La inferencia estadística puede dividirse en dos áreas principales: p Estimación de Parámetros Prueba de Hipótesis Estimación
Universidad Técnica de Babahoyo INTRODUCCIÓN A LA INFERENCIA ESTADÍSTICA
 Universidad Técnica de Babahoyo INTRODUCCIÓN A LA INFERENCIA ESTADÍSTICA Ateneo Ruperto P. Bonet Chaple UTB-Julio 2016 OBJETIVO Aplicar las técnicas de Muestreo e Inferencia Estadística Determinar el tamaño
Universidad Técnica de Babahoyo INTRODUCCIÓN A LA INFERENCIA ESTADÍSTICA Ateneo Ruperto P. Bonet Chaple UTB-Julio 2016 OBJETIVO Aplicar las técnicas de Muestreo e Inferencia Estadística Determinar el tamaño
Folleto de Estadísticas. Teoría del 2do Parcial
 Folleto de Estadísticas Teoría del 2do Parcial 2012 Variables aleatorias conjuntas continuas: Sean X y Y dos variables aleatorias continuas con ellas se asocia una función denominada función de densidad
Folleto de Estadísticas Teoría del 2do Parcial 2012 Variables aleatorias conjuntas continuas: Sean X y Y dos variables aleatorias continuas con ellas se asocia una función denominada función de densidad
METODOS ESTADÍSTICOS
 METODOS ESTADÍSTICOS Introducción. Uno de los objetivos de la asignatura de Hidrología, es mostrar a los alumnos, las herramientas de cálculo utilizadas en Hidrología Aplicada para diseño de Obras Hidráulicas.
METODOS ESTADÍSTICOS Introducción. Uno de los objetivos de la asignatura de Hidrología, es mostrar a los alumnos, las herramientas de cálculo utilizadas en Hidrología Aplicada para diseño de Obras Hidráulicas.
Técnicas de Muestreo I
 1 / 39 Técnicas de Muestreo I Patricia Isabel Romero Mares Departamento de Probabilidad y Estadística IIMAS UNAM agosto 2018 2 / 39 Temario 1. Introducción. Definición de conceptos elementales 2. Muestreo
1 / 39 Técnicas de Muestreo I Patricia Isabel Romero Mares Departamento de Probabilidad y Estadística IIMAS UNAM agosto 2018 2 / 39 Temario 1. Introducción. Definición de conceptos elementales 2. Muestreo
UNA PROPUESTA PARA LA MAXIMIZACIÓN DE LA ESTADÍSTICA Q K
 Revista Colombiana de Estadística Volumen 24 (2001) N o 1, páginas 45 a 57 UNA PROPUESTA PARA LA MAXIMIZACIÓN DE LA ESTADÍSTICA Q K JOSÉ A. JIMÉNEZ M.* Resumen En este artículo mediante el método de los
Revista Colombiana de Estadística Volumen 24 (2001) N o 1, páginas 45 a 57 UNA PROPUESTA PARA LA MAXIMIZACIÓN DE LA ESTADÍSTICA Q K JOSÉ A. JIMÉNEZ M.* Resumen En este artículo mediante el método de los
ESTUDIO COMPARATIVO DE MÉTODOS DE ESTIMACIÓN EN UN MODELO LOGIT MIXTO 1
 Leticia Hachuel Gabriela Boggio Guillermina Harvey Instituto de Investigaciones Teóricas y Aplicadas de la Escuela de Estadística ESTUDIO COMPARATIVO DE MÉTODOS DE ESTIMACIÓN EN UN MODELO LOGIT MIXTO 1
Leticia Hachuel Gabriela Boggio Guillermina Harvey Instituto de Investigaciones Teóricas y Aplicadas de la Escuela de Estadística ESTUDIO COMPARATIVO DE MÉTODOS DE ESTIMACIÓN EN UN MODELO LOGIT MIXTO 1
Regresión lineal. Marcelo Rodríguez Ingeniero Estadístico - Magíster en Estadística
 Regresión lineal Marcelo Rodríguez Ingeniero Estadístico - Magíster en Estadística Universidad Católica del Maule Facultad de Ciencias Básicas Pedagogía en Matemática Estadística I 01 de enero de 2012
Regresión lineal Marcelo Rodríguez Ingeniero Estadístico - Magíster en Estadística Universidad Católica del Maule Facultad de Ciencias Básicas Pedagogía en Matemática Estadística I 01 de enero de 2012
Cálculo de Probabilidades II Preguntas Tema 2
 Cálculo de Probabilidades II Preguntas Tema 2 1. Demuestre que la suma de n v.a. Bernuolli(p) independientes tiene una distribución Binomial con parametros (n, p). 2. Se dice que una v.a tiene una distribución
Cálculo de Probabilidades II Preguntas Tema 2 1. Demuestre que la suma de n v.a. Bernuolli(p) independientes tiene una distribución Binomial con parametros (n, p). 2. Se dice que una v.a tiene una distribución
Tema 10: Introducción a los problemas de Asociación y Correlación
 Tema 10: Introducción a los problemas de Asociación y Correlación Estadística 4 o Curso Licenciatura en Ciencias Ambientales Licenciatura en Ciencias Ambientales (4 o Curso) Tema 10: Asociación y Correlación
Tema 10: Introducción a los problemas de Asociación y Correlación Estadística 4 o Curso Licenciatura en Ciencias Ambientales Licenciatura en Ciencias Ambientales (4 o Curso) Tema 10: Asociación y Correlación
Estimación de regresión multivariante insesgada
 Estadística Española Volumen 58, número 190 / 2016, pp. 123-131 Estimación de regresión multivariante insesgada Mariano Ruiz Espejo Universidad Católica San Antonio de Murcia Resumen Proponemos un estimador
Estadística Española Volumen 58, número 190 / 2016, pp. 123-131 Estimación de regresión multivariante insesgada Mariano Ruiz Espejo Universidad Católica San Antonio de Murcia Resumen Proponemos un estimador
Resumen. Recordemos que una cópula es una función C : I 2 I tal que: C(u 2, v 2 ) C(u 2, v 1 ) C(u 1, v 2 ) + C(u 1, v 1 ) 0. (2)
 Contenido 1 2 3 Cópula Empírica Cópula Kernel Resumen Recordemos que una cópula es una función C : I 2 I tal que: 1 Para cualesquiera u, v en I := [0, 1] C(u, 0) = 0 = C(0, v), C(u, 1) = u, C(1, v) = v.
Contenido 1 2 3 Cópula Empírica Cópula Kernel Resumen Recordemos que una cópula es una función C : I 2 I tal que: 1 Para cualesquiera u, v en I := [0, 1] C(u, 0) = 0 = C(0, v), C(u, 1) = u, C(1, v) = v.
Licenciatura en Actuaría PROGRAMA DE ESTUDIO. Integral Profesional Horas teóricas: 3 Horas prácticas: 2 Total de Horas: 5 Confiabilidad
 PROGRAMA DE ESTUDIO Programa Educativo: Licenciatura en Actuaría Área de Formación : Integral Profesional Horas teóricas: 3 Horas prácticas: 2 Total de Horas: 5 Confiabilidad Total de créditos: 8 Clave:
PROGRAMA DE ESTUDIO Programa Educativo: Licenciatura en Actuaría Área de Formación : Integral Profesional Horas teóricas: 3 Horas prácticas: 2 Total de Horas: 5 Confiabilidad Total de créditos: 8 Clave:
Diseños D-óptimos bayesianos para modelos lineales heteroscedásticos
 XXVI Simposio Internacional de Estadística 2016 Sincelejo, Sucre, Colombia, 8 al 12 de Agosto de 2016 Diseños D-óptimos bayesianos para modelos lineales heteroscedásticos Catalina Patiño Bustamante 1,a,
XXVI Simposio Internacional de Estadística 2016 Sincelejo, Sucre, Colombia, 8 al 12 de Agosto de 2016 Diseños D-óptimos bayesianos para modelos lineales heteroscedásticos Catalina Patiño Bustamante 1,a,
DESCRIPCIÓN DE DATOS POR MEDIO DE GRÁFICAS
 ÍNDICE Introducción: Entrene su cerebro para la estadística... 1 La población y la muestra... 3 Estadísticas descriptivas e inferenciales... 4 Alcanzar el objetivo de estadísticas inferenciales: los pasos
ÍNDICE Introducción: Entrene su cerebro para la estadística... 1 La población y la muestra... 3 Estadísticas descriptivas e inferenciales... 4 Alcanzar el objetivo de estadísticas inferenciales: los pasos
Fundamentos para la inferencia. Estadística Prof. Tamara Burdisso
 Fundamentos para la inferencia Estadística 018 - Prof. Tamara Burdisso 1 Distribución muestral de la varianza muestral Hasta aquí nos ocupamos de hacer inferencia sobre la media y/o la proporción de una
Fundamentos para la inferencia Estadística 018 - Prof. Tamara Burdisso 1 Distribución muestral de la varianza muestral Hasta aquí nos ocupamos de hacer inferencia sobre la media y/o la proporción de una
Mathias Bourel. 2 de octubre de 2016
 Regresión Logística Mathias Bourel IMERL - Facultad de Ingeniería, Universidad de la República, Uruguay 2 de octubre de 2016 M.Bourel (IMERL, UdelaR) Regresión Logística 2 de octubre de 2016 1 / 28 Introducción
Regresión Logística Mathias Bourel IMERL - Facultad de Ingeniería, Universidad de la República, Uruguay 2 de octubre de 2016 M.Bourel (IMERL, UdelaR) Regresión Logística 2 de octubre de 2016 1 / 28 Introducción
INDICE 1. Qué es la Estadística? 2.Descripción de Datos: Distribuciones de Frecuencia y Presentación Gráfica
 INDICE 1. Qué es la Estadística? 1 Introducción 2 Qué significa estadística? 2 Por qué se estudia la estadística? 4 Tipos de estadística 5 Estadística descriptiva 5 Estadística inferencial 6 Tipos de variables
INDICE 1. Qué es la Estadística? 1 Introducción 2 Qué significa estadística? 2 Por qué se estudia la estadística? 4 Tipos de estadística 5 Estadística descriptiva 5 Estadística inferencial 6 Tipos de variables
Nota de los autores... vi
 ÍNDICE Nota de los autores... vi 1 Qué es la estadística?... 1 1.1 Introducción... 2 1.2 Por qué se debe estudiar estadística?... 2 1.3 Qué se entiende por estadística?... 4 1.4 Tipos de estadística...
ÍNDICE Nota de los autores... vi 1 Qué es la estadística?... 1 1.1 Introducción... 2 1.2 Por qué se debe estudiar estadística?... 2 1.3 Qué se entiende por estadística?... 4 1.4 Tipos de estadística...
Regresión ponderada y falta de ajuste
 Capítulo 4 Regresión ponderada y falta de ajuste 4.1. Introducción En este capítulo se presentan la regresión ponderada y la prueba de falta de ajuste como un conjunto adicional de herramientas usadas
Capítulo 4 Regresión ponderada y falta de ajuste 4.1. Introducción En este capítulo se presentan la regresión ponderada y la prueba de falta de ajuste como un conjunto adicional de herramientas usadas
Las 19 primeras diapositivas de esta clase están incluidas en la clase teórica previa: Error y expresión de resultados (diapositivas 22 a 40).
 Las 19 primeras diapositivas de esta clase están incluidas en la clase teórica previa: Error y expresión de resultados (diapositivas a 40). Definiciones fundamentales y objetivo: El resultado arrojado
Las 19 primeras diapositivas de esta clase están incluidas en la clase teórica previa: Error y expresión de resultados (diapositivas a 40). Definiciones fundamentales y objetivo: El resultado arrojado
ECONOMETRÍA II Prof.: Begoña Álvarez TEMA 1 INTRODUCCIÓN. Estimación por máxima verosimilitud y conceptos de teoría asintótica
 ECONOMETRÍA II Prof.: Begoña Álvarez 2007-2008 TEMA 1 INTRODUCCIÓN Estimación por máxima verosimilitud y conceptos de teoría asintótica 1. ESTIMACIÓN POR MÁXIMA VEROSIMILITUD (MAXIMUM LIKELIHOOD) La estimación
ECONOMETRÍA II Prof.: Begoña Álvarez 2007-2008 TEMA 1 INTRODUCCIÓN Estimación por máxima verosimilitud y conceptos de teoría asintótica 1. ESTIMACIÓN POR MÁXIMA VEROSIMILITUD (MAXIMUM LIKELIHOOD) La estimación
y k k=1 k=1 n k=1 l=1 = 1 2
 Muestreo. Tarea. Semestre 205-2. Profesora: Guillermina Eslava Gómez. Ayudante: Graciela Martínez Sánchez Fecha de entrega: viernes 27 de febrero en clase Resolver en equipos de a 6 alumnos. Las tareas
Muestreo. Tarea. Semestre 205-2. Profesora: Guillermina Eslava Gómez. Ayudante: Graciela Martínez Sánchez Fecha de entrega: viernes 27 de febrero en clase Resolver en equipos de a 6 alumnos. Las tareas
Econometría Avanzada FLACSO 2014
 Econometría Avanzada FLACSO 2014 Hemos cubierto: Mapa Planteamiento de una pregunta económica de interés Diferencias entre econometría y estadística Métodos: Lineales (MCO) revisión, variables instrumentales
Econometría Avanzada FLACSO 2014 Hemos cubierto: Mapa Planteamiento de una pregunta económica de interés Diferencias entre econometría y estadística Métodos: Lineales (MCO) revisión, variables instrumentales
BLOQUE III: INFERENCIA ESTADISTICA. X, variable aleatoria de interés sobre una determinada población
 BLOQUE III: INFERENCIA ESTADISTICA TEMA 8. MUESTREO Y DISTRIBUCIONES DE MUESTREO 1. Introducción a la Inferencia Estadística X, variable aleatoria de interés sobre una determinada población Observar el
BLOQUE III: INFERENCIA ESTADISTICA TEMA 8. MUESTREO Y DISTRIBUCIONES DE MUESTREO 1. Introducción a la Inferencia Estadística X, variable aleatoria de interés sobre una determinada población Observar el
INTERVALOS DE CONFIANZA. La estadística en cómic (L. Gonick y W. Smith)
 INTERVALOS DE CONFIANZA La estadística en cómic (L. Gonick y W. Smith) EJEMPLO: Será elegido el senador Astuto? 2 tamaño muestral Estimador de p variable aleatoria poblacional? proporción de personas que
INTERVALOS DE CONFIANZA La estadística en cómic (L. Gonick y W. Smith) EJEMPLO: Será elegido el senador Astuto? 2 tamaño muestral Estimador de p variable aleatoria poblacional? proporción de personas que
ESTADÍSTICA APLICADA A LA EDUCACIÓN (Tema 11) Asignatura de Formación Básica (FB) de 1º curso, común a los Grado en Educación Social y en Pedagogía
 ESTADÍSTICA APLICADA A LA EDUCACIÓN (Tema 11) Asignatura de Formación Básica (FB) de 1º curso, común a los Grado en Educación Social y en Pedagogía Novedades en el Plan de Trabajo Desviación típica sesgada
ESTADÍSTICA APLICADA A LA EDUCACIÓN (Tema 11) Asignatura de Formación Básica (FB) de 1º curso, común a los Grado en Educación Social y en Pedagogía Novedades en el Plan de Trabajo Desviación típica sesgada
TEMA 4 Regresión logística
 TEMA 4 Regresión logística José R. Berrendero Departamento de Matemáticas Universidad Autónoma de Madrid Análisis de Datos - Grado en Biología Esquema del tema Variable respuesta dicotómica. Ejemplo. El
TEMA 4 Regresión logística José R. Berrendero Departamento de Matemáticas Universidad Autónoma de Madrid Análisis de Datos - Grado en Biología Esquema del tema Variable respuesta dicotómica. Ejemplo. El
Estadística II Examen Final 19/06/2015 Soluciones. Responda a las preguntas siguientes en los cuadernillos de la Universidad
 Estadística II Examen Final 19/06/2015 Soluciones Responda a las preguntas siguientes en los cuadernillos de la Universidad Utilice diferentes cuadernillos para responder a cada uno de los ejercicios Indique
Estadística II Examen Final 19/06/2015 Soluciones Responda a las preguntas siguientes en los cuadernillos de la Universidad Utilice diferentes cuadernillos para responder a cada uno de los ejercicios Indique
INDICE. Capitulo Uno.
 INDICE Prefacio XIII Capitulo Uno. 1 Introducción 1.1. Estadística: La ciencia de los datos 2 1.2. Tipos de datos 5 1.3. El papel de la estadística 7 1.4. Resumen 8 Laboratorio de Computación. Introducción
INDICE Prefacio XIII Capitulo Uno. 1 Introducción 1.1. Estadística: La ciencia de los datos 2 1.2. Tipos de datos 5 1.3. El papel de la estadística 7 1.4. Resumen 8 Laboratorio de Computación. Introducción
Intervalos de Confianza Jackknife para Cuantiles en Muestreo con Probabilidades Desiguales
 Intervalos de Confianza Jackknife para Cuantiles en Muestreo con Probabilidades Desiguales Mario J. Pacheco 1 Hugo A. Brango 2 Resumen Se considera la estimación de cuantiles en poblaciones finitas mediante
Intervalos de Confianza Jackknife para Cuantiles en Muestreo con Probabilidades Desiguales Mario J. Pacheco 1 Hugo A. Brango 2 Resumen Se considera la estimación de cuantiles en poblaciones finitas mediante
Calculo del tiempo de vida con datos de degradación MC. Manuel Jesús Reyes Méndez (ITCJ) 1, Dr. Manuel A. Rodríguez Medina (ITCJ)
 Calculo del tiempo de vida con datos de degradación MC. Manuel Jesús Reyes Méndez (ITCJ) 1, Dr. Manuel A. Rodríguez Medina (ITCJ) Resumen En los productos de alta calidad es difícil de obtener suficientes
Calculo del tiempo de vida con datos de degradación MC. Manuel Jesús Reyes Méndez (ITCJ) 1, Dr. Manuel A. Rodríguez Medina (ITCJ) Resumen En los productos de alta calidad es difícil de obtener suficientes
Estimación de Parámetros. Un problema inherente al uso de modelos es el de la selección del modelo.
 Estimación de Parámetros Un problema inherente al uso de modelos es el de la selección del modelo. Este problema, cuando se recurre al empleo de familias paramétricas de modelos, se puede plantear en dos
Estimación de Parámetros Un problema inherente al uso de modelos es el de la selección del modelo. Este problema, cuando se recurre al empleo de familias paramétricas de modelos, se puede plantear en dos
Universidad de Puerto Rico Recinto de Río Piedras Facultad de Ciencias Naturales Departamento de Matemáticas
 1 Universidad de Puerto Rico Recinto de Río Piedras Facultad de Ciencias Naturales Departamento de Matemáticas Título: Introducción a la Estadística con Computadoras Codificación: MATE 3026 Número de horas
1 Universidad de Puerto Rico Recinto de Río Piedras Facultad de Ciencias Naturales Departamento de Matemáticas Título: Introducción a la Estadística con Computadoras Codificación: MATE 3026 Número de horas
Intervalos de Confianza
 Intervalos de Confianza Álvaro José Flórez 1 Escuela de Ingeniería Industrial y Estadística Facultad de Ingenierías Febrero - Junio 2012 Intervalo de Confianza Se puede hacer una estimación puntual de
Intervalos de Confianza Álvaro José Flórez 1 Escuela de Ingeniería Industrial y Estadística Facultad de Ingenierías Febrero - Junio 2012 Intervalo de Confianza Se puede hacer una estimación puntual de
donde ε es la variable aleatoria de media 0 y f(x) es una relación que tiene la siguiente expresión:
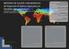 INTRODUCCIÓN Los modelos de regresión B-Splines son de tipo semiparamétrico y presentan un excelente ajuste en variables climatológicas, como se muestra en el desarrollo de este trabajo que está dividido
INTRODUCCIÓN Los modelos de regresión B-Splines son de tipo semiparamétrico y presentan un excelente ajuste en variables climatológicas, como se muestra en el desarrollo de este trabajo que está dividido
TALLER DISEÑOS DE MUESTREO ESTADÍSTICO
 TALLER DISEÑOS DE MUESTREO ESTADÍSTICO Profesor: Giovany Babativa. (Ejer..7 Lohr) Para cada una de las siguientes encuestas, describa la población objetivo, el marco de muestreo, la unidad de muestreo
TALLER DISEÑOS DE MUESTREO ESTADÍSTICO Profesor: Giovany Babativa. (Ejer..7 Lohr) Para cada una de las siguientes encuestas, describa la población objetivo, el marco de muestreo, la unidad de muestreo
Diplomado en Estadística Aplicada
 Diplomado en Estadística Aplicada Con el propósito de mejorar las habilidades para la toma de decisiones, la División de Estudios de Posgrado de la Facultad de Economía ha conjuntado a profesores con especialidad
Diplomado en Estadística Aplicada Con el propósito de mejorar las habilidades para la toma de decisiones, la División de Estudios de Posgrado de la Facultad de Economía ha conjuntado a profesores con especialidad
Fundamentos para la inferencia. Unidad 3 Parte II Estadísca Prof. Tamara Burdisso
 Fundamentos para la inferencia Estadísca 017 - Prof. Tamara Burdisso 1 Distribución muestral de la varianza muestral Hasta aquí nos ocupamos de hacer inferencia sobre la media y/o la proporción de una
Fundamentos para la inferencia Estadísca 017 - Prof. Tamara Burdisso 1 Distribución muestral de la varianza muestral Hasta aquí nos ocupamos de hacer inferencia sobre la media y/o la proporción de una
Fundamentos para la inferencia. Unidad 3 Parte II Estadísca Prof. Tamara Burdisso
 Fundamentos para la inferencia Estadísca 016 - Prof. Tamara Burdisso 1 Distribución muestral de la varianza muestral Hasta aquí nos ocupamos de hacer inferencia sobre la media y/o la proporción de una
Fundamentos para la inferencia Estadísca 016 - Prof. Tamara Burdisso 1 Distribución muestral de la varianza muestral Hasta aquí nos ocupamos de hacer inferencia sobre la media y/o la proporción de una
Auxiliar 9. MNL y MLE. Daniel Olcay. 21 de octubre de 2014 IN4402. Daniel Olcay (IN4402) Auxiliar 9 21 de octubre de / 13
 Auxiliar 9 MNL y MLE Daniel Olcay IN4402 21 de octubre de 2014 Daniel Olcay (IN4402) Auxiliar 9 21 de octubre de 2014 1 / 13 Índice Modelos no lineales Probabilidad lineal Probit Logit Máxima verosimilitud
Auxiliar 9 MNL y MLE Daniel Olcay IN4402 21 de octubre de 2014 Daniel Olcay (IN4402) Auxiliar 9 21 de octubre de 2014 1 / 13 Índice Modelos no lineales Probabilidad lineal Probit Logit Máxima verosimilitud
MODELO DE RESPUESTAS Objetivos 2, 3, 4, 5, 6, 7, Y 8.
 UNIVERSIDAD NACIONAL ABIERTA ESTADÍSTICA GENERAL 745) VICERRECTORADO ACADÉMICO INTEGRAL ÁREA DE MATEMÁTICA Fecha: 17/ 01 /009 MODELO DE RESPUESTAS Objetivos, 3, 4, 5, 6, 7, Y 8. OBJ. 1 PTA 1 Una compañía
UNIVERSIDAD NACIONAL ABIERTA ESTADÍSTICA GENERAL 745) VICERRECTORADO ACADÉMICO INTEGRAL ÁREA DE MATEMÁTICA Fecha: 17/ 01 /009 MODELO DE RESPUESTAS Objetivos, 3, 4, 5, 6, 7, Y 8. OBJ. 1 PTA 1 Una compañía
Departamento Administrativo Nacional de Estadística Dirección de Metodología y Producción Estadística-DIMPE
 Departamento Administrativo Nacional de Estadística Dirección de Metodología y Producción Estadística-DIMPE Metodología de Imputación de Novedades en Estado de Deuda Encuesta Anual Manufacturera -EAM Julio
Departamento Administrativo Nacional de Estadística Dirección de Metodología y Producción Estadística-DIMPE Metodología de Imputación de Novedades en Estado de Deuda Encuesta Anual Manufacturera -EAM Julio
1. Conceptos de Regresión y Correlación. 2. Variables aleatorias bidimensionales. 3. Ajuste de una recta a una nube de puntos
 TEMA 10 (curso anterior): REGRESIÓN Y CORRELACIÓN 1 Conceptos de Regresión y Correlación 2 Variables aleatorias bidimensionales 3 Ajuste de una recta a una nube de puntos 4 El modelo de la correlación
TEMA 10 (curso anterior): REGRESIÓN Y CORRELACIÓN 1 Conceptos de Regresión y Correlación 2 Variables aleatorias bidimensionales 3 Ajuste de una recta a una nube de puntos 4 El modelo de la correlación
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I Y II CONTENIDOS BACHILLERATO
 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I Y II CONTENIDOS BACHILLERATO BLOQUE 1. PROCESOS, MÉTODOS Y ACTITUDES EN MATEMÁTICAS Los contenidos de este bloque se desarrollan de forma simultánea al resto
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I Y II CONTENIDOS BACHILLERATO BLOQUE 1. PROCESOS, MÉTODOS Y ACTITUDES EN MATEMÁTICAS Los contenidos de este bloque se desarrollan de forma simultánea al resto
Soluciones al examen de Estadística Aplicada a las Ciencias Sociales Junio 2008 Primera semana
 Soluciones al examen de Estadística Aplicada a las Ciencias Sociales Junio 008 Primera semana Ejercicio 1. Para analizar la asociación entre el nivel de estudios y la renta calcularemos el estadístico
Soluciones al examen de Estadística Aplicada a las Ciencias Sociales Junio 008 Primera semana Ejercicio 1. Para analizar la asociación entre el nivel de estudios y la renta calcularemos el estadístico
ESTADÍSTICA APLICADA A LA EDUCACIÓN (Tema 11) Asignatura de Formación Básica (FB) de 1º curso, común a los Grado en Educación Social y en Pedagogía
 ESTADÍSTICA APLICADA A LA EDUCACIÓN (Tema 11) Asignatura de Formación Básica (FB) de 1º curso, común a los Grado en Educación Social y en Pedagogía VIDEOCLASE: Introducción a la estimación de parámetros
ESTADÍSTICA APLICADA A LA EDUCACIÓN (Tema 11) Asignatura de Formación Básica (FB) de 1º curso, común a los Grado en Educación Social y en Pedagogía VIDEOCLASE: Introducción a la estimación de parámetros
Algunos Problemas y Soluciones en el Análisis de Experimentos Ajustados con MLG s.
 Algunos Problemas y Soluciones en el Análisis de Experimentos Ajustados con MLG s. Víctor Aguirre Torres Departamento de Estadística, ITAM. Seminario de Estadística, CIMAT. 5 de Nov 2007. Créditos Trabajo
Algunos Problemas y Soluciones en el Análisis de Experimentos Ajustados con MLG s. Víctor Aguirre Torres Departamento de Estadística, ITAM. Seminario de Estadística, CIMAT. 5 de Nov 2007. Créditos Trabajo
INTRODUCCIÓN AL ANÁLISIS DE DATOS ORIENTACIONES (TEMA Nº 8) TEMA Nº 8 ESTIMACIÓN
 OBJETIVOS DE APRENDIZAJE: TEMA Nº 8 ESTIMACIÓN Conocer las relaciones entre muestra, análisis estadístico descriptivo y análisis estadístico inferencial. Conocer los conceptos de muestra aleatoria y muestra
OBJETIVOS DE APRENDIZAJE: TEMA Nº 8 ESTIMACIÓN Conocer las relaciones entre muestra, análisis estadístico descriptivo y análisis estadístico inferencial. Conocer los conceptos de muestra aleatoria y muestra
