6 - Líneas de Transmisión (cont.)
|
|
|
- María Soler Quintero
- hace 10 años
- Vistas:
Transcripción
1 Elcromgmo í d Trmó co. Adpcó d mpdc E comú qu d cocr u crg u lí d mpdc crcríc dfr. E l co xrá u od rfljd qu dmuy l poc rgd l crg y pud r fco dro l grdor, crr oro y orcorr or l lí cpc d cur dño, c. Pr r uco prolmác x do mcmo d dpcó r l lí y l crg. rmo lo má cllo coucó. Como lo hul l plcco, upodrmo qu l lí o dl o d j pérdd, por lo qu ommo rl l mpdc crcríc y l co d propgcó. Por mplcdd l roduccó mé upodrmo qu l crg rl Trformdor lí d curo d od - co co co Ju C. Frád - Dprmo d Fíc Fculd d Igrí Urdd d Buo Ar r d u roo d lí d logud y d mpdc crcríc. Pr l dpcó, rqur qu l mpdc d rd dl cojuo crg dpdor gul l mpdc crcríc d l lí orgl : ugo: co Pr qu cupl guldd d gulr por prdo l pr rl mgr d mo mmro: co co prmr cucó, l coo o ulo, rqur qu, pro o o ocurr por hpó, y qu l co o rí cr l dpcó. Eoc l guldd ólo áld π ul l coo: co π λ λ 4 λ / 4 y l logud má cor d l lí dpdor, qu por l moo llm lí d curo d od. Co codcó l o l gud cucó l y fc l guldd : qu l md gomérc d l mpdc qu qur dpr. Codrmo hor l dpcó cudo l crg complj. E co coloc l dpdor u dc d l crg pr l cul l mpdc d rd rl y oc: dpcó por méodo rl for m cll udo l cr d mh qu rmo má dl. dpcó d mpdc por lí d curo d od d pr u úc frcuc, quéll qu λ /4
2 Elcromgmo Adpdor u Much c o pol r u lí co l mpdc crcríc cr pr u dpdor d curo d od. ul ur u u, qu hulm u roo d l mm lí qu coc prllo co l cojuo lcrg pr logrr l dpcó d mpdc. Normlm l xrmo d crg xrmo ljo dl u corocrcu pr mmr l mó d rdcó lcromgéc qu podrí cur rfrc. El dño dl u co dfr l logud dl u y l pocó - d l qu d ucr. E l puo d coxó l dmc dl cojuo l um d l dmc dl u y l dmc d rd dl cojuo lícrg. E dmc d r gul / pr l dpcó. l crg r qud l cuco pr l dmc d rd: Y Y lícrg: co Y Y d Y d Y d Y d Y Y Y co co d Y d Y d Y d u: Y Y co d modo qu pr dpcó: Y Y d Y Y Y Y Y d Oprdo: Y Y Y co d dod: Y co d Y d Y -d Y Y λ d / co d Y d π Y Y d λ co co Y d Y d π E cuco prm dñr l dpcó. o áld úcm pr crg r. E l co grl d crg o r má fácl ulr l cr d mh pr dñr lo dpdor, co qu rmo má dl. Ejmplo 6.: U lí d rmó coxl d po G58 á rmd u crg d lor 75 Ω. d coplrl por mdo d u coxl dpdor d λ/4 MH. Clcul l mpdc crcríc y l logud dl dpdor. D l l d l p.6. mo qu 5Ω. mpdc crcríc dl dpdor d r: 93. 5Ω corocrcuo D l l d l p.6. qu l cl po G6 A/U l mpdc dcud. locdd d propgcó f.85c. logud dl dpdor oc : λ m 4 4 f Ejmplo 6.3: lc l dpcó dl Ejmplo pro udo u u corocrcudo d l mm lí. cuco d dño o: d / π f π f Ju C. Frád - Dprmo d Fíc Fculd d Igrí Urdd d Buo Ar
3 Elcromgmo D l l d l pág. 35 pr l cl G58: 5Ω, f.66c y oc: d / 3. 4m 3. 9m π f π f Num co l dpcó fuco u úc frcuc, porqu lo prámro d dño o proporcol l logud d od l lí l frcuc d dpcó. cm frcuc d cmr l logud dl u y u pocó. logud pud modfcr co cr fcldd, colocdo u corocrcuo mól l xrmo d crg, pro l pocó dfíclm rl. mrgo, u do o má u pol rr l frcuc d dpcó cmdo úcm u logud. Cr d mh mpdc d od rl l mpdc crcríc pud crr: ϕ ϕ w E cucó dl po: dod r x y w u. w Tl cucó cooc como u rformcó ll pud dmorr fáclm qu w y crcr porqu l lí d r co o l lí d x co rul crcufrc l plo w. Como l dgrm complo hll dro dl círculo d rdo uro. Podmo dmorr qu l form d l cur d d r co o x co o crcufrc: u u u u Prmo d: r x u u u ugo: d dod: complmo cudrdo: u r u x u u r r u r u r r u r r r r u u r r r r u r r r y flm: [ ] d dod qu l lí d r co o crcufrc d rdo / r y crd l puo r / r. mé qu l círculo pr r l cucó u y cocd co l círculo xror d l cr y qu l círculo pr r l cucó [ u ] y cocd co l puo,. Aálogm, d l cucó pr x: x u u u x x x x y flm: [ ] [ ] u / x / x r, por jmplo,. Nl r, í d Trmó, McGrw-Hll Irmrc, Méxco,. 99, pp. 8 y poror. Ju C. Frád - Dprmo d Fíc Fculd d Igrí Urdd d Buo Ar
4 Elcromgmo d dod qu l lí d x co o crcufrc d rdo / x y crd l puo,/ x. Pr x l rdo hc fo y l cur cocd co l j rl. Pr x l cucó [ u ], qu um cocd co l puo,. E dgrm lo j u, rpr l pr rl mgr dl compljo ϕ mr qu r [/ ] lor ñldo or l j horol y x Im[/ ] lor ñldo or l círculo xror o lo lor, ormldo l mpdc crcríc d l lí, d l pr rl mgr d l mpdc d od. Por cocó, l águlo ϕ dl for md dd l j rl poo do horro. rr l pocó or l lí mplc cmr l águlo d f dl compljo u,, lo qu mplc grr lr- λ hc l grdor ϕ, ϕ τ 5 ddor dl cro dl dgrm co co porqu dpd d l mpdc crcríc y d crg, pro o d l pocó l lí. - 5 λ hc l crg O Como lo águlo um cocolm l do horro, u y l do poo d l coordd hc l crg, u gro horro rpr u momo hc l crg, y l gro horro u momo hc l grdor. El círculo.5 xror dl dgrm prm mdr o dplmo, clrdo logud d od. El cro d dplmo coloc or l j rl go. Ddo qu md dfrc d logud l pocó lo lrgo d l lí rpco d l pocó d l crg o mpor dód pog l cro. cr d mh u pr clculr mpdc d rd, OE, cofc d rflxó y oro do ólo co u rgl y u compá, ur fuco rgoomérc o hprólc, lo qu fcl lo cálculo. Auqu hmo dducdo u cuco pr lí pérdd rl, pol xdr u uo lí co j pérdd. E l fgur mur u cr ádr rcho MITH.PDF. plcco d cálculo ác d l cr d mh lí pérdd o: Dd or Dd or Ddo y or y Ddo y or y Hllr poco y lor d máxmo y mímo d ó or l lí. Ju C. Frád - Dprmo d Fíc Fculd d Igrí Urdd d Buo Ar
5 Hllr l OE. Dd or Y Dd Y or Ejmplo d uo d l cr d mh Elcromgmo oprcó ác co l cr d mh co ucr u mpdc, como xplc l gu jmplo: Ejmplo 6.4: Ucr or l cr d mh l gu mpdc: U rc A 5Ω. U rcc duc X B Ω. c U rcc cpc X C -5Ω. d U 5 mpdc r D 5 Ω. U crcuo ro E. f U corocrcuo F. Ur como mpdc d ormlcó l lor 5Ω. B A A / A / 3 A D B B / X B /. B F O A E u 5 c C C / X c / C d /.3. D D D E E / E f / F F F - 5 C - Ejmplo 6.5: U lí d 5Ω á rmd - por u rc d 3Ω - r co u rcc cpc d 4Ω. Hllr: y OE, l mpdc d rd l logud d l lí. λ y c lo lor d logud d lí qu ll u mpdc d rd purm r y lo lor d mpdc. Pr ulr l cr d mh prmro xprmo l mpdc d cr- 5 g ormld l mpdc crcríc: y oc mrcmo l cr d mh l puo A l rccó C O D u d lo círculo r.6 y 5 B x -.8. l /λ A dc dd A l cro dl dgrm d.5 y l prologcó d gmo h l círculo d águlo xror d ϕ 9 ro gro. - 5 ϕ -.5 Admá OE l /λ Podmo cr l lor d OE d l cr d mh. Como dpd olm d, u crg r pur co l mmo drá l mmo OE. Ju C. Frád - Dprmo d Fíc Fculd d Igrí Urdd d Buo Ar
6 Elcromgmo Como pr > : OE y l lor dl OE cocd co l rc ormld qu d l mmo lor d. u hcho y r l cr d mh l rco d crcufrc crd l cro dl dgrm h l j x pr r >. El lor odo d r l cruc D 3 gul l OE ro rd. Pr clculr l mpdc d rd ucmo l pocó dod l rdo dl dgrm qu p por A cor l círculo prmrl mrcdo hc l grdor. ul l/λ.375. E u lor d prd rrro. hor o dplmo hc l grdor l do horro or l círculo d c. dpd olm d l crg y.λ, d curdo l ucdo dl prolm, drmo: l/λ El puo B í odo r.34 y x.4, o 7 7Ω ro ul. c Flm, l logud d l lí co mpdc d rd r corrpod lo puo d rccó or l j rl x d l crcufrc qu p por A, rcorrd l do horro. El prmr puo d cruc l C prdo dl A λ/4y lugo l D prdo dl C λ/4 ro ol. Cr d dmc Ddo qu l dmc Y / fc l mm cuco qu l mpdc d od, l cr d mh mé u dgrm d dmc ormld Y /. rformcó ll : ϕ ϕ ϕπ π Y w y ϕ ϕ ϕπ π Y w qu l mm cucó d l cr d mpdc, pro prc u águlo d f d π mulplcdo l compljo w. Por llo, u puo d l cr d mpdc á or l círculo d co.5 prdo 8 π dl puo corrpod l mm cr mdd dmc. Por or pr, l A cl o gul, d mr qu dod l rc rcc l cr d mpdc d lr coducc ucpc l d dmc. B F A D C O.5 A O C A - D E B u u E l gu jmplo u l cr d mh pr pr d mpdc dmc l co d l crg dl Ejmplo 6.4. Ejmplo 6.6: Ucr or l cr d mh l gu dmc: U rc A 5Ω. U rcc duc X B Ω. c U rcc cpc X C -5Ω. d U mpdc r D 5 Ω. U crcuo ro E. f U corocrcuo F. Ur como mpdc d ormlcó l lor 5Ω. y A YA / Y / G A / 3 A y B YB / Y / X B 5 B c yc YC / Y / X c C d y D YD / Y D / E E E f Y /Y F F F Ju C. Frád - Dprmo d Fíc Fculd d Igrí Urdd d Buo Ar
7 Elcromgmo Or poldd d rprcó d dmc Y grr odo l dgrm π, lugr d grr cd puo, co lo qu o u cr d dmc como l d l fgur. A l qurd mur u cr d mh dod duj lo círculo d mpdc rojo y d dmc ul mulám. E co o cro grr π l pocó dl puo pr pr d u cr l or, o qu co ur lo círculo dcudo rcho MITHY.PDF. E l gu jmplo dñ u u prllo d dpcó udo l cr d mh como cr d mpdc y lugo como cr d dmc. Ejmplo 6.7: Ur l cr d mh pr dñr u u d dpcó r u lí d Ω y u crg rl 5 Ω. mo ur l cr d mh d mpdc. mpdc d crg ormld : / 5 5 B - 5 d O - 5 C D - Ju C. Frád - Dprmo d Fíc Fculd d Igrí Urdd d Buo Ar gr l cr puo A. r u círculo uxlr cocérco co l cr qu p por A. E círculo l cur d y OE co. Pr dpcó dmo pr d A O, l cro dl dgrm, dod. Como mo colocr u u prllo co l lí prcpl, o co rjr co dmc. Pmo oc d A l puo corrpod B 8, dod l dmc ormld y.. Pr ucr l u o momo por l círculo d co do horro hc l grdor h llgr l círculo d dmc rl ormld gul qu cocd co l círculo d mpdc ormld gul - puo C. Pr dpcó ólo rqur grgr u ucpc prllo d lor opuo l ucpc d C. dc d.83 λ logud d od mdd or l círculo xror d l cr r lo rdo qu p por B y C l dc dd l crg l qu hy qu por l u. Pr hllr l logud dl u, or qu l mpdc ormld C y C.79, d mr qu l u d prr u dmc d rd qu ul l pr mgr: y El u corocrcudo pr u dmc d rd purm rc: l l Y l Y co l. A u
8 Elcromgmo gr co h lcr l círculo d coducc ormld ur C. md or l cl d logud d od l pocó dl u, como. ugo uc l puo D, qu url l mpdc d rd d l lí l puo d coxó dl u y md l logud cr dl u. Nurlm lo lor odo o lo mmo qu l coruccó pr. Ejmplo 6.8: Ur l cr d mh pr dñr u dpdor d curo d od r u lí d Ω y f.87c y u crg 5 Ω MH. E u co dod l uo d l cr d mh mucho má cllo qu l rolucó líc. E l ccó d dpcó mo cómo dpr u crg rl u - lí d mpdc crcríc rl, pro co mo u crg d mpdc complj. olucó co rclr l dpdor u dc d l crg, d mr qu l mpdc d rd dl cojuo lícrg rl, como mur l fgur. drmcó d pocó complc mmácm d rolr l prolm lícm, pro muy fácl co l cr d mh. 5 Commo clculdo prmro l mpdc d crg ormld: /.5.5 El lugr gomérco d mpdc mdd qu cm l l círculo xror d rdo uro qu corrpod r. Ucmo oc l puo D qu df l dmc d rd dl u or l cru- D c dl círculo d ucpc -.79 co l círculo xror, y mddo.5 or l círculo xror l dc dd l puo d dmc ormld f codcó d corocrcuo - j rl poo o.8 λ qu l logud mím rqurd dl u. rj co l cr d dmc, pr dd B y. y O B u C O B - 5 A d u y drmmo l puo A l cr. Culqur pocó l lí rá or l crcufrc crd l cr y qu p por A. Pr hllr l pocó dod d rclr l dpdor d curo d od, o momo dd A hc l grdor do horro h l prmr cruc co l j rl. Eo ocurr l puo B. Podmo lr l cl xror l logud dl rco qu o d l pocó dd pr l dpdor, y dl j rl l mpdc rl - puo, qu rá l mpdc qu - hy qu dpr l lí. Ju C. Frád - Dprmo d Fíc Fculd d Igrí Urdd d Buo Ar
9 Elcromgmo E uro co: d dod: f.56λ.56 f Ω.73m.83 83Ω λ f 3.6 m 4 4 f Aplccó crcuo d co cocrd cr d mh o ólo plcl crcuo co lí. pud ur pr dñr crcuo cocrdo co l mm mplcdd, como mur lo gu jmplo. Ejmplo 6.9: Drmr l mpdc d rd dl crcuo d l fgur. Do: 5 Ω, 5 Ω, 8 µhy, 6.5 µhy, C 3 F, C 5 F, f MH. Pr ur l cr d mh dmo ormlr l mpdc dl crcuo u lor rrro. E l co d l C lí lgmo l mpdc crcríc. E co lgrmo l lor d l rc. Agmo cd lmo l lor d u mpdc ormld l frcuc d rjo: C r r /.3 x / x 3.33 C x4 / C.6 5 C x.64 B' A C' O 5 D' C D Ju C. Frád - Dprmo d Fíc Fculd d Igrí Urdd d Buo Ar 5 Co o lor ucmo prmro l mpdc r A rx l cr d mh puo A. El gu po co hllr l mpdc rul dl prllo d co x, pr lo cul dmo rformr m mpdc dmc: A y A.5- puo A' x / x. 3 dmc rul dl prllo d y A' y pud hllr l dgrm d B mh moédoo or l círculo d coducc co.3 l do - 5 d dmc dcrc porqu - g o l do opuo l - guj dl rloj. lgmo l puo B [y B ]. Como l gu lmo comr r, olmo l dgrm d mpdc [puo B' : B.56.9 ]. Agrgmo hor l mpdc r x 4 pr lo cul o momo or l círculo d rc co l do horro d rcc dcrc porqu x 4 g h llgr l puo C: C Flm grgmo prllo l r d y C : C , qu corrpod u dmc y C Pmo l dgrm d dmc: C C' y C y grmo prmro or u círculo d coducc co.68 y lugo or u círculo d ucpc co 3.9, pr llgr l puo D y D Flm rmo l puo pr olr l dgrm d mpdc y llgmo l puo fl D' : D Ω. o lor umérco qu prc l xo l d l cr y lo lor rmdo o rqur pr l ruldo y h ddo olm pr rfrc. u
10 Elcromgmo Ejmplo 6.: Dñr u crcuo d dpcó r u grdor d mpdc r g 5 Ω y u mpdc d crg 5-3.Ω l frcuc d rjo. Pr dpcó rqur qu l mpdc d rd gul l mpdc dl grdor g. g Ucmo l cr d mh l mpdc dl grdor y l g mpdc d crg ormld g : g O A. 5 Pr pr d A O podmo r por ro cmo. Elgmo l cmo d l fgur dod mo prmro do horro or l círculo d rcc co h lcr l círculo r, y lugo por círculo h l puo O. Eo mplc grgr u mpdc r : Ω, qu u olucó rl dl prolm. 5 A O u E olucó u rpu frcuc dl po d u pjo. E pol or or oluco d dfr rpu frcuc modfcdo l cmo dd A hc O, lo qu mplc lgr oro crcuo d dpcó Ju C. Frád - Dprmo d Fíc Fculd d Igrí Urdd d Buo Ar
11 Elcromgmo í ro Admá d rmr rgí formcó d u puo oro, l lí pud ur como lmo d crcuo, fudmlm por u propdd d logrr culqur mpdc d rd fucó d u logud y u crg. E ucó muy comú l culdd, qu gr lí d rmó o guí d od chp pr mcrood. E prculr, l poldd d r od cor ll qu l lí pud ur como crcuo ro o odo. Codrmo prmro u lí upum dl corocrcud mo xrmo. El grdor coloc lgú puo rmdo qu codrrmo má dl. od cor d ó y corr l lí o:,, co co mo xpro fc l codco lo xrmo d l lí. ó ul or l xrmo d crg pro d mé ulr or l xrmo opuo -l. Eoc: λ c l l π l l f f C lo qu gfc qu, pr u dd frcuc d xccó, l logud d l lí o pud r culqur, o olm lguo d lo lor dcro l. cr, pr u lí d logud y prámro ddo, ólo pud lcr od co u cojuo dcro d frcuc: l f f C l C U lmo crcul o u crcuo qu lcco frcuc u crcuo ro o odo. Pr plccó pud ur lí qu hulm corocrcu mo xrmo pr mmr l rdcó d rfrc. Ahor podmo lr l pocó dl grdor qu lm l lí. upomo qu u grdor d ó dl mpdc r ul, y podmo colocrlo l pocó d u odo culqur d l od cor: π m - m m m 4 f C dod om lor go d m por l cocó d colocr l org d coordd or l crg. Eoc qud dfdo l lor d :, dod l ó dl grdor. l m Ergí y Q rgí lmcd l lí, qu á ocd u compo rco, pud clculr pldo l modlo crcul. Cd d d lí u ducc d y u cpcdd Cd. rgí lmcd o lmo : du, C, d C d co co Eoc: du C co co d Ju C. Frád - Dprmo d Fíc Fculd d Igrí Urdd d Buo Ar
12 Elcromgmo y omdo l promdo mporl: < du > C co d C d 4 Flm, grdo od l lí: < U > C l 4 Codrmo hor u lí co pérdd. l pérdd o j, como l co l myorí d l lí comrcl, podmo upor qu l drucó d ó y corr o rá muy dfr qu l co dl, y podmo clculr l poc prdd pr cd rmo d d l lí como: dw d, Gd, G d co co G y omdo l promdo mporl: < dw > C co d C Igrdo od l l: G < W > C co d d l C l y como π /l : π G π < > G W C co d d < W > C l l l C l l 4 C U crcuo ro como mó lmcr rgí. Cuo myor o l pérdd mor l cldd dl crcuo como ro. E crcríc ul mdr por l llmdo fcor d cldd o fcor d méro: Q π rgí mdlmcd poc md dpd por cclo < U > π < W > / f < U > < W > Udo l xpro qu hmo hlldo: C l < U > 4 π Q Q < W > G G C f G f C C l 4 C or qu pr u lí d j pérdd Q >> y qu l co cd érmo dl domdor mucho mor qu. frcuc qu prc l xpró d Q u d l pol frcuc d roc f dl crcuo, y l lor d Q clculdo corrpod frcuc. E roc, l grdor upum cocdo u odo d l ó u mpdc f cudo l lí dl. Cudo hy pérdd, l poc prdd d r umrd por l grdor, d mr qu l mpdc qu l grdor d r hor f y rl y d lor l qu l poc qu l grdor l umr gul l poc dpd l lí. Podmo clculr í l rc d rd roc d l lí por l grdor: G 4 4Q < W > C l d dod 4 C C G C λ C y flm o qud, fucó dl Q d l lí: λ Q π Ju C. Frád - Dprmo d Fíc Fculd d Igrí Urdd d Buo Ar
13 Acho d d Elcromgmo Podmo lr l compormo frcuc lrddor d l roc codrdo hor qu rmo lgrm l frcuc dl grdor rpco d u d l frcuc d l l roc dl crcuo. Pr lr l ruldo d rcó d frcuc, l crcuo pud pr como u grdor cocdo do lí prllo y corocrcud u xrmo d crg. logud d cd lí o, rpcm, l y l. E roc, logud o múlplo mpr d λ/4 y l mpdc d rd dl prllo d m lí, pro dj d r lor fur d roc. Como r d lí corocrcud d j pérdd, fur d roc u mpdc d rd o fudmlm rc, por lo qu l gu ál dprcmo momám l pr r. Como l do lí á prllo, co rjr co l dmc ucpc. E roc: [ β l co ] / / B Y co β l Fur d roc podmo crr: β / c δ / c dod u d l frcuc d roc y δ<< rpr u corrmo rlo d frcuc. δ π π ugo: β l l β l δ δ y álogm: β l δ c ugo mo: π π B Y co δ co δ π π π Pro pr mpr: co δ δ δ π π π δ y oc: B Y δ δ Y Flm, corpordo l rc d rd, l dmc qu l grdor fur d roc, proxmdm: π Y π δ π π Y / B Y Y δ Y Q Q Q π y oc: Y Y Q π Q grfcmo l módulo d l mpdc d rd fucó d l frcuc omo l clác cur d roc: El lor mímo d dmc o l máxmo d mpdc d rd d pr l roc : π Q Y Y m MAX Q π y l rc d rd y clculd. Dfmo l cho d d r l do frcuc mo ldo d l roc pr l cul l mpdc d rd c / d u lor máxmo, o lo qu lo mmo, l dmc d rd c l lor mímo: Ju C. Frád - Dprmo d Fíc Fculd d Igrí Urdd d Buo Ar
14 Elcromgmo πy πy Y m Q Q Q Q Y y flm: ± d dod: Q / f / f Q Q Podmo orr qu frcuc l pr rl y pr mgr d l dmc d rd o d l mpdc d rd o gul. cucó hlld cul lo r prámro fudml d l roc: l frcuc d roc, l cho d d y l Q. Ejmplo 6.: U lí d prámro. µhy/m, C 3 F/m,. Ω/m, G --4 /Ωm u como crcuo odo. Hllr l mím logud pr r u frcuc d roc d MH. Drmr l pol poco d l rd l crcuo. c Clculr l Q, l mpdc d rd roc y l cho d d dl crcuo odo. frcuc d roc o: f l m l 6. 35cm l C f C poco d lo odo, pol poco d rd l crcuo, o: m m m / l l / 3. 7cm 4 f C y qu ólo pud omr m. πf Q Q 5386 c.68 KΩ / G / C π f Ω f.86h 6.3 G C Q or qu l cho d d muy jo comprdo co l lor d l frcuc crl, lo qu oc l lo lor dl Q. Ejmplo 6.: U rmo d coxl G u pr crr u crcuo ro MH. Hllr l logud cr dl cl, l Q, l mpdc d rd roc y l cho d d dl crcuo odo. D l l d l p.6., lo prámro dl coxl G o: Dámro /c C α MH mm Ohm pf/m db/m logud mím dl crcuo odo : Como: πf Q / y α π f π f Q α α Q 9.5 KΩ π f f.5 MH Q l m f C f Ju C. Frád - Dprmo d Fíc Fculd d Igrí Urdd d Buo Ar
15 Troro lí Elcromgmo E muy comú l uo d lí d rmó pr propgr pulo qu codfc formcó. U r pródco d pulo pud rprr md u r d Fourr qu u uprpocó d od rmóc u pulo o pródco rqur u grl d Fourr, qu mé rpr u uprpocó d od rmóc. E pol oc lr l proco pr cd frcuc y flm uprpor lo ruldo, y qu l cuco dfrcl qu dcr l compormo d l lí d rmó o ll. E ál hc oc l domo d l frcuc. mrgo, mucho co má ruco lr l compormo d l ñl compl dcomporl por Fourr. E ál hc l domo dl mpo, y l qu mo ur ccó. -l Eoc l corr pr -l, -l, I /. Codrmo u lí pérdd qu coc u rí d mpdc r r u rc d crg. E l crr l rrupor qu coc l grdor l lí. od cl o d rrqu olm l r d y. : I-l, I / y l ó cl : Dpué d crrr l rrupor l od I y propg hc l crg co l locdd c / C. Como locdd f, l fr d c od rd l / c llgr l crg rccor co ll. E momo l ó y corr l crg rá l uprpocó d l od cd y l rfljd:, I, I dod l cofc d rflxó l crg. od rfljd - I y - j hor hc l grdor l od cd gu propgádo dd l grdor hc l crg. E l l od rfljd llg l grdor, dod l u ddpcó d mpdc cr u u od rfljd progr: l, dod I I I I l, l cofc d rflxó l grdor. E u od progr j hc l crg, dod llg pr 3, l qu gr u u od rgr: El proco d rflxo múlpl pud r má fáclm md lo dgrm d ro o dgrm d mll d Bwly, qu mur coucó: Ju C. Frád - Dprmo d Fíc Fculd d Igrí Urdd d Buo Ar
16 Elcromgmo l -l I clrm cómo form cd r d érmo qu drá l lor fl d l ó y l corr or l lí dpué d lo múlpl ro. lo lo co d grdor dl y crg corocrcuo o crcuo ro, qu produc oclco prm, como ló l ccó pr, como < cd érmo mor qu l prcd y l r flm corg u lor lím. mo lr l form d od qu o cudo coloc dr mpdc d crg. Ejmplo 6.3: lc u dgrm mporl d l ó y l corr or l grdor y l crg pr u lí d 5 Ω, cocd u grdor d ó d co rc r Ω. mpdc d crg crcuo ro. mplud d l od progr qu j por l lí lugo d crrr l rrupor o I. 67 A o cofc d rflxó o:. 667 Ju C. Frád - Dprmo d Fíc Fculd d Igrí Urdd d Buo Ar lmo l r qu dcr lo dgrm d Bwly pr or l gu gráfc o y corr A: or qu l ó y l corr l rd d l lí ocl ddo u lor fl, l,, qu corrpod l do coro d corr cou dod y o hy od jr l lí. lí codco u -, I-,, I,
17 Elcromgmo corocrcuo y l ó fl or l crg l mm qu l ó d rd gul l ó d l fu porqu o crcul corr por r l crg crcuo ro. corr or l crg mpr cro, como d r, y l corr l rd d u lor fl cro. Ejmplo 6.4: lc u dgrm mporl d l ó y l corr or l grdor d l lí dl jmplo ror pr Ω corocrcuo. o cofc d rflxó o:. 667 I lo mmo lor qu l Ejmplo pro. o dgrm mporl rul hor: 5 ó l ld mpr cro, por l corocrcuo, mr qu l rd d u lor lím ulo d corr cou. corr d mo xrmo d l lí u lor lím d cou qu l I, I l, / A A mpo fo, y o hy od jr por l lí y é compor como u corocrcuo por l qu crcul corr cor. D o jmplo or qu, l co d crg crcuo ro, l ó l xrmo dl grdor ocl lrddor dl lor lím d cou l ó dl grdor mr qu l co d crg corocrcud l ó d rd d moóom cro. mo hor qué ocurr co u mpdc d crg r f. Ejmplo 6.5: lc u dgrm mporl d l ó y l corr or l grdor d l lí dl jmplo ror pr Ω. o cofc d rflxó o: I lo mmo lor qu l Ejmplo pro. o dgrm mporl rul hor: 5 5 -,, ,, o lor d ó y corr d u lor lím d corr cou: I, I l, / 47. ma y, l, I, Ejmplo 6.6: lc u dgrm mporl d l ó y l corr or l grdor d l lí dl jmplo ror pr Ω. o cofc d rflxó o: I lo mmo lor qu l Ejmplo pro. o dgrm mporl rul hor: I-, I,.67 I-, I, Ju C. Frád - Dprmo d Fíc Fculd d Igrí Urdd d Buo Ar
18 Elcromgmo ,, I-, I, o lor d ó y corr d u lor lím d corr cou: I, I l, / 33. ma y, l, I, < l dc d ó y corr u lor fl moó- E co o, mr qu l co pro > l dc r ocl. E o do úlmo jmplo or qu < l dc d od l rl grfcd moóo hc u lor fl, mr qu > l dc ocl. Crg complj Hmo ldo l compormo d crg r. Cudo l crg u mpdc complj l dpdc mporl d lo fr d od modfc. Codrmo por jmplo u lí d mpdc crcríc rl rmd u mpdc d crg, l qu coc u rí l rd pr. El fr d od d ó j co l locdd d propgcó l lí h qu llg l crg. crg mpo l rlcó r ó y corr y gr í u od rfljd, por l ddpcó d mpdc co l mpdc crcríc d l lí. Podmo or l form d od d l od rgr uldo écc d d l rformcó d plc. lugr d rjr co l o y corr como fuco dl mpo codrmo u rformd d plc:,,, I, ± ± ± ± oc podmo crr pr l cofc d rflxó:,, Ρ, Ξ, Ξ Ξ, Ξ dod Ξ l rformd d plc d l mpdc d crg y / l rformd d plc d l fucó cló qu rpr l od progr. E xpró r um por plc pr hllr l xpró l mpo d l od d ó rgr. Ejmplo 6.7: Hll l od d ó rgr cudo l mpdc d crg : u r ; u r C; c u prllo ; d u prllo C. E co: Ξ Ju C. Frád - Dprmo d Fíc Fculd d Igrí Urdd d Buo Ar Ξ y:, Ξ / τ dod τ. rformd d xpró : / / τ, u co qu pr, y l ó or l crg l dl ro duplc l d l od cd, porqu l ducc r
19 Elcromgmo mpd l úo crmo d l corr, qu oc clm cro codcó d crcuo ro. E co: Ξ C / Ξ / C y:, Ξ / C / τ dod τ C. rformd d xpró : C / τ, u co qu pr, y qu l cpcor clm u corocrcuo y l ó or l crg dpd olm d l rlcó /. c E co: Ξ // / / Ξ y:, Ξ / τ dod τ. rformd d xpró : / / τ, u co qu pr, y qu l ducc clm u crcuo ro y l ó or l crg dpd um d l rlcó /. d E co: Ξ // C / C C Ξ C y:, Ξ C / τ dod τ C. rformd d xpró : / / τ, u co qu pr, y qu l cpcor clm u corocrcuo y l ó or l crg d ulr. form d od d l od rgr cd uo d o co rpr l gu fgur, dod r /.5,,. - / r.5 r r - / /τ /τ Ju C. Frád - Dprmo d Fíc Fculd d Igrí Urdd d Buo Ar
20 Elcromgmo / - / /τ /τ c r.5 r r d E od j hc l rd dd l mmo qu gr. dr form d od qu o cudo l mpdc d crg o r pur prm cr cocluo dl po d mpdc d crg y d org plcco écc. E lo jmplo prcd cocó u rí l lí. Dd l puo d mmáco uó u fucó cló pr dcrr l propgcó d l od l lí. Hulm lugr d r u cló í u pulo f h por l lí. Podmo ur lo ruldo odo y qu l pulo qul do clo prdo l cho mporl dl pulo y d mplud gul y d go opuo, como mur l fgur: h f h h τ. Pr lr l compormo d l propgcó d pulo u lí d rmó, dmo comprr l mpo d j lo lrgo d l lí co l cho dl pulo. l cho dl pulo mucho mor qu l mpo d j l pulo m u dd l propgcó y l form d od od l jmplo pro o plcl. l cho d pulo comprl co l mpo d ráo l prolm complc, pclm cudo hy múlpl ro, y cro u cálculo por compudor. Hwl-Pcrd Applco No 34-, Tm Dom flcomry Thory, 988 HP-AN34.PDF. Ju C. Frád - Dprmo d Fíc Fculd d Igrí Urdd d Buo Ar
21 Elcromgmo APICACION: TD El compormo d l propgcó d pulo por u lí d l d u méodo d ál d crg lí d rmó, l rflcomrí l domo dl mpo TD. E écc r u cló o u pulo dd l xrmo dl grdor dpdo l lí o hy ro l rd y orr l form d od. E l foo d l pll d u oclocopo qu gu pr u co d crcuo ro y oro d corocrcuo l xrmo d crg, co u grdor práccm dl : écc prm hllr l logud d lí r l puo d orcó y l o dod produc l rflxó por ddpcó d mpdc mddo l rlo / qu rd cmr l lcur y l mpdc dl puo d ddpcó mddo l lur dl lo [ ] d dod pud clculr y por lo o coocdo. E écc pud ur pr: coocdo l po d lí, clculr u logud. dj l xrmo d crg crcuo ro y md l rd l mpo qu rd l pulo ro. ugo: /. coocdo l logud, clculr lo prámro d l lí. crg l lí co u mpdc r coocd. locdd d propgcó clcul prr dl mpo d ro: /. lí codr d pérdd dprcl rl. Como o hy ro l rd, l ó ll : Er or plcco, écc prm dcr fll lí d rmó muy lrg mddo dd u xrmo o u puo co. í u pulo y or l form d od. rgr ro ñl d qu hy u ddpcó d mpdc. El mpo d ro d l pocó d l prmr dcoudd. form d od d l po d ddpcó y prm frr l po d fll. El ál d lo jmplo prcd pud xdr múlpl puo d ddpcó. Hy procdmo m-uomáco d dccó d fll lí muy lrg qu u dmá m d GP pr l loclcó gográfc 3. 3 Hwl-Pcrd Applco No 85, Trlg W Ful oco Powr Trmo ym, 997 HP-AN85.PDF. Ju C. Frád - Dprmo d Fíc Fculd d Igrí Urdd d Buo Ar
22 Elcromgmo EUMEN E Cpíulo prmo l écc ác d dpcó d mpdc r u lí y u crg culqur: El rformdor d curo d od coloc r l lí y l crg polm u dc pr qu l mpdc qu l rformdor rl y cumpl l cuco: Ju C. Frád - Dprmo d Fíc Fculd d Igrí Urdd d Buo Ar λ 4 E dpdor fuco olm l frcuc d dño. El u u roo d l mm lí qu coloc prllo co l crg u dc dfd. El roo o u pud rmr d dr form. mo olm l form má comú, qu l corocrcuo. cuco d dño d l pocó y logud dl u y o: -d λ d π / λ π cr d mh prm or oluco gráfc d prolm d uo d lí d rmó. l propdd d l cuco d l mpdc y dmc λ hc l grdor ϕ, ϕ τ d od lo lrgo d l lí: w u ϕ / rx O u w/ -w cr d mh pr círculo d r co rojo, círculo d x co ul y círculo d co ol. Al mor l lí l mpdc ormld rí or u círculo d co. 5 cr d mh prm clculr co fcldd odo lo prámro d u lí crgd y l λ hc l crg dpcó md rformdor o u. U lí dod x od cor compor como u crcuo ro d lo Q, co l gu crcríc: Frcuc d roc f l C corocrcuo Q Q y cho d d G C f pró u roduccó l compormo d lo roro l lí, dod cu l propdd d propgcó d pulo lo lrgo d l f
23 Elcromgmo lí. Eo d u r d poldd écc, d l cul l má comú l rflcomrí l domo dl mpo TD qu prm or l pocó y crcríc d mpdc d dcoudd l lí. E écc u, por jmplo, l dccó rmo d dfco lí d l ó y crcrcó d prámro d lí mcrorp. Iroducmo u Apédc l d rlcod co l dcrpcó d crcuo md l llmd mr d dpró y or dcrpco mrcl qul, qu o d much uldd pr lr l propgcó d od rucur complj d gudo dd u puo d crcul. Almo d l mrco d l dcrpcó d l propgcó d od lí. Ju C. Frád - Dprmo d Fíc Fculd d Igrí Urdd d Buo Ar
24 Elcromgmo APENDICE 7: Mr d Dpró Mucho m qu propg rgí formcó pud codrr como u cojuo d 4 4 puro por lo qu r y l ñl qu rpor l rgí formcó. Ex u méodo grl d dcrpcó d m ll d -puro, cudo pol lcr u rlcó ll r l ñl d rd y ld. E méodo, llmdo d l mr d dpró, plcl u gr úmro d m po y co y d mucho uo l dcrpcó d crcuo d mcrood. [,,, ] T l cor d rd y [,,, ] T l cor d ld. Eo cor á lgdo r í por l llmd mr d dpró:. o lmo j d l mr á rlcodo co do prámro qu dfmo coucó. Dcmo qu u puro u ld dpd cudo á cocdo u mpdc d crg qu o produc od rfljd qu co d xr courí u od cd or l puro. Por jmplo, l puro u ld dpd,. Aálogm, l puro u rd dpd cudo o x od l dl puro. E l co, pr puro. upogmo u m dod odo lo puro, lo l prmro, u ld dpd. Eoc >. cuco l dcrpcó d l mr d dpró rduc :,,..., d modo qu u cofc d rflxó dl prmr puro mr qu lo > o cofc d rfrc d ñl qu lg l rd l prmr puro co l ld lo oro puro. lo cooc como gc o pérdd d rcó, gú qu u módulo myor o mor qu. ul í qu lo cofc dgol d l mr d dpró o cofc d rflxó dl puro cuó y lo cofc fur d l dgol prcpl j o cofc d rfrc o rcó r do puro. Mucho m fc mé l codcó d rcprocdd: j j. E codcó gfc qu l rfrc d ñl r lo puro y j mérc o rcíproc. Dd l puo d d l poc o rgí qu propg r lo puro, podmo dcr qu, grl, pr ñl rmóc l poc md qu gr cd puro poc cd proporcol, mr qu l poc md qu l d cd puro poc rfljd proporcol. Por lo o, l poc md qu gr cd puro proporcol. Almo um l co dod odo lo puro, lo l prmro, u ld dpd. E l co,. > l m o pérdd gc d poc, od l poc qu r d lr, mr qu hy pérdd l poc qu l d r mor qu l qu r, d mr qu pr u m po: 3 Ju C. Frád - Dprmo d Fíc Fculd d Igrí Urdd d Buo Ar
25 Elcromgmo qu cd umdo rpr l frccó d poc cd l m qu propg cd puro. mo jmplfcr m d y puro pr lí d rmó. Puro d Pr jmplfcr l co d u m d u úco puro, codrmo u rmo d lí d logud d cocd u mpd- c d crg. upomo qu l lí dl pérdd d mpdc crcríc rl. rd l rmo d lí l úco puro. Dfmo, como coumr l lrur, l ñl l puro como: dod o l ó y l corr l puro. Podmo rlcor cdd co l od d ó y corr l lí d l form: d d d d d d [ ] [ ] d d d d d d [ ] [ ] d modo qu: d d d [ ] d d d d d [ ] d d ugo l rlcó d dpró : d dod pud r qu u cofc d rlxó, lo u fcor d f. Tmé qu. E cudo hy rflxó ol crg o. mpdc l puro úco : rd d l lí. d d qu l mpdc d Puro Hmo dopdo u modlo d cudrpolo d u lí d rmó pr hllr l cuco dl lgrf y, prr d ll, lr l propgcó d od l lí. E grl, pol dcrr l compormo d l lí érmo d l mr d dpró modládol - como u cojuo d cudrpolo - - ccd. Pr l -émo lmo dl cojuo dfmo u od cd y u od rfljd y l djudcmo u mpdc - crcríc. Codrr qu l mpdc crcríc rl lmo lmo d l ccd o prm lr m o uform corporr dpoo rmdo como copldor, flro, c. d Codrmo uo d lo cudrpolo como u rmo d lí dl d mpdc crcríc y logud d. El puro má crco l crg hll l pocó. Dfmo Ju C. Frád - Dprmo d Fíc Fculd d Igrí Urdd d Buo Ar
26 Elcromgmo Ju C. Frád - Dprmo d Fíc Fculd d Igrí Urdd d Buo Ar l rl d puro como l co pro 4 : Dd l puo d d l lí d rmó, l od qu cd y rflj or lo puro o: Od cd ] [ ] [ d d Od rfljd ] [ ] [ d d Eoc l rl dl puro o: ] [ ] [ d d y or oc qu: / / / / rl d puro á rlcod r í por l m ll: Pr clculr lo cofc d l mr d dpró umo l écc d dpr l ld o rd d lo puro ucm pr mplfcr l cuco. upogmo prmro qu l puro d ld á dpdo o hy od cd or l ld: Eoc: d d d d d ] [ ] [ ] [ qu l cofc d rflxó d l od l rd y u fcor d dfj roducdo l propgcó d l od progr l puro cudo l ld á dpd. Pr lí pérdd, mr qu lí co pérdd <, y qu l úmro d od oc compljo, dcdo u ucó d l od u propgcó lo lrgo dl puro. E grl, l puro pud corporr u crcuo co qu mplfqu l od cd, cuyo co drmo >. Por lo o, cooc como gc o pérdd d rcó dl puro, dc l fcor qu l puro roduc pr l od progr l propgcó. 4 Nó qu l rfr l od cd l puro -émo. Aí á ocd l od qu l dl puro, qu l od rfljd l puro.
27 Elcromgmo Ju C. Frád - Dprmo d Fíc Fculd d Igrí Urdd d Buo Ar Aálogm, hor upomo qu l rd dl puro á dpd o hy od cd or l rd: y l cuco d dpró qud: d dod: d d ] [ qu l cofc d rflxó d l od l ld quí cro érmo dl cofc d rflxó l crg d l lí y l fcor d dfj roducdo l propgcó d l od rgr l puro cudo l rd á dpd. or dmá qu:. E u codcó grl d lo puro qu cumpl l llmd rlcó d rcprocdd, qu cocpulm pud dfr como l ucó dod l puro d compor d l mm mr pr l propgcó mo do. mpdc l puro d rd : E l co d ld dpd : Aálogm: ou Y pr rd dpd : ou ou ou Alcmo l compormo d rmó d poc. poc md cd rfljd cd puro o 5 : [ ] P [ ] P poc qu fluy hc l drch dl cudrpolo : [ ] [ ] P P P Codrmo l co d ld dpd, dod : [ ] [ ] [ ] P P P l ld á dpd, cdd rá ul o hy pérdd, y qu rpr l poc qu gr l puro d rd mo l qu l dl puro d ld. hy pérdd, l poc qu r myor qu l qu l y l cdd po. Eoc: 5 Oér qu l poc rfljd l rd y l ld o d por í g, lo qu dc qu o poc qu fluy hc fur dl cudrpolo. <P > <P >
28 Elcromgmo El cofc d rflxó d poc l rd : E l co d l ld dpd qud: como pr l m d puro. lcó co or dcrpco mrcl dcrpcó d l propgcó por mdo d cudrpolo y l mr d dpró á ocd or dcrpco. mr d rmó T prm rlcor l od l ld dl cudrpolo fucó d l od u rd. E ur ocó: T T T T o cofc d l mr d rmó á rlcodo co lo d l mr d dpró por l rlco: T T / T / T / mr d rmó má cómod qu l d dpró pr rr u ccd d cudrpolo. mr d mpdc rlco l o lo puro co l corr: I I I I mr d dmc Y l r d : I Y Y Y Y Y Y I Y Y co Podmo rlcor l mr d dpró co l mr d mpdc md l gu cuco: dod j j / o l mpdc ormld l mpdc crcríc dl rmo. E dcrpco mrcl d dpoo y lí d rmó o d mporc porqu pro d u form cll d cocr uco dpoo rolr dll l cuco dl crcuo complo, y prm ulr progrm como l pc pr lr l compormo dl crcuo prr d l dcrpcó mrcl d cd loqu. Ju C. Frád - Dprmo d Fíc Fculd d Igrí Urdd d Buo Ar
29 POBEMA Elcromgmo A prr dl dgrm d mh, hllr l mpdc d rd d u ccó d lí d rmó pérdd d 5 Ω co logud d.λ, rmd u corocrcuo. Comprr co l ruldo líco. [: 36.3 Ω] 6. Empldo l cr d mh, cur l logud mím mro qu d r u lí co Ω, rmd crcuo ro pr qu l rd pr u mpdc d 3 Ω. Codr qu l prmdd rl ε r dl dlécrco d l lí l.5 y qu l frcuc d rjo d 3 Mh. [: 8.8 cm] 6.3 U lí d rmó pérdd, co mpdc crcríc d 5 Ω, á rmd u crg cuy mpdc l 5 Ω. l lí md λ/4, og l mpdc d rd prr dl dgrm d mh. [: Ω] 6.4 U lí d rmó dl, co mpdc crcríc d Ω, á rmd u crg d lor 5 5 Ω. d coplrl por mdo d u dpdor d λ/4, colocdo cr dc d l crg. Clcul l mpdc crcríc dl dpdor y l dc l qu d colocr. [: 83 Ω,.56λ] 6.5 Dd u mpdc 95 Ω, drmr qu dmc corrpod uldo l dgrm d mh. [: Y - m] 6.6 U lí d rmó dl d logud.434λ y cuy mpdc crcríc d Ω, á rmd u mpdc d 6 8 Ω. Clcul l cofc d rflxó, l ró d od cor, c l mpdc d rd y d l pocó dl lor máxmo d olj má crco l crg. [:.6/.6, 4, 69 Ω,.3λ d l crg] 6.7 U lí d rmó pérdd u mpdc crcríc d Ω y á rmd co u crg 8 Ω. d r l rflxo hc l grdor, copldo l lí co u qulrdor rco. Ecur l pocó má crc l crg or l lí prcpl dod d ur l u y og l logud dl mmo. [: l.3λ,.48λ] 6.8 coc u grdor d ó dl u lí d 5Ω,.85c, α c db/m, α d.5 db/m, λ MH. El grdor coloc λ/4 dl xrmo qurdo d l lí. o xrmo d l lí corocrcu. Drmr l xpro d l ó y l corr lo lrgo d l lí. Clculr l poc cdd por l grdor roc. c Clculr l Q y l cho d d d l lí. 6.9 U rí d 3 r co u rc d 75Ω coc ré d u lí d 5Ω y 6m d logud co u crg r d 3Ω. Dujr lo dgrm d ro d l ó y l corr. Grfcr /, I/,. c Cuál o lo lor fl d ó y corr or l crg? 6. p l prolm ror hor l grdor u fu d pulo d prodo T m y cclo úl dl 75%. Ju C. Frád - Dprmo d Fíc Fculd d Igrí Urdd d Buo Ar
CRITERIO DE ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA PARA CONTROLADORES CONMUTADOS
 CRIERIO E ESBII E E OMIIO E FRECUECI PR COROORES COMUOS Jorg Elo Mro Grcí-Sz Crlo Mol prmo d uomác y compucó Uvrdd púlc d vrr 36 Pmplo. mgz@uvrr. Rum E rículo pr u formulcó gráfc d u crro d ldd pr m ll
CRIERIO E ESBII E E OMIIO E FRECUECI PR COROORES COMUOS Jorg Elo Mro Grcí-Sz Crlo Mol prmo d uomác y compucó Uvrdd púlc d vrr 36 Pmplo. mgz@uvrr. Rum E rículo pr u formulcó gráfc d u crro d ldd pr m ll
2 Revisión de los fundamentos
 Rvó d lo udmo mmáco S cb d cr l ror cpíulo qu lo modlo d l pl o proco, rr curo, rá ddo por l cuco drcl ll y d coc co, brvádo co l crómo LI (Lr m Ivr). L drmcó dl compormo dámco dl m upo qu coocd u ucó
Rvó d lo udmo mmáco S cb d cr l ror cpíulo qu lo modlo d l pl o proco, rr curo, rá ddo por l cuco drcl ll y d coc co, brvádo co l crómo LI (Lr m Ivr). L drmcó dl compormo dámco dl m upo qu coocd u ucó
variables aleatorias discretas, la función de probabilidad conjunta del vector aleatorio ( X,..., se define como: ) A
 cors loros. só más d dos dmsos Dcó: S... rbls lors dscrs l ucó d robbldd cou dl cor loro... s d como: ddo culqur couo A R...... P... P... A...... A...... s ucó ssc ls sgus rodds:.................. orm
cors loros. só más d dos dmsos Dcó: S... rbls lors dscrs l ucó d robbldd cou dl cor loro... s d como: ddo culqur couo A R...... P... P... A...... A...... s ucó ssc ls sgus rodds:.................. orm
MODELOS DE ATMÓSFERA (teoría y problemas)
 MODLO D MÓR (or y pro) * PLN IN MÓR * MODLO MÓR NO BORBN * MODLO MÓR ON BORIÓN LIV * BLN D RDIIÓN N L IRR (PROMDIO) * JRIIO * LGUNO PROBLM D XMN RULO * PLN IN MÓR Ddd d po (W - ) Irrd, W ujo d rg d (fu:
MODLO D MÓR (or y pro) * PLN IN MÓR * MODLO MÓR NO BORBN * MODLO MÓR ON BORIÓN LIV * BLN D RDIIÓN N L IRR (PROMDIO) * JRIIO * LGUNO PROBLM D XMN RULO * PLN IN MÓR Ddd d po (W - ) Irrd, W ujo d rg d (fu:
Tema 6. Sistemas muestreados y discretos
 m 6. Sm mrdo dcro. Irodccó:. Ercr d m d corol por compdor. Mro rcorccó d ñl. L rformd 3. Dcrpcó xr d m D.L.I Dcro Ll Ivr l mpo 3. Fcó d rfrc pld 3. Fcó d rfrc d m coo mrdo co O 3.3 Dgrm d loq 4. Rp mporl
m 6. Sm mrdo dcro. Irodccó:. Ercr d m d corol por compdor. Mro rcorccó d ñl. L rformd 3. Dcrpcó xr d m D.L.I Dcro Ll Ivr l mpo 3. Fcó d rfrc pld 3. Fcó d rfrc d m coo mrdo co O 3.3 Dgrm d loq 4. Rp mporl
SENSORES DISTRIBUIDOS PARA EL DESPLAZAMIENTO VOLUMICO DE UNA PLACA DELGADA EN SOPORTE SIMPLE
 SENSORES DSTRBUDOS PARA EL DESPLAZAMENTO VOLUMCO DE UNA PLACA DELGADA EN SOPORTE SMPLE PACS: 43.4.V Coo, Pdo; Cu, Mí uo d Acúc. CSC. So 44 86 Mdd. Eñ Tl: 95 68 86 : 94 7 65 E-l: [email protected].; [email protected].
SENSORES DSTRBUDOS PARA EL DESPLAZAMENTO VOLUMCO DE UNA PLACA DELGADA EN SOPORTE SMPLE PACS: 43.4.V Coo, Pdo; Cu, Mí uo d Acúc. CSC. So 44 86 Mdd. Eñ Tl: 95 68 86 : 94 7 65 E-l: [email protected].; [email protected].
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE QUÍMICA DEPARTAMENTO DE MATEMÁTICAS Ecuaciones Diferenciales [Guia]
![UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE QUÍMICA DEPARTAMENTO DE MATEMÁTICAS Ecuaciones Diferenciales [Guia] UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE QUÍMICA DEPARTAMENTO DE MATEMÁTICAS Ecuaciones Diferenciales [Guia]](/thumbs/80/80848373.jpg) UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE QUÍMICA DEPARTAMENTO DE MATEMÁTICAS Ecucio Difrcil [Gui] E l hoj d orcio or l úmro d rgu, l drrollo qu juifiqu u ru, u ru co i crrd u rcágulo lugo u
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE QUÍMICA DEPARTAMENTO DE MATEMÁTICAS Ecucio Difrcil [Gui] E l hoj d orcio or l úmro d rgu, l drrollo qu juifiqu u ru, u ru co i crrd u rcágulo lugo u
Creación de Modelos Delphos.Net
 Crcó d Modlo lpho.nt EINSA Apdo. Potl 314-2350 S Joé, Cot Rc http://www.d.com Tléfoo (506) 2276-3380 Fx (506) 2276-3778 E-ml: [email protected] Cotdo Igro l Modlo...3 Mtmto d Prpctv...7 Mtmto d Tpo d Rpobl...10
Crcó d Modlo lpho.nt EINSA Apdo. Potl 314-2350 S Joé, Cot Rc http://www.d.com Tléfoo (506) 2276-3380 Fx (506) 2276-3778 E-ml: [email protected] Cotdo Igro l Modlo...3 Mtmto d Prpctv...7 Mtmto d Tpo d Rpobl...10
Nombre: Fecha: 1 Grado = Lee las siguientes oraciones. -El dragón vive en el castillo -El carro azul es nuevo -El caballo come pasto
 Nomb: Fh: 1 Gdo 45 32 87 31 2020= d d yo mo o g úmo 3566891002 Rz d 10 10. p b g pb bdg bogomú qo Rz dbjo d o q h dí. g oo. E dgó o E o z o E bo om po Rp g Tbg E myo m yó yo, bo m pó ó, m o po q m dmyo.
Nomb: Fh: 1 Gdo 45 32 87 31 2020= d d yo mo o g úmo 3566891002 Rz d 10 10. p b g pb bdg bogomú qo Rz dbjo d o q h dí. g oo. E dgó o E o z o E bo om po Rp g Tbg E myo m yó yo, bo m pó ó, m o po q m dmyo.
Ruta Alimentadora Sur
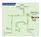 Ad Ru Ador Ad Lo Horzo Ad B A-02 ALAEDA UR Ad Lo Cd P PUENTE VILLA E o P Hy J rí E o Ovo L Cv Grd Cv ERVICIO EPECIAL CIRCUITO DE PLAYA L Gvo Hy Tr A-04 VILLA EL ALVADOR Rvou Ro A-07 AÉRICA L Uó Grd A-08
Ad Ru Ador Ad Lo Horzo Ad B A-02 ALAEDA UR Ad Lo Cd P PUENTE VILLA E o P Hy J rí E o Ovo L Cv Grd Cv ERVICIO EPECIAL CIRCUITO DE PLAYA L Gvo Hy Tr A-04 VILLA EL ALVADOR Rvou Ro A-07 AÉRICA L Uó Grd A-08
GESTIÓN POR PROCESOS MAPA DE PROCESOS CARACTERIZACIÓN DE PROCESOS
 GÓ POR PROO MP D PROO RRZÓ D PROO GÓ POR PROO B olombia Business lliance for ecure ommerce PROO Relación insumo ambio Producto RD RFORMO LD Recursos, nsumos información PROO D MBO Resultados, Producto
GÓ POR PROO MP D PROO RRZÓ D PROO GÓ POR PROO B olombia Business lliance for ecure ommerce PROO Relación insumo ambio Producto RD RFORMO LD Recursos, nsumos información PROO D MBO Resultados, Producto
2 Índice Dorian Luis Linero Segrera Universidad Nacional de Colombia, 2010
 Íd Íd... Cílo Elmo d l má d óldo r rolm ll láo..... Cmo dl dlmo l dormó ml..... Cmo dl ro... 5.. Eó o d mrl ll láo óroo: l d Hook. 6... Pro d lo ro rl... 9.. Plmo dl rolm l mdo oo....5. Elmo d l má d óldo
Íd Íd... Cílo Elmo d l má d óldo r rolm ll láo..... Cmo dl dlmo l dormó ml..... Cmo dl ro... 5.. Eó o d mrl ll láo óroo: l d Hook. 6... Pro d lo ro rl... 9.. Plmo dl rolm l mdo oo....5. Elmo d l má d óldo
Producto de convolución de las derivadas de orden k por las derivadas de orden de la delta de Dirac soportadas en x 1, x a, y x n
 Vol. 5, No., pp. 59-69/Dcmr ISSN-L 88-674 Coprgh Uvrsdd Ncol d Igrí Imprso Ncrgu. Todos los drchos rsrvdos hp://www.lmol.fo/d.php/nexo Produco d covolucó d ls drvds d ord por ls drvds d ord d l dl d Drc
Vol. 5, No., pp. 59-69/Dcmr ISSN-L 88-674 Coprgh Uvrsdd Ncol d Igrí Imprso Ncrgu. Todos los drchos rsrvdos hp://www.lmol.fo/d.php/nexo Produco d covolucó d ls drvds d ord por ls drvds d ord d l dl d Drc
Perfiles de modulación ascendentes para las tarjetas de línea para cable
 rf ucó c r rj í r c Iruccó rrru Ru z vc Ráfg c Guí rf ucó j rf ucó (zc) óg DOI.- ( y r c IO fwr rr) óg DOI.- (r ) cuó Au rf ucó Lcr hrc ( y ) Lcr Lcr Aéc A ácu ñ u r u - D Aéc frcó éc rf ucó VI G7 VI H
rf ucó c r rj í r c Iruccó rrru Ru z vc Ráfg c Guí rf ucó j rf ucó (zc) óg DOI.- ( y r c IO fwr rr) óg DOI.- (r ) cuó Au rf ucó Lcr hrc ( y ) Lcr Lcr Aéc A ácu ñ u r u - D Aéc frcó éc rf ucó VI G7 VI H
Formulario de matemáticas
 Forlro tát lgr- Sgo (+) (+) = + (-) (-) = + (+) (-) = - (-) (+) = - (+) / (+) = + (-) / (-) = + (+) / (-) = - (-) / (+) = - Fro Proto otl ftorzó ( ) ( ) ( ) ( ) ( ) ()() ()( ) ( )( ) ()( ) L lo ot rl log
Forlro tát lgr- Sgo (+) (+) = + (-) (-) = + (+) (-) = - (-) (+) = - (+) / (+) = + (-) / (-) = + (+) / (-) = - (-) / (+) = - Fro Proto otl ftorzó ( ) ( ) ( ) ( ) ( ) ()() ()( ) ( )( ) ()( ) L lo ot rl log
FAM 2004 FAM 2006 FAM 2007
 RCURO: RCCÓ PROYCO Y OBR FOO PORCO ÚP (F) 2004-2009 F 2004 FCH U CUZCÓ: 31 CBR 2010 PG 1 6 O GR OBR COR VC (%) OBR o. OBR (COVO) UBCCÓ O. CORO PZO JCUCO OO OBR FCO FCRO CRO VGCO / PCHUC OO, PyO/17/04 12/OC/2004
RCURO: RCCÓ PROYCO Y OBR FOO PORCO ÚP (F) 2004-2009 F 2004 FCH U CUZCÓ: 31 CBR 2010 PG 1 6 O GR OBR COR VC (%) OBR o. OBR (COVO) UBCCÓ O. CORO PZO JCUCO OO OBR FCO FCRO CRO VGCO / PCHUC OO, PyO/17/04 12/OC/2004
Tema 4: Regresiones lineales y no lineales TEMA 4. REGRESIONES LINEALES LINEALES Y NO. 1. 2. 3. Introducción 4. Nomenclatura
 T 4: grsos lls o lls TEMA 4. EGEIONE LINEALE LINEALE Y NO.. 3. Itroduccó 4. Nocltur 5. Llzcó Ajust grsó ll ll d últpl cucos 6. 7. 8. grsos EUMEN Progrcó o lls Mtlb Cálculo uérco Igrí T 4: grsos lls o lls.
T 4: grsos lls o lls TEMA 4. EGEIONE LINEALE LINEALE Y NO.. 3. Itroduccó 4. Nocltur 5. Llzcó Ajust grsó ll ll d últpl cucos 6. 7. 8. grsos EUMEN Progrcó o lls Mtlb Cálculo uérco Igrí T 4: grsos lls o lls.
126 l lg l g g b b t p p ñ ñ ñ l l l.. - p t p r l cl clí í í l L fc c u c i l y b ft i i cr cró ó ó l p b g,, i d,, p pm i l g i l ft i i g d r f i m
 SOBR BRE LA NEFRITIS CRON ONIC ICA DEL PERR RRO Y DEL GATO EL PELIGR IGRO DE PRACTI CTICAR CAR OPERAC RACION IONES EN LOS -BRIGH IGHTIC TICOS" Pr l Prf. HEBR BRAN ANT y Prf f. ju ANTO TOIN INE l El V r
SOBR BRE LA NEFRITIS CRON ONIC ICA DEL PERR RRO Y DEL GATO EL PELIGR IGRO DE PRACTI CTICAR CAR OPERAC RACION IONES EN LOS -BRIGH IGHTIC TICOS" Pr l Prf. HEBR BRAN ANT y Prf f. ju ANTO TOIN INE l El V r
6 REVIST REV IST IST F CU CUIT IT IT I) G R RN N MI ( ). XXX (). PERON ON EV PER 95 pi pi pi l lg g g d d c (97) 7) 7) S G G (9 S v c ll cc lu lui lu
 \ N( EN EL PERI ) N( ) (N )El NCl ("I (N \RNE\\N Y ) SR)N ("I N E TU ER ERCU CU S I) E P P Pr V VER R. TI ZIO SIV VORI Y R. MONTL LIDI E bj bj r h t d b b ci gú S v (9) ) p r ur t c pr c i l b b l l hij
\ N( EN EL PERI ) N( ) (N )El NCl ("I (N \RNE\\N Y ) SR)N ("I N E TU ER ERCU CU S I) E P P Pr V VER R. TI ZIO SIV VORI Y R. MONTL LIDI E bj bj r h t d b b ci gú S v (9) ) p r ur t c pr c i l b b l l hij
Hola, chicas y chicos! Os presentamos a. Él y sus amigos son los ganadores del concurso de ciencias de este año. . En Brasil, la selva está en
 E ryc d Pdr Hj d cividd 1 Nmbr: Fch: L rícu y cmé. NOTICIAS DEL COLE PEDRO Y SUS AMIGOS GANAN EL CONCURSO DE CIENCIAS H, chic y chic! O rm Bqu. É y u mig gdr d ccur d cici d ñ. Pdr d. E Bri, v á rqu á
E ryc d Pdr Hj d cividd 1 Nmbr: Fch: L rícu y cmé. NOTICIAS DEL COLE PEDRO Y SUS AMIGOS GANAN EL CONCURSO DE CIENCIAS H, chic y chic! O rm Bqu. É y u mig gdr d ccur d cici d ñ. Pdr d. E Bri, v á rqu á
Respuesta en régimen permanente a una entrada senoidal, resonancia y frecuencia natural de oscilación
 ur: Ig. Jrg lg - JTP Má zd Pág d 6 Fuld d Igrí Ursdd Nl d Mr dl Pl - rg spus rég pr u rd sdl, rs fru url d sló Supgs qu s u ss ll, r l p sl, rrzd pr su fuó prl, l uál grss u sñl.. s µ E grl, l sld dl ss
ur: Ig. Jrg lg - JTP Má zd Pág d 6 Fuld d Igrí Ursdd Nl d Mr dl Pl - rg spus rég pr u rd sdl, rs fru url d sló Supgs qu s u ss ll, r l p sl, rrzd pr su fuó prl, l uál grss u sñl.. s µ E grl, l sld dl ss
ANALISIS DE SISTEMAS LINEALES CONTINUOS EN EL ESPACIO DE ESTADO
 U N E X P O UNIVERSIDAD NACIONAL EXPERIMENTAL POLITECNICA ANTONIO JOSE DE SUCRE VICE RECTORADO BARQUISIMETO DEPARTAMENTO DE INGENIERIA ELECTRONICA ANALISIS DE SISTEMAS LINEALES CONTINUOS EN EL ESPACIO
U N E X P O UNIVERSIDAD NACIONAL EXPERIMENTAL POLITECNICA ANTONIO JOSE DE SUCRE VICE RECTORADO BARQUISIMETO DEPARTAMENTO DE INGENIERIA ELECTRONICA ANALISIS DE SISTEMAS LINEALES CONTINUOS EN EL ESPACIO
E N T R E V I S T A PRINCIPALES HERRAMIENTAS ENTREVISTA ESTILOS DE APRENDIZAJE HÁBITOS DE ESTUDIO
 LO D PDZJ PCPL HM HÁBO D UDO FUDMO D L OÍ Y ÉCC D L COCPO D. GÚ BGHM Y MOO, L U COCÓ, QU POPO U F DMDO, DO DL MPL PLC D L COCÓ. FUCO BÁC:. COLC DO. B. FOM. C. MO. P YMOD, L U MÉODO P U DO DU U COCÓ PD
LO D PDZJ PCPL HM HÁBO D UDO FUDMO D L OÍ Y ÉCC D L COCPO D. GÚ BGHM Y MOO, L U COCÓ, QU POPO U F DMDO, DO DL MPL PLC D L COCÓ. FUCO BÁC:. COLC DO. B. FOM. C. MO. P YMOD, L U MÉODO P U DO DU U COCÓ PD
Departamento Informática. Diputación Provincial de Soria
 3/6/ www.po. Mo éo y ogzvo Dpo Ifoá Dpu Povl So Ju Clo G www.po. Mo éo y ogzvo SORI Supf:.36 K Hb: 95. D: 9 hb/k PONTEVEDR Supf: 4.495 K Hb: 959.764 D: 4 hb/k Ju Clo G 3/6/ www.po. Mo éo y ogzvo Dbu poblol
3/6/ www.po. Mo éo y ogzvo Dpo Ifoá Dpu Povl So Ju Clo G www.po. Mo éo y ogzvo SORI Supf:.36 K Hb: 95. D: 9 hb/k PONTEVEDR Supf: 4.495 K Hb: 959.764 D: 4 hb/k Ju Clo G 3/6/ www.po. Mo éo y ogzvo Dbu poblol
$/Kg. Vivo por Clasificación Diciembre 2015
 S ST EMA NFORMAT VODE PREC OSPORC NOS P RE C OSP ORC NOS D N o d M u yf D C E MBRE2015 CONT ROLAGROPECUAR O M N S T E R ODEAGRO NDUS T R A DEL ANAC ÓN: Co R dobu y S dag u u G d yp : g Ag R dong D N o
S ST EMA NFORMAT VODE PREC OSPORC NOS P RE C OSP ORC NOS D N o d M u yf D C E MBRE2015 CONT ROLAGROPECUAR O M N S T E R ODEAGRO NDUS T R A DEL ANAC ÓN: Co R dobu y S dag u u G d yp : g Ag R dong D N o
Capítulo 3: Integral definida. Módulos 12 al 17. I. Notación sigma. En los ejercicios 1 a 5 escriba en forma de sumatoria la suma dada.
 Módulos l 7 I Nocó sgm E los jrccos scr form d sumor l sum dd + + + + + + + + 9 + + 7 6 7 8 l + l 6 + l 8 + l 6 6 Supog qu f ( ) 8, g( ) y h( ) Clcul l vlor d l prsó dcd los jrccos - c [ f ( ) g( ) h(
Módulos l 7 I Nocó sgm E los jrccos scr form d sumor l sum dd + + + + + + + + 9 + + 7 6 7 8 l + l 6 + l 8 + l 6 6 Supog qu f ( ) 8, g( ) y h( ) Clcul l vlor d l prsó dcd los jrccos - c [ f ( ) g( ) h(
gu g v C u. mró rm r mbr fum mé í írm Pró uh. m gué r - r rx L. r m r rm r mr r - m - rr, mr m gu fá v b má ér u u r b u m, fru r uó v rr m h uv C. r
 Mur ó Crv V Eér rr N r P Brá Ag V fí, ur j h ué m, vgur L g u, hum, r rr r, év E v rr mm u q R Luz Ág L. P Exr U - r M E mbé f r grr r rzr uv íqu xr r. r m m r ué ur jó f g ñr U Qu rá. mu rvur í u mur,
Mur ó Crv V Eér rr N r P Brá Ag V fí, ur j h ué m, vgur L g u, hum, r rr r, év E v rr mm u q R Luz Ág L. P Exr U - r M E mbé f r grr r rzr uv íqu xr r. r m m r ué ur jó f g ñr U Qu rá. mu rvur í u mur,
n o ó i Mi nombre: Mi numero de orden: Cuadernillo 1 periodo II MOMENTO DE LA MOVILIZACIÓN NACIONAL POR LA MEJORA DE LOS APRENDIZAJES
 l bim cm CACIÓN EDU bim cm DOS TO C u m ó i c c i d r t m m i trá d D qu d r p d i, r u q rd p l rd m p d T d 2 d u g S g prid Mi mbr: Cudrill 1 Mi umr d rd: II MOMENTO DE LA MOVILIZACIÓN NACIONAL POR
l bim cm CACIÓN EDU bim cm DOS TO C u m ó i c c i d r t m m i trá d D qu d r p d i, r u q rd p l rd m p d T d 2 d u g S g prid Mi mbr: Cudrill 1 Mi umr d rd: II MOMENTO DE LA MOVILIZACIÓN NACIONAL POR
Índice General. Disposiciones iniciales y definiciones generales
 Índice General Int r o d u c c i ó n... xxvii CAPÍTULO I Disposiciones iniciales y definiciones generales Dis p o s i c i o n e s iniciales y de f i n i c i o n e s ge n e r a l e s... 1 Capítulo II Trato
Índice General Int r o d u c c i ó n... xxvii CAPÍTULO I Disposiciones iniciales y definiciones generales Dis p o s i c i o n e s iniciales y de f i n i c i o n e s ge n e r a l e s... 1 Capítulo II Trato
r r ér r ó: ó bé í g hr r b br r b. r ró Yg hú br L Cró. ér g ó U " r: ú Sr Sr ó f Sr." Sr r bjv Rj Yg Hh Yg: v gr r g br - g. Y rf rá Yg h H b r ó br
 L CULTIVO D LA CONCNTRACIÓN I í xrr r ér Sr Cv gr Pr f frr r Pr. rí rá r r vr r hú br r x óf v r rr r ír ó Ihwr frr P. h hú v é gr "hb ír: r r "Bhgv G" í 15 rzó r v v I rz. r r r qr r á hwr rrr br g rz
L CULTIVO D LA CONCNTRACIÓN I í xrr r ér Sr Cv gr Pr f frr r Pr. rí rá r r vr r hú br r x óf v r rr r ír ó Ihwr frr P. h hú v é gr "hb ír: r r "Bhgv G" í 15 rzó r v v I rz. r r r qr r á hwr rrr br g rz
cra cla bla bra cre cle bre ble cri bli bli bri cro clo bro blo cru clu bru blu
 ba be bi bo bu bra bre bri bro bru bla ble bli blo blu ca ce ci co cu cra cre cri cro cru qui cla cle bli clo clu que da dra dla fa fra fla de dre dle fe fre fle di dri dli fi fri fli do dro dlo fo fro
ba be bi bo bu bra bre bri bro bru bla ble bli blo blu ca ce ci co cu cra cre cri cro cru qui cla cle bli clo clu que da dra dla fa fra fla de dre dle fe fre fle di dri dli fi fri fli do dro dlo fo fro
Corporación Eco Industrial y Comercial S.A. de C.V.
 Ccó Ec Idu y Cc S.A. d C.V. Ud, dccó dc, d ógc y dg Md UA8EAD...TI Cj cídc M8 d c db INO AISI 36L Dc d dccó: 50-500 Acó: d 2 5 30 VCC Sd: 0-0 V CC -20 A y u d d cucó NPN PNP, NA NC. E d dd % Rbdd 0,5%
Ccó Ec Idu y Cc S.A. d C.V. Ud, dccó dc, d ógc y dg Md UA8EAD...TI Cj cídc M8 d c db INO AISI 36L Dc d dccó: 50-500 Acó: d 2 5 30 VCC Sd: 0-0 V CC -20 A y u d d cucó NPN PNP, NA NC. E d dd % Rbdd 0,5%
Llamaremos términos amortizativos a las cuantías de los capitales financieros que componen la contraprestación: (a 1, a 2,, a n ).
 Tem 3 mortcó e prétmo Defcó y mgtue fumetle opercó e mortcó e prétmo e u opercó fcer e l ue u pero pretmt o creeor cocert etregr otr pero prettro o euor u eterm cutí e u mometo coro y el euor e compromete
Tem 3 mortcó e prétmo Defcó y mgtue fumetle opercó e mortcó e prétmo e u opercó fcer e l ue u pero pretmt o creeor cocert etregr otr pero prettro o euor u eterm cutí e u mometo coro y el euor e compromete
Mapa de los ríos de España
 p l í pñ í l l l v g í l bg í g í c g b g í ló g p í l í b ch í í í H H ñ j í í Í J j l í é í ó í gó í í í l m ü g í l í J í Jm g í ll g í g y l V í Ág Á b m Í m í É H í j í ló Í í í g í b í Ó g í í í
p l í pñ í l l l v g í l bg í g í c g b g í ló g p í l í b ch í í í H H ñ j í í Í J j l í é í ó í gó í í í l m ü g í l í J í Jm g í ll g í g y l V í Ág Á b m Í m í É H í j í ló Í í í g í b í Ó g í í í
EJERCICIOS DE DINÁMICA
 EJERCICIOS DE DIÁMICA 1. Dd un cuerd cpz de oporr un fuerz áx de 00, cuál erá l celercón áx que e podrá councr con ell un de 10 kg cundo e encuenr obre un plno horzonl n rozeno? Sol: ) 0. En un plno horzonl
EJERCICIOS DE DIÁMICA 1. Dd un cuerd cpz de oporr un fuerz áx de 00, cuál erá l celercón áx que e podrá councr con ell un de 10 kg cundo e encuenr obre un plno horzonl n rozeno? Sol: ) 0. En un plno horzonl
Variables Aleatorias. Capítulo 4: Variables Aleatorias. Distribuciones Estadística Computacional 1º Semestre Variables Aleatorias
 Uvdd Técc Fdco St Mí Dptmto d omátc L-8 Vl Alto Cpítulo 4: Vl Alto Dtuco Etdítc Computcol º Smt 3 Poo :Hécto Alld Pág : www..utm.cl/~hlld -ml : [email protected] Fucó qu g cd puto dl pco mutl u úmo l Ejmplo
Uvdd Técc Fdco St Mí Dptmto d omátc L-8 Vl Alto Cpítulo 4: Vl Alto Dtuco Etdítc Computcol º Smt 3 Poo :Hécto Alld Pág : www..utm.cl/~hlld -ml : [email protected] Fucó qu g cd puto dl pco mutl u úmo l Ejmplo
1 3 i + + A = 0, B = ½, C = 1, D = -½, dx dx de donde, :
 Hoj de Prolem Aál IV /. d L ríce de l eccó o,,,, í qe el polomo e decompoe de l form: Decompoemo e frccoe mple: D B A defcdo coefcee, e oee lo vlore: A, B ½,, D -½, Por lo qe: d d d / lclemo por eprdo
Hoj de Prolem Aál IV /. d L ríce de l eccó o,,,, í qe el polomo e decompoe de l form: Decompoemo e frccoe mple: D B A defcdo coefcee, e oee lo vlore: A, B ½,, D -½, Por lo qe: d d d / lclemo por eprdo
l ij l'; 1r" 1râ I 't i 4-1.} ,ffi,h) 4,i4 r z l,9 11,{ .Jn 1,{ 'l 'l J, J,t J,t 1,a -5^ l.{ l,{' ''' l. I, I fié \bi a j d i' .iq I '11 .J.f 3,?
 ,' ḻ.) r Ë'.' -f,.-.. =(-,, '; -'..f - ' -. -^ 0 '..'.., ḷ C. c).,' C., c. C!.c.' - ạ - C. ( rô -, '.r,.,. ',, - v ) - '.. ) r, -) '_ r Ë )'.., ^,' à ',, ' ',.' ( ) ' ',' r r ) - r c c,', ḷ,' s ) c, -
,' ḻ.) r Ë'.' -f,.-.. =(-,, '; -'..f - ' -. -^ 0 '..'.., ḷ C. c).,' C., c. C!.c.' - ạ - C. ( rô -, '.r,.,. ',, - v ) - '.. ) r, -) '_ r Ë )'.., ^,' à ',, ' ',.' ( ) ' ',' r r ) - r c c,', ḷ,' s ) c, -
Masa y composición isotópica de los elementos
 Masa y composición isotópica de los elementos www.vaxasoftware.com Z Sím A isótopo Abndancia natral Vida Prodcto 1 H 1 1,00782503207(10) 99,9885(70) 1,00794(7) estable D 2 2,0141017780(4) 0,0115(70) estable
Masa y composición isotópica de los elementos www.vaxasoftware.com Z Sím A isótopo Abndancia natral Vida Prodcto 1 H 1 1,00782503207(10) 99,9885(70) 1,00794(7) estable D 2 2,0141017780(4) 0,0115(70) estable
PRODUCTO TENSORIAL DE ESPACIOS VECTORIALES
 PRODUCTO TENSORIL DE ESPCIOS ECTORILES Poduco Teol El Fuo Poduco Teol 3 Poedde del Poduco Teol 4 Ále Teol de u Eco ecol 5 El Fuo Ále Teol Poduco Teol: Codeemo lo eco vecole oe el cueo comuvo K e χ l ceoí
PRODUCTO TENSORIL DE ESPCIOS ECTORILES Poduco Teol El Fuo Poduco Teol 3 Poedde del Poduco Teol 4 Ále Teol de u Eco ecol 5 El Fuo Ále Teol Poduco Teol: Codeemo lo eco vecole oe el cueo comuvo K e χ l ceoí
6.Co li sión de nor mas de la ley con el art. 43 de la Cons ti tu - ción Na cio nal...
 In di ce ge ne ral Pró lo go... 11 Ca pí tu lo I LOS PRO CE SOS UR GEN TES EN GE NE RAL 11....In tro duc ción 12.La no ción de pro ce so ur gen te. Cla si fi ca ción de los pro ce sos ju di cia les 13....Al
In di ce ge ne ral Pró lo go... 11 Ca pí tu lo I LOS PRO CE SOS UR GEN TES EN GE NE RAL 11....In tro duc ción 12.La no ción de pro ce so ur gen te. Cla si fi ca ción de los pro ce sos ju di cia les 13....Al
61.1 6.1. SERIES NUMÉRICAS INFINITAS 6.2. SERIES DE TÉRMINOS POSITIVOS 6.3. SERIES ALTERNANTES 6.4. SERIES DE POTENCIAS
 Cp. 6 Sris 6. 6.. SERIES NUMÉRICAS INFINITAS 6.. SERIES DE TÉRMINOS POSITIVOS 6.. SERIES ATERNANTES 6.. SERIES DE POTENCIAS Objtivo: S prtd qu l studit: Dtrmi covrgci o divrgci d sris. Empl sris pr rsolvr
Cp. 6 Sris 6. 6.. SERIES NUMÉRICAS INFINITAS 6.. SERIES DE TÉRMINOS POSITIVOS 6.. SERIES ATERNANTES 6.. SERIES DE POTENCIAS Objtivo: S prtd qu l studit: Dtrmi covrgci o divrgci d sris. Empl sris pr rsolvr
ESTRUCTURA ORGÁNICA DE LA INTENDENCIA DE MONTEVIDEO EDICIÓN:
 Gestión Humana y ecursos Materiales MÓ L FMÓ Y GÁ L M Ó: 31072013 Marcelo ebril dela iviani : ntendencia de Montevideo GÁ 31 07 2013 L GZ: ntendencia de Montevideo ágina 1 de 17 L GL Í GL Í JÍ MÉ M Í LL
Gestión Humana y ecursos Materiales MÓ L FMÓ Y GÁ L M Ó: 31072013 Marcelo ebril dela iviani : ntendencia de Montevideo GÁ 31 07 2013 L GZ: ntendencia de Montevideo ágina 1 de 17 L GL Í GL Í JÍ MÉ M Í LL
ERROR EN ESTADO ESTACIONARIO
 UNIVESIDAD AUÓNOMA DE NUEVO EÓN FACUAD DE INGENIEÍA MECÁNICA Y EÉCICA EO EN ESADO ESACIONAIO INGENIEÍA DE CONO M.C. EIZABEH GPE. AA HDZ. M.C. OSÉ MANUE OCHA NÚÑEZ UNIVESIDAD AUÓNOMA DE NUEVO EÓN FACUAD
UNIVESIDAD AUÓNOMA DE NUEVO EÓN FACUAD DE INGENIEÍA MECÁNICA Y EÉCICA EO EN ESADO ESACIONAIO INGENIEÍA DE CONO M.C. EIZABEH GPE. AA HDZ. M.C. OSÉ MANUE OCHA NÚÑEZ UNIVESIDAD AUÓNOMA DE NUEVO EÓN FACUAD
Capítulo 4: Rotaciones Multidimensionales con Operaciones Vectoriales
 Cítulo 4: Rotcos Multdmsols co Orcos ctorls Como s vo l cítulo tror s ud hcr rotr u ojto l sco D roorcodo - utos o cohrlrs s dcr s roorco l j d rotcó l cul s l rrstcó d u sml -D. E st cítulo s lz y td
Cítulo 4: Rotcos Multdmsols co Orcos ctorls Como s vo l cítulo tror s ud hcr rotr u ojto l sco D roorcodo - utos o cohrlrs s dcr s roorco l j d rotcó l cul s l rrstcó d u sml -D. E st cítulo s lz y td
ESCOGENCIA DE CARRERAS DE NIVEL DIVERSIFICADO EN INSTITUTOS NACIONALES DE EDUCACIÓN BÁSICA CERCANOS A ESCUELAS NORMALES INVESTIGACIÓN
 E og d r r r d v d v r f d o u o o d Ed u ó Bá CERCANOSAES CUEL ASNORMAL ESI NVES TI GACI ÓN D p r m oe d u v o C r od E u d od Op ó P ú b A o ó d I v g ó ye u d os o AS I E S 1 0 ª C 7 4 8Zo 9 Gu m 0
E og d r r r d v d v r f d o u o o d Ed u ó Bá CERCANOSAES CUEL ASNORMAL ESI NVES TI GACI ÓN D p r m oe d u v o C r od E u d od Op ó P ú b A o ó d I v g ó ye u d os o AS I E S 1 0 ª C 7 4 8Zo 9 Gu m 0
v,, E v lc d h 44 pr p pr xcl x c cl uiv u ivm iv m m m xi i i t í, í, x v gú ú l v b bl b l l g r r t d glá gl áu á,, g gú ú l mm gú ú l cc ó,, g m d
 APLICA CIÓN DE LA REAC ACCI CI CON DE LA CATALASA DE LA LECHE AL DIA GNÓSTI STICO DE LA MAMI MITI TS POR E. HUYN EN (Jf d tb bj d r'c u V r df Bru Tr c bl Dr. C. Nt L ii, d Ft d Agrmí mí V L I'i. 'i. Er
APLICA CIÓN DE LA REAC ACCI CI CON DE LA CATALASA DE LA LECHE AL DIA GNÓSTI STICO DE LA MAMI MITI TS POR E. HUYN EN (Jf d tb bj d r'c u V r df Bru Tr c bl Dr. C. Nt L ii, d Ft d Agrmí mí V L I'i. 'i. Er
Ejercicios de Caligrafía. ba be bi bo bu ba be bi bo bu ba be bi bo bu ba be bi bo bu ba be bi bo bu ba be bi bo bu. Sílabas
 1. bla ble bli blo blu bla ble bli blo blu bla ble bli blo blu bla ble bli blo blu bla ble bli blo blu bla ble bli blo blu.. 2. bra bre bri bro bru bra bre bri bro bru bra bre bri bro bru bra bre bri bro
1. bla ble bli blo blu bla ble bli blo blu bla ble bli blo blu bla ble bli blo blu bla ble bli blo blu bla ble bli blo blu.. 2. bra bre bri bro bru bra bre bri bro bru bra bre bri bro bru bra bre bri bro
CH1 Mi Plan 150 CH2 Mi Plan 250 CH3 Mi Plan 350 CH4 Mi Plan 500 CH6 Mi Plan 800 CH9 Mi Plan Plus 165 CI1 Mi Plan Plus 385 CI5 Mi Plan Plus 1100 CI6
 ID_PLAN PLAN CH1 Mi Plan 150 CH2 Mi Plan 250 CH3 Mi Plan 350 CH4 Mi Plan 500 CH6 Mi Plan 800 CH9 Mi Plan Plus 165 CI1 Mi Plan Plus 385 CI5 Mi Plan Plus 1100 CI6 Mi Plan Plus 1430 CI9 Pool Optimo 167 CJ0
ID_PLAN PLAN CH1 Mi Plan 150 CH2 Mi Plan 250 CH3 Mi Plan 350 CH4 Mi Plan 500 CH6 Mi Plan 800 CH9 Mi Plan Plus 165 CI1 Mi Plan Plus 385 CI5 Mi Plan Plus 1100 CI6 Mi Plan Plus 1430 CI9 Pool Optimo 167 CJ0
206 MÉTODOS NUMÉRICOS
 6 MÉTODOS UMÉRICOS.. Alguos hhos mortts r ls rs vs wto: ls sguts so lgus ls ros más mortts ls rs vs wto: (. S s u rmutó K ) ( ) K tos [ K ] [ K ] CASO PARTICULAR: [ ] [ ] ( Est ro s osu l u l olomo trolt
6 MÉTODOS UMÉRICOS.. Alguos hhos mortts r ls rs vs wto: ls sguts so lgus ls ros más mortts ls rs vs wto: (. S s u rmutó K ) ( ) K tos [ K ] [ K ] CASO PARTICULAR: [ ] [ ] ( Est ro s osu l u l olomo trolt
y variación en la Forma música del siglo XX Si hubiera que señalar dos carac Mariano Etkin Germ án Cancián
 Fm y ó mú g XX M Ek Cm y m í í O< Py mú g XX q m m P T3 á Cámó I V y T// F B A U N L P Gm á Cá P Aj g AM M /y Tj Pá mqó y Oqó / F B A U N L P C M P Mú y Cm P Aj g mó y Oqó y P Aj Cmó /V FH S A U N L P
Fm y ó mú g XX M Ek Cm y m í í O< Py mú g XX q m m P T3 á Cámó I V y T// F B A U N L P Gm á Cá P Aj g AM M /y Tj Pá mqó y Oqó / F B A U N L P C M P Mú y Cm P Aj g mó y Oqó y P Aj Cmó /V FH S A U N L P
I.E.S. Mediterráneo de Málaga Junio 2015 Juan Carlos Alonso Gianonatti OPCIÓN A
 I.E.. Mdiáno d Málg Junio Jun Clo lono Ginoni OPCIÓN.- Conido l unción dinid n l inlo [ ]. Din l cución d l c ngn l cu qu pll l c qu p po lo puno P( Q(. ( puno..- Clcul l ingl indinid iguin d d ( puno.
I.E.. Mdiáno d Málg Junio Jun Clo lono Ginoni OPCIÓN.- Conido l unción dinid n l inlo [ ]. Din l cución d l c ngn l cu qu pll l c qu p po lo puno P( Q(. ( puno..- Clcul l ingl indinid iguin d d ( puno.
Verano Cultural PROGRAMA
 V C PROGRAMA Em Dmg Ag, D Hm Uv Bg, h z bj í L Cmó Pm bgé. Cjz z mó. E q D, f G Cmó Av Uv Bg, h v Cjz, bj q h g S Dmg Ib, C Ió Cm Sg, q f v q vm fm. Em Dmg, mbé v Cg y g S J. E xó m q v Cg, x mó m q my
V C PROGRAMA Em Dmg Ag, D Hm Uv Bg, h z bj í L Cmó Pm bgé. Cjz z mó. E q D, f G Cmó Av Uv Bg, h v Cjz, bj q h g S Dmg Ib, C Ió Cm Sg, q f v q vm fm. Em Dmg, mbé v Cg y g S J. E xó m q v Cg, x mó m q my
FUNDAMENTOS MATEMÁTICOS (Grado en Ingeniería Informática) Práctica 7. INTEGRALES DEFINIDAS E IMPROPIAS
 FUNDAMENTOS MATEMÁTICOS (Grdo n Ingnirí Informátic) Práctic 7. INTEGRALES DEFINIDAS E IMPROPIAS.- L intgrl dfinid d Rimnn. L intgrl dfinid d Rimnn surg prtir dl prolm dl cálculo d árs d suprficis dlimitds
FUNDAMENTOS MATEMÁTICOS (Grdo n Ingnirí Informátic) Práctic 7. INTEGRALES DEFINIDAS E IMPROPIAS.- L intgrl dfinid d Rimnn. L intgrl dfinid d Rimnn surg prtir dl prolm dl cálculo d árs d suprficis dlimitds
smart BRABUS tailor made >> De original a pieza única.
 m BRABUS l md >> D gl pz úc. m BRABUS l md 02 03 l d P m u q y mu. h u cc U m fw mp lg pcl. C m BRABUS l md, u cch pcl cv lg úc: cfgu u m fw gú u gu y dmu u pldd l cudd. E l gu pág hm cfgud cu jmpl md
m BRABUS l md >> D gl pz úc. m BRABUS l md 02 03 l d P m u q y mu. h u cc U m fw mp lg pcl. C m BRABUS l md, u cch pcl cv lg úc: cfgu u m fw gú u gu y dmu u pldd l cudd. E l gu pág hm cfgud cu jmpl md
Un forward sobre commodities como el oro sufre una pequeña variación ya que se incluye la tasa de interés del oro (lease rate) con la variable l
 El Forward U corao fuuro o a plazo, s odo aqul cuya lqudacó o slm dfr hasa ua fcha posror spulada l msmo, s dcr s dos pas acurda hacr la rasaccó hasa u prodo fuuro dígas por jmplo 6 mss, so s u corao forward.
El Forward U corao fuuro o a plazo, s odo aqul cuya lqudacó o slm dfr hasa ua fcha posror spulada l msmo, s dcr s dos pas acurda hacr la rasaccó hasa u prodo fuuro dígas por jmplo 6 mss, so s u corao forward.
x a es una serie de la forma que el radio de convergencia de la serie geométrica es el intervalo abierto
 ERIE DE POTENCIA ERIE DE POTENCIA. Diició. U sri d pocis c s u sri d l orm c c c c... c... Por jmplo. i c y l sri d pocis om l orm....... Por jmplo. i c y l sri d pocis om l orm....... TEOREMA. El cojuo
ERIE DE POTENCIA ERIE DE POTENCIA. Diició. U sri d pocis c s u sri d l orm c c c c... c... Por jmplo. i c y l sri d pocis om l orm....... Por jmplo. i c y l sri d pocis om l orm....... TEOREMA. El cojuo
Anexo 1 Características de las haciendas en la Sierra de Alcara,z a mediados del siglo XVIII (Catastro de Ensenada)
 Aéndice Anexo 1 Características de las haciendas en la Sierra de Alcara,z a mediados del siglo XVIII (Catastro de Ensenada) Ŝ o o N r r N V 7 M N rn Ŝ.. n,. 5 v1 M o0 M v M N M N r N j 7 N M N V N 00
Aéndice Anexo 1 Características de las haciendas en la Sierra de Alcara,z a mediados del siglo XVIII (Catastro de Ensenada) Ŝ o o N r r N V 7 M N rn Ŝ.. n,. 5 v1 M o0 M v M N M N r N j 7 N M N V N 00
Testamento de Ryan Ray
 : / 2 0 1 7 é : Cá L M: Ob Pí / Of y M VS Plí m mb jg h j y m gl, m l m l mg: m wh L "g" m Al l hb h, m mg, á g L g E lg l ñm hj m b, bm l N mj Hz l L m l fml mh g m y ml, m f, m má l l ém, jgm l áb C,
: / 2 0 1 7 é : Cá L M: Ob Pí / Of y M VS Plí m mb jg h j y m gl, m l m l mg: m wh L "g" m Al l hb h, m mg, á g L g E lg l ñm hj m b, bm l N mj Hz l L m l fml mh g m y ml, m f, m má l l ém, jgm l áb C,
Tema 6.Sistemas de Telecomunicación. El ruido en los sistemas de comunicación.
 ma 6.ma d lcomucacó. l rudo lo ma d comucacó. Aál d lo ma d Comucaco Dgal dd la prpcva R y BR B rror Ra Iroduccó capíulo, la ñal y l rudo dcrb érmo d ñal alaora. Aplcarmo cálculo d probabldad. La da báca
ma 6.ma d lcomucacó. l rudo lo ma d comucacó. Aál d lo ma d Comucaco Dgal dd la prpcva R y BR B rror Ra Iroduccó capíulo, la ñal y l rudo dcrb érmo d ñal alaora. Aplcarmo cálculo d probabldad. La da báca
El límite de una función es un concepto fundamental del análisis matemático, un caso
 Lím fó E ím fó p fm á mmá, ím p f. Ifmm, hh q fó f ím L p, gf q v f p L m, m p fm, pm q. Lím mmá E mmá, ím p q b ó fó, m q pám ó fó m v. E á (pm á y mmá) p z p f p fm vg,, vó, gó,. E p p gz p póg, m p
Lím fó E ím fó p fm á mmá, ím p f. Ifmm, hh q fó f ím L p, gf q v f p L m, m p fm, pm q. Lím mmá E mmá, ím p q b ó fó, m q pám ó fó m v. E á (pm á y mmá) p z p f p fm vg,, vó, gó,. E p p gz p póg, m p
