2 Revisión de los fundamentos
|
|
|
- Eugenia de la Cruz Rodríguez
- hace 10 años
- Vistas:
Transcripción
1 Rvó d lo udmo mmáco S cb d cr l ror cpíulo qu lo modlo d l pl o proco, rr curo, rá ddo por l cuco drcl ll y d coc co, brvádo co l crómo LI (Lr m Ivr). L drmcó dl compormo dámco dl m upo qu coocd u ucó d rrc, FD, co d po LI, y l urlz dl po d rd, pobl prdcr l ñl d l ld. Obérv qu ólo oc obr m SISO (Sgl Ipu, Sgl Oupu) LI. E prdccó á bd l oprdor covolucó mmác, cuy dculd l domo mporl qud d mo u prop dcó: y x g x( τ ) g( τ ) dτ x( τ ) g( τ ) * dτ (. ) D cdd prc do po d rormd mmác (Fourr y Lplc) qu clrá l cálculo d l covolucó. Pro dmá, rormco o ólo rprco mmác o mbé gcdo dd l puo d v íco, obr odo l d Fourr qu hc u cmbo l domo rcucl. Aí rlcó co lo m, l rpu rcuc drá crcríc grl dl ucomo dámco. D oro y Dpo. Elcróc, Auomác Iormác Idurl 5
2 Cpíulo : Rvó d udmo mmáco Apu d Rgulcó Auomác dd l orí d ñl, l crcrzcó d l od rvé d u pcro rcucl á ímm lgd l rormd d Fourr. Amb rormco rljrá lo modlo d l pl LI cou orm d cuco lgbrc d vrbl complj. Dd o domo x rgl mpl qu o cpc d mpulr l cuco lgbrc y d obr l oluco u rpcvo domo. L volucó mporl obdrá plcdo l rormd corrpod. S cocluy, por o, qu o cro rolvr l cucó drcl pr prdcr l compormo dámco dl m.. El cocpo d l rormcó El cocpo d l rormcó v ímm lgdo l d corrpodc. A u drmdo grupo d lmo dl domo D l hc corrpodr u uvo grupo d lmo dl domo D. Sgú l crácr d l vrbl dl mpo,, pud dgur clm do grupo d rormco: cou, cudo l vrbl pud omr culqur vlor comprddo dro d u drmdo rvlo, o dcr cudo olm l mpo á ddo vlor cocro prdo r í dc (prodo d muro). D momo, dur prmr curmr, mplrá l rormd dd obr vrco cou l mpo. Cudo roduzc l compudor, como lmo d corol, lzrá l rormd dcr. Domo mporl L[()] F[()] L - [()] F - [()] Domo compljo Domo rcucl Fgur.. Corrpodc r domo D l rormco cou dc l rormco grl: F, b ( ) d (. ) do () l ucó cou l mpo qu d pr oro domo, mr (,) l úclo ( rl ) d l rormcó: ( ) jω, rormcó d Fourr rormcó d Lplc (. 3) 6 Dpo. Elcróc, Auomác Iormác Idurl
3 Apu d Rgulcó Auomác Cpíulo : Rvó d udmo mmáco. Sr y rormd d Fourr E l ál d l ñl y d lo m, vc, rqur rldr lo problm dl domo mporl l d l rcuc. Cudo r d ñl hbl dl pcro rcucl d é (l cmbrl dl domo mporl l rcucl); mr l udo d lo m rcuc l dom rpu rcucl. E l co má grl, u ucó pródc mporl, (), d prodo d, cod u rvlo, co u úmro o d máxmo, mímo y puo dcouo, é pud r rprd por u r d o y coo. A r l llm d Fourr: + ( ω ) + b ( ω ) co ω π (. 4) dod rpr l vlor mdo d l ucó y y b o l mplud d lo rmóco d ord. Cudo gul, rrá dl rmóco udml o d prmr ord, o, corrpod co u ucó odl o coodl cuy rcuc l vr dl prodo d l ucó covrr, (), y u mplud corrpodrá co b o, rpcvm. S hbl d rmóco, á rdo d uo, cuy rcuc vc l dl rmóco udml. El cálculo dl vlor mdo y d l mplud d lo rmóco rá dd por l gu xpro: b / / / / / / d co( ω ) ( ω ) d d (. 5) Cudo l ucó mporl, (), po drmd propdd d mrí, lo coc o b mplc. Aí, cudo () ucó pr, oc o hbrá drrollo odl y cudo mpr qudrá ccld l mplud d l r coodl: odo odo llv u combcó d rmóco qu o dgu uo d oro, pro u cojuo d u mbr o color. El cor ímbrco o rclm l có d lo compoor h l glo XVIII, y Mozr l prmro qu d orm obl hc uo d u pobldd d cor. Algu obr d Bch, El Ar d l Fug, por jmplo, u obr dr dd l puo d v ímbrco. Dpo. Elcróc, Auomác Iormác Idurl 7
4 Cpíulo : Rvó d udmo mmáco ( ) b ( ) Apu d Rgulcó Auomác (. 6) Ejmplo. U mx u() Obr l drrollo d Fourr dl r d mpulo d prodo d l gur, bdo qu l chur d pulo τ y l mplud U mx. τ Como l ñl d po pr, ólo drá u drrollo r coodl. τ / U mx τ / τ / τ / U d U mx mz τ π co d U mz π τ π Pr l co pcíco d r u prodo d m, u cho dl pulo d 5m y qu l mplud d 5V, lo coc rí: 4.5V V (4Hz) 3.8V (Hz) 5.635V (5Hz) V (Hz) 6 3 V (6Hz).6V (3Hz) 7.45V (7Hz),... A l rprcó d lo rmóco d l ucó () u dgrm, dod l j d bc l rcuc y l módulo d l mplud d lo rmóco á l j d ordd l llm l pcro rcucl d l ucó. Nó, l cmbo d l vrbl dpd, dl domo mporl,, l domo rcucl,. S mbrgo, l co má grl, l r drá drrollo uco d od y cood. Lo qu v gcr qu l domo V(w) U mx τ u() Módulo dl pcro d l ñl po r d mpulo [Hz] Fgur.. ) ñl l mpo b) pcro d l ñl (módulo) 8 Dpo. Elcróc, Auomác Iormác Idurl
5 Apu d Rgulcó Auomác Cpíulo : Rvó d udmo mmáco rcucl d vrbl complj. D hcho, or pobl prcó d l r d Fourr co u ucó d cood co mplud y d drmd pr cd rmóco. L gud orm d xprr l r d Fourr rá dd por l mplud y lo d d lo rmóco: c + c co( ω ψ ) + b b ψ rcg ω π (. 7) Empldo l rlco d Eulr obr l o y l coo l prmr orm d xprr l r d Fourr, ob or rcr xpró dl drrollo ucó d l xpocl: + / ω / jω j F( ω ) F( ω ) d (. 8).. rorm d Fourr Como d prr, l myorí d l ñl o o pródc. Pr l plccó d l r d Fourr obr ñl pródc, procd l rco mmáco d hcr qu l prodo d l ñl o, covrdo od l ñl pródc. Empldo l rcr orm d rprcó d l r d Fourr, o, xpocl, plc qu l prodo d o. jω lm dω π jω F( ω ) ω F( ω ) ω F jω ( ω ) d (. 9) (. ) E xpro cocluy co l rormd d Fourr y u vr. Vé qu hor o ólo compo dcro drmd rcuc, o qu u ucó cou odo l pcro d l rcuc. Por o dc qu hy u rormd y o u r. S mbrgo, pr qu u ucó g rormd d Fourr rqur dl cumplmo d l codcó d covrgc bolu: Dpo. Elcróc, Auomác Iormác Idurl 9
6 Cpíulo : Rvó d udmo mmáco Apu d Rgulcó Auomác + d < (. ) od l ñl d l urlz cumpl codcó, por qué o x gu u d rgí qu d crácr o. E dv, od l ñl d l Nurlz rormd d Fourr. Ejmplo. Clculr l rormd d Fourr d u ñl mpulol. U mx τ U ( ω ) τ / U mx τ / jω d ( ωτ / ) U mx U mx ω τ c ( ωτ / ) Pr l co d r u mplud d V y u cho d mpulo d µ. Nó qu c pr l cálculo d rcuc ul, ω [rd/], l plccó d H opl pr rolvr l drmcó: ( ω.) U ( ω ) U ω ( ).. V x -3 Ddd pcrl dl mpulo U(w) w[rd/] x 5 E l pág wb (couldo ocubr 7) pud corr u ppl cpz d clculr l r d Fourr d lgu ñl ípc. Fgur. 3. Appl qu drm l r d Fourr pr lgu uco ípc 3 Dpo. Elcróc, Auomác Iormác Idurl
7 Apu d Rgulcó Auomác Cpíulo : Rvó d udmo mmáco.3 rormd d Lplc Como cb d vr, l codcó d covrgc bolu upo qu much uco mporl, mpld l Corol, o rormd d Fourr. Por jmplo, l ucó l cló, l rmp o l prábol. od ll o ulzd como rd d pr vrgur l dámc d l pl o d lo proco. Vé l co d l ucó cló uro, é d como: < (. ) Nó qu ucó o pud r rormd d Fourr, l o cumplr l codcó d covrgc bolu. Pro íj mbé, qu ucó o x l urlz, pu upo u por d rgí; por dch rzó, o h puo l ombr d ñl l cló o d ucó cló. Pro, oc, por qué dcrpc r lo rl y lo órco?. Dd lugo, od l ñl íc rormd d Fourr, por qu hy ud d l rgí y por d cumplmo d l codcó d covrgc bolu. Pro por oro, l orí dl Corol mpl rco mmáco pr clr l compró voluv dl m, y qu dpdz l rpu prm d l ror. Co l propóo d r l rormd pr uco, ñd l úclo d l rormcó u xpocl moóom dcrc co l mpo, -σ. L rormd d Lplc qudrá dd por: F, d σ + jω σ jω ( σ ω ) d F (. 3) Obérv qu l lím ror d l grcó h ddo co l mpo gul cro y o dd l mo o; llo dbdo qu pr vlor d σ > l cor d covrgc dvrg cudo l mpo xd por vlor gvo d mpo. Pro o o u problm, y qu á xprdo qu l ormcó cod () dl mpo cl,, gor o codr cro. Admá, cudo u m xcdo por u rd u mpo drmdo, l rrc dl mpo pu cro l momo d cr l ímulo; o upo qu lo m íco rl o comz rpodr qu, o, l ld o prcd l mpo l rd. A o m l llm cul o mplm, ícm rlzbl. Por upuo hc rrc l od lcromgéc y qu como l d como l prurbco d u mdo qu propg l pco, rpordo rgí y cdd d movmo. Dpo. Elcróc, Auomác Iormác Idurl 3
8 Cpíulo : Rvó d udmo mmáco Apu d Rgulcó Auomác A coucó mpl l rormd d Lplc obr lgu d l uco y ñl ípc d corol: L. Fucó cló uro, L ( ) F d. :. Fucó xpocl dcrc, ( ) α L ( ) F α d ( α + ) ( α + ) ( + α ) 3. Sñl odl, U ( u ) U U mx jω ( jω ). u ω : mx ( + jω ) jω U mx ω d U mx j j ( jω ) ( + jω ) + ω :.3. orm mpor d l rormd d Lplc L plcco d l rormd d Lplc, mucho co, mplc l mplr l propdd d l rormd. E propdd pr co lo gu orm, pr lo cul o d gu dmorcó. orm : Mulplccó por u co: S u co, L F. Crcríc cogud por l propdd d l grl. ( ( )) ( ) orm : Sum y r d do uco mporl: Codr y b qu o co, L( ± b ) F ± b F. Igulm qu l orm, pobl por l propdd d l grl. orm 3: Drccó: d( ) L F lm( ) F ( ). d Cogud rvé d u grcó por pr. Mr pr l co má grl d drvd d ord, plcrá l rgl d l rcurrc: d L d d L d ( ) ( ) F F ( ) lm + ( ) d ( ) d ( ) + 3 ( ) 3 ( ) + ( ) + ( ) ( ) d d d d 3 Dpo. Elcróc, Auomác Iormác Idurl
9 Apu d Rgulcó Auomác Cpíulo : Rvó d udmo mmáco F orm 4: Igrcó: L ( ) d τ τ ; d l mm mr qu l drccó, cogu rvé d grcó por pr. Aplcdo rcurrc, l 3 F grcó d -émo ord qudrá como, ( ) L d d d... τ τ τ... τ. orm 5: orm dl vlor cl (ólo plcbl () á cod): lm lm F. ( ) ( ) orm 6: orm dl vlor l (ólo plcbl () á cod): lm lm F. ( ) ( ) L orm 7: rlcó complj: Codrdo α u co, F α. ± α ( ( )) ( ) orm 8: rlcó mporl. S u ucó mporl, (), mulplcd por or d po cló uro, u(), qudr L ( u ) F. Cudo l ñl á rrd u mpo, como l plcr u cló mbé co rro, L u F. ( ( ) ( )) ( ) orm 9: Covolucó. L covolucó d do uco mporl l covolucó d u rormd pro qu gul u * F F F F. mulplccó: ( ( ) ( )) ( ) ( ) ( ) ( ) L *.3. rormd vr d Lplc md l xpó d rcco mpl El modldo d lo m d Corol md xpro LI cou, upo qu l ucó d rrc, FD, dl m rorm d Lplc prc orm d rcco d polomo l domo compljo,. Dd oro puo d v, pud mcor qu cudo lo modlo dcrb md cuco drcl ll, l domo compljo prc xpro rcol ( l gu cpíulo dmorrá), pudédo crbr d l orm: G ( ) N D (. 4) dod N() y D() o do polomo. El grdo d D() cocd co l grdo d l cucó drcl. Por l codcó d culdd, l grdo d N() rá gul o mor dl D(). L ríc dl domdor, D(), l llm polo y l dl umrdor, N(), cro. Dpo. Elcróc, Auomác Iormác Idurl 33
10 Cpíulo : Rvó d udmo mmáco Apu d Rgulcó Auomác Por oro ldo, l ñl ípc d corol d rd (cló, rmp, odl,...), u rormd, o mbé xpro polómc. E cocluó, por plccó dl orm d l covolucó, l rormd d Lplc d l ld d o m rá coud por rcco polómc. Y odo lo lmo cro pr l procdmo d ál dl compormo dámco, cdd d clculr l cucó drcl. U vz obd l xpró d l rormd d Lplc d l ld, ólo hbrá d clculr u rormd o rormd vr, obdo l volucó mporl d l ñl d ld. L[x()] x() FD g() y() L - [Y()] X() G() Y()X()*G()X()G() Al r Y() orm d polomo l domdor y l umrdor, pud hcr u rormd vr rvé d u dcompocó rcco mpl. Hy qu codrr do co, l ríc dl domdor o mpl o hy mulplcdd lo polo. S lo polo d Y() o mpl y l grdo dl domdor, l plcrl l xpó rcco mpl qudrá como: Y ( + ) ( + ) ( + ) (. 5) por: dod l coc -émo, cuyo clculo dl rduo rá drmdo [( + ) Y ] (. 6) L olucó l domo mporl rulrá d plcr l orm d l rlcó complj: y (. 7) Ejmplo.3 Clculr l volucó mporl d l ó d ld, u (), d u cudrpolo RC, u xccó l rd, u (), d po 34 Dpo. Elcróc, Auomác Iormác Idurl
11 Apu d Rgulcó Auomác Cpíulo : Rvó d udmo mmáco cló uro. Codr codco cl ul. : L cucó drcl qu xplc l compormo dámco dl cudrpolo u Aplcdo rormd d Lplc: du RC d + A V + RC L rormd d l ñl d ld rulrá: u U U A V + RC + + RC (. 8) El cálculo d lo rduo vldrá: [ U ] + U RC / RC Rpu dl cudrpolo RC u rd cló From: U() El prmr érmo d l c. (. 8) corrpod co u ld cló uro, mr l gudo, por plccó dl orm d rlcó complj, u xpocl moóom dcrc: u / RC u() [u()] [] x -3 S hy lgú polo qu g mulplcdd, l cálculo d lo coc pr o polo gul rá dr. S l co d r u polo d mulplcdd r y l grdo dl domdor (l ro d lo polo o mpl): Y Q r A A Ar r ( + )...( + )( + ) ( + ) ( + ) ( + ) ( + ) ( + ) r r r (. 9) Dpo. Elcróc, Auomác Iormác Idurl 35
12 Cpíulo : Rvó d udmo mmáco Apu d Rgulcó Auomác Lo coc d lo polo mpl,,..., -r, clcul gú l c. (. 6); mr lo coc A, A,..., A r d lo polo d mulplcdd rá drmdo por l xpro: A A A A r r r r [( + ) Y ] d d d! d! ( r ) r ( + ) Y d d r ( + ) Y r r r ( + ) Y (. ) Ejmplo.4 Drmr l compormo dámco d u brco u rd ur l cmbo dl mó d é. Co propóo h xrído u dgrm bloqu y u modlo d compormo pr u cojuo d vlocdd váld. Aí, obrv qu l águlo δ () ddo rd dl Nm mó, provoc u pr d gro obr l brco d P 5 rd δ, l cul provoc u gro α () obr l brco gú l gu cucó drcl, α ( ) + α. P( ). Por oro ldo, l m d rmó mcác dl mó d corol, x(), l mó dl brco, δ (), rpod δ ( ) + δ x( ). x () δ () P () Prurco Prurbco α () Nor α () Corodor rmó mcác urb Brco δ () Codér codco cl ul. L xpro qu modl l compormo dámco dl m l domo compljo rá: 36 Dpo. Elcróc, Auomác Iormác Idurl
13 Apu d Rgulcó Auomác Cpíulo : Rvó d udmo mmáco G G G 3 δ X P δ α P ( + ) 5. ( + ) Por o, l rormd d Lplc dl rumbo dl brco, α(), u rd cló rá: ( ) α α El cálculo d lo rduo vldrá: ( ) X G G G ( ) + ( +. ) ( + ) (. ) [ α ] ( α ) d d [( + ) α ] [( +.) α ] L rpu dl brco u cmbo d rumbo uro rá: α 9.9. Mordo qu l brco gobrbl co rg d corol..4 Uo d Mlb l rormd d Lplc E o pu mplrá mulco umérc co Mlb. Alguo jrcco llv odo u crp corrpod bdo l oolbox d Corol-Mlb. Dpo. Elcróc, Auomác Iormác Idurl 37
14 Cpíulo : Rvó d udmo mmáco Apu d Rgulcó Auomác Aí, lguj d progrmcó pr dr l FD d lo m mplrá l comdo. S drá lo vcor l dl umrdor y dl domdor prr d lo coc dl polomo: Ejmplo.5 G N D >> g m b + b + b +... bm ( ) ([ b b b b b ], [ ]) m m Pr drmr l rpu dl cudrpolo RC dl jmplo.3 rí: >> g (,[-3 ]) >>p(g) El comdo p plc u xccó d cló uro y vulz l rpu l domo mporl. Pr l co dl brco dl jmplo.4 l ld rí: >> g (.,poly([. -])) >>p(g) L ucó poly dvulv lo coc dl polomo prr d u ríc. S d rlzr l dcompocó rcco mpl y por d mbé l cálculo d lo rduo, oprcó rlz co l comdo rdu: Y >> ( ) r( ) ( p( ) ) r( ) ( p( ) ) m Q b + b + b +... bm P [ r, p, ] rdu( [ b b b b b ] [ ]) Ejmplo.6 m, E l jmplo dl cudrpolo RC rí: >>[r,p,] rdu(,[-3 ]) Y pr l brco: m >>[r,p,] rdu(.,poly([. -])) r( ) ( p( ) ) Nó qu h ñddo u polo l org mb xpro. É l ruldo d hbr ddo u xccó d rd cló uro, crmdo l ord dl polomo dl domdor u udd Dpo. Elcróc, Auomác Iormác Idurl
15 Apu d Rgulcó Auomác Cpíulo : Rvó d udmo mmáco.5 Problm propuo Cuó. Drmr l r d Fourr d u od mrccd y doblm rccd. mbé hg lo mmo co u r d mpulo. Pr clrl l cálculo pr l grác dju d ñl hbdo bucdo lgu propdd d ucó pr mpr. Od mrccd Od doblm rccd [V].5 [V] [] [] r d mpulo [V] [] Cuó. Drmr l rormd d Lplc d l ñl d : pulo d drc, cló uro, rmp ur y prábol ur. ) Md l dcó dl oprdor d Lplc b) Aplcdo lo orm Cuó.3 Drmr l FD, gc d ó, dl cudrpolo lécrco d l gur. Codér Dpo. Elcróc, Auomác Iormác Idurl 39
16 Cpíulo : Rvó d udmo mmáco Apu d Rgulcó Auomác codco cl ul. Problm. Pr drmr lo vlor dl crcuo LC d l gur l plc u rd mpulol. Drmr ) rormd d Fourr y d Lplc d l ñl / ε ε mpulol, v. Sdo ε qu > ε d r cro. b) Expró líc, l domo dl mpo, d l ñl d ld l plcr l rd dl prdo ror. c) L ld mdd co u oclocopo y l rmóco d Hz. Drmr l vlor dl coddor l bob d mh. Rprr l ñl d ld l rd mpulol. Problm. S d rlzr l corol uomáco d lur d u globo roáco. Pr llo dpo d u qumdor d g coroldo lécrcm, d orm qu u ñl d rrc d V, dcho qumdor por Kcl g l r codo l globo. r llzr l cuco dl globo rpco d l lur dl jdo d l EUII, y d l pró y mprur mbl, ob l gu cuco qu modl u compormo: d,3 Q( ), d d Z Z( ) d E dod () l crmo, grdo Clu, d mprur dl r dl globo rpco d l mprur mbl. Z() l crmo mro d lur rpco dl jdo d l cul. Q() l crmo l lujo d clor ( Kcl g ) rpco dl puo l qu l globo prmc qulbrdo l codco d llzcó. Pr podr crrr l lzo d corol y d orm hcr l coroldor d lur r l prurbco, dpo d u límro lcróco cuyo cro h jdo l lur d llzcó d l cuco. Dcho límro d u ñl d mv m. L rrc l m d corol clm d por mdo d u pocómro ll clbrdo d orm qu u crmo d mro l rrc provoc u crmo l ó d rrc d mv. 4 Dpo. Elcróc, Auomác Iormác Idurl
17 Apu d Rgulcó Auomác Cpíulo : Rvó d udmo mmáco Drmr l dgrm d bloqu y l dámc dl globo u rd cló uro. Problm.3 El m d corol d u locomoor lécrc á bdo u rucur d rlmcó gv. L vlocdd d mdo covrd u ñl lécrc co gc ur, l cul comprd co l ó d ld d u or d vlocdd dl r, co gc D. L ñl d rror c u mplcdor d ó co gc. E p coc co l moor lécrco d l locomoor, grdo l urz d mpuj dl r. S pd:. Pr drmr l ucó d rrc dl moor, l plc u ucó cló d V l rd dl moor. L urz d mpuj rgr y dcrb l gu volucó mporl: Obr l FD dl moor. ( ) Dgrm bloqu dl m d corol d l locomoor. 3. Obr l quvl rducdo d l FD dl moor,. um 4. Empldo l quvl rducdo dl ror prdo, drmr l xpró líc d l volucó mporl d l vlocdd dl r u rd cló d V l m d rlmcó. Do M dl r 38 old,, Co d l dímo, D [V/m/]. Por l xpró mporl, l rormd d Lplc d l urz dl moor plcdo l orm d rlcó complj y dcompocó rcco mpl rá dl po: ( ) + + F Por o, plc u rd cló, l prmr rccó corrpod l xccó y l ro l FD r l ó plcd l moor y u urz: F u m + 3 m + Dpo. Elcróc, Auomác Iormác Idurl 4
18 Cpíulo : Rvó d udmo mmáco Apu d Rgulcó Auomác Pr drmr m plcrá l orm dl vlor l: lm ( F ) lm + m m 6. L rlcó r l urz plcd l locomoor y u vlocdd rá: m v v F m El dgrm bloqu qudrá como: 3. El polo dom rá l ubcdo -/3. Hbrá qu dcur l gc ác: G q 6 ( ) G q L dámc mporl rqur d br cul l FD d l rucur rlmd: 3 L rormd d l vlocdd d l locomoor : v Dpo. Elcróc, Auomác Iormác Idurl
19 Apu d Rgulcó Auomác Cpíulo : Rvó d udmo mmáco Aplcdo l rormd por dcompocó rcco mpl qudrá: v Drcho d Auor 8 Crlo Plro Duñ. Prmo pr copr, drbur y/o modcr documo bjo lo érmo d l Lcc d Documcó Lbr GNU, Vró. o culqur or vró poror publcd por l Fr Sowr Foudo; cco vr, xo d l Cubr Frol, í como l xo d l Cubr Poror. U cop d l lcc clud l ccó uld "Lcc d Documcó Lbr GNU". L Lcc d documcó lbr GNU (GNU Fr Documo Lc) u lcc co copyl pr codo bro. odo lo codo d o pu á cubro por lcc. L vro. cur hp:// L rduccó (o ocl) l cllo d l vró. cur hp:// Dpo. Elcróc, Auomác Iormác Idurl 43
6 - Líneas de Transmisión (cont.)
 Elcromgmo 4 6-33 6 - í d Trmó co. Adpcó d mpdc E comú qu d cocr u crg u lí d mpdc crcríc dfr. E l co xrá u od rfljd qu dmuy l poc rgd l crg y pud r fco dro l grdor, crr oro y orcorr or l lí cpc d cur dño,
Elcromgmo 4 6-33 6 - í d Trmó co. Adpcó d mpdc E comú qu d cocr u crg u lí d mpdc crcríc dfr. E l co xrá u od rfljd qu dmuy l poc rgd l crg y pud r fco dro l grdor, crr oro y orcorr or l lí cpc d cur dño,
variables aleatorias discretas, la función de probabilidad conjunta del vector aleatorio ( X,..., se define como: ) A
 cors loros. só más d dos dmsos Dcó: S... rbls lors dscrs l ucó d robbldd cou dl cor loro... s d como: ddo culqur couo A R...... P... P... A...... A...... s ucó ssc ls sgus rodds:.................. orm
cors loros. só más d dos dmsos Dcó: S... rbls lors dscrs l ucó d robbldd cou dl cor loro... s d como: ddo culqur couo A R...... P... P... A...... A...... s ucó ssc ls sgus rodds:.................. orm
Tema 6. Sistemas muestreados y discretos
 m 6. Sm mrdo dcro. Irodccó:. Ercr d m d corol por compdor. Mro rcorccó d ñl. L rformd 3. Dcrpcó xr d m D.L.I Dcro Ll Ivr l mpo 3. Fcó d rfrc pld 3. Fcó d rfrc d m coo mrdo co O 3.3 Dgrm d loq 4. Rp mporl
m 6. Sm mrdo dcro. Irodccó:. Ercr d m d corol por compdor. Mro rcorccó d ñl. L rformd 3. Dcrpcó xr d m D.L.I Dcro Ll Ivr l mpo 3. Fcó d rfrc pld 3. Fcó d rfrc d m coo mrdo co O 3.3 Dgrm d loq 4. Rp mporl
CRITERIO DE ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA PARA CONTROLADORES CONMUTADOS
 CRIERIO E ESBII E E OMIIO E FRECUECI PR COROORES COMUOS Jorg Elo Mro Grcí-Sz Crlo Mol prmo d uomác y compucó Uvrdd púlc d vrr 36 Pmplo. mgz@uvrr. Rum E rículo pr u formulcó gráfc d u crro d ldd pr m ll
CRIERIO E ESBII E E OMIIO E FRECUECI PR COROORES COMUOS Jorg Elo Mro Grcí-Sz Crlo Mol prmo d uomác y compucó Uvrdd púlc d vrr 36 Pmplo. mgz@uvrr. Rum E rículo pr u formulcó gráfc d u crro d ldd pr m ll
MODELOS DE ATMÓSFERA (teoría y problemas)
 MODLO D MÓR (or y pro) * PLN IN MÓR * MODLO MÓR NO BORBN * MODLO MÓR ON BORIÓN LIV * BLN D RDIIÓN N L IRR (PROMDIO) * JRIIO * LGUNO PROBLM D XMN RULO * PLN IN MÓR Ddd d po (W - ) Irrd, W ujo d rg d (fu:
MODLO D MÓR (or y pro) * PLN IN MÓR * MODLO MÓR NO BORBN * MODLO MÓR ON BORIÓN LIV * BLN D RDIIÓN N L IRR (PROMDIO) * JRIIO * LGUNO PROBLM D XMN RULO * PLN IN MÓR Ddd d po (W - ) Irrd, W ujo d rg d (fu:
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE QUÍMICA DEPARTAMENTO DE MATEMÁTICAS Ecuaciones Diferenciales [Guia]
![UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE QUÍMICA DEPARTAMENTO DE MATEMÁTICAS Ecuaciones Diferenciales [Guia] UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE QUÍMICA DEPARTAMENTO DE MATEMÁTICAS Ecuaciones Diferenciales [Guia]](/thumbs/80/80848373.jpg) UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE QUÍMICA DEPARTAMENTO DE MATEMÁTICAS Ecucio Difrcil [Gui] E l hoj d orcio or l úmro d rgu, l drrollo qu juifiqu u ru, u ru co i crrd u rcágulo lugo u
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE QUÍMICA DEPARTAMENTO DE MATEMÁTICAS Ecucio Difrcil [Gui] E l hoj d orcio or l úmro d rgu, l drrollo qu juifiqu u ru, u ru co i crrd u rcágulo lugo u
Ruta Alimentadora Sur
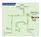 Ad Ru Ador Ad Lo Horzo Ad B A-02 ALAEDA UR Ad Lo Cd P PUENTE VILLA E o P Hy J rí E o Ovo L Cv Grd Cv ERVICIO EPECIAL CIRCUITO DE PLAYA L Gvo Hy Tr A-04 VILLA EL ALVADOR Rvou Ro A-07 AÉRICA L Uó Grd A-08
Ad Ru Ador Ad Lo Horzo Ad B A-02 ALAEDA UR Ad Lo Cd P PUENTE VILLA E o P Hy J rí E o Ovo L Cv Grd Cv ERVICIO EPECIAL CIRCUITO DE PLAYA L Gvo Hy Tr A-04 VILLA EL ALVADOR Rvou Ro A-07 AÉRICA L Uó Grd A-08
ANALISIS DE SISTEMAS LINEALES CONTINUOS EN EL ESPACIO DE ESTADO
 U N E X P O UNIVERSIDAD NACIONAL EXPERIMENTAL POLITECNICA ANTONIO JOSE DE SUCRE VICE RECTORADO BARQUISIMETO DEPARTAMENTO DE INGENIERIA ELECTRONICA ANALISIS DE SISTEMAS LINEALES CONTINUOS EN EL ESPACIO
U N E X P O UNIVERSIDAD NACIONAL EXPERIMENTAL POLITECNICA ANTONIO JOSE DE SUCRE VICE RECTORADO BARQUISIMETO DEPARTAMENTO DE INGENIERIA ELECTRONICA ANALISIS DE SISTEMAS LINEALES CONTINUOS EN EL ESPACIO
SENSORES DISTRIBUIDOS PARA EL DESPLAZAMIENTO VOLUMICO DE UNA PLACA DELGADA EN SOPORTE SIMPLE
 SENSORES DSTRBUDOS PARA EL DESPLAZAMENTO VOLUMCO DE UNA PLACA DELGADA EN SOPORTE SMPLE PACS: 43.4.V Coo, Pdo; Cu, Mí uo d Acúc. CSC. So 44 86 Mdd. Eñ Tl: 95 68 86 : 94 7 65 E-l: [email protected].; [email protected].
SENSORES DSTRBUDOS PARA EL DESPLAZAMENTO VOLUMCO DE UNA PLACA DELGADA EN SOPORTE SMPLE PACS: 43.4.V Coo, Pdo; Cu, Mí uo d Acúc. CSC. So 44 86 Mdd. Eñ Tl: 95 68 86 : 94 7 65 E-l: [email protected].; [email protected].
Respuesta en régimen permanente a una entrada senoidal, resonancia y frecuencia natural de oscilación
 ur: Ig. Jrg lg - JTP Má zd Pág d 6 Fuld d Igrí Ursdd Nl d Mr dl Pl - rg spus rég pr u rd sdl, rs fru url d sló Supgs qu s u ss ll, r l p sl, rrzd pr su fuó prl, l uál grss u sñl.. s µ E grl, l sld dl ss
ur: Ig. Jrg lg - JTP Má zd Pág d 6 Fuld d Igrí Ursdd Nl d Mr dl Pl - rg spus rég pr u rd sdl, rs fru url d sló Supgs qu s u ss ll, r l p sl, rrzd pr su fuó prl, l uál grss u sñl.. s µ E grl, l sld dl ss
Producto de convolución de las derivadas de orden k por las derivadas de orden de la delta de Dirac soportadas en x 1, x a, y x n
 Vol. 5, No., pp. 59-69/Dcmr ISSN-L 88-674 Coprgh Uvrsdd Ncol d Igrí Imprso Ncrgu. Todos los drchos rsrvdos hp://www.lmol.fo/d.php/nexo Produco d covolucó d ls drvds d ord por ls drvds d ord d l dl d Drc
Vol. 5, No., pp. 59-69/Dcmr ISSN-L 88-674 Coprgh Uvrsdd Ncol d Igrí Imprso Ncrgu. Todos los drchos rsrvdos hp://www.lmol.fo/d.php/nexo Produco d covolucó d ls drvds d ord por ls drvds d ord d l dl d Drc
Capítulo 3: Integral definida. Módulos 12 al 17. I. Notación sigma. En los ejercicios 1 a 5 escriba en forma de sumatoria la suma dada.
 Módulos l 7 I Nocó sgm E los jrccos scr form d sumor l sum dd + + + + + + + + 9 + + 7 6 7 8 l + l 6 + l 8 + l 6 6 Supog qu f ( ) 8, g( ) y h( ) Clcul l vlor d l prsó dcd los jrccos - c [ f ( ) g( ) h(
Módulos l 7 I Nocó sgm E los jrccos scr form d sumor l sum dd + + + + + + + + 9 + + 7 6 7 8 l + l 6 + l 8 + l 6 6 Supog qu f ( ) 8, g( ) y h( ) Clcul l vlor d l prsó dcd los jrccos - c [ f ( ) g( ) h(
GESTIÓN POR PROCESOS MAPA DE PROCESOS CARACTERIZACIÓN DE PROCESOS
 GÓ POR PROO MP D PROO RRZÓ D PROO GÓ POR PROO B olombia Business lliance for ecure ommerce PROO Relación insumo ambio Producto RD RFORMO LD Recursos, nsumos información PROO D MBO Resultados, Producto
GÓ POR PROO MP D PROO RRZÓ D PROO GÓ POR PROO B olombia Business lliance for ecure ommerce PROO Relación insumo ambio Producto RD RFORMO LD Recursos, nsumos información PROO D MBO Resultados, Producto
ECUACIONES DIFERENCIALES TRANSFORMADAS DE LAPLACE
 TENOÓGIO DE ESTUDIOS SUPERIORES DE EATEPE DIVISION DE INGENIERÍA EETRÓNIA Y TEEMÁTIA EUAIONES DIFERENIAES Y TRANSFORMADAS DE APAE ON APIAIONES Mrl poo pr l cro Mác M.. Aoo Slv Mríz 6 TENOÓGIO DE ESTUDIOS
TENOÓGIO DE ESTUDIOS SUPERIORES DE EATEPE DIVISION DE INGENIERÍA EETRÓNIA Y TEEMÁTIA EUAIONES DIFERENIAES Y TRANSFORMADAS DE APAE ON APIAIONES Mrl poo pr l cro Mác M.. Aoo Slv Mríz 6 TENOÓGIO DE ESTUDIOS
gu g v C u. mró rm r mbr fum mé í írm Pró uh. m gué r - r rx L. r m r rm r mr r - m - rr, mr m gu fá v b má ér u u r b u m, fru r uó v rr m h uv C. r
 Mur ó Crv V Eér rr N r P Brá Ag V fí, ur j h ué m, vgur L g u, hum, r rr r, év E v rr mm u q R Luz Ág L. P Exr U - r M E mbé f r grr r rzr uv íqu xr r. r m m r ué ur jó f g ñr U Qu rá. mu rvur í u mur,
Mur ó Crv V Eér rr N r P Brá Ag V fí, ur j h ué m, vgur L g u, hum, r rr r, év E v rr mm u q R Luz Ág L. P Exr U - r M E mbé f r grr r rzr uv íqu xr r. r m m r ué ur jó f g ñr U Qu rá. mu rvur í u mur,
ESCOGENCIA DE CARRERAS DE NIVEL DIVERSIFICADO EN INSTITUTOS NACIONALES DE EDUCACIÓN BÁSICA CERCANOS A ESCUELAS NORMALES INVESTIGACIÓN
 E og d r r r d v d v r f d o u o o d Ed u ó Bá CERCANOSAES CUEL ASNORMAL ESI NVES TI GACI ÓN D p r m oe d u v o C r od E u d od Op ó P ú b A o ó d I v g ó ye u d os o AS I E S 1 0 ª C 7 4 8Zo 9 Gu m 0
E og d r r r d v d v r f d o u o o d Ed u ó Bá CERCANOSAES CUEL ASNORMAL ESI NVES TI GACI ÓN D p r m oe d u v o C r od E u d od Op ó P ú b A o ó d I v g ó ye u d os o AS I E S 1 0 ª C 7 4 8Zo 9 Gu m 0
Hola, chicas y chicos! Os presentamos a. Él y sus amigos son los ganadores del concurso de ciencias de este año. . En Brasil, la selva está en
 E ryc d Pdr Hj d cividd 1 Nmbr: Fch: L rícu y cmé. NOTICIAS DEL COLE PEDRO Y SUS AMIGOS GANAN EL CONCURSO DE CIENCIAS H, chic y chic! O rm Bqu. É y u mig gdr d ccur d cici d ñ. Pdr d. E Bri, v á rqu á
E ryc d Pdr Hj d cividd 1 Nmbr: Fch: L rícu y cmé. NOTICIAS DEL COLE PEDRO Y SUS AMIGOS GANAN EL CONCURSO DE CIENCIAS H, chic y chic! O rm Bqu. É y u mig gdr d ccur d cici d ñ. Pdr d. E Bri, v á rqu á
Creación de Modelos Delphos.Net
 Crcó d Modlo lpho.nt EINSA Apdo. Potl 314-2350 S Joé, Cot Rc http://www.d.com Tléfoo (506) 2276-3380 Fx (506) 2276-3778 E-ml: [email protected] Cotdo Igro l Modlo...3 Mtmto d Prpctv...7 Mtmto d Tpo d Rpobl...10
Crcó d Modlo lpho.nt EINSA Apdo. Potl 314-2350 S Joé, Cot Rc http://www.d.com Tléfoo (506) 2276-3380 Fx (506) 2276-3778 E-ml: [email protected] Cotdo Igro l Modlo...3 Mtmto d Prpctv...7 Mtmto d Tpo d Rpobl...10
r r ér r ó: ó bé í g hr r b br r b. r ró Yg hú br L Cró. ér g ó U " r: ú Sr Sr ó f Sr." Sr r bjv Rj Yg Hh Yg: v gr r g br - g. Y rf rá Yg h H b r ó br
 L CULTIVO D LA CONCNTRACIÓN I í xrr r ér Sr Cv gr Pr f frr r Pr. rí rá r r vr r hú br r x óf v r rr r ír ó Ihwr frr P. h hú v é gr "hb ír: r r "Bhgv G" í 15 rzó r v v I rz. r r r qr r á hwr rrr br g rz
L CULTIVO D LA CONCNTRACIÓN I í xrr r ér Sr Cv gr Pr f frr r Pr. rí rá r r vr r hú br r x óf v r rr r ír ó Ihwr frr P. h hú v é gr "hb ír: r r "Bhgv G" í 15 rzó r v v I rz. r r r qr r á hwr rrr br g rz
Departamento de Matemática Facultad de Ingeniería Universidad Nacional de Mar del Plata
 Dprmo d Mmáic Fculd d Igirí Uivridd Nciol d Mr dl Pl Mmáic Avzd hp:://www3..ffii..mdp.du.r/mvzd [email protected] 4 Coido INRODUCCIÓN.3 EMAS DE VARIABLE COMPLEJA 8 ANÁLISIS EN EL DOMINIO EMPORAL /REAL
Dprmo d Mmáic Fculd d Igirí Uivridd Nciol d Mr dl Pl Mmáic Avzd hp:://www3..ffii..mdp.du.r/mvzd [email protected] 4 Coido INRODUCCIÓN.3 EMAS DE VARIABLE COMPLEJA 8 ANÁLISIS EN EL DOMINIO EMPORAL /REAL
126 l lg l g g b b t p p ñ ñ ñ l l l.. - p t p r l cl clí í í l L fc c u c i l y b ft i i cr cró ó ó l p b g,, i d,, p pm i l g i l ft i i g d r f i m
 SOBR BRE LA NEFRITIS CRON ONIC ICA DEL PERR RRO Y DEL GATO EL PELIGR IGRO DE PRACTI CTICAR CAR OPERAC RACION IONES EN LOS -BRIGH IGHTIC TICOS" Pr l Prf. HEBR BRAN ANT y Prf f. ju ANTO TOIN INE l El V r
SOBR BRE LA NEFRITIS CRON ONIC ICA DEL PERR RRO Y DEL GATO EL PELIGR IGRO DE PRACTI CTICAR CAR OPERAC RACION IONES EN LOS -BRIGH IGHTIC TICOS" Pr l Prf. HEBR BRAN ANT y Prf f. ju ANTO TOIN INE l El V r
n o ó i Mi nombre: Mi numero de orden: Cuadernillo 1 periodo II MOMENTO DE LA MOVILIZACIÓN NACIONAL POR LA MEJORA DE LOS APRENDIZAJES
 l bim cm CACIÓN EDU bim cm DOS TO C u m ó i c c i d r t m m i trá d D qu d r p d i, r u q rd p l rd m p d T d 2 d u g S g prid Mi mbr: Cudrill 1 Mi umr d rd: II MOMENTO DE LA MOVILIZACIÓN NACIONAL POR
l bim cm CACIÓN EDU bim cm DOS TO C u m ó i c c i d r t m m i trá d D qu d r p d i, r u q rd p l rd m p d T d 2 d u g S g prid Mi mbr: Cudrill 1 Mi umr d rd: II MOMENTO DE LA MOVILIZACIÓN NACIONAL POR
Tema 4: Regresiones lineales y no lineales TEMA 4. REGRESIONES LINEALES LINEALES Y NO. 1. 2. 3. Introducción 4. Nomenclatura
 T 4: grsos lls o lls TEMA 4. EGEIONE LINEALE LINEALE Y NO.. 3. Itroduccó 4. Nocltur 5. Llzcó Ajust grsó ll ll d últpl cucos 6. 7. 8. grsos EUMEN Progrcó o lls Mtlb Cálculo uérco Igrí T 4: grsos lls o lls.
T 4: grsos lls o lls TEMA 4. EGEIONE LINEALE LINEALE Y NO.. 3. Itroduccó 4. Nocltur 5. Llzcó Ajust grsó ll ll d últpl cucos 6. 7. 8. grsos EUMEN Progrcó o lls Mtlb Cálculo uérco Igrí T 4: grsos lls o lls.
l ij l'; 1r" 1râ I 't i 4-1.} ,ffi,h) 4,i4 r z l,9 11,{ .Jn 1,{ 'l 'l J, J,t J,t 1,a -5^ l.{ l,{' ''' l. I, I fié \bi a j d i' .iq I '11 .J.f 3,?
 ,' ḻ.) r Ë'.' -f,.-.. =(-,, '; -'..f - ' -. -^ 0 '..'.., ḷ C. c).,' C., c. C!.c.' - ạ - C. ( rô -, '.r,.,. ',, - v ) - '.. ) r, -) '_ r Ë )'.., ^,' à ',, ' ',.' ( ) ' ',' r r ) - r c c,', ḷ,' s ) c, -
,' ḻ.) r Ë'.' -f,.-.. =(-,, '; -'..f - ' -. -^ 0 '..'.., ḷ C. c).,' C., c. C!.c.' - ạ - C. ( rô -, '.r,.,. ',, - v ) - '.. ) r, -) '_ r Ë )'.., ^,' à ',, ' ',.' ( ) ' ',' r r ) - r c c,', ḷ,' s ) c, -
Corporación Eco Industrial y Comercial S.A. de C.V.
 Ccó Ec Idu y Cc S.A. d C.V. Ud, dccó dc, d ógc y dg Md UA8EAD...TI Cj cídc M8 d c db INO AISI 36L Dc d dccó: 50-500 Acó: d 2 5 30 VCC Sd: 0-0 V CC -20 A y u d d cucó NPN PNP, NA NC. E d dd % Rbdd 0,5%
Ccó Ec Idu y Cc S.A. d C.V. Ud, dccó dc, d ógc y dg Md UA8EAD...TI Cj cídc M8 d c db INO AISI 36L Dc d dccó: 50-500 Acó: d 2 5 30 VCC Sd: 0-0 V CC -20 A y u d d cucó NPN PNP, NA NC. E d dd % Rbdd 0,5%
Testamento de Ryan Ray
 : / 2 0 1 7 é : Cá L M: Ob Pí / Of y M VS Plí m mb jg h j y m gl, m l m l mg: m wh L "g" m Al l hb h, m mg, á g L g E lg l ñm hj m b, bm l N mj Hz l L m l fml mh g m y ml, m f, m má l l ém, jgm l áb C,
: / 2 0 1 7 é : Cá L M: Ob Pí / Of y M VS Plí m mb jg h j y m gl, m l m l mg: m wh L "g" m Al l hb h, m mg, á g L g E lg l ñm hj m b, bm l N mj Hz l L m l fml mh g m y ml, m f, m má l l ém, jgm l áb C,
Nombre: Fecha: 1 Grado = Lee las siguientes oraciones. -El dragón vive en el castillo -El carro azul es nuevo -El caballo come pasto
 Nomb: Fh: 1 Gdo 45 32 87 31 2020= d d yo mo o g úmo 3566891002 Rz d 10 10. p b g pb bdg bogomú qo Rz dbjo d o q h dí. g oo. E dgó o E o z o E bo om po Rp g Tbg E myo m yó yo, bo m pó ó, m o po q m dmyo.
Nomb: Fh: 1 Gdo 45 32 87 31 2020= d d yo mo o g úmo 3566891002 Rz d 10 10. p b g pb bdg bogomú qo Rz dbjo d o q h dí. g oo. E dgó o E o z o E bo om po Rp g Tbg E myo m yó yo, bo m pó ó, m o po q m dmyo.
E N T R E V I S T A PRINCIPALES HERRAMIENTAS ENTREVISTA ESTILOS DE APRENDIZAJE HÁBITOS DE ESTUDIO
 LO D PDZJ PCPL HM HÁBO D UDO FUDMO D L OÍ Y ÉCC D L COCPO D. GÚ BGHM Y MOO, L U COCÓ, QU POPO U F DMDO, DO DL MPL PLC D L COCÓ. FUCO BÁC:. COLC DO. B. FOM. C. MO. P YMOD, L U MÉODO P U DO DU U COCÓ PD
LO D PDZJ PCPL HM HÁBO D UDO FUDMO D L OÍ Y ÉCC D L COCPO D. GÚ BGHM Y MOO, L U COCÓ, QU POPO U F DMDO, DO DL MPL PLC D L COCÓ. FUCO BÁC:. COLC DO. B. FOM. C. MO. P YMOD, L U MÉODO P U DO DU U COCÓ PD
Capítulo 4: Rotaciones Multidimensionales con Operaciones Vectoriales
 Cítulo 4: Rotcos Multdmsols co Orcos ctorls Como s vo l cítulo tror s ud hcr rotr u ojto l sco D roorcodo - utos o cohrlrs s dcr s roorco l j d rotcó l cul s l rrstcó d u sml -D. E st cítulo s lz y td
Cítulo 4: Rotcos Multdmsols co Orcos ctorls Como s vo l cítulo tror s ud hcr rotr u ojto l sco D roorcodo - utos o cohrlrs s dcr s roorco l j d rotcó l cul s l rrstcó d u sml -D. E st cítulo s lz y td
ERROR EN ESTADO ESTACIONARIO
 UNIVESIDAD AUÓNOMA DE NUEVO EÓN FACUAD DE INGENIEÍA MECÁNICA Y EÉCICA EO EN ESADO ESACIONAIO INGENIEÍA DE CONO M.C. EIZABEH GPE. AA HDZ. M.C. OSÉ MANUE OCHA NÚÑEZ UNIVESIDAD AUÓNOMA DE NUEVO EÓN FACUAD
UNIVESIDAD AUÓNOMA DE NUEVO EÓN FACUAD DE INGENIEÍA MECÁNICA Y EÉCICA EO EN ESADO ESACIONAIO INGENIEÍA DE CONO M.C. EIZABEH GPE. AA HDZ. M.C. OSÉ MANUE OCHA NÚÑEZ UNIVESIDAD AUÓNOMA DE NUEVO EÓN FACUAD
Perfiles de modulación ascendentes para las tarjetas de línea para cable
 rf ucó c r rj í r c Iruccó rrru Ru z vc Ráfg c Guí rf ucó j rf ucó (zc) óg DOI.- ( y r c IO fwr rr) óg DOI.- (r ) cuó Au rf ucó Lcr hrc ( y ) Lcr Lcr Aéc A ácu ñ u r u - D Aéc frcó éc rf ucó VI G7 VI H
rf ucó c r rj í r c Iruccó rrru Ru z vc Ráfg c Guí rf ucó j rf ucó (zc) óg DOI.- ( y r c IO fwr rr) óg DOI.- (r ) cuó Au rf ucó Lcr hrc ( y ) Lcr Lcr Aéc A ácu ñ u r u - D Aéc frcó éc rf ucó VI G7 VI H
SOLUCIÓN DE LA ECUACIÓN LINEAL A COEFICIENTES CONSTANTES: CASO HOMOGÉNEO. De acuerdo a la naturaleza de las soluciones, se obtienen tres casos:
 Mri: Cálclo III Uidd III: Eccio dircil d gdo ord Nro. d pág.: Libro: Eccio dircil co pliccio Aor: Zill Di G.... SOLUCIÓN DE LA ECUACIÓN LINEAL A COEFICIENTES CONSTANTES: CASO HOMOGÉNEO L orm grl d cció
Mri: Cálclo III Uidd III: Eccio dircil d gdo ord Nro. d pág.: Libro: Eccio dircil co pliccio Aor: Zill Di G.... SOLUCIÓN DE LA ECUACIÓN LINEAL A COEFICIENTES CONSTANTES: CASO HOMOGÉNEO L orm grl d cció
FAM 2004 FAM 2006 FAM 2007
 RCURO: RCCÓ PROYCO Y OBR FOO PORCO ÚP (F) 2004-2009 F 2004 FCH U CUZCÓ: 31 CBR 2010 PG 1 6 O GR OBR COR VC (%) OBR o. OBR (COVO) UBCCÓ O. CORO PZO JCUCO OO OBR FCO FCRO CRO VGCO / PCHUC OO, PyO/17/04 12/OC/2004
RCURO: RCCÓ PROYCO Y OBR FOO PORCO ÚP (F) 2004-2009 F 2004 FCH U CUZCÓ: 31 CBR 2010 PG 1 6 O GR OBR COR VC (%) OBR o. OBR (COVO) UBCCÓ O. CORO PZO JCUCO OO OBR FCO FCRO CRO VGCO / PCHUC OO, PyO/17/04 12/OC/2004
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE NAVARRA JUNIO 2012 (GENERAL) (RESUELTOS por Antonio Menguiano) Tiempo máximo: 1 horas y 30 minutos
 IES CSTELR DJOZ nguino PRUE DE CCESO (LOGSE) UNIVERSIDD DE NVRR JUNIO (GENERL) (RESUELTOS por nonio nguino) TEÁTICS II Timpo máimo: hors minuos Rlir un d ls dos opcions propuss ( o ) OPCIÓN º) Esudi l
IES CSTELR DJOZ nguino PRUE DE CCESO (LOGSE) UNIVERSIDD DE NVRR JUNIO (GENERL) (RESUELTOS por nonio nguino) TEÁTICS II Timpo máimo: hors minuos Rlir un d ls dos opcions propuss ( o ) OPCIÓN º) Esudi l
Un forward sobre commodities como el oro sufre una pequeña variación ya que se incluye la tasa de interés del oro (lease rate) con la variable l
 El Forward U corao fuuro o a plazo, s odo aqul cuya lqudacó o slm dfr hasa ua fcha posror spulada l msmo, s dcr s dos pas acurda hacr la rasaccó hasa u prodo fuuro dígas por jmplo 6 mss, so s u corao forward.
El Forward U corao fuuro o a plazo, s odo aqul cuya lqudacó o slm dfr hasa ua fcha posror spulada l msmo, s dcr s dos pas acurda hacr la rasaccó hasa u prodo fuuro dígas por jmplo 6 mss, so s u corao forward.
2 Índice Dorian Luis Linero Segrera Universidad Nacional de Colombia, 2010
 Íd Íd... Cílo Elmo d l má d óldo r rolm ll láo..... Cmo dl dlmo l dormó ml..... Cmo dl ro... 5.. Eó o d mrl ll láo óroo: l d Hook. 6... Pro d lo ro rl... 9.. Plmo dl rolm l mdo oo....5. Elmo d l má d óldo
Íd Íd... Cílo Elmo d l má d óldo r rolm ll láo..... Cmo dl dlmo l dormó ml..... Cmo dl ro... 5.. Eó o d mrl ll láo óroo: l d Hook. 6... Pro d lo ro rl... 9.. Plmo dl rolm l mdo oo....5. Elmo d l má d óldo
Departamento Informática. Diputación Provincial de Soria
 3/6/ www.po. Mo éo y ogzvo Dpo Ifoá Dpu Povl So Ju Clo G www.po. Mo éo y ogzvo SORI Supf:.36 K Hb: 95. D: 9 hb/k PONTEVEDR Supf: 4.495 K Hb: 959.764 D: 4 hb/k Ju Clo G 3/6/ www.po. Mo éo y ogzvo Dbu poblol
3/6/ www.po. Mo éo y ogzvo Dpo Ifoá Dpu Povl So Ju Clo G www.po. Mo éo y ogzvo SORI Supf:.36 K Hb: 95. D: 9 hb/k PONTEVEDR Supf: 4.495 K Hb: 959.764 D: 4 hb/k Ju Clo G 3/6/ www.po. Mo éo y ogzvo Dbu poblol
Ejercicios de Caligrafía. ba be bi bo bu ba be bi bo bu ba be bi bo bu ba be bi bo bu ba be bi bo bu ba be bi bo bu. Sílabas
 1. bla ble bli blo blu bla ble bli blo blu bla ble bli blo blu bla ble bli blo blu bla ble bli blo blu bla ble bli blo blu.. 2. bra bre bri bro bru bra bre bri bro bru bra bre bri bro bru bra bre bri bro
1. bla ble bli blo blu bla ble bli blo blu bla ble bli blo blu bla ble bli blo blu bla ble bli blo blu bla ble bli blo blu.. 2. bra bre bri bro bru bra bre bri bro bru bra bre bri bro bru bra bre bri bro
COLEGIO WILLIAM JAMES
 COLEGIO WILLIA JAES PRIER GRADO 500 hj /C d 76 kg. ( bd) cd NO PAPEL ECOLÓGICO 1 qu d 100 hj d c 4 um md ( d g) 2 um g 2 c d c vd zu. 4 hj d f cud gd. 3 Pg d fm dmd df c 1 R d 5m. (cd) méc vd zu c 3 Pg
COLEGIO WILLIA JAES PRIER GRADO 500 hj /C d 76 kg. ( bd) cd NO PAPEL ECOLÓGICO 1 qu d 100 hj d c 4 um md ( d g) 2 um g 2 c d c vd zu. 4 hj d f cud gd. 3 Pg d fm dmd df c 1 R d 5m. (cd) méc vd zu c 3 Pg
3.-AMORTIZACIÓN DE PRÉSTAMOS
 .-MORTZÓ DE PRÉSTMOS..- Un prson solc un présmo. pr morzrlo n ños mn nuls consns pospgbls y un po nrés fcvo nul l 8%. Trnscurros ños y hbno bono l nul l rcr ño, curn uor y cror pr morzr l u pnn ls sguns
.-MORTZÓ DE PRÉSTMOS..- Un prson solc un présmo. pr morzrlo n ños mn nuls consns pospgbls y un po nrés fcvo nul l 8%. Trnscurros ños y hbno bono l nul l rcr ño, curn uor y cror pr morzr l u pnn ls sguns
x a es una serie de la forma que el radio de convergencia de la serie geométrica es el intervalo abierto
 ERIE DE POTENCIA ERIE DE POTENCIA. Diició. U sri d pocis c s u sri d l orm c c c c... c... Por jmplo. i c y l sri d pocis om l orm....... Por jmplo. i c y l sri d pocis om l orm....... TEOREMA. El cojuo
ERIE DE POTENCIA ERIE DE POTENCIA. Diició. U sri d pocis c s u sri d l orm c c c c... c... Por jmplo. i c y l sri d pocis om l orm....... Por jmplo. i c y l sri d pocis om l orm....... TEOREMA. El cojuo
Formulario de matemáticas
 Forlro tát lgr- Sgo (+) (+) = + (-) (-) = + (+) (-) = - (-) (+) = - (+) / (+) = + (-) / (-) = + (+) / (-) = - (-) / (+) = - Fro Proto otl ftorzó ( ) ( ) ( ) ( ) ( ) ()() ()( ) ( )( ) ()( ) L lo ot rl log
Forlro tát lgr- Sgo (+) (+) = + (-) (-) = + (+) (-) = - (-) (+) = - (+) / (+) = + (-) / (-) = + (+) / (-) = - (-) / (+) = - Fro Proto otl ftorzó ( ) ( ) ( ) ( ) ( ) ()() ()( ) ( )( ) ()( ) L lo ot rl log
6 REVIST REV IST IST F CU CUIT IT IT I) G R RN N MI ( ). XXX (). PERON ON EV PER 95 pi pi pi l lg g g d d c (97) 7) 7) S G G (9 S v c ll cc lu lui lu
 \ N( EN EL PERI ) N( ) (N )El NCl ("I (N \RNE\\N Y ) SR)N ("I N E TU ER ERCU CU S I) E P P Pr V VER R. TI ZIO SIV VORI Y R. MONTL LIDI E bj bj r h t d b b ci gú S v (9) ) p r ur t c pr c i l b b l l hij
\ N( EN EL PERI ) N( ) (N )El NCl ("I (N \RNE\\N Y ) SR)N ("I N E TU ER ERCU CU S I) E P P Pr V VER R. TI ZIO SIV VORI Y R. MONTL LIDI E bj bj r h t d b b ci gú S v (9) ) p r ur t c pr c i l b b l l hij
Ejemplo de convolución
 Capíulo : Rviió lo uamo x( y( Mamáico Sñal y ima Covolució: coíua icra [x(] y x * g x( g( x( g( D g( X( G( Y(X(*G(X(G( [(] - [Y(] raormaa ourir aplac [(] - [(] - [(] Domiio mporal Domiio complo Domiio
Capíulo : Rviió lo uamo x( y( Mamáico Sñal y ima Covolució: coíua icra [x(] y x * g x( g( x( g( D g( X( G( Y(X(*G(X(G( [(] - [Y(] raormaa ourir aplac [(] - [(] - [(] Domiio mporal Domiio complo Domiio
EXPRESIONES ALGEBRAICAS
 EXPRESIONES ALGEBRAICAS 1 Epresoes Algebrcs es l uó de úmeros y vrbles medte opercoes de sum, rest, multplccó, dvsó, poteccó y rdccó. Epresó lgebrc rcol: se llm sí quells e ls que ls vrbles está fectds
EXPRESIONES ALGEBRAICAS 1 Epresoes Algebrcs es l uó de úmeros y vrbles medte opercoes de sum, rest, multplccó, dvsó, poteccó y rdccó. Epresó lgebrc rcol: se llm sí quells e ls que ls vrbles está fectds
Verano Cultural PROGRAMA
 V C PROGRAMA Em Dmg Ag, D Hm Uv Bg, h z bj í L Cmó Pm bgé. Cjz z mó. E q D, f G Cmó Av Uv Bg, h v Cjz, bj q h g S Dmg Ib, C Ió Cm Sg, q f v q vm fm. Em Dmg, mbé v Cg y g S J. E xó m q v Cg, x mó m q my
V C PROGRAMA Em Dmg Ag, D Hm Uv Bg, h z bj í L Cmó Pm bgé. Cjz z mó. E q D, f G Cmó Av Uv Bg, h v Cjz, bj q h g S Dmg Ib, C Ió Cm Sg, q f v q vm fm. Em Dmg, mbé v Cg y g S J. E xó m q v Cg, x mó m q my
SISTEMAS LINEALES TABLAS. Dpto. Teoría de la Señal y Comunicaciones
 SISEMAS LIEALES ABLAS Dpo. orí d l Sñl y Comuiccios POPIEDADES DE LA ASFOMADA DE LAPLACE Propidd Sñl rsformd OC ( ) ( ) ( ) s ( s) ( s) Lilidd + b ( ) ( s) b ( s) Dsplmio l impo ( ) Dsplmio l domiio s
SISEMAS LIEALES ABLAS Dpo. orí d l Sñl y Comuiccios POPIEDADES DE LA ASFOMADA DE LAPLACE Propidd Sñl rsformd OC ( ) ( ) ( ) s ( s) ( s) Lilidd + b ( ) ( s) b ( s) Dsplmio l impo ( ) Dsplmio l domiio s
v,, E v lc d h 44 pr p pr xcl x c cl uiv u ivm iv m m m xi i i t í, í, x v gú ú l v b bl b l l g r r t d glá gl áu á,, g gú ú l mm gú ú l cc ó,, g m d
 APLICA CIÓN DE LA REAC ACCI CI CON DE LA CATALASA DE LA LECHE AL DIA GNÓSTI STICO DE LA MAMI MITI TS POR E. HUYN EN (Jf d tb bj d r'c u V r df Bru Tr c bl Dr. C. Nt L ii, d Ft d Agrmí mí V L I'i. 'i. Er
APLICA CIÓN DE LA REAC ACCI CI CON DE LA CATALASA DE LA LECHE AL DIA GNÓSTI STICO DE LA MAMI MITI TS POR E. HUYN EN (Jf d tb bj d r'c u V r df Bru Tr c bl Dr. C. Nt L ii, d Ft d Agrmí mí V L I'i. 'i. Er
EXAMEN FINAL DE I.O.E. (Curso 02/03 2º Q). Cadenas de Markov
 EXAMEN FINA DE I.O.E. (Curo / º Q. Cada d Markov S ha comrobado qu la robabldad d qu u dtrmado artdo olítco ga ua lcco dd d la gaó lo do comco mdatamt atror d la gut forma: gaó la do lcco atror toc la
EXAMEN FINA DE I.O.E. (Curo / º Q. Cada d Markov S ha comrobado qu la robabldad d qu u dtrmado artdo olítco ga ua lcco dd d la gaó lo do comco mdatamt atror d la gut forma: gaó la do lcco atror toc la
Capítulo 3: Integral definida. Módulos 12 al 17. I. Notación sigma. En los ejercicios 1 a 5 escriba en forma de sumatoria la suma dada.
 Módulos l 7 I Nocó sgm E los ejerccos escr e form de sumor l sum dd + + + + + + + + 9 + + 7 6 7 8 l + l 6 + l 8 + l 6 6 Supog que f ( ) 8, g( ) y h( ) Clcule el vlor de l epresó dcd e los ejerccos -e c
Módulos l 7 I Nocó sgm E los ejerccos escr e form de sumor l sum dd + + + + + + + + 9 + + 7 6 7 8 l + l 6 + l 8 + l 6 6 Supog que f ( ) 8, g( ) y h( ) Clcule el vlor de l epresó dcd e los ejerccos -e c
61.1 6.1. SERIES NUMÉRICAS INFINITAS 6.2. SERIES DE TÉRMINOS POSITIVOS 6.3. SERIES ALTERNANTES 6.4. SERIES DE POTENCIAS
 Cp. 6 Sris 6. 6.. SERIES NUMÉRICAS INFINITAS 6.. SERIES DE TÉRMINOS POSITIVOS 6.. SERIES ATERNANTES 6.. SERIES DE POTENCIAS Objtivo: S prtd qu l studit: Dtrmi covrgci o divrgci d sris. Empl sris pr rsolvr
Cp. 6 Sris 6. 6.. SERIES NUMÉRICAS INFINITAS 6.. SERIES DE TÉRMINOS POSITIVOS 6.. SERIES ATERNANTES 6.. SERIES DE POTENCIAS Objtivo: S prtd qu l studit: Dtrmi covrgci o divrgci d sris. Empl sris pr rsolvr
Tema 6.Sistemas de Telecomunicación. El ruido en los sistemas de comunicación.
 ma 6.ma d lcomucacó. l rudo lo ma d comucacó. Aál d lo ma d Comucaco Dgal dd la prpcva R y BR B rror Ra Iroduccó capíulo, la ñal y l rudo dcrb érmo d ñal alaora. Aplcarmo cálculo d probabldad. La da báca
ma 6.ma d lcomucacó. l rudo lo ma d comucacó. Aál d lo ma d Comucaco Dgal dd la prpcva R y BR B rror Ra Iroduccó capíulo, la ñal y l rudo dcrb érmo d ñal alaora. Aplcarmo cálculo d probabldad. La da báca
LA TRANSFORMADA DE LAPLACE
 LA RANSFORMADA DE LAPLACE (pun crio por Dr. Mnul Prgd). INRODUCCIÓN Enr l rnformcion má uul qu oprn con funcion f(x) cumplindo condicion dcud n I[,b, pr obnr or funcion n I, án por jmplo : L oprción D
LA RANSFORMADA DE LAPLACE (pun crio por Dr. Mnul Prgd). INRODUCCIÓN Enr l rnformcion má uul qu oprn con funcion f(x) cumplindo condicion dcud n I[,b, pr obnr or funcion n I, án por jmplo : L oprción D
ORGANIZACION ORGANIZACION { N-Soi~ }) PANAMERICANA' MUNDIAL u/j, DE LA SALUD DE LA SALUD
 cnsej directiv cmite reginl ORGANIZACION ORGANIZACION { N-Si~ }) PANAMERICANA' MUNDIAL u/j, DE LA SALUD DE LA SALUD XXVI Reunión Wshingtn, D.C. Snt embre-octubre 1979 XXXI Reunión INDEXED Tem 29 del pryect
cnsej directiv cmite reginl ORGANIZACION ORGANIZACION { N-Si~ }) PANAMERICANA' MUNDIAL u/j, DE LA SALUD DE LA SALUD XXVI Reunión Wshingtn, D.C. Snt embre-octubre 1979 XXXI Reunión INDEXED Tem 29 del pryect
BE FREE. energía creativa. Te presentamos la herramienta de comunicación online más innovadora!
 Gnt con nrgí crtiv. BE FREE. EL FREEBIE ONLINE: LA HERRAMIENTA DE INBOUND MARKETING MÁS CREATIVA. EL REGALO INFINITO. El frbi un hrrint d prooción y counicción onlin originl, intrctiv, virl, útil y grtuit.
Gnt con nrgí crtiv. BE FREE. EL FREEBIE ONLINE: LA HERRAMIENTA DE INBOUND MARKETING MÁS CREATIVA. EL REGALO INFINITO. El frbi un hrrint d prooción y counicción onlin originl, intrctiv, virl, útil y grtuit.
UNIDAD 3: SISTEMAS DE ECUACIONES LINEALES. 1. DEFINICIONES. Un sistema de m ecuaciones lineales con n incógnitas es una expresión de la forma:
 IE Pdr Povd (Gudi) Mtátics plicds ls CC II Dprtto d Mtátics Bloqu I: Álgr il Profsor: Ró ort Nvrro Uidd : ists d Ecucios ils UNIDD : ITEM DE ECUCIONE INEE DEFINICIONE U sist d cucios lils co icógits s
IE Pdr Povd (Gudi) Mtátics plicds ls CC II Dprtto d Mtátics Bloqu I: Álgr il Profsor: Ró ort Nvrro Uidd : ists d Ecucios ils UNIDD : ITEM DE ECUCIONE INEE DEFINICIONE U sist d cucios lils co icógits s
Mendoza - Las Grutas (Continua 1) Barda del Medio 30 Km de pavimento Km 799 9:56 hs RN 22. Cipolletti 40 Km de pavimento Km :32 hs RN 22
 v Mz ru Km 0 0:00 h RN 7 Mz 47 Km pvm Km 47 0:35 h RN 7 1.224 km S Mrí 43 Km pvm Km 90 1:07 h RP 171 147 Km pvm. Km 237 2:57 h RN 188 M má 50 Km pvm Km 287 3:34 h RN 143 r Avr 100 Km pvm Km 387 4:49 h
v Mz ru Km 0 0:00 h RN 7 Mz 47 Km pvm Km 47 0:35 h RN 7 1.224 km S Mrí 43 Km pvm Km 90 1:07 h RP 171 147 Km pvm. Km 237 2:57 h RN 188 M má 50 Km pvm Km 287 3:34 h RN 143 r Avr 100 Km pvm Km 387 4:49 h
Planes en los que aplica la promoción. COD_PLANTARIF DES_PLANTARIF Plan Mi Grupo (GSM)
 Planes en los que aplica la promoción COD_PLANTARIF DES_PLANTARIF R0 Plan Mi Grupo 4 (GSM) R1 Plan Mi Grupo (GSM) CP1 Pago x Consumo Multicolor Abie CP2 Pago x Consumo Multicolor 25 CP3 Pago x Consumo
Planes en los que aplica la promoción COD_PLANTARIF DES_PLANTARIF R0 Plan Mi Grupo 4 (GSM) R1 Plan Mi Grupo (GSM) CP1 Pago x Consumo Multicolor Abie CP2 Pago x Consumo Multicolor 25 CP3 Pago x Consumo
SISTEMAS DE ECUACIONES DIFERENCIALES DE PRIMER ORDEN
 TEMA Nº SISTEMAS DE ECUACIONES DIFERENCIALES DE PRIMER ORDEN. TEOREMA PRELIMINAR INTRODUCCIÓN.- Sism d cucios dircils lils co icógis d l orm P D P D P D P D P P D D... P... P... P D D D b b b dod ls P
TEMA Nº SISTEMAS DE ECUACIONES DIFERENCIALES DE PRIMER ORDEN. TEOREMA PRELIMINAR INTRODUCCIÓN.- Sism d cucios dircils lils co icógis d l orm P D P D P D P D P P D D... P... P... P D D D b b b dod ls P
1 IES Carlos Bousoño
 1 2 3 5 6 7 MIS DEL PP MRCELLO CREDO G.P. Palsrna 8 9 10 11 12 13 L L NN LLL LLL NN OO OO OO OO OO OO 1 PRQSUXWZY[ PRQSUXWZY[\[ ]_^UXWZY `asdcf_[ `a Sdcf_[g[ hh QYgYXWdY ML ML )! #"%$')( *+',-(./$0213(
1 2 3 5 6 7 MIS DEL PP MRCELLO CREDO G.P. Palsrna 8 9 10 11 12 13 L L NN LLL LLL NN OO OO OO OO OO OO 1 PRQSUXWZY[ PRQSUXWZY[\[ ]_^UXWZY `asdcf_[ `a Sdcf_[g[ hh QYgYXWdY ML ML )! #"%$')( *+',-(./$0213(
Índice General. Disposiciones iniciales y definiciones generales
 Índice General Int r o d u c c i ó n... xxvii CAPÍTULO I Disposiciones iniciales y definiciones generales Dis p o s i c i o n e s iniciales y de f i n i c i o n e s ge n e r a l e s... 1 Capítulo II Trato
Índice General Int r o d u c c i ó n... xxvii CAPÍTULO I Disposiciones iniciales y definiciones generales Dis p o s i c i o n e s iniciales y de f i n i c i o n e s ge n e r a l e s... 1 Capítulo II Trato
2. MÉTODO DE COEFICIENTES INDETERMINADOS.
 . MÉTODO DE COEFICIENTES INDETERMINADOS. E un étodo r hllr un olución rticulr d l cución linl colt [], u conit fundntlnt n intuir l for d un olución rticulr. No udn dr rgl n l co d cucion linl con coficint
. MÉTODO DE COEFICIENTES INDETERMINADOS. E un étodo r hllr un olución rticulr d l cución linl colt [], u conit fundntlnt n intuir l for d un olución rticulr. No udn dr rgl n l co d cucion linl con coficint
1 3 i + + A = 0, B = ½, C = 1, D = -½, dx dx de donde, :
 Hoj de Prolem Aál IV /. d L ríce de l eccó o,,,, í qe el polomo e decompoe de l form: Decompoemo e frccoe mple: D B A defcdo coefcee, e oee lo vlore: A, B ½,, D -½, Por lo qe: d d d / lclemo por eprdo
Hoj de Prolem Aál IV /. d L ríce de l eccó o,,,, í qe el polomo e decompoe de l form: Decompoemo e frccoe mple: D B A defcdo coefcee, e oee lo vlore: A, B ½,, D -½, Por lo qe: d d d / lclemo por eprdo
