SUPERFICIES DE SEGUNDO ORDEN

Transcripción

1 SUPERFICIES DE SEGUNDO ORDEN LUIS ALVARO SALAZAR SALAZAR UNIVERSIDAD NACIONAL DE COLOMBIA SECCIONAL MANIZALES DEPARTAMENTO DE CIENCIAS MARZO. 1987

2 A mi esposa A mis hijos A la Universidad Nacional de Colombia

3 TABLA DE CONTENIDO INTRODUCCION 1 FUNCION REAL DE VARIAS VARIABLES 3 GRAFICA DE UNA FUNCION REAL DE VARIAS VARIABLES 4 pág. CONJUNTOS DE NIVEL Y SECCIONES DE UNA FUNCION REAL DE VARIAS VARIABLES 9 TECNICA DE CONJUNTOS DE NIVEL Y SECCIONES PARA REPRESEN- TAR LA GRAFICA DE UNA FUNCION REAL DE VARIAS VARIABLES 28 TECNICA DE CONJUNTOS DE NIVEL Y SECCIONES PARA REPRESEN- TAR LA GRAFICA DE OTRAS SUPERFICIES 29 SUPERFICIES CUADRICAS O DE SEGUNDO ORDEN 42 SUPERFICIES CUADRICAS EN POSICION CANONICA 43 SUPERFICIES CUADRICAS TRASLADADAS 87 SUPERFICIES CUADRICAS ROTADAS 95 SUPERFICIES CUADRICAS ROTADAS Y TRASLADADAS 117 OBSERVACIONES 132 BIBLIOGRAFIA 135

4 La perfección derrotaría a la muerte porque no tendrían fin las formas de la vida. Julio Ernesto Márquez

5 INTRODUCCION Uno de los temas de matemática elemental más traginados en las carreras de aplicación como en la misma matemática es la Geometría Analítica; principalmente por el soporte gráfico que aporta en el proceso de obtención de otros conceptos de alto grado de abstracción y al mismo tiempo por la habilidad que se requiere para llevar a la imaginación elementos suyos de difícil o imposible representación gráfica. Los métodos de trabajo tradicionales de la Geometría Analítica son muy elegantes e intachables, pero han tenido dificultades con las generalizaciones y agilidad de algunos procesos. Esos mismos métodos han contribuido notablemente al desarrollo de una joven disciplina matemática llamada Algebra Lineal; la cual por su carácter algorítmico retroalimenta ahora a la Geometría Analítica con métodos mas generales y ágiles. Este trabajo se propone poner al alcance de estudiantes de primeros semestres de Carreras de aplicación de la matemática, un algoritmo proporcionado por el Algebra Lineal, para tratar con mas generalidad, agilidad y libertad unos objetos de la Geometría Analítica de no fácil manipulación por otros métodos y que se conocen como Superficies de Segundo Orden o Superficies Cuádricas. En este orden de ideas, el autor considera importante que con este tratamiento se incluya este tema en una asignatura, que por su forma de aplicar los métodos del Algebra Lineal a la Geometría Analítica, hemos denominado Geometría Vectorial, con la evidente precaución de que se estudien antes las curvas de segundo orden o cónicas.

6 FUNCION REAL DE VARIAS VARIABLES Estamos muy familiarizados con el concepto de función real de una variable real, pero probablemente no, con el concepto de función real de varias variables reales. Llamaremos función real de varias variables reales a una función f con dominio un sub-conjunto A de R n y recorrido un sub-conjunto B de R. Como un elemento X de A se nota donde cada es una variable real para las llamaremos las variables independientes de la función f. El valor de la función es otra variable real, que notaremos que depende de los valores de por lo cual esta variable se llama variable dependiente de la función. Todos estos hechos se resumen en la expresión La función f definida por la expresión donde son variables reales,ves una función real de dos variables reales. La función g definida por la expresión donde son variables reales, es una función real de 3

7 tres variables reales. En lo sucesivo para referirnos a una función real de varias variables reales diremos solamente función real de varias variables ó simplemente función de varias variables GRAFICA DE UNA FUNCION REAL DE VARIAS VARIABLES Sabemos que si f es una función de R en R con dominio D, la gráfica de f es el subconjunto de constituido por los puntos de la forma»cuando x está en D, es decir, gráfica de La gráfica de f puede ser una curva continua del plano, o puede ser la reunión de varios sectores de curvas o simplemente un conjunto de puntos separados del plano. Para una función real de varias variables de la forma la gráfica de f es el subconjunto de constituido por los puntos de la forma o con en el dominio de f, es decir, gráfica de La gráfica del f puede ser una superficie continua de, o puede ser la reunión de varios sectores de superficies ó simplemente un conjunto de puntos separados del espacio. En general la gráfica de una función real f de n variables con 4

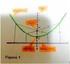
8 dominio U es el subconjunto de constituido por los puntos de la forma con gráfica de Naturalmente la gráfica de una función real de n variables, no la podemos trazar o dibujar. La gráfica de una función real de una variable la dibujamos en un plano. De la gráfica de una función real de dos variables podemos hacer una representación en el plano, aunque la gráfica es un subconjunto de. Por ejemplo la función la podemos representar en el plano como aparece en la figura 1. Una pregunta surge de inmediato: Cómo se hace una representación en el plano de la gráfica de una función real de dos variables? ó Cómo se hace la gráfica de una función real de dos variables? Las técnicas son varias y para algunas gráficas se requiere de técnicas muy especializadas como el cálculo diferencial de funciones de varias variables ó el computador. El libro CALCULO VECTORIAL de Jerrold E. Marsden y Antony J. Tromba, publicado en español por Fondo Educativo Interamericano, S.A., en 1981, muestra en sus figuras , , , , y 2.7.2, gráficas de funciones de dos variables generadas por computador. x Estudiaremos a continuación una técnica llamada de conjuntos de nivel y secciones, pero para eso debemos antes conocer que es un conjunto de nivel y que es una sección. 5

9 Figura 1. Representación en el plane de la aráfica de la funninn FIGURA NO. 1 7

10 CONJUNTOS DE NIVEL Y SECCIONES DE UNA FUNCION REAL DE VARIAS VARIABLES. Cuando los topógrafos quieren describir la forma de un terreno, en un plano, lo hacen dibujando las curvas que representan en el terreno una altura constante. Estas curvas se llaman curvas de nivel. Así una curva de nivel es la trayectoria que describimos al caminar sobre el terreno permaneciendo a una altura fija. Para cada valor de la altitud se obtiene una curva de nivel y con todas las curvas de nivel se hace el llamado mapa topográfico. Si a una montaña le asignamos un sistema coordenado x Y h, donde h representa la altura, la superficie de la montaña será posiblemende nivel y mapa topográfico de la montaña, observemos las figuras te una función Para ilustrar los conceptos de curvas 2 y 3. Cada curva de nivel está formada por los puntos del plano x Y que satisfacen la ecuación. donde X es una constante real. Las curvas de nivel son casos particulares^de conjuntos de nivel, son los conjuntos de nivel de una función real de dos variables. En general, si f es una función real de n variables con dominio D, y k es un número real fijo, el conjunto de nivel de valor k, está constituido por todos los puntos X de D para los cuales Si n = 2 los conjuntos de nivel se llaman curvas de nivel y n = 3 los conjuntos de nivel se llaman superficies de nivel. si Veamos algunos ajemplos. Ya mostrados en la figura 1 la gráfica 9

11 Figura 2. Curvas de nivel de una montaña para alturas de G, , 30, y 35 metros. FIGURA NO. 2 11

12 Figura 3. Mapa topográfico de Aquí solo se muestran de h: 0, 10, 20, 30 y la montaña mostrada en la figura 2. las curvas de nivel para los valores 35 metros. FIGURA NO. 3 13

13 de la función Analicemos para esta función algunos conjuntos de nivel. Llamemos, es decir, Z es entonces siempre mayor o igual a cero. Si Z = 0; lo cual solo es posible si x = 0 y Y = 0«el conjunto de nivel para Z = D es entonces due Si Z = 1; entonces y el conjunto de nivel es Si Z = 2; entonces y el conjunto de nivel es tales que Si Z = 3; el conjunto de nivel es tales que En general si Z = a para a un número real positivo, el conjunto de nivel es tales que En la figura 4 mostramos los conjuntos de nivel que hemos analizado Al observar la figura 4 podemos elevar mentalmente cada conjunto

14 Figura 4. Conjuntos de nivel de para los vaio res z = 0, z = 1, z = 2, z = 3, z = s. FIGURA NO. 4 17

15 de nivel a la altura indicada por Z. Y si hacemos que Z tome todos los valores reales posibles vamos formando en la mente la gráfica de la función, la cual "vaciada" en el papel nos dará lo que muestra la figura 5 ó la figura 1. Como segundo ejemplo analicemos los conjuntos de nivel de la función siendo así Z la variable dependien té, Z es entonces siempre mayor o igual a cero. Cuando y entonces pero Y es cualquier número real, así que el con- junto de nivel para es la recta Si siendo también en este caso Y cualquier número real. Luego el conjunto de nivel para Z = 1 está constituido por las rectas Analogamente el conjunto de nivel para Z = 4 está constituido por las rectas Y y para a un numero real positivo, el conjunto de nivel para está constituido por las rectas La figura 6 muestra algunas curvas de nivel de la función Si elevamos mentalmente cada curvs de nivel de la figura S a la altura indicada por Z y hacemos que Z tome todos los valores posibles, formados en la mente la gráfica que nos muestra la figura 7. Una idea intuitiva de la gráfica de la función es: una hoja de papel encurvada en forma de una parabola. La superficie que muestra la figura 7 se acostumbra a llamar cilindro parabólico. La forma de parábola que tiene la gráfica de esta función se puede percibir de otra manera distinta al mero esfuerzo mental de imaginársela. Esa manera está ligada al concepto de sección. 19

16 Figura 5. Curvas de nivel de la función la gráfica llevadas a FIGURA NO. 5 21

17 Figura 6. Curvas de nivel de la función z = x 2 FIGURA NO. 6 23

18 Figura 7. Gráfica de la Función FIGURA NO. 7

19 Para los ejemplos que hemos mostrado podemos describir les conjuntos de nivel como las intersecciones de la gráfica con planos horizontales. Haciendo una analogía con esta descripción de los conjuntos de nivel, una sección es la intersección de la gráfica con un plano vertical perpendicular a alguno de los ejes. Luego, en la función las secciones son parábolas o rectas. Pero esta es apenas una idea intuitiva de sección. Para dar una definición más formal de sección es necesario que hagamos una observación al concepto de conjunto de nivel, relacionada cor lo que hemos llamado variables dependientes e independientes de una función. Si es una función real de n variables con dominio D, un conjunto de nivel de f lo obtenemos cuando hacemos que la variable dependiente tome un valor constante. Con esta observación al concepto de conjunto de nivel, el concepto de sección de una función real de n variables asi: formalizamos Si f es una función real de n variables con dominio D, llamaremos sección al conjunto de que satisface la ecuación que se obtiene al hacer que una variable indepen diente tome un valor constante. Si el valor constante tomado por la variable independiente es cero, la sección se llama sección cero. De esta forma los conceptos de conjunto de nivel y de sección se diferencian en el hecho de que la variable aue se hace constante sea dependiente o independiente, respectivamente y en el hecho de que el conjunto de nivel es un sub-conjunto del dominio de la función y la sección no. 27

20 Técnica de Conjuntos de nivel y secciones para representar la gráfica de una función real de varias variables. Antes que todo advertimos que esta técnica no resuelve el problema de representar la gráfica de toda función de varias variables. Algunas funciones requieren del cálculo diferencial de varias variables para poder tener una representación aceptable de la gráfica. Para otras funciones no es posible representar su gráfica en un plano o en el espacio. Por ejemplo las funciones de en En las funciones de en la técnica de conjuntos de nivel y secciones, consiste en dibujar en un plano un sistema coordenado para en ese sistema coordenado, se dibujan los conjuntos de nivel cada uno a la altura señalada por la variable dependiente y sobre el plano correspondiente, en ese mismo sistema coordenado se dibujan las secciones cada uno en el plano señalado por la variable independiente; finalmente se completa la gráfica con los detalles que se consideren necesarios. Al dibujar los conjuntos de nivel y las secciones en el sistema coordenado para debe tenerse en cuenta que se está representando en un plano un subconjunto no precisamente plano de, o sea tener en cuenta la perspectiva. Analicemos ahora como ejemplo los conjuntos de nivel y las secciones de la función f(x,y) = y 2 - x 2, con el proposito de utilizarlos para dibujar la gráfica. Estudiemos primero los conjuntos de nivel. Si Z = f(x,y), Z es la variable dependiente Para se tiene que entonces resultando que el conjunto de nivel está constituido por dos rectas que se cortan en el origen. obtenemos de que el conjunto de nivel es una hipér- 28

21 bola con focos sobre el eje y asíntotas entonces focos sobre el eje y asíntotas El conjunto de nivel es una hipérbola con entonces el conjunto de nivel es la hipérbola con ecuación con focos sobre el eje x y con asíntotas el conjunto de nivel es la hipérbola con ecuación focos sobre el eje x y con asíntotas Estos conjuntos de nivel se han dibujado en la figura 8. Al hacer siendo a un número real cualquiera, el conjunto de nivel tiene como ecuación y podemos asegurar que todos los conjuntos de nivel de esta función son hipérbolas, admitiendo que un par de rectas que se cortan es un caso de degeneración de la hipérbola. De las secciones analizaremos tan solo dos: Si entonces y la sección es una parábola con vértice en el origen del plano XZ, eje de simetría el eje Z y que abre hacia abajo. Si entonces la sección es una parábola con ecuación, vertice en el origen del plano Y Z, eje de simetría el eje Z hacia arriba. y que abre La grafica de la función está dibujada en la figura 9 y se acostumbra a llamar silla de montar o también paraboloide hiperbólico. Más adelante explicaremos porque esa superficie tiene ese segundo nombre. Técnica de Conjuntos de Nivel y Secciones para representar la gráfica de otras superficies, Hasta ahora hemos estudiado la técnica de conjuntos de nivel y secciones para estudiar la gráfica de una función real de dos variables, la cual generalmente es una superficie de Pero existen superficies cuya ecuación en coordenadas cartesianas no representa a una función real de dos variables, Por ejemplo la ecuación 29

22 Figura 8. Curv/as de nivel de la función f(x,y) = y 2 _ x 2. t FIGURA NO. 8

23 Figura 9. Gráfica de la función forma de siila de montar. Observe que tiene FIGURA NO. 9 33

24 no representa a una función real de dos variables, porque si tomamos a Z como variable dependiente, al despejar Z de la ecuación obtenemos lo cual significa que para los mismos valores de se pueden obtener valores diferentes de Z, A la misma conclusión se llega si tomamos a x como variable dependiente o y como variable dependiente. Sinembargo la gráfica de la ecuación es una superficie de como podemos evidenciarlo enseguida. Con es- te propósito también utilizaremos la técnica de los conjuntos de nivel y secciones y también para mostrar un ejemplo en el cual se puede utilizar esa técnica aunque no se trate de una función. En la ecuación ninguna de las variables es función de las otras dos, entonces por conveniencia (la cual analizaremos mas adelante) tomaremos como variable dependiente Y por estar acompañada atrás por el signo menos. Las variables independientes son, por consiguiente, Con este con- venio veamos algunos conjuntos de nivel: el conjunto de nivel tiene como ecuación, cuya representación en es una elipse. Si, entonces el conjunto de nivel tiene con ecuación la cual tiene como representación en a una elipse. Si- obtiene para el conjunto de nivel es también una elipse, la misma que se 35

25 Si- para cualquier k número real, entonces el conjunto de nivel es una elipse con ecuación Concluimos asi que cualquier conjunto de nivel es una elipse. Estos conjuntos de nivel los mostramos en la figura 10. También en este caso solo necesitamos calcular dos secciones, la secy la sección ción Si la sección tiene como ecuación y que es una hipérbola con focos sobre el eje 1, Si la sección tiene como ecuación y representa en una hipérbola con focos sobre el eje x. En la figura 11 se aprecian los conjuntos de nivel y las secciones de la superficie. Esta superficie se acostumbra a llamar la hiperboloide eliptico de una hoja porque sus secciones son hipérbolas y sus conjuntos de nivel son elipses y porque la gráfica está constituida por una sola superficie. En general el lector puede verificar con esta técnica que la ecuación con a, b y c números reales positivos, tiene como gráfica un hiperboloide eliptico de una hoja. 36

26 Figura 10. Conjutos de nivel de la ecuación FIGURA NO

27 Figura 11. Gráfica de la ecuación x. 2 _ j / 2 z 2 1 A 9 16 FIGURA NO

28 Superficies Cuádratj cas ó de Segundo Orden. En el estudio de las curvas en el plano, se da un tratamiento especial a las llamadas "c6n c.ca", Etimológicamente "c6níc.a" es: intersección de un cono circular recto con un plano. Según la forma como el plano corte al cono se obtienen dos tipos diferentes de cónicas. Si el plano corta al cono sin pasar por el vértice, se obtiene una cónica "no de.gznqjia.da": hipérbola, parábola o elipse (según que el plano sea paralelo a dos, a una ó a ninguna de las generatrices del cono). Si el plano pasa por el vértice del cono se obtiene una cónica degenerada (un punto, una circunferencia, una recta, un par de rectas secantes, ó si el cono degenera en un cilindro, el vértice del cono se "atzja" al infinito,resultando entonces dos rectas paralelas). Estas curvas llamadas cónicas no degeneradas también se pueden clasificar, según la posición en la cual esten con respecto a un sistema coordenado cartesiano xy, así: En posición canónica (focos sobre uno de los ejes y centro en el origen para elipse y la hipérbola y foco sobre uno de los ejes y vértice en el origen para la parábola), transladadas (centro en un punto diferente del origen y focos sobre una recta paralela a uno de los ejes para la elipse y la hipérbola y foco sobre una recta paralela a uno de los ejes y vértice en un punto diferente del origen para la parábola), o rotadas (focos en una recta no paralela a los dos ejes centro en el origen, para la elipse y la hipérbola y vertice en el origen y foco en una recta no paralela a los dos ejes, para la parábola). Es importante notar que podemos encontrar casos de cónicas rotadas pero no transladadas, cónicas transladadas pero no rotadas y también cónicas rotadas y transladadas. A las cónicas también se les llama curvas de segundo orden porque su ecuación cartesiana siempre es de la forma ax 2 + 2b xy + cy 2 + 2dx + 2ey + f = 0, es decir, una ecuación general de segundo grado en dos variables. Además se puede demostrar que cuando el conjunto solución de la ecuación 42

29 general de segundo graao no es vacio, es una cónica (admitiendo degeneraciones). Ahora en el estudio de las superficies de CH 3, nos dedicaremos a algunos casos especiales, llamados superficies de segundo orden o super ficies cuádraticas. Para estudiar estas superficies de segundo orden, las clasificaremos inicialmente en tres tipos segün su posición con respecto a un sistema coordenado cartesiano para EK 3 : En posición canónica, transladadas y rotadas. Superficies Cuádraticas en Posición Canónica, Aunque tratemos en esta sección solamente las superficies cuádricas en posición canónica, estará implícita en este tratamiento la definición general de superficie cuádrica, ya que, como se podrá ver más adelante, una superficie cuádrica rotada o transladada siempre se podrá llevar a posición canónica con una adecuada escogencia de ejes coordenados, ó, dicho de otra forma toda superficie cuádrica está en posición canónica para algún sistema coordenado. Mostrar cómo encontrar el sistema coordenado donde una superficie cuádrica está en posición canónica, es uno de los objetivos principales' de este escrito. Apoyados en el conocimiento que ya tenemos de la técnica de conjuntos de nivel y secciones para estudiar las gráficas de superficies y funciones reales de varias variables, definimos como superficie cuádrica en posición cónica a todo conjunto de nivel no vacio o sección cero no vacío de una función f de CR 3 en ER de la forma f(x,y,z) = Ax 2 + By 2 + Cz 2 donde A, B y C son constantes reales, no todas simultáneamente iguales a cero. Como ya lo dijimos atras los conjuntos de nivel y las secciones de una función de CR 3 en D* son superficies de CR 3 y para poderlas graficar 43

30 también utilizaremos la técnica de los conjuntos de m'yel y las secciones, con lo cual, no solo podremos esbozar la gráfica, sino que también le podremos asignar un nombre» reciprocamente al conocer como son, las secciones y los conjuntos de nivel, sabremos como se llama y entonces esbozar la gráfica, Naturalmente se entiende que no nos proponemos estudiar la gráfica de la funci&n, f(x,y,z) = Ax 2 + By 2 + Cz 2 porque sabemos que es un subconjunto de CR 4 Como algunos de los conjuntos de nivel o secciones de la función f(x,y,z) = Ax 2 + By 2 + Cz 2 no representan funciones de D* 2 en $ (situación que se diversifica mucho dependiendo de cual o cuales de las constantes A, B y C sean cero ó de los signos de dichas constantes),es necesario que establezcamos un criterio para la nominación o designación de las variables dependientes o independientes para los casos en los cuales la sección o el conjunto de nivel no representa a una función. (Ya sabemos que cuando se tiene una función las variables independientes son las variables de la función). Para eso llamemos w al valor de la función f en el punto (x,y,z) o sea, f(x,y,z) = w. AsT la definición de está función toma la forma: ü) = Ax 2 + By 2 + Cz 2 Si A, B y C son todos positivos o todos negativos u> es la variable dependiente en cualquiera de las secciones de f. En los conjuntos de nivel, una cualquiera de las variables se puede fijar como dependiente y las otras dos independientes. Este mismo criterio de designación utilizaremos en el caso de que una de las constantes A, B ó C sea cero y las otras dos tengan el mismo signo. En cualquier otro caso fijaremos como variable dependiente aquella que esté precedida por signo diferente, es decir, si dos están precedidas por signo menos esas serán las independientes y la otra la dependiente 44

31 si dos están pre ce di des por signo más estas serán las independientes y la otra la dependiente, De acuerdo con estos criterios de asignación de variable dependiente e independiente les daremos los siguientes nombres a las superficies cuádricas: 1, Elipsoide, Si todas las secciones y todos los conjuntos de nivel son elipses, 2, Hiperboloide eliptico. Si las secciones son hipérbolas y los conjuntos de nivel son elipses. Se presentan dos tipos diferentes de hiperboloides elipticos: a) Todos los conjuntos de nivel son diferentes de vacio, se llama hiperboloide elíptico de una hoja. b) Algunos conjuntos de nivel son vacios, se llama hiperboloide eliptico de dos hojas. 3, Paraboloide eliptico. Si todas las secciones son parábolas y los conjuntos de nivel son elipses, 4, Paraboloide hiperbólico (o silla de montar). Si todas las secciones son parábolas y los conjuntos de nivel son hipérbolas. i 5, Cono eliptico. Si las secciones cero son pares de rectas secantes y los conjuntos de nivel son elipses. 6, Superficies cuádricas degeneradas, Cualquier otro caso diferente a los anteriores, Entre estas se encuentran los cilindros (representación gráfica en CR 3 de una ecuación cartesiana con solo dos variables). Los nombres de los cilindros pueden determinarse más exactamente al conocer su directriz. Si la directriz es una elipse se dice cilindro eliptico, si la directriz es una parábola 45

32 se dice cilindro parabólico y se dice cilindro hiperbólico si la directriz es una hipérbola, La esfera es un caso de elipsoide degenerado. Ahora si podemos comprender claramente que la superficie mostrada en la figura 11 se llama hiperboloide eliptico de una hoja (las secciones son hipérbolas y los conjuntos de nivel elipses, ninguno es vacio) y que las superficies de las figuras 7 y 9 se llaman cilindro parabólico y paraboloide hiperbólico respectivamente, Las superficies mostradas en las figuras 7, 9 y 11 son superficies cuádricas en posición canónica, A manera de ejemplo e ilustración de lo dicho hasta ahora sobre superficies cuádricas, analicemos enseguida algunos conjuntos de nivel y al gunas secciones de la función f(x,y,z) = Ax 2 + By 2 + CZ 2 determinando de antemano cuales de las constantes A o B ó C son cero y el signo de las que no son cero. 1. Si A = 1/a 2 ; B = 1/b 2 ; C = 1/c 2 para a, b y c números reales positivos, entonces u> = f(x,y,z) =-^ + X 2 +JL 2, ó, a 2 b 2 c 2 _ x 2 y 2 z 2 a 2 b 2 c 2 Estudiemos algunos conjuntos de nivel de f. Veamos el conjunto de nivel Si o» = O, entonces u> = O x% lk O a 2 b 2 c 2 Claramente el único punto de CR 3 que satisface esta igualdad es (0,0*0). Así el conjunto de nivel es un punto. 46

33 Si w = k 2, para k una constante positiva, entonces ó o Esta ecuación está describiendo el conjunto de puntos de que constituyen el conjunto de nivel w = k 2 de la función f, pero no lo podemos reconocer aún. Para poderlo reconocer hallaremos sus conjuntos de nivel y sus secciones. Como ya acordamos atrás podemos llamar variable dependiente a cualquiera de las variables. Sea z la variable dependiente. Si z = 0, el conjunto de nivel será el conjunto de puntos tales que o sea, una elipse en posición canónica con semiejes de longitud ak y bk respectivamente. Si z = h para h una constante real positiva el conjunto de nivel satisface la ecuación y es una elipse en el caso en que el valor absoluto de h es menor que ck, es un punto en el caso en que el valor absoluto de h es igual a ck y es vacio en el caso en que el valor absoluto de h es mayor que ck. Asf vemos claramente que los conjuntos de nivel de Son elipses.cuando no son vacios. x = 0 y y = 0 son Las secciones y 47

34 respectivamente. Como las secciones son elipses y los conjuntos de nivel son elipses, entonces la ecuación es la de un ELIPSOIDE, la figura 12, La gráfica de este elipsoide la mostramos en Sigamos analizando los conjuntos de nivel de f, Si u = -k 2, para k una constante real cualquiera, entonces Esta ecuación tiene solución vacía en IR 3. Resumiendo, los conjuntos de nivel de f son: Para w = 0, un punto; para w = k un elipsoide y para w = -k 2, vacio Estudiemos ahora las secciones cero de f. Si x = 0, entonces la sección será la superficie cuya ecuación es Esta superficie no la podemos reconocer, pero para hacerlo estudiemos sus conjuntos de nivel y sus secciones. Como w es función de Y y de z, entonces w es la variable dependiente y Y y z las variables independientes. Si a) = 0, el conjunto de nivel es el conjunto cuyo único elemento es (0,0). Si ai = k 2, para k una constante real positiva, entonces el conjunto 48

35 Figui-a 12. Conjunto de nivel a) = k 2 de la función Esta superficie se llama Elipsoide FIGURA NO. 12

36 de nivel será la elipse con ecuación con semiejes de longitud ak y ck respectivamente. Si y = -,k 2, para k una constante real diferente de cero, entonces el conjunto de nivel es vacio. Veamos las secciones. con ecuación Si y = 0, entonces la sección será la parábola y con vértice en (0,0) y eje simetría el eje w positivo, Si z = 0, la sección será la parábola cuya ecuación es: con vértice en (0,0) y eje de simetría el eje w positivo Como los conjuntos de nivel de son elipses,cuando no son vacios; y las secciones son parábolas, entonces esa superficie se llama un PARABOLOIDE ELIPTICO.La figura 13 muestra la gráfica del paraboloide eliptico. Las otras secciones cero de f, cuyas ecuaciones son para y = 0; z = 0 respectivamente, son también paraboloides elípticos, como efectivamente puede verificarlo el lector a manera de^e.jercició. 52

37 Figura 13. Sección x = O, de la función f(x,y,z) Esta superficie se llama Paraboloide Eliptico. FIGURA NO

38 Así hemos terminado el análisis de los conjuntos de nivel y secciones de la función 2, Si para a, b y c números reales positivos, entonces ó Estudiemos los conjuntos de nivel de f. Si uj = 0, entonces La superficie cuyos puntos satisfacen esta ecuación, tal vez no la podamos identificar en este instante. Para poderla identificar encontremos sus conjuntos de nivel y sus secciones. En este caso, ninguna de las variables es función de las otras, pero x esta precedida de signo positivo y las otras dos variables están precedidas de signo negativo, por lo cual tomamos como variable dependiente a x. Si x = 0, el conjunto de nivel se reduce al punto (0,0). Si x = k, para k cualquier número real no cero, el conjunto de nivel será una elipse con ecuación Es decir, todos los conjuntos de nivel son elipses. 56

39 Veamos ahora las secciones. Si y = 0, entonces lo cual implica que o, ecuaciones que corresponden a un par de rectas que pasan por el origen. Si z = 0, la sección está constituida por este par de rectas: y y que se cortan en el origen Como èn la superficie con ecuación > los conjuntos de nivel son elipses y las secciones cero son pares de rectas que se cortan, entonces esa superficie es un CONO ELIPTICO. La figura 14 muestra la gráfica de ese cono eliptico. Otro conjunto de nivel de f se obtiene si hacemos u> = k 2, para k cua quier constante real positiva. La ecuación de ese conjunto de nivel es: o Para esquematizar la gráfica de esa superficie de nivel, estudiemos sus curvas de nivel y sus secciones. Lo mismo que en el caso anterior, ninguna de las variables es función de las otras dos, entonces 57

40 Figura 14. Conjunto de nivel w= 0 de la función se llama Cono Eliptico Esta superficie FIGURA NO

41 por la disposición de los signos le corresponde a x ser variable dependiente. Si x = 0, la ecuación del conjunto de nivel es la cual no se satisface con ningún punto del plano Y Z, es decir el conjunto de nivel es vacio, Si x = h, para h cualquier constante real no nula, la ecuación del conjunto de nivel es:» la cual tiene solución vacía cuando el valor absoluto de h es menor que ka, tiene solución un punto cuando el valor absoluto de h es i- gual a ka y tiene como solución una elipse cuando el valor absoluto de h es mayor que ka. En síntesis algunos conjuntos de nivel de la superficie son vacios y los otros son elipses. Veamos las secciones de la superficie. Si y = 0, la ecuación de la sección es y representa a una hipérbola en posición canónica en el plano xy y con focos sobre el eje x. Si z = 0, la ecuación de la sección es 61

42 y es una hipérbola en posición canónica en el plano xy con focos sobre el eje x. Como los conjuntos de nivel de esta superficie son algunos vacios y otros son elipses y las secciones son hipérbolas, entonces la superficie es un HIPERBOLOIDE ELIPTICO DE DOS HOJAS. La figura 15 muestra la gráfica de esta superficie. Otro conjiunto de nivel de f, se obtiene cuando w = - k 2, para cualquier constante real positiva k. La ecuación de esa superficie de nivel es ó Para esbozar la gráfica de esta superficie se deben analizar los conjuntos de nivel y las secciones. Como ninguna de las variables es función de las otras dos, pero la variable x está precedida de signo menos, mientras que Y y z están precedidas de signo más, se toma a x como variable dependiente y a Y y z como variables independientes. Al hacer los cálculos correspondientes se obtiene una superficie como la que muestra la figura 11, pero con denominaciones diferentes en los ejes. Para ser más precisos mostramos en la figura 16 esta superficie de nivel llamada HIPERBOLOIDE ELIPTICO DE UNA HOJA. En la figura 17 mostramos todos los conjuntos de nivel o> = 0; w = k 2 ; cu = -k 2, de 1 a función 62

43 Figura 15. Conjunto de nivel w = k 2 de la función. Esta superficie se llama Hiperboloide Eliptico de dos hojas. FIGURA NO

44 Figura 16. Superficiede nivel u>= -k 2 de la función Esta superficie se llama Hiperboloide Eliptico ae una hoja FIGURA NO

45 Figura 17. Superficies de nivel u)= 0, œ= k 2 y uj= -k 2 de la función FIGURA NO

46 dibujados en un Onico sistema de coordenadas. Las secciones x = 0; y = 0; z = 0 de la función ftson las superficies : Paraboloide eliptico : Paraboloide hiperbólico : Paraboloide hiperbólico, respectivamente. El lector puede realizar, como ejercicios, el análisis completo de estas superficies y dibujar sus gráficas. 3. Si A = 0; para b y c números reales positivos, entonces ó Estudiemos primero los conjuntos de nivel de f. Si w = 0 ; ^, es decir, ^ ; x cualquier número real. Entonces el conjunto de nivel w = 0 está constituido por un par de planos que se cortan en el eje x. La figura 18 muestra la gráfica de esa superficie de nivel. Si «= k 2, para k, cualquier constante real positiva, entonces la ecuación de la superficie de nivel es: 70

47 Figura 18. Superficies de nivel oj=0;o)=k 2 î u)=-k 2 de la función x2 2 f(x,y,z) = -2,. tr c FIGURA NO

48 k2 = já _ $. _ «! b 2 c 2 (kb) 2 (kc) 2 con x cualquier número real. Esa superficie de nivel es entonces un cilindro hiperbólico con generatriz el eje x y que corta al eje Y en los puntos (0,kb,0) y (O^-kb.O). la figura 18. Su gráfica se muestra también en Si oj = -k 2, para k una constante real positiva calquiera, entonces la ecuación de la superficie es: k2 _ y 2 z 2 Ó z 2 y 2 = 1 b 2 c 2 (kc) 2 (kb) 2 con x cualquier número real. Esa superficie de nivel es entonces un cilindro hiperbólico con generatriz el eje x y que corta al eje z en los puntos (0,0,kc) y (0,0,-kch esta superficie de nivel. En la figura 18 también se muestra Ahora estudiemos las secciones cero de f. Sección x = 0. Si x = 0, entonces la superficie obtenida tendrá ecuación u = J 1 - z 2 b 2 c 2 y sabemos que esa superficie es un Parabolide hiperbólico o silla de montar. Para convencerse de esto el lector puede analizar las curvas de nivel y las secciones. esta sección de f. La figura 19 muestra la gráfica de Sección y = 0. Si y = 0, entonces la superficie obtenida tendrá como ecuación O) = z 2