APUNTES DE DIBUJO TÉCNICO: PRIMERO Y SEGUNDO DE BACHILLERATO. AUTOR: RAMON DEL AGUILA
|
|
|
- María Carmen Gil Domínguez
- hace 6 años
- Vistas:
Transcripción
1 Página 1 de PUNTES DE DIBUJO TÉCNICO: PRIMERO Y SEGUNDO DE BCHILLERTO. UTOR: RMON DEL GUIL α CORBLÁN ÑO 2010 G α 1 ch ( ) Los apuntes que presento solo pretenden ser un complemento a lo que presento en el UL VIRTUL del portal Por ello se omiten muchos pasos que están suficientemente explicados en el referido portal.
2 Página 2 de GENERLIDDES Y FUNDMENTO DEL SISTEM. LFBETO DEL PUNTO. En el sistema diédrico o de Monge, se debe al matemático y físico francés Gaspar Monge. Este científico es considerado como el Padre del a Geometría Descriptiva. Nació en Beauné en 1746, y murió en Paris en topografía, etc. GEOMETRI DESCRIPTIV REPRESENTR LS TRES DIMENSIONES DE UN SOBRE UN SUPERFICIE UTILIZCIÓN EN EL MUNDO DE L TECNIC E INDUSTRI PR O PROYECTR MECNISMOS, EDIFICIOS, TERRENOS, La geometría descriptiva tiene como fundamento la representación de un objeto de tres dimensiones sobre soportes que solo tienen dos, es decir superficies planas. Esta forma de expresión se utilizada en el mundo de la técnica, industria, arquitectura, Los distintos sistemas de representación se describen en el cuadro siguiente. SISTEMS DE REPRESENTCIÓN DIÉDRICO PLNOS COTDOS SISTEMS PERSPECTIVOS TÉCNICO PLICCIÓN TOPOGRÁFIC XONOMÉTRICO CBLLER CÓNICO INDUSTRI CONSTRUCCIÓN
3 Página 3 de CONVENCIONLISMOS UTILIZDOS. En el sistema diédrico intervienen dos planos, el plano horizontal y vertical. Figura 1. Estos dividen al espacio en cuatro regiones, llamadas octantes o diedros. Se numeran en sentido contrario a las agujas del reloj. La recta intersección de ambos planos, determinan la línea de tierra. Se representa por dos trazos más gruesos en sus extremos. El plano horizontal lo dividiéremos en dos partes, horizontal anterior ( PH), si se encuentra a la derecha de l línea de tierra, y horizontal posterior (PHP), si se encuentra a la izquierda. De igual forma el vertical se divide en vertical superior (PVS), si se encuentra por encima de la línea de tierra, y vertical inferior (PVI), si se encuentra por debajo del a misma, Los planos se abaten de forma que el plano vertical superior y el horizontal posterior sean coincidentes, al igual que el plano horizontal anterior y el vertical inferior l abatir los planos se abaten los puntos contenidos en los mismos, de tal forma que la proyección vertical queda por encima de la línea de tierra, y la horizontal por debajo de ella. Los puntos se representarán por letras mayúsculas. Empleando para la proyección horizontal la misma letra acompañada de un comilla p. e., y para la proyección horizontal y dos comillas, para la vertical. Figura 1. PVS PHP a C PVS c a PHP PH PVI PH Figura 1 PVI Se llama cota, a la distanciad el punto al plano horizontal. El alejamiento será la distancia del punto al vertical.
4 Página 4 de Los puntos que están situados por encima del plano horizontal, su cota es positiva. Si se encuentra por debajo será negativa. Los puntos a la derecha del plano vertical, el alejamiento es positivo. la izquierda negativo. Figura 1. El perfil X será un punto de referencia para situar el punto O. la derecha será positivo y a la izquierda negativo Planos bisectores serán aquellos que dividen al espacio en ocho regiones llamadas octantes. Estos se numeran del 1 al 8, en sentido contrario a las agujas del reloj. Figura 2.. OCT. 3º VS OCT. 2º 1.2. PUNTOS SITUDO EN LOS CUDRNTES. Figura 3 y 4. 2 do. Bisector OCT. 4º 1 er. Bisector Punto, situado en el primer cuadrante primer octante. Cota positiva. lejamiento positivo. HP H Punto B situado en el plano bisector. Cota igual al alejamiento ambos positivos OCT. 5º OCT. 6 OCT. 7 OCT. 8 Punto C situado en el primer cuadrante segundo octante. Cota y alejamiento positivos. Como puede observarse al abatir los Figura 2 planos, la proyección segunda de los puntos queda por encima de la línea de tierra y la primera por debajo. En consecuencia los puntos situados en el primer cuadrante su VS cota siempre estará por encima de la línea de tierra y el alejamiento por debajo, C" C y ambos serán positivos. B" B VS B" " c C" HP HP " a C' H c ' B' a C' ' B' VI H VI Figura 3
5 Página 5 de HP VS OCT. 3º OCT. 2º 2º BISECT. D D" 1º E E" BISECT. OCT. 4º F F" H G' I' J' K' L' ' F' E' D' L" L G" OCT. 5º G K" K H H " I I" J" J OCT. 6 OCT. 7 VI OCT. 8 Figura 4 H Punto D situado en el segundo cuadrante tercer octante. Cota positiva. lejamiento negativo. mbas proyecciones por encima de la línea de tierra. Punto E situado en el segundo bisector. Cota igual al alejamiento. Punto F, situado en el segundo cuadrante cuarto octante. lejamiento negativo y cota positiva, esta menor. Los puntos G, H, I, situados en el tercer cuadrante son inversos a los del primero. Los puntos J, K, L, situados en el cuarto cuadrante, son inversos a los del segundo. VS HP 1.3. PUNTOS SITUDOS EN LOS PLNOS DE PROYECCIÓN. D" F' E"=E' D' F" G ' I' Punto M, situado en el plano horizontal anterior. La proyección horizontal coincide con el punto. La vertical está en la línea de tierra. Cota = 0 y alejamiento +. G" H"=H' J' K"=K' L' Punto N, situado en el plano vertical. lejamiento = O y cota + VI I" J" L" H Punto P situado en el plano horizontal posterior. Cota = 0 y alejamiento negativo. Punto Q, situado en el plano vertical inferior. lejamiento = O y cota negativa 2º BISECTOR OCT. 3º VS OCT. 2º N=N" 1º BISECTOR VS N" P' HP H P OCT. 4º OCT. 5º P=P' R=R'=R" M=M' M"=N"=P"=Q' OCT. 8 H M" N' P" Q' R'=R" OCT. 6 Q=Q" OCT. 7 VI Figura 5 VI M' Q" H
6 Página 6 de Punto R, situado en la línea de tierra. Todas sus proyecciones se encontraran en ella. No tiene ni cota ni alejamiento SITUCIÓN DE PUNTOS POR MEDIO DE COORDENDS. Figura 6. Para situar los puntos por sus coordenadas, se adopta el siguiente convenio: X (perfil), Y (cota), Z (alejamiento) VS VS HP -Z + Y +Y Cota + (Y) HP lejamiento - Z(a) - o + H lejamiento +Z (a) -X O + X Cota (Y) Cota (Y) VI Figura 6 - Y VI + Z H Ejercicio: De acuerdo con el convenio establecido anteriormente. Situar los siguientes puntos en el sistema diédrico: ( -25, 20, 0), B(-15, 15, 5), C( -5, -10, 10), D ( 5, -5, -15), E(15, -20, 0) y F(25, 15, -5). Origen en el centro de la línea de tierra. Figura 7. " ' B" B ' C C" 0 D' D" E' F" F' Figura 7 E"
7 Página 7 de L RECT Una recta queda definida por dos puntos. Por tanto para su representación bastará con determinar las proyecciones de dos puntos de la recta, y unir las correspondientes proyecciones homónimas de sus puntos. Un punto pertenece a una recta si sus proyecciones homónimas se corresponden con la recta NOMENCLTUR DE L RECT. Para su denominación utilizaremos letras minúsculas acompañadas de una o dos comillas, según sea la proyección horizontal o vertical. (Por ejemplo r, r ). Los puntos que definen las rectas se designaran por letras mayúsculas. Una recta queda definida por sus trazas. Existen dos trazas una horizontal y otra vertical. Se denomina traza al punto de intersección de la recta con los planos de proyección. Traza horizontal se representa por H, su proyección será por tanto H acompañada de la letra minúscula correspondiente a la recta. Por ejemplo H r. Traza vertical se representa por V, su proyección vertical será por tanto V acompañada de la letra minúscula correspondiente a la recta. Por ejemplo V r. Como H y V siempre serán coincidentes con sus respectivas proyecciones H y V, en lo sucesivo solo emplearemos su proyecciones PROYECCIÓN DE UN RECT OBLICU DD POR DOS PUNTOS DE ELL. Se la recta r, dada por los puntos y B. Hallamos las proyecciones horizontal del os puntos y B. Seguidamente hallamos la vertical, y B. la unión de ambas nos determinará las proyecciones r y r del a recta r.
8 Página 8 de B r B r r B C r o B α B r 3 Figura PROYECCIÓN DE UN RECT OBLICU MEDINTE SUS TRZS. Sea la recta r que corta a los planos de proyección en los puntos H H r y V V r, trazas de la misma. l ser las trazas de la recta puntos de la misma, bastará con unir sus proyecciones homónimas para obtener las proyecciones r -r. El resultado será el mismo que si hubiéramos proyectado los puntos G y E, pertenecientes a la recta. Figura 9. V H G E E r H V r V H Figura 9
9 Página 9 de RECT PRLEL L PLNO VERTICL, PRIMER CUDRNTE RECT FRONTL. Tendrá una sola traza la horizontal H H, y su proyección horizontal será paralela a la línea de tierra. Y la vertical formará un determinado ángulo con el plano horizontal. Figura 10. H H H Y Y H Figura 10 Para hallar los puntos de intersección de la recta con los bisectores, bastará con buscar en la recta un punto cuya cota sea igual al alejamiento Si se encuentra en el primer o tercer bisector, o bien que ambas sean coincidentes si se encuentran en el segundo y cuarto. La recta será visible si se encuentra en el primer bisector, en caso contrario será oculta y se representará por líneas de trazos. Los referidos puntos se representarán por x o y primero y segundo bisector respectivamente PROYECCIÓN DE UN RECT PRLEL L PLNO HORIZONTL O RECT HORIZONTL. Estará contenida en un plano paralelo al horizontal. Cortará únicamente al plano vertical. Tendrá la traza vertical paralela a la línea de tierra. El punto de corte
10 Página 10 de de la recta con el segundo bisector tendrá la misma cota que alejamiento. Figura 13 a. Para hallar el punto de corte con el primer bisector trazaremos una recta auxiliar m, que formará el mismo ángulo con la línea de tierra que r. El punto X -X será el punto de corte con el primer bisector. Figura 13 b. Y' Y'' V'' r r'' X" m V' r r' X' 2ºD 1ºD Figura 11 a Figura 11 b 2.6. RECT PRLEL L PLNO VERTICL SEGUNDO CUDRNTE. Será igual que la anterior, pero no será visible. El punto de intersección con el bisector estará por encima de la línea de tierra. Figura 11. H H s H H s Figura 12
11 Página 11 de RECT PERPENDICULR L PLNO VERTICL. RECT DE PUNT (s). La proyección vertical será un punto, s que será coincidente con la traza vertical V s. La horizontal será una recta perpendicular a la línea de tierra. s Figura RECT PERPENDICULR L PLNO HORIZONTL, RECT VERTICL (r). Será contraria a la anterior RECTS PRLELS L LÍNE DE TIERR. No cortará los planos de proyección y por tanto no tendrá trazas. B B Figura 14
12 Página 12 de Para su representación tendremos que dibujar un punto cualquiera de la recta. Punto de la recta s y B de la recta r RECT r CONTENID EN EL PRIMER BISECTOR. Todas sus trazas estarán en la línea de tierra y formará 45º con los planos de proyección. Figura RECT s PRLEL L PRIMER BISECTOR. Estará contenida en un plano paralelo al bisector, su traza horizontal será paralela al bisector. Figura 15. V s V s s r r' P H PV Figura RECTS CONTENIDS EN EL SEGUNDO BISECTOR. Formará 45º con los planos de proyección, r - r serán coincidentes. mbas serán ocultas. Figura 16ª y b RECT s PRLEL L LÍNE DE TIERR. Sus proyecciones serán coincidentes. No tiene ninguna traza. Será preciso fijar un punto cualquiera de la recta. Figura 16 a y b. PH 2º B PV Figura 16 a Figura 16 b
13 Página 13 de RECT PERPENDICULR L LÍNE DE TIERR, CORTÁNDOSE CON ELL. Es un caso particular de las rectas de perfil, todas las trazas se encontrarán en la línea de tierra. Para que quede definida será preciso situar un punto cualquiera de ella. Punto. Figura 18. Estas rectas estarán contenidas en un plano perpendicular a la línea de tierra. Sus proyecciones son coincidentes en un mismo punto de la línea de tierra. Si la recta estuviera contenida en un plano bisector, recta p (p -p ), sus proyecciones serian las mismas, con la salvedad que cualquier punto de la recta p.e J, tendría la misma cota que alejamiento. " " r PVS r J" p p V"= V' H"= H' PH Figura 18 ' V"= V' H"= H' r J' RECT PERPENDICULR L LÍNE DE TIERR, CRUZÁNDOSE CON ELL. RECTS DE PERFIL. La recta s, estará contenida en un plano perpendicular a los planos de proyección. Sus trazas estarán en una línea perpendicular a la de L.T. y sus proyecciones V - H, serán coincidentes. Figura 19.
14 Página 14 de V" P s" V" s" s P V' H" s' H" V' s' H' Figura 19 H' TERCER PROYECCIÓN DE UN RECT DE PERFIL. Se denomina recta de perfil a las rectas contenidas en un plano perpendicular a la línea de tierra. Figura 20. Para poderla definir, se precisa representar la tercera proyección de la recta. V 'r r'' PP (V''r) PV '' B'' () r (B) r r B' () (r) (B) (H'r) B r ' B' H' r (`) (B`) PH (H'r) Figura 20 ' B' r' H r PP HLLR L TERCER PROYECCIÓN DE UN RECT QUE PS POR L LÍNE DE TIERR.
15 Página 15 de Sea la recta r ( r, r ) dada por los puntos (, ) y B (B, B ) Sus trazas y proyecciones están confundidas en una misma recta perpendicular a la línea de tierra. " B" r" π 2 B" ' "' 1. Elegimos un plano cualquiera de perfil π. 2. Llevamos la recta a tercera proyección, obteniendo la recta r. r' π 1 B' Figura LFBETO DEL PLNO Un plano queda definido por: dos rectas que se cortan, o paralelas, tres puntos no alineados o por una recta y un punto. Los casos anteriores se reducen a dos rectas incidentes. Un plano se representa por sus trazas. Se llama trazas de un plano a la intersección de este con los planos de proyección. α Para su representación emplearemos letras griegas. α 1 α 1 Figura 22 la traza vertical la designaremos por una letra griega ejemplo y horizontal por del α 1. En la figura 21, se representa un plano oblicuo a los de proyección.
16 Página 16 de PLNO DE CNTO β, O PERPENDICULR L VERTICL. PROYECTNTE VERTICL. β2 La traza horizontal será perpendicular a la línea de tierra, y la vertical formará un ángulo con ella. Figura 23. β 2 β 1 β 1 Figura PLNO HORIZONTL β, O PRLELO L HORIZONTL DE PROYECCIÓN PRIMER CUDRNTE. ω 2 β 2 P β ω β 2 ω 2 Tendrá una sola traza, la vertical, que será paralela a la línea de tierra.. Si el plano se encuentra en el 4º cuadrante será oculto ω. Figura 24. PV Figura PLNO FRONTL β PRLELO L VERTICL. Figura 25 a y b. tierra. l contrario que el anterior, su traza horizontal β será paralela a la línea de Si el plano se encuentra en el segundo cuadrante μ, será oculto. μ PV β μ 1 β 1 μ 1 PH β 1 Figura 25a Figura 25 b
17 Página 17 de PLNO DE PERFIL δ O PERPENDICULR L LÍNE DE TIERR. P Figura 26 δ 2 Sus trazas estarán en una misma perpendicular a la línea de tierra. Figura 26 δ 2 δ1 P δ PLNO α PRLELO L LÍNE DE TIERR. Sus trazas serán paralelas a la línea de tierra. Figura 27a y b. α2 PV Figura 27 a α1 PH la α 1 Figura 27 b 3.6. PLNO QUE PS POR L LÍNE DE TIERR Las trazas estarán confundidas con línea de tierra. Para su definición será preciso representar un punto cualquiera del plano. Por ejemplo el punto ( - ). Figura 28 a y b. El plano se representará por las proyecciones del punto y dos trazazos a cada lado de la recta que une los puntos. π α α 1 α 1 Figura 28 a Figura 28 b
18 Página 18 de DETERMINR LS TRZS DE UN PLNO DDO TRES PUNTOS DEL MISMO. H b V b Sean los puntos, B y C dados por sus proyecciones H a V 1. Utilizaremos el punto B ( B, B ) como punto común a ambas rectas. 2. Haremos pasar dos rectas a y b por dichos puntos. H H V a V 3. Hallaremos las trazas de la recta a y b. Figura 29. b α 1 Figura SITUCIÓN DE RECTS SOBRE PLNOS Una recta pertenece a un plano cuando las trazas homónimas de la recta se corresponden con las del plano. Por tanto para situar una recta sobre un plano bastará con que sus trazas se encuentren sobre las del mismo nombre del plano SITUR UN RECT OBLICU EN UN PLNO OBLICUO. Bastará con que las trazas del a recta estén situadas sobre las homónimas del plano. Figura 30.
19 Página 19 de m V" ß 2 H' r ß2 V" H V r m H' H" V' ß 1 Figura 30 ß SITUR UN RECT HORIZONTL EN UN PLNO OBLICUO. La traza horizontal de la recta será paralela a la horizontal del plano y la vertical será paralela a la línea de tierra. Esta recta recibe el nombre de recta horizontal de plano. Figura 31. δ 2 V" r r V" V' r V' r r Figura 31 δ 1 ß 2 p V" 4.3. SITUR UN RECT FRONTL EN UN PLNO OBLICUO La traza vertical de la recta será paralela a la vertical del plano y la horizontal será paralela a la línea de tierra. Figura 32. p Figura 32 H ß 1
20 Página 20 de DIBUJR UN RECT PRLEL L LÍNE DE TIERR EN UN PLNO PRLELO L LÍNE DE TIERR. r Ξr α 3 Para su representación, tendremos que dibujar la tercera proyección del plano. Figura 33. r α 1 Figura V' V" s" s β 2 H" 4.5. SITUR UN RECT s OBLICU EN UN PLNO PRLELO L LÍNE DE TIERR. Figura 34. β 1 Figura 34 H' 4.7. SITUR UN RECT n DE PERFIL EN UN PLNO PRLELO L LÍNE DE TIERR. Figura 35. H" n' n" V" V' α 1 H' Figura INTERSECCIÓN DE PLNOS Trabajaremos en el espacio. Consideremos dos planos cualquiera α y β. Figura 36.
21 Página 21 de δ Cortemos estos dos planos por otros dos cualquiera, µ y δ Seguidamente hallamos la intersección de los planos α, β, µ de tal forma que tendremos las rectas i αµ y i βµ, α rectas que determinan un punto iβµ µ común a los tres planos, punto. iαµ iαδ B iβδ β Repetimos la operación con los planos α.δ.β, Obteniendo el punto -B. La unión de los puntos y B, nos determinan la intersección de los planos α-β. Figura 36 Para facilitar esta operación en el plano se toman como planos auxiliares µ-δ, los planos horizontal y vertical del sistema INTERSECCIÓN DE DOS PLNOS OBLICUOS CULQUIER La intersección de las dos trazas horizontales α 1 y β 1 darán un punto de la intersección HΞH. Y la unión de las trazas verticales y β 2 darán el punto VΞV. Figura 37 a y b. La recta intersección de ambos planos será la recta HV=i V V i i β 2 β V i H α V H i α 1 β 1 H H Figura 37a Figura 37 b 5.2. INTERSECCIÓN DE DOS PLNOS PRLELOS L LÍNE DE TIERR.
22 Página 22 de Sus trazas serán paralelas a la línea de tierra. Se requiere de la tercera proyección para resolver el problema. Figura 38 a y b. VS α α 3 P. P. β 2 ω 2 α β 2 i I i α 1 I 3 β 3 β H α 1 β 1 i i ω 1 I β Figura 38 b Figura 38 a 5.3. RECT INTERSECCIÓN DE UN PLNO OBLICUO CON OTRO PRLELO L HORIZONTL Sea el plano oblicuo α y el paralelo al horizontal μ. Figura 39 a y b. La recta intersección i de ambos planos tendrá la traza vertical i paralela a la línea de tierra coincidiendo con la traza vertical del plano μ 2 y la horizontal i paralela a la traza horizontal del plano α 1. V i" µ 2 PVS µ 2 i" i µ V i V i' i' V i α 1 PH Figura 39 a Figura 39 b α I NTERSECCIÓN DE UN PLNO PRLELO L. T. CON OTRO QUE PS POR L L. T. 1. Representaremos ambos planos en tercera proyección.
23 Página 23 de Hallamos el punto de intersección i de ambos planos. 3. Pasamos dicho punto a primera y segunda proyección i i. Figura 40 a y b. PP PV β I" I i" " π 2 α 3 i"' ß3 "' α i β 1 β 2 i I' α 1 i' ß 1 ß 2 B" PH α 1 π 1 Figura 40 b Figura 40 a 5.5. INTERSECCIÓN DE DOS PLNOS PROYECTNTES CULQUIER La intersección será una recta i perpendicular al plano horizontal. Figura 41a y b. PV i" β 2 β 2 i" i H" H β 1 i H α 1 H i PH β 1 α 1 Figura 41 b Figura 41 a 5.6. RECT INTERSECCIÓN DE LOS PLNOS α Y β CUYS TRZS SE CORTN FUER DEL DIBUJO. (Figura 42) 1. Trazamos un plano cualquiera que corte a los dos dados, por ejemplo un plano paralelo al vertical de proyección µ.
24 Página 24 de H 'i V i a" I" 2. Hallamos la intersección del plano µ con α y β, que nos determinan las rectas a(a -a ) y b(b -b ). H i H a β 2 H "b b" V i i 3. El punto I (I - I ), será común a la intersección de los tres planos, y por tanto será uno de los puntos que buscamos. a' µ 1 H 'a β 1 H 'b b' α 1 Figura 42 I Podemos comprobar el resultado prolongando las trazas horizontales de los planos PUNTO INTERSECCIÓN DE TRES PLNOS. ( Figura 43). µ V c β 2 c V"a El punto común a tres planos dados α, β, µ, vendrá dado por la intersección de las rectas comunes a dichos planos. V b b" V'b V'c b' H b H b β 1 a" V'a H"c a' µ H"a H'a H c 1.- Hallaremos la intersección de los planos α y β, que nos determina las proyecciones a y a. 2.- Seguidamente hallamos la intersección de un plano cualquiera de los anteriores con el plano µ, resultando la recta b b. Figura 43 El punto de intersección de la recta a y b, a y b, será el punto de intersección I - I, buscado, común a los tres planos. Podemos comprobar lo realizado hallando la tercera recta c. I' I" α PUNTO INTERSECCIÓN DE RECT Y PLNO
25 Página 25 de La intersección del plano α con la recta r, se logrará de la forma siguiente: 1.- Se hace contener a la recta r en un plano cualquiera, plano β. 2. Hallamos la intersección de β con α, i β α. Dicha intersección cortará a la recta en el punto I que será el punto buscado. Figura 44a y b. r β V" r =i" I" β 2 α I αβ Figura 44 b V' i' I' r' H" β 1 Figura 44 a En el plano operamos de la misma forma. Como plano auxiliar tomaremos uno que nos facilite la resolución de forma rápida, por ejemplo uno de los proyectantes de dicha recta β (β 1- β 2 ). H 5.9. PUNTO INTERSECCIÓN DE RECT PERPENDICULR L HORIZONTL, CON UN PLNO OBLICUO. (Figura 45). La recta vendrá dada por sus proyecciones r -r. Por r haremos pasa un plano proyectante vertical δ -δ. Seguidamente determinaremos su intersección, punto I -I. V' V" i" I" r" i' r' I δ. δ H" PUNTO INTERSECCIÓN DE RECT PRLEL L LÍNE DE TIERR CON UN PLNO OBLICUO. Figura 46 Tomaremos un plano auxiliar paralelo a la línea de tierra µ (µ 1 -µ 2 ). Representamos la recta a tercera proyección y por el punto r o pasamos el plano auxiliar π (π 1 -π 2 ). H' V" µ 2 π 2 Figura 45 I" r" V' µ 1 I' i" r' i' H" H' r o µ3 α 1 π 2 Figura 46
26 Página 26 de PRLELISMO Y PERPENDICULRIDD " s 6.1. TEOREM DE LS TRES PERPENDICULRES: ' r s' r' B" B' Si dos recta r y s son perpendiculares en el espacio y una de ellas por ejemplo la s es paralela a un plano α, sus proyecciones r y s también lo serán. α Figura 47 s" I" r" K" a" b" 6.2. INCIDENCI ENTRE RECTS. s' r' b K' 1 a' Para que dos rectas r y s se corten en el espacio, las proyecciones homónimas del punto de intersección I ( I - I ) han de estar en una misma perpendicular a la línea de tierra. Figura 48a. Figura 48 a I' K' 2 Figura 48 b En caso contrario, las rectas se cruzarán en el espacio. Figura 48 b PRLELISMO ENTRE RECTS Q" a" r" Si dos rectas son paralelas en el espacio, sus proyecciones también lo son. Figura 49. Ejercicio: Trazar por un punto Q, una recta paralela a la recta r. Q' Figura 49 a r' Bastará con trazar por el punto Q -Q, dos rectas a -a, paralelas a r -r.
27 Página 27 de PRLELISMO ENTRE PLNOS V" v β 2 v V" s V" t t s V" r r H' β 1 v H' s P α 1 P H' r H' t Figura 50 Para que un plano β sea paralelo a otro α, el primero debe contener a dos rectas t y v, paralelas a otros dos s y t contenidas en el plano α. Como las trazas del plano son rectas del mismo, bastará con que estas sean paralelas TRZR POR UN PUNTO P UN PLNO β PRLELO OTRO DDO α. 1. Se hace contener en el plano α una recta cualquiera por ejemplo la recta s. 2.- Se traza por el punto P, una recta paralela a s. La traza horizontal del plano pasará por H v y será paralela a α 1. Figura PRLELISMO ENTRE RECT Y PLNO Una recta r es paralela a un plano α cuando este contiene a una recta s paralela a la r dada. Figura 52a y b. r V S H"s H's Figura 51 s" V's s' V"s α 1 β 1 β 2 H"v P" v" P' H'v Figura 52 b v' s α s" r" Figura 52 a V S s' H"s r' α 1 H's
28 Página 28 de DETERMINR LS TRZS DEL PLNO α QUE CONTENIENDO L RECT r SE PRLELO OTR RECT s. s" P" r" V"r s" 1. Por un punto P cualquiera de la recta r, trazamos una recta paralela a la dada s. H"r s' P' H"s r' H's V'r s' 2. Seguidamente hallaremos el plano que contenga a ambas rectas. Figura 53. α 1 H'r Figura PERPENDICULRIDD ENTRE RECT Y PLNO. δ M r Si una recta r y un plano β son perpendiculares, lo serán a todas las rectas contenidas en el plano, siendo la traza del mismo una de ellas. α M' α β p" α δ β Figura 54 a " p' El plano proyectantes δ que contiene a la recta será perpendicular a α y β y por tanto la recta α β y α δ serán perpendiculares. r" β 2 Por todo lo anterior, para trazar una recta perpendicular a Figura 54 b β 1 un plano, bastará con que las trazas de la recta y las del plano sean perpendiculares. Figura 54 a y b. r' ' Figura 55 α 1
29 Página 29 de TRZR POR UN PUNTO UN RECT p, PERPENDICULR UN PLNO α. Bastará con trazar una recta perpendicular a las trazas del plano que y que pase el punto. Figura TRZR POR UN PUNTO Q UN PLNO β PERPENDICULR UN RECT s. Por el punto Q trazaremos una recta horizontal de plano m (m -m ), perpendicular a s. Figura 56. s" La traza del plano pasará por V y será perpendicular a m. V V Q" m" s' PERPENDICULRIDD ENTRE DOS RECTS. Q' m' No existe a simple vista relación Figura 56 gráfica que nos permita ver la perpendicularidad entre dos rectas, tal y como podemos apreciar en la figura 57b. Por tanto nos limitaremos a trazar una recta perpendicular a s que pase por un punto cualquiera P. Elegimos un punto cualquiera P (P -P ) y trazamos un plano perpendicular α(α 1 - ) a s (s -s ). Ejercicio 57 a y b. P m s φ 2 i 1. Hacemos contener a la recta s en un plano proyectante vertical φ (φ 1 - φ 2 ). r I V S 2. Hallamos la intersección de los planos α y β. Recta i(i -i ). El punto I -I, será la intersección de la recta con el plano. 3. Uniendo I -I con P -P, tendremos la recta r(r -r ), perpendicular a s(s -s ). P H s r i m I V s s H s α1 φ 1 Figura 57 b
30 Página 30 de s P r I α Figura 57 a 7. DISTNCIS 7.1. DISTNCI ENTRE DOS PUNTOS r V B r c r B c-c c B d o La distancia entre dos puntos viene dada por el valor de la hipotenusa d o de un triángulo rectángulo cuyos catetos son la diferencia de cotas o alejamientos de los puntos ( - ) y B(B -B ) y la proyección de la recta - B. Figura 39 r a y b. B B r d o c - c r d o B Figura 58 a Figura 58 b 7.2. MÍNIM DISTNCI DE UN PUNTO UN PLNO. Figura 59a y b. P φ 1. Por el punto P se traza una recta perpendicular al plano. 2. Se hace contener a la recta en un plano, φ. 3. Se halla la intersección del plano α y el plano φ, I 4. La distancia será el segmento I - P. α i αφ Figura 59 a
31 Página 31 de La hipotenusa del triángulo rectángulo cuyos catetos son la diferencia de cotas entre el punto P y la intersección I será la verdadera magnitud de la distancia del punto al plano. β 2 V i p I c-c P 7.3. HLLR L MÍNIM DISTNCI ENTRE EL PUNTO P (P -P ).Y L RECT s (s -s ). Figura 60 a y b. V i H i 1. Trazamos un plano α que pase por el punto P y sea perpendicular a la recta s. i Para ello previamente trazaremos una P c-c recta horizontal de plano m(m -m ). 2. I do Hallamos la intersección del plano α con la recta s. Ejercicio resuelto anteriormente. φ 1 p s Figura P 59 b I H i α a-a V.M. Figura 60 a P m s δ 2 I V S 7.4. HLLR L MÍNIM DISTNCI ENTRE LOS PLNOS α Y β. Figura 61a y 61b, Sean los planos α y β. Por un cualquiera t, trazamos una perpendicular s a los planos. Hallamos la intersección de dichos planos con la recta s, que nos determinan los puntos y B, distancia entre ambos planos. a-a P α1 H s H s δ1 m i I V s s Figura 60 b Seguidamente hallaremos su verdadera magnitud.
32 Página 32 de T s" δ 2 β 2 β α B s Figura 61 a V"b V'b T" B" d c-c' V"a " a" b" V'a H" a H" b a' ' d' c-c' B' d o T' H'a s' β 1 b' α 1 Figura 61 b δ 1 H'b 8. BTIMIENTOS Decimos que abatimos un plano sobre otro, cuando hacemos superponer el primeros sobre el segundo, haciendo girar alrededor de un eje, llamado charnela, que es la intersección de ambos. Con los abatimientos se pretende obtener verdaderas magnitudes de rectas o figuras planas. 1.- Para abatir un punto P, situado en el plano α, abatimos dicho plano α que contiene al punto P, utilizando como charnela la intersección de los planos α y δ. Línea a-b. Figura 62 a. 2.- El radio de giro será la mínima distancia del punto a la charnela, la cual se halla como hipotenusa del triángulo rectángulo cuyos catetos son P M y P (P). Una vez visto el proceso en el espacio, trabajaremos en el plano. Sea el punto P ( P -P ). 1.- El primer paso será hallar el radio de giro ρ. Por P, trazamos una perpendicular y una paralela a la traza horizontal α 1, que la utilizamos como charnela.
33 Página 33 de Sobre la paralela, llevamos el valor de la cota del punto c. 3.- Haciendo centro en M y con radio ρ, trazamos un arco hasta que corte a la perpendicular P en Po, punto abatido. Hemos realizado el abatimiento en el plano horizontal, podemos repetir la operación en el vertical, la única diferencia será que uno de los catetos será, en este caso, el alejamiento en lugar de la cota. Figura 62 b. P o Figura 62 a P P N a c (P) o M P c (P) (P ) o P M b P o Figura 62 b 8.1. BTIMIENTO DE PUNTO, RECT Y TRZ DEL PLNO. 1.- Sea una recta r(r -r ). Figura 44. P Q Elegimos dos puntos cualquiera de la recta, por ejemplo, los puntos P y Q y los abatimos, caso anterior. 3.- La unión de Po y Qo, puntos abatidos será la recta ro, abatida. 3 P ρ 1 2 Q 1 O -O 4.- Para abatir las traza del plano, basta con abatir dos puntos de la misma. El punto O -O se encuentra abatido por ser punto doble, por tanto abatiremos únicamente el punto 1-1. ρ 2 3 ro Po 5.- La verdadera magnitud de la recta también puede obtenerse abatiendo las trazas de la misma La traza 3 por Qo Figura 63
34 Página 34 de encontrarse en la charnela queda batida en si mismo BTIMIENTO DE UN FIGUR CULQUIER 1.- Partimos de un pentágono irregular, de vértices 1, 2, 3, 4, 5, apoyado en el plano horizontal. 2.- Hallamos la proyección vertical, 1, 2, 3, 4, 5. del pentágono, aunque esta no es necesaria para obtener la verdadera magnitud. Lo hacemos por medio de horizontales de plano. Figura α ch ( )o que pasan por los vértices del pentágono. 4 o 5 o 3 o 2 o 1 o 3.- Para hallar la verdadera magnitud de la figura, utilizaremos como charnela la traza α 1. batimos el la traza vertical del plano. 4.- Seguidamente abatimos las rectas horizontales de plano que pasan por los vértices del pentágono. 4.- Seguidamente abatimos las rectas horizontales de plano que pasan por los vértices del pentágono. 4.- Seguidamente abatimos las rectas horizontales de plano D" C" Eo E" " E' ' o D' B" B' C' 8.3. DD UN FORM POLIGONL o, Bo, Co, Do, DETERMINR SU PROYECCIÓN HORIZONTL Y VERTICL, UTILIZNDO COMO CHRNEL L TRZ HORIZONTL DEL PLNO. 1. Hallaremos la traza vertical del plano α. Do Co Bo α ch Figura El punto por encontrarse en la charnela es un punto doble, por lo tanto o. 3. Mediante horizontales de plano hallaremos el resto de los puntos.
35 Página 35 de CMBIOS DE PLNO " N a PV a' "2 c N' PV' Los cambios de plano tienen como objetivo permaneciendo fija la posición de la figura en el espacio variar uno de los planos de proyección de forma que este se coloque en una posición adecuada que nos facilite la representación del objeto. Cuando varían los planos, cambia la posición de la línea de tierra. Esta nueva línea de tierra se representa por dos trazos gruesos. Figura 66 a y b. c " Figura 66 a PH ' c c " 2 El punto 2 cambia de posición conservando el valor de la cota c. El punto permanece fijo, variando el valor del alejamiento a. Figura 47 a y b. a ' a' Figura 66 b PV' 9.1. CMBIO DE UN RECT OBLICU PRLEL L HORIZONTL.( HORIZONTL DE PLNO) PH' ' 1 a " r 1 r" V' 1 V" Elegimos una nueva línea de tierra paralela a la traza vertical del plano ya que la proyección vertical de la recta será paralela a la L.T. Para ello cambiamos el plano horizontal. a r' V' Cambiamos dos de los puntos de la recta, por ejemplo una de sus trazas V y un punto cualquiera. Figura 67. Figura 67 '
36 Página 36 de CMBIO DE LS TRZS DE UN PLNO OBLICUO CULQUIER. N c c α 2 N Elegimos una nueva línea de tierra. 2.- Trazamos por el punto N, cruce de las dos líneas de tierra, las rectas perpendiculares a cada una de ellas. N 3.- Llevamos sobre la perpendicular a la nueva línea de tierra el valor de la cota c de punto N. Figura 68. N 1 α 1 Figura 68 PV 9.3. CMBIO DE LS TRZS DE UN PLNO OBLICUO PLNO PROYECTNTE VERTICL. Elegiremos la nueva línea de tierra perpendicular a la traza horizontal α 1. Figura 69. El resto del ejercicio es similar al anterior CMBIO DE LS TRZS DE UN PLNO OBLICUO PLNO PROYECTNTE HORIZONTL. En este caso la nueva línea de tierra será perpendicular a la traza vertical. Figura 70. α 2 N PV' N 1 N M" N 1 PH' α 1 Figura 69 M' 1 M' Figura 70 α 1 α 1
37 Página 37 de PV 10. GIROS GIRO DE UN PUNTO " a" Figura 61 a e" 1 PH e' ' e 1 ' GIRO DE UN RECT OBLICU OTR POSICIÓN DE OBLICUIDD. a' Los giros son otro de los procedimiento para obtener proyecciones en verdadera magnitud. Los resultados son los mismos que con los cambios de planos, pero en este caso los planos de proyección permanecen fijos y son los puntos los que cambian de posición. " a" e" " 1 El giro de una recta, se limita al giro de dos puntos de la misma. mbos puntos deben girarse en el mismo Sentido y con el mismo ángulo. El eje de giro puede adoptarse a cruzándose con la recta o cortándola. En ' 1 nuestro caso adoptaremos un eje de giro e -e,que corte a la recta r -r, y sea perpendicular al plano horizontal. e Figura 61 b r 1 " r" B" e" B" 1 r' e' Figura 62 B' 128 B' 1 r GIRO DE UN RECT
38 Página 38 de " OBLICU PRLEL L VERTICL. r" B e" r"1 "1 Utilizaremos un eje de giro perpendicular al plano horizontal e(e -e ) y que corte a la recta en el punto B ( B -B ). 1. Giramos el punto, el valor del ángulo preciso para dejarla paralela a la línea de tierra. Ocupando la posición Por, trazamos una recta paralela a la L.T. ' r' e' B r'1 '1 Figura El punto B ( B -B ), está abatido en si mismo. 11. PIRÁMIDE. REPRESENTCIÓN Y DESRROLLO. La pirámide está generada por una recta, que sea poya en un punto fijo, llamado vértice, y se desplaza por una superficie poligonal. Si dicha superficie es un polígono regular y el vértice se situa ene l centro del polígono, la pirámide será regular. Si el polígono del a base es irregular o la altura del a pirámide no se sitúa en el centro del mismo, será irregular DD L PIRÁMIDE RECT DE BSE HEXGONL POYD EN EL PLNO HORIZONTL. DETERMINR: V" La proyección vertical. ß 2 1 1" 6 2 6" 2" " 3" 4" " F" B" E" C" D" La sección producida por el plano β en proyecciones y verdadera magnitud. 1. Partimos de un hexágono regular -B -C - D -E -F, apoyado en el plano horizontal. Figura 64. ' F' 1' 6' 5' V' E' 4' D' 4 o 5 o 6 o 2. Hallaremos la proyección vertical de los puntos anteriores -B -C - D -E -F -, previamente B' 2' 3 C' ß 1 3 o 2 o Figura 64
39 Página 39 de determinaremos su centro V y el vértice V. 3. Por ser un plano proyectante, su proyección vertical es una línea. 4. Una ver hallada la proyección vertical determinaremos la horizontal. 5. La verdadera magnitud de la sección se halla por abatimiento. 1 o 6. La determinación de la verdadera magnitud de la arista de halla por giro de la recta V - 3 B' SECCIONR POR EL PLNO β 1 -β 2, L PIRÁMIDE DE BSE CUDRNGULR, POYD EN EL PLNO HORIZONTL DE PROYECCIÓN. DE L QUE SE CONOCE L BSE Y EL VÉRTICE V -V SE PIDE: Figura 65. a) Dibujar la proyección horizontal y vertical de la sección producida por dicho plano. b) Dibujar la verdadera forma de la sección. c) Realizar el desarrollo lateral de la transformada de la sección dando el punto V. ß ' 1" V" 3" B" " C" D" ' 1' V' 3' C' 4 ß 1 =ch 4" 3 o D' 4 o 2 o 1 o Figura 65 (ß 2 ) o 1. Partimos del cuadrado del a base, -B -C -D, apoyado ene l plano horizontal de proyección. Hallamos sus proyecciones verticales -B -C -D. y el vértice V. 2. Por tratarse de un plano oblicuo, la traza del plano β 2 no corta a las aristas del a pirámide, sin oque las cruza. 3. Por ello para hallar las intersecciones de las aristas de la pirámide con el plano β, tendremos que hacer contener a cada una de ella en un plano proyectante, y hallar las intersecciones de ambos planos. 4. hacemos pasar un plano proyectante por -C, que determina el punto 3 y 1. El punto 3-3, se encontrará en la traza β 1 y línea de tierra. 1 se obtiene por una perpendicular a la L.T.
40 Página 40 de V C 4 D 4. El punto 2 y 4, se puede hallar por homología. 5. Para obtener la verdadera forma de la sección, bastará con abatir las horizontales de plano que pasan por cada uno de los puntos Para hallar el desarrollo del a sección, tendremos que determinar la verdadera longitud el a arista de la pirámide, ya que esta es oblicua a los planos de proyección y por tanto no se encuentra en verdadera magnitud. 7. Eligiendo como eje de giro la recta que pasa por V -V, giraremos la recta B -V, hasta que esta quede paralela a la L.T. La recta 3-V, será la verdadera magnitud de la arista del a pirámide. B El resto del a construcción puede deducirse de la figura 66. Figura DD L PROYECCIÓN HORIZONTL DE L PIRÁMIDE RECT REGULR DE BSE 1, 2, 3, 4. POYD EN EL HORIZONTL: DETERMINR: EN PROYECCIÓN Y VERDDER MGNITUD L SECCIÓN PRODUCID POR EL PLNO Α ( QUE PS POR L LÍNE DE TIERR). SEGUIDMENTE DIBUJR EL DESRROLLO DE L MISM π 2 α 3 α Se dibuja un plano cualquiera de perfil π. 2.- Se halla la tercera proyección del plano α. π 1
41 Página 41 de Se halla la proyección vertical de la pirámide 4,- Pasamos la pirámide a tercera proyección. La sección en tercera proyección vendrá determinada por la intersección del plano α con las aristas de la pirámide. 5. Hallamos la proyección segunda y primera de dichos puntos. 6. La verdadera magnitud se halla trazando perpendiculares por los puntos, B, C D, y llevando sobre ellas la distancia de las segundas proyecciones al plano vertical tres HLLR L PROYECCIÓN HORIZONTL Y VERTICL DE L PIRÁMIDE HEXGONL POYD EN EL PLNO HORIZONTL, TENIENDO EN CUENT QUE L RIST 1-V ES UN RECT FRONTL. POR MEDIO DE CMBIO DE PLNO, HLLR L PROYECCIÓN HORIZONTL, VERTICL Y VERDDER MGNITUD DE L SECCIÓN PRODUCID POR EL PLNO Α. 1.- Se halla la proyección V teniendo en cuenta que es una recta frontal. 2.- Se dibuja la proyección horizontal y vertical de la pirámide. 3.- Hacemos un cambio del plano vertical, de tal forma que este se convierta en proyectante trazando una nueva línea de tierra perpendicular a la traza horizontal de α Hallamos la nueva proyección vertical de la pirámide. 5.- La sección vendrá dada por la intersección del α 2 con las aristas de la pirámide. Seguidamente se halla la proyección horizontal de dicha sección. 6.- La verdadera magnitud se obtiene trazando por los puntos -1, B -1, C -1 y D -1 perpendiculares a la traza vertical del plano y llevando sobre dichas rectas el valor del alejamiento de los puntos.
42 Página 42 de B o 55 Eo Do SE D L VERDDER MGNITUD DE L BSE DE UN PIRÁMIDE POYD EN EL PLNO Β. HLLR L PROYECCIÓN HORIZONTL Y VERTICL DE L MISM, SBIENDO QUE SU LTUR ES 30 MM. Hallamos la proyección horizontal y vertical de la base de la pirámide. Obteniendo previamente la traza vertical del plano β2. Trazamos una recta perpendicular a la trazas del plano Β (β1-β2), que pase por O - O. Elegimos un punto cualquiera de la recta anterior. a -a. Giramos dicha recta para obtener su verdadera magnitud. Llevamos sobre dicha recta la altura h de la pirámide, obteniendo el vértice Vo y seguidamente el V.
43 Página 43 de a 1 V a" h V O" a 1 3 O' 5 2o 3o a V 4 1 (β2) o O 5 o 4 o ß1=c 12. PRISM En la figura se define un prisma recto apoyado en el plano de proyección horizontal, mediante la proyección horizontal de se base y su altura. Obténgase las proyecciones horizontal y vertical del prisma. Posteriormente determinar en proyección y verdadera magnitud la sección producida por el plano α. 1.- Dibujamos el alzado del prima levantando perpendiculares por los puntos 1, 2,3,4 que nos determinan su segunda proyección. Las proyecciones 5, 6, 7 y 8, coincidirán en planta con las anteriores 2.- Por ser un prisma recto las proyección horizontal de la sección, B,C, D, debe coincidir con los puntos anteriores. Por medio de las horizontales de plano h y l se obtienen las proyecciones verticales de los puntos. 3.- Para hallar la verdadera magnitud de la sección batimos la traza vertical del plano.
44 Página 44 de α 5" 8 7 6" D 55 C B 1" 4" 3 2" 4' = 3' = 1' = 2 = α1- ch Se da un prisma oblicuo de base pentagonal apoyado en el plano horizontal de proyección. Dibujar la proyección Vertical del mismo. Determinar en proyecciones y verdadera magnitud las secciones producidas por el plano oblicuo α. 1.- Para resolver el ejercicio deben de darnos la proyección horizontal del prisma y la inclinación de una de las aristas. 2.- El ejercicio se resolverá por cambio del plano vertical hasta convertirlo en proyectante. 3.- La sección vendrá dada por los puntos 1 1, 2 1, 3 1, 4 1, 5 1. que pasados a primera y segunda proyección tendremos las secciones buscadas.
45 Página 45 de J" F" I" G" H" 1" 2" 5" 4" 3" E" " D" B" C" ' B' E' D' C' F' G H' J' I Dado un prisma de base pentagonal apoyado en el plano horizontal: Dibujar la proyección vertical del mismo. Determinar en proyecciones y verdadera magnitud las secciones producidas en el prisma por el plano β paralelo a la línea de tierra. Dibujar el desarrollo del prisma resultante como consecuencia de la intersección. 1.- Dibujamos el alzado del prisma, levantado perpendiculares por los puntos 1, 2,3,4,5. partir de las proyecciones verticales de estos puntos llevamos la altura del prisma 2.- Una paralela a la línea de tierra determina los puntos 6, 7, 8, 9 y Pasamos el prisma a tercera proyección y hallamos la intersección de este con β3. que nos determinan los puntos, B, C, D, E. Hallando a continuación las proyecciones segunda. La proyección primera debe coincidir con los puntos 1, 2,3,4, La verdadera magnitud la hallaremos por dos procedimientos
46 Página 46 de ao bo (β1)o 10" 7" 9" 6" 8" β1- ch Co a b 2" 1" 3" 5" 4" 3' 7' β3 2' 6' 4' 8' 1' 10' β1 5' 9' Hallar la proyección horizontal y la vertical del prisma regular de base hexagonal apoyado en el plano oblicuo α. En primer lugar colocamos la cara de apoyo en verdadera magnitud. Utilizando la traza α1 como charnela, hallamos las proyecciones horizontal y vertical, aplicando los procedimientos vistos, horizontales de plano, frontales, afinidad etc. Sobre la recta 2 perpendicular a la traza del plano, elegimos un punto cualquiera a - a. y giramos el punto. Sobre la recta 2 - a 1, llevamos la altura del prisma. El resto del ejercicio es evidente. 13. CONO
47 Página 47 de Se da un cono equilátero recto de revolución apoyado por su base en el plano horizontal. Dibujarle y determinar en proyecciones y verdadera magnitud las secciones interceptadas por los planos α y β. 1.- Se divide la circunferencia en doce partes iguales para obtener generatrices ficticias del cono. 2.- Hallamos la proyección vertical del cono. 3.- La sección vertical vendrá determina por la recta G, y la horizontal por la proyección horizontal de los puntos correspondientes. 4.- Para hallar la proyección horizontal de los puntos JD, se hace pasar por ellos un plano π paralelo al horizontal y hallamos su proyección horizontal que nos determinan los puntos J y D. 5.- Por último se halla la verdadera magnitud de la sección abatiendo el plano vertical- P π2 Lo N M P L 6. La intersección del plano de perfil β viene dada por la intersección de las aristas con dicho plano puntos M, N, O. 7.- También puede resolverse trazando perpendiculares por M, N,L a la traza horizontal del plano y llevando sobre las mismas el valor de las cotas de dichos puntos.
48 Página 48 de Dada una superficie cónica recta de revolución apoyada por su base en el plano horizontal de vértice V -V, dibujarla. Seguidamente hallar las secciones en proyecciones y verdadera magnitud producidas por el plano α, perpendicular al horizontal. 1.- Dividimos la base del cono en doce generatrices ficticias y hallamos la proyección vertical del mismo. α1 2.- Para hallar el punto B se traza una circunferencia con radio V B. 3.- La proyección horizontal vendrá dada por los puntos, B, C, D E, F, G. la vertical por la intersección de sus perpendiculare s a la línea de tierra con las respectivas generatrices., B, C, D E, F, G. 4.- La verdadera magnitud se halla α2 levantando perpendiculare s por los puntos, B, C, D E, F, G. y llevando sobre ellas el valor de las cotas. También se puede hallar abatiendo el plano horizontal Dada una superficie cónica recta de revolución apoyada por su base en el plano horizontal de vértice V -V, Dibujarla. Seguidamente hallar las secciones en proyecciones y verdadera magnitud producidas por el plano oblicuo α. 1.- Se divide la circunferencia en un número de partes iguales, por ejemplo ocho. Seguidamente se halla la proyección vertical.
49 Página 49 de La intersección del plano con el cono se realizará por medio de intersección de aristas con el plano y por homología. 3.- Para hallar la verdadera magnitud abatiremos el plano α2. Se utilizará el procedimiento de homología y líneas horizontales de plano. 14. CILINDRO
50 Página 50 de Se da un cilindro recto de revolución apoyado en el plano horizontal de proyección, definido por sus proyecciones vertical y horizontal. Se pide: Determinar en proyección la sección producida por el plano oblicuo α. Posteriormente determinar en Verdadera magnitud los ejes de la elipse sección. Por último construir a partir de dichos ejes obtenidos anteriormente un Óvalo de cuatro centros. C O D B Bo C1 α 1 c h C3 Oo Co Do C4 ( ) o C2 o
51 Página 51 de Se da un cilindro oblicuo apoyado en el plano horizontal definido por sus proyecciones horizontal y vertical. determinar en proyección y verdadera magnitud la sección producida por el plano para resolver se trabajará con 12 generatrices tomadas sobre la directriz del cilindro. a 2 2' 3' 4' 5' 6' 1' 7' 12' 11' 10' 9' 8 ' a1 15. POLIEDROS Se denomina poliedros a los cuerpos cuyas caras son polígonos regulares. Estos son cinco: TETREDRO: Lo componen cuatro triángulos equiláteros. Tiene cuatro vértices. OCTEDRO: Compuesto por ocho triángulos equiláteros y seis vértices. ICOSEDRO. Poliedro compuesto por veinte triángulos equiláteros. Y doce vértices.
52 Página 52 de HEXEDRO O CUBO: Sus caras son cuadradas. Tiene seis y ocho vértices. DODECEDRO: En cada vértice concurren tres son pentagonales. Tiene veinte vértices. caras que TETREDRO REGULR CON UN CR POYD EN EL PLNO HORIZONTL. Tetraedro regular es el polígono regular convexo formado por cuatro caras que son triángulos equiláteros, tiene seis aristas y cuatro vértices. Para su resolución debemos calcular el valor de la altura de mismo. Dicha altura vendrá dada por la hipotenusa del triángulo rectángulo cuyos catetos D D h B D N h a h 2/3h B C N 2/3h a son a, valor de la arista del mismo y 2/3 de la mediana. B N D h C D
53 Página 53 de TETREDRO REGULR CON DOS RISTS OPUESTS PRLELS L PLNO HORIZONTL hhh Las aristas -B y C-D, se proyectan en el plano horizontal en verdadera magnitud formando un cuadrado cuyos lados son las proyecciones de las aristas en el horizontal y sus diagonales las aristas en verdadera magnitud. C D D h B a C h C' D' C B B a D a h C o TETREDRO REGULR CON UN VÉRTICE POYDO EN PLNO HORIZONTL. La proyección horizontal del tetraedro apoyado con un vértice D en el plano horizontal, será un triángulo equilátero, cuyo lado será igual a la arista del mismo. C C D B B 2/3h h El ejercicio quedará resuelto cuando conozcamos la altura del mismo. Dicha altura se calculará de forma similar a la del tetraedro apoyado con una cara en el plano horizontal. B C h D C h B D a
54 Página 54 de TETREDRO POYDO EN EL PLNO α. 1.- Hallaremos la verdadera magnitud de la base. Para ello abatimos el triángulo, B, C, utilizando como charnela la traza vertical del plano. 2- Un vez que tenemos el triángulo equilátero correspondiente a las caras del tetraedro, hallamos la altura del mismo. 3.- Seguidamente hallamos las proyecciones, horizontal y vertical del ortocentro G. 4.- El siguiente paso, consistirá en hallar la proyección vertical del triángulo, B, C. α G 5.- Como el tetraedro se encuentra apoyado en el plano α la altura del mismo será una recta perpendicular a la traza Del plano. Una vez trazada la altura, elegimos un punto cualquiera X de la recta p. 6.- Obtenemos la verdadera magnitud del segmento G - X, Realizando un giro de la misma. α Sobre la recta G - X 1, llevamos la altura del tetraedro, que nos determinará el vértice V -V. ( HEXEDRO O CUBO. Poliedro formado por seis caras que son cuadrados, tiene doce aristas y ocho vértices, sus ángulos son rectos formando un triedro trirrectángulo. Los elementos que lo definen son: La arista a, la diagonal de la cara dc y la diagonal del cubo d. Como puede observarse, la diagonal de la cara es la hipotenusa de un triángulo rectángulo cuyos lados son las aristas del mismo.
APUNTES DE DIBUJO TÉCNICO: PRIMERO Y SEGUNDO DE BACHILLERATO. AUTOR: RAMON DEL AGUILA CORBALÁN AÑO 2010 G
 Página 1 de 59 2010 www.ramondelaguila.com α APUNTES DE DIBUJO TÉCNICO: PRIMERO Y SEGUNDO DE BACHILLERATO. AUTOR: RAMON DEL AGUILA CORBALÁN AÑO 2010 G Los apuntes que presento solo pretenden ser un complemento
Página 1 de 59 2010 www.ramondelaguila.com α APUNTES DE DIBUJO TÉCNICO: PRIMERO Y SEGUNDO DE BACHILLERATO. AUTOR: RAMON DEL AGUILA CORBALÁN AÑO 2010 G Los apuntes que presento solo pretenden ser un complemento
1º BACH SISTEMA DIÉDRICO I PUNTO, RECTA Y PLANO. PERTENENCIAS.
 1º BACH SISTEMA DIÉDRICO I PUNTO, RECTA Y PLANO. PERTENENCIAS. SISTEMA DIÉDRICO: REPRESENTACIÓN DEL PUNTO El punto se representa por dos proyecciones que están siempre alineadas en una perpendicular a
1º BACH SISTEMA DIÉDRICO I PUNTO, RECTA Y PLANO. PERTENENCIAS. SISTEMA DIÉDRICO: REPRESENTACIÓN DEL PUNTO El punto se representa por dos proyecciones que están siempre alineadas en una perpendicular a
Dibujo Técnico Sistema diédrico.- Cambios de plano, giros y ángulos. ÁNGULOS.
 30. SISTEMA DIÉDRICO.- CAMBIOS DE PLANO, GIROS Y ÁNGULOS. 30.1. Cambios de plano. Los cambios de planos de proyección consisten en tomar o elegir otros planos de proyección de forma que los elementos que
30. SISTEMA DIÉDRICO.- CAMBIOS DE PLANO, GIROS Y ÁNGULOS. 30.1. Cambios de plano. Los cambios de planos de proyección consisten en tomar o elegir otros planos de proyección de forma que los elementos que
SISTEMA DIÉDRICO PERTENENCIA VISIBILIDAD VISIBILIDAD 3º PROYECCIÓN PLANOS NO DADOS POR SUS TRAZAS
 SISTEMA DIÉDRICO PERTENENCIA 1. Dado un plano cualquiera cuya traza horizontal forma 40º con la LT y 60º la traza vertical, situar pasando por un punto A que le pertenece y de altura 30 mm, todas sus rectas
SISTEMA DIÉDRICO PERTENENCIA 1. Dado un plano cualquiera cuya traza horizontal forma 40º con la LT y 60º la traza vertical, situar pasando por un punto A que le pertenece y de altura 30 mm, todas sus rectas
S. Diédrico - 1 SISTEMAS DE PROYECCIÓN
 S. Diédrico - 1 SISTEMA DIÉDRICO El sistema diédrico es un sistema de proyecciones cilíndricas y ortogonales, es decir, que las rectas proyectantes son paralelas entre sí y perpendiculares a los planos
S. Diédrico - 1 SISTEMA DIÉDRICO El sistema diédrico es un sistema de proyecciones cilíndricas y ortogonales, es decir, que las rectas proyectantes son paralelas entre sí y perpendiculares a los planos
DIBUJO TÉCNICO BACHILLERATO TEMA 6. SISTEMA DIÉDRICO. Departamento de Artes Plásticas y Dibujo
 DIBUJO TÉCNICO BCHILLERTO TEM 6. SISTEM DIÉDRICO Departamento de rtes Plásticas y Dibujo TEM 5. CURVS. TEM 6. EL SISTEM DIÉDRICO. 1º BCH. CONCEPTOS. 1.Proyectividad y sistemas de representación Del espacio
DIBUJO TÉCNICO BCHILLERTO TEM 6. SISTEM DIÉDRICO Departamento de rtes Plásticas y Dibujo TEM 5. CURVS. TEM 6. EL SISTEM DIÉDRICO. 1º BCH. CONCEPTOS. 1.Proyectividad y sistemas de representación Del espacio
Sistema Diédrico Índice de contenido
 Sistema Diédrico Índice de contenido Sistema Diédrico Fundamentos La geometría descriptiva es la ciencia que estudia la representación de los elementos del espacio sobre el plano.... 2 El punto... 3 Conceptos
Sistema Diédrico Índice de contenido Sistema Diédrico Fundamentos La geometría descriptiva es la ciencia que estudia la representación de los elementos del espacio sobre el plano.... 2 El punto... 3 Conceptos
A(50,10,25) B(70,5,50) C(52,-10,37) A(45,15,35) B(45,-10,15) C(45,50,60) C(45,30,43) A(20,-5,70) B(45,-10,80) C(60,14,22)
 Diédrico. Pertenencia de un punto a una recta. Dados los puntos indicados. Averiguar si están o no alineados. Partes vistas y ocultas y sectorización de la recta que contiene los puntos A y B Halla los
Diédrico. Pertenencia de un punto a una recta. Dados los puntos indicados. Averiguar si están o no alineados. Partes vistas y ocultas y sectorización de la recta que contiene los puntos A y B Halla los
SISTEMA DIEDRICO. SISTEMA DIEDRICO. Planos de proyección, la línea de tierra planos bisectores.
 SISTEMA DIEDRICO. y SISTEMA DIEDRICO. Planos de proyección, la línea de tierra planos bisectores. GENERALIDADES: El Diédrico es un sistema de proyección cilíndrico ortogonal, cuyos elementos fundamentales
SISTEMA DIEDRICO. y SISTEMA DIEDRICO. Planos de proyección, la línea de tierra planos bisectores. GENERALIDADES: El Diédrico es un sistema de proyección cilíndrico ortogonal, cuyos elementos fundamentales
Carlos Quesada Dominguez ANEXO AL LIBRO DE SISTEMA DIEDRICO
 ANEXO AL LIBRO DE SISTEMA DIEDRICO 1 RECTA Y PLANO Dadas dos rectas (r y s) que se cortan y sus trazas están fuera de los limites del papel. Hallar las trazas del plano que determinan. 1º.- Trazar una
ANEXO AL LIBRO DE SISTEMA DIEDRICO 1 RECTA Y PLANO Dadas dos rectas (r y s) que se cortan y sus trazas están fuera de los limites del papel. Hallar las trazas del plano que determinan. 1º.- Trazar una
Dibujo Técnico Secciones Planas
 37. SECCIONES PLANAS 37.1. INTRODUCCIÓN. Para hallar la sección plano de un cuerpo geométrico se pueden emplear tres métodos: a.- Por intersección de aristas o generatrices del cuerpo con el plano. b.-
37. SECCIONES PLANAS 37.1. INTRODUCCIÓN. Para hallar la sección plano de un cuerpo geométrico se pueden emplear tres métodos: a.- Por intersección de aristas o generatrices del cuerpo con el plano. b.-
25. SISTEMA DIÉDRICO.- EL PLANO.
 25. SISTEMA DIÉDRICO.- EL PLANO. 25.1. Representación del Plano. Trazas del plano Se llaman trazas de un plano a las rectas que resultan de la intersección de este plano con los planos de proyección. Por
25. SISTEMA DIÉDRICO.- EL PLANO. 25.1. Representación del Plano. Trazas del plano Se llaman trazas de un plano a las rectas que resultan de la intersección de este plano con los planos de proyección. Por
27.1. Representación del Plano. Trazas del plano
 27. SISTEMA DIÉDRICO.- EL PLANO. 27.1. Representación del Plano. Trazas del plano Se llaman trazas de un plano a las rectas que resultan de la intersección de este plano con los planos de proyección. Por
27. SISTEMA DIÉDRICO.- EL PLANO. 27.1. Representación del Plano. Trazas del plano Se llaman trazas de un plano a las rectas que resultan de la intersección de este plano con los planos de proyección. Por
* * * GEOMETRÍA DESCRIPTIVA * * * ÍNDICE
 ÍNDICE 1.- CONCEPTO DE PROYECCIÓN.... 1 Proyección de un punto.... 1 Clasificación de las proyecciones.... 1 Sistema Diédrico...3 Sistema de Planos Acotados...3 Sistema Axonométrico...3 Sistema Cónico...4
ÍNDICE 1.- CONCEPTO DE PROYECCIÓN.... 1 Proyección de un punto.... 1 Clasificación de las proyecciones.... 1 Sistema Diédrico...3 Sistema de Planos Acotados...3 Sistema Axonométrico...3 Sistema Cónico...4
 OPCIÓN I PROBLEMA: SISTEMA DIÉDRICO. Los puntos A y B, vértices de un cubo, son los extremos de una de las diagonales de la base. Dicha diagonal es además línea de máxima pendiente del plano donde se apoya
OPCIÓN I PROBLEMA: SISTEMA DIÉDRICO. Los puntos A y B, vértices de un cubo, son los extremos de una de las diagonales de la base. Dicha diagonal es además línea de máxima pendiente del plano donde se apoya
27. SISTEMA DIÉDRICO.- PARALELISMO, PERPENDICULARIDAD.
 27. SISTEMA DIÉDRICO.- PARALELISMO, PERPENDICULARIDAD. 27.1. Paralelismo. 27.1.1. Paralelismo entre rectas. Dos rectas paralelas en el espacio se proyectan sobre un plano ortogonalmente sobre un plano
27. SISTEMA DIÉDRICO.- PARALELISMO, PERPENDICULARIDAD. 27.1. Paralelismo. 27.1.1. Paralelismo entre rectas. Dos rectas paralelas en el espacio se proyectan sobre un plano ortogonalmente sobre un plano
31. SISTEMA AXONOMÉTRICO. LA RECTA Y EL PLANO
 31. SISTEMA AXONOMÉTRICO. LA RECTA Y EL PLANO 31.1. Representación de la recta. Si un punto se representaba por cuatro proyecciones, la recta se representa igual por cuatro proyecciones. Tenemos la recta
31. SISTEMA AXONOMÉTRICO. LA RECTA Y EL PLANO 31.1. Representación de la recta. Si un punto se representaba por cuatro proyecciones, la recta se representa igual por cuatro proyecciones. Tenemos la recta
SISTEMA DIÉDRICO. Introducción
 Introducción SISTEMA DIÉDRICO El Sistema Diédrico o de Monge es un Sistema de Representación sobre el plano de cuerpos y elementos geométricos del espacio. Emplea la proyección cilíndrica ortogonal según
Introducción SISTEMA DIÉDRICO El Sistema Diédrico o de Monge es un Sistema de Representación sobre el plano de cuerpos y elementos geométricos del espacio. Emplea la proyección cilíndrica ortogonal según
24. SISTEMA DIÉDRICO.- LA RECTA.
 24. SISTEMA DIÉDRICO.- LA RECTA. 24.1. Representación de la Recta. Una recta queda inequívocamente determinada conocidos dos puntos de la misma; para hallar sus proyecciones bastará unir las proyecciones
24. SISTEMA DIÉDRICO.- LA RECTA. 24.1. Representación de la Recta. Una recta queda inequívocamente determinada conocidos dos puntos de la misma; para hallar sus proyecciones bastará unir las proyecciones
SISTEMA DIÉDRICO II INTERSECCIONES PARALELISMO Y PERPENDICULARIDAD ANA BALLESTER JIMÉNEZ
 SISTEMA DIÉDRICO II INTERSECCIONES PARALELISMO Y PERPENDICULARIDAD 1 SISTEMA DIÉDRICO: INTERSECCIONES. r s: Dos rectas se cortan cuando tienen un punto en común. A2 r2 y s2 A1 r1 y s1 α β: Dos planos que
SISTEMA DIÉDRICO II INTERSECCIONES PARALELISMO Y PERPENDICULARIDAD 1 SISTEMA DIÉDRICO: INTERSECCIONES. r s: Dos rectas se cortan cuando tienen un punto en común. A2 r2 y s2 A1 r1 y s1 α β: Dos planos que
2º BACH. SISTEMA DIÉDRICO [ABATIMIENTOS, CAMBIOS DE PLANOS, GIROS Y ÁNGULOS]
![2º BACH. SISTEMA DIÉDRICO [ABATIMIENTOS, CAMBIOS DE PLANOS, GIROS Y ÁNGULOS] 2º BACH. SISTEMA DIÉDRICO [ABATIMIENTOS, CAMBIOS DE PLANOS, GIROS Y ÁNGULOS]](/thumbs/53/33097240.jpg) 2º BACH. SISTEMA DIÉDRICO [ABATIMIENTOS, CAMBIOS DE PLANOS, GIROS Y ÁNGULOS] ABATIMIENTOS ABATIMIENTO DE UN PUNTO CONTENIDO EN UN PLANO. Sobre el P.H. Sobre el P.V. 1 ABATIMIENTO DE UNA RECTA CONTENIDA
2º BACH. SISTEMA DIÉDRICO [ABATIMIENTOS, CAMBIOS DE PLANOS, GIROS Y ÁNGULOS] ABATIMIENTOS ABATIMIENTO DE UN PUNTO CONTENIDO EN UN PLANO. Sobre el P.H. Sobre el P.V. 1 ABATIMIENTO DE UNA RECTA CONTENIDA
28. SISTEMA DIÉDRICO.- DISTANCIAS, VERDADERAS MAGNITUDES.
 28. SISTEMA DIÉDRICO.- DISTANCIAS, VERDADERAS MAGNITUDES. 28.1. Verdaderas magnitudes. 28.1.1. Distancia entre dos puntos. Tenemos en el espacio dos puntos A y B, la distancia entre ellos es el segmento
28. SISTEMA DIÉDRICO.- DISTANCIAS, VERDADERAS MAGNITUDES. 28.1. Verdaderas magnitudes. 28.1.1. Distancia entre dos puntos. Tenemos en el espacio dos puntos A y B, la distancia entre ellos es el segmento
TEMA VI: ÁNGULOS ENTRE ELEMENTOS
 TEMA VI: ÁNGULOS ENTRE ELEMENTOS 6.1.D Ángulo entre dos rectas El cálculo del ángulo de dos rectas que se cortan es sencillo. Si las rectas se cruzan, el ángulo es el formado entre una de las rectas y
TEMA VI: ÁNGULOS ENTRE ELEMENTOS 6.1.D Ángulo entre dos rectas El cálculo del ángulo de dos rectas que se cortan es sencillo. Si las rectas se cruzan, el ángulo es el formado entre una de las rectas y
Sistema axonométrico. Con el estudio de esta Unidad nos proponemos alcanzar los siguientes objetivos:
 UNIDAD 9 Sistema axonométrico E l sistema axonométrico se divide en ortogonal y oblicuo según sea la dirección de proyección. La axonometría ortogonal puede ser isométrica, dimétrica o trimétrica según
UNIDAD 9 Sistema axonométrico E l sistema axonométrico se divide en ortogonal y oblicuo según sea la dirección de proyección. La axonometría ortogonal puede ser isométrica, dimétrica o trimétrica según
DIBUJO TÉCNICO II EJERCICIOS DE APOYO. Prof. Jesús Macho Martínez
 DIBUJO TÉCNICO II EJERCICIOS DE APOYO Esta obra de Jesús Macho Martínez está bajo una Licencia Creative Commons Atribución- CompartirIgual 3.0 Unported 1º.- Deducir razonadamente el valor del ángulo α
DIBUJO TÉCNICO II EJERCICIOS DE APOYO Esta obra de Jesús Macho Martínez está bajo una Licencia Creative Commons Atribución- CompartirIgual 3.0 Unported 1º.- Deducir razonadamente el valor del ángulo α
GEOMETRÍA MÉTRICA Y SISTEMAS DE REPRESENTACIÓN
 SR.DR.01 Representar las proyecciones de un punto situado en: a) primer diedro e) PH anterior i) LT b) segundo diedro f) PV superior j) primer bisector (primer diedro) c) tercer diedro g) PH posterior
SR.DR.01 Representar las proyecciones de un punto situado en: a) primer diedro e) PH anterior i) LT b) segundo diedro f) PV superior j) primer bisector (primer diedro) c) tercer diedro g) PH posterior
APUNTES DE SISTEMA DIÉDRICO (1)
 APUNTES DE SISTEMA DIÉDICO (1) Departamento de Dibujo I. E. S. Jaime Ferrán SISTEMA DIÉDICO El Sistema Diédrico es un Sistema de epresentación que se basa en una Proyección Paralela o Cilíndrica Ortogonal
APUNTES DE SISTEMA DIÉDICO (1) Departamento de Dibujo I. E. S. Jaime Ferrán SISTEMA DIÉDICO El Sistema Diédrico es un Sistema de epresentación que se basa en una Proyección Paralela o Cilíndrica Ortogonal
DE LA RECTA PROYECCIONES DEL
 44 Punto, SISTEM NMÉTIC: recta, plano y cuerpos PECCINES DEL PUNT PECCINES DE L ECT PECCINES DEL PLN ECTS CNTENIDS EN PLNS Plano definido por dos rectas que se cortan INTESECCIÓN DE PLNS INTESECCIÓN DE
44 Punto, SISTEM NMÉTIC: recta, plano y cuerpos PECCINES DEL PUNT PECCINES DE L ECT PECCINES DEL PLN ECTS CNTENIDS EN PLNS Plano definido por dos rectas que se cortan INTESECCIÓN DE PLNS INTESECCIÓN DE
DIBUJO TÉCNICO II EJERCICIOS DE APOYO. Prof. Jesús Macho Martínez
 DIBUJO TÉCNICO II EJERCICIOS DE APOYO Esta obra de Jesús Macho Martínez está bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported 1º.- Deducir razonadamente el valor del ángulo α marcado
DIBUJO TÉCNICO II EJERCICIOS DE APOYO Esta obra de Jesús Macho Martínez está bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported 1º.- Deducir razonadamente el valor del ángulo α marcado
Sistema diédrico: prisma, cono y cilindro
 UNIDAD 7 Sistema diédrico: prisma, cono y cilindro Capitel basado en el prisma y el cilindro (Modificación de la fotografía de la Mezquita de las Tornerías, Toledo, de Luana Fischer Ferreira, del Banco
UNIDAD 7 Sistema diédrico: prisma, cono y cilindro Capitel basado en el prisma y el cilindro (Modificación de la fotografía de la Mezquita de las Tornerías, Toledo, de Luana Fischer Ferreira, del Banco
\ I OPCIÓN I PROBLEMA: SISTEMA DIÉDRICO.
 OPCIÓN I PROBLEMA: SISTEMA DIÉDRICO. Dadas las proyecciones horizontal y vertical de un sólido, asf como las trazas de un plano P, se pide: 1.- Determinar las proyecciones de la sección producida por el
OPCIÓN I PROBLEMA: SISTEMA DIÉDRICO. Dadas las proyecciones horizontal y vertical de un sólido, asf como las trazas de un plano P, se pide: 1.- Determinar las proyecciones de la sección producida por el
RELACIÓN DE EJERCICIOS PROPUESTOS PARA EVALUACIONES DE GEOMETRÍA DESCRIPTIVA EN LOS CURSOS , ,
 RELACIÓN DE EJERCICIOS PROPUESTOS PARA EVALUACIONES DE GEOMETRÍA DESCRIPTIVA EN LOS CURSOS 2006-2007, 2007-2008, 2008-2009 PROF: MORENO VARGAS ARQ. FEBRERO 07 DIÉDRICO. PROCEDIMIENTOS El segmento MC es
RELACIÓN DE EJERCICIOS PROPUESTOS PARA EVALUACIONES DE GEOMETRÍA DESCRIPTIVA EN LOS CURSOS 2006-2007, 2007-2008, 2008-2009 PROF: MORENO VARGAS ARQ. FEBRERO 07 DIÉDRICO. PROCEDIMIENTOS El segmento MC es
UNIDAD Nº 6 GEOMETRÍA DESCRIPTIVA PROYECCIÓN DIÉDRICA O DE MONGE
 UNIDAD Nº 6 GEOMETRÍA DESCRIPTIVA PROYECCIÓN DIÉDRICA O DE MONGE CUERPOS: POLIEDROS Se denomina superficie poliédrica aquella que está formada por varios poligonos consecutivos. Estos son las caras de
UNIDAD Nº 6 GEOMETRÍA DESCRIPTIVA PROYECCIÓN DIÉDRICA O DE MONGE CUERPOS: POLIEDROS Se denomina superficie poliédrica aquella que está formada por varios poligonos consecutivos. Estos son las caras de
Autor: Arqto. Jing Chang Lou
 SIISTEMA DIIEDRIICO A P U N T E D O C E N T E Autor: Arqto. Jing Chang Lou BIBLIOGRAFÍA SISTEMA DIÉDRICO Ferrer Muñoz, José Luis Ediciones Paraninfo (1999) GEOMETRÍA DESCRIPTIVA Izquierdo Asensi, Fernando
SIISTEMA DIIEDRIICO A P U N T E D O C E N T E Autor: Arqto. Jing Chang Lou BIBLIOGRAFÍA SISTEMA DIÉDRICO Ferrer Muñoz, José Luis Ediciones Paraninfo (1999) GEOMETRÍA DESCRIPTIVA Izquierdo Asensi, Fernando
Sistema de planos acotados
 Sistema de planos acotados 1. Fundamentos y elementos del sistema El sistema de planos acotados o sistema acotado, es una variante del sistema diédrico en el que se ha sustituido el plano Vertical de proyección
Sistema de planos acotados 1. Fundamentos y elementos del sistema El sistema de planos acotados o sistema acotado, es una variante del sistema diédrico en el que se ha sustituido el plano Vertical de proyección
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: DIBUJO TÉCNICO II
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2013-2014 MATERIA: DIBUJO TÉCNICO II INSTRUCCIONES GENERALES Y CALIFICACIÓN Después
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2013-2014 MATERIA: DIBUJO TÉCNICO II INSTRUCCIONES GENERALES Y CALIFICACIÓN Después
SISTEMA DIÉDRICO. EL PLANO
 SISTEM DIÉDRICO. EL PLNO OBJETIOS Conocer las diversas formas en que puede venir definido un plano en el espacio y su representación en la proyección diédrica. 1 2 3 Conocer y operar con rectas horizontales,
SISTEM DIÉDRICO. EL PLNO OBJETIOS Conocer las diversas formas en que puede venir definido un plano en el espacio y su representación en la proyección diédrica. 1 2 3 Conocer y operar con rectas horizontales,
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: DIBUJO TÉCNICO II
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: DIBUJO TÉCNICO II INSTRUCCIONES GENERALES Y CALIFICACIÓN Después
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: DIBUJO TÉCNICO II INSTRUCCIONES GENERALES Y CALIFICACIÓN Después
Preguntas tipo OLIMPIADA DE DIBUJO TÉCNICO MARZO 2014
 E S C U E L A T É C N I C A S U P E R I O R D E A R Q U I T E C T U R A U N I V E R S I D A D D E N A V A R R A Preguntas tipo OLIMPIADA DE DIBUJO TÉCNICO MARZO 2014 G E O M E T R Í A M É T R I C A. T
E S C U E L A T É C N I C A S U P E R I O R D E A R Q U I T E C T U R A U N I V E R S I D A D D E N A V A R R A Preguntas tipo OLIMPIADA DE DIBUJO TÉCNICO MARZO 2014 G E O M E T R Í A M É T R I C A. T
Dibujo Técnico Sistema diédrico. el punto y la recta.
 26. REPRESENTACION DEL PUNTO Y LA RECTA. 26.1. Representación del Punto. El objeto de este Sistema es representar sobre un plano, las figuras del espacio y para ello se procederá de la siguiente manera:
26. REPRESENTACION DEL PUNTO Y LA RECTA. 26.1. Representación del Punto. El objeto de este Sistema es representar sobre un plano, las figuras del espacio y para ello se procederá de la siguiente manera:
A RG. Diédrico 32. Cubo apaoyado en plano oblicuo Hoja 1/2
 Dibujar las proyecciones, con partes vistas y ocultas, de un cubo de arista 50 mm, apoyado en el plano α, dicha arista, 45 mm del vértice del plano y tiene de cota cero. El cubo está en el primer cuadrante.
Dibujar las proyecciones, con partes vistas y ocultas, de un cubo de arista 50 mm, apoyado en el plano α, dicha arista, 45 mm del vértice del plano y tiene de cota cero. El cubo está en el primer cuadrante.
Pruebas de Acceso a las Universidades de Castilla y León
 Pruebas de Acceso a las Universidades de Castilla y León DIBUJO TÉCNICO Texto para los Alumnos 9 páginas Antes de empezar a trabajar has de tener en cuenta lo siguiente: OPTATIVIDAD: Debes escoger una
Pruebas de Acceso a las Universidades de Castilla y León DIBUJO TÉCNICO Texto para los Alumnos 9 páginas Antes de empezar a trabajar has de tener en cuenta lo siguiente: OPTATIVIDAD: Debes escoger una
DIBUJO TÉCNICO. UNIDAD DIDÁCTICA VIII: Geometría 3D (IV)
 UNIDAD DIDÁCTICA VIII: Geometría 3D (IV) ÍNDICE Página: 1 SUPERFICIES DE REVOLUCIÓN 2 2 SUPERFICIE CILÍNDRICA 2 21 CILINDROS 2 22 PROYECCIONES DE UN CILINDRO 3 23 SECCIONES PLANAS 4 3 SUPERFICIES CÓNICAS
UNIDAD DIDÁCTICA VIII: Geometría 3D (IV) ÍNDICE Página: 1 SUPERFICIES DE REVOLUCIÓN 2 2 SUPERFICIE CILÍNDRICA 2 21 CILINDROS 2 22 PROYECCIONES DE UN CILINDRO 3 23 SECCIONES PLANAS 4 3 SUPERFICIES CÓNICAS
Sistema Diédrico (II). Superficies poliédricas y radiadas. Desarrollos
 Sistema Diédrico (II). Superficies poliédricas y radiadas. Desarrollos Cuando realizamos el desarrollo de una superficie estamos representando la verdadera magnitud de esta, lo que nos permitirá aplicar
Sistema Diédrico (II). Superficies poliédricas y radiadas. Desarrollos Cuando realizamos el desarrollo de una superficie estamos representando la verdadera magnitud de esta, lo que nos permitirá aplicar
INTERSECCIONES. POSICIONES RELATIVAS. DISTANCIAS
 INTERSECCIONES. POSICIONES RELATIVAS. DISTANCIAS OBJETIVOS Recordar los principios que rigen las intersecciones geo - métricas entre recta y plano y de estos entre sí, para apli - car, con dominio, el
INTERSECCIONES. POSICIONES RELATIVAS. DISTANCIAS OBJETIVOS Recordar los principios que rigen las intersecciones geo - métricas entre recta y plano y de estos entre sí, para apli - car, con dominio, el
DIÉDRICO: SECCIÓN PLANA EN UN HEXAEDRO (unidades en milímetros)
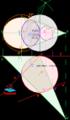 1 / 14 DIÉDRICO: SECCIÓN PLANA EN UN HEXAEDRO (unidades en milímetros) Dibujar un hexaedro apoyado en el plano horizontal de proyección diédrica de forma que su base esté inscrita en una circunferencia
1 / 14 DIÉDRICO: SECCIÓN PLANA EN UN HEXAEDRO (unidades en milímetros) Dibujar un hexaedro apoyado en el plano horizontal de proyección diédrica de forma que su base esté inscrita en una circunferencia
PROF: Jesús Macho Martínez
 DIBUJO TÉCNICO ELEMENTAL PROF: Jesús Macho Martínez 1º.- Trazar la perpendicular a r por el punto P. 2º.- Trazar la bisectriz del ángulo que forman r y s. P * r r s 3º.- Trazar las tangentes interiores
DIBUJO TÉCNICO ELEMENTAL PROF: Jesús Macho Martínez 1º.- Trazar la perpendicular a r por el punto P. 2º.- Trazar la bisectriz del ángulo que forman r y s. P * r r s 3º.- Trazar las tangentes interiores
ELEMENTOS DE GEOMETRÍA DESCRIPTIVA CURSO 2006 Prof.Sergio Weinberger. Horizontal: h // PH Frontal : f // PV De perfil : p Π LT p p Π L T L T L T
 ELEMENTOS DE GEOMETRÍA DESCRIPTIVA CURSO 2006 Prof.Sergio Weinberger RECTAS PARTICULARES: Horizontal: h // PH Frontal : f // PV De perfil : p Π LT p p Π h f A A B L T L T L T h f A B B De fuga : r PV Vertical
ELEMENTOS DE GEOMETRÍA DESCRIPTIVA CURSO 2006 Prof.Sergio Weinberger RECTAS PARTICULARES: Horizontal: h // PH Frontal : f // PV De perfil : p Π LT p p Π h f A A B L T L T L T h f A B B De fuga : r PV Vertical
PERSPECTIVA REAL - Plano del cuadro inclinado Procedimiento de las proyectantes visuales, utilizando la 2da. proyección.
 ANEP Formación Docente Uruguay Educa Comunicación Visual - Dibujo Técnico Prof. Carlos Spalvier PERSPECTIVA REAL - Plano del cuadro inclinado Procedimiento de las proyectantes visuales, utilizando la 2da.
ANEP Formación Docente Uruguay Educa Comunicación Visual - Dibujo Técnico Prof. Carlos Spalvier PERSPECTIVA REAL - Plano del cuadro inclinado Procedimiento de las proyectantes visuales, utilizando la 2da.
33. SISTEMA PLANOS ACOTADOS
 33. SISTEMA PLANOS ACOTADOS 33.1. Elementos del sistema. En el sistema de planos acotados o sistema acotado solo interviene un solo elemento el plano de proyección π. Como en los otros sistemas de representación
33. SISTEMA PLANOS ACOTADOS 33.1. Elementos del sistema. En el sistema de planos acotados o sistema acotado solo interviene un solo elemento el plano de proyección π. Como en los otros sistemas de representación
SISTEMA DIEDRICO (apuntes)
 CDU 744 SISTEMA DIEDRICO (apuntes) A. Rodríguez Alvarez INDICE. pag. 1. Generalidades. ------------------------------------ 3 2. Representación y alfabeto del punto. -------------- 4 3. Representación
CDU 744 SISTEMA DIEDRICO (apuntes) A. Rodríguez Alvarez INDICE. pag. 1. Generalidades. ------------------------------------ 3 2. Representación y alfabeto del punto. -------------- 4 3. Representación
PRIMERA EVALUACIÓN DE DIBUJO TÉCNICO I
 PRIMERA EVALUACIÓN DE DIBUJO TÉCNICO I 1. UD: TRAZADOS FUNDAMENTALES EN EL PLANO 1.1. Tipos de línea- 21 1.1.1. Línea recta 1.1.2. Línea curva 1.1.3. Línea quebrada 1.1.4. Semirrecta 1.2. Segmento 1.2.1.
PRIMERA EVALUACIÓN DE DIBUJO TÉCNICO I 1. UD: TRAZADOS FUNDAMENTALES EN EL PLANO 1.1. Tipos de línea- 21 1.1.1. Línea recta 1.1.2. Línea curva 1.1.3. Línea quebrada 1.1.4. Semirrecta 1.2. Segmento 1.2.1.
A RG. Diédrico 31. tetraedro apoyado en plano oblicuo Hoja 1/2
 A 1 A G R t 2 D 2 D' 2 L 2 B 2 t' 2 K 2 K' 2 V s2 C 2 s 2 V r2 r 2 B' 0 V V r1 V s1 A 2 L 1 B 1 ( ) 2 0 R80 A LA 1 0 t 1 t' 1 V r0 V s0 K 1 C 1 M 0 L 0 D 1 r 1 O 0 B 0 r 0 C 0 D 0 Hoja 1/2 El proceso a
A 1 A G R t 2 D 2 D' 2 L 2 B 2 t' 2 K 2 K' 2 V s2 C 2 s 2 V r2 r 2 B' 0 V V r1 V s1 A 2 L 1 B 1 ( ) 2 0 R80 A LA 1 0 t 1 t' 1 V r0 V s0 K 1 C 1 M 0 L 0 D 1 r 1 O 0 B 0 r 0 C 0 D 0 Hoja 1/2 El proceso a
D1 Generalidades: El punto
 El sistema diédrico D1 Generalidades: El punto Generalidades Proyección ortogonal de un punto sobre un plano Proyección ortogonal o, simplemente proyección de un punto sobre un plano, es el pie de la perpendicular
El sistema diédrico D1 Generalidades: El punto Generalidades Proyección ortogonal de un punto sobre un plano Proyección ortogonal o, simplemente proyección de un punto sobre un plano, es el pie de la perpendicular
MYP (MIDDLE YEARS PROGRAMME)
 MYP (MIDDLE YEARS PROGRAMME) 2014-2015 Fecha 19/05/2015 APUNTES DE GEOMETRÍA 2º ESO 1. EL TEOREMA DE PITÁGORAS El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa
MYP (MIDDLE YEARS PROGRAMME) 2014-2015 Fecha 19/05/2015 APUNTES DE GEOMETRÍA 2º ESO 1. EL TEOREMA DE PITÁGORAS El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa
Sistema Diédrico (II). Superficies poliédricas y radiadas: Representación
 Sistema Diédrico (II). Superficies poliédricas y radiadas: Representación Comenzamos una nueva unidad didáctica en la que desarrollaremos los conceptos y procedimientos sobre superficies poliédricas y
Sistema Diédrico (II). Superficies poliédricas y radiadas: Representación Comenzamos una nueva unidad didáctica en la que desarrollaremos los conceptos y procedimientos sobre superficies poliédricas y
Tema 7: Superficies regladas desarrollables. Pirámide-cono, prisma-cilindro.
 Tema 7: Superficies regladas desarrollables. Pirámide-cono, prisma-cilindro. Definición y representación diédrica. Las superficies regladas están generadas por el movimiento de una recta. En las superficies
Tema 7: Superficies regladas desarrollables. Pirámide-cono, prisma-cilindro. Definición y representación diédrica. Las superficies regladas están generadas por el movimiento de una recta. En las superficies
Superficies Curvas. Guía de clase elaborada por Ing. Guillermo Verger
 Superficies Curvas Guía de clase elaborada por Ing. Guillermo Verger www.ingverger.com.ar Superficie cilíndrica Es aquella generada por una recta llamada generatriz que se mueve en el espacio manteniendose
Superficies Curvas Guía de clase elaborada por Ing. Guillermo Verger www.ingverger.com.ar Superficie cilíndrica Es aquella generada por una recta llamada generatriz que se mueve en el espacio manteniendose
Sistema Diédrico. Punto y recta
 Sistema Diédrico. Punto y recta Dibujo Técnico Ejercicios del alumno. Uso en el Centro Pág. 1 Si un punto del espacio se encuentra por encima del plano horizontal, su cota es positiva y en el sistema diédrico
Sistema Diédrico. Punto y recta Dibujo Técnico Ejercicios del alumno. Uso en el Centro Pág. 1 Si un punto del espacio se encuentra por encima del plano horizontal, su cota es positiva y en el sistema diédrico
MINIMA DISTANCIA DE UN PUNTO A UN CONO. Y A UNA ESFERA
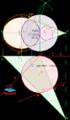 E J E R C I C I O S D E D I E D R I C O MINIMA DISTANCIA DE UN PUNTO A UN CONO. Y A UNA ESFERA Sea un cono recto apoyado en el plano horizontal y un punto exterior ( A ). 1º) Uniremos la proyección horizontal
E J E R C I C I O S D E D I E D R I C O MINIMA DISTANCIA DE UN PUNTO A UN CONO. Y A UNA ESFERA Sea un cono recto apoyado en el plano horizontal y un punto exterior ( A ). 1º) Uniremos la proyección horizontal
""' """ x. ! I I I i I I i i i J-. -"' .". -"" OPCIÓN I EJERCICIO 1 : PERSPECTIVA AXONOMÉTRICA. / ""'./ -,,- /."".
 OPCÓN EJERCCO 1 : PERSPECTVA AXONOMÉTRCA. Definida una pieza por sus tres vistas, según el método del primer diedro de proyección, a escala 3:5, se pide: Representar la perspectiva isométrica de la misma,
OPCÓN EJERCCO 1 : PERSPECTVA AXONOMÉTRCA. Definida una pieza por sus tres vistas, según el método del primer diedro de proyección, a escala 3:5, se pide: Representar la perspectiva isométrica de la misma,
TEMA 2 GEOMETRIA BASICA APLICADA
 TEM GEOMETRI SIC PLICD OPERCIONES CON SEGMENTOS.... MEDITRIZ DE UN SEGMENTO.... DIVISION DE UN SEGMENTO EN PRTES IGULES....3 PERPENDICULR UN RECT... 3.4 DIVISION DE UN RCO DE CIRCUNFERENCI EN DOS PRTES
TEM GEOMETRI SIC PLICD OPERCIONES CON SEGMENTOS.... MEDITRIZ DE UN SEGMENTO.... DIVISION DE UN SEGMENTO EN PRTES IGULES....3 PERPENDICULR UN RECT... 3.4 DIVISION DE UN RCO DE CIRCUNFERENCI EN DOS PRTES
EJERCICIOS DE DISTANCIAS PROCEDIMIENTOS DE EJECUCIÓN
 EJERCICIOS DE DISTANCIAS PROCEDIMIENTOS DE EJECUCIÓN 1-2-3.- Procedimiento: - Explicados en teoría 1) 2) 3) 4.- Procedimiento: - Trazar el plano P perpendicular a la recta R, pasando por el punto A, ayudándome
EJERCICIOS DE DISTANCIAS PROCEDIMIENTOS DE EJECUCIÓN 1-2-3.- Procedimiento: - Explicados en teoría 1) 2) 3) 4.- Procedimiento: - Trazar el plano P perpendicular a la recta R, pasando por el punto A, ayudándome
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: DIBUJO TÉCNICO II
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: DIBUJO TÉCNICO II INSTRUCCIONES GENERALES Y CALIFICACIÓN Después
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: DIBUJO TÉCNICO II INSTRUCCIONES GENERALES Y CALIFICACIÓN Después
SISTEMA DIEDRICO. Para hallar la proyección de una recta, basta unir las. homónimas de la recta. Se exceptúa de lo dicho la
 SISTEMA DIEDRICO. Representación de la recta: la recta y sus trazas. Rectas: oblicua (en el, 2, 3 y 4 cuadrante), situada en los planos de proyección, horizontal, frontal, paralela a la línea de tierra,
SISTEMA DIEDRICO. Representación de la recta: la recta y sus trazas. Rectas: oblicua (en el, 2, 3 y 4 cuadrante), situada en los planos de proyección, horizontal, frontal, paralela a la línea de tierra,
INDICE Prologo 1. Proyecciones y escalas Sistema diedrico 2. Punto y recta Recta.- 3. El plano 4. Intersecciones y paralelismo
 INDICE Prologo 7 1. Proyecciones y escalas 1.1. Proyección. Sus clases.- 1.2. Proyección cónica.- 1.3. Invariantes de 9 la proyección cónica.- 1.4. Proyección cilíndrica.- 15. Objeto de la geometría descriptiva.
INDICE Prologo 7 1. Proyecciones y escalas 1.1. Proyección. Sus clases.- 1.2. Proyección cónica.- 1.3. Invariantes de 9 la proyección cónica.- 1.4. Proyección cilíndrica.- 15. Objeto de la geometría descriptiva.
Diédrico 2. La recta
 Representar la recta, r, dada por los puntos A(-22,25,30) y B(7,10,5). Estudiar por que cuadrantes pasa Dada la recta, r, de perfil por su proyección de perfil ; situar en ella el punto A, conocida su
Representar la recta, r, dada por los puntos A(-22,25,30) y B(7,10,5). Estudiar por que cuadrantes pasa Dada la recta, r, de perfil por su proyección de perfil ; situar en ella el punto A, conocida su
A RG. Diédrico 20. Sección de un Prisma Recto por un proyectante Hoja 1/2. α 2 D 2 E 2 A 2 B 2 C 2 1' 2' 5' 3' 4' B L2 1 1 C L3 1 1
 α Dibujar la sección producida por el plano a al prisma recto regular pentagonal de altura 50 mm, obteniendo su verdadera magnitud. En la parte inferior de la lámina obtener el desarrollo del prisma y
α Dibujar la sección producida por el plano a al prisma recto regular pentagonal de altura 50 mm, obteniendo su verdadera magnitud. En la parte inferior de la lámina obtener el desarrollo del prisma y
SUPERFICIES POLIÉDRICAS CONVEXAS
 SUPERFICIES POLIÉDRICAS CONVEXAS OBJETIVOS Conocer las características y relaciones métricas del te tra - edro, hexaedro o cubo y octaedro, para su represen tación en el sistema diédrico en sus múltiples
SUPERFICIES POLIÉDRICAS CONVEXAS OBJETIVOS Conocer las características y relaciones métricas del te tra - edro, hexaedro o cubo y octaedro, para su represen tación en el sistema diédrico en sus múltiples
Perspectiva y Geometría Descriptiva I
 Cuadernillo de ejercicios y preguntas El filósofo Eric Hoffer dice: "Los que están aprendiendo heredarán la Tierra, mientras que los que ya saben estarán perfectamente equipados para vivir en un mundo
Cuadernillo de ejercicios y preguntas El filósofo Eric Hoffer dice: "Los que están aprendiendo heredarán la Tierra, mientras que los que ya saben estarán perfectamente equipados para vivir en un mundo
SISTEMA DIÉDRICO POLIEDROS REGULARES DIBUJO TÉCNICO 2º BACH.
 SISTEMA DIÉDRICO POLIEDROS REGULARES DIBUJO TÉCNICO. ANA BALLESTER JIMÉNEZ 0 SISTEMA DIÉDRICO: REPRESENTACIÓN DE POLIEDROS REGULARES DEFINICIÓN DE POLIEDRO: Sólido geométrico limitado por caras planas.
SISTEMA DIÉDRICO POLIEDROS REGULARES DIBUJO TÉCNICO. ANA BALLESTER JIMÉNEZ 0 SISTEMA DIÉDRICO: REPRESENTACIÓN DE POLIEDROS REGULARES DEFINICIÓN DE POLIEDRO: Sólido geométrico limitado por caras planas.
ESFERA. REPRESENTACIÓN Y SECCIONES
 ESFERA. REPRESENTACIÓN Y SECCIONES OBJETIVOS Representar, en el sistema diédrico, superficies esféricas; Representar, sobre la esfera, secciones planas originadas Razonar y saber representar planos tangentes
ESFERA. REPRESENTACIÓN Y SECCIONES OBJETIVOS Representar, en el sistema diédrico, superficies esféricas; Representar, sobre la esfera, secciones planas originadas Razonar y saber representar planos tangentes
Sistema Diédrico (II). Superficies poliédricas y radiadas. Secciones
 Sistema Diédrico (II). Superficies poliédricas y radiadas. Secciones En el tema anterior realizamos cambios en las superficies mediante intersecciones y tangencias con rectas o planos. Ahora vamos a ampliar
Sistema Diédrico (II). Superficies poliédricas y radiadas. Secciones En el tema anterior realizamos cambios en las superficies mediante intersecciones y tangencias con rectas o planos. Ahora vamos a ampliar
GEOMETRIA DESCRIPTIVA BASICA SISTEMAS DE REPRESENTACION EDUCACION PLASTICA Y VISUAL 3º ESO
 GEOMETRIA DESCRIPTIVA BASICA SISTEMAS DE REPRESENTACION EDUCACION PLASTICA Y VISUAL 3º ESO - 2-1. Qué es una proyección? 2. Tipos de proyección y relación con los sistemas de representación. 3. Diédrico.
GEOMETRIA DESCRIPTIVA BASICA SISTEMAS DE REPRESENTACION EDUCACION PLASTICA Y VISUAL 3º ESO - 2-1. Qué es una proyección? 2. Tipos de proyección y relación con los sistemas de representación. 3. Diédrico.
Apuntes de Dibujo Técnico
 APUNTES DE DIBUJO TÉCNICO 1. Materiales para trazados geométricos. - La Escuadra y el Cartabón. El juego de escuadra y cartabón constituye el principal instrumento de trazado. Se deben usar de plástico
APUNTES DE DIBUJO TÉCNICO 1. Materiales para trazados geométricos. - La Escuadra y el Cartabón. El juego de escuadra y cartabón constituye el principal instrumento de trazado. Se deben usar de plástico
Sistemas de representación: Sistema Diédrico. Ejercicios.
 Sistemas de representación: Sistema Diédrico. Ejercicios. Dado el plano α por las coordenadas relativas de los puntos A, B, y C, y el punto P, según las proyecciones diédricas en el método
Sistemas de representación: Sistema Diédrico. Ejercicios. Dado el plano α por las coordenadas relativas de los puntos A, B, y C, y el punto P, según las proyecciones diédricas en el método
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA
 RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
TEMA 5. CURVAS CÓNICAS.
 5.1. GENERALIDADES. TEMA 5. CURVAS CÓNICAS. Se denominan secciones cónicas a aquellas superficies que son producidas por la intersección de un plano con una superficie cónica de revolución (una superficie
5.1. GENERALIDADES. TEMA 5. CURVAS CÓNICAS. Se denominan secciones cónicas a aquellas superficies que son producidas por la intersección de un plano con una superficie cónica de revolución (una superficie
TIPOS DE RECTA (Primer Cuadrante) Recta vertical Recta frontal Recta de perfil
 SISTEMA DIÉDRICO Es un sistema de representación de proyecciones en el diedro formado mediante dos planos, el vertical y el horizontal. El diedro está dividido en cuatro cuadrantes. II III P I I P A la
SISTEMA DIÉDRICO Es un sistema de representación de proyecciones en el diedro formado mediante dos planos, el vertical y el horizontal. El diedro está dividido en cuatro cuadrantes. II III P I I P A la
El primer ejercicio se valorará sobre 4 puntos. Los dos restantes sobre 3 puntos cada uno OPCIÓN A
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2010-2011 MATERIA: DIBUJO TÉCNICO II 8 INSTRUCCIONES CRITERIOS GENERALES DE CALIFICACIÓN
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2010-2011 MATERIA: DIBUJO TÉCNICO II 8 INSTRUCCIONES CRITERIOS GENERALES DE CALIFICACIÓN
PRUEBAS DE ACCESO A LA UNIVERSIDAD MATERIAS DE MODALIDAD: FASE GENERAL Y ESPECÍFICA OPCIÓN A
 PRUEBAS DE ACCESO A LA UNIVERSIDAD MATERIAS DE MODALIDAD: FASE GENERAL Y ESPECÍFICA CURSO 2013-2014 CONVOCATORIA: JULIO MATERIA: DIBUJO TÉCNICO EL ALUMNO DEBE ELEGIR Y DESARROLLAR, OBLIGATORIAMENTE, LOS
PRUEBAS DE ACCESO A LA UNIVERSIDAD MATERIAS DE MODALIDAD: FASE GENERAL Y ESPECÍFICA CURSO 2013-2014 CONVOCATORIA: JULIO MATERIA: DIBUJO TÉCNICO EL ALUMNO DEBE ELEGIR Y DESARROLLAR, OBLIGATORIAMENTE, LOS
TEMA 7 SISTEMA AXONOMETRICO
 TEMA 7 SISTEMA AXONOMETRICO 1. AXONOMETRICO....2 2. FUNDAMENTOS Y DEFINICIONES....2 2.1 EJES Y PLANOS DE COORDENADAS....2 2.2 FUNDAMENTO DEL SISTEMA AXONOMETRICO....3 3. ESCALAS GRAFICAS DE REDUCCION....7
TEMA 7 SISTEMA AXONOMETRICO 1. AXONOMETRICO....2 2. FUNDAMENTOS Y DEFINICIONES....2 2.1 EJES Y PLANOS DE COORDENADAS....2 2.2 FUNDAMENTO DEL SISTEMA AXONOMETRICO....3 3. ESCALAS GRAFICAS DE REDUCCION....7
OBJETIVO 1 CONOCER LOS POLIEDROS Y DIFERENCIAR LOS POLIEDROS REGULARES NOMBRE: CURSO: FECHA:
 OJETIVO 1 CONOCER LOS POLIEDROS Y DIERENCIR LOS POLIEDROS REGULRES NOMRE: CURSO: ECH: CONCEPTO DE POLIEDRO Vértice Un poliedro es un cuerpo geométrico cuyas caras son polígonos. Los elementos del poliedro
OJETIVO 1 CONOCER LOS POLIEDROS Y DIERENCIR LOS POLIEDROS REGULRES NOMRE: CURSO: ECH: CONCEPTO DE POLIEDRO Vértice Un poliedro es un cuerpo geométrico cuyas caras son polígonos. Los elementos del poliedro
Tercera traza de un plano (P''): es su intersección con un plano de perfil ( ).
 El sistema diédrico D3 El plano Representación del Plano En proyección diédrica los planos se representan por sus trazas. Trazas de un plano son las rectas de intersección de ese plano con los planos de
El sistema diédrico D3 El plano Representación del Plano En proyección diédrica los planos se representan por sus trazas. Trazas de un plano son las rectas de intersección de ese plano con los planos de
(El producto de una rotación y una reflexión no es conmutativo!!!)
 HOMOTECIS (H) l numero (µ) se llama razón de la homotecia: d (O,P) / d (O, P ) = µ Si (m)>0 (es positivo), los puntos P y P están del mismo lado respecto al punto O. Si (m)
HOMOTECIS (H) l numero (µ) se llama razón de la homotecia: d (O,P) / d (O, P ) = µ Si (m)>0 (es positivo), los puntos P y P están del mismo lado respecto al punto O. Si (m)
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) Curso 2007-2008 MODELO MATERIA: DIBUJO TÉCNICO II INSTRUCCIONES GENERALES Y VALORACIÓN La prueba consiste
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) Curso 2007-2008 MODELO MATERIA: DIBUJO TÉCNICO II INSTRUCCIONES GENERALES Y VALORACIÓN La prueba consiste
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: DIBUJO TÉCNICO II Curso 2011-2012 INSTRUCCIONES Y CRITERIOS GENERALES DE CALIFICACIÓN
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: DIBUJO TÉCNICO II Curso 2011-2012 INSTRUCCIONES Y CRITERIOS GENERALES DE CALIFICACIÓN
Dimensiones Perspectivas:
 5.2. PERSPECTIVA OBLICUA O ANGULAR DE DOS PUN- TOS DE FUGA. Al igual que ocurre con la perspectiva frontal esta perspectiva queda definida por la disposición del objeto, que ha de estar situado de manera
5.2. PERSPECTIVA OBLICUA O ANGULAR DE DOS PUN- TOS DE FUGA. Al igual que ocurre con la perspectiva frontal esta perspectiva queda definida por la disposición del objeto, que ha de estar situado de manera
* * * GEOMETRÍA DESCRIPTIVA * * *
 Cambios de planos. Un cambio de plano consiste en eliminar uno de los dos planos de proyección por otro con la única condición de que el plano nuevo tiene que ser perpendicular al que permanece inmóvil.
Cambios de planos. Un cambio de plano consiste en eliminar uno de los dos planos de proyección por otro con la única condición de que el plano nuevo tiene que ser perpendicular al que permanece inmóvil.
SISTEMA DIÉDRICO: ALFABETO DEL PLANO
 SISTEMA DIÉDRICO: ALFABETO DEL PLANO Definiciones y representación Las trazas de un plano son las rectas de intersección de dicho plano con los planos de proyección H y V. Existen, por lo tanto y en general,
SISTEMA DIÉDRICO: ALFABETO DEL PLANO Definiciones y representación Las trazas de un plano son las rectas de intersección de dicho plano con los planos de proyección H y V. Existen, por lo tanto y en general,
Tema 2: Representación del punto, recta y plano, en el sistema Diédrico.
 Tema 2: Representación del punto, recta y plano, en el sistema Diédrico. Representación del punto. El punto se define por medio de sus proyecciones sobre el horizontal y el vertical. (En perspectiva caballera)
Tema 2: Representación del punto, recta y plano, en el sistema Diédrico. Representación del punto. El punto se define por medio de sus proyecciones sobre el horizontal y el vertical. (En perspectiva caballera)
CONOCIMIENTOS TEÓRICOS. 1 Características del sistema axonométrico
 9 Axonometría ortogonal y oblicua UNIDAD CONOCIMIENTOS TEÓRICOS 1 Características del sistema axonométrico 2 Proyección de los elementos fundamentales 2.1 Representación del punto 2.2 Representación de
9 Axonometría ortogonal y oblicua UNIDAD CONOCIMIENTOS TEÓRICOS 1 Características del sistema axonométrico 2 Proyección de los elementos fundamentales 2.1 Representación del punto 2.2 Representación de
REGULARES.
 Diédrico Poliedros REGULARES http://www.edu.xunta.es/contidos/premios/p2004/b/poliedros/poliedros.html POLIEDROS Los poliedros son los cuerpos geométricos limitados por polígonos. Poliedros regulares son
Diédrico Poliedros REGULARES http://www.edu.xunta.es/contidos/premios/p2004/b/poliedros/poliedros.html POLIEDROS Los poliedros son los cuerpos geométricos limitados por polígonos. Poliedros regulares son
B22 Homología. Geometría plana
 Geometría plana B22 Homología Homología y afinidad Homología: es una transformación biunívoca e inequívoca entre los puntos de dos figuras F y F'. A cada punto y recta de la figura F le corresponde un
Geometría plana B22 Homología Homología y afinidad Homología: es una transformación biunívoca e inequívoca entre los puntos de dos figuras F y F'. A cada punto y recta de la figura F le corresponde un
CUERPOS EN EL ESPACIO
 CUERPOS EN EL ESPACIO 1. Poliedros. 2. Fórmula de Euler. 3. Prismas. 4. Paralelepípedos. Ortoedros. 5. Pirámides. 6. Cuerpos de revolución. 6.1. Cilindros. 6.2. Conos. 6.3. Esferas. 6.4. Coordenadas geográficas.
CUERPOS EN EL ESPACIO 1. Poliedros. 2. Fórmula de Euler. 3. Prismas. 4. Paralelepípedos. Ortoedros. 5. Pirámides. 6. Cuerpos de revolución. 6.1. Cilindros. 6.2. Conos. 6.3. Esferas. 6.4. Coordenadas geográficas.
MATERIAS DE MODALIDAD: FASES GENERAL Y ESPECÍFICA CURSO JUNIO
 PRUEBAS DE ACCESO A LA UNIVERSIDAD MATERIAS DE MODALIDAD: FASES GENERAL Y ESPECÍFICA CURSO 2015 2016 MATERIA: DIBUJO TÉCNICO II (2) Convocatoria: JUNIO EL ALUMNO DEBE ELEGIR Y DESARROLLAR, OBLIGATORIAMENTE,
PRUEBAS DE ACCESO A LA UNIVERSIDAD MATERIAS DE MODALIDAD: FASES GENERAL Y ESPECÍFICA CURSO 2015 2016 MATERIA: DIBUJO TÉCNICO II (2) Convocatoria: JUNIO EL ALUMNO DEBE ELEGIR Y DESARROLLAR, OBLIGATORIAMENTE,
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO OPCIÓN A
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: DIBUJO TÉCNICO II Curso 2009-2010 INSTRUCCIONES GENERALES Y VALORACIÓN La prueba
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: DIBUJO TÉCNICO II Curso 2009-2010 INSTRUCCIONES GENERALES Y VALORACIÓN La prueba
SISTEMASS DE REPRESENTACIÓNN Geometría Básica
 SISTEMASS DE REPRESENTACIÓNN Geometría Básica Coordinadora de Cátedra: Ing. Canziani, Mónica Profesores: Arq. Aubin, Mónica Arq. Magenta, Gabriela Ing. Medina, Noemí Ing. Nassipián, Rosana V. Ing. Borgnia,
SISTEMASS DE REPRESENTACIÓNN Geometría Básica Coordinadora de Cátedra: Ing. Canziani, Mónica Profesores: Arq. Aubin, Mónica Arq. Magenta, Gabriela Ing. Medina, Noemí Ing. Nassipián, Rosana V. Ing. Borgnia,
* * * GEOMETRÍA DESCRIPTIVA * * *
 Superficies. Llamamos superficie a una lámina, infinitamente delgada, que recubre un cuerpo o que separa dos regiones del espacio. Una superficie puede engendrarse de dos maneras distintas: a). Como lugar
Superficies. Llamamos superficie a una lámina, infinitamente delgada, que recubre un cuerpo o que separa dos regiones del espacio. Una superficie puede engendrarse de dos maneras distintas: a). Como lugar
Problema 1. Cuántos triángulos rectángulos se pueden formar que tengan sus vértices en vértices de una caja?
 Nota4: Soluciones problemas propuestos Problema 1. Cuántos triángulos rectángulos se pueden formar que tengan sus vértices en vértices de una caja? Solución: Consideremos primero todos aquellos triángulos
Nota4: Soluciones problemas propuestos Problema 1. Cuántos triángulos rectángulos se pueden formar que tengan sus vértices en vértices de una caja? Solución: Consideremos primero todos aquellos triángulos
