Funcions i gràfiques. Objectius. Exercicis per a practicar. Per a saber-ne més. Resum. Autoavaluació. Activitats per a enviar al tutor
|
|
|
- Ana Isabel Herrero Naranjo
- hace 5 años
- Vistas:
Transcripción
1 8 Funcions i gràfiques Objectius En aquesta quinzena aprendreu a: Conéixer i interpretar les funcions i les diferents formes de presentar-les. Reconéixer el domini i el recorregut d'una funció. Determinar si una funció és contínua o discontínua. Trobar la taxa de variació i la taxa de variació mitja d'una funció en un interval. Determinar el creixement o decreixement d'una funció i trobar-ne els màxims i mínims. Reconéixer els punts d'inflexió. Comprovar la simetria d'algunes funcions respecte a l'origen i a l'eix OY. Reconéixer si una funció és periòdica. 1.Funcions reals...pàg. 13 Concepte de funció Gràfic d'una funció Domini i recorregut Funcions definides a trossos.propietats de les funcions...pàg. 136 Continuïtat i discontinuïtats Periodicitat Simetries 3.Taxa de variació i creixement...pàg. 138 Taxa de variació Creixement i decreixement Màxims i mínims Concavitat i punts d'inflexió Exercicis per a practicar Per a saber-ne més Resum Autoavaluació Activitats per a enviar al tutor MATEMÀTIQUES B 19
2 130 MATEMÀTIQUES B
3 Abans de començar El llenguatge de les gràfiques Evolució de l'ibex-35 des de 1987 Escala logarítmica Recuperació en 6 Recuperació en anys i mig 17 mesos Recuperació en 6 anys Recup. 3 anys (x,y) De les diferents formes en les quals pot presentar-se una funció, mitjançant un enunciat, una taula, una expressió algebraica o una gràfica, aquesta última és la que ens permet veure amb només una ullada el seu comportament global, és per això que és tan important. En aquest tema aprendràs a reconéixer i interpretar-ne les característiques principals. Investigueu Imagineu-vos que pugeu en una sínia el radi de la qual mesura 30 m i per tal de pujar cal ascendir 5 m des del terra. La sínia comença a girar. Com és la gràfica de la funció que dóna l'altura en la qual us trobeu segons l'angle de gir? Aneu a la cabina taronja i uns amics a la verda, com serà la seua gràfica? MATEMÀTIQUES B 131
4 1. Funcions reals Gràfic d'una funció Una funció és una correspondència entre dos conjunts numèrics, de tal manera que a cada element del conjunt inicial li correspon un element i només un del conjunt final, la imatge. Es relacionen així dues variables numèriques que solen designar-se amb x i y. f: x y=f(x) x és la variable independent y és la variable dependent km alt Gràfica d'una funció f: km recorreguts altitud en m Per tal de veure el comportament d'una funció, f:x y, recorrem a la seua representació gràfica sobre els eixos cartesians, en l'eix d'abscisses (OX) la variable independent i en el d'ordenades (OY) la independent; les coordenades de cada punt de la gràfica són: (x, f(x)). A la figura es troba representada la funció: f(x)= 0,5x +3x+3,5 Fent una taula de valors, es representen els punts obtinguts, x en l'eix d'abscisses (OX), f(x) en el d'ordenades (OY). El gràfic descriu el recorregut de la 9a Etapa de la Volta Ciclista 007, indicant els km totals i l'altitud en els punts principals del trajecte. A l'esquerra apareix la gràfica anterior traçada sobre uns eixos cartesians, per tal de simplificar-la s'han unit els punts principals mitjançant segments. Es tracta d'una funció que dóna l'altitud segons els km recorreguts, observeu la taula de valors. x f(x) -4,5 0 3,5 6 7,5 8 7,5 6 3,5 0-4,5 Hi ha uns punts que tenen interés especial, els que la gràfica talla amb els eixos coordenats. Per tal de calcular-los: Talleu amb l'eix OY: Els punts de l'eix d'ordenades tenen abscissa 0, n'hi ha prou amb fer x=0 en la fórmula de la funció. Talls amb l'eix OX: Els punts de l'eix d'abscisses tenen y=0. Es resol l'equació f(x)=0. Talls amb els eixos Eix OY:f(0)=3,5 punt (0, 3,5) Eix OX:Resolent l'equació 0,5x +3x+3,5=0 Resulta: 3 ± x = = 3 ± 4 = 0,5 Punts (7, 0) (-1, 0) MATEMÀTIQUES B
5 Dom f=[-10, 10] Calcular dominis Si l'expressió analítica de la funció és un polinomi, el domini són tots els nombres reals. f(x)=-x 4 +4x +1 Dom f = IR Im f = (-, 5] Si l'expressió analítica de la funció és un quocient, el domini són tots els reals excepte els que anul len el denominador. f(x) = x 1 Dom f = IR - {1} Im f = (-, 0) U (0, + ) Si l'expressió analítica de la funció és una arrel quadrada, el domini està format pels nombres reals per als quals el radicand és positiu o zero. f (x) = x + 3 Dom f = [-3,+ ) Im f = [0,+ ) 1 f(x) = x + Dom f = (-,+ ) Im f = (0,+ ) Domini i recorregut Donada una funció f:x y S'anomena domini de f el conjunt de valors que pren la variable independent, x. S'indica com a Dom f. El domini està format, per tant, pels valors de x per als quals existix la funció, és a dir, per als quals hi ha un f(x). El recorregut és el conjunt de valors que pot prendre la variable dependent, y, això és el conjunt de les imatges. Es representa com a Im f. Funcions i gr x f(x) = 0,5x 3,5 x < x 3 x > 3 Funcions definides a trossos Hi ha un tipus de funcions que vénen definides amb diferents expressions algebraiques segons els valors de x, es diu que estan definides a trossos. Per descriure analíticament una funció formada per trossos d'altres funcions, es donen les expressions dels diferents trams, per ordre d'esquerre a dreta, indicant en cada tram els valors de x per als quals la funció està definida. A la figura podeu veure un exemple d'aquest tipus de funcions i la seua representació gràfica. MATEMÀTIQUES B 133
6 EXERCICIS resolts 5. De les següents gràfiques indiqueu les que corresponen a una funció i les que no. Són gràfiques d'una funció a), c) i i), ja que a cada x del domini li correspon un únic valor de i. No són gràfiques d'una funció b) i d) 6. Feu una taula de valors, dibuixeu els punts obtinguts i representeu la funció a) f(x)=x-3 b) f(x)=-x +4x x f(x) x f(x) c) f(x) = x 4x + x f(x) , ,67 4 0,9 1 RECORDEU-HO: Per tal de fer una taula de valors, a partir de l'expressió d'una funció, substituïu en la fórmula la x pels valors que vulgueu, opereu i calculeu els corresponents de y=f(x). En general procureu alternar valors positius i negatius. Dibuixeu els punts (x,y) obtinguts d'aquesta manera, i uniu-los. 134 MATEMÀTIQUES B
7 EXERCICIS resolts Calculeu el domini de les següents funcions a) b) Funcions i gràfiques Dom f = IR {-, 0, 4} Dom f = IR {-1, 1, 5} En els punts indicats, en ambdós casos, no es pot trobar f(x) en la gràfica. c) f(x)= x 3 -x x +5x d) f(x)= x Dom f = IR ja que és un polinomi Dom f = IR {} e) f(x)= x 5 f) f(x)= 5 x x-5 0, x 5 Dom f = [5, + ) 5-x 0, 5 x Dom f = (-, 5] 3 1 g) f(x)= h) f(x)= x + 4 x x+4>0, x>-4 Dom f = (-4, + ) -x>0, >x Dom f = (-, ) (En aquests casos -4 i, respectivament, no són del domini ja que anul len el denominador) 3. En les següents funcions, definides a trossos, calculeu les imatges dels valors de x indicats. x f(x) 0,5x 1 si x < -4 1 a) f(x)= si x x 5 si x > x=-4 se substituïx dalt (-4 < -) x=-, x=1 i x=3 se substituïxen en la del mig, ja que són a [-,3]. x=6 se substituïx baix, o siga que 6 > ,5x + c) f(x)= x + 1 0,5x si si si x < x < x x=-6, x=- se substituïx dalt. x=0 se substituïx en la del mig, ja que són a - <0 <. x=, x=4 se substituïx baix. x f(x) MATEMÀTIQUES B 135
8 . Propietats de les funcions Continuïtat i discontinuïtats La primera idea de funció contínua és la que es pot representar d'un sol traç, sense aixecar el llapis del paper. Quan una funció no és contínua en un punt es diu que presenta una discontinuïtat. Les tres funcions dibuixades baix són discontínues en x=, però tenen diferents tipus de discontinuïtat. x + 1 f(x) = x + 5 f()=1 x < x La gràfica presenta un salt. 3 x x + x + 6 f(x) = x x= no pertany al domini. Aquesta discontinuïtat es diu "evitable". Funcions periòdiques x 6 f(x) = x x= no pertany al domini. La gràfica presenta un salt infinit En la naturalesa i en el vostre entorn habitual hi ha fenòmens que es repetixen a intervals regulars, com el cas de les marees, els pèndols i ressorts, el so... Les funcions que descriuen aquest tipus de fenòmens es diuen periòdiques. Una funció y=f(x) és contínua en x=a si: La funció està definida en x=a, existix f(a)=b. Les imatges dels valors pròxims a a tendixen a b. Hi ha diverses raons per les quals una funció no és contínua en un punt: Presenta un salt. La funció no està definida en aquest punt, o si ho està queda separat, hi ha un "forat" en la gràfica. La funció no està definida i el seu valor creix (o decreix) indefinidament quan ens apropem al punt. Una funció és periòdica quan el seu valor es repetix cada vegada que la variable independent recorre un cert interval. El valor d'aquest interval s'anomena període. f(x+període)=f(x) Dues funcions periòdiques importants: Una cisterna s'ompli i buida automàticament expulsant 6 litres d'aigua cada 5 minuts, seguint el ritme de la gràfica. Quan el dipòsit es troba buit comença l'ompliment, que costa 1 minut, està ple 3,5 minuts i es buida en 0,5 minuts. Aquest procés es repetix periòdicament. Per tal de conèixer el volum d'aigua en el dipòsit a cada instant conéixer el que ocorre en aquests primers 5 minuts. Així als 14 minuts, la quantitat d'aigua és: f(14)=f(4+ 5)=f(4)=6 En dividir 14:5, quocient= residu=5 En general, si el període és 5: f(x+5 n)=f(x) 136 MATEMÀTIQUES B
9 PAR f(-x)=f(x) Quan es plega la gràfica per l'eix d'ordenades les dues branques coincidixen. IMPAR f(-x)=-f(x) Quan es pleguen la gràfica per ambdós eixos les dues branques coincidixen. Simetries La gràfica d'algunes funcions pot presentar algun tipus de simetria que si s'estudia prèviament, en facilita el dibuix. Una funció és simètrica respecte a l'eix OY, si f(-x)=f(x). En aquest cas la funció es diu PARELLA. Una funció és simètrica respecte a l'origen de coordenades quan f( x)= f(x). En aquest cas la funció s'anomena SENAR. Observeu els gràfics per tal de reconéixer-los. EXERCICIS resolts 5. Calculeu el valor de k perquè les següents funcions siguen contínues en el punt en què canvia la gràfica: a) 0,5x + k x 4 f (x) = b) x 3 x > 4 f(4)=0,5 4+k=+k Si s'haguera definit en l'altre tram seria: f(4)=4-3=1 com que ambdós trams han de coincidir: +k=1 k=1-=-1 f (x) k = x + 1 x 1 x > 1 f(1)=k Si estiguera definida en l'altre tram seria: f(1)=-1+1=0 com que ambdós trams han de coincidir: k=0 6. Quin és el període de les funcions següents? En cada cas calculeu f(45). a) b) Període = 4 Període = 5 45= f(45)=f(1)= 45=5 9 f(45)=f(0)=0 7. D'entre les següents gràfiques seleccioneu les que corresponen a funcions parelles i a funcions senars. Parell: C Senars: A i D B no és parell ni senar 8. Les funcions següents (corresponents a les de l'exemple 7) són parelles o senars? a) f(x)=x 3 3x f(-x)=(-x) 3 3(-x)=-x 3 +3x= f(x) SENARS b) f(x)=x x- f(-x)=(-x) (-x) =x +x Ni PARELL ni SENAR c) f(x)= x 6 x 4 x f(-x)=(-x) 6 (-x) 4 (-x) =x 6 x 4 x =f(x) PARELL d) f(x)=-1/x f(-x)=-1/(-x)=1/x= f(x) SENAR MATEMÀTIQUES B 137
10 3. Taxa de variació i creixement Taxa de variació d'una funció La Taxa De variació o increment d'una funció és l'augment o disminució que experimenta una funció en passar la variable independent d'un valor a l'altre. TV[x 1,x ]=f(x 1 )-f(x ) De més utilitat resulta calcular l'anomenada taxa de variació mitjana, que ens indica la variació relativa de la funció respecte a la variable independent: TVM x [, x ] 1 f(x) f(x1) = x x 1 TV[0,30]=15 TV[17,]=4,5 La gràfica representa la distància en km recorreguda d'un ciclista en funció del temps, en minuts, emprat. La TV correspon en la distància recorreguda en un interval de temps. La TVM és la velocitat mitjana en un interval de temps determinat. 6,5 3,5 TVM = [ 5,1] = = 0, 5 TVM[15,1]=4/6 TVM[,30]=1/ 6 min 4 km 8 min 4 km Creixement i decreixement Una característica de les funcions que es pot visualitzar fàcilment en les gràfiques és la monotonia. Quan en augmentar el valor de x augmenta el valor de y=f(x), la gràfica "ascendix" i es diu que la funció és creixent. Si al contrari en augmentar x disminuïx y, la gràfica "descendix", i la funció decreix. Precisant un poc més: Una funció és creixent en un interval, quan donats dos punts qualssevol d'aquest Creixent TVM x1 f(x ) f(x ) > x x1 1 [, x ] = 0 Decreixent f(x ) f(x ) TVM x1 < x x1 1 [, x ] = 0 Si x 1 <x aleshores f(x 1 )<f(x ) I serà decreixent: Si x 1 <x aleshores f(x 1 )>f(x ) Creixent Constant x (10, 15) Decreixent x (15, 5) Totes les funcions no creixen o decreixen, de la mateixa manera. f(x)=x és la que creix més de pressa, g(x)=x té un creixement lineal, h(x)= x creix més lentament. 138 MATEMÀTIQUES B
11 Màxims i mínims Donada una funció contínua en un punt x=a, es diu que presenta un màxim relatiu, si a l'esquerre del punt esmentat la funció és creixent i a la dreta la funció és decreixent. Si, al contrari, la funció és creixent a la dreta i decreixent a l'esquerre hi ha un mínim relatiu. Màxim (6, 7) Creixent Decreixent Creixent Mínim Màxim absolut (0, 1,1) Mínim absoluto Si es verifica que f(a)>f(x) per a qualsevol valor x del domini, i no només per als valors "del voltant", es parla de màxim absolut en x=a. I anàlogament es diu que a a hi ha un mínim absolut si f(a)<(f(x) per a qualsevol x del domini. En x=0 canvia la concavitat però no hi ha punt d'inflexió, no és del domini. Convexa (0,+ ) Concavitat, convexitat i punts d'inflexió Una altra característica d'interés en les gràfiques de les funcions és la concavitat, estudiar els intervals en què la gràfica es corba cap avall o cap amunt. Una funció és còncava en un interval si el segment que unix dos punts qualssevol de la corba queda baix d'aquesta, i convexa si hi queda dalt. Els punts del domini en els quals la funció passa de còncava a convexa o viceversa, s'anomenen punts d'inflexió. Còncava (-,0) Còncava (-,13) Punt d inflexió (13, 4) Convexa (13,+ ) MATEMÀTIQUES B 139
12 EXERCICIS resolts 9. Calculeu la taxa de variació mitja de les funcions següents entre els punts indicats. Comproveu a la figura que en les funcions el gràfic de les quals és una recta la TVM és constant. a) y=x+3 b) y=0,5x ,5 3,5 TVM[1,3]= = = TVM[1,3]= = = 0, TVM[-5,-]= = = ,5 TVM[-3,0]= = 0, Las gràfiques representen l'ompliment dels diferents recipients, quina gràfica correspon a cada un? a b c d e a b 4 c 5 d 3 e Recordeu la funció que donava el "perfil" d'una etapa de la Volta, que vau veure al primer capítol, a) escriviu els intervals de creixement o decreixement; b) En quin punt quilomètric s'assoleixen els màxims relatius?, quin valor prenen?, i els mínims?; c) Hi ha absolut màxim o mínim? a) Creixent: (0,4)U(34,71)U(87,113)U(11,168) Decreixent: (4,34)U(71,87)U(113,11) km alt b) MÁX: x=4, y=180 x=71, y=190 x=113, y=100 MÍN: x=34, y=740 x=87, y=630 x=11, y=70 c) En aquest cas la funció té màxim i mínim absoluts, que s'assoleixen ambdós en els extrems del domini, com a mínim en x=0 de valor 540 m, com a màxim en x=168 de valor MATEMÀTIQUES B
13 Per a practicar Funcions i gràfiques 1. Considereu la funció que a cada nombre li assigna el seu quadrat menys 1. Escriviu la seuy expressió analítica, calculeu les imatges -1, 1 y. Calculeu també els punts de tall amb els eixos.. Considereu la funció que a cada nombre li assigna la mitat més 3. Escriviu la seuy expressió analítica, calculeu les imatges de -1, 1 y 3. Calculeu també els punts de tall amb els eixos. 3. Considereu la funció que a cada nombre li assigna el doble menys 5. Escriviu la seuy expressió analítica, calculeu les imatges -, -1 y 1. Calculeu també els punts de tall amb els eixos. 4. Calculeu el domini de les següents funcions: 7. Estudieu la simetria de les funcions: a) f(x)= x 3 x 3 +x b) f(x)= 5x c) f(x)= x x d) f(x)= x 1 4x 1 e) f(x)= + x f) f(x)= x 4-3x En cada cas la gràfica mostra un tram o període d una funció periòdica. Dibuixeu altres trams al teu quadern, trobeu el període i calculeu la imatge del punt d'abscissa que s'indica: a) f(-) a) f(x)=-x +5x-6 x b) f(x)= x 4 c) f(x)= 4x + 1 b) f(-3) d) f(x)= 4x + 0 e) f(x)= 3 x 4 5. Estudieu la continuïtat de les següents funcions: c) f(-1) a) f(x)= x x 3 b) f(x)= x x Estudieu la continuïtat de les següents funcions en los puntos que se indica: x + a) f(x)= x + x + b) f(x)= x + x 1 en x=1 x > 1 x 0 en x=0 x > 0 9. Calculeu les TVM de les funcions de la gràfica en els intervals [0,4] y [,4]. a) b) c) f(x)= x x 1 x > 1 en x=-1 d) f(x)= x x 1 x > 1 en x=-1 MATEMÀTIQUES B 141
14 10. El gráfic mostra com varia la gasolina que hi ha en el meu cotxe durant un viatge de 50 Km per una autovia. 1. El gráfic dóna l espai recorregut per dos cotxes que fan un mateix trajecte. a) Quanta gasolina hi ha al cap de 40 km? En el dipòsit, hi caben 40 litres, quan hi ha més de mig dipósit ple? b) En quantes gasolineres vaig parar?, a quina gasolinera vaig posar més gasolina? Si no em pare en cap, on em quede sense gasolina? c) Quanta gasolina utilitze per als primers 00 km? Quanta nútilitze per a tot el viatge? Quants litres consumix el meu cotxe cada 100 km en aquesta autovia? 11. La María en Jordi són dues persones més o menys típiques. En la gràfica podeu comparar com ha crescut el seu pes en els seus primers 0 anys. Quant pesava en Jordi als 8 anys?, i la Maria als 1? Quan va superar els 45 kg en Jordi? Fins quan va pesar menys de 45 kg la María? a) Quina és la distància recorreguda? Si el primer cotxe ha eixit a las 10:00 h, a quina hora ha eixit el segon? Quant temps li ha costat a cada cotxe fer el recorregut? b) Quant temps va estar parat cada cotxe? A quin km es van aturar? A quin km el segon cotxe avança el primer? A quin km el primer cotxe torna avançar el segon? c) Quina és la velocitat mitjana de cada cotxe en el trajecte total? En quin interval de temps és més alta la velocitat de cada cotxe? 13. Les gràfiques següents corresponen a les funcions I y II. I) f(x)=x 3-6x x x II) f(x)= x Calculeu-ne de cada una: a) Cuánto pesaba Jorge a los 8 años?, y María a los 1?. Cuándo superó Jorge los 45 kg?. b) A quina edat pesaven tots dos el mateix?. Quan pesava més en Jordi que la Maria? Quan pesava més la Maria que Jordi? c) Quin va ser l augment de pes de tots dos entre els 11 i els 15 anys? Quina va ser la mitjana d augment per any en el període anterior? En quin període de la seua vida la Maria va créixer més ràpidament?, i Jordi? a) El domini. b) Els punts de tall amb els eixos. c) Els valors de x per als quals la funció és positiva i negativa. d) Els intervals de creixement i decreixement. e) Els màxims i mínims. f) Quants punts d'inflexió tenen? g) Els intervals de concavitat i convexitat. 14 MATEMÀTIQUES B
15 La primera funció Funcions i gràfiques Para saber más El primer en construir una funció va ser Galileu ( ). Des de dalt de la torre inclinada de Pisa va tirar dues boles, una de ferro i una altra de fusta i va comprovar que malgrat la diferència de pes, ambdues arribaven a terra alhora, havia descobert la llei de caiguda dels cossos. Continuant el seu estudi i ocupant un artefacte curiós, va comprovar que l'espai recorregut depén del quadrat del temps, i així va escriure la primera funció de la història. Fent clic ací podeu llegir més sobre el tema. La primera definició formal de funció és gràcies a Euler, que en el llibre Introductio in analysis infinitorum, publicat el 1748, diu: Una funció d'una quantitat variable és una expressió analítica composta de qualsevol manera a partir de la quantitat variable i de nombres o quantitats constants. El 1755 en Institutiones calculi differentialis, torna a tractar el tema apropant-se més al que hui utilitzem. Una funció curiosa L'anomenada funció de Dirichlet, és la que a cada nombre real li assigna l'1 si és racional i el 0 si és irracional. És discontínua en tots els seus punts. Tangent, taxa de Variació Mitjana i pendent f (x) 1 = 0 x Q x R Q x x+h Quan el punt *PQ, la recta secant PQ tendix a la recta tangent a la corba y=f(x) en P. La pendent de la secant és la TVM[P,Q] que tendix a la de la tangent. És la derivada de la funció que f(x + h) f(x) Estudiareu en cursos posteriors. f (x) = lim h 0 h 30 45º x Observeu les dues gràfiques, ambdues funcions són periòdiques de període *, la gràfica verda està desfasada */ respecte a la taronja; fixeu-vos on assolixen els màxims i els mínims. Quan coincidixen les dues gràfiques, a quina altura estan?, x=r sin 45º=1,1 m; 1) 35-1,1=13,79 )35+1,1=56,1 MATEMÁTICAS B 143
16 Recordeu el més important Una funció és una relació entre dues variables x i y, de manera que a cada valor de la variable independent, x, se li associa un únic valor de la variable y, la dependent. El domini d'una funció és el conjunt de tots els possibles valors que pot prendre x. La gràfica d'una funció és el conjunt de punts (x,f(x)) representats en el pla. Una funció és contínua si pot representar-se amb un sol traç. És discontínua en un punt si presenta un "salt" o no està definida en aquest punt. Una funció és periòdica de període t, si la seua gràfica es repetix cada t unitats, f(x+t)=f(x). Una funció és simètrica respecte a l'eix OY, funció parella, si f(x)=f(-x); i és simètrica respecte a l'origen, funció senar, si f( x)= f(x). La taxa de variació d'una funció entre dos punts és la diferència: TV[x1,x]=f(x) f(x1) La taxa de variació mitjana és: TVM x [, x ] 1 f(x ) f(x1) = x x Una funció és creixent en un interval, quan donats dos punts qualssevol del mateix Si x 1 <x aleshores f(x 1 )<f(x ) I és decreixent Si x 1 <x aleshores f(x 1 )>f(x ) Una funció contínua en un punt x=a, presenta un màxim relatiu, si a l'esquerre de l'esmentat punt és creixent i a la dreta és decreixent. Si, al contrari, és decreixent abans i creixent després hi ha un mínim relatiu. La gràfica d'una funció pot ser còncava (avall) o convexa (amunt). Els punts del domini en què canvia la concavitat, s'anomenen punts d'inflexió. 1 Domini Tots els nombres reals excepte el 0. Continuïtat No és contínua, en 0 presenta una una discontinuïtat de salt infinit. Simetria És simètrica respecte a l'origen de coordenades, funció senar. Talls eixos A l'eix d'abscisses en (-1,0) y (1,0); no talla l'eix d'ordenades. Creixement i decreixement És creixent en (-, -,5)U(,5,+ ) I decreixent en (-,5,0)U(0,,5) Màxims i mínims Màxim en (,5,3); Mínim en (-,5,3) Concavitat i convexitat Punts d inflexió És còncava a (-, -3)U(0, 3) I convexa a (-3,0)U(3, + ) (-3,0) y (3,0) són punts d'inflexió. A x=0 canvia la concavitat però no hi ha punt d'inflexió ja que no és del domini. 144 MATEMÀTIQUES B
17 Autoavaluació 1. Calculeu la imatge de x=0 en la funció: x 1 x 3 f(x) = 5 x > 3. Calculeu el domini de la funció: x + 1 f(x) = x 4 3. Quin dels punts següents: (1,-) (3,-15) (4,-6) no pertany a la gràfica de la funció f(x)=-x -3x+?. 4. Calculeu els punts de tall amb els eixos coordenats de la recta y=-0,5x-0, Si y=f(x) és una funció SENAR i f(3)=-, Quant val f(-3)? 6. La gràfica mostra el primer tram d una funció periódica amb període 5 i expressió f(x)=-x +5x (0 x<5). Calculeu f(8). 7. Esbrineu el valor de aperquè la funció siga contínua a x=3. x + k x 3 f(x) = 6 x > 3 8. Calculeu la TVM[-3,0] de la funció f(x)=-0,5x -3x Determineu l interval en què la funció de la gràfica és decreixent. 10. Un ciclista ix d un punt A cap un altre B distant 60 km a una velocitat constant de 30 km/h. Alhora un altre ix de B cap a A, a 40 km/h. A quants km del punt A es creuen a la carretera? MATEMÀTIQUES B 145
18 Solucions dels exercicis per a practicar 1. f(x)=x -1 f(-1)=0, f()=3, f(1)=0 Tall OY: -1 Tall OX: 1 y -1 x. y= + 3 f(-1)=,5 f(1)=3,5 f(3)=4,5 Tall OY: 3 Tall OX: f(x)=x-5 f(-)=-9, f(-1)=-7, f(1)=-5 Tall OY: -5 Tall OX:,5 4. a) És un polinomi, Dom(f)=IR b) Tots els reals excepte el c) ( 3, 3 ) d) Tots els reals e) (, + ) 5. a) És discontínua en x=3 b) És discontínua en x=-3 6. a) Discontínua en 1. A l'esquerra: 3; A la dreta: 1 b) Contínua en 0. A l'esquerra: ; A la dreta: c) Contínua en -1. A l'esquerra: 4; A la dreta: 4 c) Contínua en -1. A l'esquerra: 4; A la dreta: 4 7. a) e) són senars; b) c) y f) són parells; d) no és parell ni senar 8. a) TVM[0,4]=TVM[,4]=0,5 b) TVM[0,4]=1,; TVM[,4]=1,8 9. a) b) c) 10. a) 7,5 litres; entre los km 00 i 360 i del 440 fins al 50. b) En dos, una en el km 00 i altra en el 440; en vaig posar més a la 1ª; a los 80 km c) 1,5 l; 3,5 l; 6,5 l/100 km 11. a) J. 5 kg, M. 35 kg ; a los 14 anys b) A los 11 (30 kg) i a los 15 (55 kg) J més que M: fins al 11 i des dels 15; M més que J: dels 11 a 15 c) 5kg; 6,5 kg/any; M entre els 11 i 1 (10 kg/any); J entre els 1-14 (10 kg/any) 1. a) 80 km; a las 10:15; 75 i 70 min b) 10 min en km 0, 0 min en km 30; en el km 0 i en 30 respectivament. c) 64 km/h i 68,6 km/h; 1º: min º: min i min I) a) IR; b) (0,0)(3,0) c) y>0 (0,+ ); y<0 (-,0); d) creix:(-,1)u(3,+ ), decreix:(1,3); e) màx x=1, mín x=3; f) Uno; cònc:(-,) conv: (,+ ) II) a) IR-{0}; b) No talla c) y<0 (0,+ ); y>0 (-,0); d) decreix:(-,-1)u(1,+ ), creix:(-1,0)u(0,1); e) màx x=1, mín x=-1; f) Cap; conv:(-,0) cònc: (0,+ ) Solucions de l'autoavaluació 1. f(0)= 1. IR - {, -} 3. (3, -15) 4. (0, -0,75) (-3,0) 5. f(-3)= 6. f(8)=f(3)=6 7. k=0 8. TVM[-3,0] = -,5 9. (-3, 1) 10. A partir de 4,5 min la A. No oblideu enviar les activitats al tutor 146 MATEMÀTIQUES B
Funcions i gràfiques. Objectius. 1.Funcions reals pàg. 132 Concepte de funció Gràfic d'una funció Domini i recorregut Funcions definides a trossos
 8 Funcions i gràfiques Objectius En aquesta quinzena aprendreu a: Conèixer i interpretar les funcions i les diferents formes de presentar-les. Reconèixer el domini i el recorregut d'una funció. Determinar
8 Funcions i gràfiques Objectius En aquesta quinzena aprendreu a: Conèixer i interpretar les funcions i les diferents formes de presentar-les. Reconèixer el domini i el recorregut d'una funció. Determinar
FUNCIONS REALS. MATEMÀTIQUES-1
 FUNCIONS REALS. 1. El concepte de funció. 2. Domini i recorregut d una funció. 3. Característiques generals d una funció. 4. Funcions definides a intervals. 5. Operacions amb funcions. 6. Les successions
FUNCIONS REALS. 1. El concepte de funció. 2. Domini i recorregut d una funció. 3. Característiques generals d una funció. 4. Funcions definides a intervals. 5. Operacions amb funcions. 6. Les successions
Funcions i gràfiques. Objectius. Abans de començar. 1.Funcions. pàg. 162 Concepte Taules i gràfiques Domini i recorregut
 9 Funcions i gràfiques Objectius En aquesta quinzena aprendràs a: Conèixer i interpretar les funcions i les diferents formes de representar-les. Reconèixer el domini i el recorregut d una funció. Determinar
9 Funcions i gràfiques Objectius En aquesta quinzena aprendràs a: Conèixer i interpretar les funcions i les diferents formes de representar-les. Reconèixer el domini i el recorregut d una funció. Determinar
TEMA 1 : Aplicacions de les derivades
 TEMA 1 : Aplicacions de les derivades 1.1. INFORMACIÓ EXTRETA DE LA PRIMERA DERIVADA 1.1.1 Creixement i decreixement de funcions Definició: f és creixent en x 0 existeix (x 0 - a, x 0 + a), un entorn del
TEMA 1 : Aplicacions de les derivades 1.1. INFORMACIÓ EXTRETA DE LA PRIMERA DERIVADA 1.1.1 Creixement i decreixement de funcions Definició: f és creixent en x 0 existeix (x 0 - a, x 0 + a), un entorn del
1. Què tenen en comú aquestes dues rectes? Com són entre elles? 2. En què es diferencien aquestes dues rectes?
 En la nostra vida diària trobem moltes situacions de relació entre dues variable que es poden interpretar mitjançant una funció de primer grau. La seva expressió algebraica és del tipus f(x)=mx+n. També
En la nostra vida diària trobem moltes situacions de relació entre dues variable que es poden interpretar mitjançant una funció de primer grau. La seva expressió algebraica és del tipus f(x)=mx+n. També
CARACTERÍSTIQUES DE FUNCIONS ELEMENTALS
 CARACTERÍSTIQUES DE FUNCIONS ELEMENTALS 1. FUNCIÓ CONSTANT (document d'ajuda: 1_funcio_constant.html ) Expressió algèbrica: f(x) = n. Gràfica: 2. FUNCIÓ LINEAL (document d'ajuda: 2_funcio_lineal.html )
CARACTERÍSTIQUES DE FUNCIONS ELEMENTALS 1. FUNCIÓ CONSTANT (document d'ajuda: 1_funcio_constant.html ) Expressió algèbrica: f(x) = n. Gràfica: 2. FUNCIÓ LINEAL (document d'ajuda: 2_funcio_lineal.html )
Gràficament: una funció és contínua en un punt si en aquest punt el seu gràfica no es trenca
 Funcions contínues Funcions contínues Continuïtat d una funció Si x 0 és un nombre, la funció f(x) és contínua en aquest punt si el límit de la funció en aquest punt coincideix amb el valor de la funció
Funcions contínues Funcions contínues Continuïtat d una funció Si x 0 és un nombre, la funció f(x) és contínua en aquest punt si el límit de la funció en aquest punt coincideix amb el valor de la funció
Una funció és una relació entre dues variables, de tal manera que al variar el valor d'una d'elles va variant el valor de l'altra.
 UNITAT 7: FUNCIONS. Definició Una funció és una relació entre dues variables, de tal manera que al variar el valor d'una d'elles va variant el valor de l'altra. Eemple: Completa: f() g() - h() - - (-)
UNITAT 7: FUNCIONS. Definició Una funció és una relació entre dues variables, de tal manera que al variar el valor d'una d'elles va variant el valor de l'altra. Eemple: Completa: f() g() - h() - - (-)
DERIVADES. TÈCNIQUES DE DERIVACIÓ
 UNITAT 7 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 56 Tangents a una corba y f (x) 5 5 9 4 Troba, mirant la gràfica i les rectes traçades, f'(), f'(9) i f'(4). f'() 0; f'(9) ; f'(4) 4 Digues uns altres
UNITAT 7 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 56 Tangents a una corba y f (x) 5 5 9 4 Troba, mirant la gràfica i les rectes traçades, f'(), f'(9) i f'(4). f'() 0; f'(9) ; f'(4) 4 Digues uns altres
LA RECTA. Exercicis d autoaprenentatge 1. Siga la gràfica següent:
 LA RECTA Recordeu: Una recta és una funció de la forma y = mx + n, on m i n són nombres reals. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall
LA RECTA Recordeu: Una recta és una funció de la forma y = mx + n, on m i n són nombres reals. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall
Sèrie 5. Resolució: 1. Siguin i les rectes de d equacions. a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i.
 Oficina d Accés a la Universitat Pàgina 1 de 11 Sèrie 5 1. Siguin i les rectes de d equacions : 55 3 2 : 3 2 1 2 3 1 a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i. b) Trobeu l
Oficina d Accés a la Universitat Pàgina 1 de 11 Sèrie 5 1. Siguin i les rectes de d equacions : 55 3 2 : 3 2 1 2 3 1 a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i. b) Trobeu l
Exercicis de derivades
 Variació mitjana d'una funció 1. Calcula la variació mitjana de la funció f (x) = x 2 2 x als següents intervals: a) [ 1, 3 ] b) [0, 4 ] c) [1, 5 ] 2. Donada la funció següent: a) Quina és la variació
Variació mitjana d'una funció 1. Calcula la variació mitjana de la funció f (x) = x 2 2 x als següents intervals: a) [ 1, 3 ] b) [0, 4 ] c) [1, 5 ] 2. Donada la funció següent: a) Quina és la variació
Funcions i gràfiques
 Funcions i gràfiques Continguts 1. Funciones reals Concepte de funció Gráfica d una funció Domini i recorregut Funcions definides a trossos 2. Propietats de les funcions Continuïtat i discontinuïtats Periodicitat
Funcions i gràfiques Continguts 1. Funciones reals Concepte de funció Gráfica d una funció Domini i recorregut Funcions definides a trossos 2. Propietats de les funcions Continuïtat i discontinuïtats Periodicitat
REPRESENTACIÓ DE FUNCIONS
 1. FUNCIONS PRINCIPALS REPRESENTACIÓ DE FUNCIONS 1.1 Rectes Forma: 4 5 1.2 Paràboles Forma: 1.3 Funcions amb radicals Forma: 1.4 Funcions de proporcionalitat inversa Forma: 1.5 Exponencials Forma: 2 1.6
1. FUNCIONS PRINCIPALS REPRESENTACIÓ DE FUNCIONS 1.1 Rectes Forma: 4 5 1.2 Paràboles Forma: 1.3 Funcions amb radicals Forma: 1.4 Funcions de proporcionalitat inversa Forma: 1.5 Exponencials Forma: 2 1.6
Proves d accés a la Universitat per a més grans de 25 anys Convocatòria 2013
 Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
11 Límits de funcions. Continuïtat i branques infinites
 Límits de funcions. Continuïtat i branques infinites Pàgina 7 A través d'una lupa a) A = + d " A = " + d A = 0 d "+ Soroll i silenci I = + d " 0 I = 0 d "+ Pàgina 75 a) Cert Cert Cert d) Cert e) Fals f)
Límits de funcions. Continuïtat i branques infinites Pàgina 7 A través d'una lupa a) A = + d " A = " + d A = 0 d "+ Soroll i silenci I = + d " 0 I = 0 d "+ Pàgina 75 a) Cert Cert Cert d) Cert e) Fals f)
Institut Obert de Catalunya
 Institut Obert de Catalunya v aluació contínua Qualif icació prov a TOTL Cognoms Nom: Centre: Trimestre: primavera10 M4 - Matemàtiques 4 1. (2,5 punts) SOLUCIONRI Un cotxe no s'atura de sobte al frenar
Institut Obert de Catalunya v aluació contínua Qualif icació prov a TOTL Cognoms Nom: Centre: Trimestre: primavera10 M4 - Matemàtiques 4 1. (2,5 punts) SOLUCIONRI Un cotxe no s'atura de sobte al frenar
1. RECTA TANGENT I NORMAL 2. DETERMINACIÓ DE PARÀMETRES 3. CREIXEMENT I DECREIXEMENT 4. VELOCITAT I ACELERACIÓ - PUNTS SINGULARS
 APLICACIONS DE LA DERIVADA 1. RECTA TANGENT I NORMAL. DETERMINACIÓ DE PARÀMETRES 3. CREIXEMENT I DECREIXEMENT 4. VELOCITAT I ACELERACIÓ - PUNTS SINGULARS 1. RECTA TANGENT I NORMAL 1.1 Trobeu l equació
APLICACIONS DE LA DERIVADA 1. RECTA TANGENT I NORMAL. DETERMINACIÓ DE PARÀMETRES 3. CREIXEMENT I DECREIXEMENT 4. VELOCITAT I ACELERACIÓ - PUNTS SINGULARS 1. RECTA TANGENT I NORMAL 1.1 Trobeu l equació
Institut Jaume Balmes Aplicacions de les derivades I
 MS 1) Donada la funció y 6 + 8 a) Troba la recta tangent en el seu punt d'infleió. b) Troba la recta normal en el punt de 1 (1+0,5 1,5 punts) ) A la vista de la gràfica d'aquesta funció. a) Estudia la
MS 1) Donada la funció y 6 + 8 a) Troba la recta tangent en el seu punt d'infleió. b) Troba la recta normal en el punt de 1 (1+0,5 1,5 punts) ) A la vista de la gràfica d'aquesta funció. a) Estudia la
FUNCIONS. Característiques generals. 1) Indica el domini i el recorregut de les següents funcions: a) b) c)
 4ES 4 B FUNCINS Característiques generals ) Indica el domini i el recorregut de les següents funcions: a) b) c) ) Indica els punts de discontinuïtat de les següents funcions: a) b) c) ) De cadascuna de
4ES 4 B FUNCINS Característiques generals ) Indica el domini i el recorregut de les següents funcions: a) b) c) ) Indica els punts de discontinuïtat de les següents funcions: a) b) c) ) De cadascuna de
1.4 Derivades: Unitat de síntesi (i repàs)
 1.4 Derivades: Unitat de síntesi (i repàs) 11. Problemes de: optimització, extrems ( ), punts d inflexió ( ), rectes tangents (T) i interpretació de gràfiques (G): A.- Considereu tots els prismes rectes
1.4 Derivades: Unitat de síntesi (i repàs) 11. Problemes de: optimització, extrems ( ), punts d inflexió ( ), rectes tangents (T) i interpretació de gràfiques (G): A.- Considereu tots els prismes rectes
La recta. La paràbola
 LA RECTA, LA PARÀBOLA I LA HIPÈRBOLA La recta Una recta és una funció de la forma y = m + n. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall amb
LA RECTA, LA PARÀBOLA I LA HIPÈRBOLA La recta Una recta és una funció de la forma y = m + n. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall amb
IES Valerià Pujol TEMA: FUNCIONS
 Funcions. Introducció. Objectius. Relacionar una gràfica amb una taula de valors. Introduir el concepte de funció. Introduir el concepte de imatge i antiimatge. Punts de tall amb els eixos. Introduir el
Funcions. Introducció. Objectius. Relacionar una gràfica amb una taula de valors. Introduir el concepte de funció. Introduir el concepte de imatge i antiimatge. Punts de tall amb els eixos. Introduir el
Indiqueu en quins punts Y = f(x) no és contínua, el tipus de discontinuïtats de cada cas i les asímptotes que presenta. (0,1 9 +0,8=1,7 punts)
 Generalitat de Catalunya Departament d Ensenyament Institut Jaume Balmes Nom: 1.- Trobeu la funció inversa o recíproca de la funció recorregut de la funció yf(). f ( ) Departament de Matemàtiques 1MA:
Generalitat de Catalunya Departament d Ensenyament Institut Jaume Balmes Nom: 1.- Trobeu la funció inversa o recíproca de la funció recorregut de la funció yf(). f ( ) Departament de Matemàtiques 1MA:
ANÀLISI. MATEMÀTIQUES-2
 1. ANÀLISI. Caldrà repassar alguns temes de cursos anteriors, com el tema de Funcions polinòmiques i, els de Funcions reals i Límits de funcions, caldrà recordar també els gràfics i propietats més importants
1. ANÀLISI. Caldrà repassar alguns temes de cursos anteriors, com el tema de Funcions polinòmiques i, els de Funcions reals i Límits de funcions, caldrà recordar també els gràfics i propietats més importants
FUNCIONS EXPONENCIALS I LOGARÍTMIQUES. MATEMÀTIQUES-1
 FUNCIONS EXPONENCIALS I LOGARÍTMIQUES. 1. Funcions exponencials. 2. Equacions exponencials. 3. Definició de logaritme. Propietats. 4. Funcions logarítmiques. 5. Equacions logarítmiques. 1. Funcions exponencials.
FUNCIONS EXPONENCIALS I LOGARÍTMIQUES. 1. Funcions exponencials. 2. Equacions exponencials. 3. Definició de logaritme. Propietats. 4. Funcions logarítmiques. 5. Equacions logarítmiques. 1. Funcions exponencials.
TEMA 4: Equacions exponencials i logarítmiques
 TEMA 4: Equacions exponencials i logarítmiques 4.1. EXPONENCIALS Definim exponencial de base a i exponent n:. Propietats de les exponencials: (1). (2) (3) (4) 1 (5) 4.2. EQUACIONS EXPONENCIALS Anomenarem
TEMA 4: Equacions exponencials i logarítmiques 4.1. EXPONENCIALS Definim exponencial de base a i exponent n:. Propietats de les exponencials: (1). (2) (3) (4) 1 (5) 4.2. EQUACIONS EXPONENCIALS Anomenarem
Matemàtiques Sèrie 1. Instruccions
 Proves d accés a cicles formatius de grau superior de formació professional inicial, d ensenyaments d arts plàstiques i disseny, i d ensenyaments esportius 0 Matemàtiques Sèrie SOLUCIONS, CRITERIS DE CORRECCIÓ
Proves d accés a cicles formatius de grau superior de formació professional inicial, d ensenyaments d arts plàstiques i disseny, i d ensenyaments esportius 0 Matemàtiques Sèrie SOLUCIONS, CRITERIS DE CORRECCIÓ
2 desembre 2015 Límits i número exercicis. 2.1 Límits i número
 I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 2 desembre 205 Límits i número exercicis 2. Límits i número 4. Repàs de logaritmes i exponencials: troba totes les solucions de cadascuna de les següents equacions:
I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 2 desembre 205 Límits i número exercicis 2. Límits i número 4. Repàs de logaritmes i exponencials: troba totes les solucions de cadascuna de les següents equacions:
Districte Universitari de Catalunya
 Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val
Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val
x x 1 x 11= 7) y = 6 3x-2 12) y = e 5x (3x 2-6)
 Derivació1/ 1.- Calculeu la primera derivada de les funcions següents, simplificant el resultat el màim possible. 1) y = - 4 4 + - ) y 6 4 4 = + 3 3) y = 3 + 4) y = ) 3 y = 6) y = ( + ) 1 + 7) ( 3) y =
Derivació1/ 1.- Calculeu la primera derivada de les funcions següents, simplificant el resultat el màim possible. 1) y = - 4 4 + - ) y 6 4 4 = + 3 3) y = 3 + 4) y = ) 3 y = 6) y = ( + ) 1 + 7) ( 3) y =
Aplicacions de la derivada
 Aplicacions de la derivada 1 Aplicacions de la derivada Les aplicacions de la derivada són molt àmplies; entre les més importants hi ha: Localització d extrems (màxims i mínims) d una funció Un màxim és
Aplicacions de la derivada 1 Aplicacions de la derivada Les aplicacions de la derivada són molt àmplies; entre les més importants hi ha: Localització d extrems (màxims i mínims) d una funció Un màxim és
Matemàtiques Sèrie 1. Instruccions
 Proves d accés a cicles formatius de grau superior de formació professional inicial, d ensenyaments d arts plàstiques i disseny, i d ensenyaments esportius 2011 Matemàtiques Sèrie 1 Dades de la persona
Proves d accés a cicles formatius de grau superior de formació professional inicial, d ensenyaments d arts plàstiques i disseny, i d ensenyaments esportius 2011 Matemàtiques Sèrie 1 Dades de la persona
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 PAU 2012
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 1 1 k 1.- Determineu el rang de la matriu A = 1 k 1 en funció del valor del paràmetre k. k 1 1 [2 punts] En ser la matriu
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 1 1 k 1.- Determineu el rang de la matriu A = 1 k 1 en funció del valor del paràmetre k. k 1 1 [2 punts] En ser la matriu
Oficina d Accés a la Universitat Pàgina 1 de 7 PAU 2015 Criteris de correcció Matemàtiques aplicades a les ciències socials
 Oficina d Accés a la Universitat Pàgina 1 de 7 PAU 015 SÈRIE 1. Un arbre té un volum de 0 m i, per la qualitat de la seva fusta, es ven a 50 per metre cúbic. Cada any l'arbre augmenta el volum en 5 m.
Oficina d Accés a la Universitat Pàgina 1 de 7 PAU 015 SÈRIE 1. Un arbre té un volum de 0 m i, per la qualitat de la seva fusta, es ven a 50 per metre cúbic. Cada any l'arbre augmenta el volum en 5 m.
Oficina d Accés a la Universitat Pàgina 1 de 6 PAU 2016 Criteris de correcció
 Oficina d Accés a la Universitat Pàgina 1 de 6 Criteris de correcció Matemàtiques aplicades a les ciències socials SÈRIE 3 1. Una fàbrica de mobles de cuina ven 1000 unitats mensuals d un model d armari
Oficina d Accés a la Universitat Pàgina 1 de 6 Criteris de correcció Matemàtiques aplicades a les ciències socials SÈRIE 3 1. Una fàbrica de mobles de cuina ven 1000 unitats mensuals d un model d armari
EXERCICIS MATEMÀTIQUES 1r BATXILLERAT
 Treball d estiu/r Batillerat CT EXERCICIS MATEMÀTIQUES r BATXILLERAT. Aquells alumnes que tinguin la matèria de matemàtiques pendent, hauran de presentar els eercicis el dia de la prova de recuperació.
Treball d estiu/r Batillerat CT EXERCICIS MATEMÀTIQUES r BATXILLERAT. Aquells alumnes que tinguin la matèria de matemàtiques pendent, hauran de presentar els eercicis el dia de la prova de recuperació.
DIBUIX TÈCNIC PER A CICLE SUPERIOR DE PRIMÀRIA
 DIBUIX TÈCNIC PER A CICLE SUPERIOR DE PRIMÀRIA Abans de començar cal tenir uns coneixements bàsics que estudiareu a partir d ara. PUNT: No es pot definir, però podem dir que és la marca més petita que
DIBUIX TÈCNIC PER A CICLE SUPERIOR DE PRIMÀRIA Abans de començar cal tenir uns coneixements bàsics que estudiareu a partir d ara. PUNT: No es pot definir, però podem dir que és la marca més petita que
corresponent de la primera pàgina de l examen.
 Oficina d Accés a la Universitat Pàgina 1 de 5 PAU 017 SÈRIE PAUTES PER ALS CORRECTORS RECORDEU: - Podeu valorar amb tants decimals com considereu convenient, però aconsellem no fer ho amb més de dos.
Oficina d Accés a la Universitat Pàgina 1 de 5 PAU 017 SÈRIE PAUTES PER ALS CORRECTORS RECORDEU: - Podeu valorar amb tants decimals com considereu convenient, però aconsellem no fer ho amb més de dos.
LÍMITS DE FUNCIONS. CONTINUÏTAT I BRANQUES INFINITES
 LÍMITS DE FUNCIONS. CONTINUÏTAT I BRANQUES INFINITES Pàgina 7 REFLEIONA I RESOL Aproimacions successives Comprova que: f () = 6,5; f (,9) = 6,95; f (,99) = 6,995 Calcula f (,999); f (,9999); f (,99999);
LÍMITS DE FUNCIONS. CONTINUÏTAT I BRANQUES INFINITES Pàgina 7 REFLEIONA I RESOL Aproimacions successives Comprova que: f () = 6,5; f (,9) = 6,95; f (,99) = 6,995 Calcula f (,999); f (,9999); f (,99999);
SOLUCIONARI Unitat 1. Exercicis. Comencem. 1. La gràfica velocitat-temps corresponent a dos mòbils és la que pots veure a la dreta (fig. 1.3).
 SOLUCIONARI Unitat Comencem La funció f() és decreient en l interval (, ). Fes un raonament com el que em fet anteriorment per determinar on decrei amb més rapidesa, si ens movem prop de o si o fem prop
SOLUCIONARI Unitat Comencem La funció f() és decreient en l interval (, ). Fes un raonament com el que em fet anteriorment per determinar on decrei amb més rapidesa, si ens movem prop de o si o fem prop
TEMA 5 : Derivades. Tècniques de derivació. Activitats
 TEMA 5 : Derivades. Tècniques de derivació Activitats. Calculeu, mitjançant la definició de derivada, la derivada de les funcions següents en els punts indicats: a) f() en f() + 4 5 en - c) f() 6 + 5 en
TEMA 5 : Derivades. Tècniques de derivació Activitats. Calculeu, mitjançant la definició de derivada, la derivada de les funcions següents en els punts indicats: a) f() en f() + 4 5 en - c) f() 6 + 5 en
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 PAU 2008 QÜESTIONS
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 Aquestes pautes no preveuen tots els casos que en la pràctica es poden presentar. Tampoc no pretenen donar totes les possibles
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 Aquestes pautes no preveuen tots els casos que en la pràctica es poden presentar. Tampoc no pretenen donar totes les possibles
+ 1= 0 té alguna arrel real (x en radians).
 Generalitat de Cataluna Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques n BATX MA Eamen r quadrimestre Nom i Cognoms: Grup: Data: ) Calculeu els its següents:
Generalitat de Cataluna Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques n BATX MA Eamen r quadrimestre Nom i Cognoms: Grup: Data: ) Calculeu els its següents:
( 2 3, utilitzeu la matriu inversa B 1 ( 1 4 ( 2 1. Matrius i determinants Sèrie 3 - Qüestió 4. Donada la matriu B =
 1998 - Sèrie 3 - Qüestió 4 Donada la matriu B = ( 2 3, utilitzeu la matriu inversa B 1 1 1) B X B = ( 1 4 3 2). per trobar una matriu X tal que 2004 - Sèrie 1 - Qüestió 3 Considereu les matrius Trobeu
1998 - Sèrie 3 - Qüestió 4 Donada la matriu B = ( 2 3, utilitzeu la matriu inversa B 1 1 1) B X B = ( 1 4 3 2). per trobar una matriu X tal que 2004 - Sèrie 1 - Qüestió 3 Considereu les matrius Trobeu
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 PAU 2009 QÜESTIONS
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 PAU 009 SÈRIE 4 QÜESTIONS 1. Considereu el sistema d inequacions següent: x 0, y 0 x+ 5y 10 3x+ 4y 1 a) Dibuixeu la regió de solucions
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 PAU 009 SÈRIE 4 QÜESTIONS 1. Considereu el sistema d inequacions següent: x 0, y 0 x+ 5y 10 3x+ 4y 1 a) Dibuixeu la regió de solucions
Districte Universitari de Catalunya
 Proves dʼaccés a la Universitat. Curs 2008-2009 Matemàtiques aplicades a les ciències socials Sèrie 4 Responeu a TRES de les quatre qüestions i resoleu UN dels dos problemes següents. En les respostes,
Proves dʼaccés a la Universitat. Curs 2008-2009 Matemàtiques aplicades a les ciències socials Sèrie 4 Responeu a TRES de les quatre qüestions i resoleu UN dels dos problemes següents. En les respostes,
1. Dependència entre magnituds
 FUNCIONS (I) 1. Dependència entre magnituds 1 2. Concepte de funció No és una funció.a alguns valors de x li corresponen diversos valors de y Exemple 1 : És una funció. A cada valor de x li correspon un
FUNCIONS (I) 1. Dependència entre magnituds 1 2. Concepte de funció No és una funció.a alguns valors de x li corresponen diversos valors de y Exemple 1 : És una funció. A cada valor de x li correspon un
Quan aquest límit existeix i és finit diem que f(x) és derivable en x = a.
 APLICACIONS DE LES DERIVADES Joan J. de Val 1. Definició de derivada d'una funció en un punt Recordem que la derivada de la funció f(x) en un punt d'abscissa x = a es defineix com el següent límit: Quan
APLICACIONS DE LES DERIVADES Joan J. de Val 1. Definició de derivada d'una funció en un punt Recordem que la derivada de la funció f(x) en un punt d'abscissa x = a es defineix com el següent límit: Quan
Districte Universitari de Catalunya
 Proves d Accés a la Universitat. Curs 2012-2013 Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts.
Proves d Accés a la Universitat. Curs 2012-2013 Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts.
TEMA 4 : Programació lineal
 TEMA 4 : Programació lineal 4.1. SISTEMES D INEQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITA La solució d aquest sistema és l intersecció de les regions que correspon a la solució de cadascuna de les inequacions
TEMA 4 : Programació lineal 4.1. SISTEMES D INEQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITA La solució d aquest sistema és l intersecció de les regions que correspon a la solució de cadascuna de les inequacions
CARTES DE FRACCIONS. Materials pel Taller de Matemàtiques
 CARTES DE FRACCIONS Aquesta proposta és adequada pel primer cicle d ESO perquè permet recordar mitjançant un joc, una sèrie de conceptes que ja s han treballat a l Educació Primària. Per això resulta una
CARTES DE FRACCIONS Aquesta proposta és adequada pel primer cicle d ESO perquè permet recordar mitjançant un joc, una sèrie de conceptes que ja s han treballat a l Educació Primària. Per això resulta una
Examen Final 17 de gener de 2013
 MATEMÀTIQUES FIB-UPC Examen Final 7 de gener de 03 a) Representeu gràficament la corba definida per l equació y = x 5x. b) Determineu si el conjunt C = { x R x 5x 6 } és fitat superiorment inferiorment)
MATEMÀTIQUES FIB-UPC Examen Final 7 de gener de 03 a) Representeu gràficament la corba definida per l equació y = x 5x. b) Determineu si el conjunt C = { x R x 5x 6 } és fitat superiorment inferiorment)
( b) ( a) Matemàtiques - Activitats d estiu 4t ESO + = NOMBRES REALS. 1. Calcula, extraient factors fora dels radicals:
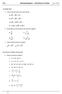 NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
TEMA 2: Divisibilitat Activitats
 TEMA 2: Divisibilitat Activitats 1. 35 és múltiple de 5?. Raoneu la resposta 2. 48 és divisible per 6?. Raoneu la resposta 3. Completeu els deu primers múltiples de 8 8, 16,, 32,,,,,, 80 4. Quines de les
TEMA 2: Divisibilitat Activitats 1. 35 és múltiple de 5?. Raoneu la resposta 2. 48 és divisible per 6?. Raoneu la resposta 3. Completeu els deu primers múltiples de 8 8, 16,, 32,,,,,, 80 4. Quines de les
= 1+ β, essent α i β paràmetres reals. a la recta r 2. i el pla Π d equació
 Problema A Setembre 0 + y z = En l espai es té la recta r i el pla Π d equacions r x + mz = 0, on x y z = 0 m és un paràmetre real a) Un vector director de la recta r b) El valor de m per al qual la recta
Problema A Setembre 0 + y z = En l espai es té la recta r i el pla Π d equacions r x + mz = 0, on x y z = 0 m és un paràmetre real a) Un vector director de la recta r b) El valor de m per al qual la recta
Gràfiques del moviment rectilini uniforme (MRU)
 x = x 0 + v (t-t 0 ) si t 0 = 0 s x = x 0 + vt D4 Gràfiques del moviment rectilini uniforme (MRU) Gràfica posició-temps Indica la posició del cos respecte el sistema de referència a mesura que passa el
x = x 0 + v (t-t 0 ) si t 0 = 0 s x = x 0 + vt D4 Gràfiques del moviment rectilini uniforme (MRU) Gràfica posició-temps Indica la posició del cos respecte el sistema de referència a mesura que passa el
DOSSIER D ACTIVITATS D ESTIU MATEMÀTIQUES 4t d ESO A I B
 DOSSIER D ACTIVITATS D ESTIU MATEMÀTIQUES 4t d ESO A I B A continuació tens una sèrie d'exercicis i activitats relacionats amb els continguts treballats durant el curs. El dossier s ha de presentar en
DOSSIER D ACTIVITATS D ESTIU MATEMÀTIQUES 4t d ESO A I B A continuació tens una sèrie d'exercicis i activitats relacionats amb els continguts treballats durant el curs. El dossier s ha de presentar en
Proporcionalitat geomètrica
 Proporcionalitat geomètrica Guió de treball de l alumne/a...del grup... Raó entre dos segments 1. Amb el GeoGebra obriu l arxiu MArao.html, us trobareu dos segments a i b, els quals podeu seleccionar les
Proporcionalitat geomètrica Guió de treball de l alumne/a...del grup... Raó entre dos segments 1. Amb el GeoGebra obriu l arxiu MArao.html, us trobareu dos segments a i b, els quals podeu seleccionar les
1.- Sabem que el vector (2, 1, 1) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c. . cx by +2z = b
 Oficina d Organització de Proves d Accés a la Universitat Pàgina de 5 PAU 0 - Sabem que el vector (,, ) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c cx by +z = b Calculeu el valor
Oficina d Organització de Proves d Accés a la Universitat Pàgina de 5 PAU 0 - Sabem que el vector (,, ) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c cx by +z = b Calculeu el valor
DOSSIER PREPARACIÓ RECUPERACIÓ MATEMÀTIQUES Setembre 3r ESO
 Generalitat de Catalunya Departament d Ensenyament Institut Pompeu Fabra DOSSIER PREPARACIÓ RECUPERACIÓ MATEMÀTIQUES Setembre 3r ESO Nom i Cognoms:... INSTRUCCIONS: - Aquest dossier serveix per a preparar
Generalitat de Catalunya Departament d Ensenyament Institut Pompeu Fabra DOSSIER PREPARACIÓ RECUPERACIÓ MATEMÀTIQUES Setembre 3r ESO Nom i Cognoms:... INSTRUCCIONS: - Aquest dossier serveix per a preparar
Funciones y gráficas. Objetivos
 8 Funciones y gráficas Objetivos En esta quincena aprenderás a: Conocer e interpretar las funciones y las distintas formas de presentarlas. Reconocer el dominio y el recorrido de una función. Determinar
8 Funciones y gráficas Objetivos En esta quincena aprenderás a: Conocer e interpretar las funciones y las distintas formas de presentarlas. Reconocer el dominio y el recorrido de una función. Determinar
4. EQUACIONS DE PRIMER GRAU AMB UNA INCÒGNITA
 Definició d'equació. Equacions de primer grau amb una incògnita 1. EQUACIONS: DEFINICIONS Equació: igualtat entre dues expressions algebraiques. L'expressió de l'esquerra de la igualtat rep el nom de PRIMER
Definició d'equació. Equacions de primer grau amb una incògnita 1. EQUACIONS: DEFINICIONS Equació: igualtat entre dues expressions algebraiques. L'expressió de l'esquerra de la igualtat rep el nom de PRIMER
UIB 2 + f (x) + f(x) ց ց ր ր Per tant, el punt ( 3. Una altra forma de veure-ho és calcular la derivada segona i mirar el signe en x = 3: 2 f (x) =
 El cas positiu no té solució. Si analitzam el cas negatiu, ens surt x = x+, d on x =. A continuació fem la taula següent per veure si el valor obtingut és un màxim, mínim o un punt de sella. x + f (x)
El cas positiu no té solució. Si analitzam el cas negatiu, ens surt x = x+, d on x =. A continuació fem la taula següent per veure si el valor obtingut és un màxim, mínim o un punt de sella. x + f (x)
Institut d Educació Secundària. x b) A partir de la gràfica d aquesta funció, indica quin és el domini i el recorregut.
 Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques MS Àlgebra i uncions I Nom: Grup: ) Resol les següents equacions: a) 7+ 3+ c) 3 +
Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques MS Àlgebra i uncions I Nom: Grup: ) Resol les següents equacions: a) 7+ 3+ c) 3 +
MATEMÀTIQUES. DOSSIER DE RECUPERACIÓ MATEMÀTIQUES 2n ESO. GRUP:2E. Nom i Cognoms (alumne):... Nom professor:...
 zz Curs: Departament d Educació Generalitat de Catalunya MATEMÀTIQUES DOSSIER DE RECUPERACIÓ MATEMÀTIQUES 2n ESO. GRUP:2E CURS 20-20 INS.PUIG CASTELLAR DATA: Nom i Cognoms (alumne):... Nom professor:...
zz Curs: Departament d Educació Generalitat de Catalunya MATEMÀTIQUES DOSSIER DE RECUPERACIÓ MATEMÀTIQUES 2n ESO. GRUP:2E CURS 20-20 INS.PUIG CASTELLAR DATA: Nom i Cognoms (alumne):... Nom professor:...
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 30 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE Activitat 1 Completa la taula següent: Graus Minuts Segons 30º 30 x 60 = 1.800 1.800 x 60 = 108.000 45º 2.700 162.000 120º 7.200 432.000 270º 16.200 972.000
30 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE Activitat 1 Completa la taula següent: Graus Minuts Segons 30º 30 x 60 = 1.800 1.800 x 60 = 108.000 45º 2.700 162.000 120º 7.200 432.000 270º 16.200 972.000
Generalitat de Catalunya Departament d Ensenyament Institut Obert de Catalunya. Avaluació contínua. Cognoms. Centre: Trimestre: Tardor 11
 Generalitat de Catalunya Departament d Ensenyament Institut Obert de Catalunya valuació contínua Qualificació prova TOTL Cognoms una lletra majúscula a cada casella: Nom: Centre: Trimestre: Tardor 11 M4
Generalitat de Catalunya Departament d Ensenyament Institut Obert de Catalunya valuació contínua Qualificació prova TOTL Cognoms una lletra majúscula a cada casella: Nom: Centre: Trimestre: Tardor 11 M4
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 9 PAU 2006 Pautes de correcció
 Oficina d Organització de Proves d Accés a la Universitat Pàgina de 9 PAU 006 SÈRIE Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
Oficina d Organització de Proves d Accés a la Universitat Pàgina de 9 PAU 006 SÈRIE Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
10 Àlgebra vectorial. on 3, -2 i 4 són les projeccions en els eixos x, y, y z respectivament.
 10 Àlgebra vectorial ÀLGEBR VECTORIL Índe P.1. P.. P.3. P.4. P.5. P.6. Vectors Suma i resta vectorial Producte d un escalar per un vector Vector unitari Producte escalar Producte vectorial P.1. Vectors
10 Àlgebra vectorial ÀLGEBR VECTORIL Índe P.1. P.. P.3. P.4. P.5. P.6. Vectors Suma i resta vectorial Producte d un escalar per un vector Vector unitari Producte escalar Producte vectorial P.1. Vectors
Institut d Educació Secundària Funcions IV i estadística d'una variable
 Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques 1MS Funcions IV i estadística d'una variable Nom: Grup: = a) Trobeu el domini i els
Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques 1MS Funcions IV i estadística d'una variable Nom: Grup: = a) Trobeu el domini i els
Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS
 Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS 2.1. Divisió de polinomis. Podem fer la divisió entre dos monomis, sempre que m > n. Si hem de fer una divisió de dos polinomis, anirem calculant les divisions
Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS 2.1. Divisió de polinomis. Podem fer la divisió entre dos monomis, sempre que m > n. Si hem de fer una divisió de dos polinomis, anirem calculant les divisions
UNITAT DIDÀCTICA 10 L ÍMITS DE FUNCIONS. CONTINUÏTAT I BRANQUES INFINITES
 7 UNITAT DIDÀCTICA 0 Refleiona i resol Aproimacions successives El valor de la funció f () = + 5 0 per a = 5 no es pot obtenir directament perquè el denominador es fa zero. L obtindrem per aproimacions
7 UNITAT DIDÀCTICA 0 Refleiona i resol Aproimacions successives El valor de la funció f () = + 5 0 per a = 5 no es pot obtenir directament perquè el denominador es fa zero. L obtindrem per aproimacions
Prova d accés a la Universitat (2013) Matemàtiques II Model 1. (b) Suposant que a = 1, trobau totes les matrius X que satisfan AX + Id = A, on Id
 UIB Prova d accés a la Universitat () Matemàtiques II Model Contestau de manera clara i raonada una de les dues opcions proposades. Es disposa de 9 minuts. Cada qüestió es puntua sobre punts. La qualificació
UIB Prova d accés a la Universitat () Matemàtiques II Model Contestau de manera clara i raonada una de les dues opcions proposades. Es disposa de 9 minuts. Cada qüestió es puntua sobre punts. La qualificació
.../... Atenció l'examen continua a l'altra pàgina
 Generalitat de Catalunya Departament d Ensenyament Institut Jaume Balmes Departament de Matemàtiques 1r BATX MA 2n quadrimestral (Global del 2n BLOC) Nom i Cognoms: Grup: Data: Nota molt important: S han
Generalitat de Catalunya Departament d Ensenyament Institut Jaume Balmes Departament de Matemàtiques 1r BATX MA 2n quadrimestral (Global del 2n BLOC) Nom i Cognoms: Grup: Data: Nota molt important: S han
16 febrer 2016 Integrals exercicis. 3 Integrals
 I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 16 febrer 2016 Integrals exercicis 3 Integrals 28. Troba una funció primitiva de les següents funcions: () = 1/ () = 3 h() = 2 () = 4 () = cos () = sin () =
I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 16 febrer 2016 Integrals exercicis 3 Integrals 28. Troba una funció primitiva de les següents funcions: () = 1/ () = 3 h() = 2 () = 4 () = cos () = sin () =
Les funcions polinòmiques
 Les funcions polinòmiques Les funcions polinòmiques Una funció polinòmica és la que té per expressió un polinomi. En general, se solen estudiar segons el grau del polinomi: Les funcions afins Una funció
Les funcions polinòmiques Les funcions polinòmiques Una funció polinòmica és la que té per expressió un polinomi. En general, se solen estudiar segons el grau del polinomi: Les funcions afins Una funció
Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes. Nom i Cognoms: Grup: Data:
 Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques n BATX MA Eamen FINAL Nom i Cognoms: Grup: Data: -5-007 r BLOC: ) Trobeu els límits:
Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques n BATX MA Eamen FINAL Nom i Cognoms: Grup: Data: -5-007 r BLOC: ) Trobeu els límits:
Examen FINAL M2 FIB-UPC 11 de gener de 2017
 Examen FINAL M FIB-UPC 11 de gener de 017 1. (3 punts) Sigui {a n } la successió tal que: a 1 = 56 i a n+1 = a n per a tot n > 1. a) Proveu que 1 a n 56, per a tot n 1. b) Proveu que {a n } és decreixent.
Examen FINAL M FIB-UPC 11 de gener de 017 1. (3 punts) Sigui {a n } la successió tal que: a 1 = 56 i a n+1 = a n per a tot n > 1. a) Proveu que 1 a n 56, per a tot n 1. b) Proveu que {a n } és decreixent.
(1,2) (1,2) (1,3) (3,0) (0,3) (2,1) (3,0) (1,3) (1,3) (2,3) (3,1) (3,0) (0,3) (1,2) (1,3) (4,0) (3,1) (3,1) (1,2) (1,3)
 1. DISTRIBUCIONS BIDIMENSIONALS Distribucions bidimensionals Moltes vegades interessa estudiar dues variables alhora dels elements d una població o mostra. En aquests casos, es recopilen dues dades per
1. DISTRIBUCIONS BIDIMENSIONALS Distribucions bidimensionals Moltes vegades interessa estudiar dues variables alhora dels elements d una població o mostra. En aquests casos, es recopilen dues dades per
Unitat 1. Nombres reals.
 Unitat 1. Nombres reals. Conjunts numèrics: - N = Naturals - Z = Enters - Q = Racionals: Són els nombres que es poden expressar com a quocient de dos nombres enters. El conjunt dels nombres racionals,
Unitat 1. Nombres reals. Conjunts numèrics: - N = Naturals - Z = Enters - Q = Racionals: Són els nombres que es poden expressar com a quocient de dos nombres enters. El conjunt dels nombres racionals,
operacions inverses índex base Per a unificar ambdues operacions, es defineix la potència d'exponent fraccionari:
 Potències i arrels Potències i arrels Potència operacions inverses Arrel exponent índex 7 = 7 7 7 = 4 4 = 7 base Per a unificar ambdues operacions, es defineix la potència d'exponent fraccionari: base
Potències i arrels Potències i arrels Potència operacions inverses Arrel exponent índex 7 = 7 7 7 = 4 4 = 7 base Per a unificar ambdues operacions, es defineix la potència d'exponent fraccionari: base
DOSSIER ESTIU 2018 MATEMÀTIQUES
 DOSSIER ESTIU 2018 MATEMÀTIQUES ELS ALUMNES AMB L ASSIGNATURA SUSPESA HAN D ENTREGAR EL DOSSIER CORRECTAMENT PER PODER REALITZAR L EXAMEN DE SETEMBRE. Has de presentar el dossier en fulls apart. S han
DOSSIER ESTIU 2018 MATEMÀTIQUES ELS ALUMNES AMB L ASSIGNATURA SUSPESA HAN D ENTREGAR EL DOSSIER CORRECTAMENT PER PODER REALITZAR L EXAMEN DE SETEMBRE. Has de presentar el dossier en fulls apart. S han
Al ser un quocient, el denominador no pot ser 0 i al ser una arrel d index senars no hi ha problema Dom = R\{x 3 +3x 2-6x-8=0}= R\{-4, 2, -1}.
 Col legi Maristes Sants-Les Corts Departament de matemàtiques Codi Sol PsP..- Troba el domini de les següents funcions. d) f ( ) 6 És un quocient de polinomis Dom R\{ -6} R\{,}. f) f ( ) És un quocient
Col legi Maristes Sants-Les Corts Departament de matemàtiques Codi Sol PsP..- Troba el domini de les següents funcions. d) f ( ) 6 És un quocient de polinomis Dom R\{ -6} R\{,}. f) f ( ) És un quocient
Fraccions. Guió de treball de l alumne/a...del grup...
 Fraccions Guió de treball de l alumne/a...del grup... Fracció: parts de la unitat 1. Amb el GeoGebra obriu l arxiu MAfraccio.html, us trobareu dos punts lliscants que permeten seleccionar dos nombres naturals
Fraccions Guió de treball de l alumne/a...del grup... Fracció: parts de la unitat 1. Amb el GeoGebra obriu l arxiu MAfraccio.html, us trobareu dos punts lliscants que permeten seleccionar dos nombres naturals
Funcions polinòmiques
 9 Funcions polinòmiques Objectius En aquesta quinzena aprendreu a: Distingir entre els diferents tipus de funcions la que tingui com a gràfica una recta i treballar amb aquestes funcions. Determinar el
9 Funcions polinòmiques Objectius En aquesta quinzena aprendreu a: Distingir entre els diferents tipus de funcions la que tingui com a gràfica una recta i treballar amb aquestes funcions. Determinar el
Definir els límits d integració en dominis 3D (R 3 ) Càlcul 2 - Aula Lliure
 Definir els límits d integració en dominis 3D (R 3 ) Càlcul 2 - Aula Lliure Quim Primavera 2017 Introducció Estem a l espai (R 3 ) i els punts del domini tenen tres components: (x, y, z). El nostre domini
Definir els límits d integració en dominis 3D (R 3 ) Càlcul 2 - Aula Lliure Quim Primavera 2017 Introducció Estem a l espai (R 3 ) i els punts del domini tenen tres components: (x, y, z). El nostre domini
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 59 Activitat 1 Llegeix atentament el teorema de Tales. Creus que també és certa la proporció següent? Per què? AB CD A B C D El teorema de Tales diu: AB (A B
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 59 Activitat 1 Llegeix atentament el teorema de Tales. Creus que també és certa la proporció següent? Per què? AB CD A B C D El teorema de Tales diu: AB (A B
2.2 Continuïtat i representació de funcions
 I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 20 gener 2016 Continuïtat i representació de funcions exercicis 2.2 Continuïtat i representació de funcions 20. Calcula la derivada que s indica en cadascun
I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 20 gener 2016 Continuïtat i representació de funcions exercicis 2.2 Continuïtat i representació de funcions 20. Calcula la derivada que s indica en cadascun
PROBLEMES DE SELECTIVITAT - MATEMÀTIQUES I - SOLUCIONS
 Si a=, compatible indeterminat amb un grau de llibertat (una recta) Si a, compatible determinat (un punt) x+y-z=6 Per a positiu: 6a) No b) Es demostra (Bolzano) 7a) Si a=-, són paral lels Si a -, es tallen
Si a=, compatible indeterminat amb un grau de llibertat (una recta) Si a, compatible determinat (un punt) x+y-z=6 Per a positiu: 6a) No b) Es demostra (Bolzano) 7a) Si a=-, són paral lels Si a -, es tallen
f x té màxims o mínims relatius. 6.- Determina els intervals de creixement i decreixement, màxims i mínims de les funcions següents: x
 4- EXERCICIS REPRESENTACIÓ DE FUNCIONS: - Estudia els intervals de monotonia (crei/decrei) de: f - Estudia si la funció f - Determina si la funció 4 té màims o mínims relatius e f té punts on la funció
4- EXERCICIS REPRESENTACIÓ DE FUNCIONS: - Estudia els intervals de monotonia (crei/decrei) de: f - Estudia si la funció f - Determina si la funció 4 té màims o mínims relatius e f té punts on la funció
= 25 = 15 =3. FITXA 1: Nombres A.1. ESCRIU AMB XIFRES AQUESTS NOMBRES: A.2. ESCRIU EL NOM D'AQUESTES QUANTITATS: A.3. COMPLETA LA TAULA:
 FITXA 1: Nombres A.1. ESCRIU AMB XIFRES AQUESTS NOMBRES: a) Cent mil dos-cents deu. b) Un milió cent mil dos-cents. c) Mil milions vuitanta mil vuit-cents. d) Nou-cents trenta mil vuitanta. e) Tres mil
FITXA 1: Nombres A.1. ESCRIU AMB XIFRES AQUESTS NOMBRES: a) Cent mil dos-cents deu. b) Un milió cent mil dos-cents. c) Mil milions vuitanta mil vuit-cents. d) Nou-cents trenta mil vuitanta. e) Tres mil
x + 2 y = 3 2 x y = 1 4 x + 3 y = k a) Afegiu-hi una equació lineal de manera que el sistema resultant sigui incompatible.
 1998 - Sèrie 3 - Qüestió 4 Discutiu el sistema d'equacions a x y + 2 z = (2 a) 2 x + 3 y z = 3a x + 2 y z = 2a segons els valors del paràmetre a. 1999 - Sèrie 1 - Qüestió 1 Resoleu el sistema següent per
1998 - Sèrie 3 - Qüestió 4 Discutiu el sistema d'equacions a x y + 2 z = (2 a) 2 x + 3 y z = 3a x + 2 y z = 2a segons els valors del paràmetre a. 1999 - Sèrie 1 - Qüestió 1 Resoleu el sistema següent per
VECTORS I RECTES AL PLA. Exercici 1 Tenint en compte quin és l'origen i quin és l'extrem, anomena els següents vectors: D
 VECTORS I RECTES AL PLA Un vector és un segment orientat que és determinat per dos punts, A i B, i l'ordre d'aquests. El primer dels punts s'anomena origen i el segons es denomina extrem, i s'escriu AB.
VECTORS I RECTES AL PLA Un vector és un segment orientat que és determinat per dos punts, A i B, i l'ordre d'aquests. El primer dels punts s'anomena origen i el segons es denomina extrem, i s'escriu AB.
Unitat 6. Introducció a les funcions
 Unitat 6. Introducció a les funcions Índex: 6.1. Representació gràfica de punts 6.2. Concepte de funció 6.3. Maneres d expressar una funció 6.4. Interpretació de funcions 6.5. Funcions de proporcionalitat
Unitat 6. Introducció a les funcions Índex: 6.1. Representació gràfica de punts 6.2. Concepte de funció 6.3. Maneres d expressar una funció 6.4. Interpretació de funcions 6.5. Funcions de proporcionalitat
TEMA 3 : Funció Exponencial i Logarítmica
 TEMA : Funció Eponencial i Logarítmica Activitats. Simplifiqueu: a) 4 b) 4 / c) ( ) 6 d) e) 5 / 5 f) ( ). Resol les equacions eponencials següents: a) = 9 j) b)5 c)0 d)7 e) f ) g)5 h)0 i) + 4 5 5 4 = 5
TEMA : Funció Eponencial i Logarítmica Activitats. Simplifiqueu: a) 4 b) 4 / c) ( ) 6 d) e) 5 / 5 f) ( ). Resol les equacions eponencials següents: a) = 9 j) b)5 c)0 d)7 e) f ) g)5 h)0 i) + 4 5 5 4 = 5
Equacions i sistemes de segon grau
 Equacions i sistemes de segon grau 3 Equacions de segon grau. Resolució. a) L àrea del pati d una escola és quadrada i fa 0,5 m. Per calcular el perímetre del pati seguei els passos següents: Escriu l
Equacions i sistemes de segon grau 3 Equacions de segon grau. Resolució. a) L àrea del pati d una escola és quadrada i fa 0,5 m. Per calcular el perímetre del pati seguei els passos següents: Escriu l
Matemàtiques Sèrie 1
 Proves d accés a cicles formatius de grau superior de formació professional inicial, d ensenyaments d arts plàstiques i disseny, i d ensenyaments esportius 013 Matemàtiques Sèrie 1 SOLUCIONS, CRITERIS
Proves d accés a cicles formatius de grau superior de formació professional inicial, d ensenyaments d arts plàstiques i disseny, i d ensenyaments esportius 013 Matemàtiques Sèrie 1 SOLUCIONS, CRITERIS
Proporcionalitat i percentatges
 Proporcionalitat i percentatges Proporcions... 2 Propietats de les proporcions... 2 Càlul del quart proporcional... 3 Proporcionalitat directa... 3 Proporcionalitat inversa... 5 El tant per cent... 6 Coneixement
Proporcionalitat i percentatges Proporcions... 2 Propietats de les proporcions... 2 Càlul del quart proporcional... 3 Proporcionalitat directa... 3 Proporcionalitat inversa... 5 El tant per cent... 6 Coneixement
