ÁLGEBRA LINEAL II Soluciones a la Práctica 4.1
|
|
|
- Carlos Vázquez Serrano
- hace 5 años
- Vistas:
Transcripción
1 ÁLGEBRA LINEAL II Soluciones a la Práctica 4.1 Cónicas (Curso ) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo y con respecto a una referencia rectangular se considera la cónica de ecuación: x 4xy + y 6x + y = 0 Calcular la ecuación de las rectas tangentes a la cónica que pasan por el punto ( 1, 3). La matriz asociada a la cónica y la de términos cuadráticos son respectivamente: A = , T = ( 1 1 ). Calculamos la recta polar del punto ( 1, 3): ( 1, 3, 1)A(x, y, 1) t = 0 x = 0 El corte de esta recta con la cónica son los puntos de tangencia de las rectas buscadas: y + y = 0 y = ó y = 0. Los puntos de tangencia son (0, 0) y (0, ). Las rectas tangentes son las polares de dichos puntos: (0, 0, 1)A(x, y, 1) t = 0 3x + y = 0, y (0,, 1)A(x, y, 1) t = 0 x y = 0.. Dada la cónica la ecuación de x + y + xy 4y = 0 respecto a una referencia rectangular, calcular centro, direcciones asintóticas, asíntotas, diámetros, ejes, vértices. Escribimos la matriz A asociada a la cónica y T de términos cuadráticos son: A = , T = ( ). i) Centro: (a, b, 1)A = (0, 0, h) a + b = 0, a + b = 0. El sistema no es compatible y por tanto no tiene centro (de hecho es una parábola). ii) Direcciones asintóticas. Son los puntos del infinito de la cónica. Basta tomar t = 0 en la ecuación homogénea de la misma: (x, y, 0)A(x, y, 0) t = 0 x + xy + y = 0 (x + y) = 0 x = y.
2 Hay una única dirección asíntotica dada por el vector (1, 1). iii) Asíntotas. Son las rectas tangentes en los puntos del infinito. En nuestro caso en (1, 1, 0): (1, 1, 0)A(x, y, 1) t = 0 = 0. Por tanto NO tien asíntotas (se trata de una parábola). iv) Diámetros. Los diámetros son las rectas polares de puntos del infinito: (a, b, 0)A(x, y, 1) y = 0 (a + b)x + (a + b)y b = 0. Es decir son todas las rectas paralelas a la recta x + y = 0. v) Ejes y vértices. Los ejes son las rectas polares de los autovectores de T asociados a autovalores no nulos. Los autvalores de T verifican: T λid = 0 λ(λ ) = 0. Por tanto el único autovalor no nulo es λ =. Calculemos los autovectores de T asociados a : x 0 (T Id) = x y = 0 S y 0 = L(1, 1). La recta polar del autovector asociado al autovalor no nulo es y por tanto el eje es: (1, 1, 0)A(x, y, 1) t = 0 x + y = 0 x + y 1 = 0. Intersecamos el eje con la cónica y obtenemos el vértice: 0 = x + y + xy 4y 0 = x + y 1 (x, y) = ( 3 4, 1 4 ). 3. Se considera la cónica dada por la ecuación: 3y 4xy + 1x 14y + 19 = 0 a) Hallar las asíntotas. La matriz asociada y de términos cuadráticos son respectivamente: A = , T = ( 0 3 Calculamos las direcciones asintóticas. Son los vectores (x, y) cumpliendo: ). (x, y)t (x, y) t = 0 3y 4xy = 0 y(3y 4x) = 0. Obtenemos las direcciones dadas por los vectores (1, 0) y (3, 4). Las asíntotas son sus rectas polares: (1, 0, 0)A(x, y, 1) t = 0 y + 6 = 0 y = 3 (3, 4, 0)A(x, y, 1) t = 0 8x + 6y 10 = 0 4x 3y + 5 = 0
3 c) Calcular las tangentes exteriores a la cónica pasando por el punto (0, 3). Calculamos la recta polar del punto dado. Esta corta a la cónica en los puntos de tangencias de las tangentes pedidas. Luego uniremos esos puntos de cortes con el punto inicial. La recta polar es: Cortamos con la ecuación de la hipérbola: (0, 3, 1)A(x, y, 1) t = 0 y = 0 y = x + 1x = 0 8x + 8 = 0 x = 1 Obtenemos un único punto de corte ( 1, 1). La recta pedida es la que une dicho punto con el (0, 3): x = y x y + 3 = 0. Observación: Aparece una sola tangente exterior, porque el punto dado está sobre la asíntota y = 3. La otra tangente exterior sería la propia asíntota Para las siguientes cónicas (1) 3x + 3y + xy 4x 4y = 0 () x + 3y 4x + 6y + 6 = 0 (3) 6y + 8xy 8x + 4y 8 = 0 (4) x + 4y 4xy + 4 = 0 (5) x y + xy + x y = 0 (6) x + y + 4x + 4 = 0 (7) x + y + xy x y = 0 (8) x + 4y 4xy + 6y = 0 (9) 4x + 4y + 8xy + 4x + 4y + 1 = 0, se pide: (a) Clasificarlas sin hallar las ecuaciones reducidas. Estudiamos los determinantes de la de términos cuadráticos T y la matriz asociada A en cada caso. (1) Se tiene que det(a) = 16, det(t ) = 8 y por tanto se trata de una elipse real. () det(t ) = 6 > 0 y det(a) = 6 > 0. Entonces dado que el término en x es positivo, se trata de una elipse imaginaria. (3) det(t ) = 16 < 0 y det(a) = 3 < 0. Se trata de una hipérbola. (4) det(t ) = 0 y det(a) = 0. Entonces se trata de dos rectas. Diagonalizando la matriz asociada queda: y vemos que se trata de dos rectas imaginarias paralelas (x + 4 = 0). (5) det(t ) = 9/4 < 0 y det(a) = 0. Se trata de dos rectas reales que se cortan. (6) det(t ) = 1 > 0 y det(a) = 0. Se trata de dos rectas imaginarias que se cortan. (7) det(t ) = 0 y det(a) = 0. Se trata de dos rectas. Diagonalizando la matriz asociada queda: 1 1 1/ 1 1 1/ / 1/ 0 0 7/3
4 por lo que se trata de dos rectas reales paralelas (x 7/3 = 0). (8) det(t ) = 0 y det(a) = 9 < 0. Se trata de una parábola. (9) det(t ) = 0, det(a) = 0. Se trata de dos rectas. Diagonalizando queda: una recta doble (4x = 0) (b) Dar las ecuaciones reducidas de las no degeneradas y las rectas que forman las degeneradas. 1 Las matrices asociada a la cónica y de términos cuadráticos son respectivamente: Se tiene que: A = y por tanto se trata de una elipse real., T = ( det(a) = 16, det(t ) = 8 Para hallar la ecuación reducida calculamos los autovalores de T : ). T λid = (3 λ) 1 = ( λ)(4 λ) de manera que los autovalores (las raíces del polinomio característico quedan): λ 1 =, λ = 4. La forma reducida es: con Queda: o en forma canónica: x + 4y + d = 0 d = det(a) ) = 16 =. λ 1 λ 8 x + 4y = 0 x + y 1 = 0 x 1 + y (1/ ) = 1. () Se trata de una elipse imaginaria. Como antes calculamos los autovalores de la matriz T de términos cuadráticos: λ λ = 0 λ = ó λ = 3 Para hallar el término independiente procedemos como en el apartado anterior: La ecuación reducida queda: λ 3 = det(a) det(t ) = 6 6 = 1 x + 3y + 1 = 0 x 1/ + y 1/3 = 1
5 (3) Ahora es una hipérbola. Pero el métdo es el mismo. Podemos simplificar primero la ecuación: 6y + 8xy 8x + 4y 8 = 0 3y + 4xy 4x + y 4 = 0 Calculamos los autovalores de T : 0 λ 3 λ = 0 λ = 4 ó λ = 1 Ahora calculamos el término independiente: La ecuación reducida queda: λ 3 = det(a) det(t ) = 4 4 = 1 x + 4y + 1 = 0 x y 1/4 = 1 Observación: En el caso de la hipérbola hacemos que el autovalor cuyo signo sea el mismo que el del determinante de la matriz asociada, vaya acompañando al término x. De esta forma los focos estarán situados sobre el eje O X. (4) Se trata de dos rectas imaginarias paralelas. En el apartado anterior hemos diagonalizado la matriz asociada de manera que obtenemos la ecuación: x + 4 = 0 (x ı)(x + ı) = 0 x ı = 0 ó x + ı = 0 Si nos fijamos en las operaciones elementales que hemos realizado vemos que la matriz de cambio de referencia es: x y = x y por tanto deshaciendo el cambio queda que las rectas tienen por ecuaciones: x y ı = 0 ó x y + ı = 0 (5) Se trata de dos rectas que se cortan. Como antes podemos diagonalizar la matriz asociada, hallar las rectas en la nueva referencia y luego deshacer el cambio. Pero usaremos otro método. Calculamos el centro, que corresponde a la intersección de ambas rectas. Luego calculamos la intersección de una recta arbritaria con la cónica y obtenemos un punto más de cada una de las rectas que la forman. Primero el centro: 1 1/ 1/ (x, y, 1) 1/ 1/ = (0, 0, t) 1/ 1/ 0 Vemos que es el punto ( 1/3, 1/3). { x + y/ + 1/ = 0 x/ y 1/ = 0 Ahora tomamos la recta x = 0 y la intersecamos con la cónica. Queda y y = 0 y = 0 ó y = 1/, x = y = 1/3 luego la intersección son los puntos (0, 0) y (0, 1/). La rectas buscadas son las que unen el centro con cada una de estos puntos: x 0 1/3 0 = y 0 1/3 0 x y = 0 x 0 1/3 0 = y + 1/ x + y + 1 = 0 1/3 + 1/
6 Podemos comprobar que la ecuación de la cónica es precisamente (x y)(x + y + 1) = 0. (6) Se trata de dos rectas imaginarias que se cortan. Podemos proceder como en el caso anterior. Simplemente hay que tener en cuenta que ahora trabajaremos con números complejos. Calculamos el centro: (x, y, 1) = (0, 0, t) 0 4 Intersecamos la recta x = 0 con la cónica: { x + = 0 y = 0 y + 4 = 0 (x, y) = (0, ı) ó (x, y) = (0, ı) Ahora calculamos las rectas que unen estos puntos con la cónica: x = y 0 x + ıy + = 0 ı 0 x = y 0 x ıy + = 0 ı 0 (x, y) = (, 0) De nuevo podemos ver que la ecuación de la cónica es (x + ıy + )(x ıy + ) = 0 (7) Se trata de dos rectas reales paralelas. Podemos actuar como en el caso (4). Pero usemos otro método. Aquí sabemos que hay una recta de centros cuya dirección es la de las rectas que buscamos: (x, y, 1) 1 1 1/ 1 1 1/ = (0, 0, t) x + y 1/ = 0 1/ 1/ Por tanto dichas rectas son de la forma x + y + a = 0. Calculamos la intersección de la cónica con una recta arbritaria, p.ej., x = 0. Obtenemos: y y = 0 y = ó y = 1 Por tanto las rectas contienen respectivamente a los puntos (0, ) y (0, 1). Son por tanto: x + y = 0 x + y + 1 = 0 Una vez más podemos comprobar que la ecuación de la cónica es (x + y )(x + y + 1) = 0. (8) Se trata de una parábola. Recordemos que, en su forma reducida ax + by = 0, la matriz asociada es: A = a b 0 b 0 donde a es el autovalor no nulo de la matriz T y det(a ) = det(a). Por tanto calculamos los autovalores de T : det(t λi) = 0 1 λ 4 λ = 0 λ = 0 ó λ = 5 y además: Por tanto la ecuación reducida queda: 9 = det(a) = det(a ) = ab = 5b b = ±3 5/5 5x y = 0
7 (9) Se trata de una recta doble. Necesariamente la ecuación es de la forma (ax + by + c) = 0 a x + b y + abxy + acx + acy + c = 0. Comparando con la ecuación que tenemos, deducimos que la recta es: x + y + 1 = 0 También podemos calcular la recta doble teniendo en cuenta que corresponde a recta de centros, es decir, viene dada por la ecuación: (x, y, 1)A = 0 Nos quedan tres ecuaciones dependientes. Tomando una sóla de ellas queda: 4x + 4y + = 0 x + y + 1 = 0 (c) En los casos en que existan, determinar: centros, puntos singulares, direcciones asintóticas, asíntotas, ejes, vértices, focos, directrices y excentricidad. Los puntos singulares sólo aparecen cuando la cónica está formada por dos rectas que se cortan (el punto singular es la intersección) o por dos rectas coincidentes (el lugar singular es la propia recta). En esos casos ya hemos hallado dichos puntos y los centros. (1) El centro es el punto (a, b) verificando: resolviendo obtenemos el punto (a, b, 1)A = (0, 0, h) 3a + b = 0, a + 3b = 0. ( 1, 1 ). Los ejes son las rectas polares de los autovectores de t asociados a autovalores no nulos. Hallamos los autovectores: - Asociados a λ 1 = : (T Id)(x, y) t = 0 (x, y) L{(1, 1)}. - Asociados a λ 4 = 4: (T 4Id)(x, y) t = 0 (x, y) L{(1, 1)}. Los ejes quedan: (1, 1, 0)A(x, y, 1) t = 0 x y = 0 x y = 0 (1, 1, 0)A(x, y, 1) t = 0 4x + 4y 4 = 0 x + y 1 = 0 Los vértices son la intersección de los ejes con la cónica. Intersecamos el primer eje: { x y = 0 3x + 3y + xy 4x 4y = 0 resolviendo obtenemos V 1 = (0, 0), V = (1, 1). Intersecamos el segundo eje: { x + y = 1 3x + 3y + xy 4x 4y = 0
8 resolviendo obtenemos V 3 = ( 1, 1 + ), V 4 = ( 1 + Los focos en la nueva referencia son (c, 0) y ( c, 0) con: c = a b = 1 1/ = /., 1 ). La ecuación de cambio de referencia es: ( x 1/ x = + y 1/ 1 1 y }{{}}{{} centro autovectores de T normalizados Cambiamos los focos de referencia mediante esa ecuación: 1/ + 1 ( ) 1 1 / 1 =. 1/ / + 1 ( ) 1 1 / 0 1/ = es decir los focos son los puntos (1, 0) y (0, 1). Finalmente la excentricidad es: c / a = = 1. ) () Vimos que se trata de una elipse imaginaria. El centro se calcula como en cualquier otra cónica: (a, b, 1) 0 { a = = (0, 0, t) 3 6 3b + 3 = 0 (a, b) = (1, 1) No tiene puntos singulares, ni asíntotas. Los ejes corresponden de nuevo a los conjugados de las direcciones de los autovectores de T : λ λ = 0 λ = ó λ = 3 Los autovectores son respectivamente (1, 0) y (0, 1). Por tanto los ejes quedan: (1, 0, 0)A(x, y, 1) t = 0 x = 0 (0, 1, 0)A(x, y, 1) t = 0 3y + 3 = 0 Lo demás no tiene sentido calcularlo, por ser una elipse imaginaria. (3) Se trata ahora de una hipérbola. Procedemos como antes. La ecuación reducida vimos que era: x + 4y + 1 = 0 x y 1/4 = 1 Calculamos los autovectores de T y el centro para escribir el cambio de referencia. Autovalor asociado a 1: ( 1 4 ) x = y 0 0 x + y = 0
9 El autovalor normalizado es (/ 5, 1/ 5). Autovalor asociado a 4: ( x y ) 4 = x y = 0 El autovalor normalizado es (1/ 5, / 5). El centro es: Ahora el cambio de referencia es: x = y (x, y, 1) = (0, 0, t) (x, y) = (, 1) Entonces, en las coordenadas (x, y ) sabemos que: - El centro es el (0, 0). ( / 5 1/ 5 1/ 5 / 5 ) x - Las direcciones asintóticas son (, 1) y (, 1) y las correspondientes asíntotas x +y = 0 y x y = 0. - Los ejes son el x = 0 e y = 0. - Los vértices (puntos de corte de la cónica con los ejes) el (1, 0) y ( 1, 0). - Para hallar los focos nos fijamos en que los vértices están sobre el eje O X. Por tanto los focos son (c, 0) y ( c, 0), donde c = a + b, a = 1 y b = 1/. Quedan ( 5/, 0) y ( 5/, 0). - Las directices son las rectas polares de los focos: x = a /c = / 5 y x = / 5. - La excentricidad es e = c a = 5. Para obtener los resultados en la referencia de partida utilizamos la ecuación de cambio de referencia. También podemos hallar algunas de ellas directamente usando la definición: - El centro es el (, 1) (ya lo hemos calculado antes). - Las direcciones asíntoticas corresponden a la intersección de la cónica con los puntos del infinito: (x, y, 0)A(x, y, 0) t = 0 6y + 8xy = 0 y = 0 ó 4x + 3y = 0 (1, 0) ó ( 3, 4) Las asíntotas corresponden a dichas direcciones pasando por el centro. Obtenemos y = 1 y 4x + 3y + 5 = 0 y - Los ejes corresponden a los conjugados de los autovectores: (, 1, 0) x y = 0 x + y 5 = (1,, 0) x y = 0 4x + 8y = Los vértices los hallamos con la ecuación de cambio de referencia. Queda: (/ 5, 1/ 5 + 1) y ( / 5, 1/ 5 + 1). - Para hallar los focos lo más cómodo es usar las fórmulas de cambio de referencia. Obtenemos: ( 1, 1/) y ( 3, 3/).
10 - Las directrices son las rectas polares de los focos: ( 1, 1/, 1) x y = 0 x + y/ 3/ = ( 3, 3/, 1) x y = 0 x y/ + 7/ = (4) Vimos que se trataba de dos rectas paralelas imaginarias. Sabemos que hay una recta de centros: (x, y, 1)A = (0, 0, h) x y = 0 No hay puntos singulares (reales) porque de hecho las rectas son imaginarias. Si los habría si trabajásemos con el plano afín imaginario. El eje corresponde al conjugado de la dirección del autovector asociado al autovalor no nulo de T : 1 λ 4 λ = 0 λ = 0 ó λ = 5 El autovalor asociado a 5 es el ( 1, ). Por tanto el eje es: ( 1,, 0)A(x, y, 1) t = 0 5x + 10y = 0 Todo lo demás no tiene sentido calcularlo en este caso. (5) Vimos que se tratan de dos rectas reales que se cortan. El centro ya lo hemos calculado ( 1/3, 1/3). El único puntos singular es precisamente la intersección de las dos rectas, es decir, el centro. Las asíntotas son las dos rectas. Los ejes corresponden a las bisectrices de dichas rectas. En cualquier caso los calculamos como siempre: tomando los conjugados de las direcciones que marcan los autovectores de T. Obtenemos que los autovalores son: y los correspondientes autovectores: y 1 10 ( 1, ) y (3 + 10, 1) Por tanto los ejes quedan: ( 1, , 0)A(x, y, 1) t = 0 x + (3 + 10)y = 0 3 (3 + 10, 1, 0)A(x, y, 1) t = 0 (3 + 10)x + y = 0 3 (6) Vimos que eran dos rectas imaginarias que se cortan: El centro ya lo hemos calculado: (, 0)
11 El único punto singular es el centro. Los ejes de nuevo son los conjugados de los autovectores de T. Dichos autovectores son (1, 0) y (0, 1) y por tanto los ejes: (1, 0, 0)A(x, y, 1) t = 0 x + = 0 (0, 1, 0)A(x, y, 1) t = 0 y = 0 (7) Se trata de dos rectas reales paralelas. Hay una recta de centros que ya hemos calculado: x + y 1/ = 0 No hay puntos singulares (propios). Las direcciones asintóticas son las de las rectas. El eje coincide en este caso con la recta de centros. (8) Se trata de una parábola. Vimos que la forma reducida era 5x y = 0 x = y En este caso (por ser una parábola) no tiene centro. Ahora, el vector traslación del cambio de referencia corresponde al vértice de la parábola. Por lo demás procedemos como en los casos anteriores: Autovalor asociado a 5: El autovalor normalizado es (1/ 5, / 5). Autovalor asociado a 0: 4 (x, y) = 0 x + y = 0 1 (x, y) El autovalor normalizado es (/ 5, 1/ 5). 1 = 0 x y = 0 4 Observación: Para que la parábola este orientada sobre el eje OY positivo comprobamos que hemos escogido la orientación correcta del autovalor asociado al 0. El signo del coeficiente de y en la expresión λ 1 x cy = 0 es: (/ 5, 1/ 5)(0, 3) t = 3/ 5 > 0 luego en lugar del vector (/ 5, 1/ 5) tomamos el vector ( / 5, 1/ 5). Ahora calculamos el eje. Corresponde al conjugado del autovector asociado al autovalor no nulo: (1,, 0) x y = 0 5x 10y 6 = El vértice es la intersección de este eje con la cónica: Resulta el punto (18/5, 6/5) Las fórmulas de cambio de referencia son: ( x 18/5 = y 6/5 10y y y 4y + 6y = ) + ( 1/ 5 / 5 / 5 1/ 5 ) x y
12 Entonces, en las coordenadas (x, y ) sabemos que: - No tiene centro. - La dirección asintótica es (1, 0); pero no hay asíntota. - El eje es el x = 0. - El vértice (puntos de corte de la cónica con los ejes) el (0, 0). - El foco es (0, p/), donde p = (3 5/5)/5. Queda (0, 3 5/50). - La directriz es la recta polar del foco: y = p/ = 3 5/50. - La excentricidad es 1. Para obtener los resultados en la referencia de partida utilizamos la ecuación de cambio de referencia. También podemos hallar algunas de ellas directamente usando la definición: - Las direcciones asíntoticas corresponde a la intersección de la cónica con los puntos del infinito: (x, y, 0)A(x, y, 0) t = 0 x + 4y 4xy = 0 (x y) = 0 (, 1) (en realidad sabemos que es la dirección correspondiente al autovector asociado al 0). - El eje ya lo calculamos: 5x 10y 6 = 0 - El vértice ya lo hemos calculado: (18/5, 6/5). - Para el foco lo más cómodo es usar las fórmulas de cambio de referencia. Obtenemos: (3/5, 3/10). - La directriz es la recta polar del foco: (3/5, 3/10, 1) x y = 0 1x + 6y 9 = (9) Se trata de una recta doble real. La recta de centros, los puntos singulares, asíntotas y el eje coinciden con la propia recta, que ya hemos caclulado antes. 6. Dada la curva de ecuación 3y + 4xy 4x 6y 1 = 0. (i) Clasificar la cónica y dar su ecuación reducida. Las matrices asociada y de términos cuadráticos de la cónica son respectivamente: Se tiene que A = 16, A = , T = ( 0 3 ). T = 4. Se trata por tanto de una hipérbola. Para hallar la ecuación reducida calculamos los autovalores de T : T λid = 0 λ 3λ 4 = 0 λ = 1 ó λ = 4. Dado que A > 0 tomamos como primer autovalores el positivo: λ 1 = 4, λ = 1.
13 La ecuación reducida queda: Es decir: (ii) Hallar el punto cuya recta polar es x 1 = 0. 4x y + d = 0, d = A λ 1 λ = 4. 4x y 4 = 0 x 1 y 4 = 1. Sea (a, b) el polo de la recta polar dada. Sabemos que: Operando: Deducimos que: (a, b, 1)A(x, y, 1) t equivale a a la recta x 1 = 0. (b )x + (a + 3b 3)y + ( a 3b 1) = 0 equivale a a la recta x 1 = 0. Resolviendo el sistema resulta: (iii) Hallar los focos. a + 3b 3 = 0, b 1 = (a, b) = ( 3, 3). a 3b 1. 1 De la ecuación reducida obtenida en el apartado 1 sabemos (con la notación usual) que a = 1, b = 4. Por tanto: c = a + b = 5, y los focos en la nueva referencia son: F 1 = ( 5, 0) R, F = ( 5, 0) R. Resta pasarlos a la referencia de partida; para ello calculamos las fórmulas de cambio de referencia. El centro es el punto (a, b) verificando: (a, b, 1)A = (0, 0, h) b = 0, a + 3b 3 = 0 (a, b) = (0, 1). Calculamos loa autovectores de T. Asociados a λ 1 = 4: x 0 (T 4Id) = x y = 0 (x, y) L{(1, )} y 0 Asociados a λ = 1: (T + Id) x = y 0 0 x + y = 0 (x, y) L{(, 1)} Los autovectores normalizados resultan: (1, ) (1, ) = 1 (1, ), 5 (, 1) (, 1) = 1 (, 1). 5 Y en definitiva la ecuación de cambio de referencia: x 0 = x y y. Cambiamos los focos de referencia: ( ) ( ) ± 5 = 0 0 ± 1 1. Los focos resultan por tanto: F 1 = (1, 3), F = ( 1, 1).
14 7. Sea A = (1, 1) y la cónica C de ecuación: 4x + y = 8 (i) Calcular los focos, la excentricidad y las directrices de C. Dividiendo la ecuación por 8 obtenemos directamente su la forma reducida: x + y x = 1 8 ( ) + y ( ) = 1. Se trata de una elipse de semiradio mayor a = y semiradio menor b =. Hay que observar también que el eje focal es el eje OY ya que el denominador del término y en la forma reducida es mayor que el del término x. Los focos tiene por tanto coordenadas (0, c) y (0, c) con Es decir F = (0, 6) y F = (0, 6). c = a b = 8 = 6. Las directrices son las rectas polares de los focos. La matriz asociada a la cónica es: B = Por tanto las directrices quedan: (0, 6, 1)B(x, y, 1) t = 0 6y 8 = 0 y La excentricidad es: (0, 6, 1)B(x, y, 1) t = 0 6y 8 = 0. e = c 6 48 a = = = = (ii) Calcular las tangentes a la cónica que pasan por el punto (, 0). Calcularemos la recta polar r P del punto P = (, 0). Las rectas tangentes son las que unen los puntos de corte de la rectar polar y la cónica con el punto P. La recta polar de P es: (, 0, 1)B(x, y, 1) t = 0 8x 8 = 0 x = 1. Cortamos tal recta con la cónica resolviendo el sistema: { x = 1 Queda: 4x + y = y = 8 y = ± 4 y así r p C = {N, M} con M = (1, ) y N = (1, ). Las tangentes pedidas son la recta P M: x 1 = y 0 0 x + y 4 = 0
15 y la recta P N: x 1 = y 0 0 x y 4 = 0 (iii) Hallar la ecuación implícita del lugar geométrico de puntos simétricos de A respecto los puntos de la cónica C. Qué tipo de curva se forma?. Hallar su centro. Sea A = (x 0, y 0 ) un punto simétrico de A respecto de un punto de la cónica. Entonces el punto medio de A y A : A + A ( x0 + 1 =, y ) debe de yacer en la cónica y por tanto satisfacer su ecuación: 4 (x 0 + 1) 4 + (y 0 + 1) 4 = 8. Simplificando queda: 4x 0 + y 0 + 8x 0 + y 0 7 = 0, que es la ecuación del lugar geométrico pedido. Se trata de nuevo de una cónica. Sus matrices asociadas y cuadrática son respectivamente: A = , T 4 0 = Se cumple que det(a) = 14 y det(t ) = 4 > 0. Por tanto es una elipse. Su centro es el punto (p, q) verificando: (p, q, 1)A = (0, 0, h) 4p + 4 = 0, q + 1 = 0. Deducimos que el centro es el punto (p, q) = ( 1, 1).
16 8. Sea la cónica de ecuación: x 4xy + y x y + 1 = 0. (i) Clasificar la cónica y hallar su ecuación reducida. La matriz asociada a la cónica A y de términos cuadráticos T son respectivamente: 1 1 A = , T = Se tiene que det(a) = 9 < 0 y det(t ) = 3 < 0 y por tanto la cónica es una hipérbola. Su ecuación reducida es de la forma: λ 1 x + λ y + c = 0, c = det(a) λ 1 λ = det(a) det(t ), siendo λ 1, λ los autovalores de T. Los calcuamos como raíces del polinomio característico: T λid = 0 (1 λ) ( ) = 0 (3 λ)( 1 λ) = 0. Obtenemos λ 1 = 3 y λ = 1; la ecuación reducida queda: 3x y + 3 = 0. (ii) Hallar los ejes y las asíntotas (si existen). Los ejes son las rectas polares de los autovectores asociados a autovalores de T no nulos. Calculemos tales autovectores. Asociados a λ 1 = 3: Asociados a λ = 1: (T 3Id)(x, y) t = (0, 0) t x y = 0 (x, y) L{(1, 1)}. (T + Id)(x, y) t = (0, 0) t x y = 0 (x, y) L{(1, 1)}. Los ejes serán: (1, 1, 0)A x y = 0 x y = 0. 1 (1, 1, 0)A x y 1 = 0 x + y + = 0. Las asíntotas son las rectas polares de las direcciones asintóticas. Estas corresponden a los puntos del infinito de la cónica: (p, q, 0)A(p, q, 0) t = 0 p 4pq + q = 0. Resolviendo queda: Las asíntotas serán: (p, q) L{( 3, 1)} ó (p, q) L{( + 3, 1)}. ( 3, 1, 0)A x y = 0 3x + ( 3 + 3)y = 0 x + ( 3)y = 0. 1 ( + 3, 1, 0)A x y = 0 3x + ( 3 3)y 3 3 = 0 x ( + 3)y 3 1 = 0. 1
17 (iii) Calcular la excentricidad de la cónica. La excentricidad de una hipérbola es: e = c a siendo c = a + b, a la distancia del vértice al centro. ecuación reducida de la hipérbola como: Para hallar tales valores reescribimos la 3x y + 3 = 0 y 3 x 1 = 1, de manera que a = 3, b = 1 y c = a + b =. La excentricidad resulta: e = 3 = Se considera la familia de cónicas dependiente del parámetro k R: x + 4y kxy + 6x + ky = 0 a) Clasificar las cónicas en función de k. Las matrices asociada a la cónica A y de términos cuadráticos T son: A = k 4 k 1 k 3 3 k 0 Clasificaremos en función de los signos de A y T. Tenemos que:, T = ( 1 k k 4 A = 7k 36, T = 4 k. Dado que k 0 se tiene que A = 7k 36 < 0 para cualquier valor de k. Por otra parte T = 4 k = 0 si k = ±. Distinguimos entonces los siguiente casos: - Si k < entonces T < 0 y A < 0. Se trata de una hipérbola. - Si k = entonces T = 0 y A < 0. Se trata de una parábola. - Si < k < entonces T > 0 y A < 0. Se trata de una elipse real. - Si k = entonces T = 0 y A < 0. Se trata de una parábola. - Si k > entonces T < 0 y A < 0. Se trata de una hipérbola. b) Para k = hallar la ecucación reducida, la excentricidad y la distancia de un vértice a un foco. Hemos visto que para k = se trata de una parábola. La excentricidad es por tanto e = 1. Para hallar la ecuación reducida comenzamos calculando los autovalores de T : La ecuación reducida es de la forma: ). T λid = 0 λ 5λ = 0 λ = 5 ó λ = 0. 5x cy = 0,
18 A = 8 5 λ 1 con c = 5. Resulta: 5x 16 5 y = 0. 5 O equivalentemente: x = y El parámetro p es p = 8 5. En una parábola la distancia del vértice al foco es p/ es decir: c) Hallar los valores de k para los cuales la recta x = 0 es tangente a la cónica. Para que la recta x = 0 sea tangente a la cónica el sistema formado por la recta y la cónica debe de tener una única solución doble. Resolvemos: { 0 = x Susituyendo la primera ecuación en la segunda: 0 = x + 4y kxy + 6x + ky 4y + ky = 0. Para que la ecuación tenga una única solución doble ha de cumplirse que el discriminante sea nulo: (k) = 0 k = Se considera la familia de cónicas que depende del parámetro m: x + m y + xy + x + my + m = 0. (i) Clasificar las cónicas en función de m. La matriz asociada y de términos cuadráticos de la cónica son respectivamente: A = m m 1 1, T = 1 m 1 m m. Para clasificar estudiamos los signos de det(a) y det(t ). En particular nos fijamos cuando se anulan; serán los puntos límite de los posibles cambios de signos. Se tiene que: det(t ) = m 1 = (m 1)(m + 1) det(a) = det m 1 m 1 = (m 1)det m = m (m 1) 0 m 1 m 1 0 m 1 m 1 Por tanto estudiamos los siguientes casos: det(t ) det(a) Tipo de cónica m < 1 > 0 < 0 Elipse real m = 1 = 0 < 0 Parábola 1 < m < 0 < 0 < 0 Hipérbola m = 0 < 0 = 0 Rectas reales que se cortan 0 < m < 1 < 0 < 0 Hipérbola m = 1 = 0 = 0 Rectas paralelas reales o complejas o recta doble m > 1 > 0 > 0 Elipse imaginaria
19 En el caso m = 1 debemos de distinguir exactamente de que tipo de cónica se trata de las tres indicadas. La matriz A es: A = Vemos que rango(a) = y por tanto se trata de rectas paralelas reales o complejas; para distinguirlas intersecamos la cónica con una recta arbitraria; por ejemplo con x = 0: y + y + = 0 y = 1 ± 1 IR. Las soluciones son complejas y por tanto se trata de dos rectas paralelas imaginarias. (ii) Para m = 1 hallar la ecuación reducida y el/los foco/focos. Para m = 1 se trata de una parábola. La ecuación reducida es de la forma: λx cy = 0. donde λ es el autovalor no nulo de T y λc = det(a). Calculamos los autovalores de T : det(t λid) = 0 El autovalor no nulo es λ = y así: La ecuación reducida queda: 1 λ 1 = λ(λ ). 1 1 λ det(a) c = =. λ x y = 0 x = y. El foco, en la nueva referencia es el punto (0, 4). Para pasarlo a la referencia de partida necesitamos las ecuaciones de cambio de referencia. Comenzamos calculando los autovectores de T : x 0 (T λid) = x + y = 0 (x, y) L{(1, 1)}. y 0 T x = y 0 0 x + y = 0 (x, y) L{(1, 1)}. Los autovectores son (1, 1) y (1, 1); el segundo, el asociado al cero, lo escogemos para que la parábola quede orientada en el semiplano positivo en su forma reducida. Debe de cumplirse que: En nuestro caso: v (1, 1) ( a13 a 3 ) < 0. 1 > 0. 1 Luego escogemos el ( 1, 1). Definitivamente los autovectores normalizados quedan: { 1 1 (1, 1), ( 1, 1)}.
20 Ahora calculamos el vértice; es la intersección del eje con la cónica. El eje es la recta polar del autovector de T asociado al autovalor no nulo: Intersecamos el eje con la cónica: (1, 1, 0)A x y 1 0 = x + y = 0 x + y = 0. 0 = x + y + xy + x y Despejando y en la primera y sustiyendo en la segunda queda: 4x = 0 x = 1/. El vértice es el punto (1/, 1/). Las ecuaciones de cambio de referencia son: Y finalmente el foco queda: x = y x = y 1/ + 1 1/ 1/ + 1 1/ ( 1 1 x 1 1 ( y ). /4 ) = ( 1/4 1/4 ). 11. Hallar las ecuaciones de (a) la cónica que pasa por A(, 0), B(0, 1), C(1, 1), D( 1, 0) y E(1, 1). Tomamos el haz de cónicas formado a partir de las cónicas degeneradas que forman las rectas AB CD y AD BC. Todas las cónicas de dicho haz pasan por estos cuatro puntos. Después basta imponer al haz que pase también por el punto E: El haz de cónicas es: Imponemos que pase el punto E, y queda: AB = x 0 0 = y + 1 x y = CD = x = y x y + 1 = 0 1 AD = y = 0 BC = x = y 1 x y 1 = α(x y )(x y + 1) + βy(x y 1) = 0 4α β = 0 podemos tomar β = y α = 1. La cónica buscada es: (x y )(x y + 1) + y(x y 1) = 0 x + y x = 0 (b) la cónica cuyo centro es C(1, 1) y tal que y = 1 es un eje y la polar del punto (, ) es la recta x + y 3 = 0.
21 Dado que un eje es y = 1, sabemos que un autovector de la matriz T asociada tiene la dirección (1, 0) y el otro (perpendicular) la (0, 1). Por tanto la matriz de la cónica es de la forma: Por ser el centro el (1, 1) se verifica: A = a 0 d 0 b e d e c (1, 1, 1)A = (0, 0, t) { a + d = 0 d = a b + e = 0 e = b Ahora imponemos la condición de polaridad: (,, 1)A = (1, 1, 3) a + d = 1 b + e = 1 d + e c = 3 Resolviendo el sistema formado por las 5 ecuaciones queda: Es decir la cónica es: a = 1; b = 1; c = 1; d = 1; e = 1 x + y x y + 1 = 0 (x 1) + (y 1) = 1 (la circunferencia de centro (1, 1) y radio 1). (c) la ecuación de una cónica que tiene por focos los puntos (0, 0) y (1, ) y por excentricidad e = 5. Dado que la excentricidad es mayor que 1 se trata de una hipérbola. Teniendo en cuenta su caracterización como lugar geométrico de puntos cuya diferencia de distancias a los focos es constante, la ecuación de la misma es de la forma: (x 0) + (y 0) (x 1) + (y ) = a, ( ) Además sabemos que: e = c/a, donde c es la distancia del centro al foco; equivalentemente c es la mitad de la distancia entre los dos focos: c = 1 5 (1 0) + ( 0) =. Susituyendo en ( ) obtenemos: Y ahora reemplazando en ( ): 5 = 5 a ( ) a = 1. x + y (x 1) + (y ) = 1. Solo resta operar: x + y 1 = (x 1) + (y ). Elevando al cuadrado: x + y + 1 x + y = x x y 4y + 4. Simplificando: x + y = x + y.
22 Elevando de nuevo al cuadrado: x + 4y + 4 4x 8y + 4xy = x + y. Y finalmente obtenemos: 3y + 4xy 4x 8y + 4 = 0. (d) Hallar la ecuación de una hipérbola que pasa por el origen, tiene por asíntota la recta x y 1 = 0 y uno de sus ejes es la recta x y 1 = 0. El eje es un eje de simetría de la cónica. Por tanto podemos calcular la otra asíntota como simétrica de la dada. Una vez que tengamos las dos asíntotas formaremos el haz de cónicas y obtendremos la cónica buscada imponiendo que pase por el origen. Para hallar la simétrica de la asíntota tenemos en cuenta que uno de sus puntos es la intersección de la misma y el eje de simetría: } x y 1 = 0 x y 1 = 0 (x, y) = (1, 0). Para hallar otro punto de la recta buscada, hallamos el simétrico de un punto cualquiera de la asíntota dada. Tomamos por ejemplo el punto A = ( 1, 1) que verifica la ecuación x y 1 = 0. Su simétrico A = (a, b) cumple: - El punto medio de A, A pertenece al eje de simetría: A + A = ( a 1, b 1 ) pertenece a la recta x y 1 = 0, de donde, a b =. - El vector AA es perpendicular al eje de simetría, de donde: (a + 1, b + 1)(1, 1) = 0 a + b =. Obtenemos A = (a, b) = (0, ). La asíntota buscada es la recta que une los puntos (1, 0) y (0, ): El haz de cónicas conocidas las dos asíntotas es: x 1 y = 1 x y = 0. (x y 1)(x y ) + c = 0. Imponiendo que pase por el origen hallamos el valor de c: ( 1)( ) + c = 0 c =. La cónica pedida queda: operando: (x y 1)(x y ) = 0, x 5xy + y 4x + 5y = 0. (e) una parábola que pasa por los puntos P = (0, ), Q = (1, 0) y tal que la recta que une P y Q es la recta polar del punto (0, 0).
23 Método I: Recordemos que la recta polar de un punto O respecto de una cónica une los puntos de tangencica de las tangentes exteriores a la cónica pasando por O. En nuestro caso esto quiere decir que las rectas uniendo O = (0, 0) con P y Q respectivamente, son tangentes a la parábola. Utilizaremos el haz de cónicas conocidas dos tangentes y los puntos de tangencia. La recta OP tiene por ecuación x = 0; la recta OQ tiene por ecuación y = 0; la recta P Q es: x = y 0 x + y = 0. El haz queda: λxy + (x + y ) = 0 4x + y + (4 + λ)xy 8x 4y + 4 = 0. Para hallar el parámetro imponemos que la cónica sea de tipo parabólico, es decir, que el determinante de la matriz de términos cuadráticos sea nulo. Obtenemos: 4 (4 + λ)/ (4 + λ)/ 1 = 0 λ 4 + λ = 0. - λ = 0, pero entonces sustituyendo en el haz nos quedaría sólo la recta doble (x + y ) = 0 que no es una parábola. - λ = 8. Entonces nos queda la ecuación: La matriz asociada es: 4x + y 4xy 8x 4y + 4 = Su determinante es no nulo, por tanto es una cónica no degenerada y en definitiva la parábola buscada. Método II: La matriz asociada a la cónica buscada es: A = a b c b d e. c e f Imponemos las condiciones del enunciado. Como los puntos P y Q pertenencen a la cónica tenemos las ecuaciones: (0,, 1)A(0,, 1) t = 0 4d + 4e + f = 0. (1, 0, 1)A(1, 0, 1) t = 0 a + c + f = 0. (I) Además la recta polar del punto (0, 0) es la recta P Q, x + y = 0: (0, 0, 1)A(x, y, 1) t = 0 x + y = 0 cx + ey + f x + y = 0. Deducimos que: Susituyendo en (I) nos queda: c = e 1 = f d = e/, c = e, f = e. a = e.
24 Y la matriz asociada: e b e A = b e/ e. e e e Imponemos que el determinante de la matriz de términos cuadráticos sea nulo para que la cónica sea de tipo parabólico: e b b e/ = 0 e = b. Tenemos dos soluciones: e = b ó e = b. Si suponemos e = b =, la matriz asociada queda: con det(a) 0. Es la parábola buscada: A = x y + 4xy + 8x + 4y 4 = 0 4x + y 4xy 8x 4y + 4 = 0. Si suponemos e = b =, la matriz asociada queda: 4 4 A = con det(a) = 0. Es degenerada y no es una parábola. (f) una cónica que tiene por eje la recta x y = 0, es tangente a x = 3 y pasa por los puntos (3, 1) y (4, 1). Dado que es tangente a x = 3 y pasa por A = (3, 1) (que cumple la ecuación de esa recta) el punto de tangencia es precisamente A. Entonces: - Usando el eje y por simetría obtendremos una segunda tangente y un segundo punto de tangencia. - Construiremos el haz de cónicas conocidas dos tangentes y los puntos de tangencia. - Impondremos que la cónica buscada pase por (, 1). El simétrico del punto A(3, 1) respecto de la recta x y = 0 es un punto A (a, b) tal que: - El vector AA = (a 3, b 1) es perpendicular al eje de simetría o equivalentemente paralelo a su vector normal: a 3 1 = b 1 - El punto medio de A y A pertenece al eje x y = 0: 3 + a b + 1 a + b 7 = 0. = 0 a b + 1 = 0. Resolviendo el sistema formado por ambas ecuaciones se obtiene A = ( 13 5, 9 5 ). La intersección B de la tangente dada con el eje es: { 0 = x y 0 = x 3 B = (x, y) = (3, 3 ).
25 El simétrico de la tangente es la recta que une A y B: x = y x + 4y 15 = 0. Formamos el haz descrito anteriormente. La primera cónica es el producto de la dos tangentes: (x 3)(3x + 4y 15) = 0 La segunda es la recta doble que une los puntos de tangencia (3, 1) y (13/5, 9/5): x = y x + y 7 = 0. El haz resulta: λ(x 3)(3x + 4y 15) + (x + y 7) = 0 Imponemos que pase por el punto (4, 1): λ(4 4)( ) + ( ) = 0 λ = 4. La cónica pedida tiene por ecuación: (x + y 7) 4(x 3)(3x + 4y 15) = 0 Simplificando: 8x + 1xy y 34y 68x = 0. (g) una cónica con vértice en el punto V (1, 1), que pasa por el punto (, 4) y tal que las rectas x + y = 0 y x = son tangentes a ella. La recta x + y = 0 pasa por el vértice V (1, 1) y por tanto es tangente a la cónica en ese punto. La perpendicular a ella es un eje de la cónica. Nos permitirá calcular el simétrico de la otra tangente. Tendremos dos tangentes y puntos de tangencia; mediante un haz de cónicas e imponiendo que la cónica pedida pase por (1, 1) obtendremos la curva pedida. 1) Calculamos primero el eje. El vector normal de x + y = 0 es (1, 1). Por tanto el eje es la recta que pasa por V (1, 1) y tiene por vector director (1, 1): x 1 1 = y 1 1 x y = 0.
26 ) Calculamos el simétrico de la recta x = por la recta x y = 0. Para ello primero intersecamos las dos rectas: x =, x y = 0 (x, y) = (, ). Calculamos ahora el simétrico del punto P (, 4) por la recta x y = 0. Tal simétrico P (p, q) cumple: P + P Eje de simetría P P Eje De donde obtenemos: + p 4 + q = 0, (p, q 4) (1, 1) = 0 y resolviendo (p, q) = (4, ). La recta simétrica es la que une (, ) y (4, ), es decir, la recta y =. 3) Formamos el haz de cónicas conocidas dos tangentes y los puntos de tangencia x = tangente en (, 4) e y = tangente en (4, ). La recta que une los puntos de tangencia es: x + y = 6. El haz queda: λ(x )(y ) + (x + y 6) = 0 4) Finalmente imponemos que pase por el punto (1, 1): λ(1 )(1 ) + ( ) = 0 λ = 16. La cónica queda: Simplificando: (x + y 6) 16(x )(y ) = 0 x + y 14xy + 0x + 0y 8 = 0. (h) una elipse sabiendo que tiene uno de sus focos en el punto ( 4, ), el vértice más alejado del mismo es el punto (, 1) y la excentricidad vale 1/. Si denotamos por a, b, c respectivamente a las longitudes del semieje mayor, menor y distancia del foco al centro, de los datos dados deducimos que: a + c = d(f, V ), c a = e = 1, siendo F = ( 4, ) y V = (, 1). Operando obtenemos: y de ahí a = 5 y c = 5. d(f, V ) = ( 4 ) + ( ( 1)) = 3 5 El otro foco F está a distancia c sobre la recta que une F y V en la dirección Operando tenemos: F = F + F V F V c. F V = (, 1) ( 4, ) = (6, 3) y F V = 6 + ( 3) = 3 5. F V, es decir,
27 de donde: F = ( 4, ) + (6, 3) = (0, 0). Finalmente para obtener la ecuación de la elipse usamos su caracterización como lugar geométrico de puntos cuya suma de distancias a los focos es constante. Tal constante sabemos además que es a. La ecuación será entonces: (x ( 4)) + (y ) + x + y = 4 5. Simplificando queda: 16x + 19y + 4xy + 60x 30y 5 = 0. (1. puntos) (i) la parábola C tal que: la recta de ecuación x + y = 0 es la tangente a C en el vértice; C pasa por el origen de coordenadas; y la recta polar del punto (, 1) con respecto a C es paralela al eje OX. El autovector asociado al autovalor no nulo de la matriz T (parte cuadrática) de la parábola, tiene la misma dirección que la tangente en el vértice, es decir, (1, 1). Teniendo en cuenta que det(t ) = 0, salvo producto por escalar, deducimos que T es de la forma: ( 1 ) y la matriz A asociada: A = 1 1 d 1 1 e d e f Dado que el origen pertenece a la cónica, deducimos que f = 0. Aplicamos ahora que la recta polar en el punto (, 1) es paralela al eje OX. Significa que: (, 1, 1)A(x, y, 1) t es paralela a y = d = 0 d = 1 Tenemos que, la ecuación de la cónica es: x + y xy x ey = 0 (x y) x + ey = 0 Para calcular el coeficiente e, aplicamos que x + y es tangente a la parábola. Su intersección con la cónica debe de ser un único punto. El punto genérico de esta recta es (λ, λ). Sustituimos en la cónica: (λ ) λ + e( λ) = 0 4λ + ( e 10)λ + (4 + 4e) = 0 Para que haya solamente una solución el discriminante ha de ser cero: ( e 10) 16(4 + 4e) = 0 e = 3 La ecuación pedida es: x + y xy x + 6y = 0
28 1. Hallar la ecuación de una hipérbola con el centro en el punto C = (1, 1), un vértice V = (, ) y una asíntota paralela a la recta x y = 0. Seguiremos los siguientes pasos: i) El eje es la recta que une el centro y el vértice. ii) Una asíntota es la recta paralela a x y = 0 y pasando por el centro. iii) La otra asíntota es la simétrica de la anterior respecto al eje calculado. iv) Usaremos finalmente el haz de cónicas conocidas dos asíntotas e impondremos que la cónica buscada pasa por el vértice. i) Comenzamos calculando el eje, la recta que une C y V : x 1 1 = y 1 1 x y = 0. ii) Calculamos una asíntota como la paralela a x y = 0 pasando por (1, 1). Será de la forma: Imponiendo que pase por (1, 1) queda: Es decir la recta: x y + 1 = 0. x y + c = c = 0 c = 1. iii) La intersercción P del eje y la asíntota es el centro (1, 1). Tomamos un punto de la asíntota A = ( 1, 0) y calculamos su simétrico A = (a, b) respecto del eje. Deberá de cumplir: A + A eje ( a 1, b ) eje a 1 b = 0, y AA eje (a + 1, b) (1, 1) a + 1 = b. Resolviendo obtenemos: A = (a, b) = (0, 1). La segunda asíntota es la recta P A : x = y x y 1 = 0. iv) El haz de cónicas conocidas dos asíntotas es: (x y + 1)(x y 1) + λ = 0. Imponemos que pase por el vértice V = (, ): ( + 1)( 1) + λ = 0 λ = 1. La ecuación queda: (x y + 1)(x y 1) + 1 = 0 x 5xy + y + x + y = 0.
29 13. En un haz de cónicas generado por dos cónicas que no son de tipo parábolico, cuál es el máximo número de parábolas que puede haber?. Un haz de cónicas se forma tomando combinaciones lineales de las ecuaciones de las cónicas generadoras: ((x, y, 1)A 1 (x, y, 1) t ) + λ((x, y, 1)A (x, y, 1) t ) = 0. (al usar un sólo parámetro omitimos una de las cónicas generadoras; pero ya sabemos que éstas no son una parábola). La condición para que sean parábolas es que el determinante de la matriz de términos cuadráticos sea nulo. Pero ese determinante al ser de orden dos y no anularse siempre (porque al menos hay una cónica que no es parábola), nos da una ecuación de grado uno o dos en la variable λ. Por tanto a lo sumo hay una o dos soluciones. El máximo número de parábolas que puede haber son dos. 14. Hallar la ecuación de una cónica que tiene por asíntota la recta x =, un vértice en el punto (1, 1) y la recta tangente en ese vértice es x + y = 0. Método I: Conocemos una asíntota y una recta tangente en un punto dado. Podemos usar el haz de cónicas en esas condiciones. Las dos cónicas que lo generan son: - La cónica formada por la asíntota y la tangente: (x )(x + y) - La cónica formada por la recta doble paralela a la asíntota pasando por el punto de tangencia: Una paralela a la asíntota es de la forma: x + k = 0. Imponemos que pase por el punto (1, 1): 1 + k = 0 k = 1. Por tanto la segunda cónica del haz es: (x 1) El haz nos queda: (x )(x + y) + λ(x 1) = 0 (1 + λ)x + xy (1 + λ)x y + λ = 0.
30 Finalmente tenemos en cuenta que uno de los ejes de la hipérbola es paralelo a la tangente en el vértice; el eje es la recta polar de su vector normal. Tal vector normal es el (1, 1). Su recta polar: (1 1 0) 1 + λ 1/ 1 + λ 1/ λ 1 λ Ha de ser paralelo al x + y = 0, y por tanto: x y 1 = (λ + 1/)x y/ + ( + λ) = 0 La cónica buscada queda: λ + 1/ 1 = 1/ 1 xy y 1 = 0. λ = 1. Método II: El eje es perpendicular a la tangente en el vértice. Por tanto es de la forma: x y + k = 0 y por pasar por (1, 1): 1 ( 1) + k = 0 k =. El eje tiene por ecuación x y = 0. Ahora el eje es un punto de simetría de la cónica; la otra asíntota es la simétrica de la dada respecto a tal eje. Para hallarla tenemos en cuenta: - Pasa por la intersección del eje y de la asíntota dada: x = 0 x y = 0 (x, y) = (, 0). - Dado P = (, 1) en la asíntota su simétrico P = (a, b) cumple: Obtenemos las ecuaciones: + a P + P eje, 1 + b Resolviendo el sistema queda a = 3, b = 0. P P eje. = 0, a + b 1 = 0. La asíntota buscada es la recta que une los puntos (, 0) y (3, 0), es decir, la recta y = 0. El haz de cónicas conocidas dos asíntotas es: y(x ) + λ = 0. Y finalmente imponemos que pase por el vértice (1, 1): 1(1 ) + λ = 0 λ = 1. La ćonica pedida queda: xy y 1 = 0.
31 15. Calcular las ecuaciones de todas las cónicas que tienen a la recta x = 0 por asíntota, un eje es la recta y x = 0 y un vértice sobre la recta x = 1. Hallamos el simétrico de la asíntota por el eje, que será la segunda asínotota de la cónica buscada. Para ello primero intersecamos el eje y la asíntota resolviendo el sistema que forman sus dos ecuaciones: x = 0, y x = 0 (x, y) = (0, 0). Ahora tomamos otro punto de la asíntota P = (0, 1) y hallamos su simétrico P = (a, b) respecto del eje. Se cumple: (0, 1) + (a, b) eje, ((a, b) (0, 1)) eje. De ahí obtenemos la ecuaciones: 1 + b Resolviendo obtenemos (a, b) = (4/5, 3/5). a = 0, a + b = 0. Por tanto la segunda asíntota es la recta que une (0, 0) y (4/5, 3/5): x 0 4/5 = y 0 3/5 0 3x 4y = 0. Formamos el haz de cónicas conocidas dos asíntotas: x(3x 4y) + λ = 0. Usamos ahora que un vértice está en la recta x = 1. Puede haber dos casos: 1) El vértice está en el eje dado. Entonces verifica las ecuaciones: y x = 0, x = 1 (x, y) = (1, ). Se trata por tanto del punto (1, ). Sustituyendo en el haz queda: 1(3 8) + λ = 0 λ = 5 y la cónica resulta: 3x 4xy + 5 = 0. ) El vértice está en el eje perpendicualar al dado. Tal eje pasa por el centro de la cónica que es la intersección del eje dado y de la asíntota, es decir, el punto (0, 0). Su vector director es el normal del eje conocido (, 1). Por tanto su ecuación es: x = y 1 x + y = 0. Intersecamos con x = 1: Sustituyendo en el haz queda: x + y = 0, x = 1 (x, y) = (1, 1/) 1(3 + ) + λ = 0 λ = 5 y la cónica resulta: 3x 4xy 5 = 0.
32 16. Hallar la ecuación de una cónica con un foco en el punto (0, 0), centro C = (1/, 1/) y excentricidad e = /. Como la excentricidad es menor que uno, se trata de una elipse. Teniendo en cuenta que ésta es simétrica respecto al centro podemos calcular el segundo foco. Si F 1 = (0, 0) entonces: F 1 + F = C F = C F 1 = (1, 1). Conocidos los dos focos usamos la caracterización geométrica de la elipse como lugar geométrico cuya suma de distancias a los focos es constante: d(p, F 1 ) + d(p, F ) = a. Para hallar a usamos la excentricidad: e = c a a = c e = d(c, F ) e = 1. La ecuación será entonces: (x 0) + (y 0) + (x 1) + (y 1) = 1. Operando: (x 1) + (y 1) = x + y. Elevando al cuadrado: x x y y + 1 = 4 + x + y 4 x + y x + y = x + y + 1 Finalmente elevando de nuevo al cuadrado y agrupando términos queda: 3x + 3y xy x y 1 = 0.
33 ÁLGEBRA LINEAL II Cónicas Problemas adicionales (Curso ) I. En el plano afín y con respecto a la referencia canónica se considera la cónica de ecuacin: Se pide: i)clasificar la cónica. x + y + 4xy + 3x + 3y + 1 = 0. La matriz asociada a la cónica y de términos cuadráticos son respectivamente: Se tiene: y por tanto es una hipérbola. ii) Hallar el centro y los ejes. El centro (a, b) cumple: Obtenemos las ecuaciones: A = 1 3/ 1 3/ 3/ 3/ 1 Resolviendo queda (a, b) = ( 1/, 1/)., T = ( 1 1 det(a) = 3/ > 0, det(t ) = 3 < 0 (a, b, 1)A = (0, 0, h). a + b + 3/ = 0, a + b + 3/ = 0 Los ejes son las rectas polares de los puntos del infinito determinados por los autovectores de T. Calculamos los autovalores: Los autovectores asociados son: ). det(t λid) = 0 λ = 3, ó λ = 1. (T 3Id) x = y 0 0 (x, y) L{(1, 1)}. y Los ejes quedan: y (T + Id) x = y 0 0 (x, y) L{( 1, 1)}. (1, 1, 0)A(x, y, 1) t = 0 x + y + 1 = 0 ( 1, 1, 0)A(x, y, 1) t = 0 x y = 0. iii)hallar la ecuación reducida y la ecuación de cambio de referencia. La ecuación reducida es de la forma: 3x y + d = 0,
34 con 3d = det(a) = 3/ de donde d = 1/. La ecuación queda: 3x y 1 = 0, o equivalentemente x ( 1/6) y ( 1/ ) = 1. La ecuación de cambio de referencia es: x = y ( 1/ 1/ ) x 1 1 y iv) Hallar la distancia entre ambos focos. La distancia focal es c con: c = a + b = = 3 es decir: /3. v) Hallar una paralela al eje focal que pase por el punto (, 0). El eje focal es, en este caso, el determinado por la recta polar del autovector asociado al autovalor positivo. Es decir: x y = 0. Una recta paralela al mismo es de la forma: Imponemos que base por (, 0): x y + c = c = 0 c =, y queda: x y = 0. II. Para cada número k R se define la cónica de ecuación: x kxy + y 1 = 0. (i) Clasificar la cónica en función de los valores de k. La matriz asociada a la cónica y de términos cuadráticos son respectivamente: A = 1 k 0 k k, T = k
35 Se tiene que: det(a) = (1 k ), det(t ) = 1 k. Por tanto det(t ) = 0 k = ±1. Distinguimos los casos: - Si k < 1, det(t ) < 0, det(a) > 0. Se trata de una hipérbola. - Si k = 1, det(t ) = 0, det(a) = 0. Se trata de un par de rectas paralelas, reales o imaginaria, o una recta doble. En particular la ecuación queda: x + xy + y 1 = 0 (x + y) 1 = 0 (x + y 1)(x + y + 1) = 0. Se trata por tanto de dos rectas paralelas reales. - Si 1 < k < 1, det(t ) > 0, det(a) < 0. Se trata de una elipse real. - Si k = 1, det(t ) = 0, det(a) = 0. Se trata de un par de rectas paralelas, reales o imaginarias, o una recta doble. En particular la ecuación queda: x xy + y 1 = 0 (x y) 1 = 0 (x y 1)(x y + 1) = 0. Se trata por tanto de dos rectas paralelas reales. - Si k > 1, det(t ) < 0, det(a) > 0. Se trata de una hipérbola. (ii) Cuando tenga sentido, calcular al excentricidad de la cónica en función de k. Tiene sentido cuando la cónica es una elipse o una hipérbola. Calculamos los autovalores de T : T λid = 0 (1 λ) k = 0 λ = 1 k ó λ = 1 + k. La ecuación reducida quedará por tanto: Distinguimos ahora los casos: (1 k)x + (1 + k)y = 1 k x 1 + k + y 1 k = 1. - Si k < 1 es una hipérbola. La excentricidad es e = c a, siendo c = a + b y a, b respectivamente la raíz cuadrada de los denominadores que acompañan a los coeficientes de x, y con signos positivo y negativo. En este caso a = 1 k, b = k 1. Por tanto: c = (1 k) + ( 1 k) = k, y e = k 1 k. - Si 1 < k < 1 es una elpise. La excentricidad es e = c a, siendo c = a b y a, b respectivamente los semiejes mayor y menor. Vemos que: Si 1 < k 0 entonces el semieje mayor es a = 1 k y el menor b = 1 + k. Si 0 k < 1 entonces el semieje mayor es a = 1 + k y el menor b = 1 k. Ambas cosas se resumen diciendo que a = 1 + k, b = 1 k. Entonces: c = (1 + k ) (1 k ) = k, y e = k 1 + k.
36 - Si k > 1 es una hipérbola. La excentricidad es e = c a, siendo c = a + b y a, b respectivamente la raíz cuadrada de los denominadores que acompañan a los coeficientes de x, y con signos positivo y negativo. En este caso a = 1 + k, b = k 1. Por tanto: c = (1 + k) + (k 1) = k, y e = k 1 + k. En resumen y en todo caso: e = k 1 + k. (1 punto) III. Se dice que una hipérbola es equilátera cuando sus asíntotas son perpendiculares. (a) Demostrar que una cónica no degenerada es una hipérbola equilátera si y sólo si es nula la traza de su matriz T de coeficientes cuadráticos, con respecto a una referencia rectangular. Sea T la matriz de términos cuadrático de una matriz no degenerada. Supongamos que la traza es nula. Entonces la suma de los autovalores de T es 0, y estos son λ y λ, donde λ 0, por ser la cónica no degenerada. Se trata de una hiṕerbola y en una referencia rectangular adecuada sabemos que su ecuación se escribe como: λx λy + c = 0 Las asíntotas son por tanto λx λy = 0 y λx + λy = 0. Vemos que son perpendiculares. Recíprocamente dada una hipérbola equilátera, sabemos que su ecuación en un sistema de referencia rectangular adecuado puede escribirse como: λ 1 x + λ y + c = 0 donde λ 1 y λ son los autovalores de T, de signos positivo y negativo respectivamente. Las asíntotas son λ1 x + λ y = 0 y λ 1 x λ y = 0. Si son perpendiculares, entonces λ 1 + λ = 0. Deducimos que la traza de T es cero. (b) Encontrar todas las hipérbolas equiláteras que tengan la recta y = x por eje focal. Recordemos primero lo siguiente. Si la ecuación reducida de una hipérbola equilátera es: λx λy + c = 0 con λ > 0 y c < 0, el eje focal es el eje OX (y = 0) y es paralelo al autovector de la matriz T asociado al autovalor positivo. Por tanto en las hipérbolas que buscamos el autovector de la matriz T asociado al autovalor positivo será el (1, ), siempre que det(a) > 0 (condición análoga a c > 0). Así por el apartado anterior, la matriz T es de la forma: a b T = b a Imponemos que (1, ) sea un autovector asociado al autovector λ: (1, )T = λ(1, ) a = 3λ/5; b = 4λ/5
ÁLGEBRA LINEAL II Algunas soluciones a la Práctica 4.1
 ÁLGEBRA LINEAL II Algunas soluciones a la Práctica 4.1 Cónicas (Curso 011 01) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 3. Dada
ÁLGEBRA LINEAL II Algunas soluciones a la Práctica 4.1 Cónicas (Curso 011 01) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 3. Dada
Examen Final Ejercicio 2 (1 hora y 30 min.) 27 de mayo de 2011
 Álgebra Lineal II Eamen Final Ejercicio 2 ( hora 30 min 27 de mao de 20 En el espacio afín euclideo usual consideramos una pirámide triangular ABCD de la cual sabemos: - A (0, 0, 0, B (, 0, 0, C (0,, -
Álgebra Lineal II Eamen Final Ejercicio 2 ( hora 30 min 27 de mao de 20 En el espacio afín euclideo usual consideramos una pirámide triangular ABCD de la cual sabemos: - A (0, 0, 0, B (, 0, 0, C (0,, -
ÁLGEBRA LINEAL II Algunas soluciones a la Práctica 4.1
 ÁLGEBRA LINEAL II Algunas soluciones a la Práctica 4.1 Cónicas (Curso 010 011) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular.. Dada
ÁLGEBRA LINEAL II Algunas soluciones a la Práctica 4.1 Cónicas (Curso 010 011) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular.. Dada
ÁLGEBRA LINEAL II Práctica 4.1
 ÁLGEBRA LINEAL II Práctica 4.1 Cónicas (Curso 2012 2013) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo
ÁLGEBRA LINEAL II Práctica 4.1 Cónicas (Curso 2012 2013) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo
NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular.
 ÁLGEBRA Práctica 15 Cónicas (Curso 2008 2009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
ÁLGEBRA Práctica 15 Cónicas (Curso 2008 2009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular.
 ÁLGEBRA Práctica 15 Cónicas (Curso 2008 2009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo y con respecto
ÁLGEBRA Práctica 15 Cónicas (Curso 2008 2009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo y con respecto
NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular.
 ÁLGEBRA Práctica 14 Cónicas (Curso 2007 2008) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
ÁLGEBRA Práctica 14 Cónicas (Curso 2007 2008) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
ÁLGEBRA Práctica Clasificar según los valores de λ IR las cónicas de los siguientes haces: 2. Para las siguientes cónicas
 ÁLGEBRA Práctica 14 Cónicas (Curso 2006 2007) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Clasificar según los valores de λ
ÁLGEBRA Práctica 14 Cónicas (Curso 2006 2007) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Clasificar según los valores de λ
ÁLGEBRA LINEAL II Práctica 4.1
 ÁLGEBRA LINEAL II Práctica 4.1 Cónicas (Curso 2010 2011) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo
ÁLGEBRA LINEAL II Práctica 4.1 Cónicas (Curso 2010 2011) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo
ÁLGEBRA Soluciones a la Práctica 15
 ÁLGEBRA Soluciones a la Práctica 15 Cónicas (Curso 008 009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 9. Calcular la ecuación
ÁLGEBRA Soluciones a la Práctica 15 Cónicas (Curso 008 009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 9. Calcular la ecuación
Examen extraordinario Ejercicio 4 (55 minutos) 4 de septiembre de 2006
 ÁLGEBRA Examen extraordinario Ejercicio 4 (55 minutos) 4 de septiembre de 006 1. Calcular la ecuación de una hipérbola que tiene por asíntota a la recta x = y, por eje la recta x+y = 1 y que pasa por el
ÁLGEBRA Examen extraordinario Ejercicio 4 (55 minutos) 4 de septiembre de 006 1. Calcular la ecuación de una hipérbola que tiene por asíntota a la recta x = y, por eje la recta x+y = 1 y que pasa por el
Cónicas. Clasificación.
 Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Lugares geométricos y cónicas
 Lugares geométricos y cónicas E S Q U E M A D E L A U N I D A D. Lugar geométrico página 6.. Definición página 6. Circunferencia página 6.. Ecuación página 6.. Casos particulares página 67. Elipse página
Lugares geométricos y cónicas E S Q U E M A D E L A U N I D A D. Lugar geométrico página 6.. Definición página 6. Circunferencia página 6.. Ecuación página 6.. Casos particulares página 67. Elipse página
Unidad 8 Lugares geométricos. Cónicas
 Unidad 8 Lugares geométricos. Cónicas PÁGINA 75 SOLUCIONES. La elipse es una cónica obtenida al cortar una superficie cónica por un plano oblicuo al eje y que corte a todas las generatrices. La hipérbola
Unidad 8 Lugares geométricos. Cónicas PÁGINA 75 SOLUCIONES. La elipse es una cónica obtenida al cortar una superficie cónica por un plano oblicuo al eje y que corte a todas las generatrices. La hipérbola
Tema 3. GEOMETRIA ANALITICA.
 Álgebra lineal. Curso 087-009. Tema. Hoja 1 Tema. GEOMETRIA ANALITICA. 1. Hallar la ecuación de la recta: a) que pase por ( 4, ) y tenga pendiente 1. b) que pase por (0, 5) y tenga pendiente. c) que pase
Álgebra lineal. Curso 087-009. Tema. Hoja 1 Tema. GEOMETRIA ANALITICA. 1. Hallar la ecuación de la recta: a) que pase por ( 4, ) y tenga pendiente 1. b) que pase por (0, 5) y tenga pendiente. c) que pase
1 CÓNICAS Cónicas. Estudio particular. 1 x y. 1 x y. a 00 a 01 a 02 a 10 a 11 a 12 a 20 a 21 a 22
 CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
( ) 2 +( 1) 2. BLOQUE III Geometría analítica plana. Resoluciones de la autoevaluación del libro de texto
 Pág. de Dados los vectores u, y v0,, calcula: a u b u + v c u v u, v0, 5 a u = = = + b u + v =, + 0, =, + 0, 6 =, c u v = u v = 0 + = Determina el valor de k para que los vectores a, y b6, k sean ortogonales.
Pág. de Dados los vectores u, y v0,, calcula: a u b u + v c u v u, v0, 5 a u = = = + b u + v =, + 0, =, + 0, 6 =, c u v = u v = 0 + = Determina el valor de k para que los vectores a, y b6, k sean ortogonales.
Autoevaluación. Bloque III. Geometría. BACHILLERATO Matemáticas I * 8 D = (3, 3) Página Dados los vectores u c1, 1m y v (0, 2), calcula:
 Autoevaluación Página Dados los vectores u c, m y v (0, ), calcula: a) u b) u+ v c) u : ( v) u c, m v (0, ) a) u c m + ( ) b) u+ v c, m + (0, ) (, ) + (0, 6) (, ) c) u :( v) () (u v ) c 0 + ( ) ( ) m 8
Autoevaluación Página Dados los vectores u c, m y v (0, ), calcula: a) u b) u+ v c) u : ( v) u c, m v (0, ) a) u c m + ( ) b) u+ v c, m + (0, ) (, ) + (0, 6) (, ) c) u :( v) () (u v ) c 0 + ( ) ( ) m 8
1. Determine el valor de la constante k para que la recta kx + (3 k)y + 7 = 0 sea perpendicular a la recta x + 7y + 1 = 0
 Universidad Técnica Federico Santa María Departamento de Matemática Campus Santiago Geometría Analítica 1. Determine el valor de la constante k para que la recta kx + (3 k)y + 7 = 0 sea perpendicular a
Universidad Técnica Federico Santa María Departamento de Matemática Campus Santiago Geometría Analítica 1. Determine el valor de la constante k para que la recta kx + (3 k)y + 7 = 0 sea perpendicular a
Este documento es de distribución gratuita y llega gracias a El mayor portal de recursos educativos a tu servicio!
 Este documento es de distribución gratuita y llega gracias a Ciencia Matemática El mayor portal de recursos educativos a tu servicio! Capítulo 5 Cónicas 5.1 Definiciones y ecuaciones reducidas Nota En
Este documento es de distribución gratuita y llega gracias a Ciencia Matemática El mayor portal de recursos educativos a tu servicio! Capítulo 5 Cónicas 5.1 Definiciones y ecuaciones reducidas Nota En
1. L U G A R E S G E O M É T R I C O S E N E L P L A N O
 L U G A R E S G E O M É T R I C O S. C Ó N I C A S 1. L U G A R E S G E O M É T R I C O S E N E L P L A N O Se define un lugar geométrico como el conjunto de puntos del plano que cumplen una determinada
L U G A R E S G E O M É T R I C O S. C Ó N I C A S 1. L U G A R E S G E O M É T R I C O S E N E L P L A N O Se define un lugar geométrico como el conjunto de puntos del plano que cumplen una determinada
ÁLGEBRA Algunas soluciones a la Práctica 14
 ÁLGEBRA Algunas soluciones a la Práctica 4 Espacios afines E y E (Curso 008 009) 9. En el espacio E dotado de un sistema de referencia rectangular, determinar la ecuación de todos los planos que contienen
ÁLGEBRA Algunas soluciones a la Práctica 4 Espacios afines E y E (Curso 008 009) 9. En el espacio E dotado de un sistema de referencia rectangular, determinar la ecuación de todos los planos que contienen
Función lineal y cuadrática. Curvas de primer y segundo grado.
 Tema 5 Función lineal y cuadrática. Curvas de primer y segundo grado. 5.0.1 Ecuaciones en dos variables. Una linea del plano es el conjunto de puntos (x, y), cuyas coordenadas satisfacen la ecuación F
Tema 5 Función lineal y cuadrática. Curvas de primer y segundo grado. 5.0.1 Ecuaciones en dos variables. Una linea del plano es el conjunto de puntos (x, y), cuyas coordenadas satisfacen la ecuación F
Bloque 2. Geometría. 4. Iniciación a las Cónicas
 Bloque 2. Geometría 4. Iniciación a las Cónicas 1. La circunferencia Se llama circunferencia al lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. Elevando al cuadrado
Bloque 2. Geometría 4. Iniciación a las Cónicas 1. La circunferencia Se llama circunferencia al lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. Elevando al cuadrado
Ejercicios de cónicas.
 Ejercicios de cónicas. 1. Demuéstrese que un rayo lanzado en cualquier dirección desde un foco de una elipse y que se refleje en la cónica pasa por el otro foco. 2. Demuéstrese que un rayo lanzado paralelamente
Ejercicios de cónicas. 1. Demuéstrese que un rayo lanzado en cualquier dirección desde un foco de una elipse y que se refleje en la cónica pasa por el otro foco. 2. Demuéstrese que un rayo lanzado paralelamente
Solución a los problemas adicionales Espacios afines E 2 y E 3 (Curso )
 ÁLGEBRA Solución a los problemas adicionales Espacios afines E 2 y E (Curso 2009 200) I. En el plano afín E 2 y con respecto a una referencia rectangular se tiene el triángulo ABC de vértices A (0, 0),
ÁLGEBRA Solución a los problemas adicionales Espacios afines E 2 y E (Curso 2009 200) I. En el plano afín E 2 y con respecto a una referencia rectangular se tiene el triángulo ABC de vértices A (0, 0),
Segundo examen parcial. Soluciones. Ejercicio 1 (1 hora y 40 minutos.) 12 de junio de 2008
 ÁLGEBRA Segundo examen parcial Soluciones Ejercicio 1 (1 hora y 40 minutos 1 de junio de 008 1 En el espacio de matrices M n n (IR consideramos las formas bilineales: f : M n n (IR M n n (IR IR, f(a, B
ÁLGEBRA Segundo examen parcial Soluciones Ejercicio 1 (1 hora y 40 minutos 1 de junio de 008 1 En el espacio de matrices M n n (IR consideramos las formas bilineales: f : M n n (IR M n n (IR IR, f(a, B
2. Distancia entre dos puntos. Punto medio de un segmento
 Geometría 1 Geometría anaĺıtica Una ecuación de primer grado con dos incógnitas x e y tiene infinitas soluciones Por ejemplo x + y = 3 tiene como soluciones (0, 3), (1, ), ( 1, 4), etc Hasta ahora se han
Geometría 1 Geometría anaĺıtica Una ecuación de primer grado con dos incógnitas x e y tiene infinitas soluciones Por ejemplo x + y = 3 tiene como soluciones (0, 3), (1, ), ( 1, 4), etc Hasta ahora se han
Es el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos llamados focos es constante.
 REPARTIDO IV - CÓNICAS Elipse Es el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos llamados focos es constante. Elementos de la elipse Focos Son los puntos fijos F
REPARTIDO IV - CÓNICAS Elipse Es el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos llamados focos es constante. Elementos de la elipse Focos Son los puntos fijos F
LA CIRCUNFERENCIA. La circunferencia es la sección producida por un plano perpendicular al eje.
 LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
LUGARES GEOMÉTRICOS. CÓNICAS
 9 LUGARES GEOMÉTRICOS. CÓNICAS Página PARA EMPEZAR, RELEXIONA Y RESUELVE Cónicas abiertas: parábolas e hipérbolas Completa la siguiente tabla, en la que α es el ángulo que forman las generatrices con el
9 LUGARES GEOMÉTRICOS. CÓNICAS Página PARA EMPEZAR, RELEXIONA Y RESUELVE Cónicas abiertas: parábolas e hipérbolas Completa la siguiente tabla, en la que α es el ángulo que forman las generatrices con el
2 Intersección de una recta y una cuádrica. 1 Definición y ecuaciones. ( x y z
 2. Cuádricas. En todo este capítulo trabajaremos en el espacio afín euclídeo E 3 con respecto a una referencia rectangular {O; ē 1, ē 2, ē 3}. Denotaremos por (x, y, las coordenadas cartesianas respecto
2. Cuádricas. En todo este capítulo trabajaremos en el espacio afín euclídeo E 3 con respecto a una referencia rectangular {O; ē 1, ē 2, ē 3}. Denotaremos por (x, y, las coordenadas cartesianas respecto
Lugar Geométrico. Se llama lugar geométrico a un conjunto de puntos que cumplen una determinada propiedad. Mediatriz
 1 Lugar Geométrico Se llama lugar geométrico a un conjunto de puntos que cumplen una determinada propiedad. Mediatriz Mediatriz de un segmento es el lugar geométrico de los puntos del plano que equidistan
1 Lugar Geométrico Se llama lugar geométrico a un conjunto de puntos que cumplen una determinada propiedad. Mediatriz Mediatriz de un segmento es el lugar geométrico de los puntos del plano que equidistan
SOLUCIONES. ÁLGEBRA LINEAL Y GEOMETRÍA (Examen Ordinario : ) Grado en Matemáticas Curso
 ÁLGEBRA LINEAL Y GEOMETRÍA Eamen Ordinario : 6--7 Grado en Matemáticas Curso 6-7 SOLUCIONES Dados tres puntos distintos alineados A, A, A A R, al número real r tal que A A = r A A lo llamaremos raón simple
ÁLGEBRA LINEAL Y GEOMETRÍA Eamen Ordinario : 6--7 Grado en Matemáticas Curso 6-7 SOLUCIONES Dados tres puntos distintos alineados A, A, A A R, al número real r tal que A A = r A A lo llamaremos raón simple
COLEGIO NUESTRA SEÑORA DEL BUEN CONSEJO. Melilla LUGARES GEOMÉTRICOS Y CÓNICAS
 LUGARES GEOMÉTRICOS Y CÓNICAS 01. Halla la ecuación de la circunferencia de centro ( 5, 12) y radio 13. Comprueba que pasa por el punto (0, 0). 02. Halla las ecuaciones de los siguientes lugares geométricos:
LUGARES GEOMÉTRICOS Y CÓNICAS 01. Halla la ecuación de la circunferencia de centro ( 5, 12) y radio 13. Comprueba que pasa por el punto (0, 0). 02. Halla las ecuaciones de los siguientes lugares geométricos:
Es la elipse el conjunto de puntos fijos cuya suma de distancias a dos puntos fijos llamados focos es constante.
 ESQUEMA LAS CÓNICAS LA PARÁBOLA ECUACIONES DE LA PARÁBOLA ECUACIÓN DE LA TANGENTE A UNA PARÁBOLA ELIPSE ECUACIONES DE LA ELIPSE PROPIEDADES DE LA ELIPSE LA HIPÉRBOLA ECUACIONES DE LA HIPÉRBOLA 10 ASÍNTOTAS
ESQUEMA LAS CÓNICAS LA PARÁBOLA ECUACIONES DE LA PARÁBOLA ECUACIÓN DE LA TANGENTE A UNA PARÁBOLA ELIPSE ECUACIONES DE LA ELIPSE PROPIEDADES DE LA ELIPSE LA HIPÉRBOLA ECUACIONES DE LA HIPÉRBOLA 10 ASÍNTOTAS
UNI DAD 4 ESPACIO BIDIMENSIONAL: CÓNICAS
 UNI DAD 4 ESPACIO BIDIMENSIONAL: CÓNICAS Objetivos Geometría analítica Introducción L cónica sección cónica Ax 2 + Bxy + Cy 2 + Dx + Ey + F = 0 A B C D E F 4.1. Circunferencia Circunferencia es el conjunto
UNI DAD 4 ESPACIO BIDIMENSIONAL: CÓNICAS Objetivos Geometría analítica Introducción L cónica sección cónica Ax 2 + Bxy + Cy 2 + Dx + Ey + F = 0 A B C D E F 4.1. Circunferencia Circunferencia es el conjunto
MATEMÁTICAS 1º BACH. C. N. Y S. 25 de enero de 2010 Geometría y Logaritmos
 MATEMÁTICAS 1º BACH. C. N. Y S. 5 de enero de 010 Geometría y Logaritmos x yz 1) Tomar logaritmos, y desarrollar, en la siguiente expresión: A 4 ab log x log b 4log a log y ) Quitar logaritmos: log A )
MATEMÁTICAS 1º BACH. C. N. Y S. 5 de enero de 010 Geometría y Logaritmos x yz 1) Tomar logaritmos, y desarrollar, en la siguiente expresión: A 4 ab log x log b 4log a log y ) Quitar logaritmos: log A )
4. Escribe la ecuación de la circunferencia de centro C(-2,3) y radio 4. Sol: (x+2) 2 +(y-3) 2 =16.
 Problemas de circunferencias 4. Escribe la ecuación de la circunferencia de centro C(-2,3) y radio 4. Sol: (x+2) 2 +(y-3) 2 =16. 10. 5. Calcula la potencia del punto P(-1,2) a la circunferencia: x 2 +y
Problemas de circunferencias 4. Escribe la ecuación de la circunferencia de centro C(-2,3) y radio 4. Sol: (x+2) 2 +(y-3) 2 =16. 10. 5. Calcula la potencia del punto P(-1,2) a la circunferencia: x 2 +y
1 + 3(0, 2) = ( 1, 2) + (0, 6) = ( 1, 4) ) ( = arc cos e 5
 utoevaluación Página Dados los vectores uc c, m v (0, ), calcula: a) u b) u + v c) u : ( v) uc c, m v (0, ) a) u c m + ( ) b) u + v c c, m + (0, ) (, ) + (0, 6) (, ) c) u : ( v) () (u v ) c 0 +( m ) (
utoevaluación Página Dados los vectores uc c, m v (0, ), calcula: a) u b) u + v c) u : ( v) uc c, m v (0, ) a) u c m + ( ) b) u + v c c, m + (0, ) (, ) + (0, 6) (, ) c) u : ( v) () (u v ) c 0 +( m ) (
TEMA 12.- RECTAS Y PLANOS EN EL ESPACIO. y una base de vectores de V cualquiera
 TEMA 12.- RECTAS Y PLANOS EN EL ESPACIO 1.- PUNTOS Y VECTORES. ESPACIO AFÍN y una base de vectores de V cualquiera {,, B = u1 u2 u} A cada punto del espacio, P, le asociamos el vector OP, que tendrá unas
TEMA 12.- RECTAS Y PLANOS EN EL ESPACIO 1.- PUNTOS Y VECTORES. ESPACIO AFÍN y una base de vectores de V cualquiera {,, B = u1 u2 u} A cada punto del espacio, P, le asociamos el vector OP, que tendrá unas
Tema 5. Cónicas. Asi, para las identificaciones habituales, (punto proyectivo recta vectorial punto de un plano afín ampliado), RP 2 R3 {0}
 Tema 5. Cónicas. Introducción. Ejemplos.- El cono C = {(x, y, z) R 3 /x 2 + y 2 = z 2 } está formado por las rectas vectoriales 0 (x 1,x 2, 1) [x 1,x 2, 1] RP 2 con (x 1,x 2, 1) C Π 1 = C 1, circunferencia
Tema 5. Cónicas. Introducción. Ejemplos.- El cono C = {(x, y, z) R 3 /x 2 + y 2 = z 2 } está formado por las rectas vectoriales 0 (x 1,x 2, 1) [x 1,x 2, 1] RP 2 con (x 1,x 2, 1) C Π 1 = C 1, circunferencia
Problemas Tema 7 Enunciados de problemas ampliación Temas 5 y 6
 página 1/13 Problemas Tema 7 Enunciados de problemas ampliación Temas 5 y 6 Hoja 1 1. Dado el segmento de extremos A( 7,3) y B(5,11), halla la ecuación de su mediatriz. 2. Halla la distancia del punto
página 1/13 Problemas Tema 7 Enunciados de problemas ampliación Temas 5 y 6 Hoja 1 1. Dado el segmento de extremos A( 7,3) y B(5,11), halla la ecuación de su mediatriz. 2. Halla la distancia del punto
Facultad de Ingeniería Facultad de Tecnología Informática. Matemática Números reales Elementos de geometría analítica. Profesora: Silvia Mamone
 Facultad de Ingeniería Facultad de Tecnología Informática Matemática Números reales Elementos de geometría analítica 0 03936 Profesora: Silvia Mamone UB Facultad de Ingeniería Facultad de Tecnología Informática
Facultad de Ingeniería Facultad de Tecnología Informática Matemática Números reales Elementos de geometría analítica 0 03936 Profesora: Silvia Mamone UB Facultad de Ingeniería Facultad de Tecnología Informática
Se quiere instalar un gran depósito de propano para abastecer a una factoría industrial y a dos urbanizaciones.
 Resuelve Página Dónde se situará el depósito? Se quiere instalar un gran depósito de propano para abastecer a una factoría industrial y a dos urbanizaciones. Han de cumplirse las siguientes condiciones:
Resuelve Página Dónde se situará el depósito? Se quiere instalar un gran depósito de propano para abastecer a una factoría industrial y a dos urbanizaciones. Han de cumplirse las siguientes condiciones:
Apellidos: Nombre: Curso: 2º Grupo: A Día: 28 - IV 14 CURSO Opción A 1.- Sean las matrices A = , B =
 S Instrucciones: EXAMEN DE MATEMATICAS II 3ª EVALUACIÓN Apellidos: Nombre: Curso: º Grupo: A Día: 8 - IV 4 CURSO 03-4 a) Duración: HORA y 30 MINUTOS. b) Debes elegir entre realizar únicamente los cuatro
S Instrucciones: EXAMEN DE MATEMATICAS II 3ª EVALUACIÓN Apellidos: Nombre: Curso: º Grupo: A Día: 8 - IV 4 CURSO 03-4 a) Duración: HORA y 30 MINUTOS. b) Debes elegir entre realizar únicamente los cuatro
Tarea 4. Geometría Analítica I
 Tarea 4. Geometría Analítica I Jesús Rodríguez Viorato 21 de noviembre de 2006 1. Ejercicios de pensar 1.- Encuentre la ecuación cartesiana del lugar geométrico de los puntos P tales que las sumas de las
Tarea 4. Geometría Analítica I Jesús Rodríguez Viorato 21 de noviembre de 2006 1. Ejercicios de pensar 1.- Encuentre la ecuación cartesiana del lugar geométrico de los puntos P tales que las sumas de las
Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad.
 LUGARES GEOMÉTRICOS. CÓNICAS. 9.1 LUGARES GEOMÉTRICOS Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad. Llamando X(,) a las coordenadas del punto genérico aplicando analíticamente
LUGARES GEOMÉTRICOS. CÓNICAS. 9.1 LUGARES GEOMÉTRICOS Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad. Llamando X(,) a las coordenadas del punto genérico aplicando analíticamente
EJERCICIOS DE GEOMETRÍA PLANA. 1. Hallar las ecuaciones paramétricas de la recta r que pasa por el punto ( 2, 2) tiene como vector director el vector
 EJERCICIOS DE GEOMETRÍA PLANA Hallar las ecuaciones paramétricas de la recta r que pasa por el punto (, ) tiene como vector director el vector v i j A y x a + vt La ecuación paramétrica de una recta es
EJERCICIOS DE GEOMETRÍA PLANA Hallar las ecuaciones paramétricas de la recta r que pasa por el punto (, ) tiene como vector director el vector v i j A y x a + vt La ecuación paramétrica de una recta es
Ejercicios de Álgebra y Geometría Analítica
 Ejercicios de Álgebra y Geometría Analítica Profr. Fausto Cervantes Ortiz Recta Dibujar las rectas indicadas 1. y = x + 1 2. y = 2x + 5 2 3. y = x + 2 4. y = x + 2 5. y = 2x 3 2 6. y = 3 2 x + 1 2 7. y
Ejercicios de Álgebra y Geometría Analítica Profr. Fausto Cervantes Ortiz Recta Dibujar las rectas indicadas 1. y = x + 1 2. y = 2x + 5 2 3. y = x + 2 4. y = x + 2 5. y = 2x 3 2 6. y = 3 2 x + 1 2 7. y
CLASIFICACIÓN AFÍN DE CÓNICAS
 Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS CLASIFICACIÓN AFÍN DE CÓNICAS Sea E un R-espacio vectorial de dimensión. Sean E = e 1, e un plano vectorial de E y e 0 un
Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS CLASIFICACIÓN AFÍN DE CÓNICAS Sea E un R-espacio vectorial de dimensión. Sean E = e 1, e un plano vectorial de E y e 0 un
Examen Final Ejercicio único (3 horas) 20 de enero de n(n 1) 2. C n,3 = n(n 3) n =
 Álgebra Lineal I Examen Final Ejercicio único (3 horas) 0 de enero de 014 1. Sea P un polígono regular de n lados. (i) Cuántas diagonales tiene el polígono?. Las diagonales son segmentos que unen pares
Álgebra Lineal I Examen Final Ejercicio único (3 horas) 0 de enero de 014 1. Sea P un polígono regular de n lados. (i) Cuántas diagonales tiene el polígono?. Las diagonales son segmentos que unen pares
ÁLGEBRA LINEAL II Algunas soluciones a la práctica 2.3
 ÁLGEBRA LINEAL II Algunas soluciones a la práctica 2. Transformaciones ortogonales (Curso 2010 2011) 1. Se considera el espacio vectorial euclídeo IR referido a una base ortonormal. Obtener la expresión
ÁLGEBRA LINEAL II Algunas soluciones a la práctica 2. Transformaciones ortogonales (Curso 2010 2011) 1. Se considera el espacio vectorial euclídeo IR referido a una base ortonormal. Obtener la expresión
CÓNICAS. 1. Dada la cónica x 2 + 2xy y 2 2x 2y + 4 = 0, se pide su clasicación y los elementos característicos de la misma. = 1
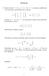 CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
Fundamentos matemáticos. Tema 3 Geometría del plano y del espacio
 Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es
Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es
Seis problemas resueltos de geometría
 Problema 1 a) Dados los puntos P(4, 2, 3) y Q(2, 0, 5), da la ecuación implícita del plano π de modo que el punto simétrico de P respecto a π es Q. b) Calcula el valor del parámetro λ R para que el plano
Problema 1 a) Dados los puntos P(4, 2, 3) y Q(2, 0, 5), da la ecuación implícita del plano π de modo que el punto simétrico de P respecto a π es Q. b) Calcula el valor del parámetro λ R para que el plano
MatemáticasI. 1. Los pasos a seguir son los siguientes, llamando AB a los montañeros que suben y abc a los que bajan.
 UNIDAD 8: Lugares geométricos. Cónicas ACTIVIDADES-PÁG. 176 1. El lugar geométrico es la mediatriz de ecuación x 5y + 3 = 0.. El circuncentro es el punto de corte de las mediatrices. Hallamos dos mediatrices:
UNIDAD 8: Lugares geométricos. Cónicas ACTIVIDADES-PÁG. 176 1. El lugar geométrico es la mediatriz de ecuación x 5y + 3 = 0.. El circuncentro es el punto de corte de las mediatrices. Hallamos dos mediatrices:
22. CURVAS CÓNICAS-ELIPSE
 22. CURVAS CÓNICAS-ELIPSE 22.1. Características generales. Las curvas cónicas son las secciones planas de un cono de revolución. El cono de revolución es la superficie que genera una recta r al girar alrededor
22. CURVAS CÓNICAS-ELIPSE 22.1. Características generales. Las curvas cónicas son las secciones planas de un cono de revolución. El cono de revolución es la superficie que genera una recta r al girar alrededor
Se llama Circunferencia al lugar geométrico de los puntos del plano equidistantes de un punto fijo llamado centro.
 Cónicas 1.- Circunferencia Definición 1 (Definición geométrica) Se llama Circunferencia al lugar geométrico de los puntos del plano equidistantes de un punto fijo llamado centro. Analíticamente la circunferencia
Cónicas 1.- Circunferencia Definición 1 (Definición geométrica) Se llama Circunferencia al lugar geométrico de los puntos del plano equidistantes de un punto fijo llamado centro. Analíticamente la circunferencia
Evaluación NOMBRE APELLIDOS CURSO Y GRUPO FECHA CALIFICACIÓN. 3 b) y 16 x Lugares geométricos y cónicas
 Evaluación NOMBRE APELLIDOS CURSO Y GRUPO FECHA CALIFICACIÓN 4 La ecuación del lugar geométrico de los puntos del plano que equidistan de la recta x y 4, y del punto P (, ) es: a) x y x y 68 0 b) 4x 9y
Evaluación NOMBRE APELLIDOS CURSO Y GRUPO FECHA CALIFICACIÓN 4 La ecuación del lugar geométrico de los puntos del plano que equidistan de la recta x y 4, y del punto P (, ) es: a) x y x y 68 0 b) 4x 9y
Para localizar un punto o un objeto en el espacio necesitamos un sistema de referencia. R es una cuaterna { O,i, j, k}
 Geometría afín del espacio MATEMÁTICAS II 1 1 SISTEMA DE REFERENCIA. ESPACIO AFÍN Para localizar un punto o un objeto en el espacio necesitamos un sistema de referencia. Definición: Un sistema de referencia
Geometría afín del espacio MATEMÁTICAS II 1 1 SISTEMA DE REFERENCIA. ESPACIO AFÍN Para localizar un punto o un objeto en el espacio necesitamos un sistema de referencia. Definición: Un sistema de referencia
A pesar de la importancia de las cónicas como secciones de una superficie cónica, para estudiar los elementos y propiedades de cada una de ellas en
 SECCIONES CÓNICAS Las secciones cónicas se pueden definir como lugares geométricos en el plano, sin embargo la definición clásica de las cónicas, que se debe a Apolonio de Perga, se hizo mediante un procedimiento
SECCIONES CÓNICAS Las secciones cónicas se pueden definir como lugares geométricos en el plano, sin embargo la definición clásica de las cónicas, que se debe a Apolonio de Perga, se hizo mediante un procedimiento
Prof. Santiago García. 1. Escuela Técnica de Atlántida 21 de febrero de 2011 Examen de Matemática B
 Prof. Santiago García. 1 Escuela Técnica de Atlántida 21 de febrero de 2011 Examen de Matemática B Ejercicio 1. Para la resolución de cada item de este ejercicio puedes escoger el método analítico o el
Prof. Santiago García. 1 Escuela Técnica de Atlántida 21 de febrero de 2011 Examen de Matemática B Ejercicio 1. Para la resolución de cada item de este ejercicio puedes escoger el método analítico o el
Ejercicios resueltos
 Ejercicios resueltos.- Comprueba que las rectas r x + y y s x y + 4 son secantes y halla el punto de intersección de las mismas., es decir, los coeficientes de las incógnitas no son proporcionales, por
Ejercicios resueltos.- Comprueba que las rectas r x + y y s x y + 4 son secantes y halla el punto de intersección de las mismas., es decir, los coeficientes de las incógnitas no son proporcionales, por
1. Clasifica las siguientes cónicas dando su ecuación reducida, centro o vértice y ejes (si es posible): (1.d) x 2 + y 2 + 2x + 1 = 0
 Clasificación de cónicas.. Clasifica las siguientes cónicas dando su ecuación reducida, centro o vértice y ejes si es posible:.a x xy + y + x y + 0.b x + xy y 6x + y 0.c x + xy + y x y 0.d x + y + x +
Clasificación de cónicas.. Clasifica las siguientes cónicas dando su ecuación reducida, centro o vértice y ejes si es posible:.a x xy + y + x y + 0.b x + xy y 6x + y 0.c x + xy + y x y 0.d x + y + x +
PAU Madrid. Matemáticas II. Año Examen modelo. Opción A. Ejercicio 1. Valor: 2 puntos.
 PAU Madrid. Matemáticas II. Año 22. Examen modelo. Opción A. Ejercicio 1. Valor: 2 puntos. Se considera una varilla AB de longitud 1. El extremo A de esta varilla recorre completamente la circunferencia
PAU Madrid. Matemáticas II. Año 22. Examen modelo. Opción A. Ejercicio 1. Valor: 2 puntos. Se considera una varilla AB de longitud 1. El extremo A de esta varilla recorre completamente la circunferencia
GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA
 ESCUELA PREPARATORIA OFICIAL No. 268 GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA Profra: Citlalli Artemisa García García 1) Qué es la pendiente? 2) Cómo es la pendiente de rectas
ESCUELA PREPARATORIA OFICIAL No. 268 GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA Profra: Citlalli Artemisa García García 1) Qué es la pendiente? 2) Cómo es la pendiente de rectas
Solución de problemas I 1
 Universidad Autónoma de Madrid Álgebra II. Físicas. Curso 5 6 Solución de problemas I Álgebra II Curso 5-6. Proyecciones en el producto escalar estándar Ejercicio 7.7. (a) Dada la ecuación x + y z, dar
Universidad Autónoma de Madrid Álgebra II. Físicas. Curso 5 6 Solución de problemas I Álgebra II Curso 5-6. Proyecciones en el producto escalar estándar Ejercicio 7.7. (a) Dada la ecuación x + y z, dar
Lugares geométricos. Cónicas
 ACTIVIDADES Si el plano es perpendicular a la generatriz del cilindro, la sección es una circunferencia. Si no es perpendicular, la sección es una elipse. Porque el plano solo corta a uno de los conos
ACTIVIDADES Si el plano es perpendicular a la generatriz del cilindro, la sección es una circunferencia. Si no es perpendicular, la sección es una elipse. Porque el plano solo corta a uno de los conos
Ejercicios resueltos
 ECUACIÓN DE LA RECTA.- PRIMERO DE BACHILLERATO.- TEORÍA Y EJERCICIOS. Pág. Ejercicios resueltos.- Comprueba que las rectas r x + y y s x y + 4 son secantes y halla el punto de intersección de las mismas.,
ECUACIÓN DE LA RECTA.- PRIMERO DE BACHILLERATO.- TEORÍA Y EJERCICIOS. Pág. Ejercicios resueltos.- Comprueba que las rectas r x + y y s x y + 4 son secantes y halla el punto de intersección de las mismas.,
Fundamentos matemáticos. Tema 3 Geometría del plano y del espacio
 Grado en Ingeniería agrícola y del medio rural Tema 3 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2017 Licencia Creative Commons 4.0 Internacional J.
Grado en Ingeniería agrícola y del medio rural Tema 3 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2017 Licencia Creative Commons 4.0 Internacional J.
1) Clasifica las siguientes cónicas y expresa sus focos y su excentricidad: a)
 Ejercicios de cónicas 1º bachillerato C 1) Clasifica las siguientes cónicas y expresa sus focos y su excentricidad: a) b) c) d) e) f) g) h) i) Soluciones: a) Circunferencia de centro ( y radio 3. Excentricidad
Ejercicios de cónicas 1º bachillerato C 1) Clasifica las siguientes cónicas y expresa sus focos y su excentricidad: a) b) c) d) e) f) g) h) i) Soluciones: a) Circunferencia de centro ( y radio 3. Excentricidad
PAU Madrid. Matemáticas II. Año Examen de junio. Opción A. Ejercicio 1. Valor: 2 puntos.
 Opción A. Ejercicio 1. Valor: 2 puntos. Calcular las edades actuales de una madre y sus dos hijos sabiendo que hace 14 años la edad de la madre era 5 veces la suma de las edades de los hijos en aquel momento,
Opción A. Ejercicio 1. Valor: 2 puntos. Calcular las edades actuales de una madre y sus dos hijos sabiendo que hace 14 años la edad de la madre era 5 veces la suma de las edades de los hijos en aquel momento,
RESUMEN TEÓRICO LUGARES GEÓMETRICOS. CÓNICAS (circunferencia y elipse)
 RESUMEN TEÓRICO LUGARES GEÓMETRICOS. CÓNICAS (circunferencia y elipse) 1. LUGARES GEOMÉTRICOS Definición: Se llama lugar geométrico a la figura que forman un conjunto de puntos que cumplen una determinada
RESUMEN TEÓRICO LUGARES GEÓMETRICOS. CÓNICAS (circunferencia y elipse) 1. LUGARES GEOMÉTRICOS Definición: Se llama lugar geométrico a la figura que forman un conjunto de puntos que cumplen una determinada
ÁLGEBRA Algunas soluciones a la Práctica 8
 ÁLGEBRA Algunas soluciones a la Práctica 8 Aplicaciones bilineales y formas cuadráticas (Curso 2008 2009 6. Sean a y b dos números reales. En el espacio P 1 de los polinomios de grado menor o igual que
ÁLGEBRA Algunas soluciones a la Práctica 8 Aplicaciones bilineales y formas cuadráticas (Curso 2008 2009 6. Sean a y b dos números reales. En el espacio P 1 de los polinomios de grado menor o igual que
ÁLGEBRA Algunas soluciones a la Práctica 8
 ÁLGEBRA Algunas soluciones a la Práctica 8 Aplicaciones bilineales y formas cuadráticas (Curso 24 25 1. Comprobar si las siguientes aplicaciones son o no bilineales y en las que resulten serlo, dar la
ÁLGEBRA Algunas soluciones a la Práctica 8 Aplicaciones bilineales y formas cuadráticas (Curso 24 25 1. Comprobar si las siguientes aplicaciones son o no bilineales y en las que resulten serlo, dar la
Tema 11: Problemas Métricos
 ..- Distancia entre dos puntos : Tema : Problemas Métricos B AB A d( A, B) AB La distancia entre dos puntos Aa (, a, a) Bbb (,, b ) es el módulo del vector que une dichos puntos: d( A, B) AB b a b a b
..- Distancia entre dos puntos : Tema : Problemas Métricos B AB A d( A, B) AB La distancia entre dos puntos Aa (, a, a) Bbb (,, b ) es el módulo del vector que une dichos puntos: d( A, B) AB b a b a b
A = [a 1 a 2 a 3. El sistema Ax = c tiene infinitas soluciones N. Existe un único vector x tal que T (x) = c X. T es suprayectiva
 Asignatura: ÁLGEBRA LINEAL Fecha: 6 de Julio de Fecha publicación notas: 6 de Julio de Fecha revisión examen: de Julio de Duración del examen: horas y media APELLIDOS Y NOMBRE: DNI: Titulación:. ( punto:,
Asignatura: ÁLGEBRA LINEAL Fecha: 6 de Julio de Fecha publicación notas: 6 de Julio de Fecha revisión examen: de Julio de Duración del examen: horas y media APELLIDOS Y NOMBRE: DNI: Titulación:. ( punto:,
Problemas Tema 7 Solución a problemas de ampliación de los Temas 5 y 6 - Hoja 13 - Todos resueltos
 página 1/9 Problemas Tema 7 Solución a problemas de ampliación de los Temas 5 y 6 - Hoja 13 - Todos resueltos Hoja 13. Problema 1 1. Sea una circunferencia de centro (0,) y radio unidades. Sea una segunda
página 1/9 Problemas Tema 7 Solución a problemas de ampliación de los Temas 5 y 6 - Hoja 13 - Todos resueltos Hoja 13. Problema 1 1. Sea una circunferencia de centro (0,) y radio unidades. Sea una segunda
Pruebas de acceso a enseñanzas universitarias oficiales de grado Castilla y León
 Selectividad Junio 14 Pruebas de acceso a enseñanzas universitarias oficiales de grado Castilla y León MATEMÁTICAS II EJERCICIO Nº páginas: INDICACIONES: 1.- OPTATIVIDAD: El alumno deberá escoger una de
Selectividad Junio 14 Pruebas de acceso a enseñanzas universitarias oficiales de grado Castilla y León MATEMÁTICAS II EJERCICIO Nº páginas: INDICACIONES: 1.- OPTATIVIDAD: El alumno deberá escoger una de
GEOMETRÍA. Septiembre 94. Determinar la ecuación del plano que pasa por el punto M (1, 0, [1,5 puntos]
![GEOMETRÍA. Septiembre 94. Determinar la ecuación del plano que pasa por el punto M (1, 0, [1,5 puntos] GEOMETRÍA. Septiembre 94. Determinar la ecuación del plano que pasa por el punto M (1, 0, [1,5 puntos]](/thumbs/86/94405582.jpg) Matemáticas II Pruebas de Acceso a la Universidad GEOMETRÍA Junio 94 1 Sin resolver el sistema, determina si la recta x y + 1 = 0 es exterior, secante ó tangente a la circunferencia (x 1) (y ) 1 Razónalo
Matemáticas II Pruebas de Acceso a la Universidad GEOMETRÍA Junio 94 1 Sin resolver el sistema, determina si la recta x y + 1 = 0 es exterior, secante ó tangente a la circunferencia (x 1) (y ) 1 Razónalo
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2006 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio 3, Opción A Reserva, Ejercicio
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio 3, Opción A Reserva, Ejercicio
Ejercicio 1 de la Opción A del modelo 6 de Solución
 Ejercicio 1 de la Opción A del modelo 6 de 2003 [2'5 puntos] Sea la función f : R R definida por f(x) = 2x 3-6x + 4. Calcula el área del recinto limitado por la gráfica de f y su recta tangente en el punto
Ejercicio 1 de la Opción A del modelo 6 de 2003 [2'5 puntos] Sea la función f : R R definida por f(x) = 2x 3-6x + 4. Calcula el área del recinto limitado por la gráfica de f y su recta tangente en el punto
E E V (P, Q) v = P Q AA + AB = AB AA = 0.
 Espacios afines. 1 Definición y propiedades. Definición 1.1 Sea E un conjunto no vacío. Se dice que E está dotado de estructura de espacio afín asociado a un espacio vectorial V, si existe una aplicación:
Espacios afines. 1 Definición y propiedades. Definición 1.1 Sea E un conjunto no vacío. Se dice que E está dotado de estructura de espacio afín asociado a un espacio vectorial V, si existe una aplicación:
ESTUDIO GRÁFICO DE LA ELIPSE.
 Curvas Cónicas para Dibujo y Matemáticas. Aplicación web Dibujo Técnico para ESO y Bachillerato Matemáticas para Bachillerato Educación Plástica y Visual Autor: José Antonio Cuadrado Vicente. ESTUDIO GRÁFICO
Curvas Cónicas para Dibujo y Matemáticas. Aplicación web Dibujo Técnico para ESO y Bachillerato Matemáticas para Bachillerato Educación Plástica y Visual Autor: José Antonio Cuadrado Vicente. ESTUDIO GRÁFICO
Circunferencias. d) A( 1, 5) y d = X = (x, y) punto genérico del lugar geométrico. b) dist (X, A) = d
 Circunferencias 6 Halla, en cada caso, el lugar geométrico de los puntos del plano cuya distancia al punto A es d. a) A(, ) y d = b) A(, ) y d = 1 c) A(, ) y d = 1 d) A( 1, ) y d = X = (x, y) punto genérico
Circunferencias 6 Halla, en cada caso, el lugar geométrico de los puntos del plano cuya distancia al punto A es d. a) A(, ) y d = b) A(, ) y d = 1 c) A(, ) y d = 1 d) A( 1, ) y d = X = (x, y) punto genérico
Definición: Se llama pendiente de una recta a la tangente de un ángulo de inclinación formado por el eje X y la
 Geometría Analítica Preliminares Identidades Trigonométricas Definición: Se llama pendiente de una recta a la tangente de un ángulo de inclinación formado por el eje X y la recta, tal que, esto es Recta
Geometría Analítica Preliminares Identidades Trigonométricas Definición: Se llama pendiente de una recta a la tangente de un ángulo de inclinación formado por el eje X y la recta, tal que, esto es Recta
B23 Curvas cónicas Curvas cónicas
 Geometría plana B23 Curvas cónicas Curvas cónicas Superficie cónica de revolución es la engendrada por una recta que gira alrededor de otra a la que corta. Curvas cónicas son las que resultan de la intersección
Geometría plana B23 Curvas cónicas Curvas cónicas Superficie cónica de revolución es la engendrada por una recta que gira alrededor de otra a la que corta. Curvas cónicas son las que resultan de la intersección
ÁLGEBRA LINEAL II Algunas soluciones a la práctica 14
 ÁLGEBRA LINEAL II Algunas soluciones a la práctica 14 Geometría afín. (Curso 013 014) 1. En un espacio afín real de dimensión 3, se consideran dos sistemas de referencia R = {O, ē 1, ē, ē 3 } y R = {P,
ÁLGEBRA LINEAL II Algunas soluciones a la práctica 14 Geometría afín. (Curso 013 014) 1. En un espacio afín real de dimensión 3, se consideran dos sistemas de referencia R = {O, ē 1, ē, ē 3 } y R = {P,
Unidad 6 Geometría euclídea. Producto escalar
 Unidad 6 Geometría euclídea Producto escalar PÁGINA 131 SOLUCIONES 1 La recta 4 x 3y + 6 = 0 tiene de pendiente 4 m = 3 4 Paralela: y 1 = ( x ) 4x 3y 5 = 0 3 4 Perpendicular: y 1 = ( x ) 3x + 4y 10 = 0
Unidad 6 Geometría euclídea Producto escalar PÁGINA 131 SOLUCIONES 1 La recta 4 x 3y + 6 = 0 tiene de pendiente 4 m = 3 4 Paralela: y 1 = ( x ) 4x 3y 5 = 0 3 4 Perpendicular: y 1 = ( x ) 3x + 4y 10 = 0
ELEMENTOS DE GEOMETRIA ANALITICA
 ELEMENTOS DE GEOMETRIA ANALITICA Derecho básico de aprendizaje: Explora y describe las propiedades de los lugares geométricos y de sus transformaciones a partir de diferentes representaciones. (ver DBA
ELEMENTOS DE GEOMETRIA ANALITICA Derecho básico de aprendizaje: Explora y describe las propiedades de los lugares geométricos y de sus transformaciones a partir de diferentes representaciones. (ver DBA
GEOMETRÍA. que pasa por el punto P y es paralelo a π. (0,9 puntos) b) Determinar la ecuación del plano π
 GEOMETRÍA 1.- Se considera la recta r : ( x, y, z) = ( t + 1, t,3 t), el plano π: x y z = 0y el punto P (1,1,1). Se pide: a) Determinar la ecuación del plano π 1 que pasa por el punto P y es paralelo a
GEOMETRÍA 1.- Se considera la recta r : ( x, y, z) = ( t + 1, t,3 t), el plano π: x y z = 0y el punto P (1,1,1). Se pide: a) Determinar la ecuación del plano π 1 que pasa por el punto P y es paralelo a
1 CUÁDRICAS Cuádricas. Estudio particular. 1 x y z. 1 x y z. a 00 a 01 a 02 a 03 a 10 a 11 a 12 a 13 a 20 a 21 a 22 a 23 a 30 a 31 a 32 a 33
 CUÁDRICAS. CUÁDRICAS.. Cuádricas. Estudio particular. Una cuádrica se dene como el lugar geométrico de los puntos del espacio euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen
CUÁDRICAS. CUÁDRICAS.. Cuádricas. Estudio particular. Una cuádrica se dene como el lugar geométrico de los puntos del espacio euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen
PAU Madrid. Matemáticas II. Año Examen de septiembre. Opción A. Ejercicio 1. Valor: 2 puntos.
 Opción A. Ejercicio. Valor: 2 puntos. Se considera la función real de variable real definida por: f(x) = a) ( punto) Determinar sus máximos y mínimos relativos x x 2 + b) ( punto) Calcular el valor de
Opción A. Ejercicio. Valor: 2 puntos. Se considera la función real de variable real definida por: f(x) = a) ( punto) Determinar sus máximos y mínimos relativos x x 2 + b) ( punto) Calcular el valor de
TEMA 7: CÓNICAS CIRCUNFERENCIA. A partir de esta ecuación podemos hallar el centro y el radio sin más que deshacer los cambios:
 TEMA 7: CÓNICAS CIRCUNFERENCIA Se define la circunferencia como el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. A dicha distancia se le llama radio de la circunferencia.
TEMA 7: CÓNICAS CIRCUNFERENCIA Se define la circunferencia como el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. A dicha distancia se le llama radio de la circunferencia.
TEMA 6 CÓNICAS CÓNICAS TEMA 6. 1.º BACHILLERATO - CIENCIAS. 1. La circunferencia. Ecuación de una circunferencia. (x - a) + (y - b) = r.
 TEMA 6 CÓNICAS Se denomina sección cónica (o simplemente cónica) a todas las curvas resultantes de las diferentes intersecciones entre un cono y un plano; si dicho plano no pasa por el vértice, se obtienen
TEMA 6 CÓNICAS Se denomina sección cónica (o simplemente cónica) a todas las curvas resultantes de las diferentes intersecciones entre un cono y un plano; si dicho plano no pasa por el vértice, se obtienen
