Análisis de Arcos Planos Isostáticos
|
|
|
- Francisca Bustamante Araya
- hace 7 años
- Vistas:
Transcripción
1 Análisis de Arcos Planos Isostáticos Diego Miramontes De León Resumen n este documento se presentarán algunos conceptos simples para E el análisis de arcos isostáticos sujetos a cargas concentradas o distribuidas. Por análisis debe entenderse el resolver el equilibrio y calcular los elementos mecánicos internos como son la fuerza axial N, fuerza cortante V y momento flexionante M a lo largo de la curva que define al arco. En un primer apartado se tratará el arco simplemente apoyado y con apoyos a la misma altura. Enseguida se tratarán arcos tri-articulados con apoyos a diferente altura. 1. Introducción 1.1. Definición Un arco es una estructura que escencialmente se diseña para que desarrolle esfuerzos de compresión a lo largo de su eje curvo, sin embargo, como elemento rígido, la flexión puede provocar tensiones. Es cierto que el trazo del arco influye directamente en la respuesta que pueda ofrecer ante las cargas aplicadas. Para que el arco sea isostático, se requiere que esté simplemente apoyado (figura 1) o que esté tri-articulado (figura ). A diferencia de los cables, en donde hay que determinar la forma que adoptará el cable, en los arcos, la geometría está por lo general completamente definida. El problema, además del equilibrio, es sobre todo el cálculo de los elementos mecánicos. La geometría está dada por el claro L, o distancia horizontal entre los apoyos, la flecha f o distancia vertical desde la horizontal al apoyo más bajo, la clave C, la cual corresponde al punto más alto sobre la curva del arco, 1
2 Figura 1: Arco simplemente apoyado es decir, ésta coincide con la flecha máxima, medida siempre desde el punto de arranque, por último el punto de arranque, quien se considerará como el punto donde se encuentre el apoyo más bajo. En la figura, el círculo sobre el arco representa una articulación. La articulación puede estar en cualquier punto, en este caso se supone localizada a una distancia b desde el apoyo izquierdo. Por último, a la línea que une los apoyos, se le da el nombre de línea de arranque y para arcos con apoyos a diferente altura puede medirse la distancia de la flecha desde ella.. Arco simplemente apoyado En este punto, interesa presentar las expresiones generales para el análisis de un arco con apoyos simples y una sola carga concentrada al centro del claro, como se muestra en la figura 1. También interesa que los apoyos estén a la misma altura, ya que representa un caso de estudio común, sobre todo como primer ejemplo. En este caso particular, no habrá reacción horizontal en ningún extremo y la reacción en cada apoyo vale la mitad de la carga. El equilibrio se resuelve pues por simetría. Fy = 0; R 1 + R = P R 1 = R = P (1)
3 Figura : Arco tri-articulado con cargas concentradas.1. Elementos mecánicos Para obtener la fuerza normal, el cortante y el momento en cualquier punto a lo largo de la curva del arco, conviene hacer uso de la matriz de rotación utilizada en análisis estructural : [R] = cosθ senθ 0 senθ cosθ () Recordando que [R] es ortogonal, será posible pasar de un sistema a otro, de modo que para un punto cualquiera localizado a una distancia (x, y) 3
4 será más sencillo realizar una suma de fuerzas a la izquierda o derecha de ese punto tomando como referencia el sistema de coordenadas global (ver figura 3), para formar el vector : {F } = R x R y M z g (3) Figura 3: Corte del arco en el punto (x, y) En la ecuación 3 R x se refiere a la resultante de la suma de las fuerzas en la dirección X a la izquierda o derecha de la sección localizada en el punto (x, y), R y se refiere a la resultante de la suma de las fuerzas en la dirección Y a la izquierda o derecha de la sección localizada en el punto (x, y) y por último, M z se refiere a la resultante de la suma de los momentos en la dirección Z a la izquierda o derecha de la sección localizada en el punto (x, y). En cada caso debe aplicarse una convención de signos, por ejemplo, N será positiva para tensión, V será positiva si sigue la dirección positiva del eje Y cuando la suma se haga a la izquierda y negativa cuando se haga a la derecha. Para el momento M se considera usualmente como positivo cuando la concavidad quede al exterior de la estructura. En vigas esto significa que la concavidad es contraria a la dirección positiva del eje Y. 4
5 A partir de las ecuaciones y 3 se obtiene : {F } l = [R] {F } g (4) Para el caso particular del arco de la figura 1, el vector de fuerzas global es simplemente : {F } = R x = 0 R y = P M z = P x g (5) Substituyendo este vector en la ecuación 5), se obtendrán directamente los valores de N, V y M. Sin embargo, dado que el ángulo θ varía en cada punto a lo largo del arco, es necesario expresar este cambio en términos de x. Para todo x, la derivada de la función y = f(x) que define la geomtería del arco, dará la pendiente en ese punto, de modo que el ángulo se calcula directamente : N x V x M x = cos(tg 1 ( dy sen(tg 1 ( dy )) dx )) dx sen(tg 1 ( dy )) 0 dx cos(tg 1 ( dy )) 0 dx R x R y M z (6).. Arcos Parábolicos Para aplicar la ecuación 6) a problemas definidos, se considerará que se conoce la distancia horizontal entre los apoyos L y la flecha máxima del arco. Esto implica que la coordenada x será L/ y la flecha será h...1. Arco parabólico de segundo grado Ahora considérese que se quiere probar un arco parabólico de segundo grado, es decir : 5
6 y = f(x) = Kx (7) Debido a la simetría, sólo se analiza la mitad, de modo que el valor de K se obtiene asignado los valores anteriores a x y y : ( ) ( ) L L y = f = h = K (8) De aquí : K = 4h L (9) La función para el arco parabólico es : ( ) 4h y = x (10) L y su derivada es : dy dx = ( ) 8h x (11) L... Arco parabólico de tercer grado Como en el caso anterior, se tendrá : y = f(x) = Kx 3 (1) 6
7 ( ) ( ) L L 3 y = f = h = K (13) De aquí : K = 8h L 3 (14) La función para el arco parabólico es : ( ) 8h y = x 3 (15) L 3 y su derivada es : dy dx = ( ) 4h x (16) L Arco parabólico de cualquier grado El procedimiento descrito antes puede generalizarse para cualquier grado, de modo que se tiene : y = Kx n (17) K = n h L n (18) ( n ) h y = x n (19) L n 7
8 dy dx = ( n n ) h x n 1 (0) L n Las expresiones dadas en este apartado sólo son válidas para arcos simplemente apoyados y con la misma altura de los apoyos, además la geometría debe ser simétrica como la mostrada en la figura 1. Para un caso más general, se analizarán arcos como el mostrado en la figura y para condiciones de carga tanto puntuales como distribuidas en puntos no simétricos. 3. Arcos tri-articulados Como parte de las estructuras isostáticas, es posible encontrar arcos con tres articulaciones, dos de las cuales están en los apoyos y una más en cualquier parte a lo largo de la curva del arco. Es frecuente que esta articulación guarde cierta estética por lo que ese punto arbitrario puede no serlo tanto. En la figura 4 se muestra uno de estos arcos en Puerto Montt, Chile. Además, en las figuras 5, se muestran los detalles de la articulación en uno de los apoyos y en la figura 6 se observa la articulación intermedia Equilibrio de arcos tri-articulados A diferencia de loas arcos simplemente apoyados, en donde el equilibrio exterior es prácticamente similar al de vigas, en los arcos tri-articulados existen cuatro reacciones externas. La articulación intermedia ofrece la ecuación adicional para resolver el equilibrio Arco con carga puntual Se analizará un arco sujeto a una carga concentrada según se muestra en la figura 7. Resolviendo el equilibrio exterior se tiene : Fx = 0; A x B x = 0 (1) 8
9 Figura 4: Arco tri-articulado (Fuente: Omar Tellez Elgueta) Fy = 0; A y B y P = 0 () M A z = 0; B x (h) + B y (L) P (a) = 0 (3) M C z = 0; B x (y c h) + B y (L x c ) = 0 (4) Las ecuaciones 3) y 4) incluyen sólo dos incógnitas (B x y B y ) por lo que pueden resolverse simultáneamente, es decir : 9
10 Figura 5: Apoyo en arco tri-articulado (Fuente: Omar Tellez Elgueta) [ h L (y c h) (L x c ) ] [ Bx B y ] = [ P (a) 0 ] (5) Conocidas B x y B y pueden resolverse 1) y ) para A x y A y. Supóngase que h = 0, es decir, los apoyos están a la misma altura. Entonces de 3) : B y = P a L (6) La ecuación 6) es similar a la reacción de una viga con una carga concentrada a la distancia a del apoyo A. De la ecuación 4) se tendría : 10
11 Figura 6: Articulacio n intermedia en arco tri-articulado (Fuente: propia) Bx = P a (L xc ) L yc (7) Pa yc (8) Si adema s xc = L/ : Bx = Para una serie de cargas concentradas P1, P,...Pn, simplemente se agregarı an a las ecuaciones anteriores Arco con carga distribuida Ahora, se analizara un arco sujeto a una carga distribuida segu n se muestra en la figura 8. Resolviendo el equilibrio exterior se tiene : 11
12 Figura 7: Arco tri-articulado bajo carga concentrada Fx = 0; A x B x = 0 (9) Fy = 0; A y B y wa = 0 (30) M A z = 0; B x (h) + B y (L) wa = 0 (31) M C z = 0; B x (y c h) + B y (L x c ) = 0 (3) 1
13 Figura 8: Arco tri-articulado bajo carga distribuida Debido a la ecuación 31), la solución sólo será válida para a x x c. Además, las ecuaciones 31) y 3) incluyen sólo dos incógnitas (B x y B y ) por lo que pueden resolverse simultáneamente, es decir : [ h L (y c h) (L x c ) ] [ Bx B y ] = [ wa 0 ] (33) Conocidas B x y B y pueden resolverse 9) y 30) para A x y A y. Nuevamente supóngase que h = 0, es decir, los apoyos están a la misma altura. Entonces de 31) : B y = wa L (34) 13
14 La ecuación 34) es similar a la reacción de una viga con una carga distribuida a la distancia a del apoyo A. De la ecuación 9) se tendría : B x = wa (L x c ) L y c (35) Si además x c = L/ : B x = wa 4y c (36) Considerando ahora que la carga va más allá del punto C, sólo se modificará la ecuación 3) : M C z = 0; B x (y c h) + B y (L x c ) w(x x c) = 0 (37) La solución para esta nueva condición es : [ h L (y c h) (L x c ) ] [ Bx B y ] [ = wa w(x x c) ] (38) Si nuevamente se considera que h = 0 se tendrá : B y = wa L (39) B x = [ wa L (L x c) w(x x c) ] 1 y c (40) 14
15 Si además, a = L B y = wl (41) B x = w(l x c) [( L L x )] c 1 yc (4) Más aun, si x c = L/ ; B x = wl 4 L 1 = wl (43) y c 8y c Deben atenderse con cuidado los límites para los cuales las soluciones dadas antes son válidas, ya que de no hacerlo, los resultados serían incorrectos. 4. Comentarios Es conveniente programar las ecuaciones dadas antes para calcular los valores de N, V y M en varios puntos. Debido a la sencillez de las expresiones y a que el cálculo es directo, puede hacerse en una hoja de cálculo, en donde se definan tantos puntos x como se quiera sobre la longitud del claro L. Puede verse que todas las expresiones sólo dependen de x. Los valores obtenidos pueden graficarse aunque no sigan la curva del arco. Aun así serán un referente para comparar el comportamiento ante cada uno de los elementos mecánicos. En forma general, se presentaron las soluciones del equilibrio exterior para un arco tri-articulado para dos casos específicos; bajo carga concentrada y bajo carga distribuida. En el primero, sólo se incluyó una carga, entendiendo que no hay dificutad en agregar tantas otras como se quiera. En el segundo se consideró la posibilidad de que la carga distribuida se aplique hasta el punto donde se encuentra la articulación o que pase de ese punto. En todos los casos expuestos se han agregado algunas condiciones expeciales como el que 15
16 los apoyos estén a la misma altura y/o que la articulación esté al centro del claro. Por último se recuerda que deben observarse detenidamente los límites para los cuales son válidas las soluciones propuestas. Referencias [1] A. Ghali y A.M. Neville (1983), Análisis estructural, Ed. Diana Técnico, 1a. Ed, 809p [] J. L. Meek, (1971), Matrix structural analysis, ISE, McGraw Hill, 481p [3] F. W. Beaufait, (1981), Análisis estructural, PH internacional, 591p [4] D. Miramontes De León, (009), Static Algorithm for Isostatic Trusses, Investigación Científica, Vol 5, No 1, ISSN
CAPÍTULO IV FUERZA CORTANTE Y MOMENTO FLEXIONANTE EN VIGAS
 CAPÍTULO IV FUERZA CORTANTE Y MOMENTO FLEXIONANTE EN VIGAS 4.1 CONCEPTOS BÁSICOS Este capítulo explica cómo las diversas fuerzas aplicadas a una viga llegan a producir fuerza cortante y momento flexionante
CAPÍTULO IV FUERZA CORTANTE Y MOMENTO FLEXIONANTE EN VIGAS 4.1 CONCEPTOS BÁSICOS Este capítulo explica cómo las diversas fuerzas aplicadas a una viga llegan a producir fuerza cortante y momento flexionante
Curvas en paramétricas y polares
 Capítulo 10 Curvas en paramétricas y polares Introducción Después del estudio detallado de funciones reales de variable real expresadas en forma explícita y con coordenadas cartesianas, que se ha hecho
Capítulo 10 Curvas en paramétricas y polares Introducción Después del estudio detallado de funciones reales de variable real expresadas en forma explícita y con coordenadas cartesianas, que se ha hecho
Figura 1. Viga simplemente apoyada
 Capítulo ESTABILIDAD E INDETERMINACIÓN. Introducción Durante los primeros cursos de estática, se aplican los principios elementales del equilibrio de sistemas de fuerza [,]. Desde entonces se plantea que
Capítulo ESTABILIDAD E INDETERMINACIÓN. Introducción Durante los primeros cursos de estática, se aplican los principios elementales del equilibrio de sistemas de fuerza [,]. Desde entonces se plantea que
Grado en Química Bloque 1 Funciones de una variable
 Grado en Química Bloque Funciones de una variable Sección.5: Aplicaciones de la derivada. Máximos y mínimos (absolutos) de una función. Sea f una función definida en un conjunto I que contiene un punto
Grado en Química Bloque Funciones de una variable Sección.5: Aplicaciones de la derivada. Máximos y mínimos (absolutos) de una función. Sea f una función definida en un conjunto I que contiene un punto
TEMA N 2 RECTAS EN EL PLANO
 2.1 Distancia entre dos puntos1 TEMA N 2 RECTAS EN EL PLANO Sean P 1 (x 1, y 1 ) y P 2 (x 2, y 2 ) dos puntos en el plano. La distancia entre los puntos P 1 y P 2 denotada por d = esta dada por: (1) Demostración
2.1 Distancia entre dos puntos1 TEMA N 2 RECTAS EN EL PLANO Sean P 1 (x 1, y 1 ) y P 2 (x 2, y 2 ) dos puntos en el plano. La distancia entre los puntos P 1 y P 2 denotada por d = esta dada por: (1) Demostración
CAPÍTULO V 10 EJERCICIOS RESUELTOS
 CAPÍTULO V 10 EJERCICIOS RESUELTOS Este último capítulo contiene 10 ejercicios complementarios (propuestos por los alumnos de la asignatura) que permiten poner en práctica los conocimientos adquiridos
CAPÍTULO V 10 EJERCICIOS RESUELTOS Este último capítulo contiene 10 ejercicios complementarios (propuestos por los alumnos de la asignatura) que permiten poner en práctica los conocimientos adquiridos
Fig. 18. Flexión asimétrica o inclinada de una viga con sección transversal doblemente simétrica
 8. Flexión Asimétrica (Biaxial) de Vigas 8.1 Introducción En esta sección, el análisis de la flexión en elementos-vigas, estudiado en las secciones precedentes, es ampliado a casos más generales. Primero,
8. Flexión Asimétrica (Biaxial) de Vigas 8.1 Introducción En esta sección, el análisis de la flexión en elementos-vigas, estudiado en las secciones precedentes, es ampliado a casos más generales. Primero,
VII. ECUACIÓN GENERAL DE SEGUNDO GRADO
 VII. ECUACIÓN GENERAL DE SEGUNDO GRADO 7.. SECCIONES CÓNICAS Cuando un plano corta a un cono circular recto de dos mantos, la sección que resulta de dicho corte determina ciertas curvas llamadas CÓNICAS.
VII. ECUACIÓN GENERAL DE SEGUNDO GRADO 7.. SECCIONES CÓNICAS Cuando un plano corta a un cono circular recto de dos mantos, la sección que resulta de dicho corte determina ciertas curvas llamadas CÓNICAS.
Aplicaciones de las integrales dobles
 Aplicaciones de las integrales dobles Las integrales dobles tienen multiples aplicaciones en física en geometría. A continuación damos una relación de alguna de ellas.. El área de una región plana R en
Aplicaciones de las integrales dobles Las integrales dobles tienen multiples aplicaciones en física en geometría. A continuación damos una relación de alguna de ellas.. El área de una región plana R en
CURSO: MECÁNICA DE SÓLIDOS II UNIVERSIDAD NACIONAL DEL CALLAO FACULTAD DE INGENIERÍA ELÉCTRICA Y ELECTRÓNICA
 UNIVERSIDAD NACIONAL DEL CALLAO FACULTAD DE INGENIERÍA ELÉCTRICA Y ELECTRÓNICA ESCUELA PROFESIONAL DE INGENIERÍA ELÉCTRICA CURSO: MECÁNICA DE SÓLIDOS II PROFESOR: ING. JORGE A. MONTAÑO PISFIL CURSO DE
UNIVERSIDAD NACIONAL DEL CALLAO FACULTAD DE INGENIERÍA ELÉCTRICA Y ELECTRÓNICA ESCUELA PROFESIONAL DE INGENIERÍA ELÉCTRICA CURSO: MECÁNICA DE SÓLIDOS II PROFESOR: ING. JORGE A. MONTAÑO PISFIL CURSO DE
2. CURVAS PLANAS, ECUACIONES PARAMÉTRICAS Y COORDENADAS POLARES
 2. CURVAS PLANAS, ECUACIONES PARAMÉTRICAS Y COORDENADAS POLARES INDICE 2.1. Curvas planas y ecuaciones paramétricas...2 2.2. Ecuaciones paramétricas de algunas curvas y su representación grafica 3 2.3.
2. CURVAS PLANAS, ECUACIONES PARAMÉTRICAS Y COORDENADAS POLARES INDICE 2.1. Curvas planas y ecuaciones paramétricas...2 2.2. Ecuaciones paramétricas de algunas curvas y su representación grafica 3 2.3.
Cálculo diferencial DERIVACIÓN
 DERIVACIÓN Definición de límite Entorno Definición. Se le llama entorno o vecindad de un punto a en R, al intervalo abierto (a - δ, a + δ ) = {a a - δ < x < a + δ }, en donde δ es semiamplitud a radio
DERIVACIÓN Definición de límite Entorno Definición. Se le llama entorno o vecindad de un punto a en R, al intervalo abierto (a - δ, a + δ ) = {a a - δ < x < a + δ }, en donde δ es semiamplitud a radio
Mecánica Vectorial Cap. 3. Juan Manuel Rodríguez Prieto I.M., M.Sc., Ph.D.
 Mecánica Vectorial Cap. 3 Juan Manuel Rodríguez Prieto I.M., M.Sc., Ph.D. Cómo tener éxito en Matemáticas? Paso 1: El trabajo duro triunfa sobre el talento natural. Paso 2: Mantenga una mente abierta.
Mecánica Vectorial Cap. 3 Juan Manuel Rodríguez Prieto I.M., M.Sc., Ph.D. Cómo tener éxito en Matemáticas? Paso 1: El trabajo duro triunfa sobre el talento natural. Paso 2: Mantenga una mente abierta.
Integrales dobles Guía electrónica de estudio para el estudiante
 Integrales dobles Guía electrónica de estudio para el estudiante Dr. M. Ranferí Gutierrez M. matematicaurl@gmail.com Introducción Esta guía electrónica de estudio le ayudará, mediante la utilización de
Integrales dobles Guía electrónica de estudio para el estudiante Dr. M. Ranferí Gutierrez M. matematicaurl@gmail.com Introducción Esta guía electrónica de estudio le ayudará, mediante la utilización de
JUNIO 2010. Opción A. 1 1.- Dada la parábola y = 3 área máxima que tiene un lado en la recta y los otros dos vértices en la gráfica de la parábola.
 Junio 00 (Prueba Específica) JUNIO 00 Opción A.- Dada la parábola y 3 área máima que tiene un lado en la recta y los otros dos vértices en la gráfica de la parábola., y la recta y 9, hallar las dimensiones
Junio 00 (Prueba Específica) JUNIO 00 Opción A.- Dada la parábola y 3 área máima que tiene un lado en la recta y los otros dos vértices en la gráfica de la parábola., y la recta y 9, hallar las dimensiones
Estática. Resultantes de Sistemas de Fuerzas
 Estática 4 Resultantes de Sistemas de Fuerzas Objetivos Concepto de momento de una fuerza en una y dos dimensiones. Método para encontrar el momento de una fuerza referido a un eje dado. Definir el momento
Estática 4 Resultantes de Sistemas de Fuerzas Objetivos Concepto de momento de una fuerza en una y dos dimensiones. Método para encontrar el momento de una fuerza referido a un eje dado. Definir el momento
Calcular el momento en el apoyo central, y dibujar los diagramas de esfuerzos. 6 m
 Elasticidad y Resistencia de Materiales Escuela Politécnica Superior de Jaén UNIVERSIDAD DE JAÉN Departamento de Ingeniería Mecánica y Minera Mecánica de Medios Continuos y Teoría de Estructuras Relación
Elasticidad y Resistencia de Materiales Escuela Politécnica Superior de Jaén UNIVERSIDAD DE JAÉN Departamento de Ingeniería Mecánica y Minera Mecánica de Medios Continuos y Teoría de Estructuras Relación
OBJETIVO: Conocer los diferentes tipos de armaduras existentes y calcular fuerzas resultantes por los métodos de juntas o nudos y secciones.
 ESTÁTICA Sesión 8 OBJETIVO: Conocer los diferentes tipos de armaduras existentes y calcular fuerzas resultantes por los métodos de juntas o nudos y secciones. 8 ESTRUCTURAS EN EQUILIBRIO 8.1. Armaduras
ESTÁTICA Sesión 8 OBJETIVO: Conocer los diferentes tipos de armaduras existentes y calcular fuerzas resultantes por los métodos de juntas o nudos y secciones. 8 ESTRUCTURAS EN EQUILIBRIO 8.1. Armaduras
2. SISTEMAS DE ECUACIONES LINEALES. Introducción
 2. SISTEMAS DE ECUACIONES LINEALES Introducción El presente curso trata sobre álgebra lineal. Al buscarla palabra lineal en un diccionario se encuentra, entre otras definiciones la siguiente: lineal, perteneciente
2. SISTEMAS DE ECUACIONES LINEALES Introducción El presente curso trata sobre álgebra lineal. Al buscarla palabra lineal en un diccionario se encuentra, entre otras definiciones la siguiente: lineal, perteneciente
APUNTES DE MATEMÁTICAS 1º BACHILLERATO TEMA 5: GEOMETRÍA AFÍN PROBLEMAS MÉTRICOS
 APUNTES DE MATEMÁTICAS TEMA 5: GEOMETRÍA AFÍN PROBLEMAS MÉTRICOS º BACHILLERATO ÍNDICE. ECUACIONES DE LA RECTA EN EL PLANO.... 4.. SISTEMAS DE REFERENCIA... 4.. COORDENADAS DE UN PUNTO... 4.3. COORDENADAS
APUNTES DE MATEMÁTICAS TEMA 5: GEOMETRÍA AFÍN PROBLEMAS MÉTRICOS º BACHILLERATO ÍNDICE. ECUACIONES DE LA RECTA EN EL PLANO.... 4.. SISTEMAS DE REFERENCIA... 4.. COORDENADAS DE UN PUNTO... 4.3. COORDENADAS
MAGNITUD VECTORIAL. Veamos un ejemplo sencillo: Es un segmento de línea recta orientada que sirve para representar a las magnitudes vectoriales.
 Capítulo 3 VECTORES MGNITUD VECTORIL Es aquella magnitud que aparte de conocer su valor numérico y su unidad respectiva, es necesario conocer también la dirección y sentido para que así dicha magnitud
Capítulo 3 VECTORES MGNITUD VECTORIL Es aquella magnitud que aparte de conocer su valor numérico y su unidad respectiva, es necesario conocer también la dirección y sentido para que así dicha magnitud
rad, y rad = 360 Ejercicio 1 Realizar las conversiones de grados a radianes y de radianes a grados de los siguientes ángulos:
 Trigonometría 1.- Ángulos En la medida de ángulos, y por tanto en trigonometría, se emplean dos unidades, si bien la más utilizada en la vida cotidiana es el grado sexagesimal, en matemáticas es el radián
Trigonometría 1.- Ángulos En la medida de ángulos, y por tanto en trigonometría, se emplean dos unidades, si bien la más utilizada en la vida cotidiana es el grado sexagesimal, en matemáticas es el radián
martilloatomico@gmail.com
 Titulo: CENTRO DE GRAVEDAD, CENTRO DE MASA Y CENTROIDE. Año escolar: Estática - Ingeniería Autor: José Luis Albornoz Salazar Ocupación: Ing Civil. Docente Universitario País de residencia: Venezuela Correo
Titulo: CENTRO DE GRAVEDAD, CENTRO DE MASA Y CENTROIDE. Año escolar: Estática - Ingeniería Autor: José Luis Albornoz Salazar Ocupación: Ing Civil. Docente Universitario País de residencia: Venezuela Correo
Funciones de varias variables.
 Funciones de varias variables. Definición. Hasta ahora se han estudiado funciones de la forma y = f (x), f :D Estas funciones recibían el nombre de funciones reales de variable real ya que su valor y dependía
Funciones de varias variables. Definición. Hasta ahora se han estudiado funciones de la forma y = f (x), f :D Estas funciones recibían el nombre de funciones reales de variable real ya que su valor y dependía
Estudio de funciones mediante límites y derivadas
 Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
CURVAS Y SUPERFICIES DE NIVEL
 CURVAS Y SUPERFICIES DE NIVEL UNIDAD NOMBRE TEMAS 4 Funciones vectorial de varias variables 4.3 Curvas y superficies de nivel. Gráfica de funciones de dos variables Existen varias maneras de visualizar
CURVAS Y SUPERFICIES DE NIVEL UNIDAD NOMBRE TEMAS 4 Funciones vectorial de varias variables 4.3 Curvas y superficies de nivel. Gráfica de funciones de dos variables Existen varias maneras de visualizar
Tema II: Programación Lineal
 Tema II: Programación Lineal Contenido: Solución a problemas de P.L. por el método gráfico. Objetivo: Al finalizar la clase los alumnos deben estar en capacidad de: Representar gráficamente la solución
Tema II: Programación Lineal Contenido: Solución a problemas de P.L. por el método gráfico. Objetivo: Al finalizar la clase los alumnos deben estar en capacidad de: Representar gráficamente la solución
3. Métodos clásicos de optimización lineal
 3. Métodos clásicos de optimización lineal Uso del método Simplex El problema que pretende resolverse es un problema de optimización lineal sujeto a restricciones. Para el modelo construido para el problema
3. Métodos clásicos de optimización lineal Uso del método Simplex El problema que pretende resolverse es un problema de optimización lineal sujeto a restricciones. Para el modelo construido para el problema
UNIDAD V LA PARÁBOLA
 UNIDAD LA PARÁBOLA OBJETIO PARTICULAR Al concluir la unidad, el alumno identificará y aplicará las propiedades relacionadas con el lugar geométrico llamado parábola, determinando los distintos parámetros,
UNIDAD LA PARÁBOLA OBJETIO PARTICULAR Al concluir la unidad, el alumno identificará y aplicará las propiedades relacionadas con el lugar geométrico llamado parábola, determinando los distintos parámetros,
El deslizamiento de un tobogán de Acuapolis, tiene la forma de un arco de. hipérbola de ecuación. como se puede apreciar en la figura siguiente:
 altura En la vida cotidiana las rectas tangentes a una curva u objeto podrán observar de muy diferentes maneras, como son el punto de contacto de la rueda de un automóvil, patineta. El deslizamiento de
altura En la vida cotidiana las rectas tangentes a una curva u objeto podrán observar de muy diferentes maneras, como son el punto de contacto de la rueda de un automóvil, patineta. El deslizamiento de
1. PRODUCTO ESCALAR. ESPACIO EUCLÍDEO
 1 1. PRODUCTO ESCALAR. ESPACIO EUCLÍDEO Muchos de los fenómenos que se investigan en la geometría utilizan nociones como las de longitud de un vector y ángulo entre vectores. Para introducir estos dos
1 1. PRODUCTO ESCALAR. ESPACIO EUCLÍDEO Muchos de los fenómenos que se investigan en la geometría utilizan nociones como las de longitud de un vector y ángulo entre vectores. Para introducir estos dos
EJEMPLOS DE CÁLCULO DE ESCALERAS DE HORMIGÓN ARMADO
 ESTRUCTURAS II FAU-UNNE: Estructura con continuidad estructural. Caso: ESCALERAS 1 EJEMPLOS DE CÁLCULO DE ESCALERAS DE HORMIGÓN ARMADO HIPÓTESIS: Se analiza solamente ESTRUCTURAS PLANAS, el eje tiene continuidad
ESTRUCTURAS II FAU-UNNE: Estructura con continuidad estructural. Caso: ESCALERAS 1 EJEMPLOS DE CÁLCULO DE ESCALERAS DE HORMIGÓN ARMADO HIPÓTESIS: Se analiza solamente ESTRUCTURAS PLANAS, el eje tiene continuidad
UNIDAD IV. LEYES DE SENOS Y COSENOS.
 UNIDAD IV. LEYES DE SENOS Y COSENOS. OBJETIVO. El estudiante resolverá problemas leyes de senos y cosenos, teóricos o prácticos de distintos ámbitos, mediante la aplicación las leyes y propiedades de Senos
UNIDAD IV. LEYES DE SENOS Y COSENOS. OBJETIVO. El estudiante resolverá problemas leyes de senos y cosenos, teóricos o prácticos de distintos ámbitos, mediante la aplicación las leyes y propiedades de Senos
1. Determinar las ecuaciones paramétricas y la ecuación continua de las rectas que pasan por el punto A y con el vector de dirección dado:
 CAPÍTULO. GEOMETRÍA AFÍN.. Problemas. Determinar las ecuaciones paramétricas y la ecuación continua de las rectas que pasan por el punto A y con el vector de dirección dado: a) A(,, ), v = (,, ) ; b) A(0,
CAPÍTULO. GEOMETRÍA AFÍN.. Problemas. Determinar las ecuaciones paramétricas y la ecuación continua de las rectas que pasan por el punto A y con el vector de dirección dado: a) A(,, ), v = (,, ) ; b) A(0,
Lección 1. Algoritmos y conceptos básicos.
 Página 1 de 8 Lección 1. Algoritmos y conceptos básicos. Objetivos. La primera lección del curs está dedicada a repasar los conceptos y algoritmos del álgebra lineal, básicos para el estudio de la geometría
Página 1 de 8 Lección 1. Algoritmos y conceptos básicos. Objetivos. La primera lección del curs está dedicada a repasar los conceptos y algoritmos del álgebra lineal, básicos para el estudio de la geometría
Fuerzas coplanares y no coplanares. Principio de transmisibilidad de las fuerzas
 2.ESTÁTICA La palabra estática se deriva del griego statikós que significa inmóvil. En virtud de que la dinámica estudia la causa que originan la causa del reposo o movimiento de los cuerpos, tenemos que
2.ESTÁTICA La palabra estática se deriva del griego statikós que significa inmóvil. En virtud de que la dinámica estudia la causa que originan la causa del reposo o movimiento de los cuerpos, tenemos que
Ec. rectas notables en un triángulo
 Ec rectas notables en un triángulo omo recordarás del curso de geometría plana (segundo semestre), las rectas notables de un triángulo son: Medianas: Una mediana es la recta que pasa por el punto medio
Ec rectas notables en un triángulo omo recordarás del curso de geometría plana (segundo semestre), las rectas notables de un triángulo son: Medianas: Una mediana es la recta que pasa por el punto medio
1. DIFERENCIABILIDAD EN VARIAS VARIABLES
 1 1. DIFERENCIABILIDAD EN VARIAS VARIABLES 1.1. DERIVADAS DIRECCIONALES Y PARCIALES Definición 1.1. Sea f : R n R, ā R n y v R n. Se define la derivada direccional de f en ā y en la dirección de v como:
1 1. DIFERENCIABILIDAD EN VARIAS VARIABLES 1.1. DERIVADAS DIRECCIONALES Y PARCIALES Definición 1.1. Sea f : R n R, ā R n y v R n. Se define la derivada direccional de f en ā y en la dirección de v como:
Coordenadas polares en el plano. Coordenadas ciĺındricas y esféricas en el espacio. Coordenadas... Coordenadas... Coordenadas...
 En el estudio de los conjuntos y las funciones es fundamental el sistema que se utilize para representar los puntos. Estamos acostumbrados a utilizar la estructura de afín o de vectorial de R n, utilizando
En el estudio de los conjuntos y las funciones es fundamental el sistema que se utilize para representar los puntos. Estamos acostumbrados a utilizar la estructura de afín o de vectorial de R n, utilizando
Universidad Alonso de Ojeda. Facultad de Ingeniería GUIA DE ESTUDIO ALGEBRA LINEAL.
 UNIDAD IV: VECTORES EN R2 Y R3 VECTOR Se puede considerar un vector como un segmento de recta con una flecha en uno de sus extremos. De esta forma lo podemos distinguir por cuatro partes fundamentales:
UNIDAD IV: VECTORES EN R2 Y R3 VECTOR Se puede considerar un vector como un segmento de recta con una flecha en uno de sus extremos. De esta forma lo podemos distinguir por cuatro partes fundamentales:
1 Ecuaciones y propiedades de la recta
 Ecuaciones propiedades de la recta Ecuaciones propiedades de la recta En esta sección estudiaremos la caracterización de la recta desde el punto de vista algebraico. A partir del concepto de pendiente
Ecuaciones propiedades de la recta Ecuaciones propiedades de la recta En esta sección estudiaremos la caracterización de la recta desde el punto de vista algebraico. A partir del concepto de pendiente
GEOMETRÍA ANALÍTICA DEL PLANO
 GEOMETRÍA ANALÍTICA DEL PLANO 1 UNIDAD DIDÁCTICA 5: Geometría analítica del plano 1. ÍNDICE 1. Sistemas de referencia y coordenadas puntuales 2. Distancia entre dos puntos del plano 3. Coordenadas del
GEOMETRÍA ANALÍTICA DEL PLANO 1 UNIDAD DIDÁCTICA 5: Geometría analítica del plano 1. ÍNDICE 1. Sistemas de referencia y coordenadas puntuales 2. Distancia entre dos puntos del plano 3. Coordenadas del
U N I V E R S I D A D A L A S P E R U A N A S FACULTAD DE INGENIERÍAS Y ARQUITECTURA ESCUELA ACADÉMICO PROFESIONAL DE INGENIERÍA INDUSTRIAL
 U N I V E R S I D A D A L A S P E R U A N A S FACULTAD DE INGENIERÍAS Y ARQUITECTURA ESCUELA ACADÉMICO PROFESIONAL DE INGENIERÍA INDUSTRIAL RESISTENCIA DE MATERIALES SILABO I. DATOS GENERALES CODIGO CARRERA
U N I V E R S I D A D A L A S P E R U A N A S FACULTAD DE INGENIERÍAS Y ARQUITECTURA ESCUELA ACADÉMICO PROFESIONAL DE INGENIERÍA INDUSTRIAL RESISTENCIA DE MATERIALES SILABO I. DATOS GENERALES CODIGO CARRERA
rad, y rad = 360 Ejercicio 1 Realizar las conversiones de grados a radianes y de radianes a grados de los siguientes ángulos:
 Trigonometría 1.- Ángulos En la medida de ángulos, y por tanto en trigonometría, se emplean dos unidades, si bien la más utilizada en la vida cotidiana es el grado sexagesimal, en matemáticas es el radián
Trigonometría 1.- Ángulos En la medida de ángulos, y por tanto en trigonometría, se emplean dos unidades, si bien la más utilizada en la vida cotidiana es el grado sexagesimal, en matemáticas es el radián
f (x) (1+[f (x)] 2 ) 3 2 κ(x) =
![f (x) (1+[f (x)] 2 ) 3 2 κ(x) = f (x) (1+[f (x)] 2 ) 3 2 κ(x) =](/thumbs/40/20918876.jpg) MATEMÁTICAS II - EXAMEN PRIMER PARCIAL - 4/11/11 Grado: Ing. Electrónica Rob. y Mec. Ing. Energía Ing. Organización Ind. Nombre y Apellidos: Ejercicio 1. La curvatura de una función f en un punto x viene
MATEMÁTICAS II - EXAMEN PRIMER PARCIAL - 4/11/11 Grado: Ing. Electrónica Rob. y Mec. Ing. Energía Ing. Organización Ind. Nombre y Apellidos: Ejercicio 1. La curvatura de una función f en un punto x viene
Anexo C. Introducción a las series de potencias. Series de potencias
 Anexo C Introducción a las series de potencias Este apéndice tiene como objetivo repasar los conceptos relativos a las series de potencias y al desarrollo de una función ne serie de potencias en torno
Anexo C Introducción a las series de potencias Este apéndice tiene como objetivo repasar los conceptos relativos a las series de potencias y al desarrollo de una función ne serie de potencias en torno
TEMA 8 GEOMETRÍA ANALÍTICA
 Tema 8 Geometría Analítica Matemáticas 4º ESO TEMA 8 GEOMETRÍA ANALÍTICA RELACIÓN ENTRE PUNTOS DEL PLANO EJERCICIO : Halla el punto medio del segmento de extremos P, y Q4,. Las coordenadas del punto medio,
Tema 8 Geometría Analítica Matemáticas 4º ESO TEMA 8 GEOMETRÍA ANALÍTICA RELACIÓN ENTRE PUNTOS DEL PLANO EJERCICIO : Halla el punto medio del segmento de extremos P, y Q4,. Las coordenadas del punto medio,
Anexo 1 ÁLGEBRA I.- Operaciones en las Expresiones Algebraicas II.- Factorización y Operaciones con las Fracciones III.- Funciones y Relaciones
 Anexo 1 ÁLGEBRA I.- Operaciones en las Expresiones Algebraicas 1.- Adición y sustracción 2.- Multiplicación 3.- División 4.- Productos especiales 5.- Triángulo de Pascal II.- Factorización y Operaciones
Anexo 1 ÁLGEBRA I.- Operaciones en las Expresiones Algebraicas 1.- Adición y sustracción 2.- Multiplicación 3.- División 4.- Productos especiales 5.- Triángulo de Pascal II.- Factorización y Operaciones
Ejercicios resueltos de tiro oblicuo
 Ejercicios resueltos de tiro oblicuo 1) Un arquero dispara una flecha cuya velocidad de salida es de 100m/s y forma un ángulo de 30º con la horizontal. Calcula: a) El tiempo que la flecha está en el aire.
Ejercicios resueltos de tiro oblicuo 1) Un arquero dispara una flecha cuya velocidad de salida es de 100m/s y forma un ángulo de 30º con la horizontal. Calcula: a) El tiempo que la flecha está en el aire.
LABORATORIO DE MECANICA LEY DE HOOKE
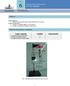 No 6 LABORATORIO DE MECANICA LEY DE HOOKE DEPARTAMENTO DE FISICA Y GEOLOGIA UNIVERSIDAD DE PAMPLONA FACULTAD DE CIENCIAS BÁSICAS Objetivos Objetivo general: Estudiar experimentalmente el comportamiento
No 6 LABORATORIO DE MECANICA LEY DE HOOKE DEPARTAMENTO DE FISICA Y GEOLOGIA UNIVERSIDAD DE PAMPLONA FACULTAD DE CIENCIAS BÁSICAS Objetivos Objetivo general: Estudiar experimentalmente el comportamiento
CAPITULO 5 LA DETERMINACIÓN DEL INGRESO DE EQUILIBRIO
 Documento elaborado por Jaime Aguilar Moreno Docente área económica Universidad del Valle Sede Buga CAPITULO 5 LA DETERMINACIÓN DEL INGRESO DE EQUILIBRIO OBJETIVO DEL CAPÍTULO Lograr que el estudiante
Documento elaborado por Jaime Aguilar Moreno Docente área económica Universidad del Valle Sede Buga CAPITULO 5 LA DETERMINACIÓN DEL INGRESO DE EQUILIBRIO OBJETIVO DEL CAPÍTULO Lograr que el estudiante
CAPÍTULO III MOMENTO DE INERCIA EN ÁREAS PLANAS. Este capítulo comprende diversas propiedades geométricas de secciones (para casos
 CAPÍTULO III MOMENTO DE INERCIA EN ÁREAS PLANAS Este capítulo comprende diversas propiedades geométricas de secciones (para casos prácticos, secciones de vigas) siendo la más importante el momento de inercia.
CAPÍTULO III MOMENTO DE INERCIA EN ÁREAS PLANAS Este capítulo comprende diversas propiedades geométricas de secciones (para casos prácticos, secciones de vigas) siendo la más importante el momento de inercia.
Introducción. El rayo B, tan pronto alcanza el arco PQ, sólo podrá saltar hacia la fase.
 Método simplificado de los dos puntos para evaluar el comportamiento de una línea de transmisión ante descargas atmosféricas Parte I Ingeniero Jairo León García Introducción Los parámetros básicos que
Método simplificado de los dos puntos para evaluar el comportamiento de una línea de transmisión ante descargas atmosféricas Parte I Ingeniero Jairo León García Introducción Los parámetros básicos que
Ecuaciones. 3º de ESO
 Ecuaciones 3º de ESO El signo igual El signo igual se utiliza en: Igualdades numéricas: 2 + 3 = 5 Identidades algebraicas: (x + 4) x = x 2 + 4 4x Fórmulas: El área, A,, de un círculo de radio r es: A =
Ecuaciones 3º de ESO El signo igual El signo igual se utiliza en: Igualdades numéricas: 2 + 3 = 5 Identidades algebraicas: (x + 4) x = x 2 + 4 4x Fórmulas: El área, A,, de un círculo de radio r es: A =
Fuerzas PROBLEMAS DE FÍSICA DE LOS PROCESOS BIOLÓGICOS RELACIÓN 2. Aula Integral de Física de los Procesos Biológicos
 Fuerzas 1. Al igual que las demás fuerzas, las fuerzas gravitatorias se suman vectorialmente. Considerar un cohete que viaja de la Tierra a la Luna a lo largo de una línea recta que une sus centros. (a)
Fuerzas 1. Al igual que las demás fuerzas, las fuerzas gravitatorias se suman vectorialmente. Considerar un cohete que viaja de la Tierra a la Luna a lo largo de una línea recta que une sus centros. (a)
MÉTODO DE LA RIGIDEZ PARA ARMADURAS PLANAS
 Instituto Tecnológico de Sonora Ciudad Obregón, Sonora. Análisis Estructural, Plan de Estudios 2009 Ing. Jesús Horacio Zazueta Villaseñor MÉTODO DE LA RIGIDEZ PARA ARMADURAS PLANAS 1 Supuestos para el
Instituto Tecnológico de Sonora Ciudad Obregón, Sonora. Análisis Estructural, Plan de Estudios 2009 Ing. Jesús Horacio Zazueta Villaseñor MÉTODO DE LA RIGIDEZ PARA ARMADURAS PLANAS 1 Supuestos para el
3.2 DIVIDIR UN POLINOMIO POR x a. REGLA DE RUFFINI
 TEMA 3 ÁLGEBRA MATEMÁTICAS CCSSI 1º BACH 1 TEMA 3 ÁLGEBRA 3.1 DIVISIÓN DE POLINOMIOS COCIENTE DE MONOMIOS El cociente de un monomio por otro monomio de grado inferior es un nuevo monomio cuyo grado es
TEMA 3 ÁLGEBRA MATEMÁTICAS CCSSI 1º BACH 1 TEMA 3 ÁLGEBRA 3.1 DIVISIÓN DE POLINOMIOS COCIENTE DE MONOMIOS El cociente de un monomio por otro monomio de grado inferior es un nuevo monomio cuyo grado es
APLICACIONES DE LAS ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN A PROBLEMAS DE TRAYECTORIAS
 APLICACIONES DE LAS ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN A PROBLEMAS DE TRAYECTORIAS 5 TRAYECTORIAS DE UN HAZ DE CURVAS: Se dice que una familia de curvas T(,, k) 0 (k una constante arbitraria)
APLICACIONES DE LAS ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN A PROBLEMAS DE TRAYECTORIAS 5 TRAYECTORIAS DE UN HAZ DE CURVAS: Se dice que una familia de curvas T(,, k) 0 (k una constante arbitraria)
Pruebas de Acceso a enseñanzas universitarias oficiales de grado Castilla y León
 Selectividad Junio 05 Pruebas de Acceso a enseñanzas universitarias oficiales de grado Castilla y León MATEMÁTICAS II EJERCICIO Nº páginas: INDICACIONES:.- OPTATIVIDAD: El alumno deberá escoger una de
Selectividad Junio 05 Pruebas de Acceso a enseñanzas universitarias oficiales de grado Castilla y León MATEMÁTICAS II EJERCICIO Nº páginas: INDICACIONES:.- OPTATIVIDAD: El alumno deberá escoger una de
P. A. U. LAS PALMAS 2005
 P. A. U. LAS PALMAS 2005 OPCIÓN A: J U N I O 2005 1. Hallar el área encerrada por la gráfica de la función f(x) = x 3 4x 2 + 5x 2 y la rectas y = 0, x = 1 y x = 3. x 3 4x 2 + 5x 2 es una función polinómica
P. A. U. LAS PALMAS 2005 OPCIÓN A: J U N I O 2005 1. Hallar el área encerrada por la gráfica de la función f(x) = x 3 4x 2 + 5x 2 y la rectas y = 0, x = 1 y x = 3. x 3 4x 2 + 5x 2 es una función polinómica
UNIDAD DIDÁCTICA 5: Geometría analítica del plano
 UNIDAD DIDÁCTICA 5: Geometría analítica del plano 1. ÍNDICE 1. Sistemas de referencia y coordenadas puntuales 2. Distancia entre dos puntos del plano 3. Coordenadas del punto medio de un segmento 4. La
UNIDAD DIDÁCTICA 5: Geometría analítica del plano 1. ÍNDICE 1. Sistemas de referencia y coordenadas puntuales 2. Distancia entre dos puntos del plano 3. Coordenadas del punto medio de un segmento 4. La
Funciones Exponenciales y Logarítmicas
 Funciones Exponenciales y Logarítmicas 0.1 Funciones exponenciales Comencemos por analizar la función f definida por f(x) = x. Enumerando coordenadas de varios puntos racionales, esto es de la forma m,
Funciones Exponenciales y Logarítmicas 0.1 Funciones exponenciales Comencemos por analizar la función f definida por f(x) = x. Enumerando coordenadas de varios puntos racionales, esto es de la forma m,
Tema 1. Cálculo diferencial
 Tema 1. Cálculo diferencial 1 / 57 Una función es una herramienta mediante la que expresamos la relación entre una causa (variable independiente) y un efecto (variable dependiente). Las funciones nos permiten
Tema 1. Cálculo diferencial 1 / 57 Una función es una herramienta mediante la que expresamos la relación entre una causa (variable independiente) y un efecto (variable dependiente). Las funciones nos permiten
FUNCIONES CUADRÁTICAS. PARÁBOLAS
 FUNCIONES CUADRÁTICAS. PARÁBOLAS 1. FUNCIONES CUADRÁTICAS Representemos, en función de la longitud de la base (x), el área (y) de todos los rectángulos de perímetro 1 metros. De ellos, cuáles son las medidas
FUNCIONES CUADRÁTICAS. PARÁBOLAS 1. FUNCIONES CUADRÁTICAS Representemos, en función de la longitud de la base (x), el área (y) de todos los rectángulos de perímetro 1 metros. De ellos, cuáles son las medidas
Análisis Estructural - 2009 Trabajo práctico de dinámica estructural: Superposición modal
 Análisis Estructural - 9 Enunciado Dada la estructura de la Figura, idealizada mediante un marco con vigas rígidas y columnas inextensibles, sometida a una carga armónica lateral de 8 t, se pide: ) Determinar
Análisis Estructural - 9 Enunciado Dada la estructura de la Figura, idealizada mediante un marco con vigas rígidas y columnas inextensibles, sometida a una carga armónica lateral de 8 t, se pide: ) Determinar
1. Sistema de coordenadas polares.
 GRADO DE INGENIERÍA AEROESPACIAL. CURSO 0.. Sistema de coordenadas polares. En esta sección estudiaremos las coordenadas polares y su relación con las coordenadas cartesianas. Un punto del plano tiene
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 0.. Sistema de coordenadas polares. En esta sección estudiaremos las coordenadas polares y su relación con las coordenadas cartesianas. Un punto del plano tiene
LA FUNCIÓN LINEAL: Ecuaciones y aplicaciones de la línea recta.
 INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMÁTICAS ASIGNATURA: GEOMETRÍA DOCENTE: JOSÉ IGNACIO DE JESÚS FRANCO RESTREPO TIPO DE GUIA: CONCEPTUAL - EJERCITACION PERIODO GRADO N FECHA
INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMÁTICAS ASIGNATURA: GEOMETRÍA DOCENTE: JOSÉ IGNACIO DE JESÚS FRANCO RESTREPO TIPO DE GUIA: CONCEPTUAL - EJERCITACION PERIODO GRADO N FECHA
CÁLCULO. Ingeniería Industrial. Curso 2009-2010. Departamento de Matemática Aplicada II. Universidad de Sevilla. Lección 3. Curvas en polares.
 CÁLCULO Ingeniería Industrial. Curso 2009-2010. Departamento de Matemática Aplicada II. Universidad de Sevilla. Lección 3. Curvas en polares. Resumen de la lección. 3.1. Gráficas en coordenadas polares.
CÁLCULO Ingeniería Industrial. Curso 2009-2010. Departamento de Matemática Aplicada II. Universidad de Sevilla. Lección 3. Curvas en polares. Resumen de la lección. 3.1. Gráficas en coordenadas polares.
Movimientos rígidos. Gonzalo Zubieta Badillo Departamento de Matemática Educativa, Cinvestav
 Movimientos rígidos Gonzalo Zubieta Badillo Departamento de Matemática Educativa, Cinvestav Resumen: Los movimientos rígidos son una parte de las transformaciones del plano en si mismo, su estudio tiene
Movimientos rígidos Gonzalo Zubieta Badillo Departamento de Matemática Educativa, Cinvestav Resumen: Los movimientos rígidos son una parte de las transformaciones del plano en si mismo, su estudio tiene
PROBLEMAS DE HOMOTECIAS Y SEMEJANZAS EN EL ESPACIO
 PROBLEMAS DE HOMOTECIAS Y SEMEJANZAS EN EL ESPACIO 82 Sea T una transformación afín definida por sus ecuaciones: = 2+ 2x y ' = 2+ 2y z' = 2+ 2z a) Clasificar T y hallar sus elementos característicos b)
PROBLEMAS DE HOMOTECIAS Y SEMEJANZAS EN EL ESPACIO 82 Sea T una transformación afín definida por sus ecuaciones: = 2+ 2x y ' = 2+ 2y z' = 2+ 2z a) Clasificar T y hallar sus elementos característicos b)
Coordenadas polares. Representación de puntos con coordenadas polares. Por ejemplo
 Instituto de Matemática Cálculo Integral Profesora Elisabeth Ramos Coordenadas polares El sistema de coordenadas polares es un sistema de coordenadas bidimensional en el cual cada punto o posición del
Instituto de Matemática Cálculo Integral Profesora Elisabeth Ramos Coordenadas polares El sistema de coordenadas polares es un sistema de coordenadas bidimensional en el cual cada punto o posición del
Clase 9 Sistemas de ecuaciones no lineales
 Clase 9 Instituto de Ciencias Básicas Facultad de Ingeniería Universidad Diego Portales Marzo, 2016 con dos incógnitas Un sistema de dos ecuaciones en el que al menos una ecuación es no lineal, se llama
Clase 9 Instituto de Ciencias Básicas Facultad de Ingeniería Universidad Diego Portales Marzo, 2016 con dos incógnitas Un sistema de dos ecuaciones en el que al menos una ecuación es no lineal, se llama
Ejercicios resueltos de trigonometría
 Ejercicios resueltos de trigonometría 1) Convierte las siguientes medidas de grados en radianes: a) 45º b) 60º c) 180º d) 270º e) 30º f) 225º g) 150º h) 135º i) -90º j) 720º 2) Expresa las siguientes razones
Ejercicios resueltos de trigonometría 1) Convierte las siguientes medidas de grados en radianes: a) 45º b) 60º c) 180º d) 270º e) 30º f) 225º g) 150º h) 135º i) -90º j) 720º 2) Expresa las siguientes razones
14.1 Introducción. 14.2 Caso 1: Area bajo una curva.
 Temas. Capacidades Calcular áreas de regiones del plano. 14.1 Introducción Area bajo una curva En esta sesión se inicia una revisión de las principales aplicaciones de la integral definida. La primera
Temas. Capacidades Calcular áreas de regiones del plano. 14.1 Introducción Area bajo una curva En esta sesión se inicia una revisión de las principales aplicaciones de la integral definida. La primera
FUERZAS DE UN FLUIDO EN REPOSO SOBRE SUPERFICIES PLANAS
 FUERZAS DE UN FLUIDO EN REPOSO SOBRE SUPERFICIES PLANAS En esta sección consideramos los efectos de la presión de un fluido, que actúa sobre superficies planas (lisas), en aplicaciones como las ilustradas.
FUERZAS DE UN FLUIDO EN REPOSO SOBRE SUPERFICIES PLANAS En esta sección consideramos los efectos de la presión de un fluido, que actúa sobre superficies planas (lisas), en aplicaciones como las ilustradas.
Celosía plana. Definición
 Celosías planas Celosía plana. Definición Modelo idealizado de una estructura reticular, formada por barras rectas de canto despreciable frente a su longitud. Barras unidas en sus extremos mediante articulaciones
Celosías planas Celosía plana. Definición Modelo idealizado de una estructura reticular, formada por barras rectas de canto despreciable frente a su longitud. Barras unidas en sus extremos mediante articulaciones
Diagonalización de matrices.
 Diagonalización de matrices. 1. Diagonalización de matrices. Definición 1.1 Sea A una matriz cuadrada,, decimos que es un autovalor de A si existe un vector no nulo tal que En esta situación decimos que
Diagonalización de matrices. 1. Diagonalización de matrices. Definición 1.1 Sea A una matriz cuadrada,, decimos que es un autovalor de A si existe un vector no nulo tal que En esta situación decimos que
Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos:
 1 CONOCIMIENTOS PREVIOS. 1 Logaritmos. 1. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Operaciones básicas con números reales. Propiedades de
1 CONOCIMIENTOS PREVIOS. 1 Logaritmos. 1. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Operaciones básicas con números reales. Propiedades de
UNIDAD II FUNCIONES. Ing. Ronny Altuve Esp.
 República Bolivariana de Venezuela Universidad Alonso de Ojeda Administración Mención Gerencia y Mercadeo UNIDAD II FUNCIONES Ing. Ronny Altuve Esp. Ciudad Ojeda, Septiembre de 2015 Función Universidad
República Bolivariana de Venezuela Universidad Alonso de Ojeda Administración Mención Gerencia y Mercadeo UNIDAD II FUNCIONES Ing. Ronny Altuve Esp. Ciudad Ojeda, Septiembre de 2015 Función Universidad
SECCIONES COMPUESTAS
 SCCONS COMPUSTS. Secciones compuestas por distintos materiales Hay casos en la práctica en los que se emplean vigas formadas por dos o más materiales diferentes. Un ejemplo de esto puede ser el de una
SCCONS COMPUSTS. Secciones compuestas por distintos materiales Hay casos en la práctica en los que se emplean vigas formadas por dos o más materiales diferentes. Un ejemplo de esto puede ser el de una
Dicho punto fijo se llama centro, a la distancia de cualquier punto de la circunferencia al centro se acostumbra a llamar radio.
 GEOMETRIA ANALITICA Capítulo 9 La Circunferencia 9.1. Definición Se llama circunferencia al lugar geométrico de los puntos de un plano que equidistan de un punto fijo del mismo plano. Dicho punto fijo
GEOMETRIA ANALITICA Capítulo 9 La Circunferencia 9.1. Definición Se llama circunferencia al lugar geométrico de los puntos de un plano que equidistan de un punto fijo del mismo plano. Dicho punto fijo
1.1 Estructuras isostáticas e hiperestáticas; cálculo de los diagramas de características en vigas, momento flector y esfuerzo de corte
 Trabajo Práctico Cálculo de Vigas. 1 Introducción 1.1 Estructuras isostáticas e hiperestáticas; cálculo de los diagramas de características en vigas, momento flector y esfuerzo de corte Como se explicó
Trabajo Práctico Cálculo de Vigas. 1 Introducción 1.1 Estructuras isostáticas e hiperestáticas; cálculo de los diagramas de características en vigas, momento flector y esfuerzo de corte Como se explicó
CAPÍTULO. 1 Conceptos básicos
 CAPÍTULO 1 Conceptos básicos 1.4.2 Curva solución de un PVI Como comentamos al hablar sobre las soluciones generales particulares de una ED, ocurre que las soluciones generales contienen una o más constantes
CAPÍTULO 1 Conceptos básicos 1.4.2 Curva solución de un PVI Como comentamos al hablar sobre las soluciones generales particulares de una ED, ocurre que las soluciones generales contienen una o más constantes
DOCUMENTO 3: DISTRIBUCIÓN DE PROBABILIDAD DE V. A. CONTINUA: LA DISTRIBUCIÓN NORMAL
 DOCUMENTO 3: DISTRIBUCIÓN DE PROBABILIDAD DE V. A. CONTINUA: LA DISTRIBUCIÓN NORMAL 3.1 INTRODUCCIÓN Como ya sabes, una distribución de probabilidad es un modelo matemático que nos ayuda a explicar los
DOCUMENTO 3: DISTRIBUCIÓN DE PROBABILIDAD DE V. A. CONTINUA: LA DISTRIBUCIÓN NORMAL 3.1 INTRODUCCIÓN Como ya sabes, una distribución de probabilidad es un modelo matemático que nos ayuda a explicar los
Ejemplo Traza la gráfica de los puntos: ( 5, 4), (3, 2), ( 2, 0), ( 1, 3), (0, 4) y (5, 1) en el plano cartesiano.
 Plano cartesiano El plano cartesiano se forma con dos rectas perpendiculares, cuyo punto de intersección se denomina origen. La recta horizontal recibe el nombre de eje X o eje de las abscisas y la recta
Plano cartesiano El plano cartesiano se forma con dos rectas perpendiculares, cuyo punto de intersección se denomina origen. La recta horizontal recibe el nombre de eje X o eje de las abscisas y la recta
3.1 Representación gráfica de curvas bidimensionales.
 Tema 3 Curvas y superficies Versión: 6 de febrero de 29 3. Representación gráfica de curvas bidimensionales. La representación gráfica de una curva en un ordenador es una linea poligonal construida uniendo
Tema 3 Curvas y superficies Versión: 6 de febrero de 29 3. Representación gráfica de curvas bidimensionales. La representación gráfica de una curva en un ordenador es una linea poligonal construida uniendo
Estructuras de acero: Problemas Vigas
 Estructuras de acero: Problemas Vigas Dimensionar con un perfil IPE una viga biapoada de 5 m de luz que soporta una sobrecarga de 0 kn/m uniformemente repartida. El acero es S75. Solución: Se supone un
Estructuras de acero: Problemas Vigas Dimensionar con un perfil IPE una viga biapoada de 5 m de luz que soporta una sobrecarga de 0 kn/m uniformemente repartida. El acero es S75. Solución: Se supone un
Tema 1: ESFUERZOS Y DEFORMACIONES
 Escuela Universitaria de Ingeniería Técnica grícola de Ciudad Real Tema 1: ESFUERZOS Y DEFORMCIONES Tipos de cargas. Tensiones: Clases. Tensiones reales, admisibles y coeficientes de seguridad. Elasticidad:
Escuela Universitaria de Ingeniería Técnica grícola de Ciudad Real Tema 1: ESFUERZOS Y DEFORMCIONES Tipos de cargas. Tensiones: Clases. Tensiones reales, admisibles y coeficientes de seguridad. Elasticidad:
V. 2 DISCUSIÓN DE UNA CURVA
 DISCUSIÓN DE ECUACIONES ALGEBRAICAS UNIDAD V Eisten dos problemas fundamentales en la Geometría Analítica:. Dada una ecuación hallar el lugar geométrico que representa.. Dado un lugar geométrico definido
DISCUSIÓN DE ECUACIONES ALGEBRAICAS UNIDAD V Eisten dos problemas fundamentales en la Geometría Analítica:. Dada una ecuación hallar el lugar geométrico que representa.. Dado un lugar geométrico definido
EI, A EI, A 2EI, A. 4.5 m. En primer lugar, definimos los nudos y los grados de libertad de la estructura.
 1. TEMA 5. MÉTODO MATRICIAL 1.1 Ejercicios resueltos 1. En la cubierta de la figura, determiar el valor de los momentos en los extremos de las barras, así como el momento máximo en ellas. (E=.1 1 11 N/m,
1. TEMA 5. MÉTODO MATRICIAL 1.1 Ejercicios resueltos 1. En la cubierta de la figura, determiar el valor de los momentos en los extremos de las barras, así como el momento máximo en ellas. (E=.1 1 11 N/m,
Actividad 12: Lectura Capítulo 7
 Actividad 12: Lectura Capítulo 7 Fecha de inicio Fecha de Cierre 17/OCT/13 00:00 09/NOV/13 23:55 La recta De las figuras geométricas la más sencilla es la recta, ya que los parámetros que la caracterizan
Actividad 12: Lectura Capítulo 7 Fecha de inicio Fecha de Cierre 17/OCT/13 00:00 09/NOV/13 23:55 La recta De las figuras geométricas la más sencilla es la recta, ya que los parámetros que la caracterizan
5.1. Recta tangente, normal e intersección de curvas. Recta tangente
 5. Aplicaciones de la Derivada 5.1. Recta tangente, normal e intersección de curvas Recta tangente Desde la escuela primaria se sabe que la recta tangente en un punto de una circunferencia es aquella recta
5. Aplicaciones de la Derivada 5.1. Recta tangente, normal e intersección de curvas Recta tangente Desde la escuela primaria se sabe que la recta tangente en un punto de una circunferencia es aquella recta
Expresiones de velocidad y aceleración en distintas coordenadas
 Apéndice B Expresiones de velocidad y aceleración en distintas coordenadas Índice B.1. Coordenadas cartesianas............... B.1 B.2. Coordenadas cilíndricas y polares......... B.2 B.3. Coordenadas esféricas................
Apéndice B Expresiones de velocidad y aceleración en distintas coordenadas Índice B.1. Coordenadas cartesianas............... B.1 B.2. Coordenadas cilíndricas y polares......... B.2 B.3. Coordenadas esféricas................
Tema 8. Geometría de la Circunferencia
 Tema 8. Geometría de la Circunferencia 1. Definición la circunferencia. Ecuación de la circunferencia 1.1 Ecuación de la circunferencia centrada en el origen 1. Ecuación de la circunferencia con centro
Tema 8. Geometría de la Circunferencia 1. Definición la circunferencia. Ecuación de la circunferencia 1.1 Ecuación de la circunferencia centrada en el origen 1. Ecuación de la circunferencia con centro
Resolución. Resolución gráfica de problemas de optimización
 Resolución de problemas de optimización Para resolver mente un problema de optimización como éste empezamos representando sus restricciones con igualdad. (0, 4) (0, 4) (4, 0) Para resolver mente un problema
Resolución de problemas de optimización Para resolver mente un problema de optimización como éste empezamos representando sus restricciones con igualdad. (0, 4) (0, 4) (4, 0) Para resolver mente un problema
Declaración de variables (integer, single, double, boolean, etc.) en Visual Basic. Dim. Ejemplos. (CU00309A)
 aprenderaprogramar.com Declaración de variables (integer, single, double, boolean, etc.) en Visual Basic. Dim. Ejemplos. (CU00309A) Sección: Cursos Categoría: Curso Visual Basic Nivel I Fecha revisión:
aprenderaprogramar.com Declaración de variables (integer, single, double, boolean, etc.) en Visual Basic. Dim. Ejemplos. (CU00309A) Sección: Cursos Categoría: Curso Visual Basic Nivel I Fecha revisión:
4. Mecánica Rotacional
 4. Mecánica Rotacional Cinemática Rotacional: (Conceptos básicos) Radián Velocidad angular Aceleración angular Frecuencia y período Velocidad tangencial Aceleración tangencial Aceleración centrípeta Torca
4. Mecánica Rotacional Cinemática Rotacional: (Conceptos básicos) Radián Velocidad angular Aceleración angular Frecuencia y período Velocidad tangencial Aceleración tangencial Aceleración centrípeta Torca
Es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado foco y de una recta llamada directriz.
 UNIDAD IV: LA PARABOLA. 4.1. Caracterización geométrica. 4.1.1. La parábola como lugar geométrico. Es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado foco y de una recta
UNIDAD IV: LA PARABOLA. 4.1. Caracterización geométrica. 4.1.1. La parábola como lugar geométrico. Es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado foco y de una recta
Modelo Académico de Calidad para la Competitividad AIND-01 92/98
 9. Matriz de Valoración ó Rúbrica MATRIZ DE VALORACIÓN O RÚBRICA Siglema: AIND-01 Nombre del Módulo: Nombre del Alumno: PSP evaluador: Grupo: Fecha: Resultado de Aprendizaje: 1.1 Determina la gráfica,
9. Matriz de Valoración ó Rúbrica MATRIZ DE VALORACIÓN O RÚBRICA Siglema: AIND-01 Nombre del Módulo: Nombre del Alumno: PSP evaluador: Grupo: Fecha: Resultado de Aprendizaje: 1.1 Determina la gráfica,
Con la ayuda de el dinamómetro implementamos el segundo método de aplicación y medición de fuerzas.
 EXPERIMENTO # 1: LEY DE HOOKE MEDICIÓN DE FUERZAS Objetivo: Estudios de las propiedades de un dinamómetro mediante la aplicación de fuerza conocidas. Fundamento Teórico: El concepto de fuerza es definido
EXPERIMENTO # 1: LEY DE HOOKE MEDICIÓN DE FUERZAS Objetivo: Estudios de las propiedades de un dinamómetro mediante la aplicación de fuerza conocidas. Fundamento Teórico: El concepto de fuerza es definido
