Análisis de Conglomerados (Cluster Analysis)
|
|
|
- Josefina Villanueva García
- hace 7 años
- Vistas:
Transcripción
1 Análisis de Conglomerados (Cluster Analysis) Ana María López Área de Metodología de las Ciencias del Comportamiento Departamento de Psicología Experimental
2 ÍNDICE 1. Introducción. Estimación Cuantitativa de la (Di)Similaridad entre Objetos.1. Medidas de distancia.1.1. Distancia Euclídea:.1.. Distancia Euclídea Binaria.1.3. Distancia para variables categóricas.. Coeficiente de Correlación de Pearson.3. Coeficientes de Asociación 3. Algoritmos de Clasificación 3.1. Algoritmos de Clasificación Jerárquicos Algoritmos de Clasificación Jerárquicos Ascendentes Método de la Distancia Mínima Método de la Distancia Máxima Método de la Distancia Media Otros métodos Determinación del método y del Número de Conglomerados en los Algoritmos Jerárquicos Ascendentes 3.. Algoritmos de Clasificación No Jerárquicos: Métodos de Partición. Agregación alrededor de Centros Móviles (K-medias) 3.3. Algoritmo en dos etapas 4. Análisis de conglomerados con SPSS
3 1. Introducción OBJETIVO: el análisis de conglomerados (cluster analysis, taxonomía numérica o procedimientos de clasificación) es un término genérico para una amplia variedad de procedimientos con un objetivo común: la formación de clases de sujetos o de variables similares. El objetivo es identificar grupos de manera que la variabilidad intraclase sea inferior a la variabilidad entreclases. En el gráfico siguiente hemos representado el resultado de una análisis de conglomerado en base a dos variables. X Conglomerado1 Conglomerado Conglomerado 3 X 1
4 1. Introducción Dado que el objetivo fundamental de una análisis de conglomerados es realizar una partición de la muestra en grupos similares, el punto de partida es una matriz de similaridades o de distancias entre los sujetos, objetos o variables que queremos agrupar. 1.. N 1... p X ik Etapas en un análisis de conglomerados 1ª. Matriz de datos 1.. N 1... N d ij ª. Matriz de (di)similaridades 3ª. Algoritmo de clasificación
5 . Estimación Cuantitativa de la (Di)Similaridad entre Objetos. Estimación Cuantitativa de la (Di)Similaridad entre Objetos.1. Medidas de distancia.1.1. Distancia Euclídea:.1.. Distancia Euclídea Binaria.1.3. Distancia para variables ordinales.. Coeficiente de Correlación de Pearson.3. Coeficientes de Asociación
6 .1.1. Distancia Euclídea La Distancia euclídea (d ij ): mide el parecido entre unidades de análisis que han sido evaluadas en un conjunto de variables métricas (cuantitativas). La distancia euclídea para dos sujetos viene dada por: d ij ( ) X X = ik jk Ejemplo 1: Calcular el parecido entre tres alumnos/as de psicología a partir de sus notas en la asignaturas de: Análisis de Datos I, Análisis de Datos II, Psicología experimental y Metodología Observacional utilizando la distancia euclídea. La matriz de datos para los tres sujetos es:
7 .1.1. Distancia Euclídea X Matriz de datos d 1 = ( 3 1) + ( 5 0) + ( 3) + ( 4 5) = 5,57 d 13 = ( 3 9) + ( 5 10) + ( ) + ( 4 5) = 7,75 Matriz de distancias S1 S S3 d 3 = ( 1 9) + ( 0 10) + ( 3 ) + ( 5 5) = 1, 85 S1 S S
8 .1.1. Distancia Euclídea Un problema de la distancia euclídea, como medida de similaridad, es su dependencia de las diferentes escalas en que estén medidas las variables. Escalas y rangos de variación diferentes pueden afectar al análisis de conglomerados. Este problema se soluciona si en vez de calcular la distancia euclídea con puntuaciones directas se calcula con puntuaciones normalizadas. Estandarizar las puntuaciones de los sujetos en las variables es uno de los procedimientos de normalización más frecuentes en análisis de datos. Un ejemplo aclarará el procedimiento de cálculo de la distancia euclídea y su dependencia de las escalas.
9 .1.1. Distancia Euclídea EJEMPLO. Supongamos que estamos interesados en agrupar a una muestra de 5 familias en base al número de hijos, al sueldo en euros al mes y al tamaño de la casa en metros cuadrados. La matriz de datos de la que partimos es: Podemos como antes calcular las distancias entre los sujetos a partir de las puntuaciones directas o bien podemos calcularlas a Partir de las variables estandarizadas. Para calcular las puntuaciones típicas utilizamos la expresión: Z ij = X ij X S j j Con SPSS directamente en el cuadro de diálogo de distancias o de análisis de conglomerados podemos optar por la matriz de distancias en puntuaciones directas o en puntuaciones estandarizadas.
10 .1.1. Distancia Euclídea Los siguientes cuadros muestran cómo obtener la matriz de distancias en puntuaciones estandarizadas. 1º. º. Insertamos en el cuadro Variables todas las que vamos a utilizar en el cálculo de la distancia 3º. Pulsamos en el botón Medidas y a continuación en la flecha del cuadro Estandarizar. Aparecen diferentes opciones de normalización. La primera es la correspondiente a Puntuaciones típicas.
11 .1.1. Distancia Euclídea Si hubiéramos utilizado la opción de no estandarizar las distancias entre las familias serían: Matriz de distancias Distancia euclídea , ,000 79,61 48,105 13, ,000,000 10,05 305, , ,61 10,05, ,19 00, , , ,19, , , ,043 00,57 605,189,000 Esta es una matriz de disimilaridades Como puede observarse, las familias más parecidas son la familia primera y la tercera. Sin embargo, son familias que salvo en que tienen un salario similar son diferentes en el resto de las variables. Si por el contrario seleccionamos la opción estandarizar la matriz de distancias que obtenemos es: Matriz de distancias Distancia euclídea ,000,773,713,388,965,773,000,77 1,745 1,537,713,77,000 4,194,09,388 1,745 4,194,000 3,56,965 1,537,09 3,56,000 Esta es una matriz de disimilaridades Con las puntuaciones estandarizadas las familias más parecidas son la primera y la segunda. Es evidente que los resultados de un análisis de conglomerados son distintos si se parte de matrices de similaridad o distancia que ordenen a los sujetos de manera distinta. Es por ello que en caso de variables medidas en escalas distintas es necesario normalizar.
12 Distancia.1.. euclídea Distancia : binaria Euclídea Binaria Versión de la distancia euclídea para variables dicotómicas. Este índice, que representaremos por d ij, se calcula a partir de una tabla de frecuencias x elaborada para cada par de sujetos o variables a clasificar. Como las variables son dicotómicas podemos codificar con 1 (presencia) a una categoría de la variable y con 0 (ausencia) a la otra categoría. Para cada par de sujetos se obtiene la siguiente tabla. Si Sj -> a b 0 c d En la tabla: a: es la frecuencia de acuerdos en el valor 1 para el conjunto de variables d: es la frecuencia de acuerdos en el valor 0 para el conjunto de variables b: es la frecuencia de desacuerdos. En las variables en las que el sujeto i tiene un 1 el sujeto j tiene un 0. c: es la frecuencia de desacuerdos. En las variables en las que el sujeto i tiene un 0 el sujeto j tiene un 1. La distancia euclídea binaria se obtiene de la tabla de frecuencias con la expresión d ij = b + c = desacuerdos La distancia así definida es un índice de la disimilaridad entre sujetos. El valor mínimo de 0 ocurre cuando todo son acuerdos y el valor máximo cuando no hay acuerdos en los sujetos comparados. Un ejemplo sencillo aclarará estos conceptos.
13 .1.. Distancia Euclídea Binaria EJEMPLO 3. Supongamos que queremos agrupar a los sujetos de una muestra (N = 5) en función de su parecido en un conjunto de variables todas ellas dicotómicas: X 1: E stado civil: soltero(1)-casado(0); X : S ituación laboral: activo(1)-parado(0); X 3: Nivel de estudios: bajo(1)-alto(0); X 4: Creencias religiosa: creyente(1)-no creyente(0); X 5: Tendencia de voto en las últimas elecciones: izquierda(1)-derecha(0). La matriz de datos de la que partimos es X 1 X X 3 X 4 X 5 S 1 S S 3 S 4 S Matriz de distancias S 1 0 S3 1 0 S4 1 0 S5 1 0 Sujeto Sujeto 1 0 Sujeto Sujeto S 1 S S 3 S 4 Tablas de frecuencias S S 3 S 4 S 5 = = = 5 = = 1 = 1 1 = 1 3 = = = 1731.
14 .1.. Distancia Euclídea Binaria En muchas ocasiones tenemos que agrupar a sujetos evaluados en variables politómicas (más de dos categorías). En estos casos podemos seguir utilizando la distancia euclídea binaria transformando las variables, previamente, en dicotómicas. Por ejemplo, imaginemos que tenemos que clasificar a una muestra de sujetos en función de su estados civil (soltero-1, casado-, y viudo-3), el sexo (hombre-1 y mujer-0) y sus creencias religiosas (no creyente-1, católico-, protestante-3 y testigo de Jehová-4) y que partimos de la siguiente matriz de datos: E.Civil Sexo C.Religiosas S 1 S S 3 S 4 S
15 .1.. Distancia Euclídea Binaria Para poder aplicar la distancia euclídea binaria tendríamos que transformar las variables politómicas de la matriz anterior en variables dicotómicas. Para transformar una variable politómica con k categorías en dicotómicas creamos k- 1 variables dicotómicas. Para el ejemplo con el que estamos trabajando la nueva matriz sería la siguiente: Solt Casado Hombre NoCreye Catól Protest
16 .1.. Distancia Euclídea Binaria Podemos transformar las variables politómicas en dicotómicas con SPSS. Los pasos a seguir serían: 1º. Seleccionamos Recodificar en distintas variables del menú Transformar º. Insertamos en Var.numérica->Var de resultado la variable que queremos transformar: creencias. 3º. Escribimos un Nombre para la primera variable dicotómica: nocreyente porque vamos a convertir en dicotómica la categoría no creyente. A continuación pinchamos en Cambiar. 4º. Pinchamos en Valores antiguos y nuevos y en el botón Valor antiguo escribimos el valor de la variable original que vamos a convertir y en Valor nuevo escribimos 1 y pulsamos en Añadir. A continuación seleccionamos Todos los demás valores y en Valor nuevo escribimos 0 y pulsamos Añadir y Continuar. Con estos pasos hemos creado una variable dicotómica de la categoría no creyente de la variable original. Para crear el resto de variable dicotómicas repetimos estos pasos dos veces.
17 .1.3. Distancia para variables categóricas En los paquetes estadísticos, no obstante, hay implementadas medidas de distancia para variables categóricas que no requieren de la transformación a dicotómicas. Concretamente, en SPSS podemos seleccionar para medir la distancia entre los sujetos evaluados en un conjuntos de variables categóricas las distancias Chi-Cuadrado o la distancia Phi-Cuadrado. Ambas se basan en el modelo de independencia. La distancia Phi-Cuadrado se obtiene dividiendo la Chi-cuadrado entre la raíz cuadrada del total de observaciones. Además de las medidas de distancia se pueden utilizar multitud de medidas de similaridad. Para variables cuantitativas se puede utilizar el coeficiente de correlación de Pearson y para variables cualitativas existen más de 100 índices derivados de la tabla de contingencia que hemos descrito anteriormente para la distancia euclídea binaria. Muchos de ellos están implementados en SPSS pero dado que las medidas de distancia descritas son las más utilizadas en análisis de conglomerados no describiremos en este documento el resto de los índices.
18 3. Algoritmos de Clasificación Una vez que se ha obtenido la matriz de (di)similaridades, el paso siguiente es aplicar una regla que nos permita agrupar a los sujetos o variables similares. Al conjunto de tales reglas se les denomina algoritmos de clasificación. De dos tipos han sido, fundamentalmente, los algoritmos de clasificación propuestos: 3.1. Algoritmos de Clasificación Jerárquicos. 3.. Algoritmos de Clasificación No Jerárquicos o basados en la partición en grupos disjuntos de los elementos a clasificar.
19 3.1. Algoritmos de Clasificación Jerárquicos Los algoritmos de clasificación jerárquicos pueden ser de tipos: Aglomerativos o ascendentes y divisivos o descendentes. Los algoritmos aglomerativos, mediante la utilización de algún criterio, van agrupando unidades de análisis en cada paso hasta llegar a un conglomerado que engloba a la totalidad. En los algoritmos divisivos se parte del conjunto total de elementos considerados como un conglomerado y, según algún criterio, se procede a dividir el grupo en grupos más pequeños llegando, en la última etapa del procedimiento, a considerar a cada elemento del grupo inicial como el conglomerado más simple y de máxima homogeneidad. En lo que sigue vamos a describir como funcionan los algoritmos de clasificación jerárquicos ascendentes.
20 Algoritmos de Clasificación Jerárquicos ascendentes La manera de proceder de los algoritmos jerárquicos ascendentes es como sigue: 1º. La primera etapa de cualquier algoritmo de clasificación ascendente trataría al conjunto de N elementos como una primera partición (C 0 ) en conglomerados de máxima homogeneidad o parecido. En esta primera etapa hay tanto conglomerados como sujetos a agrupar. º. En la segunda etapa se agrupan las clases (conglomerados) de la primera partición (C 0 ) que estén más próximas (o que sean más parecidas) según la medida de similaridad o dismilaridad que se haya definido entre los N elementos. La segunda partición (C 1 ) contiene un conglomerado menos que la primera. Se recalculan las distancias entre la nueva clase y el resto y nos encontramos en la misma situación que en la etapa 1 pero con N - 1 conglomerados. El proceso se repite hasta que en la última partición (C N-1 ) se obtiene un sólo grupo que contiene a todos los elementos. El resultado de este proceso es lo que se llama una jerarquía indexada y su representación gráfica es el dendograma. En el dendograma, o árbol de la jerarquía, se representan en el eje positivo de abscisas los elementos a agrupar y en el eje positivo de ordenadas las distancias correspondientes a los diferentes niveles de agregación denominados también índices de partición o coeficientes de agregación.
21 Algoritmos de Clasificación Jerárquicos ascendentes Para entender como proceden este tipo de algoritmos vamos a aplicarlos sobre las matrices de distancias que se dan a continuación. Este ejercicio sólo tiene utilidad didáctica. Las matrices son distancias entre 5 sujetos, denominados A, B, C, D y E, medidos en un conjunto de variables. Matriz1 Matriz A B C D E
22 Algoritmos de Clasificación Jerárquicos ascendentes Aplicación de una algoritmo de clasificación ascendente sobre la Matriz 1. Etapa 0: Se inicia el proceso con la partición: C 0 : (A), (B), (C), (D), (E) Índice de la partición: d(i)=0 Etapa 1: Agrupamos los dos sujetos más parecidos, menor distancia, formando con ellos un conglomerado. En este caso agregamos a los sujetos A y B y obtenemos la partición: C 1 : (A,B), (C), (D), (E) Índice de la partición: d(i)=0.1 En esta etapa recalculamos las distancias que afectan al nuevo conglomerado con el resto es decir: d((a,b), (C)), d((a,b), (D)), d((a,b), (E)) comparando las distancias entre los sujetos que componen los dos conglomerados y obtenemos la siguiente matriz de distancias. E 0.5 D 0.5 (A,B) (C) (D) (E) 0.4 C 0.4 (A,B) (C) (D) A 0.1 B
23 Algoritmos de Clasificación Jerárquicos ascendentes Etapa : Agrupamos los conglomerados más parecidos buscando en la nueva matriz la distancia más pequeña que en este caso corresponde a los conglomerados (A,B) y (C) y obtenemos la siguiente partición: C : (A,B,C), (D), (E) Índice de la partición: d(i)=0.3 Recalculamos, de nuevo, las distancias que afectan al nuevo conglomerado con el resto es decir: d((a,b,c)), (D)), d((a,b,c),(e)) comparando las distancias entre los sujetos que componen los dos conglomerados y obtenemos la siguiente matriz de distancias. (E) (A,B,C) (D) (E) 0.5 (D) 0.5 (A,B,C) (D) (A,B) 0.3 (C)
24 Algoritmos de Clasificación Jerárquicos ascendentes Etapa 3: Agrupamos los conglomerados más parecidos buscando en la nueva matriz la distancia más pequeña que en este caso corresponde a los conglomerados (A,B,C) y (D). El resultado de la agregación es ahora: C 3 : (A,B,C, D), (E) Índice de la partición: d(i)=0.4 Recalculamos las distancias que afectan al nuevo conglomerado con el resto es decir: d((a,b,c, D),(E)) y obtenemos la siguiente matriz de distancias. (E) (A,B,C,D) (E) (A,B,C,D) (A,B, C) 0.4 (D)
25 Algoritmos de Clasificación Jerárquicos ascendentes Etapa 4: Agrupamos los dos últimos conglomerados y obtenemos la partición: C 4 : (A,B,C, D, E) Índice de la partición: d(i)=0.5 (A,B,C,D,E) 0 (A,B,C,D,E) La representación gráfica del proceso de agregación seguido se denomina dendograma o árbol de la Jerarquía y corresponde a la figura siguiente: (A) (B) (C) (D) (E)
26 Algoritmos de Clasificación Jerárquicos ascendentes En cada etapa del procedimiento seguido para formar los grupos hemos recalculado la matriz de distancias entre clases. La distancia de cada elemento del nuevo conglomerado al resto era la misma, cuando esto ocurre para las sucesivas particiones se dice que sobre los elementos a agrupar hay definida una distancia ultramétrica, propiedad necesaria para obtener una clasificación jerárquica aglomerativa. Cuando en la matriz de distancias no se cumpla la propiedad ultramétrica, que por otro lado es lo habitual, hay que transformar la matriz en una matriz de distancias ultramétricas. Los diferentes procedimientos que permiten transformar una distancia cualquiera en ultramétrica se conocen como métodos de agregación. De los diferentes métodos propuestos los más utilizados e implementados en los paquetes estadísticos de uso más frecuentes son: a) Método de la distancia mínima (vecino más próximo en SPSS) b) Método de la distancia máxima (vecino más lejano en SPSS) c) Método de la distancia media (vinculación intergrupos en SPSS) Describiremos estos tres métodos utilizando como ejemplo la matriz.
27 Algoritmos de Clasificación Jerárquicos ascendentes El método de la distancia mínima asigna como distancia entre conglomerados el valor mínimo de las distancias entre todos los elementos que componen los conglomerados comparados. Sea (i,j) un conglomerado formado en una determinada etapa del algoritmo de clasificación. Supongamos que al recalcular la distancia entre (i,j) y (k) nos encontramos que: d(i,k) d(j,k) el método de la distancia mínima asigna como distancia entre los conglomerados (i,j) y (k) el valor más pequeño de la siguientes distancias: d((i,j),(k))=min{d(i,k), (j,k)} Aplicando este método vamos a agregar a los sujetos cuyas distancias son las de la matriz
28 Método de la Distancia Mínima Etapa 0: Se inicia el proceso con la partición: C0: (1), (), (3), (4), (5) Índice de la partición: d(i)=0 Etapa 1: Agrupamos los dos sujetos más parecidos, menor distancia, formando con ellos un conglomerado. En este caso agregamos a los sujetos 1 y y obtenemos la partición: C1: (1,), (3), (4), (5) Índice de la partición: d(i)= Antes de seguir agregando, recalculamos las distancias que afectan al nuevo conglomerado. Es decir calculamos: d((1,), (3)), d((1,), (4)), d((1,), (5)) comparando las distancias entre los sujetos que componen los dos conglomerados y obtenemos la siguiente matriz de distancias. Aplicando el método del mínimo las distancia entre los conglomerados anteriores d((1,),(3))) = min {d(1,3), d(,3)} =, (1,) (3) (4) (5) d((1,),(4))) = min {d(1,4), d(,4)} = 3 (1,) d((1,),(5))) = min {d(1,5), d(,5)} = 5 (3) y la nueva matriz de distancias sería: (4) 0 7 (5) 0
29 Método de la Distancia Mínima Etapa : Agrupamos los conglomerados más próximos buscando el índice más pequeño en la nueva matriz. Este índice corresponde a la distancia entre los conglomerados (1,) y (3). Agrupamos estos conglomerados y obtenemos la partición C : (1,,3), (4), (5) Índice de agregación es d((1,,3)) =. Volvemos a calcular las distancias entre los conglomerados d((1,,3), (4)) y d((1,,3), (5)) aplicando el método del mínimo: d((1,,3),(4)) = min [d((1,), (4)), d((3), (4))] = 3; d((1,,3),(5)) = min [d((1,), (5)), d((3), (5))] = 5 La matriz de distancias recalculada es: (1,,3) (4) (5) (1,,3) (4) 0 7 (5) 0
30 Método de la Distancia Mínima ETAPA 3: Agregamos los conglomerados más próximos tomando como referencia la última matriz de distancias calculada. Los conglomerados más próximos son ahora: (1,,3) y (4) de manera que la nueva partición es C3 : (1,,3,4), (5) el índice de la partición es d((1,,3,4)) = 3. La matriz de distancia recalculadas es: (1,,3,4) (5) (1,,3,4) 0 3 ETAPA 4: El último paso consiste en agregar los conglomerados (1,,3,4) y (5) y obtenemos la partición: C4 : (1,,3,4,5) el índice de esta partición es d((1,,3,4,5)) = 4 y la nueva matriz de distancia es (1,,3,4,5) 0 (1,,3,4,5) (1) () (3) (4) (5)
31 Método de la Distancia Máxima El método de la distancia máxima asigna como distancia entre conglomerado el valor máximo de las distancias entre todos los elementos que componen los conglomerados comparados. Sea (i,j) un conglomerado formado en una determinada etapa del algoritmo de clasificación. Supongamos que al recalcular la distancia entre (i,j) y (k) nos encontramos que: d(i,k) d(j,k) el método de la distancia máxima asigna como distancia entre los conglomerados (i,j) y (k) el valor más grande de la siguientes distancias: d((i,j),(k))=máx {d(i,k), (j,k))} Aplicando este método vamos a agregar a los sujetos cuyas distancias son las de la matriz
32 Método de la Distancia Máxima Etapa 0: Se inicia el proceso con la partición: C0: (1), (), (3), (4), (5) Índice de la partición: d(i)=0 Etapa 1: Agrupamos los dos sujetos más parecidos, menor distancia, formando con ellos un conglomerado. En este caso agregamos a los sujetos 1 y y obtenemos la partición: C1: (1,), (3), (4), (5) Índice de la partición: d(i)= Antes de seguir agregando, recalculamos las distancias que afectan al nuevo conglomerado. Es decir calculamos: d((1,), (3)), d((1,), (4)), d((1,), (5)) comparando las distancias entre los sujetos que componen los dos conglomerados y obtenemos la siguiente matriz de distancias. Aplicando el método del mínimo las distancia entre los conglomerados anteriores d((1,),(3))) = máx {d(1,3), d(,3)} = 3, d((1,),(4))) = máx {d(1,4), d(,4)} = 4 d((1,),(5))) = máx {d(1,5), d(,5)} = 6 y la nueva matriz de distancias sería: (1,) (3) (4) (5) (1,) (3) (4) 0 7 (5) 0
33 Método de la Distancia Máxima Etapa : Agrupamos los conglomerados más próximos buscando el índice más pequeño en la nueva matriz. Este índice corresponde a la distancia entre los conglomerados (1,) y (3). Agrupamos estos conglomerados y obtenemos la partición C : (1,,3), (4), (5) Índice de agregación es d((1,,3)) = 3. Volvemos a calcular las distancias entre los conglomerados d((1,,3), (4)) y d((1,,3), (5)) aplicando el método del mínimo: d((1,,3),(4)) = máx [d((1,), (4)), d((3), (4))] = 8; d((1,,3),(5)) = máx [d((1,), (5)), d((3), (5))] = 9 La matriz de distancias recalculada es: (1,,3) (4) (5) (1,,3) (4) 0 7 (5) 0
34 Método de la Distancia Máxima ETAPA 3: Agregamos los conglomerados más próximos tomando como referencia la última matriz de distancias calculada. Los conglomerados más próximos son ahora: (4) y (5) de manera que la nueva partición es C3 : (1,,3,), (4,5) el índice de la partición es d((4,5)) = 7. La matriz de distancia recalculadas es: (1,,3) (4,5) (1,,3) 0 9 (4,5) 0 ETAPA 4: El último paso consiste en agregar los conglomerados (1,,3) y (4,5) y obtenemos la partición: C4 : (1,,3,4,5) el índice de esta partición es d((1,,3,4,5)) = 9 y la nueva matriz de distancia es (1,,3,4,5) 0 (1,,3,4,5)
35 Método de la Distancia Media El método de la distancia media asigna como distancia entre conglomerado el valor medio de las distancias entre todos los elementos que componen los conglomerados comparados. Sea (i,j) un conglomerado formado en una determinada etapa del algoritmo de clasificación. Supongamos que al recalcular la distancia entre (i,j) y (k) nos encontramos que: d(i,k) d(j,k) el método de la distancia media asigna como distancia entre los conglomerados (i,j) y (k) el valor d[ ( i, j)( k) ] = (, ) + d( jk, ) dik Aplicando este método vamos a agregar a los sujetos cuyas distancias son las de la matriz
36 Método de la Distancia Media Etapa 0: Se inicia el proceso con la partición: C0: (1), (), (3), (4), (5) Índice de la partición: d(i)=0 Etapa 1: Agrupamos los dos sujetos más parecidos, menor distancia, formando con ellos un conglomerado. En este caso agregamos a los sujetos 1 y y obtenemos la partición: C1: (1,), (3), (4), (5) Índice de la partición: d(i)= Antes de seguir agregando, recalculamos las distancias que afectan al nuevo conglomerado. Es decir calculamos: d((1,), (3)), d((1,), (4)), d((1,), (5)) comparando las distancias entre los sujetos que componen los dos conglomerados y obtenemos la siguiente matriz de distancias. Aplicando el método del mínimo las distancia entre los conglomerados anteriores d d [( 1, ),() 3 ] [( 1, ),() 5 ] d = d = ( 13, ) + d( 3, ) ( 15, ) + d( 5, ) y la nueva matriz de distancias sería: ( 14, ) d( 4, ) + 3 d + = = 5.; d[ ( 1, ),( 4) ] = 6+ 5 = = = + = 35. (1,) (3) (4) (5) (1,) (3) (4) 0 7 (5) 0
37 Método de la Distancia Media Etapa : Agrupamos los conglomerados más próximos buscando el índice más pequeño en la nueva matriz. Este índice corresponde a la distancia entre los conglomerados (1,) y (3). Agrupamos estos conglomerados y obtenemos la partición C : (1,,3), (4), (5) Índice de agregación es d((1,,3)) =.5. Volvemos a calcular las distancias entre los conglomerados d((1,,3), (4)) y d((1,,3), (5)) aplicando el método de la media: d d [( 13,,),( 4) ] [( 13,,),( 5) ] ( 14, ) + ( 4, ) + ( 34, ) d d d = 3 ( ) ( ) = = 5 3 d (, 15 + d 5, + d(,) = = = La matriz de distancias recalculada es: (1,,3) (4) (5) (13) (4) 0 7 (5) 0
38 Método de la Distancia Media ETAPA 3: Agregamos los conglomerados más próximos tomando como referencia la última matriz de distancias calculada. Los conglomerados más próximos son ahora: (1,,3) y (4) de manera que la nueva partición es C3 : (1,,3,4), (5) el índice de la partición es d((1,,3,4)) = 5. La matriz de distancia recalculadas es: (1,,3,4) (5) (1,,3) (5) 0 ETAPA 4: El último paso consiste en agregar los conglomerados (1,,3,4) y (5) y obtenemos la partición: C4 : (1,,3,4,5) el índice de esta partición es d((1,,3,4,5)) = 6.75 y la nueva matriz de distancia es (1,,3,4,5) 0 (1,,3,4,5)
39 Determinación del método y del Número de conglomerados en los Algoritmos Jerárquicos Ascendentes Los diferentes métodos descritos modifican en mayor o menor medida las distancias iniciales entre sujetos. El método del mínimo aproxima a los sujetos y se denomina espacio contractivo, el método del máximo aleja a los sujetos y se denomina espacio dilatante y, por último, el método de la media suele conservar las distancias y se denomina espacio conservativo. La interpretación del resultado que proporciona un algoritmo ascendente dista mucho de referirse al grupo final sino que se refiere a un número mayor de conglomerados obtenidos en etapas intermedias del proceso de agregación. Si nos centramos en el dendograma la pregunta que cabría hacerse es qué índice de agregación o nivel de corte proporciona una solución en conglomerados óptima?. La respuesta a dicha pregunta, aunque debería constituir una etapa más del análisis de conglomerados, está entre los problemas no resueltos. Las razones para tal deficiencia son por una parte, la ausencia de una hipótesis nula y por otra la compleja naturaleza de las distribuciones muestrales multivariantes. Ante tales dificultades sólo hemos encontrado, en la literatura revisada, procedimientos basados en la inspección visual del dendograma y/o en gráficos derivados de él.
40 Determinación del método y del Número de conglomerados en los Algoritmos Jerárquicos Ascendentes El procedimiento más simple es decidir el punto de corte por inspección subjetiva. Este procedimiento no es muy satisfactorio pues está, generalmente, sesgado por las necesidades y opiniones de los investigadores acerca de la estructura correcta de sus datos. Un procedimiento más formal consiste en utilizar el gráfico de sedimentación (scree test) que ya se utiliza en análisis factorial. Para el análisis de conglomerados, este gráfico se construye colocando en el eje de abscisas los valores de los índices de agregación de las distintas etapas del algoritmo de clasificación utilizado y, en el eje de ordenadas, el número de conglomerados correspondiente a cada uno de los índices. Lo esperable es observar un primer tramo con una pendiente negativa grande donde el decaimiento es muy rápido para un intervalo de índices de agregación relativamente pequeño y, un tramo en donde la pendiente es muy pequeña y el decaimiento es muy lento. El número de conglomerados óptimo, que se recomienda como solución final, es el último valor del primer tramo del gráfico de sedimentación.
41 Determinación del método y del Número de conglomerados en los Algoritmos Jerárquicos Ascendentes (1,,3,4) (1,,3,4,5,6,7,8,) (1,,3,4,5,6,) (1,,3,4,5,6,7,8,9,10) (1,,3,4,5,6,7,8,9,) (7,8) ) número de conglomerados De la observación del gráfico de la Figura se deduce que 3 o 4 conglomerados serían una solución óptima. Otro método sencillo para determinar el número de conglomerados es el denominado tamaño de paso que consiste en determinar la mayor diferencia en índices de agregación para dos etapas sucesivas. El número de conglomerados es el de la etapa inmediatamente anterior. Podemos representar la diferencia en índices de agregación en etapas sucesivas y buscar un cambio importante.
42 Algoritmos de clasificación no jerárquicos: Métodos de partición En este conjunto de métodos, a diferencia de los jerárquicos, se forman k grupos siendo k un número que el Investigador decide a priori. Para decidir acerca del número de conglomerados se utiliza el conocimiento que se tiene de investigaciones previas o se utiliza un procedimiento de clasificación jerárquica que ayude a identificar el número de clases adecuado. Fijar un número muy pequeño puede llevar a conclusiones pobres, mientras que fijar un número demasiado grande complica la interpretación. de Lo Clasificación ideal es repetir el análisis No con distintos Jerárquicos: valores de k y seleccionar Métodos el que más satisfaga de Partic las s (K-medias) expectativas del investigador. Para llegar a la formación de conglomerados se sigue un proceso iterativo que intenta optimizar una función criterio. Se han propuesto varias funciones y una de las más eficaces consiste en la reasignación de una observación al centro más próximo. Este tipo de algoritmos comienzan con una selección de tantos sujetos como conglomerados queramos formar. Los sujetos inicialmente seleccionados constituyen los centros de las clases e inducen una primera partición por asignación del resto de los sujetos al centro más próximo. Las distintas técnicas de partición difieren en cómo se determinan los conglomerados iniciales y como son asignados a las clases. De los distintos algoritmos de clasificación no jerárquicos vamos a describir el método de k-medias o agregación alrededor de centros móviles por ser de los más utilizados e implementados en los paquetes estadísticos de uso frecuente en investigación.
43 3.. Algoritmos de Clasificación No Jerárquicos: Métodos de Partición. Agregación alrededor de Centros Móviles (K-medias) Se parte de un conjunto de sujetos a clasificar en base a sus semejanzas en p variables. Se decide un número k de clases y se procede de la siguiente manera: Etapa 0: Se determinan k centros. La forma de elegir los centros puede ser aleatoria o fija (por ejemplo los k primeros sujeto de la matriz de datos). {,,..., } I 0 I 0 1 I 0 k estos centros inducen una primera partición del conjunto de sujetos { },,..., C 0 1 C 0 C 0 k
44 3.. Algoritmos de Clasificación No Jerárquicos: Métodos de Partición. Agregación alrededor de Centros Móviles (K-medias) De tal manera que un sujeto (i) pertenece a la clase I 0 1 si está más próximo a C 1 0 que al resto de los 0 centros. La proximidad del sujeto (i) a Clase I 1 es la distancia euclídea del sujeto al centro de dicha clase. El centro de la clase -o centroide- es el vector de medias para Las p variables medidas en la investigación. Es decir, el centroide de la clase I 0 1 es { X, X,..., X p } y la distancia del sujeto (i) al centroide viene dada por p d = X ij X j= 1 I, j
45 3.. Algoritmos de Clasificación No Jerárquicos: Métodos de Partición. Agregación alrededor de Centros Móviles (K-medias) Etapa 1: Se determinan k nuevos centros {,,..., } C 1 1 C 1 C 1 k calculando el centroide de las clases de la primera partición. Los nuevos centros inducen una nueva partición { },,..., I 1 I 1 1 I 1 k Esta nueva partición se obtiene recalculando las distancias de cada sujeto a los centros de la partición y si es necesario se reasigna a los sujetos. El criterio para reasignar es que la distancia de un sujeto a otro centro sea menor que la distancia al centro de la clase a la que temporalmente se ha asignado.
46 3.. Algoritmos de Clasificación No Jerárquicos: Métodos de Partición. Agregación alrededor de Centros Móviles (K-medias) Las etapas anteriores se repiten hasta que en dos etapas sucesivas se obtiene la misma partición. Es decir, no hay reasignación de sujetos y por tanto los centroides no cambian. Otro criterio para terminar es fijar, a priori, un número máximo de etapas o un valor mínimo para las distancia entre centros. Gráficamente el algoritmo de k- medias lo hemos representado en la siguiente figura
47 Inicializa los valores de las semillas para un número k de conglomerados Se calculan las distancias de cada sujeto a los valores iniciales y se obtiene la primera partición Se calculan los nuevos centroides y se reasigna a los sujetos No hay reasignación
Medidas de asociación
 13 Medidas de asociación Irene Moral Peláez 13.1. Introducción Recurriremos a las medidas de asociación cuando queramos evaluar el grado de asociación entre dos variables y no únicamente comprobar analíticamente
13 Medidas de asociación Irene Moral Peláez 13.1. Introducción Recurriremos a las medidas de asociación cuando queramos evaluar el grado de asociación entre dos variables y no únicamente comprobar analíticamente
ANÁLISIS DE CONGLOMERADOS
 ANÁLISIS DE CONGLOMERADOS Análisis de conglomerados Autor: Manuel Terrádez Gurrea (mterradez@uoc.edu). ESQUEMA DE CONTENIDOS Análisis de conglomerados (cluster) Interpretación de dendogramas INTRODUCCIÓN
ANÁLISIS DE CONGLOMERADOS Análisis de conglomerados Autor: Manuel Terrádez Gurrea (mterradez@uoc.edu). ESQUEMA DE CONTENIDOS Análisis de conglomerados (cluster) Interpretación de dendogramas INTRODUCCIÓN
Julia García Salinero. Departamento de Investigación FUDEN. Introducción
 1 Análisis de datos en los estudios epidemiológicos V Prueba de Chi cuadrado y Análisis de la varianza. Departamento de Investigación FUDEN. Introducción Continuamos el análisis de los estudios epidemiológicos,
1 Análisis de datos en los estudios epidemiológicos V Prueba de Chi cuadrado y Análisis de la varianza. Departamento de Investigación FUDEN. Introducción Continuamos el análisis de los estudios epidemiológicos,
José Antonio Palazón Palazón Ferrando y José Francisco Calvo Sendín. Depto. Ecología e Hidrología palazon@um.es jfcalvo@um.es
 José Antonio Palazón Palazón Ferrando y José Francisco Calvo Sendín Depto. Ecología e Hidrología palazon@um.es jfcalvo@um.es Universidad de Murcia Taller Caldum, 22 de Julio de 2004 1 Observaciones, objetividad
José Antonio Palazón Palazón Ferrando y José Francisco Calvo Sendín Depto. Ecología e Hidrología palazon@um.es jfcalvo@um.es Universidad de Murcia Taller Caldum, 22 de Julio de 2004 1 Observaciones, objetividad
4. Método Simplex de Programación Lineal
 Temario Modelos y Optimización I 4. Método Simplex de Programación Lineal A- Resolución de problemas, no particulares, con representación gráfica. - Planteo ordenado de las inecuaciones. - Introducción
Temario Modelos y Optimización I 4. Método Simplex de Programación Lineal A- Resolución de problemas, no particulares, con representación gráfica. - Planteo ordenado de las inecuaciones. - Introducción
Práctica 1: Introducción a SPSS 1
 Estadística Aplicada Curso 2010/2011 Diplomatura en Nutrición Humana y Dietética Práctica 1: Introducción a SPSS 1 Este programa estadístico está organizado en dos bloques: el editor de datos y el visor
Estadística Aplicada Curso 2010/2011 Diplomatura en Nutrición Humana y Dietética Práctica 1: Introducción a SPSS 1 Este programa estadístico está organizado en dos bloques: el editor de datos y el visor
Práctica 2 Estadística Descriptiva
 Práctica 2 Estadística Descriptiva Contenido Introducción...................................... 1 Tablas de frecuencias................................. 2 Medidas de centralización, dispersión y forma...................
Práctica 2 Estadística Descriptiva Contenido Introducción...................................... 1 Tablas de frecuencias................................. 2 Medidas de centralización, dispersión y forma...................
SESIÓN PRÁCTICA 7: REGRESION LINEAL SIMPLE PROBABILIDAD Y ESTADÍSTICA. PROF. Esther González Sánchez. Departamento de Informática y Sistemas
 SESIÓN PRÁCTICA 7: REGRESION LINEAL SIMPLE PROBABILIDAD Y ESTADÍSTICA PROF. Esther González Sánchez Departamento de Informática y Sistemas Facultad de Informática Universidad de Las Palmas de Gran Canaria
SESIÓN PRÁCTICA 7: REGRESION LINEAL SIMPLE PROBABILIDAD Y ESTADÍSTICA PROF. Esther González Sánchez Departamento de Informática y Sistemas Facultad de Informática Universidad de Las Palmas de Gran Canaria
Índice de contenidos. Primera parte Introducción al SPSS. 1. Estructura del SPSS
 Índice de contenidos Primera parte Introducción al SPSS 1. Estructura del SPSS Tipos de ventanas SPSS Ventana designada versus ventana activa Cuadros de diálogo Subcuadros de diálogo Las barras de menús
Índice de contenidos Primera parte Introducción al SPSS 1. Estructura del SPSS Tipos de ventanas SPSS Ventana designada versus ventana activa Cuadros de diálogo Subcuadros de diálogo Las barras de menús
TRABAJO CON NÚMEROS EN EXCEL 2007
 Trabajar con números (Formato numérico y fórmulas) Hemos acabado ya de trabajar con palabras y vamos a comenzar a trabajar con números, aplicarles formatos y hacer operaciones matemáticas sencillas. Para
Trabajar con números (Formato numérico y fórmulas) Hemos acabado ya de trabajar con palabras y vamos a comenzar a trabajar con números, aplicarles formatos y hacer operaciones matemáticas sencillas. Para
La herramienta ArtEM: Aritmética Entera y Modular
 La herramienta ArtEM: Aritmética Entera y Modular 1. Introducción La herramienta ArtEM (Aritmética Entera y Modular) es una aplicación informática programada en Visual Basic y desarrollada con el fin de
La herramienta ArtEM: Aritmética Entera y Modular 1. Introducción La herramienta ArtEM (Aritmética Entera y Modular) es una aplicación informática programada en Visual Basic y desarrollada con el fin de
GRÁFICOS GRÁFICOS EN SPSS. Bakieva, M., González Such, J., Jornet, J., Terol, L.
 GRÁFICOS GRÁFICOS EN SPSS GRÁFICOS EN SPSS. TIPOS DE GRÁFICOS. GRÁFICOS DE BARRAS; GRÁFICOS DE LÍNEAS; GRÁFICOS DE ÁREAS; GRÁFICOS DE SECTORES; GRÁFICOS DE MÁXIMOS Y MÍNIMOS; DIAGRAMA DE CAJA; DIAGRAMAS
GRÁFICOS GRÁFICOS EN SPSS GRÁFICOS EN SPSS. TIPOS DE GRÁFICOS. GRÁFICOS DE BARRAS; GRÁFICOS DE LÍNEAS; GRÁFICOS DE ÁREAS; GRÁFICOS DE SECTORES; GRÁFICOS DE MÁXIMOS Y MÍNIMOS; DIAGRAMA DE CAJA; DIAGRAMAS
Capítulo 2. Cómo utilizar la ayuda
 Capítulo 2 Cómo utilizar la ayuda El SPSS cuenta con un completo sistema de ayuda al que puede accederse desde cualquier ventana o cuadro de diálogo. Este sistema de ayuda adopta varios formatos diferentes,
Capítulo 2 Cómo utilizar la ayuda El SPSS cuenta con un completo sistema de ayuda al que puede accederse desde cualquier ventana o cuadro de diálogo. Este sistema de ayuda adopta varios formatos diferentes,
FUNDAMENTOS METODOLÓGICOS EN PSICOLOGÍA ANÁLISIS BÁSICOS CON SPSS
 UNIVERSIDAD DE SEVILLA FACULTAD DE PSICOLOGIA FUNDAMENTOS METODOLÓGICOS EN PSICOLOGÍA PROFESORES: Gutiérrez, Mayte Martínez, Rafael J. Moreno, Rafael ANÁLISIS BÁSICOS CON SPSS INDICE: Pág. 1. Estadísticos
UNIVERSIDAD DE SEVILLA FACULTAD DE PSICOLOGIA FUNDAMENTOS METODOLÓGICOS EN PSICOLOGÍA PROFESORES: Gutiérrez, Mayte Martínez, Rafael J. Moreno, Rafael ANÁLISIS BÁSICOS CON SPSS INDICE: Pág. 1. Estadísticos
Estadística descriptiva. Representación de datos descriptivos
 6 Estadística descriptiva. Representación de datos descriptivos Alberto Rodríguez Benot Rodolfo Crespo Montero 6.1. Introducción Tal como vimos en la introducción, la estadística descriptiva comprende
6 Estadística descriptiva. Representación de datos descriptivos Alberto Rodríguez Benot Rodolfo Crespo Montero 6.1. Introducción Tal como vimos en la introducción, la estadística descriptiva comprende
Análisis de Datos CAPITULO 3: MEDIDAS DE VARIABILIDAD Y ASIMETRÍA
 1. INTRODUCCIÓN En el tema 1 veíamos que la distribución de frecuencias tiene tres propiedades: tendencia central, variabilidad y asimetría. Las medidas de tendencia central las hemos visto en el tema
1. INTRODUCCIÓN En el tema 1 veíamos que la distribución de frecuencias tiene tres propiedades: tendencia central, variabilidad y asimetría. Las medidas de tendencia central las hemos visto en el tema
P. A. U. LAS PALMAS 2005
 P. A. U. LAS PALMAS 2005 OPCIÓN A: J U N I O 2005 1. Hallar el área encerrada por la gráfica de la función f(x) = x 3 4x 2 + 5x 2 y la rectas y = 0, x = 1 y x = 3. x 3 4x 2 + 5x 2 es una función polinómica
P. A. U. LAS PALMAS 2005 OPCIÓN A: J U N I O 2005 1. Hallar el área encerrada por la gráfica de la función f(x) = x 3 4x 2 + 5x 2 y la rectas y = 0, x = 1 y x = 3. x 3 4x 2 + 5x 2 es una función polinómica
Cálculo científico y técnico con HP49g/49g+/48gII/50g Módulo 3: Aplicaciones Tema 3.2 Determinación aproximada de extremos: Método de Newton-Raphson
 Cálculo científico y técnico con HP49g/49g+/48gII/50g Módulo 3: Aplicaciones Tema 3.2 Determinación aproximada de extremos: Método de Newton-Raphson Francisco Palacios Escuela Politécnica Superior de Ingeniería
Cálculo científico y técnico con HP49g/49g+/48gII/50g Módulo 3: Aplicaciones Tema 3.2 Determinación aproximada de extremos: Método de Newton-Raphson Francisco Palacios Escuela Politécnica Superior de Ingeniería
Contenido. Página 2 de 8
 RÚBRICA Contenido INTRODUCCIÓN... 3 CONFIGURACIÓN Y GESTIÓN DE UNA RÚBRICA... 3 Definir un nuevo formulario de calificación desde cero, para crear un nuevo formulario desde cero... 4 Crear un nuevo formulario
RÚBRICA Contenido INTRODUCCIÓN... 3 CONFIGURACIÓN Y GESTIÓN DE UNA RÚBRICA... 3 Definir un nuevo formulario de calificación desde cero, para crear un nuevo formulario desde cero... 4 Crear un nuevo formulario
Análisis de fiabilidad. García-Bellido, R.; González Such, J. y Jornet Meliá, J.M.
 SPSS: ANÁLISIS DE FIABILIDAD ALFA DE CRONBACH El coeficiente Alfa de Cronbach es un modelo de consistencia interna, basado en el promedio de las correlaciones entre los ítems. Entre las ventajas de esta
SPSS: ANÁLISIS DE FIABILIDAD ALFA DE CRONBACH El coeficiente Alfa de Cronbach es un modelo de consistencia interna, basado en el promedio de las correlaciones entre los ítems. Entre las ventajas de esta
ESTADÍSTICA APLICADA. PRÁCTICAS CON SPSS. TEMA 2
 ESTADÍSTICA APLICADA. PRÁCTICAS CON SPSS. TEMA 2 1.- ANÁLISIS DE LA VARIANZA CON UN FACTOR El análisis de la varianza estudia el efecto de una o varias variables independientes denominadas factores sobre
ESTADÍSTICA APLICADA. PRÁCTICAS CON SPSS. TEMA 2 1.- ANÁLISIS DE LA VARIANZA CON UN FACTOR El análisis de la varianza estudia el efecto de una o varias variables independientes denominadas factores sobre
PROGRAMACIÓN LINEAL. 1. Introducción
 PROGRAMACIÓN LINEAL 1. Introducción La programación lineal es una técnica matemática relativamente reciente (siglo XX), que consiste en una serie de métodos y procedimientos que permiten resolver problemas
PROGRAMACIÓN LINEAL 1. Introducción La programación lineal es una técnica matemática relativamente reciente (siglo XX), que consiste en una serie de métodos y procedimientos que permiten resolver problemas
POTENCIAS. MÚLTIPLOS Y DIVISORES. MÁXIMO COMÚN DIVISOR Y MÍNIMO COMÚN MÚLTIPLO.
 1. LOS NÚMEROS NATURALES POTENCIAS. MÚLTIPLOS Y DIVISORES. MÁXIMO COMÚN DIVISOR Y MÍNIMO COMÚN MÚLTIPLO. 2. LOS NÚMEROS ENTEROS. VALOR ABSOLUTO DE UN NÚMERO ENTERO. REPRESENTACIÓN GRÁFICA. OPERACIONES.
1. LOS NÚMEROS NATURALES POTENCIAS. MÚLTIPLOS Y DIVISORES. MÁXIMO COMÚN DIVISOR Y MÍNIMO COMÚN MÚLTIPLO. 2. LOS NÚMEROS ENTEROS. VALOR ABSOLUTO DE UN NÚMERO ENTERO. REPRESENTACIÓN GRÁFICA. OPERACIONES.
DOCUMENTO 3: DISTRIBUCIÓN DE PROBABILIDAD DE V. A. CONTINUA: LA DISTRIBUCIÓN NORMAL
 DOCUMENTO 3: DISTRIBUCIÓN DE PROBABILIDAD DE V. A. CONTINUA: LA DISTRIBUCIÓN NORMAL 3.1 INTRODUCCIÓN Como ya sabes, una distribución de probabilidad es un modelo matemático que nos ayuda a explicar los
DOCUMENTO 3: DISTRIBUCIÓN DE PROBABILIDAD DE V. A. CONTINUA: LA DISTRIBUCIÓN NORMAL 3.1 INTRODUCCIÓN Como ya sabes, una distribución de probabilidad es un modelo matemático que nos ayuda a explicar los
CURSO BÁSICO DE MATEMÁTICAS PARA ESTUDIANTES DE ECONÓMICAS Y EMPRESARIALES
 Unidad didáctica. Ecuaciones, inecuaciones y sistemas de ecuaciones e inecuaciones CONCEPTOS ECUACIONES Una ecuación es una igualdad entre dos epresiones en las que aparece una o varias incógnitas. En
Unidad didáctica. Ecuaciones, inecuaciones y sistemas de ecuaciones e inecuaciones CONCEPTOS ECUACIONES Una ecuación es una igualdad entre dos epresiones en las que aparece una o varias incógnitas. En
FUNCIONES CUADRÁTICAS. PARÁBOLAS
 FUNCIONES CUADRÁTICAS. PARÁBOLAS 1. FUNCIONES CUADRÁTICAS Representemos, en función de la longitud de la base (x), el área (y) de todos los rectángulos de perímetro 1 metros. De ellos, cuáles son las medidas
FUNCIONES CUADRÁTICAS. PARÁBOLAS 1. FUNCIONES CUADRÁTICAS Representemos, en función de la longitud de la base (x), el área (y) de todos los rectángulos de perímetro 1 metros. De ellos, cuáles son las medidas
Utiliza los números ordinales al resolver problemas planteados de manera oral.
 T G CONTENIDOS APRENDIZAJES ESPERADOS ESTÁNDARES 1.2.1 Identificación y uso de los números ordinales para colocar objetos o para indicar el lugar que ocupan dentro de una colección de hasta 10 elementos.
T G CONTENIDOS APRENDIZAJES ESPERADOS ESTÁNDARES 1.2.1 Identificación y uso de los números ordinales para colocar objetos o para indicar el lugar que ocupan dentro de una colección de hasta 10 elementos.
Coeficiente de correlación semiparcial
 Coeficiente de correlación semiparcial 1.- Introducción...1.- Correlación semiparcial... 3.- Contribución específica de las distintas variables al modelo de egresión Múltiple... 3 4.- Correlación semiparcial
Coeficiente de correlación semiparcial 1.- Introducción...1.- Correlación semiparcial... 3.- Contribución específica de las distintas variables al modelo de egresión Múltiple... 3 4.- Correlación semiparcial
TEMA 2: TEORÍA DE CONJUNTOS Y CONJUNTOS NUMÉRICOS.
 TEMA 2: TEORÍA DE CONJUNTOS Y CONJUNTOS NUMÉRICOS. TEORÍA DE CONJUNTOS. Definiciones. Se define un conjunto como una colección de objetos o cosas, se nombran con letras mayúsculas (A, B...). Cada uno de
TEMA 2: TEORÍA DE CONJUNTOS Y CONJUNTOS NUMÉRICOS. TEORÍA DE CONJUNTOS. Definiciones. Se define un conjunto como una colección de objetos o cosas, se nombran con letras mayúsculas (A, B...). Cada uno de
5 Relaciones entre variables.
 ANÁLISIS EPLORATORIO DE DATOS 39 ANÁLISIS EPLORATORIO DE DATOS 40 Relaciones entre variables..1 Ejercicios. Ejercicio.1 En una muestra de 0 individuos se recogen datos sobre dos medidas antropométricas
ANÁLISIS EPLORATORIO DE DATOS 39 ANÁLISIS EPLORATORIO DE DATOS 40 Relaciones entre variables..1 Ejercicios. Ejercicio.1 En una muestra de 0 individuos se recogen datos sobre dos medidas antropométricas
Ejercicios de Excel. 2. Repetir el ejercicio anterior, pero suponiendo que los ingresos y los gastos están dados por trimestres.
 Ejercicios de Excel 1. Hacer una hoja de cálculo que permita calcular el impuesto sobre la renta, partiendo de los ingresos y los gastos, la fórmula necesaria para ello es Impuesto=(Ingresos-Gastos)*0.25,
Ejercicios de Excel 1. Hacer una hoja de cálculo que permita calcular el impuesto sobre la renta, partiendo de los ingresos y los gastos, la fórmula necesaria para ello es Impuesto=(Ingresos-Gastos)*0.25,
Tema 5: Principales Distribuciones de Probabilidad
 Tema 5: Principales Distribuciones de Probabilidad Estadística. 4 o Curso. Licenciatura en Ciencias Ambientales Licenciatura en Ciencias Ambientales (4 o Curso) Tema 5: Principales Distribuciones de Probabilidad
Tema 5: Principales Distribuciones de Probabilidad Estadística. 4 o Curso. Licenciatura en Ciencias Ambientales Licenciatura en Ciencias Ambientales (4 o Curso) Tema 5: Principales Distribuciones de Probabilidad
Determinación del tamaño muestral para calcular la significación del coeficiente de correlación lineal
 Investigación: Determinación del tamaño muestral para calcular 1/5 Determinación del tamaño muestral para calcular la significación del coeficiente de correlación lineal Autores: Pértegas Día, S. spertega@canalejo.org,
Investigación: Determinación del tamaño muestral para calcular 1/5 Determinación del tamaño muestral para calcular la significación del coeficiente de correlación lineal Autores: Pértegas Día, S. spertega@canalejo.org,
4. Medidas de tendencia central
 4. Medidas de tendencia central A veces es conveniente reducir la información obtenida a un solo valor o a un número pequeño de valores, las denominadas medidas de tendencia central. Sea X una variable
4. Medidas de tendencia central A veces es conveniente reducir la información obtenida a un solo valor o a un número pequeño de valores, las denominadas medidas de tendencia central. Sea X una variable
LECCIÓN 4 BALANCED SCORECARD
 LECCIÓN 4 BALANCED SCORECARD Creación de Elementos: Explicación de Causa-Efecto Todo Balanced Scorecard (BSC) debe alimentarse de datos para reflejar los Indicadores que el usuario necesita obtener para
LECCIÓN 4 BALANCED SCORECARD Creación de Elementos: Explicación de Causa-Efecto Todo Balanced Scorecard (BSC) debe alimentarse de datos para reflejar los Indicadores que el usuario necesita obtener para
Estadística inferencial. Aplicación con el SPSS
 Estadística inferencial. Aplicación con el SPSS Sabina Pérez Vicente Unidad de Calidad APES Hospital Costa del Sol sabina.perez.exts@juntadeandalucia.es Comparabilidad inicial de los grupos Se debe realizar
Estadística inferencial. Aplicación con el SPSS Sabina Pérez Vicente Unidad de Calidad APES Hospital Costa del Sol sabina.perez.exts@juntadeandalucia.es Comparabilidad inicial de los grupos Se debe realizar
DIPLOMADO EN RELACIONES LABORALES Estadística Asistida por Ordenador Curso 2008-2009
 Índice general 5 Análisis de datos categóricos 3 51 Tablas de contingencia 3 52 Distribuciones marginales y condicionadas 4 53 Independencia Test Chi-cuadrado Tablas 2 2 6 531 Independencia 6 532 Test
Índice general 5 Análisis de datos categóricos 3 51 Tablas de contingencia 3 52 Distribuciones marginales y condicionadas 4 53 Independencia Test Chi-cuadrado Tablas 2 2 6 531 Independencia 6 532 Test
CAPÍTULO III MOMENTO DE INERCIA EN ÁREAS PLANAS. Este capítulo comprende diversas propiedades geométricas de secciones (para casos
 CAPÍTULO III MOMENTO DE INERCIA EN ÁREAS PLANAS Este capítulo comprende diversas propiedades geométricas de secciones (para casos prácticos, secciones de vigas) siendo la más importante el momento de inercia.
CAPÍTULO III MOMENTO DE INERCIA EN ÁREAS PLANAS Este capítulo comprende diversas propiedades geométricas de secciones (para casos prácticos, secciones de vigas) siendo la más importante el momento de inercia.
UNIDAD DIDÁCTICA 5: Geometría analítica del plano
 UNIDAD DIDÁCTICA 5: Geometría analítica del plano 1. ÍNDICE 1. Sistemas de referencia y coordenadas puntuales 2. Distancia entre dos puntos del plano 3. Coordenadas del punto medio de un segmento 4. La
UNIDAD DIDÁCTICA 5: Geometría analítica del plano 1. ÍNDICE 1. Sistemas de referencia y coordenadas puntuales 2. Distancia entre dos puntos del plano 3. Coordenadas del punto medio de un segmento 4. La
GEOMETRÍA ANALÍTICA DEL PLANO
 GEOMETRÍA ANALÍTICA DEL PLANO 1 UNIDAD DIDÁCTICA 5: Geometría analítica del plano 1. ÍNDICE 1. Sistemas de referencia y coordenadas puntuales 2. Distancia entre dos puntos del plano 3. Coordenadas del
GEOMETRÍA ANALÍTICA DEL PLANO 1 UNIDAD DIDÁCTICA 5: Geometría analítica del plano 1. ÍNDICE 1. Sistemas de referencia y coordenadas puntuales 2. Distancia entre dos puntos del plano 3. Coordenadas del
ÍNDICE CAPITULO UNO CAPITULO DOS. Pág.
 ÍNDICE CAPITULO UNO Pág. Concepto de Estadística 1 Objetivo 1 Diferencia entre estadísticas y estadística 1 Uso de la estadística 1 Divisiones de la estadística 1 1. Estadística Descriptiva 1 2. Estadística
ÍNDICE CAPITULO UNO Pág. Concepto de Estadística 1 Objetivo 1 Diferencia entre estadísticas y estadística 1 Uso de la estadística 1 Divisiones de la estadística 1 1. Estadística Descriptiva 1 2. Estadística
Tema Contenido Contenidos Mínimos
 1 Números racionales - Fracciones equivalentes. - Simplificación de fracciones. - Representación y comparación de los números fraccionarios. - Operaciones con números fraccionarios. - Ordenación de los
1 Números racionales - Fracciones equivalentes. - Simplificación de fracciones. - Representación y comparación de los números fraccionarios. - Operaciones con números fraccionarios. - Ordenación de los
Lección 10: Representación gráfica de algunas expresiones algebraicas
 LECCIÓN Lección : Representación gráfica de algunas epresiones algebraicas En la lección del curso anterior usted aprendió a representar puntos en el plano cartesiano y en la lección del mismo curso aprendió
LECCIÓN Lección : Representación gráfica de algunas epresiones algebraicas En la lección del curso anterior usted aprendió a representar puntos en el plano cartesiano y en la lección del mismo curso aprendió
Microsoft Office Word 2007
 Introducción: Continuando con los temas considerados en el temario, iniciamos con el procesador de texto, usualmente llamados documentos y contienen una gran variedad de funcionalidades y entre otras cosas
Introducción: Continuando con los temas considerados en el temario, iniciamos con el procesador de texto, usualmente llamados documentos y contienen una gran variedad de funcionalidades y entre otras cosas
SISTEMAS DE NUMERACIÓN
 SISTEMAS DE NUMERACIÓN INDICE. 1. DEFINICIÓN DE SISTEMAS DE NUMERACIÓN.... 1 2. TEOREMA FUNDAMENTAL DE LA NUMERACIÓN... 3 3. SISTEMAS DECIMAL, BINARIO, OCTAL Y HEXADECIMAL.... 5 3.1. SISTEMA DECIMAL...
SISTEMAS DE NUMERACIÓN INDICE. 1. DEFINICIÓN DE SISTEMAS DE NUMERACIÓN.... 1 2. TEOREMA FUNDAMENTAL DE LA NUMERACIÓN... 3 3. SISTEMAS DECIMAL, BINARIO, OCTAL Y HEXADECIMAL.... 5 3.1. SISTEMA DECIMAL...
Unidad 1 Números. Los números naturales son aquellos que se utilizan para contar los elementos de un conjunto.
 Unidad 1 Números 1.- Números Naturales Los números naturales son aquellos que se utilizan para contar los elementos de un conjunto. El conjunto de números naturales se representa por la letra N Operaciones
Unidad 1 Números 1.- Números Naturales Los números naturales son aquellos que se utilizan para contar los elementos de un conjunto. El conjunto de números naturales se representa por la letra N Operaciones
3. Análisis univariable y bivariable
 FUOC P01/71039/00748 36 Investigación descriptiva: análisis de información 3. Análisis univariable y bivariable 3.1. Análisis univariable Como se ha visto, los métodos de análisis univariable se utilizan
FUOC P01/71039/00748 36 Investigación descriptiva: análisis de información 3. Análisis univariable y bivariable 3.1. Análisis univariable Como se ha visto, los métodos de análisis univariable se utilizan
SISTEMAS INTELIGENTES
 SISTEMAS INTELIGENTES T8: Aprendizaje basado en instancias www.aic.uniovi.es/ssii Índice Aprendizaje basado en instancias Métricas NN Vecino más próximo: Regiones de Voronoi El parámetro K Problemas de
SISTEMAS INTELIGENTES T8: Aprendizaje basado en instancias www.aic.uniovi.es/ssii Índice Aprendizaje basado en instancias Métricas NN Vecino más próximo: Regiones de Voronoi El parámetro K Problemas de
CONCEPTOS BÁSICOS DE ESTADÍSTICA
 CONCEPTOS BÁSICOS DE ESTADÍSTICA Jorge M. Galbiati Riesco La Estadística está constituida por un conjunto de métodos de análisis de datos que pueden agruparse en tres categorías: La Estadística Descriptiva,
CONCEPTOS BÁSICOS DE ESTADÍSTICA Jorge M. Galbiati Riesco La Estadística está constituida por un conjunto de métodos de análisis de datos que pueden agruparse en tres categorías: La Estadística Descriptiva,
INSTRUCCIONES PARA EL USO DEL SOFTWARE (IS)
 INSTRUCCIONES PARA EL USO DEL SOFTWARE (IS) Pantalla Inicial de DERIVE for Windows Teniendo instalado el programa DERIVE sobre Windows, podemos ingresar al sistema de las siguientes formas: Haciendo clic
INSTRUCCIONES PARA EL USO DEL SOFTWARE (IS) Pantalla Inicial de DERIVE for Windows Teniendo instalado el programa DERIVE sobre Windows, podemos ingresar al sistema de las siguientes formas: Haciendo clic
Nociones de Estadística Descriptiva. Medidas de tendencia central y de variabilidad
 Nociones de Estadística Descriptiva. Medidas de tendencia central y de variabilidad Introducción a la estadística descriptiva La estadística descriptiva ayuda a describir las características de grupos
Nociones de Estadística Descriptiva. Medidas de tendencia central y de variabilidad Introducción a la estadística descriptiva La estadística descriptiva ayuda a describir las características de grupos
Práctica 2 Métodos de búsqueda para funciones de una variable
 Práctica 2 Métodos de búsqueda para funciones de una variable Introducción Definición 1. Una función real f se dice que es fuertemente cuasiconvexa en el intervalo (a, b) si para cada par de puntos x 1,
Práctica 2 Métodos de búsqueda para funciones de una variable Introducción Definición 1. Una función real f se dice que es fuertemente cuasiconvexa en el intervalo (a, b) si para cada par de puntos x 1,
EJERCICIOS RESUELTOS TEMA 7
 EJERCICIOS RESUELTOS TEMA 7 7.1. Seleccione la opción correcta: A) Hay toda una familia de distribuciones normales, cada una con su media y su desviación típica ; B) La media y la desviaciones típica de
EJERCICIOS RESUELTOS TEMA 7 7.1. Seleccione la opción correcta: A) Hay toda una familia de distribuciones normales, cada una con su media y su desviación típica ; B) La media y la desviaciones típica de
Polinomios. 1.- Funciones cuadráticas
 Polinomios 1.- Funciones cuadráticas Definición 1 (Función polinomial) Sea n un entero no negativo y sean a n, a n 1,..., a, a 1, a 0 número s reales con a n 0. La función se denomina función polinomial
Polinomios 1.- Funciones cuadráticas Definición 1 (Función polinomial) Sea n un entero no negativo y sean a n, a n 1,..., a, a 1, a 0 número s reales con a n 0. La función se denomina función polinomial
CARTERAS MINORISTAS Sistemas de scoring: construcción y evaluación
 CARTERAS MINORISTAS Sistemas de scoring: construcción y evaluación Grupo de Tesorería y Modelos de Gestión de Riesgos Gregorio Moral Turiel Sergio Gavilá Javier Población II Seminario sobre Basilea II
CARTERAS MINORISTAS Sistemas de scoring: construcción y evaluación Grupo de Tesorería y Modelos de Gestión de Riesgos Gregorio Moral Turiel Sergio Gavilá Javier Población II Seminario sobre Basilea II
CALIDAD 1 JOSÉ MANUEL DOMENECH ROLDÁN PROFESOR DE ENSEÑANZA SECUNDARIA
 CALIDAD 1 DIAGRAMA DE CORRELACIÓN-DISPERSIÓN QUÉ ES EL DIAGRAMA DE CORRELACIÓN-DISPERSIÓN? Es una herramienta gráfica que permite demostrar la relación existente entre dos clases de datos y cuantificar
CALIDAD 1 DIAGRAMA DE CORRELACIÓN-DISPERSIÓN QUÉ ES EL DIAGRAMA DE CORRELACIÓN-DISPERSIÓN? Es una herramienta gráfica que permite demostrar la relación existente entre dos clases de datos y cuantificar
REGRESIÓN LINEAL CON SPSS
 ESCUELA SUPERIOR DE INFORMÁTICA Prácticas de Estadística REGRESIÓN LINEAL CON SPSS 1.- INTRODUCCIÓN El análisis de regresión lineal es una técnica estadística utilizada para estudiar la relación entre
ESCUELA SUPERIOR DE INFORMÁTICA Prácticas de Estadística REGRESIÓN LINEAL CON SPSS 1.- INTRODUCCIÓN El análisis de regresión lineal es una técnica estadística utilizada para estudiar la relación entre
GUÍAS. Módulo de Razonamiento cuantitativo SABER PRO 2014-1
 GUÍAS Módulo de Razonamiento cuantitativo SABER PRO 2014-1 GUÍAS Módulo Razonamiento cuantitativo Este módulo evalúa competencias relacionadas con las habilidades matemáticas que todo ciudadano debe tener,
GUÍAS Módulo de Razonamiento cuantitativo SABER PRO 2014-1 GUÍAS Módulo Razonamiento cuantitativo Este módulo evalúa competencias relacionadas con las habilidades matemáticas que todo ciudadano debe tener,
GUIA PRACTICA PARA LA APLICACIÓN DE MS EXCEL TECNOLOGIA/ INFORMATICA
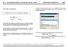 Fórmulas y funciones De la barra de menú seleccionmos la opción insertar y haciendo clic en la opción f x se desplegará el siguiente cuadro de diálogo a partir del cual escogeremos la función adecuada
Fórmulas y funciones De la barra de menú seleccionmos la opción insertar y haciendo clic en la opción f x se desplegará el siguiente cuadro de diálogo a partir del cual escogeremos la función adecuada
El uso de la Técnica de Regresión Lineal Múltiple para la evaluación de la dotación de personal en el I.N.S.S.
 El uso de la Técnica de Regresión Lineal Múltiple para la evaluación de la dotación de personal en el I.N.S.S. Establecimiento de un sistema de evaluación de la dotación de personal para las oficinas del
El uso de la Técnica de Regresión Lineal Múltiple para la evaluación de la dotación de personal en el I.N.S.S. Establecimiento de un sistema de evaluación de la dotación de personal para las oficinas del
Distribuciones bidimensionales. Regresión.
 Temas de Estadística Práctica Antonio Roldán Martínez Proyecto http://www.hojamat.es/ Tema 5: Distribuciones bidimensionales. Regresión. Resumen teórico Resumen teórico de los principales conceptos estadísticos
Temas de Estadística Práctica Antonio Roldán Martínez Proyecto http://www.hojamat.es/ Tema 5: Distribuciones bidimensionales. Regresión. Resumen teórico Resumen teórico de los principales conceptos estadísticos
SISTEMAS DE ECUACIONES LINEALES
 1 SISTEMAS DE ECUACIONES LINEALES Una ecuación es un enunciado o proposición que plantea la igualdad de dos expresiones, donde al menos una de ellas contiene cantidades desconocidas llamadas variables
1 SISTEMAS DE ECUACIONES LINEALES Una ecuación es un enunciado o proposición que plantea la igualdad de dos expresiones, donde al menos una de ellas contiene cantidades desconocidas llamadas variables
Problemas resueltos. Temas 10 y 11 11, 9, 12, 17, 8, 11, 9, 4, 5, 9, 14, 9, 17, 24, 19, 10, 17, 17, 8, 23, 8, 6, 14, 16, 6, 7, 15, 20, 14, 15.
 Temas 10 y 11. Contrastes paramétricos de hipótesis. 1 Problemas resueltos. Temas 10 y 11 1- las puntuaciones en un test que mide la variable creatividad siguen, en la población general de adolescentes,
Temas 10 y 11. Contrastes paramétricos de hipótesis. 1 Problemas resueltos. Temas 10 y 11 1- las puntuaciones en un test que mide la variable creatividad siguen, en la población general de adolescentes,
Pruebas de Acceso a Enseñanzas Universitarias Oficiales de Grado (PAEG) Matemáticas aplicadas a las Ciencias Sociales II - Junio 2011 - Propuesta B
 Pruebas de Acceso a Enseñanzas Universitarias Oficiales de Grado (PAEG) Matemáticas aplicadas a las Ciencias Sociales II - Junio 2011 - Propuesta B 1. Queremos invertir una cantidad de dinero en dos tipos
Pruebas de Acceso a Enseñanzas Universitarias Oficiales de Grado (PAEG) Matemáticas aplicadas a las Ciencias Sociales II - Junio 2011 - Propuesta B 1. Queremos invertir una cantidad de dinero en dos tipos
Contenidos mínimos 4B ESO. 1. Contenidos. Bloque I: Aritmética y álgebra.
 Contenidos mínimos 4B ESO. 1. Contenidos. Bloque I: Aritmética y álgebra. 1. Clasificar distintos tipos de números: naturales, enteros, racionales y reales. 2. Operar con números reales y aplicar las propiedades
Contenidos mínimos 4B ESO. 1. Contenidos. Bloque I: Aritmética y álgebra. 1. Clasificar distintos tipos de números: naturales, enteros, racionales y reales. 2. Operar con números reales y aplicar las propiedades
Profesor: Rafa González Jiménez. Instituto Santa Eulalia ÍNDICE
 TEMA 5: DERIVADAS. APLICACIONES. ÍNDICE 5..- Derivada de una función en un punto. 5...- Tasa de variación media. Interpretación geométrica. 5..2.- Tasa de variación instantánea. Derivada de una función
TEMA 5: DERIVADAS. APLICACIONES. ÍNDICE 5..- Derivada de una función en un punto. 5...- Tasa de variación media. Interpretación geométrica. 5..2.- Tasa de variación instantánea. Derivada de una función
Una población es el conjunto de todos los elementos a los que se somete a un estudio estadístico.
 Introducción a la Melilla Definición de La trata del recuento, ordenación y clasificación de los datos obtenidos por las observaciones, para poder hacer comparaciones y sacar conclusiones. Un estudio estadístico
Introducción a la Melilla Definición de La trata del recuento, ordenación y clasificación de los datos obtenidos por las observaciones, para poder hacer comparaciones y sacar conclusiones. Un estudio estadístico
Sistemas de Ecuaciones Lineales
 Sistemas de Ecuaciones Lineales 1 Sistemas de ecuaciones y matrices Definición 1 Una ecuación lineal en las variables x 1, x 2,..., x n es una ecuación de la forma con a 1, a 2... y b números reales. a
Sistemas de Ecuaciones Lineales 1 Sistemas de ecuaciones y matrices Definición 1 Una ecuación lineal en las variables x 1, x 2,..., x n es una ecuación de la forma con a 1, a 2... y b números reales. a
ANÁLISIS DE DATOS MULTIDIMENSIONALES
 ANÁLISIS DE DATOS MULTIDIMENSIONALES INTRODUCCIÓN DISTRIBUCIÓN DE FRECUENCIAS MULTIDIMENSIONAL DISTRIBUCIONES MARGINALES DISTRIBUCIONES CONDICIONADAS INDEPENDENCIA ESTADÍSTICA ESTUDIO ANALÍTICO DE DISTRIBUCIONES
ANÁLISIS DE DATOS MULTIDIMENSIONALES INTRODUCCIÓN DISTRIBUCIÓN DE FRECUENCIAS MULTIDIMENSIONAL DISTRIBUCIONES MARGINALES DISTRIBUCIONES CONDICIONADAS INDEPENDENCIA ESTADÍSTICA ESTUDIO ANALÍTICO DE DISTRIBUCIONES
Debemos obtener las medidas estadísticas más comunes.
 - Ejercicio: Gráficos Estadísticos Estudiando el número de hijos de 30 familias elegidas al azar en una ciudad se han obtenido los siguientes datos: 1, 2, 3, 5, 6, 0, 7, 8, 4, 1, 3, 4, 5, 2, 6, 5, 2, 3,
- Ejercicio: Gráficos Estadísticos Estudiando el número de hijos de 30 familias elegidas al azar en una ciudad se han obtenido los siguientes datos: 1, 2, 3, 5, 6, 0, 7, 8, 4, 1, 3, 4, 5, 2, 6, 5, 2, 3,
CÁLCULO DE SIGNIFICANCIA ESTADÍSTICA PARA RESULTADOS SIMCE
 CÁLCULO DE SIGNIFICANCIA ESTADÍSTICA PARA RESULTADOS SIMCE SIMCE Unidad de Currículum y Evaluación Ministerio de Educación 011 Índice 1. Antecedentes Generales 1. Comparación de puntajes promedios.1. Errores
CÁLCULO DE SIGNIFICANCIA ESTADÍSTICA PARA RESULTADOS SIMCE SIMCE Unidad de Currículum y Evaluación Ministerio de Educación 011 Índice 1. Antecedentes Generales 1. Comparación de puntajes promedios.1. Errores
D.2 ANÁLISIS ESTADÍSTICO DE LAS TEMPERATURAS DE VERANO
 Anejo Análisis estadístico de temperaturas Análisis estadístico de temperaturas - 411 - D.1 INTRODUCCIÓN Y OBJETIVO El presente anejo tiene por objeto hacer un análisis estadístico de los registros térmicos
Anejo Análisis estadístico de temperaturas Análisis estadístico de temperaturas - 411 - D.1 INTRODUCCIÓN Y OBJETIVO El presente anejo tiene por objeto hacer un análisis estadístico de los registros térmicos
ANÁLISIS CUANTITATIVO DE DATOS EN CIENCIAS SOCIALES CON EL SPSS (I) Tablas de contingencia y pruebas de asociación
 ANÁLISIS CUANTITATIVO DE DATOS EN CIENCIAS SOCIALES CON EL SPSS (I) Tablas de contingencia y pruebas de asociación Francisca José Serrano Pastor Pedro A. Sánchez Rodríguez - Implica siempre a variables
ANÁLISIS CUANTITATIVO DE DATOS EN CIENCIAS SOCIALES CON EL SPSS (I) Tablas de contingencia y pruebas de asociación Francisca José Serrano Pastor Pedro A. Sánchez Rodríguez - Implica siempre a variables
MÉTODOS DE APRENDIZAJE INDUCTIVO
 Aprendizaje Automático y Data Mining Bloque III MÉTODOS DE ARENDIZAJE INDUCTIVO 1 Índice Clasificación de métodos: Lazy Eager Árboles de decisión. Listas de reglas. Aprendizaje Bayesiano. Redes neuronales
Aprendizaje Automático y Data Mining Bloque III MÉTODOS DE ARENDIZAJE INDUCTIVO 1 Índice Clasificación de métodos: Lazy Eager Árboles de decisión. Listas de reglas. Aprendizaje Bayesiano. Redes neuronales
Conocer la forma de analizar las Medidas de Tendencia Central de una distribución con OpenOffice Calc.
 Objetivo: Conocer la forma de analizar las Medidas de Tendencia Central de una distribución con OpenOffice Calc. CALC: MEDIDAS DE TENDENCIA CENTRAL Las medidas de tendencia central sirven como puntos de
Objetivo: Conocer la forma de analizar las Medidas de Tendencia Central de una distribución con OpenOffice Calc. CALC: MEDIDAS DE TENDENCIA CENTRAL Las medidas de tendencia central sirven como puntos de
Pruebas de acceso a enseñanzas universitarias oficiales de grado Castilla y León
 Pruebas de acceso a enseñanzas universitarias oficiales de grado Castilla y León MATEMÁTICAS APLICAAS A LAS CIENCIAS SOCIALES EJERCICIO Nº Páginas 2 OPTATIVIA: EL ALUMNO EBERÁ ESCOGER UNA E LAS OS OPCIONES
Pruebas de acceso a enseñanzas universitarias oficiales de grado Castilla y León MATEMÁTICAS APLICAAS A LAS CIENCIAS SOCIALES EJERCICIO Nº Páginas 2 OPTATIVIA: EL ALUMNO EBERÁ ESCOGER UNA E LAS OS OPCIONES
ASISTENCIA TÉCNICA A LA SEGURIDAD EN PYMES DE MELILLA MANUAL GPARTED LIVECD
 ASISTENCIA TÉCNICA A LA SEGURIDAD EN PYMES DE MELILLA MANUAL GPARTED LIVECD GParted LiveCD 1. Qué es GParted? Es un interfaz gráfico para crear, eliminar, mover y redimensionar particiones de nuestros
ASISTENCIA TÉCNICA A LA SEGURIDAD EN PYMES DE MELILLA MANUAL GPARTED LIVECD GParted LiveCD 1. Qué es GParted? Es un interfaz gráfico para crear, eliminar, mover y redimensionar particiones de nuestros
Tema 3. Introducción a la estadística descriptiva: Ejercicios
 Tema 3. Introducción a la estadística descriptiva: Ejercicios Profesora Esther Chiner Sanz BIBLIOGRAÍA Amón, J. (1999): Estadística para psicólogos I. Estadística descriptiva. Madrid, España: Pirámide.
Tema 3. Introducción a la estadística descriptiva: Ejercicios Profesora Esther Chiner Sanz BIBLIOGRAÍA Amón, J. (1999): Estadística para psicólogos I. Estadística descriptiva. Madrid, España: Pirámide.
Documento elaborado por: Francisco Javier Rodríguez Cortés Matemático Facultad de Ciencias Exactas - Universidad de Antioquia INTRODUCCIÓN
 Documento elaborado por: Francisco Javier Rodríguez Cortés Matemático Facultad de Ciencias Exactas - Universidad de Antioquia INTRODUCCIÓN La Estadística se ocupa de los métodos y procedimientos para recoger,
Documento elaborado por: Francisco Javier Rodríguez Cortés Matemático Facultad de Ciencias Exactas - Universidad de Antioquia INTRODUCCIÓN La Estadística se ocupa de los métodos y procedimientos para recoger,
Estadística Descriptiva
 Estadística Descriptiva 1 Sesión No. 3 Nombre: Estadística descriptiva Contextualización Parte fundamental de la Estadística es la organización de los datos, una forma de realizar esta organización es
Estadística Descriptiva 1 Sesión No. 3 Nombre: Estadística descriptiva Contextualización Parte fundamental de la Estadística es la organización de los datos, una forma de realizar esta organización es
Julio Deride Silva. 27 de agosto de 2010
 Estadística Descriptiva Julio Deride Silva Área de Matemática Facultad de Ciencias Químicas y Farmcéuticas Universidad de Chile 27 de agosto de 2010 Tabla de Contenidos Estadística Descriptiva Julio Deride
Estadística Descriptiva Julio Deride Silva Área de Matemática Facultad de Ciencias Químicas y Farmcéuticas Universidad de Chile 27 de agosto de 2010 Tabla de Contenidos Estadística Descriptiva Julio Deride
Problemas resueltos. Tema 12. 2º La hipótesis alternativa será que la distribución no es uniforme.
 Tema 12. Contrastes No Paramétricos. 1 Problemas resueltos. Tema 12 1.- En una partida de Rol se lanza 200 veces un dado de cuatro caras obteniéndose 60 veces el número 1, 45 veces el número 2, 38 veces
Tema 12. Contrastes No Paramétricos. 1 Problemas resueltos. Tema 12 1.- En una partida de Rol se lanza 200 veces un dado de cuatro caras obteniéndose 60 veces el número 1, 45 veces el número 2, 38 veces
3. CONCEPTO Y FUNCIONES DE LA ESTADÍSTICA: DESCRIPTIVA e INFERENCIAL
 1. INTRODUCCIÓN Debemos diferenciar entre dos tipos de estadísticas: Estadística teórica: Se ocupa de los aspectos formales y normativos Estadística aplicada: Constituye la aplicación a un campo concreto.
1. INTRODUCCIÓN Debemos diferenciar entre dos tipos de estadísticas: Estadística teórica: Se ocupa de los aspectos formales y normativos Estadística aplicada: Constituye la aplicación a un campo concreto.
EXPLORACIÓN DE RESULTADOS MULTIDIMENSIONALES: ANÁLISIS DE AGRUPACIONES MEDIANTE MÉTODOS JERÁRQUICOS
 EXPLORACIÓN E RESULTAOS MULTIIMENSIONALES: ANÁLISIS E AGRUPACIONES MEIANTE MÉTOOS JERÁRQUICOS M.S. Larrechi epartament de Química Analítica i Química Orgànica. Universitat Rovira i Virgili Pl. Imperial
EXPLORACIÓN E RESULTAOS MULTIIMENSIONALES: ANÁLISIS E AGRUPACIONES MEIANTE MÉTOOS JERÁRQUICOS M.S. Larrechi epartament de Química Analítica i Química Orgànica. Universitat Rovira i Virgili Pl. Imperial
Se dice que dos monomios son semejantes cuando tienen la misma parte literal
 Expresiones algebraicas 1 MONOMIOS Conceptos Un monomio es una expresión algebraica en la que las únicas operaciones que aparecen entre las variables son el producto y la potencia de exponente natural.
Expresiones algebraicas 1 MONOMIOS Conceptos Un monomio es una expresión algebraica en la que las únicas operaciones que aparecen entre las variables son el producto y la potencia de exponente natural.
GUÍA RÁPIDA DEL PROGRAMA SPSS ver. 13.0 y superiores Programa para estudios estadísticos en general, muy completo pero de fácil manejo.
 1 GUÍA RÁPIDA DEL PROGRAMA SPSS ver. 13.0 y superiores Programa para estudios estadísticos en general, muy completo pero de fácil manejo. 3 INDICE DEL CONTENIDO 1. PREPARACIÓN DE LA MATRIZ BÁSICA DE DATOS.
1 GUÍA RÁPIDA DEL PROGRAMA SPSS ver. 13.0 y superiores Programa para estudios estadísticos en general, muy completo pero de fácil manejo. 3 INDICE DEL CONTENIDO 1. PREPARACIÓN DE LA MATRIZ BÁSICA DE DATOS.
Anexo C. Introducción a las series de potencias. Series de potencias
 Anexo C Introducción a las series de potencias Este apéndice tiene como objetivo repasar los conceptos relativos a las series de potencias y al desarrollo de una función ne serie de potencias en torno
Anexo C Introducción a las series de potencias Este apéndice tiene como objetivo repasar los conceptos relativos a las series de potencias y al desarrollo de una función ne serie de potencias en torno
2.5. Asimetría y apuntamiento
 2.5. ASIMETRÍA Y APUNTAMIENTO 59 variable Z = X x S (2.9) de media z = 0 y desviación típica S Z = 1, que denominamos variable tipificada. Esta nueva variable carece de unidades y permite hacer comparables
2.5. ASIMETRÍA Y APUNTAMIENTO 59 variable Z = X x S (2.9) de media z = 0 y desviación típica S Z = 1, que denominamos variable tipificada. Esta nueva variable carece de unidades y permite hacer comparables
Problemas de Recursividad
 Problemas de Recursividad Problema 1. El factorial de un número entero n 0, denotado como n!, se define! como!!! i = 1 2 n cuando n > 0, y 0! = 1. Por ejemplo 6! = 1 2 3 4 5 6 = 720 Diseñad una método
Problemas de Recursividad Problema 1. El factorial de un número entero n 0, denotado como n!, se define! como!!! i = 1 2 n cuando n > 0, y 0! = 1. Por ejemplo 6! = 1 2 3 4 5 6 = 720 Diseñad una método
GUÍAS. Módulo de Razonamiento cuantitativo SABER PRO 2013-1
 Módulo de Razonamiento cuantitativo Este módulo evalúa competencias relacionadas con las habilidades en la comprensión de conceptos básicos de las matemáticas para analizar, modelar y resolver problemas
Módulo de Razonamiento cuantitativo Este módulo evalúa competencias relacionadas con las habilidades en la comprensión de conceptos básicos de las matemáticas para analizar, modelar y resolver problemas
1) Características del diseño en un estudio de casos y controles.
 Departamento de Estadística Universidad Carlos III de Madrid BIOESTADISTICA (55-10536) Estudios de casos y controles CONCEPTOS CLAVE 1) Características del diseño en un estudio de casos y controles. )
Departamento de Estadística Universidad Carlos III de Madrid BIOESTADISTICA (55-10536) Estudios de casos y controles CONCEPTOS CLAVE 1) Características del diseño en un estudio de casos y controles. )
TEMA 5 FUNCIONES ELEMENTALES II
 Tema Funciones elementales Ejercicios resueltos Matemáticas B º ESO TEMA FUNCIONES ELEMENTALES II Rectas EJERCICIO. Halla la pendiente, la ordenada en el origen y los puntos de corte con los ejes de coordenadas
Tema Funciones elementales Ejercicios resueltos Matemáticas B º ESO TEMA FUNCIONES ELEMENTALES II Rectas EJERCICIO. Halla la pendiente, la ordenada en el origen y los puntos de corte con los ejes de coordenadas
TEMA III MÉTODO SIMPLEX. CONCEPTOS BÁSICOS
 TEMA III MÉTODO SIMPLE. CONCEPTOS BÁSICOS MÉTODOS CUANTITATIVOS I TEMA III. MÉTODO SIMPLE. CONCEPTOS BÁSICOS INDICE.- FACTORES PRODUCTIVOS (A i )....- VECTOR EISTENCIAS (P o )....- TÉCNICA... 4.- PROCESO
TEMA III MÉTODO SIMPLE. CONCEPTOS BÁSICOS MÉTODOS CUANTITATIVOS I TEMA III. MÉTODO SIMPLE. CONCEPTOS BÁSICOS INDICE.- FACTORES PRODUCTIVOS (A i )....- VECTOR EISTENCIAS (P o )....- TÉCNICA... 4.- PROCESO
Tema 1. Modelo de diseño de experimentos (un factor)
 Tema 1. Modelo de diseño de experimentos (un factor) Estadística (CC. Ambientales). Profesora: Amparo Baíllo Tema 1: Diseño de experimentos (un factor) 1 Introducción El objetivo del Análisis de la Varianza
Tema 1. Modelo de diseño de experimentos (un factor) Estadística (CC. Ambientales). Profesora: Amparo Baíllo Tema 1: Diseño de experimentos (un factor) 1 Introducción El objetivo del Análisis de la Varianza
LOGO Fundamentos Básicos de Estadística I
 LOGO Fundamentos Básicos de Estadística I Prof. Mariugenia Rincón mrinconj@gmail.com Definiciones Estadistica. Objetivo e Importancia Clasificación: Descriptiva e Inferencial Población y Muestra Unidad
LOGO Fundamentos Básicos de Estadística I Prof. Mariugenia Rincón mrinconj@gmail.com Definiciones Estadistica. Objetivo e Importancia Clasificación: Descriptiva e Inferencial Población y Muestra Unidad
Cómo describir e interpretar los resultados de un estudio de investigación quirúrgica? Variables cuantitativas
 Cómo describir e interpretar los resultados de un estudio de investigación quirúrgica? Variables cuantitativas Sesión de Residentes 13 de febrero, 2012 ÍNDICE Diferencia entre población y muestra. Diferencia
Cómo describir e interpretar los resultados de un estudio de investigación quirúrgica? Variables cuantitativas Sesión de Residentes 13 de febrero, 2012 ÍNDICE Diferencia entre población y muestra. Diferencia
Teoría 3_10 Gráficos!
 Teoría 3_10 Gráficos! Gráficos de columnas Ideal para mostrar cambios de datos en un período de tiempo o para ilustrar comparaciones entre elementos. En los gráficos de columnas, las categorías normalmente
Teoría 3_10 Gráficos! Gráficos de columnas Ideal para mostrar cambios de datos en un período de tiempo o para ilustrar comparaciones entre elementos. En los gráficos de columnas, las categorías normalmente
IDE y Análisis de datos
 IDE y Análisis de datos Dept. of Marine Science and Applied Biology Jose Jacobo Zubcoff Presentación Objetivos Metodología Introducción IDE y Análisis de datos 1 Planeación de la investigación Proceso
IDE y Análisis de datos Dept. of Marine Science and Applied Biology Jose Jacobo Zubcoff Presentación Objetivos Metodología Introducción IDE y Análisis de datos 1 Planeación de la investigación Proceso
El análisis de correspondencias. Ana María López Jiménez Dept. Psicología Experimental (USE)
 El análisis de correspondencias Ana María López Jiménez Dept. Psicología Experimental (USE) 4. El análisis de correspondencias 4.. Introducción 4.2. Tabla de correspondencias 4.3. Dependencia e independencia
El análisis de correspondencias Ana María López Jiménez Dept. Psicología Experimental (USE) 4. El análisis de correspondencias 4.. Introducción 4.2. Tabla de correspondencias 4.3. Dependencia e independencia
Curso Completo de Electrónica Digital. 3.7. Simplificación de funciones booleanas
 CURSO Curso Completo de Electrónica Digital Departamento de Electronica y Comunicaciones Universidad Pontifica de Salamanca en Madrid Prof. Juan González Gómez Capítulo 3 ALGEBRA DE BOOLE Continuación...
CURSO Curso Completo de Electrónica Digital Departamento de Electronica y Comunicaciones Universidad Pontifica de Salamanca en Madrid Prof. Juan González Gómez Capítulo 3 ALGEBRA DE BOOLE Continuación...
