Un algoritmo de desrefinamiento en 3D para mallas de tetraedros basado en el esqueleto
|
|
|
- Ángeles Castillo de la Fuente
- hace 7 años
- Vistas:
Transcripción
1 Vol.,, 7 8 (999) Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería Un algoritmo de desrefinamiento en D para mallas de tetraedros basado en el esqueleto Ángel Plaza y Miguel A. Padrón Departamento de Matemáticas Edificio de Matemáticas e Informática Universidad de Las Palmas de Gran Canaria Campus de Tarifa 07 Las Palmas, España Tel.: , Fax: angel@aries.dma.ulpgc.es Resumen En este trabajo, se presenta un nuevo algoritmo de desrefinamiento para mallas de tetraedros noestructuradas. El algoritmo es el inverso del algoritmo de refinamiento de Plaza y Carey. Ambos algoritmos funcionan de forma automática. El algoritmo de refinamiento se puede aplicar a cualquier malla inicial de tetraedros. De igual manera el desrefinamiento se puede usar para conseguir una malla más grosera a partir de una secuencia de mallas encajadas obtenidas por medio de la aplicación reiterada del algoritmo de refinamiento. La combinación de ambos algoritmos se puede usar para resolver problemas dependientes del tiempo en dimensión tres, de forma similar a como ya se han usado algoritmos análogos en dimensiones inferiores Ferragut et al.. A SKELETON-BASED DEREFINEMENT ALGORITHM FOR TETRAEDRAL GRIDS Summary In the present study, a novel three dimensional derefinement algorithm for nested tetrahedral grids based on bisection is presented. This algorithm is the inverse algorithm scheme first developed by Plaza and Carey. Both schemes are fully automatic. The refinement algorithm can be applied to any initial tetrahedral mesh without any preprocessing. Similarly the derefinement scheme can be used to get a coarser mesh from a sequence of nested tetrahedral meshes obtained by successive aplication of the refinement algorithm. The refinement and derefinement schemes can be easily combined to deal with time dependent problems. These combinations depend only on a few parameters that are fixed into the input data for the user, in the same manner in which anologous algorithms for lower dimensions have been already used Ferragut et al.. INTRODUCCIÓN En los últimos años se han desarrollado diferentes técnicas de refinamiento para triangulaciones bidimensionales y que posteriormente han sido extendidas a D. Incluso se han usado conceptos de geometría fractal y sistemas de funciones iteradas,. Para un tratamiento detallado sobre refinamiento local de mallas véase por ejemplo. Un algoritmo en D basado en la bisección es el T de Rivara 8,9,. LaFiguramuestra la aplicación de este algoritmo a un solo triángulo. Nótese que el primer paso, (Figura a), consiste en la bisección del triángulo por el lado mayor. c Universitat Politècnica de Catalunya (España). ISSN: 0 Recibido: Enero 999
2 7 A. Plaza y M.A. Padrón Figura. El algoritmo T de Rivara También en dimensión tres se han desarrollado algunas técnicas en los últimos años tanto para el refinamiento como para el desrefinamiento de mallas de tetraedros. Algoritmos basados en la bisección por la arista mayor son los de Rivara y Levin y el de Muthukrishnan et al.. Los algoritmos de Bänsch yliuyjoe 8,9 dividen cada tetraedro en ocho subtetraedros mediante bisección reiterada de las aristas. Otros algoritmos semejantes se encuentran en,7,0,. Sin embargo estos algoritmos no se pueden aplicar en general a cualquier malla inicial y necesitan algún tipo de pre-proceso. Recientemente Plaza y Carey,, han presentado una generalización del algoritmo - T de Rivara a dimensión tres. El algoritmo de Plaza y Carey opera en primer lugar en el esqueleto de la malla (esto es, el conjunto de las caras triangulares de los tetraedros) para dividir después el interior de cada tetraedro de forma congruente con la subdivisión de sus caras. Del mismo modo, el algoritmo de desrefinamiento aquí presentado trabaja en primer lugar en el esqueleto de la triangulación D, asegurando la conformidad de la malla que aparecerá, para finalmente, reconstruir el interior de cada tetraedro. En esta segunda tarea (la redefinición del interior de cada tetraedro) se utiliza la parte correspondiente del algoritmo de refinamiento, lo que simplifica el proceso. Ambos algoritmos se pueden aplicar a cualquier triangulación inicial y no necesitan ningún tipo de pre-proceso. El artículo está organizado como sigue: en primer lugar se recogen algunas definiciones. En la segunda sección se resume el algoritmo de refinamiento en D. Después se presentan los algoritmos de desrefinamiento en D y D basados en el esqueleto. A continuación se muestra el esquema de la combinación de ambos algoritmos para la resolución de problemas evolutivos. Por último se ofrecen algunos ejemplos numéricos. Definiciones Sea V = {X 0,X,...,X m } un conjunto de m + puntos de R n (0 m n) talesque { X 0 X i : i m} es un conjunto de vectores linealmente independientes. Entonces la envoltura cerrada convexa de V, denotada por S = V >= X 0,X,...,X m > se llama m- simplex en R n, y los puntos X 0,...,X m son llamados vértices de S. Elnúmero m se dice que es la dimensión de S. De esta manera un tetraedro (cerrado) se define por el conjunto (no ordenado) de sus vértices X 0,X,X,X >, y una cara por sus tres vértices ( X i,x j,x k >. Una arista queda definida por un par de vértices distintos X i,x j >.Vértices, arista, caras y tetraedros son, respectivamente 0,,, y símplices. Cualquier i simplex contenido en un n simplex S (con in)será denominado i símplex ó i cara de S. Sea Ω un conjunto acotado de R n (n =, aunque la definición es válida en general) con interior no vacío Ω, yfrontera Ω poligonal. Una partición de Ω en n símplices = {t,...,t n } se denominará una triangulación de Ω. Dos símplices t i,t j de se dicen adyacentes si t i tj. Si es tal que símplices adyacentes comparten una cara entera, ó una arista entera óunvértice, se dice que es una triangulación conforme. El conjunto skt() ={f : f es una (n )-cara de algún t i,cont i } se denominará (n )-esqueleto de, también denotado por (n ) skt(). Por ejemplo, el esqueleto de una triangulación en dimensión tres está compuesto por las caras triangulares de los tetraedros. Nótese que
3 Un algoritmo de desrefinamiento en D para mallas de tetraedros basado en el esqueleto 7 el concepto de una malla de símplices conforme es aplicable al skt() por estar compuesto por (n )-símplices. Por tanto, si es conforme, skt() estambién conforme. Dos triangulaciones (conformes) y de un mismo conjunto acotado Ω se llamarán encajadas ó anidadas, y escribiremos si se cumple la siguiente condición: t, t,...,t p tal que t = t... t p.diremostambién que es más grosera que, óque es más fina que. A partir de una malla inicial en la que se realizan sucesivos refinamientos por bisección, se obtiene una secuencia de triangulaciones anidadas. En una secuencia de triangulaciones encajadas, los conjuntos de nodos también son encajados. De hecho podemos hablar de nodos propios ynodosheredados como se define a continuación. Sea T = {... n } una secuencia de mallas encajadas, donde representa la malla inicial, y sea j alguna triangulación de T.UnnodoNde j se llamará nodo propio de j si ese nodo no pertenece a ningún nivel anterior de la malla. De lo contrario, N se denominará nodo heredado en j. Las aristas, caras y elementos son nombrados de la misma forma 6. Los nodos propios de j también se denominan nodos j-nuevos por Rivara 0. Figura. Envoltura de una arista relativa a la teselación Al aplicar el refinamiento por medio de la bisección de los elementos, denominamos arista entorno de un nodo N alaaristaenlacualn es el punto medio. Para cada arista E llamamos envoltura de E, y la denotamos por h(e), al conjunto de elementos que están compartiendo la arista E. Este conjunto en general es no convexo. En la Figura se dibujan la arista entorno de un nodo (en negro) y la envoltura de su arista entorno. Si la arista tiene un nodo en su punto medio, como en el caso de la figura anterior, el conjunto de nodos extremos de la envoltura (que son los puntos blancos en la figura) se denominará molécula para el nodo negro de la figura. Obsérvese que esta definición puede ser extendida a cualquier dimensión. EL PROCESO DE REFINAMIENTO El algoritmo de refinamiento en D se basa en la aplicación del algoritmo de refinamiento en D al esqueleto de una malla de tetraedros. Por eso, primero mostramos cómo trabaja la versión bidimensional. La Figura a representa una triangulación inicial en la cual el triángulo t va a ser subdividido. El primer paso del algoritmo es la subdivisión de las aristas de t (Figura b). Después el triángulo adyacente t es examinado para asegurar de esta forma la conformidad. Este proceso termina cuando ya no quedan más triángulos vecinos en los que se tenga que asegurar la conformidad (Figura c). Finalmente se divide cada triángulo en dos, tres ócuatrotriángulos-hijos, dependiendo del número de aristas divididas que contenga (Figura d).
4 7 A. Plaza y M.A. Padrón Figura. Algoritmo de refinamiento en D El pseudo-código del procedimiento que asegura la conformidad de la malla en D se expone a continuación: Para cada arista e de t, hace Marca el punto medio de e. /* sea t el triángulo vecino de t por la arista e, y l(t )laaristamayordet */ Mientras l(t) l(t ), hace Añade t alalistal. Marca el punto medio de la arista l(t ). l(t) =l(t ); t = t /* sea t el vecino de t através de la arista l(t), l(t )laaristamayordet */ Fin del mientras En la Figura se muestra el itinerario seguido para conseguir la conformidad. Las flechas indican qué triángulos vecinos han de examinarse. Figura. Comprobación de la conformidad local al refinar
5 Un algoritmo de desrefinamiento en D para mallas de tetraedros basado en el esqueleto 7 Se expone una versión del algoritmo en dimensión tres, en la que un sólo tetraedro va a ser dividido atendiendo al error local de la solución,,. Sea este tetraedro t 0. ENTRADA: {t 0,} L = { } Sea L un vector de nuevos-nodos */ /*. Subdivisión de las aristas */ Para cada arista e t 0, hace Subdivide e, siendo N e el nuevo nodo en el punto medio. L = L {N e } /*. Se asegura la conformidad */ Mientras haya un nuevo nodo N L, con arista entorno E, hace Para cada tetraedro t h(e), hace Si t es no-conforme, entonces Se divide la arista mayor de cada cara no-conforme f de t. /* Sea N f el nuevo nodo introducido */ L = L {N f } Si es el caso, e divide la arista de referencia de t. /* Sea N t el nuevo nodo introducido */ L = L {N t } Fin del si L = L {N} Fin del mientras /*. Subdivisión de las caras */ Para cada f skt() que se ha de dividir, hace Subdivide f. /*. Subdivisión de los tetraedros */ Para cada t que se ha de dividir, hace Subdivide internamente t. SALIDA: Nueva malla. La arista de referencia de cada tetraedro es la de mayor longitud, salvo en el caso en el que haya dos aristas comunes a dos caras triangulares y que sean las mayores para esas dos caras. Este caso se corresponde con un tetraedro tipo de los citados en la referencia,y puede tomarse cualquiera de esas dos aristas como la de referencia del tetraedro. La Figura muestra la aplicación del algoritmo de refinamiento a una malla inicial muy simple compuesta por tetraedros, (Figura a). El tetraedro -- - va a ser refinado de acuerdo con un indicador de error (Figura b), y a continuación el tetraedro vecino es refinado para asegurar la conformidad de la malla (ver Figura c en la que se introducen los nodos N yn). Finalmente, la Figura d presenta la división del -esqueleto y la Figura e la malla final donde se han definido los nuevos elementos. En esta última figura se han resaltado las aristas internas que aparecen en los tetraedros al subdividirlos.
6 76 A. Plaza y M.A. Padrón (a) Malla inicial (b) Paso N N (c) Paso : Conformidad (d) Paso : División del esqueleto (e) Malla final Figura. Ejemplo de aplicación del algoritmo de refinamiento en D EL ALGORITMO DE DESREFINAMIENTO Para desrefinar una malla refinada, se construye un algoritmo inverso del de refinamiento. Sin embargo, aunque este nuevo algoritmo es el inverso del de refinamiento, es importante hacer notar su mayor complejidad en el sentido de que ahora todos los niveles de la malla están implicados. Un punto importante al desrefinar es que se necesita conocer la genealogía de las aristas, caras y elementos. Es decir, es necesario saber las aristas-hijas y la arista-padre para cada arista, e igualmente para las caras y los elementos. Para los nodos, aristas, caras y elementos asignamos una serie de vectores, llamados vectores de desrefinamiento o indicadores de desrefinamiento. Estos vectores nos dan información sobre el nivel en el que cada elemento es propio, además de indicar si ese elemento geométrico debe permanecer ó ha de ser eliminado.
7 Un algoritmo de desrefinamiento en D para mallas de tetraedros basado en el esqueleto 77 La condición de desrefinamiento es aquella que un nodo N debe verificar para ser quitado. Hemos usado en D la misma condiciónquesehausadoend, es decir, la diferencia relativa (y otras veces la absoluta) entre la solución numérica en un nodo particular y la solución numérica promedio en los extremos de los nodos de la arista que contiene a dicho nodo. Si esta diferencia es menor que un pequeño parámetro ɛ>0, el nodo puede eliminarse. Esto es, si u h es la solución numérica para una malla dada, y u i h es la función interpolada de u h en la malla desrefinada, obtendremos u h u i h = sup x u h (x) u i h(x) ɛ Ciertamente, el indicador de desrefinamiento no nos permite controlar el error de discretización. En los algoritmos adaptativos el control lo realiza usualmente el indicador de error del proceso de refinamiento. La idea es que al usar un paso de tiempo de integración una buena aproximación de la solución en el tiempo t n+ = t n + t n,eslasolución en el paso de tiempo anterior t n.así que el indicador de desrefinamiento descrito se puede considerar óptimo en el sentido de que una solución dada es aproximada con un número mínimo de nodos después de desrefinar. Si δ>0 es una tolerancia dada, para el error con la norma del máximo, un criterio práctico sería elegir por ejemplo, ɛ 0.δ. De igual forma, se puede elegir ɛ como una pequeña parte de u ousaralgún otro valor característico de acuerdo con el problema que se estudia ó el rango esperado de la solución. Sin embargo se debe hacer notar que los algoritmos son independientes del criterio de refinamiento ó de la condición de desrefinamiento utilizada. También se pueden usar fórmulas más complicadas que involucren aproximaciones hasta la segunda derivada de la solución, o incluso sobre los tetraedros en lugar de los nodos. Por último llamaremos a un nodo propio N candidato a ser eliminado, si N puede ser quitado de la malla. Esto quiere decir que la conformidad se asegura manteniendo algunos nodos que de otra forma, dada la condición de desrefinamiento, podrían ser eliminados. Las ideas y definiciones anteriores son aplicables tanto al caso bidimensional como al caso tridimensional. Antes de exponer el algoritmo de desrefinamiento en D, se resume a continuación el caso bidimensional. El algoritmo de desrefinamiento en D Sea T = {... n } una secuencia de mallas triangulares encajadas, donde representa la malla inicial y n la malla más fina de la secuencia. Desrefinar la secuencia, significa obtener una nueva secuencia de mallas T m = {... m}, donde m n. Unesquemadeestealgoritmofuepropuestoen 7 como sigue: ENTRADA: Secuencia T = {... n } /* Bucle en niveles de T */ Para j = n hasta, hace Para cada nodo propio susceptible de ser eliminado N j, hace Se evalúa la condición de desrefinamiento. Se marcan los nodos y las aristas. /* Se asegura la conformidad localmente */ /* Sea c la arista entorno de N */ Para cada triángulo vecino t de c, hace Si t es no-conforme, entonces Cambia el indicador de desrefinamiento del nodo P de la arista mayor, y los nodos de la molécula de P deben permanecer. Fin del si
8 78 A. Plaza y M.A. Padrón /* Redefinición de la malla */ Si algún nodo propio de j permanece, entonces Se definen nuevas conexiones nodales. Los vectores de genealogía son modificados. En otro caso El nivel en curso j es borrado de la estructura de datos. Fin del si Los cambios son heredados para las siguentes mallas. /* Se obtiene una nueva secuencia de mallas encajadas */ SALIDA: Secuencia T m = {... m} Nótese que la conformidad se asegura localmente recorriendo los elementos vecinos de la arista-entorno de cada nodo propio. La Figura 6 muestra una secuencia de cinco niveles de malla. La columna de la izquierda representa la secuencia de entrada T = {... } del algoritmo. Las tres siguientes columnas representan el resultado del proceso al desrefinar desde el nivel más fino ( ) hasta el tercero ( ). El nivel desrefinado en cada paso es señalado por una línea punteada en la Figura 6. Los puntos negros significan que esos nodos deben permanecer en la malla por razón de la conformidad, y los blancos son nodos propios candidatos a ser eliminados en cada paso. Figura 6. Proceso de desrefinamiento en dimensiones
9 Un algoritmo de desrefinamiento en D para mallas de tetraedros basado en el esqueleto 79 El algoritmo de desrefinamiento en D El algoritmo comprende principalmente dos pasos: la aplicación del algoritmo de desrefinamiento al esqueleto, y la reconstrucción interna de los tetraedros. Como en el caso bidimensional, el concepto de adyacencia es la idea central en el algoritmo en D. Para recorrer los elementos que pertenecen a la envoltura de una arista cualquiera E, usamosla información de los elementos vecinos a cada cara, y la llamada cara base de la arista E. Entendemos por cara base de una arista E, una cara que tenga por arista la arista E. La definción de cara base no es unívoca, es decir, adjudicamos a cada arista como cara base una cualquiera de las caras triangulares que la tienen por arista. ENTRADA: Secuencia T = {... n } /* Buclē en niveles de T */ Para j = n hasta, hace Para cada nodo propio elegible N j, hace /*. Se evalúa la condición de desrefinamiento */ Se examina la condición de desrefinamiento. Se marcan los nodos y las aristas. /*. Se asegura la conformidad localmente */ /* Sea E la arista-entorno de N, yh(e) laenvoltura de E */ Para cada tetraedro t en h(e), hace Conforma el tetraedro t. /*. Se re-define el skt( j )*/ Para cada f skt( j ), hace Subdivide f por el algoritmo -T de Rivara. /*. Se redefine el interior de los tetraedros */ Para cada t j, hace Define una nueva subdivisión de t. /* Fin del bucle en niveles de malla */ SALIDA: Secuencia T m = {... m}. LA COMBINACIÓN REFINAMIENTO/DESREFINAMIENTO Los algoritmos de refinamiento y desrefinamiento se pueden combinar para obtener una estrategia adaptativa. Este procedimiento se esquematiza en lo que sigue: Generación de la malla inicial y definición de los parámetros para el refinamiento y el desrefinamiento Para npasos =,hasta N max, hace Para cada valor npasos, hace Para i =,hastan r, hace. Cálculo del nuevo paso de tiempo (t).. Solución del correspondiente sistema de ecuaciones.. Refinamiento Local.. Desrefinamiento de la malla, con tolerancia ɛ.
10 80 A. Plaza y M.A. Padrón Otra alternativa es utilizar el refinamiento y el desrefinamiento (por elementos triangulares) en el mismo punto del proceso anterior (paso ), según el indicador de error. Observaciones: i. La combinación refinamiento/desrefinamiento depende de pocos parámetros: N max, N r, (t), γ, yɛ. ii. Tanto el refinamiento como el desrefinamiento muestran una complejidad lineal: O(N). iii. La condición de desrefinamiento se evalúa en un número mínimo de nodos. iv. Por la propia naturaleza de las mallas encajadas, es relativamente fácil utilizar un método multimalla,6. v. El algoritmo de desrefinamiento se puede combinar con uno de refinamiento global para un proceso de refinamiento local. En este caso, las soluciones obtenidas por sucesivos refinamientos de las mallas, determinan un indicador de error para desrefinamientos locales, aunque el coste computacional sea mucho más alto. Sin embargo el coste computacional de esta estrategia en D es extremadamente grande. vi. Al eliminar nodos menos significativos, el número de ecuaciones involucradas en un proceso evolutivo permanece acotado. Esto es una importante propiedad porque la mayor parte del tiempo de CPU se emplea en la resolución del sistema de ecuaciones. EJEMPLOS NUMÉRICOS Un ejemplo de refinamiento Presentamos un ejemplo numérico para mostrar el comportamiento del algoritmo de refinamiento. La Figura 7a muestra una malla inicial que es localmente refinada para obtener la malla final de la Figura 7b, que contiene nodos y 06 tetraedros. (a) Malla inicial (b) Malla localmente refinada Figura 7. Ejemplo de refinamiento local Se pueden encontrar muchos ejemplos de la aplicación de la combinación del refinamiento y desrefinamiento en problemas de dos dimensiones. Aquí presentamos únicamente la simulación de un problema evolutivo en D. Este consiste en seis refinamientos locales para capturar la singularidad, seguidos de un desrefinamiento. La singularidad corresponde a un eje horizontal en la figura, que se ha ido desplazando durante el proceso. Nótese cómo el número de nodos permanece acotado en un cierto rango durante el proceso.
11 Un algoritmo de desrefinamiento en D para mallas de tetraedros basado en el esqueleto 8
12 8 A. Plaza y M.A. Padrón CONCLUSIONES Los algoritmos de refinamiento y de desrefinamiento aquí presentados son una herramienta muy útil para el tratamiento de problemas no-estacionarios en dimensión tres. La adaptatividad de la malla es particularmente importante en problemas tridimensionales porque el tamaño del problema y el coste computacional crecen muy rápidamente cuando la dimensión del dominio es mayor y el diámetro de la malla se reduce. Con la combinación refinamiento/desrefinamiento se obtienen secuencias de mallas encajadas. Esto, facilita el uso del método multimalla para la resolución del sistema de ecuaciones asociado al método de los elementos finitos 6. Estas ideas son importantes, no sólo para desarrollar métodos eficientes para resolver ecuaciones en derivadas parciales, sino que claramente pueden ser interesantes en otras áreas, tales como aproximación de superficies, visualización, compresión de datos, o modelado de sólidos. Todavía hay algunas cuestiones abiertas relacionadas con la prueba matemática de la estabilidad de las mallas obtenidas, y la existencia de un número finito de clases de tetraedros semejantes (que quizá dependa sólo de la geometría de la malla inicial). Aunque estas propiedades han sido demostradas recientemente en dimensión dos,suextensión a dimensión tres no está aún resuelta. AGRADECIMIENTOS Este trabajo ha sido financiado en parte por la DGICYES beca número PR9-80 y por la Dirección General de Universidades del Gobierno de Canarias. REFERENCIAS D.N.. Arnold, A. Mukherjee y L. Pouly, Locally adapted tetrahedral meshes using bisection, SIAM J. Sci. Comput, (997). E. Bänssch, Local mesh refinement in and dimensions, IMPACT Com. Sci. Engng., Vol., pp. 8 9, (99). S.W. Bova y G.F. Carey, Mesh generation/refinement fractal concepts and iterated fuction systems, Int. J. Num. Meth. Engng., Vol., pp. 87 0, (99). G.F. Carey, Computational grids: Generation, refinement and solution strategies, Taylor and Francis, (997). L. Ferragut, R. Montenegro y A. Plaza, Efficient refinement/derefinement algorithm of nested meshes to solve evolution problems, Comm. Num. Meth. Engng., Vol. 0, pp. 0, (99). 6 W. Hackbush, Multigrid methods and applictions, Springer Verlag, (98). 7 I. Kossaczký, A recursive approach to lacal mesh refinement in two and three dimensions, J. Comp. App. Math, Vol., pp. 7 88, (99). 8 A. Liu y B. Joe, On the shape of tetrahedra from bisection, Math. Comp., Vol. 6, pp., (99). 9 A. Liu y B. Joe, Quality local refinement of tetrahedral meshes based on bisection, SIAM J. Sci. Comput., Vol. 6, pp. 69 9, (99).
13 Un algoritmo de desrefinamiento en D para mallas de tetraedros basado en el esqueleto 8 0 J.M. Maubach, Local bisection refinement for n-simplicial grids generated by reflection, SIAM J. Sci. Stat. Comput., Vol. 6, pp. 0 7, (99). A. Mukherjee, An adaptive finite element code for elliptic boundary value problems in three dimensions with applications in numerical relativity, Ph.D. thesis, Penn, State University, (996). E. Muthukrishnan, P.S. Shiakolas, R.V. Nambiar y K.L. Lawrence, Simple algorithm for adaptive refinement of three-dimensional finite element tetrahedral meshes, AIAA Journal, Vol., pp. 98 9, (99). A. Plaza, The fractal behaviour of triangular refined/derefined meshes, Comm. Num. Meth. Engng., Vol., pp. 9 0, (996). A. Plaza y G.F. Carey, About local refinement of tetrahedral grids based on bisection, th Int. Mesh Roundtable, pp. -6, Sandia Corporation, (996). A. Plaza y G.F. Carey, A new refinement algorithm for tetrahedral grids based on bisection, Technical Report, T.I.C.A.M., (996). 6 A. Plaza, L. Ferragut y R. Montenegro, Derefinement algorithms of nested meshes, Ed. J. van Leeuwen, Algorithms, software, architecture, Elsevier Science Publishers B.V., pp. 09, North Holland, (99). 7 A. Plaza, R. Montenegro y L. Ferragut, Derefinement algorithms of nested meshes, Ed. M. Papadrakakis, Advances in post and preprocessing for finite element technology, Civil-Comp Ltd, (99). 8 M.C. Rivara, Mesh refinement on the generalized bisection of simplices, SIAM J. Num. Anal., Vol., pp. 60-6, (98). 9 M.C. Rivara, A grid generator based on -triangles conforming mesh refinement algorithms, Int. J. Num. Meth. Engng., Vol., pp., (987). 0 M.C. Rivara, Selective refinement/derefinement algorithms for sequences nested triangulations, Int. J. Num. Meth. Engng., Vol. 8, pp , (989). M.C. Rivara, Local modification meshes for adaptive and/or multigrid finite-element methods, J. Comp. and Appl. Math., Vol. 6, pp , (99). M.C. Rivara y G. Iribarren, The -triangles longest-side partition of triangles and linear refinement algorithms, Math. Comp., (997). M.C. Rivara y C. levin, A -d refinement algorithm suitable for adaptive and multigrid techniques, J. Comp. and Appl. Num. Math., Vol. 8, pp. 8 90, (99). A. Plaza y G.F. Carey, Local refinement of simplicial grids based on the skeleton, Appl. Numer. Math., Vol., N, pp. 9 8, (000).
IMPLEMENTACIÓN DE UN ALGORITMO DE REFINAMIENTO/DESREFINAMIENTO PARA MALLAS DE TETRAEDROS
 MÉTODOS COMPUTACIONAIS EM ENGENHARIA Lisboa, 31 de Maio - 2 de Junho, 2004 APMTAC, Portugal 2004 IMPLEMENTACIÓN DE UN ALGORITMO DE REFINAMIENTO/DESREFINAMIENTO PARA MALLAS DE TETRAEDROS J.M. González-Yuste
MÉTODOS COMPUTACIONAIS EM ENGENHARIA Lisboa, 31 de Maio - 2 de Junho, 2004 APMTAC, Portugal 2004 IMPLEMENTACIÓN DE UN ALGORITMO DE REFINAMIENTO/DESREFINAMIENTO PARA MALLAS DE TETRAEDROS J.M. González-Yuste
Estructuras de datos tipo Grafo en los algoritmos de Refinamiento y Desrefinamiento basados en la bisección n por el lado mayor. Aplicaciones.
 Universidad de Las Palmas de Gran Canaria Departamento de Matemáticas Estructuras de datos tipo Grafo en los algoritmos de Refinamiento y Desrefinamiento basados en la bisección n por el lado mayor. Aplicaciones.
Universidad de Las Palmas de Gran Canaria Departamento de Matemáticas Estructuras de datos tipo Grafo en los algoritmos de Refinamiento y Desrefinamiento basados en la bisección n por el lado mayor. Aplicaciones.
PROGRAMA DE CURSO. SCT Auxiliar. Personal
 PROGRAMA DE CURSO Código Nombre CC7610/ Mallas geométricas, Fundamentos y Aplicaciones CC72Y Nombre en Inglés Autor es Horas de Horas Docencia Horas de Trabajo SCT Docentes Cátedra Auxiliar Personal 6
PROGRAMA DE CURSO Código Nombre CC7610/ Mallas geométricas, Fundamentos y Aplicaciones CC72Y Nombre en Inglés Autor es Horas de Horas Docencia Horas de Trabajo SCT Docentes Cátedra Auxiliar Personal 6
Generación automática de mallas tridimensionales para la simulación numérica de procesos medioambientales
 Generación automática de mallas tridimensionales para la simulación numérica de procesos medioambientales Rafael A. Montenegro Armas Catedrático de Matemática Aplicada y Director de la División de Discretización
Generación automática de mallas tridimensionales para la simulación numérica de procesos medioambientales Rafael A. Montenegro Armas Catedrático de Matemática Aplicada y Director de la División de Discretización
Resolución de la ecuación de Difusión en 2-D y 3-D utilizando diferencias finitas generalizadas. Consistencia y Estabilidad.
 XXI Congreso de Ecuaciones Diferenciales y Aplicaciones XI Congreso de Matemática Aplicada Ciudad Real, 1-5 septiembre 009 (pp. 1 8) Resolución de la ecuación de Difusión en -D y 3-D utilizando diferencias
XXI Congreso de Ecuaciones Diferenciales y Aplicaciones XI Congreso de Matemática Aplicada Ciudad Real, 1-5 septiembre 009 (pp. 1 8) Resolución de la ecuación de Difusión en -D y 3-D utilizando diferencias
PROGRAMA DE CURSO. SCT Auxiliar. Personal (CC3301 / CC3002), CC3001 Resultados de Aprendizaje
 Código Nombre CC5501 Mallas geométricas y aplicaciones Nombre en Inglés PROGRAMA DE CURSO SCT es Horas de Horas Docencia Horas de Trabajo Docentes Cátedra Auxiliar Personal 6 10 3 1.5 5.5 Requisitos Carácter
Código Nombre CC5501 Mallas geométricas y aplicaciones Nombre en Inglés PROGRAMA DE CURSO SCT es Horas de Horas Docencia Horas de Trabajo Docentes Cátedra Auxiliar Personal 6 10 3 1.5 5.5 Requisitos Carácter
Explicación geométrica de una medida de forma de símplices n-dimensional
 Rev. Int. Mét.Num.Cálc. Dis. Ing. Vol. 18, 4, 475-480 (2002) Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería Explicación geométrica de una medida de forma de símplices n-dimensional
Rev. Int. Mét.Num.Cálc. Dis. Ing. Vol. 18, 4, 475-480 (2002) Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería Explicación geométrica de una medida de forma de símplices n-dimensional
Resolución de la ecuación de Ondas en 2-D y 3-D utilizando diferencias finitas generalizadas. Consistencia y Estabilidad.
 XXI Congreso de Ecuaciones Diferenciales y Aplicaciones XI Congreso de Matemática Aplicada Ciudad Real, 1-5 septiembre 009 (pp. 1 8) Resolución de la ecuación de Ondas en -D y 3-D utilizando diferencias
XXI Congreso de Ecuaciones Diferenciales y Aplicaciones XI Congreso de Matemática Aplicada Ciudad Real, 1-5 septiembre 009 (pp. 1 8) Resolución de la ecuación de Ondas en -D y 3-D utilizando diferencias
GENERACIÓN DE MALLAS APLICACIONES A LA INGENIERÍA
 GENERACIÓN DE MALLAS APLICACIONES A LA INGENIERÍA José Pablo Suárez Rivero Ángel Plaza de la Hoz Miguel Ángel Padrón Medina UNIVERSIDAD DE LAS PALMAS DE GRAN CANARIA Edición: Escuela Universitaria Politécnica
GENERACIÓN DE MALLAS APLICACIONES A LA INGENIERÍA José Pablo Suárez Rivero Ángel Plaza de la Hoz Miguel Ángel Padrón Medina UNIVERSIDAD DE LAS PALMAS DE GRAN CANARIA Edición: Escuela Universitaria Politécnica
El problema de la propagación del refinamiento en cuatro triángulos por la arista mayor
 Rev. Int. Mét.Num.Cálc. Dis. Ing. Vol. 22,, 3-7 (26) Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería El problema de la propagación del refinamiento en cuatro triángulos por
Rev. Int. Mét.Num.Cálc. Dis. Ing. Vol. 22,, 3-7 (26) Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería El problema de la propagación del refinamiento en cuatro triángulos por
UNIVERSIDAD DE LAS PALMAS DE GRAN CANARIA
 UNIVERSIDAD DE LAS PALMAS DE GRAN CANARIA DEPARTAMENTO DE MATEMÁTICAS TESIS DOCTORAL ESTRUCTURAS DE DATOS TIPO GRAFO EN LOS ALGORITMOS DE REFINAMIENTO Y DESREFINAMIENTO BASADOS EN LA BISECCIÓN POR EL LADO
UNIVERSIDAD DE LAS PALMAS DE GRAN CANARIA DEPARTAMENTO DE MATEMÁTICAS TESIS DOCTORAL ESTRUCTURAS DE DATOS TIPO GRAFO EN LOS ALGORITMOS DE REFINAMIENTO Y DESREFINAMIENTO BASADOS EN LA BISECCIÓN POR EL LADO
ESTRUCTURAS DE DATOS TIPO GRAFO EN LOS ALGORITMOS DE REFINAMIENTO Y DESREFINAMIENTO BASADOS EN LA BISECCIÓN POR EL LADO MAYOR. APLICACIONES.
 UNIVERSIDAD DE LAS PALMAS DE GRAN CANARIA Departamento de Matemáticas Departamento de Cartografía y Expresión Gráfica en la Ingeniería TESIS DOCTORAL ESTRUCTURAS DE DATOS TIPO GRAFO EN LOS ALGORITMOS DE
UNIVERSIDAD DE LAS PALMAS DE GRAN CANARIA Departamento de Matemáticas Departamento de Cartografía y Expresión Gráfica en la Ingeniería TESIS DOCTORAL ESTRUCTURAS DE DATOS TIPO GRAFO EN LOS ALGORITMOS DE
Resolución de la ecuación de advección-difusión en 2-D utilizando diferencias finitas generalizadas. Consistencia y Estabilidad.
 XXI Congreso de Ecuaciones Diferenciales y Aplicaciones XI Congreso de Matemática Aplicada Ciudad Real, 1-5 septiembre 009 (pp. 1 8) Resolución de la ecuación de advección-difusión en -D utilizando diferencias
XXI Congreso de Ecuaciones Diferenciales y Aplicaciones XI Congreso de Matemática Aplicada Ciudad Real, 1-5 septiembre 009 (pp. 1 8) Resolución de la ecuación de advección-difusión en -D utilizando diferencias
Capítulo 3 El Método de los Elementos de Contorno y la Formulación Hipersingular.
 Capítulo 3 El Método de los Elementos de Contorno y la Formulación Hipersingular. 3.1. Introducción El Método de los Elementos de Contorno (MEC) se ha implantado firmemente en numerosos campos de la ingeniería
Capítulo 3 El Método de los Elementos de Contorno y la Formulación Hipersingular. 3.1. Introducción El Método de los Elementos de Contorno (MEC) se ha implantado firmemente en numerosos campos de la ingeniería
Un algoritmo de detección de singularidades: señales uno-dimensionales
 XXI Congreso de Ecuaciones Diferenciales y Aplicaciones XI Congreso de Matemática Aplicada Ciudad Real, 21-25 septiembre 29 (pp. 1 8) Un algoritmo de detección de singularidades: señales uno-dimensionales
XXI Congreso de Ecuaciones Diferenciales y Aplicaciones XI Congreso de Matemática Aplicada Ciudad Real, 21-25 septiembre 29 (pp. 1 8) Un algoritmo de detección de singularidades: señales uno-dimensionales
MÉTODOS MULTIMALLA SOBRE MALLAS SEMI-ESTRUCTURADAS PARA LAS ECUACIONES DE NAVIER-STOKES
 MÉTODOS MULTIMALLA SOBRE MALLAS SEMI-ESTRUCTURADAS PARA LAS ECUACIONES DE NAVIER-STOKES Elvio Heidenreich a,b, Francisco J. Gaspar c, Francisco J. Lisbona c and Carmen Rodrigo d a Departamento de Ingeniería
MÉTODOS MULTIMALLA SOBRE MALLAS SEMI-ESTRUCTURADAS PARA LAS ECUACIONES DE NAVIER-STOKES Elvio Heidenreich a,b, Francisco J. Gaspar c, Francisco J. Lisbona c and Carmen Rodrigo d a Departamento de Ingeniería
Árboles de Partición Quadtrees Octrees K-d trees
 Árboles de Partición Quadtrees Octrees K-d trees Estructuras de Datos Andrea Rueda Pontificia Universidad Javeriana Departamento de Ingeniería de Sistemas Estructuras de Datos Geométricas Estructuras de
Árboles de Partición Quadtrees Octrees K-d trees Estructuras de Datos Andrea Rueda Pontificia Universidad Javeriana Departamento de Ingeniería de Sistemas Estructuras de Datos Geométricas Estructuras de
Programación lineal Optimización de procesos químicos DIQUIMA-ETSII
 Programación lineal PROGRAMACIÓN LINEAL PROGRAMACIÓN LINEAL se formula siguiendo el planteamiento general: Función objetivo Restricciones de igualdad Restricciones de desigualdad Límite variables PROGRAMACIÓN
Programación lineal PROGRAMACIÓN LINEAL PROGRAMACIÓN LINEAL se formula siguiendo el planteamiento general: Función objetivo Restricciones de igualdad Restricciones de desigualdad Límite variables PROGRAMACIÓN
GENERADOR DE MALLAS ADAPTADAS PARA LA SIMULACIÓN DE PROBLEMAS EN LA ATMÓSFERA
 Segones Jornades sobre Mètodes Numèrics en Ciències Aplicades i Enginyería VALL DE NÚRIA 2003 Laboratori de Càlcul Numèric (LaCàN) GENERADOR DE MALLAS ADAPTADAS PARA LA SIMULACIÓN DE PROBLEMAS EN LA ATMÓSFERA
Segones Jornades sobre Mètodes Numèrics en Ciències Aplicades i Enginyería VALL DE NÚRIA 2003 Laboratori de Càlcul Numèric (LaCàN) GENERADOR DE MALLAS ADAPTADAS PARA LA SIMULACIÓN DE PROBLEMAS EN LA ATMÓSFERA
Nuria Reguera Dpto. de Matemática y Computación, Universidad de Burgos
 Aislamiento de estructuras coherentes para la ecuación BBM discretizada mediante elementos finitos Nuria Reguera Dpto. de Matemática y Computación, Universidad de Burgos nreguera@ubu.es Isaías Alonso-Mallo,
Aislamiento de estructuras coherentes para la ecuación BBM discretizada mediante elementos finitos Nuria Reguera Dpto. de Matemática y Computación, Universidad de Burgos nreguera@ubu.es Isaías Alonso-Mallo,
Árboles de Partición Quadtrees Octrees K-d trees
 Árboles de Partición Quadtrees Octrees K-d trees Estructuras de Datos Andrea Rueda Pontificia Universidad Javeriana Departamento de Ingeniería de Sistemas Estructuras de Datos Geométricas Estructuras de
Árboles de Partición Quadtrees Octrees K-d trees Estructuras de Datos Andrea Rueda Pontificia Universidad Javeriana Departamento de Ingeniería de Sistemas Estructuras de Datos Geométricas Estructuras de
Dinámica de Fluidos Computacional: DFC Discretización temporal. Versión 0.1.0
 Dinámica de Fluidos Computacional: DFC Discretización temporal. Versión 0.1.0 Curso de adaptación al grado en ingeniería aeroespacial para ingenieros técnicos aeronáuticos Adrián Lozano Durán adrian@torroja.dmt.upm.es
Dinámica de Fluidos Computacional: DFC Discretización temporal. Versión 0.1.0 Curso de adaptación al grado en ingeniería aeroespacial para ingenieros técnicos aeronáuticos Adrián Lozano Durán adrian@torroja.dmt.upm.es
Triangulación de Polígonos. comp-420
 Triangulación de Polígonos comp-420 Triangulación de polígonos Triangulación: descomposición de un polígono simple en triángulos. Cualquier triangulación de un polígono simple con n vertices tiene n-2
Triangulación de Polígonos comp-420 Triangulación de polígonos Triangulación: descomposición de un polígono simple en triángulos. Cualquier triangulación de un polígono simple con n vertices tiene n-2
Simulación perceptual
 Simulación En ingeniería, una simulación tiene como objetivo mostrar el comportamiento de un modelo digital bajo condiciones específicas, sean estas ideales, reales o extremas, dando como resultado datos
Simulación En ingeniería, una simulación tiene como objetivo mostrar el comportamiento de un modelo digital bajo condiciones específicas, sean estas ideales, reales o extremas, dando como resultado datos
Aplicaciones de la generación de mallas
 Aplicaciones de la generación de mallas JOSÉ MARÍA ESCOBAR SÁNCHEZ RESUMEN La triangulación de Delaunay en dimensión dos y tres es uno de los métodos de generación de mallas no estructuradas que más se
Aplicaciones de la generación de mallas JOSÉ MARÍA ESCOBAR SÁNCHEZ RESUMEN La triangulación de Delaunay en dimensión dos y tres es uno de los métodos de generación de mallas no estructuradas que más se
Introducción a la Geometría Computacional. Análisis de Algoritmos
 Introducción a la Geometría Computacional Análisis de Algoritmos Geometría Computacional La Geometría Computacional surgió a finales de los 70s del área de diseño y análisis de algoritmos. Estudio sistemático
Introducción a la Geometría Computacional Análisis de Algoritmos Geometría Computacional La Geometría Computacional surgió a finales de los 70s del área de diseño y análisis de algoritmos. Estudio sistemático
Solución de la ecuación de Stokes
 REVISTA Solución de la ecuación de Stokes Doctora en Ciencias Matemáticas, Resumen Palabras clave Método de los elementos Elementos cuadriláteros Solution of the Stokes equation using the quadrilateral
REVISTA Solución de la ecuación de Stokes Doctora en Ciencias Matemáticas, Resumen Palabras clave Método de los elementos Elementos cuadriláteros Solution of the Stokes equation using the quadrilateral
Sumas subdirectas de M-matrices invertibles
 Sumas subdirectas de M-matrices invertibles Rafael Bru * Francisco Pedroche * Daniel B. Szyld ** CEDYA 00 - Congreso de Ecuaciones Diferenciales y Aplicaciones. Leganés, 19 al de Septiembre de 00. Madrid,
Sumas subdirectas de M-matrices invertibles Rafael Bru * Francisco Pedroche * Daniel B. Szyld ** CEDYA 00 - Congreso de Ecuaciones Diferenciales y Aplicaciones. Leganés, 19 al de Septiembre de 00. Madrid,
Un sistema experimental para generar mallas no-estructuradas en. irregulares.
 Un sistema experimental para generar mallas no-estructuradas en regiones planas irregulares. Facultad de Ciencias, UNAM 23-Abr-09 Planteamiento del Problema Preliminares Motivación Mallas no estructuradas
Un sistema experimental para generar mallas no-estructuradas en regiones planas irregulares. Facultad de Ciencias, UNAM 23-Abr-09 Planteamiento del Problema Preliminares Motivación Mallas no estructuradas
MÉTODO DE LOS ELEMENTOS FINITOS. Preproceso y Postproceso de Resultados
 MÉTODO DE LOS ELEMENTOS FINITOS. Preproceso y de Resultados Castillo Madrid, 18 de Enero de 2007 Índice 1 2 3 4 5 6 En la simulación computacional de un problema mediante elementos finitos, todos los pasos
MÉTODO DE LOS ELEMENTOS FINITOS. Preproceso y de Resultados Castillo Madrid, 18 de Enero de 2007 Índice 1 2 3 4 5 6 En la simulación computacional de un problema mediante elementos finitos, todos los pasos
MÉTODO DE LOS ELEMENTOS FINITOS. Preproceso y Postproceso de Resultados
 MÉTODO DE LOS ELEMENTOS FINITOS. Preproceso y de Resultados Castillo Madrid, 20 de Diciembre de 2007 Índice 1 2 3 4 5 6 En la simulación computacional de un problema mediante elementos finitos, todos los
MÉTODO DE LOS ELEMENTOS FINITOS. Preproceso y de Resultados Castillo Madrid, 20 de Diciembre de 2007 Índice 1 2 3 4 5 6 En la simulación computacional de un problema mediante elementos finitos, todos los
Ingeniería y Tecnología
 Ingeniería y Tecnología Didáctica de la programación lineal s con el método gráfico Didactic of linear programming with the graphic method (I) Fecha de recepción: 30 de marzo de 2007 Fecha de aceptación:
Ingeniería y Tecnología Didáctica de la programación lineal s con el método gráfico Didactic of linear programming with the graphic method (I) Fecha de recepción: 30 de marzo de 2007 Fecha de aceptación:
Integración múltiple
 Integración múltiple IABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice 1. Introducción 1 2. Integrales múltiples 1 3. Caso particular: la integral triple
Integración múltiple IABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice 1. Introducción 1 2. Integrales múltiples 1 3. Caso particular: la integral triple
Análisis Numérico: Soluciones de ecuaciones en una variable
 Análisis Numérico: Soluciones de ecuaciones en una variable MA2008 Contexto Uno de los problemas básicos en el área de Ingeniería es el de la búsqueda de raíces: Dada una función o expresión matemática
Análisis Numérico: Soluciones de ecuaciones en una variable MA2008 Contexto Uno de los problemas básicos en el área de Ingeniería es el de la búsqueda de raíces: Dada una función o expresión matemática
Tema 6. Tema 6. Tema 6. Modelado 3D 6.1 Introducción 6.2 Modelado plano de superficies 6.3 modelado de sólidos. 6.1 Introducción
 Tema 6 Tema 6 Tema 6. Modelado 3D 6.1 Introducción 6.3 modelado de sólidos Gràfics per Computador 2004/2005 Tema 6. Modelado 3D 1 6.1 Introducción Una escena puede contener distintos tipos de objetos (nubes,
Tema 6 Tema 6 Tema 6. Modelado 3D 6.1 Introducción 6.3 modelado de sólidos Gràfics per Computador 2004/2005 Tema 6. Modelado 3D 1 6.1 Introducción Una escena puede contener distintos tipos de objetos (nubes,
Superficies de subdivisión
 Grupo de Informática Gráfica Avanzada Universidad de Zaragoza Superficies de subdivisión Indice Introducción Subdivisión por interpolación Ventajas Subdivisión como convolución de B-splines Polígonos,
Grupo de Informática Gráfica Avanzada Universidad de Zaragoza Superficies de subdivisión Indice Introducción Subdivisión por interpolación Ventajas Subdivisión como convolución de B-splines Polígonos,
TEMA 11: INTRODUCCIÓN A LA PROGRAMACIÓN MATEMÁTICA CON VARIABLES DISCRETAS
 TEMA 11: INTRODUCCIÓN A LA PROGRAMACIÓN MATEMÁTICA CON VARIABLES DISCRETAS 1.- ECUACIONES LINEALES (MILP) 1.1.- Formulación 1.2.- Algoritmos para resolver MILPs 2.- VISIÓN GENERAL DE LOS ALGORITMOS DE
TEMA 11: INTRODUCCIÓN A LA PROGRAMACIÓN MATEMÁTICA CON VARIABLES DISCRETAS 1.- ECUACIONES LINEALES (MILP) 1.1.- Formulación 1.2.- Algoritmos para resolver MILPs 2.- VISIÓN GENERAL DE LOS ALGORITMOS DE
1) Determinar qué elección de h asegurará, a priori, que la solución numérica del P.C.: con el método de diferencias centrales, existe y es única.
 I. Resolución numérica de Problemas de Contorno en E.D.O.: Métodos en diferencias finitas 1) Determinar qué elección de h asegurará, a priori, que la solución numérica del P.C.: y (x) + 4 sen x y (x) 4
I. Resolución numérica de Problemas de Contorno en E.D.O.: Métodos en diferencias finitas 1) Determinar qué elección de h asegurará, a priori, que la solución numérica del P.C.: y (x) + 4 sen x y (x) 4
Grafos. Suponiendo que e = [u, v]. Entonces los nodos u y v se llaman extremos de e y u y v se dice que son nodos adyacentes o vecinos.
![Grafos. Suponiendo que e = [u, v]. Entonces los nodos u y v se llaman extremos de e y u y v se dice que son nodos adyacentes o vecinos. Grafos. Suponiendo que e = [u, v]. Entonces los nodos u y v se llaman extremos de e y u y v se dice que son nodos adyacentes o vecinos.](/thumbs/54/33802392.jpg) Grafos Los grafos son estructuras que constan de vértices o nodos y de aristas o arcos que conectan los vértices entre sí. Un grafo G consiste en dos cosas: 1. Un conjunto V de elementos llamados nodos
Grafos Los grafos son estructuras que constan de vértices o nodos y de aristas o arcos que conectan los vértices entre sí. Un grafo G consiste en dos cosas: 1. Un conjunto V de elementos llamados nodos
Solución aproximada del oscilador armónico simple utilizando el método de las diferencias finitas.
 Revista del programa del matemáticas (215) 59-64 Solución aproximada del oscilador armónico simple utilizando el método de las diferencias finitas. Approximate solution of simple harmonic oscillator using
Revista del programa del matemáticas (215) 59-64 Solución aproximada del oscilador armónico simple utilizando el método de las diferencias finitas. Approximate solution of simple harmonic oscillator using
Modelación de objetos 3D Parte I: Mallas de polígonos y triangulaciones
 Modelación de objetos 3D Parte I: Mallas de polígonos y triangulaciones Contenido Motivación Polígonos simples 3D Almacenamiento de mallas de polígonos OpenGl y mallas de polígonos Triangulaciones Triangulaciones
Modelación de objetos 3D Parte I: Mallas de polígonos y triangulaciones Contenido Motivación Polígonos simples 3D Almacenamiento de mallas de polígonos OpenGl y mallas de polígonos Triangulaciones Triangulaciones
Diagrama de Voronoi. Ejemplo de problemas geométricos:
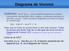 Diagrama de Voronoi Definición: Sea P={p1,p2,..,pn} un conjunto de puntos en el plano. Estos puntos son llamados sitios. Asignar a cada punto del plano el sitio más cercano. Todos los puntos asignados
Diagrama de Voronoi Definición: Sea P={p1,p2,..,pn} un conjunto de puntos en el plano. Estos puntos son llamados sitios. Asignar a cada punto del plano el sitio más cercano. Todos los puntos asignados
GENERACIÓN DE MALLAS NO ESTRUCTURADAS PARA LA IMPLEMENTACION DE MODELOS NUMÉRICOS AUTOR: DARIO FERNANDO LONDOÑO PINILLA PROYECTO DE INVESTIGACIÓN
 GENERACIÓN DE MALLAS NO ESTRUCTURADAS PARA LA IMPLEMENTACION DE MODELOS NUMÉRICOS AUTOR: DARIO FERNANDO LONDOÑO PINILLA PROYECTO DE INVESTIGACIÓN PROFESOR EDGAR CARMONA SEMINARIO DE INVESTIGACIÓN UNIVERSIDAD
GENERACIÓN DE MALLAS NO ESTRUCTURADAS PARA LA IMPLEMENTACION DE MODELOS NUMÉRICOS AUTOR: DARIO FERNANDO LONDOÑO PINILLA PROYECTO DE INVESTIGACIÓN PROFESOR EDGAR CARMONA SEMINARIO DE INVESTIGACIÓN UNIVERSIDAD
Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias.
 Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias. Dr. Rafael Morones E. Dept. de Matemáticas ITAM August 5, 2002 1 Contenido 1 Preliminares. 3 1.1 Sucesiones...............................
Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias. Dr. Rafael Morones E. Dept. de Matemáticas ITAM August 5, 2002 1 Contenido 1 Preliminares. 3 1.1 Sucesiones...............................
Diagrama de Voronoi. Ejemplo de problemas geométricos:
 Diagrama de Voronoi Definición: Sea P={p1,p2,..,pn} un conjunto de puntos en el plano. Estos puntos son llamados sitios. Asignar a cada punto del plano el sitio más cercano. Todos los puntos asignados
Diagrama de Voronoi Definición: Sea P={p1,p2,..,pn} un conjunto de puntos en el plano. Estos puntos son llamados sitios. Asignar a cada punto del plano el sitio más cercano. Todos los puntos asignados
MODELIZACIÓN DE LA CONTAMINACIÓN ATMOSFÉRICA EN EL ENTORNO DE CENTRALES TÉRMICAS
 MÉTODOS COMPUTACIONAIS EM ENGENHARIA Lisboa, 31 de Maio - 2 de Junho, 2004 APMTAC, Portugal 2004 MODELIZACIÓN DE LA CONTAMINACIÓN ATMOSFÉRICA EN EL ENTORNO DE CENTRALES TÉRMICAS G. Montero *, R. Montenegro,
MÉTODOS COMPUTACIONAIS EM ENGENHARIA Lisboa, 31 de Maio - 2 de Junho, 2004 APMTAC, Portugal 2004 MODELIZACIÓN DE LA CONTAMINACIÓN ATMOSFÉRICA EN EL ENTORNO DE CENTRALES TÉRMICAS G. Montero *, R. Montenegro,
1. El Método de Diferencias Finitas
 1. El Método de Diferencias Finitas Por Guillermo Hernández García El Método consiste en una aproximación de derivadas parciales por expresiones algebraicas envolviendo los valores de la variable dependiente
1. El Método de Diferencias Finitas Por Guillermo Hernández García El Método consiste en una aproximación de derivadas parciales por expresiones algebraicas envolviendo los valores de la variable dependiente
DIDÁCTICA DE LA MATEMÁTICA NUMÉRICA: TECNOLOGÍA Y MODELACIÓN DE PROBLEMAS
 DIDÁCTICA DE LA MATEMÁTICA NUMÉRICA: TECNOLOGÍA Y MODELACIÓN DE PROBLEMAS Eugenio Carlos Rodríguez Instituto Superior Politécnico José Antonio Echeverría (Cuba) ecarlos@tesla.cujae.edu.cu Palabras clave:
DIDÁCTICA DE LA MATEMÁTICA NUMÉRICA: TECNOLOGÍA Y MODELACIÓN DE PROBLEMAS Eugenio Carlos Rodríguez Instituto Superior Politécnico José Antonio Echeverría (Cuba) ecarlos@tesla.cujae.edu.cu Palabras clave:
Algebra lineal y conjuntos convexos 1
 Algebra lineal y conjuntos convexos Solución de sistemas. Espacios vectoriales. 3 Conjuntos convexos. 4 Soluciones básicas puntos extremos. Rango de una matriz A R m n. Reducir A a una matriz escalonada
Algebra lineal y conjuntos convexos Solución de sistemas. Espacios vectoriales. 3 Conjuntos convexos. 4 Soluciones básicas puntos extremos. Rango de una matriz A R m n. Reducir A a una matriz escalonada
02 Elementos finitos para tensión/ compresión axial. Diego Andrés Alvarez Marín Profesor Asistente Universidad Nacional de Colombia Sede Manizales
 02 Elementos finitos para tensión/ compresión axial Diego Andrés Alvarez Marín Profesor Asistente Universidad Nacional de Colombia Sede Manizales 1 El método de los elementos finitos El método de los elementos
02 Elementos finitos para tensión/ compresión axial Diego Andrés Alvarez Marín Profesor Asistente Universidad Nacional de Colombia Sede Manizales 1 El método de los elementos finitos El método de los elementos
Sobre las soluciones de las ecuaciones en diferencias lineales. J. C. Abderramán Marrero 1
 XXI Congreso de Ecuaciones Diferenciales y Aplicaciones XI Congreso de Matemática Aplicada Ciudad Real, 21-25 septiembre 2009 (pp 1 6) Sobre las soluciones de las ecuaciones en diferencias lineales J C
XXI Congreso de Ecuaciones Diferenciales y Aplicaciones XI Congreso de Matemática Aplicada Ciudad Real, 21-25 septiembre 2009 (pp 1 6) Sobre las soluciones de las ecuaciones en diferencias lineales J C
Preguntas básicas de geometría computacional. comp-420
 Preguntas básicas de geometría computacional comp-420 Bibliografía Joseph O Rourke. Computational Geometry in C. Cambridge University Press. 1994. Mark de Berg, et al. Computational Geometry. Algorithms
Preguntas básicas de geometría computacional comp-420 Bibliografía Joseph O Rourke. Computational Geometry in C. Cambridge University Press. 1994. Mark de Berg, et al. Computational Geometry. Algorithms
MÉTODO DE DIFERENCIAS FINITAS (FDM)
 MÉTODO DE DIFERENCIAS FINITAS (FDM) MÉTODO DE DIFERENCIAS FINITAS (FDM) Cambia ecuaciones diferenciales ecuaciones en diferencias finitas a Relaciona el valor de la variable dependiente en un punto a valores
MÉTODO DE DIFERENCIAS FINITAS (FDM) MÉTODO DE DIFERENCIAS FINITAS (FDM) Cambia ecuaciones diferenciales ecuaciones en diferencias finitas a Relaciona el valor de la variable dependiente en un punto a valores
REPORTES INTERNOS / Febrero de 2015
 REPORTES INTERNOS 2015-01 / Febrero de 2015 TRAZADO DE LÍNEAS DE CORRIENTE EN GEOMETRÍAS GENERALES USANDO UN MODELO MIXTO: 3D Y 2D Norberto C. Vera Guzmán Instituto de Geofísica, UNAM Ciudad Universitaria
REPORTES INTERNOS 2015-01 / Febrero de 2015 TRAZADO DE LÍNEAS DE CORRIENTE EN GEOMETRÍAS GENERALES USANDO UN MODELO MIXTO: 3D Y 2D Norberto C. Vera Guzmán Instituto de Geofísica, UNAM Ciudad Universitaria
Presas de tierra - Análisis de filtración en estado estacionario
 Manual de Ingeniería No. 32 Actualización: 04/2016 Presas de tierra - Análisis de filtración en estado estacionario Programa: Archivo: MEF Flujo de Agua Demo_manual_32.gmk Introducción Este ejemplo ilustra
Manual de Ingeniería No. 32 Actualización: 04/2016 Presas de tierra - Análisis de filtración en estado estacionario Programa: Archivo: MEF Flujo de Agua Demo_manual_32.gmk Introducción Este ejemplo ilustra
Intersección de Segmentos de Recta. Geometría Computacional, MAT-125
 Intersección de Segmentos de Recta Geometría Computacional, MAT-125 Dados dos conjuntos de segmentos de recta, calcular todas las intersecciones entre los segmentos de un conjunto y los segmentos del otro
Intersección de Segmentos de Recta Geometría Computacional, MAT-125 Dados dos conjuntos de segmentos de recta, calcular todas las intersecciones entre los segmentos de un conjunto y los segmentos del otro
Análisis de esquemas de manejo de restricciones en optimización global.
 Análisis de esquemas de manejo de restricciones en optimización global. Tesista: Daniel Trejo Pérez dtrejo@computacion.cs.cinvestav.mx Director de tesis: Dr. Carlos Artemio Coello Coello CINVESTAV-IPN
Análisis de esquemas de manejo de restricciones en optimización global. Tesista: Daniel Trejo Pérez dtrejo@computacion.cs.cinvestav.mx Director de tesis: Dr. Carlos Artemio Coello Coello CINVESTAV-IPN
Descomposicion en Polígonos Monótonos. comp-420
 Descomposicion en Polígonos Monótonos comp-420 Triangulación de Polígonos Teorema 1: Todo polígono simple admite una triangulación, y cualquier triangulación de un polígono simple con n vértices consta
Descomposicion en Polígonos Monótonos comp-420 Triangulación de Polígonos Teorema 1: Todo polígono simple admite una triangulación, y cualquier triangulación de un polígono simple con n vértices consta
Modelado de Objetos 3D I
 5 de abril de 2011 Representación de Supercies en 3D Representación Volumétrica Matriz Tridimensional de elementos espaciales Cada elemento de la discretización del espacio se conoce como Vóxel Válida
5 de abril de 2011 Representación de Supercies en 3D Representación Volumétrica Matriz Tridimensional de elementos espaciales Cada elemento de la discretización del espacio se conoce como Vóxel Válida
Un enfoque numérico en la demostración de un teorema del incremento del volumen de un cilindro de área mínima preservando su área
 Un enfoque numérico en la demostración de un teorema del incremento del volumen de un cilindro de área mínima preservando su área A numerical approach in the proof of a theorem of increasing the volume
Un enfoque numérico en la demostración de un teorema del incremento del volumen de un cilindro de área mínima preservando su área A numerical approach in the proof of a theorem of increasing the volume
4. Método del elemento finito (formulación de desplazamientos)
 4 Método del elemento finito (formulación de desplazamientos) 41 Introducción El método del elemento finito es un método numérico que permite encontrar soluciones aproximadas a problemas físicos gobernados
4 Método del elemento finito (formulación de desplazamientos) 41 Introducción El método del elemento finito es un método numérico que permite encontrar soluciones aproximadas a problemas físicos gobernados
Métodos de Subespacios. Una aproximación intuitiva
 IX Congreso de Ingeniería de Organización Gijón, 8 y 9 de septiembre de 2005 Métodos de Subespacios. Una aproximación intuitiva Segismundo S. Izquierdo Millán 1, Javier Pajares Gutiérrez 1, Cesáreo Hernández
IX Congreso de Ingeniería de Organización Gijón, 8 y 9 de septiembre de 2005 Métodos de Subespacios. Una aproximación intuitiva Segismundo S. Izquierdo Millán 1, Javier Pajares Gutiérrez 1, Cesáreo Hernández
08 Losas delgadas Teoría de Kirchhoff. Diego Andrés Alvarez Marín Profesor Asociado Universidad Nacional de Colombia Sede Manizales
 08 Losas delgadas Teoría de Kirchhoff Diego Andrés Alvarez Marín Profesor Asociado Universidad Nacional de Colombia Sede Manizales 1 Introducción Elementos laminares delgados Losas o placas (son elementos
08 Losas delgadas Teoría de Kirchhoff Diego Andrés Alvarez Marín Profesor Asociado Universidad Nacional de Colombia Sede Manizales 1 Introducción Elementos laminares delgados Losas o placas (son elementos
Estudio unificado de métodos de alto orden para ecuaciones no lineales
 XXI Congreso de Ecuaciones Diferenciales y Aplicaciones XI Congreso de Matemática Aplicada Ciudad Real, 21-25 septiembre 2009 pp. 1 6) Estudio unificado de métodos de alto orden para ecuaciones no lineales
XXI Congreso de Ecuaciones Diferenciales y Aplicaciones XI Congreso de Matemática Aplicada Ciudad Real, 21-25 septiembre 2009 pp. 1 6) Estudio unificado de métodos de alto orden para ecuaciones no lineales
Lenguaje de Programación: C++
 UG Métodos Numéricos Universidad de Guanajuato Sesión 53 En análisis numérico un algoritmo de búsqueda de raíces es un método numérico o algoritmo para encontrar las soluciones aproximadas de una ecuación
UG Métodos Numéricos Universidad de Guanajuato Sesión 53 En análisis numérico un algoritmo de búsqueda de raíces es un método numérico o algoritmo para encontrar las soluciones aproximadas de una ecuación
MCRivara/CG2008/1. MCRivara/CG2007/2MCRivara/CG2008/1 1. Modelación de Sólidos. Computación Gráfica. Modelos de sólidos
 Computación Gráfica Modelación de Sólidos Prof. María Cecilia Rivara mcrivara@dcc.uchile.cl Semestre 2009/1 Modelación de Sólidos Objetivo: Modelos matemáticos de objetos del mundo real (automóvil, motor,
Computación Gráfica Modelación de Sólidos Prof. María Cecilia Rivara mcrivara@dcc.uchile.cl Semestre 2009/1 Modelación de Sólidos Objetivo: Modelos matemáticos de objetos del mundo real (automóvil, motor,
Sensibilidad de posición de la plataforma móvil respecto de las longitudes de las bielas en un manipulador paralelo tipo 6-RUS
 Sensibilidad de posición de la plataforma móvil respecto de las longitudes de las bielas en un manipulador paralelo tipo 6-RUS J Aginaga García, I Zabalza Villava, JJ Gil Soto Universidad Pública de Navarra,
Sensibilidad de posición de la plataforma móvil respecto de las longitudes de las bielas en un manipulador paralelo tipo 6-RUS J Aginaga García, I Zabalza Villava, JJ Gil Soto Universidad Pública de Navarra,
MÉTODO DE CLASIFICACIÓN SUPERVISADA SUPPORT VECTOR MACHINE: UNA APLICACIÓN A LA CLASIFICACIÓN AUTOMÁTICA DE TEXTOS.
 Revista de Epistemología y Ciencias Humanas 37 MÉTODO DE CLASIFICACIÓN SUPERVISADA SUPPORT VECTOR MACHINE: UNA APLICACIÓN A LA CLASIFICACIÓN AUTOMÁTICA DE TEXTOS. Supervised Classification Method Support
Revista de Epistemología y Ciencias Humanas 37 MÉTODO DE CLASIFICACIÓN SUPERVISADA SUPPORT VECTOR MACHINE: UNA APLICACIÓN A LA CLASIFICACIÓN AUTOMÁTICA DE TEXTOS. Supervised Classification Method Support
Diagrama geométrico y subdivisión híbrida de triángulos
 Rev. Int. Mét. Num. Cálc. Dis. Ing. Vol. 25,, 6-78 (2009) Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería Diagrama geométrico y subdivisión híbrida de triángulos José P.
Rev. Int. Mét. Num. Cálc. Dis. Ing. Vol. 25,, 6-78 (2009) Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería Diagrama geométrico y subdivisión híbrida de triángulos José P.
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE ESTUDIOS SUPERIORES ACATLÁN LICENCIATURA EN MATEMÁTICAS APLICADAS Y COMPUTACIÓN
 UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE ESTUDIOS SUPERIORES ACATLÁN LICENCIATURA EN MATEMÁTICAS APLICADAS Y COMPUTACIÓN PROGRAMA DE ASIGNATURA ACATLÁN CLAVE: 1064 SEMESTRE: 9 (NOVENO) LÍNEA
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE ESTUDIOS SUPERIORES ACATLÁN LICENCIATURA EN MATEMÁTICAS APLICADAS Y COMPUTACIÓN PROGRAMA DE ASIGNATURA ACATLÁN CLAVE: 1064 SEMESTRE: 9 (NOVENO) LÍNEA
Inversas Aproximadas usando el producto escalar de Frobenius
 Inversas Aproximadas usando el producto escalar de Frobenius E Flórez, MD García, L González, G Montero Instituto Universitario de Sistemas Inteligentes y Aplicaciones Numéricas en Ingeniería Universidad
Inversas Aproximadas usando el producto escalar de Frobenius E Flórez, MD García, L González, G Montero Instituto Universitario de Sistemas Inteligentes y Aplicaciones Numéricas en Ingeniería Universidad
J. Estrada, V. Hernández, ICIMAF, Cuba D. Martínez, UFAL, Brasil L. Velho, IMPA, Brasil N. López, Universidad de la Habana, Cuba
 J. Estrada, V. Hernández, ICIMAF, Cuba D. Martínez, UFAL, Brasil L. Velho, IMPA, Brasil N. López, Universidad de la Habana, Cuba Cálculo de las curvas geodésicas sobre superficies Diseño de trayectorias
J. Estrada, V. Hernández, ICIMAF, Cuba D. Martínez, UFAL, Brasil L. Velho, IMPA, Brasil N. López, Universidad de la Habana, Cuba Cálculo de las curvas geodésicas sobre superficies Diseño de trayectorias
Presentación del curso
 Análisis Numérico Presentación del curso CNM-425 Departamento de Matemáticas Facultad de Ciencias Exactas y Naturales Universidad de Antioquia Copyleft c 2008. Reproducción permitida bajo los términos
Análisis Numérico Presentación del curso CNM-425 Departamento de Matemáticas Facultad de Ciencias Exactas y Naturales Universidad de Antioquia Copyleft c 2008. Reproducción permitida bajo los términos
1.IV Aproximación numérica de valores y vectores propios.
 .IV Aproximación numérica de valores y vectores propios. Manuel Palacios Departamento de Matemática Aplicada Centro Politécnico Superior. Universidad de Zaragoza Primavera 2007 Contents Introducción 2
.IV Aproximación numérica de valores y vectores propios. Manuel Palacios Departamento de Matemática Aplicada Centro Politécnico Superior. Universidad de Zaragoza Primavera 2007 Contents Introducción 2
DESCRIPCIÓN DE UN MODELO MATEMÁTICO SIMPLE DE CIRCULACIÓN DEL AGUA EN LA CUENCA DEL PACÍFICO COLOMBIANO
 DESCRIPCIÓN DE UN MODELO MATEMÁTICO SIMPLE DE CIRCULACIÓN DEL AGUA EN LA CUENCA DEL PACÍFICO COLOMBIANO Valery Tchantsev, Orientador Científico, PhD. Oceanólogo, C.C.C.P Se describe en forma detallada
DESCRIPCIÓN DE UN MODELO MATEMÁTICO SIMPLE DE CIRCULACIÓN DEL AGUA EN LA CUENCA DEL PACÍFICO COLOMBIANO Valery Tchantsev, Orientador Científico, PhD. Oceanólogo, C.C.C.P Se describe en forma detallada
IMPLEMENTACIÓN DEL MÉTODO DEL ELEMENTO FINITO EXTENDIDO PARA EL ESTUDIO DE LA PROPAGACIÓN DE GRIETAS
 IMPLEMENTACIÓN DEL MÉTODO DEL ELEMENTO FINITO EXTENDIDO PARA EL ESTUDIO DE LA PROPAGACIÓN DE GRIETAS Resumen: Marco Aurelio Fernández Torres Unidad Profesional Adolfo López Mateos Zacatenco Av. uan de
IMPLEMENTACIÓN DEL MÉTODO DEL ELEMENTO FINITO EXTENDIDO PARA EL ESTUDIO DE LA PROPAGACIÓN DE GRIETAS Resumen: Marco Aurelio Fernández Torres Unidad Profesional Adolfo López Mateos Zacatenco Av. uan de
DESARROLLO DE UN MODULO TUTORIAL DE UNA TORRE DE DESTILACIÓN BASADO EN EL MODELO MATEMÁTICO DE SOREL
 DESARROLLO DE UN MODULO TUTORIAL DE UNA TORRE DE DESTILACIÓN BASADO EN EL MODELO MATEMÁTICO DE SOREL Miguel Angel Mesa Silva y Nicolas Lallemand Najar Universidad de América, Bogotá DC Resumen. El proyecto
DESARROLLO DE UN MODULO TUTORIAL DE UNA TORRE DE DESTILACIÓN BASADO EN EL MODELO MATEMÁTICO DE SOREL Miguel Angel Mesa Silva y Nicolas Lallemand Najar Universidad de América, Bogotá DC Resumen. El proyecto
Método Simplex en Optimización de Problemas de Producción
 Método Simplex en Optimización de Problemas de Producción Pedro Piñeyro - Luis Stábile - Fernando Islas - Carlos Testuri Héctor Cancela - Antonio Mauttone Depto. Investigación Operativa. Instituto de Computación.
Método Simplex en Optimización de Problemas de Producción Pedro Piñeyro - Luis Stábile - Fernando Islas - Carlos Testuri Héctor Cancela - Antonio Mauttone Depto. Investigación Operativa. Instituto de Computación.
Optimización global en espacios restringidos mediante el sistema inmune artificial.
 Optimización global en espacios restringidos mediante el sistema inmune artificial. Tesista: Daniel Trejo Pérez dtrejo@computacion.cs.cinvestav.mx Director de tesis: Dr. Carlos Artemio Coello Coello CINVESTAV-IPN
Optimización global en espacios restringidos mediante el sistema inmune artificial. Tesista: Daniel Trejo Pérez dtrejo@computacion.cs.cinvestav.mx Director de tesis: Dr. Carlos Artemio Coello Coello CINVESTAV-IPN
ACTIVIDAD INVESTIGADORA
 UNIVERSIDAD DE LAS PALMAS DE GRAN CANARIA DEPARTAMENTO DE MATEMÁTICAS PROGRAMA DE DOCTORADO SIMULACIÓN NUMÉRICA EN CIENCIA Y TECNOLOGÍA BIENIO 97-99 ACTIVIDAD INVESTIGADORA DOCTORANDO JOSE PABLO SUÁREZ
UNIVERSIDAD DE LAS PALMAS DE GRAN CANARIA DEPARTAMENTO DE MATEMÁTICAS PROGRAMA DE DOCTORADO SIMULACIÓN NUMÉRICA EN CIENCIA Y TECNOLOGÍA BIENIO 97-99 ACTIVIDAD INVESTIGADORA DOCTORANDO JOSE PABLO SUÁREZ
CMAM - Aplicaciones de Mecánica Computacional
 Unidad responsable: Unidad que imparte: Curso: Titulación: Créditos ECTS: 2016 295 - EEBE - Escuela de Ingeniería de Barcelona Este 737 - RMEE - Departamento de Resistencia de Materiales y Estructuras
Unidad responsable: Unidad que imparte: Curso: Titulación: Créditos ECTS: 2016 295 - EEBE - Escuela de Ingeniería de Barcelona Este 737 - RMEE - Departamento de Resistencia de Materiales y Estructuras
NURBS-ENHANCED FEM PARA PROBLEMAS DE SCATTERING
 XX Congreso de Ecuaciones Diferenciales y Aplicaciones X Congreso de Matemática Aplicada Sevilla, 24-28 septiembre 2007 (pp. 1 8) NURBS-ENHANCED FEM PARA PROBLEMAS DE SCATTERING R. Sevilla, S. Fernández-Méndez
XX Congreso de Ecuaciones Diferenciales y Aplicaciones X Congreso de Matemática Aplicada Sevilla, 24-28 septiembre 2007 (pp. 1 8) NURBS-ENHANCED FEM PARA PROBLEMAS DE SCATTERING R. Sevilla, S. Fernández-Méndez
1.- Álgebra de números complejos.
 .- Álgebra de números complejos. a) Definición y representación geométrica. b) Sumas y productos de números complejos. c) Vectores y módulos en el plano complejo. d) Representación en forma exponencial.
.- Álgebra de números complejos. a) Definición y representación geométrica. b) Sumas y productos de números complejos. c) Vectores y módulos en el plano complejo. d) Representación en forma exponencial.
Problemas de complementariedad lineal. Métodos numéricos efici
 Problemas de complementariedad lineal. Métodos numéricos eficientes y aplicaciones prácticas. L. Feng (UI), V. Linetsky(NU), J. Nocedal(NU), M. Smelyanskiy(INTEL). SMMyC, Instituto de Geofísica, UNAM.
Problemas de complementariedad lineal. Métodos numéricos eficientes y aplicaciones prácticas. L. Feng (UI), V. Linetsky(NU), J. Nocedal(NU), M. Smelyanskiy(INTEL). SMMyC, Instituto de Geofísica, UNAM.
UNIVERSIDAD DEL VALLE DE MÉXICO PROGRAMA DE ESTUDIO DE LICENCIATURA PRAXIS MES XXI
 UNIVERSIDAD DEL VALLE DE MÉXICO PROGRAMA DE ESTUDIO DE LICENCIATURA PRAXIS MES XXI NOMBRE DE LA ASIGNATURA: MÉTODOS NUMÉRICOS FECHA DE ELABORACIÓN: FEBRERO 2005 ÁREA DEL PLAN DE ESTUDIOS: AS ( ) AC ( X
UNIVERSIDAD DEL VALLE DE MÉXICO PROGRAMA DE ESTUDIO DE LICENCIATURA PRAXIS MES XXI NOMBRE DE LA ASIGNATURA: MÉTODOS NUMÉRICOS FECHA DE ELABORACIÓN: FEBRERO 2005 ÁREA DEL PLAN DE ESTUDIOS: AS ( ) AC ( X
08 Losas delgadas Teoría de Kirchhoff. Diego Andrés Alvarez Marín Profesor Asistente Universidad Nacional de Colombia Sede Manizales
 08 Losas delgadas Teoría de Kirchhoff Diego Andrés Alvarez Marín Profesor Asistente Universidad Nacional de Colombia Sede Manizales 1 Introducción Elementos laminares delgados Losas o placas (son elementos
08 Losas delgadas Teoría de Kirchhoff Diego Andrés Alvarez Marín Profesor Asistente Universidad Nacional de Colombia Sede Manizales 1 Introducción Elementos laminares delgados Losas o placas (son elementos
Laboratori de Càlcul Numèric (LaCàN) Departament de Matemàtica Aplicada III Universitat Politècnica de Catalunya (Spain)
 Ceros de funciones Laboratori de Càlcul Numèric (LaCàN) Departament de Matemàtica Aplicada III Universitat Politècnica de Catalunya (Spain) http://www-lacan.upc.es Índice Objetivos Esquemas iterativos
Ceros de funciones Laboratori de Càlcul Numèric (LaCàN) Departament de Matemàtica Aplicada III Universitat Politècnica de Catalunya (Spain) http://www-lacan.upc.es Índice Objetivos Esquemas iterativos
Ingeniería Aeroespacial Computacional
 Unidad responsable: Unidad que imparte: Curso: Titulación: Créditos ECTS: 2018 205 - ESEIAAT - Escuela Superior de Ingenierías Industrial, Aeroespacial y Audiovisual de Terrassa 737 - RMEE - Departamento
Unidad responsable: Unidad que imparte: Curso: Titulación: Créditos ECTS: 2018 205 - ESEIAAT - Escuela Superior de Ingenierías Industrial, Aeroespacial y Audiovisual de Terrassa 737 - RMEE - Departamento
Una modificación del método de la Secante aplicada al problema de Lorenz.
 XXI Congreso de Ecuaciones Diferenciales y Aplicaciones XI Congreso de Matemática Aplicada Ciudad Real, 21-25 septiembre 2009 (pp. 1 8) Una modificación del método de la Secante aplicada al problema de
XXI Congreso de Ecuaciones Diferenciales y Aplicaciones XI Congreso de Matemática Aplicada Ciudad Real, 21-25 septiembre 2009 (pp. 1 8) Una modificación del método de la Secante aplicada al problema de
LA TRIANGULACIÓN DE DELAUNAY APLICADA A LOS MODELOS DIGITALES DEL TERRENO
 LA TRIANGULACIÓN DE DELAUNAY APLICADA A LOS MODELOS DIGITALES DEL TERRENO PRIEGO DE LOS SANTOS, JOSÉ ENRIQUE PORRES DE LA HAZA, M ARIA JOAQUINA Departamento de Ingeniería Cartográfica, Geodesia y Fotogrametría
LA TRIANGULACIÓN DE DELAUNAY APLICADA A LOS MODELOS DIGITALES DEL TERRENO PRIEGO DE LOS SANTOS, JOSÉ ENRIQUE PORRES DE LA HAZA, M ARIA JOAQUINA Departamento de Ingeniería Cartográfica, Geodesia y Fotogrametría
Redes de Neuronas de Base Radial
 Redes de Neuronas de Base Radial 1 Introducción Redes multicapa con conexiones hacia delante Única capa oculta Las neuronas ocultas poseen carácter local Cada neurona oculta se activa en una región distinta
Redes de Neuronas de Base Radial 1 Introducción Redes multicapa con conexiones hacia delante Única capa oculta Las neuronas ocultas poseen carácter local Cada neurona oculta se activa en una región distinta
Simulación de la calidad del aire con dispersión muy anisotrópica mediante elementos finitos adaptativos
 Simulación de la calidad del aire con dispersión muy anisotrópica mediante elementos finitos adaptativos Lluís Monforte Tutor: Agustí Pérez-Foguet Laboratori de Càlcul Numèric (LaCàN) Departament de Matemàtica
Simulación de la calidad del aire con dispersión muy anisotrópica mediante elementos finitos adaptativos Lluís Monforte Tutor: Agustí Pérez-Foguet Laboratori de Càlcul Numèric (LaCàN) Departament de Matemàtica
Análisis y Complejidad de Algoritmos. Arboles Binarios. Arturo Díaz Pérez
 Análisis y Complejidad de Algoritmos Arboles Binarios Arturo Díaz Pérez Arboles Definiciones Recorridos Arboles Binarios Profundidad y Número de Nodos Arboles-1 Arbol Un árbol es una colección de elementos,
Análisis y Complejidad de Algoritmos Arboles Binarios Arturo Díaz Pérez Arboles Definiciones Recorridos Arboles Binarios Profundidad y Número de Nodos Arboles-1 Arbol Un árbol es una colección de elementos,
Cálculo en varias variables
 Cálculo en varias variables Dpto. Matemática Aplicada Universidad de Málaga Resumen Límites y continuidad Funciones de varias variables Límites y continuidad en varias variables 1 Límites y continuidad
Cálculo en varias variables Dpto. Matemática Aplicada Universidad de Málaga Resumen Límites y continuidad Funciones de varias variables Límites y continuidad en varias variables 1 Límites y continuidad
El ente básico de la parte de la matemática conocida como ANÁLISIS, lo constituye el llamado sistema de los número reales.
 EL SISTEMA DE LOS NÚMEROS REALES Introducción El ente básico de la parte de la matemática conocida como ANÁLISIS, lo constituye el llamado sistema de los número reales. Números tales como:1,3, 3 5, e,
EL SISTEMA DE LOS NÚMEROS REALES Introducción El ente básico de la parte de la matemática conocida como ANÁLISIS, lo constituye el llamado sistema de los número reales. Números tales como:1,3, 3 5, e,
XV COPA CHAMPAGNAT DE MATEMATICAS Superior. Iván Cardona Torres, Ph.D.
 XV COPA CHAMPAGNAT DE MATEMATICAS Superior Iván Cardona Torres, Ph.D. 10 de abril de 2015 Problema. En cada diagrama ilustrado en este problema, el número sobre la recta que une dos círculos es la suma
XV COPA CHAMPAGNAT DE MATEMATICAS Superior Iván Cardona Torres, Ph.D. 10 de abril de 2015 Problema. En cada diagrama ilustrado en este problema, el número sobre la recta que une dos círculos es la suma
Novedades de software/new softwares
 REVISTA INVESTIGACIÓN OPERACIONAL VOL., 3, No. 3, 275-28, 2 Novedades de software/new softwares ALGORITMO PARA LA GENERACIÓN ALEATORIA DE MATRICES BOOLEANAS INVERSIBLES P. Freyre*, N. Díaz*, E. R. Morgado**
REVISTA INVESTIGACIÓN OPERACIONAL VOL., 3, No. 3, 275-28, 2 Novedades de software/new softwares ALGORITMO PARA LA GENERACIÓN ALEATORIA DE MATRICES BOOLEANAS INVERSIBLES P. Freyre*, N. Díaz*, E. R. Morgado**
Diagramas de Voronoi. comp-420
 Diagramas de Voronoi comp-420 http://www.ifweassume.com/2012/10/the-united-states-of-starbucks.html furthest point from a company-owned Starbucks (~140 miles). http://www.ifweassume.com/2012/10/the-united-states-of-starbucks.html
Diagramas de Voronoi comp-420 http://www.ifweassume.com/2012/10/the-united-states-of-starbucks.html furthest point from a company-owned Starbucks (~140 miles). http://www.ifweassume.com/2012/10/the-united-states-of-starbucks.html
Geometría Computacional. Dr. Antonio Marín Hernández
 Geometría Computacional Dr. Antonio Marín Hernández Centro de Investigación en Inteligencia Artificial Universidad Veracruzana anmarin@uv.mx www.uv.mx/anmarin Contenido Introducción Intersección de segmentos
Geometría Computacional Dr. Antonio Marín Hernández Centro de Investigación en Inteligencia Artificial Universidad Veracruzana anmarin@uv.mx www.uv.mx/anmarin Contenido Introducción Intersección de segmentos
