COMPETENCIA MATEMÁTICA
|
|
|
- Belén Gil Castellanos
- hace 9 años
- Vistas:
Transcripción
1 Servicio de Inspección Educativa / EVALUACIÓN DIAGNÓSTICA º DE EDUCACIÓN SECUNDARIA COMPETENCIA MATEMÁTICA 1 Nombre y apellidos:... Centro escolar:... Grupo/Aula:... Localidad:... Fecha:...
2 Instrucciones En esta prueba vas a leer una serie de textos y a responder a preguntas sobre lo que has leído. Te encontrarás con distintos tipos de preguntas. Algunas tendrán cuatro posibles respuestas y, en ellas, has de elegir la correcta y rodear la letra que se encuentre junto a ella. Por ejemplo: Cuánto suma + 5? A B 6 C 7 D 11 Si decides cambiar la respuesta, tacha con una X tu primera elección y rodea la respuesta correcta, tal como se muestra en el ejemplo: Cuánto suma + 5? A B 6 C 7 D 11 En otras preguntas te pedirán que completes la respuesta en el espacio señalado con puntos: Escribe cuántos vértices y lados tiene un triángulo... Tienes 60 minutos para hacer esta prueba.
3 Mesa de jardín Queremos construir una mesa con bancos para el jardín. Disponemos de unos listones de madera de idéntica anchura. Hemos estado mirando en un catálogo para inspirarnos y el modelo que más nos gusta es el 1. La superficie de la mesa en cada modelo es un polígono regular. Modelo 1 Modelo Modelo 3 1. Los polígonos de los modelos son: Modelo 1 Modelo Modelo 3 A. Pentágono Octógono Romboide B. Pentágono Hexágono Cuadrado C. Hexágono Pentágono Cuadrado D. Hexágono Octógono Cuadrado. Para construir la mesa del Modelo 1 utilizaremos listones de madera de igual anchura y los cortaremos con un ángulo de: A. 30 B. 45 C. 60 D. 75 3
4 3. La superficie de la mesa está compuesta de 30 piezas. De qué forma son la mayoría de esas piezas? A. Trapecios B. Triángulos C. Hexágonos D. Rombos 4. Cuántas veces cabe la pieza triangular en la pieza más larga de la mesa? Recuerda que todas las piezas son de la misma anchura. A. 11 B. 9 C. 7 D Si el lado de la mesa de la figura mide 80 cm, calcula la distancia entre dos lados opuestos de la mesa. Escribe los pasos y la solución. Recurrimos a un triángulo rectángulo, donde L es la distancia entre dos lados opuestos de la mesa: ½ L 80 cm Aplicando el Teorema de Pitágoras: 40 cm ½ L = = 69,8 cm Distancia pedida (L) = x 69,8 = 138,56 cm 4
5 Criterios de corrección Código Puntuación Respuesta/s 0 0 Respuesta incorrecta y planteamiento incorrecto. Se produce una de las siguientes situaciones: 1 1 El alumno/a identifica correctamente los datos relevantes (40 cm y 80 cm) y utiliza correctamente el Teorema de Pitágoras ( ), pero no realiza correctamente los cálculos. El alumno/a da la respuesta correcta (138,56 cm), pero no muestra la utilización del Teorema de Pitágoras. 3 3 El alumno/a identifica correctamente los datos relevantes (40 cm y 80 cm), utiliza correctamente el Teorema de Pitágoras ( ), calcula correctamente la raiz cuadrada (69,8 cm), pero no da la respuesta final (138,56 cm). El alumno/a identifica correctamente los datos relevantes (40 cm y 80 cm), utiliza correctamente el Teorema de Pitágoras ( ), y calcula correctamente la distancia requerida (138,56 cm). Nota: no se requiere que el alumno/a exprese la unidad de medida (cm). 5
6 Más o menos probable A veces nos toca tomar decisiones y no sabemos justificar por qué elegimos una opción y rechazamos las demás. Es muy importante distinguir cuando decidimos algo porque me gusta, porque me parece o porque hay algún argumento lógico que has tenido en cuenta. A continuación tienes varias situaciones o juegos que puedes resolver si reflexionas y das soluciones razonadas. 6. Tenemos 3 cajas, con bolas blancas y negras. Debes sacar una bola de una de las cajas, con los ojos cerrados. Ganas si obtienes bola blanca. De qué caja harías la extracción? Caja 1 Caja Caja 3 A. Da igual B. De la caja 1 C. De la caja D. De la caja 3 6
7 7. Tenemos un dispositivo hecho con tubos, como el de la figura. Si introducimos granos de arroz Por cuál de los orificios de salida saldrá más cantidad de arroz? A. Por 1 B. Por C. Por 3 D. Igual por los tres 8. Si lanzo la misma cantidad de arroz por cada uno de los siguientes itinerarios, en cuál saldrá más arroz por el orificio 1? A. En el Itinerario A B. En el Itinerario B C. En el Itinerario C D. Igual en los tres 7
8 9. Andrés cogió una de estas cajas y estuvo jugando. Sacaba una bola, anotaba el color y la devolvía a la caja. El resultado fue: Caja 1 Caja Con qué caja crees que es más probable que estuviese jugando? A. Con la caja 1 B. Con la caja C. Con la caja 3 D. Con la caja 4 Caja 3 Caja Idoia juega con una ruleta bien equilibrada, como la de la figura, y observa los resultados que van saliendo. En las tres primeras tiradas obtiene: verde, verde, verde. Si tira una cuarta vez. Cuál de las siguientes afirmaciones es cierta? A. Es más probable que salga rojo. B. Es más probable que salga azul. C. Es más probable que salga otra vez verde. D. Los seis colores tienen igual probabilidad de salir. 11. Si jugamos 60 veces seguidas con la ruleta anterior. Qué resultado piensas que es más fácil obtener? A. 50 veces el caballo B. 30 veces el caballo C. 10 veces el caballo D. 5 veces el caballo 8
9 Precios de alfombras Una empresa de alfombras ha lanzado un producto estrella: alfombras cuadradas con un fleco alrededor. Para calcular el precio, siguen el siguiente sistema: Alfombra: 100 el metro cuadrado Fleco que se cose alrededor: 10 el metro Servicios (transporte, mantenimiento, limpieza ): Qué precio tiene una alfombra cuadrada de 1,5 metros de lado? A. 75 B. 300 C. 35 D Se ha buscado una fórmula para calcular el precio de la alfombra según la longitud del lado. Si llamamos x a la longitud del lado y P al precio, la fórmula es: A. P = 100 x + 10 x + 40 B. P = ( ) x + 40 C. P = 100 x + 40 x + 40 D. P = (100 x + 10 x) 40 9
10 14. En la tabla siguiente se dan los precios para las alfombras de mayor venta. Qué gráfica relaciona el precio con el lado de la alfombra? Lado en metros Precio en 0, , , 3 1,8 436 A. Gráfica A B. Gráfica B C. Gráfica C D. Gráfica D 15. La relación entre el precio y el lado de la alfombra es de A. Proporcionalidad directa B. Proporcionalidad inversa C. Proporcionalidad directa e inversa D. Ni proporcionalidad directa ni inversa 10
11 16. Otra empresa lanza al mercado una oferta de alfombras cuadradas y su precio se calcula multiplicando 150 por la diagonal, en metros. Si pagas 1,13 por una alfombra, qué longitud tiene el lado? Escribe los pasos y la solución. Recurrimos a un triángulo rectángulo, donde L es la longitud del lado de la alfombra, y D su diagonal. D L L Obtenemos el valor de D a partir de la relación conocida entre precio y diagonal: Precio de la alfombra = 150 x D 1,13 = 150 x D D = 1, = 1,414 m (el alumno/a puede dar 3 cifras decimales o menos) Aplicamos el Teorema de Pitágoras y resolvemos la ecuación: D = L + L 1,414 = = L L + L L = = 1 m (el alumno/a puede dar una solución aproximada)..la longitud del lado de la alfombra es de 1 metro. 11
12 Criterios de corrección Código Puntuación Respuesta/s 0 0 El alumno/a no obtiene el valor de D, ni aplica el Teorema de Pitágoras, ni da la solución correcta. Se produce una de las siguientes situaciones: 1 1 a) El alumno/a obtiene correctamente el valor de D utilizando la relación conocida entre precio y diagonal (D = 1,414 m), y no continua con la aplicación del Teorema de Pitágoras. b) El alumno/a da la respuesta correcta (1 m), pero no ha escrito los pasos y/o el planteamiento. Se produce una de las siguientes situaciones: a) El alumno/a obtiene correctamente el valor de D utilizando la relación conocida entre precio y diagonal (D = 1,414 m), aplica correctamente el Teorema de Pitágoras, pero no resuelve correctamente la ecuación y no llega a la solución correcta. b) El alumno/a parte de un valor erróneo de D (bien por no utilizar la relación conocida entre precio y diagonal, bien por no realizar los cálculos correctamente, o bien por asignar directamente un valor incorrecto), y continua con la aplicación del Teorema de Pitágoras, resuelve la ecuación y lógicamente llega a una solución incorrecta. Es decir, parte de un valor erróneo de D y todo lo demás lo hace correctamente, aunque lógicamente llega a una solución incorrecta. 3 3 El alumno/a obtiene correctamente el valor de D utilizando la relación conocida entre precio y diagonal (D = 1,414 m), aplica correctamente el Teorema de Pitágoras, resuelve correctamente la ecuación, y obtiene la solución correcta (1 m). Notas: a) No se requiere que el alumno/a exprese la unidad de medida (m). b) Se darán por correctas soluciones aproximadas a 1 m, cuando el alumno/a trabaja con 3 cifras decimales o menos. c) La ecuación puede resolverse de diversas maneras. 1
13 Giros y simetrías Irene trabaja en Londres conduciendo un vehículo de limpieza urbana, y debe estar muy atenta a las señales que encuentra. En muchas ocasiones debe interpretar tanto las que ve directamente como las que observa a través del espejo retrovisor, se ha hecho una experta no falla nunca! 17. Si Irene ve en su espejo esta imagen, la señal real es A. B. C. D. 18. Si la señal que hay junto a la carretera es ésta, en el espejo se verá A. B. C. D. 13
14 19. De los siguientes conjuntos de letras, señala aquél en el que todas sus letras (de una en una) se verían igual a través de un espejo. A. A N C O B. M A X I C. T H S U D. V X Z O 0. Si Irene ve en el espejo la palabra AMBULANCE, la escrita en el vehículo será: A. B. C. D. 14
15 Revelado de fotos Iker quiere revelar (imprimir en papel) una selección de sus fotos digitales que tiene en el ordenador. Ha visto en Internet la siguiente oferta: 1. Si quieres revelar 60 fotos Cuál será el coste total del encargo? Escribe los pasos y la solución. Revelado de las 50 primeras fotos... Revelado de las 10 siguientes = 10 x 0, Gastos de envío... 3,99 Total... 6,99 Criterios de corrección Código Puntuación Respuesta/s 0 0 Respuesta incorrecta y planteamiento incorrecto o incompleto. 1 1 El alumno/a da la respuesta correcta (6,99 ), pero no ha escrito los pasos suficientes o no hay pasos. El alumno/a hace un planteamiento completo y correcto, pero no da la respuesta correcta porque comete un solo error en los cálculos y no llega al resultado correcto. El alumno/a hace un planteamiento completo y correcto, y da la respuesta correcta (6,99 ). 15
16 . Cuántas fotos puedes revelar sin pasarte de 10 euros de gasto, como máximo? A. 80 fotos B. 90 fotos C. 100 fotos D. 110 fotos 3. Si llamamos n al número de fotos que Iker va a encargar (entre 50 y 100), cuál de las siguientes fórmulas permitirán obtener el gasto (G) correspondiente? A. G = n B. G = + 3,99 + 0,1 n C. G = + 3,99 + 0,1 (n - 50) D. Ninguna de las anteriores 4. Identifica cuál de las siguientes gráficas refleja correctamente la relación entre el número de fotos a revelar y su coste: A. Gráfica A B. Gráfica B C. Gráfica C D. Gráfica D 16
17 5. Las dimensiones de las fotos digitales se miden en píxeles. Iker ha comprobado que sus fotos tienen 960 x 180 píxeles (ancho x alto). Cuál de los siguientes formatos de revelado en papel tiene la misma proporción que la de píxeles? A. Formato 10x15 B. Formato 11x15 C. Formato 1x16 D. Formato 15x18 17
COMPETENCIA MATEMÁTICA
 Servicio de Inspección Educativa 2 0 1 1 / EVALUACIÓN DIAGNÓSTICA 2º DE EDUCACIÓN SECUNDARIA COMPETENCIA MATEMÁTICA 1 2 Nombre y apellidos:... Centro escolar:... Grupo/Aula:... Localidad:... Fecha:...
Servicio de Inspección Educativa 2 0 1 1 / EVALUACIÓN DIAGNÓSTICA 2º DE EDUCACIÓN SECUNDARIA COMPETENCIA MATEMÁTICA 1 2 Nombre y apellidos:... Centro escolar:... Grupo/Aula:... Localidad:... Fecha:...
COMPETENCIA MATEMÁTICA
 Servicio de Inspección Educativa 2 0 1 4 / 1 5 EVALUACIÓN DIAGNÓSTICA 2º DE EDUCACIÓN SECUNDARIA COMPETENCIA MATEMÁTICA Nombre y apellidos:... Centro escolar:... Grupo/Aula:... Localidad:... Fecha:...
Servicio de Inspección Educativa 2 0 1 4 / 1 5 EVALUACIÓN DIAGNÓSTICA 2º DE EDUCACIÓN SECUNDARIA COMPETENCIA MATEMÁTICA Nombre y apellidos:... Centro escolar:... Grupo/Aula:... Localidad:... Fecha:...
POLIGONOS. Nº DE LADOS NOMBRE 3 Triángulos 4 Cuadriláteros 5 Pentágonos 6 Hexágonos 7 Heptágonos 8 Octógonos 9 Eneágonos 10 Decágonos
 1 POLIGONO POLIGONOS Polígono es la superficie plana limitada por una línea poligonal cerrada. Lados Vértices Polígono regular es el que tiene todos sus lados y ángulos iguales, mientras que polígono irregular
1 POLIGONO POLIGONOS Polígono es la superficie plana limitada por una línea poligonal cerrada. Lados Vértices Polígono regular es el que tiene todos sus lados y ángulos iguales, mientras que polígono irregular
LOS POLÍGONOS (I): TRIÁNGULOS
 Apellidos: Curso: Grupo: Nombre: Fecha: LOS POLÍGONOS (I): TRIÁNGULOS El triángulo es un polígono que tiene 3 lados, 3 vértices y 3 ángulos. Los tres ángulos de un triángulo siempre suman 180. 1. Relaciona:
Apellidos: Curso: Grupo: Nombre: Fecha: LOS POLÍGONOS (I): TRIÁNGULOS El triángulo es un polígono que tiene 3 lados, 3 vértices y 3 ángulos. Los tres ángulos de un triángulo siempre suman 180. 1. Relaciona:
TEMA 12: LONGITUDES Y ÁREAS. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco.
 009 TEMA 1: LONGITUDES Y ÁREAS. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/009 TEMA 1: Longitudes y Áreas. TEMA 1: LONGITUDES Y ÁREAS. 1.
009 TEMA 1: LONGITUDES Y ÁREAS. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/009 TEMA 1: Longitudes y Áreas. TEMA 1: LONGITUDES Y ÁREAS. 1.
CUADERNO DEL ALUMNO/A
 CUADERNO DEL ALUMNO/A PRUEBA DE EVALUACIÓN INICIAL MATEMÁTICAS PCPI 1º PCPI (nombre del centro) (población) PRUEBA DE EVALUACIÓN INICIAL MATEMÁTICAS Nombre y Apellidos Perfil Fecha 1.- LECTURA Y ESCRITURA
CUADERNO DEL ALUMNO/A PRUEBA DE EVALUACIÓN INICIAL MATEMÁTICAS PCPI 1º PCPI (nombre del centro) (población) PRUEBA DE EVALUACIÓN INICIAL MATEMÁTICAS Nombre y Apellidos Perfil Fecha 1.- LECTURA Y ESCRITURA
a) Las mediatrices de un triángulo se cortan en un punto llamado... b) Las bisectrices de un triángulo se cortan en un punto llamado...
 Geometría Plana 3º E.S.O. PARTE TEÓRICA 1.- Define para un triángulo los siguientes conceptos: Mediatriz: Bisectriz: Mediana: Altura: 2.- Completa las siguientes frases: a) Las mediatrices de un triángulo
Geometría Plana 3º E.S.O. PARTE TEÓRICA 1.- Define para un triángulo los siguientes conceptos: Mediatriz: Bisectriz: Mediana: Altura: 2.- Completa las siguientes frases: a) Las mediatrices de un triángulo
COMPETENCIA MATEMÁTICA
 Servicio de Inspección Educativa 2 0 1 0 / 1 1 EVALUACIÓN DIAGNÓSTICA 4º DE EDUCACIÓN PRIMARIA COMPETENCIA MATEMÁTICA Nombre y apellidos:... Centro escolar:... Grupo/Aula:... Localidad:... Fecha:... 2
Servicio de Inspección Educativa 2 0 1 0 / 1 1 EVALUACIÓN DIAGNÓSTICA 4º DE EDUCACIÓN PRIMARIA COMPETENCIA MATEMÁTICA Nombre y apellidos:... Centro escolar:... Grupo/Aula:... Localidad:... Fecha:... 2
FIGURAS PLANAS. Es una figura plana delimitada por una línea poligonal cerrada.
 1.- Qué es un polígono? FIGURAS PLANAS Es una figura plana delimitada por una línea poligonal cerrada. Los elementos de un polígono son: - Lado: Se llama lado a cada segmento que limita un polígono - Vértice:
1.- Qué es un polígono? FIGURAS PLANAS Es una figura plana delimitada por una línea poligonal cerrada. Los elementos de un polígono son: - Lado: Se llama lado a cada segmento que limita un polígono - Vértice:
APELLIDOS Y NOMBRE: CENTRO: CURSO: FECHA: Completa con cifras o letras según corresponda: : Noventa mil trescientas veinticuatro:
 APELLIDOS Y NOMBRE: CENTRO: CURSO: FECHA: 1.- LECTURA Y ESCRITURA DE NÚMEROS NATURALES. Completa con cifras o letras según corresponda: 5.724.372: Noventa mil trescientas veinticuatro: Un millón doscientas
APELLIDOS Y NOMBRE: CENTRO: CURSO: FECHA: 1.- LECTURA Y ESCRITURA DE NÚMEROS NATURALES. Completa con cifras o letras según corresponda: 5.724.372: Noventa mil trescientas veinticuatro: Un millón doscientas
MATEMÁTICAS EJERCICIOS DE RECUPERACIÓN 2º ESO
 MATEMÁTICAS EJERCICIOS DE RECUPERACIÓN º ESO TEMA 06 - ECUACIONES DE PRIMER Y SEGUNDO GRADO 1º. De las siguientes expresiones, identifica las que sean ecuaciones o identidades. a) x - 5 = x - 1 x + 8 b)
MATEMÁTICAS EJERCICIOS DE RECUPERACIÓN º ESO TEMA 06 - ECUACIONES DE PRIMER Y SEGUNDO GRADO 1º. De las siguientes expresiones, identifica las que sean ecuaciones o identidades. a) x - 5 = x - 1 x + 8 b)
Polígonos. Triángulos
 CLAVES PARA EMPEZAR Cada hora equivale a una abertura de 360 o : 12 30 o A las 12 h: ángulo 0 o A las 11 h y a la 1 h: ángulo 30 o A las 9 h y a las 3 h: ángulo 90 o A las 7 h y a las 5 h: ángulo 150 o
CLAVES PARA EMPEZAR Cada hora equivale a una abertura de 360 o : 12 30 o A las 12 h: ángulo 0 o A las 11 h y a la 1 h: ángulo 30 o A las 9 h y a las 3 h: ángulo 90 o A las 7 h y a las 5 h: ángulo 150 o
COMPETENCIA MATEMÁTICA
 Servicio de Inspección Educativa 2 0 1 0 / 1 1 EVALUACIÓN DIAGNÓSTICA 4º DE EDUCACIÓN PRIMARIA COMPETENCIA MATEMÁTICA Nombre y apellidos:... Centro escolar:... Grupo/Aula:... Localidad:... Fecha:... Instrucciones
Servicio de Inspección Educativa 2 0 1 0 / 1 1 EVALUACIÓN DIAGNÓSTICA 4º DE EDUCACIÓN PRIMARIA COMPETENCIA MATEMÁTICA Nombre y apellidos:... Centro escolar:... Grupo/Aula:... Localidad:... Fecha:... Instrucciones
COMPETENCIA MATEMÁTICA
 Servicio de Inspección Educativa 2 0 1 2 / 1 3 EVALUACIÓN DIAGNÓSTICA 4º DE EDUCACIÓN PRIMARIA COMPETENCIA MATEMÁTICA Nombre y apellidos:... Centro escolar:... Grupo/Aula:... Localidad:... Fecha:... 2
Servicio de Inspección Educativa 2 0 1 2 / 1 3 EVALUACIÓN DIAGNÓSTICA 4º DE EDUCACIÓN PRIMARIA COMPETENCIA MATEMÁTICA Nombre y apellidos:... Centro escolar:... Grupo/Aula:... Localidad:... Fecha:... 2
PERÍMETRO Y ÁREA DE UN POLÍGONO
 PERÍMETRO Y ÁREA DE UN POLÍGONO - Área y perímetro del triángulo - Cálculo del perímetro Es la longitud de su contorno ó la suma de sus lados. P = a + b + c Recuerda: - El perímetro de un triángulo escaleno
PERÍMETRO Y ÁREA DE UN POLÍGONO - Área y perímetro del triángulo - Cálculo del perímetro Es la longitud de su contorno ó la suma de sus lados. P = a + b + c Recuerda: - El perímetro de un triángulo escaleno
Halla los siguientes perímetros y áreas:
 73 CAPÍTULO 9: LONGITUDES Y ÁREAS.. Matemáticas 1º y º de ESO 1. TEOREMA DE PITÁGORAS 1.1. Concepto de perímetro y de área de una figura plana El perímetro de una figura plana es la suma de las longitudes
73 CAPÍTULO 9: LONGITUDES Y ÁREAS.. Matemáticas 1º y º de ESO 1. TEOREMA DE PITÁGORAS 1.1. Concepto de perímetro y de área de una figura plana El perímetro de una figura plana es la suma de las longitudes
Clasifi cación de polígonos
 Clasifi cación de polígonos Cuándo un polígono es regular? Marca la opción correcta. Sus ángulos son iguales. Sus lados son iguales. Sus lados y sus ángulos son iguales. Sus diagonales son iguales. Escribe
Clasifi cación de polígonos Cuándo un polígono es regular? Marca la opción correcta. Sus ángulos son iguales. Sus lados son iguales. Sus lados y sus ángulos son iguales. Sus diagonales son iguales. Escribe
Cuaderno: LIMPIEZA Y ORGANIZACIÓN Realización de TAREAS TEMA 12 FIGURAS PLANAS Y ESPACIALES ALUMNO/A: Nº
 Cuaderno: LIMPIEZA Y ORGANIZACIÓN Realización de TAREAS SATISFACTORIO ACEPTABLE MEJORABLE TEMA 12 FIGURAS PLANAS Y ESPACIALES ALUMNO/A: Nº Ejercicios TEMA 12 FIGURAS PLANAS Y ESPACIALES (1º ESO) Página
Cuaderno: LIMPIEZA Y ORGANIZACIÓN Realización de TAREAS SATISFACTORIO ACEPTABLE MEJORABLE TEMA 12 FIGURAS PLANAS Y ESPACIALES ALUMNO/A: Nº Ejercicios TEMA 12 FIGURAS PLANAS Y ESPACIALES (1º ESO) Página
5 = Resuelve las siguientes ecuaciones: ( punto)
 TÍTULO: ECUACIONES, PROBLEMAS. ÁREAS Y PERÍMETROS NOMBRE: CALIFICACIÓN FECHA: L-8/05/18 APELLIDOS: 1. Resuelve las siguientes ecuaciones: (0 5 + 0 5 + 0 75 + 1 punto) a) 40 = 5x b) x 5 = 4 c) 7 + x 4x
TÍTULO: ECUACIONES, PROBLEMAS. ÁREAS Y PERÍMETROS NOMBRE: CALIFICACIÓN FECHA: L-8/05/18 APELLIDOS: 1. Resuelve las siguientes ecuaciones: (0 5 + 0 5 + 0 75 + 1 punto) a) 40 = 5x b) x 5 = 4 c) 7 + x 4x
Área de Matemáticas orientadas a las enseñanzas académicas EJERCICIOS RESUELTOS DE REFUERZO TEMA 5 Ecuaciones de 2º grado
 Ejercicio nº 1 TEMA 5 Ecuaciones de º grado Resuelve las siguientes ecuaciones: b) x( x + 5) x + 7 = x x 5 5 b) x( x + 5) x + 7 = x x 5 x + 10x x + 7 = x x + 5 10x + x = 7 16 1x = 16 x = 9 Ejercicio nº
Ejercicio nº 1 TEMA 5 Ecuaciones de º grado Resuelve las siguientes ecuaciones: b) x( x + 5) x + 7 = x x 5 5 b) x( x + 5) x + 7 = x x 5 x + 10x x + 7 = x x + 5 10x + x = 7 16 1x = 16 x = 9 Ejercicio nº
A 2 TEMA 10. POLÍGONOS ÁREAS Y PERÍMETROS TRIÁNGULOS CUADRILÁTEROS POLÍGONOS REGULARES CIRCUNFERENCIA CÍRCULO TEOREMA DE PITÁGORAS:
 TEMA 10. POLÍGONOS ÁREAS Y PERÍMETROS ELEMENTOS CLASIFICACIÓN TRIÁNGULOS CUADRILÁTEROS POLÍGONOS REGULARES CIRCUNFERENCIA CÍRCULO A b h A b a A perímetro apotema A r TEOREMA DE PITÁGORAS: a b c 1 POLÍGONOS
TEMA 10. POLÍGONOS ÁREAS Y PERÍMETROS ELEMENTOS CLASIFICACIÓN TRIÁNGULOS CUADRILÁTEROS POLÍGONOS REGULARES CIRCUNFERENCIA CÍRCULO A b h A b a A perímetro apotema A r TEOREMA DE PITÁGORAS: a b c 1 POLÍGONOS
EJERCICIOS DE VERANO MATEMÁTICAS 3º ESO
 EJERCICIOS DE VERANO MATEMÁTICAS 3º ESO Página 1 de 14 Entregar el día del examen de recuperación de matemáticas. Será condición indispensable para aprobar la asignatura. 1. Calcula: NUMEROS ENTEROS. FRACCIONES.
EJERCICIOS DE VERANO MATEMÁTICAS 3º ESO Página 1 de 14 Entregar el día del examen de recuperación de matemáticas. Será condición indispensable para aprobar la asignatura. 1. Calcula: NUMEROS ENTEROS. FRACCIONES.
CAPÍTULO 9: LONGITUDES Y ÁREAS 1. PERÍMETROS Y ÁREAS DE POLÍGONOS
 88 CAPÍTULO 9: LONGITUDES Y ÁREAS 1. PERÍMETROS Y ÁREAS DE POLÍGONOS 1.1. Concepto de perímetro y de área de una figura plana El perímetro de una figura plana es la suma de las longitudes de sus lados.
88 CAPÍTULO 9: LONGITUDES Y ÁREAS 1. PERÍMETROS Y ÁREAS DE POLÍGONOS 1.1. Concepto de perímetro y de área de una figura plana El perímetro de una figura plana es la suma de las longitudes de sus lados.
COMPETENCIA MATEMÁTICA
 Servicio de Inspección Educativa 2 0 1 0 / 1 1 EVALUACIÓN DIAGNÓSTICA 2º DE EDUCACIÓN SECUNDARIA OBLIGATORIA COMPETENCIA MATEMÁTICA Nombre y apellidos:... Centro escolar:... Grupo/Aula:... Localidad:...
Servicio de Inspección Educativa 2 0 1 0 / 1 1 EVALUACIÓN DIAGNÓSTICA 2º DE EDUCACIÓN SECUNDARIA OBLIGATORIA COMPETENCIA MATEMÁTICA Nombre y apellidos:... Centro escolar:... Grupo/Aula:... Localidad:...
Tema 12: Las Áreas de figuras planas. El Teorema de Pitágoras. 1-T 12--1ºESO
 Tema 1: Las Áreas de figuras planas. El Teorema de Pitágoras. 1-T 1--1ºESO I.- Perímetro y Área de las figuras planas: Antes de ver todas y cada una de las fórmulas que nos permiten averiguar el área de
Tema 1: Las Áreas de figuras planas. El Teorema de Pitágoras. 1-T 1--1ºESO I.- Perímetro y Área de las figuras planas: Antes de ver todas y cada una de las fórmulas que nos permiten averiguar el área de
polígono 3 Triángulo 4 Cuadrilátero 5 Pentágono 6 Hexágono 7 Heptágono 8 Octógono 9 Eneágono 10 Decágono 11 Undecágono 12 Dodecágono 20 Icoságono
 TEMA: POLÍGONOS Y ÁNGULOS. POLÍGONOS REGULARES. POLÍGONOS Un polígono es una figura cerrada cuyos lados son segmentos. La palabra polígonos se puede interpretar como: figura de muchos ángulos. Los triángulos,
TEMA: POLÍGONOS Y ÁNGULOS. POLÍGONOS REGULARES. POLÍGONOS Un polígono es una figura cerrada cuyos lados son segmentos. La palabra polígonos se puede interpretar como: figura de muchos ángulos. Los triángulos,
COMPETENCIA MATEMÁTICA
 Servicio de Inspección Educativa 2 0 1 4 / 1 5 EVALUACIÓN DIAGNÓSTICA 3º DE EDUCACIÓN PRIMARIA COMPETENCIA MATEMÁTICA Nombre y apellidos:... Centro escolar:... Grupo/Aula:... Localidad:... Fecha:... Tienes
Servicio de Inspección Educativa 2 0 1 4 / 1 5 EVALUACIÓN DIAGNÓSTICA 3º DE EDUCACIÓN PRIMARIA COMPETENCIA MATEMÁTICA Nombre y apellidos:... Centro escolar:... Grupo/Aula:... Localidad:... Fecha:... Tienes
COMPETENCIA MATEMÁTICA
 Servicio de Inspección Educativa 2 0 4 / 5 EVALUACIÓN DIAGNÓSTICA 3º DE EDUCACIÓN PRIMARIA COMPETENCIA MATEMÁTICA Nombre y apellidos:... Centro escolar:... Grupo/Aula:... Localidad:... Fecha:... Tienes
Servicio de Inspección Educativa 2 0 4 / 5 EVALUACIÓN DIAGNÓSTICA 3º DE EDUCACIÓN PRIMARIA COMPETENCIA MATEMÁTICA Nombre y apellidos:... Centro escolar:... Grupo/Aula:... Localidad:... Fecha:... Tienes
IES Mata Jove. matemáticas 2ESO
 matemáticas 2ESO actividades verano 2018 3ª EVALUACIÓN: tema 5, ECUACIONES Y SISTEMAS 52. Resuelve las siguientes ecuaciones de segundo grado y sistemas de ecuaciones. x 2 = 8 2x 4x 2 + 9 = 37x ( x + 1)
matemáticas 2ESO actividades verano 2018 3ª EVALUACIÓN: tema 5, ECUACIONES Y SISTEMAS 52. Resuelve las siguientes ecuaciones de segundo grado y sistemas de ecuaciones. x 2 = 8 2x 4x 2 + 9 = 37x ( x + 1)
TEMA 10: FORMAS Y FIGURAS PLANAS. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco.
 2009 TEMA 10: FORMAS Y FIGURAS PLANAS. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/2009 TEMA 10: FORMAS Y FIGURAS PLANAS. 1. Polígonos. 2.
2009 TEMA 10: FORMAS Y FIGURAS PLANAS. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/2009 TEMA 10: FORMAS Y FIGURAS PLANAS. 1. Polígonos. 2.
ELEMENTOS DE GEOMETRÍA
 LONGITUDES Y ÁREAS. 1. Perímetro y área. 1.1. Medidas del rectángulo. 1.2. Medidas del cuadrado. 1.3. Medidas del rombo. 1.4. Medidas del romboide. 1.5. Medidas de un paralelogramo cualquiera. 1.6. Medidas
LONGITUDES Y ÁREAS. 1. Perímetro y área. 1.1. Medidas del rectángulo. 1.2. Medidas del cuadrado. 1.3. Medidas del rombo. 1.4. Medidas del romboide. 1.5. Medidas de un paralelogramo cualquiera. 1.6. Medidas
EP3. Competencia Matemática 2016/ º de Educación Primaria. Nombre y apellidos: Centro escolar: Grupo/Aula: Localidad: Fecha:
 Ebaluazio eta Kalitate Atala Sección de Evaluación y Calidad EP3 2016/2017 Nombre y apellidos: Centro escolar: Grupo/Aula: Localidad: Fecha: Competencia Matemática Tienes 45 minutos para hacer esta primera
Ebaluazio eta Kalitate Atala Sección de Evaluación y Calidad EP3 2016/2017 Nombre y apellidos: Centro escolar: Grupo/Aula: Localidad: Fecha: Competencia Matemática Tienes 45 minutos para hacer esta primera
1.SISTEMAS DE MEDIDAS: longitud, superficie, volumen. Conversiones.
 ÍNDICE DEL TEMA 1.SISTEMAS DE MEDIDAS: longitud, superficie, volumen. Conversiones. 2. FIGURAS PLANAS : 2.1. POLÍGONOS Triángulos Cuadriláteros Polígonos regulares 2.2. CIRCUNFERENCIA Y CÍRCULO: Elementos.
ÍNDICE DEL TEMA 1.SISTEMAS DE MEDIDAS: longitud, superficie, volumen. Conversiones. 2. FIGURAS PLANAS : 2.1. POLÍGONOS Triángulos Cuadriláteros Polígonos regulares 2.2. CIRCUNFERENCIA Y CÍRCULO: Elementos.
EJERCICIOS Y PROBLEMAS RESUELTOS
 Ecuaciones de Segundo Grado -- página 1 EJERCICIOS Y PROBLEMAS RESUELTOS Ejercicio 1: Indica si son ecuaciones de segundo grado las siguientes ecuaciones: a) 5 + 8 + b) + + ( )( + ) c) + 1 a) El primer
Ecuaciones de Segundo Grado -- página 1 EJERCICIOS Y PROBLEMAS RESUELTOS Ejercicio 1: Indica si son ecuaciones de segundo grado las siguientes ecuaciones: a) 5 + 8 + b) + + ( )( + ) c) + 1 a) El primer
MEP4. Competencia Matemática 2016/ º de Educación Primaria. Nombre y apellidos: Centro escolar: Grupo/Aula: Localidad: Fecha:
 Ebaluazio eta Kalitate Atala Sección de Evaluación y Calidad MEP4 2016/2017 Nombre y apellidos: Centro escolar: Grupo/Aula: Localidad: Fecha: Competencia Matemática 4º de Educación Primaria Instrucciones
Ebaluazio eta Kalitate Atala Sección de Evaluación y Calidad MEP4 2016/2017 Nombre y apellidos: Centro escolar: Grupo/Aula: Localidad: Fecha: Competencia Matemática 4º de Educación Primaria Instrucciones
Las fracciones mixtas
 I E YERMO Y PARRES Sección Carlos franco 2 Unidad didáctica periodo tres Las fracciones mixtas Grado 4 Profesora Martha Luz Ospina Muñoz DESCRIPCIÓN: En el desarrollo de esta unidad se pone énfasis en
I E YERMO Y PARRES Sección Carlos franco 2 Unidad didáctica periodo tres Las fracciones mixtas Grado 4 Profesora Martha Luz Ospina Muñoz DESCRIPCIÓN: En el desarrollo de esta unidad se pone énfasis en
Matemáticas, opción A
 1 de 9 14/09/2015 1:05 Educación Secundaria 4 Matemáticas, opción A Opción C Evaluación:...Fecha:... Ejercicio nº 1.- a) Indica cuáles de los siguientes números son naturales, cuáles son enteros, cuáles
1 de 9 14/09/2015 1:05 Educación Secundaria 4 Matemáticas, opción A Opción C Evaluación:...Fecha:... Ejercicio nº 1.- a) Indica cuáles de los siguientes números son naturales, cuáles son enteros, cuáles
Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS
 Pág. 1 Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS Halla el área y el perímetro de las figuras coloreadas de los siguientes ejercicios: 1 a) b) 5 dm 4 cm 2 cm 5 cm 8 cm 2 a) b) 5 m 8 m 17 m 15 m 3 a) b) 5
Pág. 1 Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS Halla el área y el perímetro de las figuras coloreadas de los siguientes ejercicios: 1 a) b) 5 dm 4 cm 2 cm 5 cm 8 cm 2 a) b) 5 m 8 m 17 m 15 m 3 a) b) 5
2. Calcula la suma de los 20 primeros términos en cada una de las sucesiones anteriores.
 TRABAJO DE RECUPERACIÓN DE MATEMÁTICAS PENDIENTES DE 3º ESO (APLICADAS) ª EVALUACIÓN CURSO: 4º ESO SUCESIONES 1. Di si las siguientes sucesiones son aritméticas o geométricas, calcula el término general
TRABAJO DE RECUPERACIÓN DE MATEMÁTICAS PENDIENTES DE 3º ESO (APLICADAS) ª EVALUACIÓN CURSO: 4º ESO SUCESIONES 1. Di si las siguientes sucesiones son aritméticas o geométricas, calcula el término general
FORMULARIO (ÁREAS DE FIGURAS PLANAS)
 FORMULARIO (ÁREAS DE FIGURAS PLANAS) Rectángulo Triángulo Paralelogramo Cuadrado Cuadrilátero cuyos lados forman ángulos de 90º. Es la porción de plano limitada por tres segmentos de recta. Cuadrilátero
FORMULARIO (ÁREAS DE FIGURAS PLANAS) Rectángulo Triángulo Paralelogramo Cuadrado Cuadrilátero cuyos lados forman ángulos de 90º. Es la porción de plano limitada por tres segmentos de recta. Cuadrilátero
DEPARTAMENTO DE MATEMATICAS
 1.- Halla la suma de los ángulos interiores de los siguientes polígonos convexos. a) Cuadrilátero b) Heptágono c) Octógono 2.- Halla la medida de los ángulos interiores de: a) Un octógono regular. b) Un
1.- Halla la suma de los ángulos interiores de los siguientes polígonos convexos. a) Cuadrilátero b) Heptágono c) Octógono 2.- Halla la medida de los ángulos interiores de: a) Un octógono regular. b) Un
Mª Rosa Villegas Pérez
 Mª Rosa Villegas Pérez FIGURAS PLANAS G.T. Elaboración de Materiales y Recursos Didácticos en un Centro TIC. Polígonos.- / 14 POLÍGONOS Un polígono es una figura plana y cerrada formada al unir tres o
Mª Rosa Villegas Pérez FIGURAS PLANAS G.T. Elaboración de Materiales y Recursos Didácticos en un Centro TIC. Polígonos.- / 14 POLÍGONOS Un polígono es una figura plana y cerrada formada al unir tres o
EVALUACIÓN DIAGNÓSTICA
 Departamento de Educación Servicio de Inspección Educativa 2 0 0 8 / 0 9 EVALUACIÓN DIAGNÓSTICA 2º DE EDUCACIÓN secundaria obligatoria COMPETENCIA matemática Nombre y apellidos:... Centro escolar:... Grupo/Aula:...
Departamento de Educación Servicio de Inspección Educativa 2 0 0 8 / 0 9 EVALUACIÓN DIAGNÓSTICA 2º DE EDUCACIÓN secundaria obligatoria COMPETENCIA matemática Nombre y apellidos:... Centro escolar:... Grupo/Aula:...
ESPA: Ámbito Científico Tecnológico Nivel I - Módulo II. Unidad 1: Percibimos y representamos los objetos
 ESPA: Ámbito Científico Tecnológico Nivel I - Módulo II Unidad 1: Percibimos y representamos los objetos 1.- Descripción de las figuras geométricas en el plano. Clasificación de triángulos y cuadriláteros.
ESPA: Ámbito Científico Tecnológico Nivel I - Módulo II Unidad 1: Percibimos y representamos los objetos 1.- Descripción de las figuras geométricas en el plano. Clasificación de triángulos y cuadriláteros.
10 ACTIVIDADES DE REFUERZO
 0 ACTIVIDADES DE REFUERZO. Calcula el área de estos polígonos. a) Trapecio de bases de longitud cm y 8 cm, y altura 4,5 cm. Pentágono regular de lado 4 cm y apotema 4, cm.. Halla el área de estos polígonos.
0 ACTIVIDADES DE REFUERZO. Calcula el área de estos polígonos. a) Trapecio de bases de longitud cm y 8 cm, y altura 4,5 cm. Pentágono regular de lado 4 cm y apotema 4, cm.. Halla el área de estos polígonos.
COMPETENCIA MATEMÁTICA
 Servicio de Inspección Educativa 2 0 0 9 / 1 0 EVALUACIÓN DIAGNÓSTICA 2º DE EDUCACIÓN SECUNDARIA OBLIGATORIA COMPETENCIA MATEMÁTICA Nombre y apellidos:... Centro escolar:... Grupo:... Localidad:... Fecha:...
Servicio de Inspección Educativa 2 0 0 9 / 1 0 EVALUACIÓN DIAGNÓSTICA 2º DE EDUCACIÓN SECUNDARIA OBLIGATORIA COMPETENCIA MATEMÁTICA Nombre y apellidos:... Centro escolar:... Grupo:... Localidad:... Fecha:...
EP4. Competencia Matemática 2017/ º de Educación Primaria. Nombre y apellidos: Centro escolar: Grupo/Aula: Localidad: Fecha:
 Ebaluazio eta Kalitate Atala Sección de Evaluación y Calidad EP4 217/218 Nombre y apellidos: Centro escolar: Grupo/Aula: Localidad: Fecha: Competencia Matemática 4º de Educación Primaria Instrucciones
Ebaluazio eta Kalitate Atala Sección de Evaluación y Calidad EP4 217/218 Nombre y apellidos: Centro escolar: Grupo/Aula: Localidad: Fecha: Competencia Matemática 4º de Educación Primaria Instrucciones
TEMA 6 SEMEJANZA. APLICACIONES -
 TEMA 6 SEMEJANZA. APLICACIONES - 1. SEMEJANZA: ESCALAS LECCIÓN I ESCALA: es el cociente entre cada longitud de reproducción (mapa, plano, maqueta) y la correspondiente longitud en la realidad. Es, por
TEMA 6 SEMEJANZA. APLICACIONES - 1. SEMEJANZA: ESCALAS LECCIÓN I ESCALA: es el cociente entre cada longitud de reproducción (mapa, plano, maqueta) y la correspondiente longitud en la realidad. Es, por
TRABAJO DE RECUPERACIÓN DE MATEMÁTICAS 1º ESO
 TRABAJO DE RECUPERACIÓN DE MATEMÁTICAS 1º ESO Números naturales 1. Escribe en forma de potencia de 10 los siguientes números: a) Velocidad de la luz: 300.000 km/s. b) Un año luz: 9.00.000.000.000 km/s.
TRABAJO DE RECUPERACIÓN DE MATEMÁTICAS 1º ESO Números naturales 1. Escribe en forma de potencia de 10 los siguientes números: a) Velocidad de la luz: 300.000 km/s. b) Un año luz: 9.00.000.000.000 km/s.
UNIDAD 2: ELEMENTOS GEOMÉTRICOS
 UNIDAD 2: ELEMENTOS GEOMÉTRICOS POLÍGONO Región del plano limitada por una línea poligonal cerrada. 1. Dibuja polígonos y señala los lados, vértices y ángulos. 4 lados Ángulo Vértice Lado 5 lados Este
UNIDAD 2: ELEMENTOS GEOMÉTRICOS POLÍGONO Región del plano limitada por una línea poligonal cerrada. 1. Dibuja polígonos y señala los lados, vértices y ángulos. 4 lados Ángulo Vértice Lado 5 lados Este
ARITMÉTICA. 1. Resolver las siguientes ecuaciones en Q. 2 x + 5. d) ( ) 2. g) 0,86 x 0,73 = 1. x = 1 4 3x. = x + + l) ( ) ( )( ) m) ( )( ) ( ) 2
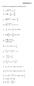 1. Resolver las siguientes ecuaciones en Q. ARITMÉTICA a) b) 3. x + 1 = 3 83 3,90x x = 3 31 c) 0,x + x 4,16 = 6 x + 3 1 + 4 = x + 1 d) ( ) e) f) x x + = 0,3 0, 6x 3 0, 6 1x + 6x = 0,3 8 g) 0,86 x 0,73
1. Resolver las siguientes ecuaciones en Q. ARITMÉTICA a) b) 3. x + 1 = 3 83 3,90x x = 3 31 c) 0,x + x 4,16 = 6 x + 3 1 + 4 = x + 1 d) ( ) e) f) x x + = 0,3 0, 6x 3 0, 6 1x + 6x = 0,3 8 g) 0,86 x 0,73
COMPETENCIA MATEMÁTICA
 Servicio de Inspección Educativa 2 0 1 1 / 1 2 EVALUACIÓN DIAGNÓSTICA 4º DE EDUCACIÓN PRIMARIA COMPETENCIA MATEMÁTICA Nombre y apellidos:... Centro escolar:... Grupo/Aula:... Localidad:... Fecha:... Instrucciones
Servicio de Inspección Educativa 2 0 1 1 / 1 2 EVALUACIÓN DIAGNÓSTICA 4º DE EDUCACIÓN PRIMARIA COMPETENCIA MATEMÁTICA Nombre y apellidos:... Centro escolar:... Grupo/Aula:... Localidad:... Fecha:... Instrucciones
Elementos del cilindro
 Definición de cilindro Un cilindro es un cuerpo geométrico engendrado por un rectángulo que gira alrededor de uno de sus lados. Desarrollo del cilindro Elementos del cilindro Eje Es el lado fijo alrededor
Definición de cilindro Un cilindro es un cuerpo geométrico engendrado por un rectángulo que gira alrededor de uno de sus lados. Desarrollo del cilindro Elementos del cilindro Eje Es el lado fijo alrededor
Tema 10: Problemas métricos en el plano
 Tema 10: Problemas métricos en el plano 10.1 Relaciones angulares Construye un polígono de cinco lados, divídelo en triángulos para averiguar la suma de los ángulos interiores del pentágono. Nuestro pentágono
Tema 10: Problemas métricos en el plano 10.1 Relaciones angulares Construye un polígono de cinco lados, divídelo en triángulos para averiguar la suma de los ángulos interiores del pentágono. Nuestro pentágono
10 SEMEJANZA. TEOREMA DE PITÁGORAS EJERCICIOS
 0 SEMEJNZ. TEOREM DE PITÁGORS EJERCICIOS Indica qué rectángulos son semejantes: a) ase cm, altura cm y base 0 cm, altura cm. b) ase 0 m, altura m y base 0 m, altura 8 m. c) ase 0,7 dm, altura 0, dm y base,0
0 SEMEJNZ. TEOREM DE PITÁGORS EJERCICIOS Indica qué rectángulos son semejantes: a) ase cm, altura cm y base 0 cm, altura cm. b) ase 0 m, altura m y base 0 m, altura 8 m. c) ase 0,7 dm, altura 0, dm y base,0
FIGURAS, ÁREAS Y PERÍMETROS
 FIGURAS, ÁREAS Y PERÍMETROS 05 Identifica propiedades de las figuras geométricas, de área y de perímetro y utiliza modelos con los que representa información matemática. Para hablar de áreas y perímetros,
FIGURAS, ÁREAS Y PERÍMETROS 05 Identifica propiedades de las figuras geométricas, de área y de perímetro y utiliza modelos con los que representa información matemática. Para hablar de áreas y perímetros,
MATEMÁTICAS 1º DE E.S.O.
 MATEMÁTICAS 1º DE E.S.O. 1 REFUERZO EDUCATIVO DE MATEMÁTICAS DE 1º DE E.S.O. TEMA 1 DIVISIBILIDAD. - Concepto de múltiplo. - Concepto de divisor. - Concepto de número primo y compuesto. - Criterios de
MATEMÁTICAS 1º DE E.S.O. 1 REFUERZO EDUCATIVO DE MATEMÁTICAS DE 1º DE E.S.O. TEMA 1 DIVISIBILIDAD. - Concepto de múltiplo. - Concepto de divisor. - Concepto de número primo y compuesto. - Criterios de
TEMA 6 SEMEJANZA. APLICACIONES -
 TEMA 6 SEMEJANZA. APLICACIONES - 1. SEMEJANZA: ESCALAS LECCIÓN I ESCALA: es el cociente entre cada longitud de reproducción (mapa, plano, maqueta) y la correspondiente longitud en la realidad. Es, por
TEMA 6 SEMEJANZA. APLICACIONES - 1. SEMEJANZA: ESCALAS LECCIÓN I ESCALA: es el cociente entre cada longitud de reproducción (mapa, plano, maqueta) y la correspondiente longitud en la realidad. Es, por
CONCEPTO DE POLÍGONO. RECONOCER Y CLASIFICAR POLÍGONOS
 OBJETIVO 1 CONCEPTO DE POLÍGONO. RECONOCER Y CLASIICAR POLÍGONOS NOMBRE: CURSO: ECHA: POLÍGONOS Varios segmentos unidos entre sí forman una línea poligonal. Una línea poligonal cerrada es un polígono.
OBJETIVO 1 CONCEPTO DE POLÍGONO. RECONOCER Y CLASIICAR POLÍGONOS NOMBRE: CURSO: ECHA: POLÍGONOS Varios segmentos unidos entre sí forman una línea poligonal. Una línea poligonal cerrada es un polígono.
EP3. Competencia Matemática 2017/ º de Educación Primaria. Nombre y apellidos: Centro escolar: Grupo/Aula: Localidad: Fecha:
 Ebaluazio eta Kalitate Atala Sección de Evaluación y Calidad EP3 2017/2018 Nombre y apellidos: Centro escolar: Grupo/Aula: Localidad: Fecha: Competencia Matemática Tienes 45 minutos para hacer esta primera
Ebaluazio eta Kalitate Atala Sección de Evaluación y Calidad EP3 2017/2018 Nombre y apellidos: Centro escolar: Grupo/Aula: Localidad: Fecha: Competencia Matemática Tienes 45 minutos para hacer esta primera
SISTEMAS DE ECUACIONES Y DE INECUACIONES
 Sistemas de Ecuaciones de Inecuaciones Departamento de Matemáticas SISTEMAS DE ECUACIONES Y DE INECUACIONES SISTEMAS LINEALES. - Resuelve por sustitución e igualación los siguientes sistemas: a) c) b)
Sistemas de Ecuaciones de Inecuaciones Departamento de Matemáticas SISTEMAS DE ECUACIONES Y DE INECUACIONES SISTEMAS LINEALES. - Resuelve por sustitución e igualación los siguientes sistemas: a) c) b)
José Gómez Penas 1 UNIDAD DIDÁCTICA. GEOMETRÍA : Triángulos y Cuadriláteros. Autor : José Gómez Penas 1º ESO.Matemáticas.
 1 UNIDAD DIDÁCTICA GEOMETRÍA : Triángulos y Cuadriláteros Autor : 1º ESO.Matemáticas. IES Miraflores CONTENIDOS: Triángulos: Teorema de Pitágoras. Áreas y Perímetros OBJETIVOS: -Comprender el teorema de
1 UNIDAD DIDÁCTICA GEOMETRÍA : Triángulos y Cuadriláteros Autor : 1º ESO.Matemáticas. IES Miraflores CONTENIDOS: Triángulos: Teorema de Pitágoras. Áreas y Perímetros OBJETIVOS: -Comprender el teorema de
ECUACIONES DE PRIMER GRADO. 3º ) Pasa todos los términos que contenga la incógnita a un lado de la igualdad y los demás al otro lado.
 ECUACIONES DE PRIMER GRADO Para resolver las ecuaciones: 1º ) Quitar denominadores, si los tiene. Para ello se multiplica ambos lados de la igualdad por el mínimo común múltiplo de los denominadores. º
ECUACIONES DE PRIMER GRADO Para resolver las ecuaciones: 1º ) Quitar denominadores, si los tiene. Para ello se multiplica ambos lados de la igualdad por el mínimo común múltiplo de los denominadores. º
NOMBRE. CURSO
 NOMBRE. CURSO 2017-18 TEOREMA DE PITÁGORAS Escribe el enunciado del teorema 1. Identifica cada lado con una letra y escribe la fórmula para calcular el valor del lado indicado 1 2. La altura de una portería
NOMBRE. CURSO 2017-18 TEOREMA DE PITÁGORAS Escribe el enunciado del teorema 1. Identifica cada lado con una letra y escribe la fórmula para calcular el valor del lado indicado 1 2. La altura de una portería
CUADERNO DEL ALUMNO/A
 CUADERNO DEL ALUMNO/A PRUEBA DE EVALUACIÓN INICIAL DE MATEMÁTICAS. 6º CURSO EDUCACIÓN PRIMARIA Evaluación Inicial de Matemáticas 6º Curso 1.- LECTURA Y ESCRITURA DE NÚMEROS NATURALES. Completa con cifras
CUADERNO DEL ALUMNO/A PRUEBA DE EVALUACIÓN INICIAL DE MATEMÁTICAS. 6º CURSO EDUCACIÓN PRIMARIA Evaluación Inicial de Matemáticas 6º Curso 1.- LECTURA Y ESCRITURA DE NÚMEROS NATURALES. Completa con cifras
El polígono es una porción del plano limitado por una línea poligonal cerrada.
 UNIDAD 12: GEOMETRÍA PLANA 12.1. Los polígonos: Elementos El polígono es una porción del plano limitado por una línea poligonal cerrada. Un polígono se nombra con las letras mayúsculas situadas en los
UNIDAD 12: GEOMETRÍA PLANA 12.1. Los polígonos: Elementos El polígono es una porción del plano limitado por una línea poligonal cerrada. Un polígono se nombra con las letras mayúsculas situadas en los
IDENTIFICAR Y RESOLVER ECUACIONES DE SEGUNDO GRADO
 IDENTIFICAR Y RESOLVER ECUACIONES DE SEGUNDO GRADO OBJETIVO Una ecuación de segundo grado con una incógnita es una ecuación que se epresa de la forma: a + b + c = 0 donde a, b y c son números reales y
IDENTIFICAR Y RESOLVER ECUACIONES DE SEGUNDO GRADO OBJETIVO Una ecuación de segundo grado con una incógnita es una ecuación que se epresa de la forma: a + b + c = 0 donde a, b y c son números reales y
EJERCICIOS-RECUPERACIÓN ESTIVAL DE MATEMÁTICAS 1º ESO
 EJERCICIOS-RECUPERACIÓN ESTIVAL DE MATEMÁTICAS 1º ESO A continuación te presentamos una serie de ejercicios que deberás realizar y presentar obligatoriamente a tu profesor/a el día del examen. Puedes consultar
EJERCICIOS-RECUPERACIÓN ESTIVAL DE MATEMÁTICAS 1º ESO A continuación te presentamos una serie de ejercicios que deberás realizar y presentar obligatoriamente a tu profesor/a el día del examen. Puedes consultar
Cálculo de perímetros y áreas
 Cálculo de perímetros y áreas 1. Calcula el perímetro de las siguientes figuras planas: 2. Calcula el perímetro de las siguientes figuras geométricas: 3. La rueda de un triciclo tiene 30 cm de radio. Cuántos
Cálculo de perímetros y áreas 1. Calcula el perímetro de las siguientes figuras planas: 2. Calcula el perímetro de las siguientes figuras geométricas: 3. La rueda de un triciclo tiene 30 cm de radio. Cuántos
COMPETENCIA MATEMÁTICA
 Servicio de Inspección Educativa 2 0 0 9 / 1 0 EVALUACIÓN DIAGNÓSTICA 4º DE EDUCACIÓN PRIMARIA COMPETENCIA MATEMÁTICA Nombre y apellidos:... Centro escolar:... Grupo:... Localidad:... Fecha:... Instrucciones
Servicio de Inspección Educativa 2 0 0 9 / 1 0 EVALUACIÓN DIAGNÓSTICA 4º DE EDUCACIÓN PRIMARIA COMPETENCIA MATEMÁTICA Nombre y apellidos:... Centro escolar:... Grupo:... Localidad:... Fecha:... Instrucciones
EJERCICIOS MÓDULO 4. Geometría plana. 1) Cuántos vértices tiene un polígono cuyo número total de diagonales es 9?
 Seminario Universitario Matemática EJERCICIOS MÓDULO 4 Geometría plana 1) Cuántos vértices tiene un polígono cuyo número total de diagonales es 9? ) Cuántos lados tiene un polígono en el cual la suma de
Seminario Universitario Matemática EJERCICIOS MÓDULO 4 Geometría plana 1) Cuántos vértices tiene un polígono cuyo número total de diagonales es 9? ) Cuántos lados tiene un polígono en el cual la suma de
TEMA 5. Geometría. Teoría. Matemáticas
 1 La Geometría trata sobre las formas y sus propiedades. A su vez, se puede dividir en: Geometría plana: trata de las figuras en el plano, (dos dimensiones) Geometría tridimensional: trata de figuras en
1 La Geometría trata sobre las formas y sus propiedades. A su vez, se puede dividir en: Geometría plana: trata de las figuras en el plano, (dos dimensiones) Geometría tridimensional: trata de figuras en
COMPETENCIA MATEMÁTICA
 Servicio de Inspección Educativa 2 0 1 2 / 1 3 EVALUACIÓN DIAGNÓSTICA 4º DE EDUCACIÓN PRIMARIA COMPETENCIA MATEMÁTICA Nombre y apellidos:... Centro escolar:... Grupo/Aula:... Localidad:... Fecha:... Instrucciones
Servicio de Inspección Educativa 2 0 1 2 / 1 3 EVALUACIÓN DIAGNÓSTICA 4º DE EDUCACIÓN PRIMARIA COMPETENCIA MATEMÁTICA Nombre y apellidos:... Centro escolar:... Grupo/Aula:... Localidad:... Fecha:... Instrucciones
2. Calcula la suma de los 20 primeros términos en cada una de las sucesiones anteriores.
 TRABAJO DE RECUPERACIÓN DE MATEMÁTICAS PENDIENTES DE 3º ESO (ACADÉMICAS) ª EVALUACIÓN CURSO: 4º ESO SUCESIONES 1. Di si las siguientes sucesiones son aritméticas o geométricas, calcula el término general
TRABAJO DE RECUPERACIÓN DE MATEMÁTICAS PENDIENTES DE 3º ESO (ACADÉMICAS) ª EVALUACIÓN CURSO: 4º ESO SUCESIONES 1. Di si las siguientes sucesiones son aritméticas o geométricas, calcula el término general
CONTENIDOS Y ESTÁNDARES DE APRENDIZAJE EVALUABLES IMPRESCINDIBLES PARA SUPERAR LA MATERIA
 DEPARTAMENTO DE MATEMÁTICAS Área: TALLER DE MATEMÁTICAS Curso: 1º E.S.O. CONTENIDOS Y ESTÁNDARES DE APRENDIZAJE EVALUABLES IMPRESCINDIBLES PARA SUPERAR LA MATERIA Los contenidos mínimos y estándares de
DEPARTAMENTO DE MATEMÁTICAS Área: TALLER DE MATEMÁTICAS Curso: 1º E.S.O. CONTENIDOS Y ESTÁNDARES DE APRENDIZAJE EVALUABLES IMPRESCINDIBLES PARA SUPERAR LA MATERIA Los contenidos mínimos y estándares de
ARITMÉTICA. 1. Resolver las siguientes ecuaciones en Q. 2 x + 5. d) ( x ) ( x ) x = x + = x. l) ( ) ( )( ) + = + + o) ( x ) 2.
 1. Resolver las siguientes ecuaciones en Q. ARITMÉTICA a) b) 3. x + 1 = 3 83 3,90x x = 3 31 c) 0,x + x 4,16 = 6 d) ( x ) ( x ) + 3 1 = + 1 4 e) f) g) x x + = 0,3 0, 6x 3 0, 6 1x + 6x = 0,3 8 0,86x 0,73
1. Resolver las siguientes ecuaciones en Q. ARITMÉTICA a) b) 3. x + 1 = 3 83 3,90x x = 3 31 c) 0,x + x 4,16 = 6 d) ( x ) ( x ) + 3 1 = + 1 4 e) f) g) x x + = 0,3 0, 6x 3 0, 6 1x + 6x = 0,3 8 0,86x 0,73
PRUEBA DE EVALUACIÓN INICIAL ÁREA DE MATEMÁTICAS. 2º CURSO DE ED. SECUNDARIA CUADERNILLO DE EJERCICIOS APELLIDOS Y NOMBRE: CENTRO: CURSO: FECHA:
 PRUEBA DE EVALUACIÓN INICIAL ÁREA DE MATEMÁTICAS. 2º CURSO DE ED. SECUNDARIA CUADERNILLO DE EJERCICIOS APELLIDOS Y NOMBRE: CENTRO: CURSO: FECHA: 1.- LECTURA Y ESCRITURA DE NÚMEROS NATURALES. Completa con
PRUEBA DE EVALUACIÓN INICIAL ÁREA DE MATEMÁTICAS. 2º CURSO DE ED. SECUNDARIA CUADERNILLO DE EJERCICIOS APELLIDOS Y NOMBRE: CENTRO: CURSO: FECHA: 1.- LECTURA Y ESCRITURA DE NÚMEROS NATURALES. Completa con
Figuras planas. Definiciones
 Figuras planas Definiciones Polígono: definición Un polígono es una figura plana (yace en un plano) cerrada por tres o más segmentos. Los lados de un polígono son cada uno de los segmentos que delimitan
Figuras planas Definiciones Polígono: definición Un polígono es una figura plana (yace en un plano) cerrada por tres o más segmentos. Los lados de un polígono son cada uno de los segmentos que delimitan
Mayo Evaluación de 3er. curso de Educación Primaria. Prueba de competencia matemática + = + = =
 1 Mayo 2015 Evaluación de 3er. curso de Educación Primaria Prueba de competencia matemática + = + = 3 1 4 5 5 5 8 + 5-2 = INSTRUCCIONES En esta prueba tendrás que responder a preguntas relacionadas con
1 Mayo 2015 Evaluación de 3er. curso de Educación Primaria Prueba de competencia matemática + = + = 3 1 4 5 5 5 8 + 5-2 = INSTRUCCIONES En esta prueba tendrás que responder a preguntas relacionadas con
MEDIDAS DE LONGITUDES Y SUPERFICIES_ADAPT (6ºEP)
 Adaptación Unidad 11 _La longitud y la superficie. Página 1 LA LONGITUD. Copia en tu cuaderno y aprende. Adaptación Unidad 11 _La longitud y la superficie. Página 2 1. Copia y completa: metros (m) centímetros
Adaptación Unidad 11 _La longitud y la superficie. Página 1 LA LONGITUD. Copia en tu cuaderno y aprende. Adaptación Unidad 11 _La longitud y la superficie. Página 2 1. Copia y completa: metros (m) centímetros
CUADERNILLO RECUPERACIÓN DE PENDIENTES
 Cuadernillo de recuperación. ª Evaluación Curso 017/018 CUADERNILLO RECUPERACIÓN DE PENDIENTES CURSO 017/018 MATEMÁTICAS ORIENTADAS A LAS ENSEÑANZAS APLICADAS 3º E.S.O. ª EVALUACIÓN Los ejercicios deben
Cuadernillo de recuperación. ª Evaluación Curso 017/018 CUADERNILLO RECUPERACIÓN DE PENDIENTES CURSO 017/018 MATEMÁTICAS ORIENTADAS A LAS ENSEÑANZAS APLICADAS 3º E.S.O. ª EVALUACIÓN Los ejercicios deben
TEMA 6: GEOMETRÍA PLANA
 TEMA 6: GEOMETRÍA PLANA 1. INTRODUCCIÓN A LA GEOMETRÍA En nuestro entorno podemos visualizar objetos que se relacionan con elementos geométricos: por ejemplo la ventana de nuestra casa tiene forma rectangular.
TEMA 6: GEOMETRÍA PLANA 1. INTRODUCCIÓN A LA GEOMETRÍA En nuestro entorno podemos visualizar objetos que se relacionan con elementos geométricos: por ejemplo la ventana de nuestra casa tiene forma rectangular.
Ámbito Científico-Matemático MATEMÁTICAS 3º E.S.O.
 CUADERNILLO RECUPERACIÓN DE PENDIENTES CURSO 2017/2018 Ámbito Científico-Matemático MATEMÁTICAS º E.S.O. 1ª EVALUACIÓN Los ejercicios deben ser entregados en A4 blancos al profesor correspondiente en la
CUADERNILLO RECUPERACIÓN DE PENDIENTES CURSO 2017/2018 Ámbito Científico-Matemático MATEMÁTICAS º E.S.O. 1ª EVALUACIÓN Los ejercicios deben ser entregados en A4 blancos al profesor correspondiente en la
Nombre: Fecha: Curso: ^ C
 REPASO 1 Mide los siguientes ángulos con un transportador e indica de qué tipo son. ^ A ^B ^ C ^ D ^E Â = 90 recto, Bˆ = 60 agudo, Ĉ = 45 agudo, Dˆ = 120 obtuso, Ê = 100 obtuso. 2 Indica si las siguientes
REPASO 1 Mide los siguientes ángulos con un transportador e indica de qué tipo son. ^ A ^B ^ C ^ D ^E Â = 90 recto, Bˆ = 60 agudo, Ĉ = 45 agudo, Dˆ = 120 obtuso, Ê = 100 obtuso. 2 Indica si las siguientes
Ejercicios de verano 2º ESO
 Ejercicios de verano º ESO 1 ACTIVIDADES DE REFUERZO 1. Descompón en factores primos el número 4.. Halla el máximo común divisor y el mínimo común múltiplo de los números 40 y 504.. Ordena los siguientes
Ejercicios de verano º ESO 1 ACTIVIDADES DE REFUERZO 1. Descompón en factores primos el número 4.. Halla el máximo común divisor y el mínimo común múltiplo de los números 40 y 504.. Ordena los siguientes
COMPETENCIA MATEMÁTICA
 Servicio de Inspección Educativa 2 0 1 1 / 1 2 EVALUACIÓN DIAGNÓSTICA 4º DE EDUCACIÓN PRIMARIA COMPETENCIA MATEMÁTICA Nombre y apellidos:... Centro escolar:... Grupo/Aula:... Localidad:... Fecha:... Instrucciones
Servicio de Inspección Educativa 2 0 1 1 / 1 2 EVALUACIÓN DIAGNÓSTICA 4º DE EDUCACIÓN PRIMARIA COMPETENCIA MATEMÁTICA Nombre y apellidos:... Centro escolar:... Grupo/Aula:... Localidad:... Fecha:... Instrucciones
Miguel Ángel Ladrón de Guevara Editorial TUTOR FORMACIÓN
 97 Polígonos Definiciones Un polígono es una figura geométrica plana limitada al menos por tres segmentos rectos consecutivos no alineados llamados lados. Un polígono se llama regular si todos sus lados
97 Polígonos Definiciones Un polígono es una figura geométrica plana limitada al menos por tres segmentos rectos consecutivos no alineados llamados lados. Un polígono se llama regular si todos sus lados
7 Geometría del plano. Movimientos
 Qué tienes que saber? 7 QUÉ tienes que saber? Lugares geométricos ctividades Finales 7 Teorema de Pitágoras. plicaciones Ten en cuenta Dos rectas secantes forman dos ángulos adyacentes si son consecutivos
Qué tienes que saber? 7 QUÉ tienes que saber? Lugares geométricos ctividades Finales 7 Teorema de Pitágoras. plicaciones Ten en cuenta Dos rectas secantes forman dos ángulos adyacentes si son consecutivos
Guía didáctica 1º TRIMESTRE CRITERIOS DE EVALUACIÓN
 Guía didáctica 1º TRIMESTRE BL2.1. Interpretar los números naturales, enteros, fraccionarios, decimales y porcentajes sencillos, y sus propiedades (orden, recta real, divisibilidad, etc.) y utilizarlos
Guía didáctica 1º TRIMESTRE BL2.1. Interpretar los números naturales, enteros, fraccionarios, decimales y porcentajes sencillos, y sus propiedades (orden, recta real, divisibilidad, etc.) y utilizarlos
Matemática III Trimestre PRÁCTICA PARA LA SEGUNDA PRUEBA CORTA SOLUCIONARIO
 Matemática III Trimestre PRÁCTICA PARA LA SEGUNDA PRUEBA CORTA SOLUCIONARIO I parte. Concepto de áreas y de perímetro. 1. Repinte de azul el perímetro y coloree de rojo el área en las siguientes figuras
Matemática III Trimestre PRÁCTICA PARA LA SEGUNDA PRUEBA CORTA SOLUCIONARIO I parte. Concepto de áreas y de perímetro. 1. Repinte de azul el perímetro y coloree de rojo el área en las siguientes figuras
Problemas de repaso. 2. Sabiendo que los puntos P, Q y R están sobre una circunferencia de centro C, determina la medida del ángulo P RQ de la figura.
 Matemáticas II Magisterio (rimaria) urso 2015-2016 1. alcula la medida del ángulo a de la figura. roblemas de repaso 116 105 a ol: a = 49. 2. abiendo que los puntos, y están sobre una circunferencia de
Matemáticas II Magisterio (rimaria) urso 2015-2016 1. alcula la medida del ángulo a de la figura. roblemas de repaso 116 105 a ol: a = 49. 2. abiendo que los puntos, y están sobre una circunferencia de
ÁREAS DE FIGURAS PLANAS
 6. ÁREAS DE FIGURAS PLANAS EN ESTA UNIDAD VAS A APRENDER ÁREAS POLÍGONOS RECTÁNGULO CUADRADO PARALELOGRAMO TRIÁNGULO TRAPECIO ROMBO POLÍGONO IRREGULAR FÓRMULA RESOLUCIÓN DE PROBLEMAS CÍRCULO FÓRMULA FIGURAS
6. ÁREAS DE FIGURAS PLANAS EN ESTA UNIDAD VAS A APRENDER ÁREAS POLÍGONOS RECTÁNGULO CUADRADO PARALELOGRAMO TRIÁNGULO TRAPECIO ROMBO POLÍGONO IRREGULAR FÓRMULA RESOLUCIÓN DE PROBLEMAS CÍRCULO FÓRMULA FIGURAS
Guía del estudiante. Clase 36 Tema: Teorema de Pitágoras. Actividad 1
 MATEMÁTICAS Grado Séptimo Bimestre III Semana 8 Número de clases 36-39 Clase 36 Tema: Teorema de Pitágoras Actividad 1 Halle la medida, en centímetros, de la hipotenusa de un triángulo rectángulo, cuos
MATEMÁTICAS Grado Séptimo Bimestre III Semana 8 Número de clases 36-39 Clase 36 Tema: Teorema de Pitágoras Actividad 1 Halle la medida, en centímetros, de la hipotenusa de un triángulo rectángulo, cuos
Unidad 7 Figuras planas. Polígonos
 Polígonos 1.- Halla la suma de los ángulos interiores de los siguientes polígonos convexos. a) Cuadrilátero b) Heptágono c) Octógono.- Halla la medida de los ángulos interiores de: a) Un octógono regular.
Polígonos 1.- Halla la suma de los ángulos interiores de los siguientes polígonos convexos. a) Cuadrilátero b) Heptágono c) Octógono.- Halla la medida de los ángulos interiores de: a) Un octógono regular.
13Soluciones a los ejercicios y problemas PÁGINA 250
 PÁGINA 50 Pág. 1 Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS Halla el área y el perímetro de las figuras coloreadas de los siguientes ejercicios: 1 a) b) 5 dm 4 cm cm 5 cm 8 cm a) 5 5 dm b) 8 8 cm P 5 4 0
PÁGINA 50 Pág. 1 Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS Halla el área y el perímetro de las figuras coloreadas de los siguientes ejercicios: 1 a) b) 5 dm 4 cm cm 5 cm 8 cm a) 5 5 dm b) 8 8 cm P 5 4 0
EJERCICIOS. 4 6 e) Si en una caja hay 2 fichas blancas y 3 fichas negras, la probabilidad de sacar una ficha negra es. 2 3
 . La probabilidad de obtener un número mayor que en el lanzamiento de un dado es: EJERCICIOS. Si en una caja hay fichas blancas y fichas negras, la probabilidad de sacar una ficha negra es.. Si elegimos
. La probabilidad de obtener un número mayor que en el lanzamiento de un dado es: EJERCICIOS. Si en una caja hay fichas blancas y fichas negras, la probabilidad de sacar una ficha negra es.. Si elegimos
