Series y transformadas de Fourier
|
|
|
- Laura Robles Toledo
- hace 9 años
- Vistas:
Transcripción
1 Capítulo Series transformadas de Fourier Las series de Fourier son series de términos coseno seno surgen en la tarea práctica de representar funciones periódicas generales. Como aplicación constituen una herramienta mu importante en la solución de problemas en los que intervienen ecuaciones diferenciales ordinarias parciales. La teoría de las series de Fourier es bastante complicada, pero la aplicación de estas series es simple. Las series de Fourier son, en cierto sentido, más universales que las series de Talor, a que muchas funciones periódicas discontinuas pueden desarrollarse en serie de Fourier, pero, desde luego, no tienen representaciones en serie de Talor. La introducción de las series de Fourier ( de las integrales de Fourier) fue uno de los maores avances jamas realizados en la física matemática en sus aplicaciones en la ingeniería, a que las series de Fourier ( las integrales de Fourier) son probablemente la herramienta más importante en la solución de problemas con valores en la frontera. Esto se eplicará en el capítulo siguiente. La transformada de Laplace es con mucho la transformada integral más importante en ingeniería. Desde el punto de vista de las aplicaciones, las si guientes en importancia serían quizás la transformada de Fourier, aún cuando su manejo resulta un tanto más difícil que la transformada de Laplace.1. Series trigonométricas Diremos que una función () es periódica, o periódica, si está definida para todo R sieiste0, talque ( + ) = () para todo R. (.1) 1
2 Domingo Alcaraz Candela Al número lo llamaremos periodo de (). Lagráfica de esta función se obtiene por repetición periódica de su gráfica en cualquier intervalo de longitud. Ejemplo 1 Las funciones sin cos son funciones periódicas de periodo. Las funciones constantes son funcionesperiódicasdecualquierperiodo (en el sentido de la definición). Ejemplo de funciones que no son periódicas son,, ln. Si () () tienen periodo, entonces la función () = ()+ () con R, también tiene periodo. Por (.1) se tiene que para cualquier Z ( + ) = () para todo R por tanto, 3 también son periodos 1 de (). El problema principal de este capítulo será la representación de varias funciones de periodo = en términos de las funciones simples, de periodo, {1 cos sin cos () sin () cos () sin () } llamado sistema trigonométrico cos cos cos 3 1 Si una función periódica () tiene un periodo 0 que es el más pequeño de todos, este se denomina el periodo primitivo de (). Por ejemplo, el periodo primitivo de sin es el periodo primitivo de sin () es. Una función periódica sin periodo primitivo es.
3 .1 Series Trigonométricas sin El sistema trigonométrico -1.0 sin -1.0 sin 3 1 cos sin cos () sin () cos () sin () es ortogonal en el intervalo [ ] (, en consecuencia, en cualquier intervalo de longitud, debido a la periodicidad). Por definición esto significa que la integral del producto de cualesquiera dos de estas funciones diferentes sobre dicho intervalo es cero, es decir, para todo N, Z 1cos() = Z 1sin() =0 (.) Z cos ()sin() =0 (.3) Z Z 0 si 6=, cos ()cos() = si =. 0 si 6=, sin ()sin() = si =. Las series que surgirán serán de la forma (.4) (.5) cos + 1 sin + cos ()+ = X ( cos ()+ sin ()) Recordar que sin ± sin = sin ± cos cos +cos = cos + cos cos cos = sin + sin =1 (.6)
4 4 Domingo Alcaraz Candela donde son constantes reales. Estas series se llaman series trigonométricas 3 aloscoeficientes { } + =0 { } + =1 se les llama coeficientes de la serie. Cada término de la serie (.6) tiene periodo. Portantosilaserie(.6) converge, su suma será una función de periodo... Serie de Fourier Las funciones periódicas que se presentan en problemas prácticos con frecuencia son bastante complicadas es deseable representarlas en términos de funciones periódicas simples. Se verá que casi cualquier función periódica () de periodo que aparezca en las aplicaciones (por ejemplo, con relación a vibraciones) puede representarse por una serie trigonométrica la cual se denominará serie de Fourier de. Las series de Fourier surgen de la tarea práctica de representar una función periódica () dada en términos de funciones coseno seno. Estas series son trigonométricas cuos coeficientes se determinan a partir de () mediante ciertas fórmulas (fórmulas de Euler), las cuales se establecerán primero. Después se considerará la teoría de las series de Fourier...1. Fórmulas de Euler para los coeficientes de Fourier Supongamos que () es una función periódica de periodo que puede representarse por una serie trigonométrica () = X ( cos ()+ sin ()), (.7) =1 es decir, se supone que esta serie converge que tiene a () como su suma. Dada una función () como esta, quieren determinarse los coeficientes de la serie trigonométrica correspondiente. Determinemos 0. Al integrar ambos miembros de (.7) se obtiene Z Z " + # 0 () = + X ( cos ()+ sin ()) =1 3 Recordar que cualquier situación en la que está involucrada una serie funcional su convergencia requiere preocuparse por el comportamiento de sus sumas parciales () = 0 + ( cos ()+ sin ()). =1
5 . Series de Fourier 5 Si es posible realizar la integración término a término de la serie 4,se obtiene Z () = Z 0 + X Z Z + µ cos () + sin (). =1 Claramente el primer término del segundo miembro 0 Z = 0. Además sabemos de (.) que las integrales del segundo miembro son cero. Consecuentemente, Z () = 0, es decir, 0 = 1 Z () Determinemos ahora 1 1 Multipliquemos (.7) por cos (), donde Z +,eintegremosde a : Z Z Ã! + X ()cos() = 0 + ( cos ()+ sin ()) cos () =1 Al integrar término a término, se observa que el segundo miembro queda Z 0 cos () Z Z µ cos ()cos() + sin ()cos(). + + =1 Sabemos de (.) que la primera integral es cero. Además de (.4) + X =1 Z cos ()cos() = de (.3) + X =1 Z sin ()cos() =0. 4 La idea consiste en suponer que la serie es uniformemente convergente, lo que permite integrar término a término.
6 6 Domingo Alcaraz Candela Consecuentemente Z ()cos() = para todo Z +. Para determinar 1 se razona de manera análoga a lo anterior pero ahora multiplicando (.7) por sin (), donde Z + Al escribir en lugar de, se obtienen las llamadas fórmulas de Euler = 1 R ()cos() para todo 0. = 1 R (.8) ()sin() para todo 0. Los números dados por (.8) se denominan coeficientes de Fourier de (). La serie trigonométrica () = X ( cos ()+ sin ()) (.9) =1 con coeficientes { } + =0 { } + =1 dados por (.8) se denomina serie de Fourier de () (sin atender la convergencia, ésta la discutiremo más adelante) Ejemplo Onda cuadrada Determinar los coeficientes de Fourier de la función 5 si 0, () = si 0. ( +) = () Las gráficas de las cuatro primeras sumas parciales { } 4 =1 de la Serie 5 Funciones de este tipo se presentan como fuerzas eternas que actúan sobre sistemas mecánicos, fuerzas electromotrices en circuitos eléctricos, etc (el valor de () en un sólo puntonoafectalaintegral,porloquepuededejarseindefinida () en =0 = ±)
7 . Series de Fourier 7 de Fourier de esta serie son = 4 sen = 4-4 µsen + 13 sen = 4 P = sen ( +1) 4 = 4 3P = sen ( +1)... Convergencia de la serie de Fourier Supongamos que () es cualquier función periódica dada de periodo para la que eisten las integrales de (.8); por ejemplo, () es continua o tan sólo continua a trozos. Entonces pueden calcularse los coeficientes de Fourier (.8) de () utilizarlos para formar la serie de Fourier (.9) de (). Sería mu conveniente que la serie así obtenida convergiera tuviera la suma 6 (). La maoría de las funciones que se presentan en las aplicaciones son tales que esto se cumple (salvo en los saltos de (), los cuales discutiremos a continuación). En este caso, cuando la serie de Fourier () 6 Pero no siempre ocurre así, pues eisten muchas funciones integrables e incluso continuas, cua serie de fourier converge en uno o más puntos.
8 8 Domingo Alcaraz Candela de () representa a (), seescribe () = () con un signo de igualdad. Si la serie de Fourier de () no tiene la suma () o no converge, escribiremos () () con una tilde, lo que indica que la serie trigonométrica del segundo miembro tiene los coeficientes de Fourier de () como coeficientes 7,porloque se trata de la serie de Fourier de () Elsiguientepasoesplantearelproblemadelaconvergenciadelaserie de Fourier: hasta qué punto la serie de Fourier de una función es una representación válida de la misma. Nuestro propósito es presentar de manera adecuada un conjunto de condiciones que garanticen que la serie de Fourier de una función no solamente converja, sino que además converja alafunción considerada. Teorema..1 Condición suficiente de convergencia puntual de una serie de Fourier Sea () una función -periódica 8, continua a trozos en el intervalo [ [ que tiene derivada por la izquierda por la derecha en todo punto de dicho intervalo. Entonces la serie de Fourier de () converge su suma 9 es X ( cos ()+ sin ()) = (+ )+( ). =1 Ejemplo 3 Onda cuadrada 7 Empezaremos por poner de manifiesto que la serie de Fourier de una función integrable en el intervalo [ ] no está determinada biunívocamente por la función. Por ejemplo, dos funciones que coinciden en todo el intervalo [ ], salvoenunnúmerofinito de puntos, definen la misma serie de Fourier. 8 Por tanto al considerar series de Fourier, asumiremos que la función está definida en el intervalo (o bien en el intervalo ) que para los otros valores de la variable, viene determinada por la condición ( +) =(). 9 Observar que si () es continua en 0, entonces 0 Fourier converge a ( 0) a que ( + 0 )+( 0 ) = ( 0)+( 0 ) = + 0 = (0 ) laseriede = ( 0).
9 .3 Otras formas de las series de Fourier 9 La onda cuadrada del Ejemplo tiene un salto en 0 =0.Enestepunto su límite por la izquierda es su límite por la derecha es, porloque el promedio de estos límites es 0. La serie de Fourier de la onda cuadrada converge en realidad a este valor cuando =0a que entonces todos sus términos son cero. Se procede de manera similar para los otros saltos. (Esto concuerda con el Teorema..1).3. Otras formas de las series de Fourier La forma canónica de las series de Fourier es la que hemos estado utilizando hasta el momento, donde la función en cuestión estaba definida sobre el intervalo [ [,.3.1. Serie de Fourier para una función de periodo En muchas ocasiones es deseable adaptar la forma de una serie de Fourier a funciones periódicas de periodo =0 en el intervalo [ [. Esto se consigue gracias a un cambio de variable. Sea () una función periódica de periodo. Para desarrollar en serie de Fourier en [ [ hacemos un cambio de variable, poniendo entonces Si definimos =, () = () = µ µ claramente la función es una función periódica de de periodo a que ( +) = µ µ µ ( +) = + = = (). De esta forma si el desarrollo en serie de Fourier de la función () es () = µ X ( cos ()+ sin ()) (.10) =1
10 10 Domingo Alcaraz Candela con coeficientes de Fourier = 1 R ()cos() para todo 0. = 1 R (.11) ()sin() para todo N. entonces, como = sustituendo en (.10) (.11) se obtiene ³ µ = = () X µ µ cos + sin = 1 = 1 µ R ()cos µ R ()sin =1 para todo 0. para todo N. µ, (.1) Generalmente se escribe 0 =,porlotanto, con () X ( cos ( 0 )+ sin ( 0 )), =1 = 1 R ()cos( 0) para todo 0. = 1 R ()sin( 0 ) para todo N. Ejemplo 4 Onda cuadrada periódica Determinar la serie de Fourier de la función 0 si 1 () = si 1 1 con = =4, =. 0 si 1
11 .3 Otras formas de las series de Fourier Series de Fourier de funciones pares e impares A continuación pasamos a considerar el desarrollo en serie trigonométrica de funciones pares e impares. En principio los conceptos desarrollados hasta ahora podrían haberse realizado en cualquier intervalo de longitud. No obstante, el intervalo tienen importantes ventajas a la hora de aprovechar las propiedades simétricas de las funciones. Recordemos que una función (), definida en un intervalo [ ] con 0, es una función par 10 si () = () para todo [ ].Diremos que es una función impar 11 si () = () para todo [ ]. Las funciones cos () son pares las funciones sin () son impares. También sabemos que si es par, entonces si es impar, entonces Z () = Z Z 0 () =0. (). Además es obvio que el producto = de una función par una función impar es impar, a que () = (). µ Consecuentemente, si () es par, entonces el integrando ()sin en (.1) esµ impar, =0. De manera similar, si () es impar, entonces ()cos en (.1) es impar, =0. De esto deducimos el siguiente resultado Teorema.3.1 SeriedeFourierdefuncionespareseimpares Sea una función -periódica integrable de Riemann en [ ]. (i) Si esparlaseriedefourierde es una serie de Fourier de cosenos () X ³ cos (.13) =1 donde los coeficientes { } + =0 se determinan a partir de la función según las fórmulas = Z 0 ()cos() para todo 0 (.14) 10 La gráfica de esta función es simétrica con respecto al eje. 11 la gráfica de una función impar es simétrica respecto del origen de coordenadas
12 1 Domingo Alcaraz Candela (ii) Si es impar la serie de Fourier de es una serie de Fourier de senos + X =1 ³ sin (.15) cuos coeficientes { } + =1 se determinan a partir de la función según las fórmulas = Z 0 ³ ()sin para todo =1 (.16) Ejemplo 5 Obtener la serie de Fourier de la función 1 () = en [ [ Teorema.3. Suma de funciones Los coeficientes de Fourier de una suma 1 + son las sumas de los coeficientes de Fourier de 1 correspondientes. Los coeficientes de Fourier de son el producto de loscoeficientes de Fourier de correspondientes. Ejemplo 6 Pulso rectangular (pag40)
13 .3 Otras formas de las series de Fourier 13 La función () de la siguiente gráfica k es la suma de la función () del Ejemplo la constante. Por tanto, a partir de dicho ejemplo del Teorema.3. se conclue que () = + 4 µsin + 13 sin (3)+15 sin (5)+. Ejemplo 7 Onda diente de sierra (pag41) Determinar la serie de Fourier de la función () = + si ( +) = () Serie de Fourier en notación compleja Supongamos que la función () satisface las condiciones suficientes de desarrollabilidad en serie de Fourier. Entonces es posible representarla en [[ mediante la serie del tipo () X ( cos ()+ sin ()) (.17) =1
14 14 Domingo Alcaraz Candela Aprovechando las fórmulas de Euler =cos + sin hallamos, con =, que =cos sin cos () = sin () =. (.18) Sustituendo ahora (.18) en (.17) se obtiene si denotamos () = X =1 + X =1 µ µ entonces 0 = 0 o equivalentemente () 0 + = + X =1 + + = () 0 + = 0 + = = + X =0 + X + X =1 + X =1 = X 1 + X = + =1 1 X = + Esta es la llamada forma compleja de la serie de Fourier o serie compleja de Fourier. Determinemos ahora la epresión de los coeficientes. Sabemos que = = +
15 .3 Otras formas de las series de Fourier 15 para todo N, entonces = 1 Z = 1 = 1 Z Z = 1 Z = 1 = 1 Z Z ()cos() 1 Z ()sin() ()(cos() sin ()) () 0 ()cos() + 1 Z ()sin() ()(cos()+ sin ()) () para todo N. Claramente también podemos escribir = 1 Z (). para todo Z. Estoscoeficientes reciben el nombre de coeficientes complejos de Fourier de (). Para una función de periodo, el razonamiento anterior da como resultado la serie compleja de Fourier () = + X = ( ), = 1 Z () ( ). Ejemplo 8 Serie compleja de Fourier Encontrar la serie compleja de Fourier de () = si ( +) = () a partir de ella obtener la serie (común de Fourier).
16 16 Domingo Alcaraz Candela.4. Transformada de Fourier Dada una función : R C llamaremos transformada de Fourier de a la función compleja F [ ()] () = (). (.19) para todo R donde la epresión anterior tenga sentido, es decir, donde la integral impropia anterior sea convergente 1. Esta convergencia es más dificil de verificar que en el caso de la transformada de Laplace. Supongamos por ejemplo que son reales, por lo que =cos() sin (), que como sabemos tiene módulo 1. Si () es también real, para garantizar la convergencia absoluta de la integral anterior debe satisfacerse que lím ± () = lím () =0 ± por lo que las funciones reales que tendrán transformada de Fourier tienen 1 La integral impropia + () = () + + () para todo R, se dice que eiste o es convergente si eisten los límites = lím + () = lím () entonces Si + () = +. + =+ (+ ) la integral no es convergente, pero si eiste lím () + a éste límite le llamaremos valor principal de Cauch de la integral impropia. Este valor principal coincide con el de la integral cuando ésta es convergente, por lo que en la integral impropia de la integral de Fourier se considera su valor principal.
17 .4 Transformada de Fourier 17 que tener una gráfica como la siguiente o bien ser nulas fuera de un intervalo compacto [ ]. Ejemplo 9 Determinar la transformada de Fourier de la función () = () (), donde () es la función de Heaviside (etendida a R) para () F [ ()] () Ejemplo 10 Determinar la transformada de Fourier de la función () =.
18 18 Domingo Alcaraz Candela () F [ ()] () Ejemplo 11 Determinar la transformada de Fourier de la función () = () F [ ()] ().4.1. Propiedades Eistencia Las dos condiciones siguientes son suficientes para la eistencia de la transformada de Fourier de un función () definida en R son: 1. () es continua a trozos en R.
19 .4 Transformada de Fourier 19. () es absolutamente integrable 13 en R. Linealidad de la transformación de Fourier Para cualesquiera funciones () () cuas transformadas de Fourier eisten para constantes cualesquiera F [ ()+ ()] () =F [ ()] ()+F [ ()] (). (.0) La prueba de esta propiedad viene directamente de la linealidad de la integral a que F [ ()+ ()] () = = ( ()+ ()) () + = F [ ()] ()+F [ ()] (). () Ejemplo 1 Determinar la transformada de Fourier de la función () = () ()+. Transformada de Fourier de la derivada Sea una función continua absolutamente integrable en R con lím () =0 + 0 continua a trozos en R. Entonces F 0 () () =F [ ()] () (.1) La demostración de este resultado se realiza mediante la fórmula de integración por partes F 0 () () = 13 () + R 0 () = () =+ = + () = F [ ()] ()
20 0 Domingo Alcaraz Candela a que lím + () = lím () =0 + Mediante dos aplicaciones sucesivas de (.1) se obtiene F h i 00 () () =F 0 () () =() F [ ()] () = F [ ()] (). Se aplicará lo mismo para derivadas superiores obteniendo que para 1 F h i ) () () =() F [ ()] (). Ejemplo 13 Determinar la transformada de Fourier de. Cambio de escala Sea 0. Si es una función continua absolutamente integrale en R, entonces F [ ()] () = 1 ³ F [ ()] La demostración de este resultado se realiza mediante el cambio de variable = donde = como0 Por lo tanto F [ ()] () = si + = = +, si = =. = 1 = 1 () () () = 1 F [ ()] ³. Ejemplo 14 Determinar la transformada de Fourier de con 0.
21 .5 Transformada de Fourier inversa 1 Derivada de la transformada Si es una función continua absolutamente integrale en R, entonces F [ ()] () =F [ ()] () Ejemplo 15 Determinar la transformada de Fourier de. Convolución El objetivo es el mismo que en el caso de la transformada de Laplace : la convolución de funciones corresponde a la multiplicación de sus transformadas de Fourier Sean dos funciones continuas por secciones, acotadas absolutamente integrables. Entonces F ( ) =F () F(). (.) Como F () F() = = µ µ () () () (+) () haciendo ahora el cambio de variable + = F () F() = = = µ ( ) () ( ) () ( ) = F ( ).5. Transformada de Fourier inversa Sea () una función compleja de variable real que verifica:
22 Domingo Alcaraz Candela 1. Es continua o continua a trozos en cualquier intervalo finito de R. Si es continua a trozos, en los puntos de discontinuidad 14 está definida por: () = Contiene un número finito de etremos relativos. 3. Eiste () + entonces se verifica lafórmuladelaintegraldefourier () = 1 µ (). Sabemos que la transformada de Fourier de la función es F [ ()] () = () = () por lo tanto la fórmula de la integral de Fourier puede escribirse como () = 1 () escribimos F 1 [ ()] () = 1 () que es la epresión de la transformada inversa de Fourier. Esquemáticamente () F F 1 () Si () es una función dada, la epresión () = 1 () 14 Si no se cumple esta condición diremos que la fórmula integral de Fourier es válida o se cumple casí por todas partes. En las discontinuidades (que son de dalto finito) la fórmula converge a:
23 .6 Ejercicios propuestos 3 es una ecuación integral de función incognita (), de tipo singular por ser la integral impropia. La solución de esta ecuación integral es () = (). A () se le llama también función espectral de la función (). Por tratarse de una fórmula integral hereda las propiedades de la integración, en particular la linealidad F 1 [ ()+ ()] () =F 1 [ ()] ()+F 1 [ ()] () para todo R. Ejemplo 16 Consideremos la función 1 si () = 0 si Se pide: 1. Determinar su transformada de Fourier.. Utilizar el apartado anterior para evaluar sen ()cos() 3. Deducir el valor de 0 sen..6. Ejercicios propuestos 1. Verificar la ortogonalidad del sistema trigonométrico.. Rectificador de media onda Un voltaje senoidal sin (), donde es el tiempo, se hace pasar por un rectificador de media onda que corta la porción negativa de la onda. Encontrar la serie de Fourier de la función periódica resultante 0 si 0, () = con = = 4, =. sin () si 0,
24 4 Domingo Alcaraz Candela 3. Consideremos la función () =. Sepide: a) Determinar la serie de Fourier de la etensión periódica de () en el intervalo [ [. b) Usar el desarrollo obtenido para sumar la serie + 1 =0 ( +1). 4. Consideremos la función 0 si 5 0 () = 3 si 0 5 ( + 10) = (). Se pide: a) Determinar los coeficientes de Fourier de la función. b) Escribir la serie de Fourier. c) Comodeberíadefinirse () cuando = 5, =0 =5para que la serie converga a () en Determinar la serie de Fourier de la función () =, 0 ( +) = (). Con el resultado obtenido verificar que = Desarrollos de medio rango En varias aplicaciones eiste la necesidad práctica de usar series de Fourierenrelaciónconfunciones () que están dadas solamente en algún intervalo, por ejemplo, 0 0 L Podría etenderse () periódicamente con periodo para después representar la función etendida por una serie de Fourier, la cual en general incluiría tanto términos coseno como seno. Sin embargo, ha una alternativa mejor mediante la cual se obtiene siempre una serie de
25 .6 Ejercicios propuestos 5 cosenos al etender primero () de 0 como una función par en el intervalo, L 0 L L para después etender esta nueva función como una función periódica de periodo, como es par, representarla como una serie de Fourier de cosenos. O puede etenderse () como una función impar en el intervalo, comoenlafigura L 0 L L para después etender esta nueva función como una función periódica de periodo, como es impar, representarla por una serie de Fourier de senos. Estas dos series se llaman los dos desarrollos de medio rango de la función (), lacualestádadasóloen lamitaddelrango (la mitad del intervalo de periodicidad de estas series). Encontrar los dos desarrollos de medio rango de la función () = si 0 ( ) si,
26 6 Domingo Alcaraz Candela k 0 L/ L 7. Eplica razonadamente porque no eiste la transformada de Fourier de la función () =1con R. Es absolutamenteintegrableen R? 8. Determinar la transformada de Fourier de la función 1 si 1 () = 0 si 1 9. Aplicando el resultado del ejercicio anterior determinar el valor de la integral µ cos sen cos Para cualquier función par () la transformada de Fourier es la transformada de Fourier de coseno F [ ()] () = su transformada inversa () = 0 0 ()cos() F [ ()] ()cos(). Resolver la ecuación integral 1 si 0 1 ()cos() = 0 0 si Utilizar el ejercicio anterior para demostrar que 0 sen =.
27 .7 Ejercicios complementarios 7.7. Ejercicios complementarios 1. Encuentra la transformada de Fourier de las siguientes funciones cos a) () = 0 b) () = 0 0 c) () = d) () = 0 µ + 1 e) () = µ 1 µ µ µ 0 1 sin () sen () f ) () = 0 0 g) () = cos (); 0 0 h) () = 1. Calculalaconvolución( )() en los siguientes casos: 1 a) () = 0 b) () = 0
28 8 Domingo Alcaraz Candela 3. Calcula la transformada de Fourier inversa de la función () = Encuentra los desarrollos en serie de Fourier de las siguientes funciones periódicas (se da su valor en el intervalo [ [ siendo =,con su periodo. (a) () = ½ 1 [ 1 0[ 1 [0 1[ (b) () = ½ [ 0[) 0 [0 [ (c) () = [ 1 1[ (d) () = 1 [ 0[ (e) () = 0 [0 1[ 1 [1 [ (f) () = ½ [ 1 0[ [0 1[ ½ 0 [ 1[ 1 [1 [ ½ 0 [ 0[ (g) () = [0[ ½ [ 0[ (h) () = [0[
Integral de Fourier y espectros continuos
 9 2 2 2 Esta expresión se denomina forma de Angulo fase (o forma armónica) de la serie de Fourier. Integral de Fourier y espectros continuos Las series de Fourier son una herramienta útil para representar
9 2 2 2 Esta expresión se denomina forma de Angulo fase (o forma armónica) de la serie de Fourier. Integral de Fourier y espectros continuos Las series de Fourier son una herramienta útil para representar
La función, definida para toda, es periódica si existe un número positivo tal que
 Métodos con series de Fourier Definición: Función periódica La función, definida para toda, es periódica si existe un número positivo tal que para toda. El número en un periodo de la función. Si existe
Métodos con series de Fourier Definición: Función periódica La función, definida para toda, es periódica si existe un número positivo tal que para toda. El número en un periodo de la función. Si existe
( + )= ( ) ( ) tiene periodo si es cualquier periodo de ( ). + =cos( +2 )=cos + = ( +2 )=. cosnt+ sinnt) ( )~ Métodos con series de Fourier
 Métodos con series de Fourier Definición: Función periódica La función (), definida para toda, es periódica si existe un número positivo tal que (+)=() para toda. El número en un periodo de la función.
Métodos con series de Fourier Definición: Función periódica La función (), definida para toda, es periódica si existe un número positivo tal que (+)=() para toda. El número en un periodo de la función.
Series de potencias y de Fourier
 Capítulo 2. Series de potencias y de Fourier En este capítulo estudiaremos dos casos particulares, pero muy importantes, de series de funciones: las series de potencias y las series de Fourier. Ambas series
Capítulo 2. Series de potencias y de Fourier En este capítulo estudiaremos dos casos particulares, pero muy importantes, de series de funciones: las series de potencias y las series de Fourier. Ambas series
INDICE Capitulo 1. Números Capitulo 2. Secuencias Capitulo 3. Funciones, Límites y Continuidad
 INDICE Capitulo 1. Números 1 Conjuntos 1 Números reales 1 Representación decimal de los números reales 2 Representación geométrica de los números reales 2 Operación con los números reales 2 Desigualdades
INDICE Capitulo 1. Números 1 Conjuntos 1 Números reales 1 Representación decimal de los números reales 2 Representación geométrica de los números reales 2 Operación con los números reales 2 Desigualdades
Series de Fourier Trigonométricas
 Capítulo 4 Series de Fourier Trigonométricas En el capítulo anterior hemos visto que toda función f L ([, ];R) se puede desarrollar en serie trigonométrica de senos y cosenos del tipo a + X (a n cos nx
Capítulo 4 Series de Fourier Trigonométricas En el capítulo anterior hemos visto que toda función f L ([, ];R) se puede desarrollar en serie trigonométrica de senos y cosenos del tipo a + X (a n cos nx
Lección: Ortogonalidad y Series de Fourier
 Lección: Ortogonalidad y Series de Fourier Dr. Miguel Angel Uh Zapata, Centro de Investigación en Matemáticas, Unidad Mérida Facultad de Matemáticas, UADY Octubre 2015 Miguel Uh Lección: Ortogonalidad
Lección: Ortogonalidad y Series de Fourier Dr. Miguel Angel Uh Zapata, Centro de Investigación en Matemáticas, Unidad Mérida Facultad de Matemáticas, UADY Octubre 2015 Miguel Uh Lección: Ortogonalidad
Ecuaciones Diferenciales Tema 4. Series de Fourier
 Ecuaciones Diferenciales Ester Simó Mezquita Matemática Aplicada IV 1 1. Funciones periódicas 2. Serie de Fourier de una función periódica 3. Convergencia. Teorema de Dirichlet. Fenómeno de Gibbs 4. Forma
Ecuaciones Diferenciales Ester Simó Mezquita Matemática Aplicada IV 1 1. Funciones periódicas 2. Serie de Fourier de una función periódica 3. Convergencia. Teorema de Dirichlet. Fenómeno de Gibbs 4. Forma
Una matriz es un arreglo rectangular de números. Los números en el arreglo se llaman elementos de la matriz. ) ( + ( ) ( )
 MATRICES Una matriz es un arreglo rectangular de números. Los números en el arreglo se llaman elementos de la matriz. Ejemplo 1. Algunos ejemplos de matrices ( + ( ) ( + ( ) El tamaño o el orden de una
MATRICES Una matriz es un arreglo rectangular de números. Los números en el arreglo se llaman elementos de la matriz. Ejemplo 1. Algunos ejemplos de matrices ( + ( ) ( + ( ) El tamaño o el orden de una
PROGRAMA DETALLADO VIGENCIA TURNO UNIVERSIDAD NACIONAL EXPERIMENTAL POLITÉCNICA DE LA FUERZA ARMADA 2009 DIURNO INGENIERIA ELECTRICA ASIGNATURA
 PROGRAMA DETALLADO VIGENCIA TURNO UNIVERSIDAD NACIONAL EXPERIMENTAL POLITÉCNICA DE LA FUERZA ARMADA 2009 DIURNO INGENIERIA ELECTRICA SEMESTRE ASIGNATURA 3er TRANSFORMADAS INTEGRALES CÓDIGO HORAS MAT-20254
PROGRAMA DETALLADO VIGENCIA TURNO UNIVERSIDAD NACIONAL EXPERIMENTAL POLITÉCNICA DE LA FUERZA ARMADA 2009 DIURNO INGENIERIA ELECTRICA SEMESTRE ASIGNATURA 3er TRANSFORMADAS INTEGRALES CÓDIGO HORAS MAT-20254
7.FUNCIÓN REAL DE VARIABLE REAL
 7.FUNCIÓN REAL DE VARIABLE REAL 7.1 CONCEPTOS PREVIOS Dados dos conjuntos A={ 1,, 3,...} y B={y 1, y, y 3,...}, el par ordenado ( m, y n ) indica que el elemento m del conjunto A está relacionado con el
7.FUNCIÓN REAL DE VARIABLE REAL 7.1 CONCEPTOS PREVIOS Dados dos conjuntos A={ 1,, 3,...} y B={y 1, y, y 3,...}, el par ordenado ( m, y n ) indica que el elemento m del conjunto A está relacionado con el
ƒ : {(1, 4), (2, 5), (3, 6), (4, 7)}.
 SECCIÓN 5. Funciones inversas 5. Funciones inversas Verificar que una función es la inversa de otra. Determinar si una función tiene una función inversa. Encontrar la derivada de una función inversa. f
SECCIÓN 5. Funciones inversas 5. Funciones inversas Verificar que una función es la inversa de otra. Determinar si una función tiene una función inversa. Encontrar la derivada de una función inversa. f
José Humberto Serrano Devia Página 1
 Similitudes entre el espacio y las series de Fourier Funciones Ortogonales En esta sección se muestra la forma en que los conceptos vectoriales de producto interno, o producto escalar, y el de ortogonalidad
Similitudes entre el espacio y las series de Fourier Funciones Ortogonales En esta sección se muestra la forma en que los conceptos vectoriales de producto interno, o producto escalar, y el de ortogonalidad
ÍNDICE Capítulo 2 La transformada de Laplace 1 Capítulo 2 Series de Fourier 49 Capítulo 3 La integral de Fourier y las transformadas de Fourier 103
 ÍNDICE Capítulo 2 La transformada de Laplace... 1 1.1 Definición y propiedades básicas... 1 1.2 Solución de problemas con valores iniciales usando la transformada de Laplace... 10 1.3 Teoremas de corrimiento
ÍNDICE Capítulo 2 La transformada de Laplace... 1 1.1 Definición y propiedades básicas... 1 1.2 Solución de problemas con valores iniciales usando la transformada de Laplace... 10 1.3 Teoremas de corrimiento
Capítulo VI. Diferenciabilidad de funciones de varias variables
 Capítulo VI Diferenciabilidad de funciones de varias variables La definición de diferenciabilidad para funciones el cociente no tiene sentido, puesto que no está definido, porque el cociente entre el vector
Capítulo VI Diferenciabilidad de funciones de varias variables La definición de diferenciabilidad para funciones el cociente no tiene sentido, puesto que no está definido, porque el cociente entre el vector
1. Se trata en primer lugar de calcular la transformada de Fourier F[f]. Para ello
![1. Se trata en primer lugar de calcular la transformada de Fourier F[f]. Para ello 1. Se trata en primer lugar de calcular la transformada de Fourier F[f]. Para ello](/thumbs/73/68677028.jpg) 1. Enunciados 1.1. Primer ejercicio Sea f(x := e x, x R. 1. Se trata en primer lugar de calcular la transformada de Fourier F[f]. Para ello a Asegurar que existe probando que la función f es absolutamente
1. Enunciados 1.1. Primer ejercicio Sea f(x := e x, x R. 1. Se trata en primer lugar de calcular la transformada de Fourier F[f]. Para ello a Asegurar que existe probando que la función f es absolutamente
Cálculo I (Grado en Ingeniería Informática) Problemas adicionales resueltos
 Cálculo I (Grado en Ingeniería Informática) - Problemas adicionales resueltos Calcula el ĺımite lím ( n + n + n + ) n Racionalizando el numerador, obtenemos L lím ( n + n + n (n + n + ) (n + ) + ) lím
Cálculo I (Grado en Ingeniería Informática) - Problemas adicionales resueltos Calcula el ĺımite lím ( n + n + n + ) n Racionalizando el numerador, obtenemos L lím ( n + n + n (n + n + ) (n + ) + ) lím
Índice. Tema 8: Series de Fourier. Funciones periódicas. Algunas funciones periódicas. Marisa Serrano, José Ángel Huidobro
 Índice Marisa Serrano, José Ángel Huidobro 1 Universidad de Oviedo email: [email protected] email: [email protected] Funciones periódicas Algunas funciones periódicas f : R R es una función periódica
Índice Marisa Serrano, José Ángel Huidobro 1 Universidad de Oviedo email: [email protected] email: [email protected] Funciones periódicas Algunas funciones periódicas f : R R es una función periódica
UNIDAD 1 NUMEROS COMPLEJOS
 UNIDAD 1 NUMEROS COMPLEJOS El conjunto de los números complejos fue creado para poder resolver algunos problemas matemáticos que no tienen solución dentro del conjunto de los números reales. Por ejemplo
UNIDAD 1 NUMEROS COMPLEJOS El conjunto de los números complejos fue creado para poder resolver algunos problemas matemáticos que no tienen solución dentro del conjunto de los números reales. Por ejemplo
Ecuaciones Diferenciales Ordinarias
 Ecuaciones Diferenciales Ordinarias (Transformada de Laplace) Julio López [email protected] Depto Ingeniería Matemática, Universidad de Chile Verano 2010, Resumen clases Julio López EDO 1/30 Introducción
Ecuaciones Diferenciales Ordinarias (Transformada de Laplace) Julio López [email protected] Depto Ingeniería Matemática, Universidad de Chile Verano 2010, Resumen clases Julio López EDO 1/30 Introducción
7.- Teorema integral de Fourier. Transformada de Fourier
 7.- Teorema integral de Fourier. Transformada de Fourier a) Introducción. b) Transformada de Fourier. c) Teorema integral de Fourier. d) Propiedades de la Transformada de Fourier. e) Teorema de Convolución.
7.- Teorema integral de Fourier. Transformada de Fourier a) Introducción. b) Transformada de Fourier. c) Teorema integral de Fourier. d) Propiedades de la Transformada de Fourier. e) Teorema de Convolución.
Teoría de la Integración
 Licenciatura en Matemáticas y Física Universidad de Antioquia 1 Introducción 2 3 Introducción Para toda persona con formación matemática superior, es conocida la teoría de la integración de Riemann. Sin
Licenciatura en Matemáticas y Física Universidad de Antioquia 1 Introducción 2 3 Introducción Para toda persona con formación matemática superior, es conocida la teoría de la integración de Riemann. Sin
f: D IR IR x f(x) v. indep. v. dependiente, imagen de x mediante f, y = f(x). A x se le llama antiimagen de y por f, y se denota por x = f -1 (y).
 TEMA 8: FUNCIONES. 8. Función real de variable real. 8. Dominio de una función. 8.3 Características de una función: signo, monotonía, acotación, simetría y periodicidad. 8.4 Operaciones con funciones:
TEMA 8: FUNCIONES. 8. Función real de variable real. 8. Dominio de una función. 8.3 Características de una función: signo, monotonía, acotación, simetría y periodicidad. 8.4 Operaciones con funciones:
CONCEPTOS BASICOS DE LA TRANSFORMADA DE LAPLACE LA TRANSFORMADA DE LAPLACE
 LA TRANSFORMADA DE LAPLACE Por cálculo integral sabemos que cuando vamos a determinar una integral impropia de la forma,su desarrollo se obtiene realizando un cambio de variable en el límite superior de
LA TRANSFORMADA DE LAPLACE Por cálculo integral sabemos que cuando vamos a determinar una integral impropia de la forma,su desarrollo se obtiene realizando un cambio de variable en el límite superior de
Funciones reales de variable real
 Tema Funciones reales de variable real Introducción El objetivo fundamental de este tema es recordar conceptos ya conocidos acerca de las funciones reales de variable real.. Conceptos Generales Definición.
Tema Funciones reales de variable real Introducción El objetivo fundamental de este tema es recordar conceptos ya conocidos acerca de las funciones reales de variable real.. Conceptos Generales Definición.
Tema 1: Matrices. El concepto de matriz alcanza múltiples aplicaciones tanto en la representación y manipulación de datos como en el cálculo numérico.
 Tema 1: Matrices El concepto de matriz alcanza múltiples aplicaciones tanto en la representación y manipulación de datos como en el cálculo numérico. 1. Terminología Comenzamos con la definición de matriz
Tema 1: Matrices El concepto de matriz alcanza múltiples aplicaciones tanto en la representación y manipulación de datos como en el cálculo numérico. 1. Terminología Comenzamos con la definición de matriz
+ = 0, siendo z=f(x,y).
 Ecuaciones diferenciales de primer orden ECUACIONES DIFERENCIALES Definición. Se llama ecuación diferencial a toda ecuación que inclua una función, que es la incógnita, alguna de sus derivadas o diferenciales.
Ecuaciones diferenciales de primer orden ECUACIONES DIFERENCIALES Definición. Se llama ecuación diferencial a toda ecuación que inclua una función, que es la incógnita, alguna de sus derivadas o diferenciales.
Estabilidad de ecuaciones diferenciales
 Capítulo 3 Estabilidad de ecuaciones diferenciales En este tema estudiaremos como resolver sistema de ecuaciones diferenciales lineales de coeficientes constantes utilizando la transformada de Laplace,
Capítulo 3 Estabilidad de ecuaciones diferenciales En este tema estudiaremos como resolver sistema de ecuaciones diferenciales lineales de coeficientes constantes utilizando la transformada de Laplace,
CAPITULO 7.SERIES DE FOURIER. 7.1. Sistemas de funciones ortogonales
 CAPITULO 7.SERIES DE FOURIER La publicación por Fourier (1768-1830) de la " Teoría analítica del calor ", fue de una influencia decisiva en las matemáticas posteriores. Se supone en ella que cualquier
CAPITULO 7.SERIES DE FOURIER La publicación por Fourier (1768-1830) de la " Teoría analítica del calor ", fue de una influencia decisiva en las matemáticas posteriores. Se supone en ella que cualquier
Para qué x de ese intervalo alcanza F su valor máximo? Y el valor mínimo?
 Análisis I (A y B) febrero9 Consideremos f() = sen() arctg( 3 Calcular el límite de f cuando tiende a Sea la sucesión ) a n = cosn Es convergente? Determinar el límite, si eiste, de la sucesión {f(a n
Análisis I (A y B) febrero9 Consideremos f() = sen() arctg( 3 Calcular el límite de f cuando tiende a Sea la sucesión ) a n = cosn Es convergente? Determinar el límite, si eiste, de la sucesión {f(a n
Así tenemos el siguiente teorema: Sea f una función analítica en un disco Entonces f admite la representación de potencias:
 Así tenemos el siguiente teorema: Sea f una función analítica en un disco Entonces f admite la representación de potencias: donde conocida como serie de Taylor (o serie de Maclaurin cuando ). Además la
Así tenemos el siguiente teorema: Sea f una función analítica en un disco Entonces f admite la representación de potencias: donde conocida como serie de Taylor (o serie de Maclaurin cuando ). Además la
8. Consecuencias de la Teoría de Cauchy.
 Funciones de variable compleja. Eleonora Catsigeras. 8 Mayo 2006. 77 8. Consecuencias de la Teoría de Cauchy. 8.1. Principio del módulo máximo. Definición 8.1.1. Sea f una función continua en Ω. Se dice
Funciones de variable compleja. Eleonora Catsigeras. 8 Mayo 2006. 77 8. Consecuencias de la Teoría de Cauchy. 8.1. Principio del módulo máximo. Definición 8.1.1. Sea f una función continua en Ω. Se dice
TEORIA MATEMATICAS 5 PRIMER PARCIAL
 Def: Grafica de una función TEORIA MATEMATICAS 5 PRIMER PARCIAL Sea:. Definimos la grafica de f como el subconjunto de formado por los puntos, de en los que es un punto de U. Simbólicamente grafica es:
Def: Grafica de una función TEORIA MATEMATICAS 5 PRIMER PARCIAL Sea:. Definimos la grafica de f como el subconjunto de formado por los puntos, de en los que es un punto de U. Simbólicamente grafica es:
Funciones: Límites y continuidad.
 Límites finitos de sucesiones. Funciones: límites y continuidad Matemáticas I Funciones: Límites y continuidad. + Decimos que una sucesión numérica ( ) n= tiene por límite r R y se escribe =r o de forma
Límites finitos de sucesiones. Funciones: límites y continuidad Matemáticas I Funciones: Límites y continuidad. + Decimos que una sucesión numérica ( ) n= tiene por límite r R y se escribe =r o de forma
UNIVERSIDAD NACIONAL ABIERTA VICERRECTORADO ACADÉMICO SUBPROGRAMA DE DISEÑO ACADÉMICO ÁREA MATEMATICA PLAN DE CURSO
 UNIVERSIDAD NACIONAL ABIERTA VICERRECTORADO ACADÉMICO SUBPROGRAMA DE DISEÑO ACADÉMICO ÁREA MATEMATICA PLAN DE CURSO I. Identificación Nombre: MATEMÁTICA V Código: 739 U.C: 05 Carreras: Ingeniería de Sistemas
UNIVERSIDAD NACIONAL ABIERTA VICERRECTORADO ACADÉMICO SUBPROGRAMA DE DISEÑO ACADÉMICO ÁREA MATEMATICA PLAN DE CURSO I. Identificación Nombre: MATEMÁTICA V Código: 739 U.C: 05 Carreras: Ingeniería de Sistemas
CÁLCULO II. Grado M+I. Sucesiones y series de funciones. Sucesiones y series de funciones 1 / 27. Grado M+I () CÁLCULO II
 CÁLCULO II Grado M+I Sucesiones y series de funciones Sucesiones y series de funciones 1 / Sucesiones funciones. Convergencia puntual Sucesión de funciones Definición Una sucesión de funciones será cualquier
CÁLCULO II Grado M+I Sucesiones y series de funciones Sucesiones y series de funciones 1 / Sucesiones funciones. Convergencia puntual Sucesión de funciones Definición Una sucesión de funciones será cualquier
un conjunto cuyos elementos denominaremos vectores y denotaremos por es un espacio vectorial si verifica las siguientes propiedades:
 CAPÍTULO 2: ESPACIOS VECTORIALES 2.1- Definición y propiedades. 2.1.1-Definición: espacio vectorial. Sea un cuerpo conmutativo a cuyos elementos denominaremos escalares o números. No es necesario preocuparse
CAPÍTULO 2: ESPACIOS VECTORIALES 2.1- Definición y propiedades. 2.1.1-Definición: espacio vectorial. Sea un cuerpo conmutativo a cuyos elementos denominaremos escalares o números. No es necesario preocuparse
Capítulo V. Valores y vectores propios. Diagonalización de operadores lineales.
 Capítulo V Valores y vectores propios. Diagonalización de operadores lineales. Hemos visto que la aplicaciones lineales de en están definidas a través de una expresión de la forma ; pero esta fórmula puede
Capítulo V Valores y vectores propios. Diagonalización de operadores lineales. Hemos visto que la aplicaciones lineales de en están definidas a través de una expresión de la forma ; pero esta fórmula puede
Límites y Continuidad
 Tema 2 Límites y Continuidad Introducción En este tema se trata el concepto de límite de una función real de variable real y sus propiedades, así como algunas de las técnicas fundamentales para el cálculo
Tema 2 Límites y Continuidad Introducción En este tema se trata el concepto de límite de una función real de variable real y sus propiedades, así como algunas de las técnicas fundamentales para el cálculo
MODELACION EN VARIABLES DE ESTADO
 CAPÍTULO VIII INGENIERÍA DE SISTEMAS I MODELACION EN VARIABLES DE ESTADO 8.1. DEFINICIONES Estado: El estado de un sistema dinámico es el conjunto más pequeño de variables de modo que el conocimiento de
CAPÍTULO VIII INGENIERÍA DE SISTEMAS I MODELACION EN VARIABLES DE ESTADO 8.1. DEFINICIONES Estado: El estado de un sistema dinámico es el conjunto más pequeño de variables de modo que el conocimiento de
CAPÍTULO 2 TRANSFORMACIONES LINEALES
 CAPÍULO RANSFORMACIONES LINEALES ransformación Sean V W espacios vectoriales. La función : V W recibe el nombre de transformación, los espacios V W se llaman dominio codominio de la transformación, respectivamente.
CAPÍULO RANSFORMACIONES LINEALES ransformación Sean V W espacios vectoriales. La función : V W recibe el nombre de transformación, los espacios V W se llaman dominio codominio de la transformación, respectivamente.
Variable Compleja I ( ) Ejercicios resueltos. Las convergencias puntual y uniforme de sucesiones y series de funciones
 Variable Compleja I (205-6) Ejercicios resueltos Las convergencias puntual y uniforme de sucesiones y series de funciones Recordemos la definición de la convergencia uniforme: f n (z) f (z) en un conjunto
Variable Compleja I (205-6) Ejercicios resueltos Las convergencias puntual y uniforme de sucesiones y series de funciones Recordemos la definición de la convergencia uniforme: f n (z) f (z) en un conjunto
FUNCIONES DE UNA VARIABLE
 FUNCIONES DE UNA VARIABLE 1- Definiciones 2- Algunas funciones reales 3- Ecuaciones de curvas planas en coordenadas cartesianas 4- Coordenadas polares 5- Coordenadas paramétricas 6- Funciones hiperbólicas
FUNCIONES DE UNA VARIABLE 1- Definiciones 2- Algunas funciones reales 3- Ecuaciones de curvas planas en coordenadas cartesianas 4- Coordenadas polares 5- Coordenadas paramétricas 6- Funciones hiperbólicas
Convergencia y existencia de la serie de Fourier
 A Convergencia y existencia de la serie de Fourier A.1. Convergencia de la serie de Fourier* Posiblemente una de las mayores controversias respecto al desarrollo de Fourier fue su afirmación que cualquier
A Convergencia y existencia de la serie de Fourier A.1. Convergencia de la serie de Fourier* Posiblemente una de las mayores controversias respecto al desarrollo de Fourier fue su afirmación que cualquier
MATEMÁTICAS. Posgrado en Nanotecnología. Dr. Roberto Pedro Duarte Zamorano 2016 Departamento de Física
 MATEMÁTICAS Posgrado en Nanotecnología Dr. Roberto Pedro Duarte Zamorano 016 Departamento de Física TEMARIO 3. Transformada de Fourier 1. Transformadas integrales.. La Transformada de Fourier. 3. Teorema
MATEMÁTICAS Posgrado en Nanotecnología Dr. Roberto Pedro Duarte Zamorano 016 Departamento de Física TEMARIO 3. Transformada de Fourier 1. Transformadas integrales.. La Transformada de Fourier. 3. Teorema
REPRESENTACIÓN DE FUNCIONES
 REPRESENTACIÓN DE FUNCIONES Página 5 REFLEXIONA Y RESUELVE Descripción de una gráfica Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos, y sin mirar la gráfica que aparece al principio,
REPRESENTACIÓN DE FUNCIONES Página 5 REFLEXIONA Y RESUELVE Descripción de una gráfica Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos, y sin mirar la gráfica que aparece al principio,
1. Para la función f(x) = x sen x, halle su polinomio de Taylor de orden 2 en a = 0. x x3 3!, x x3
 Cálculo I (Grado en Ingeniería Informática) Problemas resueltos, - y -4 (tercera parte) Preparado por los profesores de la asignatura: Pablo Fernández, Dragan Vukotić (coordinadores), Luis Guijarro, Kazaros
Cálculo I (Grado en Ingeniería Informática) Problemas resueltos, - y -4 (tercera parte) Preparado por los profesores de la asignatura: Pablo Fernández, Dragan Vukotić (coordinadores), Luis Guijarro, Kazaros
Ecuaciones Diferenciales II. Series de Fourier
 Ecuaciones Diferenciales II Series de Fourier José C. Sabina de Lis Universidad de La Laguna La Laguna, 9 de noviembre de 23 . Problemas de Contorno y series de autofunciones. A) Series de Fourier en senos.
Ecuaciones Diferenciales II Series de Fourier José C. Sabina de Lis Universidad de La Laguna La Laguna, 9 de noviembre de 23 . Problemas de Contorno y series de autofunciones. A) Series de Fourier en senos.
FUNCIONES. Función. π k π +, k } (los puntos que quitamos anulan el coseno). 2. tg x: {x / x =
 Función FUNCIONES Es una relación entre dos magnitudes variables, de tal manera que a cada valor de la primera, llamada independiente, le corresponde un único valor de la segunda, llamada dependiente.
Función FUNCIONES Es una relación entre dos magnitudes variables, de tal manera que a cada valor de la primera, llamada independiente, le corresponde un único valor de la segunda, llamada dependiente.
Tema 5. Series de Potencias
 Tema 5. Series de Potencias Prof. William La Cruz Bastidas 21 de noviembre de 2002 Tema 5 Series de Potencias Definición 5.1 La sucesión de números complejos {z n } tiene un límite o converge a un número
Tema 5. Series de Potencias Prof. William La Cruz Bastidas 21 de noviembre de 2002 Tema 5 Series de Potencias Definición 5.1 La sucesión de números complejos {z n } tiene un límite o converge a un número
Alonso Fernández Galián
 Alonso Fernández Galián TEMA 3: ESTUDIO Y REPRESENTACIÓN DE FUNCIONES Para representar gráficamente una función deben estudiarse los siguientes aspectos: i) Dominio. ii) Puntos de corte con los ejes de
Alonso Fernández Galián TEMA 3: ESTUDIO Y REPRESENTACIÓN DE FUNCIONES Para representar gráficamente una función deben estudiarse los siguientes aspectos: i) Dominio. ii) Puntos de corte con los ejes de
Funciones, Límites y Continuidad
 Tema Funciones, Límites y Continuidad Introducción El objetivo fundamental de este tema es recordar conceptos ya conocidos acerca de las funciones reales de variable real, así como de los límites en dichas
Tema Funciones, Límites y Continuidad Introducción El objetivo fundamental de este tema es recordar conceptos ya conocidos acerca de las funciones reales de variable real, así como de los límites en dichas
10. Series de potencias
 FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 7-2 Basado en el apunte del curso Cálculo (2do semestre), de Roberto Cominetti, Martín Matamala y Jorge San
FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 7-2 Basado en el apunte del curso Cálculo (2do semestre), de Roberto Cominetti, Martín Matamala y Jorge San
Matemáticas de 2º de bachillerato página 1 Integral indefinida. Integral indefinida
 Matemáticas de º de bachillerato página Integral indefinida Integral indefinida.introducción.- La integración es el proceso recíproco de la derivación, es decir, en la derivación se trata de hallar la
Matemáticas de º de bachillerato página Integral indefinida Integral indefinida.introducción.- La integración es el proceso recíproco de la derivación, es decir, en la derivación se trata de hallar la
Límite de una función Funciones continuas
 Límite de una función Funciones continuas Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid 2014-2015 1 LÍMITE CUANDO LA VARIABLE TIENDE A INFINITO. 3 1. Límite cuando la variable tiende
Límite de una función Funciones continuas Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid 2014-2015 1 LÍMITE CUANDO LA VARIABLE TIENDE A INFINITO. 3 1. Límite cuando la variable tiende
TEMA 4. Series de potencias
 TEMA 4 Series de potencias. Introducción En el tema anterior hemos estudiado la aproximación polinómica local de funciones mediante el polinomio de Taylor correspondiente. En particular, vimos para la
TEMA 4 Series de potencias. Introducción En el tema anterior hemos estudiado la aproximación polinómica local de funciones mediante el polinomio de Taylor correspondiente. En particular, vimos para la
(Apuntes en revisión para orientar el aprendizaje) INTEGRALES IMPROPIAS
 (Apuntes en revisión para orientar el aprendizaje) INTEGRALES IMPROPIAS En integración se pide que la función sea continua en el intervalo considerado que además éste sea finito. En este tema se pretende
(Apuntes en revisión para orientar el aprendizaje) INTEGRALES IMPROPIAS En integración se pide que la función sea continua en el intervalo considerado que además éste sea finito. En este tema se pretende
Definición: Dos matrices A y B son iguales si tienen el mismo orden y coinciden los elementos que ocupan el mismo lugar.
 UNIDAD 03: MATRICES Y DETERMINANTES. 3.1 Conceptos de Matrices. 3.1.1 Definición de matriz. Definición: Se lama matriz de orden m x n a un arreglo rectangular de números dispuestos en m renglones y n columnas.
UNIDAD 03: MATRICES Y DETERMINANTES. 3.1 Conceptos de Matrices. 3.1.1 Definición de matriz. Definición: Se lama matriz de orden m x n a un arreglo rectangular de números dispuestos en m renglones y n columnas.
Tema 2: Teorema de estructura de los grupos abelianos finitamente generados.
 ESTRUCTURAS ALGEBRAICAS GRADO EN MATEMÁTICAS. CURSO 215/216 Tema 2: Teorema de estructura de los grupos abelianos finitamente generados. 1.1. Grupo abeliano libre. Bases. Definición 1.1. El grupo Z n con
ESTRUCTURAS ALGEBRAICAS GRADO EN MATEMÁTICAS. CURSO 215/216 Tema 2: Teorema de estructura de los grupos abelianos finitamente generados. 1.1. Grupo abeliano libre. Bases. Definición 1.1. El grupo Z n con
2. Método de separación de variables
 APUNTES DE AMPIACIÓN DE MATEMÁTICAS II PARA INGENIEROS DE TEECOMUNICACIONES Elaborados por Arturo de Pablo, Domingo Pestana y José Manuel Rodríguez 2. Método de separación de variables 2.1. Separación
APUNTES DE AMPIACIÓN DE MATEMÁTICAS II PARA INGENIEROS DE TEECOMUNICACIONES Elaborados por Arturo de Pablo, Domingo Pestana y José Manuel Rodríguez 2. Método de separación de variables 2.1. Separación
T0. TRANSFORMADAS DE LAPLACE
 ESCUELA TÉCNICA SUPERIOR DE NÁUTICA Y MÁQUINAS NAVALES / NAUTIKAKO ETA ITSASONTZI MAKINETAKO GOI ESKOLA TEKNIKOA MATEMATICAS T0. TRANSFORMADAS DE LAPLACE Mediante transformadas de Laplace (por Pierre-Simon
ESCUELA TÉCNICA SUPERIOR DE NÁUTICA Y MÁQUINAS NAVALES / NAUTIKAKO ETA ITSASONTZI MAKINETAKO GOI ESKOLA TEKNIKOA MATEMATICAS T0. TRANSFORMADAS DE LAPLACE Mediante transformadas de Laplace (por Pierre-Simon
f, y el Funciones de varias variables Función de dos variables Definición. Es una función f que asigna a cada pareja ordenada ( xy, ) de D un
 Funciones de varias variables Función de dos variables Definición. Es una función f que asigna a cada pareja ordenada (, ) de D un único número real f (, ). El conjunto D es el dominio de f, el correspondiente
Funciones de varias variables Función de dos variables Definición. Es una función f que asigna a cada pareja ordenada (, ) de D un único número real f (, ). El conjunto D es el dominio de f, el correspondiente
Curso Propedéutico de Cálculo Sesión 1: Funciones
 Curso Propedéutico de Cálculo Sesión 1: Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico Esquema 1 2 Esquema 1 2 El cálculo se basa en las propiedades de los
Curso Propedéutico de Cálculo Sesión 1: Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico Esquema 1 2 Esquema 1 2 El cálculo se basa en las propiedades de los
11. Integrales impropias
 11. Integrales impropias 11.1. Definición de Integrales Impropias Las denominadas integrales impropias son una clase especial de integrales definidas (integrales de Riemann) en las que el intervalo de
11. Integrales impropias 11.1. Definición de Integrales Impropias Las denominadas integrales impropias son una clase especial de integrales definidas (integrales de Riemann) en las que el intervalo de
Sistemas de Ecuaciones Lineales y Matrices
 Capítulo 4 Sistemas de Ecuaciones Lineales y Matrices El problema central del Álgebra Lineal es la resolución de ecuaciones lineales simultáneas Una ecuación lineal con n-incógnitas x 1, x 2,, x n es una
Capítulo 4 Sistemas de Ecuaciones Lineales y Matrices El problema central del Álgebra Lineal es la resolución de ecuaciones lineales simultáneas Una ecuación lineal con n-incógnitas x 1, x 2,, x n es una
CÁLCULO DE DERIVADAS
 TEMA 4 CÁLCULO DE DERIVADAS Contenidos Criterios de Evaluación 1. Función derivada.. Derivadas sucesivas. 3. Derivadas elementales. 4. Álgebra de derivadas. 5. La Regla de la Cadena. 6. Continuidad y derivabilidad.
TEMA 4 CÁLCULO DE DERIVADAS Contenidos Criterios de Evaluación 1. Función derivada.. Derivadas sucesivas. 3. Derivadas elementales. 4. Álgebra de derivadas. 5. La Regla de la Cadena. 6. Continuidad y derivabilidad.
Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones
![Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones](/thumbs/49/25360651.jpg) Semana 09 [1/28] 29 de abril de 2007 Semana 09 [2/28] Definición Sucesión Una sucesión real es una función: f : N R n f (n) Observaciones Para distinguir a una sucesión de las demás funciones, se ocupará
Semana 09 [1/28] 29 de abril de 2007 Semana 09 [2/28] Definición Sucesión Una sucesión real es una función: f : N R n f (n) Observaciones Para distinguir a una sucesión de las demás funciones, se ocupará
Tema 7.0. Repaso de números reales y de funciones
 Matemáticas II (Bachillerato de Ciencias) Análisis: Repaso de números reales y de funciones 47 Tema 70 Repaso de números reales y de funciones El conjunto de los números reales El conjunto de los números
Matemáticas II (Bachillerato de Ciencias) Análisis: Repaso de números reales y de funciones 47 Tema 70 Repaso de números reales y de funciones El conjunto de los números reales El conjunto de los números
Máximos y mínimos de una función real de dos variables reales
 Máimos mínimos de una unción real Deinición Sea D una región del plano Sea :D R Se dice que alcanza su valor máimo absoluto M en un punto P (, ) D cuando M (, ) (,) (,) D Se dice que tiene un máimo relativo
Máimos mínimos de una unción real Deinición Sea D una región del plano Sea :D R Se dice que alcanza su valor máimo absoluto M en un punto P (, ) D cuando M (, ) (,) (,) D Se dice que tiene un máimo relativo
C A P Í T U L O 5 PROPUESTA DE ENSEÑANZA: SECUENCIAS DIDÁCTICAS. Neevia docconverter 5.1
 C A P Í T U L O PROPUESTA DE ENSEÑANZA: SECUENCIAS DIDÁCTICAS CAPÍTULO. PROPUESTA DE ENSEÑANZA: SECUENCIAS DIDÁCTICAS. En este capítulo se mostrarán las diferentes secuencias didácticas o instrumentos
C A P Í T U L O PROPUESTA DE ENSEÑANZA: SECUENCIAS DIDÁCTICAS CAPÍTULO. PROPUESTA DE ENSEÑANZA: SECUENCIAS DIDÁCTICAS. En este capítulo se mostrarán las diferentes secuencias didácticas o instrumentos
ECUACIONES DIFERENCIALES INTRODUCCIÓN A LAS ECUACIONES EN DERIVADAS PARCIALES
 ECUACIONES DIFERENCIALES INTRODUCCIÓN A LAS ECUACIONES EN DERIVADAS PARCIALES Objetivo: El alumno conocerá las ecuaciones en derivadas parciales y aplicará el método de separación de variables en su resolución.
ECUACIONES DIFERENCIALES INTRODUCCIÓN A LAS ECUACIONES EN DERIVADAS PARCIALES Objetivo: El alumno conocerá las ecuaciones en derivadas parciales y aplicará el método de separación de variables en su resolución.
Raíz cuadrada. Superficies de Riemann
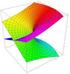 Raíz cuadrada Superficies de Riemann Aplicación: Circuito RLC (a) (b) Aplicación: Circuito RLC Para el circuito (a): De la ley de Ohm con Aplicación: Circuito RLC Es más conveniente utilizar un voltaje
Raíz cuadrada Superficies de Riemann Aplicación: Circuito RLC (a) (b) Aplicación: Circuito RLC Para el circuito (a): De la ley de Ohm con Aplicación: Circuito RLC Es más conveniente utilizar un voltaje
9 Continuidad. Solucionario ACTIVIDADES INICIALES EJERCICIOS PROPUESTOS. 9.I. Dibuja la gráfica de las siguientes funciones.
 Solucionario 9 Continuidad 9.I. Dibuja la gráfica de las guientes funciones. ACTIVIDADES INICIALES a) < f( ) > b) f ( ) a) Si (, ). El segmento de recta pasa por el punto (, ) y se acerca al (, ). Si [,
Solucionario 9 Continuidad 9.I. Dibuja la gráfica de las guientes funciones. ACTIVIDADES INICIALES a) < f( ) > b) f ( ) a) Si (, ). El segmento de recta pasa por el punto (, ) y se acerca al (, ). Si [,
Series de Laurent. En la práctica, los coeficientes de una serie de Laurent se obtienen por métodos distintos a las expresiones integrales a n
 Series de Laurent En la práctica, los coeficientes de una serie de Laurent se obtienen por métodos distintos a las expresiones integrales a n y b n dadas anteriormente. Además se puede demostrar que la
Series de Laurent En la práctica, los coeficientes de una serie de Laurent se obtienen por métodos distintos a las expresiones integrales a n y b n dadas anteriormente. Además se puede demostrar que la
Cálculo I. Índice Continuidad. Julio C. Carrillo E. * 1. Introducción Continuidad puntual Continuidad en un intervalo 8
 2.4. Continuidad Julio C. Carrillo E. * Índice 1. Introducción 1 2. Continuidad puntual 2 3. Continuidad en un intervalo 8 4. Conclusiones 18 * Profesor Escuela de Matemáticas, UIS. 1. Introducción Las
2.4. Continuidad Julio C. Carrillo E. * Índice 1. Introducción 1 2. Continuidad puntual 2 3. Continuidad en un intervalo 8 4. Conclusiones 18 * Profesor Escuela de Matemáticas, UIS. 1. Introducción Las
Teoremas de Convergencia
 Capítulo 24 Teoremas de Convergencia El teorema de la convergencia monótona (Lema 21.3) establece ciertas condiciones sobre una sucesión de funciones medibles para que se puedan permutar los símbolos y
Capítulo 24 Teoremas de Convergencia El teorema de la convergencia monótona (Lema 21.3) establece ciertas condiciones sobre una sucesión de funciones medibles para que se puedan permutar los símbolos y
Principio de Superposición
 1 Sistemas en tiempo continuo discreto Un sistema en tiempo continuo discreto e puede ver como una transformación que se aplica a una señal de entrada en tiempo continuo discreto y produce una señal de
1 Sistemas en tiempo continuo discreto Un sistema en tiempo continuo discreto e puede ver como una transformación que se aplica a una señal de entrada en tiempo continuo discreto y produce una señal de
Funciones en explícitas
 Funciones en eplícitas.- Sea la función f() e, se pide:. Dominio.. Signo de f() en función de.. Asíntotas. 4. Crecimiento y decrecimiento. Máimos y mínimos relativos. 5. Concavidad y conveidad. Puntos
Funciones en eplícitas.- Sea la función f() e, se pide:. Dominio.. Signo de f() en función de.. Asíntotas. 4. Crecimiento y decrecimiento. Máimos y mínimos relativos. 5. Concavidad y conveidad. Puntos
TEMA 1. MATRICES, DETERMINANTES Y APLICACIÓN DE LOS DETERMINANTES. CONCEPTO DE MATRIZ. LA MATRIZ COMO EXPRESIÓN DE TABLAS Y GRAFOS.
 TEMA 1. MATRICES, DETERMINANTES Y APLICACIÓN DE LOS DETERMINANTES. 1. MATRICES. CONCEPTO DE MATRIZ. LA MATRIZ COMO EXPRESIÓN DE TABLAS Y GRAFOS. DEFINICIÓN: Las matrices son tablas numéricas rectangulares
TEMA 1. MATRICES, DETERMINANTES Y APLICACIÓN DE LOS DETERMINANTES. 1. MATRICES. CONCEPTO DE MATRIZ. LA MATRIZ COMO EXPRESIÓN DE TABLAS Y GRAFOS. DEFINICIÓN: Las matrices son tablas numéricas rectangulares
TEMA 2. FUNCIONES REALES DE VARIABLE REAL 2.5. GRÁFICAS DE FUNCIONES REALES DE VARIABLE REAL
 TEMA. FUNCIONES REALES DE VARIABLE REAL.5. GRÁFICAS DE FUNCIONES REALES DE VARIABLE REAL . FUNCIONES REALES DE VARIABLE REAL.5. GRÁFICAS DE FUNCIONES REALES DE VARIABLE REAL.5.1. DOMINIO, CORTES CON LOS
TEMA. FUNCIONES REALES DE VARIABLE REAL.5. GRÁFICAS DE FUNCIONES REALES DE VARIABLE REAL . FUNCIONES REALES DE VARIABLE REAL.5. GRÁFICAS DE FUNCIONES REALES DE VARIABLE REAL.5.1. DOMINIO, CORTES CON LOS
Espacios vectoriales reales.
 Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
CALCULO INTEGRAL CONCEPTOS DE AREA BAJO LA CURVA. (Se utiliza el valor de la función en el extremo izquierdo de cada subintervalo)
 CALCULO INTEGRAL CONCEPTOS DE AREA BAJO LA CURVA El problema del área, el problema de la distancia tanto el valor del área debajo de la gráfica de una función como la distancia recorrida por un objeto
CALCULO INTEGRAL CONCEPTOS DE AREA BAJO LA CURVA El problema del área, el problema de la distancia tanto el valor del área debajo de la gráfica de una función como la distancia recorrida por un objeto
Producto Escalar. AMD Grado en Ingeniería Informática. AMD Grado en Ingeniería Informática (UM) Producto Escalar 1 / 31
 Producto Escalar AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Producto Escalar 1 / 31 Objetivos Al finalizar este tema tendrás que: Saber usar el producto escalar. Calcular
Producto Escalar AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Producto Escalar 1 / 31 Objetivos Al finalizar este tema tendrás que: Saber usar el producto escalar. Calcular
1. LÍMITE DE UNA FUNCIÓN REAL
 INSTITUCION EDUCATIVA DISTRITAL RODRIGO DE BASTIDAS Resolución Nº 88 de noviembre.8/ Secretaria De Educación Distrital REGISTRO DANE Nº-99 Teléfono 6 Barrio Bastidas Santa Marta DEPARTAMENTO DE MATEMATICAS
INSTITUCION EDUCATIVA DISTRITAL RODRIGO DE BASTIDAS Resolución Nº 88 de noviembre.8/ Secretaria De Educación Distrital REGISTRO DANE Nº-99 Teléfono 6 Barrio Bastidas Santa Marta DEPARTAMENTO DE MATEMATICAS
32 EJERCICIOS de CONTINUIDAD 2º BACH.
 3 EJERCICIOS de CONTINUIDAD º BACH. RECORDAR: f() continua en = a lim f(a) Es decir: Una función es continua en un punto si el límite a coincide con la imagen en dicho punto. A efectos prácticos, para
3 EJERCICIOS de CONTINUIDAD º BACH. RECORDAR: f() continua en = a lim f(a) Es decir: Una función es continua en un punto si el límite a coincide con la imagen en dicho punto. A efectos prácticos, para
Sucesiones y series de funciones
 Sucesiones y series de funciones Renato Álvarez Nodarse Departamento de Análisis Matemático Facultad de Matemáticas. Universidad de Sevilla http://euler.us.es/ renato/ 8 de octubre de 2012 Sucesiones y
Sucesiones y series de funciones Renato Álvarez Nodarse Departamento de Análisis Matemático Facultad de Matemáticas. Universidad de Sevilla http://euler.us.es/ renato/ 8 de octubre de 2012 Sucesiones y
Un resultado de Leonhard Euler relativo a series infinitas
 Miscelánea Matemática 33 2) 57 67 SMM Un resultado de Leonhard Euler relativo a series infinitas Gonzalo Aguilar Quiroz Departamento de Física y Matemáticas Universidad de las Américas Puebla MÉXICO [email protected]
Miscelánea Matemática 33 2) 57 67 SMM Un resultado de Leonhard Euler relativo a series infinitas Gonzalo Aguilar Quiroz Departamento de Física y Matemáticas Universidad de las Américas Puebla MÉXICO [email protected]
Funciones y Función lineal
 Profesorado de Nivel Medio Superior en Biología Funciones Función lineal Analicemos los siguientes ejemplos: 1) El gráfico que figura más abajo muestra la evolución de la presión arterial de un paciente
Profesorado de Nivel Medio Superior en Biología Funciones Función lineal Analicemos los siguientes ejemplos: 1) El gráfico que figura más abajo muestra la evolución de la presión arterial de un paciente
V = v 1 +2v 2 +3v 3. v 2. v 1
 Coordenadas Hay muchas maneras de darle coordenadas a los puntos del espacio, las ecuaciones de las curvas o superficies dependen de las coordenadas que utilicemos y eligiendo las coordenadas adecuadas
Coordenadas Hay muchas maneras de darle coordenadas a los puntos del espacio, las ecuaciones de las curvas o superficies dependen de las coordenadas que utilicemos y eligiendo las coordenadas adecuadas
Anexo 1 ( Momentos de segundo orden )
 .1 neo 1 ( Momentos de segundo orden ) 1. Momento de inercia En muchas de las fórmulas empleadas en ingeniería aparecen epresiones analíticas de la forma ρ d, siendo ρ la distancia de un elemento diferencial
.1 neo 1 ( Momentos de segundo orden ) 1. Momento de inercia En muchas de las fórmulas empleadas en ingeniería aparecen epresiones analíticas de la forma ρ d, siendo ρ la distancia de un elemento diferencial
Tema 3. LÍMITES Y CONTINUIDAD DE FUNCIONES
 1 Tema LÍMITES Y CONTINUIDAD DE FUNCIONES Límite de una función en un punto Vamos a estudiar el comportamiento de las funciones f ( ) g( ) ENT[ ] h ( ) i ( ) 4 en el punto = Para ello, damos a valores
1 Tema LÍMITES Y CONTINUIDAD DE FUNCIONES Límite de una función en un punto Vamos a estudiar el comportamiento de las funciones f ( ) g( ) ENT[ ] h ( ) i ( ) 4 en el punto = Para ello, damos a valores
Unidad 3: Razones trigonométricas.
 Unidad 3: Razones trigonométricas 1 Unidad 3: Razones trigonométricas. 1.- Medida de ángulos: grados y radianes. Las unidades de medida de ángulos más usuales son el grado sexagesimal y el radián. Se define
Unidad 3: Razones trigonométricas 1 Unidad 3: Razones trigonométricas. 1.- Medida de ángulos: grados y radianes. Las unidades de medida de ángulos más usuales son el grado sexagesimal y el radián. Se define
Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS
 Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS Grado en Matemáticas Curso 203-204 . Ecuaciones lineales con coeficientes constantes Ecuaciones de primer orden. Encontrar la solución de los siguientes
Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS Grado en Matemáticas Curso 203-204 . Ecuaciones lineales con coeficientes constantes Ecuaciones de primer orden. Encontrar la solución de los siguientes
PROYECTO MATEM CÁLCULO I PLANEAMIENTO ANUAL
 Universidad de Costa Rica Instituto Tecnológico de Costa Rica PROYECTO MATEM CÁLCULO I PLANEAMIENTO ANUAL 2016 Coordinadores: Licda. Elizabeth Díaz G. (U.C.R) y Mag. Randall Blanco B. (TEC) Parcial I II
Universidad de Costa Rica Instituto Tecnológico de Costa Rica PROYECTO MATEM CÁLCULO I PLANEAMIENTO ANUAL 2016 Coordinadores: Licda. Elizabeth Díaz G. (U.C.R) y Mag. Randall Blanco B. (TEC) Parcial I II
REPRESENTACIÓN DE FUNCIONES
 8 REPRESENTACIÓN DE FUNCIONES Página 86 Descripción de una gráfica. Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos y sin mirar la gráfica que aparece al principio, representa esta
8 REPRESENTACIÓN DE FUNCIONES Página 86 Descripción de una gráfica. Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos y sin mirar la gráfica que aparece al principio, representa esta
12.1 CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO
 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES. CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO TASA DE VARIACIÓN MEDIA Deinición Se llama tasa de variación media (T.V.M.) de una unción, y = () en un intervalo
INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES. CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO TASA DE VARIACIÓN MEDIA Deinición Se llama tasa de variación media (T.V.M.) de una unción, y = () en un intervalo
Derivadas de orden superior
 Tema 6 Derivadas de orden superior 6 Polinomios de Taylor Nuestro objetivo es aproimar una función dada mediante funciones polinómicas Resulta conveniente estudiar las funciones polinómicas con más detenimiento
Tema 6 Derivadas de orden superior 6 Polinomios de Taylor Nuestro objetivo es aproimar una función dada mediante funciones polinómicas Resulta conveniente estudiar las funciones polinómicas con más detenimiento
ECUACIÓN DE CAUCHY-EULER 2013
 ECUACIÓN DE CAUCHY-EULER 3 LA ECUACIÓN DE CAUCHY-EULER Se trata de una ecuación con coeficientes variables cua solución general siempre se puede epresar en términos de potencias, senos, cosenos, funciones
ECUACIÓN DE CAUCHY-EULER 3 LA ECUACIÓN DE CAUCHY-EULER Se trata de una ecuación con coeficientes variables cua solución general siempre se puede epresar en términos de potencias, senos, cosenos, funciones
