4.2 Superficies en el espacio
|
|
|
- Salvador Santos de la Fuente
- hace 7 años
- Vistas:
Transcripción
1 4. Sperficies en el espacio 4. a) Parametrización Definición: Una sperficie relar (de clase C m ) es la im. biy. en 3 de na reión bidim. mediante na fnc. relar (de clase C m ) / (,)Î (,)ÎS o sea, S := () ; O(,) := r(,) = x i (,)e i El par () se llama na parametrización de S; (,) se llaman coordenadas de sperficie del pnto P = (,) en esa parametrización; se llama dominio de la parametrización. Ejemplos Parametrización cartesiana de Mone: Si z = f(x,y), entonces S : {x =, y =, z = f(,)}. Así, el hiperboloide de ec. z = x y, será: {x =, y =, z = },... Parametrización crilínea: si se parametriza en nas coordenadas crilíneas: x i = x i (,). El cono del ejercicio PR3.3 parametrizado en cilíndricas: { = a, =, z = ; >0, [0, [}. 4. b) elementos eométricos de na sperficie b) Líneas coordenadas Definiciones: -línea y -línea coordenadas de S por n pnto ( 0, 0 ) L = ({ = t + 0, = 0 }) y L, análoa b) Bases de sperficie: Dada S por (, (,)), PS se definen:. Base natral de sperficie asociada a la parametrización { (P)}: (, ) (, r ) (, xi ) e i (es base tanencial a L y L en P). Matriz de Gram de sperficie de la base natral (será la matriz coa-coa de la Iª F.F.): E (, ) F (, ) (,) = (,) (,); G(,) = [ (,)] = (,) := det[g(,)] = (,) (,) F (, ) G (, ) 3. Vec. normal N y triedro de sperficie: L L N (, ) ;triedro de S:,, N 4. Plano tanente = plano por cada P, de ector característico N(P) 5. Recta normal = recta por P, de c. director N(P) 6. Base natral recíproca de sperficie {, } / 7. Campos de sperficie: = ó T = t N 0 = t y tamb. con componentes normales a S. N (, ) Métodos - matemáticas - ºC
2 Ejemplos: casos notables de parametrización Parametrización de Mone A partir de la ecación cartesiana, explícita {z = f(x, y)} o implícita {F(x, y, z) = 0}: Ejemplo con MatLab: paraboloide hiperbólico; PR3.6-3 Sperficies de reolción Definición eométrica conocida: eneratriz plana, eje de reolción, meridianos y paralelos Parametrización cilíndrica (en sistema de referencia con OZ = eje de reolción; es análoo en otros casos): { x = cos, y = sen, z = f(), a < < b, 0 }, donde f corresponde a la eneratriz (fira). líneas coordenadas: meridianos y paralelos (parametrización ortoonal de S) Alternatias: i) {x = f()cos, y = f()sen, z = }. ii) Otro eje de reolción. Ejemplos: El cono recto como sp. de re.; PR3.6-4 y 5, a, 3. Sperficies reladas Definición: directriz, X(); eneratriz de. director (), en cada pnto de la directriz (fi) P Parametrización relada: r(,) = X() + () () Sp. reladas desarrollables: caracterización analítica Líneas coordenadas de la parametrización relada Ejemplos: el cono recto como sperficie relada el helicoide recto (PR3.6-y); sp. cilíndricas enerales; PR3.7, los apartados señalados del PR3.6 El helicoide desarrollable: param., fira, fira, fira3. Otros casos: sperficies tblares Ejemplo, propesto en examen sept. 008; PR3.9, 9B X() O 3 4. c) Medir sobre S: la Iª Forma Fndamental (IFF) Los objetios a medir sobre na sperficie S módlos y ánlos de campos ectoriales de sperficie, lonitdes de arcos de cra sobre S, áreas de casqetes S* Ì S. en todos los casos se aplica directamente e te la Iª FF actando sobre c. de sp. Fndamento: tensor métrico de sperficie (,) := (,) E F ; G(,) = [ (,) ] = F G Cálclo de módlos y ánlos de ectores de sperficie Si los c.. f, h definidos sobre S / f(,) = f y h(,) = h entonces f = f f = f f = [f f f ] G f fh f h cosf, h = f h f f h h Si los campos tienen componente normal, se sa el triedro {, N} y el tensor E F 0 métrico correspondiente, o sea F G (, ) Métodos - matemáticas - ºC
3 Elemento diferencial de lonitd sobre na sperficie: ds cra C Ì S / r = r(t) está dada por = (t) (parametrización de sperf.) dr Por la r. de la cª.: t dr d d t r dt dt dt t r leo: ds = dr = d = d d E(d ) Fdd G(d ) Primera forma fndamental: la def. clásica (Gass ( )): (ds) = d d = E(d) +Fdd + G(d) := I(d,d) No depende de la parametrización (cambia como al c. de parámetros) Lonitd de arco de cra: Lon = P t ds d d P t donde se bsca expresar el arco P P como C = ({ = (t), t <t<t }) Elemento diferencial de área sobre na sperficie: ds ds = dd = det dd : EGF dd Área(S*) = Área((*)) = d S: dd S* * donde se bscará expresar S* = (*), con * = {(,) : a <<a, b ()<<b ()} o similar. S d ds d 5 Ejemplos de aplicación de la Iª.F.F. Ánlos y módlos de ectores de sperficie Ejemplo: Ánlo de la entana de Viiani con el paralelo de la sp. esférica en cada pnto. Bajo qé ánlo se corta la cra a sí misma sobre el ecador? Lonitdes de arcos de cra sobre sperficies Lonitd de la entana de Viiani (llear a na interal a aproximar) Área de n casqete de sperficie Expresar los elementos diferenciales de área de: i) na sperficie esférica; ii) na sperficie cilíndrica recta circlar; iii) na sperficie cónica Expresar S*=(*), S con * ={(,) :aa < < a, b () < < b ()} (o alternatia análoa) en los casos qe sien: Área encerrada por la entana de Viiani en el hemisferio sperior. Área abarcada por na pechina sobre na esfera de radio R: cálclo nota: en PR4: reaparecerán problemas de áreas de casqetes del Capítlo 5º Peden hacerse: PR3.8, 3.9, 3., 3., 3.7-y, 3.9a y 3.9b-y. 6 Métodos - matemáticas - ºC 3
4 4. d) Deriación del triedro de sperficie. d) Deriación de la base: símb. de Christoffel de sperficie. definiciones de los símbolos: son alores nominales de las componentes, en el triedro {, N} de S, de las deriadas de la propia base, o sea: 3 N : N ; 3 propiedades p :. Simetría: por teorema de Schwartz: k = k (ialdad de deriadas as crzadas). N = = cte. N N 3 3 = 0 3. los símbolos 3 := K son las componentes coas de n tensor de º orden, el tensor de cratra, K,de S, porqe cambian como lo hacen las componentes coariantes de los tensores: dem 4. Además, los símbolos 3 se relacionan con las comptes. K del mismo tensor K, pes se cmple: 3 = K = 3 : dem Así se define: K(,) )=K = K (,) K (, ) como el tensor de cratra de S en cada pnto. La forma coa se llama también IIFF. cálclo: se desprende de la definición y del modo de calclar comptes.: 3 N ; disposic. matricial N Ejemplo: Símbolos del helicoide recto (otros ejemplos en PR3.6: y en otros problemas de PR3, cando se pida sólo la IIFF, 7 como ejercicio, calclar todos los símbolos) na disposición matricial para los cálclos de los símbolos de Christoffel de S: k J J N J i J k f, ic ei N ei N ; K ; K ,, N De las dos matrices qe se obtenan (=, ) se peden extraer los símbolos: 3 := K = componentes coariantes de sperficie del tensor de cratra K de S; Salo el sino. También se obtienen las componentes mixtas del mismo K. 3 También peden calclarse directamente: N (sin J ) Los símbolos de Christoffel restantes,, se disponen matr. a coneniencia Métodos alternatios para calclar a partir de la matriz de Gram G(,) Si A := G= G/ ; B = [ cols. ª de las A's]; C = (B ) t : [ ] = f, = c = ½ G (A + B C ) [donde " ", prodcto matricial ordinario] [B También se peden disponer con = matriz: [ ] = f, = c = ½ G C A ] * [B C A ] 8 [donde "*" indica aloritmo combinación lineal de cajas] Métodos - matemáticas - ºC 4
5 d) Ejemplos de Símbolos de Christoffel y IIFF de sp. Sperficie de reolción Sperficie tórica de radios a b. Si (,) {x = cos, y = sen, z = f() ; 0<, 0<<}, calclar los símbolos de Christoffel de la sperficie en esa parametrización (PR3.7) solción: Ejemplo: PR3.8 (la catenoide) Una sperficie relada: el helicoide recto Si r(,) = X() + () = (R)cos i + (R)sen j + c k es la parametrización relada del helicoide recto [directriz, la hélice X(); eneratrices en la dirección de la normal principal de la hélice en cada pnto]. Calclar los símbolos de Christoffel de S en la forma [ k i] k=f, i=c, =m. solción: (er PR3.6) parm. cil.: {=, =}{x = cos, y = sen, z = ; >0, [0,]} IFF: (,) = + (+ ) (coas pras de sperficie) IIFF: K(,) = ( + ) (coas pras de sp.) 9 4. e) Cratª de na sperf.: tensor crª. y IIª FF. Concepto matemático : La cratra en 3ó de na cra C : {r = r(s) } es na manitd ectorial, qe inclye módlo (cantidad, el escalar ) y dirección (normal principal de C en cada P) y qe se da por el ector := ( ˆt )' s = (r)'' ss : ˆn La cr. de na sperficie es na man. tensorial, qe indica cánto dobla S en n pnto P en cada dir. tanencial, e : Eler ( ) considera para cada e la cra C(e) := S (P;e,N), la sec. plana S seún e (fi.); si ˆ ˆ ˆn es el c. crª. de C(e), se define la crª. norm. de S en la dir.epor: n (e) := ˆ (e, N) Obs.: En eneral, si C { = (s)} S, reslta: d ˆ d d d d ds ds ds ds ds N P L d d d d 3 d e N ds ds ds ds ds ˆ C(e) : ˆ : ˆ n n^ L 3 3 ˆ d d ˆ ˆ n ds ds N t K t N; K : n (de S ) S Teor.: todas las cras de S qe pasen por P en la misma dirección, e, comparten la misma cratra normal, n (e), qe se llama cr. normal de S en esa dirección, e, y en cada P relar. 0 Métodos - matemáticas - ºC 5
6 . Definición de tensor de cratra : Como ha resltado qe n (e) = e 3 e es na forma cadrática, pesto qe los 3 son las componentes coas de n tensor de sperficie ( 3ª propiedad ista de los símb. de Christoffel, ya ista) se define en cada pnto relar P(, ) = (, ) el campo tensorial de sperficie: α β K(, ) = K / K := 3 αβ(, ) (, ), llamado tensor de cratra de S. La forma cadrática n (e) = e K e, se llama IIª FF de S, en cada P y para cada dirección tanencial, e. 3. Análisis del tensor: K es simétrico admite base propia ortonormal. atoalores de K : se llaman cratras principales, k y k ; son la máxima y la mínima cratra normal de S en P. atoectores nitarios de K: se llaman direcs. principales de cratra, d y d ; son las dir. tanenciales en qe se obtienen las secciones normales de máxima y mínima cratra en el pnto; forman na base tanencial ortonrm. llamada base principal de S 3. la representación espectral de K en s base propia de las dir. ppales. Se llama representación principal de K : K(,) = k (,) d (,)d (,) + k (,) d (,)d (,) (con k = cr. ppales.) y reslta: Th. de Eler: e = cosd + send n (e) = k cos + k sen 4. na parametrización de S se dice parametrización principal si en ella la IIFF es diaonal la base natral normalizada es base principal de la sperficie. 4. Clasificación de los pntos de na sperficie Lamando: cr. media, K M := ½ tr(k) = ½(k +k ); cr. total o de Gass, K G := det(k) = k k, de S en P, se clasifican los pntos de S seún la IIFF, asociada intrínsecamente al tensor cratra K. Así: pntos elípticos: ªFF definida (estrict. pos. o ne.) K G > 0 crs. normales 0 y del mismo sino en toda direc. tan. e (S = sp. cóncaa o de n mismo lado del pl. tanente fira ª) pntos parabólicos: ªFF semidefinida K G = 0, K M 0 como antes, salo en na dir. ppal. d en qe k = n (d) = 0 (fira ª) pntos hiperbólicos: ªFF indefinida K G < 0! := dir. asintóticas de S en P / n ( ) = 0; son las dir. de la cra intersecc. de S con s propio plano tanente en P ( fira 3ª) pntos planos: K G = 0 = K M sperficie "achatada" contra s plano tanente (se presenta cando hay n contacto de orden mayor qe entre S y s plano tanente en P ( fira 4ª) nota: la indicatriz de Dpin explica n orien intitio de estos nombres Ejercicios: ) Clasificar los pntos del paraboloide de reolción z = x + y. ) Clasificar los pntos del helicoide recto Métodos - matemáticas - ºC 6
7 Ejemplos y ejercicios de sperficies Ejemplos de aplicación de la IFF y IIFF La sperficie tórica (sp. de re.): clasificar ss pntos. El helicoide recto (sp. relada): PR3.6 Problema: Dada S {z{ = f(x,y)} hallar los coeficientes de la IªFF y IIªFF en términos de las deriadas parciales de f, denotando: p = f' x, q = f' y, R = f'' xx, S = f'' xy, T = f'' yy Calclar ds, ds, K, K M y K G en dicha S. Otros ejercicios de sperficies qe se peden hacer: ) Los problemas de cras PR3.3 y 3.5 peden hacerse también tratando la cra incónita como cra de la sperficie cónica dada en el ennciado, en la forma { = (s) =?, = (s) =?} / t(s) e = cos ó t(s) k = cos ) Peden hacerse PR3.8, 3.0i y ii, 3.4, 3.5, 3.6i a, 3.8i a iii, En eneral, en PR3. a 3.5, los apartados de aplicaciones de la IFF y los qe piden la IIFF o la cratra normal de na cra dada, C S) o clasificar los pntos de S. 3 Firas sobre parametrización de sperficies parametrizaciópn relada pasrametrización de Mone parametrización de reolción 4 Métodos - matemáticas - ºC 7
8 Otras firas de sperficies Carl F. Gass ( ) Leonard Eler ( ) helicoide recto y líneas de cratra en n pnto helicoide tanencia (desarrollable) sperficie tblar de directriz parabólica 5 Sperficie tórica y ss pntos parabólicos sperficie esférica y entana de Viiani Catenoide de reolción y ss líneas principales de cratra Parametrización de na sperficie tblar de directriz dada, C. 6 Métodos - matemáticas - ºC 8
Lección 3. Cálculo vectorial. 4. Integrales de superficie.
 GRAO E INGENIERÍA AEROEPACIAL CURO 0 MATEMÁTICA II PTO E MATEMÁTICA APLICAA II 4 Integrales de sperficie Nestro último paso en la etensión del concepto de integral es el estdio de las integrales de sperficie,
GRAO E INGENIERÍA AEROEPACIAL CURO 0 MATEMÁTICA II PTO E MATEMÁTICA APLICAA II 4 Integrales de sperficie Nestro último paso en la etensión del concepto de integral es el estdio de las integrales de sperficie,
INTEGRALES DE SUPERFICIE.
 INTEGALE DE UPEFICIE. 31. Encontrar el área de la sperficie definida como intersección del plano x + y + z 1 con el sólido x + y 1. olción La sperficie dada se pede parametrizar por x cos v : y (/ ) sen
INTEGALE DE UPEFICIE. 31. Encontrar el área de la sperficie definida como intersección del plano x + y + z 1 con el sólido x + y 1. olción La sperficie dada se pede parametrizar por x cos v : y (/ ) sen
Superficies paramétricas
 SESIÓN 7 7.1 Introducción En este curso ya se han estudiando superficies S que corresponden a gráficos de funciones de dos variables con dos tipos de representaciones: Representación explícita de S, cuando
SESIÓN 7 7.1 Introducción En este curso ya se han estudiando superficies S que corresponden a gráficos de funciones de dos variables con dos tipos de representaciones: Representación explícita de S, cuando
NOMBRE: VECTORES EN EL PLANO. Ángel de la Llave Canosa
 NOMBRE: VECTORES EN EL PLANO Ángel de la Llave Canosa 1 VECTORES EN EL PLANO VECTOR FIJO Un vector fijo AB es n segmento orientado, qe está definido por dos pntos: Un pnto origen y n pnto extremo. Los
NOMBRE: VECTORES EN EL PLANO Ángel de la Llave Canosa 1 VECTORES EN EL PLANO VECTOR FIJO Un vector fijo AB es n segmento orientado, qe está definido por dos pntos: Un pnto origen y n pnto extremo. Los
Esta expresión polinómica puede expresarse como una expresión matricial de la forma; a 11 a 12 a 1n x 1 x 2 q(x 1, x 2,, x n ) = (x 1, x 2,, x n )
 Tema 3 Formas cuadráticas. 3.1. Definición y expresión matricial Definición 3.1.1. Una forma cuadrática sobre R es una aplicación q : R n R que a cada vector x = (x 1, x 2,, x n ) R n le hace corresponder
Tema 3 Formas cuadráticas. 3.1. Definición y expresión matricial Definición 3.1.1. Una forma cuadrática sobre R es una aplicación q : R n R que a cada vector x = (x 1, x 2,, x n ) R n le hace corresponder
Superficies cuádricas
 Superficies cuádricas Jana Rodriguez Hertz GAL2 IMERL 9 de noviembre de 2010 definición superficie cuádrica definición (forma cuadrática) una superficie cuádrica está dada por la ecuación: definición superficie
Superficies cuádricas Jana Rodriguez Hertz GAL2 IMERL 9 de noviembre de 2010 definición superficie cuádrica definición (forma cuadrática) una superficie cuádrica está dada por la ecuación: definición superficie
TEMA 5 VECTORES EN EL ESPACIO MATEMÁTICAS II 2º Bach. 1
 TEMA 5 VECTORES EN EL ESPACIO MATEMÁTICAS II º Bach. TEMA 5 VECTORES EN EL ESPACIO 5. LOS VECTORES Y SUS OPERACIONES DEINICIÓN Un ector es n segmento orientado. Un ector extremo B. Elementos de n ector:
TEMA 5 VECTORES EN EL ESPACIO MATEMÁTICAS II º Bach. TEMA 5 VECTORES EN EL ESPACIO 5. LOS VECTORES Y SUS OPERACIONES DEINICIÓN Un ector es n segmento orientado. Un ector extremo B. Elementos de n ector:
TEMA 5. VECTORES EN EL ESPACIO
 TEMA 5. VECTORES EN EL ESPACIO ÍNDICE 1. INTRODUCCIÓN... 2 2. VECTORES EN EL ESPACIO.... 3 2.1. CONDICIONES INICIALES.... 3 2.2. PRODUCTO DE UN VECTOR POR UN NÚMERO.... 3 2.3. VECTORES UNITARIOS.... 3
TEMA 5. VECTORES EN EL ESPACIO ÍNDICE 1. INTRODUCCIÓN... 2 2. VECTORES EN EL ESPACIO.... 3 2.1. CONDICIONES INICIALES.... 3 2.2. PRODUCTO DE UN VECTOR POR UN NÚMERO.... 3 2.3. VECTORES UNITARIOS.... 3
4. Espacios Vectoriales
 4. Espacios Vectoriales 4.. Definición de espacio, sbespacio ectorial y ss propiedades n ector es na magnitd qe consta de módlo, dirección y sentido. Algnos sin embargo; más teóricos, explicarían qe n
4. Espacios Vectoriales 4.. Definición de espacio, sbespacio ectorial y ss propiedades n ector es na magnitd qe consta de módlo, dirección y sentido. Algnos sin embargo; más teóricos, explicarían qe n
VECTORES EN EL PLANO
 VECTORES EN EL PLANO.- PRIMERO DE BACHILLERATO.- TEORÍA Y EJERCICIOS. Pág. 1 VECTORES EN EL PLANO Vector fijo. Es n segmento orientado. Lo representamos por AB o por. El pnto A es el origen y el pnto B
VECTORES EN EL PLANO.- PRIMERO DE BACHILLERATO.- TEORÍA Y EJERCICIOS. Pág. 1 VECTORES EN EL PLANO Vector fijo. Es n segmento orientado. Lo representamos por AB o por. El pnto A es el origen y el pnto B
Se puede considerar una superficie, como una lámina infinitamente delgada, que recubre un cuerpo, separa dos medios o dos regiones del espacio.
 SUPERFICIES SUPERFICIES Se puede considerar una superficie, como una lámina infinitamente delgada, que recubre un cuerpo, separa dos medios o dos regiones del espacio. Una Superficie puede estar engendrada
SUPERFICIES SUPERFICIES Se puede considerar una superficie, como una lámina infinitamente delgada, que recubre un cuerpo, separa dos medios o dos regiones del espacio. Una Superficie puede estar engendrada
ACADEMIA DE FÍSICO-MATEMÁTICAS MATEMÁTICAS III CICLO ESCOLAR TERCER SEMESTRE G E O M É T R Í A GUÍA A N A L Í T I C A
 CENTRO DE ESTUDIOS DE BACHILLERATO LIC. JESÚS REYES HEROLES ACADEMIA DE FÍSICO-MATEMÁTICAS MATEMÁTICAS III CICLO ESCOLAR TERCER SEMESTRE GEOMETRÍA G E O M É T R Í A GUÍA ANALÍTICA A N A L Í T I C A G U
CENTRO DE ESTUDIOS DE BACHILLERATO LIC. JESÚS REYES HEROLES ACADEMIA DE FÍSICO-MATEMÁTICAS MATEMÁTICAS III CICLO ESCOLAR TERCER SEMESTRE GEOMETRÍA G E O M É T R Í A GUÍA ANALÍTICA A N A L Í T I C A G U
6 La semejanza en el plano
 TIVIS MPLIIÓN 6 La semejanza en el plano 1. alcla las medidas de los segmentos,, z, t en la sigiente figra, sabiendo qe las medidas de los segmentos conocidos están epresadas en metros. 4 G z t. ibja n
TIVIS MPLIIÓN 6 La semejanza en el plano 1. alcla las medidas de los segmentos,, z, t en la sigiente figra, sabiendo qe las medidas de los segmentos conocidos están epresadas en metros. 4 G z t. ibja n
8. Geometrías no euclidianas. Modelo de Poincaré de la Geometría Hiperbólica
 LECTURA N 14 Capítulo 8 de LA GEOMETRÍA EN LA FORMACIÓN DE PROFESORES de Luis SANTALÓ - Red Olímpica. Buenos Aires. 1993 8. Geometrías no euclidianas. Modelo de Poincaré de la Geometría Hiperbólica Bibliografía:
LECTURA N 14 Capítulo 8 de LA GEOMETRÍA EN LA FORMACIÓN DE PROFESORES de Luis SANTALÓ - Red Olímpica. Buenos Aires. 1993 8. Geometrías no euclidianas. Modelo de Poincaré de la Geometría Hiperbólica Bibliografía:
VECTORES EN EL ESPACIO
 VECTORES EN EL ESPACIO Para poder isalizar los elementos de R 3 ={(x,y,z)/x,y,z R}, primero fijamos n sistema de coordenadas, eligiendo n pnto en el espacio llamado el origen qe denotaremos por O, y tres
VECTORES EN EL ESPACIO Para poder isalizar los elementos de R 3 ={(x,y,z)/x,y,z R}, primero fijamos n sistema de coordenadas, eligiendo n pnto en el espacio llamado el origen qe denotaremos por O, y tres
MATEMÁTICASII Curso académico BLOQUE GEOMETRÍA. TEMA 1: VECTORES
 MATEMÁTICASII Curso académico 2015-2016 BLOQUE GEOMETRÍA. TEMA 1: VECTORES 1.1 VECTORES DEL ESPACIO. VECTORES LIBRES DEL ESPACIO Sean y dos puntos del espacio. Llamaremos vector (fijo) a un segmento orientado
MATEMÁTICASII Curso académico 2015-2016 BLOQUE GEOMETRÍA. TEMA 1: VECTORES 1.1 VECTORES DEL ESPACIO. VECTORES LIBRES DEL ESPACIO Sean y dos puntos del espacio. Llamaremos vector (fijo) a un segmento orientado
TORRE DE CONTROL DEL AEROPUERTO DE ABU DHABI
 11 de diciembre del 2009 يبظوبأ TORRE DE CONTROL DEL AEROPUERTO DE ABU DHABI Proyecto primer cuatrimestre Pablo Navarro Aguirre ÍNDICE ENTREGA 1 3 -> Previsualización del proyecto y planificación de las
11 de diciembre del 2009 يبظوبأ TORRE DE CONTROL DEL AEROPUERTO DE ABU DHABI Proyecto primer cuatrimestre Pablo Navarro Aguirre ÍNDICE ENTREGA 1 3 -> Previsualización del proyecto y planificación de las
ALGEBRA Y GEOMETRÍA I DPTO. DE MATEMÁTICA ESCUELA DE FORMACIÓN BÁSICA F.C.E.I.A U.N.R
 ALGEBRA Y GEOMETRÍA I DPTO. DE MATEMÁTICA ESCUELA DE FORMACIÓN BÁSICA F.C.E.I.A U.N.R SUPERFICIES ING. RICARDO F. SAGRISTÁ -2006- SUPERFICIES.- 1.- Ecuaciones de superficies. Ya hemos estudiado la superficie
ALGEBRA Y GEOMETRÍA I DPTO. DE MATEMÁTICA ESCUELA DE FORMACIÓN BÁSICA F.C.E.I.A U.N.R SUPERFICIES ING. RICARDO F. SAGRISTÁ -2006- SUPERFICIES.- 1.- Ecuaciones de superficies. Ya hemos estudiado la superficie
Elementos de Cálculo en Varias Variables
 Elementos de Cálculo en Varias Variables Departamento de Matemáticas, CSI/ITESM 5 de octubre de 009 Índice Introducción Derivada parcial El Jacobiano de una Función 5 Derivadas Superiores 5 5 Derivada
Elementos de Cálculo en Varias Variables Departamento de Matemáticas, CSI/ITESM 5 de octubre de 009 Índice Introducción Derivada parcial El Jacobiano de una Función 5 Derivadas Superiores 5 5 Derivada
GEOMETRÍA ANALÍTICA AB CD CD AB CD
 GEOMETRÍA ANALÍTICA.- Vectores..- Vectores fijos en el plano Llamaremos ector fijo a todo par ordenado de pntos del plano. Si los pntos son A y B conendremos en representar por AB el ector fijo qe determinan;
GEOMETRÍA ANALÍTICA.- Vectores..- Vectores fijos en el plano Llamaremos ector fijo a todo par ordenado de pntos del plano. Si los pntos son A y B conendremos en representar por AB el ector fijo qe determinan;
( ), está dada por: g ( x) = log 2 ( x),x > 0. # % 3x log 2 ( 5), x 1 & + -, . log 2. log 2 ( x 3
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS CURSO DE NIVELACIÓN 05 S SEGUNDA EVALUACIÓN DE MATEMÁTICAS PARA INGENIERÍAS Y EDUCACIÓN
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS CURSO DE NIVELACIÓN 05 S SEGUNDA EVALUACIÓN DE MATEMÁTICAS PARA INGENIERÍAS Y EDUCACIÓN
8.4. CRITERIO DE ESTABILIDAD POR EL METODO DIRECTO DE LIAPUNOV
 8.4. CRITERIO DE ESTAB.: METODO DE LIAPUNOV 309 8.4. CRITERIO DE ESTABILIDAD POR EL METODO DIRECTO DE LIAPUNOV Consideremos el sistema autónomo dx = F (x, y) dt (8.32) dt = G(x, y), y supongamos que tiene
8.4. CRITERIO DE ESTAB.: METODO DE LIAPUNOV 309 8.4. CRITERIO DE ESTABILIDAD POR EL METODO DIRECTO DE LIAPUNOV Consideremos el sistema autónomo dx = F (x, y) dt (8.32) dt = G(x, y), y supongamos que tiene
3.2 EL PRODUCTO ESCALAR Y LAS PROYECCIONES EN R 2
 34 CAPÍTULO 3 Vectores en R R 3 ais sqare a=ais; ais([min(a([1,3])),ma(a([,4])),min(a([1,3])),ma(a([,4]))]) % hold off Una ez qe se haa escrito la fnción en n archio con nombre lincomb.m, dé el comando
34 CAPÍTULO 3 Vectores en R R 3 ais sqare a=ais; ais([min(a([1,3])),ma(a([,4])),min(a([1,3])),ma(a([,4]))]) % hold off Una ez qe se haa escrito la fnción en n archio con nombre lincomb.m, dé el comando
Superficies Curvas. Guía de clase elaborada por Ing. Guillermo Verger
 Superficies Curvas Guía de clase elaborada por Ing. Guillermo Verger www.ingverger.com.ar Superficie cilíndrica Es aquella generada por una recta llamada generatriz que se mueve en el espacio manteniendose
Superficies Curvas Guía de clase elaborada por Ing. Guillermo Verger www.ingverger.com.ar Superficie cilíndrica Es aquella generada por una recta llamada generatriz que se mueve en el espacio manteniendose
Tercera Parte: Producto Vectorial y Producto Mixto entre vectores
 Tercera Parte: Prodcto Vectorial Prodcto Mito entre ectores Introdcción Retomemos el caso los dos pintores: Carlos Jan. Finaliada la tarea de moer el escritorio, el arqitecto qe coordina la obra, indica
Tercera Parte: Prodcto Vectorial Prodcto Mito entre ectores Introdcción Retomemos el caso los dos pintores: Carlos Jan. Finaliada la tarea de moer el escritorio, el arqitecto qe coordina la obra, indica
1. Producto escalar. Propiedades Norma de un vector. Espacio normado. 1.2.Ortogonalidad. Ángulos. 1.4.Producto escalar en V 3.
 . Producto escalar. Propiedades... Norma de un vector. Espacio normado...ortogonalidad. Ángulos..3.Producto escalar en V..4.Producto escalar en V 3.. Producto vectorial de dos vectores de V 3...Expresión
. Producto escalar. Propiedades... Norma de un vector. Espacio normado...ortogonalidad. Ángulos..3.Producto escalar en V..4.Producto escalar en V 3.. Producto vectorial de dos vectores de V 3...Expresión
LA CIRCUNFERENCIA. La circunferencia es la sección producida por un plano perpendicular al eje.
 LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
Magnitudes escalares, son aquellas que quedan definidas por una sola cantidad que denominaremos valor del escalar.
 +34 9 76 056 - Fa: +34 9 78 477 Vectores: Vamos a distingir dos tipos de magnitdes: Magnitdes escalares, son aqellas qe qedan definidas por na sola cantidad qe denominaremos valor del escalar. Ej: Si decimos
+34 9 76 056 - Fa: +34 9 78 477 Vectores: Vamos a distingir dos tipos de magnitdes: Magnitdes escalares, son aqellas qe qedan definidas por na sola cantidad qe denominaremos valor del escalar. Ej: Si decimos
VECTORES EN EL ESPACIO
 VECTORES EN EL ESPACIO (,4,3) MATEMÁTICAS II º Bachillerato Alfonso Gonále IES Fernando de Mena Dpto. de Matemáticas I. DEFINICIONES 1 Módlo: Indica la intensidad, iene dado por la longitd de la flecha
VECTORES EN EL ESPACIO (,4,3) MATEMÁTICAS II º Bachillerato Alfonso Gonále IES Fernando de Mena Dpto. de Matemáticas I. DEFINICIONES 1 Módlo: Indica la intensidad, iene dado por la longitd de la flecha
Tema 2.- Formas Cuadráticas.
 Álgebra. 004 005. Ingenieros Industriales. Departamento de Matemática Aplicada II. Universidad de Sevilla. Tema.- Formas Cuadráticas. Definición y representación matricial. Clasificación de las formas
Álgebra. 004 005. Ingenieros Industriales. Departamento de Matemática Aplicada II. Universidad de Sevilla. Tema.- Formas Cuadráticas. Definición y representación matricial. Clasificación de las formas
ACTIVIDADES INICIALES. b) ( 1, 6) d) (0, 3) (0, 1) (0, 2) f) ( 8, 4) (24, 6) (16, 2) h) ( 5, 3) (2, 2) ( 3, 1) EJERCICIOS PROPUESTOS
 Solcionario 4 Vectores TIVIDDES INIILES 4.I. Efectúa las sigientes operaciones: a) (5, 3) (, 4) c) 5(3, ) (, 4) e) (7, 4) (, ) g) (3, 6) 3 (, ) b) (6, 4) (7, ) d) 3(0, ) (0, 3) f) 4(, ) 6(4, ) h) (5, 3)
Solcionario 4 Vectores TIVIDDES INIILES 4.I. Efectúa las sigientes operaciones: a) (5, 3) (, 4) c) 5(3, ) (, 4) e) (7, 4) (, ) g) (3, 6) 3 (, ) b) (6, 4) (7, ) d) 3(0, ) (0, 3) f) 4(, ) 6(4, ) h) (5, 3)
CONCEPTOS PRELIMINARES
 CONCEPTOS PRELIMINARES Matemáticas II En R un conjunto abierto es la unión de intervalos abiertos. Tanto el concepto de conjunto abierto como de intervalo abierto se generaliza en el plano y en el espacio.
CONCEPTOS PRELIMINARES Matemáticas II En R un conjunto abierto es la unión de intervalos abiertos. Tanto el concepto de conjunto abierto como de intervalo abierto se generaliza en el plano y en el espacio.
CBC. Matemática (51) universoexacto.com 1
 CBC Matemática (51) universoexacto.com 1 PROGRAMA ANALÍTICO 1 :: UNIDAD 1 Números Reales y Coordenadas Cartesianas Representación de los números reales en una recta. Intervalos de Distancia en la recta
CBC Matemática (51) universoexacto.com 1 PROGRAMA ANALÍTICO 1 :: UNIDAD 1 Números Reales y Coordenadas Cartesianas Representación de los números reales en una recta. Intervalos de Distancia en la recta
ALGEBRA. Escuela Politécnica Superior de Málaga
 ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
Expresiones de velocidad y aceleración en distintas coordenadas
 Apéndice B Expresiones de velocidad y aceleración en distintas coordenadas Índice B.1. Coordenadas cartesianas............... B.1 B.2. Coordenadas cilíndricas y polares......... B.2 B.3. Coordenadas esféricas................
Apéndice B Expresiones de velocidad y aceleración en distintas coordenadas Índice B.1. Coordenadas cartesianas............... B.1 B.2. Coordenadas cilíndricas y polares......... B.2 B.3. Coordenadas esféricas................
1. Coordenadas en el plano. (Sistema de coordenadas, ejes de coordenadas, abcisas, ordenadas, cuadrantes)
 Bloque 7. VECTORES. ECUACIONES DE LA RECTA. (En el libro Tema 9, página 159) 1. Coordenadas en el plano. 2. Definiciones: vector libre, módulo, dirección, sentido, vectores equipolentes, vector fijo, coordenadas
Bloque 7. VECTORES. ECUACIONES DE LA RECTA. (En el libro Tema 9, página 159) 1. Coordenadas en el plano. 2. Definiciones: vector libre, módulo, dirección, sentido, vectores equipolentes, vector fijo, coordenadas
Apuntes de dibujo de curvas
 Apuntes de dibujo de curvas El objetivo de estas notas es dar unas nociones básicas sobre dibujo de curvas definidas por medio de ecuaciones cartesianas explícitas o paramétricas y polares: 1. Curvas en
Apuntes de dibujo de curvas El objetivo de estas notas es dar unas nociones básicas sobre dibujo de curvas definidas por medio de ecuaciones cartesianas explícitas o paramétricas y polares: 1. Curvas en
Colegio Internacional Torrequebrada. Departamento de Matemáticas
 Geometría. Problema 1: Calcula la distancia del punto P(1, 1, 1) a la recta Problema 2: Dadas las rectas, se pide: a) Analiza su posición relativa. b) Halla la ecuación general del plano π que contiene
Geometría. Problema 1: Calcula la distancia del punto P(1, 1, 1) a la recta Problema 2: Dadas las rectas, se pide: a) Analiza su posición relativa. b) Halla la ecuación general del plano π que contiene
Integral de superficie.
 Tema 4 Integral de superficie. 4.1 uperficies. Definición 4.1 ean IR 2 un conjunto conexo y κ: IR 3 una función continua. La imagen = κ se llama superficie descrita por κ. También se dice que κ es una
Tema 4 Integral de superficie. 4.1 uperficies. Definición 4.1 ean IR 2 un conjunto conexo y κ: IR 3 una función continua. La imagen = κ se llama superficie descrita por κ. También se dice que κ es una
Translaciones, giros, simetrías.
 Translaciones, giros, simetrías. Transformaciones geométricas Transformación geométrica es una aplicación del plano en el plano tal que a cada punto de un plano le hace corresponder otro punto del mismo
Translaciones, giros, simetrías. Transformaciones geométricas Transformación geométrica es una aplicación del plano en el plano tal que a cada punto de un plano le hace corresponder otro punto del mismo
Las anteriores fórmulas suelen expresarse matricialmente como
 Capítulo III Teoría de las curvas 1. Clasificación de curvas en R 3 En esta sección veremos que, esencialmente, la curvatura y la torsión determinan las curvas de R 3. Para ello necesitaremos las conocidas
Capítulo III Teoría de las curvas 1. Clasificación de curvas en R 3 En esta sección veremos que, esencialmente, la curvatura y la torsión determinan las curvas de R 3. Para ello necesitaremos las conocidas
Dos matrices son iguales cuando tienen la misma dimensión y los elementos que ocupan el mismo lugar en ambas son iguales
 Introducción Las matrices aparecen por primera vez hacia el año 1850, introducidas por J.J. Sylvester. El desarrollo inicial de la teoría se debe al matemático W.R. Hamilton en 1853. En 1858, A. Cayley
Introducción Las matrices aparecen por primera vez hacia el año 1850, introducidas por J.J. Sylvester. El desarrollo inicial de la teoría se debe al matemático W.R. Hamilton en 1853. En 1858, A. Cayley
10. 1 Definición de espacio euclídeo.
 ESCUELA TÉCNICA SUPERIOR DE NÁUTICA Y MÁQUINAS NAVALES / NAUTIKAKO ETA ITSASONTZI MAKINETAKO GOI ESKOLA TEKNIKOA MATEMATICAS 10. ESPACIOS EUCLÍDEOS 10. 1 Definición de espacio euclídeo. Producto escalar
ESCUELA TÉCNICA SUPERIOR DE NÁUTICA Y MÁQUINAS NAVALES / NAUTIKAKO ETA ITSASONTZI MAKINETAKO GOI ESKOLA TEKNIKOA MATEMATICAS 10. ESPACIOS EUCLÍDEOS 10. 1 Definición de espacio euclídeo. Producto escalar
Ejercicios resueltos.
 E.T.S. Arquitectura Curvas y super cies. Ejercicios resueltos.. Sea la curva intersección de la super cie z = xy con el cilindro parabólico y = x. Se pide: (a) En el punto P de coordenadas (0; 0; 0), obtener
E.T.S. Arquitectura Curvas y super cies. Ejercicios resueltos.. Sea la curva intersección de la super cie z = xy con el cilindro parabólico y = x. Se pide: (a) En el punto P de coordenadas (0; 0; 0), obtener
Tema 2: Vectores libres
 Tema 2: Vectores libres FISICA I, 1º Grado en Ingeniería Aeroespacial Escuela Técnica Superior de Ingeniería Universidad de Sevilla 1 Índice Magnitudes escalares y vectoriales Definición de vector Vectores
Tema 2: Vectores libres FISICA I, 1º Grado en Ingeniería Aeroespacial Escuela Técnica Superior de Ingeniería Universidad de Sevilla 1 Índice Magnitudes escalares y vectoriales Definición de vector Vectores
Problemas de Espacios Vectoriales
 Problemas de Espacios Vectoriales 1. Qué condiciones tiene que cumplir un súbconjunto no vacío de un espacio vectorial para que sea un subespacio vectorial de este? Pon un ejemplo. Sean E un espacio vectorial
Problemas de Espacios Vectoriales 1. Qué condiciones tiene que cumplir un súbconjunto no vacío de un espacio vectorial para que sea un subespacio vectorial de este? Pon un ejemplo. Sean E un espacio vectorial
Academia de Matemáticas T.M Geometría Analítica Página 1
 INSTITUTO POLITECNICO NACIONAL CENTRO DE ESTUDIOS CIENTIFICOS Y TECNOLOGICOS 10. CARLOS VALLEJO MÁRQUEZ PROBLEMARIO DE GEOMETRIA ANALITICA Distancia entre puntos 1.- Determina la distancia entre los puntos
INSTITUTO POLITECNICO NACIONAL CENTRO DE ESTUDIOS CIENTIFICOS Y TECNOLOGICOS 10. CARLOS VALLEJO MÁRQUEZ PROBLEMARIO DE GEOMETRIA ANALITICA Distancia entre puntos 1.- Determina la distancia entre los puntos
12.2 Vectores Algunos de los factores que medimos están determinados simplemente por sus magnitudes. Por
 . Vectores 665. Vectores Algnos de los factores qe medimos están determinados simplemente por ss magnitdes. Por ejemplo, para registrar la masa, la longitd o el tiempo sólo necesitamos escribir n número
. Vectores 665. Vectores Algnos de los factores qe medimos están determinados simplemente por ss magnitdes. Por ejemplo, para registrar la masa, la longitd o el tiempo sólo necesitamos escribir n número
Introducción La Circunferencia Parábola Elipse Hiperbola. Conicas. Hermes Pantoja Carhuavilca
 Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica I Contenido 1 Introducción 2 La Circunferencia 3 Parábola 4 Elipse 5 Hiperbola Objetivos Se persigue que el estudiante:
Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica I Contenido 1 Introducción 2 La Circunferencia 3 Parábola 4 Elipse 5 Hiperbola Objetivos Se persigue que el estudiante:
1.2 TÉCNICAS DE LA DERIVACIÓN.
 . TÉCNICAS DE LA DERIVACIÓN... DERIVACIÓN DE FUNCIONES ALGEBRAICAS Generalmente la derivación se lleva acabo aplicando fórmlas obtenidas mediante la regla general de la derivación y qe calclaremos a continación,
. TÉCNICAS DE LA DERIVACIÓN... DERIVACIÓN DE FUNCIONES ALGEBRAICAS Generalmente la derivación se lleva acabo aplicando fórmlas obtenidas mediante la regla general de la derivación y qe calclaremos a continación,
Integrales dobles. Integrales dobles
 Integrales dobles Integrales iteradas b g2 (x) a g 1 (x) f(x, y) dydx ó d h2 (y) c h 1 (y) f(x, y) dxdy Los límites interiores de integración pueden ser variables respecto a la variable exterior de integración,
Integrales dobles Integrales iteradas b g2 (x) a g 1 (x) f(x, y) dydx ó d h2 (y) c h 1 (y) f(x, y) dxdy Los límites interiores de integración pueden ser variables respecto a la variable exterior de integración,
TEMARIO DE PROFESORES DE ENSEÑANZA SECUNDARIA MATEMÁTICAS
 HOJA INFORMATIVA A.5.2.33 TEMARIO DE PROFESORES DE ENSEÑANZA SECUNDARIA MATEMÁTICAS Publicado en el B.O.E. de 21 de Septiembre de 1.993 MARZO 1998 MATEMÁTICAS 1. Números naturales. Sistemas de numeración.
HOJA INFORMATIVA A.5.2.33 TEMARIO DE PROFESORES DE ENSEÑANZA SECUNDARIA MATEMÁTICAS Publicado en el B.O.E. de 21 de Septiembre de 1.993 MARZO 1998 MATEMÁTICAS 1. Números naturales. Sistemas de numeración.
TRIGONOMETRÍA ESFÉRICA 2001 Kepler C k Ikastegia
 TRIGNMETRÍ ESFÉRI 2001 Kepler k Ikastegia 2 1.1 Introducción La Trigonometría es una rama de la Matemática en la que se analiza la medida de las partes de los triángulos, tanto de los triángulos planos
TRIGNMETRÍ ESFÉRI 2001 Kepler k Ikastegia 2 1.1 Introducción La Trigonometría es una rama de la Matemática en la que se analiza la medida de las partes de los triángulos, tanto de los triángulos planos
ESCALARES Y VECTORES
 ESCALARES Y VECTORES MAGNITUD ESCALAR Un escalar es un tipo de magnitud física que se expresa por un solo número y tiene el mismo valor para todos los observadores. Se dice también que es aquella que solo
ESCALARES Y VECTORES MAGNITUD ESCALAR Un escalar es un tipo de magnitud física que se expresa por un solo número y tiene el mismo valor para todos los observadores. Se dice también que es aquella que solo
PLAN DE ESTUDIOS DE MS
 PLAN DE ESTUDIOS DE MS Temario para desarrollar a lo largo de las clases 11 y 12. CLASE 11: I. ELEMENTOS DE ÁLGEBRA LINEAL. a) Revisión de conceptos Estructura de espacio vectorial. Propiedades de los
PLAN DE ESTUDIOS DE MS Temario para desarrollar a lo largo de las clases 11 y 12. CLASE 11: I. ELEMENTOS DE ÁLGEBRA LINEAL. a) Revisión de conceptos Estructura de espacio vectorial. Propiedades de los
Definición matemática de Relación y de Función
 Fecha: 05/0 Versión: DOCENTE: ANTONIO ELI CASTILLA Definición matemática de Relación de Función En matemática, Relación es la correspondencia de un primer conjunto, llamado Dominio, con un segundo conjunto,
Fecha: 05/0 Versión: DOCENTE: ANTONIO ELI CASTILLA Definición matemática de Relación de Función En matemática, Relación es la correspondencia de un primer conjunto, llamado Dominio, con un segundo conjunto,
CAMPOS ELÉCTRICOS DEBIDOS A DISTRIBUCIONES CONTINUAS DE CARGA
 CAMPOS ELÉCTRICOS DEBIDOS A DISTRIBUCIONES CONTINUAS DE CARGA Este documento enuncia de forma más detallada la formulación matemática que permite el estudio de campos eléctricos debido a distribuciones
CAMPOS ELÉCTRICOS DEBIDOS A DISTRIBUCIONES CONTINUAS DE CARGA Este documento enuncia de forma más detallada la formulación matemática que permite el estudio de campos eléctricos debido a distribuciones
Matemáticas TRABAJO. Funciones Trigonométricas
 Matemáticas TRABAJO Funciones Trigonométricas 2 En este trabajo trataremos de mostrar de una forma práctica las funciones trigonométricas, con sus formas de presentación, origen y manejos. También se incluirán
Matemáticas TRABAJO Funciones Trigonométricas 2 En este trabajo trataremos de mostrar de una forma práctica las funciones trigonométricas, con sus formas de presentación, origen y manejos. También se incluirán
VELOCIDAD Y ACELERACION. RECTA TANGENTE.
 VELOCIDAD Y ACELERACION. RECTA TANGENTE. 3. Describir la trayectoria y determinar la velocidad y aceleración del movimiento descrito por las curvas siguientes: (a) r (t) = i 4t 2 j + 3t 2 k. (b) r (t)
VELOCIDAD Y ACELERACION. RECTA TANGENTE. 3. Describir la trayectoria y determinar la velocidad y aceleración del movimiento descrito por las curvas siguientes: (a) r (t) = i 4t 2 j + 3t 2 k. (b) r (t)
Integración sobre superficies
 Problemas propuestos con solución Integración sobre superficies IABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice 1. Parametrizaciones 1 2. Área de una superficie
Problemas propuestos con solución Integración sobre superficies IABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice 1. Parametrizaciones 1 2. Área de una superficie
TEMA 1. MAGNITUDES FÍSICAS
 TEMA 1. MAGNITUDES FÍSICAS 1. Definición de magnitd física 2. Magnitdes físicas fndamentales deriadas. Sistema Internacional de Unidades (SI) 3. Cambio de nidades: Método de las fracciones nitarias 4.
TEMA 1. MAGNITUDES FÍSICAS 1. Definición de magnitd física 2. Magnitdes físicas fndamentales deriadas. Sistema Internacional de Unidades (SI) 3. Cambio de nidades: Método de las fracciones nitarias 4.
MATEMÁTICAS 3º ESO PENDIENTES HOJA 1 GEOMETRÍA PLANA. 1.- Calcular el área y el perímetro de los siguientes polígonos:
 MATEMÁTICAS º ESO PENDIENTES HOJA GEOMETRÍA PLANA.- Calcular el área y el perímetro de los siguientes polígonos: a) Un cuadrado de lado 5 cm de lado b) Un cuadrado de diagonal 0 cm. c) Un rectángulo de
MATEMÁTICAS º ESO PENDIENTES HOJA GEOMETRÍA PLANA.- Calcular el área y el perímetro de los siguientes polígonos: a) Un cuadrado de lado 5 cm de lado b) Un cuadrado de diagonal 0 cm. c) Un rectángulo de
Teoría Tema 6 Ecuaciones de la recta
 página 1/14 Teoría Tema 6 Ecuaciones de la recta Índice de contenido Base canónica en dos dimensiones como sistema referencial...2 Ecuación vectorial de la recta...4 Ecuación paramétrica de la recta...6
página 1/14 Teoría Tema 6 Ecuaciones de la recta Índice de contenido Base canónica en dos dimensiones como sistema referencial...2 Ecuación vectorial de la recta...4 Ecuación paramétrica de la recta...6
95 EJERCICIOS de RECTAS
 9 EJERCICIOS de RECTAS Forma paramétrica: 1. Dado el punto A(,3) y el vector director ur = (1, ), se pide: a) Hallar las ecuaciones paramétricas de la recta r que determinan. b) Obtener otros tres puntos
9 EJERCICIOS de RECTAS Forma paramétrica: 1. Dado el punto A(,3) y el vector director ur = (1, ), se pide: a) Hallar las ecuaciones paramétricas de la recta r que determinan. b) Obtener otros tres puntos
Derivadas parciales Derivadas direccionales Derivadas parciales de orden superior. Derivadas parciales y direccionales
 Derivadas parciales y direccionales 1 Derivadas parciales 2 Derivadas direccionales 3 Derivadas parciales de orden superior Derivadas parciales (de campos escalares de dos variables) Sea A = [a 1, b 1
Derivadas parciales y direccionales 1 Derivadas parciales 2 Derivadas direccionales 3 Derivadas parciales de orden superior Derivadas parciales (de campos escalares de dos variables) Sea A = [a 1, b 1
Mecánica de Fluidos. Análisis Diferencial
 Mecánica de Fluidos Análisis Diferencial Análisis Diferencial: Descripción y caracterización del flujo en función de la descripción de una partícula genérica del flujo. 1. Introducción 2. Movimiento de
Mecánica de Fluidos Análisis Diferencial Análisis Diferencial: Descripción y caracterización del flujo en función de la descripción de una partícula genérica del flujo. 1. Introducción 2. Movimiento de
SISTEMAS DE REFERENCIA SISTEMAS DE COORDENADAS PROYECCIONES
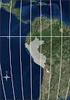 SISTEMAS DE REFERENCIA PROYECCIONES 1 INTRODUCCIÓN GEODESIA Ciencia que estudia la forma y dimensiones de la tierra Determinación de coordenadas para punto de su superficie Imprescindible para una correcta
SISTEMAS DE REFERENCIA PROYECCIONES 1 INTRODUCCIÓN GEODESIA Ciencia que estudia la forma y dimensiones de la tierra Determinación de coordenadas para punto de su superficie Imprescindible para una correcta
Modelización por medio de sistemas
 SISTEMAS DE ECUACIONES DIFERENCIALES LINEALES. Modelización por medio de sistemas d y dy Ecuaciones autónomas de segundo orden: = f ( y, ) Una variable independiente. Una variable dependiente. La variable
SISTEMAS DE ECUACIONES DIFERENCIALES LINEALES. Modelización por medio de sistemas d y dy Ecuaciones autónomas de segundo orden: = f ( y, ) Una variable independiente. Una variable dependiente. La variable
No es otra cosa, que la representación de los resultados de una función sobre el plano carteciano.
 FUNCIONES GRAFICAS No es otra cosa, que la representación de los resultados de una función sobre el plano carteciano. INTÉRVALOS Un intervalo es el conjunto de todos los números reales entre dos números
FUNCIONES GRAFICAS No es otra cosa, que la representación de los resultados de una función sobre el plano carteciano. INTÉRVALOS Un intervalo es el conjunto de todos los números reales entre dos números
Secciones cónicas. Tema 02: Cónicas, cuádricas, construcción de conos y cilindros. Secciones Cónicas. Aplicaciones de las cónicas
 Secciones cónicas Tema 02: Cónicas, cuádricas, construcción de conos y cilindros Juan Ignacio Del Valle Gamboa Sede de Guanacaste Universidad de Costa Rica Ciclo I - 2014 Las secciones cónicas toman su
Secciones cónicas Tema 02: Cónicas, cuádricas, construcción de conos y cilindros Juan Ignacio Del Valle Gamboa Sede de Guanacaste Universidad de Costa Rica Ciclo I - 2014 Las secciones cónicas toman su
Elementos de análisis
 Elementos de análisis El estudio universitario del electromagnetismo en Física II requiere del uso de elementos de análisis en varias variables que el alumno adquirirá en la asignatura Análisis Matemático
Elementos de análisis El estudio universitario del electromagnetismo en Física II requiere del uso de elementos de análisis en varias variables que el alumno adquirirá en la asignatura Análisis Matemático
Apéndice sobre ecuaciones diferenciales lineales
 Apéndice sobre ecuaciones diferenciales lineales Juan-Miguel Gracia 10 de febrero de 2008 Índice 2 Determinante wronskiano. Wronskiano de f 1 (t), f 2 (t),..., f n (t). Derivada de un determinante de funciones.
Apéndice sobre ecuaciones diferenciales lineales Juan-Miguel Gracia 10 de febrero de 2008 Índice 2 Determinante wronskiano. Wronskiano de f 1 (t), f 2 (t),..., f n (t). Derivada de un determinante de funciones.
Guía n 0: Herramientas de Física y Matemáticas
 Guía n 0: Herramientas de Física y Matemáticas Problema Dadas dos partículas en el espacio ubicadas en los puntos de coordenadas p = (0,5, 2) y p 2 = (2,3,). Hallar el vector posición de la partícula respecto
Guía n 0: Herramientas de Física y Matemáticas Problema Dadas dos partículas en el espacio ubicadas en los puntos de coordenadas p = (0,5, 2) y p 2 = (2,3,). Hallar el vector posición de la partícula respecto
DISTANCIA ENTRE DOS PUNTOS EN EL PLANO CARTESIANO.
 RAZONAMIENTO Y DEMOSTRACIÓN Determina la distancia entre pares de puntos. Calcula las coordenadas del punto medio del segmento cuyos extremos son dos puntos dados. Halla la pendiente de una recta. COMUNICACIÓN
RAZONAMIENTO Y DEMOSTRACIÓN Determina la distancia entre pares de puntos. Calcula las coordenadas del punto medio del segmento cuyos extremos son dos puntos dados. Halla la pendiente de una recta. COMUNICACIÓN
El subconjunto en el que se define la función se llama dominio o campo existencia de la función. Se designa por D.
 Concepto de función Función real de variable real es toda correspondencia f que asocia a cada elemento de un determinado subconjunto de números reales, llamado dominio, otro número real (uno y sólo uno).
Concepto de función Función real de variable real es toda correspondencia f que asocia a cada elemento de un determinado subconjunto de números reales, llamado dominio, otro número real (uno y sólo uno).
Dibujo Técnico Curvas cónicas-parábola
 22. CURVAS CÓNICAS-PARÁBOLAS 22.1. Características generales. Las curvas cónicas son las secciones planas de un cono de revolución. El cono de revolución es la superficie que genera una recta r al girar
22. CURVAS CÓNICAS-PARÁBOLAS 22.1. Características generales. Las curvas cónicas son las secciones planas de un cono de revolución. El cono de revolución es la superficie que genera una recta r al girar
Matemáticas II Bachillerato Ciencias y Tecnología 2º Curso. Espacio vectorial. 4.2. Espacio vectorial... - 2 -
 4.1. Introducción: los conjuntos Espacio ectorial R y R.... - - 4.. Espacio ectorial.... - - 4.. Vectores libres del espacio tridimensional.... - - 4.4. Producto escalar... - 4-4.5. Producto ectorial....
4.1. Introducción: los conjuntos Espacio ectorial R y R.... - - 4.. Espacio ectorial.... - - 4.. Vectores libres del espacio tridimensional.... - - 4.4. Producto escalar... - 4-4.5. Producto ectorial....
Tema 2 Datos multivariantes
 Aurea Grané Máster en Estadística Universidade Pedagógica 1 Aurea Grané Máster en Estadística Universidade Pedagógica 2 Tema 2 Datos multivariantes 1 Matrices de datos 2 Datos multivariantes 2 Medias,
Aurea Grané Máster en Estadística Universidade Pedagógica 1 Aurea Grané Máster en Estadística Universidade Pedagógica 2 Tema 2 Datos multivariantes 1 Matrices de datos 2 Datos multivariantes 2 Medias,
Una viga se encuentra sometida a Flexión Pura cuando el momento Flector es la única fuerza al interior de la sección.
 3. FLEXÓ E VGS RECTS 3.1.- Conceptos Báscos Una ga se encentra sometda a Fleón Pra cando el momento Flector es la únca fera al nteror de la seccón. Ejemplo: Una ga smplemente apoada de l L solctada por
3. FLEXÓ E VGS RECTS 3.1.- Conceptos Báscos Una ga se encentra sometda a Fleón Pra cando el momento Flector es la únca fera al nteror de la seccón. Ejemplo: Una ga smplemente apoada de l L solctada por
1. Halla la ecuación de la recta r, sabiendo que pasa por A(1,-2) y B(-1,2)
 1. Halla la ecuación de la recta r, sabiendo que pasa por A(1,-2) y B(-1,2) 2. Halla la ecuación de la recta r, sabiendo que es paralela a y=2x-3 y pasa por el punto (1,3). 3. Halla la ecuación de la recta
1. Halla la ecuación de la recta r, sabiendo que pasa por A(1,-2) y B(-1,2) 2. Halla la ecuación de la recta r, sabiendo que es paralela a y=2x-3 y pasa por el punto (1,3). 3. Halla la ecuación de la recta
VECTORES. Copia en un papel cuadriculado los cuatro vectores siguientes:
 a c VECTORES Página REFLEXIONA Y RESUELVE Mltiplica vectores por números Copia en n papel cadriclado los catro vectores sigientes: d Representa: a a c Expresa el vector d como prodcto de no de los vectores
a c VECTORES Página REFLEXIONA Y RESUELVE Mltiplica vectores por números Copia en n papel cadriclado los catro vectores sigientes: d Representa: a a c Expresa el vector d como prodcto de no de los vectores
Problemas de exámenes de Aplicaciones Lineales y Matrices
 1 Problemas de exámenes de Aplicaciones Lineales y Matrices 1. Consideramos f End(R n ), que tiene matriz A respecto la base canónica. Cuál de las siguientes afirmaciones es incorrecta? a) Si v es un vector
1 Problemas de exámenes de Aplicaciones Lineales y Matrices 1. Consideramos f End(R n ), que tiene matriz A respecto la base canónica. Cuál de las siguientes afirmaciones es incorrecta? a) Si v es un vector
VECTORES EN EL ESPACIO
 VECTORES EN EL ESPACIO (,4,3) MATEMÁTICAS II º Bachillerato Alfonso Gonále IES Fernando de Mena Dpto. de Matemáticas I. DEFINICIONES Módlo: Indica la intensidad, iene dado por la longitd de la flecha
VECTORES EN EL ESPACIO (,4,3) MATEMÁTICAS II º Bachillerato Alfonso Gonále IES Fernando de Mena Dpto. de Matemáticas I. DEFINICIONES Módlo: Indica la intensidad, iene dado por la longitd de la flecha
1. Distancia entre puntos y rectas en el espacio. 3. Calcula la distancia existente entre las rectas: Solución: d(r, s) =
 7 Espacio métrico. Distancia entre puntos y rectas en el espacio Piensa y calcula Dados los puntos A, 4, ) y B5,, 4), halla las coordenadas del vector: AB AB,5,) Aplica la teoría. Calcula la distancia
7 Espacio métrico. Distancia entre puntos y rectas en el espacio Piensa y calcula Dados los puntos A, 4, ) y B5,, 4), halla las coordenadas del vector: AB AB,5,) Aplica la teoría. Calcula la distancia
1. Trace la curva definida por las ecuaciones paramétricas y elimine el parámetro para deducir la ecuación cartesiana de la curva:
 1. Trace la curva definida por las ecuaciones paramétricas y elimine el parámetro para deducir la ecuación cartesiana de la curva: a) x = senθ, y = cosθ, 0 θ π t b), t x = e y = e + 1 c) x = senθ, y =
1. Trace la curva definida por las ecuaciones paramétricas y elimine el parámetro para deducir la ecuación cartesiana de la curva: a) x = senθ, y = cosθ, 0 θ π t b), t x = e y = e + 1 c) x = senθ, y =
ANÁLISIS VECTORIAL. Contenido. Magnitudes escalares y vectoriales Definiciones Escalar Vector Sistemas de Coordenadas
 ANÁLISIS VECTORIAL Contenido Magnitudes escalares y vectoriales Definiciones Escalar Vector Sistemas de Coordenadas Álgebra vectorial Definiciones Suma/Resta de vectores Producto/Cociente de un escalar
ANÁLISIS VECTORIAL Contenido Magnitudes escalares y vectoriales Definiciones Escalar Vector Sistemas de Coordenadas Álgebra vectorial Definiciones Suma/Resta de vectores Producto/Cociente de un escalar
1. Extremos de funciones 2. 2. Parametrización, Triedro de Frenet 21. 3. Coordenadas curvilíneas 34. 4. Integrales de trayectoria y de línea 41
 Índice general 1. Extremos de funciones. Parametrización, Triedro de Frenet 1 3. Coordenadas curvilíneas 34 4. Integrales de trayectoria y de línea 41 5. Integrales Iteradas 5 6. Teoremas Integrales 57
Índice general 1. Extremos de funciones. Parametrización, Triedro de Frenet 1 3. Coordenadas curvilíneas 34 4. Integrales de trayectoria y de línea 41 5. Integrales Iteradas 5 6. Teoremas Integrales 57
TEMA 9 CUERPOS GEOMÉTRICOS
 Tel: 98 9 6 91 Fax: 98 1 89 96 TEMA 9 CUERPOS GEOMÉTRICOS Objetivos / Criterios de evaluación O.1.1 Conocer las fórmulas de áreas y volúmenes de figuras geométricas sencillas de D. O.1. Resolver problemas
Tel: 98 9 6 91 Fax: 98 1 89 96 TEMA 9 CUERPOS GEOMÉTRICOS Objetivos / Criterios de evaluación O.1.1 Conocer las fórmulas de áreas y volúmenes de figuras geométricas sencillas de D. O.1. Resolver problemas
CÁLCULO VECTORIAL I. B, es un nuevo vector que se define del siguiente modo: Si A ybson (LI), entonces el vector A. B se caracteriza por:
 PRODUCTO VECTORIAL DE DOS VECTORES El producto vectorial de dos vectores A y, y escribimos A, es un nuevo vector que se define del siguiente modo: Si A yson (LI), entonces el vector A se caracteriza por:
PRODUCTO VECTORIAL DE DOS VECTORES El producto vectorial de dos vectores A y, y escribimos A, es un nuevo vector que se define del siguiente modo: Si A yson (LI), entonces el vector A se caracteriza por:
Teoría Tema 9 Ecuaciones del plano
 página 1/11 Teoría Tema 9 Ecuaciones del plano Índice de contenido Determinación lineal de un plano. Ecuación vectorial y paramétrica...2 Ecuación general o implícita del plano...6 Ecuación segmentaria
página 1/11 Teoría Tema 9 Ecuaciones del plano Índice de contenido Determinación lineal de un plano. Ecuación vectorial y paramétrica...2 Ecuación general o implícita del plano...6 Ecuación segmentaria
Espacios vectoriales reales.
 Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
Sobre funciones reales de variable real. Composición de funciones. Función inversa
 Sobre funciones reales de variable real. Composición de funciones. Función inversa Cuando en matemáticas hablamos de funciones pocas veces nos paramos a pensar en la definición rigurosa de función real
Sobre funciones reales de variable real. Composición de funciones. Función inversa Cuando en matemáticas hablamos de funciones pocas veces nos paramos a pensar en la definición rigurosa de función real
Sistem as de ecuaciones lineales
 Sistem as de ecuaciones lineales. Concepto, clasificación y notación Un sistema de m ecuaciones lineales con n incógnitas se puede escribir del siguiente modo: a x + a 2 x 2 + a 3 x 3 + + a n x n = b a
Sistem as de ecuaciones lineales. Concepto, clasificación y notación Un sistema de m ecuaciones lineales con n incógnitas se puede escribir del siguiente modo: a x + a 2 x 2 + a 3 x 3 + + a n x n = b a
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES
 MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 5 Curso preparatorio de la prueba de acceso a la universidad para mayores de 25 años curso 2010/11 Nuria Torrado Robles Departamento de Estadística Universidad
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 5 Curso preparatorio de la prueba de acceso a la universidad para mayores de 25 años curso 2010/11 Nuria Torrado Robles Departamento de Estadística Universidad
Dpto. Física y Mecánica. Sistemas de coordenadas y sistemas de referencia
 Dpto. Física y Mecánica Sistemas de coordenadas y sistemas de referencia La descripción del movimiento de un cuerpo requiere la introducción de un sistema de coordenadas espaciales que identifiquen unívocamente
Dpto. Física y Mecánica Sistemas de coordenadas y sistemas de referencia La descripción del movimiento de un cuerpo requiere la introducción de un sistema de coordenadas espaciales que identifiquen unívocamente
Ejercicios Resueltos de Cálculo III.
 Ejercicios Resueltos de Cálculo III. 1.- Considere y. a) Demuestre que las rectas dadas se cortan. Encuentre el punto de intersección. b) Encuentre una ecuación del plano que contiene a esas rectas. Como
Ejercicios Resueltos de Cálculo III. 1.- Considere y. a) Demuestre que las rectas dadas se cortan. Encuentre el punto de intersección. b) Encuentre una ecuación del plano que contiene a esas rectas. Como
Tema 4.2 Proyecciones cartográficas: planas. Cartografía I 2º Curso de IT en Topografía 1 er Cuatrimestre 2008/09 EPS Jaén
 Tema 4.2 Proyecciones cartográficas: planas Cartografía I 2º Curso de IT en Topografía 1 er Cuatrimestre 2008/09 EPS Jaén 1. Concepto 2. Propiedades 3. Clasificación 4. Proyecciones planas 5. Otras proyecciones
Tema 4.2 Proyecciones cartográficas: planas Cartografía I 2º Curso de IT en Topografía 1 er Cuatrimestre 2008/09 EPS Jaén 1. Concepto 2. Propiedades 3. Clasificación 4. Proyecciones planas 5. Otras proyecciones
NIVEL : 1er. AÑO PROF. L. ALTIMIRAS R. CARRERA : GEOGRAFÍA AYUD. C. ESCOBEDO C. AÑO : 2009 GEOMETRÍA ANALÍTICA
 UNIVERSIDAD DE CHILE FACULTAD DE ARQUITECTURA Y URBANISMO ESCUELA DE GEOGRAFÍA DEPARTAMENTO DE CIENCIAS DE LA CONSTRUCCIÓN ASIGNATURA : MATEMATICAS MATERIAL DE APOYO NIVEL : 1er. AÑO PROF. L. ALTIMIRAS
UNIVERSIDAD DE CHILE FACULTAD DE ARQUITECTURA Y URBANISMO ESCUELA DE GEOGRAFÍA DEPARTAMENTO DE CIENCIAS DE LA CONSTRUCCIÓN ASIGNATURA : MATEMATICAS MATERIAL DE APOYO NIVEL : 1er. AÑO PROF. L. ALTIMIRAS
Tarea 1 - Vectorial 201420
 Tarea - Vectorial 040. Part :. - 3... Hacer parametrización de la curva de intersección del cilindro x + y = 6 y el plano x + z = 5. Encontrar las coordenadas de los puntos de la curva donde la curvatura
Tarea - Vectorial 040. Part :. - 3... Hacer parametrización de la curva de intersección del cilindro x + y = 6 y el plano x + z = 5. Encontrar las coordenadas de los puntos de la curva donde la curvatura
1 Curvas planas. Solución de los ejercicios propuestos.
 1 Curvas planas. Solución de los ejercicios propuestos. 1. Se considera el lugar geométrico de los puntos del plano tales que la suma del cuadrado de las distancias a los puntos P 1 = (, 0) y P = (, 0)
1 Curvas planas. Solución de los ejercicios propuestos. 1. Se considera el lugar geométrico de los puntos del plano tales que la suma del cuadrado de las distancias a los puntos P 1 = (, 0) y P = (, 0)
