Apuntes de la asignatura Química Física II (Licenciatura en Química) Tema 6: Momento angular
|
|
|
- Elisa Lucero Fuentes
- hace 7 años
- Vistas:
Transcripción
1 Apuntes de la asignatura Química Física II Licenciatura en Química) Tema 6: Momento angular Ángel José Pére Jiméne Dept. de Química Física Univ. Alicante) Índice 1. Momento angular en Mecánica Clásica Definición del momento angular de una partícula en Mecánica Clásica Significado físico del momento angular Tratamiento mecano-cuántico del momento angular orbital Operadores del momento angular en coordenadas cartesianas Operadores del momento angular en coordenadas esféricas Autofunciones autovalores de ˆL ˆL Separación de variables Autofunciones autovalores de ˆL Autofunciones autovalores de ˆL Armónicos esféricos Epresión anaĺıtica de los armónicos esféricos Armónicos esféricos reales Representación gráfica de los armónicos esféricos Problemas 16
2 2 Tema 6: Momento angular 1. Momento angular en Mecánica Clásica Definición del momento angular de una partícula en Mecánica Clásica Se define como el vector, L, que resulta del producto vectorial entre su vector de posición, r, su vector momento lineal p ver Figura 1) L = r p 1) L r θ p=mv Figura 1: Momento angular de una partícula. Cuas tres componentes cartesianas son L = p p 2) L = p p 3) L = p p 4) que pueden deducirse de la epresión L = i j k p p p 5) Y cuo módulo viene dado por: L = r p senθ r,p 6)
3 2 Tratamiento mecano-cuántico del momento angular orbital Significado físico del momento angular Momento angular giro de una partícula. L caracteria el cambio de orientación de una partícula: Su dirección es la del eje de giro: perpendicular al plano formado por los vectores r p. Su sentido se obtiene de aplicar la regla del sacacorchos sentido del giro. Su longitud es tanto maor cuanto más pronunciado es dicho giro: maor velocidad maor desalineamiento entre r p. Momento angular torque sobre la partícula. La derivada respecto al tiempo del momento angular de una partícula es igual al momento de la fuera que actúa sobre ésta torque): M d L dt = d r p) dt = v p + r d p dt = r F 7) Conservación del momento angular. Por tanto, si la fuera F que actúa sobre la partícula tiene la misma dirección que r el torque es nulo L es constante: Si F r r p = 0 = d L dt L = const. 8) El caso anterior sucede en los llamados problemas de campo central, en los que el potencial es independiente de la orientación de r sólo depende de su módulo), como le sucede al electrón en el átomo de hidrógeno. 2. Tratamiento mecano-cuántico del momento angular orbital Operadores del momento angular en coordenadas cartesianas Operadores del momento angular. Empleando las reglas de construcción de operadores introducidas en el Tema 4, los operadores correspondientes a las tres componentes cartesianas del operador momento angular de su módulo al cuadrado son: ˆL = ŷˆp ẑ ˆp = i h ) 9) ˆL = ẑ ˆp ˆˆp = i h ) 10) ˆL = ˆˆp ŷˆp = i h ) 11) ˆL 2 = ˆL 2 + ˆL 2 + ˆL 2 12)
4 4 Tema 6: Momento angular Reglas de conmutación. Empleando las epresiones anteriores es posible demostrar que: [ˆL, ˆL = i hˆl 13) [ˆL, ˆL = i hˆl 14) [ˆL, ˆL = i hˆl 15) [ˆL2, ˆL = 0 16) [ˆL2, ˆL = 0 17) [ˆL2, ˆL = 0 18) De forma que: No es posible asignar valores precisos de manera simultánea a más de una componente del momento angular si se conoce con precisión el valor de una de las componentes, las otras dos quedan indeterminadas Es posible determinar simultáneamente el valor del cuadrado del momento angular una de sus componentes Operadores del momento angular en coordenadas esféricas Epresión de los operadores en coordenadas polares esféricas. En los problemas donde el momento angular es importante, como sucede con potenciales de campo central, las coordenadas cartesianas no son el sistema de coordenadas más apropiado. En problemas con simetría esférica es conveniente trabajar con coordenadas esféricas ver figura 2) θ,,) o r, θ,φ) r φ Figura 2: Coordenadas esféricas.
5 3 Autofunciones autovalores de ˆL ˆL 2. 5 = r sen θ cos φ r = ) = r sen θ senφ θ = arc cos r 20) = r cos θ cuos rangos de definición son: φ = arctan 21) 0 r 22) 0 θ π 23) 0 φ 2π 24), además dτ = ddd = r 2 senθdrdθdφ 25) Conviene, pues, epresar los operadores del momento angular en función de coordenadas esféricas r, θ, φ), empleando sus definiciones la regla de la cadena, para llegar a: ˆL = i h senφ ) + cot θ cos φ 26) θ φ ˆL = i h cos φ ) cot θsenφ 27) θ φ Variables angulares. ˆL = i h φ ˆL 2 = h 2 2 θ 2 + cot θ θ + 1 sen 2 θ 2 ) φ 2 Obsérvese que los operadores ˆL, ˆL, ˆL ˆL 2 sólo dependen de las variables angulares θ φ. En particular ˆL sólo depende φ, por lo que habitualmente se aborda la determinación de las autofunciones autovectores comunes a ˆL ˆL Autofunciones autovalores de ˆL ˆL Separación de variables Vamos a determinar las funciones propias comunes de ˆL ˆL 2, denominadas armónicos esféricos: 28) 29) ˆL Y = by 30) ˆL 2 Y = cy 31) 32)
6 6 Tema 6: Momento angular Como ˆL ˆL 2 sólo dependen de las variables angulares θ φ, sus correspondientes autofunciones comunes son funciones de dichas variables, de forma que: h 2 2 Y θ, φ) Y θ, φ) + cot θ + 1 θ 2 θ sen 2 θ Y θ, φ) i h φ = by θ, φ) 33) 2 Y θ, φ) ) = cy θ, φ) 34) φ 2 Puesto que ˆL sólo depende de φ podemos buscar una solución que tenga la forma: Y θ, φ) = Θθ)Φφ) 35) 3.2. Autofunciones autovalores de ˆL Solución general. Introduciendo la epresión para Y θ, φ) dada por 35) en la ecuación de autovalores de ˆL, teniendo en cuenta que éste sólo actúa sobre φ, se llega a: cua solución general es: i h dφφ) dφ = bφφ) 36) Φφ) = Ae ibφ/ h 37) Condiciones de contorno. Para ser aceptable la función Φφ) debe ser unievaluada: Φ0) = Φ2π) A = Ae ib2π/ h 1 = e ib2π/ h = cos 2πb h 2πb h 2πb + isen h = m2π); m = 0, ±1, ±2, ±3,... 1 = cos 2πb h 0 = sen 2πb h Cuantiación normaliación. En otras palabras, los autovalores de la componente del momento angular están cuantiados: ˆL Φ m φ) = m hφ m φ); m = 0, ±1, ±2, ±3,... 38) Finalmente, para determinar A aplicamos la condición de normaliación sobre Φ m φ): 2π 1 = Φ m Φ m = A 2 e imφ e imφ dφ = 2π A 2 39) 0 A = 1 2π 40) de forma que: Φ m φ) = 1 2π e imφ 41)
7 3 Autofunciones autovalores de ˆL ˆL 2. 7 Conjunto ortonormal. Puesto que las funciones Φ m φ) son autofunciones no degeneradas de un operador Hermítico, forman un conjunto ortonormal: Φ m Φ m = 2π 3.3. Autofunciones autovalores de ˆL 2 Ecuación diferencial para Θθ). 0 Φ mφ)φ m φ)dφ = δ m,m 42) Introduciendo la epresión para Y θ, φ) dada por 35) en la ecuación de autovalores de ˆL 2 se llega a: [ h 2 Φφ) 2 Θθ) + Φφ) cot θ Θθ) + Θθ) 2 Φφ) = cθθ)φφ) 43) θ 2 θ sen 2 θ) φ 2 Introduciendo la forma de Φφ) deducida en el apartado anterior, dada por 41), en la ecuación 43) reagrupando se tiene que: d 2 Θθ) + cot θ dθθ) c ) + dθ 2 dθ h 2 m2 Θθ) = 0 44) sen 2 θ que es una ecuación diferencial homogénea de segundo orden con coeficientes variables. Haciendo el cambio de variable introduciendo la función w = cos θ; obsérvese que 1 w +1) 45) epresando las derivadas de θ en función de las de w: Zw) = Θθ) 46) d dθ = senθ d dw 47) d 2 dθ = cos θ d 2 dw + sen2 θ d2 dw 2 48) la ecuación diferencial se transforma en: c ) 1 w 2 )Z 2wZ + h 2 m2 Z = 0 1 w 2 49) Polinomios asociados de Legendre. La ecuación anterior es análoga a la denominada ecuación diferencial asociada de Legendre: ) 1 w 2 )P 2wP + m2 ll + 1) 1 w 2 P = 0 50) cuas soluciones son los denominados polinomios asociados de Legendre de grado l orden m, P m l w): ver tabla 1.
8 8 Tema 6: Momento angular Tabla 1: Algunos polinomios asociados de Legendre. l m P m l cos θ) cos θ 1 1 sen θ cos 2 θ 1)/ cos θsen θ 2 2 3sen 2 θ cos 3 θ 3 cos θ)/ sen θ5 cos 3 θ 1)/ sen 2 θ cos θ sen 3 θ Dichos polinomios son funciones aceptables pues no divergen, a que cada polinomio se trunca hasta un cierto orden, lo que conduce a la cuantiación de los valores de l: a la siguiente relación entre m l: l = 0, 1, 2, 3,... 51) m l m = 0, ±1, ±2, ±3,..., ±l 52) La igualdad entre ambas ecuaciones diferenciales 49) 50) requiere, pues que los autovalores de ˆL 2 estén cuantiados: c = ll + 1) h 2 ; l = 0, 1, 2, 3,... 53) Finalmente, de todo lo anterior tras imponer la condición de normaliación, se deduce que la función Θθ) viene dada por: ) 1/2 Θ l,m θ) = 1) m 2l + 1)l m )! P m l cos θ) 54) 2l + m )! 4. Armónicos esféricos 4.1. Epresión anaĺıtica de los armónicos esféricos En resumen: las autofunciones comunes de ˆL ˆL 2, denominadas armónicos esféricos se pueden epresar como: ) 1/2 Y l,m θ, φ) = 1) m 2l + 1)l m )! P m l cos θ)e imφ 55) 4πl + m )! algunas de las cuales se presentan en la Tabla 2.
9 4 Armónicos esféricos 9 Tabla 2: Algunos armónicos esféricos l m Y l,m θ, φ) ) 1/ /4π) ) 1/ /4π) cos θ 1 ± 1 3/8π) ) 1/2 sen θ ep±iφ) ) 1/ /16π) cos 2 θ 1) 2 ± 1 15/8π) ) 1/2 cos θsen θ ep±iφ) ) 1/2sen 2 ± 2 15/32π) 2 θ ep±2iφ) ) 1/ /16π) cos 3 θ 3 cos θ) 3 ± 1 21/64π) ) 1/2 sen θ5 cos 3 θ 1) ep±iφ) ) 1/2sen 3 ± 2 105/32π) 2 θ cos θ ep±2iφ) 3 ± 3 35/64π) ) 1/2 sen 3 θ ep±3iφ) Recordemos que tanto el módulo como la componente del momento angular están cuantiados: ˆL 2 Y l,m = ll + 1) h 2 Y l,m L = h ll + 1) l = 0, 1, 2, 3,... 56) ˆL Y l,m = m hy l,m L = hm m = 0, ±1, ±2,..., ±l 57) La relación entre m l establece que, por cada valor de l ha 2l + 1 posibles valores distintos de m los armónicos esféricos presentan una degeneración 2l + 1 respecto a ˆL 2. Recordemos también que Y l,m θ, φ) no son autofunciones de ˆL componentes del momento angular están indeterminadas. ˆL, por lo que dichas Por esta raón es frecuente usar una representación gráfica del momento angular como la de la figura 3, de manera que el momento angular de una partícula sería cualquiera de los infinitos vectores de módulo ll + 1) h componente m h que definen el cono representado en dicha figura: mh L ll+1) h Figura 3: Representación vectorial del momento angular de una partícula.
10 10 Tema 6: Momento angular Los armónicos esféricos formarán parte de las funciones de onda que describen el movimiento de los electrones en átomos moléculas, de ahí su importancia en Química Cuántica. Una notación habitual de los armónicos esféricos emplea la letra s, p, d, f,... según el valor de l = 0, 1, 2, 3... un subíndice según el valor de m. Por ejemplo: Y l=3,m= 2 f Armónicos esféricos reales Los armónicos esféricos son funciones complejas cuando m 0. Sin embargo es posible combinar Y l,+ m con Y l, m para obtener dos nuevas funciones reales denominadas armónicos esféricos reales ver tabla 3): Y l,+ = 1 2 Yl,+ m + Y l, m ) Y l, = 1 i ) Yl,+ m Y l, m 2 58) 59) Dichas funciones siguen siendo autofunciones de ˆL 2 pues son combinaciones lineales de funciones con el mismo valor propio de ˆL 2. Sin embargo los armónicos esféricos reales no son autofunciones de ˆL por la raón contraria. Tabla 3: Algunos armónicos esféricos reales Notación l m Y ± l m θ, φ) Pol. cartesiano ) 1/2 s 0 0 1/4π) 1 ) 1/2 p 1 0 3/4π) cos θ ) 1/2sen p 1 1 3/4π) θ cos φ ) 1/2sen p 1 1 3/4π) θsen φ ) 1/23 d /16π) cos 2 θ 1) ) 1/2 d /4π) cos θsen θ cos φ ) 1/2 d /4π) cos θsen θsen φ d ) 1/2sen 15/16π) 2 θ cos 2φ 2 2 ) 1/2sen d /16π) 2 θsen 2φ En la tabla anterior se inclue también: Su epresión en coordenadas cartesianas, pues resulta especialmente sencilla. La notación habitual de estas funciones, que emplea la letra s, p, d, f,... según el valor de l = 0, 1, 2, 3... un subíndice que corresponde al término más alto del polinomio cartesiano correspondiente.
11 4 Armónicos esféricos Representación gráfica de los armónicos esféricos Dada su importancia es conveniente representar gráficamente los armónicos esféricos. Dicha representación se suele realiar mediante gráficos polares: para cada dirección definida por los valores de θ φ se representa un segmento de longitud igual al valor absoluto del armónico esférico o su módulo al cuadrado. Figura 4: Representación en coordenadas polares esféricas del módulo al cuadrado de algunos armónicos esféricos. De iquierda a derecha: Y 0,0 2, Y 1,0 2, Y 1,1 2 = Y 1, 1 2.
12 12 Tema 6: Momento angular Figura 5: Arriba: representación en coordenadas polares esféricas del módulo al cuadrado del armónico esférico real s. Abajo: corte transversal.
13 4 Armónicos esféricos 13 Figura 6: Arriba, de iquierda a derecha: representación en coordenadas polares esféricas del módulo al cuadrado de los armónicos esféricos reales p, p p. Abajo: cortes transversales.
14 14 Tema 6: Momento angular Figura 7: Arriba, de iquierda a derecha: representación en coordenadas polares esféricas del módulo al cuadrado de los armónicos esféricos reales d 2, d d. Abajo: cortes transversales.
15 4 Armónicos esféricos 15 Figura 8: Arriba, de iquierda a derecha: representación en coordenadas polares esféricas del módulo al cuadrado de los armónicos esféricos reales d 2 2 d. Abajo: cortes transversales.
16 16 Tema 6: Momento angular 5. Problemas 1: Calcular el valor de los siguientes conmutadores: [ˆL, ˆL, [ˆL, ˆL, [ˆL, ˆL, [ˆL2, ˆL evaluar el producto vectorial ˆ L ˆ L. 2: Calcular, si es posible, los valores propios de ˆL 2 ˆL para las funciones: Considerar ˆL ˆL 2 en coordenadas polares. ˆL = h i Ψ 1 = N cos θ Ψ 2 = Nsenθ cos ϕ Ψ 3 = Nsenθsenϕ Ψ 4 = Ψ 2 + iψ 3 ϕ ˆL 2 = h 2 2 θ + cot θ 2 θ + 1 ) 2 sen 2 θ ϕ 2 3: Una partícula de masa m está restringida a moverse sobre una circunferencia de radio r, sin estar sometida a ningún potencial. Si en unidades atómicas tenemos que: ˆp = i sin ϕ r ϕ ˆp = i cos ϕ r ϕ E cinética = p2 + p 2 2m donde 0 ϕ 2π. Obtener la epresión de la energía de la función de onda aceptable normaliada para los estados estacionarios del sistema. 4: Sabiendo que los denominados operadores escalera se definen como ˆL ± = ˆL ±iˆl, encontrar el valor de: [ˆL, ˆL ±, [L 2, ˆL ±, [ˆL +, ˆL, [ˆL, ˆL +
1.1 DEFINICIÓN CLÁSICA DEL MOMENTO ANGU- LAR
 Chapter MOMENTO ANGULAR La teoría del momento angular en mecánica cuántica es de gran importancia tanto por el número como por la variedad de sus consecuencias. A partir de la espectroscopía rotacional,
Chapter MOMENTO ANGULAR La teoría del momento angular en mecánica cuántica es de gran importancia tanto por el número como por la variedad de sus consecuencias. A partir de la espectroscopía rotacional,
0 si dos índices coinciden 1 si jkl es permutación impar de 123. = εjkl i X l (2) = εjkl i P l (3) = εjkl i L l (4)
 Momento angular Operador momento angular L = R P, L j = ε jkl X k P l (1) Tensor antisimétrico ε jkl = 0 si dos índices coinciden 1 si jkl es permutación par de 123 1 si jkl es permutación impar de 123
Momento angular Operador momento angular L = R P, L j = ε jkl X k P l (1) Tensor antisimétrico ε jkl = 0 si dos índices coinciden 1 si jkl es permutación par de 123 1 si jkl es permutación impar de 123
Lección: Modelos cuánticos útiles en Química
 Lección: Modelos cuánticos útiles en Química TEMA: Introducción 1 Adolfo Bastida Pascual Universidad de Murcia. España. I. La partícula en una caja de potencial.. 2 I.A. Ecuación de Schrödinger...........
Lección: Modelos cuánticos útiles en Química TEMA: Introducción 1 Adolfo Bastida Pascual Universidad de Murcia. España. I. La partícula en una caja de potencial.. 2 I.A. Ecuación de Schrödinger...........
Vibración y rotación en mecánica cuántica
 Vibración y rotación en mecánica cuántica Antonio M. Márquez Departamento de Química Física Universidad de Sevilla Ultima actualización de marzo de 017 Índice 1. Oscilador armónico monodimensional 1. Cuantización
Vibración y rotación en mecánica cuántica Antonio M. Márquez Departamento de Química Física Universidad de Sevilla Ultima actualización de marzo de 017 Índice 1. Oscilador armónico monodimensional 1. Cuantización
2. MECANICA CUANTICA DE SISTEMAS ELEMENTALES.
 . MECANICA CUANTICA DE SISTEMAS EEMENTAES... MOVIMIENTO TRASACIONA. A PARTÍCUA IBRE. Partícula de masa m moviéndose en la dimensión no sometida a fueras eternas: V( 0 Operador amiltoniano del sistema:
. MECANICA CUANTICA DE SISTEMAS EEMENTAES... MOVIMIENTO TRASACIONA. A PARTÍCUA IBRE. Partícula de masa m moviéndose en la dimensión no sometida a fueras eternas: V( 0 Operador amiltoniano del sistema:
Apuntes de la asignatura Química Física II (Licenciatura en Química) Tema 4: Postulados de la Mecánica Cuántica
 Apuntes de la asignatura Química Física II (Licenciatura en Química) Tema 4: Postulados de la Mecánica Cuántica Ángel José Pérez Jiménez Dept. de Química Física (Univ. Alicante) Índice 1. Descripción de
Apuntes de la asignatura Química Física II (Licenciatura en Química) Tema 4: Postulados de la Mecánica Cuántica Ángel José Pérez Jiménez Dept. de Química Física (Univ. Alicante) Índice 1. Descripción de
FÍSICA 4 PRIMER CUATRIMESTRE DE 2015 GUÍA 9: POTENCIALES EN 2-D Y 3-D, MOMENTO ANGULAR, ÁTOMO DE HIDRÓGENO, ESPÍN
 FÍSICA 4 PRIMER CUATRIMESTRE DE 2015 GUÍA 9: POTENCIALES EN 2-D Y 3-D, MOMENTO ANGULAR, ÁTOMO DE HIDRÓGENO, ESPÍN 1. Considere el siguiente potencial (pozo infinito): { 0 x a; y b y z c V(x)= sino Escribiendo
FÍSICA 4 PRIMER CUATRIMESTRE DE 2015 GUÍA 9: POTENCIALES EN 2-D Y 3-D, MOMENTO ANGULAR, ÁTOMO DE HIDRÓGENO, ESPÍN 1. Considere el siguiente potencial (pozo infinito): { 0 x a; y b y z c V(x)= sino Escribiendo
El átomo de hidrógeno
 El átomo de hiógeno Antonio. árquez Departamento de Química Física Universidad de Sevilla Curso 017/018 Índice 1. Ecuación de Schrodinger 1. Orbitales hiogenoides 5 3. Función de distribución radial 7
El átomo de hiógeno Antonio. árquez Departamento de Química Física Universidad de Sevilla Curso 017/018 Índice 1. Ecuación de Schrodinger 1. Orbitales hiogenoides 5 3. Función de distribución radial 7
ESTRUCTURA DE LA MATERIA
 7/03/18 FUNDAMENTOS DE LA MECÁNICA CUÁNTICA 0 7/03/18 FUNDAMENTOS DE LA MECÁNICA CUÁNTICA 1 7/03/18 FUNDAMENTOS DE LA MECÁNICA CUÁNTICA 1 7/03/18 FUNDAMENTOS DE LA MECÁNICA CUÁNTICA 3 7/03/18 FUNDAMENTOS
7/03/18 FUNDAMENTOS DE LA MECÁNICA CUÁNTICA 0 7/03/18 FUNDAMENTOS DE LA MECÁNICA CUÁNTICA 1 7/03/18 FUNDAMENTOS DE LA MECÁNICA CUÁNTICA 1 7/03/18 FUNDAMENTOS DE LA MECÁNICA CUÁNTICA 3 7/03/18 FUNDAMENTOS
HOJA DE PROBLEMAS 1: ENUNCIADOS
 Tema: ESTRUCTURA ELECTRÓNICA DE LOS ÁTOMOS HOJA DE PROBLEMAS 1: ENUNCIADOS 1. ( ) Para describir el estado fundamental de una partícula que se encuentra en una caja de potencial unidimensional definida
Tema: ESTRUCTURA ELECTRÓNICA DE LOS ÁTOMOS HOJA DE PROBLEMAS 1: ENUNCIADOS 1. ( ) Para describir el estado fundamental de una partícula que se encuentra en una caja de potencial unidimensional definida
EL ÁTOMO DE HIDRÓGENO
 EL ÁTOMO DE HIDRÓGENO El átomo de hidrógeno constituye uno de los pocos sistemas de interés químico que admite una solución exacta de la ecuación de Schröedinger. Para todos los demás sólo es factible
EL ÁTOMO DE HIDRÓGENO El átomo de hidrógeno constituye uno de los pocos sistemas de interés químico que admite una solución exacta de la ecuación de Schröedinger. Para todos los demás sólo es factible
Capítulo 3. Átomos Hidrogenoides.
 Capítulo 3. Átomos Hidrogenoides. Objetivos: Introducción del concepto de orbital atómico Descripción de los números cuánticos en los orbitales atómicos Justificación cualitativa de la cuantización de
Capítulo 3. Átomos Hidrogenoides. Objetivos: Introducción del concepto de orbital atómico Descripción de los números cuánticos en los orbitales atómicos Justificación cualitativa de la cuantización de
El ÁTOMO de HIDRÓGENO
 El ÁTOMO de HIDRÓGENO Dr. Andres Ozols Dra. María Rebollo FIUBA 006 Dr. A. Ozols 1 ESPECTROS DE HIDROGENO espectros de emisión espectro de absorción Dr. A. Ozols ESPECTROS DE HIDROGENO Secuencias de las
El ÁTOMO de HIDRÓGENO Dr. Andres Ozols Dra. María Rebollo FIUBA 006 Dr. A. Ozols 1 ESPECTROS DE HIDROGENO espectros de emisión espectro de absorción Dr. A. Ozols ESPECTROS DE HIDROGENO Secuencias de las
TEMA 2. Modelo mecanocuántico. ntico del átomo de
 TEMA. Modelo mecanocuántico ntico del átomo de hidrógeno Aunque la teoría de Bohr y la etensión de Somerfeld conducen a resultados satisfactorios para el átomo de hidrógeno su aplicación tropezaba con
TEMA. Modelo mecanocuántico ntico del átomo de hidrógeno Aunque la teoría de Bohr y la etensión de Somerfeld conducen a resultados satisfactorios para el átomo de hidrógeno su aplicación tropezaba con
Química Física II. Curso Serie L02. Problemas de una partícula
 Química Física II. Curso 009-00. Serie L0. Problemas de una partícula. La función de onda de una partícula libre que se mueve en una dimensión con energía constante es Ψ k (x, t) = ψ k (x)e iωt = Ae ikx
Química Física II. Curso 009-00. Serie L0. Problemas de una partícula. La función de onda de una partícula libre que se mueve en una dimensión con energía constante es Ψ k (x, t) = ψ k (x)e iωt = Ae ikx
Estructura de la Materia. Átomo de Hidrógeno. Martha M. Flores Leonar FQ UNAM. 16 de abril de 2018
 Estructura de la Materia Átomo de Hidrógeno Martha M. Flores Leonar FQ UNAM 16 de abril de 2018 ÁTOMO DE HIDRÓGENO z θ r φ y x Ψ (r, θ, φ) = R (r) Θ (θ) Φ (φ) (1) Ĥ = 2 2µ 2 kze2 r (2) ĤΨ (r, θ, φ) = EΨ
Estructura de la Materia Átomo de Hidrógeno Martha M. Flores Leonar FQ UNAM 16 de abril de 2018 ÁTOMO DE HIDRÓGENO z θ r φ y x Ψ (r, θ, φ) = R (r) Θ (θ) Φ (φ) (1) Ĥ = 2 2µ 2 kze2 r (2) ĤΨ (r, θ, φ) = EΨ
Examen de Física Cuántica I
 UNIVERSIDAD COMPLUTENSE DE MADRID FACULTAD DE CIENCIAS FISICAS 9 de Junio de 2017 Examen de Física Cuántica I Nombre y Apellidos: Firma y DNI: Los alumnos que se presentan a toda la asignatura tienen que
UNIVERSIDAD COMPLUTENSE DE MADRID FACULTAD DE CIENCIAS FISICAS 9 de Junio de 2017 Examen de Física Cuántica I Nombre y Apellidos: Firma y DNI: Los alumnos que se presentan a toda la asignatura tienen que
Apuntes del Modelo del átomo hidrogenoide.
 Apuntes del Modelo del átomo hidrogenoide. Dr. Andrés Soto Bubert Un átomo hidrogenoide es aquel que tiene un solo electrón de carga e, rodeando un núcleo de carga +Ze. Átomos que cumplen esta descripción
Apuntes del Modelo del átomo hidrogenoide. Dr. Andrés Soto Bubert Un átomo hidrogenoide es aquel que tiene un solo electrón de carga e, rodeando un núcleo de carga +Ze. Átomos que cumplen esta descripción
UNIVERSIDAD SANTO TOMAS SECCIONAL BUCARAMANGA. División de Ingenierías - Facultad de Química Ambiental
 UNIVERSIDAD SANTO TOMAS SECCIONAL BUCARAMANGA División de Ingeniería Facultad de Química Ambiental Nombre de Asignatura: QUÍMICA CUÁNTICA Àrea: Básicas de Química Fisicoquímica Créditos: 3 Modalidad: Teórica
UNIVERSIDAD SANTO TOMAS SECCIONAL BUCARAMANGA División de Ingeniería Facultad de Química Ambiental Nombre de Asignatura: QUÍMICA CUÁNTICA Àrea: Básicas de Química Fisicoquímica Créditos: 3 Modalidad: Teórica
Para establecer la relación entre coordenadas cartesianas y polares es suficiente proyectar r sobre los ejes x e y. De la gráfica se sigue que:
 COORDENADAS POLARES. Algunas veces conviene representar un punto P en el plano por medio de coordenadas polares planas (r, ), donde r se mide desde el origen y es el ángulo entre r y el eje x (ver figura).
COORDENADAS POLARES. Algunas veces conviene representar un punto P en el plano por medio de coordenadas polares planas (r, ), donde r se mide desde el origen y es el ángulo entre r y el eje x (ver figura).
Física cuántica I Grupo C 2015/16 Examen final 22 de junio de 2016
 UNIVERSIDAD COMPLUTENSE DE MADRID DEPARTAMENTO DE FÍSICA TEÓRICA I GRADO EN FÍSICA Física cuántica I Grupo C 15/1 Examen final de junio de 1 Nombre: Soluciones Firma: Problema 1 (1 punto). Un haz de radiación
UNIVERSIDAD COMPLUTENSE DE MADRID DEPARTAMENTO DE FÍSICA TEÓRICA I GRADO EN FÍSICA Física cuántica I Grupo C 15/1 Examen final de junio de 1 Nombre: Soluciones Firma: Problema 1 (1 punto). Un haz de radiación
Hoja de Problemas 5. Física Atómica.
 Hoja de Problemas 5. Física Atómica. Fundamentos de Física III. Grado en Física. Curso 25/26. Grupo 56. UAM. 3-3-26 Problema En 896 el astrónomo americano Edward Charles Pickering observó unas misteriosas
Hoja de Problemas 5. Física Atómica. Fundamentos de Física III. Grado en Física. Curso 25/26. Grupo 56. UAM. 3-3-26 Problema En 896 el astrónomo americano Edward Charles Pickering observó unas misteriosas
Química Física II. Tema II
 Química Física II. Tema II TEMA II: LA ECUACIÓN DE SCHRÖDINGER 1. La ecuación de Schrödinger independiente del tiempo 2. La ecuación de Schrödinger dependiente del tiempo 3. Principio de incertidumbre
Química Física II. Tema II TEMA II: LA ECUACIÓN DE SCHRÖDINGER 1. La ecuación de Schrödinger independiente del tiempo 2. La ecuación de Schrödinger dependiente del tiempo 3. Principio de incertidumbre
Bases para el estudio del movimiento mecánico
 Vectores 1 ases para el estudio del movimiento mecánico SR: Cuerpos que se toman como referencia para describir el movimiento del sistema bajo estudio. Se le asocia z(t) (t) (t) Observador Sistema de Coordenadas
Vectores 1 ases para el estudio del movimiento mecánico SR: Cuerpos que se toman como referencia para describir el movimiento del sistema bajo estudio. Se le asocia z(t) (t) (t) Observador Sistema de Coordenadas
Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) x u + f
 1 228 Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) z u = f x x u + f y y u z v = f x x v + f y y v z w = f x
1 228 Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) z u = f x x u + f y y u z v = f x x v + f y y v z w = f x
Movimiento vibracional
 ESPECTROSCOPÍA Movimiento vibracional El oscilador armónico como modelo de la vibración molecular Los sistemas que vibran a nivel molecular incluyen las vibraciones internas de una molécula y las vibraciones
ESPECTROSCOPÍA Movimiento vibracional El oscilador armónico como modelo de la vibración molecular Los sistemas que vibran a nivel molecular incluyen las vibraciones internas de una molécula y las vibraciones
El Atomo de Hidrógeno (2)
 1 El Atomo de Hidrógeno (2) 2 Ψ n l m (r,θ,ϕ) = R n l (r) Θ l m (θ) Φ m (ϕ) Θ l m (θ) Φ m (ϕ) = Y m = Armónicos esféricos m = 0 Y m función real Solución matemática = Orbital Atómico m 0 Y m función imaginaria
1 El Atomo de Hidrógeno (2) 2 Ψ n l m (r,θ,ϕ) = R n l (r) Θ l m (θ) Φ m (ϕ) Θ l m (θ) Φ m (ϕ) = Y m = Armónicos esféricos m = 0 Y m función real Solución matemática = Orbital Atómico m 0 Y m función imaginaria
Para ser considerada una función aceptable, la función de onda debe ser:
 Cualquier estado de un sistema dinámico de N partículas puede ser descrito por la llamada función de onda de las 3N coordenadas espaciales y del tiempo: (1) Para ser considerada una función aceptable,
Cualquier estado de un sistema dinámico de N partículas puede ser descrito por la llamada función de onda de las 3N coordenadas espaciales y del tiempo: (1) Para ser considerada una función aceptable,
Respuestas de la Serie 2
 Respuestas de la Serie 2 1. N h 2 Ĥ = 2 2M I I=1 }{{} A n h 2 2 + 2m i }{{} B N N I=1 J>I kz 2 e 2 R I R J } {{ } C N n kze 2 I } i R I r i {{} D + n n ke 2 r j>i i r j }{{} E a) En el orden en el que
Respuestas de la Serie 2 1. N h 2 Ĥ = 2 2M I I=1 }{{} A n h 2 2 + 2m i }{{} B N N I=1 J>I kz 2 e 2 R I R J } {{ } C N n kze 2 I } i R I r i {{} D + n n ke 2 r j>i i r j }{{} E a) En el orden en el que
LOS POSTULADOS DE LA MECÁNICA CUÁNTICA
 LOS POSTULADOS DE LA MECÁNICA CUÁNTICA POSTULADO I Cualquier estado de un sistema dinámico de N partículas puede ser descrito por una función de las 3N coordenadas y del tiempo: La cantidad Ψ(q 1, q 2,...,
LOS POSTULADOS DE LA MECÁNICA CUÁNTICA POSTULADO I Cualquier estado de un sistema dinámico de N partículas puede ser descrito por una función de las 3N coordenadas y del tiempo: La cantidad Ψ(q 1, q 2,...,
r = r + a O O y r y r son los vectores de posición de los puntos de la distribución con respecto a cada uno de los orígenes.
 192 5.3. Problemas 5-1. Demuestre: a) Que si la carga total Q de una distribución es nula, el momento dipolar no depende del origen. b) Que si Q = 0 y p = 0, el momento cuadripolar tampoco depende del
192 5.3. Problemas 5-1. Demuestre: a) Que si la carga total Q de una distribución es nula, el momento dipolar no depende del origen. b) Que si Q = 0 y p = 0, el momento cuadripolar tampoco depende del
Espectroscopía atómica
 C A P Í T U L O 6 Espectroscopía atómica 6.. ENUNCIADOS Y SOLUCIONES DE LOS PROBLEMAS PROBLEMAS 6. Demuestre la regla de selección angular del átomo hidrogenoide m = 0, ±. Para m m 2π 0 e im Φ e imφ dφ
C A P Í T U L O 6 Espectroscopía atómica 6.. ENUNCIADOS Y SOLUCIONES DE LOS PROBLEMAS PROBLEMAS 6. Demuestre la regla de selección angular del átomo hidrogenoide m = 0, ±. Para m m 2π 0 e im Φ e imφ dφ
Ayudantía 11: Resumen Mecánica Cuántica
 Pontificia Universidad Católica de Chile Facultad de Física FIZ03 Física Cuántica I Ayudantía 11: Resumen Mecánica Cuántica Fabián Cádiz 0.1. Principios 0.1.1. El espacio de Hilbert La primera etapa en
Pontificia Universidad Católica de Chile Facultad de Física FIZ03 Física Cuántica I Ayudantía 11: Resumen Mecánica Cuántica Fabián Cádiz 0.1. Principios 0.1.1. El espacio de Hilbert La primera etapa en
Electromagnetismo I. Semestre: TAREA 1 Y SU SOLUCIÓN Dr. A. Reyes-Coronado
 Electromagnetismo I Semestre: 01- TAREA 1 Y SU SOLUCIÓN Dr. A. Reyes-Coronado Solución por Carlos Andrés Escobar Ruí 1.- Problema: (5pts) (a) Doce cargas iguales q se encuentran localiadas en los vérices
Electromagnetismo I Semestre: 01- TAREA 1 Y SU SOLUCIÓN Dr. A. Reyes-Coronado Solución por Carlos Andrés Escobar Ruí 1.- Problema: (5pts) (a) Doce cargas iguales q se encuentran localiadas en los vérices
Cuestiones de Autoevaluación
 Cuestiones de Autoevaluación Temas 1-5 Razone cuál de las respuestas es correcta en cada caso 1. En un experimento fotoeléctrico que se realiza con fotones de energías superiores a la función trabajo del
Cuestiones de Autoevaluación Temas 1-5 Razone cuál de las respuestas es correcta en cada caso 1. En un experimento fotoeléctrico que se realiza con fotones de energías superiores a la función trabajo del
El átomo de hidrógeno
 El átomo de hiógeno Antonio M. Márquez Departamento de Química Física Universidad de Sevilla Curso 15-16 Problema 1 Calcule la probabilidad de que un electrón 1s del H se encuentre entre r r. La probabilidad
El átomo de hiógeno Antonio M. Márquez Departamento de Química Física Universidad de Sevilla Curso 15-16 Problema 1 Calcule la probabilidad de que un electrón 1s del H se encuentre entre r r. La probabilidad
Ψ también debe existir.
 Primer postulado de la mecánica cuántica El estado de un sistema puede ser descrito por una función llamada función de onda. Las funciones de onda en la mecánica cuántica se simbolian con (psi). Por raones
Primer postulado de la mecánica cuántica El estado de un sistema puede ser descrito por una función llamada función de onda. Las funciones de onda en la mecánica cuántica se simbolian con (psi). Por raones
+V(x,y,z).ψ(x,y,z,t) = i.h
 Ecuación n de Schrödinger -h ( Ψ Ψ Ψ ) m Ψ +V(x,y,z).ψ(x,y,z,t) = i.h x y z t h = h / π i = (-1) 1/ ψ(x,y,z,t)... función (compleja) de onda V(x,y,z)... función de energía potencial ψ (x,y,z,t)... puede
Ecuación n de Schrödinger -h ( Ψ Ψ Ψ ) m Ψ +V(x,y,z).ψ(x,y,z,t) = i.h x y z t h = h / π i = (-1) 1/ ψ(x,y,z,t)... función (compleja) de onda V(x,y,z)... función de energía potencial ψ (x,y,z,t)... puede
El átomo de hidrógeno
 El átomo de hiógeno Antonio M. Márquez Departamento de Química Física Universidad de Sevilla Curso 16-17 Problema 1 Calcule la probabilidad de que un electrón 1s del H se encuentre entre r y r. Solución
El átomo de hiógeno Antonio M. Márquez Departamento de Química Física Universidad de Sevilla Curso 16-17 Problema 1 Calcule la probabilidad de que un electrón 1s del H se encuentre entre r y r. Solución
Examen de Física-1, 1 Ingeniería Química Examen final. Enero de 2011 Problemas (Dos puntos por problema).
 Examen de Física-1, 1 Ingeniería Química Examen final Enero de 2011 Problemas (Dos puntos por problema) Problema 1 (Primer parcial): Un muelle de constante k =10 4 N/m está comprimido 20 cm Al liberarlo
Examen de Física-1, 1 Ingeniería Química Examen final Enero de 2011 Problemas (Dos puntos por problema) Problema 1 (Primer parcial): Un muelle de constante k =10 4 N/m está comprimido 20 cm Al liberarlo
Matemática Avanzada. Clase Nro. 22
 Matemática Avanzada Clase Nro. 22 Octavio Miloni Facultad de Cs. Astronómicas y Geofísicas - Universidad Nacional de La Plata / 28 Aplicaciones a la Física Matemática Teoria del Potencial Problema de Contorno
Matemática Avanzada Clase Nro. 22 Octavio Miloni Facultad de Cs. Astronómicas y Geofísicas - Universidad Nacional de La Plata / 28 Aplicaciones a la Física Matemática Teoria del Potencial Problema de Contorno
VIII. MOMENTOS DE INERCIA
 VIII. MOMENTOS DE INERCIA Recordemos que el momento estático es la suma de los productos de cada elemento de un cuerpo por su distancia a un eje. El momento de inercia, es cambio es la suma de los productos
VIII. MOMENTOS DE INERCIA Recordemos que el momento estático es la suma de los productos de cada elemento de un cuerpo por su distancia a un eje. El momento de inercia, es cambio es la suma de los productos
a) Analice la continuidad en (1,0). E1) Dada F : IR 2 π g : D IR 2 I R 2 2 2
 Ejemplos de parcial de Análisis Matemático II Los ítems E1, E, E3 E4 corresponden a la parte práctica Los ítems T1 T son teóricos (sólo para promoción) T1) Sea F : IR IR diferenciable tal que F(,) 00 =
Ejemplos de parcial de Análisis Matemático II Los ítems E1, E, E3 E4 corresponden a la parte práctica Los ítems T1 T son teóricos (sólo para promoción) T1) Sea F : IR IR diferenciable tal que F(,) 00 =
Serie de problemas para el curso. Química Cuantica I
 erie de problemas para el curso Química Cuantica I Matemáticas Tema Resuelva todos los problemas del capítulo de la referencia B6 y compare sus resultados con las soluciones que se incluyen al final de
erie de problemas para el curso Química Cuantica I Matemáticas Tema Resuelva todos los problemas del capítulo de la referencia B6 y compare sus resultados con las soluciones que se incluyen al final de
, SZ } como. i de estados propios de { ˆ s
 Función de onda de spin de una partícula de spin S Si ψ es la función de onda de spin de una partícula de spin S, puede expandirse en la base Sσ de estados propios de {ˆ S, SZ } como ψ = S σ= S C σ Sσ.
Función de onda de spin de una partícula de spin S Si ψ es la función de onda de spin de una partícula de spin S, puede expandirse en la base Sσ de estados propios de {ˆ S, SZ } como ψ = S σ= S C σ Sσ.
Bárbara Cánovas Conesa
 67 70 11 1 Junio 006 Dos cargas puntuales q1 = + 0 nc y q = 1 0 nc están fijas y separadas una distancia de 8 cm. Calcular: a) El campo eléctrico en el punto T situado en el punto medio entre las cargas
67 70 11 1 Junio 006 Dos cargas puntuales q1 = + 0 nc y q = 1 0 nc están fijas y separadas una distancia de 8 cm. Calcular: a) El campo eléctrico en el punto T situado en el punto medio entre las cargas
Práctico 2: Mecánica lagrangeana
 Mecánica Anaĺıtica Curso 2016 Práctico 2: Mecánica lagrangeana 1. La polea y la cuerda de la figura son ideales y los bloques deslizan sin roce. Obtenga las aceleraciones de los bloques a partir de las
Mecánica Anaĺıtica Curso 2016 Práctico 2: Mecánica lagrangeana 1. La polea y la cuerda de la figura son ideales y los bloques deslizan sin roce. Obtenga las aceleraciones de los bloques a partir de las
Rotor Rígido. Ley de la palanca para dos cuerpos. Ileana Nieves Martínez QUIM m x X m x X 3/16/2014
 3/16/014 Rotor Rígido Ileana Nieves Martínez QUIM 404 1 Ley de la palanca para dos cuerpos 1 x1 X x X 1 1 0 x X x X Physical Cheistry 006 P.W. Atkins & J. de Paula W.H. Freean & Copany; 8va. edición 1
3/16/014 Rotor Rígido Ileana Nieves Martínez QUIM 404 1 Ley de la palanca para dos cuerpos 1 x1 X x X 1 1 0 x X x X Physical Cheistry 006 P.W. Atkins & J. de Paula W.H. Freean & Copany; 8va. edición 1
SEMINARIO 1: ELEMENTOS DIFERENCIALES DE LÍNEA, SUPERFICIE Y VOLUMEN
 SEMINARIO 1: ELEMENTOS DIFERENCIALES DE LÍNEA, SUPERFICIE Y VOLUMEN Sistemas de coordenadas 3D Transformaciones entre sistemas Integrales de línea y superficie SISTEMA COORDENADO CARTESIANO O RECTANGULAR
SEMINARIO 1: ELEMENTOS DIFERENCIALES DE LÍNEA, SUPERFICIE Y VOLUMEN Sistemas de coordenadas 3D Transformaciones entre sistemas Integrales de línea y superficie SISTEMA COORDENADO CARTESIANO O RECTANGULAR
Principios de Estructura de la Materia Equipo 4. Solución de la ecuación de Schrödinger para un rotor rígido
 Principios de Estructura de la Materia Equipo 4 Ramírez Palma Lillian Gisela Rendón Gaytán Fernando Torres Alcalá Andrea Villanueva Sánchez Luis Felipe Solución de la ecuación de Schrödinger para un rotor
Principios de Estructura de la Materia Equipo 4 Ramírez Palma Lillian Gisela Rendón Gaytán Fernando Torres Alcalá Andrea Villanueva Sánchez Luis Felipe Solución de la ecuación de Schrödinger para un rotor
Sistemas de coordenadas
 Sistemas de coordenadas. Introducción En un sistema de coordenadas un punto se representa como la intersección de tres superficies ortogonales llamadas superficies coordenadas del sistema: u u u = cte
Sistemas de coordenadas. Introducción En un sistema de coordenadas un punto se representa como la intersección de tres superficies ortogonales llamadas superficies coordenadas del sistema: u u u = cte
Otras distribuciones multivariantes
 Trabajo A Trabajos Curso -3 Otras distribuciones multivariantes Clase esférica de distribuciones en R p Definición. Dado un vector aleatorio X = X,..., X p t, se dice que se distribuye en la clase esférica
Trabajo A Trabajos Curso -3 Otras distribuciones multivariantes Clase esférica de distribuciones en R p Definición. Dado un vector aleatorio X = X,..., X p t, se dice que se distribuye en la clase esférica
De órbitas a orbitales. De órbitas a orbitales
 De órbitas de Bohr a orbitales de Schrödinger Una consecuencia muy importante de la naturaleza dual de la materia es un hecho estudiado por Heisenberg, enunciado en 97. Este fenómeno muestra que es imposible
De órbitas de Bohr a orbitales de Schrödinger Una consecuencia muy importante de la naturaleza dual de la materia es un hecho estudiado por Heisenberg, enunciado en 97. Este fenómeno muestra que es imposible
La energía cinética de un sistema constituido por dos masas m A y m B cuyas coordenadas son x A, y A, z A y x B, y B, z B, respectivamente, es:
 1 EL ROTOR RÍGIDO E rotor rígido es un sistema formado por dos cuerpos A y B unidos por una barra sin masa, de argo R, y girando en cuaquier dirección pero con e centro de masa fijo. La energía cinética
1 EL ROTOR RÍGIDO E rotor rígido es un sistema formado por dos cuerpos A y B unidos por una barra sin masa, de argo R, y girando en cuaquier dirección pero con e centro de masa fijo. La energía cinética
CAPITULO 1. Introducción a la Mecánica Cuántica. 1) Naturaleza de la luz. Dualidad onda-corpúsculo
 CAPITULO. Introducción a la Mecánica Cuántica ) Naturaleza de la luz. Dualidad onda-corpúsculo Naturaleza ondulatoria: Eistencia de difracción e interferencias. La luz puede ser polarizada. La luz no tiene
CAPITULO. Introducción a la Mecánica Cuántica ) Naturaleza de la luz. Dualidad onda-corpúsculo Naturaleza ondulatoria: Eistencia de difracción e interferencias. La luz puede ser polarizada. La luz no tiene
Geometría de masas: Cálculos del tensor de Inercia
 Departamento: Física Aplicada Mecánica acional (ngeniería ndustrial) Curso 007-08 eometría de masas: Cálculos del tensor de nercia Tensor de inercia de una varilla delgada. Calculo del tensor de inercia
Departamento: Física Aplicada Mecánica acional (ngeniería ndustrial) Curso 007-08 eometría de masas: Cálculos del tensor de nercia Tensor de inercia de una varilla delgada. Calculo del tensor de inercia
Vectores. 1) Magnitudes físicas
 Vectores 1) Magnitudes físicas Eisten magnitudes físicas que quedan perfectamente definidas mediante un número epresado en sus unidades correspondientes. Ejemplos de este tipo de magnitud son: la masa
Vectores 1) Magnitudes físicas Eisten magnitudes físicas que quedan perfectamente definidas mediante un número epresado en sus unidades correspondientes. Ejemplos de este tipo de magnitud son: la masa
Unidad 5: Geometría analítica del plano.
 Geometría analítica del plano 1 Unidad 5: Geometría analítica del plano. 1.- Vectores. Operaciones con vectores. Un vector fijo es un segmento entre dos puntos, A y B del plano, al que se le da una orientación
Geometría analítica del plano 1 Unidad 5: Geometría analítica del plano. 1.- Vectores. Operaciones con vectores. Un vector fijo es un segmento entre dos puntos, A y B del plano, al que se le da una orientación
Fuerzas de un Campo Magnético sobre Cargas Eléctricas en Movimiento
 Fuerzas de un Campo Magnético sobre Cargas Eléctricas en Movimiento Ejercicio resuelto nº 1 Un electrón penetra perpendicularmente desde la izquierda en un campo magnético uniforme vertical hacia el techo
Fuerzas de un Campo Magnético sobre Cargas Eléctricas en Movimiento Ejercicio resuelto nº 1 Un electrón penetra perpendicularmente desde la izquierda en un campo magnético uniforme vertical hacia el techo
La ecuación lineal de primer grado con dos incógnitas. La recta en el plano afín
 La ecuación lineal de primer grado con dos incógnitas. La recta en el plano afín Una ecuación lineal es una ecuación polinómica de grado uno con una o varias incógnitas. Si la ecuación solamente tiene
La ecuación lineal de primer grado con dos incógnitas. La recta en el plano afín Una ecuación lineal es una ecuación polinómica de grado uno con una o varias incógnitas. Si la ecuación solamente tiene
APUNTES DE FÍSICA I Profesor: José Fernando Pinto Parra UNIDAD 2 ÁLGEBRA VECTORIAL
 Vectores y escalares. REPÚBLICA BOLIVARIANA DE VENEZUELA APUNTES DE FÍSICA I Profesor: José Fernando Pinto Parra UNIDAD 2 ÁLGEBRA VECTORIAL Las magnitudes escalares son aquellas magnitudes físicas que
Vectores y escalares. REPÚBLICA BOLIVARIANA DE VENEZUELA APUNTES DE FÍSICA I Profesor: José Fernando Pinto Parra UNIDAD 2 ÁLGEBRA VECTORIAL Las magnitudes escalares son aquellas magnitudes físicas que
Capítulo 10. Rotación de un Cuerpo Rígido
 Capítulo 10 Rotación de un Cuerpo Rígido Contenido Velocidad angular y aceleración angular Cinemática rotacional Relaciones angulares y lineales Energía rotacional Cálculo de los momentos de inercia Teorema
Capítulo 10 Rotación de un Cuerpo Rígido Contenido Velocidad angular y aceleración angular Cinemática rotacional Relaciones angulares y lineales Energía rotacional Cálculo de los momentos de inercia Teorema
Apuntes de la asignatura Química Física II (Licenciatura en Química) Tema 7: El átomo de hidrógeno
 Apuntes de la asignatura Química Física II (Licenciatura en Química) Tema 7: El átomo de hidrógeno Ángel José Pérez Jiménez Dept. de Química Física (Univ. Alicante) Índice 1. Partícula sometida a un potencial
Apuntes de la asignatura Química Física II (Licenciatura en Química) Tema 7: El átomo de hidrógeno Ángel José Pérez Jiménez Dept. de Química Física (Univ. Alicante) Índice 1. Partícula sometida a un potencial
Lección: Introducción a la Química Cuántica
 Lección: Introducción a la Química Cuántica TEMA: Introducción 1....................... 2 I.A. Espectro discreto............... 2 I.B. Espectro continuo...............8 II. Mecánica Cuántica...............
Lección: Introducción a la Química Cuántica TEMA: Introducción 1....................... 2 I.A. Espectro discreto............... 2 I.B. Espectro continuo...............8 II. Mecánica Cuántica...............
Mecánica Clásica (B) 2do. cuatrimestre de 2017 AD Primer parcial (con soluciones) 12/10
 Mecánica Clásica B) do. cuatrimestre de 017 AD Primer parcial con soluciones) 1/10 Problema 1. El marco exterior de un giróscopo rota con velocidad angular constante ω = ωẑ, como muestra la figura, donde
Mecánica Clásica B) do. cuatrimestre de 017 AD Primer parcial con soluciones) 1/10 Problema 1. El marco exterior de un giróscopo rota con velocidad angular constante ω = ωẑ, como muestra la figura, donde
1. Obtener las coordenadas cartesianas del punto B simétrico del punto A(5,30 ), respecto al polo.
 SEMESTRE 018-1 SERIE CURVAS EN EL PLANO POLAR 1. Obtener las coordenadas cartesianas del punto B simétrico del punto A(5,30 ), respecto al polo.. Determinar las coordenadas polares del punto C simétrico
SEMESTRE 018-1 SERIE CURVAS EN EL PLANO POLAR 1. Obtener las coordenadas cartesianas del punto B simétrico del punto A(5,30 ), respecto al polo.. Determinar las coordenadas polares del punto C simétrico
Física I. TEMA I. Vectores. Ing. Alejandra Escobar UNIVERSIDAD FERMÍN TORO VICE RECTORADO ACADÉMICO FACULTAD DE INGENIERÍA
 Física I TEMA I. Vectores UNIVERSIDAD FERMÍN TORO VICE RECTORADO ACADÉMICO FACULTAD DE INGENIERÍA Ing. Alejandra Escobar TEMA I. VECTORES Magnitudes Una magnitud se define como toda aquella propiedad que
Física I TEMA I. Vectores UNIVERSIDAD FERMÍN TORO VICE RECTORADO ACADÉMICO FACULTAD DE INGENIERÍA Ing. Alejandra Escobar TEMA I. VECTORES Magnitudes Una magnitud se define como toda aquella propiedad que
EJERCICIOS COMPLEMENTARIOS DE ELASTICIDAD AÑO ACADÉMICO
 EJERCICIOS COMPLEMENTARIOS DE ELASTICIDAD AÑO ACADÉMICO 2011-2012 Prob 1. Sobre las caras de un paralepípedo elemental que representa el entorno de un punto de un sólido elástico existen las tensiones
EJERCICIOS COMPLEMENTARIOS DE ELASTICIDAD AÑO ACADÉMICO 2011-2012 Prob 1. Sobre las caras de un paralepípedo elemental que representa el entorno de un punto de un sólido elástico existen las tensiones
Tema 14 11/02/2005. Tema 8. Mecánica Cuántica. 8.1 Fundamentos de la mecánica cuántica
 Tema 14 11/0/005 Tema 8 Mecánica Cuántica 8.1 Fundamentos de la mecánica cuántica 8. La ecuación de Schrödinger 8.3 Significado físico de la función de onda 8.4 Soluciones de la ecuación de Schrödinger
Tema 14 11/0/005 Tema 8 Mecánica Cuántica 8.1 Fundamentos de la mecánica cuántica 8. La ecuación de Schrödinger 8.3 Significado físico de la función de onda 8.4 Soluciones de la ecuación de Schrödinger
ATOMO DE HIDROGENO. o = permitividad al vacío = 8.85 X C 2 N -1 cm -1. = metros. F = Newtons 2. Ó (3)
 ATOMO DE HIDROGENO I. Atomo de hidrógeno A. Descripción del sistema: Dos partículas que interaccionan por atracción de carga eléctrica y culómbica. 1. Ley de coulomb: a. En el sistema cgs en unidades de
ATOMO DE HIDROGENO I. Atomo de hidrógeno A. Descripción del sistema: Dos partículas que interaccionan por atracción de carga eléctrica y culómbica. 1. Ley de coulomb: a. En el sistema cgs en unidades de
Esta relación se obtiene mediante el denominado modelo dinámico, que relaciona matemáticamente:
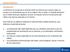 Introducción La dinámica se ocupa de la relación entre las fuerzas que actúan sobre un cuerpo y el movimiento que en el se origina. Por lo tanto, el modelo dinámico de un robot tiene por objetivo conocer
Introducción La dinámica se ocupa de la relación entre las fuerzas que actúan sobre un cuerpo y el movimiento que en el se origina. Por lo tanto, el modelo dinámico de un robot tiene por objetivo conocer
d x e z d y Z d Ecuación de Schroedinger tridimensional en coordenadas cartesianas x, y, z. El operador Hamiltoniano (H), ahora es:
 1 Ecuación de Schroedinger tridimensional E e z d y d x d h r Z d d d m 0 4 8 en coordenadas cartesianas x, y, z. El operador Hamiltoniano (H), ahora es: z d y d x d h d d d m 8 El primer término de esta
1 Ecuación de Schroedinger tridimensional E e z d y d x d h r Z d d d m 0 4 8 en coordenadas cartesianas x, y, z. El operador Hamiltoniano (H), ahora es: z d y d x d h d d d m 8 El primer término de esta
Átomo de hidrógeno. z = r cos θ B = A = r sen θ x = A cos φ = r sen θ cos φ y = A sen φ = r sen θ sen φ
 Coordenadas esféricas polares La ecuación de Schroedinger para el átoo de hidrógeno debe resolverse en coordenadas esféricas polares (r θφ) que guardan la siguiente relación con las coordenadas cartesianas
Coordenadas esféricas polares La ecuación de Schroedinger para el átoo de hidrógeno debe resolverse en coordenadas esféricas polares (r θφ) que guardan la siguiente relación con las coordenadas cartesianas
Momento angular de una partícula. Momento angular de un sólido rígido
 Momento angular de una partícula Se define momento angular de una partícula respecto de del punto O, como el producto vectorial del vector posición r por el vector momento lineal mv L=r mv Momento angular
Momento angular de una partícula Se define momento angular de una partícula respecto de del punto O, como el producto vectorial del vector posición r por el vector momento lineal mv L=r mv Momento angular
Métodos Matemáticos en Física Lección 7A: Coordenadas curvilíneas (app_d_apl)
 Lección 7A: Coordenadas curvilíneas (app_d_apl) Operadores diferenciales: gradiente, divergencia y laplaciano Recordatorio: Coordenadas cartesianas Gradiente 1 Divergencia 2 1 Leccion: Coordenadas curvilíneas
Lección 7A: Coordenadas curvilíneas (app_d_apl) Operadores diferenciales: gradiente, divergencia y laplaciano Recordatorio: Coordenadas cartesianas Gradiente 1 Divergencia 2 1 Leccion: Coordenadas curvilíneas
Dpto. Física y Mecánica. Operadores diferenciales
 Dpto. Física y Mecánica Operadores diferenciales Se denominan líneas coordenadas de un espacio euclídeo tridimensional a aquellas que se obtienen partiendo un punto dado P de coordenadas (q 1, q 2, q 3
Dpto. Física y Mecánica Operadores diferenciales Se denominan líneas coordenadas de un espacio euclídeo tridimensional a aquellas que se obtienen partiendo un punto dado P de coordenadas (q 1, q 2, q 3
REPRESENTACIÓN ANALÍTICA DE UNA RECTA Una recta puede ser representada de las siguientes formas:
 LA RECTA Una recta queda definida en el espacio si se conocen: 1) Un punto de ella y la dirección de la recta, definiéndose ésta con un vector; o bien 2) Dos puntos de la recta; o 3) Dos planos no paralelos
LA RECTA Una recta queda definida en el espacio si se conocen: 1) Un punto de ella y la dirección de la recta, definiéndose ésta con un vector; o bien 2) Dos puntos de la recta; o 3) Dos planos no paralelos
CURSO EN MÉTODOS DE LA FÍSICA
 CURSO EN MÉTODOS DE LA FÍSICA TEÓRICA P. L. Torres Escuela de Física, Facultad de Ciencias, Universidad Central de Venezuela, Caracas, Venezuela. pltorres42@gmail.com pltorres@fisica.ciens.ucv.ve 3 de
CURSO EN MÉTODOS DE LA FÍSICA TEÓRICA P. L. Torres Escuela de Física, Facultad de Ciencias, Universidad Central de Venezuela, Caracas, Venezuela. pltorres42@gmail.com pltorres@fisica.ciens.ucv.ve 3 de
Problemas de Mecánica Cuántica (para el Exámen Predoctoral)
 Problemas de Mecánica Cuántica (para el Exámen Predoctoral) 1 Formalismo general 1. Problema: Consideremos un sistema cuántico que contiene sólo dos estados linealmente independientes 1 y 2, 1 = 2 = (
Problemas de Mecánica Cuántica (para el Exámen Predoctoral) 1 Formalismo general 1. Problema: Consideremos un sistema cuántico que contiene sólo dos estados linealmente independientes 1 y 2, 1 = 2 = (
Métodos Matemáticos en Física
 Lección 7A: Coordenadas curvilíneas (app_d_apl) Operadores diferenciales: gradiente, divergencia y laplaciano Recordatorio: Coordenadas cartesianas Gradiente 1 Divergencia 2 1 Leccion: Coordenadas curvilíneas
Lección 7A: Coordenadas curvilíneas (app_d_apl) Operadores diferenciales: gradiente, divergencia y laplaciano Recordatorio: Coordenadas cartesianas Gradiente 1 Divergencia 2 1 Leccion: Coordenadas curvilíneas
1 CÓNICAS Cónicas. Estudio particular. 1 x y. 1 x y. a 00 a 01 a 02 a 10 a 11 a 12 a 20 a 21 a 22
 CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
Profesores de Enseñanza Secundaria. MATEMÁTICAS. ANDALUCÍA 2018
 ANDALUCÍA 8 PROBLEMA Dados la matriz A R, el vector b R, α R y el subespacio F de R A =, b = y F + = α + + = α a) Discutir y resolver cuando sea compatible el sistema AX=b con X R. b) Sea E el espacio
ANDALUCÍA 8 PROBLEMA Dados la matriz A R, el vector b R, α R y el subespacio F de R A =, b = y F + = α + + = α a) Discutir y resolver cuando sea compatible el sistema AX=b con X R. b) Sea E el espacio
7. Cambio de variables en integrales triples.
 GRADO DE INGENIERÍA AEROESPACIAL. CURSO 011 1. Lección. Integrales múltiples. 7. Cambio de variables en integrales triples. El teorema del cambio de variables para integrales triples es análogo al de integrales
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 011 1. Lección. Integrales múltiples. 7. Cambio de variables en integrales triples. El teorema del cambio de variables para integrales triples es análogo al de integrales
Tema 2. Los átomos: estructura electrónica.
 Tema 2. Los átomos: estructura electrónica. 1. Introducción. 2. Antecedentes de la mecánica ondulatoria. 3. Mecánica ondulatoria. 4. Orbitales atómicos. 5. Configuraciones electrónicas. 1. Introducción
Tema 2. Los átomos: estructura electrónica. 1. Introducción. 2. Antecedentes de la mecánica ondulatoria. 3. Mecánica ondulatoria. 4. Orbitales atómicos. 5. Configuraciones electrónicas. 1. Introducción
Mecánica Cuántica. Curso propedéutico Mauricio Fortes 21/10/09 IFUNAM. mfb (IFUNAM) MQ-3 21/10/09 1 / 30
 Mecánica Cuántica Curso propedéutico 2009 Mauricio Fortes IFUNAM 21/10/09 mfb (IFUNAM) MQ-3 21/10/09 1 / 30 Sitio web http://www.fisica.unam.mx/personales/fortes mfb (IFUNAM) MQ-3 21/10/09 2 / 30 Postulados
Mecánica Cuántica Curso propedéutico 2009 Mauricio Fortes IFUNAM 21/10/09 mfb (IFUNAM) MQ-3 21/10/09 1 / 30 Sitio web http://www.fisica.unam.mx/personales/fortes mfb (IFUNAM) MQ-3 21/10/09 2 / 30 Postulados
A. VECTORES 1. VECTORES FIJOS Y VECTORES LIBRES
 RESUMEN DE GEOMETRÍA MATEMÁTICAS II A. VECTORES 1. VECTORES FIJOS Y VECTORES LIBRES Un vector fijo de origen A y extremo B, siendo A y B puntos del espacio, es un segmento orientado caracterizado por:
RESUMEN DE GEOMETRÍA MATEMÁTICAS II A. VECTORES 1. VECTORES FIJOS Y VECTORES LIBRES Un vector fijo de origen A y extremo B, siendo A y B puntos del espacio, es un segmento orientado caracterizado por:
Definición 13.1 Definimos el conjunto de los polinomios de Laguerre {L n (t)} n N 0 mediante una cualquiera de las siguientes ecuaciones:
 Capítulo 13 Polinomios de Laguerre 13.1 Definición Definición 13.1 Definimos el conjunto de los polinomios de Laguerre {} n N mediante una cualquiera de las siguientes ecuaciones: = e t dn ( t n e t) =
Capítulo 13 Polinomios de Laguerre 13.1 Definición Definición 13.1 Definimos el conjunto de los polinomios de Laguerre {} n N mediante una cualquiera de las siguientes ecuaciones: = e t dn ( t n e t) =
Planos y Rectas. 19 de Marzo de 2012
 el Geometría en el Planos y Rectas Universidad Autónoma Metropolitana Unidad Iztapalapa 19 de Marzo de 2012 el Anteriormente vimos que es posible encontrar un número infinito de vectores, no paralelos
el Geometría en el Planos y Rectas Universidad Autónoma Metropolitana Unidad Iztapalapa 19 de Marzo de 2012 el Anteriormente vimos que es posible encontrar un número infinito de vectores, no paralelos
Tema 5: Tensor de Inercia
 Tema 5: Tensor de Inercia Mecánica Racional, 2º, Grado en Ingeniería Civil Escuela Técnica Superior de Ingenieros Universidad de Sevilla 1 Índice Introducción Momentos de inercia de cuerpos continuos Tensor
Tema 5: Tensor de Inercia Mecánica Racional, 2º, Grado en Ingeniería Civil Escuela Técnica Superior de Ingenieros Universidad de Sevilla 1 Índice Introducción Momentos de inercia de cuerpos continuos Tensor
Vibraciones Linealización de ecuaciones diferenciales
 Vibraciones Linealización de ecuaciones diferenciales MScAA Marcos Knoblauch Departamento de Aeronáutica Universidad Nacional de La Plata Introducción Este documento contiene las ecuaciones y conceptos
Vibraciones Linealización de ecuaciones diferenciales MScAA Marcos Knoblauch Departamento de Aeronáutica Universidad Nacional de La Plata Introducción Este documento contiene las ecuaciones y conceptos
Posición de un Cuerpo. Elementos para la descripción del movimiento. Vector de Posición y Vector Desplazamiento
 1 Bárbara Cánovas Conesa 637 70 113 www.clasesalacarta.com 1 Cinemática Posición de un Cuerpo Coordenadas Cartesianas Coordenadas Polares Vector de Posición (,, z) r, q r Elementos para la descripción
1 Bárbara Cánovas Conesa 637 70 113 www.clasesalacarta.com 1 Cinemática Posición de un Cuerpo Coordenadas Cartesianas Coordenadas Polares Vector de Posición (,, z) r, q r Elementos para la descripción
Física cuántica I - Colección de ejercicios cortos
 Física cuántica I - Colección de ejercicios cortos http://teorica.fis.ucm.es En las siguientes cuestiones una y sólo una de las cuatro respuestas ofrecidas es correcta. Dígase cuál. Es conveniente hacer
Física cuántica I - Colección de ejercicios cortos http://teorica.fis.ucm.es En las siguientes cuestiones una y sólo una de las cuatro respuestas ofrecidas es correcta. Dígase cuál. Es conveniente hacer
Física 2º Bto. (A y B) Movimiento ondulatorio. Campos gravitatorio y eléctrico 19 marzo 2008
 Alumno o alumna: Puntuación: 1. El oscilador armónico Una partícula de 1,4 kg de masa se conecta a un muelle de masa despreciable y constante recuperadora k = 15 N/m, de manera que el sistema se mueve
Alumno o alumna: Puntuación: 1. El oscilador armónico Una partícula de 1,4 kg de masa se conecta a un muelle de masa despreciable y constante recuperadora k = 15 N/m, de manera que el sistema se mueve
sea a lo largo de la curva solución de la ecuación diferencial xy, = 5x
 1. Hallar κ de manera que el flujo saliente del campo f ( x, = (x + y + z, 6y a través de la frontera del cuerpo x + y + z 16 x + y κ, 0 < k < 4 f : R R un campo vectorial definido por:. Sea γ ( t ) =
1. Hallar κ de manera que el flujo saliente del campo f ( x, = (x + y + z, 6y a través de la frontera del cuerpo x + y + z 16 x + y κ, 0 < k < 4 f : R R un campo vectorial definido por:. Sea γ ( t ) =
Solución de la ecuación de Schrödinger para el oscilador armónico
 Solución de la ecuación de Schrödinger para el oscilador armónico Erika Armenta Jaime Francisco Barrera Raul Camiña Blando Geraldyne L. Castro Herrera Antecedentes Max Plank (1900) propone que la emisión
Solución de la ecuación de Schrödinger para el oscilador armónico Erika Armenta Jaime Francisco Barrera Raul Camiña Blando Geraldyne L. Castro Herrera Antecedentes Max Plank (1900) propone que la emisión
b) Cuantos microestados y cuantos niveles de energía existen en una configuración.
 EXMEN DE SEPTIEMRE DE QUÍMI FÍSI (3º urso de Químicas): 13/9/11 (ula 11). 1) a) Sea una caja de potenciales de paredes infinitas bidimensional de tamaño a b, tal que b a /. Indicar la energía del sistema.
EXMEN DE SEPTIEMRE DE QUÍMI FÍSI (3º urso de Químicas): 13/9/11 (ula 11). 1) a) Sea una caja de potenciales de paredes infinitas bidimensional de tamaño a b, tal que b a /. Indicar la energía del sistema.
Webpage: Departamento de Física Universidad de Sonora
 Mecánica fluidos Webpage: http://paginas.fisica.uson.m/qb 2007 Departamento de Física Universidad de Sonora 1 Temario III.- VECTORES. 1. Clasificación de cantidades físicas: Escalares vectores. 2. Representación
Mecánica fluidos Webpage: http://paginas.fisica.uson.m/qb 2007 Departamento de Física Universidad de Sonora 1 Temario III.- VECTORES. 1. Clasificación de cantidades físicas: Escalares vectores. 2. Representación
